一道高考题的巧证、加强与变式

试题研究２０２４年１月上半月㊀㊀㊀四点共面,链接教材,变式拓展以一道高考题为例◉江苏省张家港市沙洲中学㊀陶㊀贤㊀㊀空间中的四点共面的判断与证明是空间向量与立体几何部分的一个基本知识点,也是一大难点,历年高考数学试题中较少涉及,没有引起大家的高度重视．而在２０２０年高考数学全国卷Ⅲ的文科和理科试题中,都出现了空间四点共面的证明问题,也充分说明了该部分知识的基础性与重要性．借助空间中四点共面的判断与证明,很好地考查考生的数形结合思想㊁空间想象能力与推理论证能力,以及直观想象㊁逻辑推理等数学核心素养．１真题呈现图１高考真题㊀(２０２０年高考数学全国卷Ⅲ理科第１９题)如图１,在长方体A B C D ＧA １B １C １D １中,点E ,F 分别在棱D D １,B B １上,且２D E ＝E D １,B F ＝２F B １．(１)证明:点C １在平面A E F 内．(２)若A B ＝２,A D ＝１,A A １＝３,求二面角A ＧE F ＧA １的正弦值．此题以长方体为问题背景,通过相应线段的长度关系,证明点在平面内(其实就是证明四点共面)以及求解二面角的平面角的正弦值,改变以往传统的证明直线与平面之间的平行或垂直关系,令人耳目一新．图２２问题破解(Ⅰ)第(１)问的证法如下:证法１:几何法．如图２,在棱C C １上取点G ,使得C １G ＝１２C G ,连接D G ,F G ,C １E ,C １F ．在长方体A B C D ＧA １B １C １D １中,A D ʊBC 且AD ＝B C ,B B １ʊC C １且B B １＝C C １．由C １G ＝１２C G ,B F ＝２F B １,可得C G ＝２３C C １＝２３B B １＝B F ,所以四边形B C G F 为平行四边形,则G F ʊB C 且G F ＝B C ．又B C ʊA D 且B C ＝A D ,所以A D ʊG F 且A D ＝G F ,即四边形A F D G 是平行四边形,则A F ʊD G 且A F ＝D G ．同理可证,四边形D E C １G 为平行四边形,则C １E ʊD G 且C １E ＝D G ．所以C １E ʊA F 且C １E ＝A F ,则四边形A E C １F为平行四边形．因此,点C １在平面A E F 内．证法２:基底法１共面向量定理．在长方体A B C D ＧA １B １C １D １中,B B １ʊC C １ʊD D １且B B １＝C C １＝D D １,结合２DE ＝E D １,BF ＝２F B １,可得E D １＝B F ．由A C １ң＝A C ң＋C C １ң＝A B ң＋A D ң＋D E ң＋E D １ң＝A B ң＋A D ң＋D E ң＋B F ң＝(A B ң＋B F ң)＋(A D ң＋D E ң)＝A F ң＋A E ң,知A ,E ,F ,C １四点共面,所以点C １在平面A E F 内．证法３:基底法２共面向量定理的推论．设D １A １ң＝a ,D １C １ң＝b ,D １D ң＝c ,则D １A ң＝a ＋c ,D １E ң＝２３c ,可得c ＝３２D １E ң,于是a ＝D １A ң－３２D １E ң．由D １F ң＝D １A １ң＋A １B １ң＋B １F ң＝D １A １ң＋D １C １ң＋１３B １B ң＝D １A １ң＋D １C １ң＋１３D １D ң＝a ＋b ＋１３c ＝(D １A ң－３２D １E ң)＋D １C １ң＋１３ˑ３２D １E ң＝D １A ң＋D １C １ң－D １E ң(其中１＋１－１＝１),知A ,E ,F ,C １四点共面,所以点C １在平面A E F 内．图３证法４:坐标法．设A B ＝a ,A D ＝b ,A A １＝c ,如图３所示,以C １为坐标原点,C １D １ң的方向为x 轴正方向,建立空间直角坐标系C １Ｇx yz ．连接C １F ,则C １(０,０,０),A (a ,b ,c ),E (a ,０,２３c ),F (０,b ,１３c ),于８６２０２４年１月上半月㊀试题研究㊀㊀㊀㊀是E A ң＝(０,b ,１３c ),C １F ң＝(０,b ,１３c ),可得E A ң＝C １F ң,因此E A ʊC １F ,即A ,E ,F ,C １四点共面,所以点C １在平面A E F 内．点评:证明空间中的四点共面问题,常见的证明方法就是以上三大类 (１)利用空间几何图形的特征,借助几何法的推理与论证,通过空间问题平面化来证明;(２)利用共面向量定理或推论,借助空间向量的基底法,通过向量的线性运算与转化来证明;(３)利用空间直角坐标系的建立,借助坐标法的运算,通过向量的平行判断与转化来证明等．特别地,对于共面向量定理及其推论,是立体几何中的一个重要的定理,可以用来处理一些与之相关的问题,往往可以使问题处理得更加简捷㊁巧妙．(Ⅱ)第(２)问的解法如下:解:以C １为坐标原点,C １D １ң的方向为x 轴正方向,建立空间直角坐标系C １Ｇx yz ,则由已知可得A (２,１,３),E (２,０,２),F (０,１,１),A １(２,１,０),则A E ң＝(０,－１,－１),A F ң＝(－２,０,－２),A １E ң＝(０,－１,２),A １F ң＝(－２,０,１)．设平面A E F 的法向量为m ＝(x １,y １,z １)．由m A E ң＝０,m A F ң＝０,{得－y １－z １＝０,－２x １－２z １＝０,{取z １＝－１,得x １＝y １＝１,则m ＝(１,１,－１)．设平面A １E F 的法向量为n ＝(x ２,y ２,z ２)．由n A １E ң＝０,n A １F ң＝０,{得－y ２＋２z ２＝０,－２x ２＋z ２＝０,{取z ２＝２,得x ２＝１,y ２＝４,则n ＝(１,４,２)．所以c o s ‹m ,n ›＝m n |m ||n |＝１＋４－２３ˑ２１＝７７．设二面角A ＧE F ＧA １的平面角为θ,则|c o s θ|＝７７,可得s i n θ＝１－c o s ２θ＝４２７．因此,二面角A ＧE F ＧA １的正弦值为４２７．点评:坐标法是求解二面角的平面角的三角函数值问题中一个比较常见的方法,借助空间直角坐标系的建立,以及对应的点㊁向量的坐标的表示,结合相应两半平面的法向量的设置与确定,结合向量的数量积公式的转化与应用来确定相应的二面角的平面角问题．坐标法实现了用代数方法处理立体几何问题中的四点共面㊁线面位置关系㊁空间角㊁距离等几何推理与求解问题．３链接教材以上基于向量的四点共面的判断,其对应的共面向量定理及其推论是数学教材中的一个基本知识点,来源于教材,又服务于证明,可以很好地证明或求解与四点共面有关的数学问题．普通高中课程标准实验教科书«数学 选修２－１»(人教A 版)第８７页:结论１:共面向量定理．空间一点P 位于平面A B C 内的充要条件是存在有序实数对(x ,y ),使A P ң＝xA B ң＋y A C ң．普通高中课程标准实验教科书«数学 选修２－１»(人教A 版)第８８页思考 :结论２:共面向量定理的推论．空间任意一点O 和不共线的三点A ,B ,C 满足向量关系式O P ң＝xO A ң＋y O B ң＋zO C ң(x ＋y ＋z ＝１)的点P 与点A ,B ,C 共面．共面向量定理是共线向量定理在空间中的推广与拓展,共线向量定理用来证明三点共线,共面向量定理用来证明四点共面．４变式拓展图４高考真题㊀(２０２０年高考数学全国卷Ⅲ文科第１９题)如图４,在长方体A B C D ＧA １B １C １D １中,点E ,F分别在棱D D １,B B １上,且２D E ＝E D １,BF ＝２F B １．证明:(１)当A B ＝B C 时,E F ʅA C ;(２)点C １在平面A E F 内．证明:(１)连接B D ,B １D １．因为A B ＝B C ,所以四边形A B C D 为正方形,故A C ʅB D ．又因为B B １ʅ平面A B C D ,于是B B １ʅA C ,而B D ,B B １Ì平面B B １D １D ,所以A C ʅ平面B B １D １D ．因为E F ÌB B １D １D ,所以E F ʅA C ．(２)可以参照上述理科真题第(１)问的证明方法．５解后反思新一轮课程改革的核心就是培育学生的核心素养,发展学生的综合能力．承载着 立德树人㊁服务选才和引导教学 功能的数学高考,应借助试题 情境 的变革,夯实基础,以教材为本并超越教材,着眼于基础知识㊁基本技能㊁基本方法的考查,特别重视对数学思想方法㊁关键能力和学科素养的考查．因而在平时的数学教学与复习中,教师应在拓展延伸中紧扣课本,链接教材,注重归类迁移能力培养,聚焦思维品质,培养关键能力,从而有效实现学生数学素养的渐进式提升．Z９６。

2024届大题强化训练及变式训练（13）4(1)求b 的值；(2)求ACD 的周长的取值范围.变式：已知条件：①23sin 32cos 2CC =-从三个条件中任选一个，补充在下面的问题中，并解答.问题：在ABC 中，角(1)求角C 的大小；(2)若23c =，ABC ∠注：如果选择多个条件分别作答，按第一个解答计分大题强化训练及变式训练（13）-2024届高三数学二轮复习大题强化训练及变式训练（新高考九省联考题型）（解析版）2．如图，将边长为2的菱形ABDC沿其对角线BC对折，使得点A、D分别位于边长为2的等边PBC所在平面的两侧，且PA=，PD=．设E是PA的中点．（1）证明：平面PBC⊥平面ABC；（2）求平面EBD与平面ABC夹角的正弦值．变式：已知矩形ABCD中，点E在边CD上，且2AD DE CE===．现将ADEV沿AE向上翻折，使点D到点P的位置，构成如图所示的四棱锥P ABCE-．（1）若点F在线段AP上，且//EF平面PBC，求AFFP的值；（2）若2PB=，求锐二面角P EC A--的余弦值．3．如图，一个质点在随机外力的作用下，从原点O 出发，随机移动n 次，每次等可能地向左或向右移动一个单位长度，n 次移动结束后，质点到达的位置的数字记为X .（1）若2n =，求()0P X =;（2）若6n =，求X 的分布列和()E X 的值.变式：一个质点在一条直线上“随机游走”，向左走一步和向右走一步的概率均为12，试探讨下列问题：（1）若质点进行了4次“随机游走”，在其中恰有2次向右游走的情况下，求第二次向左游走的概率；（2）记()P i 为()2,3,4,,2i i n =+ 次游走中恰有2次向右游走的概率，令()()()232Y P P P n =++++ .记()2,3,,n ξξ= 为不超过n 次游走的情况下，向右游走2次后停止游走（若向右游走一直不足2次，在游走到n 次时也停止游走），此时一共游走的次数，ξ的数学期望为()E ξ.请比较()E ξ与2Y 的大小，并说明理由.4．已知函数()()23ln 40f x x ax x a =+->．（1）讨论函数()f x 的单调性；（2）当12a =时，若方程()f x b =有三个不相等的实数根123,,x x x ，且123x x x <<，证明：4x x -<．5．已知双曲线2212:1y C x b -=经过椭圆2222:1x C y a +=的左、右焦点12,F F ，设12,C C 的离心率分别为12,e e ，且1262e e =．（1）求12,C C 的方程；（2）设P 为1C 上一点，且在第一象限内，若直线1PF 与2C 交于,A B 两点，直线2PF 与2C 交于,C D两点，设,AB CD 的中点分别为,M N ，记直线MN 的斜率为k ，当k 取最小值时，求点P 的坐标．变式：已知抛物线21:44C y x =-与双曲线22222:1(0)4x y C a a a-=>-相交于两点,,A B F 是2C 的右焦点，直线AF 分别交12,C C 于,C D 两点（不同于,A B 点），直线,BC BD 分别交x 轴于,P Q 两点.（1）求a 的取值范围；（2）记AQF 的面积为1,S CQP 的面积为2S ，当123S S =时，求a 的值.2024届大题强化训练及变式训练（13）4(1)求b 的值；(2)求ACD 的周长的取值范围.【答案】(1)3(2)(2【解析】（1）若选①，因为()tan sin cos 0C b A A ⋅-⋅=，由正弦定理可得()sin sin sin cos 0cos CB C A C A C⋅⋅=，显然sin 0C >，所以sin sin cos 0B C A C A -+⋅=，即()sin 3cos 0B C A ++=，所以sin 0B B -=，所以tan B =()0,πB ∈，所以π3B =，因为ABC 外接圆的半径1R =，所以2sin b R B ==若选②，因为()2cos cos 2sin sin tan C A C A A +=-⋅，所以()sin 2cos cos 2sin sin cos AC A C A A+=-⋅，即222cos cos cos 2sin sin sin C A A C A A +=-，所以222cos cos 2sin sin sin cos C A C A A A -=--，所以()2cos 1C A +=-，所以1cos 2B =，又()0,πB ∈，所以π3B =，因为ABC 外接圆的半径1R =，所以2sin b R B ==若选③，ABC 的面积为)2224a c b +-，则)2221sin 24S ac B a c b ==+-，由余弦定理可得2222cos a c b ac B =+-，所以1sin cos 22ac B ac B =，所以tan B =，又()0,πB ∈，所以π3B =，因为ABC 外接圆的半径1R =，所以2sin b R B ==（2）由题知2π3ADC ∠=，设CAD α∠=，03α<<，由正弦定理22πsin sin sin sin3AC AD CD ADC ACD CAD ====∠∠∠，所以2sin CD α=，π2sin 3AD α⎛⎫=- ⎪⎝⎭，所以π2sin 2sin 3ACD C a =++)3(απ-ππ2sin 2sin cos 2cos sin 33a a a=+-sin 2sin a a a ==)3(απ-，因为π03α<<，所以ππ2π333α<+<，所以πsin 123α⎛⎫<+≤ ⎪⎝⎭，所以ACD C Î∈2⎤+【答案】(1)条件选择见解析，3C =；(2)4+.【解析】（1）选择条件①，22cos a b c B =+，在ABC 中，由余弦定理得222222222a c b a c b a b c b ac a+-+-=+⋅=+，整理得222a bc ab +-=，则2221cos 22a b c C ab +-==，又()0,πC ∈，所以π3C =.选择条件②，2sin cos sin 2cos a A B bA C +=，于是sin cos sin cos cos a AB b A AC +=，在ABC 中，由正弦定理得，2sin cos sin sin coscos A B A B A A C +=，因为sin 0A ≠，则sin cossin cos cos A B B A C +，即()sin A B C +=，因为πA B C ++=，因此sin C C =，即tan C =()0,πC ∈，所以3C π=.232cos 2C C =-，在ABC 22(2cos 1)2cos 2C C C =--=-cos 2C C +=，则πsin 16C ⎛⎫+= ⎪⎝⎭，又()0,πC ∈，即有ππ7π,666C ⎛⎫+∈ ⎪⎝⎭，则ππ62C +=，所以π3C =.（2）由（1）知，π3C =，有2π3ABC BAC ∠+∠=，而BAC ∠与ABC ∠的平分线交于点I ，即有π3ABI BAI ∠+∠=，于是2π3AIB ∠=，设ABI θ∠=，则π3BAI θ∠=-，且π03θ<<，在ABI △中，由正弦定理得，4π2πsin sin sin()sin33BI AI AB AIB θθ===∠-，所以)4sin π3(BI θ=-，4sin AI θ=，所以ABI △的周长为34sin(4si π)n θθ-+1sin )4sin 22θθθ=-+π2sin 4sin()3θθθ=++=++，由π03θ<<，得ππ2π333θ<+<，则当ππ32θ+=，即π6θ=时，ABI △的周长取得最大值4+，所以ABI △周长的最大值为4+2．如图，将边长为2的菱形ABDC 沿其对角线BC 对折，使得点A 、D 分别位于边长为2的等边PBC所在平面的两侧，且PA =，PD =．设E 是PA的中点．（1）证明：平面PBC ⊥平面ABC ；（2）求平面EBD 与平面ABC 夹角的正弦值．【答案】（1）证明见解析（2）217【分析】（1）取BC 的中点O ，根据题意，分别证得OP BC ⊥和OP OA ⊥，利用线面垂直的判定定理，证得OP ⊥平面ABC ，进而证得平面PBC ⊥平面ABC ．（2）以O 为原点，建立空间直角坐标系，根据题意，分别求得平面ABC 和EBD 得到法向量(0,0,1)m =和()n = ，结合向量的夹角公式，即可求解.【解析】（1）证明：取BC 的中点O ，连接OA 、OP ，如图所示．因为四边形ABDC 是边长为2的菱形，PBC 是边长为2的等边三角形，所以ABC 也是边长为2的等边三角形，在等边PBC 中，O 是BC 的中点，可得OP BC ⊥且OA OP ==又因为PA =222PA OA OP =+，所以OP OA ⊥，因为⋂=OA BC O ，且,OA BC ⊂平面ABC ，所以OP ⊥平面ABC ；又因为OP ⊂平面PBC ，故平面PBC ⊥平面ABC ．（2）由（1）知，OP BC ⊥，OP OA ⊥．因为O 是等边ABC 的BC 边中点，可得OA BC ⊥．所以，以O 为原点，分别以,,OA OB OP 所在直线为x 、y 、z 轴，建立空间直角坐标系，如图所示，则,(0,1,0)(0,1,0),A B C -，可得33,0,22E ⎛⎫⎪ ⎪⎝⎭，因为DBC △是边长为2的等边三角形，故OD OP PD ===，所以60POD ∠=︒，且OD BC ⊥，又因为OP BC ⊥，OD OP O ⋂=，故BC ⊥平面DOP ，则D 在平面xOz 内，可得33,0,22D ⎛⎫- ⎪ ⎪⎝⎭，所以33,1,22BE ⎛⎫=- ⎪ ⎪⎝⎭ ，33,1,22BD ⎛⎫=-- ⎪ ⎪⎝⎭ ，设平面ABC 的法向量为(,,)m a b c = ，显然可令(0,0,1)m =；设平面EBD 的法向量为(,,)n x y z = ，则3302233022n BE x y z n BE x y z ⎧⋅=-+=⎪⎪⎨⎪⋅=--+=⎪⎩，令2z =，则0x =，y =，即()n =，所以27cos ,7m m m n m n⋅==，设平面EBD 与平面ABC 的夹角为θ，则21s in 7θ=，故平面EBD 与平面ABC的夹角的正弦值为7．变式：已知矩形ABCD 中，点E 在边CD 上，且22AD DE CE ===．现将ADE V 沿AE 向上翻折，使点D 到点P 的位置，构成如图所示的四棱锥P ABCE -．（1）若点F 在线段AP 上，且//EF 平面PBC ，求AFFP的值；（2）若142PB =，求锐二面角P EC A --的余弦值．【答案】（1）2（2）33【分析】1）点F 为线段AP 上靠近点P 的三等分点，过点F 作//FG AB 交PB 于点G ，连接CG ，可证//CE AB ，进而可证四边形FGCE 为平行四边形，可证//EF 平面PBC ．（2）取AE 中点O ，以O 为坐标原点建立空间直角坐标系，用向量法可求锐二面角P EC A --的余弦值．【解析】（1）点F 为线段AP 上靠近点P 的三等分点，满足//EF 平面PBC ，证明如下：如图，过点F 作//FG AB 交PB 于点G ，连接CG ，则13FG AB =，又2DE CE =，13CE AB =，所以13FG CE AB ==．因为//CE AB ，所以//CE FG ，所以四边形FGCE 为平行四边形，有//EF CG ，又EF ⊄平面PBC ，CG ⊂平面PBC ，所以//EF 平面PBC ．此时有2AFFP= .（2）2DE CE ==ADE V 为等腰直角三角形，322AB =，2AE =，135CEA ∠= ，45BAE ∠= ．取AE 的中点O ，以O 为坐标原点，OE 为x 轴建立如图所示的空间直角坐标系，设()0,,P m n ，()1,0,0E ，31,,022⎛⎫- ⎪⎝⎭C ，13,,022B ⎛⎫- ⎪⎝⎭，则()0,,OP m n = ，13,,22PB m n ⎛⎫=---⎪⎝⎭，因为1OP =，2PB =，所以22222211314222m n m n ⎧+=⎪⎪⎛⎫⎨⎛⎫⎛⎫+++= ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭⎩，解得0,1m n ==，则(0,0,1)P ，(1,0,1)PE =-，11,,022EC ⎛⎫=- ⎪⎝⎭，设平面PEC 的法向量为(),,m a b c =，则011022m PE a c m EC a b ⎧⋅=-=⎪⎨⋅=-=⎪⎩，不妨取1a =，则1,1b c ==，()1,1,1m =，设平面ECA 的一个法向量为()0,0,1n =，则cos ,||||3m n m n m n ⋅===⋅，则锐二面角P EC A --的的余弦值为33．3．如图，一个质点在随机外力的作用下，从原点O 出发，随机移动n 次，每次等可能地向左或向右移动一个单位长度，n 次移动结束后，质点到达的位置的数字记为X .（1）若2n =，求()0P X =;（2）若6n =，求X 的分布列和()E X 的值.【答案】（1）12（2）分布列见解析，0【分析】（1）由()12022c P X ==⨯可直接得到结果；（2）首先求出X 的所有可能取值以及对应的概率，再结合离散型随机变量的期望公式求答案即可.【解析】（1）()1210222c P X ===⨯；（2）设Y 表示6次移动中向左移动的次数，则()1166322Y B E Y ⎛⎫~=⨯= ⎪⎝⎭，，，质点最后到达的数字62X Y =-，则：()()6061160264P X P Y C ⎛⎫===== ⎪⎝⎭，()()6161341232P X P Y C ⎛⎫=====⎪⎝⎭，()()62611522264P X P Y C ⎛⎫=====⎪⎝⎭，()()6361503216P X P Y C ⎛⎫===== ⎪⎝⎭，()()16664P X P X =-===，()()34432P X P X =-===，()()152264P X P X =-===，X ∴的分布列为：X6-4-2-0246P16433215645161564332164()()()62620E X E Y E Y =-=-=.变式：一个质点在一条直线上“随机游走”，向左走一步和向右走一步的概率均为12，试探讨下列问题：（1）若质点进行了4次“随机游走”，在其中恰有2次向右游走的情况下，求第二次向左游走的概率；（2）记()P i 为()2,3,4,,2i i n =+ 次游走中恰有2次向右游走的概率，令()()()232Y P P P n =++++ .记()2,3,,n ξξ= 为不超过n 次游走的情况下，向右游走2次后停止游走（若向右游走一直不足2次，在游走到n 次时也停止游走），此时一共游走的次数，ξ的数学期望为()E ξ.请比较()E ξ与2Y 的大小，并说明理由.【答案】（1）12（2）()2E Y ξ≥，理由见解析【分析】（1）设出事件，求出相应概率，利用条件概率公式求出答案；（2）先计算出()()112i i i P i +-=，进一步得求和式()22122n ii i i Y +=-=∑，另一方面若2,3,,1k n =- 时停止游走，最后一次必然向右游走，可以得出()12k k P k ξ-==，从而()2311221222n n P n ξ--⎛⎫==-+++ ⎝⎭ ，结合错位相减法、等比数列求和公式得()P n ξ=的表达式，进一步结合期望公式得()()2112122n kn k k k n E ξ--=-=+∑，将()E ξ与2Y 作差即可比较大小.【解析】（1）设事件n A 表示共有()0,1,2,3,4n n =次向右游走，事件B 表示第二次向左游走，则2BA 表示一共向右游走2次，且第二次向左游走，则从剩余的三次选择两次向右游走，故()22321113C 22216P BA =⨯⨯=，2A 表示一共向右游走2次，故()22422113C 228P A =⨯=，则()()()2223116328P BA P B A P A ===.（2）根据题意可知()()2212111C 222i i ii i P i -+-⎛⎫⎛⎫=⨯⨯= ⎪ ⎪⎝⎭⎝⎭，()()()()()22122112222322222n n i ii i i i i i Y P P P n +++==--=++++==∑∑ .若2,3,,1k n =- ，最后一次必然向右游走，故()2111111C 2222k k k k P k ξ---⎛⎫==⨯⨯= ⎪⎝⎭，()2311221222n n P n ξ--⎛⎫==-+++ ⎪⎝⎭ ，记231122222n n n S --=+++ ①.3411222222n n n S -=+++ ②.两式相减得2311111112214212222222212n n n n n n n n nS ----=+++-=-=-- ，112n n n S -∴=-，()111122n n n nP n ξ--∴==-+=.所以()()()()211122122n n kn k k k k n E kP k nP n ξξξ---==-==+==+∑∑；()()()()()()()221211122211112122222222n n i n i n n n n k i k k i i n n n n n n n n E Y ξ-+--++==---+++-=+-=--∑∑()()()()()()()()()1222121212112022222n n n n n n n n n n n n n n n ++++++++-+++-=-==≥，故()2E Y ξ≥.4．已知函数()()23ln 40f x x ax x a =+->．（1）讨论函数()f x 的单调性；（2）当12a =时，若方程()f x b =有三个不相等的实数根123,,x x x ，且123x x x <<，证明：314x x -<．【答案】（1）答案见解析（2）证明见解析【分析】（1）求导，分0∆≤和0∆>两种情况，结合导数符号判断函数单调性；（2）根据题意分析可知：()f x 在()()0,1,3,+∞内单调递增，在()1,3内单调递减，123013x x x <<<<<，利用极值点偏离证明122x x +>和236x x +<，即可得结果.【解析】（1）由题意可知：()f x 的定义域为()0,∞+，()2324324ax x f x ax x x-+'=+-=，且0a >，令()0f x '=，可得22430ax x -+=，当01624a =-≤∆，即23a ≥时，可知22430ax x -+≥在()0,∞+内恒成立，即()0f x '≥在()0,∞+内恒成立，所以()f x 在()0,∞+内单调递增；当01624a =->∆，即023a <<时，由22430ax x -+=解得12462x a-=或222x a +=，由1212230,02x x x x a a+=>=>可知120x x <<，若()()120,,x x x ∞∈⋃+，()0f x ¢>；若()12,x x x ∈，()0f x '<；所以()f x 在()()120,,,x x +∞内单调递增，在()12,x x 内单调递减；综上所述：当23a ≥时，()f x 在()0,∞+内单调递增；当023a <<时，()f x 在2462460,,,22a a ⎛⎫⎛⎫++∞ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭内单调递增，在22,22a a ⎛+ ⎝⎭内单调递减.（2）当12a =时，可得()213ln 42f x x x x =+-，()34f x x x +'=-，由（1）可知：()f x 在()()0,1,3,+∞内单调递增，在()1,3内单调递减，由题意可得：123013x x x <<<<<，因为()()()123f x f x f x b ===，令()()()2,01g x f x f x x =--<<，则()()()()()233612024242x x x x g x f x f x x x x ⎛⎫+-+-- ⎪--⎛⎫'''=+-=+=> ⎪-⎝⎭⎭⎝，可知()g x 在()0,1内单调递增，则()()10g x g <=，可得()()2f x f x <-在()0,1内恒成立，因为101x <<，则()()()1212f x f x f x =<-，且12122,13x x <-<<<，()f x 在()1,3内单调递减，则122x x -<，即122x x +>；令()()()6,13h x f x f x x =--<<，则()()()()()233636064646x x x x g x f x f x x x x ⎛⎫+-+-- ⎪--⎛⎫'''=+-=+=> ⎪-⎝⎭⎭⎝，可知()h x 在()1,3内单调递增，则()()30h x h <=，可得()()6h x h x <-在()1,3内恒成立，因为213x <<，则()()()2326f x f x f x =<-，且23365,3x x <-<>，()f x 在()3,+∞内单调递增，则236x x ->，即236x x +<；由【解析】（1）函数()ln f x x ax =-的定义域为()0,∞+，导函数11()'-=-=axf x a x x，①当0a ≤时，()0f x '>，则()f x 在()0,+∞上单调递增；②当0a >时，令1()0f x a x ¢=-=，则1x a=，∴当10x a <<时，()0f x '>，函数()f x 在10,a ⎛⎫⎪⎝⎭上单调递增，当1x a >时，()0f x '<，函数()f x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减；（2）由（1）知，方程ln 0x ax -=的两个不等的正实根12,x x ，即1122ln ,ln x ax x ax ==，亦即()2121ln ln x x a x x -=-，从而2121ln ln x x a x x -=-，设21x t x =，又1202x x <<，即2t >，要证20x ->，即证2128x x <，只需证122ln x x <，即证123ln 22ax ax +<，即证()2123ln 2a x x ->，即证()212121ln ln 23ln2x x x x x x -->-，即证1222112ln 3ln 2x x x x x x -⋅>-，即证22121121ln 3ln21x x xx x x -⋅>-，即证21ln 3ln 21t t t -⋅>-，令()()21ln 21t g t t t t -=>-，则()()()212ln 3,21t t t g t t t +--=>-'设()()12ln 3,2F t t t t t =+-->，则()()()222111120t t F t t t t +-=--=>'则()F t 在()2,+∞上单调递增，有()()32ln 202F t F >=->，于是()0g t '>，即有()g t 在()2,+∞上单调递增，因此()()23ln2g t g >=，即21ln 3ln21t t t -⋅>，所以2128x x <成立，即20x ->．5．已知双曲线2212:1y C xb -=经过椭圆2222:1x C y a +=的左、右焦点12,F F ，设12,C C 的离心率分别为12,e e ，且122e e =．（1）求12,C C 的方程；（2）设P 为1C 上一点，且在第一象限内，若直线1PF 与2C 交于,A B 两点，直线2PF 与2C 交于,C D两点，设,AB CD 的中点分别为,M N ，记直线MN 的斜率为k ，当k 取最小值时，求点P 的坐标．【答案】（1）1C 的方程为2221,2y x C -=的方程为2212xy +=（2）)P 【解析】（1）依题意可得211a -=，得22a =，由1262e e =，得222212211312b a e e a +-=⋅=，解得22b =，故1C 的方程为2221,2y x C -=的方程为2212x y +=．（2）易知()()121,0,1,0F F -，设()00,P x y ，直线12,PF PF 的斜率分别为12,k k ，则200012122000,,111y y y k k k k x x x ===+--，()00,P x y在221:12y C x -=，即有220012y x -=，可得20122021y k k x ==-为定值．设直线1PF 的方程为：()11y k x =+，联立2212x y +=可得()()2222111214210,Δ0k x k x k +++-=>恒成立，设()()1122,,,A x y B x y ，则有211221421k x x k -+=+，可求得21122112,2121k k M k k ⎛⎫- ⎪++⎝⎭，设直线2PF 的方程为：()()()233441,,,,y k x C x y D x y =-，同理可得22222222,2121k k N k k ⎛⎫- ⎪++⎝⎭，则()()()()122222122112222222121221221221212121222212212121k k k k k k k k k k k k k k k k k ++++++=-=-++++++()()()()()()1212121222222221212121212212182822k k k k k k k k k k k k k k k k k k ++++=-=-⎡⎤++++-⎣⎦由122k k =可得：()()122125242k k k k k +=-++，点P 在第一象限内，故210k k >>，()121255324242k k k k k =-≥=-+++当且仅当()1212242k k k k=++，即12k k+=时取等号，而12k k +>=，故等号可以取到．即当k 取最小值时，12k k +=122k k=，可解得121,1k k =-=+，故1PF 的方程为：)()211,y x PF =-+的方程为：)()11y x =+-，联立可解得2x y ⎧=⎪⎨=⎪⎩)P．说明：第（2）问中未说明能取到最小值扣1分，另外可以分别设直线方程11x t y =-和21x t y =+求解，此时：121222221122221,,,,22222t t M N t t t t t t ⎛⎫⎛⎫--=⎪ ⎪++++⎝⎭⎝⎭()()()()()12121222212122528412t t t t t t k t t t t +++=-=-++++也可以直接通过()00,P x y 的横纵坐标代换来求解，此时：()()()()()()2200000022222222000000001122,,,12121212y x y x y y M N x y x y x y x y ⎛⎫⎛⎫+--- ⎪ ⎪⎪ ⎪++++-+-+⎝⎭⎝⎭()2222000000000022222200000000214114522422242243x x y x y x y x x y k y x y y x y x y -++=-⋅=-⋅=-⋅+++++都可以根据相应步骤给分．变式：已知抛物线21:44C y x =-与双曲线22222:1(0)4x y C a a a-=>-相交于两点,,A B F 是2C 的右焦点，直线AF 分别交12,C C 于,C D 两点（不同于,A B 点），直线,BC BD 分别交x 轴于,P Q 两点.（1）求a 的取值范围；（2）记AQF 的面积为1,S CQP 的面积为2S ，当123S S =时，求a 的值.【答案】（1）())11,2a ∈-⋃a =【解析】（1）由双曲线方程222214x y a a -=-，则22040a a ⎧>⎨->⎩，得到()0,2a ∈，联立㘯物线与双曲线方程222221444x y a a y x ⎧-=⎪-⎨⎪=-⎩，得到()2224440a x a x a --+=，，记()()()()2224224422f x a x a x a a x a a x a ⎡⎤⎡⎤=--+=+---⎣⎦⎣⎦，可知()0f x =有两个根22aa +和22a a -，其中212a a <+，则212a a>-，解得()1,2a ∈.又直线AF 分别交12,C C 于,C D （不同于,A B 点），即,,A B F 三点不共线，当2x =时，代入抛物线方程得到()2,2A ，将()2,2A 代入双曲线方程得到224414a a-=-，解得26a =-故1a =-.综上，())11,2a ∈⋃（2）由()()1122,,,A x y C x y 是直线AF 与抛物线21:44C y x =-的两个交点，显然直线AF 不垂直y 轴，点()2,0F ，故设直线AF 的方程为2x my =+，由2244x my y x =+⎧⎨=-⎩消去x 并整理得2440y my --=，所以124y y =-为定值.设()11,B x y -，直线BC 的斜率21212221212144444y y y y y y x x y y ++==++---，方程为()11214y y x x y y +=--，令0y =，得点P 的横坐标()2121112440444P y y y y y y x -++=+==，设()33,D x y ，由2222214x my x ya a =+⎧⎪⎨-=⎪-⎩消去x 得()()()2222222244440m m a a y m a y a --+-+-=，()()()()()2222222222222222240Δ1644444140m m a a m a am m a a a m a ⎧--≠⎪⎨=-----=+->⎪⎩，()()222131322222222444,44m a a y y y y m m a am m a a ---+==----，而直线BD 的方程为()311131y y y y x x x x ++=--，依题意0m ≠，令0y =，得点Q 的横坐标()()()13113113113131Q y x x y x x x y y x x y y y y --++=+=++133113y x y x y y +=+()()()1331131313132222y my y my my y y y y y y y +++++==++()()()2222222222222222248444444m a m a m m a a m m a a m a m m a a ---+----=----()2244122a a --==-，因此22112,22QF a PQ a =-=.联立抛物线与双曲线方程222221444x y a a y x ⎧-=⎪-⎨⎪=-⎩，得到()2224440a x a x a --+=，解得点A 的坐标2,2a a ⎛ -⎝，由122144,y y y y -=-==.根据123S S =，则1212312A CQF y S S PQ y⋅==⋅，代入得到2122122312a y a y ⎛⎫-⋅ ⎪⎝⎭=⋅，即()22121243a y a y y -⋅=⋅，化简得()()()222144122a a a a a+--⋅=-解得34a =，故a =。

专题01 “陷阱”类题型——巧用排除法目录一、题型解读二、热点题型归纳【题型1】偷换概念【题型2】表述夸张【题型3】无中生有【题型4】逻辑错误三、最新模考题组练在高中生物学科内选择题部分常常设置“陷阱”以混淆迷惑，因此在答题时，首先需要敏锐洞察题目中涵盖的“陷阱”信息，避免上当。

尤其是对于细菌、等原核生物、病毒类生物或者是植物的根尖细胞等等特殊的生物和细胞而言，应该保持高度注意。

学生应谨记原核生物不具备核膜、高尔基体等细胞器，没有生物膜系统，但可能会形成细胞壁。

常见的陷阱设置包括：偷换概念、表述夸张、无中生有、答非所问和逻辑错误等。

【题型1】偷换概念【典例分析1】（2023·湖南·统考高考真题）“油菜花开陌野黄，清香扑鼻蜂蝶舞。

”菜籽油是主要的食用油之一，秸秆和菜籽饼可作为肥料还田。

下列叙述错误的是（）A．油菜花通过物理、化学信息吸引蜂蝶B．蜜蜂、蝴蝶和油菜之间存在协同进化C．蜂蝶与油菜的种间关系属于互利共生D．秸秆和菜籽饼还田后可提高土壤物种丰富度陷阱提示：将“原始合作”偷换成“互利共生”。

【变式演练1-1】（2023·海南·高考真题）我国航天员乘坐我国自主研发的载人飞船，顺利进入空间实验室，并在太空中安全地生活与工作。

航天服具有生命保障系统，为航天员提供了类似地面的环境。

下列有关航天服及其生命保障系统的叙述，错误的是（）A．能清除微量污染，减少航天员相关疾病的发生B．能阻隔太空中各种射线，避免航天员机体细胞发生诱发突变C．能调控航天服内的温度，维持航天员的体温恒定不变D．能控制航天服内的压力，避免航天员的肺由于环境压力变化而发生损伤【变式演练1-2】（2023·山东·高考真题）某种植株的非绿色器官在不同O2浓度下，单位时间内O2吸收量和CO2释放量的变化如图所示。

若细胞呼吸分解的有机物全部为葡萄糖，下列说法正确的是（）A．甲曲线表示O2吸收量B．O2浓度为b时，该器官不进行无氧呼吸C．O2浓度由0到b的过程中，有氧呼吸消耗葡萄糖的速率逐渐增加D．O2浓度为a时最适合保存该器官，该浓度下葡萄糖消耗速率最小【题型2】表述绝对【典例分析2】（2023·浙江·统考高考真题）浙江浦江县上山村发现了距今1万年的稻作遗址，证明我国先民在1万年前就开始了野生稻驯化。

由一道高考题看数学变式教学作者：邓谦棠来源：《师道·教研》2013年第07期纵观每年的高考试卷，我们都可以发现许多“似曾相识”的题，其实，他们都是从课本上的习题变式而来。

那么，怎样进行课本习题的变式教学呢？这是我们每个数学教师必须认真思考的问题，下面我将与大家一起来就习题变式教学谈谈自己的看法。

1. 变式教学的目的高中数学学习的内容跨度大、抽象性强，只有促进高中生对数学知识的深刻理解，才能达到掌握和灵活运用数学知识的目的。

在数学学习中，教师通过变式教学，可以把一个看似孤立的问题从不同角度向外扩散，并形成一个有规律可行的系列，帮助学生在问题的解答过程中去寻找解此类问题的思路和方法，有意识地展现教学过程中教师与学生数学思维活动的过程，充分调动学生学习的积极性，培养学生独立思考问题、分析问题和解决问题的能力，培养学生的创新意识以及创造性的逻辑思维方式。

同时，通过变式教学，学生不需要做大量地、重复地同一种题型的练习，减轻了学生的学业负担，提高了学习效率。

2. 变式教学的方法叶圣陶先生曾说：“教材只能作为教课的依据，要教得好，使学生受到实益，还要靠教师的善于运用”。

教材是教学的重要资源，课本中的每一个例题和习题都是经过“千锤百炼”的，有很高的教育价值，因此在教学中我们要精心设计和挖掘课本的例题和习题，编制一题多变、一题多解、一题多用和多题一解，以提高学生灵活运用知识的能力。

下面以课本《数学》必修4第91页的第6题为例，谈谈习题变式教学的方法。

原题：已知向量■，■，求作向量■，使■+■+■=0.表示■，■，■的有向线段能构成三角形吗？分析：如图1，设■=■，■=■，以AB、AD为邻边作平行四边形ABCD，由向量加法的平行四边形法则可知■+■=■，即■=■.显然，当■，■不共线时，表示■，■，■的有向线段能构成三角形。

2.1 创设新情境，培养学生思维的灵活性创设新情境是指把条件放在一些特殊的情境中，使问题得以深化.而且，在新的情境中，解决问题的方法不仅仅拘泥于原题的方法，这就要求学生有扎实的基础，有变通的能力，培养了学生思维的灵活性。

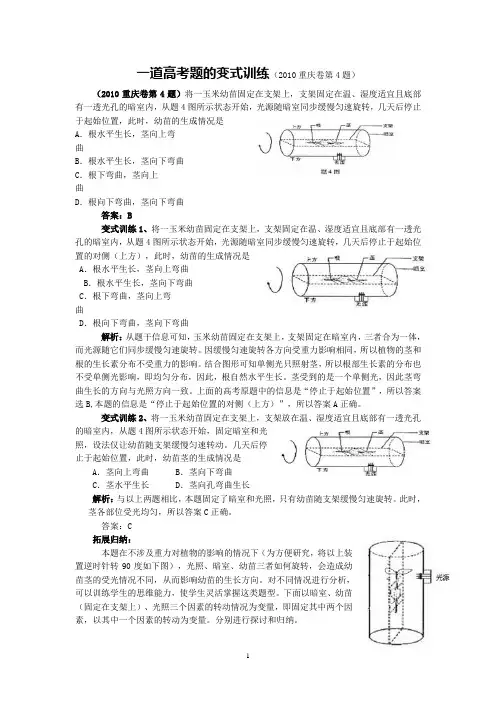
一道高考题的变式训练（2010重庆卷第4题）（2010重庆卷第4题）将一玉米幼苗固定在支架上，支架固定在温、湿度适宜且底部有一透光孔的暗室内，从题4图所示状态开始，光源随暗室同步缓慢匀速旋转，几天后停止于起始位置，此时，幼苗的生成情况是A．根水平生长，茎向上弯曲B．根水平生长，茎向下弯曲C．根下弯曲，茎向上曲D．根向下弯曲，茎向下弯曲答案：B变式训练1、将一玉米幼苗固定在支架上，支架固定在温、湿度适宜且底部有一透光孔的暗室内，从题4图所示状态开始，光源随暗室同步缓慢匀速旋转，几天后停止于起始位置的对侧（上方），此时，幼苗的生成情况是A．根水平生长，茎向上弯曲B．根水平生长，茎向下弯曲C．根下弯曲，茎向上弯曲D．根向下弯曲，茎向下弯曲解析：从题干信息可知，玉米幼苗固定在支架上，支架固定在暗室内，三者合为一体，而光源随它们同步缓慢匀速旋转。

因缓慢匀速旋转各方向受重力影响相同，所以植物的茎和根的生长素分布不受重力的影响。

结合图形可知单侧光只照射茎，所以根部生长素的分布也不受单侧光影响，即均匀分布，因此，根自然水平生长。

茎受到的是一个单侧光，因此茎弯曲生长的方向与光照方向一致。

上面的高考原题中的信息是“停止于起始位置”，所以答案选B,本题的信息是“停止于起始位置的对侧（上方）”，所以答案A正确。

变式训练2、将一玉米幼苗固定在支架上，支架放在温、湿度适宜且底部有一透光孔的暗室内，从题4图所示状态开始，固定暗室和光照，设法仅让幼苗随支架缓慢匀速转动。

几天后停止于起始位置，此时，幼苗茎的生成情况是A．茎向上弯曲B．茎向下弯曲C．茎水平生长D．茎向孔弯曲生长解析：与以上两题相比，本题固定了暗室和光照，只有幼苗随支架缓慢匀速旋转。

此时，茎各部位受光均匀，所以答案C正确。

答案：C拓展归纳：本题在不涉及重力对植物的影响的情况下（为方便研究，将以上装置逆时针转90度如下图），光照、暗室、幼苗三者如何旋转，会造成幼苗茎的受光情况不同，从而影响幼苗的生长方向。

2024届大题强化训练及变式训练（6）1．如图，在四棱台1111ABCD A B C D -中，下底面ABCD 是平行四边形，120ABC ∠=︒，1122AB A B ==，8BC =，1A A =1DD DC ⊥，M 为BC的中点．（1）求证：平面11CDD C ⊥平面1D DM ；（2）若14D D =，求直线DM 与平面11BCC B 所成角的正弦值．变式：如图，圆台上底面圆1O 半径为1，下底面圆2OAB 为圆台下底面的一条直径，圆2O 上点C 满足1,AC BC PO =是圆台上底面的一条半径，点,P C 在平面1ABO 的同侧，且1//PO BC.（1）证明：平面PAC ⊥平面ABC ；（2）若圆台的高为2，求直线1AO 与平面PBC 所成角的正弦值.大题强化训练及变式训练（6）-2024届高三二轮复习大题强化训练及变式训练（新高考九省联考题型）（解析版）2．已知数列{}n a 满足，()()1214126n n n n a a na +-++⋅⋅⋅+=．（1）求数列{}n a 的通项公式；（2）若对任意*1212,333n n a a a n m ∈≥++⋅⋅⋅+N ，求m 的最小整数值．变式：已知数列{}n a 的前n 项和为n S ，194a =-，且14391n n S S +=-．(1)求数列{}n a 的通项；(2)设数列{}n b 满足3(4)0n n b n a +-=，记{}n b 的前n 项和为n T ，若n n T b λ≤对任意N n *∈恒成立，求λ的范围．3．某商场举行“庆元宵，猜谜语”的促销活动，抽奖规则如下：在一个不透明的盒子中装有若干个标号为1，2，3的空心小球，球内装有难度不同的谜语．每次随机抽取2个小球，答对一个小球中的谜语才能回答另一个小球中的谜语，答错则终止游戏．已知标号为1，2，3的小球个数比为1：2：1，且取到异号球的概率为57．（1）求盒中2号球的个数；（2）若甲抽到1号球和3号球，甲答对球中谜语的概率和对应奖金如表所示，请帮甲决策猜谜语的顺序（猜对谜语的概率相互独立）球号1号球3号球答对概率0.80.5奖金100500变式：某公司生产某种出口商品，为严把质量关，对每件商品请3位专家进行质量把关，质量把关程序如下：（i）若一件商品3位专家都认为质量过关，则该商品质量为A 级；（ii）若仅有1位专家认为质量不过关，再由另外2位专家进行第二次质量把关，若第二次质量把关这2位专家都认为质量过关，则该商品质量为B 级，若第二次质量把关这2位专家中有1位或2位认为质量不过关，则该商品质量为C 级；（iii）若有2位或3位专家认为质量不过关，则该商品质量为D 级．已知每一次质量把关中一件商品被1位专家认为质量不过关的概率为13，各商品质量是否过关相互独立．（1）对两件商品进行质量把关，求两件商品质量均为D 级的概率；（2）若一件商品质量为,,A B C 级，则该商品可出口外销，且利润分别为1000元，500元，200元，若一件商品质量为D 级，则不能出口外销，利润记为10元．记1件商品的利润为X 元，求X 的分布列与数学期望．4．已知矩形ABCD 中，,,,AB BC E F G H ==分别是矩形四条边的中点，以矩形中心O 为原点，HF 所在直线为x 轴，EG 所在直线为y 轴，建立如图所示的平面直角坐标系.直线,HF BC 上的动点,R S 满足(),OR OF CS CF λλλ==∈R .（1）求直线ER 与直线GS 交点P 的轨迹方程；（2）当λ=R 的直线m （与x 轴不重合）和点P 轨迹交于,M N 两点，过点N 作直线:3l x =-的垂线，垂足为点Q .设直线MQ 与x 轴交于点K ，求KMN △面积的最大值.变式：已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ，点31,2P ⎛⎫ ⎪⎝⎭在椭圆C 上，且PF 垂直于x 轴．（1）求椭圆C 的方程；（2）直线l 斜率存在，交椭圆C 于,A B 两点，,,A B F 三点不共线，且直线AF 和直线BF 关于PF 对称．（ⅰ）证明：直线l 过定点；（ⅱ）求ABF △面积的最大值．5．已知函数()()2e 0x f x ax a =->．（1）若函数()f x 有3个不同的零点，求a 的取值范围；（2）已知()f x '为函数()f x 的导函数，()f x '在R 上有极小值0，对于某点()()00,P x f x ，()f x 在P 点的切线方程为()y g x =，若对于R x ∀∈，都有()()()00x x f x g x -⋅-≥⎡⎤⎣⎦，则称P 为好点．①求a 的值；②求所有的好点．变式：帕德近似是法国数学家亨利．帕德发明的用有理多项式近似特定函数的方法．给定两个正整数m ，n ，函数()f x 在0x =处的[,]m n 阶帕德近似定义为：011()1mm n n a a x a x R x b x b x+++=+++ ，且满足：(0)(0)f R =，(0)(0)f R ''=，(0)(0)f R ''''=，…，()()(0)(0)m n m n f R ++=．（注：[]()()f x f x '='''，[]()()f x f x ''''''=，[](4)()()f x f x ''''=，(5)(4)()()f x f x '⎡⎤=⎣⎦，…；()()n f x 为(1)()n f x -的导数）已知()ln(1)f x x =+在0x =处的[]1,1阶帕德近似为()1ax R x bx =+．（1）求实数a ，b 的值；（2）比较()f x 与()R x 的大小；（3）若()1()()()2f x h x m f x R x ⎛⎫=-- ⎪⎝⎭在(0,)+∞上存在极值，求m 的取值范围．2024届大题强化训练及变式训练（6）1．如图，在四棱台1111ABCD A B C D -中，下底面ABCD 是平行四边形，120ABC ∠=︒，1122AB A B ==，8BC =，1A A =1DD DC ⊥，M 为BC 的中点．（1）求证：平面11CDD C ⊥平面1D DM ；（2）若14D D =，求直线DM 与平面11BCC B 所成角的正弦值．【答案】（1）证明见解析；（2）67.【分析】（1）利用平行四边形性质及余弦定理求出DM ，进而证得DM CD ⊥，再利用线面垂直、面面垂直的判定推理即得.（2）由已知证得1D D ⊥平面ABCD ，再以D 为原点建立空间直角坐标系，利用线面角的向量求法求解即得.【解析】（1）在ABCD Y 中，由120ABC ∠=︒，得60DCM ∠=︒，而2,4DC CM ==，在DCM △中，由余弦定理，得DM ==，则222DM CD CM +=，即DM CD ⊥，又1，1DM D = ，1,DD DM ⊂平面1D DM ，因此CD ⊥平面1D DM ，而CD ⊂平面11CDD C ，所以平面11CDD C ⊥平面1D DM .（2）在四棱台1111ABCD A B C D -中，由112AB AB =，得1128AD A D ==，有114A D =，在梯形11ADD A 中，18,4AD DD ==，过1A 作11//A E D D 交AD 于点E ，则14,4AE A E ==，又1AA =，显然22211AE A E AA +=，则1A E AD ⊥，即1D D AD ⊥，又1,,,D D CD AD CD D AD CD ⊥=⊂ 平面ABCD ，于是1D D ⊥平面ABCD ，以D 为坐标原点，以1,,DM DC DD 的方向分别为,,x y z 轴的正方向建立空间直角坐标系D xyz -，1(0,0,0),(0,2,0),(0,1,4),D C C M，1(2,0),(0,1,4)MC CC =-=- ，设平面11BCC B 的法向量为(,,)n x y z = ，则120 40MC n y CC n y z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ ，令z =，得n = ，而DM = ，设DM 与平面11BCC B 所成角大小为θ，因此||467sin |cos ,|67||||DM n DM n DM n θ⋅=〈〉== ，所以直线DM 与平面11BCC B 所成角的正弦值为46767.变式：如图，圆台上底面圆1O 半径为1，下底面圆2OAB 为圆台下底面的一条直径，圆2O 上点C 满足1,AC BC PO =是圆台上底面的一条半径，点,P C 在平面1ABO 的同侧，且1//PO BC.（1）证明：平面PAC ⊥平面ABC ；（2）若圆台的高为2，求直线1AO 与平面PBC 所成角的正弦值.【答案】（1）证明见解析（2）15【分析】（1）取AC 中点M ，四边形12PO O M 为平行四边形，从而得到12//PM O O ，根据12O O ⊥平面ABC 可得PM ⊥平面ABC ，从而得到需求证的面面垂直.（2）建立如图所示的空间直角坐标系，求出1AO 及平面PBC 的法向量后可求线面角的正弦值.【解析】（1）取AC 中点M ，由题意，121,22PO BC AB ===，又1//PO BC ，故1111//,22PO BC PO BC =.又2211//,22O M BC O M BC =，故1212//,PO O M PO O M =，所以四边形12PO O M 为平行四边形，则12//PM O O .由12O O ⊥平面ABC ，故PM ⊥平面ABC ，又PM ⊂面PAC ，故平面PAC ⊥平面ABC .（2）以2O 为坐标原点，2221,,O B O C O O的方向为,,x y z 轴的正方向，建立如图所示的空间直角坐标系.则有：())()()1,,,,,2,0,0,222A B C P O ⎛⎫- ⎪ ⎪⎝⎭，故)12.AO = 设平面PBC 的法向量(),,n x y z =而()22,,,222BC CP ⎛⎫==-- ⎪ ⎪⎝⎭ ，故0222022n BC n CP x y z ⎧⋅==⎪⎨⋅=--+=⎪⎩ ，令1z =，得).n = 设所求角的大小为θ，则111230sin cos ,15AO n AO n AO n θ⋅====⋅ .所以直线1AO 与平面PBC所成角的正弦值为15.2．已知数列{}n a 满足，()()1214126n n n n a a na +-++⋅⋅⋅+=．（1）求数列{}n a 的通项公式；（2）若对任意*1212,333n n a a a n m ∈≥++⋅⋅⋅+N ，求m 的最小整数值．【答案】（1）()*21n a n n =-∈N （2）1【分析】（1）作差法，计算得到21n a n =-，验证1n =是否成立，进而得到数列{}n a 的通项公式；（2）令1212333n n n a a a S =++⋅⋅⋅+，利用错位相减法得到113n n n S +=-，即可求得m 的最小整数值．【解析】（1）因为()()1214126n n n n a a na +-++⋅⋅⋅+=，①当2n ≥时，()()()121145216n n n n a a n a ---++⋅⋅⋅+-=，②①-②得()()()()14114566n n n n n n n na +---=-=22n n -，即21n a n =-．当1n =时，11a =也符合上式，所以()*21n a n n =-∈N ．（2）因为21n a n =-，所以2133n n n a n -=，令121223135213333333n n n n a a a n S -=++⋅⋅⋅+=+++⋅⋅⋅+，所以231411353333213n n n S +=+++⋅⋅⋅+-，两式相减得211121133212221121222133333333313n n n n n n n n n S +++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭--+⎢⎥⎣⎦=++⋅⋅⋅+-=--=--，所以()*113n n n S n +=-∈N ．因为103n n +>，所以1n S <，所以m 1≥，故m 的最小整数值为1．变式：已知数列{}n a 的前n 项和为n S ，194a =-，且14391n n S S +=-．(1)求数列{}n a 的通项；(2)设数列{}n b 满足3(4)0n n b n a +-=，记{}n b 的前n 项和为n T ，若n n T b λ≤对任意N n *∈恒成立，求λ的范围．【答案】(1)33()4n n a =-⋅；(2)31λ-≤≤．【解析】(1)当1n =时，1214()39a a a +=-，229272749,4416a a =-=-∴=-，当2n ≥时，由1439n n S S +=-①，得1439n n S S -=-②，①-②得143n n a a +=122730,0,164n n n a a a a +=-≠∴≠∴=，又213,{}4n a a a =∴是首项为94-，公比为34的等比数列，1933(3()444n n n a -∴=-⋅=-⋅；(2)由3(4)0n nb n a +-=，得43(4)()34n n n n b a n -=-=-，所以234333333210(4)44444n n T n +⎛⎫⎛⎫⎛⎫⎛⎫=-⨯-⨯-⨯⨯++-⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ ，2413333333321(5)(4)444444n n n T n n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-⨯-⨯-⨯++-⋅+-⋅ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ ，两式相减得234113333333(4)4444444n n n T n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-⨯++++--⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 1193116493(4)34414n n n -+⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=-+-- ⎪⎝⎭-111993334(4)44444n n n n n +++⎛⎫⎛⎫⎛⎫=-+---⋅=-⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以134(4n n T n +=-⋅，由n n T b λ≤得1334()(4)()44n nn n λ+-⋅≤-⋅恒成立，即(4)30n n λ-+≥恒成立，4n =时不等式恒成立；4n <时，312344n n n λ≤-=----，得1λ≤；4n >时，312344n n n λ≥-=----，得3λ≥-；所以31λ-≤≤．3．某商场举行“庆元宵，猜谜语”的促销活动，抽奖规则如下：在一个不透明的盒子中装有若干个标号为1，2，3的空心小球，球内装有难度不同的谜语．每次随机抽取2个小球，答对一个小球中的谜语才能回答另一个小球中的谜语，答错则终止游戏．已知标号为1，2，3的小球个数比为1：2：1，且取到异号球的概率为57．（1）求盒中2号球的个数；（2）若甲抽到1号球和3号球，甲答对球中谜语的概率和对应奖金如表所示，请帮甲决策猜谜语的顺序（猜对谜语的概率相互独立）球号1号球3号球答对概率0.80.5奖金100500【答案】（1）4个（2）推荐甲先回答3号球中的谜语再回答1号球中的谜语【分析】（1）由取到异号球的概率为57，设1，2，3号球的个数分别为n ，2n ，n ，列方程求解；（2）分先回答1号球中的谜语和先回答3号球中的谜语两种情况，分别计算奖金的数学期望，比较后得结论.【解析】（1）由题意可设1，2，3号球的个数分别为n ，2n ，n ，则取到异号球的概率11112242C C C C 5C 7n n n nnP +==，22554(41)7n n n ⋅∴=-，即22n n =．解得2n =．所以盒中2号球的个数为4个．（2）若甲先回答1号球再回答3号球中的谜语，因为猜对谜语的概率相互独立，记X 为甲获得的奖金总额，则X 可能的取值为0元，100元，600元，(0)0.2P X ==，(100)0.8(10.5)0.4P X ==⨯-=，(600)0.80.50.4P X ==⨯=．X 的分布列为X 0100600P0.20.40.4X 的均值为()280E X =，若甲先回答3号球再回答1号球，因为猜对谜语的概率相互独立，记Y 为甲获得的奖金总额，则Y 可能的取值为0元，500元，600元，()00.5P Y ==．()()5000.510.80.1P Y ==⨯-=()6000.80.50.4P Y ==⨯=Y 的分布列为Y 0500600P0.50.10.4Y 的均值为()290E Y =，因为()()E Y E X >，所以推荐甲先回答3号球中的谜语再回答1号球中的谜语．变式：某公司生产某种出口商品，为严把质量关，对每件商品请3位专家进行质量把关，质量把关程序如下：（i）若一件商品3位专家都认为质量过关，则该商品质量为A 级；（ii）若仅有1位专家认为质量不过关，再由另外2位专家进行第二次质量把关，若第二次质量把关这2位专家都认为质量过关，则该商品质量为B 级，若第二次质量把关这2位专家中有1位或2位认为质量不过关，则该商品质量为C 级；（iii）若有2位或3位专家认为质量不过关，则该商品质量为D 级．已知每一次质量把关中一件商品被1位专家认为质量不过关的概率为13，各商品质量是否过关相互独立．（1）对两件商品进行质量把关，求两件商品质量均为D 级的概率；（2）若一件商品质量为,,A B C 级，则该商品可出口外销，且利润分别为1000元，500元，200元，若一件商品质量为D 级，则不能出口外销，利润记为10元．记1件商品的利润为X 元，求X 的分布列与数学期望．【答案】（1）49729（2）分布列见解析；期望为1207027【分析】（1）根据相互独立事件概率计算公式求得所求概率.（2）根据（1）求得X 的分布列，进而求得数学期望.【解析】（1）由题意，对一件商品进行质量把关，其质量为A 级的概率为318(1)327-=，质量为B 级的概率为122311116C (1)(1)33381⨯⨯-⨯-=，质量为C 级的概率为1212321111120C (1)[C (1)()]3333381⨯⨯-⨯⨯⨯-+=，质量为D 级的概率为816207127818127---=．对两件商品进行质量把关，两件商品质量均为D 级的概率77492727729⨯=．（1）X 的分布列为：X100050020010P82716812081727数学期望为8162073621012070()100050020010278181278127E X =⨯+⨯+⨯+⨯==．4．已知矩形ABCD 中，,,,AB BC E F G H ==分别是矩形四条边的中点，以矩形中心O为原点，HF 所在直线为x 轴，EG 所在直线为y 轴，建立如图所示的平面直角坐标系.直线,HF BC上的动点,R S 满足(),OR OF CS CF λλλ==∈R.（1）求直线ER 与直线GS 交点P 的轨迹方程；（2）当3λ=-时，过点R 的直线m （与x 轴不重合）和点P 轨迹交于,M N 两点，过点N 作直线:3l x =-的垂线，垂足为点Q .设直线MQ 与x 轴交于点K ，求KMN △面积的最大值.【答案】（1）221(62x y +=不含点(0,；（2）34.【分析】（1）根据给定条件，借助向量共线用λ表示点,R S ，再求出直线,ER GS 的方程，联立消去参数λ即得.（2）设出直线m 的方程，与点P 的轨迹方程联立，借助韦达定理求出点K 坐标，再建立三角形面积的函数关系，并求出最大值即得.【解析】（1）依题意，(()0,,0,,,E G FC，设点)(,),(,0),R S P x y R x S y ，由OR OF λ=，得R x =，即,0)R ，由CS CF λ=，得)S y λ=-，即))S λ-，当0λ≠时，直线:ER y x =，直线:GS y x =+，联立消去参数λ得21(3y y x +-=-，即221(0)62x y x +=≠，当0λ=时，得交点P ，满足上述方程，所以直线ER 与直线GS 交点P 的轨迹方程:221(62x y +=不含点(0,.（2）当3λ=-时，点(2,0)R -，过点R 的直线m可设为2(x ty t =-≠，由22236x ty x y =-⎧⎨+=⎩消去x 得：22(2)36ty y -+=，即22(3)420t y ty +--=，设1112)(,,)(,M x y N x y ，则12122242,33t y y y y t t -+==++，依题意，2()3,Q y -，直线1221:(3)3y y MQ y y x x --=++，令0y =，得点K 横坐标()212111212333K y x y x y x y y y y -+--=-=--，又111212)2,2(x ty ty y y y =-=-+，则122112211122112121212155(23(2)32352222)Ky y y y y y y ty y ty y y y x y y y y y y y y ++--+----+-=====-----，因此直线MQ 过定点5(,0)2K -，显然1212||11||||24KMN S KR y y y y =-=- ，而12||y y-===，令21(1)n t n =+≥，12y y -=≤=当且仅当2n =，即1t =±取等号，此时34KMN S = ，所以KMN △面积的最大值为34.变式：已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ，点31,2P ⎛⎫ ⎪⎝⎭在椭圆C 上，且PF 垂直于x轴．（1）求椭圆C 的方程；（2）直线l 斜率存在，交椭圆C 于,A B 两点，,,A B F 三点不共线，且直线AF 和直线BF 关于PF对称．（ⅰ）证明：直线l 过定点；（ⅱ）求ABF △面积的最大值．【答案】（1）22143x y +=（2）（ⅰ）证明见解析；（ⅱ）334【分析】（1）由焦点坐标和椭圆上的点，求椭圆C 的方程；（2）设直线方程，与椭圆方程联立，由0AF BF k k +=，结合韦达定理得系数间的关系，可得直线所过定点，利用面积公式表示出ABF △的面积，由基本不等式求最大值.【解析】（1）点31,2P ⎛⎫⎪⎝⎭在椭圆C 上，且PF 垂直于x 轴，则有()1,0F 设椭圆C 的焦距为()20c c >，则1c =，点31,2P ⎛⎫ ⎪⎝⎭代入椭圆方程，有()222219191441a b a a +=+=-，解得2a =，则222413b a c =-=-=，所以椭圆C 的方程为22143x y +=.（1）（ⅰ）设直线l 的方程为y kx m =+，由22143y y k x x m=+⎧⎪⎨⎪+⎩=，消去y ，整理得()2223484120kxkmx m +++-=，因为l 交椭圆C于,A B 两点，所以()22Δ48430k m =-+>，设()()1122,,,A x y B x y ，所以21212228412,3434km m x x x x k k -+=-=++，因为直线AF 和直线BF 关于PF 对称，所以()()()()12121212121212220111111AF BF kx x m k x x my y kx m kx m k k x x x x x x +-+-+++=+=+==------所以()()()21212224128222203434m kmkx x m k x x m k m k m k k --+-+-=⨯+-⨯-=++所以222282488860km k km k m mk m --+--=解得4m k =-.所以直线l 的方程为()44y kx k k x =-=-，所以直线l 过定点()4,0.（ⅱ）设直线l 的方程为4x ny =+，由224143x ny x y =+⎧⎪⎨+=⎪⎩，消去x ，整理得()223424360n y ny +++=，因为l 交椭圆C于,A B 两点，所以()()()222Δ241443414440n n n =-+=->，解得24n >，1212222436,3434n y y y y n n +=-=++，所以()222121212222243612444343434n n y y y y y y n n n -⎛⎫-=+-=--⨯= ⎪+++⎝⎭，所以()22122221344318223434ABFn n S y y n n--=⨯-=⨯=⨯++ 令()24,0n t t -=>则()213318182564316996ABC tS t t t==⨯+++ ，当且仅当163t =时取等号，所以ABF △面积的最大值为334.5．已知函数()()2e 0xf x ax a =->．（1）若函数()f x 有3个不同的零点，求a 的取值范围；（2）已知()f x '为函数()f x 的导函数，()f x '在R 上有极小值0，对于某点()()00,P x f x ，()f x 在P 点的切线方程为()yg x =，若对于R x ∀∈，都有()()()00x x f x g x -⋅-≥⎡⎤⎣⎦，则称P 为好点．①求a 的值；②求所有的好点．【答案】（1）2e ,4∞⎛⎫+ ⎪⎝⎭（2）①e2a =；②e 1,2⎛⎫ ⎪⎝⎭【分析】（1）首先讨论当0x ≤时，有1个零点，当0x >时，参变分离为e xa x=存在两个根，再利用导数分析函数()2e xu x x=的图象，即可求解a 的取值范围；（2）①利用二次导数求函数()f x '的极小值，根据极小值为0，即可求解a 的值；②首先求函数在点P 处的切线方程，再根据好点的定义，讨论0x x >和0x x <两种情况，求好点.【解析】（1）当0x ≤，()f x 单调递增，且()01f =，当x →-∞时，()f x ∞→-，因此()f x 在区间(],0-∞上存在唯一零点，当0x >时，只要2e 0xax -=存在两个根即可，即2e xa x=存在两个根，设()2e x u x x =，则()()32e x x u x x-'=，当()0,2x ∈时，()0u x '<，函数()u x 单调递减，当()2,x ∞∈+时，()0u x '>，函数()u x 单调递增，由()2e 24u =，当0x →时，()u x ∞→+，当x →+∞时，()u x ∞→+，所以当2e 4a >时，在区间()0,∞+有2个零点，因此a 得到取值范围是2e ,4∞⎛⎫+ ⎪⎝⎭；（2）①()()2e 0xf x axa =->，()e 2x f x ax ='-，令()()x f x ϕ='，则()e 2xx a ϕ='-，令()0x ϕ'=，得ln 2x a =，当(),ln 2x a ∞∈-时，()0x ϕ'<，()f x '单调递减，当()ln 2,x a ∞∈+时，()0x ϕ'>，()f x '单调递增，故()()ln 2ln 2e2ln 221ln 20af a a a a a =-=-='，得e 2a =，②设()()00,P x f x 为好点，对于任意x ∈R ，都有()()()00x x f x g x ⎡⎤-⋅-≥⎣⎦，当0x x =时，00≥成立，当0x x ≠时，即为当0x x ≥时，()()0f x g x -≥，当0x x <时，()()0f x g x -≤成立，因为()f x 在P 点的切线方程为()()()()000g x f x f x x x '-=-，所以()()()()000g x f x x x f x -'=+，设()()()h x f x g x =-，即()()()()()000h x f x f x x x f x =---'，()()()0h x f x f x ''-'=，又因为()f x '在(),1x ∞∈-上单调递减，()1,x ∞∈+上单调递增，故分情况讨论，（1）当0x x >时，因为P 为好点，所以()()()0h x f x g x =-≥恒成立，1 若01x ≥，()f x '在()0,x x ∞∈+上单调递增，()()0f x f x '>'，()()()00h x f x f x =-''>'，所以()h x 在0x x >时单调递增，()()()()0000h x h x f x g x >=-=，满足条件，故01x ≥时成立；2 若01x <，()f x '在()0,1x x ∈上单调递减，在()1,x ∞∈+上单调递增，当()0,1x x ∈时，()()0f x f x '<'，()()()00h x f x f x =-''<'，所以()h x 在()0,1x x ∈时单调递减，()()()()0000h x h x f x g x <=-=，矛盾，不满足条件；（2）当0x x <时，因为P 为好点，所以()()()0h x f x g x =-≤恒成立，1 若01x ≤，()f x '在()0,x x ∞∈-上单调递减，()()0f x f x '>'，()()()00h x f x f x =-''>'，所以()h x 在0x x <时单调递增，()()()()0000h x h x f x g x <=-=，满足条件，故01x ≤时成立；2 若01x >，()f x '在(),1x ∞∈-上单调递减，在()01,x x ∈上单调递增，当()01,x x ∈时，()()0f x f x '<'，()()()00h x f x f x =-''<'，所以()h x 在()01,x x ∈时单调递减，()()()()0000h x h x f x g x >=-=，矛盾，不满足条件；综上可知，由（1）（2）可得，01x ≥且01x ≤，即01x =，所以只有一个好点e 1,2⎛⎫⎪⎝⎭.变式：帕德近似是法国数学家亨利．帕德发明的用有理多项式近似特定函数的方法．给定两个正整数m ，n ，函数()f x 在0x =处的[,]m n 阶帕德近似定义为：011()1mm nn a a x a x R x b x b x +++=+++ ，且满足：(0)(0)f R =，(0)(0)f R ''=，(0)(0)f R ''''=，…，()()(0)(0)m n m n f R ++=．（注：[]()()f x f x '='''，[]()()f x f x ''''''=，[](4)()()f x f x ''''=，(5)(4)()()f x f x '⎡⎤=⎣⎦，…；()()n f x 为(1)()n f x -的导数）已知()ln(1)f x x =+在0x =处的[]1,1阶帕德近似为()1axR x bx=+．（1）求实数a ，b 的值；（2）比较()f x 与()R x 的大小；（3）若()1()()()2f x h x m f x R x ⎛⎫=-- ⎪⎝⎭在(0,)+∞上存在极值，求m 的取值范围．【答案】（1）1a =，12b =；（2）答案见解析；（3）10,2⎛⎫ ⎪⎝⎭．【分析】（1）由(0)(0)f R ''=，(0)(0)f R ''''=，列方程组求实数a ，b 的值；（2）令()()()x f x R x ϕ=-利用导数研究单调性，又(0)(0)(0)0f R ϕ=-=，可比较()f x 与()R x 的大小；（3）由()h x 在(0,)+∞上存在极值，所以()h x '在(0,)+∞上存在变号零点，通过构造函数分类讨论，对()h x '的零点进行分析．【解析】（1）由()ln(1)f x x =+，()1axR x bx=+，有(0)(0)f R =，可知1()1f x x '=+，21()(1)f x x ''=-+，2()(1)a R x bx '=+，32()(1)ab R x bx -''=+，由题意，(0)(0)f R ''=，(0)(0)f R ''''=，所以121a ab =⎧⎨-=-⎩，所以1a =，12b =．（2）由（1）知，2()2x R x x =+，令2()()()ln(1)(1)2xx f x R x x x x ϕ=-=+->-+，则22214()01(2)(1)(2)x x x x x x ϕ'=-=>++++，所以()ϕx 在其定义域(1,)-+∞内为增函数，又(0)(0)(0)0f R ϕ=-=，0x ∴≥时，()()()(0)0x f x R x ϕϕ=-≥=；10x -<<时，()()()(0)0x f x R x ϕϕ=-<=；所以0x ≥时，()()f x R x ≥；10x -<<时，()()f x R x <．（3）由()11()()ln(1)()2f x h x m f x m x R x x ⎛⎫⎛⎫=--=++ ⎪ ⎪⎝⎭⎝⎭，222111(1)ln(1)()ln(1)1(1)mx x x x h x x m x x x x x +-++⎛⎫∴=-+++=+' ⎪+⎝⎭．由()1()()()2f x h x m f x R x ⎛⎫=-- ⎪⎝⎭在(0,)+∞上存在极值，所以()h x '在(0,)+∞上存在变号零点．令2()(1)ln(1)g x mx x x x =+-++，则[]()21ln(1)12ln(1)g x mx x mx x =+-++=-+'，1()21g x m x ''=-+．①0m <时，()0g x ''<，()g x '为减函数，()(0)0g x g ''<=，()g x 在(0,)+∞上为减函数，()(0)0g x g <=，无零点，不满足条件．②当21m >，即12m >时，()0g x ''>，()g x '为增函数，()(0)0g x g ''>=，()g x 在(0,)+∞上为增函数，()(0)0g x g >=，无零点，不满足条件．③当021m <<，即102m <<时，令()0g x ''=即121m x =+，112x m∴=-．当1012x m <<-时，()0g x ''<，()g x '为减函数；112x m>-时，()0g x ''>，()g x '为增函数，min 111()121ln 1112ln 2222g x g m m m m m m ⎛⎫⎛⎫⎛⎫∴=-=---+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝'⎭'；令()1ln H x x x =-+，01x <<，1()1H x x '=-+，1()10H x x '=-+>在01x <<时恒成立，()H x 在()0,1上单调递增，()(1)0H x H <=，11(12)ln 202g m m m ⎛⎫∴-=-+< ⎪⎝⎭'恒成立；0x >，01m <<，(1)0x m ∴-<，则()()221111mx mx mx x x mx ->-+-=+-，2111mx mx x -∴>-+，211ln(1)ln(1)1mx x mx x x -∴+-+>-++；2()(1)ln(1)1mx x g x x x x ⎡⎤+=+-+⎢⎥+⎣⎦，令221()ln(1)1ln(1)ln(1)(1)ln(1)11mx x mx l x x x mx x m x x m x x +-=-+=+-+>-+=+-+-++，令())ln(1)0F x x x =+->，()11011F x x x -=-=++'<，则()F x 在()0,∞+是单调递减，()()02F x F <=-，所以ln(1)x +<，()(1)(1)(1)22m m l x m x m x m x ⎡∴>+-=+-++-⎢⎣，令2161x m =-，则2161x m +=，(1)02m x ∴+-≥，81(1)0022m x m m m m ⎛⎫+-=-><< ⎪⎝⎭．()0l x ∴>，即21610l m ⎛⎫-> ⎪⎝⎭．由零点存在定理可知，()l x 在11,2m ∞⎛⎫-+⎪⎝⎭上存在唯一零点021161,12x m m ⎛⎫∈-- ⎪⎝⎭，又由③知，当1012x m<<-时，()0g x ''<，()g x '为减函数，(0)0g '=，所以此时，()0g x '<，在10,12m ⎛⎫- ⎪⎝⎭内无零点，()g x ∴在(0,)+∞上存在变号零点，综上所述实数m 的取值范围为10,2⎛⎫⎪⎝⎭．。

机械能守恒定律的综合运用(含典型例题变式练习题和答案)一.教学内容：机械能守恒定律的综合运用二.学习目标：1、掌握机械能守恒定律的表达式及应用机械能守恒定律解题的一般方法和步骤。

2、深刻掌握关于机械能守恒定律的习题类型及其相关解法。

三•考点地位：机械能守恒定律的综合应用问题是高考考查的重点和难点，题目类型通常为计算题目形式，从出题形式上常与牛顿定律、圆周运动、电磁学、热学等问题进行综合，从习题模型化的角度上来看，常与线、轻杆、弹簧等模型综合，题目灵活性很强，在高考当中常做为压轴题形式出现，2007年天津理综卷第5题，2006年全国H卷理综卷第23题、2006年广东大综合卷第34题、2006年北京理综卷第22题、2005年北京理综卷的第23题均通过大型计算题目形式考查。

知识体系：(一)机械能守恒定律的表达式：当系统满足机械能守恒的条件以后，常见的守恒表达式有以下几种：①二打f二-匕，-二，即初状态的动能与势能之和等于末状态的动能与势能之和。

②△ \ =—―耳,或△匕」 - -I-,即动能(或势能)的增加量等于势能(或动能)的减少量。

③△ - - ■二-:•，即卩A物体机械能的增加量等于B物体机械能的减少量。

(二)应用机械能守恒定律解题的步骤及方法：(1)根据题意选取研究对象(物体或系统) 。

(2)明确研究对象的运动过程，分析对象在运动过程中的受力情况，弄清各力做功的情况，判断机械能是否守恒。

(3)恰当地选取零势面，确定研究对象在运动过程中的始态和末态的机械能。

(4)根据机械能守恒定律的不同表达式列方程，并求解结果。

说明：(1)机械能守恒定律只关心运动的初、末状态，而不必考虑这两个状态之间变化过程的细节，因此，如果能恰当地选择研究对象和初、末状态，巧妙地选定势能参考平面，问题就能得到简捷、便利的解决，可避免直接应用牛顿定律可能遇到的困难，机械能守恒定律为解决力学问题提供了一条简捷的途径。

(2)如果物体运动由几个不同的物理过程组成，则应分析每个过程机械能是否守恒，还要分析过程的连接点有无能量损失，只有无机械能损失才能对整体列机械能守恒式，否则只能列出每段相应的守恒关系。

巧辨高考试题中形形色色的强调句型甘肃省临泽一中 734200 陈明华英语中“It is/was +被强调部分+who/that+其它”是强调句型的基本构成。

这种结构在中学英语课本中频频出现，引起高考命题者的格外关注。

强调句的基本句型是：“It is/was+被强调部分+that/who从句。

”可强调的句子成分通常为主语,状语,宾语等,不能用来强调谓语动词, 表语(主语补语), 定语，让步状语, 条件状语等。

被强调部分可以是单词，短语，也可以是从句。

一、具体用法:1.强调句型用于强调陈述句。

形式：It is/was + 被强调部分+ that/who…例：（1）It was there, the police believe,___ she was able to activate the recorder she kept in her bag .A. untilB. whichC. thatD. when解析：选C 被强调部分为地点状语there，the police believe为插入语（2）It was after he got what he had desired___ he realized it was not so important.A. thatB. whenC. sinceD. as解析：选A 被强调的是时间状语after he got what he had desired2.强调句型用于强调一般疑问句。

形式：Is/Was it+被强调部分+that/who…?例： Was it form the lake___ he often went fishing___ he saved the drowning girl?A. that; thatB. where; whereC. where;thatD. that; where解析：选C 解答此题关键是能够对句型进行正确的分析和判断。

一道高考题的溯源与变式作者：王思俭来源：《新高考·高三数学》2012年第05期问题1 （人教 A 版必修1第133页复习参考题第8题）已知如图1,ABCD是半径为2的半圆O的内接等腰梯形,下底AB为直径,C,D在圆弧上.设 BD= x,等腰梯形的周长为y,试求y关于x的函数解析式,并指出函数定义域.图2问题2 （人教 A 版必修1第27页练习1.2.2第5题）已知如图2,圆O的半径为5,ABCD是其内接矩形,求矩形面积的最大值.将上述两问题中的圆改为椭圆再结合起来就构成了2007年北京理科卷第18题.图3原题如图3,有一块半椭圆形钢板,其长半轴长为4r,短半轴长为r.计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记C D=2x,梯形面积为S.（1）求面积S以x为自变量的函数解析式,并写出其定义域；（2）求面积S的最大值.这两个问题是属于同一类问题,即二次曲线（圆、椭圆或抛物线）内接矩形或等腰梯形的面积、周长等问题.由此引发一些思考,得出如下变式问题.变式1 在图1中,求等腰梯形面积的最大值.●分●析策略一：连结BC，OC，在△BO C中,利用面积法求出等腰梯形的高h,建立面积的函数关系式,再利用求值域的方法求解；策略二：设∠AO C=θ,将等腰梯形的面积建立为关于θ的函数,再利用三角函数法求解；策略三：建立直角坐标系,写出圆的方程,选择点C的横坐标为自变量,建立目标函数.●解●析●一连结BC，OC，在△BOC中,由等面积法,可知12x4－x 24=12×2h,所以有h= x2·4－x 24,从而有CD= 24－x 244－x 24 =22－x 24.－x 24,0所以梯形ABCD的面积为S=4+4－x 222·x2·4－x 24=4－x 24· x2· 4令4－x 24=t∈(2,4),可得S=4－x 24 3x 24=t 3(4－t)=－t 4+4t 3.令g(t)=－t 4+4t 3,则g′(t)=－4t 3+12t 2=4t 2(3－t).当20,g(t)单调递增；当3●解●题●回●顾这三种解法都是常见的方法,但解法二、三较简单,涉及了函数、三角、不等式等知识以及函数最大值的求法导数法、基本不等式法、三角函数的有界性法,是一道较好的小型综合题.图5变式2 如图5,ABCD是半径为2的半圆内接矩形,且A,B在直径上,C,D在半圆周上,求矩形周长L及面积S的最大值.●分●析选取BC=x为自变量,可建立L与S关于x的函数,若连结OC，选取∠BO C=θ为自变量,则可以建立L与S关于θ的函数.变式3 如图6,已知ABCD为抛物线段y=4－x 2 （－2≤x≤2)的内接矩形,A,B在x轴上,C,D 在抛物线上,求矩形面积S的最大值.图6图7变式4 如图7,已知ABCD为抛物线段y=4－x 2 （－2≤x≤2)的内接等腰梯形,A(－2,0),B(2,0),C,D在抛物线上,求等腰梯形面积S的最大值.图8变式5 如图8,在变式4中,设ABCD绕y轴旋转一周所得的几何体的体积为V,当V取得最大值时,CD的近似值为多少？（精确到0.001）首先确定自变量,由于CD的平行移动引起等腰梯形的变化,于是选择点C的横坐标为自变量x；其次确定几何体的形状,等腰梯形绕y轴旋转一周得到的几何体是圆台,将圆台的体积建立为关于x的函数；最后利用导数法求取最大值时x的值,需要解三次方程,这是我们无法完成的,但题目要求近似解,于是想到二分法.●解等腰梯形绕y轴旋转一周得到的几何体是圆台,上底半径r 1=x,下底半径r 2=2,高h=4－x 2,则V=13 π (x 2+2 2+2x)(4－x 2)=13 π (－x 4－2x 3+8x+16)（0－4)（0＜x 对V求导，得V′(x)=13 π (－4x 3－ 6x 2+8) = －2 π 3 (2x 3+3x 2＜2）.令g(x)=2x 3+3x 2－4,00,所以g(x)在(0,2)内单调递增.又因为g(0)=-4,g(1)=1,所以g(x)=0在（0,1）内有且只有一个解x 0.当00, V(x) 单调递增；当x 00,V′(x)所以当x=x 0时,V有最大值V(x 0).下面用二分法求x 0的近似解.因为G（0）=－4,G（1）=1,G12= －3,所 以x 0∈12,1,又有G34取x 0=3132,得 C D= 2x 0=3116≈1.938.●解●题●回●顾利用圆台体积公式很容易建立目标函数V(x),运用导数法求出驻点,讨论其极值.但由于V′(x)=0是三次方程,没有简便的求根公式,于是利用函数图象研究方程根的分布情况,再利用二分法确定极大值点x 0的近似范围,从而得出近似解.变式6 如图9,等腰梯形ABCD的两腰及上底CD与半圆O均相切,下底AB落在直径上,已知半圆的半径为R,求等腰梯形的周长L及面积S的最小值.图9因为四边形ABCD是半圆O的内切等腰梯形,等腰梯形的周长、面积的变化与∠BCD有关,即与∠EOF有关,于是选取∠EOF为自变量,将周长、面积都建立为∠EOF的函数,再利用三角、导数、基本不等式等知识求解.变题7 如图10,抛物线y=4－x 2 （－2≤x≤2）,等腰梯形ABCD的两腰BC,DA及上底CD 与抛物线段相切,A,B在x轴上,求梯形ABCD的面积S的最小值.图10图11变题8 如图11,函数y= 21－x 2 （-1≤x≤1）的 图象,等腰梯形ABCD的两腰BC,DA 及上底CD与与函数图象均相切,A,B在x轴上,且CD∥AB,求梯形ABCD的面积S的最小值.●分●析等腰梯形的变化是由BC边上的切点E引起的,设E（t, 21－t 2） ,利用导数求出切线斜率及切线方程,继而求出B,C两点坐标,于是就建立了面积S关于t的函数,再利用导数知识求出函数的最小值.●解设BC与函数图象的切点为E（t, 21－t 2）, 对y=21－x 2求导，得y′= －2x1－x 2 ,所以k=－2t1－t 2，可得切线方程y-21－t 2=－2t1－t 2（x－t）.令y=0,得x B=t+1－t 2t=1t.令 y= 2,得x C=1t－1－t 2t,0于是得S=2×22t－1－t 2t2= 22t－ 1t 2－1=22u－u 2－1（令1t=u>1）.对S求导,得S′（u）=22－uu 2－1.令S′（u）=0,解得u=23.当1当u>23时,S′>0,S是单调增函数.所以当u=23,即t=32时,S有极小值,也是最小值,即S min =23.●解●题●回●顾首先,要建立等腰梯形的面积S的目标函数,关键是如何选取自变量,等腰梯形的变化是由切点E变化而引起的,所以就选择切点E的横坐标为自变量；其次,求函数的最小（大）值,利用化归思想化繁为简；最后,利用导数知识求解函数的最小（大）值.本题也可以采用三角换元法求解,先令t= sin θ0再利用三角函数知识或数形结合方法，求出当θ= π 3时,即2(2－ cos θ) sin θ,t=32时,S有最小值.从上述各题可以看出,高考题在课本上都是有其原型的,所以我们在学习过程中要善于变更问题的形式,扩大问题的思维“容量”,实现以少胜多.在学习新知识的时候,同学们虽然也掌握了某种解题模式,但在一定阶段内往往只会机械地模仿、照搬这个固定模式解题.对此,如果不予以注意,很可能形成某种心理定势,造成思维的呆板和僵化,因而在学习过程中,当我们获得某种解题的基本方法以后,应及时将原题的条件、结论、情境或方法延伸变通,使我们进一步理解和掌握典型问题所阐述的概念、原理、规律、数量关系或解题方法,从而极大地开拓思维空间,以达到学会创造性解题的目的.。

巧用错题，开展变式教学张鑫一．研究背景本人对所教两个班级进行了一个调查，其中80%的同学小学做过错题本，到目前为止，还能坚持做错题本的同学占到20%.能够坚持做错题本的同学，主要有以下几种原因：1.选择性归纳错题，所以能够坚持；2.因为家长和老师要检查；3.认为考试前复习错题具有针对性；4.归纳错题以后成绩有进步，尝到了归纳错题的甜头。

放弃归纳错题的同学主要有以下几种原因：1.小学比较闲，现在没时间；2.认为归纳错题太麻烦，不如直接翻资料看；3.因为错题太多；4.认为归纳错题时，抄题时间太多，有这个时间不如多做几道题5.认为搞懂就算了，没必要做错题.到底学生是否真正理解了题目考察的知识点？错题只停留在揪因吗？学生如何能够做到真正举一反三？带着这些问题，我想：能否和学生一起，归纳日常学习中出现的错题，利用错题这种生成性资源，在每节课开始的10-15分钟时间，评讲作业错题，利用变式，从而开展有效教学.二．研究的主要内容平常批改作业及试卷中，对于学生易错的地方，用“正”字统计，错误人数超过十个以上的题目，确定要重点讲评.用错题进行变式教学的基本思想：共享学习；抓住本质；建立联系；形成思想；探讨方法；创新思维用错题进行变式教学的基本策略：错误分享—投影典型错误，归纳错误原因正确解法—分享一题多法，拓展学生思维归纳规律—画龙点睛，总结差异和共性举一反三—变式训练，知识迁移案例1.对于学生形成的共性错误，需要老师与学生一起找到错误的本质，帮学生扫清知识障碍.【《勤学早》2-3页二次根式的性质】=_______错误答案：错因分析：1.看错题目；2.对于=性质中，底数a的取值范围虽然清晰，呈现形式没有辨析清楚，不会活用公式；3.忘记师生活动：学生1讲解方法：学生2讲解方法：教师比较两种方法，提出最优法建议.变式1.=_______ 变式2.=_______ 变式3.=_______变式教学设计目的：针对该知识点，通过变式1，对公式方法初步掌握；再通过变式2，对二次根式的性质及公式辨识清晰；最后，通过字母变式，提升学生的抽象思维.教学反思：此处三个变式，学生很快做出，学习最弱的孩子三十秒钟都可以解决，尤其是变式3，提问最弱的孩子，能够解对，说明此设计合理.案例2.学生对于数学方法的运用，不可能一蹴而就，在错误中总结经验，通过多个变式，不断强化方法.【勤学早22页勾股定理】如图，在 ,CD平分交AB于点D,AB=5,BC=4,求CD的长.错误体现：大部分学生不会做.错误原因：大部分学生不能想到面积法及其它方法着手解决.师生活动：学生1阐述解法：过D分别作于M,于N,利用面积法,可求,在等腰直角三角形DCM中，求得.学生2阐述解法：设AD=x,则BD=5-x,由角平分线定理2得,解得,作,则AF=CF=,在中，由勾股定理得DF=,所以CD=CF+DF=.教师根据学生的解答，肯定学生1，面积法是解决线段长度的一种常用方法，遇到角平分线时，可以往这个角度去考虑，同时肯定学生2，课外知识丰富，思维灵活，对于角平分线定理2，大家遇到相关问题，可以考虑使用该知识解决问题.变式1.如图，在 ,CD平分交AB于点D,AC=5,AB=13,求CD的长.变式2.如图，在 ,CD平分交AB于点D,AB=a,BC=b,求变式3.如图，在 ,BE平分交AC于点E,AB=5,BC=4,求AE的长.变式教学目的：变式1只是改变数据，考察学生是否真正掌握面积法；变式2，把数字换成字母，训练学生的抽象思维能力；变式3，改变位置，考察学生灵活运用知识的能力.教学反思：学生1,2提供的方法，为同学们打开思维的闸门，很多学生能够马上运用两种方法解决变式1和变式2，变式3回归到常规问题上来，有学生通过作辅助线用勾股定理列方程解决问题，也有很多学生不作辅助线用角平分线性质定理2解决问题,达到了教学目的.本节课反思：学生在训练变式1时，有几个学生主动跟我说，老师这个题目我想到了其它方法，也是面积法.如图，作垂足为M,作，垂足为N,因为CD平分交AB于点D,AC=5,所以,在中，求得，同理可求,由面积法可得，,解得：.本节课教学反思：学生产生的新的解法，是前面学生解法1的创新，这样的教学开展下去，日积月累，相信学生的数学思维会有质的提升！教学反思：讲解该题目时，在第一个班，我只是讲解第一种方法，然后让学生去处理变式，五分钟后调查完成情况，发现只有十个同学做出来；第二个班讲完以后，追问有没有其它方法，学生2和学生3积极的讲解自己的方法，这两位同学刚讲完，全班同学自觉的报以热烈的掌声.而后第二个班级的学生练习变式，五分钟后调查情况，有三十个同学做出来.实践证明,巧用错题，开展变式教学，可以引导学生摆脱“题海”，变被动思维为主动思维，形成“趣学”、“乐学”的氛围，让学生成为学习的主人。

题型30 句子的表达效果以句式为主的表达效果比较分析题，是新高考全国卷中的新题型。

这种题型常见的提问方式为：“文中画波浪线的句子可以改写成：‘×××。

’从语义上看二者基本相同，为什么说原文表达效果更好？”这种题型是融合了各种表达知识甚至结构的综合赏析题，而“句式效果”是其中一个考查点。

赏析句子表达效果的常见思维角度子曰：“言之无文，行而不远。

”苏轼也说过：“凡文字，少小时须气象峥嵘，色彩绚烂。

”作文要力求词汇丰富，特别要恰当地运用修饰语。

要在文中善于变换多种句式，长句和短句结合，整句和散句兼行或散中见骈；能巧妙使用排比、反复、比喻、拟人等修辞手法，作文往往就能“气象峥嵘，色彩绚烂”。

锤炼语言可以提高我们运用语言的能力,帮助我们更确切地表达思想感情。

一、锤炼语言，要推敲词语。

用词贴切，就是要求从几个可用的词语中，选出最恰当、最准确、最生动的那一个，把所要表达的意思恰如其分地表达出来。

文章用词贴切才能准确地表情达意。

如何能在作文时准确地运用最恰当的词语呢？1．锤炼词语，使之形象生动很多文学家都非常讲究“炼”字。

宋代词人宋祁《木兰花》中的“红杏枝头春意闹”一句是世人传诵的绝美佳句，王国维的评价是：“一个‘闹’字境界全出。

”王维的“大漠孤烟直，长河落日圆”中“直”与“圆”二字将直线美与浑圆美融为一体，形象地描绘了塞外苍凉壮观的景象，其他字确实难以代替。

法国作家福楼拜说：“我们不论要描写什么事物，要把它表现出来,只有唯一的名词；要赋予它运动，只有唯一的动词；要赋予它性质，只有唯一的形容词。

人们应苦心探索，非要找到这唯一的名词、动词、形容词不可！”文章用词精当，讲究炼字，不仅能准确地表意，准确地勾勒出事物的特点，更能使语言简明精练、含蓄隽永，达到言有尽而意无穷的诗意效果。

如“人生是忙碌交织的，需要让心灵翱翔于天空，接受和风细雨的洗礼；需要让心灵驰骋于大漠，接受黄沙漫天的洗礼；需要让心灵游弋于海洋，接受雪白浪花的洗礼……”这是一段摘自优秀作文《风筝不断线》中的文字，其中“翱翔”“驰骋”“游弋”等动词准确地表达了心灵的自由，形象生动，极富语言张力。

www 中学数学教学参考（下旬〉2021年第4期@多解探究15妙归納—以_道解析几何题的探索为例邵明冠(河南省兰考县第一高级中学）摘要：直线与圆锥曲线的位置关系问题，新颖多样，能综合考查相关知识，具有较高的选拔性与区分度，备受命题者的青睐，通过深入探究与变式拓展、归纳总结，可达到综合提升的目的。

关键词：橢圆；直线；平行；四边形；最大值；弦长文章编号：1002-2171 (2021)4-0051-03直线与圆锥曲线的位置关系中，涉及最值或取值 范围的问题是高考和竞赛中的一个热点内容，形式新 颖，通过转化，利用平面几何中的三角形或四边形、平 面向量的线性关系或数量积、线段的乘积或比值等关 系式，以及直线的倾斜角或斜率等加以巧妙设置，能 综合考查相关知识，具有较高的选拔性与区分度，备 受命题者的青睐，通过进一步挖掘问题的潜在功能，为进一步的探究、拓展与归纳提供条件。

1问题呈现为 j c =A (:^，％ )，B (:c2，火），联立-m y—,|x2消元并整理可得（m2+4)y ——4+y=1,1=0,根据根与系数关系可得M+力!+4，而 I A B丨=\/l+m2 |y\一y2 \= \/l+w2 V(^1 +^2 )2—4^1 yi=\/\+rrf2\[3n2+4/m2+4(2020届河南省普通高中毕业班高考适应性测试数学理科第16题）设F,,F2是椭圆C:^+/=l 的两个焦点，过P\，F2分别作直线，且A//2，若 G与橢圆C交于A，B两点，匕与椭圆C交于C，D两 点（点八，0在^轴上方），则四边形A B C D面积的最 大值为________。

该题涉及椭圆内接四边形的面积，点、线等元素 较多，离不开系统的逻辑推理与繁杂的代数运算，能 很好地激发学生和教师的解题兴趣。

2解法探究解法1:(弦长公式法）由题意可得a==2,6=l,当直线斜率不存在时，易得四边形A B C D 面积为2 W，当直线6斜率存在时，设直线A的方程4(l+m2)m2+4°又点〇到直线/,的距离为结合y i+m2A//&及椭圆的对称性，可知四边形A B C D是平行四边形，且点〇是A C与B D的交点，所以 ^C J A B C D=4S a〇4b = 4 X — |A B |= 4 X -r- X X/ Z m十4 V3 =8V3y i +m2=_______8^/3 〈y i T^w2+4~y i+^+—^、V l + m2—-—-—=^=4,当且仅当2 L/Y T^x-3V\/l+所2、3 ,,即m2=2,亦即m=士#时等号成立，所以V l+m2四边形A B C D面积的最大值为4。

2024届高三二轮复习大题强化训练及变式训练（5）1．某小区在2024年的元旦举办了联欢会，现场来了1000位居民．联欢会临近结束时，物业公司从现场随机抽取了20位幸运居民进入摸奖环节，这20位幸运居民的年龄用随机变量X 表示，且()~45,225X N ．（1）请你估计现场年龄不低于60岁的人数（四舍五入取整数）；（2）奖品分为一等奖和二等奖，已知每个人摸到一等奖的概率为40%，摸到二等奖的概率为60%，每个人摸奖相互独立，设恰好有()020n n ≤≤个人摸到一等奖的概率为()P n ，求当()P n 取得最大值时n 的值．附：若()2~,X N μσ，则{||}0.6827,{||2}0.9545P X P X μσμσ-<=-<=．变式：已知某客运轮渡最大载客质量为4000kg ，且乘客的体重（单位：kg ）服从正态分布()60,100N ．（1）记X 为任意两名乘客中体重超过70kg 的人数，求X 的分布列及数学期望（所有结果均精确到0.001）；（2）设随机变量()1,2,,i X i n = 相互独立，且服从正态分布()2,N μσ，记niXn μξ-=∑，则当20n ≥时，可认为ξ服从标准正态分布()0,1N ．若保证该轮渡不超载的概率不低于97.7%，求最多可运载多少名乘客．附：若随机变量η服从正态分布()2,N μσ，则0.68()26P μσημσ-<<+=；若ξ服从标准正态分布()0,1N ，则(2)0.977P ξ<=；20.15870.0252≈，20.84130.7078≈，0.15870.84130.1335⨯≈．2．如图，在四棱锥P -ABCD 中，底面ABCD 为正方形，PA ⊥底面ABCD ，2PA AB ==，E 为线段PB 的中点，F 为线段BC 上的动点．（1）证明：平面AEF ⊥平面PBC ；（2）若直线AF 与平面PAB ，求点P 到平面AEF 的距离．变式：如图，多面体ABCDEF 是由一个正四棱锥A BCDE -与一个三棱锥F ADE -拼接而成，正四棱锥A -BCDE 的所有棱长均为//AF CD .（1）在棱DE 上找一点G ，使得面ABC ⊥面AFG ，并给出证明;（2）当12AF CD =时，求点F 到面ADE 的距离;（3）若13AF CD =，求直线DF 与面ABC 所成角的正弦值.3．已知函数()2ln f x ax x x =--．（1）讨论()f x 的单调性；（2）若不等式()0f x ≥恒成立，求a 的取值范围；（3）当0a =时，试判断函数()()2sin 2F x x f x x =--的零点个数，并给出证明．变式：已知函数()e sin 1x f x x =--.（1）讨论函数()f x 在区间(0,)+∞上的单调性;（2）证明函数()f x 在区间(π,0]-上有且仅有两个零点.4．已知椭圆E ：22221x y a b+=（0a b >>）中，点A ，C 分别是E 的左、上顶点，AC =且E 的焦距为．（1）求E 的方程和离心率；（2）过点()1,0且斜率不为零的直线交椭圆于R ，S 两点，设直线RS ，CR ，CS 的斜率分别为k ，1k ，2k ，若123k k +=-，求k 的值．变式：已知椭圆E ：()222210x y a b a b+=>>过点81,3⎛⎫ ⎪⎝⎭，且其离心率为13．（1）求椭圆E 的方程；（2）过点()1,0-的斜率不为零的直线与椭圆E 交于C ，D 两点，A ，B 分别为椭圆E 的左、右顶点，直线AC ，BD 交于一点P ，M 为线段PB 上一点，满足OM PA ∥，问⋅OA OM 是否为定值，若是，求出该定值；若不是，说明理由（O 为坐标原点）．5．对于数列{}()*n a n ∈N，记1Δnn n aa a +=-，称数列{}Δn a 为数列{}n a 的一阶差分数列；记()21ΔΔΔΔΔn n n n a a a a +==-，称数列{}2Δn a 为数列{}n a 的二阶差分数列，…，一般地，对于k ∈N ，记()11ΔΔΔΔΔk k k k n n n n a a a a ++==-，规定：01Δ,ΔΔn n n n a a a a ==，称{}Δkn a 为数列{}n a 的k 阶差分数列．对于数列{}n a ，如果Δ0k n a d =≠（d 为常数），则称数列{}n a 为k 阶等差数列．（1）数列{}2n是否为k 阶等差数列，如果是，求k 值，如果不是，请说明为什么？（2）请用231111,Δ,Δ,Δ,a a a a 表示34,a a ，并归纳出表示n a 的正确结论（不要求证明）；（3）请你用（2）归纳的正确结论，证明：如果数列{}n a 为k 阶等差数列，则其前n 项和为123211111C C ΔC ΔC Δk kn n n n n S a a a a +=++++ ；（4）某同学用大小一样的球堆积了一个“正三棱锥”，巧合用了2024个球．第1层有1个球，第2层有3个，第3层有6个球，…，每层都摆放成“正三角形”，从第2层起，每层“正三角形”的“边”都比上一层的“边”多1个球，问：这位同学共堆积了多少层？变式：已知n 为正整数，数列12:,,,n X x x x ，记()12n S X x x x =+++ .对于数列X ，总有{}0,1,1,2,,k x k n ∈= ，则称数列X 为n 项01 数列.若数列1212:,,,,:,,,n n A a a a B b b b ，均为n 项01 数列，定义数列12:,,,n A B m m m ⊗ ，其中1,1,2,,k k k m a b k n =--= .（1）已知数列:1,1,1,0,:0,0,1,1A B ，求()()S A A S A B ⊗⊗的值；（2）若数列,A B 均为n 项01 数列，求证：()()()SA B A S B ⊗⊗=；（3）对于任意给定的正整数n ，是否存在n 项01 数列,,A B C ，使得()()()2S A B S A C S B C n ⊗+⊗+⊗=，并说明理由.2024届高三二轮复习大题强化训练及变式训练（5）1．某小区在2024年的元旦举办了联欢会，现场来了1000位居民．联欢会临近结束时，物业公司从现场随机抽取了20位幸运居民进入摸奖环节，这20位幸运居民的年龄用随机变量X 表示，且()~45,225X N ．（1）请你估计现场年龄不低于60岁的人数（四舍五入取整数）；（2）奖品分为一等奖和二等奖，已知每个人摸到一等奖的概率为40%，摸到二等奖的概率为60%，每个人摸奖相互独立，设恰好有()020n n ≤≤个人摸到一等奖的概率为()P n ，求当()P n 取得最大值时n 的值．附：若()2~,X N μσ，则{||}0.6827,{||2}0.9545P X P X μσμσ-<=-<=．【答案】（1）159（2）()P n 取得最大值时n 的值为8【分析】（1）利用正态分布的对称性可求(60)P X ≥，故可估算年龄不低于60岁的人数.（2）利用不等式组()(1)()(1)P n P n P n P n ≥+⎧⎨≥-⎩可求()P n 取得最大值时n 的值.【解析】（1）因为~(45,225)X N ，所以15σ=，则10.6827(60)()0.158652P X P X μσ-≥=≥+==，所以现场年龄不低于60岁的人数大约为10000.15865159⨯≈(人)．（2）依题意可得，2020()C 0.40.6n n nP n -=⨯，设()(1)()(1)P n P n P n P n ≥+⎧⎨≥-⎩，所以20111920202011212020C 0.40.6C 0.40.6C 0.40.6C 0.40.6n n n n n n n n n n n n -++-----⎧⨯≥⨯⎨⨯≥⨯⎩，所以200.41,10.6210.41,0.6n n n n -⎧⋅≤⎪⎪+⎨-⎪⋅≥⎪⎩所以374255n ≤≤，因n 为整数，所以8n =，所以当()P n 取得最大值时n 的值为8．变式：已知某客运轮渡最大载客质量为4000kg ，且乘客的体重（单位：kg ）服从正态分布()60,100N ．（1）记X 为任意两名乘客中体重超过70kg 的人数，求X 的分布列及数学期望（所有结果均精确到0.001）；（2）设随机变量()1,2,,i X i n = 相互独立，且服从正态分布()2,N μσ，记niXn μξ-=∑，则当20n ≥时，可认为ξ服从标准正态分布()0,1N ．若保证该轮渡不超载的概率不低于97.7%，求最多可运载多少名乘客．附：若随机变量η服从正态分布()2,N μσ，则0.68()26P μσημσ-<<+=；若ξ服从标准正态分布()0,1N ，则(2)0.977P ξ<=；20.15870.0252≈，20.84130.7078≈，0.15870.84130.1335⨯≈．【答案】（1）分布列见解析，期望值为0.317；（2）64【分析】（1）首先求得乘客体重大于70kg 的概率为0.1587，再利用二项分布可求得概率得分布列和期望值；（2）根据(2)0.977P ξ<=可得保证该轮渡不超载的概率不低于97.7%等价于2ξ=≥，解不等式可得64n ≤.【解析】（1）由乘客的体重（单位：kg ）服从正态分布()60,100N 可得60,10μσ==，则可得()())0.6821(1700.1586722P P P X X X μσμσμσ-<<-->=>+==+=，即任意一名乘客体重大于70kg 的概率为0.1587，则X 的所有可能取值为0,1,2，()()2010.15870.708P X ==-≈，()()121C 10.15870.15870.267P X ==-⨯≈，()220.15870.025P X ==≈所以X 的分布列为X012P0.7080.2670.025期望值为()00.70810.26720.0250.317E X ≈⨯+⨯+⨯=（2）设i X 为第()1,2,,i i n = 位乘客的体重，则()2,i XNμσ ，其中60,10μσ==，所以1400097.7%i n i P X P ξ=⎛⎫⎛≤=≤≥ ⎪ ⎝⎝⎭∑，由(2)0.977P ξ<=可得2ξ=≥，即32000n -≤，可得)2580≤8≤，64n ≤.所以保证该轮渡不超载的概率不低于97.7%，最多可运载64名乘客.2．如图，在四棱锥P -ABCD 中，底面ABCD 为正方形，PA ⊥底面ABCD ，2PA AB ==，E 为线段PB 的中点，F 为线段BC 上的动点．（1）证明：平面AEF ⊥平面PBC ；（2）若直线AF 与平面PAB 255，求点P 到平面AEF 的距离．【答案】（1）证明见解析（2）63．【分析】(1)利用面面垂直的判定定理或利用平面的法向量数量积等于零证明；(2)利用坐标运算求点到平面的距离，或者用等体积法的思想求解.【解析】（1）方法一：因为PA ⊥底面ABCD ，BC ⊂平面ABCD ，所以PA BC ⊥．因为ABCD 为正方形，所以AB BC ⊥，又因为PA AB A = ，PA ⊂平面PAB ，AB ⊂平面PAB ，所以BC ⊥平面PAB ．因为AE ⊂平面PAB ，所以AE BC ⊥．因为PA AB =，E 为线段PB 的中点，所以AE PB ⊥，又因为PB BC B ⋂=，PB ⊂平面PBC ，BC ⊂平面PBC ，所以⊥AE 平面PBC ．又因为AE ⊂平面AEF ，所以平面AEF ⊥平面PBC ．方法二：因为PA ⊥底面ABCD ，PA ⊂平面PAB ，所以平面PAB ⊥底面ABCD又平面PAB ⋂底面ABCD AB =，BC AB ⊥，BC ⊂平面ABCD ，所以BC ⊥平面PAB ．因为AE ⊂平面PAB ，所以AE BC ⊥．因为PA AB =，E 为线段PB 的中点，所以AE PB ⊥．因为PB BC B ⋂=，PB ⊂平面PBC ，BC ⊂平面PBC ，所以⊥AE 平面PBC，又因为AE ⊂平面AEF ，所以平面AEF ⊥平面PBC解法三：因为PA ⊥底面ABCD ，AB AD ⊥，以A 为坐标原点，以,,AB AD AP的方向分别为x 轴，y 轴，z 轴的正方向，建立如图所示的空间直角坐标系A -xyz ，则()()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,0,2,1,0,1A B C D P E ，设([0,2])BF t t =∈，则()2,,0F t ，所以(1,0,1)AE = ，(2,,0)AF t = ，(2,0,2)PB =- ，(0,2,0)BC =，设()111,,n x y z =为平面AEF 的法向量，则0,0,n AE n AF ⎧⋅=⎪⎨⋅=⎪⎩所以11110,20,x z x ty +=⎧⎨+=⎩取12y =，则1x t =-，1z t =，则(,2,)n t t =-，设()222,,m x y z =为平面PBC 的法向量，则0,0,m PB m BC ⎧⋅=⎪⎨⋅=⎪⎩所以222220,20,x z y -=⎧⎨=⎩取21x =，则20y =，21z =，则(1,0,1)m = 因为00n m t t ⋅=-++= ，所以n m ⊥ ,所以平面AEF ⊥平面PBC.（2）（基于（1）解法一、二）因为PA ⊥底面ABCD ，AB AD ⊥，以A 为坐标原点，以,,AB AD AP的方向分别为x 轴，y 轴，z 轴的正方向，建立如图所示的空间直角坐标系A -xyz，则()()()()0,0,0,2,0,0,0,0,2,1,0,1A B P E ，易知(0,1,0)u =是平面PAB 的法向量设([0,2])BF t t =∈，则()2,,0F t ，所以(1,0,1)AE = ，(2,,0)AF t =，所以|||cos ,|||||AF u AF u AF u ⋅==5=，得1t =，所以(2,1,0)AF = ，设()111,,n x y z = 为平面AEF 的法向量，则0,0,n AE n AF ⎧⋅=⎪⎨⋅=⎪⎩所以平面AEF 的法向量(1,2,1)n =-，又因为(0,0,2)AP =所以点P 到平面AEF 的距离为||||AP n d n ⋅=，63==所以点P 到平面AEF的距离为3．（另解）由（1）可知，BAF ∠是直线AF 与平面PAB 所成的角，所以cos 5AB BAF AF ∠===解得1122BF AB BC ==，故F 是BC 的中点．所以AF ==12AE PB ==EF ==AEF △的面积为1622AEF S AE EF =⋅= 因为2PA AB ==，PAE △的面积为11124PAE PAB S S PA AB ==⋅= 设点P 到平面AEF 的距离为h ，则有16113633P AEF AEF F PAE PAE V S h h V S BF --=⋅===⋅=解得63h =所以点P 到平面AEF的距离为63．（基于（1）解法三）易知(0,1,0)u =是平面PAB 的法向量所以|||cos ,|||||AF u AF u AF u ⋅== 55=，解得1t =所以(1,2,1)n =-，又因为(0,0,2)AP =所以点P 到平面AEF 的距离为||||AP n d n ⋅=，63==所以点P 到平面AEF的距离为63．变式：如图，多面体ABCDEF 是由一个正四棱锥A BCDE -与一个三棱锥F ADE -拼接而成，正四棱锥A -BCDE 的所有棱长均为//AF CD .（1）在棱DE 上找一点G ，使得面ABC ⊥面AFG ，并给出证明;（2）当12AF CD =时，求点F 到面ADE 的距离;（3）若13AF CD =，求直线DF 与面ABC 所成角的正弦值.【答案】（1）当点G 为DE 中点时，证明见解析（3）21【分析】（1）当点G 为DE 中点时，面ABC ⊥面AFC ，利用面面垂直的判定即可证明；（2）首先证明AF ⊥面DEF ，再利用等体积法即可；（3）建立合适的空间直角坐标系，利用线面角的空间向量求法即可.【解析】（1）当点G 为DE 中点时，面ABC ⊥面AFC ，证明如下：因为四棱锥A BCDE -是正四棱锥，所以,AD AE AG DE =⊥.在正方形BCDE 中，//DE BC ，所以AG BC ⊥，在正方形BCDE 中，CD BC ⊥，因为//AF CD ，所以AF BC ⊥，因为,,AF AG A AF AG ⋂=⊂面AFG ，所以BC ⊥面AFG ，因为BC ⊂面ABC ，所以面ABC ⊥面AFG .（2）连接BD ，CE 交于点O ，连接AO ，OG ，则//AF OG ，又因为四棱锥A BCDE -是正四棱锥，所以AO ⊥面BCDE ，所以四边形AOGF 为矩形，AF FG ∴⊥，又,AF DE DE FG G ⊥⋂=，,DE FG ⊂面DEF ，AF ∴⊥面DEF ，又1132193,333222A FDE FDE FG AO V AF S -==∴=⋅⋅=⨯⨯= ，设点F 到面ADE 的距离为9,2F ADE A FDE h V V --==，即2139342h ⨯⋅=，h ∴=，所以，点F 到面ADE.（3）因为四棱锥A BCDE -是正四棱锥，所以OC ，OD ，OA 两两垂直，以O 为坐标原点，建立如图所示的空间直角坐标系，则(0,0,3),(0,3,0),(3,0,0),(0,3,0),(1,1,3)A B C D F --，所以(0,3,3),(3,0,3),(1,2,3)BA CA DF ==-=--，设平面ABC 的法向量为(,,)n x y z = ，则有330330n BA y z n CA x z ⎧⋅=+=⎪⎨⋅=-+=⎪⎩取1z =，则1,1y x =-=，故(1,1,1)n =-，设直线DF 与平面ABC 所成角为θ，则242sin 21||||DF n DF n θ⋅==⋅，所以直线DF 与平面ABC 所成角的正弦值为24221.3．已知函数()2ln f x ax x x =--．（1）讨论()f x 的单调性；（2）若不等式()0f x ≥恒成立，求a 的取值范围；（3）当0a =时，试判断函数()()2sin 2F x x f x x =--的零点个数，并给出证明．【答案】（1）答案见解析（2）[)1,+∞（3）有且仅有2个零点，证明见解析【分析】（1）对()f x 求导，再分0a ≤与0a >两种情况分类讨论()f x 的单调性即可求解；（2）根据条件，分离常量得到21ln xa x x≥+，构造()21ln (0)x g x x x x =+>，将问题转化成求()g x 的最大值，即可解决问题；（3）构造函数，利用导数研究函数的单调性，结合零点存在定理即可求解．【解析】（1）因为()()2ln ,0,f x ax x x x =--∈+∞，所以()212121ax x f x ax x x-'-=--=，当0a ≤时，2210ax x --<恒成立，所以()0f x '<；当0a >时，令210x --=，解得1184ax a++=（舍去负根），令()0f x ¢>，得1184a x a ++>；令()0f x '<，得11804ax a++<<．综上所述，当0a ≤时，()f x 在()0,∞+上单调递减；当0a >时，()f x 在1180,4a a ⎛⎫++ ⎪ ⎪⎝⎭上单调递减，在118,4a a ⎛⎫++∞ ⎪ ⎪⎝⎭上单调递增．（2）由()0f x ≥恒成立，得2ln ax x x ≥+在()0,∞+上恒成立，所以21ln xa x x≥+在()0,∞+上恒成立．令()21ln (0)xg x x x x=+>，则()2423312ln 112ln 12ln x x x x x xg x x x x x x '---+-=-+=-+=．令()2ln 1(0)h x x x x =--+>，易知()2ln 1h x x x =--+在()0,∞+上单调递减．又()10h =，所以当()0,1x ∈时，()()0,0h x g x '>>，当()1,x ∈+∞时，()()0,0h x g x '<<，所以()g x 在()0,1上单调递增，在()1,+∞上单调递减，所以()g x 在1x =处取得极大值，也是最大值，即()max ()11g x g ==，所以1a ≥，即a 的取值范围为[)1,+∞．（3）当0a =时，()2sin ln 2ln 2sin ,0F x x x x x x x x x =++-=-+>，则()112cos F x x x=-+'，令()()112cos ,0G x F x x x x ==-+>'，则()212sin G x x x'=--，当()0,πx ∈时，()0G x '<，所以()F x '在()0,π上单调递减．又()π212cos10,102πF F ⎛⎫=>=-<⎪⎝⎭''，所以()F x '在()0,π上存在唯一的零点．设()F x '在()0,π上的零点为00π12x x ⎛⎫<< ⎪⎝⎭，可得当()00,x x ∈时，()0F x '>，()F x 单调递增；当()0,πx x ∈时，()()0,F x F x '<单调递减，解法一：11111ln 2sin ln222222F ⎛⎫=-+=--+⎪⎝⎭12sin 2，因为1π26<，所以1π1sin sin 262<=，故12sin 12<．又1ln212--<-，所以102F ⎛⎫< ⎪⎝⎭．又πππln 20222F ⎛⎫=-+> ⎪⎝⎭，所以()F x 在1π,22⎛⎫⎪⎝⎭上有一个零点．又()πlnππ0F =-<，所以()F x 在π,π2⎛⎫⎪⎝⎭上有一个零点．当3ππ,2x ⎡⎤∈⎢⎥⎣⎦时，()112cos 0F x x x =-+<'，所以()F x 在3ππ,2⎡⎤⎢⎥⎣⎦上没有零点．当3π2x >时，令()ln (e)exW x x x =->，则()11e 0e e xW x x x-='=-<，所以()W x 在()e,+∞上单调递减，所以()e lne 0e W x <-=，所以ln e 2x x x <<，所以()ln 2sin 2sin 2x F x x x x x x =-+<-+2sin 2xx =-，而113π2sin 2,2222x x ≤>⨯>，所以()0F x <，故()F x 在3π,2⎛⎫+∞ ⎪⎝⎭上没有零点．综上所述，()F x 在定义域()0,∞+上有且仅有2个零点．解法二：因为22211122sin 0e e e F ⎛⎫=--+<⎪⎝⎭，πππln 0333F ⎛⎫=-+> ⎪⎝⎭，所以()F x 在21π,e 3⎛⎫⎪⎝⎭上有一个零点．又()πlnππ0F =-<，所以()F x 在π,π3⎛⎫⎪⎝⎭上有一个零点，当[]π,2πx ∈时，()ln 2sin ln F x x x x x x =-+≤-，易证ln 1x x <-，所以ln 110x x x x -<--=-<，从而()0F x <在[]π,2π上恒成立，故()F x 在[]π,2π上没有零点．当()2π,x ∈+∞时，()ln 2sin ln 2F x x x x x x =-+≤-+，设()ln 2(2π)H x x x x =-+>，则()110H x x-'=<，所以()H x 在()2π,+∞上单调递减．又()()2πln 2π2π20H =-+<，则()0H x <在()2π,+∞上恒成立，所以()0F x <在()2π,+∞上恒成立，故()F x 在()2π,+∞上没有零点．综上所述，()F x 在定义域()0,∞+上有且仅有2个零点．变式：已知函数()e sin 1x f x x =--.（1）讨论函数()f x 在区间(0,)+∞上的单调性;（2）证明函数()f x 在区间(π,0]-上有且仅有两个零点.【答案】（1）单调递增；（2）证明见解析.【分析】（1）求出函数()f x 的导数，再判断导函数值的正负即得.（2）利用导数，结合零点存在性定理推理论证即可.【解析】（1）函数()e sin 1x f x x =--，当0x >时，()e cos 1cos 0x f x x x '=->->，所以()f x 在(0,)+∞上的单调递增.（2）由（1）知，()e cos x f x x '=-，当ππ,2(x --∈时，()0f x '>，函数()f x 在(π,2]π--上单调递增，π(π)e 10f --=-<，π2π(e 02f --=>，因此函数()f x 在(π,2π--上有唯一零点；当]π(,02x -∈时，令()e cos x g x x =-，求导得()e sin x g x x '=+，()g x '在π(,0]2-上单调递增，π2π()e 10,(0)102g g -''-=-<=>，则存在0π(,0)2x ∈-，使得00()g x '=，当0π(,)2x x ∈-时，()0g x '<，函数()g x ，即()f x '单调递减，当0(,0)x x ∈时，()0g x '>，函数()g x ，即()f x '单调递增，又π2π()e 02f -'-=>，0()(0)0f x f ''<=，则存在01)π,(2x x -∈，使得1()0f x '=，当1π(,)2x x ∈-时，()0f x '>，函数()f x 单调递增，当1(,0)x x ∈时，()0f x '<，函数()f x 单调递减，而π2π()e 02f --=>，(0)0f =，因此函数()f x π(,0]2-上有唯一零点，所以函数()f x 在区间(π,0]-上有且仅有两个零点.4．已知椭圆E ：22221x y a b+=（0a b >>）中，点A ，C 分别是E 的左、上顶点，AC =且E的焦距为．（1）求E 的方程和离心率；（2）过点()1,0且斜率不为零的直线交椭圆于R ，S 两点，设直线RS ，CR ，CS 的斜率分别为k ，1k ，2k ，若123k k +=-，求k 的值．【答案】（1）2214x y +=，32e =（2）3【分析】（1）由||AC 的值，可得a ，b 的关系，再由焦距可得c 的值，又可得a ，b 的关系，两式联立，可得a ，b 的值，即求出椭圆的方程；（2）设直线RS 的方程，与椭圆的方程联立，消元、列出韦达定理，求出直线CR ，CS 的斜率之和，由题意整理可得参数的值，进而求出直线RS 的斜率的大小．【解析】（1）由题意可得(,0)A a -，(0,)C b ，可得AC，2c =c =可得2223a b c -==，225a b +=，解得24a =，21b =，所以离心率2c e a ==，所以椭圆的方程为2214x y +=，离心率32e =；（2）由（1）可得(0,1)C ，由题意设直线RS 的方程为1x my =+()0m ≠，则1k m=，设()11,R x y ，()22,S x y ()120x x ≠，联立22141x y x my ⎧+=⎪⎨⎪=+⎩，整理可得22(4)230m y my ++-=，显然0∆>，且12224my y m +=-+，12234y y m =-+，直线CR ，CS 的斜率1111y k x -=，2221y k x -=，则12211212121211(1)(1)(1)(1)(1)(1)y y my y my y k k x x my my --+-++-+=+=++1212212122(1)()2()1my y m y y m y y m y y +-+-=+++22222322(1)2244321144m m m m m m m m m m m --⋅+-⋅-++==---⋅+⋅+++，因为123k k +=-，即231m -=-，解得13m =，所以直线RS 的斜率13k m==．即k的值为3．变式：已知椭圆E ：()222210x y a b a b+=>>过点81,3⎛⎫ ⎪⎝⎭，且其离心率为13．（1）求椭圆E 的方程；（2）过点()1,0-的斜率不为零的直线与椭圆E 交于C ，D 两点，A ，B 分别为椭圆E 的左、右顶点，直线AC ，BD 交于一点P ，M 为线段PB 上一点，满足OM PA ∥，问⋅OA OM 是否为定值，若是，求出该定值；若不是，说明理由（O 为坐标原点）．【答案】（1）22198x y +=（2）是定值，定值为9【分析】（1）将点代入椭圆方程，以及联立离心率可求得椭圆方程；（2）首先设过点()1,0-的直线为1x my =-，与椭圆方程联立，利用坐标分别表示直线AC 和BD方程，并求得点P 的坐标，利用几何关系，转化⋅OA OM ，即可求解.【解析】（1）由题意可知，222221316419c a a b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩，解得：21c =，28b =，29a =，所以椭圆E 的方程为22198x y +=；（2）设过点()1,0-的直线为1x my =-，()11,C x y ，()22,D x y ，()3,0A -，()3,0B ，联立221198x my x y =-⎧⎪⎨+=⎪⎩，得()228916640m y my +--=，1221689m y y m +=+，12264089y y m -=∆>+，，113AC y k x =+，所以()11:33ACy l y x x =++，()22:33BD y k y x x =--，联立直线AC 和BD 方程，得()()()()2121122121212132233344y x y my my y y x x y x y my my y y ++++===----，22222212222226432322189898964643216242289898989m m my y y m m m m m m m y y y m m m m ---++++++====---⎛⎫-+-- ⎪++++⎝⎭，所以3132x x +=-，得9x =-，1163y y x -=+，即1169,3y P x ⎛⎫-- ⎪+⎝⎭因为点O 是AB 的中点，//OM PA ，所以12OM AP =，所以()116113,06,9223y OA OM OA AP x ⎛⎫-⋅=⋅=-⋅-= ⎪+⎝⎭ .所以⋅OA OM 是定值，且定值为9.5．对于数列{}()*n a n ∈N，记1Δnn n aa a +=-，称数列{}Δn a 为数列{}n a 的一阶差分数列；记()21ΔΔΔΔΔn n n n a a a a +==-，称数列{}2Δn a 为数列{}n a 的二阶差分数列，…，一般地，对于k ∈N ，记()11ΔΔΔΔΔk k k k n n n n a a a a ++==-，规定：01Δ,ΔΔn n n n a a a a ==，称{}Δkn a 为数列{}n a 的k 阶差分数列．对于数列{}n a ，如果Δ0k n a d =≠（d 为常数），则称数列{}n a 为k 阶等差数列．（1）数列{}2n是否为k 阶等差数列，如果是，求k 值，如果不是，请说明为什么？（2）请用231111,Δ,Δ,Δ,a a a a 表示34,a a ，并归纳出表示n a 的正确结论（不要求证明）；（3）请你用（2）归纳的正确结论，证明：如果数列{}n a 为k 阶等差数列，则其前n 项和为123211111C C ΔC ΔC Δk kn n n n n S a a a a +=++++ ；（4）某同学用大小一样的球堆积了一个“正三棱锥”，巧合用了2024个球．第1层有1个球，第2层有3个，第3层有6个球，…，每层都摆放成“正三角形”，从第2层起，每层“正三角形”的“边”都比上一层的“边”多1个球，问：这位同学共堆积了多少层？【答案】（1）数列{}2n是二阶等差数列，2（2）231112ΔΔa a a a =++，4a =2311113Δ3ΔΔa a a a +++，1221111111ΔC ΔC Δk k n n n n a a C a a a ---=++++ （3）证明见详解（4）22【分析】（1）由新定义可直接证明数列{}2n 是二阶等差数列；（2）由()12112111ΔΔΔΔ0,ΔΔ0k k k k n a a a a a ++-=-==== 的关系，递推可得答案；（3）首先证明数列1230,,,,,n S S S S ⋅⋅⋅为1k +阶等差数列，再结合（2）可得123211111C C ΔC ΔC Δk k n n n n n S a a a a +=++++ ；（4）由（3）得：2222123n ++++ ()()11216n n n =++，方法一：结合等差数列的前n 项和公式可得答案；方法二：结合组合数的性质可得答案.【解析】（1）因为221Δ(1)21n n n a a a n n n +=-=+-=+，而()()()()2ΔΔΔΔ212112120n n a a n n n ==+=++-+=≠，所以2k =，数列{}2n是二阶等差数列．（2）因为数列{}n a 为k 阶等差数列，则Δ0k n a d =≠，则()12112111ΔΔΔΔ0,ΔΔ0k k k k n a a a a a ++-=-==== ，则211Δa a a =+，()()223221111111ΔΔΔΔ2ΔΔa a a a a a a a a a =+=+++=++，()()2243311122Δ2ΔΔΔΔa a a a a a a a =+=++++()()()222311111112ΔΔΔΔΔΔa a a a a a a =++++++2311113Δ3ΔΔa a a a =+++．归纳得一般结论：1221111111C ΔC ΔC Δk k n n n n a a a a a ---=++++ ①．（3）设数列：1230,,,,,n S S S S ⋅⋅⋅，因为()11111Δ2,Δ0n n n n a S S S n S S a --=-=≥=-=，所以数列1230,,,,,n S S S S ⋅⋅⋅为1k +阶等差数列，由（2）中①得：122111110C ΔC ΔC Δk k n n n n S S S S ++=-+++ ，因为()1111ΔΔΔΔk k k S S a +==所以123211111C C ΔC ΔC Δk k n n n n n S a a a a +=++++ ．【小问4详解】由（1）知数列{}2n 为二阶等差数列，且()()()()211213221Δ413,ΔΔΔ94412a a a a a a a a =-==-=---=---=，则由（3）得：2222123n ++++ ()()()123112C 1C 3C 23226n n n n n n n n n ---=⨯+⨯+⨯=+⨯+⨯()()11216n n n =++②．设共堆积了n 层，第n 层共有n a 个球，第1层有1个球，因为每层的“边”比上一层多1个球，所以第n 层的“边”共有n 个球，则第n 层的球数为()11232n n n a n +=++++= ．则这n 层所有球的个数为()11362n n n S +=++++．【法一】由②式得：()()()22221113612312322n n n S n n +⎡⎤=++++=++++++++⎣⎦ ()()()111211202462n n n n n =++++=．解得：22n =．答：这位同学共堆积了22层．【法二】()222223411136C C C C 2n n n n S ++=++++=++++ 32223223223341441551C C C C C C +C C C C n n n +++=++++=++⋅⋅⋅=+++ ()()3221C 20246n n n n+++==== ．解得：22n =．答：这位同学共堆积了22层．变式：已知n 为正整数，数列12:,,,n X x x x ，记()12n S X x x x =+++ .对于数列X ，总有{}0,1,1,2,,k x k n ∈= ，则称数列X 为n 项01 数列.若数列1212:,,,,:,,,n n A a a a B b b b ，均为n 项01 数列，定义数列12:,,,n A B m m m ⊗ ，其中1,1,2,,k k k m a b k n =--= .（1）已知数列:1,1,1,0,:0,0,1,1A B ，求()()S A A S A B ⊗⊗的值；（2）若数列,A B 均为n 项01 数列，求证：()()()S A B A S B ⊗⊗=；（3）对于任意给定的正整数n ，是否存在n 项01 数列,,A B C ，使得()()()2S A B S A C S B C n ⊗+⊗+⊗=，并说明理由.【答案】（1）4（2）证明见解析（3）答案见解析【分析】（1）根据数列A B ⊗的定义分别求出A A ⊗,A B ⊗,进一步计算即可得到答案；（2）记数列12:,,,n A B c c c ⊗⋅⋅⋅数列()12:,,,n A B A d d d ⊗⊗⋅⋅⋅，分别考虑1k a =，0k a =两种情况，从而得出结论；（3）分别讨论n 为奇数和偶数两种情况，根据定义分析运算，从而得到结论.【解析】（1）根据题中定义知，数列：:1,1,1,1A A ⊗，数列:0,0,1,0A B ⊗，所以()()11114;00101S A A S A B ⊗=+++=⊗=+++=,故()()4S A A S A B ⊗=⊗.（2）对于01 数列1212:,,,,:,,,n n A a a a B b b b ，记数列12:,,,n A B c c c ⊗⋅⋅⋅对于(),1,2,,k c k n =⋅⋅⋅，若1k a =，则1,1k k k k k k k a b b c a b b -=-=--=，若0k a =，则,11k k k k k k k a b b c a b b -==--=-，故对于数列()12:,,,n A B A d d d ⊗⊗⋅⋅⋅，若1k a =，则k k k d c b ==；若0k a =，则()111k k k k d c b b =-=--=，所以数列()A B A ⊗⊗与数列B 是同一数列，故()()()S A B A S B ⊗⊗=.（3）若n 是奇数，则不存在满足条件的n 项01 数列,,A B C ，证明如下：对于3个n 项01 数列,,A B C ，记()3,0,1,i i i i i i i x a b b c c a i n =------=⋅⋅⋅，则()()()12n S A B S A C S B C x x x ⊗+⊗+⊗=++⋅⋅⋅+，当i i i a b c ==时，33i i i i i i i x a b b c c a =------=，当,,i i i a b c 中有一个不同于其他两个时，31i i i i i i i x a b b c c a =------=，所以i x 是奇数，则()()()12n S A B S A C S B C x x x ⊗+⊗+⊗=++⋅⋅⋅+为奇数个奇数之和，仍为奇数，不可能为2n ；若n 为偶数，即()*2Nn k k =∈,可构造：:1,1,,1n A ⋅⋅⋅ ，:1,1,,1n B ⋅⋅⋅ ,:0,0,,0,1,1,,1k k C ⋅⋅⋅⋅⋅⋅ ，此时数列A B ⊗为1,1,,1n ⋅⋅⋅ ，数列,A C B C ⊗⊗相同，都是0,0,,0,1,1,,1k k⋅⋅⋅⋅⋅⋅ ，所以有()()()2S A B S A C S B C n k k n ⊗+⊗+⊗=++=，综上所述，当n 为偶数时，()()()S A B S A C S B C ⊗+⊗+⊗有可能为2n ；当n 为奇数时，不可能成立.。