小学五年级下册数学试题-奥数专题：第三节 速算与巧算(二)全国通用

第二讲 小数的速算与巧算（二）【知识概述】若干个数排成一列称为“数列”，数列中的每一个数称为一项，其中第一项称为首项（1a ），最后一项称为末项（n a ）。

从第二项开始，后项与前项之差都相等的数列称为“等差数列”，后项与前项之差称为公差（d ），数列中的数的个数称为项数（n ）。

对于等差数列，我们要熟练运用三个公式：通项公式：第n 项＝首项＋（项数－1）×公差项数公式：项数＝（末项－首项）÷公差＋1求和公式：和＝（首项＋末项）×项数÷21、对于一个数除以两个或者两个以上的数，我们可以把多个除数先用乘积的方式算出结果，再用被除数除以所求的结果，得到最后的商例1 计算8.376÷3.2÷2.5解析：8.376除以3.2再除以2.5也就是8.376除以3.2与2.5的乘积练习 计算7.68÷2.5÷0.42、 一个数除以另一个数就等于这个数乘以这个数的倒数，即a ÷b=a ×1/b=a/b 例2 计算（4.8×7.5×8.1）÷（2.4×2.5×2.7）解析 ：因为乘除是同一级运算，我们可以把式子拆开，看作是（4.8÷2.4）×（7.5÷2.5）×（8.1÷2.7）练习 1.1÷（1.1÷1.2）÷（1.2÷1.3）÷（1.3÷1.4）3.数列通项公式：第n项＝首项＋（项数－1）×公差，项数公式：项数＝（末项－首项）÷公差＋1，求和公式：和＝（首项＋末项）×项数÷2等差数列就是一列数，后面的数减去前面的数所得的差都是相等的例3 已知等差数列0.2，0.5，0.8，1.1，1.4，…。

（1）这个数列的第13项是多少？（2）4.7是其中的第几项？解析：第13项等于首项+（n-1）×公差=0.2+（13-1）×0.3, 4.7=0.2+(n-1) ×0.3,求得的n就是第几项练习：有一列数0.1，0.5，0.9，1.3，1.7，…。

五年级奥数速算、巧算方法及习题五年级奥数速算、巧算方法及习题数的概念自然数：0，1，2，3，4……叫自然数。

整数：正整数，0，负整数统称整数。

……-4，-3，-2，-1，0，1，2，3，4……1、整除：整数a除以整数b，如果除得的商是整数，而余数为0，我们就说a能被b整除，或者说b能整除a。

如果整数a能被整数b整除（b不等于0），a就叫b的倍数，b 就叫a的约数（因数）。

2、整除的条件：（1）、除数被除数都是整数( 2 )、被除数除以除数，商是整数，而且余数为零，除数不为零。

4、整除的特征：(1)、0能整除任意非零的整数，1能整除任意整数(2)、能被2整除的数的特征：一个数的末尾数字是0，2，4，6，8(3)、能被3（或9）整除的数的特征：各位数字的和能被3（或9）整除(4)、能被4（或25）整除的数的特征：末尾两位能被4（或25）整除(5)、能被5整除的数的特征：一个数的末尾是0或5(6)、能被6整除的数的特征：同时能被2或3整除(7)、能被7整除的数的特征：去掉个位数字，再从剩下的数中减去个位数字的2倍，差是7的倍数(8)、能被8（或125）整除的数的特征：末尾3位能被8（或125）整除(9)、能被10整除的数的特征：末尾数字是0(10)、能被11整除的数的特征：奇位上的数字的和与偶位上数字的和的差能被11整除(11)、能被7、11、13整除的数的特征：一个整数，如果他的末三位数与末三位以前的数字所组成的数的差能被7、11、13整除(12)、能被16（或625）整除的数的特征：末尾四位数能被16或625整除。

练习1：(1)、判断下列哪些数能被2整除？21 44 56 65 98(2)、判断下列哪些数能被3整除111 135 186 **** ****(3)、判断下列哪些数能被4整除？84 200 1984 1978 2008 200912456 37212 7800 5408(4)、判断下列哪些数能被5整除？135 65 80 4246 15360 95556 50058(5)、判断下列哪些数能被25整除？75 125 7800 178 197 2050 2029 2350 65325(6)、判断下列哪些数能被10整除？9060 4140 1531 95856 56340(7)、判断下列哪些数能被100整除？1200 170 110 200 2029(8)、判断下列哪些数能被7整除？判断下列哪些数能被11整除？判断下列哪些数能被13整除？128114 94146 64152 238231 413412 242231 439417(9) 判断下列哪些数能被8整除？判断下列哪些数能被125整除？1880 1978 1997 2008 2009 178 197 2250 2029 672520 333640 78500 987000 333420(10)、判断下列哪些数能被9整除？1161 4248 15310 95856 56349 73265 64585 6723 661232：（1）、在□中填入合适的数字，使组成的数能被4整除78□4 7653□ 863□□（2）、在□中填入合适的数字，使组成的数能被25整除98□5 765□ 667□ 874□0（3）、在□中填入合适的数字，使组成的数能被8整除32□80 789□2□ 664□（4）、在□中填入合适的数字，使组成的数能被125整除662□0 887□0 4525□□ 6673□□（5）、在□中填入合适的数字，使组成的数能被9整除78□3 68□4 322□（6）、在□中填入合适的数字，使852□7能被7整除，7630□2能被11整除，890□能被13整除。

小学数学《速算与巧算》练习题（含答案）【复习1】（我爱数学夏令营）计算：6.11+9.22+8.33+7.44+5.55+4.56+3.67+2.78+1.89分析：原式=（6.11+1.89）+（9.22+2.78）+（8.33+3.67）+（7.44+4.56）+5.55=8+12+12+12+5.55=49.55【复习2】（06香港圣公会小学奥林匹克）计算：3.72-2.73+4.6+5.28-0.27+6.4分析：原式=（3.72+5.28）+（4.6+6.4）-（2.73+0.27）=9+11-3=17 .【复习3】(华罗庚学校五年级入学考试试题)8×(3.1-2.85)×12.5×(1.62＋2.38)-3.27分析：初看这道题好像不能用简便方法进行计算.但是里面有特殊数8、12.5,所以可以先算一步,再用简便方法进行计算.原式=8×0.25×12.5×4－3.27=(8×12.5)×(0.25×4)-3.27=100-3.27=96.73【复习4】（04陈省身杯数学邀请赛）（56789+67895+78956+89567+95678）÷7分析：原式=（5+6+7+8+9）×11111÷7=5×11111=55555 . 观察可知5、6、7、8、9在万、千、百、十、个位各出现过一次 .【复习5】计算：l-2+3-4+5-6+…+2005-2006+2007分析：原式= l+3-2+5-4+7-6+…+2005+2007-2006=1+1×1003=1004 ，分组求和的思路.在速算的过程中，如果加入运算律的应用，会有意想不到的效果！我们一起先来看看常用的一些运算律和结论吧！在计算过程中，最常用的技巧之一是灵活熟练地运用运算律.运算律有：（1）加法交换律：a＋b=b＋a（2）加法结合律：(a＋b)＋c=a＋(b＋c)（3）乘法交换律：ab=ba（4）乘法结合律：(ab)c=a(bc)（5）分配律： a(b＋c)=ab＋ac （反过来就是提取公因数）（6）减法（括号）的性质：a-b-c=a-(b＋c)（7）除法的性质：a÷(b×c)=a÷b÷c(a＋b) ÷c=a÷c＋b÷c(a-b) ÷c=a÷c-b÷c和不变的规律：如果一个加数增加另一个加数减少同一个数，它们的和不变.积不变的规律：如果一个因数扩大几倍，另一个因数缩小相同的倍数，积不变.商不变的规律：如果除数和被除数同时扩大或缩小相同的倍数，商不变.【例1】（04陈省身杯数学邀请赛）计算：3.1415×252-3.1415×152分析：（法1）：题中的三项都有因数34.5，容易想到把34.5作为公因数提取出来(把乘法分配律反过来用)，从而使计算简便.原式=34.5×(8.23＋2.77—1)=34.5×10=345.（法2）：原式=3.1415×（252-152）=3.1415×（25+15）×（25-15）=3.1415×40×10=1256.6 应用下面的平方差公式【回忆巩固】ａ、ｂ代表任意数字，（ａ＋ｂ）×（ａ－ｂ）＝ａ×ａ－ｂ×ｂ，这个公式在数学上称为平方差公式。

小学五年级奥数题——速算与巧算在日常生活和解答数学问题时,经常要进行计算,在数学课里我们学习了一些简便计算的方法 ,但如果善于观察、勤于思考 ,计算中还能找到更多的巧妙的计算方法 ,不仅使你能算得好、算得快 ,还可以让你变得聪明和机敏 .例 1：计算： 9.996＋ 29.98＋ 169.9＋ 3999.5算式中的加法看来无法用数学课中学过的简算方法计算,但是 ,这几个数每个数只要增加一点 ,就成为某个整十、整百或整千数,把这几个数“凑整”以后,就容易计算了.当然要记住 ,“凑整”时增加了多少要减回去.9.996＋ 29.98＋ 169.9＋ 3999.5=10＋ 30＋ 170＋ 4000－（ 0.004＋ 0.02＋ 0.1＋ 0.5）=4210－ 0.624=4209.376例 2：计算： 1＋ 0.99－ 0.98－ 0.97＋ 0.96＋ 0.95－ 0.94－0.93 ＋＋ 0.04＋ 0.03－ 0.02－ 0.01 式子的数是从 1 开始 ,依次减少0.01, 直到最后一个数是0.01, 因此 ,式中共有100 个数而式子中的运算都是两个数相加接着减两个数,再加两个数 ,再减两个数这样的顺序排列的 .由于数的排列、运算的排列都很有规律,按照规律可以考虑每 4 个数为一组添上括号 ,每组数的运算结果是否也有一定的规律?可以看到把每组数中第 1 个数减第 3 个数 ,第 2 个数减第 4 个数 ,各得 0.02, 合起来是 0.04,那么 ,每组数（即每个括号）运算的结果都是0.04,整个算式 100 个数正好分成 25 组 ,它的结果就是25 个 0.04 的和 .1＋ 0.99－ 0.98－ 0.97＋ 0.96＋ 0.95 － 0.94－ 0.93 ＋＋ 0.04＋0.03 －0.02 －0.01 =（ 1＋ 0.99－ 0.98－ 0.97）＋（ 0.96＋ 0.95 －0.94－ 0.93 ）＋＋（ 0.04＋ 0.03－ 0.02－ 0.01 ）=0.04× 25=1如果能够灵活地运用数的交换的规律,也可以按下面的方法分组添上括号计算：1＋ 0.99－ 0.98－ 0.97＋ 0.96＋ 0.95 － 0.94－ 0.93 ＋＋ 0.04＋0.03 －0.02 －0.01 =1＋（ 0.99－ 0.98－ 0.97＋ 0.96）＋（0.95 －0.94－ 0.93 ＋ 0.92）＋＋（ 0.03－ 0.02－ 0.01 ）=1例 3：计算： 0.1＋ 0.2＋ 0.3＋＋ 0.8 ＋0.9＋0.10 ＋ 0.11＋ 0.12＋＋ 0.19＋ 0.20这个算式的数的排列像一个等差数列,但仔细观察 ,它实际上由两个等差数列组成,0.1＋0.2＋ 0.3＋＋ 0.8＋ 0.9 是第一个等差数列,后面每一个数都比前一个数多0.1,而 0.10＋ 0.11＋0.12＋＋ 0.19＋ 0.20 是第二个等差数列,后面每一个数都比前一个数多0.01, 所以 ,应分为两段按等差数列求和的方法来计算.0.1＋ 0.2＋ 0.3＋＋ 0.8＋0.9＋ 0.10＋ 0.11 ＋ 0.12＋＋0.19＋ 0.20=（ 0.1＋ 0.9）×9÷ 2＋（ 0.10＋0.20 ）× 11÷2=4.5＋ 1.65=6.15例 4：计算： 9.9× 9.9＋ 1.99算式中的 9.9× 9.9 两个因数中一个因数扩大10 倍 ,另一个因数缩小10 倍 ,积不变 ,即这个乘法可变为99× 0.99； 1.99 可以分成0.99＋ 1 的和 ,这样变化以后 ,计算比较简便.9.9× 9.9＋ 1.99=99× 0.99＋ 0.99＋ 1=（ 99＋ 1）× 0.99 ＋1=100例 5：计算： 2.437× 36.54＋ 243.7× 0.6346虽然算式中的两个乘法计算没有相同的因数,但前一个乘法的 2.437 和后一个乘法的243.7 两个数的数字相同,只是小数点的位置不同,如果把其中一个乘法的两个因数的小数点.按相反方向移动同样多位,使这两个数变成相同的,就可以运用乘法分配律进行简算了2.437× 36.54＋ 243.7× 0.6346=2.437× 36.54＋ 2.437× 63.46=2.437×（ 36.54＋ 63.46）=243.7* 例 6：计算： 1.1×1.2 ×1.3× 1.4×1.5算式中的几个数虽然是一个等差数列,但算式不是求和,不能用等差数列求和的方法来计算这个算式的结果.平时注意积累计算经验的同学也许会注意到7、 11 和 13 这三个数连乘的积是1001,而一个三位数乘1001,只要把这个三位数连续写两遍就是它们的积,例如 578× 1001=578578,这一题参照这个方法计算,能巧妙地算出正确的得数.1.1× 1.2× 1.3× 1.4× 1.5=1.1× 1.3× 0.7× 2× 1.2× 1.5=1.001× 3.6=3.6036计算下列各题并写出简算过程：1． 5.467＋ 3.814＋ 7.533＋ 4.1862． 6.25× 1.25× 6.43． 3.997＋ 19.96＋ 1.9998 ＋ 199.74． 0.1＋ 0.3＋＋ 0.9＋ 0.11＋ 0.13＋ 0.15＋＋ 0.97＋ 0.995． 199.9× 19.98－ 199.8× 19.976． 23.75× 3.987＋ 6.013× 92.07＋ 6.832× 39.87*7 ． 20042005 × 20052004 － 20042004 ×20052005 *8 ．（1＋ 0.12＋ 0.23）×（ 0.12＋ 0.23＋ 0.34）－（ 1＋ 0.12＋ 0.23＋ 0.34）×（ 0.12＋ 0.23 ）计算下列各题并写出简算过程：1． 6.734－ 1.536＋ 3.266－ 4.4642． 0.8÷ 0.1253． 89.1＋ 90.3＋ 88.6＋ 92.1＋ 88.9＋ 90.84． 4.83× 0.59＋ 0.41× 1.59－ 0.324× 5.95． 37.5× 21.5× 0.112＋ 35.5× 12.5× 0.112包含与排除1、某班有40 名学生 ,其中有 15 人参加数学小组,18 人参加航模小组,有 10 人两个小组都参加. 那么有多少人两个小组都不参加?两个小组共有（15+18） -10=23 （人） ,都不参加的有40-23=17（人）答：有 17 人两个小组都不参加 .--2、某班45 个学生参加期末考试,成绩公布后 ,数学得满分的有 10 人 ,数学及语文成绩均得满分的有 3 人 ,这两科都没有得满分的有29 人.那么语文成绩得满分的有多少人?45-29-10+3=9 （人）答：语文成绩得满分的有9 人 .3、 50 名同学面向老师站成一行.老师先让大家从左至右按1,2,3,,49,50 依次报数；再让报数是 4 的倍数的同学向后转,接着又让报数是 6 的倍数的同学向后转 .问：现在面向老师的同学还有多少名 ?4 的倍数有 50/4 商 12 个 ,6 的倍数有 50/6 商 8个,既是 4又是 6的倍数有 50/12 商 4 个.4 的倍数向后转人数 =12,6 的倍数向后转共8 人 ,其中 4 人向后 ,4 人从后转回 .面向老师的人数 =50-12=38（人）答：现在面向老师的同学还有38 名.4、在游艺会上 ,有 100 名同学抽到了标签分别为 1 至 100 的奖券 .按奖券标签号发放奖品的规则如下：（ 1）标签号为 2 的倍数 ,奖 2 支铅笔；（ 2）标签号为 3 的倍数 ,奖 3 支铅笔；（ 3 ）标签号既是 2 的倍数 ,又是 3 的倍数可重复领奖；（ 4）其他标签号均奖 1 支铅笔 .那么游艺会为该项活动准备的奖品铅笔共有多少支?2 的倍数有100/2 商 50 个 ,3 的倍数有100/3 商 33 个 ,2 和 3 人倍数有100/6 商 16 个 .领 2 支的共准备（ 50— 16）*2=68, 领 3 支的共准备（ 33— 16）*3=51, 重复领的共准备16*（ 2+3）=80,其余准备100-（ 50+33-16 ） *1=33共需要 68+51+80+33=232（支）答：游艺会为该项活动准备的奖品铅笔共有232 支.5、有一根长为180 厘米的绳子 ,从一端开始每隔后将标有记号的地方剪断.问绳子共被剪成了多少段3 厘米作一记号?,每隔 4 厘米也作一记号,然3 厘米的记号：180/3=60, 最后到头了不划,60-1=59 个4 厘米记号： 180/4=45,45-1=44 个 ,重复的记号：180/12=15,15-1=14 个 ,所以绳子中间实际有记号 59+44-14=89 个 .剪 89 次 ,变成 89+1=90 段答：绳子共被剪成了 90 段 .6、东河小学画展上展出了许多幅画,其中有 16 幅画不是六年级的 ,有 15 幅画不是五年级的 . 现知道五、六年级共有25 幅画 ,那么其他年级的画共有多少幅?1,2,3,4,5 年级共有 16,1,2,3,4,6 年级共有 15,5,6 年级共有 25所以总共有（ 16+15+25） /2=28 （幅） ,1,2,3,4 年级共有28-25=3 （幅）答：其他年级的画共有 3 幅.---7、有若干卡片 ,每张卡片上写着一个数 ,它是 3 的倍数或 4 的倍数 ,其中标有 3 的倍数的卡片占 2/3, 标有 4 的倍数的卡片占 3/4, 标有 12 的倍数的卡片有15 张 .那么 ,这些卡片一共有多少张?12 的倍数有2/3+3/4-1=5/12,15/（5/12）=36（张）答：这些卡片一共有36 张.----8、在从 1 至 1000 的自然数中 ,既不能被 5 除尽 ,又不能被7 除尽的数有多少个?5 的倍数有1000/5 商 200 个 ,7 的倍数有 1000/7 商 142 个,既是 5 又是 7 的倍数有1000/35商 28 个 .5 和 7 的倍数共有 200+142-28=314 个 .1000-314=686答：既不能被 5 除尽 ,又不能被 7 除尽的数有686 个.---9、五年级三班学生参加课外兴趣小组,每人至少参加一项 .其中有 25 人参加自然兴趣小组 ,35 人参加美术兴趣小组 ,27 人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12 人, 参加自然同时又参加美术兴趣小组的有8 人 ,参加自然同时又参加语文兴趣小组的有9 人,语文、美术、自然 3 科兴趣小组都参加的有 4 人 .求这个班的学生人数 .25+35+27-（ 8+12+9） +4=62（人）答：这个班的学生人数是62 人.-- --10、如图 8-1,已知甲、乙、丙 3 个圆的面积均为 30,甲与乙、乙与丙、甲与丙重合部分的面积分别为 6,8,5,而 3 个圆覆盖的总面积为 73.求阴影部分的面积 .甲、乙、丙三者重合部分面积=73+（ 6+8+5） -3*30=2阴影部分面积=73-（ 6+8+5） +2*2=58答：阴影部分的面积是58.11、四年级一班有 46 名学生参加 3 项课外活动 .其中有 24 人参加了数学小组 ,20 人参加了语文小组 ,参加文艺小组的人数是既参加数学小组又参加文艺小组人数的 3.5 倍 ,又是 3 项活动都参加人数的 7 倍 ,既参加文艺小组也参加语文小组的人数相当于 3 项都参加的人数的 2 倍 , 既参加数学小组又参加语文小组的有10 人 .求参加文艺小组的人数 .设参加文艺小组的人数是X,24+20+X-（ X/305+2/7*X+10 ） +X/7=46, 解得 X=21答：参加文艺小组的人数是21 人.________________________________________-12、图书室有 100 本书 ,借阅图书者需要在图书上签名.已知在 100 本书中有甲、乙、丙签名的分别有 33,44 和 55 本 ,其中同时有甲、乙签名的图书为29 本 ,同时有甲、丙签名的图书有25 本,同时有乙、丙签名的图书有36 本 .问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过 ?三个人一共看过的书的本数是：甲 +乙 +丙（-甲乙 +甲丙 +乙丙）+甲乙丙 =33+44+55（- 29+25+36）+甲乙丙 =42+甲乙丙 ,当甲乙丙最大时 ,三人看过的书最多,因为甲、丙共同看过的书只有25 本,比甲乙和乙丙共同看到的都少,所以甲乙丙最多共同看过25 本.三人总共看过最多有42+25=67（本） ,都没看过的书最少有100-67=33 （本）答：这批图书中最少有33 本没有被甲、乙、丙中的任何一人借阅过.________________________________________13、如图 8-2,5 条同样长的线段拼成了一个五角星.如果每条线段上恰有1994 个点被染成红色,那么在这个五角星上红色点最少有多少个?五条线上右发有 5*1994=9970 个红点 ,如果所有交叉点上都放一个红点,则红点最少 ,这五条线有 10 个交叉点 ,所以最少有9970-10=9960 个红点答：在这个五角星上红色点最少有9960 个 .14、甲、乙、丙同时给100 盆花浇水 .已知甲浇了 78 盆 ,乙浇了 68 盆 ,丙浇了 58 盆 ,那么 3 人都浇过的花最少有多少盆?甲和乙必有 78+68-100=46 盆共同浇过 ,丙有 100-58=42 没浇过 ,所以 3 人都浇过的最少有46-42=4（盆）答： 3 人都浇过的花最少有 4 盆 .15、甲、乙、丙都在读同一本故事书 ,书中有100 个故事 .每个人都从某一个故事开始,按顺序往后读 .已知甲读了 75 个故事 ,乙读了 60 个故事 ,丙读了 52 个故事 .那么甲、乙、丙 3 人共同读过的故事最少有多少个?乙和丙共同读过的故事至少有60+52-100=12（个） ,甲无论从哪里开始都必定要读这12 个故事.答：甲、乙、丙 3 人共同读过的故事最少有12 个.15、甲、乙、丙都在读同一本故事书 ,书中有100 个故事 .每个人都从某一个故事开始,按顺序往后读 .已知甲读了 75 个故事 ,乙读了 60 个故事 ,丙读了 52 个故事 .那么甲、乙、丙 3 人共同读过的故事最少有多少个?乙和丙共同读过的故事至少有60+52-100=12（个） ,甲无论从哪里开始都必定要读这12 个故事.答：甲、乙、丙 3 人共同读过的故事最少有12 个.________________________________________-8、在从 1 至 1000 的自然数中 ,既不能被 5 除尽 ,又不能被 7 除尽的数有多少个 ?5 的倍数有 1000/5 商 200 个 ,7 的倍数有1000/7 商 142 个,既是 5 又是 7 的倍数有 1000/35 商 28 个 .5 和 7 的倍数共有 200+142-28=314 个 .1000-314=686答：既不能被 5 除尽 ,又不能被7 除尽的数有686 个 .题中的除尽应该是整除吧.11、四年级一班有46 名学生参加 3 项课外活动 .其中有 24 人参加了数学小组,20 人参加了语文小组 ,参加文艺小组的人数是既参加数学小组又参加文艺小组人数的 3.5 倍 ,又是 3 项活动都参加人数的7 倍 ,既参加文艺小组也参加语文小组的人数相当于 3 项都参加的人数的 2 倍 , 既参加数学小组又参加语文小组的有10 人 .求参加文艺小组的人数.设参加文艺小组的人数是X,24+20+X-（ X/305+2/7*X+10 ） +X/7=46, 解得 X=21答：参加文艺小组的人数是21 人.。

五年级计算题(巧算与速算)五年级计算题练习一一、直接写出得数。

101－201= 2＋21= 41＋43－51= 97 －92=1－21－51= 51＋21－51= 31＋35－2= 52＋101=二、解方程或比例。

① 0.3χ= 45 ②52χ＋53χ=28 ③χ－54=125 三、计算，要写出主要计算过程，能用简便方法的要用简便方法计算。

51＋21＋31 21＋31－41 51＋21＋542－125－127 79＋61＋65＋75 1513－（1513－52）五年级计算题练习二一．直接写出得数。

21＋21= 31＋32= 1－65= 65－65=51＋51= 54－51= 83＋83= 1－21=二．解方程Ⅹ－21=54 61＋Ⅹ=21 2Ⅹ－65=61三．计算下列各题，要写出主要计算过程，能用简便方法的要用简便方法计算。

（18分）（1）54 ＋（83－41） （2）2－73－74 (3)85－31＋125（4）68－ 7.5 ＋ 32－2.5 （5）125 －（121 －21）五年级计算题92＋21= 76－32= 103＋41= 73＋91= 31－51=① 1720 －（720 ＋512 ） ② 89 －（29 ＋13 ） ③ 29 + 45 + 79 + 15④ 7- 57 - 57 ⑤ 45 + 1115 + 310 ⑥ 6- （34 - 25）五年级计算题练习五一、直接写出得数。

（4分）87+21＝ 21+31＝ 81－91＝ 43－21＝ 1+136＝53+52＝ 32－61＝ 81+31＝ 103+32＝ 87－43＝ 52+103＝ 1－1511＝ 74－21＝ 41+41＝ 72+141＝ 62＝ 53＝ 0.125×8＝ 6.25×13＝ 28÷56＝二、解方程或比例。

（9分）37 χ＋ 18 = 12 4χ－1.6χ＝36 X ＋73=43三、递等式计算，怎样简便就怎样算。

速算与巧算一、考点、热点回顾：1、掌握小学数学中常用的速算方法，并根据数字特点选择恰当方法计算。

二、典型例题：例1计算72.19＋6.48＋27.81－1.38－5.48－0.62。

解：观察发现，有些加数可以凑整；有的加数和减数尾数相同，可以抵消。

于是：72.19＋6.48＋27.81－1.38－5.48－0.62＝(72.19＋27.81)＋(6.48－5.48)－(1.38＋0.62)＝100＋1－2＝99例2用简便方法计算 1.25×67.875＋125×6.7875＋1250×0.053375。

解：观察发现：相加的三个乘积中分别有1.25、125、250，因此想到利用积不变的性质，使三个积有相同的因数。

于是：1.25×67.875＋125×6.7875＋1250×0.053375＝1.25×67.875＋1.25×678.75＋1.25×53.375＝1.25×(67.875＋678.75＋53.375)＝1.25×800＝1000例3计算1999＋199.9＋19.99＋1.999。

解法一：观察发现，构成这四个加数的数字和排列顺序完全相同，因此可以把它们都看作1999与某个数的积，于是：1999＋199.9＋19.99＋1.999＝1999×(1＋0.1＋0.01＋0.001)＝1999×1.111＝(2000－1)×1.111＝2222－1.111＝2220.889解法二：观察发现这四个加数分别接近2000、200、20、2，于是1999＋199.9＋19.99＋1.999＝2000＋200＋20＋2－1.111＝2220.889例4计算(1＋0.33＋0.44)×(0.33＋0.44＋0.55)－(1＋0.33＋0.44＋0.55)×(0.33＋0.44)。

【五年级奥数举一反三一全国通用】测评卷01《速算和巧算》试卷满分：100分考试时间：100分钟姓名:.班级:.得分:一.选择题（共7小题，满分21分，每小题3分）1.（2015•创新杯）计算：2.34-0.084-1.25=（）2.A.230 B.23 C. 2.3 D.0.23（2009-华罗庚金杯）下面有四个算式:®0.6+n1n；2揭0.625=旦@＞且+旦旦X41=142 U.［况U.3-814214+2162■755其中正确的算式是（）A.①和②B.②和④ D.①和④3.（2003•创新杯）2003+2002-2001-2000+1999+1998-1997-1996+・・・+7+6-5-4+3+2-1的计算结果是A.2002B.2003C.2004D.40054.0.65X201=0.65X（200+1）=0.65X200+0.65运用了乘法的（）5. 6.A.交换律 B.结合律 C.分配律与0.456X2.1的结果相同的算式是（）A. 4.56X21B.21X0.0456C.45.6X0.21D.456X0.021与61.2H-3.4II-算结果相同的是（）A. 6.124-0.34B.61290.34C.0.612X0.034D.6124-347.105X18=100X18+5X18运用了（）A.乘法交换律B.乘法结合律C.乘法分配律二.填空题（共10小题，满分30分，每小题3分）8.（2018*其他模拟）计算:3-5+7-9+11-13+-+I995-1997+1999=9.（2018*其他模拟）。

=1997个。

4,5=1997个025,则a+h=，aXb=,a7b=10.（2017-育苗杯）计算39.07-22.78+3.4=11.（2018*迎春杯）算式（20.17-12.024-6）X6的计算结果是.12.（2017-其他杯赛）计算:（2017-1）+（2016-2）+…+（2011-7）13.（2016・其他杯赛）计算：91.5+19.8+80.2=.14.（2016-其他杯赛）计算：（102.4+89.6・38X5）X（2016-126X16）=.15.（2018-陈省身杯）计算200・（16+17+18+・・・+23+24）=.16.（2018-其他模拟）计算：53.34-0.234-0.91X16.14-0.82=.17.（2007•迎春杯）计算：379X0.00038+159X0.00621+3.79X0.121=.三.计算题（共6小题，满分18分，每小题3分）18.（2016-中环杯）计算：（20.15+40.3）X33+20.15.19.计算（1）24X2X125X25（2）125X32X25X201320.（2018・学而思杯）2.8X27+28X2.9+2.8X4421.（2017-春蕾杯）计算©0.8：9+0.1：9=；②201.7X4.5+2017X0.35+20.17X20=；③]0.1+0.2+0.3+0.4）X（1+0.1+0.2+0.3）-（1+0.1+0.2+03+0.4）X（0.1+0.2+0.3）=22.计算：2015+201.5+20.15+985+98.5+9.85.23.（2003•创新杯）计算：0.79X0.46+7.9X0.24+11.4X0.079.四.解答题（共6小题，满分31分）24.（5分）（2015・奥林匹克）计算：（12X21X45X10.2）4-（15X4X0.7X51）25.（5分）（2018・学而思杯）903+899+902+897+904+89826.（5分）（1996*其他杯赛）376+385+391+380+377+389+383+374+366+378=27.（5分）（1995*其他杯赛）0.873个0X01122个0=28.（5分）（2015・春蕾杯）（1）10.444-1.2X0.3=（2）[0.5X（6+0.6）-0.5]4-2.5=.29.（6分）（2017・学而思杯）（1）解方程：3（15-2x）+12=85-10v（2）计算:4.02X16+33X4.02-4.9X20.2.测评卷01《速算和巧算》试卷满分：100分考试时间：100分钟姓名：班级：得分：一.选择题（共7小题，满分21分，每小题3分）（请将答案填写在各试题的答题区内）1234567二.填空题（共10小题，满分30分，每小题3分）（请在各试题的答题区内作答）8._____________________________________9._____________________________________10.______________________________________11.______________________________________12.______________________________________13.______________________________________14.______________________________________15.______________________________________16.______________________________________17.______________________________________计算题（共6小题，满分18分，每小题3分）（请在各试题的答题区内作答）三.18.答：20.答:21.答:22.答:四.解答题（共6小题，满分31分）（请在各试题的答题区内作答）24.答：25.答:26.答:28.答:29.答:【五年级奥数举一反三一全国通用】测评卷01《速算和巧算》试卷满分：100分考试时间：100分钟姓名：班级：得分：一.选择题（共7小题，满分21分，每小题3分）1.（2015・创新杯）计算：2.340.08：1.25=（）A.230B.23C. 2.3D.0.23【分析】根据除法的性质简算即可.【解答】解:2.34-0.084-1.25=2.3：（0.08X1.25）=2.34-0.1=23故选：B.2.（2009-华罗庚金杯）下面有四个算式：®0.6+n120=n；々赢.625=§（§）§+旦旦X4_l=142u・u.58「14214+2162755其中正确的算式是（）A.①和②B.②和④C.②和③D.①和④【分析】①循环小数加、减要根据“四舍五入”取其近似值再计算，0.6中的6不能与o.中的循环节中的1相加，答案不正确.②把分数&化成小数，用分子除以分母5^8=0.625：或把小数0.625化成分数并化简是答案正确.88③根据分数加、减法的计算法则，把异分数分母化成同分数分数再加、减，分子不变，只把分子相加、减，答案不正确.④把两个带分数化成假分数再相乘，结果再化成带分数，正确.【解答】解：®0-6+Q e133=0.733*正确；②0.625=旦正确；8③且+旦=鱼臣-=旦=>1不正确：14214+2162④3旦X4—=14—正确.755故选：B.3.(2003・创新杯)2003+2002-2001-2000+1999+1998-1997・1996+・・・+7+6-5-4+3+2-1的计算结果是()A.2002B.2003C.2004D.4005【分析】四个数一组相互抵消，2000是被4整除的，也就是说2000以后的数都可以相互抵消，因为2002：2=1001,不是偶数组，即有一组不能被抵消，最后剩下2003+2002-2001=2004.【解答】解：2003+2002-2001-2000+1999+1998-1997・1996+•••+7+6-5-4+3+2-1=2003+(2002-2001)+(-2(X)0+1999)+(1998-1997)+…+(6-5)+(-4+3)+(2-1)=2003+1-1+1+-+1-1+1=2003+1=2004故选：C.4.0.65X201=0.65X(200+1)=0.65X200+0.65运用了乘法的()A.交换律B.结合律C.分配律【分析】本题考查的是乘法运算律的运用.【解答】解：乘法分配律：(q+0)Xc=aXc+bXc所以0.65X201=0.65X(200+1)=0.65X200+0.65运用了乘法的分配律.故选：C.5.与0.456X2.1的结果相同的算式是()A. 4.56X21B.21X0.0456C.45.6X0.21D.456X0.021【分析】根据积不变的规律，其中一个因数的小数点向右(左)移动多少位，另一个因数的小数点就要向左(右)移动多少位，据此分析解答即可.【解答】解：0.456X2.1=4.56X0.21=0.0456X21=45.6X0.021=456X0.0021故选：B.6.与61.24-3.4计算结果相同的是（)A. 6.12H-0.34B.612：0.34C.0.612X0.034D.612934【分析】根据商不变的性质，被除数和除数同时乘以或除以一个数（0除外），商不变，据此分析解答即可.【解答】解：61.24-3.4=6124-34故选：D.7.105X18=100X18+5X18运用了（）A.乘法交换律B.乘法结合律C.乘法分配律【分析】本题考查的是乘法运算律的运用.【解答】解:105X18=（100+5）X18=100X18+5X18运用了乘法分配律.故选：C.二.填空题（共10小题，满分30分，每小题3分）8.（2018*其他模拟）计算：3-5+7-9+11-13+-+1995-1997+1999=1001.【分析】本题可以从后往前算.【解答】解：3-5+7-9+11-13+.......+1995-1997+1999=1999-1997+1995-1993+......+11-9+7-5+3=（1999-1997）+（1995-1993）+.......+（II-9）+（7-5）+3=2+2+2+......+2+3=2X499+3=10019.（2018*其他模拟）。

五年级奥数：速算与巧算例1：计算236×37×27分析与解答：在乘除法的计算过程中，除了常常要将因数和除数“凑整”，有时为了便于口算，还要将一些算式凑成特殊的数。

例如，可以将27变为“3×9”，将37乘3得111，这是一个特殊的数，这样就便于计算了。

236×37×27=236×（37×3×9）=236×（111×9）=236×999=236×（1000－1）=236000－236=235764例2：计算333×334＋999×222分析与解答：表面上，这道题不能用乘除法的运算定律、性质进行简便计算，但只要对数据作适当变形即可简算。

333×334＋999×222=333×334＋333×（3×222）=333×（334＋666）=333×1000=333000例3：计算20012001×2002－20022002×2001分析与解答：这道题如果直接计算，显得比较麻烦。

根据题中的数的特点，如果把20012001变形为2001×10001，把20022002变形为2002×10001，那么计算起来就非常方便。

20012001×2002－20022002×2001=2001×10001×2002－2002×10001×2001=0例4：不用笔算，请你指出下面哪个得数大。

163×167 164×166分析与解答：仔细观察可以发现，第二个算式中的两个因数分别与第一个算式中的两个因数相差1，根据这个特点，可以把题中的数据作适当变形，再利用乘法分配律，然后进行比较就方便了。

163×167 164×166=163×（166＋1） =（163＋1）×166=163×166＋163 =163×166＋166所以，163×167＜164×166例5：888…88[1993个8]×999…99[1993个9]的积是多少？分析将999…99[1993个9]变形为“100…0[1993个0]－1”，然后利用乘法分配律来进行简便计算。

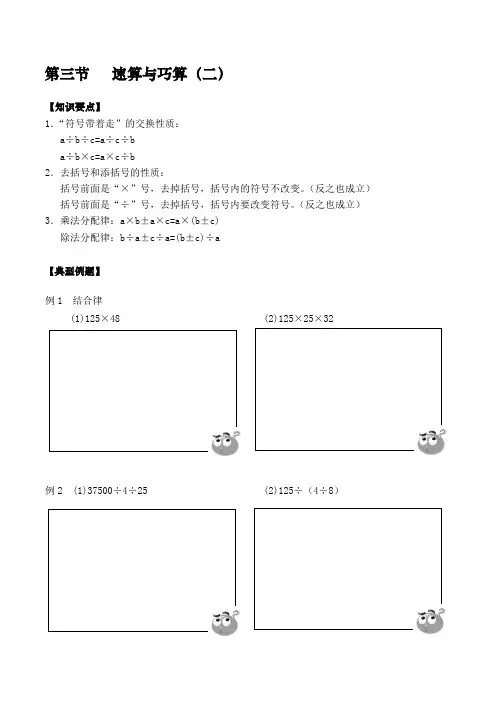
第三节速算与巧算（二）【知识要点】1．“符号带着走”的交换性质：a÷b÷c=a÷c÷ba÷b×c=a×c÷b2．去括号和添括号的性质：括号前面是“×”号，去掉括号，括号内的符号不改变。

（反之也成立）括号前面是“÷”号，去掉括号，括号内要改变符号。

（反之也成立）3．乘法分配律：a×b±a×c=a×(b±c)除法分配律：b÷a±c÷a=(b±c)÷a【典型例题】例1 结合律(1)125×48 (2)125×25×32例2 (1)37500÷4÷25 (2)125÷（4÷8）例3 (1)121×99÷（11×33）(2)46×72×23÷46÷23÷72例4 (1)33×89＋33×11 (2)2861315613÷-÷例5 (1)4421552121⨯+⨯+(2)23×666+54×333趣味题1．一副扑克牌有54张，两人轮流拿，每人每次只能拿1到4张，谁拿到最后一张牌就算输，问先拿的人怎样才能确保获胜？随堂小测1．124×25 125×5×32×5 2．91000÷125÷8 520÷（2×52）3．（48×75）÷（24×25）4444×505÷1111 4．123×456÷789÷456×789÷1235．89×10＋89×93－89×3 19×1001－19 6．2÷9＋3÷9＋4÷97．999×222＋333×334课后作业1．125×32×8 6000÷125÷8 2．37÷8＋5÷8＋6÷8－8÷8125÷（10÷8）3．（38×56）÷（19×28）4．16×80＋16×18＋16×2 99×15 5．328×93-328×31-328×426．95×98＋95×3－957．68×52－34×4割圆术数学意义：“割圆术”，则是以“圆内接正多边形的面积”，来无限逼近“圆面积”。