3一元一次方程讲义

一元一次方程复习讲义1．方程的有关概念2．等式的基本性质3．解一元一次方程的基本步骤：4.应用一元一次方程解决实际问题的一般步骤（1)审 （2）找 （3）设 （4)列 (5）解 （6）验 （7）答1．下列方程是一元一次方程的有哪些? x+2y=9 x 2－3x=111=x x x 3121=- 2x=1 3x –5 3+7=10 x 2+x=12、解下列方程:⑴ 103.02.017.07.0=--x x ⑵16110312=+-+x x⑶03433221=-+++++x x x ⑷2362132432⎪⎭⎫ ⎝⎛+--=+--x x x x x(5)｜5x 一2｜＝33、8=x 是方程a x x 2433+=- 的解，又是方程 ()[]b x b x x x +=⎥⎦⎤⎢⎣⎡---913131的解，求 b4、小张在解方程1523=-x a （x 为未知数)时，误将 - 2x 看成 2x 得到的解为3=x ，请你求出原来方程的解5、已知关于x 的方程 ()()x n x m 121232+=-+无穷多解，求m 、n1、(本题7分）按要求完成下面题目：323221+-=--x x x解:去分母，得424136+-=+-x x x ……① 即 8213+-=+-x x ……②移项，得 1823-=+-x x ……③合并同类项，得 7=-x ……④∴ 7-=x ……⑤上述解方程的过程中，是否有错误？答：__________；如果有错误，则错在__________步。

如果上述解方程有错误,请你给出正确的解题过程：2、（本题7分）请阅读下列材料:让我们来规定一种运算：bcad dc ba -=，例如：5432=2×5－3×4=10－12=－2. 按照这种运算的规定，若2121x x-=23，试用方程的知识求x 的值。

3、检修一处住宅区的自来水管,甲单独完成需要14天，乙单独完成需18天，丙单独完成需要12天。

一元一次方程的讲义-CAL-FENGHAI.-(YICAI)-Company One1乐杰数理化教师辅导讲义基础知识回顾：有理数1．一元一次方程：只含有一个未知数，并且未知数的次数是1，并且含未知数项的系数不是零的整式方程是一元一次方程.2．一元一次方程的标准形式： ax+b=0（x 是未知数，a 、b 是已知数，且a ≠0）.3．一元一次方程解法的一般步骤： 整理方程 …… 去分母 …… 去括号 …… 移项 …… 合并同类项 …… 系数化为1 …… （检验方程的解）.4．列一元一次方程解应用题：（1）读题分析法:………… 多用于“和，差，倍，分问题”仔细读题，找出表示相等关系的关键字，例如：“大，小，多，少，是，共，合，为，完成，增加，减少，配套-----”，利用这些关键字列出文字等式，并且据题意设出未知数，最后利用题目中的量与量的关系填入代数式，得到方程.5．列方程解应用题的常用公式：（1）行程问题： 距离=速度·时间 时间距离速度= 速度距离时间=； （2）工程问题： 工作量=工效·工时 工时工作量工效=工效工作量工时=； （3）比率问题： 部分=全体·比率 全体部分比率= 比率部分全体=； （4）顺逆流问题： 顺流速度=静水速度+水流速度，逆流速度=静水速度-水流速度；（5）商品价格问题： 售价=定价·折·101 ，利润=售价-成本， %100⨯-=成本成本售价利润率； （6）周长、面积、体积问题：C 圆=2πR ，S 圆=πR 2，C 长方形=2(a+b)，S 长方形=ab ， C 正方形=4a ， S 正方形=a 2，S 环形=π(R 2-r 2),V 长方体=abc ，V 正方体=a 3，V 圆柱=πR 2h ，V 圆锥=31πR 2h. 经典例题1、下列方程中，一元一次方程有几个① 2210x x --= ② 223x y -= ③ 11x --= ④120x -= 2、若关于x 的方程3x 4n －7＋5＝17是一元一次方程，求n ．3、．已知：y 1＝4x －3，y 2＝12－x ，当x 为何值时，(1)y 1＝y 2；(2)y 1与y 2互为相反数；(3)y 1比y 2小4．4、已知关于y 的方程y ＋3m ＝24与y ＋4＝1的解相同，则m 的值是( )．5、已知2232012x x +=，求代数式2466x x --+的值。

一元一次方程的应用讲义用一元一次方程解决实际问题的一般步骤（1）审：审题，分析题中已知什么、求什么，明确各数量之间的关系；（2）找：找出能够表示应用题全部含义的一个相等关系；（3）设：设未知数（一般求什么，就设什么）；（4）列：根据相等关系列出需要的代数式，从而列出方程；（5）解：解所列的方程，求出未知数的值；（6）检：检查所求解是否符合题意；（7）答：写出答案（包括单位名称）.水箱变高了长方形的周长=_________，面积=__________ ．长方体的体积=_________，正方体的体积=__________．圆的周长=___________；面积=_______________．圆柱的体积=_______________．例：把直径6cm ，长16cm的圆钢锻造成半径为4cm的圆钢，求锻造后的圆钢的长？这个问题中的等量关系是：解：设锻造后圆钢的高为x 厘米，填写下表：随堂检测：将一个底面直径是10厘米，高为36厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖”形圆柱，高变成了多少？这个问题中的等量关系是：设锻压后圆柱的高为x 厘米，填写下表：例：用一根250cm 长的铁丝恰好能围成一个长方形，且长方形的长比宽多25cm,求长方形的宽？ 等量关系：随堂练习：用一根长为60cm 的铁丝围成一个长方形，若长方形的宽是长的32，求这个长方形的长和宽？打折销售（1）进价：购进商品时的价格（有时也叫成本价）（2）售价：在销售商品时的售出价（有时称成交价，卖出价）（3）标价：在销售时标出的价（有时称原价，定价）（4）利润：在销售商品的过程中纯收入即：利润=售价－进价（5）利润率：利润占进价的百分率，即：利润率=利润÷进价×100%（6）打折：卖货时，按照标价乘以十分之几或百分之几十，则称打了几折，或理解为：销售价占标价的百分率。

例如某种服装打8 折即按标价的百分之八十出售。

龙文教育个性化辅导
学生： 陈树帆 时间： 2010 年 月 日 段
一.列方程
1.某水果店有苹果与香蕉共134千克，其中苹果的数量是香蕉的5倍，求该水果店的苹果与香蕉各有多少千克？
2.有一所监狱，安排监舍时，如果每间监舍住8人，有10个人没有床位；如果每间监舍安排住9人，就有300人没有床位，问有多少人？
3.一个数与它的一半的和是3
2，求这个数。

4.一个正方形的边长为x 厘米，周长为4y 厘米。

5.小丽3月赚工资12560元，她花掉了x 元，还剩下4500元。

6. 5
9减去x 的一半是y 。

二.解一元一次方程
(1)25(3-x )+15(3-x )=25x -15x (2)1.005(3678+x )=1.005(x 6
735-)+20.1
(3)x -2123614331
12)(+=-+x x (4) 92391627y 61⨯+⨯+=y
(5)3.5(m -1)=8.7(2-2m )-12.15(5m -5) (6)2{[4(5x -1)-8]-20}-7=1
(7)已知5:4:3::=z y x ,且3x -4y +z =-4,求式子x -3y +5z 的值。

（8）已知关于x 的方程)0(17231≠=-++x x x n 是一元一次方程，试求n 的值。

（9）讨论关于x 的方程（a -2）x =b 的值。

（10）如果关于x 的方程83)1(2=+-m x
m 是一元一次方程，球m ，n 。

第三章：一元一次方程本章板块⎪⎪⎪⎩⎪⎪⎪⎨⎧程实际问题与一元一次方方程的解解方程等式的基本性质定义一元一次方程.5.4.3.2.1 知识梳理【知识点一：方程的定义】方程：含有未知数的等式就叫做方程。

注意未知数的理解，n m x ,,等，都可以作为未知数。

题型：判断给出的代数式、等式是否为方程 方法：定义法例1、判定下列式子中，哪些是方程？（1）4=+y x （2）2>x （3）642=+（4）92=x （5）211=x【知识点二：一元一次方程的定义】一元一次方程：①只含有一个未知数(元)；②并且未知数的次数都是1(次)；③这样的整式方程叫做一元一次方程。

题型一：判断给出的代数式、等式是否为一元一次方程 方法：定义法例2、判定下列哪些是一元一次方程？0)(22=+-x x x ，712=+x π，0=x ，1=+y x ，31=+xx ，x x 3+，3=a题型二：形如一元一次方程，求参数的值方法：2x 的系数为0；x 的次数等于1；x 的系数不能为0。

例3、如果()051=+-mx m 是关于x 的一元一次方程，求m 的值例4、若方程()05122=+--ax x a 是关于x 的一元一次方程，求a 的值【知识点三：等式的基本性质】等式的性质1：等式两边都加上(或减去)同个数(或式子)，结果仍相等。

即：若a=b ，则a ±c=b ±c等式的性质2：等式两边同时乘以同一个数，或除以同一个不为0的数，结果仍相等。

即：若b a =，则bc ac =；若b a =，0≠c 且cb c a = 例5、运用等式性质进行的变形，不正确的是（ ）A 、如果a=b ，那么a-c=b-cB 、如果a=b ，那么a+c=b+cC 、如果a=b ，那么cbc a = D 、如果a=b ，那么ac=bc 【知识点四：解方程】方程的一般式是：()00≠=+a b ax 题型一：不含参数，求一元一次方程的解 方法：步骤具体做法 依据 注意事项1.去分母在方程两边都乘以各分母的最小公倍数等式基本性质2防止漏乘（尤其整数项），注意添括号； 2.去括号先去小括号，再去中括号，最后去大括号 去括号法则、分配律括号前面是“+”号，括号可以直接去，括号前面是“-”号，括号里的每一项都要变号3.移项把含有未知数的项都移到方程的一边，其他项都移到方程的另一边(移项一定要变号)等式基本性质1 移项要变号，不移不变号；4.合并同类项将方程化简成()0≠=a b ax合并同类项法则计算要仔细5.化系数为1 方程两边同时除以未知数的系数a ，得到方程的解 等式基本性质2 计算要仔细，分子分母勿颠倒例7、解方程2583243=--+x x练习1、()()()35123452+--=-+-x x x x练习2、14.01.05.06.01.02.0=+--x x 练习3、x =+⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+221413223题型二：解方程的题中，有相同的含x 的代数式方法：利用整体思想解方程，将相同的代数式用另一个字母来表示，从而先将方程化简，并求值。

第三章一元一次方程复习讲义知识点1．等式：用“=”号连接而成的式子叫等式.2．等式的性质：等式性质1：等式两边都加上(或减去)同一个数或同一个整式，所得结果仍是等式；等式性质2：等式两边都乘以(或除以)同一个不为零的数，所得结果仍是等式.例1(1)怎样从等式x-5=y-5得到等式x=y?(2)怎样从等式3+x=1得到等式x=-2?(3)怎样从等式4x=12得到等式x=3?例2利用等式的性质解下列方程：(1)x+7=26(2)-5x=203．方程：只含有一个未知数，未知数的次数是1，等号两边都是整式，这样的方程叫做一元一次方程.4．方程的解：使等式左右两边相等的未知数的值叫方程的解；注意：“方程的解就能代入”！5．移项：改变符号后，把方程的项从一边移到另一边叫移项.移项的依据是等式性质1. 6．一元一次方程：只含有一个未知数，并且未知数的次数是1，并且含未知数项的系数不是零的整式方程是一元一次方程.7.一元一次方程的标准形式：ax+b=0(x是未知数，a、匕是已知数，且aW0).8．一元一次方程解法的一般步骤：化简方程分数基本性质去分母同乘(不漏乘)最简公分母去括号先去小括号,再去中括号,最后去大括号.依据是去括号法则和乘法分配律，注意符号变化移项把含有未知数的项移到一边,常数项移到另一边.“过桥变号”，依据是等式性质一合并同类项将未知数的系数相加，常数项相加.依据是乘法分配律合并后注意符号系数化为1在方程的两边除以未知数的系数.依据是等式性质二.例1解下列方程[1]用合并同类项的方法解一元一次方程(1)2x-£%=6-8;(2)7x—2.5x+3x-1.5x=-15x4—6x3.[2]用移项的方法解一元一次方程(1)7-2x=3-4x(2)4x+10=6x[3]利用去括号解一元一次方程去括号法则：去掉“+()”，括号内各项的符号不变.去掉“-()”，括号内各项的符号改变.用三个字母a、b、c表示去括号前后的变化规律：a+(b+c)=a+b+ca-(b+c)=a—b—c(1)2x-(x+10)=5x+2(x—1)(2)3x—7(x—1)=3—2(x+3)[4]利用去分母解一元一次方程(总结：像上面这样的方程中有些系数是分数，如果能化去分母，把系数化为整数，则可以使解方程中的计算更方便些.)2x+2x+7x+x=33(2)3x+x-1=3-2x-1(1)^要点归纳1.去分母时，应在方程的左右两边乘以分母的最小公倍数；2.去分母的依据是等式性质2，去分母时不能漏乘没有分母的项；3.去分母与去括号这两步分开写，不要跳步，防止忘记变号.10．列一元一次方程解应用题：(1)读题分析法:多用于“和，差，倍，分问题”仔细读题，找出表示相等关系的关键字，例如：“大，小，多，少，是，共，合，为，完成，增加，减少，配套”，利用这些关键字列出文字等式，并且据题意设出 未知数，最后利用题目中的量与量的关系填入代数式，得到方程.（2）画图分析法:…………多用于“行程问题”利用图形分析数学问题是数形结合思想在数学中的体现，仔细读题，依照题意画出有关图形，使图形各部分具有特定的含义，通过图形找相等关系是解决问题的关键，从而取得列方程的依据，最后利用量与量之间的关系（可把未知数看做已知量），填入有关的代数式是获得方程的基础.11.列方程（组）的应用题的一般步骤：审：审清题意，分清题中的已知量、未知量．设：设未知数，设其中某个未知量为x.列：根据题意寻找等量关系列方程．解：解方程．验：检验方程的解是否符合题意．答：写出答案（包括单位）．［注意］审题是基础，找等量关系是关键.11．解实际应用题：知识点1:市场经，^、打折销售问题（1）商品利润=商品售价一商品成本价（3）商品销售额=商品销售价X 商品销售量（4）商品的销售利润=（销售价一成本价）X 销售量例1一商店在某一时间以每件60元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，卖这两件衣服总的是盈利还是亏损，或是不盈不亏?变式1.某琴行同时卖出两台钢琴，每台售价为960元.其中一台盈利20%，另一台亏损20%.这次琴行是盈利还是亏损，或是不盈不亏？例2一件服装先将进价提高25%出售，后进行促销活动，又按标价的8折出售,此时售价为60元.请问商家是盈是亏，还是不盈不亏？例3.某商品的进价是1000元，售价是1500元，由于销售情况不好，商店决定降价出 售，但又要保证利润率不低于5%,那么商店最多可打几折出售此商品？（2） 商品利润率= 商品利润 商品成本价X 100%例4.某商场国庆节搞促销活动，购物不超过200元不给优惠，超过200元但不超过500元的优惠10%，超过500元，其中500元按9折优惠，超过的部分按8折优惠。

第四类：调配（分配）与比例问题 调配与比例问题在日常生活中十分常见，比如合理安排工人生产，按比例选取工程材料，调剂人数或货物等。

调配问题中关键是要认识清楚部分量、总量以及两者之间的关系。

在调配问题中主要考虑“总量不变”；而在比例问题中则主要考虑总量与部分量之间的关系，或是量与量之间的比例关系。

（第一类）：调配问题：这类问题的关键是找对分配的两类物体的数量关系【例1】某车间有16名工人，每人每天可加工甲种零件5个或乙种零件4个．在这16名工人中，一部分人加工甲种零件，其余的加工乙种零件．•已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元．若此车间一共获利1440元，•求这一天有几个工人加工甲种零件．解：设这一天有x 名工人加工甲种零件，则这天加工甲种零件有5x 个，乙种零件有4（16-x ）个．根据题意，得16×5x+24×4（16-x ）=1440 解得x=6、 有两个工程队，甲工程队有32人，乙工程队有28人，如果是甲工程队的人数是工程队人数的2倍，需从乙工程队抽调多少人到甲工程队？2、某班同学利用假期参加夏令营活动，分成几个小组，若每组7人还余1人，若每组8人还缺6人，问该班分成几个小组，共有多少名同学？3、一堆玩具分给若干个小朋友，若每人分3件，则剩余4件，若前面每人分4件，则最后一人得到的玩具最多3件，问小朋友的人数至少有多少人？。

（第二类）：比例分配问题比例分配问题的一般思路为：设其中一份为x ，利用已知的比，写出相应的代数式。

常用等量关系：各部分之和=总量地板砖厂的坯料由白土、沙土、石膏、水按25∶2∶1∶6的比例配制搅拌而成。

现已将前三种料称好，共5600千克，应加多少千克的水搅拌？前三种料各称了多少千克？分析：解决比例问题的一般方法是：按比例设未知数，并根据题设中的相等关系列出方程进行求解。

本题中，由四种坯料比例25∶2∶1∶6，设四种坯料分别为25x 、2x 、x 、6x 千克，由前三种坯料共5600千克，有 25x+2x+x=5600 解得：x=200 ∴ 6x=12001500台，已知A 、B 、C 三种型号的洗衣机的数量比是2：3：5，则三种型号的洗衣机各生产多少台？初中数学基础知识讲义—一元一次方程各类题型解法分析： （三）（第三类）：配套问题：这类问题的关键是找对配套的两类物体的数量关系：某车间22名工人参加生产一种螺母和螺丝。

一元一次方程的解法一、知识梳理1．只含有一个未知数，并且未知数的次数是1，系数不等于0的一类方程叫做一元一次方程．（一个未知数，最高次数为1，整式方程）23．一元一次方程的标准形式ax+b=0（其中x 是未知数，a 、b 是已知数，并且a≠0） 4．等式的基本性质及用等式的性质解方程。

性质1：m b m a b a ±=±=,性质2：)0(;,≠=⋅=⋅=d dbd a m b m a b a 性质3：a b b a ==,性质4：)(,,传递性则c a c b b a ===（性质是解题的依据，在使用时注意等式性质成立的条件） 5搬硬套．为了检验解方程时的计算有没有错误，可以把求得的解代入原方程，看左、右两边的值是否相等，这叫验根，一元一次方程的验根过程可以不写出来． 6．一元一次方程的基本变形与它的解法（1）变形：同加、同减、同乘、同除（不为0），解不变。

（2）步骤：去分母; (2)去括号; (3)移项; (4)合并同类项; (5)系数化为1.（3）注意：过“桥”变号 7.方程ax=b 的解的讨论1）当a ≠0时，方程ax=b 有惟一解x=ba(此时方程为一元一次方程，ax=b(a ≠0))是一元一次方程的最简形式.2）当a=0,b ≠0时，方程ax=b 无解(此方程不是一元一次方程).3）当a=0,b=0时，方程ax=b 有无穷多解(此方程不是一元一次方程).二、典例剖析（一）概念问题 例1：（武汉二中模拟）下列方程中是一元一次方程的是（ ）。

A.3+7=10 B.2x-5 C.-x+3=1 D.2x+7y=0 变式1：下列各式中，是方程的个数为（ ）。

（1）－3－3＝－7 （2）3x －5＝2x ＋1 （3）2x ＋6 （4）x －y ＝0 （5）a ＋b>3 （6）a 2＋a －6＝0A ．1个B ．2个C ．3个D ．4个变式2：下列说法中，正确的是。

（ ）A 、 代数式是方程B 、方程是代数式C 、等式是方程D 、方程是等式变式3：若2x 3-2k+2k=41是关于x 的一元一次方程，则k= （二）分母化整问题 例2：（1）解方程：43160.20.5x x +--=- （2）解方程：431625x x +--=-变式训练： 1.511241263x x x +--=+x x 238)4121(3443.2=⎥⎦⎤⎢⎣⎡--3.x 41-132x 43=+ 4.[1－2x+（3x －5）]=x（三）方程的解问题例3：若x=0是方程2002x-a=2003x+3的解，那么代数式的值是-a 2+2变式1：已知关于x 的方程23()2,ax a x x a -=+=的解是求的值. 变式2：已知5x 61y ,1x 32y 21-=+-=,若12y +y 20=,则x=( ) A.-30 B.-48 C.48 D.301212（四）同解问题例4：如果方程6x+3a=22与方程3x+5=11的解相同，那么a=（ ）A. 103B. 310C. -103D.- 310 变式1：与方程3523=-x 的解相同的方程是（ ）A 、163=xB 、133=xC 、83=xD 、43=x变式2：已知关于x 的方程3[x-2（x-3a ）]=4x 和123a x +-851x-=1有相同的解，求这个解。

《一元一次方程》讲义一、什么是一元一次方程在数学的世界里，方程就像是一座神秘的桥梁，连接着已知和未知。

而一元一次方程，则是这座桥梁中较为基础和常见的一种。

一元一次方程，简单来说，就是指含有一个未知数，并且未知数的最高次数是 1 的整式方程。

我们可以用一个通用的形式来表示一元一次方程：ax ＋ b ＝ 0 （其中a ≠ 0 ）。

这里的“x”就是我们要寻找的未知数，“a”是未知数的系数，“b”则是常数项。

比如说，3x ＋ 5 ＝ 14 就是一个一元一次方程。

在这个方程中，未知数是 x ，系数是 3 ，常数项是 5 和 14 。

二、一元一次方程的求解接下来，让我们一起来探索如何求解一元一次方程。

求解一元一次方程的基本思路就是通过一系列的运算，将方程变形，最终求出未知数的值。

以方程 2x ＋ 7 ＝ 15 为例，我们的目标是让 x 单独在等号的一边。

首先，我们要把常数项 7 移到等号的右边，这时候要注意，移项时要变号，所以得到 2x ＝ 15 7 ，即 2x ＝ 8 。

然后，将方程两边同时除以系数 2 ，得到 x ＝ 4 。

再来看一个稍微复杂一点的方程，比如 5(x 3) ＋ 2 ＝ 17 。

第一步，先把括号展开，得到 5x 15 ＋ 2 ＝ 17 。

接着，合并同类项，5x 13 ＝ 17 。

然后，把－13 移到等号右边，5x ＝ 17 ＋ 13 ，即 5x ＝ 30 。

最后，两边同时除以 5 ，解得 x ＝ 6 。

三、一元一次方程的应用一元一次方程在我们的日常生活中有着广泛的应用。

比如，购物时计算折扣和价格。

假设一件商品原价为 x 元，打 8 折后的价格是 160 元，那么可以列出方程 08x ＝ 160 ，解得 x ＝ 200 ，就知道这件商品的原价是 200 元。

再比如，行程问题。

如果一辆汽车以每小时 60 千米的速度行驶，行驶了 x 小时后，总共行驶了 300 千米，那么可以列出方程 60x ＝300 ，解得 x ＝ 5 ，也就是这辆汽车行驶了 5 小时。

第三章一元一次方程本章小结小结1 本章内容概览本章的主要内容包括：一元一次方程及其相关的概念，一元一次方程的解法，利用一元一次方程分析与解决实际问题．其课标要求是：了解一元一次方程及其相关的概念和性质，掌握一元一次方程的解法和一般步骤，初步认识方程与现实生活的联系，建立列方程解决实际问题的数学模型，感受方程的应用价值，提高分析问题、解决问题的能力．小结2 本章重点、难点：本章重点是一元一次方程的解法和列一元一次方程解应用题．难点是根据具体问题中的数量关系列一元一次方程．小结3 本章学法点津1．学好本章的关键在于正确理解方程及方程的解的概念和等式的两个性质，了解算术和代数的主导思想的区别及找准问题中的等量关系．2．在学习本章时，要深刻理解方程的思想，即未知量可以和已知量一起表示数量关系，找到数量之间的等量关系就可列方程，即建立数学模型．“建模思想”和解方程中蕴涵的“化归思想”是本章渗透的主要数学思想．另外，要加强练习，巩固好基础知识和基本技能．因为一元一次方程是最基本的代数方程，学好它对于后续学习(其他的方程以及不等式、函数等)具有重要的作用．知识网络结构图重点题型总结及应用题型一 灵活解一元一次方程解一元一次方程的一般步骤是：(1)去分母；(2)去括号；(3)移项；(4)合并同类项；(5)把系数化为1．根据方程的特点，可灵活运用五个步骤，以简化运算． 例1 解方程：1121(1)3232x x x ⎡⎤⎛⎫--=- ⎪⎢⎥⎣⎦⎝⎭．分析：此题中括号外的系数是分数，小括号外的系数也是分数，这种类型的方程解法比较灵活，可以先去括号，再去分母；也可以先去分母，再去括号． 解法1：去中括号，得()112113632x x x ⎛⎫--=- ⎪⎝⎭． 去小括号，得1112136633x x x -+=-． 去分母，得2x － x ＋1=4 x －2．移项，得2 x － x －4 x ＝－2－1．合并同类项，得－3 x ＝－3．系数化为1，得x ＝1． 解法2：方程两边同乘6，得112(1)422x x x ⎡⎤⎛⎫--=- ⎪⎢⎥⎣⎦⎝⎭． 去中括号，得2x －(x －1)=4(x －12)．去小括号，得2x － x ＋1=4 x －2． 移项，得2 x － x －4 x =－2－1．合并同类项，得－3 x ＝－3．系数化为1，得x ＝1． 点拨若方程中合有多层括号，则应按照分配律先由内向外(或由外向内)去括号，再去分母，但也有时先去分母，再去括号会更简便，这取决于所给方程的特点，因此解方程时，应灵活地选取方法，尽量使过程简单，而又不产生错误. 例2 解方程：21101136x x ++-=． 分析：本题按照常规的解方程的步骤，应先去分母，但考虑本题特点，可把213x +拆成2133x +，把1016x +-拆成10166x --来解．解：原方程可写成2133x +10166x --=1.约分，移项，得25111.3336x x -=-+合并同类项，得－x ＝56.系数化为1，得x ＝－56.评注本题采用的是“拆项法”，此方法比常规方法简便，但这种方法不是对所有的一元一次方程都适用，需要根据方程的特点灵活应用．题型二 方程的解的应用例3 关于x 的方程2x －4＝3m 和x ＋2＝m 有相同的解，则m 的值是( )A．10 B．－8 C．－10 D．8解析：解方程2x－4=3m，得x=342m+．解方程x＋2＝m，得x＝m－2．由两方程解相同，得342m+＝m－2，解得m＝－8．答案：B例4 已知y＝3是6＋14(m－y)＝2y的解，那么关于x的方程2m(x－1)＝(m＋1)(3x－4)的解是多少?分析：把y＝3代入第一个方程，使这个方程转化为关于m的方程，解出m的值，再代入第二个方程，求出x的值．解：y＝3代入方程6＋14(m－y)＝2y，得6＋14(m－3)＝6．解得m＝3．将m＝3代入2m(x－1)＝(m＋1)(3x－4)，得2×3(x－1)＝(3＋1)(3x－4)．解得x＝53.方法先利用第一个方程求出字母m的值，再把m值代入第二个方程解第二个方程，培养思考问题的综合能力．题型三一元一次方程的应用例5一通讯员骑摩托车需要在规定时间，把文件送到某地，若每小时走60千米，就早到12分钟；若每小时走50千米，则要迟到7分钟，求路程．分析：如果设规定时间为x小时，当每小时走60千米时，则路程为601260x⎛⎫-⎪⎝⎭千米；当每小时走50千米时，则路程为50760x⎛⎫+⎪⎝⎭千米．这时可用路程相等列出方程．解：设规定时间为x小时，根据题意，得601260x⎛⎫-⎪⎝⎭=50760x⎛⎫+⎪⎝⎭．解得10760x=．所以路程为61260x⎛⎫-⎪⎝⎭=60×107126060⎛⎫-⎪⎝⎭＝95千米．答：路程为95千米．例6某校校长暑假将带领该校市级“三好学生”去北京旅游，甲旅行社说：“如果校长买全票一张，则其余学生可享受半价优惠”．乙旅行社说：“包括校长在内全部按全票价的六折优惠”，若全票价为240元，(1)设学生数为x，甲旅行社收费为y甲，乙旅行社收费为y乙，分别计算两家旅行社的收费(建立表达式)；(2)当学生数是多少时，两家旅行社的收费一样?分析：(1)问分别用含x的式子表示y甲、y乙. (2)问是当y甲=y乙时求x.解：(1)因为全票价为240元，所以半票价为120元，这样甲旅行社收费为y甲＝120x＋240．又因为全票价为240元，所以全票价的60％为240×60100=144(元)，这样乙旅行社收费为y乙＝144x＋144．(2)因为甲旅行社收费为y甲，乙旅行社收费为y乙，所以当两家旅行社收费一样时，即有方程120x＋240＝144x＋144．解这个方程，得x＝4．答：当学生数为4时，两家旅行社收费一样．例7某商场将彩电先按原价提高40％，然后在广告中写上“大酬宾，八折优惠”，结果每台彩电比原价多赚了270元，那么每台彩电原价是多少元?分析：假设每台彩电原价是x元，则提高40％后为(1＋40％) x元，八折为(1＋40％) x·80％元，也就是现售价为(1＋40％) x·80％元．解：设每台彩电原价是x元，根据售价与原价之差等于270，列方程得x (1＋40％)·80％－x＝270，解得x＝2 250．答：每台彩电原价是2 250元．例8某中学租用两辆汽车(设速度相同)同时送1名带队老师及7名九年级的学生到县城参加数学竞赛，每辆限坐4人(不包括司机)．其中一辆小汽车在距离考场15千米的地方出现故障，此时离截止进考场的时间还有42分，这时唯一可利用的交通工具是另一辆小汽车，且这辆车的平均速度是60千米／时，人步行的速度是5千米／时(上、下车时间忽略不计)．(1)若小汽车送4人到达考场，然后再回到出故障处接其他人，请你通过计算说明他们能否在截止进考场的时间前到达考场；(2)假如你是带队的老师，请你设计一种运送方案，使他们能在截止进考场的时间前到达考场，并通过计算说明方案的可行性．分析：本题是一道开放性的方案设计问题，解答时应注意分各种情况进行讨论．解：(1)1560×3=34(时)=45(分)．因为45＞42，所以不能在限定时间内到达考场．(2)方案：先将4人用车送到考场，另外4人同时步行前往考场，汽车到考场后返回到与另外4人的相遇处再载他们到考场．先将4人用车送到考场所需时间为1560＝14(时)＝15(分)．14时另外4人步行了1．25千米，此时他们与考场的距离为15－1．25＝13．75(千米)．设汽车返回t(时)后与步行的4人相遇，则有5t＋60t=13．75，解得t=2.75 13．汽车由相遇点再去考场所需时间也是2.7513小时．所以用这一方案送这8人到考场共需15＋2×2.7513×60≈40．4(分)＜42(分)．所以这8个人能在截止进考场的时间前赶到．题型四图表类应用题例9(1)七年级(1)班43人参加运土劳动，共有30根扁担，要安排多少人抬土，多少人挑土，可使扁担和人数相配不多不少?若设有x人挑土，填写下表：挑土抬土人数／人扁担／根即可知两个等量关系：挑土人数＋抬土人数＝43人，挑土用扁担数＋抬土用扁担数＝30根．根据等量关系，列方程，解得x＝，因此挑土人数为，抬土人数为．你能用其他方法计算这道题吗?(2)如果参加劳动的人数不变，扁担数为20根可以吗?为什么?分析：有x人挑土，则用扁担x根，剩余的(43－x)人抬土，需用扁担数为12(43－x)根，可列方程为x＋12(43－x)＝30，解得x＝17，即有挑土人数为17，抬土人数为43－17=26．还可以利用“挑土人数＋抬土人数＝43人”列方程．解：(1)列表如下：挑土抬土人数／人x 43－x扁担／根x 12(43－x)x＋12(43－x)=30；17；17；26．能．设挑土用x根扁担，则抬土用(30－x)根扁担，挑土用x人，抬土用2(30－x)人．根据题意，得x＋2(30－x)＝43．解得x =17．因此，挑土人数为17，抬土人数为2(30－17)＝26．(2)不可以，因为若20根扁担用于挑土，则需20人＜43人；若20根扁担用于抬土，则需40人＜43人，因此，人员有剩余．所以参加劳动的人数不变，扁担数为20根不可以．点拨此题关键是如何利用人数与扁担数的关系列方程．由生活常识可知，挑土1人用l根扁担，抬土2人用l根扁担．例10下面是甲商场电脑产品的进货单，其中进价一栏被墨水污染，读了进货单后，请你求出这台电脑的进价．甲商场商品进货单供货单位乙单位品名P4200商品代码DN—63DT商品所属电脑专柜标价 5 850元折扣八折利润210元分析：本题应先读懂图表所提供的信息，明确题目的条件和所求，此题等量关系为：售价－进价=利润．解：设这台电脑的进价为x元．根据题意，得5 850×0．8－x＝210．解得x＝4 470．答：这台电脑的进价为4 470元．注意商品打八折后的售价等于标价×0．8．思想方法归纳方程体现了数学建模思想，主要培养同学们的运算能力、观察能力和灵活运用所学知识解决实际问题的能力，体会数学的价值．主要解题思想方法如下：1．转化思想本部分内容在转化思想上的主要体现是利用方程的概念求代数式的值、巧解方程等．例1已知方程3x2－9x＋m＝0的一个解是1，则m的值为．分析：根据方程解的定义，把方程的解x＝1代入方程成立，然后解关于m的方程即可．解：把x=1代入原方程，得3×12－9×1＋m＝0，解得m=6．答案：6方法解题依据是方程的定义，解题方法是把方程的解代入原方程，转化为关于待定系数的方程．例2 如果4x2＋3x－5＝kx2－20x＋20k是关于x的一元一次方程，那么k= ，方程的解是．解析：要判断一个方程是不是一元一次方程，首先应先化为最简形式，原方程化为一般形式得(4－k) x2＋23 x－5－20 k＝0．由一元一次方程的定义知4－x＝0，解得k＝4．把k＝4代入方程得23 x－85＝0，解得x＝8523．答案：4；x＝8523技巧判断一个方程是不是一元一次方程，应先化为最简形式，再根据一元一次方程的定义来判断．2．方程思想本部分内容方程思想的体现主要是列方程解决实际问题．解决问题的关键是分析题意，找出题目中的相等关系，列出一元一次方程，解出方程，得出答案．例3某中学甲、乙两班学生在开学时共有90人，如果从甲班转入乙班4人，结果甲班的学生人数是乙班的80％，问开学时两班各有学生多少人?解：设开学时甲班有x人，则乙班有(90－x)人，根据题意，得x－4=(90－x＋4)×80％，5x－20＝360－4x＋16，即x＝44，90－x＝46．答：开学时甲班有44人，乙班有46人．点拨调配问题是：一方增多，另一方要减少，注意变化前后的关系是列方程的关键．例4如图3－5－1所示，在水平桌面上有甲、乙两个内部呈圆柱形的容器，内部底面积分别为80 cm2、100 cm2，且甲容器装满水，乙容器是空的．若将甲中的水全部倒入乙中，则乙中的水位高度比原先甲的水位高度低了8 cm，则甲的容积为( )A．1 280 cm3B．2 560 cm3C．3 200 cm3D．4 000 cm3解析：设甲容器的高度为x cm，则乙容器中水的高度为(x－8)cm．根据两容器中水的体积不变可得80x=100(x－8)．解得x＝40．所以甲容器的容积为80×40＝3 200(cm3)．故选C．答案：C点拨在等积问题中，物体的形状改变了，但体积不变，根据体积相等列方程求解．中考热点聚焦考点1 一元一次方程的解考点突破：在中考中对一元一次方程的解的考查，一般以填空题的形式出现．已知一元一次方程的解，求未知字母的值．解决此类问题的思路是：将解代入一元一次方程，转化成关于未知字母的方程，从而求解．例1 (2010·江苏宿迁中考)已知5是关于x 的方程3x －2a ＝7的解，则a 的值为 ． 解析：因为5是关于x 的方程3x －2a ＝7的解，所以3× 5－2a ＝7．所以a ＝4． 答案：4例2 (20l0·湖南怀化中考)已知关于x 的方程3x －2m ＝4的解是x ＝m ，则m 的值是 ．解析：把x ＝m 代入3x －2m ＝4，得3m －2m ＝4，所以m ＝4． 答案：4 考点2 解一元一次方程考点突破：一元一次方程是初中数学方程与方程组的基础，是中考命题的重点，解一元一次方程一般难度不大，只要牢记解一元一次方程的步骤，就能求出正确的解． 例3 (2010·福建泉州中考)方程2x ＋8＝0的解是 ．解析：由2x ＋8＝0，2x ＝－8，得x ＝－4． 答案：x ＝－4 考点3 一元一次方程的应用考点突破：一元一次方程在生活中应用广泛，一元一次方程的应用在中考中时常出现，解一元一次方程的应用题，要明确已知量与未知量，找出题目中的相等关系，就能列出元一次方程，进而求解． 一、选择题1. （2011山东日照，4，3分）某道路一侧原有路灯106盏，相邻两盏灯的距离为36米，现计划全部更换为新型的节能灯，且相邻两盏灯的距离变为70米，则需更换的新型节能灯有（ ） A ．54盏 B ．55盏 C ．56盏 D ．57盏 考点：一元一次方程的应用。

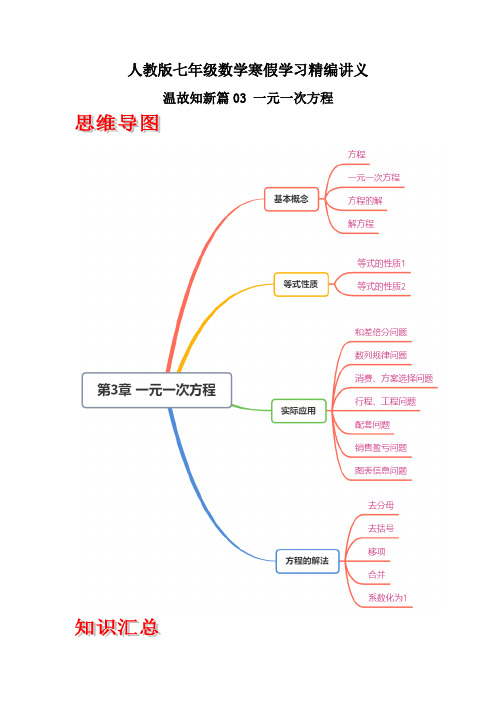
人教版七年级数学寒假学习精编讲义温故知新篇03 一元一次方程知识点1：方程的有关概念1．定义：含有的等式叫做方程.细节剖析：判断一个式子是不是方程，只需看两点：一.是；二.是含有．2．方程的解：使方程左右两边的值的未知数的值，叫做方程的解.细节剖析：判断一个数（或一组数）是否是某方程的解，只需看两点：①.它（或它们）是方程中的值；②将它（或它们）分别代入方程的和，若左边右边，则它们是方程的，否则不是．3．解方程：求方程的的过程叫做解方程.4．方程的两个特征：（1）.方程是；（2）.方程中必须含有（或）. 知识点2:一元一次方程的有关概念定义：只含有一个（元），并且未知数的次数都是，这样的方程叫做一元一次方程.要点诠释：“元”是指，“次”是指未知数的，一元一次方程满足条件：①首先是一个 ;②其次是必须只含有一个 ;③未知数的指数是 ;④分母中不含有．知识点3：等式的性质1．等式的概念：用符号“=”来表示的式子叫做等式.2．等式的性质：等式的性质1：等式两边加（或减）同一个数（或式子），结果仍 .即：如果，那么 (c为一个数或一个式子) .等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍 .即：如果，那么；如果，那么.细节剖析：（1）根据等式的两条性质，对等式进行，等式两边必须同时进行完全的变形；(2) 等式性质1中，强调的是整式，如果在等式两边同加的不是整式，那么变形后的等式不一定成立，如x＝0中，两边加上得x＋，这个等式 ;(3) 等式的性质2中等式两边都除以时，这个除数不能为．知识点4：解一元一次方程的一般步骤变形名称 具体做法 注意事项去分母 在方程两边都乘以各分母的 (1)不要漏乘不含 的项(2)分子是一个 的，去分母后应加上去括号 先去 ，再去 ，最后去 (1)不要漏乘括号里的项 (2)不要弄错移项 把含有 的项都移到方程的一边，其他项都移到方程的另一边(记住移项要 )(1)移项要(2)不要丢 合并同类项把方程化成 (a ≠0)的形式 字母及其 不变 系数化成1 在方程两边都除以未知数的系数 ，得到方程的解b x a =． 不要把 、 写颠倒细节剖析：（1）解方程时，表中有些变形步骤可能用不到，而且也不一定要按照自上而下的顺序，有些步骤可以合并简化．(2) 去括号一般按由内向外的顺序进行，也可以根据方程的特点按由外向内的顺序进行.（3）当方程中含有 或 形式的分母时，一般先利用分数的性质将分母变为 后再去 ，注意去分母的依据是等式的性质，而分母化整的依据是分数的性质，两者不要混淆．知识点5：解特殊的一元一次方程1.含绝对值的一元一次方程解此类方程关键要把绝对值化去，使之成为一般的一元一次方程，化去 的依据是绝对值的意义．细节剖析： 此类问题一般先把方程化为ax b c +=的形式，再分类讨论：(1)当0c <时， ；（2）当0c =时，原方程化为：0ax b +=；（3）当0c >时，原方程可化为：ax b c +=或ax b c +=-.2.含字母的一元一次方程此类方程一般先化为最简形式 再分三种情况分类讨论：（1）当a ≠0时， ；（2）当a ＝0，b ＝0时，x 为任意 ；（3）当a ＝0，b ≠0时，方程 ．知识点6：用一元一次方程解决实际问题的一般步骤列方程解应用题的基本思路为：问题−−−→分析抽象方程−−−→求解检验解答．由此可得解决此类 题的一般步骤为：审、设、列、解、检验、答．细节剖析：（1）“审”是指读懂题目，弄清题意，明确哪些是已知量，哪些是未知量，以及它们之间的关系，寻找等量关系；（2）“设”就是设未知数，一般求什么就设什么为x ，但有时也可以间接设未知数；（3）“列”就是列方程，即列代数式表示相等关系中的各个量，列出方程，同时注意方程两边是同一类量，单位要统一；（4）“解”就是解方程，求出 的值；（5）“检验”就是指检验方程的解是否符合实际意义，当有不符合的解时，及时指出，舍去即可；（6）“答”就是写出 ，注意单位要写清楚．知识点7：常见列方程解应用题的几种类型1．和、差、倍、分问题（1）基本量及关系：增长量＝原有量× ，现有量＝原有量+ ，现有量＝ -降低量．（2）寻找相等关系：抓住关键词列方程，常见的关键词有：多、少、和、差、不足、剩余以及倍，增长率等．2．行程问题（1）三个基本量间的关系： 路程=速度×（2）基本类型有：①相遇问题（或相向问题）：Ⅰ．基本量及关系：相遇路程=速度和×Ⅱ．寻找相等关系：甲走的路程+ ＝两地距离．②追及问题：Ⅰ．基本量及关系：追及路程=速度差×Ⅱ．寻找相等关系：第一， 同地不同时出发：前者走的路程＝第二， 第二，同时不同地出发：前者走的路程+ ＝追者走的路程．③航行问题：Ⅰ．基本量及关系：顺流速度=静水速度+ ，逆流速度=静水速度－顺水速度－逆水速度＝2×Ⅱ．寻找相等关系：抓住两地之间距离不变、水流速度不变、船在静水中的速度不变来考虑．（3）解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系，并且还常常借助画草图来分析．3．工程问题如果题目没有明确指明总工作量，一般把总工作量设为1．基本关系式：（1）总工作量=工作效率×（2）总工作量=4．调配问题寻找关系的方法：抓住调配后甲处的数量与乙处的数量间的关系去考虑．5．存贷款问题（1）利息=本金××期数（2）本息和（本利和）＝本金＋＝本金＋本金××期数＝本金×（3）实得利息=利息-（4）利息税=利息×（5）年利率＝×121（6）月利率＝×126.数字问题已知各数位上的数字，写出两位数，三位数等这类问题一般设间接未知数，例如：若一个两位数的个位数字为a，十位数字为b，则这个两位数可以表示为7．方案问题选择设计方案的一般步骤：（1）运用一元一次方程解应用题的方法求解两种方案值相等的情况．（2）用特殊值试探法选择方案，取小于（或大于）一元一次方程解的值，比较两种方案的优劣性后下结论．一．选择题1．（2021秋•黔西南州期末）小亮和家人计划元旦节报团去贞丰县城境内的“圣母峰”游玩，由于节假日旅游旺季，酒店房源紧张，只有混合民宿（一人一个床位）可以选择：若每间房住4人，则有8人无法入住；若每间房住5人，则有一间房空了3个床位．设小亮所在旅游团共有x人，则可列方程为（）A．B．C．D．4x+8＝5x﹣3 2．（2021秋•南岗区校级月考）下列说法：①小明小时走了2千米，小红小时走了千米，所以小明走得快些；②两个分数相除，商一定大于被除数；③用一根长120cm的铁丝围成一个长方形，长和宽的比是7：5，则长是35cm；④一头大象重3000千克，一个橙子重300克，所以大象与橙子质量比是10：1．其中正确的个数是（）A．1 B．2 C．3 D．43．（2021秋•澧县期中）根据等式的性质，下列变形中正确的为（）A．若x2＝5x，则x＝5 B．若，则ax＝ayC．若a2x＝a2y，则x＝y D．若，则k＝﹣124．（2021秋•澧县期中）若方程（m﹣3）x＝1是关于x的一元一次方程，则m的值是（）A．m≠﹣3 B．m≠0 C．m≠3 D．m＞35．（2021秋•富裕县期末）A、B两地相距350千米，甲、乙两车分别从A、B两地同时出发，相向而行，已知甲车速度为60千米/时，乙车速度为40千米/时，经过t小时两车相距50千米，则t的值是（）A．3.5 B．3.5或2.5 C．4 D．3或4 6．（2020秋•拱墅区期末）某超市有线上和线下两种销售方式．去年10月份该超市线下销售额比线上销售额多a元．与去年相比，该超市今年10月份线上销售额增长35%，线下销售额减少10%．若该超市今年10月份的销售总额比去年10月份的销售总额增加了10%，则今年10月份线上销售额与当月销售总额的比为（）A．B．C．D．7．（2021秋•邢台月考）鸡兔同笼问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”图是嘉淇解题过程，需要补足横线上符号所代表的内容，则下列判断不正确的是（）A．□代表（35﹣x）B．☆代表鸡的足数C．〇代表2 D．△代表28．（2019秋•镇江期末）某超市在“元旦”活动期间，推出如下购物优惠方案：①一次性购物在100元（不含100元）以内，不享受优惠；②一次性购物在100元（含100元）以上，350元（不含350元）以内，一律享受九折优惠；③一次性购物在350元（含350元）以上，一律享受八折优惠；小敏在该超市两次购物分别付了90元和270元，如果小敏把这两次购物改为一次性购物，则小敏至少需付款（）元A．288 B．296 C．312 D．3209．如图，正方形ABCD的轨道上有两个点甲与乙，开始时甲在A处，乙在C处，它们沿着正方形轨道顺时针同时出发，甲的速度为每秒1cm，乙的速度为每秒5cm，已知正方形轨道ABCD的边长为2cm，则乙在第2018次追上甲时的位置（）A．AB上B．BC上C．CD上D．AD上二．填空题10．（2021秋•南岗区校级月考）一艘轮船在水中由A地开往B地，顺水航行用了4小时，由B地开往A地，逆水航行比顺水航行多用了1小时，已知此船在静水中速度是18千米/时，水流速度为千米/小时．11．（2021秋•崇川区校级月考）如图，数轴上线段AB＝2，CD＝4，点A在数轴上表示的数是﹣10，点C在数轴上表示的数是16，若线段AB以6个单位长度/秒的速度向右匀速运动，同时线段CD以2个单位长度/秒的速度向左匀速运动．当B点运动到线段CD上时，P是线段AB上一点，且有关系式BD﹣AP＝3PC成立，则线段PD的长为．12．（2020秋•赫山区期末）互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品进价为180元，按标价的八折销售，仍可获利60元，求这件商品的标价为．13．（2021•海安市二模）众所周知，中华诗词博大精深，集大量的情景情感于短短数十字之间，或豪放，或婉约，或思民生疾苦，或抒发己身豪情逸致，文化价值极高．而数学与古诗词更是有着密切的联系．古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗，每句都是七个字．有一本诗集，其中五言绝句比七言绝句多13首，总字数却反而少了20个字．问两种诗各多少首？设七言绝句有x首，根据题意，可列方程为．14．（2021春•肇源县期末）程大位《直指算法统宗》：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完．试问大、小和尚各多少人？设大和尚有x人，依题意列方程得．15．（2020秋•商河县校级期末）一台收割机收割一块麦田，上午收割了麦田的25%，下午收割了麦田的20%，结果还剩下6.6公顷麦田未收割，这块麦田一共有公顷．16．（2019秋•九江期中）九江市城区的出租车收费标准如下：2公里内起步价为7元，超过2公里以后按每公里1.4元计价．若某人坐出租车行驶x公里，应付给司机21元，则x ＝．17．（2015秋•镇江期末）图1是边长为30cm的正方形纸板，裁掉阴影部分后将其折叠成如图2所示的长方体盒子，已知该长方体的宽是高的2倍，这个长方体的高为cm．18．甲、乙、丙三人分别拿出相同数量的钱，合伙购买某种商品若干件．商品买来后，乙比甲少拿了4件，丙比甲多拿了13件，最后结算时，三人要求按所得商品的实际数量付钱，进行多退少补，已知丙付给甲60元，那么丙应付给乙元．三．解答题19．（2021秋•富裕县期末）解方程．（1）2（1﹣y）﹣5（y﹣2）＝2y﹣3．（2）﹣＝1．20．（2021秋•南岗区校级月考）某工厂车间有28个工人，生产A零件和B零件，每人每天可生产A零件18个或B零件12个（每人每天只能生产一种零件），一个A零件配两个B 零件，且每天生产的A零件和B零件恰好配套．工厂将零件批发给商场时，每个A零件可获利10元，每个B零件可获利5元．（1）求该工厂有多少工人生产A零件？（2）因市场需求，该工厂每天要多生产出一部分A零件供商场零售使用，现从生产B零件的工人中调出多少名工人生产A零件，才能使每日生产的零件总获利比调动前多600元？21．（2021秋•肇源县期末）笑笑买一套运动服，共用去540元，裤子的价格是上衣的80%，上衣多少元？（用方程解答）22．（2021秋•江油市期末）如图，已知在数轴上有三个点A、B、C，O是原点，满足OA＝AB ＝BC＝20cm，动点P从点O出发向右以每秒2cm的速度匀速运动；同时，动点Q从点C 出发，在数轴上向左匀速运动，速度为v（v＞1）；运动时间为t．（1）求：点P从点O运动到点C时，运动时间t的值．（2）若Q的速度v为每秒3cm，那么经过多长时间P，Q两点相距30cm？此时|QB﹣QC|是多少？（3）当|PA+PB|＝2|QB﹣QC|＝24时，请直接写出点Q的速度v的值．23．（2019秋•绵阳期末）小刚和小强从A、B两地同时出发，小刚骑自行车，小强步行，沿同一条路线相向匀速而行，出发后2h两人相遇，相遇时小刚比小强多行进24km，相遇后0.5h小刚到达B地，两人的行进速度分别是多少？相遇后经过多少时间小强到达A地？24．（2020秋•黄冈期末）佳佳平价商场经销的甲、乙两种商品，甲种商品每件售价70元，利润率为40%；乙种商品每件进价40元，售价60元．（1）甲种商品每件进价为元，每件乙种商品利润率为；（2）若该商场同时购进甲、乙两种商品共30件，恰好总进价为1320元，求购进乙种商品多少件？（3）在“元旦”期间，该商场只对甲种商品进行如下的优惠促销活动：打折前一次性购物总金额优惠措施少于等于560元不优惠按售价打九折超过560元，但不超过700元超过700元其中700元部分八点七折优惠，超过700元的部分打三折优惠按上述优惠条件，若顾客小贺一次性购买甲种商品实际付款630元，求小贺在该商场购买甲种商品多少件？25．（2020秋•九龙坡区期末）若在一个两位正整数A的个位数与十位数字之间添上数字6，组成一个新的三位数，我们称这个三位数为A的“至善数”，如13的“至善数”为163；若将一个两位正整数B加6后得到一个新数，我们称这个新数为B的“明德数”，如13的“明德数”为19．（1）38的“至善数”是，“明德数”是；（2）若一个两位正整数M的“明德数”的各位数字之和是M的“至善数”各位数字之和的一半，求出满足条件的所有两位正整数M的值．26．（2021秋•乌兰察布期末）如图，已知点A，B，C是数轴上三点，O为原点，点C对应的数为3，BC＝2，AB＝6．（1）求点A，B对应的数；（2）动点M，N分别同时从AC出发，分别以每秒3个单位和1个单位的速度沿数轴正方向运动．P为AM的中点，Q在CN上，且CQ＝CN，设运动时间为t（t＞0）．①求点P，Q对应的数（用含t的式子表示）；②t为何值时OP＝BQ．27．（2020秋•杭州期末）数轴上A点对应的数为﹣10，B点在A点右边，甲、乙在B分别以2个单位/秒，1个单位/秒的速度向左运动，丙在A以3个单位/秒的速度向右运动．（1）若它们同时出发，经过5秒丙和乙相遇，求B点表示的数；（2）在（1）的条件下，设它们同时出发的时间为t秒，是否存在t（t＞0）的值，使得甲、乙、丙三个点中的其中一个点，到另外两个点的距离相等．28．（2020秋•涪城区校级期末）如图，数轴上点A表示数a，点C表示数c，且多项式x3﹣3xy29﹣20的常数项是a，次数是c．我们把数轴上两点之间的距离用表示两点的大写字母表示，比如，点A与点C之间的距离记作AC．（1）求a，c的值；（2）若数轴上有一点D满足CD＝2AD，求D点表示的数为多少？（3）动点B从数1对应的点开始向右运动，速度为每秒1个单位长度，同时点A，C在数轴上运动，点A，C的速度分别为每秒2个单位长度，每秒3个单位长度，运动时间为t秒．若点A向左运动，点C向右运动，AB＝BC，求t的值．。

一元一次方程储蓄利息问题类型9 储蓄利息问题常思用公式利息＝本金×利率×期数；本息和＝本金＋利息＝本金＋本金×利率×期数＝本金×（1＋利率×期数）。

典例精析例：小明爸爸为小明存了一个3 年期的教育储蓄（3 年期的年利率为2.7%）。

若3年后能取出5405 元，则小明爸爸开始存人了多少元？审题指导1、转化条件已知量：①3 年期：教育储蓄的期数；②2.7%：年利率；③5405 元：3年后的本息和。

未知量：④开始存入的本金（可设为x元）2、画图梳理关系由线段图，得本金＋利息＝本息和，即本金×（1＋利率×期数）＝本息和。

解：设小明爸爸开始存人了x元根据题意，得x（1＋2.7%×3）＝5405，解得x＝5 000。

答：小明爸爸开始存人了5 000元。

习题精练1.小杰妈妈去银行存款，银行一年定期储蓄的年利率是1.5%，两年后取出的本息和为61800元。

设小杰妈妈存人银行的本金为x元，那么下列方程正确的是（）。

A.1.5%x×2＝61800B.x＋1.5%x×2＝61800C.x.（1＋1.5%）×2＝61800D.（1＋1.5%x）×2＝618002.将一笔资金按一年定期存人银行，若年利率为2%，元，则到期支取时，共得本息和为7140元，则这笔资金为（）。

3，妈妈把20000元存入银行，定期三年，年利率是2.6%。

若三年后用所得利息买一部价值1500元的，则利息还剩（）。

A.60元B.100元4. 某人存人银行3 000 元，定期5 年，到期后本息和为3375 元，则年利率为（）%。

5.某同学把积攒的零用钱1000 元存人银行，月利率是0.24%。

如果到期后他连本带利可取回1024元，那么他一共存了几个月？6.小明将已经到期的存了3年的3000元压岁钱取出，本息和为3247.5元，求他存款的年利率。