立体几何训练题

课题：立体几何综合训练个性化教学辅导教案学生姓名年级学科数学上课时间教师姓名课题立体几何综合训练教学过程教师活动1.若三个平面两两相交，有三条交线，则下列命题正确的是（）A．三条交线为异面直线B．三条交线两两平行C．三条交线交于一点D．三条交线两两平行或交于一点2.回顾下直线，平面的平行判断与性质。

3.回顾下直线，平面垂直的性质和判定方法。

4.求线面所成角与二面角的一般步骤是什么？5.若已知条件中，已知三角形中两线段相等，你会想到什么？遇到中点呢？立体几何综合训练例1 如图，直三棱柱111ABC A B C - 中，90BAC ∠=，2AB AC ==，11AA =，点,M N 分别为1A B 和11B C 的中点．(1)证明：MN ∥平面11A ACC ； (2)求三棱锥1A MNC -的体积例2 如图，已知111ABC A B C -是正三棱柱，棱长均为5，E 、F 分别是AC 、11A C 的中点． （1）求证：平面1AB F ∥平面1BEC ； （2）求点A 到平面1BEC 的距离．例3 如图，在直角梯形SABC 中，∠B=∠C=π2，D 为边SC 上的点，且AD ⊥SC ，现将△SAD 沿AD 折起到达PAD 的位置（折起后点S 记为P ），并使得PA ⊥AB ． （1）求证：PD ⊥平面ABCD ；（2）已知PD=AD ，PD +AD +DC=6，G 是AD 的中点，当线段PB 取得最小值时，则在平面PBC 上是否存在点F ，使得FG ⊥平面PBC ？若存在，确定点F 的位置，若不存在，请说明理由．立体几何综合训练教学过程： 突破1： 1.线面平行：①定义：直线与平面无公共点.②判定定理：（线线平行线面平行）③性质定理：（线面平行线线平行）④判定或证明线面平行的依据：（i ）定义法（反证）：（用于判断）；////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭⇒////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭⇒//l l αα=∅⇒（ii ）判定定理：“线线平行面面平行”（用于证明）；（iii ）“面面平行线面平行”（用于证明）； （4）（用于判断）；3.面面平行： ①定义：；②判定定理：如果一个平面内的两条相交直线都平行于另一个平面，那么两个平面互相平行； 符号表述： 【如下图①】图① 图②推论：一个平面内的两条相交直线分别平行于另一个平面的两条直线，那么这两个平面互相平行 符号表述：【如上图②】判定2：垂直于同一条直线的两个平面互相平行. 符号表述：.【如右图】③判定与证明面面平行的依据：（1）定义法；（2）判定定理及推论（常用）（3）判定2 ④面面平行的性质： （1）（面面平行线面平行）； （2）；（面面平行线线平行）（3）夹在两个平行平面间的平行线段相等。

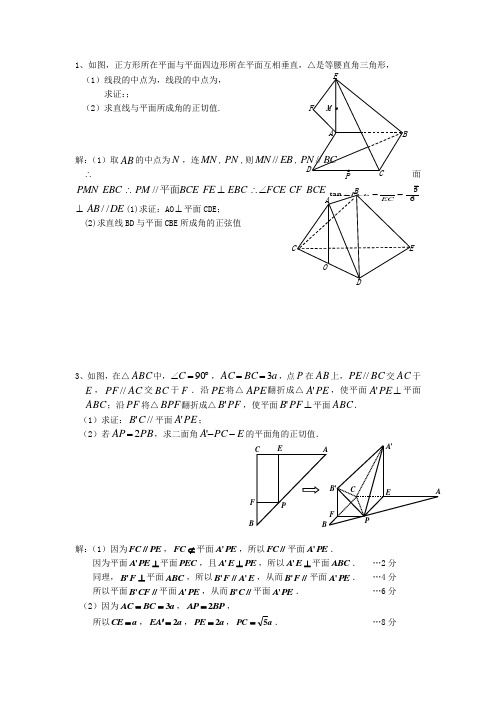
1、如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（1）线段的中点为，线段的中点为，求证：；（2）求直线与平面所成角的正切值.解：（1）取AB 的中点为N ，连MN ,PN ,则//MN EB ,//PN BC∴PMN EBC ∴//PM BCE 平面FE ⊥EBC FCE ∴∠⊥//AB DE (1)求证：AO ⊥平面CDE ；(2)求直线BD 与平面CBE 所成角的正弦值3、如图，在△ABC 中，︒=∠90C ，a BC AC 3==，点P 在AB 上，BC PE //交AC 于E ，AC PF //交BC 于F ．沿PE 将△APE 翻折成△PE A '，使平面⊥PE A '平面ABC ；沿PF 将△BPF 翻折成△PF B '，使平面⊥PF B '平面ABC ． （1）求证：//'C B 平面PE A '；（2）若PB AP 2=，求二面角E PC A --'的平面角的正切值．解：（1）因为PE FC //，⊄FC 平面PE A '，所以//FC 平面PE A '．因为平面⊥PE A '平面PEC ，且PE E A ⊥'，所以⊥E A '平面ABC ． …2分 同理，⊥F B '平面ABC ，所以E A F B '//'，从而//'F B 平面PE A '． …4分 所以平面//'CF B 平面PE A '，从而//'C B 平面PE A '．…6分（2）因为a BC AC 3==，BP AP 2=，所以a CE =，a A E 2='，a PE 2=，a PC 5=．…8分ABCDE FM .. C BF PAF C'B 'A EABCDEP M过E 作PC EM ⊥，垂足为M ，连结M A '．由（1）知ABC E A 平面⊥'，可得PC E A ⊥'， 所以EM A PC '⊥面，所以PC M A ⊥'．所以ME A '∠即为所求二面角E PC A --'的平面角，可记为θ． …12分在Rt △PCE 中，求得a EM 552=， 所以55522tan =='=a aEM E A θ． …15分4、如图，⊥DA 平面ABC ，⊥ED 平面BCD ，DE=DA=AB=AC.0120=∠BAC ，M 为BC 中点. (1)求直线EM 与平面BCD 所成角的正弦值； (2)P 为线段DM 上一点，且⊥AP DM ，求证：AP解：(1) ED ⊥平面BCD ，为在平面上的射影， 为与平面所成角．……………………2分 DA ⊥Q 平面ABC ，， 设，又=Q DA AB =AC ，． 在△ABC 中，Q ，， 又Q 为中点，∴⊥DM BC ，12==BM BC ，∴．…5分 在Rt △EDM中，EM =32a =， PABF C'B 'A E（第20题）MA BCDE A 1C 1sin EMD ∠=32DE a EM a =23=． ………………………7分 （2）=AB AC ，M 为BC 中点，∴⊥BC AM ．又⊥DA 平面ABC ， ∴⊥BC DA ，平面． ……………………9分又平面，， ……………………11分 又，平面． ……………………13分 又ED ⊥平面BCD ，． ……………………14分5、如图，已知ABCD 是边长为1的正方形，AF⊥平面ABCD ，CE∥AF，)1(>=λλAF CE ．（1）证明：BD⊥EF；（2）若AF ＝1，且直线BE 与平面ACE 所成角的正弦值为1023，求λ的值．解：（1）连结BD 、AC ，交点为Ｏ．∵ABCD 是正方形∵AF⊥平面ABCD ∴AF⊥BD ……4分 ∴BD⊥平面ACEF ……6分 ∴BD⊥EF ……7分（2）连结OE ，由（1）知，BD⊥平面ACEF ，所以∠BEO 即为直线BE 与平面ACE 所成的角． ……10分 ∵AF⊥平面ABCD ，CE∥AF ，∴CE⊥平面ABCD ，CE⊥BC， ∵BC =1，AF ＝1，则CE ＝λ，BE ＝21λ+，BO ＝22， ∴Rt△BEO 中， 1023122sin 2=λ+==∠BE BO BEO ， …13分 因为1>λ，解得34=λ． ……15分6、如图，在几何体中，⊥1AA 平面ABC ，,2,//,111===⊥AA BC AB AA CC BC AB E D CC ,,11=分别是1,AA AB 的中点. (1)求证：//1BC 平面CDE ；(2)求二面角A DC E --的平面角的正切值.解：（1）连接ACR 1R 交EC 于点F ，由题意知四边形ACCR 1RE 是矩形，则F 是ACR 1R 的中点，连接DF ，∵D 是AB 的中点，∴DF 是△ABCR 1R 的中位线，∴ BCR 1R ⊄⊂ 7分 (2) 作AH ⊥直线CD ，垂足为H ，连接HE ， ∵ AAR 1R ⊥平面ABC ，∴ AAR 1R ⊥DC ，∴ CD ⊥平面AHE ， ∴ CD ⊥EH ，∴ ∠AHE 是二面角E – CD – A 的平面角. 11分 ∵ D 是AB 的中点，∴ AH 等于点B 到CD 的距离，在△BCD 中，求得：AH ＝552， 在△AEH 中， 25tan ==∠AH AE AHE 即所求二面角的正切值为25.7、如图，已知平面与直线均垂直于所在平面，且, （1）求证：平面；（2）若，求与平面所成角的正弦值.解：（1）证明：过点作于点，∵平面⊥平面，∴平面……2分 又∵⊥平面∴∥, ………………2分 又∵平面∴∥平面 ………………6分（2）∵平面 ∴，又∵∴ ∴ ………………8分 ∴点是的中点，连结，则 ∴平面 ∴∥，∴四边形是矩形 ………………10分 设QPABCABCA 1B 1C 1DE 得：， 又∵，∴，从而，过作于点，则：∴是与平面所成角 ………………………………………………12分 ∴，∴与平面所成角的正弦值为…………………………14分8、如图，在直三棱柱111C B A ABC -中，ABC ∆是等腰直角三角形，090=∠ACB ，侧棱AA 1=2，D ，E 分别为CC 1与A 1B 的中点，点E 在平面ABD 上的射影是ABD ∆的重心. (1)求证：DE9、如图，在侧棱垂直于底面的三棱柱ABC —A 1B 1C 1中，底面△ABC 为等腰直角三角形，∠B=90°,D 为棱BB 1的中点。

高中数学必修二第八章立体几何初步考点精题训练单选题1、南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148．5m时，相应水面的面积为140．0km2；水位为海拔157．5m时，相应水面的面积为180．0km2，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148．5m上升到157．5m时，增加的水量约为（√7≈2.65）（）A．1.0×109m3B．1.2×109m3C．1.4×109m3D．1.6×109m3答案：C分析：根据题意只要求出棱台的高，即可利用棱台的体积公式求出．依题意可知棱台的高为MN=157.5−148.5=9(m)，所以增加的水量即为棱台的体积V．棱台上底面积S=140.0km2=140×106m2，下底面积S′=180.0km2=180×106m2，∴V=13ℎ(S+S′+√SS′)=13×9×(140×106+180×106+√140×180×1012)=3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m3)．故选：C．2、如图已知正方体ABCD−A1B1C1D1，M，N分别是A1D，D1B的中点，则（）A．直线A1D与直线D1B垂直，直线MN//平面ABCDB．直线A1D与直线D1B平行，直线MN⊥平面BDD1B1C．直线A1D与直线D1B相交，直线MN//平面ABCDD．直线A1D与直线D1B异面，直线MN⊥平面BDD1B1答案：A分析：由正方体间的垂直、平行关系，可证MN//AB,A1D⊥平面ABD1，即可得出结论.连AD1，在正方体ABCD−A1B1C1D1中，M是A1D的中点，所以M为AD1中点，又N是D1B的中点，所以MN//AB，MN⊄平面ABCD,AB⊂平面ABCD，所以MN//平面ABCD.因为AB不垂直BD，所以MN不垂直BD则MN不垂直平面BDD1B1，所以选项B,D不正确；在正方体ABCD−A1B1C1D1中，AD1⊥A1D，AB⊥平面AA1D1D，所以AB⊥A1D，AD1∩AB=A，所以A1D⊥平面ABD1，D1B⊂平面ABD1，所以A1D⊥D1B，且直线A1D,D1B是异面直线，所以选项C错误，选项A正确.故选：A.小提示：关键点点睛：熟练掌握正方体中的垂直、平行关系是解题的关键，如两条棱平行或垂直，同一个面对角线互相垂直，正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.3、在正方体ABCD −A 1B 1C 1D 1中，三棱锥A −B 1CD 1的表面积为4√3，则正方体外接球的体积为（ ）A ．4√3πB ．√6πC ．32√3πD ．8√6π答案：B解析：根据三棱锥的表面积进一步求出正方体的棱长，最后求出正方体的外接球的半径，进一步求出结果． 解：设正方体的棱长为a ，则B 1D 1=AC =AB 1=AD 1=B 1C =D 1C =√2a ，由于三棱锥A −B 1CD 1的表面积为4√3，所以S =4S △AB 1C =4×12×√32(√2a)2=4√3所以a =√2所以正方体的外接球的半径为√(√2)2+(√2)2+(√2)22=√62， 所以正方体的外接球的体积为43π·(√62)3=√6π故选：B ．小提示：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.4、已知三棱锥P −ABC ，其中PA ⊥平面ABC ，∠BAC =120°，PA =AB =AC =2，则该三棱锥外接球的表面积为（ ）A ．12πB ．16πC ．20πD ．24π答案：C分析：根据余弦定理、正弦定理，结合球的性质、球的表面积公式进行求解即可.根据题意设底面△ABC 的外心为G ，O 为球心，所以OG ⊥平面ABC ，因为PA ⊥平面ABC ，所以OG//PA ，设D 是PA 中点，因为OP =OA ，所以DO ⊥PA ，因为PA ⊥平面ABC ，AG ⊂平面ABC ，所以AG ⊥PA ，因此OD//AG ，因此四边形ODAG 是平行四边形，故OG =AD =12PA =1，由余弦定理，得BC =√AB 2+AC 2−2AB ⋅AC ⋅cos120°=√4+4−2×2×2×(−12)=2√3，由正弦定理，得2AG =√3√32⇒AG =2，所以该外接球的半径R 满足R 2=(OG )2+(AG )2=5⇒S =4πR 2=20π，故选：C ．小提示：关键点睛：运用正弦定理、余弦定理是解题的关键.5、牟合方盖是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，该方法不直接给出球体的体积，而是先计算牟合方盖的体积.刘徽通过计算，“牟合方盖”的体积与球的体积关系为V 牟V 球=4π，并且推理出了“牟合方盖”的八分之一的体积计算公式，即V 牟8=r 3−V 方盖差，从而计算出V 球=43πr 3.如果记所有棱长都为r 的正四棱锥的体积为V ，则V 方差盖:V =（ ）A．√22B．1C．√2D．2√2答案：C分析：计算出V方盖差，V，即可得出结论.由题意，V方盖差=r3−18V牟=r3−18×4π×43×π×r3=13r3，所有棱长都为r的正四棱锥的体积为V正=13×r×r×r2−(√2r2)2=√26r3，∴V方盖差V正=13r3√2r36=√2，故选：C．6、如图，已知正方体的棱长为a，沿图1中对角面将它分割成两个部分，拼成如图2的四棱柱，则该四棱柱的全面积为（）A．(8+2√2)a2B．(2+4√2)a2C．(4+2√2)a2D．(6−4√2)a2答案：C分析：拼成的几何体比原正方体的表面增加了两个截面，减少了原来两个正方形面，据此变化，进行求解. 由题意，拼成的几何体比原正方体的表面增加了两个截面，减少了原来两个正方形面，由于截面为矩形，长为√2a，宽为a，所以面积为√2a2，所以拼成的几何体的表面积为4a2+2√2a2=(4+2√2)a2.故选：C.7、如图所示的正方形SG1G2G3中，E ， F分别是G1G2，G2G3的中点，现沿SE，SF，EF把这个正方形折成一个四面体，使G1，G2，G3重合为点G，则有（）A．SG⊥平面EFG B．EG⊥平面SEFC．GF⊥平面SEF D．SG⊥平面SEF答案：A解析：根据正方形的特点，可得SG⊥FG，SG⊥EG，然后根据线面垂直的判定定理，可得结果. 由题意：SG⊥FG，SG⊥EG，FG∩EG=G，FG，EG⊂平面EFG所以SG⊥平面EFG正确，D不正确；.又若EG⊥平面SEF，则EG⊥EF，由平面图形可知显然不成立；同理GF⊥平面SEF不正确；故选：A小提示：本题主要考查线面垂直的判定定理，属基础题.8、如图，PA垂直于矩形ABCD所在的平面，则图中与平面PCD垂直的平面是（）A．平面ABCD B．平面PBCC．平面PAD D．平面PCD答案：C分析：由线面垂直得到线线垂直，进而证明出线面垂直，面面垂直.因为PA⊥平面ABCD，CD⊂平面ABCD，所以PA⊥CD，由四边形ABCD为矩形得CD⊥AD，因为PA∩AD=A，所以CD⊥平面PAD．又CD⊂平面PCD，所以平面PCD⊥平面PAD．故选：C多选题9、沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图，某沙漏由上(细管长度忽略不下两个圆锥组成，圆锥的底面直径和高均为8cm，细沙全部在上部时，其高度为圆锥高度的23计).假设该沙漏每秒钟漏下0.02cm3的沙，且细沙全部漏入下部后，恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是（）A．沙漏中的细沙体积为1024πcm381B．沙漏的体积是128πcm3C．细沙全部漏入下部后此锥形沙堆的高度约为2.4cmD．该沙漏的一个沙时大约是1565秒(π≈3.14)答案：AC解析：A．根据圆锥的体积公式直接计算出细沙的体积；B．根据圆锥的体积公式直接计算出沙漏的体积；C．根据等体积法计算出沙堆的高度；D．根据细沙体积以及沙时定义计算出沙时.A.根据圆锥的截面图可知：细沙在上部时，细沙的底面半径与圆锥的底面半径之比等于细沙的高与圆锥的高之比，所以细沙的底面半径r=23×4=83cm，所以体积V=13⋅πr2⋅2ℎ3=13⋅64π9⋅163=1024π81cm3B.沙漏的体积V=2×13×π×(ℎ2)2×ℎ=2×13×π×42×8=2563πcm3；C.设细沙流入下部后的高度为ℎ1，根据细沙体积不变可知：1024π81=13×(π(ℎ2)2)×ℎ1，所以1024π81=16π3ℎ1,所以ℎ1≈2.4cm；D.因为细沙的体积为1024π81cm3，沙漏每秒钟漏下0.02cm3的沙，所以一个沙时为：1024π810.02=1024×3.1481×50≈1985秒.故选：AC.小提示：该题考查圆锥体积有关的计算，涉及到新定义的问题，难度一般.解题的关键是对于圆锥这个几何体要有清晰的认识，同时要熟练掌握圆锥体积有关的计算公式.10、(多选题)在四棱锥A－BCDE中，底面四边形BCDE为梯形，BC∥DE.设CD，BE，AE，AD的中点分别为M，N，P，Q，则（）A．PQ＝1MN B．PQ∥MN2C．M，N，P，Q四点共面D．四边形MNPQ是梯形答案：BCD分析：根据中位线的性质，结合平行的性质逐个判定即可DE，且DE≠MN，由题意知PQ=12所以PQ≠1MN，故A不正确；又PQ∥DE，DE∥MN，2所以PQ∥MN，又PQ≠MN，所以B，C，D正确.故选：BCD11、给出以下关于斜二测直观图的结论，其中正确的是（）A．水平放置的角的直观图一定是角B．相等的角在直观图中仍然相等C．相等的线段在直观图中仍然相等D．两条平行线段在直观图中仍是平行线段答案：AD分析：根据直观图和斜二测画法的规则，判断选项.水平放置的角的直观图一定是角，故A正确；角的大小在直观图中都会发生改变，有的线段在直观图中也会改变，比如正方形的直方图中，故BC错误；由斜二测画法规则可知，直观图保持线段的平行性，所以D正确.故选：AD填空题12、如图所示，P为平行四边形ABCD所在平面外一点，E为AD的中点，F为PC上一点，若PA//平面EBF，则PF=_______FC答案：12##0.5 分析：连接AC 交BE 于点M ，连接FM ，由线面平行的性质得线线平行，由平行线性得结论． 连接AC 交BE 于点M ，连接FM ，∵PA//平面EBF ，PA ⊂平面PAC ，平面PAC ∩平面EBF =EM ，∴PA//EM ，又AE//BC ，∴PF FC =AM MC =AE BC =12. 所以答案是：12． 13、已知一个圆锥的底面半径为6，其体积为30π则该圆锥的侧面积为________.答案：39π分析：利用体积公式求出圆锥的高，进一步求出母线长，最终利用侧面积公式求出答案. ∵V =13π62⋅ℎ=30π∴ℎ=52∴l =√ℎ2+r 2=√(52)2+62=132 ∴S 侧=πrl =π×6×132=39π. 所以答案是：39π.14、如图，拿一张矩形纸片对折后略微展开，竖立在桌面上，折痕与桌面的关系是______．答案：垂直分析：根据给定条件，利用线面垂直的判定推理作答.令桌面所在的平面为α，折痕所在直线为l，纸片与桌面公共部分所在直线为a,b，如图，依题意有a∩b=A，因l⊥a,l⊥b，a,b⊂α，所以l⊥α，所以折痕与桌面垂直.所以答案是：垂直解答题15、如图，四棱锥P−ABCD的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PB⊥AM．（1）证明：平面PAM⊥平面PBD；（2）若PD=DC=1，求四棱锥P−ABCD的体积．答案：（1）证明见解析；（2）√23．分析：（1）由PD⊥底面ABCD可得PD⊥AM，又PB⊥AM，由线面垂直的判定定理可得AM⊥平面PBD，再根据面面垂直的判定定理即可证出平面PAM⊥平面PBD；（2）由（1）可知，AM⊥BD，由平面知识可知，△DAB~△ABM，由相似比可求出AD，再根据四棱锥P−ABCD的体积公式即可求出．（1）因为PD⊥底面ABCD，AM⊂平面ABCD，所以PD⊥AM，又PB⊥AM，PB∩PD=P，所以AM⊥平面PBD，而AM⊂平面PAM，所以平面PAM⊥平面PBD．（2）[方法一]：相似三角形法由（1）可知AM⊥BD．于是△ABD∽△BMA，故ADAB =ABBM．因为BM=12BC,AD=BC,AB=1，所以12BC2=1，即BC=√2．故四棱锥P−ABCD的体积V=13AB⋅BC⋅PD=√23．[方法二]：平面直角坐标系垂直垂直法由（2）知AM⊥DB,所以k AM⋅k BD=−1．建立如图所示的平面直角坐标系，设BC =2a(a >0)．因为DC =1，所以A(0,0)，B(1,0)，D(0,2a)，M(1,a)．从而k AM ⋅k BD =a−01−0×2a−00−1=a ×(−2a)=−2a 2=−1． 所以a =√22，即DA =√2．下同方法一.[方法三]【最优解】：空间直角坐标系法建立如图所示的空间直角坐标系D −xyz ，设|DA|=t ，所以D(0,0,0)，C(0,1,0)，P(0,0,1)，A(t,0,0)，B(t,1,0)．所以M (t 2,1,0)，PB ⃑⃑⃑⃑⃑ =(t,1,−1)，AM ⃑⃑⃑⃑⃑⃑ =(−t 2,1,0)．所以PB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =t ⋅(−t 2)+1×1+0×(−1)=−t 22+1=0． 所以t =√2，即|DA|=√2．下同方法一.[方法四]：空间向量法由PB ⊥AM ，得PB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0．所以(PD⃑⃑⃑⃑⃑ +DA ⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ )⋅AM ⃑⃑⃑⃑⃑⃑ =0． 即PD ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +DA ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0．又PD ⊥底面ABCD ，AM 在平面ABCD 内，因此PD ⊥AM ，所以PD ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0．所以DA ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0，由于四边形ABCD 是矩形，根据数量积的几何意义，得−12|DA ⃑⃑⃑⃑⃑ |2+|AB ⃑⃑⃑⃑⃑ |2=0，即−12|BC ⃑⃑⃑⃑⃑ |2+1=0． 所以|BC⃑⃑⃑⃑⃑ |=√2，即BC =√2．下同方法一. 【整体点评】(2)方法一利用相似三角形求出求出矩形的另一个边长，从而求得该四棱锥的体积；方法二构建平面直角坐标系，利用直线垂直的条件得到矩形的另一个边长，从而求得该四棱锥的体积；方法三直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的另一个边长,为最常用的通性通法，为最优解；方法四利用空间向量转化求得矩形的另一边长.。

空间几何体的结构及其三视图和直观图一、选择题1．下列命题中正确的个数是()①由五个面围成的多面体只能是四棱锥；②用一个平面去截棱锥便可得到棱台；③仅有一组对面平行的五面体是棱台；④有一个面是多边形，其余各面是三角形的几何体是棱锥．A．0个B．1个C．2个D．3个【解析】对于①，五个面围成的多面体也可以是三棱柱或三棱台，故①错；对于②，当平面与棱锥底面不平行时，截得的几何体不是棱台，故②错；对于③，仅有一组对面平行的五面体也可能是三棱柱，故③错；对于④，当三角形面没有一个公共顶点时，也不是棱锥，故④错．【答案】 A2．(2013·青岛质检)将长方体截去一个四棱锥，得到的几何体如图7－1－11所示，则该几何体的侧视图为()图7－1－11【解析】如图所示，点D1的投影为C1，点D的投影为C，点A的投影为B，故选D.【答案】 D3．如图7－1－12所示正三棱柱ABC—A1B1C1的主视图(又称正视图)是边长为4的正方形，则此正三棱柱的侧视图(又称左视图)的面积为()图7－1－12A．16 B．2 3C．4 3 D．8 3【解析】由主视图知，正三棱柱底面边长为4，侧棱长为4，则正三棱柱的侧视图是高为4，底边长为23的矩形，从而侧视图的面积为S＝4×23＝侧8 3.【答案】 D4．(2013·武汉模拟)如图7－1－13是一正方体被过棱的中点M、N和顶点A、D、C1的两个截面截去两个角后所得的几何体，则该几何体的正视图为()图7－1－13【解析】由几何体知，边界线AM可视，DC1不可视，且点M在正方体后侧面上的射影是边的中点，故选B.【答案】 B5．(2013·郑州模拟)已知正三棱锥V—ABC的主视图、俯视图如图7－1－14所示，其中VA＝4，AC＝23，则该三棱锥的左视图的面积为()图7－1－14A．9 B．6C．3 3 D.39【解析】由主视图和俯视图知，正三棱锥的底面边长为23，侧棱长为4，由俯视图知，正三棱锥的左视图是以BC为底边的等腰三角形，其高为正三棱锥的高，因为正三棱锥的高h＝23，故左视图的面积S左＝12×23×23＝6.【答案】 B6．对于长和宽分别相等的两个矩形，给出下列三个命题：①存在三棱柱，其正(主)视图、俯视图如图7－1－15所示；②存在四棱柱，其正(主)视图、俯视图如图7－1－15所示；③存在圆柱，其正(主)视图、俯视图如图7－1－15所示．其中真命题的个数是()图7－1－15A．3 B．2C．1 D．0【解析】只要把底面为等腰直角三角形的直三棱柱的一个侧面放在水平面上，就可以使得这个三棱柱的正视图和俯视图符合要求，故命题①是真命题；把一个正四棱柱的一个侧面放置在水平面上，即可使得这个四棱柱的正视图和俯视图符合要求，命题②是真命题；只要把圆柱侧面的一条母线放置在水平面即符合要求，命题③也是真命题．【答案】 A二、填空题7．如图7－1－16，在正方体ABCD—A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P—ABC的主视图与左视图的面积的比值为________．图7－1－16【解析】三棱锥P—ABC的主视图与左视图为底边和高均相等的三角形，故它们的面积相等，面积比值为1.【答案】 18．已知△ABC是边长为a的等边三角形，则其直观图△A′B′C′的面积为________．【解析】如图所示，设△A′B′C′为△ABC的直观图，O′为A′B′的中点．由直观图的画法知A′B′＝a，O′C′＝12·3a2＝3a4，∴S△A′B′C′＝12·A′B′·(O′C′·sin 45°)＝12·a·(3a4×22)＝616a2.即边长为a的等边三角形的直观图的面积为6a2 16.【答案】6a2 169．(2013·长春模拟)已知一几何体的三视图如图7－1－17所示，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是(写出所有正确结论的编号)________．图7－1－17①矩形；②不是矩形的平行四边形；③有三个面为直角三角形，有一个面为等腰三角形的四面体；④每个面都是等腰三角形的四面体；⑤每个面都是直角三角形的四面体．【解析】由该几何体的三视图可知该几何体为底面边长为a，高为b的长方体，这四个顶点的几何形体若是平行四边形，则一定是矩形，故②不正确．【答案】①③④⑤三、解答题10．已知：图①是截去一个角的长方体，试按图示的方向画出其三视图；图②是某几何体的三视图，试说明该几何体的构成．图7－1－18【解】图①几何体的三视图为：图②所示的几何体是上面为正六棱柱，下面为倒立的正六棱锥的组合体． 11．如下的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出(单位：cm)．图7－1－19(1)在正视图下面，按照画三视图的要求画出该多面体的俯视图； (2)按照给出的尺寸，求该多面体的体积； 【解】 (1)如图．(2)所求多面体的体积V ＝V 长方体－V 正三棱锥＝4×4×6－13×(12×2×2)×2＝2843(cm 3)． 12．如图7－1－20是一个几何体的正视图和俯视图．图7－1－20(1)试判断该几何体是什么几何体；(2)画出其侧视图，并求该平面图形(侧视图)的面积．【解】 (1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥． (2)该几何体的侧视图，如图．其中AB ＝AC ，AD ⊥BC ，且BC 的长是俯视图正六边形对边间的距离，即BC ＝3a ，AD 是正棱锥的高，则AD ＝3a ，所以该平面图形(侧视图)的面积为 S ＝12×3a ×3a ＝32a 2.课后作业(四十一) 空间几何体的表面积与体积一、选择题1．(2012·课标全国卷)如图7－2－11，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为( )图7－2－11A ．6B ．9C ．12D ．18【解析】 由题意知，此几何体是三棱锥，其高h ＝3，相应底面面积为S ＝12×6×3＝9，∴V ＝13Sh ＝13×9×3＝9.【答案】 B2．长方体的三个相邻面的面积分别为2,3,6，这个长方体的顶点都在同一个球面上，则这个球的面积为( )A.72πB ．56πC ．14πD ．64π【解析】设长方体的过同一顶点的三条棱长分别为a ，b ，c ，则⎩⎨⎧ab ＝2bc ＝3ac ＝6，得⎩⎨⎧a ＝2b ＝1，c ＝3令球的半径为R ，则(2R )2＝22＋12＋32＝14， ∴R 2＝72，∴S 球＝4πR 2＝14π. 【答案】 C3．如图7－2－12所示，已知三棱柱ABC —A 1B 1C 1的所有棱长均为1，且AA 1⊥底面ABC ，则三棱锥B 1—ABC 1的体积为( )图7－2－12A.312B.34C.612D.64【解析】 在△ABC 中，BC 边长的高为32，即棱锥A —BB 1C 1上的高为32，又S △BB 1C 1＝12，∴VB 1—ABC 1＝VA —BB 1C 1＝13×32×12＝312. 【答案】 A4．(2013·西安八校联考)若一个底面是正三角形的三棱柱的正视图如图7－2－13所示，其顶点都在一个球面上，则球的表面积为( )图7－2－13A.43πB.163πC.19π3D.19π12【解析】 如图所示，F 、H 是正三棱柱上下底面的中心，则球心O 是FH 的中点，由三视图知AB ＝2，FH ＝1，则AE ＝3， AF ＝233，OF ＝12， ∴OA ＝(12)2＋(233)2＝1912，∴球的表面积S 球＝4πOA 2＝19π3. 【答案】 C5．(2013·潍坊模拟)如图7－2－14为某个几何体的三视图，则该几何体的侧面积为( )图7－2－14A ．16＋4πB ．12＋4πC ．16＋8πD ．12＋8π【解析】 易知该几何体是一个半圆柱和一个三棱柱的组合体，其侧面积为4π＋6＋10＝16＋4π.【答案】 A6．(2013·广州模拟)如图7－2－15，某几何体的正视图(主视图)，侧视图(左视图)和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为( )图7－2－15A ．4 3B ．4C ．2 3D ．2【解析】 由三视图知，该几何体为四棱锥，如图所示．依题意AB ＝23，菱形BCDE 中BE ＝EC ＝2.∴BO ＝22－12＝3，则AO ＝AB 2－BO 2＝3， 因此V A —BCDE ＝13·AO ·S 四边形BCDE ＝13×3×2×232＝2 3. 【答案】 C 二、填空题7．(2012·辽宁高考)一个几何体的三视图如图7－2－16所示，则该几何体的表面积为________．图7－2－16【解析】 根据三视图可知几何体是一个长方体挖去一个圆柱，所以S ＝2×(4＋3＋12)＋2π－2π＝38.【答案】 388．圆锥的全面积为15π cm 2，侧面展开图的圆心角为60°，则该圆锥的体积为________cm 3.【解析】 设底面圆的半径为r ，母线长为a ，则侧面积为12×(2πr )a ＝πra .由题意得⎩⎪⎨⎪⎧πra ＋πr 2＝15ππra ＝16πa 2，解得⎩⎪⎨⎪⎧r 2＝157a 2＝36×157，故圆锥的高h ＝a 2－r 2＝53，所以体积为V ＝13πr 2h ＝13π×157×53＝2537π(cm 3)．【答案】 2573π9．一个几何体的三视图如图7－2－17，该几何体的表面积为________．图7－2－17【解析】 该几何体的直观图如图所示，将小长方体的上底面补到大长方体被遮住的部分，则所求的表面积为小长方体的侧面积加上大长方体的表面积，∴S ＝S 侧＋S 表＝6×8×2＋2×8×2＋(2×8＋2×10＋8×10)×2＝360. 【答案】 360 三、解答题10．若一个底面边长为62，侧棱长为6的正六棱柱的所有顶点都在一个球面上，求该球的体积和表面积．【解】 在底面正六边形ABCDEF 中，连接BE 、AD 交于O ，连接BE 1， 则BE ＝2OE ＝2DE ，∴BE ＝6，在Rt △BEE 1中， BE 1＝BE 2＋E 1E 2＝23， ∴2R ＝23，则R ＝3，∴球的体积V 球＝43πR 3＝43π，球的表面积S 球＝4πR 2＝12π. 11．如图7－2－18，已知某几何体的三视图如下(单位：cm)．图7－2－18(1)画出这个几何体的直观图(不要求写画法)； (2)求这个几何体的表面积及体积． 【解】 (1)这个几何体的直观图如图所示．(2)这个几何体可看成是正方体AC 1及直三棱柱B 1C 1Q —A 1D 1P 的组合体． 由P A 1＝PD 1＝2，A 1D 1＝AD ＝2，可得P A 1⊥PD 1. 故所求几何体的表面积S ＝5×22＋2×2×2＋2×12×(2)2＝(22＋42)(cm 2)，所求几何体的体积V ＝23＋12×(2)2×2＝10(cm 3)．12．如图7－2－19，已知平行四边形ABCD 中，BC ＝2，BD ⊥CD ，四边形ADEF 为正方形，平面ADEF ⊥平面ABCD ，G ，H 分别是DF ，BE 的中点．记CD ＝x ，V (x )表示四棱锥F —ABCD 的体积．图7－2－19(1)求V (x )的表达式； (2)求V (x )的最大值．【解】 (1)∵平面ADEF ⊥平面ABCD ，交线为AD 且F A ⊥AD ，∴F A ⊥平面ABCD .∵BD ⊥CD ，BC ＝2，CD ＝x ， ∴F A ＝2，BD ＝4－x 2(0＜x ＜2)， ∴S ▱ABCD ＝CD ·BD ＝x 4－x 2，∴V (x )＝13S ▱ABCD ·F A ＝23x 4－x 2(0＜x ＜2)． (2)V (x )＝23x 4－x 2＝23－x 4＋4x 2 ＝23－(x 2－2)2＋4.∵0＜x ＜2，∴0＜x 2＜4，∴当x 2＝2，即x ＝2时，V (x )取得最大值，且V (x )max ＝43.课后作业(四十二) 空间点、直线、平面之间的位置关系一、选择题阿1．(2013·台州模拟)以下四个命题中 ①不共面的四点中，其中任意三点不共线；②若点A 、B 、C 、D 共面，点A 、B 、C 、E 共面，则点A 、B 、C 、D 、E 共面；③若直线a 、b 共面，直线a 、c 共面，则直线b 、c 共面； ④依次首尾相接的四条线段必共面． 正确命题的个数是( ) A ．0 B ．1 C ．2D ．3【解析】 ①中显然是正确的；②中若A 、B 、C 三点共线则A 、B 、C 、D 、E 五点不一定共面．③构造长方体或正方体，如图显然b 、c 异面故不正确．④中空间四边形中四条线段不共面，故只有①正确．【答案】 B2．已知异面直线a，b分别在平面α，β内，且α∩β＝c，那么直线c一定() A．与a，b都相交B．只能与a，b中的一条相交C．至少与a，b中的一条相交D．与a，b都平行【解析】若c与a，b都不相交，则c与a，b都平行，则a∥b与a，b异面相矛盾．【答案】 C3．如图7－3－8所示，ABCD—A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论正确的是()图7－3－8A．A，M，O三点共线B．A，M，O，A1不共面C．A，M，C，O不共面D．B，B1，O，M共面【解析】连接A1C1，AC，则A1C1∥AC，∴A1，C1，A，C四点共面，∴A1C⊂平面ACC1A1，∵M∈A1C，∴M∈平面ACC1A1，又M∈平面AB1D1，∴M在平面ACC1A1与平面AB1D1的交线上，同理O在平面ACC1A1与平面AB1D1的交线上．∴A，M，O三点共线．【答案】 A4．如图是正方体或四面体，P，Q，R，S分别是所在棱的中点，这四个点不共面的一个图是( )【解析】 在A 图中分别连接PS ，QR ， 易证PS ∥QR ，∴P ，Q ，R ，S 共面； 在C 图中分别连接PQ ，RS ， 易证PQ ∥RS ，∴P ，Q ，R ，S 共面．如图，在B 图中过P ，Q ，R ，S 可作一正六边形，故四点共面； D 图中PS 与QR 为异面直线，∴四点不共面，故选D. 【答案】 D5．(2013·青岛质检)如图7－3－9，正三棱柱ABC —A 1B 1C 1的各棱长(包括底面边长)都是2，E ，F 分别是AB ，A 1C 1的中点，则EF 与侧棱C 1C 所成的角的余弦值是( )图7－3－9A.55B.255C.12D ．2【解析】 如图，取AC 中点G ，连FG 、EG ，则FG ∥C 1C ，FG ＝C 1C ；EG ∥BC ，EG ＝12BC ，故∠EFG 即为EF 与C 1C 所成的角，在Rt △EFG 中，cos ∠EFG ＝FG FE ＝25＝255.【答案】 B6．设A，B，C，D是空间四个不同的点，在下列命题中，不正确的是() A．若AC与BD共面，则AD与BC共面B．若AC与BD是异面直线，则AD与BC是异面直线C．若AB＝AC，DB＝DC，则AD＝BCD．若AB＝AC，DB＝DC，则AD⊥BC【解析】由公理1知，命题A正确．对于B，假设AD与BC共面，由A正确得AC与BD共面，这与题设矛盾，故假设不成立，从而结论正确．对于C，如图，当AB＝AC，DB＝DC，使二面角A—BC—D的大小变化时，AD与BC不一定相等，故不正确．对于D，如图，取BC的中点E，连接AE，DE，则由题设得BC⊥AE，BC ⊥DE.根据线面垂直的判定定理得BC⊥平面ADE，从而AD⊥BC.故D正确．【答案】 C二、填空题7．(2013·合肥质检)如图7－3－10是正四面体的平面展开图，G、H、M、N 分别为DE、BE、EF、EC的中点，在这个正四面体中，图7－3－10①GH与EF平行；②BD与MN为异面直线；③GH与MN成60°角；④DE与MN垂直．以上四个命题中，正确命题的序号是________．【解析】还原成正四面体知GH与EF为异面直线，BD与MN为异面直线，GH与MN成60°角，DE⊥MN.【答案】②③④8．(2013·杭州模拟)设a，b，c是空间中的三条直线，下面给出五个命题：①若a∥b，b∥c，则a∥c；②若a⊥b，b⊥c，则a∥c；③若a与b相交，b与c相交，则a与c相交；④若a⊂平面α，b⊂平面β，则a，b一定是异面直线；⑤若a，b与c成等角，则a∥b.上述命题中正确的命题是________(只填序号)．【解析】由公理4知①正确；当a⊥b，b⊥c时，a与c可以相交、平行，也可以异面，故②不正确；当a与b相交，b与c相交时，a与c可以相交、平行，也可以异面，故③不正确；a⊂α，b⊂β，并不能说明a与b“不同在任何一个平面内”，故④不正确；当a，b与c成等角时，a与b可以相交、平行，也可以异面，故⑤不正确．【答案】①9．如图7－3－11所示，在正三棱柱ABC—A1B1C1中，D是AC的中点，AA1∶AB＝2∶1，则异面直线AB1与BD所成的角为________．图7－3－11【解析】 取A 1C 1的中点D 1，连接B 1D 1， 因为D 是AC 的中点， 所以B 1D 1∥BD ，所以∠AB 1D 1即为异面直线AB 1与BD 所成的角． 连接AD 1，设AB ＝a ， 则AA 1＝2a ，所以AB 1＝3a ，B 1D 1＝32a ， AD 1＝14a 2＋2a 2＝32a .所以cos ∠AB 1D 1＝3a 2＋34a 2－94a 22×3a ×32a ＝12，所以∠AB 1D 1＝60°. 【答案】 60° 三、解答题10．如图7－3－12所示，在正方体ABCD —A 1B 1C 1D 1中，E ，F 分别为CC 1，AA 1的中点，画出平面BED 1F 与平面ABCD 的交线．图7－3－12【解】 在平面AA 1D 1D 内，延长D 1F ， ∵D 1F 与DA 不平行，∴D 1F 与DA 必相交于一点，设为P ，则P∈D1F，P∈DA.又∵D1F⊂平面BED1F，AD⊂平面ABCD，∴P∈平面BED1F，P∈平面ABCD.又B为平面ABCD与平面BED1F的公共点，连接PB，∴PB即为平面BED1F与平面ABCD的交线．如图所示．11．如图7－3－13所示，在正方体ABCD—A1B1C1D1中，E，F分别为A1A，C1C的中点，求证：四边形EBFD1是菱形．图7－3－13【证明】如图所示，取B1B的中点G，连接GC1，EG，∵GB∥C1F，且GB＝C1F，∴四边形C1FBG是平行四边形，∴FB∥C1G，且FB＝C1G，∵D1C1∥EG，且D1C1＝EG，∴四边形D1C1GE为平行四边形．∴GC1∥D1E，且GC1＝D1E，∴FB∥D1E，且FB＝D1E，∴四边形EBFD1为平行四边形．又∵FB＝FD1，∴四边形EBFD1是菱形．12．已知正方体ABCD—A1B1C1D1中，E、F分别为D1C1、C1B1的中点，AC∩BD＝P，A1C1∩EF＝Q.求证：(1)D、B、F、E四点共面；(2)若A1C交平面DBFE于R点，则P、Q、R三点共线．【证明】(1)如图所示，因为EF是△D1B1C1的中位线，所以EF∥B1D1.在正方体AC1中，B1D1∥BD，所以EF∥BD.所以EF，BD确定一个平面，即D、B、F、E四点共面．(2)在正方体AC1中，设平面A1ACC1确定的平面为α，又设平面BDEF为β.因为Q∈A1C1，所以Q∈α.又Q∈EF，所以Q∈β.则Q是α与β的公共点，同理，P点也是α与β的公共点．所以α∩β＝PQ.又A1C∩β＝R，所以R∈A1C，R∈α且R∈β.则R∈PQ，故P、Q、R三点共线．课后作业(四十三) 直线、平面平行的判定及其性质一、选择题1．(2013·威海模拟)设α、β是两个不同的平面，m、n是平面α内的两条不同直线，l1，l2是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是()A．m∥β且l1∥αB．m∥β且n∥l2C．m∥β且n∥βD．m∥l1且n∥l2【解析】m∥l1，且n∥l2⇒α∥β，但α∥βD/⇒m∥l1且n∥l2，∴“m∥l1，且n∥l2”是“α∥β”的一个充分不必要条件．【答案】 D2．在空间四边形ABCD中，E、F分别是AB和BC上的点，若AE∶EB＝CF∶FB＝1∶2，则对角线AC和平面DEF的位置关系是() A．平行B．相交C．在平面内D．不能确定【解析】如图，由AEEB＝CFFB得AC∥EF.又因为EF⊂平面DEF，AC⊄平面DEF，所以AC∥平面DEF.【答案】 A3．(2013·西安模拟)设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊥α，n∥α，则m⊥n；②若α∥β，β∥γ，m⊥α，则m⊥γ；③若m∥α，n∥α，则m∥n；④若α⊥γ，β⊥γ，则α∥β.其中正确命题的序号是()A．①和②B．②和③C．③和④D．①和④【解析】对于①，由线面平行的性质及线面垂直的定义可知正确；对于②，由α∥β，β∥γ知α∥γ，由m⊥α知m⊥γ，故②正确；对于③，m与n可能平行，相交或异面，故③错；对于④，α与β可能相交，故④错．【答案】 A4．(2013·石家庄模拟)给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题：①若l与m为异面直线，l⊂α，m⊂β，则α∥β；②若α∥β，l⊂α，m⊂β，则l∥m；③若α∩β＝l，β∩γ＝m，γ∩α＝n，l∥γ，则m∥n.其中真命题的个数为()A ．3B ．2C ．1D ．0【解析】 ①中当α与β不平行时，也可能存在符合题意的l 、m . ②中l 与m 也可能异面．③中⎭⎬⎫l ∥γl ⊂ββ∩γ＝m ⇒l ∥m ，同理l ∥n ，则m ∥n ，正确． 【答案】 C5．如图7－4－10所示，若Ω是长方体ABCD —A 1B 1C 1D 1被平面EFGH 截去几何体EFGHB 1C 1后得到的几何体，其中E 为线段A 1B 1上异于B 1的点，F 为线段BB 1上异于B 1的点，且EH ∥A 1D 1，则下列结论中不正确的．．．．是()图7－4－10A ．EH ∥FGB ．四边形EFGH 是矩形C ．Ω是棱柱D ．Ω是棱台【解析】 ∵EH ∥A 1D 1，∴EH ∥B 1C 1， ∴EH ∥平面BB 1C 1C .由线面平行性质，EH ∥FG . 同理EF ∥GH .且B 1C 1⊥面EB 1F .由直棱柱定义知几何体B 1EF —C 1HG 为直三棱柱， ∴四边形EFGH 为矩形，Ω为五棱柱．故选D. 【答案】 D6．在三棱锥P —ABC 中，点D 在P A 上，且PD ＝12DA ，过点D 作平行于底面ABC 的平面，交PB ，PC 于点E ，F ，若△ABC 的面积为9，则△DEF 的面积是( )A ．1B ．2C ．4D.94【解析】 由于平面DEF ∥底面ABC ，因此DE ∥AB ，DF ∥AC ，EF ∥BC ，所以DE AB ＝DF AC ＝EFBC ，所以△DEF ∽△ABC ，所以S △DEF S △ABC ＝(13)2，而S △ABC ＝9，所以S △DEF ＝1，故选A.【答案】 A 二、填空题7．在四面体A —BCD 中，M 、N 分别是△ACD 、△BCD 的重心，则四面体的四个面中与MN 平行的是________．【解析】 如图，取CD 的中点E .则EM ∶MA ＝1∶2，EN ∶BN ＝1∶2， 所以MN ∥AB .所以MN ∥面ABD ，MN ∥面ABC . 【答案】 面ABD 与面ABC8．如图7－4－11所示，棱柱ABC —A 1B 1C 1的侧面BCC 1B 1是菱形，设D 是A 1C 1上的点且A 1B ∥平面B 1CD ，则A 1D ∶DC 1的值为________．图7－4－11【解析】 设BC 1∩B 1C ＝O ，连接OD ，∵A1B∥平面B1CD且平面A1BC1∩平面B1CD＝OD，∴A1B∥OD，∵四边形BCC1B1是菱形，∴O为BC1的中点，∴D为A1C1的中点，则A1D∶DC1＝1.【答案】 19．(2013·徐州模拟)如图7－4－12所示，在四面体ABCD中，截面PQMN 是正方形，则在下列结论中，错误的为________．图7－4－12(1)AC⊥BD；(2)AC∥截面PQMN；(3)AC＝BD；(4)异面直线PM与BD所成的角为45°.【解析】∵PQMN是正方形，∴MN∥PQ，则MN∥平面ABC，由线面平行的性质知MN∥AC，则AC∥平面PQMN，同理可得MQ∥BD，又MN⊥QM，则AC⊥BD，故(1)(2)正确．又∵BD∥MQ，∴异面直线PM与BD所成的角即为∠PMQ＝45°，故(4)正确．【答案】(3)三、解答题10．在多面体ABCDEF中，点O是矩形ABCD的对角线的交点，三角形CDE是等边三角形，棱EF∥BC且EF＝12BC.求证：FO∥平面CDE.图7－4－13 【证明】取CD中点M，连接OM，EM，在矩形ABCD中，OM∥BC且OM＝12BC，又EF∥BC且EF＝12BC，则EF∥OM且EF＝OM.所以四边形EFOM为平行四边形，所以FO∥EM.又因为FO⊄平面CDE，且EM⊂平面CDE，所以FO∥平面CDE.11．在长方体ABCD—A1B1C1D1中，AB＝BC＝1，AA1＝2，点M是BC的中点，点N是AA1的中点．图7－4－14(1)求证：MN∥平面A1CD；(2)过N，C，D三点的平面把长方体ABCD—A1B1C1D1截成两部分几何体，求所截成的两部分几何体的体积的比值．【解】(1)证明取AD的中点P，A1D的中点E，连接NE、EC.又∵N是AA1的中点，∴NE 綊AP 綊MC ，∴四边形NECM 为平行四边形， ∴MN ∥EC ，又∵EC ⊂平面A 1CD ， MN ⊄平面A 1CD ， ∴MN ∥平面A 1CD .(2)取BB 1的中点Q ，连接NQ 、CQ 、ND ， 因为点N 是AA 1的中点，所以NQ ∥AB . 因为AB ∥CD ，所以NQ ∥CD ，所以过N 、C 、D 三点的平面NQCD 把长方体ABCD —A 1B 1C 1D 1截成两部分几何体，其中一部分几何体为直三棱柱QBC —NAD ，另一部分几何体为直四棱柱B 1QCC 1—A 1NDD 1.所以S △QBC ＝12QB ·BC ＝12×1×1＝12. 所以直三棱柱QBC —NAD 的体积 V 1＝S △QBC ·AB ＝12.因为长方体ABCD —A 1B 1C 1D 1的体积V ＝1×1×2＝2. 所以直四棱柱B 1QCC 1—A 1NDD 1的体积 V 2＝V －V 1＝32，所以V 1V 2＝1232＝13.所以所截成的两部分几何体的体积的比值为13.12．如图7－4－15所示，在四面体ABCD 中，截面EFGH 平行于对棱AB和CD .图7－4－15(1)判断截面的形状；(2)试问截面在什么位置时其截面面积最大． 【解】 (1)∵AB ∥平面EFGH ，平面EFGH 与平面ABC 和平面ABD 分别交于FG 、EH . ∴AB ∥FG ，AB ∥EH ，∴FG ∥EH ，同理可证EF ∥GH ，∴截面EFGH 是平行四边形． (2)设AB ＝a ，CD ＝b ，∠FGH ＝α.又设FG ＝x ，GH ＝y ， 则由平面几何知识可得x a ＝CG BC ，y b ＝BGBC ， 两式相加得x a ＋y b ＝1，即y ＝ba (a －x )， ∴S ▱EFGH ＝FG ·GH ·sin α＝x ·b a ·(a －x )·sin α＝b sin αa x (a －x )≤ab sin α4. ∵x ＞0，a －x ＞0，且x ＋(a －x )＝a 为定值． ∴当且仅当x ＝a －x ， x ＝a 2时，S ▱EFGH 最大为ab sin α4.即当截面EFGH 的顶点E 、F 、G 、H 为棱AD 、AC 、BC 、BD 的中点时，截面面积最大．课后作业(四十四) 直线、平面垂直的判定及其性质一、选择题1．(2013·宝鸡模拟)α、β、γ为不同的平面，m ，n ，l 为不同的直线，则m ⊥β的一个充分条件是()A．n⊥α，n⊥β，m⊥αB．α∩γ＝m，α⊥γ，β⊥γC．α⊥γ，β⊥γ，m⊥αD．α⊥β，α∩β＝l，m⊥l【解析】由n⊥α，n⊥β知α∥β，又m⊥α，∴m⊥β，但当m⊥β时，n⊥α，n⊥β不一定成立，故选A.【答案】 A2．(2013·深圳模拟)设a，b是两条不同的直线，α、β是两个不同的平面，则下列四个命题中正确命题的个数是()①若a⊥b，a⊥α，b⊄α，则b∥α；②若a∥α，a⊥β，则α⊥β；③若a⊥β，α⊥β，则a∥α或a⊂α；④若a⊥b，a⊥α，b⊥β，则α⊥β.A．1 B．2C．3 D．4【解析】由空间线面位置关系容易判断①②③④均正确．【答案】 D3．如图7－5－9，P A⊥正方形ABCD，下列结论中不正确的是()图7－5－9A．PB⊥BC B．PD⊥CDC．PD⊥BD D．P A⊥BD【解析】由CB⊥BA，CB⊥P A，P A∩BA＝A，知CB⊥平面P AB，故CB ⊥PB，即A正确；同理B正确；由条件易知D正确，故选C.【答案】 C4．(2013·银川模拟)如图7－5－10正方体ABCD—A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF＝12，则下列结论中错误的是()图7－5－10A．AC⊥BEB．EF∥平面ABCDC．三棱锥A—BEF的体积为定值D．△AEF的面积与△BEF的面积相等【解析】连接BD，则AC⊥平面BB1D1D，BD∥B1D1，从而A、B、C正确．因为点A、B到直线B1D1的距离不相等，所以△AEF与△BEF的面积不相等，故选D.【答案】 D5．如图7－5－11所示，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A—BCD.则在三棱锥A—BCD中，下列命题正确的是()图7－5－11A．AD⊥平面BCD B．AB⊥平面BCDC．平面BCD⊥平面ABC D．平面ADC⊥平面ABC【解析】在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD ＝90°，∴BD⊥CD，又平面ABD⊥平面BCD，且平面ABD∩平面BCD＝BD，∴CD⊥平面ABD，∴CD⊥AB，又AD⊥AB，故AB⊥平面ADC，从而平面ABC⊥平面ADC.【答案】 D6．(2013·杭州模拟)如图7－5－12，正三角形P AD所在平面与正方形ABCD 所在平面互相垂直，O为正方形ABCD的中心，M为正方形ABCD内一点，且满足MP＝MC，则点M的轨迹为()图7－5－12【解析】取AD的中点E，连接PE，PC，CE.由PE⊥AD知PE⊥平面ABCD，从而平面PEC⊥平面ABCD，取PC、AB的中点F、G，连接DF、DG、FG，由PD＝DC知DF⊥PC，由DG⊥EC知，DG⊥平面PEC，又PC⊂平面PEC，∴DG⊥PC，DF∩DG＝D，∴PC⊥平面DFG，又点F是PC的中点，因此线段DG上的点满足MP＝MC，故选A.【答案】 A二、填空题7．(2012·江苏高考)如图7－5－13，在长方体ABCD－A1B1C1D1中，AB＝AD ＝3 cm，AA1＝2 cm，则四棱锥A－BB1D1D的体积为________cm3.图7－5－13【解析】关键是求出四棱锥A－BB1D1D的高．连接AC 交BD 于O ，在长方体中，∵AB ＝AD ＝3，∴BD ＝32且AC ⊥BD .又∵BB 1⊥底面ABCD ，∴BB 1⊥AC .又DB ∩BB 1＝B ，∴AC ⊥平面BB 1D 1D ，∴AO 为四棱锥A －BB 1D 1D 的高且AO ＝12BD ＝322.∵S 矩形BB 1D 1D ＝BD ×BB 1＝32×2＝62，∴VA －BB 1D 1D ＝13S 矩形BB 1D 1D ·AO ＝13×62×322＝6(cm 3)．【答案】 68．如图7－5－14所示，在四棱锥P —ABCD 中，P A ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)．图7－5－14【解析】 由定理可知，BD ⊥PC .∴当DM ⊥PC 时，即有PC ⊥平面MBD ，而PC ⊂平面PCD .∴平面MBD ⊥平面PCD .【答案】 DM ⊥PC (答案不唯一)9．如图7－5－15所示，P A ⊥圆O 所在的平面，AB 是圆O 的直径，C 是圆O 上的一点，E 、F 分别是点A 在PB 、PC 上的正投影，给出下列结论：图7－5－15①AF ⊥PB ；②EF ⊥PB ；③AF ⊥BC ；④AE ⊥平面PBC .其中正确结论的序号是________．【解析】由题意知P A⊥平面ABC，∴P A⊥BC，又AC⊥BC，P A∩AC＝A，∴BC⊥平面P AC.∴BC⊥AF.∵AF⊥PC，BC∩PC＝C，∴AF⊥平面PBC，∴AF⊥PB，AF⊥BC.又AE⊥PB，AE∩AF＝A，∴PB⊥平面AEF.∴PB⊥EF.故①②③正确．【答案】①②③三、解答题10．(2012·江苏高考)如图7－5－16，在直三棱柱ABC－A1B1C1中，A1B1＝A1C1，D，E分别是棱BC，CC1上的点(点D不同于点C)，且AD⊥DE，F为B1C1的中点．图7－5－16求证：(1)平面ADE⊥平面BCC1B1；(2)直线A1F∥平面ADE.【证明】(1)因为ABC－A1B1C1是直三棱柱，所以CC1⊥平面ABC.又AD⊂平面ABC，所以CC1⊥AD.又因为AD⊥DE，CC1，DE⊂平面BCC1B1，CC1∩DE＝E，所以AD⊥平面BCC1B1.又AD⊂平面ADE，所以平面ADE⊥平面BCC1B1.(2)因为A1B1＝A1C1，F为B1C1的中点，所以A1F⊥B1C1.因为CC1⊥平面A1B1C1，且A1F⊂平面A1B1C1，所以CC1⊥A1F.又因为CC1，B1C1⊂平面BCC1B1，CC1∩B1C1＝C1，所以A 1F ⊥平面BCC 1B 1.由(1)知AD ⊥平面BCC 1B 1，所以A 1F ∥AD .又AD ⊂平面ADE ，A 1F ⊄平面ADE ，所以A 1F ∥平面ADE .11．(2013·济南模拟)如图7－5－17，在四棱锥S —ABCD 中，平面SAD ⊥平面ABCD .四边形ABCD 为正方形，且P 为AD 的中点，Q 为SB 的中点．图7－5－17(1)求证：CD ⊥平面SAD ；(2)求证：PQ ∥平面SCD ；(3)若SA ＝SD ，M 为BC 的中点，在棱SC 上是否存在点N ，使得平面DMN ⊥平面ABCD ，并证明你的结论．【解】 (1)证明 因为四边形ABCD 为正方形，所以CD ⊥AD .又平面SAD ⊥平面ABCD ，且平面SAD ∩平面ABCD ＝AD ，所以CD ⊥平面SAD .(2)证明 取SC 的中点R ，连接QR ，DR .由题意知：PD ∥BC 且PD ＝12BC .在△SBC 中，Q 为SB 的中点，R 为SC 的中点，所以QR ∥BC 且QR ＝12BC .所以QR ∥PD 且QR ＝PD ，则四边形PDRQ 为平行四边形，所以PQ ∥DR .又PQ ⊄平面SCD ，DR ⊂平面SCD ，所以PQ ∥平面SCD .(3)存在点N 为SC 的中点，使得平面DMN ⊥平面ABCD .连接PC 、DM 交于点O ，连接PM 、SP 、NM 、ND 、NO ，因为PD ∥CM ，且PD ＝CM ，所以四边形PMCD为平行四边形，所以PO＝CO.又因为N为SC的中点，所以NO∥SP.易知SP⊥AD，因为平面SAD⊥平面ABCD，平面SAD∩平面ABCD＝AD，并且SP⊥AD，所以SP⊥平面ABCD，所以NO⊥平面ABCD.又因为NO⊂平面DMN，所以平面DMN⊥平面ABCD.12．(2012·江西高考)如图7－5－18所示，在梯形ABCD中，AB∥CD，E、F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB＝12，AD＝5，BC＝42，DE＝4.现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合于点G，得到多面体CDEFG.图7－5－18(1)求证：平面DEG⊥平面CFG；(2)求多面体CDEFG的体积．【解】(1)证明因为DE⊥EF，CF⊥EF，所以四边形CDEF为矩形．由GD＝5，DE＝4，得GE＝GD2－DE2＝3.由GC＝42，CF＝4，得FG＝GC2－CF2＝4，所以EF＝5.在△EFG中，有EF2＝GE2＋FG2，所以EG⊥GF.又因为CF⊥EF，CF⊥FG，所以CF⊥平面EFG.所以CF⊥EG，所以EG⊥平面CFG.又EG⊂平面DEG，所以平面DEG⊥平面CFG.(2)如图，在平面EGF中，过点G作GH⊥EF于点H，则GH＝EG·GFEF＝125.因为平面CDEF ⊥平面EFG ， 所以GH ⊥平面CDEF ，所以V 多面体CDEFG ＝13S 矩形CDEF ·GH ＝16.。

立几大题训练题一、解答题（共50题；共505分）1. ( 10分) 已知四棱锥S−ABCD中，四边形ABCD为梯形，∠BCD=∠ADC=∠SAD=90°,平面SAD⊥平面ABCD，E为线段AD的中点，AD=2BC=2CD.（1）证明：BD⊥平面SAB；（2）若SA=AD=2，求点E到平面SBD的距离.2. ( 10分) 如图，平面ABCD∩平面ABEF=AB，四边形ABCD和ABEF都是边长为2的正方形，点M，N分别是AF，AB的中点，二面角D−AB−F的大小为60°.（1）求证：MN//平面BCF；（2）求直线DE与平面BCF所成角的正弦值.3. ( 10分) 如图，四棱锥P-ABCD的底面是正方形，E为AB的中点，PD⊥CE,AE=1,PD=3,PC=√13（1）证明：AD⊥平面PCD．（2）求DA与平面PCE所成角的正弦值.4. ( 10分) 如图所示，直三棱柱ABC−A1B1C1的各棱长均相等，点E为AA1的中点.（1）证明：EB1⊥BC1；（2）求二面角C1−EB1−C的余弦值.AD，G是PB的中点，5. ( 10分) 已知在四棱锥P−ABCD中，AD//BC，AB=BC=CD=12ΔPAD是等边三角形，平面PAD⊥平面ABCD.（1）求证：CD⊥平面GAC；（2）求二面角P−AG−C的余弦值.6. ( 10分) 如图，多面体ABCE中，平面AEC⊥平面ABC，AC⊥BC，AE⊥CD四边形BCDE 为平行四边形.（1）证明：AE⊥EC；（2）若AE=EC=CB=√2，求二面角D−AC−E的余弦值.7. ( 10分) 如图,在三棱锥A−BCD中, △ABC是等边三角形, ∠BAD=∠BCD=90°,点P是AC 的中点,连接BP,DP．（1）证明:平面ACD⊥平面BDP;（2）若BD=√6,且二面角A−BD−C为120°,求直线AD与平面BCD所成角的正弦值．8. ( 10分) 如图，在四棱锥P−ABCD中，AP⊥平面PCD，AD//BC，AB⊥BC，AP=AB=AD，E为AD的中点，AC与BE相交于点O.BC=12（1）证明：PO⊥平面ABCD.（2）若OB=1，求点C到平面PAB的距离.9. ( 10分) 如图，在斜三棱柱ABC−A1B1C1中，平面ABC⊥平面A1ACC1，CC1=2，△ABC，△ACC1，均为正三角形，E为AB的中点.（1）证明: AC1//平面B1CE，（2）求直线AC1与平面B1BAA1所成角的正弦值.10. ( 10分) 如图，四棱锥P−ABCD中，底面ABCD是边长为2的正方形，平面PAB⊥平面ABCD，AP=PB，AP⊥PB，E为CP的中点.（1）求证：AP//平面BDE；（2）求点D到平面ACP的距离.11. ( 10分) 在三棱柱ABC−A1B1C1中，已知AB=AC=AA1=√5，BC=4，O为BC的中点，A1O⊥平面ABC（1）证明四边形BB1C1C为矩形；（2）求直线AA1与平面A1B1C所成角的余弦值.12. ( 10分) 如图，四棱锥P−ABCD的底面是正方形，PA⊥平面ABCD，AE⊥PD.（1）证明：AE⊥平面PCD；（2）若AP=AB，求二面角B−PC−D的余弦值.13. ( 10分) 在直角梯形ABCD（如图1），∠ABC=90°，BC//AD，AD=8，AB=BC=4，M为线段AD中点.将△ABC沿AC折起，使平面ABC⊥平面ACD，得到几何体B−ACD（如图2）.（1）求证：CD⊥平面ABC；（2）求AB与平面BCM所成角θ的正弦值.14. ( 15分) 如图，四棱锥S−ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，SD=1.（1）求证BC⊥SC；（2）求平面SBC与平面ABCD所成二面角的大小；（3）设棱SA的中点为M，求异面直线DM与SB所成角的大小.15. ( 10分) 已知菱形ABCD的边长为4, AC∩BD=O, ∠ABC=60°,将菱形ABCD沿对角线BD折起,使AC=a,得到三棱锥A−BCD,如图所示.⇒（1）当a=2√2时,求证: AO⊥平面BCD;（2）当二面角A−BD−C的大小为120°时,求直线AD与平面ABC所成的正切值.16. ( 10分) 在四棱锥P–ABCD中，AB//CD，CD=2AB．⇀=mAP⇀(m>0)，且MN//平面PCD，求实数m的值；（1）设AC与BD相交于点M，AN（2）若AB=AD=DP，∠BAD=60°，PB=√2AD，且PD⊥AD，求二面角A−PC−B的余弦值．17. ( 10分) 如图，在四棱锥P−ABCD中，PA⊥平面ABCD，ABCD是正方形，E是CD中点，点F在BC上，且BF=3FC.（1）证明：EF⊥平面PAE；（2）若PA=AB=4，求点C到平面PEF的距离.18. ( 10分) 如图，在四棱锥P−ABCD中，PA⊥平面ABCD，ABCD是正方形，E是CD中点，点F在BC上，且BF=3FC.（1）证明EF⊥平面PAE；AB，求平面PAB与平面PEF所成二面角的正弦值.（2）若PA=5419. ( 10分) 如图（1），在平面五边形EADCB中，已知四边形ABCD为正方形，ΔEAB为正三角形.沿着AB将四边形ABCD折起得到四棱锥E−ABCD，使得平面ABCD⊥平面EAB，设F在线段AD上且满足DF=2AF，G在线段CF上且满足FG=CG，O为ΔECD的重心，如图（2）.（1）求证：GO//平面ABE；（2）求直线CF与平面BCE所成角的正弦值.20. ( 10分) 如图所示，在矩形ABCD中，AB=4，AD=2，E是CD的中点，O为AE的中点，以AE为折痕将ΔADE向上折起，使D点折到P点，且PC=PB.（1）求证: PO⊥面ABCE；（2）求AC与面PAB所成角θ的正弦值.21. ( 10分) 如图，在以A，B，C，D，E，F为顶点的多面体中，四边形ACDF是菱形，∠FAC=600,AB//DE,BC//EF,AB=BC=3,AF=2√3,BF=√15（1）求证：平面ABC⊥平面ACDF（2）求平面AEF与平面ACE所成的锐二面角的余弦值22. ( 10分) 已知四棱锥E−ABCD，AB=3，BC=4，CD=12，AD=13，cos∠ADC= 12，EC⊥平面ABCD.13（1）求证：平面ABE⊥平面EBC；（2）当CE=60时，求直线AC和平面ADE所成角的正弦值.23. ( 10分) 如图，在四棱锥P−ABCD中，四边形ABCD是直角梯形，AB⊥AD，AB//CD，PC⊥底面ABCD，AB=2AD=2CD=4，PC=2a，E是PB的中点.（1）求证：AC⊥平面PBC；，求直线PA与平面EAC所成角的正弦值.（2）若二面角P−AC−E的余弦值为√6324. ( 10分) 如图1，在等腰梯形ABF1F2中，两腰AF2=BF1=2，底边AB=6，F1F2=4，D，C是AB的三等分点，E是F1F2的中点.分别沿CE，DE将四边形BCEF1和ADEF2折起，使F1，F2重合于点F，得到如图2所示的几何体.在图2中，M，N分别为CD，EF的中点.（1）证明：MN⊥平面ABCD.（2）求直线CN与平面ABF所成角的正弦值.25. ( 15分) 如图，在四棱锥P一ABCD中，已知AB=BC=√5,AC=4,AD=DC=2√2，点Q为AC中点，PO⊥底面ABCD, PO=2，点M为PC的中点.（1）求直线PB与平面ADM所成角的正弦值；（2）求二面角D-AM-C的正弦值；（3）记棱PD的中点为N，若点Q在线段OP上，且NQ//平面ADM，求线段OQ的长.26. ( 10分) 如图，已知ΔABC为等边三角形，ΔABD为等腰直角三角形，AB⊥BD，平面ABC⊥平面ABD，点E与点D在平面ABC的同侧，且CE//BD，BD=2CE.点F为AD中点，连接EF.（1）求证：EF//平面ABC；（2）求二面角C−AE−D的余弦值.27. ( 10分) 如图，在四棱锥S−ABCD中，底面ABCD是直角梯形，AD//BC，AB⊥BC，ΔSAB 是等边三角形，侧面SAB⊥底面ABCD，AB=2√3，BC=3，AD=1，点M、点N分别在棱SB、棱CB上，BM=2MS，BN=2NC，点P是线段MN上的任意一点.（1）求证：AP//平面SCD；（2）求二面角S−CD−B的大小.28. ( 15分) 如图，四棱锥P−ABCD的底面是正方形，PA⊥底面ABCD，PA=AD=2，点M,N分别在棱PD,PC上，且PC⊥平面AMN.（1）求证：AM⊥PD；（2）求直线CD与平面AMN所成角的正弦值.（3）求二面角C−AM−N的余弦值29. ( 10分) 如图,四棱锥P−ABCD中, PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB= 60°, AB=2, AD=1.（1）求证: PA⊥BD;（2）若∠PCD=45°,求点D到平面PBC的距离ℎ.30. ( 10分) 在长方体ABCD−A1B1C1D1中，底面ABCD是边长为2的正方形，E是AB的中点，F是BC的中点.（1）求证：EF//平面A1DC1；（2）若AA1=2√3，求平面A1DC1与平面B1EF所成二面角的正弦值.31. ( 10分) 如图，在四棱锥P−ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，且PD= CD=1，过棱PC的中点E，作EF⊥PB交PB于点F.（1）证明：PA//平面EDB；，求PA与面ABCD所成角的正弦值．（2）若面DEF与面ABCD所成二面角的大小为π332. ( 5分) 如图，在三棱柱ABC−A1B1C1中，AA1⊥平面ABC，D是AB的中点，BC=AC，AB=2DC=2√2，AA1=4.（Ⅰ）求证：BC1//平面A1CD；（Ⅱ）求平面BCC1B1与平面A1CD所成锐二面角的平面角的余弦值.33. ( 10分) 如图，在三棱柱ABC−A1B1C1中，AA1⊥平面ABC，点D是AB的中点，BC= AC，AB=2DC=2，AA1=√3.（1）求证：平面A1DC⊥平面ABB1A1；（2）求点A到平面A1DC的距离.34. ( 10分) 如图，在平行六面体ABCD﹣A1B1C1D1中，AA1＝A1D，AB＝BC，∠ABC＝120°.（1）证明：AD⊥BA1；（2）若平面ADD1A1⊥平面ABCD，且A1D＝AB，求直线BA1与平面A1B1CD所成角的正弦值.35. ( 10分) 如图,在四棱锥P−ABCD中, PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP= 4,AB=BC=2, M,N为线段PC,AD上一点不在端点.AD，求证：MN∥面PBA（1）当M为中点时，AN=14，若存在（2）当N为AD中点时，是否存在M，使得直线MN与平面PBC所成角的正弦值为2√55求出M的坐标，若不存在，说明理由.36. ( 10分) 如图，正方体ABCD−A1B1C1D1的棱长为2，E为棱CC1的中点.（1）求 AD 1 与 DB 所成角的大小；（2）求 AE 与平面 ABCD 所成角的正弦值.37. ( 20分 ) 如图， E 是以 AB 为直径的半圆 O 上异于 A,B 的点，矩形 ABCD 所在的平面垂直于半圆 O 所在的平面，且 AB =2 ， AD =3（1）求证：平面 EAD ⊥ 平面 EBC ；（2）若 EB ⌢ 的长度为 π3，求二面角 A −DE −C 的正弦值． 38. ( 5分 ) 如图1，在直角梯形 ABCD 中，AB ∥CD ， AB ⊥AD ，且 AB =AD =12CD =1 ．现以 为一边向梯形外作正方形 ADEF ，然后沿边 AD 将正方形 ADEF 翻折，使平面 ADEF 与平面 ABCD 垂直，如图2．（Ⅰ）求证：BC ⊥平面DBE ；（Ⅱ）求点D 到平面BEC 的距离.39. ( 10分 ) 如图，扇形 AOB 的半径为 2 ，圆心角 ∠AOB =120∘ ，点 C 为弧 AB 上一点， PO ⊥ 平面 AOB 且 PO =√5 ，点 M ∈PB 且 BM =2MP ， PA ∥平面 MOC ．（1）求证：平面MOC⊥平面POB；（2）求平面POA和平面MOC所成二面角的正弦值的大小.40. ( 10分) 如图，已知四边形ABCD为等腰梯形，BDEF为正方形，平面BDEF⊥平面ABCD，AD//BC,AD=AB=1，∠ABC=60°.（1）求证:平面CDE⊥平面BDEF；（2）点M为线段EF上一动点，求BD与平面BCM所成角正弦值的取值范围.41. ( 10分) 如图，在四棱锥P-ABCD中，AD=2√3,AB=3,AP=√3,AD//BC，AD⊥平面PAB，∠APB=90°，点E满足PE⇀=23PA⇀+13PB⇀.（1）证明：PE⊥DC；（2）求二面角A-PD-E的余弦值.42. ( 10分) 在斜三棱柱ABC−A1B1C1中，侧面AC1⊥平面ABC，AA1=√2a，A1C=CA=AB=a，AB⊥AC，D是AA1的中点．（1）求证：CD⊥平面AB1；（2）在侧棱BB1上确定一点E，使得二面角E−A1C1−A的大小为π．343. ( 10分) 如图,在四棱锥P−ABCD中,侧面PAD⊥底面ABCD,底面ABCD为梯形，AB//CD,=2.∠ABC=∠BCD=90°,BC=CD=AB2（1）证明: BD⊥PD;（2）若△PAD为正三角形,求二面角A−PB−C的余弦值.44. ( 10分) 如图，已知四棱锥P−ABCD的底面为直角梯形，∠ADC为直角，AP⊥平面ABCD，BC:AD:CD=5:4:2，且CD=1.（1）求证：BP⊥AC；（2）若AP=CD，求二面角D−PC−B的余弦值.45. ( 10分) 如图，在四棱锥P−ABCD中，底面ABCD是矩形，PA⊥平面ABCD,PA=AD=2,AB=1, AM⊥PD于点M，连接BM.（1）求证：PD⊥BM；（2）求直线CD与平面ACM所成角的正弦值.BC=1，E是BC的中46. ( 10分) 如图所示1，已知四边形ABCD满足AD//BC，BA=AD=DC=12点.将△BAE沿着AE翻折成△B1AE，使平面B1AE⊥平面AECD，F为CD的中点，如图所示2.（1）求证：EF⊥平面AB1E；（2）求AE到平面CB1D的距离.47. ( 10分) 如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,∠BCD=135°,PA⊥平面ABCD,AB=AC=PA=2,E,F,M分别为线段BC,AD,PD的中点.（1）求证:直线EF⊥平面PAC;（2）求平面MEF与平面PBC所成二面角的正弦值.48. ( 5分) 如图，三棱柱A1B1C1−ABC中，BB1⊥平面ABC，AB⊥BC，AB=2，BC= 1，BB1=3，D是CC1的中点，E是AB的中点.（Ⅰ）证明：DE//平面C1BA1；（Ⅱ）F是线段CC1上一点，且直线AF与平面ABB1A1所成角的正弦值为1，求二面角F−3BA1−A的余弦值.49. ( 5分) 如图,在四棱锥P−ABCD中, PA⊥平面ABCD, AD⊥CD,AD//BC,BC=4,PA= AD=CD=2,点E为PC的中点.(I) 证明：DE//平面PAB;(II)求直线PB与平面PCD所成角的正弦值.50. ( 10分) 如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上的一点.（1）求证：平面PAC⊥平面PBC；（2）若AB=2 , AC=PA=1，求直线PA与平面PBC所成角的正弦值.答案解析部分一、解答题1.【答案】（1）解：由题意知∠BCD=∠ADC=90°，BC//ED,且BC=CD=12AD=DE，所以四边形BCDE是正方形，连接CE，所以BD⊥CE，又因为BC//AE，BC=AE，所以四边形ABCE是平行四边形，所以CE//AB，则BD⊥AB.因为平面SAD⊥平面ABCD，∠SAD=90°，平面SAD∩平面ABCD=AD，故SA⊥平面ABCD.所以SA∩AB=A，所以SA⊥BD，又因为SA∩AB=A，则BD⊥平面SAB.（2）解：∵SA=AD=2，BE=DE=1，∴△BDE的面积为12，又由（1）知SA⊥平面ABCD，∴V S−BDE=13×12×2=13，又在RtΔSAB中，SA=2，AB=DB=√2，∴SB=√6，由（1）知BD⊥SB，∴ΔSBD的面积为12×√2×√6=√3，设点E到平面SBD的距离为ℎ，则13S△BDS⋅ℎ=13，即ℎ=√33.【考点】直线与平面垂直的判定，点、线、面间的距离计算【解析】【分析】（1)利用线面垂直的判定定理，即可证得BD⊥平面SAB.（2）由（1）知SA⊥平面ABCD，求得V S−BDE=13，再根据等体积法，即可求解点点E到平面SBD的距离.2.【答案】（1）证明：∵M，N分别是AF，AB的中点，∴MN∥BF.∵MN⊄平面BCF，BF⊂平面BCF，∴MN//平面BCF.（2）解：∵四边形ABCD和ABEF都是边长为2的正方形，∴DA⊥AB，FA⊥AB，∴∠DAF就是二面角D−AB−F的平面角，∴∠DAF=60°.连接DM，在△DAM中，DA=2，AM=1，∠DAM=60°，∴DM2=AM2+AD2−2AM⋅AD⋅cos60°=3，∴DM=√3.∴DM2+AM2=AD2，∴DM⊥AM.∵DA⊥AB，FA⊥AB，FA∩DA=A，∴AB ⊥ 平面 ADM ， ∴AB ⊥DM .∴DM ⊥ 平面 ABEF .以点 M 为原点， MF ， MG （ G 是 BE 中点）， MD 所在直线分别为 x 轴， y 轴， z 轴建立如图空间直角坐标系，如图所示：则 D(0,0,√3) ， E(1,2,0) ， B(−1,2,0) ， F(1,0,0) ， A(−1,0,0) ，DE ⃗⃗⃗⃗⃗ =(1,2,−√3) ， BF ⃗⃗⃗⃗⃗ =(2,−2,0) ， BC ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ =(1,0,√3) .设平面 BCF 的法向量为 m⃗⃗ =(x,y,z) ， 则 {m ⇀⋅BF ⇀=2x −2y =0m ⇀⋅BC⇀=x +√3z =0 ，取 m ⃗⃗ =(√3,√3,−1) . 设直线 DE 与平面 BCF 所成角为 θ ，则 sinθ=|m⃗⃗⃗ ⋅DE ⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||DE ⃗⃗⃗⃗⃗⃗ |=√427 ，∴ 直线 DE 与平面 BCF 所成角的正弦值为 √427. 【考点】直线与平面平行的判定，用空间向量求直线与平面的夹角【解析】【分析】（1）根据三角形的中位线，有 MN ∥BF ，再利用线面平行的判定定理证明.（2）根据点 M ， N 分别是 AF ， AB 的中点，二面角 D −AB −F 的大小为60°，证明 DM ⊥ 平面 ABEF ，然后以点 M 为原点， MF ， MG （ G 是 BE 中点）， MD 所在直线分别为 x 轴， y 轴， z 轴建立如图空间直角坐标系，再求得平面 BCF 的一个法向量，利用线面角的向量求法求解.3.【答案】 （1）证明：因为E 为AB 的中点， AE =1 ，所以 CD =AB =2 ，所以 CD 2+PD 2=PC 2 ，从而 PD ⊥CD .又 PD ⊥CE ， CD ∩CE =C ，所以 PD ⊥ 底面ABCD ， 所以 PD ⊥AD .因为四边形ABCD 是正方形，所以 AD ⊥CD .又 CD ∩PD =D ，所以 AD ⊥ 平面PCD.（2）解：以D 为坐标原点，建立空间直角坐标系 D −xyz ，如图所示，则 A(2,0,0) ， P(0,0,3) ， E(2,1,0) ， C(0,2,0) ，所以 PE ⃗⃗⃗⃗⃗ =(2,1,−3) ， EC ⃗⃗⃗⃗⃗ =(−2,1,0) ， DA ⃗⃗⃗⃗⃗ =(2,0,0) .设平面PCE 的法向量为 n⃗ =(x,y,z) ， 则 PE ⃗⃗⃗⃗⃗ ⋅n ⃗ =EC ⃗⃗⃗⃗⃗ ⋅n ⃗ =0 ，即 {2x +y −3z =0−2x +y =0 ，令 x =3 ，得 n ⃗ =(3,6,4) . cos〈n ⃗ ,DA ⃗⃗⃗⃗⃗ 〉=n ⃗ ⋅DA ⃗⃗⃗⃗⃗⃗ |n ⃗ ||DA ⃗⃗⃗⃗⃗⃗ |=3√6161 ， 故DA 与平面PCE 所成角的正弦值为 3√6161 .【考点】直线与平面垂直的判定，用空间向量求直线与平面的夹角【解析】【分析】（1）通过证明 PD ⊥AD ， AD ⊥CD 即可证明线面垂直；（2）建立空间直角坐标系，利用向量方法求解线面角的正弦值.4.【答案】 （1）证明：设 BC 1 与 CB 1 交点为 O ，连接 OE ， BE .由题可知四边形 BCC 1B 1 为正方形，所以 BC 1⊥CB 1 ，且 O 为 BC 1 中点.又因 BE 2=AB 2+AE 2 ， C 1E 2=A 1E 2+A 1C 12 ，所以 BE =C 1E ，所以 BC 1⊥OE .又因为 OE ∩CB 1=O ，所以 BC 1⊥ 平面 EB 1C .因为 EB 1⊂ 平面 EB 1C ，所以 BC 1⊥EB 1 .（2）解：取 AB 的中点 O ′ ，连接 O ′C ， O ′C ⊥AB ，在平面 ABB 1A 1 过点 O ′ 内作 AB 的垂线，如图所示，建立空间直角坐标系 O ′−xyz .设 AB =2 ，则 E(0,−1,1) ， B 1(0,1,2) ， B(0,1,0) ， C 1(−√3,0,2) .所以 EB 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,1) ， EC 1⃗⃗⃗⃗⃗⃗⃗ =(−√3,1,1) .设平面 C 1EB 1 的一个法向量为 n ⃗ =(x,y,z) ，则 {n ⇀⋅EB1⇀=2y +z =0n ⇀⋅EC 1⇀=−√3x +y +z =0 ，令 y =√3 ，则 n ⃗ =(−1,√3,−2√3) . 由（1）可知平面 CEB 1 的一个法向量为 BC 1⃗⃗⃗⃗⃗⃗⃗ =(−√3,−1,2) ， 则 |cos〈BC 1⃗⃗⃗⃗⃗⃗⃗ ,n⃗ 〉|=|n ⃗ ⋅BC 1⃗⃗⃗⃗⃗⃗⃗⃗ ||n ⃗ |⋅|BC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=√3√3+1+4⋅√1+3+12=√64.由图可知二面角 C 1−EB 1−C 为锐角，所以其余弦值为 √64.【考点】空间中直线与直线之间的位置关系，用空间向量求平面间的夹角【解析】【分析】（1）通过证明 BC 1⊥ 平面 EB 1C 即可证得；（2）建立空间直角坐标系，利用向量求解.5.【答案】 （1）证明：取 AD 的中点为 O ，连结 OP ， OC ， OB ，设 OB 交 AC 于 H ，连结 GH . 因为 AD//BC ， AB =BC =CD =12AD ， 四边形 ABCO 与四边形 OBCD 均为菱形， ∴OB ⊥AC ， OB//CD ， CD ⊥AC ， 因为 △PAD 为等边三角形， O 为 AD 中点， ∴PO ⊥AD ，因为平面 PAD ⊥ 平面 ABCD ，且平面 PAD ∩ 平面 ABCD =AD .PO ⊂ 平面 PAD 且 PO ⊥AD ， ∴PO ⊥ 平面 ABCD 因为 CD ⊂ 平面 ABCD ， ∴PO ⊥CD ，因为H ， G 分别为 OB ， PB 的中点， ∴GH//PO ， ∴GH ⊥CD .又因为 GH ∩AC =H ， AC,GH ⊂ 平面 GAC ， ∴CD ⊥ 平面 GAC .（2）解：取 BC 的中点为 E ，以 O 为空间坐标原点，分别以 OE ⇀,OD ⇀,OP ⇀ 的方向为 x 轴、 y 轴、 z 轴的正方向，建立如图所示的空间直角坐标系 O −xyz .设 AD =4 ，则 P(0,0,2√3) ， A(0,−2,0) ， C(√3,1,0) ， D(0,2,0) ， G(√32,−12,√3)AP ⃗⃗⃗⃗⃗ =(0,2,2√3) ， AG ⇀=(√32,32,√3) ， 设平面 PAG 的一法向量 n →=(x,y,z) .由 {n ⇀⋅AP⇀=0n ⇀⋅AG ⇀=0 ⇒{2y +2√3z =0√32x +32y +√3z =0⇒{y =−√3z x =z .令 z =1 ，则 n ⃗ =(1,−√3,1) . 由（1）可知，平面 AGC 的一个法向量 CD ⃗⃗⃗⃗⃗ =(−√3,1,0) ， cos〈n ⇀,CD⇀〉=n ⇀⋅CD ⇀|n⇀||CD ⇀|=−√155∴ 二面角 P −AG −C 的平面角的余弦值为 −√155.【考点】直线与平面垂直的判定，用空间向量求平面间的夹角【解析】【分析】（1）取 AD 的中点为 O ，连结 OP ， OC ， OB ，设 OB 交 AC 于 H ，连结 GH .证明 AC ⊥CD ， GH ⊥CD ，即可证 CD ⊥ 平面 GAC ；（2）取 BC 的中点为 E ，以 O 为空间坐标原点，分别以 OE⇀,OD ⇀,OP ⇀ 的方向为 x 轴、 y 轴、 z 轴的正方向，建立如图所示的空间直角坐标系 O −xyz .设 AD =4 ，利用向量法求二面角 P −AG −C 的余弦值.6.【答案】 （1）解：因为平面 AEC ⊥ 平面 ABC ，交线为 AC ，又 AC ⊥BC ， 所以 BC ⊥ 平面 AEC ， ∴BC ⊥AE ，又 AE ⊥CD ， CD ∩BC =C ， 则 AE ⊥ 平面 BCDE ， EC ⊂ 平面 BCDE ， 所以， AE ⊥EC ；（2）解：取 AC 的中点 O ， AB 的中点 F ，连接 OE ， OF ，则 OE ⊥ 平面 ABC ， OF ⊥ 平面 AEC ；以点 O 为坐标原点，分别以 OA ， OF ， OE 为 x 轴， y 轴， z 轴建立空间直角坐标系如图所示，已知 AE =EC =CB =√2 ，则 AC =2 ， OE =1 ， O(0,0,0) ， A(1,0,0) ， C(−1,0,0) ， D(0,−√2,1) ， 则 AC⃗⃗⃗⃗⃗ =(−2,0,0) ， AD ⃗⃗⃗⃗⃗ =(−1,−√2,1) ， 设平面 DAC 的一个法向量 m⃗⃗ =(x,y,z) ， 由 {m ⇀⋅AC⇀=0,m ⇀⋅AD ⇀=0 得 {−2x =0,−x −√2y +z =0令 y =√2 ，则 x =0 ， z =2 ，即 m ⃗⃗ =(0,√2,2) ；平面 ECA 的一个法向量为 n ⃗ =(0,1,0) ； cos〈m ⃗⃗ ,n ⃗ 〉=m⃗⃗⃗ ⋅n ⃗ |m ⃗⃗⃗ ||n ⃗ |=√2√2+4=√33.所以二面角 D −AC −E 的余弦值为 √33.【考点】空间中直线与直线之间的位置关系，用空间向量求平面间的夹角【解析】【分析】（1）先通过平面 AEC ⊥ 平面 ABC 得到 BC ⊥AE ，再结合 AE ⊥CD ，可得 AE ⊥ 平面 BCDE ，进而可得结论；（2）取 AC 的中点 O ， AB 的中点 F ，连接 OE ， OF ，以点 O 为坐标原点，分别以 OA ， OF ， OE 为 x 轴， y 轴， z 轴建立空间直角坐标系，求出平面 DAC 的一个法向量以及平面 ECA 的一个法向量，求这两个法向量的夹角即可得结果. 7.【答案】 （1）证明:因为 △ABC 是等边三角形, ∠BAD =∠BCD =90° , 所以 Rt △ABD ≅Rt △CBD ,可得 AD =CD ． 因为点 P 是 AC 的中点,则 PD ⊥AC , PB ⊥AC , 因为 PD ∩PB =P , PD ⊂ 平面PBD, PB ⊂ 平面 PBD , 所以 AC ⊥ 平面 PBD ,因为 AC ⊂ 平面 ACD , 所以平面 ACD ⊥ 平面 BDP ．（2）解：如图,作 CE ⊥BD ,垂足为 E 连接 AE ．因为 Rt △ABD ⊆Rt △CBD ,所以 AE ⊥BD, AE =CE, ∠AEC 为二面角A-BD-C 的平面角． 由已知二面角 A −BD −C 为 120° ,知 ∠AEC =120° ． 在等腰三角形 AEC 中,由余弦定理可得 AC =√3AE ． 因为 △ABC 是等边三角形,则 AC =AB ,所以 AB =√3AE ． 在 Rt △ABD 中,有 12AE ⋅BD =12AB ⋅AD ,得 BD =√3AD , 因为 BD =√6 ,所以 AD =√2 ． 又 BD 2=AB 2+AD 2 ,所以 AB =2 ． 则 AE =2√33, ED =√63．以 E 为坐标原点,以向量 EC ⃗⃗⃗⃗⃗ , ED ⃗⃗⃗⃗⃗ 的方向分别为 x 轴, y 轴的正方向, 以过点 E 垂直于平面 BCD 的直线为 z 轴,建立空间直角坐标系 E −xyz ,则 D(0,√63,0) , A(−√33,0,1) ,向量 AD ⃗⃗⃗⃗⃗ =(√33,√63,−1) ,平面 BCD 的一个法向量为 m⃗⃗ =(0,0,1) , 设直线 AD 与平面 BCD 所成的角为 θ , 则 cos〈m ⃗⃗ ,AD ⃗⃗⃗⃗⃗ 〉=m⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ |m⃗⃗⃗ ||AD ⃗⃗⃗⃗⃗⃗ |=√2×1=−√22, sinθ=|cos〈m ⃗⃗ ,AD⃗⃗⃗⃗⃗ 〉|=√22所以直线 AD 与平面 BCD 所成角的正弦值为 √22．【考点】平面与平面垂直的判定，直线与平面所成的角，二面角的平面角及求法【解析】【分析】（1）由 △ABC 是等边三角形, ∠BAD =∠BCD =90° ,得 AD =CD ．再证明 PD ⊥AC , PB ⊥AC ,从而和证明 AC ⊥ 平面 PBD ,故平面 ACD ⊥ 平面 BDP 得证．（2）作 CE ⊥BD ,垂足为 E 连接 AE ．由 Rt △ABD ⊆Rt △CBD ,证得 AE ⊥BD, AE =CE, 结合二面角 A −BD −C 为 120° ,可得 AB =2 , AE =2√33, ED =√63 .建立空间直角坐标系,求出点的坐标则 D(0,√63,0) , A(−√33,0,1) ,向量AD ⃗⃗⃗⃗⃗ =(√33,√63,−1) ,即平面 BCD 的一个法向量 m ⃗⃗ =(0,0,1) ,运用公式 cos〈m ⃗⃗ ,AD ⇀〉=m ⃗⃗⃗ ⋅AD ⇀|m⃗⃗⃗ ||AD ⇀| 和 sinθ=|cos〈m ⃗⃗ ,AD ⇀〉| ,即可得出直线 AD 与平面 BCD 所成角的正弦值． 8.【答案】 （1）证明：∵ AP ⊥ 平面 PCD ，∴ AP ⊥CD . ∵ AD//BC ， BC =12AD ，∴四边形 BCDE 为平行四边形， ∴ BE//CD ， ∴ AP ⊥BE .又∵ AB ⊥BC ， AB =BC =12AD ，且 E 为 AD 的中点， ∴四边形 ABCE 为正方形，∴ BE ⊥AC .又 AP ∩AC =A ，∴ BE ⊥ 平面 APC ，则 BE ⊥PO . ∵ AP ⊥ 平面 PCD ，∴ AP ⊥PC ，又 AC =√2AB =√2AP ， ∴ ΔPAC 为等腰直角三角形， O 为斜边 AC 上的中点， ∴ PO ⊥AC 且 AC ∩BE =O ，∴ PO ⊥ 平面 ABCD .（2）解：∵ OB =1 ，∴ PA =PB =AB =√2 . 设 C 到平面 PAB 的距离为 d ， 由 V C−PAB =V P−ABC ，得 13×√34×(√2)2×d =13×12×(√2)2×1 ，解得 d =2√33.【考点】直线与平面垂直的判定，点、线、面间的距离计算【解析】【分析】（1）首项通过证明 AP ⊥CD,CD//BE ，证得 AP ⊥BE ，然后通过证明四边形 ABCE 是正方形证得 BE ⊥AC ，由此证得 BE ⊥ 平面 APC ，所以 BE ⊥PO .通过证明 ΔPAC 为等腰直角三角形证得 PO ⊥AC ，由此证得 PO ⊥ 平面 ABCD .（2）利用等体积法，由 V C−PAB =V P−ABC 列方程，解方程求得点 C 到平面 PAB 的距离.9.【答案】 （1）解：如图，连接 BC 1 ，交 B 1C 于点M ，连接ME ，则 ME//AC 1 . 因为 AC 1⊄ 平面 B 1CE ， ME ⊂ 平面 B 1CE ，所以 AC 1// 平面 B 1CE .（2）解：设O 是AC 的中点，连接 OC 1 ，OB.因为 △ACC 1 为正三角形， 所以 OC 1⊥AC ，又平面 ABC ⊥ 平面 A 1ACC 1 ，平面 ABC ∩ 平面 A 1ACC 1=AC ， 所以 OC 1⊥ 平面ABC.由已知得 AC =2 .如图，分别以射线OB ，OA ， OC 1 的方向为x ，y ，z 轴的正方向，建立空间直角坐标系，则有 A(0,1,0) ， B(√3,0,0) ， C 1(0,0,√3) ， A 1(0,2,√3) ， 故 AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,−1,√3) ， AB ⃗⃗⃗⃗⃗ =(√3,−1,0) ， AA 1⃗⃗⃗⃗⃗⃗⃗ =(0,1,√3) ， 设平面 B 1BAA 1 的一个法向量为 m⃗⃗ =(x,y,z) ，则 {AB ⇀⋅m ⇀=0AA 1⇀⋅m ⇀=0 ， 所以 {√3x −y =0y +√3z =0 令 x =1 ，则 m ⃗⃗ =(1,√3,−1) .设直线 AC 1 与平面 B 1BAA 1 所成的角为 θ ， 则 sinθ=|AC⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ ||AC⃗⃗⃗⃗⃗1|⋅|m⃗⃗⃗ |=√32×5=√155，故直线 AC 1 与平面 B 1BAA 1 所成角的正弦值为 √155.【考点】直线与平面平行的判定，直线与平面所成的角【解析】【分析】（1）如图，连接 BC 1 ，交 B 1C 于点M ，连接ME ，则 ME//AC 1 ，再利用线面平行的判定定理，即可证明线面平行；（2）设O 是AC 的中点，连接 OC 1 ，OB ，分别以射线OB ，OA ， OC 1 的方向为x ，y ，z 轴的正方向，建立空间直角坐标系，求出平面 B 1BAA 1 的一个法向量为 m ⃗⃗ =(1,√3,−1) ，设直线 AC 1 与平面 B 1BAA 1 所成的角为 θ ，代入公式 sinθ=|AC ⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ ||AC ⃗⃗⃗⃗⃗ 1|⋅|m⃗⃗⃗ | 运算，即可得答案.10.【答案】 （1）解：如图，连接 AC 交 BD 于 O ，连接 OE ，则 O 为 AC 的中点.又E为CP上的中点，所以OE//PA.又AP⊄平面BDE，OE⊂平面BDE，所以AP//平面BDE（2）解：如图，取AB的中点M，连接PM，因为AP⊥PB，AP=PB，所以PM⊥AB，PM=12AB=1，AP=PB=√2，又平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，PM⊂平面PAB，所以PM⊥平面ABCD.同理可得BC⊥平面PAB，∵AP、BP⊂平面PAB，∴BC⊥AP，BC⊥BP. 又因为AP⊥BP，BC∩BP=B，所以AP⊥平面BCP，∵PC⊂平面BCP，则AP⊥PC，所以PC=√PB2+BC2=√6，所以SΔAPC=12AP⋅PC=12×√2×√6=√3，又SΔACD=12×2×2=2，设点D到平面ACP的距离为ℎ，由V D−APC=V P−ACD，得13⋅SΔAPC⋅ℎ=13⋅PM⋅SΔACD，所以ℎ=3=2√33，即点D到平面ACP的距离为2√33.【考点】直线与平面平行的判定，点、线、面间的距离计算【解析】【分析】（1）连接AC交BD于O，则O为AC的中点，利用中位线的性质可得出OE//PA，然后利用直线与平面平行的判定定理可证明出AP//平面BDE；（2）取AB的中点M，连接PM，利用面面垂直的性质定理可得出PM⊥平面ABCD，由此可计算出三棱锥P−ACD的体积，并计算出ΔAPC的面积，并设点D到平面ACP的距离为ℎ，由V P−ACD=13SΔACP⋅ℎ可计算出点D到平面ACP的距离的值.11.【答案】（1）解：连接AO，因为O为BC的中点，可得BC⊥AO，∵ A 1O ⊥ 平面 ABC ， BC ⊂ 平面 ABC ，∴ A 1O ⊥BC ， 又∵ AO ∩A 1O =O ，∴ BC ⊥ 平面 AA 1O ，∴ BC ⊥AA 1 ， ∵ BB 1//AA 1 ， ∴ BC ⊥BB 1 ， 又∵四边形 BB 1C 1C 为平行四边形， ∴四边形 BB 1C 1C 为矩形；（2）解：如图，分别以 OA,OB,OA 1 所在直线为 x,y,z 轴，建立空间直角坐标系，则 A(1,0,0),B(0,2,0),C(0,−2,0),Rt △AOB 中， AO =√AB 2−BO 2=1 ， Rt △AA 1O 中， A 1O =√AA 12−AO 2=2 ，A 1(0,0,2) ，∴ AA 1⃗⃗⃗⃗⃗⃗⃗ =(−1,0,2) ， A 1C ⃗⃗⃗⃗⃗⃗⃗ =(0,−2,−2) ， A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ =(−1,2,0) ，设平面 A 1B 1C 的法向量是 n⃗ =(x,y,z) ， 由 {n ⇀⋅AB⇀=0,n ⇀⋅A 1C ⇀=0, 得 {−x +2y =0,−2y −2z =0, 即 {x =2y,z =−y, ，可取 n ⃗ =(2,1,−1) ， 设直线 AA 1 与平面 A 1B 1C 所成角为 θ ，则 θ∈[0,π2] ，sinθ=|cos <AA 1⃗⃗⃗⃗⃗⃗⃗ ,n ⃗ >| =|AA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||AA 1⃗⃗⃗⃗⃗⃗⃗⃗ |⋅|n ⃗ |=√5⋅√6=215√30 ， ∵ θ∈[0,π2] ，∴ cosθ=√1−sin 2θ=√10515，即直线 AA 1 与平面 A 1B 1C 所成角的余弦值为 √10515．【考点】直线与平面所成的角【解析】【分析】（1）连接 AO ，可得 BC ⊥AO ，易证 A 1O ⊥BC ，则 BC ⊥ 平面 AA 1O ，从而可证 BC ⊥BB 1 ，由此即可得出结论；（2）以 OA,OB,OA 1 所在直线分别为 x,y,z 轴建立空间直角坐标系，利用法向量解决问题．12.【答案】 （1）证明:因为 PA ⊥ 平面 ABCD , CD ⊂ 平面 ABCD , 所以 PA ⊥CD ,因为底面 ABCD 是正方形,所以 AD ⊥CD , 又 PA ∩AD =A ,所以 CD ⊥ 平面 PAD , 因为 AE ⊂ 平面 PAD ,所以 CD ⊥AE ,又因为 AE ⊥PD,CD ∩PD =D , CD,PD ⊂ 平面 PCD , 所以 AE ⊥ 平面 PCD（2）解：因为 PA ⊥ 平面 ABCD ,底面 ABCD 为正方形,所以 PA ⊥AB,PA ⊥AD,AB ⊥AD ,以 A 为原点,分别以 AB 、AD 、AP 所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系 A −xyz （如图所示）,设 PA =AB =1 ,则 A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,1) , 因为 AE ⊥PD ,所以 E 为 PD 中点,所以 E(0,12,12) , 所以 PB ⃗⃗⃗⃗⃗ =(1,0,−1),PC ⃗⃗⃗⃗⃗ =(1,1,−1),AE ⃗⃗⃗⃗⃗ =(0,12,12) , 由（1）得 AE ⃗⃗⃗⃗⃗ =(0,12,12) 为平面 PCD 的一个法向量, 设平面 PBC 的一个法向量为 m⃗⃗ =(x,y,z) , 由 {PB ⇀⋅m ⃗⃗ =0PC ⇀⋅m ⃗⃗ =0 ,即 {x −z =0x +y −z =0 ,令 x =1 ,则 z =1,y =0 ,所以 m ⃗⃗ =(1,0,1) , 因此 cos〈m⃗⃗ ,AE ⃗⃗⃗⃗⃗ 〉=m⃗⃗⃗ ⋅AE ⃗⃗⃗⃗⃗ |m⃗⃗⃗ |⋅|AE ⃗⃗⃗⃗⃗ |=12√2×√12=12, 由图可知二面角 B −PC −D 的大小为钝角, 故二面角 B −PC −D 的余弦值为 −12【考点】直线与平面垂直的判定，用空间向量求平面间的夹角【解析】【分析】（1）由 PA ⊥ 平面 ABCD 及底面 ABCD 是正方形可证得 CD ⊥ 平面 PAD ,则 CD ⊥AE ,又由 AE ⊥PD ,即可求证；（2）以 A 为原点,分别以 AB 、AD 、AP 所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系 A −xyz ,由（1）可知 AE ⃗⃗⃗⃗⃗ 为平面 PCD 的一个法向量,求得平面 PBC 的一个法向量 m ⃗⃗ ,进而利用数量积求解即可13.【答案】 （1）解：由题设可知 AC =4√2 ， CD =4√2 ， AD =8 ∴ AD 2=CD 2+AC 2 ∴ CD ⊥AC又∵平面 ABC ⊥ 平面 ACD ，平面 ABC ∩ 平面 ACD =AC ∴ CD ⊥ 面 ABC .（2）解：法一、等体积法取 AC 的中点 O 连接 OB ，由题设可知 △ABC 为等腰直角三角形，所以 OB ⊥ 面 ACM ∵ V B−ACM =V A−BCM 且 V B−ACM =13S ACM ⋅BO =16√23而 S ΔBCM =4√3∴ A 到面 BCM 的距离 ℎ=4√63，所以 sinθ=ℎAB =√63.法二、向量法取 AC 的中点 O 连接 OB ，由题设可知 △ABC 为等腰直角三角形，所以 OB ⊥ 面 ACM ，连接 OM ，因为 M 、O 分别为 AB 和 AC 的中点，所以 OM//CD ，由（1）可知 OM ⊥AC ，故以 OM 、OC 、OB 所在直线为 x 轴、 y 轴、 z 轴建立空间直角坐标系，如图所示. 则 A(0,−2√2,0) ， B(0,0,2√2) ， C(0,2√2,0) ， M(2√2,0,0) ∴ CB⃗⃗⃗⃗⃗ =(0,−2√2,2√2) CM ⃗⃗⃗⃗⃗⃗ =(2√2,−2√2,0) BA ⃗⃗⃗⃗⃗ =(0,−2√2,−2√2) ∴面 BCM 的一个法向量 n ⃗ =(1,1,1) ∴ sinθ=|BA⃗⃗⃗⃗⃗ ⋅n ⃗ ||BA ⃗⃗⃗⃗⃗ ||n⃗ |=√63【考点】直线与平面垂直的判定，直线与平面所成的角【解析】【分析】（1）通过计算结合勾股定理的逆定理可以证明 CD ⊥AC ，再根据面面垂直的性质定理进行证明即可；（2）法一、取 AC 的中点 O 连接 OB ，根据 V B−ACM =V A−BCM ，结合三棱锥的体积公式进行求解即可；法二、取 AC 的中点 O 连接 OB ，由题设可知 △ABC 为等腰直角三角形，所以 OB ⊥ 面 ACM ，连接 OM ，因为 M 、O 分别为 AB 和 AC 的中点，所以 OM//CD ，由（1）可知 OM ⊥AC ，故以 OM 、OC 、OB 所在直线为 x 轴、 y 轴、 z 轴建立空间直角坐标系，如图所示.运用向量法求解即可.14.【答案】 （1）证明：∵底面 ABCD 是正方形， ∴ BC ⊥CD ，∵ SD ⊥ 底面 ABCD ， BC ⊂ 底面 ABCD ，∴ SD ⊥BC ，又 DC ∩SD =D ， ∴ BC ⊥ 平面 SDC ，∵ SC ⊂ 平面 SDC ，∴ BC ⊥SC .（2）解：由（1）知 BC ⊥SC ，又 CD ⊥BC ，∴ ∠SCD 为所求二面角的平面角， 在 RtΔDSC 中，∵ SD =DC =1 ，∴ ∠SCD =45° .（3）解：取AB中点P，连结MP,DP，在ΔABS，由中位线定理得MP//SB，∴∠DMP或其补角是异面直线DM与SB所成角，∵MP=12SB=√32，DM=√22,DP=√1+14=√52，所以ΔDMP中，有DP2=MP2+DM2，∴∠DMP=90°.【考点】直线与平面垂直的判定，二面角的平面角及求法【解析】【分析】（1）根据题意，由线面垂直证线线垂直，再根据线面垂直的判定定理，证明线面垂直，再证线线垂直.（2）由（1）中线面垂直，可知所求二面角的平面角为∠SCD，根据题意可求角度.（3）利用中位线将异面直线平移，则∠DMP或其补角是异面直线DM与SB所成角，根据勾股定理，即可求解.15.【答案】（1）解：在△AOC中, OA=OC=2,AC=a=2√2,∴OA2+OC2=AC2∴∠AOC=90°,即AO⊥OC,∵AO⊥BD,且AO∩BD=O,∴AO⊥平面BCD（2）解：由(1)知, OC⊥OD,以O为原点, OC,OD所在的直线分别为x轴, y轴建立如图的空间直角坐标系O−xyz:则 Q(0,0,0), B(0,−2√3,0), C(2,0,0), D(0,2√3,0) . ∵AO ⊥BD,CO ⊥BD∴∠AOC 为二面角 A −BD −C 的平面角, ∴∠AOC =120° ∴ 点 A(−1,0,√3)AD⃗⃗⃗⃗⃗ =(1,2√3,−√3) , BA ⃗⃗⃗⃗⃗ =(−1,2√3,√3) , BC ⃗⃗⃗⃗⃗ =(2,2√3,0) 设平面 ABC 的法向量为 n⃗ =(x,y,z) ,则 ∴ {n ⃗ ⋅BC ⇀=0n ⃗ ⋅BA ⇀=0 故 {2x +2√3y =0x +2√3y +√3z =0 取 x =1 ,则 y =−√33,z =√3∴ n ⃗ =(1,−√33,√3)设直线 AD 与平面 ABC 所成的角为 θ , sinθ=|AD⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||AD ⃗⃗⃗⃗⃗⃗ ||n ⃗ |=4√133=√313 ∴cosθ=√1−sin 2θ=√1013 ∴tanθ=sinθcosθ=√310=√3010∴ 直线 AD 与平面 ABC 所成的正切值: √3010【考点】直线与平面垂直的判定，用空间向量求直线与平面的夹角，用空间向量求平面间的夹角 【解析】【分析】(1)根据线面垂直定义,即可求得答案.(2)由于平面 ABC 不是特殊的平面,故建系用法向量求解,以 O 为原点建系, OC,OD 所在的直线分别为 x 轴, y 轴,求出平面 ABC 的法向量 n ⃗ ,求解 AD ⃗⃗⃗⃗⃗ 和 n⃗ 的夹角,即可求得答案. 16.【答案】 （1）解：因为 AB//CD ，所以 AMMC =ABCD =12 ，即AM AC=13.因为 MN// 平面PCD ， MN ⊂ 平面PAC ，平面 PAC ∩ 平面 PCD =PC ， 所以 MN//PC ． 所以 ANAP =AM AC=13 ，即 m =13（2）解：因为 AB =AD ， ∠BAD =60° ，可知 △ABD 为等边三角形， 所以 BD =AD =PD ，又 BP =√2AD ， 故 BP 2=PD 2+DB 2 ，所以 PD ⊥DB ．由已知 PD ⊥AD ， AD ∩BD =D ，所以 PD ⊥ 平面ABCD ，如图，以D 为坐标原点， DA ⃗⃗⃗⃗⃗ ,DP⃗⃗⃗⃗⃗ 的方向为x ， y 轴的正方向建立空间直角坐标系，设 AB =1 ，则 AB =AD =DP =1 ， CD =2 ， 所以 A(1,0,0) ， B(12,0,√32) ， P(0,1,0) ， C(−1,0,√3) ，则 PB ⃗⃗⃗⃗⃗ =(12,−1,√32) ， PC ⃗⃗⃗⃗⃗ =(−1,−1,√3) ， PA ⃗⃗⃗⃗⃗ =(1,−1,0) 设平面PBC 的一个法向量为 n 1⃗⃗⃗⃗ =(x 1,y 1,z 1) ，则有 {n 1⇀⋅PB⇀=0n 1⇀⋅PC ⇀=0 即 {x 1−2y 1+√3z 1=0x 1+y 1−√3z 1=0. 令 x 1=1 ，则 y 1=2,z 1=√3 ，即 n 1⃗⃗⃗⃗ =(1,2,√3) ， 设平面APC 的一个法向量为 n 2⃗⃗⃗⃗ =(x 2,y 2,z 2) ，则有{n 2⇀⋅PA ⇀=0n 2⇀⋅PC ⇀=0，即 {x 2−y 2=0−x 2−y 2+√3z 2=0 令 x 2=y 2=√3 ，则 z 2=2 ，即 n 2⃗⃗⃗⃗ =(√3,√3,2) ． 所以 cos <n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ >=n 1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ |n 1⃗⃗⃗⃗⃗ |⋅|n 2⃗⃗⃗⃗⃗ |=√32√2×√10=√154设二面角 A −PC −B 的平面角为 θ ，则 cosθ=√154【考点】向量的共线定理，直线与平面平行的性质，用空间向量求平面间的夹角 【解析】【分析】（1）由AB ∥CD ， 得到AM AC=13 ，由MN ∥平面PCD ， 得MN ∥PC ， 从而 ANAP =AM AC=13，由此能实数m 的值；（2）由AB ＝AD ， ∠BAD ＝60°，知△ABD 为等边三角形，推导出PD ⊥DB ， PD ⊥AD ， 从而PD ⊥平面ABCD ， 以D 为坐标原点， DA ⃗⃗⃗⃗⃗ ，DP ⃗⃗⃗⃗⃗ 的方向为x ， y 轴的正方向建立空间直角坐标系，由此能求出二面角B ﹣PC ﹣B 的余弦值．17.【答案】 （1）证明：因为 PA ⊥ 平面 ABCD ， EF ⊂ 平面 ABCD ，故可得 EF ⊥PA ； 设底面正方形的边长为4，故可得 AE =√AD 2+DE 2=√16+4=2√5 ， EF =√FC 2+CE 2=√1+4=√5 ， AF =√AB 2+BF 2=√16+9=5 ， 故在 △AFE 中，满足 AE 2+EF 2=AF 2 ，故可得 AE ⊥EF ； 又 PA,AE ⊂ 平面 PAE ，且 PA ∩AE =A ， 则 EF ⊥ 平面 PAE ，即证.（2）解：因为 PA ⊥ 平面 ABCD ，故 PA 为三棱锥 P −EFC 底面上的高线.故可得V P−EFC=13S∆EFC×PA=13×12×1×2×4=43.在△PEF中，因为PE=√PA2+AE2=6，EF=√5，由（1）可知EF⊥平面PAE，又PE⊂平面PAE，故可得EF⊥PE，则S△PEF=12×EF×PE=3√5，设点C到平面PEF的距离为ℎ，故可得V P−EFC=V C−PEF=13×S∆PEF×ℎ=43，解得ℎ=4√515.即点C到平面PEF的距离为：4√515.【考点】直线与平面垂直的判定，点、线、面间的距离计算【解析】【分析】（1）根据PA⊥平面ABCD，可得EF⊥PN，再证EF⊥AE，即可由线线垂直推证线面垂直；（2）转换三棱锥顶点，用等体积法求点面距离即可.18.【答案】（1）证明：因为PA⊥平面ABCD，EF⊂平面ABCD，故可得EF⊥PA；设底面正方形的边长为4，故可得AE=√AD2+DE2=√16+4=2√5，EF=√FC2+CE2=√1+4=√5，AF=√AB2+BF2=√16+9=5，故在△AFE中，满足AE2+EF2=AF2，故可得AE⊥EF；又PA,AE⊂平面PAE，且PA∩AE=A，则EF⊥平面PAE，即证.（2）解：因为PA⊥平面ABCD, AB,AD⊂平面ABCD，故可得PA⊥AB,PA⊥AD，又底面ABCD为正方形，故可得AB⊥AD，故以A为坐标原点，以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系如下图所示：设AB=4，故可得A(0,0,0),P(0,0,5),B(4,0,0),E(2,4,0),F(4,3,0)设平面PEF的法向量为m⃗⃗ =(x,y,z)，则{m⃗⃗ ⋅EF⇀=0m⃗⃗ ⋅PE⇀=0，则{2x−y=02x+4y−5z=0取y=2，则m⃗⃗ =(1,2,2).不妨取平面PAB的法向量n⃗=(0,1,0).则cos〈m⃗⃗ ,n⃗ 〉=m⃗⃗⃗ ⋅n⃗|m⃗⃗⃗ ||n⃗ |=√9×1=23.。

1、如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（1）线段的中点为，线段的中点为，求证：；（2）求直线与平面所成角的正切值.解：（1）取的中点为，连,,则,面/面, .............. 分5（2）先证出面，.............. 分8为直线与平面所成角，................ 分11................ 分142、己知多面体ABCDE中，DE平面ACD,, AC=AD=CD=DE=2 AB =1, O 为CD 的中点.（1）求证：AO平面CDE（2）求直线BD与平面CBE所成角的正弦值3、如图，在△中，，，点在上，交于，交于•沿将△翻折成△，使平面平面；沿将△翻折成△ ，使平面平面．（ 1 ）求证：平面；（2 ）若，求二面角的平面角的正切值.解：（1）因为，平面，所以平面.因为平面平面，且，所以平面. …2分同理，平面，所以，从而平面. …4分所以平面平面，从而平面.2)因为，，所以，，，．过E作，垂足为M，连结.由( 1)知，可得，所以，所以.所以即为所求二面角的平面角，可记为.在Rt△中，求得，所以. …4、如图，平面ABC,平面BCD, DE=DA=AB=AC,. M(1) 求直线EM与平面BCD所成角的正弦值；(2) P为线段DM上一点，且DM，求证：AP//DE. (12)分15 分为BC中点.解：(1) 平面,为在平面上的射影,为与平面所成角. …分2平面,, 设,又,. 在△中，，，又为中点，， ,.…5分在△中，，．……………………分 (7)2),为中点, ．又平面, ,平面．又平面,,分11 …分9又，平面. .............. 分13又平面，. .............. 分145、如图，已知ABCD是边长为1的正方形，AF丄平面ABCD, CE// AF,(1)证明：BD丄EF;(2)若AF= 1，且直线BE与平面ACE所成角的正弦值为,求的值.解：(1)连结BD、AC,交点为O. •/ ABCD是正方形/• BD丄AC ……2分•/ AF丄平面ABCD A AF丄BD ……4分••• BD丄平面ACEF (6)A BD丄EF ……7分(2)连结0E,由(1)知，BD丄平面ACEF所以/ BEO即为直线BE与平面ACE所成的角. ……10分•/ AF丄平面ABCD, CE// AF , • CE丄平面ABCD, CE1 BC,•/ BC =1 , AF= 1 ,贝U CE= , BE= , B0=,• RtA BEO 中，，…1盼因为解得. …… 15分6、如图在几何体中平面ABC分别是的中点.(1) 求证：平面CDE；(2) 求二面角的平面角的正切值.解：(1)连接ACR1R交EC于点F ,由题意知四边形ACCR1RE是矩形,贝U F是ACR1R的中连接DF, •/ D是AB的中点，•ABCR1R勺中位线，a BCR1R//DF， 4 分•/ BCR1RF面EDC DF平面EDC,• BCR1R//平面CDE. 7 分(2)作AH丄直线CD,垂足为H ,连接HE,•/ AAR1R丄平面ABC, • AAR1RL DC,CD丄平面AHE,CD丄EH ,••• AHE是二面角E -CD -A的平面角. 11分•/ D是AB的中点，• AH等于点B到CD的距离，在厶BCD中，求得：AH=, 在厶AEH中，即所求二面角的正切值为.7、如图，已知平面与直线均垂直于所在平面，且,( 1 )求证：平面；(2)若，求与平面所成角的正弦值.解：(1)证明：过点作于点，•••平面丄平面，•平面……2分又•••丄平面•- 〃 , ......... 分又•••平面• 〃平面 ......... 分(2) •••平面•,又•/••………………分8•点是的中点，连结，则•平面•//,•四边形是矩形………………分10设得：，又•••，•，从而，过作于点，则：•是与平面所成角…………………………………………分…… •，• 与平面所成角的正弦值为…………………………分14&如图，在直三棱柱中，是等腰直角三角形，，侧棱AA仁2, D, E分别为点，点E在平面ABD上的射影是的重心.(1) 求证：DE// 平面ACB；(2) 求A1B与平面ABD所成角的正弦值.12CC1 与A1B 的中9、如图，在侧棱垂直于底面的三棱柱ABC-A1B1中，底面△ ABC为等腰直角三角形，/ B=90°D为棱BB1的中点。

高中数学必修二第八章立体几何初步专项训练题单选题1、直角三角形的三边满足a<b<c，分别以a，b，c三边为轴将三角形旋转一周所得旋转体的体积记为V a、V b、V c，则（）A．V c<V b<V a B．V a<V b<V c C．V c<V a<V b D．V b<V a<V c答案：A解析：求出V a=b×13abπ，V b=a×13abπ，V c=abc×13abπ，推导出abc<a<b，从而得到V c<V b<V a．∵直角三角形的三边满足a<b<c，分别以a、b、c三边为轴将三角形旋转一周所得旋转体的体积记为V a、V b、V c，∴V a=13×π×b2×a=13πab2=b×13abπ，V b=13×π×a2×b=13πa2b=a×13abπ，该直角三角形斜边上的高ℎ满足12ab=12cℎ，可得ℎ=abc，V c=13×π×(abc)2×c=13π⋅a2b2c=abc×13abπ，∵abc −a=ab−acc<0，abc−b=ab−bcc<0，∴abc<a<b，∴V c<V b<V a，故选：A.小提示：关键点点睛：本题考查旋转体体积的大小比较，解题的关键就是确定旋转体的形状，并据此求出对应的旋转体的体积，结合作差法比较即可.2、如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱的底面是顶角为120°，腰为3的等腰三角形，则该几何体的体积为（）A．23B．24C．26D．27答案：D分析：作出几何体直观图，由题意结合几何体体积公式即可得组合体的体积.该几何体由直三棱柱AFD −BHC 及直三棱柱DGC −AEB 组成，作HM ⊥CB 于M ，如图，因为CH =BH =3,∠CHB =120∘，所以CM =BM =3√32,HM =32， 因为重叠后的底面为正方形，所以AB =BC =3√3,在直棱柱AFD −BHC 中，AB ⊥平面BHC ，则AB ⊥HM ,由AB ∩BC =B 可得HM ⊥平面ADCB ，设重叠后的EG 与FH 交点为I,则V I−BCDA =13×3√3×3√3×32=272,V AFD−BHC =12×3√3×32×3√3=814则该几何体的体积为V =2V AFD−BHC −V I−BCDA =2×814−272=27.故选：D. 3、直三棱柱ABC −A 1B 1C 1中，若∠BAC =90°，AB =AA 1=1，AC =2，E 是棱A 1C 1上的中点，则点A 到平面BCE 的距离是（ ）A ．1B ．√23C ．√63D ．√33答案：C分析：作出草图，根据题意易证A 1C 1⊥平面AA 1BB 1，可得A 1C 1⊥BA 1，再根据勾股定理分别求出A 1B ，BE ，CE，BC的值，再根据V A−BCE=V E−ABC，即可求出点A到平面BCE的距离.如图，在直三棱柱ABC−A1B1C1中，连接BA1,CE,AE,BE，由题知，AA1⊥平面A1B1C1，AA1⊥A1C1,AA1⊥A1B1，又∠CAB=∠C1A1B1=90°，∴B1A1⊥A1C1又AA1∩B1A1=A1，所以A1C1⊥平面AA1BB1，所以A1C1⊥BA1，由于AB=AA1=CC1=1,A1C1=AC=2，E点是棱AC上的中点，根据勾股定理，A1B=√AB2+AA12=√12+12=√2，BE=√A1B2+A1E2=√(√2)2+12=√3 CE=√(C1C)2+(C1E)2=√12+12=√2，BC=√AB2+AC2=√12+22=√5，所以BE2+CE2=BC2，即BE⊥CE.设E到平面ABC的距离为d，则d=1，设点A到平面BCE的距离为ℎ，在四面体A−BCE中，V A−BCE=V E−ABC，V E−ABC=13×S△ABC×d=13×(12×1×2)×1=13V A−BCE=13×S△BCE×ℎ=13×(12×√3×√2)×ℎ=√66ℎ则√66ℎ=13，解得ℎ=√63.故选：C.4、如图1，已知PABC是直角梯形，AB∥PC，AB⊥BC，D在线段PC上，AD⊥PC．将△PAD沿AD折起，使平面PAD⊥平面ABCD，连接PB，PC，设PB的中点为N，如图2．对于图2，下列选项错误的是（）A．平面PAB⊥平面PBC B．BC⊥平面PDCC．PD⊥AC D．PB＝2AN答案：A分析：由已知利用平面与平面垂直的性质得到PD⊥平面ABCD，判定C正确；进一步得到平面PCD⊥平面ABCD，结合BC⊥CD判定B正确；再证明AB⊥平面PAD，得到△PAB为直角三角形，判定D正确；可证明平面PBC⊥平面PDC，若平面PAB⊥平面PBC，则平面PAB与平面PDC的交线⊥平面PBC，矛盾，可判断A图1中AD⊥PC，则图2中PD⊥AD，又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，∴PD⊥平面ABCD，则PD⊥AC，故选项C正确；由PD⊥平面ABCD，PD⊂平面PDC，得平面PDC⊥平面ABCD，而平面PDC∩平面ABCD＝CD，BC⊂平面ABCD，BC⊥CD，∴BC⊥平面PDC，故选项B正确；∵AB⊥AD，平面PAD⊥平面ABCD，且平面PAD∩平面ABCD＝AD，∴AB⊥平面PAD，则AB⊥PA，即△PAB是以PB为斜边的直角三角形，而N为PB的中点，则PB＝2AN，故选项D正确．由于BC⊥平面PDC，又BC⊂平面PBC∴平面PBC⊥平面PDC若平面PAB ⊥平面PBC ，则平面PAB 与平面PDC 的交线⊥平面PBC由于AB//平面PDC ，则平面PAB 与平面PDC 的交线//AB显然AB 不与平面PBC 垂直，故A 错误故选：A5、在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑A −BCD 中，AB ⊥平面BCD ，BC ⊥CD ，且AB =BC =CD =4，M 为AD 的中点，则异面直线BM 与CD 夹角的余弦值为（ ）A ．√32B ．√34C ．√33D ．√24答案：C分析：画出图形，取AC 的中点N ，连接MN ，BN ，可得MN //CD ，则所求为∠BMN ，易证△BMN 是直角三角形，则可得BM ，进而求解.如图，取AC 的中点N ，连接MN ，BN ，由题，AB =BC =CD =4，M 为AD 的中点，所以MN //CD ，MN =2，则∠BMN 为所求，由AB ⊥平面BCD ，则AB ⊥CD ，又BC ⊥CD ，AB ∩BC =B ，所以CD ⊥平面ABC ，则MN ⊥平面ABC ，所以△BMN 是直角三角形，即∠MNB =90°，又BM =12AD =12√AB 2+BD 2=2√3，所以cos∠BMN =MN BM =2√3=√33， 故选：C6、若直线a //平面α，A ∉α，且直线a 与点A 位于α的两侧，B ，C ∈a ，AB ，AC 分别交平面α于点E ，F ，若BC =4，CF =5，AF =3，则EF 的长为（ ）A ．3B ．32C ．34D ．23 答案：B分析：根据线面平行可得线线平行，从而可求EF =32. ∵BC //α，BC ⊂平面ABC ，平面ABC ∩α=EF ，∴EF //BC ，∴AF AC =EF BC ，即35+3=EF 4，∴EF =32. 故选：B.7、一个正方体的平面展开图及该正方体的直观图如图所示，在正方体中，设BC 的中点为M ，GH 的中点为N ，下列结论正确的是（ ）A ．MN//平面ABEB ．MN//平面ADEC ．MN//平面BDHD ．MN//平面CDE答案：C解析：根据题意，得到正方体的直观图及其各点的标记字母，取FH的中点O,连接ON,BO，可以证明MN‖BO,利用BO与平面ABE的关系可以判定MN与平面ABE的关系，进而对选择支A作出判定；根据MN与平面BCF的关系，利用面面平行的性质可以判定MN与平面ADE的关系，进而对选择支B作出判定；利用线面平行的判定定理可以证明MN与平面BDE的平行关系，进而判定C；利用M,N在平面CDEF的两侧，可以判定MN与平面CDE 的关系，进而对D作出判定.根据题意，得到正方体的直观图及其各点的标记字母如图所示，取FH的中点O,连接ON,BO，易知ON与BM平行且相等，∴四边形ONMB为平行四边形，∴MN‖BO,∵BO与平面ABE（即平面ABFE)相交，故MN与平面ABE相交，故A错误；∵平面ADE‖平面BCF,MN∩平面BCF=M,∴MN与平面ADE相交，故B错误；∵BO⊂平面BDHF,即BO‖平面BDH,MN‖BO,MN⊄平面BDHF,∴MN‖平面BDH,故C正确；显然M,N在平面CDEF的两侧，所以MN与平面CDEF相交，故D错误.故选：C.小提示：本题考查从面面平行的判定与性质，涉及正方体的性质，面面平行，线面平行的性质，属于小综合题，关键是正确将正方体的表面展开图还原，得到正方体的直观图及其各顶点的标记字母，并利用平行四边形的判定与性质找到MN的平行线BO.8、已知正方体ABCD−A1B1C1D1的棱长为2，点P在棱AD上，过点P作该正方体的截面，当截面平行于平面B1D1C且面积为√3时，线段AP的长为（）A．√2B．1C．√3D．√32答案：A分析：过点P作DB，A1D的平行线，分别交棱AB，AA1于点Q，R，连接QR，BD，即可得到△PQR为截面，且为等边三角形，再根据截面面积求出PQ的长度，即可求出AP；解：如图，过点P作DB，A1D的平行线，分别交棱AB，AA1于点Q，R，连接QR，BD，因为BD//B1D1，所以PQ//B1D1，B1D1⊂面B1D1C，PQ⊄面B1D1C，所以PQ//面B1D1C因为A1D//B1C，所以PR//B1C，B1C⊂面B1D1C，PR⊄面B1D1C，所以PR//面B1D1C又PQ∩PR=P，PQ,PR⊂面PQR，所以面PQR//面B1D1C，则PQR为截面，易知△PQR是等边三角形，则12PQ2⋅√32=√3，解得PQ=2，∴AP=√22PQ=√2.故选：A.多选题9、如图，在菱形ABCD中，AB＝2，∠BAD＝60°，将△ABD沿对角线BD翻折到△PBD位置，连结PC，则在翻折过程中，下列说法正确的是（）A．PC与平面BCD所成的最大角为45°B．存在某个位置，使得PB⊥CDC．当二面角P﹣BD﹣C的大小为90°时，PC=√6D．存在某个位置，使得B到平面PDC的距离为√3答案：BC分析：A，取BD的中点O，连接OP、OC，则OP＝OC=√3．可得PC与平面BCD所成的角为∠PCO，当PC=√3时∠PCO＝60°＞45°，即可判断；B，当点P在平面BCD内的投影为△BCD的重心点Q时，可得PB⊂平面PBQPB⊥CD，即可判断；C，当二面角P﹣BD﹣C的大小为90°时，平面PBD⊥平面BCD，即可得△POC为等腰直角三角形，即可判断；D，若B到平面PDC的距离为√3，则有DB平面PCD，即DB⊥CD，与△BCD是等边三角形矛盾．解：选项A，取BD的中点O，连接OP、OC，则OP＝OC=√3．由题可知，△ABD和△BCD均为等边三角形，由对称性可知，在翻折的过程中，PC与平面BCD所成的角为∠PCO，当PC=√3时，△OPC为等边三角形，此时∠PCO＝60°＞45°，即选项A错误；选项B，当点P在平面BCD内的投影为△BCD的重心点Q时，有PQ⊥平面BCD，BQ⊥CD，∴PQ⊥CD，又BQ∩PQ＝Q，BQ、PQ⊂平面PBQ，∴CD⊥平面PBQ，∵PB⊂平面PBQ，∴PB⊥CD，即选项B正确；选项C，当二面角P﹣BD﹣C的大小为90°时，平面PBD⊥平面BCD，∵PB＝PD，∴OP⊥BD，∵平面PBD∩平面BCD＝BD，∴OP⊥平面BCD，∴OP⊥OC，又OP＝OC=√3，∴△POC为等腰直角三角形，∴PC=√2OP=√6，即选项C正确；选项D，∵点B到PD的距离为√3，点B到CD的距离为√3，∴若B到平面PDC的距离为√3，则平面PBD⊥平面PCD．平面CBD⊥平面PCD，则有DB平面PCD，即DB⊥CD，与△BCD是等边三角形矛盾．故选：BC．10、如图是正方体的平面展开图，在这个正方体中，下列结论正确的是（）A．BM与ED平行B．CN⊥AFC．CN与BM成60°D．四条直线AF、BM、CN、DE中任意两条都是异面直线答案：BCD分析：还原成正方体之后根据正方体性质分析线线位置关系.根据展开图还原正方体如图所示：BM与ED不平行，所以A错误；正方体中CN⊥DM，DM//FA，所以CN⊥AF，所以B正确；CN//EB，CN与BM成角就是∠EBM，△EBM是等边三角形，所以∠EBM=60°，所以C正确；由图可得四条直线AF、BM、CN、DE中任意两条既不想交也不平行，所以任意两条都是异面直线. 故选：BCD11、下图是一个正方体的平面展开图，则在该正方体中（）A．AE//CD B．CH//BE C．DG⊥BH D．BG⊥DE答案：BCD分析：由平面展开图还原为正方体，根据正方体性质即可求解.由正方体的平面展开图还原正方体如图，由图形可知，AE⊥CD，故A错误；由HE//BC,HE=BC，四边形BCHE为平行四边形，所以CH//BE，故B正确；因为DG⊥HC,DG⊥BC,HC∩BC=C,所以DG⊥平面BHC,所以DG⊥BH，故C正确；因为BG//AH，而DE⊥AH,所以BG⊥DE，故D正确.故选：BCD填空题12、已知a，b表示两条直线，α，β，γ表示三个不重合的平面，给出下列命题：①若α∩γ=a，β∩γ=b，且a//b，则α//β；②若a，b相交且都在α，β外，a//α，b//β，则α//β；③若a//α，a//β，则α//β；④若a⊂α，a//β，α∩β=b，则a//b.其中正确命题的序号是________.答案：④分析：根据线线、线面、面面之间的位置关系即可得出结果.解析：①错误，α与β也可能相交；②错误，α与β也可能相交；③错误，α与β也可能相交；④正确，由线面平行的性质定理可知.所以答案是：④13、中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知PA⊥平面ABCE，四边形ABCD为正方形，AD=√5，ED=√3，若鳖臑P−ADE 的外接球的体积为9√2π，则阳马P−ABCD的外接球的表面积等于______.答案：20π解析：求出鳖臑P−ADE的外接球的半径R1，可求出PA，然后求出正方形ABCD的外接圆半径r2，利用公式R2=√(PA2)2+r22可求出阳马P−ABCD的外接球半径R2，然后利用球体的表面积公式可得出答案.∵四边形ABCD是正方形，∴AD⊥CD，即AD⊥CE，且AD=√5，ED=√3，所以，ΔADE的外接圆半径为r1=AE2=√AD2+ED22=√2，设鳖臑P−ADE的外接球的半径R1，则43πR13=9√2π，解得R1=3√22.∵PA⊥平面ADE，∴R1=√(PA2)2+r12，可得PA2=√R12−r12=√102，∴PA=√10.正方形ABCD的外接圆直径为2r2=AC=√2AD=√10，∴r2=√102，∵PA⊥平面ABCD，所以，阳马P−ABCD的外接球半径R2=√(PA2)2+r22=√5，因此，阳马P−ABCD的外接球的表面积为4πR22=20π.所以答案是：20π.小提示：本题考查球体表面积和体积的计算，同时也涉及了多面体外接球问题，解题时要分析几何体的结构特征，考查分析问题和解决问题的能力，属于中等题.14、词语“堑堵”、“阳马”、“鳖臑”等出现自中国数学名著《九章算术・商功》，是古代人对一些特殊锥体的称呼．在《九章算术・商功》中，把四个面都是直角三角形的四面体称为“鳖臑”．现有如图所示的“鳖臑”四面体PABC，其中PA⊥平面ABC，PA=AC=2，BC=2√2，则四面体PABC的外接球的表面积为______．答案：16π分析：确定外接球球心求得球半径后可得表面积．由于PA⊥平面ABC，因此PA与底面上的直线AC,AB,BC都垂直，从而AC与AB不可能垂直，否则△PBC是锐角三角形，由于AC<BC，因此有AC⊥BC，而PA与AC是平面PAC内两相交直线，则BC⊥平面PAC，PC⊂平面PAC，所以BC⊥PC，所以PB的中点O到P,A,B,C四个点的距离相等，即为四面体PABC的外接球球心．PB2=PA2+AB2=PA2+AC2+BC2=22+22+(2√2)2=16，PB=4，)2=4π×22=16π．所以所求表面积为S=4π×(PB2所以答案是：16π．解答题15、如图，四边形ABCD是一个半圆柱的轴截面，E，F分别是弧DC，AB上的一点，EF//AD，点H为线段AD 的中点，且AB=AD=4，∠FAB=30°，点G为线段CE上一动点.(1)试确定点G的位置，使DG//平面CFH，并给予证明；(2)求三棱锥E−CFH的体积.答案：(1)点G为线段CE中点，证明见解析；.(2)8√33分析：（1）点G为线段CE中点，取CF中点M，证明DG//HM，再利用线面平行的判定推理作答.（2）根据给定条件，证得CE⊥平面ADEF，再结合等体积法即可求出三棱锥E−CFH的体积作答.（1）当点G为线段CE中点时，DG//平面CFH，取CF中点M，连接HM,GM，如图，则GM//EF，GM=12EF，因E，F分别是弧DC，AB上的一点，EF//AD，则EF是半圆柱的一条母线，即EF=AD，而点H为线段AD的中点，于是得GM//DH,GM=DH，即四边形DGMH为平行四边形，则DG//HM，而DG⊄平面CFH，HM⊂平面CFH，所以DG//平面CFH.（2）依题意，AB是半圆柱下底面半圆的直径，则∠AFB=90∘，而∠FAB=30°，有AF=√32AB=2√3,BF=12AB=2，显然CD是半圆柱上底面半圆的直径，则CE⊥DE，由（1）知EF是半圆柱的一条母线，则EF⊥平面CDE，而CE⊂平面CDE，即有CE⊥EF，DE∩EF=E，DE,EF⊂平面ADEF，因此，CE⊥平面ADEF，而EF//BC,EF=BC，即四边形BCEF是平行四边形，CE=BF=2，又点H为线段AD的中点，则S△EFH=12AD⋅AF=4√3，所以三棱锥E−CFH的体积V E−CFH=V C−EFH=13⋅S△EFH⋅CE=13×4√3×2=8√33.。

2021 级数学科自主学习提升课程（一）立体几何综合训练1、如图，在三棱锥 A - BCD 中，平面 ABD ⊥ 平面 BCD ， AB = AD ， O 为 BD 的中点. （1）证明： OA ⊥ CD ；（2）若 OCD 是边长为 1 的等边三角形，点 E 在棱 AD 上， DE = 2EA ，且二面角 E - BC - D 的大小为 45︒ ， 求三棱锥 A - BCD 的体积.2、如图，四棱锥 P - ABCD 的底面是矩形， PD ⊥ 底面 ABCD ，M 为 BC 的中点，且 PB ⊥ AM ．（1）证明：平面 PAM ⊥ 平面 PBD ；（2）若 PD = DC = 1 ，求四棱锥 P - ABCD 的体积．3、如图，在四棱锥 P - ABCD 中，底面 ABCD 是平行四边形， ∠ABC = 120︒, AB = 1, BC = 4, PA = N 分别为 BC, PC 的中点， PD ⊥ DC , PM ⊥ MD . （1）证明： AB ⊥ PM ；（2）求直线 AN 与平面 PDM 所成角的正弦值.M ，4、如图，在四棱锥P﹣ABCD 中，PC⊥底面ABCD，底面ABCD 是直角梯形，AB⊥AD，AB∥CD，AB＝2，AD＝CD＝1，E 是PB 的中点．（Ⅰ）求证：平面EAC⊥平面PBC；（Ⅱ）若PC＞1，直线PA 与平面EAC 所成角的正弦值为，求二面角P﹣AC﹣E 的余弦值．5、如图，在四棱锥P﹣ABCD 中，AB∥CD，且∠BAP＝∠CDP＝90°．（1）证明：AD⊥CD；（2）已知CD＝PD＝4，AB＝AD＝3，∠ADP＝90°．在棱AB 上是否存在一点E，使得平面PAD 与平面PCE 所成的锐二面角的余弦值为？若存在，求出的值，若不存在，请说明理由．6、如图，在四棱锥P﹣ABCD 中，AB∥CD，且∠BAP＝∠CDP＝90°．（1）证明：平面PAD⊥平面ABCD；（2）若PA＝PD＝AB＝CD＝2，∠APD＝90°，求点C 到平面BDP 的距离．7、如图，在梯形ABCD 中，AB∥CD，AD＝DC＝CB，∠ABC＝60°，四边形ACEF 是矩形．（Ⅰ）求证：AC⊥EB；（Ⅱ）若CE＝BC，且CE⊥BC，求EB 与平面FBD 所成角的正弦值．8、如图，在四棱锥P﹣ABCD 中，PA＝PB＝AB，且∠PBC＝2∠PAD＝90°．（1）求证：平面PAD⊥平面ABCD；（2）求平面PAB 与平面PBC 所成锐二面角的余弦值．9、如图，在四棱锥P﹣ABCD 中，PA⊥平面ABCD，AD∥BC，PA＝AD＝CD＝3，E为PD 的中点，点F 在PC 上，且；（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）求二面角F﹣AE﹣P 的余弦值；（Ⅲ）设点G 在PB 上，且，判断直线AG 是否在平面AEF 内，说明理由．10、如图，四棱锥P﹣ABCD 中，平面PCD⊥平面ABCD，AB∥CD，AB＝3DC＝6，BM＝2MP．（1）求证：CM∥平面PAD；（2）若AD＝1，AD⊥DC，PD⊥PC 且PD＝PC．求直线CM 与平面PAB 所成的角．11、已知平面四边形ABCD 中，AB⊥AC，AB＝AC＝AD＝CD＝2，现将△ABC沿AC 折起，使得点B 移至点P 的位置（如图），且PC＝PD．（1）求证：CD⊥PA；（2）若M 为PD 的中点，求点D 到平面ACM 的距离．12、在四棱锥P﹣ABCD 中，四边形ABCD 为平行四边形，以BC 为直径的圆O（O 为圆心）过点A，且AO＝AC ＝AP＝2，PA 底面ABCD，M 为PC 的中点．（1）证明：平面OAM⊥平面PCD；（2）求二面角O﹣MD﹣C 的余弦值．13、在三棱柱ABC﹣A1B1C1 中，M，N 分别为BC，AB1 的中点．（Ⅰ）证明：MN∥平面ACC1A1；（Ⅱ）若AB＝AC＝AA＝，BC＝2，且A1 在底面ABC 上的正投影恰为点M，求二面角N﹣BC﹣C1 的正弦值．114、如图，在多面体ABCDE 中，平面ACDE⊥平面ABC，四边形ACDE 为直角梯形，CD∥AE，AC⊥AE，∠ABC＝60°，CD＝1，AE＝AC＝2，F 为BE 的中点．（1）当BC 的长为多少时，DF⊥平面ABE．（2）求平面ABE 与平面BCD 所成的锐二面角的大小．15、在四棱台ABCD﹣A1B1C1D1 中，底面为矩形，平面AA1D1D⊥平面CC1D1D，且CC1＝CD＝DD1＝C1D1＝1．（1）证明：AD⊥平面CC1D1D；（2）若AC 与平面CC1D1D 所成角为，求二面角C﹣AA1﹣D 的余弦值．116、在如图所示的几何体中，EA⊥平面ABCD，四边形ABCD 为等腰梯形，AD∥BC，AD＝BC，AD＝1，∠ABC＝60°，EF∥AC，EF＝AC．（1）证明：AB⊥CF；（2）当二面角B﹣EF﹣D 的余弦值为时，求线段CF 的长．17、如图，在四棱锥P﹣ABCD 中，BC⊥平面PAB，AB∥CD，若DC＝DP＝2，BC＝，AP＝1，AB＝3．（Ⅰ）求证：AP⊥AB；（Ⅱ）求直线PC 与平面ADP 所成的角的正弦值．18、如图1，在梯形ABCD 中，AD∥BC，AB⊥AD，AD＝AB＝BC＝2，将△ABD沿BD 折起，使得A 到P 的位置，且二面角P﹣BD﹣C 是直二面角，如图2．（1）求证：CD⊥PB．（2）求二面角P﹣BC﹣D 的余弦值．19、在直角梯形ABCD 中，∠ABC＝90°，BC∥AD，AD＝4，AB＝BC＝2，M为线段AD 中点．将△ABC沿AC 折起，使平面ABC⊥平面ACD，得到几何体B﹣ACD．（Ⅰ）求证：AB⊥平面BCD；（Ⅱ）求直线BD 与平面BCM 所成角的正弦值．20、如图所示，四棱锥S﹣ABCD 中，△SAB为等边三角形，四边形ABCD 为菱形，，二面角S﹣AB﹣C 为直二面角，点E 为线段AB 的中点．（1）求证：SC⊥CD；（2）求直线BC 与平面SCD 所成角的余弦值．21、已知正△ABC的边长为3，点D、E 分别是AB、AC 上的三等分点（点E 靠近点A，点D 靠近点B）（如图1），将△ADE沿DE 折起到△ADE的位置，使二面角A1﹣DE﹣B 的平面角为90°，连接A1B，A1C（如图2）．1（1）求证：AE⊥平面BCED；1（2）在线段BC 上是否存在点P，使得直线PA1 与平面A1EC 所成的角为60°？若存在，求出CP 的长；若不存在，请说明理由．22、如图，AB⊥平面ADE，AB∥CD，AD＝CD＝AB＝AE＝3，∠DAE＝120°，四边形ABCD 的对角线交于点M，N 为棱DE 上一点，且MN∥平面ABE．（1）求的值；（2）求二面角B﹣AC﹣N 的余弦值．23、如图，在四棱锥P﹣ABCD 中，△PBC为正三角形，底面ABCD 为直角梯形，AD∥BC，∠ADC＝90°，AD＝CD＝3，BC＝4，点M，N 分别在线段AD 和PC 上，且．（1）求证：PM∥平面BDN；（2）设二面角P﹣AD﹣B 为θ．若，求直线PA 与平面PBC 所成角的正弦值．24、如图：P⊥平面ABCD，四边形ABCD 为直角梯形，��//��，∠���= 90 ∘，P = P = 2P = 2A = 2.求证：平面���⊥平面PBC；求二面角�−��−�的余弦值；在棱PA 上是否存在点Q，使得��//平面PBC？若存在，求��的值，若不存在，请说明理由.��25、如图，AB 是半圆O 的直径，C 是半圆O 上除A，B 外的一个动点，DC 垂直于半圆O 所在的平面，DC∥EB，DC＝EB＝1，AB＝4．（1）证明：平面ADE⊥平面ACD；（2）当C 点为半圆的中点时，求二面角D﹣AE﹣B 的余弦值．。

高中数学立体几何经典题型专题训练试题姓名 班级 学号 得分说明：１、本试卷包括第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分100分。

考试时间120分钟。

２、考生请将第Ⅰ卷选择题的正确选项填在答题框内，第Ⅱ卷直接答在试卷上。

考试结束后，只收第Ⅱ卷第Ⅰ卷（选择题）评卷人得　分一．单选题（共10小题，每题3分，共30分）1、如图，在正方体中ABCD-A1B1C1D1，M为BC的中点，点N在四边形CDD1C1及其内部运动．⊥1C1，则N点的轨迹为（ ）若MN AA．线段B．圆的一部分C．椭圆的一部分D．双曲线的一部分2、如图，正方体ABCD-A1B1C1D1的棱长为1，过点A作平面A1BD的垂线，垂足为H，则以下命题中，错误的是（ ）A．点H是△A1BD的垂心B．直线AH与CD1的成角为900C．AH的延长线经过点C1D．直线AH与BB1的成角为4503、如图，正方体ABCD-A1B1C1D1中，点P为线段AD1上一动点，点Q为底面ABCD内（含边界）一动点，M为PQ的中点，点M构成的点集是一个空间几何体，则该几何体为（　）A．棱柱B．棱锥C．棱台D．球4．下列说法中正确的是（ ）A．棱柱的面中，至少有两个面互相平行B．棱柱中两个互相平行的平面一定是棱柱的底面C．棱柱中一条侧棱就是棱柱的高D．棱柱的侧面一定是平行四边形，但它的底面一定不是平行四边形5．用一个平面去截一个正方体，所得截面不可能是（1）钝角三角形；（2）直角三角形；（3）菱形；（4）正五边形；（5）正六边形．下述选项正确的是（ ）A．（1）（2）（5）B．（1）（2）（4）C．（2）（3）（4）D．（3）（4）（5）6、如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=，则下列结论中错误的是（ ）⊥A．AC BEB．A1C⊥平面AEFC．三棱锥A-BEF的体积为定值D．异面直线AE、BF所成的角为定值7．已知一个正六棱锥的体积为12，底面边长为2，则它的侧棱长为（ ）A．4B．C．D．28．一正四棱锥的高为2，侧棱与底面所成的角为45°，则这一正四棱锥的斜高等于（）A．2B．C．2D．29、如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误的是（ ）A．D1O∥平面A1BC1B．D1O⊥平面AMCC．异面直线BC1与AC所成的角等于60°D．点B到平面AMC的距离为10．如图，E为正方体的棱AA1的中点，F为棱AB上的一点，且∠C1EF=90°，则AF：FB=（）A．1：1B．1：2C．1：3D．1：4第Ⅱ卷（非选择题）评卷人得　分二．填空题（共14小题，每题3分，共42分）11、正方体ABCD-A1B1C1D1中，M，N分别是AA1和BB1的中点，G是BC上一点，使⊥，则∠D1NG=______．C1N MG12、已知如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为棱DD1，AB上的点（不含顶点）．则下列说法正确的是______．①A1C⊥平面B1EF；②△B1EF在侧面上的正投影是面积为定值的三角形；③在平面A1B1C1D1内总存在与平面B1EF平行的直线；④平面B1EF与平面ABCD所成的二面角（锐角）的大小与点E位置有关，与点F位置无关；⑤当E，F分别为中点时，平面B1EF与棱AD交于点P，则三棱锥P-DEF的体积为．⊥，∠BAC=θ（0＜θ≤），且13、如图，三棱锥A-BCD中，AB AD⊥，AC ADAB=AC=AD=2，E、F分别为AC、BD的中点，则EF的最大值为______．14、如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记，，那么M，N的大小关系是______．15．若空间四边形ABCD的两条对角线AC，BD的长分别为4，6，过AB的中点E且平行BD，AC的截面四边形的周长为______．⊥1D则EF和BD1的关系是______．16、正方体ABCD-A1B1C1D1中，EF AC⊥，EF A17、已知正方体AC1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，则线段PQ的长为______．18、如图，正方体ABCD-A1B1C1D1中，E，F分别为棱DD1，AB上的点．已知下列判断：①A1C⊥平面B1EF；②△B1EF在侧面BCC1B1上的正投影是面积为定值的三角形；③在平面A1B1C1D1内总存在与平面B1EF平行的直线；④平面B1EF与平面ABCD所成的二面角（锐角）的大小与点E的位置有关，与点F的位置无关．其中正确结论的序号为______（写出所有正确结论的序号）．19、如图，正方体ABCD-A1B1C1D1的棱长为4，E，F分别是棱CD、C1D1的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A1B1C1D1上运动，则线段MN 的中点P的轨迹（曲面）与二面角D-C1D1-B1所围成的几何体的体积为______．∈1，且AM=BN，有以下四个结论：20、如图，正方体ABCD-A1B1C1D1中，点M AB∈1，N BC⊥；①AA1MN∥；②A1C1MN③MN与面A1B1C1D1成0°角；④MN与A1C1是异面直线．其中正确结论的序号是______．21、在正方体ABCD-A1B1C1D1中，过对角线BD1的一个平面交AA1于点E，交CC1于F，①四边形BFD1E一定是平行四边形②四边形BFD1E有可能是正方形③四边形BFD1E在底面ABCD内的投影一定是正方形④四边形BFD1E点有可能垂直于平面BB1D以上结论正确的为______（写出所有正确结论的编号）22、如图，正方体ABCD-A1B1C1D1中，对角线BD1与过A1、D、C1的平面交于点M，则=______．23．设A是自然数集的一个非空子集，如果k2A∉，且A，那么k是A的一个“酷元”，⊆，且集合M中的两个元素都是“酷元”那么这样的结给定S={0，1，2，3，4，5}，设M S合M有______个．24、如图，AC为圆O的直径，B为圆周上不与A、C重合的点，SA⊥圆O所在的平面，连接SB、SC、AB、BC，则图中直角三角形的个数是______．评卷人得　分三．简答题（共28分）25、四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，点P为平面ABCD所在平面外的⊥．一点，若△PAD为等边三角形，求证：PB AD26、如图，设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°，又∠BAC=60°，且⊥．SA BC（1）求证：S-ABC为正三棱锥；（2）已知SA=a，求S-ABC的全面积．27、如图，E、F、G、H分别是空间四边形ABCD四边上的中点．（1）若BD=2，AC=6，则EG2+HF2等于多少？（2）若AC与BD成30°的角，且AC=6，BD=4，则四边形EFGH的面积等于多少？28、已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c，设O 为S在底面ABC上的射影．求证：（1）O为△ABC的垂心；（2）O在△ABC内；（3）设SO=h，则++=．29．已知正三棱锥的高为1，底面边长为2，其内有一个球和该三棱锥的四个面都相切，求：（1）棱锥的全面积；（2）球的半径R．30、如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC 的中点，F在棱AC上，且AF=3FC．（1）求三棱锥D-ABC的表面积；（2）求证AC⊥平面DEF；（3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N 的位置；若不存在，试说明理由．参考答案评卷人得　分一．单选题（共__小题）1、如图，在正方体中ABCD-A1B1C1D1，M为BC的中点，点N在四边形CDD1C1及其内部运动．⊥1C1，则N点的轨迹为（ ）若MN AA．线段B．圆的一部分C．椭圆的一部分D．双曲线的一部分答案：A解析：解：正方体中ABCD-A1B1C1D1中，M为BC的中点，点N在四边形CDD1C1及其内部运动；如图所示，取CD、C1D1的中点Q、P，连接PQ，⊥1C1；当点N在线段PQ上时，MN A因为正方体ABCD-A1B1C1D1中，⊥1D1，连接B1D1，交A1C1于点O，∴B1D1A取B1C1的中点E，连接PE，则PE B∥1D1，⊥1C1；∴PE A∥1，又CC1⊥平面A1B1C1D1，PQ CC∴PQ⊥平面A1B1C1D1，∵A1C1⊂平面A1B1C1D1，⊥1C1；∴PQ A且PQ∩PE=P，∴A1C1⊥平面PQME，PQ⊂平面PQME，⊥；∴A1C1PQ∴N点的轨迹为线段PQ．故选：A．2、如图，正方体ABCD-A1B1C1D1的棱长为1，过点A作平面A1BD的垂线，垂足为H，则以下命题中，错误的是（ ）A．点H是△A1BD的垂心B．直线AH与CD1的成角为900C．AH的延长线经过点C1D．直线AH与BB1的成角为450答案：D解析：解：由ABCD-A1B1C1D1是正方体，得A-A1BD是一个正三棱锥，因此A点在平面A1BD上的射影H是三角形A1BD的中心，故A正确；⊥1B，又CD1A∥1B，可得直线AH与CD1的成角为90°，故B正确；∵AH⊥面A1BD，∴AH A连接AC1，由三垂线定理及线面垂直的判定可得AC1⊥面A1DB，再由过一点与已知平面垂直的直线有且只有一条可得AH与AC1重合，可得C正确；直线AH与BB1所成的角，即为AH与AA1所成的角，设为θ，由正方体棱长为1，可得正三棱锥的底面边长为，从而求得AH=，则cos，∴D错误．故选：D．3、如图，正方体ABCD-A1B1C1D1中，点P为线段AD1上一动点，点Q为底面ABCD内（含边界）一动点，M为PQ的中点，点M构成的点集是一个空间几何体，则该几何体为（　）A．棱柱B．棱锥C．棱台D．球答案：A解析：解：∵Q点不能超过边界，若P点与A点重合，设AB中点E、AD中点F，移动Q点，则此时M点的轨迹为：以AE、AF为邻边的正方形；下面把P点从A点向上沿线段AD1移动，在移动过程中可得M点轨迹为正方形，…，最后当P点与D1点重合时，得到最后一个正方形，故所得几何体为棱柱，故选：A4．下列说法中正确的是（ ）A．棱柱的面中，至少有两个面互相平行B．棱柱中两个互相平行的平面一定是棱柱的底面C．棱柱中一条侧棱就是棱柱的高D．棱柱的侧面一定是平行四边形，但它的底面一定不是平行四边形答案：A解析：解：棱柱的定义是，有两个面互相平行，其余各面都是四边形，相邻的公共边互相平行，有这些面围成的几何体是棱柱；可以判断A正确；B不正确，例如正六棱柱的相对侧面；C 不正确，只有直棱柱满足C的条件；D不正确，例如长方体．故选A5．用一个平面去截一个正方体，所得截面不可能是（1）钝角三角形；（2）直角三角形；（3）菱形；（4）正五边形；（5）正六边形．下述选项正确的是（ ）A．（1）（2）（5）B．（1）（2）（4）C．（2）（3）（4）D．（3）（4）（5）答案：B解析：解：如图所示截面为三角形ABC，OA=a，OB=b，OC=c，AC2=a2+c2，AB2=a2+b2，BC2=b2+c2∠=＞0，∴cos CAB=∴∠CAB为锐角，同理∠ACB与∠ABC也为锐角，即△ABC为锐角三角形；如右图，取相对棱的中点，得到的四边形是菱形；正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，如图为正六边形；经过正方体的一个顶点去切就可得到5边形．但此时不可能是正五边形．故不可能是（1）（2）（4）．故选：B．6、如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=，则下列结论中错误的是（ ）⊥A．AC BEB．A1C⊥平面AEFC．三棱锥A-BEF的体积为定值D．异面直线AE、BF所成的角为定值答案：D解析：解：∵AC⊥平面BB1D1D，又BE⊂平面BB1D1D，⊥．故A正确．∴AC BE∵EF垂直于直线AB1，AD1，∴A1C⊥平面AEF．故B正确．C中由于点B到直线B1D1的距离不变，故△BEF的面积为定值．又点A到平面BEF的距离为，故V A-BEF为定值．C正确当点E在D1处，F为D1B1的中点时，异面直线AE，BF所成的角是∠FBC1，当E在上底面的中心时，F在C1的位置，异面直线AE，BF所成的角是∠EAA1显然两个角不相等，D不正确．故选D．7．已知一个正六棱锥的体积为12，底面边长为2，则它的侧棱长为（ ）A．4B．C．D．2答案：A解析：解：由于正六棱锥可知底面是六个正三角形组成，∴底面积S=6×=6，∴体积V==12，∴h=，夺直角三角形SOB中，侧棱长为SB=．故选A．8．一正四棱锥的高为2，侧棱与底面所成的角为45°，则这一正四棱锥的斜高等于（）A．2B．C．2D．2答案：C解析：解：如图PO⊥底面ABCD，连接OA，取AD的中点E，连接OE，PE，则PE为斜高．∠PAO为侧棱与底面所成的角，且为45°，在直角△PAO中，PO=2，AO=2，PA=4，在直角△AEO中，AE=2，故在直角△PEA中，PE==2．故选C．9、如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误的是（ ）A．D1O∥平面A1BC1B．D1O⊥平面AMCC．异面直线BC1与AC所成的角等于60°D．点B到平面AMC的距离为答案：D解析：解：如图，∥，连接B1D1，交A1C1于N，则可证明OD1BN由OD1⊄面A1BC1，BN⊂面A1BC1，可得D1O∥面A1BC1，A正确；⊥，由三垂线定理的逆定理可得OD1AC设正方体棱长为2，可求得OM2=3，，，⊥，由线面垂直的判定可得D1O⊥平面AMC，B正确；则，有OD1OM由正方体的面对角线相等得到△A1BC1为正三角形，即∠A1C1B=60°，∴异面直线BC1与AC所成的角等于60°，C正确；设点B到平面AMC的距离为d，正方体的棱长为2a，则，，由V B-AMC=V A-BCM，得，即，解得：d=，D错误．故选：D．10．如图，E为正方体的棱AA1的中点，F为棱AB上的一点，且∠C1EF=90°，则AF：FB=（）A．1：1B．1：2C．1：3D．1：4答案：C解析：解：解：设正方体的棱长为：2，由题意可知C1E==3，∠C1EF=90°，所以设AF=x，12+x2+C1E2=22+22+（2-x）2，解得：x=，所以AF：FB=：=1：3；故选：C．评卷人得　分二．填空题（共__小题）11、正方体ABCD-A1B1C1D1中，M，N分别是AA1和BB1的中点，G是BC上一点，使⊥，则∠D1NG=______．C1N MG答案：90°解析：解：连接MN，∵M，N分别是AA1和BB1的中点，∥1D1，由正方体的几何特征可得MN C在正方体ABCD-A1B1C1D1中，D1C1⊥平面B1C1CB∵C1N⊂平面B1C1CB⊥1N∴D1C1C⊥1N∴MN C⊥，MN∩MG=M，MD1，MG⊂平面MNG又∵C1N MG∴C1N⊥平面MNG又∵NG⊂平面MNG⊥∴C1N NG故∠D1NG=90°故答案为：90°12、已知如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为棱DD1，AB上的点（不含顶点）．则下列说法正确的是______．①A1C⊥平面B1EF；②△B1EF在侧面上的正投影是面积为定值的三角形；③在平面A1B1C1D1内总存在与平面B1EF平行的直线；④平面B1EF与平面ABCD所成的二面角（锐角）的大小与点E位置有关，与点F位置无关；⑤当E，F分别为中点时，平面B1EF与棱AD交于点P，则三棱锥P-DEF的体积为．答案：②③⑤解析：解：对于①A1C⊥平面B1EF，不一定成立，因为A1C⊥平面AC1D，而两个平面面B1EF与面AC1D不一定平行．对于②△B 1EF 在侧面BCC 1B 1上 的正投影是面积为定值的三角形，此是一个正确的结论，因为其投影三角形的一边是棱BB 1，而E 点在面上的投影到此棱BB 1的距离是定值，故正确；对于③在平面A 1B 1C 1D 1内总存在与平面B 1EF 平行的直线，此两平面相交，一个面内平行于两个平面的交线一定平行于另一个平面，此结论正确；对于④平面B 1EF 在平面ABCD 中的射影为△DFB ，面积为定值，但△B 1EF 的面积不定，故不正确；对于⑤由面面平行的性质定理可得EQ B ∥1F ，故D 1Q=，B 1Q PF ∥，故AP=，所以三棱锥P-DEF 的体积为，故正确故答案为：②③⑤．13、如图，三棱锥A-BCD 中，AB AD ⊥，AC AD ⊥，∠BAC=θ（0＜θ≤），且AB=AC=AD=2，E 、F 分别为AC 、BD 的中点，则EF 的最大值为______．答案：解析：⊥，垂足为G，连接GE，解：过F作FG AB⊥，∵AD AB∥，∴G为AB的中点，∴AD FG∴FG=1，AG=1，∵E为AC的中点，∴AE=1，∠BAC=θ，∴EG=∵AD⊥平面ABC，∴FG⊥平面ABC，△中，EF===，在Rt FGE∵0，∴EF≤．故答案是．14、如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记，，那么M，N的大小关系是______．答案：M=N解析：解：根据平面中直角三角形的勾股定理类比得，S ABC△2=S PAB△2+S PBC△2+S PAC△2①，由等体积法得，∴②，①÷②整理得M=N．故答案为：M=N．15．若空间四边形ABCD的两条对角线AC，BD的长分别为4，6，过AB的中点E且平行BD，AC的截面四边形的周长为______．答案：10解析：解：设截面四边形为EFGH，F、G、H分别是BC、CD、DA的中点，∴EF=GH=2，FG=HE=3，∴周长为2×（2+3）=10．故答案为：10．16、正方体ABCD-A1B1C1D1中，EF AC⊥，EF A⊥1D则EF和BD1的关系是______．答案：平行解析：解：法一：根据图象可知：⊥，AC∩B1C=C，⊥1D，A1D B∥1C，B1C EFEF AC⊥，EF A∥．∴EF⊥面AB1C，而BD1⊥面AB1C，即BD1EF法二：建立以D1为原点的空间直角坐标系D1-xyz，且设正方形的边长为1所以就有D1（0，0，0），B（1，1，0），A1（1，0，0），D（0，0，1），A（1，0，1），C（0，1，1）所以=（-1，0，1），=（-1，1，0），=（-1，-1，1）⊥1，所以•=-1+1=0 所以A1D BD⊥1，•=1-1=0 所以AC BD所以BD1与A1D和AC都垂直又∵EF是AC、A1D的公共垂线，∥．∴BD1EF故答案为：平行．17、已知正方体AC1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，则线段PQ的长为______．答案：解析：解：∵正方体AC1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，连结AD1，AB1，∴由正方体的性质，得：AD1∩A1D=P，P是AD1的中点，∥1，PQ AB∴PQ=AB1==．故答案为：．18、如图，正方体ABCD-A1B1C1D1中，E，F分别为棱DD1，AB上的点．已知下列判断：①A 1C ⊥平面B 1EF ；②△B 1EF 在侧面BCC 1B 1上的正投影是面积为定值的三角形；③在平面A 1B 1C 1D 1内总存在与平面B 1EF 平行的直线；④平面B 1EF 与平面ABCD 所成的二面角（锐角）的大小与点E 的位置有关，与点F 的位置无关．其中正确结论的序号为______（写出所有正确结论的序号）．答案：②③解析：解：若A 1C ⊥平面B 1EF ，则A 1C B ⊥1F ，由三垂线逆定理知：B 1F A ⊥1B ，又当F 与A 不重合时，B 1F 与A 1B 不垂直，∴①错误；∵E 在侧面BCC 1B 1上的投影在CC 1上，F 在侧面BCC 1B 1上的投影是B ，∴△B 1EF 在侧面BCC 1B 1上的正投影是三角形，三角形的面积S=×棱长×棱长为定值．∴②正确；设平面A 1B 1C 1D 1∩平面B 1EF=l ，∵平面A 1B 1C 1D 1内总存在与l 平行的直线，由线面平行的判定定理得与l 平行的直线，与平面B 1EF 平行，∴③正确；设E 与D 重合，F 位置变化，平面B 1EF 与平面ABCD 所成的二面角（锐角）的大小也在变化，∴④错误．故答案为：②③．19、如图，正方体ABCD-A 1B 1C 1D 1的棱长为4，E ，F 分别是棱CD 、C 1D 1的中点，长为2的线段MN 的一个端点M 在线段EF 上运动，另一个端点N 在底面A 1B 1C 1D 1上运动，则线段MN 的中点P 的轨迹（曲面）与二面角D-C 1D 1-B 1所围成的几何体的体积为______．答案：解析：解：依题意知|FP|=|MN|=1，因此点P的轨迹是以点F为球心、1为半径的球的．∴所求几何体的体积是×π×13=．故答案为：．∈1，且AM=BN，有以下四个结论：∈1，N BC20、如图，正方体ABCD-A1B1C1D1中，点M AB⊥；①AA1MN∥；②A1C1MN③MN与面A1B1C1D1成0°角；④MN与A1C1是异面直线．其中正确结论的序号是______．答案：①③解析：解：当M 为A ，N 为B ，排除②；当M 为B 1，N 为C 1，排除④．作MM′A ⊥1B 1于M′，作NN′B ⊥1C 1于N′，易证|MM′|=|NN′|，MM′NN′∥∴MN M′N′∥，由此知①③正确．故答案为：①③21、在正方体ABCD-A 1B 1C 1D 1中，过对角线BD 1的一个平面交AA 1于点E ，交CC 1于F ，①四边形BFD 1E 一定是平行四边形②四边形BFD 1E 有可能是正方形③四边形BFD 1E 在底面ABCD 内的投影一定是正方形④四边形BFD 1E 点有可能垂直于平面BB 1D以上结论正确的为______（写出所有正确结论的编号）答案：①③④解析：解：如图：①由平面BCB 1C 1∥平面ADA 1D 1，并且B 、E 、F 、D 1四点共面，∴ED 1BF ∥，同理可证，FD 1EB ∥，故四边形BFD 1E 一定是平行四边形，故①正确；②若BFD 1E 是正方形，有ED 1BE ⊥，这个与A 1D 1BE ⊥矛盾，故②错误；③由图得，BFD 1E 在底面ABCD 内的投影一定是正方形ABCD ，故③正确；④当点E 和F 分别是对应边的中点时，平面BFD 1E ⊥平面BB 1D 1，故④正确．故答案为：①③④．22、如图，正方体ABCD-A 1B 1C 1D 1中，对角线BD 1与过A 1、D 、C 1的平面交于点M ，则=______．答案：2解析：解：由正方体的性质可得：D 1B ⊥平面DA 1C 1，∴D 1M 是三棱锥D 1-A 1DC 1的高．不妨设正方体的棱长为1．∵=，∴=，解得D 1M==．∴=2．故答案为：2．∉，且A，那么k是A的一个“酷元”，23．设A是自然数集的一个非空子集，如果k2A⊆，且集合M中的两个元素都是“酷元”那么这样的结给定S={0，1，2，3，4，5}，设M S合M有______个．答案：5解析：解：∵S={0，1，2，3，4，5}，由题意可知：集合M不能含有0，1，也不能同时含有2，4故集合M可以是{2，3}、{2，5}、{3，5}、{3，4}、{4，5}，共5个故答案为：524、如图，AC为圆O的直径，B为圆周上不与A、C重合的点，SA⊥圆O所在的平面，连接SB、SC、AB、BC，则图中直角三角形的个数是______．答案：4解析：解：题题意SA⊥圆O所在的平面，AC为圆O的直径，B为圆周上不与A、C重合的点，可得出AB，BC垂直由此两个关系可以证明出CB垂直于面SAB，由此可得△ADB，△SAC，△ABC，△SBC都是直角三角形故图中直角三角形的个数是4个故答案为：4．评卷人得　分三．简答题（共__小题）25、四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，点P为平面ABCD所在平面外的⊥．一点，若△PAD为等边三角形，求证：PB AD答案：证明：如图，连结BD ，取AD 的中点E ，连结PE ，BE ；从而易知△ABD 也是等边三角形，又∵△PAD 为等边三角形，∴AD PE ⊥，AD BE ⊥，又∵PE∩BE=E ；故AD ⊥平面PBE ；故AD PB ⊥．解析：证明：如图，连结BD ，取AD 的中点E ，连结PE ，BE ；从而易知△ABD 也是等边三角形，又∵△PAD 为等边三角形，∴AD PE ⊥，AD BE ⊥，又∵PE∩BE=E ；故AD ⊥平面PBE ；故AD PB ⊥．26、如图，设三棱锥S-ABC 的三个侧棱与底面ABC 所成的角都是60°，又∠BAC=60°，且SA BC ⊥．（1）求证：S-ABC 为正三棱锥；（2）已知SA=a ，求S-ABC 的全面积．答案：（1）证明：正棱锥的定义中，底面是正多边形；顶点在底面上的射影是底面的中心，两个条件缺一不可．作三棱锥S-ABC 的高SO ，O 为垂足，连接AO 并延长交BC 于D ．因为SA BC ⊥，所以AD BC ⊥．又侧棱与底面所成的角都相等，从而O 为△ABC 的外心，OD 为BC 的垂直平分线，所以AB=AC ．又∠BAC=60°，故△ABC 为正三角形，且O 为其中心．所以S-ABC 为正三棱锥．（2）解：在Rt SAO △中，由于SA=a ，∠SAO=60°，所以SO=a ，AO=a ．因O 为重心，所以AD=AO=a ，BC=2BD=2ADcot60°=a ，OD=AD=a ．在Rt SOD △中，SD 2=SO 2+OD 2=（a ）2+（a ）2=，则SD=a ．于是，（S S-ABC ）全=•（a ）2sin60°+3••a•a=a 2．解析：（1）证明：正棱锥的定义中，底面是正多边形；顶点在底面上的射影是底面的中心，两个条件缺一不可．作三棱锥S-ABC 的高SO ，O 为垂足，连接AO 并延长交BC 于D ．因为SA BC ⊥，所以AD BC ⊥．又侧棱与底面所成的角都相等，从而O 为△ABC 的外心，OD 为BC 的垂直平分线，所以AB=AC ．又∠BAC=60°，故△ABC 为正三角形，且O 为其中心．所以S-ABC 为正三棱锥．（2）解：在Rt SAO △中，由于SA=a ，∠SAO=60°，所以SO=a ，AO=a ．因O 为重心，所以AD=AO=a ，BC=2BD=2ADcot60°=a ，OD=AD=a ．在Rt SOD △中，SD 2=SO 2+OD 2=（a ）2+（a ）2=，则SD=a ．于是，（S S-ABC ）全=•（a ）2sin60°+3••a•a=a 2．27、如图，E 、F 、G 、H 分别是空间四边形ABCD 四边上的中点．（1）若BD=2，AC=6，则EG 2+HF 2等于多少？（2）若AC 与BD 成30°的角，且AC=6，BD=4，则四边形EFGH 的面积等于多少？答案：解：（1）∵E 、F 、G 、H 分别是空间四边形ABCD 四边上的中点，∴EH BD ∥，且EH=BD ；FG BD ∥，且FG=BD ；∴EH FG ∥，且EH=FG ，∴四边形EFGH 是平行四边形；又BD=2，AC=6，∴EH=BD=1，EF=AC=3，在△EFG 和△HFG 中，由余弦定理得，EG 2=EF 2+FG 2-2EF•FG•cos EFG∠=32+12-2×3×1×cos EFG∠=10-6cos EFG ∠，HF 2=HG 2+FG 2-2HG•FG•cos FGH∠=32+12-2×3×1×cos （π-EFG ∠）=10+6cos EFG ∠，∴EG 2+HF 2=20；（2）∵AC 与BD 成30°的角，且EF AC ∥，FG BD ∥，∴∠EFG=30°，又AC=6，BD=4，∴EF=AC=3，FG=BD=2；∠．∴四边形EFGH的面积为S=EF•FG•sin EFG=3×2×sin30°=3解析：解：（1）∵E、F、G、H分别是空间四边形ABCD四边上的中点，∥，且EH=BD；∴EH BDFG BD∥，且FG=BD；∥，且EH=FG，∴EH FG∴四边形EFGH是平行四边形；又BD=2，AC=6，∴EH=BD=1，EF=AC=3，在△EFG和△HFG中，由余弦定理得，∠EG2=EF2+FG2-2EF•FG•cos EFG∠=32+12-2×3×1×cos EFG∠，=10-6cos EFG∠HF2=HG2+FG2-2HG•FG•cos FGH∠）=32+12-2×3×1×cos（π-EFG=10+6cos EFG∠，∴EG2+HF2=20；（2）∵AC 与BD 成30°的角，且EF AC ∥，FG BD ∥，∴∠EFG=30°，又AC=6，BD=4，∴EF=AC=3，FG=BD=2；∴四边形EFGH 的面积为S=EF•FG•sin EFG=3×2×sin30°=3∠．28、已知三棱锥S-ABC 的三条侧棱SA 、SB 、SC 两两互相垂直且长度分别为a 、b 、c ，设O 为S 在底面ABC 上的射影．求证：（1）O 为△ABC 的垂心；（2）O 在△ABC 内；（3）设SO=h ，则++=．答案：证明：（1）∵SA SB ⊥，SA SC ⊥，∴SA ⊥平面SBC ，BC ⊂平面SBC ．∴SA BC ⊥．而AD 是SA 在平面ABC 上的射影，∴AD BC ⊥．同理可证AB CF ⊥，AC BE ⊥，故O 为△ABC 的垂心．（2）证明△ABC 为锐角三角形即可．不妨设a≥b≥c ，则底面三角形ABC 中，AB=为最大，从而∠ACB 为最大角．用余弦定理求得cos ACB=∠＞0，∴∠ACB 为锐角，△ABC 为锐角三角形．故O 在△ABC 内．（3）SB•SC=BC•SD ，故SD=，=+，又SA•SD=AD•SO ，∴===+=++=．解析：证明：（1）∵SA SB ⊥，SA SC ⊥，∴SA ⊥平面SBC ，BC ⊂平面SBC ．∴SA BC ⊥．而AD 是SA 在平面ABC 上的射影，∴AD BC ⊥．同理可证AB CF ⊥，AC BE ⊥，故O 为△ABC 的垂心．（2）证明△ABC 为锐角三角形即可．不妨设a≥b≥c ，则底面三角形ABC 中，AB=为最大，从而∠ACB 为最大角．用余弦定理求得cos ACB=∠＞0，∴∠ACB 为锐角，△ABC 为锐角三角形．故O 在△ABC 内．（3）SB•SC=BC•SD ，故SD=，=+，又SA•SD=AD•SO ，∴===+=++=．29．已知正三棱锥的高为1，底面边长为2，其内有一个球和该三棱锥的四个面都相切，求：（1）棱锥的全面积；（2）球的半径R．答案：解：（1）设正三棱锥的底面中心为H，由题意知PH=1，边长BC=2，取BC中点E，连接HE、PE，则HE=S全=3×=9⊥于点G，（2）过O作OG PE∽△，且OG=OH=R，则△POG PEH∴，∴R=解析：解：（1）设正三棱锥的底面中心为H，由题意知PH=1，边长BC=2，取BC中点E，连接HE、PE，则HE=S全=3×=9⊥于点G，（2）过O作OG PE∽△，且OG=OH=R，则△POG PEH∴，∴R=30、如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC 的中点，F在棱AC上，且AF=3FC．（1）求三棱锥D-ABC 的表面积；（2）求证AC ⊥平面DEF ；（3）若M 为BD 的中点，问AC 上是否存在一点N ，使MN ∥平面DEF ？若存在，说明点N 的位置；若不存在，试说明理由．答案：解：（1）∵AB ⊥平面BCD ，∴AB BC ⊥，AB BD ⊥．∵△BCD 是正三角形，且AB=BC=a ，∴AD=AC=．设G 为CD 的中点，则CG=，AG=．∴，，．三棱锥D-ABC 的表面积为．（2）取AC 的中点H ，∵AB=BC ，∴BH AC ⊥．∵AF=3FC ，∴F 为CH 的中点．∵E 为BC 的中点，∴EF BH ∥．则EF AC ⊥．∵△BCD 是正三角形，∴DE BC ⊥．∵AB ⊥平面BCD ，∴AB DE ⊥．∵AB∩BC=B ，∴DE ⊥平面ABC ．∴DE AC ⊥．∵DE∩EF=E ，∴AC ⊥平面DEF ．（3）存在这样的点N ，当CN=时，MN ∥平面DEF ．连CM ，设CM∩DE=O ，连OF ．由条件知，O 为△BCD 的重心，CO=CM ．∴当CF=CN 时，MN OF ∥．∴CN=．解析：解：（1）∵AB ⊥平面BCD ，∴AB BC ⊥，AB BD ⊥．∵△BCD 是正三角形，且AB=BC=a ，∴AD=AC=．设G 为CD 的中点，则CG=，AG=．∴，，．三棱锥D-ABC 的表面积为．（2）取AC 的中点H ，∵AB=BC ，∴BH AC ⊥．∵AF=3FC ，∴F 为CH 的中点．∵E 为BC 的中点，∴EF BH ∥．则EF AC ⊥．∵△BCD 是正三角形，∴DE BC ⊥．∵AB ⊥平面BCD ，∴AB DE ⊥．∵AB∩BC=B ，∴DE ⊥平面ABC ．∴DE AC ⊥．∵DE∩EF=E ，∴AC ⊥平面DEF ．（3）存在这样的点N ，当CN=时，MN ∥平面DEF ．连CM ，设CM∩DE=O ，连OF ．由条件知，O 为△BCD 的重心，CO=CM ．∴当CF=CN 时，MN OF ∥．∴CN=．。

立体几何大题训练题一、解答题（共17题；共150分）1.如图，在四棱锥P-ABCD中，PA⊥平面ABCD，在四边形ABCD中，∠ABC= ，AB=4，BC=3，CD= ，AD=2 ，PA=4.（1）证明：CD⊥平面PAD；（2）求二面角B-PC-D的余弦值..2.如图，在四棱锥中，平面，在四边形中，，，，，，.（1）证明：平面；（2）求B点到平面的距离3.如图，在四棱锥中，底面为长方形，底面，，，为的中点，F 为线段上靠近B 点的三等分点.（1）求证：平面；（2）求平面与平面所成二面角的正弦值.4.如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.（1）证明：平面平面;（2）求与平面所成角的正弦值.5.如图，在三角锥中，, , 为的中点.（1）证明：平面;（2）若点在棱上，且MC=2MB，求点C到平面POM的距离.6.如图，在三角锥中，, , 为的中点.（1）证明：平面;（2）若点在棱上，且二面角为，求与平面所成角的正弦值. 7.如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（12分）（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．8.如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值.9.如图，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，BAD=60°，E，M，N分别是BC，BB1，A1D的中点（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N的正弦值。

10.已知三棱柱，底面三角形为正三角形，侧棱底面，，为的中点，为中点.（1）求证：直线平面；（2）求平面和平面所成的锐二面角的余弦值.11.如图，已知三棱柱ABC-A1B1C1，平面A1AC1C⊥平面ABC，∠ABC=90°.∠BAC=30°，A1A=A1C=AC，E，F 分别是AC，A1B1的中点（1）证明：EF⊥BC（2）求直线EF与平面A1BC所成角的余弦值.12.如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（Ⅰ）证明：平面ACD⊥平面ABC；（Ⅱ）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C 的余弦值．13.如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC= AD，∠BAD=∠ABC=90°，E是PD的中点．（Ⅰ）证明：直线CE∥平面PAB；（Ⅱ）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．14.如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（Ⅰ）证明：AB1⊥平面A1B1C1；（Ⅱ）求直线AC1与平面ABB1所成的角的正弦值．15.如图所示多面体中，AD⊥平面PDC，四边形ABCD为平行四边形，点E，F分别为AD，BP的中点，AD ＝3，AP＝3 ，PC ．（1）求证：EF//平面PDC；（2）若∠CDP＝120°，求二面角E﹣CP﹣D的平面角的余弦值．16.如图，四棱锥中，侧棱垂直于底面，，，为的中点，平行于，平行于面，.（1）求的长；（2）求二面角的余弦值.17.如图，在斜三棱柱中，侧面，，，，．（Ⅰ）求证：平面平面；（Ⅱ）若为中点，求二面角的正切值．答案解析部分一、解答题1.【答案】（1）解：连接，由∠ABC= ，AB=4，BC=3，则，又因为CD= ，AD=2 ，所以，即，因为PA⊥平面ABCD，平面ABCD，所以，因为，所以CD⊥平面PAD；（2）解：以点D为坐标原点，的延长线为x，为y轴，过点D与平行线为z轴，建立空间直角坐标系，如图：作交与点G，，即，所以，，所以，所以，，，，则，，，设平面的一个法向量为，则，即，令，则，，即，设平面的一个法向量为，则，即，令，则，，即，由，所以二面角B-PC-D的余弦值为.【解析】【分析】（1）连接，证出，利用线面垂直的性质定理可得，再利用线面垂直的判定定理即可证出.（2）以点D为坐标原点，的延长线为x，为y轴，过点D与平行线为轴，建立空间直角坐标系，分别求出平面的一个法向量与平面的一个法向量，利用向量的数量积即可求解.2.【答案】（1）解：在平面中，，，，则，又，∴，即，又平面，则，又，∴平面.（2）解：在平面中，过A作BC的平行线交CD的延长线于M，因为，，，则,又因为，,所以.所以又，则，所以,在中，.因为,则面,所以由可知：，,所以，则，因此P点到平面的距离为.【解析】【分析】(1)在三角形中，由勾股定理可证得，由平面，可得，根据线面垂直的判定定理即可证得结论；(2) 在平面中，过A作BC的平行线交CD 的延长线于M，因为利用等体积转换即可求得距离.3.【答案】（1）证明：，为线段中点，.平面，平面，.又底面是长方形，.又，平面.平面，. 又，平面.（2）解：由题意，以为轴建立空间直角坐标系，则，，，，，.所以, ，，，设平面的法向量，则，即，令，则，，，同理可求平面的法向量，，，即平面与平面所成角的正弦值为.【解析】【分析】（1）通过，可证明平面，进而可得，结合证明线面垂直.（2）以为轴建立空间直角坐标系，可求出平面的法向量，平面的法向量，则可求出两向量夹角的余弦值，从而可求二面角的正弦值.4.【答案】（1）解：由已知可得，BF⊥PF，BF⊥EF，又，∴BF⊥平面PEF.∴又平面ABFD，平面PEF⊥平面ABFD.（2）解：作PH⊥EF，垂足为H.由（1）得，PH⊥平面ABFD.以H为坐标原点，的方向为y轴正方向，为单位长，建立如图所示的空间直角坐标系H−xyz.由（1）可得，DE⊥PE.又DP=2，DE=1，所以PE= .又PF=1，EF=2，故PE⊥PF.可得.则为平面ABFD的法向量. 设DP与平面ABFD所成角为，则.∴DP与平面ABFD所成角的正弦值为.【解析】【分析】(1)在翻折过程中,作于H,由得到,从而得到面面垂直;(2)DP与平面所成的角就是,在三角形中求其正弦值.5.【答案】（1）∵PA=PC=AC=4 且O是AC的中点∴PO⊥AC∵AB=BC=2 ，AC=4,∴∴∠ABC=90°连接BO则OB=OC∴PO2+BO2=PB2PO⊥OB，PO⊥OCOB∩OC=O∴PO⊥平面ABC（2）过点C作CH⊥OM交OM于点H又∵PO⊥平面ABC∴∴CH的长度为点C到平面POM的距离在△COM中，CM= ，OC=2，∠OCM=45°∴∴OM=∴【解析】【分析】（1）由线面垂直的判定定理易得；（2）由线面垂直可得面面垂直，易找点面距，可求.6.【答案】（1）PA=PC=AC=4 且O是AC的中点PO⊥AC∵AB=BC=2 ，AC=4,∴∴∠ABC=90°连接BO则OB=OC∴PO2+BO2=PB2PO⊥OB，PO⊥OCOB∩OC=O∴PO⊥平面ABC（2）∵PO⊥平面ABC，∴PO⊥OB∴AB=BC=2 O是AC的中点∴OB⊥AC OB⊥平面PAC如图所示以O为坐标原点，为x轴正方向建立如图所示的直角坐标系O-xyz则P（0,0，）A（,0，-2,0），C（0,2,0），B（2,0,0）平面PAC法向量为=（1,0,0）设M（x，2-x，0）平面PAC法向量为=（1，λ，μ），=（0，2，）, = （x，4-x，0）则即即得到，∴x=-4（舍），x=即M∴PAM的法向量记PC与平面PAM所成的角为θ∴即PC与平面PAM所成的角为的正弦值为.【解析】【分析】（1）由线面垂直的判定定理易得；（2）先由条件建系，找到点M的位置，再用公式求线面角.7.【答案】（1）证明：∵∠BAP=∠CDP=90°，∴PA⊥AB，PD⊥CD，∵AB∥CD，∴AB⊥PD，又∵PA∩PD=P，且PA⊂平面PAD，PD⊂平面PAD，∴AB⊥平面PAD，又AB⊂平面PAB，∴平面PAB⊥平面PAD；（2）解：∵AB∥CD，AB=CD，∴四边形ABCD为平行四边形，由（1）知AB⊥平面PAD，∴AB⊥AD，则四边形ABCD为矩形，在△APD中，由PA=PD，∠APD=90°，可得△PAD为等腰直角三角形，设PA=AB=2a，则AD= ．取AD中点O，BC中点E，连接PO、OE，以O为坐标原点，分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系，则：D（），B（），P（0，0，），C（）．，，．设平面PBC的一个法向量为，由，得，取y=1，得．∵AB⊥平面PAD，AD⊂平面PAD，∴AB⊥AD，又PD⊥PA，PA∩AB=A，∴PD⊥平面PAB，则为平面PAB的一个法向量，．∴cos＜＞= = ．由图可知，二面角A﹣PB﹣C为钝角，∴二面角A﹣PB﹣C的余弦值为．【解析】【分析】（1.）由已知可得PA⊥AB，PD⊥CD，再由AB∥CD，得AB⊥PD，利用线面垂直的判定可得AB⊥平面PAD，进一步得到平面PAB⊥平面PAD；（2.）由已知可得四边形ABCD为平行四边形，由（1）知AB⊥平面PAD，得到AB⊥AD，则四边形ABCD 为矩形，设PA=AB=2a，则AD= ．取AD中点O，BC中点E，连接PO、OE，以O为坐标原点，分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系，求出平面PBC的一个法向量，再证明PD⊥平面PAB，得为平面PAB的一个法向量，由两法向量所成角的余弦值可得二面角A﹣PB﹣C的余弦值．8.【答案】（1）解：由已知得，平面，平面，故．又，所以平面．（2）由（1）知．由题设知，所以，故，．以为坐标原点，的方向为x轴正方向，为单位长，建立如图所示的空间直角坐标系D-xyz，则C（0，1，0），B（1，1，0），（0，1，2），E（1，0，1），，．设平面EBC的法向量为=（x，y，x），则即所以可取= .设平面的法向量为=（x，y，z），则即所以可取=（1，1，0）．于是．所以，二面角的正弦值为．【解析】【分析】（1）根据题意由线面垂直的性质得出线线垂直，再由线线垂直的判定定理出线面垂直。

1、如图，正方形 ABCD 所在平面与平面四边形 ABEF 所在平面互相垂直，△ ABE 是等腰E(1) 线段CD 的中点为P ,线段AE 的中点为M ，求证：PM Zz 平面BCE ；(2) 求直线CF 与平面BCE 所成角的正切值•D解：（1）取 AB 的中点为 N ,连 MN , P N 则MN/∕EB ,PN∕∕BC P.面 PMN //面 EBC ,. PM // 平面 BCE⑵先证出FE _面EBC ，■ Z FCE 为直线CF 与平面BCE 所成角，FE _ 6^~6~2、己知多面体 ABCDE 中，DE _ 平面 ACD , AB//DE , AC=AD=CD=DE=2 , AB =1 , O 为CD 的中点.⑴求证：AO-平面CDE ;(2)求直线BD 与平面CBE 所成角的正弦值解：(I)证明；THC =才D, O 为QD 的中点I ^AO 丄C D. 又 DE 丄平面 ACD. Ad^ACD t AOLDE, :、AO 丄平面CDE ・ 一(in E Φ 点F,连接 A 尸、DF t山已知可得，ABHDE 且用月=丄DE,2在 ∖CDE 中.OF //DE 且OF=ZD £』2Λ四边形ABFO 是平行四边形..∖ BF f/ AO f 宙(I)知.BF 丄平面 CDE. TCD = D E ,二 DF 丄 CE. :、DF 丄平面 CBE . ：.Z r DBF 就是直线BD 与平面CBE 所成角• …・直角三角形， AB =AE =2,FA =FE,. AEF =45 tan . FCE(第19题)12分MC 分BE7分E即口线BD与平面CBE所咸角的正弦值为零.*<(此题证ZQBF为所求角，方法较多，酌情给分)3、如图，在厶ABC 中，.C =90 , AC=BC=3a ,点P 在AB 上，PE//BC 交AC 于E , PF // AC交BC于F •沿PE将厶APE翻折成△ A' PE ,使平面A' PE _平面ABC ；沿PF将厶BPF翻折成△ B'PF ,使平面B'PF _平面ABC •(1)求证：B'C//平面A'PE ;(2)若AP =2PB ,求二面角A'-PC -E的平面角的正切值.解：（1）因为FC // PE , FC二平面A' PE ,所以FC //平面A PE •因为平面A'PE _平面PEC ,且A'E _ PE ,所以A'E _平面ABC . 同理，B'F —平面ABC ,所以B'F //A'E ,从而B'F //平面A' PE . 所以平面B'CF //平面A'PE ,从而B'C//平面A'PE .（2）因为AC=BC= 3a , AP=2BP ,所以CE =a , EA =2a , PE =2a , PC= 5a .过E作EM _ PC ,垂足为M ,连结A M .在ΛBDF中.DF = √2 J5D = √5由(1)知A' E _平面ABC ,可得A E _ PC , 所以PC _面AEM ,所以AM _ PC .所以.A'ME即为所求二面角A'-PC - E的平面角，可记为二. …12分在Rt△ PCE 中，求得EM =^-5aAC EB- P（第20 题）5............. 9分又 AP 平面 DAM , BC _ AP ,又 AP _ DM , AP _ 平面 BCD .又 ED _ 平面 BCD ,AP//DE .5、如图，已知ABCD 是边长为1的正方形，AF 丄平面ABCD (1) 证明：BD 丄EF;(2) 若AF = 1,且直线BE 与平面ACE 所成角的正弦值所以 ta ^ =EMr…15分DA _平面 .EMD 为 EM ,DA _ 平面 ABC , DA _ AB,DA _ AC ,设 AB = a ,又.DA = AB= AC , DC = DB 在厶 ABC 中， BAC =120， BC = 又.M 为BC 中点，.DM _ BC ，35a, DM a .…5 分 2 21 BM BC =2在 Rt △ EDM 中，EM=.DE 2 DM 2Si n EMD(2) AB=AC ,BC _ DA ,=匹_EM 3a 2M 为BC 中点，.BC _ AM .又.BC _ 平面 DAM .DA _ 平面 ABC ,11分 13分 14分,CE // AF , C^ AFC 1).C与平面BCD 所成角.2分4、如图, 中占I 八、、ABC ， ED _ 平面 BCD ，DE=DA=AB=AC. . BAC =120°，M 为 BC CMD为302 ,求•的值∙解：(1)连结BD、AC,交点为O.∙∙∙ ABCD是正方形∕∙ BD丄AC ……2分∙∙∙ AF丄平面 ABCD ∙∙∙ AF丄BD ……4分∙∙∙ BD丄平面 ACEF ……6分∙ BD丄EF ……7分(2)连结OE,由(1)知，BD丄平面ACEF ,所以∠ BEO即为直线BE与平面ACE所成的角. ……10分∙∙∙ AF 丄平面 ABCD , CE // AF , ∙ CE 丄平面ABCD , CE⊥ BC,∙∙∙ BC =1 , AF = 1,贝U CE = . , BE =、1 ∙2 , BO = -2 ,2∙Rt△ BEO 中，Sin. BEO=B O -—2一二3^2 , …13 分BE 2胡丘104因为■ ∙1 ,解得，. ……15分36、如图，在几何体中,AA1 _ 平面 ABC , AB _ BC,CC1 // AA1, AB = BC = AA1 = 2, CC1 =1,D,E分别是AB, AA1的中点.(1) 求证：BC1 // 平面 CDE ;(2) 求二面角E -DC-A的平面角的正切值解：(1)连接ACR 1R交EC于点F ,由题意知四边形 ACCR I RE是矩形，则F是ACR 1R 的中点，连接DF ,∙∙∙ D是AB的中点，∙ DF是厶ABCR I R的中位线，∙ BCR I RzzDF , 4 分∙∙∙ BCR 1R 二平面 EDC , DF 平面 EDC , ∙ BCR I RZZ平面 CDE.⑵作AH 丄直线CD ,垂足为H ,连接HE ,∙∙∙ AAR ιR⊥平面 ABC ,∙'∙ AAR i R 丄 DC, ∙∙∙ CD 丄平面AHE ,∙ CD 丄 EH ,又∙.∙ PA 丄平面ABC∙ QD // PA,......... 2 分又∙∙∙ QD 平面QBC ∙ PA //平面 QBC......... 6 分(2)∙∙∙ PQ _ 平面 QBC∙ PQB =∕PQC =90 ,又∙.∙ PB= PC ) PQ= PQ∙ PQB = PQC ∙ BQ =CQ .......................... 8 分 ∙点D 是BC 的中点，连结AD ,则AD — BC ∙ AD —平面 QBC ∙ PQ // AD , AD _ QD ∙四边形PADQ 是矩形 ........... 10分设 PA = AB = AC= 2a 得：PQ=AD = .2a , PD= 6a又∙∙∙ BC — PA l BC — PQ ,∙ BC —平面 PADQ ,ZAHE 是二面角 E -CD -A 的平面角. 11分D 是AB 的中点，AH 等于点B 到CD 的距离， 在厶BCD 中，求得:AH = 2^5AE J5 在厶 AEH 中，tan EAHE =AH 27、如图，已知平面 QBC 与直线PA 均垂直于Rt ABC 所在平面，且 PA=AB = AC ,(1)求证：PA //平面QBC ;即所求二面角的正切值为A从而 平面PBC _平面PADQ ,过Q 作QH _ PD 于点H ,则：QH _平面PBC ∙ . QCH 是CQ 与平面PBC 所成角2、2a 2 "3• ∙ QHa , CQ= BQ胚 3QH 2.3 12 sinQCHCQ 3 ^/63&如图，在直三棱柱 ABC-AB iG 中，UBC 是等腰直角三角形，∙ ACB = 90° ,侧棱 AA ι=2，D ，E 分别为CC i 与A l B 的中点，点E 在平面ABD 上的射影是 ABD 的重心.⑴求证：DE//平面ACB ；(2)求A i B 与平面ABD 所成角的正弦值.＜【)取中点d 普EF 、FU 、曲已知可得 EF 汙2^DC //A i A r 所以购边形DEFC 为平打凹边形 则EDHCF冈为EDU 平面虫BC. FC ⊂ T ：面ABC,ClD 过E 作£H 丄QF 于∕Λ连结HR.12=.6a∙∙∙ CQ 与平面PBC 所成角的正弦值为14分CC I 丄平面di?LABCL VnS ABC卜n CG 丄AB^2分AC = BC …—F n AB丄CF tAF —κCF∩CD = C,CΛCD⊂平^DEFC∖所^AB丄平面DEFC∖ EH U 平^DEFC所以丄EH t义EH丄DF,DFn Ali = FM/DF U T所⅛E/7 1 平［ii∖A BD t为州B与平面』EQ所成角的平面角，.......... Ii分H为Zvl j8D的巫心,在E∆DEFΨ EF2= FH FDJFDj所以^ro = √3,∕∕r -= √2ψFB= √2t£2? = Λ铤血ZEBH二醫=冬所ft J1/?与ip UiMBD所成饬的iE弦值为辱........... 诂分9、如图，在侧棱垂直于底面的三棱柱ABC — A i B i C i中，底面△ ABC为等腰直角三角形,∠ B=90° ,D为棱BB i的中点。

六年级数学专题思维训练—立体几何1、下面四个图形都是由六个相同的正方形组成的，其中，折叠后不能围成正方体的是______________．（填序号）2、如下图所示，棱长分别为1厘米、2厘米、3厘米的三个正方体紧贴在一起，则所得到的立体图形的表面积是平方厘米．3、下图是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形，问这个直三棱柱的体积是多少？4、有一个足够深的水槽，底面是长为16厘米、宽为12厘米的长方形，原本在水槽里盛有6厘米深的水和6厘米深的油（油在水的上方）．在水槽中放人一个长、宽、高分别为8厘米、8厘米、12厘米的铁块，那么此时油层的层高是厘米。

5、圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是立方厘米。

（结果用兀表示）6、如下图所示，从正方形ABCD 上截去长方形DEFG ，其中AB=1厘米，DE=21厘米， DG=31厘米，将ABCGFE 以GC 边为轴旋转一周，所得几何体的表面积是 平方厘米，体积是 _____________ 立方厘米。

（结果用兀表示）7、若长方体的三个侧面的面积分别是6，8，12，则长方体的体积是 。

8、一个圆柱和一个圆锥（如下图所示），它们的高和底面直径都标在图上，单位是厘米。

请回答：圆锥体积与圆柱体积的比是多少？9、如下图所示，一个圆柱体形状的木棒，沿着底面直径竖直切成两部分，已知这两部分的表面积之和比圆柱体的表面积大2008平方厘米，则这个圆柱体木棒的侧面积是 平方厘米。

（兀取3. 14）10、两个同样材料做成的球A 和B ，一个实心，一个空心。

A 的直径为7、重量为22，B 的直径为10.6、重量为33.3。

问：哪个球是实心球？（球的体积公式V=34πr ³）11、铁路油罐车由两个半球面和一个圆柱面钢板焊接而成，尺寸如下图所示．问：该油罐车的容积是多少立方米？（兀=3. 1416）（球的体积公式V=34πr ³）12、某工厂原用长4米，宽1米的铁皮围成无底无顶的的正方体形状的围栏，现要将围栏容量增加27%，问：能否还用原来的铁皮围成？13、一个正方体的纸盒中，恰好能放人一个体积为6. 28立方厘米的圆柱体，纸盒的容积有多大？（兀=3. 14）．14、用若干个小正方体拼成下图所示的造型．其中有一个小孔分别由左至右、由上至下以及由前至后穿透整个造型．拼成此造型共需使用多少个小正方体？15、一个圆锥形容器甲与一个半球形容器乙，它们圆形口的直径与容器的高的尺寸如下图所示，若用甲容器取水来注满乙容器，问：至少要注水多少次？（球的体积公式：V=34πr ³）16、下图是一个直圆柱形状的玻璃杯，一个长为12厘米的直棒状细吸管（不考虑吸管粗细）放在玻璃杯内，当吸管一端接触圆柱下底面时，另一端沿吸管最少可露出上底面边缘2厘米，最多能露出4厘米．则这个玻璃杯的容积为立方厘米．（取兀=3. 14）17、威力集团生产的某种洗衣机的外形是长方体，装衣物部分是圆柱形的桶，直径40厘米，深36厘米，已知该洗衣机装衣物的空间占洗衣机体积的25% ，长方体外形的长为52厘米，宽50厘米．问：高是多少厘米？（兀取3. 14，结果保留整数）18、有两个高度一样的水瓶，瓶子的底部被钉子分别戳了一个同样大的小洞．粗瓶子的水12分钟可以漏完，细瓶子的水8分钟可以漏完．若两个瓶子同时漏水，过了一段时间后，粗瓶子中水的高度是细瓶子中的2倍．这两个瓶子同时漏了分钟．19、世界上最早的灯塔建于公元270年，塔分三层，如下图所示，每层都高27米，底座呈正四棱柱，中间呈正八棱柱，上部呈正圆锥．上部的体积是底座的体积的 。

立体几何综合训练1. 一个长方体仓库从里面量约长10米，宽5米，高6米，如果放入棱长是2米的正方体木箱，至多可以放进多少个？【解答】分别从长、宽、高三个方向进行考虑：10÷2＝5（个）长这个方向可以放5个；5÷2＝2（个）……1（米），宽这个方向可以放2个；6÷2＝3（个），高这个方向可以放3个，5×2×3＝30（个），所以至多可以放30个。

2. 如图，用棱长是1厘米的立方体拼成如图所示的立体图形，这个立体图形的表面积是多少平方厘米？上、下底面：3×5×2＝30（平方厘米）左、右侧面：6×2＝12（平方厘米）前、后侧面：8×2＝16（平方厘米）立体图形的表面积：30＋12＋16＝58（平方厘米）3. 如图（单位：厘米），要将一个圆锥形的零件用一个长方体硬纸板的盒子包装起来，至少需要多少平方厘米的硬纸板？（接头处忽略不计）。

5×2＝10（厘米），长＝宽＝高10（厘米）硬纸板面积＝10×10×6＝600（平方厘米）立体几何综合训练4. 如图，甲圆柱体容器是空的，乙长方体容器中水深6.28厘米，将容器乙中的水全部倒入甲容器后水深8厘米，则甲容器的底面半径是多少厘米？【解答】水从乙容器倒入甲容器体积不变，找准这一点。

水的体积＝10×10×6.28＝628（立方厘米）S甲＝V÷h＝628÷8＝78.5（平方厘米）因为S甲＝78.5＝πr²，那么r²＝78.5÷3.14＝25＝5²，则r＝5（厘米）5. 用铁皮做一个如图所示的水管（单位：厘米），需用铁皮多少平方厘米？铁皮围成的物体的体积是多少？如图，把两根一样的水管拼接成一根圆柱形水管，r＝18÷2＝9（厘米），h＝45＋55＝100（厘米）S铁皮＝2mrh÷2＝2×3.14×9×100÷2＝2826（平方厘米）V＝πr²h÷2＝3.14×9²×100÷2＝12717（立方厘米）立体几何综合训练 6. 如图是一个棱长为6厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个棱长1厘米的正方体，做成一种零件，问它的表面积是多少？体积是多少？原表面积＝6×6×6＝216（平方厘米）新增表面积＝1×1×4×6＝24（平方厘米） 零件的表面积＝216＋24＝240（平方厘米） 原体积＝6×6×6＝216（立方厘米）减少的体积＝1×1×1×6＝6（立方厘米） 零件的体积＝216－6＝210（立方厘米）答：它的表面积是240平方厘米，体积是 210立方厘米。

1立体几何大题训练（1）1．如图，已知△ABC 是正三角形，EA ，CD 都垂直于平面ABC ，且EA ＝AB ＝2a ，DC ＝a ，F 是BE 的中点．(1）FD ∥平面ABC ；(2）AF ⊥平面EDB ．2．已知线段PA ⊥矩形ABCD 所在平面，M 、N 分别是AB 、PC 的中点。

（1)求证：MN //平面PAD ; （2）当∠PDA ＝45°时，求证：MN ⊥平面PCD ；FCB A E D2AB CDEF立体几何大题训练(2）3．如图，在四面体ABCD 中，CB=CD,BD AD ⊥，点E,F 分别是AB,BD 的中点．求证： （1)直线EF// 面ACD ； （2)平面⊥EFC 面BCD ．4．在斜三棱柱A 1B 1C 1—ABC 中，底面是等腰三角形，AB =AC ，侧面BB 1C 1C ⊥底面ABC （1）若D 是BC 的中点,求证 AD ⊥CC 1；（2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ,若AM =MA 1， 求证 截面MBC 1⊥侧面BB 1C 1C ；（3)AM =MA 1是截面MBC 1⊥平面BB 1C 1C 的充要条件吗？请你叙述判断理由]C13立体几何大题训练（3)5。

如图，在正方体ABCD-A 1B 1C 1D 1中,M 、N 、G 分别是A 1A ，D 1C,AD 的中点． 求证:(1）MN//平面ABCD; （2）MN ⊥平面B 1BG ．6。

如图，在正方体ABCD －A 1B 1C 1D 1中，E 、F 为棱AD 、AB 的中点． （1）求证：EF ∥平面CB 1D 1；（2）求证：平面CAA 1C 1⊥平面CB 1D 1．_ G_ M _ D_1_ C_1_ B_1_ A_1_ N _ D_ C_ B_ ABA 1F4立体几何大题训练(4）7、如图,在直四棱柱ABCD —A 1B 1C 1D 1中，底面ABCD 为等腰梯形,AB ∥CD ，AB=4，BC=CD=2，AA 1=2，E 、E 1分别是棱AD 、AA 1的中点（1）设F 是棱AB 的中点，证明：直线EE 1∥面FCC 1；（2)证明:平面D 1AC ⊥面BB 1C 1C 。

数学立体几何练习题一、选择题:本大题共8小题,每小题５分，共40分．在每小题给出的四个选项中,只有一个是符合题目要求的.1.如图,在正方体ABC Ｄ-A 1B 1Ｃ１D 1中，棱长为a ，Ｍ、N 分别为A 1Ｂ和AC 上的点，A 1Ｍ=AN ＝错误!，则M Ｎ与平面BB 1C 1C 的位置关系是（ ） A.相交 B.平行 C ．垂直 Ｄ.不能确定2.将正方形ＡBCD 沿对角线B Ｄ折起，使平面ABD ⊥平面CBD,Ｅ是CD 中点，则AED ∠的大小为（ ） ﻩA ．45 Ｂ.30C.60ﻩD.90３.ＰA ，PB,PC 是从P 引出的三条射线，每两条的夹角都是6０º，则直线PC 与平面P ＡB所成的角的余弦值为（ )A.12B 。

3ﻩC 。

3ﻩＤ。

6４.正方体ＡB ＣD —A 1B 1Ｃ1Ｄ1中，Ｅ、F 分别是A Ａ1与CC 1的中点,则直线ED 与D １F 所成角的余弦值是A ．15ﻩＢ。

13C 。

12D 。

3 5． 在棱长为2的正方体1111D C B A ABCD -中，O 是底面ABC Ｄ的中心,Ｅ、F 分别是1CC 、A Ｄ的中点，那么异面直线OE 和1FD 所成的角的余弦值等于（ )ﻩＡ.510 B ．32 ﻩＣ.55ﻩD ．515 6．在正三棱柱AB Ｃ-A 1B 1C 1中，若AB=2,A A 1=1，则点Ａ到平面A １BC 的距离为(ﻩ）A.43ﻩB.23ﻩＣ．433ﻩD.3 ７．在正三棱柱ABC-A 1B 1Ｃ1中，若ＡB=错误!BB 1,则AB 1与Ｃ1Ｂ所成的角的大小为（ ）A.60ºﻩ B ． 90º ﻩＣ．１0５º ﻩD. 75º８.设E ，Ｆ是正方体AC 1的棱ＡB 和D 1C 1的中点,在正方体的１2条面对角线中,与截面Ａ1EＣF 成60°角的对角线的数目是（ ） A ．0 B.2 C.4 ﻩＤ.6 二、填空题：本大题共6小题,每小题5分,共3０分．9.在正方体ABC Ｄ-A １B 1C 1D 1中,M 、Ｎ分别为棱ＡＡ1和B Ｂ1的中点,则ｓin 〈CM ,1D N 〉的值为___＿__＿_＿．１０.如图，正方体的棱长为1,C 、D 分别是两条棱的中点， A 、B 、M 是顶点,AM DCAB CDP 那么点M 到截面ＡB ＣD 的距离是 .１1．正四棱锥Ｐ-A ＢCD 的所有棱长都相等，E 为PC 中点,则直线AC 与截面BDE 所成的角为 .12.已知正三棱柱A ＢC-Ａ1B 1Ｃ1的所有棱长都相等，D 是Ａ1C 1的中点,则直线AD 与平面Ｂ1DC 所成角的正弦值为 . 13．已知边长为的正三角形A ＢＣ中，Ｅ、F 分别为ＢＣ和AC 的中点，PA ⊥面ＡBC ，且PA=2,设平面α过PF 且与AE 平行,则AE 与平面α间的距离为 ． 14.棱长都为2的直平行六面体A ＢＣD —A 1B 1C 1D １中,∠BA Ｄ=60°,则对角线A 1C 与侧面DCC 1D 1所成角的余弦值为__＿__＿__.三、解答题:本大题共6小题，共80分。

立体几何小题基础练-新高考数学复习分层训练（新高考通用）一、单选题1．（2023·广东·统考一模）已知一个圆锥和圆柱的底面半径和高分别相等，若圆锥的轴截面是等边三角形，则这个圆锥和圆柱的侧面积之比为（）A．12B．2C．3D2．（2023·山东济南·一模）已知正三角形边长为2，用斜二测画法画出该三角形的直观图，则所得直观图的面积为（）A．4B．4C．D．3．（2023·广东惠州·统考模拟预测）已知互不重合的三个平面α、β、γ，其中a αβ⋂=，b βγ= ，c γα= ，且a b P = ，则下列结论一定成立的是（）A ．b 与c 是异面直线B ．a 与c 没有公共点C ．//b cD ．b c P= 【答案】D【分析】根据题设条件可得相应的空间图形，从而可得正确的选项.【详解】∵a b P = ，∴P a ∈，P b ∈，∵a αβ= ，b βγ= ，∴P α∈，P β∈，P γ∈，∵c αγ⋂=，∴P c ∈，∴b c P = ，∴a c P ⋂=，如图所示：故A ，B ，C 错误；故选：D ．4．（2023·浙江嘉兴·统考模拟预测）《九章算术·商功》中记载：“斜解立方，得两堑堵..”我们可以翻译为：取一长方体，分成两个一模一样的直三棱柱，称为堑堵.再沿堑堵的一顶点与相对的棱剖开，得一个四棱锥和一个三棱锥，这个四棱锥称为阳马，这个三棱锥称为鳖臑.现已知某个鳖臑的体积是1，则原长方体的体积是（）A ．8B ．6C ．4D ．35．（2023·辽宁阜新·校考模拟预测）已知矩形ABCD 中，AB =8，取AB 、CD 的中点E 、F ，沿直线EF 进行翻折，使得二面角A EF B --的大小为120°，若翻折后A 、B 、C 、D 、E 、F 都在球O 上，且球O 的体积为288π，则AD =（）A ．B ．C ．4D ．2记三角形CDF 外接圆的圆心为因为二面角A EF B --的大小为且,EF DF EF CF ⊥⊥，所以所以30DCF ∠=o ，由正弦定理可得sin DFDCF∠6．（2023·山东日照·统考一模）红灯笼，起源于中国的西汉时期，两千多年来，每逢春节人们便会挂起象征美好团圆意义的红灯笼，营造一种喜庆的氛围.如图1，某球形灯笼的轮廓由三部分组成，上下两部分是两个相同的圆柱的侧面，中间是球面除去上下两个相同球冠剩下的部分.如图2，球冠是由球面被平面截得的一部分，垂直于截面的直径被截得的部分叫做球冠的高，若球冠所在球面的半径为R，球冠的高为h，则球冠的面积S Rh=.如图1，已知该灯笼的高为58cm，圆柱的高为5cm，圆柱的底面圆直径为14cm，2π则围成该灯笼中间球面部分所需布料的面积为（）A．21940πcm B．22400πcm D．22540πcm2350πcm C．27．（2023·山东·烟台二中校考模拟预测）已知圆锥的侧面积为，高为，若圆锥可在某球内自由运动，则该球的体积最小值为（）A．B．8πC．9πD．【答案】D【分析】由圆锥侧面积公式及勾股定理可得圆锥半径r与母线l长，求该圆锥的外接球体积即可.【详解】解：设圆锥的底面半径为r，母线长为l，则8．（2023·山东威海·统考一模）已知圆锥的侧面展开图是一个半径为4，弧长为4π的扇形，则该圆锥的表面积为（）A ．4πB ．8πC ．12πD ．20π9．（2023·山东聊城·统考一模）在正方体1111ABCD A B C D -中，直线m 、n 分别在平面ABCD 和11ABB A ，且m n ⊥，则下列命题中正确的是（）A ．若m 垂直于AB ，则n 垂直于AB B ．若m 垂直于AB ，则n 不垂直于ABC ．若m 不垂直于AB ，则n 垂直于ABD ．若m 不垂直于AB ，则n 不垂直于AB【答案】C【分析】根据线面垂直的判定定理及直线位置关系来判定选项即可.【详解】如图所示：A 选项，若m 垂直于AB ，则面11ABB A 内的所有直线均与m 垂直，无法证明,AB n 的关系，故A 选项错误，B 选项与A 同理；C 选项，若m 不垂直于AB ，因为1BB m ⊥，所以当m n ⊥时，1//BB n ，又因为1BB AB ⊥，所以n 垂直于AB ；D 选项与C 同理.故选：C10．（2023·江苏徐州·徐州市第七中学校考一模）则三棱锥-P ABC 中，PA ⊥平面π,6,3,6ABC PA BC CAB ==∠=，则三棱锥-P ABC 的外接球半径为（）A ．3B．C ．D ．611．（2023·湖北武汉·统考模拟预测）某车间需要对一个圆柱形工件进行加工，该工件底面半径15cm ，高10cm ，加工方法为在底面中心处打一个半径为r cm 且和原工件有相同轴的圆柱形通孔.r 的值应设计为（）A ．BC ．4D ．5【答案】D【分析】表示出表面积后，根据二次函数性质可得.【详解】大圆柱表面积为2215π10215π750π⨯+⨯⨯=小圆柱侧面积为102πr ⨯，上下底面积为22πr 所以加工后物件的表面积为2750π20π2πr r +-，当=5r 时表面积最大.故选：D12．（2023·湖北·统考模拟预测）截角四面体是一种半正八面体，可由四面体经过适当的截角而得到．如图，将棱长为6的正四面体沿棱的三等分点作平行于底面的截面截角得到所有棱长均为2的截角四面体，则该截角四面体的体积为（）A．B ．2023C D ．13．（2023·湖北·荆州中学校联考二模）甲、乙两个圆锥的底面积相等，侧面展开图的圆心角之和为2π，侧面积分别为S 甲、S 乙，体积分别为V 甲、V 乙，若2S S =甲乙，则V V 甲乙等于（）A B ．5C ．5D14．（2023·湖南湘潭·统考二模）已知,,A B C为球O球面上的三个点，若3AB BC AC===，球O的表面积为36π，则三棱锥O ABC-的体积为（）A B．4C．4D．415．（2023·湖南·湖南师大附中校联考模拟预测）如图所示，一个球内接圆台，已知圆台上､下底面的半径分别为3和4，球的表面积为100π，则该圆台的体积为（）A．175π3B．75πC．238π3D．259π3因为圆台上､下底面的半径分别为所以4OB OA ==，1O B 所以2211OO OB O B =-所以127O O =，16．（2023·广东茂名·统考一模）蒙古包是蒙古族牧民居住的一种房子，建造和搬迁都很方便，适于牧业生产和游牧生活，蒙古包下半部分近似一个圆柱，高为2m ；上半部分近似一个与下半部分同底的圆锥，其母线长为，轴截面（过圆锥旋转轴的截面）是面积为2的等腰钝角三角形，则该蒙古包的体积约为（）A ．321πmB ．318πm C ．(318πm+D ．(320πm+【答案】C因为其轴截面（过圆锥旋转轴的截面）是腰长为()2211sin 23sin 3l αα=⨯⨯=17．（2023·广东茂名·统考一模）已知菱形ABCD 的各边长为2，=60B ∠︒.将ABC 沿AC 折起，折起后记点B 为P ，连接PD ，得到三棱锥P ACD -，如图所示，当三棱锥P ACD -的表面积最大时，三棱锥P ACD -的外接球体积为（）A ．π3B ．π3C ．D ．π34+【点睛】结论点睛：若三棱锥有两个面为共斜边的直角三角形，则三棱锥的外接球的球心为该斜边的中点.18．（2023·江苏·统考一模）已知正四面体-P ABC 的棱长为1，点O 为底面ABC 的中心，球О与该正四面体的其余三个面都有且只有一个公共点，且公共点非该正四面体的顶点，则球O 的半径为（）A B C ．9D ．3二、多选题19．（2023·浙江·统考一模）已知三棱柱ABC DEF -的棱长均相等，则（）A ．AB CF ⊥B ．AE BD ⊥C ．60ABC ∠=︒D ．60ADE ∠=︒【答案】BC【分析】根据题意结合异面直线夹角逐项分析判断.【详解】对A ：∵AD CF ，则AB 与CF 的夹角为BAD ∠，不一定是直角，A 错误；对B ：由题意：ABED 为菱形，则AE BD ⊥，B 正确；对C ：由题意：AB BC CA ==，则60ABC ∠=︒，C 正确；对D ：由题意：ABED 为菱形，则()0,πADE ∠∈，即ADE ∠大小无法确定，D 错误.故选：BC.20．（2023·江苏泰州·统考一模）在棱长为2的正方体1111ABCD A B C D -中，AC 与BD 交于点O ，则（）A ．1AD //平面1BOCB ．BD ⊥平面1COC C ．1C O 与平面ABCD 所成的角为45 D ．三棱锥1C BOC -的体积为23【答案】ABD【分析】根据线面平行判定定理判断A ，利用线面垂直判定定理判断B ，利用线面夹角的定义判断C ，根据等体积法判断D.【详解】∵111//,AD BC AD ⊄平面11,BOC BC ⊂平面1,BOC 1∴AD //平面1BOC ，A 对；21．（2023·辽宁葫芦岛·统考一模）已知a ，b 为空间中两条不同直线，α，β为空间中两个不同的平面，则下列命题一定成立的是（）A ．αβ∥，a α⊂，b a b β⊥⇒⊥B ．αβ∥，a α⊥，b a b β⊥⇒∥C ．αβ⊥，a αβ⋂=，b a b β⇒∥∥D ．αβ⊥，a α⊥，b a b β⊥⇒⊥22．（2023·江苏南通·统考模拟预测）已知点P 是正方体1111ABCD A B C D -侧面11BB C C （包含边界）上一点，下列说法正确的是（）A ．存在唯一一点P ，使得DP //1AB B ．存在唯一一点P ，使得AP //面11ACD C ．存在唯一一点P ，使得1A P ⊥1B D D ．存在唯一一点P ，使得1D P ⊥面11AC D 【答案】AD【分析】建立空间直角坐标系，设()1,,1,AD P x z =，写成点的坐标，A 选项，根据向量平行得到方程组，得到0,1x z ==，存在唯一一点P ，使得DP //1AB ，A 正确；B 选项，证明出1BD ⊥ 平面11AC D ，从而得到10AP BD ⋅=，列出方程，解得：x z =，得到P 点轨迹为线段1B C ；C 选项，由向量数量积为0列出方程，得到P 在线段1BC 上，满足条件的P 有无数个；D 选项，在1BD ⊥平面11AC D 的基础上，得到,P B 重合，D 正确.【详解】如图建系，令()1,,1,AD P x z =，则()()()()()()()11111,0,0,1,0,1,0,1,1,0,0,0,1,1,0,0,0,1,1,1,1A A C D B D B ，对于A ，()()1,1,,0,1,1DP x z AB == ，若1//DP AB ，则01x z λλλ=⋅⎧⎪=⎨⎪=⎩，解得：0,1x z ==故()0,1,1P 满足要求，与1C 重合，存在唯一一点P ，使得DP //1AB ，A 对.对于B ，因为()()1111,1,11,1,0110B AC D ⋅=--⋅-=-= ，()()111,1,11,0,1110BD A D ⋅=--⋅--=-=，因为1111A C A D A ⋂=，111,A C A D ⊂平面11AC D ，所以1BD ⊥ 平面11AC D ，又AP //平面11AC D ，则10AP BD ⋅=，()()1,1,11,1,110x z x z --⋅-=--+=，解得：x z =，故P 点轨迹为线段1B C ，满足条件的P 有无数个，B 错，对于C ，()()11111,1,1,1,1,1,11110A P x z DB A P DB x z x z =--=⋅=-++-=+-= ，P 在线段1BC 上，满足条件的P 有无数个，C 错.对于D ，由B 选项可知：1BD ⊥ 平面11AC D ，而1D P ⊥面11AC D ，又1D P 与1BD共线，故,P B 重合，D 对.故选：AD.23．（2023·山东青岛·统考一模）下列说法正确的是（）A ．若直线a 不平行于平面α，a α⊄，则α内不存在与a 平行的直线B ．若一个平面α内两条不平行的直线都平行于另一个平面β，则αβ∥C ．设l ，m ，n 为直线，m ，n 在平面α内，则“l α⊥”是“l m ⊥且l n ⊥”的充要条件D ．若平面α⊥平面1α，平面β⊥平面1β，则平面α与平面β所成的二面角和平面1α与平面1β所成的二面角相等或互补24．（2023·湖南常德·统考一模）已知平面α，β，直线l ，m ，则下列命题正确的是（）A ．若αβ⊥，,,m l m l αβα⋂=⊥⊂，则l β⊥B ．若l αβα⊂∥，，m β⊂，则//l mC ．若m α⊂，则“l α⊥”是“l m ⊥”的充分不必要条件D ．若m α⊂，l α⊄，则“l α∥”是“l m ”的必要不充分条件【答案】ACD【分析】根据面面垂直的性质定理可判断A,根据线面平行的判断以及性质可判断BD,根据线面垂直的性质可判断C.【详解】由面面垂直的性质定理可知A 正确,对于B,若l αβα⊂∥，，m β⊂，则//l m ,或者,l m 异面，故B 错误,对于C,若m α⊂,l α⊥则l m ⊥,故充分性成立,但是l m ⊥，m α⊂，不能得到l α⊥，故C 正确，对于D,若m α⊂，l α⊄，l α∥,不能得到l m ,因为,l m 有可能异面，但是l m ，m α⊂，l α⊄，则l α∥，故D 正确，故选：ACD25．（2023·广东茂名·统考一模）已知空间中三条不同的直线a 、b 、c ，三个不同的平面αβγ、、，则下列说法中正确的是（）A ．若a b ∥，a α⊥，则b α⊥B ．若a αβ⋂=，b βγ= ，c αγ⋂=，则a b c ∥∥C ．若αβ⊥，a α⊄，a β⊥，则a αP D ．若c β⊥，c γ⊥，则βγ∥如图，正方体两两相交的三个平面平面ABCD ⋂平面11ABB A =平面11ABB A 平面11ADD A =对于C ，若αβ⊥，a β⊥，则αP三、填空题26．（2023·江苏南通·校联考模拟预测）中国某些地方举行婚礼时要在吉利方位放一张桌子，桌子上放一个装满粮食的升斗，斗面用红纸糊住，斗内再插一杆秤、一把尺子，寓意粮食满园、称心如意、十全十美，下图为一种婚庆升斗的规格，该升斗外形是一个正四棱台，上、下底边边长分别为20cm ，10cm ，侧棱长为10cm ，忽略其壁厚，则该升斗的容积为_________3cm ．【详解】上下底面对角线的长度分别为：202,10上底面的面积2120400S ==()2cm ，下底面的面积四棱台的体积27．（2023·江苏宿迁·江苏省沭阳高级中学校考模拟预测）在直角梯形ABCD 中，//AB CD ，AD AB ⊥，22AB DC ==，E 为AD 的中点.将EAB 和ECD 分别沿,EB EC 折起，使得点A ，D 重合于点F ，构成四面体FBCE .若四面体FBCE 的四个面均为直角三角形，则其外接球的半径为_________.故答案为：324.28．（2023·山东·烟台二中校联考模拟预测）已知在正方体1111ABCD A B C D -中，12AM AD =，平面11A BC ⋂平面1CC M l =，则直线l 与1D M 所成角的余弦值为__________．【答案】3030【分析】作出辅助线，找到1C G 即为直线l ，建立空间直角坐标系，设出点的坐标，利用异面直线夹角余弦公式求出答案.【详解】作出图形，如图所示．延长DC 至E ，使得DC CE =，则1A AB △≌1C CE △，111D A C≌CBE △，故11A B C E =，11A C BE =，故四边形11A C EB 为平行四边形，连接BE ，延长MC ，BE 交于点G ，连接1C G ，则1C G 即为直线l ．以D 为坐标原点，DA ，DC ，1DD 分别为x ，y ，z 轴建立如图所示的空间直角坐标系，设2AD =，过点G 作GN ⊥y 轴于点N ，则MDC △∽GNC △，且相似比为1:2，故24CN CD ==，22GN DM ==，则()10,2,2C ，()2,6,0G -，()1,0,0M ，()10,0,2D ，29．（2023·湖北·校联考模拟预测）葫芦是一种爬藤植物，在我国传统文化中，其枝密集繁茂，象征着儿孙满堂、同气连枝；其音近于“福禄”，寓意着长寿多福、事业发达；其果口小肚大，代表着心胸开阔、和谐美满．如图，一个葫芦的果实可以近似看做两球相交所得的几何体Ω，其中Ω的下半部分是半径为1O 的一部分，Ω的上半部分是半径为3的球2O 的一部分，且126O O =，则过直线12O O 的平面截Ω所得截面的面积为__________．30．（2023·湖北武汉·华中师大一附中校联考模拟预测）已知圆台的侧面积与轴截面的面积之比为23π3，若上、下底面的半径分别为1和2，则母线长为__________．【答案】2【分析】设圆台的母线长为l ．解得2故答案为：2.。

立体几何大题1.空间中的平行关系（1）线线平行（2）线面平行的判定定理：平面外一直线与平面内一直线平行，则线面平行（3）线面平行的性质定理若线面平行，经过直线的平面与该平面相交，则直线与交线平行（4）面面平行的判定定理判定定理1：一个平面内有两条相交直线分别平行于另一个平面，则面面平行判定定理2：一个平面内有两条相交直线分别于另一个平面内两条相交直线平行，则面面平行（5）面面平行的性质定理性质定理1：两平面互相平行，一个平面内任意一条直线平行于另一个平面性质定理2：两平面互相平行，一平面与两平面相交，则交线互相平行6.空间中的垂直关系（1）线线垂直（2）线面垂直的判定定理一直线与平面内两条相交直线垂直，则线面垂直（3）线面垂直的性质定理性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线性质定理2：垂直于同一个平面的两条直线平行（4）面面垂直的判定定理一个平面内有一条直线垂直于另一个平面，则两个平面垂直(或：一个平面经过另一个平面的垂线，则面面垂直)（5）面面垂直的性质定理两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角，a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角，sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ，n 为平面α，β的法向量).9.点B 到平面α的距离d =|AB ⋅n | |n |(n 为平面α的法向量，AB 是经过面α的一条斜线，A ∈α).模拟训练一、解答题1(22·23下·湖南·二模)如图，在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2,AC =BB ，点D 为棱BB 的中点，AE =13AC ．(1)求DE 的长度；(2)求平面CDE 与平面BDE 夹角的余弦值．【答案】(1)393(2)34【分析】(1)在△ABC 中，用余弦定理可得到AC =23，在△ABE 中，用余弦定理可得BE =233，即可求得DE =DB 2+BE 2=393；(2)以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立空间直角坐标系，求出平面CDE 与平面BDE 的法向量，即可求解【详解】(1)因为在直三棱柱ABC -A B C 中，∠ABC =120°,AB =BC =2，在△ABC 中，由余弦定理得cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC=22+22-AC 22×2×2=-12，解得AC =23，则AE =13AC =233，在△ABE 中，由余弦定理得cos ∠BAE =AB 2+AE 2-BE 22AB ⋅AE =22+233 2-BE 22×2×233=32，解得BE =233，又AC =BB =23，所以BD =12BB =3，因为BB ⊥平面ABC ，BE ⊂平面ABC ，所以BB ⊥BE ，在直角三角形DBE 中，DE =DB 2+BE 2=(3)2+233 2=393；(2)因为AE =BE =233，所以∠ABE =∠BAE =30°，则∠CBE =∠ABC -∠ABE =120°-30°=90°，则BE ,BC ,BB 两两互相垂直，以B 为原点，分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立如下图所示的空间直角坐标系：则点C 0,2,0 ,D 0,0,3 ,E 233,0,0 ，则CD =0,-2,3 ,CE =233,-2,0 ，设平面CDE 的法向量为n =x ,y ,z ，由n ⋅CD =x ,y ,z ⋅0,-2,3 =-2y +3z =0n ⋅CE =x ,y ,z ⋅233,-2,0 =233x -2y =0 ，得z =233y x =3y，令y =3，得平面CDE 的一个法向量为n =3,3,2 ；平面BDE 的一个法向量为m =0,1,0 ．设平面CDE 与平面BDE 夹角的大小为θ，则cos θ=m ⋅n m n =0,1,0 ⋅3,3,2 1×4=34，故平面CDE 与平面BDE 夹角的余弦值为34．2(22·23下·绍兴·二模)如图，在多面体ABCDE 中，DE ⊥平面BCD ,△ABC 为正三角形，△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证：AE ⊥BC ；(2)若AE ⎳平面BCD ，求直线BE 与平面ABC 所成的线面角的正弦值.【答案】(1)证明见解析(2)63【分析】(1)由线面垂直的性质定理和判定定理即可证明；(2)法一：由分析可知，∠EBH 就是直线BE 与平面ABC 所成的线面角，设∠AFD =α，当α<90°时，O 与D 重合，可得A ,E 两点重合，不符合题意，当α>90°时，求出EH ,BE ，即可得出答案；法二：建立空间直角坐标系，求出直线BE 的方向向量与平面ABC 的法向量，由线面角的向量公式代入即可得出答案.【详解】(1)设F 为BC 中点，连接AF ,EF ，则由△ABC 为正三角形，得AF ⊥BC ；DE ⊥平面BCD ，且△BCD 为等腰直角三角形，计算可得：BE =CE =2,∴EF ⊥BC .EF ∩AF =F ,EF ,AF ⊂面AEF ，于是BC ⊥面AEF ，AE ⊂面AEF ，从而BC ⊥AE .(2)法一：由(1)可知，过点E 作EH ⊥AF ，垂足为H ，则∠EBH 就是直线BE 与平面ABC 所成的线面角.当AE ⎳平面BCD 时，可得A 到平面BCD 的距离为 2.设∠AFD =α，所以AF ⋅sin α=2，可得sin α=63，当α<90°时，cos α=33，不妨设A 在底面BCD 射影为O ，则FO =1，此时O 与D 重合，可得A ,E 两点重合，不符合题意，舍去；当α>90°时，FO =1，此时O 在DF 的延长线上，作EH ⊥AF ，由于AODE 为矩形，可得AE =DO =2,AE ∥OD ，可得sin ∠EAH =63，可得EH =263.于是sin ∠EBH =EH BE=63.法二：建立如图坐标系，可得F 0,0,0 ,B 1,0,0 ，C -1,0,0 ,D 0,1,0 ,E 0,1,2 ,A 0,a ,b由AF =3，解得a 2+b 2=3，又∵AE ⎳平面BCD ，令n =0,0,1 ，可得AB ⋅n =0，解得b =2,a =±1.当a =1时A ,E 重合，所以a =-1，此时A 0,-1,2 .不妨设平面ABC 的法向量为m =x ,y ,z ，则CB ⋅m =0CA ⋅m =0代入得x -y +2z =02x =0 ，令z =1，则y =2，所以m =0,2,1 .由于BE =-1,1,2 ，不妨设所成角为θ，则sin θ=∣cos BE ,m |=63.3(22·23·张家口·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为菱形，∠CBB 1=60°，AB =BC =2，AC =AB 1=2.(1)证明：平面ACB 1⊥平面BB 1C 1C ；(2)求平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值.【答案】(1)证明见解析；(2)57.【分析】(1)利用面面垂直的判定定理进行证明；(2)利用垂直关系建立空间直角坐标系，用向量法进行求解.【详解】(1)如图，连接BC 1，交B 1C 于O ，连接AO .因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1，且O 为BC 1的中点.又AC =AB 1=2，故AO ⊥B 1C .又AB =BC =2，且∠CBB 1=60°，所以CO =1,BO =3，所以AO =AC 2-CO 2=1.又AB =2，所以AB 2=BO 2+AO 2，所以AO ⊥BO .因为BO ,CB 1⊂平面BB 1C 1C ，BO ∩CB 1=O ，所以AO ⊥平面BB 1C 1C .又AO ⊂平面ACB 1，所以平面ACB 1⊥平面BB 1C 1C .(2)由(1)知，OA ,OB ,OB 1两两互相垂直，因此以O 为坐标原点，OB ,OB 1,OA 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系O -xyz ，则A (0,0,1)，B (3,0,0)，C (0,-1,0)，C 1(-3,0,0).故CC 1 =(-3,1,0)，CA =(0,1,1)，CB =(3,1,0).设n =(x 1,y 1,z 1)为平面ACC 1A 1的一个法向量，则有n ⋅CC 1 =0n ⋅CA =0 ，即-3x 1+y 1=0y 1+z 1=0 ，令x 1=1，则n =(1,3,-3).设m =(x 2,y 2,z 2)为平面ABC 的一个法向量，则有m ⋅CA =0m ⋅CB =0，即y 2+z 2=03x 2+y 2=0 ，令x 2=1，则m =(1,-3,3).因为平面A 1B 1C 1∥平面ABC ，所以m =(1,-3,3)也是平面A 1B 1C 1的一个法向量.所以cos <n ,m > =n ⋅m n m=1-3-3 7×7=57.所以平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值57. 4(22·23·湛江·二模)如图1，在五边形ABCDE 中，四边形ABCE 为正方形，CD ⊥DE ，CD =DE ，如图2，将△ABE 沿BE 折起，使得A 至A 1处，且A 1B ⊥A 1D ．(1)证明：DE ⊥平面A 1BE ；(2)求二面角C -A 1E -D 的余弦值．【答案】(1)证明见解析(2)63【分析】(1)由已知易得DE ⊥BE ，即可证明线面垂直；(2)建立空间直角坐标系，用坐标公式法求解即可．【详解】(1)由题意得∠BEC =∠CED =π4，∠BED =π2，DE ⊥BE ，因为AB ⊥AE ，则A 1B ⊥A 1E ，又A 1B ⊥A 1D ，A 1E ∩A 1D =A 1,A 1E ,A 1D ⊂面A 1ED ，所以A 1B ⊥面A 1ED ，又DE ⊂面A 1ED ，则DE ⊥A 1B ，又DE ⊥BE ，A 1B ∩BE =B ，A 1B ⊂平面A 1BE ，BE ⊂平面A 1BE ，所以DE ⊥平面A 1BE ．(2)取BE 的中点O ，可知BE =2CD ,OE =CD ，由DE ⊥BE ，且CD ⊥DE 可得OE ⎳CD ，所以四边形OCDE 是平行四边形，所以CO ∥DE ，则CO ⊥平面A 1BE ，设BE =2，以点O 为坐标原点，OB ,OC ,OA 1所在直线为坐标轴建立空间直角坐标系，如图，则A 1(0,0,1),E (-1,0,0),B (1,0,0),C (0,1,0),D (-1,1,0)，EA 1 =(1,0,1),EC =(1,1,0),ED =(0,1,0)，设平面A 1EC 的一个法向量为n 1 =(x 1,y 1,z 1)，则n 1 ⋅EA 1 =0n 1 ⋅EC =0 ，即x 1+z 1=0x 1+y 1=0 ，取x 1=1，则n 1 =(1,-1,-1)，设平面A 1ED 的一个法向量为n 2 =(x 2,y 2,z 2)，则n 2 ⋅E 1A =0n 2 ⋅ED =0 ，即x 2+z 2=0y 2=0 ，取x 2=1，则n 2 =(1,0,-1)，所以cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2=63，由图可知，二面角C -A 1E -D 为锐角，所以面角C -A 1E -D 的余弦值为63．5(22·23下·长沙·三模)如图，在多面体ABCDE 中，平面ACD ⊥平面ABC ，BE ⊥平面ABC ，△ABC 和△ACD 均为正三角形，AC =4，BE =3，点F 在AC 上.(1)若BF ⎳平面CDE ，求CF ；(2)若F 是AC 的中点，求二面角F -DE -C 的正弦值.【答案】(1)CF =1(2)8517【分析】(1)记AC 中点为M ，连接DM 、BM ，依题意可得DM ⊥AC ，根据面面垂直的性质得到DM ⊥平面ABC ，如图建立空间直角坐标系，求出平面CDE 的法向量，设F a ,0,0 ，a ∈2,-2 ，依题意可得BF ⋅n =0求出a 的值，即可得解；(2)依题意点F 与点M 重合，利用空间向量法计算可得.【详解】(1)记AC 中点为M ，连接DM 、BM ，△ACD 为正三角形，AC =4，则DM ⊥AC ，且DM =2 3.因为平面ACD ⊥平面ABC ，平面ACD ∩平面ABC =AC ，DM ⊂平面ACD ，所以DM ⊥平面ABC ，又△ABC 为正三角形，所以BM ⊥AC ，所以BM =23，如图建立空间直角坐标系，则B 0,23,0 ，C -2,0,0 ，D 0,0,23 ，E 0,23,3 ，所以CD =2,0,23 ，CE =2,23,3 ，设平面CDE 的法向量为n =x ,y ,z ，则n ⋅CD =2x +23z =0n ⋅CE =2x +23y +3z =0，令x =3，则z =-3，y =-32，则n =3,-32,-3 ，设F a ,0,0 ，a ∈-2,2 ，则BF =a ,-23,0 ，因为BF ⎳平面CDE ，所以BF ⋅n =3a +-23 ×-32+0×-3 =0，解得a =-1，所以F 为CM 的中点，此时CF =1.(2)若F 是AC 的中点，则点F 与点M 重合，则平面FDE 的一个法向量可以为m =1,0,0 ，设二面角F -DE -C 为θ，显然二面角为锐角，则cos θ=m ⋅n m ⋅n=332+-32 2+-3 2=651，所以sin θ=1-cos 2θ=1-651 2=8517，所以二面角F -DE -C 的正弦值为8517.6(22·23下·湖北·二模)如图，S 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322，AM =2MS ,AS =3,PQ 为⊙O 的一条弦，且SB ⎳平面PMQ .(1)求PQ 的最小值；(2)若SA ⊥PQ ，求直线PQ 与平面BCM 所成角的正弦值.【答案】(1)22(2)3010【分析】(1)作出辅助线，找到符合要求的PQ ，并利用垂径定理得到最小值；(2)在第一问基础上，得到当PQ 取得最小值时，SA ⊥PQ ，并建立空间直角坐标系，利用空间向量求解线面角.【详解】(1)过点M 作MH ⎳SB 交AB 于点H ，过点H 作PQ ⊥AB ，此时满足SB ⎳平面PMQ ，由平面几何知识易知，PQ =2r 2-d 2，当弦心距d 最大时，d =OH ，弦长最短，即PQ 取得最小值，因为AM =2MS ,AS =3，所以AH =2HB ，因为AC ⊥BC ,AC =BC =322，由勾股定理得AB =322⋅2=3，故AH =2,HB =1，连接OQ ，则OQ =32，由勾股定理得HQ =OQ 2-OH 2=94-14=2，所以PQ =2HQ =22；(2)连接OS ，则OS ⊥平面ACB ，因为PQ ⊂平面ACB ，故OS ⊥PQ ，而SA ⊥PQ ，OS ∩SA =S ，所以PQ ⊥平面AOS ，即有PQ ⊥AB .以O 为坐标原点，过点O 且平行PQ 的直线为x 轴，OB 所在直线为y 轴，OS 所在直线为z 轴，建立空间直角坐标系，则P -2,12,0 ,Q 2,12,0 ,B 0,32,0 ,C 32,0,0 ,M 0,-12,3 ，设平面BCM 的法向量为m =x ,y ,z ，则m ⋅CB =x ,y ,z ⋅-32,32,0 =-32x +32y =0m ⋅MB =x ,y ,z ⋅0,2,-3 =2y -3z =0，令x =1，则y =1,z =233，故m =1,1,233，设直线PQ 与平面BCM 所成角的大小为θ，则sin θ=cos PQ ,m =PQ ⋅m PQ ⋅m =22,0,0 ⋅1,1,233 22×1+1+43=3010.故直线PQ与平面BCM所成角的正弦值为30 10.7(22·23·深圳·二模)如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD,PA= AD=2AB，点M是PD的中点.(1)证明：AM⊥PC；(2)设AC的中点为O，点N在棱PC上(异于点P，C)，且ON=OA，求直线AN与平面ACM所成角的正弦值.【答案】(1)证明见解析(2)1510【分析】(1)由等腰三角形的性质可得AM⊥PD，由面面垂直的性质可得CD⊥平面PAD，则CD⊥AM，所以由线面垂直的判定可得AM⊥平面PCD，从而可得结论；(2)以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，利用空间向量求解即可.【详解】(1)证明：因为PA=AD，点M是PD的中点，所以AM⊥PD.因为PA⊥平面ABCD,PA⊂平面PAD，所以平面PAD⊥平面ABCD，因为四边形ABCD为矩形，所以CD⊥AD，因为平面PAD∩平面ABCD=AD，CD⊂平面ABCD，所以CD⊥平面PAD，所以CD⊥AM，因为PD∩CD=D，PD,CD⊂平面PCD，所以AM⊥平面PCD，因为PC⊂平面PCD，所以AM⊥PC.(2)解：由题意可得AB,AD,AP两两垂直，设AB=1，如图，以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系，则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,2)，因为点M是PD的中点，所以M0,22,22，所以AM =0,22,22 ,AC =1,2,0 ，设平面ACM 的法向量为n =x ,y ,z ，则AM ⋅n =22y +22z =0AC ⋅n =x +2y =0，令y =-1可得x =2,z =1，所以平面ACM 的一个法向量n =2,-1,1 .PC =1,2,-2 ，设N x N ,y N ,z N ,PN =λPC =λ,2λ,-2λ (0<λ<1)，即x N ,y N ,z N -2 =λ,2λ,-2λ ，所以N λ,2λ,2-2λ .又O 12,22,0 ,ON =OA =32，所以λ-12 2+2λ-22 2+(2-2λ)2=34，化简得5λ2-7λ+2=0，解得λ=25或λ=1(舍去).所以AN =25,225,325，设直线AN 与平面ACM 所成的角为θ，则sin θ=n ⋅AN n ⋅AN=3252+1+1×425+825+1825=1510，所以直线AN 与平面ACM 所成角的正弦值为1510.8(22·23下·温州·二模)已知三棱锥D -ABC 中，△BCD 是边长为3的正三角形，AB =AC =AD ,AD 与平面BCD 所成角的余弦值为33．(1)求证：AD ⊥BC ；(2)求二面角D -AC -B 的平面角的正弦值．【答案】(1)证明见解析(2)223【分析】(1)取BC 的中点E ，连接AE ,DE ，证明BC ⊥平面ADE ，即可得证；(2)取正三角形BCD 的中心O ，连接OA ，从而可得OA ⊥平面BCD ，则∠ODA 即为AD 与平面BCD 所成角的平面角，进而可得AB =AC =AD =3，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，解△BDH 即可得解.【详解】(1)取BC 的中点E ，连接AE ,DE ，因为AB =AC ，所以AE ⊥BC ，因为△BCD 是边长为3的正三角形，所以DE ⊥BC ，又AE ∩DE =E ,AE ,DE ⊂平面ADE ，所以BC ⊥平面ADE ，因为AD ⊂平面ADE ，所以AD ⊥BC ；(2)取正三角形BCD 的中心O ，连接OA ，则点O 在DE 上，且OD =23DE ，由AB =AC =AD ，△BCD 是正三角形，得三棱锥A -BCD 为正三棱锥，则OA ⊥平面BCD ，故∠ODA 即为AD 与平面BCD 所成角的平面角，又AD 与平面BCD 所成角的余弦值为33，所以OD AD =3×32×23AD=33，即AB =AC =AD =3，即三棱锥A -BCD 是正四面体，取AC 中点为H ，连接DH ,BH ，则DH ⊥AC ,BH ⊥AC ，故∠BHD 即为二面角D -AC -B 的平面角，在△BDH 中，BH =DH =332,BD =3，则cos ∠BHD =BH 2+DH 2-BD 22⋅BH ⋅DH =274+274-92×332×332=13，所以sin ∠BHD =1-cos 2∠BHD =223，所以二面角D -AC -B 的平面角的正弦值223．9(22·23下·浙江·二模)如图，四面体ABCD ,AD ⊥CD ,AD =CD ,AC =2,AB =3,∠CAB =60°，E 为AB 上的点，且AC ⊥DE ,DE 与平面ABC 所成角为30°，(1)求三棱锥D -BCE 的体积；(2)求二面角B -CD -E 的余弦值.【答案】(1)答案见解析；(2)答案见解析．【分析】(1)取AC 中点F ，可证明AC ⊥平面DEF ，得平面ABC ⊥平面DEF ，DE 在平面ABC 内的射影就是直线EF ，∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，由正弦定理求得∠FDE ，有两个解，在∠FDE =60°时可证DF ⊥平面ABC ，在∠FDE =120°时，取FE 中点H 证明DH ⊥平面ABC ，然后由棱锥体积公式计算体积；(2)建立如图所示的空间直角坐标系，用空间向量法求二面角．【详解】(1)取AC 中点F ，连接FE ,FD ，因为AD =CD ，所以DF ⊥AC ，又AC ⊥DE ，DE ∩DF =D ，DE ,DF ⊂平面DEF ，所以AC ⊥平面DEF ，而FE ⊂平面DEF ，所以AC ⊥FE ，由已知AF =1，∠BAC =60°，所以EF =3，AE =2，BE =1，由AC ⊥平面DEF ，AC ⊂平面ABC 得平面ABC ⊥平面DEF ，因此DE 在平面ABC 内的射影就是直线EF ，所以∠DEF 是DE 与平面ABC 所成的角，即∠DEF =30°，AD =CD ,AC =2，因此DF =12AC =1，在△DEF 中，由正弦定理EF sin ∠FDE =DF sin ∠DEF 得1sin30°=3sin ∠FDE ，sin ∠FDE =32，∠FDE 为△DEF 内角，所以∠FDE =60°或120°，S △ABC =12AB ×AC ×sin ∠BAC =12×3×2×sin60°=333，S △CBE =BE BAS △ABC =3-23×332=32，若∠FDE =60°，则∠DFE =90°，即DF ⊥FE ，AC ∩FE =F ，AC ,FE ⊂平面ABC ，所以DF ⊥平面ABC ，V D -BCE =13S △BCE ⋅DF =13×32×1=36；若∠FDE =120°，则∠DFE =30°，DF =DE =1，取EF 中点H ，连接DH ，则DH ⊥EF ，因为平面ABC ⊥平面DEF ，平面ABC ∩平面DEF =EF ，而DH ⊂平面DEF ，所以DH ⊥平面ABC ，DH =DF sin ∠DFE =1×sin30°=12，所以V D -BCE =13S △BCE ⋅DF =13×32×12=312；(2)若∠FDE =60°，以FA ,FE ,FD 为x ,y ,z 轴建立如图所示的空间直角坐标系F -xyz ，则D (0,0,1)，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =(1,0,1)，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-33，即m =(33,-1,-33)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+955×7=19385385，所以二面角B -CD -E 的余弦值是19385385；若∠FDE =120°，以FA 为x 轴，FE 为y 轴，过F 且平行于HD 的直线为z 轴建立如图所示的空间直角坐标系F -xyz ，FH =12FE =32，则D 0,32,12 ，C (-1,0,0)，A (1,0,0)，E (0,3,0)，AE =(-1,3,0)，EB =12AE =-12,32,0 ，所以B 点坐标为-12,332,0 ，CD =1,32,12 ，CB =12,332,0 ，CE =(1,3,0)，设平面DBC 的一个法向量是m =(x 1,y 1,z 1)，则m ⋅CD =x 1+32y 1+12z 1=0m ⋅CB =12x 1+332y 1=0，取y 1=-1，则x 1=33，z 1=-53，即m =(33,-1,-53)，设平面DEC 的一个法向量是n =(x 2,y 2,z 2)，则n ⋅CD =x 2+32y 2+12z 2=0n ⋅CE =x 2+3y 2=0，取y 2=-1，则x 2=3，z 2=-3，即m =(3,-1,-3)，cos m ,n =m ⋅n m n =9+1+15103×7=25721721，所以二面角B -CD -E 的余弦值是25721721．10(22·23下·襄阳·三模)如图，在三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为矩形，∠BAC =90°，AB =AC =2，AA 1=4，A 1在底面ABC 的射影为BC 的中点N ，M 为B 1C 1的中点.(1)求证：平面A 1MNA ⊥平面A 1BC ；(2)求平面A 1B 1BA 与平面BB 1C 1C 夹角的余弦值.【答案】(1)证明见解析(2)23015【分析】(1)利用线面垂直和面面垂直的判定定理证明；(2)利用空间向量的坐标运算求面面夹角的余弦值.【详解】(1)如图，∵A 1N ⊥面ABC ，连AN ，则AN ⊥A 1N ，又AB =AC =2，∴AN ⊥BC ，又AN ∩BC =N ，A 1N ⊂面A 1BC ，BC ⊂面A 1BC ，于是AN ⊥面A 1BC ，又AN ⊂面A 1MN ，，所以面A 1BC ⊥面A 1MNA .(2)由(1)可得，以NA ,NB ,NA 1 为x ,y ,z 轴，建系如图，∠BAC =90°，AB =AC =2，BC =22则A (2,0,0),B (0,2,0),C (0,-2,0),因为AA 1=4,AN =2,所以A 1N =14,则A 1(0,0,14),因为NB 1 =NB +BB 1 =NB +AA 1 =0,2,0 +-2,0,14 =-2,2,14 ,所以B 1-2,2,14 ,设平面A 1BB 1的一个法向量为m =(x ,y ,z )，因为A 1B =(0,2,-14),B 1B =(2,0,-14),所以A 1B ⋅m =2y -14z =0B 1B ⋅m =2x -14z =0 ，令y =7，则x =7,z =1，所以m =(7,7,1)，设平面BCC 1B 1的一个法向量为n =(a ,b ,c )，因为BC =(0,-22,0),BB 1 =(-2,0,14),所以BC ⋅n =-22b =0BB 1 ⋅n =-2a +14c =0，令a =7，则b =0,c =1，所以n =(7,0,1)，设平面A 1BB 1与平面BCC 1B 1夹角为θ，则cos θ=cos <m ,n >=m ⋅n m n=7+0+17+7+1×7+0+1=23015，所以平面A 1BB 1与平面BCC 1B 1夹角的余弦值为23015.11(22·23·唐山·二模)如图，在三棱柱ABC -A 1B 1C 1中，△ABC 是等边三角形，侧面ACC 1A 1⊥底面ABC ，且AA 1=AC ，∠AA 1C 1=120°，M 是CC 1的中点．(1)证明：A 1C ⊥BM ．(2)求二面角A 1-BC -M 的正弦值．【答案】(1)证明见解析(2)45【分析】(1)根据菱形的性质、结合面面垂直的性质，线面垂直的判定定理进行证明即可；(2)建立空间直角坐标系，运用空间向量夹角公式进行求解即sk .【详解】(1)取AC 的中点O ，连接OM ，OB ，AC 1．在三棱柱ABC -A 1B 1C 1中，由AA 1=AC ，得四边形ACC 1A 1为菱形，所以A 1C ⊥AC 1，易知OM ∥AC 1，则A 1C ⊥OM ．由△ABC 是等边三角形，知OB ⊥AC ，又平面ACC 1A 1⊥平面ABC ，平面ACC 1A 1∩平面ABC =AC ，OB ⊂平面ABC ，知OB ⊥平面ACC 1A 1，则OB ⊥A 1C ，又OB ∩OM =O ,OB ,OM ⊂平面OBM ，得A 1C ⊥平面OBM ，又BM ⊂平面OBM ，故A 1C ⊥BM ．.(2)连接OA 1，因为侧面ACC 1A 1为菱形，∠AA 1C 1=120°，则∠A 1AC =60°，则△A 1AC 为等边三角形，所以A 1O ⊥AC ，又由(1)易知OA 1，OB ，AC 两两垂直，故以O 为坐标原点，分别以OB ，OC ，OA 1 的方向为x 轴、y 轴、z 轴的正方向，建立空间直角坐标系．不妨设AB =2，则O 0,0,0 ，B 3,0,0 ，C 0,1,0 ，A 10,0,3 ，C 10,2,3 ，BA 1 =-3,0,3 ，BC =-3,1,0 ，CC 1 =0,1,3 ，设平面A 1BC 的法向量为n =x ,y ,z ，则n ⋅BC =-3x +y =0n ⋅BA 1 =-3x +3z =0 ，令x =1，得n =1,3,1 ，设平面BCC 1的法向量为m =a ,b ,c ，则m ⋅BC =-3a +b =0m ⋅CC 1 =b +3c =0，令a =1，得m =1,3,-1 ，所以cos n ,m =n ⋅m n ⋅m=35⋅5=35，即二面角A 1-BC -M 的正弦值为45．12(22·23下·盐城·三模)如图，该几何体是由等高的半个圆柱和14个圆柱拼接而成，点G 为弧CD 的中点，且C ，E ，D ，G 四点共面.(1)证明：平面BDF ⊥平面BCG ；(2)若平面BDF 与平面ABG 所成二面角的余弦值为155，且线段AB 长度为2，求点G 到直线DF 的距离.【答案】(1)证明见解析(2)62【分析】(1)过G 作GH ⎳CB ，交底面弧于H ，连接HB ，有HBCG 为平行四边形，根据题设可得FB ⊥HB ，即FB ⊥CG ，再由线面垂直的性质可得CB ⊥FB ，最后根据线面、面面垂直的判定即可证结论.(2)构建如下图示空间直角坐标系A -xyz ，令半圆柱半径为r ，高为h ，确定相关点坐标，进而求平面BDF 、平面ABG 的法向量，利用空间向量夹角的坐标表示及已知条件可得h =2r ，即可求出点G 到直线DF 的距离.【详解】(1)过G 作GH ⎳CB ，交底面弧于H ，连接HB ，易知：HBCG 为平行四边形，所以HB ⎳CG ，又G 为弧CD 的中点，则H 是弧AB 的中点，所以∠HBA =45°，而由题设知：∠ABF =45°，则∠HBF =∠HBA +∠ABF =90°，所以FB ⊥HB ，即FB ⊥CG ，由CB ⊥底面ABF ，FB ⊂平面ABF ，则CB ⊥FB ，又CB ∩CG =C ，CB ,CG ⊂平面BCG ，所以FB ⊥平面BCG ，又FB ⊂平面BDF ，所以平面BDF ⊥平面BCG .(2)由题意，构建如下图示空间直角坐标系A -xyz ，令半圆柱半径为r ，高为h ，则B 0,2r ,0 ，F 2r ,0,0 ，D 0,0,h ，G -r ,r ,h ，所以FD =-2r ,0,h ，BD =0,-2r ,h ，AB =0,2r ,0 ，AG =-r ,r ,h ，若m =x ,y ,z 是面BDF 的一个法向量，则m ⋅FD =-2rx +hz =0m ⋅BD =-2ry +hz =0 ，令z =2r ，则m =h ,h ,2r ，若n =a ,b ,c 是面ABG 的一个法向量，则n ⋅AB =2rb =0n ⋅AG =-ra +rb +hc =0 ，令c =r ，则n =h ,0,r ，所以cos m ,n =m ⋅n m n=h 2+2r 22h 2+4r 2×h 2+r 2=155，整理可得h 2-4r 2 h 2+2r 2 =0，则h =2r ，又AB =2，由题设可知，此时点G -1,1,2 ，D 0,0,2 ，F 2,0,0 ，则DF =2,0,-2 ，DG =-1,1,0 ，所以点G 到直线DF 的距离d =DG 2-DG ⋅DF 2DF2=62.13(22·23下·江苏·三模)如图，圆锥DO 中，AE 为底面圆O 的直径，AE =AD ，△ABC 为底面圆O 的内接正三角形，圆锥的高DO =18，点P 为线段DO 上一个动点.(1)当PO =36时，证明：PA ⊥平面PBC ；(2)当P 点在什么位置时，直线PE 和平面PBC 所成角的正弦值最大.【答案】(1)证明见解析；(2)P 点在距离O 点36处【分析】(1)利用勾股定理证明出AP ⊥BP 和AP ⊥CP ，再用线面垂直的判定定理证明出PA ⊥平面PBC ；(2)建立空间直角坐标系，利用向量法求解.【详解】(1)因为AE =AD ，AD =DE ，所以△ADE 是正三角形，则∠DAO =π3，又DO ⊥底面圆O ，AE ⊂底面圆O ，所以DO ⊥AE ，在Rt △AOD 中，DO =18，所以AO =DO 3=63，因为△ABC 是正三角形，所以AB =AO ×32×2=63×3=18，AP =AO 2+PO 2=92，BP =AP ，所以AP 2+BP 2=AB 2，AP ⊥BP ，同理可证AP ⊥CP ，又BP ∩PC =P ，BP ，PC ⊂平面PBC ，所以PA ⊥平面PBC .(2)如图，建立以O 为原点的空间直角坐标系O -xyz .设PO =x ，(0≤x ≤18)，所以P 0,0,x ，E -33,9,0 ，B 33,9,0 ，C -63,0,0 ，所以EP =33,-9,x ，PB =33,9,-x ，PC =-63,0,-x ，设平面PBC 的法向量为n =a ,b ,c ，则n ⋅PB =33a +9b -cx =0n ⋅PC =-63a -cx =0，令a =x ，则b =-3x ，c =-63，故n =x ,-3x ,-63 ，设直线PE 和平面PBC 所成的角为θ，则sin θ=cos EP ,n =33x +93x -63x 108+x 2⋅x 2+3x 2+108=63x 108+x 2⋅4x 2+108=634x 2+1082x 2+540≤6324x 2⋅1082x 2+540=13，当且仅当4x 2=1082x 2，即PO =x =36时，直线PE 和平面PBC 所成角的正弦值最大，故P 点在距离O 点36处.14(22·23下·镇江·三模)如图，四边形ABCD 是边长为2的菱形，∠ABC =60°，四边形PACQ 为矩形，PA =1，从下列三个条件中任选一个作为已知条件，并解答问题(如果选择多个条件分别解答，按第一个解答计分).①BP ,DP 与平面ABCD 所成角相等；②三棱锥P -ABD 体积为33；③cos ∠BPA =55(1)平面PACQ ⊥平面ABCD ；(2)求二面角B -PQ -D 的大小；(3)求点C 到平面BPQ 的距离.【答案】(1)证明见解析(2)2π3(3)32【分析】(1)若选①，则作PA ⊥面ABCD ，证明A 和A 重合从而得到PA ⊥面ABCD ，从而得到面面垂直；若选②，计算得到P 到面ABD 的距离h =1=PA ，得到PA ⊥面ABCD ，从而得到面面垂直；若选③，通过余弦定理计算得到PA ⊥AB ，再通过PA ⊥面ABCD ，从而得到面面垂直；(2)通过建立空间直角坐标系，求出两个平面的法向量，结合二面角计算公式计算即可；(3)通过点面距离的计算公式直接计算即可.【详解】(1)选①，连接BD ，作PA ⊥面ABCD ，垂足为A .∵BP ,DP 与平面ABCD 所成角相等，∴A B =A D ，∴A 在BD 的中垂线AC 上，∵在平面PACQ 内，PA ⊥AC ,PA ⊥AC ,∴A 和A 重合，∴PA ⊥面ABCD ，又PA ⊂面PACQ ，∴面PACQ ⊥面ABCD若选②，设P 到面ABD 的距离为h ，∵V P -ABD =13S △ABD ⋅h =13×3⋅h =33，得h =1=PA ，∴PA 即为P 到面ABD 的距离，即PA ⊥面ABCD ，又PA ⊂面PACQ ，∴面PACQ ⊥面ABCD .若选③，由余弦定理得，cos ∠BPA =PB 2+PA 2-AB 22PB ⋅PA =55，∴BP =5,∴BP 2=AP 2+AB 2∴PA ⊥AB ，又PA ⊥AC ,AC ∩AB =A ,AC ,AB ⊂面ABCD∴PA ⊥面ABCD ，又PA ⊂面PACQ∴面PACQ ⊥面ABCD(2)因为PA ⊥面ABCD ，OB ,OC ⊂面ABCD ，所以PA ⊥OB ,PA ⊥OC ，取PQ 中点G ，则OG ⎳PA ，所以OG ⊥OB ,OG ⊥OC ，又因为OB ⊥OC ，所以建立如下图所示空间直角坐标系，∵B 3,0,0 ,P 0,-1,1 ,D -3,0,0 ,Q 0,1,1 ，∴BQ =-3,1,1 ,DQ =3,1,1 ,DP =3,-1,1 ，设平面BPQ 的一个法向量为m =x ,y ,z ，则m⋅BP =0m ⋅BQ =0 ，即-3x -y +z =0-3x +y +z =0 ，令x =3，则y =0,z =3,∴m =3,0,3 ，设平面DPQ 的一个法向量为n =x 1,y1,z 1 ，则n ⋅DP=0n ⋅DQ =0 ，即3x 1-y 1+z 1=3x 1+y 1+z 1=0，令x1=3，则y 1=0,z 1=-3,∴n =3,0,-3 ，∴cos m ,n =m ⋅n m ⋅ n =-623×23=-12，∵m ,n ∈0,π ,∴m ,n =2π3，由图可知二面角B -PQ -D 是钝角，所以二面角B -PQ -D 的大小为2π3.(3)∵C 0,1,0 ,Q 0,1,1 ，∴CQ =0,0,1 ,∵平面BPQ 的一个法向量为m =3,0,3 ，∴点C 到平面BPQ 的距离d =CQ ⋅m m=323=32.15(22·23下·江苏·一模)在三棱柱ABC -A 1B 1C 1中，平面A 1B 1BA ⊥平面ABC ，侧面A 1B 1BA 为菱形，∠ABB 1=π3，AB 1⊥AC ，AB =AC =2，E 是AC 的中点.(1)求证：A 1B ⊥平面AB 1C ；(2)点P 在线段A 1E 上(异于点A 1，E )，AP 与平面A 1BE 所成角为π4，求EP EA 1的值.【答案】(1)证明见解析(2)EP EA 1=25【分析】(1)作B 1O ⊥AB 交AB 于O 点，由面面垂直的性质可得B 1O ⊥平面ABC ，可得B 1O ⊥AC ，再由线面垂直的判定定理得AC ⊥平面A 1B 1BA ，从而得到AC ⊥A 1B ，再由线面垂直的判定定理可得答案；(2)以A 为原点，AB 、AC 、AO 1所在的直线分别为x 、y 、z 轴，建立空间直角坐标系，设EP =λEA 1 ，可得AP =-λ,1-λ,3λ ，求出平面A 1BE 的一个法向量，由线面角的向量求法可得答案.【详解】(1)因为侧面A 1B 1BA 为菱形，∠ABB 1=π3，AB =AC =2，所以△ABB 1、△AA 1B 1为边长为2的等边三角形，作B 1O ⊥AB 交AB 于O 点，则O 点为AB 的中点，因为平面A 1B 1BA ⊥平面ABC ，平面A 1B 1BA ∩平面ABC =AB ，B 1O ⊂平面A 1B 1BA ，所以B 1O ⊥平面ABC ，AC ⊂平面ABC ，可得B 1O ⊥AC ，又AB 1⊥AC ，B 1O ∩AB 1=B 1，B 1O 、AB 1⊂平面A 1B 1BA ，可得AC ⊥平面A 1B 1BA ，因为A 1B ⊂平面A 1B 1BA ，所以AC ⊥A 1B ，因为侧面A 1B 1BA 为菱形，所以B 1A ⊥A 1B ，AB 1∩AC =A ，AB 1、AC ⊂平面AB 1C ，所以A 1B ⊥平面AB 1C ；(2)由(1)知，AC ⊥平面A 1B 1BA ，∠BAC =π2，取做A 1B 1的中点O 1，连接AO 1，则B1O ⎳AO 1，所以AO 1⊥平面ABC ，以A 为原点，AB 、AC 、AO 1所在的直线分别为x 、y 、z 轴，建立空间直角坐标系，则A 0,0,0 ，A 1-1,0,3 ，B 2,0,0 ，E 0,1,0 ，A 1B =3,0,-3 ，EA 1 =-1,-1,3 ，设EP =λEA 1 ，可得P -λ,1-λ,3λ ，所以AP =-λ,1-λ,3λ ，设平面A 1BE 的一个法向量为n=x ,y ,z ，则A 1B ⋅n=0EA 1 ⋅n =0，即3x -3z =0-x -y +3z =0 ，令z =3，可得n =1,2,3 ，可得sin π4=cos n ,AP =n ⋅AP n AP=-λ+2-2λ+3λ 1+4+3λ2+1-λ 2+3λ2，解得λ=0舍去，或λ=25，所以EP EA 1=25.16(22·23下·河北·三模)如图，四棱锥P -ABCD 的底面ABCD 是菱形，其对角线AC ,BD 交于点O ，且PO ⊥平面ABCD ,OC =1,OD =OP =2,M 是PD 的中点，N 是线段CD 上一动点．(1)当平面OMN ⎳平面PBC 时，试确定点N 的位置，并说明理由；(2)在(1)的前提下，点Q 在直线MN 上，以PQ 为直径的球的表面积为214π．以O 为原点，OC ,OD ,OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系O -xyz ，求点Q 的坐标．【答案】(1)N 是CD 的中点(2)12,1,0 ，-1310,1,185 【分析】(1)根据面面平行的性质证明MN ⎳PC ，即可得解；(2)先根据球的体积求出PQ ，然后根据空间中两点间的距离公式即可得解.【详解】(1)因为平面OMN ⎳平面PBC ，平面OMN ∩平面PCD =MN ，平面PBC ∩平面PCD =PC ，所以MN ⎳PC ，因为M 是PD 的中点，所以N 是CD 的中点；(2)由题意4π×PQ 22=214π，解得PQ =212，设MQ =λMN,λ∈R ，由题意，P 0,0,2 ,M 0,1,1 ,N 12,1,0 ，则PM =0,1,-1 ,MN =12,0,-1 ，则PQ =PM +MQ =0,1,-1 +λ12,0,-1 =λ2,1,-λ-1 ，则λ24+1+-λ-1 2=212，解得λ=1或λ=-135，当λ=1时，MQ =MN ，则Q 12,1,0 ，当λ=-135时，MQ =-135MN =-1310,0,135，设Q x ,y ,z ，则MQ =x ,y -1,z -1 =-1310,0,135，所以x =-1310y -1=0z -1=135 ，解得x =-1310y =1z =185 ，则Q -1310,1,185 ，综上所述点Q 的坐标为12,1,0，-1310,1,185 .17(22·23·汕头·三模)如图，圆台O 1O 2的轴截面为等腰梯形A 1ACC 1，AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点.(1)在平面BCC 1内，过C 1作一条直线与平面A 1AB 平行，并说明理由；(2)若四棱锥B -A 1ACC 1的体积为23，设平面A 1AB ∩平面C 1CB =l ,Q ∈l ，求CQ 的最小值.【答案】(1)作图见解析，理由见解析(2)7【分析】(1)根据线面平行的判定和中位线定理即可求解;(2)根据几何关系或空间向量方法即可求解.【详解】(1)取BC 中点P ，作直线C 1P 即为所求，取AB 中点H ，连接A 2H ,PH ，则有PH ∥AC ,PH =12AC ，如图，在等腰梯形A 1ACC 1中，A 1C 1=12AC ，有HP ∥A 1C 1,HP =A 1C 1，则四边形A 1C 1PH 为平行四边形，即有C 1P ∥A 1H ，又A 1H ⊂平面A 1AB ,C 1P⊄平面A 1AB ，所以C 1P ∥平面A 1AB .(2)法一：延长AA 1,CC 1交于点O ，故O ∈AA 1⊂平面ABA 1,O ∈CC 1⊂平面CC 1B故平面A 1AB ∩平面C 1CB =BO ,BO 即l ,在△OBC 中，OC ,OB 均为圆锥母线.过点B 作BO ⊥AC 于O .在等腰梯形A 1ACC 1中，AC =2AA 1=2A 1C 1=4，此梯形的高h =AA 21-AC -A 1C 122=3,∴等腰梯形A 1ACC 1的面积为S =122+4 3=33，所以四棱锥B -A 1ACC 1的体积V =13S ×BO =13×33×BO =23，解得BO =2，故点O 与O 2重合，BC =22由AC =2AA 1=2A 1C 1，得OC =2CC 1，且∠C 1CA =60°，故OC =AC =4=OB .△OBC 中，O 到BC 距离h 1=OB 2-BC 22=14.则△OBC 面积=12OB ⋅CQ min =12BC ⋅h 1,得：CQ 的最小值为：CQ min =22⋅144=7.法二：同法一求出B 的位置.以O 2为原点，OB ,OC ,O 2O 1方向为x ,y ,z 轴正向建立空间直角坐标系，C 0,2,0 ,B 2,0,0 ,AA 1 =0,1,3 ,AB =2,2,0 ,CC 1 =0,-1,3 ,BC=-2,2,0设面A 1AB 的法向量为a=x 1,y 1,z 1a ⋅AA 1=y 1+3z 1=0a ⋅AB=2x 1+2y 1=0，取z 1=1，有a=3,-3,1 ；同理可得面C 1CB 的法向量为β=3,3,1 ,由l =面C 1CB ∩面A 1AB ，可知B ∈l ，设l 的方向向量为l=x ,y ,z ，故l ⋅a =3x -3y +z =0,l ⋅β=3x +3y +z =0取l=1,0,3 ,下面分2个方法求|CQ |min求|CQ |min 方法1：BQ =l=t ,0,3t ,，∵B 2,0,0 ,∴Q t -2,0,3t∴CQ =(t -2)2+22+(3t )2=4t 2-4t +8，当t =12时，CQ 取最小值为7.求CQ min 方法2：BC 在l 上的投影向量的模为BC ⋅l l =-2×1+2×0+0×32=1故CQ 的最小值即C 到l 的距离为BC 2-12=7.法三:在三角形△BCO 中，BO =CO =4,BC =22,cos ∠CBO =42+(22)2-422×4×22=122⋅sin ∠CBO =1-1222=722,所以CQ ≥CB sin ∠CBO =722×22=7.18(19·20下·临沂·二模)如图①，在Rt △ABC 中，B 为直角，AB =BC =6，EF ∥BC ，AE =2，沿EF 将△AEF 折起，使∠AEB =π3，得到如图②的几何体，点D 在线段AC 上．(1)求证：平面AEF ⊥平面ABC ；(2)若AE ⎳平面BDF ，求直线AF 与平面BDF 所成角的正弦值．【答案】(1)证明见解析；(2)64.【分析】(1)由余弦定理计算证明EA ⊥AB ，再利用线面垂直的判定、性质，面面垂直的判定推理作答.(2)以A 为原点，建立空间直角坐标系，利用空间向量求线面角的正弦作答.【详解】(1)在△ABE 中，AE =2,BE =4，∠AEB =π3，由余弦定理得：AB 2=AE 2+BE 2-2AE ⋅BE cos ∠AEB =4+16-2×2×4×12=12，则AB =23，有EB 2=EA 2+AB 2，于是∠EAB =π2，即有EA ⊥AB ，又EF ⊥EB ,EF ⊥EA ,EA ∩EB =E ,EA ,EB ⊂平面ABE ，因此EF ⊥平面ABE ，而AB ⊂平面ABE ，则EF ⊥AB ，又因为EA ∩EF =E ,EA ,EF ⊂平面AEF ，从而AB ⊥平面AEF ，而AB ⊂平面ABC ，所以平面AEF ⊥平面ABC .(2)以A 为原点，以AB ,AE 分别为x ,y 轴，过点A 垂直于平面ABE 的直线为z 轴，建立空间直角坐标系，如图，由(1)知，EF ⊥平面ABE ，而EF ⎳BC ，则有BC ⊥平面ABE ，则A (0,0,0),B (23,0,0),E (0,2,0),F (0,2,2),C (23,0,6)，AF =(0,2,2),FB =(23,-2,-2),AC=(23,0,6)，连接EC 与FB 交于点G ，连接DG ，因为AE ⎳平面BDF ，AE ⊂平面AEC ，平面AEC ∩平面BDF =DG ，则AE ⎳GD ，有GC GE =DCDA，在四边形BCFE 中，由EF ⎳BC ，得GC GE =BC EF =3，即DC DA=3，AD =14AC =32,0,32 ，FD =AD -AF =32,-2,-12，设平面BDF 的法向量为n =(x ,y ,z )，则n ⋅FD =32x -2y -12z =0n ⋅FB =23x -2y -2z =0，令x =1，得n =(1,0,3)，设直线AF 与平面BDF 所成角为θ，于是sin θ=|cos ‹n ,AF ›|=|n ⋅AF ||n ||AF |=2322×2=64，所以直线AF 与平面BDF 所成角的正弦值为64.19(22·23下·广州·三模)如图，四棱锥P -ABCD 的底面为正方形，AB =AP =2，PA ⊥平面ABCD ，E ,F 分别是线段PB ,PD 的中点，G 是线段PC 上的一点.(1)求证：平面EFG ⊥平面PAC ；(2)若直线AG 与平面AEF 所成角的正弦值为13，且G 点不是线段PC 的中点，求三棱锥E -ABG 体积.【答案】(1)证明见解析(2)19【分析】(1)由线面垂直判定可证得BD ⊥平面PAC ，由中位线性质知EF ⎳BD ，从而得到EF ⊥平面PAC ，由面面垂直判定可得结论；(2)以A 为坐标原点可建立空间直角坐标系，设PG =λPC ，λ∈0,12 ∪12,1 ，由线面角的向量求法可构造方程求得λ，结合垂直关系可得G 平面PAB 的距离为16BC =13，利用棱锥体积公式可求得结果.【详解】(1)连接BD ，∵E ,F 分别是线段PB ,PD 的中点，∴EF ⎳BD ，∵底面四边形ABCD 为正方形，∴BD ⊥AC ，∵PA ⊥平面ABCD ，BD ⊂平面ABCD ，∴PA ⊥BD ，又PA ∩AC =A ，PA ,AC ⊂平面PAC ，∴BD ⊥平面PAC ，∵EF ⎳BD ，∴EF ⊥平面PAC ，又EF ⊂平面EFG ，∴平面EFG ⊥平面PAC .(2)以A 为坐标原点，分别以AB ,AD ,AP 所在直线为x ,y ,z 轴建立空间直角坐标系，则A 0,0,0 ，E 1,0,1 ，F 0,1,1 ，P 0,0,2 ，C 2,2,0 ，设PG =λPC ，λ∈0,12 ∪12,1 ，则AG =AP +PG =0,0,2 +2λ,2λ,-2λ =2λ,2λ,2-2λ ，AE =1,0,1 ，AF =0,1,1 ，设平面AEF 的一个法向量为n=x ,y ,z ，则n ⋅AE=x +z =0n ⋅AF=y +z =0，令z =-1，解得：x =1，y =1，∴n =1,1,-1 ；设直线AG 与平面AEF 所成角为θ，sin θ=cos n ,AG =n ⋅AGn ⋅AG=6λ-2 3⋅4λ2+4λ2+2-2λ 2=13，解得：λ=16或λ=12(舍)，∴PG =16PC ，∵PA ⊥平面ABCD ，BC ⊂平面ABCD ，∴PA ⊥BC ；∵BC ⊥AB ，PA ∩AB =A ，PA ,AB ⊂平面PAB ，∴BC ⊥平面PAB ，∴G 到平面PAB 的距离为16BC =13，∴V E -ABG =V G -ABE =13S △ABE ⋅16BC =13×12×12×2×2×13=19.20(22·23下·长沙·一模)斜三棱柱ABC -A 1B 1C 1的各棱长都为2，∠A 1AB =60°，点A 1在下底面ABC 的投影为AB 的中点O ．(1)在棱BB 1(含端点)上是否存在一点D 使A 1D ⊥AC 1若存在，求出BD 的长；若不存在，请说明理由；(2)求点A 1到平面BCC 1B 1的距离．【答案】(1)存在，BD =25(2)2155【分析】(1)连接OC ，以O 点为原点，如图建立空间直角坐标系，设BD =tBB 1 ,t ∈0,1 ，根据AC 1 ⋅A 1D=0，求出t 即可；(2)利用向量法求解即可.【详解】(1)连接OC ，因为AC =BC ，O 为AB 的中点，所以OC ⊥AB ，由题意知A 1O ⊥平面ABC ，又AA 1=2，∠A 1AO =60°，所以A 1O =3，以O 点为原点，如图建立空间直角坐标系，则A 10,0,3 ，A 1,0,0 ，B -1,0,0 ，C 0,3,0 ，由AB =A 1B 1得B 1-2,0,3 ，同理得C 1-1,3,3 ，设BD =tBB 1,t ∈0,1 ，得D -1-t ,0,3t ，又AC 1 =-2,3,3 ，A 1D =-1-t ,0,3t -3 ，由AC 1 ⋅A 1D=0，得-2-1-t +33t -3 =0，得t =15，又BB 1=2，∴BD =25，∴存在点D 且BD =25满足条件；(2)设平面BCC 1B 1的法向量为n=x ,y ,z ，BC =1,3,0 ，CC 1 =-1,0,3 ，则有n ⋅BC=x +3y =0n ⋅CC 1=-x +3z =0，可取n =3,-1,1 ，又BA 1=1,0,3 ，∴点A 1到平面BCC 1B 1的距离为d =BA 1 cos BA 1 ,n =BA 1 ×3+0+3BA 1×5=2155，∴所求距离为2155.21(22·23下·长沙·三模)如图，三棱台ABC -A 1B 1C 1，AB ⊥BC ，AC ⊥BB 1，平面ABB 1A 1⊥平面ABC ，AB =6,BC =4，BB 1=2，AC 1与A 1C 相交于点D ，AE =2EB，且DE ∥平面BCC 1B 1.(1)求三棱锥C -A 1B 1C 1的体积；(2)平面A 1B 1C 与平面ABC 所成角为α，CC 1与平面A 1B 1C 所成角为β，求证：α+β=π4.【答案】(1)2(2)证明见解析【分析】(1)通过证明线线和线面垂直，并结合已知条件即可得出三棱锥C -A 1B 1C 1的体积；(2)建立空间直角坐标系，表达出各点的坐标，求出所成角为α与β的正余弦值，即可证明结论.【详解】(1)由题意，∵平面ABB 1A 1⊥平面ABC ，且平面ABB 1A 1∩平面ABC =AB ，AB ⊥BC ，BC ⊂平面ABC ∴BC ⊥平面ABB 1A 1，∵BB 1⊂平面ABB 1A 1，∴BC ⊥BB 1，又AC ⊥BB 1，BC ∩AC =C ，BC ,AC ⊂平面ABC ∴BB 1⊥平面ABC ，连接C 1B ，∵DE ⎳平面BCC 1B 1，DE ⊂平面ABC 1，平面ABC 1∩平面BCC 1B 1=C 1B ，∴DE ∥C 1B ，∵AE =2EB ，∴AD =2DC 1 ，∴A 1C 1=12AC .∴三棱锥C -A 1B 1C 1底面A 1B 1C 1的面积S 1=12×2×3=3，高h =BB 1=2，。

立体几何大题训练(1)1.如图，已知ZkABC是正三角形，EA, CD都垂直于平面ABC∙且EA=AB=Za. DC=a, F是BE的(1)FD〃平面ABC： (2) AF丄平而EDB.2.己知线段PA丄矩形ABCD所在平而，M、N分别是AB. PC的中点。

(1)求证：MN//平面PAD： (2)当ZPDA=45°时，求证：MN丄平面PCD；3.如图，在四面体ABCD中，CB=CD,ADdBD.点E, F分别是AB1BD的中点•求证:(1)直线EF//面ACD： (2)平面EFC丄面BCD.4.在斜三棱柱A l B l C l-ABC中，底面是等腰三角形，AB=AC,侧面BB l C l C丄底面ABC(1)若D是BC的中点，求证AD±CC1:(2)过侧面BB l C l C的对角线BC l的平面交侧棱于M,若扯仁M&, 求证截面MBCl丄侧面BBiCiC:(3)AM=MA l是截面MBCI丄平面BB l CIC的充要条件吗？请你叙述判断理由5.如图，在正方体ABCD-A l BXC I Dl >, M、N、G分别是A1A, D i C, AD的中点. 求证：(1) MN//平面ABCD：(2) MN丄平面B1BG.D6.如图，在正方体ABCD-AlBlClDI中，E、F为⅛AD. AB的中点•(1)求证：EF 〃平面CB1D1:(2)求证：平面CAAlCl丄平面CBiDi.7.如图，在直四棱柱ABCD-A1B1C1D11I1,底面ABCD 为等腰梯形，AB/7CD, AB=4, BC=CD=2, AA1=Z, E、El分别是棱AD、AAI的中点(1)设F是棱AB的中点，证明：直线EEl〃面FCCi:C)证明：平面DIAC丄面BBlClCoDBl EI8.如图，在四棱锥P-ABCD中•F分别在PD, Be上，且PE：(1)求证：PA丄平面ABCD：底面ABCD是菱形，ZABC=60°ED=BF: FCO(2)求证：EF//平面PAB。