全等三角形2

专题02 全等三角形专题详解专题02 全等三角形专题详解 (1)12.1 全等三角形 (2)知识框架 (2)一、基础知识点 (2)知识点1 全等形的概念及性质 (2)知识点2 全等形的定义和表示方法 (2)知识点3 全等三角形的性质与拓展 (2)知识点4 全等变换的保形性 (2)12.2三角形全等的判定 (3)知识框架 (3)一、基础知识点 (3)知识点1 全等三角形判定条件 (3)二、典型题型 (4)题型1 全等三角形的判定 (4)三、添加辅助线方法 (5)方法1 关于中点的辅助线 (5)方法2 作垂线构造全等求点的坐标 (12)方法3 截长补短法（往往需证2次全等） (14)12.3角平分线的性质 (17)知识框架 (17)一、基础知识点 (17)知识点1 角平分线的性质 (17)知识点2 角平分线的判定 (17)知识点3 三角形的内心和旁心 (17)二、典型题型 (17)题型1 角平分线的性质和定义的应用 (17)题型2 三角形内心的应用 (18)三、添加辅助线方法 (20)方法1 角平分线上的点向两边作垂线 (20)方法2 过边上的点向两边作垂线 (22)方法3 过平分线上的点作一条边平行线构造等腰三角形 (24)方法4 利用角平分线的性质，在角两边截长补短 (25)12.1 全等三角形知识框架一、基础知识点知识点1 全等形的概念及性质1）全等形：能够完全重合的两个图形2）全等形的性质：①形状相同；②大小相同注：①全等图形与其所在的位置无关（只要通过平移、旋转、翻折后能够使两个图形完成重合即可）。

对称图形要求更苛刻些。

②因两图形完全相等，故图形所有对应条件都相同（例：周长、面积、对应角角度等皆相等）知识点2 全等形的定义和表示方法1）全等三角形：能够完全重合的三角形（长得完全一样的三角形）2）表示方法：①△ABC≌△DEF（读作：三角形ABC全等于三角形DEF）②顶点需要一一对应（即长得一样的在描述中至于同等地位）③从书写中，我们根据一一对应的关系，可得：a.点A与点D为对应顶点，点B与点E为对应顶点，点C与点F为对应顶点；b.∠A与∠D为对应角，∠B与∠E为对应角，∠C与∠F为对应角；c.AB与DE为对应边，AC与DF为对应边，BC与EF为对应边。

例01．如图，已知：21∠=∠，43∠=∠. 求证：BCD ADC ∆≅∆.分析：ADC ∆与BCD ∆的对应边是DC 与DC ，AD 与BC ，AC 与BD . 对应角是1∠与2∠，ADC ∠与BCD ∠，DAC ∠与CBD ∠. 由条件已有一对应边DC 与DC ，和一对应角1∠和2∠相等，只需证明BCD ADC ∠=∠，就可以证明两三角形全等.证明：21∠=∠，43∠=∠（已知），∴ 4231∠+∠=∠+∠. 即BCD ADC ∠=∠ 在ADC ∆与BCD ∆中，⎪⎩⎪⎨⎧∠=∠=∠=∠)(12)()(已知公共边已证CD DC BCD ADC ∴ )(ASA BCD ADC ∆≅∆例02．已知：如图，21∠=∠，C B ∠=∠. 求证：COD BOE ∆≅∆.分析：欲证COD BOE ∆≅∆，已有两组条件，即C B ∠=∠和COD BOE ∠=∠. 因此，必须再具备一组对应边相等这一条件. BE 和CD 是在BOE ∆和COD ∆中，但直接证明CE BE =比较困难. 若证OE 和OD 相等或OB 和OC 相等，可以分别转化到证明AOD AOE ∆≅∆和AOC AOB ∆≅∆. 由已知条件，不难证出这两对三角形分别全等.证明：∵ 21∠=∠（已知），DOC EOB ∠=∠（对顶角相等）， ∴ DOC EOB ∠+∠=∠+∠21. 即 AOC AOB ∠=∠. 在AOB ∆与AOC ∆中，⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(公共边已证已知AO AO AOC AOB C B ∴ )(AAS AOC AOB ∆≅∆. ∴CO BO =在EOB ∆与COD ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(已知已证对顶角相等C B CO BO COD EOB∴ COD BOE ∆≅∆（ASA ）例03．如图，已知：AB 与CD 相交于点O ，且OD OC BD AC =,//，E 、F 为AB 上两点，且BF AE =.求证：DOF COE ∆≅∆.分析：欲证DOF COE ∆≅∆，已具备了两个条件，OD OC =和DOF COE ∠=∠. 所以只需证另一对角相等或证明OF OE =，即可. 证明另一对角相等，比较困难. 所以就证明OF OE =. 因为有BF AE =. 要证OF OE =只需证OB OA =即可. 由已知条件容易证得BOD AOC ∆≅∆，从而证明OB OA =.证明：∵BD AC //（已知）∴B A ∠=∠（两直线平行，内错角相等） 在AOC ∆与BOD ∆中，⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知对顶角相等已证OD OC BOD AOC B A ∴)(AAS BOD AOC ∆≅∆∴BO AO =（全等三角形的对应边相等） ∵BF AE =（已知）， ∴BF BO AE AO -=-. 即OF OE =在COE ∆与DOF ∆中，⎪⎩⎪⎨⎧=∠=∠=)()()(已证对顶角相等已知OE OE DOE COE DO CO ∴)(SAS DOF COE ∆≅∆例04．如图，已知：CE BD ACE ABD DAE BAC =∠=∠∠=∠,,. 求证：AE AD =.分析：欲证相等的两条线段AD ，AE 分别在ABD ∆和ACE ∆中，由于CE BD =，ACE ABD ∠=∠，所以只需再证CAE BAD ∠=∠即可，这由已知条件DAE BAC ∠=∠容易得到.证明：∵DAE BAC ∠=∠（已知） ∴DAC DAE DAC BAC ∠-∠=∠-∠ 即CAE BAD ∠=∠ 在ABD ∆与ACE ∆中，⎪⎩⎪⎨⎧∠=∠∠=∠=)()()(已证已知已知CAE BAD ACE ABD CE BD ∴)(AAS ACE ABD ∆≅∆∴AE AD =（全等三角形的对应边相等）例05．已知：（如图）21,∠=∠∠=∠D A . 求证：DO AD =分析：要证DO AD =，只要证DOC AOB ∆≅∆即可，在AOB ∆和DOC ∆中，已知D A ∠=∠，DOC AOB ∆=∆，只要再证一边对应相等即可，根据已知可得DCB ABC ∆≅∆，从而可证DC AB =，进而可证DO AO =，思路即为：DO AO =⇐DOC AOB ∆≅∆⇐DC AB =⇐DCB ABC ∆≅∆⇐“AAS ”证明：在ABC ∆和DCB ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(21公共边已知已知CB BC D A ∴)(AAS DCB ABC ∆≅∆∴DC AB =（全等三角形的对应边相等）在AOB ∆和DOC ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已证已知对顶角相等DC AB D A DOC AOB ∴ )(AAS DOC AOB ∆≅∆∴ DO AO =（全等三角形的对应边相等）例06．求证：三角形的一边的两端到这边的中线或中线的延长线的距离相等.分析：这是一道了题，必须先根据题意画出图形，再结合题意写出已知，求证，再证明.已知：AD 是ABC ∆的中线. 如图，且AD CF ⊥于F ，AD BE ⊥的延长线于E ， 求证：CF BE =证明：∵AD 为ABC ∆的中线（已知） ∴ CD BD =（中线定义）∵ AD BE ⊥ AD CF ⊥（已知）∴ ︒=∠=∠90CFD BED （等于定义） 在BED ∆与CFD ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()(21)(已证对顶角相等已知CD BD CFD BED ∴CFD BED ∆≅∆（AAS ）∴CF BE =（全等三角形对应边相等）说明 本题还可利用面积相等来证明，提示，过A 作BC AN ⊥于N ，希同学们自己来证明.例07．已知：如图，BC AD CD AB //,//， 求证：CD AB =.分析：因为四边形，我只学过三角形的有关知识，因此只要连结四边形的对角线从而把四边形的总是转化为三角形的总是来解决.证明：连结AC∵BC AD CD AB //,//（已知）∴43,21∠=∠∠=∠（两直线平行内错角相等）在ABC ∆和CDA ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已证公共边已知CA AC∴ )(ASA CDA ABC ∆≅∆∴CD AB =（全等三角形的对应边相等）例08．已知：如图，AO CO DO BO ==,求证：OF OE =证明：在BOC ∆和DOA ∆中⎪⎩⎪⎨⎧=∠=∠=)()()(已知对顶角相等已知OA OC DOA BOC DO BO ∴ )(SAS DOA BOC ∆≅∆∴ D B ∠=∠（全等三角形的对应角相等） 在BOE ∆和DOF ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(对顶角相等已知已证DOF BOE DO BO D B ∴)(ASA DOF BOE ∆≅∆∴OF OE =（全等三角形的对应边相等）说明 找到题目中的隐性条件并加以应用是关键.例09．如图，在ABC ∆和DBC ∆中，43,21∠=∠∠=∠，P 是BC 上任意一点， 求证：PD PA =.证明：在ABC ∆和DBC ∆中，⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已知公共边已知BC BC ∴ )(ASA DBC ABC ∆=∆∴ DB AB =（全等三角形对应边相等） 在ABP ∆和DBP ∆中，⎪⎩⎪⎨⎧=∠=∠=)()(21)(公共边已知已证BP BP DB AB ∴ )(SAS DBP ABP ∆≅∆∴ PD PA =（全等三角形对应边相等）说明：本题也可通过DBC ABC ∆≅∆，得到DC AC =，从而证DCP ACP ∆≅∆，得到PD PA =.选择题（1）已知ABC Rt ∆与C B A Rt '''∆，︒=∠90C ，︒='∠90C ，B A '∠=∠.B A AB ''=.那么下列结论正确的是（ ）（A ）C A AC ''= （B ）C B BC ''= （C ）C B AC ''= （D ）以上答案都不对（2）在ABC ∆和C B A '''∆，甲：B A AB ''=；乙：C B BC ''=；丙：C A AC ''=；丁：A A '∠=∠；戊：B B '∠=∠；己：C C '∠=∠，则不能保证ABC ∆≌C B A '''∆成立的条件为（ ）（A ）丙、丁、己 （B ）甲、丙、戊 （C ）甲、乙、戊 （D ）乙、戊、己 （3）如图，已知ABD ∆和ACE ∆均为等边三角形，那么ADC ∆≌ABE ∆的根据是（ ）（A ）ASA （B ）SAS（C ）AAS （D ）以上都不对（4）如图，C 是BE 上一点，CD AB =，D A ∠=∠，E BCA ∠=∠，那么（ ）（A ）ECD B ∠=∠ （B ）C 是BE 的中点 （C ）CD AB //（D ）以上结论都正确参考答案：（1）C （2）B （3）B （4）D填空题（1）如图，已知：21∠=∠，D C ∠=∠. 求证：AD AC =.证明：在ACB ∆与ADB ∆中，⎪⎩⎪⎨⎧=∠=∠∠=∠) _______()()(21AB D C 已知已知 ∴ACB ∆≌ADB ∆（ ） ∴AD AC =（2）如图，已知：BC AB ⊥，DC AD ⊥，垂足分别为B ，D .21∠=∠. 求证：AD AB =.证明：在ABC ∆与ADC ∆中，⎪⎩⎪⎨⎧=∠=∠∠=∠) ()(21)(AC AC ADC ABC ∴ ABC ∆≌ADC ∆（ ） ∴AD AB =（ ）（3）如图，已知：CE AE =，C A ∠=∠.求证：ADE ∆≌CEB ∆.证明：在AED ∆与CEB ∆中，⎪⎩⎪⎨⎧==∠=∠) _____(______)()(已知CE AE C A ∴ AED ∆≌CEB ∆（ASA ）（4）如图，已知：C B ∠=∠，AD AE =.求证：AEC ∆≌ADB ∆.证明：在AEC ∆与ADB ∆中，⎪⎩⎪⎨⎧=∠=∠∠=∠) ()()(AE AE C B A A 已知 ∴AEC ∆≌ADB ∆（ ）参考答案：（1）AB ；公共边；AAS ；全等三角形的对应边相等（2）垂直定义；已知；公共边；AAS ；全等三角形的对应边相等. （3）已知：AED ∠；CEB ∠；对顶角相等 （4）公共角；已知；AAS证明题1．如图，已知，21∠=∠，DCB ABC ∠=∠. 求证：DC AB =.2．如图，已知：E D ∠=∠，AM EM CN DN ===. 求证：点B 是线段AC 的中点.3．如图，已知：21∠=∠，AE AD =. 求证：OC OB =.4．如图，已知：在ABC ∆中，AD 是BAC ∠的平分线，AB DE ⊥于E ，AC DF ⊥于C ，求证：AF AE =.5．如图，已知：E 在AC 上，21∠=∠，43∠=∠. 求证：DE BE =.6．如图，已知：BC AD //，21∠=∠，43∠=∠，直线DC 过E 点交AD 于D ，交BC 于C .求证：AB BC AD =+.7．求证：三角形一边的两个端点到这边上的中线的距离相等. 8．如图，已知：DE AB =，直线AE ，BD 相交于点C ，︒=∠+∠180D B ，DE AF //，交BD 于F .求证：CD CF =.9．如图，已知：AB 与CD 相交于点O ，O 是AB ，CD 的中点，过点O 引直线EF 分别与AD ，BC 相交于E 、F 两点.求证：BF AE =.参考答案：1．证：由DCB ABC =∠，21∠=∠，可得ACB DBC ∠=∠.易证ABC ∆≌DCB ∆，∴ DC AB =2．证：易证DNB ∆≌EMB ∆，∴ EB DB =，由此可证：EA DC =.因此，可证DCB ∆≌EAB ∆.∴BC AB =，∴B 是AC 的中点.3．易证ABE ∆≌ACD ∆，∴C B ∠=∠，AC AB =，又∵AE AD =，∴CE BD =.由此可证BOD ∆≌COE ∆，∴OC OB =4．︒=∠=∠90AFD AED ，FAD EAD ∠=∠，AD AD =，∴AFD AED ∆≅∆，∴AF AE =.5．∵ 21∠=∠，AC AC =，43∠=∠，∴ABC ∆≌ADC ∆，∴AD AB =，又∵21∠=∠,AE AE =，∴ADE ABE ∆≅∆，∴DE BE =6．在AB 上取一点F ，使BF BC =，又∵43∠=∠，EB EB =，∴EC B EFB ∆≅∆，∴C EFB ∠=∠，又∵BC AD //，由此可推出D EFA ∠=∠.可证AFE ADE ∆≅∆，∴AF AD =，∴BC AD AB +=.7．已知：如图，AD 为ABC ∆的中线，AD BF ⊥于F ，AD CE ⊥于E . 求证：CE BF =.证：︒=∠=∠90BFD CED ，BDF CDE ∠=∠，BD CD =，∴ BFD CED ∆≅∆,∴ CE BF =8．证：∵ DE AF //， ∴AFC D ∠=∠，又∵︒=∠+∠180AFB AFC ，︒=∠+∠180D B ，∴ AFB B ∠=∠∴ DE AF AB ==，∴ 可证ECD ACF ∆≅∆，∴CD CF =9．证：BO AO =，BOC AOD ∠=∠，CO DO =，∴B O C A O D ∆≅∆，∴B A ∠=∠.而BOF AOE ∠=∠，BO AO =，∴BOF AOE ∆≅∆，∴ BF AE =能力：1、如图1，已知：AD 平分∠BAC ，AB=AC ，连接BD ，CD ，并延长相交AC 、AB 于F 、E 点.则图形中有（ ）对全等三角形.A 、2B 、3C 、4D 、5答案：C.2、如图2，已知：∠1=∠2，AB=DC ，图中全等三角形的对数是（ ）A 、0B 、1C 、2D 、3答案：A3、如图3，已知：△ABC 中，DF=FE ，BD=CE ，AF ⊥BC 于F ，则此图中全等三角形共有（ ）A 、5对B 、4对C 、3对 D2对答案：C.1、如图4，已知：在△ABC 中，AD 是BC 边上的高，AD=BD ，DE=DC ，延长BE 交AC 于F ，求证：BF 是△ABC 中边上的高. 图1 A B B 、E F D C AD B O C 1 2 图2 图3 D FE C AF C D B E 图4提示：关键证明△ADC ≌△BFC2、如图5，已知：∠D=∠E ，DN=EM ，AM=CN ，求证：点B 是线段AC 的中点.提示：欲证点B 是线段AC 的中点，只需证AB ＝BC.选择AB 、BC 所在的两个三角形，然后证这两个三角形△AMB ≌△CNB.由条件可得△EMB ≌△DNB ，所以得到∠EMB ＝∠DNB ，MB ＝NB由此易证△AMB ≌△CNB.3、如图6，已知：AB=CD ，∠A=∠D.求证：∠ABC=∠DCB提示：欲证∠ABC=∠DCB ，选择这两个角所在的三角形，只需证△ABC ≌△DBC由条件可知△ADC ≌△DAB ，所以得到∠DAC ＝∠ADB ，BD ＝AC ，加之条件利用边角边公理可证△ABC ≌△DBC4、如图7，已知：在△ABC 中，∠ACB=090,AC=BC ，AE 是BC 边上的中线过C 作CF ⊥AE ，垂足为F ，过B 作BD ⊥BC 交CF 的延长线于点D.（1）求证：AE=CD.（2）AC=12cm ，求BD 的长.提示：欲证AE=CD ，只需证△ACE ≌△CBD 由条件可知∠CAE ＝∠BCD （同角的余角相等）加之其它两个条件易证得结论.由E 是BC 的中点，EC ＝BE又BD ＝EC ，BC ＝AC 知BD ＝6 cm5、如图8，已知：在△ABC 中，AB=AC ，∠A=90，BD 平分∠ABC 交AC 于D ，CE ⊥BD 交BD 的延长线于E ，求证：BD=2CE提示：本题的关键是从结论BD=2CE 出发，想到构造线段CF ＝2CE ，再证BD ＝CFA M N E C DB 图5 A D BC 图6 O E ┛ ┓ ┏D A CF 图7 B A E C D 图8 F。

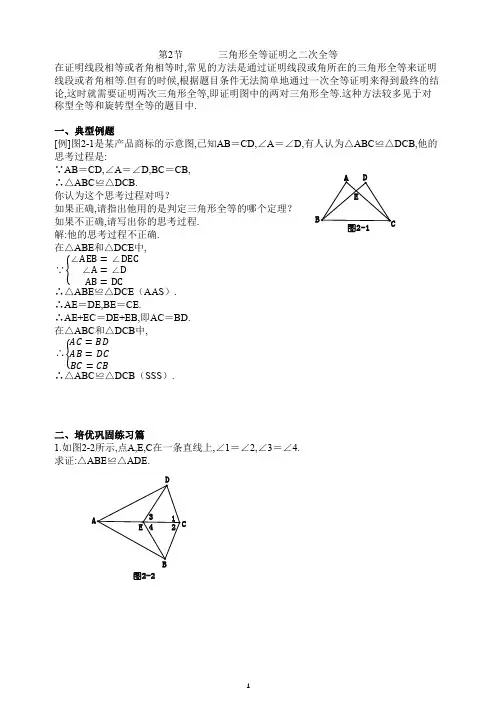
第2节 三角形全等证明之二次全等在证明线段相等或者角相等时,常见的方法是通过证明线段或角所在的三角形全等来证明线段或者角相等.但有的时候,根据题目条件无法简单地通过一次全等证明来得到最终的结论,这时就需要证明两次三角形全等,即证明图中的两对三角形全等.这种方法较多见于对称型全等和旋转型全等的题目中.一、典型例题[例]图2-1是某产品商标的示意图,已知AB ＝CD,∠A ＝∠D,有人认为△ABC ≌△DCB,他的思考过程是:∵AB ＝CD,∠A ＝∠D,BC ＝CB,∴△ABC ≌△DCB.你认为这个思考过程对吗？如果正确,请指出他用的是判定三角形全等的哪个定理？如果不正确,请写出你的思考过程.解:他的思考过程不正确.在△ABE 和△DCE 中,∵{∠AEB =∠DEC∠A =∠D AB =DC∴△ABE ≌△DCE （AAS ）.∴AE ＝DE,BE ＝CE.∴AE+EC ＝DE+EB,即AC ＝BD.在△ABC 和△DCB 中,∴{AC =BDAB =DC BC =CB∴△ABC ≌△DCB （SSS ）.二、培优巩固练习篇1.如图2-2所示,点A,E,C 在一条直线上,∠1＝∠2,∠3＝∠4.求证:△ABE ≌△ADE.图2-2图2-12.如图2-3所示,点A,E,F,C 在一条直线上,AE ＝CF,分别过点E,F 作DE ⊥ AC,BF ⊥AC,连接AB,CD,且AB ∥CD,连接BD 交AC 于点C.求证:△DEG ≌△BFG.3.如图2-4所示,AB ＝AC,DB ＝DC,F 是AD 延长线上的一点.求证:BF ＝CF.4.如图2-5所示,AE 是∠BAC 的角平分线,EB ⊥AB 于点B,EC ⊥AC 于点C,点D 是AE 上一点.求证:BD ＝CD.5.如图2-6所示,DE ⊥AC,BF ⊥AC,AD ＝BC,DE ＝BF.求证:AB ∥DC.图2-3C图2-4图2-5图2-66.如图2-7所示,点E,F 在BD 上,且AB ＝CD,BF ＝DE,AE ＝CF.求证:AO ＝CO.7.如图2-8所示,AB 之间有一条河.想要测量AB 的长,但无法过河接近点A,于是在AB 外任取一点D,在AB 的延长线上任取一点E,连接ED 和BD,并延长BD 到点G,使DG ＝DB,延长ED 到点F,使DF ＝DE,连接FG,并延长FG 到点H,使点H,D,A 在一条直线上,则HG ＝AB.试说明这种测量方法的原理.8.如图2-9所示,在Rt △ABC 和Rt △ADE 中,∠ABC ＝∠ADE ＝90°,BC 与DE 相交于点F,且AB ＝AD,AC ＝AE,连接CD,EB.求证:(1)∠CAD ＝∠EAB;（2）CF ＝EFDH图2-8图2-99.如图2-10所示,在等边△ABC 内取一点D,使DA ＝DB,在△ABC 外取一点E,使∠DBE ＝∠DBC,且BE ＝BA,则∠BED ＝_______°.10.如图2-11所示,∠BAC 是钝角,AB ＝AC,点D,E 分别在AB,AC 上,且CD ＝BE.试说明:∠ADC ＝∠AEB.一个同学的解法是这样的: 在△ACD 和△ABE 中, ∵{AB =AC BE =CD ∠BAE =∠CAD ∴△ABE ≌△ACD.∴∠ADC ＝∠AEB.这种解法遭到了其他同学的质疑.理由是错在不能用“SSA ”判定三角形全等.请你给出正确的解法.图2-10CB AC B答案解析1.证明:在△DEC和△BEC中,{∠1=∠2 EC=EC ∠3=∠4∴△DEC≌△BEC（ASA）.∴DE＝BE.∵∠3＝∠4,∴∠DEA＝∠BEA.在△ABE和△ADE中,{AE=AE∠AEB=∠AEDBE=DE∴△ABE≌△ADE（SAS）.2.证明:∵DE⊥AC,BF⊥AC, ∴∠AFB＝90°＝∠CED. ∵AE＝CF,∴AE+EF＝CF+FE,即AF＝CE.∵AB∥CD,∴∠A＝∠C.在△ABF和△CDE中,{∠A=∠C AF=CE∠AFB=∠CED ∴△ABF≌△CDE（ASA）.∴DE＝BF.在△BFG和△DEG中,{∠BFG=∠DEG ∠BGF=∠DGE BF=DE∴△BFG≌△DEG（AAS）.3.证明:在△ABD和△ACD中,{AB=AC BD=CD AD=AD∴△ABD≌△ACD（SSS）.∴∠BAD＝∠CAD.在△BAF和△CAF中,{AB=AC∠BAF=∠CAF AF=AF∴△BAF≌△CAF（SAS）.∴BF＝CF.4.证明:∵AE是∠BAC的角平分线, ∴∠CAE＝∠BAE. ∵EB⊥AB,EC⊥AC, ∴∠ECA＝∠EBA＝90°.在△CAE和△BAE中,{∠CAE=∠BAE ∠ECA=∠EBA AE=AE∴△CAE≌△BAE（AAS）.∴AC＝AB.在△CAD和△BAD中,{AC=AB ∠CAD＝∠BAD AD=AD∴△CAD≌△BAD（SAS）.∴BD＝CD.5.证明:∵DE ⊥AC,BF ⊥AC, ∴∠AED ＝∠CFB ＝90°, ∠AFB ＝∠CED ＝90°, 在Rt △ADE 和Rt △CBF 中,∵{AD =CB DE =BF ∴Rt △ADE ≌Rt △CBF （HL ）.∴AE ＝CF.∴AE+EF ＝CF+FE,即AF ＝CE.在△AFB 和△CED 中,∵{AF =CE∠AFB =∠CED DE =BF∴△AFB ≌△CED （SAS ）. ∴∠BAF ＝∠DCE.∴AB ∥DC.∴AO ＝CO.6.证明:∵BF ＝DE, ∴BF-EF ＝DE-FE,即BE ＝DF. 在△ABE 和△CDF 中, {AB =CDAE =CF BE =DF∴△ABE ≌△CDF （SSS ）.∴∠B ＝∠D.在△AOB 和△COD 中,{∠AOB =∠COD∠B =∠D AB =CD∴△AOB ≌△COD （AAS ）7.解:在△BED 和△GFD 中,{DB =DG∠BDE =∠GDF DE =DF∴△BED ≌△GFD （SAS ）.∴∠EBD ＝∠FGD.∴∠ABD ＝∠HGD.在△ABD 和△HGD 中,{∠ABD =∠HGDBD =GD∠BDA =∠GDH∴△ABD ≌△HGD （ASA ）.∴HG ＝AB.8.证明:（1）在Rt △ABC 和Rt △ADE 中,{AC =AE AB =AD ∴Rt △ABC ≌Rt △ADE （HL ）.∴∠BAC ＝∠DAE.∴∠BAC-∠DAB ＝∠DAE-∠DAB,即∠CAD ＝∠EAB.（2）在△ACD 与△AEB 中, {AC =AE∠CAD =∠EAB AD =AB∴△ACD ≌△AEB （SAS ）.∴CD ＝BE,∠ACD ＝∠AEB.∵Rt △ABC ≌Rt △ADE （HL ）, ∴∠ACB ＝∠AED.∴∠ACB-∠ACD ＝∠AED-∠AEB,即∠DCF ＝∠BEF.又∵∠DFC ＝∠BFE, ∴△DFC ≌△BFE （AAS ）.∴CF ＝EF.9.解:如图2所示,连接CD.∵△ABC是等边三角形, ∴AB＝BC＝CA.∵BE＝BA,BA＝BC, ∴BE＝BC.在△BDC和△BDE中,{BD=BD∠DBE=∠DBC BE=BC∴△BDC≌△BDE（SAS）. ∴∠BED＝∠BCD.在△BCD和△ACD中,{BC=AC BD=AD CD=CD∴△BCD≌△ACD（SSS）.∴∠BCD＝∠ACD＝30°.∴∠BED＝30°.10.证明:因为∠BAC是钝角,故过点B,C分别作CA,BA的垂线,垂足分别为点F, G,如图3所示.在△ABF和△ACG中,{∠F=∠G=90°∠FAB=∠GACAC=AB∴△ABF≌△ACG（AAS）.∴BF＝CG.在Rt△BEF和Rt△CDG中,{BF=CGBE=CD∴Rt△BEF≌Rt△CDG（HL）.∴∠ADC＝∠AEBEDC BA。

《数学思维与能力训练》辅导讲义姓名 辅导时间全 等 三 角 形 (2)【知识要点】1、能够完全重合的两个图形叫做全等形，两个三角形重合后，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角，全等用符号“≌”表示，全等三角形对应边相等，对应角相等。

判断两个三角形全等的定理有：① 边角边（SAS ）② 角边角（ASA ）③ 角角边（AAS ）④ 边边边（SSS ）⑤ 斜边直角边（HL ）2、全等三角形的对应边、对应角、对应中线、对应角平分线、对应高等对应线段或角全都相等，所以可利用三角形全等证明某些等式成立，如线段相等、角相等等。

【拓展探究】［例题1］如图所示，在ΔABC 中，∠C = 90°，∠A = 30°，分别以AB 、AC 为边在ΔABC 外侧作正ΔABE 和正ΔACD ，DE 与AB 相交于F ，求证：EF = FDF A E B C D［例题2］如图所示，ΔABC 中，∠ACB = 90°，AD ⊥AB ，AD = AB ，BE ⊥DC ，AF ⊥AC ，求证：CF 平分∠ACB［例题3］如图所示，ΔABC 中，若AB = 6，AC = 4，求BC 边上的中线AD 长的范围DC A FB E A CD B〖小试牛刀〗1、如图所示，AD 、A 1D 1 分别是ΔABC 和ΔA 1B 1C 1 的中线，已知AB = A 1B 1，AC = A 1C 1，AD = A 1D 1，求证：ΔABC ≌ ΔA 1B 1C 12、如图所示，AB = AD ，BC = DC ，E 、F 在AC 上，AC 与BD 交于P 点，请找出图中共有多少对全等三角形，并简述全等的理由。

B DC A E P F A B CD3、如图所示，在∠AOB 的OA 边上取两点P 和S ，再在OB 边上取两点Q 和T ，使OQ = OP ，OT = OS ，PT 与QS 相交于点C ，求证：OC 平分∠AOB4、(1) 如图所示，A 、B 、C 三点在一直线上，分别以AB 、BC 为边在AC 同侧作等边ΔABD 和等边ΔBCE ，AE 交BD 于点F ，DC 交BE 于点G ，求证：AE = DC ，BF = BG(2) 如图所示，如果A 、B 、C 不在同一直线上，那么这时AE = DC ，BF = BG 是否仍然成立？如果成立，请加以证明；如果不成立，请说明理由。

八年级数学暑期辅导全等三角形性质教学目标：1.理解全等形和全等三角形的概念，并能准确的表示全等三角形，找出对应边和对应角2.掌握全等形的三种变换：平移、翻折和旋转3.掌握三角形全等及其性质，能用符号正确地表示两个三角形全等，运用全等三角形的性质灵活解决相关问题4.学生通过观察、发现生活中的全等形和实际操作中获得全等三角形的体验在探索和运用全等三角形性质的过程中感受到数学的乐趣。

教学重难点：重点：全等三角形的概念和性质；难点：找全等三角形的对应边、对应角。

掌握几种常见的全等三角形类型教学过程：一、三角形相关知识点回顾知识点1.三角形的概念：1、由直线上的三条线段组成的图形叫三角形2、三角形的基本元素：三角形有条边个顶点个内角三角形的分类：按边可分为三角形和三角形，按角可分为三角形三角形三角形【注意：等边三角形属于特殊的三角形，锐角三角形和钝角三角形有时称为三角形】知识点2.三角形的性质：1、三角形的内角和是三角形的任意一个外角和它不相交两个内角的和三角形的一个外角任意一个和它不相邻的内角2、三角形任意两边之和第三边，任意两边之差第三边3、三角形具有性注意：1、三角形的外角是指三角形一边和另一边的组成的角，三角形的外角和是2、三角形三边关系定理是确定三条线段是否构成三角形和判断限度间不等关系的主要依据1、角平分线：三角形的三条角平分线都在三角形部且交于一点，这些是三角形的心它到得距离相等2、中线：三角形的三条中线都在三角形部，且交于一点3、高线：不同三角形的三条高线位置不同，锐角三角形三条高都连三角形直角三角形有一条高线在部，另两条河重合，钝角三角形有一条高线在三角形部，两条在三角形部4、中位线：连接三角形任意两边的线段叫做三角形的中位线。

定理：三角形的中位线第三边且等于第三边的【注意：三角形的平分线、中线、高线、中位线都是且都有条】二、知识点梳理1．全等形的概念：能够完全重合的两个图形叫做全等形．2．全等形的性质：（1）形状相同．（2）大小相等．3．全等三角形的概念：能够完全重合的两个三角形叫做全等三角形．4．全等三角形的表示：（1）两个全等的三角形重合时：重合的顶点叫做对应顶点；重合的边叫做对应边；重合的角叫做对应角．（2）如图，和全等，记作．通常对应顶点字母写在对应位置上．5.对应顶点，对应边，对应角：对应顶点，对应边，对应角定义两个全等三角形重合在一起，重合的顶点叫对应顶点，重合的边叫对应边，重合的角叫对应角.注意：在写两个三角形全等时，通常把对应顶点的字母写在对应位置上，这样容易找出对应边、对应角.如下图，△ABC与△DEF全等，记作△ABC≌△DEF，其中点A和点D，点B和点E，点C和点F是对应顶点；AB和DE，BC和EF，AC和DF是对应边；∠A和∠D，∠B和∠E，∠C 和∠F是对应角.找对应边、对应角的方法（重点）（1）全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边；（2）全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角；（3）有公共边的，公共边是对应边；（4）有公共角的，公共角是对应角；（5）有对顶角的，对顶角一定是对应角；（6）两个全等三角形中一对最长的边（或最大的角）是对应边（或角），一对最短的边（或最小的角）是对应边（或角），等等.6．全等三角形的性质：（1）全等三角形的对应边相等；全等三角形的对应角相等．（2）全等三角形的周长、面积相等．7．全等变换：只改变位置，不改变形状和大小的图形变换．平移、翻折（对称）、旋转变换都是全等变换．8．全等三角形基本图形翻折：找到中心线经此翻折后能互相重合的两个三角形，易发现其对应元素旋转：两个三角形绕某一定点旋转一定角度能够重合时，易于找到对应元素将两个三角形沿某一直线推移能重合时也可找到对应元素三、常考点分析考点一、全等形和全等三角形的概念例1 下列每组中的两个图形，是全等图形的为（）A． B．C．D．总结归纳：是不是全等形，既要看形状是否相同，还要看大小是否相等.同类练习：如图，在5个条形方格图中，图中由实线围成的图形与①全等的有______________.类型二、全等三角形的对应边，对应角例2 如图，△ABN≌△ACM，∠B和∠C是对应角，AB与AC是对应边，写出其他对应边和对应角.总结归纳：全等三角形对应角所对的边是对应边；全等三角形对应边所对的角是对应角.全等，记作 ，其中点A 和点 ，点B 和点 ，点 和点D 是对应点， 边AB 和 ， 和ED ，AC 和 是对应边；例4 分别写出下列三组全等三角形的对应点和对应边： 分析:注意问题：1、把两个全等的三角形重合在一起，重合的顶点叫做对应顶点；重合的边叫 做对应边；重合的叫做对应角。

当我们在日常办公时，经常会遇到一些不太好编辑和制作的资料。

这些资料因为用的比较少，所以在全网范围内，都不易被找到。

您看到的资料，制作于2021年，是根据最新版课本编辑而成。

我们集合了衡中、洋思、毛毯厂等知名学校的多位名师，进行集体创作，将日常教学中的一些珍贵资料，融合以后进行再制作，形成了本套作品。

本套作品是集合了多位教学大咖的创作经验，经过创作、审核、优化、发布等环节，最终形成了本作品。

本作品为珍贵资源，如果您现在不用，请您收藏一下吧。

因为下次再搜索到我的机会不多哦！12.1 全等三角形教学目标知识与技能通过实例理解全等形的概念和特征，并能识别图形的全等．②知道全等三角形的有关概念，能正确地找出对应顶点、对应边、对应角；掌握全等三角形对应边相等，对应角相等的性质．③能运用性质进行简单的推理和计算，解决一些实际问题．过程与方法通过两个重合的三角形变换其中一个的位置，使它们呈现各种不同位置的活动，让学生从中了解并体会图形变换的思想，逐步培养学生动态的研究几何图形的意识．情感态度价值观培养学生的观察能力、动手操作能力和自主学习能力，发展学生的空间观念。

教学重点掌握全等三角形对应边相等、对应角相等的性质教学难点理解全等三角形边、角之间的对应关系．教学准备复写纸、剪刀、半透明的纸、多媒体课件(几个重要片断中使用)．教学过程（师生活动）设计理念问题情境1．展现生活中的大量图片或录像片断。

丰富的图形容易引起学生的注意，使他们能很快地投入到学习的情境中．它反映了现实生活中存在着大量的全等图形．2．学生讨论：(1)从上面的片断中你有什么感受?(2)你能再举出生活中的一些类似例子吗?教师明晰，建立模型观察下列图案，指出这些图案中中形状与大小相同的图形问题：你还能举出生活中一些实际例子吗？这些形状、大小相同的图形放在一起能够完全重合。

能够完全重合的两个图形叫做全等形能够完全重合的两个三角形叫做全等三角形通过构图，为学生理解全等三角形的有关概念奠定基础．解析、应用与拓广1.学生用半透明的纸描绘下图中左边的△ABC，然后按要求在三个图中依次操作．体验“平移、翻折、旋转前后的两个图形全等”．你发现变换前后的两个三角形有什么关系？结论：一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小都没有改变，即平移、翻折、旋转前后的图形全等。