初三上期末 丰台 2015 1

丰台区2014～2015学年度第一学期期末练习初三化学相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 P-31 Cl-35.5 Ti-48 Fe-56 一、选择题（每小题只有一个选项符合题意，共25个小题，每小题1分，共25分。

）1．空气成分中，体积分数约占78%的是A．氮气B．氧气C．二氧化碳D．稀有气体2．下列金属的活动性最弱的是A．银B．铜C．铝D．钠3．地壳中含量最多的金属元素是A．氧B．硅C．铝D．铁4．加碘食盐中的“碘”指的是A．元素B．原子C．分子D．单质5．决定元素种类的是A．中子数B．质子数C．核外电子数D．最外层电子数6．下列措施不利于．．．保护环境的是A．使用清洁能源B．使用无氟冰箱C．提倡使用私家车D．提倡垃圾分类7．下列物质中，属于纯净物的是A．自来水B．汽水C．液态氧气D．液态空气8．下列物质在氧气中燃烧，产生大量白烟的是A．木炭B．甲烷C．蜡烛D．红磷9．下列图标中，表示“禁止烟火”的是ABCD10．下列符号中，表示2个氢分子的是A ．H 2B ．2H 2C ．H 2OD ．2H11．下列实验操作中，正确的是A ．点燃酒精灯B ．倾倒液体C ．称量固体D ．加热液体12．下列物质性质的表述中，属于化学性质的是A. 干冰易升华B. 水通电能分解C. 五氧化二磷是白色固体D. 食盐易溶于水13.在元素周期表中，镁元素的信息如右图所示，对图中信息解释不正确．．．的是 A ．原子序数为12 B ．核外电子数为 24C ．元素符号为MgD ．相对原子质量为24.3114．下列物质的化学式书写不正确．．．的是 A ．氯化钠 NaClB ．氧化铝 Al 2O 3C ．碳酸钠 NaCO 3D ．氢氧化钾 KOH15．卫星运载火箭的动力由高氯酸铵（NH 4ClO 4）发生反应提供，化学方程式为：2NH 4ClO 4高温N 2↑+Cl 2↑+2O 2↑+4X 。

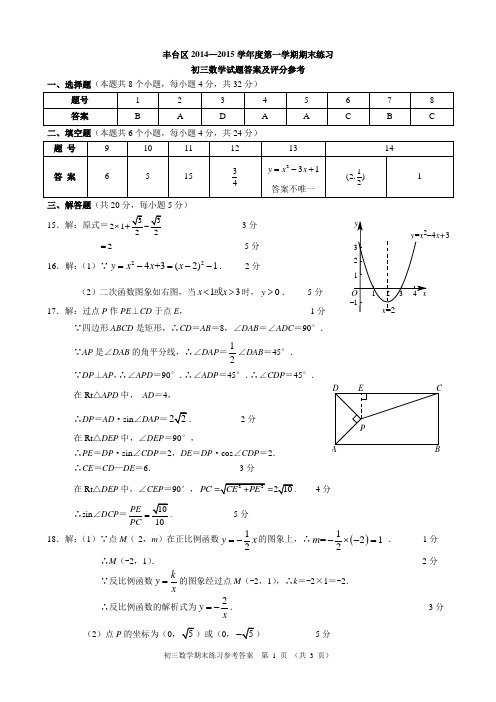
x+3丰台区2014—2015学年度第一学期期末练习初三数学试题答案及评分参考一、选择题（本题共8个小题，每小题4分，共32分）二、填空题（本题共6个小题，每小题4分，共24分）三、解答题（共20分，每小题5分） 15．解：原式＝21⨯ ------3分 2= ------5分16．解：（1）∵224+3(2)1y x x x =-=--．------2分（2）二次函数图象如右图，当13x x <>或时，0y >．------5分17．解：过点P 作PE ⊥CD 于点E ， ------1分∵四边形ABCD 是矩形，∴CD ＝AB ＝8，∠DAB ＝∠ADC ＝90°． ∵AP 是∠DAB 的角平分线，∴∠DAP ＝12∠DAB ＝45°． ∵DP ⊥AP ，∴∠APD ＝90°．∴∠ADP ＝45°．∴∠CDP ＝45°．在Rt △APD 中，AD ＝4，∴DP ＝AD ·sin ∠DAP ＝ ------2分在Rt △DEP中，∠DEP ＝90°，∴PE ＝DP ·sin ∠CDP ＝2，DE ＝DP ·cos ∠CDP ＝2． ∴CE ＝CD —DE ＝6． ------3分在Rt △DEP 中，∠CEP ＝90°，PC 分 ∴sin ∠DCP ＝PE PC =. ------5分 18．解：（1）∵点M （-2，m ）在正比例函数12y x =-的图象上，∴()1=212m -⨯-= ． ------1分 ∴M （-2，1）．------2分∵反比例函数ky x=的图象经过点M （-2，1），∴k ＝-2×1＝-2． ∴反比例函数的解析式为2y x=-． ------ 3分（2）点P 的坐标为（00， -------5分PDCBAE四、解答题（本题共22分，第19，22题每小题5分，第20， 21题每小题6分） 19．解：（1）(20)(20)(280)W y x x x =-=--+ ------- 1分 221201600x x =-+-． ------- 3分（2） ()2230200W x =--+． ------4分∴当销售单价定为30元时，工厂每天获得的利润最大，最大利润是200元．------5分20．解：过点C 作CD ⊥AB ，交AB 延长线于点D ．由题意可知，------- 1分在△ABC 中，∠CAB ＝30°，∠ABC ＝90°＋30°＝120°， ∴∠ACB ＝30°，BC ＝AB ＝20 ． ------- 3分 在Rt △CBD 中，∠CBD ＝60°，∴CD ＝CB ·sin ∠CBD＝． ------- 5分∵12，∴这艘渔船继续向东航行追赶鱼群不会进入危险区． ------- 6分21．（1）证明：如图，联结OA ，OB ．∵PB 是⊙O 的切线，∴ ∠PBO ＝90°． ------- 1分 ∵ OA ＝OB ，BA ⊥PE 于点D ， ∴ ∠POA ＝∠POB ． ------- 2分 又∵ PO ＝PO ，∴ △P AO ≌△PBO ．∴ ∠P AO ＝∠PBO ＝90°． ∴P A ⊥OA ．∴ 直线P A 为⊙O 的切线． ------- 3分 （2）在Rt △ADE 中，∠ADE ＝90°，∵tan ∠AEP ＝AD DE ＝12，∴设AD ＝x ，DE ＝2x ．----- 4分 ∴OE ＝2x —3．在Rt △AOD 中，由勾股定理 ，得(2x －3)2＝x 2＋32． ------5分解得，x 1＝4，x 2＝0（不合题意，舍去）．∴ AD ＝4，OA ＝OE ＝2x －3＝5．即⊙O 的半径的长5． ------ 6分 22．解：（1）同，异，同． ------3分（2） 1或2． ------5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．解：（1）根据题意得，Δ440m =+>， ------1分解得 1.m >- ------2分（2）由题意知，抛物线对称轴为直线x ＝1，点A 和点B 是抛物线上的两个对称点，则()311(1)n n +-=--，解得0.n = ------3分 ∴点A （-1，0），∴22 3.y x x =-- ------5分（3）2060.k << ------7分24．解：（1）如图1， ------1分∠AEB ＝∠CEB ． ------2分 （2）b a 21=. ------3分 证明：如图2，作过点A 作AF ⊥BE 于点F ， ------4分∵ AB ＝AE ，∴1.2BF BE =∵∠AFB ＝∠C =90°，∠ABE ＝∠CEB ， ∴△ABF ∽△BEC . ------5分∴ABBFBE EC =． ------6分 ∴ABBEBE EC 21=， 即12a b =． ------7分 25.解：（1）①90°； ------1分②60°或120°． ------3分（2）如图，当⊙P 与x 轴相切，G 为切点时，∠DGE 最大．------4分由题意知，点P 在线段ED 的垂直平分线上，∴PG ＝2.5. ------5分过点P 作PH ⊥DE 于点H ， ∴11.5.2EH DE == ------6分∵PG ⊥x 轴，∴四边形PHOG 为矩形.联结PE ，在Rt △PEH 中， PE ＝PG ＝2.5，EH ＝1.5，∴PH ＝2． 所以点G （2，0）． ------8分。

丰台区2014～2015学年度第一学期期末练习初三化学 2015．01相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 P-31 Cl-35.5 Ti-48 Fe-56 一、选择题（每小题只有一个选项符合题意，共25个小题，每小题1分，共25分。

） 1．空气成分中，体积分数约占78%的是A ．氮气B ．氧气C ．二氧化碳D ．稀有气体 2．下列金属的活动性最弱的是A ．银B ．铜C ．铝D ．钠3．地壳中含量最多的金属元素是A ．氧B ．硅C ．铝D ．铁4．加碘食盐中的“碘”指的是A ．元素B ．原子C ．分子D ．单质 5．决定元素种类的是A ．中子数B ．质子数C ．核外电子数D ．最外层电子数6．下列措施不利于．．．保护环境的是 A ．使用清洁能源B ．使用无氟冰箱C ．提倡使用私家车D ．提倡垃圾分类7．下列物质中，属于纯净物的是A ．自来水B ．汽水C ．液态氧气D ．液态空气 8．下列物质在氧气中燃烧，产生大量白烟的是A ．木炭B ．甲烷C ．蜡烛D ．红磷 9．下列图标中，表示“禁止烟火”的是ABCD10．下列符号中，表示2个氢分子的是A ．H 2B ．2H 2C ．H 2OD ．2H11．下列实验操作中，正确的是A ．点燃酒精灯B ．倾倒液体C ．称量固体D ．加热液体12．下列物质性质的表述中，属于化学性质的是A. 干冰易升华B. 水通电能分解C. 五氧化二磷是白色固体D. 食盐易溶于水13.在元素周期表中，镁元素的信息如右图所示，对图中信息解释不正确．．．的是 A ．原子序数为12 B ．核外电子数为 24C ．元素符号为MgD ．相对原子质量为24.3114．下列物质的化学式书写不正确．．．的是[A ．氯化钠 NaClB ．氧化铝 Al 2O 3C ．碳酸钠 NaCO 3D ．氢氧化钾 KOH15．卫星运载火箭的动力由高氯酸铵（NH 4ClO 4）发生反应提供，化学方程式为：2NH 4ClO 4高温N 2↑+Cl 2↑+2O 2↑+4X 。

丰台区2014-2015学年度第一学期期末练习初 三 英 语2015.1听力理解（共26分）一、听对话，从下面各题所给的A 、B 、C 三幅图片中选择与对话内容相符的图片。

每段对话你将听两遍。

（共4分，每小题1分）1．A ．B ．C ．2．A ．B ．C ．3.A ．B ．C ． 4．A．B．C．二、听对话或独白，根据对话或独白的内容，从下面各题所给的A、B、C三个选项中选择最佳选项。

每段对话或独白你将听两遍。

(共12分，每小题1分) 请听一段对话，完成第5至第6小题。

5. What does Mike often do in his spare time?A. He goes swimming.B. He reads books.C. He plays basketball.6. What does Mike like to do during the trip?A. To buy presents.B. To take photos.C. To taste food.请听一段对话，完成第7至第8小题。

7. How long has the woman learned English?A. For one year.B. For two years.C. For three years.8. What problem does the man have in his English study?A. Grammar.B. Pronunciation.C. Listening.请听一段对话，完成第9至第10小题。

9. When will the visitors come?A. At the end of May.B. In the middle of June.C. At the beginning of July.10. How many days will the visitors spend on the visit?A. Three.B. Four.C. Five.请听一段对话，完成第11至第13小题。

丰台区2014-2015学年度第一学期初三数学期末练习一、选择题（共8个小题，每小题4分，共32分） 1. 如果45(0)x y y =≠，那么下列比例式成立的是A ．45x y= B ．54x y = C ．45x y =D ．54x y= 2．二次函数2(3)1y x =--+的最大值为A ．1B ．－1C ．3D ．－33．⊙O 1和⊙O 2的半径分别为2cm 和3cm ，如果O 1O 2=5cm ，那么⊙O 1和⊙O 2的位置关系是 A ．内含 B ．内切 C ．相交 D ．外切4. 如图，A ，B ，C 是⊙O 上的三个点，如果∠BAC =30°，那么∠BOC 的度数是 A ．60○ B ．45○ C ．30○ D ．15○5. 如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB 于点D ，如果AC =3， AB =6， 那么AD 的值为 A.32 B. 92 C.2D. 6．如图，扇形折扇完全打开后，如果张开的角度（∠BAC ）为120°，骨柄AB 的长为30cm ，扇面的宽度BD 的长为20cm ，那么这把折扇的扇面面积为 A ．2400πcm 3 B ．2500πcm 3 C ．2800πcm 3D ．2300πcm7. 如果点A ()11y -,，B ()22y ,，C ()33y ,都在反比例函数3y x=的图象上，那么 A ．123y y y << B ．132y y y << C ．213y y y << D ．321y y y << 8．如图，在平面直角坐标系中，点C 的坐标为（0，2），动点A 以每秒1个单位长的速度从点O 出发沿x 轴的正方向运动，M 是线段AC 的中点，将线段AM 以点A 为中心，沿顺时针方向旋转︒90得到线段AB ．联结CB ．设△ABC 的面积为S ，运动时间为t 秒，则下列图象中，能表示S 与t 的函数关系的图象大致是D CA ABCOBCAA BC D二、填空题（共6个小题，每小题4分，共24分）9．如图，在△ABC 中，点D ，E 分别在AB ，AC 边上，且 DE ∥BC ，如果 AD ∶DB =3∶2， EC =4，那么AE 的长等于 ．10．如图，AB 是⊙O 的弦，OC ⊥AB 于点C ，如果 AB=8，OC=3，那么⊙O 的半径等于 ．11．在某一时刻，测得一身高为1.80m 的人的影长为3m ，同时测得一根旗杆的影长为25m ，那么这根旗杆的高度为 m ．12．在正方形网格中，ABC △的位置如图所示，则tan B 的值为__________． 13．关于x 的二次函数22y x kx k =-+-的图象与y 轴的交点在x 轴的上方，请写出一．个．满足条件的二次函数的表达式： ． 14．在平面直角坐标系xOy 中，对于点(),P x y ，其中0≠y ，我们把点)11,1(y x P -+-'叫做点P 的衍生点.已知点1A 的衍生点为2A ，点2A 的衍生点为3A ，点3A 的衍生点为4A ，…，这样依次得到点1A ，2A ，3A ，…，n A ，…，如果点1A 的坐标为)1,2(-，那么点3A 的坐标为________；如果点1A 的坐标为()b a ,，且点2015A 在双曲线xy 1=上， 那么=+ba 11________． 三、解答题（本题共20分，每小题5分） 15．计算：2tan45sin60cos30︒+︒-︒. 16．已知二次函数y = x 2－4x ＋3.（1）把这个二次函数化成2()y a x h k =-+的形式； （2）画出这个二次函数的图象，并利用图象写出当x 为何值时，y>0．E A CBD17．如图，矩形ABCD 中，AP 平分∠DAB ，且AP ⊥DP 于点P ，联结CP ，如果AB ﹦8， AD ﹦4，求sin ∠DCP 的值.18．如图，正比例函数12y x =-的图象与反比例函数k y x =的图象分别交于M ，N 两点，已知点M （-2，m ）. （1）求反比例函数的表达式；（2）点P 为y 轴上的一点，当∠MPN 为直角时，直接写出点P 的坐标．四、解答题（本题共22分，第19，22题每小题5分，第20， 21题每小题6分）19．某工厂设计了一款产品，成本为每件20元．投放市场进行试销，经调查发现，该种产品每天的销售量y （件）与销售单价x （元）之间满足280y x =-+ （20≤x ≤40），设销售这种产品每天的利润为W （元）.（1）求销售这种产品每天的利润W （元）与销售单价x （元）之间的函数表达式； （2）当销售单价定为多少元时, 每天的利润最大？最大利润是多少元？20. 如图，一艘渔船正自西向东航行追赶鱼群，在A 处望见岛C 在船的北偏东60°方向，前进20海里到达B 处，此时望见岛C 在船的北偏东30°方向，以岛C 为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能. （参考数据:1.4 1.7≈≈）21．如图，PB 切O 于点B ，联结PO 并延长交O 于点E ，过点B 作BA ⊥PE 交O 于点A ，联结AP ，AE ． （1）求证：P A 是O 的切线； （2）如果OD ＝3，tan ∠AEP ＝12，求O 的半径．ABCD P22．对于两个相似三角形，如果对应顶点沿边界按相同方向顺序环绕，那么称这两个三角形互为同相似，如图1，111A B C ∆∽ABC ∆，则称111A B C ∆与ABC ∆互为同相似；如果对应顶点沿边界按相反方向顺序环绕，那么称这两个三角形互为异相似，如图2，222A B C ∆∽ABC ∆，则称222A B C ∆与ABC ∆互为异相似.11BC 22图1 图2（1）在图3、图4和图5中，△ADE ∽△ABC ， △HXG ∽△HGF ，△OPQ ∽△OMN ，其中△ADE 与△ABC 互为 相似，△HXG 与△HGF 互为 相似，，△OPQ 与△OMN 互为 相似；BEA DCG XHFNQOPM图3 图4 图5（2）在锐角△ABC 中，∠A <∠B <∠C ，点P 为AC 边上一定点（不与点A ，C 重合），过这个定点P 画直线截△ABC ，使截得的一个三角形与△ABC 互为异相似．．．，符合条件的直线有_____条. 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23. 已知抛物线22y x x m =--与x 轴有两个不同的交点． （1）求m 的取值范围；（2）如果A 2(1,)n n -、B 2(3,)n n +是抛物线上的两个不同点，求n 的值和抛物线的表达式； （3） 如果反比例函数ky x=的图象与（2）中的抛物线在第一象限内的交点的横坐标为0x ， 且满足4<0x <5，请直接写出k 的取值范围. 24. 已知：如图，矩形ABCD 中，AB >AD .BC（1）以点A 为圆心，AB 为半径作弧，交DC 于点E ，且AE ＝AB ，联结AE ，BE ，请补全图形，并判断∠AEB 与∠CEB 的数量关系； （2）在（1）的条件下，设EC a BE =，BEb AB=，试用等式表示a 与b 间的数量关系并加以 证明.25．我们规定：线段外一点和这条线段两个端点连线所构成的角叫做这个点对这条线段的视角.如图1，对于线段AB 及线段AB 外一点C ，我们称∠ACB 为点C 对线段AB 的视角. 如图2，在平面直角坐标系xOy 中，已知点D （0，4），E （0，1）. （1）⊙P 为过D ，E 两点的圆， F 为⊙P 上异于点D ，E 的一点.①如果DE 为⊙P 的直径，那么点F 对线段DE 的视角∠DFE 为______度；②如果⊙P，那么点F 对线段DE 的视角∠DFE 为_________度；（2）点G 为x 轴正半轴上的一个动点，当点G 对线段DE 的视角∠DGE 最大时，求点G 的坐标.丰台区2014—2015学年度第一学期期末练习初三数学试题答案及评分参考一、选择题（本题共8个小题，每小题4分，共32分）DCBAx+3二、填空题（本题共6个小题，每小题4分，共24分）三、解答题（共20分，每小题5分） 15．解：原式＝21⨯ ------3分 2= ------5分16．解：（1）∵224+3(2)1y x x x =-=--．------2分（2）二次函数图象如右图，当13x x <>或时，0y >．------5分17．解：过点P 作PE ⊥CD 于点E ， ------1分∵四边形ABCD 是矩形，∴CD ＝AB ＝8，∠DAB ＝∠ADC ＝90°． ∵AP 是∠DAB 的角平分线，∴∠DAP ＝12∠DAB ＝45°． ∵DP ⊥AP ，∴∠APD ＝90°．∴∠ADP ＝45°．∴∠CDP ＝45°．在Rt △APD 中，AD ＝4，∴DP ＝AD ·sin ∠DAP ＝． ------2分在Rt △DEP中，∠DEP ＝90°，∴PE ＝DP ·sin ∠CDP ＝2，DE ＝DP ·cos ∠CDP ＝2． ∴CE ＝CD —DE ＝6． ------3分在Rt △DEP 中，∠CEP ＝90°，PC =分 ∴sin ∠DCP ＝PE PC =. ------5分 18．解：（1）∵点M （-2，m ）在正比例函数12y x =-的图象上，∴()1=212m -⨯-= ． ------1分 ∴M （-2，1）．------2分∵反比例函数ky x=的图象经过点M （-2，1），∴k ＝-2×1＝-2． ∴反比例函数的解析式为2y x=-． ------ 3分（2）点P 的坐标为（00， -------5分四、解答题（本题共22分，第19，22题每小题5分，第20， 21题每小题6分） 19．解：（1）(20)(20)(280)W y x x x =-=--+ ------- 1分221201600x x =-+-． ------- 3分PDCBAE（2） ()2230200W x =--+． ------4分∴当销售单价定为30元时，工厂每天获得的利润最大，最大利润是200元．------5分20．解：过点C 作CD ⊥AB ，交AB 延长线于点D ．由题意可知，------- 1分在△ABC 中，∠CAB ＝30°，∠ABC ＝90°＋30°＝120°， ∴∠ACB ＝30°，BC ＝AB ＝20 ． ------- 3分 在Rt △CBD 中，∠CBD ＝60°，∴CD ＝CB ·sin ∠CBD＝． ------- 5分∵12，∴这艘渔船继续向东航行追赶鱼群不会进入危险区． ------- 6分21．（1）证明：如图，联结OA ，OB ．∵PB 是⊙O 的切线，∴ ∠PBO ＝90°． ------- 1分 ∵ OA ＝OB ，BA ⊥PE 于点D ， ∴ ∠POA ＝∠POB ． ------- 2分 又∵ PO ＝PO ，∴ △PAO ≌△PBO ．∴ ∠PAO ＝∠PBO ＝90°． ∴PA ⊥OA ．∴ 直线PA 为⊙O 的切线． ------- 3分 （2）在Rt △ADE 中，∠ADE ＝90°，∵tan ∠AEP ＝AD DE ＝12，∴设AD ＝x ，DE ＝2x ．----- 4分 ∴OE ＝2x —3．在Rt △AOD 中，由勾股定理 ，得 (2x －3)2＝x 2＋32． ------5分 解得，x 1＝4，x 2＝0（不合题意，舍去）．∴ AD ＝4，OA ＝OE ＝2x －3＝5．即⊙O 的半径的长5． ------ 6分 22．解：（1）同，异，同． ------3分（2） 1或2． ------5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．解：（1）根据题意得，Δ440m =+>， ------1分解得 1.m >- ------2分（2）由题意知，抛物线对称轴为直线x ＝1，点A 和点B 是抛物线上的两个对称点，则()311(1)n n +-=--，解得0.n = ------3分 ∴点A （-1，0），∴22 3.y x x =-- ------5分（3）2060.k << ------7分24．解：（1）如图1， ------1分∠AEB ＝∠CEB ． ------2分 （2）b a 21=. ------3分 证明：如图2，作过点A 作AF ⊥BE 于点F ， ------4分∵ AB ＝AE ，∴1.2BF BE =∵∠AFB ＝∠C =90°，∠ABE ＝∠CEB ， ∴△ABF ∽△BEC . ------5分∴ABBFBE EC =． ------6分 ∴ABBEBE EC 21=， 即12a b =． ------7分25.解：（1）①90°； ------1分②60°或120°． ------3分（2）如图，当⊙P与x轴相切，G为切点时，∠DGE最大．------4分由题意知，点P在线段ED的垂直平分线上，∴PG＝2.5. ---5分过点P作PH⊥DE于点H，∴11.5.2EH DE==------6分∵PG⊥x轴，∴四边形PHOG为矩形.联结PE，在Rt△PEH中，PE＝PG＝2.5，EH＝1.5，∴PH＝2．所以点G（2，0）．------8分4* 七月的天山教学时间教学目标（一）知识与技能：认识8 个生字。

丰台区2014-2015学年度第一学期初三数学期末练习一、选择题（共8个小题，每小题4分，共32分） 1. 如果45(0)x y y =≠，那么下列比例式成立的是A ．45x y= B ．54x y = C ．45x y = D ．54x y= 2．二次函数2(3)1y x =--+的最大值为A ．1B ．－1C ．3D ．－33．⊙O 1和⊙O 2的半径分别为2cm 和3cm ，如果O 1O 2=5cm ，那么⊙O 1和⊙O 2的位置关系是 A ．内含 B ．内切 C ．相交 D ．外切4. 如图，A ，B ，C 是⊙O 上的三个点，如果∠BAC =30°，那么∠BOC 的度数是 A ．60○ B ．45○ C ．30○ D ．15○5. 如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB 于点D ，如果AC =3， AB =6， 那么AD 的值为 A.32 B. 92 C.D. 6．如图，扇形折扇完全打开后，如果张开的角度（∠BAC ）为120°，骨柄AB 的长为30cm ，扇面的宽度BD 的长为20cm ，那么这把折扇的扇面面积为 A ．2400πcm 3 B ．2500πcm 3 C ．2800πcm 3D ．2300πcm7. 如果点A ()11y -,，B ()22y ,，C ()33y ,都在反比例函数3y x=的图象上，那么 A ．123y y y << B ．132y y y << C ．213y y y << D ．321y y y << 8．如图，在平面直角坐标系中，点C 的坐标为（0，2），动点A 以每秒1个单位长的速度从点O 出发沿x 轴的正方向运动，M 是线段AC 的中点，将线段AM 以点A 为中心，沿顺时针方向旋转︒90得到线段AB ．联结CB ．设△ABC 的面积为S ，运动时间为t 秒，则下列图象中，能表示S 与t 的函数关系的图象大致是D CA ABCOBCAA BC D二、填空题（共6个小题，每小题4分，共24分）9．如图，在△ABC 中，点D ，E 分别在AB ，AC 边上，且 DE ∥BC ，如果 AD ∶DB =3∶2， EC =4，那么AE 的长等于 ．10．如图，AB 是⊙O 的弦，OC ⊥AB 于点C ，如果 AB=8，OC=3，那么⊙O 的半径等于 ．11．在某一时刻，测得一身高为1.80m 的人的影长为3m ，同时测得一根旗杆的影长为25m ，那么这根旗杆的高度为 m ．12．在正方形网格中，ABC △的位置如图所示，则tan B 的值为__________． 13．关于x 的二次函数22y x kx k =-+-的图象与y 轴的交点在x 轴的上方，请写出一．个．满足条件的二次函数的表达式： ． 14．在平面直角坐标系xOy 中，对于点(),P x y ，其中0≠y ，我们把点)11,1(y x P -+-'叫做点P 的衍生点.已知点1A 的衍生点为2A ，点2A 的衍生点为3A ，点3A 的衍生点为4A ，…，这样依次得到点1A ，2A ，3A ，…，n A ，…，如果点1A 的坐标为)1,2(-，那么点3A 的坐标为________；如果点1A 的坐标为()b a ,，且点2015A 在双曲线xy 1=上， 那么=+ba 11________． 三、解答题（本题共20分，每小题5分） 15．计算：2tan 45sin 60cos30︒+︒-︒. 16．已知二次函数y= x 2－4x ＋3.（1）把这个二次函数化成2()y a x h k =-+的形式； （2）画出这个二次函数的图象，并利用图象写出当x 为何值时，y>0．E A CBD17．如图，矩形ABCD 中，AP 平分∠DAB ，且AP ⊥DP 于点P ，联结CP ，如果AB ﹦8， AD ﹦4，求sin ∠DCP 的值.18．如图，正比例函数12y x =-的图象与反比例函数k y x =的图象分别交于M ，N 两点，已知点M （-2，m ）. （1）求反比例函数的表达式；（2）点P 为y 轴上的一点，当∠MPN 为直角时，直接写出点P 的坐标．四、解答题（本题共22分，第19，22题每小题5分，第20， 21题每小题6分）19．某工厂设计了一款产品，成本为每件20元．投放市场进行试销，经调查发现，该种产品每天的销售量y （件）与销售单价x （元）之间满足280y x =-+ （20≤x ≤40），设销售这种产品每天的利润为W （元）.（1）求销售这种产品每天的利润W （元）与销售单价x （元）之间的函数表达式； （2）当销售单价定为多少元时, 每天的利润最大？最大利润是多少元？20. 如图，一艘渔船正自西向东航行追赶鱼群，在A 处望见岛C 在船的北偏东60°方向，前进20海里到达B 处，此时望见岛C 在船的北偏东30°方向，以岛C 为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能. （参考数据:1.4 1.7≈≈）21．如图，PB 切O 于点B ，联结PO 并延长交O 于点E ，过点B 作BA ⊥PE 交O 于点A ，联结AP ，AE ． （1）求证：P A 是O 的切线；（2）如果OD ＝3，tan ∠AEP ＝12，求O 的半径．ABCD P22．对于两个相似三角形，如果对应顶点沿边界按相同方向顺序环绕，那么称这两个三角形互为同相似，如图1，111A B C ∆∽ABC ∆，则称111A B C ∆与ABC ∆互为同相似；如果对应顶点沿边界按相反方向顺序环绕，那么称这两个三角形互为异相似，如图2，222A B C ∆∽ABC ∆，则称222A B C ∆与ABC ∆互为异相似.11BC22图1 图2（1）在图3、图4和图5中，△ADE ∽△ABC ， △HXG ∽△HGF ，△OPQ ∽△OMN ，其中△ADE 与△ABC 互为 相似，△HXG 与△HGF 互为 相似，，△OPQ 与△OMN 互为 相似；BEA DCG XHFNQOPM图3 图4 图5（2）在锐角△ABC 中，∠A <∠B <∠C ，点P 为AC 边上一定点（不与点A ，C 重合），过这个定点P 画直线截△ABC ，使截得的一个三角形与△ABC 互为异相似．．．，符合条件的直线有_____条. 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23. 已知抛物线22y x x m =--与x 轴有两个不同的交点． （1）求m 的取值范围；（2）如果A 2(1,)n n -、B 2(3,)n n +是抛物线上的两个不同点，求n 的值和抛物线的表达式； （3） 如果反比例函数ky x=的图象与（2）中的抛物线在第一象限内的交点的横坐标为0x ， 且满足4<0x <5，请直接写出k 的取值范围. 24. 已知：如图，矩形ABCD 中，AB >AD .BC（1）以点A 为圆心，AB 为半径作弧，交DC 于点E ，且AE ＝AB ，联结AE ，BE ，请补全图形，并判断∠AEB 与∠CEB 的数量关系； （2）在（1）的条件下，设EC a BE =，BEb AB=，试用等式表示a 与b 间的数量关系并加以 证明.25．我们规定：线段外一点和这条线段两个端点连线所构成的角叫做这个点对这条线段的视角.如图1，对于线段AB 及线段AB 外一点C ，我们称∠ACB 为点C 对线段AB 的视角. 如图2，在平面直角坐标系xOy 中，已知点D （0，4），E （0，1）. （1）⊙P 为过D ，E 两点的圆， F 为⊙P 上异于点D ，E 的一点.①如果DE 为⊙P 的直径，那么点F 对线段DE 的视角∠DFE 为______度；②如果⊙P，那么点F 对线段DE 的视角∠DFE 为_________度；（2）点G 为x 轴正半轴上的一个动点，当点G 对线段DE 的视角∠DGE 最大时，求点G 的坐标.丰台区2014—2015学年度第一学期期末练习初三数学试题答案及评分参考一、选择题（本题共8个小题，每小题4分，共32分）DCBAx+3二、填空题（本题共6个小题，每小题4分，共24分）三、解答题（共20分，每小题5分） 15．解：原式＝21⨯+------3分 2= ------5分16．解：（1）∵224+3(2)1y x x x =-=--．------2分（2）二次函数图象如右图，当13x x <>或时，0y >．------5分17．解：过点P 作PE⊥CD 于点E ， ------1分∵四边形ABCD 是矩形，∴CD ＝AB ＝8，∠DAB ＝∠ADC ＝90°． ∵AP 是∠DAB 的角平分线，∴∠DAP ＝12∠DAB ＝45°． ∵DP ⊥AP ，∴∠APD ＝90°．∴∠ADP ＝45°．∴∠CDP ＝45°．在Rt △APD 中，AD ＝4，∴DP ＝AD ·sin ∠DAP ＝ ------2分在Rt △DEP中，∠DEP ＝90°，∴PE ＝DP ·sin ∠CDP ＝2，DE ＝DP ·cos ∠CDP ＝2． ∴CE ＝CD —DE ＝6． ------3分在Rt △DEP 中，∠CEP ＝90°，PC 分 ∴sin ∠DCP ＝PE PC =. ------5分 18．解：（1）∵点M （-2，m ）在正比例函数12y x =-的图象上，∴()1=212m -⨯-= ． ------1分 ∴M （-2，1）．------2分∵反比例函数ky x=的图象经过点M （-2，1），∴k ＝-2×1＝-2． ∴反比例函数的解析式为2y x=-． ------ 3分（2）点P 的坐标为（00， -------5分四、解答题（本题共22分，第19，22题每小题5分，第20， 21题每小题6分） 19．解：（1）(20)(20)(280)W y x x x =-=--+ ------- 1分221201600x x =-+-． ------- 3分PDCBAE（2） ()2230200W x =--+． ------4分∴当销售单价定为30元时，工厂每天获得的利润最大，最大利润是200元．------5分20．解：过点C 作CD ⊥AB ，交AB 延长线于点D ．由题意可知，------- 1分在△ABC 中，∠CAB ＝30°，∠ABC ＝90°＋30°＝120°， ∴∠ACB ＝30°，BC ＝AB ＝20 ． ------- 3分 在Rt △CBD 中，∠CBD ＝60°，∴CD ＝CB ·sin ∠CBD＝． ------- 5分∵12，∴这艘渔船继续向东航行追赶鱼群不会进入危险区． ------- 6分21．（1）证明：如图，联结OA ，OB ．∵PB 是⊙O 的切线，∴ ∠PBO ＝90°． ------- 1分 ∵ OA ＝OB ，BA ⊥PE 于点D ， ∴ ∠POA ＝∠POB ． ------- 2分 又∵ PO ＝PO ，∴ △PAO ≌△PBO ．∴ ∠PAO ＝∠PBO ＝90°． ∴PA ⊥OA ．∴ 直线PA 为⊙O 的切线． ------- 3分 （2）在Rt △ADE 中，∠ADE ＝90°，∵tan ∠AEP ＝AD DE ＝12，∴设AD ＝x ，DE ＝2x ．----- 4分 ∴OE ＝2x —3．在Rt △AOD 中，由勾股定理 ，得 (2x －3)2＝x 2＋32． ------5分 解得，x 1＝4，x 2＝0（不合题意，舍去）．∴ AD ＝4，OA ＝OE ＝2x －3＝5．即⊙O 的半径的长5． ------ 6分 22．解：（1）同，异，同． ------3分（2） 1或2． ------5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．解：（1）根据题意得，Δ440m =+>， ------1分解得 1.m >- ------2分（2）由题意知，抛物线对称轴为直线x ＝1，点A 和点B 是抛物线上的两个对称点，则()311(1)n n +-=--，解得0.n = ------3分 ∴点A （-1，0），∴22 3.y x x =-- ------5分（3）2060.k << ------7分24．解：（1）如图1， ------1分∠AEB ＝∠CEB ． ------2分 （2）b a 21=. ------3分 证明：如图2，作过点A 作AF ⊥BE 于点F ， ------4分∵ AB ＝AE ，∴1.2BF BE =∵∠AFB ＝∠C =90°，∠ABE ＝∠CEB ， ∴△ABF ∽△BEC . ------5分∴ABBFBE EC =． ------6分 ∴ABBEBE EC 21=， 即12a b =． ------7分25.解：（1）①90°； ------1分②60°或120°． ------3分（2）如图，当⊙P与x轴相切，G为切点时，∠DGE最大．------4分由题意知，点P在线段ED的垂直平分线上，∴PG＝2.5. ---5分过点P作PH⊥DE于点H，∴11.5.2EH DE==------6分∵PG⊥x轴，∴四边形PHOG为矩形.联结PE，在Rt△PEH中，PE＝PG＝2.5，EH＝1.5，∴PH＝2．所以点G（2，0）．------8分课时安排：2 课时笛的呢？（展示课件第四屏）2.思考：为什么爷爷的芦笛声会让强强感到一股浓浓的海水味呢？想象中的爷爷的芦笛声到底给了强强怎样的感受呢？3.带着美好的憧憬，齐读第一小节。

丰台区2014-2015学年度第一学期期末练习试卷答案初三英语2015年1月听力理解（共26分）一、听对话选图。

（共4小题，每小题1分）1. A2. B3. B4. C二、听对话或独白选择答案。

（共12小题，每小题1分）5. A6. C7. C8. B9. A 10. B 11. A 12. A 13. C 14. B15. A 16. B三、听对话记录关键信息。

（共5小题，每小题2分）评分标准：字母拼写错误不给分，大小写错误不扣分。

17. Kate 18. large 19. money 20. oranges 21. 84658723知识运用（共25分）四、单项填空（共13小题，每小题1分）22. C 23. A 24. C 25. B 26. D 27. A 28. B 29. C 30. A 31. D32. C 33. D 34. B五、完形填空（共12小题，每小题1分）35. B 36. A 37. C 38. D 39. B 40. A 41. B 42. A 43.C 44. B45. C 46. D阅读理解（共48分）六、阅读短文选择最佳选项。

（共15小题，每小题2分）47. B 48. D 49. B 50. B 51. A 52. D 53. C 54. A 55. A 56. B57. D 58. A 59. D 60. C 61. B七、阅读短文，根据短文内容，从短文后的五个选项中选出能填入空白处的最佳选项。

选项中有一项为多余选项。

（共4小题，每小题2分）62. C 63. E 64. A 65. D八、阅读短文回答问题。

（共5小题，每小题2分）评分标准：达意2分，大小写、拼写、语法错3个以上扣0.5分（扣在66题处）。

66. In 1971.67. She fell through the trees and landed on the ground (and had a bad cut on herarm).68. She stood up and started to look for help.69. Because she often had to walk or swim through dangerous water full ofcrocodiles. And when the animals attacked her, she fought them with a stick.70. Her knowledge about the forest (Her experience of living in the forest) andher spirit of being brave to fight against the difficulties.书面表达（共21分）九、完成句子（共3小题，每小题2分）评分标准：大小写错误不扣0.5分。

丰台区 2014-2015学年度第一学期期末练习初三语文2015.1一、基础·运用(共23分)(一)选择。

下面各题均有四个选项，其中只有一个符合题意。

选出答案后在答题卡上用铅笔把对应题目的选项字母涂黑涂满。

(共12分，每小题2分)1.“说好普通话，圆梦你我他”是第17届全国“推广普通话宣传周”的主题。

目前，推广普通话面临的主要问题是常见字的字音误读，请找出下列语句中加点字读音有误．．的一项A.那块白玉雕琢细致，晶莹剔．（tī）透，好似是女娲补天用的神石。

B.她已经有点懊悔了，不过因为性情太倔．（jué）强，就是不肯认错。

C.以零容忍态度惩．（chěng）治腐败，充分表明了中央反腐的坚定决心。

D．“校园阅读节”倡导师生共读好书，营造了浓厚的书香氛．（fēn）围。

2.下列词语中没有错别．．．．字．的一项是A.严峻震慑奔驰不屑置辩B.荒费戳穿蔑视众志成诚C.秘诀蒙蔽侧隐拔山涉水D.谴责干躁严厉完壁归赵3.下面这段文字中加点词语使用不恰当．．．的一项是北京地铁的建设速度和发展成就令人瞩目．．．．，仅2014年一年就新建了四段轨道交通线，新增通车里程总计62公里。

地铁沿线的社区居民和商家成为首当其冲．．．．的受益者，体验到出行的便捷。

北京地铁的建设以低耗环保为原则，一些线路因地制宜．．．．设置节能坡，使列车进出站时自然减速、加速，从而达到低碳减排的目的。

地铁站点的装饰设计也别具匠心．．．．，各有特色，充分体现出北京深厚的文化底蕴。

A.令人瞩目B.首当其冲C.因地制宜D.别具匠心4.2014年12月13日，是我国首个南京大屠杀死难者国家公祭日。

为铭记日本侵华战争给中国人民带来的深重灾难，激励同学们为国家的发展做出贡献，学校举办了“勿忘国耻，振兴中华”主题活动，同学们纷纷发表自己的看法。

下列发言中，语言不得体．．．的一句是A.学生甲：忘记历史就意味着背叛，前事不忘，后事之师，我们难道不该牢记历史吗？B.学生乙：我非常赞同设立国家公祭日，种瓜得瓜，种豆得豆，我们不能不忘记历史。

2015年北京市丰台区九年级（上）期末物理试卷一、单项选择题（下列各小题均有四个选项，其中只有一个选项符合题意．共28分，每小题2分）1．(★★★★)下列的单位中电流的单位是（）A．安培B．伏特C．欧姆D．瓦特2．(★★★★★)家庭电路中，电能表可直接测量（）A．电功B．电阻C．电流D．电压3．(★★★★★)小青把以下物品分成两类：①铅笔芯、铜线、盐水；②塑料尺、橡皮擦、油．他分成两类后的物品分别属于（）A．固体和液体B．导体和绝缘体C．金属和非金属D．晶体和非晶体4．(★★★★★)如图所示电器中，利用电流热效应的是（）A．电视机B．洗衣机C．电风扇D．电热水壶5．(★★★★)如图所示的事例中，符合安全用电原则的是（）A．用湿布擦正在发光的日光灯B．有人触电时应立即切断电源C．在高压线附近玩耍D．电线接触或靠近高温物体6．(★★★★★)欧姆定律表明（）A．导体电阻大小是由电流和电压决定的B．导体两端的电压跟电流成正比，跟电阻成反比C．导体中的电流，跟导体两端的电压成正比，跟导体的电阻成反比D．导体电阻大小跟电压成正比，跟电流成反比7．(★★★★)如图所示的几种家用电器正常工作时，消耗的电功率接近25W的是（）A．电饼铛B．台灯C．电饭锅D．电暖器8．(★★★★)下列关于磁场和磁感线的说法正确的是（）A．将小磁针放在地球周围某一空间，若小磁针静止时偏离南北方向，说明这个空间存在磁场B．在研究磁场强弱分布时，放不放铁屑磁感线都存在C．在磁场中某点放一小磁针，小磁针静止时，其S极的指向为该点磁场方向D．在磁体外部，磁感线总是从S极出发回到N极9．(★★★)如图所示是学习电磁现象过程中做过的几个实验，其中能反映电动机工作原理的是（）A．线圈转动，电流表指针偏转B．导体AB左右摆动，电流表指针偏转C．线圈通电，吸住铁块D．闭合开关，导体ab运动起来10．(★★★★)新交通法规于2013年1月1日施行，驾驶员不系安全带记3分，罚100元．汽车上设置了“安全带指示灯”，提醒驾驶员系好安全带．当安全带系好时，相当于闭合开关，指示灯不亮；安全带未系好时，相当于断开开关，指示灯发光．图中符合上述要求的电路图是（）A．B．C．D．11．(★★★)小明同学按照如图所示的电路进行实验探究，两个灯的规格相同．当开关闭合时，其中一个灯亮，一个灯不亮，电压表有示数．则故障原因可能是（）A．L1短路B．L1断路C．L2短路D．L2断路12．(★★★)关于标有“12V 24W”的白炽灯，下列说法正确的是（）A．该灯泡实际工作时的实际功率是24WB．该灯泡工作时，其两端电压是12VC．该灯泡正常发光时，其灯丝电阻是6ΩD．该灯泡工作时，通过其灯丝的电流是2A13．(★★★)给电炉通电后电炉丝热得发红，而与电炉丝相连的导线却不是很热，主要原因是（）A．通过电炉丝的电流比通过导线的电流大B．通过电炉丝的电流比通过导线的电流小C．导线的电阻比电炉丝的电阻小，相同时间内产生的热量少D．电炉丝的电阻比导线的电阻小，相同时间内产生的热量少14．(★★)如图所示的电路中，闭合开关，灯泡L 1、L 2均发光．将滑动变阻器的滑片P向b端滑动，则下列说法正确的是（）A．电流表示数变大B．电压表V1示数变大C．电压表V2示数变大D．灯泡L1、L2均变亮二、多项项选择题（下列各小题均有四个选项，其中符合题意的选项均多于一个．本题共12分，每小题3分．每小题全选对的得3分，选项对但不全的得2分，有错选的不得分）15．(★★)下列说法正确的是（）A．电荷的移动形成电流B．电荷定向移动的方向为电流的方向C．电源是在电路中提供电能的装置D．电压的作用是使导体中的自由电荷定向移动形成电流16．(★★★)定值电阻R 1和R 2的阻值之比为5：2，将它们以某种方式连接在电源两端，若定值电阻的阻值不随温度变化，下列说法中正确的是（）A．若电阻R1和R2串联，则它们的电功率之比为5：2B．若电阻R1和R2串联，则它们的电功率之比为2：5C．若电阻R1和R2并联，则它们的电功率之比为2：5D．若电阻R1和R2并联，则它们的电功率之比为5：217．(★)关于电与磁的有关知识，下列说法正确的是（）A．静电复印利用了异种电荷相互吸引的原理B．大头针被磁铁吸引的同时也被磁化成小磁体C．电动机工作时，主要的能量转化是将电能转化为机械能D．导体在磁场中做切割磁感线运动时，导体中一定产生感应电流18．(★)能源、材料和信息是现代社会发展的三大支柱．关于能源、材料和信息，下列说法错误的是（）A．核电站以核反应堆来代替火电站的锅炉B．“北斗”卫星导航系统是利用超声波进行定位和导航的C．卫星通信、移动通信是利用电磁波来传递信息的D．LED灯的核心元件发光二极管是由超导材料制成的三、填空题（共12分，每小题2分）19．(★★★★)大量实验表明，不高于 36 V的电压对人体来说一般是安全，称为安全电压．20．(★★★)家庭电路中各用电器的连接方式是并联，这种电路连接方式的好处是用电器可各自独立工作．21．(★★★)电阻R 1与R 2串联起来接在电压为6V且不变的电源两端．已知电阻R 1两端的电压是2V，电阻R 2=8Ω，则电阻R 1是 4 Ω．22．(★★★)某养鸡场新购进一台电热孵卵器，其电阻为110Ω不变，在额定电压下工作时通过孵卵器的电流是2A，则该孵卵器正常工作10s所产生的热量为 4400 J．23．(★★)2012年10月1日起，我国分阶段逐步禁止进口和销售白炽灯，并将在2018年淘汰白炽灯．节能灯比白炽灯节能60%-80%，且使用寿命长．一只标有“220V 60W”的白炽灯与“220V 15W的节能灯光效相同．则1kW•h的电能，可供“220V 15W”的节能灯正常发光 66.7 h．（结果保留一位小数）24．(★★)图1中，小灯泡L的额定电压为6V，将粗细均匀的电阻丝AB（其阻值不随温度变化）通过滑片P连入电源电压不变的电路．闭合开关S后，滑片P从A滑到最右端B的过程中，小灯泡L的I-U关系图象图2所示．当小灯泡消耗的功率为0.75W时，电阻丝AB连入电路的电阻阻值是 9 Ω．四、实验与探究题（共35分，25-27、30、33题各2分，28、29题各5分，31题3分，32、34、35题各4分）25．(★★★★)如图所示，电能表的示数是 8352.8 kW•h．26．(★★★★)通电螺线管中的电流方向如图所示，则通电螺线管左端的磁极是 N 极．27．(★★★★)如图所示，电阻箱的示数是 1358 Ω．28．(★★★)小岩利用“伏安法”测量定值电阻R的阻值．（1）请你添加一条导线，将图甲的实物图补充完整；（2）闭合开关S前，应把图甲中滑动变阻器的滑片P置于最右（选填“左”或“右”）端；（3）检查电路连接正确后，闭合开关S，滑动变阻器的滑片P滑动到某一位置时，电压表的示数如图乙，电流表的示数如图丙，则电压表的示数为 2.6 V，电流表的示数为 0.26 A，电阻R的阻值为 10Ω．29．(★★★)在探究影响导体电阻大小的因素时，小明作出了如下猜想：导体的电阻可能与①导体的长度有关；②导体的横截面积有关；③导体的材料有关．实验室提供发4根电阻丝，其规格、材料如表所示．（1）按照图1所示“探究影响导体电阻大小因素”的实验电路，在M、N之间分别接上不同的导体，则通过观察电流表示数来比较导体电阻的大小．（2）为了验证猜想①，应该选用编号 A、B 两根电阻丝分别接入电路进行实验；（3）分别将A和D两电阻丝接入图1电路中M、N两点间．电流表示数不相同．由此初步得到的结论是：当长度和横截面积相同时，导体电阻跟导体的材料有关．（4）要进一步研究导体材料的导电性能，就需要测量导体的电阻．小明的实验方案的操作过程均正确，两表的连接的示数如图2所示．但通过观察发现电流表指针偏转角度过小．这样会导致实验误差较大，解决这一问题的措施是电流表改用小量程．30．(★★★)小芳用导线及两个相同的铁钉自制了甲、乙两个电磁铁，通过如图所示的电路来探究“影响电磁铁磁性强弱的因素”．将两个电磁铁串联接入电路是为了探究电磁铁磁性强弱与电磁铁线圈匝数是否有关；当滑动变阻器的滑片依次向左滑动到几个不同位置时，电磁铁甲、乙吸引大头针的个数都会逐渐增多，说明电流越大，电磁铁磁性越强．（选填“大”或“小”）31．(★★★)某同学在探究电流与电压关系时，取一个定值电阻（其阻值不随温度变化）和一只小灯泡做为研究对象，并分别测量了多组通过它们的电流与其两端对应的电压，然后根据测得的数据在坐标纸上分别画出如图所示的甲、乙两条I-U图线．根据图线可知，乙（选填“甲”或“乙”）是定值电阻的I-U图线；这个定值电阻阻值的测量值是15 Ω；小灯泡的电阻随其两端电压的升高而变大（选填“大”或“小”）．32．(★★★)在探究“电流通过导体产生的热量与哪些因素有关”时，把两段电热丝A、B分别放在如图所示的甲、乙两个完全相同烧瓶并接入电路，在烧瓶中加入质量、初温均相同的煤油，再分别插入相同的温度计．闭合开关通电一定时间，可以通过观察温度计的示数变化，了解电热丝产生热量多少．已知A、B两电热丝的电阻分别为R A、R B，且R A＞R B．这个方案是用来探究电流和通电时间相同时，电流通过电热丝产生的热量与电阻大小的关系．请你应用所学知识推断实验过程中甲（选填“甲”或“乙”）烧瓶内煤油的温度升高得快．33．(★★)你有没有留神过，我们写字的时候，笔的上端都会小弧度的来回摇摆．有设计师就发现了这个细微的动作，根据物理学原理设计出一款“收音机钢笔”如图所示．希望给在繁重功课压力下的同学增添一些乐趣．这支钢笔内置有电池．当你书写的时候，笔端摇摇摆摆产生电流，就能给电池储存电量．钢笔上面的频道调节、音量调节、耳机插孔、音响等配置一个也不少．如此一来，枯燥的学习中你便可以听听音乐或是新闻，以缓和学习的压力．但是家长应该不会赞同这样的设计吧，说好的，乖乖做功课呢？请回答下列问题：（1）文中括号部分是基于哪个物理原理或规律制成的： C ．A欧姆定律 B焦耳定律 C电磁感应 D静电现象（2）给内置电池充电过程发生的能量转化情况是： A ．A．电能转化为化学能 B．化学能转化为电能 C．机械能转化为电能 D．电能转化为机械能．34．(★★)实验桌上有如下器材：电源、额定电压为2.5V的小灯泡、滑动变阻器、已调零的电流表和电压表、开关、导线若干．小明利用这些器材进行如下实验：（1）测量小灯泡的额定功率：实验电路如图1所示．①连接电路前，开关应断开，并将滑动变阻器的滑片调到阻值最大处；②连接好电路后，闭合开关，调节滑动变阻器，使电压表示数为2.5V ；此时电流表的示数如图乙所示，则小灯泡的功率P= 0.5 W．（2）小明调节滑动变阻器测出多组数据，绘出了小灯泡电压与电流关系的图象如图3所示，则图中有关小灯泡功率P的图象正确的是 B （选填“A”、“B”或“C”）．35．(★★★)实验桌上提供了下列符合要求的实验器材：电源一个（电源两端电压不变）、电阻两只R 1和R 2、电压表三个、滑动变阻器一个、开关一个、导线若干．在电阻R 1和R 2串联的这段电路中，R 1两端的电压为U 1，R 2两端的电压为U 2，R 1和R 2串联的这段电路两端的总电压为U．小英利用提供的实验器材设计了证明U=U 1+U 2的实验．请你完成下列题：（1）画出实验电路图．（2）在这个探究实验中，自变量是 U 1+U 2，因变量是 U ．（3）通过改变滑动变阻器滑片的位置改变接入电路中的电阻实现自变量的改变．（4）画出实验记录表．12五、计算题（共13分，36题6分，37题7分）36．(★★)为了防止酒驾事故的出现，酒精测试仪已被广泛应用．交警使用的某型号酒精测试仪的工作原理如图所示．电源电压恒为8V，传感器电阻R 2的电阻值随酒精气体浓度的增大而减小，当酒精气体的浓度为0时，R 2的电阻为60Ω．使用前要通过调零旋扭（即滑动变阻器R 1的滑片）对酒精测试仪进行调零，此时电压表的示数为6V．（1）电压表的示数为6V时，电流表的示数为多少？（2）电压表的示数为6V时，滑动变阻器R 1的电阻值为多少？（3）调零后，R 1的电阻保持不变．某驾驶员对着酒精测试仪吹气10s，若电流表的示数达到0.2A，表明驾驶员酒驾，此时电压表的示数为多少？37．(★★)如图1所示，小灯泡L上标有“6V 3W”字样，电流表量程为0～0.6A，电压表的量程为0～15V，变阻器R的最大电阻为100Ω．只闭合S 1，滑片置于a点时（a点未标出），变阻器连入电路中的电阻为R a，电流表示数为I a；只闭合S 2，移动滑片，变阻器两端电压与其连入电路的电阻关系如图2所示，当滑片置于b点时（b点未标出），电压表示数U b=8V，电流表示数为I b．已知R a：R 0=12：5，I a：I b=3：5．（灯丝电阻不随温度变化）求：（1）小灯泡的电阻；（2）只闭合S 2，滑片置于b点时的电流表示数I b和电源电压；（3）在电表的示数不超过量程，灯泡两端的电压不超过额定值的情况下，只闭合S 1时，变阻器连入电路的最小值和电路消耗的最小功率．。

丰台区2014-2015学年度第一学期期末练习初 三 英 语2015.1一、听对话，选择与对话内容相符的图片。

每段对话你将听两遍。

1．A ．B ．C ．2．A ．B ．C ．3.A ．B ．C ．4．A ．B ．C ．四、单项填空（共13分，每小题1分）22. This is my sister. ______ name is Jane.A. MyB. ItsC. HerD. His23. — When is the school sports meeting this term, Ann?— It’s ______ September 30th.A. onB. inC. ofD. at24. — ______ do you visit your grandparents, Mike?— Once a week.A. How soonB. How longC. How oftenD. How far25. Tom missed the school bus, ______ he was late for class.A. orB. soC. becauseD. but26. My friends and I ______ going to Happy Valley this weekend.A. beB. amC. isD. are 27. ______ from your office phoned you. Here is the message.A. SomebodyB. NobodyC. AnybodyD. Everybody28. My sister is good at sports. She can jump ______ than me.A. highB. higherC. highestD. the highest29. —Can you ride a motorbike, Peter? —No, I ____.A. needn’tB. mustn’tC. can’tD. shouldn’t30. My father ______ newspapers after dinner every day instead of watching TV.A. readsB. readC. will readD. is reading31. — Tell me something about the new library.— It ______ last year and it has a lot of books.A. buildsB. builtC. is builtD. was built32. We __________ in the same school since three years ago.A. studyB. were studyingC. have studiedD. will study33. My mother ______ dinner when I got home yesterday.A. cooksB. will cookC. is cookingD. was cooking34. — Could you tell me______? — Two hours ago.A. when you finish your workB. when you finished your workC. when do you finish your workD. when did you finish your work五、完形填空（共12分，每小题1分）I am sitting in front of the computer. I need to 35 what Iam going to do during the beautiful fall coming up in New York. Iam nervous because I think that my life at this moment depends onhow much I learnt in the intensive English during the last fourmonths.All my life I have been a fighter. When I was 5, I had a very 36 convulsion (痉挛) with high fever. I had the wrong medicine, which caused me to 37 my speech. The doctor told my mother that I would never be able to speak well again or to learn another language.My mother, 38 , was a fighter. She sent me to a lot of 39 . Finally, she sent me to Maria. She was a very nice person. She believed in me, and thought that I would speak again.The most amazing thing was that she taught me to read by mouth. I remember that I spent hours in front of the mirror and tried to 40 every word that I learnt. Imaginelosing your speech and having to learn everything again. For me it was like being 41 again. I learnt to talk and speak my native language: Spanish.Now, I am studying English in New York. I can’t believe that I am learning another 42 . But, I am! I am crying because studying here makes me feel 43 , and it makes me smile when I remember wh at the doctors said to my mom: “She will never be able to speak well again or to learn another language.”I’ll always remember the beautiful words my mom said to me when I was a child and learnt to speak again after all. “You did something that nobody 44 you could do. You made an impossible dream that people said you would never do come true. I will always be proud of you, and you will always be my 45 .”Now, I'm thinking about the beautiful fall leaf that is coming and what is going to happen to me. Just as every leaf is going to fall from the trees, I am going to take every 46 in my studies and in my life. I try to think about this and be a grateful person.35. A. draw B. write C. watch D. explain36. A. serious B. strange C. important D. interesting37. A. improve B. change C. lose D. end38. A. luckily B. maybe C. suddenly D. however39. A. doctors B. teachers C. reporters D. friends40. A. repeat B. find C. copy D. record41. A. saved B. born C. taught D. raised42. A. language B. method C. subject D. skill43. A. nervous B. sad C. happy D. comfortable44. A. imagined B. thought C. remembered D. expected45. A. future B. child C. hero D. honor46. A. chance B. exam C. class D. step阅读理解（共48分）六、阅读下列短文，根据短文内容，选择最佳选项。

丰台区 2014～ 2015 学年度第一学期期末练习初三化学2015． 01考1．本试卷共 8 页，共四道大题，35 个小题，满分80 分。

考试时间 100 分钟。

2．在答题卡上正确填写学校名称、姓名和考试号。

生3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

须4．本答题卡中的选择题用 2B 铅笔作答，其余试题用黑色笔迹署名笔作答。

知5.考试结束，将本试卷、答题卡和底稿纸一并交回。

相对原子质量： H-1 C-12 N-14 O-16 Na-23 Mg-24 P-31 Cl-35.5 Ti-48 Fe-56一、选择题（每题只有一个选项切合题意，共25 个小题，每题 1 分，共 25 分。

）1．空气成分中，体积分数约占78% 的是A．氮气 B ．氧气 C ．二氧化碳 D ．罕有气体21世纪教育网版权所有2．以下金属的活动性最弱的是A．银B．铜C．铝D．钠3．地壳中含量最多的金属元素是A．氧B．硅C．铝D．铁4．加碘食盐中的“碘”指的是A．元素 B ．原子 C ．分子 D ．单质 21 教育网5．决定元素种类的是A．中子数B．质子数C．核外电子数D．最外层电子数6．以下举措不利于保护环境的是．．．A．使用洁净能源B．使用无氟冰箱C．倡导使用私人车D．倡导垃圾分类7．以下物质中，属于纯净物的是A．自来水B．汽水C．液态氧气D．液态空气8．以下物质在氧气中焚烧，产生大批白烟的是A ．木炭B．甲烷C．蜡烛D．红磷2-1-c-n-j-y9．以下图标中，表示“严禁烟火”的是A B C D10．以下符号中，表示 2 个氢分子的是A．H2B． 2H2C． H2 O D． 2H11．以下实验操作中，正确的选项是A ．点燃酒精灯B ．倾倒液体C ．称量固体D ．加热液体12．以下物质性质的表述中，属于化学性质的是A. 干冰易升华B. 水通电能分解C. 五氧化二磷是白色固体D. 食盐易溶于水13. 在元素周期表中，镁元素的信息如右图所示，对图中信息解说不正确 ．．．的是A ．原子序数为 12B ．核外电子数为 24C ．元素符号为 MgD ．相对原子质量为24.3114．以下物质的化学式书写不正确 的是 [．．．A ．氯化钠 NaClB ．氧化铝 Al2 O3C ．碳酸钠 NaCOD ．氢氧化钾 KOH315．卫星运载火箭的动力由高氯酸铵（NH 4ClO 4）发生反响供给，化学方程式为：高温 N 2↑ +Cl 2↑ ↑ +4X 。

丰台区2014—2015学年度第一学期期末练习参考答案初三语文2015.1 一、基础·运用（共23分）（一）选择（每小题2分，共12分）（二）填空（共11分）7．默写（共6分）（1）白露未晞（1分）（2）绿杨阴里白沙堤（1分）（3）会当凌绝顶（1分）（4）了却君王天下事（1分）（5）沉舟侧畔千帆过，病树前头万木春(2分)评分说明：每空1分，出现错别字该空不得分。

8．名著阅读（共5分）参考答案：①三国演义（1分）；②赤壁之战（1分）；③黄盖（1分）；④一个愿打，一个愿挨（1分）；⑤诸葛亮草船借箭（或：舌战群儒、借东风、曹操横槊赋诗、曹操败走华容道、关羽义释曹操等）（1分）评分说明：第①－④空填写错误或有错别字不得分；第⑤空内容只要与“赤壁之战”相关即可。

二、文言文阅读（共12分）9.（3分）参考答案：（1）志：志趣，心意（1分）；（2）卒：通“猝”，突然（1分）；（3）于：向（1分）评分说明：意思对即可。

10.（4分）（1）参考译文：只要是伯牙心里所想的，钟子期必定能够领会。

评分说明：“所念”、“得之”为得分点，每点1分，共2分。

（2）参考译文：不是文王谁能做到这样呢！评分说明：“为此”、反问句式为得分点，每点1分，共2分。

11.（3分）参考答案：①心志（或“情怀”、“旨趣”、“理想”、“志向”均可）；②得其为人；③伯牙所念，钟子期必得之（或“曲每奏，钟子期辄穷其趣”、“志想象犹吾心也”、“吾于何逃声哉”均可）。

评分说明：每空1分，共3分。

12.（2分）B评分说明：选择正确即得2分。

三、现代文阅读（共35分）（一）《协管何大拿》（共15分）13．（4分）答案要点：①刚当上协管员，管理小商贩占道经营；②关切；③齐齐站立，一起鼓掌；④亲近（或“喜爱”“热爱”）。

评分说明：每空1分，共４分。

意思相近即可。

14.（4分）答案要点：①第③－⑥段具体交代了何大拿专业技术过硬，仅凭听力就能辨识机器故障（2分），②为后文写他准确识别肇事车辆做了铺垫。

2015-2016 学年北京市丰台区九年级（上）期末数学试卷一、选择题（本题共 30 分，每小题 3 分，）下列各题均有四个选项，其中只有 一个是符合题意的．1．（ 3 分 ） 如 图 ， 在 Rt △ ABC 中 ， ∠ C=90°， BC=3， AB=4， 则 cosB 的 值 是 （）B ．C ．D ．2．（3 分）如图，在△ABC 中，D 、E 分别是 AB 、AC 上的点，且 DE ∥BC ，若 AD ：DB=3：2，则 AE ：AC 等于（）A ．3：2B ．3：1C ．2：3D ．3：53．（3 分）⊙O 的半径为 3cm ，如果圆心 O 到直线 l 的距离为 d ，且 d=5cm ，那 么⊙O 和直线 l 的位置关系是（ ）A ．相交B ．相切C ．相离D ．不确定4．（3 分）抛物线 y=（x ﹣2）2+3 的顶点坐标是（ ）A ．（2，3）B ．（﹣2，3）C ．（2，﹣3）D ．（﹣2，﹣3）5．（3 分）如果△ABC ∽△DEF ，相似比为 2：1，且△DEF 的面积为 4，那么△ ABC 的面积为（ ） A ．1B ．4C ．8D ．166．（3 分）如图，四边形 ABCD 内接于⊙O ，∠BCD=120°，则∠BAD 的度数是 （）A ．A．30°B．60°C．80°D．120°7．（3 分）对于反比例函数，下列说法正确的是（）A．图象经过点（2，﹣1）B．图象位于第二、四象限C．当x＜0 时，y 随x 的增大而减小D．当x＞0 时，y 随x 的增大而增大8．（3分）如图，为了测量某棵树的高度，小明用长为2m 的竹竿作测量工具，移动竹竿，使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点．此时竹竿与这一点相距5m，与树相距10m，则树的高度为（）A．5m B．6m C．7m D．8m9．（3 分）小宏用直角三角板检查某些工件的弧形凹面是否是半圆，下列工件的弧形凹面一定是半圆的是（）A．B．C．D．10．（3 分）如图，点A、B、C、D、E、F 为⊙O 的六等分点，动点P 从圆心O出发，沿OE 弧EFFO 的路线做匀速运动，设运动的时间为t，∠BPD 的度数为y，则下列图象中表示y 与t 之间函数关系最恰当的是（）A．B．C．D．二、填空题（本题共22 分，第11 题3 分，第12 题3 分，第13-16 题，每小题3 分）11．（3 分）如果∠A 是锐角，且sinA=，那么∠A= °．12．（3 分）若2x=5y，则=．13．（4 分）圆心角是60°的扇形的半径为6，则这个扇形的面积是．14．（4 分）排水管的截面为如图所示的⊙O，半径为5m，如果圆心O 到水面的距离是3m，那么水面宽AB= m．15．（4 分）请写出一个符合以下三个条件的二次函数的解析式：．①过点（1，1）；②当x＞0 时，y 随x 的增大而减小；③当自变量的值为3 时，函数值小于0．16．（4 分）阅读下面材料：在数学课上，老师请同学思考如下问题：小亮的作法如下：老师说：“小亮的作法正确．” 请你回答：小亮的作图依据是．三、解答题（本题共24 分，每小题6 分）17．（6 分）计算：2cos30°﹣tan45°+sin60°．18．（6 分）函数y=mx3m﹣1+4x﹣5 是二次函数．（1）求m 的值；（2）写出这个二次函数图象的对称轴：；将解析式化成y=a（x﹣h）2+k 的形式为：．19．（6 分）如图，在△ABC 中，D 是AB 上一点，连接CD，且∠ACD=∠ABC．（1）求证：△ACD∽△ABC；（2）若AD=6，AB=10，求AC 的长．20．（6 分）如图，直线y1=x+2 与双曲线相交于A，B 两点其中点A 的纵坐标为3，点B 的纵坐标为﹣1．（1）求k 的值；（2）若y1＜y2，请你根据图象确定x 的取值范围．四、解答题（本题共28 分，每小题7 分）21．（7 分）如图，某小区在规划改造期间，欲拆除小区广场边的一根电线杆AB，已知距电线杆AB 水平距离14 米处是观景台，即BD=14 米，该观景台的坡面CD 的坡角∠CDF 的正切值为2，观景台的高CF 为2 米，在坡顶C 处测得电线杆顶端A 的仰角为30°，D、E 之间是宽2 米的人行道，如果以点B 为圆心，以AB 长为半径的圆形区域为危险区域．请你通过计算说明在拆除电线杆AB 时，人行道是否在危险区域内？（≈1.73）22．（7 分）如图，D 为⊙O 上一点，点C 在直径BA 的延长线上，∠CDA=∠CBD．（1）求证：CD 是⊙O 的切线；（2）过点B 作⊙O 的切线交CD 的延长线于点E，若AB=6，tan∠CDA=，依题意补全图形并求DE 的长．23．（7 分）某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A 处的正上方，如果每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球从发射出到第一次落在桌面的运行过程中，设乒乓球与端点 A 的水平距离为x（米），距桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：（1）如果y 是t 的函数，①如图，在平面直角坐标系tOy 中，描出了上表中y 与t 各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；②当t 为何值时，乒乓球达到最大高度？（2）如果y 是关于x 的二次函数，那么乒乓球第一次落在桌面时，与端点A 的水平距离是多少？24．（7 分）如图，⊙O 为△ABC 的外接圆，直线l 与⊙O 相切与点P，且l∥ BC．（1）请仅用无刻度的直尺，在⊙O 中画出一条弦，使这条弦将△ABC 分成面积相等的两部分（保留作图痕迹，不写作法）；（2）请写出证明△ABC 被所作弦分成的两部分面积相等的思路．五、解答题（本题共16 分，每小题8 分）25．（8 分）已知抛物线G1：y=ax2+bx+c 的顶点为（2，﹣3），且经过点（4，1）．（1）求抛物线G1 的解析式；（2）将抛物线G1 先向左平移3 个单位，再向下平移1 个单位后得到抛物线G2，且抛物线G2 与x 轴的负半轴相交于A 点，求A 点的坐标；（3）如果直线m 的解析式为，点B 是（2）中抛物线G2 上的一个点，且在对称轴右侧部分（含顶点）上运动，直线n 过点A 和点B．问：是否存在点B，使直线m、n、x 轴围成的三角形和直线m、n、y 轴围成的三角形相似？若存在，求出点B 的坐标；若不存在，请说明理由．26．（8 分）在平面直角坐标系xOy 中，定义点P（x，y）的变换点为P′（x+y，x﹣y）．（1）如图1，如果⊙O 的半径为，①请你判断M（2，0），N（﹣2，﹣1）两个点的变换点与⊙O 的位置关系；②若点P 在直线y=x+2 上，点P 的变换点P′在⊙O 的内，求点P 横坐标的取值范围．（2）如图2，如果⊙O 的半径为1，且P 的变换点P′在直线y=﹣2x+6 上，求点P 与⊙O 上任意一点距离的最小值．2015-2016 学年北京市丰台区九年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共 30 分，每小题 3 分，）下列各题均有四个选项，其中只有 一个是符合题意的．1．（ 3 分 ） 如 图 ， 在 Rt △ ABC 中 ， ∠ C=90°， BC=3， AB=4， 则 cosB 的 值 是 （）B ．C ．D ．【分析】根据在直角三角形中，锐角的余弦为邻边比斜边，可得答案． 【解答】解：cosB= =，故选：C ．【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦 为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2．（3 分）如图，在△ABC 中，D 、E 分别是 AB 、AC 上的点，且 DE ∥BC ，若 AD ：DB=3：2，则 AE ：AC 等于（）A ．3：2B ．3：1C ．2：3D ．3：5【分析】由 DE ∥CB ，根据平行线分线段成比例定理，可求得 AE 、AC 的比例关系．【解答】解：∵DE ∥BC ，AD ：DB=3：2， ∴AE ：EC=3：2， ∴AE ：AC=3：5．A ．故选：D．【点评】此题主要考查了平行线分线段成比例定理，根据已知得出AE 与EC 的关系是解题关键．3．（3 分）⊙O 的半径为3cm，如果圆心O 到直线l 的距离为d，且d=5cm，那么⊙O 和直线l 的位置关系是（）A．相交B．相切C．相离D．不确定【分析】根据直线和圆的位置关系的判定方法判断即可．【解答】解：∵⊙O 的半径为3cm，圆心O 到直线l 的距离为d=5cm，∴r＜d，∴直线l 与⊙O 的位置关系是相离，故选：C．【点评】本题考查了直线和圆的位置关系的应用，注意：已知⊙O 的半径为r，如果圆心O 到直线l 的距离是d，当d＞r 时，直线和圆相离，当d=r 时，直线和圆相切，当d＜r 时，直线和圆相交．4．（3 分）抛物线y=（x﹣2）2+3 的顶点坐标是（）A．（2，3）B．（﹣2，3）C．（2，﹣3）D．（﹣2，﹣3）【分析】已知解析式为顶点式，可直接根据顶点式的坐标特点，求顶点坐标，从而得出对称轴．【解答】解：y=（x﹣2）2+3 是抛物线的顶点式方程，根据顶点式的坐标特点可知，顶点坐标为（2，3）．故选：A．【点评】此题主要考查了二次函数的性质，关键是熟记：顶点式y=a（x﹣h）2+k，顶点坐标是（h，k），对称轴是x=h．5．（3 分）如果△ABC∽△DEF，相似比为2：1，且△DEF 的面积为4，那么△ABC 的面积为（）A．1 B．4 C．8 D．16【分析】根据相似三角形面积的比等于相似比的平方解答即可．【解答】解：∵△ABC∽△DEF，相似比为2：1，∴△ABC 和△DEF 的面积比为4：1，又△DEF 的面积为4，∴△ABC 的面积为16．故选：D．【点评】本题考查的是相似三角形的性质，掌握相似三角形面积的比等于相似比的平方是解题的关键．6．（3 分）如图，四边形ABCD 内接于⊙O，∠BCD=120°，则∠BAD 的度数是（）A．30°B．60°C．80°D．120°【分析】直接根据圆内接四边形的性质即可得出结论．【解答】解：∵四边形ABCD 内接于⊙O，∠BCD=120°，∴∠BAD=180°﹣120°=60°．故选：B．【点评】本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．7．（3 分）对于反比例函数，下列说法正确的是（）A．图象经过点（2，﹣1）B．图象位于第二、四象限C．当x＜0 时，y 随x 的增大而减小D．当x＞0 时，y 随x 的增大而增大【分析】根据反比例函数的性质即可直接作出判断．【解答】解：A、把x=2 代入y=得，y=1，则（2，﹣1）不在图象上，选项错误；B、图象位于第一、三象限，选项错误；C、当x＜0 时，y 随x 的增大而减小，选项正确；D、当x＞0 时，y 随x 的增大而减小，选项错误．故选：C．【点评】本题考查了反比例函数的性质：（1）反比例函数y=（k≠0）的图象是双曲线；（2）当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y 随x 的增大而减小；（3）当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y 随x 的增大而增大．8．（3分）如图，为了测量某棵树的高度，小明用长为2m 的竹竿作测量工具，移动竹竿，使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点．此时竹竿与这一点相距5m，与树相距10m，则树的高度为（）A．5m B．6m C．7m D．8m【分析】先判定△OAB 和△OCD 相似，再根据相似三角形对应边成比例列式求解即可．【解答】解：如图所示：∵AB⊥OD，CD⊥OD，∴AB∥CD，∴△OAB∽△OCD，∴，即，解得：CD=6（米）；即树的高度为6m；故选：B．【点评】本题考查了相似三角形的应用，判断出三角形相似并根据相似三角形对应边成比例得出比例式是解题的关键．9．（3 分）小宏用直角三角板检查某些工件的弧形凹面是否是半圆，下列工件的弧形凹面一定是半圆的是（）A．B．C．D．【分析】根据90°的圆周角所对的弧是半圆，从而得到答案．【解答】解：根据90°的圆周角所对的弧是半圆，显然A 正确，故选：A．【点评】本题考查了圆周角定理、圆周角的概念；理解圆周角的概念，掌握圆周角定理的推论，把数学知识运用到实际生活中去．10．（3 分）如图，点A、B、C、D、E、F 为⊙O 的六等分点，动点P 从圆心O 出发，沿OE 弧EFFO 的路线做匀速运动，设运动的时间为t，∠BPD 的度数为y，则下列图象中表示y 与t 之间函数关系最恰当的是（）A．B．C．D．【分析】利用点A、B、C、D、E、F 为⊙O 的六等分点可得到∠BOC=∠ COD=60°，所以P 在O 点时，∠BPD=120°，P 在弧EF 上时，∠BPD=∠BOD=60°，然后分类讨论：当点P 从O 点运动到E 点时，易得y 由120°逐渐减小到60°；当点P 在弧EF 上运动时，y=60°；当点P 从F 点运动到O 点时，易得y 由60°逐渐增大到120°，根据此特征可对四个选项进行判断．【解答】解：因为点A、B、C、D、E、F 为⊙O 的六等分点，所以∠BOC=∠COD=60°，当P 在O 点时，∠BPD=120°，当P 在弧EF 上时，∠BPD=∠BOD=60°，当点P 从O 点运动到E 点时，y 由120°逐渐减小到60°；当点P 在弧EF 上运动时，y 的值不变，为60°；当点P 从F 点运动到O 点时，y 由60°逐渐增大到120°．故选：C．【点评】本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．解决本题的关键是圆周角定理的应用．二、填空题（本题共22 分，第11 题3 分，第12 题3 分，第13-16 题，每小题3 分）11．（3 分）如果∠A 是锐角，且sinA=，那么∠A= 30 °．【分析】直接利用特殊角的三角函数值得出答案．【解答】解：∵∠A 是锐角，且sinA=，∴∠A=30°．故答案为：30．【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．12．（3 分）若2x=5y，则= ．【分析】根据内项之积等于外项之积即可求解．【解答】解：∵2x=5y，∴=．故答案为：．【点评】考查了比例的性质，是基础题型，比较简单．13．（4 分）圆心角是60°的扇形的半径为6，则这个扇形的面积是6π．【分析】根据扇形的面积公式S= 计算，即可得出结果．【解答】解：该扇形的面积S==6π．故答案为：6π．【点评】本题考查了扇形面积的计算，属于基础题．熟记公式是解题的关键．14．（4 分）排水管的截面为如图所示的⊙O，半径为5m，如果圆心O 到水面的距离是3m，那么水面宽AB= 8 m．【分析】过O 点作OC⊥AB，连接OB，由垂径定理可得出AB=2BC，在Rt△OBC 中利用勾股定理即可得出BC 的长，进而可得出AB 的长．【解答】解：过O 点作OC⊥AB，连接OB，如图所示：x 2+ ∴AB=2BC ，在 Rt △OBC 中，BC 2+OC 2=OB 2，∵OB=5m ，OC=3m ，∴BC= =4m ，∴AB=2BC=8m ．即水面宽 AB 为 8m ；故答案为：8．【点评】本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．15．（4 分）请写出一个符合以下三个条件的二次函数的解析式： y=﹣．①过点（1，1）；②当 x ＞0 时，y 随 x 的增大而减小；③当自变量的值为 3 时，函数值小于 0．【分析】设解析式为：y=ax 2+b ，根据该函数的增减性确定其与 x 轴交点的取值，然后代入已知点后即可求得其解析式．【解答】解：∵当 x ＜0 时，y 随 x 的增大而增大，∴设解析式为：y=ax 2+b ，∵函数过点（1，1），∴a +b=1…①，∵当自变量的值为 3 时，函数值小于 0．∴设当 x=2 时，y=0，∴4a +b=0…②， 由①②知可 a=﹣，b= ，∴函数的解析式为：y=﹣x2+ ．答案为y=﹣x2+．【点评】此题是一道开放性题，主要考查二次函数的基本性质，函数的增减性及用待定系数法来确定函数的解析式．16．（4 分）阅读下面材料：在数学课上，老师请同学思考如下问题：小亮的作法如下：老师说：“小亮的作法正确．” 请你回答：小亮的作图依据是垂径定理．【分析】利用垂径定理得出任意两弦的垂直平分线交点即可．【解答】解：根据小亮作图的过程得到：小亮的作图依据是垂径定理．故答案是：垂径定理．【点评】此题主要考查了复杂作图以及垂径定理，熟练利用垂径定理的性质是解题关键．三、解答题（本题共24 分，每小题6 分）17．（6 分）计算：2cos30°﹣tan45°+sin60°．【分析】根据特殊角三角函数值，可得实数的运算，根据实数的运算，可得答案．【解答】解：原式=2×﹣1+= ﹣1．【点评】本题考查了特殊角三角函数值，熟记特殊角三角函数知识解题关键．18．（6 分）函数y=mx3m﹣1+4x﹣5 是二次函数．（1）求m 的值；（2）写出这个二次函数图象的对称轴：直线x=2 ；将解析式化成y=a （x﹣h）2+k 的形式为：y=﹣（x﹣2）2﹣1 ．【分析】（1）直接利用二次函数的定义得出m 的值；（2）利用配方法求出二次函数顶点坐标与对称轴即可．【解答】解：（1）∵函数y=mx3m﹣1+4x﹣5 是二次函数，∴3m﹣1=2，解得：m=1；（2）由（1）得：y=x2+4x﹣5=（x+2）2﹣9故这个二次函数图象的对称轴为：直线x=﹣2；将解析式化成y=a（x﹣h）2+k 的形式为：y=（x+2）2﹣9．故答案为：（1）m=1；（2）直线x=﹣2；y=﹣（x+2）2﹣9．【点评】此题主要考查了二次函数的定义以及配方法求二次函数的顶点坐标与对称轴，正确掌握配方法求二次函数顶点坐标是解题关键．19．（6 分）如图，在△ABC 中，D 是AB 上一点，连接CD，且∠ACD=∠ABC．（1）求证：△ACD∽△ABC；（2）若AD=6，AB=10，求AC 的长．【分析】（1）根据相似三角形的判定得出即可；（2）根据相似得出比例式，代入求出即可．【解答】（1）证明：∵∠A=∠A，∠ACD=∠B，∴△ACD∽△ABC；（2）解：∵△ACD∽△ABC，∴=，∴AC2=AD×AB，∵AD=6，AB=10，∴AC=2 ．【点评】本题考查了相似三角形的性质和判定的应用，能求出△ACD∽△ABC 是解此题的关键．20．（6 分）如图，直线y1=x+2 与双曲线相交于A，B 两点其中点A 的纵坐标为3，点B 的纵坐标为﹣1．（1）求k 的值；（2）若y1＜y2，请你根据图象确定x 的取值范围．【分析】（1）将A，B 的纵坐标代入直线y1=x+2 求出横坐标，确定出A，B 的坐标，将A 坐标代入反比例函数的解析式即可求出k 的值；（2）根据图象即可得到结论．【解答】解：（1）把y=3 代入y1=x+2 得x=1，把y=﹣1 代入y1=x+2 得x=﹣3，∴A（1，3），B（﹣3，﹣1），把A（1，3）代入得k=3；（2）由图象知：当x＜﹣3，或0＜x＜1 时，y1＜y2，即若y1＜y2，x 的取值范围为：x＜﹣3，或0＜x＜1．【点评】此题考查了反比例函数与一次函数的交点问题，熟练掌握待定系数法是解本题的关键．四、解答题（本题共28 分，每小题7 分）21．（7 分）如图，某小区在规划改造期间，欲拆除小区广场边的一根电线杆AB，已知距电线杆AB 水平距离14 米处是观景台，即BD=14 米，该观景台的坡面CD 的坡角∠CDF 的正切值为2，观景台的高CF 为2 米，在坡顶C 处测得电线杆顶端A 的仰角为30°，D、E 之间是宽2 米的人行道，如果以点B 为圆心，以AB 长为半径的圆形区域为危险区域．请你通过计算说明在拆除电线杆AB 时，人行道是否在危险区域内？（≈1.73）【分析】根据已知条件得到DF=1 米，BG=2 米；得到BF=GC=15 米；在Rt△AGC 中，由tan30°=，得到AG=15×=5 ≈5×1.732=8.660 米；于是得到结论．【解答】解：由tan∠CDF==2，CF=2 米，∴DF=1 米，BG=2 米；∵BD=14 米，∴BF=GC=15 米；在Rt△AGC 中，由tan30°= ，∴AG=15×=5≈5×1.732=8.660 米；∴AB=8.660+2=10.66 米；而BE=BD﹣ED=12 米，∴BE＞AB；因此不需要封人行道．【点评】本题考查了解直角三角形﹣俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．22．（7 分）如图，D 为⊙O 上一点，点C 在直径BA 的延长线上，∠CDA=∠CBD．（1）求证：CD 是⊙O 的切线；（2）过点B 作⊙O 的切线交CD 的延长线于点E，若AB=6，tan∠CDA=，依题意补全图形并求DE 的长．【分析】（1）连OD，OE，根据圆周角定理得到∠ADO+∠1=90°，而∠CDA=∠CBD，∠CBD=∠1，于是∠CDA+∠ADO=90°；（2）根据切线的性质得到ED=EB，OE⊥BD，推出AD∥OE，∠OEB=∠ADC，即可解决问题；【解答】（1）证明：连OD，OE，如图1 所示，∵AB 为直径，∴∠ADB=90°，即∠ADO+∠BDO=90°，又∵∠CDA=∠CBD，而∠CBD=∠BDO，∴∠BDO=∠CDA，∴∠CDA+∠ADO=90°，即∠CDO=90°，∴CD⊥OD，∴CD 是⊙O 的切线；（2）解：如图2 所示，连接EO．∵EB 为⊙O 的切线，ED 为切线，∴∠OED=∠OEB，∵AD⊥BD，OE⊥BD，∴AD∥OE，∴∠ADC=∠OED=∠OEB，∴tan∠OEB= =，∵OB=3，∴BE= ．【点评】本题考查了切线的判定与性质、圆周角定理的推论、三角形相似的判定与性质、勾股定理；熟练掌握切线的判定与性质，由三角函数和证明三角形相似是解决问题（2）的关键．23．（7 分）某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A 处的正上方，如果每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球从发射出到第一次落在桌面的运行过程中，设乒乓球与端点A 的水平距离为x（米），距桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：（1）如果y 是t 的函数，①如图，在平面直角坐标系tOy 中，描出了上表中y 与t 各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；②当t 为何值时，乒乓球达到最大高度？（2）如果y 是关于x 的二次函数，那么乒乓球第一次落在桌面时，与端点A 的水平距离是多少？【分析】（1）①根据描出了上表中y 与t 各对对应值为坐标的点，画出该函数的图象即可；②利用网格中数据直接得出乒乓球达到最大高度时的时间；（2）首先求出函数解析式，进而求出乒乓球落在桌面时，与端点A 的水平距离．【解答】解：（1）①如图所示，②由表格中数据可得，t=0.4（秒），乒乓球达到最大高度；（2）由表格中数据，可设y=a（x﹣1）2+0.45，将（0，0.25）代入，可得：a=﹣，则y=﹣（x﹣1）2+0.45，当y=0 时，0=﹣（x﹣1）2+0.45，解得：x1=，x2=﹣（舍去），即乒乓球与端点A 的水平距离是m．【点评】此题主要考查了二次函数对应用以及根的判别式和一元二次方程的解法等知识，利用图表中数据得出函数解析式是解题关键．24．（7 分）如图，⊙O 为△ABC 的外接圆，直线l 与⊙O 相切与点P，且l∥ BC．（1）请仅用无刻度的直尺，在⊙O 中画出一条弦，使这条弦将△ABC 分成面积相等的两部分（保留作图痕迹，不写作法）；（2）请写出证明△ABC 被所作弦分成的两部分面积相等的思路．【分析】（1）连结PO 并延长交BC 于E，过点A、E 作弦AD 即可；（2）由于直线l 与⊙O 相切于点P，根据切线的性质得OP⊥l，而l∥BC，则PE ⊥BC，根据垂径定理得BE=CE，所以弦AE 将△ABC 分成面积相等的两部分．【解答】解：（1）如图所示：（2）∵直线l 与⊙O 相切与点P，∴OP⊥l，∵l∥BC，∴PE⊥BC，∴BE=CE，∴弦AE 将△ABC 分成面积相等的两部分．【点评】此题主要考查了复杂作图，以及切线的性质，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图．五、解答题（本题共16 分，每小题8 分）25．（8 分）已知抛物线G1：y=ax2+bx+c 的顶点为（2，﹣3），且经过点（4，1）．（1）求抛物线G1 的解析式；（2）将抛物线G1 先向左平移3 个单位，再向下平移1 个单位后得到抛物线G2，且抛物线G2 与x 轴的负半轴相交于A 点，求A 点的坐标；（3）如果直线m 的解析式为，点B 是（2）中抛物线G2 上的一个点，且在对称轴右侧部分（含顶点）上运动，直线n 过点A 和点B．问：是否存在点B，使直线m、n、x 轴围成的三角形和直线m、n、y 轴围成的三角形相似？若存在，求出点B 的坐标；若不存在，请说明理由．【分析】（1）先设为顶点式，再把顶点坐标和经过的点（4，1）代入即可解决，（2）根据平移规则直接写出抛物线G2 的解析式，令y=0，即可求出点A 的坐标，（3）分为交点咋x 轴上方，与下方进行分析，根据相似确定角的大小，进一步得到直线n 的斜率，求出与y 轴的交点坐标，由点A（﹣3，0），运用待定系数法，确定直线n 的解析式，联立抛物线G2，解方程组即可求解．【解答】解：由抛物线G1：y=ax2+bx+c 的顶点为（2，﹣3），且经过点（4，1），可设抛物线G1：y=a（x﹣2）2﹣3，把（4，1）代入得：1=4a﹣3，解得：a=1，所以抛物线G1：y=（x﹣2）2﹣3=x2﹣4x+1，（2）抛物线G1：y=（x﹣2）2﹣3 先向左平移3 个单位，再向下平移1 个单位后得到抛物线G2：y=（x+1）2﹣4，令y=0，得：0=（x+1）2﹣4，解得：x=﹣3，或x=1（舍去），所以点A（﹣3，0）．（3）直线m 与x 轴，y 轴的交点分别为F，E，当直线n 与G2 交点在x 轴上方时，直线n 与x 轴，y 轴的交点为A，D，与抛物线交点B，与直线m 交与点C，当直线n 与G2 交点在x 轴下方时，直线n1 与x 轴，y 轴的交点为A，H，与抛物线交点B1，与直线m 交与点L，当直线n 与G2 交点在x 轴上方时，如图1：由题意△CDE∽△CFA，此时有：∠CDE=∠CFA，直线m 的解析式为，当x=0 时，y=3，当y=0 时，x=﹣6，∴点E（0，3），点F（﹣6，0），∴OF=6，OE=3，∴tan∠CDE=tan∠CFA= ，∴=，∵OA=3，∴OD=6，点D（0，6），设直线n：y=mx+n，把D（0，6），点A（﹣3，0）代入得：，解得：，∴直线n：y=2x+6，联立直线n 和抛物线G2 得：，解得：x=3，或x=﹣3（舍去）此时y=12，所以：点B（3，12），当直线n 与G2 交点在x 轴下方时，如图2：由题意△HLE∽△FLA，此时有：∠ELH=∠FLA=90°，∠EHA=∠LFA，直线m 的解析式为，当x=0 时，y=3，当y=0 时，x=﹣6，∴点E（0，3），点F（﹣6，0），∴OF=6，OE=3，∴tan∠EHA=tan∠LFA= ，∴=，∵OA=3，∴OH=6，点H（0，﹣6），设直线n：y=mx+n，把D（0，﹣6），点A（﹣3，0）代入得：解得：，∴直线n：y=﹣2x﹣6，联立直线n 和抛物线G2 得：，解得：x=﹣1，或x=﹣3（舍去）此时y=﹣4，所以：点B1（﹣1，﹣4），综上所述：存在点B，使直线m、n、x 轴围成的三角形和直线m、n、y 轴围成的三角形相似，点B 的坐标为（3，12）和（﹣1，﹣4）．【点评】此题主要考查二次函数的综合问题，会运用待定系数法求函数解析式，会根据相似判断出相等的对应角，并会根据三角函数求出线段的值进一步表示点的坐标，是解题的关键．26．（8 分）在平面直角坐标系xOy 中，定义点P（x，y）的变换点为P′（x+y，x﹣y）．（1）如图1，如果⊙O 的半径为，①请你判断M（2，0），N（﹣2，﹣1）两个点的变换点与⊙O 的位置关系；②若点P 在直线y=x+2 上，点P 的变换点P′在⊙O 的内，求点P 横坐标的取值范围．（2）如图2，如果⊙O 的半径为1，且P 的变换点P′在直线y=﹣2x+6 上，求点P 与⊙O 上任意一点距离的最小值．【分析】（1）①根据新定义得到点M 的变换点M′的坐标为（2，2），于是根据勾股定理计算出OM′=2，则根据点与圆的位置关系的判定方法可判断点M 的变换点在⊙O 上；同样方法可判断点N（﹣2，﹣1）的变换点在⊙O 外②利用一次函数图象上点的坐标特征，设P 点坐标为（x，x+2），利用新定义得到P 点的变换点为P′的坐标为（2x+2，﹣2），则根据勾股定理计算出OP′=，然后利用点与圆的位置关系得到＜2 ，解不等式得﹣2＜x＜0；（2）设点P′的坐标为（x，﹣2x+6），P（m，n），根据新定义得到m+n=x，m﹣n=﹣2x+6，消去x 得3m+n=6，则n=﹣3m+6，于是得到P 点坐标为（m，﹣3m+6），则可判断点P 在直线y=﹣3x+6 上，设直线y=﹣3x+6 与x 轴相交于点A，与y 轴相交于点B，过O 点作OH⊥AB 于H，交⊙O 于C，如图2，易得A（2，0），B（0，6），利用勾股定理计算出AB=2，再利用面积法计算出OH= ，所以CH=﹣1，当点P 在H 点时，PC 为点P 与⊙O 上任意一点距离的最小值．【解答】解：（1）①M（2，0）的变换点M′的坐标为（2，2），则OM′= =2，所以点M（2，0）的变换点在⊙O 上；N（﹣2，﹣1）的变换点N′的坐标为（﹣3，﹣1），则ON′= =＞2，所以点N（﹣2，﹣1）的变换点在⊙O 外；②设P 点坐标为（x，x+2），则P 点的变换点为P′的坐标为（2x+2，﹣2），则OP′=，∵点P′在⊙O 的内，∴＜2，∴（2x+2）2＜4，即（x+1）2＜1，∴﹣1＜x+1＜1，解得﹣2＜x＜0，即点P 横坐标的取值范围为﹣2＜x＜0；（2）设点P′的坐标为（x，﹣2x+6），P（m，n），根据题意得m+n=x，m﹣n=﹣2x+6，∴3m+n=6，即n=﹣3m+6，∴P 点坐标为（m，﹣3m+6），∴点P 在直线y=﹣3x+6 上，设直线y=﹣3x+6 与x 轴相交于点A，与y 轴相交于点B，过O 点作OH⊥AB 于H，交⊙O 于C，如图2，则A（2，0），B（0，6），∴AB= =2，∵OH•AB= OA•OB，∴OH= = ，∴CH= ﹣1，即点P 与⊙O 上任意一点距离的最小值为﹣1．【点评】本题考查了圆的综合题：熟练掌握点与圆的位置关系和一次函数图象上点的坐标特征；会运用勾股定理定理和面积法计算线段的长；提高阅读理解能力．。