非线性振动特性分析及其应用研究

第１５卷第１期　２０１５年３月　南京工业职业技术学院学报　Ｊｏｕｒｎａｌ　ｏｆ　Ｎａｎｊｉｎｇ　Ｉｎｓｔｉｔｕｔｅ　ｏｆ　Ｉｎｄｕｓｔｒｙ　Ｔｅｃｈｎｏｌｏｇｙ　Ｖｏ１．１５，Ｎｏ．１　Ｍｉｌｌ＂．，２０１５　

油气悬架车辆振动非线性特性分析与仿真研究　

丁继斌　

（南京工业职业技术学院机械工程学院，江苏　南京２１００２３）　

摘要：建立了二自由度汽车油气悬架系统模型，分析了油气悬架和车身模型的非线性特性。运用ＡＭＥｓｉｍ仿真软　件，通过模型对不同的激振频率的时域和频谱响应分析，验证了油气悬架非线性振动模型的正确性。结果表明振动状　态不稳定是由于系统产生了接近激振频率分数或整数倍的频率分量，这些频率分量使得系统产生了亚谐波或超谐波　共振。　关键词：油气悬架；振动；非线性；车身；ＡＭＥｓｉｍ；仿真　中图分类号：Ｕ４６３．３３　文献标识码：Ａ　文章编号：１６７１—４６４４（２０１５）０１—０００１—０４　

作为车辆悬架的发展方向之一，油气悬架车辆　使用越来越广泛，国内外学者对其进行了深入研究，　

建立了油气悬架的数学模型，运用计算机仿真、虚拟　

样机等手段对油气悬架的各种特性进行了深入分　

析　，但目前大多只限于对油气悬架本身的研　究　。由于悬架的性能对操纵稳定性、乘坐舒适性　

有直接影响，由于目前对车辆平顺性、舒适性要求的　

越来越高，汽车整车振动特性的研究也越来越受到　

重视。因此，有必要对主要影响车辆平顺性、舒适性　

的悬架系统进行深入研究。　本文以汽车油气悬架车辆车身振动为研究对　

象，分析油气悬架的非线性特性对车身振动特性的　

影响，对油气悬架系统车辆的车身的幅频特性进行　研究，运用ＡＭＥｓｉｍ仿真软件，验证不同频率输入下　

油气悬架车身的振动的非线性特性。　

１油气悬架系统模型　

根据车辆振动情况做简化模型：只考虑垂直方　

向的振动，将汽车简化为二自由度油气悬架振动模　型（图１）。车身质量由弹簧和蓄能器控制的液压油　

缸支撑，根据牛顿定律，其相应的运动微分方　程为ＩＳ］：　

第４７卷第５期　２０１７年５月　雹焊娥　

Ｅｌｅｃｔｒｉｃ　Ｗｅｌｄｉｎｇ　Ｍａｃｈｉｎｅ　Ｖｏ１．４７　Ｎｏ．５　Ｍａｖ　２０ｌ７　

本文参考文献引用格式：余震．董浩明，徐桂芳，等．常规工况下塔机整体钢结构应力分析及其振动特性研究『Ｊ１＿电焊机，２０１７，４７（０５）：２２—２６，３ｌ　

常　鳙规整体钢　掬麈　橱　

余震－　。董浩明３。徐桂芳３，饶刚１，２　

（１．武汉科技大学冶金装备及其控制教育部重点实验室，湖北武汉４３００８ｌ；２．武汉科技　

大学机械传动与制造工程湖北省重点实验室，湖北武汉４３００８ｌ；３。武汉市特种设备监　

督检验所。湖北武汉４３００１９）　

摘要：塔式起重机是建筑施工中重要的施工设备，它在使用过程中的金属结构安全Ｊ陛能评估直接影响到使　

用安全，同时为了避免塔机结构在运行过程中产生共振现象，也有必要对塔机进行振动特Ｊ陆研究。以某塔　

式起重机为研究对象，根据常规典型工况进行有限元模型构建和应力分析，并完成整机的模态分析，得到　

塔机在常规工况下的应力状况与前六阶固有频率和振型，分析出塔机在工作过程中的关键检测位置，为塔　

机的优化设计提供理论支撑。研究结果对塔机的优化设计及安全使用具有重要的意义。　

关键词：有限元法；塔式起重机；模态；振动特性；应力分析　

中图分类号：ＴＨ２１３．３　文献标志码：Ａ　文章编号：１００ｌ一２３０３（２０１７）０５－００２２—０６　

ＤＯＩ：１０．７５１２／ｊ．ｉｓｓｎ．１００１—２３０３．２０１７．０５．０５　

Ｒｅｓｅａｒｃｈ　ｏｆ　ｓｔｒｅｓｓ　ａｎｄ　ｖｉｂｒａｔｉｏｎ　ｏｆ　ｔｈｅ　ｗｈｏｌｅ　ｓｔｅｅｌ　ｓｔｒｕｃｔｕｒｅ　ｆｏｒ　

ｔｏｗｅｒ　ｃｒａｎｅ　ｕｎｄｅｒ　ｎｏｒｍａｌ　ｌｏａｄｉｎｇ　

ＹＵ　Ｚｈｅｎ　，ＤＯＮＧ　Ｈａｏｍｉｎｇ：，ＸＵ　Ｇｕｉｆａｎｇ　，ＲＡＯ　Ｇａｎｇ　

（１．Ｋｅｙ　Ｌａｂｏｒａｔｏｒｙ　ｏｆ　Ｍｅｔａｌｌｕｒｇｉｃａｌ　Ｅｑｕｉｐｍｅｎｔ　ａｎｄ　Ｃｏｎｔｒｏｌ　Ｔｅｃｈｎｏｌｏｇｙ　ｏｆ　Ｍｉｎｉｓｔｒｙ．ｏｆ　Ｅｄｕｃａｔｉｏｎ．Ｗｕｈａｎ　Ｕｎｉｖｅｒｓｉｔｙ　

第３７卷第３期　２０１７年３月　隧道建设　

Ｔｕｎｎｅｌ　Ｃｏｎｓｔｒｕｃｔｉｏｎ　Ｖ０１．３７　Ｎｏ．３　Ｍａｒ．２０１７　

一种大尺度让压锚杆特性分析及其应用研究　

杨喻声　

（１．同济大学地下建巩ｋＡ＂与工程系，上海２０００９２；２．同济大学岩土及地下工程教育部重点实验室，上海２０００９２）　

摘要：随着众多深、大、长隧道的建设，软岩挤压性大变形问题日益突出。让压锚杆是一种治理大变形问题的有效手段。介绍大尺　

度让压锚杆的结构及支护过程，并采用ＡＮＳＹＳ软件验证大尺度让压锚杆弹性变形、滑动让压、杆体受拉３阶段的工作特性。采用　

基于Ｈｏｅｋ隧洞挤压预测经验公式的概率分析方法和ＡＢＡＱＵＳ软件分别对让压锚杆的让压力和让压量研究，结果表明：１）锚杆让　

压力存在下限值，岩体抗压强度越高，下限值越低；２）让压量增大到一定程度后，再增加相同的让压量，二次衬砌压力降幅减小。　

利用大尺度让压锚杆的受拉阶段，实现“边支边让，先柔后刚”，可有效控制围岩大变形，提高隧洞的长期稳定性。　

关键词：大尺度让压锚杆；软岩大变形；Ｈｏｅｋ经验公式；让压力；让压量　

ＤＯＩ：１０．３９７３／ｊ．ｉｓｓｎ．１６７２—７４１Ｘ．２０１７．０３．０１０　

中图分类号：Ｕ　４５５．７　２　文献标志码：Ａ　文章编号：１６７２—７４１Ｘ（２０１７）０３—０３２１—０９　

Ｓｔｕｄｙ　ｏｆ　Ｐｅｒｆｏｒｍａｎｃｅ　ａｎｄ　Ａｐｐｌｉｃａｔｉｏｎ　ｏｆ　Ｙｉｅｌｄｉｎｇ　Ａｎｃｈｏｒ　

Ｂｏｌｔ　ｗｉｔｈ　Ｌａｒｇｅ　Ａｌｌｏｗａｂｌｅ　Ｄｅｆｏｒｍａｔｉｏｎ　

ＹＡＮＧ　Ｙｕｓｈｅｎｇ　＇　

（１。Ｄｅｐａｒｔｍｅｎｔ　ｏｆ　Ｇｅｏｔｅｃｈｎｉｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ，Ｔｏｎｇｊｉ　Ｕｎｉｖｅｒｓｉｔｙ，Ｓｈａｎｇｈａｉ　２０００９２，Ｃｈｉｎａ；　

２．Ｋｅｙ　Ｌａｂｏｒａｔｏｒｙ　ｏｆ　Ｇｅｏｔｅｃｈｎｉｃａｌ　ａｎｄ　Ｕｎｄｅｒｇｒｏｕｎｄ　Ｅｎｇｉｎｅｅｒｉｎｇ（Ｔｏｎｇｆｉ　Ｕｎｉｖｅｒｓｉｔｙ）　

落叶灌木省沽油的特性分析及其应用价值研究

作者：金文豪

来源：《种子科技》 2017年第10期

摘 要：介绍了省沽油的生物学特性、生态习性，论述了省沽油的食用价值、油用价值、药用价值、观赏价值等可开发利用价值，并分析其开发利用前景，对省沽油资源的保护提出了科学合理的建议。

关键词：省沽油；价值；开发

近年来，随着我国经济的快速发展，人们生活水平有了较大的提高，对生活的品质也有了更高的追求。当前，山野菜以其营养丰富、富含各种氨基酸和微量元素、具有较高的药用价值、能治疗或者抑制各种疾病而深受城市居民的喜爱，已逐渐成为蔬菜产业中的热点[1,2]。省沽油是多年生落叶灌木，它的叶、枝、根、花、果都具有较高的营养和药用价值，特别是省沽油的嫩芽及花蕾含有丰富的蛋白质、矿质元素和多种营养成分，至少含有17种氨基酸，其中7种为人体必需的氨基酸，其蛋白质、镁、钠、铁、锰、锌含量较高[3]。因此，开发利用省沽油山野菜将会产生较大的经济效益和社会效益。

1 省沽油的特性

1.1 形态特征

省沽油为多年生植物，平均株高达162.5 cm，骨干地径为1.9 cm，茎光滑无绒毛，树皮浅紫红色或青棕色。小枝灰褐色，初被短毛，枝条形成一簇，丛生，多从基部生长，枝条密度大。叶片为单叶或奇数羽状复叶，对生，复叶叶柄基部腋芽芽孢明显突出，3片小叶卵圆形或披针形，边缘呈波纹状，叶缘有细小锯齿，小叶顶端尖锐，基部广楔形，中央小叶叶柄略长，两侧小叶叶柄稍短，复叶叶柄较长。花整齐而密集，为总状花序或圆锥花序，每个花序具有25～40个小花蕾。花瓣5个，子房2室，内有2～3颗种子，种子呈不规则圆形，种皮坚硬。

1.2 开花结实习性

省沽油每年3月上旬在两年生枝条上的潜伏芽开始萌动发芽，一般3月中旬至4月中上旬会生出花蕾，4—5月初开始开花，全株枝条的大多数嫩芽均可生出花序。省沽油花白中泛红，有芳香，因其花与种子跟珍珠很相似，因此，老百姓一般称之为“珍珠花”。5月中旬至6月中上旬开始结果，一般在每个花序上会生出4～6个膀胱状蒴果，两裂顶尖向外斜伸，幼果嫩绿色。一般6月下旬至7月初果实开始成熟，呈不规则椭圆形，成熟果实呈浅红色或紫红色。在11月上旬省沽油的叶子开始慢慢枯黄，到了冬天省沽油枝干处于休眠状态。

非线性时间序列分析的关键技术及其应用研究　

谢红梅俞卞章　

（西北工业大学电子工程系，西安７１００７２）　

Ｅ－ｍａｉｌ：Ｘｉｅｈｍ＠ｎｗｐｕ．ｅｄｕ．ｃｎ　

摘要非线性时间序列分析是近几年发展起来的一个崭新的研究领域，在物理、生物、地理、医学、经济等领域具有广　

泛的应用前景。文章介绍了时间序列分析的线性和非线性分析方法各自的特点，由于非线性时间序列分析是个比较新　

的领域，该文对非线性处理技术进行了初步探讨，阐述了其研究意义，分析了其关键技术、应用前景等。最后讨论了在这　

一新的研究领域中值得注意的几个问题。　

关键词　非线性系统混沌　时间序列分析　

文章编号１ｏ０２—８３３１一（２ｏ０２）１４一ｏ０７９—０３　文献标识码Ａ　中图分类号ＴＰ２７４　

Ｔｈｅ　Ｋｅｙ　Ｔｅｃｈｎｉｑｕｅｓ　ａｎｄ　Ａｐｐｌｉｃａｔｉｏｎ　ｏｆ　Ｎｏｎｌｉｎｅａｒ　Ｔｉｍｅ　Ｓｅｒｉｅｓ　

Ｘｉｅ　Ｈｏｎｇｍｅｉ　Ｙｕ　Ｂｉａｎｚｈａｎｇ　

（Ｎｏｒｔｈｗｅｓｔｅｒｎ　Ｐｏｌｙｔｅｃｈｎｉｃ　Ｕｎｉｖｅｒｓｉｔｙ。Ｘｉｒａｎ　７　１００７２）　

Ａｂｓｔｒａｃｔ：　Ａｓ　ａ　ｎｅｗｌｙ　ｄｅｖｅｌｏｐｅｄ　ｒｅｓｅａｒｃｈ　ｆｉｅｌｄ，ｎｏｎｌｉｎｅａｒ　ｔｉｍｅ　ｓｅｒｉｅｓ　ａｎａｌｙｓｉｓ　ｈａｓ　ａ　ｖａｓｔ　ａｐｐｌｉｃａｔｉｏｎ　ｉｎ　ｍａｔｈｅｍａｔｉｃｓ，　

ｐｈｙｓｉｃｓ　ａｎｄ　ｅｃｏｎｏｍｙ　ｐｒｏｂｌｅｍｓ．Ｉｎ　ｔｈｉｓ　ｐａｐｅｒ　ｔｈｅ　ａｕｔｈｏｒｓ　ｂｒｉｅｆｌｙ　ｄｉｓｃｕｓｓ　ｔｈｅ　ｌｉｎｅａｒ　ａｎｄ　ｎｏｎｌｉｎｅａｒ　ｔｉｍｅ　ｓｅｒｉｅｓ　ａｎａｌｙｓｉｓ　

ｔｅｃｈｎｉｑｕｅ　ｒｅｓｐｅｃｔｉｖｅｌｙ　ｂｙ　ａｎ　ｅｘａｍｐｌｅ．Ｓｉｎｃｅ　ｎｏｎｌｉｎｅａｒ　ｔｉｍｅ　ｓｅｒｉｅｓ　ａｎａｌｙｓｉｓ　ｉｓ　ａ　ｎｅｗ　ｆｉｅｌｄ，ｔｈｅ　ａｕｔｈｏｒｓ　ｇｉｖｅ　ｏｕｔ　ｉｔｓ　ｋｅｙ　

ｔｅｃｈｎｉｑｕｅｓ　ａｎｄ　ｆｕｔｕｒｅ　ａｐｐｌｉｃａｔｉｏｎｓ．Ｆｉｎａｌｌｙ，ｓｏｍｅ　ｏｆ　ｐｏｔｅｎｔｉａｌ　ｒｅｓｅａｒｃｈ　ｐｒｏｂｌｅｍｓ　ａｒｅ　ｄｉｓｃｕｓｓｅｄ．　

龙源期刊网

镍基耐蚀合金特性及其应用研究分析

作者：贾成涛

来源：《中国新技术新产品》2017年第01期

摘 要：镍基耐蚀合金属于一种高性能的耐蚀材料。针对防腐蚀问题，笔者主要总结了纯镍的性质和耐蚀特点，探究了镍基耐蚀合金与镍铬不锈钢及镍基高温合金之间的区别与联系，同时阐述了目前在工程中使用镍基耐蚀合金的种类及其应用现状，突出了高性能通用型镍铬钼合金的特征与实际情况。

关键词：镍基耐蚀合金；镍铬不锈钢；纯镍；镍基高温合金

中图分类号：TB37 文献标识码：A

1.腐蚀问题和抗腐蚀材料

腐蚀属于机械零部件3种主要失效方式（磨损、腐蚀、疲劳）中的一种。金属腐蚀指的是周围介质对金属材料的表面产生作用从而发生状态变化同时转变为新相或是别的物质，使得零件慢慢地受到损毁的一种现象。零件应用于各行各业的机械、设备之中，因此研究腐蚀问题意义重大，其直接牵涉到国民经济的每个领域，零部件的使用时间长短对于整个设备质量和使用寿命都有着至关重要的作用。据笔者查阅资料发现，腐蚀给合金材料造成的直接损失巨大，从而造成了极大的资源浪费和成本支出。目前，每年全世界因为腐蚀造成的金属报废总量达到了一亿吨以上，是每年金属产量的五分之一左右。同时，随着工业化的不断推进，世界各国的腐蚀问题都呈现严重上涨的趋势。美国的腐蚀消耗（材料消耗与腐蚀）1950年为45亿美元，到1975年已经上涨到了900亿美元，到1990年已经高达1800亿美元，和1950年相比已经翻了几十倍。对比美国，尽管中国的经济体量、基础建设都远远不如，但是中国因腐蚀所带来的经济损失每年也超过了300亿人民币。国际金属腐蚀会议每3年召开一次，同时地区性的国际会议也很活跃，全球各国关于腐蚀方面出版的正规学术刊物已经超过了40种。当前，怎样加强设备的可靠性并延长使用周期，减少材料的使用量，就成为世界各国的关注重点，所以腐蚀与防护科学受到各国的普遍重视，从而寻求对于腐蚀的有效控制，以加强设备的耐用度，延长设备寿命。此外，近些年来随着环境和生态逐渐恶化以及人们环保理念的不断提升，各国都开始注重可持续发展理念，以寻求保护人类生存的家园。从微观角度出发，环境保护包括水污染和大气污染的治理以及对固体废弃物的有效处理等，而污水、废水、垃圾等污染基本上都属于腐蚀性极强的介质，所以采取高性能的耐蚀材料，能够有效减少腐蚀物的产生、避免由于腐蚀破坏所导致的物质泄漏。因此，对于镍基耐蚀合金的研究与应用对于环境保护技术也有着重要意义。

第２９卷第６期　振动与冲击　ＪＯＵＲＮＡＬ　ＯＦ　ＶＩＢＲＡＴＩＯＮ　ＡＮＤ　ＳＨＯＣＫ　

谱相关技术及其在潜艇结构振动信号传递特性分析中的应用　

成玮　，张周锁　，何正嘉　，王衍学　，陈略　

（１．西安交通大学机械制造系统工程国家重点实验室，西安７１００４９；２．西安交通大学机械工程学院，西安７１００４９）　

摘　要：由于潜艇结构的复杂性，有限元方法和时域相关方法在分析结构振动信号传递特性时精度欠佳。针对上　述问题，提出了定量分析结构振动信号传递特性的谱相关技术，该技术通过结构两侧振动信号分析结构对振动信号组成　成分的影响，避免了有限元精确建模困难与振动信号通过复杂结构时波形失真较大的难题。将该技术应用于潜艇缩比模　型不同结构振动信号传递特性分析中，定量分析结果表明该技术能很好地分析不同结构的振动信号传递特性。　关键词：潜艇结构；振动信号；传递特性；谱相关技术；定量分析　中图分类号：ＴＨ１７；ＴＪ８　文献标识码：Ａ　

潜艇航行时辐射到水中的噪声对潜艇的隐蔽性构　

成严重威胁，直接影响到潜艇的作战性能甚至生死存　

亡。因此，噪声源识别以及振动噪声的传播途径分析　对于振动噪声控制具有重要意义¨　』。　

低速航行状态下，潜艇的机械噪声是辐射噪声的　主要来源　Ｊ。常用的噪声源识别方法主要有自适应噪　

声抵消法　Ｊ、盲源分离方法　、虚拟样本法　Ｊ、多输人　

多输出（ＭＩＭＯ）量化分析模型方法　等。这些方法分　

析了振动噪声的来源，但未对结构的振动传递特性进　

行定量分析。已有分析结果表明，复杂的壳体结构使　

得利用有限元分析方法　和时域相关分析方法在求　

解振动信号传递特性的计算精度很低。　

针对上述问题，本文提出了研究潜艇结构振动信　号传递特性的谱相关分析技术，谱相关分析技术综合　

考虑到了设备运行信息与结构传递特征信息在频谱上　的分布特性。即不同结构的传递特性是不同的，对于　

足够带宽的信号，经过结构传递后信号特定频段谱线　

将发生变化，通过谱相关分析定量分析结构两侧信号　

中国新技术新产品　

镍基耐蚀合金特性及其应用研究分析　

贾成涛　

（青岛新力通ｏｒ－，＿ｌｋ有限责任公司，山东青岛２６６７０６）　

摘要：镍基耐蚀合金属于一种高性能的耐蚀材料。针对防腐蚀问题，笔者主要总结了纯镍的性质和耐蚀特点，探　

究了镍基耐蚀合金与镍铬不锈钢及镍基高温合金之间的区别与联系，同时阐述了目前在工程中使用镍基耐蚀合金　

的种类及其应用现状，突出了高性能通用型镍铬钼合金的特征与实际情况。　

关键词：镍基耐蚀合金；镍铬不锈钢；纯镍；镍基高温合金　

中图分类号：ＴＢ３７　文献标识码：Ａ　

１．腐蚀问题和抗腐蚀材料　

腐蚀属于机械零部件３种主要失效方式（磨损、腐蚀、　

疲劳）中的一种。金属腐蚀指的是周围介质对金属材料的　表面产生作用从而发生状态变化同时转变为新相或是别的　

物质，使得零件慢慢地受到损毁的一种现象。零件应用于　

各行各业的机械、设备之中，因此研究腐蚀问题意义重　

大，其直接牵涉到国民经济的每个领域，零部件的使用时　

间长短对于整个设备质量和使用寿命都有着至关重要的作　

用。据笔者查阅资料发现，腐蚀给合金材料造成的直接损　

失巨大，从而造成了极大的资源浪费和成本支出。目前，　

每年全世界因为腐蚀造成的金属报废总量达到了一亿吨以　

上，是每年金属产量的五分之一左右。同时，随着工业　

化的不断推进，世界各国的腐蚀问题都呈现严重上涨的趋　

势。美国的腐蚀消耗（材料消耗与腐蚀）１９５０年为４５亿美　

元，到１９７５年已经上涨到了９００亿美元，到１９９０年已经高达　

１８００亿美元，和１９５０年相比已经翻了几十倍。对比美国，　

尽管中国的经济体量、基础建设都远远不如，但是中国因　

腐蚀所带来的经济损失每年也超过了３００亿人民币。国际金　属腐蚀会议每３年召开一次，同时地区性的国际会议也很活　

跃，全球各国关于腐蚀方面出版的正规学术刊物已经超过　了４Ｏ种。当前，怎样加强设备的可靠性并延长使用周期，　

减少材料的使用量，就成为世界各国的关注重点，所以腐　

摘要

摘要

水果在贮运过程中的损伤问题在当今引起越来越多的关注，减少损伤是现代农业技术的重要研究课题之一。针对果品在重复受载时出现软化并产生累积损伤的现象，本文以水蜜桃

为研究对象，通过准静态压缩试验确定其压缩破坏临界变形量后，在临界变形量范围内研究

其峰值力松弛特性。建立水蜜桃动态松弛特性的三单元力学模型，并结合试验数据进行模型

表征。

从果品实际运输环境出发，简要地分析了果品在运输中的受载特性，并综合农业物料中常见的损伤机理，指出果品在振动条件下的损伤模式为疲劳累积损伤。以水晶梨为例，通过

实验求出水晶梨的疲劳损伤常数和疲劳损伤阀值，为预测果品的机械损伤提供合理参数。

根据建立的三单元力学模型，以粘弹性理论为基础，求解出果品在稳态振动条件下的耗

能特性。基于模型间耗散能不变的原理，对果品的力学模型进行简化。对单自由度有阻尼系

统的频响特性和能耗特性分析后，结合实验确定了水晶梨的损伤系数，为水晶梨的损伤预测

提供依据。 实验采用了工Ｎｖ３０６虚拟仪器系统和ＤＡＳ尸模态分析软件，通过定频振动试验，对果品的

粘弹特性和损伤特性做了初步的阐述。根据振动系统的共振频率和峰值传递率测得水晶梨和

Ｂ型单瓦楞纸板的刚度系数与阻尼系数。并将果品与缓冲材料一起看成一个两自由度有阻尼

系统，通过对其频响特性的理论分析，提出了一套适合果品的防振包装设计以及合理选取缓

冲材料的方法。

本文采用果品在运输过程中累积耗散能来定义果品的疲劳累积损伤时，山于实验条件的限制，对果品的品种、大小、成熟度、形状等对模型的影响缺乏深入的研究。后期的工作应

增加模型的影响因子，更好地满足工程应用。

关键词：果品，流变模型，水蜜桃，水晶梨，振动，疲劳损伤，减损包装

Ａｂｓｌｒａｃｔ

Ａｂｓｔｒａｃｔ

ＴｈｅｄａｍａｇｅＰｒｏｂｌｅｍｏｆｆｒｕｉｔｉｓＰａｉｄｍｏｒｅａｎｄｍｏｒｅａｔｔｅｎｔｉｏｎｓｎｏｗａｄａｙｓｄｕｒｉｎｇｓｔｏｒｉｎｇａｎｄ

ｔｒａｎｓＰｏｒｔｉｎｇ．ＲｅｄｕｃｉｎｇｄａｍａｇｅｉｓｏｎｅｏｆｔｈｅｉｍＰｏｒｔａｎｔｓｕｂｊｅｃｔｓｆｏｒｒｅｓｅａｒｃｈ，ｗｈｉｃｈｉｓｔｈｅｍｏｄｅｒｎ

结晶器振动波形分析及其应用研究　５３　

文章编号：１００６—１３５５（２００７）０２—００５３—０２　

结晶器振动波形分析及其应用研究　

涂福泉　，陈奎生　，杨　波　，曹　铭　，付曙光　

（１．武汉科技大学机械自动化学院，武汉４３００８１；２．武汉钢铁（集团）公司矿业公司，武汉４３００８１）　

摘要：在连铸连轧生产过程中，结晶器振动方式对铸坯的质量起到关键作用。结合结晶器的工艺特性，首先　在理论上对正弦振动和非正弦振动两种方式的波形进行了分析比较，得出非正弦振动方式在结晶器振动过程更有　利于提高铸坯质量结论，然后通过一应用实例证明了理论分析的正确性与合理性。　关键词：振动与波；结晶器；正弦振动；非正弦振动　中图分类号：０４２２　文献标识码：Ａ　

Ｔｈｅ　Ａｎａｌｙｓｉｓ　ａｎｄ　Ａｐｐｌｉｃａｔｉｏｎ　ｏｆ　Ｏｓｃｉｌｌａｔｉｏｎ　Ｗａｖｅｆｏｒｍ　Ｍｏｌｄ　

Ｆｕ．ｑｕａｎ　，ＣＨＥＮ　Ｋｕｉ．ｓｈｅｎｇ　。ＹＡＮＧ　Ｂｏ。，ＣＡＯ　Ｍｉｎ　。ＦＵ　Ｓｈｕ．ｇｕａｎｇ　（１．Ｃｏｌｌｅｇｅ　ｏｆ　Ｍａｃｈｉｎｅｒｙ＆Ａｕｔｏｍａｔｉｏｎ，Ｗｕｈａｎ　Ｕｎｉｖｅｒｓｉｔｙ　ｏｆ　Ｓｃｉｅｎｃｅ　ａｎｄ　Ｔｅｃｈｎｏｌｏｇｙ，Ｗｕｈａｎ　４３００８　１，Ｃｈｉｎａ；　２．Ｃｏｍｐａｎｙ　ｏｆ　Ｉｒｏｎ　Ｍｉｎｅ，Ｗｕｈａｎ　Ｉｒｏｎ　ａｎｄ　ｓｔｅｅｌ　Ｃｏ．，Ｌｔｄ．，Ｗｕｈａｎ　４３００８１，Ｃｈｉｎａ）　

Ａｂｓｔｒａｃｔ：Ｔｈｅ　ｍｏｄｅ　ｏｆ　ｍｏｌｄ　Ｏｓｃｉｌｌａｔｉｏｎ　ｈａｓ　ａ　ｋｅｙ　ｅｆｆｅｃｔ　ｔｏ　ｔｈｅ　ｓｌａｂ　ｑｕａｌｉｔｙ　ｉｎ　ｔｈｅ　ｃｏｎｔｉｎｕｏｕｓ　ｃａｓｔ　ｐｒｏｃｅｓｓ．Ｉｎ　ｔｈｅ　ｐａｐｅｒ．ｔｈｅ　ｏｓｃｉｌｌａｔｉｏｎ　ｍｏｄｅｓ　ｂｅｔｗｅｅｎ　ｎｏｎｓｉｎｕｓｏｉｄａｌ　ｏｓｃｉｌｌａｔｉｏｎ　ａｎｄ　ｓｉｎｕｓｏｉｄａｌ　ｏｓｃｉｌｌａｔｉｏｎ　ｗｅｒｅ　ｃｏｍｐａｒｅｄ　ａｎｄ　ａｎａｌｙｚｅｄ　ｉｎ　ｔｈｅｏｒｙ．ａｎｄ　ｔｈｅ　ｃｏｎｃｌｕｓｉｏｎ　ｔｈａｔ　ｎｏｎｓｉｎｕｓｏｉｄａｌ　ｏｓｃｉｌｌａｔｉｏｎ　ｉＳ　ｂｅｔｔｅｒ　ｆｏｒ　ｔｈｅ　ｉｍｐｒｏｖｅｍｅｎｔ　ｏｆ　ｓｌａｂ　ｑｕａｌｉｔｙ．Ｏｎ　ｔｈｅ　ｂａｓｅ　ｏｆ　ｉｔ，ａｎ　ａｐｐｌｉｃａｔｉｏｎ　ｗａｓ　ｐｒｏｐｏｓｅｄ　ｔｏ　ｐｒｏｖｅ　ｔｈｅ　ｃｏｒｒｅｃｔｎｅｓｓ　ａｎｄ　ｐｒｏｐｅｒ　ｏｆ　ｔｈｅ　ａｎａｌｙｓｉｓ．　Ｋｅｙ　ｗｏｒｄｓ：ｖｉｂｒａｔｉｏｎ　ａｎｄ　ｗａｖｅ；ｍｏｌｄ；ｓｉｎｕｓｏｉｄａｌ　ｏｓｃｉｌｌａｔｉｏｎ；ｎｏｎｓｉｎｕｓｏｉｄａｌ　ｏｓｃｉｌｌａｔｉｏｎ　

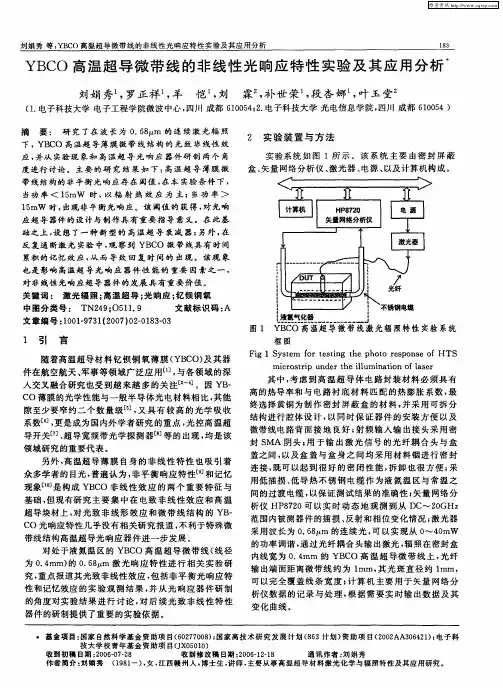
刘娟秀等：ＹＢＣＯ高温超导微带线的非线性光响应特性实验及其应用分析　１８３　

ＹＢＣＯ高温超导微带线的非线性光响应特性实验及其应用分析　

刘娟秀　，罗正祥　，羊　恺　，刘　霖　，补世荣　，段杏娜　，叶玉堂　

（１．电子科技大学电子工程学院微波中心，￣ｔ）ｌｌ成都６１００５４￣２．电子科技大学光电信息学院，四川成都６１００５４）　

摘　要：　研究了在波长为０．６８　ｍ的连续激光辐照　

下，ＹＢＣＯ高温超导薄膜微带线结构的光致非线性效　

应，并从实验现象和高温超导光响应器件研制两个角　

度进行讨论。主要的研究结果如下：高温超导薄膜微　

带线结构的非平衡光响应存在阈值，在本实验条件下，　

当功率＜１５ｍＷ时，以辐射热效应为主；当功率＞　

１５ｍＷ时，出现非平衡光响应。该闲值的获得，对光响　

应超导器件的设计与制作具有重要指导意义。在此基　

础之上，设想了一种新型的高温超导衰减器；另外，在　

反复通断激光实验中，观察到ＹＢＣＯ微带线具有时间　

累积的记忆效应，从而导致回复时间的出现。该现象　

也是影响高温超导光响应器件性能的重要因素之一，　对非线性光响应超导器件的发展具有重要价值。　

关键词：激光辐照；高温超导；光响应；钇钡铜氧　

中图分类号：ＴＮ２４９；Ｏ５１１．９　文献标识码：Ａ　

文章编号：１００１－９７３１（２００７）０２—０１８３－０３　

１　引　言　

随着高温超导材料钇钡铜氧薄膜（ＹＢＣＯ）及其器　

件在航空航天、军事等领域广泛应用［１］，与各领域的深　

入交叉融合研究也受到越来越多的关注［２　］。因ＹＢ－　

ＣＯ薄膜的光学性能与一般半导体光电材料相比，其能　

隙至少要窄约二个数量级［５］，又具有较高的光学吸收　

系数［６］，更是成为国内外学者研究的重点，光控高温超　

导开关［７］、超导宽频带光学探测器［８　等的出现，均是该　

领域研究的重要代表。　

另外，高温超导薄膜自身的非线性特性也吸引着　

众多学者的目光，普遍认为，非平衡响应特性［９　和记忆　

目录

1.两端铰支偏置转子的瞬态涡动分析 ........................................................................................... 1

1.1转子动力学模型三维立体示意图：（UG） ...................................................................... 3

1.2转子动力学模型二维平面示意图：（CAD） .................................................................... 4

1.3导出两端弹性支承刚性薄单盘偏置转子的瞬态涡动微分方程： ................................. 5

1.3.1偏置转子在平动坐标系中的动量矩 ...................................................................... 5

1.3.2在平动坐标系中外力矩的表达 .............................................................................. 7

1.3.3在平动坐标系中定点转动微分方程 ...................................................................... 7

1.4形心稳态自由涡动时的频率方程，画出涡动角速度与自转角速度的关系曲线图： . 8

1.4.1同步涡动的临界转速： .......................................................................................... 9

非线性动力学方法在机械系统分析中的应用

在现代机械工程领域，对机械系统的性能和行为进行准确分析是至关重要的。随着科学技术的不断发展，非线性动力学方法逐渐成为研究机械系统的有力工具。

机械系统中的非线性现象广泛存在。例如，零部件之间的接触和摩擦、材料的非线性特性、系统的几何非线性等。这些非线性因素使得机械系统的行为变得复杂且难以预测。传统的线性分析方法在处理这些复杂情况时往往存在局限性，无法准确描述系统的真实动态特性。

非线性动力学方法为解决这些问题提供了新的途径。其中，混沌理论是一个重要的分支。混沌现象是指在确定性系统中出现的貌似随机的不规则运动。在机械系统中，如某些旋转机械的运行过程中，可能会由于参数的变化而进入混沌状态，表现出不规则的振动和噪声。通过对混沌现象的研究，可以更好地理解机械系统的稳定性和可靠性。

分岔理论也是非线性动力学中的关键内容。分岔意味着系统在参数变化时，其动态行为发生质的改变。比如，在机械传动系统中，随着负载或转速的改变，系统可能会从稳定的运行状态分岔到不稳定状态，甚至出现故障。通过分析分岔点和分岔行为，可以提前预测系统的性能变化，为优化设计和故障诊断提供依据。

相空间重构是一种常用的非线性动力学分析技术。它将机械系统的时间序列数据转换到高维相空间中，从而揭示系统的隐藏结构和动态特性。通过观察相空间中的轨迹，可以判断系统是否处于稳定状态、是否存在周期运动或混沌行为。

在实际应用中，非线性动力学方法为机械系统的设计和优化带来了显著的优势。例如，在汽车悬架系统的设计中，考虑非线性因素可以更好地改善车辆的行驶舒适性和操控稳定性。通过对悬架系统的非线性动力学分析，可以优化弹簧和阻尼的参数，使车辆在不同路况下都能保持良好的性能。

在航空航天领域，发动机的叶片振动是一个关键问题。由于叶片的材料特性和复杂的工作环境，其振动呈现出明显的非线性特征。利用非线性动力学方法，可以准确地模拟叶片的振动行为，预测可能出现的故障模式，从而为发动机的设计和维护提供重要的参考。

非线性振动分析的切比雪夫谱元法

毛虎平;王伟能;续彦芳;张艳岗;董小瑞

【摘 要】为了进一步探索Chebyshev时间谱元法求解非线性的振动问题，从Bubnov-Galerkin方法出发，在第二类Chebyshev正交多项式极点处；用重心Lagrange插值来构造节点基函数及其特性，推导了非线性振动问题的伽辽金谱元离散方案，借助Newton-Raphson法求解非线性方程组。对于非线性单摆，还需要将二分法和重心Lagrange插值结合求解角频率。以Duffing型非线性振动和非线性单摆振动问题为例，验证了此方法具有现实可行和高精度的优点。%The

solution of nonlinear vibration problems was studied by using Chebyshev

spectral elements method. The node-based functions were constructed by

barycentric Lagrange interpolation at the pole points of Chebyshev

orthogo-nal polynomials of the 2nd kind which characteristics were

analyzed by using Bubnov-Galerkin method. Galerkin discretiza-tion

scheme for the nonlinear vibration problems was derived. Finally, the

nonlinear equations were solved by Newton-Raph-son method. For

nonlinear single pendulums, the angular frequencies were solved using the

列车-桥梁耦合系统非线性随机振动分析

晋智斌;李小珍;朱艳;强士中

【摘 要】在轨道不平顺激励下,列车过桥时发生车-桥耦合振动.由于轨道不平顺激励源是随机过程,而轮轨接触关系又是非线性的,因此,车-桥耦合振动属于非线性随机振动问题.用统计线性化方法分析车-桥非线性随机振动.轮轨接触几何关系用5个非线性函数描述,推导车-桥系统非线性振动方程.对车-桥非线性振动方程中的非线性函数进行统计线性化,得到时变的线性车-桥耦合振动方程.用虚拟激励法求解线性车-桥系统的随机响应,提出一种"显式"统计线性化方法,该法在每个时间步均无需作统计线性化迭代.最后,用Monte Carlo法验证了车-桥统计线性化随机振动分析方法具有较高的精度.算例表明,轮轨非线性接触对车辆和桥梁的随机响应影响很大,车-桥随机振动分析应合理考虑轮轨非线性接触.%Due to the excitation from

the rail irregularity,the vehicle-bridge coupling vibration occurs when rail-way trains traverse the bridge.Since the rail irregularity is random

process,and the wheel-rail contact is non-linear,the railway vehicle-bridge

dynamic interaction should be classified as the random vibration of

nonlinear systems.This study analyzed the nonlinear vehicle-bridge

random vibration using the statistical linearization method.This nonlinear

第35卷第3期2022年6月振动工程学报JournalofVibrationEngineeringVol.35No.3Jun.2022

弹性边界约束矩形板的振动特性分析：

理论、有限元和实验

柴玉阳，杜绍君，李凤明

（哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001）

摘要:提出一种有效的理论方法研究弹性边界约束矩形板的振动特性，并设计实验测试不同边界矩形板的固有频率。矩形板的弹性边界约束采用一系列的均布线性弹簧模拟，用特征正交多项式来表示矩形板的位移容许函数，并采用瑞利‐里茨法获得弹性边界约束矩形板的固有频率和固有振型。通过改变边界弹簧的刚度即可模拟矩形板不同的边界条件，提高计算效率。基于理论方法计算获得结构固有频率并和有限元及实验结果进行对比，验证所提理论方法的正确性。此外，通过实验测试的方法分析弹性‐简支、弹性‐固支等不同边界组合条件下矩形板的振动特性，分析调整不同边界弹簧刚度对矩形板振动特性的影响。

关键词:矩形板；弹性边界约束；特征正交多项式；瑞利‐里茨法；振动特性中图分类号:O327文献标志码:A文章编号:1004-4523（2022）03-0577-08DOI：10.16385/ki.issn.1004-4523.2022.03.007

引言

矩形板作为一种典型的结构，广泛应用于飞行

器、船舶、海洋平台以及高速列车等结构中。为了避

免矩形板结构在动态载荷作用下的不利振动影响，

开展矩形板结构振动特性的理论和实验研究具有重

要的实际意义。

目前很多学者针对矩形板的振动特性开展了大

量的理论研究。Leissa［1］系统地研究了多种简单边

界（自由、简支和固支）组合情况下矩形板的振动特

性，研究发现对于6种对边简支情况的矩形板可以

获得精确的固有振动特征方程。Liew等［2］利用瑞利‐

里茨法分析了不同边界条件下厚矩形板的振动特

性。基于微分求积法，Li等［3］研究了正交各向异性

板的非线性振动特性。Aksu等［4］基于有限差分法