常用材料弹性模量 E 和 泊松比 ν

更全面的常用材料的弹性模量与泊松比材料的弹性模量和泊松比是描述材料弹性性质的两个重要物理量。

弹性模量（Young's modulus）是材料在拉伸应力下单位面积变形的比例系数，常用符号为E，单位为帕斯卡（Pa）或兆帕（MPa）。

弹性模量越大，说明材料的刚度越大，抗拉性能越好，不易发生变形。

泊松比（Poisson's ratio）是材料沿一个方向受到拉伸应力时，在垂直于该方向的平面上产生的应变与沿该方向的应变的比值。

泊松比的取值范围在[-1，0.5]之间，常用符号为ν。

下面将介绍几种常见材料的弹性模量和泊松比。

1.钢材钢是一种常见的结构材料，具有优良的机械性能。

一般来说，钢材的弹性模量在200GPa至210GPa之间，泊松比在0.27至0.35之间。

2.铝合金铝合金是一种轻质、高强度的材料，在航空航天、汽车等行业中广泛应用。

铝合金的弹性模量大约在70GPa至80GPa之间，泊松比大约在0.3至0.33之间。

3.铜材铜是一种导电性能良好的金属材料，在电子、电器等领域中广泛应用。

铜材的弹性模量约为110GPa至130GPa，泊松比约为0.32至0.354.塑料塑料是一种可塑性材料，具有较低的强度和硬度。

一般来说，塑料的弹性模量在0.1GPa至4GPa之间，泊松比在0.3至0.5之间。

不同种类的塑料具有不同的弹性模量和泊松比。

5.混凝土混凝土是一种常见的建筑材料，具有一定的强度和耐久性。

混凝土的弹性模量约为30GPa至50GPa，泊松比约为0.15至0.36.陶瓷陶瓷是一种脆性材料，具有很高的硬度和耐高温性。

陶瓷的弹性模量大约在100GPa至400GPa之间，泊松比约为0.2至0.3。

CAE常用各种材料的弹性模量及泊松比弹性模量（Young's modulus）是描述材料在受力作用下发生弹性变形程度的物理量，常用符号为E。

弹性模量表示单位面积的材料受力后的伸长或收缩程度，单位为帕斯卡（Pa）或兆帕（MPa）。

泊松比（Poisson's ratio）表示材料在受力作用下的横向收缩与纵向伸长的比例，无单位。

本文将介绍一些常用材料的弹性模量和泊松比。

1.金属材料：-铜：弹性模量为110-130GPa，泊松比为0.33-0.36-铝：弹性模量为68-79GPa，泊松比为0.33-钢（低碳钢）：弹性模量为200-210GPa，泊松比为0.27-0.30。

-钛：弹性模量为95-120GPa，泊松比为0.292.玻璃材料：-常规玻璃：弹性模量为60-90GPa，泊松比为0.20-0.27-硼硅酸盐玻璃：弹性模量为80-90GPa，泊松比为0.20-0.25-石英玻璃：弹性模量为70-80GPa，泊松比为0.173.塑料材料：-聚乙烯：弹性模量为0.1-0.3GPa，泊松比为0.42-聚丙烯：弹性模量为0.8-1.6GPa，泊松比为0.40-0.45-聚氯乙烯（PVC）：弹性模量为2.5-3.0GPa，泊松比为0.42-0.45 -聚苯乙烯（PS）：弹性模量为3.0-3.5GPa，泊松比为0.35-0.384.复合材料：-碳纤维增强复合材料：弹性模量为200-400GPa，泊松比为0.2-0.3 -玻璃纤维增强复合材料：弹性模量为25-40GPa，泊松比为0.255.高分子材料：-聚苯乙烯（PS）：弹性模量为3.0-3.5GPa，泊松比为0.35-0.38-聚氨酯：弹性模量为15-30GPa，泊松比为0.30-0.45-聚酰胺（尼龙）：弹性模量为2.5-4.0GPa，泊松比为0.35-0.42需要注意的是，在实际工程中，材料的弹性模量和泊松比可能会因具体材料牌号、制造工艺和温度等因素而有所差异。

常用材料的弹性模量与泊松比弹性模量是一个材料对外加力产生形变的抵抗能力的度量，而泊松比是衡量材料在拉伸或压缩时横向收缩或扩展程度的因素。

不同材料的弹性模量和泊松比对于工程设计和材料选择非常重要。

以下是一些常用材料的弹性模量和泊松比的示例：1.金属材料：金属具有较高的弹性模量和较低的泊松比，使其具有很好的强度和刚性。

-钢：弹性模量通常在200-220GPa之间，泊松比约为0.3-铝：弹性模量约为70-80GPa，泊松比约为0.33-铜：弹性模量约为110-140GPa，泊松比约为0.342.陶瓷材料：陶瓷材料通常是非金属的，具有高硬度和低弹性模量。

-瓷砖：弹性模量约为60-80GPa，泊松比约为0.2至0.3-氧化铝陶瓷：弹性模量约为350-400GPa，泊松比约为0.2至0.25 -碳化硅陶瓷：弹性模量约为400-500GPa，泊松比约为0.1至0.2 3.高分子材料：高分子材料具有较低的弹性模量和较高的泊松比，使其具有较好的延展性和柔韧性。

-聚乙烯：弹性模量约为0.1-0.3GPa，泊松比约为0.42至0.49-聚丙烯：弹性模量约为0.8-2.0GPa，泊松比约为0.36至0.42-聚苯乙烯：弹性模量约为2.5-3.5GPa，泊松比约为0.39至0.43 4.合成材料：合成材料通常由不同类型的材料组合而成，其弹性模量和泊松比可能因组合方式而有所不同。

-碳纤维增强复合材料：弹性模量约为130-330GPa，泊松比约为0.2至0.4-玻璃纤维增强复合材料：弹性模量约为20-45GPa，泊松比约为0.2至0.3-聚合物混凝土：弹性模量约为20-40GPa，泊松比约为0.17至0.22需要注意的是，上述数值仅为常见材料的一般范围，具体数值可能会因材料的制备方法、组分和结构等因素而有所不同。

另外，弹性模量和泊松比还可以通过实验测量来获取，因此具体的数值可以在实验室中精确测定。

00EA A P==εσε弹性模量E 和泊松比µ的测定拉伸试验中得到的屈服极限бb 和强度极限бS ，反映了材料对力的作用的承受能力，而延伸率δ 或截面收缩率ψ，反映了材料缩性变行的能力，为了表示材料在弹性范围内抵抗变行的难易程度，在实际工程结构中，材料弹性模量E 的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变性量来判断其刚度的。

一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中 A 0为零件的横截面积。

由上式可见，要想提高零件的刚度 E A 0,亦即要减少零件的弹性变形，可选用高弹性模量的材料和适当加大承载的横截面积，刚度的重要性在于它决定了零件服役时稳定性，对细长杆件和薄壁构件尤为重要。

因此，构件的理论分析和设计计算来说，弹性模量E 是经常要用到的一个重要力学性能指标。

在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。

纵向应力与纵向应变的比例常数就是材料的弹性模量E ，也叫杨氏模量。

横向应变与纵向应变之比值称为泊松比µ，也叫横向变性系数，它是反映材料横向变形的弹性常数。

因此金属才料拉伸时弹性模量E 地测定是材料力学最主要最基本的一个实验，下面用电测法测定低碳钢弹性模量E 和泊松比µ。

(一） (一） 试验目的1．1．用电测方法测定低碳钢的弹性模量E 及泊松比µ；2．2．验证虎克定律；3．3．掌握电测方法的组桥原理与应用。

(二） (二） 试验原理1．测定材料弹性模量E 一般采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其荷载与变形关系为：0EA PL L ∆=∆ （1）若已知载荷ΔP 及试件尺寸，只要测得试件伸长ΔL 即可得出弹性模量E 。

（2）由于本试验采用电测法测量，其反映变形测试的数据为应变增量，即（3）所以（2）成为:)(A L PL E ∆∆∆=0)(L L ∆∆=∆ε（4）式中： ΔP ——载荷增量，kN ；A 0-----试件的横截面面积，cm为了验证力与变形的线性关心，采用增量法逐级加载，分别测量在相同载荷增量 ΔP 作用下试件所产生的应变增量Δε。

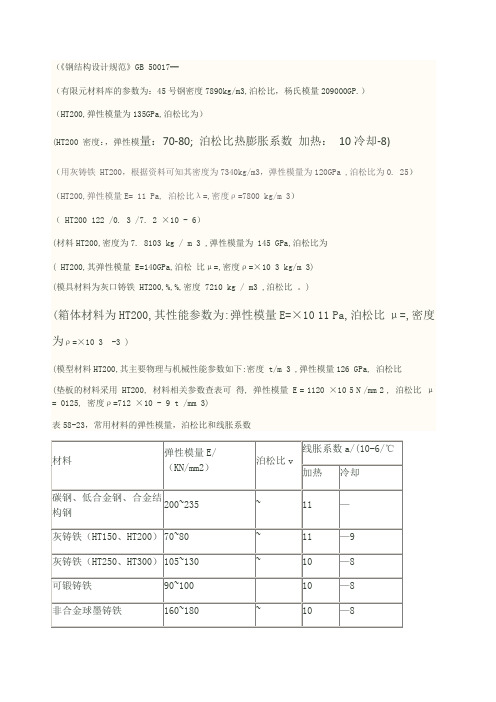
（《钢结构设计规范》GB 50017━（有限元材料库的参数为：45号钢密度7890kg/m3,泊松比，杨氏模量209000GP.）（HT200,弹性模量为135GPa,泊松比为）(HT200 密度：，弹性模量：70-80; 泊松比热膨胀系数加热：10冷却-8)（用灰铸铁 HT200，根据资料可知其密度为7340kg/m3，弹性模量为120GPa ,泊松比为0. 25）（HT200,弹性模量E= 11 Pa, 泊松比λ=,密度ρ=7800 kg/m 3）（ HT200 122 /0. 3 /7. 2 ×10 - 6）(材料HT200,密度为7. 8103 kg / m 3 ,弹性模量为 145 GPa,泊松比为( HT200,其弹性模量 E=140GPa,泊松比μ=,密度ρ=×10 3 kg/m 3)(模具材料为灰口铸铁 HT200,%,%,密度 7210 kg / m3 ,泊松比。

)(箱体材料为HT200,其性能参数为:弹性模量E=×10 11 Pa,泊松比μ=,密度为ρ=×10 3 -3 )(模型材料HT200,其主要物理与机械性能参数如下:密度 t/m 3 ,弹性模量126 GPa, 泊松比(垫板的材料采用 HT200, 材料相关参数查表可得, 弹性模量 E = 1120 ×10 5 N /mm 2 , 泊松比μ= 0125, 密度ρ=712 ×10 - 9 t /mm 3)表58-23，常用材料的弹性模量，泊松比和线胀系数常用弹性模量及泊松比━━━━━━━━━━━━━━━━━━名称弹性模量E 切变模量G 泊松比μ GPa GPa──────────────────镍铬钢 206合金钢 206碳钢 196-206 79铸钢 172-202球墨铸铁 140-154 73-76灰铸铁 113-157 44白口铸铁 113-157 44冷拔纯铜 127 48轧制磷青铜 113 41轧制纯铜 108 39轧制锰青铜 108 39铸铝青铜 103 41冷拔黄铜 89-97 34-36 轧制锌 82 31硬铝合金 70 26轧制铝 68 25-26铅 17 7玻璃 55 22混凝土 14-23纵纹木材横纹木材橡胶电木尼龙可锻铸铁 152拔制铝线 69大理石 55花岗石 48 石灰石 41 尼龙1010夹布酚醛塑料石棉酚醛塑料高压聚乙烯低压聚乙烯聚丙烯。

00EA A P==εσε弹性模量E 和泊松比µ的测定拉伸试验中得到的屈服极限бb 和强度极限бS ，反映了材料对力的作用的承受能力，而延伸率δ 或截面收缩率ψ，反映了材料缩性变行的能力，为了表示材料在弹性范围内抵抗变行的难易程度，在实际工程结构中，材料弹性模量E 的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变性量来判断其刚度的。

一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中 A 0为零件的横截面积。

由上式可见，要想提高零件的刚度E A 0,亦即要减少零件的弹性变形，可选用高弹性模量的材料和适当加大承载的横截面积，刚度的重要性在于它决定了零件服役时稳定性，对细长杆件和薄壁构件尤为重要。

因此，构件的理论分析和设计计算来说，弹性模量E 是经常要用到的一个重要力学性能指标。

在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。

纵向应力与纵向应变的比例常数就是材料的弹性模量E ，也叫杨氏模量。

横向应变与纵向应变之比值称为泊松比µ，也叫横向变性系数，它是反映材料横向变形的弹性常数。

因此金属才料拉伸时弹性模量E 地测定是材料力学最主要最基本的一个实验，下面用电测法测定低碳钢弹性模量E 和泊松比µ。

(一） (一） 试验目的1．1．用电测方法测定低碳钢的弹性模量E 及泊松比µ；2．2．验证虎克定律；3．3．掌握电测方法的组桥原理与应用。

(二） (二） 试验原理1．测定材料弹性模量E 一般采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其荷载与变形关系为：0EA PL L ∆=∆ （1）若已知载荷ΔP 及试件尺寸，只要测得试件伸长ΔL 即可得出弹性模量E 。

（2）由于本试验采用电测法测量，其反映变形测试的数据为应变增量，即（3） 所以（2）成为:)(A L PL E ∆∆∆=0)(L L ∆∆=∆ε（4） 式中： ΔP ——载荷增量，kN ；A 0-----试件的横截面面积，cm为了验证力与变形的线性关心，采用增量法逐级加载，分别测量在相同载荷增量 ΔP 作用下试件所产生的应变增量Δε。

常用材料的弹性模量、泊松比、密度材料名称弹性模量E 切变模量G 泊松比密度Gpa Gpa g/cm3(t/m3)灰铸铁118-126 44.3 0.3 7白口铸铁113-157 44 0.23-0.27 7.55球墨铸铁173 73-76 0.3 7.3延性铁120 7.7 0.31 7.3金屬鎂45 0.33 1.74鎂合金 1.74鈦(Ti) 105-120碳钢206 79.4 0.24-0.28 7.3-7.85铸钢202 0.3 7.8镍铬钢206 79.4 0.25-0.3 7.9合金钢206 79.4 0.25-0.3 7.9高速钢（含WW9%）8.3高速钢（含WW18%） 8.7轧制纯铜（紫铜）108 39.2 0.31-0.34 8.9冷拔纯铜（紫铜）127 48 8.9轧制磷锡青铜113 41.2 0.32-0.35 8.8冷拔黄铜89-97 34.3-36.3 0.32-0.42 8.4-8.85铸造黄铜8.62轧制锰青铜108 39.2 0.35 8.8铸锡青铜103 0.3 8.7-8.9铸铝青铜103 11.1 0.3工业用铝、铝镍合金 2.7可铸铝合金 2.7轧制铝68 25.5-26.5 0.32-0.36 2.7拔制铝线69 2.7硬铝合金70 26.5 0.3 2.7轧制锌82 31.4 0.27 7.1铅16 6.8 0.42 11.37鎢(W) 400-410 7.29碳化鎢（WC）450-650镍8.9金19.32银10.5锡7.29汞13.55碳化硅（SiC）450 3.1硅铜片7.55-7.8锡基轴承合金7.34-7.75铅基轴承合金9.33-10.67硬质合金（钨钴）14.4-14.9硬质合金（钨钴钛）9.5-12.4鑽石1,050-1,200玻璃55 1.96 0.25有机玻璃（PMMA） 2.35-29.42 1.18-1.19橡胶0.0078 2.9 0.47胶木板、纤维板 1.3-1.4电木 1.96-2.94 0.69-2.06 0.35-0.38 1.2夹布酚醛塑料 3.92-8.83 13-1.45赛璐珞 1.71-1.89 0.69-0.98 0.4 1.4材料名称弹性模量E 切变模量G 泊松比密度Gpa Gpa g/cm3(t/m3)ABS 0.2 0.3189 0.394ABS、PC合金 2.41 0.862 0.3897PC高密度 2.32 0.829 0.3902聚丙烯PP 1.5-2PP共聚物0.896 0.3158 0.4103尼龙1010 1.07 0.34-0.35 1.04-1.06尼龙66 8.3 3.2 0.28 1.14-1.15PA6 2.32 0.97 0.34 1.13PE高密度 1.07 0.377 0.4101PE低/中密度0.172 0.0594 0.439低压聚乙烯PE 0.54-0.75高压聚乙烯PE 0.147-0.245硬聚氯乙烯（PVC） 3.14-3.92 1.35-1.40聚苯乙烯0.91聚四氯乙烯 1.14-1.42丙烯酸（中耐冲力） 2.4 0.89 0.35PBT 1.93 0.69 0.3902POM已缩醛共聚物 2.6 0.09328 0.38569P/S中高流量2.28 0.8173 0.387PVC0.007塑化0.006 0.002 0.47PVC僵化 2.41 0.866 0.3825聚对苯二甲酸乙二酯PET 2-2.5 1.38聚苯乙烯PS 3-3.5碳纤维强化塑料（单向颗粒表面）150混凝土13.73-39.2 4.9-15.69 0.1-0.18 1.8-2.45---------------------作者：无穷山色来源：CSDN原文：https:///dxuehui/article/details/52497907 版权声明：本文为博主原创文章，转载请附上博文链接！。

00EA A P==εσε弹性模量E 和泊松比µ的测定拉伸试验中得到的屈服极限бb 和强度极限бS ，反映了材料对力的作用的承受能力，而延伸率δ 或截面收缩率ψ，反映了材料缩性变行的能力，为了表示材料在弹性范围内抵抗变行的难易程度，在实际工程结构中，材料弹性模量E 的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变性量来判断其刚度的。

一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中 A 0为零件的横截面积。

由上式可见，要想提高零件的刚度E A 0,亦即要减少零件的弹性变形，可选用高弹性模量的材料和适当加大承载的横截面积，刚度的重要性在于它决定了零件服役时稳定性，对细长杆件和薄壁构件尤为重要。

因此，构件的理论分析和设计计算来说，弹性模量E 是经常要用到的一个重要力学性能指标。

在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。

纵向应力与纵向应变的比例常数就是材料的弹性模量E ，也叫杨氏模量。

横向应变与纵向应变之比值称为泊松比µ，也叫横向变性系数，它是反映材料横向变形的弹性常数。

因此金属才料拉伸时弹性模量E 地测定是材料力学最主要最基本的一个实验，下面用电测法测定低碳钢弹性模量E 和泊松比µ。

(一） (一） 试验目的1．1．用电测方法测定低碳钢的弹性模量E 及泊松比µ；2．2．验证虎克定律；3．3．掌握电测方法的组桥原理与应用。

(二） (二） 试验原理1．测定材料弹性模量E 一般采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其荷载与变形关系为：0EA PL L ∆=∆ （1）若已知载荷ΔP 及试件尺寸，只要测得试件伸长ΔL 即可得出弹性模量E 。

（2）由于本试验采用电测法测量，其反映变形测试的数据为应变增量，即（3） 所以（2）成为:)(A L PL E ∆∆∆=0)(L L ∆∆=∆ε（4） 式中： ΔP ——载荷增量，kN ；A 0-----试件的横截面面积，cm为了验证力与变形的线性关心，采用增量法逐级加载，分别测量在相同载荷增量 ΔP 作用下试件所产生的应变增量Δε。

常用材料的弹性模量与泊松比弹性模量（Young's modulus）和泊松比（Poisson's ratio）是材料力学性质的重要参数，用于描述材料的弹性行为和变形特性。

弹性模量是衡量材料抵抗形变的刚度的物理量。

它表示单位面积内的应力（力与单位面积的比值）与应变（形变与初始尺寸的比值）之间的比例关系。

弹性模量的单位为帕斯卡（Pa）或兆帕（MPa）。

不同材料的弹性模量差异很大。

下面是一些常见材料的弹性模量范围：-铁：200-211GPa-钢：200-210GPa-铝：68.9GPa-铜：110-128GPa-钛：116GPa-水泥：14-40GPa-玻璃：65-85GPa泊松比是描述材料体积在受力同时沿一个轴向收缩而沿另一个轴向膨胀的能力的无量纲物理量。

一般来说，泊松比的值在0到0.5之间。

常见材料的泊松比一般在以下范围内：-铁：0.28-0.33-钢：0.27-0.30-铝：0.33-0.34-铜：0.33-钛：0.34-0.37-水泥：大于0.05小于0.3-玻璃：0.2-0.3需要注意的是，这些数值是一个大致的估计范围，因为弹性模量和泊松比会受到很多因素的影响，例如材料的微结构、温度等。

有了弹性模量和泊松比的数值，我们可以通过应力-应变关系来计算材料在外力作用下的变形行为。

例如，对于线弹性材料，可以根据胡克定律（Hooke's law）来计算应力和应变之间的关系：应力=弹性模量×应变同时，泊松比也可以用于描述应变在材料中的传播情况。

例如，当材料拉伸时，在拉伸方向上产生的应变将会导致在垂直方向上的压缩应变，而泊松比可以描述这种相互作用的程度。

总之，弹性模量和泊松比是常用材料力学性质的重要参数，能够在工程设计和材料选择过程中提供有价值的信息。

然而，不同材料的实际弹性模量和泊松比还会受到更多因素的影响，包括应力状态、变形速率和温度等。

因此，在具体的工程应用中，还需要对具体材料的力学性质进行更详细的研究和测试。

常用材料的弹性模量及泊松比
弹性模量是材料的一项重要力学性质，它描述了材料在受力时的变形能力。

而泊松比则是描述材料压缩时横向变形与纵向变形的比值。

以下是一些常用材料的弹性模量及泊松比。

1.金属材料：
-铁：弹性模量为190-210GPa，泊松比为0.27-0.30；
-铝：弹性模量为69GPa，泊松比为0.33；
-铜：弹性模量为117-130GPa，泊松比为0.33；
-不锈钢：弹性模量为190-210GPa，泊松比为0.3；
-钛：弹性模量为100-116GPa，泊松比为0.32
2.非金属材料：
-塑料（聚合物）：弹性模量为1-3GPa，泊松比为0.3；
-橡胶：弹性模量为0.01-0.1GPa，泊松比为0.45；
-玻璃：弹性模量为60-90GPa，泊松比为0.23；
-水泥：弹性模量为20-40GPa，泊松比为0.2-0.25；
-石头（大理石、花岗岩）：弹性模量为70-90GPa，泊松比为0.2-0.25
3.复合材料：
-碳纤维复合材料：弹性模量为250-500GPa，泊松比为0.2-0.3；
-玻璃纤维复合材料：弹性模量为20-45GPa，泊松比为0.2-0.3；
-蜂窝结构复合材料：弹性模量为1-10GPa，泊松比为0.1-0.3
需要注意的是，这些数值都是估算值，实际数值可能会因具体材料的不同而有所变化。

此外，弹性模量与泊松比也可能因材料的制备工艺和温度等条件而发生变化。

弹性模量和泊松比是许多工程设计和材料选择的重要参数。

通过了解材料的弹性模量和泊松比，可以在设计过程中准确预测和控制材料的力学性能，确保结构的稳定性和可靠性。

常用材料弹性模量及泊松比常用材料的弹性模量及泊松比是工程设计和材料选择时需要考虑的重要参数。

弹性模量是材料抵抗形变的能力，泊松比则是材料在受力时沿垂直方向的收缩程度与沿加载方向的伸长程度之比。

以下是一些常用材料的弹性模量及泊松比：1.钢铁：弹性模量：约为200GPa泊松比：约为0.3钢铁是一种常用的结构材料，其弹性模量高、强度大、塑性好，具有良好的韧性和可塑性。

泊松比为0.3，意味着在受力时有一定的横向收缩。

2.铝合金：弹性模量：约为70GPa泊松比：约为0.33铝合金重量轻、耐腐蚀性好，广泛应用于航空、汽车、电子等领域。

其弹性模量略低于钢铁，但仍具有较高的强度和刚度。

3.铜：弹性模量：约为110GPa泊松比：约为0.33铜导电性好、耐腐蚀性好、导热性好，在电子、通讯、电力等领域得到广泛应用。

其弹性模量与铝合金相近，但比铝合金更韧性。

4.混凝土：弹性模量：约为30GPa泊松比：约为0.15混凝土是一种重要的建筑材料，其弹性模量相对较低，但具有较高的耐久性和承载能力。

由于泊松比较小，混凝土的体积变化较小，适用于抵抗大变形。

5.玻璃：弹性模量：约为70GPa泊松比：约为0.22玻璃是一种无机非晶体材料，透明、硬度高、耐热性好。

其弹性模量较低，但比较脆性，易于破碎。

6.聚合物：弹性模量：约为1-10GPa泊松比：约为0.3-0.4聚合物材料轻、耐腐蚀性好、绝缘性能好，在包装、建筑、电子等行业应用广泛。

弹性模量较低，但具有良好的可塑性和韧性。

以上材料的弹性模量和泊松比均为约值，实际数值可能会有些差异。

此外，不同类型和牌号的材料也可能具有不同的弹性特性。

因此，在具体设计和选择材料时，需要根据实际情况进行综合考虑。

精心整理常用材料的弹性模量及泊松比序号材料名称弹性模量\E\Gpa切变模量\G\Gpa泊松比μ1镍铬钢、合金钢20679.380.25～0.32碳钢196～206790.24～0.283铸钢172～202-0.34球墨铸铁140～15473～76-5灰铸铁、白口铸铁113～157440.23～0.276冷拔纯铜12748-7轧制磷青铜113410.32～0.358轧制纯铜108390.31～0.349轧制锰青铜108390.3510铸铝青铜10341-11冷拔黄铜89～9734～360.32～0.4212轧制锌82310.2713硬铝合金7026-14轧制铝6825～260.32～0.3615铅1770.4216玻璃55220.2517混凝土14～234.9～15.70.1～0.1818纵纹木材9.8～120.5-19横纹木材0.5～0.980.44～0.64-20橡胶0.00784-0.4721电木1.96～2.940.69～2.060.35～0.3822尼龙28.310.10.423可锻铸铁152--24拔制铝线69--25大理石55--26花岗石48--27石灰石41--28尼龙10101.07--29夹布酚醛塑料4～8.8--30石棉酚醛塑料1.3--31高压聚乙烯0.15～0.25--32低压聚乙烯0.49～0.78--33聚丙烯1.32～1.42--常用金属材料的密度表材料名称密度,克/立方厘米材料名称密度,克/立方厘米灰口铸铁6.6~7.4不1Crl8NillNb、Cr23Ni187.9 白口铸铁7.4~7.72Cr13Ni4Mn98.5锈可锻铸铁7.2~7.43Cr13Ni7Si28.0钢铸钢7.8纯铜材8.9精心整理工业纯铁7.8759、62、65、68黄铜8.5普通碳素钢7.8580、85、90黄铜8.7优质碳素钢7.8596黄铜8.8碳素工具钢7.8559-1、63-3铅黄铜8.5易切钢7.8574-3铅黄铜8.7锰钢7.8190-1锡黄铜8.815CrA铬钢7.7470-1锡黄铜8.5420Cr、30Cr、40Cr铬钢7.8260-1和62-1锡黄铜8.538CrA铬钢7.8077-2铝黄铜8.6铬钒、铬镍、铬镍钼、铬锰、硅、铬锰硅镍、硅锰、硅铬钢7.8567-2.5、66-6-3-2、60-1-1铝黄铜8.5镍黄铜8.5铬镍钨钢7.80锰黄铜8.5铬钼铝钢7.65硅黄铜、镍黄铜、铁黄铜8.5 含钨9高速工具钢8.35-5-5铸锡青铜8.8含钨18高速工具钢8.73-12-5铸锡青铜8.69 高强度合金钢`7.826-6-3铸锡青铜8.82轴承钢7.817-0.2、6.5-0.4、6.5-0.1、4-3锡青铜8.80Cr13、1Cr13、2Cr13、3Cr13、4Cr13、Cr17Ni2、Cr18、9Cr18、7.754-0.3、4-4-4锡青铜8.9 Cr25Cr28、不Cr14Cr177.74-4-2.58.75、锡青铜锈Cr18Ni91Cr18Ni9、、钢1Cr18Ni9Ti、2Cr18Ni91Cr18Ni11Si4A1Ti7.52锻LD82.777铝青铜7.8铝LD7、LD9、LD102.819-2铝青铜7.6超硬铝2.859-4、10-3-1.5铝青铜7.5LT1特殊铝2.7510-4-4铝青铜7.46工业纯镁1.74铍青铜8.3MB11.76变3-1硅青铜8.47MB2、MB81.78形1-3硅青铜8.6MB31.79镁1铍青铜8.8MB5、MB6、MB7、MB151.80.5镉青铜8.9铸镁1.80.5铬青铜8.9工业纯钛（TA1、TA2、TA3）4.51.5锰青铜8.8TA4、TA5、TC64.455锰青铜8.6TA64.4B5、B19、B30、BMn40-1.58.9TA7、TC54.46钛白铜B Mn3-128.4TA84.56合金BZN15-208.6TB1、TB24.89BA16-1.58.7TC1TC24.55、BA113-38.5TC3、TC44.43精心整理纯铝2.7TC74.4LF2、LF432.68TC84.48防LF32.67TC94.52锈LF5、LF10、LF112.65TC104.53铝LF62.64纯镍、阳极镍、电真空镍8.85LF212.73镍铜、镍镁、镍硅合金8.85LY1、LY2、LY4、LY62.76镍铬合金8.72硬铝L Y32.73锌锭（Zn0.1、Zn1、Zn2、Zn3）7.15 LY7、LY8、LY10、LY11、LY142.8铸锌6.86 LY9LY122.784-16.9、铸造锌铝合金LY16、LY172.844-0.5铸造锌铝合金6.75锻铝L D2、LD302.7铅和铅锑合金11.37LD42.65铅阳极板11.33LD52.75弹性模量与热物理性质序号材料名称弹性模量(×105MPa)5MPa)剪切模量(×105MPa)5MPa)泊松比熔点(o C)o C)线膨胀系数(×10-6/K)-6/K)热导率(W/(m·k))比热容(J/(kgK)·)1灰口铸铁/白口铸铁1.13-1.570.450.23-0.2712008.5-11.639.2470 2可锻铸铁1.550.4581.1/纯铁455/纯铁3碳钢2.0-2.10.79-0.810.25-0.281400-150011.3-1349.84654镍铬钢、合金钢2.060.79-0.810.25-0.311.5-14.5154605铸钢1.750.349.84706轧制纯铜1.080.390.31-0.34108317.53983867冷拔纯铜1.270.4-0.48108317.54074188轧制磷青铜1.130.410.32-0.3517.922.2镍青铜410/镍青铜9冷拔黄铜0.90-0.97034-0.370.32-0.42108318.810637710轧制锰青铜1.080.390.3524.8锡青铜343/锡青铜序号材料名称弹性模量(×105MPa)5MPa)剪切模量(×105MPa)5MPa)泊松比熔点(o C)o C)线膨胀系数(×10-6/K)-6/K)热导率(W/(m·k))比热容(J/(kgK)·)11轧制铝0.690.26-0.270.32-0.36658238/纯铝902/纯铝12铸铝青铜1.030.410.317.95642013硬铝合金0.70.270.323.6162/硅铝871/硅铝14轧制锌0.820.310.2712138815铅0.170.070.423273512616球墨铸铁1.4-1.540.73-0.7617玻璃0.550.2-0.220.254-11.518混凝土0.14-0.230.049-0.1570.1-0.1810-1419纵纹木材0.098-0.120.00520横纹木材0.005-0.000.0044-0.0064序号材料名称弹性模量(×105MPa)5MPa)剪切模量(×105MPa)5MPa)泊松比熔点(o C)o C)线膨胀系数(×10-6/K)-6/K)热导率(W/(m·k))比热容(J/(kgK)·)21橡胶0.00007840.4722电木0.0196-0.02940.0069-0.02060.35-0.38 23尼龙0.02830.01010.424大理石0.5525花岗岩0.4826尼龙10100.010727夹布酚醛塑料0.04-0.08828石棉酚醛塑料0.01329高压聚乙烯0.015-0.02530低压聚乙烯0.0049-0.0078序号材料名称弹性模量(×105MPa)5MPa)剪切模量(×105MPa)5MPa)泊松比熔点(o C)o C)线膨胀系数(×10-6/K)-6/K)热导率(W/(m·k))比热容(J/(kgK)·)31聚丙烯0.0132-0.014232不锈钢24.551033灰口铸铁/白口铸铁1.13-1.570.450.23-0.2712008.5-11.639.2470 34可锻铸铁1.550.4581.1/纯铁455/纯铁35碳钢2.0-2.10.79-0.810.25-0.281400-150011.3-1349.846536镍铬钢、合金钢2.060.79-0.810.25-0.311.5-14.51546037铸钢1.750.349.847038轧制纯铜1.080.390.31-0.34108317.539838639冷拔纯铜1.270.4-0.48108317.540741840轧制磷青铜1.130.410.32-0.3517.922.2镍青铜410/镍青铜序号材料名称弹性模量(×105MPa)5MPa)剪切模量(×105MPa)5MPa)泊松比熔点(o C)o C)线膨胀系数(×10-6/K)-6/K)热导率(W/(m·k))比热容(J/(kgK)·)41冷拔黄铜0.90-0.97034-0.370.32-0.42108318.810637742轧制锰青铜1.080.390.3524.8锡青铜343/锡青铜43轧制铝0.690.26-0.270.32-0.36658238/纯铝902/纯铝44铸铝青铜1.030.410.317.95642045硬铝合金0.70.270.323.6162/硅铝871/硅铝46轧制锌0.820.310.2712138847铅0.170.070.423273512648球墨铸铁1.4-1.540.73-0.7649玻璃0.550.2-0.220.254-11.550混凝土0.14-0.230.049-0.1570.1-0.1810-14序号材料名称弹性模量剪切模量泊松比熔点线膨胀系数热导率比热容(×105MPa)(×150MPa)(o C)(×1-60/K)(W/(m·k))(J/(kgK)·) 51纵纹木材0.098-0.120.00552横纹木材0.005-0.000.0044-0.006453橡胶0.00007840.4754电木0.0196-0.02940.0069-0.02060.35-0.3855尼龙0.02830.01010.456大理石0.5557花岗岩0.4858尼龙10100.010759夹布酚醛塑料0.04-0.08860石棉酚醛塑料0.013序号材料名称弹性模量(×105MPa)5MPa)剪切模量(×105MPa)5MPa)泊松比熔点(o C)o C)线膨胀系数(×10-6/K)-6/K)热导率(W/(m·k))比热容(J/(kgK)·)61高压聚乙烯0.015-0.025 62低压聚乙烯0.0049-0.0078 63聚丙烯0.0132-0.014264不锈钢24.5510。

材料弹性模量E和泊松⽐实验测定实验三材料弹性模量E 和泊松⽐µ的测定实验⼀、实验⽬的1、测定常⽤⾦属材料的弹性模量E 和泊松⽐µ。

2、验证胡克（Hooke ）定律。

⼆、实验仪器设备和⼯具1、组合实验台中拉伸装置2、XL2118系列⼒＆应变综合参数测试仪三、实验原理和⽅法试件采⽤矩形截⾯试件，电阻应变⽚布⽚⽅式如图3-1。

在试件中央截⾯上，沿前后两⾯的轴线⽅向分别对称的贴⼀对轴向应变⽚R1、R1ˊ和⼀对横向应变⽚R2、R2ˊ，以测量轴向应变ε和横向应变εˊ。

补偿块图 3-1 拉伸试件及布⽚图1、弹性模量E 的测定由于实验装置和安装初始状态的不稳定性，拉伸曲线的初始阶段往往是⾮线性的。

为了尽可能减⼩测量误差，实验宜从⼀初载荷00(0)P P ≠开始，采⽤增量法，分级加载，分别测量在各相同载荷增量P ?作⽤下，产⽣的应变增量ε?，并求出ε?的平均值。

设试件初始横截⾯⾯积为0A ，⼜因L L ε=?，则有A E P ε??=0上式即为增量法测E 的计算公式。

式中 0A — 试件截⾯⾯积ε? — 轴向应变增量的平均值组桥⽅式采⽤1/4桥单臂测量⽅式，应变⽚连接见图3-2。

补偿⽚图3-2 1/4桥连接⽅式实验时，在⼀定载荷条件下，分别对前、后两枚轴向应变⽚进⾏单⽚测量，并取其平均值'11()2εεε+=。

显然ε代表载荷P 作⽤下试件的实际应变量。

⽽且前后两⽚应变⽚可以相互抵消偏⼼弯曲引起的测量误差。

2、泊松⽐µ的测定利⽤试件上的横向应变⽚和纵向应变⽚合理组桥，为了尽可能减⼩测量误差，实验宜从⼀初载荷00(0)P P ≠开始，采⽤增量法，分级加载，分别测量在各相同载荷增量△P 作⽤下，横向应变增量ε'?和纵向应变增量ε?。

求出平均值，按定义'εµε= 便可求得泊松⽐µ。

四、实验步骤1、明确试件尺⼨的基本尺⼨，宽30mm ，厚5mm 。

2、调整好实验加载装置。

（《钢结构设计规》GB 50017━2003表3.4.3统一取弹性模量206000MPa。

泊松比约为0.3 ）（有限元材料库的参数为：45号钢密度7890kg/m3,泊松比0.269，氏模量209000GP.）（HT200,弹性模量为135GPa,泊松比为0.27）(HT200 密度：7.2-7.3，弹性模量：70-80; 泊松比0.24-0.25 ;热膨胀系数加热： 10冷却-8)（用灰铸铁 HT200，根据资料可知其密度为7340kg/m3，弹性模量为120GPa ,泊松比为0. 25）（HT200,弹性模量E=1.22e 11 Pa, 泊松比λ=0.25,密度ρ=7800 kg/m 3）（ HT200 122 /0. 3 /7. 2 ×10 - 6）(材料HT200,密度为7. 8103 kg / m 3 ,弹性模量为 145 GPa,泊松比为0.3)( HT200,其弹性模量 E=140GPa,泊松比μ=0.25,密度ρ=7.8×10 3 kg/m 3)(模具材料为灰口铸铁 HT200,C-3.47%,Si-2.5%,密度 7210 kg / m3 ,泊松比 0.27。

)(箱体材料为HT200,其性能参数为:弹性模量E=1.4×10 11 Pa,泊松比μ=0.3,密度为ρ=7.8×10 3 kg.m -3 )(模型材料HT200,其主要物理与机械性能参数如下:密度7.25 t/m 3 ,弹性模量126 GPa, 泊松比0.3)(垫板的材料采用 HT200, 材料相关参数查表可得, 弹性模量 E = 1120 ×10 5 N /mm 2 , 泊松比μ= 0125, 密度ρ=712 ×10 - 9 t /mm 3)表58-23，常用材料的弹性模量，泊松比和线胀系数非合金球墨铸铁160~180 0.28~0.29 10 —8 青铜85 0.35 17 —15 黄铜80 0.36~0.37 18 —16 铝合金69 0.32~0.36 21 —20 镁铝合金40 0.25~0.30 25.5 —25常用材料弹性模量与泊松比━━━━━━━━━━━━━━━━━━名称弹性模量E 切变模量G 泊松比μGPa GPa──────────────────镍铬钢 206 79.38 0.25-0.30合金钢 206 79.38 0.25-0.30碳钢 196-206 79 0.24-0.28铸钢 172-202 0.3球墨铸铁 140-154 73-76 0.23-0.27灰铸铁 113-157 44 0.23-0.27白口铸铁 113-157 44 0.23-0.27冷拔纯铜 127 48轧制磷青铜 113 41 0.32-0.35轧制纯铜 108 39 0.31-0.34轧制锰青铜 108 39 0.35铸铝青铜 103 41冷拔黄铜 89-97 34-36 0.32-0.42轧制锌 82 31 0.27硬铝合金 70 26轧制铝 68 25-26 0.32-0.36铅 17 7 0.42玻璃 55 22 0.25混凝土 14-23 4.9-15.7 0.1-0.18纵纹木材 9.8-12 0.5横纹木材 0.5-0.98 0.44-0.64橡胶 0.00784 0.47电木 1.96-2.94 0.69-2.06 0.35-0.38 尼龙 28.3 10.1 0.4可锻铸铁 152拔制铝线 69石 55花岗石 48石灰石 41尼龙1010 10.7夹布酚醛塑料 4-8.8石棉酚醛塑料 1.3高压聚乙烯 0.15-0.25低压聚乙烯 0.49-0.78聚丙烯 1.32-1.42。

00EA A P==εσε弹性模量E 和泊松比µ的测定拉伸试验中得到的屈服极限бb 和强度极限бS ，反映了材料对力的作用的承受能力，而延伸率δ 或截面收缩率ψ，反映了材料缩性变行的能力，为了表示材料在弹性范围内抵抗变行的难易程度，在实际工程结构中，材料弹性模量E 的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变性量来判断其刚度的。

一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中 A 0为零件的横截面积。

由上式可见，要想提高零件的刚度E A 0,亦即要减少零件的弹性变形，可选用高弹性模量的材料和适当加大承载的横截面积，刚度的重要性在于它决定了零件服役时稳定性，对细长杆件和薄壁构件尤为重要。

因此，构件的理论分析和设计计算来说，弹性模量E 是经常要用到的一个重要力学性能指标。

在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。

纵向应力与纵向应变的比例常数就是材料的弹性模量E ，也叫杨氏模量。

横向应变与纵向应变之比值称为泊松比µ，也叫横向变性系数，它是反映材料横向变形的弹性常数。

因此金属才料拉伸时弹性模量E 地测定是材料力学最主要最基本的一个实验，下面用电测法测定低碳钢弹性模量E 和泊松比µ。

(一） (一） 试验目的1．1．用电测方法测定低碳钢的弹性模量E 及泊松比µ；2．2．验证虎克定律；3．3．掌握电测方法的组桥原理与应用。

(二） (二） 试验原理1．测定材料弹性模量E 一般采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其荷载与变形关系为：0EA PL L ∆=∆ （1）若已知载荷ΔP 及试件尺寸，只要测得试件伸长ΔL 即可得出弹性模量E 。

（2）由于本试验采用电测法测量，其反映变形测试的数据为应变增量，即（3） 所以（2）成为:)(A L PL E ∆∆∆=0)(L L ∆∆=∆ε（4） 式中： ΔP ——载荷增量，kN ；A 0-----试件的横截面面积，cm为了验证力与变形的线性关心，采用增量法逐级加载，分别测量在相同载荷增量 ΔP 作用下试件所产生的应变增量Δε。

常⽤⾦属材料的弹性模量及泊松⽐常⽤材料的弹性模量及泊松⽐名称弹性模量E切变模量G泊松⽐µ备注GPa GPa灰、⽩⼝铸铁115～160 45 0.23 ～0.27球墨铸铁151～160 61 0.25 ～0.29碳钢200～220 81 0.24-0.28合⾦钢210 81 0.25 ～0.3铸钢175 70-84 0.25 ～0.29轧制磷青铜115 42 0.32 ～0.35轧制锰黄铜110 40 0.35铸铝青铜105 42 0.25⽹上下载硬铝合⾦71 27冷拔黄铜91～99 35-37 0.32 ～0.42轧制纯铜110 40 0.31 ～0.34轧制锌84 32 0.27轧制铝69 26-27 0.32 ～0.36铅17 7 0.42钢207 0.29铝71.7 0.33铸铁100 0.211不锈钢190 0.305镁44.8 0.35镍207 0.291玻璃46.2 0.245 黄铜106 0.324 摘⾃adams 材料库铜119 0.326 右墨36.5 0.425 钛102.04 0.3 钨344.7 0.28 ⽊材11 0.33 钛的热膨胀系数为(9.41～10.3) ×10-6/℃Ti-6Al-4V 的线膨胀系数只有8.8×10-6K-1.杨⽒模量剪切模量泊松⽐Cr 250 115 0.12Pt 169 61 0.38Co 210 83 0.32以上杨⽒模量（E）和剪切模量（G）的单位为GPa 材料线膨胀系数(x0.000001/ °C)⼀般铸铁9.2-11.8⼀般碳钢10~13铬钢10~13镍铬钢13-15铁12-12.5 铜18.5青铜17.5黄铜18.5铝合⾦23.8⾦14.2⾦属铬常温25 摄⽒度下：线膨胀系数 6.2x10exp （-6）/K体膨胀系数是线膨胀系数的三倍。

铜17.7X10^-6/ 。

C ⽆氧铜18.6X10^-8/ 。