高一下学期5月月考试题 数学(湖南省)

2023-2024学年湖南省衡阳一中高一（下）第一次月考数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知，，若集合，则的值为()A.B.C.1D.22.已知命题p ：任意，，命题q ：存在，若“p 且q ”是假命题，则实数a 的取值范围是()A. B.C.D.3.设正实数x ，y ，z 满足，则的最大值为()A.4 B.2C.3D.14.，则当t 变化时，的最小值为()A.2020B.2019C.2018D.20175.已知函数，其中，，若对任意，恒成立，则的最小值为()A.B.C.D.6.如图所示，矩形ABCD 中，，点E 为AB 中点，若，则()A.B.C.3D.7.已知函数定义域为，，对任意的，，当时，有若，则实数a 的取值范围是()A. B.C.D.8.将函数的图象向右平移个单位长度后得到函数的图象，若的图象关于直线对称，则下列结论正确的是()A. B.是奇函数C.在上单调递增D.二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，部分选对的得2分，有选错的得0分。

9.已知函数的部分图象如图所示，若，，则()A.B.的单调递增区间为C.的图象关于点对称D.的图象关于直线对称10.已知函数其中表示不大于x的最大整数，则()A.是奇函数B.是周期函数C.在上单调递增D.的值域为11.在中，D为BC边上的中点，是边AB上的一个定点，，且对于AB上任一点P，恒有，则下列结论中正确的是()A. B.存在点P，使C. D.三、填空题：本题共3小题，每小题5分，共15分。

12.已知，点M是内一点且，则的面积为______.13.函数的最小值______.14.已知，，，，且，则的最小值为______.四、解答题：本题共5小题，共77分。

解答应写出文字说明，证明过程或演算步骤。

15.本小题13分已知的内角所对的边分别为，且，若，求的值；若的面积，求的值．16.本小题15分已知函数的最小正周期为将化简成的形式；设函数，求函数在上的值域.17.本小题15分已知，我们定义函数表示不小于x的最小整数，例如：，若，求实数x的取值范围；求函数的值域，并求满足的实数x的取值范围.18.19.本小题17分在中，a，b，c分别为内角A，B，C的对边，且求A；点D在边BC上，且，，求面积的最大值.答案和解析1.【答案】B【解析】解：因为，所以，解得，或，，当时，不满足集合元素的互异性，故，，故选：根据集合相等的定义求出m，n，即可得解．本题主要考查了集合相等条件的应用，属于基础题．2.【答案】D【解析】解：命题p为真时，恒成立，即，，，则；命题q为真时，，即，解得：或命题“p且q”是真命题时，可得或，所以命题“p且q”是假命题时，可得且，即故选：首先分别求两个命题为真命题时a的取值范围，取其补集即可得答案．本题考查复合命题的真假判断与应用，考查运算求解能力，是基础题．3.【答案】D【解析】解：因为正实数x，y，z满足，则，当且仅当时取等号．故选：先把代入到所求式子，然后进行分离变形，结合基本不等式即可求解．本题主要考查了基本不等式在最值求解中的应用，属于基础题．4.【答案】D【解析】解：函数，对称轴为，当，在上单调递增，所以；当，即时，在上单调递减，；当，即时，此时，，无最小值；当，即时，，综上知，的最小值为故选：根据对称轴和区间的位置关系对t的值进行讨论，从而求出，继而求出其最小值即可．本题考查二次函数在动区间上的最值，考查了分类讨论思想，属于难题．5.【答案】C【解析】解：，①当时，，对称轴为，在上单调递增，所以，则，所以②当时，，对称轴为，在上递增，在上递减，所以，则，所以③当时，若，，；若，，当时，，，，；当时，，，，综上所述：的最小值为故选：先按a的不同取值区间分类讨论在上的最大值，得到a与b的关系，结合a的范围，求得的最小值，再取不同情况下最小值中的最小者即可．本题主要考查了不等式恒成立与最值关系的转化，体现了分类讨论及转化思想的应用，属于中档题．6.【答案】B【解析】【分析】本题考查了向量的垂直与数量积的关系、模的计算公式，属于基础题．如图所示，建立直角坐标系．利用，可得，再利用向量模的计算公式即可得出．【解答】解：如图所示，建立直角坐标系．则，设，，，，，解得故选：7.【答案】D【解析】解：由题意可知，当时，有，即，令，则当时，，则函数在上单调递减，由，可得，即，所以，解得，即实数a 的取值范围是故选：根据题意，构造函数，即可得到函数在上单调递增，结合函数的单调性求解不等式，即可得到结果．本题主要考查利用导数研究函数的单调性，属于中档题．8.【答案】C 【解析】解：将函数的图象向右平移个单位长度后，得到函数的图象．若的图象关于直线对称，则，，求得，故，故A 、B 错误．在上，，函数单调递增，故C 正确．由于，故D 错误．故选：由题意，利用函数的图象变换规律，得到的解析式，再根据正弦函数的图象和性质，得出结论．本题主要考查函数的图象变换规律，正弦函数的图象和性质，属于中档题．9.【答案】AD【解析】解：根据已知函数的部分图象可得：，因为，，所以，所以，即，所以，将代入解析式中得：，所以，即，因为，所以，所以，故A正确；令，得，故B不正确；因为，所以的图象不关于点对称，故C不正确；因为，所以的图象关于直线对称，故D正确．故选：根据已知函数的部分图象可得，再结合函数的周期可得，然后将代入求得，即可求得函数的解析式，进而判断选项A的正误；利用三角函数的图象与性质求出函数的单调区间，即可判断选项B的正误；利用代入验证法判断函数的对称中心和对称轴即可判断选项C、D的正误．本题考查由三角函数的部分图象求函数的解析式、三角函数的图象与性质，考查学生的逻辑思维能力和直观想象能力，属中档题．10.【答案】BD【解析】解：由题意，表示不大于x的最大整数，则，所以，则函数是以3为周期的函数，当时，；当时，，又是以3为周期的函数，则的值域为，B和D均正确；，，所以，故不是奇函数，A错误；当时，，故在上无单调性，C错误．故选：结合已知定义，结合函数的奇偶性，单调性及周期性检验各选项即可判断．本题以新定义为载体，主要考查了函数的周期性，奇偶性及单调性的判断，属于中档题．11.【答案】ACD【解析】解：A：，故A正确．B：由A知，，又恒成立，，即恒成立，不正确．C：由恒成立，是点D与直线AB上各点距离的最小值，，，正确．D：取AB的中点为O，，为OB中点，，，为等腰三角形，，正确．故选：由题意画出图形，利用平面向量的加减运算及数量积运算逐一分析4个命题得答案．本题考查平面向量的数量积运算，考查命题的真假判断与应用，考查逻辑思维能力与推理论证能力，是中档题．12.【答案】【解析】解：取AC的中点D，由，得，即，即，可知点M为BD的中点，所以故答案为：根据题意，取AC的中点D，利用平面向量的线性运算法则判断出点M的位置，进而利用三角形面积公式算出的面积．本题主要考查平面向量的线性运算法则、三角形的面积公式及其性质等知识，属于基础题．13.【答案】【解析】解：，当且仅当，即，时取等号．故答案为：先对已知函数进行变形，然后结合乘1法及基本不等式即可求解．本题主要考查了乘1法及基本不等式在最值求解中的应用，属于中档题．14.【答案】【解析】解：根据，可得，所以，由，得，结合且，可得，所以当且仅当，即时，等号成立．因此，的最小值为，可得的最小值为，的最小值为故答案为：根据题意，取对数得，然后利用基本不等式与“1的代换”，算出的最小值为，由此得出的最小值，进而可得的最小值．本题主要考查对数的运算法则、利用基本不等式求最值等知识，考查了计算能力、逻辑推理能力，属于中档题．15.【答案】解：Ⅰ为的内角，且，，，，由正弦定理得：；Ⅱ，，【解析】本题考查正弦定理、余弦定理的运用，考查学生分析解决问题的能力，属于中档题．Ⅰ先求出，再利用正弦定理求的值；Ⅱ由的面积求c的值，利用余弦定理求b的值．16.【答案】解：，根据题意可得，解得，故；由知，则，所以当或时，取得最小值，最小值为，当时，取得最大值，最大值为，故在上的值域为【解析】利用二倍角公式和辅助角公式化简函数，利用周期性求解，即可解答；利用诱导公式求得，然后根据正弦函数性质求解值域即可．本题主要考查了三角函数恒等变换，以及正弦函数的性质的综合应用，考查了转化思想和函数思想的应用，属于中档题．17.【答案】解：由表示不小于x的最小整数，，得，所以实数x的取值范围是；函数定义域为而函数在上单调递增，值域为因此，即，所以函数的值域为显然由，得，则有，而时，不等式不成立，则，必有，即，因此，，解得，所以实数x的取值范围【解析】由已知定义即可得x的范围；由已知结合基本初等函数的性质先求出的值域，再由已知建立不等式关系即可得关于x的不等式，即可求．本题以新定义为载体，主要考查了函数值域的求解，属于中档题．18.【答案】【解析】19.【答案】解：，，即，，；由题意得，两边平方得，整理得，，当且仅当，时，等号成立，，故面积的最大值为【解析】由正弦定理角化边，再结合余弦定理，即可得出答案；由向量建立等量关系，结合基本不等式，即可得出答案．本题考查解三角形，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．。

大联考湖南师大附中2025届高三月考试卷（一）数学命题人：高三数学备课组 审题人：高三数学备课组时量：120分钟 满分：150分一､选选选：本选共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，1. 已知{}()260,{lg 10}Axx x B x x =+−≤=−<∣∣，则A B = （ ）A. {}32xx −≤≤∣ B. {32}x x −≤<∣ C. {12}x x <≤∣D. {12}x x <<∣2. 若复数z 满足()1i 3i z +=−+（i 是虚数单位），则z 等于（ ）A.B.54C.D.3. 已知平面向量()()5,0,2,1ab ==−，则向量a b +在向量b上投影向量为（ ）A. ()6,3−B. ()4,2−C. ()2,1−D. ()5,04. 记n S 为等差数列{}n a 的前n 项和，若396714,63a a a a +==，则7S =（ ） A. 21B. 19C. 12D. 425. 某校高二年级下学期期末考试数学试卷满分为150分，90分以上（含90分）为及格．阅卷结果显示，全年级1200名学生的数学成绩近似服从正态分布，试卷的难度系数（难度系数=平均分/满分）为0.49，标准差为22，则该次数学考试及格的人数约为（ ）附：若()2,X Nµσ∼，记()()p k P k X k µσµσ=−≤≤+，则()()0.750.547,10.683p p ≈≈．A 136人 B. 272人C. 328人D. 820人6. 已知()π5,0,,cos ,tan tan 426αβαβαβ∈−=⋅=，则αβ+=（ ） A.π6 B.π4C.π3D.2π37. 已知12,F F 是双曲线22221(0)x y a b a b−=>>的左､右焦点，以2F 为圆心，a 为半径的圆与双曲线的一条的.渐近线交于,A B 两点，若123AB F F >，则双曲线的离心率的取值范围是（ ）A.B.C. (D. (8. 已知函数()220log 0x a x f x x x ⋅≤= > ，，，，若关于x 的方程()()0f f x =有且仅有两个实数根，则实数a 的取值范围是（ ） A. ()0,1B. ()(),00,1−∞∪C. [)1,+∞D. ()()0,11,+∞二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分9. 如图，在正方体111ABCD A B C D −中，E F M N ，，，分别为棱111AA A D AB DC ，，，的中点，点P 是面1B C 的中心，则下列结论正确的是（ ）A. E F M P ，，，四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN10. 已知函数()5π24f x x=+，则（ ）A. ()f x 的一个对称中心为3π,08B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象 C. ()f x 在区间5π7π,88上单调递增 D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点，则5π13π,24m∈11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++−=，则（ ）A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =−=∑ 三､填空题：本题共3小题，每小题5分，共15分.12. 6(31)x y +−的展开式中2x y 的系数为______．13. 已知函数()f x 是定义域为R 的奇函数，当0x >时，()()2f x f x ′−>，且()10f =，则不等式()0f x >的解集为__________.14. 已知点C 为扇形AOB 弧AB 上任意一点，且60AOB ∠=，若(),R OC OA OB λµλµ=+∈，则λµ+的取值范围是__________.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ，已知22cos a b c B +=． （1）求角C ；（2）若角C 的平分线CD 交AB于点,D AD DB =，求CD 的长．16. 已知1ex =为函数()ln af x x x =的极值点． （1）求a 的值； （2）设函数()ex kxg x =，若对()120,,x x ∀∈+∞∃∈R ，使得()()120f x g x −≥，求k 的取值范围． 17. 已知四棱锥P ABCD −中，平面PAB ⊥底面,ABCD AD∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥==为AB 的中点，F 为棱PC 上异于,P C 的点．的（1）证明：BD EF ⊥；（2）试确定点F 的位置，使EF 与平面PCD18. 在平面直角坐标系xOy 中，抛物线21:2(0)C ypx p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长，点P 在抛物线1C 上，圆222:(2)E x y r −+=（其中01r <<）.（1）若1,2r Q =为圆E 上的动点，求线段PQ 长度的最小值； （2）设()1,D t 是抛物线1C 上位于第一象限的一点，过D 作圆E 的两条切线，分别交抛物线1C 于点,M N .证明：直线MN 经过定点.19. 龙泉游泳馆为给顾客更好的体验，推出了A 和B 两个套餐服务，顾客可选择A 和B 两个套餐之一，并在App 平台上推出了优惠券活动，下表是该游泳馆在App 平台10天销售优惠券情况． 日期t 12345678910销售量千张 1.9 1.98 2.2 2.36 2.43 2.59 2.68 2.76 2.7 04经计算可得：10101021111 2.2,118.73,38510i i i i i i i y y t y t ======∑∑∑ （1）因为优惠券购买火爆，App 平台在第10天时系统出现异常，导致当天顾客购买优惠券数量大幅减少，已知销售量y 和日期t 呈线性关系，现剔除第10天数据，求y 关于t 的经验回归方程结果中的数值用分数表示；（2）若购买优惠券的顾客选择A 套餐的概率为14，选择B 套餐的概率为34，并且A 套餐可以用一张优惠券，B 套餐可以用两张优惠券，记App 平台累计销售优惠券为n 张的概率为n P ，求n P ； （3）记（2）中所得概率n P 的值构成数列{}()N n P n ∗∈.①求n P 的最值；②数列收敛的定义：已知数列{}n a ，若对于任意给定的正数ε，总存在正整数0N ，使得当0n N >时，n a a ε−<，（a 是一个确定的实数），则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛．..参考公式： ()()()1122211ˆˆ,n ni ii ii i n n i i i i x x y y x y nx yay bx x xx nx====−−−==−−−∑∑∑∑.大联考湖南师大附中2025届高三月考试卷（一）数学命题人：高三数学备课组 审题人：高三数学备课组时量：120分钟 满分：150分一､选选选：本选共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，1. 已知{}()260,{lg 10}Axx x B x x =+−≤=−<∣∣，则A B = （ ）A. {}32xx −≤≤∣ B. {32}x x −≤<∣ C. {12}x x <≤∣ D. {12}x x <<∣【答案】D 【解析】【分析】通过解一元二次不等式和对数函数的定义域，求出集合,A B ，再求交集． 【详解】集合{}()32,{lg 10}{12}A x x B x x x x =−≤≤=−<=<<∣∣∣，则{12}A B xx ∩=<<∣， 故选：D ．2. 若复数z 满足()1i 3i z +=−+（i 是虚数单位），则z 等于（ ）A.B.54C.D.【答案】C 【解析】【分析】由复数的除法运算计算可得12i z =−+，再由模长公式即可得出结果. 【详解】依题意()1i 3i z +=−+可得()()()()3i 1i 3i 24i12i 1i 1i 1i 2z −+−−+−+====−+++−，所以z =. 故选：C3. 已知平面向量()()5,0,2,1a b ==−，则向量a b +在向量b上的投影向量为（ ）A. ()6,3−B. ()4,2−C. ()2,1−D. ()5,0【答案】A 【解析】【分析】根据投影向量的计算公式即可求解.【详解】()()7,1,15,a b a b b b +=−+⋅==所以向量a b +在向量b 上的投影向量为()()236,3||a b b b bb +⋅==− .故选：A4. 记n S 为等差数列{}n a 的前n 项和，若396714,63a a a a +==，则7S =（ ） A. 21 B. 19C. 12D. 42【答案】A 【解析】【分析】根据等差数列的性质，即可求解公差和首项，进而由求和公式求解.【详解】{}n a 是等差数列，396214a a a ∴+==，即67a =，所以67769,a a a a == 故公差76162,53d a a a a d =−=∴=−=−，()767732212S ×∴=×−+×=， 故选：A5. 某校高二年级下学期期末考试数学试卷满分为150分，90分以上（含90分）为及格．阅卷结果显示，全年级1200名学生的数学成绩近似服从正态分布，试卷的难度系数（难度系数=平均分/满分）为0.49，标准差为22，则该次数学考试及格的人数约为（ ）附：若()2,X Nµσ∼，记()()p k P k X k µσµσ=−≤≤+，则()()0.750.547,10.683p p ≈≈．A. 136人B. 272人C. 328人D. 820人【答案】B 【解析】【分析】首先求出平均数，即可得到学生的数学成绩2~(73.5,22)X N ，再根据所给条件求出(5790)P X ≤≤，即可求出(90)P X ≥，即可估计人数．【详解】由题得0.4915073.5,22µσ=×==，()()(),0.750.547p k P k X k p µσµσ=−≤≤+≈ ，()5790P X ∴≤≤ ()0.750.547p ≈，()()900.510.5470.2265P X ≥×−，∴该校及格人数为0.22651200272×≈（人），故选：B ． 6. 已知()π5,0,,cos ,tan tan 426αβαβαβ∈−=⋅=，则αβ+=（ ） A.π6 B.π4C.π3D.2π3【答案】D 【解析】【分析】利用两角差的余弦定理和同角三角函数的基本关系建立等式求解，再由两角和的余弦公式求解即可．【详解】由已知可得5cos cos sin sin 6sin sin 4cos cos αβαβαβαβ⋅+⋅=⋅ =⋅ ， 解得1cos cos 62sin sin 3αβαβ⋅=⋅=，，()1cos cos cos sin sin 2αβαβαβ∴+=⋅−⋅=−，π,0,2αβ∈，()0,παβ∴+∈， 2π,3αβ∴+=，故选：D ．7. 已知12,F F 是双曲线22221(0)x y a b a b−=>>的左､右焦点，以2F 为圆心，a 为半径的圆与双曲线的一条渐近线交于,A B 两点，若123AB F F >，则双曲线的离心率的取值范围是（ ）A.B.C. (D. (【答案】B 【解析】【分析】根据双曲线以及圆的方程可求得弦长AB =，再根据不等式123AB F F >整理可得2259c a <，即可求得双曲线的离心率的取值范围.【详解】设以()2,0F c 为圆心，a 为半径的圆与双曲线的一条渐近线0bx ay −=交于,A B 两点， 则2F 到渐近线0bx ay −=的距离d b，所以AB =， 因为123AB F F >，所以32c ×>，可得2222299a b c a b −>=+， 即22224555a b c a >=−，可得2259c a <，所以2295c a <，所以e <，又1e >，所以双曲线的离心率的取值范围是 .故选：B8. 已知函数()220log 0x a x f x x x ⋅≤= > ，，，，若关于x 的方程()()0f f x =有且仅有两个实数根，则实数a 的取值范围是（ ） A. ()0,1 B. ()(),00,1−∞∪C. [)1,+∞D. ()()0,11,+∞【答案】C 【解析】【分析】利用换元法设()u f x =，则方程等价为()0f u =，根据指数函数和对数函数图象和性质求出1u =，利用数形结合进行求解即可． 【详解】令()u f x =，则()0f u =．�当0a =时，若()0,0u f u ≤=；若0u >，由()2log 0f u u==，得1u =． 所以由()()0ff x =可得()0f x ≤或()1f x =．如图所示，满足()0f x ≤的x 有无数个，方程()1f x =只有一个解，不满足题意；�当0a ≠时，若0≤u ，则()20uf u a =⋅≠；若0u >，由()2log 0f u u==，得1u =． 所以由()()0ff x =可得()1f x =，当0x >时，由()2log 1f x x==，可得2x =， 因为关于x 的方程()()0f f x =有且仅有两个实数根，则方程()1f x =在(,0∞−]上有且仅有一个实数根，若0a >且()(]0,20,xx f x a a ≤=⋅∈，故1a ≥； 若0a <且()0,20xx f x a ≤=⋅<，不满足题意．综上所述，实数a 的取值范围是[)1,+∞， 故选：C ．二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分9. 如图，在正方体111ABCD A B C D −中，E F M N ，，，分别为棱111AA A D AB DC ，，，的中点，点P 是面1B C 的中心，则下列结论正确的是（ ）A. E F M P ，，，四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN【答案】BD 【解析】【分析】可得过,,E F M 三点的平面为一个正六边形，判断A ；分别连接,E F 和1,B C ，截面1C BEF 是等腰梯形，判断B ；分别取11,BB CC 的中点,G Q ，易证EF 显然不平行平面QGMN ，可判断C ；EM ⊥平面PMN ，可判断D.【详解】对于A ：如图经过,,E F M 三点的平面为一个正六边形EFMHQK ，点P 在平面外，,,,E F M P ∴四点不共面，∴选项A 错误；对于B ：分别连接,E F 和1,B C ，则平面PEF 即平面1C BEF ，截面1C BEF 是等腰梯形，∴选项B 正确；对于C ：分别取11,BB CC 的中点,G Q ，则平面PMN 即为平面QGMN ， 由正六边形EFMHQK ，可知HQ EF ，所以MQ 不平行于EF ，又,EF MQ ⊂平面EFMHQK ，所以EF MQ W = ，所以EF I 平面QGMN W =， 所以EF 不平行于平面PMN ，故选项C 错误；对于D ：因为,AEM BMG 是等腰三角形，45AME BMG ∴∠=∠=°， 90EMG ∴∠=°，EMMG ∴⊥，,M N 是,AB CD 的中点，易证MN AD ∥，由正方体可得AD ⊥平面11ABB A ，MN ∴⊥平面11ABB A ，又ME ⊂平面11ABB A ，EM MN ∴⊥，,MG MN ⊂ 平面PMN ，EM ∴⊥平面GMN ，EM ⊂ 平面MEF ，∴平面MEF ⊥平面,PMN 故选项D 正确．���BD ．10. 已知函数()5π24f x x=+，则（ ）A. ()f x 的一个对称中心为3π,08B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象 C. ()f x 在区间5π7π,88上单调递增 D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点，则5π13π,24m∈【答案】BD 【解析】【分析】代入即可验证A ，根据平移可得函数图象，即可由正弦型函数的奇偶性求解B ，利用整体法即可判断C ，由5πcos 24x+求解所以根，即可求解D.【详解】对于A ，由35π3π2π0848f =+×=≠，故A 错误；对于B ，()f x 的图象向右平移3π8个单位长度后得： 3π3π5ππ228842y f x x x x=−−++，为奇函数，故B 正确； 对于C ，当5π7π,88x∈时，则5π5π2,3π42x +∈ ，由余弦函数单调性知，()f x 在区间5π7π,88 上单调递减，故C 错误；对于D ，由()1f x =，得5πcos 24x+ππ4x k =+或ππ,2k k +∈Z ， ()y f x =在区间()0,m 上与1y =有且只有6个交点，其横坐标从小到大依次为：ππ5π3π9π5π,,,,,424242， 而第7个交点的横坐标为13π4， 5π13π24m ∴<≤，故D 正确. 故选：BD11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++−=，则（ ）A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =−=∑ 【答案】ABC 【解析】【分析】根据函数奇偶性以及所满足的表达式构造方程组可得()()222f x f x ++−=，即可判断A 正确；利用对称中心表达式进行化简计算可得B 正确，可判断()g x 也是以8为周期的周期函数，即C 正确；根据周期性以及()()42f x f x ++=计算可得20241(42)2024k f k =−=∑，可得D 错误. 【详解】由题意()()()(),f x f x g x g x −=−=−，且()()()00,21g f x g x =++−=， 即()()21f x g x +−=①， 用x −替换()()21f x g x ++−=中的x ，得()()21f x g x −+=②， 由①+②得()()222f x f x ++−=， 所以()f x 的图象关于点(2,1)对称，且()21f =，故A 正确；由()()222f x f x ++−=，可得()()()()()42,422f x f x f x f x f x ++−=+=−−=−， 所以()()()()82422f x f x f x f x +=−+=−−= ， 所以()f x 是以8为周期的周期函数，故B 正确； 由①知()()21g x f x =+−，则()()()()882121g x f x f x g x +=++−=+−=，故()()8g x g x +=，因此()g x 也是以8为周期的周期函数， 所以()()202400g g ==，C 正确；又因为()()42f x f x ++−=，所以()()42f x f x ++=， 令2x =，则有()()262f f +=，令10x =，则有()()10142,f f +=…， 令8090x =，则有()()809080942f f +=， 所以1012(2)(6)(10)(14)(8090)(8094)2222024f f f f f f ++++++=+++=个所以20241(42)(2)(6)(10)(14)(8090)(8094)2024k f k f f f f f f =−=++++++=∑ ，故D 错误.故选：ABC【点睛】方法点睛：求解函数奇偶性、对称性、周期性等函数性质综合问题时，经常利用其中两个性质推得第三个性质特征，再进行相关计算.三､填空题：本题共3小题，每小题5分，共15分.12. 6(31)x y +−的展开式中2x y 的系数为______． 【答案】180− 【解析】【分析】根据题意，由条件可得展开式中2x y 的系数为213643C C (1)⋅−，化简即可得到结果． 【详解】在6(31)x y +−的展开式中， 由()2213264C C 3(1)180x y x y ⋅⋅−=−，得2x y 的系数为180−. 故答案为：180−．13. 已知函数()f x 是定义域为R 的奇函数，当0x >时，()()2f x f x ′−>，且()10f =，则不等式()0f x >的解集为__________.【答案】()()1,01,−∪+∞ 【解析】【分析】根据函数奇偶性并求导可得()()f x f x ′′−=，因此可得()()2f x f x ′>，可构造函数()()2xf x h x =e并求得其单调性即可得()f x 在()1,+∞上大于零，在()0,1上小于零，即可得出结论. 【详解】因为()f x 为奇函数，定义域为R ，所以()()f x f x −=−，两边同时求导可得()()f x f x ′′−−=−，即()()f x f x ′′−=且()00f =，又因为当0x >时，()()2f x f x ′−>，所以()()2f x f x ′>. 构造函数()()2xf x h x =e，则()()()22x f x f x h x ′−′=e ， 所以当0x >时，()()0,h x h x ′>在()0,∞+上单调递增，又因为()10f =，所以()()10,h h x =在()1,+∞上大于零，在()0,1上小于零， 又因为2e 0x >，所以()f x 在()1,+∞上大于零，在()0,1上小于零， 因为()f x 为奇函数，所以()f x 在(),1∞−−上小于零，在()1,0−上大于零， 综上所述，()0f x >的解集为()()1,01,−∪+∞. 故答案为：()()1,01,−∪+∞14. 已知点C 为扇形AOB 的弧AB 上任意一点，且60AOB ∠=，若(),R OC OA OB λµλµ=+∈，则λµ+的取值范围是__________.【答案】【解析】【分析】建系设点的坐标，再结合向量关系表示λµ+，最后应用三角恒等变换及三角函数值域求范围即可. 【详解】方法一：设圆O 的半径为1，由已知可设OB 为x 轴的正半轴，O 为坐标原点，过O 点作x 轴垂线为y 轴建立直角坐标系，其中()()1,1,0,cos ,sin 2A B C θθ ，其中π,0,3BOC θθ ∠=∈ ， 由(),R OC OA OB λµλµ=+∈，即()()1cos ,sin 1,02θθλµ =+，整理得1cos sin 2λµθθ+=，解得cos λµθ=，则ππcos cos ,0,33λµθθθθθ+=++=+∈，ππ2ππ,,sin 3333θθ+∈+∈所以λµ +∈ . 方法二：设k λµ+=，如图，当C 位于点A 或点B 时，,,A B C 三点共线，所以1k λµ=+=； 当点C 运动到AB的中点时，k λµ=+，所以λµ +∈故答案为：四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ，已知22cos a b c B +=． （1）求角C ；（2）若角C 的平分线CD 交AB于点,D AD DB =，求CD 的长．【答案】（1）2π3C = （2）3CD = 【解析】【分析】（1）利用正弦定理及两角和的正弦定理整理得到()2cos 1sin 0C B +=，再利用三角形的内角及正弦函数的性质即可求解；（2）利用正弦定理得出3b a =，再由余弦定理求出4a =，12b =，再根据三角形的面积建立等式求解． 【小问1详解】 由22cos a b c B +=，根据正弦定理可得2sin sin 2sin cos A B C B +=，则()2sin sin 2sin cos B C B C B ++=，所以2sin cos 2cos sin sin 2sin cos B C B C B C B ++=，整理得()2cos 1sin 0C B +=， 因为,B C 均为三角形内角，所以(),0,π,sin 0B C B ∈≠， 因此1cos 2C =−，所以2π3C =． 【小问2详解】因为CD 是角C的平分线，AD DB=所以在ACD 和BCD △中，由正弦定理可得，,ππsin sin sin sin 33AD CD BD CDA B ==， 因此sin 3sin BADA BD==，即sin 3sin B A =，所以3b a =， 又由余弦定理可得2222cos c a b ab C =+−，即222293a a a =++， 解得4a =，所以12b =．又ABCACD BCD S S S =+△△△，即111sin sin sin 222ab ACB b CD ACD a CD BCD ∠∠∠=⋅⋅+⋅⋅， 即4816CD =，所以3CD =． 16. 已知1ex =为函数()ln af x x x =的极值点． （1）求a 的值； （2）设函数()ex kxg x =，若对()120,,x x ∀∈+∞∃∈R ，使得()()120f x g x −≥，求k 的取值范围． 【答案】（1）1a = （2）(]()10,−∞−+∞ , 【解析】【分析】（1）直接根据极值点求出a 的值；（2）先由（1）求出()f x 的最小值，由题意可得是求()g x 的最小值，小于等于()f x 的最小值，对()g x 求导，判断由最小值时的k 的范围，再求出最小值与()f x 最小值的关系式，进而求出k 的范围． 【小问1详解】()()111ln ln 1a a f x ax x x x a x xα−−==′+⋅+，由1111ln 10e e e a f a −=+=′，得1a =， 当1a =时，()ln 1f x x =′+，函数()f x 在10,e上单调递减，在1,e∞ +上单调递增， 所以1ex =为函数()ln af x x x =的极小值点， 所以1a =． 【小问2详解】由（1）知min 11()e ef x f ==−． 函数()g x 的导函数()()1e xg x k x −=−′ �若0k >，对()1210,,x x k ∞∀∈+∃=−，使得()()12111e 1e k g x g f x k=−=−<−<−≤，即()()120f x g x −≥，符合题意． �若()0,0kg x =，取11ex =，对2x ∀∈R ，有()()120f x g x −<，不符合题意．�若0k <，当1x <时，()()0,g x g x ′<在(),1∞−上单调递减；当1x >时，()()0,g x g x ′>在(1,+∞)上单调递增，所以()min ()1ekg x g ==， 若对()120,,x x ∞∀∈+∃∈R ，使得()()120f x g x −≥，只需min min ()()g x f x ≤， 即1e ek ≤−，解得1k ≤−． 综上所述，k 的取值范围为(](),10,∞∞−−∪+．17. 已知四棱锥P ABCD −中，平面PAB ⊥底面,ABCD AD ∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥==为AB 的中点，F 为棱PC 上异于,P C 的点．（1）证明：BD EF ⊥；（2）试确定点F 的位置，使EF 与平面PCD【答案】（1）证明见解析 （2）F 位于棱PC 靠近P 的三等分点 【解析】【分析】（1）连接,,PE EC EC 交BD 于点G ，利用面面垂直的性质定理和三角形全等，即可得证； （2）取DC 的中点H ，以E 为坐标原点，分别以,,EB EH EP 所在直线为,,x y z 轴建立，利用线面角公式代入即可求解．小问1详解】如图，连接,,PE EC EC 交BD 于点G ．因为E 为AB 的中点，PA PB =，所以PE AB ⊥．因为平面PAB ⊥平面ABCD ，平面PAB ∩平面,ABCD AB PE =⊂平面PAB ， 所以PE ⊥平面ABCD ，因为BD ⊂平面ABCD ，所以PE BD ⊥．因为ABD BCE ≅ ，所以CEB BDA ∠∠=，所以90CEB ABD ∠∠+= ， 所以BD EC ⊥，因为,,PE EC E PE EC ∩=⊂平面PEC ， 所以BD ⊥平面PEC ．因为EF ⊂平面PEC ，所以BD EF ⊥． 【小问2详解】如图，取DC 的中点H ，以E 为坐标原点，分别以,,EB EH EP 所在直线为,,x y z 轴建立空间直角坐标系，【设2AB =，则2,1,BC AD PA PB ====则()()()()0,0,1,1,2,0,1,1,0,0,0,0P C D E −，设(),,,(01)F x y z PF PC λλ=<<， 所以()(),,11,2,1x y z λ−=−，所以,2,1x y z λλλ===−，即(),2,1F λλλ−．则()()()2,1,0,1,2,1,,2,1DC PC EF λλλ==−=−，设平面PCD 的法向量为(),,m a b c =，则00DC m PC m ⋅=⋅=，，即2020a b a b c += +−= ，，取()1,2,3m =−− ， 设EF 与平面PCD 所成的角为θ，由cos θ=sin θ=．所以sin cos ,m EF m EF m EF θ⋅===整理得2620λλ−=，因为01λ<<，所以13λ=，即13PF PC = ，故当F 位于棱PC 靠近P 的三等分点时，EF 与平面PCD18. 在平面直角坐标系xOy 中，抛物线21:2(0)C ypx p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长，点P 在抛物线1C 上，圆222:(2)E x y r −+=（其中01r <<）.（1）若1,2r Q =为圆E 上的动点，求线段PQ 长度的最小值；（2）设()1,D t 是抛物线1C 上位于第一象限的一点，过D 作圆E 的两条切线，分别交抛物线1C 于点,M N .证明：直线MN 经过定点.【答案】（1（2）证明见解析【解析】【分析】（1）根据椭圆的短轴可得抛物线方程2y x =，进而根据两点斜率公式，结合三角形的三边关系，即可由二次函数的性质求解，（2）根据两点坐标可得直线,MN DM 的直线方程，由直线与圆相切可得,a b 是方程()()()2222124240r x r x r −+−+−=的两个解，即可利用韦达定理代入化简求解定点. 【小问1详解】 由题意得椭圆的方程：221116y x +=，所以短半轴14b = 所以112242p b ==×=，所以抛物线1C 的方程是2y x =. 设点()2,P t t ，则111222PQ PE ≥−=−=≥， 所以当232ι=时，线段PQ . 【小问2详解】()1,D t 是抛物线1C 上位于第一象限的点，21t ∴=，且()0,1,1t D >∴设()()22,,,M a a N b b ，则： 直线()222:b a MN y a x a b a −−=−−，即()21y a x a a b −=−+，即()0x a b y ab −++=. 直线()21:111a DM y x a −−=−−，即()10x a y a −++=. 由直线DMr =，即()()()2222124240r a r a r −+−+−=..同理，由直线DN 与圆相切得()()()2222124240r b r b r −+−+−=. 所以,a b 是方程()()()2222124240r x r x r −+−+−=的两个解， 22224224,11r r a b ab r r −−∴+==−− 代入方程()0x a b y ab −++=得()()222440x y r x y +++−−−=， 220,440,x y x y ++= ∴ ++= 解得0,1.x y = =− ∴直线MN 恒过定点()0,1−.【点睛】圆锥曲线中定点问题的两种解法（1）引进参数法：先引进动点的坐标或动线中系数为参数表示变化量，再研究变化的量与参数何时没有关系，找到定点.（2）特殊到一般法：先根据动点或动线的特殊情况探索出定点，再证明该定点与变量无关.技巧：若直线方程为()00y y k x x −=−,则直线过定点()00,x y ;若直线方程为y kx b =+ (b 为定值),则直线过定点()0,.b 19. 龙泉游泳馆为给顾客更好的体验，推出了A 和B 两个套餐服务，顾客可选择A 和B 两个套餐之一，并在App 平台上推出了优惠券活动，下表是该游泳馆在App 平台10天销售优惠券情况． 日期t 1 2 3 4 5 6 7 8 9 10 销售量千张 1.9 1.98 2.2 2.36 2.43 259 2.68 2.76 2.7 0.4经计算可得：10101021111 2.2,118.73,38510i i i i i i i y y t y t ======∑∑∑. （1）因为优惠券购买火爆，App 平台在第10天时系统出现异常，导致当天顾客购买优惠券数量大幅减少，已知销售量y 和日期t 呈线性关系，现剔除第10天数据，求y 关于t 的经验回归方程结果中的数值用分数表示；..（2）若购买优惠券的顾客选择A 套餐的概率为14，选择B 套餐的概率为34，并且A 套餐可以用一张优惠券，B 套餐可以用两张优惠券，记App 平台累计销售优惠券为n 张的概率为n P ，求n P ；（3）记（2）中所得概率n P 的值构成数列{}()Nn P n ∗∈. ①求n P 的最值；②数列收敛的定义：已知数列{}n a ，若对于任意给定的正数ε，总存在正整数0N ，使得当0n N >时，n a a ε−<，（a 是一个确定的实数），则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛．参考公式： ()()()1122211ˆˆ,n ni ii i i i n n ii i i x x y y x y nx y ay bx x x x nx ====−−−==−−−∑∑∑∑. 【答案】（1）673220710001200y t + （2）433774n n P =+⋅−（3）①最大值为1316，最小值为14；②证明见解析 【解析】 【分析】（1）计算出新数据的相关数值，代入公式求出 ,ab 的值，进而得到y 关于t 的回归方程； （2）由题意可知1213,(3)44n n n P P P n −−=+≥，其中12113,416P P ==，构造等比数列，再利用等比数列的通项公式求解；（3）①分n 为偶数和n 为奇数两种情况讨论，结合指数函数的单调性求解；②利用数列收敛的定义，准确推理、运算，即可得证． 【小问1详解】 解：剔除第10天的数据，可得2.2100.4 2.49y ×−==新， 12345678959t ++++++++=新， 则9922111119.73100.4114,73,38510285i i i i t y t = =−×==−= ∑∑新新，所以912922119114,7395 2.4673ˆ2859560009i i i i t y t y b t t == − −×× ==−× − ∑∑新新新新新， 可得6732207ˆ 2.4560001200a =−×=，所以6732207ˆ60001200y t +. 【小问2详解】 解：由题意知1213,(3)44n n n P P P n −−=+≥，其中12111313,444416P P ==×+=， 所以11233,(3)44n n n n P P P P n −−−+=+≥，又由2131331141644P P ++×， 所以134n n P P − +是首项为1的常数列，所以131,(2)4n n P P n −+=≥ 所以1434(),(2)747n n P P n −−=−−≥，又因为1414974728P −=−=−， 所以数列47n P − 是首项为928−，公比为34−的等比数列， 故1493()7284n n P −−=−−，所以1934433()()2847774n n n P −=−−+=+−. 【小问3详解】 解：①当n 为偶数时，19344334()()28477747n n n P −=−−+=+⋅>单调递减， 最大值为21316P =； 当n 为奇数时，19344334()()28477747n n n P −=−−+=−⋅<单调递增，最小值为114P =， 综上可得，数列{}n P 的最大值为1316，最小值为14. ②证明：对任意0ε>总存在正整数0347[log ()]13N ε=+，其中 []x 表示取整函数， 当 347[log ()]13n ε>+时，347log ()34333333()()()7747474n n n P εε−=⋅−=⋅<⋅=， 所以数列{}n P 收敛.【点睛】知识方法点拨：与新定义有关的问题的求解策略：1、通过给出一个新的定义，或约定一种新的运算，或给出几个新模型来创设新问题的情景，要求在阅读理解的基础上，依据题目提供的信息，联系所学的知识和方法，实心信息的迁移，达到灵活解题的目的；2、遇到新定义问题，应耐心读题，分析新定义的特点，弄清新定义的性质，按新定义的要求，“照章办事”，逐条分析、运算、验证，使得问题得以解决.方法点拨：与数列有关的问题的求解策略：3、若新定义与数列有关，可得利用数列的递推关系式，结合数列的相关知识进行求解，多通过构造的分法转化为等差、等比数列问题求解，求解过程灵活运用数列的性质，准确应用相关的数列知识.。

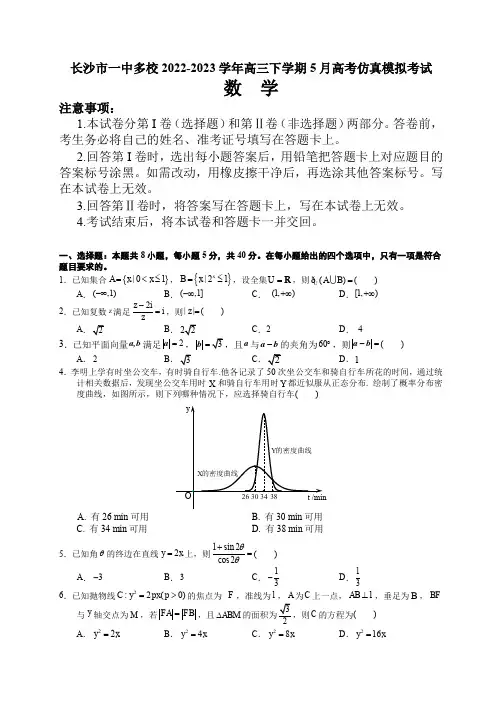
长沙市一中多校2022-2023学年高三下学期5月高考仿真模拟考试数 学注意事项：1.本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答第I 卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3.回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。

4.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{}|01A x x =<≤，{}|21xB x =≤，设全集U =R ，则()U AB =ð( ) A ．(,1)-∞ B ．(,1]-∞C ． (1,)+∞D ．[1,)+∞2．已知复数z 满足2ii z z-=，则||z =( )AB．C ．2 D ． 43．已知平面向量a,b 满足2=a，=b ，且a 与-a b 的夹角为60︒，则-=a b ( )A ．2 B．CD ．14．李明上学有时坐公交车，有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间，通过统计相关数据后，发现坐公交车用时X 和骑自行车用时Y 都近似服从正态分布. 绘制了概率分布密度曲线，如图所示，则下列哪种情况下，应选择骑自行车( )A. 有26 min 可用B. 有30 min 可用C. 有34 min 可用D. 有38 min 可用5．已知角θ的终边在直线2y x =上，则1sin 2cos2θθ+=( )A ．3-B ．3C ．1- D ．17．如图，一个由四根细铁杆PA 、PB 、PC 、PD 组成的支架（PA 、PB 、PC 、PD 按照逆时针排布），若π3APB BPC CPD DPA ∠=∠=∠=∠=，一个半径为1的球恰好放在支架上与四根细铁杆均有接触，则球心O 到点P 的距离是( )A ．2B ．32C ．D ．8．已知实数,,p q r 满足：()()()527395log (23)log 53,log (35)log 75,log (57)log 79.p p p p q qr r r q r q ⎧+=-⎪⎪+=-⎨⎪⎪+=-⎩则( )A ．p q r <<B ．r p q <<C ．p r q <<D ．r q p <<二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符15.直线:240l x y ＋－＝与椭圆11x y m m+=+(m >0)有且仅有一个公共点P ，则m ＝ ，点P 的坐四、解答题：本题共6小题，共70分。

2023-2024学年湖南省长沙一中高一（下）第三次月考数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.若复数a +3i2+i 是纯虚数，则实数a =( )A. −32B. 32C. −23D. 232.某校举行“勇士杯”学生篮球比赛，统计高一年级部分班级的得分数据如下： 班级12345678得分2834343026282832则下列说法正确的是( )A. 得分的众数为34 B. 得分的中位数为28C. 得分的75%分位数为33D. 得分的极差为63.已知平面α、β，直线l ⊂α，直线m 不在平面α上，下列说法正确的是( )A. 若α//β，m//β，则l//m B. 若α//β，m ⊥β，则l ⊥m C. 若l//m ，α//β，则m//βD. 若l ⊥m ，m//β，则α⊥β4.已知a >0，b >0，则“a +b >1”是“ab >14”( )A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.已知正六棱柱ABCDEF−A 1B 1C 1D 1E 1F 1的所有棱长均为1，则这个棱柱侧面对角线E 1D 与BC 1所成的角的余弦值为( )A. 12B.64C. 14D. 06.已知cos (α+π8)+2cos(α−3π8)=0，则tan (2α+π4)=( )A. 12B. 43C. −1D. −437.已知m ∈R ，若函数f(x)=1x +1−mx−m−3(−1<x ≤0)在定义域内有且仅有两个不同的零点，则m 的取值范围是( )A. (−94,−2)B. (−94,−2]C. (−114,−2)D. (−114,−2]8.已知集合I ⊆{a|a =(x,y)，x ，y ∈R}，若对于任意m ，n ∈I ，以及任意λ∈[0,1]，满足λm +(1−λ)n ∈I ，则称集合I 为“类圆集”.下列说法正确的是( )A. 集合A ={a|a =(x,y)，y ≥x 3}为“类圆集”B. 集合B ={a|a =(x,y)，y ≤lnx}为“类圆集”C. 集合C ={a|a =(x,y)，y ≥x 2}不为“类圆集”D. 若A ，B 都是“类圆集”，则A ∪B 也一定是“类圆集”二、多选题：本题共3小题，共18分。

长沙市一中2024届高三月考试卷（七）数学试卷一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．样本数据15、13、12、31、29、23、43、19、17、38的中位数为（）A ．19B ．23C ．21D ．182．已知集合{}22e 1x xA x -=≤，{}1,0,1B =-，则集合A B 的非空子集个数为（）A ．4B ．3C ．8D ．73．已知实部为3的复数z 满足()12i z ⋅-为纯虚数，则z =（）A ．2B ．32C ．352D 4．已知数列{}n a 满足()*3,n a n b n b =-∈∈N R ，则“3b <”是“{}n a 是递增数列”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．已知tan 2θ=，则22sin 22cos 4sin θθθ=+（）A ．13B ．2C ．1D ．296．过抛物线()2:20E y px p =>的焦点F 的直线交E 于点A ，B ，交E 的准线l 于点C ，AD l ⊥，点D 为垂足．若F 是AC 的中点，且3AF =，则AB =（）A ．4B ．C ．D ．37．已知双曲线22:1C kx y -=的左焦点为F ，()()3,40P m m m ->为C 上一点，且P 与F 关于C 的一条渐近线对称，则C 的离心率为（）A ．2B ．C ．2D 8．已知函数()f x 的定义域为R ，且满足()()34f x f x +-=，()f x 的导函数为()g x ，函数()1y g x =-的图象关于点()2,1中心对称，则()320242f g ⎛⎫+= ⎪⎝⎭（）A ．3B ．3-C ．1D ．1-二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．9．已知函数()11cos 2sin 222f x x x =+，则（）A ．函数8f x π⎛⎫- ⎪⎝⎭关于原点对称B ．曲线()y f x =的对称轴为122k x ππ=+，k ∈Z C ．()f x 在区间5,88ππ⎛⎫⎪⎝⎭单调递减D ．曲线()y f x =在点()()0,0f 处的切线方程为2210x y -+=10．已知二面角A —CD —B 的大小为23π，AC CD ⊥，BD CD ⊥，且1CD =，2AC BD +=，则（）A ．ABC △是钝角三角形B ．异面直线AD 与BC 可能垂直C ．线段AB 长度的取值范围是⎡⎣D ．四面体A —BCD 体积的最大值为411．甲、乙两同学参加普法知识对抗赛，规则是每人每次从题库中随机抽取一题回答．若回答正确，得1分，答题继续；若回答错误，得0分，同时换成对方进行下一轮答题．据经验统计，甲、乙每次答题正确的概率分别是12和23，且第1题的顺序由抛掷硬币决定．设第i 次答题者是甲的概率为i P ，第i 次回答问题结束后中甲的得分是i K ，则（）A ．214P =B ．()25124PK ==C ．11163i i P P +=+D ．()()1122i i i EK P K i -=+≥三、填空题：本题共3小题，每小题5分，共15分．12．()()83x y x y +-的展开式中36x y 的系数为______．13．已知动点P 在圆()()22:11M x m y m -++-=上，动点Q 在曲线ln y x =上．若对任意的m ∈R ，PQ n ≥恒成立，则n 的最大值是______．14．已知正六棱锥的高是底面边长的倍，侧棱长为，正六棱柱内接于正六棱锥，即正六棱柱的所有顶点均在正六棱锥的侧棱或底面上，则该正六棱柱的外接球表面积的最小值为______．四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．盒中有形状、大小均相同的卡片6张，卡片依次标记数字1，2，2，3，3，3．（1）若随机一次取出两张卡片，求这两张卡片标记数字之差为1的概率；（2）若每次随机取出两张卡片后不放回，直到将所有标记数字为2的卡片全部取出，记此时盒中剩余的卡片数量X ，求X 的分布列和()E X ．16．如图三棱锥P —ABC 中，PA BC =，AB PC =，AC PB ⊥．（1）证明：AB BC =；（2）若平面PAC ⊥平面ABC ，AC =，求二面角A —PB —C 的余弦值．17．已知定义在()0,π上的函数()2cos sin f x x x =+．（1）求()f x 的极大值点；（2）证明：对任意()0,1x ∈，()42114f x x x >-+．18．已知椭圆()2222:10x y C a b a b+=>>的上、下顶点分别为()0,1A ，()0,1B -，其右焦点为F ，且FA BA FA FB ⋅=⋅．（1）求椭圆C 的方程；（2）若点()2,1P -，在直线BP 上存在两个不同的点1P ，2P 满足212PP PP PB ⋅= ．若直线1AP 与直线2AP 分别交C 于点M ，N （异于点A ），证明：P ，M ，N 三点共线．19．定义ABC △三边长分别为a ，b ，c ，则称三元无序数组(),,a b c 为三角形数．记D 为三角形数的全集，即(),,a b c D ∈．（1）证明：“(),,a b c D ∈”是“D ∈”的充分不必要条件；（2）若锐角ABC △内接于圆O ，且0xOA yOB zOC ++=，设()(),,,,0I x y z x y z =>．①若()3,4,5I =，求:AOB AOC S S △△；②证明：I D ∈．长沙市一中2024届高三月考试卷（七）数学参考答案一、选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）题号12345678答案CBCADADA1．C 【解析】将这10个数据从小到大排列为12，13，15，17，19，23，29，31，38，43，所以这组数据的中位数是1923212+=．故选：C ．2．B 【解析】因为{}{}22002A x x x x x =-≤=≤≤，{}1,0,1B =-，因此{}0,1A B = ．故该集合的非空子集个数为2213-=个，故选：B ．3．C 【解析】由题意可设3i z b =+，则()()()()12i 3i 12i 326i z b b b ⋅-=+⋅-=++-，所以320,60,b b +=⎧⎨-≠⎩解得32b =-，故2z ==，故选：C ．4．A 【解析】当3b <时，30n a n b =->，则330n a n b n b =-=->，所以{}n a 是递增的等差数列；反之，数列{}n a 递增，则20a >，且12a a <，解得92b <．所以“3b <”是“{}n a 是递增数列”的充分不必要条件．故选A ．5．D 【解析】由题意可得tan 2θ=，所以22222sin 22sin cos 2tan 422cos 4sin 2cos 4sin 24tan 2449θθθθθθθθθ====++++⨯，故选D ．6．A 【解析】如图，设准线l 与x 轴交于点M ．由抛物线的定义知3AD AF ==．因为F 是线段AC 的中点，所以22AD MF p ==，所以23p =，解得32p =，所以抛物线E 的方程为23y x =．由112cos 2AD AFx AF ∠==，得60AFx ∠=︒．直线AF的方程为34y x ⎫=-⎪⎭，将此方程与23y x =联立后消去y 并整理，得2164090xx -+=，设()11,A x y ，()22,B x y ，则1252x x +=，所以1253422AB x x p =++=+=．故选A．7．D 【解析】双曲线C 的方程可设为22221x y a b-=，222a b c +=，0a >，0b >，0c >，左焦点为F ，O 为坐标原点，连接OP ．因为双曲线221kx y -=上的一点()()3,40P m m m ->与C 的左焦点F 关于C的一条渐近线对称，所以5OP OF c m ===，则()5,0F m -．又直线PF 的斜率为()41352m m m -=---，直线PF 与渐近线垂直，所以该条渐近线的斜率为2b a =，所以2224c a a -=，则225c a=，所以C的离心率c e a ==．故选D ．8．A 【解析】因为()()34f x f x +-=，则函数()f x 的图象关于点3,22⎛⎫⎪⎝⎭中心对称，且322f ⎛⎫= ⎪⎝⎭．由()()30f x f x ''--=，()()f x g x '=，得()()3g x g x =-，所以函数()g x 的图象关于32x =对称，()()12g g =．根据图象变换的规律，由()1y g x =-的图象关于点()2,1中心对称，得()g x 的图象关于点()1,1中心对称，()11g =，则()g x 的周期为34122T ⎛⎫=⨯-= ⎪⎝⎭，()()()2024211g g g ===，故()320242132f g ⎛⎫+=+= ⎪⎝⎭．故选A ．二、选择题（本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）题号91011答案ACDACBCD9．ACD 【解析】由题意可得()11cos 2sin 2sin 22224f x x x x π⎛⎫=+=+ ⎪⎝⎭．对于选项A ：sin 2sin 282442f x x x πππ⎛⎫⎛⎫-=+-= ⎪ ⎪⎝⎭⎝⎭为奇函数，关于原点对称，故A 正确；对于选项B ：令242x k πππ+=+，k ∈Z ，得82k x ππ=+，k ∈Z ，故B 错误；对于选项C ：对于()sin 224f x x π⎛⎫=+ ⎪⎝⎭，令24t x π=+，则sin 2y t =，因为5,88x ππ⎛⎫∈⎪⎝⎭，所以32,422t x πππ⎛⎫=+∈ ⎪⎝⎭，而sin 2y t =在3,22ππ⎛⎫⎪⎝⎭上单调递减，所以函数()f x 在区间5,88ππ⎛⎫⎪⎝⎭上单调递减，故C 正确；对于选项D ：易得()102f =，()24f x x π⎛⎫'=+ ⎪⎝⎭，()01f '=，故曲线()y f x =在点()()0,0f 处的切线方程为2210x y -+=，故D 正确，故选：ACD ．10．AC 【解析】因为()2cos 03DA DB DC CA DB CA DB CA DB π⋅=+⋅=⋅=< ，所以ADB ∠是钝角，则ABD △是钝角三角形，故A 正确；因为()()22cos 103AD BC AC CD BD CD AC BD CD AC BD π⋅=+⋅-=⋅-=-< ，所以异面直线AD 与BC 不可能垂直，故B 错误；()222222221AB AC CD DBAC CD DB AC DB AC DB AC DB =++=+++⋅=+++ ()21AC DBAC DB =+-+．设AC x =，由2AC BD +=，得2BD x =-，其中02x <<，所以()2222514AB x x x =-+=-+，则线段AB 长度的取值范围是⎡⎣，故C 正确；四面体A －BCD 的体积为211sin 3231212212AC BD CD BD AC AC BD π+⎛⎫⨯⨯⨯⨯⨯=⋅≤⨯= ⎪⎝⎭，当且仅当1AC BD ==时，等号成立，故D 错误．故选AC ．11．BCD 【解析】设“第i 次答题者是甲，且甲答对”为事件i A ，“第i 次答题者是乙，且乙答对”为事件i B ，第2次答题是甲分两类：①第一次是甲，且甲回答正确；②第一次是乙，且乙回答错误，所以()()21111115222312P A P A B =+=⨯+⨯=，故A 错误；()()212121111115122223224P K P A A B A =+=⨯⨯+⨯⨯=，故B 正确；第1i +次答题者是甲包含两种情况：①甲第i 次回答，且回答正确；②乙第i 次回答，且回答错误，所以()1111112363i i i i P P P P +=⋅+-⋅=+，故C 正确；第i 次答题结束后，甲得分可分为两种情况：①第i 次答题后甲的得分加上1分，则第i 次必由甲答题且得1分；②第i 次答题后甲的得分加上0分，则第i 次由甲答题且不得分或第i 次由乙答题，所以()()11111111222i i i i i i i i E K P K P P K P K ---⎛⎫=+++-=+ ⎪⎝⎭，其中2i ≥，故D 正确．故选BCD ．三、填空题（本题共3小题，每小题5分，共15分）12．140-【解析】()8x y -的展开式的通项为()88C rrrxy --，所以原式的展开式中含36x y 的项为()()65625388C 3C x x y y x y ⋅-+⋅-，所以36x y 的系数为()56588C 3C 1140+-=-．131-【解析】由题意可知M 的圆心()1,M m m -在直线1y x =+上，曲线ln y x =在1x =处的切线与之平行，故曲线ln y x =上的动点Q 到直线1y x =+，因此min 1PQ =，故n 1-．14．3π【解析】设正六棱锥为P —ABCDEF ，底面中心为2O ，正六棱柱为111111222222A B C D E F A B C D E F -，其中与底面重合的面为222222A B C D E F ，面111111A B C D E F 的中心为1O ，外接球球心为O ，由题意得，面222222A B C D E F 的中心为2O ，面111111A B C D E F 的边均在正六棱锥的侧棱上．作截面PAD 的平面图，由题意得，2AP ===，所以21AO =，2PO =．设22A O x =，21AA x =-，由题意得tan A =，故)1221A A x ==-，)212112OO A A x ==-，外接球半径的平方222222222233463444R A O A O OO x x x ⎛⎫==+=-+=-+ ⎪⎝⎭，当且仅当34x =时取得最小值34，此时外接球表面积243SR ππ==，故正六棱柱的外接球表面积的最小值为3π．四、解答题（本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤）15．【解析】（1）若取出的两张卡片标记数字分别为1和2，此时126122C 15P ⨯==，若取出的两张卡片标记数字分别为2和3，此时226232C 5P ⨯==，故这两张卡片标记数字之差为1的概率12815P P P =+=；（2）由题意可得X 所有可能取值为0，2，4，其中()26114C 15PX ===，()2422226464C 1241312C C C C 3P X ⨯⨯==⨯+⨯=，()()()301425P X P X P X ==-=-==，故X 的分布列为X 024P3513115()31114024531515E X =⨯+⨯+⨯=．16．【解析】（1）作PO AC ⊥，O 为垂足，由AC PB ⊥，AC PO ⊥，PB PO P = ，PB PBO ⊂平面，PO PBO ⊂平面得，AC PBO ⊥平面，∴AC BO ⊥，又PA BC =，PC BA =，AC AC =，∴PAC BCA ≌△△，∴PO BO =，AO CO ===，∴O 为AC 中点，∴PA PC =，BA BC =；（2）由（1）BO AC ⊥，又平面PAC ABC AC = 平面，BO ABC ⊂平面，∴BO APC ⊥平面，∴BO PO ⊥，∴PO ，BO ，AC 两两垂直．由AC =，AB BC =，得222cos 02AB BC AC ABC AB BC+-∠==⋅，∴2ABCπ∠=，以O 为原点建立如图所示的空间直角坐标系，不妨设2AC =，则()0,1,0A -，()1,0,0B ，()0,1,0C ，()0,0,1P ，()1,0,1PB =- ，()0,1,1PA =-- ，()0,1,1PC =-，令(),,m x y z = ，(),,n d l s =分别为平面APB ，平面PBC 的法向量，则0,0,m PB m PA ⎧⋅=⎪⎨⋅=⎪⎩ 即0,0,x z y z -=⎧⎨+=⎩令1x =得()1,1,1m =-为平面PAB 的一个法向量．0,0,n PB n PC ⎧⋅=⎪⎨⋅=⎪⎩ 即0,0,d s l s -=⎧⎨-=⎩令1d =得()1,1,1n =为平面PBC 的一个法向量．设θ为二面角A —PB —C 的平面角，则111cos cos ,3m n m n m n θ⋅===⋅，由图观察可得二面角所成角为钝角，故二面角A —PB —C 的余弦值为13-．17．【解析】（1）()()2sin cos cos cos 12sin f x x x x x x '=-+=-，x0,6π⎛⎫ ⎪⎝⎭6π,62ππ⎛⎫ ⎪⎝⎭2π5,26ππ⎛⎫ ⎪⎝⎭56π5,6ππ⎛⎫ ⎪⎝⎭()f x '＋0－0＋0－单调性↗极大值↘极小值↗极大值↘故()f x 有两个极值点，为6x π=和56x π=；（2）令()()42114h x f x x x =-+-，()()()22cos 12sin h x x x x x '=-+-，①当10,2x ⎛⎤∈ ⎥⎝⎦时，因为1026x π<≤<，所以1sin 2x <，()0h x '>成立，令()32r x x x =-+，则()232r x x '=-+，令()0r x '=，解得63x =（负值舍去），故()r x 在0,3⎛⎫ ⎪ ⎪⎝⎭上单调递增，,13⎛⎫ ⎪ ⎪⎝⎭上单调递减；②当1,23x ⎛∈ ⎝⎦时，()()7cos 12sin 8h x x x '>+-，令()sin F x x x =-，则()1cos 0F x x '=-≥恒成立，故()()00F x F >=，进一步()()715cos 122088h x x x x '>+->->；③当,13x ⎛⎫∈ ⎪ ⎪⎝⎭时，()()1cos 12sin 220h x x x x '>+->->，综上所述，()0h x '>在()0,1x ∈上恒成立，则()()00h x h >=，也即()42114f x x x >-+成立．【评分细则】1．第一问不用列出表格，只要求导后单调性和最终极值点分析正确即可满分2．第二问用其他方法证明出来也可以，根据具体方法酌情给分18．【解析】（1）由题意知1b =，由FA BA FA FB ⋅=⋅ ，得()0FA BA FB ⋅-=，即()()220BA FB BA FB BA FB +⋅-=-= ，所以AB BF =．又BF a =，所以22a b ==，故椭圆C 的方程为2214x y +=．（2）证明：因为点()2,1P -，所以2124PP PP PB ⋅== ．设()11,1P x -，()22,1P x -，则()()12224x x --=，即()()12122*x x x x =+．显然，直线MN 的斜率一定存在，设直线MN 的方程为y kx m =+，()33,M x y ，()44,N x y ，联立221,4x y y kx m ⎧+=⎪⎨⎪=+⎩得()222148440k x kmx m +++-=．则()()()222222641614116410k m k m k m ∆=-+-=-+>，且342814km x x k +=-+，23424414m x x k-=+．因为直线AM 过点()11,1P x -，所以31312y x x -=--，解得331332211x x x y kx m ==---+，同理可得42421x x kx m =--+．代入（*）式，得()()()3434121k x x m x x +=-+，所以()()()2124481k m km m +-=--．因为M ，N 异于点A ，所以1m ≠，从而()()1212k m km ++=，所以210k m ++=，则直线MN 的方程为21y kx k =--，恒过点()2,1P -，因此，P ，M ，N 三点共线．19．【解析】（1）(),,a b c D ∈，则a b c +>，即22+->，∴22+>+>D ∈成立，若D ∈+>a b c ++>，又因为a b +≥，则()2c a b <+，不能证明a b c +>．∴“(),,a b c D ∈”是“D ∈”的充分不必要条件．（2）①()3,4,5I =，则3450OA OB OC ++= ，∴2222222591624cos ,1692530cos ,OC OA OB OA OB AOB OB OA OC OA OC AOC ⎧=++⋅⋅∠⎪⎨⎪=++⋅⋅∠⎩又因为OA OB OC ==，∴cos 0,3cos 5AOB AOC ∠=⎧⎪⎨∠=-⎪⎩∴sin 1,4sin 5AOB AOC ∠=⎧⎪⎨∠=⎪⎩记R OA =，∴2211:sin :sin 5:422AOB AOC S S R AOB R AOC ⎛⎫⎛⎫=⋅∠⋅∠= ⎪ ⎪⎝⎭⎝⎭△△；②由zOC xOA yOB -=+ ，∴()222222cos z R x y xy AOB R ⋅=++∠⋅，∴222cos 2z x y AOB xy --∠=，∵()0,AOB π∠∈，即222112z x y xy---<<，∴()()222x y z x y -<<+，在∴x y z x y -<<+，同理得y z x y z -<<+，x z y x z -<<+，∴x ，y ，z 可组成三角形，∴I D ∈．。

2023级高一年级第二学期开学考试数学试题（答案在最后）时量：120分钟分值：150分考试内容：必修一，必修二第六章1-3节命题人：一､单项选择题：本题共8小题，每小题5分，共40分．在每个小题给出的四个选项中，只有一项是符合题目要求的．1.如图，U 是全集，,M N 是U 的两个子集，则图中的阴影部分可以表示为（）A.M N ⋂B.()UM N⋃ð C.()U M N⋂ð D.()U N M N ⋂⋂ð【答案】D 【解析】【分析】根据给定的图形，利用集合的交并补运算即可求解.【详解】观察图形知，阴影部分在集合N 中，且不在集合M ，在()U M N ⋂ð中，ABC 不可选，也不在M N ⋂中，所以阴影部分可表示为()U N M N ⋂⋂ð.故选：D 2.函数3ln y x x=-的零点所在区间是（）A.()3,4 B.()2,3 C.()1,2 D.()0,1【答案】B 【解析】【分析】根据解析式判断函数单调性，再应用零点存在性定理确定所在区间即可.【详解】由3,ln y y x x==-在(0,)+∞上递减，所以3ln y x x=-在(0,)+∞上递减，又3(2)ln 2ln 022f =-=>，e (3)1ln 3ln 03f =-=<，所以零点所在区间为()2,3.故选：B3.函数()3e 1x x f x =+的部分图象大致为（）A. B.C. D.【答案】B 【解析】【分析】由函数的奇偶性与函数值符号判断．【详解】∵函数()3e 1x x f x =+为非奇非偶函数，∴其图象既不关于原点对称，也不关于y 轴对称，故选项C 错误；当0x <时，()30e 1x x f x =<+，故A ，D 错误，故选：B4.已知()1,3P 为角α终边上一点，则()()()()2sin πcos πsin 2π2cos αααα-++=++-（）A.17-B.1C.2D.3【答案】B 【解析】【分析】应用诱导公式及由弦化切化简目标式为2tan 1tan 2αα-+，结合三角函数的定义求得tan 3α=，即可求值.【详解】由()()()()2sin πcos π2sin cos 2tan 1sin 2π2cos sin 2cos tan 2αααααααααα-++--==++-++，又tan 3α=，所以2tan 12311tan 232αα-⨯-==++.故选：B5.已知2169log 3,2,log 2a b c -===，则,,a b c 的大小关系为（）A.a c b >>B.c b a >>C.a b c >>D.c a b>>【答案】A 【解析】【分析】利用对数换底公式，结合对数函数性质及媒介数比较大小即得.【详解】依题意，1633111log 3log log 31627a ==>=，922111log 2log 9log 38c ==<=，又291log 2log 24c b -=>===，所以,,a b c 的大小关系为a c b >>.故选：A 6.已知()()1241,2(0,1)2,2x a x a x f x a a ax -⎧-++≤=>≠⎨>⎩．若()f x 存在最小值，则实数a 的取值范围为（）A.10,2⎛⎤ ⎥⎝⎦B.30,4⎛⎤ ⎥⎝⎦C.10,(1,2)2⎛⎤ ⎥⎝⎦D.30,(1,2)4⎛⎤⋃ ⎥⎝⎦【答案】A 【解析】【分析】通过对参数a 分类讨论，研究()f x 在(,2]-∞和(2,)+∞的单调性，再结合已知条件，即可求解.【详解】解：由题意，不妨令()(2)41g x a x a =-++，(,2]x ∈-∞；1()2x h x a -=，(2,)x ∈+∞，①当01a <<时，()(2)41g x a x a =-++在(,2]-∞上单调递减，1()2x h x a -=在(2,)+∞上单调递减，易知1()2x h x a -=在(2,)+∞上的值域为(0,2)a ，又因为()f x 存在最小值，只需(2)(2)2410g a a =-⨯++≤，解得12a ≤，又由01a <<，从而102a <≤；②当12a <<时，()(2)41g x a x a =-++在(,2]-∞上单调递减，1()2x h x a -=在(2,)+∞上单调递增，又因为()f x 存在最小值，故(2)(2)g h ≤，即(2)2412a a a -⨯++≤，解得，34a ≤，这与12a <<矛盾；③当2a =时，9,2()2,2x x f x x ≤⎧=⎨>⎩，易知()f x 的值域为(4,)+∞，显然()f x 无最小值；④当2a >时，()(2)41g x a x a =-++在(,2]-∞上单调递增，1()2x h x a -=在(2,)+∞上单调递增，从而()f x 无最小值.综上所述，实数a 的取值范围为10,2⎛⎤ ⎥⎝⎦.故选：A.7.如图，在ABC 中，1AC =，2AB =，60BAC ∠=︒，BC ，AB 边上的两条中线AD ，CE 相交于点P ，则cos DPE ∠=（）A.14B.7C.17D.14【答案】D 【解析】【分析】由题得ABC 为直角三角形，建立平面直角坐标系，将问题转化为求AD 与CE夹角的余弦即可.【详解】因为1AC =，2AB =，60BAC ∠=︒，由余弦定理得，2222cos 41221cos603BC AB AC AB AC BAC =+-⋅∠=+-⨯⨯⨯︒=，得到BC =，又222BC AC AB +=，所以ABC 为直角三角形，建立如图所示的平面直角坐标系，则有(1,0),3),(0,0)A B C ，又,D E 分别为,BC AB 中点，所以313(0,),(,)222D E ，故313(1,(,)222AD CE =-= ，所以13724cos cos ,143131444AD CEDPE AD CE AD CE-+⋅∠===⋅+⋅+，故选：D.8.已知点,024A π⎛⎫⎪⎝⎭在函数()()cos f x x ωϕ=+（0ω>且，*ω∈N ，0ϕπ<<）的图像上，直线6x π=是函数()f x 图像的一条对称轴.若()f x 在区间,63ππ⎛⎫⎪⎝⎭上单调，则ϕ=（）A.6π B.4π C.3πD.23π【答案】C 【解析】【分析】由()f x 在区间,63ππ⎛⎫⎪⎝⎭内单调求出ω的范围，先由函数零点与对称轴之间的关系求出周期，进而求得ω，利用对称轴即可求出ϕ.【详解】∵()f x 在区间,63ππ⎛⎫⎪⎝⎭内单调，3662T πππ∴-=≤，得1226ππω⨯≥，所以06ω<≤∵24x π=是函数()()cos f x x ωϕ=+的零点，直线6x π=是函数()f x 的图象的一条对称轴，∴6248πππ-=，若84T π=，则2T π=，此时22ππω=，得4ω=，满足条件，若384T π=，则6T π=，此时26ππω=，得12ω=，不满足条件，综上可知，函数()()cos 4f x x ϕ=+，∵6x π=是函数()f x 的图象的一条对称轴，∴4,6k k Z πϕπ⨯+=∈，即2,3k k Z πϕπ=-∈，∵0ϕπ<<，∴3πϕ=，故选：C【点睛】关键点点睛：本题主要考查三角函数性质的应用，结合的单调区间以及对称轴对称中心之间的关系求出周期和ω是解决本题的关键，属于一般题.二､多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.下列说法正确的是（）A.若不等式220ax x c ++>的解集为{}|12x x -<<，则2a c +=B.若命题p ：()0,x ∀∈+∞，1ln x x ->，则p 的否定为()0,x ∃∈+∞，1ln x x-≤C.已知函数()()()2511x ax x f x a x x⎧---≤⎪=⎨>⎪⎩在(),-∞+∞上是增函数，则实数a 的取值范围是[]3,1--D.已知()()2ln 21f x mx x =++.若()f x 的值域为R ，则实数m 的取值范围(]0,1【答案】AB 【解析】【分析】对于A ，不等式解集的端点即对应方程的根，可求出a ，c 判断正误；对于B ，使用含有一个量词的命题的否定的知识进行判断；对于C ，结合函数单调性的定义，结合分段函数单调性知识进行判断；对于D ，可使用复合函数的值域知识进行判断.【详解】对于A ，不等式220ax x c ++>的解集为{}12x x -<<，则1-和2是方程220ax x c ++=的两个根，故20440a c a c -+=⎧⎨++=⎩，解得2a =-，4c =所以2a c +=，故A 正确；对于B ，全称量词命题“x M ∀∈，()p x ”的否定为存在量词命题“x M ∃∈，()p x ⌝”因此命题():0,,1ln p x x x ∞∀∈+->，则其否定为()0,,1ln x x x ∃∈+∞-≤，故B 正确；对于C ，因为()f x 是增函数，需满足当1x ≤时，25y x ax =---为增函数，当1x >时，ay x=为增函数，且当1x =时，25a x ax x ---≤，所以12015a a a a⎧-≥⎪⎪<⎨⎪---≤⎪⎩，解得32a --≤≤，故C 不正确；对于D ，令ln y t =，221t mx x =++，()f x 的值域为R ，则ln y t =的值域为R ，即(0,)+∞为221t mx x =++值域的子集，当0m =时，21t x =+，值域为R ，满足题意，当0m ≠时，需00m >⎧⎨∆≥⎩，即0440m m >⎧⎨-≥⎩，解得01m <≤，综上所述，实数m 的取值范围是01m ≤≤，故D 不正确.故选：AB.10.下列说法正确的是（）A.函数()228f x x x =+-的零点是()()4,0,2,0-B.方程e 3x x =+有两个解C.函数313,log xy y x-==的图象关于y x =对称D.用二分法求方程3380x x +-=在()1,2x ∈内的近似解的过程中得到()()10, 1.50f f <>，()1.250f <，则方程的根落在区间()1,1.25上【答案】BC 【解析】【分析】对于A ，由零点的定义即可得解；对于BD ，由零点存在定理即可判断；对于C ，由互为反函数的两个函数图象的位置关系即可判断.【详解】对于A ，零点不是点，而是函数图象与x 轴交点的横坐标，故A 错误；对于B ，令()e 3xx f x =--，则()()232e10,3e 0f f ---=-<-=>，()()1010020,10e 1321310241310110f f =-<=->-=-=>，所以由零点存在定理可知()e 3xx f x =--（其图象连续不断）在()()3,2,0,10--内各有一个零点，故B正确；对于C ，若331log log 3xx y x y y -⇔-=⇔==，所以函数313,log xy y x-==互为反函数，所以函数313,log xy y x-==的图象关于y x =对称，故C 正确；由零点存在定理可知方程的根落在区间()1.25,1.5，故D 错误.故选：BC.11.给出下列命题，其中正确的选项有（）A.等边ABC 中，向量AC 与向量BC的夹角为60B.()2,1a =r ，()3,1b =- ，则向量a 在向量b 上的投影向量为31,22⎛⎫- ⎪⎝⎭C.非零向量,a b 满足a b a b ==- ，则a 与a b + 的夹角为30D.若()3,4OA =- ，()6,3OB =- ，()5,3OC m m =---，ABC ∠为锐角，则实数m 的取值范围为34m >-【答案】ABC 【解析】【分析】由向量夹角定义知A 正确；由投影向量定义，结合向量坐标运算知B 正确；根据向量线性运算的几何意义可确定C 正确；由cos BA BCABC BA BC⋅∠=⋅ ，根据ABC ∠为锐角可构造不等式组求得D 错误.【详解】对于A ，,AC BC C =∠ ，ABC 为等边三角形，,60AC BC ∴=，A 正确；对于B，cos ,2a b a a b b ⋅===- ，3,1,1010b b ⎛-==- ⎝⎭，a ∴r 在b 上的投影向量为31cos ,,22b a a b b ⎛⎫⋅=- ⎪⎝⎭，B 正确；对于C ，a b a b ==-，∴以,,a b a b - 构成如图所示的等边三角形ABC ，其中AB a =，AC b =，CB a b =- ，以,AB AC 为邻边作平行四边形ABCD ，则a b AD +=，四边形ABCD 为菱形，,a a b BAD ∴+=∠，又60CAB ∠= ，AD 平分CAB ∠，,30a a b BAD ∴+=∠=，C 正确；对于D ，()3,1BA OA OB =-=-- ，()1,BC OC OB m m =-=---，()()22cos 101BA BC ABC BA BC m m ⋅∴∠==⋅⋅--+- ABC ∠ 为锐角，cos 0cos 1ABC ABC ∠>⎧∴⎨∠≠⎩，解得：34m >-且12m ≠，D 错误.故选：ABC.12.已知函数()sin sin f x x x =⋅，则下列说法正确的是（）.A.()f x 是周期函数B.ππ,22⎡⎤-⎢⎣⎦是函数()f x 的一个单调递增区间C.若()()120f x f x +=，则()12πZ x x k k +=∈D.不等式sin 2πsin 2πcos 2πcos 2πx x x x ⋅>⋅的解集为15,88k k ⎛⎫++ ⎪⎝⎭，Z k ∈【答案】ABD 【解析】【分析】利用正弦型函数的图象与性质逐一判断即可.【详解】对于A ，因为()()()()2πsin 2πsin 2πsin sin f x x x x x f x +=+⋅+=⋅=，所以2π是()f x 的一个周期，正确；对于B ，因为()()()()sin sin sin sin f x x x x x f x -=-⋅-=-⋅=-，且函数()f x 的定义域为R ，所以()f x 是奇函数，当π0,2x ⎡⎤∈⎢⎥⎣⎦时，()21cos 2sin 2x f x x -==单调递增，又因为()f x 是奇函数且过原点，所以ππ,22⎡⎤-⎢⎥⎣⎦是函数()f x 的一个单调递增区间，正确；对于C ，由AB 可画出函数()f x 在ππ,22⎡⎤-⎢⎣⎦上的图象，又因为ππ22f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭，所以()f x 的图像关于π2x =对称，可画出函数()f x 在π3π,22⎡⎤⎢⎥⎣⎦上的图象，即得到函数()f x 在π3π,22⎡⎤-⎢⎥⎣⎦上的图象，即一个周期的图象，如图：则π13π1,4242f f ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭，满足π3π044f f ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭，但π3ππ442-+=，错误；对于D ，先求不等式sin 2πsin 2πcos 2πcos 2πx x x x ⋅>⋅在一个周期内的解集，取区间[]0,2π，因为sin 2πsin 2πcos 2πcos 2πx x x x ⋅>⋅，所以()π2π2π2f x f x ⎛⎫>+⎪⎝⎭，则π2π4π7π2π24x x ⎧>⎪⎪⎨⎪+<⎪⎩，则在整个定义域上有π2π2π4π7π2π2π24x k x k ⎧>+⎪⎪⎨⎪+<+⎪⎩，解得15,Z 88k x k k +<<+∈，正确.故选：ABD.【点睛】关键点点睛：对于新的三角函数，往往先画出一个周期的函数图象，进而得到整个函数图象，利用三角函数图象不仅解决三角函数性质问题，还可以解不等式、方程零点个数等问题.三､填空题：本题共4小题，每小题5分，共计20分．13.51log 22661611742log 3log 4cos4953π-⎛⎫⎛⎫⨯++-+= ⎪⎝⎭⎝⎭__________．【答案】9【解析】【分析】由指数与对数的运算法则以及诱导公式即可求解.【详解】原式512266log 2414[()]log 9log 4cos(6)753-π=⨯++-+π-16414()log 36cos723-π=⨯+-+1172922=+-+=故答案为：914.若扇形的弧长为8，圆心角为4rad ，则扇形的面积为__________.【答案】8【解析】【分析】由弧长公式求出扇形的半径r ，再由扇形的面积公式求解即可.【详解】解：8,4,l α== 2,lr α∴==182S rl ∴==.故答案为：815.a b c >>，*N n ∈，且11n a b b c a c+≥---恒成立，则n 的最大值为__．【答案】4【解析】【分析】将不等式变形分离出n ，不等式恒成立即n 大于等于右边的最小值；由于a c a b b c -=-+-，凑出两个正数的积是常数，利用基本不等式求最值．【详解】解：由于11n a b b c a c+≥---恒成立，且a c >即a c a cn a b b c --≤+--恒成立只要a c a cn a b b c--≤+--的最小值即可a c a c ab bc a b b ca b b c a b b c---+--+-+=+----2b c a ba b b c--=++--a b c>> 0a b ∴->，0b c ->，故4a c a c a b b c ⎛⎫--+≥ ⎪--⎝⎭，因此4n ≤故答案为：4．16.如图，ABC 是等边三角形，边长为2,P 是平面上任意一点．则()PA PB PC ⋅+的最小值为__________．【答案】32-【解析】【分析】取BC 的中点D ，AD 的中点O ，利用向量数量积的运算律计算即得.【详解】在边长为2的在ABC 中，取BC 的中点D ，连接AD 并取其中点O ，连接PO ，则1322OD AD ==，于是)22()()(PA PB PC PA PD PO OA PO OD ⋅+=⋅=+⋅+ 222332()()222()22PO OD PO OD PO OD =-⋅+=-≥-⨯=- ，当且仅当点P 与点O 重合时取等号，所以()PA PB PC ⋅+ 的最小值为32-.故答案为：32-四､解答题：本题共6小题，共计70分．解答时应写出文字说明､证明过程或演算步骤．17.如图所示，已知在△AOB 中，BC =2AC ，OD =2DB ，DC 和OA 交于点E ，设OA a = ，OB b =．（1）用a和b 表示向量OC 、DC；（2）若OE OA λ=，求实数λ的值【答案】（1）2OC a b =- ；523DC a b=-（2）4=5λ【解析】【分析】（1）结合向量的加法、减法法则运算即可（2）根据向量的减法法则可得()2EC a b λ=-- 、523DC a b =-，结合平行向量的基本定理计算即可.【小问1详解】由题意知，A 是BC 的中点，且23OD OB =，由平行四边形法则，2OB OC OA +=，所以22OC OA OB a b =-=-，()252233DC OC OD a b b a b =-=--=-.【小问2详解】因为//EC DC ，又()()22EC OC OE a b a a b λλ=-=--=--，523DC a b =- ，所以22λ-＝153--，解得4=5λ．18.已知函数π()sin()0,0,2f x A x A ωϕωϕ⎛⎫=+>>≤⎪⎝⎭在一个周期内的图象如图所示，其中，点P 的坐标为(6,0)-，点Q 是()f x 图象上的最低点且坐标为(2,3)--，点R 是()f x 图象上的最高点.（1）求函数()f x 的解析式；（2）记RPO α∠=，QPO β∠=（α，β均为锐角），求()tan 2αβ+的值.【答案】（1）()ππ3sin 84f x x ⎛⎫=-⎪⎝⎭（2）7736【解析】【分析】（1）由图象可得A ，由函数()y f x =的最小正周期求得ω的值，利用正弦函数的对称中心结合ϕ的取值范围可求得ϕ的值，即可求得函数()f x 的解析式；（2）利用函数周期求得(6,3)R ，由两点式斜率公式及诱导公式求得1tan 4α=，3tan 4β=，进而利用二倍角正切公式和两角和的正切公式求解即可.【小问1详解】由图象及(6,0)P -，(2,3)Q --可知，3A =，又函数()f x 的最小正周期()42616T ⎡⎤=---=⎣⎦，所以2ππ8T ω==，因为点(6,0)P -为函数()f x 的一个对称中心，所以()π6π,Z 8k k ϕ⨯-+=∈，即3ππ,Z 4k k ϕ=+∈，又π2ϕ≤，所以π0,4k ϕ==-，所以()ππ3sin 84f x x ⎛⎫=- ⎪⎝⎭.【小问2详解】由（1）函数周期及最值知(6,3)R ，因为RPO α∠=，QPO β∠=，(6,0)P -，(2,3)Q --，所以()301tan 664PR k α-===--，()()303tan πtan 264PQ k ββ---=-===----，即3tan 4β=，所以22122tan 84tan 21tan 15114ααα⨯===-⎛⎫- ⎪⎝⎭，所以()83tan 2tan 77154tan 2831tan 2tan 361154αβαβαβ+++===-⋅-⋅.19.为了预防流感病毒，某中学对教室进行药熏消毒，室内每立方米空气中的含药量y （单位：毫克）随时间x （单位：h ）的变化情况如图所示，在药物释放过程中，y 与x 成正比，药物释放完毕后，y 与x 的函数关系式为18x ay -⎛⎫= ⎪⎝⎭（a 为常数），根据图中提供的信息，回答下列问题：（1）写出从药物释放开始，y 与x 之间的函数关系；（2）据测定，当空气中每立方米的含药量降低至0.25毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能回到教室（精确到0.01）.【答案】（1）0.110,00.11,0.18x x x y x -≤≤⎧⎪=⎨⎛⎫> ⎪⎪⎝⎭⎩（2）0.77【解析】【分析】（1）根据已知图象过的点的坐标，即可直接求出相应解析式；（2）令0.25y =，即可得出结果.【小问1详解】由题知，药物释放过程中，设y kx =，将()0.1,1代入解析式可得，0.11k =，解得10k =，以及0.1118a-⎛⎫= ⎪⎝⎭，解得0.1a =，所以从药物释放开始，0.110,00.11,0.18x x x y x -≤≤⎧⎪=⎨⎛⎫> ⎪⎪⎝⎭⎩.【小问2详解】由（1）知，0.110,00.11,0.18x x x y x -≤≤⎧⎪=⎨⎛⎫> ⎪⎪⎝⎭⎩，令0.110.258x -⎛⎫< ⎪⎝⎭，则20.10.773x >+≈，所以从药物释放开始，至少需要经过约0.77小时后，学生才能回到教室.20.已知函数()211f x x x =---．（1）求函数()f x 的零点以及不等式()0f x ≤的解集M ；（2）设M 中的最大数是m ，正数a b ､满足3a b m +=，求225b aa b++的最小值．【答案】（1）20,3⎡⎤⎢⎥⎣⎦（2）132【解析】【分析】（1）将函数写为分段函数的形式，再根据范围依次解不等式即可.（2）确定2a b +=，变换224659b a a b a b=+++-，再利用均值不等式计算得到最值.【小问1详解】,1121132,121,2x x y x x x x x x ⎧⎪≥⎪⎪=---=-<<⎨⎪⎪-≤⎪⎩，当1x ≥时，0x ≤，解得∅；当112x <<时，320x -≤，解得23x ≤，即12,23x ⎛⎤∈ ⎥⎝⎦；当12x ≤时，0x -≤，解得102x ≤≤，即10,2x ⎡⎤∈⎢⎥⎣⎦；综上所述：20,3x ⎡⎤∈⎢⎣⎦，即20,3M ⎡⎤=⎢⎥⎣⎦.【小问2详解】23m =，2a b +=，()()22222222555949486a b b a b a a b a b a b a a b a a b a b --++=++=++=++=-()1941194113622222b a a b a b a b ⎛⎫⎛⎫=++-=++≥+ ⎪ ⎪⎝⎭⎝⎭.当且仅当94b a a b=，即65a =，45b =时等号成立.21.已知()()()4,0,0,4,cos ,sin ,(0π)A B C ααα<<．（1）若OA OC += （O 为坐标原点），求OB 与OC的夹角；（2）若⊥AC BC ，求33sin cos ,sin cos αααα-+的值．【答案】21.6π22.sin cos 4αα-=，33sin cos αα+47128=【解析】【分析】（1）根据向量模长以及夹角的坐标公式计算即可；（2）由向量垂直得到数量积为0，进而得到1sin cos 4αα+=，通过平方得到2sin cos αα，进而可得()2sin cos αα-，再根据α的范围确定正负，开方得解；再利用立方和公式展开33sin cos αα+，进而得解.【小问1详解】由OA OC += 得()224+cos sin 21αα+=，1cos 2α=，又0πα<<，3πα∴=，1,22C ⎛⎫ ⎪ ⎪⎝⎭，设OB 与OC的夹角为β,()0πβ≤≤，则cos OB OC OB OC β⋅=23342==,又0πβ≤≤，故OB 与OC的夹角β为6π.【小问2详解】由⊥ AC BC 得0AC BC ⋅=，即()()cos 4cos sin sin 40αααα-+-=，1sin cos 4αα∴+=，152sin cos 016αα-∴=<，故ππ2α<<,()21531sin cos 11616αα-∴-=-=，sin cos 4αα∴-=.又33sin cos αα+()()22sin cos sin sin cos cos αααααα=+-+1151432⎛⎫=⨯+ ⎪⎝⎭47128=.22.已知函数()()12log 2sin 1 3.f x x =+-（1）求f (x )的定义域；（2）若0,6x π⎡⎤∈⎢⎥⎣⎦，求f (x )的值域;（3）设R a ∈，函数()2232g x x a x a =--，[0,1]x ∈，若对于任意10,6x π⎡⎤∈⎢⎥⎣⎦，总存在唯一的0[0,1]x ∈，使得()()01 g x f x =成立，求a 的取值范围.【答案】（1）7{|22Z}66x k x k k ππππ-<<+∈；（2）[4,3]--；（3）53(,][1,]32-∞- .【解析】【分析】（1）由对数函数的意义，列出不等式，再求解作答.（2）求出函数2sin 1y x =+在[0,]6π上的值域，再结合对数函数单调性求解作答.（3）利用二次函数对称轴分类，结合（2）的结论列出不等式，求解作答.【小问1详解】函数12()log (2sin 1)3=+-f x x 有意义，有2sin 10x +>，即1sin 2x >-，解得722,Z 66k x k k ππππ-<<+∈，所以函数f (x )的定义域为7{|22Z}66x k x k k ππππ-<<+∈.【小问2详解】当06x π≤≤时，10sin 2x ≤≤，则12sin 12x ≤+≤，121log (2sin 1)0x -≤+≤，4()3f x -≤≤-，所以f (x )的值域是[4,3]--.【小问3详解】由（2）知，1[0,]6x π∈，14()3f x -≤≤-，函数()2232g x x a x a =--图象对称轴232a x =，而[0,1]x ∈，当2312a ≤，即33a -≤≤时，显然(0)233g a =-≥->-，因为任意10,6x π⎡⎤∈⎢⎥⎣⎦，总存在唯一的0[0,1]x ∈，使得()()01g x f x =成立，则必有2(1)1324g a a =--≤-，解得53a ≤-或1a ≥，显然无解，当2312a >，即3a <-或3a >时，函数()2232g x x a x a =--在[0,1]上单调递减，()()()10g g x g ≤≤，因为任意10,6x π⎡⎤∈⎢⎥⎣⎦，总存在唯一的0[0,1]x ∈，使得()()01g x f x =成立，则(0)3(1)4g g ≥-⎧⎨≤-⎩，于是得2231324a a a -≥-⎧⎨--≤-⎩，解得53a ≤-或312a ≤≤，满足3a <-或3a >，因此53a ≤-或312a ≤≤，所以a 的取值范围是53(,[1,]32-∞- .【点睛】结论点睛：若[]1,x a b ∀∈，[]2,x c d ∃∈，有()()12f x g x =，则()f x 的值域是()g x 值域的子集．。

2025届高三月考试卷（一）数学（答案在最后）本试卷共8页.时量120分钟.满分150分.一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.设集合[),A a =+∞，()1,2B =-，若A B =∅ ，则（）A.1>-aB.2a > C.1a ≥- D.2a ≥【答案】D 【解析】【分析】根据题意，结合集合的交集的运算，即可求解.【详解】由集合[),A a =+∞，()1,2B =-，因为A B =∅ ，则满足2a ≥.故选：D.2.已知复数z 满足22z -=，z 的取值范围为（）A.[]0,2 B.()0,2 C.[]0,4 D.()0,4【答案】C 【解析】【分析】根据题意，利用复数模的几何意义，得到复数z 在复平面内对应的轨迹，进而结合圆的性质，即可求解.【详解】由题意知复数z 满足22z -=，可得复数z 在复平面内对应的轨迹为以(2,0)A 为圆心，2r =为半径的圆，且z 表示圆上的点到原点(0,0)O 的距离，则max min 224,220z OA r z OA r =+=+==-=-=，所以z 的取值范围为0,4.故选：C.3.在ABC V 中，若2AB BC BC CA CA AB ⋅=⋅=⋅，则AB BC=A.1B.2C.2D.2【答案】C 【解析】【分析】根据题意，由AB BC BC CA ⋅=⋅uu u v uu u v uu u v uu v可以推得AB AC =，再利用向量运算的加法法则，即可求得结果．【详解】由题意得，AB BC BC CA ⋅=⋅uu u v uu u v uu u v uu v ，即A A =0+BC B C ⋅uu u v uu u v uuu v（），设BC 的中点为D ，则AD BC ⊥，即ABC V 为等腰三角形，B=C AB AC =∠∠，又因为2BC CA CA AB⋅=⋅uu u v uu v uu v uu u v即2222222C C cos 2C 2C cos 112C +22232C 2AB BC CA A B AB BC B A CA B C BC A BC A BC⋅=⋅-=-+-=-+⨯=uu u v uu u v uu v uu u v uuv uu u v uu u v uu u v uu v uuvuu u v uu u v uu u v uu u v uu u v （）所以2AB BC=uu u v uu u v ．【点睛】本题主要考查平面向量的线性运算．4.若函数()2211x x f x x ++=+的最大值为M ，最小值为N ，则M N +=（）A.1 B.2 C.3D.4【答案】B 【解析】【分析】将函数解析式化为()211xf x x =++，令()21xg x x =+，判断()g x 的奇偶性，然后利用函数的奇偶性求解即可.【详解】()2222221111111x x xf x x x x x x x +==+=+++++++，令()21x g x x =+，则其定义域为R ，又()()()2211x x g x g x x x --==-=-+-+，所以()21xg x x =+为奇函数，则()()max min 0g x g x +=，所以()()()()max min max min 112f x f x g x g x +=+++=，则2M N +=.故选：B.5.如图，点N 为正方形ABCD 的中心，ECD ∆为正三角形，平面ECD ⊥平面AB,是线段ED 的中点，则A.BM EN =，且直线,BM EN 是相交直线B.BM EN ≠，且直线,BM EN 是相交直线C.BM EN =，且直线,BM EN 是异面直线D.BM EN ≠，且直线,BM EN 是异面直线【答案】B 【解析】【分析】利用垂直关系，再结合勾股定理进而解决问题．【详解】如图所示，作EO CD ⊥于O ，连接ON ，过M 作MF OD ⊥于F ．连BF ， 平面CDE ⊥平面ABCD ．,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴∆与EON ∆均为直角三角形．设正方形边长为2，易知12EO ON EN ===，5,,22MF BF BM ==∴=．BM EN ∴≠，故选B ．【点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形．6.tan10tan503tan50︒+︒+︒︒的值为（）A.3B.3C.3D.33【答案】B 【解析】【分析】利用正切的和角公式，逆用即可求出结果.【详解】tan10tan503tan10tan50︒+︒︒︒()()tan 10501tan10tan 503tan 50=︒+︒-︒︒+︒︒)31tan10tan503tan 50=-︒︒+︒︒33tan10tan503tan50=-︒︒︒︒3=故选：B.7.一枚质地均匀的正方体骰子，其六个面分别刻有1，2，3，4，5，6六个数字，投掷这枚骰子两次，设事件M =“第一次朝上面的数字是奇数”，则下列事件中与M 相互独立的是（）A.第一次朝上面的数字是偶数B.第一次朝上面的数字是1C.两次朝上面的数字之和是8D.两次朝上面的数字之和是7【答案】D 【解析】【分析】根据题意，由相互独立事件的定义，对选项逐一判断，即可得到结果.【详解】抛掷骰子两次，共有6636⨯=个基本事件数，则()()()()()()()()()()()(){1,1,1,2,1,3,1,4,1,5,1,6,3,1,3,2,3,3,3,4,3,5,3,6M =，()()()()()()}5,1,5,2,5,3,5,4,5,5,5,6共18个基本事件，则()181362P M ==，设事件E 为第一次朝上面的数字是偶数，则事件M 与事件E 是对立事件，故A 错误；设事件F 为第一次朝上面的数字是1，则F M ⊆，故B 错误；设事件N 为两次朝上面的数字之和是8，则()()()()(){}2,6,3,5,4,4,5,3,6,2N =共5个基本事件，则()536P N =，且()(){}3,5,5,3MN =，则()213618P MN ==，()()()P MN P M P N ≠⋅，所以C 错误；设事件Q 两次朝上面的数字之和是7，则()()()()()(){}1,6,2,5,3,4,4,3,5,2,6,1Q =，则()61366P Q ==，且()()(){}1,6,3,4,5,2MQ =，则()313612P MQ ==，因为()()()P MQ P M P Q =⋅，所以事件M 与事件Q 相互独立.故选：D8.一只蜜蜂从蜂房A 出发向右爬，每次只能爬向右侧相邻的两个蜂房（如图），例如：从蜂房A 只能爬到1号或2号蜂房，从1号蜂房只能爬到2号或3号蜂房，…，以此类推，用n a 表示蜜蜂爬到n 号蜂房的方法数，则10a =（）A.10B.55C.89D.99【答案】C 【解析】【分析】根据给定条件，求出数列{}n a 的递推公式，再依次计算求出10a .【详解】依题意，12n n n a a a --=+（*n ∈N ，3n ≥），11a =，22a =，所以34567893,5,8,13,21,34,55,a a a a a a a =======1089a =.故选：C二、选择题（本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.）9.已知一组样本数据1x ，2x ，…，()201220x x x x ≤≤≤ ，下列说法正确的是（）A.该样本数据的第60百分位数为12x B.若样本数据的频率分布直方图为单峰不对称，且在右边“拖尾”，则其平均数大于中位数C.剔除某个数据i x （1i =，2，…，20）后得到新样本数据的极差不大于原样本数据的极差D.若1x ，2x ，…，10x 的均值为2，方差为1，11x ，12x ，…，20x 的均值为6，方差为2，则1x ，2x ，…，20x 的方差为5【答案】BC 【解析】【分析】由百分位数的定义即可判断A ；由极差的定义即可判断C ，由频率分布直方图中中位数、平均数的求法画出图形即可判断B ；由方差计算公式即可判断D.【详解】对于A ，由2060%12⨯=，所以样本数据的第60百分位数为12132x x +，故A 错误；对于B ，数据的频率分布直方图为单峰不对称，向右边“拖尾”，大致如下图，由于“右拖”时最高峰偏左，中位数靠近高峰处，平均数靠近中点处，此时平均数大于中位数，故B 正确；对于C ，剔除某个数据i x （1i =，2，…，20）后得到新样本数据的极差不大于原样本数据的极差，故C 正确；对于D ，由10102642020x =⨯+⨯=，则()()22210101112426420202s ⎡⎤⎡⎤=+-++-=⎣⎦⎣⎦，所以则1x ，2x ，…，20x 的方差为112，故D 错误.故选：BC.10.在平面直角坐标系中，O 为坐标原点，抛物线()220y px p =>的焦点为F ，点()1,2M ，()11,A x y ，()22,B x y 都在抛物线上，且0FA FB FM ++=ruu r uu r uuu r ，则下列结论正确的是（）A.抛物线方程为22y x= B.F 是ABM 的重心C .6FA FM FB ++= D.2223AFO BFO MFO S S S ++=△△△【答案】BCD 【解析】【分析】把点代入可得抛物线的方程，结合向量运算可得F 是ABM 的重心，利用抛物线的定义可得6FA FM FB ++= ，利用三角形面积公式及122x x +=，可得2223AFO BFO MFO S S S ++=△△△.【详解】对于A ，由()1,2M 在抛物线上可得42p =，即抛物线方程为24y x =，错误；对于B ，分别取,AB AM 的中点,D E ，则2FA FB FD +=uu u u r uu r u r ，2FM FD =-uuu r uu u r，即F 在中线MD 上，同理可得F 也在中线BE 上，所以F 是ABM 的重心，正确；对于C ，由抛物线的定义可得121,2,1FA x FM FB x =+==+uu r uuu r uu r，所以124++=++FA FM FB x x uu r uuu r uu r.由()10F ,是ABM 的重心，所以12113x x ++=，即122x x +=，所以1246++=++=FA FM FB x x uu r uuu r uu r，正确；对于D ，112AFO S OF y =△，221114AFO S y x ==△；同理222214BFOSy x ==△,21MFO S =△，所以2221213AFO BFO MFO S S S x x ++=++=△△△，正确.故选：BCD.11.已知函数()()()322,,R ,f x x ax bx c a b c f x =-++'∈是()f x 的导函数，则（）A.“0a c ==”是“()f x 为奇函数”的充要条件B.“0a b ==”是“()f x 为增函数”的充要条件C.若不等式()0f x <的解集为{1xx <∣且1}x ¹-，则()f x 的极小值为3227-D.若12,x x 是方程()0f x '=的两个不同的根，且12111x x +=，则0a <或3a >【答案】ACD 【解析】【分析】根据函数的奇偶性和充分、必要条件的判定方法，可判定A 正确；结合导数和函数的单调性间的关系，结合充分、必要条件的判定方法，可判定B 错误；利用导数求得函数()f x 的单调性，进而求得()f x 的极小值，可判定C 正确；结合二次函数的性质，结合0∆>，列出不等式，可判定D 正确．【详解】对于A 中，当0a c ==时，函数()3f x x bx =+，则满足()()3f x x bx f x -=--=-，所以()f x 为奇函数，所以充分性成立；若()f x 为奇函数，则()322f x x ax bx c -=---+=()322f x x ax bx c -=-+--，则24ax -20c =恒成立，所以0a c ==，所以必要性成立，所以A 正确；对于B 中，当0a b ==时，()3f x x c =+，可得()230f x x '=≥，所以()f x 为增函数；由()234f x x ax b =-+'，当()f x 为增函数时，216120a b ∆=-≤，所以“0a b ==”是“()f x 为增函数”的充分不必要条件，所以B 错误；对于C 中，由()234f x x ax b =-+'，若不等式()0f x <的解集为{|1x x <且1}x ¹-，则()f x 在R 上先增后减再增，则()1f '-=()()0,110f f =-=，解得21a b c ===-，故()()()232111f x x x x x x =+--=+-，可得()()()2321311f x x x x x '=+-=-+，令()0f x '=，解得=1x -或13x =，当(),1x ∈-∞-内，()0f x '>，()f x 单调递增；当11,3x ⎛⎫∈- ⎪⎝⎭内，()0f x '<，()f x 单调递减；当1,3x ⎛⎫∈+∞ ⎪⎝⎭内，()0f x '>，()f x 单调递增，所以()f x 的极小值为2111321133327f ⎛⎫⎛⎫⎛⎫=+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以C 正确．对于D 中，由()234f x x ax b =-+'，因为12,x x 是方程()0f x '=的两个不同的根，所以216120a b ∆=->，即2430a b ->，且1x +2124,33a bx x x ==，由12111x x +=，可得1x +212x x x =，所以433a b =，即4b a =，联立方程组，可得230a a ->，解得0a <或3a >，所以D 正确．故选：ACD ．三、填空题（本大题共3小题，每小题5分，共15分.）12.点M 在椭圆221259x y +=上，F 是椭圆的一个焦点，N 为MF 的中点，3ON =，则MF =_________.【答案】4【解析】【分析】根据椭圆的对称性，利用三角形中位线定理求得||MF '，再由椭圆定义求解||MF 即可．【详解】如图，根据椭圆的对称性，不妨设F 为左焦点，F '为右焦点，由椭圆221259x y +=，得5a =，210a =，N Q 是MF 的中点，O 是FF '的中点，ON ∴为FMF ' 的中位线，||2||6MF ON ∴'==，∴由椭圆的定义得||2||1064MF a MF =-'=-=．故答案为：4．13.如图，将一个各面都涂了油漆的正方体切割为125个同样大小的小正方体.经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X ，则X 的均值()=E X ______.【答案】65【解析】【分析】根据题意得出X 的所有可能取值为0,1,2,3，然后分析出涂3面油漆，2面油漆，1面油漆，0面油漆的各有多少个小正方体，从而计算X 取每个值时的概率，从而求X 的均值.【详解】X 的所有可能取值为0,1,2,3，大正方体8个顶点处的8个小正方体涂有3面油漆；每一条棱上除了两个顶点处的小正方体外剩余的都涂有两面油漆，所以涂有两面油漆的有31236⨯=个；每个表面去掉四条棱上的16个小正方体，还剩9个小正方体，这9个都是一面涂漆，所以一共有9654⨯=个小正方体涂有一面油漆；剩余的()1258365427-++=个内部的小正方体6个面都没有涂油漆，所以()270125P X ==，()541125P X ==，()362125P X ==，()83125P X ==，()()()()()00112233E X P X P X P X P X =⨯=+⨯=+⨯=+⨯=2754368150601231251251251251255=⨯+⨯+⨯+⨯==.故答案为：65.14.若函数()()52cos sin 2f x a x x x =-+在R 上单调递增，则a 的取值范围是_________.【答案】11,22⎡⎤-⎢⎥⎣⎦【解析】【分析】求导，根据()0f x '≥在R 上恒成立，即可结合二次函数的性质求解.【详解】根据题意，()22259cos 2sin 2cos cos 4cos 22f x a x x x a x x '=+-+=-+，()f x 在R 上单调递增，()0f x '∴≥在R 上恒成立，令cos x t =，[]1,1t ∈-，则()f x '可写为()2942g t at t =-+，[]1,1t ∈-，根据题意()g t 在[]1,1-上的最小值非负，∴()()10,10,g g ⎧-≥⎪⎨≥⎪⎩解得1122a -≤≤.故答案为：11,22⎡⎤-⎢⎥⎣⎦四、解答题（本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.）15.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知向量(),sin m b a C =-- ，(),sin sin n c b A B =++，满足//m n u r r ．（1）求A ；（2）若角A 的平分线交边BC 于点D ，AD 长为2，求△ABC 的面积的最小值．【答案】（1）23A π=（2）【解析】【分析】（1）由//m n u r r 得出等式，再由正、余弦定理即可解出；（2）把ABC 的面积用等积法表示可得,b c 关系，再利用基本不等式得出bc 的最小值，即得面积最小值．【小问1详解】因为//m n u r r ，所以()()()()sin sin sin b a A B c b C -+=+-，由正弦定理得()()()()b a a b c b c -+=+-，所以222b c a bc +-=-，所以2221cos 222b c a bc A bc ab +--===-，因为()0,A π∈，故23A π=.【小问2详解】∵AD 平分∠BAC ，∴123BAD CAD BAC π∠=∠=∠=，∵ABD ACD ABC S S S +=△△△，∴1sin 2AB AD BAD ⋅⋅∠11sin sin 22AC AD CAD c A +⋅⋅∠=⋅⋅，即22sin 2sin sin 333c b bc πππ+=，∴22c b bc+=由基本不等式可得：22bc b c =+≥，∴16bc ≥，当且仅当4b c ==时取“=”，∴1sin 2ABC S bc A ==≥ 即ABC V的面积的最小值为.16.如图，已知点P 在圆柱1OO 的底面圆O 上，120AOP ∠=o ，圆O 的直径4AB =，圆柱的高13OO =.（1）求点A 到平面1A PO 的距离；（2）求二面角1A PB O --的余弦值大小.【答案】（1）32；（2）277.【解析】【分析】（1）根据等体积法，由11A AOP A A OP V V --=即可求出点A 到平面1A PO 的距离；（2）先证明PB AP ⊥，1PB AA ⊥，由线面垂直的判定定理可得PB ⊥面1AA P ，进而可得1A PA ∠即为所求二面角的平面角，在1Rt A PA 中，计算11cos AP A PA A P∠=即可求解.【详解】（1）因为113AA OO ==，122AO AB ==，所以1AO ===在AOP中，由余弦定理可得：AP ===所以1A P ==，2OP =，在1AOP中，由余弦定理可得222111121cos 27A P OP A O A PO A P OP +-∠===⋅，所1sin7A PO∠==，所以11227A OPS=⨯=，设点A到平面1A PO的距离为d，由11A AOP A A OPV V--=，得111133AOP AO PS AA S d⋅⋅=⋅⋅，即1111233223d⨯⨯⨯⨯=，解得：32d=，所以点A到平面1A PO的距离为32；（2）二面角1A PB O--即二面角1A PB A--，因为AB是圆O的直径，点P在圆柱1OO的底面圆O上，所以PB AP⊥，因为1AA⊥面ABP，PB⊂面ABP，可得1PB AA⊥，因为1AP AA A⋂=，所以PB⊥面1AA P，因为1A P⊂面1AA P，AP⊂面1AA P，所以PB⊥AP，PB⊥1A P，所以1A PA∠即为二面角1A PB O--的平面角，在1Rt A PA中，1A P=，AP=所以11cos7APA PAA P∠===，所以二面角1A PB O--的余弦值为7.17.双曲线()2222:10,0x yC a ba b-=>>的左顶点为A，焦距为4，过右焦点F作垂直于实轴的直线交C于B、D两点，且ABD△是直角三角形．（1）求双曲线C的方程；（2）M、N是C右支上的两动点，设直线AM、AN的斜率分别为1k、2k，若122k k=-，求点A到直线MN的距离d的取值范围．【答案】（1）2213y x -=（2）(⎤⎦【解析】【分析】（1）根据等腰直角三角形的性质，转化为,,a b c 的方程，即可求解；（2）首先设直线MN 的方程为x my n =+，与双曲线方程联立，利用韦达定理表示122k k =-，并根据2m 的取值范围，求点到直线的距离的取值范围.【小问1详解】依题意，90BAD ∠=，焦半径2c =，由AF BF =，得2b ac a+=，得22222a a a +=-，解得：1a =（其中20a =-<舍去），所以222413b c a =-=-=，故双曲线C 的方程为2213y x -=；【小问2详解】显然直线MN 不可能与轴平行，故可设直线MN 的方程为x my n =+，联立2233x my n x y =+⎧⎨-=⎩，消去x 整理得()()222316310m y mny n -++-=，在条件2310Δ0m ⎧-≠⎨>⎩下，设()11,M x y ，()22,N x y ，则122631mn y y m +=--，()21223131n y y m -=-，由122k k =-，得()()12122110y y x x +++=，即()()12122110y y my n my n +++++=，整理得()()()()2212122121210m y y m n y y n ++++++=，代入韦达定理得，()()()()()22222312112121310n m m n n n m -+-+++-=，化简可消去所有的含m 的项，解得：5n =或1n =-（舍去），则直线MN 的方程为50x my --=，得d =又,M N 都在双曲线的右支上，故有2310m -<，2103m ≤<，此时1≤<，(d ⎤=⎦，所以点A 到直线MN 的距离d的取值范围为(⎤⎦.18.已知函数()()e xf x x a =-，a ∈R .（1）当1a =时，求()f x 的极值；（2）若函数()()ln g x f x a x =-有2个不同的零点1x ，2x .（i ）求a 的取值范围；（ii ）证明：12112e x x a x x +->.【答案】（1）极小值为0，无极大值（2）（i ）()e,+∞；（ii ）证明见解析【解析】【分析】（1）将1a =代入函数解析式，求导，判断其单调性，进而得出极值；（2）（i ）化简函数()g x 的解析式，令e x t x =，问题可转化为()ln h t t a t =-在(0,)t ∈+∞有2个零点1t ，2t ，再利用导数研究函数()h t 的性质即可得出答案；（ii ）等价于证明21e a t t >，再利用极值点偏移法即可得证．【小问1详解】1a =时，()()e 1xf x x =-，()()1e 1x f x x =+'- ，令()()()(),2e xm x f x m x x ''=∴=+，(),2x ∞∴∈--，()0m x '<；()2,x ∞∈-+，()0m x '>，()f x ∴'在(),2∞--单调递减，()2,∞-+单调递增，x →-∞ 时，10x +<，e 0x >，则′<0，()21210ef '--=-<，()00f '=，x →+∞时，()f x ∞'→+，(),0x ∞∴∈-时，′<0；∈0,+∞，′>0，∴在(),0∞-单调递减，在0,+∞单调递增，∴的极小值为()00f =，无极大值.【小问2详解】（i ）()()()()ln e ln e ln e x x x g x f x a x x a x x x a x =-=-+=-，∈0,+∞，令e x t x =，()0,t ∞∈+，()1e 0x t x =+'> ，e x t x ∴=在0,+∞单调递增，令()ln h t t a t =-，即()h t 在()0,t ∞∈+有2个零点1t ，2t ，且111e x t x =，222e xt x =，()1a t a h t t t-='-= ，0a ∴≤时，()0h t '>，()h t 在()0,t ∞∈+单调递增，不存在2个零点，0a ∴>，()0,t a ∈ 时，()0h t '<；(),t a ∞∈+时，()0h t '>，()h t ∴在()0,a 单调递减，在(),a ∞+单调递增，0t → 时，()h t ∞→+；t →+∞时，()h t ∞→+，()()()min 1ln 0h t h a a a ∴==-<，()e,a ∞∴∈+.（ii ）设12t t <，()110h => ，()e e 0h a =-<，∴由（i ）知，121e t a t <<<<，即证：12e t t a >，即证：21e a t t >，2t a > ，1e a a t >，()h t 在(),a ∞+单调递增，∴即证：()21e 0a h t h t ⎛⎫=> ⎪⎝⎭，11ln t a t = ，()1111111e e e e e e ln ln ln ln 1ln a a a h a a a t t t t t t t ⎛⎫⎛⎫⎡⎤∴=-=-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，令()()111e ln ln 1p t t t =+-，()11,e t ∈，即证：()10p t <，()1112211111eln e 1ln ln t t p t t t t t t -=='-+，令()111eln q t t t =-，()11,e t ∈，()1111e e 10t q t t t -=-='< ，()1q t ∴在()1,e 单调递减，()()1e 0q t q >=，()10p t ∴'>，()1p t ∴在()1,e 单调递增，()()1e 0p t p ∴<=，【点睛】方法点睛：利用导数证明或判定不等式问题：1．通常要构造新函数，利用导数研究函数的单调性与极值（最值），从而得出不等关系；2．利用可分离变量，构造新函数，直接把问题转化为函数的最值问题，从而判定不等关系；3．适当放缩构造法：根据已知条件适当放缩或利用常见放缩结论，从而判定不等关系；4．构造“形似”函数，变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.19.已知集合{}()1,2,3,,,3A n n n =∈≥ N ，W A ⊆，若W 中元素的个数为()2m m ≥，且存在u ，()v W u v ∈≠，使得()2k u v k +=∈N ，则称W 是A 的()P m 子集.（1）若4n =，写出A 的所有()3P 子集；（2）若W 为A 的()P m 子集，且对任意的s ，()t W s t ∈≠，存在k ∈N ，使得2k s t +=，求m 的值；（3）若20n =，且A 的任意一个元素个数为m 的子集都是A 的()P m 子集，求m 的最小值.【答案】（1）{}{}1,2,3,1,3,4；（2）2；（3）13.【解析】【分析】（1）根据()P m 子集的定义，即可容易求得；（2）取{}1,3W =，求得2m =，再利用反证法假设3m ≥，推得10a <与11a ≥矛盾即可；（3）令{}020,19,18,17,11,10,9,3,16,8,4,2W =，讨论12m ≤时不满足题意，再验证13m ≥时的情况满足题意，即可求得m 的最小值.【小问1详解】当4n =时，{}1,2,3,4A =，A 的所有()3P 子集为{}{}1,2,3,1,3,4.【小问2详解】当3n ≥时，取{}1,3W =，因为2132+=，所以W 是A 的()2P 子集，此时2m =；若3m ≥，设123,,a a a W ∈且1231a a a ≤<<，根据题意，3121213232,2,2kk k a a a a a a +=+=+=，其中123,,N k k k ∈；因为121323a a a a a a +<+<+，所以312222k k k <<，所以123k k k <<；又因为123,,N k k k ∈，所以321k k ≥+；因为()3121232222k k k a a a ++=++，所以()31212312222k k k a a a ++=++，所以()()3331212111222222222k k k k k k k a =++-=+-；因为3122221222222k k k k k k ++<+=≤，所以3122220k k k +-<，所以10a <，与11a ≥矛盾.综上所述，2m =.【小问3详解】设{}{}{}{}{}1234520,12,19,13,18,14,17,15,11,5,A A A A A ====={}{}{}{}{}{}{}678123410,6,9,7,1,3,2,4,8,16A A AB B B B =======，设W 的元素个数为m ，若W 不是A 的()P m 子集，则W 最多能包含1238,,,,A A A A 中的一个元素以及1234,,,B B B B 中的元素；令{}020,19,18,17,11,10,9,3,16,8,4,2W =，易验证0W 不是A 的()12P 子集，当12m ≤时，0W 的任意一个元素个数为m 的子集都不是A 的()P m 子集，所以，若A 的任意一个元素个数为m 的子集都是A 的()P m 子集，则13m ≥；当13m ≥时，存在{}1,2,3,4,5,6,7,8i ∈，使得W 中必有两个元素属于i A ，同时i A 中两个元素之和为2的某个正整数指数幂，P m子集；所以W是A的()所以，m的最小值为13.P m子集的定义，【点睛】关键点点睛：本题考查集合新定义问题，处理问题的关键是充分把握题中对()同时要熟练的使用证明方法，属综合困难题.。

长沙市一中2023届高三月考试卷（六）数学时量：120分钟 满分：150分一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 已知集合，，则（ ） {}32,Z M x x n n ==-∈{}2,1,0,1,2N =--M N ⋂=A. B. C.D. {}2,1-{}1,2-{}1,1-{}2,0,2-2. 已知复数满足，为虚数单位，则（ ）z ()1i 1i z -=+i z =A. B. C. D. i 11i 22+1i +3. 已知，，，一束光线从点出发经AC 反射后，再经BC 上点D 反射，()30A -,()3,0B ()0,3C ()1,0F -落到点上．则点D 的坐标为（ ）()1,0E A. B. C. D. 15,22⎛⎫ ⎪⎝⎭33,22⎛⎫ ⎪⎝⎭()1,2()2,14. 若，且，则（ ） ππ,24α⎛⎫∈-- ⎪⎝⎭23π1cos cos 222αα⎛⎫++=- ⎪⎝⎭tan α=A. B. C. D. 2-3--5. 据一组样本数据，求得经验回归方程为，且．现发现()(()1122,,,,,,n n x y x y x y ⋅⋅⋅ 1.20.4y x =+3x =这组样本数据中有两个样本点和误差较大，去除后重新求得的经验回归直线的斜率为()1.2,0.5()4.8,7.5l 1.1，则（ ）A. 去除两个误差较大的样本点后，的估计值增加速度变快y B. 去除两个误差较大的样本点后，重新求得的回归方程对应直线一定过点()3,5C. 去除两个误差较大的样本点后，重新求得的回归方程为1.10.7y x =+D. 去除两个误差较大的样本点后，相应于样本点的残差为0.1()2,2.76. 在四面体中，，，，，则该四面体的PABC PA AB ⊥PA AC ⊥120BAC ∠=︒2AB AC AP ===外接球的表面积为（ ）A. B. C. D.12π16π18π20π7. 已知圆O 的半径为1，A 为圆内一点，，B ，C 为圆O 上任意两点，则的最小值是12OA =AC BC ⋅（ ）A. B. C. D. 18-116-116188. 设是定义在上的函数，若是奇函数，是偶函数，函数()f x R ()2f x x +()f x x -，若对任意的，恒成立，则实数的最大值为()()[]()(),0,121,1,f x x g x g x x ∞⎧∈⎪=⎨-∈+⎪⎩[]0,x m ∈()3g x ≤m （ ） A. B. C. D. 133********二、多项选择题（本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．）9. 已知函数在区间上有且仅有3条对称轴，给出下列四个结论，正确()()πsin 04f x x ωω⎛⎫=+> ⎪⎝⎭[]0,π的是（ ）A. 的取值范围是 ω913,44⎡⎫⎪⎢⎣⎭B. 在区间上有且仅有3个不同的零点()f x ()0,πC. 的最小正周期可能是 ()f x 4π5D. 在区间()f x π0,15⎛⎫ ⎪⎝⎭10. 已知抛物线C ：的焦点为F ，准线为，A ，B 是C 上异于点O 的两点，O 为坐标原点，则22x y =l （ ）A. 的方程为 l 12x =-B. 若，则 32AF =AOF AC. 若，则0OA OB ⋅= 9OA OB ⋅≥D. 若，过AB 的中点D 作于点E ，则的最小值为 120AFB ∠=︒DE l ⊥AB DE11. 如图，正方体中，顶点在平面内，其余顶点在的同侧，顶点到1111ABCD A B C D -A αα1,,B C A α的距离分别为，则（ ）1,2,3A. 平面BD A αB. 平面平面1A AC ⊥αC. 直线与所成角比直线与所成角大1AB α1AA αD.12. 已知，为正实数，且，则（ ）a b 26ab a b ++=A. 的最大值为2B. 的最小值为5 ab 2a b +C. 的最小值为D. 1211a b +++98()0,3a b -∈三、填空题（本题共4小题，每小题5分，共20分．）13. 设直线是曲线的一条切线，则_________．10x y ++=ln y a x =-=a 14. 楼道里有8盏灯，为了节约用电，需关掉3盏互不相邻的灯，则关灯方案有_________种．15. 过双曲线：右焦点作直线，且直线与双曲线的一条渐近线垂直，C ()222210x y a b a b-=>>F l l C 垂足为A ，直线与另一条渐近线交于点B ．且点A ，B 位于x 轴的异侧，O 为坐标原点，若的内切l OAB A 圆的半径为，则双曲线C 的离心率为__________． 23b 16. 小说《三体》中，一个“水滴”摧毁了人类整个太空舰队，当全世界第一次看到“水滴”的影像时，所有人都陶醉于它那绝美的外形．这东西真的是太美了，像梦之海中跃出的一只镜面海豚，仿佛每时每刻都在宇宙之夜中没有尽头地滴落着．有科幻爱好者为“水滴”的轴截面设计了二维数学图形，已知集合．由集合中所有的点组成的图形如图中阴影部分()()(){}22,cos sin 4,0P x y x y θθθπ=-++=≤≤P所示，中间白色部分就如美丽的“水滴”．则图中“水滴”外部阴影部分的面积为_________．四、解答题（本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17. 记为正项数列的前项和，已知是4与的等比中项．n S {}n a n 1n a +n S （1）求的通项分式；{}n a （2）证明：． 2222123111154n a a a a +++⋅⋅⋅+<18. 已知a ，b ，c 分别为三个内角A ，B ，C 的对边，且．ABCA cos sin a C C b c +=+（1）求A ；（2）已知M 为BC 的中点，且，的平分线交BC 于N ，求线ABC A AM =BAC ∠段AN 的长度．19. 近日，某芯片研发团队表示已自主研发成功多维先进封装技术XDFOI ，可以实现4nm 手机SOC 芯片的封装，这是中国芯片技术的又一个重大突破，对中国芯片的发展具有极为重要的意义．可以说国产4nm 先进封装技术的突破，激发了中国芯片的潜力，证明了知名院士倪光南所说的先进技术是买不来的、求不来的，自主研发才是最终的出路．研发团队准备在国内某著名大学招募人才，准备了3道测试题，答对两道就可以被录用，甲、乙两人报名参加测试，他们通过每道试题的概率均为，且相互独立，若()01p p <<甲选择了全部3道试题，乙随机选择了其中2道试题，试回答下列问题．（所选的题全部答完后再判断是否被录用）（1）求甲和乙各自被录用的概率；（2）设甲和乙中被录用的人数为，请判断是否存在唯一的值，使得？并说明理由． ξp 0p () 1.5E ξ=20. 如图，四棱锥的底面是边长为2的正方形，． P ABCD -ABCD 2PA PB ==（1）证明：；PAD PBC ∠=∠（2）当直线PA 与平面PCD 所成角的正弦值最大时，求此时二面角的大小．P AB C --21. 已知，D 是圆C ：上的任意一点，线段DF 的垂直平分线交DC 于点P ． ()1,0F -()22116x y -+=（1）求动点P 的轨迹的方程：Γ（2）过点的直线与曲线相交于A ，B 两点，点B 关于轴的对称点为，直线交轴于(),0M t l Γx B 'AB 'x 点，证明：为定值．N OM ON ⋅ 22. 已知函数，． ()1e ln axf x x x-=+a ∈R （1）当时，求函数的最小值；1a =()f x x -（2）若函数的最小值为，求的最大值．()f x xa a长沙市一中2023届高三月考试卷（六）数学时量：120分钟 满分：150分一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 已知集合，，则（ ） {}32,Z M x x n n ==-∈{}2,1,0,1,2N =--M N ⋂=A.B. C. D. {}2,1-{}1,2-{}1,1-{}2,0,2-【答案】A【解析】【分析】利用列举法及交集的定义即可求解.【详解】,{}}{32,Z ...,5,2,1,4,7,M x x n n ==-∈=-- 所以.{}2,1M N =- 故选：A.2. 已知复数满足，为虚数单位，则（ ）z ()1i 1i z -=+i z =A.B. C. D. i 11i 22+1i +【答案】B【解析】【分析】根据向量的除法和向量模的求法，变形的，即可求解. 1i 1i z +==-【详解】， 1i 1i z +===+-故选：B3. 已知，，，一束光线从点出发经AC 反射后，再经BC 上点D 反射，()30A -,()3,0B ()0,3C ()1,0F -落到点上．则点D 的坐标为（ ）()1,0E A. B. C. D.15,22⎛⎫ ⎪⎝⎭33,22⎛⎫ ⎪⎝⎭()1,2()2,1【答案】C【解析】【分析】根据入射光线与反射光线的性质可知方程，由与的交点可得D ，求坐标即可.GH GH BC【详解】根据入射光线与反射光线关系可知，分别作出关于的对称点,,F E ,AC BC ,G H 连接，交于，则D 点即为所求，如图，GH BCD因为所在直线方程为，，设，AC 3y x =+(1,0)F -()G x y ,则，解得，即， 132211y x y x -⎧=+⎪⎪⎨⎪=-⎪+⎩3,2x y =-=(3,2)G -由所在直线方程为，，同理可得，BC 3y x =-+(1,0)E (3,2)H 所以直线方程为，由解得， GH 2y =32y x y =-+⎧⎨=⎩(1,2)D 故选：C4. 若，且，则（ ） ππ,24α⎛⎫∈-- ⎪⎝⎭23π1cos cos 222αα⎛⎫++=- ⎪⎝⎭tan α=A.B. C. D. 2-3--【答案】C【解析】【分析】利用三角函数的诱导公式及二倍角的正弦公式，结合三角函数的齐次式法即可求解.【详解】因为，所以， ππ,24α⎛⎫∈-- ⎪⎝⎭tan 1α<-由，得，即， 23π1cos cos 222αα⎛⎫++=- ⎪⎝⎭21cos sin 22αα+=-222cos 2sin cos 1cos sin 2ααααα+=-+所以，即，解得 212tan 11tan 2αα+=-+2tan 4tan 30αα++=或(舍).tan 3α=-tan 1α=-故选：C.5. 据一组样本数据，求得经验回归方程为，且．现发现()()()1122,,,,,,n n x y x y x y ⋅⋅⋅ 1.20.4y x =+3x =这组样本数据中有两个样本点和误差较大，去除后重新求得的经验回归直线的斜率为()1.2,0.5()4.8,7.5l1.1，则（ ）A. 去除两个误差较大的样本点后，的估计值增加速度变快y B. 去除两个误差较大的样本点后，重新求得的回归方程对应直线一定过点()3,5C. 去除两个误差较大的样本点后，重新求得的回归方程为1.10.7y x =+D. 去除两个误差较大的样本点后，相应于样本点的残差为0.1()2,2.7【答案】C【解析】【分析】根据直线的斜率大小判断A ；求出判断B ；再求出经验回归方程判断C ；计算残差判断D 作l y 答.【详解】对于A ，因为去除两个误差较大的样本点后，经验回归直线的斜率变小，则的估计值增加速l y 度变慢，A 错误；对于B ，由及得：，因为去除的两个样本点和， 1.20.4y x =+3x =4y =()1.2,0.5()4.8,7.5并且，因此去除两个样本点后，样本的中心点仍为， 1.2 4.80.57.53,422++==(3,4)因此重新求得的回归方程对应直线一定过点，B 错误；(3,4)对于C ，设去除后重新求得的经验回归直线的方程为，由选项B 知，，解得l ˆ1.1y x a=+ˆ4 1.13a =⨯+， ˆ0.7a=所以重新求得的回归方程为，C 正确；1.10.7y x =+对于D ，由选项C 知，，当时，，则， 1.10.7y x =+2x = 1.120.72.9y =⨯+= 2.7 2.90.2-=-因此去除两个误差较大的样本点后，相应于样本点的残差为，D 错误.()2,2.70.2-故选：C6. 在四面体中，，，，，则该四面体的PABC PA AB ⊥PA AC ⊥120BAC ∠=︒2AB AC AP ===外接球的表面积为（ ）A.B. C. D. 12π16π18π20π【答案】D【解析】【分析】由线面垂直的判定定理可得平面，设底面的外心为，外接球的球心为，PA ⊥ABC ABC A G O 为的中点，可得四边形为平行四边形，所以，在中，由余弦定理及正弦定理D PA ODAG 1OG =ABC 可求，故可求外接球的半径，根据球的表面积公式即可求解.AG 【详解】因为，，平面,PA AB ⊥PA AC ⊥,,AB AC A AB AC =⊂ ABC 所以平面.PA ⊥ABC设底面的外心为，外接球的球心为，则平面，所以. ABC A G O OG ⊥ABC //PA OG 设为的中点，DPA因为，所以.OP OA =DO PA ⊥因为平面，平面,PA ⊥ABC AG ⊂ABC 所以，所以.PA ⊥AG //OD AG 因此四边形为平行四边形，所以. ODAG 112OG AD PA ===因为，，120BAC ∠=︒2AB AC ==所以,BC ===由正弦定理，得. 242AG AG ==⇒=所以该外接球的半径满足,R )()2225R OG AG =+=故该外接球的表面积为.24π20πS R ==故选:D.7. 已知圆O 的半径为1，A 为圆内一点，，B ，C 为圆O 上任意两点，则的最小值是12OA =AC BC ⋅ （ ）A.B. C. D. 18-116-11618【答案】A【解析】 【详解】首先设与所成角为，根据题意得到OA BC θ，再根据()1cos cos 2AC BC OC OA BC OC BC OA BC BC BCO BC θ⋅=-⋅=⋅-⋅=∠- 求解即可. 221111cos 2222BC BC BC BC θ-≥-【点睛】如图所示：设与所成角为，OA BCθ因为， ()1cos cos 2AC BC OC OA BC OC BC OA BC BC BCO BC θ⋅=-⋅=⋅-⋅=∠- 因为，112cos 2BC BCO BC OC ∠== 所以 211cos 22AC BC BC BC θ⋅=- 因为，当时，等号成立. 221111cos 2222BC BC BC BC θ-≥- 0θ= 因为，所以当时，取得最小值为， 02BC ≤≤ 12BC = 21122BC BC - 18-所以当时，取得最小值为. 12BC = AC BC ⋅ 18-故选：A8. 设是定义在上的函数，若是奇函数，是偶函数，函数()f x R ()2f x x +()f x x -，若对任意的，恒成立，则实数的最大值为()()[]()(),0,121,1,f x xg x g x x ∞⎧∈⎪=⎨-∈+⎪⎩[]0,x m ∈()3g x ≤m （ ）A. B. C. D. 133********【答案】B【解析】【分析】由是奇函数，是偶函数，求出，再根据()2f x x +()f x x -()2f x x x =-，作出函数的图象即可求解. ()()[]()(),0,121,1,f x xg x g x x ∞⎧∈⎪=⎨-∈+⎪⎩()g x【详解】因为是奇函数，是偶函数， ()2f x x +()f x x -所以，解得，()()()()()22f x x f x x f x x f x x⎧-+-=--⎪⎨-+=-⎪⎩()2f x x x =-由， ()()[]()(),0,121,1,f x x g x g x x ∞⎧∈⎪=⎨-∈+⎪⎩当时，则，所以， ()1,2x ∈()10,1x -∈()()()2121gx g x f x =-=-同理：当时，，()2,3x ∈()()()()214242g x g x g x f x =-=-=-以此类推，可以得到的图象如下：()gx由此可得，当时，，()4,5x ∈()()164g x f x =-由，得，解得或， ()3g x ≤()()16453x x --≤174x ≤194x ≥又因为对任意的，恒成立，[]0,x m ∈(3g x ≤所以，所以实数的最大值为. 1704m <≤m 174故选：B.【点睛】本题考查了奇函数与偶函数的性质，抽象函数的周期性，通过递推关系分析出每一个区间的解析式是本题的关键，数形结合是解题中必须熟练掌握一种数学思想，将抽象转化为形象，有助于分析解决抽象函数的相关问题. 二、多项选择题（本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．）9. 已知函数在区间上有且仅有3条对称轴，给出下列四个结论，正确()()πsin 04f x x ωω⎛⎫=+> ⎪⎝⎭[]0,π的是（ ）A. 的取值范围是 ω913,44⎡⎫⎪⎢⎣⎭B. 在区间上有且仅有3个不同的零点()f x ()0,πC. 的最小正周期可能是 ()f x 4π5D. 在区间上单调递增 ()f x π0,15⎛⎫ ⎪⎝⎭【答案】ACD【解析】【分析】由，得，再根据函数在区间上有且仅有条对称轴，[]0,πx ∈πππ,π444x ωω⎡⎤+∈+⎢⎥⎣⎦()f x []0,π3可得，可求出的取值范围判断A ，再利用三角函数的性质可依次判断BCD ． 5ππ7ππ242ω≤+<ω【详解】由，得， []0,πx ∈πππ,π444x ωω⎡⎤+∈+⎢⎥⎣⎦因为函数在区间上有且仅有条对称轴，()f x []0,π3所以，解得，故A 正确； 5ππ7ππ242ω≤+<91344ω≤<对于B ，，， (0,π)x ∈ ∴πππ,π444x ωω⎛⎫+∈+ ⎪⎝⎭， ∴π5π7ππ,422ω⎛⎫+∈ ⎪⎝⎭当时，在区间上有且仅有个不同的零点； π5π,3π42x ω⎛⎤+∈ ⎥⎝⎦()f x (0,π)2当时，在区间上有且仅有个不同的零点，故B 错误； π7π3π,42x ω⎛⎫+∈ ⎪⎝⎭()f x (0,π)3对于C ，周期，由，则， 2πT ω=91344ω≤<414139ω<≤， ∴8π8π139T <≤又，所以的最小正周期可能是，故C 正确； 84ππ58π,139⎛⎤∈ ⎥⎝⎦()f x 4π5对于D ，，， π0,15x ⎛⎫∈ ⎪⎝⎭∴ππππ,44154x ωω⎛⎫+∈+ ⎪⎝⎭又，， 91344ω≤<∴ππ2π7ππ,0,1545152ω⎡⎫⎛⎫+∈⊆⎪ ⎪⎢⎣⎭⎝⎭所以在区间上一定单调递增，故D 正确． ()f x π0,15⎛⎫ ⎪⎝⎭故选：ACD.10. 已知抛物线C ：的焦点为F ，准线为，A ，B 是C 上异于点O 的两点，O 为坐标原点，则22x y =l （ ）A. 的方程为 l 12x =-B. 若，则 32AF =AOF AC. 若，则0OA OB ⋅= 9OA OB ⋅≥D. 若，过AB 的中点D 作于点E ，则的最小值为 120AFB ∠=︒DE l ⊥AB DE【答案】BD【解析】【分析】A 选项，由抛物线方程得到准线方程，A 错误；由焦半径公式得到，进而求出1A y =A x =从而得到的面积，B 正确；由得到，，表达出AOF A 0OA OB ⋅=4A B x x =-4A B y y =，结合基本不等式求出最值，C 错误；作出辅助线，设()2222232A B A B OA OB x y y x ⋅=++，由焦半径公式得到，结合余弦定理，基本不等式得到的最小值. ,AF a BF b ==2a b DE +=AB DE【详解】的焦点为，准线方程为，故A 错误； 22x y =F ⎛ ⎝12y =-由焦半径公式可知：，解得， 1322A AF y =+=1A y =故，故 222A A x y ==A x =所以的面积为，B 正确； AOF A 111222A OF x ⋅=⨯=若，则，即，解得：， 0OA OB ⋅= 0A B A B x x y y +=22104A B A B x x x x +=4A B x x =-则，4A B y y =故 ()()()2222222223232A A B B AB A B OA OB x y x y x y y x ⋅=++=++≥+，32264A B A B x x y y =+⋅=故，当且仅当时，等号成立，C 错误；8OA OB ⋅≥A B A B x y y x =过点作⊥l 于点，过点B 作⊥l 于点，A 1AA 1A 1BB 1B设，所以， ,AF a BF b ==2a b DE +=因为()2222222cos AB a b ab AFB a b ab a b ab =+-∠=++=+-， ()()22223342a b a b a b DE ++⎛⎫≥+-== ⎪⎝⎭所以. AB ≥故选：BD【点睛】圆锥曲线中最值或范围问题的常见解法：（1）几何法，若题目的条件和结论能明显体现几何特征和意义，则考虑利用几何法来解决；（2）代数法，若题目的条件和结论能体现某种明确的函数关系，则可首先建立目标函数，再求这个函数的最值或范围．11. 如图，正方体中，顶点在平面内，其余顶点在的同侧，顶点到1111ABCD A B C D -A αα1,,B C A α的距离分别为，则（ ）1,2,3A. 平面BD A αB. 平面平面1A AC ⊥αC. 直线与所成角比直线与所成角大1AB α1AA αD.【答案】ABD【解析】【分析】根据点到面的距离的性质，结合线面垂直的判定定理、线面角的定义、面面相交的性质进行求解判断即可.【详解】解：设的交点为，显然是、的中点，,AC BD O O AC BD 因为平面，到平面的距离为，所以到平面的距离为，ABCD A α= C α2O α1又到平面的距离为，B α1所以平面，即平面，即A 正确；//BO α//BD α设平面，ABCD l α= 所以，//BD l 因为是正方形，所以，ABCD AC BD ⊥又因为平面，平面，1AA ⊥ABCD BD ⊂ABCD 所以，因为平面，1AA BD ⊥11,,AA AC A AA AC ⋂=⊂1A AC 所以平面，因此有平面，而，BD ⊥1A AC l ⊥1A AC l ⊂α所以平面平面，因此选项B 正确；1A AC ⊥α设到平面的距离为，1B αd 因为平面，是正方形，点，B 到的距离分别为，1，11AA B B A α= 11AA B B 1A α3所以有， 31422d d +=⇒=设正方体的棱长为，1111ABCD A B CD -a设直线与所成角为，所以， 1AB αβ14sin AB β===设直线与所成角为，所以， 1AA αγ133sin AA aγ==因为，因此选项C 不正确；3>sin sin βγβγ<⇒<因为平面平面，平面平面，1A AC ⊥α1A AC ⋂A α=所以在平面的射影与共线，1,C A α,E F A显然，如图所示：1112,3,,,CE A F AC AA a AA AC ====⊥由，11ECA CAE CAE A AF ECA A AF ∠+∠=∠+∠⇒∠=∠， 111cos ,sin A F CE ECA A AF AC AA ∠=∠=由， 2212249cos sin 112ECA A AF a a a ∠+∠=⇒+=⇒=因此选项D 正确，故选：ABD 12. 已知，为正实数，且，则（ ）a b 26ab a b ++=A. 的最大值为2B. 的最小值为5 ab 2a b +C. 的最小值为D. 1211a b +++98()0,3a b -∈【答案】AC【解析】【分析】由已知条件结合基本不等式及相关结论分别检验各选项即可求解.【详解】依题意，对于A ：因为，26ab a b ++=所以，62ab a b ab =++≥+当且仅当时取等号，2a b =令，则有，0t =>260t +-≤解得，又因为， t -≤≤0t =>所以，即0t <≤0<≤的最大值为2，故A 选项正确；ab 对于B ：因为，26ab a b ++=所以， ()221162222224a b ab a b ab a b a b +=++=⨯++≤⨯++当且仅当时取等号，2a b =令，则有，20t a b =+>28480t t +-≥解得或（舍去），4t ≥t 12≤-即，所以的最小值为4，24a b +≥2a b +故B 选项错误；对于C ：因为，26ab a b ++=所以， 12111888b b a ++==++所以，81221119888111a b b b +++≥=+++=++当且仅当，即时等式成立， 2118b b +=+3b =所以的最小值为，故C 选项正确； 1211a b +++98对于D ：当，时，， 14a =225b =()4.150,3a b -=∉所以D 选项错误；故选：AC.三、填空题（本题共4小题，每小题5分，共20分．）13. 设直线是曲线的一条切线，则_________．10x y ++=ln y a x =-=a 【答案】2-【解析】【分析】设切点为，根据导数的几何意义求出切点的横坐标，再根据切点即在曲线上又在切线上()00,x y 即可得解.【详解】设切点为，()00,x y ， 1y x '=-则，所以， 0011x x y x ==-=-'01x =所以切点为，()1,a 又切线为，10x y ++=所以，解得.110a ++=2a =-故答案为：.2-14. 楼道里有8盏灯，为了节约用电，需关掉3盏互不相邻的灯，则关灯方案有_________种．【答案】20【解析】【分析】根据题意，原问题等价于在5盏亮灯的6个空隙中插入3盏不亮的灯，由组合公式计算即可求解.【详解】依题意，原问题等价于在5盏亮灯的6个空隙中插入3盏不亮的灯，则有种方案.36C 20=故答案为：20. 15. 过双曲线：右焦点作直线，且直线与双曲线的一条渐近线垂直，C ()222210,0x y a b a b-=>>F l l C 垂足为A ，直线与另一条渐近线交于点B ．且点A ，B 位于x 轴的异侧，O 为坐标原点，若的内切l OAB A 圆的半径为，则双曲线C 的离心率为__________． 23b【解析】 【分析】作出图象，设的内切圆的圆心为，易知在的平分线上，过分别作OAB A M M AOB ∠Ox M 于，于，则有四边形为正方形，则，MN OA ⊥N MT AB ⊥T MTAN 2||||3b NA MN ==2||3b ON a =-，由，可得，由斜率公式即可得答案. tan MNb AOF ON a∠==2a b =【详解】解：如图所示：设A 在第一象限，由题意可知，其中为点到渐近线的距离，， AF d b ===d (c,0)F b y x a =||OF c =所以， ||OA a ===设的内切圆的圆心为，OAB A M 则在的平分线上，M AOB ∠Ox 过分别作于，于，M MN OA ⊥N MT AB ⊥T 又因为于，FA OA ⊥A 所以四边形为正方形，MTAN所以， 2||||3b NA MN ==所以， 2||||||3b ON OA NA a =-=-又因为， 2||3tan 2||3bMN b AOF b ON aa ∠===-所以， 2233a b a =-，2a b =所以，22225c a b b =+=所以， c =所以. c e a ===. 16. 小说《三体》中，一个“水滴”摧毁了人类整个太空舰队，当全世界第一次看到“水滴”的影像时，所有人都陶醉于它那绝美的外形．这东西真的是太美了，像梦之海中跃出的一只镜面海豚，仿佛每时每刻都在宇宙之夜中没有尽头地滴落着．有科幻爱好者为“水滴”的轴截面设计了二维数学图形，已知集合．由集合中所有的点组成的图形如图中阴影部分()()(){}22,cos sin 4,0P x y x y θθθπ=-++=≤≤P 所示，中间白色部分就如美丽的“水滴”．则图中“水滴”外部阴影部分的面积为_________．【答案】 16π3+【解析】【分析】根据图形与，建立直角坐标系，画出图形，()()(){}22,cos sin 4,0πP x y x y θθθ=-+-=≤≤求出相应的坐标，先求第一、二象限的阴影面积，再求第三象限的阴影面积，再求和即可求解.【详解】根据题意，建立直角坐标系，如图所示：在方程，中， ()()22cos sin 4x y θθ-+-=0πθ≤≤令，则有， 0x =222cos 2sin sin 4y y θθθ+-+=所以，其中， 12sin y yθ=-0πθ≤≤所以，所以， []sin 0,1θ∈[]12sin 0,2y y θ=-∈解得，1y ⎡⎤⎤∈-⎣⎦⎦所以，，，， (A ()0,3E ()0,1G -(0,D 令，则有，0θ=()2214x y -+=所以，，()1,0C ()3,0N 令，则有πθ=()2214x y ++=所以，. ()1,0B -()3,0M -由，，易得与线段()3,0M -()3,0N ()0,3E A MEN MN 组成的图形为的上半圆，229x y +=由此可知，在第一、第二象限中的阴影面积是由 的上半圆减去上半圆 229x y +=()2214x y -+=与上半圆相交的部分形成， ()2214x y ++=即与线段组成的面积，设为. A BACBC S 水滴上部由，，三点易得 (A ()1,0B -()1,0C 为边长为2的等边三角形，ABC A所以 212ππ263ABC AnC S S =⨯⨯-=-A 弓形所以，4π23ABC AnC S S S =+=A 弓形水滴上部设第一、二象限的阴影面积为， 1S 则. 19π9π4π19π2236S S =-=-+=+水滴上部由，，易得与线段 ()1,0B -()1,0C ()0,1G -A BGCBC 组成的图形为的下半圆， 221x y +=设在第三象限中的阴影面积为， 2S 则有， 2π4MOD MpD S S S =+-A 弓形由图知11322MOD S MO OD =⨯⨯=⨯=A ，，11222MBD S MB OD =⨯⨯=⨯=A 2π3MBD ∠=所以，214ππ233MBD MpD S S =⨯⨯-=A 弓形所以，2π4ππ13π43412MOD MpD S S S =+-=+-=A 弓形所以图中“水滴”外部阴影部分的面积为：. 1219π13π16π226123S S S ⎛=+=⨯=+ ⎝故答案为：. 16π3+【点睛】本题考查了圆与三角函数综合的知识点，可以根据图形的对称性建立直角坐标系，将图形转化为实际的数据，割补法是求阴影面积常用的方法，需要考生有一定的分析转化能力.四、解答题（本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17. 记为正项数列的前项和，已知是4与的等比中项． n S {}n a n 1n a +n S （1）求的通项分式；{}n a （2）证明：． 2222123111154n a a a a +++⋅⋅⋅+<【答案】（1）21n a n =-（2）证明见解析 【解析】【分析】(1)由等比中项得，进而由递推式计算出，并得到，得数列()214n n a S +=11a =12n n a a --=是等差数列，进而可求解；{}n a (2)由，从第二项开始放缩即可证明. ()22111114121n a n n n ⎛⎫=<- ⎪-⎝⎭-【小问1详解】∵是4与的等比中项，∴①． 1n a +n S ()214n n a S +=当时，，∴． 1n =()2111144a S a +==11a =当时，②，2n ≥()21114n n a S --+=由①-②得，， ()()()22111144n n n n n a a S S a --+-+=-=∴， ()()1120n n n n a a a a ----+=∵，∴，0n a >12n n a a --=∴数列是首项为l ，公差为2的等差数列， {}n a ∴的通项公式． {}n a 21n a n =-【小问2详解】由（1）得，2111a =当时，，2n ≥()222111111444121n a n n n n n ⎛⎫==<=- ⎪--⎝⎭-∴ 22222221232311111111n na a a a a a a +++⋅⋅⋅+=+++⋅⋅⋅+1111111115151114122314444n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫<+-+-+⋅⋅⋅+-=+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦18. 已知a ，b ，c 分别为三个内角A ，B ，C 的对边，且．ABC A cos sin a C C b c +=+（1）求A ；（2）已知M 为BC 的中点，且，的平分线交BC 于N ，求线ABC A AM =BAC ∠段AN 的长度． 【答案】（1） π3A =（2） AN =【解析】【分析】（1）根据题意，由正弦定理的边角互化将原式化简，再结合三角恒等变换即可求得结果； （2）根据题意，可得，再结合三角形()22222242AMAB ACAB AB AC AC c b bc =+=+⋅+=++的面积公式，代入计算，即可得到结果. 【小问1详解】由题意知中，， ABC A cos sin a C C b c +=+由正弦定理边角关系得：则sin cos sin A C A C，()sin sin sin sin sin cos cos sin sin B C A C C A C A C C =+=++=++， sin cos sin sin A C A C C =+∵，()0,πC ∈∴， sin 0C ≠cos 1A A -=∴，∴， π2sin 16A ⎛⎫-= ⎪⎝⎭π1sin 62A ⎛⎫-= ⎪⎝⎭又，， ()0,πA ∈ππ5π,666A ⎛⎫-∈- ⎪⎝⎭所以，即． ππ=66A -π3A =【小问2详解】如下图所示，在中，为中线，ABC A AM∴， 2AM AB AC =+∴，()22222242AMAB ACAB AB AC AC c b bc =+=+⋅+=++ ∴． 2212b c bc ++=∵， ABC S =△1sin 2bc A ==3bc =∴，b c +==∵， ABC ABN ACN S S S =+△△△，∴． ()1πsin 26b c AN AN =+=AN =19. 近日，某芯片研发团队表示已自主研发成功多维先进封装技术XDFOI ，可以实现4nm 手机SOC 芯片的封装，这是中国芯片技术的又一个重大突破，对中国芯片的发展具有极为重要的意义．可以说国产4nm 先进封装技术的突破，激发了中国芯片的潜力，证明了知名院士倪光南所说的先进技术是买不来的、求不来的，自主研发才是最终的出路．研发团队准备在国内某著名大学招募人才，准备了3道测试题，答对两道就可以被录用，甲、乙两人报名参加测试，他们通过每道试题的概率均为，且相互独立，若()01p p <<甲选择了全部3道试题，乙随机选择了其中2道试题，试回答下列问题．（所选的题全部答完后再判断是否被录用）（1）求甲和乙各自被录用的概率；（2）设甲和乙中被录用的人数为，请判断是否存在唯一的值，使得？并说明理由． ξp 0p () 1.5E ξ=【答案】（1）甲被录用的概率为，乙被录用的概率为2332p p -2333p p -（2）不存在；理由见解析 【解析】【分析】(1)分析已知，甲被录用符合二项分布，乙被录用符合组合排列，分别利用对应求概率公式计算即可.(2)先分析的可能取值，然后分别求解对应概率，再利用离散型数学期望的公式表示出数学期望，然后构ξ造函数，利用求导分析函数单调性，进而判断即可. 【小问1详解】由题意，设甲答对题目的个数为，得， X ()~3,X B p 则甲被录用的概率为，()2232313C 132P pp p p p =-+=-乙被录用的概率为． ()222332C 133P p p p p =-=-【小问2详解】的可能取值为0，1，2，ξ则，()()()12011P P P ξ==--， ()()()1212111P P P P P ξ==-+-，()122P PP ξ==∴ ()()()()()121212*********E P P P P P P PPξ=⨯--+⨯-+-+⨯⎡⎤⎣⎦，23232312323365 1.5P P p p p p p p =+=-+-=-=，32101230p p ∴-+=设，()()321101230f p p p p +=<<-则．()23024f p p p '=-∴当时，单调递减，405p <<()f p 当时，单调递增，415p <<()f p 又，，，()03f =()11f =4110525f ⎛⎫=> ⎪⎝⎭所以不存在的值，使得.p 0p ()00f p =20. 如图，四棱锥的底面是边长为2的正方形，．P ABCD -ABCD 2PA PB ==（1）证明：；PAD PBC ∠=∠（2）当直线PA 与平面PCD 所成角的正弦值最大时，求此时二面角的大小． P AB C --【答案】（1）证明见解析（2）6π【解析】【分析】(1) 分别取，的中点，，连接，，，证明出，可得AB CD E F PE EF PF PC PD =，由此可证得结论成立；PAD PBC ≌△△(2)先根据条件推出为二面角的平面角，设，建立空间直角坐标系，利用PEF ∠P AB C --PEF α∠=空间向量法结合基本不等式求出直线与平面所成角的正弦值的最大值，求出对应的角的值，即PA PCD 可求解. 【小问1详解】分别取，的中点，，连接，，， AB CD E F PE EF PF ∵，为的中点，∴．PA PB =E AB PE AB ⊥∵四边形为正方形，则且，∴． ABCD AB CD ∥AB CD =CD PE ⊥∵，分别为，的中点，∴，∴，E F AB CD EF AD ∥EF CD ⊥∵，∴平面．EF PE E ⋂=CD ⊥PEF∵平面，∴． PF ⊂PEF CD PF ⊥在中，PCD A ∵为的中点，，∴． F CD CD PF ⊥PC PD =又∵，，∴， PA PB =AD BC =PAD PBC ≌△△从而可得． PAD PBC ∠=∠【小问2详解】由（1）可知，，PE AB ⊥EF AB ⊥∴为二面角的平面角，且，PEF ∠P AB C --PE ==以点为坐标原点，，所在直线分别为x ，轴建立如下图所示的空间直角坐标系，E EB EFy设，其中，PEF α∠=0απ<<则，，，，，，()1,0,0A -()1,0,0B ()1,2,0C ()1,2,0D -()0,2,0F ()P αα，，．()AP αα= ()2,0,0DC =u u ur()FP αα=- 设平面的法向量为，PCD (),n x y z =由，即，取， 00n DC n FP ⎧⋅=⎪⎨⋅=⎪⎩202)0x y z αα=⎧⎪⎨-⋅=⎪⎩y α=则，，∴，2z α=-0x=(),2n αα=-cos ,n AP n AP n AP⋅<>==⋅==令，(77t α-=∈-+则， cos α=则，cos ,n AP <>==≤=当且仅当时，即当时，等号成立．1t =cos α=6πα=所以当直线与平面所成角的正弦值最大时，二面角为．PA PCD P AB C --6π21. 已知，D 是圆C ：上的任意一点，线段DF 的垂直平分线交DC 于点P ． ()1,0F -()22116x y -+=（1）求动点P 的轨迹的方程：Γ（2）过点的直线与曲线相交于A ，B 两点，点B 关于轴的对称点为，直线交轴于(),0M t l Γx B 'AB 'x 点，证明：为定值． N OM ON ⋅【答案】（1）22143x y +=（2）证明见解析 【解析】【分析】（1）由中垂线性质，可知，得动点P 的轨迹以，F 42PC PF PC PD DC FC +=+==>=C 为焦点的椭圆；（2）将直线与曲线方程联立，利用韦达定理及题目条件表示出点N 坐标，后可得答案. l Γ【小问1详解】圆：，圆心为，半径为4，C ()22116x y -+=)1,0因为线段DF 的垂直平分线交DC 于P 点，所以， PD PF =所以， 42PC PF PC PD DC FC +=+==>=所以由椭圆定义知，P 的轨迹是以，F 为焦点的椭圆， C 则，，.242a a =⇒=221c c =⇒=2223b a c =-=故轨迹方程为：．22143x y +=【小问2详解】依题意，直线不垂直于坐标轴，设直线的方程为，将其与方程联立：l l ()0x my t m =+≠Γ，消去x 得. 22143x my tx y =+⎧⎪⎨+=⎪⎩()2223463120m y mty t +++-=方程判别式，设，，则，()2248430m t+->()11,A x y ()22,B x y ()22,B x y '-由韦达定理有，，122634mt y y m -+=+212231234t y y m -=+则直线的方程为，AB '()121112y y y y x x x x +-=--令()1212211212N 121212202my y t y y x y x y y yy x m t y y y y y y +++=⇒===⋅++++，则，得.2312426t m t mt t -=⋅+=-40,N t ⎛⎫ ⎪⎝⎭()400,，,OM t ON t ⎛⎫== ⎪⎝⎭∴．即为定值4．44OM ON t t ⋅=⋅= OM ON ⋅ 22. 已知函数，．()1e ln axf x x x-=+a ∈R （1）当时，求函数的最小值； 1a =()f x x -（2）若函数的最小值为，求的最大值． ()f x xa a 【答案】（1）0（2）1【分析】（1）当时，令，求得，根据在不同区间1a =()()F x f x x =-()()()121e x x x x F x --=-'()F x '的符号判断的单调性，由单调性即可求出的最小值；()F x ()()F x f x x =-（2）将等价变换为，借助第（1）问中判断的符号时()≥f x a x ()0f x ax -≥()()()121e x x xx F x --=-'构造的在时取最小值，取，将问题转化为有解问题即可.()1ex g x x -=-1x =()ln g ax x -ln 1ax x -=【小问1详解】当时，令，，1a =()()1e ln x x x F xf x x x-+=--=()0,x ∈∞则，()()()()()11112221e e 11e e 11x x x x x x x x x x x x F xx x ------+-'==-⋅-+-=令，，则，()1ex g x x -=-x ∈R ()1e 1x g x -'=-易知在上单调递增，且，()g x 'R ()10g '=∴当时，，在区间上单调递减，且，()0,1x ∈()0g x '<()g x ()0,1()()110e x g x x g -=->=当时，，在区间上单调递增，且，()1,x ∈+∞()0g x '>()g x ()1,+∞()()110e x g x x g -=->=∴当时，，在区间上单调递减， ()0,1x ∈()()()121e 0x x x F x x --'=-<()F x ()0,1当时，，在区间上单调递增，()1,x ∈+∞()()()121e 0x x x F xx --'=->()F x ()1,+∞当时，取得极小值，也是最小值，，1x =()F x ()()11mine 1ln1101F x F -==+-=∴当时，函数的最小值为. 1a =()f x x -0【小问2详解】由已知，的定义域为， ()f x ()0,∞+若函数的最小值为，则有，∴，， ()f x x a ()≥f x a x()f x ax ≥()0f x ax -≥令，即的最小值为，()()h x f x ax =-()()1e ln ax x ax h x x ax xf -+=--=0由第（1）问知，当且仅当时，取最小值，1x =()1ex g x x -=-()10g =∴当且仅当时，取得最小值， ln 1ax x -=()ln g ax x -0又∵，()()()l 1l 1n 1n n e e ln ln ln ee ax ax ax x x g ax x ax x x ax x ax h x x-----=--=+-=+-=∴只需令有解，即有解， ln 1ax x -=ln 1x a x+=令，，则， ()ln 1x H x x+=()0,x ∈+∞()()221ln 1ln x x x x H x x x ⋅-+'==-当时，，在区间上单调递增， ()0,1x ∈()2ln 0xH x x '=->()H x ()0,1当时，，在区间上单调递减， ()1,x ∈+∞()2ln 0xH x x'=-<()H x ()1,+∞∴， ()()ln 111x a H x H x+==≤=综上所述，若函数的最小值为，则的最大值为. ()f x xa a 1【点睛】在导数压轴题中，常常会使用前问的结论或某一步构造的函数，解决后面的问题.本题第（2）问中直接求导分析的单调性较为困难，这里使用了换元思想，借助第()()1e ln ax x ax h x x ax xf -+=--=（1）问构造的，使，以达到简化运算的目的.()1ex g x x -=-()()ln g ax x h x -=。

大联考湖南师大附中2024届高三月考试卷（五）数学一､选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知集合{}{}2,,1,9A a a B =-=-，若{}1,1,9A B ⋃=-，则=a （）A .3B.1C.-1D.-32.已知复数231ii 2i iz -=--，则z 的虚部为（）A.-1B.12-C.12D.13.二项式741x ⎫⎪⎭的展开式中常数项为（）A .7- B.21- C.7D.214.已知函数()()()321222xxa x a x f x --+-=+为偶函数，则=a （）A.2B.1C.1- D.2-5.已知F 为双曲线2222:1(0,0)x y C a b a b-=>>的左焦点，直线33y x a =+与C 交于,A B 两点，且BF x ⊥轴，则C 的离心率为（）A.B.C.2D.36.已知函数()cos ln f x x a x =+在区间π0,2⎛⎫⎪⎝⎭上单调递增，则a 的最小值为（）A.π8 B.π4 C.π2D.π7.已知31sin cos ,cos sin 33αβαβ+=-=-，则()cos 22αβ-=（）A.4781B.4781-C.1781D.1781-8.在数列{}n a 中的相邻两项n a 与()*1n a n +∈N 之间插入一个首项为1n a n -，公差为1n-的等差数列的前n项，记构成的新数列为{}n b ，若21n a n =+，则{}n b 前65项的和为（）A.252-B.-13C.272- D.-14二､多选题（本大题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.）9.已知S 为圆锥的顶点，AB 为该圆锥的底面圆O 的直径，45,SAB C ∠= 为底面圆周上一点，60,BAC SC ∠==，则（）A.该圆锥的体积为π3B.AC =C.该圆锥的侧面展开图的圆心角大于180D.二面角A BC S --10.已知椭圆2222:1(0)x y C a b a b+=>>的左､右焦点分别为12,F F ，直线y x =+经过C 的一个焦点和一个顶点，且与C 交于,A B 两点（点A 在第三象限），则（）A.2a b =B.2ABF △的周长为8C.83AB =D.以2AF 为直径的圆过点B11.若函数()()ln 0cf x ax b x a x=+-≠在x c =处取得极值，则（）A.240b ac ->B.ac b +为定值C.当0<a 时，()f x 有且仅有一个极大值D.若()f x 有两个极值点，则1x a=是()f x 的极小值点12.今年是共建“一带一路”倡议提出十周年.某校进行“一带一路”知识了解情况的问卷调查，为调动学生参与的积极性，凡参与者均有机会获得奖品.设置3个不同颜色的抽奖箱，每个箱子中的小球大小相同质地均匀，其中红色箱子中放有红球3个，黄球2个，绿球2个；黄色箱子中放有红球4个，绿球2个；绿色箱子中放有红球3个，黄球2个，要求参与者先从红色箱子中随机抽取一个小球，将其放入与小球颜色相同的箱子中，再从放入小球的箱子中随机抽取一个小球，抽奖结束.若第二次抽取的是红色小球，则获得奖品，否则不能获得奖品，已知甲同学参与了问卷调查，则（）A.在甲先抽取的是黄球的条件下，甲获得奖品的概率为47B.在甲先抽取的不是红球的条件下，甲没有获得奖品的概率为1314C.甲获得奖品的概率为2449D.若甲获得奖品，则甲先抽取绿球的机会最小三､填空题（本大题共4小题，每小题5分，共20分.）13.已知向量()1,1a =- ，向量b 满足22b a b -= ，则⋅= a b __________.14.已知正三棱台的上､和为__________.15.已知直线10x y -+=与圆()22:8C x m y -+=交于,A B 两点，则满足“ABC的面积为”的m 的一个值为__________.16.已知函数()()sin (0,0,0π)f x A x B A ωϕωϕ=++>><<的部分图象如图所示，且32MN =，则不等式()1f x ≥+[]0,4上的解集为__________.四､解答题（本大题共6个小题，共70分.解答应写出文字说明､证明过程或演算步骤.）17.记ABC 的内角,,A B C 的对边分别为,,a b c ，已知1tan tan 3B C =.（1）求222c b a-的值；（2）若a =，且ABC的周长为3，求边b 上的高.18.记n S 为正项数列{}n a 的前n 项和，且113a =，()231nn n S a =-.（1）求数列{}n a 的通项公式；（2）设()111n n n n a b a S ++=-，记数列{}n b 的前n 项和为n T ，证明：38n T ≥.19.为检验预防某种疾病的A B ､两种疫苗的免疫效果，随机抽取接种A B ､疫苗的志愿者各100名，化验其血液中某项医学指标（该医学指标范围为[]0,100)，统计如下：该项医学指标[)0,25[)25,50[)50,75[]75,100接种A 疫苗人数10m+105030m-接种B 疫苗人数10m-304020m+个别数据模糊不清，用含字母()m m ∈N 的代数式表示.（1）为检验该项医学指标在[)0,50内的是否需要接种加强针，先从医学指标在[)25,50的志愿者中，按接种A B ､疫苗分层抽取8人，再次抽血化验进行判断.从这8人中随机抽取4人调研医学指标低的原因，记这4人中接种B 疫苗的人数为X ，求X 的分布列与数学期望；（2）根据（1）化验研判结果，医学认为该项医学指标低于50，产生抗体较弱，需接种加强针，该项医学指标不低于50，产生抗体较强，不需接种加强针.请先完成下面的22⨯列联表，若根据小概率0.025α=的独立性检验，认为接种A B ､疫苗与志愿者产生抗体的强弱有关联，求m 的最大值.疫苗抗体合计抗体弱抗体强A 疫苗B 疫苗合计附：()()()()22()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.α0.250.0250.005x α1.3235.0247.87920.如图，在直三棱柱111ABC A B C -中，1BC =，点D 为11B C 上一点，且1CD BC ⊥.（1）证明：1AC 平面1A BD ；（2）若AC AB =，求直线CD 与平面1A BD 所成角的正弦值.21.已知抛物线E 的顶点在坐标原点，对称轴为坐标轴，且经过()()12312,1,2,2,1,4A A A ⎛⎫-- ⎪⎝⎭三点中的两点.（1）求抛物线E 的方程；（2）设O 为坐标原点，E 的焦点为F ，过F 的直线BC 与E 交于,B C 两点，过F 的直线PQ 与E 交于,P Q 两点，点,P B 都在第二象限，记直线,BC PQ 的倾斜角分别为,αβ，且90αβ-=.若直线PB 与直线CQ 交于点M ，不同于点M 的点N 满足MN y ⊥轴，当ON PQ 时，设,NBC OBC 的面积分别为,m n ，求m nmn-的取值范围.22.已知函数()()2ln 2f x a x x a x =---.（1）求函数()f x 的极值；（2）设()f x 的导函数为()f x '，若()1212,x x x x <为()f x 的两个零点，证明：()()211f x f x ''>-.大联考湖南师大附中2024届高三月考试卷（五）数学一､选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知集合{}{}2,,1,9A a a B =-=-，若{}1,1,9A B ⋃=-，则=a （）A.3 B.1C.-1D.-3【答案】B 【解析】【分析】由{}{}1,1,9,1,9A B B ⋃=-=-，得到1A ∈求解.【详解】解：因为{}{}1,1,9,1,9A B B ⋃=-=-，所以1A ∈，当21a =时，1a =±，根据元素的互异性可知，1a =；当1a -=时，1a =-，不满足元素的互异性，舍去，故选：B.2.已知复数231ii 2i iz -=--，则z 的虚部为（）A.-1 B.12-C.12D.1【答案】C 【解析】【分析】根据复数除法的运算法则、复数乘方的法则，结合共轭复数和复数虚部的定义进行求解即可.【详解】因为()()()2231i 1i 1i 12i 11ii 2i i i 2i 21i 1i 42z -----=====---+++-所以1i 2z =，所以z 的虚部为12，故选：C.3.二项式741x ⎫⎪⎭的展开式中常数项为（）A.7- B.21- C.7D.21【答案】A 【解析】【分析】根据二项式通项公式进行求解即可.【详解】二项式741x ⎫-⎪⎭的通项公式为()14147317741C C 1rrrr rrr T x x --+⎛⎫=⋅⋅-=⋅-⋅ ⎪⎝⎭，令1414013rr -=⇒=，所以常数项为()17C 17⋅-=-，故选：A4.已知函数()()()321222xxa x a x f x --+-=+为偶函数，则=a （）A.2B.1C.1- D.2-【答案】B 【解析】【分析】结合偶函数定义与指数幂的运算计算即可得.【详解】因为()f x 为偶函数，所以()()f x f x -=，即()()()()323212122222xx xxa x a x a x a x ----+--+-=++，整理得()3210a x -=恒成立，所以()210a -=，则1a =.故选：B.5.已知F 为双曲线2222:1(0,0)x y C a b a b-=>>的左焦点，直线33y x a =+与C 交于,A B 两点，且BF x ⊥轴，则C 的离心率为（）A.B.C.2D.3【答案】C 【解析】【分析】根据题意直线过双曲线的左顶点得(),0A a -，再由BF x ⊥求出2,b B c a ⎛⎫-- ⎪⎝⎭，然后利用点B 也在直线上得到2c a =，从而求解.【详解】易知直线33y x a =+经过C 的左顶点(),0A a -，设(),0F c -，因为BF x ⊥轴，所以22221c y a b -=，解得2b y a =-，或2b y a =（舍去），所以点B 坐标为2,b c a ⎛⎫-- ⎪⎝⎭，则233b c a a -=-+，整理得2233ac a b -=，所以22233ac a c a -=-，即22320c ac a -+=，解得c a =（舍去），或2c a =，所以C 的离心率为2ce a==，故C 正确.故选：C.6.已知函数()cos ln f x x a x =+在区间π0,2⎛⎫⎪⎝⎭上单调递增，则a 的最小值为（）A.π8 B.π4 C.π2D.π【答案】C 【解析】【分析】由题意可得()0f x '≥在区间π0,2⎛⎫ ⎪⎝⎭上恒成立，即sin ≥a x x 在区间π0,2⎛⎫⎪⎝⎭上恒成立，设()πsin ,0,2g x x x x ⎛⎫=∈ ⎪⎝⎭，利用导数求出max ()g x 可得答案.【详解】()sin sin 0-'=-+=≥a a x x f x x x x在区间π0,2⎛⎫ ⎪⎝⎭上恒成立，即sin ≥a x x 在区间π0,2⎛⎫⎪⎝⎭上恒成立，设()πsin ,0,2g x x x x ⎛⎫=∈ ⎪⎝⎭，则()sin cos 0'=+>g x x x x ，所以()g x 在π0,2⎛⎫⎪⎝⎭上单调递增，则()max π()2g x g x <=，所以π2a ≥，则a 的最小值为π2.故选：C.7.已知31sin cos ,cos sin 33αβαβ+=-=-，则()cos 22αβ-=（）A.4781 B.4781-C.1781D.1781-【答案】D 【解析】【分析】分别将3sin cos 3αβ+=和1cos sin 3αβ-=-分别平方相加求出sin cos cos sin αβαβ-，然后逆用正弦两角差公式并结合倍角公式从而求解.【详解】由sin cos 3αβ+=得，221sin cos 2sin cos 3αβαβ++=，由1cos sin 3αβ-=-得，221cos sin 2cos sin 9αβαβ+-=，两式相加得，()422sin cos cos sin 9αβαβ+-=，则()7sin 9αβ-=-，所以()()22717cos 2212sin 12981αβαβ⎛⎫-=--=-⨯-=- ⎪⎝⎭，故D 正确.故选：D.8.在数列{}n a 中的相邻两项n a 与()*1n a n +∈N 之间插入一个首项为1nan -，公差为1n-的等差数列的前n 项，记构成的新数列为{}n b ，若21n a n =+，则{}n b 前65项的和为（）A.252-B.-13C.272-D.-14【答案】A 【解析】【分析】根据题意，得到数列{}n b 中n a 及其后面n 项的和为n S ，()()1112n n n n S n a n+=+-求解.【详解】解：数列{}n b 为：1122233331121,1,,,1,,,,1,,,233n n a a a a a a a a a a a n------- ，1231,,,,1,,n n n n n n a a a a a n n n+----- ，设n a 及其后面n 项的和为n S ，则()()()1111123222n n n n n S n a n n ++=+-⨯=-=-，所以数列{}n S 是以1为首项，公差为12-的等差数列.所以{}n b 前65项的和为1210710125222S S S ⎛⎫- ⎪⎝⎭+++==-，故选：A.二､多选题（本大题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.）9.已知S 为圆锥的顶点，AB 为该圆锥的底面圆O 的直径，45,SAB C ∠=为底面圆周上一点，60,BAC SC ∠== ，则（）A.该圆锥的体积为π3B.AC =C.该圆锥的侧面展开图的圆心角大于180D.二面角A BC S --【答案】AC 【解析】【分析】求得该圆锥的体积判断选项A ，求得AC 的长度判断选项B ，求得该圆锥的侧面展开图的圆心角判断选项C ，求得二面角A BC S --的正切值判断选项D.【详解】如图，因为45SAB ∠= ，所以SAB △为等腰直角三角形，又SC =，则SA SB ==，所以2AB ==，则1r AO SO ===，所以该圆锥的体积为21ππ,A 33V r SO =⋅=正确；易知ABC 为直角三角形，且90ACB ∠= ，又60BAC ∠= ，则30ABC ∠= ，所以11,B 2AC AB ==错误；该圆锥的侧面展开图为一扇形，其弧长为2πl =，扇形半径为R SA ==，设扇形圆心角为α，所以πlRα==>，所以该圆锥的侧面展开图的圆心角大于180,C 正确；取BC 的中点D ，连接,SD OD ，则,SD BC OD ⊥为ABC 的中位线，所以11,22OD BC OD AC ⊥==，所以ODS ∠为二面角A BC S --的平面角，易知SOD 为直角三角形，所以tan 2,D SOODS OD∠==错误.故选：AC .10.已知椭圆2222:1(0)x y C a b a b+=>>的左､右焦点分别为12,F F ，直线y x =+经过C 的一个焦点和一个顶点，且与C 交于,A B 两点（点A 在第三象限），则（）A.2a b =B.2ABF △的周长为8C.83AB =D.以2AF 为直径的圆过点B【答案】BCD 【解析】【分析】根据条件求出,,a b c 的值，判定A 错误；由椭圆定义可得2ABF △的周长为8，判定B 正确；联立方程组求出(2,3A B ⎛⎫- ⎪ ⎪⎝⎭，可得83AB =，判定C 正确；2221212BF BF F F +=，所以1290F BF ∠= ，判定D 正确.【详解】易知直线y x =+经过C的焦点()1F和顶点(B ，所以b c ==，则a ==2，所以,A a =错误；由椭圆的定义可知，2ABF △的周长为48,B a =正确；由上可知C 的方程为22142x y +=，由221,42x y y x ⎧+=⎪⎨⎪=⎩解得120,x x ==，则(,3A B ⎛⎫- ⎪ ⎪⎝⎭，所以8,C 3AB ==正确；由12122,BF BF F F ===得，2221212BF BF F F +=，所以1290F BF ∠= ，则以2AF 为直径的圆过点,D B 正确.故选：BCD .11.若函数()()ln 0cf x ax b x a x=+-≠在x c =处取得极值，则（）A.240b ac ->B.ac b +为定值C.当0<a 时，()f x 有且仅有一个极大值D.若()f x 有两个极值点，则1x a=是()f x 的极小值点【答案】ABC 【解析】【分析】求导()22ax bx cf x x++='，由题意可知，x c =是方程20ax bx c ++=的一个变号实数根，则Δ0>，即可判断A ；由20ac bc c ++=判断B ；当a<0时，可得，当()0,x c ∈时()0f x ¢>，当(),x c ∈+∞时()0f x '<，即可判断C ；将1b ac =--代入20ax bx c ++=整理得()10x x c a ⎛⎫--= ⎪⎝⎭，则方程有不相等的实数根1a 与c ，分类讨论，结合极值点的定义可判断D.【详解】()f x 的定义域为()0,∞+，则0x c =>，()222b c ax bx cf x a x x x++=++='，由题意可知，x c =是方程20ax bx c ++=的一个变号实数根，则2Δ40b ac =->，故A 正确；由20ac bc c ++=得，1ac b +=-，故B 正确；当a<0时，因为0c >，所以函数2y ax bx c =++开口向下，且与x 轴正半轴只有一个交点，当()0,x c ∈时，()0f x ¢>，当(),x c ∈+∞时，()0f x '<，所以()f x 在()0,c 上单调递增，在(),c +∞上单调递减，则()f x 有且仅有一个极大值，故C 正确；将1b ac =--代入20ax bx c ++=整理得()10x x c a ⎛⎫--= ⎪⎝⎭，则方程有不相等的实数根1a 与c ，即1c a≠，当10c a <<时，()10,,x c a ∞⎛⎫∈+ ⎪⎝⎭ 时，()10,,f x x c a ⎛⎫>∈ ⎪⎝⎭'时，()0f x '<，所以()f x 在()10,,,c a ∞⎛⎫+ ⎪⎝⎭上单调递增，在1,c a ⎛⎫ ⎪⎝⎭上单调递减，则1x a=是()f x 的极大值点，x c =是()f x 的极小值点，当10c a <<时，()10,,x c a ∞⎛⎫∈+ ⎪⎝⎭ 时，()0f x ¢>；当1,x c a ⎛⎫∈ ⎪⎝⎭时，()0f x '<，所以()f x 在()10,,,c a ⎛⎫+∞⎪⎝⎭上单调递增，在1,c a ⎛⎫ ⎪⎝⎭上单调递减，则x c =是()f x 的极大值点，1x a=是()f x 的极小值点，故D 错误，故选：ABC.12.今年是共建“一带一路”倡议提出十周年.某校进行“一带一路”知识了解情况的问卷调查，为调动学生参与的积极性，凡参与者均有机会获得奖品.设置3个不同颜色的抽奖箱，每个箱子中的小球大小相同质地均匀，其中红色箱子中放有红球3个，黄球2个，绿球2个；黄色箱子中放有红球4个，绿球2个；绿色箱子中放有红球3个，黄球2个，要求参与者先从红色箱子中随机抽取一个小球，将其放入与小球颜色相同的箱子中，再从放入小球的箱子中随机抽取一个小球，抽奖结束.若第二次抽取的是红色小球，则获得奖品，否则不能获得奖品，已知甲同学参与了问卷调查，则（）A.在甲先抽取的是黄球的条件下，甲获得奖品的概率为47B.在甲先抽取的不是红球的条件下，甲没有获得奖品的概率为1314C.甲获得奖品的概率为2449D.若甲获得奖品，则甲先抽取绿球的机会最小【答案】ACD【解析】【分析】设出事件后，结合条件概率与全概率公式逐个计算即可得.【详解】设A 红，A 黄，A 绿，分别表示先抽到的小球的颜色分别是红、黄、绿的事件，设B 红表示再抽到的小球的颜色是红的事件，在甲先抽取的是黄球的条件下，甲获得奖品的概率为：()()()24477277P B A P B A P A ⨯===红黄红黄黄∣，故A 正确；在甲先抽取的不是红球的条件下，甲没有获得奖品的概率为：()()()()()()23211377724287P A B P A B P A B P B A P A P A ⨯+⨯+====红红红红绿黄红红红红∣，故B 错误；由题意可知，()()()()()32234,,,,77777P A P A P A P B A P B A =====红红红红绿黄黄∣∣，()12P B A =红绿∣，由全概率公式可知，甲获得奖品的概率为：P =()()()()()()P A P B A P A P B A P A P B A +⋅+⋅红红红红红绿绿黄黄∣∣∣3324212477777249=⨯+⨯+⨯=，故C 正确；因为甲获奖时红球取自哪个箱子的颜色与先抽取小球的颜色相同，则()()()()3349377248P A P B A P A B P B ⋅==⨯⨯=红红红红红红∣∣，()()()()2449177243P A P B A P A B P B ⋅===红黄黄红黄红∣∣，()()()()21497722424P A P B A P A B P B ⋅===红绿绿红绿红∣∣，所以甲获得奖品时，甲先抽取绿球的机会最小，故D 正确.故选：ACD.三､填空题（本大题共4小题，每小题5分，共20分.）13.已知向量()1,1a =- ，向量b 满足22b a b -= ，则⋅= a b __________.【答案】12##0.5【解析】【分析】由22b a b -=平方求解.【详解】解：由()1,1a =- ，得a = 由22b a b -= ，得222444b a b a b -⋅+= ，则242a b a ⋅== ，所以12a b ⋅= .故答案为：1214.已知正三棱台的上､和为__________.【答案】4【解析】【分析】根据正三棱台的性质及题中条件分别求出侧面的高h 和正三棱台的高H ，然后利用棱台体积公式即可求解.【详解】设该正三棱台侧面的高为h ，由题意可知，12h +⋅=h =该正三棱台的上底面的面积为21322⨯⨯=下底面的面积为213273224⨯⨯=，设正三棱台的高为H ，则1H ==，故该正三棱台的体积为11344V =+⨯=⎝.故答案为：4.15.已知直线10x y -+=与圆()22:8C x m y -+=交于,A B 两点，则满足“ABC 的面积为”的m 的一个值为__________.【答案】1（或3-，或1-±）【解析】【分析】由ABC 的面积为，得到60ACB ∠= 或120ACB ∠= ，进而得到圆心C 到直线AB 的距离为d =d =.【详解】解：由ABC 的面积为(21sin 2ACB ⨯∠=，解得3sin 2ACB ∠=，则60ACB ∠= 或120ACB ∠= ，易知圆心C 到直线AB 的距离为d =或d ==，或=，解得1m =-±1m =或3m =-.故答案为：1(或3-，或1-±)16.已知函数()()sin (0,0,0π)f x A x B A ωϕωϕ=++>><<的部分图象如图所示，且32MN =，则不等式()1f x ≥+[]0,4上的解集为__________.【答案】51,416⎡⎤⎢⎥⎣⎦【解析】【分析】根据函数的最高点和最低点，结合函数的零点、正弦型函数的单调性进行求解即可.【详解】由图可知，3,1,A B A B +=⎧⎨-+=-⎩解得2,1A B ==，由图可知，12sin +12sin 2ϕϕ=⇒=，又0πϕ<<，所以π6ϕ=或5π6ϕ=，当π6ϕ=时，()π2sin 16f x x ω⎛⎫=++ ⎪⎝⎭，因为0ω>，所以当0x >时，显然有ππ66x ω+>，因此函数先是增函数，显然不符合图象，当5π6ϕ=时，()5π2sin 16f x x ω⎛⎫=++ ⎪⎝⎭因为0ω>，所以当0x >时，显然有5π5π66x ω+>，因此函数先是减函数，符合图象特征，令()15π5π15π7π2sin 10sin 2π66266f x x x x k ωωω⎛⎫⎛⎫=++=⇒+=-⇒+=- ⎪ ⎪⎝⎭⎝⎭，或()25π11π2πZ 66x k k ω+=-∈，因为32MN =，所以212π32π4π3239x x ωωω-=⇒⋅=⇒=，即()4π5π2sin 196f x x ⎛⎫=++⎪⎝⎭，由()4π5π4π5π12sin 11sin ,96962f x x x ≥⎛⎫⎛⎫≥+⇒++≥++ ⎪ ⎪⎝⎭⎝⎭所以有()()π4π5π3π921932π2πZ Z 4964216216m m m x m m x m +≤+≤+∈⇒-≤≤-∈，因为[]0,4x ∈，所以令1m =，则有9219351692162161616x x -≤≤-⇒≤≤，而[]0,4x ∈，所以51416x ≤≤，故答案为：51,416⎡⎤⎢⎥⎣⎦【点睛】关键点睛：本题的关键是根据函数的单调性确定ϕ的值.四､解答题（本大题共6个小题，共70分.解答应写出文字说明､证明过程或演算步骤.）17.记ABC 的内角,,A B C 的对边分别为,,a b c ，已知1tan tan 3B C =.（1）求222c b a -的值；（2）若a =，且ABC 的周长为3，求边b 上的高.【答案】（1）12（2）2【解析】【分析】（1）根据题意，得到3sin cos sin cos B C C B =，结合正弦、余弦定理，求得2224()2c b a -=，即可求解；（2）根据题意得到3b c +=，结合（1）得到1c b -=，联立方程组求得2,1c b ==，再由余弦定cos A 的值，利用sin h c A =，即可求解.【小问1详解】解：由1tan tan 3B C =，可得sin sin cos 3cos B CB C =，所以3sin cos sin cos B C C B =，又由正弦定理和余弦定理，可得222222322a b c a c b b c ab ac +-+-⋅=⋅，整理得2224()2c b a -=，所以22212c b a -=.【小问2详解】解：由a =，且ABC 的周长为3，可得3b c +=，又由（1）可知，222123c b a -==，即()()3c b c b +-=，所以1c b -=，联立方程组31b c c b +=⎧⎨-=⎩，解得2,1c b ==，所以22222212(6)1cos 22124b c a A bc +-+-===-⨯⨯，则15sin 4A ===，所以边b 上的高为1515sin 242h c A ==⨯=.18.记n S 为正项数列{}n a 的前n 项和，且113a =，()231nn n S a =-.（1）求数列{}n a 的通项公式；（2）设()111n n n n a b a S ++=-，记数列{}n b 的前n 项和为n T ，证明：38n T ≥.【答案】（1）13nn a ⎛⎫= ⎪⎝⎭（2）证明见解析【解析】【分析】（1）由()231nn n S a =-退位相减可得13n n a a -=，又10,a ≠可得113n n a a -=，继而可知数列{}n a 为等比数列，则通项可求；（2）由（1）可得1n a +、1n S +继而可求n b ，并将其裂项再求和，即可证明不等式.【小问1详解】因为()231nn n S a =-，所以，当2n ≥时，()111231n n n S a ---=-，两式相减得，()()111223131nn n n n n S S a a ----=---，化简可得()()1133310nn n n a a -----=，所以130n n a a --=，即13n n a a -=，又110,3a =≠可得113n n a a -=，所以数列{}n a 是以13为首项，13为公比的等比数列，可得1111333n nn a -⎛⎫⎛⎫=⋅= ⎪⎪⎝⎭⎝⎭【小问2详解】由（1）可知，1113n n a ++⎛⎫= ⎪⎝⎭，1113311112313nn n S ⎡⎤⎛⎫-⎢⎥ ⎪⎡⎤⎝⎭⎢⎥⎛⎫⎣⎦==-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦-所以1111123n n S ++⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，则()1111131********n n n n n n n a b a S ++++⎛⎫⎪⎝⎭==-⎛⎫⎡⎤⎛⎫⎛⎫-⨯- ⎪⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎣⎦，111=111133nn +-⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，123n n T b b b b =++++ 12231111111111111111111333333n n +=-+-++⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫------ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ ，1312113n +=-⎛⎫- ⎪⎝⎭，因为118139n +⎛⎫-≥⎪⎝⎭，所以1198113n +≤⎛⎫- ⎪⎝⎭，则38n T ≥.19.为检验预防某种疾病的A B ､两种疫苗的免疫效果，随机抽取接种A B ､疫苗的志愿者各100名，化验其血液中某项医学指标（该医学指标范围为[]0,100)，统计如下：该项医学指标[)0,25[)25,50[)50,75[]75,100接种A 疫苗人数10m+105030m-接种B 疫苗人数10m-304020m+个别数据模糊不清，用含字母()m m ∈N 的代数式表示.（1）为检验该项医学指标在[)0,50内的是否需要接种加强针，先从医学指标在[)25,50的志愿者中，按接种A B ､疫苗分层抽取8人，再次抽血化验进行判断.从这8人中随机抽取4人调研医学指标低的原因，记这4人中接种B 疫苗的人数为X ，求X 的分布列与数学期望；（2）根据（1）化验研判结果，医学认为该项医学指标低于50，产生抗体较弱，需接种加强针，该项医学指标不低于50，产生抗体较强，不需接种加强针.请先完成下面的22⨯列联表，若根据小概率0.025α=的独立性检验，认为接种A B ､疫苗与志愿者产生抗体的强弱有关联，求m 的最大值.疫苗抗体合计抗体弱抗体强A 疫苗B 疫苗合计附：()()()()22()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.α0.250.0250.005x α1.3235.0247.879【答案】（1）分布列见解析，()3E X =（2）列联表见解析，2【解析】【分析】（1）由抽样调查性质可得抽取接种A B 、疫苗人数，计算出X 的所有可能取值的对应概率可得分布列，由分布列可计算期望；（2）结合2χ的计算公式计算出对应m 的范围即可得.【小问1详解】从医学指标在[)25,50的志愿者中，按接种A B 、疫苗分层抽取8人中，接种A 疫苗有2人，接种B 疫苗有6人，由题意可知，X 可能取值为2,3,4，()()()221304262626444888C C C C C C 3432,34C 14C 7C 14P X P X P X =========，X 的分布列为：X234P31447314则()343234314714E X =⨯+⨯+⨯=；【小问2详解】22⨯列联表如下：疫苗抗体合计抗体弱抗体强A 疫苗20m +80m -100B 疫苗40m-60m+100合计60140200则()()()()()222200804060202101001001406021m m m m m χ⎡⎤---++-⎣⎦==⨯⨯⨯，由题意可知，()20.025210 5.02421m x -≥=，整理得，()21052.752m -≥，解得2m ≤或18,m m ≥∈N ，又100,m m -≥∈N ，则10,m m ≤∈N ，所以2,m m ≤∈N ，故m 的最大值为2.20.如图，在直三棱柱111ABC A B C -中，1BC =，点D 为11B C 上一点，且1CD BC ⊥.（1）证明：1AC 平面1A BD ；（2）若AC AB =，求直线CD 与平面1A BD 所成角的正弦值.【答案】（1）证明见解析（2）223【解析】【分析】（1）利用空间向量的线性运算与数量积运算法则求得D 为1B C 的中点，再利用线面平行的判定定理即可得证；（2）建立空间直角坐标系，然后利用空间向量法求出直线CD 与平面1A BD 所成角的正弦值，从而求解.【小问1详解】设()11101C D tC B t =≤≤ ，则11111CD CC C D CC tC B =+=+ ，1111111111C B C B B B C B C C C B CC =+=+=- ，所以()()()221111111111111··1·CD C B CC tC B C B CC t CC C B CC tC B =+-=--+ ，因为11111,,2CD BC CC C B BC ⊥⊥=，所以()()21210t AA -=，解得12t =，则点D 为1B C 的中点.连接1AB ，设11A B AB E = ，连接DE ，因为四边形11ABB A 为矩形，所以E 为1AB 的中点，在11AB C △中，DE 为中位线，所以DE 1AC ，又1AC ⊄平面1,A BD DE ⊂平面1A BD ，所以1AC 平面1A BD ..【小问2详解】取BC 的中点O ，连接,OD OA ，则DO 1BB ，所以OD BC ⊥，由AC AB =可知，AO BC ⊥，易知四边形1AA DO 为平行四边形，又1AA ⊥平面ABC ，所以DO ⊥平面ABC ，所以DO OA ⊥.以O 为坐标原点，分别以,,OC OA OD 所在直线为x 轴､y 轴､z 轴建立如图所示的空间直角坐标系O xyz -，如图，设1(0),(0)OA m m BC a =>==>，所以1,CC a BC ==，则()()1220,,,,0,0,0,0,,,0,022A m a B a D a C a ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，所以()1220,,0,,0,,0,22DA m DB a a DC a a ⎛⎫⎛⎫==--=⋅- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ，设平面1A BD 的一个法向量为(),,n x y z =r，由10,0,DA n DB n ⎧⋅=⎪⎨⋅=⎪⎩得0,0,2my ax az =⎧⎪⎨--=⎪⎩取x =，则)1n =-r ，设直线CD 与平面1A BD 所成角为θ，则22sin cos ,3DC n θ===.故直线CD 与平面1A BD 所成角的正弦值为223.21.已知抛物线E 的顶点在坐标原点，对称轴为坐标轴，且经过()()12312,1,2,2,1,4A A A ⎛⎫-- ⎪⎝⎭三点中的两点.（1）求抛物线E 的方程；（2）设O 为坐标原点，E 的焦点为F ，过F 的直线BC 与E 交于,B C 两点，过F 的直线PQ 与E 交于,P Q 两点，点,P B 都在第二象限，记直线,BC PQ 的倾斜角分别为,αβ，且90αβ-=.若直线PB 与直线CQ 交于点M ，不同于点M 的点N 满足MN y ⊥轴，当ON PQ 时，设,NBC OBC 的面积分别为,m n ，求m nmn-的取值范围.【答案】（1）24x y =（2）10,4⎛⎫ ⎪⎝⎭【解析】【分析】（1）根据抛物线的对称性，分类讨论进行求解即可；（2）根据直线的斜率公式、一元二次方程根与系数关系，结合三角形面积公式、点到直线距离公式、基本不等式进行求解即可.【小问1详解】因为()12,1A 关于y 轴对称的点为()12,1A -，所以拋物线E 经过12,A A 两点中的一点，由题意可知，抛物线E 经过311,4A ⎛⎫- ⎪⎝⎭，当抛物线E 的方程为22(0)y px p =->时，将点311,4A ⎛⎫- ⎪⎝⎭代入E 的方程得，()21214p ⎛⎫=-⨯- ⎪⎝⎭，解得132p =，验证可知，抛物线21:16E y x =-不经过点12,A A ，不满足题意；当抛物线E 的方程为22(0)x py p =>时，将点311,4A ⎛⎫- ⎪⎝⎭代入E 的方程得，()21124p -=⨯，解得2p =，验证可知，抛物线2:4E x y =经过点1A ，不经过点2A ，满足题意，故抛物线E 的方程为24x y =.【小问2详解】由（1）可知，()0,1F ，设BC 的方程为()10y kx k =+≠，设()()1122,,,B x y C x y ，由21,4,y kx x y =+⎧⎨=⎩得2440x kx --=，12124,4x x k x x +==-，因为90αβ-=，所以BC PQ ⊥，设()()3344,,,P x y Q x y ，同理可知，34344,4x x x x k+=-=-.直线BP 的斜率为223131313131444BPx x y y x x k x x x x --+===--，其方程()2311144x x x y x x +-=-，即311344x x x x y x +=-①同理可知直线CQ 的方程422444x x x xy x +=-，即31311313134444444x x x x x x y x x x x x x ⎛⎫⎛⎫-⋅--- ⎪ ⎪+⎝⎭⎝⎭=-=--②由①②解得，1y =-，所以点M 在直线1y =-上，由MN y ⊥轴可知，点N 在直线1y =-上，设()0,1N x -，由ON PQ 可知，ON BC ⊥，则1ON BCk k ⋅=-，所以011x k-=-，解得0x k =，由上可知，()212122444BC y y k x x k =++=++=+，原点O 到直线BC的距离为1d =，N 到直线BC的距离为2d =所以221112222m BC d k n BC d =⋅=+=⋅=则11m n mn n m -=-=2=()211111122422k ==⋅≤⋅+，=，即0k =取得等号，因为0k ≠，所以14m n mn -<，由0m n ->得，104m n mn -<<，故m n mn -的取值范围为10,4⎛⎫⎪⎝⎭.【点睛】关键点睛：本题的关键是对m nmn-的表达式进行变形，用基本不等式进行求解.22.已知函数()()2ln 2f x a x x a x =---.（1）求函数()f x 的极值；（2）设()f x 的导函数为()f x '，若()1212,x x x x <为()f x 的两个零点，证明：()()211f x f x ''>-.【答案】（1）极大值为2ln 42a aa a +-.（2）证明见解析【解析】【分析】（1）先利用导数求得()f x 的单调区间，再利用极值定义即可求得函数()f x 的极值；（2）先将不等式()()211f x f x ''>-转化为2121212ln 0x x x x x x -->，再构造函数()12ln (1)g t t t t t=-->，并利用导数证得()()10g t g >=，进而证得原不等式成立.【小问1详解】()f x 的定义域为()0,∞+，()()()()2122x a x af x x a x x-+=---=-'，当0a ≤时，()0f x '<在()0,∞+上恒成立，所以()f x 在()0,∞+上单调递减，此时()f x 无极值；当0a >时，当0,2a x ⎛⎫∈ ⎪⎝⎭时，()0f x ¢>，当,2a x ⎛⎫∈+∞⎪⎝⎭时，()0f x '<，所以()f x 在0,2a ⎛⎫ ⎪⎝⎭上单调递增，在,2a ⎛⎫+∞ ⎪⎝⎭上单调递减，故()f x 只存在极大值且为2ln 242a aa f a a ⎛⎫=+- ⎪⎝⎭.【小问2详解】由()1212,x x x x ≠为()f x 的两个零点得，()()22111222ln 2ln 2a x x a x a x x a x ---=---，所以()()()2221212121ln ln 2a x x x x x x x x ⎡⎤-+-=-+-⎣⎦，则()()()()()()22212121212212121122ln ln lnx x x x x x x x a x x x x x x x x -+--++==-+-+-，又()()()()1212122222a af x f x x a x a x x +=---+--'-'()121211222a x x x x ⎛⎫=++-++ ⎪⎝⎭()()()()212112212211211222ln x x x x x x xx x x x x -++⎛⎫=++-++ ⎪⎝⎭+-.由（1）可知，()f x 在0,2a ⎛⎫ ⎪⎝⎭上单调递增，在,2a ⎛⎫+∞ ⎪⎝⎭上单调递减，若()1212,x x x x <为()f x 的两个零点，则120,,,22a a x x ∞⎛⎫⎛⎫∈∈+ ⎪ ⎪⎝⎭⎝⎭，所以()()120,0f x f x >'<'.要证()()211f x f x ''>-，需证()()120f x f x ''+>，需证()()()()2121122122112112220ln x x x x x x xx x x x x -++⎛⎫++-++> ⎪⎝⎭+-，又12220x x ++>>，即证()2121221111220ln x x x x x x x x ⎛⎫-++-> ⎪⎝⎭+-，因为120x x <<，则211x x >，则()2211ln 0xx x x +->，所以需证()()221211211122ln 0x x x x x x x x ⎛⎫⎡⎤-++-+->⎪⎢⎥⎝⎭⎣⎦，即证2121212ln 0x x x x x x -->，令21(1)x t t x =>，需证12ln 0t t t-->，设()12ln (1)g t t t t t =-->，则()22212(1)10t g t t t t-=+-=>'，所以()g t 在()1,+∞上单调递增，所以()()10g t g >=，则12ln 0t t t-->，故()()211f x f x ''>-.。

长沙市2023—2024学年度高一第二学期开学自主检测数学（答案在最后）时量：120分钟满分：150分一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}139x A x =≤<，集合{}30log1B x x =≤<，则A B = （）A.[)1,2 B.[)0,2 C.[)0,3 D.[)1,3【答案】A 【解析】【分析】解指对数不等式化简集合,A B ，再利用集合的交集运算即可得解.【详解】因为{}{}{}0213933302xx A x x x x =≤<=≤<=≤<，{}{}{}33330log 1log 1log log 313B x x x x x x =≤<=≤<=≤<，所以{}[)121,2A B x x ⋂=≤≤=.故选：A.2.函数()1312⎛⎫=- ⎪⎝⎭xf x x 的零点一定位于下列的哪个区间（）A.()2,3 B.()1,2 C.()0,1 D.()1,0-【答案】C 【解析】【分析】由根的存在性定理求端点值的正负性，可知零点所在区间．【详解】因为函数()1312xf x x ⎛⎫=- ⎪⎝⎭,是连续单调函数，且()01310010,2f ⎛⎫=-=> ⎪⎝⎭()113111110,22f ⎛⎫=-=-< ⎪⎝⎭，∴函数()1312xf x x ⎛⎫=- ⎪⎝⎭的零点一定位于区间()0,1.故选:C ．3.已知a →,b →为非零向量，则“0a b →→∙>”是“a →与b →夹角为锐角”的A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件【答案】B 【解析】【详解】根据向量数量积的定义式可知，若0a b ⋅>，则a 与b 夹角为锐角或零角，若a 与b夹角为锐角，则一定有0a b ⋅> ，所以“0a b ⋅> ”是“a与b夹角为锐角”的必要不充分条件，故选B.4.已知函数()f x 的图象如图所示，则()f x 可以为（）A.()exxf x = B.()exf x x = C.()exf x x=D.()exx f x =【答案】D 【解析】【分析】先由图象得到()f x 的定义域、奇偶性与单调性，再结合指数函数的性质，逐一分析各选项即可得解.【详解】由图象可知，()f x 是定义在R 上的奇函数，则()()f x f x -=-，同时，()f x 在()0,∞+上先增后减，对于A ，()11e f =，()111e ef ---==-，不满足题意，故A 错误；对于B ，当120x x <<时，120e e x x <<，即210e e x x <<，所以1212ee x xx x <，即()()12f x f x <，所以()f x 在()0,∞+上单调递增，故B 错误；对于C ，显然，()exf x x=在0x =处无意义，故C 错误；对于D ，()exx f x =的定义域为R ，又()()e ex x x xf x f x ---==-=-，则()f x 是奇函数，经检验，()f x 的单调性也满足题意，故D 正确.故选：D.5.已知3log 2a =，4log 3b =，5log 4c =，则（）A.a b c >> B.b a c>> C.c b a>> D.a c b>>【答案】C 【解析】【分析】做差，利用换底公式，基本不等式，对数的性质进行大小比较.【详解】2222243ln 2ln 4ln 3ln 3ln 2ln 3ln 2ln 4ln ln 2log 3log 20ln 4ln 3ln 3ln 4ln 3ln 4ln 3ln 4b a +⎛⎫- ⎪-⎝⎭-=-==>=>22254ln 3ln 5ln 4ln 4ln 3ln 4ln 3ln 5ln ln 2log 4log 30ln 5ln 4ln 5ln 4ln 5ln 4ln 5ln 4c b +⎛⎫- ⎪--⎝⎭-=-=-=>=>所以c b a >>.故选：C.6.已知tan 2tan A B =，()1sin 4A B +=，则()sin A B -=（）A.13B.14 C.112D.112-【答案】C 【解析】【分析】根据题意，切化弦，结合两角和的正弦公式分别求出cos ,cos i s n n i s B A A B 的值，代入两角差的正弦公式即可求解.【详解】因为tan 2tan A B =，即sin sin 2cos cos A BA B=，所以sin cos 2sin cos A B B A =，因为()1sin sin cos cos sin 4A B A B A B +=+=，即13cos sin 4A B =，解得11cos sin ,sin cos 126A B A B ==，因为()sin A B -=sin cos cos sin A B A B -，所以()111sin 61212A B -=-=.故选：C【点睛】本题考查两角和与差的正弦公式；考查运算求解能力；熟练掌握两角和与差的正弦公式是求解本题的关键；属于中档题.7.如图，在ABC 中，满足条件1,3AD DB AE EC == ，若DE BA BC λμ=+ ，则11λμ+=（）A.8B.4C.2D.12【答案】A 【解析】【分析】利用向量加法的三角形法则，结合已知条件，可得1144DE BA BC =+ ，求出11,44λμ==，从而得出答案.【详解】因为DE DA AE =+ ，1,3AD DB AE EC ==,所以()11112424DE BA AC BA BC BA ==++-，即1144DE BA BC =+ ，又DE BA BC λμ=+ ，所以11,44λμ==，故118λμ+=.故选：A.8.设函数()()()1sin 02f x x ωϕω=+->，若对于任意实数ϕ，函数()f x 在区间[]0,2π上至少有2个零点，至多有3个零点，则ω的取值范围是（）A.1,13⎡⎫⎪⎢⎣⎭ B.41,3⎡⎫⎪⎢⎣⎭C.51,3⎡⎫⎪⎢⎣⎭D.45,33⎡⎫⎪⎢⎣⎭【答案】B 【解析】【分析】根据题意，将问题转化为研究1sin 2y x ω=-在任意一个长度为2π的区间上的零点问题，分别求得相邻三个零点之间的距离，相邻四个零点之间的最小距离，从而得到关于ω的不等式组，解之即可得解.【详解】因为ϕ为任意实数，故函数()f x 的图象可以任意平移，从而研究函数()f x 在区间[]0,2π上的零点问题，即研究函数1sin 2y x ω=-在任意一个长度为2π02π-=的区间上的零点问题，令1sin 2y x ω=-0=，得1sin 2x ω=，则它在y 轴右侧靠近坐标原点处的零点分别为π6ω，5π6ω，13π6ω，17π6ω，25π6ω，L ，则它们相邻两个零点之间的距离分别为2π3ω，4π3ω，2π3ω，4π3ω，L ，故相邻三个零点之间的距离为2πω，相邻四个零点之间的最小距离为8π3ω，所以要使函数()f x 在区间[]0,2π上至少有2个零点，至多有3个零点，则需相邻三个零点之间的距离不大于2π，相邻四个零点之间的最小距离大于2π，即2π2π8π2π3ωω⎧≤⎪⎪⎨⎪>⎪⎩，解得413ω≤<，即41,3ω⎡⎫∈⎪⎢⎣⎭.故选：B【点睛】关键点点睛：在求解复杂问题时，要善于将问题进行简单化，本题中的ϕ以及区间[]0,2π是干扰因素，所以排除干扰因素是解决问题的关键所在.二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.9.已知a ，b ，R c ∈，则下列结论正确的是（）A.若0a b >>，则11a b < B.若a b >，则22ac bc >C .若0a b >>，则11a b b a+<+ D.若0a >，0b >，2324a b a b +=+，则a b>【答案】AD 【解析】【分析】利用作差法可以判断AC ，举反例可排除B ，构造函数()23xf x x =+，利用其单调性可判断D ，从而得解.【详解】对A ，因为0a b >>，所以110b a a b ab--=<，则11a b <，故A 正确；对B ，当0c =，则220ac bc ==，故B 错误；对C ，因为()()1111a b a b a b a b b a ab ab -⎛⎫⎛⎫+-+=-+=-+ ⎪ ⎪⎝⎭⎝⎭，而0a b >>，则10,10a b ab->+>，所以110a b b a ⎛⎫+-+> ⎪⎝⎭，即11a b b a+>+，故C 错误；对D ，因为0b >，所以232423a b b a b b +=+>+，令()23xf x x =+，则()()f a f b >，易知()23xf x x =+在R 上单调递增，所以a b >，故D 正确.故选：AD.10.汽车的“燃油效率”是指汽车每消耗1L 汽油行驶的里程，如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况．下列叙述中正确的是（）A.消耗1L 汽油，乙车最多可行驶5kmB.甲车以80km/h 的速度行驶1h 消耗约8L 汽油C.以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多D.某城市机动车最高限速80千米/小时．相同条件下，在该市用丙车比用乙车更省油【答案】BD【解析】【分析】结合图象逐项分析即得.【详解】由题可知，当乙车速度大于40km/h 时，乙车每消耗1升汽油，行驶里程都超过5km ，A 错误；甲车以80km/h 的速度行驶时，燃油效率为10km/L,则行驶1h 消耗8L 汽油，B 正确；以相同速度行驶相同路程，燃油效率越高耗油越少，故三辆车中甲车消耗汽油最少，C 错误；在机动车最高限速80km/h 在相同条件下，丙车比乙车燃油效率更高，所以更节油，D 正确；故选：BD11.已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，下列说法正确的是（）A.函数()y f x =的图象关于直线π3x =-对称B.函数()y f x =在5ππ,6⎡⎤--⎢⎥⎣⎦上单调递减C.函数π6y f x ⎛⎫=+⎪⎝⎭是偶函数D.该函数的图象可由2cos y x =的图象向左平行移动π6个单位长度得到【答案】BC 【解析】【分析】先根据函数图象，结合三角函数的性质可确定函数的解析式，利用代入检验法可判断AB ，利用余弦函数的奇偶性可判断C ，利用三角函数平移的性质可判断D.【详解】由图象可知：2A =，37ππ3π4632T ⎛⎫=--= ⎪⎝⎭，则2πT =，故2π1Tω==，所以()()2sin f x x ϕ=+，又7π7π2sin 266f ϕ⎛⎫⎛⎫=+=-⎪ ⎪⎝⎭⎝⎭，则7π3π2π,Z 62k k ϕ+=+∈，所以ππ,Z k k ϕ=+∈23，由于π,2ϕ<所以π3ϕ=，故()π2sin 3f x x ⎛⎫=+ ⎪⎝⎭，对于A ，πππ2sin 02333f ⎛⎫⎛⎫-=-+=≠± ⎪ ⎪⎝⎭⎝⎭，故A 错误，对于B ，当5ππ,6x ⎡⎤∈--⎢⎣⎦时，π2πππ,π,3322x ⎡⎤⎡⎤+∈--⊆--⎢⎥⎢⎥⎣⎦⎣⎦，故()y f x =在5ππ,6⎡⎤--⎢⎥⎣⎦上单调递减，故B 正确，对于C ，ππππ2sin 2sin 2cos 6632y f x x x x ⎛⎫⎛⎫⎛⎫=+=++=+= ⎪ ⎪⎝⎭⎝⎭⎝⎭，显然π6y f x ⎛⎫=+⎪⎝⎭是偶函数，故C 正确，对于D ，2cos y x =的图象向左平行移动π6个单位长度得()π2π2cos 2sin 63y x x f x ⎛⎫⎛⎫=+=+≠ ⎪ ⎪⎝⎭⎝⎭，故D 错误，故选：BC.12.已知定义域为()0,∞+的函数()f x 满足：（1）对任意()0,x ∈+∞，()()22f x f x =恒成立；（2）当(]1,2x ∈时，()2f x x =-，则下列选项正确的有（）A.对任意m Z ∈，有()2mf =B.函数()f x 的值域为[)0,∞+C.存在Z n ∈，使得()219nf +=D.函数()f x 在区间(),a b 上单调递减的充要条件是：存在Z k ∈，使得()()1,2,2kk a b +⊆.【答案】ABD 【解析】【分析】利用条件(1)判断A ；利用条件(2)判断B ；利用反证法判断C ；结合以上推导判断D ．【详解】对于选项A ，()()()()11122222220mm m m f f f f ---=⋅=⋅⋅⋅===，A 正确；对于选项B ，当(12,2mm x +⎤∈⎦时，(]1,22m x ∈，[)20,122m m x x f ⎛⎫=-∈ ⎪⎝⎭，从而())1220,2222mm mm f x x x x f f +⎛⎫⎛⎫⎡=⋅⋅⋅==-∈ ⎪ ⎪⎣⎝⎭⎝⎭＝，所以函数()f x 的值域为[)0,∞+，B 正确；对于选项C ，因为(1212,2nn n +⎤+∈⎦，所以()12122121n n n nf +-+==--，假设存在n 使()219nf +=，则12210n n +-=，所以210n =，满足条件的整数不存在，C 错误；对于选项D ，若()()1,2,2kk a b +⊆，当(),x a b ∈时，()12k f x x +=-，函数()f x 在区间(),a b 上单调递减，若函数()f x 在区间(),a b 上单调递减，不妨设122k k a +≤<，Z k ∈，若22k b +>，则()122,2,k k a b ++∈，1222k k ++<，()()12220k k f f ++==，与已知矛盾，若1222k k b ++<≤，则()12,k a b +∈，当()102,k x b +∈，102k x +>，但()()2100220k k f x x f ++=-<=，与已知矛盾，故12k b +≤，故()()1,2,2kk a b +⊆，故函数()f x 在区间(),a b 上单调递减的充要条件是：存在Z k ∈，使得()()1,2,2k k a b +⊆，D 正确，故选：ABD.【点睛】本题解决的关键在于分区间求出函数的解析式，再结合函数的性质判断.三、填空题：本题共4小题，每小题5分，共20分13.3log 712lg5lg 43⎛⎫-++= ⎪⎝⎭______.【答案】87##117【解析】【分析】利用指数对数的运算性质计算即可.【详解】33log 7log 71182lg 5lg 42lg 52lg 21321377-⎛⎫--++=+-+=-+= ⎪⎝⎭.故答案为：87.14.设函数()y f x =的定义域为R ，则函数()1y f x =-与()1y f x =-的图象关于______对称.【答案】1x =【解析】【分析】先确定()y f x =与()y f x =-的图象关系，再同时向右平移一个单位可得答案.【详解】由于R x ∈，恒有()y f x =与()y f x =-的图象关于y 轴对称，又()y f x =向右平移一个单位得()1y f x =-，()y f x =-向右平移一个单位得()1y f x =-，故函数()1y f x =-与()1y f x =-的图象关于1x =对称.故答案为：1x =.15.函数()sin cos sin2f x x x x =-+在区间π0,2⎡⎤⎢⎥⎣⎦上的值域是__________．【答案】51,4⎡⎤-⎢⎥⎣⎦【解析】【分析】令sin cos t x x =-，根据同角的三角函数关系式求出关于sin2x 的表达式，最后利用二次函数2()1g t t t =-++的单调性求出函数的值域.【详解】令πsin cos 4t x x x =-=-，因为π0,2x ⎡⎤∈⎢⎥⎣⎦，πππ,444x ⎡⎤-∈-⎢⎥⎣⎦，所以[1,1]t ∈-，()22sin cos sin2sin cos (sin cos )11f x x x x x x x x t t =-+=---+=-+，设2()1,[1,1]g t t t t =-++∈-，显然一元二次函数2()1g t t t =-++在区间1[1,]2-上单调递增，在区间1[,1]2上单调递减，所以max min 15(,(1)124g g =-=-，所以函数()sin cos sin2f x x x x =-+的值域为5[1,4-.故答案为：5[1,4-.16.已知边长为的正三角形ABC 的中心为O ，正方形MNPQ ，且线段MP 与NQ 相交于点O ，则BM CP +=______.【答案】2【解析】【分析】结合图形，利用向量的加减运算化简BM CP +，再在正ABC 中求得OD ，从而得解.【详解】记BC 中点为D ，连接,,OB OC OD ，如图，因为在正方形MNPQ 中，MP 与NQ 相交于点O ，则O 是MP 的中点，所以0OM OP += ，则2BM CP BO OM CO OP OB OC OD +=+++=--=-，在正ABC 中，BC =，O 为ABC 的中心，所以1113232OD BC =⨯=⨯⨯=，则22BM CP OD +== .故答案为：2.【点睛】关键点点睛，本题解决的关键是充分用点O 的性质，利用向量的线性运算即可得解.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.已知向量(1,2)a = ，(3,2)b =- ．（1）求a b - ；（2）已知c = (2)a c c +⊥ ，求向量a 与向量c 的夹角．【答案】（1）（2）3π4【解析】【分析】（1）根据向量的坐标运算求向量的模即可；（2）由向量的模，根据向量的数量积公式转化求向量的夹角即可.【小问1详解】由题知，(1,2)a = ，(3,2)b =- 所以(2,4)a b -=-，所以a b -== 【小问2详解】由题知，(1,2)a = ，c = (2)a c c +⊥，所以a = (2)0a c c +⋅= ，所以220a c c ⋅+= ，所以22||||cos ,)||0a c a c c 〈+= ，所以2cos ,100a c +=，所以cos ,2a c 〈>=- ，因为[],)0,πa c ∈ ，向量a 与向量c 的夹角为3π4.18.已知函数()21ax b f x x +=+是定义域为R 的奇函数，且满足()()1012f f +=.（1）求a ，b 的值，判断函数()f x 在区间()0,∞+上的单调性（不需要证明）；（2）已知1x ∀，()20,x ∈+∞，且12x x <，若()()12f x f x =，求124x x +的取值范围.【答案】（1）1,0a b ==，()f x 的单调性见解析（2）()5,+∞【解析】【分析】（1）利用奇函数的性质与()()1012f f +=可求得,a b 的值，从而得到()f x 的解析式，再利用函数单调性的定义，结合作差法即可得解；（2）利用()()12f x f x =得121=x x ，再分析得21x >，将124x x +转化为关于2x 的表达式，从而利用对勾函数的性质即可得解.【小问1详解】因为函数2()1ax b f x x +=+是定义域为R 的奇函数，所以()00f =，又()()1012f f +=，则()112f =，所以00011112b a b +⎧=⎪⎪+⎨+⎪=⎪+⎩，解得10a b =⎧⎨=⎩，所以2()1x f x x =+，此时其定义域为R ，又2()()1x f x f x x --==-+，则函数()f x 是定义域为R 的奇函数，所以1,0a b ==，此时()f x 在()0,1上单调递增，在()1,+∞上单调递减，证明如下：设1201x x <<<，则()()()()22122112122222121211()()1111+-+-=-=++++x x x x x x f x f x x x x x ()()()()12212212111x x x x x x --=++，因为1201x x <<<，所以21211,0x x x x <->，所以()()()()122122121011x x x x x x --<++，12()()f x f x <，所以函数()f x 在()0,1上单调递增；同理可证在()1,+∞上单调递减.【小问2详解】因为()()12f x f x =，2()1x f x x =+，则有2112122212()(1)()()0(1)(1)x x x x f x f x x x ---==++，因为120x x <<，所以1210x x -=，即121=x x ，所以21x >，且121x x =，所以1222144x x x x +=+，令()141y x x x=+>，由对勾函数的性质可知，14y x x =+在()1,+∞上单调递增，所以1144151y x x =+>⨯+=，所以1254x x +>，即124x x +的取值范围为()5,+∞.19.如图所示，已知点()1,0A ，()1,0D -，点B ，C 在单位圆O 上，且3BOC π∠=.（1）若点34,55B ⎛⎫ ⎪⎝⎭，求cos AOC ∠的值；（2）设203AOB x x π⎛⎫∠=<<⎪⎝⎭，四边形ABCD 的周长为y ，将y 表示成x 的函数，并求出y 的最大值.【答案】（1）310-（2）23sin 323x y π⎛⎫=++⎪⎝⎭，max 5y =【解析】【分析】（1）根据任意角三角函数定义，由终边上的34,55B ⎛⎫ ⎪⎝⎭，可得43sin ,cos 55AOB AOB ∠=∠=，再由余弦的和角公式，可得答案；（2）根据圆直径的性质和锐角三角函数，可得弦,AB CD ，根据周长公式，可得函数，再根据三角恒等变换，可得周长y 关于x 的函数.【小问1详解】因为34,55B ⎛⎫ ⎪⎝⎭，且为AOB ∠终边上一点，所以43sin ,cos 55AOB AOB ∠=∠=，由3BOC π∠=，可得：1sin ,cos 22BOC BOC ∠=∠=，()cos cos cos cos sin sin AOC AOB BOC AOB BOC AOB BOC∠=∠+∠=∠∠-∠∠3143525210-=⨯-⨯=【小问2详解】由3BOC π∠=，易知等边BOC ，则1BC =，连接,AC BD ，作图如下：易知12,,2223x ABD ACD BDA AOB COD x ππ∠=∠=∠=∠=∠=-，即1232x CAD COD π∠=∠=-，则在Rt △ABD 中，sin 2sin 2x AB AD ADB =⋅∠=，同理，sin 2sin 32x CD AD CAD π⎛⎫=⋅∠=- ⎪⎝⎭，则122sin 12sin 32sin 2cos sin 23222222x x x x x y π⎛⎫⎛⎫=+++-=++- ⎪ ⎪ ⎪⎝⎭⎝⎭32sin sin 3sin 2sin 32222223x x x x x x π⎛⎫=+-=++=++ ⎪⎝⎭，由203x π<<，可得323x πππ<+<，根据正弦函数的性质，当232x ππ+=，即3x π=，则max 5y =.20.某医药公司研发的一种新药，如果成年人按规定的剂量服用，由监测数据可知，服用后6小时内每毫升血液中含药量y （单位：微克）与时间t （单位：小时）之间的关系满足如图所示的曲线，当[]0,1.5t ∈时，曲线是二次函数图象的一部分，当[]1.5,6t ∈时，曲线是函数()()log 2.550,1a y t a a =++>≠图象的一部分，根据进一步测定，每毫升血液中含药量不少于2微克时，治疗有效.（1）试求服药后6小时内每毫升血液中含药量y 与时间t 之间的函数关系式；（2）问服药多久后开始有治疗效果？治疗效果能持续多少小时？（精确到0.1）1.414≈）【答案】（1）2124(1)4,0 1.5log ( 2.5)5,1.56t t y t t ⎧--+≤<⎪=⎨++≤≤⎪⎩（2）0.3小时后，5.2小时【解析】【分析】（1）当0 1.5t ≤<时，设2(1)4y k t =-+，再将(0,0)代入即可求出k 的值，当1.56t ≤≤时，将点(1.5,3)的坐标代入函数表达式()log 2.55a y t =++即可求出a 的值，则可写出答案；（2）分段求出2y ≥时，对应的x 的取值范围，即可写出答案.【小问1详解】当0 1.5t ≤<时，由图象可设()214y k t =-+，将点()0,0的坐标代入函数表达式，解得4k =-，即当0 1.5t ≤<时，()2414y t =--+，当1.56t ≤≤时，将点()1.5,3的坐标代入函数()log 2.55a y t =++，得3log 45a =+，解得12a =，所以12log ( 2.5)5y t =++，故2124(1)4,0 1.5log ( 2.5)5,1.56t t y t t ⎧--+≤<⎪=⎨++≤≤⎪⎩.【小问2详解】当0 1.5t ≤<时，24(1)4y t =--+，令2y ≥，即()24142t --+≥，解得1122t -≤≤+，即0.3 1.7t ≤<，又0 1.5t ≤<，∴0.3 1.5t ≤≤，故服药0.3小时之后开始有治疗效果，当1.56t ≤≤时，12log ( 2.5)5y t =++，令2y ≥，即()12log 2.552t ++≥，解得 2.5 5.5t -≤≤，又1.56t ≤≤，∴1.5 5.5t ≤≤，综上，0.3 5.5t ≤≤，所以服药后的治疗效果能持续5.2小时.21.已知向量()()1cos ,sin (0),,,22a x x b f x a b ωωω⎛⎫=>==⋅ ⎪ ⎪⎝⎭.（1）当π6x =时，函数()f x 取得最大值，求ω的最小值及此时()f x 的解析式；（2）现将函数()f x 的图象沿x 轴向左平移3ωπ个单位，得到函数()g x 的图象.已知,,A B C 是函数()f x 与()g x 图象上连续相邻的三个交点，若ABC 是锐角三角形，求ω的取值范围.【答案】（1）min 2ω=，()πcos 23f x x ⎛⎫=- ⎪⎝⎭（2）π3ω>【解析】【分析】（1）根据数量积的坐标公式结合辅助角公式化简，再根据余弦函数的最值即可得解；（2）先根据平移变换得到函数()g x 的解析式，作出两个函数的图象，不妨设B 在x 轴下方，D 为AC 的中点，根据πcos cos 3x x ωω⎛⎫-= ⎪⎝⎭，求得BD ，再由ABC 为锐角三角形时，只需要π4ACB ∠>即可，即可得解.【小问1详解】()13cos sin 22f x a b x x ωω=⋅=+ ππcos cos sin sin 33x x ωω=+πcos 3x ω⎛⎫=- ⎪⎝⎭，当π6x =时，函数()f x 取得最大值，即()ππ2πZ 63k k ω-=∈，解得()122Z k k ω=+∈，且0ω>，则min 2ω=，此时()πcos 23f x x ⎛⎫=-⎪⎝⎭；【小问2详解】由函数()f x 的图象沿x 轴向左平移3ωπ个单位，得到()ππcos cos 33g x x x ωωω⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦，由（1）知()πcos 3f x x ω⎛⎫=- ⎪⎝⎭，作出两个函数图象，如图：,,A B C 为连续三交点，（不妨设B 在x 轴下方），D 为AC 的中点，由对称性可得ABC 是以B ∠为顶角的等腰三角形，根据图像可得2π2AC T CD ω===，即πCD ω=，由两个图像相交可得πcos cos 3x x ωω⎛⎫-= ⎪⎝⎭，即ππcos cos sin sin cos 33x x x ωωω+=，化简得sinx x ωω=，再结合22sin cos 1x x ωω+=，解得3cos 2x ω=±，故2C B y y =-=，可得BD =，当ABC 为锐角三角形时，只需要π4ACB ∠>即可，由tan 1πBD ACB DC ∠==>，故ω的取值范围为π3ω>.【点睛】关键点点睛：作出两个函数()(),f x g x 的图象，根据πcos cos 3x x ωω⎛⎫-= ⎪⎝⎭，求出等腰三角形ABC 底边上的高是解决本题的关键.22.已知函数()2e e x x f x a =-，()ln g x x =.（1）若存在()1,0x ∈-∞，对任意21,e e x ⎡⎤∈⎢⎥⎣⎦，()()12f x g x ≠，求实数a 的取值范围；（2）若函数()()()F x f x f x =+-，求函数()F x 零点的个数.【答案】（1）2a >或0a ≤（2）答案见解析【解析】【分析】（1）将问题转化为不等式有解问题，然后再将有解问题转化为最值求解即可；（2）()()()2e e e e 2x x x x F x a a --=+-+-，令e e x x p -=+，则()22h p ap p a =--，进而讨论方程220p a p a --=大于等于2的解的个数即可.【小问1详解】由21,e e x ⎡⎤∈⎢⎥⎣⎦得()[]21,1g x ∈-，因为存在()1,0x ∞∈-，对任意21,e e x ⎡⎤∈⎢⎥⎣⎦，()()12f x g x ≠，所以112e e 1x x a ->或112e e 1x x a -<-在()1,0x ∞∈-上有解，即11211e e x x a >+或11211e e x x a <-在()1,0x ∞∈-上有解，令111ex t =>，所以2a t t >+或2a t t <-在()1,∞+上有解，又22t t +>，20t t -<，所以2a >或a<0；【小问2详解】()()()()()222e e e e e e e e 2x x x x x x x x F x f x f x a a a a ----=+-=-+-=+-+-，令e e x x p -=+，2p ≥，则()()22,2h p F x ap p a p ==--≥，故只需要讨论方程220p a p a --=大于等于2的解，①当0a =时，0p -=，方程无大于等于2的解，函数()F x 无零点；②当0a >时，()020h a =-<，若()2220h a =->，即1a >时，方程无大于等于2的解，函数()F x 无零点；若()2220h a =-=，即1a =时，方程有一个等于2的解，此时e e 2x x -+=，解得0x =，函数()F x 有一个零点；若()2220h a =-<，即01a <<时，方程有一个大于2的解，此时e e x x p -+=，即2e e 10x x p -+=，此时240010p p ⎧->⎪>⎨⎪>⎩，方程有2根，即函数()F x 有两个零点；③当a<0时，()020h a =->，()2220h a =-<，此时方程无大于等于2的解，函数()F x 无零点；综上所述：当1a =时，函数()F x 有一个零点；当01a <<时，函数()F x 有两个零点；当0a ≤或1a >时，函数()F x 无零点.。

长沙市2023~2024学年高一年级期末考试数学试卷（答案在最后）2024年7月时量：120分钟满分：150分命题：高一数学组审题：高一数学组一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知复数2i z =-，则zz z =-（）A.1i 2-+ B.1i 2- C.1i 2+ D.1i 2--2.有一组互不相等的样本数据126,,,x x x ，平均数为x .若随机剔除其中一个数据，得到一组新数据，记为125,,,y y y ，平均数为y ，则下列说法错误的是（）A.新数据的极差可能等于原数据的极差B.新数据的中位数不可能等于原数据的中位数C.若x y =，则新数据的方差一定大于原数据方差D.若x y =，则新数据的40%分位数一定大于原数据的40%分位数3.设ABC 的内角A B C ､､所对边分别为,,a b c ，若π3A =，且不等式(230x x -+<的解集为{}x b x a <<∣，则B =（）A.π6B.5π6C.π6或5π6 D.2π34.在侧棱长为S ABC -中，40ASB BSC CSA ∠∠∠=== ，过A 作截面AEF ，则截面的最小周长为（）A. B.4C.6D.105.设,a b 是非零向量，则“存在实数λ，使得b a λ= ”是“a b a b +=+ ”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件6.如图，在直三棱柱111ABC A B C -中，1,AC BC CC AC BC ==⊥，点D 是AB 的中点，则直线1B B 和平面1CDB 所成角的正切值为（）A.22B.3222D.227.在正方体1111ABCD A B C D -中边长为2，点P 是上底面1111A B C D 内一动点，若三棱锥P ABC -的外接球表面积恰为41π4，则此时点P 构成的图形面积为（）A.πB.25π16C.41π16D.2π8.已知平面向量12312312,,,1,,60e e e e e e e e ====.若对区间1,12⎡⎤⎢⎥⎣⎦内的三个任意的实数123,,λλλ，都有11223312312e e e e e e λλλ++≥++，则向量13,e e 夹角的最大值的余弦值为（）A.366-B.356+-C.366-D.356-二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分.9.一个正八面体的八个面上分别标以数字1到8，将其随机抛掷两次，记与地面接触面上的数字依次为12,x x ，事件A =“13x =”，事件B =“26x =”，事件12“9C x x =+=”，则（）（）A.AB C ⊆B.AC B ⊆C.,B C 互斥D.,B C 独立10.已知函数()23sin 2sin (0)2xf x x ωωω=+>的图象在区间[]0,π上有且仅有三个对称中心，则（）A.ω的取值范围是102,3⎡⎫⎪⎢⎣⎭B.()f x 的图象在区间[]0,π上有2条或3条对称轴C.()f x 在区间π0,4⎛⎫⎪⎝⎭上的最大值不可能为3D.()f x 在区间π0,6⎛⎫⎪⎝⎭上为增函数11.如图，已知正方体1111ABCD A B C D -的棱长为1,,,E F G 分别为棱11,,AA CC BC 上的点，()10,1A E CF CG λ===∈，则（）A.EG GF⊥B.平面EFG 经过棱AB 的中点HC.平面EFG 截该正方体，截面面积的最大值为4D.点D 到平面EFG 距离的最大值为2三､填空题：本题共3小题，每小题5分，共15分.12.如图，函数()()2sin (0,0π)f x x ωϕωϕ=+><<的图象与坐标轴交于点,,A B C ，直线BC 交()f x 的图象于点,D O （坐标原点）为ABD 的重心（三条边中线的交点），其中()π,0A -，则ABD 的面积为__________.13.明德中学为提升学校食堂的服务水平，组织全校师生对学校食堂满意度进行评分，按照分层抽样方法，抽取200位师生的评分（满分100分）作为样本，在这200个样本中，所有学生评分样本的平均数为x ，方差为2x s ，所有教师评分样本的半均数为y ，方差为2y s ，总样本的平均数为z ，方差为2s ，若245x y x s y s s ==，抽取的学生样本多于教师样本，则总样本中学生样本的个数至少为__________.14.正四棱锥的外接球半径为R ，内切球半径为r ，则Rr的最小值为__________.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）在四棱锥P ABCD -中，平面PAB ⊥平面,2,22,,ABCD PA AB PB AD BC AB BC AD =====⊥∥,BC M 为棱AP 的中点.（1）求证：BM ∥平面PCD ；（2）求直线PC 与平面BCM 所成角的正弦值.16.（15分）在ABC 中，角,,A B C 的对边分别为,,a b c ，且满足cos sin 3a b C C =-.（1）求B 的大小；（2）若ABC 的面积为，且3BC BD =，当线段AD 的长最短时，求AC 的长.17.（15分）袋中装有除颜色外完全相同的黑球和白球共7个，其中白球3个，现有甲､乙两人从袋中轮流摸球，甲先取，乙后取，然后甲再取，...，取后不放回，直到两人中有一人取到白球时终止.每个球在每一次被取出的机会是等可能的.（1）求取球2次即终止的概率：（2）求甲取到白球的概率.18.（17分）如图，已知四边形ABCD 为菱形，四边形ACEF 为平行四边形，且6AB =，60BAD BAF DAF ∠∠∠=== .（1）证明：直线BD ⊥平面ACEF ；（2）设平面BEF ⋂平面ABCD l =，且二面角E l D --的平面角为26,tan 3θθ=，设G 为线段AF 的中点，求DG 与平面ABCD 所成角的正弦值.19.（17分）点A 是直线PQ 外一点，点M 在直线PQ 上（点M 与,P Q 两点均不重合），我们称如下操作为“由A 点对PQ 施以视角运算”：若点M 在线段PQ 上，记()sin ,;sin AP PAM P Q M AQ MAQ∠∠=；若点M 在线段PQ 外，记()sin ,;sin AP PAM P Q M AQ MAQ∠∠=-.（1）若M 在正方体1111ABCD A B C D -的棱AB 的延长线上，且22AB BM ==，由1A 对AB 施以视角运算，求(),;A B M 的值：（2）若M 在正方体1111ABCD A B C D -的棱AB 上，且2AB =，由1A 对AB 施以机角运算，得到()1,;2A B M =，求AM MB的值；（3）若1231,,,,n M M M M - 是ABC 的边BC 的()2n n ≥等分点，由A 对BC 施以视角运算，证明：()()(),;,;11,2,3,,1k n k B C M B C M k n -⨯==- .长沙市2023~2024学年高一年级期末考试数学答案题号12345678答案ADACBDAA【解析】因为2i z =-，所以2i z =+，所以()()()2i i 2i 2i 12i 1i 2i 2i 2i 2i i 22z z z +⋅++-+=====-+---+--⋅.故选：A.2.【答案】D【解析】不妨设原数据126x x x <<< ，新数据.125y y y <<< .，A ：例如原数据为1,2,3,4,5,6，新数据为，此时极差均为615-=，故A 正确；B ：原数据中位数为342x x +，新数据中位数为3y ，可知33y x =或34y x =，若33y x =，可得34332x x x y +>=；若34y x =，可得34432x xx y +<=；综上所述：新数据的中位数不可能等于原数据的中位数，故B 正确；C ：若x y =，可知去掉的数据为x ，则652211(()i i x x y y ==-=-∑∑，可得652211111,3,4,5,6()()65i i x x y y ==-<-∑∑，所以新数据的方差一定大于原数据方差，故C 正确；D：若x y =，可知去掉的数据为x ，因为640% 2.4⨯=，可知原数据的40%分位数为第3位数，540%2⨯=，可知新数据的40%分位数为第2位数与第3位数的平均数，例如原数据为2,2,3,4,5,6-，新数据为2,2,4,5,6-，此时新数据的40%分位数､原数据的40%分位数均为3，故D 错误；故选：ABC.3.【答案】A【解析】不等式(230x x -+<即()(30x x -<3x <<，所以，3,a b ==，由正弦定理可得sin sin b a B A=，所以，πsin 13sin 32b A B a ===，b a < ，所以B A <，可得B 是锐角，所以π6B =，故选A .4.【答案】C【解析】如图三棱锥以及侧面展开图，要求截面AEF 的周长最小，就是侧面展开图中AG 的距离，因为侧棱长为2的正三棱锥V ABC -的侧棱间的夹角为40,120AVG ∠=，所以由余弦定理可知22222cos12036,6AG VA VG VA VG AG =+-⋅==∴= ，故选C.5.【答案】B【解析】若“a b a b +=+，则平方得2222|2||2|a a b b a a b b +⋅+=+⋅+ ，即a b a b ⋅=⋅ ，即cos ,a b a b a b a b ⋅=⋅=⋅ ，则cos ,1a b = ，即,0a b = ，即,a b同向共线，则存在实数λ使得b a λ= ；反之当,πa b = 时，存在0λ<，满足b a λ= ，但“a b a b +=+ ”不成立，即“存在实数λ使得b a λ= ”是“a b a b +=+ ”的必要不充分条件.故选：B.6.【答案】D【解析】由题意，以C 为坐标原点，以1,,CA CB CC 为,,x y z 轴建立空间坐标系，如下图所示：令12AC BC CC ===，则()0,0,0C ，()()()()12,0,0,0,2,0,1,1,0,0,2,2A B D B 故()()()110,0,2,1,1,0,0,2,2B B CD CB =-==设(),,n x y z = 为平面1CDB 的一个法向量，则100CD n CB n ⎧⋅=⎪⎨⋅=⎪⎩ ，即0220x y y z +=⎧⎨+=⎩令1x =，则1,1y z =-=，从而()1,1,1n =-，设直线1B B 和平面1CDB 所成角为θ，则111sin cos ,3||n B B n B B n B Bθ⋅=<>==⋅，故cos 3θ=，从而tan 2θ=.故选：D.7.【答案】A【解析】如下图所示，设三棱锥P ABC -的外接球为球O '，分别取11AC A C ､的中点1O O ､，则点O '在线段1OO 上，由于正方体1111ABCD A B C D -的棱长为2，则ABC的外接圆的半径为OA =O 的半径为R ，则2414ππ4R =，解得4R =.所以，34OO =='，则1135244OO OO OO '=-=-=，易知，点P 在上底面1111A B C D 所形成的轨迹是以1O为圆心的圆，由于4O P R =='，所以，11O P ==，因此，点P 所构成的图形的面积为21ππO P ⨯=.故选：A.8.【答案】A【解析】设()cos ,sin C θθ，如图，不妨设()()12311,0,,,cos ,sin 22e OA e OB e CO θθ⎛⎫======-- ⎪ ⎪⎝⎭.设M 为AB 的中点，G 为OC 的中点，F 为BD 的中点，E 为AD 的中点.则()1233111,,cos ,sin ,44222M G e e e GO OM GM θθ⎛⎫⎛⎫++=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，设112233e e e HO OP HP λλλ++=+=，点P 在平行四边形EDFM 内（含边界）.由题知HP GM ≥恒成立.为了使13,e e最大，则思考13,e e为钝角，即思考C 点在第一或第四象限.思考临界值即P 与M 重合，G 与H 重合，且GM 不能充当直角三角形斜边，否则可以改变H 的位置，使得HM GM <，此时θ最小，所以GM OC ⊥ ，即()311cos ,sin cos ,sin 04242θθθθ⎛⎫--⋅= ⎪⎪⎝⎭，即22311cos cos sin 04242θθθθ-+-=.即331cos sin 1222θθ⎛⎫+= ⎪ ⎪⎝⎭，即π1cos 262θ⎛⎫-= ⎪⎝⎭.所以πcos 63θ⎛⎫-= ⎪⎝⎭.所以ππππππcos cos cos cos sin sin 666666θθθθ⎡⎤⎛⎫⎛⎫⎛⎫=-+=---⋅ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦1332326+=⨯+=，其中向量1e 与3e 夹角为πθ-，故1e 与3e 夹角的最大值的余弦值为36+-.故选：A.9.【答案】ABD【解析】AB =“13x =且26x ="，事件C 的基本事件有121212121,8;2,7;3,6;4,5x x x x x x x x ========；121212125,4;6,3;7,2;8,1x x x x x x x x ========共8个，所以AB C ⊆，故A 正确；AC ="13x =且129"x x +=="13x =且26"x =，所以AC B ⊆，故B 正确；对于C ，当13x =且26x =时，事件,B C 同时发生，所以,B C 不互斥，故C 错误；对于()()181D,,8888P B P C ===⨯，而BC =“13x =且26x =”，则()164P BC =，所以()()()P BC P B P C =，所以,B C 独立，故D 正确.故选：ABD.10.【答案】BD【解析】()1cos π2cos 12sin 126xf x x x x x ωωωωω-⎛⎫=+⨯=-+=-+ ⎪⎝⎭，令()ππ6x k k ω-=∈Z ，得()()61πππ66k k x k ωωω+=+=∈Z ，由()()61π0π6k k ω+≤≤∈Z 结合0ω>，得()1166k k ω-≤≤-∈Z ，依题意.k .有且只有三个整数值，所以1236ω≤-<，得131966ω≤<，故A 不正确；令()πππ62x k k ω-=+∈Z ，得()()32ππ2π33k k x k ωωω+=+=∈Z ，由()()32π0π3k k ω+≤≤∈Z 结合0ω>，得()2233k k ω-≤≤-∈Z ，当13863ω≤<时，32223ω≤-<，此时0k =或1k =，函数()f x 的图象在区间[]0,π上有2条对称轴，为2π5π,33x x ωω==，当81936ω≤<时，25232ω≤-<，此时0k =或1k =或2k =，函数()f x 的图象在区间[]0,π上有2条对称轴，为2π5π8π,,333x x x ωωω===，所以()f x 的图象在区间[]0,π上有2条或3条对称轴，故B 正确；当π0,4x ⎛⎫∈ ⎪⎝⎭时，ππππ,6646x ωω⎛⎫-∈-- ⎪⎝⎭，因为131966ω≤<，所以ππ3π5π,4688ω⎡⎫-∈⎪⎢⎣⎭，所以当ππ62x ω-=，即2π3x ω=时，()f x 取得最大值3，故C 不正确；由π0,6x ⎛⎫∈ ⎪⎝⎭，得ππππ,6666x ωω⎛⎫-∈-- ⎪⎝⎭，因为131966ω≤<，所以ππ7π13π,663636ω⎡⎫-∈⎪⎢⎣⎭，因为0ω>，所以()f x 在区间π0,6⎛⎫⎪⎝⎭上为增函数，故D 正确.故选：BD11.【答案】ABD【解析】记M 为11D C 的中点，棱AB 的中点H ，取线段11A D 上的点N 使得1A N λ=，正方体1111ABCD A B C D -的中心为O .则根据对称性，E 和,F G 和,N H 和M 分别关于点O 对称.从而O 在平面EFG 内，而FG ∥1BC ∥HM ，故FG ∥HO ，从而H 在平面EFG 内.由于前面的对称性，及,,,,E F G H O 在平面EFG 内，知平面EFG 截该正方体的截面就是中心为O 的六边形EHGFMN ，从而H 一定在平面EFG 内，至此我们得到选项B 正确.前面已经证明FG ∥MH ，同理有NE ∥MH ，故FG ∥MH ∥NE .由于11A N A E CF CG λ====，故111D N AE C F BG λ====-，同时显然有1112AH BH D M C M ====.从而EN FG λ===，MN MF EH GH =====由于,EN FG HM FG λ==<=∥MH ∥NE ，故四边形ENMH 和GFMH 都是等腰梯形，从而,OE ON OF OG ==.这表明线段EF 和GN 互相平分且长度相等，所以四边形是EGFN 矩形，故EG GF ⊥，至此我们得到选项A 正确.由于四边形ENMH 和GFMH λ，下底均为，.所以它们的面积都等于(11122λλ⋅+=+故截面EHGFMN 的面积(1S λ=+.当34λ=时，(7321411644S λ⋅=+=>，至此我们得到选项C 错误.由于1122DO DB ==，且O 在平面EFG 内，故点D 到平面EFG的距离不超过2.而当12λ=时，,,,,,E H G F M N分别是各自所在棱的中点，从而DE DF DG ===而2OE OF OG ===，这表明点D 和点O 到,,E F G 三点的距离两两相等.故点D 和点O 在平面EFG 的投影同样满足到,,E F G 三点的距离两两相等，从而点D 和点O 在平面EFG 的投影都是EFG 的外心，所以由点D 和点的投影是同一点，知DO 垂直于平面EFG .从而由O 在平面EFG 内，知点D 到平面EFG 的距离就是DO 的长，即32.所以，点D 到平面EFG 的距离的最大值是32，至此我们得到选项D 正确.故选：ABD.12.【答案】2【解析】因为O 为ABD 的重心，且()π,0A -，可得2π3OA AC ==，解得3π2AC =，所以π,02C ⎛⎫ ⎪⎝⎭，所以()1π3ππ222T =--=，所以3πT =，所以2π3πω=，解得23ω=，可得()22sin 3f x x ϕ⎛⎫=+ ⎪⎝⎭，由()π0f -=，即()2sin π03ϕ⎡⎤⋅-+=⎢⎥⎣⎦，可得()2π2π3k ϕ⨯-+=，解得2π2π,3k k ϕ=+∈Z ，又由0πϕ<<，所以2π3ϕ=，所以()22π2sin 33f x x ⎛⎫=+ ⎪⎝⎭，于是()22π02sin 033OB f ⎛⎫==⨯+= ⎪⎝⎭，故ABD的面积为13π2222S =⨯⨯.故答案为：2.13.【答案】160【解析】假设在样本中，学生､教师的人数分别为,(1200,,)m n n m m n ≤<<∈N ，记样本中所有学生的评分为(),1,2,3,,i x i m =⋯，所有教师的评分为(),1,2,3,,j y j n =⋯，由x y =得mx ny z x y m n +===+，所以()()222111200m n i j i j s x z y z ==⎡⎤=-+-⎢⎥⎣⎦∑∑()()()222211114,2002005m n i j x y x y i j x x y y ms ns s s ==⎡⎤=-+-=+=⎢⎥⎣⎦∑∑，所以22160x y x y ms ns s s +=，即160y x y xs s m n s s +=，令x ys t s =，则()21600,Δ2560042560042000mt t n mn m m -+==-=--≥，即220064000m m -+≥，解得40m ≤或160m ≥，因为1200n m ≤<<且200m n +=，得100m >，所以160m ≥.所以总样本中学生样本的个数至少为160.故答案为：160.14.1+【解析】设正四棱锥P ABCD -底面边长为a ，高为h ，底面ABCD 的中心为M ，连接,PM BM，则,2BM a PM h ==，所以PB ==，设外接球球心为1O ，内切球球心为2O ，则12,O O 在PM 上，因为11PO BO R ==，所以11O M PM PO h R =-=-，在1Rt O MB中，222()2h R a R ⎛⎫-+= ⎪ ⎪⎝⎭，化简得2224h a R h +=，因为22111143332P ABCDV a h a r -==+⨯⨯所以r =，所以()22222222244h a h a a a R h a a h ahr h ah ++++===2222224ha h +⋅=，令h k a =，则222221h R a r ⎛⎫+ ⎪=，令1)t t =>，则()2121R t r t +=-，令1(0)m tm =->，则222111122R m m m r m m ++==++≥+=+，当且仅当12m m =，即m =时取等号，所以R r1+.1+.15.【解析】（1）取PD 的中点N ，连接,MN CN ，则MN ∥AD 且12MN AD =，又BC ∥AD 且12BC AD =，所以MN ∥BC 且MN BC =，故四边形BCNM 为平行四边形，所以BM ∥CN ，又BM ⊄平面,PCD CN ⊂平面PCD ，所以BM ∥平面PCD（2）由2,2AB PA PB ===222AB PA PB +=，所以PA AB ⊥，又平面PAB ⊥平面ABCD ，平面PAB ⋂平面,ABCD AB PA =⊂平面PAB ，所以PA ⊥平面ABCD ，又AC ⊂平面ABCD ，所以PA AC ⊥.由2,1,AB BC AB BC ==⊥，得225AC AB BC =+=，所以223PC AC PA =+=，22226,5CM AM AC BM AM AB =+==+=，得222CM BM BC =+，则BC BM ⊥，所以1522MBC S BM BC =⋅= .又()()111121213323P MBC P ABC M ABC ABC V V V S PA MA ---=-=-=⋅⋅⋅⋅-= ，设P 到平面MBC 的距离为h ，直线PC 与平面MBC 的所成角为θ，则1536P MBC MBC V hS -== ，所以1536h =，解得55h =，所以5255sin 315h PC θ===，即直线PC 与平面MBC 的所成角的正弦值为515.16.【解析】（1）因为3cos sin 3a b C C =-，由正弦定理可得3sin sin cos sin 3A B C B C =-，又()()sin sin πsin sin cos cos sin A B C B C B C B C ⎡⎤=-+=+=+⎣⎦，所以sin cos cos sin sin cos sin sin 3B C B C B C B C +=-，所以cos sin sin 3B C B C =-，又()0,πC ∈，所以sin 0C >，所以cos sin 3B B =-，即tan B =，又()0,πB ∈，所以2π3B =；（2）因为ABC 的面积为，即1sin 2ac B =，即12πsin 23ac =11222ac ac ⨯==，因为3BC BD = ，所以13BD BC = ，在ABD 中2222cos AD BA BD BA BD B =+-⋅，即2221121123333AD c a ac ca ac ac ⎛⎫=++≥+== ⎪⎝⎭，当且仅当13c a =，即6,2a c ==时取等号，所以AD ≥AD 的最小值为6,2a c ==，则2222212cos 62262522b a c ac B ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭，所以b =，即AC =17.【解析】（1）设事件A 为“取球2次即终止”.即甲第一次取到的是黑球而乙取到的是白球，借助树状图求出相应事件的样本点数：因此，()432767P A ⨯==⨯.（2）设事件B 为“甲取到白球”，“第i 次取到白球”为事件1,2,3,4,5i =，因为甲先取，所以甲只可能在第1次，第3次和第5次取到白球.借助树状图求出相应事件的样本点数：所以()()()()135135()P B P A A A P A P A P A =⋃⋃=++343343213361227765765437353535⨯⨯⨯⨯⨯⨯=++=++=⨯⨯⨯⨯⨯⨯18.【解析】（1）设AC BD O ⋂=，连接,DF OF ，四边形ABCD 为菱形，则,,AB AD AC BD BO OD =⊥=，又60BAF DAF ∠∠== ，易得BAF DAF ≅ ，所以BF DF =，则BD OF ⊥，又,,AC OF O AC OF ⋂=⊂平面ACEF ，所以直线BD ⊥平面ACEF（2）过F 点作FH AC ⊥于H 点，过H 点作HM l ⊥于M 点，连接FM ，过H 点作HN AD ⊥于N 点，连接FN ，由（1）易证，,FM l FN AD ⊥⊥，则FMH ∠为二面角E l D --的平面角，在直角FHM 中，6tan 3FH HM θ==，又3HM BO ==，可得6FH =，设2AF a =，则,33AN a NH FN a ===，直角FHN 中，222(26)3)3a +=，可得6AF =，G 为线段AF 的中点，则G 到平面ABCD 的距离6d =，又33DG =，设直线DG 与平面ABCD所成角为,sin 3d DG αα==，直线DG 与平面ABCD所成角的正弦值为3.19.【解析】（1）如图1，因为22AB BM ==，所以113,AM A B A M ===.由正方体的定义可知1AA AB ⊥，则190A AB ∠= ，故11sin 22AA B AA B ∠∠==，11sin 1313AA M AA M ∠∠==.因为111BA M AA M AA B ∠∠∠=-，所以11111sin sin cos cos sin 26BA M AA M AA B AA M AA B ∠∠∠∠∠=-=，则()11112sin 13,;3sin A A AA M A B M A B MA B ∠∠⨯=-=--.（2）如图2，设()02AM a a =≤≤，则1122sin ,cos 44AA M AA M a a ∠∠==++.因为111BA M AA B AA M ∠∠∠=-，所以()()()()()()22111sin sin 224/24BA M AA B AA M a a a ∠∠∠=-=-++，则()211112sin 14,;sin 22A A AA M a a A B M A B MA B a ∠∠⨯===-，解得23a =，故122AM a MB a ==-.（3）证明：如图3，因为1231,,,,n M M M M - 是BC 的n 等分点，所以k n k BM CM -=,n k k k n k BC BM CM BC n n --===.在k ABM 中，由正弦定理可得sin sin k k k BM AB BAM AM B ∠∠=，则sin sin k k k AB BAM BM AM B ∠∠=.在k ACM 中，同理可得sin sin k k k AC CAM CM AM C ∠∠=.因为πk k AM B AM C ∠∠+=，所以sin sin k k AM B AM C ∠∠=，则()sin sin ,;sin sin k k k k k k k k k AB BAM BM AM B BM k B C M AC CAM CM AM C CM n k∠∠∠∠====-.同理可得(),;n k n k n k BM n k B C M CM k ----==.。

2023年下学期高一第一次月考数学（答案在最后）（时量：120分钟分值：150分）一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.命题“200,1x x ∃∈≠R ”的否定是（）A.2,1x x ∀∈=RB.2,1x x ∀∉=RC.200,1x x ∃∈=R D.200,1∃∉=x x R 【答案】A 【解析】【分析】由特称命题的否定是全称命题，可得出答案.【详解】根据特称命题的否定是全称命题，可知命题“200,1x x ∃∈≠R ”的否定是“2,1x x ∀∈=R ”.故选：A.2.设集合A 含有2-，1两个元素，B 含有1-，2两个元素，定义集合A B ，满足1x A ∈，2x B ∈且12x x A B ∈e ，则A B 中所有元素之积为（）A.8- B.16- C.8D.16【答案】C 【解析】【分析】根据集合A B 的定义先求出集合A B ，然后再把集合中所有元素相乘即可求解.【详解】由题意{}2,1A =-，{}1,2B =-，由集合A B 的定义可知，集合A B 中有以下元素：①()212-⨯-=，②224-⨯=-，③()111⨯-=-，④122⨯=，根据集合中元素满足互异性去重得{}4,1,2A B =--e ，所以A B 中所有元素之积为()4128-⨯-⨯=.故选：C.3.若函数()31y f x =+的定义域为[]2,4-，则()y f x =的定义域是（）A.[]1,1- B.[]5,13- C.[]5,1- D.[]1,13-【答案】B 【解析】【分析】根据函数()31y f x =+中[]2,4x ∈-，即可得出[]315,13x +∈-，即可选出答案.【详解】因为函数()31y f x =+的定义域为[]2,4-，即24x -≤≤所以53+113x -≤≤所以()y f x =的定义域是[]5,13-故选:B.【点睛】本题考查隐函数的定义域，属于基础题.解本题的关键在于正确理解函数的定义域是x 的取值范围与同一个函数其括号里面的取值范围一样.4.下列命题正确的是（）A.“a b >”是“22a b >”的充分条件B.“a b >”是“22a b >”的必要条件C.“a b >”是“22ac bc >”的充分条件D.“a b >”是“22ac bc >”的必要条件【答案】D 【解析】【分析】根据充分条件、必要条件的定义判断即可；【详解】解：对于A ：由a b >推不出22a b >，如0a =，1b =-满足a b >，但是22a b <，故A 错误；对于B ：由22a b >推不出a b >，如1a =-，0b =满足22a b >，但是a b <，即a b >不是22a b >的必要条件，故B 错误；对于C ：由a b >推不出22ac bc >，当0c =时220ac bc ==，故C 错误；对于D ：若22ac bc >，则20c ≠，即20c >，所以a b >，即a b >是22ac bc >的必要条件，故D 正确；故选：D5.用C (A )表示非空集合A 中的元素个数，定义A *B ＝()()()()()()()(),,C A C B C A C B C B C A C A C B ⎧-≥⎪⎨-<⎪⎩若A ＝{1，2}，B ＝{x |(x 2＋ax )·(x 2＋ax ＋2)＝0}，且A *B ＝1，设实数a 的所有可能取值组成的集合是S ，则C (S )等于（）A.1B.3C.5D.7【答案】B 【解析】【分析】根据题意可得()1C B =或()3C B =，进而讨论a 的范围，确定出()C B ，最后得到答案.【详解】因为()2C A =，*1A B =，所以()1C B =或()3C B =，由20x ax +=，得120,x x a ==-，关于x 的方程220x ax ++=，当=0∆时，即a =±()3C B =，符合题意；当0>∆时，即a <-或a >0，-a 不是方程220x ax ++=的根，故()4C B =，不符合题意；当<0∆时，即a -<<时，方程220x ax ++=无实根，若a =0，则B ={0}，()1C B =，符合题意，若0a -<<或0a <<，则()2C B =，不符合题意.所以{0,S =-，故()3C S =.故选：B .【点睛】对于新定义的问题，一定要读懂题意，一般理解起来不难，它一般和平常所学知识和方法有很大关联；另外当<0∆时，容易遗漏a =0时的情况，注意仔细分析题目.6.函数[]y x =在数学上称为高斯函数，也叫取整函数，其中[]x 表示不大于x 的最大整数，如[1.5]1,[2.3]3,[3]3=-=-=．那么不等式24[]12[]50x x -+≤成立的充分不必要条件是（）A.15[,22B.[1,2]C.[1,3)D.[1,3]【答案】B 【解析】【分析】先解不等式，再结合充分条件和必要条件的定义求解即可.【详解】因为24[]12[]50x x -+≤，则[]()[]()21250x x --≤，则[]1522x ≤≤，又因为[]x 表示不大于x 的最大整数，所以不等式24[]12[]50x x -+≤的解集为：13x ≤<，因为所求的时不等式24[]12[]50x x -+≤成立的充分不必要条件，所以只要求出不等式24[]12[]50x x -+≤解集的一个非空真子集即可，选项中只有[1,2]⫋[)1,3.故选：B .7.已知1,0,0x y y x +=>>，则121x x y ++的最小值为（）A.54B.0C.1D.2【答案】A 【解析】【分析】根据“1”技巧，利用均值不等式求解.【详解】1x y += ，12x y ∴++=，1(1)11221441x y x y x x y x y +++∴+=++++，0,0y x >> ，10,041y x x y +∴>>+，111152144144x y x x y x y +∴+=++≥+++，当且仅当141y x x y +=+，即23x =，13y =时等号成立，故选：A8.黎曼函数()R x 是由德国数学家黎曼发现并提出的，在高等数学中有着广泛的应用，()R x 在[]0,1上的定义为：当q x p =（p q >，且p ，q 为互质的正整数）时，()1R x p=；当0x =或1x =或x 为()0,1内的无理数时，()0R x =.已知a ，b ，[]0,1a b +∈，则（）注：p ，q 为互质的正整数()p q >，即q p为已约分的最简真分数.A.()R x 的值域为10,2⎡⎤⎢⎥⎣⎦B.()()()R a b R a R b ⋅≥⋅C.()()()R a b R a R b +≥+ D.以上选项都不对【答案】B 【解析】【分析】设q A x x p ⎧⎫==⎨⎩⎭，（p q >，且p ，q 为互质的正整数），B ＝{x |x ＝0或x ＝1或x 是[0，1]上的无理数}，然后对A 选项，根据黎曼函数()R x 在[]0,1上的定义分析即可求解；对B 、C 选项：分①a A ∈，b A ∈；②a B ∈，b B ∈；③a A b B ∈⎧⎨∈⎩或a Bb A ∈⎧⎨∈⎩分析讨论即可．【详解】解：设q A x x p ⎧⎫==⎨⎬⎩⎭，（p q >，且p ，q 为互质的正整数），B ＝{x |x ＝0或x ＝1或x 是[0，1]上的无理数}，对A 选项：由题意，()R x 的值域为1110,,,,,23p ⎧⎫⎨⎬⎩⎭，其中p 是大于等于2的正整数，故选项A 错误；对B 、C 选项：①当a A ∈，b A ∈，则()()()R a b R a R b +≤+，()()()R a b R a R b ⋅≥⋅；②当a B ∈，b B ∈，则()()()R a b R a R b +=+，()()()R a b R a R b ⋅≥⋅＝0；③当a A b B ∈⎧⎨∈⎩或a B b A ∈⎧⎨∈⎩，则()()()R a b R a R b +≤+，()()()R a b R a R b ⋅≥⋅，所以选项B 正确，选项C 、D 错误，故选：B.【点睛】关键点点睛：本题解题的关键是牢牢抓住黎曼函数()R x 在[]0,1上的定义去分析.二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．9.若不等式20ax bx c -+>的解集是(1,2)-，则下列选项正确的是（）A.0b <且0c >B.0a b c -+>C.0a b c ++> D.不等式20ax bx c ++>的解集是{|21}x x -<<【答案】ABD 【解析】【分析】根据一元二次不等式的解集可判断出a 的正负以及,,a b c 的关系，由此可判断各选项的对错.【详解】因为20ax bx c -+>的解集为()1,2-，解集属于两根之内的情况，所以a<0，又因为0420a b c a b c ++=⎧⎨-+=⎩，所以2b ac a =⎧⎨=-⎩；A ．0,20b a c a =<=->，故正确；B ．因为()11,2∈-，所以0a b c -+>，故正确；C ．因为解集为()1,2-，所以0a b c ++=，故错误；D ．因为20ax bx c ++>即为2220ax ax a +->，即220x x +-<，解得()2,1x ∈-，故正确；故选：ABD.10.命题:p x ∃∈R ，2220x x m ++-<为假命题，则实数m 的取值可以是（）A.1- B.0 C.1D.2【答案】ABC 【解析】【分析】先求出命题为真命题时实数m 的取值范围，然后利用补集思想求出命题为假命题时m 的取值范围，由此可得出合适的选项.【详解】若命题:p x ∃∈R ，2220x x m ++-<为真命题，则()2Δ242440m m =--=->，解得1m >，所以当命题:p x ∃∈R ，2220x x m ++-<为假命题时，1m £，符合条件的为A 、B 、C 选项.故选：A BC.11.设a ，b 为两个正数，定义a ，b 的算术平均数为()2a bA a b +=,，几何平均数为()G a b =,，则有：()(),,G a b A a b ≤，这是我们熟知的基本不等式．上个世纪五十年代，美国数学家D ．H ．Lehmer 提出了“Lehmer 均值”，即()11,p pp p p a b L a b a b--+=+，其中p 为有理数．如：()0.50.50.50.50.5,11a b L a b a b --+==+．下列关系正确的是（）A.()()0.5,,L a b A a b ≤ B.()()0,,L a b G a b ≥C.()()21,,L a b L a b ≥D.()()1,,n n L a b L a b +≤【答案】AC 【解析】【分析】根据新定义逐个选项代入，化简后根据基本不等式与柯西不等式判断即可.【详解】A ：()()0.5,,112a bL a b A a b +===，故A 对；B：001102(,)(,)a b ab L a b G a b a b a b --+==≤++，故B 错；C ：()222,a b L a b a b+=+，()1,2a b L a b +=，而()()()()()22222222222222122,1,22a b a b L a b a b a b L a b a b ab a b aba b +++++===≥+++++，故C 对；D ：由柯西不等式，()()()()()112111112211(,)1(,)n n n n n n n n n n n n n n n n n n n n a b a b a b a b L a b a b a b L a b a b a b a b++++--+--+++++==≥=++++，故D 错.故选：AC.12.已知集合{}20,0x x ax b a ++=>有且仅有两个子集，则下面正确的是（）A.224a b -≤B.214a b+≥C.若不等式20x ax b +-<的解集为()12,x x ，则120x x >D.若不等式2x ax b c ++<的解集为()12,x x ，且124x x -=，则4c =【答案】ABD 【解析】【分析】根据集合{}20,0x x ax b a ++=>子集的个数列方程，求得,a b 的关系式，对A ，利用二次函数性质可判断；对B ，利用基本不等式可判断；对CD ，利用不等式的解集及韦达定理可判断.【详解】由于集合{}20,0x x ax b a ++=>有且仅有两个子集，所以2240,4a b a b ∆=-==，由于0a >，所以0b >.A ，()22224244a b b b b -=-=--+≤，当2,b a ==时等号成立，故A 正确.B ，21144a b b b +=+≥=，当且仅当114,,2b b a b ===时等号成立，故B 正确.C ，不等式20x ax b +-<的解集为()12,x x ，120x x b =-<，故C 错误.D ，不等式2x ax b c ++<的解集为()12,x x ，即不等式20x ax b c ++-<的解集为()12,x x ，且124x x -=，则1212,x x a x x b c +=-=-，则()()22212121244416x x x x x x a b c c -=+-=--==，4c ∴=，故D 正确，故选：ABD三、填空题：本大题共4小题，每小题5分，共20分．13.已知111f x x ⎛⎫=⎪+⎝⎭，那么f (x )的解析式为________.【答案】()(0,1)1xf x x x x=≠≠-+.【解析】【分析】用1x代换已知式中的x ，可得，注意x 有取值范围．【详解】解：由111f x x ⎛⎫=⎪+⎝⎭可知，函数的定义域为{x |x ≠0，x ≠﹣1}，用1x代换x ，代入上式得：f (x )=111x+=1x x +，故答案为：()(0,1)1xf x x x x=≠≠-+．【点睛】本题考查求函数解析式，掌握函数这定义是解题关键．求解析式时要注意自变量的取值范围．14.设集合{43}M xx =-<<∣，={+2<<21,}N x t x t t -∈R ∣，若M N N ⋂=，则实数t 的取值范围为____________．【答案】(],3-∞【解析】【分析】由M N N ⋂=可知N M ⊆，讨论N =∅与N ≠∅，即可求出答案.【详解】因为M N N ⋂=，所以N M ⊆，当N =∅时：2213t t t +≥-⇒≤，满足题意；当N ≠∅时：+2<21>34+262132t t t t t t t --≤⇒≥--≤≤⎧⎧⎪⎪⎨⎨⎪⎪⎩⎩，无解；所以实数t 的取值范围为(],3-∞.故答案为：(],3-∞15.已知函数()2f x x =-，()()224R g x x mx m =-+∈，若对任意[]11,2x ∈，存在[]24,5x ∈，使得()()12g x f x =，则m 的取值范围______．【答案】54⎡⎢⎣【解析】【分析】由题意可判断(){}(){},12,45y y g x x y y f x x =≤≤⊆=≤≤，由此求出()[]2,3f x ∈，可得相应不等式恒成立，转化为函数最值问题，求解即可.【详解】由题意知(){}(){},12,45y y g x x y y f x x =≤≤⊆=≤≤；当[]4,5x ∈时，()[]2,3f x ∈，故()()224R g x x mx m =-+∈需同时满足以下两点：①对[]1,2x ∀∈时，()2243g x x mx =-+≤∴12m x x≥+恒成立，由于当[]1,2x ∀∈时，1y x x=+为增函数，∴1522,24m m ≥+∴≥；②对[]1,2x ∀∈时，()2242g x x mx =-+≥，∴22m x x≤+恒成立，由于2x x+≥2x x =，即[1,2]x =时取得等号，∴2m m ≤∴≤∴54m ⎡∈⎢⎣，故答案为：54⎡⎢⎣16.若,a b R ∈，且22231a ab b +-=，则22a b +的最小值为_______.【答案】14【解析】【分析】根据a 2+2ab ﹣3b 2=1得到(a +3b )(a ﹣b )=1，令x =a +3b ，y =a ﹣b ，用x ，y 表示a ，b ，然后代入a 2+b 2，利用均值不等式求解.【详解】由a 2+2ab ﹣3b 2=1得(a +3b )(a ﹣b )=1，令x =a +3b ，y =a ﹣b ，则xy =1且a 34x y +=，b 4x y-=，所以a 2+b 2=(34x y +)2+(4x y -)22252184x y ++=≥，当且仅当x 2=，y 25=时取等号.故答案为14.【点睛】本题主要考查均值不等式的应用，还考查了转化求解问题的能力，属于中档题.四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．（其中第17题10分，18~22题每题12分，共70分）17.已知全集U =R ，集合502x A x x ⎧⎫-=≤⎨⎬-⎩⎭，{}11,B x a x a a =-<<+∈R .（1）当2a =时，求()()U UA B ⋂痧；（2）若x A ∈是x B ∈的必要不充分条件，求实数a 的取值范围.【答案】（1）()(){1U UA B x x ⋂=≤痧或}5x >（2）{}34a a ≤≤【解析】【分析】（1）当2a =时，求出集合A 、B ，利用补集和交集的定义可求得集合()()U U A B ⋂痧；（2）分析可知，BA ，利用集合的包含关系可得出关于实数a 的不等式组，由此可解得实数a 的取值范围.【小问1详解】因为{}50252x A x x x x ⎧⎫-=≤=<≤⎨⎬-⎩⎭，当2a =时，{}13B x x =<<，因为全集U =R ，则{2U A x x =≤ð或}5x >，{1U B x x =≤ð或}3x ≥，因此，()(){1U U A B x x ⋂=≤痧或}5x >.【小问2详解】易知集合{}11,B x a x a a =-<<+∈R 为非空集合，因为x A ∈是x B ∈的必要不充分条件，则BA ，所以，1215a a -≥⎧⎨+≤⎩，解得34a ≤≤.因此，实数a 的取值范围是{}34a a ≤≤.18.已知a ，b ，c 均为正实数，且1a b c ++=．（1）求证：1111118a b c ⎛⎫⎛⎫⎛⎫---≥⎪⎪⎪⎝⎭⎝⎭⎝⎭；（2）求111a b c++的最小值．【答案】（1）证明见解析（2）9【解析】【分析】（1）根据111111111++++++⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫---=---⎪⎪⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭a b c a b c a b c a b c a b c 结合基本不等式即可得证；（2）根据111a b c a b c a b c a b c a b c++++++++=++结合基本不等式即可得解.【小问1详解】原式111a b c a b c a b c a b c ++++++⎛⎫⎛⎫⎛⎫=--- ⎪⎪⎪⎝⎭⎝⎭⎝⎭()()()b c a c a b abc+++=222bc ac ababc≥8abc abc=8=.当且仅当13a b c ===是取等号，所以1111118a b c ⎛⎫⎛⎫⎛⎫---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭；【小问2详解】原式a b c a b c a b c a b c++++++=++3b a c a c b a b a c b c ⎛⎫⎛⎫⎛⎫=++++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3≥2339=⨯+=.当且仅当13a b c ===是取等号，所以111a b c++的最小值为9．19.已知x >0，y >0，且2x +8y -xy =0，求：（1）xy 的最小值；（2）x +y 的最小值..【答案】（1）64（2）18【解析】【分析】（1）利用基本不等式构建不等式即可得结果；（2）将28x y xy +=变形为分式型281y x +=，利用“1”的代换和基本不等式可得结果.【小问1详解】∵0x >，0y >，280x y xy +-=，∴28xy x y =+≥=，当且仅当28x y =时取等号，8≥∴64xy ≥，当且仅当416x y ==时取等号，故xy 的最小值为64.【小问2详解】∵28x y xy +=，则281y x+=，又∵0x >，0y >，∴2828()()101018x y x y x y y x y x +=++=++≥+=，当且仅当212x y ==时取等号，故x y +的最小值为18.20.济南市地铁项目正在加火如荼的进行中，通车后将给市民出行带来便利，已知某条线路通车后，列车的发车时间间隔t （单位：分钟）满足220t ≤≤，经市场调研测算，列车载客量与发车时间间隔t 相关，当1020t ≤≤时列车为满载状态，载客量为500人，当210t ≤<时，载客量会减少，减少的人数与(10)t -的平方成正比，且发车时间间隔为2分钟时的载客量为372人，记列车载客量为()p t .（1）求()p t 的表达式，并求当发车时间间隔为5分钟时，列车的载客量；（2）若该线路每分钟的净收益为()()8265660p t Q t t -=-（元），问当发车时间间隔为多少时，该线路每分钟的净收益最大，并求出最大值.【答案】（1）2300+402,2<10()=500,1020t t t p t t -≤≤≤⎧⎨⎩；450（2）发车时间间隔为4分钟时，每分钟的净收益最大为132元.【解析】【分析】（1）由题设，有2()500(10)p t k t =--且(2)=372p ，求k 值，进而写出其分段函数的形式即可.（2）由（1）写出()Q t 解析式，讨论210t ≤<、1020t ≤≤求最大值即可.【小问1详解】由题设，当210t ≤<时，令2()500(10)p t k t =--，又发车时间间隔为2分钟时的载客量为372人，∴2(2)500(102)372p k =--=，解得=2k .∴2300+402,2<10()=500,1020t t t p t t -≤≤≤⎧⎨⎩，故=5t 时，2(5)5002(105)450p =-⨯-=，所以当发车时间间隔为5分钟时，列车的载客量为450人.【小问2详解】由（1）知：25626016,2<10()=134460,1020t t t Q t t t--≤-≤≤⎧⎪⎪⎨⎪⎪⎩，∵210t ≤<时，()260132Q t ≤-当且仅当=4t 等号成立，∴210t ≤<上max ()(4)132Q t Q ==，而1020t ≤≤上，()Q t 单调递减，则max ()(10)74.4Q t Q ==，综上，时间间隔为4分钟时，每分钟的净收益最大为132元.21.已知二次函数22y ax bx =++（a ，b 为实数）（1）若1x =时，1y =且对()2,5x ∀∈，0y >恒成立，求实数a 的取值范围；（2）若1x =时，1y =且对[]2,1a ∀∈--，0y >恒成立，求实数x 的取值范围．【答案】（1）3a >-（2）11,44⎛⎫-+ ⎪ ⎪⎝⎭【解析】【分析】（1）由题意求出1b a =--可得()2120y ax a x =-++>对()2,5x ∀∈恒成立，分离参数，即得2max 2x a x x -⎛⎫> ⎪-⎝⎭，令()20,3t x =-∈，则可得()123f t t t=++，利用基本不等式即可求得答案；（2）由题意()212y ax a x =-++，变更主元：令a 为主元，视x 为参数，则()()220g a x x a x =-+->，对[]2,1a ∀∈-恒成立，由此可得不等式组，即可求得答案.【小问1详解】将1x =，1y =代入得1,1a b b a +=-∴=--∴()2120y ax a x =-++>对()2,5x ∀∈恒成立，即()22a x x x ->-对()2,5x ∀∈恒成立，当()2,5x ∈时，由于2y x x =-在()2,5上单调递增，故22220x x ->->，∴2max2x a x x -⎛⎫> ⎪-⎝⎭，()2,5x ∀∈，令()20,3t x =-∈，则()()()2213232223t t f t t t t t t t ===≤=-+++-+++，当且仅当2t t=，即()0,3t =时等号成立，∴3a >-【小问2详解】由题意()()21,12b a y ax a x =-+∴=-++，变更主元：令a 为主元，视x 为参数，令()()22g a x x a x =-+-，对[]2,1a ∀∈-，()()220g a x x a x =-+->恒成立，故只需()()()2222220120g x x x g x x x ⎧-=-++->⎪⎨-=--+->⎪⎩，即2222020x x x ⎧--<⎨-<⎩，解得1111,,4444x x x ⎧⎛⎫<<+⎪∴∈ ⎪⎨ ⎪⎝⎭⎪<<⎩.22.已知函数()f x =，()g x =．（1）求函数()f x 的定义域和值域；（2）已知a 为非零实数，记函数()()()x x h f g x a =-的最大值为()m a ，求()m a ．【答案】（1）[]0,2，2⎤⎦（2）12,0211(),2222a a am a a aaa⎧⎛⎫⎪-<≠⎪⎪⎝⎭⎪⎛⎪=+≤≤⎨⎝⎭⎪⎛⎫>⎪⎪⎝⎭⎩且【解析】【分析】（1）根据根式的概念可得()f x定义域，再计算()22f x=+求解可得()f x值域；（2）令2t⎤=⎦，设函数()22aF t t t a=-++，2t⎤∈⎦，再根据二次函数对称轴与区间的位置关系分类讨论求解即可.【小问1详解】定义域：[]0,220xxx≥⎧⇒∈⎨-≥⎩，()222f x x x=+=+-+2=+当[]0,2x∈时，()[]2110,1x--+∈，∴()[]()22,4,0f x f x∈≥，∴()2f x⎤∈⎦；【小问2详解】()h x=-2t⎤=+⎦，则22222tt-=+，设()22222t aF t t a t t a-=-=-++，2t⎤∈⎦，1°若a<0，此时二次函数对称轴10ta=<<()()max2F t F=2a=-.2°若0a >，此时对称轴：10t a =>，①当12a >即102a <<时，开口向下，则()()max 2F t F =2a =-；12a ≤≤即122a ≤≤，对称轴1t a =，开口向下，则()max 1F t F a ⎛⎫= ⎪⎝⎭12a a =+，③1a <即2a >时，开口向下，()max F t F==综上：12,0211(),2222a a a m a a a a a ⎧⎛⎫⎪-<≠ ⎪⎪⎝⎭⎪⎛⎫⎪=+≤≤ ⎪⎨ ⎪⎝⎭⎪⎛⎫> ⎪ ⎪⎝⎭⎩且.。

2023-2024学年湖南省永州市道县第二中学高一下学期第一次月考数学试卷1.若复数满足，则的共轭复数是A．B．C．D．2.已知向量，，若，则的值为（）A．B．C．D．3.已知向量，，是线段AB的中点，则点的坐标是（）A．B．C．D．4.欧拉公式把自然对数的底数、虚数单位和三角函数联系在一起，充分体现了数学的和谐美，被誉为“数学中的天桥”.若复数，则（）A．B．C．D．5.在中，，且，是的中点，是线段的中点，则的值为（）A．0B．C．D．6.桂林日月塔又称金塔银塔､情侣塔，日塔别名叫金塔，月塔别名叫银塔，所以也有金银塔之称.如图1，这是金银塔中的金塔，某数学兴趣小组成员为测量该塔的高度，在塔底的同一水平面上的两点处进行测量，如图2.已知在处测得塔顶的仰角为60°，在处测得塔顶的仰角为45°，米，，则该塔的高度（）A．米B．米C．50米D．米7.已知非零向量，满足，，若，则向量在向量方向上的投影向量为（）A．B．C．D．8.如图，在中，，是上的一点，若，则实数的值为()A．B．C．1D．39.已知i为虚数单位，复数z满足，则下列说法正确的是（）A．复数z的模为B．复数z的共轭复数为C．复数z的虚部为D．复数z在复平面内对应的点在第一象限10.已知角A，B，C是三角形ABC的三个内角，下列结论一定成立的有（）A．B．C．若，则D．若，则11.蜜蜂的巢房是令人惊叹的神奇天然建筑物．巢房是严格的六角柱状体，它的一端是平整的六角形开口，另一端是封闭的六角菱形的底，由三个相同的菱形组成，巢中被封盖的是自然成熟的蜂蜜，如图是一个蜂巢的正六边形开口，则下列说法正确的有（）A．B．C．在上的投影向量为D．12.已知为虚数单位，若复数为纯虚数，则___________.13.在中内角所对边分别是若，则的形状一定是__________．14.已知，表示两个夹角为的单位向量，为平面上的一个固定点，为这个平面上任意一点，当时，定义为点的斜坐标.设点的斜坐标为，则______.15.已知，，三点的坐标分别为，，，且，．(1)求点，的坐标(2)判断与是否共线．16.已知向量，，．（1）求向量与所成角的余弦值；（2）若，求实数的值．17.如图，在矩形中，，，点为的中点，点在上，且．（1）求；（2）若（，），求的值.18.在中，内角A、B、C所对边的长分别为a、b、c，已知向量，且满足.(1)求A的大小；(2)若，，求的周长.19.在中，角所对的边分别为，已知．(1)求；(2)若，求面积的取值范围．。

2024年高一数学阶段检测卷姓名：___________班级：___________考号：___________一、选择题（40分）1.已知某扇形的圆心角为，其所对的弦长为，则该扇形的面积为（ ）A.B. C. D.2.已知，则（ ）A. B.D.3.已知函数在上单调递增，则（ ）A.B.C.D.4.函数，的值域是（ ）A. B. C. D.5.函数，的值域为（ ）A. B. C. D.6.已知且为第二象限角，则（ ）A.B. C. D.7.若函数在上有零点，则实数的取值范围为（ ）A. B. C. D.π36π18π()()1cos 0,π3θθ=-∈3πcos 2θ⎛⎫-= ⎪⎝⎭13-13()()()2cos 4102πf x x ϕϕ=+-<<0,π4⎡⎤⎢⎥⎣⎦ϕ=π8π4π2ππcos 3y x ⎛⎫=+⎪⎝⎭,02πx ⎡⎤∈-⎢⎥⎣⎦1,12⎡⎤⎢⎥⎣⎦⎤⎥⎦12⎡⎢⎣⎡⎤⎢⎥⎣⎦()26π3tan f x x ⎛⎫=+⎪⎝⎭0,12πx ⎡⎤∈⎢⎥⎣⎦3sin 5α=αsin cos sin 2cos αααα+=-111111-75-75()sin cos 2sin cos 1f x x x x x a =+-+-3π,44π⎡⎤--⎢⎥⎣⎦a 2⎡⎤⎣⎦94⎡⎤⎢⎥⎣⎦⎡-⎣94⎤⎥⎦8.已知函数的部分图象如图所示，若，，则正整数的取值为（ ）A.1B.2C.3D.4二、多项选择题（18分）9.已知，则（ ）A.的最小正周期为B.的图象的对称轴方程为C.D.在上单调递减10.关于函数，下列说法中正确的有（ ）A.是奇函数B.在区间上单调递增C.为其图象的一个对称中心D.最小正周期为11.已知函数，则下列结论正确的是（ ）A.是的一个周期 B.的图象关于点对称C.为奇函数 D.在区间上的最大值为3()()cos 0π,02f x x ωϕωϕ⎛⎫=+><<⎪⎝⎭x ∀∈R ()()f x m f x +=-m ()26π2cos f x x ⎛⎫=- ⎪⎝⎭()f x π()f x ()2π3πx k k =-∈Z ()2023πf =()f x 3π,22π⎛⎫-- ⎪⎝⎭πtan 3y x ⎛⎫=-⎪⎝⎭6π,6π⎛⎫-⎪⎝⎭5π,06⎛⎫⎪⎝⎭π()23π3cos f x x ⎛⎫=-⎪⎝⎭π2()f x ()f x 0π,12⎛⎫-⎪⎝⎭6πf x ⎛⎫-⎪⎝⎭()f x 2π,3π⎡⎤-⎢⎥⎣⎦三、填空题（15分）12.已知，，则_________.13.形如的式子叫做行列式，其运算法则为，则行列式___________.14.若方程的两个根分别是，，则_________.四、解答题（77分）15.（13分）（1）已知，，且为第一象限角，为第二象限角，求的值.（2）已知，，，求与的值.16.（15分）已知函数的最小正周期为.（1）求的值，并求的单调递减区间；（2）求的对称轴；（3）求在上的值域.17.（15分）已知，且（1的值；（2）求的值.18.（17分）某学习小组在一次研究性学习中发现，以下三个式子的值都等于同一个常数.；3cos 5α=3π,2π2α⎛⎫∈⎪⎝⎭sin 2α=a b c d a b ad bc c d =-sin15cos15︒︒212π12π0x x +-=αβcos cos cos sin sin sin αβαβαβαβ-=3sin 5α=5cos 13β=-αβ()sin αβ+4π3π2βα<<<()12cos 13αβ-=()3sin 5αβ+=-sin 2αcos 2α()()0π2cos 23f x x ωω⎛⎫=+> ⎪⎝⎭πω()f x ()f x ()f x 0,π2⎡⎤⎢⎥⎣⎦()0,πθ∈1sin cos 5θθ+=1sin 2cos 21tan θθθ+-+22cos 15cos 15sin15︒+︒-︒︒；.（1）求出这个常数；（2）结合（1）的结果，将该小组的发现推广为一个三角恒等式，并证明你的结论.19.（17分）已知函数（1）当时，求的最值；（2）当时，关于的不等式有解，求实数的取值范围.()()22cos 80cos 5080sin 50︒+-︒︒-︒()()22cos 170cos 140sin 140︒+-︒-︒-︒()2sin cos cos 3344ππππf x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=-+++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,3ππ3x ⎡⎤∈-⎢⎥⎣⎦()f x π6π5,6x ⎡⎤∈⎢⎥⎣⎦x 14212ππ6af x f x ⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭≥a。

湖南省常德市汉寿县第一中学2023-2024学年高一下学期5月月考数学试题一、单选题 1．已知条件p ：411x ≤--，条件q ：22x x a a +≤-，且p 的一个充分不必要条件是q ，则a 的取值范围是（ ）A ．[]1,2-B ．1,22⎡⎤⎢⎥⎣⎦C ．12,2⎡⎤--⎢⎥⎣⎦D ．()1,2-2．若i 为虚数单位，则复数311i i-+的模是（ ）A ．BC ．5D 3．若函数()2()lg 2f x ax x a =-+的定义域为R ，则实数a 的取值范围为（ ）A ．(1,0)-B ．[1,1]-C ．(0,1)D ．(1,)+∞4．已知143a -=，121log 3b =，31log 5c =，则A ．b c a >>B ．a b c >>C ．b a c >>D ．c b a >>5．我国著名数学家华罗庚先生曾说：数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来琢磨函数的图象特征，如函数()21||x x x f =-的图象大致为（ ） A ． B ．C ．D ．6．中国传统扇文化有着极其深厚的底蕴.按如下方法剪裁(如图1)，扇面形状较为美观.从半径为R 的圆面中剪下扇形OAB ，使扇形OAB ，再从扇形OAB 中剪下扇环形ABDC 制作扇面，使扇环形ABDC 的面积与扇形OAB 的面积比.若为一个按上述方法制作的扇面装饰品装裱边框(如图2)，则需要边框的长度为（ ）A ．(31)R +B ．(31)R +C ．1)πRD ．1)πR7．在ABC ∆中，角A ､B ､C 的对边分别是a ､b ､c ，若2a =，b =解，则角A 的取值范围是（ ） A ．0,4π⎛⎫ ⎪⎝⎭B ．,42ππ⎛⎫ ⎪⎝⎭C ．3,44ππ⎛⎫ ⎪⎝⎭D ．,43ππ⎛⎫ ⎪⎝⎭8．已知函数()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭0,2π⎡⎤⎢⎥⎣⎦上有且仅有三个零点，则正实数ω的取值范围是（ ） A ．1014,33⎡⎫⎪⎢⎣⎭B ．1014,33⎡⎤⎢⎥⎣⎦C ．144,3⎡⎤⎢⎥⎣⎦D ．144,3⎡⎫⎪⎢⎣⎭二、多选题9．已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，()1112f x f π⎛≥⎫⎪⎝⎭恒成立，且()f x 的最小正周期为π，那么（ ）A ．()sin 23πf x x ⎛⎫=- ⎪⎝⎭B ．()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为1-C ．将()f x 的图象向左平移56π个单位长度后得到的函数图象关于y 轴对称 D ．()f x 在0,3π⎛⎫⎪⎝⎭上单调递增10．在ABC V 中，内角,,A B C 的对边分别为,,a b c ，则下列说法正确的是（ ）A ．若sin sin AB =，则ABC V 为等腰三角形 B ．sin sin sin sin a a b c A A B C++=++ C ．若2220a b c +-<，则ABC V 是锐角三角形D ．若π2,3bc A ==，则ABC V 的面积为ABC S V 11．（多选）对于实数a ，b ，c ，下列命题为真命题的是（ ）A ．若a b >，则2a ba b +>> B ．若0a b >>，则a b > C ．若0a b <<，0c >，则b c b a c a->- D ．若0ac <，a b c <<，则0b ca-<三、填空题12．已知函数 ()y f x =的表达式为()()ln ,036,36x x f x f x x ⎧<≤⎪=⎨-<<⎪⎩，若方程 ()f x m =有四个不相等的实根 ()1,2,3,4i x i =，且1234x x x x <<<，则()2221234x x x x +++取值范围是.13．已知平面向量34,,55a b a ⎛⎫= ⎪⎝⎭r r r 与b r 夹角为45o，则向量a r 在b r 方向上的投影为.14．如图，设,A B 两点在河的两岸，在A 所在河岸边选一定点C ，测量AC 的距离50m ，30ACB ︒∠=，105CAB ︒∠=则可以计算,A B 两点间的距离是四、解答题15．已知O 为坐标原点，对于函数()sin cos f x a x b x =+，称向量(),OM a b =u u u u r为函数()f x 的伴随向量，同时称函数()f x 为向量OM u u u u r的伴随函数．(1)设函数()2πsin sin 3g x x x ⎛⎫=++ ⎪⎝⎭，试求()g x 的伴随向量OM u u u u r ；(2)记向量()0,1ON =u u u r 的伴随函数为()f x ，在ABC V 中，π3B =，()35f C =，求()sin B A -的值；(3)记向量)OP =u u u r 的伴随函数为()f x ，函数()()2h x f x =，函数()h x 在区间π,4t t ⎡⎤+⎢⎥⎣⎦上的最大值为t M ，最小值为t m ，设函数()t t H t M m =-，若ππ[,)126t ∈，求函数()H t 的值域．16．已知集合{|121}A x a x a =-<<+，集合{}268|0B x x x =-+≥．(1)当3a =时，求A B ⋂；(2)若A B ⋃=R ，求实数a 的取值范围．17．某公园为了吸引更多的游客，准备进一步美化环境．如图，准备在道路AB 的一侧进行绿化，线段AB 长为4百米，C ，D 都设计在以AB 为直径的半圆上．设COB θ∠=．（1）现要在四边形ABCD 内种满郁金香，若3COD π∠=，则当θ为何值时，郁金香种植面积最大；（2）为了方便游客散步，现要铺设一条栈道，栈道由线段BC ，CD 和DA 组成，若BC ＝CD ，则当θ为何值时，栈道的总长l 最长，并求l 的最大值（单位：百米）．18．在ABC V 中，A ，B ，C 的对边分别为a ，b ，c ，已知sin cos b A B =． （1）求角B 的大小；（2）若2ABC S =△，求角C 的大小． 19．在ABC V 中，角A ，B ，C 所对的边分别为a ，b ，c ．AD 为BC 边上的中线，点E ，F 分别为边AB ，AC 上动点，EF 交AD 于G ．已知4b =，且12si n c o s s i n s i n s i n 4c A B a A b B bC =-+．(1)求c 边的长度；(2)若cos BAD ∠BAC ∠的余弦值； (3)在（2）的条件下，若4ABC AEF S S =△△，求AG EF ⋅u u u r u u u r的取值范围．。

2023-2024学年湖南省郴州一中等校联考高一（下）月考数学试卷（5月份）一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.设集合，，则()A. B. C.D.2.若，则()A.B.C.D.3.已知奇函数在R 上单调递增，且，则不等式的解集为()A.B.C. D.4.某班同学利用课外实践课，测量A ，B 两地之间的距离，在C 处测得A ，C 两地之间的距离是4千米，B ，C 两地之间的距离是6千米，且，则A ，B 两地之间的距离是()A.千米B.千米C.千米D.千米5.已知命题p ：函数在内有零点，则命题p 成立的一个必要不充分条件是()A. B. C.D.6.()A.B.C.D.7.如图，在正方体中，，E 在线段上，则的最小值是()A. B. C. D.8.已知长方体的底面ABCD 是边长为1的正方形，侧棱，在矩形内有一动点P 满足，且，则的最小值为()A.B.C.D.2二、多选题：本题共3小题，共18分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，部分选对的得2分，有选错的得0分。

9.已知m ，n 是两条不同的直线，，是两个不同的平面，下列结论不正确的是()A.若，，，，则B.若，，则C.若，，，则D.若，，则10.已知函数，则下列结论正确的是()A.的图象向左平移个单位长度后得到函数的图象B.直线是图象的一条对称轴C.在上单调递减D.的图象关于点对称11.已知三棱锥的所有棱长都是6，D ，E 分别是三棱锥外接球和内切球上的点，则()A.三棱锥的体积是B.三棱锥内切球的半径是C.DE 长度的取值范围是D.三棱锥外接球的体积是三、填空题：本题共3小题，每小题5分，共15分。

12.某连锁超市在A ，B ，C 三地的数量之比为2：m ：4，现采用分层抽样的方法抽取18家该连锁超市进行调研，已知A 地被抽取了4家，则B 地被抽取的数量是______.13.若实数，则的最小值为______，此时______.14.在长方形ABCD 中，，，点E 在线段AB 上，，沿DE 将折起，使得，此时四棱锥的体积为______.四、解答题：本题共5小题，共77分。