2014届高考一轮复习备考之知能演练高分跨栏(新课标通用)第一章第二节知能演练高分跨栏
- 格式:doc
- 大小:99.00 KB
- 文档页数:5

1.一定条件下,在恒容密闭容器中,能表示反应X(g)+2Y(g)2Z(g)一定达到化学平衡状态的是( )①X 、Y 、Z 的物质的量之比为1∶2∶2②X 、Y 、Z 的浓度不再发生变化③容器中的压强不再发生变化④单位时间内生成n mol Z ,同时生成2n mol YA .①②B .①④C .②③D .③④解析:选C 。
根据化学平衡状态的概念可知,可逆反应达平衡时,正、逆反应速率相等,故④错误;对于反应前后气体总体积不等的反应,其压强不再发生变化,各组分的浓度不再变化,故②、③正确;但它们的物质的量之比不一定等于其化学计量数之比,①错误,故选C 。
2.实验室用4 mol SO 2与2 mol O 2进行下列反应:2SO 2(g)+O 2(g)2SO 3(g) ΔH =-196.64 kJ/mol ,当放出314.624 kJ 热量时,SO 2的转化率为( )A .40%B .50%C .80%D .90%解析:选C 。
根据放出314.624 kJ 的热量可知参加反应的SO 2的物质的量为:314.624 kJ 196.64 kJ/mol×2=3.2 mol ,故SO 2的转化率为:3.2 mol 4 mol×100%=80%。
3.(2013·石家庄教学质量检测)在一定温度下的定容密闭容器中,当物质的下列物理量不再变化时,不能说明反应A(s)+2B(g)C(g)+D(g)已达平衡状态的是( )A .混合气体的压强B .混合气体的密度C .B 的物质的量浓度D .气体的平均相对分子质量解析:选A 。
解答该题,首先明确:反应条件——定温定容,反应特点——A 为固体,气体体积不变。
气体的体积不变,则反应过程中压强始终不变,A 不能说明;气体的密度ρ=m V,气体的相对分子质量M r =m n,V 、n 不变,反应未达到平衡时气体的m 发生变化,ρ、M r 随之发生变化,平衡时m 不变,ρ、M r 不变,B 、D 能说明;C 项属于根本标志,能说明。

1.(2013·吉林高三检测)改变下列条件,一定能促进盐类水解的是( ) A .升高温度 B .增大压强 C .加酸 D .加碱解析:选A 。
盐类的水解反应吸热,升高温度水解程度增大,A 正确。
2.下列离子反应方程式中,属于水解反应的是( ) A .CN -+H 2O HCN +OH -B .NH 3·H 2O NH +4+OH -C .HCO -3+H 2OH 3O ++CO 2-3D .H 2CO 3HCO -3+H +解析:选A 。
B 、C 、D 项均属于电离,故错误。
3.下列溶液在空气中加热、蒸干、灼烧后,所得固体为原溶液中的溶质的是( ) A .NaHCO 3 B .KMnO 4 C .FeCl 3 D .NaCl解析:选D 。
NaHCO 3溶液加热后得到Na 2CO 3;KMnO 4溶液最后得到K 2MnO 4和MnO 2;FeCl 3溶液最后得到Fe 2O 3。
4.(2013·茂名高三调研)下列说法中,错误的是( )A .NaHCO 3溶液中碳元素主要以HCO -3存在B .Na 2CO 3溶液中滴加酚酞呈红色,加热红色变深C .NH 4Cl 溶液呈酸性这一事实能说明一水合氨为弱碱D .在稀醋酸中加醋酸钠固体能促进醋酸的电离 解析:选D 。
A 选项,碳酸氢钠电离出的碳酸氢根离子的电离和水解均相当微弱;B 选项,加热使水解程度增大,碱性增强,红色加深;C 选项,铵根离子结合水电离出的氢氧根离子生成弱电解质(一水合氨),使溶液呈酸性;D 选项,增加了醋酸根离子的浓度,醋酸的电离受到抑制。
5.(2013·益阳高三检测)在一定条件下,Na 2CO 3溶液存在CO 2-3+H 2O HCO -3+OH -平衡。
下列说法不正确的是( )A .稀释溶液c (HCO -3)·c (OH -)c (CO 2-3)增大 B .通入CO 2,溶液pH 减小 C .升高温度,此平衡常数增大D .加入NaOH 固体,c (HCO -3)c (CO 2-3)减小解析:选A 。

1.若圆锥的主视图是正三角形,则它的侧面积是底面积的( ) A. 2 倍 B .2倍 C .3倍 D .5倍解析:选B.设圆锥的底面半径为r ,母线长为l ,则l =2r ,侧面积S 1=πr ·l =2πr 2,而底面积S 2=πr 2,故侧面积与底面积之比为S 1S 2=2.2.(2013·吉林高一检测)已知圆锥的侧面展开图为半圆,半圆的面积为S ,则圆锥的底面面积是( )A .2S B.S2C.2SD.22S解析:选B.设圆锥的母线长为l ,则侧面展开图半圆的半径R =l .∴S =12πR 2=12πl 2,∴l =2Sπ,∴圆锥的底面周长C =πR =πl =2πS ,∴圆锥的底面半径r =C 2π=2πS 2π=S2π,∴圆锥的底面积为S ′=πr 2=S2,故选B.3.(2013·临沂高一检测)若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于( )A .6B .2 3 C. 3 D .2解析:选A.由正视图可知底面边长为2,高为1,因为三棱柱底面为等边三角形,所以其侧面积S =6×1=6.4.(2013·西安交大附中月考)正三棱锥的底面边长为a ,高为66a ,则三棱锥的侧面积等于( )A.34a 2B.32a 2C.334a 2D.332a 2 解析:选A.VO =66a ,OA =a 2·33=36a ,∵VA =12a ,∴S 侧=12·3a ·12a =34a 2,故选A.5.(2012·高考北京卷)某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+6 5B .30+6 5C .56+12 5D .60+12 5解析:选B.由题中的三视图知,该三棱锥的直观图如图所示.由题中所给条件,可求得S △ABD =12×4×5=10,S △ACD =S △BCD =12×4×5=10,AC =BC=41,AB =25,可求得△ABC 中AB 边上的高为41-5=6,所以S △ABC =12×6×25=6 5.综上可知,该三棱锥的表面积为S △ABD +S △ACD +S △BCD +S △ABC =30+6 5. 6.若圆台的上、下底面半径和母线长的比为1∶4∶5,高为8,则其侧面积为__________. 解析:不妨设上、下底面半径和母线长分别为k 、4k 、5k (k >0),高为8,如图:则母线l =(4k -k )2+64=9k 2+64,可得:9k 2+64=5k ,解得k =2,∴上、下底面半径r 1=2、r 2=8,母线长l =10,因此S 圆台侧=π(r 1+r 2)l =π×10×10=100π.答案:100π7.已知正四棱柱的高为 3 cm ,对角线长为17 cm ,则该正四棱柱的侧面积为__________.解析:设正四棱柱的底面边长为a cm ,则: 2a 2+9=17,∴a =2,∴侧面积S =4a ×3=12×2=24 cm 2. 答案:24 cm 28.长方体的高等于h ,底面积等于Q ,垂直于底面的对角面的面积等于M ,此长方体的侧面积等于________.解析:设底面两边长分别为x ,y ,则⎩⎨⎧xy =Qh ·x 2+y 2=M⇒(x +y )2=x 2+y 2+2xy =(M h )2+2Q ,S 侧=2h (x +y )=2h (Mh)2+2Q =2M 2+2h 2Q .答案:2M2+2h2Q9.有一根长为3π cm、底面半径为1 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为多少?解:把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD(如图),由题意知BC=3πcm,AB=4π cm,点A与点C分别是铁丝的起、止位置,故线段AC的长度即为铁丝的最短长度.AC=AB2+BC2=5π cm,故铁丝的最短长度为5π cm.10.已知正三棱锥V ABC的主视图,俯视图如图所示,其中VA=4,AC=23,求该三棱锥的表面积.解:由主视图与俯视图可得正三棱锥的直观图如图,且VA=VB=VC=4,AB=BC=AC=23,取BC的中点D,连接VD,则VD=VB2-BD2=42-(3)2=13.∴S△VBC=12·VD·BC=12×13×23=39,S△ABC=12×(23)2×32=33,∴三棱锥V ABC的表面积为3S △VBC+S△ABC=339+33=3(39+3).1.底面是菱形的直棱柱,它的体对角线的长分别是9和15,高是5,则这个棱柱的侧面积是()A.130 B.140C.150 D.160解析:选D.如图,直棱柱ABCD A 1B 1C 1D 1,AA 1=BB 1=CC 1=DD 1=5,BD 1=9,A 1C =15,可求得AC =A 1C 2-AA 21=152-52=102,BD =BD 21-DD 21=92-52=214. 所以AB =BC =C 1B 1=A 1B 1 =50+14=8.所以棱柱侧面积为4×5×8=160.2.正四棱锥底面正方形边长为4 cm ,高与斜高的夹角为30°,则正四棱锥的侧面积为__________ cm 2.解析:由题意可得,高PO 与斜高PE 的夹角∠OPE =30°,在Rt △POE 中,OE =2 cm ,∠OPE =30°,则PE =OEsin 30°=4 cm ,∴S △P AB =12AB ·PE =12×4×4=8 cm 2,∴S 侧=4S △P AB =32 cm 2. 答案:323.有一个蒙古包形状的帐篷,其形状是一个圆柱与圆锥的组合体,尺寸如下图所示,请你帮助算出要搭建这样的一个蒙古包至少需要多少平方米的篷布?(精确到0.01 m 2)解:上部分圆锥体的母线长为 1.22+2.52,其侧面积为S 1=π×52× 1.22+2.52.下部分圆柱体的侧面积为S 2=π×5×1.8. S =S 1+S 2=π×52× 1.22+2.52+π×5×1.8≈50.03(m 2).所以,要搭建这样的一个蒙古包至少需要约50.03 m 2的篷布. 4.正四棱台的两底面边长分别是a 和b (a <b ).(1)若侧棱所在直线与上、下底面正方形中心的连线所成的角为45°,求棱台的侧面积; (2)若正四棱台的侧面积等于两底面积之和,求它的高. 解:(1)如图所示,设O ′,O 分别为上、下底面的中心,过C 1作C 1E ⊥AC 于E ,过E 作EF ⊥BC 于F , 连接C 1F ,则C 1F 为正四棱台的斜高. 由题意知,∠C 1CO =45°,所以CE =CO -EO =CO -C 1O ′=22(b -a ).在Rt △C 1CE 中,C 1E =CE =22(b -a ),又EF =CE ·sin 45°=12(b -a ),所以C 1F =C 1E 2+EF 2=32(b -a ),所以S 侧=12(4a +4b )×32(b -a )=3(b 2-a 2),即棱台的侧面积为3(b 2-a 2).(2)由S 侧=a 2+b 2,得12(4a +4b )·h 斜=a 2+b 2,所以h 斜=a 2+b 22(a +b ).又因为EF =b -a 2,所以h =h 2斜-EF 2=ab a +b, 即棱台的高为aba +b .。

【优化方案】(新课标)2016高考数学一轮复习 第2讲 知能训练轻松闯关(选修4-4)1.(2014·高考江苏卷)在平面直角坐标系xOy 中,已知直线l 的参数方程为⎩⎪⎨⎪⎧x =1-22t ,y =2+22t (t 为参数),直线l 与抛物线y 2=4x 相交于A ,B 两点,求线段AB 的长. 解:将直线l的参数方程⎩⎪⎨⎪⎧x =1-22t ,y =2+22t 代入抛物线方程y 2=4x ,得⎝⎛⎭⎪⎫2+22t 2=4⎝ ⎛⎭⎪⎫1-22t ,解得t 1=0,t 2=-82. 所以AB =|t 1-t 2|=82.2.在直角坐标系xOy 中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,设点A ,B 分别在曲线C 1:⎩⎪⎨⎪⎧x =3+cos θ,y =4+sin θ(θ为参数)和曲线C 2:ρ=1上,求|AB |的最小值.解:曲线C 1:⎩⎪⎨⎪⎧x =3+cos θ,y =4+sin θ(θ为参数)的直角坐标方程为(x -3)2+(y -4)2=1,知C 1是以(3,4)为圆心,1为半径的圆;曲线C 2:ρ=1的直角坐标方程是x 2+y 2=1,可知C 2是以原点为圆心,1为半径的圆,题意就是求分别在两个圆C 1和C 2上的两点A ,B 的最短距离.由圆的方程知,这两个圆相离,所以|AB |min =(3-0)2+(4-0)2-1-1=5-1-1=3.3.(2015·东北三校联合模拟)在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知曲线C 1的极坐标方程为ρ2=21+sin 2θ,直线l 的极坐标方程为ρ=42sin θ+cos θ.(1)写出曲线C 1与直线l 的直角坐标方程;(2)设Q 为曲线C 1上一动点,求Q 点到直线l 距离的最小值. 解:(1)C 1:x 2+2y 2=2,l :2y +x =4.(2)设Q (2cos θ,sin θ),则点Q 到直线l 的距离d =|2sin θ+2cos θ-4|3=|2sin (θ+π4)-4|3≥23=233,当且仅当θ+π4=2k π+π2(k ∈Z ),即θ=2k π+π4(k ∈Z )时取等号.4.(2015·山西省忻州市第一次联考)在直角坐标平面内,直线l 过点P (1,1),且倾斜角α=π4.以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,已知圆C 的极坐标方程为ρ=4sin θ.(1)求圆C 的直角坐标方程;(2)设直线l 与圆C 交于A 、B 两点,求|PA |·|PB |的值.解:(1)∵ρ=4sin θ,∴ρ2=4ρsin θ,则x 2+y 2-4y =0,即圆C 的直角坐标方程为x 2+y 2-4y =0. (2)由题意,得直线l 的参数方程为⎩⎪⎨⎪⎧x =1+22t y =1+22t (t 为参数).将该方程代入圆C 方程x 2+y 2-4y =0, 得(1+22t )2+(1+22t )2-4(1+22t )=0, 即t 2=2,∴t 1=2,t 2=-2.即|PA |·|PB |=|t 1t 2|=2.5.(2015·石家庄第一次模拟)在直角坐标系中,曲线C 1的参数方程为:⎩⎨⎧x =2cos αy =2sin α(α为参数),以原点为极点,x 轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C 2的极坐标方程为:ρ=cos θ.(1)求曲线C 2的直角坐标方程;(2)若P ,Q 分别是曲线C 1和C 2上的任意一点,求|PQ |的最小值. 解:(1)∵ρ=cos θ, ∴x 2+y 2=x ,即(x -12)2+y 2=14.(2)设P (2cos α,2sin α),易知C 2(12,0),∴|PC 2|= (2cos α-12)2+(2sin α)2=4cos 2α-2cos α+14+2sin 2α=2cos 2α-2cos α+94,当cos α=12时,|PC 2|取得最小值,|PC 2|min =72,∴|PQ |min =7-12. 6.(2015·河北唐山模拟)极坐标系的极点为直角坐标系xOy 的原点,极轴为x 轴的正半轴,两种坐标系中的长度单位相同,已知曲线C 的极坐标方程为ρ=2(cos θ+sin θ).(1)求C 的直角坐标方程;(2)直线l :⎩⎪⎨⎪⎧x =12t ,y =1+32t (t 为参数)与曲线C 交于A ,B 两点,与y 轴交于E ,求|EA |+|EB |的值.解:(1)在ρ=2(cos θ+sin θ)中,两边同乘ρ,得ρ2=2(ρcos θ+ρsin θ),则C 的直角坐标方程为x 2+y 2=2x +2y ,即(x -1)2+(y -1)2=2.(2)将l 的参数方程代入曲线C 的直角坐标方程,化简得t 2-t -1=0, 点E 对应的参数t =0,设点A ,B 对应的参数分别为t 1,t 2, 则t 1+t 2=1,t 1t 2=-1,所以|EA |+|EB |=|t 1|+|t 2|=|t 1-t 2|=(t 1+t 2)2-4t 1t 2=5.1.(2015·新乡许昌平顶山第二次调研)已知直线l :⎩⎪⎨⎪⎧x =1+12t y =32t (t 为参数),曲线C 1:⎩⎪⎨⎪⎧x =cos θy =sin θ(θ为参数). (1)设l 与C 1相交于A ,B 两点,求|AB |;(2)若把曲线C 1上各点的横坐标压缩为原来的12,纵坐标压缩为原来的32,得到曲线C 2,设点P 是曲线C 2上的一个动点,求它到直线l 的距离的最小值.解:(1)l 的普通方程为y =3(x -1),C 1的普通方程为x 2+y 2=1. 联立方程⎩⎨⎧y =3(x -1)x 2+y 2=1,解得l 与C 1的交点为A (1,0),B ⎝ ⎛⎭⎪⎫12,-32, 则|AB |=1.(2)C 2的参数方程为⎩⎪⎨⎪⎧x =12cos θy =32sin θ(θ为参数).故点P 的坐标是⎝ ⎛⎭⎪⎫12cos θ,32sin θ.从而点P 到直线l 的距离d =⎪⎪⎪⎪⎪⎪32cos θ-32sin θ-32=34⎪⎪⎪⎪⎪⎪2sin (θ-π4)+2, 当sin ⎝⎛⎭⎪⎫θ-π4=-1时,d 取得最小值,且最小值为64(2-1).2.(2013·高考辽宁卷)在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系.圆C 1,直线C 2的极坐标方程分别为ρ=4sin θ,ρcos (θ-π4)=22.(1)求C 1与C 2交点的极坐标;(2)设P 为C 1的圆心,Q 为C 1与C 2交点连线的中点.已知直线PQ 的参数方程为⎩⎪⎨⎪⎧x =t 3+a ,y =b 2t 3+1(t ∈R 为参数),求a ,b 的值.解:(1)圆C 1的直角坐标方程为x 2+(y -2)2=4,直线C 2的直角坐标方程为x +y -4=0.解⎩⎪⎨⎪⎧x 2+(y -2)2=4,x +y -4=0,得⎩⎪⎨⎪⎧x 1=0,y 1=4,⎩⎪⎨⎪⎧x 2=2,y 2=2. 所以C 1与C 2交点的极坐标为(4,π2),(22,π4).注:极坐标系下点的表示不唯一.(2)由(1)可得,P 点与Q 点的直角坐标分别为(0,2),(1,3). 故直线PQ 的直角坐标方程为x -y +2=0, 由参数方程可得y =b 2x -ab2+1.所以⎩⎪⎨⎪⎧b2=1,-ab 2+1=2,解得⎩⎪⎨⎪⎧a =-1,b =2.3.(2015·贵州省六校联考)在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :ρsin 2θ=2a cos θ(a >0),过点P (-2,-4)的直线l :⎩⎪⎨⎪⎧x =-2+22t y =-4+22t (t 为参数)与曲线C 相交于M ,N 两点.(1)求曲线C 的直角坐标方程和直线l 的普通方程; (2)若|PM |,|MN |,|PN |成等比数列,求实数a 的值.解:(1)把⎩⎪⎨⎪⎧x =ρcos θy =ρsin θ代入ρsin 2θ=2a cos θ,得y 2=2ax (a >0),由⎩⎪⎨⎪⎧x =-2+22t y =-4+22t (t 为参数),消去t 得x -y -2=0,∴曲线C 的直角坐标方程和直线l 的普通方程分别是y 2=2ax (a >0),x -y -2=0. (2)将⎩⎪⎨⎪⎧x =-2+22t y =-4+22t (t 为参数)代入y 2=2ax ,整理得t 2-22(4+a )t +8(4+a )=0.设t 1,t 2是该方程的两根,则t 1+t 2=22(4+a ),t 1·t 2=8(4+a ),∵|MN |2=|PM |·|PN |,∴(t 1-t 2)2=(t 1+t 2)2-4t 1·t 2=t 1·t 2,∴8(4+a )2-4×8(4+a )=8(4+a ),∴a =1.4.(2015·吉林长春调研)已知直线l 的参数方程为⎩⎪⎨⎪⎧x =-1-3t2,y =3+12t (t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为ρ=4sin ⎝⎛⎭⎪⎫θ-π6.(1)求圆C 的直角坐标方程;(2)点P (x ,y )是直线l 与圆面ρ≤4sin ⎝ ⎛⎭⎪⎫θ-π6的公共点,求3x +y 的取值范围.解:(1)因为圆C 的极坐标方程为ρ=4sin ⎝ ⎛⎭⎪⎫θ-π6, 所以ρ2=4ρsin ⎝ ⎛⎭⎪⎫θ-π6=4ρ⎝ ⎛⎭⎪⎫32sin θ-12cos θ.又ρ2=x 2+y 2,x =ρcos θ,y =ρsin θ,所以x 2+y 2=23y -2x ,所以圆C 的直角坐标方程为x 2+y 2+2x -23y =0. (2)设z =3x +y ,由圆C 的方程x 2+y 2+2x -23y =0,得(x +1)2+(y -3)2=4, 所以圆C 的圆心是(-1,3),半径是2.将⎩⎪⎨⎪⎧x =-1-32t ,y =3+12t代入z =3x +y ,得z =-t ,又直线l 过C (-1,3),圆C 的半径是2,所以-2≤t ≤2, 所以-2≤-t ≤2,即3x +y 的取值范围是[-2,2].。

1.下列关于电解质的叙述正确的是()A.强酸、强碱及大部分盐类属于强电解质,弱酸、弱碱属于弱电解质B.所有的离子化合物都是强电解质,所有的共价化合物都是弱电解质C.强电解质溶液的导电能力一定比弱电解质溶液的导电能力强D.CO2的水溶液能导电,所以CO2是电解质解析:选A。
H2SO4、HCl等都是共价化合物,溶于水完全电离是强电解质,B错;溶液的导电能力的强弱取决于溶液中离子浓度的大小和离子所带电荷数,与电解质强弱没有必然联系,C错;CO 2的水溶液导电,是因为CO2+H2O H2CO3,H2CO3H++HCO-3,H2CO3是电解质,CO2是非电解质,D错。
2.下列物质在水溶液中的电离方程式书写正确的是()A.CH 3COOH H++CH3COO-B.NaHSO 4Na++HSO-4C.H 3PO43H++PO3-4D.NaHCO 3Na++H++CO2-3解析:选A。
B项应为NaHSO4===Na++H++SO2-4;C项中H3PO4为多元弱酸,其电离方程式应分步书写;D项应为NaHCO 3===Na++HCO-3、HCO-3H++CO2-3。
故A项正确。
O H++OH-。
下列叙述正3.(2013·聊城高三检测)室温下,水的电离达到平衡:H确的是()A.将水加热,平衡向正反应方向移动,K w不变B.向水中加入少量盐酸,平衡向逆反应方向移动,c(H+)增大C.向水中加入少量NaOH固体,平衡向逆反应方向移动,c(OH-)降低D.向水中加入少量CH3COONa固体,平衡向正反应方向移动,c(OH-)=c(H+)解析:选B。
H2O电离吸热,加热促进水的电离,K W增大,A不正确;加入NaOH,c(OH -)增大,C不正确;加入CHCOONa,因CH3COO-与H+结合生成CH3COOH,使c(OH-)>3c(H+),D不正确。
4.(2013·秦皇岛高三检测)高氯酸、硫酸、硝酸和盐酸都是强酸,其酸性在水溶液中差别从以上表格中判断以下说法中不正确的是()A.在冰醋酸中这四种酸都没有完全电离B.在冰醋酸中高氯酸是这四种酸中最强的酸C.在冰醋酸中硫酸的电离方程式为H2SO4===2H++SO2-4D.水对于这四种酸的强弱没有区分能力,但醋酸可以区别这四种酸的强弱解析:选C。

1.(2012·高考上海卷)氮氧化铝(AlON)属原子晶体,是一种超强透明材料,下列描述错误的是()A.AlON和石英的化学键类型相同B.AlON和石英晶体类型相同C.AlON和Al2O3的化学键类型不同D.AlON和Al2O3晶体类型相同解析:选D。
石英主要成分的化学式为SiO2,是原子晶体,而原子晶体中的化学键为共价键,选项A、B正确;AlON晶体中存在共价键,而Al2O3晶体中存在离子键,故D错误。
2.钡在氧气中燃烧时得到一种钡的氧化物晶体,结构如图所示,有关说法不正确的是() A.该晶体属于离子晶体B.晶体的化学式为Ba2O2C.该晶体晶胞结构与NaCl相似D.与每个Ba2+距离相等且最近的Ba2+共有12个解析:选B。
对比NaCl晶体结构发现此晶体相当于用Ba2+代替Na+,O2-2代替Cl-,故Ba2+与O2-2物质的量之比为1∶1,化学式为BaO2。
3.在通常条件下,下列各组物质的性质排列正确的是()A.熔点:CO2>KCl>SiO2B.水溶性:HCl>H2S>SO2C.沸点:乙烷>戊烷>丁烷D.热稳定性:HF>H2O>NH3解析:选D。
选项A,SiO2是原子晶体,熔点最高。
选项B,HCl、SO2、H2S分子中键的极性依次减弱,在极性溶剂H2O中的溶解性也依次减小。
选项C,戊烷的相对分子质量最大,其沸点最高。
选项D,元素非金属性越强,其氢化物越稳定,正确。
4.以下关于晶体的说法中正确的是()A.晶体根据结构和性质只可分为分子晶体、原子晶体、离子晶体和金属晶体四大类B.任何晶体中都含有化学键,如离子键、共价键、金属键、氢键等C.含有阳离子的晶体一定是离子晶体D.干冰和冰都属于分子晶体解析:选D。
A项,还有混合型晶体,如石墨;B项,由稀有气体组成的分子晶体中不含任何化学键,只有范德华力,且氢键不属于化学键;C项,金属晶体中含有金属阳离子。

1.(2013·长沙高三质检)下列溶液中溶质的物质的量浓度为1 mol·L -1的是( )A .将58.5 g NaCl 溶解于1 L 水中配成的溶液B .将80 g SO 3溶于水并配成1 L 溶液C .将0.5 mol·L -1的NaNO 3溶液100 mL 加热蒸发掉50 g 水后的溶液D .含K +为2 mol 的K 2SO 4溶液解析:选B 。
A 中“1 L 水”,溶液体积不一定为1 L ;C 中蒸发掉50 g 水后,溶液的体积不一定是50 mL ;D 中未指明溶液体积。
2.关于0.2 mol·L -1的NaOH 溶液,下列说法不正确的是( )A .100 mL 该溶液中含0.8 g NaOHB .200 mL 该溶液与100 mL 0.2 mol·L -1的硫酸溶液反应形成中性溶液C .100 mL 该溶液中约含0.02×6.02×1023个Na +D .配制含1 L 水的该溶液,需NaOH 的质量为8 g 解析:选D 。
8 g NaOH 溶于1 L 水配制成的溶液,其物质的量浓度小于0.2 mol·L -1。
3.(2013·大庆一中高三月考)在80 g 密度为d g·cm -3的硫酸铁溶液中,含有2.8 g Fe 3+,则此溶液中SO 2-4的物质的量浓度为( )A.1516dB.516d C.38d D.58d 解析:选A 。
n (Fe 3+)=0.05 mol ,n [Fe 2(SO 4)3]=0.025 mol ,n (SO 2-4)=0.075 mol ,V (溶液)=801 000d L ,c (SO 2-4)=n (SO 2-4)V (溶液)=0.075 mol 801 000dL =1516d 。
4.在无土栽培中,需配制1 L 含0.50 mol·L -1的NH 4Cl 、0.16 mol·L -1 KCl 、0.24 mol·L-1 K 2SO 4的混合溶液,但当时没有K 2SO 4固体,若用(NH 4)2SO 4固体代替,需用KCl 、NH 4Cl 、(NH 4)2SO 4三种固体的物质的量(单位为 mol)分别为( )A .0.40、0.50、0.12B .0.66、0.50、0.24C .0.64、0.50、0.24D .0.64、0.02、0.24解析:选D 。

2014届高考一轮化学复习备考之知能演练高分跨栏(新课标通用):选修3第一节1.下列有关表达正确的是( )A.硫离子的电子排布式:1s22s22p63s23p4B.H2O的电子式:C.N原子最外层电子的排布图:D.的名称:2乙基丙烷解析:选B。
S2-的电子排布式为1s22s22p63s23p6,A错;1s不属最外层,C错;名称应为2甲基丁烷,D错。
2.下列有关认识正确的是( )A.各能级的原子轨道数按s、p、d、f的顺序分别为1、3、5、7B.各能层的能级都是从s能级开始至f能级结束C.各能层含有的能级数为n-1D.各能层含有的电子数为2n2解析:选A。
各能层的能级之间存在着交错现象,B错;各能层含有的能级数为n,C 错;2n2是各能层中可最多容纳的电子数,很多情况下电子达不到这个数。
3.(2013·大同高三第一次模拟)下列各组原子中,彼此化学性质一定相似的是( ) A.原子核外电子排布式为1s2的X原子与原子核外电子排布式为1s22s2的Y原子B.原子核外M层上仅有两个电子的X原子与原子核外N层上仅有两个电子的Y原子C.2p轨道上只有2个电子的X原子与3p轨道上只有2个电子的Y原子D.最外层都只有一个电子的X、Y原子解析:选C。
本题考查的是核外电子排布的知识。
A项中1s2结构的原子为He,1s22s2结构的原子为Be,两者性质不相似。
B项X原子为Mg,Y原子N层上有2个电子的有多种元素,如第四周期中Ca、Fe等相符合,化学性质不一定相似。
C项为同主族的元素,化学性质一定相似。
D项最外层只有1个电子的第ⅠA族元素都可以,过渡元素中也有很多最外层只有1个电子,故性质不一定相似。
4.下列叙述中正确的是( )A.在一个基态多电子的原子中,可以有两个运动状态完全相同的电子B.在一个基态多电子的原子中,不可能有两个能量完全相同的电子C.在一个基态多电子的原子中,M层上的电子能量肯定比L层上的电子能量高D.如果某一基态原子3p能级上仅有2个电子,它们的自旋状态必然相反解析:选C。

1.若两个平面互相垂直,在第一个平面内的一条直线a垂直于第二个平面内的一条直线b,那么()A.直线a垂直于第二个平面B.直线b垂直于第一个平面C.直线a不一定垂直于第二个平面D.过a的平面必垂直于过b的平面解析:选C.对于两平面,无论关系如何,在两平面内一定可以找到互相垂直的两条直线,因此直线a不一定是第二个平面的垂线,故选C.2.如果直线a与平面α不垂直,那么平面α内与直线a垂直的直线有()A.0条B.1条C.无数条D.任意条解析:选C.可构造图形,若a∥α,a′α,且a′∥a,则在平面α内有无数条直线垂直于a′,故平面α内有无数条直线垂直于直线a.3.若平面α⊥平面β,平面β⊥平面γ,则()A.α∥γB.α⊥γC.α与γ相交但不垂直D.以上都有可能解析:选D.结合图形,可考虑出α与γ有以下几种情况:α∥γ或α⊥γ,也可以α与γ相交但不垂直,故选D.4.在三棱锥P ABC中,P A=PB=PC,且PO⊥平面ABC,O为垂足,则O是△ABC 的()A.外心B.内心C.垂心D.重心解析:选A.如图所示,可以证明Rt△POA≌Rt△POB≌Rt△POC,∴OA=OB=OC,即O为△ABC外接圆的圆心.故选A.5.如图(1)所示,四边形ABCD中,AD∥BC,AD=AB,∠DCB=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体A-BCD(如图(2)所示),则在四面体A-BCD中,下列命题正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析:选D.因为∠BAD=90°,所以AD⊥AB.又因为∠BCD=45°,AB=AD,∠BAD=90°,AD∥BC,所以∠DBC=45°,所以∠BDC=90°,即BD⊥CD.而平面ABD⊥平面BCD,所以CD⊥平面ABD,所以CD⊥AB,所以AB⊥平面ACD,所以平面ABC⊥平面ADC.6.如图,平面ABC⊥平面ABD,∠ACB=90°,CA=CB,△ABD是正三角形,O为AB中点,则图中直角三角形的个数为__________.解析:△ACB,△ACO,△COB,△AOD,△BOD,△COD均为直角三角形.答案:67.已知α,β是两个平面,m,n是两条直线,给出如下四个论断:①m⊥α;②n∥β;③α⊥β;④m∥n.现以其中三个论断作为条件,余下一个论断作为结论,请写出一个正确的说法__________.解析:由m⊥α,m∥n可知n⊥α,结合n∥β可得α⊥β,应填①②④⇒③.答案:①②④⇒③8.已知P A垂直于平行四边形ABCD所在平面,若PC⊥BD,平行四边形ABCD一定是________.解析:易知,BD⊥平面P AC,∴BD⊥AC,又四边形ABCD是平行四边形,∴ABCD一定是菱形.答案:菱形9.(2013·吉林高一检测)如图,△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,CE=CA=2BD,M是EA的中点,N是EC的中点,求证:平面DMN∥平面ABC.证明:∵M、N分别是EA与EC的中点,∴MN∥AC,又AC平面ABC,MN平面ABC,∴MN∥平面ABC.∵DB⊥平面ABC,EC⊥平面ABC,∴BD∥EC,四边形BDEC为直角梯形.∵N为EC中点,EC=2BD,∴NC BD,∴四边形BCND为矩形,∴DN∥BC,又∵DN平面ABC,BC平面ABC,∴DN∥平面ABC.又∵MN∩DN=N,且MN、DN平面DMN,∴平面DMN∥平面ABC.10.已知:平面α⊥平面β,平面α⊥平面γ,且β∩γ=l,求证:l⊥α.证明:法一:如图(1),在α内任取一点P,过点P分别作β,γ与α交线的垂线,垂足分别为A,B.∵β⊥α,γ⊥α,∴P A⊥β,PB⊥γ.∴P A⊥l,PB⊥l.又∵P Aα,PBα,P A∩PB=P,∴l⊥α.法二:如图(2),在l上任取一点Q,作QC⊥α于C,∵β∩γ=l,∴Q∈β.∵β⊥α,∴QCβ.同理可证QCγ.∴QC=β∩γ.即QC与l重合,∴l⊥α.法三:如图(3),在β,γ内分别取点M,N,过M,N分别作α,β的交线及α,γ的交线的垂线c,d,则c⊥α,d⊥α.∴c∥d.∴c∥γ.又β∩γ=l,∴l∥c,∴l⊥α.1.(2011·高考浙江卷)下列命题中错误的是()A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γD.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β解析:选D.两个平面α,β垂直时,设交线为l,则在平面α内与l平行的直线都平行于平面β,故A正确;如果平面α内存在直线垂直于平面β,那么由面面垂直的判定定理知α⊥β,故B正确;两个平面都与第三个平面垂直时,易证交线与第三个平面垂直,故C正确;两个平面α,β垂直时,平面α内与交线平行的直线与β平行,故D错误.2.已知a,b为不垂直的异面直线,α是一个平面,则a,b在α上的射影有可能是(1)两条平行直线,(2)两条互相垂直的直线,(3)同一条直线,(4)一条直线及其外一点.在上面的结论中,正确结论的编号是________.(写出所有正确结论的编号).解析:(1)当且仅当直线垂直于平面时,直线在平面上的射影是一点.(2)当一条线在平面上的射影是一直线时,则该线必在以这条直线为交线的该平面的垂面内.对(3),可得a、b共面,故不正确,对(1)、(2)、(3)、(4)均可想象出或画出以射影直线为交线的α的垂面或以射影点为垂足的α的垂线.(1)、(2)、(4)三种情况都有可能出现(如图).答案:(1)(2)(4)3.如图,已知矩形ABCD,沿对角线AC将其折起,使B点在平面ACD上的射影O恰落在AD上.求证:AB⊥平面BCD.证明:∵四边形ABCD是矩形,∴AB⊥BC.∵BO⊥平面ACD,∴平面ABD⊥平面ACD.又∵CD⊥AD,∴CD ⊥平面ABD ,∴AB ⊥CD .∴由AB ⊥BC ,AB ⊥CD 可得AB ⊥平面BCD .4.如图,在四棱锥P -ABCD 中,底面ABCD 为菱形,∠BAD =60°,Q为AD 的中点.(1)若P A =PD ,求证:平面PQB ⊥平面P AD ;(2)点M 在线段PC 上,PM =tPC ,试确定t 的值,使P A ∥平面MQB .解:(1)证明:连接BD ,如图.∵四边形ABCD 为菱形,∴AB =AD ,又∠BAD =60°,∴△ABD 为等边三角形.∵Q 为AD 中点,∴AD ⊥BQ .又P A =PD ,∴PQ ⊥AD .又BQ ∩PQ =Q ,∴AD ⊥平面PQB ,而AD 平面P AD ,∴平面PQB ⊥平面P AD .(2)当t =13时,P A ∥平面MQB . 连接AC 交BQ 于N ,由AQ ∥BC 可得,△ANQ ∽△BNC ,∴AQ BC =AN NC =12. ∵P A ∥平面MQB ,P A 平面P AC ,平面P AC ∩平面MQB =MN , ∴P A ∥MN ,∴PM MC =12. ∴t =PM PC =13.。

1.(改编题)第三十届奥运会开幕式于2012年7月27日晚20时12分(伦敦时间)在伦敦举行,所有比赛历时17天.以上记录的数据分别指的是()A.时刻和时间间隔B.时间间隔和时刻C.都是时刻D.都是时间间隔解析:选A.2012年7月27日晚20时12分指的是开幕的时刻;17天是所有比赛所用的时间,指的是时间间隔.故选A.2.下列说法表示同一时刻的是()A.第2 s末和第3 s初B.前3 s内和第3 s内C.第3 s末和第2 s初D.第1 s内和第1 s末解析:选A.同一时刻在时间轴上对应同一个点,所以仅选项A正确.3.如图所示,一物体沿3条不同的路径由A运动到B,则关于位移大小的说法正确的是()A.沿1较大B.沿2较大C.沿3较大D.都一样解析:选D.三条路径的初位置、末位置相同,位移一样,故选D.4.(2013·吕梁高一检测)下列关于位移和路程关系的说法正确的是()A.物体沿直线向某一方向运动,通过的路程就是位移B.物体沿直线运动,通过的路程等于位移的大小C.质点通过一段路程,其位移可能是0D.物体通过一段路程,位移一定不为零解析:选C.路程是标量,位移是矢量,即便路程和位移的大小相等,两者也是不同的,A错误.只有物体向一个方向沿直线运动,路程才等于位移的大小,B错误.若物体从某一点出发,最后又回到该点,其位移为0,C正确,D错误.故选C.5.气球升到离地面80 m高时,从气球上掉下一物体,物体又上升了10 m后才开始下落,规定向上为正方向,讨论并回答下列问题.(1)物体从离开气球到落到地面的路程是多少?(2)物体从离开气球到落到地面时的位移大小是多少?方向如何?解析:(1)物体在整个运动过程中的路程s=10 m+90 m=100 m.(2)物体从离开气球到落到地面时的位移x=-80 m,方向竖直向下.答案:(1)100 m(2)80 m方向竖直向下一、选择题1.(单选)下列物理量中是矢量的是()A.质量B.路程C.位移D.时间答案:C2.(单选)关于时刻和时间,下列说法正确的是()A.作息时间表上的数字均表示时间B.1 min只能分成60个时刻C.手表上指针指示的是时间D.“宁停三分,不抢一秒”指的是时间解析:选D.作息时间表上的数字表示的是起床、就餐、上下课的时刻,A错误.1 min 能分成无数多个时刻,B错误.手表上指针指示的是时刻,C错误,“宁停三分,不抢一秒”指的是时间,D正确.故选D.3.(多选)(2013·哈师大附中高一检测)关于位移和路程,下列说法正确的是()A.在某一段时间内物体运动的位移为零,则该物体一定是静止的B.在某一段时间内物体运动的路程为零,则该物体一定是静止的C.在直线运动中,物体的位移大小可能等于其路程D.在曲线运动中,物体的位移大小一定小于路程解析:选BCD.位移为零,表明该运动过程的初、末位置相同,物体不一定静止,A错误;路程为零,表明运动轨迹长度为零,物体一定静止,B正确;单向直线运动时,物体的位移大小等于其路程,C正确;曲线运动时,初、末位置直线距离小于轨迹长度,所以位移大小小于路程,D正确.故选BCD.4.(多选)(2013·攀枝花高一检测)北京时间2012年10月25日23时33分,中国在西昌卫星发射中心用“长征三号丙”运载火箭,将第16颗北斗导航卫星成功送入太空预定轨道.这标志着中国北斗卫星导航系统工程建设又迈出重要一步,北斗卫星导航系统将免费提供定位、测速和授时服务,定位精度10 m,测速精度0.2 m/s.以下说法正确的是() A.北斗导航卫星定位提供的是被测物体的位移B.北斗导航卫星定位提供的是被测物体的位置C.北斗导航卫星授时服务提供的是时间间隔D.北斗导航卫星授时服务提供的是时刻解析:选BD.由位置、位移、时间间隔、时刻的定义可知,北斗导航卫星定位提供的是一个点,是位置,不是位置的变化,A错误、B正确.北斗导航卫星授时服务提供的是时刻,C错误,D正确.故选BD.5. (单选)如图所示,某人站在楼房顶层从O点竖直向上抛出一个小球,上升的最大高度为20 m,然后落回到抛出点O下方25 m处的B点,则小球在这一运动过程中通过的路程和位移分别为(规定竖直向上为正方向)()A.25 m、25 mB.65 m、25 mC.25 m、-25 mD.65 m、-25 m解析:选D.通过的路程s=(20+20+25) m=65 m,通过的位移为x=-25 m,故选D.6.(单选)如图所示,是一位晨练者每天早晨进行锻炼时的行走路线,从A点出发,沿半径分别为3 m和5 m的半圆经B点到达C点,则他的位移和路程分别为() A.16 m,方向从A到C;16 mB.8 m,方向从A到C;8π mC.8π m,方向从A到C;16 mD.16 m,方向从A到C;8π m解析:选D.位移是矢量,大小等于A、C之间的线段长度.即x=AB+BC=2×3 m+2×5 m=16 m,方向由A指向C;路程是标量,等于两个半圆曲线的长度和,即l=(3π+5π) m=8π m,故选D.7.(单选)在田径赛场上,甲、乙两运动员分别参加了400 m和100 m田径决赛,且两人都是在最内侧跑道完成了比赛,则两人在各自的比赛过程中通过的位移大小x甲、x乙和通过的路程大小s甲、s乙之间的关系是(标准体育场内侧跑道为400 m)() A.x甲>x乙,s甲<s乙B.x甲<x乙,s甲>s乙C.x甲>x乙,s甲>s乙D.x甲<x乙,s甲<s乙解析:选B.甲运动员参加400 m田径决赛,其位移大小为0,路程为400 m;乙运动员参加100 m田径决赛,其位移大小为100 m,路程为100 m.故选B.8.(多选)下列关于位移和温度的说法中,正确的是()A.两运动物体的位移大小均为30 m,这两个位移不一定相同B.做直线运动的两物体的位移x甲=3 m,x乙=-5 m,则x甲>x乙C.温度计读数有正有负,其正负号表示温度方向D.温度计读数的正负号表示温度的高低,不能说表示方向解析:选AD.两物体的位移大小虽然均为30 m,但由于不知其方向关系,两个位移不一定相同,A正确.比较物体位移大小应比较其绝对值,B错误.温度无方向,其正负表示温度的高低,不能说表示方向,C错误,D正确.故选AD.☆9.(单选)(2013·宿州高一检测)如图所示,自行车的车轮半径为R,车轮沿直线无滑动地滚动,当气门芯由轮子的正上方第一次运动到轮子的正下方时,气门芯位移的大小为() A.πR B.2RC.2πR D.R4+π2解析:选D.如图所示,气门芯由轮子的正上方第一次运动到轮子的正下方的过程中,初末位置之间的距离,也就是位移大小为x=(2R)2+(πR)2=R4+π2,故选D.二、非选择题10.一汽艇在广阔的湖面上先向东行驶了6 km,接着向南行驶了8 km.那么汽艇全过程的位移大小是多少?方向如何?解析:汽艇在湖面上运动,它的位置及位置变化用一个平面坐标系来描述.选向东为x 轴的正方向,向南为y轴的正方向,以起点为坐标原点.汽艇向东行驶了6 km,位移设为x1;再向南行驶了8 km,位移设为x2;全过程汽艇的位移设为x,汽艇的位置及位置变化情况如图所示.由图中的几何关系可知汽艇全过程的位移大小为x=x21+x22=62+82km=10 km由tan α=43得α=53°,所以位移方向是东偏南53°. 答案:10 km 东偏南53° 11.如图所示,在运动场的一条直线跑道上,每隔5 m 放置一个空瓶子,运动员在进行往返跑训练,从O 点处出发,跑向右侧最近的空瓶将其扳倒后再返回扳倒出发点处的第一个瓶子,之后再往返到前面的最近处的瓶子,依次进行下去,当他扳倒第6个空瓶时,他跑过的路程多大?位移是多大?解析:从O 点出发,画出运动员的运动示意图如图所示,路程s =OA +AO +OB +BC +CD +DE =(5+5+10+15+20+25) m =80 m.而位移大小为从O 点到E 点的距离,即x =OE =10 m ,方向由O 点指向E 点. 答案:80 m 10 m☆12.一个人晨练,按如图所示走半径为R 的中国古代的八卦图,中央的S 部分是两个直径为R 的半圆,BD 、CA 分别为西东、南北指向.他从A 点出发沿曲线ABCOADC 行进,则当他走到D 点时,求他的路程和位移的大小分别为多少?位移的方向如何?解析:路程是标量,等于半径为R 与半径为R 2两圆周长之和减去半径为R 的圆周长的14,即2πR +2π·R 2-14·2πR =52πR .位移是矢量,大小为AD 线段长度,由直角三角形知识得AD =2R ,方向由A 指向D ,即东南方向.答案:52πR 2R 东南方向。

1.用一平面去截体积为43π的球,所得截面的面积为π,则球心到截面的距离为( ) A .2 B. 3 C. 2 D .1解析:选C.由已知得球的半径为R =3,又πr 2=π,∴r =1,∴d =R 2-r 2= 2.2.(2012·高考课标全国卷)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A.6π B .43πC .46πD .63π解析:选B.设球的半径为R ,由球的截面性质得R =(2)2+12=3,所以球的体积V =43πR 3=43π. 3.(2011·高考陕西卷)某几何体的三视图如图所示,则它的体积为( )A .8-2π3B .8-π3C .8-2π D.2π3解析:选A.主视图与左视图一样是边长为2的正方形,里面有两条虚线,俯视图是边长为2的正方形与直径为2的圆相切,其直观图为棱长为2的正方体中挖掉一个底面直径为2的圆锥.V 正方体=23=8,V 圆锥=13πr 2·h =13π×2=2π3, 由于该几何体的体积为正方体的体积与圆锥的体积之差,所以该几何体的体积为V 正方体-V 圆锥=8-2π3,故选A. 4.如果两个球的体积之比为8∶27,那么这两个球的表面积之比为( )A .8∶27B .2∶3C .4∶9D .2∶9 解析:选C.∵V 1V 2=R 31R 32,∴⎝⎛⎭⎫R 1R 23=827,∴R 1R 2=23, ∴S 1S 2=4πR 214πR 22=⎝⎛⎭⎫R 1R 22=⎝⎛⎭⎫232=49,故选C. 5.已知半球内有一个内接正方体,则这个半球的体积与正方体的体积之比为( )A.62π B.63π C.62 D.63解析:选A.设正方体棱长为a ,则球的半径R =a 2+⎝⎛⎭⎫22a 2=62a . ∴V 半球=23π⎝⎛⎭⎫62a 3=62πa 3, ∴V 半球∶V 正方体=62πa 3∶a 3=62π. 6.若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为________. 解析:由题意可得球的直径d 即为正方体的体对角线,则d =32+32+32=33,故球的表面积为S =4π(332)2=27π. 答案:27π7.棱长为2的正方体内有一个球,并且该球与正方体的六个面相切,则球的体积是__________.解析:球的直径等于正方体的棱长,则球的半径为1,故球的体积为43π×13=4π3. 答案:4π38.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为__________. 解析:设球的半径为R ,截面圆的半径为R 2-1, 截面圆的面积S =π(R 2-1)2=(R 2-1)π=π,∴R 2=2⇒R =2,球的体积V =43πR 3=82π3. 答案:82π39.某个几何体的三视图如图所示(单位:m).(1)求该几何体的表面积(结果保留π);(2)求该几何体的体积(结果保留π).解:由三80视图可知,该几何体的下半部分是棱长为2 m 的正方体,上半部分是半径为1 m 的半球.(1)该几何体的表面积为S =12×4π×12+6×22-π×12=24+π(m 2). (2)该几何体的体积为V =23+12×43×π×13=8+2π3(m 3). 10.据说伟大的阿基米德死了以后,敌军将领马塞拉斯给他建了一块墓碑.在墓碑上刻了一个如图所示的图案,图案中球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点是圆柱上底面的圆心,圆锥的底面是圆柱的下底面.试计算出图形中圆锥、球、圆柱的体积比.解:设圆柱的底面半径为r ,高为h ,则V 圆柱=πr 2h .圆锥的底面半径为r ,高为h ,则V 圆锥=13πr 2h .球的半径为r , 所以V 球=43πr 3.又h =2r , 所以V 圆锥∶V 球∶V 圆柱=⎝⎛⎭⎫13πr 2h ∶⎝⎛⎭⎫43πr 3∶(πr 2h ) =⎝⎛⎭⎫23πr 3∶⎝⎛⎭⎫43πr 3∶(2πr 3)=1∶2∶3.1.(2011·高考湖北卷)设球的体积为V 1,它的内接正方体的体积为V 2,下列说法中最合适的是( )A .V 1比V 2大约多一半B .V 1比V 2大约多两倍半C .V 1比V 2大约多一倍D .V 1比V 2大约多一倍半解析:选D.设正方体的棱长为a ,则球的半径为32a ,得正方体的体积为a 3,球的体积为4π3⎝⎛⎭⎫32a 3=3π2a 3.则3π2a 3-a 3≈1.7a 3.故选D. 2.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.解析:设球的半径为r cm ,则由题意可得3V 球+V 水=V 柱,即3×43πr 3+πr 2×8=πr 2×6r ,解得r =4.答案:43.有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.解:设正方体的棱长为a .(1)正方体的内切球球心是正方体的中心,切点是六个面的中心,经过四个切点及球心作截面如图(1),所以有2r 1=a ,r 1=a 2,所以S 1=4πr 21=πa 2.(2)球与正方体的各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,如图(2),2r 2=2a ,r 2=22a ,所以S 2=4πr 22=2πa 2. (3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图(3),所以有2r 3=3a ,r 3=32a ,所以S 3=4πr 23=3πa 2. 综上可得S 1∶S 2∶S 3=1∶2∶3.4.高为24的四棱锥S ABCD 的底面是边长为1的正方形,点S ,A ,B ,C ,D 均在半径为1的一个球面上(如图所示),其中⊙O 1为正方形ABCD 的外接圆,⊙O 2所在的平面平行于⊙O 1所在平面.求:(1)SO 1的长度;(2)以O 为顶点,⊙O 2为底面的圆锥的表面积及体积.解:(1)由球的性质可得:O 1O ,O 2O 与⊙O 1,⊙O 2所在的平面都是垂直的. ∵四边形ABCD 为边长为1的正方形,∴BD =2,∴O 1B =12BD =22. 连接OB ,则△O 1OB 为Rt △,且OB =1,BO 1=22,则OO 1=OB 2-BO 21=22.又∵四棱锥S -ABCD 的高为24,∴O 2O 1=24,∴O 2为OO 1的中点, 连接OS ,O 2S ,∵O 2为OO 1的中点,且O 2S ⊥O 1O ,∴△O 1SO 为等腰三角形,且OS =SO 1,∴SO 1=OS =1.(2)由(1)知OO 2=12OO 1=24,且OO 2⊥⊙O 2所在平面, 在Rt △OO 2S 中,OO 2=24,OS =1,则O 2S =OS 2-OO 22=1-216=144,即⊙O 2的半径r =144.∴以O 为顶点,⊙O 2所在平面为底面的圆锥的表面积为: S =πrl +πr 2=π×144×1+π×78=7+2148π, 体积为:V =13πr 2·OO 2=13π×78×24=72π96.。

第二讲文言虚词知能演练场一、阅读下面的文言文,完成后面的题目。
掣肘宓子贱治亶父,恐鲁君之听谗人,而令己不得行其术也,将辞而行,请近吏二人于鲁君,与之俱至于亶父。
邑吏皆朝,宓子贱令吏二人书。
吏方将书,宓子贱从旁时掣摇其肘。
吏书之不善,宓子贱为之怒。
吏甚患之,辞而请归。
宓子贱曰:“子之书甚不善,子勉归矣。
”二吏归报于君,曰:“宓子贱不可为书。
”君曰:“何故?”对曰:“宓子贱使臣书,而时掣摇臣之肘,书恶而有甚怒。
吏皆笑宓子,此臣所以辞而去也。
”鲁君太息而叹曰:“宓子以此谏寡人之不肖也!寡人之乱宓子,而令宓子不得行其术,必数有之矣。
微二人,寡人几过!”遂发所爱,而令之亶父,告宓子曰:“自今以来,亶父非寡人之有也,子之有也。
有便于亶父者,子决为之矣。
”下列句子中加点的虚词解释有误的一项是()A.与之俱至于.亶父于:动词,到B.二吏归报于.君于:介词,向C.寡人之.乱宓子之:代词,代“寡人”D.而令之.亶父之:动词,到解析:C项,“之”,助词,用在主谓之间,取消句子独立性。
答案:C[参考译文]宓子贱被派往亶父为官,他担心鲁国国君听信小人谗言,从而会使自己无法按自己的方法治理亶父,要动身的时候,他请求鲁国国君,派两名身旁的人一同前往。
(亶父)当地的官吏都来拜见宓子贱,宓子贱让那两人书写记录。
他们每次准备要写时,宓子贱就从旁边时不时地拽摇他们的手肘。
他们写的字很难看,宓子贱就为这事生气。
那两人很怕他,请求让他们回去。
宓子贱说:“你们的字写得太差了,你们赶快回去吧。
”两个人回去后向鲁国国君汇报,说:“宓子贱不让我们好好写字。
”鲁国国君说:“怎么回事呢?”回答说:“宓子贱让我们写字(记事),却总是拽摇我们的手肘,字很难看他又生气。
那些官吏都笑宓子贱,所以我们就要求回来了。
”鲁国国君叹息道:“宓子贱用这个办法来提醒我的不是啊!我扰乱他的治理方案,使他无法按照他自己的办法治理的情况,肯定有很多次了。
没有你们两个人,我几乎要犯错误啊!”于是打发亲信,让他们到亶父去传达旨意,告诉宓子贱说:“从现在开始,亶父不是我国君所管,归你管了。

1.在冶金工业上,均不能用化学还原剂制得的一组金属是( )A .Na 、Mg 、AlB .Na 、K 、Zn 、FeC .Zn 、Fe 、Cu 、AgD .Mg 、Al 、Zn 、Fe解析:选A 。
热还原法不适合冶炼活泼金属,选项A 的所有金属只能用电解法冶炼。
2.(2013·广州高三月考)煤是一种重要的能源,含有硫元素,燃烧时会生成SO 2,下列说法正确的是( )A .煤是含硫化合物B .煤是一种可再生能源C .在用水吸收SO 2的过程中只发生物理变化D .SO 2是酸性氧化物,被云雾吸收后可转化成酸雨解析:选D 。
煤是由多种无机物和有机物组成的复杂混合物,其作为一种化石燃料是不可再生的,A 、B 错误。
SO 2是一种酸性氧化物,其溶于水中部分SO 2和H 2O 发生反应生成H 2SO 3,也可被云雾吸收形成酸雨,C 不正确,D 正确。
3.氧化还原反应广泛应用于金属冶炼,下列说法不正确的是( )A .电解熔融氯化钠制取金属钠的反应中,钠离子被还原B .湿法炼铜与火法炼铜的反应中,铜元素都发生还原反应C .用磁铁矿炼铁的反应中,1 mol Fe 3O 4被CO 还原成Fe ,转移9 mol 电子D .铝热法还原铁的反应中,放出的热量能使铁熔化解析:选C 。
用磁铁矿炼铁的反应为Fe 3O 4+4CO=====△3Fe +4CO 2,当有1 mol Fe 3O 4被CO 还原成Fe 时,转移8 mol 电子。
4.海洋是一巨大的化学资源宝库,下列有关海水综合利用的说法正确的是( )A .海水中含有钾元素,只需经过物理变化就可以得到钾单质B .海水蒸发制海盐的过程中只发生了化学变化C .从海水中可以得到氯化钠,电解熔融氯化钠可制备氯气D .利用潮汐发电是将化学能转化为电能解析:选C 。
海水中钾以离子形式存在,必须经过化学变化才能得到钾单质,A 错误;海水蒸发制海盐没有发生化学变化,B 错误;潮汐发电是将潮汐能转化为电能,D 错误。
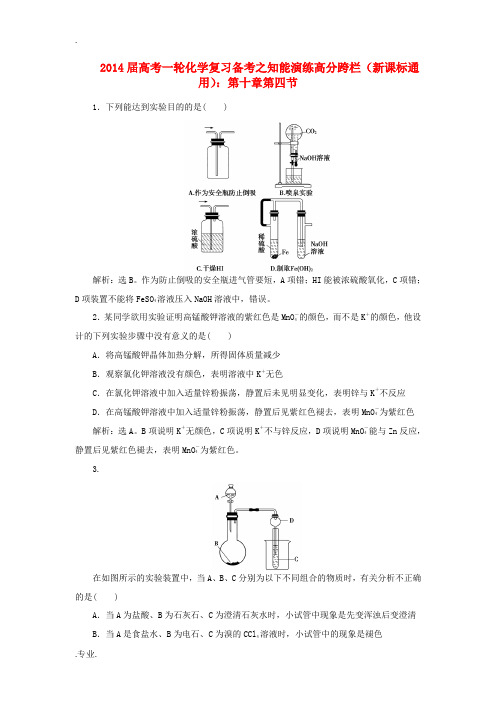
2014届高考一轮化学复习备考之知能演练高分跨栏(新课标通用):第十章第四节1.下列能达到实验目的的是( )解析:选B。
作为防止倒吸的安全瓶进气管要短,A项错;HI能被浓硫酸氧化,C项错;D项装置不能将FeSO4溶液压入NaOH溶液中,错误。
2.某同学欲用实验证明高锰酸钾溶液的紫红色是MnO-4的颜色,而不是K+的颜色,他设计的下列实验步骤中没有意义的是( )A.将高锰酸钾晶体加热分解,所得固体质量减少B.观察氯化钾溶液没有颜色,表明溶液中K+无色C.在氯化钾溶液中加入适量锌粉振荡,静置后未见明显变化,表明锌与K+不反应D.在高锰酸钾溶液中加入适量锌粉振荡,静置后见紫红色褪去,表明MnO-4为紫红色解析:选A。
B项说明K+无颜色,C项说明K+不与锌反应,D项说明MnO-4能与Zn反应,静置后见紫红色褪去,表明MnO-4为紫红色。
3.在如图所示的实验装置中,当A、B、C分别为以下不同组合的物质时,有关分析不正确的是( )A.当A为盐酸、B为石灰石、C为澄清石灰水时,小试管中现象是先变浑浊后变澄清B.当A是食盐水、B为电石、C为溴的CCl4溶液时,小试管中的现象是褪色C.若A为硫酸、B为Na2SO3、C为品红溶液,实验时当小试管中出现褪色现象时,向烧杯中加入沸水,试管中不会产生变化D.若A为浓氨水、B为氧化钙、C为AgNO3和乙醛的混合溶液,实验时当小试管中出现沉淀又恰好溶解时,向烧杯中加入热水,试管中生成光亮的银镜解析:选C。
A项制备的是CO2,通入澄清石灰水先变浑浊后变澄清,正确;B项制备的是C2H2,能使溴的CCl4溶液褪色,正确;C项小试管中品红溶液先褪色,加热后恢复红色,不正确;D项产生的氨气通入硝酸银溶液生成了银氨溶液,小试管中先出现沉淀后沉淀消失,烧杯中加入热水提供水浴加热条件,所以片刻后看到试管壁上生成光亮的银镜,正确。
4.(2011·高考广东卷)某同学通过系列实验探讨Mg及其化合物的性质,操作正确且能达到目的的是( )A.将水加入浓硫酸中得稀硫酸,置镁片于其中探讨Mg的活泼性B.将NaOH溶液缓慢滴入MgSO4溶液中,观察Mg(OH)2沉淀的生成C.将Mg(OH)2浊液直接倒入已装好滤纸的漏斗中过滤,洗涤并收集沉淀D.将Mg(OH)2沉淀转入表面皿中,加足量稀盐酸,加热蒸干得无水MgCl2固体解析:选B。

1.(2012·高考湖南卷)某几何体的正视图和左视图均如图所示,则该几何体的俯视图不可能是()解析:选D.对于选项A,两个圆柱的组合体符合要求;对于选项B,一个圆柱和一个正四棱柱的组合体符合要求;对于选项C,底面为等腰直角三角形的直三棱柱符合要求,故选D.2.下列说法正确的是()A.任何物体的三视图都与物体的摆放位置有关B.任何物体的三视图都与物体的摆放位置无关C.有的物体的三视图与物体的摆放位置无关D.正方体的三视图一定是三个全等的正方形解析:选C.对于A,球的三视图与物体的摆放位置无关,故A错;对于B,D,正方体的三视图与摆放位置有关,故B,D错;故选C.3.下图所示几何体的一个俯视图是下列选项中的()解析:选C.该几何体是由一个长方体和一个截去一个角的三棱柱组成的,结合轮廓线和交线知它的俯视图应为C.4.(2013·赣州一中质检)下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④解析:选D.利用排除法:正方体的三视图都是正方形,所以①不符合题意,可排除A、B、C,只能选D.5.(2011·高考江西卷)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为()解析:选D.被截去的四棱锥的三条可见侧棱中有两条为长方体的面对角线,它们在右侧面上的投影与右侧面(正方形)的两条边重合,另一条为长方体的对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图及对角线方向,只有选项D符合.6.①若一个几何体的三视图是完全相同的,则这个几何体一定是正方体;②若一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;③若一个几何体的三视图都是矩形,则这个几何体是长方体;④若一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台.其中正确的说法是__________.解析:①不正确,因为球的三视图也完全相同.②不正确,因为一个横放在水平位置的圆柱,其主视图和俯视图都是矩形.④不正确,因为一个正四棱台的主视图和左视图也都是等腰梯形.③正确.答案:③7.如图①,直三棱柱的侧棱长和底面边长均为2,主视图和俯视图如图②所示,则其左视图的面积为__________.解析:左视图为矩形,边长如图,所以其面积为2 3.答案:2 38.如图所示,(1)(2)(3)是图(4)所表示的几何体的三视图,其中,图(1)是______,图(2)是________,图(3)是________.(说出视图的名称)解析:根据三视图的特点:主俯一样长,主左一样高,俯左一样宽可知.答案:主视图俯视图左视图9.根据图中所给出的一个物体的三视图,试画出它的形状.解:对应的几何体是一个正六棱锥,其所对应的空间几何体的图形为:10.根据如图所示的几何体的组合体,画出它的三视图.解:这个组合体的三视图如图所示:1.(2012·高考陕西卷)将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为()解析:选B.左视图中能够看到线段AD1,画为实线,看不到线段B1C,画为虚线,而且AD1与B1C不平行,投影为相交线,所以选择B.2.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为________.解析:由三视图得到直观图(如图),从而最长的棱长是2 3.答案:2 33.如图是一个几何体的三视图,试画出其直观图.解:由三视图的主视图、左视图与俯视图,容易想到该几何体可以由正方体切割而得到,连结正方体的三个顶点,切去一个角,则可得相应的几何体,也可以是切掉对应位置的两个角,如图所示:4.如图是底边为2 cm,侧棱长为4 cm的正四棱锥.(1)画出其三视图,并把其尺寸标注在图中;(2)求该正四棱锥的高及各侧面三角形的高(即斜高).解:(1)三视图如图所示:(2)在等腰△SAC中,SA=SC=4 cm,AC=22+22=2 2 cm,此时等腰△SAC底边AC 的高即为正四棱锥的高h,所以:h=42-(2)2=14 cm(如图);在等腰△SAB中,SA=SB=4 cm,AB=2,此时底边AB上的高即为各侧面三角形的高h′,所以:h′=42-12=15 cm.综上,该四棱锥的高为14 cm,各侧面三角形的高为15 cm.。

1.(2013·北京市东城区高三测试)下列说法正确的是()A.金属单质在反应中只能作还原剂,非金属单质只能作氧化剂B.失电子多的金属还原性强C.某元素从化合态到游离态,该元素一定被还原D.金属阳离子被还原不一定得到金属单质解析:选D。
A错,金属单质在反应中只能失电子,只能作还原剂,但非金属单质往往处于中间价态,既可作氧化剂又可作还原剂,如S、N2等;B错,氧化性、还原性的强弱是指得失电子的难易而不是指得失电子的多少;C错,如2H2S+SO2===3S↓+2H2O中,S单质既是氧化产物又是还原产物;D正确,如2Fe3++Fe===3Fe2+中,Fe3+被还原为Fe2+。
2.(2013·乌鲁木齐高三质检)在酸性溶液中,高锰酸钾发生的反应是MnO-4+5e-+8H+===Mn2++4H2O。
下列离子能让此反应过程发生的是()①Fe2+②C2O2-4③SiO2-3④IO-3A.①②B.①③C.②③D.③④解析:选A。
Fe2+和C2O2-4都具有还原性,都能被高锰酸钾溶液氧化。
3.(创新题)图中两圆圈相交的阴影部分表示圆圈内物质相互发生的反应,其中属于氧化还原反应,但水既不作氧化剂也不作还原剂的是()A.甲B.乙C.丙D.丁解析:选A。
甲中发生的反应为3NO2+H2O===2HNO3+NO,水既不作氧化剂也不作还原剂,A正确。
乙中水作氧化剂,不符合题意。
丙、丁中发生的反应都不是氧化还原反应,也不符合题意。
4.下列叙述正确的是()A.发生化学反应时失去电子数越多的金属原子,其还原能力越强B.工业制备Si、Fe没有发生氧化还原反应C.铝热反应常被用于野外焊接钢轨,说明铝的氧化性很强D.某溶液用盐酸酸化无明显现象,再滴加氯化钡溶液有白色沉淀产生,说明溶液中有SO2-4解析:选D。
A中,金属原子的还原能力只与失电子的难易程度有关,而与失电子数目的多少无关;B中,工业制备Si、Fe均发生了氧化还原反应;C中,铝热反应说明铝的还原性很强。

1.下列有关沉淀溶解平衡的说法中正确的是()A.在AgCl沉淀溶解平衡体系中加入蒸馏水,K sp(AgCl)增大B.在CaCO3的沉淀溶解平衡体系中加入稀盐酸,平衡不移动C.可直接根据K sp的数值大小比较难溶物在水中的溶解度大小D.25 ℃时,K sp(AgCl)>K sp(AgI),向AgCl的悬浊液中加入KI固体,有黄色沉淀生成解析:选D。
K sp的大小只与温度有关,A项错误;CaCO3(s)Ca2+(aq)+CO2-3(aq),加入稀盐酸,CO2-3与H+反应,导致溶解平衡正向移动,B项错误;只有比较相同温度下、相同组成形式的难溶电解质的K sp的数值大小,才可比较难溶物在水中的溶解度大小。
2.已知Ca(OH)2的溶解度随温度升高而降低。
将某温度下饱和澄清石灰水:①加入少量生石灰后恢复到原来温度;②降低温度。
这两种情况下,前后均保持不变的是() A.溶液的质量B.Ca(OH)2的溶解度C.溶液中Ca2+的数目D.溶液中溶质的质量分数解析:选D。
饱和澄清石灰水中加入少量生石灰,生石灰和水反应:CaO+H2O===Ca(OH)2,消耗一部分水,使部分溶质析出,则水溶液的质量减少,溶液中的Ca2+的数目减少,但溶液仍为该温度下的饱和溶液,所以溶解度和溶质的质量分数不变。
若降低温度,由于Ca(OH)2的溶解度随温度升高而降低,所以溶液本身没有变化,只有溶解度变大。
总结上述两种情况,前后均不变的是溶液中溶质的质量分数。
3.(2013·合肥高三模拟)某酸性化工废水中含有Ag+、Pb2+等重金属离子。
有关数据如下:在废水排放之前,用沉淀法除去这两种离子,应该加入的试剂是()A.氢氧化钠B.硫化钠C.碘化钾D.氢氧化钙解析:选B。
根据表格中的数据知,硫化银和硫化铅的溶度积很小,加入硫化钠能完全除去这两种金属离子。
4.(原创题)将AgCl分别加入盛有:①5 mL水;②6 mL 0.5 mol/L NaCl溶液;③10 mL 0.2 mol/L CaCl2溶液;④50 mL 0.1 mol/L盐酸的烧杯中,均有固体剩余,各溶液中c(Ag+)从大到小的顺序排列正确的是()A.④③②①B.②③④①C.①④③②D.①③②④解析:选C。

1.(2012·高考山东卷)下列关于原子结构、元素性质的说法正确的是()A.非金属元素组成的化合物中只含共价键B.ⅠA族金属元素是同周期中金属性最强的元素C.同种元素的原子均有相同的质子数和中子数D.ⅦA族元素的阴离子还原性越强,其最高价氧化物对应水化物的酸性越强解析:选B。
非金属元素组成的化合物中可以含有离子键,如NH4Cl;B项正确;同种元素的原子质子数相同,中子数不一定相同;ⅦA族元素的阴离子还原性越强,对应元素的非金属性越弱,其最高价氧化物对应水化物的酸性越弱,如:非金属性:Cl>I,还原性:I->Cl -,酸性:HClO4>HIO4。
2.(2013·阳泉高三综合检测)短周期元素X、Y的原子序数相差7,下列有关判断错误的是()A.X和Y可能处于同一周期B.X和Y可能处于相邻周期C.X和Y可能处于同一主族D.X和Y可能处于相邻主族解析:选C。
同一主族上下相邻短周期的元素,其原子序数之差为2、8,故C项错误。
3.(2013·乌鲁木齐高三模拟)门捷列夫在描述元素周期表时,许多元素尚未发现,但他为第四周期的三种元素留下了空位,并对它们的一些性质做了预测,X是其中的一种“类硅”元素,后来被德国化学家文克勒发现,并证实门捷列夫当时的预测相当准确。
根据元素周期律,下列有关X的性质的描述中正确的是()A.X单质易与水反应B.X形成的氧化物易与水反应生成酸C.X易形成氧化物XOD.XH4的稳定性比SiH4的低解析:选D。
第ⅣA族元素有碳、硅、锗、锡、铅;第四周期元素是锗,其化学性质“类硅”,硅不和水反应,锗也不和水反应,A项错误;二氧化硅不能与水反应生成硅酸,二氧化锗也不能,B项错误;Si的常见价态为+4,形成氧化物SiO2,C错误;同主族元素,原子序数越小,非金属性越强,其简单氢化物的稳定性越强,氢化物稳定性:SiH4>GeH4,D项符合题意。
4.已知X、Y、Z、W四种短周期主族元素在周期表中的相对位置如图所示,下列说法正确的是()A.Z元素的原子半径可能比Y元素的小B.Z元素的最高化合价可能比Y元素的高C.W的气态氢化物的稳定性一定比Y的强D.Z的最高价氧化物对应的水化物的酸性一定比W的强解析:选B。
1.(2013·长沙高三质检)下列溶液中溶质的物质的量浓度为1 mol·L -1的是( )A .将58.5 g NaCl 溶解于1 L 水中配成的溶液B .将80 g SO 3溶于水并配成1 L 溶液C .将0.5 mol·L -1的NaNO 3溶液100 mL 加热蒸发掉50 g 水后的溶液D .含K +为2 mol 的K 2SO 4溶液解析:选B 。
A 中“1 L 水”,溶液体积不一定为1 L ;C 中蒸发掉50 g 水后,溶液的体积不一定是50 mL ;D 中未指明溶液体积。
2.关于0.2 mol·L -1的NaOH 溶液,下列说法不正确的是( )A .100 mL 该溶液中含0.8 g NaOHB .200 mL 该溶液与100 mL 0.2 mol·L -1的硫酸溶液反应形成中性溶液C .100 mL 该溶液中约含0.02×6.02×1023个Na +D .配制含1 L 水的该溶液,需NaOH 的质量为8 g解析:选D 。
8 g NaOH 溶于1 L 水配制成的溶液,其物质的量浓度小于0.2 mol·L -1。
3.(2013·大庆一中高三月考)在80 g 密度为d g·cm -3的硫酸铁溶液中,含有2.8 g Fe 3+,则此溶液中SO 2-4的物质的量浓度为( )A.1516dB.516d C.38d D.58d 解析:选A 。
n (Fe 3+)=0.05 mol ,n [Fe 2(SO 4)3]=0.025 mol ,n (SO 2-4)=0.075 mol ,V (溶液)=801 000d L ,c (SO 2-4)=n (SO 2-4)V (溶液)=0.075 mol 801 000dL =1516d 。
4.在无土栽培中,需配制1 L 含0.50 mol·L -1的NH 4Cl 、0.16 mol·L -1 KCl 、0.24 mol·L -1K 2SO 4的混合溶液,但当时没有K 2SO 4固体,若用(NH 4)2SO 4固体代替,需用KCl 、NH 4Cl 、(NH 4)2SO 4三种固体的物质的量(单位为 mol)分别为( )A .0.40、0.50、0.12B .0.66、0.50、0.24C .0.64、0.50、0.24D .0.64、0.02、0.24解析:选D 。
根据离子的物质的量来判断:n (NH +4)=0.50 mol ,n (Cl -)=(0.50+0.16) mol=0.66 mol ,n (K +)=(0.16+0.24×2) mol =0.64 mol ,n (SO 2-4)=0.24 mol ,0.64 mol K +来自KCl ,则n (KCl)=0.64 mol ,SO 2-4只能来自(NH 4)2SO 4,则(NH 4)2SO 4为0.24 mol,0.66 mol Cl -由KCl和NH 4Cl 共同提供,而0.64 mol KCl 提供了0.64 mol Cl -,故0.02 mol Cl -由NH 4Cl 提供,此时NH +4恰好为 (0.02+0.24×2) mol =0.50 mol 。
5.(2013·大同高三调研)向100 mL 的FeBr 2溶液中通入标准状况下Cl 2 3.36 L ,反应后溶液中Cl -和Br -的物质的量浓度相等,则原FeBr 2溶液的物质的量浓度为( )A .2 mol·L -1B .1.5 mol·L -1C .1 mol·L -1D .0.75 mol·L -1解析:选A 。
氯气先氧化Fe 2+,现在溶液中Cl -和Br -的物质的量浓度相等,表明溶液中无Fe 2+,有FeBr 3、FeCl 3,n (Cl -)=(3.36÷22.4)×2=0.3 (mol)=n (Br -),根据原子守恒得n (Fe)=0.2 mol ,则c (FeBr 2)=0.2 mol÷0.1 L =2 mol·L -1,A 正确。
6.(2013·黄石高三月考)实验室里需用480 mL 0.1 mol·L -1的硫酸铜溶液,现选取500 mL容量瓶进行配制,以下操作正确的是( )A .称取7.68 g 硫酸铜,加入500 mL 水B .称取12.0 g 胆矾配成500 mL 溶液C .称取8.0 g 硫酸铜,加入500 mL 水D .称取12.5 g 胆矾配成500 mL 溶液解析:选D 。
溶液体积为500 mL ,n (CuSO 4)=0.05 mol ,m (CuSO 4)=8.0 g 或m (CuSO 4·5H 2O)=12.5 g ,然后配成500 mL 溶液, D 正确。
7.使用容量瓶配制溶液时,由于操作不当,会引起误差,下列情况会使所配溶液浓度偏低的是( )①用天平(使用游码)称量时,被称量物与砝码的位置放颠倒了②用滴定管量取液体时,开始时平视读数,结束时俯视读数③溶液转移到容量瓶后,烧杯及玻璃棒未用蒸馏水洗涤④转移溶液前容量瓶内有少量蒸馏水⑤定容时,仰视容量瓶的刻度线⑥定容后摇匀,发现液面降低,又补加少量水,重新达到刻度线A .①③⑤⑥B .①②⑤⑥C .②③④⑥D .③④⑤⑥解析:选A 。
①用天平称量时,被称量物与砝码位置放颠倒,将会使称得的物质的质量偏小,溶液浓度偏低;②中操作所得到的溶液体积偏大,使所配溶液浓度偏高;③中烧杯及玻璃棒未洗涤,残留的溶质未转移至容量瓶,使结果偏低;④转移溶液前容量瓶内有少量水对结果无影响;⑤定容时,仰视刻度线会使溶液体积偏大,浓度偏低;⑥摇匀后又加水,造成溶液体积偏大,浓度偏低。
8.t ℃,将w g 化合物A 放入水中充分溶解,制得y g 饱和溶液,化合物A 的相对分子质量为m ,饱和溶液密度为d g·cm -3,其质量分数为a %,t ℃时,A 的饱和溶液的物质的量浓度为( )A.10da m mol·L -1B.100w d ymmol·L -1 C.w da ym mol·L -1 D.da mmol·L -1 解析:选A 。
取1 L 溶液,由物质的量浓度的定义可得:c =n V =1 000 mL ×d g·cm -3×a %m g·mol -1×1 L=10da m mol·L -1。
9.(2013·江南十校联考)36.5 g HCl 溶解在1 L 水中(水的密度近似为1 g/mL),所得溶液的密度为ρ g/mL ,质量分数为w ,物质的量浓度为c ,N A 表示阿伏加德罗常数,则下列叙述中正确的是( )A .所得溶液的物质的量浓度:c =1 mol/LB .所得溶液中含有N A 个HCl 分子C .36.5 g HCl 气体占有的体积为22.4 LD .所得溶液的质量分数:w =36.5c /(1 000ρ)解析:选D 。
c = 1 mol (36.5+1 000) g 1 000ρ g/L= 1 000ρ36.5+1 000mol/L ,A 项错误;HCl 溶于水后完全电离为H +和Cl -,溶液中不存在HCl 分子,B 项错误;36.5 g HCl 在标准状况下体积为22.4 L ,C项错误;设溶液体积为V L ,则w =36.5cV 1 000Vρ×100%=36.5c 1 000ρ,D 项正确。
10.(2013·江西九校联考)试回答下列问题:(1)已知24 g A 和40 g B 恰好完全反应生成0.4 mol C 和32 g D ,则C 的摩尔质量为________。
(2)把1 mol Na 和1 mol Mg 分别投入到等量且过量的盐酸中,分别得到溶液a 和b ,则溶液a 和b 的质量关系为m a ________ m b 。
(3)如图为实验室某浓盐酸试剂瓶的标签上的有关数据,试根据标签上的有关数据回答下列问题:盐酸HCl的质量分数:36.5%①该浓盐酸中HCl的物质的量浓度为________ mol·L-1。
②标准状况下,1.00 L水(密度为1.00 g·cm-3)吸收________ L的HCl可制得上述浓盐酸。
解析:(1)由质量守恒定律可知生成m(C)=24 g+40 g-32 g=32 g,故M(C)=32 g/0.4 mol =80 g/mol。
(2)把1 mol Na和1 mol Mg分别投入到等量且过量的盐酸中,充分反应后均引起溶液增重22 g,故反应后两溶液质量仍相等。
(3)①假设取该盐酸1 L,则溶液中含有n(HCl)=[(1 000 mL×1.19 g·mL-1)×36.5%]/36.5g·mol-1=11.9 mol,故其物质的量浓度为11.9 mol/L。
②设需吸收x L HCl,则x L22.4 L·mol-1÷[(36.5g·mol-1×x L22.4 L·mol-1+1 000 g)÷1.19 g·mL-1×10-3 L/mL]=11.9 mol/L,解得x≈353。
答案:(1)80 g/mol(2)=(3)①11.9②35311.实验室配制460 mL 0.4 mol·L-1的NaCl溶液,有如下操作步骤:①把称量好的NaCl晶体放入小烧杯中,加适量蒸馏水溶解。
②把①所得溶液小心转入一定容积的容量瓶中。
③继续向容量瓶中加蒸馏水至液面距刻度线1~2 cm处,改用胶头滴管小心滴加蒸馏水至溶液凹液面与刻度线相切。
④用少量蒸馏水洗涤烧杯和玻璃棒2~3次,每次洗涤的液体都小心转入容量瓶,并轻轻摇匀。
⑤将容量瓶瓶塞塞紧,充分摇匀。
请填写下列空白:(1)操作步骤的正确顺序为(填序号)________________________________________________________________________。
(2)实验室有如下规格的容量瓶:①100 mL,②250 mL,③500 mL,④1 000 mL,本实验选用________(填序号)。
(3)本实验用到的基本实验仪器除容量瓶、玻璃棒外还有________________________。
(4)需要使用玻璃棒的操作有________(填序号),其作用为________________________________。