一类特殊图的邻点可区别全染色

2020年10月第40卷第5期天水师范学院学报Journal of Tianshui Normal UniversityOct.，2020V〇1.40 No.5r-型六角系统的邻点可区别/-全色数杨随义(天水师范学院数学与统计学院，甘肃天水741001)摘要：图G的邻点可区别/-全染色是一个满足相邻顶点色集合不同的/-全染色，其中任意一点的色集 合为该顶点及其关联边所染颜色构成的集合.将其所需颜色的最小数称为邻点可区别/-全色数，记为;^(G).运 用数学归纳法研究了 r-型六角系统厂>多0)的邻点可区别/-全染色，并证明了当n多0时，；^(7\)=3;当n这1时，獻)=4.关键词：r-型六角系统；邻点可区别/-全染色；邻点可区别/-全色数中图分类号：0157.5 文献标识码：A1预备知识图染色作为图论研究的重要方向之一，被广 泛应用于信息计算科学、通信网络、交通运输等领 域，为实际问题的解决提供了重要的理论依据和 最优策略.图染色最早起源于四色问题的研究，随后一系列经典染色如点染色、边染色以及全染色 等相继被提出.m点染色是若干种颜色在顶点(边）上的一个分配，且相邻顶点（边）分配不同的 颜色，将所用的最少颜色数称为点（边）色数.图的全染色是若干种颜色同时在顶点和边上的一个分 配，且满足相邻顶点与相邻边以及关联元素分配不 同的颜色，类似地，将所用的最少颜色数称为全 色数.1941年，Brooks证明任意一个既不是奇圈 也不是完全图的连通图，其点色数不超过A.1964 年前后，Vizing和Gupta分别独立证明了任意一个 图的边色数不超过A+1.此外，Vizing还猜测：任意一个图的全色数不超过A+ 2,即后来众所周 知的全染色猜想（T C C).染色问题已被证明是一 个N P-难问题，因此，为了进一步探索T C C猜 想，国内外学者随后又相继提出了一系列可区别染 色.2005年，张忠辅等"]提出了图的邻点可区别 全染色的概念，并给出了圈、完全图、完全二部 图等一些特殊图类的邻点可区别全色数，并猜测 图的邻点可区别全色数A+ 2.此后，国内外学者 针对这一猜想展开了研究.[2_31为了推动邻点可区文章编号：1671-1351 (2020) 05-0019-03别全色数猜想的研究，张忠辅等[41在邻点可区别全 染色的基础上，提出了邻点可区别/-全染色的概 念.随后王继顺M研究了蛛网图、渔网图以及联图 及的邻点可区别/-全染色.张婷、赵慧霞等171给出了图（75乂见…的邻点可区别/- 全色数•六角系统作为化学图论中重要的研究对象，受到了国内外学者的广泛关注.六角系统图是由正 六边形所组成的平面图网络，其构型多种多样，不 同的构型其化学性质也各不相同.r-型六角系统 是一类特殊的六角系统，它是由一个正六边形中心 分别向3个间隔方向延伸n个正六边形直链所构成 的对称图，简称》阶r-型六角系统链.最近，王 文杰等181首先研究了 r-型六角系统链的点可区别边 染色.本文以此为动机，研究了:r-型六角系统的邻点可区别/-全色数，并得到了其邻点可区别 /-全色数.定义1.1[”设6是阶至少为2的连通图，&是正 整数，/是V(G)U£(C)到{1，2，"•，叼的映射，对任意ueK(G)，记C(u) = {/(“)}“託.如果(1)对于任意肌，有f(uv)¥^f{vw);⑵对于任意有/(u)^f(v),f{u)t^/M ;则称/为C的正常全染色，进一步，如果 /还满足收稿日期：2020-09-17作者简介：杨随义（1977-),男，甘肃天水人，天水师范学院数学与统计学院副教授，硕士。

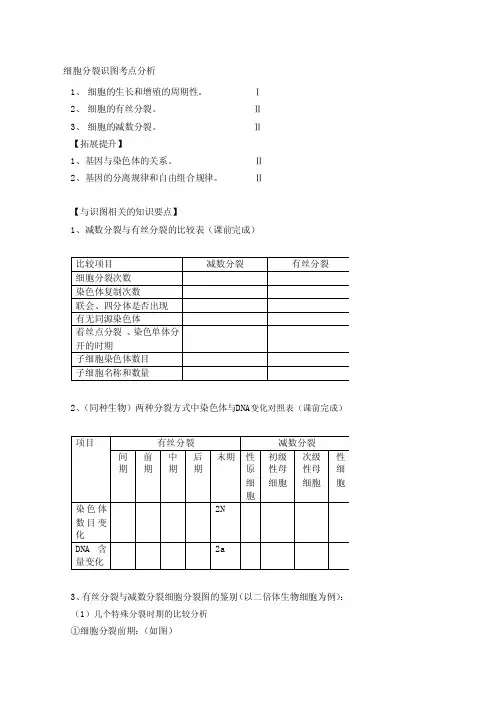
细胞分裂识图考点分析1、细胞的生长和增殖的周期性。

Ⅰ2、细胞的有丝分裂。

Ⅱ3、细胞的减数分裂。

Ⅱ【拓展提升】1、基因与染色体的关系。

Ⅱ2、基因的分离规律和自由组合规律。

Ⅱ【与识图相关的知识要点】1、减数分裂与有丝分裂的比较表（课前完成）比较项目减数分裂有丝分裂细胞分裂次数染色体复制次数联会、四分体是否出现有无同源染色体着丝点分裂、染色单体分开的时期子细胞染色体数目子细胞名称和数量2、（同种生物）两种分裂方式中染色体与DNA变化对照表（课前完成）项目有丝分裂减数分裂间期前期中期后期末期性原细胞初级性母细胞次级性母细胞性细胞染色体数目变化2NDNA含量变化2a3、有丝分裂与减数分裂细胞分裂图的鉴别（以二倍体生物细胞为例）：（1）几个特殊分裂时期的比较分析①细胞分裂前期：（如图）②细胞分裂中期：（如图）③细胞分裂后期：（如图）③有丝分裂、减数分裂图形辨析（以二倍体为例）4、其他与减数分裂和有丝分裂有关的图形题分析4.1坐标曲线图坐标曲线图一般用于考查细胞分裂过程中染色体及DNA含量关系的判断及分裂时期的判断。

例1、下列图示中，横轴表示细胞周期，纵轴表示一个细胞核中DNA含量或染色体数目的变化，请分析图示，表示有丝分裂DNA含量变化、染色体数目的变化和减数分裂DNA含量变化、染色体数目的变化的依次是（）4.2柱形图柱形图常用于考查细胞分裂各时期的染色体、染色单体及DNA等的数量关系特点。

熟悉细胞分裂各时期中染色体、染色单体及DNA的变化特点是解答此类问题的关键。

例2．下图A、B、C、D分别表示某哺乳动物细胞（2n）进行减数分裂的不同时期，其中a表示细胞数目。

请判断b、c、d依次代表（）A．DNA分子数、染色体数、染色单体数B．染色体数、DNA分子数、染色单体数C．DNA分子数、染色单体数、染色体数D．染色单体数、染色体数、DNA分子4.3扇形图扇形图常用于考查细胞分裂各时期的判断。

例3.下图表示细胞有丝分裂一个细胞周期所用的时间，下列说法正确的是（）①甲→乙过程中着丝点会分裂②乙→甲的过程有蛋白质合成③一个细胞周期是指甲→甲的全过程④一个细胞周期是指乙→乙的全过程A、①②③B、①②④C、③D、④4.4细胞分裂模式图和坐标曲线图相结合细胞分裂模式图常用于考查细胞分裂各时期染色体变化的特点，如根据图中细胞的特点判断细胞属于有丝分裂还是减数分裂的哪个时期、判断细胞的雌雄性等。

度逻辑判断一、图推常考：1、数量规律（重点）2、空间规律（重点）3、属性规律4、特殊规律：功能元素，图形间位置关系5、位置/样式规律较少,结合有点二、定义常考：1、单定义占90%2、多定义占10%三、类比常考：1、对应关系（50%）2、比喻象征3、包容关系：包容+对应4、近义关系、语法关系四、逻辑常考：1、加强论证（40%）2、削弱论证（20%）3、日常结论（20%）4、翻译推理，真假推理，其他（整体很少）图形推理一、图推考点：（注意图形特征匹配考点）1、位置规律：元素组成相同优先考虑位置（1）、平移（就近看图形变化，）方向：A直线（上下，左右，对角线），B绕圈（顺逆时针）步数：恒定，递增（等差递增）（2）、旋转（看选项差异，排除选项）方向：顺逆时针常见角度：45，90，180（3）、翻转左右翻转：图形沿竖轴对称（不必区别向左还是向右翻，因为图形都一样）上下翻转：图形沿横轴对称对比思维，看选项差异，排除选项，如遇到九宫格题目，可以直接看第二列规律，不必把每一列规律都推出来。

2、样式规律：元素组成似，元素重复出现；线条重复出现（1）遍历——缺啥补啥（相同元素重复出现，九宫格和两组图居多）注：1、外框缺啥补啥，2、内部图案缺啥补啥3、相减和求异不严格区分（2）、加减同异：相加相减、求异（去同求异）、求同（去异求同）A、相加、相减B、求异（去同求异）C相同图形重复出现，优先考虑加减。

求异和旋转一起出现（3）、黑白运算：图形轮廓和分割区域相同，不同区域“黑白”颜色不同且黑块数量不成规律。

方法：相同位置做运算注意：黑块数量相同，优先考虑位置平移黑块位置不同，优先考虑黑白运算“坑”：黑+白与白+黑未必一样3、属性规律：元素组成不相同、不相似、优先属性（1）、对称性A：轴对称（两侧一样）考点：对称轴方向和数量特征图：（出现箭头优先考虑轴对称）B：中心对称（绕某点，旋转180度，跟原图一样，考试中卷子倒过来看，跟原图一样就是中心对称图形）特征图：N Z S有2条垂直的对称轴，则该图既是轴对称又是中心对称轴对称图形一、新特征图图形两侧一样二、新考法1、对称轴的方向和数量（运算）2、对称轴与图形的线条关系（平行或者垂直）4、两个对称轴的线条关系（平行或垂直）三、技巧：把对称轴画出来（2）、曲直性A：全曲线B：全直线C：曲+直（3）、开闭性1、全封闭例如：2、全开放例如：完整图形留了小开口，可以考虑封闭性4、数量规律（点线角面素）：元素组成不相同不相似、数量规律明显（元素组成不相同、不相似优先考虑属性，不行再数量）（1）、点：点的数量（交点）A：与线的交点，直曲相交的切点也属于交点B：直曲线的两个端点不属于交点数点特征图：Ⅰ、线条交叉明显（大树杈）Ⅱ、乱糟糟一团线交叉Ⅲ、相切较多细化考点：出现数点特征图，但整体数点无规律，考虑曲直交点（2）、线：线的数量A：直线数特征图形：多边形，单一直线（为了补充直线规律，有时候单一画个直线）B：曲线数：特征图形：曲线图形（全曲图形、圆、弧）注：单一直线或者曲线，可以看做直曲图形特征图内外框组合图形：外框直线和内框图形直线可以分开数看规律C：一笔画：线条不重复情况下，可以一笔画成，线条不能重复特征图形：一笔画：一笔画问题：A：线条之间连通。

特殊图类的彩虹点染色1 前言1.1课题背景图论是数学中的一个重要的分支。

它以图为研究的对象。

图论原本是应用数学的一个重要的分支，为此，历史上曾有许多位数学家独自地建立过图论。

早在1736年欧拉的著作中就出现了关于图论的文字记载，最初他所思考的图论问题都有很强的现实背景。

著名的柯尼斯堡七桥问题就是图论的起源。

欧拉证明了这个题目没有解，并且把这个题目进行推广，给出了对于一个给定的图可以以某种方法走遍的判定规则。

这项研究所取得的成果奠定了欧拉图论〔及拓扑学〕创始人的地位。

染色问题是图论的一类重要的题目，具有重要的实际意义和理论意义。

不同类型的图的染色问题一直是图论中的热点题目，而连通图的染色问题又是其中一种很重要的分支。

染色问题就是给定一个图，把它所有顶点或所有的边染上颜色，使得相邻顶点或边的颜色都不相同时所需要的最少的不同的颜色数，边的染色题目可以转化为点染色题目，它们都能归于将一个图划分为独立子集的理论。

目前，伴随着图的染色问题在实际问题中被广泛的应用，研究这类问题的学者在逐渐的增多。

对不同图类的染色问题的研究，已经有了比较丰富的成果，并且这些结论还在不断的完善之中。

连通性是图论中最重要的性质之一，2008年，Chartrand，Johns等人首次提出了图的彩虹连通性的概念，是经典连通性概念的一种加强。

作为一个自然的组合概念，彩虹连通数不但有其了理论意义，而且在网络问题中起到了非常重要的作用。

事实上，它产生于政府机构之间机密信息的安全传输，在网络安全等实际问题中有很多的应用。

假如我们需要在一个蜂窝网络中进行信息的传输。

在网络中的任意两点在之间都要有一条路相连接，而且在该路径上的每段都被分配一个独特的频道（例如，不同的频率）。

显而易见，我们需要求出的是能在网络中所使用的最少的（不同）频道个数。

而这个最少个数恰好是这个网络所对应无向图的彩虹连通数。

彩虹点连通的概念是由Krivelevich，Yuster 首次提出的，是彩虹连通性的一种重要推广。

图的染色标号问题及超图中的彩色匹配图的染色理论和极值图论一直是图论研究领域中的重要分支,在组合最优化、计算机科学以及模式匹配等方面有着广泛的应用,因此长久以来备受关注。

本文旨在讨论图的染色问题、标号问题以及超图中关于匹配的彩虹Turan问题。

在本文中,除特殊声明外,我们所提到的图均为无向、有限、非空的简单图。

给定一个图G,我们分别用V(G)、E(G)、△((G)、δ(G)和mad(G)(或简便起见,用V、E、△、δ和mad)来表示图的点集、边集、最大度、最小度和最大平均度。

首先,我们研究了图的邻积可区别全染色问题。

给定一个图G=(V,E),图G的一个正常[k]-全染色c是指图G的一个正常全染色c:V ∪ E{1,2,...,kk}。

我们用p(v)表示所有与点v相关联的边的颜色及点v本身颜色的乘积,即p(v)=c(v)Пuv∈E(G)C(uv)。

若对于图G中任意一条边uv,均有p(v)≠p(u)成立,则我们称染色c以乘积区分相邻点,并且称c为图G的一个邻积可区别全染色。

使得图G存在一个邻积可区别全染色的最小整数kk,我们称之为邻积可区别全色数,记作x"П(G)。

关于邻积可区别全染色,我们猜想对于包含至少两个点的连通图G,其邻积可区别全色数至多是△(G)+3。

在第二章,我们证明了对于最大度至少为10的平面图,其邻积可区别全色数至多为max{△((G)+2,13};对于最大平均度小于3的图,其邻积可区别全色数至多为max{△({+2,7}。

图的标号问题是一类特殊的图染色问题。

在本文中,我们主要研究了图的反魔幻标号问题。

图G的反魔幻标号是指从图G的边集E(GE到集合{1,2,...,|E(G)|}的一个双射,使得图中任意两个点的点和均不同,其中,点和是指该点的邻边标号之和。

如果图G存在一个这样的反魔幻标号,那么我们就称图G是反魔幻的。

1990年,Hartsfield和Ringel提出了这样一个猜想:除K2外所有的连通图均是反魔幻的。

与图的顶点染色数有关的几个问题张祥波【摘要】设x(G)是无向简单图G(V,E)的顶点染色数,证明了:若|S|＞P/2且|S|=p-m,则图G不存在第p-q类图,其中:q≥2m+1,m≥3且m∈z+;若|S|=p-4,则x(G)≤ p-3;若|S|=p-4,则x(G)≤4θ(G)+θ2(G)-1.【期刊名称】《高师理科学刊》【年(卷),期】2016(036)003【总页数】4页(P17-20)【关键词】顶点染色数;第k类图;最大团;图的厚度【作者】张祥波【作者单位】临盘中学,山东临邑251507【正文语种】中文【中图分类】O157.51 引言及预备知识本文中有关术语和符号参见文献[1]，所指图均为有限无向简单图．用，，，分别表示图的顶点数、厚度、顶点染色数和最大团的顶点数；图含有的所有最大团的公共顶点及它们在图中的边构成的子图，记作图，简称图；是图含有的所有最大团的公共顶点集；表示从中删去的所有顶点及其与中顶点关联的一切边后得到的图．关于图的顶点染色，较多的文献研究特殊图的顶点染色[2-5]，尚未找到很好的方法研究一般图的顶点染色．文献[6]提出猜想：，文献[7]初步证明了时，猜想是成立的．文献[8]进一步证明了时猜想是成立的，文献[9]给出了时图的各种顶点染色数．本文研究一般图的顶点染色，主要解决上述文献中一些有待解决的问题，从而改进和推广文献[7-9]中已有的结果．具体表现在3个方面：（1）若且，则图不存在第类图，其中：，且；（2）若，则；（3）若，则．定义[9]11 如果图含有的所有最大团存在公共顶点，且公共顶点的个数为，则称此图为第类图．引理1[7]36 若，则图含有的所有最大团必存在公共顶点．引理2[8]67 当时，图含最大团，若不存在奇圈，则；若存在奇圈，则．引理3[7]36 若，则．引理4[8]67 当时，图含有最大团，．引理5[7]36 若，则．引理6[10]215 ，；，其中：是完全图．2 主要结果及证明2.1 关于第类图定理1 若且，则图不存在第类图，其中：且．证明使用反证法证明．假设图是第类图，由定义可知，图中所有最大团有个公共顶点．考虑其中一个最大团，则图中必有个顶点不是最大团的顶点．不妨设这个顶点分别是，，，…，；．于是这个顶点中至少有一个顶点是其它最大团的顶点．考虑2种情况：情况1 ，，，…，都是最大团的顶点，则图的顶点与图的顶点都相邻．将图的所有顶点及其边删掉，必得到一个顶点数是，含最大团的图．由于，故情况2 设，，，…，中有个顶点在除之外的最大团中，有个顶点不在任何最大团中，设这个顶点分别是，，…，．将图的所有顶点及其边删掉，得到一个顶点数是的图，而图含有顶点数是的团．在图中将顶点，，…，全部删掉，于是得到一个顶点数是，含最大团的顶点数是的图．由于，故．所以综上可知，假设不成立，定理得证．证毕．推论对于且的图，有且仅有以下若干类图：第类图，第类图，……，第类图及只有一个最大团的图．例对于且的图，有且仅有第类图，第类图，第类图，第类图及只有一个最大团的图．2.2 时猜想的证明定理2 若，则．证明易知．（1）当时，则，显然成立．（2）当时，图顶点数为6，含最大团的图．图中至少有一对顶点不相邻，设这2个顶点分别是和，将和删掉，得到一个顶点数是4的图，而图至多含最大团，故，添上顶点和，色数最多增加1，从而，结论成立．（3）当时，图顶点数是7，含最大团的图．图中至少有一对顶点不相邻，设这2个顶点分别是和，将和删掉，得到一个顶点数是5的图，而图含最大团或者含最大团．若图含最大团，由引理2可知，；若图含最大团，由引理3可知，．添上顶点和，色数最多增加1，故，结论成立．（4）当时，图顶点数是8，含最大团的图．将图中一对不相邻的顶点和删掉，得到顶点数是6，含最大团或者含最大团的图．若图含最大团，由引理4可知，；若图含最大团，由引理3可知，．添上顶点和，色数最多增加1，故，结论成立．（5）当时，则．图中至少有一对顶点不相邻，设这2个顶点是和，将和删掉，得到一个顶点数是的图，而图含最大团或者含最大团．若图含最大团，由引理3可知，；若图含最大团，由引理5可知，．添上顶点和，色数最多增加1，故．综上可知，，则．证毕．定理3 若，则．证明易知．（1）当时，由定理2的证明可知，，故．（2）当时，由定理2的证明可知，．若，则．若，由于平面图的点染色数不超过4，所以图必是非平面图，于是．从而（3）当时，因为图含最大团，所以．由引理6可知，若，则．于是，由定理2可知，，而．所以，当时，对于和10的情况，令，其中：是正整数．若，则由定理2可知，．由引理6可知，，故对于的情况，同理有．若，则由定理2可知，．由引理6可知，，故综上可知，若，则．证毕．本文主要证明了时，猜想：若，则；是正确的．这些结果为进一步研究图的顶点染色提供了一些参考．[1] 谢政，戴丽．组合图论[M]．长沙：国防科技大学出版社，2003[2] 亢莹利，王应前．平面图3色可染的一个充分条件[J]．中国科学·数学，2013，43（4）：409-421[3] 彩春丽，谢德政．平面图3-可着色的3个充分条件[J]．河南师范大学学报：自然科学版，2011，39（6）：4-6[4] 刘配配，王应前．不含4-圈与7-圈的平面图是（2，0，0）-可染的[J]．中国科学·数学，2014，44（11）：1153-1164[5] 刘广德．双外平面图的点染色[J]．枣庄学院学报，2013，30（5）：63-65[6] 张祥波．研究四色问题的意义及理论构想[J]．数学理论与应用，2012，32（3）：24-28[7] 张祥波，魏志芹．关于图的色数与厚度的一些新结果[J]．高师理科学刊，2013，33（5）：35-37[8] 张祥波．一类特殊图的顶点染色及其猜想的证明[J]．重庆工商大学学报：自然科学版，2015，32（9）：66-70[9] 张祥波．一类特殊图的顶点染色数[J]．安庆师范学院学报：自然科学版，2015，21（3）：11-13[10] 卜月华．图论及其应用[M]．南京：东南大学出版社，2002。

组合数学中有关图形染色问题在优化组合中，有一类关键问题为染色问题，最为出名的则是”四色定理”，也就是用四种不相同的颜色将地图上各个国家标出，保证相邻的国家颜色互不相同。

染色问题针对的模型就是给n个区域染色，有N种颜色可供选择，要求相邻的区域颜色不同，一共有多少种不同染色方法？关于解法无非有具体针对的两类。

一，颜色备用型，就是颜色可以不用完。

1，如果是直链型，第一个有N种剩下的都为N-1种，则直链型共有N乘以(N-1)的（n-1）次方。

2，如果区域是地图型，如一个大圆，里边还有一个小圆，将圆环分为四个部分，给这五个区域染色，推导过程:（1），给公共相邻的区域先染色，共有N种不同方法。

（2），给其中一个区域染色，则共有N-1种方法。

（3），给另一个区域染色。

则共有N-2种方法。

（4），给再一个区域染色则当与第二个区域相同时，则有一种方法，与第二个不同时，则有N-3种方法。

（5），给最后一个区域染色，则与上个与第二个相同时，则有N-3种方法，当不同时则有N-3种方法。

综上则根据加法与乘法原理得共有N(N-1)(N-2)[(N-2)+(N-3)(N-3)]。

3，当图形为正方体时，给六个面染色时，利用上面相同的推导原理，根据加法与乘法原理得染色计算方法运算关系为N(N-1)(N-2)(N-2)+2N(N-1)(N-2)(N-3)+N(N-1)(N-3) (N-4)(N-4)种不同染色方法。

二，颜色用完型，也就是颜色必须用完，对于此类问题N必须小于等于n，如是区域种植问题，还是上面第一类图形，大圆中有个小圆，圆环有四部分，用四种颜色图，共有多少种不同染色方法，根据推导过程，根据乘法与加法原理得共有48种不同染色问题。

区域种植问题还是上面第一类图形，大圆中有个小圆，圆环有五部分，用四种颜色图，共有多少种不同染色方法，根据推导过程，根据乘法与加法原理得共有120种不同染色问题。

如果是直链型，如三种作物种五块地，根据乘法与加法原理得共有42种不同染色问题。

地图着色同学们对地图是很熟悉的，但你是否注意到地图中各国或者各省的颜色数目？1852年，刚从伦敦大学毕业的弗南西斯·葛斯里在对英国地图着色时发现，对无论多么复杂的地图，只需用四种颜色就足够将相邻的区域分开。

这个千万人屡见不鲜的有趣事实引起了他的注意，他感到这种现象决非偶然，可能隐藏着深刻的科学道理。

他把他的想法告诉了他的哥哥弗德雷克。

弗德雷克是著名数学家德·摩根的学生，他对这个问题极感兴趣，凭他的数学敏锐性，他感到这是个数学问题，于是便设法证明。

可是，尽管他绞尽脑汁，仍百思不得其解，于是他以“四色定理”为名，请他的老师德·摩根证明。

德·摩根写信请著名数学家哈密尔顿帮助解答，这位智慧超群的人也被这个简单的问题弄得一筹莫展，他冥思苦想了13年，直至逝世仍毫无结果。

在1876年，当时很有名望的数学家凯莱在数学年会上把这个问题归纳为“四色猜想”提出，并征求问题的解答。

于是“四色猜想”开始引人注目。

“四色猜想”的难度一开始并未引起人们的注意。

爱因斯坦的老师闵可夫斯基平时为人很谦虚，偏偏有一次给大学生上课时在这个问题上出了洋相。

他在课堂上，一时兴起，便说：“四色猜想之所以一直没有解决，那仅仅是由于当今世界上第一流的数学家没有研究它，其实要解决这一猜想并不见得会有多难。

”说着拿起粉笔竟要在课堂上即兴推演，以为可以一挥而就。

没想到越写越多，越写越复杂，最后竟不由自主地“挂”起黑板来(讲不下去了)。

但他仍胸有成竹，确信可证明此问题。

可是一连几个星期的课，他都以失败而告终。

有一天，他疲惫不堪地走进教室，当时正值惊雷震耳，暴雨滂沱，他十分愧疚地对同学说：“唉，看来上帝也在责怪我的狂妄自大！四色猜想真难呀，我简直拿他毫无办法。

”此后，数学家们开始沿着这条艰难的道路攀登，1890年希伍德首先解决了“五色问题”。

科学家们此后的进展是：1922年证明了一张地图国家不超过25个时，定理成立，1938年证明了地图国家数为32个，1940年又提高到35个，1969年提高到39个。

一类特殊图的顶点染色数张祥波【摘要】If there are common vertexes in all the maximum cliques of graph, and there are k common vertexes, then we call graph is the k class graph. Hereby, this paper gives a new method to study vertex coloring of graph. According to this method, this paper studies a class vertex coloring of special graphs, and gives vertex coloring number of some graphs.%如果图G含有的所有最大团存在公共顶点,且公共顶点的个数为k,就称此图为第k类图。

据此,本文给出了研究图的顶点染色的一种新方法,并以此研究了一类特殊图的顶点染色及一些图的顶点染色数。

【期刊名称】《安庆师范学院学报（自然科学版）》【年(卷),期】2015(000)003【总页数】4页(P11-13,30)【关键词】最大团;顶点染色数;第k类图;图的厚度【作者】张祥波【作者单位】临盘中学，山东临邑 251507【正文语种】中文【中图分类】O157.5给定一个无向简单图G(V,E)(以下简称图G)，使得任意相邻顶点染不同颜色，这种染色所需要的最小数目，叫做图G的顶点染色数，记为χ(G)。

图的顶点染色较为复杂，这是一个NPC问题。

关于这个方面的研究主要包括它的求解算法[1-5]和特殊图的顶点染色[6-11](尤以平面图的染色较多[12-18])两个方面。

本文则提出了第k类图的概念，对图的结构进行统一分类，给出了研究图的顶点染色的一种新方法。

按照这种方法，本文研究了|S|且|S|=p-3时，图G的顶点染色，并给出了其中4类图的顶点染色数。

高考数学中的染色问题的解题策略安徽省太湖县牛镇高中 黄军华近几年来，数学高考以能力立意来命题，每年都出现一批立意独特、情景新颖脱俗的有关染色问题的试题。

染色问题常以生活实际为背景，其背景公平，突出了数学思维能力和学习潜能的考查，是高考的热点素材之一，但是学生解答并不理想，症结在哪里呢？（1）对问题的背景不熟悉，染色问题情景生动有趣，虽然源于生活实际，但学生的阅历浅，从未见过，更无具体模式可套，因此倍觉破题困难；（2）不能正确地选好分类标准和优化分类顺序；（3）不能正确地将染色问题模型化、构造转化为熟悉的数学问题。

针对染色问题的特点和学生解答染色问题时存在的问题，下面本文将从两方面入手谈谈染色问题的常用解题策略。

1、选好分类标准，优化分类顺序的策略分类讨论是一种重要的数学思想方法，当问题所给对象不能进行统一研究时，就需要对研究的对象进行分类，将整体问题划分为局部问题，把复杂问题转化为单一问题，然后分而治之、各个击破，最后综合各类的结果得到整个问题的解答。

因此，采用分类策略解答染色问题时，我们可以从三个方面入手考虑：1.1从确定染色顺序入手 根据染色问题的要求，先确定好区域的染色顺序，对各个区域分步染色，再由乘法原理计算出染色的种数，是处理这类问题最基本的方法。

例1 如图(1)所示，用五种不同的颜色分别为A 、B 、C 、D 、E 五部分染色，相邻区域不能用同一种颜色，但同一种颜色可以反复使用，也可不使用，求符合这种要求的不同染色方法的种数。

分析：按照分步计数原理，先为A 染色共有5种，再为B 染色有4种（不能与A 同色），接着为C 染色有3种（不与A 、B同色），同理依次为D 、E 染色各有3种，所以不同染色方法的种数为5×4×33=540（种）1.2从使用颜色的种类入手 按照染色问题中的题设要求，从使用了多少种颜色分类讨论入手，分别计算出各种情形的种类，再用分类计数原理求出不同的染色方法的种数。

7-2-3乘法原理之染色问题1.使学生掌握乘法原理主要内容，掌握乘法原理运用的方法；2.使学生分清楚什么时候用乘法原理，分清有几个必要的步骤，以及各步之间的关系．3.培养学生准确分解步骤的解题能力；乘法原理的数学思想主旨在于分步考虑问题，本讲的目的也是为了培养学生分步考虑问题的习惯．一、乘法原理概念引入老师周六要去给同学们上课，首先得从家出发到长宁上8点的课，然后得赶到黄埔去上下午1点半的课．如果说申老师的家到长宁有5种可选择的交通工具（公交、地铁、出租车、自行车、步行），然后再从长宁到黄埔有2种可选择的交通工具（公交、地铁），同学们，你们说老师从家到黄埔一共有多少条路线？我们看上面这个示意图，老师必须先的到长宁，然后再到黄埔．这几个环节是必不可少的，老师是一定要先到长宁上完课，才能去黄埔的．在没学乘法原理之前，我们可以通过一条一条的数，把线路找出来，显而易见一共是10条路线．但是要是老师从家到长宁有25种可选择的交通工具，并且从长宁到黄埔也有30种可选择的交通工具，那一共有多少条线路呢？这样数，恐怕是要耗费很多的时间了．这个时候我们的乘法原理就派上上用场了．二、乘法原理的定义完成一件事，这个事情可以分成n个必不可少的步骤（比如说老师从家到黄埔，必须要先到长宁，那么一共可以分成两个必不可少的步骤，一是从家到长宁，二是从长宁到黄埔），第1步有A种不同的方法，第二步有B种不同的方法，……，第n步有N种不同的方法.那么完成这件事情一共有A x B x……x N种不同的方法．结合上个例子，老师要完成从家到黄埔的这么一件事，需要2个步骤，第1步是从家到长宁，一共5种选择；第2步从长宁到黄埔，一共2种选择；那么老师从家到黄埔一共有5x2个可选择的路线了，即10条.三、乘法原理解题三部曲1、完成一件事分N个必要步骤；2、每步找种数（每步的情况都不能单独完成该件事）；3、步步相乘四、乘法原理的考题类型1、路线种类问题——比如说老师举的这个例子就是个路线种类问题；2、字的染色问题——比如说要3个字，然后有5种颜色可以给每个字然后，问3个字有多少种染色方法；3、地图的染色问题——同学们可以回家看地图，比如中国每个省的染色情况，给你几种颜色，问你一张包括几个部分的地图有几种染色的方法；4、排队问题——比如说6个同学，排成一个队伍，有多少种排法；5、数码问题——就是对一些数字的排列，比如说给你几个数字，然后排个几为数的偶数，有多少种排法．【例1】地图上有A, B, C, D四个国家（如下图），现有红、黄、蓝三种颜色给地图染色，使相邻国家的颜色不同，但不是每种颜色都必须要用，问有多少种染色方法？【考点】乘法原理之染色问题【难度】3星【题型】解答【解析】A有3种颜色可选；当B, C取相同的颜色时，有2种颜色可选，此时D也有2种颜色可选.根据乘法原理，不同的涂法有3x 2x 2=12种；当B, C取不同的颜色时，B有2种颜色可选，C仅剩1种颜色可选，此时D也只有1种颜色可选（与A相同）.根据乘法原理，不同的涂法有3x2x 1 x 1=6种.综上，根据加法原理，共有12 + 6=18种不同的涂法.【答案】18【巩固】如果有红、黄、蓝、绿四种颜色给例题中的地图染色,使相邻国家的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法？【考点】乘法原理之染色问题【难度】3星【题型】解答【解析】第一步，首先对A进行染色一共有4种方法，然后对B、C进行染色，如果B、C取相同的颜色，有三种方式，D 剩下3种方式，如果B、C取不同颜色，有3x2=6种方法，D剩下2种方法，对该图的染色方法一共有4x（3x3 + 3x2x2）= 84种方法.【注意】给地图染色问题中有的可以直接用乘法原理解决，有的需要分类解决，前者分类做也可以解决问题. 【答案】84【例2】在右图的每个区域内涂上A、B、C、D四种颜色之一，使得每个圆里面恰有四种颜色，则一共有 __________ 种不同的染色方法．【考点】乘法原理之染色问题【难度】4星【题型】解答【解析】因为每个圆内4个区域上染的颜色都不相同，所以一个圆内的4个区域一共有4x3x2=24种染色方法.如右图所示，当一个圆内的1、2、3、4四个区域的颜色染定后，由于6号区域的颜色不能与2、3、4三个区域的颜色相同，所以只能与1号区域的颜色相同，同理5号区域只能与4号区域的颜色相同，7号区域只能与2号区域的颜色相同，所以当1、2、3、4四个区域的颜色染定后，其他区域的颜色也就相应的只有一种染法，所以一共有24种不同的染法.【答案】24【例3】如图，地图上有A，B，C，D四个国家，现用五种颜色给地图染色，要使相邻国家的颜色不相同，有多少种不同染色方法?ABC D【考点】乘法原理之染色问题 【难度】3星 【题型】解答【解析】为了按要求给地图上的这四个国家染色，我们可以分四步来完成染色的工作：第一步：给A 染色，有5种颜色可选.第二步：给B 染色，由于B 不能与A 同色，所以B 有4种颜色可选.第三步：给C 染色，由于C 不能与A 、B 同色，所以C 有3种颜色可选.第四步：给D 染色，由于D 不能与B 、C 同色，但可以与A 同色，所以D 有3种颜色可选. 根据分步计数的乘法原理，用5种颜色给地图染色共有5 x 4 x 3 x 3=180种不同的染色方法. 【答案】180 【巩固】如图，一张地图上有五个国家A , B , C , D , E ，现在要求用四种不同的颜色区分不同国家，要求相邻的国家不能使用同一种颜色，不同的国家可以使用同—种颜色，那么这幅地图有多少着色 方法？【考点】乘法原理之染色问题 【难度】3星 【题型】解答【解析】第一步，给A 国上色，可以任选颜色，有四种选择；第二步，给B 国上色，B 国不能使用A 国的颜色，有三种选择；第三步，给C 国上色，C 国与B , A 两国相邻，所以不能使用A , B 国的颜色，只有两种选择；第四步，给D 国上色，D 国与B , C 两国相邻，因此也只有两种选择；第五步，给E 国上色，E 国与C , D 两国相邻，有两种选择.共有4x 3x 2x 2x 2=96种着色方法.【答案】96【例 4】 如图：将一张纸作如下操作，一、用横线将纸划为相等的两块，二、用竖线将下边的区块划为相等的两块，三、用横线将最右下方的区块分为相等的两块，四、用竖线将最右下方的区块划为相等的两块……，如此进行8步操作，问：如果用四种颜色对这一图形进行染色，要求相邻区块颜色不同，应该有多少种不同的染色方法？【解析】对这张纸的操作一共进行了8次，每次操作都增加了一个区块，所以8次操作后一共有9个区块， 我们对这张纸，进行染色就需要9个步骤，从最大的区块从大到小开始染色，每个步骤地染色方法 有：4、3、2、2、2 ，所以一共有：4x 3x 2x 2x 2x 2x 2x 2x 2 = 1536 种.【答案】1536 【巩固】用三种颜色去涂如图所示的三块区域，要求相邻的区域涂不同的颜色，那么共有几种不同的涂法？【考点】乘法原理之染色问题 【题型】解答【难度】3星【考点】乘法原理之染色问题 【难度】2星 【题型】解答【解析】涂三块毫无疑问是分成三步.第一步，涂A 部分，那么就有三种颜色的选择；第二步，涂B 部分， 由于要求相邻的区域涂不同的颜色，A 和B 相邻，当A 确定了一种颜色后，B 只有两种颜色可选择 了；第三步，涂C 部分，C 和A 、B 都相邻，A 和B 确定了两种不相同的颜色，那么C 只有一种颜 色可选择了.然后再根据乘法原理.3x 2x 1=6【答案】6【例 5】 如图，有一张地图上有五个国家，现在要用四种颜色对这一幅地图进行染色，使相邻的国家所染的颜色不同，不相邻的国家的颜色可以相同.那么一共可以有多少种染色方法？【考点】乘法原理之染色问题 【难度】3星 【题型】解答【解析】这一道题实际上就是例题，因为两幅图各个字母所代表的国家的相邻国家是相同的，如果将本题中的地图边界进行直角化就会转化为原题，所以对这幅地图染色同样一共有4x 3x 2x 2x 2=96种方法.【讨论】如果染色步骤为C - A - B - D - E ,那么应该该如何解答？答案：也是4x 3x 2x 2x 2=96种方法.如果染色步骤为C - A - D - B - E 那么应该如何解答？答案：染色的前两步一共有4x3种方法，但染第 三步时需要分类讨论，如果D 与A 颜色相同，那么B 有2种染法，E 也有2种方法，如果D 与A 染 不同的颜色，那么D 有2种染法那么B 只有一种染法，E 有2种染法，所以一共应该有4x 3x （1x 2x 2 + 2x 1 x 2） = 96种方法，（教师应该向学生说明第三个步骤用到了分类讨论和加法原理，加法原理在下一讲中将会讲授），染色步骤选择的经验方法：每一步骤所染的区块应该尽量和之前所 染的区块相邻.【答案】96 【巩固】某沿海城市管辖7个县，这7个县的位置如右图．现用红、黑、绿、蓝、紫五种颜色给右图染色，要求任意相邻的两个县染不同颜色，共有多少种不同的染色方法?为了便于分析，把地图上的7个县分别编号为A 、B 、C 、D 、E 、F 、G （如左下图）.为了便于观察，在保持相邻关系不变的情况下可以把左图改画成右图.那么，为了完成地图染色这 件工作需要多少步呢【考点】乘法原理之染色问题 【难度】4星 【题型】解答 【解析】由于有7个区域，我们不妨按A 、B 、C 、D 、E 、F 、G 的顺序，用红、黑、绿、蓝、紫五种颜 色依次分7步来完成染色任务．第1步：先染区域A ，有5种颜色可供选择;再染区域B ，由于B 不能与A 同色，所以区域B 的染色方式有4种； 染区域C ，由于C 不能与B 、A同色，所以区域C 的染色方式有3种； 染区域D ，由于D 不能与C 、A 同色，所以区域D 的染色方式有3种; 染区域E ，由于E 不能与D 、A 同色，所以区域E 的染色方式有3种； 染区域F ，由于F 不能与E 、A 同色，所以区域F 的染色方式有3种; 染区域G ，由于G 不能与C 、D 同色，所以区域G的染色方式有3种.根据分步计数的乘法原理，共有5 x 4 x 3 x 3 x 3 x 3 x 3=4860种不同的染色方法.【答案】4860【例6】 用3种颜色把一个3x 3的方格表染色，要求相同行和相同列的3个格所染的颜色互不相同，一共有 ____ 种不同的染色法.【考点】乘法原理之染色问题 【难度】3星 【题型】解答【解析】根据题意可知，染完后这个3x 3的方格表每一行和每一列都恰有3个颜色.用3种颜色染第一行，有P 3=6种染法；染完第一行后再染第一列剩下的2个方格，有2种染法； 当第一行和第一列都染好后3，再根据每一行和每一列都恰有3个颜色对剩下的方格进行染色，可知 其余的方格都只有唯一一种染法.所以，根据乘法原理，共有3 x 2=6种不同的染法.【答案】6【例7】 如右图，有A 、B 、C 、D 、E 五个区域，现用五种颜色给区域染色，染色要求：每相邻两个区域不同色，每个区域染一色．有多少种不同的染色方式？【解析】先采用分步：第一步给A 染色，有5种方法；第二步给B 染色，有4种方式；第三步给C 染色，有 3种方式；第四步给D 染色，有3种方式；第五步，给E 染色，由于E 不能与A 、B 、D 同色，但可 以和C 同色.此时就出现了问题：当D 与B 同色时，E 有3种颜色可染；而当D 与B 异色时，E 有 2种颜色可染.所以必须从第四步就开始分类：第一类，D 与B 同色.E 有3种颜色可染，共有5 x 4 x 3 x 3=180 （种）染色方式；第二类，D 与B 异色.D 有2种颜色可染，E 有2种颜色可染，共有5x 4x 3x 2x 2=240 （种）染色 方式.根据加法原理，共有180 + 240=420 （种）染色方式.【注意】给图形染色问题中有的可以直接用乘法原理解决，但如果碰到有首尾相接的图形往往需要分类解决. 【答案】420【巩固】如右图，有A , B , C , D 四个区域，现用四种颜色给区域染色，要求相邻区域的颜色不同，每个区域染一色．有多少种染色方法？【考点】乘法原理之染色问题 【难度】3星 【题型】解答【解析】A 有4种颜色可选，然后分类：第一类：B , D 取相同的颜色.有3种颜色可染，此时D 也有3种颜色可选.根据乘法原理，不同 的染法有4x 3x 3=36 （种）；第二类：当B , D 取不同的颜色时，B 有3种颜色可染，C 有2种颜色可染，此时D 也有2种颜色 可染.根据乘法原理，不同的染法有4x 3x 2x 2=48 （种）.根据加法原理，共有36 + 48=84（种）染色方法.第2步 第3步 第4步 第5步 第6步 第7步 【考点】 乘法原理之染色问题 【难度】3星 【题型】解答【答案】84 【巩固】用四种颜色对右图的五个字染色，要求相邻的区域的字染不同的颜色，但不是每种颜色都必须要用．问：共有多少种不同的染色方法?【解析】第一步给“而”上色，有4种选择；然后对“学”染色，“学”有3种颜色可选； 当“奥”，“数”取相同的颜色时，有 2 种颜色可选，此时“思”也有 2 种颜色可选，不同的涂法有3 x 2 x 2 = 12 种；当“奥”，“数”取不同的颜色时，“奥”有2种颜色可选，“数”剩仅1种颜色可选，此时“思”也只有1种 颜色可选（与“学”相同），不同的涂法有3 x 2 x 1x 1=6种.所以，根据加法原理，共有4x 3x （2x 2 + 2） = 72种不同的涂法.【答案】72分别用五种颜色中的某一种对下图的A , B , C , D , E , F 六个区域染色，要求相邻的区域染不同的颜色，但不是每种颜色都必须要用．问：有多少种不同的染法？【解析】先按A , B , D , C , E 的次序染色，可供选择的颜色依次有5, 4, 3, 2, 3种，注意E 与D 的颜 色搭配有3 x 3=9（种），其中有3种E 和D 同色，有6种E 和D 异色.最后染F ，当E 与D 同色时 有3种颜色可选，当E 与D 异色时有2种颜色可选，所以共有5x 4x 2x （3x 3 + 6x 2） = 840种染法.【答案】840【例9】 将图中的。