算法初步流程图基本算法语句二轮复习专题练习(一)含答案新高考高中数学

算法算法是高中数学课程中的新增内容，是中国数学课程内容的一个新特色．“算法”过程是指机械式地按照某种确定的步骤行事，通过一系列小的简单计算操作完成复杂计算的过程．算法的学习内容大致可分为三个步骤：用自然语言描述算法；精确刻画算法(程序框图)；计算机实现执行算法(程序语言的描述过程)．算法思想贯穿高中数学课程的相关部分．【知识要点】1．算法：算法可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤，或者看成按照要求设计好的有限的确切的计算序列，并且这样的步骤或序列能够解决一类问题．现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤．2．程序框图程序框图：用一些通用的符号构成一张图来表示算法，这种图称为程序框图(程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形)．用框图表示算法步骤的一些常用的图形符号：程序框名称功能终端框(起止框) 表示一个算法的起始和结束输入、输出框表示一个算法输入和输出的信息处理框(执行框) 赋值、计算判断框判断某一条件是否成立，成立时在出口处标明“是”，不成立时标明“否”↓→流程线(指向线) 指引流程图的方向连接点连接另一页或另一部分的框图程序框图的三种基本逻辑结构：顺序结构：描述的是最简单的算法结构，语句与语句之间、框与框之间按从上到下的顺序进行(如图9－1)．图9－1条件分支结构：依据指定条件选择执行不同指令的控制结构(如图9－2)．图9－2循环结构：根据指定条件决定是否重复执行一条或多条指令的控制结构(如图9－3)．图9－33．几种基本算法语句任何一个程序设计语言中，都包含五种基本的算法语句，即输入语句、输出语句、赋值语句、条件语句、循环语句．输入语句和输出语句分别用来实现算法的输入信息、输出结果的功能；赋值语句是用来表明赋给某一个变量一个具体的确定值的语句；条件语句是处理条件分支逻辑结构的算法语句；循环语句是用来处理算法中的循环结构的语句．4．中国古代算法案例：更相减损之术、辗转相除法：求两个正数的最大公因数的方法．辗转相除法算法步骤：第一步：用两数中较大数除以较小数，求商和余数．第二步：用除数除以余数．第三步：重复第二步，直到余数为0．第四步，得出两数的最大公约数，即余数0之前的余数．更相减损术算法步骤：第一步：用较大数减去较小数，得到差．第二步：比较减数与差的大小，再用较大数减去较小数．第三步：重复第二步，直到差与减数相等为止．第四步：相等数即为最大公约数．割圆术：用正多边形的面积逐渐逼近圆面积的算法求圆周率π． 秦九韶算法：求一元多项式的值的一种方法，递推关系为),,2,1(10n k a x v v a v k n k kn=⎩⎨⎧+==-- 【复习要求】1．了解算法的含义，了解算法的思想．2．理解程序框图的三种基本逻辑结构：顺序结构、条件分支结构、循环结构．3．理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义．【例题分析】例1 如图(图9－4)所示，将一系列指令用框图的形式表示，箭头指向下一步的操作．请按照框图回答问题：图9－4(1)这个框图表示了怎样的算法?(2)输出的数是多少?【分析】由框图中的文字及图形符号表示的操作内容可知：此算法是“求1到50的和”，由此可以算出输出的数．解：(1)此框图表示的算法为：求1＋2＋3＋…＋50的和；(2)易知所求和为1275．【评析】程序框图主要包括三部分：表示相应操作的框，带箭头的流程线和框外必要的说明．读框图时要从这三个方面研究，流程线反映了命令执行的先后顺序，主要看箭头方向，框及内外的文字说明表明了操作内容．常用这种方式考察对算法的理解和应用．例2 (1)如图9－5所示的是一个算法的程序框图，已知a1＝3，输出的结果为7，则a2的值为______．图9－5(2)如图9－6所示的是某个函数求值的程序框图，则满足该程序的函数解析式为_____．图9－6(3)如图9－7所示的是求某个数列和的程序框图，此程序输出的结果为_____．图9－7【分析】这三个小题的重点在于读懂框图．(1)只含有顺序结构，(2)含有条件分支结构，表明函数的定义域为R ，当x ＜0时，遵从解析式f (x )＝3x －1，否则(即当x ≥0时)，遵从解析式f (x )＝2－5x ；(3)中有两个循环变量S 、I ，S 是累加变量，I 是计数变量；另外还要判断I 的奇偶性，以此决定是加还是减．解：(1)112=a ；(2)⎩⎨⎧≥-<-=)0(52)0(13)(x x x x x f ；(3)S ＝12－22＋32－42＋…＋992－1002＝－5050．【评析】题(1)，只含有顺序结构，所表示的算法比较简单，只需按照框图箭头方向依次读出即可．题(2)含有条件分支结构，这是一个与分段函数有关的算法，框图中含有判断框．读包含有判断框的框图时，要特别重视判断框内的条件和框外的文字说明，对应的下一步操作会依条件不同而改变．题(3)含有循环结构，当解决一些有规律的科学计算问题，尤其是累加和累乘时，往往可以利用循环结构来实现算法．循环结构有两种，读包含有循环结构的框图时，除关注判断框内外的说明外，一般要从开始依顺序做几次循环，观察变量的变化规律来帮助读懂算法的含义．例3 (1)已知平面上的一点P 0(x 0，y 0)和直线l ：Ax ＋By ＋C ＝0，求点P 0到直线l 的距离d ，并画出程序框图．(2)用条件分支结构写“已知三个数a 、b 、c ，找出其中最大数”的算法及框图．(3)写出求n131211++++的和的算法，画出程序框图，并写出相应程序(选做)． 【分析】正确分析“算理”，才能选择恰当的算法结构，有条理的表达算法．(1)在已知点到直线距离公式的前提下，适合用顺序结构表示；(2)涉及比大小，必须用到条件分支结构；(3)中分母有规律的递增，可以引入累加变量S 和计数变量i ，且S ＝S ＋1/i 是反复进行的，可以用循环结构表示．解：(1)算法及框图为：S1 输入x 0，y 0；A ，B ，C ； S2 计算m ＝A 2＋B 2；S3 计算n ＝Ax 0＋By 0＋C ； S4 计算mn d ||=； S5 输出d ；(2)算法及框图为：S1 输入a ，b ，c ； S2 令x ＝a ；S3 若b ＞x ，则令x ＝b ；否则，执行S4；S4 若c ＞x ，则令x ＝c ；否则，执行S5； S5 输出x ；(3)算法及框图为：S1 输入i ＝1，S ＝0； S2 当i ≤n 时，,1iS S += i ＝i ＋1；否则执行S3； S3 输出S ；程序如下； S ＝0For i ＝1:1:n S ＝S ＋1/i i ＝i ＋1 endprint(％io (2)，S )【评析】书写算法时，一步一步的程序化步骤，即“算则”固然重要，但这些步骤的依据，即“算理”有着更基本的作用，“算理，，是“算则”的基础，“算则”是“算理”的表现．这三道小题由于算理不同，所蕴含的算法结构也不同．通过实例，模仿、操作、探索，经历通过设计程序框图表达解决问题的过程，可以更好的理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句，体会和理解算法的含义，了解算法语言的基本构成．本例中涉及的“利用公式求点到直线的距离”、“实数排序求最值问题”、“求数列的和或积的问题”，还包括“二分法求函数零点”、“质数的判定”，“求π的近似值”等等，都是算法的典型案例，学习时要给予充分的重视．一般算法的表示方法并不唯一．不同的算法语言的书写形式是有差别的．本书所采用的是Scilab 语言，学习时要了解赋值语句、输入输出语句、if 语句、while 和for 语句的基本含义及表达方式，能够读懂语句表示的算法过程．例4 (1)用辗转相除法计算56和264的最大公约数时，需要做的除法次数是______． (2)用更相减损术求56和98的最大公约数时，操作如下：(98，56)(56，42)(42，14)(28，14)(14，14)，由此可知两数的最大公约数为______．(3)用秦九韶算法求得多项式f (x )＝x 6－2x 5＋3x 3＋4x 2－6x ＋5当x ＝2时函数值为______．解：(1)8216816240164015640564264+⨯=+⨯=+⨯=+⨯=所以最大公约数为8，需做的除法次数是4；(2)最大公约数为14； (3)33． 【评析】书上所涉及的古代基本算法案例包括：更相减损术与辗转相除法、秦九韶算法、割圆术．辗转相除法与更相减损术都是求最大公约数的方法，辗转相除法又叫欧几里得方法，计算上以除法为主，更相减损术以减法为主，计算次数上，前者相对较少，特别是两个整数相差较大时区别尤其明显；辗转相除法以余数为0结束，更相减损术则以减数与差相等结束．秦九韶算法的特点是把求n 次多项式的值转化为求n 个一次多项式的值，运算时只有加法和乘法，而且运算的次数比较少，求一个n 次多项式的值最多需要进行n 次加法、n 次乘法．割圆术是由中国古代数学家刘徽提出的，是当时计算圆周率比较先进的算法，“算理”明确，即用圆内接正多边形和外切正多边形逼近圆周率，重点是确定递推关系．例5 (09辽宁)某店一个月的收入和支出总共记录了N 个数据，其中收入记为正数，支出记为负数．该店用下边的程序框图计算月总收入S 和月净盈利V ．那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的( )A ．A ＞0，V ＝S －TB ．A ＜0，V ＝S －TC ．A ＞0，V ＝S ＋TD ．A ＜0，V ＝S ＋T【分析】本题要注意三点：a k 有正有负；S 为总收入，是所有正数的和；T 为总支出，是所有非正数的和．答案为C【评析】本题结合实际背景，强调算法的应用价值，是一种比较新的题型，应引起关注．练习9一、选择题1．任何一个算法都必须有的基本结构是( )A．顺序结构B．条件分支结构C．循环结构D．以上三个都要有2．下面给出对程序框图的几种说法：①任何一个程序框图都必须有起止框；②判断框有一个入口，有不止一个出口；③对于一个算法来说，判断框内的条件表达方式是唯一的；其中正确的有( )A．0个B．1个C．2个D．3个3．在算法的逻辑结构中，要求进行逻辑判断并根据结果进行不同处理的是哪种结构( ) A．顺序结构B．条件分支结构和循环结构C．顺序结构和条件分支结构D．顺序结构和循环结构4．算法：S1 输入n；S2 判断n是否是2；若n＝2，则n满足条件，若n＞2，则执行S3；S3 依次从2到n－1检验能否整除n，若都不能整除，则n满足条件；满足上述算法的n是( )A．奇数B．偶数C．质数D．合数二、填空题5．阅读下面两个程序框图，框图1输出的结果为______；框图2输出的结果为______．框图1 框图26．(08广东)阅读图9－8的程序框图，若输入m＝4，n＝6，则输出a＝______，i＝______．图9－8 图9－97．阅读图9－9的程序框图，若输入的n是100，则输出的变量S和T的值依次是______．8．“x＝3*5”和“x＝x＋1”是某个程序中的先后相邻两个语句，下列说法中①“x＝3*5”是将数值15赋给x，而不是普通运算“x＝3*5＝15”；②“x＝3*5”可以写成“3*5＝x”③语句“x＝x＋1”在执行时，“＝”右边x为15，“＝”左边x为16；正确的有______．三、解答题9．分别用辗转相除法和更相减损术求189和81的最大公约数．10．用循环语句书写求1＋2＋3＋…＋n＞1000的最小自然数n的算法，画出程序框图，并写出相应的程序(选做)．11．(09宁夏)为了测量两山顶MN间的距离，飞机沿水平方向在AB两点进行测量，MN在同一个铅垂平面内(如图)．飞机能够测量的数据有俯角和AB间的距离，请你设计一个方案，包括：指出需要测量的数据(用字母表示，并在图中标出)；用文字和公式写出计算MN间距离的步骤．专题九 算法参考答案练习9一、选择题1．A 2．C 3．B 4．C 二、填空题5．27，21 6．12，3 7．2550，2500 8．①③． 三、解答题9．解：辗转相除法：3278127281189 ⨯=⨯=，所以最大公约数为27．更相减损术：189－81＝108，108－81＝27，81－27＝54，54－27＝27， 所以最大公约数为27． 10．解：S1 输入S ＝0，i ＝1； S2 S ＝S ＋i ，i ＝i ＋1；S3 若S ≤1000，重复执行S2； 若 S ＞1000，输出i ．S ＝0，i ＝1； While S ≤1000 S ＝S ＋i ； i ＝i ＋1； endprint （%io （2），i ）11．解：如图(1)需要测量的数据有：A 点到M 、N 的俯角α1，β1；B 点到M 、N 的俯角α 2，β 2；A 、B 的距离d ．11 / 11 (2)第一步：计算BM ，由正弦定理)sin(sin 211ααα+=d BM ； 第二步：计算BN ，由正弦定理)sin(sin 121βββ-=d BN ； 第三步：计算MN ，由余弦定理 )cos(22122αβ+++=⋅⋅BN BM BN BM MN ．。

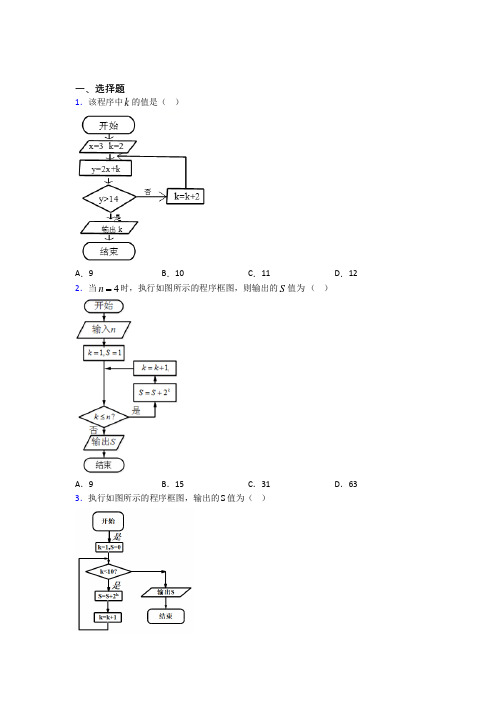
一、选择题1．该程序中k的值是（）A．9 B．10 C．11 D．12 n 时，执行如图所示的程序框图，则输出的S值为（）2．当4A．9 B．15 C．31 D．633．执行如图所示的程序框图，输出的S值为（）A ．511B ．512C ．1022D ．10244．执行如图所示的程序框图，则输出S 的值为（ ）A ．-1010B ．-1009C ．1009D ．10105．某程序框图如图所示，其中21()g n n n =+，若输出的20192020S =，则判断框内可以填入的条件为（ ）A ．2020?n <B ．2020?nC ．2020?n >D ．2020?n 6．朱世杰是我国元代伟大的数学家，其传世名著《四元玉鉴》中用诗歌的形式记载了下面这样一个问题：我有一壶酒，携着游春走.遇务①添一倍，逢店饮斛九②.店务经四处，没了这壶酒.借问此壶中，当原多少酒？①“务”：旧指收税的关卡所在地；②“斛九”：1.9斛.下图是解决该问题的算法程序框图，若输入的x 值为0，则输出的x 值为（ ）A．5740B．13380C．5732D．5893207．程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作．卷八中第33问：“今有三角果一垛，底阔每面七个．问该若干？”如图是解决该问题的程序框图．执行该程序框图，求得该垛果子的总数S为（）A．28 B．56 C．84 D．1208．若执行如图所示的程序框图，输出S 的值为511，则输入n 的值是（ ）A ．7B ．6C ．5D ．49．如图，执行程序框图后，输出的结果是（ ）A ．140B ．204C ．245D ．30010．对任意非零实数a 、b ，若a b ⊗的运算原理如图所示，则121log 43-⎛⎫⊗ ⎪⎝⎭的值为（ ）A ．13B ．1C ．43D ．2 11．定义语句“mod r m n =”表示把正整数m 除以n 所得的余数赋值给r ，如7mod31=表示7除以3的余数为1，若输入56m =，18n =，则执行框图后输出的结果为（ ）A ．6B ．4C ．2D ．112．执行如图的程序框图，则输出x 的值是 ( )A．2018B．2019C．12D．2二、填空题13．已知某程序框图如图所示，则执行该程序后输出的结果是_____14．一个算法的伪代码如下图所示，执行此算法，若输出的y值为1，则输入的实数x的值为________.15．执行如图所示的程序框图，输入l=2，m=3，n=5，则输出的y的值____16．已知流程图如图，则输出的i＝________．17．阅读如图所示的流程图，运行相应的程序，则输出n的值为______．18．一个算法的程序框图如下图所示，若该程序输出的结果为，则判断框中应填入的条件是____．x ，则输出i的值是 .19．如图所示的程序框图中，若520．阅读如图所示的程序框图，该程序输出的结果是__________.三、解答题21．如图所示的程序框图，根据该图和下列各小题的条件回答下面的几个小题．(1)该程序框图解决的是一个什么问题？(2)当输入的x的值为0和4时，输出的值相等，问当输入的x的值为3时，输出的值为多大？(3)在(2)的条件下要想使输出的值最大，输入的x的值应为多大？22．已知程序框图如图所示,用“直到型循环”写出程序框图所对应的算法语句23．现有一个算法框图如图所示。

一、选择题1．执行如图所示的程序框图，则输出的S=（）A．1-B．2-C．2D．1 22．运行下图所示的程序框图，如果输入的2020n=，则输出的n=（）A．6 B．7 C．63 D．64 3．如图所示的程序框图输出的结果是（）A．34 B．55 C．78 D．894．执行如图所示的程序框图，若输入x=9，则循环体执行的次数为（）A．1次B．2次C．3次D．4次5．明代数学家程大位（1533~1606年），有感于当时筹算方法的不便，用其毕生心血写出《算法统宗》，可谓集成计算的鼻祖．如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题．执行该程序框图，若输出的y的值为2，则输入的x的值为（）A ．74B ．5627C ．2D ．164816．某程序框图如图所示，其中21()g n n n =+，若输出的20192020S =，则判断框内可以填入的条件为（ ）A ．2020?n <B ．2020?nC ．2020?n >D ．2020?n 7．鸡兔同笼，是中国古代著名的趣味题之一.《孙子算经》中就有这样的记载：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各有几何？设计如右图的算法来解决这个问题，则判断框中应填入的是（ ）A ．94m >B ．94m =C ．35m = D ．35m ≤8．如图，执行程序框图后，输出的结果是（ ）A ．140B ．204C ．245D ．300 9．如图给出的是计算1111246102+++⋅⋅⋅+的值的一个程序框图，其中判断框中应填入的是（ ）A ．102i >B ．102i ≤C ．100i >D ．100i ≤ 10．执行如图所示的程序框图,若输入的6n =，则输出S =A ．514B ．13C ．2756D ．31011．《数书九章》是我国宋代数学家秦九韶的著作，其中给出了求多项式的值的秦九韶算法，如图所示的程序框图给出了一个利用秦九韶算法求某多项式值的实例，若输入的13x =，输出的12181=y 则判断框“”中应填入的是（ ）A ．2?k ≤B ．3?k ≤C ．4?k ≤D ．5?≤k 12．执行如下图的程序框图，那么输出S 的值是( )A ．2B ．1C ．12D ．-1二、填空题13．执行下面的程序框图，若输入的a ，b ，k 分别为1，2，3，则输出的M =_____14．执行如图所示的程序框图若输人x 的值为3，则输出y 的值为______．15．执行如图所示的伪代码，若输出的y的值为10，则输入的x的值是________．16．我国元朝著名数学家朱世杰在《四元玉鉴》中有一首诗：“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经三处，没有壶中酒，借问此壶中，当原多少酒？”用程序x=，问一开始输入的x=______斗.遇店添一倍，逢框图表达如图所示，即最终输出的0友饮一斗，意思是碰到酒店就把壶里的酒加1倍，碰到朋友就把壶里的酒喝一斗，店友经三处，意思是每次都是遇到店后又遇到朋友，一共是3次．17．如图是一个算法流程图，则输出的S的值为______．18．如图所示的程序框图，输出S的结果是__________．19．运行如图所示的程序，输出结果为___________.20．一个算法的程序框图如图所示，则该程序运行后输出的结果是．三、解答题21．如图所示，已知底角为45°的等腰梯形ABCD，底边BC长为7 cm，腰长为22cm，当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时，直线l把梯形分成两部分，令BF＝x(0≤x≤7)，左边部分的面积为y，求y与x之间的函数关系式，画出程序框图，并写出程序．22．用程序框图描述算法：已知梯形的两底边长分别为a，b，高为h，求梯形面积．23．下面程序的功能是输出1~100之间的所有偶数．程序：i=1DOm=iMOD2IF①THENPRINTiENDIF②LOOPUNTILi>100END（1）试将上面的程序补充完整；（2）改写为WHILE型循环结构程序．24．已知函数f(x)＝221(0)25(0)x xx x⎧-≥⎨-<⎩每输入一个x值，都得到相应的函数值，画出程序框图并写出程序．25．分别标有1,2,3,4,5,6六个号码的小球,有一个最重,写出挑出最重球的算法,并画出程序框图.26．写出计算102+202+…+1 0002的算法程序,并画出相应的程序框图.【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】列举出前四次循环，可知，该算法循环是以3为周期的周期循环，利用周期性可得出输出的S 的值.【详解】第一次循环，02020k =≤成立，1112S ==--，011k =+=； 第二次循环，12020k =≤成立，()11112S ==--，112k =+=； 第三次循环，22020k =≤成立，12112S ==-，213k =+=；第四次循环，32020k =≤成立，1112S ==--，314k =+=； 由上可知，该算法循环是周期循环，且周期为3，依次类推，执行最后一次循环，20202020k =≤成立，且202036731=⨯+，此时12S =， 202012021k =+=，20212020k =≤不成立，跳出循环体，输出S 的值为12. 故选：D.【点睛】本题考查利用程序框图计算输出结果，推导出循环的周期性是解题的关键，考查计算能力，属于中等题.2．A解析：A【分析】根据题中所给的框图，模拟执行程序框图，求得结果.【详解】输入2020100n =>，且不是奇数，赋值1010100n =>，且不是奇数，赋值505100n =>，且是奇数，赋值252100n =>，且不是奇数，赋值126100n =>，且不是奇数，赋值63100n =<，赋值()2log 6316n =+=，输出6.故选：A【点睛】该题考查的是有关程序框图的问题，涉及到的知识点有计算程序框图的输出结果，属于简单题目.3．B解析：B【分析】通过不断的循环赋值，得到临界值，即可得解.【详解】1,1,21,2,32,3,53,5,85,8,138,13,2113,21,3421,34,55x y z x y z x y z x y z x y z x y z x y z x y z ======================== 不满足50z ≤，输出即可，故选：B.【点睛】本题考查了程序框图循环结构求输出结果，考查了计算能力，属于中当题.4．C解析：C【分析】根据程序框图依次计算得到答案.【详解】9,5x y ==，41y x -=>；115,3x y ==，413y x -=>； 1129,39x y ==，419y x -=<；结束. 故选：C .【点睛】本题考查了程序框图的循环次数，意在考查学生的理解能力和计算能力.5．C解析：C【分析】根据程序框图依次计算得到答案.【详解】34y x =-，1i =；34916y y x =-=-，2i =；342752y y x =-=-，3i =； 3481160y y x =-=-，4i =；34243484y y x =-=-，此时不满足3i ≤，跳出循环，输出结果为243484x -，由题意2434842y x =-=，得2x =．故选:C【点睛】本题考查了程序框图的计算，意在考查学生的理解能力和计算能力.6．A解析：A【分析】因为()()2111111g n n n n n n n ===-+++，此程序框图是对函数()g n 求和，利用裂项相消法求和，可知201912020n S n ==+，可知2019满足条件进入循环，2020不满足条件没有进入循环，根据选项得到正确结果.【详解】 由2221111111112019(1111222231112020n S n n n n n n ⎫⎛⎫⎛⎫=++⋯+=-+-+⋯+-=-==⎪ ⎪ ⎪++++++⎭⎝⎭⎝⎭，解得2019n =，可得n 的值为2019时.满足判断框内的条件，当n 的值为2020时，不满足判断框内的条件，退出循环，输出S 的值，故判断框内可以填人的条件为“2020n <？”.故选A.【点睛】本题考查根据循环框图的输出结果填写判断框的内容，关键是分析出满足输出结果时的n 值，再根据选项判断结果.7．B解析：B【分析】由题意知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意可得出判断条件.【详解】由题意可知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意知，在程序框图中，当计算足的数量为94时，算法结束，因此，判断条件应填入“94m =”.故选B.【点睛】本题考查算法程序框图中判断条件的填写，考查分析问题和解决问题的能力，属于中等题. 8．B【分析】根据程序框图列举出算法的每一步，可得出输出结果.【详解】18n =>不成立，执行第一次循环，211b ==，011s =+=，112n =+=；28n =>不成立，执行第二次循环，224b ==，145s =+=，213n =+=； 38n =>不成立，执行第三次循环，239b ==，5914s =+=，314n =+=； 48n =>不成立，执行第四次循环，2416b ==，141630s =+=，415n =+=； 58n =>不成立，执行第五次循环，2525b ==，302555s =+=，516n =+=； 68n =>不成立，执行第六次循环，2636b ==，553691s =+=，617n =+=； 78n =>不成立，执行第七次循环，2749b ==，9149140s =+=，718=+=n ； 88n =>不成立，执行第八次循环，2864b ==，14064204s =+=，819n =+=； 98n =>成立，跳出循环体，输出s 的值为204，故选B.【点睛】本题考查程序框图运行结果的计算，一般利用算法程序框图将算法的每一步列举出来，考查计算能力，属于中等题.9．B解析：B【解析】【分析】 根据题目所求表达式1111246102+++⋅⋅⋅+中最后一个数字1102，确定填写的语句. 【详解】 由于题目所求是1111246102+++⋅⋅⋅+，最后一个数字为1102，即当102i =时，判断是，继续循环，2104i i =+=，判断否，退出程序输出S 的值，由此可知应填102i ≤.故选B.【点睛】本小题主要考查填写程序框图循环条件，属于基础题. 10．B解析：B【解析】【分析】首先确定流程图所实现的功能，然后利用裂项求和的方法即可确定输出的数值.【详解】 由流程图可知，程序输出的值为：1111023344556S =++++⨯⨯⨯⨯， 即1111111123344556S ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭111263=-=.【点睛】本题主要考查流程图功能的识别，裂项求和的方法等知识，意在考查学生的转化能力和计算求解能力.11．C解析：C【解析】【分析】模拟程序的运行过程，即可得出输出y 的值时判断框中应填入的是什么．【详解】模拟程序的运行过程如下， 输入114,1,11333x k y ===⨯+=， 41132,1339k y ==⨯+=， 131403,19327k y ==⨯+=， 4011214,127381k y ==⨯+=， 此时不满足循环条件，输出12181=y ； 则判断框中应填入的是4?k ≤． 故选：C ．【点睛】本题考查了算法与程序框图的应用问题，理解框图的功能是解题的关键，是基础题． 12．A解析：A【解析】【分析】模拟程序的运行，依次写出每次循环得到的k 和S 值，根据题意即可得到结果.【详解】程序运行如下，k=0, S ＝112-＝﹣1， k ＝1，S ＝()111--＝12； k ＝2，S ＝12112=-；k ＝3，S ＝11-2＝-1… 变量S 的值以3为周期循环变化，当k=2018时，s=2，K=2019时，结束循环，输出s 的值为2．故选：A ．【点睛】本题考查程序框图，是当型结构，即先判断后执行，满足条件执行循环，不满足条件，跳出循环，算法结束，解答的关键是算准周期，是基础题．二、填空题13．12【分析】由题意可知从开始判断框条件成立执行第一次循环得到一组新的的值再从开始判断框条件成立执行第一次循环得到一组新的的值当时判断条件框不成立输出此时的值即可得出答案【详解】当时执行程序框图得；当 解析：12【分析】由题意可知，从1n =开始，判断框条件成立，执行第一次循环，得到一组新的,,M a b 的值，再从2n =开始，判断框条件成立，执行第一次循环，得到一组新的,,M a b 的值，当3n =时，判断条件框不成立，输出此时M 的值，即可得出答案．【详解】当1n =时，执行程序框图得，1225,2,5M a b =+⨯===；当2n =时，执行程序框图得，22512,5,12M a b =+⨯===；当3n =时，不满足判断条件框，直接输出 12M =．故答案为12．【点睛】本题主要考查了根据程序框图写出执行结果的问题，对于这类题目，首先要弄清框图的结构和执行过程，本题为循环结构的程序框图．14．63【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量y 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】解：模拟程序的运行可得x=3y=7不满足条件|x-y|解析：63【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量y 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】解：模拟程序的运行，可得x=3y=7不满足条件|x-y|＞31，执行循环体，x=7，y=15不满足条件|x-y|＞31，执行循环体，x=15，y=31不满足条件|x-y|＞31，执行循环体，x=31，y=63此时，满足条件|x-y|＞31，退出循环，输出y 的值为63．故答案为63．【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．15．3【解析】【分析】分析出算法的功能是求分段函数的值根据输出的值为10分别求出当时和当时的值即可【详解】由程序语句知：算法的功能是求的值当时解得(或不合題意舍去)；当时解得舍去综上的值为3故答案为3【 解析：3【解析】【分析】分析出算法的功能是求分段函数22,31,3x x y x x <⎧=⎨+≥⎩的值，根据输出的值为10 ,分别求出当3x <时和当3x ≥时的x 值即可.【详解】由程序语句知：算法的功能是求22,31,3x x y x x <⎧=⎨+≥⎩的值， 当3x ≥时，2110y x =+=，解得3x =(或3- ,不合題意舍去)；当3x <时，210y x ==,解得5x = ,舍去，综上，x 的值为3，故答案为3 .【点睛】本题主要考查条件语句以及算法的应用，属于中档题 .算法是新课标高考的一大热点，其中算法的交汇性问题已成为高考的一大亮，这类问题常常与函数、数列、不等式等交汇自然，很好地考查考生的信息处理能力及综合运用知识解决问題的能力，解决算法的交汇性问题的方：（1）读懂程序框图、明确交汇知识，(2）根据给出问题与程序框图处理问题即可. 16．【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件输出令即可得结果【详解】第一次输入执行循环体执行循环体执行循环体输出的值为0解得：故答案为【点睛】本题主要考查程序框图的 解析：78【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件输出87x -，令870x -=即可得结果.【详解】第一次输入x x =，1i =执行循环体，21x x =-，2i =，执行循环体，()221143x x x =--=-，3i =，执行循环体，()243187x x x =--=-，43i =>，输出87x -的值为0，解得：78x =， 故答案为78． 【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可. 17．【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】模拟程序的运行可得满足条件执行循环体满足条件执行循 解析：7【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】模拟程序的运行，可得1S =，1i =满足条件4i <，执行循环体，2S =，2i =满足条件4i <，执行循环体，4S =，3i =满足条件4i <，执行循环体，7S =，4i =此时，不满足条件4i <，退出循环，输出S 的值为7．故答案为7．【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.18．【解析】阅读流程图可得该流程图计算的数值为：解析：【解析】阅读流程图可得，该流程图计算的数值为：sin 0sin 1sin 5262626S ππππππ⎛⎫⎛⎫⎛⎫=⨯++⨯+++⨯+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 19．【详解】试题分析：第一次运行条件成立；第二次运行条件成立；第三次运行条件成立；第四次运行条件不成立；输出故答案应填：1考点：算法及程序语言解析：1【详解】试题分析：第一次运行，5,4s n ==条件14s <成立；第二次运行，9,3s n ==条件14s <成立；第三次运行，12,2s n ==条件14s <成立；第四次运行，14,1s n ==条件14s <不成立；输出1n =，故答案应填：1．考点：算法及程序语言．20．4【分析】执行程序当时循环结束即可得出【详解】因为第一次进入循环后；第二次进入循环后；第三次进入循环后；第四次进入循环后循环结束所以输出的结果为4【点睛】本题主要考查了程序框图求输出的值做题时要仔细 解析：4【分析】执行程序，当4K =时循环结束，即可得出【详解】因为第一次进入循环后1,1S K ==；第二次进入循环后3,2S K ==；第三次进入循环后11,3S K ==；第四次进入循环后2059,4S K ==，循环结束，所以输出的结果为4【点睛】本题主要考查了程序框图求输出的值，做题时要仔细点，属于基础题．三、解答题21．221,02222,251(7)10,572x x y x x x x ⎧≤≤⎪⎪=-<≤⎨⎪⎪-+<<⎩，程序框图和程序见解析． 【分析】根据直线l 将梯形分割的左边部分的形状进行分类讨论，求出函数关系式，即可根据条件结构画出程序框图，并写出程序．【详解】过点A ，D 分别作AG ⊥BC ，DH ⊥BC ，垂足分别是G ，H .∵四边形ABCD 是等腰梯形，底角是45°，AB ＝2cm ，∴BG ＝AG ＝DH ＝HC ＝2 cm .又BC ＝7cm ，∴AD ＝GH ＝3cm ，当02x ≤≤时，212yx =； 当25x <≤时，22y x =-； 当57x <<时，21(7)102y x =-+， 所以221,02222,251(7)10,572x x y x x x x ⎧≤≤⎪⎪=-<≤⎨⎪⎪-+<<⎩ ． 程序框图如下：程序：INPUT “x ＝”；xIF x >＝0 AND x <＝2 THENy ＝0.5 *x ^2ELSEIF x <＝5 THENy ＝2*x -2ELSEy =-0.5*(x -7) ^2+10END IFEND IFPRINT yEND【点睛】本题主要考查分段函数解析式的求法、程序框图的画法以及程序语句的书写，意在考查学生分类讨论思想和算法语句的理解和书写．22．答案详见解析．【分析】分三步完成，先输入上下底和高，再计算面积S ，最后输出计算结果S.【详解】梯形面积S =12（上底+下底）×高， ∵梯形的两底边长分别为a ，b ，高为h ，∴程序算法如下：第一步：输入a ，b ，h 的值，第二步：计算S =()2a b h +， 第三步：输出S ，程序框图如下：【点睛】本题主要考查了算法及程序框图，属于中档题.23．（1）①m=0②i=i+1；（2）见解析【分析】（1）如果除以2的余数为零，则为偶数，故填0m =.i 每次增加1，故填1i i =+.（2）根据WHILE 型循环的结构，对原有程序进行改写.【详解】（1）①m=0②i=i+1（2）改写为WHILE 型循环程序如下：i=1WHILE i<=100m=I MOD 2IF m=0 THENPRINT iEND IFi=i+1WENDEND【点睛】本小题主要考查循环结构的两种编写程序的方法，属于基础题.24．见解析【分析】由条件可得函数为分段函数，这样就要进行判断，然后进行求解【详解】用变量x y ，分别表示自变量和函数值，步骤如下：第一步，输入x 的值第二步，判断x 的范围，若0x ≥，则用解析式21y x =-求函数值；否则，用225y x =-求函数值第三步，输出y 的值程序框图和程序如下．【点睛】本题考查的知识点是设计程序解决问题，由已知条件不难发现函数为分段函数，故需要进行对输入值的判定，然后再代入求解．25．见解析【解析】分析：挑最重的球需要把最重的一个球与其它都想比较，运用循环结构即可得出结果.详解：设六个小球的重量分别为ω1,ω2,…,ω6.算法如下:S1将1号球放在天平左边,2号球放在天平右边.S2比较两球的重量后,若两球一样重,则淘汰天平右边的球;若两球不一样重,则淘汰较轻的球,将较重的球放在天平左边.S3将下一号球放在天平右边比较重量,重复执行S2.S4最后留在天平左边的球是最重的球.程序框图如下图所示:点睛：本题的重点是掌握算法流程图书写的基本步骤，书写规范和方法，当需要解决的问题需要多次重复的相同的步骤时，实现算法需要通过循环结构来实现，在写算法和流程图时注意语言的表达要清晰，步骤要简洁完整.26．见解析【解析】试题分析：确定循环体为：S=S+i^2，i=i+10，再确定初始值和结束的条件即可试题程序如下:S=0;i=10;while i<=1000S=S+i^2;i=i+10;endprint(%io(2),S);程序框图如图所示:。

高一数学算法初步试题答案及解析1.我国《算经十书》之一《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二.问物几何？答曰：二十三.”你能用程序解决这个问题吗？【答案】见解析。

【解析】设物共m个，被3，5，7除所得的商分别为x、y、z，则这个问题相当于求不定方程的正整数解.m应同时满足下列三个条件：（1）m MOD 3=2；（2）m MOD 5=3；（3）m MOD 7=2.因此，可以让m从2开始检验，若3个条件中有任何一个不成立，则m递增1，一直到m同时满足三个条件为止.程序：m=2f=0WHILE f=0IF m MOD 3=2 AND m MOD 5=3AND m MOD 7=2 THENPRINT “物体的个数为：”；mf=1ELSEm=m+1END IFWENDEND【考点】本题主要考查算法的基本概念及算法的程序语言。

点评：经典题目。

在理解解方程组算理的基础上，首先用语言表示算法，再写出程序语言。

2.下面程序的运行结果不为4的【答案】C【解析】本题考查的是简单程序语言的运行。

A考查的是条件语句，由a←3，b←5得b＞a，应执行c←， Print c所以运行结果为4。

B考查的也是条件语句，由a←3，b←4得，应执行a←a+1，Print a所以运行结果为4。

C考查的是条件语句，由a←3，b←4得a≤b，应执行c←a+b，Print c运行结果为7。

故应选C。

【考点】程序中条件语句，赋值语句的运行。

点评：解决此类问题，先根据变量的初始值判断条件是否成立，然后再根据“是”和“否”分别执行的语句来计算运行结果。

3.设计一个解关于x的方程：ax+b=0的程序．图中给出了程序的一部分，请在横线上填上适当的语句，使程序完整．【答案】①：x= -；②：“方程无解”；③：“解为一切实数”【解析】根据题意要解关于x的方程应先判断a是否为0，如a≠0，则方程的根为所以①为；若，再判断把是否为0，若输b≠0，方程无解，②应为“方程无解”；若，则方程为，则“解为一切实数”。

算法初步本章达标测评(总分:150分;时间:120分钟)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面对算法的描述正确的一项是( )A.算法只能用自然语言来描述B.算法只能用图形语言来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同2.执行如图所示的框图,输入N=5,则输出S的值为( )A.54B.45C.65D.563.下面一段程序执行后的结果是( )A.6B.4C.8D.104.算式1 010(2)+10(2)的值是( )A.1 011(2)B.1 100(2)C.1 101(2)D.1 000(2)5.执行如图所示的程序框图,当输入的值为3时,输出的结果是( )A.3B.8C.12D.206.若如图所示的程序框图的功能是计算1×12×13×14×15的结果,则在空白的执行框中应该填入( )A.T=T·(i+1)B.T=T·iC.T=T·1i+1D.T=T·1i7.已知7 163=209×34+57,209=57×3+38,57=38×1+19,38=19×2.根据上述一系列等式,可确定7 163和209的最大公约数是( )A.57B.3C.19D.348.已知44(k)=36,则把67(k)转化成十进制数为( )A.8B.55C.56D.629.执行如图所示的程序框图,若输出的k=5,则输入的整数p的最大值为( )A.7B.15C.31D.6310.用秦九韶算法求多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4时的值时,其中v4的值为( )A.-57B.124C.-845D.22011.某程序框图如图所示,若该程序运行后输出的值是9,则( )5A.a=4B.a=5C.a=6D.a=712.执行如图所示的程序框图,则输出的n的值是( )A.29B.31C.61D.63二、填空题(本大题共4小题,每小题4分,共16分,把正确答案填在题中横线上)13.输入8,则下列程序运行后输出的结果是.化成十进制数,结果为,再将该结果化成七进制数,结14.将二进制数110 101(2)果为.15.执行如图所示的程序框图,则输出结果S= .16.阅读下面程序,当输入x的值为3时,输出y的值为.(其中e为自然对数的底数)三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(12分)下面给出一个用循环语句编写的程序:(1)指出程序所用的是何种循环语句,并指出该程序的算法功能;(2)请用另一种循环语句的形式把该程序写出来.18.(12分)输入10个数,找出其中最大的数并输出,画出程序框图,并写出程序.19.(12分)如图所示,在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动(不与A、B重合).设点P运动的路程为x,△APB的面积为y,求y与x之间的函数关系式,画出程序框图,写出程序.20.(12分)把区间[0,1]10等分,求函数y=√2x+1+|x-2|在各分点(包括区间端点)的函数值,写出程序.21.(12分)设计一个程序求11×4+13×6+15×8+…+199×102的值.22.(14分)“角谷猜想”是由日本学者角谷静夫首先提出的,所以称为“角谷猜想”.猜想的内容是:对于任意一个大于1的整数n,如果n 为偶数就除以2,如果n 是奇数,就将其乘3再加1,然后将得到的结果再进行以上处理,则最后结果总是1.试设计一个算法的程序框图,对任意输入的整数n(n≥2)进行检验,要求输出每一步的结果,直到结果为1时结束.附加题1.(2015河北石家庄一模,★★☆)执行下面的程序框图,如果输入的依次是1,2,4,8,则输出的S 为( )A.2B.2√2C.4D.62.(2015山西四校联考三,★★☆)执行如图的程序框图,则输出S 的值为( )D.-1 A.2 016 B.2 C.12一、选择题1.C 算法可以用自然语言、图形语言和程序语言来描述;同一个问题可以有不同的算法,但算法的结果相同.2.D 第一次循环,S=0+11×2=12,k=2;第二次循环,S=12+12×3=23,k=3;第三次循环,S=23+13×4=34,k=4;第四次循环,S=34+14×5=45,k=5;第五次循环,S=45+15×6=56,此时k=5不满足判断框内的条件,跳出循环,输出S=56,选D.3.A 由程序知a=2,2×2=4,4+2=6,故最后输出a 的值为6,故选A.4.B 1 010(2)+10(2)=(1×23+0×22+1×21+0×20)+(1×21+0×20)=12=1 100(2).5.B 3<5,执行y=x 2-1,所以输出结果为8.故选B.6.C 程序框图的功能是计算1×12×13×14×15的结果,依次验证选项可得选项C 正确. 7.C 由辗转相除法的思想可得结果. 8.B 由题意得,36=4×k 1+4×k 0,所以k=8. 则67(k)=67(8)=6×81+7×80=55.9.B 由程序框图可知:①S=0,k=1;②S=1,k=2;③S=3,k=3;④S=7,k=4;⑤S=15,k=5,输出k,此时S=15≥p,则p 的最大值为15,故选B. 10.D由已知,得a 0=12,a 1=35,a 2=-8,a 3=79,a 4=6,a 5=5,a 6=3,所以v 0=3,v 1=3×(-4)+5=-7,v 2=(-7)×(-4)+6=34,v 3=34×(-4)+79=-57,v 4=(-57)×(-4)-8=220.11.A 此程序框图的作用是计算S=1+11×2+12×3+…+1a (a+1)的值,由已知得S=95,即S=1+1-12+12-13+…+1a -1a+1=2-1a+1=95,解得a=4.12.D 开始:p=5,n=1;p=9,n=3;p=15,n=7;p=23,n=15;p=31,n=31;p=31,n=63,此时log 3163>1,结束循环,输出n=63. 二、填空题 13.答案 0.7解析 这是一个用条件语句编写的程序,由于输入的数据为8,8<-4不成立,所以c=0.2+0.1×(8-3)=0.7. 14.答案 53;104(7)解析 110 101(2)=1×25+1×24+0×23+1×22+0×21+1×20=53,然后用除7取余法得53=104.(7)15.答案 1 007解析根据程序框图知,S=(-1+2)+(-3+4)+…+(-2 013+2 014)=1 007,故输出的S的值为1 007.16.答案 1.5解析当输入x=3时,由于3>e,故执行y=0.5x,即y=0.5×3=1.5.三、解答题17.解析(1)本程序所用的循环语句是WHILE循环语句,其功能是计算12+22+32+…+92的值.(2)用UNTIL语句改写程序如下:18.解析程序框图如图.程序:19.解析 函数关系式为 y={2x (0<x ≤4),8(4<x ≤8),2(12-x )(8<x <12).程序框图如图所示:程序:20.解析把区间[0,1]10等分,故步长为0.1,∴用“x=x+0.1”表达,y=√2x+1+|x-2|,用“y=SQR(2*x+1)+ABS(x-2)”表达,循环控制条件x≤1.程序如下:21.解析程序:22.解析程序框图如图:附加题1.B 由程序框图可知,S=1,i=1;S=1,i=2;S=√2,i=3;S=2,i=4;S=2√2,i=5,此时跳出循环,输出S=2√2.故选B.2.B 循环前S=2,k=0,第一次循环,得S=11-2=-1,k=1;第二次循环,得S=11-(-1)=12,k=2;第三次循环,得S=11-12=2,k=3;……,由此可知S 的值的变化周期为3,又2 016=672×3,所以输出S 的值为2,故选B.。

描述：例题：高中数学必修3(人教A版)知识点总结含同步练习题及答案第一章 算法初步 1.1 算法与程序框图一、学习任务1. 了解算法的含义，了解算法的基本思想，能用自然语言描述解决具体问题的算法．2. 了解设计程序框图表达解决问题的过程，了解算法和程序语言的区别；了解程序框图的三种基本逻辑结构，会用程序框图表示简单的常见问题的算法．二、知识清单算法 程序框图三、知识讲解1.算法算法（algorithm）是指按照一定规则解决某一类问题的明确和有限的步骤 ．可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤，或者看成按照要求设计好的有限的确切的计算序列，并且这样的步骤或序列能够解决一类问题.描述算法可以有不同的方式．例如，可以用自然语言和数学语言加以描述，也可以借助形式语言（算法语言）给出精确的说明，也可以用框图直观地显示算法的全貌.算法的要求：(1)写出的算法，必须能解决一类问题，并且能重复使用；(2)算法过程要能一步一步执行，每一步执行的操作必须确切，不能含混不清，而且经过有限步后能得到结果.下列对算法的理解不正确的是（ ）A．一个算法应包含有限的步骤，而不能是无限的B．算法中的每一个步骤都应当是确定的，而不应当是含糊的、模棱两可的C．算法中的每一个步骤都应当是有效地执行，并得到确定的结果D．一个问题只能设计出一种算法解：D算法的有限性是指包含的步骤是有限的，故 A 正确；算法的确定性是指每一步都是确定的，故 B正确；算法的每一步都是确定的，且每一步都应有确定的结果，故 C 正确；对于同一个问题可以有不同的算法，故 D 错误．下列叙述能称为算法的的个数为（ ）描述：2.程序框图程序框图简称框图，是一种用程序框、流程线及文字说明来表示算法的图形．其中，起、止框是任何流程不可少的，表明程序的开始和结束．输入和输出框可用在算法中任何需要输入、输出的位置．算法中间要处理数据或计算，可分别写在不同的处理框内．一个算法步骤到另一个算法步骤用流程线连接．如果一个框图需要分开来画，要在断开处画上连接点，并标出连接的号码．①植树需要运苗、挖坑、栽苗、浇水这些步骤；②依次进行下列运算：，，，，；③从枣庄乘火车到徐州，从徐州乘飞机到广州；④ ；⑤求所有能被 整除的正整数，即 ．A． B． C． D．解：B①、②、③为算法．1+1=22+1=33+1=4⋯99+1=1003x >x +133,6,9,12,⋯2345写出解方程组的一个算法．解：方法一：代入消元法．　第一步，由 得 ；第二步，将 代入 ，得 ，解得 ；第三步，将 代入方程 ，得 ；第四步，得到方程组的解为 ．方法二：加减消元法．第一步，方程 两边同乘以 ，得 ；第二步，将第一步所得的方程与方程 作差，消去 ，得 ，解得 ；第三步，将 代入方程 ，得 ，解得 ；第四步，得到方程组的解为 ．{2x +y =74x +5y =112x +y =7y =7−2x y =7−2x 4x +5y =114x +5(7−2x )=11x =4x =4y =7−2x y =−1{x =4y =−12x +y =7510x +5y =354x +5y =11y 6x =24x =4x =42x +y =72×4+y =7y =−1{x =4y =−1例题：画程序框图的规则（1）使用标准的图形符号．（2）框图一般按从上到下、从左到右的方向画．（3）除判断框外，大多数流程图符号只有一个进入点和一个退出点．判断框是具有超过一个退出点的惟一符号．（4）判断框分两大类，一类判断框是“是”与“否”两分支的判断，而且有且仅有两个结果；另一类是多分支判断，有几种不同的结果．（5）在图形符号内描述的语言要非常简练清楚．算法的三种基本逻辑结构顺序结构：语句与语句之间，框与框之间按从上到下的顺序进行．条件分支结构：在一个算法中，经常会遇到一些条件的判断，算法的流程条件是否成立有不同的流向，条件结构就是处理这种过程的结构．循环结构：在一些算法中，经常会出现从某处开始，按照一定的条件反复执行某些步骤的情况，这就是循环结构．下列程序框图分别是解决什么问题的算法．解：（1）已知圆的半径，求圆的面积的算法．（2）求两个实数加法的算法．执行如图的程序框图，输出的 ______ ．解：T =30四、课后作业 （查看更多本章节同步练习题，请到快乐学）某程序框图如图所示，若输出的 ，则判断框内为（ ）A． B． C． D．解：AS =57k >4?k >5?k >6?k >7?已知函数 ，对每次输入的一个值，都得到相应的函数值，画出程序框图．解：f (x )={2x +3,3−x ,x 2x ⩾0x <0x答案：1. 关于算法的说法中，正确的是 A ．算法就是某个问题的解题过程B ．算法执行后可以产生不确定的结果C ．解决某类问题的算法不是唯一的D ．算法可以无限地操作下去不停止C()答案：解析：2. 下列运算不属于我们所讨论算法范畴的是 A ．已知圆的半径求圆的面积B ．随意抽 张扑克牌算到二十四点的可能性C ．已知坐标平面内两点求直线方程D ．加减乘除法运算法则B注意算法需按照一定的顺序进行．()4答案：解析：3. 执行如图所示的程序框图，如果输入的 ，则输出的 属于 ．A ．B ．C ．D ．D取 ，得输出的 ，即可判断．t ∈[−2,2]S ()[−6,−2][−5,−1][−4,5][−3,6]t =−2S =64. 某批发商按客户订单数额的大小分别给予不同的优惠折扣．计算客户应付货款的算法步骤如下： ：输入订单数额 （单位：件）；输入单价 （单位：元）；：若 ，则折扣率 ；若 ，则折扣率 ；若 ，则折扣率 ；若 ，则折扣率 ；：计算应付货款 （单位：元）；：输出应付货款 ．S 1x A S 2x <250d =0250⩽x <500d =0.05500⩽x <1000d =0.10x ⩾1000d =0.15S 3T =Ax (1−d )S 4T。

第九章算法初步、统计与统计案例第一节算法与程序框图[考纲传真]1．了解算法的含义，了解算法的思想． 2.理解程序框图的三种基本逻辑结构：顺序、条件、循环． 3.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义．1．算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．(2)应用：算法通常可以编成计算机程序，让计算机执行并解决问题．2．程序框图定义：程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形．3．三种基本逻辑结构及相应语句1．(夯基释疑)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)程序框图中的图形符号可以由个人来确定．( )(2)一个程序框图一定包含顺序结构，但不一定包含条件结构和循环结构．( ) (3)5＝x 是赋值语句．( )(4)输入语句可以同时给多个变量赋值．( )[解析] 图形符号不能个人确定，(1)不正确；赋值语句只能给变量赋值，(3)不正确． [答案] (1)× (2)√ (3)× (4)√2．(教材改编)根据给出的程序框图，计算f(－1)＋f(2)＝( )图9­1­1A ．0B ．1C ．2D ．4[解析] 输入－1，满足x≤0，所以f(－1)＝4×(－1)＝－4；输入2，不满足x≤0，所以f(2)＝22＝4，即f(－1)＋f(2)＝0.[答案]A3．运行如图所示的程序，可得A的输出值为( )A＝20A＝A*2－30PRINT AENDA．30 B．20 C．10 D．－10[解析]A＝20×2－30＝10.[答案]C4．(2014·天津高考)阅读下边的框图，运行相应的程序，输出S的值为________．图9­1­2[解析]S＝0，n＝3，S＝0＋(－2)3＝－8，n＝3－1＝2≤1不成立；故S＝－8＋(－2)2＝－4，n＝2－1＝1≤1成立．故输出S的值为－4.[答案]－45．(2014·福建高考改编)阅读如图9­1­3所示的程序框图，运行相应的程序，输出的n的值为________．图9­1­3[解析]当n＝1时，21>12；当n＝2时，22>22不成立，结束循环．因此输出n＝2.[答案] 2考向1程序框图的基本结构与应用【典例1】(1)执行下面的程序框图，如果输入的t∈[－1，3]，则输出的s属于( ) A．[－3，4] B．[－5，2]C．[－4，3] D．[－2，5]图9­1­4图9­1­5(2)(2014·浙江高考)若某程序框图如图9­1­5所示，当输入50时，则该程序运行后输出的结果是________．[解析] (1)由程序框图知s ＝⎩⎪⎨⎪⎧3t ，（t<1），4t －t 2，（t≥1），①当－1≤t<1时，－3≤s<3；②当1≤t≤3时，s ＝－(t －2)2＋4.∴3≤s≤4. 由①②知，s 的取值范围属于[－3，4]． (2)第一次循环，S ＝1，i ＝2； 第二次循环，S ＝4，i ＝3；第三次循环，S ＝2×4＋3＝11，i ＝4； 第四次循环，S ＝2×11＋4＝26，i ＝5；第五次循环，S ＝2×26＋5＝57，i ＝6，此时S>50，退出循环． 所以输出的结果i ＝6. [答案] (1)A (2)6 【规律方法】1．对条件结构，无论判断框中的条件是否成立，都只能执行两个分支中的一个，不能同时执行两个分支．2．利用循环结构表示算法，第一要确定是利用当型还是直到型循环结构；第二准确表示累计变量；第三要注意从哪一步开始循环．弄清进入或终止的循环条件、循环次数是做题的关键．【变式训练1】 (1)如图9­1­6所示的程序框图，运行相应的程序．若输入x 的值为1，则输出S 的值为________．图9­1­6(2)(2014·陕西高考)根据下边框图，对大于2的整数N，输出的数列的通项公式是( )图9­1­7A．a n＝2n B．a n＝2(n－1) C．a n＝2n D．a n＝2n－1[解析](1)第1次运行：x＝1，S＝0＋13＝1<50；第2次运行：x＝2，S＝1＋23＝9<50；第3次运行：x＝4，S＝9＋43＝73>50，满足S≥50，跳出循环．输出S＝73.(2)由程序框图可知第一次运行：i＝1，a1＝2，S＝2；第二次运行：i＝2，a2＝4，S＝4；第三次运行：i＝3.a3＝8，S＝8；第四次运行：i＝4，a4＝16，S＝16.故选C.[答案](1)73 (2)C考向2程序框图的识别与完善(高频考点)命题视角程序框图的识别与完善是高考命题的热点，主要以客观题的形式呈现．主要命题角度：(1)根据程序框图确定输出结果；(2)补充程序框图中判断框或执行框；(3)依据程序框图及运行结果求输入变量的初始值等．【典例2】 (1)如图9­1­8所示是计算某年级500名学生期末考试(满分为100分)及格率q 的程序框图，则图中空白框内应填入________．图9­1­8 图9­1­9(2)(2014·重庆高考)执行如图9­1­9所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是( )A ．s>12B ．s>35C ．s>710D ．s>45[思路点拨] (1)根据程序框图的功能，应确定及格率q 与及格人数M 之间的关系；(2)依次执行程序框图，根据输出结果确定判断框内的控制条件．[解析] (1)由判断框输出可知，M 表示及格人数，N 表示不及格人数， ∴及格率q ＝M M ＋N ，因此执行框为“q＝M M ＋N”．(2)第一次循环：s ＝1×910＝910，k ＝8，s ＝910应满足条件；第二次循环：s ＝910×89＝810，k ＝7，s ＝810应满足条件，排除选项D ；第三次循环：s ＝810×78＝710，k ＝6，故这时程序不再满足条件，结束循环，因此判断框中的条件为s>710.[答案] (1)q ＝MM ＋N(2)C 【通关锦囊】1．(1)第1题的关键在于理解程序框图的功能；(2)第2题要明确何时进入或退出循环体，以及累乘变量的变化．2．解答此类题目：(1)要明确程序框图的顺序结构，条件结构和循环结构；(2)理解程序框图的功能；(3)要按框图中的条件运行程序，按照题目的要求完成解答．【变式训练2】 (2015·潍坊质检)执行如图9­1­10所示的程序框图，若输出的S 是2 047，则判断框内应填写()图9­1­10A ．n ≤9？B ．n ≤10?C ．n ≥10?D ．n ≥11?[解析] 由程序框图的功能知，题目的实质是数列{2n}(n∈N )求和． ∵{2n }的首项为20＝1，公比为2.∴当n ＝9时，S ＝1＋2＋22＋…＋29＝1－2101－2＝1 023.当n ＝10时，S ＝1＋2＋22＋…＋210＝1－2111－2＝2 047.此时输出S ＝2 047，跳出循环，所以判断框的条件为n ≤9. [答案] A考向3 基本算法语句【典例3】 根据下列算法语句，当输入x 为60时，输出y 的值为( )A ．25B ．30C ．31D ．61[解析] 由题意，得y ＝⎩⎪⎨⎪⎧0.5x ，x ≤50，25＋0.6（x －50），x>50.当x ＝60时，y ＝25＋0.6×(60－50)＝31. ∴输出y 的值为31. [答案] C ,【规律方法】1．本题主要考查条件语句，输入与输出语句，要注意赋值语句一般格式中的“＝”不同于等式中的“＝”，其实质是计算“＝”右边表达式的值，并将该值赋给“＝”左边的变量．2．解决此类问题关键要理解各语句的含义，以及基本算法语句与算法结构的对应关系． 【变式训练3】 运行下面的程序时，WHILE 循环语句的执行次数是( )A ．3B ．4C ．18D ．19[解析] 0<20，1<20，2×2<20，5×5>20，程序结束， 故WHILE 循环语句共执行了3次． [答案] A掌握1条规律 每个算法结构都含有顺序结构，循环结构中必定包含一个条件结构，用于确定何时终止循环体．循环结构和条件结构都含有顺序结构．注意1个区别 当型循环与直到型循环的区别：直到型循环是“先循环，后判断，条件满足时终止循环”；当型循环是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．勿忘2点注意 1.赋值号左边只能是变量(不是表达式)，在一个赋值语句中只能给一个变量赋值． 2.利用循环结构表示算法，要明确是利用当型循环结构，还是直到型循环结构．要注意：(1)选择好累计变量；(2)弄清在哪一步开始循环，满足什么条件不再执行循环体．易错辨析之10程序框图中“变量”的含义理解不清致误(2014·课标全国卷Ⅰ)执行下面的程序框图，若输入的a ，b ，k 分别为1，2，3，则输出的M ＝( )图9­1­11A .203 B .72 C .165 D .158[错解] n ＝1，M ＝1＋12＝32，a ＝2，b ＝32；n ＝2，M ＝2＋23＝83，a ＝32，b ＝83；n ＝3，M ＝32＋38＝158，a ＝83，b ＝158；n ＝4，M ＝83＋815＝4815＝165，a ＝158，b ＝165，此时不满足条件，跳出循环，输出M ＝165.[答案] C 【智慧心语】错因分析：(1)循环变量n 与累加变量M 计算不对立，或混淆当型循环，误认为直到型循环结构，导致错解．(2)对循环体中各执行框的含义不清，错误赋值，错选A 或B .防范措施：(1)要分清是当型循环结构还是直到型循环结构；要理解循环结构中各变量的具体含义以及变化规律．具体求解时，把每次循环中各个变量的值对应起来，并要清楚的写下来，再根据条件判断是否结束循环．(2)在处理含有循环结构的算法问题时，关键是确定循环的次数，循环中有哪些变量，且每一次循环之后的变量S 、k 值都要被新的S 、k 值所替换．[正解] 第一次执行循环后：M ＝1＋12＝32，a ＝2，b ＝32，n ＝2；第二次执行循环后：M ＝2＋23＝83，a ＝32，b ＝83，n ＝3.第三次执行循环后：M ＝32＋38＝158，a ＝83，b ＝158，n ＝4.这时n ＝4，跳出循环．输出M 的值158.[答案] D【类题通关】 (2014·北京高考)当m ＝7，n ＝3时，执行如图9­1­12所示的程序框图，输出的S 值为( )图9­1­12A．7 B．42 C．210 D．840[解析]程序框图的执行过程如下：m＝7，n＝3时，m－n＋1＝5，k＝m＝7，S＝1，S＝1×7＝7；k＝k－1＝6＞5，S＝6×7＝42；k＝k－1＝5＝5，S＝5×42＝210；k＝k－1＝4＜5，输出S＝210.故选C.[答案]C课后限时自测[A级基础达标练]一、选择题1．(2014·课标全国卷Ⅱ)执行如图9­1­13所示的程序框图，如果输入的x，t均为2，则输出的S＝( )图9­1­13A ．4B ．5C ．6D ．7[解析] x ＝2，t ＝2，M ＝1，S ＝3，k ＝1. k ≤t ，M ＝11×2＝2，S ＝2＋3＝5，k ＝2；k ≤t ，M ＝22×2＝2，S ＝2＋5＝7，k ＝3；3>2，不满足条件，输出S ＝7. [答案] D2．(2014·湖南高考)执行如图9­1­14所示的程序框图，如果输入的t∈[－2，2]，则输出的S 属于( )图9­1­14A ．[－6，－2]B ．[－5，－1]C ．[－4，5]D ．[－3，6][解析] 由程序框图知，当0≤t≤2时，输出S ＝t －3，此时S∈[－3，－1]；当－2≤t<0时，执行t ＝2t 2＋1后1<t≤9，执行1<t≤9时，输出S ＝t －3，此时S∈(－2，6]．因此输出S 的值属于[－3，6]．[答案] D3．某程序框图如图9­1­15所示，若输出的结果S＝57，则判断框内应填入的条件是( )图9­1­15A．k＞4? B．k＞5? C．k＞6? D．k＞7?[解析]由程序框图可知，k＝1时，S＝1；k＝2时，S＝2×1＋2＝4；k＝3时，S＝2×4＋3＝11；k＝4时，S＝2×11＋4＝26；k＝5时，S＝2×26＋5＝57.[答案]A4．阅读如图9­1­16所示的程序框图，运行相应的程序，则输出S的值为( )图9­1­16A．8 B．18 C．26 D．80[解析]执行一次循环S＝2，n＝2；执行第二次循环：S＝2＋32－31＝8，n＝3；执行第3次循环：S＝8＋33－32＝26，n＝4；满足n≥4，故输出S＝26.[答案]C5．(2014·安徽高考)如图9­1­17所示，程序框图(算法流程图)的输出结果是( )图9­1­17A．34 B．55 C．78 D．89[解析]当输入x＝1，y＝1，执行z＝x＋y及z≤50，x＝y，y＝z后，x，y，z的值依次对应如下：x＝1，y＝1，z＝2；x＝1，y＝2，z＝3；x＝2，y＝3，z＝5；x＝3，y＝5，z＝8；x＝5，y＝8，z＝13；x＝8，y＝13，z＝21；x＝13，y＝21，z＝34；x＝21，y＝34，z＝55.由于55≤50不成立，故输出55.故选B.[答案]B二、填空题6．运行下列的程序，当输入a，b分别为2，3时，最后输出的m的值为________．[解析]∵a＝2，b＝3，满足a＜b，∴应把b值赋给m，∴m的值为3.[答案] 37．(2014·山东高考)执行如图9­1­18所示的程序框图，若输入的x的值为1，则输出的n的值为________．图9­1­18[解析]按照程序框图逐一执行．由x2－4x＋3≤0，解得1≤x≤3.当x＝1时，满足1≤x≤3，所以x＝1＋1＝2，n＝0＋1＝1；当x＝2时，满足1≤x≤3，所以x＝2＋1＝3，n＝1＋1＝2；当x＝3时，满足1≤x≤3, 所以x＝3＋1＝4，n＝2＋1＝3；当x＝4时，不满足1≤x≤3，所以输出n＝3.[答案] 38．(2015·临沂模拟)图9­1­19(1)是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到第14次的考试成绩依次记为A1，A2，…，A14.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是________．(1) (2)图9­1­19[解析]从算法流程图可知，该图表示统计成绩大于或等于90分的考试次数．由茎叶图可知输出的结果为10.[答案]10三、解答题9．某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表格所示：图9­1­20统计该6名队员在最近三场比赛中投进的三分球总数的程序框图如图9­1­20所示．(1)试在判断框内填上条件；(2)求输出的s的值．[解](1)依题意，程序框图是统计6名队员投进的三分球的总数．∴判断框内应填条件“i≤6？”．(2)6名队员投进的三分球数分别为a1，a2，a3，a4，a5，a6.故输出的s＝a1＋a2＋…＋a6.10．三月植树节，林业管理部门在植树前，为了保证树苗的质量，都会对树苗进行检测．现从甲，乙两种树苗中各抽测了10株树苗，量出它们的高度如下：(单位：厘米) 甲：37，21，31，20，29，19，32，23，25，33；乙：10，30，47，27，46，14，26，10，44，46.(1)画出两组数据的茎叶图，并根据茎叶图对甲，乙两种树苗的高度作比较，写出两个统计结论．(2)设抽测的10株甲种树苗高度平均值为x －，将这10株树苗的高度依次输入，按程序框图(如图9­1­21)进行运算，问输出的S 大小为多少？并说明S 的统计学意义．图9­1­21[解] (1)茎叶图如下：统计结论：①甲种树苗的平均高度小于乙种树苗的平均高度； ②甲种树苗比乙种树苗长得整齐；③甲种树苗的中位数为27，乙种树苗的中位数为28.5；④甲种树苗的高度基本上是对称的，而且大多数集中在均值附近．(任写两条即可) (2)x －＝27，S ＝35；S 表示10株甲种树苗高度的方差，是描述树苗高度离散程度的量．S 值越小，表示长得越整齐，S 值越大，表示长得越参差不齐．[B 级 能力提升练]1．(2015·济南质检)已知函数f(x)＝ax 3＋12x 2在x ＝－1处取得极大值，记g(x)＝1f ′（x ）.程序框图如图9­1­22所示，若输出的结果S>2 0142 015，则判断框中可以填入的关于n 的判断条件是( )图9­1­22A ．n ≤ 2 014?B ．n ≤2 015?C ．n>2 014?D ．n>2 015?[解析] 由题意得f′(x)＝3ax 2＋x ，由f′(－1)＝0得a ＝13，∴f ′(x)＝x 2＋x ，即g(x)＝1x 2＋x ＝1x （x ＋1）＝1x －1x ＋1. 由程序框图可知S ＝0＋g(1)＋g(2)＋…＋g(n)＝1－1n ＋1， 由1－1n ＋1>2 0142 015，得n>2 014. 因此条件应为n≤2 015? [答案] B2．执行如图9­1­23所示的程序框图，若输入n 的值为4，则输出s 的值为________．图9­1­23[解析] 第一步运算结果：s ＝1，i ＝2(i≤4成立)；第二步运算结果：s ＝2，i ＝3(i≤4成立)；第三步运算结果：s ＝4，i ＝4(i≤4成立)；第四步运算结果：s ＝7，i ＝5(i≤4不成立)，程序结束，故输出s 的值为7.[答案] 73．已知数列{a n }的各项均为正数，观察程序框图如图9­1­24所示，若k ＝5，k ＝10时，分别有S ＝511和S ＝1021，试求数列{a n }的通项公式．图9­1­24[解] 由程序框图可知，数列{a n }是等差数列，首项为a 1，公差为d. S i ＝1a 1a 2＋1a 2a 3＋…＋1a i a i ＋1＝1d (1a 1－1a 2＋1a 2－1a 3＋…＋1a i －1a i ＋1) ＝1d ⎝ ⎛⎭⎪⎫1a 1－1a i ＋1. 当k ＝5时，S ＝⎝ ⎛⎭⎪⎫1a 1－1a 61d ＝5a 1a 6＝511.∴a 1a 6＝11，即a 1(a 1＋5d)＝11；①当k ＝10时，S ＝⎝ ⎛⎭⎪⎫1a 1－1a 111d ＝10a 1a 11＝1021，∴a 1a 11＝21，即a 1(a 1＋10d)＝21，② 由①②联立，得a 1＝1，d ＝2， 因此a n ＝a 1＋(n －1)d ＝2n －1.第二节 随机抽样[考纲传真]1．理解随机抽样的必要性和重要性． 2.会用简单随机抽样方法从总体中抽取样本． 3.了解分层抽样和系统抽样方法．1．简单随机抽样(1)设一个总体含有N 个个体，从中逐个不放回地抽取n 个个体作为样本(n≤N)，如果每次抽取时总体内的各个个体被抽到的机会都相等，就把这种抽样方法叫做简单随机抽样．(2)常用简单随机抽样的方法：抽签法和随机数表法． 2．系统抽样的步骤假设要从容量为N 的总体中抽取容量为n 的样本． (1)先将总体的N 个个体编号．(2)确定分段间隔k ，对编号进行分段，当N n 是整数时，取k ＝N n ，当Nn 不是整数时，随机从总体中剔除余数．(3)在第1段用简单随机抽样确定第一个个体编号l(l≤k)． (4)按照一定的规则抽取样本， 3．分层抽样(1)定义：在抽样时，将总体分成互不交叉的层，然后按照一定的比例，从各层独立地抽取一定数量的个体，将各层取出的个体合在一起作为样本，这种抽样方法是分层抽样．(2)应用范围：总体是由差异明显的几个部分组成时．1．(夯基释疑)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)简单随机抽样是从总体中逐个不放回的抽取抽样．( ) (2)简单随机抽样每个个体被抽到的机会不一样，与先后有关．( ) (3)系统抽样在起始部分抽样时采用简单随机抽样．( )(4)分层抽样中，每个个体被抽到的可能性与层数及分层有关．( )[解析] 由简单随机抽样，系统抽样，分层抽样的意义，知(1)与(3)正确，(2)与(4)不正确．[答案] (1)√ (2)× (3)√ (4)×2．(2014·广东高考)为了解1 000名学生的学习情况，采用系统抽样的方法，从中抽取容量为40的样本，则分段的间隔为( )A ．50B ．40C ．25D ．20[解析] 根据系统抽样的特点可知分段间隔为1 00040＝25，故选C .[答案] C3．(2015·青岛调研)为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学，初中，高中三个学段学生的视力情况有较大差异，而男女视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是( )A ．简单随机抽样B ．按性别分层抽样C ．按学段分层抽样D ．系统抽样[解析] 由于三个学段学生的视力情况差别较大，故需按学段分层抽样． [答案] C4．(2014·湖南高考)对一个容量为N 的总体抽取容量为n 的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为p 1，p 2，p 3，则( )A ．p 1＝p 2<p 3B ．p 2＝p 3<p 1C ．p 1＝p 3<p 2D ．p 1＝p 2＝p 3[解析] 由于三种抽样过程中，每个个体被抽到的概率都是相等的，因此p 1＝p 2＝p 3. [答案] D5．某学校高一，高二，高三年级的学生人数之比为3∶3∶4，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取________名学生．[解析] 设应从高二年级抽取x 名学生，则x∶50＝3∶10.解得x ＝15. [答案] 15考向1简单随机抽样【典例1】(1)下列抽取样本的方式属于简单随机抽样的个数为( )①盒子里共有80个零件，从中选出5个零件进行质量检验．在抽样操作时，从中任意拿出一个零件进行质量检验后再把它放回盒子里．②从20件玩具中一次性抽取3件进行质量检验．③某班有56名同学，指定个子最高的5名同学参加学校组织的篮球赛．A．0 B．1 C．2 D．3(2)(2013·江西高考)总体由编号为01，02，…，19，20的20个个体组成，利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为( )A.08 B．07 C．02 D．01[解析](1)①②③中都不是简单随机抽样，这是因为：①是放回抽样，②中是“一次性”抽取，而不是“逐个”抽取，③中“指定个子最高的5名同学”，不存在随机性，不是等可能抽样．(2)由随机数表法的随机抽样的过程可知选出的5个个体是08，02，14，07，01，所以第5个个体的编号是01.[答案](1)A(2)D【规律方法】1．简单随机抽样是从含有N(有限)个个体的总体中，逐个不放回地抽取样本，且每次抽取时总体内的各个个体被抽到的机会都相等．2．(1)一个抽样试验能否用抽签法，关键看两点：一是制签是否方便；二是号签是否易搅匀，一般地，当总体容量和样本容量都较小时可用抽签法．(2)随机数表法适用于总体中个体数较多的情形：随机数表法的操作要点：编号，选起始数，读数，获取样本．【变式训练1】下列抽样试验中，适合用抽签法的有________．①从某厂生产的5 000件产品中抽取600件进行质量检测； ②从某厂生产的两箱(每箱18件)产品中抽取6件进行质量检验； ③从甲，乙两厂生产的两箱(每箱18件)产品中抽取6件进行质量检测； ④从某厂生产的5 000件产品中抽取10件进行质量检测． [解析] ①，④中总体的个体数较大，不适用抽签法．对于③中，甲，乙两厂的产品质量可能差别较大，不一定能够达到搅拌均匀的条件，不适宜用抽签法．②中为同厂的产品，且样本容量较小，可用抽签法． [答案] ②考向2 系统抽样及其应用【典例2】 (1)(2015·淄博调研)用系统抽样法要从160名学生中抽取容量为20的样本，将160名学生随机地从1～160编号，按编号顺序平均分成20组(1～8号，9～16号，…，153～160号)，若第16组抽出的号码为126，则第1组中用抽签的方法确定的号码是________．(2)(2013·陕西高考)某单位有840名职工，现采用系统抽样方法抽取42人做问卷调查，将840人按1，2，…，840随机编号，则抽取的42人中，编号落入区间[481，720]的人数为( )A ．11B ．12C ．13D ．14[解析] (1)设第1组抽取的号码为b ，由系统抽样则第n 组抽取的号码为8(n －1)＋b ， ∴8×(16－1)＋b ＝126，∴b ＝6， 故第1组抽取的号码为6.(2)抽样间隔为84042＝20.设在1，2，…，20中抽取号码x 0(x 0∈[1，20])，在[481，720]之间抽取的号码记为20k ＋x 0，则481≤20k＋x 0≤720，k ∈N *.∴24120≤k ＋x 020≤36.∵x 020∈⎣⎢⎡⎦⎥⎤120，1，∴k ＝24，25，26，…，35， ∴k 值共有35－24＋1＝12(个)，即所求人数为12. [答案] (1)6 (2)B 【规律方法】1．如果总体容量N 能被样本容量n 整除，则抽样间隔为k ＝Nn，否则，可随机地从总体中剔除余数，然后按系统抽样的方法抽样．特别注意，每个个体被抽到的机会均是n N.2．系统抽样中依次抽取的样本对应的号码就是一个等差数列，首项就是第1组所抽取样本的号码，公差为间隔数，根据等差数列的通项公式就可以确定每一组内所要抽取的样本号码．【变式训练2】 (2015·威海质检)采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为1，2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中，编号落入区间[1，450]的人做问卷A ，编号落入区间[451，750]的人做问卷B ，其余的人做问卷C .则抽到的人中，做问卷B 的人数为( )A ．7B ．9C ．10D ．15[解析] 由系统抽样知：抽取号码的间隔为96032＝30，∵第一组抽取的号码为9，∴抽取的第n 个号码为a n ，则a n ＝9＋30(n －1)， 由451≤a n ≤750，得151115≤n ≤25710，注意到n ∈N *，∴落入区间[451，750]的号码共10个， 因此做问卷B 的有10人． [答案] C考向3 分层抽样及应用(高频考点)命题视角 分层抽样是抽样方法考查的重点，主要以客观题的形式呈现，命题的主要角度：(1)求各层的个体容量；(2)根据某层的容量求总体容量；(3)分层抽样的简单应用．【典例3】 (1)(2015·日照联考)某工厂甲，乙，丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n 的样本进行调查，其中从丙车间的产品中抽取了3件，则n ＝( )A ．9B ．10C ．12D ．13(2)(2014·湖北高考)甲、乙两套设备生产的同类型产品共4 800件，采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测．若样本中有50件产品由甲设备生产，则乙设备生产的产品总数为________件．[思路点拨] (1)利用抽样比为定值，列方程求解；(2)利用分层抽样，先求出总体中甲设备生产的产品数量，再计算乙设备生产的产品数量．[解析] (1)依题意得360＝n120＋80＋60，故n ＝13.(2)由题设，抽样比为804 800＝160.设甲设备生产的产品为x 件， 则x60＝50，∴x ＝3 000. 故乙设备生产的产品总数为4 800－3 000＝1 800. [答案] (1)D (2)1 800 【通关锦囊】1．分层抽样中分多少层，如何分层要视具体情况而定，总的原则是：层内样本的差异要小，两层之间的样本差异要大，且互不重叠．2．为了保证每个个体被抽到的可能性是相同的，这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比，即n i ∶N i ＝n∶N.分层抽样的有关计算，转化为按比例列方程或算式求解．【变式训练3】 (1)某个年级有男生560人，女生420人，用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，则此样本中男生人数为________．(2)(2014·重庆高考)某中学有高中生3 500人，初中生1 500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n 的样本，已知从高中生中抽取70人，则n 为( )A ．100B ．150C ．200D ．250[解析] (1)抽样比为280560＋420＝280980＝27，所以样本中男生人数为560×27＝160.(2)法一：由题意可得70n －70＝3 5001 500，解得n ＝100.法二：由题意，抽样比为703 500＝150，总体容量为3 500＋1 500＝5 000，故n ＝5 000×150＝100.[答案] (1)160 (2)A掌握2条规律 1.三种抽样方法的共同点都是等概率抽样，即抽样过程中每个个体被抽到的概率相等，体现了这三种抽样方法的客观性和公平性．若样本容量为n ，总体容量为N ，每个个体被抽到的概率是nN. 2.系统抽样抽取的个体编号从小到大成等差数列．熟记3个范围 1.简单随机抽样：总体容量较少，尤其是样本容量较少． 2.系统抽样：适用于元素个数很多且均衡的总体． 3.分层抽样：适用于总体由差异明显的几部分组成的情形．勿忘3点注意 1.简单随机抽样中，易忽视样本是从总体中逐个抽取，是不放回抽样，且每个个体被抽到的概率相等． 2.系统抽样中，易忽视抽取的样本数也就是分段的段数，当Nn 不是整数时，注意剔除，剔除的个体是随机的． 3.分层抽样中，易忽视每层抽取的个体的比例是相同的．易错辨析之11 图表信息求解的误区(2014·广东高考改编)已知某地区中小学生人数和近视情况分别如图9­2­1①和图②所示．为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为________．图9­2­1[错解] 由图①知，样本容量为(2 000＋3 500＋4 500)×2%＝200， 根据图②知，高中学生的近视人数为200×50%＝100. 或根据图②知，高中近视人数为50人． 【智慧心语】错因分析：(1)误把样本容量200认为高中学生的样本数量，或将条形图中近视率误为近视人数．(2)不能从图表中提取有效信息，有的考生无从入手，或者未抓住分层抽样的特点：“各层抽取的个体数依各层个体之比来分配”而无法正确完成高中近视人数的计算求值．防范措施：(1)加强识图能力的培养，如本题中纵轴表示的近视率分别为10%，30%，50%.(2)理解分层抽样的概念，首先分层抽样是等概率抽样，因此，各层的抽样比应相等，可以利用这个等比关系计算求值．[正解] 易知，样本容量为(3 500＋4 500＋2 000)×2%＝200.又样本中高中学生共有2 000×2%＝40人．利用图②知，高中学生的近视率为50%.因此所抽样本中高中学生的近视人数为40×50%＝20人．[答案]200 20【类题通关】从某小学随机抽样100名学生，将他们的身高(单位：厘米)数据绘制成频率分布直方图(如图9­2­2所示)，由图中数据可知a＝________．若要从身高在[120，130)，[130，140)，[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140，150]内的学生中选取的人数应为________．图9­2­2[解析]∵0.005×10＋0.035×10＋a×10＋0.020×10＋0.010×10＝1，∴a＝0.030.设身高在[120，130)，[130，140)，[140，150]内的三组学生各有x，y，z人，则x100＝0.030×10，y100＝0.020×10，z100＝0.01×10.∴x＝30，y＝20，z＝10.由分层抽样的意义，抽样比为1830＋20＋10＝30%.因此从身高在[140，150]内的学生中选取10×30%＝3(人)．[答案](1)0.030 (2)3课后限时自测[A 级 基础达标练]一、选择题1．(2014·四川高考)在“世界读书日”前夕，为了了解某地5 000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析．在这个问题中，5 000名居民的阅读时间的全体是( )A ．总体B ．个体C ．样本的容量D ．从总体中抽取的一个样本[解析] 调查的目的是“了解某地5 000名居民某天的阅读时间”，所以“5 000名居民的阅读时间的全体”是调查的总体．[答案] A2．从2 007名学生中选取50名学生参加全国数学联赛，若采用下面的方法选取：先用简单随机抽样从2 007人中剔除7人，剩下的2 000人再按系统抽样的方法抽取，则每人入选的概率( )A ．不全相等B ．均不相等C ．都相等，且为502 007D ．都相等，且为140[解析] 从N 个个体中抽取M 个个体，每个个体被抽到的概率均为MN .[答案] C3．某学校有男，女学生各500名，为了解男，女学生在学习兴趣与业余爱好方面是否存在显著差异，拟从全体学生中抽取100名学生进行调查，则宜采用的抽样方法是( )A ．抽签法B ．随机数法C ．系统抽样法D ．分层抽样法[解析] 由于是调查男，女学生在学习兴趣与业余爱好方面是否存在差异，因此用分层抽样法．[答案] D4．(2015·潍坊一模)高三某班有学生56人，现将所有同学随机编号，用系统抽样的方。

第一章算法初步1.1算法与程序框图1.1.1算法的概念1．下面的结论正确的是【】A.一个程序的算法步骤是可逆的B.一个算法可以无止境地运算下去的C.完成一件事情的算法有且只有一种D.设计算法要本着简单方便的原则2．下面对算法描述正确的一项是【】A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同3．下面哪个不是算法的特征【】A.抽象性B.精确性C.有穷性D.唯一性4．算法的有穷性是指【】A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限D.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(10min)、听广播(8min)几个步骤,从下列选项中选最好的一种算法【】A.S1洗脸刷牙、S2刷水壶、S3烧水、S4泡面、S5吃饭、S6听广播B.S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5听广播C. S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭同时听广播D.S1吃饭同时听广播、S2泡面；S3烧水同时洗脸刷牙；S4刷水壶6.看下面的四段话,其中不是解决问题的算法是【】A.从济南到北京旅游,先坐火车,再坐飞机抵达B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.方程210x-=有两个实根D.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为157．写出求1+2+3+4+5+6+…+100的一个算法.可运用公式1+2+3+…+n=(1)2n n+直接计算.第一步______①_______；第二步_______②________；第三步输出计算的结果.8.写出1×2×3×4×5×6的一个算法.1．1．2 程序框图1．算法的三种基本结构是【】A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2．给出以下四个问题,①输入x, 输出它的相反数；②求面积为6的正方形的周长；③在三个不等实数,,a b c中，求一个数的最大数；④求函数1,0()2,0x xf xx x-≥⎧=⎨+<⎩的函数值。

新高中数学第一章算法初步1-1算法与程序框图1-1-1算法的概念课时作业新人教B版必修31.1.1算法的概念A级基础巩固一、选择题1．下列语句中是算法的是导学号 95064017( A )A．解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1B．吃饭C．做饭D．写作业[解析]选项A是解一元一次方程的具体步骤，故它是算法，而B、C、D是说的三个事实，不是算法．2．计算下列各式中的S值，能设计算法求解的是导学号 95064018( B )①S＝1＋2＋3＋ (100)②S＝1＋2＋3＋…＋100＋…；③S＝1＋2＋3＋…＋n(n≥1，且n∈N)．A．①②B．①③C．②D．②③[解析]由算法的确定性、有限性知选B．3．早上从起床到出门需要洗脸、刷牙(5 min)，刷水壶(2 min)，烧水(8 min)，泡面(3 min)，吃饭(10 min)，听广播(8 min)几个过程，下列选项中最好的一种算法是导学号 95064019( C )A．第一步，洗脸刷牙；第二步，刷水壶；第三步，烧水；第四步，泡面；第五步，吃饭；第六步，听广播B．第一步，刷水壶；第二步，烧水同时洗脸刷牙；第三步，泡面；第四步，吃饭；第五步，听广播C．第一步，刷水壶；第二步，烧水同时洗脸刷牙；第三步，泡面；第四步，吃饭同时听广播D．第一步，吃饭同时听广播；第二步，泡面；第三步，烧水同时洗脸刷牙；第四步，刷水壶[解析]因为A选项共用时36 min，B选项共有时31 min，C选项共用时23 min，选项D 的算法步骤不符合常理，所以最好的一种算法为C 选项．4．对于一般的二元一次方程组⎩⎪⎨⎪⎧a 1x ＋b 1y ＝c 1a 2x ＋b 2y ＝c 2，在写求此方程组解的算法时，需要我们注意的是导学号 95064020( C )A ．a 1≠0B ．a 2≠0C ．a 1b 2－a 2b 1≠0D ．a 1b 1－a 2b 2≠0[解析] 由二元一次方程组的公式算法即知C 正确． 5．下面是对高斯消去法的理解： ①它是解方程的一种方法； ②它只能用来解二元一次方程组； ③它可以用来解多元一次方程组；④用它来解方程组时，有些方程组的答案可能不准确． 其中正确的是导学号 95064021( A ) A ．①② B ．②④ C ．①③D ．②③[解析] 高斯消去法是只能用来解二元一次方程组的一种方法，故①②正确． 6．一个算法步骤如下： S1 S 取值0，i 取值2；S2 如果i ≤10，则执行S3，否则执行S6； S3 计算S ＋i 并将结果代替S ； S4 用i ＋2的值代替； S5 转去执行S2； S6 输出S .运行以上步骤输出的结果为导学号 95064022( B ) A ．25 B ．30 C ．35D ．40[解析] 按算法步骤一步一步地循环计算替换，该算法作用为求和S ＝2＋4＋6＋8＋10＝30.二、填空题7．已知直角三角形两条直角边长分别为a 、b ，求斜边长c 的算法如下：导学号 95064023S1 输入两直角边长a 、b 的值．S2 计算c＝a2＋b2的值；S3 ____________.将算法补充完整，横线处应填__输出斜边长c的值__．[解析]算法要有输出，故S3应为输出c的值．8．一个算法步骤如下：导学号 95064024S1 S取值0，i取值1；S2 如果i≤12，则执行S3，否则执行S6；S3 计算S＋i并将结果代替S；S4 用i＋3的值代替i；S5 转去执行S2；S6 输出S.运行以上步骤输出的结果为S＝__22__.[解析]由以上算法可知：S＝1＋4＋7＋10＝22.三、解答题9．某年青歌赛流行唱法个人组决赛中，某歌手以99.19分夺得金奖．青歌赛在计算选手最后得分时，要去掉所有评委对该选手所打分数中的最高分和最低分，试设计一个找出最高分的算法.导学号 95064025[解析]S1 先假定其中一个为“最高分”；S2 将第二个分数与“最高分”比较，如果它比“最高分”还高，就假定这个分数为“最高分”；否则“最高分”不变；S3 如果还有其他分数，重复S2；S4 一直到没有可比的分数为止，这时假定的“最高分”就是所有评委打分中的最高分．10．一个人带三只狼和三只羚羊过河，只有一条船，同船最多可容纳一个人和两只动物，没有人在的时候，如果狼的数量不少于羚羊的数量，狼就会吃掉羚羊．请设计过河的算法.导学号 95064026[解析]算法如下：S1 人带两只狼过河；S2 人自己返回；S3 人带一只羚羊过河；S4 人带两只狼返回；S5 人带两只羚羊过河；S6 人自己返回；S7 人带两只狼过河；S8 人自己返回；S9 人带一只狼过河．B级素养提升一、选择题1．算法：S1 输入n；S2 判断n是否是2.若n＝2，则n满足条件；若n>2，则执行S3；S3 依次从2到n－1检验能不能整除n，若不能整除n，则满足条件．上述满足条件的数是导学号 95064027( A )A．质数B．奇数C．偶数D．4的倍数[解析]根据算法可知，如果n＝2直接就是满足条件的数．n不是2时，验证从2到n －1有没有n的因数，如果没有就满足条件．显然，满足这个算法中条件的数是质数．故选A．2．现用若干张扑克牌进行扑克牌游戏．小明背对小亮，让小亮按下列四个步骤操作：第一步：分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；第二步：从左边一堆拿出两张，放入中间一堆；第三步：从右边一堆拿出一张，放入中间一堆；第四步：左边一堆有几张牌，就从中间一堆拿出几张牌放入左边一堆．这时，小明准确地说出了中间一堆牌现有的张数，你认为中间一堆牌的张数是导学号 95064028( B )A．4 B．5C．6 D．8[解析]按各放3张，可以算出答案是5，各放x张答案也是一样的．二、填空题3．下面算法运行后输出结果为__720__.导学号 95064029S1 设i＝1，P＝1；S2 如果i≤6则执行S3，否则执行S5；S3 计算P×i，并将结果代替P的值；S4 用i＋1的值代替i的值，转去执行S2；S5 输出P.[解析]该算法包含一个循环结构，计数变量i的初值为1，每次循环它的值增加1.由1变到6.P 是一个累乘变量，每一次循环得到一个新的结果，并用新的结果替代原值．第一次循环i ＝1，P ＝1.第二次循环i ＝2，P ＝2.第三次循环i ＝3，P ＝6.第四次循环i ＝4，P ＝24.第五次循环i ＝5，P ＝120.第六次循环i ＝6，P ＝720.4．下面是解决一个问题的算法：导学号 95064030 S1 输入x ；S2 若x ≥4，转到S3；否则转到S4； S3 输出2x －1； S4 输出x 2－2x ＋3.当输入x 的值为__1__输出的数值最小值为__2__.[解析] 所给算法解决的问题是求分段函数f (x )＝⎩⎪⎨⎪⎧2x －1 (x ≥4)x 2－2x ＋3 (x ＜4)的函数值的问题当x ≥4时，f (x )＝2x －1≥2×4－1＝7；当x ＜4时，f (x )＝x 2－2x ＋3＝(x －1)2＋2≥2.所以f (x )min ＝2，此时x ＝1.即当输入x 的值为1时，输出的数值最小，且最小值是2.三、解答题5．设计一个算法，求表面积为16π的球的体积. 导学号 95064031 [解析] S1 取S ＝16π； S2 计算R ＝S4π(由于S ＝4πR 2)；S3 计算V ＝43πR 3；S4 输出运算结果．6．设火车托运行李，当行李重量为m (kg)时，每千米的费用(单位：元)标准为y ＝⎩⎪⎨⎪⎧0.3m (m ≤30 kg )0.3×30＋0.5(m －30)(m >30 kg)，试写出当托运路程为S 千米时计算运费的算法.导学号 95064032[解析] 算法如下： S1 输入m ；S2 若m ≤30，则执行S3，若m >30，则执行S4； S3 输出0.3m ×S ；S4 输出[0.3×30＋0.5(m －30)]×S .C 级 能力拔高1．已知函数y ＝⎩⎪⎨⎪⎧2x－1(x ≤－1)log 2(x ＋1)(－1<x <2)x 2(x ≥2)，请设计一个算法，输入x 的值，求对应的函数值.导学号 95064033[解析] 算法如下： S1 输入x 的值；S2 当x ≤－1时，计算y ＝2x－1，否则执行S3； S3 当x <2时，计算y ＝log 2(x ＋1)，否则执行S4； S4 计算y ＝x 2； S5 输出y .2．试描述判断圆(x －x 0)2＋(y －y 0)2＝r 2和直线Ax ＋By ＋C ＝0的位置关系的算法.导学号 95064034[解析] S1 输入圆心的坐标(x 0，y 0)，直线方程的系数A ，B ，C 和半径r ； S2 计算z 1＝Ax 0＋By 0＋C ； S3 计算z 2＝A 2＋B 2； S4 计算d ＝|z 1|z 2；S5 如果d >r ，则相离；如果d ＝r ，则相切；如果d <r ，则相交．。

广州大学附中2013年创新设计高考数学二轮简易通全套课时检测：算法初步与框图本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．点)1,2,3(-M 关于面yoz 对称的点的坐标是( )A ．)1,2,3(--B ．)1,2,3(--C ．)1,2,3(-D ．)1,2,3(--- 【答案】A2．某几何体的三视图如图所示，则它的体积是( )A ．283π-B ．83π-C ．82π-D ．23π 【答案】A3．圆柱的一个底面积为S ，侧面展开图是一个正方形，那么这个圆柱的侧面积是( )A ．S πB ．S π2C ．S π4D ．S π332 【答案】C4．下面图形中是正方体展开图的是( )【答案】A5．下列命题中错误的是( )A ．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βB ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βC ．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l ，那么l ⊥平面γD ．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β 【答案】D6．给出下列命题：①有两个面平行，其余各面都是平行四边形所围成的几何体一定是棱柱； ②有一个面是多边形，其余各面都是三角形所围成的几何体是棱锥； ③用一个平行于棱锥底面的平面去截棱锥，得到的几何体叫棱台.以上命题中真命题的个数为( ) A ．0 B ．1C ．2D ．3【答案】A7．已知空间四边形OABC 中，，，===，点M 在OA 上，且OM=2MA ，N 为BC 中点，则=( ) A ．213221+- B ．212132++- C ．212121-+ D ．213232-+【答案】B8．一个三棱锥的正视图和侧视图及其尺寸如图所示，则该三棱锥俯视图的面积为( )123侧视图正视图A ．1B ．2C ．3D ．1或2【答案】D9．O 为空间任意一点，若818143++=，则A ，B ，C ，P 四点( ) A ．一定不共面 B ．一定共面C ．不一定共面D ．无法判断【答案】B10．已知空间四边形OABC 中，，，===，点M 在OA 上，且OM=2MA ，N 为BC 中点，则=( ) A ．213221+-B ．212132++-C ．212121-+D ．213232-+ 【答案】B11．已知△ABC 的三个顶点为A （3，3，2），B （4，－3，7），C （0，5，1），则BC 边上的中线长为( )A ．2B ．3C ．4D ．5 【答案】B12．如图是正方体的平面展开图，则在这个正方体中①BM ∥DE ②CN 与BE 是异面直线③CN 与BM 成600角 ④DM 与BN 是异面直线以上命题中，正确命题的序号是( )A ．①②③B ．②④C ．③④D ．②③④ 【答案】C第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．以正方体的顶点为顶点所构成的四棱锥和四面体的个数之差的绝对值是 。

1．1 算法与程序框图1．1.1算法的概念内容标准学科素养1。

通过回顾解二元一次方程组的方法，了解算法的思想。

2。

了解算法的含义和特征。

3.会用自然语言表述简单的算法。

提升数学运算发展逻辑推理应用数学抽象授课提示:对应学生用书第1页［基础认识]知识点一算法的概念预习教材P2－3,思考并完成以下问题一个大人和两个小孩一起渡河,渡口只有一条小船，每次只能渡1个大人或两个小孩，他们三人都会划船,但都不会游泳．（1)试问他们怎样渡过河去?提示：第一步,两个小孩同船过河去；第二步，一个小孩划船回来；第三步，一个大人划船过河去;第四步，对岸的小孩划船回来;第五步，两个小孩同船渡过河去．（2）设计的过河方法有什么特点？提示:由于船小，不能同时坐三个人，这样就需要遵循这一规则，然后按照一定的步骤一步一步的把三人运到河对岸．知识梳理在数学中，算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．现在,算法通常可以编成计算机程序，让计算机执行并解决问题．知识点二算法与计算机知识梳理计算机解决任何问题都要依赖于算法．只有将解决问题的过程分解为若干个明确的步骤,即算法，并用计算机能够接受的“语言”准确地描述出来，计算机才能够解决问题．思考：与一般的解决问题的过程相比，算法最重要的特征是什么？提示：最重要的特征是步骤的有序性、明确性和有限性．［自我检测］下列叙述不能称为算法的是(）A．从北京到上海先乘汽车到飞机场，再乘飞机到上海B．解方程4x＋1＝0的过程是先移项再把x的系数化成1C．利用公式S＝πr2计算半径为2的圆的面积得π×22D．解方程x2－2x＋1＝0解析：A、B两选项给出了解决问题的方法和步骤，是算法．C项，利用公式计算也属于算法．D项，只提出问题没有给出解决的方法，不是算法．答案：D授课提示：对应学生用书第2页探究一算法的概念［例1]下列关于算法的说法，正确的个数为(）①求解某一类问题的算法是唯一的；②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义或模糊；④算法执行后一定产生确定的结果．A．1B．2C．3 D．4［解析］由于算法具有有限性、确定性、输出性等特点,因而②③④正确，而解决某类问题的算法不一定唯一，从而①错．［答案］ C方法技巧1。

算法初步【学法导航】算法是高中数学课程中的新内容，本章的重点是算法的概念和算法的三种逻辑结构。

以选择题或填空题的形式出现，分值在5分左右，考察的热点是算法的概念【典例精析】1.自然语言表示的算法【内容解读】通过对解决具体问题过程与步骤的分析，体会算法的思想，理解算法的含义；对于某一问题往往能够设计出多种算法，通过选用步骤最少的、结构最好的算法【命题规律】以选择题或解答题的题型为主，难度不大。

例1、烧水泡茶需要洗刷茶具(5 min)、刷水壶(2 min)、烧水(8 min)、泡茶(2 min)等个步骤、从以下选项中选最好的一种算法( )（A）第一步：洗刷茶具；第二步：刷水壶；第三步：烧水；第四步：泡茶（B）第一步：刷水壶；第二步：洗刷茶具；第三步：烧水；第四步：泡茶（C）第一步：烧水；第二步：刷水壶；第三步：洗刷茶具；第四步：泡茶（D）第一步：烧水；第二步：烧水的同时洗刷茶具和刷水壶；第三步：泡茶解：烧水要8分钟，这时刚好刷茶具和水壶，可节省时间。

所以选（D）点评：一个问题的算法有多种，我们应该选择结构最好的算法。

例2、已知直角三角形的两直角边长分别为a b，，设计一个求该三角形周长的算法．解：由勾股定理，可求出斜边22=+++．l a b a bc a b=+，从而周长22算法步骤如下：第一步：输入实数a b，；第二步：计算22+的结果，并将这个结果赋给c；a b第三步：执行计算：l a b c=++；第四步：输出l．点评：用自然语言描绘算法，然后才能画出程序框图，写出程序。

所以，用自然描绘算法是程序设计的基础2.程序框图【内容解读】顺序结构、选择结构和循环结构是算法的三种基本逻辑结构．在画流程图时，首先要实行逻辑结构的选择，若求只含有一个关系式的解析式的函数的函数值时，只用顺序结构就能解决，顺序结构是任何一个算法中必不可少的结构．选择结构主要用在一些需要依据选择实行判断的算法中，如分段函数的求值、数据的大小关系比较等问题．循环结构主要用在一些有规律的重复计算的算法中，如累加求和、累乘求积等问题．用循环结构表达算法，关键要做好以下三点：①确定循环变量和初始值；②确定算法中反复执行的局部，即循环体；③确定循环的终止选择．循环结构又分为当型（Ｗhile型）和直到型（Until型）两种．当型循环在每次执行循环体前对控制循环的选择实行判断，当选择满足时执行循环体，不满足则停止；直到型循环在执行了一次循环体之后，对控制循环的选择实行判断，当选择不满足时执行循环体，满足则停止．两种循环仅仅实现循环的不同方法，它们是能够互相转换的．对同一个问题假如分别用当型循环和直到型循环来处理的话，那么两者判断的条件恰好相反．【命题规律】考查程序框图的知识经常出现在高考的选择题或填空题中，理解程序框图中，程序的流向，执行步骤。

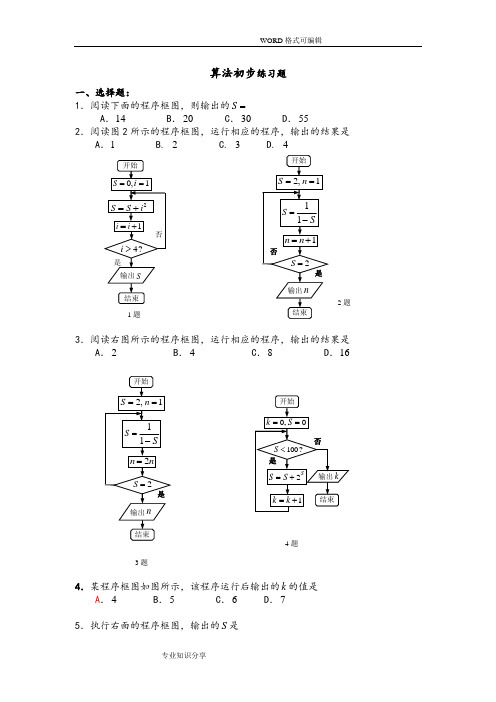
算法初步练习题一、选择题：1．阅读下面的程序框图，则输出的S =A ．14B ．20C ．30D ．552．阅读图2所示的程序框图，运行相应的程序，输出的结果是A ．1 B. 2 C. 3 D. 43．阅读右图所示的程序框图，运行相应的程序，输出的结果是A ．2B ．4C ．8D ．164．某程序框图如图所示，该程序运行后输出的k 的值是A ．4B ．5C ．6D ．75．执行右面的程序框图，输出的S 是3题 2题1题4题A ．378-B ．378C ．418-D ．4186．如图的程序框图表示的算法的功能是A ．计算小于100的奇数的连乘积B ．计算从1开始的连续奇数的连乘积C ．从1开始的连续奇数的连乘积，当乘积大于100时，计算奇数的个数D ．计算100531≥⨯⋅⋅⋅⨯⨯⨯n 时的最小的n 值.7．右图是把二进制数)2(11111化为十进制数的一个程序框图,判断框内应填入的 条件是 A ．4i > B ．4i ≤ C ．5i > D ．5i ≤8．某程序框图如图所示，则该程序运行后输出的B 等于 A ．15 B ．29 C ．31 D ．635题6题9．如果执行右边的程序框图，输入2,0.5x h =-=，那么输出的各个数的和等于 A ．3 B ．3.5 C ．4 D ．4.510．某店一个月的收入和支出总共记录了N 个数据1a ，2,,N a a ⋅⋅⋅，其中 收入记为 正数，支出记为负数。

该店用右边的程序框图计算月总收入S 和月 净盈利V ，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中 的A ．0,A V S T >=-B ．0,A V S T <=-C ．0,A V S T >=+D ．0,A V S T <=+ 11. 如图1所示，是关于闰年的流程，则 以下年份是闰年的为A ．1996年B ．1998年C ．2010年D ．2100年12. 某流程如右上图所示，现输入如下四个函数，则可以输出的函数是11题A ．2)(x x f =B ．xx f 1)(=C ．62ln )(-+=x x x fD ．x x f sin )(=二、填空题：13．程序框图（即算法流程图）如图所示，其输出结果是_______. 14．执行右边的程序框图，输出的T = .14题12题13题15．下面的程序框图表示的算法的结果是 1616．阅读右上面的流程图，若输入6,1a b ==，则输出的结果是 217右面的程序框图，如果输入三个实数a ，b ，c ，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的 ①c x > ②x c > ③C ．c b > ④b c >15题三、解答题：18．已知数列{a n }的各项均为正数，观察程序框图，若10,5==k k 时，分别有2110115==S S 和 （1）试求数列{a n }的通项； （2）令m a n b b b b n +++=...,221求的值.参考答案1．C ．【解读与点评】当1=i 时， S =1;当i =2时， S =5;循环下去，当i =3时， S =14； 当i =4时,S =30；本试题考查了程序框图的运用．2．D 【解读与点评】本题考查是算法的重新框图与算法的语句识别．易错点是 不懂得运行顺序．当1,2n S ==代入程序中运行第一次是1S =-，然后赋值此时2n =；返回运 行第二次可得111(1)2S ==--，然后赋值3n =； 再返回运行第三次可得12112S ==-，然后赋值4n =，判断可知此时2S =，故输出4n =．故选D ．3．C 【解读与点评】本题考查是算法的重新框图与算法的语句识别．考查学生 运算求解能力．本题的易错点是要注意是先赋值再输出．当1,2n S ==代入程序中运行第一次是1S =-，然后赋值此时2n =；返回运 行第二次可得111(1)2S ==--，然后赋值4n =； 再返回运行第三次可得12112S ==-，然后赋值8n =，判断可知此时2S =，故输出8n =．4．A ．【解读与点评】对于0,1,k s ==1k ∴=.对于1,3,2k s k ==∴=，则2,38,3k s k ==+∴=，后面是113,382,4k s k ==++∴=，不符合条件时输出 的4k =．此题是新课程新增内容，考查了程序语言的概念和基本的应用，通 过对程序语言的考查，充分体现了数学程序语言中循环语言的关键． 9．B ．【解读与点评】循环9次，对应输出值如下表。

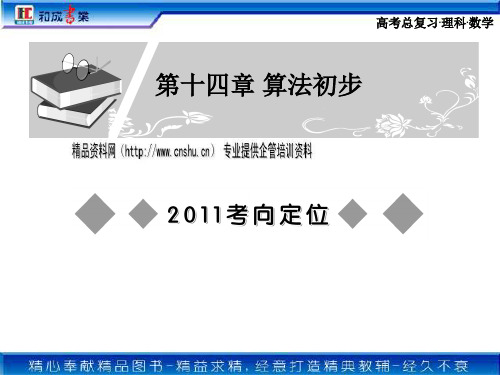
高中数学-算法初步测试练习题1. 下列说法正确的是（）A.算法就是某个问题的解题过程B.算法执行后可以产生不同的结果C.解决某一个具体问题算法不同结果不同D.算法执行步骤的次数不可以为很大，否则无法实施2. 将两个数a=2，b=−6交换，使a=−6，b=2，下列语句正确的是（）A.a=b，b=aB.c=a，a=b，b=cC.b=a，a=bD.a=c，c=b，b=a3. 算法：S1m=aS2若b<m，则m=bS3若c<m，则m=cS4若d<m，则m=dS5输出m，则输出m表示（）A.a，b，c，d中最大值B.a，b，c，d中最小值C.将a，b，c，d由小到大排序D.将a，b，c，d由大到小排序4. 观察下列各式：，则的末四位数为（）A.3125B.5624C.0625D.81255. 给出下列问题：(1)求面积为1的正三角形的周长；(2)求键盘所输入的三个数的算术平均数；(3)求键盘所输入两个数的最小数；(4)求函数f(x)={2xx2(x≥3)(x<3)当自变量取相应值时的函数值．其中不需要用条件语句描述的算法的问题有（）A.1个B.2个C.3个D.4个6. 执行如下的程序框图，则输出的结果是（）A.1 132B.833C.1112D.147. 阅读如图所示的程序框图，若输入m=2020，则输出S为()A.20202B.10092C.10102D.101128. 某程序的框图如图所示，若执行该程序，输出的S值为( )A.45B.36C.25D.169. 图中程序是计算2+3+4+5+6的值的程序．在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是（）A.①i>1②i=i−1B.①i>1②i=i+1C.①i>=1②i=i+1D.①i>=1②i=i−110. 如图，程序运行后输出的结果为（）A.3B.5C.2D.011. 下面的流程图中，能实现数据A，B互相交换的有________．（要求把符合条件的图形序号全填上）12. 用辗转相除法求324和243的最大公约数为________．13. 下列给出的几个式子中，正确的赋值语句是（填序号）________．①3←A；②M←−M；③B←A←2；④x+y←0．14. 已知一个学生的语文成绩为89，数学成绩为96，外语成绩为99．求他的总分和平均成绩的一个算法为：第一步：取A=89，B=96，C=99；第二步：________；第三步：________；第四步：输出计算的结果．15. 用秦九韶算法计算多项式f(x)=1+8x+7x2+5x4+4x5+3x6在x=5时所对应的v4的值为________．16. 用辗转相除法求294和84的最大公约数时，需要做除法的次数是________．17. 写出下列语句的运行结果：输入aif a<0tℎen输出“是负数”else t=√a输出ta=−4，输出结果为________，a=9，输出结果为________．18. 阅读程序框图，则输出的S=________．19. 若二进制数100y011和八进制数x03相等，则x+y=________．20. 用秦九韶算法求多项式f(x)=4x5+2x4−3x2+1，当x=3时，v3=________．21. 某居民区的物业管理部门每月向居民收取卫生费，计费方法如下：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出1人加收1.2元．设计一个算法，根据输入的人数，计算应收取的卫生费只需画出程序框图即可．22. 在程序语言中，下列符号分别表示什么运算*；\；∧；SQR；ABS？23. 执行如图所示的伪代码，则输出的S值为________.24. x的取值范围为[0, 10]，给出如图所示程序框图，输入一个数x．求：（1）输出的x(x<6)的概率；（2）输出的x(6<x≤8)的概率．25. 已知10b1（2）=a02（3），求数字a，b的值．参考答案与试题解析高中数学-算法初步测试练习题一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】B【考点】算法的概念【解析】广义的算法是指完成某项工作的方法和步骤，那么我们可以说洗衣机的使用说明书是操作洗衣机的算法，菜谱是做菜的算法等等．在数学中，现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成，根据算法的定义进行逐一判定即可．【解答】解：选项A，算法不能等同于解法，故不正确；选项B，判断一个整数是否为偶数，结果为“是偶数”和“不是偶数”两种，故正确；选项C，解决某一个具体问题算法不同结果应该相同，否则算法构造得有问题，故不正确；选项D，算法可以为很多次，但不可以无限次，故不正确.故选B.2.【答案】B【考点】赋值语句【解析】要实现两个变量a，b值的交换，需要借助中间量c，先把a的值赋给中间变量c，这样c=2，再把b的值赋给变量a，这样a=−6，把c的值赋给变量b，这样a=2．问题解决．【解答】解：先把a的值赋给中间变量c，这样c=a，再把b的值赋给变量a，把c的值赋给变量b，故选：B3.【答案】B【考点】算法的概念【解析】逐步分析算法图中的各语句的功能，第二步条件结构是比较a，b的大小，并将a，b中的较小值保存在变量m中，第三步条件结构是比较m，c的大小，并将m，c中的较小值保存在变量m中，第四步条件结构是比较m，d的大小，并将m，d中的较小值保存在变量m中，故变量m的值最终为a，b，c中的最小值．由此不难推断程序的功能．【解答】解：逐步分析框图中的各框语句的功能，第二步条件结构是比较a，b的大小，并将a，b中的较小值保存在变量m中，→第三步条件结构是比较m，c的大小，并将m，c中的较小值保存在变量m中，→第四步条件结构是比较m，d的大小，并将m，d中的较小值保存在变量m中，故变量m的值最终为a，b，c中的最小值．由此程序的功能为求a，b，c三个数的最小数．故选B4.【答案】C【考点】进位制排序问题与算法的多样性用辗转相除计算最大公约数【解析】由54=3125,54=15.5=78.53=390625,55=195312510=97676.562…可以看出这些幂的最后四位是以4为周期进行变化的，因此52016的末四位数0625，故选C．【解答】此题暂无解答5.【答案】B【考点】条件语句算法的概念【解析】由于条件语句适用于不同前提条件下不同处理方式的问题的解决，可依次对四个问题进行分析找出具有不同前提条件下不同处理方式这一特征的问题，即可得到正确选项【解答】解：(1)求面积为1的正三角形的周长用顺序结构即可，故不需要用条件语句描述；(2)求键盘所输入的三个数的算术平均数用顺序结构即可解决问题，不需要用条件语句描述；(3)求键盘所输入两个数的最小数，由于要作出判断，找出最小数，故本问题的解决要用到条件语句描述；(4)求函数f(x)={2xx2(x≥3)(x<3)当自变量取相应值时的函数值，由于此函数是一个分段函数，所以要用条件结构选择相应的函数解析式，需要用条件语句描述．综上，(3)(4)两个问题要用到条件语句描述，(1)，(2)不需要用条件语句描述故选B6.【答案】C程序框图循环结构的应用【解析】此题暂无解析【解答】解：开始：T=0，S=0，n=1：T=2，S=12=1−12；n=2：T=2×3，S=12+12×3=12+12−13=1−13；n=3：T=3×4，S=12+12×3+13×4=12+12−13+13−14=1−14；…n=11：T=11×12，S=1−112，此时满足n>10，跳出循环结构，输出S=1112.故选C.7.【答案】D【考点】程序框图【解析】此题暂无解析【解答】解：当输入m=2020时，执行第1次循环，S=1，i<m，i=1+2=3，执行第2次循环，S=1+3=4，i<m，i=3+2=5，执行第3次循环，S=4+5=9，i<m，i=5+2=7，⋯由此可得，当i>m时，i=2021，此时S=0+1+3+⋯+2021=1011(1+2021)2=10112.故选D.8.【答案】D【考点】程序框图【解析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．解：由题意模拟程序的运行，可得k=1,s=0，满足条件k≤8，执行循环体，S=1，k=3；满足条件k≤8，执行循环体，S=4，k=5；满足条件k≤8，执行循环体，S=9，k=7；满足条件k≤8，执行循环体，S=16，k=9;此时，不满足条件k≤8，退出循环，输出S的值为16.故选D．9.【答案】A【考点】循环语句【解析】根据流程图所表示的算法功能可知求2+3+4+5+6的和，从而应该利用累积加的表达式，以及数i是逐一减小的，可得处理框应填的内容．【解答】解：程序框图是计算2+3+4+5+6的和则第一个处理框应为i>1，i是减小1个，i=i−1从而答案为：①i>1②i=i−1．故选A．10.【答案】A【考点】输入、输出语句【解析】分析已知中程序的语句及结构，我们易得本程序的功能是利用循环判断2∼12中，4的倍数的个数，根据约束的定义，即可求出答案．【解答】解：根据伪代码所示的顺序，逐框分析程序中各变量、各语句的作用可知：该程序的作用是利用循环判断2∼12中，4的倍数的个数，由于2∼12中，4的倍数有4，8，12三个故选A．二、填空题（本题共计 10 小题，每题 3 分，共计30分）11.【答案】①②③【考点】顺序结构的应用【解析】对三个图形的运算过程进行分析，根据运行的顺序检验运算的结果，可判断出正确结果【解答】解：①中引入了一个中间量，先把A记入C，再把B赋给A，然后把C赋给B，实现数据交换；②先把两者的和记到A 里，再用和减去B 赋给B ，此过程把A 记到B 中了，再计算A −B ，此时差为原来的B ，将其赋给A ，可以实现数据交换；③同理可得，③也可以实现数据交换，故①②③都正确故答案为①②③12.【答案】81【考点】辗转相除法【解析】用较大的数字除以较小的数字，得到商和余数，然后再用上一式中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约数．【解答】解：∵ 324÷243=1⋯⋯81，243÷81=3，∴ 324和243的最大公约数是81.故答案为：81.13.【答案】②【考点】赋值语句【解析】根据赋值语句的功能和格式，逐一分析四个答案中四个赋值语句，根据赋值号左边只能是变量，右边可以是任意表达式，即可得到答案．【解答】解：赋值号的左边是常量，故①错误；赋值语句不能连续赋值，故③错误；x +y =0中，赋值号的左边是表达式，故④错误；只有②是正确的赋值语句，故答案为：②14.【答案】S =A +B +C ,x ¯=A+B+C 3【考点】算法的概念【解析】由题意，第二步，求和，第三步，计算平均成绩．【解答】解：由题意，第二步，求和S =A +B +C ，第三步，计算平均成绩x ¯=A+B+C 3． 故答案为：S =A +B +C ；x ¯=A+B+C 3．15.【答案】2507【考点】秦九韶算法【解析】首先把一个n次多项式f(x)写成(…（(a[n]x+a[n−1])x+a[n−2]）x+...+a[1]）x+ a[0]的形式，然后化简，求n次多项式f(x)的值就转化为求n个一次多项式的值，求出V4的值．【解答】解：∵f(x)=1+8x+7x2+5x4+4x5+3x612+35x−8x2+79x3+6x4+5x5+3x6=(（（（(3x+4)x+5）x+0）x+7）x+8)x+1，∴v0=a6=3，x=5时，v1=v0x+a5=3×5+4=19，v2=v1x+a4=19×5+5=100，v3=v2x+a3=100×5+0=500，v4=v3x+a4=500×5+7=2507∴V4的值为2507；故答案为：2507．16.【答案】2【考点】用辗转相除计算最大公约数辗转相除法【解析】用大数除以小数，得到商和余数，再用上面的除数除以余数，又得到商和余数，继续做下去，知道刚好能够整除为止，得到两个数的最大公约数，从而得到需要做除法的次数．【解答】解：∵294÷84=3...42，84÷42=2，∴用辗转相除法求294和84的最大公约数时，需要做除法的次数2．故答案为217.【答案】负数,3【考点】条件语句输入、输出语句【解析】根据所给的语句看出运行结果的表达式，根据所写的表达式在两种不同的情况下分别求解，得到结果．【解答】解：由语句可知，这是一个条件语句，对应的输出运行结果的表达式是t ={负数，a <0√a ，a ≥0当输入的值是−4时，选择代入的表达式，输出结果为负数当输入的值是9时，选择代入的表达式，输出结果为√9=3故答案为：负数；3．18.【答案】40【考点】循环结构的应用【解析】写出前5次循环的结果，判断出各次得到的结果是否满足判断框中的条件，直到满足判断框中的条件执行输出结果．【解答】解：经过第一次循环得到的结果为T =2，S =2，i =2，不满足判断框中的条件，执行“否”经过第二次循环得到的结果为T =5，S =7，i =3，不满足判断框中的条件，执行“否” 经过第三次循环得到的结果为T =8，S =15，i =4，不满足判断框中的条件，执行“否”经经过第四次循环得到的结果为T =11，S =26，i =5，不满足判断框中的条件，执行“否”过第五次循环得到的结果为T =14，S =40，i =6，满足判断框中的条件，执行“是”，输出40．故答案为：40．19.【答案】1【考点】进位制【解析】将二进制、八进制转化为十进制，利用两数相等及进制数的性质，即可解得x ，y 的值，从而得解．【解答】解：∵ 100y011（2）=1+1×21+y ×23+1×26=67+8y ，x03（8）=3+x ×82=3+64x ，∴ 由3+64x =67+8y ，解得：8+y =8x ，∵ y ∈{0, 1}，x ∈{0, 1, 2, 3, 4, 5, 6, 7, }，∴ 解得：x =1，y =0．x +y =1．故答案为：1．20.【答案】【考点】秦九韶算法【解析】此题暂无解析【解答】此题暂无解答三、解答题（本题共计 5 小题，每题 10 分，共计50分）21.【答案】解：依题意得，费用y与人数n之间的关系为：y={5(n≤3)5+1.2(n−3)(n>3)．程序框图如图所示：【考点】程序框图的三种基本逻辑结构的应用【解析】本题考查的知识点是设计程序框图解决实际问题，我们根据题目已知中应收取的卫生费计费方法，然后可根据分类标准，设置两个判断框的并设置出判断框中的条件，再由各段的输出，确定判断框的“是”与“否”分支对应的操作，由此即可画出流程图，再编写满足题意的程序．【解答】解：依题意得，费用y与人数n之间的关系为：y={5(n≤3)5+1.2(n−3)(n>3)．程序框图如图所示：22.【答案】解：“*”表示乘法运算；“\”表示除法运算；“∧”表示乘方运算；“SQR()”表示求算术平方根运算；“ABS()”表示求绝对值运算．【考点】输入、输出语句【解析】由程序语句中各种运算符表示的意义对题目中的各运算符逐一进行判断，即可得到答案．【解答】解：“*”表示乘法运算；“\”表示除法运算；“∧”表示乘方运算；“SQR()”表示求算术平方根运算；“ABS()”表示求绝对值运算．23.【答案】30【考点】伪代码（算法语句）【解析】此题暂无解析【解答】解：模拟程序的运行过程如下：i=1，S=2；S=2，i=3；S=6，i=5；S=30，i=7；此时不满足循环条件，故输出S=30.故答案为：30.24.【答案】解：（1）由已知中的程序框图可得该程序的功能是计算并输出分段函数y ={x −1,x >7x +1,x ≤7的值， 当x <6时，输出x +1，此时输出的结果满足x +1<6，所以x <5，所以输出的x(x <6)的概率为5−010−0=12；（2）当x ≤7时，输出x +1，此时输出的结果满足6<x +1≤8解得5<x ≤7；当x >7时，输出x −1，此时输出的结果满足6<x −1≤8解得7<x ≤9；综上，输出的x 的范围中5<x ≤9．则使得输出的x 满足6<x ≤8的概率为9−510=25．【考点】程序框图【解析】（1）由已知中的程序框图，我们根据选择结构的功能，可能分析出程序的功能是计算并输出分段函数y ={x −1,x >7x +1,x ≤7的值，输出的x(x <6)，可得x <5，即可求出输出的x(x <6)的概率；（2）由输出的结果在区间6<x ≤8上，我们可以分当x ≤7时和x >7时两种情况，分别讨论满足条件的x 的取值范围，得到输出结果的范围，最后根据输入x 的取值范围利用几何概型求出概率即可．【解答】解：（1）由已知中的程序框图可得该程序的功能是计算并输出分段函数y ={x −1,x >7x +1,x ≤7的值， 当x <6时，输出x +1，此时输出的结果满足x +1<6，所以x <5，所以输出的x(x <6)的概率为5−010−0=12；（2）当x ≤7时，输出x +1，此时输出的结果满足6<x +1≤8解得5<x ≤7；当x >7时，输出x −1，此时输出的结果满足6<x −1≤8解得7<x ≤9；综上，输出的x 的范围中5<x ≤9．则使得输出的x 满足6<x ≤8的概率为9−510=25．25.【答案】解：10b1（2）=1×20+b ×21+0×22+1×23=9+2b ．a02（3）=2×30+0×31+a×32=9a+2，∵10b1（2）=a02（3），b∈{0, 1}，a∈{0, 1, 2}，且9+2b=9a+2∴a=b=1．【考点】进位制【解析】把两个数都化为10进制，即可求出结果．【解答】解：10b1（2）=1×20+b×21+0×22+1×23=9+2b．a02（3）=2×30+0×31+a×32=9a+2，∵10b1（2）=a02（3），b∈{0, 1}，a∈{0, 1, 2}，且9+2b=9a+2∴a=b=1．。

专题十二算法初步探考情悟真题【真题探秘】【考情探究】考点内容解读5年考情预测热度考题示例考向关联考点程序框图与算法语句(1)了解算法的含义和思想.(2)理解程序框图的三种基本逻辑结构:顺序结构、条件结构、循环结构.(3)理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义2019课标Ⅰ,8,5分补全程序框图★★★2018课标Ⅱ,7,5分补全程序框图数列2017课标Ⅰ,8,5分补全程序框图2016课标Ⅰ,9,5分2015课标Ⅰ,9,5分求循环结构的输出值2017课标Ⅲ,7,5分求循环结构的输入值2015课标Ⅱ,8,5分条件结构的程序框图分析解读从近五年的考查情况来看,本专题内容一般以选择题、填空题的形式出现,分值为5分,难度中等偏下.主要的命题角度有条件结构与分段函数相结合,求循环结构的输入值、输出值,补全程序框图等.考查学生的数学运算能力和逻辑推理能力.破考点练考向【考点集训】考点程序框图与算法语句1.(2020届陕西百校联盟九月联考,8)《九章算术》卷七——盈不足中有如下问题:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”翻译为:现有几个人一起买羊,若每人出五钱,还差四十五钱,若每人出七钱,还差三钱,问人数、羊价分别是多少?为了研究该问题,设置了如图所示的程序框图,若要输出人数和羊价,则判断框中应该填()第1题图A.k>20B.k>21C.k>22D.k>23答案A2.(2020届河南南阳中学第二次考试,6)执行如图所示的程序框图,如果输入的n=6,那么输出的S=()A.167B.168C.104D.105答案B3.(2019福建泉州1月单科质检,6)执行如图所示的程序框图,若输入的x∈[-2,1],则输出的y的取值范围是()A.[-8,0]B.[-8,2]C.[-7,2]D.[-1,2]答案B炼技法提能力【方法集训】方法程序框图功能的识读1.(2020届安徽高三开学考试,6)阅读如图所示的程序框图,若输入的k=10,则该算法的功能是()A.计算数列{2n-1}的前9项和B.计算数列{2n-1}的前10项和C.计算数列{2n-1}的前10项和D.计算数列{2n-1}的前9项和答案B2.(2019河南郑州第二次质量检测,3)南宋数学家秦九韶在《数书九章》中提出的秦九韶算法至今仍是多项式求值比较先进的算法,已知f(x)=2019x2018+2018x2017+…+2x+1,程序框图设计的是求f(x0)的值,在M处应填的执行语句是()A.n=2018-iB.n=2019-iC.n=i+1D.n=i+2答案B3.(2019福建厦门第一中学3月模拟,5)我国古代典籍《九章算术》第七章“盈不足”中有一问题:“今有蒲生一日,长三尺.莞生一日,长一尺.蒲生日自半.莞生日自倍.问几何日而长等?”(蒲常指一种多年生草本植物,莞指水葱一类的植物)现欲知几日后,莞高超过蒲高一倍.为了解决这个新问题,设计如图所示的程序框图,输入A=3,a=1.那么在①处应填()A.T>2S?B.S>2T?C.S<2T?D.T<2S?答案B【五年高考】A 组 统一命题·课标卷题组1.(2019课标Ⅲ,9,5分)执行如图所示的程序框图,如果输入的ε为0.01,则输出s 的值等于( )A.2-124B.2-125C.2-126D.2-127答案 C2.(2018课标Ⅱ,7,5分)为计算S=1-12+13-14+…+199-1100,设计了如图所示的程序框图,则在空白框中应填入 ( )A.i=i+1B.i=i+2C.i=i+3D.i=i+4答案 B3.(2017课标Ⅰ,8,5分)如图所示的程序框图是为了求出满足3n -2n >1 000的最小偶数n,那么在和两个空白框中,可以分别填入( )A.A>1 000和n=n+1B.A>1 000和n=n+2C.A≤1000和n=n+1D.A≤1000和n=n+2答案DB组自主命题·省(区、市)卷题组1.(2019北京,2,5分)执行如图所示的程序框图,输出的s值为()A.1B.2C.3D.4答案B2.(2018天津,3,5分)阅读如图所示的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1B.2C.3D.4答案B3.(2017山东,6,5分)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为()A.0,0B.1,1C.0,1D.1,0答案D4.(2019江苏,3,5分)如图是一个算法流程图,则输出的S的值是.答案5C组教师专用题组1.(2018北京,3,5分)执行如图所示的程序框图,输出的s值为()A.12B.56C.76D.712答案B2.(2017课标Ⅱ,8,5分)执行下面的程序框图,如果输入的a=-1,则输出的S=()A.2B.3C.4D.5答案B3.(2017课标Ⅲ,7,5分)执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为()A.5B.4C.3D.2答案D4.(2017天津,3,5分)阅读下面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为()A.0B.1C.2D.3答案C5.(2017北京,3,5分)执行如图所示的程序框图,输出的s值为()A.2B.32C.53D.85答案C6.(2016课标Ⅰ,9,5分)执行下面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足()A.y=2xB.y=3xC.y=4xD.y=5x答案C7.(2016课标Ⅲ,7,5分)执行下面的程序框图,如果输入的a=4,b=6,那么输出的n=()A.3B.4C.5D.6答案B8.(2016四川,6,5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为()A.9B.18C.20D.35答案B9.(2016北京,3,5分)执行如图所示的程序框图,若输入的a值为1,则输出的k值为()A.1B.2C.3D.4答案B10.(2016天津,4,5分)阅读下边的程序框图,运行相应的程序,则输出S的值为()A.2B.4C.6D.8答案B11.(2015课标Ⅰ,9,5分)执行下面的程序框图,如果输入的t=0.01,则输出的n=()A.5B.6C.7D.8答案C12.(2015课标Ⅱ,8,5分)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()A.0B.2C.4D.14答案B13.(2015湖南,3,5分)执行如图所示的程序框图.如果输入n=3,则输出的S=()A.67B.37C.89D.49答案B14.(2015福建,6,5分)阅读如图所示的程序框图,运行相应的程序,则输出的结果为()A.2B.1C.0D.-1答案C15.(2015重庆,7,5分)执行如图所示的程序框图,若输出k的值为8,则判断框内可填入的条件是()A.s≤34B.s≤56C.s≤1112D.s≤2524答案C16.(2015北京,3,5分)执行如图所示的程序框图,输出的结果为()A.(-2,2)B.(-4,0)C.(-4,-4)D.(0,-8)答案B17.(2015天津,3,5分)阅读下边的程序框图,运行相应的程序,则输出S的值为()A.-10B.6C.14D.18答案B18.(2014课标Ⅰ,7,5分)执行下面的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=()A.203B.72C.165D.158答案D19.(2014课标Ⅱ,7,5分)执行下面的程序框图,如果输入的x,t均为2,则输出的S=()A.4B.5C.6D.7答案D20.(2017江苏,4,5分)下图是一个算法流程图.若输入x的值为1,则输出y的值是.16答案-221.(2016山东,11,5分)执行如图所示的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为.答案322.(2015山东,13,5分)执行下边的程序框图,输出的T的值为.答案11623.(2015江苏,4,5分)根据如图所示的伪代码,可知输出的结果S为.答案7【三年模拟】一、选择题(每小题5分,共35分)1.(2020届山西学情调研,7)如图是解方程12+22+…+n2=(n+1)(n+2)的程序框图,输出的i为()A.3B.4C.5D.6答案B2.(2020届河南百校联盟9月联合检测,8)《周髀算经》向来被认为是中国最古老的天文学及数学著作,《周髀算经》的内容是以商高与周公的问答形式陈述而成,主要阐明当时的盖天说、四分历法.由《周髀算经》中关于影长的问题,可以得到从冬至起,小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气日影长依次构成等差数列,若冬至的日影长为13.5尺,现在我们用如图所示的程序框图来求解这十二个节气日影长的和,执行该程序框图,则输出的结果是()A.94尺B.95尺C.96尺D.97尺答案C3.(2020届宁夏银川一中第二次月考,9)记不超过实数x的最大整数为[x],则函数f(x)=[x]称作取整函数,取整函数在科学和工程上有广泛应用.如图所示的程序框图是与取整函数有关的求和问题,若输出的S的值为5,则判断框内填入的条件可以是()A.k≤6?B.k≤4?C.k≤5?D.k≤3?答案C4.(2020届云南师大附中第一次月考,8)如图,执行程序框图后,输出的结果是()A.140B.204C.245D.300答案B5.(2018河南郑州高中毕业班第二次质量预测,5)《九章算术》是中国古代第一部数学专著,是《算经十书》中最重要的一种,成于公元1世纪左右.“更相减损术”便是《九章算术》中记录的一种求最大公约数的算法,按其算理流程有如图所示的程序框图,若输入的a、b分别为96、36,则输出的i为()A.4B.5C.6D.7答案A6.(2019安徽安庆二模,9)执行如图所示的程序框图,则输出的结果是()A.171B.342C.683D.341答案C7.(2018陕西宝鸡金台期中,8)执行如图所示的程序框图,如果输入的a=0.6,b=0.5,c=1.5,那么输出m的值是()A.0.5B.0.6C.1.5D.都有可能答案A二、填空题(共5分)8.(2020届江西新余四中高三月考(文))执行如图所示的程序框图,则输出S的值为.答案2。