基于哈夫曼编码的通信系统的设计与实现

哈夫曼编码的实现及应用哈夫曼编码（Huffman Coding）是一种用于数据压缩的编码技术，它可以将数据中频繁出现的字符或符号用较短的编码表示，从而减小数据的存储或传输开销。

以下是哈夫曼编码的实现和应用：实现哈夫曼编码：1. 构建哈夫曼树：首先，需要收集数据中不同字符或符号的频率信息，然后根据这些频率构建哈夫曼树。

在哈夫曼树中，频率较高的字符位于树的较低部分，频率较低的字符位于树的较高部分。

2. 分配编码：从根节点开始，沿着哈夫曼树的路径向下，为每个字符分配唯一的编码。

左子树通常表示0，右子树表示1。

这确保了编码是前缀编码，即没有一个编码是另一个编码的前缀。

3. 编码数据：使用分配的编码，将原始数据中的字符替换为相应的编码，从而生成压缩的数据。

哈夫曼编码的应用：1. 数据压缩：哈夫曼编码广泛用于数据压缩领域，包括压缩文件、图像、音频和视频数据。

由于频率较高的字符使用较短的编码，哈夫曼编码可以显著减小文件大小。

2. 通信系统：在通信系统中，数据通常需要在网络上传输。

使用哈夫曼编码可以减小数据传输的带宽要求，提高通信效率。

3. 文本编辑器：哈夫曼编码可用于实现字典压缩，减小文本文件的大小，使其更容易存储和传输。

4. 图像压缩：JPEG图片格式使用了哈夫曼编码来压缩图像数据，减小图像文件的大小。

5. 音频压缩：MP3音频格式中的音频数据也使用了哈夫曼编码，以减小音频文件的大小。

6. 存储设备：存储设备，如硬盘和闪存驱动器，通常使用哈夫曼编码来提高存储效率，减小数据的物理存储需求。

哈夫曼编码是一种有效的数据压缩方法，可以在多个领域中应用，以减小数据的大小并提高数据传输和存储的效率。

不同应用领域可能会采用不同的编码方式，但核心原理是一致的。

基于哈夫曼编码的通信系统的设计与实现一、实验目的（1）掌握二叉树的存储结构及其相关操作。

（2）掌握构造哈夫曼树的基本思想，及其编码/译码过程。

二、实验内容利用哈夫曼编码进行通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。

但是，这要求在发送端通过一个编码系统对待传输数据预先编码，在接收端将传来的数据进行译码。

对于双工信道，每端都需要一个完整的编/译码系统。

试为这样的信息收发站设计一个基于哈夫曼编码的通信系统。

一个完整的系统应具有以下功能1）初始化处理：建立通信系统（1）建立有100句中文的信息集合，每个句子称为一条信息。

（2）输入编码参数：①从终端输入编码字符集大小n，字符编码长度m（设n为4，m为8）；②从终端输入编码字符（设为A,B,C,D）;（3）生成每条信息的字符编码，构造字符编码集合；（4）计算每个字符编码集合中出现的概率；（5）根据字符概率构造哈夫曼树，求出每个字符的二进制编码。

2）发送端信息编码（1）用户从信息集合中选择一条信息，找到该信息对应的字符编码；（2）根据该信息的字符编码，哈夫曼树求出的每个字符的二进制编码，构造出该信息的二进制编码，记录二进制比编码。

3）接受端信息译码（1）根据得到的信息的二进制编码，利用哈夫曼树求出每个字符的二进制编码还原出信息的字符编码；（2）根据信息的字符编码，找到对应的信息。

三、源程序代码#include<stdio.h>#include<malloc.h>#include<stdlib.h>char *codechar;int ncodechar,lcodechar;int *arraychar[100];char *temp;float *proba;char pass[50];int passl;struct node{float pro;int num;struct node* p;struct node* lc;struct node* rc;char *res;int length;}*hc;char message[100][20]={{"人之初"}, {"性本善"}, {"性相近"}, {"习相远"}, {"苟不教"}, {"性乃迁"},{"教之道"}, {"贵以专"}, {"昔孟母"}, {"择邻处"}, {"子不学"}, {"断机杼"},{"窦燕山"}, {"有义方"}, {"教五子"}, {"名俱扬"}, {"养不教"}, {"父之过"},{"教不严"}, {"师之惰"}, {"子不学"}, {"非所宜"}, {"幼不学"}, {"老何为"},{"玉不琢"}, {"不成器"}, {"人不学"}, {"不知义"}, {"为人子"}, {"方少时"},{"亲师友"}, {"习礼仪"}, {"香九龄"}, {"能温席"}, {"孝于亲"}, {"所当执"},{"融四岁"}, {"能让梨"}, {"弟于长"}, {"宜先知"}, {"首孝弟"}, {"次见闻"},{"知某数"}, {"识某文"}, {"一而十"}, {"十而百"}, {"百而千"}, {"千而万"},{"三才者"}, {"天地人"}, {"三光者"}, {"日月星"}, {"三纲者"}, {"君臣义"},{"父子亲"}, {"夫妇顺"}, {"曰春夏"}, {"曰秋冬"}, {"此四时"}, {"运不穷"},{"曰南北"}, {"曰西东"}, {"此四方"}, {"应乎中"}, {"曰水火"}, {"木金土"},{"此五行"}, {"本乎数"}, {"曰仁义"}, {"礼智信"}, {"此五常"}, {"不容紊"},{"稻粱菽"}, {"麦黍稷"}, {"此六谷"}, {"人所食"}, {"马牛羊"}, {"鸡犬豕"},{"此六畜"}, {"人所饲"}, {"曰喜怒"}, {"曰哀惧"}, {"爱恶欲"}, {"七情具"},{"匏土革"}, {"木石金"}, {"丝与竹"}, {"乃八音"}, {"高曾祖"}, {"父而身"},{"身而子"}, {"子而孙"}, {"自子孙"}, {"至玄曾"}, {"乃九族"}, {"人之伦"},{"父子恩"}, {"夫妇从"}, {"兄则友"}, {"弟则恭"}} ;int zifushengcheng();int probability();int huffman();int Exchange(struct node *a,struct node *b);int Exchangenum(int *a,int *b);int Exchangepoint(struct node **a,struct node ** b);int produce(struct node *a,int *b);int sent();int receive();int main(){int i;char t;printf("初始化通讯系统:\n请输入编码字符集大小n,字符编码长度m(以n m格式来输入):\n");scanf("%d %d",&ncodechar,&lcodechar);codechar=(char *)malloc(sizeof(char)*ncodechar);proba=(float *)malloc(sizeof(float)*ncodechar);for(i=0;i<ncodechar;i++){proba[i]=0;}for(i=0;i<100;i++){arraychar[i]=(int *)malloc(sizeof(int )*lcodechar);}hc=(struct node*)malloc(sizeof(struct node)*(ncodechar*2-1));temp=(char *)malloc(sizeof(char)*(ncodechar));printf("请输入编码字符(以A B C D的格式来输入):\n");for(i=0;i<ncodechar;i++){scanf("%c",&t);if(t=='\n'||t==' '){i--;continue;}codechar[i]=t;}zifushengcheng();probability();huffman();sent();receive();return 1;}int sent(){int i,j,k,x;printf("\n--------------------------------发送方------------------------------------\n");for(i=0;i<100;i++){printf("%d:",i+1);for(j=0;j<20;j++){printf("%c",message[i][j]);}printf(" 相应的字符编码:");for(k=0;k<lcodechar;k++){printf("%c",codechar[arraychar[i][k]]);}printf("\n");}printf("请从以上100条信息中选择发送的信息，输入你的信息号:");scanf("%d",&x);printf("你选择发送的信息是:");for(j=0;j<20;j++){printf("%c",message[x-1][j]);}printf("\n相应的字符编码是:");for(i=0;i<lcodechar;i++){printf("%c",codechar[arraychar[x-1][i]]);}printf("\n根据哈夫曼树得到的哈夫曼编码是:");for(i=0;i<lcodechar;i++){for(j=0;j<ncodechar*2-1;j++){if(arraychar[x-1][i]==hc[j].num){for(k=0;k<hc[j].length;k++){printf("%c",hc[j].res[k]);pass[passl]=hc[j].res[k];passl++;}}}}return 1;}int receive(){int i,j,k=0,m;int *get=(int *)malloc(sizeof(int)*lcodechar);printf("\n--------------------------------接收方------------------------------------\n接收到的哈夫曼编码是:");for(i=0;i<passl;i++){printf("%c",pass[i]);}i=0;while(i!=lcodechar){for(j=0;(j<ncodechar*2-1);j++){for(m=0;m<hc[j].length;m++,k++){if(hc[j].res[m]!=pass[k]){break;}}if(m==hc[j].length){get[i]=hc[j].num;i++;break;}k=k-m;}}printf("\n根据哈夫曼树转换出的字符编码为:\n");for(i=0;i<lcodechar;i++){printf("%c",codechar[get[i]]);}for(i=0;i<100;i++){for(j=0;j<lcodechar;j++){if(get[j]!=arraychar[i][j])break;}if(j==lcodechar){printf("\n字符编码转换后得到的信息是:\n");for(k=0;k<20;k++){printf("%c",message[i][k]);}break;}}printf("\n接收结束，谢谢使用!");return 1;}int zifushengcheng(){int i,j=0,k=0,yushu,x;int *b[100];for(i=0;i<100;i++){b[i]=(int *)malloc(sizeof(int)*lcodechar);for(j=0;j<lcodechar;j++){b[i][j]=0;}for(i=0;i<100;i++){x=i;do{yushu=x%ncodechar;x=(int)(x/ncodechar);b[i][j]=yushu;j++;}while(x!=0);for(j=ncodechar-1;j>=0;j--,k++){arraychar[i][k]=b[i][j];}j=0;k=0;}for(i=0;i<100;i++){for(j=ncodechar;j<lcodechar;j++){arraychar[i][j]=rand()%ncodechar;}}/*for(i=0;i<100;i++){for(j=0;j<lcodechar;j++){printf("%d ",arraychar[i][j]);}printf(" ");for(j=0;j<lcodechar;j++){printf("%c",codechar[arraychar[i][j]]);}printf("\n");}*/return 1;}int probability(){for(i=0;i<100;i++){for(j=0;j<lcodechar;j++){for(k=0;k<ncodechar;k++){if(arraychar[i][j]==k){proba[k]++;}}}}printf("随机生成的字符编码概率:\n");for(i=0;i<ncodechar;i++){proba[i]=proba[i]/(100*lcodechar);printf("%c:%f ",codechar[i],proba[i]);}return 1;}int huffman(){int i,j,k,l=0;for(i=0;i<(ncodechar*2-1);i++){hc[i].lc=NULL;hc[i].rc=NULL;hc[i].p=NULL;hc[i].num=i;if(i<ncodechar){hc[i].pro=proba[i];continue;}hc[i].pro=0;}for(i=0;i<ncodechar-1;i++){for(j=i*2;j<(ncodechar+i);j++){for(k=j+1;k<(ncodechar+i);k++){if(hc[k].pro<hc[j].pro&&hc[k].pro!=0){Exchange(&hc[k],&hc[j]);}}}hc[i+ncodechar].pro=hc[i*2].pro+hc[i*2+1].pro;hc[i+ncodechar].lc=&hc[i*2];hc[i+ncodechar].rc=&hc[i*2+1];hc[i*2].p=&hc[i+ncodechar];hc[i*2+1].p=&hc[i+ncodechar];}printf("\n构造的哈夫曼树:");for(i=0;i<ncodechar*2-1;i++){printf("\nchar:%c num:%d pro:%f",codechar[hc[i].num],hc[i].num,hc[i].pro);printf(" lc:");if(hc[i].lc==NULL){printf(" ");}else{printf("%d,",hc[i].lc->num);}printf(" rc:");if(hc[i].rc==NULL){printf(" ");}else{printf("%d,",hc[i].rc->num);}printf(" p:");if(hc[i].p==NULL){printf(" ");}else{printf("%d,",hc[i].p->num);}}produce(&hc[ncodechar*2-2],&l);printf("\n生成的哈夫曼编码是:");for(i=0;i<ncodechar*2-1;i++){printf("\nchar:%c num:%d length:%d code:",codechar[hc[i].num],hc[i].num,hc[i].length);for(j=0;j<hc[i].length;j++){printf("%c",hc[i].res[j]);}}return 1;}int produce(struct node*a,int *b){int i;a->length=(*b);a->res=(char *)malloc(sizeof(char)*(*b));for(i=0;i<(*b);i++){a->res[i]=temp[i];}if(a->lc!=NULL&&a->rc!=NULL){temp[(*b)]='0';(*b)++;produce((a->lc),b);temp[(*b)]='1';(*b)++;produce((a->rc),b);}(*b)--;return 1;}int Exchange(struct node*a,struct node*b){float t;t=a->pro;a->pro=b->pro;b->pro=t;Exchangenum(&a->num,&b->num);Exchangepoint(&a->p,&b->p);Exchangepoint(&a->lc,&b->lc);Exchangepoint(&a->rc,&b->rc);return 1;}int Exchangepoint(struct node **a,struct node ** b) {struct node *t;t=*a;*a=*b;*b=t;return 1;}int Exchangenum(int *a,int *b){int t;t=*a;*a=*b;*b=t;return 1;}参考至《百度文库》四、结果分析本次实验是学习编程以来接触的最大程序，参考了较多相关源文件，对c语的函数引用有了更深刻的了解，初步掌握了二叉树的存储结构及其相关操作。

20180902一、需求分析1、问题描述利用哈夫曼编码进行通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。

但是，这要求在发送端通过一个编码系统对待传数据预先编码，在接收端将传来的数据进行译码（解码）。

对于双工信道（即可以双向传输信息的信道），每端都需要一个完整的编/译码系统。

试为这样的信息收发站设计一个哈夫曼编译码系统。

2、基本要求（1）初始化（Initialzation）。

从数据文件DataFile.txt中读入字符及每个字符的权值，建立哈夫曼树HuffTree；（2）编码（EnCoding）。

用已建好的哈夫曼树，对文件ToBeTran.txt 中的文本进行编码形成报文，将报文写在文件Code.txt中；（3）译码（Decoding）。

利用已建好的哈夫曼树，对文件CodeFile.txt 中的代码进行解码形成原文，结果存入文件Textfile.txt中；（4）输出（Output）。

输出DataFile.txt中出现的字符以及各字符出现的频度（或概率）；输出ToBeTran.txt及其报文Code.txt；输出CodeFile.txt及其原文Textfile.txt；二、概要设计1.数据结构本程序需要用到以一个结构体HTNode，以及一个二维数组HuffmanCode。

2.程序模块本程序包含两个模块，一个是实现功能的函数的模块，另一个是主函数模块。

系统子程序及功能设计本系统共有七个子程序，分别是：a.int min1(HuffmanTree t,int i)//进行比较b.void select(HuffmanTree t,int i,int *s1,int *s2)//求权值最小的两个数c.void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,char *u,int n)///* w存放n个字符的权值(均>0),构造赫夫曼树HT,并求出n 个字符的赫夫曼编码HC */d.void Initialzation(HuffmanTree *HT,HuffmanCode *HC)//初始化e.int EnCoding(HuffmanTree *HT,HuffmanCode *HC)//对文件ToBeTran.txt中的文本进行编码形成报文，将报文写在文件Code.txt 中f.int pipei(char *c,int n,HuffmanCode *HC)//在huffmancode寻找匹配的编码g.void Decoding(HuffmanTree *HT,HuffmanCode *HC)//对文件CodeFile.txt中的代码进行解码形成原文，结果存入文件Textfile.txt中3.各模块之间的调用关系以及算法设计主函数调用Initialzation，EnCoding，Decoding。

课程设计任务书2010—2011学年第一学期专业：通信工程学号：070110101 姓名：苟孟洛课程设计名称：信息论与编码课程设计设计题目：哈夫曼编码的分析与实现完成期限：自2010 年12月20 日至2010 年12 月26 日共1 周一．设计目的1、深刻理解信源编码的基本思想与目的；2、理解哈夫曼编码方法的基本过程与特点；3、提高综合运用所学理论知识独立分析和解决问题的能力；4、使用MATLAB或其他语言进行编程。

二．设计内容假设已知一个信源的各符号概率，编写适当函数，对其进行哈夫曼编码，得出码字，平均码长和编码效率，总结此编码方法的特点和应用。

三．设计要求1、编写的函数要有通用性；2、信源可以自由选择，符号信源与图像信源均可。

四．设计条件计算机、MATLAB或其他语言环境五、参考资料[1]曹雪虹，张宗橙.信息论与编码.北京：清华大学出版社，2007.[2]王慧琴.数字图像处理.北京：北京邮电大学出版社，2007.指导教师（签字）：教研室主任（签字）：批准日期：年月日摘要哈夫曼编码(Huffman Coding)是一种编码方式，以哈夫曼树—即最优二叉树，带权路径长度最小的二叉树，经常应用于数据压缩。

在计算机信息处理中，“哈夫曼编码”是一种一致性编码法（又称"熵编码法"），用于数据的无损耗压缩。

这一术语是指使用一张特殊的编码表将源字符（例如某文件中的一个符号）进行编码。

这张编码表的特殊之处在于，它是根据每一个源字符出现的估算概率而建立起来的（出现概率高的字符使用较短的编码，反之出现概率低的则使用较长的编码，这便使编码之后的字符串的平均期望长度降低，从而达到无损压缩数据的目的）。

本课题通过MATLAB编写适当的函数，对一个随机信源进行哈夫曼编码，得出码字，平均码长和编码效率。

从而理解信源编码的基本思想与目的以及哈夫曼编码方法的基本过程与特点，并且提高综合运用所学理论知识独立分析和解决问题的能力。

哈夫曼编码（Huffman Coding）是一种常见的数据压缩算法，它通过构建哈夫曼树（Huffman Tree）来实现。

以下是一个简单的哈夫曼编码算法的实现示例，使用Python 语言：pythonCopy codeimport heapqfrom collections import defaultdictclass HuffmanNode:def __init__(self, char, frequency):self.char = charself.frequency = frequencyself.left = Noneself.right = Nonedef __lt__(self, other):return self.frequency < other.frequencydef build_huffman_tree(data):frequency = defaultdict(int)for char in data:frequency[char] += 1priority_queue = [HuffmanNode(char, freq) for char, freq in frequency.items()]heapq.heapify(priority_queue)while len(priority_queue) > 1:node1 = heapq.heappop(priority_queue)node2 = heapq.heappop(priority_queue)merged_node = HuffmanNode(None, node1.frequency + node2.frequency)merged_node.left = node1merged_node.right = node2heapq.heappush(priority_queue, merged_node)return priority_queue[0]def build_huffman_codes(root, current_code="", codes={}):if root:if root.char is not None:codes[root.char] = current_codebuild_huffman_codes(root.left, current_code + "0", codes)build_huffman_codes(root.right, current_code + "1", codes)return codesdef huffman_encoding(data):if not data:return None, Noneroot = build_huffman_tree(data)codes = build_huffman_codes(root)encoded_data = "".join([codes[char] for char in data])return encoded_data, rootdef huffman_decoding(encoded_data, root):if not encoded_data or not root:return Nonecurrent_node = rootdecoded_data = ""for bit in encoded_data:if bit == "0":current_node = current_node.leftelse:current_node = current_node.rightif current_node.char is not None:decoded_data += current_node.charcurrent_node = rootreturn decoded_data# 示例data = "abracadabra"encoded_data, tree_root = huffman_encoding(data) decoded_data = huffman_decoding(encoded_data, tree_root)print("Original data:", data)print("Encoded data:", encoded_data)print("Decoded data:", decoded_data)。

哈夫曼编解码算法设计1.引言1.1 概述概述部分将对哈夫曼编解码算法进行简要介绍，包括该算法的产生背景、主要特点以及应用领域等方面的内容。

哈夫曼编解码算法是一种基于权重分布的压缩算法，它通过对输入的数据流进行编码和解码来实现数据的压缩和恢复。

该算法由大卫·哈夫曼（David A. Huffman）于1952年提出，是一种被广泛应用于信息论和数据压缩领域的有效算法。

该算法的主要特点是根据输入数据的权重分布构建一棵哈夫曼树，通过不等长的编码方式来表示输入数据中出现频率较高的字符或数据块。

编码时，出现频率较高的字符使用较短的二进制编码，而出现频率较低的字符则使用较长的二进制编码，以此来实现数据的压缩效果。

哈夫曼编码算法在数据压缩领域有着广泛的应用。

由于压缩后的数据长度较短，可以大大节省存储空间和传输带宽，因此被广泛应用于各种数据传输和存储场景中，如文件压缩、图像压缩、语音压缩等。

此外，哈夫曼编码算法的设计思想也对后续的数据压缩算法提供了重要的借鉴和参考价值。

本文将详细介绍哈夫曼编码算法的原理、设计与实现，并通过实例和实验验证算法的性能和效果。

通过对哈夫曼编码算法的研究与分析，可以更好地理解该算法的优势和不足，并为后续的算法改进和优化提供参考。

最后，本文将总结哈夫曼编码算法的主要特点和应用场景，并对未来的研究方向提出展望。

1.2 文章结构文章结构部分主要介绍本文的各个部分以及每个部分的内容安排。

在本文中，共包含引言、正文和结论三个部分。

引言部分主要介绍了整篇文章的背景和目的。

在概述部分，简要说明了哈夫曼编解码算法的概念和作用，以及该算法在通信领域的重要性。

然后，文章结构部分具体说明了本文的组织结构，以便读者能够清晰地了解文章的整体脉络。

正文部分是本文的主体，分为两个部分：哈夫曼编码算法原理和哈夫曼编码算法设计与实现。

在哈夫曼编码算法原理部分，将详细介绍哈夫曼编码算法的基本原理，包括频率统计、构建哈夫曼树和生成哈夫曼编码等步骤。

哈夫曼编码算法哈夫曼编码算法是一种基于编码理论的高效数据压缩算法。

它是由美国数学家大卫·哈夫曼于1952年提出的，被广泛应用于数据压缩、图像处理、音频处理、通信传输等领域。

哈夫曼编码算法的核心思想是利用字符出现的频率来设计一种最优的编码方式，使得压缩后的数据长度最短。

具体来说，它将出现频率较高的字符用较短的编码表示，而将出现频率较低的字符用较长的编码表示，从而实现了数据的压缩。

在哈夫曼编码算法中，首先需要统计待压缩数据中各个字符出现的频率，并将其构建成一棵二叉树。

在构建二叉树的过程中，每个字符都被看作是一个叶子节点，其出现频率越高，其在二叉树中的位置越靠近根节点。

构建完二叉树后，再对每个叶子节点进行编码，将其路径上的0和1分别表示为0和1的编码序列，这样就得到了每个字符的哈夫曼编码。

对于任意一段待压缩数据，可以根据字符的哈夫曼编码将其转换为一串由0和1组成的二进制序列。

由于哈夫曼编码是一种前缀编码，即任何一个字符的编码序列都不是另一个字符的编码序列的前缀，因此在解压缩时，可以根据编码序列逐位识别出每个字符，并将其还原成原始数据。

哈夫曼编码算法的优点在于它能够实现高效的数据压缩，尤其是对于出现频率较高的字符，其编码长度非常短，可以显著减少数据的存储空间。

此外，哈夫曼编码算法还具有良好的可扩展性和适应性，能够适应不同类型、不同大小的数据集。

然而，哈夫曼编码算法也存在一些限制和缺陷。

首先，由于需要统计字符出现的频率，因此在压缩较小的数据集时，其效果可能不如其他压缩算法。

其次，由于哈夫曼编码算法需要在解压缩时构建二叉树，因此对于大规模数据集，其解压缩的时间复杂度可能较高。

为了克服哈夫曼编码算法的这些限制和缺陷，研究者们提出了许多改进和优化的方法。

例如，可以利用哈夫曼编码算法的可扩展性，将其与其他压缩算法结合使用，以实现更高效的数据压缩。

此外，还可以利用多种哈夫曼编码算法的优点，设计出更加灵活、高效的数据压缩方案。

哈夫曼编\译码的设计与实现一、简介1．设计目的：通过对简单哈夫曼编/译码系统的设计与实现来熟练掌握树型结构在实际问题中的应用。

2．问题的描述：利用哈夫曼编码进行通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。

但是，这要求在发送端通过一个编码系统对待传数据预先编码，在接收端将传来的数据进行译码。

系统应该具有如下的几个功能：接收原始数据、编码、译码、打印编码规则。

二、数据结构的设计：1.哈夫曼结点结构体：typedef struct HtNode{int weight;int parent, lchild, rchild;}HtNode;2.哈夫曼树结构体：typedef struct HtTree{struct HtNode ht[MAXNODE+1];int root;}HtTree, *PHtTree;三、功能（函数）设计：总体上划分为四个模块，具体功能描述如下：1．初始化功能模块：接收输入信息，并正确输出2．建立哈夫曼树的功能模块：按照构造哈夫曼树的算法构造哈夫曼树，将HuffNode数组中的各个位置的各个域都添上相关的值3．哈夫曼编码的功能模块：根据输入的相关字符信息进行哈夫曼编码，然后将结果存入，同时将字符与0、1代码串的一一对应关系打印到屏幕上。

4．译码的功能模块：接收需要译码的0、1代码串，按照哈夫曼编码规则将其翻译成字符集中的字符所组成的字符串形式，将翻译的结果在屏幕上输出四、界面设计：该界面操做简单，内容详细，便于程序使用者根据提示轻松上手。

简洁明朗是该界面最大的特点。

哈夫曼编/译码请逐个输入结点和结点的权值>>>按Enter键开始根据此提示界面进入程序使用阶段。

请输入结点个数：根据用户输入结点个数，动态输入并存储字符及权值然后输出字符与0、1代码串的对应关系。

进入以下界面，进行后续操作1----------------------------编码2----------------------------译码3----------------------------重新输入权值;0----------------------------退出用户键入“0”，即可出编码译码操作五、程序设计：1．函数功能说明及其程序流程图的描述：1>:main函数：控制整个程序的整个流程。

哈夫曼编码系统的设计与实现
哈夫曼编码是一种用于数据压缩的编码方式，通过将出现频率高的字符用较短的编码表示，从而实现对数据的压缩。

哈夫曼编码系统的设计与实现包括以下几个步骤：
1. 字符频率统计：根据待压缩的数据，统计每个字符出现的频率。

可以使用哈希表或数组来记录每个字符的频率。

2. 构建哈夫曼树：根据字符的频率构建哈夫曼树。

首先将每个字符及其频率作为叶子节点，并按照频率的大小构建一个最小堆。

然后，每次从最小堆中取出两个频率最小的节点，将它们作为子节点构建一个新的节点，频率为子节点频率之和。

将新的节点放回最小堆中，重复上述步骤，直到最小堆中只剩下一个节点，即为哈夫曼树的根节点。

3. 构建编码表：通过遍历哈夫曼树，可以得到每个字符对应的哈夫曼编码。

一种常用的方式是，从根节点开始，每次向左走为0，向右走为1，直到叶子节点，将走过的路径记录下来，即为该字符的哈夫曼编码。

可以使用哈希表来存储每个字符及其对应的哈夫曼编码。

4. 数据压缩：根据构建好的哈夫曼编码表，将待压缩的数据中的每个字符替换为对应的哈夫曼编码，并将编码后的数据保存起来。

由于哈夫曼编码的特性，编码后的数据长度会变短，从而实现对数据的压缩。

5. 数据解压缩：使用相同的哈夫曼树和哈夫曼编码表，将压缩后的数据中的每个哈夫曼编码替换为对应的字符，从而实现对数据的解压缩。

要注意的是，设计和实现哈夫曼编码系统需要考虑到字符频率统计的效率、哈夫曼树的构建算法选择、编码表的存储结构选择等问题。

此外，还需要注意对压缩后的数据进行合理的保存和传输，以便于解压缩时能够正确恢复原始数据。

一、概述哈夫曼编码是一种被广泛应用于数据压缩和传输领域的编码方法，由David A. Huffman于1952年提出。

其独特的编码方式能够使得频率较高的字符用较短的编码表示，从而实现对数据的高效压缩。

在本文中，我们将探讨哈夫曼编码的研究历程以及针对某某程序的实现。

二、哈夫曼编码的原理哈夫曼编码的原理主要基于字符的出现频率。

在给定的字符集中，将频率较高的字符用较短的编码表示，而频率较低的字符用较长的编码表示，从而实现数据的压缩。

哈夫曼编码的主要步骤包括：建立字符的频率统计表、构建哈夫曼树、生成哈夫曼编码表和进行编解码。

通过这些步骤，我们可以利用哈夫曼编码对数据进行高效的压缩和传输。

三、哈夫曼编码的研究历程哈夫曼编码作为一种经典的编码方法，其研究历程可以追溯到上世纪50年代。

当时，David A. Huffman提出了哈夫曼编码的概念，并通过其论文《A Method for the Construction of Minimum-Redundancy Codes》详细阐述了这一编码方法的原理和算法。

随后，哈夫曼编码被广泛应用于通信、数据存储和图像压缩等领域，成为了数据压缩技术中的重要组成部分。

四、某某程序的实现在现实应用中，我们经常需要对数据进行压缩和传输，而哈夫曼编码正是其中一种常用的方法。

针对某某程序的实现，我们可以通过以下步骤来实现哈夫曼编码的功能：1. 构建字符的频率统计表在实现某某程序时，首先需要对给定的字符集进行频率统计，以便后续的编码操作。

可以利用哈希表或数组来记录每个字符的出现次数，并按照频率进行排序。

2. 构建哈夫曼树基于字符的频率统计表，我们可以构建哈夫曼树。

哈夫曼树的构建需要借助最小堆或优先队列等数据结构，通过不断合并频率最小的节点来构建一棵树，直到所有字符都被合并为止。

3. 生成哈夫曼编码表一旦构建好哈夫曼树，就可以根据树的结构来生成哈夫曼编码表。

通过遍历哈夫曼树，可以得到每个字符对应的哈夫曼编码，从而实现对数据的编码操作。

算法与数据结构课程设计哈夫曼编码和译码的设计与实现1.问题描述利用哈夫曼编码进行通信可以大大提高信道的利用率，缩短信息传输时间，降低传输成本。

但是，这要求在发送端通过一个编码系统对待传数据预先编码，在接收端将传来的数据进行译码（复原）。

对于双工信道（即可以双向传输信息的信道），每端都需要一个完整的编/译码系统。

试为这样的信息收发站设计一个哈夫曼码的编/译码系统。

2.基本要求a.编/译码系统应具有以下功能：（1）I：初始化（Initialization）。

从终端读入字符集大小n，以及n个字符和n个权值，建立哈夫曼树，并将它存于文件hfmTree中。

（2）E：编码（Encoding）。

利用已建好的哈夫曼树（如不在内存，则从文件hfmTree中读入），对文件ToBeTran中的正文进行编码，然后将结果存入文件CodeFile中。

（3）D：译码（Decoding）。

利用已建好的哈夫曼树将文件CodeFile中的代码进行译码，结果存入文件TextFile中。

（4）P：印代码文件（Print）。

将文件CodeFile以紧凑格式显示在终端上，每行50个代码。

同时将此字符形式的编码文件写入文件CodePrin中。

（5）T：印哈夫曼树（Tree printing）。

将已在内存中的哈夫曼树以直观的方式（树或凹入表形式或广义表）显示在终端上，同时将此字符形式的哈夫曼树写入文件TreePrint中。

b.测试数据（1）利用下面这道题中的数据调试程序。

某系统在通信联络中只可能出现八种字符，其概率分别为0.25，0.29，0.07，0.08，0.14，0.23，0.03，0.11，试设计哈夫曼编码。

（2）用下表给出的字符集和频度的实际统计数据建立哈夫曼树，并实现以下报文的编码和译码：“THIS PROGRAM IS MY FAVORITE”。

字符空格 A B C D E F G H I J K L M频度 186 64 13 22 32 103 21 15 47 57 1 5 32 20字符 N O P Q R S T U V W X Y Z频度57 63 15 1 48 51 80 23 8 18 1 16 13．需求分析3.1程序的基本功能本程序可以对任何大小的字符型文件进行Huffman编码，生成一个编码文件。

数据结构哈夫曼编码器课程设计报告哈夫曼编码器课程设计报告设计目标：本课程设计的目标是实现一个哈夫曼编码器，能够实现对给定文本文件进行压缩和解压缩操作。

通过使用哈夫曼编码，可以使文本文件的大小大幅度减小，从而节约存储空间。

设计原理及实现方法：本设计主要包括以下几个步骤：1、文本文件的读取：首先需要从外部文件中读取待压缩的文本文件，读取过程可以通过使用文件输入流进行操作。

读取的文本内容将用于构建哈夫曼树和编码表。

2、构建哈夫曼树：哈夫曼树是通过给定文本中的字符出现频率来构建的，出现频率更高的字符将拥有更短的编码。

构建哈夫曼树的过程可以通过使用优先队列和二叉树来实现。

3、编码表：在构建哈夫曼树的过程中，每个字符都会有一个唯一的编码。

根据哈夫曼树的特性，左子树的编码为0，右子树的编码为1，根据这个规则可以通过遍历哈夫曼树来编码表。

4、压缩文本文件：在编码表后，可以利用编码表来对文本文件进行压缩操作。

遍历文本文件中的每个字符，通过编码表将字符转换为对应的哈夫曼编码，并将编码存储在一个压缩文件中。

5、解压缩文本文件：解压缩操作是压缩操作的逆过程。

根据编码表将压缩文件中的哈夫曼编码逐个解码为字符，并将解码后的字符写入解压缩文件中。

附件说明：本文档的附件包括以下内容：1、源代码文件：- HuffmanEncoder：java：包含了哈夫曼编码器的主要实现代码。

- Mn：java：包含了测试哈夫曼编码器的主函数。

2、示例文本文件：- input：txt：用于测试的示例文本文件。

法律名词及注释：本文档中涉及的法律名词及注释如下：1、哈夫曼编码：用于数据压缩的一种编码方式，旨在通过减少字符的编码长度来节省存储空间。

2、压缩：将原始文件经过编码转换为较短的文件，从而减小存储空间的占用。

3、解压缩：将压缩文件经过解码转换为原始文件，恢复原始文件的过程。

全文结束。

哈夫曼编码的设计与实现
哈夫曼编码是一种数据压缩算法，通过构建最小生成树来实现编码和解码操作。

下面是哈夫曼编码的设计和实现步骤：
1. 统计每个字符在文本中出现的频率。

2. 根据字符频率构建哈夫曼树：
a. 创建一个优先队列（最小堆），将每个字符的频率作为优先级。

b. 将每个字符作为一个单独的树节点，并插入优先队列中。

c. 重复以下步骤直到优先队列中只剩一个节点：
- 从优先队列中弹出两个频率最小的树节点。

- 创建一个新的树节点，将弹出的两个节点作为子节点，并将其频率之和作为新节点的频率。

- 将新节点插入优先队列中。

d. 最后一个剩下的节点即为哈夫曼树的根节点。

3. 构建字符和编码的映射表：
a. 从根节点出发，遍历哈夫曼树的所有路径。

b. 按照字符出现的顺序，记录每个字符对应的编码序列。

4. 对原文本进行编码：
a. 遍历原文本中的每个字符，根据映射表将其替换为对应的编码序列。

b. 将所有编码序列连接在一起，形成最终的编码结果。

5. 对编码结果进行解码：
a. 从哈夫曼树的根节点开始，遍历编码结果中的每个编码位。

b. 根据当前位的值，选择进入左子节点或右子节点。

c. 如果当前节点是叶子节点，则找到了一个字符，将其添加到解码结果中，并返回根节点继续解码。

d. 重复以上步骤直到遍历完整个编码结果。

6. 完成解码后，得到原始的文本内容。

以上是哈夫曼编码的设计和实现步骤，实际的实现可能需要使用递归、数据结构等相关知识。

设计一个利用哈夫曼算法的编码系统(总4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--设计一个利用哈夫曼算法的编码系统，重复地显示并处理以下项目，直到选择退出为止。

【基本要求】1) 将权值数据存放在数据文件(文件名为，位于执行程序的当前目录中)2) 初始化：键盘输入字符集大小n、n个字符和n个权值，建立哈夫曼树；3) 编码：利用建好的哈夫曼树生成哈夫曼编码；4) 输出（1）各个字符的编码；（2）1111111;;;;;;#include<>#include<>#include<>#define M 50#define MAX 1000;typedef struct{int weight;arent=ht[i].lchild=ht[i].rchild=0;if(i<=n)ht[i].weight=weight[i];elseht[i].weight=0;}for(i=1;i<n;i++)eight<m1)&&(ht[j].parent==0)){m2=m1;x2=x1;m1=ht[j].weight;x1=j;}else if((ht[j].weight<m2)&&(ht[j].parent==0)){m2=ht[j].weight;x2=j;}}k=n+i;ht[x1].parent=ht[x2].parent=k;ht[k].weight=m1+m2;ht[k].lchild=x1;ht[k].rchild=x2;}return ht;}void huffmancoding(const int n,HUFFMANCODE hc,HUFFMANTREE ht,char str[]){int i,start,child,father;char *cd;hc=(HUFFMANCODE)malloc((n+1)*sizeof(char*));arent;father!=0;child=f ather,father=ht[father].parent)/*从叶子结点到根结点求逆向编码*/ if(ht[father].lchild==child)cd[--start]='0';elsecd[--start]='1';hc[i]=(char*)malloc((n-start)*sizeof(char));arent=ht[i].lchild=ht[i].rchild=0;if(i<=n)ht[i].weight=weight[i];elseht[i].weight=0;}for(i=1;i<n;i++)eight<m1)&&(ht[j].parent==0)){m2=m1;x2=x1;m1=ht[j].weight;x1=j;}else if((ht[j].weight<m2)&&(ht[j].parent==0)){m2=ht[j].weight;x2=j;}}k=n+i;ht[x1].parent=ht[x2].parent=k;ht[k].weight=m1+m2;ht[k].lchild=x1;ht[k].rchild=x2;}return ht;}void huffmancoding(const int n,HUFFMANCODE hc,HUFFMANTREE ht,charstr[]){int i,start,child,father;char *cd;hc=(HUFFMANCODE)malloc((n+1)*sizeof(char*));arent;father!=0;child=f ather,father=ht[father].parent)/*从叶子结点到根结点求逆向编码*/ if(ht[father].lchild==child)cd[--start]='0';elsecd[--start]='1';hc[i]=(char*)malloc((n-start)*sizeof(char));eight); ht[i].parent=0;}for(;i<=2*n-1;i++)ht[i].parent=ht[i].lchild=ht[i].rchild=0;for(i=n+1;i<=2*n-1;i++){m1=m2=30000;s1=s2=0;for(k=1;k<=i-1;k++){if(ht[k].parent==0 && ht[k].weight<m1){m2=m1;s2=s1;m1=ht[k].weight;s1=k;}else if(ht[k].parent==0 && ht[k].weight<m2){m2=ht[k].weight;s2=k;}}ht[s1].parent=ht[s2].parent=i;ht[i].lchild=s1;ht[i].rchild=s2;ht[i].weight=ht[s1].weight+ht[s2].weight;}for(i=1;i<=n;i++){=n-1;c=i;f=ht[i].parent;while(f){if(ht[f].lchild==c)[]='0';else []='1';c=f;f=ht[f].parent;}hcd[i]=d;}printf("输出哈夫编码:");for(i=1;i<=n;i++){printf("%d ",ht[i].weight);for(k=hcd[i].start;k<n-1;k++) printf("%c",hcd[i].cd[k]);printf(" ");}printf("\n");}。

课程设计任务书学生：王鸣专业班级：信息sy1001班指导教师：洪涛工作单位：信息工程学院题目:基于哈夫曼编码的图像编解码系统设计及实现初始条件：计算机Windows8操作系统MATLAB7.8.0软件要求完成的主要任务:设计哈夫曼编码的图像编解码系统、利用软件编写程序、仿真实现时间安排：第1-18周：理论讲解第19周：理论设计，实验室安装调试以及撰写设计报告答辩：时间：7月2日地点: 鉴主15楼通信实验室四指导教师签名：年月日系主任（或责任教师）签名：年月日目录目录 (I)摘要 (II)ABSTRACT (III)1引言 (1)1.1图像数据压缩的目的 (1)1.2图像数据压缩的原理 (1)1.3常用的压缩编码方法 (3)2哈夫曼编码 (3)2.1 哈夫曼编码简介 (3)2.2哈夫曼编码步骤 (3)2.3 哈夫曼编码的缺点 (5)3基于哈夫曼编码的图像编解码系统的程序设计 (6)3.1 分块程序设计分析 (6)3.2主程序 (8)3.3程序函数 (8)3.3.1编码函数 (8)3.3.2解码函数 (12)3.3.3符号概率计算函数 (13)3.3.4节点添加函数 (14)3.3.5解码返回符号函数 (14)4系统仿真结果 (15)4.1程序运行结果 (15)4.2 程序运行结果分析 (16)5.总结 (18)参考文献 (19)摘要本论文首先介绍了图像压缩相关知识。

随后，分析概述了哈夫曼压缩编码的原理及方法，并采用 MATLAB 软件对两幅图片进行压缩编码程序设计，获得压缩信息及哈夫曼编码表，分析压缩后的图像像素数据及压缩比。

关键词：图像压缩；MATLAB；哈夫曼编码;无损压缩编码ABSTRACTThis paper firstly introduces the theoretical knowledge of image compression. Then, it analyses the principle and method of Huffman coding and using Huffman coding principle and methods, compression coding design is made for two images on the MATLAB software. Also gain the compression information and Huffman coding table. What’s more, compressed image pixel data and compression ratio are analyzed.Key words： Image compression; MATLAB; Huffman encoding;Lossless compression coding1引言1.1图像数据压缩的目的数字图像通常要求很大的比特数，这给图像的传输和存储带来相当大的困难。

哈夫曼编/译码的设计与实现实验报告问题描述利用哈夫曼编码进行通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。

但是，这要求在发送端通过一个编码系统对待传数据预先编码，在接收端将传来的数据进行译码（复原）。

对于双工信道（即可以双向传输信息的信道），每端都需要一个完整的编/译码系统。

试为这样的信息收发编写一个哈夫曼码的编/译码系统。

基本要求（1）接收原始数据：从终端读入字符集大小n，以及n个字符和n个权值，建立哈夫曼树，并将它存于文件hfmtree.dat中。

（2）编码：利用已建好的哈夫曼树（如不在内存，则从文件hfmtree.dat中读入），对文件中的正文进行编码，然后将结果存入文件codefile.dat中。

（3）译码：利用已建好的哈夫曼树将文件codefile.dat中的代码进行译码，结果存入文件textfile.dat中。

（4）打印编码规则：即字符与编码的一一对应关系。

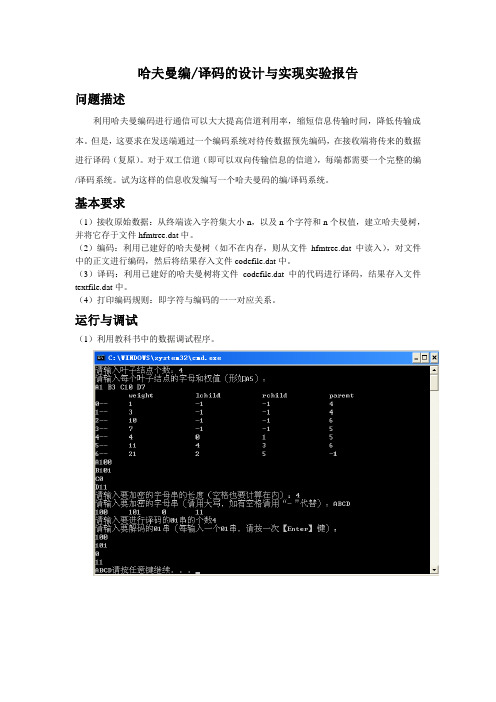
运行与调试（1）利用教科书中的数据调试程序。

（2）用下表给出的字符集和频度的实际统计数据建立哈夫曼树，并实现以下报文的编码和译码：“THIS-PROGRAM-IS-MY-FA VORITE”。

字符 A B C D E F G H I J K L M 频度186 64 13 22 32 103 21 15 47 57 1 5 32 20 字符N O P Q R S T U V W X Y Z频度57 63 15 1 48 51 80 23 8 18 1 16 1实验小结通过这次实验，让我对于树的应用多了认识，在读取文件时，遇到的一些困难，不过在和同学交流的过程中，解决了这个问题，我觉的自己对于树及文件的应用又有了一些进步。

通过这次实验，感觉收获很大。

源程序// 哈夫曼编译码的设计与实现.cpp : 定义控制台应用程序的入口点。

//#include "stdafx.h"#include<iostream>#include<fstream>#include<string>#define Maxvalue 10000#define MAXBIT 200using namespace std;struct node{char letter;string num;};typedef struct{char letter;int weight; //结点权值int parent;int lchild;int rchild;}HnodeType;typedef struct{int bit[MAXBIT];int start;}HcodeType;HnodeType *HaffmanTree(int n){HnodeType *HuffNode;HuffNode=new HnodeType[2*n-1];int i,j;int m1,m2,x1,x2;for(i=0;i<2*n-1;i++) //数组HuffNode[]初始化{HuffNode[i].weight=0;HuffNode[i].parent=-1;HuffNode[i].lchild=-1;HuffNode[i].rchild=-1;}cout<<"请输入每个叶子结点的字母和权值（形如A5）："<<endl;for(i=0;i<n;i++)cin>>HuffNode[i].letter>>HuffNode[i].weight; //输入n个叶子结点的权值for(i=0;i<n-1;i++) //构造哈夫曼树{m1=m2=Maxvalue;x1=x2=0;for(j=0;j<n+i;j++) //选取最和次小两个权值{if(HuffNode[j].parent==-1&&HuffNode[j].weight<m1){m2=m1;x2=x1;m1=HuffNode[j].weight;x1=j;}else{if(HuffNode[j].parent==-1&&HuffNode[j].weight<m2){m2=HuffNode[j].weight;x2=j;}}}//将找出的两棵子树合并为一棵子树HuffNode[x1].parent=n+i;HuffNode[x2].parent=n+i;HuffNode[n+i].weight=HuffNode[x1].weight+HuffNode[x2].weight;HuffNode[n+i].lchild=x1;HuffNode[n+i].rchild=x2;}cout<<" weight"<<" lchild"<<" rchild"<<" parent"<<endl; for(i=0;i<2*n-1;i++)cout<<i<<"--"<<" "<<HuffNode[i].weight<<" "<<HuffNode[i].lchild<<" "<<HuffNode[i].rchild<<" "<<HuffNode[i].parent<<endl;ofstream outFile("hfmtree.dat",ios::out);if(!outFile)cerr<<"文件打开失败！"<<endl;else{outFile<<" weight"<<" lchild"<<" rchild"<<"parent"<<endl;for(i=0;i<2*n-1;i++)outFile<<i<<"--"<<" "<<HuffNode[i].weight<<""<<HuffNode[i].lchild<<" "<<HuffNode[i].rchild<<""<<HuffNode[i].parent<<endl;outFile.close();}return HuffNode;}void HaffmanCode(HnodeType *HuffNode,int n){HcodeType *HuffCode,cd;HuffCode=new HcodeType[2*n-1];int c,p,i,j;for(i=0;i<n;i++){cd.start=n-1;c=i;p=HuffNode[c].parent;while(p!=-1){if(HuffNode[p].lchild==c)cd.bit[cd.start]=0;elsecd.bit[cd.start]=1;cd.start--;c=p;p=HuffNode[c].parent;}for(j=cd.start+1;j<n;j++)HuffCode[i].bit[j]=cd.bit[j];HuffCode[i].start=cd.start;}for(i=0;i<n;i++){cout<<HuffNode[i].letter;for(j=HuffCode[i].start+1;j<n;j++)cout<<HuffCode[i].bit[j];cout<<endl;}ofstream outFile1("codefile.dat",ios::out|ios::binary);if(!outFile1)cerr<<"文件打开失败！"<<endl;else{for(i=0;i<n;i++){outFile1<<HuffNode[i].letter;for(j=HuffCode[i].start+1;j<n;j++)outFile1<<HuffCode[i].bit[j];outFile1<<endl;}outFile1.close();}}int _tmain(int argc, _TCHAR* argv[]){HnodeType *HuffNode;int n,i;cout<<"请输入叶子结点个数：";cin>>n;if(cin.fail()){cout<<"输入有误！"<<endl;return 0;}HuffNode=HaffmanTree(n);HaffmanCode(HuffNode,n);int num;cout<<"请输入要加密的字母串的长度（空格也要计算在内）：";cin>>num;char *l1;char l;node l2[27];l1=new char[num];cout<<"请输入要加密的字母串（请用大写，如有空格请用“-”代替）：";for(int n=0;n<num;n++)cin>>l1[n];ofstream outFile2("bianma.dat",ios::out|ios::binary);if(!outFile2)cerr<<"文件打开失败！"<<endl;else{for(i=0;i<num;i++)outFile2<<l1[i];outFile2.close();}ifstream inFile1("codefile.dat",ios::in|ios::binary);ifstream inFile2("bianma.dat",ios::in|ios::binary);cerr<<"读取文件失败！"<<endl;if(!inFile2)cerr<<"读取文件失败！"<<endl;else{while(inFile2.peek ()!=EOF){inFile2>>l;for(i=0;i<2*n-1;i++){inFile1>>l2[i].letter;inFile1>>l2[i].num;}for(i=0;i<n;i++){if(l2[i].letter==l)cout<<l2[i].num<<" ";}}inFile1.close();inFile2.close();}delete []l1;cout<<endl;int a;cout<<"请输入要进行译码的串的个数：";cin>>a;string *s;s=new string[a];cout<<"请输入要解码的串（每输入一个串，请按一次【Enter】键）："<<endl; for(i=0;i<a;i++)cin>>s[i];ofstream outFile4("yima.dat",ios::out);if(!outFile4)cerr<<"文件打开失败！"<<endl;else{for(i=0;i<a;i++)outFile4<<s[i]<<endl;outFile4.close();}ifstream inFile3("codefile.dat",ios::in|ios::binary);cerr<<"读取文件失败！"<<endl;else{for(i=0;i<2*n-1;i++){inFile3>>l2[i].letter;inFile3>>l2[i].num;}ifstream inFile4("yima.dat",ios::in);if(!inFile4)cerr<<"读取文件失败！"<<endl;else{for(int j=0;j<a;j++)inFile4>>s[j];}for(int j=0;j<a;j++){for(i=0;i<n;i++){if(l2[i].num==s[j])cout<<l2[i].letter;}}inFile3.close();}return 0;}。