流体力学5-3、4

第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d ＝100 mm ，通过流量Q ＝4 L/s ，水温T ＝20℃；(2)条件与以上相同，但管道中流过的是重燃油，其运动粘度6215010m /s ν-=⨯。

试判别以上两种情况下的流态。

解：(1) 200C 时，水的运动粘性系数ν=1.007×10-6m 2/s ，24Q u d π=水的雷诺数Re 为：-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1mud Q v v d π⨯⨯====>⨯⨯⨯，紊流 (2) 石油：-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1m ud Q v v d π⨯⨯====<⨯⨯⨯，层流 5—2 温度为0℃的空气，以4 m/s 的速度在直径为l00 mm 的圆管中流动，试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。

若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水，问水在管中呈何流态?解：空气的雷诺数Re 为：-524 m/s 0.1m Re 2919720001.3710m /sud v ⨯===>⨯，紊流 水的雷诺数Re 为：-624 m/s 0.1m Re 223 21420001.79210m /sud v ⨯===>⨯，紊流 5—3 (1)一梯形断面排水沟，底宽0.5m ，边坡系数cot θ＝1.5(θ为坡角)，水温为20℃，水深0.4m ，流速为0.1m ／s ，试判别其流态；(2)如果水温保持不变，流速减小到多大时变为层流?解：200C 时，水的运动粘性系数ν=1.007×10-6m 2/s 水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯ 4-620.1m/s 0.23m Re 2.24101.00710m /sR uR ν⨯===⨯⨯，42.24102000⨯>，湍流 水流为层流时Re 500uR ν≤=(明渠流)，故 63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯ 5—4 由若干水管组装成的冷凝器，利用水流经过水管不断散热而起到冷凝作用。

4-2 用式（4-3）证明压强差△p 、管径d 、重力加速度g 三个物理量是互相独立的。

解： dim p ∆ = 12ML T -- dim d = L dim g = 2LT -将p ∆、d 、g 的量纲幂指数代入幂指数行列式得112010012--- = -2 ≠ 0 因为量纲幂指数行列式不为零，故p ∆、d 、g 三者独立。

4-4 用量纲分析法，证明离心力公式为F= kWv 2 / r 。

式中，F 为离心力；M 为作圆周运动物体的质量；υ为该物体的速度；d 为半径；k 为由实验确定的常数。

解：设F kM r αβγυ= 2MLTM L T L αββγ--=据量纲一致性原则求指数α、β、γ： M ： 1 = αα = 1L ： 1 = βγ+β = 2T ： -2 = -β γ = -1故 2M F k rυ=4-6 有压管道流动的管壁面切应力w τ，与流动速度υ、管径D 、动力粘度μ和流体密度ρ有关，试用量纲分析法推导切应力w τ的表达式。

解：选υ、D 、ρ为基本量，故可组成两个π数，即12(,)ϕππ = 0其中，1π = 111w D αβγυρτ 2π = 222D αβγυρμ 求出两个π数O O O M L T = 11111132L T L M L ML T ααβγγ----M ： 0 = 1γ + 1 12α=- L ：0 = 11131αβγ+--10β=T ：0 = -12α- 11γ=-得 1wDτπρυ=同理可得12e R Dμπρυ-==将w τ解出得21()w e R τρυϕ=4-7 一直径为 d 、密度为1ρ的固体颗粒，在密度为ρ、动力粘度为μ的流体中静止自由沉降，其沉降速度(,,,,)f d p g υρμ=∆，其中g 为重力加速度，1ρρ∆=-ρ为颗粒与流体密度之差。

试用量纲分析法，证明固体颗粒沉降速度由下式表示：1()d υρυμ= 解：选υ、d 、ρ为基本量，故可组成3个π数，即123(,,)0ϕπππ= 其中，1111d g αβγπυρ= 2222d αβγπυρμ= 3333d p αβγπυρ=∆ 求解各π数， 1111113002M L T L T L M L LT ααβγγ--=1111:0:031:02M L T γαβγα=⎫⎪=+-+⎬⎪=--⎭111210αβγ=-⎧⎪=⎨⎪=⎩ 即 12gdπυ=对于2π，22222300011M L T L T L M L ML T ααβγγ----=22222:01:031:01M L T γαβγα=+⎫⎪=+--⎬⎪=--⎭222111αβγ=-⎧⎪=-⎨⎪=-⎩即 2d μπυρ=对于3π，3333330003M L T L T L M L ML ααβγγ---=33333:01:033:0M L T γαβγα=+⎫⎪=+--⎬⎪=-⎭33301αβγ=⎧⎪=⎨⎪=-⎩即 3pπρ∆=故2(,,)gdpd μϕυρρυ∆=0化简整理，解出υ211(,)e pR gdυπϕρ-∆==又υ与p ∆成正比，将pρ∆提出，则22()e pR gdυϕρ∆=33()()e e R R υ== 4-8 设螺旋浆推进器的牵引力F 取决于它的直径D 、前进速度υ、流体密度ρ、粘度μ和螺旋浆转速度n 。

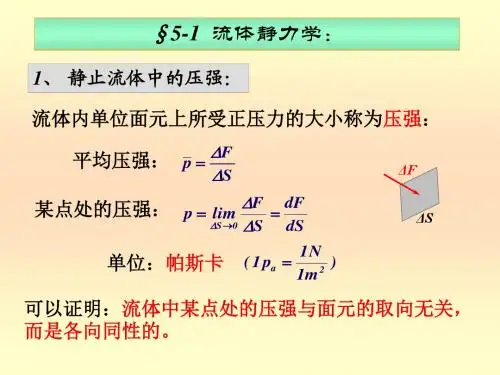
流体力学泵与风机部分习题答案 2-15解：（1）当1γ为空气 21p p = ()A B p h z p =++γ ()h z p p p B A +=-=∆γ 3.010008.9⨯⨯= kpa pa 94.22940== （2）当1γ为油 31p p =()z H h p p A +++=γ1 ()H h p p B γγ++=13H h z H h p p p p p B A γγγγγ--+++-=-=∆131h z h 1γγγ-+=1.090002.010008.91.010008.9⨯-⨯⨯+⨯⨯= kpa pa 04.22040== 2-16 解：21p p =()211h h H p p M +++=水γ 212h h p p a 汞油γγ++=()2121h h p h h H p a M 汞油水γγγ++=+++()2.010008.96.1378502.05.110008.998011⨯⨯⨯+⨯=++⨯⨯+-h h 26656785098002.098005.1980098011+=+⨯+⨯+-h h 1960147009802665619501--+=hm h 63.51= 2-28解：()21h h p -=γ()()()b h h h b h h h h P 02210212145sin 45sin 21-+--=γγ ()()145sin 22310008.9145sin 232310008.92100⨯-⨯⨯+⨯-⨯-⨯⨯⨯= kN N 65.343465022510008.9==⨯⨯=()()()Pbl h h h bl h h h h l D D D 2022110212145sin 45sin 21-+--=γγ m 45.222510008.9222210008.92322210008.9=⨯⨯⨯⨯⨯+⨯⨯⨯=2-32 解：b h h b h h P 02202145sin 2145sin γγ+= 2222210008.9212222110008.9⨯⨯⨯⨯⨯+⨯⨯⨯⨯=kN N 8576.1106.1108572810008.9==⨯⨯=Ph h b h h h h b h h l D 02102202102145sin 3245sin 2145sin 245sin ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=γγ 2810008.92372410008.9222410008.9⨯⨯⨯⨯⨯+⨯⨯⨯=2613= 26722613=-=p lT P G l T l P l G ⨯=⨯+⨯22672810008.9162.19⨯=⨯⨯⨯+⨯T kN T 31.10134.27481.9=+= 2-41解：245sin 0=⨯=r hb h h P x ⨯⨯⋅⋅=21γ 4212210008.9⨯⨯⨯⨯⨯=kN N 2.3939200==V P z γ=b r r r⎪⎭⎫⎝⎛⨯⨯⨯-=00245cos 45sin 2136045πγ 4212281214.310008.92⨯⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯= kN N 344.2222344==kN P 1.45344.222.3922=+=03057.0arctan 2.39344.22arctan arctan≈===x z P P α3-3解：（1）s m v d Q /0049.010025.04432323=⋅⋅=⋅=ππs kg Q /9.4=ρ（2）s m v d d v /625.032131=⎪⎪⎭⎫⎝⎛= s m v d d v /5.232232=⎪⎪⎭⎫ ⎝⎛=3-5解：s m h m Q /778.2/1000033==s m d Qv /2042≤=π所以，177.04=≥πv Qd 所以，mm m d 45045.0== 此时，s m d Q d Qv /4.1763585.0112.114422====ππ3-6解：22543212054d d A A A A A ππ======22114012021d d A A ππ=⋅="=' 22224012021d d A A ππ=⋅="='22334012021d d A A ππ=⋅="='22444012021d d A A ππ=⋅="='22554012021d d A A ππ=⋅="='2214014d d ππ=d d 1011=d r 10211= 2224034d d ππ=d d 1032= d r 10232= 2234054d d ππ=d d 1053= d r 10253= 2244074d d ππ=d d 1074= d r 10274=2254094d d ππ=d d 1035=d r 10235= ()()54321254321220240u u u u u d u u u u u d Q G ++++=++++==πρπρρ3-7解：干管前端的质量流量为：42562.2211111d A v Q πρρ⨯⨯==()s kg /128544.005.042562.22=⨯⨯⨯=πs kg Q Q Q /064272.02132===ρρρ ()s m A Q v /247.2204.043.2064272.022222=⋅⋅==πρρ()s m A Q v /05.18045.0424.2064272.023333=⋅⋅==πρρ 3-10解：将基准面建立在B 点经过的水平面上，列能量方程：gv p z gv p z 222222221111αγαγ++=++其中，m z 2.11= m p 5.11=γ s m v /21= s m v d d v /5.4122212== 121==αα gp g 25.40225.12.1222++=++γ871.125.4225.12.1222=-++=gg p γ 3-11解：将2点所在的水平面作为基准面，列能量方程： gv p z gv p z 222222221111αγαγ++=++31=z 02=zγγ21p p =s m v /31=gv p g p 2023322221++=++γγ s m gh v /2.83222=+=32.822112=⎪⎪⎭⎫ ⎝⎛=d d v v 所以，m d 12.02= 3-14解：以水面为基准面，列0-0和D-D 的能量方程：gv p z gv p z DD DD 22220000αγαγ++=++00=z00=γp02200=gv α 4-=D z0=γDpgv DD 2040002α++-=++ 所以，422=gv DD α，即，s m v D /85.88.924=⋅⋅=所以，s m v d Q D /017368.085.805.044322=⋅⋅==ππ81:1:2:24422==A D DD A A d d gv gv αα列0-0和A-A 断面的能量方程：gv p z gv p z AA AA 22220000αγαγ++=++8147000++-=++γAp 所以，8147-=γAp 所以，kpa p A 1.68= 列0-0和B-B 断面的能量方程：gv p z gv p z BB BB 22220000αγαγ++=++kpa p B 484.08.9814-=⋅-= 列0-0和C-C 断面的能量方程：gv p z gv p z CC CC 22220000αγαγ++=++kpa p C 1.208.98142-=⨯⎪⎭⎫ ⎝⎛+-=0=D p3-18解：将基准面建在管道所在的水平面上，列能量方程：21222222111122-+++=++l h gv p z gv p z αγαγ128.998.0008.9490222+++=++g v α9.3222=gv s m v /74.82= 3-19 解：（1）（a ）将基准面建在A 所在的水平面上，列0-0和C-C 断面的能量方程：gv p z gv p z CC CC 2222000αγαγ++=++gv CC 2000042α++=++422=gv CC α s m v C /85.88.98=⨯=1:4:2:22222==B C CC B B s s gv gv αα122=gv BB α s m v /43.48.921=⨯= 且 B A v v =（b ）（c ）gv p z gv p z AA AA 22220000αγαγ++=++10004++=++γAp3=γAp kpa p A 4.29=（2）（a ）2122000022-+++=++l CC CC h gv p z gv p z αγαγ其中，gv g v h l 2324222121+=-g v g v g v 223200004222222++++=++54222=g v 所以，s m v /96.32= s m v v /96.12121==（b ）（c ）gv g v p z g v p z 2222212111120000+++=++αγαγ 5300041++=++γp5341-=γp kpa p 32.331= gv g v g v p z g v p z 223242222222222220000++++=++αγαγ5423545400042⋅++++=++γp kpa p 76.112=3-20 解：()()212221221122-++=--++l a p v p z z v p ργγρs m d Qv /38.2005.014.34202.042221=⨯⨯⨯==πs m d Qv /19.1005.014.3402.04222=⨯⨯==π2423222121v v p l ρρ+=-()()242322222122212211v v v p z z v p a ρρργγρ+++=--++22214v v =()()8.930306.02.1224232300212221221⨯+---+++=v v v v p ρρρρ()()8.930306.02.12424212230022222222⨯+---+++=v v v v ρρρρ8.9606.019.1026.0133002⨯⨯-⨯⨯+= pa 16.352= mm p h 6.449.716.3521===γ3-22解：s kN h kN G /048944.0/2.176==s m GQ /1347.77.08.910048944.033=⨯⨯==γs m d Q d Qv /09.914.31347.7444222=⨯===ππ()2122221122-++=-++l a p v p H v p ργγρ其中，01≈v ，pa h p 988.9101010331=⨯⨯⨯==-γ()γgv d H H 2035.0209.97.008.97.02.1098222+⨯+=⨯⨯-++-()8.97.08.9209.9035.0209.97.008.97.02.109822⨯⨯⨯+⨯+=⨯⨯-++-H HH H 0122.19.289.498+=+-所以，m H 64.32=()212211212212-++=-++l M M a p v p H v p ργγρ()8.97.08.9209.9164.322035.0209.97.064.328.97.02.12109822⨯⨯⨯+⨯+=⨯⨯-++-M p 科技52.169.28968.7998++=+-M p 所以，pa p M 45.63-=3-263-28解：列连续性方程：s m D Qv /18.34.014.344.04221=⨯⨯==π s m d Q v /96.501.014.344.04222=⨯⨯==π列能量方程： g v p z g v p z 222222221111αγαγ++=++ g v g v p 222112221ααγ-=m 98.1318.9218.396.5022=⨯-= kpa p 404.12938.998.1311=⨯=列动量方程：()12v vQ F -=∑ρ ()12222144v v Q R d p D p -=-⨯-⨯ρππ()18.396.504.04.04404.12932-⨯=-⨯⨯R πkN R 339.14378.474.04.04404.12932=⨯-⨯⨯=π kN R 94.1112=3-33解：列能量方程：g v p z g v p z 222222221111αγαγ++=++ 其中，5321=v v 2221259v v = g v g v 209.0205.1222211αα++=++gv g v 225926.02222-= s m v /3.42= s m v /58.21=()12v v Q F -=∑ρ()1222212121v v Q R b h b h -=--ργγ 其中，s m Q /644.45.12.158.23=⨯⨯= 72.1644.410009.0108.9215.1108.9212323⨯⨯=-⨯⨯⨯-⨯⨯⨯R N R 2.480=4-2 （1） m mm d 1.0100== s kg Q /10=ρs m Q Q /01.03==ρρs m d Q v /274.11.014.301.04422=⨯⨯==π s m /10519.126-⨯=ν 8387110519.11.0274.1Re 6=⨯⨯==-νvd （紊流） （2） s kg Q /10=ρ s m Q Q /011765.0850103===ρρ s m d Q v /4987.11.014.3011765.04422=⨯⨯==π s m /1014.124-⨯=ν 13151014.11.04987.1Re 4=⨯⨯==-νvd 4-3 解：m d 3.0= C T 020= s m /107.1526-⨯=νs m d v /1067.1043.0107.152000Re 36max --⨯=⨯⋅=⋅=ν s m A v Q /103947.743.014.31067.1043323max max --⨯=⨯⨯⨯=⋅= h kg Q /9.3136002.1103947.73=⨯⨯⨯=-ρ4-4 解：212=d d 4212221==d d v v 222111Re 2214Re ===ννd v d v 所以，2Re Re 21= 4-12 紊流粗糙区，5106Re ⨯> νvd=Re ，所以，s m d v /14.325.010308.1106Re 65=⨯⨯⨯==-ν s m d v Q /154.0425.014.314.34322=⨯==π 4-13 s m s L Q /2.0/20031==s m d Q v /076433.44211==π 661107791.010308.125.0076433.4Re ⨯=⨯⨯==-νvd s L Q /202= s m v /4076433.02=4210791.7Re ⨯=s L Q /53= s m v /1019.03= 43109478.1Re ⨯=查尼氏图，得到， 5106Re ⨯=u 4104Re ⨯=l123Re Re Re Re Re <<<<u l ，所以，1Q 属于紊流粗糙区，2Q 属于紊流过渡区，3Q 属于紊流光滑区，（1） 对于1Q ，采用希弗林松公式，02326.025.0105.011.011.025.0325.01=⎪⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=-d K λm g v d l h f 888.78.92076433.425.010002326.0222111=⨯⨯⨯==λ （2） 对于2Q ，采用阿公式，02547.010791.76825.0105.011.0Re 6811.025.04325.02=⎪⎪⎭⎫ ⎝⎛⨯+⨯=⎪⎭⎫ ⎝⎛+=-d K λ m g v d l h f 086.08.924076433.025.010002547.0222222=⨯⨯⨯==λ（3） 对于3Q ，采用布公式02678.05.194773164.0Re 3164.025.025.03===λ m g v d l h f 005676.08.9244076433.025.010002678.0222333=⨯⎪⎭⎫ ⎝⎛⨯⨯==λ 4-15 5102Re ⨯=u 4000Re =lm d 05.0= m K 31025.0-⨯= s m d v u /028.405.010007.1102Re 65max =⨯⨯⨯==-νs L d v Q /905.7405.014.3028.4422max max =⨯==π 26min 10056.805.010007.14000Re --⨯=⨯⨯==d v l ν s L s m d v Q /1581.0/1001581.0405.014.310056.8432222min min =⨯=⨯⨯==--π 4-21 （1） a d d =21 2211av v = gv d l d v g v d l g v d l h f 2642Re 64221111211121111νλ=== 4212221211ad d v v h h f f == 19.1=a （2）75.425.12275.12122225.0225.0225.021125.0125.0125.021123164.023164.0a d d v v gv d l d v g v d l d v h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==νν 16.1=a （3）25.525.11222122225.0221125.01211211.0211.0a d d v v g v d l d K g v d l d K h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛= 14.1=a 4-24 解：s m Q /002742.0602329.03=⨯=s m d Q v /3972.105.014.3002742.04422=⨯⨯==π 629.022=⎪⎭⎫ ⎝⎛+g v d l ζλ ()629.08.923972.162=⨯+ζ 3151.0=ζ 4-26 解：（1） 突然缩小375.03145.7815.015.0121=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζmm m g v h j 5.760765.08.922375.022211==⨯==ζ （2）5.02=ζmm m g v h j 102102.08.9225.022222==⨯==ζ （3）1693145.781122213=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζ mm m h j 115115.08.92216923==⨯= （4）14=ζ mm m h j 204204.08.922124==⨯= 4-27 解：()()gv v g v v h h m m j j 222121-+-=''+' ()()()()02212221=-+--=''+'gv v g v v h h m m vm j j 所以，221v v v m += 此时，()j j j h gv v g v v v g v v v h h 2221222222121212211=-=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛+-=''+' 4-29 解：s m h m Q /1044.4/16333-⨯== s m d Q v /2624.205.014.31044.44423211=⨯⨯⨯==-π s m d Q v /5656.01.014.31044.44423222=⨯⨯⨯==-π m g v v p p h j 140674.08.925656.02624.28.910001739.522222121=⨯-+⨯⨯-=-+-=γ g v h j 2211ζ= 5387.01=ζ gv h j 2222ζ= 619.82=ζ5-17 解：5.6082.014.32.12.01002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 7.30422.014.32.12.05002.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 973671.014.32.11.05002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 3.101018973677.30425.608321=++=++=p p p p S S S S 22211/91.227215.03.101018m N Q S p p =⨯==22222/1.258616.03.101018m N Q S p p =⨯==5-25 解：()()⎪⎩⎪⎨⎧=++=++=1021520232322223221SQ Q Q S SQ Q Q S SQ 610=S解得，s m Q /10472.4331-⨯= s m Q /1041.2332-⨯= s m Q /1063.0333-⨯=5-27 解：94.10348.92.014.32.020002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 8.206988.91.014.31.0100025.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 78.37258.92.014.32.072002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 038035.087.14311705.321111211=+=+='S S S 所以，25.6911='S 1）()H Q S S =+'231s m S S H Q /10186.604417163331-⨯==+'=2）H SQ =2 H Q S =⎪⎭⎫ ⎝⎛'221 1325133831432=+'=-'=S S S S gd πζ ()1.25688.92.014.31325142=⨯⨯⨯=ζ 5-28 解：286.1368.93.014.383.020002.084242=⨯⨯⨯⨯==g d d l S AB AB AB AB πλ 029.1098.93.014.383.016002.084242=⨯⨯⨯⨯==g d d l S AC AC AC AC πλ 34.328.94.014.384.020002.084242=⨯⨯⨯⨯==g d d l S AD AD AD AD πλ 772.818.93.014.383.012002.084242=⨯⨯⨯⨯===g d d l S S BC BC BC CD BC πλ 5108.2⨯=A p2AB AB A Q S p γ= s m S p Q AB A AB /457868.08.91000286.136108.235=⨯⨯⨯==γ 2AD AD A Q S p γ= s m S p Q AD A AD /93993.08.9100034.32108.235=⨯⨯⨯==γ ()()222BC BC BC AC A Q S Q S p += ()s m S S p Q Q BC AC A CD BC /23488.043=+==γs m Q Q Q BC AB /69275.022=+= s m Q Q Q CD AD /17481.123=+=s m Q Q Q /86756.13321=+= 22/2.44m kN Q S p BC BC C ==γ。

《流体力学》习题（五）5－ 1 水流经变截面管道，已知细管直径d1，粗管直径d2＝ 2d1，试问哪个截面的雷诺数大?两截面雷诺数的比值 Re1/Re2是多少？5－ 2 水管直径 d＝ 10cm，管中流速u＝ 1.0m/s，水温为10℃，试鉴别流态。

又流速u 等于多少时，流态将发生变化？5－ 3 通风管道直径为250mm，输送的空气温度为20℃，试求保持层流的最大流量。

若输送空气的质量流量为 200kg/h ，其流态是层流仍是紊流？5－ 4 有一矩形截面的小排水渠，水深15cm，底宽 20cm，流速 0.15m/s ，水温 10℃，试鉴别流态。

5－ 5 散热器由 8× 12mm2的矩形截面水管构成，水的运动粘性系数为0.0048cm2/s，要保证每根水管中的流态为紊流 (取 Re≥ 4000) 以利散热，试问水管中的流量应为多少？5－ 6 输油管的直径 d＝ 150mm，流量 Q＝ 16.3m3/h，油的运动粘性系数ν＝ 0.2cm2/s，试求每公里管长的沿程压头损失。

5－ 7 应用细管式粘度计测定油的粘度，已知细管直径d＝ 6mm，丈量段长 l ＝ 2m，实测油的流量Q＝77cm3/s，水银压差计读数 h＝ 30cm，油的重度γ＝8.83kN/m 3，试求油的运动粘性系数ν和动力粘性系数μ。

5－ 8 为了确立圆管内径，在管内经过ν为 0.013cm2/s 的水，实测流量为 35cm3/s，长 15m 管段上的压头损失为 2cm 水柱，试求此圆管的内径。

5－ 9 要求用毕托管一次测出半径为r0的圆管层流的截面均匀流速，试求毕托管测口应搁置的地点。

题 5－7 图题5－9图题5－10图5－ 10 油管直径为75mm，已知油的重度为8.83kN/m 3，运动粘性系数为0.9cm2/s，在管轴地点安置连结水银压差计的毕托管，水银面高差h＝ 20mm，水银重度为133.38kN/m 3，试求油的流量。

第5章流体力学基础思考题5-l 图5-17中三个容器的底面积相同，液面高度相同，容器底面受到的压力是否相同?它们对台面的压力是否相同?图5-17思考题5-1用图答：因为液面高度相同，所以容器底面处的压强相等．又由于底面积相同，故容器底面受到的压力相同．因为各容器内液体的重量不同，所以它们对台面的压力不相同．5-2 流线和迹线有什么区别与联系？答：流体力学中把流体微团的轨迹称为迹线，它是流体微团实际运动的轨迹．流线是为了形象地描述流场而引进的一系列假想曲线，曲线上任一点的切线方向和流经该点的流体微团的速度方向一致．各流线不会相交，且只能是光滑的曲线．一般情况下，流线的形状分布随时间而变化，但在定常流动条件下，流线的形状及分布不随时间变化．在定常流动中，任一条流线便表示了初始时刻位于该流线起点上的那一个流体微团的迹线，即任一条迹线必然是一条流线，因此，定常流动中流线和迹线是重合的．然而，在非定常流动中，微团不一定沿着流线运动，即流线和迹线一般是不重合的．5-3在流体力学中引入流管这一概念有什么意义?答：流管是由一组流线所围成的细管，它可以形象地描述流体的运动．对于定常流动，流管的位置和形状保持不变．这样，可将流体看成由若干个流管组成．只要知道每一个流管中流体的运动规律，就能了解整个流体的运动规律．从而把对整个流体的研究转化为对某一选定的流管中流体的研究．5-4在定常流动中，空间任一确定点流体的速度矢量是恒定不变的，那么，流体微团是否可能有加速度?答：定常流动是指空间各点流体微团的速度、加速度、压强等不随时间变化的流动．但速度、加速度、压强等会随空间变化，故速度矢量随空间点是变矢量，所以在定常流动中，流体微团也可能有加速度．5-5从水龙头徐徐流出的水流，下落时逐渐变细，为什么？答：据连续性原理知，流速大处截面积小．下落时水的流速逐渐增大，所以面积逐渐减少而变细.5-6两船相距较近而并行前进时就容易相撞，试说明之．答：两船平行前进时，两条流线方向相同．如果靠得较近，两船之间的水的流速将大于两船外侧的流速．根据伯努利方程可知，两船之间压强将小于两船外侧的压强．这样两船都将受到一个指向对方的一个压力的作用，极易造成两船碰撞．5-7流体从粗管流向细管时，流速增大，使流体微团获得加速度的动力从何而来? 答：由连续性方程可知流体从粗管流向细管时，流速增大．这是由于截面积的减小，使单位体积的压强能转化为动能，从而使流速增大．5-8如图5-18所示，在漏斗中放一乒乓球，颠倒过来，再通过漏斗管向下吹气，则发现乒乓球不但不被吹掉，反而牢牢地留在漏斗内，这是什么原因?答：因为球与漏斗壁之间的通道狭窄，此处空气相对于球的流速大于其它区域（球的下部）空气的流速．根据伯努利方程可知，此处的压强将小于球下部的压强，这样，球将受到 一个向上的举力．5-9图5-19为水流抽气机的简图，试说明其工作原理?答：根据伯努利方程可知，当水流高速通过水流抽气机细管口时，使其产生负压，把外面的气体吸入随水流带出去，达到抽气的目的．5-10俗话说：“好船家会使八面风”，有经验的水手能够使用风力开船逆风行进，试用伯努利原理解释这一现象?水水和图5-19 水流抽气机图5-18 思考题5-8用图答：如右图所示，当船逆风时（实际并不完全逆风，风向与船行进方向有一夹角），气流经过弯曲的帆（不是平的，一侧凸起，一侧凹陷）时，在帆凸起的一侧，气流速率要大些，而在凹进的一侧气流速率要小些．这样根据伯努利方程可知，在帆凹进的一侧气流的压强要大于帆凸起一侧气流的压强，于是对帆就产生一个推力，该力指向船头的分力可以使船前进．5-11如图5-20所示，有3根竖直的管子连在一等截面的水平管道上，水平管道中流动着不可压缩的粘性液体，但3根竖直管中的液面高度却表明压强沿着管道逐步下降．试说明之．答：这是因为粘性液体在水平管道中流动时需要消耗能量，且流程愈长，消耗能量愈多所致．为了维持粘性流体在管道中作的流动，要么必须在管子的两端维持一定的压强差以克服粘滞力的作用．习题5-1水坝横截面如图5-21所示，坝长1088m L =，水深5m h =，水的密度为31.010ρ=⨯解：将坝身迎着水坡沿垂直纸面方向分成长度为坝长L 、宽度为d l 的许多狭长面积元，其面积为d d S L l =．则作用在此面积元上的力为d d S d F ρgh ρghL l == 由于d d sin h l α=，α为斜坡倾角，代入上式得d d dS sin h F ρgh ρghLα==d F 方向与斜坡垂直，其沿水平方向的分力为图5-20 思考题5-11用图图5-21 习题5-1用图d d dS sin sin sin h F ρgh αρghLαα==水平作用在坝身的水平推力为21d 2h F ρghL h ρgL h ==⎰水平 代入数据，得 32811.0109.810885N 1.3310N2F =⨯⨯⨯⨯⨯=⨯ 5-2 地球被包围在大气中，若认为大气温度不随高度而变，则大气密度ρ与压强p 成正比，试求大气压强随高度的变化．可认为重力加速度g 为一恒量．解：由题意知 d d p ρg h =- ○1 大气密度与大气压强成正比，即ρp ρp =式中为00ρp ρp 、、、分别表示海平面及某一高度的大气密度和大气压强，则00p ρρp =把上式代入○1，并积分得00g d d p h p ρp h pp =-⎰⎰所以 00g 0ρhp p p e-=5-3 用一根跨过水坝的粗细均匀的虹吸管从水库里取水，如图5-22所示，已知水库的水深A 2.0m h =，虹吸管出水口的高度B 1.0m h =，坝高C 2.5m h =，设水在管内作定常流动．⑴ 求A B C 、、三个位置处管内的压强； ⑵ 若虹吸管的截面积427.010m S -=⨯，求从虹吸管流出的水的体积流量；⑶ 虹吸管跨过河坝的最高点C 最多能高出出水口多少米?设大气压为51.01310Pa ⨯．图5-22习题5-3用图AD解：在水库内的水面上取一点D ．连接D 与虹吸管口（浸没在水库中的一端）作一条流线，其与虹吸管内的流线ABC ，形成一条完整的流线，如图中红色虚线所示．在这条流线上运用伯努利方程．⑴对D 、B 两处应用伯努利方程，有221122D D A B B B p ρυρgh p ρυρgh ++=++由于水库截面积很大，液面下降速度为零，即0D υ≈．又D 、B 两处压强均为大气压强，即0B D p p p ==，所以有50 1.01310Pa B p p ==⨯m s 4.43m s B υ==≈又由于在吸管内各处的流速相同，对A 、B 两处应用伯努利方程，则有0A A B p ρgh p ρgh +=+所以可得()()5350 1.01310 1.010 1.0 2.0Pa 0.91510Pa A B A p p ρg h h =+-=⨯+⨯⨯-≈⨯对C 、B 两处应用伯努利方程，有0C C B p ρgh p ρgh +=+所以可得()()5350 1.01310 1.010 1.0 2.5Pa 0.86610Pa C B C p p ρg h h =+-=⨯+⨯⨯-≈⨯⑵从虹吸管流出的水的体积流量为43337.0104.43ms 3.1010ms B Q S υ--==⨯⨯≈⨯⑶ 最高点C 的压强取决与它与出水口的距离，当点C 的压强为零时，点C 的位置距出水口最高，此时，对C 、B 两处应用伯努利方程，有0C B ρgh p ρgh =+所以()50max 31.01310m 10.34m 1.0109.8C C B p h h h ρg⨯=-==≈⨯⨯5-4 水从管1流入，通过支管2和3流人管4，管4的出口与大气相通，整个管道系统在同一水平面内，如图5-23所示.已知各管的横截面积分别是2115cm S =，2235cm S S ==，2410cm S =，管1中的体积流量31600cms Q =．求：⑴ 各管中的流速；⑵ 各管中的压强与大气压强之差． 解：⑴ 根据连续性原理，有111223344Q S υS υ+S υS υ===各管中的流速分别为111600cm s 0.4m s 15Q υS ===1232600cm s 0.6m 225Q υυS ====⨯144600cm s 0.6m 10Q υS ===⑵由伯努利方程知22221122334411112222p ρυp ρυp ρυp ρυ+=+=+=+由于管4的出口与大气相通，所以40p p =，于是()()22322110144111Δ 1.0100.60.4Pa =100Pa 22p p p p p ρυυ=-=-=-=⨯⨯⨯-()()22322220244211Δ 1.0100.60.6P a =0P a 22p p p p p ρυυ=-=-=-=⨯⨯⨯-()()22322330344311Δ 1.0100.60.6P a =0P a 22p p p p p ρυυ=-=-=-=⨯⨯⨯-440Δ=0Pa p p p =-图5-23习题5-4用图5-5 如图5-24所示为一空吸装置，已知水平管道的中心线与容器A 中的液面的高度差h ，与容器B 中的液面的高度差b h ，管口d 处截面积d S ，收缩段c 处截面积为c S ，试问d S 与c S 满足什么条件方能发生空吸作用？解：在容器A 和水平管道中取一流线，流线的一端在A 中的液面处，一端在管口d 处，对c 、d 两处应用伯努利方程，有221122c cd d p ρυp ρυ+=+由于容器A 截面积很大，液面下降速度为零，对容器A 的液面处和管道出口d 处应用伯努力方程，有2012d d p ρgh p ρυ+=+管口d 处压强为大气压强，即0d p p =，所以d 处的流速为22d υgh =对c 、d 两处应用连续性原理，有c cd d υS υS =以上各式联立，可得201d c d c c S p p p p ρgh S ⎡⎤⎛⎫⎢⎥-=-=- ⎪⎢⎥⎝⎭⎣⎦○1 由于d c S S >，所以0c p p <，这时容器B 中的液体将沿着竖直管上升，只要满足0b c p ρgh p -> ○2容器B 中的液体就会被吸到水平管道中，从而发生空吸作用．将○1式代入○2式，可得发生空吸作用的条件d cS S >5-6 欲使灭火水枪喷出的水柱能达到15 m 的高度，灭火水枪所接主水管的计示压强应为多少？设主水管管径比灭火水枪出水口管径大得多，并略去水枪出水口与主水管的高度差．图5-24 习题5-5用图解：设主水管的计示压强为p ，灭火水枪出水口管处的喷水速度为υ．沿主水管与灭火水枪出水口管的轴线作一流线，根据伯努利方程，且主水管管径比灭火水枪出水口管径大得多，并略去水枪出水口与主水管的高度差，则可得212p ρυ=设喷出的水柱能达到的高度用h 表示，由题意有22υgh =两式联立并代入数据，有351.0109.8Pa 15 1.4710Pa p ρgh ==⨯⨯⨯=⨯5-7 一喷泉坚直喷出高度为H 的水流，喷泉的喷嘴具有上细下粗的截圆锥形状，上截面的直径为d ，下截面的直径为D ，喷嘴高为h ，设大气压强为0p ，求：⑴ 水的体积流量Q ； ⑵ 喷嘴的下截面处的压强．解：沿喷嘴轴线作一条流线，设上、下截面处分别为1、2两点，根据连续性方程及伯努利方程，有1122υS υS = ，2201221122p ρυρgh p ρυ++=+由题意知 212υgH =又知 11Q υS =，21π4d S =，22π4D S =解得Q =，42041d p p ρgh ρgH D ⎛⎫=++- ⎪⎝⎭5-8 一柱容器的截面积为22510m -⨯、高为1 m ，容器中装满水，在容器的底部有一面积为42210m -⨯的小孔，试求使容器内水流尽需要多少时间？设在整个过程中，水的流动可视为定常流动．解：设某时刻水面到小孔的深度为h ，由连续性方程，得1122υS υS =式中12S S 、分别表示容器、小孔两处的横截面积，12υυ、分别表示容器、小孔两处的流速．由伯努利方程可得2211021122p ρυρgh p ρυ++=+联立两式，得12υS =式中h 为变量．1d d h υt=-，负号表示液面高度随时间下降，代入上式，得d d h S t-=上式可改写为00d t Ht h =-⎰其中1m H =，对上式积分，代入数据，得21.110st ==≈⨯5-9 由于飞机机翼形状的关系，在机翼上面的气流速度大于下面的流速，在机翼上、下两面间就形成压强差，因而使机翼产生上升的力．假定空气流过机翼是稳恒流动，并假定空气的密度不变，等于331.2910g cm -⨯．如果机翼下面的气流速率为100m s ，问机翼要得到1000 Pa 的压强差，机翼上面的气流速率应该是多少？解：根据伯努利方程得2211221122p ρυp ρυ+=+机翼上面的气流速率为2m s 107m s υ==≈5-10 一条半径为3.0 mm 的小动脉内出现一硬斑块，此处的有效半径为2.0 mm ，平均血流速度为0.5 m/s ，求：⑴ 未变窄处的平均血流速度； ⑵ 狭窄处会不会发生湍流?(已知血液的粘滞系数为3310Pa s -⨯⋅，密度为331.0510kg m ⨯)解：⑴用12r r 、分别表示血管未变窄、狭窄两处的半径，12υυ、分别表示未变窄、狭窄两处的血液流速．由连续性方程，得221122ππυr υr =则 2222212221120.5m s 0.22m s 3r r υυυr r ⎛⎫⎛⎫===⨯≈ ⎪ ⎪⎝⎭⎝⎭⑵由雷诺数的定义e ρυr R η=，代入相应数据，得3331.05100.5210350310e R --⨯⨯⨯⨯==⨯此处的雷诺数远小于流体作湍流流动的临界值，故不发生湍流．5-11 从油槽经过1.2 km 长的钢管将油输送到储油罐中，已知钢管的内直径为12 cm ，油的粘滞系数为0.32Pa s ⋅，密度为30.91g cm ，如果要维持235.210ms -⨯的流量，试问油泵的功率应为多大?解：首先根据泊肃叶公式求出油被输送到1.2 km 处所需要的压强差()()32612442880.32 1.210 5.210Pa 3.910Pa π 3.14610ηlQ p p R--⨯⨯⨯⨯⨯-==≈⨯⨯⨯为保持一定的流量．油泵的功率为()()12126253.910 5.210W2.010WP F υp p S υp p Q-==-=-=⨯⨯⨯≈⨯。

第一章1-190610500453.06=⨯==-V m ρkg/m 3906.01000906==d1—2 544.0140027327334.11013252732730=⨯+⨯=+=p t ρρkg/m 31-3 1121211V V V t t V dV dt V--==α98.616060)2080(10550)(611122=+⨯-⨯⨯=+-=-V V t t V V αm 3/h1-4933666112121051011011099510102111----⨯=⨯⨯-⨯-⨯-=---=-=V V V p p V dV dp κ1/Pa1-5 47109.26781028.4--⨯=⨯⨯==νρμ Pa·s1—6 63103.14.999103.1--⨯=⨯==ρμνm 2/s1—7 （1)17.266050001.014.360=⨯⨯==dnu π m/s521023.510005.017.260⨯=⨯=-=-δu dy du 1/s(2）222ddy du dL d dy du A d FM μπμ===35221033.51023.5108.01.014.35.322-⨯=⨯⨯⨯⨯⨯==du dy L d M πμ Pa·s(3)3531079.21023.51033.5⨯=⨯⨯⨯==-dyduμτPa1—8 (1)y dydu μμτ2==（2)μμμμτ2122=⨯===y dydu 1-9 (1）hu bL dy duAF 022μμ==(2） 当2h y =时,h u dy duμμτ== (3)当h y 23=时，0u u = 所以0==dy duμτ 1—102903.03.0133)(112121=⨯⨯==+=+=μμμμdy du A dy du AF F F N967.01=μ Pa·s 933.1212==μμPa·s1-11drr r dr r r r dA dy du r dF dM αδπωμαπδωμμsin 2sin 203=-=⋅=⋅=αδαπωμααδπωμαδπωμαδπωμαααcos 24)(sin 2sin 2sin 234403030tg H Htg dr r dr r dM M Htg Htg Htg =====⎰⎰⎰1-1262.26020025.014.360=⨯⨯==dnu πm/s3925.050.025.014.3=⨯⨯==dL A πm 2331022.4102.0062.23925.082.0⨯=⨯-⨯⨯==-dy du AF μN 05.1162.21022.43=⨯⨯==Fu P kW 1-130841.0100092.0109144.04=⨯⨯⨯==-νρμ Pa·s 1459.03048.01524.014.3=⨯⨯==dL A πm 22.7361024.1526.152061459.00841.03=⨯--⨯⨯==-dydu AF μN42.462.736=⨯==Fv P kW1—14dr r r r rdr r dy du dAr dF dM 3202δμπωδωπμμ=-⋅==⋅=δμπωδμπω3224203d dr r dM M d A===⎰⎰ 1-15785.0125.014.3=⨯⨯==dL A πm 23610258.4001.003.0785.01008.18--⨯=-⨯⨯⨯==dy du AF μN 1—161884.03.02.014.3=⨯⨯==Db A πm 2δμδμμ20u Au u A u dy du A Fu N =-=== 9374.01884.0245.01008.07.502=⨯⨯⨯==-A N u μδm/s9056.892.014.39374.06060≈=⨯⨯==D u n πr/min 1-17082.091810893.04=⨯⨯==-νρμ Pa·s75.14103.003.01.08.1082.03=⨯-⨯⨯⨯==-dy du AF μN1—18 由1-14的结果得2.791023.096046.09014.31044003032323424424=⨯⨯⨯⨯⨯⨯=⨯==--δμπδμπωnd d M N·m1—19dy du AF 00μ=dyduA F 120120μ= %7.86015.0002.0015.00120001200=-=-=-μμμF F F1-203.29105.0324.0105.08.910000728.098.1324.098.1332=⨯⨯-⨯⨯⨯⨯=-=--r gr h O H ρσmm1—217.11)105.0216.0105.08.91000513.053.1()216.053.1(33=⨯⨯-⨯⨯⨯⨯-=--=--r gr h Hg ρσmm1—22 由2642322δδδδρσ-++=RR g h 得δδδδρσ4622223+⎪⎪⎭⎫ ⎝⎛-+=R R h g其中 ()θθδsin 1cos -=R则 ()⎥⎦⎤⎢⎣⎡+++=22sin 13sin 21cos 2θθθρσR h gR1-23 根据牛顿内摩擦定律 drdV μτ-= 由于流速随半径的增加而减小，即drdu是负值，为了使为正值,上式在等号右端取负号根据已知条件 r r D drd 2)]4(4[22βμβμτ=--= 在管壁处2D r = 则4221DDββτ==当4D r =时 4222DDββτ==管壁处的阻力 L D DL DA F 21414βππβτ===1—24maF G =- 其中18.98.990===g Gm （kg ）则 )61.0(18.990-⨯=-F 60.95=F N 由dydu A F μ= 其中0583.01219.015228.014.3=⨯⨯==DL A πm 2 6.248979100245.001.603=⨯-=-=-δu dy du 1/s 则310586.6006586.06.2489790583.06.95-⨯==⨯==dydu A F μ Pa·s第二章2—1112.2128.08.910009.08.913600105122=⨯⨯-⨯⨯+=-+=gh gh p p OH HgaAρρkPa2-2 08.140599.08.91594)0(=⨯⨯=∆--=-=h g p p evρPa 92.8726508.14059101325=-=-=v ap p p Pa2-3 gh gh p BAeρρ=+ 且 1.015.025.0=-=h m （a) 9801.08.91000)(=⨯⨯=≈-=gh gh p BABeρρρPa 102305980101325=+=+=e ap p p Pa(b) 4.8131.08.9100083.0)(=⨯⨯⨯=≈-=gh gh p BABeρρρPa 4.1021384.813101325=+=+=e ap p p Pa(c) 123481.08.9)100013600()(=⨯⨯-=-=gh p ABeρρPa 11367312348101325=+=+=eap p p Pa2-4 设A 点到下水银面的距离为h 1，B点到上水银面的距离为h 2 BOH HgOH Ap gh gh gh p =+-+2122ρρρ04.348.521+=+-h h h 即44.221+=+h h h305.18.9)100013600(8.9100044.210)372.1744.2()(44.2522=⨯-⨯⨯+⨯-=-+-=gg p p h O H Hg OH B A ρρρm 2—544.03000027.025.10027.025.1=⨯-=-=s s t ρkg/m 3gHp gH p a a s s ρρ-=-6.166208.9)44.029.1()(=⨯⨯-=-=-gH p p s a s a ρρPa2—64.1340638.9100012.08.913600312.02=⨯⨯+⨯⨯-=⨯+⨯-=g g p OH HgeρρPa 2-7 223311gh gh p gh p B A ρρρ++=+ （1)112233100010001000gh d gh d gh d p p B A -++=16.08.983.0100008.08.96.13100012.08.983.010********.68⨯⨯⨯-⨯⨯⨯+⨯⨯⨯+⨯=287.79=kPa （2) 332211100010001000gh d gh d gh d pp AB--+=12.08.983.0100008.08.96.13100016.08.983.010*******.137⨯⨯⨯-⨯⨯⨯-⨯⨯⨯+⨯=96.127562=Pa563.319600096.127562=-=-=a B Be p p p kPa2—8 设401=h cm 22=h m 33=h m)(32112h h g p gh gh gh p BBHgAAA+-=+--ρρρρ 11232)(gh gh gh h h g p p HgAABBAρρρρ-+++-=4.08.9136004.08.97.85628.97.856)32(8.93.1254200000⨯⨯-⨯⨯+⨯⨯++⨯⨯-=377.105=kPa2-9 (1)93.138545sin 2.08.91000sin =⨯⨯⨯==-αρgL p p BAPa（2)3530sin 8.980093.1385sin =⨯⨯=-=αρg p p L BA cm 2—10666405.08.9136001=⨯⨯=∆=h g p Hg ρPa68.08.91000666422=⨯==∆gph O H ρm2—11 1022gh p gh p O H Hg a ρρ+=+4032gh p gh p O H Hg a ρρ+=+整理得)(1321422h h h h Hg Hg O H OH ρρρρ+-=)3.0136002.0136005.01000(10001⨯+⨯-⨯=86.1=m 2—12)()()(112342h H g h h g h h g p p O H Hg Hg a ---+-+=ρρρ)5.15.3(8.91000)5.15.2(8.913600)0.13.2(8.913600105-⨯⨯--⨯⨯+-⨯⨯+=386944=Pa2-13 ghh g p Hg A ρρ=++)84.0(85.1138.9)100075.013600(84.08.9100075.010372.1)(84.05=⨯⨯-⨯⨯⨯+⨯=-⨯+=g g p h Hg A ρρρcm 2-14)0.343.3(1000)74.22.3(1000-⨯-=-⨯+g d g d p B A862.043.08.9100046.08.9100060.110845=⨯⨯-⨯⨯⨯+-=B d2-15 59.0)59.0(22⨯++-=-g z g p gz p Hg O H B O H A ρρρ整理：853.7259.08.9)100013600(59.059.02=⨯⨯-=⨯-⨯=-g g p p OH HgBAρρkPa 2—16 设差压计中的工作液体密度为)()()(213241h h g h h g p h h g p B A -'---=--ρρρ)()(213241h h g h h h h g p p p B A -'-+--=-=∆ρρ)48.381.3(8.9100075.0)00.348.310.081.3(8.910005.1-⨯⨯⨯-+--⨯⨯⨯=5.45055Pa065.38.910005.15.45055=⨯⨯=∆g p ρm2-17112233100010001000gh d gh d gh d p p A B ---=44.28.975.0100052.18.9110006.08.96.131000274600⨯⨯⨯-⨯⨯⨯-⨯⨯⨯-=161802=Pa2—1882.38)34.01360053.0100025.1(8.934.053.0-=⨯-⨯⨯⨯=⨯-⨯=g g p HgA ρρkPa2—19 (1） 981010018.910004=⨯⨯⨯⨯==-ghA F ρN（2） 95.1)99.01001.001.0(8.910004=⨯+⨯⨯⨯==-gV G ρN 2-20 证明：如书中证明过程。

精心整理牛顿流体 作用在流体上的切向应力与它所引起的角变形速度之间的关系符合牛顿内摩擦定律的流体，1-2: 什么是连续介质模型？为什么要建立？1） 将流体作为由无穷多稠密、没有间隙的流体质点构成的连续介质，于是可将流体视为在时间和空间连续分布的函数。

2） ①可以不考虑流体复杂的微观粒子运动，只考虑在外力作用下的微观运动；②可以用连续函数的解析方法等数学工具去研究流体的平衡和运动规律。

1-3：流体密度、相对密度概念，它们之间的关系？1） 密度：单位体内流体所具有的质量，表征流体的质量在空间的密集程度。

相对密度：在标准大气压下流体的密度与4℃时纯水的密度的比值。

2） 性质：在静止流体中，作用于任意点的质量力垂直于经过该点的等压面。

水头:单位重量流体所具有的能量也可以用液柱高来表示帕斯卡原理：施于在重力作用下不可压缩流体表面上的压强，将以同样大小传到液体内部任意点上2-4：写出流体静力学基本方程的几种表达式。

说明流体静力学基本方程的适用范围以及物理意义、几何意义。

1c g p z =+ρ；gp z g p z ρρ2211+=+适用于不可压缩重力流体的平衡状态；物理意义：当连续不可压缩的重力流体处于平衡状态时,在流体中的任意点上,单位重量流体的总势能为常数。

几何意义：不可压缩的重力流体处于平衡状态时,静水头线或者计示静水头线为平行于基准面的水平线。

2-5：什么是绝对压强、计时压强和真空？它们之间有什么关系？1）绝对压强：以完全真空为基准计量的压强。

2）计示压强：（相对压强，表压强）以当地大气压强为基准计量的压强。

3）大气压强体处于真空状态。

1）迹线是同一流体质点在不同时刻的位移曲线，流线是同一时刻、不同流体质点速度向量的包络线，流线是流场中某一顺势的光滑曲线，该曲线上的流体质点的运动方向和该曲线相切。

1流线不能彼此相交和转折，只能平滑过渡。

2流线越密集流速越大。

3在定常流动中，流线不随时间改变其位置和形状，流线和迹线重合。

流体力学泵与风机2-15解：（1）当为空气（2）当为油2-16解：2-28 解：2-32 解：2-41 解：3-3解：（1）（2）3-5 解：所以，所以，此时，3-6 解：3-7解：干管前端的质量流量为：3-10解：将基准面建立在B点经过的水平面上，列能量方程：其中，3-11解：将2点所在的水平面作为基准面，列能量方程：所以，3-14解：以水面为基准面，列0-0和D-D的能量方程：所以，，即，所以，列0-0和A-A断面的能量方程：所以，所以，列0-0和B-B断面的能量方程：列0-0和C-C断面的能量方程：3-18解：将基准面建在管道所在的水平面上，列能量方程：3-19解：（1）（a）将基准面建在A所在的水平面上，列0-0和C-C断面的能量方程：且（b）（c）（2）（a）其中，所以，（b）（c）3-20 解：3-22解：其中，，所以，所以，3-263-28解：列连续性方程：列能量方程：列动量方程：3-33解：列能量方程：其中，其中，4-2 （1）（紊流）（2）4-3 解：4-4 解：所以，4-12 紊流粗糙区，，所以，4-13查尼氏图，得到，，所以，属于紊流粗糙区，属于紊流过渡区，属于紊流光滑区，（1）对于，采用希弗林松公式，（2）对于，采用阿公式，（3）对于，采用布公式4-154-21 （1）（2）（3）4-24 解：4-26 解：（1）突然缩小（2）（3）（4）4-27 解：所以，此时，4-29 解：5-17 解：5-25 解：解得，5-27 解：所以，1）2）5-28 解：继续阅读。