2011年第九届小学希望杯初赛四年级组试题
- 格式:doc
- 大小:611.00 KB
- 文档页数:12

四年级希望杯选题1.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷___ 3003 __ 。
2.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书__ 66 ____ 本。
3.在 a=20032003×2002和 b=20022003×2003中,较大的数是_b_____ ,它比较小的数大_2003_____ 。
4.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是__乙____ 。
5.在一个正方形水池的四周,环绕着一条宽2米的路(如图),这条路的面积是120平方米,那么水池的面积是__169____ 平方米。
6.甲、乙两辆汽车从A、B两地同时相向开出,出发后2小时,两车相距141千米;出发后5小时,两车相遇。
A、B两地相距_235_____ 千米。
7.小琴、小惠、小梅三人报名参加运动会的跳绳,跳高和短跑这三个项目的比赛,每人参加一项,报名的情况有__27____ 种。
8.下图是一个正方体木块。
M是AB的中点,N是AD的中点。
用一把锋利的锯,过M、N、G 三个点将木块锯成两块,使截面是平的,这个截面是_5_____ 边形。
9.下图是一所小学的科技数,它有4层,正面每层的三个圆形窗户由左向右表示一个三位数,这些三位数是:837、571、206、439,但是不知道这四个数和哪一层的窗户对应,请你观察一下,然后画出表示2008的四个窗户。
10.星期天,妈妈从超市买了4支小梦龙和3支可爱多冰淇淋,用去24元钱。
妈妈对小丽说:“上星期天我买了3支小梦龙和5支可爱多冰淇淋用去29元钱,你算一算,小梦龙每支 __3______元,可爱多冰淇淋每支___4_____ 元。


2010年第八届小学“希望杯”全国数学邀请赛四年级第1试试题1.计算:8×7÷8×7=。
2.将一些半径相同的小圆按如图1所示的规律摆放:第1个图形中有6个小圆,第2个图形中有10个小圆,第3个图形中有16个小圆,第4个图形中有24个小圆,…,依此规律,第6个图形中有个小圆。
3.地球与月球的平均距离大约是384400000米,把这个数改写成用“亿”作单位的数是亿米。
4.如果两个自然数的和与差的积是23,那么这两个自然数的和除以这两个数的差的商是。
5.已知8个数的平均数是8,如果把其中一个数改为8后这8个数的平均数变为7,那么这个被改动的数原来是。
6.某校的学生的属相有鼠、牛、龙、蛇、马、羊、猴、鸡、狗、猪。
那么至多选出位学生,就一定能找到属相相同的两位学生。
7.某养鸡场的母鸡只数是公鸡只数的6倍,后来公鸡、母鸡各增加60只,母鸡的只数变成公鸡只数的4倍。
则养鸡场原来一共养了只鸡。
8.将几个大小相同的正方体木块放成一堆,从正面看到的视图是图2(a),从左向右看到的视图是图2(b),从上向下看到的视图是图2(c),则这堆木块最多共有块。
9.将边长为10厘米的五张正方形纸片如图3那样放置,每张小正方形纸片被盖住的部分是一个较小的正方形,它的边长是原正方形边长的一半,则图3中的图形外轮廓(图中粗线条)的周长为厘米。
10.几百年前,哥伦布发现美洲新大陆,那年的年份的四个数字各不相同,它们的和等于16。
如果十位数字加1,则十位数字恰等于个位数字的5倍,那么哥伦布发现美洲新大陆是在公元年。
11.某年的8月份有5个星期一,4个星期二。
则这年的8月8日是星期。
12.一栋居民楼里的住户每户都订了2份不同的报纸。
如果该居民楼的住户只订了甲、乙、丙三种报纸,其中甲报30份,乙报34份,丙报40份。
那么既订乙报又订丙报的有户。
13.由1,2,3,4,5五个数字组成不同的五位数有120个,从大到小排列起来第95个数是。

2011年第9届小学“希望杯”全国数学邀请赛试卷(四年级第2试)一、填空(每小题5分,共60分)1.(5分)计算:234+432﹣4×8+330÷5=.2.(5分)四(1)班全体同学站成一排,当从左往右报数时,小华报:18;当从右往左报数时,小华报:13.那么,该班有学生名.3.(5分)如果25×口÷3×15+5=2005,那么口.4.(5分)如图是由25个面积等于1的小正方形组成的大正方形,图中面积是6的长方形有个.5.(5分)在括号内填上两个相邻的整数,使等式成立.6.(5分)由数字0,3,6组成的所有三位数的和.7.(5分)某种品牌的电脑降价20%后,每台售价为4592元,则该品牌电脑降价前每台售价元.8.(5分)已知两个自然数的积是35,差是2,则这两个自然数的和是.9.(5分)把1991,1992,1993,1994,1995分别填入图中的5个方格中,使得横排的三个方格中的数的和等于竖列的三个方格中的数的和.则中间方格中能填的数是.10.(5分)图是3×3的正方形方格,∠1与∠2相比,较大的是.11.(5分)小明从家出发,先向东偏北30°的方向跑了350米到达点A,接着向北偏西30°的方向跑了200米到达点B,然后又向西偏南30°的方向跑了350米到达点C,这时小明距家米.12.(5分)在图的九个方格里,每行、每列、每条对角线上的三个数的和都相等,则N=.二、解答题(每小题15分,共60分)每题都要写出推算过程.13.(15分)将一副三角板摆放在一起(可以叠放),使同时出现15°,30°,45°,60°,75°,90°,105°这七个角,请画图说明并表示出这些角.14.(15分)连续写出从1开始的自然数,写到2008时停止,得到一个多位数:123456789…2008请说明:这个多位数除以3,得到的余数是几?为什么?15.(15分)甲、乙、丙三辆车同时从A地出发驶向B地,依次在出发后5小时、5小时、6小时与迎面驶来的一辆卡车相遇.已知甲、乙两车的速度分别是80千米/时和70千米/时,求丙车和卡车的速度.16.(15分)将66个乒乓球放入10个盒子中,要求每只盒子都要有乒乓球,有且只有两个盒子中的乒乓球的个数相同,能办到吗?若能办到,请说明一种具体方法.若办不到,请说明理由.2011年第9届小学“希望杯”全国数学邀请赛试卷(四年级第2试)参考答案与试题解析一、填空(每小题5分,共60分)1.(5分)计算:234+432﹣4×8+330÷5=700.【分析】先计算算式中的乘法与除法,得到算式234+432﹣32+66,将这个算式中66使用加法交换律使它与234相加,然后再按照整数的四则混合运算进行计算即可得到答案.【解答】解:234+432﹣4×8+330÷5,=234+432﹣32+66,=234+66+432﹣32,=300+432﹣32,=732﹣32,=700.故答案为:700.2.(5分)四(1)班全体同学站成一排,当从左往右报数时,小华报:18;当从右往左报数时,小华报:13.那么,该班有学生30名.【分析】根据题意,可知小华的左边有17人,右边有12人,由此即可求得该班总人数.【解答】解:小华的左边有17人,右边有12人,17+12+1=30(人);答:该班有学生30名.故答案为:30.3.(5分)如果25×口÷3×15+5=2005,那么口16.【分析】由题目可以看出:25×口÷3×15是2005与5的差,即为2000;25×口÷3是2000与15的商,即为2000÷15;25×口是2000÷15与3的积,即为400;由此可以求出□的值.【解答】解:25×口÷3×15=2005﹣5=200,25×口÷3=2000÷15,25×口=2000÷15×3=400,25×口=400,□=16;答:ϖ应是16.故此题答案为:16.4.(5分)如图是由25个面积等于1的小正方形组成的大正方形,图中面积是6的长方形有24个.【分析】根据方类数图形的计数原理和方法,分别计算出行、列所包含的面积是6的长方形的个数,然后合并起来即可.【解答】解:图形中行所包含的面积是6的长方形是:3×4=12(个);图形中列所包含的面积是6的长方形也是12个;一共有:12+12=24(个);答:图中面积是6的长方形有24个.故答案为:24.5.(5分)在括号内填上两个相邻的整数3、4,使等式成立.【分析】根据题意,由分析分数的拆项,,就可以求出结果.【解答】解:由可知,这两个连续的自然数的积是12,因3×4=12,所以,==,故答案是:3、4.6.(5分)由数字0,3,6组成的所有三位数的和1899.【分析】根据题干,利用枚举法列举出0,3,6可以组成的所有三位数,①0不能为最高位;②3为最高位时可以组成:360;306;③6为最高位时可以组成:603;630.即可计算得出正确答案.【解答】解:根据题干分析可得:360+306+630+603=1899,答:由数字0,3,6组成的所有三位数的和是1899.故答案为:1899.7.(5分)某种品牌的电脑降价20%后,每台售价为4592元,则该品牌电脑降价前每台售价5740元.【分析】“降价20%”是把电脑原来的价格看作单位“1”,按原来价格的1﹣20%=80%出售,所以原来的价格为4592÷80%.【解答】解:4592÷(1﹣20%),=4592÷80%,=5740(元);答:该品牌电脑降价前每台售价5740元.故答案为:5740.8.(5分)已知两个自然数的积是35,差是2,则这两个自然数的和是12.【分析】因为两个自然数的积是35,所以这两个数一定是5和7,故和为:5+7=12.【解答】解:设这两个数分别为a和b,则a×b=35.又a、b都是自然数,在自然数范围内,积为35的只有5和7.所以a+b=12.故答案为:12.9.(5分)把1991,1992,1993,1994,1995分别填入图中的5个方格中,使得横排的三个方格中的数的和等于竖列的三个方格中的数的和.则中间方格中能填的数是1991,1993,1995.【分析】为了便于计算研究,我们把这五个数只取个位上的数字分别为:1、2、3、4、5.因为在横竖排的和中都含有中间的数字,设中间的数字为a,所以根据题意可表示出每排三个数字的和:(1+2+3+4+5+a)÷2=(15+a)÷2,要使(15+a)能被2整除,a只能等于1或3或5;故中间方格中能填的数是:1991,1993,1995.【解答】解:为了便于计算研究,我们把这五个数只取个位上的数字分别为:1、2、3、4、5.设中间的数字为a,所以根据题意可表示出每排三个数字的和:(1+2+3+4+5+a)÷2,=(15+a)÷2,要使(15+a)能被2整除,又因为这五个数是整数,所以a只能等于1或3或5;也就是代表的原数1991,1993,1995.故答案为:1991,1993,1995.10.(5分)图是3×3的正方形方格,∠1与∠2相比,较大的是∠1.【分析】借助正方形和线段构成的角来比较角的大小.:∠1=180°﹣(∠3+∠4),∠2=180°﹣(∠4+∠5)=180°﹣2∠4.很明显∠3<∠4,所以180°﹣(∠3+∠4)>180°﹣2∠4.即∠1>∠2.【解答】解:∠1=180°﹣(∠3+∠4),∠2=180°﹣(∠4+∠5)=180°﹣2∠4.很明显∠3<∠4,所以180°﹣(∠3+∠4)>180°﹣2∠4.即∠1>∠2.11.(5分)小明从家出发,先向东偏北30°的方向跑了350米到达点A,接着向北偏西30°的方向跑了200米到达点B,然后又向西偏南30°的方向跑了350米到达点C,这时小明距家200米.【分析】可根据上北下南,左西右东的方法进行作图,如图可连接C点与小明的家,可以看出小明跑过的路程为一个长方形,根据长方形的对边相等的性质,小明家距离C点有200米.【解答】解:如图小明站在C点时距离小明家的距离=点A到点B的距离,故答案为:200.12.(5分)在图的九个方格里,每行、每列、每条对角线上的三个数的和都相等,则N=18.【分析】先确定每行、每列、每条对角线上的三个数的和,8+6+16=30;再确定对角线上的中心数:30﹣8﹣12=10,然后求出右上角的数:30﹣16﹣10=4;最后得出第一行中间的数N=30﹣8﹣4=18.【解答】解:每行、每列、每条对角线上的三个数的和是:8+6+16=30;中心数是:30﹣8﹣12=10,右上角的数是:30﹣16﹣10=4;第一行中间的数是:N=30﹣8﹣4=18.二、解答题(每小题15分,共60分)每题都要写出推算过程.13.(15分)将一副三角板摆放在一起(可以叠放),使同时出现15°,30°,45°,60°,75°,90°,105°这七个角,请画图说明并表示出这些角.【分析】30°、45°、60°、90°的角在三角板中能找出,可直接利用三角板画出,15°、75°、105°的角要用两个三角板中的角组合画出.【解答】解:所要画出的角如下图:14.(15分)连续写出从1开始的自然数,写到2008时停止,得到一个多位数:123456789…2008请说明:这个多位数除以3,得到的余数是几?为什么?【分析】能被3整除的数的特征,各位数字和被3整除的数,本身能被3整除.各位数字和被3除余几,原数被3除就余几.【解答】解:(1+2+3+ (2008)=(1+2008)×2008÷2=2017036.(2+1+7+3+6)÷3,=19÷3,=6…1;则可推得原数字123…2008被3除余1.答:这个多位数除以3,得到的余数是1.15.(15分)(2010•拱墅区校级自主招生)甲、乙、丙三辆车同时从A地出发驶向B地,依次在出发后5小时、5小时、6小时与迎面驶来的一辆卡车相遇.已知甲、乙两车的速度分别是80千米/时和70千米/时,求丙车和卡车的速度.【分析】已知三车与卡车的相遇时间及甲乙两车的速度,因此可先据速度差×时间=路程差求出甲车与卡车相遇时比乙车多行的路程,即此时卡车和乙车的距离,然后再据路程÷相遇时间=速度和,即能求出卡车的速度;求出卡的速度后再据和丙车的相遇时间即能求出丙的速度.【解答】解:卡车的速度为:[(80﹣70)×5]÷(55)﹣70=50﹣70,=120﹣70,=50(千米/小时).丙车的速度为:[(80+50)×5]÷﹣50=650÷﹣50,=100﹣50,=50(千米).答:卡车的速度与丙车的速度同为每小时50千米.16.(15分)将66个乒乓球放入10个盒子中,要求每只盒子都要有乒乓球,有且只有两个盒子中的乒乓球的个数相同,能办到吗?若能办到,请说明一种具体方法.若办不到,请说明理由.【分析】每个盒子都放,且数目都不一样,至少用1+2+…+10=55个乒乓球,还剩下66﹣55=11个,从1﹣﹣9个的里面任取一个盒子,再放入一个球,例如在放了4个的里面再放一个,这样就有两个盒子有5个球,然后把剩下的10个球都放入最后一个盒子,由此即可得出10个盒子里面的数目.【解答】解:此题的答案有很多,只要把66拆成符合条件的10个数相加即可,这里只说一种方法,首先每个盒子都放,且数目都不一样,至少用的乒乓球的个数是:1+2+…+10=55(个),还剩下:66﹣55=11(个),从1﹣﹣9个的里面任取一个盒子,再放入一个球例如在放了4个的里面再放一个,这样就有两个盒子有5个球,然后把剩下的10个球都放入最后一个盒子,10个盒子里面的数目为:1,2,3,5,5,6,7,8,9,20,答:能将66个乒乓球放入10个盒子中,每只盒子都要有乒乓球,并且只有两个盒子中的乒乓球的个数相同.参与本试卷答题和审题的老师有:pyzq;xiaosh;rdhx;姜运堂;吴涛;齐敬孝;xuetao;春暖花开;admin;zhuyum(排名不分先后)菁优网2017年2月8日第11页(共11页)。

目录四年级 (2)2011年第九届小学“希望杯”全国数学邀请赛四年级第1试试题答案 (2)2011年第九届小学“希望杯”全国数学邀请赛四年级第2试试题答案 (4)2012年第十届小学“希望杯”全国数学邀请赛四年级第1试试题答案 (8)2012年第十届小学“希望杯”全国数学邀请赛四年级第2试试题答案 (11)2013年第十一届小学“希望杯”全国数学邀请赛四年级第1试试题答案 (13)2013年第十一届小学“希望杯”全国数学邀请赛四年级第2试试题答案 (16)五年级 (18)2011年第九届小学“希望杯”全国数学邀请赛五年级第1试试题答案 (18)2011年第九届小学“希望杯”全国数学邀请赛五年级第2试试题答案 (19)2012年第十届小学“希望杯”全国数学邀请赛五年级第1试试题答案 (22)2012年第十届小学“希望杯”全国数学邀请赛五年级第2试试题答案 (25)2013年第十一届小学“希望杯”全国数学邀请赛五年级第1试试题答案 (27)2013年第十一届小学“希望杯”全国数学邀请赛五年级第2试试题答案 (31)六年级 (35)2011年第九届小学“希望杯”全国数学邀请赛六年级第1试试题答案 (35)2011年第九届小学“希望杯”全国数学邀请赛六年级第2试试题答案 (36)2012年第十届小学“希望杯”全国数学邀请赛六年级第1试试题答案 (42)2012年第十届小学“希望杯”全国数学邀请赛六年级第2试试题答案 (44)2013年第十一届小学“希望杯”全国数学邀请赛六年级第1试试题答案 (46)2013年第十一届小学“希望杯”全国数学邀请赛六年级第2试试题答案 (50)四年级2011年第九届小学“希望杯”全国数学邀请赛四年级第1试试题答案2011年第九届小学“希望杯”全国数学邀请赛四年级第2试试题答案2012年第十届小学“希望杯”全国数学邀请赛四年级第1试试题答案2012年第十届小学“希望杯”全国数学邀请赛四年级 第2试试题答案答案:1.【解析】后3个和比前3个和大9,则前3个和为9,所以6数为2,3,4,5,6,7,最大数为7。
真题到底有什么用呢?是不是真题全部会做了,考试就没问题了呢?真题最明显的作用呢,就是能知道考试题型以及分值喽!但还可以更深层的挖掘一下:通过分析真题,能知道考试会考察到哪些知识点,以及各知识点的考察比重;通过做真题,可以查漏补缺,发现自己哪块知识点掌握得不好,及时加强,进一步完善自己的知识体系。
但真题也不是万能的,毕竟题目数量有限,而设计多变,所以关键还是要在熟练掌握知识点的基础上多见识各种各样的题目设计。
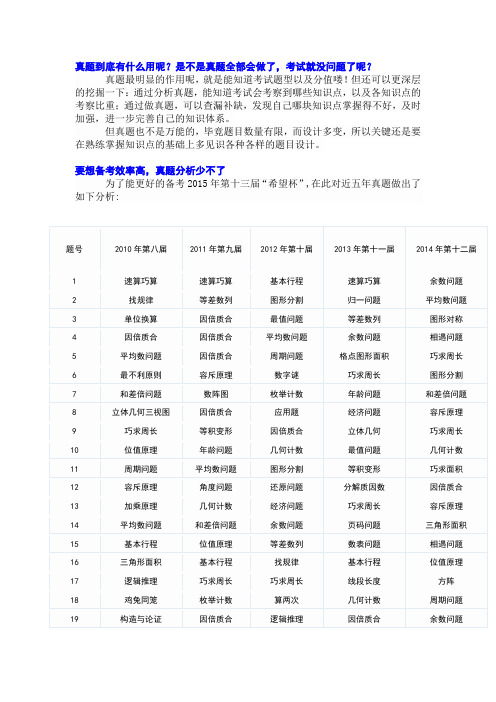
要想备考效率高,真题分析少不了为了能更好的备考2015年第十三届“希望杯”,在此对近五年真题做出了如下分析:题号2010年第八届2011年第九届2012年第十届2013年第十一届2014年第十二届1速算巧算速算巧算基本行程速算巧算余数问题2找规律等差数列图形分割归一问题平均数问题3单位换算因倍质合最值问题等差数列图形对称4因倍质合因倍质合平均数问题余数问题相遇问题5平均数问题因倍质合周期问题格点图形面积巧求周长6最不利原则容斥原理数字谜巧求周长图形分割7和差倍问题数阵图枚举计数年龄问题和差倍问题8立体几何三视图因倍质合应用题经济问题容斥原理9巧求周长等积变形因倍质合立体几何巧求周长10位值原理年龄问题几何计数最值问题几何计数11周期问题平均数问题图形分割等积变形巧求面积12容斥原理角度问题还原问题分解质因数因倍质合13加乘原理几何计数经济问题巧求周长容斥原理14平均数问题和差倍问题余数问题页码问题三角形面积15基本行程位值原理等差数列数表问题相遇问题16三角形面积基本行程找规律基本行程位值原理17逻辑推理巧求周长巧求周长线段长度方阵18鸡兔同笼枚举计数算两次几何计数周期问题19构造与论证因倍质合逻辑推理因倍质合余数问题20追及问题逻辑推理加乘原理角度问题因倍质合一试真题分析附加题1找规律附加题2几何计数上表是对近五年“希望杯”一试真题的分析。
一试题型为20道填空题,每题6分,满分120分。
通过上表可以发现“希望杯”考察的知识面非常的广,基本上小学数学中的七大模块都会涉及到,这同时也反映出进入四年级后,学习到的知识量会加大,知识面会更广。

第九届小学“希望杯”全国数学邀请赛获奖名单黑龙江省哈尔滨市来成文化学校一等奖(7名)四年级:哈尔滨市荣智小学李超然五年级:哈尔滨市香安小学宁昆鹏哈尔滨市继红小学单希政哈尔滨市复华小学郭涛鸣:哈尔滨市锅炉小学郎天宇:哈尔滨市花园小学尹泽霖:哈尔滨市铁岭小学李佳泽:二等奖(13名)四年级:哈尔滨市新阳路小学闫正邦哈尔滨市师范附小刘照一、葛佳琳赵万博哈尔滨市工农兵小学宁作宇哈尔滨市经纬小学刘锦徽哈尔滨市继红小学刘泽辉哈尔滨市复华小学宋晓斌哈尔滨市保国一校唐昊翔五年级哈尔滨市复华小学白雨萌哈尔滨市马家沟小学石昊天哈尔滨市雷锋小学祝明玥哈尔滨市新疆二校李文博三等奖(共370名)四年级:中英小学李容舟中英小学于海波中英小学齐颢然中英小学崔启元中英小学宋宣毅中英小学张瀚予中英小学霍鸣霄中英小学沈卓然正阳南小学陈可心兆麟小学郭凡漪兆麟小学李东泓兆麟小学赵健百兆麟小学丁瑞姝兆麟小学于盛麟兆麟小学高珊兆麟小学沈超凡育英小学张悦育民小学张雨菲育民小学王彬羽育红小学吴崎菲育才小学王佳旭应诺文化学校王胤博应诺文化学校陈智蕾逸夫小学王子嘉兴华小学李响兴华小学王鸿飞兴华小学衣凌克兴华小学姜永翔兴华小学杨宇航兴华小学张镇乾兴华小学马皓轩兴华小学宁民福新阳路小学杨澜新民小学赵文博新民小学阿文卓龙新疆二校周姿谕新成小学朱峰香坊小学杨天睿香坊小学孙嘉彤香坊小学刘津楚凡香坊小学张瀚文香坊小学王嘉旭香滨小学任忠麒香滨小学刘昕羽香滨小学李政润香滨小学张昊香安小学田爽文昌小学张振文王兆新村欧睿泽王兆新村庞博文王兆新村秦澜嘉王兆新村刘天泽通达小学毕皇辰通达小学张金岩铁岭小学于浩铁岭小学谷彧潇天天文化学校周建识泰山小学杨思宇泰山小学李杰豪泰山小学陈泳佐泰山小学刘世祺绥化尚志小学周博文苏宁小学杨笑迎苏宁小学王子恩苏宁小学刘湘禹实验小学曲晟师范附小侯冠廷师范附小陈曦师范附小刘思睿师范附小宫逸师范附小宋佳璐师范附小王圣与师范附小刘鼎坤师范附小孙可盈师范附小黄睿师范附小董浩廷师范附小周泽昱师范附小张芸鹏师范附小刘熠龙师范附小田宇迪师范附小韩谨谦师范附小许思远师范附小齐天宇师范附小费小溪师范附小马天翔师范附小吕鑫栋师范附小周翀尚志小学张雯雯清滨小学杨岱鑫汽轮小学韩志诚南市小学刘梓淇南马小学刘宇轩马家沟小学林晟宇龙江小学丁浩楠柳树小学王曦卓柳树小学刘渤雷锋小学李泽琛雷锋小学张天慧经纬小学吴尚哲经纬小学尹祎阳经纬小学莫奥博经纬小学甘岳林解放小学赵鹏建国小学孟祥鑫建国小学杜健洋继红小学王本宇继红小学方辛月继红小学王涵宇继红小学史涵帅继红小学于灿继红小学潘醍继红小学邵世龙继红小学刘明帆继红小学刘迪航继红小学焦阳继红小学侯冰俏继红小学王玥晴继红小学胡继元淮河小学聂君心桦树小学么恩泽花园小学刘昱彤花园小学黄之冠花园小学王军尧花园小学赵睿毅花园小学项品湜花园小学王心艺花园小学李昊霖花园小学于海昕花园小学王冠骐虹桥小学石晓熠虹桥小学卜祥滨虹桥小学刘志淮虹桥小学王宇鹏虹桥小学程蒋慧一虹桥小学郝俊雄虹桥小学付俊淳虹桥小学刘文俊虹桥小学张超虹桥小学张靖崧虹桥小学陈淞潇锅炉小学孟子佳公园小学彭涧明公园小学夏宇航公滨小学王津浩公滨小学王梓睿公滨小学林泽瀚公滨小学韩博公滨小学林子淇公滨小学王然公滨小学金树林公滨小学董天泽公滨小学郭剑锋公滨小学刘家汐高潮小学吕善鹏复华小学田雨泰复华小学赵澍淇风华小学马瑞成风华小学王禹诺风华小学季可儿风华小学王铭玥风华小学张嘉臣范清军奥数王祺动力小学张子华动力小学马赫东风小学孙明宇东风小学姜馨雨东风小学徐斐然东方红小学杨博涵电工小学孟月冰大同小学沙雨桐大同小学张智博长虹小学林南伟保国一校张淙彧奥林文化孟炜棋奥林文化张瀚一安静小学张邵亦安静小学王晶博安静小学于康萌安广小学叶润泽爱国小学赵文煊五年级:电工小学李震东风小学李伊冉香安小学李咏航大同小学孟祥泓中英小学赵宇轩花园小学毛星茏继红小学冯奕博复华小学孙源泽育红小学李昱林香安小学彭梓越新疆一校孙浩然南市小学王源继红小学李禹辰电工小学司恒宇范清军奥数刘心亿范清军奥数王应泽新阳路小学张奥凯新阳路小学郑博文长虹小学张鹤龙公滨小学韩一楠兴华小学纪霖琦复华小学吕泽明公滨小学温克寒友协三校孙浩然公滨小学孙白羽虹桥小学关博麟中英小学李阔然继红小学刘泽宇马家沟小学崔博睿育红小学吴尚思南马路小学宋嘉龙新阳路小学徐培文师范附小王仲博继红小学王晓瞳文化小学常云鹏南马路小学李晓生锅炉小学刘宏旭继红小学王俊博靖宇小学李季玉靖宇小学刘天祎奥林文化刘焱继红小学郭晋东复华小学孙嘉良复华小学陈思潼奥林文化苏冠荣继红小学刘世豪范清军奥数陈峻洋风华小学李潇锅炉小学王延明香滨小学沙湧瀚香安小学张可欣范清军奥数王嘉莹继红小学姜焯文继红小学王梓懿继红小学刘睿轩师大附小李应东师范附小王婧怡清滨小学羿天阳和兴小学刘畅电工小学王馨平友协二校张一宸电工小学唐诗范清军奥数刘函范清军奥数孙文龙红岩小学钱星瑞奋斗小学张子扬桥南小学杨宁虹桥小学刘涵智香坊小学姜君继红小学鲍海航百利小学赵杨师范附小宋冠禹雷锋小学单航电工小学姜宝洋中英小学刘昊贤苏宁小学李政萱师范附小刘泓辰民生路小学郑博文尚志小学孙泽铭继红小学张雨桐安静小学王松颢香滨小学栗延坤师范附小刘适涵兆麟小学潘浩泽闽江小学温胜伦继红小学姜博师范附小闫艺桐南马路小学赵文昊安阳小学杨少朕新疆二校喜泽昕花园小学王彩璇苏宁小学刘子雍泰山小学高唯珂复华小学东添建文小学袁宇宸香坊小学韩易达香坊小学姜宇昊桥南小学孙鹏宇花园小学佟文宇铁岭小学余泓霄雷锋小学吴桐师范附小王禹东风小学张岩松神龙文化学校李佳芯大同小学宋玥达保国二校杨万宝复华小学侯雨晴经纬小学陈雨辰继红小学刘天一师范附小王志乾兆麟小学程实继红小学薛添元新华小学林海杰香滨小学郭雨杨复华小学张佳钰电工小学丛佳文南直小学徐璐范清军奥数姜鹏飞继红小学邹雨辰马家沟小学王昕昊师范附小关昊育英小学徐华鹏大同小学梁炜悦新疆二校于涵花园小学王宇昂铁岭小学王志鹏奋斗小学丁家华泰山小学胡千禧团结小学王子皓经纬小学郝泽宇师范附小赵元硕新苗小学张银朵闽江小学黄婧育英小学徐子昂师范附小张馨予马家沟小学王鸣谦铁岭小学任金香滨小学杜宜聪闽江小学李仕隆育红小学张恩霆育英小学温金城香红小学庞博新疆二校黄禹瑞公滨小学刘泽宇实验小学刘永晟萧红小学吴雨奇复华小学姚烁香二小学张彤中英小学滕杨师大附小赵睿馨复华小学谢天丁兆麟小学吕正钦雷锋小学黄健马家沟校张康然虹桥小学苏章德隆兴华小学岳文涛长虹小学白东鑫兴华小学金宗贤公滨小学邓子睿苏宁小学徐宁泽经纬小学孙宇彤文昌小学任天翔闽江小学王法鹏闽江小学周子正建国小学徐昕钰康富小学孙琳昊南马路小学王睿东风小学张修琪东方红小学张健铭公滨小学王昕宇建国小学郭鑫泽新民小学杨雅涵师大附小张馨月通乡小学白英博香滨小学刘思源剑桥小学于志成团结小学王宇轩东风小学毕然风华小学张雨森公园小学柏金龙汽轮小学段世杰泰山小学柳思齐优秀辅导员:许波吕明蒋石春杨曦敏左春梅马洪峰杜良胤范清军薛晨亮蔡荣欣王丽孙莹英张蕊夏晓炜刘琦李英华张晶芦丽王丽英肖碧松林琳郭阳白晓双夏秀明高静娴张华高天苏嘉韩文静韩玉柱李强张圣龙刘亚男李天奇杨新月李昕烨胡玉福刘冬强李姝车美丽成诚杨慧娟张蕊姚宁宇简晓冬刘宁张代臣牟丹张静吕力赵淑珍边淑蓉陆甜甜陈丽娜黄龙刘天一张利王文玲王磊毕蕾王宏阎伟黄大勇陈维冲李芒陈立威王立枢尹龙艳朱春瑜王瑶吴丹王维华赵淞萍吕庭波邰慧尚颖韩忠生历海波沈丽刘卓顾惠敏丁宝田左春梅董荣张代臣陈悦张玉华王倩何华赵洁莹李婉嫔李冰路琳尹龙艳韩忠生张旭王丽焕姚文蕾赵洁莹张云凯郝庆多白晓双牟宏宇季威张丹丹刘松玲孙彦广孙爽英马静芝于志敏马丽赵丽娜赵桂荣郑露汤丽彦郑少妍王元静贝景南金晶晶崔昆王学丽蔡运生周凤英王雁黎孟晋温与寒王秀玲于志敏孙彦津王立枢丘立华历海波丁宝田王燕平王金波。

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
]](https://img.taocdn.com/s1/m/f473ed0e0912a21614792942.png)
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。

2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第2试)一、填空题(每小题5分,共60分)1.(5分)计算:(70÷4+90÷4)÷4=.2.(5分)计算:898+9898+99898+999898=.3.(5分)对运算⊙和㊣,规定:a⊙b=a×b+b,a㊣b=a×b﹣a,那么(2⊙3)⊙(2㊣4)=.4.(5分)若一个能被5整除的两位数既不能被3整除,又不能被4整除,它的97倍是偶数,十位数字不小于6,则这个两位数是.5.(5分)如图中每一横行右面的一个数减去它左面相邻的一个数所得的差都相等,每一数列下面的一个数除以它上面相邻的一个数所得的商都相等,则a+b×c=.6.(5分)如果一个两位数的3倍与4的差是10的倍数,它的4倍与15的差大于60且小于100,则这个两位数是.7.(5分)若四位数的各个数位上的数字都是偶数,并且百位上的数字是2,则这样的四位数有个.8.(5分)将长为12厘米,宽为8厘米的长方形纸片剪去4个同样大小的等腰直角三角形,剩余部分的面积至少是平方厘米.9.(5分)一个除法运算,被除数是10,除数比10小,则可能出现的所有不同的余数的和是.10.(5分)苹果和梨各有若干个,若每袋5个苹果和3个梨,则当梨恰好装完时,还多4个苹果;若每袋装7个苹果和3个梨,则当苹果恰好装完时,梨还多12个,那么苹果和梨共有个.11.(5分)如图,在△ABC中,AB=BC=CA,D、E、F分别是三边的中点,AD、BE、CF交于点O,则图中有个三角形;他们的面积有个不同的值.12.(5分)A、B、C、D四人带着一个手电筒,要通过一个黑暗的只容2人走的隧道,每次先让2人带着手电筒通过,再由一人送回手电筒,又由2人带着手电筒通过…,若A、B、C、D四人单独通过隧道分别需要3、4、5、6分钟,则他们4人都通过至少需要分钟.二、解答题(每小题15分,共60分)13.(15分)摩托车行驶120千米与汽车行驶180千米所用的时间相同,7小时内摩托车行驶的路程比6小时内汽车行驶的路程少80千米,若摩托车先出发2小时,然后汽车从同一出发点开始追赶,那么汽车出发后几小时内可以追上摩托车?14.(15分)将1,10,11,15,18,37,40这7个数分别填入图中的7个圆圈内(每个数都用到),能否使其中两条直线上的三个数的和相等,并且等于另一条直线上的三个数的和的3倍?若可以,请给出一种填法;若不能,请说明理由.15.(15分)100人参加速算测试,共10题.每题答对的人数如下表所示:题号 1 2 3 4 5 6 7 8 9 1093 90 86 91 80 83 72 75 78 59答对人数规定:答对6题或6题以上,为及格,根据上表计算至少有多少人及格.16.(15分)如图,甲乙两只小虫分别从每边长20厘米不透明的正五角星围墙的顶点A、B出发,沿外侧按逆时针方向爬行,甲每秒爬行5厘米,乙每秒爬行4厘米.问:在甲从出发到第一次爬到B的过程中,乙能看到甲的时间有多少秒?2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第2试)参考答案与试题解析一、填空题(每小题5分,共60分)1.(5分)计算:(70÷4+90÷4)÷4=10 .【分析】可以先从括号里开始运算,而括号里两个除式,可以化成分数的形式,最后再算结果.【解答】解:根据分析,原式=(70÷4+90÷4)÷4=(70+90)÷4÷4=160÷4÷4=40÷4=10.故答案是:10.【点评】本题考查了四则运算的巧算,突破点是,将括号里的运算进行巧算,再求最后的结果.2.(5分)计算:898+9898+99898+999898=1110592 .【分析】此题一看便知,这式子里的数都接近整数,用凑整法把它变成:(898+2﹣2)+(9898+2﹣2)+(99898+2﹣2)+(999898+2﹣2)=(900﹣2)+(9900﹣2)+(99900﹣2)+(999900﹣2)=900+9900+99900+999900﹣8.再根据特点易想到把这些凑整的数化成乘积的形式,便发现了乘法的分配律的运用,计算就简便了.【解答】898+9898+99898+999898=(900﹣2)+(9900﹣2)+(99900﹣2)+(999900﹣2)=900+9900+99900+999900﹣8=9×100+99×100+999×100+9999×100﹣8=(9+99+999+9999)×100﹣8=(10+100+1000+10000﹣4)×100﹣8=(11110﹣4)×100﹣8=11110×100﹣4×100﹣8=1111000﹣400﹣8=1110600﹣8=1110592【点评】此题是反复运用凑整法和乘法的分配律.并且是在解题过程中不断发现所用的运算定律.3.(5分)对运算⊙和㊣,规定:a⊙b=a×b+b,a㊣b=a×b﹣a,那么(2⊙3)⊙(2㊣4)=60 .【分析】按题意,则2⊙3=2×3+3=9;2㊣4=2×4﹣2=6,则(2⊙3)⊙(2㊣4)=9⊙6=9×6+6=60.【解答】解:根据分析,则2⊙3=2×3+3=9,2㊣4=2×4﹣2=6,则(2⊙3)⊙(2㊣4)=9⊙6=9×6+6=60,故答案是:60.【点评】本题考查了定义新运算,突破点是:分别算出2⊙3和2㊣4,再算出结果.4.(5分)若一个能被5整除的两位数既不能被3整除,又不能被4整除,它的97倍是偶数,十位数字不小于6,则这个两位数是70 .【分析】显然,能被5整除,则个位只能是0或5,而它的97倍是偶数,说明此两位数是一个偶数,故可以断定此两位数个位数字为0,而十位不小于6,只能是6、7、8、9,因不能被4整除,则十位不能是6、8,故十位只能是7或9,又因为不能被3整除,故十位上只能是7.【解答】解:根据分析,能被5整除,则个位只能是0或5,而它的97倍是偶数,说明此两位数是一个偶数,故可以断定此两位数个位数字为0,而十位不小于6,只能是6、7、8、9,因不能被4整除,则十位不能是6、8,故十位只能是7或9,又因为不能被3整除,故十位上只能是7.综上,此两位数是70,故答案是:70.【点评】本题考查了数的整除特征,突破点是:从题中已知条件推测出个位数字和十位数字.5.(5分)如图中每一横行右面的一个数减去它左面相邻的一个数所得的差都相等,每一数列下面的一个数除以它上面相邻的一个数所得的商都相等,则a+b×c=540 .【分析】首先分析题意,横行为等差,竖列为等比数列,找到第一行公差和数列的公比即可.【解答】解:依题意可知:横行为等差,竖列为等比.根据横行为等差数列可知第一行的数字为2,4,6,8.竖行是等比数列,故18÷2=9.所以c是2 的3倍即是6.a是4的27倍.4×27=108.b是8的9倍72.a+b×c=108+72×6=540.故答案为:540【点评】本题考查对幻方的理解和运用,关键问题是找到公差和公比问题解决.6.(5分)如果一个两位数的3倍与4的差是10的倍数,它的4倍与15的差大于60且小于100,则这个两位数是28 .【分析】显然,两位数的3倍与4的差是10的倍数,可知此两位数的三倍得到的数的个位数是4,而乘以3得到个位为4的两位数个位数为8,由它的4倍与15的差大于60且小于100,可求得此两位数的范围,不难求得此两位数.【解答】解:根据分析,两位数的3倍与4的差是10的倍数,可知此两位数的三倍得到的数的个位数是4,而乘以3得到个位为4的两位数个位数为8;由它的4倍与15的差大于60且小于100,可求得此两位数的范围:大于:=,小于:=,综上,此两位数为:28.故答案是:28.【点评】本题考查了因数与倍数,突破点是:根据因数与倍数的性质,以及两位数的范围求得两位数.7.(5分)若四位数的各个数位上的数字都是偶数,并且百位上的数字是2,则这样的四位数有100 个.【分析】四位数的最高位是千位,最高位上不能为0,那么可以是2,4,6,8,而百位上只是2,固定好了,那么十位和个位上可以是0,2,4,6,8,根据排列的特点可知:共有4×5×5个不同的四位数.【解答】解:千位可取2,4,6,8,十位和各位都可以取0,2,4,6,8 所以4×5×5=100(个)故答案为:100.【点评】本题考查每个数位数字的特点,注意千位上不能取0.8.(5分)将长为12厘米,宽为8厘米的长方形纸片剪去4个同样大小的等腰直角三角形,剩余部分的面积至少是24 平方厘米.【分析】长为12厘米,宽为8厘米的长方形纸片,显然最多只能剪下4个直角边为6的等腰直角三角形,故剩下的面积不难求得.【解答】解:根据分析,如图,长为12厘米,宽为8厘米的长方形纸片,最多只能剪下4个直角边为6的等腰直角三角形,故剩下的部分的面积至少=12×(8﹣6)=24.故答案是:24【点评】本题考查剪切和拼接,突破点是:利用长方形的长和宽的值,剪切时取最大值,则剩下的部分面积最小.9.(5分)一个除法运算,被除数是10,除数比10小,则可能出现的所有不同的余数的和是10 .【分析】除数比10小,可以将10除以1~9,得出的余数中有2个是0即除以1、5时余数为0,不同的余数为1、2、3、4,再求和即可.【解答】解:根据分析,10÷6=1…4;10÷7=1…3;10÷8=1…2;10÷9=1…1;而10÷3和10÷9余数都是1,10÷4和10÷8余数都是2,故不同的余数只有:1、2、3、4,可能出现的所有不同的余数的和=1+2+3+4=10.故答案是:10【点评】本题考查带余除法,突破点是:将10除以1~9,得出的余数中有2个是0即除以1、5时余数为0,不同的余数为1、2、3、4,再求和.10.(5分)苹果和梨各有若干个,若每袋5个苹果和3个梨,则当梨恰好装完时,还多4个苹果;若每袋装7个苹果和3个梨,则当苹果恰好装完时,梨还多12个,那么苹果和梨共有132 个.【分析】首先分析根据梨的数量是多12个,证明袋子少了12÷3=4袋.再根据少的4袋苹果数量为20加上剩余的4个就是24个平均每袋多2个共12袋子,即可求解.【解答】解:依题意可知:根据梨的数量是多12个,证明袋子少了12÷3=4袋.苹果差是4×5+4=24个.24÷(7﹣5)=12袋,水果总数为10×12+12=132.故答案为:132.【点评】本题考查对分配盈亏问题的理解和运用,关键问题是找到梨的数量差找到袋子的数量差.问题解决.11.(5分)如图,在△ABC中,AB=BC=CA,D、E、F分别是三边的中点,AD、BE、CF交于点O,则图中有16 个三角形;他们的面积有 4 个不同的值.【分析】要求三角形的个数和不同的面积的取值,可以分情况讨论,从只含有一个小三角形的三角形开始算起,面积的不同取值也不难求得.【解答】解:根据分析,由题可知,AB=BC=CA,D、E、F分别是三边的中点,①只含有1个小三角形的三角形有:6个,且每个三角形的面积均相等,且均等于三角形ABC面积的;②含有2个小三角形的三角形有:3个,且每个三角形的面积均相等,且均等于三角形ABC面积的;③含有3个小三角形的三角形有:6个,且每个三角形的面积均相等,且均等于三角形ABC面积的;④含有6个小三角形的三角形有:1个,即三角形ABC,综上,则图中有16个三角形;他们的面积有4个不同的值.故答案是:16、4【点评】本题考查了三角形的面积,突破点是:根据图形的三角形的特点,分情况讨论,不难求得结果.12.(5分)A、B、C、D四人带着一个手电筒,要通过一个黑暗的只容2人走的隧道,每次先让2人带着手电筒通过,再由一人送回手电筒,又由2人带着手电筒通过…,若A、B、C、D四人单独通过隧道分别需要3、4、5、6分钟,则他们4人都通过至少需要21 分钟.【分析】四人要通过的时间要少,过隧道花费时间少的来回跑,即可得出结论.【解答】解:分两种情况讨论:第一种:A和B过,A回,4+3=7(分钟)C和D过,B回,6+4=10(分钟)A和B过,4(分钟)共用7+10+4=21(分钟);第二种:A和B过,A回,4+3=7(分钟)A和C过,A回,5+3=8(分钟)A和D过,6(分钟)共用7+8+6=21分钟.所以,至少需要21分钟;故答案为21.【点评】此题是最大与最小问题,解本题的关键是安排过隧道花费时间少的送手电.二、解答题(每小题15分,共60分)13.(15分)摩托车行驶120千米与汽车行驶180千米所用的时间相同,7小时内摩托车行驶的路程比6小时内汽车行驶的路程少80千米,若摩托车先出发2小时,然后汽车从同一出发点开始追赶,那么汽车出发后几小时内可以追上摩托车?【分析】首先分析两车的路程比即是速度比,根据路程差除以速度差即可求解.【解答】解:依题意可知:摩托车速度:汽车的速度=120:180=2:3.每一份的路程为:80÷(3×6﹣2×7)=20(千米).摩托车7小时的路程为:20×7×2=280(千米).摩托车的速度为:280÷7=40(千米/小时).汽车6小时的路程为:20×6×3=360(千米).汽车的速度是:360÷6=60(千米/小时).40×2÷(60﹣40)=4(小时)答:那么汽车出发后4小时内可以追上摩托车.【点评】本题考查对追及问题的理解和运用,关键问题是找到路程差与速度差问题解决.14.(15分)将1,10,11,15,18,37,40这7个数分别填入图中的7个圆圈内(每个数都用到),能否使其中两条直线上的三个数的和相等,并且等于另一条直线上的三个数的和的3倍?若可以,请给出一种填法;若不能,请说明理由.【分析】首先根据这7个数字求和为132.再根据这些数字除以7的余数和132除以7的余数组成7的倍数即可,【解答】解:依题意可知:设最小的和为1份,那么其他的为3份,最后加的数字和为7的倍数才行.1+10+11+15+18+37+40=132.这7个数字除以7的余数分别为1,3,4,1,4,2,5.132÷7=18…6.根据中间数字多加2次,那么数字和为7的倍数,那么余数是4的可以构成7的倍数.132+11+11=154.154÷7=21.故答案为:【点评】本题考查对凑数谜的理解和运用,关键是找到数字和是7的倍数,问题解决.15.(15分)100人参加速算测试,共10题.每题答对的人数如下表所示:题号 1 2 3 4 5 6 7 8 9 10答对 93 90 86 91 80 83 72 75 78 59人数规定:答对6题或6题以上,为及格,根据上表计算至少有多少人及格.【分析】先确定出答错的总人次,不及格的至少答错5道,即可得出得出结果.【解答】解:各题答错的总人次数为7+10+14+9+20+17+28+25+22+41=193,每有一个人不及格,则他至少答错5题,193÷5=38…3,所以至多有38人不及格,至少有62人及格.为说明是可以的,注意41正好比38多3,所以这38个人全都在第10题上答错,剩余的答错次数恰好平均分配到其他9题上.答:至少有62人及格.【点评】此题是最大与最小问题,主要考查了数的除法,确定出各题答错的总人次是解本题的关键.16.(15分)如图,甲乙两只小虫分别从每边长20厘米不透明的正五角星围墙的顶点A、B出发,沿外侧按逆时针方向爬行,甲每秒爬行5厘米,乙每秒爬行4厘米.问:在甲从出发到第一次爬到B的过程中,乙能看到甲的时间有多少秒?【分析】设五角星的五个顶点按逆时针方向标为B、B1、B2、B3、B4,形成顶点B﹣﹣顶点B1的区间一,顶点B1﹣﹣顶点B2的区间二,以此类推到区间五.根据题意,乙能看到甲的情况是他们必须在同一时间都行走在同一区间.在区间一看到的时间:20÷5=4(秒);区间二看到的时间:20×2÷4=10(秒),20×3﹣10×5=60﹣50=10(厘米),10÷5=2(秒);区间三的情况:甲到达B3的时间是(10+20+20)÷5=10(秒),乙移动距离10×4=40(厘米),此时乙到达B2,乙能看到甲的时间是0,据此可解答.【解答】解:区间一看到的时间:20÷5=4(秒);区间二看到的时间:20×2÷4=10(秒),20×3﹣10×5=60﹣50=10(厘米),10÷5=2(秒);区间三能看到的时间:0总共乙能看到甲的时间有2+4=6(秒)答:乙能看到甲的时间有6秒.【点评】此题一定要结合生活实际去想去思考(什么情况下乙能看到甲),然后确定解题思路,就能顺利解答,这真是生活中的数学.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/4/22 16:48:13;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。

简单方程例1 某数加上6,然后乘以6,再减去6,最后除以6,其结果等于6,则这个数是多少?例2 将4放在一个两位数的右端,得到一个三位数,这个三位数比原来的两位数大445,问原来的两位数是多少?例3 一个数除以8后再减3,得到的数比原来的数少66,问原来的数是多少?例4 一个三位数,个位数字比十位数字大1,比百位数字大3,百位上与十位上的数字交换位置后得到一个新数,这两个三位数的和为787,问原来的三位数是多少?例5 甲筐苹果个数比乙筐苹果多64个,问从甲筐中取出多少个苹果放入乙筐,可使乙筐苹果比甲筐苹果多12个?例6 有三堆棋子,第二堆比第一堆的3倍多4个,第三堆比第一堆的4倍少1个,问当第一堆棋子是多少时,第二、三堆的棋子数相等?例7 有一架飞机,能在空中连续飞行9小时,飞出时的速度是每小时740千米,返回时每小时925千米,问这架飞机最多飞出多少千米就应返回?例8 少年乐团中有170人不是五年级,有135人不是六年级,已知五、六年级学生共205人,则少年乐团中除五、六年级以外的学生共有多少人?习题1 一个四位数abc 2扩大到3倍后,变成了8abc ,问这个四位数是多少?习题2 铁路旁的一条平行小路上,有一汽车人和一开车人同向行进,骑车人速度为每小时14.4千米,开车人速度为每小时72千米.这时有一列火车从他们背后开过来,火车通过骑车人用8秒,通过开车人用24秒,问这列火车车身长多少米?习题3 星期天,妈妈从超市买了4支小梦龙和3支可爱多冰淇淋,用去24元钱.妈妈对小丽说:“上星期我买3支小梦龙和5支可爱多冰淇淋用去29元钱,你算一算,小梦龙和可爱多每支各多少钱?”答:“小梦龙冰淇淋每支______元;可爱多冰淇淋每支_____元.习题4 有兄弟两人今年的年龄之和是50岁,但曾经有一年,哥哥的年龄是弟弟今年的年龄,那时哥哥的岁数恰好是弟弟当年岁数的2倍,问哥哥、弟弟今年分别多少岁?习题5 小明买鸡蛋买了5.40元,后来他觉得鸡蛋太小,又叫小贩无偿添加了2个鸡蛋.这样一来,平均每个鸡蛋降了3分钱,小明共带回多少个鸡蛋?习题6 某工人和老板签了一份30天的劳务合同:工作一天可得报酬48元,休息一天则要从所得报酬中扣掉12元.该工人合同到期后并没有拿到报酬,则他最多工作了多少天?习题7 小明做一道计算题,原题是一个数除以7,再加上72,由于粗心,他把除以算成了乘,加算成了减,凑巧得数是对的,这道题的得数是多少?习题8 将786个桃子分成四堆,第一堆比第二堆多24个,比第三堆多16个,比第四堆多46个,那么第四堆有多少个?习题9 在一堆球中有红、白、黑三种颜色的球,白球和红球合起来是16个,红球比黑球多7个,黑球比白球多5个,那么黑球有多少个?习题10 甲、乙、丙三人参加一次智力测试,甲答对题目最多,他们中任意两个人答对的题目数之和分别是39,50,47.那么甲答对多少到题?应用题1.简单的应用题例1 有一座六层的塔,每一层的灯的盏数都是上一层的3倍,最顶层点了一盏灯,则这座塔一共点了多少盏灯?例2 生产一吨含20%水分的苹果果脯,需要4吨新鲜苹果。

小学四年级希望杯数学竞赛第一届至十一届全部试题与答案第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+=2002÷3.观察1,2,3,6,12,23,44,某,164的规律,可知某=4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定ab=13某a-b÷8,那么1724的最后结果是6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在a=20032003某2002和b=20022003某2003中,较大的数是,它比较小的数大12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。

第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。

2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)一、解答题(共20小题,满分114分)1.(6分)计算:(7777+8888)÷5﹣(888﹣777)×3=.2.(6分)计算:1+11+21+…+1991+2001+2011=.3.(6分)在小于30的质数中,加3以后是4的倍数的是.4.(6分)小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的倍.5.既是6的倍数又是8的倍数的所有两位数的和是.6.(6分)四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这个小组中既不会打乒乓球又不会下象棋的有人.7.(6分)按照左侧四个图中数的规律,在第五个图中填上适当的数:8.(6分)已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200,则这两个被改动的数以外的7个数的乘积是.9.(6分)如图,△ABC的面积为36,点D在AB上,BD=2AD,点E在DC 上,DE=2EC,则△BEC的面积是.10.(6分)今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大岁.11.(6分)某次考试,A、B、C、D、E五人的平均分是90分.若A、B、C 的平均分是86分,B、D、E的平均分是95分,则B的得分是分.12.(6分)如图,已知直线AB和CD交于点O,若∠AOC=20°,∠EOD=60°,则∠AOE=,∠BOC=.13.(6分)如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G 在一条直线上,则图中共有个正方形,个等腰直角三角形.14.(6分)一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水千克,桶重千克.15.(6分)某个两位数的个位数字和十位数字的和是12,个位数和十位数字交换后所得两位数比原数小36,则原数是.16.(6分)王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么,他来回都坐车,则需分钟.17.(6分)图中“C”形图形的周长是厘米.18.(6分)如图,从1,2,3,4,5,6中选出5个数填在图中空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有种不同的填法.19.(6分)三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是.20.(6分)甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D,第五名是E.”乙:“第二名是A,第四名是C.”丙:“第三名是D,第四名是A”,丁:“第一名是C,第三名是B.”戊:“第二名是C,第四名是B.”若每个人都是只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是.2011年第九届小学“希望杯”全国数学邀请赛试卷(四年级第1试)参考答案与试题解析一、解答题(共20小题,满分114分)1.(6分)计算:(7777+8888)÷5﹣(888﹣777)×3=3000 .【分析】把7777+8888与888﹣777,拆成两个数的乘积,再根据乘法分配律进行计算即可.【解答】解:(1111×7+1111×8)÷5﹣(111×8﹣111×7)×3,=1111×(7+8)÷5﹣111×(8﹣7)×3,=1111×(15÷5)﹣111×1×3,=1111×3﹣111×3,=(1111﹣111)×3,=1000×3,=3000.故答案为:3000.【点评】本题主要考查乘法分配律的灵活运用,根据数字特点找出巧算的方法进行计算即可.2.(6分)计算:1+11+21+…+1991+2001+2011=203212 .【分析】通过观察,相邻两个数的差是10,这是一个等差数列,可以用高斯求和公式进行简算.这一数列共有(2011﹣1)÷10+1=202个数,然后运用公式计算即可.【解答】解:1+11+21+…+1991+2001+2011,=(1+2011)×[(2011﹣1)÷10+1]÷2,=2012×202÷2,=203212.故答案为:203212.【点评】此题的关键是先探索出这是一个等差数列,运用“项数=(末项﹣首项)÷公差+1”算出项数.3.(6分)在小于30的质数中,加3以后是4的倍数的是5,13,17,29 .【分析】根据质数的意义,一个自然数,如果只有1和它本身两个因数,这样的数叫做质数.30以内的质数有:2,3,5,7,11,13,17,19,23,29;4的倍数特征是个位上的数是偶数;由此解答.【解答】解:5+3=8;13+3=16;17+3=20;29+3=32;8,16,20,32都是4的倍数;故答案为:5,13,17,29.【点评】此题的解答主要明确质数的意义,掌握30以内的10个质数,和4的倍数的特征.4.(6分)小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的 2 倍.【分析】此题要找出小于100的最大自然数是99,大于300的最小自然数是301,不大于200(即小于或等于200)的最大自然数是200,由此本题可以看做是:“99和301的和是200的多少倍?”.【解答】解:(99+301)÷200,=400÷200,=2;答:是不大于200的最大的自然数的2倍.故答案为:2.【点评】解决此题的关键是,根据题干先得出“小于100的最大的自然数”是99、“大于300的最小的自然数”是301,“不大于200的最大的自然数”是200.5.既是6的倍数又是8的倍数的所有两位数的和是240 .【分析】既是6的倍数,又是8的倍数,先分解质因数,6分为2×3,8分为2×2×2,再找出最小公倍数,两位数的公倍数只有四个数:24,48,72,96,相加即得答案240.【解答】解:根据分析,先分解质因数6=2×3,8=2×2×2,则两者的最小公倍数即为24,符合条件的所有两位数公倍数为:24,48,72,96;所有这些两位数之和:24+48+72+96=240,故答案为:240.【点评】本题考查了公倍数和数的整除运算知识,本题突破点是:找出两者之间的最小公倍数.6.(6分)四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这个小组中既不会打乒乓球又不会下象棋的有 2 人.【分析】只要从总人数12人中,把会打乒乓球和会下象棋的人数减掉,剩下的就是这个小组中既不会打乒乓球又不会下象棋的人数;此题可以画图分析:5+8=13人,这里重复加了一次既会打乒乓球有会下象棋的3人,所以会打乒乓球和会下象棋的人数为13﹣3=10人,则剩下的12=2人就是这个小组中既不会打乒乓球又不会下象棋的人数.【解答】解:12﹣(5+8﹣3)=2(人),答:这个小组中既不会打乒乓球又不会下象棋的有 2人.故答案为:2.【点评】此题考查了利用容斥原理解决实际问题的灵活应用.7.(6分)按照左侧四个图中数的规律,在第五个图中填上适当的数:【分析】(1)根据题干,图中1的位置变化规律是:按顺时针方向依次移动一个格;(2)数字排列规律是:分别按1、3、5、2、4、6的顺序排列的,而且第奇数幅是按顺时针排列,第偶数幅是按逆时针排列;第五幅图是第奇数幅,所以按顺时针排列.【解答】解:根据题干分析可得:(1)图中1的位置变化规律是:按顺时针方向依次移动一个格;所以先确定1的位置如下图所示;(2)第五幅图是第奇数幅,所以按顺时针排列,所以可以在图中添上正确的数字如下图所示:【点评】根据题干得出1的位置变化规律和图中数字1、3、5、2、4、6的排列特点是解决此题的关键.8.(6分)已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200,则这两个被改动的数以外的7个数的乘积是10 .【分析】只要求出被改动的两个数是多少,即能求出这两个被改动的数以外的7个数的乘积是多少.已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,积缩小了800÷200=4(倍),则这个被改动的数也被缩小了4倍,则被改动的这个数为:4×4=16;同理,1200÷200=6,积扩大了6倍,第二个被改动的数也被扩大了6倍,其原来应为:30÷6=5,所以则这两个被改动的数以外的7个数的乘积是:800÷(16×5)=10.【解答】解:第一个数原来为:(800÷200)×4=16;第二个数原来为:30÷(1200÷200)=5;则两个被改动的数以外的7个数的乘积是:800÷(16×5)=10.故答案为:10.【点评】在乘法算式,其中一个因数扩大(或缩小)多少倍,积也相应的扩大(或缩小)多少倍.9.(6分)如图,△ABC的面积为36,点D在AB上,BD=2AD,点E在DC 上,DE=2EC,则△BEC的面积是8 .【分析】(1)△ABC的面积是36,BD=2AD,根据高一定时,三角形的面积与底成正比的性质即可得出:△ABC的面积:△BDC的面积=3:2,所以:△BDC的面积是:36×2÷3=24;(2)△BDC的面积是36×2÷3=24,DE=2EC,根据高一定时,三角形的面积与底成正比的性质即可得出:△BEC的面积:△BDC的面积=1:3,所以△BEC的面积是24÷3=8.【解答】解:因为BD=2AD,根据高一定时,三角形的面积与底成正比的性质即可得出:△ABC的面积:△BDC的面积=3:2,故△BDC的面积是36×2÷3=24;因为DE=2EC,同理可得:△BEC的面积:△BDC的面积=1:3,故△BEC的面积是24÷3=8.答:△BEC的面积是8.故答案为:8.【点评】此题反复考查了高一定时,三角形的面积与底成正比的性质的灵活应用.10.(6分)今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大28 岁.【分析】4年后,李林和他爸爸的年龄之和是50+4×2=58岁,设李林4年后的年龄为x岁,则爸爸的年龄是3x﹣2岁,根据他们的年龄之和是58岁列出方程即可解决问题.【解答】解:设李林4年后的年龄为x岁,则爸爸的年龄是3x﹣2岁,根据题意可得方程:x+3x﹣2=50+4×2,4x=60,x=15,3×15﹣2=43(岁),43﹣15=28(岁),答:李林的爸爸比他大28岁.故答案为:28.【点评】此题也可以这样分析,4年后,李林和爸爸的年龄之和就是58岁,把李林的年龄看做1份,那么爸爸的年龄就是3份少2岁,由此可以求出1份即李林的年龄为:(58+2)÷4=15(岁),由此可得爸爸58﹣15=43岁,则爸爸比李林大28岁.11.(6分)某次考试,A、B、C、D、E五人的平均分是90分.若A、B、C 的平均分是86分,B、D、E的平均分是95分,则B的得分是93 分.【分析】根据“平均数×数量=总数”分别计算出A、B、C三个数的和与B、D、E三个数的和与这五个数的和,进而用“A、B、C三个数的和+B、D、E三个数的和﹣五个数的和”进行解答即可.【解答】解:(86×3+95×3)﹣(90×5),=543﹣450,=93(分);故答案为:93.【点评】解答此题的关键:根据平均数和数量、总量之间的关系进行分析解答.12.(6分)如图,已知直线AB和CD交于点O,若∠AOC=20°,∠EOD=60°,则∠AOE=100°,∠BOC=160°.【分析】由图可知,∠AOC=20°、∠EOD=60°与∠AOE相加等于180°,由此即可求得∠AOE的度数;∠BOC与∠AOC=20°互为补角,根据补角的定义即可解答.【解答】解:∠AOE=180°﹣∠AOC﹣∠EOD=180°﹣20°﹣60°=100°.∠BOC=180°﹣∠AOC=180°﹣20°=160°.故答案为:100°;160°.【点评】本题主要考查角的度量与补角的定义,根据几个角的和差关系进行计算是解题关键.13.(6分)如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G 在一条直线上,则图中共有 3 个正方形,22 个等腰直角三角形.【分析】根据图形可知,正方形有:ABCD、CEFG、BEGD三个;在正方形ABCD、CEFG和BEGD中,单一三角形是10个,有两个小三角形组成的是8个;由3个三角形组成的等腰直角三角形是4个;由此解答.【解答】解:图中共有正方形3个;等腰直角三角形有:10+8+4=22(个);故答案为:3;22【点评】此题主要考查通过分类、观察、思考探寻事物规律的能力.14.(6分)一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水 3 千克,桶重 4 千克.【分析】根据题意知道,桶的重量不变,(22﹣16)千克的水就是水原来的(6﹣4)倍,由此即可求出原来的水的千克数,那桶的重量即可求出.【解答】解:桶内原有水:(22﹣16)÷(6﹣4),=6÷2,=3(千克),桶重:16﹣4×3,=16﹣12,=4(千克);答:桶内原有水3千克,桶重4千克.故答案为:3,4.【点评】解答此题的关键是,根据题意,找出对应的数和对应的倍数,由此列式解答即可.15.(6分)某个两位数的个位数字和十位数字的和是12,个位数和十位数字交换后所得两位数比原数小36,则原数是84 .【分析】设个位数字是x,则十位数字是12﹣x,所以可得:原来两位数是10(12﹣x)+x,交换位置后的新两位数是10x+12﹣x;根据新数比原数小36,列出方程即可解决问题.【解答】解:设个位数字是x,则十位数字是12﹣x,那么原来两位数是10(12﹣x)+x,交换位置后的新两位数是10x+12﹣x;根据题意可得方程:10(12﹣x)+x﹣(10x+12﹣x)=36,18x=72,x=4;12﹣4=8,答:原数是84.故答案为:84.【点评】此题设出个位数字和十位数字,从而得出原两位数和新两位数是解决本题的关键.16.(6分)王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么,他来回都坐车,则需30 分钟.【分析】来回都步行,需要2个半小时说明王强步行单程用:2.5÷2=1.25(小时),又因为步行去公园,回来时坐车,往返用了一个半小时,则坐车单程用:1.5﹣1.25=0.25(小时),则来回都坐车用时:0.25×2=0.5(小时).【解答】解:(1.5﹣2.5÷2)×2,=0.25×2,=0.5(小时);0.5小时=30分钟.故答案为:30.【点评】完成本题的关健是:在求出步行单程所用时间的基础上,求出坐车单程所用时间.17.(6分)图中“C”形图形的周长是32 厘米.【分析】如图,将内部的2厘米边平移到外面红色线段处,这样这个图形的周长就是这个边长为6厘米的正方形的边长与内部横着的两条长为6﹣2=4厘米的线段的长度之和,由此利用正方形周长公式代入数据即可解决问题.【解答】解:根据题干分析可得:6×4+(6﹣2)×2,=24+8,=32(厘米),答:这个图形的周长是32厘米.故答案为:32.【点评】借助平移的性质将图形中的某些线段移动到规则图形的边上,使求这个不规则图形的周长转化成求规则图形的周长是解决此类题目的主要解题思路.18.(6分)如图,从1,2,3,4,5,6中选出5个数填在图中空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有30 种不同的填法.【分析】此题根据乘法原理进行解答,从6个数中选出5个进行填空,共有6×5种.【解答】解:从6个数中选出5个进行填空,共有:6×5=30(种);故答案为:30.【点评】此题运用了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有m n种不同的方法,那么完成这件事共有N=m1×m2×m3×…×m n种不同的方法.19.(6分)三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是1488 .【分析】据题意可知,这是三个相连的自然数,又7、8、9也是相连的自然数,因此先找到7、8、9的最小公倍数:7×8×9=504,则减9是9的倍数,减8是8的倍数,减7是7的倍数,得到495、496、497是符合要求的.【解答】解:7、8、9的最小公倍数为:7×8×9=504;504﹣7=497,504﹣8=496,504﹣9=495;495+496+497=1488.故填:1488.【点评】任何三个连续自然数(零除外)的最小公倍分别减(或加)这三个数得到的三个连续的自然数分别是这三数的倍数.20.(6分)甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D,第五名是E.”乙:“第二名是A,第四名是C.”丙:“第三名是D,第四名是A”,丁:“第一名是C,第三名是B.”戊:“第二名是C,第四名是B.”若每个人都是只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是CADBE .【分析】本题可用假设法分两步进行推理:第一步:假设甲说的前半句是真的,那么D是第1名,那么此时丙说的前半句错,后半句对.则A是第4名.同理乙的后半句对,C是第4名.矛盾.由此可知甲的后半句对.第二步:已知E是第5名,D不是第1名.和第一名有关的话只剩下丁说的,设C是第1名.则戊:“第2名是c,第4名是B”.可知前错后对,B 是第4名.且有乙:“第二名是A,第四名是c”.可知,A是第2名.D是第3名.【解答】解:第一步:假设甲说的前半句是真的,那么D是第1名,那么此时丙说的前半句错,后半句对.则A是第4名.同理乙的后半句对,C是第4名.矛盾.由此可知甲的后半句对.即第五名是E;第二步:已知E是第5名,D不是第1名.和第一名有关的话只剩下丁说的,设C是第1名.则戊:“第2名是c,第4名是B”.可知前错后对,B是第4名.且有乙:“第二名是A,第四名是c”.可知,A是第2名.D是第3名.综上可知,第一、二、三、四、五名分别是CADBE.【点评】完成此类题目思路要清晰,根据所给条件中的逻辑关系细心推理,从而得出结论.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/4/22 16:49:14;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。

2011年第九届希望杯四年级培训题100题2011年第九届希望杯四年级培训题2011年2月1、计算:123+456+789+987+654+321=_________ ____ 2、计算:7+97+997+9997+99997=_____________ 3、若两个相同的自然数的和与积相等,求这个自然数。
4、计算:(1×2×3×?×11)÷(1+2+3+?+11)=_______________ 5、计算:125×70-5×28×2+4×5×9=_____________________6、有一个两位数,它除以3,得余数2,它乘以3,乘积的个位数字是4,百位数字是2,求这个两位数。
7、乘积是160的两个数的和比这两个数的差大4,求这两个数的和。
8、算式8888?8 ×9999?9的结果中有多少个1?2010个8 2010个9 9、图1中,以点A,B,C,D,E,F,G,H为端点的线段有多少条?图1 10、一个六位数,从左到右的第三个数字开始,每个数字恰好都是前两个数字的积,求符合此条件的六位数的个数。
11、甲、乙、丙三人拿出同样多的钱共买回一筐苹果。
甲和丙都比乙多拿了15千克苹果,并且分别给了乙30元,问:每千克苹果多少元?12、妈妈带儿子小虎到超市习了两件商品,小虎把一件商品标价中个位上的零忽略了,他付给收银员162元,但是收银员说应当付270元,求这两种商品的单价分别是多少?13、一人匀速地在公路上散步,从第1根电线杆走到第15根,用了15分钟,则这人如果按这速度走30分钟可从第1根电线杆走到第几根电线杆处?14、赵明步行去公园回来时坐车,途中用了一个半小时,如果他去公园时,来、回都坐车,则只需半小时,如果他来去都步行,需要多少小时?15、某影院一号播放厅有20排座位,第七排有42个座位,从第二排起后面一排总比前一排多2个座位,求这个播放厅的座位总数。

第九届小学“希望杯”数学邀请赛四年级第2试2011年4月10日上午9:00---11:00一.填空题(每小题5分,共60分)1.计算:(70÷4+90÷4)÷4=()2.计算:898+9898+99898+999898=()3.对运算符号⊙和⊕规定:a⊙b=a×b+b,a⊕b=a×b-a,那么(2⊙3)⊙(2⊕4)=()4.若一个能被5整除的两位数既不能被3整除也不能被4整除,它的97倍是偶数,十位数字不小于6,则这个两位数是()5.图1中每一横行右面的一个数减去它左面相邻的一个数所得到的差都相等,每一竖行下面的一个数除以它上面相邻的一个数所得到的商都相等,则a+b×c=()4 8c18 ba 1626.如果一个两位数的3倍与4的差是10的倍数,它的4倍与15的差大于60,小于100,则这个两位数是()???7.若四位数的各个数位上的数都是偶数,且百位数字是2,则这样的四位数有()个。
8.将长为12厘米宽为8厘米的长方形纸片剪去4个同样大小的等腰直角三角形,剩下部分的面积至少是()平方厘米9.一个除法运算,被除数是10,除数比10小,则可能出现的所有不同的余数的和是()10.苹果和梨各有若干个,若每袋装5个苹果和3个梨,则梨恰好装完,还多4个苹果;若每袋装7个苹果和3个梨,则苹果恰好装完,梨还多12个。
那么苹果和梨共有()个。
11.如图,在△ABC中,AB=BC=CA,D,E,F是三边的中点,AD、BE、CF交于点O,则图中有()个三角形,它们的面积有()个不同的值。
12.A,B,C,D四人带一个手电筒,要通过一个黑暗的只能容2人走的隧道,每次先让2人带着手电筒过去,再由一人送回手电筒、、、、、,若A,B,C,D四人单独通过隧道各需要3、4、5、6分钟,则他们四人都通过隧道至少需要()分钟。
二.解答题(每题15分,共60分,每题都要写出推算过程)13.摩托车行驶120千米与汽车行驶180千米所用的时间相同,7小时内摩托车行驶的路程比6小时汽车行驶的路程少80千米,若摩托车先出发2小时,然后汽车从同一出发点开始追赶,问汽车出发后几小时可以追上摩托车?14.将1,10,11,15,18,37,40这7个数分别填入图中的7个圆圈内,每个数都要用,能否让其中两条直线上的三个数的和相等,并且等于另一条直线上的三个数的和的3倍?若可以,请给出一种填法,若不可能,请说明理由。
来源:本站原创 2011-03-13 09:38:14 [标签:希望杯答案试卷]奥数精华资讯免费订阅答案:一. 小强由家里到学校,如果每分钟走50米,上课就要迟到3分钟;如果每分钟走60米,就可以比上课时间提前2分钟到校。
小强家到学校的路程是多少米?【分析】迟到3分钟转化成米数:50×3=150(米),提前2分钟到校转化成米数:60×2=120(米),距离上课时间为:(150+120)÷(60-50)=27(分钟),家到学校的路程为:50×(27+3)=1500(米)。
二. 200720072007÷22302230223原式=(2007×100010001)÷(223×100010001)=2007÷223=9三. 甲乙两个油桶各装了15千克油.售货员卖了14千克.后来,售货员从剩下较多油的甲桶倒一部分给乙桶使乙桶油增加一倍;然后从乙桶倒一部分给甲桶,使甲桶油也增加一倍,这时甲桶油恰好是乙桶油的3倍.问:售货员从两个桶里各卖了多少千克油?解题关键是求出甲、乙两个油桶最后各有油多少千克.已知"甲、乙两个油桶各装油15千克.售货员卖了14千克".可以求出甲、乙两个油桶共剩油15×2-14=16(千克).又已知"甲、乙两个油桶所剩油"及"这时甲桶油恰是乙桶油的3倍".就可以求出甲、乙两个油桶最后有油多少千克.求出甲、乙两个油桶最后各有油的千克数后,再用倒推法并画图求甲桶往乙桶倒油前甲、乙两桶各有油多少千克,从而求出从两个油桶各卖出多少千克.解:①甲乙两桶油共剩多少千克?15×2-14=16(千克)②乙桶油剩多少千克?16÷(3+1)=4(千克)③甲桶油剩多少千克?4×3=12(千克)四. 在下面的算式中,不同的字母代表不同的数字,相同的字母代表相同的数字,求这道题可以从个位开始,比较等式两边的数,逐个确定各个(100000+x)×3=10x+1,300000+3x=10x+1,7x=299999,x=42857。
五. 李明和王亮同时分别从两地骑车相向而行,李明每小时行18 千米,王亮每小时行16 千米,两人相遇时距全程中点3千米.问全程长多少千米?李明走了全程的一半多3千米,王亮走了全程的一半少3千米,李明比王亮实际多走了3× 2 = 6(千米).由已知李明每小时比王亮多走18 ?16 = 2 (千米),李明比王亮多行6千米需要6 ÷ 2 = 3 (小时),这就是两人的相遇时间,有了相遇时间,全程是:(18 +16)×3 =102 (千米六. 马小虎在做一道整数减法题时,把减数个位上的1看成7,把十位上的7看成1,得出差为111,则正确答案是?七. 张阿姨给幼儿园两个班的孩子分水果,大班每人分得5个橘子和2个苹果,小班每人分得3个橘子和2个苹果.张阿姨一共分出了135个橘子和70个苹果,那么小班有多少个孩子?解首先,大班,小班每人都分2苹果,一共70个苹果,我们可以求得大班小班一共有70÷2=35(人)那这道题,就变为了一道鸡兔同笼问题了:大班每人5个橘子,小班每人3个橘子,共有35人,135个橘子假设每人都是5个橘子那应该是5×35=175(个)所以小班人数为(175-135)÷(5-3)=20(个)八. 少先队员去植树,如果每人挖5个树坑,还有3个树坑没人挖;如果其中两人各挖4个树坑,其余每人挖6个树坑,就恰好挖完所有的树坑。
请问,共有多少名少先队员?共挖了多少树坑?盈亏问题答案:解这道题的关键在于条件的转换,把"如果其中两人各挖4个树坑,其余每人挖6个树坑,就恰好挖完所有的树坑",转换成"每人挖6个树坑,还差2×(6-4)个树坑。
"则本题成为"一盈一亏"的盈亏问题。
所以〔3+2×(6-4)〕÷(6-5)=7(人),7×5+3=38(个)树坑。
盈亏问题公式:总差÷分差=份数。
一盈一亏中:盈+亏=总差;在双盈或双亏中:大数-小数=总差;份数在不同的题目中表示不同的意思。
此题表示参与分配的人数。
九. 在下图中的几个圈内各填一个数,使每一条直线上的三个数中,当中的数是两边两个数的平均数,现在已经填好两个数,那么______.数字迷答案:如下图所示,将剩下的圆圈内标上字母于是A=(13+17)÷2=15,由题意可得B+15=D+17=2C,因此B-D=2.于是2D=B+13=D+ 2+13,故D=15.从而C=(17+15)÷2=16,X=2C-13=19。
解数字谜时,出现的条件较少时,通过设未知量表示出其中的隐含关系往往是解题的关键。
十. 四年级有三个班,每班有两个班长,开班会时,每次每班只要一个班长参加。
第一次到会的有A,B,C;第二次到会的有B,D,E;第三次到会的有A,E,F。
请问哪两位班长是同班的?用数字"1"表示到会,用数字"0"表示没到会,可列下表从第一次到会的情况看,A只能和D,E,F同班从第二次到会的情况看,A只能和D,E同班从第三次到会的情况看,A只能和D同班利用上述表格,仿照上述方法,推出与B,C分别同班的同学。
十一. 有一根长为180厘米的绳子,从一端开始每隔3厘米作一个记号,每隔4厘米也作一个记号,然后将标有记号的地方剪断。
问绳子共被剪成了多少段。
解答:1-180中,3的倍数有60个,4的倍数有45个,而既是3的倍数又是4的倍数的数一定是12的倍数,这样的数有180÷12=15个。
注意到180厘米处无法标上记号,所以标记记号有:(60-1)+(45-1)-(15-1)=89,绳子被剪成90段。
例1求图1正六边形的面积。
(单位:厘米)分析与解将正六边形按图2所示等分成3个平行四边形。
所以,正六边形的面积为:37.5×(65÷2)×3=3656.25(平方厘米)例2如图3,四边都相等的两个完全相同的四边形,在两边的中点处部分重合。
已知重合部分的面积是8平方厘米。
求阴影部分的面积。
分析与解将图3按图4所示等分成7个棱形。
所以,阴影部分的面积为:8×6=48(平方厘米)二、运用梯形定义等分例3如图5所示,求出中队旗的面积。
(单位:厘米)分析与解将图5按图6所示等分成2个梯形。
所以,中队旗的面积为:(60+80)×30÷2×2=4200(平方厘米)例4将正方形的四条边分别向两端各延长一倍,连接8个端点得到一个八边形(如图7),求阴影部分的面积。
分析与解将八边形按图8所示等分成4个梯形。
所以,阴影部分的面积为:(2+2×2)×2÷2×4=24(平方厘米)三、运用三角形面积法等分。
例5如图9,梯形的面积是36平方厘米,BE是BC的一半。
求阴影部分的面积。
分析与解将梯形按图10所示等分成3个等底等高的三角形。
所以,阴影部分的面积为:36÷3=12(平方厘米)例6如图11,平行四边形的面积是49平方厘米,E是底边上的中点。
求阴影部分的面积。
分析与解将平行四边形按图12所示等分成4个等底等高的三角形。
所以,阴影部分的面积为:49÷4=12.25(平方厘米)四、运用中点性质等分例7如图13,长方形ABCD的长是10厘米,宽是6厘米,E、F分别是AB和AD的中点。
求阴影部分的面积。
分析与解将阴影部分等分成与△AEF完全相等的3个三角形(如图14)。
所以,阴影部分的面积为:(10÷2)×(6÷2)÷2×3=22.5(平方厘米)所谓假设法,就是假设题中的某几个数量相等,或假设要求的一个未知量是已知数量,把复杂问题化为简单问题处理,再进行推算,以求出原题的答案。
其解题思路可用下图表示。
假设思想方法是一种重要的数学思维方法,掌握它能使要解决的问题更形象、更具体,从而丰富解题的思路。
下面举例说明用假设法解题的常见类型。
一、条件假设在解题时,有些题目数量关系比较隐蔽,如果对某些条件作出假设,则往往能顺利找到解题途径。
例1 有黑、白棋子一堆,黑子个数是白子个数的2倍,现从这堆棋子中每次取出黑子4个,白子3个,待到若干次后,白子已经取尽,而黑子还有16个。
求黑、白棋子各有多少个?分析与解假设每次取出的黑子不是4个,而是6个,也就是说每次取出的黑子个数也是白子的2倍。
由于这堆棋子中黑子个数是白子的2倍,所以,待取到若干次后,黑子、白子应该都取尽。
但是实际上当白子取尽时,剩下黑子还有16个,这是因为实际每次取黑子是4个,和假定每次取黑子6个相比,相差2个。
由此可知,一共取的次数是(16÷2=)8(次)。
故白棋子的个数为:(3×8=)24个),黑棋子个数为(24×2=)48(个)。
25吨,问甲、乙两堆货物原来各有多少吨?把这种假设的情形与题中已知情形作出比较,发现多了(27.5-25=)2.5吨。
=50(吨),所以甲堆货物有60吨。
二、问题假设当直接解一些题目似乎无从下手时,可对问题提出假设性答案,然后进行推算,当所得结果与题目的条件出现差异时,再进行调整,直至与题目的条件符合,从而得出正确答案。
例3 有一妇女在河边洗碗,掌管桥梁的官吏路过这里,问她:“你怎么洗这么多碗?”,妇女回答:“家里来了客人”。
官吏又问:“有多少个客人?”妇女回答:“2个人共一碗饭,3个人共一碗羹,4个人共一碗肉,一共65只碗”。
问共有多少客人?(选自《孙子算经》)分析与解假设有12个客人(因为[2,3,4]=12),由题设知:12个人共用了(12÷2=)6(只)饭碗、(12÷3=)4(只)羹碗、(12÷4=)3(只)肉碗,所以12个人共用了(6+ 4+3=)13(只)碗。
而题目的条件是65只碗,是根据假设进行计算所得结果的5倍,因此,客人数一共有(12×5=)60(人)。
三、单位假设解答某些应用题时,可假设某个数量为单位“1”或几,进而列式求解。
苹果?分析与解假设甲筐有苹果5(重量单位),卖出3/5后,还剩(5量单位)。
因此甲筐苹果比乙筐少(6.4-5=)1.4(重量单位),但实际上甲筐苹果比乙筐少7千克,所以每1(重量单位)相当于(7÷1.4=)5(千克)。
所以甲筐苹果重(5×5=)25(千克),乙筐苹果重(5×6.4=)32(千克)。