第01章 基础知识

第一章计算机基础知识[目的要求]1、掌握计算机的定义、用途、特点、发展历史、分类，熟练掌握计算机系统的基本组成、结构和常用外设的使用。

[课时安排]本章总教学课时为8节，其中理论课时6节，上机课时2节。

[教学手段]使用计算机多媒体设备进行教学，使用计算机设备进行实践训练。

[教学内容]1.1 计算机概述1.1.1 计算机的概念计算机是一种能够高速且自动地执行算术运算和逻辑运算的数字化电子设备，它能够按照人们预先编写的程序高效准确地处理信息。

1.1.2 计算机的发展世界上第一台电子计算机称为ENIAC(Electronic Numerical Integrator And Calculator)，即电子数字积分计算机，它于1946年诞生于美国。

计算机”是一种非冯·诺伊曼型计算机，其目标是使计算机具有人工智能，使其能模拟甚至替代人的智能，具有人—机自然交流的能力。

1.1.3未来计算机的发展趋势1．巨型化2．微型化3．网络化4．智能化1.1.4 计算机的特点1.记忆能力强2.运算速度快且精度高3.具有逻辑判断能力4.在程序控制下自动完成各种操作1.1.5 计算机的分类电子计算机是一种通过电子线路对信息进行加工处理以实现其计算功能的机器，按照不同的原则可以有多种分类方法。

1.按信息在计算机内的表示形式划分2.按计算机的大小、规模、性能划分3.按计算机使用范围来划分4.按计算机的字长位数来划分1.1.6 计算机的应用1. 科学计算2. 数据处理3.辅助技术CAI、CAD、CAM等。

4.自动控制5.人工智能6.网络应用7.多媒体技术1.2 数制与编码1.2.1 计算机中的进位计数制在生产实践和日常生活中人们创造了多种表示数的方法，这些数的表示规则就称为数制。

为区分不同的数制本书约定对于任一R进制的数N记作：（N）R。

如：(1100)2表示二进制数1100，(567)8表示八进制数567，(ABCD)16表示十六进制数ABCD。

第一章计算机基础知识一、判断题1. 计算机的应用可分为科学计算、信息处理、过程控制、计算机辅助设计/辅助教学和人工智能等多个方面。

（ T ）2. 计算机病毒是一种人为编制、特殊的能够自我繁殖的计算机程序。

（ T ）3. 运算器是完成算术和逻辑运算的核心部件，通常称之为CPU。

（ F）4. 显示器既是输入设备又是输出设备。

（ F ）5. 某微机的配置是：P4/1G/320G，其中P4是指CPU的型号。

（T ）6. 键盘是标准的输入设备。

（ T ）7. 可以利用键盘上的Ctrl+Alt+Del组合键重启电脑。

（ T ）8. 计算机中统一指挥和控制计算机各部分自动、连续、协调一致运行的部件是控制器。

（ T ）9. 鼠标是计算机必不可少的输入设备。

（ F ）10. 微型计算机的性能主要取决于微处理器的性能。

（ T ）11. 键盘上主键盘区的数字键与小键盘区的数字键都可以输入数字。

（T ）12. 按住Alt键不放再去按双字符键，可以输入上档字符。

（ F ）13. 杀毒软件通常都滞后于计算机病毒。

（ T ）14. 键盘、显示器都是输入设备。

（ F ）15. 字节的英文名称是Byte。

（ T ）16. 多媒体计算机能够处理文字、图片、图形图像、动画、声音和视频等类型的信息。

（ T ）17. 用一种杀毒软件能够清除任何病毒。

（ F ）18. 计算机和人进行国际象棋比赛，属于计算机应用中的“人工智能”。

（ T ）19. 显示器显示的信息既有用户输入的内容，又有计算机输出的结果，所以显示器既是输入设备，又是输出设备。

（ F ）20. 键盘上的Ctrl键单独按下不起作用。

（ T ）21. 正版的杀毒软件都能免费更新病毒库。

（ T ）22. 银行用计算机处理客户的存款，属于计算机应用中的“数值计算”。

（ F ）23. 触摸屏属于输入设备。

（ T ）24. 微型计算机的CPU包括运算器、控制器。

（ T ）25. 硬盘存储数据的可靠性比软盘高得多。

第一章微型计算机基础知识第一章微型计算机基础知识第一章微机基础知识1.1计算机中的数和编码1.1.1计算机中的数制计算机最初是作为一种计算工具出现的，所以它最基本的功能是处理和处理对数。

数字由机器中设备的物理状态表示。

具有两种不同稳定状态和相互转换的设备可用于表示1位二进制数。

二进制数具有操作简单、物理实现方便、节省设备等优点。

因此，目前，几乎所有的二进制数都用计算机来表示。

然而，二进制数太长，无法写入，不容易阅读和记忆；此外，目前大多数微机是8位、16位或32位，是4的整数倍，4位二进制数是1位十六进制数；因此，在微型计算机中，二进制数被缩写为十六进制数。

十六进制数使用16个数字，例如0~9和a~F来表示十进制数0~15。

8位二进制数由2位十六进制数表示，16位二进制数由4位十六进制数表示。

这便于书写、阅读和记忆。

然而，十进制数是最常见和最常用的。

因此，我们应该熟练掌握十进制数、二进制数和十六进制数之间的转换。

表1-1列出了它们之间的关系。

表1-1十进制数、二进制数及十六进制数对照表十进制二进制十六进制012345678910111213141500000001001000110100010101100111100010011010101111001101 111011110123456789abcdef为了区别十进制数、二进制数及十六进制数3种数制，可在数的右下角注明数制，或者在数的后面加一字母。

如b(binary)表示二进制数制；d(decimal)或不带字母表示十进制数制；h(hexadecimal)表示十六进制数制。

1.二进制数和十六进制数之间的转换根据表1-1所示的对应关系即可实现它们之间的转换。

二进制整数被转换成十六进制数。

方法是将二进制数从右（最低位）到左分组：每4位为一组。

如果最后一组少于4位，则在其左侧加0以形成一个4位组。

每组由一位十六进制数表示。

例如：1111111000111b→1111111000111b→0001111111000111b=1fc7h要将十六进制数转换为二进制数，只需使用4位二进制数而不是1位十六进制数。

第一章焊接基础知识§1－1 概述焊接是金属材料连接的最基本方法之一，它具有低成本、永久性、可靠性高的特点。

目前，焊接广泛应用于金属材料间的连接，并对所焊产品产生更大的附加值。

焊接作为一种现代的先进主导制造工艺技术，正逐步集成到产品的主寿命过程，即从设计开发、工艺制定、制造生产，到运行服役、失效分析、维护、再循环等产品的各个阶段。

焊接作为一种广泛的系统工程，大量应用于机械制造、电力建设、石油化工、交通运输设备、建筑工程、航天航空、电子器件、家用电器、医疗器械、通讯工程等众多领域。

几乎有金属应用的地方，都有焊接现象。

一、焊接装备焊接装备包括焊接电源设备、焊接辅机具和切割设备。

近几年来，我国焊接装备的技术水平和制造能力不断提高，绝大多数焊接装备能满足国内市场的需要，一些专机、成套设备和部分通用焊接设备还向国外出口，但是仍然存在很多问题。

1、焊接设备结构不合理在电弧焊机中交流弧焊机所占比例仍较大，以逆变焊机为代表的直流焊机所占比例还有待提高。

2、焊接设备的自动、半自动化程度不高。

以电弧焊机为例，自动、半自动焊机所占比例较小。

3、数控切割机的制造已形成一定的规模，但配套的等离子切割电源还要大量进口，专用的数控切割设备品种不多。

4、焊接机器人制造能力、制造水平和推广应用有待进一步提高。

国内投产使用的焊接机器人绝大部分从国外进口，与日本、美国、西欧等工业发达国家相比，焊接机器人的数量极少，焊接机器人的正常运行率不理想。

5、焊接装备水平相对落后我国在特种焊机、成套设备及其他焊接装备方面发展较慢，满足不了焊接生产的需要。

很多国产新型焊接设备自行研制开发的少，仿制、组装的多。

6、焊接设备、TIG、CO焊枪和配件制造的自动化程度不高，手工作业2较多，产品性能稳定性和一次合格率有待提高。

二、焊接技术应用在重型机械、冶金机械、矿山工程机械、电站锅炉、压力容器、石油化工、机车车辆、汽车等行业，普遍应用了数控切割技术以及埋弧焊、电气保焊、TIG焊、MIG焊、MAG焊、电阻焊、钎焊等焊接方法。

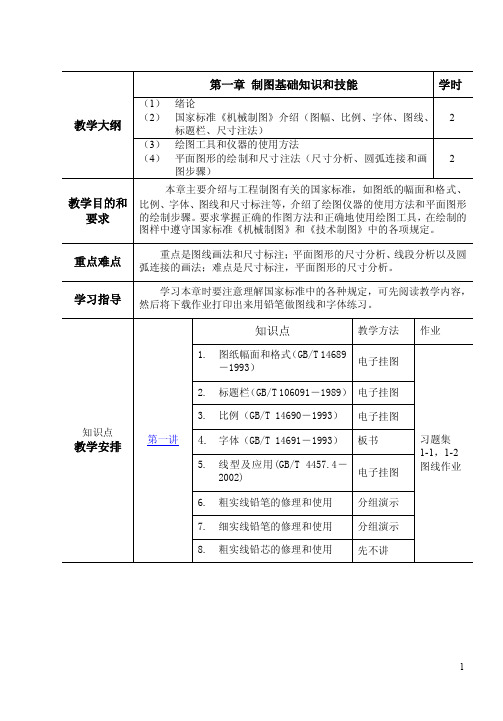
第一讲绘图仪器的使用与《机械制图》国家标准1．本讲知识要点：（1）图纸幅面和格式（GB/T 14689－1993）（2）标题栏（GB/T 106091－1989）（3）比例（GB/T 14690－1993）（4）字体（GB/T14691－1993）（5）线型及应用(GB/T 4457.4－2002)（6）粗实线铅笔的修理和使用（7）细实线铅笔的修理和使用（8）粗实线铅芯的修理和使用2．教学内容设计图纸幅面、格式、标题栏、比例：首先用电子挂图说明国家标准对图纸幅面、格式、标题栏、比例等规定，然后展示以往学生的不同幅面的图纸作业，再展示生产上使用的蓝图，同时讲解图纸的折叠。

（2）字体：先介绍国家标准对字体的规定，重点介绍铅笔制图字体的写法，然后以标题栏为例在黑板上介绍标题栏的填写和习题集作业的签名方法。

（3）线形及其应用：主要介绍粗实线、细实线、虚线、点画线和底稿线5种线形，其他线形今后用到时再介绍。

粗实线铅笔的修理和使用先用电子挂图观看修理的形状，然后用动画演示粗实线铅笔的使用，再分组演示铅笔的修理和使用。

（4）粗实线铅芯的修理和使用不讲，在讲回转曲面时介绍，本讲以只介绍直线的画法。

3．课前准备收集以往学生的作业若干张，到工厂收集一些生产上使用图纸。

准备一篇教师的铅笔制图字体和图线范例，将电子挂图和动画用PowerPoint制作成演示文档。

因为是第一次课，所以课前要告诉同学上课时带好绘图仪器。

教师图线练习学生图线作业生产上用的蓝图教师铅笔手写制图字体4．本讲作业习题集上的字体和图线练习，在A4图纸上作图线练习。

5．教学内容【内容概要】本讲主要介绍与工程制图有关的国家标准，如图纸的幅面和格式、比例、字体、图线和尺寸标注等，介绍了绘图仪器的使用方法和平面图形的绘制步骤。

要求掌握正确的作图方法和正确地使用绘图工具，在绘制的图样中遵守国家标准《机械制图》和《技术制图》中的各项规定。

1.1机械图样的一般规定为适应生产发展和技术交流的需要，对图样的绘制方法、绘图格式及绘图规则等作出统一的规定，为此我国在1959年发布了国家标准《机械制图》，之后又作了几次重大修改，使其进一步向国际标准化组织靠拢，有利于工程技术的国际交流。

必修1第一章集合与函数基础知识点整理第1讲 §1.1.1 集合的含义与表示¤知识要点：1. 把一些元素组成的总体叫作集合（set ），其元素具有三个特征，即确定性、互异性、无序性.2. 集合的表示方法有两种：列举法，即把集合的元素一一列举出来，并用花括号“{ }”括起来，基本形式为123{,,,,}n a a a a ⋅⋅⋅，适用于有限集或元素间存在规律的无限集.描述法，即用集合所含元素的共同特征来表示，基本形式为{|()x A P x ∈}，既要关注代表元素x ，也要把握其属性()P x ，适用于无限集.3. 通常用大写拉丁字母,,,A B C ⋅⋅⋅表示集合. 要记住一些常见数集的表示，如自然数集N ，正整数集*N 或N +，整数集Z ，有理数集Q ，实数集R .4. 元素与集合之间的关系是属于（belong to ）与不属于（not belong to ），分别用符号∈、∉表示，例如3N ∈，2N -∉.¤例题精讲：【例1】试分别用列举法和描述法表示下列集合：（1）由方程2(23)0x x x --=的所有实数根组成的集合；（2）大于2且小于7的整数.解：（1）用描述法表示为：2{|(23)0}x R x x x ∈--=；用列举法表示为{0,1,3}-.（2）用描述法表示为：{|27}x Z x ∈<<；用列举法表示为{3,4,5,6}.【例2】用适当的符号填空：已知{|32,}A x x k k Z ==+∈，{|61,}B x x m m Z ==-∈，则有：17 A ； －5 A ； 17 B .解：由3217k +=，解得5k Z =∈，所以17A ∈；由325k +=-，解得73k Z =∉，所以5A -∉；由6117m -=，解得3m Z =∈，所以17B ∈. 【例3】试选择适当的方法表示下列集合：（教材P 6 练习题2， P 13 A 组题4）（1）一次函数3y x =+与26y x =-+的图象的交点组成的集合； （2）二次函数24y x =-的函数值组成的集合；（3）反比例函数2y x=的自变量的值组成的集合. 解：（1）3{(,)|}{(1,4)}26y x x y y x =+⎧=⎨=-+⎩. （2）2{|4}{|4}y y x y y =-=≥-. （3）2{|}{|0}x y x x x ==≠.点评：以上代表元素，分别是点、函数值、自变量. 在解题中不能把点的坐标混淆为{1,4}，也注意对比（2）与（3）中的两个集合，自变量的范围和函数值的范围，有着本质上不同，分析时一定要细心.*【例4】已知集合2{|1}2x a A a x +==-有唯一实数解，试用列举法表示集合A ．A B B A A B A B A ． B ． C ． D ． 解：化方程212x a x +=-为：2(2)0x x a --+=．应分以下三种情况： ⑴方程有等根且不是2±：由 △=0，得94a =-，此时的解为12x =，合． ⑵方程有一解为2，而另一解不是2-：将2x =代入得2a =-，此时另一解12x =-，合． ⑶方程有一解为2-，而另一解不是2：将2x =-代入得2a =，此时另一解为21x =+，合．综上可知，9{,2,2}4A =--．点评：运用分类讨论思想方法，研究出根的情况，从而列举法表示. 注意分式方程易造成增根的现象.第2讲 §1.1.2 集合间的基本关系¤知识要点：1. 一般地，对于两个集合A 、B ，如果集合A 中的任意一个元素都是集合B 中的元素，则说两个集合有包含关系，其中集合A 是集合B 的子集（subset ），记作A B ⊆（或B A ⊇），读作“A 含于B ”（或“B 包含A ”）.2. 如果集合A 是集合B 的子集（A B ⊆），且集合B 是集合A 的子集（B A ⊇），即集合A 与集合B 的元素是一样的，因此集合A 与集合B 相等，记作A B =.3. 如果集合A B ⊆，但存在元素x B ∈，且x A ∉，则称集合A 是集合B 的真子集（proper subset ），记作A ≠⊂B （或B ≠⊃A ）.4. 不含任何元素的集合叫作空集（empty set ），记作∅，并规定空集是任何集合的子集.5. 性质：A A ⊆；若A B ⊆，B C ⊆，则A C ⊆；若A B A =，则A B ⊆；若A B A =，则B A ⊆.¤例题精讲：【例1】用适当的符号填空：（1）{菱形} {平行四边形}； {等腰三角形} {等边三角形}.（2）∅ 2{|20}x R x ∈+=； 0 {0}； ∅ {0}； N {0}. 解：（1）， ；（2）=， ∈， ，.【例2】设集合1,,}22{|,{|n n x n n A x x B x =∈=+∈==Z}Z ，则下列图形能表示A 与B 关系的是（ ）. 解：简单列举两个集合的一些元素，3113{,1,,0,,1,,}2222A =⋅⋅⋅---⋅⋅⋅，3113{,,,,,}2222B =⋅⋅⋅--⋅⋅⋅， 易知B ≠⊂A ，故答案选A ． 另解：由21,}2{|n x n B x +=∈=Z ，易知B ≠⊂A ，故答案选A ． 【例3】若集合{}{}2|60,|10M x x x N x ax =+-==-=，且N M ⊆，求实数a 的值. 解：由26023x x x +-=⇒=-或，因此，{}2,3M =-.（i ）若0a =时，得N =∅，此时，N M ⊆；（ii ）若0a ≠时，得1{}N a =. 若N M ⊆,满足1123a a==-或，解得1123a a ==-或. 故所求实数a 的值为0或12或13-. 点评：在考察“A B ⊆”这一关系时，不要忘记“∅” ，因为A =∅时存在A B ⊆. 从而需要分情况讨论. 题中讨论的主线是依据待定的元素进行.【例4】已知集合A ={a ,a +b ,a +2b }，B ={a ,ax ,ax 2}. 若A =B ，求实数x 的值.解：若22a b ax a b ax+=⎧⎨+=⎩⇒a +ax 2-2ax =0, 所以a (x -1)2=0，即a =0或x =1. 当a =0时，集合B 中的元素均为0，故舍去；当x =1时，集合B 中的元素均相同，故舍去.若22a b ax a b ax⎧+=⎨+=⎩⇒2ax 2-ax -a =0. 因为a ≠0，所以2x 2-x -1=0, 即(x -1)(2x +1)=0. 又x ≠1，所以只有12x =-.经检验，此时A =B 成立. 综上所述12x =-.点评：抓住集合相等的定义，分情况进行讨论. 融入方程组思想，结合元素的互异性确定集合.第3讲 §1.1.3 集合的基本运算（一）¤知识要点：集合的基本运算有三种，即交、并、补，学习时先理解概念，并掌握符号等，再B （读作“B （读作“U A （读作“ ¤例题精讲：】设集合,{|15},{|39},,()U U R A x x B x x A B A B ==-≤≤=<<求解：在数轴上表示出集合A 、B ，如右图所示： {|35}A B x x =<≤，(){|1,9}U C A B x x x =<-≥或，【例2】设{|||6}A x Z x =∈≤，{}{}1,2,3,3,4,5,6B C ==，求：（1）()A B C ； （2）()A A B C .解：{}6,5,4,3,2,1,0,1,2,3,4,5,6A =------.（1）又{}3B C =，∴()A B C ={}3；（2）又{}1,2,3,4,5,6B C =，得{}()6,5,4,3,2,1,0A C B C =------. U∴ ()A A C B C {}6,5,4,3,2,1,0=------.【例3】已知集合{|24}A x x =-<<，{|}B x x m =≤，且A B A =，求实数m 的取值范围.解：由A B A =，可得A B ⊆.在数轴上表示集合A 与集合B ，如右图所示：由图形可知，4m ≥. 点评：研究不等式所表示的集合问题，常常由集合之间的关系，得到各端点之间的关系，特别要注意是否含端点的问题.【例4】已知全集*{|10,}U x x x N =<∈且，{2,4,5,8}A =，{1,3,5,8}B =，求()U C A B ，()U C A B ，()()U U C A C B ， ()()U U C A C B ，并比较它们的关系.解：由{1,2,3,4,5,8}A B =，则(){6,7,9}U C A B =.由{5,8}A B =，则(){1,2,3,4,6,7,9}U C A B =由{1,3,6,7,9}U C A =，{2,4,6,7,9}U C B =，则()(){6,7,9}U U C A C B =，()(){1,2,3,4,6,7,9}U U C A C B =.由计算结果可以知道，()()()U U U C A C B C A B =，()()()U U U C A C B C A B =.另解：作出Venn 图，如右图所示，由图形可以直接观察出来结果.点评：可用Venn 图研究()()()U U U C A C B C A B =与()()()U U U C A C B C A B = ，在理解的基础记住此结论，有助于今后迅速解决一些集合问题.第4讲 §1.1.3 集合的基本运算（二） ¤知识要点：1. 含两个集合的Venn 图有四个区域，分别对应着这两个集合运算的结果. 我们需通过Venn 图理解和掌握各区域的集合运算表示，解决一类可用列举法表示的集合运算. 通过图形，我们还可以发现一些集合性质：()()()U U U C A B C A C B =,()()()U U U C A B C A C B =.2. 集合元素个数公式：()()()()n A B n A n B n A B =+-.3. 在研究集合问题时，常常用到分类讨论思想、数形结合思想等. 也常由新的定义考查创新思维.¤例题精讲：【例1】设集合{}{}24,21,,9,5,1A a a B a a =--=--，若{}9A B =，求实数a 的值. 解：由于{}{}24,21,,9,5,1A a a B a a =--=--，且{}9A B =，则有：当219 a -＝时，解得5a ＝，此时={4, 9, 25}={9, 0, 4}A B －，－，不合题意，故舍去； 当29a ＝时，解得33a ＝或－.3 ={4,5,9} ={9,2,2}a A B ＝时，－，－－，不合题意，故舍去；3={4, 7 9}={9, 8, 4}a A B ＝－，－－，，－，合题意.所以，3a ＝－.【例2】设集合{|(3)()0,}A x x x a a R =--=∈，{|(4)(1)0}B x x x =--=，求A B , A B .（教材P 14 B 组题2）解：{1,4}B =.当3a =时，{3}A =，则{1,3,4}A B =，A B =∅；当1a =时，{1,3}A =，则{1,3,4}A B =，{1}A B =；当4a =时，{3,4}A =，则{1,3,4}A B =，{4}A B =；-2 4 m x B A当3a ≠且1a ≠且4a ≠时，{3,}A a =，则{1,3,4,}A B a =，A B =∅.点评：集合A 含有参数a ，需要对参数a 进行分情况讨论. 罗列参数a 的各种情况时，需依据集合的性质和影响运算结果的可能而进行分析，不多不少是分类的原则.【例3】设集合A ={x |240x x +=}， B ={x |222(1)10x a x a +++-=，a R ∈}，若A B =B ，求实数a 的值．解：先化简集合A ={4,0}-. 由A B =B ，则B ⊆A ，可知集合B 可为∅，或为{0}，或{－4}，或{4,0}-.(i )若B =∅，则224(1)4(1)0a a ∆=+--<，解得a ＜1-；(ii )若0∈B ，代入得2a 1-=0⇒a =1或a =1-，当a =1时，B =A ，符合题意；当a =1-时，B ={0}⊆A ，也符合题意．(iii )若－4∈B ，代入得2870a a -+=⇒a =7或a =1，当a =1时，已经讨论，符合题意；当a =7时，B ={－12，－4}，不符合题意．综上可得，a =1或a ≤1-．点评：此题考查分类讨论的思想，以及集合间的关系的应用. 通过深刻理解集合表示法的转换，及集合之间的关系，可以把相关问题化归为解方程的问题，这是数学中的化归思想，是重要数学思想方法．解该题时，特别容易出现的错误是遗漏了A =B 和B =∅的情形，从而造成错误．这需要在解题过程中要全方位、多角度审视问题.【例4】对集合A 与B ，若定义{|,}A B x x A x B -=∈∉且，当集合*{|8,}A x x x N =≤∈，集合{|(2)(5)(6)0}B x x x x x =---=时，有A B -= . （由教材P 12 补集定义“集合A 相对于全集U 的补集为{|,}U C A x x x A =∈∉且”而拓展）解：根据题意可知，{1,2,3,4,5,6,7,8}A =，{0,2,5,6}B =由定义{|,}A B x x A x B -=∈∉且，则{1,3,4,7,8}A B -=.点评：运用新定义解题是学习能力的发展，也是一种创新思维的训练，关键是理解定义的实质性内涵，这里新定义的含义是从A 中排除B 的元素. 如果再给定全集U ，则A B -也相当于()U A C B .第5讲 §1.2.1 函数的概念¤知识要点：1. 设A 、B 是非空的数集，如果按某个确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有唯一确定的数y 和它对应，那么就称f ：A →B 为从集合A 到集合B 的一个函数（function ），记作y =()f x ，x A ∈．其中，x 叫自变量，x 的取值范围A 叫作定义域（domain ），与x 的值对应的y 值叫函数值，函数值的集合{()|}f x x A ∈叫值域（range ）.2. 设a 、b 是两个实数，且a <b ，则：{x |a ≤x ≤b }＝[a ,b ] 叫闭区间； {x |a <x <b }＝(a ,b ) 叫开区间；{x |a ≤x <b }＝[,)a b ， {x |a <x ≤b }＝(,]a b ，都叫半开半闭区间.符号：“∞”读“无穷大”；“－∞”读“负无穷大”；“+∞”读“正无穷大”. 则{|}(,)x x a a >=+∞，{|}[,)x x a a ≥=+∞，{|}(,)x x b b <=-∞，{|}(,]x x b b ≤=-∞，(,)R =-∞+∞.3. 决定函数的三个要素是定义域、值域和对应法则. 当且仅当函数定义域、对应法则分别相同时，函数才是同一函数.¤例题精讲：【例1】求下列函数的定义域： （1）121y x =+-；（2）y =.解：（1）由210x +-≠，解得1x ≠-且3x ≠-，所以原函数定义域为(,3)(3,1)(1,)-∞----+∞.（2）由3020x -≥⎧⎪≠，解得3x ≥且9x ≠， 所以原函数定义域为[3,9)(9,)+∞.【例2】求下列函数的定义域与值域：（1）3254x y x+=-； （2）22y x x =-++. 解：（1）要使函数有意义，则540x -≠，解得54x ≠. 所以原函数的定义域是5{|}4x x ≠.32112813(45)233233305445445445444x x x y x x x x ++-+==⨯=⨯=-+≠-+=-----，所以值域为3{|}4y y ≠-. （2）22192()24y x x x =-++=--+. 所以原函数的定义域是R ，值域是9(,]4-∞. 【例3】已知函数1()1x f x x-=+. 求：（1）(2)f 的值； （2）()f x 的表达式 解：（1）由121x x -=+，解得13x =-，所以1(2)3f =-. （2）设11x t x -=+，解得11t x t -=+，所以1()1t f t t -=+，即1()1x f x x -=+. 点评：此题解法中突出了换元法的思想. 这类问题的函数式没有直接给出，称为抽象函数的研究，常常需要结合换元法、特值代入、方程思想等. 【例4】已知函数22(),1x f x x R x =∈+. （1）求1()()f x f x+的值；（2）计算：111(1)(2)(3)(4)()()()234f f f f f f f ++++++. 解：（1）由2222222221111()()1111111x x x x f x f x x x x x x ++=+=+==+++++. （2）原式11117(1)((2)())((3)())((4)())323422f f f f f f f =++++++=+= 点评：对规律的发现，能使我们实施巧算. 正确探索出前一问的结论，是解答后一问的关键.第6讲 §1.2.2 函数的表示法¤知识要点：1. 函数有三种表示方法：解析法（用数学表达式表示两个变量之间的对应关系，优点：简明，给自变量可求函数值）；图象法（用图象表示两个变量的对应关系，优点：直观形象，反应变化趋势）；列表法（列出表格表示两个变量之间的对应关系，优点：不需计算就可看出函数值）.2. 分段函数的表示法与意义（一个函数，不同范围的x ，对应法则不同）.3. 一般地，设A 、B 是两个非空的集合，如果按某一个确定的对应法则f ，使对于集合A 中的任意一个元素x ，在集合B 中都有唯一确定的元素y 与之对应，那么就称对应:f A B →为从集合A 到集合B 的一个映射（mapping ）．记作“:f A B →”. 判别一个对应是否映射的关键：A 中任意，B 中唯一；对应法则f . ¤例题精讲： 【例1】如图，有一块边长为a 的正方形铁皮，将其四个角各截去一个边长为x 的小正方形，然后折成一个无盖的盒子，写出体积V 以x 为自变量的函数式是_____，这个函数的定义域为_______．解：盒子的高为x ，长、宽为2a x －，所以体积为V ＝2(2)x a x －.又由20a x >－，解得2a x <.所以，体积V 以x 为自变量的函数式是2(2)V x a x =－，定义域为{|0}2a x x <<.【例2】已知f (x )=333322x x x x-⎧++⎪⎨+⎪⎩ (,1)(1,)x x ∈-∞∈+∞，求f [f (0)]的值. 解：∵ 0(,1)∈-∞， ∴ f (0)=32. 又 ∵ 32>1，∴ f (32)=(32)3+(32)-3=2+12=52，即f [f (0)]=52.【例3】画出下列函数的图象：（1）|2|y x =-； （教材P 26 练习题3）（2）|1||24|y x x =-++.解：（1）由绝对值的概念，有2,2|2|2,2x x y x x x -≥⎧=-=⎨-<⎩. 所以，函数|2|y x =-的图象如右图所示. （2）33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩，所以，函数|1||24|y x x =-++的图象如右图所示.点评：含有绝对值的函数式，可以采用分零点讨论去绝对值的方法，将函数式化为分段函数，然后根据定义域的分段情况，选择相应的解析式作出函数图象.【例4】函数()[]f x x =的函数值表示不超过x 的最大整数，例如[3.5]4-=-，[2.1]2=，当( 2.5,3]x ∈-时，写出()f x 的解析式，并作出函数的图象.解：3, 2.522,211,10()0,011,122,233,3x x x f x x x x x --<<-⎧⎪--≤<-⎪--≤<⎪=≤<⎨⎪≤<⎪≤<⎪=⎩. 函数图象如右：点评：解题关键是理解符号[]m 的概念，抓住分段函数的对应函数式.第7讲 §1.3.1 函数的单调性 ¤知识要点： 1. 增函数：设函数y =f (x )的定义域为I ，如果对于定义域I 内的某个区间D 内的任意两个自变量x 1，x 2，当x 1<x 2时，都有f (x 1)<f (x 2)，那么就说f (x )在区间D 上是增函数（increasingfunction ）. 仿照增函数的定义可定义减函数.2. 如果函数f (x )在某个区间D 上是增函数或减函数，就说f (x )在这一区间上具有（严格的）单调性，区间D 叫f(x )的单调区间. 在单调区间上，增函数的图象是从左向右是上升的（如右图1），减函数的图象从左向右是下降的（如右图2）. 由此，可以直观观察函数图象上升与下降的变化趋势，得到函数的单调区间及单调性.3. 判断单调性的步骤：设x 1、x 2∈给定区间，且x 1<x 2；→计算f (x 1)－f (x 2) →判断符号→下结论.¤例题精讲：【例1】试用函数单调性的定义判断函数2()1x f x x =-在区间（0，1）上的单调性. 解：任取12,x x ∈(0,1)，且12x x <. 则1221121212222()()()11(1)(1)x x x x f x f x x x x x --=-=----. 由于1201x x <<<，110x -<，210x -<，210x x ->，故12()()0f x f x ->，即12()()f x f x >.所以，函数2()1x f x x =-在（0，1）上是减函数. 【例2】求二次函数2()(0)f x ax bx c a =++<的单调区间及单调性. 解：设任意12,x x R ∈，且12x x <. 则22121122()()()()f x f x ax bx c ax bx c -=++-++221212()()a x x b x x =-+-1212()[()]x x a x x b =-++.若0a <，当122b x x a <≤-时，有120x x -<，12b x x a+<-，即12()0a x x b ++>，从而12()()0f x f x -<，即12()()f x f x <，所以()f x 在(,]2b a-∞-上单调递增. 同理可得()f x 在[,)2b a-+∞上单调递减. 【例3】求下列函数的单调区间：（1）|1||24|y x x =-++；（2）22||3y x x =-++.解：（1）33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩，其图象如右.由图可知，函数在[2,)-+∞上是增函数，在(,2]-∞-上是减函数.（2）22223,02||323,0x x x y x x x x x ⎧-++≥⎪=-++=⎨--+<⎪⎩，其图象如右. 由图可知，函数在(,1]-∞-、[0,1]上是增函数，在[1,0]-、[1,)+∞上是减函数.点评：函数式中含有绝对值，可以采用分零点讨论去绝对值的方法，将函数式化为分段函数. 第2小题也可以由偶函数的对称性，先作y 轴右侧的图象，并把y 轴右侧的图象对折到左侧，得到(||)f x 的图象. 由图象研究单调性，关键在于正确作出函数图象.第8讲 §1.3.1 函数最大（小）值 ¤知识要点： 1. 定义最大值：设函数()y f x =的定义域为I ，如果存在实数M 满足：对于任意的x ∈I ，都有()f x ≤M ；存在x 0∈I ，使得0()f x = M . 那么，称M 是函数()y f x =的最大值（Maximum Value ）. 仿照最大值定义，可以给出最小值（Minimum Value ）的定义.2. 配方法：研究二次函数2(0)y ax bx c a =++≠的最大（小）值，先配方成224()24b ac b y a x a a -=++后，当0a >时，函数取最小值为244ac b a-；当0a <时，函数取最大值244ac b a-. 3. 单调法：一些函数的单调性，比较容易观察出来，或者可以先证明出函数的单调性，再利用函数的单调性求函数的最大值或最小值.4. 图象法：先作出其函数图象后，然后观察图象得到函数的最大值或最小值. ¤例题精讲：【例1】求函数261y x x =++的最大值. 解：配方为2613()24y x =++，由2133()244x ++≥，得260813()24x <≤++. 所以函数的最大值为8.【例2】某商人如果将进货单价为8元的商品按每件10元售出时，每天可售出100件. 现在他采用提高售出价，减少进货量的办法增加利润，已知这种商品每件提价1元，其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚得的利润最大？并求出最大利润.解：设他将售出价定为x 元，则提高了(10)x -元，减少了10(10)x -件，所赚得的利润为(8)[10010(10)]y x x =---.即2210280160010(14)360y x x x =-+-=--+. 当14x =时，max 360y =.所以，他将售出价定为14元时，才能使每天所赚得的利润最大, 最大利润为360元.【例3】求函数21y x x =+-的最小值.解：此函数的定义域为[)1,+∞，且函数在定义域上是增函数，所以当1x =时，min 2112y =+-=，函数的最小值为2.点评：形如y ax b cx d =+±+的函数最大值或最小值，可以用单调性法研究，也可以用换元法研究.【另解】令1x t -=，则0t ≥，21x t =+，所以22115222()48y t t t =++=++，在0t ≥时是增函数，当0t =时，min 2y =，故函数的最小值为2.【例4】求下列函数的最大值和最小值：（1）25332,[,]22y x x x =--∈-； （2）|1||2|y x x =+--.解：（1）二次函数232y x x =--的对称轴为2b x a =-，即1x =-.画出函数的图象，由图可知，当1x =-时，max 4y =； 当32x =时，min 94y =-. 所以函数25332,[,]22y x x x =--∈-的最大值为4,最小值为94-. （2） 3 (2)|1||2|2 1 (12)3 (1)x y x x x x x ≥⎧⎪=+--=--<<⎨⎪-≤-⎩.作出函数的图象，由图可知，[3,3]y ∈-. 所以函数的最大值为3, 最小值为-3. 点评：二次函数在闭区间上的最大值或最小值，常根据闭区间与对称轴的关系，结合图象进行分析. 含绝对值的函数，常分零点讨论去绝对值，转化为分段函数进行研究. 分段函数的图象注意分段作出.第9讲 §1.3.2 函数的奇偶性¤知识要点：1. 定义：一般地，对于函数()f x 定义域内的任意一个x ，都有()()f x f x -=，那么函数()f x 叫偶函数（even function ）. 如果对于函数定义域内的任意一个x ，都有()()f x f x -=-），那么函数()f x 叫奇函数（odd function ）.2. 具有奇偶性的函数其定义域关于原点对称，奇函数的图象关于原点中心对称，偶函数图象关于y 轴轴对称.3. 判别方法：先考察定义域是否关于原点对称，再用比较法、计算和差、比商法等判别()f x -与()f x 的关系.¤例题精讲：【例1】判别下列函数的奇偶性：（1）31()f x x x=-； （2）()|1||1|f x x x =-++；（3）23()f x x x =-.解：（1）原函数定义域为{|0}x x ≠，对于定义域的每一个x ，都有3311()()()()f x x x f x x x -=--=--=--， 所以为奇函数. （2）原函数定义域为R ，对于定义域的每一个x ，都有()|1||1||1||1|()f x x x x x f x -=--+-+=-++=，所以为偶函数.（3）由于23()()f x x x f x -=+≠±，所以原函数为非奇非偶函数.【例2】已知()f x 是奇函数，()g x 是偶函数，且1()()1f x g x x -=+，求()f x 、()g x . 解：∵ ()f x 是奇函数，()g x 是偶函数，∴ ()()f x f x -=-，()()g x g x -=.则1()()11()()1f x g x x f x g x x ⎧-=⎪⎪+⎨⎪---=⎪-+⎩，即1()()11()()1f x g x x f x g x x ⎧-=⎪⎪+⎨⎪--=⎪-+⎩. 两式相减，解得2()1x f x x =-；两式相加，解得21()1g x x =-.。

01章农业化学分析的基础知识农业化学分析是农业科学的一个重要分支，它研究的是农业中的化学成分、化学性质以及化学过程。

通过对种植物、土壤、植物病害等进行化学分析，可以帮助农民提高农产品的产量和质量，优化土壤肥力，预防和控制植物病害等。

下面将介绍一些农业化学分析的基础知识。

首先是植物化学分析。

植物化学分析主要研究植物体内的营养元素和次要营养元素的含量。

这些元素对植物的生长发育和产量质量有着重要影响。

常用的植物化学分析包括植物中氮、磷、钾、钙、镁、锌、铁等元素的含量分析。

通过分析植物的养分含量，可以为农民提供科学的施肥建议，帮助提高作物的产量和品质。

其次是土壤化学分析。

土壤是作物生长的基础，土壤中的养分含量和化学性质直接影响着作物的生长发育和产量质量。

土壤化学分析主要研究土壤中养分元素的含量、土壤酸碱度、有机质含量等参数。

常用的土壤化学分析方法包括土壤氮、磷、钾、酸度、碱度、有机质含量等的分析。

这些分析结果可以为农民提供合理的施肥和调整土壤pH值的建议，帮助提高土壤肥力和作物产量。

另外，农业化学分析还包括植物病害的化学分析。

植物病害对作物产量和质量的影响非常大，通过化学分析可以帮助农民及时发现和诊断植物病害，并采取相应的防治措施。

常用的植物病害化学分析方法包括病原菌的鉴定、病害的病原体摄取、病原体的生长抑制等。

这些分析结果可以为农民提供科学的防治建议，帮助减少病害对作物产量的影响。

在农业化学分析中，采样和样品处理是非常重要的环节。

采样要准确代表分析对象的特征，避免污染和样品损失。

样品处理要根据具体的分析目的进行选择，包括样品的研磨、滤液、制备溶液等。

此外，农业化学分析还需要选择合适的分析方法和仪器设备，比如光谱分析、色谱分析、质谱分析等，以获取准确可靠的分析结果。

总之，农业化学分析是农业科学中非常重要的一部分，它可以帮助农民了解作物和土壤的养分状况和化学性质，为农业生产提供科学依据，提高农产品的产量和质量。