《电磁场与电磁波》试题4与答案
- 格式:doc
- 大小:192.73 KB
- 文档页数:8


如题图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为,求槽内的电位函数。
解根据题意,电位满足的边界条件为①②③根据条件①和②,电位的通解应取为题图由条件③,有两边同乘以,并从0到对积分,得到故得到槽内的电位分布两平行无限大导体平面,距离为,其间有一极薄的导体片由到。
上板和薄片保持电位,下板保持零电位,求板间电位的解。
设在薄片平面上,从到,电位线性变化,。
题图解应用叠加原理,设板间的电位为其中,为不存在薄片的平行无限大导体平面间(电压为)的电位,即;是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:①②③根据条件①和②,可设的通解为由条件③有两边同乘以,并从0到对积分,得到故得到求在上题的解中,除开一项外,其他所有项对电场总储能的贡献。
并按定出边缘电容。
解在导体板()上,相应于的电荷面密度则导体板上(沿方向单位长)相应的总电荷相应的电场储能为其边缘电容为如题图所示的导体槽,底面保持电位,其余两面电位为零,求槽内的电位的解。
解根据题意,电位满足的边界条件为①题图②③根据条件①和②,电位的通解应取为由条件③,有两边同乘以,并从0到对积分,得到故得到槽内的电位分布为一长、宽、高分别为、、的长方体表面保持零电位,体积内填充密度为的电荷。
求体积内的电位。
解在体积内,电位满足泊松方程(1)长方体表面上,电位满足边界条件。
由此设电位的通解为代入泊松方程(1),可得由此可得或(2)由式(2),可得故如题图所示的一对无限大接地平行导体板,板间有一与轴平行的线电荷,其位置为。
求板间的电位函数。
解由于在处有一与轴平行的线电荷,以为界将场空间分割为和两个区域,则这两个区域中的电位和都满足拉普拉斯方程。
而在的分界面上,可利用函数将线电荷表示成电荷面密度。
电位的边界条件为题图①②③由条件①和②,可设电位函数的通解为由条件③,有(1)(2)由式(1),可得(3)将式(2)两边同乘以,并从到对积分,有(4)由式(3)和(4)解得故如题图所示的矩形导体槽的电位为零,槽中有一与槽平行的线电荷。
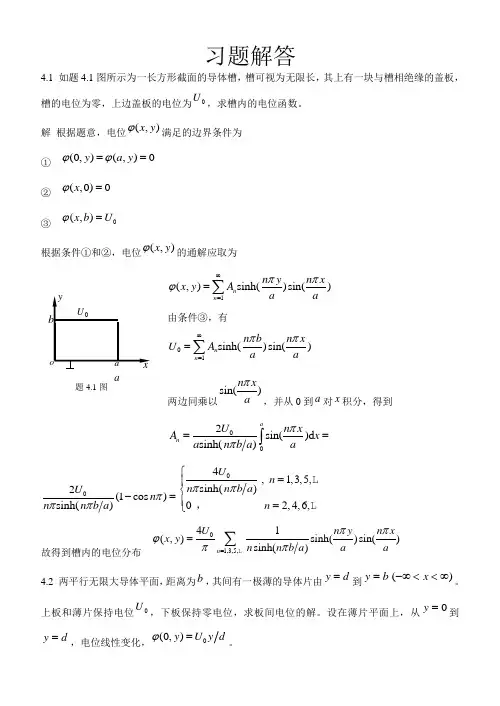
习题解答4.1 如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为 ① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ= ③0(,)x b U ϕ=根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a a ππϕ∞==∑由条件③,有01sinh()sin()n n n b n x U A a a ππ∞==∑两边同乘以sin()n x a π,并从0到a 对x 积分,得到002sin()d sinh()an U n xA x a n b a a ππ==⎰02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩L L ,故得到槽内的电位分布1,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a a ππϕππ==∑L4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
a题4.1图解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为: ①22(,0)(,)0x x b ϕϕ==②2(,)0()x y x ϕ=→∞③002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b d b ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩根据条件①和②,可设2(,)x y ϕ的通解为 21(,)sin()en x bn n n y x y A b ππϕ∞-==∑由条件③有00100(0)sin()()n n U U y y d n y b A U U b y yd y b d b π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n yb π,并从0到b 对y 积分,得到0002211(1)sin()d ()sin()d dbn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d b ππ故得到 (,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d n b b ππππ∞-=+∑4.3 求在上题的解中,除开0U y 一项外,其他所有项对电场总储能的贡献。

2010-2011-2学期《电磁场与电磁波》课程考试试卷参考答案及评分标准命题教师:李学军 审题教师:米燕一、判断题(10分)(每题1分)1.旋度就是任意方向的环量密度 ( × )2. 某一方向的的方向导数是描述标量场沿该方向的变化情况 ( √ )3. 点电荷仅仅指直径非常小的带电体 ( × )4. 静电场中介质的相对介电常数总是大于 1 ( √ )5. 静电场的电场力只能通过库仑定律进行计算 ( × )6.理想介质和导电媒质都是色散媒质 ( × )7. 均匀平面电磁波在无耗媒质里电场强度和磁场强度保持同相位 ( √ )8. 复坡印廷矢量的模值是通过单位面积上的电磁功率 ( × )9. 在真空中电磁波的群速与相速的大小总是相同的 ( √ ) 10 趋肤深度是电磁波进入导体后能量衰减为零所能够达到的深度 ( × ) 二、选择填空(10分)1. 已知标量场u 的梯度为G ,则u 沿l 方向的方向导数为( B )。
A. G l ⋅B. 0G l ⋅ C. G l ⨯2. 半径为a 导体球,带电量为Q ,球外套有外半径为b ,介电常数为ε的同心介质球壳,壳外是空气,则介质球壳内的电场强度E 等于( C )。
A.24Q r π B. 204Q r πε C. 24Qr πε3. 一个半径为a 的均匀带电圆柱(无限长)的电荷密度是ρ,则圆柱体内的电场强度E 为( C )。
A.22aE r ρε=B. 202r E a ρε= C. 02r E ρε= 4. 半径为a 的无限长直导线,载有电流I ,则导体内的磁感应强度B 为( C )。
A.02I r μπB. 02Ir a μπC. 022Ir aμπ 5. 已知复数场矢量0x e E =E ,则其瞬时值表述式为( B )。
A.()0cos y x e E t ωϕ+ B. ()0cos x x e E t ωϕ+ C. ()0sin x x e E t ωϕ+6. 已知无界理想媒质(ε=9ε0, μ=μ0,σ=0)中正弦均匀平面电磁波的频率f=108 Hz ,则电磁波的波长为( C )。

电磁场与微波技术基础试题一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题2分,共20分)1.设一个矢量场 =x x+2y y+3z z,则散度为( )A. 0B. 2C. 3D. 62.人们规定电流的方向是( )运动方向。
A.电子B.离子C.正电荷D.负电荷3.在物质中没有自由电子,称这种物质为( )A.导体B.半导体C.绝缘体D.等离子体4.静电场能量的来源是( )A.损耗B.感应C.极化D.做功5.对于各向同性介质,若介电常数为ε,则能量密度we为( )A. •B. E2C. εE2D. εE26.电容器的大小( )A.与导体的形状有关B.与导体的形状无关C.与导体所带的电荷有关D.与导体所带的电荷无关7.电矩为的电偶极子在均匀电场中所受的作用力和库仑力矩为( )A. =0,Tq= •B. =0, = ×C. = • ,= ×D. = • , =08.在 =0的磁介质区域中的磁场满足下列方程( )A. × =0, • =0B. × ≠0, • ≠0C. × ≠0, • =0D. × =0, • ≠09.洛伦兹条件人为地规定的( )A.散度B.旋度C.源D.均不是10.传输线的工作状态与负载有关,当负载短路时,传输线工作在何种状态?( )A.行波B.驻波C.混合波D.都不是二、填空题(每空2分,共20分)1.两个矢量的乘法有______和______两种。
2.面电荷密度ρs( )的定义是______,用它来描述电荷在______的分布。
3.由库仑定律可知,电荷间作用力与电荷的大小成线性关系,因此电荷间的作用力可以用______原理来求。
4.矢量场的性质由它的______决定。
5.在静电场中,电位相同的点集合形成的面称为______。
6.永久磁铁所产生的磁场,称之为______。
7.在电场中电介质在外电场的作用下会产生______,使电场发生变化。

电磁场与电磁波习题及答案电磁场与电磁波习题及答案电磁场和电磁波是物理学中非常重要的概念,它们广泛应用于电子工程、通信技术等领域。
在学习电磁场和电磁波的过程中,习题是非常重要的一环。
通过解答习题,我们可以更好地理解和掌握相关知识。
本文将为大家提供一些电磁场和电磁波的习题及答案,希望对大家的学习有所帮助。
1. 电磁场的基本概念(1) 什么是电磁场?答案:电磁场是由电荷和电流所产生的一种物质性质,它可以通过电磁场力作用于其他电荷或电流。
电场和磁场是电磁场的两个基本成分。
(2) 电场和磁场有何区别?答案:电场是由电荷产生的,它的作用是使电荷受力;磁场是由电流产生的,它的作用是使电流受力。
电场和磁场都是电磁场的一部分,它们之间通过麦克斯韦方程组相互联系。
2. 电磁波的基本特性(1) 什么是电磁波?答案:电磁波是一种由变化的电场和磁场相互耦合而产生的波动现象。
它具有电磁场的传播特性,可以在真空中传播。
(2) 电磁波有哪些基本特性?答案:电磁波具有波长、频率、速度和能量等基本特性。
波长是指电磁波的一个完整周期所对应的距离,通常用λ表示;频率是指单位时间内电磁波的周期数,通常用ν表示;速度是指电磁波在介质中传播的速度,通常用c表示;能量是指电磁波传播时携带的能量。
3. 电磁场和电磁波的应用(1) 电磁场和电磁波在通信技术中的应用有哪些?答案:电磁场和电磁波在通信技术中起到至关重要的作用。
无线通信技术利用电磁波在空间中传播的特性,实现了远距离的信息传输。
例如,无线电、手机、卫星通信等都是基于电磁波传播原理的。
(2) 电磁场和电磁波在医学中的应用有哪些?答案:电磁场和电磁波在医学中有广泛的应用。
例如,核磁共振成像(MRI)利用强大的磁场和无线电波来获取人体内部的影像;电磁波在治疗癌症中也有应用,如放射疗法利用高能电磁波杀死癌细胞。
4. 电磁场和电磁波的数学描述(1) 请简述麦克斯韦方程组的含义。
答案:麦克斯韦方程组是描述电磁场和电磁波的基本方程。


电磁学试题库试题4一、填空题(每小题2分,共20分)1、一均匀带电球面,电量为Q,半径为R,在球内离球心R/2处放一电量为q 的点电荷,假定点电荷的引入并不破坏球面上电荷的均匀分布,整个带电系统在球外P点产生的电场强度( )。
2、一无限长均匀带电直线(线电荷密度为λ)与另一长为L ,线电荷密度为η的均匀带电直线AB 共面,且互相垂直,设A 端到无限长均匀带电线的距离为a ,带电线AB 所受的静电力为( )。
3、如图所示,金属球壳内外半径分别为a 和b ,带电量为Q ,球壳腔内距球心O 为r 处置一电量为q 的点电荷,球心O 点的电势(4、平行板电容器充电后两极板的面电荷密度分别为+σ与-σ,极板上单位面积的受力( )5、一电路如图所示,已知V 121=ε V 92=ε V 83=ε Ω===1321r r rΩ====25431R R R R Ω=32R 则Uab =( )6、两条无限长的平行直导线相距a ,当通以相等同向电流时,则距直导线距离都为a 的一点P 的磁感应强度的大小是( )7、通过回路所圈围的面积的磁通量发生变化时,回路中就产生感应电动势,引起磁通量变化的物理量是( )R R 33r ε54I a Pa a I8、0C C r ε=成立的条件是( )。
9、铁介质的主要特征是( )。
10、麦克斯韦在总结前人电磁学全部成就的基础上,提出了两条假设。
一、选择题(每小题2分,共20分)1、在用试探电荷检测电场时,电场强度的定义为:0q FE =则( )(A )E 与q o 成反比(B )如果没有把试探电荷q o 放在这一点上,则E=0(C )试探电荷的电量q o 应尽可能小,甚至可以小于电子的电量 (D )试探电荷的体积应尽可能小,以致可以检测一点的场强 2、一点电荷q 位于边长为d 的立方体的顶角上,通过与q 相连的三个平面的电通量是( )(A )04εq (B )08εq(C )010εq (D )03、两个平行放置的带电大金属板A 和B ,四个表面电荷面密度为4321σσσσ、、、如图所示,则有( ) (A )3241σ-=σσ=σ,(B )3241σ=σσ=σ, (C )3241σ-=σσ-=σ, (D )3241σ=σσ-=σ,4、如图所示,图中各电阻值均为R ,AB R 为( ) (A )Ω=4AB R (B )Ω=2AB R(C ) R R AB 43=(D ) R R AB 23=5、一圆线圈的半径为R ,载有电流I ,放在均匀外磁场中,如图所示,线圈导线上的张力是:( ) (A )T=2RIB (B )T=IRB (C )T=0(D )T=RIB π26、一个分布在圆柱形体积内的均匀磁场,磁感应强度为B ,方向沿圆柱的轴线,圆柱Q Q 1234A B的半径为R ,B 的量值以κ=dt dB 的恒定速率减小,在磁场中放置一等腰形金属框ABCD (如图所示)已知AB=R ,CD=R/2,线框中总电动势为:( )(A )K R 21633 顺时针方向(B )KR 21633 逆时针方向 (C )KR 243 顺时针方向 (D )KR 243 逆时针方向7、一个介质球其内半径为R ,外半径为R+a ,在球心有一电量为0q 的点电荷,对于R <r <R+a 电场强度为:( )(A )2004r q r επε (B)2004r q πε (C)204r q π (D)2041r q r r πε-ε)(8、在与磁感应强度为B 的均匀恒定磁场垂直的平面内,有一长为L 的直导线ab ,导线绕a 点以匀角速度ω转动,转轴与B 平行,则ab 上的动生电动势为:( )(A )221BL ω=ε(B )2BL ω(C )241BL ω=ε(D )ε=09、放在平滑桌面上的铁钉被一磁铁吸引而运动,其产生的动能是因为消耗了( ) (A )磁场能量; (B )磁场强度; (C )磁场力; (D )磁力线。

第一章习题解答1.1 给定三个矢量A 、B 和C 如下: 23x y z =+-A e e e4y z =-+B e e52x z =-C e e求:(1)A a ;(2)-A B ;(3)A B g ;(4)AB θ;(5)A 在B 上的分量;(6)⨯A C ;(7)()⨯A B C g 和()⨯A B C g ;(8)()⨯⨯A B C 和()⨯⨯A B C 。
解 (1)23A x y z +-===+e e e A a e e e A (2)-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e(3)=A B g (23)x y z +-e e e (4)y z -+=e e g -11 (4)由cos AB θ===A B A B g ,得1cos AB θ-=(135.5=o (5)A 在B 上的分量 B A =A cos ABθ==A B B g (6)⨯=A C 123502x yz-=-e e e 41310x y z ---e e e(7)由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C g (23)x y z +-e e e g (8520)42x y z ++=-e e e ()⨯=A B C g (1014)x y z ---e e e g (52)42x z -=-e e(8)()⨯⨯=A B C 1014502x yz---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。
(1)判断123PP P ∆是否为一直角三角形;(2)求三角形的面积。

一、选择题1.(0分)[ID:129187]关于电磁波的下列说法正确的是()A.T射线(1THz=1012Hz)是指频率从0.3~10THz、波长介于无线电波中的毫米波与红外线之间的电磁辐射,它的波长比可见光波长短B.电磁波可以通过电缆、光缆进行有线传输,但不能实现无线传输,光缆传递的信息量最大,这是因为频率越高可以传递的信息量越大C.太阳辐射的能量大部分集中在可见光及附近的区域D.调制的方法分调幅和调频,经过调制后的电磁波在空间传播得更快2.(0分)[ID:129185]如图所示,一细束白光通过玻璃三棱镜折射后分为各种单色光,取其中a、b、c三种色光,下列说法正确的是()A.把温度计放在c的下方,示数增加最快B.若分别让a、b、c三色光通过一双缝装置,则a光形成的干涉条纹的间距最大C.a、b、c三色光在玻璃三棱镜中的传播速度依次越来越小D.若让a、b、c三色光以同一入射角,从空气中某方向射入一介质,b光恰能发生全反射,则c光也一定能发生全反射3.(0分)[ID:129179]关于电磁场和电磁波,下列说法正确的是()A.把带电体和永磁体放在一起,可在其周围空间中产生电磁波B.手机、电视、光纤通信都是通过电磁波来传递信息的C.医院中用于检查病情的“B超”是利用了电磁波的反射原理D.车站、机场安全检查时“透视”行李箱的安检装置利用的是红外线4.(0分)[ID:129178]关于电磁场和电磁波,下列说法中正确的是()A.麦克斯韦认为变化的电场产生变化的磁场B.红外线、可见光和紫外线是由原子的外层电子受激发产生的C.电磁波由真空进入介质传播时,波长变大D.电磁波按频率由高到低的正确排列顺序是:无线电波、红外线、可见光、紫外线、X 射线,γ射线5.(0分)[ID:129176]关于波和波的现象解释,下列说法中正确的有()A.电磁波的传播速度恒为8⨯310m/sB.雷达工作时利用了声波的反射C.增透膜使得两列反射光波相消,但透射光强并没有增加D.声源与观察者相对靠近时,观察者按收到的频率大于声源发出的频率6.(0分)[ID:129170]要提高LC振荡电路辐射电磁波的本领,应该采取的措施是()A.增加辐射波的波长B.使振荡电容器的正对面积足够小C.尽可能使电场和磁场分散开D.增加回路中的电容和电感7.(0分)[ID:129157]如图所示,L为电感线圈,C为电容器,R为定值电阻,线圈及导线电阻均不计。

1. 写出非限定情况下麦克斯韦方程组的微分形式,并简要说明其物理意义。
2.答非限定情况下麦克斯韦方程组的微分形式为,,0,D B H J E B D t tρ∂∂∇⨯=+∇⨯=-∇⋅=∇⋅=∂∂,(3分)(表明了电磁场和它们的源之间的全部关系除了真实电流外,变化的电场(位移电流)也是磁场的源;除电荷外,变化的磁场也是电场的源。
1. 写出时变电磁场在1为理想导体与2为理想介质分界面时的边界条件。
2. 时变场的一般边界条件 2n D σ=、20t E =、2t s H J =、20n B =。
(或矢量式2n D σ=、20n E ⨯=、2s n H J ⨯=、20n B =)1. 写出矢量位、动态矢量位与动态标量位的表达式,并简要说明库仑规范与洛仑兹规范的意义。
2. 答矢量位,0B A A =∇⨯∇⋅=;动态矢量位A E t ϕ∂=-∇-∂或AE tϕ∂+=-∇∂。
库仑规范与洛仑兹规范的作用都是限制A 的散度,从而使A 的取值具有唯一性;库仑规范用在静态场,洛仑兹规范用在时变场。
1. 简述穿过闭合曲面的通量及其物理定义 2.sA ds φ=⋅⎰⎰ 是矢量A 穿过闭合曲面S 的通量或发散量。
若Ф> 0,流出S 面的通量大于流入的通量,即通量由S 面内向外扩散,说明S 面内有正源若Ф< 0,则流入S 面的通量大于流出的通量,即通量向S 面内汇集,说明S 面内有负源。
若Ф=0,则流入S 面的通量等于流出的通量,说明S 面内无源。
1. 证明位置矢量x y z r e x e y e z =++ 的散度,并由此说明矢量场的散度与坐标的选择无关。
2. 证明在直角坐标系里计算 ,则有()()xy z x y z r r e e e e x e y e z x y z ⎛⎫∂∂∂∇⋅=++⋅++ ⎪∂∂∂⎝⎭3x y z x y z∂∂∂=++=∂∂∂ 若在球坐标系里计算,则 232211()()()3r r r r r r r r r∂∂∇⋅===∂∂由此说明了矢量场的散度与坐标的选择无关。
电磁场与电磁波期末考试复习资料11.圆柱坐标系中单位矢量 , 。
2.对于矢量A ,若 ,则=+•y x a y x a x )(2 ,=⨯x z a y a x 2 。
3.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为 ,矢量B A ⋅= 。
4.已知直角坐标系中点P 1(5,-2,1),P 2(3,1,2),则P1的位置矢量为 ,P1到P2的距离矢量为 。
5.已知球坐标系中单位矢量 。
6.在两半无限大导电平面组成的直角劈形中间放置一点电荷,此时点电荷的镜像电荷个数为 。
7.点电荷q 在自由空间任一点r 处电场强度为 。
8.静电场中导体内的电场为 ,电场强度与电位函数的关系为 。
9.高斯散度定理的积分式为 ,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
10.已知任意一个矢量场A ,则其旋度的散度为 。
11.真空中静电场的基本方程的微分形式为 、 、 。
12.分析恒定磁场时,在无界真空中,两个基本场变量为 ,它们之间的关系为 。
13.斯托克斯定理为 ,它表明矢量场A 的旋度沿曲面S 的方向分量的面积分等于该矢量沿围绕此面积曲线边界的线积分。
14.任意一个标量场u ,则其梯度的旋度为 。
15.对于某一矢量 ,它的散度定义式为 ,用哈密顿算子表示为 。
16.介质中静电场的基本方程的积分式为 , , 。
17.介质中恒定磁场的基本方程的微分形式为 、 、 。
18.介质中恒定磁场的基本方程的积分式为 , , 。
19.静电场中两种介质分界面的边界条件是 , 。
20.在无限大的导体平面上方d 处放一点电荷q ,则其镜像电荷电量为 ,位置位于 ;如果一个点电荷置于两平行导体中间,则此点电荷有 镜像电荷。
21.矢量场223z a yz a y x a A z y x ++=在点P(1,1,0)的散度为 。
22.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为 ,位置位于 ;当点电荷q 向无限远处运动时,其镜像电荷向 运动。
4.2 电磁场与电磁波一、选择题1.(单选)下列四个选项中的四种磁场变化情况,能产生如图所示电场的是( )【答案】 B【解析】由麦克斯韦电磁场理论知均匀变化的磁场才能产生稳定的电场,选项B正确。
方法总结均匀(非均匀)变化的磁场(电场)、恒定的磁场(电场)的比较(1)变化的磁场产生的电场,叫作感应电场,它的电场线是闭合的。
而静电荷周围产生的电场叫作静电场,它的电场线由正电荷或无限远出发,终止于无限远或负电荷,是不闭合的。
(2)恒定的电场不产生磁场,恒定的磁场不产生电场。
(3)均匀变化的磁场周围产生恒定的电场,均匀变化的电场周围产生恒定的磁场。
(4)不均匀变化的磁场产生变化的电场,不均匀变化的电场产生变化的磁场。
2.(单选)如图所示的四种变化电场,能发射电磁波的是()【答案】 D【解析】图A是稳定的电场,不能产生磁场;图B与图C是均匀变化的电场,产生恒定的磁场,也不能形成电磁波;图D是周期性变化的电场,会产生同频率周期性变化的磁场,能形成电磁场,向外发射电磁波,选项D正确,A、B、C错误。
3.(多选)甲、乙两种磁场的磁感应强度B随时间t变化的规律如图所示,下列说法正确的是()A.磁场甲能够产生电场B.磁场甲能够产生电磁波C.磁场乙的磁感应强度最大时产生的电场最强D.磁场乙的磁感应强度为零时产生的电场最强【答案】AD【解析】根据麦克斯韦的电磁场理论,均匀变化的磁场甲能产生稳定的电场,不能产生电磁波,选项A 正确,B错误;周期性变化的磁场产生同频率周期性变化的电场,磁场乙的磁感应强度最大时,产生的电场最弱,磁场乙的磁感应强度为零时,产生的电场最强,选项C错误,D正确。
4.(单选)电磁波在传播时,不变的物理量是()A.振幅B.频率C.波速D.波长【答案】 B【解析】离波源越远,振幅越小,电磁波在不同介质中的波速不一样,波长也不一样。
频率是由发射电磁波的波源决定的,与介质无关。
5.(单选)电磁场理论是以下哪位科学家提出的()A.法拉第B.赫兹C.麦克斯韦D.安培【答案】 C【解析】由图示电流方向知电容器在充电,振荡电流减小,电容器极板上的电荷量正在增强,极板间的场强在增强,磁场能正在向电场能转化,选项C正确,A、B、D错误。
电磁波与电磁场第四版答案一、单选题1.垂直于匀强磁场放置一长为1m的通电直导线,导线中电流为2A,所受安培力大小为0.1N,则该磁场的磁感应强度大小为() [单选题] *A.0.05T(正确答案)B.0.1TC.0.2TD.2T2.某一区域的磁感线分布如图所示,M、P为磁场中的两个点,下列说法正确的是()[单选题] *A.M点的磁场方向和P点的磁场方向相反B.M点的磁场方向和P点的磁场方向相同C.M点的磁感应强度小于P点的磁感应强度(正确答案)D.M点的磁感应强度大于P点的磁感应强度3.如图所示,小磁针静止在导线环中。
当导线环通过沿逆时针方向的电流时,忽略地磁场影响,小磁针最后静止时N极所指的方向()[单选题] *A.水平向右B.水平向左C.垂直纸面向里D.垂直纸面向外(正确答案)4.面积为0.75m2的线圈放在匀强磁场中,线圈平面与磁感线垂直,已知穿过线圈平面的磁通量是1.50Wb,那么这个磁场的磁感应强度是() [单选题] *A.0.05T B.1.125T C.2.0T(正确答案)D.0.02T5.首先发现电流的磁效应的物理学家是() [单选题] *A.安培B.法拉第C.奥斯特(正确答案)D.密立根6.某个磁场的磁感线如图所示,如果把一个小磁针放入磁场中,小磁针将()[单选题] *A.顺时针转动(正确答案)B.逆时针转动C.向右移动D.向左移动7.关于定义式(其中B表示磁感应强度,F表示通电导体棒受到的磁场力,I表示通过导体棒的电流强度,L表示导体棒的长度),下列说法正确的是() [单选题] *A.B与F成正比B.I越大,则B越小C.F的方向就是B的方向D.B的大小和方向与IL无关,由磁场本身决定(正确答案)8.如图,通电螺线管轴线上a、b、c三点的磁感应强度大小分别为Ba、Bb、Bc,则()[单选题] *A.Bc>Ba>Bb B.Bb>Bc>BaC.Ba>Bb>Bc(正确答案)D.Ba=Bb=Bc9.下列选项中通电直导线周围磁感线分布正确的是()[单选题] *A.⑴(正确答案)B.⑵ C. ⑶D.⑷10.把螺线管与电源连接,发现小磁针N极向螺线管偏转,静止时所指方向如图所示。
《电磁场与电磁波》知识点及参考答案第1章 矢量分析1、如果矢量场F 的散度处处为0,即0F∇⋅≡,则矢量场是无散场,由旋涡源所产生,通过任何闭合曲面S 的通量等于0。
2、如果矢量场F 的旋度处处为0,即0F ∇⨯≡,则矢量场是无旋场,由散度源所产生,沿任何闭合路径C 的环流等于0。
3、矢量分析中的两个重要定理分别是散度定理(高斯定理)和斯托克斯定理, 它们的表达式分别是:散度(高斯)定理:SVFdV F dS ∇⋅=⋅⎰⎰和斯托克斯定理:sCF dS F dl∇⨯⋅=⋅⎰⎰。
4、在有限空间V 中,矢量场的性质由其散度、旋度和V 边界上所满足的条件唯一的确定。
( √ )5、描绘物理状态空间分布的标量函数和矢量函数,在时间为一定值的情况下,它们是唯一的。
( √ )6、标量场的梯度运算和矢量场的旋度运算都是矢量。
( √ )7、梯度的方向是等值面的切线方向。
(× )8、标量场梯度的旋度恒等于0。
( √ ) 9、习题1.12, 1.16。
第2章 电磁场的基本规律(电场部分)1、静止电荷所产生的电场,称之为静电场;电场强度的方向与正电荷在电场中受力的方向相同。
2、在国际单位制中,电场强度的单位是V/m(伏特/米)。
3、静电系统在真空中的基本方程的积分形式是:V V sD d S d V Q ρ⋅==⎰⎰和0lE dl ⋅=⎰。
4、静电系统在真空中的基本方程的微分形式是:V D ρ∇⋅=和0E∇⨯=。
5、电荷之间的相互作用力是通过电场发生的,电流与电流之间的相互作用力是通过磁场发生的。
6、在两种媒质分界面的两侧,电场→E 的切向分量E 1t -E 2t =0;而磁场→B 的法向分量B 1n -B 2n =0。
7、在介电常数为e 的均匀各向同性介质中,电位函数为 2211522x y z ϕ=+-,则电场强度E=5x y zxe ye e --+。
8、静电平衡状态下,导体内部电场强度、磁场强度等于零,导体表面为等位面;在导体表面只有电场的法向分量。
《电磁场与电磁波》(第四版)习题集:第4章时变电磁场第4章时变电磁场在时变的情况下,电场和磁场相互激励,在空间形成电磁波,时变电磁场的能量以电磁波的形式进行传播。
电磁场的波动方程描述了电磁场的波动性,本章首先对电磁场的波动方程进行讨论。
在时变电磁场的情况下,也可以引入辅助位函数来描述电磁场,使一些复杂问题的分析求解过程得以简化。
本章对时变电磁场的位函数及其微分方程进行了讨论。
电磁能量一如其它能量服从能量守恒原理,本章将讨论电磁场的能流和表征电磁场能量守恒关系的坡印廷定理。
本章在最后讨论了随时间按正弦函数变化的时变电磁场,这种时变电磁场称为时谐电磁场或正弦电磁场。
4. 1 波动方程由麦克斯韦方程可以建立电磁场的波动方程,揭示了时变电磁场的运动规律,即电磁场的波动性。
下面建立无源空间中电磁场的波动方程。
在无源空间中,电流密度和电荷密度处处为零,即0ρ=、0=J 。
在线性、各向同性的均匀媒质中,E 和H 满足的麦克斯韦方程为t ε=?EH (4.1.1) tμ=-?HE (4.1.2) 0?=H (4.1.3) 0?=E (4.1.4)对式(4.1.2)两边取旋度,有()()tμ=-E H 将式(4.1.1)代入上式,得到22()0t με+=?EE利用矢量恒等式2()()=??-?E E E 和式(4.1.4),可得到2220tμε??-=?EE (4.1.5)此式即为无源区域中电场强度矢量E 满足的波动方程。
同理可得到无源区域中磁场强度矢量H 满足的波动方程为2220tμε??-=?H H (4.1.6)无源区域中的E 或H 可以通过求解式(4.1.5)或式(4.1.6)的波动方程得到。
在直角坐标系中,波动方程可以分解为三个标量方程,每个方程中只含有一个场分量。
例如,式(4.1.5)可以分解为222222220x x x xE E E E x y z tμε++-= (4.1.7) 222222220yyyyE E E E x y z t με++-= (4.1.8)222222220z z z zE E E E x y z t με++-= (4.1.9)在其它坐标系中分解得到的三个标量方程都具有复杂的形式。
《电磁场与电磁波》试题(4)一、填空题(每小题 1 分,共 10 分)1.矢量的大小为 。
2.由相对于观察者静止的,且其电量不随时间变化的电荷所产生的电场称为 。
3.若电磁波的电场强度矢量的方向随时间变化所描绘的轨迹是直线,则波称为 。
4.从矢量场的整体而言,无散场的 不能处处为零。
5.在无源区域中,变化的电场产生磁场,变化的磁场产生电场,使电磁场以 的形式传播出去,即电磁波。
6.随时间变化的电磁场称为 场。
7.从场角度来讲,电流是电流密度矢量场的 。
8.一个微小电流环,设其半径为、电流为,则磁偶极矩矢量的大小为 。
9.电介质中的束缚电荷在外加 作用下,完全脱离分子的内部束缚力时,我们把这种现象称为击穿。
10.法拉第电磁感应定律的微分形式为 。
二、简述题 (每小题 5分,共 20 分)11.简述恒定磁场的性质,并写出其两个基本方程。
12.试写出在理想导体表面电位所满足的边界条件。
13.试简述静电平衡状态下带电导体的性质。
14.什么是色散?色散将对信号产生什么影响?三、计算题 (每小题10 分,共30分)15.标量场,在点处 (1)求出其梯度的大小 (2)求梯度的方向 16.矢量,,求(1)(2)17.矢量场的表达式为(1)求矢量场的散度。
(2)在点处计算矢量场的大小。
z y x e e eA ˆˆˆ++=ϖa I ()ze y x z y x +=32,,ψ()0,1,1-P y x e eA ˆ2ˆ+=ϖz x e eB ˆ3ˆ-=ϖB A ϖϖ⨯B A ϖϖ+A ϖ2ˆ4ˆy e x eA y x -=ϖA ϖ()1,1A ϖ四、应用题 (每小题 10分,共30分)18.一个点电荷位于处,另一个点电荷位于处,其中。
(1) 求出空间任一点处电位的表达式;(2) 求出电场强度为零的点。
19.真空中均匀带电球体,其电荷密度为,半径为,试求(1) 球内任一点的电位移矢量 (2) 球外任一点的电场强度20. 无限长直线电流垂直于磁导率分别为的两种磁介质的交界面,如图1所示。
(1) 写出两磁介质的交界面上磁感应强度满足的方程 (2) 求两种媒质中的磁感应强度。
五、综合题 (10分)21. 设沿方向传播的均匀平面电磁波垂直入射到理想导体,如图2所示,入射波电场的表达式为(1)试画出入射波磁场的方向 (2)求出反射波电场表达式。
《电磁场与电磁波》试题(4)参考答案二、简述题 (每小题 5分,共 20 分)q +()0,0,a -q 2-()0,0,a 0>a ()z y x ,,ρa I 21μμ和21B B 和z +z j y e E eE β-=0ˆϖ图2图11B ϖ2B ϖ1μ2μ11.答:恒定磁场是连续的场或无散场,即磁感应强度沿任一闭合曲面的积分等于零。
产生恒定磁场的源是矢量源。
(3分)两个基本方程:⎰=⋅SS d B 0ϖϖ (1分)I l d H C=⋅⎰ϖϖ (1分)(写出微分形式也对)12.答:设理想导体内部电位为2φ,空气媒质中电位为1φ。
由于理想导体表面电场的切向分量等于零,或者说电场垂直于理想导体表面,因此有SS 21φφ= (3分)σφε-=∂∂Sn10(2分)13.答:静电平衡状态下,带电导体是等位体,导体表面为等位面;(2分)导体内部电场强度等于零,在导体表面只有电场的法向分量。
(3分)14.答:在导电媒质中,电磁波的传播速度随频率变化的现象称为色散。
(3分)色散将使信号产生失真,从而影响通信质量。
(2分)三、计算题 (每小题10分,共30分)15.标量场()ze y x z y x +=32,,ψ,在点()0,1,1-P 处(1)求出其梯度的大小 (2)求梯度的方向解:(1)ze y e x ez y x ∂∂+∂∂+∂∂=∇ψψψψˆˆˆ (2分)z y x Pe e eˆ3ˆ2ˆ++-=∇ψ(2分)梯度的大小: 14=∇Pψ (1分)(2)梯度的方向z z y x e e y x e xy eˆ3ˆ2ˆ223++=∇ψψψ∇∇=nˆ (3分) 14ˆ3ˆ2ˆˆz y x e e en++-= (2分)16.矢量y x e e A ˆ2ˆ+=ϖ,z x e e B ˆ3ˆ-=ϖ,求 (1)B A ϖϖ⨯ (2)B A ϖϖ+解:(1)根据zyxz y xz y x B B B A A A eeeB A ˆˆˆ=⨯ϖϖ (3分) 所以2ˆ3ˆ6ˆ31021ˆˆˆz y x z y xe e e ee eB A -+-=-=⨯ϖϖ (2分) (2)z x y x e e e eB A ˆ3ˆˆ2ˆ-++=+ϖϖ (2分) z y x e e e B A ˆ3ˆ2ˆ2-+=+ϖϖ (3分) 17.矢量场A ϖ的表达式为2ˆ4ˆy e x eA y x -=ϖ(1)求矢量场A ϖ的散度。
(2)在点()1,1处计算矢量场A ϖ的大小。
解:(1)分)(分)(2243yz A y A x A A zy x -=∂∂+∂∂+∂∂=⋅∇ϖ(2)在点()1,1处 矢量 y x e eA ˆ4ˆ-=ϖ(2分)所以矢量场Aϖ在点()1,1处的大小为()171422=-+=A(3分)四、应用题(每小题 10分,共30分)18.一个点电荷q+位于()0,0,a-处,另一个点电荷q2-位于()0,0,a处,其中0>a。
求(3)求出空间任一点()z yx,,处电位的表达式;(4)求出电场强度为零的点。
解:(1)建立如图18-1所示坐标空间任一点的电位⎪⎪⎭⎫⎝⎛-=12214rrqπεφ(3分)其中,()2221zyaxr++-=(1分)()2222zyaxr+++=(1分)(2)根据分析可知,电场等于零的位置只能位于两电荷的连线上的q+的左侧,(2分)设位于x处,则在此处电场强度的大小为()()⎪⎪⎭⎫⎝⎛+--=22214axaxqEπε(2分)令上式等于零得()()2221axax+=-求得()ax223+-=(1分)图18-119.真空中均匀带电球体,其电荷密度为ρ,半径为a ,试求 (3) 球内任一点的电位移矢量 (4) 球外任一点的电场强度解:(1)作半径为r 的高斯球面,在高斯球面上电位移矢量的大小不变, (2分)根据高斯定理,有ρππ32344r r D =(2分)r D ϖϖ3ρ= a r < (1分)(2)当a r >时,作半径为r 的高斯球面,根据高斯定理,有 ρππ32344a r D =(2分) r ra D ϖϖ333ρ= (2分)电场强度为r ra E ϖϖ3033ερ= (1分) 20. 无限长直线电流I 垂直于磁导率分别为21μμ和的两 种磁介质的交界面,如图1所示。
试(3) 写出两磁介质的交界面上磁感应强度满足的方程 (4) 求两种媒质中的磁感应强度21B B 和。
解:(1)磁感应强度的法向分量连续n n B B 21= (2分)根据磁场强度的切向分量连续,即t t H H 21= (1分)因而,有2211μμttB B =(2分)图11B ϖ2B ϖ1μ 2μ(2)由电流在区域1和区域2中所产生的磁场均为ϕeˆ,也即是分界面的切向分量,再根据磁场强度的切向分量连续,可知区域1和区域2中的磁场强度相等。
(2分) 由安培定律I l d H C=⋅⎰ϖϖ得 rI H π2=(1分)因而区域1和区域2中的磁感应强度分别为rIeB πμϕ2ˆ11=ϖ(1分) r IeB πμϕ2ˆ22=ϖ (1分) 五、综合题 (10分)21. 设沿z +方向传播的均匀平面电磁波垂直入射到理想导体,如图2所示,入射波电场的表达式为 z j y e E eE β-=0ˆϖ(1)试画出入射波磁场的方向 (2)求出反射波电场表达式。
解:(1)入射波磁场的方向如图21-1所示。
(2)设反射波电场z j r y r e E eE βˆ=ϖ区域1中的总电场为)(ˆ0z j r zj y r e E e E eE E ββ+=+-ϖϖ (2分)根据0=z 导体表面电场的切向分量等于零的边界条件得图2图21-1Hϖ0E E r -= (2分)因此,设反射波电场为z j y r e E eE β0ˆ-=ϖ(1分)。