2011年高三桂林市第一次调研考试数学(理)试题
- 格式:doc
- 大小:671.50 KB
- 文档页数:8

桂林中学2011届高三第三次月考数学理科试题命题人: 伊 洁 审题人: 龙飞跃 命题时间: 2010年11月7日本套试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间:120分钟.第Ⅰ卷(选择题,共60分)一、选择题:(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{}R x x xA ∈≤=,1,{}Rx x y y B ∈==,2,则=B A ( )A 。
{}11≤≤-x x B. {}0≥x x C. {}10≤≤x x D 。
φ2.复数32322323i i i i +--=-+( )A. 0B. 2C. —2i D 。
2i . 3。
若5232250ππsinlog ,log ,.===c b a ,则( )A 。
c b a >> B 。
b c a >>C 。
a b c >>D 。
b a c >>高)考资源&网 4。
.已知条件21:≤-x p ,条件034:>--x x q ,则┓p 是 ┓q 的 ( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分也非必要条件5. 为了得到函数3lg 10x y +=的图像,只需把函数lg y x =的图像上所有的点( )A .向左平移3个单位长度,再向上平移1个单位长度B .向右平移3个单位长度,再向上平移1个单位长度C .向左平移3个单位长度,再向下平移1个单位长度D .向右平移3个单位长度,再向下平移1个单位长度高)考资源&网6。
已知函数22log (2)()24(22a x x f x x x x x +≥⎧⎪==⎨-<⎪-⎩当时在点处当时)连续,则=++∞→11lim 222n a an n ( ) 高)考资源&网A。
21B。
31 C。
3 D. 27. 在R 上定义的函数)(x f 是偶函数,且)2()(x f x f -=。
广西桂林市中山中学2025届高三数学第一学期期末学业质量监测试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
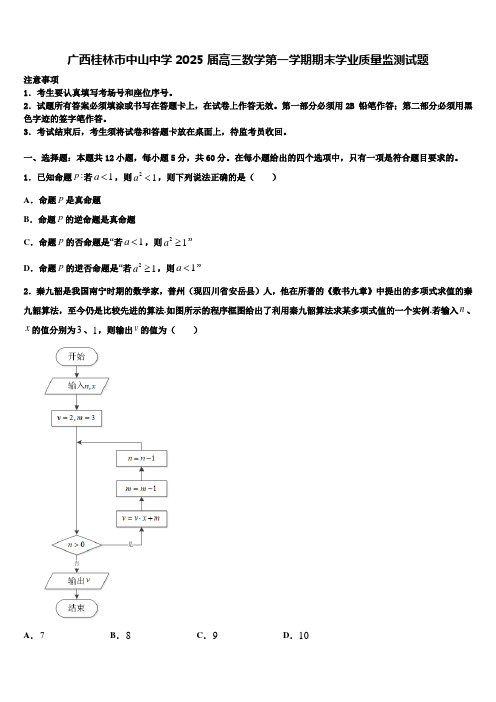
1.已知命题:p 若1a <,则21a <,则下列说法正确的是( )A .命题p 是真命题B .命题p 的逆命题是真命题C .命题p 的否命题是“若1a <,则21a ≥”D .命题p 的逆否命题是“若21a ≥,则1a <”2.秦九韶是我国南宁时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n 、x 的值分别为3、1,则输出v 的值为( )A .7B .8C .9D .103.已知函数log ()a y x c =+(a ,c 是常数,其中0a >且1a ≠)的大致图象如图所示,下列关于a ,c 的表述正确的是( )A .1a >,1c >B .1a >,01c <<C .01a <<,1c >D .01a <<,01c <<4.在直角坐标平面上,点(),P x y 的坐标满足方程2220x x y -+=,点(),Q a b 的坐标满足方程2268240a b a b ++-+=则y b x a--的取值范围是( ) A .[]22-, B .474733⎡--+⎢⎣⎦C .13,3⎡⎤--⎢⎥⎣⎦D .676733⎡+⎢⎣⎦ 5.若点(3,4)P -是角α的终边上一点,则sin 2α=( )A .2425-B .725-C .1625D .856.已知三棱锥P ABC -中,ABC ∆是等边三角形,43,25,AB PA PC PA BC ===⊥,则三棱锥P ABC -的外接球的表面积为( )A .25πB .75πC .80πD .100π7.已知定义在R 上的函数()f x 满足()()f x f x =-,且在(0,)+∞上是增函数,不等式()()21f ax f +≤-对于[]1,2x ∈恒成立,则a 的取值范围是A .3,12⎡⎤--⎢⎥⎣⎦B .11,2⎡⎤--⎢⎥⎣⎦C .1,02⎡⎤-⎢⎥⎣⎦D .[]0,18.5G 网络是一种先进的高频传输技术,我国的5G 技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款5G 手机,现调查得到该款5G 手机上市时间x 和市场占有率y (单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出y 关于x 的线性回归方程为0.042y x a =+.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款5G 手机市场占有率能超过0.5%(精确到月)( )A .2020年6月B .2020年7月C .2020年8月D .2020年9月9.小王因上班繁忙,来不及做午饭,所以叫了外卖.假设小王和外卖小哥都在12:00~12:10之间随机到达小王所居住的楼下,则小王在楼下等候外卖小哥的时间不超过5分钟的概率是( )A .12B .45C .38D .3410.若直线不平行于平面,且,则( )A .内所有直线与异面B .内只存在有限条直线与共面C .内存在唯一的直线与平行D .内存在无数条直线与相交 11.已知复数z 满足32i z i ⋅=+(i 是虚数单位),则z =( )A .23i +B .23i -C . 23i -+D . 23i --12.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为5的概率为A .15B .625C .825D .25二、填空题:本题共4小题,每小题5分,共20分。

广西桂林市2011届高三第一次联合调研考试英语本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考试结束后,将本试题卷和答题卡一并交回。
第I卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
第一部分:听力(共两节,满分30分)做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Where is the woman going?A.To a dance. B.To a lecture. C.To the Student Center.2.What does Jack’s girlfriend do?A.She organizes concerts. B.She plays the piano. C.She sells pianos.3.What’s the man going to do?A.Buy a ticket.B.Go back home from abroad.C.Make a journey.4.How many new dress does the woman have?A.One. B.Three. C.Four.5.What did the man mean?A.He was glad to meet Martha.B.He agreed the woman had written the poem by herself.C.He didn’t think the woman had written the poem by herself.第二节(共15小题;每题1.5分,满分22.5分)听下面5段对话或独白。

桂林市、防城港市高三第一次调研数 学 试 题(文)本试卷分第I 卷和第II 卷(非选择题)两部分。
考试结束后,将本试卷和答题卡一并交回。
第I 卷注意事项: 1.答题前,考生在答题卡务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
3.第I 卷共12小题,第小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一、选择题1.已知集合{1,2,3,4,5,6},{1,4,5},{2,3,4}U S T ===,则U S C T 等于 ( )A .{1,4,5,6}B .{1,5}C .{4}D .{1,2,3,4,5} 2.不等式302x x -<+的解集为( )A .{|23}x x -<<B .{|2}x x <-C .{|23}x x x <->或D .{|3}x x > 3.函数3()lg 1f x o x =+的反函数是 ( )A .11()3(0)x f x x --=> B .1()31(0)x f x x -=->C .11()3()x fx x R --=∈D .1()31()x fx x R -=-∈4.已知a ,b 都是实数,那么“22a b >”是“a b >”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件5.已知3,,sin 25παπα⎛⎫∈= ⎪⎝⎭,则tan()4πα+的值为( )A .17 B .7C .17-D .7- 6.已知向量(1,2),(,2),,||a b x a b b =-=⊥若则=( )A .5B .25C .5D .207.已知数列{}n a 是等比数列,其前n 项和为n S ,若公比42,1q S ==,则8S = ( )A .17B .16C .15D .2568.过点(5,0)的椭圆22221(0)x y a b a b +=>>与双曲线2213x y -=有共同的焦点,则该椭圆的短轴长为( )A .21B .221C .23D .2239.已知n S 是等差数列{}n a 的前n 项和,且11635S S =+,则17S 的值为 ( )A .117B .118C .119D .120 10.若33ln 2,log 2,log tan 3a b c π===,则( )A .b c a >>B .b a c >>C .c a b >>D .a b c >>11.将co s2y x =的图像向左平移(0)ϕϕπ<<个单位长度,得到2cos(2)3y x π=+的图像,若ABC ∆中三边a 、b 、c 所对内角依次为A 、B 、C ,且222,3A c a b ab ϕ==+-,则ABC ∆是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形12.双曲线22221(0,0)x y a b a b-=>>的右支上存在一点,它到右焦点及左准线的距离相等,则双曲线离心率的取值范围是( )A .(1,2⎤⎦B .)2,⎡+∞⎣C .(1,21⎤+⎦D .)21,⎡++∞⎣第II 卷二、填空题:本大题共4小题,每小题5分,共20分。

桂林十八中11级高三第一次月考试卷理科数学注意:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间:120分钟.答卷前,考生务必将自己的姓名和考号填写或填涂在答题卷指定的位置。
2、选择题答案用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试题卷上.3、主观题必须用黑色字迹的钢笔或签字笔在答题卷上作答,答案必须写在答题卷各题目指定区域内的相应位置上,超出指定区域的答案无效;如需改动,先划掉原来的答案,然后再写上新的答案.Ⅰ卷 (共60分)一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集{}1,2,3,4U =,集合{}=12A ,,{}=23B ,,则()=U A B ðA.{}134,,B.{}34,C. {}3D. {}4 2. 已知a 是实数,i1ia +-是纯虚数,则a = A.1- B.1D.3. 已知双曲线C :22221x y a b -=(0,0a b >>)则C 的渐近线方程为A .14y x =±B .13y x =±C .12y x =±D .y x =±4. 设变量x 、y 满足约束条件0230063x y x y y ≥--≤+-⎧-≤⎪⎨⎪⎩,则目标函数2z y x =-的最小值为A .-7B .-4C .1D .25. 若21()nx x-展开式中的所有二项式系数和为512,则该展开式中的常数项为A .-84B .84C .-36D .366.函数2)y x =≤≤反函数是A.1(11)y x =+-≤≤B. )10( 112≤≤--=x x yC.111)y x =--≤≤D. 11)y x =+≤≤7. 已知点()()1,3,4,1,A B AB -则与向量同方向的单位向量为A .3455⎛⎫ ⎪⎝⎭,-B .4355⎛⎫ ⎪⎝⎭,-C .3455⎛⎫- ⎪⎝⎭,D .4355⎛⎫- ⎪⎝⎭, 8.已知数列{}n a 中,12a =,113n n na a a +=+ ()*n N ∈,则4a =A .165 B .219 C .85 D .879.将函数()sin y x x x R =+∈的图像向左平移()0m m >个长度单位后,所得到的图像关于y 轴对称,则m 的最小值是 Ks5u A.12π B.6π C.3π D.56π10. 已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的半径为A.2B.C .132D.11. 设F 为抛物线x y C 4:2=的焦点,过点)0,1(-P 的直线l 交抛物线C 于两点B A ,,点Q 为线段AB 的中点,若2||=FQ ,则直线l 的斜率等于Ks5uAB .1C .1±D.12. )0)()((),(≠x g x g x f 分别是定义在R 上的奇函数和偶函数,当0x <时,()()()()f x g x f x g x ''<,且0)()(,0)2(<=-x g x f f 则不等式的解集为Ks5u A .(-∞,-2)∪(2,+∞) B .(-2,0)∪(0,2)C .(-2,0)∪(2,+∞)D .(-∞,-2)∪(0,2)Ⅱ卷 (共90分)二、填空题:本大题共4小题,每小题5分.把答案填在题中横线上.Ks5u13. 设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是_________. Ks5u14. 函数()sin ((0,2))x f x e x x π=∈的极值点是_________.15. 将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________. (用数字作答)16. 在矩形ABCD中,1,DC AD ==在DC 上截取1DE =,沿AE 将AED ∆翻折得到1AED ∆,使点1D 在平面ABC 上的射影落在AC 上,则二面角1D AE B --的平面角的余弦值为_________.三、解答题:解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分10分) (注意:在试..题卷上作答无效.......) 设△ABC 的内角,,A B C 所对的边分别为,,a b c ,且6a c +=,2b =,7cos 9B =. (Ⅰ)求,a c 的值; (Ⅱ)求ABC ∆的面积.18. (本小题满分12分) (注意:在试题卷上作答无效.........) 已知数列{}n a ,{}n b 分别为等差和等比数列,且11a =,0d >,22a b =,53a b =,144(*)a b n N =∈.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设n n n c a b =⋅,求数列{}n c 的前n 项和.19. (本小题满分12分) (注意:在试题卷上作答无效.........) 如图,在直四棱柱1111ABCD A BC D -中,底面ABCD 为平行四边形,且2AD =,14AB AA ==,60BAD ∠= ,E 为AB 的中点. (Ⅰ)证明:1AC ∥平面1EBC ; (Ⅱ)求1ED 与平面1EBC 所成的角的大小.20. (本小题满分12分) (注意:在试题卷上作答无效.........) ABCA 1B 1C 1D 1D在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手. 各位观众须彼此独立地在选票上选3名歌手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.(Ⅰ) 求观众甲选中3号歌手且观众乙未选中3号歌手的概率;(Ⅱ) ξ表示3号歌手得到观众甲、乙、丙的票数之和, 求ξ的分布列和数学期望.21. (本小题满分12分) (注意:在试题卷上作答无效.........) 已知椭圆C :22221,(0)x y a b a b+=>>的两个焦点分别为12(1,0),(1,0)F F -,且椭圆C 经过点41(,)33P .(Ⅰ)求椭圆C 的离心率;(Ⅱ)过点2F 的直线l 与椭圆C 相交于 P Q 、两点,且11F P FQ ⊥,求直线l 的方程.22. (本小题满分12分) (注意:在试题卷上作答无效.........) 设函数11()ln(0)2(1)x xf x a a x +-=+>+. (Ⅰ) 若函数()f x 在[1,)+∞上为增函数, 求实数a 的取值范围; (Ⅱ) 求证:当n N *∈且2n ≥时,1111ln 234n n++++< .桂林十八中11级高三第一次月考试卷理科数学参考答案一、选择题二、填空题37,44ππ 15.96 16.2 三、解答题17.解:(Ⅰ)由余弦定理2222cos b a c ac B =+-,得()222(1cos )b a c ac B =+-+, 又6a c +=,2b =,7cos 9B =,所以9ac =,解得3a =,3c =. (Ⅱ)在△ABC中,sin 9B ==,因此112s i n 332222ABC S ac B ∆==⨯⨯⨯=18.解:(I )由2a 、5a 、14a 成等比数列,知()()()2111134a d a d a d ++=+,解得212a d d =,由11a =,且0d >得2d =; ……………………3分 ∴21,(*)n a n n N =-∈, ……………………4分又由223b a ==,359b a ==,知13,(*)n n b n N -=∈;……………6分 ⑵由()1213n n n n c a b n -=⋅=-⋅,设n S 是{}n c 的前n 项和,则()012112133353213n n n S c c c n -=+++=⋅+⋅+⋅++-⋅ Ks5u ()1233133353213n n S n ⋅=⋅+⋅+⋅++-⋅两式相减得:()12121232323213n n n S n --=+⋅+⋅++⋅--⋅()()()1313212132132232n n n n S n n ---=--⋅+⨯-=-⋅-故()131nn S n =-+ (*)n N ∈. ……………………12分19. 解:(Ⅰ) 证明:连接1BC ,11B C BC F = 因为AE EB =,1FB FC =,所以EF ∥1AC 2分 因为1AC ⊄面1EBC ,EF ⊂面1EBC 所以1AC ∥面1EBC ······················································· 4分(Ⅱ)设1AC 与1ED 交于点G ,连DE,1AC ∥面1EBC ∴ G 与1C 到平面1EBC 的距离相等,设为h , ······························6分 则1ED =52,352=EG ············································ 7分 1B ECS ∆,点E 到平面11CC B 距离为3又 C B C E EC B C V V 1111--=∴3451=h 174=∴h … ······································· 10分ABC A 1B 1C 1D 1D EFG设直线1ED 与面1EBC 所成角为α,则sin h GE α=. 所以直线1ED 与面1EBC 所成角为arcsin 85856 ························································· 12分 解法二 :作DH AB ⊥,分别令1,,DH DC DD 为x 轴,y 轴,z 轴, 如图建立坐标系┉1分因为60BAD ∠=,2AD =,所以1AH =,DH =所以,1,0)E 1(0,0,4)D ,(0,4,0)C,1B ,)0,1,3(-A )4,4,0(1C ···················· 3分(Ⅰ))4,1.3(1--=ED ,)0,3,3(),4,2,0(1-==EB )4,5,3(1-=AC ········································································· 4分 设面1EBC 的法向量为(,,)x y z =n ,所以10EB =n ,0EC = n化简得240,30y z y +=⎧⎪⎨+=⎪⎩令1y =,则1)2=-n . ········· 6分10AC =n ,1AC ⊄面1EBC ,∴1AC ∥面1EBC . ········································································································ 8分(Ⅱ)设1,ED θ= n,则11cos ED ED θ==⋅n n 10分 设直线1ED 与面1EBC 所成角为α,则cos cos(90)sin θαα=+=- .即sin α= ·············································································································· 11分∴直线1ED 与面1EBC 所成角为arcsin 85856. ······························································· 12分20. 解:(Ⅰ) 设事件A 表示:观众甲选中3号歌手且观众乙未选中3号歌手.观众甲选中3号歌手的概率为32,观众乙未选中3号歌手的概率为53-1. 所以P(A) = 15453-132=⋅)(. 因此,观众甲选中3号歌手且观众乙未选中3号歌手的概率为154 (Ⅱ) X 表示3号歌手得到观众甲、乙、丙的票数之和,则X 可取0,1,2,3.观众甲选中3号歌手的概率为32,观众乙选中3号歌手的概率为53. 当观众甲、乙、丙均未选中3号歌手时,这时ξ=0,P(ξ = 0) = 754)531()321(2=-⋅-.当观众甲、乙、丙中只有1人选中3号歌手时,这时ξ=1,P(ξ =1)= Ks5u75207566853)531(321()531(53321()531(322=++=⋅-⋅-+-⋅⋅-+-⋅)). 当观众甲、乙、丙中只有2人选中3号歌手时,这时ξ=2,P(ξ=2) =A7533751291253)531(325353321()531(5332=++=⋅-⋅+⋅⋅-+-⋅⋅). 当观众甲、乙、丙均选中3号歌手时,这时ξ=3,P(ξ=3) = 7518)53(322=⋅.ξ的分布列如下表:4203318206654280123757575757515E ξ++=⋅+⋅+⋅+⋅== 所以,数学期望2815E ξ=21. 解:(Ⅰ)122a PF PF =+=所以,a =又由已知,1c =, 所以椭圆C的离心率c e a ===()II 由()I 知椭圆C 的方程为2212x y +=. Ks5u当直线l 的斜率不存在时,其方程为1x =,不符合题意;当直线的斜率存在时,设直线l 的方程为(1)y k x =-. Ks5u由22(1)12y k x x y =-⎧⎪⎨+=⎪⎩ 得2222(21)42(1)0k x k x k +-+-=. 设1122( ) ( )P x y Q x y ,,,,则 Ks5u2212121111222242(1) (1 ) (1 )2121k k x x x x F P x y FQ x y k k -+===+=+++ ,,,,, 因为11F P FQ ⊥ ,所以110F P FQ ⋅=,即 Ks5u 21212121212(1)(1)()1(1)(1)x x y y x x x x k x x +++=++++--2221212(1)(1)()1k x x k x x k =+--+++ 2271021k k -==+,解得217k =,即7k =±. 故直线l的方程为10x -=或10x -=. 22.解: 2221(1)(1)12()++22[(1)]2(1)a x a x f x x a x x a x -+---'=⋅=++++ 222(1)(1)2(1)(1)x a x a a x x --+-==++,(1)x >-2 分 ()f x ∴在2(1,1)a --上为减函数,在2(1,)a -+∞为增函数,()f x ∴在21x a=-处取得极小值. 4 分(Ⅰ)依题: 2110,a a ⎧-≤⎪⎨⎪>⎩⇒1a ≥;6 分()II 由(Ⅰ)知:当1a =时,11()ln,21x xf x x +-=++在[1,)+∞上为增函数, ∴当1x >时,有()(1)0f x f >=,即11ln ,(1)21x xx x +->->+,取11(2)1x n x n --=≥+,则111n x n +=>-,121x n n +=-, 即有:1l n ,(2)1n n n n>≥-,∴111134ln 2ln ln ln ln 234231n n n n ++++<++++=- .12 分。

2012年高考桂林市第一次模拟考试理科数学参考答案及评分标准评分说明:1. 第一题选择题,选对得分,不选、错选或多选一律得0分. 2. 第二题填空题,不给中间分.3. 解答与证明题,本答案给出了一种或几种解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分参考制订相应的评分细则.4. 对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.5. 解答右侧所注分数,表示考生正确做到这一步应得的累加分数. 6. 只给整数分数.一. 选择题二.填空题 (13) 132-. (14)2-. (15) 32. (16)163. 三.解答与证明题(17) (本小题满分10分)解: sin ,sin ,sin A B C 成等比数列∴由正弦定理得 2b ac =. ··················································································· 2分 又a c ac bc 22-=-,∴+-=b c a bc 222. ················································ 3分在∆ABC 中,由余弦定理得cos A b c a bc bc bc =+-==2222212······················· 5分60A ∴=︒ ············································································································· 6分在∆ABC 中,由正弦定理得sin sin B b Aa= ························································ 7分260b ac A ==︒ , , ∴=︒=︒=b Bc b ca sin sin sin 2606032····················· 10分 (18) (本小题满分12分)解:(Ⅰ)当且仅当小球一直向左落下或一直向右落下时小球才会落入B 袋中, ······ 2分故33111()224P B ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭. ················································································· 4分答:小球落入B 袋中的概率为14. ········································································ 5分 (Ⅱ)记“小球落入A 袋中”为事件A ,“小球落入B 袋中”为事件B ,则事件A 与事件B 为对立事件,从而13()1()144P A P B =-=-=.················································································· 6分 显然,ξ的取值为0,1,2, ············································································· 7分且2211(0)416P C ξ⎛⎫==⨯= ⎪⎝⎭;12316(1)()()4416P C ξ===;22239(2)()416P C ξ===.······················································································· 9分 ξ的分布列为······························································································ 10分故1693012.1616162E ξ=⨯+⨯+⨯= ········································································ 12分 (或由随机变量32,4B ξ⎛⎫⎪⎝⎭,故332.42E ξ=⨯=)19.(本小题满分12分)解法一:(Ⅰ) 证明:连接1BC ,11B C BC F =因为AE EB =,1FB FC =,所以EF ∥1AC ························································ 2分 因为1AC ⊄面1EBC ,EF ⊂面1EBC 所以1AC ∥面1EBC ················································ 4分 (Ⅱ)设1AC 与1ED 交于点G ,连DE, 1AC ∥面1EBC , ∴ G 与1C 到平面1EBC 的距离相等,设为h , ···················· 6分 则1ED =52,352=EG . ······························· 7分1B ECS ∆, 点E 到平面11CC B 距离为3.又 C B C E EC B C V V 1111--= ,∴3451=h .174=∴h . ···························· 10分设1ED 与面1EBC 所成角为α,则sin h GE α==. 所以1ED 与面1EBC 所成角为arcsin 85856. ·················································· 12分 解法二:作DH AB ⊥,分别令1,,DH DC DD 为x 轴,y 轴,z 轴, 如图建立坐标系┉1分因为60BAD ∠=,2AD =,所以1AH =,DH所以,0)E 1(0,0,4)D ,(0,4,0)C,1B ,)0,1,3(-A )4,4,0(1C3分(Ⅰ))4,1.3(1--=ED ,)0,3,3(),4,2,0(1-==EB )4,5,3(1-=AC ·········· 4分ABCA 1B 1C 1D 1D EFG设面1EBC 的法向量为(,,)x y z =n ,所以10EB =n ,0EC = n化简得240,30y z y +=⎧⎪⎨+=⎪⎩令1y =,则1)2=-n . ····· 6分10AC =n ,1AC ⊄面1EBC ,∴1AC ∥面1EBC . ······ 8分 (Ⅱ)设1,ED θ=n ,则11cos ED ED θ==⋅ n n ·········································· 10分 设直线1ED 与面1EBC 所成角为α,则cos cos(90)sin θαα=+=- .即sin α=·········································································································· 11分 ∴直线1ED 与面1EBC 所成的角的大小为arcsin 85856. ············································· 12分 (20) (本小题满分12分)解:(Ⅰ)函数()f x 的定义域为{}|0x x >,21()a f x x x '=+. ·································· 2分 又曲线()y f x =在点(1,(1))f 处的切线与直线20x y +=垂直,所以(1)12f a '=+=,即1a =. ··········································································· 5分(Ⅱ)当1a =时,1(1)ln(1)1f x x x -=---,[)2,x ∈+∞. 令1()ln(1)251g x x x x =---+-. 2211(21)(2)()21(1)(1)x x g x x x x --'=+-=----. ·············································· 8分当2x >时,()0g x '<,()g x 在(2,)+∞单调递减.又(2)0g =,所以()g x 在(2,)+∞恒为负. ······································· 10分所以当[2,)x ∈+∞时,()0g x ≤.即1ln(1)2501x x x ---+-≤. 故 当1a =,且2x ≥时,(1)25f x x --≤成立. ·················································· 12分 (21) (本小题满分12分)解:(Ⅰ) ∵P (-1,3)在⊙O :x 2+y 2=b 2上,∴b 2=4. ············································ 1分又∵P A 是⊙O 的切线,∴P A ⊥OP ,∴0OP AP =. ············································ 3分即(-1,3)·(-1+a ,3)=0,解得a =4. ························································· 5分∴椭圆C 的方程为x 216+y 24=1. ···················································································6分(Ⅱ) 设P (x 1,y 1),F (-c,0),且c 2=a 2-b 2,A要使得||||PA PF 是常数,不妨令()()22112211x a y x c y λ++=++(λ是常数). 即()()222212a c x b c b a λλ-=+--. ····································································· 8分 ∴ b 2+a 2=λ(b 2+c 2),a =λc . ················································································· 9分 故cb 2+ca 2=a (b 2+c 2),即ca 2-c 3+ca 2=a 3,即e 3-2e +1=0. ····································································································· 10分 也就是(e -1)(e 2+e -1)=0,符合条件的解为e =5-12. ∴这样的椭圆存在,离心率为5-12. ···································································· 12分 (22) (本小题满分12分)解:(Ⅰ)()()()2211221+=+-+++=-=∆+n n n n n a a a n n n ,12n n a a +∆-∆=,且14a ∆=, ············································································ 2分 ∴{}n a ∆是首项为4,公差为2的等差数列,不是等比数列. ························· 3分∵ ()()2222122=+-++=∆n n a n ,∴由定义知,{}n a 2∆是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列. ····························································· 6分(Ⅱ)n n n n a a a 212-=+∆-∆+,即n n n n n a a a a 211-=+∆-∆-∆++,即n n n a a 2=-∆,又1n n n a a a +∆=-,∴n n n a a 221+=+. ······················································································· 9分∵11=a ,∴12224⨯==a ,232312⨯==a ,342432⨯==a ,猜想12-⋅=n n n a . ···················································································· 10分证明:ⅰ)当1=n 时,01211⨯==a ;ⅱ)假设k n =时,则12-⋅=k k k a .当1+=k n 时,()()111222212k k k k k k a a k k +-+=+=⋅+=+ .结论也成立.∴由ⅰ)、ⅱ)可知,12n n a n -=⋅. ······························································· 12分。

广西桂林市(新版)2024高考数学人教版考试(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题若焦点在轴上的椭圆的离心率为,则()A.5B.4C.3D.2第(2)题设命题:,,则为()A.,B.,C.,D.,第(3)题函数的图象大致是()A.B.C.D.第(4)题已知是定义在上的函数,且为偶函数,是奇函数,当时,,则等于()A.B.C.D.1第(5)题与圆及圆都外切的圆的圆心在()A.一个圆上B.一个椭圆上C.一条抛物线上D.双曲线的一支上第(6)题已知圆,点在线段()上,过点作圆的两条切线,切点分别为,,以为直径作圆,则圆的面积的最大值为().A.B.C.D.第(7)题如图程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a,b分别为35、28,则输出的a=()A.1B.14C.7D.28第(8)题设a,b是两条不同的直线,,是两个不同的平面,若,,,则“”是“”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题在三棱锥中,,,且,则()A.当为等边三角形时,,B.当,时,平面平面C.的周长等于的周长D.三棱锥体积最大为第(2)题在棱长为2的正方体中,点分别是棱的中点,,,过点的平面截正方体所得图形为,则()A.,使得B.,使得为四边形C.三棱锥体积的取值范围是D.的面积的取值范围是第(3)题某灯具配件厂生产了一种塑胶配件,该厂质检人员某日随机抽取了100个该配件的质量指标值(单位:分)作为一个样本,得到如下所示的频率分布直方图,则(同一组中的数据用该组区间的中点值作代表)()A.B.样本质量指标值的平均数为75C.样本质量指标值的众数小于其平均数D.样本质量指标值的第75百分位数为85三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题若将函数表示成,则a 3的值等于__第(2)题已知平面向量,满足,,,则______.第(3)题已知抛物线的焦点为,第一象限的、两点在抛物线上,且满足,.若线段中点的纵坐标为4,则抛物线的方程为________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知的内角的对边分别为.(1)求;(2)若为线段上一点,且,求的长.第(2)题已知椭圆C:()和圆O:.C的焦距为,过C的右顶点作圆O的切线,切线长为.(1)求椭圆C的方程;(2)设圆O的切线l与椭圆C交于A,B两点,求面积的最大值.第(3)题当前移动网络已融入社会生活的方方面面,深刻改变了人们的沟通、交流乃至整个生活方式.4G网络虽然解决了人与人随时随地通信的问题,但随着移动互联网快速发展,其已难以满足未来移动数据流量暴涨的需求,而5G作为一种新型移动通信网络,不但可以解决人与人的通信问题,而且还可以为用户提供增强现实、虚拟现实、超高清(3D)视频等更加身临其境的极致业务体验,更重要的是还可以解决人与物、物与物的通信问题,从而满足移动医疗、车联网、智能家居、工业控制、环境监测等物联网应用需求,为更好的满足消费者对5G网络的需求,中国电信在某地区推出了六款不同价位的流量套餐,每款套餐的月资费x(单位:元)与购买人数y(单位:万人)的数据如下表:套餐A B C D E F月资费x(元)384858687888购买人数y(万人)16.818.820.722.424.025.5对数据作初步的处理,相关统计量的值如下表:75.324.618.3101.4其中,且绘图发现,散点集中在一条直线附近.(1)根据所给数据,求出关于的回归方程;(2)已知流量套餐受关注度通过指标来测定,当时相应的流量套餐受大众的欢迎程度更高,被指定为“主打套餐”.现有一家四口从这六款套餐中,购买不同的四款各自使用.记四人中使用“主打套督”的人数为,求随机变量的分布列和期望.附:对于一组数据,其回归方程的斜率和截距的最小二乘估计值分别为.第(4)题函数 .(1)当时,讨论的单调性;(2)若函数有两个极值点,且,证明: .第(5)题如图,在三棱柱中,底面是等腰三角形,且,又侧棱,面对角线,点分别是棱的中点,.(1)证明:平面;(2)求二面角的正切值.。

2011年广西桂林市高三第一次调研数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分) 1. 已知复数Z 的共轭复数Z ¯=2+i 1−i,则复数Z 对应的点位于( )A 第一象限B 第二象限C 第三象限D 第四象限2. 设全集I =R ,集合M ={x||x|<2},N ={x|xx−2<0},则(∁I N)∩M =( ) A [−2, 0] B (−2, 0]∪[2, +∞) C (−2, 0] D [0, 2) 3. 设0<b <a <1,则下列不等式恒成立的是( )A ab <b 2<1B log 12b <log 12a <0 C 2<2a <2b D |a|−|b|=|a −b|4. 已知函数f(x)=2x 的反函数为f −1(x),若f −1(a)+f −1(b)=4,则1a+1b的最小值为( )A 1B 12C 13D 145. 已知向量满足|a →|=2|b →|,若p :关于x 的方程x 2+|a →|x +a →⋅b →=0没有实数根;q :向量a →,b →的夹角θ∈[0, π6),则p 是q 的( )A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件 6. 已知点M 在曲线x 2+y 2+4x +3=0,点N 在不等式组{x −2≤03x +4y ≥4y −3≤0所表示的平面区域上,那么|MN|的最小值是( ) A 1 B2√103 C 2√103−1 D 27. 如果|cosθ|=15,5π2<θ<3π,那么sin θ2的值为( )A√105 B √155 C −√105 D −√1558. 在等比数列{a n }中,a 1=2,前n 项和为S n ,若数列{a n +1}也是等比数列,则S n 等于( )A 2n+1−2B 3nC 2nD 3n −19. 曲线y =2sin(x +π4)cos(x −π4)和直线y =12在y 轴右侧的交点按横坐标从小到大依次记为P 1,P 2,P 3,…,则|P 2P 4|等于( ) A π2 B 3π4 C π D 2π10. 若椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1、F 2,线段F 1F 2被抛物线y 2=2bx 的焦点F 分成3:1两段,则此椭圆的离心率为( ) A 12 B √22 C 13 D √3311. 设向量m →=(sinB, √3cosB),n →=(√3cosC, sinC),且A 、B 、C 分别是△ABC 的三个内角,若m →⋅n →=1+cos(B +C),则A =( ) A 5π6 B π3 C 2π3 D π612. 函数y =f(x)(x ∈R)满足:对一切x ∈R,f(x)≥0,f(x +1)=√7−f 2(x),当x ∈[0,1)时,f(x)={x +2(0≤x <√5−2)√5(√5−2≤x <1)则f(2011−√3)=( )A √2B 2−√3C 2+√3D 2√2√3−3二、填空题(共4小题,每小题5分,满分20分) 13. 不等式3−√1−x >√33的解集是________. 14. 已知双曲线C :x 29−y 216=1的左、右焦 点分别为F 1、F 2,P 为C 的右支上一点,且|PF 2→|=|F 1F 2→|,则△PF 1F 2的面积等于________.15. 已知直线l :y =−12x +m 与曲线C :y =12√|4−x 2|仅有三个交点,则实数m 的取值范围是________.16. 已知函数f(x)的导数f′(x)=a(x +1)⋅(x −a),若f(x)在x =a 处取到极大值,则a 的取值范围是________.三、解答题(共6小题,满分70分)17. 设函数f(x)=cosωx(sinωx +cosωx),其中0<ω<2. (1)若f(x)的周期为π,求当−π6≤x ≤π3时,f(x)的值域(2)若函数f(x )的图象的一条对称轴为x =π3,求ω的值.18. 学校决定对教学楼部分房间配制现代化的电子教学设备,并对其中两种电子设备配备外壳,现有A 种电子装置45台,B 种电子装置55台,需用到两种规格的薄金属板;甲种薄金属板每张面积2m 2,可做A 、B 的外壳分别为3个和5个,乙种薄金属板每张面积3m 2,可做A 、B 的外壳各6个,求两种薄金属板各用多少线时,才能使用料总的面积最小.19. 在数列{a n }中,已知a 1=1,S n 是数列{a n }的前n 项和,且对任意正整数n ,S n+1=4a n +2.(1)令b n =a n+1−2a n (n =1, 2,…),证明{b n }是等比数列,并求{b n }的通项公式; (2)令f(x)=xln(1+x)−a(x +1),为数列{1log2c n+2⋅log 2c n+1}的前n 项和,求limn →∞T n.20. 已知函数f(x)=xln(1+x)−a(x +1),其中a 为常数.(1)当x ∈[1, +∞)时,f ′(x)>0恒成立,求实数a 的取值范围;(2)求g(x)=f′(x)−axx+1的单调区间.21. 在直角坐标平面内,已知点A(2, 0),B(−2, 0),P是平面内一动点,直线PA、PB斜率之积为−34.(1)求动点P的轨迹C的方程;(2)过点(12, 0)作直线l与轨迹C交于E、F两点,线段EF的中点为M,求直线MA的斜率k 的取值范围.22. 已知函数y=f(x),x∈N∗,y∈N∗满足:①对于任意a,b∈N∗,a<b,都有af(a)+bf(b)>af(b)+bf(a);②对任意n∈N∗,都有f[f(n)]=3n.(1)证明:f(x)为N∗上的单调增函数;(2)求f(1),f(2),f(3)的值;(3)令a n=f(3n),n∈N∗,证明:n4n+2≤1a1+1a2+⋯+1a n<14.2011年广西桂林市高三第一次调研数学试卷(理科)答案1. A2. C3. D4. B5. B6. A7. D8. C9. C10. B11. C12. A13. (34, 1]14. 4815. (1, √2)16. (−1, 0)17. 解:f(x)=√32sin2ωx+12cos2ωx+12=sin(2ωx+π6)+12.(1)因为T=π,所以ω=1.∴ f(x)=√32sin2ωx+12cos2ωx+12=sin(2x+π6)+12当−π6≤x≤π3时,2x+π6∈[−π6, 5π6],所以f (x)的值域为[0, ].(2)因为f(x)的图象的一条对称轴为x=π3,所以2ω(π3)+π6=kπ+π2(k∈Z),ω=32k+12(k∈Z),又0<ω<2,所以−13<k<1,又k∈Z,所以k=0,ω=12.18. 两种薄金属板各用5张时,才能使用料总的面积最小.19. 解(1)a n+1=S n+1−S n=4(a n−a n−1)①∵ b n=a n+1−2a n∴ b n+1=a n+2−2a n+1由①得b n+1=4(a n+1−a n)−2a n+1=2(a n+1−2a n)∴ b n+1b n =2(a n+1−2a n)a n+1−2a n=2∴ b n}是公比为2的等比数列∵ b1=a2−2a1=3∴ b n=3×2n−1(2)∵ C n=b n3=2n−1∴ 1log2c n+2⋅log2c n+1=1n(n+1)∴ T n=(1−12)+(12−13)+⋯+(1n−1n+1)=1−1n+1∴ limn→∞T n=limn→∞(1−1n+1)=120. 解:(1)由f′(x)=ln(1+x)+x1+x−a>0得a<ln(1+x)+x1+x,令ℎ(x)=ln(1+x)+x1+x ,则ℎ′(x)=11+x+1(1+x)2.当x∈[1, +∞)时,ℎ′(x)>0,ℎ(x)在[1, +∞)上递增,∴ a<ℎ(1)=12+ln2.∴ 实数a的取值范围是(−∞, 12+ln2).(2)g(x)=ln(1+x)+(1−a)xx+1−a,x∈(−1, +∞)则g′(x)=11+x −1−a(x+1)2=x+2−a(x+1)2①当a>1时,x∈(−1, a−2),g′(x)<0,g(x)是减函数,x∈(a−2, +∞)时,g′(x)>0,g(x)是增函数.②当a ≤1时,x ∈(−1, +∞),g ′(x)>0,g(x)是增函数.所以:当a >1时,减区间为(−1, a −2),增区间为(a −2, +∞); 当a ≤1时,增区间为(−1, +∞). 21. 解:(1)设P 点的坐标为(x, y), 依题意,有y x−2⋅yx+2=−34(x ≠±2).化简并整理,得x 24+y 23=1(x ≠±2).∴ 动点P 的轨迹C 的方程是x 24+y 23=1(x ≠±2).(2)依题意,直线l 过点(12,0)且斜率不为零,故可设其方程为x =my +12,由方程组{x =my +12x 24+y 23=1消去x ,并整理得4(3m 2+4)y 2+12my −45=0设E(x 1, y 1),F(x 2, y 2),M(x 0, y 0),则 ∴ y 1+y 2=−3m3m 2+4, ∴ y 0=y 1+y 22=−3m2(3m 2+4)∴ x 0=my 0+12=23m 2+4,∴ k =y 0x 0−2=m4m 2+4,①当m =0时,k =0; ②当m ≠0时,k =14m+4m∵ |4m +4m |=4|m|+4|m|≥8,∴ 0<1|4m+4m|≤18.∴ 0<|k|≤18.∴ −18≤k ≤18且k ≠0.综合①②可知直线MA 的斜率k 的取值范围是:−−18≤k ≤18.22. 解:(1)由①知,对任意a ,b ∈N ∗,a <b ,都有(a −b)(f(a)−f(b))>0, 由于a −b <0,从而f(a)<f(b), 所以函数f(x)为N ∗上的单调增函数.(2)令f(1)=a ,则a ≥1,显然a ≠1,否则f (f(1))=f(1)=1,与f (f(1))=3矛盾.从而a >1,而由f (f(1))=3, 即得f(a)=3.又由(1)知f(a)>f(1)=a,即a<3.于是得1<a<3,又a∈N∗,从而a=2,即f(1)=2.进而由f(a)=3知,f(2)=3.于是f(3)=f(f(2))=3×2=6,(3)f(a n)=f(f(3n))=3×3n=3n+1,a n+1=f(3n+1)=f(f(a n))=3a n,a1= f(3)=6.即数列{a n}是以6为首项,以3为公比的等比数列.∴ a n=6×3n−1=2×3n(n=1, 2, 3).于是1a1+1a2+⋯+1a n=12(13+132+⋯+13n)=12×13(1−13n)1−13=14(1−13n),显然14(1−13n)<14,另一方面3n=(1+2)n=1+C n1×2+C n2×22+...+C n n×2n≥1+2n,从而14(1−13n)≥14(1−12n+1)=n4n+2.综上所述,n4n+2≤1a1+1a2+⋯+1a n<14.。

广西桂林市、防城港市2011年考第一次联合模拟考试数 学 试 题(理)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答题前,考生在答题卡上备必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作作无效.........。
3.第I 卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题要求。
参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B )如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k次的概率P n (k )=k n k k n P P C --)1(球的体积公式:334R V π=(其中R 表示球的半径) 球的表面积公式S=4πR 2(其中R 表示球的半径)一、选择题1.设复数z 满足2zi i =-,其中i 为虚数单位,则z=( )A .-1+2iB .-1-2iC .1+2iD .1-2i2.设全集为R ,集合{}(){}()B A C x y x B x x A B ⋂-==≤-=则,1lg ,32为( )A .{|15}x x <≤B .{|15}x x x ≤->或C .{|15}x x x ≤>或D .{|15}x x -≤≤3.若函数()f x 的反函数121()log 1),()2fx f -=则= ( )A 1B .1C .1-D .3-4.为了做一项调查,在A 、B 、C 、D 四个单位回收的问卷数依次成等差数列,再从回收的问卷中按单位分层抽取容量为100的样本,若在B 单位抽取20份问卷,则在D 单位抽取的问卷份数是( )A .30份B .35份C .40份D .65份5.函数tan()42y x ππ=-的部分图像如图1所示, 则()OA OB AB +⋅= ( )A .4B .6C .1D .2 6.设2234sin sin 2,sin ,25cos cos 2a a a a a aππ+<<=-+则的值为 ( )A .20B .-20C .4D .-47.在正三棱柱ABC —A 1B 1C 1中,AB=1,若二面角C —AB —C 1的大小为60°,则点C 到平面C 1AB 的距离为( )A .34B .12C .2D .18.设F 为抛物线214y x =-的焦点,与抛物线相切于点P (-4,-4)的直线l 与x 轴的交点为Q ,则PQF ∠等于( )A .30°B .45°C .60°D .90°9.某地招募了11名翻译人员,其中5名英语翻译员 ,4名日语翻译员,另2人英语、日语都精通。
广西桂林市2009届高三上学期第一次调研考试理科数学注意事项:1.本试题卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共4页,总分150分,考试时间120分钟2.答题前,考生必须将自己的姓名、准考证号、考场号、座位号填写在答题卡上指定的位置上。
3.选择题的每小题选出答案后,用2B 铅笔将答题卡上对应的题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上4.非选择题必须使用0.5毫米的黑色字迹的签字笔在答题卡上书写,字体工整,字迹清楚。
5.非选择题必须按照题号顺序在答题卡上各题目的答题区域内作答,超出答题区域或在其他题的答题区域内书写的答案无效;在草稿纸、本试卷上打题无效。
6.考试结束,将本试卷和答题卡一并交回。
A .B .C .D .第I 卷(选择题 60分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.i 是虚数单位,则复数221ii i++等于 A .1 B .-1 C .i D .i- 2. 若b<a<0,则下列结论不正确的是A .22a b < B .2ab b < C .2b aa b+> D .a b a b -=- 3.设U 为全集,M 、P 是U 的两个子集,且()CuM ∩P=P ,则M ∩P=A .MB .PC .CuPD .φ 4.函数1(01)xy a a =+<<的反函数的图象大致是5.已知条件2:12,:0,3x p x q x -+><-条件则┓p 是 ┓q 的 A .充分非必要条件 B .必要非充分条件C .充要条件D .既非充分也非必要条件6.已知直线22:1()1x l a R x y a +=∈+=与圆相切,则直线l 与两坐标轴所围成的三角形的面积等于A .1或3B .1322或 C .1 D .327.3sin()45x π-=,则sin2x 的值为 A .725 B .1425 C .1625 D .19258.数列{}n a 是公差不为零的等差数列,并且5a ,8a ,13a 是等比数列{}n b 的相邻三项,若25b =,则n b 等于A .515·()3n - B .315·()3n - C .3 13·()5n - D .5 13·()5n -9.已知函数sin()y A wx m ϕ=++的最大值是4,最小值是0,最小正周期是2π,直线x= 2π是其图象的一条对称轴,则下列符合条件的函数的解析式是 A .4sin(4)6y x π=+ B .2sin(2)23y x π=++C .2sin(4)23y x π=++D .2sin(4)26y x π=++10.若向量a,b 满足2,a b ==且(a-b )⊥a, 则|a+b|=A . 3B .C .10D 11.已知双曲线22122:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ,抛物线c :的顶点在原点,它的准线与双曲线1C ,的左准线重合,若双曲线1C ,与抛物线2C 的交点P 满足PF 2⊥12F F 则双曲线1C 的离心率为A .B C .3D .12.设2()|4|,0,()(),f x x m n f m f n m n =-<<=+若且则的取值范围是A . (0,4)B .(4)C .(0,D .4)第Ⅱ卷(非选择题共90分)注意事项:1.第Ⅱ卷共3页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效。

广西桂林市、崇左市、北海市、防城港市2014届高三第二次联合调研考试数学(理)试卷(必修+选修I)本试卷分第I 卷和第Ⅱ巷(非选择题)两部分第I 卷1至2页第Ⅱ卷3至4页考试结束后,将本试卷和答题卡一并交回第I 卷注意事项:1答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证 号填写清楚,并贴好争形码请认真核准争形码上的准考证号、姓名和科目2每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号潦黑,如需改动,用 橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效。
3第I 卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一.选择题(1)已知全集U R =,集合{}{}2|21|340x A x B x x x =>=-->,则A B =(A) {}|0x x > (B){}|4x x >(C) {}|10x x x <->或 (D){}|14x x -≤≤(2)复数22()1i i=+(A)2i (B)-2i (C)2 (D)-2(3)函数()ln(1)(1)f x x x =->的反函数为(A)11()(0)x fx e x -+=> (B)11()()x f x e x R -+=∈ (C)1()1()x f x e x R -=+∈ (D)1()1(0)x f x e x -=+>(4)已知等比数列数列{}n a 的前n 项和n S ,若232a a =1a ,且4a 与72a 的等差中项为54,则5S = (A)35 (B)33 (C)31 (D)29(5)已知向量a ,b 满足1a b -=,且(3,4)b =,则a 的取值范围是(A)[4,5] (B)[5,6] (C)[3,6] (D)[]4,6(6)已知实数0.20.33log 3,log 0.2,log 2a b c ===,则a,b,c 的大小关系为(A)b<a<c (B)a<b<c (C)c<a<b (D)a<c<b(7)在直三棱柱111ABC A B C -中,1,2,B AC BC ===分别是1AC 和1BB 的中点,则直线DE 与平面11BBC C 所在角为(A)6π (B) 4π (C)3π (D)2π (8)设变量x ,y 满足约束条件1,1,22,x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩.目标函数2z ax y =+处取得最小值,则a 的取值范围为(A)(-1,2) (B)(-2,4) (C)(-4,0] (D)(-4,2)(9)已知O 为坐标原点,1P 、2P 是双曲线22194x y -=上的点.P 是线段12PP 的中点,直线OP 、12PP 的斜率分别为1k 、2k ,若124k ≤≤=,则2k 的取值范围是(A)12,33⎡⎤⎢⎥⎣⎦ (B)12,99⎡⎤⎢⎥⎣⎦ (C) 14,39⎡⎤⎢⎥⎣⎦ (D)42,93⎡⎤⎢⎥⎣⎦(10)设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则()f x(A)在(0,)2π单调递减 (B)在3(,)44ππ单调递减 (C)在(0,)2π单调递增 (D )在3(,)44ππ单调递增 (11)一名同学想要报考某大学,他必须从该校的7个不同的专业中选出5个,并按第一志愿,第二志愿,……,第五志愿顺序填进志愿表,若A 专业不能作为第一志愿,B 专业不能作为第二志愿,且A 、B 专业不能相邻,则不同的填法种数有( A)1560 (B)1500 (C)1080 (D)960(12)已知球O 的半径为4,圆M 与圆N 为该球的两个小圆,AB 为圆M 与圆N 的公共弦,AB=4若OM= ON.则两圆圆心的距离MN 的最大值为(A)(B)(C) (D)3理科数学(必修+选修I)第Ⅱ卷注意事项:l.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证 号填写清楚,然后贴好条形码.请认真核准条形码上的准考证号、姓名和科目2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作 答。

2011-2012学年广西某校高三第一次调研联考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 复数2−i 2+i表示复平面内的点位于( )A 第一象限B 第二象限C 第三象限D 第四象限 2. 已知集合M ={m 2,m},N ={x|x+12x−3<0,x ∈Z},若M ∩N ≠ϕ,则实数m 等于( )A 2B −1或1C −1D 0或13. 已知等差数列{a n }的前n 项和S n ,且S 2n −S 2n−2+a 3+a 2=848,n ∈N ∗且n >1,则a n+1等于( )A 212B 424C 848D 10164. 已知函数f(x)=log 2(x +ax −1)(x >0),则函数f(x)的值域为[0, +∞)的充要条件是正实数a 等于( )A 1B 2C 3D 45. 设向量a →,b →满足|a →|=2,a →⋅b →=32,|a →+b →|=2√2,则|b →|等于( )A 1B 32 C 2 D 86. 已知cosx +sinx =1,则tan x2等于( )A 0B 1C −1D 0或17. 曲线y =e −2x +1在点(0, 2)处的切线在x 上的截距等于( ) A −12e B 12e C 1 D 2e8. (x +2)2(1−x)5中x 7的系数与常数项之差的绝对值为( ) A 5 B 3 C 2 D 09. 已知函数f(x)=x 2cosθ−√2xsinθ+34对于任意的实数x 恒有f(x)>0,且θ是三角形中的一个锐角,则θ的取值范围是( ) A (0,π6) B (π6,π2) C (0,π3) D (π3,π2)10. 定义在R 上的奇函数f(x)满足对任意的x 都有f(x −1)=f(4−x)且f(x)=x,x ∈(0,32),则f(2012)−f(2010)等于( ) A −1 B 0 C 1 D 211. 已知实数s ,t 满足不等式(s −t)(s +t −2)≥0.若1≤s ≤4,则ts 的取值范围是( )A [−14,1] B (−14,1] C [−12,1] D (−12,1]12. 已知锐角△ABC 内有一点O ,满足OA =OB =OC ,且∠A =60∘,若cosB sinCAB →+cosC sinBAC →=2mAO →,则m 等于( )A 12 B √32C √3D 无法确定二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13. 若直线y =1与函数y =3sin2x 在区间(0,π2)内有两个交点A 、B ,则线段AB 中点的坐标为________.14. 一支田径队有男运动员44人,女运动员33人,若用分层抽样的方法从该队的全体运动员中抽取一个容量为14的样本,则抽取女运动员的人数为________.15. 已知函数f(x)={−x 2+4x −10,(x ≤2)log 3(x −1)−6,(x >2),若f(6−a 2)>f(a),则实数a 的取值范围是________.16. 定义在[1, +∞)上的函数f(x)满足:①f(3x)=cf(x)(c 为正常数);②当3≤x ≤9时,f(x)=1−|x −6|,若函数的所有极大值点均落在同一条直线上,则c =________.三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17. 已知等比数列{a n }中,a 2=2,a 5=128. (1)求通项a n ;(2)若b n =log 2a n ,数列{b n }的前n 项和为S n ,且S n =360,求n 的值.18. 已知△ABC 的内角A 、B 、C 的对边分别为a ,b ,c ,且a :b :c =2:√3:√5. (1)若△ABC 的面积为2√11,求△ABC 的周长;(2)若△ABC 的BC 边上的中线长为3,求BC 边上的高.19. 今年夏季酷暑难熬,某品牌饮料抓住这一时机举行夏季促销活动,若瓶盖中印有“再来一瓶”字样,则可以兑换同样的饮料一瓶(兑换的饮料中率率为0),如果这种饮料每瓶成本2元,投入市场按照每瓶3元销售,“再来一瓶”综合中奖率为10%.(1)甲购买该饮料3瓶,乙购买该饮料2瓶,求乙所购买的饮料中奖瓶数比甲多的概率. (2)若该厂生产这种饮料10万瓶,盈利的期望值是多少?20. 如图五面体中,平面ABCD ⊥平面BFEC ,AB =AD =BF =EF =1,CB =CD =CE =√3,AB ⊥BC ,FB ⊥BC ,AD ⊥DC ,FE ⊥EC . (1)证明:AF // DE ;(2)求二面角E−AD−B的余弦值.21. 已知椭圆C:x24+y2=1,直线l与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点.(1)证明:点O到直线AB的距离为定值;(2)求|OA|⋅|OB|的最小值.22. 已知函数f(x)=kxlnx,k∈R.(1)求函数f(x)的单调区间;(2)当函数g(x)=f(x)−kxe x ,x∈[e,3]的最大值为1e2时,求k的值.2011-2012学年广西某校高三第一次调研联考数学试卷(理科)答案1. D2. C3. A4. A5. A6. D7. C8. A9. C10. C11. C12. B13. (π4, 1)14. 615. (−3, 2)16. 1或317. 解:(1)设公比为q,由a2=2,a5=128及a5=a2q3得128=2q3,∴ q=4∴ a n=a2q n−2=2⋅4n−2=22n−3(2)∵ b n=log222n−3=2n−3,∴ 数列{b n}是以−1为首项,2为公差的等差数列∴ S n=n(−1)+n(n−1)2⋅2=n2−2n令n2−2n=360得n1=20,n2=−18(舍)故n=20为所求.18. 解:由题意可设a=2m,b=√3m,c=√5m,m≠0,(1)∵ a=2m,b=√3m,c=√5m,∴ cosC=a2+b2−c22ab =2222⋅2m⋅√3m=√36,又C为三角形的内角,∴ sinC=√1−cos2C=√336,∴ S=12absinC=12⋅2m⋅√3m⋅√336=2√11,解得:m=2,∴ a=4,b=2√3,c=2√5,则△ABC的周长为a+b+c=4+2√3+2√5;(2)设BC边上的中点为D,BC边上的高为ℎ,则AD=3,又由(1)得cosC=√36,则AD2=b2+(a2)2−2⋅b⋅a2cosC=3m2+m2−2⋅√3m⋅m⋅√36=3m2=9,解得:m=√3,∴ S△ABC=12absinC=12⋅2m⋅√3m⋅√336=√112m2=3√112,又12aℎ=3√112,且a=2m=2√3,则BC边上的高ℎ=√112√3=√332.19. 解:(1)“甲购买的饮料都没有中奖,乙购买的饮料有1瓶中奖”的概率为:P1=C30×(1−0.1)3×C21×0.1×(1−0.1)=0.13122,“甲购买的饮料都没有中奖,乙购买的饮料有2瓶中奖”的概率为:P2=C30×(1−0.1)3×C22×0.12=0.00729,“甲购买的饮料恰有1瓶中奖,乙购买的饮料有2瓶中奖”的概率为:P3=C31×0.1×(1−0.1)2×C22×0.12=0.00243,∴ 乙所购买的饮料中奖瓶数比甲多的概率为P=P1+P2+P3=0.14094(2)设生产1瓶这种饮料盈利为ξ,则ξ=−1,1P(ξ=−1)=0.1,P(ξ=1)=0.9生产这种饮料10万瓶,盈利的期望值Eξ=(−1×0.1+1×0.9)×10=8万元20. (1)证明:∵ 平面ABCD⊥平面BFEC,AB⊥BC,平面ABCD∩平面BFEC=BC,∴ AB⊥平面BFEC∵ FB⊂平面BFEC∴ AB⊥FB∵ AB⊥BC,FB⊥BC,∴ 四边形ABCD和四边形BCEF中∠BCD=∠BCE=60∘过D 作DM ⊥BC 于M ,连接EM ,在△DMC 和△EMC 中,∠MCD =∠MCE =60∘,CD =CE ,CM =CM∴ △DMC ≅△EMC∴ ∠DMC =∠EMC =90∘ ∴ EM ⊥BC∵ AB ⊥BC ,FB ⊥BC ∴ EM // BF ,DM // AB∵ EM ,DM ⊂平面DEM ,BF ,AB ⊄平面DEM ∴ AB // 平面DEM ,BF // 平面DEM ∵ AB ∩BF =B∴ 平面ABF // 平面DEM∵ 平面ADEF 与平面ABF 、平面DEM 的交线分别为AF ,DE ∴ AF // DE ;(2)解:作MN ⊥AD ,垂足为N ,连接EN ,则EN ⊥AD ,所以∠ENM 为所求二面角的平面角由(1)知EM =MD =32,在△DMN 中,MN =3√34,∴ tan∠ENM =2√33∴ cos∠ENM =√21721. (1)证明:设A(x 1, y 1),B(x 2, y 2),①当直线AB 斜率不存在时,由椭圆的对称性可知x 1=x 2,y 1=−y 2, ∵ 以AB 为直径的圆D 经过坐标原点,∴ OA →⋅OB →=0∴ x 1x 2+y 1y 2=0,∴ x 12−y 12=0 ∵ x 12+4y 12=4,∴ |x 1|=|y 1|=2√55 ∴ 原点O 到直线的距离为d =|x 1|=2√55②当直线AB 斜率存在时,设直线AB 的方程为y =kx +m ,代入椭圆方程,消元可得(1+4k 2)x 2+8kmx +4m 2−4=0 ∴ x 1+x 2=−8km1+4k 2,x 1x 2=4m 2−41+4k 2∵ 以AB 为直径的圆D 经过坐标原点,∴ OA →⋅OB →=0 ∴ x 1x 2+y 1y 2=0,∴ (1+k 2)4m 2−41+4k 2−km ×8km 1+4k 2+m 2=0∴ 5m 2=4(k 2+1) ∴ 原点O 到直线的距离为d =√k 2+1=2√55综上,点O 到直线AB 的距离为定值;(2)由(1)可知,在直角△OAB 中,点O 到直线AB 的距离|OH|=2√55,设∠OAH =θ,则∠BOH =θ ∴ |OA|=|OH|sinθ,|OB|=|OH|cosθ∴ |OA||OB|=85sin2θ∴ 2θ=π2,即θ=π4时,|OA||OB|取得最小值为8522. 解:(1)由题意知函数定义域为(0, +∞),f′(x)=k(1+lnx); 当k =0时,f(x)=0,所以函数无单调区间;当k >0时,令f′(x)=k(1+lnx)>0,则x >1e,所以函数f(x)在(0, 1e]上单调递减,在[1e , +∞)上单调递增;当k <0时,令f′(x)=k(1+lnx)>0,则0<x <1e ,所以函数f(x)在(0, 1e ]上单调递增,在[1e , +∞)上单调递减;(2)因为g(x)=f(x)−kx e x,所以g′(x)=k(lnx+x−xlnx)e x令u(x)=lnx +x −xlnx ,所以u′(x)=1x −lnx∵ x ∈[e, 3],∴ lnx ≥1,1x ≤1e <1,∴ u′(x)<0,即u(x)为减函数,可得u(x)min =u(3)=3−3ln3=lne 39>0∴ x ∈[e, 3]时,lnx +x −xlnx >0当k >0时,g′(x)>0,可得g(x)在x ∈[e, 3]时为增函数,g(x)max =g(3)=1e 2,所以k =e 3(ln3−1);当k =0时,g(x)的最大值是0,不合题意;当k <0时,g′(x)<0,g(x)在x ∈[e, 3]上为减函数,g(x)的最大值是0,不合题意 故当函数g(x)的最大值为1e 2时,k 的值为e3(ln3−1).。