数学人教A版选修2-2预习导航：1.6 微积分基本定理 Word版含解析

1.6微积分基本定理一、教材分析1、地位与作用“微积分基本定理”是高中人教版选修2-2第一章第6节的内容。

这节课的主要内容是：微积分基本定理的形成，以及用它求定积分。

在本节课之前教材已经引入导数和定积分的概念，并研究了其性质。

该定理揭示了导数和定积分之间的内在联系，同时也提供计算定积分的一种有效方法。

本节内容不仅是本书一个非常重要的内容，也是整个数学学习中的一块重要知识，该定理为下一节定积分的应用的学习奠定了基础，同时也为学生深入研究数学作了一个知识储备。

2、教学目标根据以上的教材分析，确定本节课的教学目标如下：知识与技能：（1）了解微积分基本定理，学会应用微积分基本定理求定积分；（2）通过对本课学习，培养应用微积分思想解决实际问题的能力。

过程与方法：（1）通过自主探究速度与位移的关系对图像的研究，巩固数形结合的方法，；（2）通过设问，探究速度与位移的关系，培养化整为零，以直代曲的思想。

情感态度与价值观：（1）感知寻求计算定积分新方法的必要性，激发求知欲；（2）通过对定理的应用，体会微积分基本定理的优越性；（3）帮助建立微观与宏观的联系桥梁。

3、教学重点根据教材分析，及教学目标我对本节课确定了以下重点：通过探究变速直线运动中的速度和位移的关系导出出微积分基本定理，以及对微积分基本定理的应用。

二、学情分析1、已有的知识与能力学生是在高二时学习该定理，因此学生具备了以下知识和能力储备（1）学生在学习本节内容之前，变速直线运动中的位移、速度、时间三者的关系已经很熟悉；（2）已经熟练掌握高中导数的知识，并能应用这些知识解决问题； （3）理解了定积分的定义及其几何意义，并能按定积分的定义求解定积分； （4）相对高一而言具有更好地抽象思维能力和计算、化简能力。

2、学生可能遇到的困难（1）学生在本学期才开始接触微分和逐步逼近的思想，所以大部分学生微积分基本定理的形成还是比较困难的，因此只要求学生通过实例了解微积分基本定理；（2）在用微积分基本定理计算定积分时，部分学生对该定理的条件的理解和找满足()()x f x F ='的()x F 还是存在困难，但在高中对此要求不高，故提醒学生不必深究。

1.6 微积分基本定理[学习目标]1．直观了解并掌握微积分基本定理的含义． 2．会利用微积分基本定理求函数的定积分． [知识链接]1．导数与定积分有怎样的联系？答 导数与定积分都是微积分学中两个最基本、最重要的概念，运用它们之间的联系，我们可以找出求定积分的方法，求导数与定积分是互为逆运算．2．在下面图(1)、图(2)、图(3)中的三个图形阴影部分的面积分别怎样表示？答 根据定积分与曲边梯形的面积的关系知： 图(1)中S ＝⎠⎛ab f (x )d x ，图(2)中S ＝－⎠⎛ab f (x )d x ，图(3)中S ＝⎠⎛0b f (x )d x －⎠⎛a0f (x )d x .[预习导引] 1．微积分基本定理如果f (x )是区间[a ，b ]上的连续函数，并且F ′(x )＝f (x )，那么⎠⎛ab f (x )d x ＝F (b )－F (a )．2．函数f (x )与其一个原函数的关系 (1)若f (x )＝c (c 为常数)，则F (x )＝cx ； (2)若f (x )＝x n (n ≠－1)，则F (x )＝1n ＋1·x n ＋1；(3)若f (x )＝1x ，则F (x )＝ln_x (x >0)；(4)若f (x )＝e x ，则F (x )＝e x ；(5)若f (x )＝a x，则F (x )＝a xln a(a >0且a ≠1)；(6)若f (x )＝sin x ，则F (x )＝－cos_x ； (7)若f (x )＝cos x ，则F (x )＝sin_x .要点一 求简单函数的定积分 例1 计算下列定积分 (1)⎠⎛123d x ； (2)⎠⎛02(2x ＋3)d x ；(3)⎠⎛3－1(4x －x 2)d x ； (4)⎠⎛12(x －1)5d x .解 (1)因为(3x )′＝3，所以⎠⎛123d x ＝(3x )⎪⎪⎪21＝3×2－3×1＝3. (2)因为(x 2＋3x )′＝2x ＋3， 所以⎠⎛2(2x ＋3)d x ＝(x 2＋3x )⎪⎪⎪2＝22＋3×2－(02＋3×0)＝10. (3)因为⎝⎛⎭⎫2x 2－x33′＝4x －x 2， 所以⎠⎛3－1(4x －x 2)d x ＝⎝⎛⎭⎫2x 2－x 33⎪⎪⎪3－1 ＝⎝⎛⎭⎫2×32－333－⎣⎡⎦⎤2×(－1)2－(－1)33＝203.(4)因为⎣⎡⎦⎤16(x －1)6′＝(x －1)5， 所以⎠⎛21(x －1)5d x＝16(x －1)6⎪⎪⎪21＝16(2－1)6－16(1－1)6 ＝16. 规律方法 (1)用微积分基本定理求定积分的步骤： ①求f (x )的一个原函数F (x )； ②计算F (b )－F (a )． (2)注意事项：①有时需先化简，再求积分；②f (x )的原函数有无穷多个，如F (x )＋c ，计算时，一般只写一个最简单的，不再加任意常数c .跟踪演练1 求下列定积分： (1)∫π20(3x ＋sin x )d x ；(2)⎠⎛21⎝⎛⎭⎫e x －1x d x . 解 (1)∵⎝⎛⎭⎫32x 2－cos x ′＝3x ＋sin x ， ∴∫π20(3x ＋sin x )d x ＝⎝⎛⎭⎫32x 2－cos x ⎪⎪⎪⎪π20＝⎣⎡⎦⎤32×⎝⎛⎭⎫π22－cos π2－⎝⎛⎭⎫32×0－cos0＝3π28＋1； (2)∵(e x －ln x )′＝e x －1x，∴⎠⎛21(e x－1x )d x ＝()e x －ln x ⎪⎪⎪21＝(e 2－ln2)－(e －0) ＝e 2－e －ln2.要点二 求较复杂函数的定积分 例2 求下列定积分：(1)⎠⎛41x (1－x )d x ； (2)∫π202cos 2x2d x ；(3)⎠⎛41(2x ＋1x)d x . 解 (1)∵x (1－x )＝x －x ， 又∵⎝⎛⎭⎫23x 32－12x 2′＝x －x .∴⎠⎛41x (1－x )d x ＝⎝⎛⎭⎫23x 32－12x 2⎪⎪⎪41 ＝⎝⎛⎭⎫23×432－12×42－⎝⎛⎭⎫23－12＝－176. (2)∵2cos 2x2＝1＋cos x ，(x ＋sin x )′＝1＋cos x ，∴原式＝∫π20(1＋cos x )d x ＝(x ＋sin x )⎪⎪⎪⎪π20＝π2＋1.(3)∵⎝⎛⎭⎫2xln2＋2x ′＝2x ＋1x，∴⎠⎛41(2x ＋1x)d x ＝⎝⎛⎭⎫2xln2＋2x ⎪⎪⎪41＝⎝⎛⎭⎫24ln2＋24－⎝⎛⎭⎫2ln2＋2＝14ln2＋2. 规律方法 求较复杂函数的定积分的方法：(1)掌握基本初等函数的导数以及导数的运算法则，正确求解被积函数的原函数，当原函数不易求时，可将被积函数适当变形后求解，具体方法是能化简的化简，不能化简的变为幂函数、正、余弦函数、指数、对数函数与常数的和与差． (2)确定积分区间，分清积分下限与积分上限． 跟踪演练2 计算下列定积分： (1)∫π30(sin x －sin2x )d x ；(2)⎠⎛0ln 2e x (1＋e x )d x .解 (1)sin x －sin2x 的一个原函数是－cos x ＋ 12cos2x ，所以∫π30(sin x －sin2x )d x ＝⎝⎛⎭⎫－cos x ＋12cos2x ⎪⎪⎪⎪π30＝⎝⎛⎭⎫－12－14－⎝⎛⎭⎫－1＋12＝－14. (2)∵e x (1＋e x )＝e x ＋e 2x ， ∴⎝⎛⎭⎫e x ＋12e 2x ′＝e x ＋e 2x ， ∴⎠⎛0ln 2e x (1＋e x )d x ＝⎠⎛0ln 2()e x ＋e 2x d x＝⎝⎛⎭⎫e x ＋12e 2x ⎪⎪⎪ln2＝e ln2＋12e 2ln2－e 0－12e 0＝2＋12×4－1－12＝52.要点三 定积分的简单应用例3 已知f (a )＝⎠⎛10(2ax 2－a 2x )d x ，求f (a )的最大值．解 ∵⎝⎛⎭⎫23ax 3－12a 2x 2′＝2ax 2－a 2x ，∴⎠⎛10(2ax 2－a 2x )d x ＝⎝⎛⎭⎫23ax 3－12a 2x 2⎪⎪⎪10＝23a －12a 2， 即f (a )＝23a －12a 2＝－12⎝⎛⎭⎫a 2－43a ＋49＋29 ＝－12⎝⎛⎭⎫a －232＋29， ∴当a ＝23时，f (a )有最大值29.规律方法 定积分的应用体现了积分与函数的内在联系，可以通过积分构造新的函数，进而对这一函数进行性质、最值等方面的考查，解题过程中注意体会转化思想的应用． 跟踪演练3 已知f (x )＝ax 2＋bx ＋c (a ≠0)，且f (－1)＝2，f ′(0)＝0，⎠⎛10f (x )d x ＝－2，求a 、b 、c 的值．解 由f (－1)＝2，得a －b ＋c ＝2. ① 又f ′(x )＝2ax ＋b ，∴f ′(0)＝b ＝0， ②而⎠⎛10f (x )d x ＝⎠⎛10(ax 2＋bx ＋c )d x ＝⎝⎛⎭⎫13ax 3＋12bx 2＋cx ⎪⎪⎪1＝13a ＋12b ＋c ， ∴13a ＋12b ＋c ＝－2， ③由①②③式得a ＝6，b ＝0，c ＝－4. 要点四 求分段函数的定积分 例4 计算下列定积分：(1)若f (x )＝⎩⎪⎨⎪⎧x 2 (x ≤0)cos x －1 (x >0)，求∫π2－1f (x )d x ；(2)⎠⎛30|x 2－4|d x .解 (1)∫π2－1f (x )d x ＝⎠⎛0－1x 2d x ＋∫π20(cos x －1)d x ，又∵⎝⎛⎭⎫13x 3′＝x 2，(sin x －x )′＝cos x －1∴原式＝13x 3⎪⎪⎪0－1＋(sin x －x )⎪⎪⎪⎪π20＝⎝⎛⎭⎫0＋13＋⎝⎛⎭⎫sin π2－π2－(sin0－0) ＝43－π2.(2)∵|x 2－4|＝⎩⎪⎨⎪⎧x 2－4 (x ≥2或x ≤－2)，4－x 2 (－2<x <2)，又∵⎝⎛⎭⎫13x 3－4x ′＝x 2－4，⎝⎛⎭⎫4x －13x 3′＝4－x 2， ∴⎠⎛30|x 2－4|d x ＝⎠⎛20(4－x 2)d x ＋⎠⎛32(x 2－4)d x＝⎝⎛⎭⎫4x －13x 3⎪⎪⎪20＋⎝⎛⎭⎫13x 3－4x ⎪⎪⎪32 ＝⎝⎛⎭⎫8－83－0＋(9－12)－⎝⎛⎭⎫83－8＝233. 规律方法 (1)求分段函数的定积分时，可利用积分性质将其表示为几段积分和的形式； (2)带绝对值的解析式，先根据绝对值的意义找到分界点，去掉绝对值号，化为分段函数； (3)含有字母参数的绝对值问题要注意分类讨论． 跟踪演练4 求⎠⎛3－3(|2x ＋3|＋|3－2x |)d x .解 ∵|2x ＋3|＋|3－2x |＝⎩⎪⎨⎪⎧－4x ，x <－32，6，－32≤x ≤32，4x ，x >32，∴⎠⎛3－3(|2x ＋3|＋|3－2x |)d x＝∫－32－3(－4x )d x ＋∫32－326d x ＋∫3324x d x＝－2x 2⎪⎪⎪⎪－32－3＋6x ⎪⎪⎪32－32＋2x 2⎪⎪⎪⎪332＝45.1．∫π2－π2(1＋cos x )d x 等于( )A ．πB ．2C ．π－2D ．π＋2答案 D解析 ∵(x ＋sin x )′＝1＋cos x ， ∴⎪⎪∫π2－π2(1＋cos x )d x ＝(x ＋sin x )π2－π2＝π2＋sin π2－⎣⎡⎦⎤－π2＋sin ⎝⎛⎭⎫－π2＝π＋2. 2．若⎠⎛1a ⎝⎛⎭⎫2x ＋1x d x ＝3＋ln2，则a 的值是( ) A ．5 B ．4 C ．3 D ．2答案 D解析 ⎠⎛1a ⎝⎛⎭⎫2x ＋1x d x ＝⎠⎛1a 2x d x ＋⎠⎛1a 1xd x ＝x 2|a 1＋ ln x 错误!＝a 2－1＋ln a ＝3＋ln2，解得a ＝2. 3．⎠⎛02⎝⎛⎭⎫x 2－23x d x ＝________. 答案 43解析 ⎠⎛02⎝⎛⎭⎫x 2－23x d x ＝⎠⎛02x 2d x －⎠⎛0223x d x ＝x 33⎪⎪⎪⎪20－x 2320＝83－43＝43. 4．已知f (x )＝⎩⎨⎧4x －2π，0≤x ≤π2，cos x ，π2<x ≤π，计算⎠⎛0πf (x )d x .解 ⎠⎛0πf (x )d x ＝∫π20f (x )d x ＋错误!f (x )d x＝∫π20(4x －2π)d x ＋错误!cos x d x ，取F 1(x )＝2x 2－2πx ，则F 1′(x )＝4x －2π； 取F 2(x )＝sin x ，则F 2′(x )＝cos x .所以∫π20(4x －2π)d x ＋错误!cos x d x ＝(2x 2－2πx )错误!＋sin x 错误!，即错误!f (x )d x ＝－错误!π2－1.1．求定积分的一些常用技巧(1)对被积函数，要先化简，再求积分．(2)若被积函数是分段函数，依据定积分“对区间的可加性”，分段积分再求和． (3)对于含有绝对值符号的被积函数，要去掉绝对值符号才能积分．2．由于定积分的值可取正值，也可取负值，还可以取0，而面积是正值，因此不要把面积理解为被积函数对应图形在某几个区间上的定积分之和，而是在x 轴下方的图形面积要取定积分的相反数.一、基础达标1．已知物体做变速直线运动的位移函数s ＝s (t )，那么下列命题正确的是( ) ①它在时间段[a ，b ]内的位移是s ＝s (t )⎪⎪ba ； ②它在某一时刻t ＝t 0时，瞬时速度是v ＝s ′(t 0)； ③它在时间段[a ，b ]内的位移是s ＝li m n →∞i ＝1nb －ans ′(ξi )； ④它在时间段[a ，b ]内的位移是s ＝⎠⎛ab s ′(t )d t .A ．①B ．①②C ．①②④D ．①②③④答案 D2．若F ′(x )＝x 2，则F (x )的解析式不正确的是( ) A ．F (x )＝13x 3B ．F (x )＝x 3C ．F (x )＝13x 3＋1D ．F (x )＝13x 3＋c (c 为常数)答案 B解析 若F (x )＝x 3，则F ′(x )＝3x 2，这与F ′(x )＝x 2不一致，故选B. 3．⎠⎛01(e x ＋2x )d x 等于( )A ．1B ．e －1C ．eD ．e ＋1答案 C解析 ⎠⎛01(e x ＋2x )d x ＝(e x ＋x 2)|10＝(e 1＋12)－(e 0＋02)＝e. 4．已知f (x )＝⎩⎪⎨⎪⎧x 2，－1≤x ≤0，1，0<x ≤1，则⎠⎛1－1f (x )d x 的值为( )A.32 B ．43C ．23D ．－23答案 B解析 ⎠⎛1－1f (x )d x ＝⎠⎛0－1x 2d x ＋⎠⎛011d x ＝⎪⎪x 330－1＋1＝13＋1＝43，故选B. 5．设函数f (x )＝ax 2＋c (a ≠0)，若⎠⎛01f (x )d x ＝f (x 0)，0≤x 0≤1，则x 0的值为________．答案33解析 由已知得13a ＋c ＝ax 20＋c ，∴x 20＝13，又∵0≤x 0≤1，∴x 0＝33. 6．(2013·湖南)若⎠⎛0T x 2d x ＝9，则常数T 的值为________．答案 3解析 ⎠⎛0T x 2d x ＝⎪⎪13x 3T 0＝13T 3＝9，即T 3＝27，解得T ＝3. 7．已知⎠⎛1－1(x 3＋ax ＋3a －b )d x ＝2a ＋6且f (t )＝⎠⎛0t (x 3＋ax ＋3a －b )d x 为偶函数，求a ，b 的值．解 ∵f (x )＝x 3＋ax 为奇函数， ∴⎠⎛1－1(x 3＋ax )d x ＝0，∴⎠⎛1－1(x 3＋ax ＋3a －b )d x＝⎠⎛1－1(x 3＋ax )d x ＋⎠⎛1－1(3a －b )d x＝0＋(3a －b )[1－(－1)]＝6a －2b . ∴6a －2b ＝2a ＋6，即2a －b ＝3， ①又f (t )＝⎪⎪⎣⎡⎦⎤x 44＋a 2x 2＋(3a －b )x t0 ＝t 44＋at 22＋(3a －b )t 为偶函数， ∴3a －b ＝0，②由①②得a ＝－3，b ＝－9. 二、能力提升8．∫π20sin 2x2d x 等于( )A.π4 B ．π2－1C ．2D ．π－24答案 D解析 ∫π20sin 2x 2d x ＝∫π201－cos x 2d x ＝⎪⎪12(x －sin x )π20＝π－24，故选D. 9．(2013·江西)若S 1＝⎠⎛12x 2d x ，S 2＝⎠⎛121x d x ，S 3＝⎠⎛12e x d x ，则S 1，S 2，S 3的大小关系为( )A ．S 1＜S 2＜S 3B ．S 2＜S 1＜S 3C ．S 2＜S 3＜S 1D ．S 3＜S 2＜S 1答案 B 解析 S 1＝⎠⎛12x 2d x ＝13x 3⎪⎪21＝73，S 2＝⎪⎪⎪⎠⎛121x d x ＝ln x 21＝ln2＜1，S 3＝⎠⎛12e x d x ＝e x |21＝e 2－e ＝e(e －1)＞73，所以S 2＜S 1＜S 3，选B.10．设f (x )＝⎩⎪⎨⎪⎧lg x ，x ＞0，x ＋⎠⎛0a 3t 2d t ，x ≤0.若f [f (1)]＝1，则a ＝________.答案 1解析 因为x ＝1>0，所以f (1)＝lg1＝0.又x ≤0时，f (x )＝x ＋⎠⎛0a 3t 2d t ＝x ＋t 3|a 0＝x ＋a 3，所以f (0)＝a 3.因为f [f (1)]＝1，所以a 3＝1，解得a ＝1.11．设f (x )是一次函数，且⎠⎛01f (x )d x ＝5，⎠⎛01xf (x )d x ＝176，求f (x )的解析式．解 ∵f (x )是一次函数，设f (x )＝ax ＋b (a ≠0)，则 ⎠⎛01f (x )d x ＝⎠⎛01(ax ＋b )d x ＝⎠⎛01ax d x ＋⎠⎛01b d x ＝12a ＋b ＝5， ⎠⎛01xf (x )d x ＝⎠⎛01x (ax ＋b )d x ＝⎠⎛01(ax 2)d x ＋⎠⎛a1b x d x ＝13a ＋12b ＝176. 由⎩⎨⎧12a ＋b ＝513a ＋12b ＝176，得⎩⎪⎨⎪⎧a ＝4b ＝3.即f (x )＝4x ＋3.12．若函数f (x )＝⎩⎪⎨⎪⎧x 3，x ∈[0，1]，x ，x ∈(1，2]，2x ，x ∈(2，3].求⎠⎛03f (x )d x 的值．解 由积分的性质，知：经典小初高讲义小初高优秀教案 ⎠⎛03f (x )d x ＝⎠⎛01f (x )d x ＋⎠⎛12f (x )d x ＋⎠⎛23f (x )d x ＝⎠⎛01x 3d x ＋⎠⎛12x d x ＋⎠⎛232x d x ＝x 44⎪⎪⎪⎪10＋23x 3221 ⎪⎪＋2x ln232 ＝14＋432－23＋8ln2－4ln2＝－512＋432＋4ln2. 三、探究与创新13．求定积分⎠⎛3－4|x ＋a |d x . 解 (1)当－a ≤－4即a ≥4时，原式＝⎠⎛3－4(x ＋a )d x ＝ ⎪⎪⎝⎛⎭⎫x 22＋ax 3－4＝7a －72. (2)当－4＜－a ＜3即－3＜a ＜4时， 原式＝⎠⎛－4－a [－(x ＋a )]d x ＋⎠⎛3－a(x ＋a )d x ＝⎝⎛⎭⎫－x 22－ax ⎪⎪－a －4＋ ⎪⎪⎝⎛⎭⎫x 22＋ax 3－a ＝a 22－4a ＋8＋⎝⎛⎭⎫a 22＋3a ＋92 ＝a 2－a ＋252. (3)当－a ≥3即a ≤－3时，原式＝⎠⎛3－4[－(x ＋a )]d x ＝ ⎪⎪⎝⎛⎭⎫－x 22－ax 3－4＝ －7a ＋72. 综上，得⎠⎛3－4|x ＋a |d x ＝⎩⎪⎨⎪⎧ 7a －72(a ≥4)，a 2－a ＋252(－3＜a ＜4)，－7a ＋72(a ≤－3).。

1.6 微积分基本定理1．了解导数与定积分的关系以及微积分基本定理的含义．(重点、易混点) 2．掌握微积分基本定理，会用微积分基本定理求定积分．(重点、难点)[基础·初探]教材整理1 微积分基本定理阅读教材P 51～P 53“例1”以上内容，完成下列问题．1．内容：如果f (x )是区间[a ，b ]上的__________函数，并且F ′(x )＝f (x )，那么⎠⎛ab f (x )d x ＝__________.这个结论叫做微积分基本定理，又叫做____________． 2．表示：为了方便，常常把F (b )－F (a )记成__________，即⎠⎛a bf (x )dx ＝______________＝______________.【答案】 1.连续 F (b )－F (a ) 牛顿-莱布尼茨公式 2．F (x )|b a F (x )|b a F (b )－F (a )1．判断(正确的打“√”，错误的打“×”)(1)微积分基本定理中，被积函数f (x )是原函数F (x )的导数．( )(2)应用微积分基本定理求定积分的值时，为了计算方便通常取原函数的常数项为0.( ) (3)应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数．( ) 【答案】 (1)√ (2)√ (3)√2．若a ＝⎠⎛01(x －2)d x ，则被积函数的原函数为( )A ．f (x )＝x －2B ．f (x )＝x －2＋C C ．f (x )＝12x 2－2x ＋CD ．f (x )＝x 2－2x【答案】 C3．⎠⎜⎛π2cos x d x ＝________. 【解析】⎠⎜⎛0π2cos x d x ＝sin x ⎪⎪⎪π20＝sinπ2－sin 0＝1. 【答案】 1教材整理2 定积分与曲边梯形面积的关系 阅读教材P 53“例2”以下部分～P 54的内容，完成下列问题．设曲边梯形在x 轴上方的面积为S 上，在x 轴下方的面积为S 下，则(1)当曲边梯形在x 轴上方时，如图1-6-1①，则⎠⎛a b f (x )d x ＝__________.(2)当曲边梯形在x 轴下方时，如图1-6-1②，则⎠⎛ab f (x )d x ＝________.① ② ③图1-6-1(3)当曲边梯形在x 轴上方、x 轴下方均存在时，如图1-6-1③，则⎠⎛ab f (x )d x ＝______________.特别地，若S 上＝S 下，则⎠⎛ab f (x )d x ＝______.【答案】 (1)S 上 (2)－S 下 (3)S 上－S 下1．如图1-6-2，阴影部分的面积为________．图1-6-2【解析】 根据定积分的几何意义知S 阴影＝－⎠⎜⎛π232πcos x d x ＝－sin x ⎪⎪⎪⎪32ππ2＝－⎝⎛⎭⎪⎫sin 32π－sin π2＝2. 【答案】 22．如图1-6-3，定积分⎠⎛a b f (x )d x 的值用阴影面积S 1，S 2，S 3表示为⎠⎛ab f (x )d x ＝________.图1-6-3【解析】 根据定积分的几何意义知⎠⎛a b f (x )d x ＝S 1－S 2＋S 3.【答案】 S 1－S 2＋S 3[小组合作型](1)⎠⎛0A ．e ＋2 B ．e ＋1 C ．eD ．e －1(2)求下列定积分．①⎠⎛12(x 2＋2x ＋3)d x ；②⎠⎜⎛0π2 sin 2x 2d x . 【自主解答】 (1)⎠⎛01(2x ＋e x)d x ＝(x 2＋e x)⎪⎪⎪10＝(12＋e)－(02＋e 0)＝1＋e －1＝e.【答案】 C(2)①⎠⎛12(x 2＋2x ＋3)d x ＝⎠⎛12x 2d x ＋⎠⎛122x d x ＋⎠⎛123d x ＝x33⎪⎪⎪ 21＋x 2⎪⎪⎪21＋3x ⎪⎪⎪21＝253. ②sin 2x 2＝1－cos x 2，而⎝ ⎛⎭⎪⎫12x －12sin x ′＝12－12cos x ＝sin 2x 2，∴⎠⎜⎛0π2sin 2x 2d x ＝⎝ ⎛⎭⎪⎫12x －12sin x ⎪⎪⎪π2＝π4－12＝π－24.求简单的定积分关键注意两点1．掌握基本函数的导数以及导数的运算法则，正确求解被积函数的原函数，当原函数不易求时，可将被积函数适当变形后再求解．2．精确定位积分区间，分清积分下限与积分上限．[再练一题]1．(1)若⎠⎛01(kx ＋1)d x ＝2，则k 的值为( )A ．1B ．2C ．3D ．4(2)⎠⎛12x －1x2d x ＝________.【导学号：62952051】【解析】 (1)⎠⎛01(kx ＋1)d x ＝⎝ ⎛⎭⎪⎫12kx2＋x ⎪⎪⎪10＝12k ＋1＝2，∴k ＝2. (2)⎠⎛12x －1x2d x ＝⎠⎛12⎝ ⎛⎭⎪⎫1x －1x2d x＝⎝ ⎛⎭⎪⎫ln x ＋1x ⎪⎪⎪21＝⎝ ⎛⎭⎪⎫ln 2＋12－(ln 1＋1)＝ln 2－12.【答案】 (1)B (2)ln 2－12(1)f (x )＝⎩⎪⎨⎪⎧sin x ，0≤x<π2，1，π2≤x≤2，x －1，2<x≤4，求⎠⎛04f (x )d x ； (2)⎠⎛02|x 2－1|d x . 【精彩点拨】 (1)按f (x )的分段标准，分成⎣⎢⎡⎭⎪⎫0，π2，⎣⎢⎡⎦⎥⎤π2，2，(2,4]三段求定积分，再求和．(2)先去掉绝对值号，化成分段函数，再分段求定积分． 【自主解答】(1)⎠⎛04f (x )d x ＝⎠⎜⎛π2sin x d x ＋⎠⎜⎛π221d x +⎠⎛24(x －1)d x ＝(－cos x )⎪⎪⎪⎪ π20＋x ⎪⎪⎪2π2＋⎝ ⎛⎭⎪⎫12x2－x ⎪⎪⎪42＝1＋⎝⎛⎭⎪⎫2－π2＋(4－0)＝7－π2.(2)⎠⎛02|x 2－1|d x ＝⎠⎛01(1－x 2)d x ＋⎠⎛12(x 2－1)d x＝⎝⎛⎭⎪⎫x －13x3⎪⎪⎪10＋⎝ ⎛⎭⎪⎫13x3－x ⎪⎪⎪21＝2.1．本例(2)中被积函数f (x )含有绝对值号，可先求函数f (x )的零点，结合积分区间，分段求解．2．分段函数在区间[a ，b ]上的定积分可分成n 段定积分和的形式，分段的标准可按照函数的分段标准进行．3．带绝对值号的解析式，可先化为分段函数，然后求解．[再练一题]2．计算定积分：⎠⎛-33(|2x ＋3|＋|3－2x |)d x . 【解】 设f (x )＝|2x ＋3|＋|3－2x |，x ∈[－3,3]，则f (x )＝⎩⎪⎨⎪⎧－4x ，－3≤x<－32，6，－32≤x≤32，4x ，32<x≤3.所以⎠⎛-33 (|2x ＋3|＋|3－2x |)d x＝⎠⎜⎛-3－32(－4x )d x ＋⎠⎜⎜⎛－3232 6 d x ＋⎠⎜⎛323 4x d x ＝－2x 2⎪⎪⎪－32-3＋6x⎪⎪⎪⎪32－32＋2x 2⎪⎪⎪332＝－2×⎝ ⎛⎭⎪⎫94－9＋6×⎝ ⎛⎭⎪⎫32＋32＋2×⎝⎛⎭⎪⎫9－94＝45.[探究共研型]探究 如何求使⎠⎛01(【提示】 令y ＝⎠⎛01(x 2＋cx ＋c )2d x ，则y ＝⎠⎛01(x 4＋2cx 3＋c 2x 2＋2cx 2＋2c 2x ＋c 2)d x＝⎝ ⎛⎭⎪⎫15x5＋c 2x4＋c2＋2c 3x3＋c2x2＋c2x ⎪⎪⎪1＝15＋76c ＋73c 2＝73⎝⎛⎭⎪⎫c ＋142－73×116＋15.∵73>0，∴当c ＝－14时，⎠⎛01(x 2＋cx ＋c )2d x 最小． 已知f (x )是一次函数，其图象过点(1,4)，且⎠⎛01f (x )d x ＝1，求f (x )的解析式．【精彩点拨】 设出函数解析式，由题中条件建立两方程，联立求解．【自主解答】 设f (x )＝kx ＋b (k ≠0)，因为函数的图象过点(1,4)，所以k ＋b ＝4. ① 又⎠⎛01f (x )d x ＝⎠⎛01(kx ＋b )d x ＝⎝ ⎛⎭⎪⎫k 2x2＋bx ⎪⎪⎪10＝k 2＋b ，所以k2＋b ＝1. ②由①②得k ＝6，b ＝－2，所以f (x )＝6x －2.1．含有参数的定积分可以与方程、函数或不等式综合起来考查，先利用微积分基本定理计算定积分是解决此类综合问题的前提．2．计算含有参数的定积分，必须分清积分变量与被积函数f (x )、积分上限与积分下限、积分区间与函数F (x )等概念．[再练一题]3．上例中，若把“已知f (x )是一次函数”改为“已知f (x )＝ax 2＋bx (a ≠0)”，其余条件不变，求f (x )的解析式．【解】 ∵函数的图象过点(1,4)，∴a ＋b ＝4， ① 又⎠⎛01f (x )d x ＝⎠⎛01(ax 2＋bx )d x ＝⎝ ⎛⎭⎪⎫a3x3＋b 2x2⎪⎪⎪10＝a 3＋b2， ∴a 3＋b2＝1， ②由①②得a ＝6，b ＝－2，所以f (x )＝6x 2－2x .1．下列值等于1的是( ) A.⎠⎛01x d x B.⎠⎛01(x ＋1)d x C.⎠⎛011d x D.⎠⎛0112d x 【解析】 选项A ，因为⎝ ⎛⎭⎪⎫x22′＝x ，所以⎠⎛01x d x ＝x22⎪⎪⎪10＝12； 选项B ，因为⎝ ⎛⎭⎪⎫x22＋x ′＝x ＋1，所以⎠⎛01(x ＋1)d x ＝⎝ ⎛⎭⎪⎫x22＋x ⎪⎪⎪10＝32；选项C ，因为x ′＝1，所以⎠⎛011d x ＝x ⎪⎪⎪10＝1；选项D ，因为⎝ ⎛⎭⎪⎫12x ′＝12，所以⎠⎛0112d x ＝12x ⎪⎪⎪10＝12. 【答案】 C2．⎠⎜⎛-π2π2 (sin x ＋cos x )d x 的值是( ) A ．0 B.π4C ．2D ．4【解析】 ⎠⎜⎛-π2π2 (sin x ＋cos x )d x ＝⎠⎜⎛-π2π2sin x d x ＋⎠⎜⎛-π2π2cos x d x＝(－cos x )| π2－π2＋sin x⎪⎪⎪⎪π2-π2＝2.【答案】 C3．计算⎠⎛01x 2d x ＝________.【导学号：62952052】【解析】 由于⎝ ⎛⎭⎪⎫13x3′＝x 2，所以⎠⎛01x 2d x ＝13x 3⎪⎪⎪10＝13. 【答案】 134．已知2≤⎠⎛12(kx ＋1)d x ≤4，则实数k 的取值范围为________.【解析】 ⎠⎛12(kx ＋1)d x ＝⎝ ⎛⎭⎪⎫12kx2＋x ⎪⎪⎪21＝(2k ＋2)－⎝ ⎛⎭⎪⎫12k ＋1＝32k ＋1，所以2≤32k ＋1≤4，解得23≤k ≤2.【答案】 ⎣⎢⎡⎦⎥⎤23，25．已知f (x )＝ax ＋b ，且⎠⎛-11 f 2(x )d x ＝1，求f (a )的取值范围．【解】 由f (x )＝ax ＋b ，⎠⎛-11 f 2(x )d x ＝1，得2a 2＋6b 2＝3,2a 2＝3－6b 2≥0，所以－22≤b ≤22， 所以f (a )＝a 2＋b ＝－3b 2＋b ＋32＝－3⎝ ⎛⎭⎪⎫b －162＋1912，所以－22≤f (a )≤1912.。

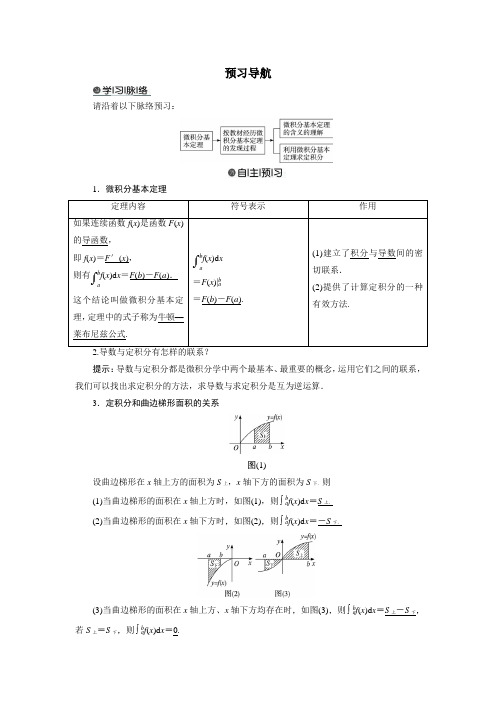
预习导航请沿着以下脉络预习：1．微积分基本定理提示：导数与定积分都是微积分学中两个最基本、最重要的概念，运用它们之间的联系，我们可以找出求定积分的方法，求导数与求定积分是互为逆运算．3．定积分和曲边梯形面积的关系图(1)设曲边梯形在x 轴上方的面积为S 上，x 轴下方的面积为S 下．则 (1)当曲边梯形的面积在x 轴上方时，如图(1)，则⎰b a f (x )d x ＝S 上． (2)当曲边梯形的面积在x 轴下方时，如图(2)，则⎰b a f (x )d x ＝－S 下．(3)当曲边梯形的面积在x 轴上方、x 轴下方均存在时，如图(3)，则⎰b a f (x )d x ＝S 上－S 下，若S 上＝S 下，则⎰ba f (x )d x ＝0.4．如何理解微积分基本定理？提示：利用微积分基本定理计算定积分⎰b a f (x )d x 的关键是找到使F ′(x )＝f (x )成立的F (x )，通常是逆向考虑基本初等函数的求导公式和导数的四则运算法则，求出F (x )．这个过程与求导运算互为逆运算，为避免出错，在求出F (x )后，可利用F ′(x )＝f (x )对F (x )进行求导验证．提醒：求F (x )使得F ′(x )＝f (x )时，只求一个最简单的F (x )即可，因为⎰b a f (x )d x ＝F (x )|b a ＝(F (x )＋C )|b a ＝F (b )－F (a )．5．如何正确使用牛顿—莱布尼兹公式？提示：以运用微积分基本公式求定积分⎰10x 2d x 为例，先求出f (x )＝x 2的一个原函数(一个即可，并非所有的)F (x )＝13x 3，并计算F (x )在其端点x ＝0和x ＝1处函数值的差13×13－13×03，这要比用定积分的定义去求定积分简单得多，从而使学生体会到利用微积分基本定理计算定积分的优越性．上述解法可用等式表示出来，解题格式为： 解析：⎠⎛01x 2d x ＝13x 3|10＝13×13－13×03＝13. 一般地，⎠⎛ab f (x )d x ＝F (x )|b a ＝F (b )－F (a )(其中F (x )为f (x )的一个原函数)，要注意将积分上限、下限代入原函数时，要按步骤进行，以免发生符号错误．1．若F ′(x )＝x 2，则F (x )的解析式不正确的是( )． A ．F (x )＝13x 3B ．F (x )＝x 3C ．F (x )＝13x 3＋1D ．F (x )＝13x 3＋c (c 为常数)答案：B解析：对选项B ，F ′(x )＝(x 3)′＝3x 2，与已知矛盾． 2. ⎰π－πsin 2x d x 等于( )．A ．0B ．2πC ．4πD ．4 答案：A解析：⎰π－πsin 2x d x ＝－12cos 2x ⎰π－π ＝－12[cos 2π－cos 2(－π)]＝0.3．若⎰10(2x ＋k )d x ＝2，则k ＝__________.答案：1解析：⎰10(2x ＋k )d x ＝(x 2＋kx )10＝1＋k ＝2，∴k ＝1.4．设f (x )＝⎩⎪⎨⎪⎧x 2，0≤x ≤1，2－x ，1<x ≤2，则⎰20f (x )d x 等于__________．答案：56解析：⎰20f (x )d x ＝⎰10x 2d x ＋⎰21(2－x )d x＝x 33|10＋⎝⎛⎭⎫2x －x 22|21 ＝13＋⎣⎡⎦⎤⎝⎛⎭⎫2×2－222－⎝⎛⎭⎫2－12＝56. 5．求下列定积分：(1) ⎰10(x 2－x )d x ； (2) ⎰3－1(3x 2－2x ＋1)d x ； (3) ⎰π20cos x d x . 解：(1) ⎰10(x 2－x )d x ＝⎝⎛⎭⎫13x 3－12x 2|10＝－16； (2) ⎰3－1(3x 2－2x ＋1)d x ＝(x 3－x 2＋x )|3－1＝24； (3) ⎰π20cos x d x ＝sin x |π20＝1.。

1.6微积分基本定理（1）【学习目标】1.通过实例(变速运动物体在某段时间内的速度与路程的关系)，直观了解微积分基本定理的含义；2.了解微积分基本定理；3.会用微积分基本定理求函数的定积分．【新知自学】知识回顾：1.定积分的概念：一般地，设函数()f x 在区间[,]a b 上连续，用分点012a x x x =<<< …1i i x x -<<<…n x b <=将区间[,]a b 等分成n 个小区间，每个小区间长度为x ∆=______，在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ= ，作和式：11()()n nn i i i i b a S f x f nξξ==-=∆=∑∑.如果x ∆无限接近于0（亦即n →+∞）时，上述和式n S 无限趋近于常数S ，那么称该常数S 为________________．记为_______. 2．定积分的几何意义：______________________ ___________________ .新知梳理：1.微积分基本定理:一般地，如果)(x f 是区间[]b a ,上的连续函数，并且，)()(x f x F ='，那么=⎰dx x f ba)(________．这个结论叫做微积分基本定理，又叫做牛顿一莱布尼兹公式．为了方便，常把)()(b F a F -记成_________，即()()|bbaaf x dx F x ==⎰________________________．2．利用微积分基本定理计算定积分dx x f ba⎰)(的关键是找到满足____________的函数)(x F ，通常，可以用基本初等函数的求导公式和导数的四则运算法则从 _______上求出)(x F ．3．求导数运算与求原函数运算互为 ___ ． 在微积分基本定理中函数)(x F 叫函数)(x f 在区间[]b a ,上的一个原函数．因为[])()(x F C x F '='+，所以C x F +)(也是函数_________的原函数．对点练习：1.已知)()(x f x F ='，则下列等式正确的是 ( ) A.⎰-=ba a Fb F dx x f )()()( B.⎰-=ba b F a F dx x f )()()(C.)(lim )(1i ni ban F nab dx x f ξ∑⎰=∞→-=D.x F nab dx x f i ni ban ∆-=∑⎰=∞→)(lim )(1ξ． 2．已知⎩⎨⎧<<≤≤-=10,101,)(2x x x x f ，则⎰-11)(dx x f 的值为 ( )A.23B.32- C.32 D.34 3．设⎰⎰⎰===11132sin ,,xdx c dx x b dx x a ，则c b a ,,的大小关系是( )A.c b a <=B.c b a >=C.c a b <<D.a b c >> 4.计算下列定积分：（1）dx x 3131）（⎰；（2）dx x⎰211.【合作探究】典例精析：例1. 求下列定积分: (1) dx x x ⎰-12)(；(2) dx x x ⎰+20)sin 3(π；变式练习：求下列定积分: (1) dx x x⎰+232)43(；(2)dx ⎰1x .例2.求下列定积分: (1) ⎰πcos xdx ；π变式练习：求下列定积分:（1）dx x x 2202cos 2sin ⎰⎪⎭⎫ ⎝⎛+π；（2）xdx ⎰22-2cos ππ.规律总结：利用微积分基本定理求定积分,实质上是求导数逆运算，即求导数等于被积函数的一个函数，求解时注意以下两个方面：（1）熟练掌握基本函数导数及导数的运算法则，学会逆运算；（2）当被积函数较为复杂，不容易找到原函数时，可适当变形后再求解.【课堂小结】1. 由抛物线x y =2和直线x =1所围成的图形的面积等于（ ）A.1B.34 C.32D.312.如果⎰⎰-==1201)(,1)(dx x f dx x f ，则⎰=21)(dx x f ．3.（1）dx x ⎰πsin =________；（2）dx x ⎰π20sin =_________．4.求下列定积分的值 (1)dx x⎰311；（2）dx e x ⎰22.【课时作业】1.dx x1312⎰=_____________. 2.⎰-=-1121dx x ． 3.dx x x10⎰=___________________.4.求下列定积分的值 (1) dx x e ⎰++1211；（2）dx xx x⎰-20sin cos 2cos π;(3) dx x x ⎰⎪⎭⎫ ⎝⎛-31212.5.已知()623113+=-++⎰-a dx b a ax x且()d x b a ax x t f t⎰-++=033)(为偶函数，求b a ,的值.赠送初中数学几何模型【模型二】半角型：图形特征：45°4321DAC1FDAB正方形ABCD 中，∠EAF =45° ∠1=12∠BAD 推导说明：1.1在正方形ABCD 中，点E 、F 分别在BC 、CD 上，且∠F AE ＝45°，求证：EF ＝BE +DF45°DBa +b-aa45°ABE1.2在正方形ABCD 中，点E 、F 分别在BC 、CD 上，且EF ＝BE +DF ，求证：∠F AE ＝45°Da +b-aa45°E挖掘图形特征：a+bx-aa 45°DEa +bx -b-ab45°A运用举例：1．正方形ABCD 的边长为3，E 、F 分别是AB 、BC 边上的点,且∠EDF =45°.将△DAE 绕点D 逆时针旋转90°，得到△DCM .（1）求证：EF =FM（2）当AE =1时，求EF 的长．DE3．如图，梯形ABCD中，AD∥BC，∠C＝90°，BC＝CD＝2AD＝4，E为线段CD上一点，∠ABE＝45°. （1）求线段AB的长；（2）动点P从B出发，沿射线．．BE运动，速度为1单位/秒，设运动时间为t，则t为何值时，△ABP为等腰三角形；（3）求AE－CE的值.DC变式及结论：4.在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图1），求证：△AEG≌△AEF；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图3），请你直接写出线段EF，BE，DF之间的数量关系．AB CFEDCDC。

预习课本～，思考并完成下列问题()微积分基本定理的内容是什么？()被积函数()的原函数是否是唯一的？．微积分基本定理如果()是区间[，]上的连续函数，并且′()＝()，那么()＝()－()．这个结论叫做微积分基本定理，又叫做牛顿莱布尼茨公式．—为了方便，我们常常把()－()记为()，即()＝()＝()－()．[点睛]对微积分基本定理的理解()微积分基本定理表明，计算定积分()的关键是找到满足′()＝()的函数()，通常，我们可以运用基本初等函数的求导公式和导数的四则运算法则从反方向上求出()．()牛顿－莱布尼茨公式指出了求连续函数定积分的一般方法，把求定积分的问题，转化成求原函数(()叫做()的原函数)的问题，提示了导数和定积分的内在联系，同时也提供计算定积分的一种有效方法．．定积分和曲边梯形面积的关系设曲边梯形在轴上方的面积为上，在轴下方的面积为下．则()当曲边梯形的面积在轴上方时，如图①，则()＝上．()当曲边梯形的面积在轴下方时，如图②，则()＝－下．()当曲边梯形的面积在轴上方、轴下方均存在时，如图③，则()＝上－下，若上＝下，则()＝.．判断(正确的打“√”，错误的打“×”)()微积分基本定理中，被积函数()是原函数()的导数．( )()应用微积分基本定理求定积分的值时，为了计算方便通常取原函数的常数项为.( )()应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数．()答案：()√ ()√ ()√．下列积分值等于的是( )(＋)答案：．计算： ＝( )．－． ． ．答案：错误!定积分的求法[典例]()定积分(＋)的值为( ) ．＋ ．＋ ．．－()()＝(\\(＋，≤≤，，<≤，))求().[解析]()(＋)＝(＋)＝(＋)－(＋)＝，因此选. 答案： ()解：()＝()＋() ＝(＋)＋＝(＋)＋ ＝＋＋(－)＝.．由微积分基本定理求定积分的步骤当被积函数为两个函数的乘积时，一般要转化为和的形式，便于求得函数()，再计算定积分，具体步骤如下．第一步：求被积函数()的一个原函数()； 第二步：计算函数的增量()－()．。

预习导航1．微积分基本定理(1)定理内容：一般地，如果f(x)是区间[a，b]上的连续函数，并且F′(x)＝f(x)，那么b⎰f(x)d x＝F(b)－F(a)．a这个结论叫做微积分基本定理，又叫做牛顿—莱布尼茨公式．(2)符号表示：b a⎰f(x)d x＝F(x)|b a＝F(b)－F(a)．(3)作用：建立了积分与导数间的密切联系，并提供了计算定积分的有效方法．思考1满足F′(x)＝f(x)的函数F(x)是唯一的吗？这影响微积分基本定理的正确性吗？提示：满足F′(x)＝f(x)的函数F(x)不是唯一的，这些函数之间相差一个常数，即[F(x)＋c]′＝f(x)，但这并不影响微积分基本定理，因为bf(x)d x＝[F(x)＋c]|b aa＝[F(b)＋c]－[F(a)＋c]＝F(b)－F(a)，所以用一个最简单的原函数F(x)就可以．思考2求导数运算与求原函数运算有什么关系？提示：求导数运算与求原函数运算可以看做是互逆的运算，但一个函数的导函数是唯一的，而一个导函数的原函数却不止一个，这些原函数之间仅相差一个常数，在利用微积分基本定理计算定积分时，只要选用最简单的一个即可．2．定积分和曲边梯形面积的关系设曲边梯形在x轴上方的面积为S上，在x轴下方的面积为S下，则(1)当曲边梯形在x轴上方时，如图①，则b⎰f(x)d x＝S上．a(2)当曲边梯形在x轴下方时，如图②，则b⎰f(x)d x＝－S下．a(3)当曲边梯形在x轴上方、x轴下方均存在时，如图③，则b⎰f(x)d x＝S上－S下．a若S上＝S下，则b⎰f(x)d x＝0.a。

选修2-2 1.6 微积分基本定理一、选择题1．下列积分正确的是( )[答案] AA.214 B.54 C.338D.218[答案] A[解析] ⎠⎛2－2⎝⎛⎭⎫x 2＋1x 4d x ＝⎠⎛2－2x 2d x ＋⎠⎛2－21x 4d x ＝13x 3| 2－2＋⎝⎛⎭⎫－13x －3| 2－2 ＝13(x 3－x －3)| 2－2 ＝13⎝⎛⎭⎫8－18－13⎝⎛⎭⎫－8＋18＝214.故应选A.3.⎠⎛1－1|x |d x 等于( )A.⎠⎛1－1x d xB.⎠⎛1－1d xC.⎠⎛0－1(－x )d x ＋⎠⎛01x d xD.⎠⎛0－1x d x ＋⎠⎛01(－x )d x[答案] C[解析] ∵|x |＝⎩⎪⎨⎪⎧x (x ≥0)－x (x <0)∴⎠⎛1－1|x |d x ＝⎠⎛0－1|x |d x ＋⎠⎛01|x |d x＝⎠⎛0－1(－x )d x ＋⎠⎛01x d x ，故应选C.4．设f (x )＝⎩⎪⎨⎪⎧x 2 (0≤x <1)2－x (1≤x ≤2)，则⎠⎛02f (x )d x 等于( )A.34 B.45 C.56D ．不存在[答案] C[解析] ⎠⎛02f (x )d x ＝⎠⎛01x 2d x ＋⎠⎛12(2－x )d x取F 1(x )＝13x 3，F 2(x )＝2x －12x 2，则F ′1(x )＝x 2，F ′2(x )＝2－x ∴⎠⎛02f (x )d x ＝F 1(1)－F 1(0)＋F 2(2)－F 2(1)＝13－0＋2×2－12×22－⎝⎛⎭⎫2×1－12×12＝56.故应选C. 5.⎠⎛ab f ′(3x )d x ＝( )A ．f (b )－f (a )B ．f (3b )－f (3a ) C.13[f (3b )－f (3a )]D ．3[f (3b )－f (3a )][答案] C[解析] ∵⎣⎡⎦⎤13f (3x )′＝f ′(3x ) ∴取F (x )＝13f (3x )，则⎠⎛ab f ′(3x )d x ＝F (b )－F (a )＝13[f (3b )－f (3a )]．故应选C. 6.⎠⎛03|x 2－4|d x ＝( )A.213 B.223 C.233D.253[答案] C[解析] ⎠⎛03|x 2－4|d x ＝⎠⎛02(4－x 2)d x ＋⎠⎛23(x 2－4)d x＝⎝⎛⎭⎫4x －13x 3| 20＋⎝⎛⎭⎫13x 3－4x | 32＝233.A ．－32 B ．－12C.12D.32[答案] D[解析] ∵1－2sin 2θ2＝cos θ8．函数F (x )＝⎠⎛0x cos t d t 的导数是( )A ．cos xB ．sin xC ．－cos xD ．－sin x[答案] A[解析] F (x )＝⎠⎛0x cos t d t ＝sin t | x0＝sin x －sin0＝sin x .所以F ′(x )＝cos x ，故应选A. 9．若⎠⎛0k (2x －3x 2)d x ＝0，则k ＝( )A ．0B ．1C ．0或1D ．以上都不对[答案] C[解析] ⎠⎛0k (2x －3x 2)d x ＝(x 2－x 3)| k0＝k 2－k 3＝0，∴k ＝0或1.10．函数F (x )＝⎠⎛0x t (t －4)d t 在[－1,5]上( )A ．有最大值0，无最小值B ．有最大值0和最小值－323C ．有最小值－323，无最大值D ．既无最大值也无最小值 [答案] B[解析] F (x )＝⎠⎛0x (t 2－4t )d t ＝⎝⎛⎭⎫13t 3－2t 2| x0＝13x 3－2x 2(－1≤x ≤5)． F ′(x )＝x 2－4x ，由F ′(x )＝0得x ＝0或x ＝4，列表如下：x (－1,0) 0 (0,4) 4 (4,5) F ′(x ) ＋0 － 0 ＋F (x )极大值极小值可见极大值F (0)＝0，极小值F (4)＝－323.又F (－1)＝－73，F (5)＝－253∴最大值为0，最小值为－323. 二、填空题 11．计算定积分： ①⎠⎛1－1x 2d x ＝________②⎠⎛23⎝⎛⎭⎫3x －2x 2d x ＝________ ③⎠⎛02|x 2－1|d x ＝________ ④⎠⎛0－π2|sin x |d x ＝________[答案] 23；436；2；1[解析] ①⎠⎛1－1x 2d x ＝13x 3| 1－1＝23.②⎠⎛23⎝⎛⎭⎫3x －2x 2d x ＝⎝⎛⎭⎫32x 2＋2x | 32＝436.③⎠⎛02|x 2－1|d x ＝⎠⎛01(1－x 2)d x ＋⎠⎛12(x 2－1)d x＝⎝⎛⎭⎫x －13x 3| 10＋⎝⎛⎭⎫13x 3－x | 21＝2.[答案] 1＋π213．(2010·陕西理，13)从如图所示的长方形区域内任取一个点M (x ，y )，则点M 取自阴影部分的概率为________．[答案] 13[解析] 长方形的面积为S 1＝3，S 阴＝⎠⎛013x 2dx ＝x 3| 10＝1，则P ＝S 1S 阴＝13.14．已知f (x )＝3x 2＋2x ＋1，若⎠⎛1－1f (x )d x ＝2f (a )成立，则a ＝________.[答案] －1或13[解析] 由已知F (x )＝x 3＋x 2＋x ，F (1)＝3，F (－1)＝－1， ∴⎠⎛1－1f (x )d x ＝F (1)－F (－1)＝4，∴2f (a )＝4，∴f (a )＝2.即3a 2＋2a ＋1＝2.解得a ＝－1或13.三、解答题15．计算下列定积分： (1)⎠⎛052x d x ；(2)⎠⎛01(x 2－2x )d x ；(3)⎠⎛02(4－2x )(4－x 2)d x ；(4)⎠⎛12x 2＋2x －3x d x .[解析] (1)⎠⎛052x d x ＝x 2| 50＝25－0＝25.(2)⎠⎛01(x 2－2x )d x ＝⎠⎛01x 2d x －⎠⎛012x d x＝13x 3| 10－x 2| 10＝13－1＝－23.(3)⎠⎛02(4－2x )(4－x 2)d x ＝⎠⎛02(16－8x －4x 2＋2x 3)d x＝⎝⎛⎭⎫16x －4x 2－43x 3＋12x 4| 20 ＝32－16－323＋8＝403.(4)⎠⎛12x 2＋2x －3x d x ＝⎠⎛12⎝⎛⎭⎫x ＋2－3x d x ＝⎝⎛⎭⎫12x 2＋2x －3ln x | 21＝72－3ln2. 16．计算下列定积分：[解析] (1)取F (x )＝12sin2x ，则F ′(x )＝cos2x＝12⎝⎛⎭⎫1－32＝14(2－3)． (2)取F (x )＝x 22＋ln x ＋2x ，则F ′(x )＝x ＋1x＋2.∴⎠⎛23⎝⎛⎭⎫x ＋1x 2d x ＝⎠⎛23⎝⎛⎭⎫x ＋1x ＋2d x ＝F (3)－F (2)＝⎝⎛⎭⎫92＋ln3＋6－⎝⎛⎭⎫12×4＋ln2＋4 ＝92＋ln 32. (3)取F (x )＝32x 2－cos x ，则F ′(x )＝3x ＋sin x17．计算下列定积分： (1)⎠⎛0－4|x ＋2|d x ；(2)已知f (x )＝，求⎠⎛3－1f (x )d x 的值．[解析] (1)∵f (x )＝|x ＋2|＝∴⎠⎛0－4|x ＋2|d x ＝－⎠⎛－4－2(x ＋2)d x ＋⎠⎛0－2(x ＋2)d x＝－⎝⎛⎭⎫12x 2＋2x | －2－4＋⎝⎛⎭⎫12x 2＋2x | 0－2 ＝2＋2＝4.(2)∵f (x )＝∴⎠⎛3－1f (x )d x ＝⎠⎛0－1f (x )d x ＋⎠⎛01f (x )d x ＋⎠⎛12f (x )d x ＋⎠⎛23f (x )d x ＝⎠⎛01(1－x )d x ＋⎠⎛12(x －1)d x＝⎝⎛⎭⎫x －x 22| 10＋⎝⎛⎭⎫x 22－x | 21 ＝12＋12＝1. 18．(1)已知f (a )＝⎠⎛01(2ax 2－a 2x )d x ，求f (a )的最大值；(2)已知f (x )＝ax 2＋bx ＋c (a ≠0)，且f (－1)＝2，f ′(0)＝0，⎠⎛01f (x )d x ＝－2，求a ，b ，c的值．[解析] (1)取F (x )＝23ax 3－12a 2x 2则F ′(x )＝2ax 2－a 2x ∴f (a )＝⎠⎛01(2ax 2－a 2x )d x＝F (1)－F (0)＝23a －12a 2＝－12⎝⎛⎭⎫a －232＋29∴当a ＝23时，f (a )有最大值29.(2)∵f (－1)＝2，∴a －b ＋c ＝2① 又∵f ′(x )＝2ax ＋b ，∴f ′(0)＝b ＝0② 而⎠⎛01f (x )d x ＝⎠⎛01(ax 2＋bx ＋c )d x取F (x )＝13ax 3＋12bx 2＋cx则F ′(x )＝ax 2＋bx ＋c∴⎠⎛01f (x )d x ＝F (1)－F (0)＝13a ＋12b ＋c ＝－2③解①②③得a ＝6，b ＝0，c ＝－4.。

第一章 1．6 微积分基本定理提能达标过关一、选择题1.⎠⎛02(x 2＋1)d x ＝( ) A.143 B ．6 C ．8D ．10解析：⎠⎛02(x 2＋1)d x ＝⎝ ⎛⎭⎪⎫13x 3＋x ＝83＋2－0＝143，故选A.答案：A 2．sin 2x d x 等于( )A.π4 B.π2－1 C ．2D.π－24解析：sin 2x ＝1－cos 2x2.∵⎝ ⎛⎭⎪⎫12x －14sin 2x ′＝12－12cos 2x ， ∴sin 2x d x ＝＝⎝ ⎛⎭⎪⎫12×π2－14sin π－⎝ ⎛⎭⎪⎫0－14sin 0 ＝π4. 答案：A3．设f (x )是一次函数，且⎠⎛01f (x )d x ＝5，⎠⎛01xf (x )d x ＝176，则f (x )＝( )A ．4x ＋3B ．3x ＋4C ．－4x ＋2D ．－3x ＋4解析：设f (x )＝ax ＋b (a ≠0)，∴⎠⎛01f (x )d x ＝⎝ ⎛⎪⎪⎪⎭⎪⎫12ax 2＋bx 10，⎠⎛01xf (x )d x ＝⎝⎛⎪⎪⎪⎭⎪⎫13ax 3＋12bx 210，∴⎩⎪⎨⎪⎧12a ＋b ＝5，13a ＋12b ＝176，解得a ＝4，b ＝3，故f (x )＝4x ＋3.答案：A4．已知一个二次函数f (x )的图象如图所示，那么f (x )d x ＝( )A ．1 B.π2 C.43D ．2解析：由图象可知二次函数f (x )＝－x 2＋1， ∴f (x )d x ＝(－x 2＋1)d x ＝⎝ ⎛⎭⎪⎫－13x 3＋x＝⎝ ⎛⎭⎪⎫－13＋1－⎝ ⎛⎭⎪⎫13－1＝43，故选C. 答案：C5．已知a ＝⎠⎛01e x d x ，b ＝1－x 2d x ，c ＝⎠⎛1e 2x d x ，则a 、b 、c 的大小关系为( )A ．b<c<aB ．a<b<cC ．b<a<cD ．c<b<a解析：依题意，a＝⎠⎛1e x d x＝e x10＝e1－e0＝e－1，b ＝1－x2d x＝12×π×12＝π2，∵π2<e－1<2，∴b<a<c，故选C.答案：C二、填空题6．(2019·南昌第二中学高二期末)16－x2d x＋x3d x＝________.解析：由于y＝16－x2表示圆心在原点，半径为4的圆的上半部分，故16－x2d x＝12×π×42＝8π.x3d x＝＝0.故原式＝8π.答案：8π7．(2019·西安高二期末)如图，在边长为1的正方形中随机撒一粒黄豆，则它落在阴影部分的概率为________．解析：由题意，结合定积分可得阴影部分的面积为由几何概型的计算公式可得，黄豆在阴影部分的概率为P＝131×1＝13.答案：138．设f (x )＝⎩⎪⎨⎪⎧lg x (x ＞0)，x ＋⎠⎛0a 3t 2d t (x ≤0).若f [f (1)]＝1，则a ＝________.解析：∵f (1)＝lg 1＝0. ∴f [f (1)]＝f (0)＝0＋⎠⎛0a 3t 2d t ＝1.即⎠⎛0a 3t 2d t ＝1.答案：1 三、解答题9．(2019·山西沁县中学高二期中)计算由直线y ＝6－x ，曲线y ＝8x 以及x 轴所围图形的面积．解：作出直线y ＝6－x ，曲线y ＝8x 的草图， 所求面积为图中阴影部分的面积．解方程组⎩⎨⎧y ＝6－x ，y ＝8x ，得直线y ＝6－x 与曲线y ＝8x 交点的坐标为(2,4)，直线y ＝6－x 与x 轴的交点坐标为(6,0)． 若选x 为积分变量，所求图形的面积 S ＝S 1＋S 2＝⎠⎛028x d x ＋⎠⎛26(6－x )d x＝ ⎪⎪⎪⎝ ⎛⎭⎪⎫8×23x 3220＋⎪⎪⎪⎝ ⎛⎭⎪⎫6x －12x 262＝163＋⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫6×6－12×62－⎝ ⎛⎭⎪⎫6×2－12×22＝163＋8＝403.10．已知(x3＋ax＋3a－b)d x＝2a＋6且f(t)＝⎠⎛t(x3＋ax＋3a－b)d x为偶函数，求a，b的值．解：∵f(x)＝x3＋ax为奇函数，∴(x3＋ax)d x＝0，∴(x3＋ax＋3a－b)d x＝(x3＋ax)d x＋(3a－b)d x＝0＋(3a－b)[1－(－1)]＝6a－2b.∴6a－2b＝2a＋6，即2a－b＝3，①＝t44＋at22＋(3a－b)t为偶函数，∴3a－b＝0，②由①②得a＝－3，b＝－9.。

高中数学学习材料鼎尚图文*整理制作§1.6微积分基本定理教学目标：1、能说出微积分基本定理。

2、能运用微积分基本定理计算简单的定积分。

3、能掌握微积分基本定理的应用。

4、会用牛顿-莱布尼兹公式求简单的定积分。

教学重点： 通过探究变速直线运动物体的速度与位移的关系，使学生直观了解微积分基本定理的含义，并能正确运用基本定理计算简单的定积分；教学难点：微积分基本定理的含义．教学过程设计（一）、复习引入，激发兴趣。

【教师引入】同学们，我们来复习一下上节课的内容，请同学们回答以下几个问题: 1. 我们如何确定曲线上一点处切线的斜率呢？2. 如何求曲线下方的面积？3. 用“以直代曲”解决问题的思想和具体操作过程是什么呢？求由连续曲线y=f(x)对应的曲边梯形面积的方法。

我们讲过用定积分定义计算定积分,但其计算过程比较复杂，所以不是求定积分的一般方法。

我们必须寻求计算定积分的新方法，也是比较一般的方法。

(二)、探究新知，揭示概念变速直线运动中位置函数与速度函数之间的联系设一物体沿直线作变速运动，在时刻t 时物体所在位置为S(t),速度为v(t)（()v t o ），则物体在时间间隔12[,]T T 内经过的路程可用速度函数表示为21()T T v t dt ⎰。

另一方面，这段路程还可以通过位置函数S （t ）在12[,]T T 上的增量12()()S T S T -来表达，即 21()T T v t dt ⎰=12()()S T S T -而()()S t v t '=。

对于一般函数()f x ，设()()F x f x '=，是否也有()()()b a f x d x F b F a =-⎰（三）、分析归纳，抽象概括若上式成立，我们就找到了用()f x 的原函数（即满足()()F x f x '=）的数值差()()F b F a -来计算()f x 在[,]a b 上的定积分的方法。