圆的复习练习题

高考圆复习题一、选择题1. 圆的标准方程是：A. \((x-a)^2+(y-b)^2=r^2\)B. \(x^2+y^2=r^2\)C. \((x-a)^2+(y-b)^2=1\)D. \(x^2+y^2=1\)2. 已知圆的半径为5，圆心到直线的距离为3，那么直线与圆的位置关系是：A. 相切B. 相交C. 相离D. 内切3. 圆的切线与半径垂直，切点到圆心的距离等于：A. 半径的长度B. 切线的长度C. 圆心到切点的距离D. 半径的一半二、填空题4. 若圆的方程为 \(x^2+y^2=9\)，圆心坐标为（0，0），半径为3，则圆上任意一点P(x,y)到圆心的距离为______。

5. 圆 \(x^2+y^2+Dx+Ey+F=0\) 与直线 \(Ax+By+C=0\) 相切，则\(D^2+E^2-4F=\) ______。

三、解答题6. 已知圆 \((x-2)^2+(y+1)^2=9\)，求圆心坐标和半径。

7. 证明：圆的任意一条直径所对的圆周角是直角。

8. 已知圆心在原点，半径为4的圆，求经过点P(3,2)的圆的切线方程。

四、综合题9. 圆 \(x^2+y^2-4x-6y-10=0\) 与直线 \(2x+3y-11=0\) 相交于A、B 两点，求弦AB的长度。

10. 已知圆 \(x^2+y^2=16\) 内接于一个矩形，求矩形的面积最大值。

【答案】1. A2. B3. A4. 35. \(AB^2\)6. 圆心坐标为(2,-1)，半径为3。

7. 证明略。

8. 切线方程为 \(x+3y-7=0\) 或 \(3x-y-5=0\)。

9. 弦AB的长度为 \(\sqrt{65}\)。

10. 矩形面积最大值为32。

【结束语】通过以上题目的练习，相信同学们对圆的方程、性质、与直线的位置关系等知识点有了更深刻的理解和掌握。

希望同学们能够继续努力，不断巩固和提高自己的数学能力，为即将到来的高考做好充分的准备。

圆的练习题一．选择题1．⊙O是△ABC的外接圆，直线EF切⊙O于点A,若∠BAF=40°，则∠C等于（)A、20°B、40°C、50°D、80°2．如图,BC是⊙O的直径，P是CB延长线上一点，P A切⊙O于点A，如果P A＝, PB＝1，那么∠APC等于(）3．某工件形状如图所示，圆弧BC的度数为，AB＝6厘米，点B到点C的距离等于AB,∠BAC＝,则工件的面积等于（)(A)4π（B）6π(C）8π(D）10π4．下列语句中正确的是（)(1）相等的圆心角所对的弧相等;(2)平分弦的直径垂直于弦；(3）长度相等的两条弧是等弧；（4)经过圆心的每一条直线都是圆的对称轴．（A）1个（B)2个(C)3个(D)4个5．如图,两个等圆⊙O和⊙的两条切线OA、OB，A、B是切点，则∠AOB等于() (A）(B）（C）(D）6．如图，⊙A、⊙B、⊙C、⊙D、⊙E相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE,则图中五个扇形（阴影部分）的面积之和是(）(A）π（B）1。

5π（C)2π（D）2。

5π7。

在Rt△ABC中，已知AB＝6，AC＝8,∠A＝．如果把Rt△ABC绕直线AC旋转一周得到一个圆锥，其表面积为S;把Rt△ABC绕直线AB旋转一周得到另一个圆锥,其表面积为S，那么S∶S（）(A）2∶3(B)3∶4(C)4∶9（D)5∶128．圆锥的母线长为13cm，底面半径为5cm，则此圆锥的高线长为() A．6 cm B．8 cm C．10 cm D．12 cm9．已知⊙O1和⊙O2相外切，它们的半径分别是1厘米和3厘米．那么半径是4厘米，且和⊙O1、⊙O2都相切的圆共有（）(A）1个(B)2个（C)5个(D)6个10．已知圆的半径为6。

5厘米，如果一条直线和圆心距离为6。

5厘米，那么这条直线和这个圆的位置关系是()（A）相交（B)相切（C)相离（D)相交或相离二．填空题1．已知：如图，AB是⊙O的直径，弦CD⊥AB于P，CD＝10cm,AP︰PB＝1︰5．则：⊙O的半径为。

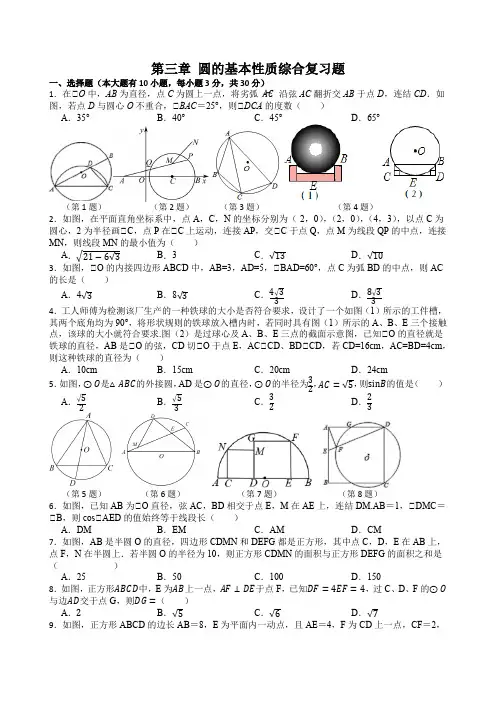
第三章圆的基本性质综合复习题一、选择题（本大题有10小题，每小题3分，共30分）1．在⊙O中，AB为直径，点C为圆上一点，将劣弧AC⌢沿弦AC翻折交AB于点D，连结CD．如图，若点D与圆心O不重合，⊙BAC＝25°，则⊙DCA的度数（）A．35°B．40°C．45°D．65°（第1题）（第2题）（第3题）（第4题）2．如图，在平面直角坐标系中，点A，C，N的坐标分别为（-2，0），（2，0），（4，3），以点C为圆心，2为半径画⊙C，点P在⊙C上运动，连接AP，交⊙C于点Q，点M为线段QP的中点，连接MN，则线段MN的最小值为（）A．√21−6√3B．3C．√13D．√103．如图，⊙O的内接四边形ABCD中，AB=3，AD=5，⊙BAD=60°，点C为弧BD的中点，则AC 的长是（）A．4√3B．8√3C．4√33D．8√334．工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图（1）所示的工件槽，其两个底角均为90°，将形状规则的铁球放入槽内时，若同时具有图（1）所示的A、B、E三个接触点，该球的大小就符合要求.图（2）是过球心及A、B、E三点的截面示意图，已知⊙O的直径就是铁球的直径，AB是⊙O的弦，CD切⊙O于点E，AC⊙CD、BD⊙CD，若CD=16cm，AC=BD=4cm，则这种铁球的直径为（）A．10cm B．15cm C．20cm D．24cm5．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，⊙O的半径为32，AC=√5，则sinB的值是（）A．√52B．√53C．32D．23（第5题）（第6题）（第7题）（第8题）6．如图，已知AB为⊙O直径，弦AC，BD相交于点E，M在AE上，连结DM.AB＝1，⊙DMC＝⊙B，则cos⊙AED的值始终等于线段长（）A．DM B．EM C．AM D．CM7．如图，AB是半圆O的直径，四边形CDMN和DEFG都是正方形，其中点C，D，E在AB上，点F，N在半圆上．若半圆O的半径为10，则正方形CDMN的面积与正方形DEFG的面积之和是（）A．25B．50C．100D．1508．如图，正方形ABCD中，E为AB上一点，AF⊥DE于点F，已知DF=4EF=4，过C、D、F的⊙O 与边AD交于点G，则DG=（）A．2B．√5C．√6D．√79．如图，正方形ABCD的边长AB＝8，E为平面内一动点，且AE＝4，F为CD上一点，CF＝2，连接EF，ED，则2EF+ED的最小值为（）A．12√3B．12√2C．12D．1010．如图，将边长为6的正六边形ABCDEF沿HG折叠，点B恰好落在边AF的中点上，延长B′C′交EF 于点M，则C′M的长为（）A．1B．65C．56D．9 5（第9题）（第10题）（第11题）（第12题）二、填空题（本大题有6小题，每小题4分，共24分）11．如图，正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH 的边长为6，则正六边形ABCDEF的边长为.12．如图，△ABC内接于⊙O，AH⊥BC于点H，若AC=10，AH=8，⊙O的半径为7，则AB=．13．如图，在平面直角坐标系中，点A（－1，0），点B（1，0），点M（3，4），以M为圆心，2为半径作⊙M.若点P是⊙M上一个动点，则PA2＋PB2的最大值为（第13题）（第14题）（第15题）（第16题）14．如图，ABCD为圆O的内接四边形，且AC⊙BD，若AB=10，CD=8，则圆O的面积为. 15．如图，AB是⊙O的直径，点M是⊙O内的一定点，PQ是⊙O内过点M的一条弦，连接AM，AP，AQ，若⊙O的半径为4，AM=√5，则AP⋅AQ的最大值为．16．如图，点A，C，D，B在⊙O上，AC＝BC，⊙ACB＝90°．若CD＝a，tan⊙CBD＝13，则AD的长是．三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）17．如图，AB是⊙O的直径，C是的中点，CE⊙AB于E，BD交CE于点F，（1）求证：CF＝BF；（2）若CD＝12，AC＝16，求⊙O的半径和CE的长。

北师大版六年级上册数学圆的复习练习题圆的复习（一）一、填写：1、用圆规画一个周长50.24厘米的圆,圆规两脚之间的距离是（）厘米,所画的圆的面积是（）平方厘米。

2、圆的半径扩大3倍,直径扩大（）倍,周长扩大（）倍；面积扩大（）倍。

3、一根铁丝正好围成一个直径2米的圆,这根铁丝长（）米；如果改围成一个正方形,正方形的边长是（）米,面积是（）平方米。

4、小圆半径6厘米,大圆半径8厘米。

大圆和小圆半径的比是（）；直径的比是（）；周长的比是（）；面积的比是（）。

二、解决问题：1、一辆自行车轮胎外直径50厘米,如果自行车每分钟转120周,这辆自行车每小时能行多少千米？（得数保留整千米）2、在长8分米宽6分米的长方形中画一个最大的圆,圆的周长和面积各是多少？3、在长8分米宽6分米的长方形中画一个最大的半圆,半圆的周长和面积各是多少？4、一个圆形喷水池的周长62.8米,在水池外边有一条0.5米宽的水泥路。

路的面积是多少平方米？三、判断：1、圆的半径有无数条。

…………………………………………………………（）2、圆的直径是半径的2倍。

……………………………………………………（）3、圆有无数条对称轴。

………………………………………………………（）4、圆的半径都相等。

…………………………………………………………（）5、直径4厘米的圆与半径2厘米的圆一样大。

………………………………（）6、半径2分米的圆的周长和面积一样大。

…………………………………（）圆的复习（二）一、选择：1、圆周率π的值（）。

A 等于3.14B 大于3.14C 小于3.142、一个圆的半径2米,那么它的周长和面积相比,（）。

A 面积大B 周长大C 同样大D 无法比较3、直径是通过圆心并且两端都在圆上的（）。

A 线段B 直线C 射线4、把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长（）。

A 等于圆周长B 大于圆周长C 小于圆周长D 无法比较5、圆的直径扩大2倍,它的面积扩大（）。

圆精选练习题及答案一一、选择题(共8题，每题有四个选项，其中只有一项符合题意。

每题3分，共24 分):1. 下列说法正确的是()A.垂直于半径的直线是圆的切线B. 经过三点一定可以作圆C.圆的切线垂直于圆的半径D. 每个三角形都有一个内切圆2. 在同圆或等圆中，如果AB = 2CD ，则AB与CD的关系是()(A)AB > 2CD (B)AB = 2CD (C)AB V 2CD (D)AB = CD3. 如图(1),已知PA切O O于B,OP交AB于C,则图中能用字母表示的直角共有()个A.3B.4C.5D.6⑵4. 已知O O的半径为10cm,弦AB// CD,AB=12cm,CD=16cr则AB和CD的距离为()A.2cmB.14cmC.2cm 或14cmD.10cm 或20cm5. 在半径为6cm的圆中，长为2 - cm的弧所对的圆周角的度数为()A.30 °B.100C.120°D.130 °6. 如图(2),已知圆心角/ AOB勺度数为100° ,则圆周角/ ACB的度数是()A.80 °B.100 °C.120°D.130 °7. O O的半径是20cm,圆心角/ AOB=120 ,AB是O O弦,则S. AOB等于()A.25 .3 cmB.50 、3 cnfC.100 \ 3 cn iD.200 、3 cnf8. 如图(3),半径0A 等于弦AB,过B 作O 0的切线BC,取BC=AB,O 交O 0于E,AC 交O 0于点D,则BD 和DE 的度数分别为()、填空题:(每小题4分,共20分):11. 一条弦把圆分成1 ：3两部分，贝U 劣弧所对的圆心角的度数为 12. 如果O O 的直径为10cm,弦AB=6cm 那么圆心O 到弦AB 的距离为 13. 在O O 中，弦AB 所对的圆周角之间的关系为 14. 如图(4), 。

《圆》知识点及练习题一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；A四、圆与圆的位置关系外离（图1）⇒ 无交点 ⇒ d R r >+； 外切（图2）⇒ 有一个交点 ⇒ d R r =+； 相交（图3）⇒ 有两个交点 ⇒ R r d R r -<<+； 内切（图4）⇒ 有一个交点 ⇒ d R r =-； 内含（图5）⇒ 无交点 ⇒ d R r <-；五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； （2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧 以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。

圆的复习练习题
一、解决问题。

1、一个圆的半径是4厘米，这个圆的周长是多少厘米？
2、农场里有一个自动旋转喷水器，喷水器的射程是6米，请问喷灌面积是多少平方米？
3、有一个直径是4米圆形的花坛，在花坛的外面修一条宽为1米的环形小路，小路的面积是多少平方米？
4、在一个圆形花坛的周围安装电线杆，每两根电线杆之间的距离是1.256米，先安装了20根，这个圆的半径是多少米？
5、有一根铁丝刚好可以围成一个半径是6厘米的圆，如果
用这根铁丝围成一个正方形，围成的正方形的边长是多少厘米？
二、填空题。

1、半径为10厘米的半圆，它的周长是（）。

2、用一根28.26厘米的铁丝围成一个圆，围成的圆的半径是（）厘米，面积是（）平方厘米。

3、在一块草地的中间用一根2米长的绳子拴着一头牛，牛能吃到的草的面积是（）平方米。

4、甲乙两个圆的半径分别是8厘米和10厘米，甲乙两个圆的面积比是（）。

5、以四分之一圆为弧的扇形的圆心角是（）。

6、一个钟面的分针长30厘米，从10：00到10：30，分子尖端走过的距离是（）厘米。

7、把一个周长是31.4厘米的圆的半径增加2厘米，它的周长增加（）厘米。

8、画一个直径9厘米的圆，圆规的两脚要张开（）厘米，画出的圆的周长是（）。

圆的练习题及答案圆是几何学中的重要概念，它在我们的生活中随处可见。

无论是在建筑设计中的圆形窗户，还是在日常生活中的圆形饼干，圆形都扮演着重要的角色。

为了更好地理解和应用圆，我们需要进行一些练习题。

在本文中，我将为大家提供一些圆的练习题及其答案，希望能够帮助大家更好地掌握这一知识点。

练习题一：计算圆的面积和周长1. 已知圆的半径为5cm，求其面积和周长。

答案：圆的面积公式为πr²，其中π取3.14，半径r为5cm。

所以面积为3.14 * 5² = 78.5cm²。

圆的周长公式为2πr，所以周长为2 * 3.14 * 5 = 31.4cm。

2. 已知圆的直径为12cm，求其面积和周长。

答案：圆的直径是半径的两倍，所以半径r为12cm的一半，即6cm。

根据上述公式，可以计算出面积为3.14 * 6² = 113.04cm²，周长为2 * 3.14 * 6 =37.68cm。

练习题二：判断圆的位置关系1. 判断以下两个圆的位置关系：圆A的半径为10cm，圆心坐标为(0, 0)；圆B 的半径为5cm，圆心坐标为(8, 0)。

答案：首先，我们可以通过计算两个圆心之间的距离来判断它们的位置关系。

两个圆心的坐标分别为(0, 0)和(8, 0)，所以它们的横坐标之差为8-0=8，纵坐标之差为0-0=0。

根据勾股定理，两个圆心之间的距离为√(8²+0²)=8。

由于两个圆的半径之和为10+5=15，大于圆心之间的距离8，所以这两个圆相交。

2. 判断以下两个圆的位置关系：圆A的半径为6cm，圆心坐标为(0, 0)；圆B的半径为3cm，圆心坐标为(10, 0)。

答案：同样地，我们计算两个圆心之间的距离。

两个圆心的坐标分别为(0, 0)和(10, 0)，横坐标之差为10-0=10，纵坐标之差为0-0=0。

根据勾股定理，两个圆心之间的距离为√(10²+0²)=10。

人教版六年级数学上册第五单元：圆的复习题圆有关计算公式：1、圆的周长公式：C=πd 或C=2πr 。

（d=C ÷π r=C ÷π÷2）2、圆的面积公式：Ｓ＝πｒ² 或者S=π（d ÷2）² 或者S=π（C ÷π ÷2）²3、圆环的面积公式：S=πR ²－πｒ² 或 S=π（R ²－ｒ²）。

（其中R ＝r ＋环的宽度）4、半圆的周长等于圆的周长的一半加直径。

半圆周长公式：Ｃ＝πd ÷2＋d 或Ｃ＝πr ＋2r5、半圆面积＝圆面积÷2 公式为：Ｓ＝πｒ²÷26、如果两个圆的半径比是2：3，那么这两个圆的直径比和周长比都是2：3，而面积比是4：9。

强化练习：一、填空题。

1、圆的半径扩大2倍，直径就扩大（ ）倍，周长就扩大（ ）倍，面积就扩大（ ）倍。

2、一个圆的的直径是12厘米，它的半径是（ ）厘米，周长是（ ）厘米。

3、用圆规画一个周长50.24cm 的圆，圆规两脚尖之间的距离应是（ ）cm ，画出的这个圆的面积是（ ）cm ²。

4、一个时钟的时针长5厘米，它转动一周形成的图形是（ ），这根时针的尖端转动一昼夜所走的路程是（ ）厘米。

5、在一个长10cm 宽8cm 的长方形内画一个最大的圆，这个圆的周长是（ ）cm ,面积是（ ）cm 2 。

6、圆有（ ）条对称轴，长方形有（ ）条对称轴，正方形有（ ）条对称轴，等边三角形有（ ）对称轴。

7、下图是把圆平均分成若干等份后拼成的一个近似的长方形。

已知长方形的宽是4厘米，求这个长方形的长是（ ）厘米，面积是（ ）平方厘米。

8、在右图中，大圆的半径是（ ）cm ，直径是（ ）cm ；小圆的半径是（ ）cm ，直径是（ ）cm ；阴影部分的周长是（ ）cm ，面积是（ ）cm ²。

第五单元圆第1课时圆的认识（1）【过基础关】教材知识巩固练1.我会填。

（1）（）决定圆的位置,（）决定圆的大小。

（2）在同一个圆里,所有的半径（）,所有的（）都相等,直径等于半径的（）。

（3）用圆规画一个直径20cm的圆,圆规两脚间的距离是（）cm。

2.我会判。

（1）从圆心到圆周上任意一点的距离都相等。

（）（2）圆内有无数条直径,只有8条半径。

( )（3）直径永远等于半径的2倍。

( )（4）直径是一个圆中最长的线段。

( )（5）直径为5厘米的圆比半径为3厘米的圆大。

（）3.我会选。

（1）半径是2厘米的圆,直径是( )。

A．2cm B．4cm C．6cm（2）以一个点为圆心,可以画( )个圆。

A．1 B．2 C．无数（3）在一个边长为10cm 的正方形中,画一个最大的圆,圆的半径是( )。

A．10cm B．5cm C．15cm（4）如右图,正方形内有4个同样大小的圆,每个圆的半径是（）厘米。

A.10B.5C.2.54.画一个半径为2厘米的圆,并用字母标出它的圆心、半径和直径。

5.看图计算。

（1）（2）d＝ r＝大圆的直径是小圆的半径是【过能力关】思维拓展提升练6.如下图,这个长方形的周长和面积分别是多少?参考答案1.（1）圆心半径（2）都相等直径 2倍（3）102.（1）√（2）×（3）×（4）√（5）×3.（1）B (2)C (3)B (4)C4.略5.（1）8cm 4cm （2）6cm 4.5cm6. 4×6=24（cm） 4×2=8（cm）周长：（24+8）×2=64（cm）面积：24×8=192（cm2）。

圆的认识练习题
圆是几何中的一个基本概念，广泛应用在数学、物理等领域。

了解和熟悉圆的性质和相关概念对于学习几何非常重要。

为此，以下是一些关于圆的认识练习题，帮助巩固和加深对圆的理解。

练习题1：基本概念
1. 圆是什么形状？
2. 圆的特点有哪些？
3. 请描述一下圆的半径和直径的关系。

4. 圆的周长公式是什么？
5. 圆的面积公式是什么？
练习题2：圆的性质
1. 判断下列说法是否正确：如果两个圆的半径相等，那么它们的面积一定相等。

2. 判断下列说法是否正确：如果两个圆的半径相等，那么它们的周长一定相等。

3. 如果一个圆的半径是3cm，那么它的直径是多少？
4. 如果一个圆的直径是8cm，那么它的半径是多少？
5. 如果一个圆的周长是12π cm，那么它的半径是多少？
6. 如果一个圆的周长是30 cm，那么它的半径是多少？
练习题3：圆和其他几何图形的关系
1. 判断下列说法是否正确：圆是正方形的一种特殊情况。

2. 判断下列说法是否正确：圆不是任何一种多边形。

练习题4：圆的应用
1. 将一个正方形分成四等分，可以得到4个什么形状的区域？
2. 请描述一下如何用圆型盖子来覆盖一个长方形饼干盒？
3. 请描述一下如何用圆来构建一个简单的钟表表盘。

练习题5：圆的建模
1. 请描述一下如何用数学表达式定义一个圆。

2. 设计一个程序，在屏幕上绘制一个圆。

通过完成上述练习题，你可以加深对圆的认识和理解。

同时，练习题也有助于培养你的解题思维和分析能力。

希望这些练习题能对你在几何学习中有所帮助！。

初中圆的简单练习题及答案一、选择题1．如图，BC是⊙O的直径，P是CB延长线上一点，PA 切⊙O于点A，如果PA＝，PB＝1，那么∠APC等于153045602．如果圆柱的高为20厘米，底面半径是高的1，那么这个圆柱的侧面积是100π平方厘米00π平方厘米500π平方厘米00平方厘米3．“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题，“今在圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言表述是：“如图，CD为⊙O的直径，弦AB⊥CD，垂足为E，CE＝1寸，AB＝10寸，求直径CD的长”．依题意，CD长为25寸13寸25寸26寸4．已知：如图，⊙O半径为5，PC切⊙O于点C，PO 交⊙O于点A，PA＝4，那么PC的长等于62225．如果圆锥的侧面积为20π平方厘米，它的母线长为5厘米，那么此圆锥的底面半径的长等于2厘米22厘米4厘米8厘米6．相交两圆的公共弦长为16厘米，若两圆的半径长分别为10厘米和17厘米，则这两圆的圆心距为7厘米 16厘米 1厘米27厘米7．如图，⊙O为△ABC的内切圆，∠C＝90，AO的延长线交BC于点D，AC＝4，DC＝1，，则⊙O的半径等于4534468．一居民小区有一正多边形的活动场．为迎接“AAPP”会议在重庆市的召开，小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台，花台都以多边形的顶点为圆心，比多边形的内角为圆心角，花台占地面积共为12π平方米．若每个花台的造价为400元，则建造这些花台共需资金2400元2800元3200元3600元9．如图，AB是⊙O直径，CD是弦．若AB＝10厘米，CD＝8厘米，那么A、B两点到直线CD的距离之和为12厘米 10厘米厘米6厘米10．某工件形状如图所示，圆弧BC的度数为60?，AB ＝6厘米，点B到点C的距离等于AB，∠BAC＝30?，则工件的面积等于4π6π8π 10π11．如图，PA切⊙O于点A，PBC是⊙O的割线且过圆心，PA＝4，PB＝2，则⊙O的半径等于312．已知⊙O的半径为3厘米，⊙O?的半径为5厘米．⊙O与⊙O?相交于点D、E．若两圆的公共弦DE的长是6厘米，则两圆的圆心距OO?的长为2厘米 10厘米2厘米或10厘米4厘米13．如图，两个等圆⊙O和⊙O?的两条切线OA、OB，A、B是切点，则∠AOB等于304560014．如图，AB是⊙O的直径，∠C＝30，则∠ABD＝304050015．弧长为6π的弧所对的圆心角为60，则弧所在的圆的半径为621 1816．如图，在△ABC中，∠BAC＝90，AB＝AC＝2，以AB为直径的圆交BC于D，则图中阴影部分的面积为1 1+－417．已知圆的内接正六边形的周长为18，那么圆的面积为18πππ3π18．如图，点P是半径为5的⊙O内一点，且OP＝3，在过点P的所有弦中，长度为整数的弦一共有2条条条5条19．如图，正六边形ABCDEF的边长的上a，分别以C、F为圆心，a为半径画弧，则图中阴影部分的面积是a a2a2a220．过⊙O内一点M的最长的弦长为6厘米，最短的弦长为4厘米，则OM的长为3厘米厘米2厘米5厘米21．已知圆锥的底面半径是3，高是4，则这个圆锥侧面展开图的面积是12π 15π30π24π22．已知⊙O的直径AB与弦AC的夹角为30，过C点的切线PC与AB延长线交P．PC＝5，则⊙O的半径为16132343510623．如图：PA切⊙O于点A，PBC是⊙O的一条割线，有PA＝32，PB＝BC，那么BC的长是24．如图，⊙A、⊙B、⊙C、⊙D、⊙E相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE，则图中五个扇形的面积之和是π1.5ππ .5π25．正六边形的半径为2厘米，那么它的周长为6厘米 12厘米24厘米122厘米26．一个圆柱形油桶的底面直径为0.6米，高为1米，那么这个油桶的侧面积为0.09π平方米 0.3π平方米 0.6平方米 0.6π平方米27．一个形如圆锥的冰淇淋纸筒，其底面直径为6厘米，母线长为5厘米，围成这样的冰淇淋纸筒所需纸片的面积是66π平方厘米0π平方厘米8π平方厘米 15π平方厘米28．在半径为2的⊙O中，圆心O到弦AB的距离为1，则弦AB所对的圆心角的度数可以是60 0 120 15029．将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面，，则桶底的面积为1600平方厘米 1600π平方厘米6400平方厘米400π平方厘米30．如图，已知AB是⊙O的直径，弦CD⊥AB于点P，CD＝10厘米，AP∶PB＝1∶5，那么⊙O的半径是6厘米厘米8厘米53厘米31．在Rt△ABC中，已知AB＝6，AC＝8，∠A＝90．如果把Rt△ABC绕直线AC旋转一周得到一个圆锥，其表面积为S1；把Rt△ABC绕直线AB旋转一周得到另一个圆锥，其表面积为S2，那么S1∶S2等于2∶33∶44∶9∶1232．如图，⊙O的弦AB＝8厘米，弦CD平分AB于点E．若CE＝2厘米．ED长为8厘米厘米4厘米2厘米33．如图，四边形ABCD内接于⊙O，若∠BOD＝160，则∠BCD＝160 100802034．如图，正方形ABCD内接于⊙O，E为DC的中点，直线BE交⊙O于点F．若⊙O的半径为2，则BF的长为2 255．如图，AB是⊙O的直径，∠ACD＝15，则∠BAD的度数为70536．已知：点P直线l的距离为3，以点P为圆心，r 为半径画圆，如果圆上有且只有两点到直线l的距离均为2，则半径r的取值范围是r＞1 r＞＜r＜1＜r＜537．边长为a的正方边形的边心距为a a aa38．如图，以圆柱的下底面为底面，上底面圆心为顶点的圆锥的母线长为4，高线长为3，则圆柱的侧面积为30π67π20π47π39．如图，扇形的半径OA＝20厘米，∠AOB＝135，用它做成一个圆锥的侧面，则此圆锥底面的半径为3.75厘米 .5厘米 15厘米 0厘米40．如图，正六边形ABCDEF中．阴影部分面积为12平方厘米，则此正六边形的边长为2厘米4厘米厘米厘米41．已知扇形的弧长是2π厘米，半径为12厘米，则这个扇形的圆心角是6002042．圆锥的高线长是厘米，底面直径为12厘米，则这个圆锥的侧面积是48π厘米 4平方厘米48平方厘米0π平方厘米43．如图，AB是⊙O的直径，点P在BA的延长线上，PC是⊙O的切线，C为切点，PC＝26，PA＝4，则⊙O的半径等于1 244．已知圆柱的母线长为5厘米，表面积为28π平方厘米，则这个圆柱的底面半径是5厘米厘米2厘米3厘米45．半径相等的圆内接正三角形、正方形、正六边形的边长之比为1∶2∶∶2∶13∶2∶11∶2∶346．如图，若四边形ABCD是半径为1和⊙O的内接正方形，则图中四个弓形的面积和为厘米厘米厘米厘米47．如图，已知圆心角∠BOC＝100，则圆周角∠BAC的度数是初中数学-圆习题及答案1. 已知AB为⊙O的直径，BD?2CD，CE//AB切⊙O于C 点，交AD延长线于E点，若⊙O半径为2cm，求AE2.如图，PC、PD为大⊙O 求证：CE?BE?AC3. 如图，⊙O1和⊙O2交于A、B两点，小圆的圆心O1在大圆⊙O2上，直线PEC切⊙O1于点C，交⊙O2于点P，E4.如图，?ABC⊥AK.5、如图1和图2，MN是⊙O的直径，弦AB、CD?相交于MN?上的一点P，?∠APM=∠CPM．由以上条件，你认为AB和CD大小关系是什么，请说明理由．若交点P在⊙O的外部，上述结论是否成立？若成立，加以证明；若不成立，请说明理由．P6、2.已知：如图等边△ABC内接于⊙O，点P是劣弧PC上的一点若AP过圆心O，如图①，请你判断△PDC是什么三角形？并说明理由．若AP不过圆心O，如图②，△PDC 又是什么三角形？为什么？7.如图OA、OB是⊙O的两条半径，且OA⊥OB，点C 是OB延长线上任意一点：过点C作CD切⊙O于点D，连结AD交DC于点E．求证：CD=CE若将图中的半径OB所在直线向上平行移动交OA于F，交⊙O于B’，其他条件不变，那么上述结论CD=CE还成立吗?为什么?若将图中的半径OB所在直线向上平行移动到⊙O外的CF，点E是DA的延长线与CF的交点，其他条件不变，那么上述结论CD=CE还成立吗?为什么图①D图②8、如图，在⊙O中，AB是直径，CD是弦，AB⊥CD。

(完整版)圆形基础练习题圆形基础练题（完整版）本文档提供了一系列圆形基础练题，旨在帮助练者掌握圆形相关的基本概念和计算方法。

以下是题目及其答案，供参考和练。

1. 计算圆的面积给定一个圆的半径为r，计算其面积。

答案：圆的面积公式为A = π * r^2，其中π为圆周率，近似取值为3.14。

故圆的面积为A = 3.14 * r^2。

2. 计算圆的周长给定一个圆的半径为r，计算其周长。

答案：圆的周长公式为C = 2 * π * r，其中π为圆周率，近似取值为3.14。

故圆的周长为C = 2 * 3.14 * r。

3. 计算圆柱的体积给定一个圆柱的底面半径为r，高度为h，计算其体积。

答案：圆柱的体积公式为V = π * r^2 * h，其中π为圆周率，近似取值为3.14。

故圆柱的体积为V = 3.14 * r^2 * h。

4. 计算圆的弧长给定一个圆的半径为r，扇形度数为θ，计算圆的弧长。

答案：圆的弧长公式为L = (2 * π * r * θ) / 360，其中π为圆周率，近似取值为3.14。

故圆的弧长为L = (2 * 3.14 * r * θ) / 360。

5. 计算圆环的面积给定一个圆环的外半径为R，内半径为r，计算其面积。

答案：圆环的面积公式为A = π * (R^2 - r^2)，其中π为圆周率，近似取值为3.14。

故圆环的面积为A = 3.14 * (R^2 - r^2)。

6. 计算圆心角的弧度给定一个圆的半径为r，圆心角的度数为θ，计算圆心角的弧度。

答案：圆心角的弧度公式为α = (π * θ) / 180，其中π为圆周率，近似取值为3.14。

故圆心角的弧度为α = (3.14 * θ) / 180。

以上是本文档提供的圆形基础练习题，通过练习这些问题，您可以更好地掌握圆形的基础知识和计算方法。

祝您练习顺利！。

圆的复习题及答案一、选择题1. 圆的周长公式是（）。

A. C = 2πrB. C = πdC. C = πr²D. C = 2πd答案：A、B2. 圆的面积公式是（）。

A. S = πr²B. S = 2πrC. S = πd²D. S = πr² + r²答案：A3. 半径为5的圆的周长是（）。

A. 10πB. 15πC. 20πD. 25π答案：D4. 半径为3的圆的面积是（）。

A. 9πB. 18πC. 27πD. 36π答案：A二、填空题1. 半径为r的圆的直径是_________。

答案：2r2. 如果一个圆的周长是44π，那么这个圆的半径是_________。

答案：223. 一个圆的面积是28.26平方厘米，那么这个圆的半径是_________。

答案：3厘米三、计算题1. 一个圆的半径是7厘米，计算它的周长和面积。

答案：周长= 2 × π × 7 = 14π 厘米面积= π × 7² = 49π 平方厘米2. 如果一个圆的面积是78.5平方厘米，求这个圆的半径。

答案：半径= √(面积/ π) = √(78.5 / π) 厘米四、简答题1. 为什么圆的周长和面积公式中都包含π？答案：圆的周长和面积公式中包含π是因为π是一个无理数，表示圆的周长与直径的比值。

这个比值对于所有圆都是相同的，因此π在圆的周长和面积公式中起到了一个通用的常数的作用。

2. 如何用圆规画一个半径为10厘米的圆？答案：首先，将圆规的两个脚分开，使它们之间的距离为10厘米。

然后，将其中一个脚作为圆心固定在纸上，旋转另一个脚，使其围绕固定脚画一个完整的圆，这样就画出了一个半径为10厘米的圆。

五、应用题1. 一个圆形花坛的直径是20米，如果绕花坛走一圈，需要走多少米？答案：花坛的周长= π × 直径= π × 20米= 20π 米因此，绕花坛走一圈需要走大约 62.8 米（取π ≈3.14）。

圆的练习题及答案练习题一：1. 设圆O的半径为5cm，求其直径、周长和面积。

解答：直径：直径是通过圆心的一条线段，等于半径的两倍，所以直径=2 ×半径 = 2 × 5cm = 10cm。

周长：周长等于圆的周长，即2 × π × 半径= 2 × 3.14 × 5cm ≈31.4cm。

面积：面积等于圆的面积，即π × 半径² = 3.14 × 5cm × 5cm ≈78.5cm²。

2. 已知圆O的直径为16cm，求其半径、周长和面积。

解答：半径：半径等于直径的一半，所以半径=直径 ÷ 2 = 16cm ÷ 2 = 8cm。

周长：周长等于圆的周长，即2 × π × 半径= 2 × 3.14 × 8cm ≈50.24cm。

面积：面积等于圆的面积，即π × 半径² = 3.14 × 8cm × 8cm ≈201.06cm²。

3. 若一圆的周长为15πcm，求其半径和面积。

解答：已知周长=2 × π × 半径所以半径=周长÷ (2 × π) = 15πcm ÷ (2 × π) = 7.5cm。

面积等于圆的面积，即π × 半径² = 3.14 × 7.5cm × 7.5cm ≈ 176.625cm²。

练习题二：1. 设圆O的半径为r，若圆周长等于其面积的2倍，求r的值。

解答：已知周长=2 × π × 半径，面积=π × 半径²根据题意，2 ×周长 = 面积，可以得到2 × 2 × π × r = π × r²。

圆的经典练习题及答案一、填空题1. （2011浙江省舟山，15，4分）如图，AB 是半圆直径，半径OC ⊥AB 于点O ，AD 平分∠CAB 交弧BC 于点D ，连结CD 、OD ，给出以下四个结论：①AC ∥OD ；②OE CE =；③△ODE ∽△ADO ；④AB CE CD ⋅=22．其中正确结论的序号是．【答案】①④2. （2011安徽，13，5分）如图，⊙O 的两条弦AB 、CD 互相垂直，垂足为E ，且AB =CD ，已知CE =1，ED =3，则⊙O 的半径是 ．【答案】3. （2011江苏扬州，15,3分）如图，⊙O 的弦CD 与直径AB 相交，若∠B AD=50°，则∠ACD=【答案】40°4. （2011山东日照，14，4分）如图，在以AB 为直径的半圆中，有一个边长为1的内接正方形CDEF ，则以AC 和BC 的长为两根的一元二次方程是 ．【答案】如：x 2-5x +1=0；5. （2011山东泰安，23 ，3分）如图，P A 与⊙O 相切，切点为A ，PO 交⊙O 于点C ，点B 是优弧CBA 上一点，若∠ABC ==320，则∠P 的度数为 。

（第16题） A B DCOE【答案】2606. （2011山东威海，15，3分）如图，⊙O 的直径AB 与弦CD 相交于点E ，若AE =5,BE =1,42CD ,则∠AED= .【答案】 30°7. （2011山东烟台，16,4分）如图，△ABC 的外心坐标是__________.【答案】（－2，－1） 8. （2011浙江杭州，14，4）如图，点A ，B ，C ，D 都在⊙O 上，O x yB C A的度数等于84°，CA是∠OCD的平分线，则∠ABD十∠CAO= °．【答案】53°9. （2011浙江温州，14，5分）如图，AB是⊙O的直径，点C，D都在⊙O上，连结CA，CB，DC，DB．已知∠D=30°，BC＝3，则AB的长是．【答案】610．（2011浙江省嘉兴，16，5分）如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB分别交OC于点E，交弧BC于点D，连结CD、OD，给出以下四个结论：①S△AEC =2S△DEO；②AC=2CD；③线段OD是DE与DA的比例中项；④ABCECD⋅=22．其中正确结论的序号是．【答案】①④11. （2011福建泉州，16，4分）已知三角形的三边长分别为3，4，5，则它的边与半径为1的圆的公共点个数所有可能的情况是.（写出符合的一种情况即可）【答案】 2（符合答案即可）12. （2011甘肃兰州，16，4分）如图，OB 是⊙O 的半径，点C 、D 在⊙O 上，∠DCB=27°，则∠OBD=度。

圆的相关练习题1、 已知：弦AB 把圆周分成1: 5的两部分，这弦AB 所对应的圆心角的度数为2、 如图：在。

O 中，/ AOB 的度数为1200，贝U 的长是圆周的1 3、 已知：。

O 中的半径为4cm ,弦AB 所对的劣弧为圆的-，则弦AB 的长为3C . 2个D . 3个二”的度数是60°，求弦AB 的弦心距。

8 已知：如图，O O 中，AB 是直径，CO 丄AB ，D 是CO 的中点，DE / AB ， 求证：I ：:二卩9. 已知：AB 交圆O 于C 、D ，且AC = BD.你认为OA = 为什么？10. 如图所示，是一个直径为650mm 的圆柱形输油管的 若油cm 。

AB 的弦心距为 4、 如图，在O O 中，AB //CD ，川 的度数为45°，则/ COD 的度数为5、 如图, 在三角形ABC 中, / A=700，O O 截厶ABC 的三边所得的弦长相等，则 / BOC= ( )。

A . 140°B . 135C . 130°D . 125°&下列语句中，正确的有((1)相等的圆心角所对的弧相等;(2)平分弦的直径垂直于弦; (3)长度相等的两条弧是等弧;(4)圆是轴对称图形，任何一条直径都是对称轴 A . 0个 B . 1个 7、已知：在直径是10的。

O 中, OB 吗?横截面, 0 600 AIB (第2题图)CiC D (第4题图) L J B(第5题图)面宽AB=600mm，求油面的最大深度。

11. 如图所示，AB 是圆0的直径，以OA 为直径的圆C 与圆0的弦AD 相交于点E 你认为图中有哪些相等的线段？为什么？答案：1.60度22.- 34.90 度5. D6. A7.2.58. 提示：连接0E ，求出角COE 的度数为60度即可9. 略10.100毫米11.AC=0C ， OA=OB ，AE=ED3. 4.3。

有关圆的练习题一、选择题（每题2分，共20分）1. 圆的周长公式是：A. C = 2πrB. C = πdC. C = 2πdD. C = πr2. 圆的面积公式是：A. A = πr²B. A = 2πrC. A = πd²D. A = π(2r)²3. 半径为2厘米的圆的周长是：A. 4厘米B. 8厘米C. 12.56厘米D. 25.12厘米4. 半径为3厘米的圆的面积是：A. 28.26平方厘米B. 45平方厘米C. 9平方厘米D. 28平方厘米5. 一个圆的直径是10厘米，那么它的半径是：A. 5厘米C. 20厘米D. 15厘米6. 圆内接四边形的对角线所夹的圆心角的度数是：A. 90度B. 180度C. 360度D. 无法确定7. 圆的切线与半径在切点处垂直，这是因为：A. 切线与半径平行B. 切线与半径垂直C. 切线与圆相切D. 切线与圆相交8. 一个圆的半径增加1厘米，它的面积将增加：A. π平方厘米B. 2π平方厘米C. π(2r+1)平方厘米D. π(r+1)²平方厘米9. 圆的内接正六边形的边长等于圆的半径，这是因为：A. 正六边形的每个内角都是120度B. 正六边形的每个内角都是90度C. 正六边形的每个外角都是60度D. 正六边形的每个外角都是120度10. 圆的外接正三角形的边长是圆的半径的：A. 1/2倍B. 1/3倍D. 3倍二、填空题（每题2分，共20分）11. 半径为r的圆的周长是________。

12. 半径为r的圆的面积是________。

13. 圆的直径是半径的________倍。

14. 圆的周长与直径的比值是________。

15. 半径为5厘米的圆的周长是________厘米。

16. 半径为5厘米的圆的面积是________平方厘米。

17. 圆的切线与半径在切点处的关系是________。

18. 圆内接正六边形的边长与圆的半径的关系是________。