光学主要公示总结
- 格式:docx
- 大小:146.10 KB
- 文档页数:3

光学公式汇总(总10页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--光学公式汇总一、 几何光学1、折射公式(斯涅耳公式)211212sin sin n i n n i == 2、全反射临界角211sin c i n n =⎛⎫ ⎪⎝⎭3、棱镜色散·最小偏向角12m i δα=-4、棱镜色散·由最小偏向角求棱镜折射率sin 2sin2m n αδα+⎛⎫ ⎪⎝⎭=5、折射率和光速关系211212n v n n v == 6、单个折射球面的物像距公式'''n n n ns s r-+=7、轴上物点成像的普遍物像距公式'1'f f s s +=('nr f n n =-,'''n rf n n=-)8、傍轴条件下反射球面成像的普遍物像距公式112's s r +=-9、傍轴条件下反射球面成像的焦距公式'2rf f ==-10、 横向放大率''''y ns s V y n s s==-=- 11、 薄透镜物像方折射率相等时的物像距公式高斯形式111's s f+=12、 薄透镜物像距公式牛顿形式''xx ff = 13、 放大镜、显微镜、望远镜的视角放大率'M ωω= 14、 放大镜视角放大率公式0s M f=15、 显微镜视角放大率公式O E M V M = 16、 望远镜视角放大率公式OEf M f =- 17、 发光强度的微分表示式d I d Φ=Ω(坎德拉,cd ) 18、 光度学亮度cos cos dI d B dS d dS θθΦ==Ω(熙提,sb ) 19、 照度''d E dS Φ=(勒克斯,lx )20、 点光源产生的照度2'cos ''d I E dS r θΦ==(勒克斯,lx ) 21、 面光源产生的照度2cos cos 'BdS E r θθ=⎰⎰光源表面(勒克斯,lx )二、 波动光学基础22、 普通的定态波表达式()()(),cos U P t A P t P ωϕ=-⎡⎤⎣⎦ 23、 普通的定态波复数表达式()()(),i t P U P t A P e ωϕ--⎡⎤⎣⎦=24、 复振幅()()()i P U P A P e ϕ= 25、 平面波复振幅()()0x y z i k x k y k z U P Ae ϕ⎡⎤+++⎣⎦=26、 球面波振幅()aA P r=27、 位相形式()0P ϕϕ=⋅+k r 28、 球面波复振幅()()()00exp i kr a U P e i rϕϕ⎡⎤+⎣⎦⎡⎤==⎢⎥⎣⎦(以上的0ϕ可略去,因为我们感兴趣的是相位的变化) 29、 光强的振幅表示()()2I P A P =⎡⎤⎣⎦ 30、 光强的复振幅表示()()()*I P U P U P =三、 光的干涉31、 干涉条纹的反衬度12122221212221M m M m A A I I A A I I A A A A γ⎛⎫ ⎪-⎝⎭===++⎛⎫+ ⎪⎝⎭32、 双光束干涉场光强的振幅表示式()22121202cos 1cos I A A A A I δγθ=++=+33、 干涉场强度为极大值的条件L m λ∆=,2m δπ=34、 干涉场强度为极小值的条件212m L λ-∆=,212m δπ-=35、 两束平行光的干涉场在0z =的波前上位相分布()()1111022220cos cos cos cos k x y k x y ϕαβϕϕαβϕ=++=++36、 两束平行光的干涉场在0z =的波前上沿x 方向的条纹间距()12122cos cos cos cos x k πλαααα∆==--37、 两束平行光的干涉场在0z =的波前上沿y 方向的条纹间距()12122cos cos cos cos y k πλββββ∆==--38、 两束平行光干涉场在0z =的波前上沿x 方向的空间频率12cos cos 1x f x ααλ-==∆ 39、 两束平行光干涉场在0z =的波前上沿y 方向的空间频率12cos cos 1y f y ββλ-==∆ 40、 杨氏双缝条纹间距D x d λ∆= 41、 杨氏双缝干涉明条纹条件xdm Dλ= 42、 杨氏双缝干涉暗条纹条件212xd m D λ-= 43、 菲涅耳双面镜条纹间距()2B C x Bλα+∆=44、 菲涅耳双棱镜条纹间距()()21B C x n Bλα+∆=- 45、 洛埃镜条纹间距2D x aλ∆=46、 移过固定场点P 的干涉条纹数目()L N δλ∆= 47、 杨氏实验条纹位移与点源位移关系D x s Rδδ= 48、 杨氏双缝光源的临界宽度1R b dλ= 49、 相干孔径角公式0b θλ∆(空间相干性的反比公式)50、 时间相干性反比公式01ντ∆= 51、 薄膜干涉明条纹条件2cos 2nh i m λλ±= 52、 薄膜干涉暗条纹条件212cos 22m nh i λλ-±= 53、 每经过一个明(暗条纹),薄膜厚度改变量2h nλ∆=54、 楔形空气薄膜条纹间隔2x λα∆= 55、 楔形薄膜条纹竖直间隔2d n λ∆=56、 劈尖干涉明条纹条件122d k n λ⎛⎫=- ⎪⎝⎭57、 劈尖干涉暗条纹条件2k d nλ=58、 牛顿环暗环半径k r =59、 牛顿环元件的曲率半径22k m k r r R m λ+-=60、 等倾干涉光程差2cos L nh i ∆= 61、 等倾干涉倾角余弦值公式cos 2k k i nhλ=62、 等倾干涉相邻条纹倾角余弦值差公式1cos cos 2k k i i nhλ+-=63、 等倾干涉条纹间距12sin k k kr r r nh i λ+-∆=-=64、 法--珀多光束干涉表观光程差2cos L nh i ∆=65、 法--珀多光束干涉相邻光线位相差24cos nh iL ππδλλ=∆=66、 法--珀多光束干涉透射光强()224sin 211T I I R R δ=⎛⎫⎪⎝⎭+-67、 法--珀多光束干涉反射光强()022114sin 2R T I I I I R R δ=-=-+⎛⎫⎪⎝⎭68、 法--珀干涉条纹的半值宽度21R ε-=69、 单色扩展光入射时,法--珀第k 级明纹的角宽度k i ∆=70、 非单色平行光入射时,法--珀多光束干涉波长极大满足2k nh k λ= 71、 非单色平行光入射,法--珀多光束干涉在极大处频率满足2k kc kcnhνλ== 72、 非单色平行光入射,法--珀多光束干涉相邻极强的频率间隔12k k c nh ννν+∆=-= 73、 非单色平行光入射,法--珀多光束干涉纵模谱线宽度k λ∆=74、 非单色平行光入射,法--珀多光束干涉纵模谱线宽度的频率表示k ν∆=75、法--珀干涉仪色分辨本领1k Rλπδλ=-四、光的衍射76、 菲涅耳衍射公式()()()00,ikre U P K U Q F d rθθ=∑⎰⎰ 77、 基尔霍夫衍射公式()()()000cos cos 2ikri e U P U Q d r θθλ∑-=+∑⎰⎰ 78、 巴俾涅原理()()()0a b U P U P U P += 79、 巴俾涅原理的光强推论()()a b I P I P = 80、 菲涅耳波带片第k个半波带的半径k ρ=81、 菲涅耳半波带的透镜作用111R b f+= 82、 夫琅和费单缝衍射光程差sin L a θ∆= 83、 夫琅和费单缝衍射矢量图解圆心角公式22sin 2aL ππδθαλλ=∆==84、 夫琅和费单缝衍射矢量图解半角公式sin aπαθλ= 85、 夫琅和费单缝衍射振幅公式0sin A A θαα=86、 夫琅和费单缝衍射光强公式(单缝衍射因子)20sin I I θαα⎛⎫= ⎪⎝⎭87、 夫琅和费矩孔衍射光强公式()220sin sin I P I αβαβ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭88、 夫琅和费单缝衍射暗纹位置,0m m απ=≠,sin ,0m m aλθ=≠89、 夫琅和费单缝衍射亮斑的半角宽度a θλ∆=90、 夫琅和费圆孔衍射半角宽度(爱里班) 1.22Dλθ∆=91、 望远镜的最小分辨角 1.22m Dλδθ=92、 N 缝夫琅和费衍射总振幅sin sin N A a θθββ= 93、 N 缝夫琅和费光强222220sin sin sin sin sin N N I a a θθβαββαβ⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭94、 多缝夫琅和费衍射矢量图解β角公式sin dπβθλ=95、 多缝夫琅和费衍射主极强位置(光栅公式)sin k dλθ=96、 N 缝夫琅和费次极强位置(缝间干涉因子零点)m k N βπ⎛⎫=+ ⎪⎝⎭,即sin m k N d λθ⎛⎫=+ ⎪⎝⎭97、 N 缝夫琅和费主极强的半角宽度cos kNd λθθ∆=98、 光栅的角色散本领定义D θδθδλ=99、 光栅的线色散本领定义l lD δδλ=100、线色散本领和角色散本领的关系l D fD θ= 101、光栅的角色散本领公式cos k kD d θθ=102、光栅的线色散本领公式cos l kkfD d θ=103、光栅的色分辨本领定义R λδλ=104、光栅能分辨的最小波长差kNλδλ=105、光栅的色分辨本领公式R kN =106、最大待测波长与光栅常数的关系M d λ< 107、光栅光谱仪工作波段上限与下限关系2M m λλ>108、光栅缺级d j k a=109、平行光沿槽面法线入射时相邻槽面光程差2sin b L d θ∆= 110、平行光沿光栅平面法线入射时相邻槽面光程差sin 2b L d θ∆=五、光的偏振111、部分偏振光偏振度定义+I I P I I -=极大极小极大极小112、马吕斯定律210=cos I I θ113、偏振光在x 和y 方向的分量()cos cos x x y y E A tE A t ωωδ=⎧⎨=+⎩114、线偏振光()cos cos x x y y E A tE A t k ωωπ=⎧⎨=+⎩115、圆偏振光cos 21cos 2x y E A t k E A t ωωπ=⎧⎪+⎨⎛⎫=+ ⎪⎪⎝⎭⎩ 116、正椭圆偏振光cos 21cos 2x x yy E A t k E A t ωωπ=⎧⎪+⎨⎛⎫=+ ⎪⎪⎝⎭⎩117、椭圆偏振光()cos ,cos x x yy E A tk E A t ωδπωδ=⎧≠⎨=+⎩11 118、菲涅耳反射折射公式()()()()()12211211121121212121122111221111122211112211112221tan cos cos 'cosi cos tan 2cos cos cos sin cos cos 'cos cos sin 2cos 2cos sin cos cos sin P P P P P s s s s s s i i n i n i E E E n n i i i n i E E n i n i i i n i n i E E E n i n i i i n i i i E E E n i n i i i -⎧-==++=+⎨--==++==++⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩119、振幅反射率1111''Pp Pss sE r E E r E ⎧=⎪⎪⎨⎪=⎪⎩120、光强反射率211211''P PPPss ssI R r I I R r I ⎧==⎪⎪⎨⎪==⎪⎩121、能流反射率1111''PP PPs s ssW R W W R W ⎧ℜ==⎪⎪⎨⎪ℜ==⎪⎩122、振幅透射率2121PPP s s sE t E E t E ⎧=⎪⎪⎨⎪=⎪⎩123、光强透射率2211222211P P P P s s s s I n T t I n I n T t I n ⎧==⎪⎪⎨⎪==⎪⎩124、能流透射率22112211cos cos cos cos PP PP s s ss W i T W i W i T W i ⎧==⎪⎪⎨⎪==⎪⎩125、布儒斯特角121tan B n i n -=。


光学公式高中光学公式是高中物理学中的重要内容,用于描述光的传播、成像和折射等现象。
本文将介绍一些常见的光学公式,并拓展讨论其应用。
首先,我们来介绍一下光的传播公式。
在光学中,光的传播速度通常用光速c来表示,其数值约为3.00×10^8 m/s。
当光在介质中传播时,其速度会发生改变,这可以由光的折射率n来描述。
光的传播速度可以用以下公式表示:v = c/n其中,v为光在介质中的传播速度,c为光速,n为介质的折射率。
接下来,我们来讨论成像公式。
在光学中,当光线通过透镜或反射面时,会发生成像现象。
成像公式可用于计算成像点的位置。
对于薄透镜而言,成像公式可以表示为:1/f = 1/v + 1/u其中,f为透镜的焦距,v为像距,u为物距。
根据成像公式,我们可以计算出透镜成像的位置和大小。
除了成像公式,折射公式也是光学中的重要内容。
折射公式用于描述光线从一个介质折射到另一个介质时的偏折情况。
折射公式的数学表达式为:n1*sinθ1 = n2*sinθ2其中,n1和n2分别为两个介质的折射率,θ1和θ2分别为入射角和折射角。
根据折射公式,我们可以计算出光线在不同介质中的传播方向和角度。
除了上述公式,还有许多其他的光学公式,如反射公式、杨氏双缝干涉公式、多普勒效应公式等等。
这些公式在光学实验和现象的研究中都具有重要的应用价值。
总之,光学公式是高中物理学中不可或缺的内容,它们用于描述光的传播、成像和折射等现象。
通过学习和理解这些公式,我们可以更好地理解光学原理,并应用于实际问题的解决中。

光学常用公式范文光学是研究光的传播和相互作用的科学领域,涉及到许多光学常用公式。
下面是一些光学领域常见的公式:1.光速公式:光在真空中的速度为c=299,792,458m/s。
2. 折射定律:当光从一种介质射入另一种介质时,入射角θ1、折射角θ2和两种介质的折射率n1、n2之间满足康斯特定律:n1sinθ1 =n2sinθ23.球面镜成像公式:对凸透镜和凹透镜而言,成像公式为1/f=1/v+1/u,其中f为焦距,v为像距,u为物距。
4.薄透镜公式:对于无限薄的透镜,成像公式可以简化为1/f=(n2-n1)(1/R1-1/R2),其中n1、n2为透镜两侧的折射率,R1、R2为曲率半径。
5. 光谱衍射公式:在光通过一个狭缝或光栅时,光的衍射现象遵循衍射公式:mλ = d sinθ,其中m为衍射级次,λ为波长,d为狭缝或光栅的间距,θ为衍射角。
6.杨氏双缝干涉公式:当光通过两个间距为d的狭缝时,干涉现象满足干涉公式:y=mλL/d,其中y为干涉条纹的位置,m为干涉级次,λ为波长,L为狭缝到屏幕的距离。
7. 薄膜干涉公式:当光在薄膜上反射和折射时,干涉现象满足薄膜干涉公式:2nt = mλ,其中n为薄膜的折射率,t为薄膜的厚度,m为干涉级次,λ为波长。
8.瑞利判据:用于判断两个光源是否可以被分辨为两个点光源。
根据瑞利判据,两个光源的最小可分辨角度为θ=1.22λ/d,其中λ为波长,d为光路的孔径直径。
9. 空气中的大气折射公式:当光穿过大气层时,受大气折射的影响,光线在水平方向上会发生弯曲。
大气折射公式可以用来计算偏折角度:tanδ ≈ V / d,其中V为大气折射率变化率,d为光线传播距离。
10. 斯涅尔定律:当光从一种介质射入另一种介质时,入射角θ1、折射角θ2和两种介质的折射率n1、n2之间满足斯涅尔定律:n1sinθ1= n2sinθ2这只是光学中的一小部分常用公式,实际上光学是一个非常广泛且复杂的科学领域,在不同的光学现象和应用中还有许多其他的公式和定律。

光学计算公式高中
光学是物理学的一个分支,主要研究光的性质和行为。
在高中物理中,光学是一个重要的部分,涉及到光在自然界中的传播、反射、折射、干涉和衍射等现象。
以下是一些光学计算公式,供您参考:
1. 光速公式:C = 299792458 m/s
光速是光在真空中的速度,是一个基本的物理学常数。
光速公式可以帮助我们计算光在不同介质中的传播速度,例如在空气中的速度约为 3×10^8 m/s,在水中的速度约为2×10^8 m/s。
2. 反射和折射定律:R = R0 / (1 + n2/n1)
R 表示反射率,R0 表示真空中的反射率,n1 和 n2 分别表示介质的折射率。
这个公式可以帮助我们计算光在反射和折射时的角度和反射率。
3. 菲涅尔公式:F = (2/n)^(1/2) * (1 - cosθ)
F 表示菲涅尔常数,n 表示介质的折射率,θ表示入射角。
这个公式可以帮助我们计算光在反射和折射时的传播距离和角度。
4. 干涉和衍射公式:I = I0 * |cosθ|
I 表示干涉或衍射的强度,I0 表示真空中的干涉或衍射强度,θ表示干涉或衍射的角度。
这个公式可以帮助我们计算干涉或衍射的强度和时间。
以上是一些基本的光学计算公式,它们在高中物理光学课程中具有重要的应用。
在实际应用中,光学计算公式还有很多,例如光的偏振、光纤通信、光学传感器等。


光学公式总结光学是研究光的传播、偏振、反射、折射和干涉等现象的科学领域。
在光学研究中,有许多重要的公式被使用,这些公式帮助我们理解和描述光的行为。
本文将对常见的光学公式进行总结,以便读者更好地理解和运用这些公式。
1. 光的速度公式:光的速度(v)在真空中是一个恒定值,通常用c表示,其数值为299,792,458米/秒。
2. 光的传播公式:光线按照直线传播,并且在真空中以光速传播。
光线传播距离(d)等于速度(v)乘以时间(t),即d = v × t。
3. 焦距公式:当光线通过一块薄透镜时,它会被聚焦在焦点上。
薄透镜的焦距(f)与物体距透镜的距离(do)和像距离(di)之间存在如下关系:1/f =1/do + 1/di。
4. 折射定律:当光线从一种介质折射到另一种介质中时,它会发生折射。
折射定律指出入射角(θ1)、折射角(θ2)和两种介质的折射率(n1和n2)之间满足如下关系:n1*sin(θ1) = n2*sin(θ2)。
5. 牛顿环公式:牛顿环是干涉现象的一种,常见于透明薄片与平面介质接触时形成的环形彩色条纹。
牛顿环半径(R)与光的波长(λ)、透明薄片与平面介质之间的距离(d)之间满足如下关系:R = (√(n * λ * d)) / 2。
6. 球面镜成像公式:当光线通过球面镜时,会发生折射和反射,形成像。
球面镜成像的关系由下列公式描述:1/f = (n - 1) * (1/R1 - 1/R2),其中f是焦距,R1和R2分别是球面镜的曲率半径。
7. 力学公式:在光学实验中,一些力学公式也被应用。
例如,力(F)可以通过牛顿第二定律表示为F = m * a,其中m表示质量,a表示加速度。
8. 干涉条纹公式:干涉现象中的条纹间距(d)与光的波长(λ)、光程差(ΔL)之间存在关系:d = λ / 2 * (ΔL)。
9. 各向异性介质的折射率:各向异性介质的折射率通常用一个张量来表示。
这个张量可以通过一个矩阵来描述,其中的元素被称为折射率的主值。

光学公式总结范文光学公式是用于描述光学现象和光的传播行为的数学关系式。
它们是基于光学定律和几何关系得出的,能够帮助我们理解光的折射、反射、干涉、衍射等现象,并应用于光学器件的设计和光学实验的分析。
下面是一些常见的光学公式的总结:1. 反射定律:入射角等于反射角。
即sin(θi) = sin(θr),其中θi是入射角,θr是反射角。
2. 折射定律:折射角的正弦与入射角的正弦和折射率的比例相等。
即sin(θi)/sin(θr) = n,其中θi是入射角,θr是折射角,n是折射率。
3.光程差定理:光程差等于两个波面之间的几何距离差乘以介质的折射率。
即Δr=n*Δl,其中Δr是光程差,n是折射率,Δl是几何距离差。
4.光的干涉条件:当两个波源的相干波面相交时,两波的光程差等于(2m+1)*λ/2,其中m是整数,λ是波长。
5. 双缝干涉光强分布:双缝干涉的光强分布可由Young公式表示:I = I1 + I2 + 2√(I1 * I2) * cos(2π * Δr/λ),其中I1和I2是单缝的光强,Δr是两缝之间的光程差,λ是波长。
6. 衍射公式:衍射的光强分布可以由Fresnel-Kirchhoff衍射公式表示:I = [A * (sinc(φ/2))^2]^2,其中A是入射光的振幅,Φ是衍射角,sinc(x) = sin(x)/x是sinc函数。
7.薄透镜公式:薄透镜的公式可以表示为1/f=1/v-1/u,其中f是透镜的焦距,v是像距离,u是物距离。
8.放大倍率公式:显微镜和望远镜的放大倍率可分别表示为M=-v/u和M=v/u,其中v是像距离,u是物距离。
9.折射球面的公式:折射球面的公式可以表示为n1/v+n2/u=(n2-n1)/R,其中n1和n2是两个介质的折射率,v是像距离,u是物距离,R 是球面的曲率半径。
10. 偏振光公式:偏振器通过的光强可以由马吕斯定律表示:I = I0 * cos^2(θ),其中I0是入射光的强度,θ是光的偏振角。

高中物理公式汇总一、质点的运动(1)------直线运动1)匀变速直线运动1.平均速度V平=s/t(定义式)2.有用推论Vt2-Vo2=2as3.中间时刻速度Vt/2=V平=(Vt+Vo)/24.末速度Vt=Vo+at5.中间位置速度Vs/2=[(Vo2+Vt2)/2]1/26.位移s=V平t=Vot+at2/2=Vt/2t7.加速度a=(Vt-Vo)/t {以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0}8.实验用推论Δs=aT2 {Δs为连续相邻相等时间(T)内位移之差}9.主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s=3.6km/h。
注:(1)平均速度是矢量;(2)物体速度大,加速度不一定大;(3)a=(Vt-Vo)/t只是量度式,不是决定式;(4)其它相关内容:质点、位移和路程、参考系、时间与时刻/s--t图、v--t 图/速度与速率、瞬时速度。
2)自由落体运动1.初速度Vo=02.末速度Vt=gt3.下落高度h=gt2/2(从Vo位置向下计算)4.推论Vt2=2gh注:(1)自由落体运动是初速度为零的匀加速直线运动,遵循匀变速直线运动规律;(2)a=g=9.8m/s2≈10m/s2(重力加速度在赤道附近较小,在高山处比平地小,方向竖直向下)。
3)竖直上抛运动1.位移s=Vot-gt2/22.末速度Vt=Vo-gt (g=9.8m/s2≈10m/s2)3.有用推论Vt2-Vo2=-2gs4.上升最大高度Hm=Vo2/2g(抛出点算起)5.往返时间t=2Vo/g (从抛出落回原位置的时间)注:(1)全过程处理:是匀减速直线运动,以向上为正方向,加速度取负值;(2)分段处理:向上为匀减速直线运动,向下为自由落体运动,具有对称性;(3)上升与下落过程具有对称性,如在同点速度等值反向等。


光学简单计算公式光学是研究光的传播、反射、折射、干涉、衍射等规律的一门学科。
在光学中,有许多简单的计算公式可以帮助我们理解光的行为和性质。
本文将介绍一些常见的光学计算公式,并解释它们的应用。
1. 光速公式。
光速是光在真空中传播的速度,通常用符号c表示。
光速在真空中的数值约为3.00×10^8米/秒。
光速公式可以表示为:c = λν。
其中,c为光速,λ为光的波长,ν为光的频率。
这个公式表明了光速与波长和频率之间的关系。
当波长增大时,频率减小,光速保持不变。
2. 折射定律。
折射定律描述了光线从一种介质进入另一种介质时的偏折规律。
折射定律可以表示为:n1sinθ1 = n2sinθ2。
其中,n1和n2分别为两种介质的折射率,θ1和θ2分别为入射角和折射角。
这个公式表明了入射角和折射角之间的关系,以及两种介质的折射率对光线偏折的影响。
3. 焦距公式。
焦距是光学中一个重要的概念,它描述了透镜或镜片对光线的聚焦能力。
焦距公式可以表示为:1/f = 1/do + 1/di。
其中,f为焦距,do为物体距离透镜或镜片的距离,di为像距离。
这个公式表明了物体距福镜或镜片的距离、像距离和焦距之间的关系。
4. 色散公式。
色散是光在经过不同介质时,不同波长的光线受到不同折射角的现象。
色散公式可以表示为:n = c/v。
其中,n为介质的折射率,c为光速,v为光在介质中的速度。
这个公式表明了介质的折射率与光速之间的关系,从而解释了色散现象的物理机制。
5. 透镜公式。
透镜公式描述了透镜对光线的成像规律。
透镜公式可以表示为:1/f = 1/do + 1/di。
其中,f为透镜的焦距,do为物体距透镜的距离,di为像距离。
这个公式表明了透镜的焦距与物体距福镜的距离、像距离之间的关系。
以上是一些光学中常见的简单计算公式,它们可以帮助我们理解光的行为和性质,以及光在不同介质中的传播规律。
通过这些公式的应用,我们可以更好地设计光学系统、解决光学问题,以及开发光学技术。

初中物理光学公式
初中物理光学公式包括以下内容:
1. 光的反射定律:反射角α等于入射角i,即α=i。
2. 光的折射定律:绝对折射率n等于光在真空中的光速c除以光在介质中
的光速v,即n=c/v。
另外,光的色散现象中,可见光中红光的折射率最小。
3. 全反射的条件:当光从介质中进入真空或空气中时,如果入射角等于或大于临界角C,则会发生全反射。
此时,sinC=1/n。
4. 电功率公式:P=W/t,其中P表示电功率,W表示电功,t表示时间。
另外,电功率也可以用P=UI来表示,其中U表示电压,I表示电流。
5. 额定电压和额定功率:额定电压是指用电器正常工作的电压,额定功率是指用电器在额定电压下的功率。
6. 实际电压和实际功率:实际电压是指实际加在用电器两端的电压,实际功率是指用电器在实际电压下的功率。
这些公式是初中物理光学的重要知识点,对于理解光学现象和解决相关问题具有重要意义。
同时,也需要注意公式的适用条件和单位换算等问题。

高中物理公式光学光学是物理学的一个分支,研究光的传播、反射、折射、干涉、衍射、偏振等现象。
光学中常用的公式有折射定律、反射定律、光程差等等。
下面将介绍一些常用的光学公式及其应用。
1. 折射定律折射定律是光学中最基础的公式之一,描述光线从一种介质进入到另一种介质时的偏折规律。
根据折射定律,入射角和折射角的正弦值之比等于两种介质的折射率之比。
这个公式可以用于解释光在棱镜中的偏折、光在水中的折射等现象。
2. 反射定律反射定律是描述光线从一种介质反射到另一种介质时的规律。
根据反射定律,入射角和反射角相等。
这个公式可以用于解释镜面反射的现象。
3. 光程差光程差是光学中一个重要的概念,指的是两束光线从一个点出发到达另一个点所经过的光程差。
在干涉、衍射等现象中,光程差的大小决定了干涉条纹的位置和衍射图样的形状。
计算光程差时,需要考虑光线传播路径的长度和两束光线的相位差。
4. 线性偏振光的式子线性偏振光是指振动方向固定的光,其振动方向可以沿任意方向。
线性偏振光可以用一个复数表示,其实部表示光的振幅,虚部表示振动方向。
线性偏振光的式子可以用于解释偏振器的作用,以及光在晶体中的双折射现象。
5. 薄透镜公式薄透镜公式是描述光线通过薄透镜时的偏折规律的公式。
根据薄透镜公式,光线通过薄透镜后的焦距和透镜的曲率半径、介质折射率有关。
薄透镜公式可以用于计算透镜成像的位置和大小。
以上是一些在高中物理学习中常用的光学公式,这些公式在解释光学现象、设计光学器件等方面都有重要的应用。
在学习光学公式时,需要理解公式的物理意义,掌握公式的推导过程和应用方法。
同时,还需要结合实验和实际应用,加深对光学公式的理解和掌握。

光学公式知识点总结1. 折射定律折射定律是描述光线在两种介质交界面上发生折射现象的定律,它的数学表达式为:n1*sin(θ1) = n2*sin(θ2)其中,n1和n2分别是两种介质的折射率,θ1和θ2分别是入射角和折射角。
折射定律的应用非常广泛,比如在设计光学元件时需要考虑介质折射率的影响,以及在物体在水中或其它介质中的看起来位置的视差修正等方面都需要用到折射定律。
2. 薄透镜公式薄透镜公式是描述透镜成像规律的重要公式,它的数学表达式为:1/f = 1/v + 1/u其中,f是透镜的焦距,v是像距,u是物距。
薄透镜公式是设计光学系统和计算成像位置的重要工具,它可以用来计算透镜成像的倍率、位置和质量等参数,通常在相机、显微镜等设备的设计和调整中应用广泛。
3. 光的干涉和衍射公式光的干涉和衍射是光学的重要现象,它们的数学表达式为:干涉:δ = 2π*(t/λ)*(n2-n1)衍射:a*sin(θ) = m*λ其中,δ是光程差,t是光程差产生的源波长度,λ是光波长,n1和n2分别是两种介质的折射率;a是衍射光栅的间距,θ是衍射角,m是衍射级数。
光的干涉和衍射公式是用来描述光的波动性质和在光学系统中的应用的重要工具,比如在研究光栅和干涉条纹、衍射成像和光波的相位调制等方面应用广泛。
4. 光学薄膜公式光学薄膜公式是描述薄膜光学性质的数学表达式,它的数学表达式和特殊设计形式非常丰富,比如薄膜反射率表达式、薄膜产生的光程差、薄膜的谐振条件等。
光学薄膜公式在光学薄膜设计和应用中发挥非常重要的作用,比如在太阳能光伏薄膜、光学薄膜滤波器和激光薄膜反射镜等领域都有广泛的应用。
总结:光学公式是描述光学现象的数学表达式,它们在光学理论和实践中发挥着非常重要的作用。
折射定律描述了光线在介质交界面上的折射现象,薄透镜公式描述了透镜的成像规律,光的干涉和衍射公式描述了光的波动性质,光学薄膜公式描述了薄膜的光学性质。
这些公式在光学系统的设计、计算和优化过程中都有广泛的应用。

常用光学计算公式光学是研究光的发射、传播、反射、折射和干涉等现象的学科,是物理学的一个重要分支。
在光学中,我们经常需要进行各种计算。
下面是一些常用的光学计算公式。
1.光速公式光速是光在真空中传播的速度,用c表示,其数值为299,792,458米/秒。
2.光的折射公式光的折射公式可以用来计算光在不同介质之间的折射现象。
公式如下:n1sin(θ1) = n2sin(θ2)其中,n1和n2分别表示两个介质的折射率,θ1表示入射角,θ2表示折射角。
3.球面镜公式球面镜是由一个镜面围绕一个球面形成的镜子。
对于一个球面镜,其焦距f和物距u、像距v之间的关系可以用以下公式表示:1/f=1/v-1/u其中,f表示焦距,u表示物距,v表示像距。
4.单缝衍射公式单缝衍射是光通过一个缝隙之后发生的衍射现象。
单缝衍射公式可以用以下公式表示:sin(θ) = mλ/d其中,θ表示衍射角,m表示衍射级别,λ表示波长,d表示缝隙的宽度。
5.多缝衍射公式多缝衍射是光通过多个缝隙之后发生的衍射现象。
多缝衍射公式可以用以下公式表示:λ = d(sin(θ) + sin(θ'))其中,λ表示波长,d表示两个缝隙之间的距离,θ和θ'分别表示缝隙两侧的入射角。
6.群速公式群速是光在介质中传播的速度,与光的频率和介质的折射率有关。
群速公式可以用以下公式表示:v=c/n其中,v表示群速,c表示光速,n表示介质的折射率。
7.球面透镜公式球面透镜是由一个球面形成的透镜。
对于一个球面透镜,其焦距f和物距u、像距v之间的关系可以用以下公式表示:1/f=1/v-1/u其中,f表示焦距,u表示物距,v表示像距。
8.瓣射光现象公式瓣射光是在光通过行走波状过程中发生的现象。
瓣射光现象公式可以用以下公式表示:sin(θ) = mλ/a其中,θ表示瓣射角,m表示瓣射级别,λ表示波长,a表示光的孔径。
以上是一些常用的光学计算公式,使用这些公式可以进行光学相关的计算。

常用光学计算公式文章来源:未知(发布时间:2012-07-03)1. 焦距:反向延长的轴上成像锥形光束与延长的入射光束相交形成一个平面,从像到该平面的沿光轴距离就是焦距。
焦距f、通光孔径D与f/#(F数)之间的关系:2.视场角:由光学系统主平面与光轴交点看景物或看成像面的线长度时所张的角度。
全视场角2ω、像面尺寸2y与焦距f之间的关系:像面尺寸=像素数×像元尺寸ω=arctg(像素数×像元尺寸/2f)视场角分为水平视场角和垂直视场角,没有特殊说明是指由像面对角线尺寸计算出的视场角。
3. 分辨率:反映光学系统分辨物体细节的能力,通常将光学系统能够分辨名义物距处两个靠近的有间隙点源的能力定义为分辨率。
瑞利判据指出,两个靠近的有间隙点源通过光学系统成像,每个点都形成一个衍射斑。
如果两个衍射斑之间的距离等于艾里斑半径,两个点像是可以分辨的,此时像面上两个点的间距d 为:4.空间分辨率:探测器的张角,为像元尺寸与焦距的比值,单位为mrad。
空间分辨率=像元尺寸/f5. 尼奎斯特频率:是像素化传感器可以成功记录的最大空间频率,为1/(2像素周期),以lp/mm为单位。
例如,某传感器的像元尺寸为25um,其尼奎斯特频率为:1000/(2×25)=20lp/mm6.视觉放大率:视觉光学系统的放大倍率,其定义为有光学系统(即通过光学系统观察)时目标所张的角度与无光学系统(即用肉眼直接观察)时目标所张的角度之比。
在人眼为探测器的目视光学系统中,在250mm距离处定义放大倍率为1。
目镜视觉放大率Г=250/f7.数值孔径:就是到达轴上像的边缘光线的半锥角的正弦,即来自轴上物点的半锥角的正弦。
8.红外系统识别和探测距离的计算:其中,d s—识别距离d t—探测距离h—物体尺寸f—光机系统焦距n—识别或者探测所需像素数d0—像元尺寸9. 光焦度:焦距的倒数。
用Φ表示:其中,n—透镜的折射率r1,r2—透镜的两个曲率半径d—透镜的中心厚度对于薄透镜,光焦度Φ为:两个组合光学系统的光焦度Φ为:其中,f—组合系统的焦距Φ1,Φ2—两个系统的光焦度d—两个系统主平面之间的距离10. 平行平板:是个无光焦度的光学元件,不会使物体放大或者缩小,在光学系统中对总光焦度的贡献为零。

光学中的概念和公式一、光的基本概念1.1 光的传播光是一种电磁波,它在真空中的传播速度为 (3 10^8) 米/秒。
光在空气或其他介质中的传播速度会因为介质的折射率而有所不同。
1.2 光的波动性光的波动性可以通过双缝干涉、单缝衍射等实验证明。
光的波动性决定了它的亮度和颜色。
1.3 光的粒子性光同时具有粒子性,这一性质可以通过光电效应、康普顿效应等实验证明。
光的粒子性决定了它的能量和动量。
二、光学基本公式2.1 波动光学公式2.1.1 波动方程波动方程描述了光波在空间中的传播。
对于一维光波,波动方程可以表示为: = c^2其中,() 表示光波的振幅,(c) 表示光在介质中的传播速度,(t) 表示时间,(x) 表示空间坐标。
2.1.2 干涉公式干涉现象发生在两个或多个光波重叠时。
对于两个相互干涉的光波,干涉公式可以表示为:= _1 + _2其中,(_1) 和 (_2) 分别表示两个光波的振幅。
2.1.3 衍射公式衍射现象发生在光波通过一个孔径或遇到一个障碍物时。
对于夫琅禾夫衍射,衍射公式可以表示为:= (kr - )其中,(A) 表示光波的振幅,(r) 表示距离,(k) 表示波数,() 表示相位差。
2.2 粒子光学公式2.2.1 光电效应公式光电效应是指当光子照射到金属表面时,将电子从金属中逸出的现象。
光电效应公式可以表示为:E_{km} = h- W_0其中,(E_{km}) 表示电子的动能,(h) 表示普朗克常数,() 表示光的频率,(W_0) 表示金属的逸出功。
2.2.2 康普顿效应公式康普顿效应是指光子与电子发生散射时,光子的能量和动量发生改变的现象。
康普顿效应公式可以表示为:= (1 - )其中,() 表示光子波长的变化,(m_e) 表示电子的质量,(c) 表示光速,() 表示散射角。
三、光学元件和现象3.1 凸透镜和凹透镜凸透镜对光有会聚作用,可以将平行光聚焦到一个焦点上。
凹透镜对光有发散作用,可以将平行光发散。

光学物理公式
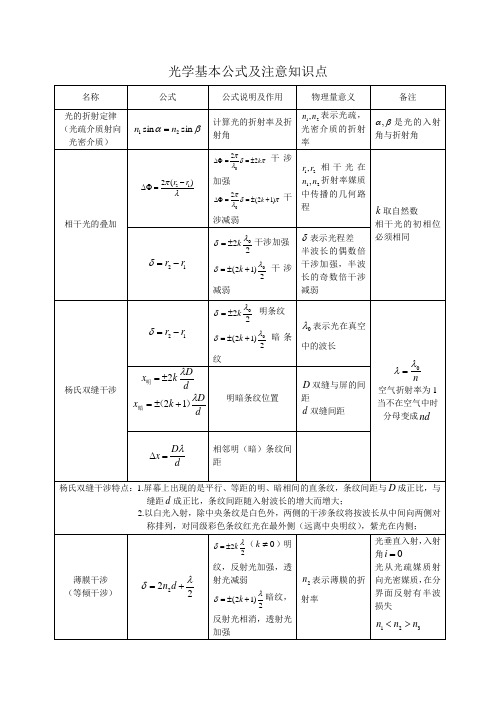
大学物理光学公式波动光学杨氏双缝干涉x=kDλ/d,薄膜干涉2ne + λ/2 =kλ(亮纹)单缝衍射a sinΨ=kλ(暗纹)asinΨ=(2k+1)λ/2 亮纹光栅方程(a+b)sinΨ=kλ。
1,透镜的等光程性,使用透镜不会产生附加光程差,半波损失,入射光从光疏(n1小)掠射(入射角约90°) 或正射(入射角约0°) 到光密媒质(n2 大)的界面时,产生半波损失。
光密→光疏无半波损失。
折射无半波损失。
2,条纹特点单色光照射:一系列平行的明暗相间的条纹;θ不太大时条纹等间距,中间级次低;Δx ∝λ。
白光照射:零级明纹为白色,其它亮纹构成彩带,由紫到红,第二级开始重合。
3,牛顿第一定律:任何物体都保持静止或匀速直线运动状态,除非它受到作用力而被迫改变这种状态。
牛顿第二定律:物体受到外力作用时,所获得的加速度a的大小与外力F的大小成正比,与物体的质量m成反比;加速度的方向与外力的方向相同。
1.37 F=ma牛顿第三定律:若物体A以力F作用与物体B,则同时物体B必以力F2作用与物体A;这两个力的大小相等、方向相反,而且沿同一直线。