2010年初中数学第二次模拟考试题(2)

一、选择题1．(0分)[ID ：68030]下列代数式的书写，正确的是（ ） A ．5nB ．n5C ．1500÷tD ．114x 2y 2．(0分)[ID ：68053]如图，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y 与n 之间的关系是（）A ．y=2n+1B ．y=2n +nC ．y=2n+1+nD ．y=2n +n+13．(0分)[ID ：68052]有一组单项式如下：﹣2x ，3x 2，﹣4x 3，5x 4……，则第100个单项式是（ ） A ．100x 100 B ．﹣100x 100C ．101x 100D ．﹣101x 1004．(0分)[ID ：68041]化简2a -[3b -5a -（2a -7b ）]的值为（ ）A ．9a -10bB ．5a +4bC ．-a -4bD ．-7a +10b5．(0分)[ID ：68040]下列去括号正确的是（ ） A ．112222x y x y ⎛⎫ =⎭-⎪⎝--- B ．()12122x y x y ++=+- C ．()16433232x y x y --+=-++ D ．()22x y z x y z +-+=-+6．(0分)[ID ：68025]观察下列单项式：223344191920202,2,2,2,,2,2,x x x x x x ---，则第n 个单项式是（ ） A ．2n n xB ．(1)2n n n x -C ．2n n x -D ．1(1)2n n n x +-7．(0分)[ID ：68021]1261年，我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律，比欧洲的相同发现要早三百多年，我们把这个三角形称为“杨辉三角”，请观察图中的数字排列规律，则,,a b c 的值分别为（ ）1111211464115101051331151161a b c A ．1,6,15a b c ===B ．6,15,20a b c ===C ．15,20,15a b c ===D ．20,15,6a b c ===8．(0分)[ID ：68015]已知132n x y +与4313x y 是同类项，则n 的值是（ ） A ．2B ．3C ．4D ．59．(0分)[ID ：68009]已知有理数1a ≠,我们把11a-称为a 的差倒数,如:2的差倒数是1112=--,1-的差倒数是()11112=--.如果12a =-,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数…依此类推,那么2020a 的值是（ ） A ．2-B ．13C ．23D ．3210．(0分)[ID ：68003]下面去括号正确的是（ ） A ．2()2y x y y x y +--=+- B ．2(35)610a a a a --=-+ C ．()y x y y x y ---=+-D ．222()2x x y x x y +-+=-+11．(0分)[ID ：67992]下列去括号正确的是（ ） A ．221135135122x y x x y y ⎛⎫--+=-++⎪⎝⎭B ．()8347831221a ab b a ab b --+=---C ．()()222353261063x y x x y x +--=+-+ D ．()()223423422x y x x y x --+=--+12．(0分)[ID ：67980]代数式21a b-的正确解释是（ ） A ．a 与b 的倒数的差的平方 B ．a 与b 的差的平方的倒数C ．a 的平方与b 的差的倒数D ．a 的平方与b 的倒数的差13．(0分)[ID ：67978]有20个数排成一行，对于任意相邻的三个数，都有中间的数等于前后两数的和．如果第一个数是0，第二个数是2，这20个数的和是（ ） A ．2B ．﹣2C ．0D ．414．(0分)[ID ：67977]下列关于多项式21ab a b --的说法中，正确的是（ ） A ．该多项式的次数是2 B ．该多项式是三次三项式 C ．该多项式的常数项是1D ．该多项式的二次项系数是1-15．(0分)[ID ：67963]小明乘公共汽车到白鹿原玩，小明上车时，发现车上已有（6a ﹣2b ）人，车到中途时，有一半人下车，但又上来若干人，这时车上共有（10a ﹣6b ）人，则中途上车的人数为（ ） A ．16a ﹣8bB ．7a ﹣5bC ．4a ﹣4bD ．7a ﹣7b二、填空题16．(0分)[ID ：68154]如果多项式32242(176)x x kx x +-+-中不含2x 的项，则k 的值为__．17．(0分)[ID ：68148]已知整数a 1，a 2，a 3，a 4…满足下列条件：a 1=0，a 2=﹣|a 1+1|，a 3=﹣|a 2+2|，a 4=﹣|a 3+3|，…，依此类推，则a 2016的值为_______.18．(0分)[ID ：68147]在同一平面中，两条直线相交有一个交点，三条直线两两相交最多有3个交点，四条直线两两相交最多有6个交点……由此猜想，当相交直线的条数为n 时，最多可有的交点数m 与直线条数n 之间的关系式为：m =_____.（用含n 的代数式填空） 19．(0分)[ID ：68145]观察下面的一列单项式：2342,4,8,16,,x x x x --根据你发现的规律，第n 个单项式为__________． 20．(0分)[ID ：68135]在多项式422315x xx x 中，同类项有_________________；21．(0分)[ID ：68131]m ，n 互为相反数，则（3m –2n ）–（2m –3n ）=__________． 22．(0分)[ID ：68129]某商店经销一种品牌的洗衣机，其中某一型号的洗衣机每台进价为a 元，商店将进价提高20%后作为零售价进行销售，一段时间后，商店又以9折优惠价促销，这时该型号洗衣机的零售价为__元．23．(0分)[ID ：68118]将连续正整数按以下规律排列，则位于第 7 行第 7 列的数 x 是________________．?13 61015 2128 2 5 9 1420 27 ? 4813 19 26 ?? 7121825 ?? 1117 24?? 1623 ??22?????x?24．(0分)[ID ：68104]在如图所示的运算流程中，若输出的数3y =，则输入的数x =________________．25．(0分)[ID ：68084]已知5a b -=，3c d +=，则()()b c a d +--的值等于______. 26．(0分)[ID ：68083]一个长方形的周长为68a b +，其一边长为23a b +，则另一边长为______.27．(0分)[ID ：68081]为了鼓励节约用电，某地对用户用电收费标准作如下规定：如果每户用电不超过50度，那么每度电按a 元收费，如果超过50度，那么超过部分按每度()0.5a +元收费，某居民在一个月内用电98度，他这个月应缴纳电费______元.三、解答题28．(0分)[ID ：67777]先化简，再求值：-2x 2-2[3y 2-2(x 2-y 2)+6]，其中x =-1，y =-2. 29．(0分)[ID ：67763]有这样一道题，计算()()4322433222422xx y x y x x y y x y -----+的值，其中0.25x =，1y =-；甲同学把“0.25x =”，错抄成“0.25x =-”，但他的计算结果也是正确的，你说这是为什么？ 30．(0分)[ID ：67759]已知多项式﹣x 2y 2m +1+xy ﹣6x 3﹣1是五次四项式，且单项式πx n y 4m ﹣3与多项式的次数相同，求m ，n 的值．【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1．A 2．B 3．C 4．A6．B7．B8．B9．A10．B11．C12．D13．A14．B15．B二、填空题16．2【分析】先去括号再根据不含的项列出式子求解即可得【详解】由题意得：解得故答案是：2【点睛】本题考查了去括号多项式中的无关型问题熟练掌握去括号法则是解题关键17．﹣1008【解析】a2=−|a1+1|=−|0+1|=−1a3=−|a2+2|=−|−1+2|=−1a4=−|a3+3|=−|−1+3|=−2a5=−|a4+4|=−|−2+4| =−2…所以n是奇数18．【分析】根据题意3条直线相交最多有3个交点4条直线相交最多有6个交点5条直线相交最多有10个交点而3=1+26=1+2+310=1+2+3+4故可猜想n条直线相交最多有1+2+3+…+（n-1）=个19．【分析】分别从单项式的系数与次数两方面总结即可得出规律进而可得答案【详解】解：由已知单项式的排列规律可得第n个单项式为：故答案为：【点睛】本题考查了单项式的规律探求通过所给的单项式找到规律并能准确的20．-2x5x【分析】根据同类项：所含字母相同并且相同字母的指数也相同进行判断即可【详解】解：-2x与5x是同类项；故答案为：-2x5x【分析】本题考查了同类项的知识解题的关键是掌握同类项的定义21．0【解析】由题意m+n=0所以(3m－2n)－(2m－3n)=3m-2n-2m+3n=m+n=0【点睛】本题考查相反数去括号法则等解题的关键是根据题意得出m+n=0然后再对所求的式子进行去括号合并同22．08a【解析】试题分析：根据题意得：a•（1+20）×90=108a；故答案为108a考点：列23．【分析】先根据第一行的第一列的数以及第二行的第二列的数第三行的第三列数第四行的第四列数进而得出变化规律由此得出结果【详解】第一行的第一列的数是1;第二行的第二列的数是5=1+4;第三行的第三列的数是24．或【分析】由运算流程可以得出有两种情况当输入的x为偶数时就有y=x当输入的x 为奇数就有y=（x+1）把y=3分别代入解析式就可以求出x的值而得出结论【详解】解：由题意得当输入的数x是偶数时则y=x当25．-2【分析】把原式去括号转化为含有(a-b)和(c+d)的式子然后代入求值即可【详解】故答案为：-2【点睛】本题考查了整式的化简求值把原式转化为含有(a-b)和(c+d)的式子是解决此题的关键26．【分析】根据长方形的周长公式列出代数式求解即可【详解】解：由长方形的周长=2×（长+宽）可得另一边长为：故答案为：a+b【点睛】本题考查了整式的加减长方形的周长公式列出代数式是解决此题的关键27．【分析】98度超过了50度应分两段进行计费第一段50每度收费a元第二段(98-50)度每度收费(a+05)元据此计算即可【详解】解：由题意可得：（元）故答案为：(98a+24)【点睛】本题考查了列代三、解答题28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题解析：A【分析】直接利用代数式书写方法分析得出答案．【详解】解：A、5n，书写正确，符合题意；B、n5，书写错误，不合题意；C、1500÷t，应为1500t，故书写错误，不合题意；D、114x2y=54x2y，故书写错误，不合题意；故选：A．【点睛】此题主要考查了代数式，正确把握代数式的书写方式是解题关键．2．B解析：B【详解】∵观察可知：左边三角形的数字规律为：1，2，…，n，右边三角形的数字规律为：2，22，…，2n，下边三角形的数字规律为：1+2，222+， (2)n+，∴最后一个三角形中y与n之间的关系式是y=2n+n.故选B．【点睛】考点：规律型：数字的变化类．3．C解析：C【分析】由单项式的系数，字母x的指数与序数的关系求出第100个单项式为101x100．【详解】由﹣2x，3x2，﹣4x3，5x4……得，单项式的系数的绝对值为序数加1，系数的正负为（﹣1）n，字母的指数为n，∴第100个单项式为（﹣1）100（100+1）x100＝101x100，故选C．【点睛】本题综合考查单项式的概念，乘方的意义，数字变化规律与序数的关系等相关知识点，重点掌握数字的变化与序数的关系．4．A【解析】2a －[3b －5a －(2a －7b)]=2a-(3b-5a-2a+7b)=2a-(10b-7a)=2a-10b+7a=9a-10b ， 故选A.【点睛】本题考查去括号，合并同类项，解题的关键是按运算的顺序先去括号，然后再进行合并同类项.5．D解析：D 【分析】根据整式混合运算法则和去括号的法则计算各项即可． 【详解】 A. 112222x y x y ⎛⎫ =⎭-⎪⎝--+，错误； B. ()12122x y x y ++=++，错误； C. ()136433222x y x y --+=-+-，错误； D. ()22x y z x y z +-+=-+，正确； 故答案为：D ． 【点睛】本题考查了整式的混合运算，掌握整式混合运算法则和去括号的法则是解题的关键．6．B解析：B 【分析】要看各单项式的系数和次数与该项的序号之间的变化规律．本题中，奇数项符号为负，偶数项符号为正，数字变化规律是（-1）n 2n ，字母变化规律是x n ． 【详解】因为第一个单项式是1112(1)2x x -=-⨯； 第二个单项式是222222(1)2x x =-⨯； 第三个单项式是333332(1)2x x -=-⨯， …，所以第n 个单项式是(1)2n n n x -． 故选：B ． 【点睛】本题考查了单项式的系数和次数的规律探索，确定单项式的系数和次数时，把一个单项式改写成数字因数和字母因式的积，是找准单项式的系数和次数的关键．分别找出单项式的系数和次数的规律也是解决此类问题的关键．7．B【分析】由数字排列规律可得：除去每行两端的数字外，每个数字都等于上一行的左右两个数字之和，据此解答即可． 【详解】解：根据图形得：除去每行两端的数字外，每个数字都等于上一行的左右两个数字之和， 所以156a =+=，51015,101020b c =+==+=． 故选：B ． 【点睛】本题以“杨辉三角”为载体，主要考查了与整式有关的数字类规律探索，找准规律是关键．8．B解析：B 【分析】根据同类项的概念可得关于n 的一元一次方程，求解方程即可得到n 的值. 【详解】 解：∵132n x y +与4313x y 是同类项， ∴n+1=4， 解得，n=3， 故选：B. 【点睛】本题考查了同类项，解决本题的关键是判断两个项是不是同类项，只要两看，即一看所含有的字母是否相同，二看相同字母的指数是否相同．9．A解析：A 【分析】求出数列的前4个数，从而得出这个数列以-2，13，32依次循环，用2020除以3，再根据余数可求a 2020的值． 【详解】∵a 1=-2， ∴2111(3)3a ==--，3131213a ==-， 412312a ==-- ∴每3个结果为一个循环周期 ∵2020÷3=673⋯⋯1，∴202012a a ==- 故选：A. 【点睛】本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．10．B解析：B 【分析】根据去括号法则对四个选项逐一进行分析,要注意括号前面的符号,以选用合适的法则. 【详解】A. 2()2y x y y x y +--=--,故错误;B. 2(35)610a a a a --=-+,故正确;C. ()y x y y x y ---=++,故错误;D. 222()22x x y x x y +-+=-+,故错误; 故选:B 【点睛】本题考查去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘;括号前是“+”，去括号后，括号里的各项都不改变符号;括号前是“一”，去括号后，括号里的各项都改变符号.11．C解析：C 【分析】依据去括号法则计算即可判断正误. 【详解】 A. 221135135122x y x x y x ⎛⎫--+=-+-⎪⎝⎭，故此选项错误；B. ()8347831221a ab b a ab b --+=-+-，故此选项错误；C. ()()222353261063x y x x y x +--=+-+，此选项正确；D. ()()223423422x y x x y x --+=---，故此选项错误；故选：C. 【点睛】此题考查整式的化简，注意去括号法则.12．D解析：D 【分析】说出代数式的意义，实际上就是把代数式用语言叙述出来．叙述时，要求既要表明运算的顺序，又要说出运算的最终结果． 【详解】解：代数式21a b-的正确解释是a 的平方与b 的倒数的差. 故选：D.用语言表达代数式的意义，一定要理清代数式中含有的各种运算及其顺序．具体说法没有统一规定，以简明而不引起误会为出发点．13．A解析：A【分析】根据题意可以写出这组数据的前几个数，从而发现数字的变化规律，再利用规律求解.【详解】解：由题意可得，这列数为：0，2，2，0，﹣2，﹣2，0，2，2，…，∴这20个数每6个为一循环，且前6个数的和是：0+2+2+0+（﹣2）+（﹣2）＝0，∵20÷6＝3…2，∴这20个数的和是：0×3+（0+2）＝2.故选：A．【点睛】本题考查了数字的变化规律，正确理解题意，发现题目中数字的变化规律：每6个数重复出现是解题的关键.14．B解析：B【分析】直接利用多项式的相关定义进而分析得出答案．【详解】A、多项式21ab a b--次数是3，错误；B、该多项式是三次三项式，正确；C、常数项是-1，错误；D、该多项式的二次项系数是1，错误；故选：B．【点睛】此题考查多项式，正确掌握多项式次数与系数的确定方法是解题关键．15．B解析：B【分析】根据题意表示出途中下车的人数，再根据车上总人数即可求得中途上车的人数．【详解】由题意可得：（10a﹣6b）﹣[（6a﹣2b）﹣（3a﹣b）]＝10a﹣6b﹣6a+2b+3a﹣b＝7a﹣5b．故选B．【点睛】本题考查了整式加减的应用，根据题意正确列出算式是解决问题的关键.16．2【分析】先去括号再根据不含的项列出式子求解即可得【详解】由题意得：解得故答案是：2【点睛】本题考查了去括号多项式中的无关型问题熟练掌握去括号法则是解题关键 解析：2【分析】先去括号，再根据“不含2x 的项”列出式子求解即可得．【详解】3223242(176)4(2)176x x kx x x k x x +-+-=+--+，由题意得：20k -=，解得2k =，故答案是：2．【点睛】本题考查了去括号、多项式中的无关型问题，熟练掌握去括号法则是解题关键． 17．﹣1008【解析】a2=−|a1+1|=−|0+1|=−1a3=−|a2+2|=−|−1+2|=−1a4=−|a3+3|=−|−1+3|=−2a5=−|a4+4|=−|−2+4|=−2…所以n 是奇数解析：﹣1008【解析】a 2=−|a 1+1|=−|0+1|=−1，a 3=−|a 2+2|=−|−1+2|=−1，a 4=−|a 3+3|=−|−1+3|=−2，a 5=−|a 4+4|=−|−2+4|=−2，…，所以n 是奇数时，a n =−12n -；n 是偶数时，a n =−2n ； a 2016=−20162=−1008. 故答案为-1008. 点睛：此题考查数字的变化规律，根据所给出的数，观察出n 为奇数与偶数时的结果的变化规律是解题的关键. 探寻数列规律：认真观察、席子思考、善用联想是解决问题的方法.利用方程解决问题.当问题中有多个未知数时，可先设其中一个为x ，再利用它们之间的关系，设出其它未知数，然后列方程.18．【分析】根据题意3条直线相交最多有3个交点4条直线相交最多有6个交点5条直线相交最多有10个交点而3=1+26=1+2+310=1+2+3+4故可猜想n 条直线相交最多有1+2+3+…+（n-1）=个解析：()12n n - 【分析】根据题意，3条直线相交最多有3个交点，4条直线相交最多有6个交点，5条直线相交最多有10个交点．而3=1+2，6=1+2+3，10=1+2+3+4，故可猜想，n条直线相交，最多有1+2+3+…+（n-1）=()12n n-个交点．【详解】解：∵3条直线相交最多有3个交点，4条直线相交最多有6个交点．而3=1+2，6=1+2+3，10=1+2+3+4，∴可猜想，n条直线相交，最多有1+2+3+…+（n-1）=()12 n n-个交点．即()12n nm-=故答案为：()12n n-．【点睛】本题主要考查了相交线，图形的规律探索，此题着重培养学生的观察、实验和猜想、归纳能力，掌握从特殊向一般猜想的方法．19．【分析】分别从单项式的系数与次数两方面总结即可得出规律进而可得答案【详解】解：由已知单项式的排列规律可得第n个单项式为：故答案为：【点睛】本题考查了单项式的规律探求通过所给的单项式找到规律并能准确的解析：(2)n n x-【分析】分别从单项式的系数与次数两方面总结即可得出规律，进而可得答案．【详解】解：由已知单项式的排列规律可得第n个单项式为：(2)n n x-．故答案为：(2)n n x-．【点睛】本题考查了单项式的规律探求，通过所给的单项式找到规律，并能准确的用代数式表示是解题的关键．20．-2x5x【分析】根据同类项：所含字母相同并且相同字母的指数也相同进行判断即可【详解】解：-2x与5x是同类项；故答案为：-2x5x【分析】本题考查了同类项的知识解题的关键是掌握同类项的定义解析：-2x，5x【分析】根据同类项：所含字母相同，并且相同字母的指数也相同，进行判断即可．【详解】解： -2x与5x是同类项；故答案为：-2x，5x．【分析】本题考查了同类项的知识，解题的关键是掌握同类项的定义．21．0【解析】由题意m+n=0所以(3m－2n)－(2m－3n)=3m-2n-2m+3n=m+n=0【点睛】本题考查相反数去括号法则等解题的关键是根据题意得出m+n=0然后再对所求的式子进行去括号合并同解析：0【解析】由题意m+n=0，所以(3m－2n)－(2m－3n)=3m-2n-2m+3n=m+n=0.【点睛】本题考查相反数、去括号法则等，解题的关键是根据题意得出m+n=0，然后再对所求的式子进行去括号，合并同类项，整体代入数值即可.22．08a【解析】试题分析：根据题意得：a•（1+20）×90=108a；故答案为108a考点：列代数式解析：08a【解析】试题分析：根据题意得：a•（1+20%）×90%=1.08a；故答案为1.08a．考点：列代数式．23．【分析】先根据第一行的第一列的数以及第二行的第二列的数第三行的第三列数第四行的第四列数进而得出变化规律由此得出结果【详解】第一行的第一列的数是1;第二行的第二列的数是5=1+4;第三行的第三列的数是解析：85【分析】先根据第一行的第一列的数，以及第二行的第二列的数，第三行的第三列数，第四行的第四列数，进而得出变化规律，由此得出结果．【详解】第一行的第一列的数是 1;第二行的第二列的数是 5=1+4;第三行的第三列的数是 13=1+4+8;第四行的第四列的数是 25=1+4+8+12;......第n行的第n列的数是1+4+8+12+...+4(n-1)=1+4[1+2+3+...+(n+1)]=1+2n(n-1);∴第七行的第七列的数是1+2×7×（7-1）=85;故答案为：85．【点睛】本题考查数字的变化规律，学生通过观察、分析、归纳发现其中的规律，从而利用规律解决问题．24．或【分析】由运算流程可以得出有两种情况当输入的x为偶数时就有y=x当输入的x为奇数就有y=（x+1）把y=3分别代入解析式就可以求出x的值而得出结论【详解】解：由题意得当输入的数x是偶数时则y=x当解析：5或6【分析】由运算流程可以得出有两种情况，当输入的x为偶数时就有y=12x，当输入的x为奇数就有y=12（x+1），把y=3分别代入解析式就可以求出x的值而得出结论．【详解】解：由题意，得当输入的数x是偶数时，则y=12x，当输入的x为奇数时，则y=12（x+1）．当y=3时，∴3=12x或3=12（x+1）．∴x=6或5故答案为：5或6【点睛】本题考查了有理数的混合运算，解答此题的关键是，根据流程图，列出方程，解方程即可得出答案.25．-2【分析】把原式去括号转化为含有(a-b)和(c+d)的式子然后代入求值即可【详解】故答案为：-2【点睛】本题考查了整式的化简求值把原式转化为含有(a-b)和(c+d)的式子是解决此题的关键解析：-2【分析】把原式去括号转化为含有(a-b)和(c+d)的式子，然后代入求值即可．【详解】()()()()532b c a d b c a d b a c d+--=+-+=-++=-+=-.故答案为：-2．【点睛】本题考查了整式的化简求值，把原式转化为含有(a-b)和(c+d)的式子是解决此题的关键．26．【分析】根据长方形的周长公式列出代数式求解即可【详解】解：由长方形的周长=2×（长+宽）可得另一边长为：故答案为：a+b【点睛】本题考查了整式的加减长方形的周长公式列出代数式是解决此题的关键解析：+a b【分析】根据长方形的周长公式列出代数式求解即可．【详解】解：由长方形的周长=2×（长+宽）可得，另一边长为：()()68223a b a b a b +÷-+=+. 故答案为：a +b ．【点睛】本题考查了整式的加减，长方形的周长公式列出代数式是解决此题的关键．27．【分析】98度超过了50度应分两段进行计费第一段50每度收费a 元第二段(98-50)度每度收费(a+05)元据此计算即可【详解】解：由题意可得：（元）故答案为：(98a+24)【点睛】本题考查了列代解析：()9824a +【分析】98度超过了50度，应分两段进行计费，第一段50，每度收费a 元，第二段(98-50)度，每度收费(a +0.5)元，据此计算即可．【详解】解：由题意可得：()()5098500.59824a a a +-+=+（元）.故答案为：(98a +24)．【点睛】本题考查了列代数式，根据题意，列出代数式是解决此题的关键．三、解答题28．2221012x y --，－50．【分析】根据整式的加减及合并同类项先对原式进行化简，得到2221012x y --，再将1,2x y =-=-代入即可求解，需要注意本题中两次遇到去括号，注意符号的改变.【详解】原式=2222223226x y x y ⎡⎤---++⎣⎦=2222264412x y x y --+--=2222246412x x y y -+---=2221012x y --，当1,2x y =-=-时，原式=222(1)10(2)1250⨯--⨯--=-.【点睛】本题主要考查了去括号，整式的加减，合并同类项，乘法的分配律等相关内容，熟练掌握各项计算法则是解决本题的关键，注意去括号中符号的改变原则. 29．化简后为32y ，与x 无关.【分析】原式去括号合并得到最简结果中不含x ，可得出x 的取值对结果没有影响．【详解】解：()()4322433222422x x y x y x x y y x y -----+ =43224332224242x x y x y x x y y x y ---+++=32y ，原式化简后为32y ，跟x 的取值没有关系．因此不会影响计算结果．【点睛】本题考查了整式的加减——化简求值，正确的将原式去括号合并同类项是解决此题的关键．30．m ＝1，n ＝4．【分析】根据多项式的次数是多项式中次数最高的单项式的次数，可得m 的值，根据单项式的次数是单项式中所有字母指数和，可得n 的值．【详解】∵多项式﹣x 2y 2m +1+xy ﹣6x 3﹣1是五次四项式，且单项式πx n y 4m ﹣3与多项式的次数相同， ∴2+2m +1＝5，n +4m ﹣3＝5，解得m ＝1，n ＝4．【点睛】本题考查了多项式，利用多项式的次数是多项式中次数最高的单项式的次数，单项式的次数是单项式中所有字母指数和得出m 、n 的值是解题关键．。

广东省初中学业水平考试第二次模拟测试卷数学一、选择题（本大题共10小题，每小题3分，共30分）1. ﹣3的相反数是（ ） A. 13− B. 13 C. 3− D. 3【答案】D【解析】 【分析】相反数的定义是：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，0的相反数还是0．【详解】根据相反数的定义可得：－3的相反数是3，故选D ．【点睛】本题考查相反数，题目简单，熟记定义是关键．2. 如图是由4个大小相同的小立方块搭成的几何体，这个几何体的左视图是（ ）A.B. C. D.【答案】A【解析】 【分析】本题主要考查了几何体的三种视图和学生的空间想象能力，视图中每一个闭合的线框都表示物体上的一个平面，而相连的两个闭合线框常不在一个平面上，根据左视图的作法求解即可．【详解】解：这个几何体的左视图有2行，第一行有1个正方形，第二行有2个正方形，第1列有2个正方形，第2列有1个正方形故选：A ．3. 在平面直角坐标系中，点()5,2P −−关于y 轴对称的点的坐标是（ ）A. ()5,2−B. ()2,5−C. ()2,5−D. ()5,2−【答案】D【解析】【分析】本题主要考查了平面直角坐标系中对称点的规律，解决本题的关键是掌握好对称点的坐标规律：（1）关于x 轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y 轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．【详解】解：点()5,2P −−关于y 轴对称的点的坐标是()5,2−，故选：D ．4. 若一个凸多边形的内角和为720°，则这个多边形的边数为( )A. 4B. 5C. 6D. 7 【答案】C【解析】【分析】设这个多边形的边数为n ，根据多边形的内角和定理得到(n ﹣2)×180°=720°，然后解方程即可．【详解】设这个多边形的边数为n ，由多边形的内角和是720°，根据多边形的内角和定理得（n －2）180°=720°．解得n =6.故选C.【点睛】本题主要考查多边形的内角和定理，熟练掌握多边形的内角和定理是解答本题的关键. 5. 已知点P （m-2，2m-1）在第二象限，且m 为整数，则m 的值是（ ）A. 0B. 1C. 2D. 3 【答案】B【解析】【分析】根据第二象限内的点的坐标特征：横坐标小于0，纵坐标大于0列不等式组可求出m 的取值范围，根据m 为整数即可确定m 的值．【详解】∵点P （m-2，2m-1）在第二象限，∴20210m m −< −> ， 解得：122m <<， ∵m 为整数，∴m=1，故选：B ．【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点．四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．6. 如图，ABC 是等腰直角三角形，a b ∥．若1125∠=°，则2∠的度数是（ ）A. 30°B. 35°C. 40°D. 45°【答案】B【解析】 【分析】本题考查的是角的和差运算，平行线的性质，先证明12ABC ∠=∠+∠，从而可得答案．【详解】解：∵a b ∥，∴12ABC ∠=∠+∠，∵1125∠=°，90ABC ∠=°， ∴2135ABC ∠=∠−∠=°，故选B7. 某小组在一次“在线测试”中做对的题数分别是10869878，，，，，，，对于这组数据，下列判断错误的是（ ）A. 众数是8B. 中位数是8C. 平均数是8D. 方差是8 【答案】D【解析】【分析】根据平均数，众数，中位数，方差的定义求解判断即可．【详解】解：把这组数据从小到大排列为67888910，，，，，，，处在最中间的数是8，∴这组数据的中位数为8，故B 不符合题意；∵这组数据中8出现了3次，出现的次数最多，∴这组数据众数为8，故A 不符合题意； 这组数据的平均数为1086987887++++++=，故C 不符合题意； 这组数据的方差为 ()()()()()2222268788889810810877−+−+×−+−+−=≠，故D 符合题意； 故选D ． 【点睛】本题主要考查了求平均数，众数，中位数，方差，熟知平均数，众数，中位数，方差的定义是解的题的关键．8. 已知x=1是关于x 的方程(1-k)x 2+k 2x-1=0的根,则常数k 的值为 ( )A. 0B. 1C. 0或1D. 0或-1 【答案】C【解析】【详解】解：当k =1时，方程（1﹣k ）x 2+k 2x ﹣1=0为一元一次方程，解为x =1；k ≠1时，方程（1﹣k ）x 2+k 2x ﹣1=0为一元二次方程，把x =1代入方程（1﹣k ）x 2+k 2x ﹣1=0可得：1﹣k +k 2﹣1=0，即﹣k +k 2=0，可得k （k ﹣1）=0，即k =0或1（舍去）；故选C ．点睛：该题应注意方程与一元二次方程的区别，此题1﹣k 可为0，同时此题也考查了因式分解．9. 如图，已知矩形ABCD 的边AB =，3BC =，E 为边CD 上一点．将BCE 沿BE 所在的直线翻折，点C 恰好落在AD 边上的点F 处，过点F 作FM BE ⊥，垂足为点M ，取AF 的中点N ，连接MN ，则MN 的长为（ ）A. 3B.C. －1D. 【答案】D【解析】 【分析】连接AC ，FC ，由折叠的性质得出CF BE ⊥，由勾股定理求出AC ，利用三角形的中位线定理解决问题即可．【详解】解：如图所示连接AC ，FC ．由翻折的性质可知，BE 垂直平分线段CF ，CF BE ∴⊥，又FM BE ⊥ ，F ∴，M ，C 共线，FM MC ∴=，四边形ABCD 是矩形，90ABC ∴∠=°，AC ∴，N 是AF 的中点，M 是CF 的中点，MN ∴是ACF △的中位线，12MN AC ∴==．故选：D ．【点睛】本题考查翻折变换，矩形的性质，勾股定理，三角形的中位线定理等知识，解题的关键是学会添加常用辅助线，构造三角形中位线解决问题．10. 如图1，在Rt ABC △中，点D 为AC 的中点，动点P 从点D 出发，沿着D A B →→的路径以每秒1个单位长度的速度运动到点B ，在此过程中线段CP 的长度y 随着运动时间x 的函数关系如图2所示，则BC 的长为（ ）A.B.C.D. 【答案】C【解析】【分析】本题考查了动点问题的函数图象、解直角三角形、勾股定理，当0x =时，点P 在点D 处，此时3y PC PA ===，则6AC =，当3x =+时，PC AB ⊥，求出AP =，由勾股定理得出4CP =，求出tan =A tan BC AC A =⋅计算即可得解． 【详解】解：当0x =时，点P 点D 处，此时3y PC PA ===，则6AC =，当3x =+时，PC AB ⊥，在，则33AP x AD =−=+−=，4CP ∴===，tan CP A AP ∴=，tan 6BC AC A ∴=⋅， 故选：C ． 二、填空题（本大题共5小题，每小题3分，共15分）11. 国家统计局公布了2023年的人口数据：2023年末全国人口140967万人，比上年末减少208万人，其中208万用科学记数法表示为______．【答案】62.0810×【解析】【分析】本题主要考查了科学记数法的表示方法，熟练掌握科学记数法的表示方法是解题的关键．科学记数法的表现形式为10n a ×的形式，其中1||10,a n ≤<为整数，确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n 是正整数，当原数绝对值小于1时，n 是负整数；由此进行求解即可得到答案．【详解】解：∵208万2080000=，∴208万用科学记数法表示为62.0810×．故答案为：62.0810×．12. 因式分解：2312x −=________________． 【答案】()()322x x +−【解析】【分析】此题主要考查了提取公因式法与公式法的综合运用，正确运用平方差公式是解题关键．首先提取公因式3，再利用平方差公式分解因式即可．【详解】解：原式()234x =− ()()322x x =+−．故答案为：()()322x x +−．13. 如图，将ABC 放在每个小正方形边长为1的网格中，点A ，B ，C 均在格点上，则tan A 的值是______． 【答案】12##05 【解析】 【分析】根据题意，作BD AC ⊥于点D ，可以求得BD 、AD 的长，从而可以求出tan A 的值．【详解】作BD ⊥AC 于点D ，如图所示：2BC =，AC ，点A 到BC 的距离为3，AB =322AC BD BC ××∴=232×=，.BD ∴，AD ∴=1tan =2BD A AD ∴==， 故答案是：12．【点睛】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边，构造直角三角形是本题的关键．14. 如图，菱形ABCD 的边长为4cm ，∠A ＝60°，弧BD 是以点A 为圆心，AB 长为半径的弧，弧CD 是以点B 为圆心，BC 长为半径的弧，则阴影部分的面积为______【答案】2【解析】【分析】连接BD ，判断出△ABD 是等边三角形，根据等边三角形的性质可得∠ABD=60°，再求出∠CBD=60°=S △ABD ，计算即可得解． 【详解】解：如图，连接BD ，∵四边形ABCD 是菱形，∴AB=AD ，∵∠A=60°，∴△ABD 是等边三角形，∴∠ABD=60°，又∵菱形的对边AD ∥BC ，∴∠ABC=180°-60°=120°，∴∠CBD=120°-60°=60°，∴S 阴影=S 扇形BDC -（S 扇形ABD -S △ABD )， ∵AB=CD ，∠CBD=∠A=60°，∴S 扇形BDC =S 扇形ABD ，∴S 阴影=S △ABD 142×cm 2．故答案为2．【点睛】本题考查了菱形的性质，扇形的面积的计算，熟记性质并作辅助线构造出等边三角形是解题的关键．15. 如图，AB 是半圆O 的直径，点C 在半圆上，AB ＝5，AC ＝4，D 是 BC上的一个动点，连接AD ．过点C 作CE ⊥AD 于E ，连接BE ，则BE 的最小值是_____．2−【解析】【分析】取AC 的中点O ′，连接,,BO BC EO ′′，先利用圆周角定理判断出点E 在以AC 为直径的一段弧上运动，从而可得2O E O C ′′==，再利用圆周角定理、勾股定理可得O B ′=，然后根据两点之间线段最短即可求得最小值．【详解】解：如图，取AC 的中点O ′，连接,,BO BC EO ′′，则122O C AC ′==，CE AD ⊥ ，90AEC ∴∠=°，∴在点D 移动的过程中，点E 在以AC 为直径的一段弧上运动，即O ′ 上运动， 2O E O C ′′∴==，AB 是直径，90ACB ∴∠=°，在Rt ABC 中，4,5AC AB ==，3BC ∴=，在Rt BCO ′ 中，O B ′==，由两点之间线段最短可知，当点,,O E B ′共线时，O E BE ′+取得最小值，最小值为O B ′=，所以BE 的最小值为2O B O E ′′−=，2−．【点睛】本题考查了圆周角定理、勾股定理、两点之间线段最短等知识点，正确判断出点E 的运动轨迹是解题关键．三、解答题（一）（本大题共2小题，每小题5分，共10分）16. 2013)4sin 302−° −+−【答案】3【解析】【分析】根据零指数幂，负整数指数幂和特殊的三角函数值计算即可. 【详解】解：原式121442=−+−×=3． 17. 如图，在Rt ABC 中，90B ∠=°，AD 为BAC ∠的平分线．（1）尺规作图：过点D 作AC 的垂线DE ，交AC 于点E ．(不写作法，保留作图痕迹)（2）若30C ∠=°，3AB =，则 ACD 的面积是 ．【答案】（1）见解析 （2）【解析】【分析】本题考查了作垂线，含30度角的直角三角形的性质，勾股定理；（1）根据题意，过点D ，作AC 的垂线DE ，交AC 于点E ；（2）根据题意得出60BAC ∠=°，根据AD 为BAC ∠的平分线，得出30BAD ∠=°，进而勾股定理求得BD ，即可得出DC ，根据三角形的面积公式，即可求解． 【小问1详解】解：如图所示，DE 即为所求；【小问2详解】解：∵在Rt ABC 中，90B ∠=°，30C ∠=°，∴60BAC ∠=°，12AB AC =，则BC ==∵AD 为BAC ∠的平分线， ∴30BAD ∠=°， ∴12BD AD =，∴D B A =，∵3AB =，∴BD =，∴CD BC BD =−==，∴ ACD 的面积是11322CD AB ××=×=． 四、解答题（二）（本大题共3小题，每小题7分，共21分）18. 先化简，再求值：2226911x x x x x ⎛⎫-+ ⎪-÷ ⎪--⎝⎭，其中x =3+．【答案】3xx −，1+【解析】【分析】本题考查了分式的化简求值，分母有理化；先根据分式的加减计算括号内的，同时将除法转化为乘法，再根据分式的性质化简，最后将字母的值代入求解．【详解】解：2226911x x x x x ⎛⎫-+ ⎪-÷ ⎪--⎝⎭=212(1)1(3)x x x x x −−−⋅−−=23(1)1(3)x x x x x −−⋅−− =3xx −，当x =3时，原式1．19. 的小正方形纸片沿中间对角线剪开，拼成一个大正方形．（1）大正方形的边长是______cm ．（2）丽丽同学想用这块大正方形纸片裁剪出一块面积为212cm 且长和宽之比为3:2的长方形纸片，她能裁出来吗？请说明理由．【答案】（1）4 （2）不能裁出，理由见解析 【解析】【分析】（1）已知两个正方形的面积之和就是大正方形的面积，根据面积公式即可求出大正方形的边长； （2）先设长方形纸片的长为()3x cm ，宽为：()2x cm ，根据面积公式列方程，求出长方形的边长，将长方形的长与正方形边长进行比较即可判断． 【小问1详解】解：两个正方形的面积之和为：()22216cm ×=，∴拼成的大正方形的面积为：()216cm ，∴大正方形的边长为：4cm ， 故答案为：4； 【小问2详解】解：设长方形纸片的长为()3x cm ，宽为：()2x cm ，∴3212x x ⋅=，解得x =，∴34x =>，∴不能使裁下的长方形纸片的长宽之比为：3:2，且面积为()212cm．【点睛】本题考查算术平方根的实际应用，能根据题意列出算式是解题的关键．20. 为了解中考体育科目训练的效果，九年级学生中随机抽取了部分学生进行了以此中考体育科目测试（把测试结果分为四个等级，A等：优秀；B等：良好；C等：及格；D等：不及格），并将结果汇成了如图1、2所示两幅不同统计图，请根据统计图中的信息解答下列问题：（1）本次抽样测试的学生人数是人；（2）图1扇形图中D等所在的扇形的圆心角的度数是，并把图2条形统计图补充完整；（3）已知得A等的同学有一位男生，体育老师想从4名同学中随机选择两位同学向其他同学介绍经验，请用列表法或画树状图的方法求出选中的两人刚好是一男一女的概率．【答案】（1）25 （2）43.2°，条形图见解析（3）12【解析】【分析】本题考查了列表法与树状图法求概率，条形统计图与扇形统计图信息关联，求扇形统计图圆心角，画条形统计图．（1）用B等级的人数除以它所占的百分比即可得到调查的总人数；（2）用总人数分别减去A、B、C等级的人数得到D等级人数，然后用360°乘以D等级所占的百分比得D 等所在的扇形的圆心角的度数，再补全条形统计图；（3）画树状图展示所有12种等可能的结果数，再找出选中的两人刚好是一男一女的结果数，然后根据概率公式求解．【小问1详解】解：抽取B等成绩的人数为10人，所占比例为40%，∴本次抽样测试学生人数是10=2540%（人），故答案为：25；【小问2详解】D等级的人数为2541083−−−=（人），所以D等所在的扇形的圆心角的度数336043.2 25×°=°，的条形图如下图：【小问3详解】画树状图为：共有12种等可能的结果数，其中选中的两人刚好是一男一女的结果数为6， 所以选中的两人刚好是一男一女的概率为61=122． 五、解答题（三）（本大题共3小题，每小题8分，共24分）21. 某学校准备购进一批足球和篮球，从体育商城了解到：足球单价比篮球单价少25元，用250元购买足球与用375元购买篮球的数量相等． （1（2）若该学校准备同时购进这两种足球和篮球共80个，并且足球的数量不多于篮球数量的3倍，求本次购买最少花费多少钱．【答案】（1）足球的单价是50元，篮球的单价是75元 （2）本次购买最少花费4500元 【解析】【分析】本题考查了分式方程以及一元一次不等式，一次函数的应用，正确掌握相关性质内容是解题的关键．（1）先设足球的单价是x 元，则篮球的单价是()25x +元，根据题意列式25037525x x =+，进行作答即可．（2）先列不等式得出60m ≤，再设总费用w ，依题意得出()507580w m m =+−，结合一刹那函数的性质进行作答． 【小问1详解】解：设足球的单价是x 元，则篮球的单价是()25x +元， 根据题意得：25037525x x =+， 解得：50x =，经检验50x =是所列方程的解，且符合题意， ∴25502575x +=+=（元）． 答：足球的单价是50元，篮球的单价是75元； 【小问2详解】设购买足球m 个，则购买篮球()80m −个， 根据题意得：()380m m ≤−， 解得：60m ≤，设学校购买足球和篮球的总费用为w 元，则()507580w m m =+−， 即256000w m =−+， ∵250−<，∴w 随m 的增大而减小，∴当60m =时，w 取得最小值，为4500元 ∴本次购买最少花费4500元．22. 独轮车（图1）俗称“手推车”，又名辇、鹿车等，西汉时已在一些田间隘道上出现．北宋时正式出现独轮车名称，在北方，几乎与毛驴起同样的运输作用．如图2所示为从独轮车中抽象出来的几何模型．在ABC 中，AB BC =，以ABC 的边AB 为直径作O ，交AC 于点P ，且PD BC ⊥，垂足为点D ．（1）求证：PD 是O 的切线；（2）若1tan ,22C BD ==，求O 的半径． 【答案】（1）见详解 （2）5 【解析】【分析】（1）连接OP ，由等腰三角形的性质可得OP BC ∥，继而可证明PD 是O 的切线；（2）连接PB ，可证C BPD ∠=∠，则由1tan tan 2BPD C ∠==可求PD ，再运用勾股定理求得BP =，最后由BDP BPC △∽△即可求解． 【小问1详解】 证明：连接OP ，∵AB BC =， ∴A C ∠=∠， ∵OA OP =， ∴OPA A ∠=∠， ∴OPA C ∠=∠， ∴OP BC ∥ ∴PDC OPD ∠=∠， 又∵PD BC ⊥， ∴90PDC ∠=°， ∴90OPD ∠=°， 即PD OP ⊥， ∴PD 是O 的切线； 【小问2详解】 解：连接PB ，如图，∵AB 为直径， ∴90APB ∠=°，∴90C PBC ∠+∠=°， 又∵90BPD PBC ∠+∠=°， ∴C BPD ∠=∠， 在Rt PBD △中， ∵21tan tan 2BD BPD C PD PD ∠====， ∴4PD =，∴BP∵,BDP BPC DBP PBC ∠=∠∠=∠， ∴BDP BPC △∽△， ∴BP BD BC BP=，=解得：10BC =， ∴10BA BC ==， ∴O 的半径为5．【点睛】本题考查了圆的切线的判定，等腰三角形性质，平行线的判定与性质，相似三角形的判定与性23. 如图，ABO 中，()0,4A ，()3,0B −，AB 绕点B 顺时针旋转与BC 重合，点C 在x 轴上，连接AC ，若反比例函数my x=与直线AC 仅有一个公共点E（1）求直线AC 和反比例函数my x=的解析式； （2）把ACB △沿直线AC 翻折到ACD ，AD 与反比例函数交于点F ，求FCD 的面积．【答案】（1）直线AC 解析式为24y x =−+，反比例函数解析式为2y x=（2）9 【解析】【分析】（1）先利用勾股定理求出5AB =，进而利用旋转的性质得到5BC AB ==，则()20C ，，再利用待定系数法求出直线AC 的解析式，联立直线AC 的解析式和反比例函数解析式得到的一元二次方程只有一个实数根，据此求解即可；（2）先由折叠的性质证明四边形ABCD 是菱形，得到AD BC ∥，求出142F，，得到92DF =，则11949222FCD S DF OA =⋅=××=△． 【小问1详解】解：∵()0,4A ，()3,0B −， ∴43OA OB ==，，∴5AB ，由旋转的性质可得5BC AB ==， 又∵点C 在x 轴上， ∴2OC =，∴()20C ，， 设直线AC 解析式为y kx b =+， ∴204k b b +== ，∴24k b =− =， ∴直线AC 解析式24y x =−+， 联立24y x my x =−+=得24m x x =−+，即2240x x m −+=， ∵反比例函数my x=与直线AC 仅有一个公共点E ， ∴方程2240x x m −+=只有一个实数根，为∴()2480m ∆=−−=，∴2m =，∴反比例函数解析式为2y x=； 【小问2详解】解：由折叠的性质可得AB AD CB CD ==，， 又∵5BC AB ==，∴5AB AD CB CD ====， ∴四边形ABCD 是菱形， ∴AD BC ∥， 在2y x =中，当4y =时，12x =， ∴142F，， ∴92DF AD AF =−=， ∴11949222FCD S DF OA =⋅=××=△．【点睛】本题主要考查了反比例函数与一次函数综合，菱形的性质与判定，折叠的性质，旋转的性质，勾股定理等等，灵活运用所学知识是解题的关键．六、解答题（四）（本大题共2小题，每小题10分，共20分）24. 在边长为1的正方形ABCD 中，点E 为线段BC 上一动点，连接AE ．（1）如图①，过点B 作BF AE ⊥于点G ，交直线CD 于点F ．以点F 为直角顶点在正方形ABCD 的外部作等腰Rt CFH △，连接AH EH ，．求证：AEH △是等腰直角三角形； （2）如图②，在（1）的条件下，记AH EH 、分别交CD 于点P Q 、，连接PE ． ①试探究PE BE DP 、、之间的数量关系；②设BE m =，PQE 中边PE 上的高为h ，请用含m 的代数式表示h ．并求h 的最大值．【答案】（1）见解析 （2）①PE BE PD =+；②21124h m =−−+，h 最大值为14 【解析】【分析】（1）根据正方形的性质和全等三角形的判定与性质得出AE BF BE CF ==，，进而利用平行四边形的判定和性质解答即可；（2）①将ADP △绕点A 顺时针旋转90°得到ABT ，则C B T ，，共线，利用全等三角形的性质证明PE ET =，即可得出结论；②利用相似三角形的性质构建二次函数，利用二次函数的性质求解即可．【小问1详解】证明：∵四边形ABCD 是正方形， ∴90AB BC ABE BCF ===°，∠∠， ∵BF AE ⊥， ∴90AGB ∠=°，∴90BAE ABG ∠+∠=°， ∵90ABG CBF ∠+∠=°， ∴BAE CBF ∠=∠， ∴()ASA ABE BCF ≌， ∴AE BF BE CF ==，， ∵CF FH =， ∴BE FH =， ∵BC FH ∥，∴四边形BEHF 为平行四边形，∴BF EH =，∴AE EH =，∴BF EH BF AE ⊥∥，，∴AE EH ⊥，∴90AEH ∠=°，∴AEH △是等腰直角三角形；【小问2详解】解：①结论：PE BE PD =+．理由：如图②中，将ADP △绕点A 顺时针旋转90°得到ABT ，则C B T ，，共线．图②∵四边形ABCD 是正方形，∴90BAD ∠=°，∵EAH 是等腰直角三角形，∴45EAH ∠=°，∴45EAT BAT BAE DAP BAE ∠=∠+∠=∠+∠=°，∴EAT EAP ∠=∠，∵AE AE AT AP ==，，∴()SAS EAT EAP ≌，∴PE ET =，∵ET BT BE PD BE =+=+，∴PE BE PD =+．②∵EAT EAP ≌，∴AET AEP ∠=∠，∵90AEH ∠=°，∴9090AET CEQAEP PEQ ∠+∠=°∠+∠=°，， ∴CEQ PEQ ∠=∠， ∴点Q 到PE 的距离的长CQ h =，∵90AEB BAE ∠+∠=°，∴BAE CEQ ∠=∠， ∴BAE CEQ ∽，AB BE EC CQ ∴=， 11m m h∴=−， ∴221124h m m m =−+=−−+∵10−<， ∴12m =时，h 的值最大，最大值为14． 【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，二次函数的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会构建二次函数解决最值问题．25. 已知抛物线2y x bx c =++经过点(1,0)A −和点(0,3)C −，与x 轴交于另一点B ．（1）求抛物线的解析式；（2）点P 为第四象限内抛物线上的点，连接CP AP AC 、、，如图1，若ACP △的面积为1，求P 点坐标；（3）设点M 为抛物线上的一点，若2MAB ACO ∠=∠时，求M 点坐标．【答案】（1）2=23y x x −−（2）4(1)P −，（3）M 的坐标为939,416 −或1557,416 【解析】【分析】（1）用待定系数法即可求解；（2）过点P 作PQ y ∥轴交直线AC 于点Q ，先求出2PQ =，再求出直线AC 的解析式，设点223P m m m −−（,），则点33Q m m −−（，），求得22PQ m m =+=，进而求解； （3）取点(1,0)D ，连接CD ，在CD 上取一点E ，使得AE AD =，连接AE ，并延长交抛物线于点M ，求出直线CD 的解析式为33y x =−，设(,33)E n n −，由AE 的长可求出36(,)55E −，设直线AE 的解析式为12y k x b =+，求出直线AE 的解析式，联立2334423y x y x x =−− =−− ，解方程组可得出答案．【小问1详解】将点A 、C 的坐标代入抛物线表达式得，103b c c −+= =−， 解得23b c =− =− ， 故抛物线的表达式为2=23y x x −−；【小问2详解】如图所示，过点P 作PQ y ∥轴交直线AC 于点Q ，112ACP S PQ OA ∴=⋅⋅= ， 又∵1OA =，∴2PQ =，设直线AC 为y kx b =+， 03k b b −+= =− ，解得33k c =− =− ， ∴33y x =−−， 设点223P m m m −−（,），则点33Q m m −−（，）， ∴22PQ m m =+=，解得1m =或2m =−（舍去）， ∴14P −（，）； 【小问3详解】如图，取点(1,0)D ，连接CD ，在CD 上取一点E ，使得AE AD =，连接AE ，并延长交抛物线于点M ，(1,0)A − ，点D 关于y 轴对称，AC DC ∴=，ACO DCO ∠=∠， 2ACD ACO MAB ∴∠=∠=∠，CAD CDA ∠=∠，AE AD = ，ADE AED CAD CDA ∴∠=∠=∠=∠，CAD AED ∴∆∆∽，2EAD ACD ACO ∴∠=∠=∠，设直线CD 的解析式为1y kx b =+，∴1103k b b += =− ，∴133k b = =− ，∴直线CD 的解析式为33y x =−，设(,33)E n n −，2222(1)(33)2AE n n ∴=++−=， 解得35n =或1n =（舍去），36(,)55E ∴−，设直线AE 的解析式为12y k x b =+， ∴121203655k b k b −+=+=− ， ∴123434k b =− =− ，∴直线AE 的解析式为3344y x =−−， 联立2334423y x y x x=−− =−− ，得2590 44x x−−=，解得94x=或=1x−（舍去），M∴点的坐标为9(4，39)16−，由对称性可知F点的坐标为3(5，6)5时，直线AF与抛物线的另一个交点也满足题意，同理可求出此时M点的坐标为15(4，57)16，综上所述，点M的坐标为9(4，39)16−或15(4，57)16．【点睛】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，待定系数法，等腰三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题，属于中考压轴题．。

ABC DE①第6题图②DCBAO第7题图2010年初中学业质量检查数学试题（试卷满分：150分；考试时间：120分钟）一、选择题（每小题3分，共21分）每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡上相应题目的答题区域内作答，答对的得3分，答错、不答或答案超过一个的一律得0分.1.31的倒数是( ).A.31B.31- C. 3 D.3-2. 下列计算正确的是( ).A.aaa632=+ B. 2632aaa=+ C. aaa532=+ D. 2532aaa=⋅3. 若x21+有意义，则 ( ) .A.x≤21- B. x≥21- C. x＜21- D. x＞21-4. 不等式组⎩⎨⎧-≤<1,2xx的解集是( ) .A.2<x B.1-≤x C.21<≤-x D.无解5. 把正三角形、正方形、正六边形进行组合，其中不能铺满地面的是( ) .A. 正三角形与正方形B. 正三角形与正六边形C. 正方形与正六边形D. 正三角形、正方形与正六边形6. 如图，所有的三角形都是全等的等边三角形，若把图①中的一条边与图②中的下列某条线段重合，则不．能构成．．．正三棱锥的展开图的是 ( ).A. ABB. AEC. CDD. BC7. 已知：如图，A、B、C是⊙O上的三点，D是BO与AC的交点，若︒=∠108ODC,且AB∥OC，则OCD∠的度数是( )A. ︒20 B. ︒26 C. ︒25 D.︒24二、填空题（每小题4分，共40分）在答题卡上相应题目的答题区域内作答.8. 计算：().______30=-9. 计算：.________35=÷aa≤≤≤ABCDO第15题O A BCD10．截至2010年4月25日青海玉树共接受各界捐赠资金近3500000000元，用科学记数法表示各界捐赠资金约为_____________元.11．已知一组数据2, 1，－1，2, 3，则这组数据的众数是______.12. 某服装店一套夏装的进价为120元，要获利20%，则该套服装的标价为______元. 13．二元一次方程组⎩⎨⎧=-=+26y x y x 的解是___________.14．在右图方格纸中，ABC ∆≌'''C B A ∆，把ABC ∆向右平移_____格后可得到'''C B A ∆.15．如图，在平行四边形ABCD 中，请再添加一个．．条件，使它成 为菱形，则该条件可以是： . 16．已知圆锥的底面圆的半径是cm 8，母线长 是cm 10，则圆锥的侧面积是2______cm .17．如图，第(1)个多边形由正三角形“扩展”而来，边数记为123=a .第(2)个多边形由正方形“扩展”而来，边数记为204=a ，…，依此类推，由正n 边形“扩展”而来 的多边形的边数记为n a （n ≥3），则5a ＝ ；当na a a a 1111543++++ 的结果 是30097时，n 的值为 ．第17题图三、解答题（共89分）在答题卡上相应题目的答题区域内作答. 18.（9分）计算：()542921-+-⨯---.19.（9分）请从下列三个代数式中，任意选取两个式子相加，组成一个新的式子并进行分解因式.xy x 32-，()x y y -4，()y x y +9A ’A BCB ’C ’第14题图20.（9分）如图，已知点M 是AB 的中点，BC ∥MN ，且AB BC 21=，MN AB =， 求证：ABC ∆≌NMB ∆.21.（9分）如图，桌面上放置了三张不透明的扑克牌，正面朝上，我们做蒙眼睛翻扑克牌（正面朝上的翻后为背面朝上，背面朝上的翻后为正面朝上）的游戏，在每次翻牌前，都要把扑克牌搅匀.（1）若三张扑克牌都是背面朝上，随机翻一张扑克牌，求翻到黑桃A 的概率；（2）开始时，三张扑克牌都是正面朝上，可记为（正，正，正），随机翻一张扑克牌，接着从这三张扑克 牌中再随机翻一张，请利用树状图（或列表法） 求出两次翻牌后三张扑克牌恰好全部正面朝上的概率.22．（9分）某校研究性学习小组为了了解2010届九年级学生市质检的数学成绩，随机抽查了年段部分同学的数学成绩，成绩分为A 、B 、C 、D 四个等级. 把抽查数据绘制成如图所示不完整的扇形统计图和频数分布直方图. 请你根据图中提供的信息,解答以下问题: （1）被抽查的同学共有多少人？ （2）请把条形统计图补充完整；（3）若该校九年级共有学生800人，试估计数学成绩B 级以上（含B 级和A 级）的同学比B 级以下的同学多了多少人？正面背面A 等级C 等级 14%D 等级 10% B 等级 36%ABCNM等级A 人数(人)20105 B C D15 20 25 18723．（9分）已知：如图， 在直角梯形ABCD 中，︒=∠90C ，AD ∥BC ，4==AD AB ，6=BC ，以A 点为圆心，在梯形内画一个扇形，使扇形所在的圆与BC 相切于点E ．（1）求BE 的长； （2）求图中扇形的面积．24. （9分）某种待填充的煤气罐，需要4分钟才能把煤气罐充满（按额定的压力填充，否则压力过大会有危险），据测算，该煤气罐从填充开 始，罐内的气体质量y (千克)与时间x （分钟）成一 次函数关系；充气完成后，煤气罐投入使用进入放气 阶段，罐内剩余的气体y (千克)与时间x （分钟）成 反比例关系. 已知该煤气罐在充气前罐内的气体质量 为0.3千克，充气完成后罐内的气体质量为15千克． （1）分别求出充气和放气阶段，y 与x 的函数关系式； （2）当煤气罐“放完”气（罐内外气压平衡，此时罐内还有0.3千克的气体）时，应进行第二次充气， 那么从充．．满．气．开始．．到．“．放完．．”．气．结束．．，经过了多少分钟？y (千克)x （分钟）O0.3 415ABCDE25. （13分）某住宅小区，为美化环境，提高居民区生活质量，要建居民广场（平面图如图所示）. 其中四边形ABCD 是矩形，分别以AB 、BC 、CD 、DA 为边向外作正方形，若整个广场的周长为600米，设矩形ABCD 的边长y AB =（米），x BC =（米）. （1）试用含x 的代数式表示y ；（2）现计划在矩形ABCD 区域上种植花草及铺设鹅卵石，平均每平方米造价为400元；在四个正方形的区域上种植草坪及铺设花岗岩，平均每平方米造价为300元； ①设该工程的总造价为W （元），求W 关于x 的函数关系式；②若该工程的银行贷款为350万元，问仅靠银行贷款能否完成该工程的建设任务？若能，请列出设计方案；若不能请说明理由；③若该工程在银行贷款350万元的基础上，又增加居民募捐资金82万元，但小区居民 要求矩形的边BC 的长不超过AB 长的21，且所有资金需 要全部恰好用来建设广场，问能否完成该工程的建设任务？若能，请列出所有可能的设计方案；若不能，请说明理由.A BCDAP26. （13分）如图，在ABC Rt ∆中，︒=∠90C ，20=AB ，12=AC ，D 、E 、F 分别是AC 、AB 、BC 的中点. 点P 从点D 出发沿折线CD FC EF DE ---以每秒7个单位长度的速度匀速运动；点Q 从点B 出发沿折线BA 以每秒4个单位长度的速度匀速运动，过点Q 作射线AB QK ⊥，交折线CA BC -于点G . 点P 、Q 同时出发，当点P 绕行一周回到点D 时停止运动，点Q 也随之停止. 设点P 、Q 运动的时间是t 秒()0>t .（1）求DF 的长；（2）当t 为何值时，射线QK 把四边形CFED 分成面积相等的两部分？（3）是否存在某个时刻t ，使得点P 运动过程中恰好又落在射线QK 上？若存在，请求出t 的值；若不存在，试说明理由.四、附加题（共10分）在答题卡上相应题目的答题区域内作答.友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况.如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷总分已经达到或超过90分，则本题的得分不计入全卷总分. 1．如图， ︒=∠50AOB ，OP 平分AOB ∠，则AOP ∠等于 度. 2．一元一次方程25-=-x 的解是_____.ACBDEFPQ KCBFADE2010年初中学业质量检查数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神 进行评分.（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分. （三）以下解答各行右端所注分数表示正确做完该步应得的累计分数. 一、选择题（每小题3分，共21分）1. C ；2. C ；3.B ；4.B ；5. C ；6.B ；7. D ； 二、填空题（每小题4分，共40分）8. 1； 9.2a ； 10. 9105.3⨯； 11. 2； 12. 144； 13.⎩⎨⎧==2,4y x ； 14.2； 15.BD AC ⊥或AD AB =（答案不惟一）； 16. 80π； 17. (1) 30；(2) 99. 三、解答题（共89分） 18.（本小题9分） 解：原式58321++-=……………………………………………………（8分） 2110=………………………………………………………………（9分）19.（本小题9分）解一：()x y y xy x -+-432原式=xy y xy x -+-2243 …………………………………………………………（3分）= 2244y xy x +-………………………………………………………………（6分） =()22y x -………………………………………………………………………（9分）解二：()y x y xy x ++-932原式=22993y xy xy x ++- …………………………………………………………（3分）2269x xy y =++…………………………………………………………（6分）=()23y x +…………………………………………………………………………（9分）解三：()()y x y x y y ++-94原式=22994y xy xy y ++- …………………………………………………………（3分）=xy y 8132+ …………………………………………………………（6分） =()x y y 813+ …………………………………………………………（9分） 20.（本小题9分）证明：∵ 点M 是AB 的中点∴AB BM 21=……………………………………………………………………………（1分） 又AB BC 21=∴BC BM =………………………………………………………………………………（3分） ∵BC ∥MN∴BMN ABC ∠=∠………………………………………………………………………（6分） ∵BC BM =，BMN ABC ∠=∠，MN AB =∴ABC ∆≌NMB ∆………………………………………………………………（9分） 21. （本小题9分） 解：（解法一）(1) 31)A (＝翻到黑桃P ；…………………………………………………………………（3分） (2) （解法一）将扑克牌正面朝上用“正”表示，扑克牌背面朝上用“反”表示，列举所有等可能结果，画出树状图如下：（正，正，正）（正，正，反）（正，反，反） （反，正，反） （正，正，正） （正，反，正）（正，正，正） （反，反，正） （正，反，反） （反，正，正）（反，反，正） （正，正，正）（反，正，反）………………………………………………………………………………………………（6分） 由上图可知，所有等可能结果共有9种. 其中恰好全部正面朝上的有3种.∴3193)(＝＝全部正面朝上P …………………………………………………………（9分） （解法二） 列表如下第一次 （正，正，反） （正，反，正） （反，正，正） 第二次（正，正，正） （正，反，反） （反，正，反） （正，反，反） （正，正，正） （反，反，正） （反，正，反）（反，反，正）（正，正，正）……………………………………………………………………………………………（6分） 由上表可知，所有等可能结果共有9种. 其中恰好全部正面朝上的有3种.∴3193)(＝＝全部正面朝上P ………………………………………………………（9分） 22．（本小题9分）解: (1)50%3618=÷(人)被抽查的同学共有50人. ……………………………（3分） (2) 补图正确得2分. …………………………………（5分） (3)样本的数学成绩在B 级以上（含B 级和A 级）的同学比B 级以下的同学多了()%52%10%14%365020=+-⎪⎭⎫⎝⎛+，由此可以估计，800个同学的数学成绩在B 级以上（含B 级和A 级）的比B 级以下的多了416800%52=⨯（人）. ……………………………………………………………（9分） 23.（本小题9分） 解:（1）连结AE ，∵BC 与⊙A 相切于点E ，∴AE ⊥BC ………………………………………（2分） ∵︒=∠90C ，AD ∥BC ， ∴90AEC C D ∠=∠=∠=︒ ∴四边形ADCE 是矩形， ∴EC ＝AD ＝4BE ＝BC －EC ＝BC －AD ＝2 ……………………………（4分） （2）在Rt △ABE 中，BE ＝2，AB ＝4，∴21sin 42BE BAE AB ∠=== 2 等级A 人数(人) 02010 5B C D1520 25 1875∴30BAE ∠=︒ …………………………………（6分） ∴120BAD ∠=︒，224223AE =-= ………………………（7分）∴扇形的面积＝2120(23)4360ππ=………………………………………（9分）24.（本小题9分）解：(1)设充气阶段y 与x 的函数关系式为：b kx y +=()0≠k 又过点()3.0,0、()15,4，∴⎩⎨⎧=+=154,3.0b k b ， 解得：⎩⎨⎧==3.0,675.3b k .∴y 与x 的函数关系式为：3.0675.3+=x y ()40≤≤x .………………………………（3分） 设放气阶段y 与x 的函数关系式为：xmy =()0≠m ， 把()15,4代入xmy =，得60=m . ∴y 与x 的函数关系式为：xy 60=()4>x .……………………………………………（6分） (2)当3.0=y 时，x 603.0=，解得2003.060==x （分钟）…………………………（8分） 即该煤气罐从充满气到放完气，经过了196分钟. ………………………………………（9分）25.（本小题13分） 解： (1)66x y +＝600100y x =-………………………………（3分）(2) ①2240023002300W xy x y =+⨯⋅+⨯⋅ ……………………（5分） 由100y x =-得，22400(100)600600(100)W x x x x =-++-＝2680080000610x x -+⨯………………………（7分）②266800(50)410 3.510W x =-+⨯>⨯∴仅靠银行贷款不能完成该工程的建设任务……………………………………（9分）③由题意得，x ≤12y ，即x ≤1(100)2x - 解得，x ≤1003∴0＜x ≤1003………………………………（10分）由6563.5108.210 4.3210W =⨯+⨯=⨯得，266800(50)410 4.3210x -+⨯=⨯解得170x =，230x =∵0＜x ≤1003∴只取30x = ……………………………………（12分）故设计方案为：矩形的长为70米，宽为30米，再分别以各边向外作正方形．……（13分） 26.（本小题13分）(1)∵D 、F 分别是AC 、BC 的中点，∴1DF AB 102＝＝；……………………………………（3分） (2)如图1，连结DF ，过点F 作AB FH ⊥，垂足为H .由四边形CDEF 为矩形，可知QK 过DF 的中点O 时，QK 把矩形CDEF 分为面积相等的两部分.(利用全等三角形借助割补法或用中心对称等方法说明，同样可酌情得分)此时5102121=⨯===DF OF QH .………………………（6分） ∵B B ∠=∠，︒=∠=∠90C FHB∴FHB ∆∽ACB ∆.∴AB BF BC HB =，20816=HB∴532=HB . 故85.244.65=+=t (秒) …………………………………………（8分）(3)①当点P 在DE 上（807t <≤）时，∵8DE =，10BE =，74DE BE<∴当点P 在DE 上时，不可能落在射线QK 上．…………………………（9分）A C BD E F P Q KGHO 图1②当点P 在EF 上（278≤≤t ）时，如图2，t QB 4=，t EP DE 7=+，则87-=t EP ，t QE 410-=.∵︒=∠=∠90C PQE ，A PEQ ∠=∠ ∴PQE ∆∽BCA ∆ ∴CAQE BA EP = ∴124102087t t -=-，解得4174=t .……………………………（10分） ③当点P 在FC 上（7222≤≤t ）时，如图3，t QB 4=，714876PB PF BF t t =+=-+=- 由PQB ∆∽ACB ∆，可得BCQBAB PB =，∴7642016t t-=， 解得3=t . …………………………（11分）④当点P 在CD 上（2247t ≤≤）时，如图4， 204AQ t =-，12(722)347AP t t =--=-由APQ ∆∽ABC ∆得，AQ AP AC AB =即2043471220t t--= 解得2t =，不合题意，舍去． …………………………（12分） 综上，存在4174=t 秒或3秒，使得点P 运动过程中恰好又落在射线QK 上. ……………………………………………………………………………（13分）四、附加题（共10分）1．（5分）25……………………………………………………………………（5分） 2．（5分）3=x ………………………………………………………………（5分）ACBD E F PQK 图2图3 A C BDE F PQ K 图4 ACBD EF P Q K。

2024云南年省初中学业水平考试模拟卷二（万唯卷）(全卷三个大题，共27个小题，共8页，满分100分，考试用时120分钟)注意事项：1. 本卷为试题卷。

考生必须在答题卡上解题作答。

答案应书写在答题卡的相应位置上，在试题卷、草稿纸上作答无效。

2. 考试结束后，请将试题卷和答题卡一并交回。

一、选择题(本大题共15小题，每小题只有一个正确选项，每小题2分，共30分)1.-3的相反数是A.-3B.3C.D.2 . 2023年12月25 日，在国家统计局公布的全国棉花产量数据显示，2023 年全国棉花总产5618000吨.数据5618000用科学记数法表示为A.0.5618×10⁷B.5.618×10⁷C.5.618×10⁶D.56.18×10⁵3.下面圆锥的主视图(主视图也称正视图)是4. 不等式2x+1<5的解集是A.x<2B.x<3C.x>2D.x>35. 二十四节气是中国劳动人民独创的文化遗产.下列四个图形中，是中心对称图形的是6. 下列计算正确的是A.a+a=a²B.(π-3.14)⁰=0C.a⁴÷a=a³(a≠0)D.3-1=-37. 将一把直尺和一个三角板按如图方式叠合在一起(三角板的直角顶点在直尺的边上),若∠1=28°，则∠2的度数为A.73°B.62°C.52°D,45°8. 按一定规律排列的单项式：2x,4x3,6x5,8x7,10x9,…, 第n 个单项式是A.2nx n+1B.2nx 2n+1C.2nx n -lD.2nx 2n -19. 一个多边形的外角和是内角和的一半，这个多边形的边数是A.4B.5C.6D.710. 下列成语所描述的事件属于不可能事件的是 A. 海底捞月 B. 水涨船高 C. 旭日东升 D.水滴石穿 11. 如图，△ABC 中，AB=AC=5,BC=6, 观察尺规作图的痕迹，则AD 的长为A.6B.5C.4D.312. 若对于反比例函数 ,在每个象限内，y 随 x 的增大而增大，则下列四个点可能在该函数图象上的是 A.(2,4) B.(1,-1) C.(-2,-2) D.(-1,0)13. 如图，在矩形ABCD 中，E 是边BC 的中点，连接AE 交对角线 BD 于点F, 若AD=4,则的值为A. 32B.31C.21 D.4314. 函数的自变量x 的取值范围是A.x≠2B.x>2C.x<2D.x=215. 如图，AB 是⊙0的切线，连接OB 交⊙0于点C,若⊙0的半径为2,∠B=40°,连接OA,则图中阴影部分的面积为A.3πB.95πC.32πD.97π 二、填空题(本大题共4小题，每小题2分，共8分)16. 分解因式：x ²+2x+1=17.某校运会百米预赛用抽签方式确定赛道.若琪琪第一个抽签，她从1-8号中随机抽取一签，则抽到8号赛道的概率是18. 在科学活动课上，同学们用圆心角为120°,半径为12cm 的扇形纸片，卷成一个无底圆锥形小帽，则这个小纸帽的底面半径为 cm. 19..写出一个比5大且比17小的整数三、解答题(本大题共8小题，共62分)20.(本小题满分7分)先化简，再求值：,其中x=5.21.(本小题满分6分)如图，AB=AC,点 D 在AB上，点E 在AC上，AE=AD.连接BE,CD.求证：∠B=∠C.22.(本小题满分7分)云南中药材种植面积、产量、农业产值等主要经济指标连续5年位居全国第一，素有药材宝库的美誉.某中医诊所计划花费900元购进一批茯苓，由于货源供应充足，茯苓的进价在原进价的基础上打了八折，结果用同样的钱比预期多购进15斤.求茯苓打折前每斤的价格.23. (本小题满分6分)跳绳是我国的民间传统体育项目，某校为了了解九年级学生跳绳情况，从九年级学生中随机抽取40名学生进行1分钟跳绳测试(每分钟不低于180个为满分),并对测试成绩进行整理绘制成如下表：数量/个 0<x<64 64≤x<108 108≤x<140 140≤x<180 x≥180 等级 不合格 合格 良好 优秀 满分 频数2a111210测试成绩位于140≤x<180(单位：个)145,148,150,153,157,160,160,166,168,169,173,177 请根据以上信息，解答下列问题：(1)a= ,样本数据的中位数为 ；(2)这次测试成绩的平均数是147个，甲的测试成绩是148个.乙说：“甲的成绩高于平均数，所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.24.(本小题满分8分)如图，AB 是◎O 的直径，C,D 是◎0上的点，连接DO 并延长交◎0于点E,交AC 于点F,且∠BCD= ∠CDE,连接CE. (1)求证：△CEF ∽△DEC;(2)若 3,tan 43==∠EF BCD ,求O F 的长，25 . (本小题满分8分)食糖是关系国计民生的重要农产品，是我国蔗糖产业发展的基本国策.某地的甘蔗出苗率y ( 单位：%)与播种后20天累计降雨量x (单位：毫米)的关系如下图所示.该地某种植园购买了一批甘蔗种子共计2000颗，购买费用为800 元，有如下两种种植方案：方案一：在室外种植，只靠降雨提供水分；方案二：在室内种植，人工可提供水分，使得出苗率达到最高，但成本需要500 元.已知成功出苗的甘蔗每株可售卖2元.(1)求y与x 之间的函数解析式；(2)甘蔗种子种植后20天累计降雨量不少于100毫米但不超过150毫米，若要使该种植园的收益W最大，应该选择哪种方案?26.(本小题满分8分)包知二次函数y=m²-2mx+3,其中m≠0(1)求二次函数图象的顶点坐标(用含有m 的代数式表示);(2)在二次函数图象上任取两点(x₁,y₁),(x₂,y₂), 当a-1≤x₁<x₂≤a+1时，总有y₁<y₂, 求a的取范围.27.(本小题满分12分)如图，菱形ABCD 中，点E,F,G,H 分别是边AD,AB,BC,CD 的中点，且菱形ABCD 的面积为24,85AD AC ,O 是AC 的中点.(1)求证：四边形 EFGH 为矩形； (2)求四边形 EFGH 的面积；(3)M,N 分别为边EF 和 EH 上一点，且∠MON=90° 求 EM 的长.。

12010年全国初中数学联合竞赛试题参考答案第一试一、选择题：（本题满分42分，每小题7分）1．若a ，b ，c 均为整数且满足1010()()1a b a c -+-=，则||||||a b b c c a -+-+-=（ ）A ．1B ．2C ．3D ．4【答案】 B【解析】 因为()()10101a b a c ---=，而左边的两个加数都是非负整数，所以一个等于0，另一个等于1，也就是说，a ，b ，c 三个数中有两个相等，另一个和它们相差1．因此，所求的和式中，两项等于1，另一项等于2，结果为2．2．若实数a ，b ，c 满足等式3||6a b =，49||6a b c =，则c 可能取的最大值为（ ）A ．0B ．1C ．2D ．3【答案】 C【解析】 为了使c 尽量大，a 应该尽量大，b 应该尽量小．因为它们都是非负数，3a ，0b =，不难观察到所求答案为2．3．若a ，b 是两个正数，且1110,a b b a--++= 则（ ）2A ．103a b <+≤B ．113a b <+≤C ．413a b <+≤D ．423a b <+≤. 【答案】 C【解析】 去分母之后得到()()110a a b b ab -+-+=，即220a ab b a b ++--=．给定a 和b 是两个正数，那么如果让它们中的一个等于0，则另一个等于0或14．若方程2310x x --=的两根也是方程420x ax bx c +++=的根，则2a b c +-的值为 （ ）A ．13-B ．9-C ．6D ．0【答案】 A【解析】 这需要使得前者是后者的因式，用综合除法可得，余式为()()33310a b x a c +++++，它应该等于0．所以两个系数都为0，特别地，()()333210a b a c ++-++，所以所求答案为13-．5．在ABC △中，已知60CAB ∠=︒，D ，E 分别是边AB ，AC 上的点，且60AED ∠=︒，ED DB CE +=，2CDB CDE ∠=∠,则DCB ∠= ( )A ．15oB ．20oC ．25oD ．30o【答案】 B【解析】 观察可得ADE △为正三角形，6．对于自然数n ，将其各位数字之和记为n a ，如2009200911a =+++=，201020103a =+++=，则312320092010a a a a a +++++=L （ ）A ．28062B ．28065C ．28067D ．28068.【答案】 D【解析】 根据弃九法，它和1到2010的和被9除的余数相等．每连续9个自然数之和被9整除，2010被9除余3，1236++=，所以只有D 符合．二、填空题：（本题满分28分，每小题7分）1．已知实数x ，y 满足方程组33191x y x y ⎧+=⎨+=⎩，，则22x y += ．【答案】 13【解析】 第一式除以第二式可得2219x xy y -+=，第二式平方可得2221x xy y ++=，那么所求答案就是()1921313⨯+÷=．2．二次函数2y x bx c =++的图象与x 轴正方向交于A ，B 两点，与y 轴正方向交于点C ．已知3AB ，30CAO ∠=︒，则c = ．【答案】 19【解析】 观察可知A 必须在B 左边，否则B 会跑到x 轴负半轴上．设A 的横坐标为a ，则C 的纵坐标3，23AC =，2AB a =．因此，考虑两根之积，33a a ⨯，3a =319=． 3．在等腰直角ABC △中，5AB BC ==，P 是ABC △内一点，且5PA ，5PC =，则PB = ．4【答案】 10【解析】 设()00B ，，()50A ，，()05C ，，根据熟知的勾三股四弦五，可观察到()31P ，，（另一个点在三角形外，不符合），所以10PB =．4．将若干个红、黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放，最多可以摆放 个球．【答案】 15【解析】 也就是说，编号之差为6或11的两个球颜色相同．下面从1号球开始，依次写出颜色相同的球的编号：11261711516104159314821371→→→→→→→→→→→→→→→→→也就是说，如果有17个球，则全部同色；如果超过17个，则任何连续17个同色，也不行．如果有16个，则上面的圈去掉17号球仍然是一条链，仍然不行；如果有15个，则上面的圈去掉17号球和16号球后断成两部分，所以可以．第二试 （A ）一．（本题满分20分）设整数()a b c a b c ≥≥，，为三角形的三边长，满足22213a b c ab ac bc ++---=，求符合条件且周长5不超过30的三角形的个数．【解析】 由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=，b c n -=，则a c m n -=+，其中m ，n 均为自然数.于是，等式①变为222()26m n m n +++=，即2213m n mn ++= ②由于m ，n 均为自然数，判断易知，使得等式②成立的m ，n 只有两组：31m n =⎧⎨=⎩，，和13.m n =⎧⎨=⎩，⑴ 当3m =，1n =时，1b c =+，34a b c =+=+．又a ，b ，c 为三角形的三边长，所以b c a +>，即(1)4c c c ++>+，解得3c >．又因为三角形的周长不超过30，即(4)(1)30a b c c c c ++=++++≤，解得253c ≤． 因此2533c <≤， 所以c 可以取值4，5，6，7，8，对应可得到5个符合条件的三角形.6⑵ 当1m =，3n =时，3b c =+，14a b c =+=+．又a ，b ，c 为三角形的三边长，所以b c a +>，即(3)4c c c ++>+，解得1c >．又因为三角形的周长不超过30，即(4)(3)30a b c c c c ++=++++≤，解得233c ≤． 因此2313c <≤， 所以c 可以取值2，3，4，5，6，7，对应可得到6个符合条件的三角形．综合可知：符合条件且周长不超过30的三角形的个数为5611+=．二．（本题满分25分）已知等腰三角形ABC △中，AB AC =，C ∠的平分线与AB 边交于点P ，M 为ABC △的内切圆I e 与BC 边的切点，作MD AC ∥，交I e 于点D ．证明：PD 是I e 的切线．【解析】 过点P 作I e 的切线PQ （切点为Q ）并延长，交BC 于点N ．因为CP 为ACB ∠的平分线，所以ACP BCP ∠=∠．又因为PA 、PQ 均为I e 的切线，所以APC NPC ∠=∠．IP QNB7又CP 公共，所以ACP NCP △≌△，所以PAC PNC ∠=∠．由NM QN =，BA BC =，所以QNM BAC △≌△，故NMQ ACB ∠=∠，所以MQ AC ∥．又因为MD AC ∥，所以MD 和MQ 为同一条直线．又点Q 、D 均在I e 上，所以点Q 和点D 重合，故PD 是I e 的切线．三．（本题满分25分）已知二次函数2y x bx c =+-的图象经过两点()1P a ，，()210Q a ，． ⑴ 如果a ，b ，c 都是整数，且8c b a <<，求a ，b ，c 的值．⑵ 设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ，与y 轴的交点为C ．如果关于x 的方程20x bx c +-=的两个根都是整数，求ABC △的面积．【解析】 点()1P a ，、()210Q a ，在二次函数2y x bx c =+-的图象上，故1b c a +-=，4210a c a +-=，解得93b a =-，82c a =-．⑴ 由8c b a <<知8293938a a a a -<-⎧⎨-<⎩，，解得13a <<．又a 为整数，所以2a =，9315b a =-=，8214c a =-=．⑵ 设m ，n 是方程的两个整数根，且m n ≤，旗开得胜8由根与系数的关系可得39m n b a +=-=-，28mn c a =-=-，消去a ，得98()6mn m n -+=-，两边同时乘以9，得8172()54mn m n -+=-，分解因式，得(98)(98)10m n --=．所以9819810m n -=⎧⎨-=⎩，，或982985m n -=⎧⎨-=⎩，，或9810981m n -=-⎧⎨-=-⎩，，或985982m n -=-⎧⎨-=-⎩，，解得12m n =⎧⎨=⎩，，或109139m n ⎧=⎪⎪⎨⎪=⎪⎩，，或2979m n ⎧=-⎪⎪⎨⎪=⎪⎩，，或19323m n ⎧=⎪⎪⎨⎪=⎪⎩，，又m ，n 是整数，所以后面三组解舍去，故1m =，2n =．因此，()3b m n =-+=-，2c mn =-=-，二次函数的解析式为232y x x =-+．易求得点A 、B 的坐标为()10，和()20，，点C 的坐标为()02，， 所以ABC △的面积为1(21)212⨯-⨯=．第二试 （B ）旗开得胜9一．（本题满分20分）设整数a ，b ，c 为三角形的三边长，满足22213a b c ab ac bc ++---=，求符合条件且周长不超过30的三角形的个数（全等的三角形只计算1次）．【解析】 不妨设a b c ≥≥，由已知等式可得222()()()26a b b c a c -+-+-= ①令a b m -=，b c n -=，则a c m n -=+，其中m ，n 均为自然数.于是，等式①变为222()26m n m n +++=，即2213m n mn ++= ②由于m ，n 均为自然数，判断易知，使得等式②成立的m ，n 只有两组：31m n =⎧⎨=⎩，，和13.m n =⎧⎨=⎩，⑴ 当3m =，1n =时，1b c =+，34a b c =+=+．又a ，b ，c 为三角形的三边长，所以b c a +>，即(1)4c c c ++>+，解得3c >．又因为三角形的周长不超过30，即(4)(1)30a b c c c c ++=++++≤，解得253c ≤． 因此2533c <≤，旗开得胜10所以c 可以取值4，5，6，7，8，对应可得到5个符合条件的三角形.⑵ 当1m =，3n =时，3b c =+，14a b c =+=+．又a ，b ，c 为三角形的三边长，所以b c a +>，即(3)4c c c ++>+，解得1c >．又因为三角形的周长不超过30，即(4)(3)30a b c c c c ++=++++≤，解得233c ≤． 因此2313c <≤， 所以c 可以取值2，3，4，5，6，7，对应可得到6个符合条件的三角形．综合可知：符合条件且周长不超过30的三角形的个数为5611+=．二．（本题满分25分）题目和解答与（A ）卷第二题相同.三．（本题满分25分）题目和解答与（A ）卷第三题相同.第二试 （C ）11一．（本题满分20分）题目和解答与（B ）卷第一题相同.二．（本题满分25分）题目和解答与（A ）卷第二题相同.三．（本题满分25分）设p 是大于2的质数，k 为正整数．若函数2(1)4y x px k p =+++-的图象与x 轴的两个交点的横坐标至少有一个为整数，求k 的值．【解析】 由题意知，方程2(1)40x px k p +++-=的两根1x ，2x 中至少有一个为整数．由根与系数的关系可得12x x p +=-，12(1)4x x k p =+-，从而有()()()()12121222241x x x x x x k p ++=+++=- ①⑴ 若1k =，则方程为22(2)0x px p ++-=，它有两个整数根2-和2p -．⑵ 若1k >，则10k ->.因为12x x p +=-为整数，如果1x ，2x 中至少有一个为整数，则1x ，2x 都是整数.又因为p 为质数，由①式知1|2p x +或2|2p x +．不妨设1|2p x +，则可设12x mp +=（其中m 为非零整数），则由①式可得212k x m-+=，12故()()12122k x x mp m -+++=+，即1214k x x mp m-++=+． 又12x x p +=-，所以14k p mp m--+=+， 即1(1)4k m p m-++= ② 如果m 为正整数，则(1)(11)36m p ++⨯=≥，10k m->， 从而1(1)6k m p m-++>，与②式矛盾. 如果m 为负整数，则(1)0m p +<，10k m-<， 从而1(1)0k m p m-++<，与②式矛盾. 因此，1k >时，方程2(1)40x px k p +++-=不可能有整数根．综上所述，1k =．旗开得胜13。

一、选择题1．(0分)[ID ：67647]下列计算中，错误的是（ ） A ．(2)(3)236-⨯-=⨯= B ．()144282⎛⎫÷-=⨯-=- ⎪⎝⎭C ．363(6)3--=-++=D ．()()2399--=--=2．(0分)[ID ：67643]在-1，2，-3，4，这四个数中，任意三数之积的最大值是（ ） A ．6B ．12C ．8D ．243．(0分)[ID ：67632]已知n 为正整数，则()()2200111n-+-=（ ）A ．-2B ．-1C ．0D ．24．(0分)[ID ：67623]计算4(8)(4)(1)+-÷---的结果是( ) A ．2B ．3C ．7D ．435．(0分)[ID ：67610]下列有理数的大小比较正确的是（ ） A ．1123< B ．1123->- C ．1123->- D ．1123-->-+ 6．(0分)[ID ：67608]绝对值大于1小于4的整数的和是（ ） A ．0B ．5C ．﹣5D ．107．(0分)[ID ：67600]计算2136⎛⎫--- ⎪⎝⎭的结果为（ ） A ．-12B ．12C ．56D ．568．(0分)[ID ：67597]如果用＋0.02克表示一只乒乓球质量超出标准质量0.02克，那么一只乒乓球质量低于标准质量0.02克记作（）. A ．＋0.02克B ．－0.02克C ．0克D ．＋0.04克9．(0分)[ID ：67594]下列关系一定成立的是（ ） A ．若|a|＝|b|，则a ＝b B ．若|a|＝b ，则a ＝b C ．若|a|＝﹣b ，则a ＝bD ．若a ＝﹣b ，则|a|＝|b|10．(0分)[ID ：67592]某种细菌在培养过程中，每半小时分裂一次（由一个分裂成两个）．经过3个小时，这种细菌由1个可分裂为（ ） A ．8个B ．16个C ．32个D ．64个11．(0分)[ID ：67583]下列说法中错误的有（ ）个 ①绝对值相等的两数相等．②若a ，b 互为相反数，则ab=﹣1．③如果a 大于b ，那么a 的倒数小于b 的倒数．④任意有理数都可以用数轴上的点来表示．⑤x 2﹣2x ﹣33x 3+25是五次四项．⑥两个负数比较大小，绝对值大的反而小．⑦一个数的相反数一定小于或等于这个数．⑧正数的任何次幂都是正数，负数的任何次幂都是负数．A ．4个B ．5个C ．6个D ．7个12．(0分)[ID ：67581]当A 地高于海平面152米时，记作“海拔+152米”，那么B 地低于海平面23米时，记作（ ） A ．海拔23米B ．海拔﹣23米C ．海拔175米D ．海拔129米13．(0分)[ID ：67580]据《经济日报》2018年5月21日报道：目前，世界集成电路生产技术水平最高已达到7nm （1nm=10﹣9m ），主流生产线的技术水平为14～28nm ，中国大陆集成电路生产技术水平最高为28nm ．将28nm 用科学记数法可表示为（ ） A ．28×10﹣9mB ．2.8×10﹣8mC ．28×109mD ．2.8×108m 14．(0分)[ID ：67566]按键顺序是的算式是( )A ．(0.8＋3.2)÷45＝B ．0.8＋3.2÷45＝C ．(0.8＋3.2)÷45＝ D ．0.8＋3.2÷45＝ 15．(0分)[ID ：67573]有理数a ，b 在数轴上表示如图所示，则下列各式中正确的是（ ）A ．0ab >B ．b a >C ．a b ->D ．b a <二、填空题16．(0分)[ID ：67754]绝对值小于2的整数有_______个，它们是______________. 17．(0分)[ID ：67744]23(2)0x y -++=，则x y 为______．18．(0分)[ID ：67724]大肠杆菌每过20分钟便由1个分裂成2个，经过3小时后这种大肠杆菌由1个分裂成_____个．19．(0分)[ID ：67675]校运动会的拔河比赛真是紧张刺激！规定拔河时，任意一方拉过30cm 就算获胜．小胖他们班在每次喊过“拉”声之后都可拉过7cm ，但又会被拉回3cm ．如此下去，该班在第________次喊过“拉”声后就可获得胜利．20．(0分)[ID ：67673]计算：(1)(2)(3)(4)(2019)(2020)++-+++-++++-=_____．21．(0分)[ID ：67671]点A 表示数轴上的一个点，将点A 向右移动10个单位长度，再向左移动8个单位长度，终点恰好是原点，则点A 到原点的距离为______． 22．(0分)[ID ：67669]有理数a ，b ，c 在数轴上的位置如图所示：填空：+a b ________0，1b -_______0，a c -_______0，1c -_______0．23．(0分)[ID ：67661]下列各组式子：①a ﹣b 与﹣a ﹣b ，②a +b 与﹣a ﹣b ，③a +1与1﹣a ，④﹣a +b 与a ﹣b ，互为相反数的有__．24．(0分)[ID ：67751]在－1，2，－3，0，5这五个数中，任取两个数相除，其中商最小是________．25．(0分)[ID ：67746]点A ，B 表示数轴上互为相反数的两个数，且点A 向左平移8个单位长度到达点B ，则这两点所表示的数分别是____________和___________．26．(0分)[ID ：67723]如果数轴上原点右边 8 厘米处的点表示的有理数是 32，那么数轴上原点左边 12 厘米处的点表示的有理数是__________． 27．(0分)[ID ：67722]已知太阳与地球之间的平均距离约为150000000千米，用科学记数法表示为______千米．三、解答题28．(0分)[ID ：67946]计算：|﹣2|﹣32＋（﹣4）×（12-）3 29．(0分)[ID ：67936]阅读下面材料：在数轴上6与1-所对的两点之间的距离：6(1)7--=； 在数轴上2-与3所对的两点之间的距离：235--=； 在数轴上8-与4-所对的两点之间的距离：(8)(4)4---=；在数轴上点A 、B 分别表示数a 、b ，则A 、B 两点之间的距离AB a b b a =-=-． 回答下列问题：（1）数轴上表示2-和5-的两点之间的距离是_______； 数轴上表示数x 和3的两点之间的距离表示为_______； 数轴上表示数_______和_______的两点之间的距离表示为2x +；（2）七年级研究性学习小组在数学老师指导下，对式子23x x ++-进行探究： ①请你在草稿纸上画出数轴，当表示数x 的点在2-与3之间移动时，32x x -++的值总是一个固定的值为：_______．②请你在草稿纸上画出数轴，要使327x x -++=，数轴上表示点的数x =_______．30．(0分)[ID ：67924]计算： （1）23(2)14⎛⎫-⨯-⎪⎝⎭；（2）2331(2)592-+-⨯--÷．【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1．C2．B3．C4．C5．B6．A7．A8．B9．D10．D11．C12．B13．B14．B15．C二、填空题16．3;－101等【分析】当一个数为非负数时它的绝对值是它本身；当这个数是负数时它的绝对值是它的相反数【详解】绝对值小于2的整数包括绝对值等于0的整数和绝对值等于1的整数它们是0±1共有3个故答案为(117．﹣8【分析】根据绝对值的非负性和偶次方的非负性求出xy的值然后代入代数式中计算即可【详解】解：∵∴x-3=0y+2=0解得：x=3y=﹣2∴==﹣8故答案为：﹣8【点睛】本题考查代数式求值绝对值乘方18．512【解析】分析：由于3小时有9个20分而大肠杆菌每过20分便由1个分裂成2个那么经过第一个20分钟变为2个经过第二个20分钟变为22个然后根据有理数的乘方定义可得结果详解：∵3小时有9个20分而19．7【分析】根据题意得到当喊到第6次时一共拉过了离胜利还差所以再喊一次后拉过超过了即可取得胜利【详解】解：由题意得喊过一次拉声之后可拉过当喊到第6次时一共拉过了离胜利还差所以再喊一次后拉过超过了即可取20．【分析】第1个数与第2个数相结合第3个数与第4个数相结合……第2019个数与第2020个数相结合进行计算即可【详解】原式故答案为：【点睛】本题考查了加法的结合律根据加数的特点将从第一个开始的每相邻两21．2【分析】设点A表示的数为x然后根据向右平移加向左平移减列出方程再解方程即可得出答案【详解】设A表示的数是x依题意可得：x+10-8=0解得：x=-2则点A到原点的距离为2故答案为：2【点睛】本题主22．<<<＞【分析】数轴上右边表示的数总大于左边表示的数左边的数为负数右边的数为正数；根据有理数减法法则进行判断即可【详解】由题图可知所以故答案为：<<<＞【点睛】考核知识点：有理数减法掌握有理数减法法23．②④【分析】直接利用互为相反数的定义分析得出答案【详解】解：①a-b与-a-b=-（a+b）不是互为相反数②a+b与-a-b是互为相反数③a+1与1-a不是相反数④-a+b与a-b 是互为相反数故答案24．－5【分析】所给的五个数中最大的数是5绝对值最小的负数是-1所以取两个相除其中商最小的是:5÷（-1）=-5【详解】∵-3<-1<0<2<5所给的五个数中最大的数是5绝对值最小的负数是-1∴任取两个25．-4【解析】试题26．﹣48【分析】数轴上原点右边8厘米处的点表示的有理数是32即单位长度是cm即1cm表示4个单位长度数轴左边12厘米处的点表示的数一定是负数再根据1cm表示4个单位长度即可求得这个数的绝对值【详解】数27．5×108【分析】科学记数法的表示形式为a×10n的形式其中1≤|a|<10n为整数确定n的值时要看把原数变成a时小数点移动了多少位n的绝对值与小数点移动的位数相同当原数绝对值>1时n是正数；当原数三、解答题28．29．30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1．C 解析：C 【分析】根据有理数的运算法则逐一判断即可． 【详解】(2)(3)236-⨯-=⨯=，故A 选项正确；()144282⎛⎫÷-=⨯-=- ⎪⎝⎭，故B 选项正确； 363(6)9--=-+-=-，故C 选项错误； ()()2399--=--=，故D 选项正确；故选C ． 【点睛】本题考查了有理数的运算，重点是去括号时要注意符号的变化．2．B解析：B 【分析】三个数乘积最大时一定为正数，二2和4的积为8，因此一定要根据-1和-3相乘，积为3，然后和4相乘，此时三数积最大． 【详解】∵乘积最大时一定为正数 ∴-1，-3，4的乘积最大为12 故选B ． 【点睛】本题考查了有理数的乘法，两个负数相乘积为正数，先将两个负数化为正数是本题的关键．3．C解析：C【解析】【分析】根据-1的偶次幂等于1，奇次幂等于-1，即可求得答案.【详解】∵n为正整数，∴2n为偶数.∴（-1）2n+(-1)2001=1+(-1)=0故选C.【点睛】此题考查了有理数的乘方，关键点是正确的判定-1的偶次幂等于1，奇次幂等于-1. 4．C解析：C【分析】先计算除法、将减法转化为加法，再计算加法可得答案．【详解】解：原式421=++7=，故选：C．【点睛】本题主要考查有理数的混合运算，解题的关键是掌握有理数的混合运算顺序和运算法则．5．B解析：B【分析】根据有理数大小的比较方法逐项判断即得答案．【详解】解：A、1123>，故本选项大小比较错误，不符合题意；B、因为1122-=，1133-=，1123>，所以1123->-，故本选项大小比较正确，符合题意；C、因为1122-=，1133-=，1123>，所以1123-<-，故本选项大小比较错误，不符合题意；D、因为1122--=-，1133-+=-，1123-<-，所以1123--<-+，故本选项大小比较错误，不符合题意．故选：B ． 【点睛】本题考查了有理数的大小比较和有理数的绝对值，属于基础题型，掌握比较大小的方法是解题的关键．6．A解析：A 【解析】 试题绝对值大于1小于4的整数有：±2；±3． -2+2+3+（3）=0． 故选A ．7．A解析：A 【分析】根据有理数加减法法则计算即可得答案． 【详解】2136⎛⎫--- ⎪⎝⎭=2136-+ =12-． 故选：A ． 【点睛】本题考查有理数的加减，有理数加法法则：同号两数相加，取相同的符号，并把绝对值相加；绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值，一个数同零相加，仍得这个数，有理数减法法则：减去一个数，等于加上这个数的相反数．8．B解析：B 【解析】 －0.02克，选A.9．D解析：D 【分析】根据绝对值的定义进行分析即可得出正确结论． 【详解】选项A 、B 、C 中，a 与b 的关系还有可能互为相反数，故选项A 、B 、C 不一定成立，D.若a＝﹣b，则|a|＝|b|，正确，故选D．【点睛】本题考查了绝对值的定义，熟练掌握绝对值相等的两个数的关系是相等或互为相反数是解题的关键．10．D解析：D【分析】每半小时分裂一次，一个变为2个，实际是21个．分裂第二次时，2个就变为了22个．那么经过3小时，就要分裂6次．根据有理数的乘方的定义可得．【详解】26=2×2×2×2×2×2=64．故选D．【点睛】本题考查了有理数的乘方在实际生活中的应用，应注意观察问题得到规律．11．C解析：C【分析】分别根据有理数、绝对值、相反数的定义及数轴的特点对各小题进行逐一判断.【详解】解：①绝对值相等的两数相等或互为相反数，故本小题错误；②若a，b互为相反数，则ab=-1在a、b均为0的时候不成立，故本小题错误；③∵如果a=2，b=0，a＞b，但是b没有倒数，∴a的倒数小于b的倒数不正确，∴本小题错误；④任意有理数都可以用数轴上的点来表示，故本小题正确；⑤x2-2x-33x3+25是三次四项，故本小题错误；⑥两个负数比较大小，绝对值大的反而小，故本小题正确；⑦负数的相反数是正数，大于负数，故本小题错误；⑧负数的偶次方是正数，故本小题错误，所以④⑥正确，其余6个均错误．故选C.【点睛】本题考查的是有理数、绝对值、相反数的定义及数轴的特点，熟知以上知识是解答此题的关键.12．B解析：B【解析】由已知，当A 地高于海平面152米时，记作“海拔+152米”，那么B 地低于海平面23米时，则应该记作“海拔-23米”， 故选B.13．B解析：B 【解析】【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|<10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值>1时，n 是正数；当原数的绝对值<1时，n 是负数．【详解】28nm =28×10﹣9m = 2.8×10﹣8m ，所以28nm 用科学记数法可表示为：2.8×10﹣8m ， 故选B ．【点睛】本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|<10，n 为整数，表示时关键要正确确定a 的值以及n 的值．14．B解析：B 【分析】根据计算器的使用方法，结合各项进行判断即可． 【详解】解：按下列按键顺序输入：则它表达的算式是0.8＋3.2÷45＝， 故选：B ． 【点睛】此题主要考查了计算器的应用，根据有理数的输入方法正确输入数据是解题关键．15．C解析：C 【分析】根据数轴可得0a b <<且a b >，再逐一分析即可． 【详解】由题意得0a <，0b >，a b >，A 、0ab <，故本选项错误；B 、a b >，故本选项错误；C 、a b ->，故本选项正确；D 、b a >，故本选项错误． 故选：C ． 【点睛】本题考查数轴，由数轴观察出0a b <<且a b >是解题的关键．二、填空题16．3;－101等【分析】当一个数为非负数时它的绝对值是它本身；当这个数是负数时它的绝对值是它的相反数【详解】绝对值小于2的整数包括绝对值等于0的整数和绝对值等于1的整数它们是0±1共有3个故答案为(1解析：3; －1，0，1等.【分析】当一个数为非负数时，它的绝对值是它本身；当这个数是负数时，它的绝对值是它的相反数．【详解】绝对值小于2的整数包括绝对值等于0的整数和绝对值等于1的整数，它们是0，±1，共有3个．故答案为(1). 3; (2). －1，0，1等．【点睛】本题考查了绝对值，熟悉掌握绝对值的定义是解题的关键．17．﹣8【分析】根据绝对值的非负性和偶次方的非负性求出xy 的值然后代入代数式中计算即可【详解】解：∵∴x-3=0y+2=0解得：x=3y=﹣2∴==﹣8故答案为：﹣8【点睛】本题考查代数式求值绝对值乘方解析：﹣8【分析】根据绝对值的非负性和偶次方的非负性求出x 、y 的值，然后代入代数式中计算即可．【详解】解：∵23(2)0x y -++=，∴x-3=0，y+2=0，解得：x=3，y=﹣2，∴x y =3(2)-=﹣8，故答案为：﹣8．【点睛】本题考查代数式求值、绝对值、乘方运算，熟练掌握绝对值和偶次方的非负性是解答的关键． 18．512【解析】分析：由于3小时有9个20分而大肠杆菌每过20分便由1个分裂成2个那么经过第一个20分钟变为2个经过第二个20分钟变为22个然后根据有理数的乘方定义可得结果详解：∵3小时有9个20分而解析：512【解析】分析：由于3小时有9个20分，而大肠杆菌每过20分便由1个分裂成2个，那么经过第一个20分钟变为2个，经过第二个20分钟变为22个，然后根据有理数的乘方定义可得结果．详解：∵3小时有9个20分，而大肠杆菌每过20分便由1个分裂成2个，那么经过第一个20分钟变为2个，经过第二个20分钟变为22个，⋯经过第九个20分钟变为29个，即：29=512个．所以，经过3小时后这种大肠杆菌由1个分裂成512个．故答案为512.点睛：乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．19．7【分析】根据题意得到当喊到第6次时一共拉过了离胜利还差所以再喊一次后拉过超过了即可取得胜利【详解】解：由题意得喊过一次拉声之后可拉过当喊到第6次时一共拉过了离胜利还差所以再喊一次后拉过超过了即可取解析：7【分析】⨯-=，离胜利还差根据题意得到当喊到第6次时，一共拉过了6(73)24(cm)30246(cm)-=，所以再喊一次后拉过7cm，超过了30cm，即可取得胜利.【详解】解：由题意得喊过一次“拉”声之后可拉过4cm.⨯-=.当喊到第6次时，一共拉过了6(73)24(cm)-=，离胜利还差30246(cm)所以再喊一次后拉过7cm，超过了30cm，即可取得胜利.故答案为:7.【点睛】此题考查了有理数的混合运算的应用，正确理解题意，掌握有理数的各运算法则是解题的关键.20．【分析】第1个数与第2个数相结合第3个数与第4个数相结合……第2019个数与第2020个数相结合进行计算即可【详解】原式故答案为：【点睛】本题考查了加法的结合律根据加数的特点将从第一个开始的每相邻两-解析：1010【分析】第1个数与第2个数相结合，第3个数与第4个数相结合，……，第2019个数与第2020个数相结合进行计算即可.【详解】=-+-++-=-----=-．原式(12)(34)(20192020)11111010-.故答案为：1010【点睛】本题考查了加法的结合律，根据加数的特点，将从第一个开始的每相邻两个数结合是解决此题的关键.21．2【分析】设点A 表示的数为x 然后根据向右平移加向左平移减列出方程再解方程即可得出答案【详解】设A 表示的数是x 依题意可得：x+10-8=0解得：x=-2则点A 到原点的距离为2故答案为：2【点睛】本题主解析：2【分析】设点A 表示的数为x ，然后根据向右平移加，向左平移减列出方程，再解方程即可得出答案.【详解】设A 表示的数是x ，依题意可得：x+10-8=0，解得：x=-2，则点A 到原点的距离为2.故答案为：2.【点睛】本题主要考查的是数轴，解题时需注意点在数轴上移动，向右平移加，向左平移减. 22．<<<＞【分析】数轴上右边表示的数总大于左边表示的数左边的数为负数右边的数为正数；根据有理数减法法则进行判断即可【详解】由题图可知所以故答案为：<<<＞【点睛】考核知识点：有理数减法掌握有理数减法法解析：< < < ＞【分析】数轴上右边表示的数总大于左边表示的数．左边的数为负数，右边的数为正数；根据有理数减法法则进行判断即可．【详解】由题图可知01b a c <<<<，所以0,10,0,10a b b a c c +<-<-<->故答案为：<，<，<，＞【点睛】考核知识点：有理数减法．掌握有理数减法法则是关键．23．②④【分析】直接利用互为相反数的定义分析得出答案【详解】解：①a -b 与-a-b=-（a+b ）不是互为相反数②a+b 与-a-b 是互为相反数③a+1与1-a 不是相反数④-a+b 与a-b 是互为相反数故答案解析：②④【分析】直接利用互为相反数的定义分析得出答案．【详解】解：①a -b 与-a-b=-（a+b ），不是互为相反数，②a+b 与-a-b ，是互为相反数，③a+1与1-a，不是相反数，④-a+b与a-b，是互为相反数．故答案为：②④．【点睛】本题考查了互为相反数，正确把握相反数的定义是解题的关键．24．－5【分析】所给的五个数中最大的数是5绝对值最小的负数是-1所以取两个相除其中商最小的是:5÷（-1）=-5【详解】∵-3<-1<0<2<5所给的五个数中最大的数是5绝对值最小的负数是-1∴任取两个解析：－5【分析】所给的五个数中,最大的数是5,绝对值最小的负数是-1,所以取两个相除,其中商最小的是:5÷（-1）=-5.【详解】∵-3<-1<0<2<5,所给的五个数中,最大的数是5,绝对值最小的负数是-1,∴任取两个相除,其中商最小的是:5÷（-1）=-5,故答案为:-5．【点睛】本题主要考查有理数的大小比较和有理数除法,解决本题的关键是要熟练掌握有理数大小比较和有理数除法法则.25．-4【解析】试题解析：-4【解析】试题两点的距离为8，则点A、B距离原点的距离是4，∵点A，B互为相反数，A在B的右侧，∴A、B表示的数是4，-4．26．﹣48【分析】数轴上原点右边8厘米处的点表示的有理数是32即单位长度是cm即1cm表示4个单位长度数轴左边12厘米处的点表示的数一定是负数再根据1cm表示4个单位长度即可求得这个数的绝对值【详解】数解析：﹣48【分析】数轴上原点右边 8厘米处的点表示的有理数是 32，即单位长度是14cm，即 1cm表示 4个单位长度，数轴左边12厘米处的点表示的数一定是负数，再根据 1cm表示 4个单位长度，即可求得这个数的绝对值．【详解】数轴左边 12 厘米处的点表示的有理数是﹣48．故答案为﹣48．【点睛】本题主要考查了在数轴上表示数．借助数轴用几何方法化简含有绝对值的式子，比较有关数的大小既直观又简捷．27．5×108【分析】科学记数法的表示形式为a×10n的形式其中1≤|a|<10n为整数确定n的值时要看把原数变成a时小数点移动了多少位n的绝对值与小数点移动的位数相同当原数绝对值>1时n是正数；当原数解析：5×108【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．【详解】150 000 000将小数点向左移8位得到1.5，所以150 000 000用科学记数法表示为：1.5×108，故答案为1.5×108．【点睛】本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．三、解答题28．162-【分析】有理数的混合运算，注意先算乘方，然后算乘除，最后算加减，有小括号先算小括号里面的．【详解】解：|﹣2|﹣32＋（﹣4）×（12 -）3＝2﹣9＋（﹣4）×（﹣18）＝2＋（﹣9）＋1 2＝162 -．【点睛】本题考查有理数的混合运算，掌握运算顺序和计算法则正确计算是解题关键．29．（1）3；|x−3|；x ，-2；（2）5；−3或4．【分析】（1）根据题意找出数轴上任意点间的距离的计算公式，然后进行计算即可；（2）①先化简绝对值，然后合并同类项即可；②分为x ＞3和x ＜−2两种情况讨论．【详解】解：（1）数轴上表示−2和−5的两点之间的距离为：|−2−（−5）|=3；数轴上表示数x 和3的两点之间的距离为：|x−3|；数轴上表示数x 和−2的两点之间的距离表示为：|x ＋2|；故答案为：3，|x−3|，x ，-2；（2）①当x 在-2和3之间移动时，|x ＋2|＋|x−3|=x ＋2＋3−x=5；②当x ＞3时，x−3＋x ＋2=7，解得：x=4，当x ＜−2时，3−x−x−2＝7．解得x=−3，∴x=−3或x=4．故答案为：5；−3或4．【点睛】本题主要考查的是绝对值的定义和化简，根据题意找出数轴上任意两点之间的距离公式是解题的关键．30．（1）1-；（2）47-．【分析】（1）原式先计算乘方和括号内，然后再计算乘法即可得到答案；（2）原式先计算乘方和化简绝对值，再计算乘除法，最后计算加减运算即可得到答案．【详解】解：（1）23(2)14⎛⎫-⨯- ⎪⎝⎭ 3414⎛⎫=⨯- ⎪⎝⎭ 144⎛⎫=⨯- ⎪⎝⎭1=-．（2）2331(2)592-+-⨯--÷ 21(8)593=-+-⨯-⨯ 1406=---47=-．【点睛】此题主要考查了有理数的混合运算，熟练掌握运算法则是解答此题的关键．。

初中数学竞赛题汇编（代数部分2）江苏省泗阳县李口中学 沈正中 精编、解答例1：已知a 2＋b 2＝6ab ，且a ＞b ＞0，求 。

解：由已知得 (a ＋b)2＝8ab ， (a －b)2＝4ab ，所以 ＝2，因a ＞b ＞0，所以a ＋b 、a －b 均为正数，故 ＝ 。

例2：计算 的值 。

解：因＝2， 所以 ＝ 。

例3：已知 ，求解：由已知得 2(a ＋b)2＝ab ，即 ＝－所以 ＝ ＝ 。

例4：已知 ， ，求 ＝？解：由 得 ，由 得 ，所以 ＝ ＋ ＝1。

例5：已知若abc =1，求证 。

分析：所要求证的等式的左边是三个分母差异很大的式子，因而变形比较困难。

可以充分利用abc=1，将它们化成同分母。

在1++a ab a 的分子、分母上同乘c ，化成1++=++c ca ca c ac abc ac ，将1++b bc b的分母1111=++++++++c ca c b bc b a ab a中的“1”换成abc 得cac abc b bc b ++=++11，然后再相加即可得证。

证明：∵ abc =1 ∴ = + = =1 。

例6：已知bc=ad ，求证：ab(c 2-d 2)=(a 2-b 2)cd证明：因bc=ad ，所以 由比例的性质得……① ……② ……③ ①×②×③得 ， 所以ab(c 2-d 2)=(a 2-b 2)cd∴ab(c 2-d 2)=(a 2-b 2)cd 。

例7：已知x=by+cz ，y=cz+ax ，z=ax+by ，且x+y+z ≠0，. 证明：1111=+++++cc b b a a 证明：解方程组⎪⎩⎪⎨⎧+=+=+=(3) (2)(1) by ax z ax cz y cz by x (2)+(3)-(1) 得y+z-x=2ax ，所以xz y x a x x z y a 21 2++=+-+=则 所以 z y x x z y a a ++-+=+1 同理可得，z y x y z x b b ++-+=+1，z y x z y x c c ++-+=+1 所以 1111=++++=+++++zy x z y x c c b b a a 例8：已知x 、y 、z 满足关系式1=+++++y x z x z y z y x ， 证明：0222=+++++yx z x z y z y x 证明：将已知等式分别乘以x 、y 、z 得111++++++++c ca c b bc b a ab a 1++c ca ca 1+++c ca c ca c ++1111++++c ca cca ()()()()b d ad c d c d b c b a b a 22-+=-+x yx xz x z xy z y x =+++++2 ① y yx yz x z y z y xy =+++++2 ② z yx z x z yz z y xz =+++++2③ ①+②+③ 得zy x y x yz y x xz x z yz x z xy z y xz z y xy y x z x z y z y x ++=+++++++++++++++++)()()(222所以z y x z y x yx z x z y z y x ++=++++++++222 即：0222=+++++yx z x z y z y x 例9：试用关于（x-1）的各次幂表示多项式322435x x x -+-。

2011——2012年初中数学第二次模拟试题亲爱的同学们，请你在答题之前，一定要仔细阅读以下说明：1.试题由第Ⅰ卷和第Ⅱ卷组成，共6页，第Ⅰ卷为选择题，36分；第Ⅱ卷为非选择题，84分，共120分，考试时间为120分钟.2.将试题的答案直接写在答卷上.3.不允许使用计算器。

愿你放松心情，认真审题，缜密思考，细心演算，交一份满意的答卷。

第Ⅰ卷（选择题 共36分）一、选择题（本题共12个小题，每小题3分.在每小题给出的四个选项中，只有一项符合题目要求）1.（－2）2的算术平方根是 （ ）A.2B.±2C.－2D. 22.下列图形中，既是轴对称图形又是中心对称图形的是（ ）A B C D 3. 某种鲸的体重约为13.6万kg ．用科学记数法表示（ ）A.1.36×105kgB.1.36×106kgC.1.36×107kgD.1.36×108kg4. 在平行四边形ABCD 中，若点E 为AD 的中点，连接BE ，交AC 于点F ，则AF ︰CF ＝ （ ）A. 1︰2B. 1︰3C. 2︰3D. 2︰5第4题图第1页 共6页5.若121-+x x有意义，则x 的取值范围为 （ ） A. x ≤21B. x ≥21C. x ≤21且x ≠1 D. x ≥21且x ≠1 6.在1,2,3，-4这四个数中，任选两个数的积作为k 的值，使反比例函数y ＝xk的图象在第二、四象限的概率是 （ ） Ａ.41 Ｂ.21 Ｃ.32 Ｄ.837.下列语句正确的有（ ）①相等的圆心角所对的弧相等； ②平分弦的直径垂直于弦；③长度相等的两条弧是等弧；④经过圆心的每一条直线都是圆的对称轴.Ａ. 1个 Ｂ. 2个 Ｃ. 3个 Ｄ. 4个8.如果点P （ｍ，1－2ｍ）在第四象限，那么ｍ的取值范围是（ ）Ａ. 0＜ｍ＜2 Ｂ.-21＜ｍ＜0 Ｃ. ｍ＜0 Ｄ. ｍ＞21 9.有13位同学参加学校组织的才艺表演比赛，已知他们所得的分数互不相同，共设7个获奖名额.某同学知道自己的比赛分数后，要判断自己能否获奖，在下列13名同学成绩的统计量中只需知道一个量，它是 （ ） A. 众数 B.方差 C.中位数 D.平均数10.如图，在△ABC 中，点D 、E 、F分别是AB 、AC 、BC 的中点．已知AB ＝6,BC＝9,则四边形BFEDA.6B.9C.12D.15第11题图 第2页 共6页B NC 学校-----------------------------------------------------------班级----------------------姓名---------------------考号-------------------------------- ---------------------------------密-----------------------------------------------封-----------------------------------------线-----------------------------A11.如图，将边长为8㎝的正方形纸片ABCD 折叠，使点B 落在CD 中点E 处，点A 落在F 处，折痕为MN ，则线段CN 的长是 （ ）A.2B.3C.4D.512.如图，在正方形ABCD 中，AB=3cm ，动点M 自A 点出发沿AB 方向以每秒 1cm 的速度运动，同时动点N 自A 点出发沿折线AD-DC-CB 以每秒3cm 的速度 运动，到达B 点时运动同时停止．设△AMN 的面积为y （cm 2）．运动时间为x （秒），则下列图象中能大致反映y 与x 之间函数关系的是（ ）第12题图 A B C D 第Ⅱ卷（非选择题 共84分） 二、填空题（本题共5个小题，每小题3分，共15分.只要求填写最后结果）13. 3(2)412 1.3-x x x x -≤-⎧⎪+⎨>-⎪⎩，的解集为 。

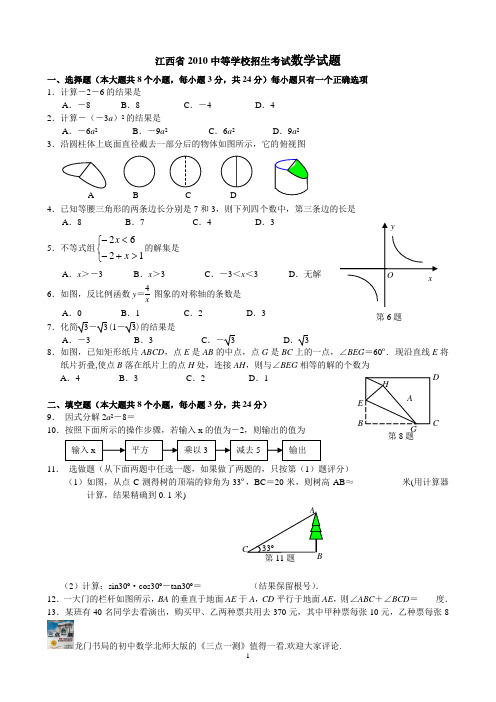
AB CD E H第8题输入x 平方 乘以3 减去5 输出 江西省2010中等学校招生考试数学试题一、选择题（本大题共8个小题，每小题3分，共24分）每小题只有一个正确选项 1．计算－2－6的结果是A ．－8B ．8C ．－4D ．4 2．计算－（－3a ）2的结果是A ．－6a 2B ．－9a 2C ．6a 2D ．9a 2 3．沿圆柱体上底面直径截去一部分后的物体如图所示，它的俯视图4．已知等腰三角形的两条边长分别是7和3A ．8 B ．7 C ．4 D ．35．不等式组⎩⎨⎧>+-<-1262x x 的解集是A ．x ＞－3B ．x ＞3C ．－3＜x ＜3D ．无解 6．如图，反比例函数y ＝4x图象的对称轴的条数是A ．0B ．1C ．2D ．37．化简3－3(1－3)的结果是A ．－3B ．3C ．－3D ． 38．如图，已知矩形纸片ABCD ，点E 是AB 的中点，点G 是BC 上的一点，∠BEG ＝60º. 现沿直线E 将纸片折叠,使点B 落在纸片上的点H 处，连接AH ，则与∠BEG 相等的解的个数为A ．4B ．3C ．2D ．1二、填空题（本大题共8个小题，每小题3分，共24分）9． 因式分解2a 2－8＝___________10．按照下面所示的操作步骤，若输入x 的值为－2，则输出的值为___________11． 选做题（从下面两题中任选一题，如果做了两题的，只按第（1）题评分）（1）如图，从点C 测得树的顶端的仰角为33º，BC ＝20米，则树高AB ≈___________米(用计算器计算，结果精确到0.1米)（2）计算：sin30º·cos30º－tan30º＝___________（结果保留根号）．12．一大门的栏杆如图所示，BA 的垂直于地面AE 于A ，CD 平行于地面AE ，则∠ABC ＋∠BCD ＝____度． 13．某班有40名同学去看演出，购买甲、乙两种票共用去370元，其中甲种票每张10元，乙种票每张8A B C D AB C33º第11题xyO第6题元．设购买了甲种票x 张，乙种票y 张，由此可列出方程组：_________________． 14．如图所示，半圆AB 平移到半圆CD 的位置时所扫过的面积为_________________．15．如图，以点P 为圆心的圆弧与x 轴交于A 、B 两点，点P 的坐标为（4，2），点A 的坐标为（2，0）则点B 的坐标为_________________．16．如图，一根直立于水平地面上的木杆AB 在灯光下形成影子，当木杆绕点A 按逆时针方向旋转直至到达地面时，影子的长度发生变化．设垂直于地面时的影长为AC （假定AC ＞AB ），影长的最大值为m ，最小值为n ，那么下列结论：①m ＞AC ；②m ＝AC ；③n ＝AB ；④影子的长度先增大后减小．其中正确结论的序号是（多填或错填的得0分，少填的酌情给分）三、（本大题共3个小题，第17小题6分，第18、19小题各7分，共20分） 17．已知直线经过点（1，2）和点（3，0），求这条直线的解析式． 18，解方程：x －2x ＋2 ＋4x 2－4＝1．19．如图所示的转盘，分成三个相同的扇形，指针位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置，并相应得到一个数（指针指向两个扇形的交线时，当作指向右边的扇形）． （1）求事件“转动一次，得到的数恰好是0”发生的概率； （2）写出此情境下一个．．不可能发生的事件； （3）用树状图或列表法，求事件“转动两次，第一次得到的数与第二次得到的数绝对值相等”发生的概率．四、（本大题共2个小题，每小题各8分，共16分）20．某校九年级全体500名女生进行仰卧起坐训练，下面两图是随机抽取的若干名女生训练前后“1分钟仰卧起坐”测试的成绩统计图（其中，右下图不完整）．A B0 1 －1 xyAB 第15题 ·OP x y A B D C1 －1 1 12 O（1）根据上图提供的信息，补全右上图；（2）根据上图提供的信息判断，下列说法不正确．．．的是A．训练前各成绩段中人数最多的是第三成绩段B．“33—35”成绩段中，训练前成绩的平均数一定大于训练后成绩的平均数C．训练前后成绩的中位数所落在成绩段由第三成绩到了第四成绩段（3）规定39个以上（含39个）为优秀等级，请根据两次测试成绩，估算该校九年级全体女生优秀等级人数训练后比训练前增加了多少人．21．剃须刀由刀片和刀架组成．某时期，甲、乙两厂家分别生产老式剃须刀（刀片不可更换）和新式剃须刀（刀片可更换）．有关销售策略与售价等信息如下表所示：老式剃须刀新式剃须刀刀架刀片售价2.5(元/把) 1(元/把) 0.55(元/片)成本2(元/把) 5(元/把) 0.5(元/片)某段时间内，甲厂家销售了8400把剃须刀，乙厂家销售的刀片数量是刀架数量的50倍，乙厂家获得的利润是甲厂家的两倍，问这段时间内乙厂家销售了多少把刀架？多少片刀片？五、（本大题共2个小题，第22小题8分，第23小题9分，共17分）22．“6”字形图中，FM是大⊙O的直径，BC与大⊙O相切于B，OB与小⊙O相交于A，AD∥BC，CD ∥BH∥FM，DH⊥BH于H，设∠FOB＝α，OB＝4，BC＝6．（1）求证：AD为小⊙O的切线；（2）在图中找出一个．．可用α表示的角，并说明你这样表示的理由；（根据所写结果的正确性及所需推理过程的难易程度得分略有差异）（3）当α＝30º时，求DH的长（结果保留根号）．23．图1所示的遮阳伞，伞柄垂直于水平地面，其示意图如图2．当伞收紧时，点P 与点A 重合；当伞慢慢撑开时，动点P 由A 向B 移动；当点P 到达点B 时，伞张得最开．已知伞在撑开的过程中，总有PM ＝PN ＝CM ＝CN ＝6.0分米，CE ＝CF ＝18.0分米，BC ＝2.0分米．设AP ＝x 分米． （1）求x 的取值范围；（2）若∠CPN ＝60º，求x 的值；（3）设阳光直射下，伞下的阴影（假定为圆面）面积为y ，求y 关于x 的关系式（结果保留）．六、（本大题共2个小题，第24小题9分，第25小题10分，共19分）24．如图，已知经过原点的抛物线y ＝－2x 2＋4x 与x 轴的另一交点为A ，现将它向右平移m （m ＞0）个单位，所得抛物线与x 轴交于C 、D 两点，与原抛物线交于点P ． （1）求点A 的坐标，并判断△PCA 存在时它的形状（不要求说理）；（2）在x 轴上是否存在两条相等的线段，若存在，请一一找出，并写出它们的长度（可用含m 的式子表示）；若不存在，主说明理由；（3）设△CDP 的面积为S ，求S 关于m 的关系式．25．课题：两个重叠的正多形，其中的一个绕某一顶点旋转所形成的有关问题．实验与论证OAB C DEFH G MxyD A C O P设旋转角∠A 1A 0B 1＝α（α＜∠A 1A 0 A 2），θ3、θ4、θ5、θ6所表示的角如图所示．图1 图2 图3 图4ααααθ4θ6θ5θ3HHHHB 4A 4B 23345A 5A 4B 3A 3A 3A 3A 22A 2B 2B 2B 1B 1B 1A A 0A 1A A 1A 2B 2A 0B 11（1）用含α的式子表示解的度数：θ3＝_______，θ4＝_______，θ5＝_______；（2）图1—图4中，连接A 0H 时，在不添加其他辅助线的情况下，是否存在与直线A 0H 垂直且被它平分的线段？若存在，请选择其中的一个图给出证明；若不存在，请说明理由；归纳与猜想设正n 边形A 0A 1 A 2…A n －1与正n 边形A 0B 1 B 2…B n －1重合（其中，A 1与B 1重合），现将正边形A 0B 1B 2…B n －1绕顶点A 0逆时针旋转α（0º＜α＜180ºn）．（3）设θn 与上述“θ3、θ4、…”的意义一样，请直接写出θn 的度数；（4）试猜想在正n 边形的情形下，是否存在与直线A 0H 垂直且被它平分的线段？若存在，请将这条线段用相应的顶点字母表示出来（不要求证明）；若不存在，请说明理由．江西省2010中等学校招生考试数学试题参考答案及评分意见一、选择题（本大题共8个小题，每小题3分，共24分）每小题只有一个正确选项 1．A 2．B 3．D 4．B 5．B 6．C 7．A 8．B 二、填空题（本大题共8个小题，每小题3分，共24分） 9．2(a ＋2)(a －2) 10．7 11．(1)13.0 (2) －31212．270 13．⎩⎨⎧=+=+370810,40y x y x 14．6 15．(6,0) 16．①③④说明：（1）第11题（1）题中填成了“13”，不扣分；（2）第16题，填了②的，不得分；未填②的，①、③、④中每填一个得1分． 三、（本大题共3个小题，第17小题6分，第18、19小题各7分，共20分） 17．解：设这条直线的解析式为y ＝kx ＋b ，把两点的坐标（1，2），（3，0）代入，得⎩⎨⎧=+=+.03,2b k b k ………………………………2分 解得⎩⎨⎧=-=.3,1b k ………………………………5分所以这条直线的解析式为y ＝－x ＋3……6分 18．解：方程两边同乘以x 2－4，得(x －2)2＋4＝ x 2－4…………………………3分 解得x ＝3……………………………………6分 检验：x ＝3，x 2－4≠0所以，是原分式方程的解……………………7分19．解：（1）P （所指的数为0）= 13 ； …………………2分（2）（答案不唯一）如：事件“转动一次，得到的数恰好是3” …………………4分或事件“转动两次，第一次得到的数与第二次得到的数之和为2” …………………4分 （3）方法一：画树状图如下：第一次 －1 0 1第二次 －1 0 1 －1 0 1 －1 0 1 ……………6分 所有可能出现的结果共有9种，其中满足条件的结果有5种所以，P （所指的两数的绝对值相等）= 59 ……………7分－1 0 1 －1 (－1, －1) (－1, 0) (－1, 1) 0 (0, －1) (0,0) (0, 1) 1(1, －1)(1,0)(1,1)……………6分所有可能出现的结果共有9种，其中满足条件的结果有5种所以，P （所指的两数的绝对值相等）= 59……………7分20．解：（1）如图所示：第二次第一次························································· 2分 （2）B ． ···················································· 3分 （3）依题意知：50050911500502010⨯+-⨯+ ＝100（人）答：估计该校九年级全体女生训练后优秀等级增加的人数为100人. ·················· 5分 21．解：设这段时间内乙厂家销售了x 把刀架.依题意，得8400)25.2(2)51(50)05.055.0(⨯-⨯=-+•-x x . ················ 3分 解得400=x . ·························· 4分 销售出的刀片数：50×400=20000片刀片.答：这段时间内乙厂家销售了400把刀架，20000片刀片 ······················· 5分说明：列二元一次方程解答的，参照给分. 22．解：（1）证明：∵BC 是大⊙O 的切线，∴∠CBO ＝90°.∵BC ∥AD , ∴∠BAD ＝90°.即OA ⊥AD . 又∵点A 在小⊙O 上，∴AD 是小⊙O 的切线. ······························· 2分 (2)∵CD ∥BG ，CB ∥DG ,∴四边形BGDC 是平行四边形. ∴6==BC DG . ··································································· 3分 ∵BH ∥FM ，∴︒=∠=∠30FOB GBO .∴︒=∠60DGH . 又∵BH DH ⊥,∴33660sin =⨯=︒DH . ····································································· 5分 23.解：（1）∵,12,2=+==PN CN AC BC∴10212=-=AB∴AP 的取值范围为：0≤AP ≤10. ················································ 1分 (2)∵,60,︒=∠=CPN PN CN ∴PCN ∆等边三角形. ∴6=CP . ∴6612=-=-=PC AC AP .即当︒=∠60CPN 时，6=x 分米. ··················································· 2分（3）伞张得最开时，点P 与点B 重合. 连接MN ，EF .分别交AC 于H O , ∵CN CM BN BM ===，∴四边形为BNCM 菱形，∴AC BC MN ,⊥是ECF ∠的平分线，1222===BC OC . 在Rt CON ∆中 3516222=-=-=OC CN ON .∵CF CE =,AC 是ECF ∠的平分线， ∴EF AC ⊥.∴CON ∆～CHF ∆. ∴CFCNHF ON =.∴18635=HF 。

2024年中考第二次模拟考试（徐州卷）数学·全解全析注意事项：1．本试卷共6页．全卷满分140分．考试时间为120分钟．考生答题全部答在答题卡上，答在本试卷上无效．2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效．4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．第Ⅰ卷一、选择题（本大题共8个小题，每小题3分，共24分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）1．2024年夏季奥运会将在法国巴黎举行，平移如图所示的巴黎奥运会图标可以得到的图形是（）A．B．C．D．【答案】D【解析】解：由图形可知，选项D与原图形完全相同．故选：D2．8-的倒数是（）A．8B．18C．18-D．8-【答案】C【解析】解：∵1818⎛⎫-⨯-= ⎪⎝⎭，∴8-的倒数为18-，故选：C ．3．餐桌边的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约1700万吨．将数据1700万用科学记数法表示为（）A ．71.710⨯B ．80.1710⨯C ．81.710⨯D ．71710⨯【答案】A【解析】解：将数据1700万用科学记数法表示为71.710⨯．故选：A ．4．下列运算正确的是（）A ．()325a a -=-B ．3515a a a ⋅=C ．22321a a -=D ．()22346a b a b -=【答案】D【解析】解：A 、()326a a -=-，故A 不正确，不符合题意；B 、358a a a ⋅=，故B 不正确，不符合题意；C 、22232a a a -=，故C 不正确，不符合题意；D 、()22346a b a b -=，故D 正确，符合题意；故选：D ．5．一个含45︒的三角板和一个直尺按如图所示方式叠合在一起，若1123=︒∠，则2∠的度数是（）A ．67︒B ．68︒C ．77︒D ．78︒【答案】D【解析】解：1=123∠︒ ，123EFB ∴∠=︒，EF BD ∥，123EFB ∠=︒，18012357ABD ∴∠=︒-︒=︒，又90ABC ∠=︒ ，905733DBC ∴∠=︒-︒=︒，2453378C DBC ∠=∠+∠=︒+︒=︒．故选：D ．6．如图，,OA OB 是O 的两条半径，点C 在O 上，连接,AC BC ，若36C ∠=︒，则AOB ∠的度数为（）A ．72︒B ．62︒C ．54︒D ．36︒【答案】A 【解析】解：∵36C ∠=︒，∴272AOB C ∠︒=∠=，故选：A ．7．某校射击比赛所用的靶子有8环，9环，10环三个环次，每一环又有10个小环，小新、小华、小宇三人每人射击三次，成绩如图所示，则射击成绩的平均数约为9.0环的是（）A ．小新B ．小宇C ．小华D ．三人都有可能【答案】C 【解析】解：由图可知：小新的成绩2个在10环上，一个在9环上，平均成绩不可能为9.0环；小宇的成绩一个在10环，一个接近10环，一个接近9环，平均数不可能为9.0环；小华的成绩均在9环附近，射击成绩的平均数约为9.0环；故选C ．8．如图，在平面直角坐标系中，矩形ABOC 的顶点C 在y 轴上，A 在x 轴上，把矩形ABOC 沿对角线BO 所在的直线翻折，点A 恰好落在反比例函数()0k y k x=≠的图象上点D 处，BD 与y 轴交于点E ，点D 恰好是BE 的中点．已知A 的坐标为()4,0，则反比例函数的表达式为（）A ．232y =B ．43y =C ．4y x =D ．1633y x=【答案】B 【解析】解：∵矩形ABOC ，A 的坐标为()4,0，∴4OA =，点B 的横坐标为4，∵折叠，∴4OD OA ==，∵E 在y 轴上，D 为BE 的中点，∴点D 的横坐标为2，过点D 作DF OA ⊥，∴2OF =，∴2223DF OD OF =-，∴(2,23D ，∴22343k =⨯=∴反比例函数的表达式为43y =故选B ．第Ⅱ卷二、填空题（本大题共10个小题，每小题3分，共30分）9．0.0081的平方根是．【答案】0.09±【解析】解：因为20.090.0081()±=，所以0.0081的平方根是0.09±；故答案为：0.09±．10．当x =时，分式43xx --无意义．【答案】3【解析】 分式43xx --无意义30x ∴-=3x ∴=．故答案为：3．11．如图，由三个正方形拼成的图形中，字母B 所代表的正方形面积是．【答案】144【解析】解：由勾股定理得，字母B 所代表的正方形面积16925144=-=．故答案为：144．12．如图，第4套人民币中菊花1角硬币采用“外圆内凹正九边形”设计，则内凹正九边形的外角的度数为．【答案】40︒【解析】解：内凹正九边形的外角的度数为360940︒÷=︒，故答案为：40︒．13．若分式方程12x x a +=+的解是3x =，则=a ．【答案】1-【解析】解：分式方程去分母得：122x x a +=+，由分式方程的解为3x =，代入整式方程得：31232a +=⨯+，解得：1a =-，故答案为：1-．14．某节活动课上，安安用一张半径为18cm 的扇形纸板做了一个圆锥形帽子（如图，接缝处忽略不计）．若圆锥形帽子的半径为10cm ，则这张扇形纸板的面积为cm²．【答案】180π【解析】解：解：这张扇形纸板的面积为121018180cm²2ππ⨯⨯⨯=，故答案为：180π．15．已知20ax bx c ++=的两根为2，3，则20cx bx a -+=的两个根分别为．【答案】121123x x =-=-，【解析】解：∵20ax bx c ++=的两根为2，3，∴235236bca a -=+==⨯=，，∴56b a c a =-=，，∴方程20cx bx a -+=即为2560a ax x a ++=，∴26510x x +=+，∴()()21310x x ++=，解得121123x x =-=-，，故答案为：121123x x =-=-，．16．如图，边长为1的正方形ABCD 绕点A 逆时针旋转60︒得到正方形AEFG ，连接CF ，则CF 的长是．2【解析】解：如图所示，连接AC 、AF ，∵四边形AEFD 是四边形ABCD 逆时针旋转60︒，∴AC AF =，60CAF ∠=︒，∴ACF △是等边三角形，∴AC CF AF ==，在Rt ABC △中，222AC AB BC =+=∴2AC CF =2．17．如图，在矩形ABCD 中，4AB =，2AD =，点E 是AD 边的中点，连接,AC BE 交于点,F CAD ∠的平分线AG 交CD 边于点G ，点A 关于过点E 的某条直线的对称点H 恰好在AG 上，且点H 不与点A 重合，连接FH ，则FH 的长为．46363【解析】解：∵在矩形ABCD 中，4AB =，42AD =E 是AD 边的中点，∴90BAD ∠=︒，122AE ED AD ===∴222tan 42AE ABE AB ∠==，2tan 242CD CAD AD ∠=，∴tan tan ABE CAD ∠=∠，∴ABE CAD ∠=∠，∴90ABE BAF CAD BAF BAD ∠+∠=∠+∠=∠=︒，∴90BFA ∠=︒，即BE AC ⊥，∵在矩形ABCD 中，4AB =，22AE =∴()224226BE =+AE BC ∥，∴AEF CBF ∽△△，∴12EF AE BF BC ==，∴12633EF BE =，连接EH ，∵点A 关于过点E 的某条直线的对称点H 恰好在AG 上，∴2AE EH ==∴EAH EHA ∠=∠，∵AG 是CAD ∠的平分线，∴EAH CAH ∠=∠，∴EHA CAH ∠=∠，∴HE AC ∥，∵BE AC ⊥，∴BE EH ⊥，即90FEH ∠=︒，∴()222224622633FH EF EH ⎛⎫=+=+= ⎪⎝⎭463．18．如图，在矩形ABCD 中，6,10AB BC ==，点E 是AD 边的中点，点F 是线段AB 上任一点，连接EF ，以EF 为直角边在AD 下方作等腰直角EFG ，FG 为斜边，连接DG ，则DEG 周长最小值为．【答案】555【解析】解：如图，过点G 作GH AD ⊥于点H ，∵四边形ABCD 是矩形，∴90,6,10A AB CD AD BC ∠=︒====，∴5AE ED ==，∵90A FEG GHE ∠∠∠===︒，∴90,90AEF GEH GEH EGH ∠∠∠∠+=︒+=︒，∴AEF EGH ∠∠=，∵EF EG =，∴(AAS)AEF GHE ≌ ，∴5GH AE ==，过点G 作直线l AD ∥，∵5GH =，GH AD ⊥，∴点G 在直线l 上运动，作点D 关于直线l 的对称点T ，连接ET ，在Rt EDT 中，90,5,10DET DE DT ∠=︒==，∴2255ET DE DT +=∵GD GT =，∴GE GD EG GT ET +=+≥，∴55GE GD +≥，∴GE GD +的最小值为55，∴DEG 周长最小值为555，故答案为：555．三、解答题（本大题共10个小题，共86分．解答应写出文字说明，证明过程或演算步骤）19．计算．(1)()()220240221π433-⎛⎫-+--- ⎪⎝⎭；(2)21111x x x ⎛⎫-÷ ⎪+-⎝⎭．【解析】（1）解：原式411199=+--39=13=；（2）原式21111x x x x+--=⨯+(1)(1)1x x x x x+-=⨯+1x =-．20．解方程或方程组：(1)解方程：2450x x --=；(2)解不等式组：()432123x x x x ⎧+≤+⎪⎨-<⎪⎩①②．【解析】（1）解：因式分解得，(5)(1)0x x -+=，∴10x +=或50x -=，∴15=x ，21x =-；（2）解：解不等式①得，1x ≥-，解不等式②得，3x <，∴不等式组的解集为：13x -≤<．21．一个不透明的笔袋里装有若干支黑色、红色和蓝色这三种颜色的中性笔（除笔芯颜色外，其余都相同），其中黑色中性笔有2支，红色中性笔有1支，从中任意摸出的一支笔是黑色中性笔的概率为12．(1)求笔袋中蓝色中性笔有多少支？(2)第一次任意摸出一支笔（不放回），第二次再摸出一支笔，请用树状图或列表法求出两次摸到的都是黑色中性笔的概率．【解析】（1）解：122112÷--=（支），答：笔袋中蓝色中性笔有1支．（2）解：解法一：树状图法由树状图可知，共有12种等可能的结果，其中两次摸到的都是黑色中性笔的情形有2种，∴两次摸到的都是黑色中性笔的概率为21126=．解法二：列表法第一次第二次黑1黑2红蓝黑1（黑1，黑2）（黑1，红）（黑1，蓝）黑2（黑2，黑1）（黑2，红）（黑2，蓝）红（红，黑1）（红，黑2）（红，蓝）蓝（蓝，黑1）（蓝，黑2）（蓝，红）由列表可知，共有12种等可能的结果，其中两次摸到的都是黑色中性笔的情形有2种，∴两次摸到的都是黑色中性笔的概率为21126=．22．某市教育局为了解“双减”政策落实情况，随机抽取几所学校部分初中生进行调查、统计他们平均每天完成作业的时间，并根据调查结果绘制如下不完整的统计图：请根据图表中提供的信息，解答下面的问题：(1)在调查活动中，教育局采取的调查方式是（填写“普查”或“抽样调查”）；(2)教育局抽取的初中生有人，扇形统计图中m的值是；(3)若该市共有初中生12000人，则平均每天完成作业时长在“7080t≤<”分钟的初中生约有多少人．【解析】（1）解：抽查方式为随机抽取几所学校部分初中生进行调查，则在调查活动中，教育局采取的调查方式是抽样调查，故答案为：抽样调查；（2）解：4515%300÷=人，∴教育局抽取的初中生有300人，∴每天完成作业时长在“7080t≤<”分钟的初中生人数有3004513521990----=人，∴90%100%30%300m=⨯=，∴30m=，故答案为：300；30；（3）解：1200030%3600⨯=人，∴平均每天完成作业时长在“7080t≤<”分钟的初中生约有3600人．23．新能源汽车因其废气排放量比较低，被越来越多的家庭所喜爱，老疆车行销售甲、乙两种型号的新能源汽车，十月的第一周售出1辆甲型车和3辆乙型车，销售额为65万元；第二周售出4辆甲型车和5辆乙型车，销售额为155万元．(1)求每辆甲型车和乙型车的售价各为多少万元？(2)茅溪科技发展有限公司准备向老疆车行购买甲、乙两种型号的新能源汽车共8辆，其购车费用不少于145万元，且不超过153万元，问有哪几种购车方案？【解析】（1）解：设每辆甲型车的售价为x 万元，每辆乙型车的售价为y 万元，根据题意得：36545155x y x y +=⎧⎨+=⎩解得：2015x y =⎧⎨=⎩，答：每辆甲型车的售价为20万元，每辆乙型车的售价为15万元；（2）解：设购买甲型车a 辆，则购买乙型车为()8a -辆，依题意得：()14520158153a a ≤+-≤，解得：5 6.6a ≤≤∵a 为正整数，∴a 取5或6．∴有两种购车方案：方案一：购买甲型车5辆，购买乙型车3辆，此时的费用是145万元，；方案二：购买甲型车6辆，购买乙型车2辆，此时的费用是150万元；24．如图，AC 是菱形ABCD 的对角线．(1)在AC 上求作一点E ，使得BEC BCD ∠=∠（尺规作图，不写作法，保留作图痕迹）；(2)在（1）的条件下，若140D ∠=︒，求CBE ∠的度数．【解析】（1）解：如图，点E 即为所求；（2）解： 四边形ABCD 是菱形，AD CB ∴∥，ACD ACB ∠=∠，180D BCD ︒∴∠+∠=，18014040BCD ∴∠=︒-︒=︒，20ACD ACB ∴∠=∠=︒，又∵40BEC BCD ∠=∠=︒，1801802040120CBE ACB BEC ∴∠=︒-∠-∠=︒-︒-︒=︒．25．如图，CD 是O 的直径，点B 在O 上，点A 为DC 延长线上一点，过点O 作OE BC ∥交AB 的延长线于点E ，且D E∠=∠(1)求证：AE 是O 的切线；(2)若线段OE 与O 的交点F 是OE 的中点，O 的半径为3，求阴影部分的面积．【解析】（1）证明：连接OB ，∵CD 是O 的直径，∴BC BD ⊥，即90CBD ∠=︒，∵OE BC ∥，∴90DGO CBD ∠=∠=︒，∴90BGE DGO ∠=∠=︒，90D DOG ∠+∠=︒，∵D E ∠=∠，∴DOE DBE ∠=∠，∵OD OB =，∴D OBD ∠=∠，∴90OBD DBE D DOG ∠+∠=∠+∠=︒，∴90OBE ∠=︒，∵OB 是O 的半径，∴AE 是O 的切线；（2）解：连接BF ，∵90OBE ∠=︒，F 是OE 的中点，∴BF OF =，∵O 的半径为3，90∠=︒DGO ，∴3BF OF OB ===，18090BGO DGO ∠=︒-∠=︒，∴OBF 是等边三角形，∴60BOF ∠=︒，∴9030OBG BOF ∠=︒-∠=︒，∴1322OG OB ==，2222333322BG OB OG ⎛⎫=-=-= ⎪⎝⎭，∴阴影部分的面积为：2603133339336022228OBG OBF S S ⨯π⨯π-=-⨯=-扇形△，∴阴影部分的面积为39328π26．如图，山区某教学楼后面紧邻着一个土坡，坡面BC 平行于地面AD ，斜坡AB 的坡比为51:12i =，且26AB =米．为了防止山体滑坡，保障安全，学校决定对该土坡进行改造．经地质人员勘测，当坡角不超过53︒时，可确保山体不滑坡．(1)求改造前坡顶与地面的距离BE 的长．(2)为了消除安全隐患，学校计划将斜坡AB 改造成AF （如图所示），那么BF 至少是多少米？（结果精确到1米）（参考数据：sin530.8︒≈，cos530.6︒≈，tan 53 1.33︒≈，cot 530.75)︒≈．【解析】（1）解： 斜坡AB 的坡比为51:12i =，:12:5BE EA ∴=，设12BE x =，则5EA x =，由勾股定理得，222BE EA AB +=，即222(12)(5)26x x +=，解得，2x =，则1224BE x ==，510AE x ==，答：改造前坡顶与地面的距离BE 的长为24米；（2）解：作FH AD ⊥于H ，则tan FH FAH AH ∠=，24181.33AH ∴=≈，18108BF ∴=-=，答：BF 至少是8米．27．如图，在ABC 中，10AB AC ==，45BC =AD BC ⊥于点D ，点P 从点A 出发，沿折线AC CD →向终点D 运动，点P 在AC 上以每秒5个单位长度的速度匀速运动，在CD 5匀速运动，当点P 不与点A 、D 重合时，作PQ AB ∥，PQ 与射线AD 交于点Q ，以PQ 为一边向左侧作正方形PQMN ．设点P 的运动时间为()s t ．(1)直接写出AD =______．(2)求sin BAC ∠的值．(3)当正方形PQMN 与ABC 重叠部分图形是四边形时，直接写出t 的取值范围．(4)连接BM ，直接写出BM AB ⊥时t 的值．【解析】（1）解：∵,=⊥AB AC AD BC ，∴1145522BD BC ==⨯=在Rt △ABD 中，根据勾股定理得：2245AD AB BD -=故答案为：45（2）解：如图1，作CE AB ⊥于点E ．分别以AB BC 、为底表示ABC 的面积两式相等，可得：8BC ADCE AB ⋅==；∴4sin 5CEBAC AC ∠==；（3）解：正方形PQMN 与ABC 重叠部分图形随着t 的变化而变化．①如图2，当Q 点与D 点重合时，正方形PQMN 与ABC 重叠部分图形，由四边形变为五边形．∵PQ AB ∥，∴1APBDPC DC ==，∴此时：1215ACt ==．②如图3：当MQ 经过B 点时，正方形PQMN 与ABC重叠部分图形，由五边形变为四边形．∵4sin 5BAC ∠=，∴243cos 155BAC ⎛⎫∠=-= ⎪⎝⎭；∵,PQ AB PN PQ ⊥∥，∴PN AB ⊥．∴此时，cos AP BAC PQ AB ⋅∠+=，即355105t t ⨯+=，解得：54t =．如图4：当P 与C 重合时，正方形PQMN 与ABC 重叠部分图形，由四边形变为三角形．此时，1025t ==．综上：t 的取值范围为：01t <≤或524t ≤<；（4）解：由（3）可知54t =时，MQ 经过点B 时BM AB ⊥；另外当P 在DC 上时，也会出现BM AB ⊥，如图5．∵,PQ AB MQ PQ ⊥∥；∴MQ AB ⊥，∴ABD BQD QPD ∽∽ ．∴::::::AB BQ PQ AD BD QD BD QD PD ==，即10::45225:BQ PQ QD QD PD ==；得：52PD =∴535452522CP BC PD BD =--=-=；∴3572225t ==．故BM AB ⊥时t 的值为：54，72．28．如图，抛物线2y x bx c =-++交x 轴于A 、B 两点（点A 在点B 的左侧）坐标分别为()2,0-，()4,0，交y 轴于点C ．(1)求出抛物线解析式；(2)如图1，过y 轴上点D 作BC 的垂线，交直线BC 于点E ，交抛物线于点F ，当355EF =F 的坐标；(3)如图2，点H 的坐标是()0,2，点Q 为x 轴上一动点，点()2,8P 在抛物线上，把PHQ 沿HQ 翻折，使点P 刚好落在x 轴上，请直接写出点Q 的坐标．【解析】（1）解：将()2,0-，()4,0代入表达式得：4201640b c b c --+=⎧⎨-++=⎩，解得：28b c =⎧⎨=⎩，∴抛物线解析式为228y x x =-++；（2）过点F 作x 轴的垂线交BC 于N ，交x 轴于M ，∵FNE BNM ∠=∠，90FNE EFN BNM MBN ∠+∠=∠+∠=︒，∴EFN MBN ∠=∠，在Rt BOC 中，90BOC ∠=︒，由勾股定理得：22224845BC OB OC =+=+=∴cos cos OB EF EFN MBN BC FN ∠=∠=35545FN =，∴3FN =，∵()4,0B ，()0,8C ，∴直线BC ：28y x =-+，设()2,28F m m m -++，(),28N m m -+，∴()228283m m m -++--+=或()28²283m m m -+--++=，∴243m m -+=或243m m -+=-，解得：11m =，23m =，327m =427m =，∴()1,9F 或()3,5或(27,17-或()27,271其中()1,9F 和(27,17-两点所对应的E 点不在线段BC 上，所以舍去，∴点F 的坐标为()3,5或()27,271；（3）分两种情况讨论：①如图所示，当点Q 位于x 轴负半轴时，过点P 作PM y ∥轴交x 轴于点M ，作PN x ∥轴交y 轴于点N ，则四边形OMPN 为矩形，∵()2,8P ，∴2NP OM ==，8ON PM ==，∵()0,2H ，∴826NH =-=，∴222226210PH NP NH =+=+=，由折叠可知：210PH HP '==QP QP '=，∴()222221026OP P H OH =--'='，设OQ x =，∴6QP QP x '==+，2QM x =+，∵222P M Q M P Q +=，∴()()222826x x ++=+，∴4x =，∴Q 点的坐标为()4,0-；②如图所示，当点Q 位于x 轴正半轴时，过点P 作PM y ∥轴交x 轴于点M ，作PN x ∥轴交y 轴于点N ，由①得：210PH P H '==，P Q PQ '=，∴()222221026OP P H OH =--'='，设OQ m =，则6P Q PQ m '==+，2QM m =-，∵222P M Q M P Q +=，∴()()222286m m -+=+，∴2m =，∴Q 点的坐标为()2,0，综上所述，Q 点的坐标为()4,0-或()2,0．。

2024届安徽省黄山市初中毕业学业模拟考试数学试题（二模）一、选择题（本大题共10小题，每小题4分，满分40分.在每小题所给的四个选项中,只有一项正确. 请在答题卷的相应区域答题.）1. 4的相反数是A ．B ．C ．D ．2±14-4-142.计算的正确结果为()23(3)2x x -⋅-A ．B ．C ．D ．518x 536x518x-536x-3. 大庆油田发现预测地质储量亿吨的页岩油，这标志着我国页岩油勘探开发取得重大1268.战略突破.数字用科学记数法表示为1268000000A. B. C. D.9126810.⨯8126810.⨯7126810.⨯6126810.⨯4．将一个机器零件按如图方式摆放，则它的俯视图为A ．B ．C ．D ．5. 如图，将直尺与含角的三角尺叠放在一起，若，则的大小是30︒155∠=︒2∠A ．B ．C ．D ．65︒70︒75︒80︒6.如图，电路图上有四个开关和一个小灯泡，则任意闭合其中两个开关，小灯A B C D 、、、泡发光的概率是A. B. C. D.1214第4题图第5题图第6题图7．“房住不炒”多次出现在政府报告中，明确了要稳地价、稳房价、稳预期．为响应中央“房住不炒”的基本政策，某房企连续降价两次后的平均价格比降价之前减少了19%，则平均每次降价的百分率为A ．9.5%B ．10%C ．10.5%D ．11%8．如图，平行四边形中,分别是的中点,,，ABCD G H 、AD BC 、AE BD ⊥CF BD ⊥四边形是矩形，若,，则GEHF 5AB =8AD =BD A ．B ．C ．82231529. 如图，边长为4的正方形中，为边ABCD E AD 动点，将线段绕点顺时针旋转得到线段EF F 90︒FG B ．4C ．10.对于一个函数，自变量取时，函数值等于0x c y 的二次函数x 210y x x m =--+(0)m ≠方程有两个不相等的非零实数根21020x x m +--=3x 定正确的是A ．B ．C ．1301x x <<131x x >240x x <二、填空题（本大题共4小题，每小题5分，满分20分. 11．的解集为．412x -<12. 分解因式 ：．324x xy -=13. 如图，正比例函数与反比例函数()110y k x k =≠E 第8题图第13题图的图象交于，()220k y k x =≠()6,A m (),8B n -两点，点C 是坐标系中的一点，若，90ACB ∠=︒则的长为．OC 14.如图，在中，，将绕Rt ABC ∆90ACB ∠=︒ABC ∆点顺时针旋转得到,和相交于点，C DEC ∆BC DE O 点落在线段上，连接．D AB BE （1）若，则；20ABC ∠=︒BCE=∠（2）若，则．BEBD =tan ABC=∠三、（本大题共2小题，每小题8分，满分16分. 请在答题卷的相应区域答题.）15.计算：111452cos -⎛⎫-︒+ ⎪⎝⎭16.如图，三个顶点的坐标分别为．ABC ∆(2,4),(1,1),(4,3)A B C （1）请画出关于x 轴对称的；ABC ∆111A B C ∆（2）请画出绕点逆时针旋转后的；ABC ∆B 90︒22A BC ∆（3）仅用无刻度直尺作图（保留作图痕迹），求作线段的中点．AB P 第14题图ABC四、（本大题共2小题，每小题8分，满分16分. 请在答题卷的相应区域答题.）17．《九章算术》中有记载：今有甲乙二人持钱不知其数．甲得乙半而钱五十，乙得甲太半而亦钱五十，问甲、乙持钱各几何？大意是：今有甲、乙两人持钱不知有多少．若甲得到乙所有钱的，则有50钱；若乙得到甲所有钱的，则也有50钱，问甲、乙各12持钱多少？请解答此问题．18．观察以下等式：第1个等式：；第2个等式：21131232-=⨯⨯31182343-=⨯⨯第3个等式：；第4个等式：411153454-=⨯⨯511244565-=⨯⨯……按照以上规律，解决下列问题：（1）写出第5个等式：_______________________；（2）写出你猜想的第n 个等式：__________________（用含n 的等式表示），并证明．五、（本大题共2小题，每小题10分，满分20分. 请在答题卷的相应区域答题.）19．如图，O 为的外接圆，直线与O 相切于点，弦,与ABC ∆MN C BD MN ∥AC 相交于点．BD E （1）求证：；CAB CBD ∠=∠（2）若，求O 的半径．58BC ,BD == 20.现有一张宽为12cm 练习纸，相邻两条格线间的距离均为0.8cm ．调皮的小聪在纸的左上角用印章印出一个矩形卡通图案，图案的顶点恰好在四条格线上（如图），测得．32α∠=︒（1）求矩形图案的面积；（2）若小聪在第一个图案的右边以同样的方式继续盖印（如图），最多能印________个完整的图案？请直接写出答案.（参考数据：，，3205.sin ︒≈3208.cos ︒≈）3206.tan ︒≈六、（本大题满分12分. 请在答题卷的相应区域答题.）21.为了解某校九年级学生的理化实验操作情况，随机抽查一部分同学实验操作的得分．根据获取的样本数据，制作了如下的不完整的条形统计图和扇形统计图．请根据相关信息，解答下列问题：（1）抽查的人数为________，6分所在的扇形的圆心角的大小是________度；请补全条形统计图；（2）样本数据的平均数为________分，众数为________分，中位数为________分；（3）该校九年级共有1200名学生，估计该校理化实验操作得满分10分有多少人．七、（本大题满分12分. 请在答题卷的相应区域答题.）22.某建筑物的窗户如图所示，上半部分是等腰三角形,,AF ∶BF 3∶4，点ABC ∆AB AC =分别是边的中点，下半部分四边形是矩形，G H F 、、AB AC BC 、、BCDE ，制造窗户框的材料总长为16米(图中所有黑线的长度和),设BE IJ MNCD ∥∥∥米，米．BF x =BE y =（1）求与之间的函数关系式，并求出自变量的取值范围；x x （2）当为多少时，窗户透过的光线最多(窗户的面积最大)，并计算窗户的最大面积．x八、（本大题满分14分.请在答题卷的相应区域答题.）23.如图1，在正方形中，分别为边的中点，连接交于ABCD E F 、AB BC 、AF DE 、点．G （1）求证：；AFDE ⊥（2）如图2，连接，求证：平分；BG BG EGF ∠（3）如图3，连接，若的面积为，求证：．BG ADG ∆S 22BG S =答案及评分标准一、选择题（本大题共10小题，每小题4分，满分40分.）12345678910CCABAABDDA二、填空题（本大题共4小题，每小题5分，满分20分. 请在答题卷的相应区域答题.）11.12.13. 1014.6x ＜()()22x x y x y +﹣40︒1-三、解答题（本大题共2小题，每小题8分，满分16分）15.解：111452cos -⎛⎫-︒+ ⎪⎝⎭222212+⨯--=2212+--=…………………………………………………………………………8分1=16.（1）如图所示，即为所求.………………………………………2分111A B C ∆（2）如图所示，即为所求.…………………………………………5分22A BC ∆（3）如图所示，点即为所求.…………………………………………8分P 四、（本大题共2小题，每小题8分，满分16分）17.解：设甲、乙的持钱数分别为x ，y ，根据题意可得：，15022503x y y x ⎧+=⎪⎪⎨⎪+=⎪⎩解得：，37.525x y =⎧⎨=⎩答：甲、乙的持钱数分别为37.5，25．…………………………………………8分18.解：（1）；……………………………………………………2分611355676-=⨯⨯（2）；……………………………………4分111(2)(1)(2)1n n n n n n n +-=++++证明：∵等式左边()()()11212n n n n n n +=-+++()()()21112n n n n +-=++()()2212n n n n n +=++()()()212n n n n n +=++11n =+又∵等式右边=，11+n ∴等式左边=等式右边，∴成立.………8分()()()1111212n n n n n n n +-=++++五、（本大题共2小题，每小题10分，满分20分）19.解：（1）连接，交于点OC BD F ∵直线与相切于点，MN O C ∴，OC MN ⊥∵，BD MN ∥∴，OC BD ⊥∴，BC CD =∴；…………………………………………………4分CAB CBD ∠=∠（2）连接,由（1）知，OB OC BD ⊥8BD =∴4BFDF ==∴在中得Rt BCF∆3CF ===设半径为,在中，r Rt BOF ∆3OF r =-根据勾股定理可得，解得.……………10分()22234r r-+=256r =20.解：（1）如图，在中，∵，Rt BCE ∆CE sin BC α=∴，081605CE .BC .sin .α===∵四边形是矩形，ABCD ∴，90BCD ∠=︒∴，90BCE FCD ∠+∠=︒又∵在中，Rt BCE ∆∴，90EBC BCE ∠+∠=︒∴32FCD EBC ∠=∠=在中，∵，Rt FCD ∆FC cos FCD CD ∠=∴，1623208FC .CD cos .===︒∴矩形图案的长和宽分别为2cm 和1.6cm ，∴面积＝2×1.6＝3.2（）………………………………………7分2cm （2）5. ………………………………………………………………………10分六、（本大题满分12分）21．（1）40，36，补全图形如下………………………………………………3分（2）8.3，9，8 ； …………………………………………………………9分（3）解：（人），7120021040⨯=答：该校九年级共有1200名学生，估计该校理化实验操作得满分10分有210人．…………………………………………………………………………………12分七、（本大题满分12分）22．解：（1）∵是等腰三角形，是的中点，ABC ∆F BC ∴，BF CF ,AF BC,AB AC =⊥=∵米，BF x =∴米，米，CF x =22BC BF x ==∵∶∶，AF 3BF =4∴米，34AF x =在中，由勾股定理得(米） Rt AFB54AB x ===∴米，54AC AB x ==∵点分别是边的中点，，G H 、AB AC 、90AFB AFC ∠=∠=︒∴米，米，1528FG AB x ==1528FH AC x ==∵四边形是矩形，BCDE ∴米，米，2ED BC x ==BE CD y ==∵，BE IJ MN CD ∥∥∥∴米，BE IJ MN CD y ====∵制造窗户框的材料总长为16米，∴米，16AB AC FG FH AF BC ED BE IJ MN CD ++++++++++=∴，555532241644884x x x x x x x y +++++++=整理得；1748y x =-+由题意得，017408x x ⎧⎪⎨-+⎪⎩＞＞解得；………………………………………………………6分32017x＜＜（2）2113322244ABC S BC AF x x x ∆=⋅=⋅⋅= ，2171724884BCDE S BC BE x x x x ⎛⎫=⋅=⋅-+=-+ ⎪⎝⎭矩形设窗户的面积为平方米，W 则ABC BCDEW S S ∆=+矩形22223178447827832277x x x x x x =-+=-+⎛⎫=--+ ⎪⎝⎭，702- ＜有最大值，W ∴当米时，最大，最大值为平方米． ……………………12分87x =W 327八、（本大题满分14分）23.（1）∵四边形是正方形，ABCD ∴，90AD AB BC,DAE ABF ==∠=∠=︒∵分别为边的中点，E F 、AB BC 、∴，AE BF =∴，DAE ABF ≌∴，ADE BAF ∠=∠∵，90DAG EAG ∠+∠=︒∴，90DAG ADG ∠+∠=︒∴，90AGD ∠=︒∴；………………………………………………………………4分AF DE ⊥（2）如图2，过点作，垂足为，B BMAF ⊥M ∵，则，AFDE ⊥BM GE ∥∵，AE BE =∴，AGGM =设，则，BFa=2AB a,AF====∵,1122ABF S AB BF AF BM =⋅=⋅ ∴，2a a BM ⋅=⋅∴，BM =∴，AM ==∴，GM BM ==∴为等腰直角三角形，BMG ∴，45904545BGM ,BGE ∠=︒∠=︒-︒=︒∴，BGM BGE ∠=∠∴平分；……………………………………………………9分BG EGF ∠（3）的面积为，则，ADG S 2AG DG S ⋅=过点作，垂足为，B BM AF ⊥M 由（2）知：，22122GM AG,BM AM ,BG BM ===∵，90AGD AMB ,ADG BAM ,AB AD ∠=∠=︒∠=∠=∴，DAG ABM ≌∴，BM AG,AM DG ==∴，21222AG DG,AG DG AG S =⋅==即，2AG S =∴，2BM S =∴．…………………………………………………14分2222BG BM S ==。

（北师大版）初中九年级数学下学期中考复习模拟考试试题卷（含答案详解）（满分150分 时间：120分钟）一.单选题。

（共40分） 1.16的算术平方根是（ ）A.±2B.2C.4D.±4 2.下面四个几何体中，左视图为圆的是（ ）A. B. C. D.3.据5月17日消息，全国各地约42600名医务人员支援湖北抗击新冠肺炎疫情，将42600用科学记数法表示为（ ）A.0.426×105B.4.26×105C.42.6×104D.4.26×1044.如图，直线a ∥b ，直线c 分别交a ，b 于点A ，C ，∠BAC 的平分线交直线b 于点D ，若∠1=50°，则∠2的度数是（ ）A.50°B.70°C.80°D.110°（第4题图） （第9题图） （第10题图） 5.下列图形中，既是轴对称图形又是中心对称图形的是（ ）A. B. C. D.6.化简a 2a －1－1－2a 1－a的结果为（ ）A.a+1a －1B.a ﹣1C.aD.17.从甲、乙、丙、丁四人中抽调两人参加“寸草心”志愿服务队，恰好抽到甲和乙的概率是（ ）A.112 B.18 C.16 D.128.在同一直角坐标系中，函数y=kx 和y=kx ﹣3的图象大致是（ ）A. B. C. D.9.在直角坐标系中，等腰直角三角形AOB 在如图所示的位置，点B 的横坐标为2，将△AOB 绕点O 按逆时针方向旋转90°，得到△A’OB’，则点A’的坐标为（ ） A.（1，1） B.（√2，√2） C.（﹣1，1） D.（﹣√2，√2）10.在平面直角坐标系内，已知点A （﹣1，0），点B （1，1）都在直线y ＝12x+12上，若抛物线y ＝ax 2﹣x+1（a ≠0）与线段AB 有两个不同的交点，则a 的取值范围是（ ） A.a ≤﹣2 B.a ＜98 C.1≤a ＜98或a ≤﹣2 D.﹣2≤a ＜98 二.填空题。

高桥初中教育集团第一学期第二次质量检测九年级数学试题卷请同学们注意：1、考试卷分试题卷和答题卷两部分，满分120分，考试时间为90分钟．2、所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应．3、考试结束后，只需上交答题卷。

祝同学们取得成功！ 一、仔细选一选（本题有10小题，每题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的。

注意可以用多种不同的方法来选取正确答案。

1．下列各点中在反比例函数的图象上的点是（ ） A ．（-1，-2）B ．（1，-2）C ．（1，2）D ．（2，1）2．抛物线的对称轴是（ ） A ．直线B ．直线C ．直线D ．直线 3．有三个二次函数，甲：；乙：；丙：。

则下列叙述中正确的是（ ） A ．甲的图形经过适当的平行移动后，可以与乙的图形重合 B ．甲的图形经过适当的平行移动后，可以与丙的图形重合 C ．乙的图形经过适当的平行移动后，可以与丙的图形重合 D ．甲，乙，丙3个图形经过适当的平行移动后，都可以重合 4．下列函数：①；②；③；④中，随的增大而减小的函数有（ ）A ．1个B ．2个C ．3个D ．4个 5．在反比例函数的图像上有两点（-1，y 1），（-，y 2），则y 1-y 2的值是（ ）A ．负数B ．非正数C ．正数D ．不能确定 6．二次函数的图象可能是（ ）xy 2-=242+-=x y 2-=x 41-=x 0=x 41=x 12-=x y 12+-x 122-+=x x y 12-=x y ()01<-=x x y ()01682>--=x x x y 34x y =y x ()0<=k xky 41122-++=a x ax yA B CD7．二次函数的图象如图所示，则的值是（ ） A ．-8 B ．8 C ． ±8 D ．68．已知二次函数中，其函数与自变量之间的部分对应值如下表所示：… 0 1 2 3 4 ……4114…点A （，）、B （，）在函数的图象上，则当，时，与的大小关系正确的是（ ）A ．B ．C ．D ． 9．如图，Rt △OAB 的顶点A （-2，4）在抛物线y=ax 2上，将Rt △OAB 绕点O 顺时针旋转90°，得到△OCD ，边CD 与该抛物线交于点P ，则点P 的坐标为（ ） A ．（，） B ．（2，4） C ．（，2）D ．（2，）10．如图，反比例函数（x ＞0）的图象经过矩形OABC 对角线的交点M ，分别于AB 、BC交于点D 、E ，若四边形ODBE 的面积为9，则k 的值为（ ） A ． 1 B ． 2 C ． 3 D ． 4二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案． 11．若双曲线的图象经过第二、四象限，则的取值范围是 822++=mx x y m c bx ax y ++=2y x x y 1x 1y 2x 2y 211<<x 432<<x 1y 2y 21y y ≥21y y ≤21y y >21y y <2222xk y 12-=k （第7题）（第10题） （第9题）12．若函数与轴的一个交点坐标是（2，0），则它与轴的另一个交点坐标是 13．已知，当时，的取值范围是 14．将抛物线的图象先向右平移个单位，再向上平移个单位，得到的抛物线经过点（1，3），（4，9）则= ，=15．已知函数的图象与轴有一个交点，则的值是 ．16．如图，是二次函数的图象的一部分，图象过A 点（3，0），对称轴为，给出三个结论：①；②；③的两根分别为-1和3；④。

2023年广西初中学业水平考试模拟（二）数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列实数中是无理数的是（）A ．πB ．227C ．3-D ．2．下列几何体中，主视图与俯视图的形状不一样的几何体是（）A ．B ．C ．D ．3．下列运算中，正确的是（）A ．235a a a +=B ．3515a a a ⋅=C ．632a a a ÷=D ．43a a a-=4．据广西壮族自治区统计局消息根据地区生产总值统一核算结果，2022年全区生产总值26300.87亿元，按不变价格计算，比上年增长2.9％．数据26300用科学记数法表示为（）A ．32.6310⨯B ．42.6310⨯C ．52.6310⨯D ．62.6310⨯5．下列图形中，既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．6．下列事件中，属于必然事件的是（）A ．随机购买一张彩票，中奖100万B ．抛掷硬币时，反面朝上C ．三角形的两边之和大于第三边D ．经过红绿灯路口，遇到绿灯7．如图，要把河中的水引到水池A 中，应在河岸B 处（AB ⊥CD ）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（）A ．两点之间线段最短B ．点到直线的距离C ．两点确定一条直线D ．垂线段最短8）A ．1x >-B ．1x >C ．1x ≥-D ．1x ≥9．为了解某中学八年级600名学生的身高情况，抽查了其中100名学生的身高进行统计分析．下面叙述正确的是（）A ．以上调查属于全面调查B ．每名学生是总体的一个个体C ．100名学生的身高是总体的一个样本D ．600名学生是总体10．不等式组21{30x x +≥-≥①②的解集在数轴上表示正确的是（）A ．B ．C ．D ．11．我国是最早了解勾股定理的国家之一.下面四幅图中，不能用来证明勾股定理的是（）A ．B ．C ．D ．12．对于任意实数m ，n ，如果满足2424m n m n++=+，那么称这一对数m ，n 为“完美数对”，记为(),m n ．若(),a b 是“完美数对”，则()()332a b a b +-+-的值为（）A ．2B ．3C ．4-D ．6-二、填空题13．点()23A -，关于x 轴的对称点A '的坐标为_________．14．已知关于x 的一元二次方程240x x m -+=有两个相等的实数根，则m =_________．15．如图，在等边ABC 中，D 是边AC 上一点，连接BD ，将BCD △绕点B 逆时针旋转60︒得到BAE ，连接ED ，若8BC =，7BD =，则AED △的周长是______．16．圆周率π是无限不循环小数．历史上，祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究．目前，超级计算机已计算出π的小数部分超过31.4万亿位．有学者发现，随着π小数部分位数的增加，09～这10个数字出现的频率趋于稳定接近相同，从π的小数部分随机取出一个数字，估计数字是6的概率为______．17．如图，已知双曲线()0ky x x=<经过矩形OABC 边AB 的中点F ，交BC 于点E ，且四边形OEBF 的面积为3，则k =______．18．如图所示，在ABC 中，30A ∠=︒，M 为线段AB 上一定点，P 为线段AC 上一动点．当点P 在运动的过程中，满足12PM AP +的值最小时，则APM ∠=______．三、解答题1913322-+÷-．20．解方程：28124x x x -=--．21．如图，在平面直角坐标系中，已知△ABC 三个顶点的坐标分别是A （2，2），B （4，0），C （4，﹣4）．（1）请在图中，画出△ABC 向左平移6个单位长度后得到的△A 1B 1C 1；（2）以点O 为位似中心，将△ABC 缩小为原来的12，得到△A 2B 2C 2，请在图中y 轴右侧，画出△A 2B 2C 2，并求出∠A 2C 2B 2的正弦值．22．某中学举办“垃圾分类知识答题竞赛”，七年级和八年级根据初赛成绩各选出5名选手参加学校决赛，成绩如图所示．平均分中位数众数方差七年级a 85b s 2八年级85c100160(1)直接写出a 、b 、c 的值；(2)结合两个年级成绩的平均数和中位数进行分析，哪个年级的决赛成绩好；(3)计算七年级决赛成绩的方差s 2，并判断哪个年级的选手成绩较为稳定．23．在Rt ABC △中，∠BAC ＝90°，D 是BC 的中点，E 是AD 的中点，过点A 作AF BC ∥交BE 的延长线于点F ．(1)求证：AEF DEB ≌△△；(2)证明：四边形ADCF 是菱形：(3)若AC ＝3，AB ＝4，求菱形ADCF 的面积．24．为了提高同学们学习数学的兴趣，某中学开展主题为“感受数学魅力，享受数学乐趣”的数学活动．并计划购买A 、B 两种奖品奖励在数学活动中表现突出的学生，已知购买1件A 种奖品和2件B 种奖品共需64元，购买2件A 种奖品和1件B 种奖品共需56元．(1)每件A 、B 奖品的价格各是多少元？(2)根据需要，该学校准备购买A 、B 两种奖品共80件，设购买a 件A 种奖品，所需总费用为w 元，求w 与a 的函数关系式，并直接写出a 的取值范围；(3)在（2）的条件下，若要求购买的A 种奖品的数量不超过B 种奖品数量的3倍，求所需总费用的最小值．25．筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理：如图1，其原理是利用流动的河水，推动水车转动，水斗舀满河水，将水提升，等水斗转至顶空后再倾入接水槽，水流源源不断，流入田地，以利灌溉．如图2，筒车O 与水面分别交于点A ，B ，筒车上均匀分布着若干盛水筒，P 表示筒车的一个盛水筒．接水槽MN 所在的直线是O 的切线，且与直线AB 交于点M ，当点P 恰好在NM 所在的直线上时．解决下面的问题：(1)求证：BAP MPB ∠=∠；(2)若AB AP =，8MB =，12MP =，求BP 的长．26．已知二次函数2y x x 2=--的图象与x 轴交于点A ，点B ，与y 轴交于点C ．(1)直接写出点A 和点B 的坐标．(2)如图1，若点P 是二次函数图象上位于BC 下方的一个动点，连接OP 交BC 于点Q ．设点P 的横坐标为t ，设PQw OQ=，求w 的最大值．(3)如图2，已知点()1,2D -，P 是二次函数图象上不同于点D 的一个动点，连接CD 、PB 、PC ，当DBC △的面积等于PBC 时，求点P 的坐标．参考答案：1．A【分析】先计算零次幂，然后根据有理数和无理数的概念加以判断即可．【详解】解：在π，227，3-，0=1中，π是无理数，其余的数是有理数，故选：A ．【点睛】本题主要考查了无理数的定义，解题的关键是熟练掌握无限不循环小数是无理数．2．C【分析】根据各个几何体的主视图和左视图进行判定即可．【详解】解：A ．正方体的主视图与俯视图都是正方形，故该选项不符合题意；B ．圆柱的主视图与俯视图都是长方形，故该选项不符合题意；C ．圆锥的主视图是等腰三角形，俯视图是圆，故该选项符合题意；D ．球的主视图与俯视图都是圆，故该选项不符合题意；故选：C ．【点睛】本题考查简单几何体的三视图，掌握各种几何体的三视图的形状是正确判断的关键．3．D【分析】根据合并同类项，同底数幂的乘法，同底数幂的除法法则进行计算，进而得出答案．【详解】解：A ，2a 和3a 底数相同，但指数不同，不是同类项，不能合并，故选项错误；B ，同底数幂相乘，底数不变，指数相加，因此358a a a ⋅=，故选项错误；C ，同底数幂相除，底数不变，指数相减，因此633a a a ÷=，故选项错误；D ，4a 和a 是同类项，可以合并，43a a a -=，故选项正确．故答案为：D【点睛】本题考查合并同类项和同底数幂的乘除法，熟练掌握运算法则是解题的关键．4．B【分析】科学记数法的表现形式为10n a ⨯的形式，其中110a ≤<，n 为整数，确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n 是正数，当原数绝对值小于1时n 是负数；由此进行求解即可得到答案．【详解】解：426300 2.6310⨯=,故选B ．【点睛】本题主要考查了科学记数法，解题的关键在于能够熟练掌握科学记数法的定义．5．D【分析】根据轴对称图形和中心对称图形的定义进行逐一判断即可：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．【详解】解：A、不是轴对称图形，是中心对称图形，不符合题意；B、是轴对称图形，不是中心对称图形，不符合题意；C、是轴对称图形，不是中心对称图形，不符合题意；D、既是轴对称图形，也是中心对称图形，符合题意；故选D．【点睛】本题主要考查了轴对称图形和中心对称图形的识别，熟知二者的定义是解题的关键．6．C【分析】根据必然事件：一定条件下，一定发生的事件即为必然事件，可能发生也可能不发生的为随机事件，一定不发生的为不可能事件；据此判断即可．【详解】解：A、随机购买一张彩票，中奖100万，是随机事件，不符合题意；B、抛掷硬币时，反面朝上，是随机事件，不符合题意；C、三角形的两边之和大于第三边，是必然事件，符合题意；D、经过红绿灯路口，遇到绿灯，是随机事件，不符合题意；故选：C．【点睛】本题考查了事件类型的判断，熟练掌握相关事件的定义是解本题的关键．7．D【分析】根据垂线段的性质：垂线段最短进行解答．【详解】解：要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是：垂线段最短，故选：D.【点睛】本题考查垂线段的性质：垂线段最短，熟练掌握垂线段的定义是解题的关键. 8．D【分析】根据二次根式有意义的条件可得x-1≥0，再解即可．【详解】由题意得：x-1≥0，解得：x≥1，故选D．【点睛】此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．9．C【分析】总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．据此对每个选项进行判断即可．【详解】A．是抽样调查，故A不符合题意；B．每名学生的身高是个体，故B不符合题意；C．100名学生的身高是总体的一个样本，故C符合题意；D．600名学生的身高是总体，故D不符合题意；故选：C【点睛】本题考查了总体、个体、样本、样本容量，全面调查与抽样调查的概念．10．B【详解】解：解不等式①得x≥-1解不等式②得x≤3∴不等式组的解集是﹣1≤x≤3，其数轴上表示为：故选B．【点睛】本题考查在数轴上表示不等式的解集；解一元一次不等式组．11．C【分析】根据A、B、C、D各图形结合勾股定理一一判断可得答案.【详解】解:A、有三个直角三角形,其面积分别为12ab,12ab和21c2,还可以理解为一个直角梯形,其面积为1(a+b)(a+b)2，由图形可知:1(a+b)(a+b)2=12ab+12ab+21c 2，整理得:(a+b)2=2ab+c 2,∴a 2+b 2+2ab=2ab+c 2,a 2+b 2=c 2∴能证明勾股定理;B 、中间正方形的面积=c 2,中间正方形的面积=(a+b)2-4⨯12⨯ab=a 2+b 2,∴a 2+b 2=c 2,能证明勾股定理;C 、不能利用图形面积证明勾股定理,它是对完全平方公式的说明.D 、大正方形的面积=c 2,大正方形的面积=(b-a)2+4⨯12⨯ab =a 2+b 2,,∴a 2+b 2=c 2,能证明勾股定理;故选C.【点睛】本题主要考查勾股定理的证明，解题的关键是利用构图法来证明勾股定理.12．A【分析】先根据“完美数对”的定义2424a b a b ++=+，从而可得40a b +=，再去括号，计算整式的加减，然后将40a b +=整体代入即可得解．【详解】解：由题意得：2424a b a b ++=+，即40a b +=，则3(3)(2)932a b a b a b a b +-+-=+--+，822a b =++，2(4)2a b =++，202=⨯+，2=；故选：A ．【点睛】本题考查了整式加减中的化简求值，掌握理解“完美数对”的定义是解题关键．13．()23-，-【分析】关于x 轴对称的点，横坐标相同，纵坐标互为相反数．由此可解．【详解】解：点()23A -，关于x 轴的对称点A '的坐标为()23-，-．故答案为：()23-，-．【点睛】本题考查了关于x 轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x 轴对称的点，横坐标相同，纵坐标互为相反数；关于y 轴对称的点，纵坐标相同，横坐标互为相反数．14．4【分析】一元二次方程20(0)ax bx c a ++=≠的根与24b ac ∆=-有如下关系：当0∆>时，方程有两个不相等的实数根；当Δ0=时，方程有两个相等的实数根；当Δ0<时，方程无实数根．利用判别式的意义得到2(4)40m ∆=--=，然后解关于m 的方程即可．【详解】解：根据题意得2(4)40m ∆=--=，解得m =4．故答案为：4．【点睛】本题主要考查了一元二次方程的根的判别式，理解并熟练掌握一元二次方程的根的判别式是解题关键．15．15【分析】先根据旋转的性质得BE BD =，AE CD =，60DBE ∠=︒，于是可判断BDE 为等边三角形，则有7DE BD ==，所以AED △的周长DE AC =+，再利用等边三角形的性质得8AC BC ==，即可求得AED △的周长．【详解】解：BCD 绕点B 逆时针旋转60︒得到BAE ，BE BD ∴=，AE CD =，60DBE ∠=︒，BDE ∴ 为等边三角形，7DE BD ∴==，AED ∴ 的周长DE AE AD DE CD AD DE AC =++=++=+，ABC 为等边三角形，8AC BC ∴==，AED ∴ 的周长7815DE AC =+=+=，故答案为：15．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的判定与性质．16．110##0.1【分析】从π的小数部分随机取出一个数字共有10种等可能的结果，其中出现数字6的只有1种结果，利用概率公式求解即可．【详解】解： 随着π小数部分位数的增加，09～这10个数字出现的频率趋于稳定接近相同，∴从π的小数部分随机取出一个数字共有10种等可能的结果，其中出现数字6的只有1种结果，P ∴(数字是6)110=．故答案为：110．【点睛】本题考查了利用频率估计概率，掌握大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率是解题的关键．17．3-【分析】设点(,)k E m m ，根据中点表示出(2,)2k F m m ，求出矩形的面积，根据反比例函数k 的几何意义求出OEC △与OAF △面积，即可得到答案；【详解】解：设点(,k E m m ，∵F 是AB 的中点，∴(2,)2k F m m，∵四边形OABC 是矩形，∴22OABC k S m k m =⨯=-，∵22OEC k k S ==- ，22OAF k k S ==- ，∴222OEBF OABC OAF OEC k k S S S S k k =--=-++=- ，∵四边形OEBF 的面积为3，∴3k -=，∴3k =-，故答案为3-；【点睛】本题考查反比例函数k 的几何意义，解题的关键是设出点的坐标计算出表示出矩形的面积．18．120︒【分析】作CAF CAB ∠=∠，过M 作MD AF ⊥交AC 于一点即为点P ，结合三角形内外角关系即可得到答案；【详解】解：作CAF CAB ∠=∠，过M 作MD AF ⊥交AC 于一点即为点P ，∵30CAB ∠=︒，∴30CAF CAB ∠=∠=︒，∴1DP AP 2=，∴当MD AF ⊥时12PM AP +的值最小，∴在ADP △中，9030120APM ∠=︒+︒=︒,故答案为120︒；【点睛】本题考查垂线段最短及直角三形30︒角所对直角边等于斜边的一半，解题的关键是作辅助线找到最小距离点．19．5【分析】先计算负整数指数幂，然后根据实数的混合计算法则求解即可．13322-+÷-13823=⨯+÷14=+5=．【点睛】本题主要考查了实数的混合计算，负整数指数幂，熟知相关计算法则是解题的关键．20．无解【分析】根据解分式方程的步骤去解答：去分母将分式方程化为整式方程、解整式方程、检验、回答．【详解】解：原方程可化为：812(2)(2)x x x x -=-+-．方程两边同时乘以(2)(2)x x +-，得(2)(2)(2)8x x x x +-+-=．化简，得248x +=．解得2x =．检验：2x =时(2)(2)0x x +-=，所以2x =不是原分式方程的解，所以原分式方程无解．【点睛】本题考查解分式方程，熟练掌握解分式方程的步骤，尤其是检验是解分式方程的重要步骤．21．（1）见解析（2【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）利用位似图形的性质得出对应点位置，再利用锐角三角三角函数关系得出答案．【详解】（1）如图所示：△A 1B 1C 1，即为所求；（2）如图所示：△A 2B 2C 2，即为所求，由图形可知，∠A 2C 2B 2=∠ACB ，过点A 作AD ⊥BC 交BC 的延长线于点D ，由A （2，2），C （4，﹣4），B （4，0），易得D （4，2），故AD =2，CD =6，AC ==，∴sin10AD ACB AC ∠=，即222sin A C B ∠【点睛】此题考查了作图−位似变换，平移变换，以及解直角三角形，熟练掌握位似及平移的性质是解本题的关键．22．(1)85、85、80(2)七年级的决赛成绩较好(3)七年级决赛成绩的方差S 2为70，七年级的选手成绩较为稳定【分析】（1）根据平均数的计算公式和众数、中位数的定义分别进行求解即可；（2）根据平均数相同的情况下，中位数高的那个队的决赛成绩较好进行解答即可；（3）根据方差公式先算出七年级选手成绩的方差，然后根据方差的意义即可解答．【详解】（1）解：七年级5名选手的平均分a =（75+80+85+85+100）÷5=85，由八年级成绩中85分学生数最多，则众数b =85，八年级5名选手的成绩按从低到高排列为：70，75，80，100，100，则中位数c =80；（2）解：由表格可知七年级与八年级的平均分相同，七年级的中位数较高，故七年级的决赛成绩较好；（3）解：222221(7585)(8085)2(8585)(10085)70,5s ⎡⎤=⨯-+-+⨯-+-=⎣⎦七年级∵22s s 七年级八年级＜∴七年级的选手成绩较为稳定．【点睛】本题主要考查方差、中位数、平均数与众数等知识点，掌握方差是反映了一组数据的波动大小且方差越大，波动性越大．23．(1)见解析(2)见解析(3)6【分析】(1)根据AAS 证AEF DEB ≌△△；(2)利用全等三角形的对应边相等得到AF ＝DB ，证出四边形ADCF 是平行四边形，再由“直角三角形斜边的中线等于斜边的一半”得到AD =DC ，从而得出结论；(3)由Rt △ABC 与菱形有相同的高，根据等积变形求出这个高，代入菱形面积公式可求出结论．【详解】（1）证明：∵AF BC ∥，∴∠AFE ＝∠DBE ，∵E 是AD 的中点，∴AE ＝DE ，在△AEF 和△DEB 中，AFE DBE FEA BED AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AEF DEB AAS ≌△△；（2）证明：由（1）知，AFE DBE △△≌，则AF ＝DB ，∵DB ＝DC ，∴AF ＝CD ，∵AF BC ∥，∴四边形ADCF 是平行四边形∵∠BAC ＝90°，D 是BC 的中点，∴12AD DC BC ==，∴四边形ADCF 是菱形；（3）解：连接DF ，如图所示：∵AF BD ∥，AF BD =，∴四边形ABDF 是平行四边形，∴DF ＝AB ＝4，∵四边形ADCF 是菱形，∴菱形ADCF 的面积1134622D C F A =⋅=⨯⨯=．【点睛】本题考查了全等三角形的性质和判定，平行四边形的判定，菱形的判定的应用，菱形的面积计算；熟练掌握菱形的判定与性质，证明三角形全等是解决问题的关键．24．(1)A 奖品的价格为16，B 奖品的价格为24；(2)81920w a =-+（080a ≤≤，且是整数）；(3)1440元；【分析】（1）设A 奖品的价格为x ，B 奖品的价格为y ，根据买1件A 种奖品和2件B 种奖品共需64元，购买2件A 种奖品和1件B 种奖品共需56元列方程组求解即可得到答案；（2）根据金额=单价⨯数量即可得到答案；（3）根据A 种奖品的数量不超过B 种奖品数量的3倍，求出a 的取值范围，结合函数性质求解即可得到答案；【详解】（1）解：设A 奖品的价格为x 元，B 奖品的价格为y 元，由题意可得，264256x y x y +=⎧⎨+=⎩，解得：1624x y =⎧⎨=⎩，答：A 奖品的价格为16，B 奖品的价格为24；（2）解：由题意可得，∵购买A 、B 两种奖品共80件，购买a 件A 种奖品，∴B 种奖品(80)a -件，∴1624(80)1619202481920w a a a a a =+⨯-=+-=-+（080a ≤≤，且是整数）；（3）解：∵A 种奖品的数量不超过B 种奖品数量的3倍，∴3(80)a a ≤-，解得：60a ≤，∴060a ≤≤，且是整数，∵81920w a =-+，∵80k =-<，∴w 随a 的增大而减小，∴当60a =时，w 最小，∴min 86019201440w =-⨯+=（元）；【点睛】本题考查二元一次方程组解应用题及一次函数择优方案问题，解题的关键是找到等量关系式．25．(1)见解析(2)203【分析】（1）由圆周角定理得出90BPC BCP ∠+∠=︒，由切线的性质得出90MPB BPC ∠+∠=︒，进而得出MPB BCP ∠=∠，由对顶角的性质得出BCP BAP ∠=∠，即可证明BAP MPB ∠=∠；（2）先证明MPA MBP ∽，得出MA MP AP MP MB PB==，由AB AP =，8MB =，12MP =，求出18MA =，进而求出10AP =，即可求出BP【详解】（1）证明：PC 是O 的直径，90PBC ∴∠=︒，90BPC BCP ∴∠+∠=︒，MN 所在的直线是O 的切线，点P 恰好在NM 所在的直线上，MP PC ∴⊥，90MPC ∴∠=︒，90MPB BPC ∴∠+∠=︒，MPB BCP ∴∠=∠，BCP BAP ∠=∠ ，BAP MPB ∴∠=∠；（2）解：MAP MPB ∠=∠ ，M M ∠=∠，MPA MBP ∴ ∽，∴MA MP AP MP MB PB== AB AP =，8MB =，12MP =，2212188MP MA MB ∴===18810AP AB MA MB ∴==-=-=，∴121020183MP AP BP MA ⋅⨯===【点睛】本题考查了切线的判定与性质，圆周角定理，掌握圆周角定理，切线的性质，相似三角形的判定与性质是解决问题的关键．26．(1)()1,0A -，()2,0B (2)12(3)(1或(1【分析】（1）根据次函数2y x x 2=--的图象与x 轴交于点A ，点B ，令0y =，即220x x --=，解方程即可；（2）过点P 作PN AB ⊥于点N ，交BC 于点M ，二次函数2y x x 2=--的图象与y 轴交于点C ，求出点C 的坐标为()0,2-，由B 、C 点坐标求出直线BC 的解析式为2y x =-，可得(),2M t t -，再结合()2,2P t t t --，求出2=2PM t t -+，根据证明OQC PQM ，可得22==2PQ PM t t OQ OC -+，即()211=122w t --+，即可求出结果；（3）可分为点P 在直线BC 的上方或下方两种情况，设点P 的坐标分别为()2,2m m m --或()2,n n n n --，分别表示出BPC △的面积，根据1PBC DCB S S == ，列出方程求解，即可求出点P 的坐标．【详解】（1）解：∵次函数2y x x 2=--的图象与x 轴交于点A ，点B ，0y ∴=时，220x x --=，解得：11x =-，22x =，∴A 点坐标为()1,0-，B 点坐标为()2,0．（2）解：如图，过点P 作PN AB ⊥于点N ，交BC 于点M ，∵二次函数2y x x 2=--的图象与y 轴交于点C ，0x ∴=时，=2y -，∴点C 的坐标为()0,2-，设直线BC 的解析式为2y kx =-，∵直线BC 的图象过点()2,0B ，∴把点()2,0B 代入直线BC 的解析式为2y kx =-，即220k -=，解得1k =，∴直线BC 的解析式为2y x =-，()2,t 2P t t -- ，(),2M t t -，()()22=22=2PM t t t t t ∴-----+，PN CO ∥ ，=MPQ COQ ∴∠∠，=OQC PQM ∠∠，OQC PQM ∴ ，22==2PQ PM t t OQ OC -+∴，()22211==1222t t w t -+∴--+，∴1t =时，w 的最大值为12．（3）解；如图，当点P 在直线BC 的上方时，过点P 作PF y ∥轴，交BC 于点F ，PF 的延长线交x 轴于点E ，设点P 的坐标为()2,2m m m --，则点F 的坐标为(),2m m -，111222PBC PBF PCF S S S BE PF OE PF OB PF =-=⋅-⋅=⋅ ，2OB = ，()()22=22=2PF m m m m m -----，()2212222PBC S m m m m ∴=⨯⨯-=- ，∵点()1,2D -，点C 的坐标为()0,2-，1DC ∴=，12112DBC S ∴=⨯⨯= ，DBC PBC S S = ，221m m ∴-=，解得：1m =∴点1m =y 1m =y =答案第15页，共15页(1P ∴+或(1P ；当点P 在BC 的下方时，过点P 作PH AB ⊥，交AB 于点G ，延长PH 交CD 的延长线于点L ，设点P 的坐标为()2,n n n n --，则点G 的坐标为(),2n n -，()()22=22=2PG n n n n n ∴-----+，()111222PBC BGP CPG S S S HB GP CL GP GP HB CL =+=⨯⋅+⋅⋅=+ ,==2HB CL OB + ，122PBC S GP GP ∴=⨯⨯= ，1PBC DCB S S == ，1GP \=，22=1n n ∴-+，解得1n =，1n = 时，2=112=2y ---，此时点P 与点D 重合，故舍去，∴点P的坐标为(1或(1．【点睛】本题考查了二次函数的图象和性质、求一次函数的解析式、相似三角形的性质和判定、解一元二次方程，作出辅助线，构造相似三角形是解题的关键．。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:某小区现有一块等腰直角三角形形状的绿地，腰长为100米，直角顶点为A．小区物业管委会准备把它分割成面积相等的两块，有如下的分割方法：方法一：在底边BC上找一点D，连接AD作为分割线；方法二：在腰AC上找一点D，连接BD作为分割线；方法三：在腰AB上找一点D，作DE∥BC，交AC于点E，DE作为分割线；方法四：以顶点A为圆心，AD为半径作弧，交AB于点D，交AC于点E，弧DE作为分割线．这些分割方法中分割线最短的是（）A．方法一 B．方法二 C．方法三 D．方法四试题2:如图，要在一块形状为直角三角形（∠C为直角）的铁皮上裁出一个半圆形的铁皮，需先在这块铁皮上画出一个半圆，使它的圆心在线段AC上，且与AB、BC都相切.请你用直尺和圆规画出来（要求用尺规作图，保留作图痕迹，不要求写作法）．评卷人得分试题3:已知线段a和直角∠α：（1）用尺规作△ABC，使得∠C＝，BC＝a , AB＝2a（保留作图痕迹，不写画法）；（2）用尺规作△ABC的中线CD和角平分线CE（保留作图痕迹，不写画法）；（3）求出∠DCE的度数．试题4:新余某区拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示．请在答题卷的原图上利用尺规作出音乐喷泉M 的位置．(要求：不写已知、求作、作法和结论，只保留作图痕迹，必须用铅笔作图)试题5:已知：如图，点C、E均在直线AB上.（1）在图中作∠FEB，使∠FEB=∠DCB（保留作图痕迹，不写作法）；（2）请说出射线EF与射线CD的位置关系.试题6:如图，利用尺规求作所有点，使点同时满足下列两个条件：点到两点的距离相等；②点到直线的距离相等.(要求保留作图痕迹, 不必写出作法)试题7:如图，已知△ABC，且∠ACB＝90°。