下载文档原格式
数论-整除-整除的基本概念-1星题课程目标学问提要整除的基本概念•定义假如整数a除以整数b（b≠ 0），除得的商是整数且没有余数，我们就说a能被b整除，也可以说b能整除a，记作b∣a．留意：假如除得的结果有余数，我们就说a不能被b整除，也可以说b不能整除a．•整除的性质性质1：假如a、b都能被c整除，那么它们的和与差也能被c整除。
性质2：假如b与c的积能整除a，那么b与c都能整除a。
性质3：假如b、c都能整除a，且b和c互质，那么b与c的积能整除a。
性质4：假如c能整除b，b能整除a，那么c能整除a。
精选例题整除的基本概念1. 再过12天就到2016年了，昊昊感慨地说：我到目前只经过2个闰年，并且我诞生的年份是9的倍数，那么2016年昊昊是岁．【答案】9【分析】依据题意“我到目前只经过2个闰年”可得我的诞生年份在2005 2008,这之间只有2007是9的倍数，则昊昊是2007年诞生，则2016年昊昊是2016−2007=9岁.2. 若六位数201ab7能被11和13整除，则两位数ab=．【答案】48【分析】由11的整除特征可知：(7+a+0)−(2+1+b)=a+4−b=0或11,若a+4−b=11,a−b=7,只有8−1=9−2=7,六位数201817、201927都不能被13整除．若a+4−b=0,则a+4=b,只有0+4=4，1+4=5，2+4=6，3+4=7，4+4=8，5+4=9等状况，构成的六位数201047，201157，201267，201377，201487，201597中只有201487能被13整除，则ab=48．3. 一个电子钟表上总把日期显示为八位数，如2011年1月1日显示为20110101．假如2011年最终一个能被101整除的日子是2011ABCD，那么2011ABCD是多少？【答案】20111221【分析】试除法得出答案：20111231÷101=199121⋯⋯10，31−10=21，所以ABCD=1221．4. 若4b+2c+d=32，试问abcd能否被8整除？请说明理由．【答案】见解析．【分析】由能被8整除的特征知，只要后三位数能被8整除即可．bcd=100b+10c+d，有bcd−(4b+2c+d)=96b+8c=8(12b+c)能被8整除，而4b+2c+d=32也能被8整除，所以abcd能被8整除．。
数的整除性规律【能被2或5整除的数的特征】（见小学数学课本，此处略）【能被3或9整除的数的特征】一个数，当且仅当它的各个数位上的数字之和能被3和9整除时，这个数便能被3或9整除。
例如，1248621各位上的数字之和是1+2+4+8+6+2+1=243｜24，则3｜1248621。
又如，372681各位上的数字之和是3+7+2+6+8+1=279｜27，则9｜372681。
【能被4或25整除的数的特征】一个数，当且仅当它的末两位数能被4或25整除时，这个数便能被4或25整除。
例如，173824的末两位数为24，4｜24，则4｜173824。
43586775的末两位数为75，25｜75，则25｜43586775。
【能被8或125整除的数的特征】一个数，当且仅当它的末三位数字为0，或者末三位数能被8或125整除时，这个数便能被8或125整除。
例如，32178000的末三位数字为0，则这个数能被8整除，也能够被125整除。
3569824的末三位数为824，8｜824，则8｜3569824。
214813750的末三位数为750，125｜750，则125｜214813750。
【能被7、11、13整除的数的特征】一个数，当且仅当它的末三位数字所表示的数，与末三位以前的数字所表示的数的差（大减小的差）能被7、11、13整除时，这个数就能被7、11、13整除。
例如，75523的末三位数为523，末三位以前的数字所表示的数是75，523-75=448，448÷7=64，即7｜448，则7｜75523。
又如，1095874的末三位数为874，末三位以前的数字所表示的数是1095，1095-874=221，221÷13=17，即13｜221，则13｜1095874。
再如，868967的末三位数为967，末三位以前的数字所表示的数是868，967-868=99，99÷11=9，即11｜99，则11｜868967。
奥数思维训练题库---计算【分组】【2】计算：1－2＋3－4＋5－……－1994＋1995=【答案】998【分组】【2】计算：1－2＋3－4＋5－……－2014＋2015=【答案】1008【分组】【2】计算：（2＋4＋6＋…＋1996）－（1＋3＋5＋…＋1995）=【答案】998【分组】【2】计算：（2＋4＋6＋…＋2014）－（1＋3＋5＋…＋2013）=【答案】1007【分组】【2】3－5+7－9+11－13+…+2011－2013+2015=【答案】1009【提取公因数】【2】计算：222＋333＋444＋555＋666=【答案】2220444×5=2220【提取公因数】【2】计算：111＋222＋333＋444＋555＋666=【答案】2331【位值原理】【2】（123456＋234561＋345612＋456123＋561234＋612345）÷111111= 【答案】21【提取公因数】【2】计算：1÷2015+2÷2015+3÷2015+…+2014 ÷2015+2015÷2015= 【答案】1008【提取公因数】【乘法凑整】【2】计算：3.6×31.4＋(31.4＋12.5)×6.4=【答案】394【提取公因数】【乘法凑整】【2】计算：3.6×30.4＋(30.4＋12.5)×6.4=【答案】384【提取公因数】【分拆】【3】计算：161.8×6.18＋2618×0.382=【答案】2000【提取公因数】【3】计算：(4.16×84－2.08×54－0.15×832)÷0.32【答案】1248【分拆】【凑整】【2】计算:0.75＋9.75＋99.75＋999.75＋1=【答案】1111【分拆】【提取公因数】【3】7210810846(118142118134)⨯+⨯-⨯-⨯【答案】11800【提取公因数】【2】计算：0.9999×0.7+0.1111×2.7=【答案】0.9999【提取公因数】【2】1994.5×81+0.24×800+2.4+8.1×31=【答案】162000【凑整】【1】计算：98＋998＋9998＋99998=【答案】111092【凑整】【1】计算：8＋998＋9998＋99998=【答案】111002【提取公因数】【凑整】【2】计算：（8.88+8.88+8.88+8.88）×1.25= 【答案】44.4【提取公因数】【2】20.14×37－201.4×1.9＋2.014×820=【答案】2014【提取公因数】【2】计算：17.48×37－174.8×1.9＋1.748×820=【答案】1748【提取公因数】【2】计算：2098－5.5×7.5－0.25×55－45=【答案】19982098－5.5×7.5－0.25×55－45=2098－55×(0.75＋0.25)－45=2098－(55＋45)=1998【提取公因数】【2】8.1×1.3－8÷1.3+1.9×1.3+11.9÷1.3=【答案】10【提取公因数】【2】999.99×222.22+333.33×333.34 =【答案】333330【提取公因数】【2】51.2×32.5+512×6.74+5.12=【答案】5120【分拆】【2】325.24+425.24+625.24+925.24+525.24=【答案】2826.2【分拆】【提取公因数】【3】计算：333×332332333－332×333333332【答案】665【分拆】【重码数】【3】19501950×2010－20112011×1949=【答案】61061【提取公因数】【2】计算：9.99×0.13－0.111×2.7【答案】0.999【定义新运算】【3】对于任意两个自然数A 和B 、规定一种新运算“※”：A ※B=A （A ＋1）（A ＋2）……（A ＋B －1）。
数的整除之四大方法综合应用知识要点一、整除的定义：当两个整数a和b(b≠0)，a被b除的余数为零时(商为整数)，则称a被b整除或b整除a，也把a叫做b的倍数，b叫a的约数，记作b|a，如果a被b除所得的余数不为零，则称a不能被b整除，或b不整除a，记作b…a。
二、数的整除性质：⑴对称性：若甲数能被乙数整除，乙数也能被甲数整除，那么甲、乙两数相等。
记作：a|b，b|a，则a＝b。
⑵传递性：若甲数能被乙数整除，乙数能被丙数整除，那么甲数能被丙数整除。
记作：若a|b，b|c，则a|c。
⑶若两个数能被一个自然数整除，那么这两个数的和与差都能该自然数整除。
记作：若a|b，a|c，则a|(bc)。
⑷几个数相乘，若其中有一个因子能被某一个数整除，那么它们的积也能被该数整除。
⑸若一个数能被两个互质数中的每一个数整除，那么这个数也能分别被这两个互质数的积整除。
记作：若a|b，c|b，(a，c)＝1，则ac|b。
⑹若一个数能被两个互质数的积整除，那么，这个数也能分别被这两个互质数整除。
记作：若ac|b，(a，c)＝1，则a|b，c|b。
⑸若一个整数的末位是0或5，则这个数能被5整除。
⑹若一个整数能被2和3整除，则这个数能被6整除。
⑺若一个质数能整除两个自然数的乘积，那么这个质数至少能整除这两个自然数中的一个。
⑻若a|b，m≠0，则am|bm。
⑼若am|bm，m≠0，则a|b。
⑽若c|a，c|b，则c|(ma＋nb)，其中m、n为任意整数(这一性质还可以推广到更多项的和)三、整除特征⑴1与0的特性：1是任何整数的约数，即对于任何整数a，总有1/a。
0是任何非零整数的倍数，a≠0，a为整数，则a/0。
⑵若一个整数的末位是0、2、4、6或8，则这个数能被2整除。
⑶若一个整数的数字和能被3整除，则这个整数能被3整除。
⑷若一个整数的末尾两位数能被4整除，则这个数能被4整除。
⑸若一个整数的末位是0或5，则这个数能被5整除。
⑹若一个整数能被2和3整除，则这个数能被6整除。
小学奥数（含答案）质数与合数一般地，如a、b、c为整数，b≠0，且a÷b＝c，即整数a除以整数b(b不等于0)，除得的商c正好是整数而没有余数(或者说余数是0)，我们就说，a能被b整除否则，称为a不能被b整除，(或b不能整除a)。
如果整数a能被整数b整除，a就叫做b的倍数，b就叫做a的约数。
一、自然数除0和1外，按约数的个数分为质数和合数两类。
质数：一个数除了1和它本身，不再有别的约数，这个数叫做质数(也叫做素数)。
合数：一个数除了1和它本身，还有别的约数，这个数叫做合数。
二、质数与合数重要知识点⑴要特别记住：0和1不是质数，也不是合数。
⑵任何一个合数都可以写成几个质数相乘的形式。
⑶最小的质数是2 ，2是唯一的偶质数，其他质数都为奇数；最小的合数是4。
⑷质数是一个数，是含有两个约数的自然数。
互质数是指两个数，是公约数只有1的两个数，组成互质数的两个数：可能是两个质数(3和5)，可能是一个质数和一个合数(3和4)，可能是两个合数(4和9)或1与另一个自然数。
⑸如果一个质数是某个数的约数，那么就说这个质数是这个数的质因数。
把一个合数用质因数相乘的形式表示出来，叫做分解质因数。
例1请找出100以内的所有质数。
例2若将17拆成若干个不同的质数之和，使得这些质数的乘积尽可能大，那么这个最大的乘积是多少？例3将八个不同的合数填入下面的括号中，如果要求相加的两个合数互质，那么A最小是几？A＝( )＋( )＝( )＋( )＝( )＋( )＝( )＋( )今有17、23、31、41、53、67、79、83、101、103共10个质数。
如果把它们分成两组，使每一组5个数，并且每组的5个数之和相等，那么把含有101的这组数从小到大排列，第2个数是多少？从小到大写出5个质数，使后面的数都比前面的数大12。
这样的数有几组？如果某整数同时具备如下三条性质：①这个数与1的差是质数，②这个数除以2所得的商也是质数，③这个数除以9所得的余数是5，那么我们称这个整数为幸运数。
第八讲最大与最小在实际生活与生产实践中，人们总是想用最少的财力、物力、人力以及时间等在可能的范围内取得最佳效益。
况且，在许多现实问题中有时很难确定或者就不需要具体的每个数值，有时只关心最大、最小等极值。
这一讲就来研究某个量在一定条件下取得最大值或最小值问题。
这类问题题目中经常出现“最小”、“至少”、“至多”等术语。
经常只能根据具体问题，综合运用所学知识进行求解。
例1某校六年级一班准备用100元钱买圣诞树装饰品。
在花店这样的装饰品成束出售，由20朵花组成的花束每束价值4元，由35朵花组成的花束每束价值6元，由50朵花组成的花束每束价值9元，请问每种花束各买多少才能买到最多的花朵？分析：想用100元钱买到最多的花朵，题目中有三种花束：A种：由20朵花组成的花束价值4元B种：由35朵花组成的花束价值6元C种：由50朵花组成的花束每束价值9元平均1元钱可买A种花朵5朵或B种花朵5.8朵或C种花朵5.5朵，为了买到最多的花朵，应该多买B种花束解：经分析可知由35朵花组成的B种花束中的花朵最便宜，宜多买。
由于每束6元，故100元钱可买16束，还剩4元钱，这4元钱恰好买一束由20朵花组成的A种花束，这时共买花朵：16×35+20=580（朵），若B种花束少买几束，增加A种或C种花束的数量，都不能使花朵数达到580朵。
因此，应买由35朵花组成的花束16束和由20朵花组成的花束1束，可使花朵数量最多：580朵。
说明：此题也可设A种、B种、C种花束各买x束、y束、z束时，可使花朵最多，列方程：4x+6y+9z=100，x，y，z是自然数可以先缩小字母的取值范围。
例如12元能买3束A种花束或2束B种花束，分别得到60朵花和70朵花，于是很清楚在最优解中A种花束不应超过2束。
同理，比较B种花束和C种花束，发现要使花朵最多，C种花束不应超过1束，即x≦2，z≦1，下面只有很少的几种情况了，可以一一列举，同样可以求得x=1，z=0，y=16例2有一类自然数，从第三个数字开始，每个数字恰好是它前面两个数字之和，如134，1459等等，求这类数中最大的自然数和最小的自然数。
第12讲行程问题（二）在四年级的教材中，我们已经对于相遇问题、追及问题、水流问题和车长及桥长等问题，进行了较为细致的研究。
在这一讲中，我们将进一步就环行路上的行程问题以及多次相遇等问题进行研究。
行程问题在小学的应用题中是变化最多的类型之一。
对于行程问题的研究是小学综合运用知识解决问题的一个重要的内容。
因为行程问题的变化可谓是丰富多彩，不仅在小学，而且在中学的数学和物理的学习中，也是极其重要的内容。
一、环行路上的行程问题环行路上的行程问题，有着它独特的方面，由于环行的道路是封闭的，因此，环行路上的运动，计算行程时，通常与环行道路的周长有关。
例1在400米的环行跑道上，A、B两点相距100米，甲、乙两人分别从A、B两点同时出发，按逆时针方向跑步。
甲每秒跑5米，乙每秒跑4米，他们每人跑100米，都要停10秒钟。
求甲追上乙需要多少秒？分析：这道题初看时，由于他们每人跑100米，都要停10秒钟。
似乎不太好解决。
但如果将二人看成不停的跑，就很容易算出甲追上乙的时间，这时再考虑在这期间所停留的时间，问题的解决就比较简单了。
解答：如果甲、乙不停的跑步，甲追上乙共需：100÷（5－4）=100（秒），甲在100秒中共跑：5×100=500（米），而甲在跑100米、200米、300米、400米时共停留了4次，到了500米处恰好追上乙。
不必计算停留的时间。
所以，甲追上乙所需的时间是：100＋4×10=140（秒）说明：甲跑到500米处时，正好是乙跑完400米，并且休息完10秒时。
当甲跑到时，乙恰好要出发，他们两个在这一瞬间正好相遇。
例2 如图，A、B是圆直径的两个端点，小华在点A，小明在点B，他们同时出发，反向而行。
他们在C点第一次相遇，C点离A点100米；在D点第二次相遇，D点离B点80米。
求这个圆的周长。
分析：第一次相遇，两人合起来走了半圈，第二次相遇，两人合起来走了一圈，因此，从开始出发到第二次相遇，两人合起来走了一圈半。
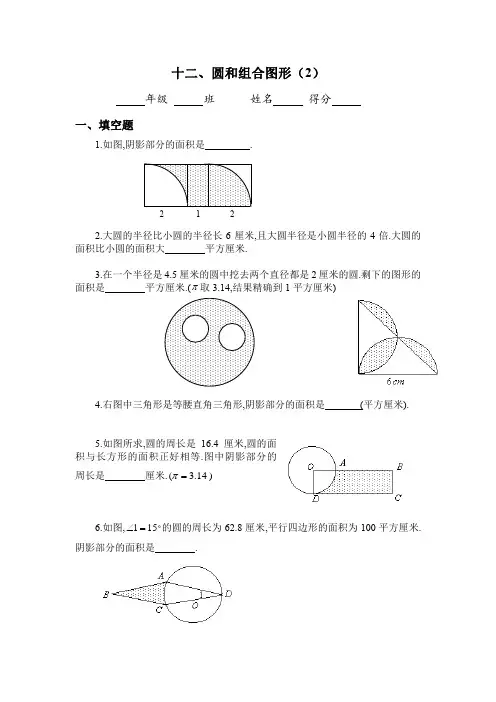
212十二、圆和组合图形（2）年级班姓名得分一、填空题1.如图,阴影部分的面积是.2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是(平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是.E D C B A GF O D CA B7.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)2 甲乙12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、CD 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?120 ABCD 1 2A B Ca1 OC B A ED———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠, 又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.⌒E D C B AG F① ②花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ,解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米).11. 如图,小正方形的边长为2r,则①的面积为:72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯,②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,①和②的面积和为2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=S x ,解得S=6.③① ②14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:)420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).ABD12。
一、 知识点概述：分数应用题是研究数量之间份数关系的典型应用题，一方面它是在整数应用题上的延续和深化，另一方面，它有其自身的特点和解题规律．在解这类问题时，分析中数量之间的关系，准确找出“量”与“率”之间的对应是解题的关键．关键：分数应用题经常要涉及到两个或两个以上的量，我们往往把其中的一个量看作是标准量．也称为：单位“1”，进行对比分析。
在几个量中，关键也是要找准单位“1”和对应的百分率，以及对应量三者的关系例如：（1）a 是b 的几分之几，就把数b 看作单位“1”．（2）甲比乙多18，乙比甲少几分之几？ 方法一：可设乙为单位“1”，则甲为19188+=，因此乙比甲少191889÷=. 方法二：可设乙为8份，则甲为9份，因此乙比甲少1199÷=. 二、 怎样找准分数应用题中单位“1”（一）、部分数和总数在同一整体中，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，那么总数就是单位“1”。
例如：我国人口约占世界人口的几分之几？——世界人口是总数，我国人口是部分数，世界人口就是单位“1”。
解答题关键：只要找准总数和部分数，确定单位“1”就很容易了。
（二）、两种数量比较分数应用题中，两种数量相比的关键句非常多。
有的是“比”字句，有的则没有“比”字，而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。
例如：六（2）班男生比女生多——就是以女生人数为标准（单位“1”），解题关键：在另外一种没有比字的两种量相比的时候，我们通常找到分率，看“占”谁的，“相知识框架分数、百分数应用题（二）当于”谁的，“是”谁的几分之几。
这个“占”，“相当于”，“是”后面的数量——谁就是单位“！”。
（三）、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。
这类分数应用题的单位“1”比较难找。
第2讲数的整除特征（二）知识网络上一章我们已经学习了被2、3、5、8、9、25、125等整除的数的特征和一些整除的基本性质，但作为奥林匹克竞赛仅仅掌握以上知识还不够，这一讲继续学习有关数的整除知识。
（1）能被7、11和13整除的数的特征：如果一个数的末三位数字所表示的数与末三以前的数字所表示的差（一定要大数减小数）能被7、11或13整除，那么这个数就能被7、11或13整除。
（2）能被11整除的数的特征还有：一个数的奇数位上的数字之和与偶数位上的数字之和的差（大减小）是11的倍数。
重点·难点同学们在牢记上面整除的数的特征的同时，重点应弄清楚能被7、11、13整除的数为什么有上面的特征。
学法指导上面数的整除特征可以结合例子来理解。
例如：443716，判断它能否被7、11、13整除的方法是：716－443=273。
因为273能被7整除，所以443716能被7整除；因为273不能被11整除，所以443716不能被11整除；因为273能被13整除，所以443716能被13整除。
记忆要理论联系实际。
经典例题[例1]用1、9、8、8这四个数字能排成几个被11除余8的四位数？思路剖析能被11整除的数的特征是这个数的奇位数字之和与偶位数字之和的差能被11整除。
一个数要能被11除余8，那么这样的数加上3后，就能被11整除了，于是得到被11除余8的数的特征是：将偶位数字相加得到一个和数，再将奇位数字相加再加上3，得到另一个和数，如果这两个和数之差能被11整除，那么这个数就是被11除余8的数。
解答要把1、9、8、8排成被11除余8的四位数，可以把这四个数字分成两组，每组两个数字，其中一组作为千位和十位数，它们的和记作p，另外一组作为百位和个位数，它们之和加上3记作q，且p和q的差能被11整除，满足要求的分组只可能是p=1+8=9，q=（9+8）+3=20，q－p=20－9=11，所以1988是被11除余8的四位数。
如果一个数被11除余8，那么在奇位的任意两介数字互换，或者在偶位的任意两个数字互换，得到的新数被11除也余8，因此除1988外，还有1889、8918与8819共四个被11除余8的四位数。
[例2]如果下面这个41位数□能被7整除，那中间方格内的数字是几?思路剖析对于数555555，由于555–555=0是7的倍数，根据能被7整除的数的特征，555555也能被7整除；同理999999也能被7整除，所以和也能被7整除，所以我们可以把这个41位数分成几个数的和，其中部分能被7整除。
解答□=+55□99，上式等号右边的三个加数中，第一个和第三个加数都能被7整除，由此可推出55□99能被7整除，所以55□99能被7整除。
根据能被7整除的数的特征，□99－55=□44也能被7整除，可推理得□内应为6。
[例3]有一堆苹果，要装在46个箱子里，其中有45个大箱子和一个小箱子，而小箱子装的苹果只相当于大箱装的数量的一半，现有个苹果，如果规定按箱子大小平均分装苹果数是否能办到？思路剖析由于大小箱子装的苹果的数量不一致，不便于解题，所以我们可以统一成小箱子，则应有2×45+1=91个小箱子，那么是否恰好装完，并符合要求，关键是看总苹果数能否被91整除，由于91=7×13，所以由整除的性质，只需要考虑7、13是否能整除总苹果数。
由于13整除4979，而7整除497949794979，那么必定有91整除497949794979，因为99÷3=33，所以容易推出91整除，所以能把苹果按规定装入箱子中。
解答2×45+1=91（个），7×13=91，因为13整除4979，7整除497949794979，所以91整除497949794979，则91整除。
答：可以做到按箱子大小平均分装苹果。
[例4]求能被26整除的六位数。
思路剖析因为26=2×13，所以由整除的性质得能分别被2和13整除。
所以解此题可以从2整除入手。
解答因为2整除，所以y可能取0、2、4、6、8。
又因为13整除，所以13能整除与的差。
当y=0时，由于13整除910，而13又要整除与910之差，所以13整除。
又因为=100x+19=（7×13+9）x+19=7×13x+9x+13+6，所以根据数的整除性质得13整除9x+6，经试验可知，只有当x=8时，13整除9x+6，所以当y=0时，符合题意的六位数是819910。
当y=2时，因为13整除，所以13整除与912之差，而912=910+2，所以13整除与2之差；与前面的相仿，=7×13x+13+9x+6，所以13整除9x+6－2，即13整除9x+4。
经试验可得，只有当x=1时，13整除9x+4。
所以当y=2时，符合题意的六位数是119912。
同理，当y=4时，13整除9x+6－4，即13整除9x+2，经试验可知，当x=7时，13整除9x+2，所以当y=4时，符合题意的六位数是719914。
同理，当y=6时，13整除9x+6－6，即13整除9x。
经试验可知，x无解（因为x是的最高位数码，所以x≠0）。
所以当y=6时，找不到符合题意的六位数。
同理，当y=8时，13整除9x+6—8，即13整除9x—2。
经试验得，只有当x=6时，13整除9x—2。
所以当y=8时，符合题意的六位数是619918。
答：满足本题意条件的六位数共有819910、119912、719914和619918四个。
[例5]从0、1、2、3、4、5、6、7、8、9这十个数中选出5个不同的数，组成一个五位数，使它能被3、5、7、13同时整除，这个数最大是多少？思路剖析这道题如果从10个数字中选出5个不同的数，组成一个五位数，再逐个判断每个五位数能否同时被3、5、7、13整除，那是非常麻烦的。
可以先从整体上考虑，因为3、5、7、13这四个数两两互质，且3×5×7×13=1365，那么我们要找的数就是在五位数中能被1365整除的最大的那个数。
那我们只需用一个自然数去与1365相乘，使积尽可能大且是一个五位数即可（注意，五位数中不能出现相同数字）。
解答设1365×a（a是自然数）的积是要求的五位数，可知：1365×a<100000，则a≤73。
当a=73时，这个五位数是1365×73=99645，数字重复了，舍去；当a=72时，这个五位数是1365×72=98280，数字重复；当a=71时，这个五位数是1365×71=96915，数字重复；当a=70时，这个五位数是95550，数字重复；当a=69时，这个五位数是94185，符合题目条件。
所以，这个数是94185。
点津这道题从整体入手，先用3、5、7、13相乘得1365，在五位数中通过找1365的最大倍数得到解答。
最后用枚举的方法时，虽然要计算1365与73、72、71、70、69的积，但比起漫无边际地去找这样的五位数要简便得多。
[例6]求能被26整除的六位数。
思路剖析由于26=2×13，所以原数能被26整除，转化为原数既能被2整除，又能被13整除。
解答因为要求的数能被2整除，所以个位数字只能是0、2、4、6、8。
（1）当B=0时，数能被13整除。
根据能被13整除的数的特征，必有（930－=□11）是13的倍数。
试算知13×47=611。
所以差数是611，逆推出A=3。
（2）当B=2时，数能被13整除，必有（932—A19=□13）是13的倍数。
试算知13×1=13，所以差数为13，逆推出A=9。
（3）当B=4时，数能被13整除，必有（934—A19=□15）是13的倍数。
试算知13×55=715，所以差为715，逆推出A=2。
（4）当B=6时，数能被13整除，必有（936—A19=□17）是13的倍数。
试算知117是13的倍数，逆推出A=8。
（5）当B=8时，数能被13整除，必有（938—A19=□19）是13的倍数，试算知819是13的倍数，从而推出A=1。
所以，所求的六位数共有五个，即：319930，919932，219934，819936，119938。
[例7]用数字6、7、8各两个组成一个六位数，使它被168整除。
这个六位数是多少？思路剖析168=3×56，3与56互质。
因为6+6+7+7+8+8=42，42是3的倍数，所以用6、7、8各两个组成的所有六位数都能被3整除。
问题转化为使组成的六位数能被56整除。
因为56=7×8，7与8互质，所以只要组成的数能被7整除，又能被8整除即可。
要能被8整除，只要看末三位数，如果能仅用6、7、8各一个数组成能被8整除的三位数，那么把它连写两遍得到的六位数就合乎要求。
而用6、7、8各一个数不难组成被8整除的三位数。
解答768能被8整除，768768也就能被8整除，它又能被7整除，而7与8互质，所以它能被7与8的积56整除。
7+6+8+7+6+8=42，3整除42，所以768768能被3整除，由于3与56也互质，因此，768768就能被3与56的积168整除。
点津本题初看无处下手，但是我们应用整除性质“一个数能被互质的两个自然数整除，就一定能被这两个互质数的积整除”，把问题逐步转化，实现了化难为易的目的。
[例8]甲、乙两人进行了下面的游戏。
两人先约定一个整数N，然后由甲开始，轮流用0、1、2、3、4、5、6、7、8、9这十个数字之一组成一个六位数的一位，数字可重复。
如果这个六位数能被N 整除，就算乙胜；如果这个六位数不能被N整除，就算甲胜。
设N小于15，那么当N取哪几个数时，乙才能取胜？思路剖析我们列出乙不能获胜的N的取值情况。
N取偶数，甲可以在最右边方格里填一个奇数（六位数的个位），就能使六位数不能被N整除，乙不能获胜。
N=5，甲可以在六位数的个位填一个不是0或5的数，甲就获胜。
解答如果N=1，很明显乙必获胜。
如果N=3或9，那么乙在填最后一全数时，总是把六位数字之和凑成3的整倍数或9的整倍数。
因此乙必获胜。
当N=7、11、13时是本题最困难的情况。
注意到1001=7×11×13，乙就有一种必胜的办法。
我们从左到右数这六位数，把第一位与第四位，第二位与第五位，第三位与第六位配对，甲在一对数位的一位上填上某一个数字后，乙就在这一对数位的另一位上填同样的数字，这就保证所填成的六位数能被1001整除，因为若按我们的方法得到的六位数是，由于。
这个六位数就能被7、11或13整除，所以乙就能获胜。
综合起来，使乙获胜的N是1、3、7、9、11、13。
[例9]四名学生做加法练习：任写一个六位数，把它的个位数字（不等于0）拿到这个数的最左边一位数字的左边得到一个新的六位数，然后与原六位数相加，它们的得数分别是172536、568741、620708、845267，结果其中哪一个可能是正确的，为什么？思路剖析初看时，觉得困难，因为是任意写的六位数，不好找正确的一个结果。
