湖南省永州市2020届高三第三次模拟考试数学(理)试题及详细解析

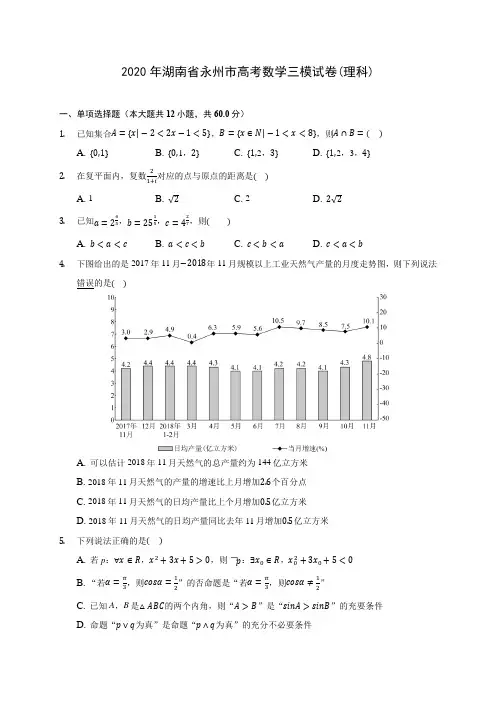
永州市2020年高考第三次模拟考试试卷数学（理科）参考答案一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中， 只有一项是符合题目要求的．1．解析：2N {|}{|1110}x x x x x ==-><->或，M N I ＝3}|1{x x <<，选C. 2．解析：12(1255(12))(12)12z i i i i i ++--===-，在第四象限，选D. 3．解析：0.30.40.30.3>，即b c >，而0.30.30.44()()10.33a b ==>，即a b >， a b c ∴>>，选B.4．解析：由图表易知，选C.5．解析：“p q ∨”为真，则命题p,q 有可能一真一假，则“p q ∧”为假，故选项A 说法不正确；命题“0x ∀>，10x e x -->”的否定应该是“00x ∃>，0010x e x --≤”，故选项B 说法不正确；因命题“若1x ≥，则11x≤”为真命题，则其逆否命题为真命题，故选项C 说法正确；因21560x x x =-⇒--=，但256016x x x x --=⇒=-=或，所以“1x =-”是“2560x x --=”的充分不必要条件，选项D 说法不正确；选C.6．解析：sin cos sin cos 2sin cos B C C B C C -=Q ，sin()sin 2B C C ∴-=，2B C C ∴-=，3B C ∴=，32C π∴<且42B C C π+=>，86C ππ∴<<选A.7．解析：||1=a ，||1=b ，||+a b2333()()=()()||||=222+⋅-⋅+-+⋅=-+⋅≤++⋅-+a b b c a b b a b c a b c a b c 当且仅当+a b 与c 反向时取等号.选C.8．解析：先计算半片花瓣面积：22260=(3606R R ππ22=12(=(26阴ππ∴-S R R 故所求概率为2(2)2阴π=S R B. 9．解析：依题意作出()f x 的图象，()=+y f x a 的图象可以看成是()=y f x 的图象向左(a>0时)或向右(a<0时)平移|a|个单位而得.当a>0时，()=y f x 的图象至少向左平移6个单位(不含6个单位)才能满足()()f x a f x +>成立，当a<0时，()=y f x 的图象向右平移至多2个单位（不含2个单位）才能满足()()f x a f x +>成立(对任意的[1,2]x ∈-),故(2,0)(6,)∈-+∞U x ，选D.10．解析：不妨设P 在第二象项，FM m =，(0,)(0)H h h >，由3HN OH =-u u u r u u u r知(0,2)N h -，由AFM ∆~AON ∆，得2m c a h a -=（1），由BOH ∆ ~BFM ∆，得h a m c a=+（2） (1),(2)两式相乘得12c ac a-=+，即3c a =，离心率为3.选B. 11．解析：[]0,x π∈Q ，,333x πππωωπ⎡⎤∴+∈+⎢⎥⎣⎦，令3z x πω=+，则,33z ππωπ⎡⎤∈+⎢⎥⎣⎦由题意，1sin 2z =在,33ππωπ⎡⎤+⎢⎥⎣⎦上只能有两解5=6z π和136z π=1317636πππωπ∴≤+<，（*）因为在,33z ππωπ⎡⎤∈+⎢⎥⎣⎦上必有3sin sin 222ππ=－，故在(0,)π上存在12,x x 满足 ()()122f x f x -=；①成立；2z π=对应的x （显然在[]0,π上）一定是最大值点，因52z π=对应的x 值有可能在[]0,π上，故②结论错误；解（*）得11562ω≤<，所以④成立；当(0,)15x π∈时，,3153z πωππ⎡⎤∈+⎢⎥⎣⎦，由于11562ω≤<，故,,315332z πωππππ⎡⎤⎡⎤∈+⊆⎢⎥⎢⎥⎣⎦⎣⎦，此时sin y z =是增函数，从而()f x 在(0,)15π上单调递增.综上，①③④成立，选B.12．解析：求导得21()(21)xx f x e x t x-'⎡⎤=-+⎣⎦有两个零点等价于函数()x 21x e x t ϕ-+（）=有一个不等于1的零点，分离参数得()21x e t h x x ==+，令()(0)21=>+xe h x x x221()(21)xx h x e x -'=+，()h x 在1(0,)2递减，在1(+)2，∞递增，显然在12x =取得最小值2，作()h x 的图像，并作y=t 的图象，注意到h(0)=1，(1)13=<eh ，（原定义域x>0,这里为方便讨论，考虑h(0)），当1≥t 时直线y=t 与()21=+xe h x x 只有一个交点即x （）ϕ只有一个零点（该零点值大于1）；当=t 时21()(21)x x f x e x t x -'⎡⎤=-+⎣⎦在12x =两侧附近同号，12x =不是极值点；当3=et 时函数()x 21x e x t ϕ-+（）=有两个不同零点(其中一个零点等于1)，但此时21()(21)xx f x e x t x-'⎡⎤=-+⎣⎦在1=x 两侧附近同号,使得1=x 不是极值点不合.选D.二、填空题：本大题共4小题，每小题5分，共20分． 把答案填在答题卡中对应题号后的横线上．13．80- 14．24015．23 16．4[0,]513．解析：展开式通项5352552()()(2)rr rr rC x r C x x ---=-，依题意，5322-=-r ，得r =3，2x -的系数是335(2)80C -=-.14．解析：依题意，先选出一个重灾区（有14C 种选法），分配有两个医疗队，有25C 种分配法，另3个重灾区各分配一个医疗队，有33A 种分配法，所以不同的分配方案数共有123453240C C A =.15．解析：设准线l 与x 轴交于E. 易知F (1,0),由抛物线定义知|MN |=|MF |,由于=60NMF ∠o ,所以NMF ∆为等边三角形，三角形边长为||2||4NM FE ==，又OD 是FEN ∆的中位线，MD 就是该等边三角形的高，||23MD =16．解析：易证AB CD ^，又GE ∥CD ，GF ∥AB ∴GE GF ^，得5EF =.当四面体绕AB 旋转时，由GF ∥AB 即EF 绕GF 旋转，故EF 与直线l 所成角的范围为[90,90]GFE 鞍-?，直线EF 与直线l 夹角的余弦值的取值范围是4[0,]5三、解答题：本大题共70分，解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）命题意图：第1问考查等差、等比数列基本量的运算求数列通项公式；第2问考查利用裂项相消法求数列前n 和.解：（1）2193a a a ⋅=Q 1分 1a d ∴= 2分 3336S a d =+=Q 3分 11a d ∴== 4分所以数列{}n a 是以1为首项和公差的等差数列，故综上*,n a n n =∈N 5分 （2）（裂项相消）：由上题可知()()241111412121nn n n b n n n ⎛⎫=-=-+ ⎪--+⎝⎭7分 所以11111111113355723212121n P n n n n =--++--+-+++---+L8分 1121n =-++， 9分 所以211201914120042n P n n +=<⇒>+，10分 故n 的最小值为505. 12分18．（本小题满分12分）命题意图：第1问考查线线平行与垂直的证明；第2问考查利用线线、线面垂直的判定，求二面角.解：（1）证明：取AC 中点为G ，连接GE 和GF ，因为//GF BC ，且12GF BC =，又因为//DE BC ，且12DE BC =，故//GF DE ，且GF DE =， 即四边形GFDE 为平行四边形，故//GE DF 2分CE AE =Q ， GE AC ∴⊥，又//GE DF ，则DF AC ⊥ 4分（2）Q 平面BCED ⊥平面ABC ，平面BCED I 平面ABC BC =,DB BC ⊥，DB ∴⊥平面ABC ，又AC ⊂Q 平面ABC ，DB ∴⊥AC ，又DF AC ⊥BD DF D =Q I ，BD ，DF ⊂平面ABD ∴AC ⊥平面ABD AC AB ∴⊥Q =2AB AC =，BC ∴=，DE取BC 中点O 连接OE 和OA ，四边形BCED 为直角梯形，则OE ∥DB ， DB ⊥Q 平面ABCOE ∴⊥平面ABC ，故OE BC ⊥，OE OA ⊥,Q AB AC =,OA BC ⊥所以可以以OA 为x 轴，OB 为y 轴，OE 为z 轴建立空间直角坐标系 6分CE AE =Q 1OE ∴=则D ，(0,0,1)E，A，(0,C ，(AD =u u u r，(AE =u u u r，CA =u u u r，则CA =u u u r为平面ABD 的一个法向量， 8分设平面ADE 的一个法向量为(,,)n x y z =r，则 00n AD n AE ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u r，即00z z ⎧+=⎪⎨+=⎪⎩， 令1x =，则z =0y =，则n =r， 10分 设二面角B AD E --为θ，则cos |cos ,|||||n CA n CA n CA θ⋅=<>==⨯r u u u rr u u u r u u r u u u r ， 故二面角B AD E --． 12分19．（本小题满分12分）命题意图：第1问考查求椭圆的标准方程；第2问考查直线与圆锥曲线位置关系.解：（1）如图，由题意知(1,0)F -，因而1c =，即221a b =+，又两曲线在第二象限内的交点(,)Q Q Q x y 到F 的距离是它到直线4x =-的距离的一半，即42(1)Q Q x x +=-+，得23Q x =-，则283Q y =，代入到椭圆方程，得2248193a b+=2分由2222481931a ba b ⎧+=⎪⎨⎪=+⎩，解得224,3a b ==，所以所求椭圆的方程为22143x y +=． 5分（2）当直线AB 的斜率存在，且不为0时，设直线AB 的方程为(1)y k x =+， 由22(1)143y k x x y =+⎧⎪⎨+=⎪⎩，得2222(34)84120k x k x k +++-=， 6分设00(,)M x y ，11(,)A x y ，22(,)B x y ，则122834kx x k -+=+，212241234k x x k -⋅=+，由于OABM 为平行四边形，则OM OA OB =+u u u u r u u u r u u u r，故20122012111228346(1)(1)(2)34k x x x k k y y y k x k x k x x k ⎧-=+=⎪⎪+⎨⎪=+=+++=++=⎪+⎩， 8分若点M 在椭圆C 上，则2200143x y +=，代入得422216121(34)k k k +=+，解得k 无解， 若点M 在抛物线D 上，则200:4D y x =-，代入得222223632(34)34k k k k=++解得k 无解10分 当直线斜率不存在时，易知存在点M (2,0)-在椭圆C 上故不存在直线l ，使点M 落在抛物线D 上，存在直线l ，使点M (2,0)-落在椭 圆C ．12分20．（本小题满分12分）命题意图：第1问考查频率分布直方图；第2问考查概率、分布列、数学期望.解：（1）X 在[70,100)内，按组距为5可分成6个小区间分别是[70，75），[75，80），[80，85），[85，90）， [90，95), [95，100)因70100≤<X ，由55(1)≤<+n X n ，*∈n N ， 得14,15,16,17,18,19=n每个小区间对应的频率值分别是810914,15,16605115.,17,18,19320n n P Y k n n -⎧=⎪⎪==⎨⎪-=⎪-⎩，（1） 2分311191115(1)160606032+++-++=k ，解得350=k . 4分 故n 的取值是14，15，16，17，18，19，350=k 5分(2) (i)由于参赛学生很多，可以把频率视为概率，由（1）知，学生B 的分数属于区间[70，75），[75，80），[80，85），[85，90）， [90，95), [95，100)的概率分别是3111914112,,,606060606060，，，我们用符号i j A (或i j B )表示学生A(或B)在第一轮获奖等级为i ，通过附加赛最终获奖等级为j, 其中,,1,2,3（）≤=j i i j , 记W=“学生B 最终获奖等级不低于学生A 的最终获奖等级”， 则P(W)=12122223222()+++P B B B A B A =12122223222()()()()()()+++P B P B P B P A P B P A =2111111010141105160601160111160711+⋅+⋅⋅+⋅⋅=分(ii) 学生A 最终获得一等奖的概率是211()=11P A ， 学生B 最终获得一等奖的概率是12121111()=2727119''++⋅=P B B ，1180(=0)=(1)(1)11999ξ--=P ， 9分 111118(=1)=(1)(1)11911999ξ-+-=P ， 10分 111(=2)=11999ξ⋅=P ， 11分ξ的分布列为8018120()012999999ξ=⋅+⋅+⋅=E 12分21．（本小题满分12分）命题意图：第1问考查不等式恒成立问题；第2问考查不等式放缩求参数取值范围.解：（1）令()()21ln(1)2x x mx x x ϕ=+-++ ，()ln(1)1x x m x ϕ'=+-+-，1()101x x ϕ''=->+ 1分()x ϕ'∴在[0,)+∞上单调递增，且(0)1m ϕ'=-，若1m ≥， ()x ϕ在[0,)+∞上单调递增，()(0)0x ϕϕ∴≥=，即1m ≥满足条件 3分 若1m <，(0)10m ϕ=-<，()x ϕ存在单调递减区间0[0,]x ，又(0)0ϕ=Q所以存在0x 使得0()0x ϕ<与已知条件矛盾，所以1m ≥，m 的最小值为1 5分（2）由（1）知22x f x x ≤+（），如果22x x g x ≤+（），则必有()f x ≤()g x 成立． 令2()=)2x h x g x x -+（）(，则()=(1)cos (1cos )h x a x x x x a x --=--， 6分()(1cos )0h x x a x =--≥，则1cos 0a x --≥，1+cos a x ≥，2a ≥．若()0h x ≥，必有()f x ()g x ≤恒成立，故当2a ≥时，()()f x g x ≤恒成立 8分下面证明2a <时，()()f x g x ≤不恒成立． 令1()()(1)ln(1)f x f x x x x x ==++－－，1()ln(1)f x x '=+，当x ＞0时，1()ln(1)f x x '=+＞0， 1()f x 在区间［0,1］上单调递增，故1()f x ≥1(0)f ＝0，即1()=()0f x f x x -≥，故x ()f x ≤. 9分()()()g x f x g x x -≤-＝2(1)cos 2x a x x x -+-＝(1cos )2xx a x -+-，令()1cos 2xt x a x =-+-，1()sin 2t x x '=+＞0， 10分()t x 在[0,1]上单调递增，(0)20t a =-<，则一定存在区间(0,)m (其中01m <<)，当(0,)x m ∈时，()0t x <，则()()g x f x -≤x ()t x ＜0，故()()f x g x ≤不恒成立．综上所述：实数a 取值范围是[2,)+∞． 12分． 22．（本小题满分10分）命题意图：第1问考查曲线的普通方程化极坐标方程和解极坐标方程组；第2问考查三角函数的最值问题.解：（1）曲线C 的极方程：2cos ρθ= 2分联立2cos 3ρθπθ=⎧⎪⎨=⎪⎩得，(0,0)M ，(1,)3N π 5分 （2）易知1MN =，直线:l y =. 6分 设点(2cos ,sin )P αα，则点P 到直线l的距离d =∴`12PMN S MN d ∆=⋅⋅ tan ϕ=. 9分∴PMN ∆.10分 23.（本小题满分10分）命题意图：第1问考查利用分类讨论思想解绝对值不等式；第2问考查分段函数求最值、构造法和基本不等式等.解：（1）当0x <时，|2|()x f x x >等价于22|1|2x x +->-，该不等式恒成立， 1分当01x <≤时，|2|()x f x x >等价于220x x ->，该不等式解集为φ， 2分当1x >时，|2|()x f x x>等价于2222x x +->，解得1x >， 3分综上，0x <或1x ， 所以不等式|2|()x f x x>的解集为(,0)1,)-∞-+∞U ． 5分 （2）⎪⎩⎪⎨⎧<+-≥-+=-+=12212212)(222x x x x x x x x x f ，，，易得)(x f 的最小值为1，即1==++M c b a 7分 因为a ，b ，+∈R c ，所以b ac b c a 222≥+，c ab c a b 222≥+，abca b c 222≥+， 所以⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+≥+++++a bc b ac a bc c ab c ab bac a b c c a b b c a 222222 2222=++≥c b a ， 9分当且仅当31===c b a 时等号成立. 10分。

2020年湖南省永州市高考数学三模试卷(理科)一、单项选择题（本大题共12小题，共60.0分）1.已知集合A={x|−2<2x−1<5}，B={x∈N|−1<x<8}，则A∩B=()A. {0,1}B. {0,1，2}C. {1,2，3}D. {1,2，3，4}2.在复平面内，复数21+i对应的点与原点的距离是()A. 1B. √2C. 2D. 2√23.已知a=245，b=2515，c=427，则()A. b<a<cB. a<c<bC. c<b<aD. c<a<b4.下图给出的是2017年11月−2018年11月规模以上工业天然气产量的月度走势图，则下列说法错误的是()A. 可以估计2018年11月天然气的总产量约为144亿立方米B. 2018年11月天然气的产量的增速比上月增加2.6个百分点C. 2018年11月天然气的日均产量比上个月增加0.5亿立方米D. 2018年11月天然气的日均产量同比去年11月增加0.5亿立方米5.下列说法正确的是()A. 若p：∀x∈R，x2+3x+5>0，则￢p：∃x0∈R，x02+3x0+5<0B. “若α=π3，则cosα=12”的否命题是“若α=π3，则cosα≠12”C. 已知A，B是△ABC的两个内角，则“A>B”是“sinA>sinB”的充要条件D. 命题“p∨q为真”是命题“p∧q为真”的充分不必要条件6. 在△ABC 中，若ccosB =bcosC 且cosA =23，则sinB =( )A. √66B. √36C. √156D. √306 7. 设向量a ⃗ ,b ⃗ 均为单位向量，且a ⃗ 与b ⃗ 的夹角为60°，则(a ⃗ +b ⃗ )⋅b ⃗ 等于( )A. 1B. √32+1C. 32D. 4−√38. 在正方形内任取一点，则该点在正方形的内切圆内的概率为( )A. π12B. π4C. π3D. π2 9. 设奇函数f(x)在[−1,1]上是减函数，且f(−1)=2，若存在x ∈[−1,1]使不等式f(x)≤x +a 成立，则实数a 的取值范围是( )A. [−1,+∞)B. [3,+∞)C. [1,+∞)D. [−3,+∞) 10. 已知双曲线C ：x 2a 2−y 2b 2=1的左、右焦点分别是F 1，F 2，正三角形△AF 1F 2的顶点A 在y 轴上，边AF 1与双曲线左支交于点B ，且AF 1⃗⃗⃗⃗⃗⃗⃗ =4BF 1⃗⃗⃗⃗⃗⃗⃗ ，则双曲线C 的离心率的值是( )A. √32+1B. √13+13C. √133+1D. √3+12 11. 关于函数f(x)=4sin(2x +π3),(x ∈R)有下列命题：其中正确的是( )①由f(x 1)=f(x 2)=0可得x 1−x 2必是π的整数倍；②f(x)的表达式可改写为f(x)=4cos(2x −π6)；③f(x)的图象关于点(−π6,0)对称；④f(x)的图象关于直线x =π3对称；⑤f(x)在区间(−π3,π12)上是增函数． A. ②③⑤B. ①②③C. ②③④D. ①③⑤ 12. 已知函数f(x)=e x x −k(1x +lnx)有两个极值点，则实数k 的取值范围是( )A. (−∞,0]B. (1,e)∪(e,+∞)C. (0,e)∪(e,+∞)D. (e,+∞)二、填空题（本大题共4小题，共20.0分）13. 已知在(1−2x)n 的展开式中，各项的二项式系数之和是64，则(1+2x)n (1−2x 2)的展开式中，x 4项的系数是__________．14. 5名大学生分配到3个公司实习，每个公司至少一名．则不同的分配方案有______ (用数字作答)15.已知抛物线E：y2=4x的焦点为F，准线为l，l交x轴于点T，A为E上一点．AA1垂直l，垂足为A1，A1F交y轴于点S，若ST//AF，则|AF|=______．16.在三棱锥S−ABC中，AB⊥AC,AB=AC=SA,SA⊥平面ABC，D为BC中点，则异面直线AB与SD所成角的余弦值为________．三、解答题（本大题共7小题，共82.0分）17.已知公差不为0的等差数列{a n}，其中a1=2，若a1，a3，a11是等比数列{b n}的前三项．(1)求等差数列{a n}的通项公式；(2)求等比数列{b n}的前n项和S n．18.如图，已知边长为2的正三角形ABE所在的平面与菱形ABCD所在的平面垂直，且∠DAB=60°，点F是BC的中点．(1)求证：BD⊥EF；(2)求二面角E−DF−B的余弦值．19.已知椭圆C：x2a2+y2b2=1(a>b>0)的左焦点为F，点A(0,−13)，B(0,13)三等分椭圆C的短轴，且sin∠FAB=3√1010．(1)求椭圆C的标准方程；(2)过点A作与x轴不垂直的直线l与椭圆C交于点M，N，椭圆C上是否存在点P，使得恒有PM⊥PN？若存在，求出点P坐标；若不存在，请说明理由．20.为选拔选手参加“中国谜语大会”，某中学举行了一次“谜语大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数作为样本(样本容量为n)进行统计．按照[50,60)，[60,70)，[70,80)，[80,90)，[90,100]的分组作出频率分布直方图，并作出样本分数的茎叶图(图中仅列出了得分在[50,60)，[90,100]的数据)．(Ⅰ)求样本容量n和频率分布直方图中的x、y的值；(Ⅱ)在选取的样本中，从竞赛成绩在80分以上(含80分)的学生中随机抽取3名学生参加“中国谜语大会”，设随机变量X 表示所抽取的3名学生中得分在(80,90].内的学生人数，求随机变量X 的分布列及数学期望．21. 已知函数f(x)=x −2·sin x ．(1)当x >0时，求f(x)的最小值；(2)若x ∈[0,π]时，f(x)≤(1−a)x −x ·cos x ，求实数a 的取值范围．22. 在直角坐标系xOy 中，曲线C 1的参数方程为{x =2cosθy =sinθ(θ为参数).在以原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2极坐标方程为ρ2=4ρsinθ−3．(1)写出曲线C 1的普通方程和C 2的直角坐标方程；(2)若分别为曲线C 1和C 2上的动点，求|PQ |的最大值．23.已知函数f(x)=|x+2|−|x−1|．(1)求不等式f(x)≥−2的解集；(2)设a，b，c为正实数，若函数f(x)的最大值为m，且a+b+2c=m，求证ab+ac+bc+c2≤9．4【答案与解析】1.答案：B解析：本题主要考查交集的运算，属于基础题．可求出集合A，B，然后进行交集的运算即可．解：由题意得A={x|−12<x<3}，B={0,1，2，3，4，5，6，7}，∴A∩B={0,1，2}．故选：B．2.答案：B解析：解：21+i=1−i则1+i对应的点为(1,1)，到原点的距离为√2．故选B．化简21+i即得．本题考查复数的运算，属于基础题．3.答案：D解析：本题考查指数函数及其性质，属于基础题．解：a=245=425，b=2515=525，c=427=247，所以a=245=425<b=2515=525，a=245>c=427=247则c<a<b．故选D．4.答案：D解析：本题考查了统计图表，属于基础题．利用统计图表对其进行分析判断正误即可得．解：因为11月份有30天，故11月份天然气的总产量约为4.8×30=144亿立方米，故A正确，2018年11月份天然气的产量的增速为10.1%．2018年10月份天然气的产量的增速为7.5%．因为10.1%−7.5%=2.6%，故B正确，2018年11月份天然气的日均产量为4.8亿立方米，比10月份增加0.5亿立方米，故C正确，2018年11月天然气的日均产量同比去年11月增加0.6亿立方米，故D错误．故选D．5.答案：C解析：解：若p：∀x∈R，x2+3x+5>0，则￢p：∃x0∈R，x02+3x0+5≤0，故A错误；“若α=π3，则cosα=12”的否命题是“若α≠π3，则cosα≠12”，故B错误；已知A，B是△ABC的两个内角，由A>B⇔a>b⇔sinA>sinB，可知，“A>B”是“sinA>sinB”的充要条件，故C正确；命题“p∨q为真”是命题，说明p、q中至少有一个为真命题，反之，若“p∧q为真”，则p、q均为真，∴命题“p∨q为真”是命题“p∧q为真”的必要不充分条件，故D错误．故选：C．写出全称命题的否定判断A；写出命题的否命题判断B；由充分必要条件的判定方法判断C；由复合命题的真假判断与充分必要条件的判定方法判断D．本题考查命题的真假判断与应用，考查命题的否定与否命题，考查充分必要条件的判定方法，是基础题．6.答案：D解析：本题考查了正弦定理，两角差的正弦函数公式，半角公式，属于中档题．已知等式利用正弦定理化简，再利用两角差的正弦函数公式整理后得到B=C，用A表示出B，再将cosA=23代入计算即可得到结果．解：在△ABC中，ccosB=bcosC，利用正弦定理化简得：sinCcosB=sinBcosC，即sinCcosB−sinBcosC=sin(C−B)=0，∴C−B=0，即C=B，B为锐角，则sinB=sinπ−A2=cos A2=√1+cosA2=√306，故选D．7.答案：C解析：本题考查平面向量的数量积的运算，是基础题．直接应用数量积计算求值．解：∵向量a⃗,b⃗ 均为单位向量，且a⃗与b⃗ 的夹角为60°，∴(a⃗+b⃗ )⋅b⃗ =a⃗·b⃗ +b⃗ 2=12+1=32，故选C．8.答案：B解析：解：设圆的半径为r，则正方形的边长为2r ∴圆的面积为πr2，正方形的面积为4r2以面积为测度，可得点P落在⊙O内的概率为πr24r2=π4故选：B．以面积为测度，计算圆的面积，正方形的面积，即可求得点P落在⊙O内的概率．本题考查几何概型，考查面积的计算，属于基础题．9.答案：D解析：本题主要考查函数的奇偶性和单调性以及数形结合的思想方法，属于中等题。

永州市2020年高考第三次模拟考试试卷理科综合能力测试生物部分第I卷一、选择题：本题共13小题，每小题6分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.下列有关细胞器的叙述，正确的是A.常用密度梯度离心法从细胞中分离出各种细胞器B.花瓣细胞液泡中色素种类和含量可影响花的颜色C.正常生理状态下溶酶体不会分解自身机体的细胞结构D.细菌分泌的蛋白质类外毒素需经内质网的合成和加工2.在适宜温度和大气CO2浓度条件下，测得甲、乙两种植物的光补偿点(光合速率等于呼吸速率时的光照强度)分别为E1和E2，且E1小于E2；甲、乙两种植物的光饱和点(达到最大光合速率所需的最小光照强度)分别为E3和E4，且E3小于E4。

下列有关叙述正确的是A.若持续保持光照强度为E1，则乙种植物能正常生长，甲种植物停止生长B.若持续保持光照强度为E2，则甲种植物能正常生长，乙种植物停止生长C.光照强度低于E3时，限制甲种植物光合速率的环境因素是CO2浓度D.光照强度高于E4时，限制乙种植物光合速率的环境因素是光照强度3.核酸是生物的遗传物质，通过复制、转录和翻译等过程传递遗传信息。

下列有关叙述错误的是A.DNA分子复制合成的两条子链的碱基序列相同B.转录时，RNA聚合酶能识别DNA中特定的碱基序列C.在细胞的生命历程中，mRNA的种类会不断发生变化D.一个mRNA分子上可以结合多个核糖体，同时进行多条肽链的合成4.人类ABO血型由9号染色体上的3个复等位基因(I A，I B和i)决定，血型的基因型组成见下表。

若一个O型血红绿色盲男性和一个AB型血红绿色盲携带者的女性婚配，下列有关叙述正确的是A.他们生的儿子患色盲的概率为1/4B.他们生B型血色盲女孩的概率为1/4C.他们B型血色盲儿子和A型血色盲正常女性婚配，不可能生出O型血色盲女儿D.他们A型血色盲女儿和O型血色觉正常男性婚配，生A型血色盲男孩的概率为1/45.人体内存在由非糖类物质转化为葡萄糖的糖异生途径，据报道，科学家已发现了参与糖异生的一种关键性酶——PEPCKI，其作用过程如下图所示。

永州市2020年高考第三次模拟考试试卷数学（理科）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合{}|13M x x =-<<，(){}2|lg 1N x y x ==-，则M N =I （ ）A. {}|13x x -<<B. {}|11x x -<<C. {}|13x x <<D.{}|11x x -<≤2. 已知复数z 满足()1234z i i ⋅+=-（i 为虚数单位），则在复平面内复数z 对应的点位于（ ） A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 已知0.30.4a =，0.30.3b =，0.40.3c =，则（ ） A. a c b >>B. a b c >>C. c a b >>D. b c a >>4. 图1为某省2019年1至4月快递业务量统计图，图2是该省2019年1至4月快递业务收入统计图，下列对统计图理解错误．．的是（ ）（“同比”指与去年同月相比）A. 2019年1至4月的快递业务收入在3月最高，2月最低，差值超过20000万元B. 2019年1至4月的快递业务收入同比增长率不低于30%，在3月最高C. 从1至4月来看，该省在2019年快递业务量同比增长率月增长D. 从两图来看2019年1至4月中的同一个月快递业务量与收入的同比增长率不完全一致 5. 下列说法正确的是（ ）A. 若“p q ∨”为真命题，则“p q ∧”为真命题B. 命题“0x ∀>，10x e x -->”的否定是“00x ∃≤，0010xe x --≤” C. 命题“若1x ≥，则11x≤”的逆否命题为真命题 D. “1x =-”是“2560x x --=”的必要不充分条件6. 在锐角ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos 2cos b C c B c C -=⋅，则角C 的取值范围为（ ） A. ,86ππ⎛⎫⎪⎝⎭ B. 0,6π⎛⎫⎪⎝⎭C. ,62ππ⎛⎫⎪⎝⎭ D. ,82ππ⎛⎫⎪⎝⎭ 7. 已知平面向量a r ，b r ，c r 均为单位向量，若12a b ⋅=r r ，则()()a b b c +⋅-r r r r 的最大值是（ ）A. 13+B. 3C. 332+D. 1232+8. 我国传统的房屋建筑中，常会出现一些形状不同的窗棂，窗棂上雕刻有各种花纹，构成种类繁多的精美图案.如图所示的窗棂图案，是将边长为2R 的正方形的内切圆六等分，分别以各等分点为圆心，以R 为半径画圆弧，在圆的内部构成的平面图形.若在正方形内随机取一点，则该点在窗棂图案上阴影内的概率为（ ）A. 331π-B.3324π-C. 332π-D.324π-9. 已知函数()f x 是定义在R 上的奇函数，当0x <时，()22f x x =-+.若对任意的[]1,2x ∈-，()()f x a f x +>成立，则实数a 的取值范围是（ ）A. ()0,2B. ()()0,2,6-∞UC. ()2,0-D. ()()2,06,-+∞U10. 已知双曲线C ：()222210,0x y a b a b-=>>的左、右顶点分别为A ，B ，左焦点为F ，P为C 上一点，且PF x ⊥轴，过点A 的直线l 与线段PF 交于点M （异于P ，F ），与y 轴交于点N ，直线MB 与y 轴交于点H ，若3HN OH =u u u r u u u r（O 为坐标原点），则C 的离心率为（ ） A. 2B. 3C. 4D. 511. 已知函数()()sin 03f x x πωω⎛⎫=+> ⎪⎝⎭，()12f x =在区间[]0,π上有且仅有2个零点，对于下列4个结论：①在区间()0,π上存在1x ，2x ，满足()()122f x f x -=；②()f x 在区间()0,π有且仅有1个最大值点；③()f x 在区间0,15π⎛⎫⎪⎝⎭上单调递增；④ω的取值范围是115,162⎡⎫⎪⎢⎣⎭，其中所有正确结论的编号是（ ） A. ①③B. ①③④C. ②③D. ①④12. 设函数()1ln 2x e t x x x x f x ⎛⎫=+-- ⎪⎝⎭恰有两个极值点，则实数t 的取值范围是（ ）A. ()1,+∞⎪⎪⎩⎭U B. [)1,3e ⎧⎫+∞⎨⎬⎩⎭UC. [)1,3e ⎫⎪+∞⎬⎪⎪⎩⎭U D. [)1,+∞ 二、填空题：本大题共4小题，每小题5分，共20分.13. 二项式52x ⎫⎪⎭的展开式中2x -的系数是______.14. 在今年的疫情防控期间，某省派出5个医疗队去支援武汉市的4个重灾区，每个重灾区至少分配一个医疗队，则不同的分配方案共有______种.（用数字填写答案）15. 已知抛物线24y x =的焦点为F ，准线为l ，过点F 的直线交抛物线于点M（M 在第一象限），MN l ⊥，垂足为N ，直线NF 交y 轴于点D ，则MD =______. 16. 在四面体ABCD 中，CA CB =，DA DB =，6AB =，8CD =，AB ⊂平面α，l ⊥平面α，E ，F 分别为线段AD ，BC 的中点，当四面体以AB 为轴旋转时，直线EF 与直线l 夹角的余弦值的取值范围是______.三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.第17题~第21题为必考题，考生都必须作答，第22、23题为选考题，考生根据要求作答. （一）必做题：60分.17. 已知n S 是公差不为零的等差数列{}n a 的前n 项和，36S =，3a 是1a 与9a 的等比中项. （1）求数列{}n a 的通项公式； （2）设数列()*24(1)41n n n a b n N n =-∈-，数列{}n b 的前2n 项和为2n P ，若2112020n P +<，求正整数n 的最小值.18. 在如图的空间几何体中，四边形BCED 为直角梯形，90DBC ∠=︒，2BC DE =，2AB AC ==，3CE AE ==，且平面BCED ⊥平面ABC ，F 为棱AB 的中点.（1）证明：DF AC ⊥；（2）求二面角B AD E --的正弦值.19. 已知椭圆C ：()222210x y a b a b+=>>与抛物线D ：24y x =-有共同的焦点F ，且两曲线的公共点到F 的距离是它到直线4x =-（点F 在此直线右侧）的距离的一半. （1）求椭圆C 的方程；（2）设O 为坐标原点，直线l 过点F 且与椭圆交于A ，B 两点，以OA ，OB 为邻边作平行四边形OAMB .是否存在直线l ，使点M 落在椭圆C 或抛物线D 上？若存在，求出点M 坐标；若不存在，请说明理由.20. 为丰富学生课外生活，某市组织了高中生钢笔书法比赛，比赛分两个阶段进行：第一阶段由评委给出所有参赛作品评分，并确定优胜者；第二阶段为附加赛，参赛人员由组委会按规则另行确定.数据统计员对第一阶段的分数进行了统计分析，这些分数X 都在[)70,100内，在以组距为5画分数的频率分布直方图（设“Y =频率组距”时，发现Y 满足8109,1630011,161520n n Y k n n -⎧≤⎪⎪=⎨⎪-⋅>⎪-⎩，*n N ∈，()551n X n ≤<+.（1）试确定n 的所有取值，并求k ；（2）组委会确定：在第一阶段比赛中低于85分的参赛者无缘获奖也不能参加附加赛；分数在[)95,100的参赛者评为一等奖；分数在[)90,95的同学评为二等奖，但通过附加赛有111的概率提升为一等奖；分数在[)85,90的同学评为三等奖，但通过附加赛有17的概率提升为二等奖（所有参加附加赛的获奖人员均不降低获奖等级）.已知学生A 和B 均参加了本次比赛，且学生A 在第一阶段评为二等奖.（i ）求学生B 最终获奖等级不低于学生A 的最终获奖等级的概率；（ii ）已知学生A 和B 都获奖，记A ，B 两位同学最终获得一等奖的人数为ξ，求ξ的分布列和数学期望.21. 已知函数()()()1ln 1f x x x =++，()2cos 2x g x ax x x =+-. （1）当0x ≥时，总有()22x f x mx ≤+，求m 的最小值； （2）对于[]0,1中任意x 恒有()()f x g x ≤，求a 的取值范围.（二）选考题：10分.请考生在第22、23题中任选一题作答.如果多做，则按所做第一题计分. 22. 选修4-4：坐标系与参数方程在平面直角坐标系xoy 中，曲线C 的方程为2220x x y -+=.以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为()3R πθρ=∈.（1）写出曲线C 的极坐标方程，并求出直线l 与曲线C 的交点M ，N 的极坐标；（2）设P 是椭圆2214x y +=上的动点，求PMN △面积的最大值.23. 选修4-5：不等式选讲 已知()221f x x x =+-.（1）解关于x 的不等式：()2x f x x>； （2）若()f x 的最小值为M ，且(),,a b c M a b c R +++=∈，求证：2222222a b a c c b c b a+++++≥.永州市2020年高考第三次模拟考试试卷数学（理科）参考答案一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1-5：CDBCC6-10：ACBDB11-12：BD1. 详细分析：{}{}2|10|11N x x x x x =->=><-或，{}|13M N x x =<<I ，选C. 2. 详细分析：55(12)1212(12)(12)i z i i i i -===-++-，在第四象限，选D. 3. 详细分析：0.30.40.30.3>，即b c >，而0.30.30.4410.33a b ⎛⎫⎛⎫==> ⎪⎪⎝⎭⎝⎭，即a b >，∴a b c >>，选B.4. 详细分析：由图表易知，选C.5. 详细分析：“p q ∨”为真，则命题p ，q 有可能一真一假，则“p q ∧”为假，故选项A说法不正确；命题“0x ∀>，10x e x -->”的否定应该是“00x ∃>，0010x e x --≤”，故选项B 说法不正确；因命题“若1x ≥，则11x≤”为真命题，则其逆否命题为真命题，故选项C 说法正确；因21560x x x =-⇒--=，但25601x x x --=⇒=-或6x =，所以“1x =-”是“2560x x --=”的充分不必要条件，选项D 说法不正确；选C. 6. 详细分析：∵sin cos sin cos 2sin cos B C C B C C -=，∴()sin sin 2B C C -=，∴2B C C -=，∴3B C =，∴32C π<且42B C C π+=>，∴86C ππ<<，选A.7. 详细分析：1a =r ，1b =r ，a b +==r r ，()()()()232a b b c a b b a b c a b c +⋅-=⋅+-+⋅=-+⋅r r r r r r r r r r r r r 3322a b c ≤++⋅-=r r r当且仅当a b +r r 与c r反向时取等号.选C.8. 详细分析：先计算半片花瓣面积：22260360464R R R ππ⎛-=- ⎝⎭，∴2212(264R S R ππ⎛=-=- ⎝⎭阴，故所求概率为2(2)2S R π==阴，选B. 9. 详细分析：依题意作出()f x 的图象，()y f x a =+的图象可以看成是()y f x =的图象向左（0a >时）或向右（0a <时）平移a 个单位而得.当0a >时，()y f x =的图象至少向左平移6个单位（不含6个单位）才能满足()()f x a f x +>成立，当0a <时，()y f x =的图象向右平移至多2个单位（不含2个单位）才能满足()()f x a f x +>成立（对任意的[]1,2x ∈-），故()()2,06,x ∈-+∞U ，选D.10. 详细分析：不妨设P 在第二象项，FM m =，()()0,0H h h >，由3HN OH =-u u u r u u u r 知()0,2N h -，由AFM AON :△△，得2m c a h a -=（1），由BOH BFM :△△，得h am c a=+（2）（1），（2）两式相乘得12c ac a-=+，即3c a =，离心率为3.选B. 11. 详细分析：∵[]0,x π∈，∴,333x πππωωπ⎡⎤+∈+⎢⎥⎣⎦，令3z x πω=+，则,33z ππωπ⎡⎤∈+⎢⎥⎣⎦，由题意，1sin 2z =在,33ππωπ⎡⎤+⎢⎥⎣⎦上只能有两解56z π=和136z π=，∴1317636πππωπ≤+<，（*）因为在,33z ππωπ⎡⎤∈+⎢⎥⎣⎦上必有3sin sin 222ππ-=，故在()0,π上存在1x ，2x 满足()()122f x f x -=；①成立；2z π=对应的x （显然在[]0,π上）一定是最大值点，因52z π=对应的x 值有可能在[]0,π上，故②结论错误；解（*）得11562ω≤<，所以④成立；当0,15x π⎛⎫∈ ⎪⎝⎭时，,3153z πωππ⎡⎤∈+⎢⎥⎣⎦，由于11562ω≤<，故,,315332z πωππππ⎡⎤⎡⎤∈+⊆⎢⎥⎢⎥⎣⎦⎣⎦，此时sin y z =是增函数，从而()f x 在0,15π⎛⎫⎪⎝⎭上单调递增.综上，①③④成立，选B. 12. 详细分析：求导得()()21'21xx f x e x t x -⎡⎤=-+⎣⎦有两个零点等价于函数()()21xx e x t ϕ=-+有一个不等于1的零点，分离参数得()21xe t h x x ==+，令()()021xe h x x x =>+，()()221'21xx h x e x -=+，()h x 在10,2⎛⎫ ⎪⎝⎭递减，在1,2⎛⎫+∞ ⎪⎝⎭递增，显然在12x =作()h x 的图像，并作y t =的图象，注意到()01h =，()113eh =<，（原定义域0x >，这里为方便讨论，考虑()0h ），当1t ≥时直线y t =与()21xe h x x =+只有一个交点即()x ϕ只有一个零点（该零点值大于1）；当t =时()()21'21x x f x e x t x -⎡⎤=-+⎣⎦在12x =两侧附近同号，12x =不是极值点；当3e t =时函数()()21xx e x t ϕ=-+有两个不同零点（其中一个零点等于1），但此时()()21'21xx f x e x t x -⎡⎤=-+⎣⎦在1x =两侧附近同号，使得1x =不是极值点不合.选D.二、填空题：本大题共4小题，每小题5分，共20分. 把答案填在答题卡中对应题号后的横线上.13. -80 14. 240 15. 16. 40,5⎡⎤⎢⎥⎣⎦13. 详细分析：展开式通项5352552()(2)rr rr r C x r C x x --⎛⎫-=- ⎪⎝⎭，依题意，5322r -=-，得3r =，2x -的系数是()335280C -=-.14. 详细分析：依题意，先选出一个重灾区（有14C 种选法），分配有两个医疗队，有25C 种分配法，另3个重灾区各分配一个医疗队，有33A 种分配法，所以不同的分配方案数共有123453240C C A =.15. 详细分析：设准线l 与x 轴交于E .易知()1,0F ，由抛物线定义知MN MF =，由于60NMF ∠=︒，所以NMF △为等边三角形，三角形边长为24NM FE ==，又OD 是FEN △的中位线，MD 就是该等边三角形的高，23MD =.16. 详细分析：易证AB CD ⊥，又//GE CD ，//GF AB ，∴GE GF ⊥，得5EF =.当四面体绕AB 旋转时，由//GF AB 即EF 绕GF 旋转，故EF 与直线l 所成角的范围为[]90,90GFE ︒-∠︒，直线EF 与直线l 夹角的余弦值的取值范围是40,5⎡⎤⎢⎥⎣⎦.三、解答题：本大题共70分，解答应写出文字说明、证明过程或演算步骤. 17. 命题意图：第1问考查等差、等比数列基本量的运算求数列通项公式； 第2问考查利用裂项相消法求数列前n 和.解：（1）∵2193a a a ⋅=，∴1a d =，∵3336S a d =+=， ∴11a d ==.所以数列{}n a 是以1为首项和公差的等差数列，故综上n a n =，*n N ∈.（2）（裂项相消）：由上题可知()()241111412121nn n n b n n n ⎛⎫=-=-+ ⎪--+⎝⎭，所以11111111113355723212121n P n n n n =--++--+-+++---+L1121n =-++， 所以211201914120042n P n n +=<⇒>+， 故n 的最小值为505.18. 命题意图：第1问考查线线平行与垂直的证明； 第2问考查利用线线、线面垂直的判定，求二面角.解：（1）证明：取AC 中点为G ，连接GE 和GF ，因为//GF BC ，且12GF BC =，又因为//DE BC ，且12DE BC =，故//GF DE ，且GF DE =， 即四边形GFDE 为平行四边形，故//GE DF .∵CE AE =，∴GE AC ⊥，又//GE DF ，则DF AC ⊥.（2）∵平面BCED ⊥平面ABC ，平面BCED I 平面ABC BC =，DB BC ⊥， ∴DB ⊥平面ABC ，又∵AC ⊂平面ABC ，∴DB AC ⊥，又DF AC ⊥， ∵BD DF D =I ，,BD DF ⊂平面ABD ，∴AC ⊥平面ABD ， ∴AC AB ⊥，∵2AB AC ==，∴BC =DE =取BC 中点O 连接OE 和OA ，四边形BCED 为直角梯形，则//OE DB ， ∵DB ⊥平面ABC ，∴OE ⊥平面ABC ，故OE BC ⊥，OE OA ⊥，∵AB AC =，OA BC ⊥， 所以可以以OA 为x 轴，OB 为y 轴，OE 为z 轴建立空间直角坐标系，∵CE AE ==1OE =，则()D ，()0,0,1E，)A，()0,C ，()AD =u u u r，()AE =u u u r，)CA =u u u r ，则)CA =u u u r 为平面ABD 的一个法向量，设平面ADE 的一个法向量为(),,n x y z =r，则00n AD n AE ⎧⋅=⎪⎨⋅=⎪⎩r u u u rr u u u r，即00z z ⎧++=⎪⎨+=⎪⎩， 令1x =，则z =0y =，则(n =r，设二面角B AD E --为θ，则cos cos ,n CA n CA n CAθ⋅===⨯r u u u rr u u u r r u u u r ， 故二面角B AD E --的正弦值为6. 19. 命题意图：第1问考查求椭圆的标准方程； 第2问考查直线与圆锥曲线位置关系.解：（1）如图，由题意知()1,0F -，因而1c =，即221a b =+，又两曲线在第二象限内的交点(),Q Q Q x y 到F 的距离是它到直线4x =-的距离的一半，即42(1)Q Q x x +=-+，得23Q x =-，则283Q y =，代入到椭圆方程，得2248193a b+=.由2222481931a ba b ⎧+=⎪⎨⎪=+⎩，解得24a =，23b =，所以所求椭圆的方程为22143x y +=. （2）当直线AB 的斜率存在，且不为0时，设直线AB 的方程为()1y k x =+，由22(1)143y k x x y =+⎧⎪⎨+=⎪⎩，得2222(34)84120k x k x k +++-=，设00(,)M x y ，11(,)A x y ，22(,)B x y ，则122834kx x k-+=+，212241234k x x k -⋅=+， 由于OABM 为平行四边形，则OM OA OB =+u u u u r u u u r u u u r ， 故20122012111228346(1)(1)(2)34k x x x k k y y y k x k x k x x k ⎧-=+=⎪⎪+⎨⎪=+=+++=++=⎪+⎩，若点M 在椭圆C 上，则2200143x y +=，代入得422216121(34)k k k +=+，解得k 无解， 若点M 在抛物线D 上，则D ：2004y x =-，代入得222223632(34)34k k k k=++解得k 无解 当直线斜率不存在时，易知存在点()2,0M -在椭圆C 上，故不存在直线l ，使点M 落在抛物线D 上，存在直线l ，使点()2,0M -落在椭圆C . 20. 命题意图：第1问考查频率分布直方图； 第2问考查概率、分布列、数学期望.解：（1）X 在[)70,100内，按组距为5可分成6个小区间分别是[)70,75，[)75,80，[)80,85，[)85,90，[)90,95，[)95,100，因70100X ≤<，由()551n X n ≤<+，*n N ∈，得14,15,16,17,18,19n =，每个小区间对应的频率值分别是8109,14,15,1660115,17,18,193052n n k n P n Y -⎧=⎪⎪=⎨⎪-⋅=-⎩=⎪（1）3111911151160606032k ⎛⎫+++-++= ⎪⎝⎭，解得350k =， 故n 的取值是14，15，16，17，18，19，350k =. （2）（i ）由于参赛学生很多，可以把频率视为概率，由（1）知，学生B 的分数属于区间[)70,75，[)75,80，[)80,85，[)85,90，[)90,95，[)95,100的概率分别是360，1160，1960，1460，1160，260，我们用符号ij A （或ij B ）表示学生A （或B ）在第一轮获奖等级为i ，通过附加赛最终获奖等级为j ，其中(),1,2,3j i i j ≤=，记W =“学生B 最终获奖等级不低于学生A 的最终获奖等级”，则()()12122223222P B B B A P B A W =+++()()()()()()12122223222P B P B P B P A P B P A =+++2111111010141105160601160111160711220=+⋅+⋅⋅+⋅⋅=. （ii ）学生A 最终获得一等奖的概率是()21111P A =， 学生B 最终获得一等奖的概率是()''121211112727119P B B +=+⋅=， 1180(0)1111999P ξ⎛⎫⎛⎫==--= ⎪⎪⎝⎭⎝⎭，111118(1)1111911999P ξ⎛⎫⎛⎫==-+-= ⎪ ⎪⎝⎭⎝⎭， 111(2)11999P ξ==⋅=，ξ的分布列为()01299999999E ξ=⋅+⋅+⋅=. 21. 命题意图：第1问考查不等式恒成立问题； 第2问考查不等式放缩求参数取值范围.解：（1）令()()21ln(1)2x x mx x x ϕ=+-++ ，()()'ln 11x x m x ϕ=+-+-， ()1''101x x ϕ=->+， ∴()'x ϕ在[)0,+∞上单调递增，且()'01m ϕ=-，若1m ≥，()x ϕ在[)0,+∞上单调递增，∴()()00x ϕϕ≥=， 即1m ≥满足条件，若1m <，()010m ϕ=-<，()x ϕ存在单调递减区间[]00,x ，又∵()00ϕ=， 所以存在0x 使得()00x ϕ<与已知条件矛盾，所以1m ≥，m 的最小值为1.（2）由（1）知()22x f x x ≤+，如果()22x x g x +≤，则必有()()f x g x ≤成立. 令()()22x h x g x x ⎛⎫=-+ ⎪⎝⎭，则()(1)cos (1cos )h x a x x x x a x =--=--， ()(1cos )0h x x a x =--≥，则1cos 0a x --≥，1cos a x ≥+，2a ≥.若()0h x ≥，必有()()f x g x ≤恒成立，故当2a ≥时，()()f x g x ≤恒成立， 下面证明2a <时，()()f x g x ≤不恒成立. 令1()()(1)ln(1)f x f x x x x x =-=++-，()()'1ln 1f x x =+，当0x >时，()()'1ln 10f x x =+>， ()1f x 在区间[]0,1上单调递增，故()()1100f x f ≥=，即()()10f x f x x =-≥，故()x f x ≤.2()()()(1)cos 2x g x f x g x x a x x x -≤-=-+-1cos 2x x a x ⎛⎫=-+- ⎪⎝⎭，令()1cos 2x t x a x =-+-，()1'sin 02t x x =+>， ()t x 在[]0,1上单调递增，()020t a =-<，则一定存在区间()0,m （其中01m <<），当()0,x m ∈时，()0t x <，则()()()0g x f x xt x -≤<，故()()f x g x ≤不恒成立.综上所述：实数a 取值范围是[)2,+∞.22. 命题意图：第1问考查曲线的普通方程化极坐标方程和解极坐标方程组； 第2问考查三角函数的最值问题.解：（1）曲线C 的极方程：2cos ρθ=，联立2cos 3ρθπθ=⎧⎪⎨=⎪⎩得，(0,0)M ，(1,)3N π. （2）易知1MN =，直线l：y =.设点(2cos ,sin )P αα，则点P 到直线l的距离d =，∴∴12PMNS MN d ∆=⋅⋅=（其中tan ϕ=.∴PMN △面积的最大值为4. 23. 命题意图：第1问考查利用分类讨论思想解绝对值不等式； 第2问考查分段函数求最值、构造法和基本不等式等. 解：（1）当0x <时，()2x f x x>等价于2212x x +->-，该不等式恒成立， 当01x <≤时，()2x f x x>等价于220x x ->，该不等式解集为∅，当1x >时，()2x f x x >等价于2222x x +->，解得1x >， 综上，0x <或1x >，所以不等式()2xf x x>的解集为()),01,-∞+∞U .（2）()22222,12122,1x x x f x x x x x x ⎧+-≥⎪=+-=⎨-+<⎪⎩，易得()f x 的最小值为1，即1a b c M ++==， 因为,,a b c R +∈，所以222a c ac b b +≥，222b a ab c c+≥，222c b bca a +≥， 所以222222a c b a c b ac ab ab bc ac bc b c a bc c a b a +++⎛⎫⎛⎫⎛⎫++≥+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2222a b c ≥++=，当且仅当13a b c ===时等号成立.。

湖南省永州市高三下学期第三次模拟考试数学（理）试题 第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合}0,{a A =，}1,2{+=a B ，若}0{=B A ，则=B A （ ） A ．}2,0,1{- B ．}2,1,0{ C ．}2,0{ D ．}2,1,0,1{- 2．若复数z 是纯虚数，且i a z i +=-)1(（R a ∈，i 是虚数单位），则=a （ ） A ．2- B ．1- C ．1 D ．22．的报告明确提出：在共享经济等领域培育增长点、形成新动能.共享经济是公众将闲置资源通过社会化平台与他人共享，进而获得收入的经济现象.为考察共享经济对企业经济活跃度的影响，在四个不同的企业各取两个部门进行共享经济对比试验，根据四个企业得到的试验数据画出如下四个等高条形图，最能体现共享经济对该部门的发展有显著效果的图形是（ ）4．双曲线11322=-+-ay a x 的焦点x 轴上，若焦距为4，则a 等于（ ） A ．1 B ．23C ．4D ．10 5．运行如图所示的程序框图，设输出的数据构成集合A ，从集合A 中任取一个元素a ，则函数ax y =在),0(+∞是增函数的概率为（ ）A ．21 B ．52 C ．32D ．43 6．3)3)(1(xx x x +-的展开式中的常数项为（ ）A ．6-B ．6C ．12D ．187．设ABC ∆的内角C B A ,,的对边分别为c b a ,,，已知B c B b A b tan 2tan tan =+，则=A （ ） A ．6π B ．4π C ．3π D ．2π 8．在ABC ∆中，060=∠BAC ，5=AB ，6=AC ，D 是AB 上一点，且5-=⋅CD AB ，则||BD 等于（ ） A. 1B. 2C. 3D.49．某几何体的三视图如图所示，则该几何体的体积为（ ）A ．1B ．2C ．3D ．610．已知椭圆C ：)0(12222>>=+b a by a x 的右焦点为2F ，O 为坐标原点，M 为y 轴上一点，点A 是直线2MF 与椭圆C 的一个交点，且||3||||2OM OF OA ==，则椭圆C 的离心率为（ ） A ．410 B ．610 C ．55 D ．35 11．三棱锥BCD A -的所有棱长都相等，N M ,别是棱BC AD ,的中点，则异面直线BM 与AN 所成角的余弦值为（ ）A ．31 B ．42 C ．33 D ．3212．若曲线)11()1ln(1)(41-<<-+=e x e x a x f 和)0()1()(22<-=x x x x g 上分别存在点A和点B ，使得AOB ∆是以原点O 为直角顶点的直角三角形，且斜边AB 的中点在y 轴上，则实数a 的取值范围是（ ）A ．),2[2e eB ．),2(2e e C ．)4,2[e e D ．),4(2e e二、填空题（每题4分，满分20分，将答案填在答题纸上）13．中国有个名句：“运筹帷幄之中，决胜千里之外”.其中“筹”的原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵、横两种形式，下表只给出了1~6的纵、横两种表示法：表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位、百位、万位数用纵式表示，十位、千位、十万位用横式表示，以此类推，请观察表中纵横两种表示法的特征，并用算筹表示628为 .14．已知实数y x ,满足条件⎪⎩⎪⎨⎧≤≥-+≥+-30203x y x y x ，则22)1(y x z ++=的最小值为 .15．函数)2||,0)(sin()(πϕωϕω<>+=x A x f 的部分图象如图所示，将函数)(x f 的图象向右平移125π个单位后得到函数)(x g 的图象，若函数)(x g 在区间],6[θπ-上的值域为]2,1[-，则 .16．记n S 为正项等比数列}{n a 的前n 项和，若2224=-S S ，则46S S -的最小值为 . 三、解答题 （本大题共6题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17．在等比数列}{n a 中，首项81=a ，数列}{n b 满足n n a b 2log =，且15321=++b b b . （1）求数列}{n a 的通项公式；（2）记数列}{n b 的前n 项和为n S ，又设数列}1{n S 的前n 项和为n T ，求证：43<n T . 18．如图，在多面体ABCDEF 中，四边形ABCD 是菱形，AC EF //，1=EF ，060=∠ABC ，⊥CE 平面ABCD ，3=CE ，2=CD ，G 是DE 的中点.（1）求证：平面//ACG 平面BEF ；（2）求直线AD 与平面ABF 所成的角的正弦值.19．某保险公司对一个拥有20000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金，保险公司把企业的所有岗位共分为C B A ,,三类工种，从事这三类工种的人数分别为12000，6000，2000，由历史数据统计出三类工种的赔付频率如下表（并以此估计赔付概率）：已知C B A ,,三类工种职工每人每年保费分别为25元、25元、40元，出险后的赔偿金额分别为100万元、100万元、50万元，保险公司在开展此项业务过程中的固定支出为每年10万元. （1）求保险公司在该业务所或利润的期望值； （2）现有如下两个方案供企业选择：方案1：企业不与保险公司合作，职工不交保险，出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工，企业开展这项工作的固定支出为每年12万元；方案2：企业与保险公司合作，企业负责职工保费的70%，职工个人负责保费的30%，出险后赔偿金由保险公司赔付，企业无额外专项开支. 请根据企业成本差异给出选择合适方案的建议.20．设斜率不为0的直线l 与抛物线y x 42=交于B A ,两点，与椭圆14622=+y x 交于D C ,两点，记直线OD OC OB OA ,,,的斜率分别为4321,,,k k k k . （1）求证：4321k k k k ++的值与直线l 的斜率的大小无关；（2）设抛物线y x 42=的焦点为F ，若OB OA ⊥，求FCD ∆面积的最大值.21．已知2ln 22)(1b x a aex f x -+=-,222222ln 22)(a b x ex g x +-+=-. （1）若对任意的实数a ，恒有)()(x g x f <，求实数b 的取值范围； （2）当a b a 10,42-=<<时，求证：方程x x e ex f +=-12)(恒有两解.请考生在22、23二题中任选一题作答，如果都做，则按所做的第一题记分. 22．选修4-4：坐标系与参数方程在直角坐标系中，直线l 过点)2,1(P ，且倾斜角为α，)2,0(πα∈.以直角坐标系的原点O为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为12)sin 3(22=+θρ. （1）求直线l 的参数方程和曲线C 的直角坐标方程，并判断曲线C 是什么曲线；（2）设直线l 与曲线C 相交与N M ,两点，当2||||=⋅PN PM ，求α的值. 23．选修4-5：不等式选讲已知函数3|2|)(|,3||2|)(+-=++-=x x g x a x x f . （1）解不等式6|)(|<x g ；（2）若对任意的R x ∈2，均存在R x ∈1，使得)()(21x f x g =成立，求实数a 的取值范围.永州市高考第三次模拟考试试卷 数学（理科）参考答案及评分标准一、选择题（每小题5分，共60分）1～5 ACDCC 6～10 BCCBA 11～12 DA 二、填空题（每小题5分，共20分）13．14．9215．3π 16．8三、解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．解：（Ⅰ）由2log =n n b a 和12315b b b ++=得2123log ()15a a a =，所以151232a a a =， 设等比数列}{n a 的公比为q ，18=a ， 18-∴=n n a q ，2158882∴⋅⋅=q q 解得4=q ． （4=-q 舍去）， 184-∴=⋅n n a 即212+=n n a ．（Ⅱ）由（Ⅰ）得21=+n b n ，易知}{n b 为等差数列，235...(21)2=++++=+n S n n n ,则11111()(2)22n S n n n n ==-++， =n T 111111[(1)()()]23242n n -+-++-+1311()2212n n =--++， 34∴<n T ．18．解：（Ⅰ）连接BD 交AC 于O ，易知O 是BD 的中点，故OG //BE ，BE ⊂面BEF ，OG 在面BEF 外，所以OG//面BEF ；又EF //AC ，AC 在面BEF 外，A C//面BEF ，又AC 与OG 相交于点O ，面ACG 有两条相交直线与面BEF 平行，故面A C G ∥面BEF ；（Ⅱ）如图，以O 为坐标原点，分别以OC 、OD 、OF 为x 、y 、z 轴建立空间直角坐标系，则(1,0,0)A -，(0,3,0)B - ， (0,3,0)D ，(0,0,3)F ， (1,3,0)AD =，(1,3,0)AB =-，(1,0,3)AF =，设面ABF 的法向量为(,,)m a b c =，依题意有m m AB AF ⊥⊥⎧⎪⎨⎪⎩，(,,)(1,)(,,)(1,0,)3,030330a b c a a b c a b c ⋅-=-⋅=+⎧=⎪⎨=⎪⎩，令3a =，1b =，1c =-，(,1,)31m =-，3315cos ,5441m AD =+<>=⨯+，直线AD 与面ABF 成的角的正弦值是155．19．（本小题满分12分）解：（Ⅰ）设工种A 、B 、C 职工的每份保单保险公司的收益为随机变量X 、Y 、Z ，则X 、Y 、Z的分布列为X 2542510010-⨯P51110-5110Y 2542510010-⨯P52110-5210Z 404405010-⨯P41110-4110保险公司的期望收益为45511()25(1)(2510010)151010E X =-+-⨯⨯=； 45522()25(1)(2510010)51010E Y =-+-⨯⨯=； 44411()40(1)(405010)101010E Z =⨯-+-⨯⨯=-； 保险公司的利润的期望值为12000()6000()2000()10000090000E X E Y E Z ⨯+⨯+⨯-=， 保险公司在该业务所获利润的期望值为9万元．（Ⅱ）方案1：企业不与保险公司合作，则企业每年安全支出与固定开支共为：4444455412112000100106000100102000501012104610101010⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯=⨯， 方案2：企业与保险公司合作，则企业支出保险金额为：4(1200025600025200040)0.737.110⨯+⨯+⨯⨯=⨯， 44461037.110⨯>⨯，故建议企业选择方案2．20．（本小题满分12分）解：解：（Ⅰ）设直线l ：=+y kx m ，11(,)A x y ，22(,)B x y ，33(,)C x y ，44(,)D x y ．联立=+y kx m 和24=x y ，得2440--=x kx m ，则124+=x x k ，124=-x x m ，121212+=+=y y k k x x 1244+=x x k ， 联立=+y kx m 和22164+=x y 得222(23)63120+++-=k x kmx m ， 在22222(6)4(23)(312)0(46)km k m k m ∆=-+->⇒+>此式可不求解)的情况下，342623-+=+km x x k ，234231223-=+m x x k ，233443422343434()682223124y m x x y m m km kk k k k k x x x x x x m m +--+=+=++=+=+=--，所以 2123448+-=-+k k m k k 是一个与k 无关的值． （Ⅱ）由（Ⅰ）知124+=x x k ，124=-x x m ，而由OA OB ⊥得12120x x y y +=22212124016∴+=-+=x x x x m m 得m =4（m =0显然不合题意），此时202∆>⇒>k ， 3422423k x x k -+=+，3423623x x k =+， 2341CD kx x =+-222(1)(2)1223k k k +-=⋅+， 点(0,1)F 到直线CD 的距离21=+d k所以212182∆-=⋅=FCDk S CD d （求面积的另法：将直线l 与y 轴交点（0,4）记为E ，则341||2FCD S EF x x ∆=⋅- 234343()42x x x x =+-2218FCD k S ∆-= 220-=>k t ，则22183638238FCD t S t t ∆=≤=+⋅， 当且仅当83=t ，即143k =时，OCD S ∆36．21．（本小题满分12分）解：（Ⅰ）要使f (x )＜g (x )恒成立，即使21222222ln 22ln 22x x b baea x ex a --+-<+-+成立，整理成关于a 的二次不等式221222ln )(22ln 22()02x x ba e x ex ba --+++--+>， 只要保证△＜0，21222222122ln )4(22ln ln 8ln 224()44202x x x x bex ex e x e x b bb ----∆=+-+-+++=---<，整理为22212ln 2ln 11022x x e x e x b b ---++->，122(ln )1122x e x b b -->- （i ）下面探究（i ）式成立的条件，令1()ln x t x ex --=，1()1x t x e x-'-=，(1)0t '=，当(0,1)x ∈时，()0t x '<，()t x 单调递减；当(1,)x ∈+∞时，()0t x '<，()t x 单调递增，x =1时()t x 有最小值(1)1t =，222min 111(()(())122)b b t x t -<==，220b b --<，12b -<<．实数b 的取值范围是（－1,2）．（Ⅱ）方程1()2x x f x ae e -=+化为2ln 50x e a x a --=， 令()2ln 5x h x e a x a =--，2()x a h x e x'=-，()h x '在（0，＋∞）上单调递增，(1)20h e a '=-<，2(2)0h e a '=->，存在0(1,2)x ∈使0()0h x '=，即002x a e x =，002xa x e =，()h x 在0(0,)x 上单调递减，在0(,)x +∞上单调递增， ()h x 在0x 处取得最小值．00022()2ln 52ln5x x a a h x e a x a a a x e=--=--0012()2ln 25a x a a a x =+--，001(2,)52x x +∈，0()2ln 2h x a a <-＜0，33()0eh e ea --=+>，22()90eh e e a =->，()h x 在03(,)e x -和02(,)x e 各有一个零点，故方程1()2x x f x ae e -=+恒有两解．22.（本小题满分10分） 解：(Ⅰ)直线l 的参数方程为⎪⎭⎫⎝⎛∈⎩⎨⎧+=+=2,0),(sin 2,cos 1πααα为参数t t y t x .曲线C 的直角坐标方程为124322=+y x ，即13422=+y x ， 所以曲线C 是焦点在x 轴上的椭圆. (Ⅱ)将l 的参数方程⎪⎭⎫⎝⎛∈⎩⎨⎧+=+=2,0),(sin 2,cos 1πααα为参数t t y t x 代入曲线C 的直角坐标方程为124322=+y x得07)sin 16cos 6()sin 4cos 3(222=++++t t αααα，11 / 11 1222723cos 4sin PM PN t t αα∴⋅=⋅==+， 得21sin 2α=， 0,2πα⎛⎫∈ ⎪⎝⎭，4πα∴= 23.（本小题满分10分）解：(Ⅰ)由236x -+<|，得6236x -<-+<，∴923x -<-<，得不等式的解为15x -<< .(Ⅱ)()()()232323f x x a x x a x a =-++≥--+=+，()233g x x =-+≥， 对任意的2x R ∈均存在1x R ∈，使得21()()f x g x =成立，∴{}{}()()y y f x y y g x =⊆=，∴233a +≥，解得0a ≥或3a ≤-，即实数a 的取值范围为：0a ≥或3a ≤-．。

湖南省永州市2023年高考第三次适应性考试数学试题及答案解析一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若复数z 满足z i z =-3，则复数z 的虚部为（）A .23B .23-C .i 23D .i23-2.设集合(){}x y y x A 2,==，(){}3,x y y x B ==，则A ∩B 的元素个数是（）A .1B .2C .3D .43.已知012cos cos =--θθ，⎪⎭⎫ ⎝⎛∈20πθ，，则=θcos （）A .21-B .21C .0D .14.窗花是贴在窗纸或窗户玻璃上的剪纸，是中国古老的传统民间艺术.图1是一张由卷曲纹和回纹构成的正六边形剪纸窗花，如图2所示其外框是边长为2的正六边形ABCDEF ，内部圆的圆心为该正六边形的中心O ，圆O 的半径为1，点P 在圆O 上运动，则OE PE ⋅的最小值为（）A .1-B .2-C .1D .25.在二项式641⎪⎪⎭⎫ ⎝⎛+x x 的展开式中，把所有的项进行排列，有理项都互不相邻，则不同的排列方案为（）A .2655A A 种B .3544A A 种C .2755A A 种D .2244A A 种6.若函数()x f y =和()x f y -=在区间[]n m ,上的单调性相同，则把区间[]n m ,叫做()x f y =的“稳定区间”.已知区间[]2023,1，为函数a y x+⎪⎭⎫⎝⎛=21的“稳定区间”，则实数a 的可能取值是（）A .49-B .45-C .21D .237.已知正项数列{}n a 满足11=a ，11++-⋅=n n n n n a a a a a ，其前200项和为200S ，则（）A .5667200<<S B .4556200<<S C .3445200<<S D .2334200<<S 8.已知函数()()()()()0,4ln >++++-+=a b a bx a x e aa x a x f ，对于定义域的任意x 恒有()0≤x f ，则ab的最大值为（）A .e2-B .e-C .1-e D .e二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.9.已知R c b a ∈,,，下列命题为真命题的是（）A .若0<<a b ，则22c a c b ⋅<⋅B .若c a b >>>0，在bc a c <C .若0>>>a b c ，则bc ba c a ->-D .若0>>>c b a ，则c b ca b a ++>10.已知四面体ABCD 的所有棱长均为2，N M ,分别为棱BC AD ,的中点，F 为棱AB 上异于B A ,的动点，点G 为线段MN 上的动点，则（）A .线段MN 的长度为1B .FMN ∆的周长的最小值为12+C .MFN ∠的余弦值的取值范围为⎥⎦⎤⎢⎣⎡310，D .直线FG 与直线CD 互为异面直线11.已知抛物线()022>=p px y C ：的焦点为F ，直线l 与C 交于()11,y x A ，()22,y x B 两点，其中A 在第一象限，点M 是AB 的中点，MN 垂直准线于N ，则下列结论正确的是（）A .若FB AF 3=，则直线l 的倾斜角为3πB .点M 到准线距离为2AB C .若直线l 经过焦点F 且12-=⋅OB OA ，则4=p D .若以AB 为直径的圆M 经过焦点F ，则MNAB 的最小值为212.若()⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+=x x x f 6sin 23sin 2ππ，⎦⎤⎢⎣⎡∈1225,0πx 时，函数()()b x f x g +=2（b 是实常数）有奇数个零点，记为()*12221,,,Nn x x x x n n ∈+ ，⎥⎦⎤⎢⎣⎡-∈0,125,21πaa 且21a a ≠，则（）A .()x f 的最小正周期是πB .()x f 的对称轴方程为()Z k k x ∈-=124ππC .()22122212≥+=+--+n x x x x n n n n D .对任意的R x ∈，21,a a ∃使得()[]()()()2,10122==+-k a f x f x f k 三、填空题：本题共4小题，每小题5分，共20分13.已知等比数列{}n a ，其前n 项和为n S ，若82=a ，283=S ，则=3a .14.现有四家工厂生产同一产品，已知它们生产该产品的日产量分别占日产量总和的%15，%20，%30和%35，且产品的不合格率分别为05.0，04.0，03.0和02.0.现从四家工厂一天生产的所有产品中任取一件，则抽到不合格品的概率是.15.已知双曲线()0,012222>>=-Ωb a by a x ：，圆2222b a y x O +=+：与x 轴交于B A ,两点，N M ,是圆O 与双曲线在x 轴上方的两个交点，点M A 、在y 轴的同侧，且AM 交BN 于点C .若ON MA CN OM +=+，则双曲线Ω的离心率为.16.在棱长为1的正方体1111D C B A ABCD -中，动点P 在平面1ACD 上运动，且341=P B ，三棱锥ACD B -1外接球球面上任意一点Q 到点P 的距离记为PQ ，当平面P AD 与平面1ADB 夹角的正切值为6时，则PQ 的最大值为.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（本题满分10分）记正项数列{}n a 的前n 项积为n T ，且nn T a 411-=.（1）证明：数列{}n T 是等差数列；（2）记()1681+⋅+⋅-=n n nn T T n b ，求数列{}n b 的前n 2项和n S 2.18.（本题满分12分）在ABC ∆中，C B A ,,的对边分别为c b a ,,且b a Ac A c +=⋅+⋅sin 3cos .（1）求C 的值；（2）若AB 边上的点M 满足MA BM 2=，3=c ，7=CM ，求ABC ∆的周长.19.（本题满分12分）已知底面为菱形的平行六面体1111D C B A ABCD -中，1==BD AB ，四边形11B BDD 为正方形，11C A 交11D B 于点M .（1）证明：CM BD ⊥；（2）若31=AB ，求直线1CD 与平面11B BDD 所成角的余弦值.20.（本题满分12分）为了精准地找到目标人群，更好地销售新能源汽车，某S 4店对近期购车的男性与女性各100位进行问卷调查，并作为样本进行统计分析，得到如下列联表（40≤m ，N m ∈）：（1）当0=m 时，将样本中购买传统燃油车的购车者按性别采用分层抽样的方法抽取6人，再从这6人中随机抽取3人调查购买传统燃油车的原因，记这3人中女性的人数为X ，求X 的分布列与数学期望；（2）定义()()N j i j i B B AKijij ij∈≤≤≤≤-=∑,,32,3222，其中ij A 为列联表中第i 行第j 列的实际数据，ij B 为列联表中第i 行第j 列的总频率之积再乘以列联表的总频数得到的理论频数.基于小概率值α的检验规则：首先提出零假设0H （变量Y X ,相互独立），然后计算2K 的值，当αx K ≥2时，我们推断0H 不成立，即认为Y X ,不独立，该推断犯错误的概率不超过α；否则，我们没有充分证据推断0H 不成立，可以认为Y X ,独立.根据2K 的计算公式，求解下面的问题：（i ）当0=m 时，依据小概率值005.0=α的独立性检验，请分析性别与是否喜爱购买新能源汽车有关；（ii ）当10<m 时，依据小概率值1.0=α的独立性检验，若认为性别与是否喜爱购买新能源汽车有关，则至少有多少名男性喜爱购买新能源汽车？附：α0.10.0250.005αx 2.7065.0247.87921.（本题满分12分）已知椭圆14822=+y x C ：，其右焦点为F ，过点F 的直线与椭圆C 交于B A ,两点，与y 轴交于点P ，AF P A λ=，BF PB μ=.（1）求证：μλ+为定值；（2）若点P 不在椭圆C 的内部，点Q 是点P 关于原点O 额对称点，试求QAB ∆面积的最小值.22.（本题满分12分）已知函数()a xex f xln ⋅=-，()x x g sin =.（1）若0=x 是函数()()()x ag x f x h +=的极小值点，讨论()x h 在区间()π，∞-上的零点个数；（2）英国数学家泰勒发现了如下公式：()()()()()*264202!21!6!4!21!21cos N n n x x x x n x x nnn nn∈+-++-+-=-=∑∞= 这个公式被编入计算工具，计算足够多的项时就可以确保显示值的精确性，现已知() ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=ππππππππn x n x x x x x x x x x g 113131212111，利用上述知识，试求∑∞=121n n 的值.答案解析一、单项选择题题号12345678答案BCB D A BC A7.解析：令1n =，则可得214a =，故2001254S a a >+=，将两边倒数得1na =，所以{}n a 为递减数列.所以1n a ≤.可得1n a -=≥12≤，112n -⎛⎫=⎪⎝⎭，所以11()4n n a -≤，根据等比数列求和公式得01199199200114114()()...()(4443343S <+++=-⋅<，综上，2005443S <<8.解析：两边同时除以a 得()()1ln 4b x a b x e x a a ⎛⎫++≤-+ ⎪+⎝⎭，令t =x +a ,原不等式等价于：14ln b t t a et+≤-，设1()ln g t t et =-，()4bk t t a=+，对()g t 求导并画出函数图像，当直线()k t 与曲线()g t 相切时，解得2e ba=-，选D二、多项选择题题号9101112答案BDABACDBC11.解析：A 选项，因为3AF FB =，所以,,A F B 三点共线，即直线l 经过抛物线焦点.当直线l 的斜率为0时，此时，直线l 与C 只有1个交点，不合题意，故设直线:2pl x my =+，与22y px =联立得：2220y pmy p --=，故21212,2y y pm y y p +==-，因为3AF FB = ，所以123y y =-，代入21212,2y y pm y y p +==-中，得到2222,3y pm y p =--=-，即213m =，因为点A 在第一象限，所以10y >，故20y <，即0pm -<，0m >，解得：3m=故直线l 的斜率为1m =，设直线l 的倾斜角为()0πθθ≤<，则tan θ=π3θ=，A 正确；B 选项，当直线l 不经过焦点p ,02F ⎛⎫⎪⎝⎭时，设m AF =，n BF =，由三角形三边关系可知：AB BF AF >+，由抛物线定义可知：AB MN BF AF >=+2，即2AB MN >，B 不正确；C 选项，由题意得：,02p F ⎛⎫⎪⎝⎭，准线方程为2p x =-，当直线l 的斜率为0时，此时，直线l 与C 只有1个交点，不合题意，故设直线:2p l x my =+，与22y px =联立得：2220y pmy p --=，故21212,2y y pm y y p +==-，则()221212244y y p x x p ==，所以221212124O p x x y y A OB p =⋅+=--= ，解得：4p =，C 正确；D 选项，设,AF m BF n ==，过点A 作AQ ⊥准线于点Q ，过点B 作BP ⊥准线于点P ，因为以AB 为直径的圆M 经过焦点F ，所以AF ⊥BF ，则AB =222AQ BP AF BF m nMN +++===，由基本不等式得：222m n mn +≥，则()()2222222m n mn m n m n +≥++=+，当且仅当m n =时，等号成立，2AB m n MN m n ==≥++，D 正确；故选：ACD 12.解析：由题设()2|sin()|2|sin()|2|sin()|2|cos()|3633f x x x x x ππππ=++=+++，所以22()4(1|sin(2)|)4(1|cos(2)|)36f x x x =++=++ππ，故()f x =A 选项由cos 2y x =的最小正周期为π，知|cos 2|y x =的最小正周期为2π，同理y =π，则()f x 的最小正周期为2π，A 不正确；对于()f x ，令262k x ππ+=，则对称轴方程为412k x ππ=-且Z k ∈，B 正确；由()0g x =可转化为()f x 与2b y =-交点横坐标，而250,12x π⎡⎤∈⎢⎥⎣⎦上()f x 图象如下：6312b ≤-≤，此时共有9个零点，1226x x π+=、235212x x π+=、34223x x π+=、4511212x x π+=、56726x x π+=、6717212x x π+=、78523x x π+=、8923212x x π+=、22413πx x x x =-=-,24635πx x x x =-=-,26857πx x x x =-=-，()22122212≥+=+-+n x x x x n -n n n ，所以C 正确.对任意x 有()[2,22]f x ∈，a ∃∈R ，215,,012a a π⎡⎤∃∈-⎢⎥⎣⎦且12a a ≠满足12()()()k f a f x f x =+592[,24∈且()1,2k =，而5,012x π⎡⎤∈-⎢⎥⎣⎦的()f x 图象如下：所以(4,26]31),2)2()k f a ∈ ，4294>12()()()k f a f x f x ∴≠+即()()()()212210k f x f x f a k -+≠⎡⎤=⎣⎦，，D 错误；三、填空题13．4或1614．0.031515．13+16．1933616.解析：设11CD C D O =I ，连接1B D ，AO ，且11B D AO O = ，所以1B D ⊥平面1ACD ，设正方体的棱长为1，则可知11B ACD -2所以1O 为等边三角形1的中心，由题可得362AO =1263AO AO =11B O =233又1B P 与平面1ACD 所成角为π3，则111tan 3B O O P π==可求得123O P =，即P 在以1O 为圆心，半径23r =的圆上，且圆在平面1ACD 内，由1B D ⊥平面1ACD ，又1B D ⊂ 平面11AB C D ，∴平面11AB C D ⊥平面1ACD ，且两个平面的交线为AO ，把两个平面抽象出来，如图：作PM AO ⊥于M 点，过点M 作MN AD ⊥交AD 于N 点，连接PN ，Q 平面11AB C D ⊥平面1ACD ，PM ⊂平面1ACD ，平面11AB C D 平面1ACD AO =，PM ∴⊥平面11AB C D ，AD ⊂平面11AB C D ，PM AD ∴⊥，又MN AD ⊥，MN 与PM 为平面PMN 中两相交直线，故AD ⊥平面PMN ，PN ⊂平面PMN ，AD PN ∴⊥，PNM ∴∠为二面角1P AD B --的平面角，即为角θ，设AM x =，当M 与点1O 不重合时，在1Rt PMO中，可得PM 若M 与点1O重合时，即当3x =时，可求得123PM PO ==，也符合上式，故PM =MN AD ⊥ ，OD AD ⊥，//MN OD ∴，MN AM OD AO ∴=OD AM MN x AO ⨯∴=tanPM MN θ∴==解得：12x =，9x =再取1B D 的中点F ，连接PF ,在Rt 三角形PFM 和Rt 三角形1FMO 中利用勾股定理得PF =，所以PQ 的最大值为6PQ =.四、解答题17．（本题满分10分）解：（1）证明：由题意得1nn n T a T -=()2≥n ，…………………1分因为nn T a 411-=，所以，nn n T T T 411-=-()2≥n …………………2分即41-=-n n T T ()2≥n ，…………………3分所以41=--n n T T ()2≥n ．当1=n 时，11T a =，所以11411T T -=，解得51=T ，…………………4分故{}n T 是以5为首项，4为公差的等差数列．…………………5分（2）由（1）可知，()14415+=⨯-+=n n T n ，…………………6分所以()1681+⋅+⋅-=n n nn T T n b ()()()5414681+++⋅-=n n n n ()⎪⎭⎫ ⎝⎛+++⋅-=5411411n n n …………………8分⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛++--+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-=5811811813811711311319191512n n n n S n 58151++-=n 25408+-=n n…………………10分18．（本题满分12分）解：（1）由正弦定理得：BA A C A C sin sin sin sin 3cos sin +=+…………………1分在三角形中，()C A πB +-=()C A A A C A C ++=+sin sin sin sin 3cos sin …………………2分C A C A A A C A C sin cos cos sin sin sin sin 3cos sin ++=+…………………3分1C cos C 3=-sin 216C =⎪⎭⎫ ⎝⎛-πsin …………………4分()0C ∈πQ ，…………………5分366πC ππC ==-∴…………………6分（2）2BM MA =uuu r uuu rQ 12==∴AM BM ，由余弦定理得C cos 2222⋅-+=ab b a c 则 ab b a -+=229①…………………7分又CM =Q 由于CB CA CM 3132+=()CB CA CB CACM ⋅++=949194222则 ab b a 246322++=②…………………8分①7⨯=②即ab b a ab b a 247772222++=-+03222=+-b ab a 亦即()()02=--b a b a 则b a =或2ba =…………………9分当b a =时，代入①得33==b a ，周长9=++=c b a L …………………10分当2ba =时，代入①得323==b a ，…………………11分周长333+=++=c b a L …………………12分19．（本题满分12分）解：（1）连接AC 交BD 于点O,连接OM四边形ABCD 为菱形AC BD ⊥∴…………………1分 M 为11C A 中点1OM//BB ∴…………………2分 四边形11B BDD 为正方形OM BD BB BD ⊥⊥∴，1…………………3分 O OM AC = ⊥∴BD 平面11A ACC …………………4分⊂CM 平面11A ACC CMBD ⊥∴…………………5分（2）以O 为坐标原点，OA 所在直线为x 轴，OB 所在直线为y 轴，过O 且垂直于平面ABCD的直线为z轴，得A ⎫⎪⎪⎝⎭，10,,02D ⎛⎫- ⎪⎝⎭．…………………6分1AB =1C 11==D B A ，由（1）知，⊥BD 平面11A ACC ⊥11D B 平面11A ACC ，CM D B ⊥11，11D CB ∆是等边三角形CM ……………7分点M 作NH 垂直OC 于点H ，在OMC∆中，1OM =，CM CO =可得CM，由等面积法可得OC边上的高MH，由勾股定理可得OH ，…………………8分故M ⎝⎭，112D ⎛- ⎝⎭，,0C ⎛⎫ ⎪ ⎪⎝⎭10,,02OD ⎛⎫=- ⎪⎝⎭ ，112OD ⎛= ⎝⎭，⎪⎪⎭⎫ ⎝⎛-=36,21,631CD …………………9分设平面11B D D B 的法向量为(),,n x y z = ，则10n OD n OD ⎧⋅=⎪⎨⋅=⎪⎩ ，即102102y y ⎧=⎪⎪⎨⎪++=⎪⎩，取1z =，平面11BDD B的一个法向量为)n =．……………………10分设直线1CD 与平面11BDD B 所成角为θ，则2s in 2θ==，c o s 2θ=……………………11分∴直线1CD 与平面11B BDD所成角的余弦值2……………………12分20．（本题满分12分）解：（1）当=0时，用分层抽样的方法抽取购买传统燃油车的6人中，男性有2人，女性有4人.……………1分由题意可知，X 的可能取值为1，2，3..5136C 34C 02)3(,5336C 24C 12C )2(,51C C C )1(361422=========C X P X P X P ……………3分X 的分布列如下表X 123P515351……………4分131()1232555E X =⨯+⨯+⨯=……………5分（2）（i ）零假设为0H ：性别与是否购买新能源汽车独立，即性别与是否购买新能源汽车无关联.当=0时，302003.05.0B 2070803,23,22,22,2=⨯⨯====，，，A B A ，，602,3=A 302003.05.040702007.05.03,33,32,3=⨯⨯===⨯⨯=B A B ，，…………6分3,323,33,32,322,32,33,223,23,22,222,22,22)()()()(B B A B B A B B A B B A K -+-+-+-=524.92120030)3040(70)7060(30)3020(70)7080(2222≈=-+-+-+-=…………7分,879.7524.9005.0x => …………8分005.0=∴α根据小概率值的独立性检验，我们推断0H 不成立，即认为性别与是否购买新能源汽车有关联，此推断犯错误的概率不超过0.005.…………9分（ii ）30)3040(70)7060(30)3020(70)7080(22222--+-++-++--=m m m m K 21)10(22m -=…………10分由题意可知，（706.221)1022≥-m …………11分整理得210)28.413m -≥（，10m N m ∈<又，，4m ∴≤所以m 的最大值为4，又804=76-，∴至少有76名男性购买新能源汽车…………12分21．（本题满分12分）解：（1）证明：如图所示，设),0(),,(),,2211t P y x B y x A （.由λy λλx AF λP A +=+==1t,12,11得.……………1分又点A 在椭圆C 上，故14181222=⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+λt λλ……………2分整理得048222=+-+t λλ……………3分由,BF μPB =同理可得048222=+-+t μμ……………4分由于B A ,不重合，即,μλ≠因此0482,22=+-+t x x μλ是方程的两个根，所以4-=+μλ为定值。

永州市2024年高考第三次模拟考试数 学注意事项：1．本试卷共150分，考试时量120分钟．2．全部答案在答题卡上完成，答在本试题卷上无效．3．考试结束后，只交答题卡．一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一3． 已知非零数列}{n a 满足02221=-++n n n n a a ，则20212024a a=A ．8B ．16C ．32D ．644． 61tan ⎪⎭⎫ ⎝⎛-x x θ的展开式中第四项的系数为540，则θ2cos 的值为A ．3735-B ．3735C ．54-D ．545． 为迎接2024年在永州举行的中国龙舟公开赛，一位热情好客的永州市民准备将9份一样的永州特产分给甲、乙、丙三名幸运观众，若每人至少分得一份，且甲、乙两人分得的份数不相同，则不同的分法总数为7． 已知函数2sin )(+-+-=-x x e e x f x x ，其中e 是自然对数的底数.若4)3()(log 21>+f t f ，则实数t 的取值范围是A ．⎪⎭⎫ ⎝⎛810，B ．18⎛⎫+∞ ⎪⎝⎭，C ．），（80D ．），（∞+88． 已知1F ，2F 分别是双曲线)0,0(12222>>=-b a by a x 的左、右焦点，点O 为坐标原点，过1F 的直线分别交双曲线左、右两支于A ,B 两点，点C 在x 轴上，A F CB 23=，2BF 平分BC F 1∠，其中一条渐近线与线段AB 交于点P ,则=∠2sin POF A ．741B ．742C ．743D ．7112二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9． 下列说法正确的是A ．已知随机变量),2(~2σN X ，若(02)0.4P X <<=，则(4)0.1P X >=B ．设0>a ，0>b ，则“3log 3log a b >”成立的充要条件是“1>>b a ”C ．已知21)|(=A B P ，83)(=AB P ，则163)(=A P D ．若()61=AB P ，31)(=A P ，41)(=B P ，则事件A 与B 相互独立10．已知抛物线y x C 2:2=的焦点为F ，过点F 且倾斜角为锐角的直线l 与抛物线C 相交于A ，B 两点（点A 在第一象限），过点A 作抛物线C 的准线的垂线，垂足为M ，直线l 与抛物线C 的准线相交于点N ，则A ．BF AF +的最小值为2 B ．当直线l 的斜率为3时，8=AB C ．设直线BM ，MF 的斜率分别为1k ，2k ，则2121=k k D ．过点B 作直线AM 的垂线，垂足为Q ，BQ 交直线MF 于点P ，则PQ BP =11．在平面四边形ABCD 中，2==AB ,AD AB ⊥,BCD ∆为等边三角形，将ABD∆沿BD 折起，得到三棱锥BCD A -1，设二面角C BD A --1的大小为α．则下列说法正确的是A ．当︒=150α时，M ，N 分别为线段BD ，C A 1上的动点，则MN 的最小值为1421B ．当︒=120α时，三棱锥BCD A -1外接球的直径为313C ．当︒=90α时，以C A 1为直径的球面与底面BCD 的交线长为π33D ．当︒=60α时，AD 绕D 点旋转至D A 1所形成的曲面面积为π32三、填空题：本题共3小题，每小题5分，共15分．12．已知复数i )65(221+--=m m m z ，i )3(1022m m z --=，若21z z <（z 为z 的共轭复数），则实数m 的取值范围为 ．13．已知在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，且C c A b B a cos 2cos cos -=+，87)62sin(=+πA ，则=-)cos(B A ．14．已知函数)(x f 的定义域为R ，1)1()(=-+x f x f ，)7(2)(xf x f =，且对于1021≤≤≤x x ，恒有)()(21x f x f ≤，则=)20241(f ．四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（本题满分13分）绿化祖国要扩绿、兴绿、护绿并举．某校植树节分别在甲，乙两块不同的土地上栽种某品种树苗各500株．甲地土质含有M 元素，乙地土质不含有M 元素，其它土质情况均相同，一段时间后，为了弄清楚该品种树苗的成活情况与M 元素含量是否有关联，分别在甲，乙两块土地上随机抽取树苗各50株作为样本进行统计分析．经统计，甲地成活45株，乙地成活40株．（1）根据所给数据，完成下面的2⨯2列联表（单位：株），并判断依据小概率值α=0.10的独立性检验，能否认为该品种树苗成活与M 元素含量有关联？（2）若将频率视为概率，从样本中不成活的树苗中随机抽取3株，其中取自甲地的株数为X ，求X 的分布列及方差．参考公式：()()()()()22,n ad bc n a b c da b c d a c b d χ-==+++++++参考数据：16．（本题满分15分）如图，在多面体ABCDEF 中，底面ABCD 为直角梯形，CD AB //，BC AB ⊥，ABCD EC 平面⊥，442===AB BC CD ．（1）证明：AE BD ⊥；（2）若BF EC 2=，EC BF //，且多面体ABCDEF 的体积为311，求直线AC 与平面AEF 所成角的正弦值．2⨯2列联表类别树苗成活情况合计成活不成活含M 元素不含M 元素合计17．（本题满分15分）已知函数x b x x f ln 33|13|---=）（.（1）当1=b 时，求)(x f 在），（∞+31的单调区间及极值.（2）若0)(≥x f 恒成立，求b 的取值范围.18．（本题满分17分）已知数列}{n a 为等比数列，}{n b 为等差数列，且211==b a ,588a a =,84b a =．（1）求}{n a ，}{n b 的通项公式；（2）数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⋅-⎥⎦⎤⎢⎣⎡+-21)42sin(2211n n b ππ）（的前n 项和为n S ，集合⎭⎬⎫⎩⎨⎧∈≥⋅⋅=*++N n t a n b S n A n n n ,224共有5个元素，求实数t 的取值范围；（3）若数列}{n c 中，11=c ，)2(1log 2412≥-=n b a c nnn ，求证：112123c c c c c c +⋅+⋅⋅+⋅⋅⋅1232n c c c c +⋅⋅⋅⋅⋅⋅⋅⋅<．19．（本题满分17分）已知O 为坐标原点，动点M 在椭圆12:22=+y x C 上，动点N满足ON =N 的轨迹为E ．（1）求轨迹E 的方程；（2）在轨迹E 上是否存在点T ，使得过点T 作椭圆C 的两条切线互相垂直？若存在，求点T 的坐标；若不存在，请说明理由；（3）过点M 的直线)0(≠+=m m kx y 交轨迹E 于A ，B 两点，射线OM 交轨迹E 于点P ，射线MO 交椭圆C 于点Q ，求四边形APBQ 面积的最大值．永州市2024年高考第三次模拟考试数学参考答案及评分标准一、单项选择题题号12345678答案ADDCCA CB二、多项选择题题号91011答案ADBCDACD三、填空题12．}3{13．8714．1617.解析：0cos 11cos 21cos )(≥+=-+⋅≥-++='--x x e e x e e x f x x x x ．)(x f ∴在R 上单调递增．令2)()(g -=x f x ，)(x g 为奇函数，)(g x ∴在R 上单调递增，2)()(+=x g x f ．则4)3()(log 21>+f t f 化为42)3(2)(log 21>+++g t g ．3log )3()(log )3()(log 212121->⇔->⇔->t g t g g t g ．解得80<<t ．)8,0(∈∴t ．8.解析：如图A F CB 23= ，BC F AF F 121~∆∆∴,c F F 2||21=，c CF 4||2=设t AF =||1，则t BF 3||1=，t AB 2||=2BF 平分BC F 1∠,2||||||||2121==∴F F C F BF BC ,t BF BC 6||2||1==，t BC AF 2||31||2==,由双曲线定义可知a t AF AF 2||||12==-，a BF BF 2||||21=-,a AB AF BF 4||22===∴，B CAO2F 1F0260=∠ABF ,在21BF F ∆中，由余弦定理知aa c a a B F B F F F B F B F BF F 462)2()4()6(||||2||||||cos 22221221222121⋅⋅-+=⋅-+=∠化简得a c 7=，由222c b a =+得742=c b ，abPOF =∠2tan ，742sin 2==∠∴c b POF .11.解析：当M 为BD 中点且C A MN 1⊥时，MN 长度最短，由等面积法求得最小值为1421．故A 对．半径为313．故B 错．如图，过1A 作BD E A ⊥1，连接EC ，过球心O 作EC OO ⊥1则1O 为EC 的中点，且211=OO ，又球半径为1，球与BCD ∆的一交点为H ，则23=OH ，又过1O 作BC F O ⊥1，431=F O ，球与底面BCD ∆的交线如图，交线长为ππ333332=⋅，故C 对．转过的曲面为圆锥的一部分侧面积，该圆锥母线长为2，底面圆半径为1，故面积为πππ32312=⋅⋅．故D 对．EODO 1A 1F HC B060DBO 1C FH14.解析：)7(2)71(21)1(1)(x f x f x f x f =--=--=，217()71(=+-∴x f x f 21)71()0(=+f f ，1)1()0(=+f f ，2171()1(=-∴f f ，71(2)71(21)1(f f f =+=21)71(=f ，∴当)21,71(∈x 时，21)(=x f ，而），（21712024343∈161)2024343(81)202449(4120247(21)20241(====∴f f f f .四、解答题15．（本题满分13分）解：（1）依题意可得2⨯2列联表如下：…………………2分零假设为0H :该品种树苗成活与M 元素含量无关联．…………………3分根据列联表中的数据，10.022706.2961.15110015855050)5401045(100x =<≈=⨯⨯⨯⨯-⨯⨯=χ．…………………5分根据小概率值10.0=α的独立性检验，没有充分证据推断0H 不成立，因此可以认为0H 成立，即认为该品种树苗成活与M 元素含量无关联．…………………6分（2）由题意知，不成活的树苗共有15株，甲地不成活的树苗有5株，X 的可能取值为0，1，2，3…………………7分故9124)0(31531005===C C C X P ，9145)1(31521015===C C C X P ，类别树苗成活情况合计成活不成活含M 元素45550不含M 元素401050合计85151009120)2(31511025===C C C X P ，912)3(31501035===C C C X P ．故X 的分布列为…………………11分（一个概率1分）期望19123912029145191240)(=⨯+⨯+⨯+⨯=X E （另解：易知X 服从超几何分布，则11553)(=⨯=X E ）…………………12分方差74)13(912)12(9120)11(9145)10(9124)(2222=-⨯+-⨯+-⨯+-⨯=X D ．…………………13分16.（本题满分15分）解：（1）在BCD Rt ∆中，21tan ==∠CD BC BDC ，…………………1分在ABC Rt ∆中，21tan ==∠BC AB ACB ，ACB BDC ∠=∠∴，…………………2分︒=∠+∠=∠+∠∴90ACD ACB ACD BDC ，…………………3分∴BD AC ⊥，…………………4分又⊥EC 平面ABCD ，⊂BD 平面ABCD ，∴BD EC ⊥，又C EC AC = ，AC ⊂平面AEC ，EC ⊂平面AEC ，…………………5分⊥∴BD 平面AEC ，…………………6分又AE ⊂平面AEC ，AE BD ⊥∴．……………7分（其他方法酌情给分）（2）设多面体ABCDEF 的体积为V ，x BF EC 22==．X0123P912491459120912则311423131313131=⋅⋅+⋅⋅=⋅⋅+⋅⋅=+=∆--x x S EC S AB V V V ACD BCEF ACD E BCEF A 四边形求得1=x ．…………………9分如图，以C 为坐标原点，CD ，CB ，CE 所在直线分别为x ，y ，z 轴建立空间直角坐标系，…………10分则)0,2,1(A ，)2,0,0(E ，)1,2,0(F ，)0,0,0(C )1,2,0(-=EF ，)1,0,1(-=AF ，)0,2,1(--=AC …………11分设平面AEF 的法向量),,(z y x n =，则有0AF n EF n ⎧⋅=⎪⎨⋅=⎪⎩，即⎩⎨⎧=-=+-020z y z x ，令2=z ，则2=x ，1=y ，即)2,1,2(=n …………………12分设直线AC 与平面AEF 所成角为θ，那么1554354|,cos |sin =⋅==><=n AC θ．…………………15分17．（本题满分15分）解：（1）当1=b ，31>x 时，4ln 33ln 3313)(--=---=x x x x x f …………………1分xx x x f )1(333)(-=-='…………………2分令0)(>'x f ，解得1>x ，令0)(<'x f ，解得131<<x ，…………………4分)(x f ∴的单调递减区间为)1,31(，单调递增区间为),1(+∞)(x f ∴在1=x 处取得极小值1)1(-=f ，无极大值．…………………7分（2）依题意x b x x f ln 3313)(---=，对任意),0(+∞∈x ，0)(≥x f 恒成立，即x x b ln 3133--≤，…………………8分令x x x g ln 313)(--=，yxzEDF CBA当]31,0(∈x 时，x x x g ln 331)(--=，)(x g 单调递减．…………………9分当）+∞∈,31(x 时，x x x g ln 313)(--=，x x x x g 3333)(-=-='，…………………10分令0)(>'x g ，解得1>x ，令0)(<'x g ，解得131<<x ，…………………11分综上所述，)(x g 在)1,0(上单调递减，在),1(+∞上单调递增…………………13分因此2)1()(min ==g x g ，23≤∴b ，即32≤b 故b 的取值范围为]32，（∞-．…………………15分18．（本题满分17分）解：（1）设数列}{n a 公比的为q ，数列}{n b 公差的为d则由588a a =,283=∴=q q ，n n n q a a 211==∴-，…………………2分1684==b a ，即216728=∴=+=d d b ，n n b n 22)1(2=-+=∴．………………4分（2）设21)42sin(2211nn n b d ⋅-=⎥⎦⎤⎣⎡+-ππ）（则48128234224214243424144-=--+=+++------n b b b b d d d d n n n n n n n n ………………6分2)8048128()(414243443214+-=++++⋅⋅⋅++++=∴---n n d d d d d d d d S n n n n n ）（(6416)n n =+…………………7分nn n n n n n n n a n b S 2)2)(832(22216642224++=+⋅+=⋅⋅∴+++）（）（…………………8分令nn n n f 2)2)(832()(++=，则112)42)(832(2)3)(4032()()1(++++-++=-+n n n n n n n f n f nn n n n n 2)114(4288832212+--=+--=+，可得)()4()3()2()1(n f f f f f >⋅⋅⋅>>><，故当2=n 时，)(n f 最大.…………………11分60)1(=f 且，4147)5(=f ，25)6(=f ，∴414725≤<t ，即t 的取值范围为]414725，（．…………………12分（3）由11=c ，)2()1)(1(12≥-+=-=n n n nn n c n ，则当2≥n 时，)1(543)1)(1(423312121+⨯⨯⋅⋅⋅⨯⨯⨯=+-⨯⋅⋅⋅⨯⋅⨯⋅⨯=⋅⋅⋅n n n n n n c c c n 2111122(1)!(1)!!(1)!n n n n n n ⎡⎤⎡⎤+-===-⎢⎥⎢⎥+++⎣⎦⎣⎦…………………14分当1=n 时，11=c 也满足上式）（*∈⎥⎦⎤⎢⎣⎡+-=⋅⋅⋅∴N n n n c c c n )!1(1!1221…………………15分nc c c c c c c c c c ⋅⋅⋅⋅⋅+⋅⋅⋅+⋅⋅+⋅+∴3213212112)!1(22)!1(1!131212112<+-=⎦⎤⎢⎣⎡+-+⋅⋅⋅+-+-=n n n ！！！故原不等式成立.…………………17分19．（本题满分17分）解：（1）设),(00y x M ，）（y x N ,，则(,)ON x y =,00(,)OM x y =．由ON得00(,),)x y x y =，即30x x =，30y y =，…………………2分又),(00y x M 在椭圆C 上，所以122020=+y x .代入化简得22163x y +=所以点N 的轨迹E 的方程为22163x y +=．…………………4分（2）当两条切线的斜率存在时，设过00(,)T x y 点的切线为()00y y k x x -=-联立()002212y y k x x x y ⎧-=-⎪⎨+=⎪⎩，消去y 得()()()2220000124220k x k y kx x y kx ++-+--=则由判别式()22008120k y kx ⎡⎤∆+--=⎣⎦=…………………6分得()22200002210x k x y k y --+-=，设两条切线的斜率分别为1k ，2k ，依题意得201220112y k k x -⋅==--，即22003x y +=，…………………7分又点T 在轨迹E 上，2002163x y ∴+=解得000x y ==，T ∴或…………………8分当两条切线的斜率有一条不存在时，结合图像得不合题意．…………………9分综上，存在满足条件的点T ，且点T的坐标为或．…………10分（3）设()()1122,,,A x y B x y 将y kx m =+代入轨迹E 的方程，可得()222124260k x kmx m +++-=由222222164(12)(26)8(63)0k m k m k m ∆=-+-=+->，可得2236m k <+①且2121222426,1212km m x x x x k k -+=-=++…………………12分所以12212x x k -=+…………………13分因为直线y kx m =+与y 轴交点的坐标为()0,m所以OAB ∆的面积01212S m x x =⋅-==…………………14分将y kx m =+代入椭圆C 的方程可得()222124220k x kmx m +++-=由228(12)0k m ∆=+-≥，可得2212m k ≤+②令2212m t k=+,由①②可知01t <≤…………………15分因此0S ,故02S ≤当且仅当1t =，即2212m k =+时，0S 取得最大值2…………………16分由题知,OP =ABP ∴∆的面积101)S S =,又易知ABQ ∆面积202S S =从而四边形APBQ 的面积120=+=1S S S S ），所以四边形APBQ 面积的最大值为2）．…………………17分。

永州市2024年高考第三次模拟考试数学参考答案及评分标准一、单项选择题题号12345678答案ADDCCA CB二、多项选择题题号91011答案ADBCDACD三、填空题12．}3{13．8714．1617.解析：0cos 11cos 21cos )(≥+=-+⋅≥-++='--x x e e x e e x f x x x x ．)(x f ∴在R 上单调递增．令2)()(g -=x f x ，)(x g 为奇函数，)(g x ∴在R 上单调递增，2)()(+=x g x f ．则4)3()(log 21>+f t f 化为42)3(2)(log 21>+++g t g ．3log )3()(log )3()(log 212121->⇔->⇔->t g t g g t g ．解得80<<t ．)8,0(∈∴t ．8.解析：如图A F CB 23= ，BC F AF F 121~∆∆∴,c F F 2||21=，c CF 4||2=设t AF =||1，则t BF 3||1=，t AB 2||=2BF 平分BC F 1∠,2||||||||2121==∴F F C F BF BC ,t BF BC 6||2||1==，t BC AF 2||31||2==,由双曲线定义可知a t AF AF 2||||12==-，a BF BF 2||||21=-,a AB AF BF 4||22===∴，B CAO2F 1F0260=∠ABF ,在21BF F ∆中，由余弦定理知aa c a a B F B F F F B F B F BF F 462)2()4()6(||||2||||||cos 22221221222121⋅⋅-+=⋅-+=∠化简得a c 7=，由222c b a =+得742=c b ，abPOF =∠2tan ，742sin 2==∠∴c b POF .11.解析：当M 为BD 中点且C A MN 1⊥时，MN 长度最短，由等面积法求得最小值为1421．故A 对．半径为313．故B 错．如图，过1A 作BD E A ⊥1，连接EC ，过球心O 作EC OO ⊥1则1O 为EC 的中点，且211=OO ，又球半径为1，球与BCD ∆的一交点为H ，则23=OH ，又过1O 作BC F O ⊥1，431=F O ，球与底面BCD ∆的交线如图，交线长为ππ333332=⋅，故C 对．转过的曲面为圆锥的一部分侧面积，该圆锥母线长为2，底面圆半径为1，故面积为πππ32312=⋅⋅．故D 对．EODO 1A 1F HC B060DBO 1C FH14.解析：)7(2)71(21)1(1)(x f x f x f x f =--=--=，217()71(=+-∴x f x f 21)71()0(=+f f ，1)1()0(=+f f ，2171()1(=-∴f f ，71(2)71(21)1(f f f =+=21)71(=f ，∴当)21,71(∈x 时，21)(=x f ，而），（21712024343∈161)2024343(81)202449(4120247(21)20241(====∴f f f f .四、解答题15．（本题满分13分）解：（1）依题意可得2⨯2列联表如下：…………………2分零假设为0H :该品种树苗成活与M 元素含量无关联．…………………3分根据列联表中的数据，10.022706.2961.15110015855050)5401045(100x =<≈=⨯⨯⨯⨯-⨯⨯=χ．…………………5分根据小概率值10.0=α的独立性检验，没有充分证据推断0H 不成立，因此可以认为0H 成立，即认为该品种树苗成活与M 元素含量无关联．…………………6分（2）由题意知，不成活的树苗共有15株，甲地不成活的树苗有5株，X 的可能取值为0，1，2，3…………………7分故9124)0(31531005===C C C X P ，9145)1(31521015===C C C X P ，类别树苗成活情况合计成活不成活含M 元素45550不含M 元素401050合计85151009120)2(31511025===C C C X P ，912)3(31501035===C C C X P ．故X 的分布列为…………………11分（一个概率1分）期望19123912029145191240)(=⨯+⨯+⨯+⨯=X E （另解：易知X 服从超几何分布，则11553)(=⨯=X E ）…………………12分方差74)13(912)12(9120)11(9145)10(9124)(2222=-⨯+-⨯+-⨯+-⨯=X D ．…………………13分16.（本题满分15分）解：（1）在BCD Rt ∆中，21tan ==∠CD BC BDC ，…………………1分在ABC Rt ∆中，21tan ==∠BC AB ACB ，ACB BDC ∠=∠∴，…………………2分︒=∠+∠=∠+∠∴90ACD ACB ACD BDC ，…………………3分∴BD AC ⊥，…………………4分又⊥EC 平面ABCD ，⊂BD 平面ABCD ，∴BD EC ⊥，又C EC AC = ，AC ⊂平面AEC ，EC ⊂平面AEC ，…………………5分⊥∴BD 平面AEC ，…………………6分又AE ⊂平面AEC ，AE BD ⊥∴．……………7分（其他方法酌情给分）（2）设多面体ABCDEF 的体积为V ，x BF EC 22==．X0123P912491459120912则311423131313131=⋅⋅+⋅⋅=⋅⋅+⋅⋅=+=∆--x x S EC S AB V V V ACD BCEF ACD E BCEF A 四边形求得1=x ．…………………9分如图，以C 为坐标原点，CD ，CB ，CE 所在直线分别为x ，y ，z 轴建立空间直角坐标系，…………10分则)0,2,1(A ，)2,0,0(E ，)1,2,0(F ，)0,0,0(C )1,2,0(-=EF ，)1,0,1(-=AF ，)0,2,1(--=AC …………11分设平面AEF 的法向量),,(z y x n =，则有0AF n EF n ⎧⋅=⎪⎨⋅=⎪⎩，即⎩⎨⎧=-=+-020z y z x ，令2=z ，则2=x ，1=y ，即)2,1,2(=n …………………12分设直线AC 与平面AEF 所成角为θ，那么1554354|,cos |sin =⋅==><=n AC θ．…………………15分17．（本题满分15分）解：（1）当1=b ，31>x 时，4ln 33ln 3313)(--=---=x x x x x f …………………1分xx x x f )1(333)(-=-='…………………2分令0)(>'x f ，解得1>x ，令0)(<'x f ，解得131<<x ，…………………4分)(x f ∴的单调递减区间为)1,31(，单调递增区间为),1(+∞)(x f ∴在1=x 处取得极小值1)1(-=f ，无极大值．…………………7分（2）依题意x b x x f ln 3313)(---=，对任意),0(+∞∈x ，0)(≥x f 恒成立，即x x b ln 3133--≤，…………………8分令x x x g ln 313)(--=，yxzEDF CBA当]31,0(∈x 时，x x x g ln 331)(--=，)(x g 单调递减．…………………9分当）+∞∈,31(x 时，x x x g ln 313)(--=，x x x x g 3333)(-=-='，…………………10分令0)(>'x g ，解得1>x ，令0)(<'x g ，解得131<<x ，…………………11分综上所述，)(x g 在)1,0(上单调递减，在),1(+∞上单调递增…………………13分因此2)1()(min ==g x g ，23≤∴b ，即32≤b 故b 的取值范围为]32，（∞-．…………………15分18．（本题满分17分）解：（1）设数列}{n a 公比的为q ，数列}{n b 公差的为d则由588a a =,283=∴=q q ，n n n q a a 211==∴-，…………………2分1684==b a ，即216728=∴=+=d d b ，n n b n 22)1(2=-+=∴．………………4分（2）设21)42sin(2211nn n b d ⋅-=⎥⎦⎤⎣⎡+-ππ）（则48128234224214243424144-=--+=+++------n b b b b d d d d n n n n n n n n ………………6分2)8048128()(414243443214+-=++++⋅⋅⋅++++=∴---n n d d d d d d d d S n n n n n ）（(6416)n n =+…………………7分nn n n n n n n n a n b S 2)2)(832(22216642224++=+⋅+=⋅⋅∴+++）（）（…………………8分令nn n n f 2)2)(832()(++=，则112)42)(832(2)3)(4032()()1(++++-++=-+n n n n n n n f n f nn n n n n 2)114(4288832212+--=+--=+，可得)()4()3()2()1(n f f f f f >⋅⋅⋅>>><，故当2=n 时，)(n f 最大.…………………11分60)1(=f 且，4147)5(=f ，25)6(=f ，∴414725≤<t ，即t 的取值范围为]414725，（．…………………12分（3）由11=c ，)2()1)(1(12≥-+=-=n n n nn n c n ，则当2≥n 时，)1(543)1)(1(423312121+⨯⨯⋅⋅⋅⨯⨯⨯=+-⨯⋅⋅⋅⨯⋅⨯⋅⨯=⋅⋅⋅n n n n n n c c c n 2111122(1)!(1)!!(1)!n n n n n n ⎡⎤⎡⎤+-===-⎢⎥⎢⎥+++⎣⎦⎣⎦…………………14分当1=n 时，11=c 也满足上式）（*∈⎥⎦⎤⎢⎣⎡+-=⋅⋅⋅∴N n n n c c c n )!1(1!1221…………………15分nc c c c c c c c c c ⋅⋅⋅⋅⋅+⋅⋅⋅+⋅⋅+⋅+∴3213212112)!1(22)!1(1!131212112<+-=⎦⎤⎢⎣⎡+-+⋅⋅⋅+-+-=n n n ！！！故原不等式成立.…………………17分19．（本题满分17分）解：（1）设),(00y x M ，）（y x N ,，则(,)ON x y =,00(,)OM x y =．由ON得00(,),)x y x y =，即30x x =，30y y =，…………………2分又),(00y x M 在椭圆C 上，所以122020=+y x .代入化简得22163x y +=所以点N 的轨迹E 的方程为22163x y +=．…………………4分（2）当两条切线的斜率存在时，设过00(,)T x y 点的切线为()00y y k x x -=-联立()002212y y k x x x y ⎧-=-⎪⎨+=⎪⎩，消去y 得()()()2220000124220k x k y kx x y kx ++-+--=则由判别式()22008120k y kx ⎡⎤∆+--=⎣⎦=…………………6分得()22200002210x k x y k y --+-=，设两条切线的斜率分别为1k ，2k ，依题意得201220112y k k x -⋅==--，即22003x y +=，…………………7分又点T 在轨迹E 上，2002163x y ∴+=解得000x y ==，T ∴或…………………8分当两条切线的斜率有一条不存在时，结合图像得不合题意．…………………9分综上，存在满足条件的点T ，且点T的坐标为或．…………10分（3）设()()1122,,,A x y B x y 将y kx m =+代入轨迹E 的方程，可得()222124260k x kmx m +++-=由222222164(12)(26)8(63)0k m k m k m ∆=-+-=+->，可得2236m k <+①且2121222426,1212km m x x x x k k -+=-=++…………………12分所以12212x x k -=+…………………13分因为直线y kx m =+与y 轴交点的坐标为()0,m所以OAB ∆的面积01212S m x x =⋅-==…………………14分将y kx m =+代入椭圆C 的方程可得()222124220k x kmx m +++-=由228(12)0k m ∆=+-≥，可得2212m k ≤+②令2212m t k=+,由①②可知01t <≤…………………15分因此0S ,故02S ≤当且仅当1t =，即2212m k =+时，0S 取得最大值2…………………16分由题知,OP =ABP ∴∆的面积101)S S =,又易知ABQ ∆面积202S S =从而四边形APBQ 的面积120=+=1S S S S ），所以四边形APBQ 面积的最大值为2）．…………………17分。