最新一轮优化探究理数(苏教版)练习：第二章 第八节 幂函数与二次函数

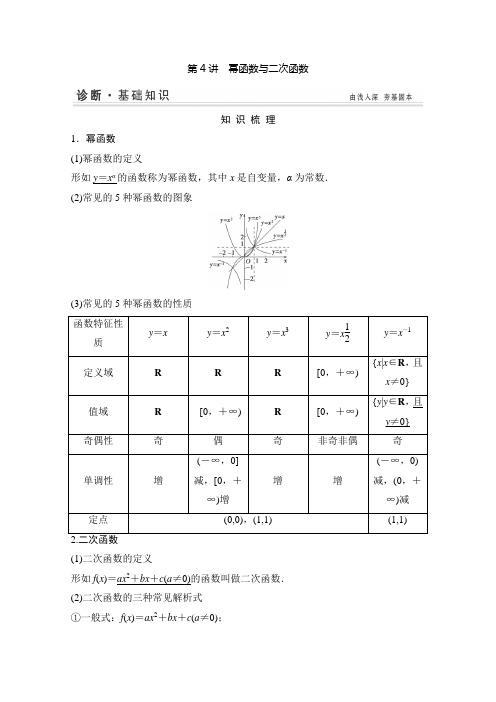
第4讲幂函数与二次函数知识梳理1．幂函数(1)幂函数的定义形如y＝xα的函数称为幂函数，其中x是自变量，α为常数．(2)常见的5种幂函数的图象(3)常见的5种幂函数的性质函数特征性质y＝x y＝x2y＝x3y＝x12y＝x－1定义域R R R[0，＋∞){x|x∈R，且x≠0} 值域R[0，＋∞)R[0，＋∞){y|y∈R，且y≠0} 奇偶性奇偶奇非奇非偶奇单调性增(－∞，0]减，[0，＋∞)增增增(－∞，0)减，(0，＋∞)减定点(0,0)，(1,1) (1,1) (1)二次函数的定义形如f(x)＝ax2＋bx＋c(a≠0)的函数叫做二次函数．(2)二次函数的三种常见解析式①一般式：f(x)＝ax2＋bx＋c(a≠0)；②顶点式：f (x )＝a (x －m )2＋n (a ≠0)，(m ，n )为顶点坐标；③两根式：f (x )＝a (x －x 1)(x －x 2)(a ≠0)其中x 1，x 2分别是f (x )＝0的两实根． (3)二次函数的图象和性质函数二次函数y ＝ax 2＋bx ＋c (a ，b ，c 是常数，a ≠0)图象a >0a <0定义域 RR值域 y ∈⎣⎢⎡⎭⎪⎫4ac －b 24a ，＋∞y ∈⎝⎛⎦⎥⎤－∞，4ac －b 24a 对称轴 x ＝－b2a 顶点 坐标 ⎝ ⎛⎭⎪⎫－b 2a，4ac －b 24a奇偶性 b ＝0⇔y ＝ax 2＋bx ＋c (a ≠0)是偶函数 递增 区间 ⎝ ⎛⎭⎪⎫－b 2a ，＋∞ ⎝ ⎛⎭⎪⎫－∞，－b 2a 递减 区间⎝ ⎛⎭⎪⎫－∞，－b 2a ⎝ ⎛⎭⎪⎫－b 2a ，＋∞ 最值当x ＝－b2a 时，y 有最小值y min＝4ac －b 24a当x ＝－b2a 时，y 有最大值y max ＝4ac －b 24a1．对幂函数的认识(1)函数f (x )＝x 2与函数f (x )＝2x 2都是幂函数．(×) (2)幂函数的图象都经过点(1,1)和(0,0)．(×) (3)幂函数的图象不经过第四象限．(√) 2．对二次函数的理解(4)二次函数y ＝ax 2＋bx ＋c ，x ∈R ，不可能是偶函数．(×)(5)(教材习题改编)函数f (x )＝12x 2＋4x ＋6，x ∈[0,2]的最大值为16，最小值为－2.(×) (6)(2011·陕西卷改编)设n ∈N *，一元二次方程x 2－4x ＋n ＝0有整数根的充要条件是n ≤4.(×) [感悟·提升]三个防范 一是幂函数的图象最多出现在两个象限内，一定会经过第一象限，一定不经过第四象限，若与坐标轴相交，则交点一定是原点，但并不是都经过(0,0)点，如(2)、(3)．二是二次函数的最值一定要注意区间的限制，不要盲目配方求得结论，如(5)中的最小值就忽略了函数的定义域．三是一元二次方程有实根的充要条件为Δ≥0，但还要注意n ∈N *，如(6).考点一 幂函数的图象与性质的应用【例1】 (1)(2014·济南模拟)已知幂函数y ＝f (x )的图象过点⎝ ⎛⎭⎪⎫12，22，则log 4f (2)的值为________．(2)函数y ＝13x 的图象是________．解析 (1)设f (x )＝x α，由图象过点⎝ ⎛⎭⎪⎫12，22，得⎝ ⎛⎭⎪⎫12α＝22＝⇒α＝12，log 4f (2)＝＝14.(2)显然f (－x )＝－f (x )，说明函数是奇函数，同时由当0＜x ＜1时，13x ＞x ；当x＞1时，13x＜x，知只有②符合．答案(1)14(2)②规律方法(1)幂函数解析式一定要设为y＝xα(α为常数)的形式；(2)可以借助幂函数的图象理解函数的对称性、单调性；(3)在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较，准确掌握各个幂函数的图象和性质是解题的关键．【训练1】比较下列各组数的大小：⑴1 21.1，120.9，1；⑵2322⎛⎫- ⎪⎝⎭，23107-⎛⎫- ⎪⎝⎭，()431.1-.解(1)把1看作，幂函数y＝在(0，＋∞)上是增函数．∵0＜0.9＜1＜1.1，∴即幂函数y＝在(0，＋∞)上是增函数，且7 10＜22＜1.21.∴考点二二次函数的图象与性质【例2】(2013·浙江七校模拟)如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A(－3,0)，对称轴为x＝－1.给出下面四个结论：①b2＞4ac；②2a－b＝1；③a－b＋c＝0；④5a＜b.其中正确的是________．解析因为图象与x轴交于两点，所以b2－4ac＞0，即b2＞4ac，①正确；对称轴为x＝－1，即－b2a＝－1,2a－b＝0，②错误；结合图象，当x＝－1时，y＞0，即a－b＋c＞0，③错误；由对称轴为x＝－1知，b＝2a.又函数图象开口向下，所以a＜0，所以5a＜2a，即5a＜b，④正确．答案①④规律方法解决二次函数的图象问题有以下两种方法：(1)排除法，抓住函数的特殊性质或特殊点；(2)讨论函数图象，依据图象特征，得到参数间的关系．【训练2】(2012·山东卷改编)设函数f(x)＝1x，g(x)＝－x2＋bx，若y＝f(x)的图象与y＝g(x)的图象有且仅有两个不同的公共点A(x1，y1)，B(x2，y2)，则x1＋x2________0，y1＋y2________0(比较大小)．解析 由题意知满足条件的两函数图象如图所示．作B 关于原点的对称点B ′，据图可知：x 1＋x 2>0，y 1＋y 2<0. 答案 ＞ ＜考点三 二次函数的综合运用【例3】 若二次函数f (x )＝ax 2＋bx ＋c (a ≠0)满足f (x ＋1)－f (x )＝2x ，且f (0)＝1. (1)求f (x )的解析式；(2)若在区间[－1,1]上，不等式f (x )>2x ＋m 恒成立，求实数m 的取值范围． 审题路线 f (0)＝1求c →f (x ＋1)－f (x )＝2x 比较系数求a ，b →构造函数g (x )＝f (x )－2x －m →求g (x )min →由g (x )min ＞0可求m 的范围． 解 (1)由f (0)＝1，得c ＝1.∴f (x )＝ax 2＋bx ＋1. 又f (x ＋1)－f (x )＝2x ，∴a (x ＋1)2＋b (x ＋1)＋1－(ax 2＋bx ＋1)＝2x ， 即2ax ＋a ＋b ＝2x ，∴⎩⎨⎧ 2a ＝2，a ＋b ＝0，∴⎩⎨⎧a ＝1，b ＝－1. 因此，f (x )＝x 2－x ＋1.(2)f (x )>2x ＋m 等价于x 2－x ＋1>2x ＋m ，即x 2－3x ＋1－m >0，要使此不等式在[－1,1]上恒成立，只需使函数g (x )＝x 2－3x ＋1－m 在[－1,1]上的最小值大于0即可． ∵g (x )＝x 2－3x ＋1－m 在[－1,1]上单调递减， ∴g (x )min ＝g (1)＝－m －1，由－m －1>0得，m <－1. 因此满足条件的实数m 的取值范围是(－∞，－1)．规律方法 二次函数、二次方程与二次不等式统称“三个二次”，它们常结合在一起，有关二次函数的问题，数形结合，密切联系图象是探求解题思路的有效方法．一般从：①开口方向；②对称轴位置；③判别式；④端点函数值符号四个方面分析. 【训练3】 (2014·盐城检测)设二次函数f (x )＝ax 2＋bx ＋c (a ≠0)在区间[－2,2]上的最大值、最小值分别是M ，m ，集合A ＝{x |f (x )＝x }． (1)若A ＝{1,2}，且f (0)＝2，求M 和m 的值；(2)若A ＝{1}，且a ≥1，记g (a )＝M ＋m ，求g (a )的最小值． 解 (1)由f (0)＝2可知c ＝2.又A ＝{1,2}， 故1,2是方程ax 2＋(b －1)x ＋2＝0的两实根． 所以⎩⎪⎨⎪⎧ 1＋2＝1－ba ，2＝2a .解得a ＝1，b ＝－2.所以f (x )＝x 2－2x ＋2＝(x －1)2＋1，x ∈[－2,2]． 当x ＝1时，f (x )min ＝f (1)＝1，即m ＝1. 当x ＝－2时，f (x )max ＝f (－2)＝10，即M ＝10.(2)由题意知，方程ax 2＋(b －1)x ＋c ＝0有两相等实根x ＝1. 所以⎩⎪⎨⎪⎧1＋1＝1－b a ，1＝ca ，即⎩⎨⎧b ＝1－2a ，c ＝a .所以f (x )＝ax 2＋(1－2a )x ＋a ，x ∈[－2,2]，其对称轴方程为x ＝2a －12a ＝1－12a .又a ≥1，故1－12a ∈⎣⎢⎡⎭⎪⎫12，1.所以M ＝f (－2)＝9a －2.m ＝f ⎝⎛⎭⎪⎫2a －12a ＝1－14a . g (a )＝M ＋m ＝9a －14a －1.又g (a )在区间[1，＋∞)上单调递增，所以当a ＝1时，g (a )min ＝314.1．对于幂函数的图象的掌握只要抓住在第一象限内三条线分第一象限为六个区域，即x ＝1，y ＝1，y ＝x 分区域．根据α＜0,0＜α＜1，α＝1，α＞1的取值确定位置后，其余象限部分由奇偶性决定．2．二次函数的综合应用多涉及单调性与最值或二次方程根的分布问题，解决的主要思路是等价转化，多用到数形结合思想与分类讨论思想．3．对于与二次函数有关的不等式恒成立或存在问题注意等价转化思想的运用．答题模板2——二次函数在闭区间上的最值问题【典例】 (12分)(经典题)求函数f (x )＝－x (x －a )在x ∈[－1,1]上的最大值．[规范解答] 函数f (x )＝－⎝ ⎛⎭⎪⎫x －a22＋a24的图象的对称轴为x ＝a 2，应分a 2＜－1，－1≤a 2≤1，a2＞1，即a ＜－2，－2≤a ≤2和a ＞2三种情形讨论．(2分)(1)当a ＜－2时，由图(1)可知f (x )在[－1,1]上的最大值为f (－1)＝－1－a ；(5分)(2)当－2≤a ≤2时，由图(2)可知f (x )在[－1,1]上的最大值为f ⎝ ⎛⎭⎪⎫a 2＝a24；(8分)(3)当a ＞2时，由图(3)可知f (x )在[－1,1]上的最大值为f (1)＝a －1.(11分)综上可知，f (x )max＝⎩⎪⎨⎪⎧－a －1，a ＜－2，a24，－2≤a ≤2，a －1，a ＞2.(12分)[反思感悟] (1)二次函数在闭区间上的最值主要有三种类型：轴定区间定、轴动区间定、轴定区间动，不论哪种类型，解题的关键是对称轴与区间的关系，当含有参数时，要依据对称轴与区间的关系进行分类讨论．(2)部分学生易出现两点错误：①找不到分类的标准，无从入手；②书写格式不规范，漏掉结论f (x )max ＝⎩⎪⎨⎪⎧－a －1，a＜－2，a24，－2≤a ≤2，a －1，a ＞2.答题模板 第一步：配方，求对称轴.第二步：分类，将对称轴是否在给定区间上分类讨论.第三步：求最值.第四步：下结论.【自主体验】已知函数f (x )＝－4x 2＋4ax －4a －a 2在区间[0,1]内有一个最大值－5，求a 的值． 解 f (x )＝－4⎝ ⎛⎭⎪⎫x －a 22－4a ，对称轴为x ＝a 2，顶点为⎝ ⎛⎭⎪⎫a 2，－4a .①当a2≥1，即a ≥2时，f (x )在区间[0,1]上递增． ∴y max ＝f (1)＝－4－a 2.令－4－a 2＝－5， ∴a ＝±1＜2(舍去)．②当0＜a2＜1，即0＜a ＜2时，y max ＝f ⎝ ⎛⎭⎪⎫a 2＝－4a ，令－4a ＝－5，∴a ＝54∈(0,2)．③当a2≤0，即a ≤0时，f (x )在区间[0,1]上递减， 此时f (x )max ＝f (0)＝－4a －a 2.令－4a －a 2＝－5，即a 2＋4a －5＝0，∴a ＝－5或a ＝1(舍去)．综上所述，a ＝54或a ＝－5.基础巩固题组 (建议用时：40分钟)一、填空题1．幂函数的图象过点⎝ ⎛⎭⎪⎫2，14，则它的单调递增区间是______．解析 设幂函数y ＝x α，则2α＝14，解得α＝－2，所以y ＝x －2，故函数y ＝x －2的单调递增区间是(－∞，0)． 答案 (－∞，0)2．(2013·浙江七校模拟)二次函数y ＝－x 2＋4x ＋t 图象的顶点在x 轴上，则t 的值是________．解析 二次函数图象的顶点在x 轴上，所以Δ＝42－4×(－1)×t ＝0，解得t ＝－4. 答案 －43．(2014·扬州检测)若函数f (x )＝x 2＋ax ＋b 的图象与x 轴的交点为(1,0)和(3,0)，则函数f (x )的单调递增区间为________．解析 由已知可得该函数的图象的对称轴为x ＝2，又二次项系数为1＞0，所以f (x )在(－∞，2]上是递减的，在[2，＋∞)上是递增的． 答案 [2，＋∞)4．若a ＜0，则0.5a,5a,5－a 的大小关系是________． 解析 5－a ＝⎝⎛⎭⎪⎫15a ，因为a ＜0时，函数y ＝x a 单调递减，且15＜0.5＜5，所以5a ＜0.5a ＜5－a .答案 5a ＜0.5a ＜5－a5．(2014·南阳一中月考)函数f (x )＝log a (6－ax )在[0,2]上为减函数，则a 的取值范围是________．解析 若0＜a ＜1，则f (x )不可能为减函数，当a ＞1时，由函数(f )x ＝log a (6－ax )在[0,2]上为减函数，知6－ax ＞0在[0,2]恒成立，等价于(6－ax )min ＞0，即6－2a ＞0，得a ＜3，所以a 的取值范围是(1,3)． 答案 (1,3)6．二次函数y ＝f (x )满足f (3＋x )＝f (3－x )(x ∈R )，且f (x )＝0有两个实根x 1，x 2，则x 1＋x 2＝________.解析 由f (3＋x )＝f (3－x )，知函数y ＝f (x )的图象关于直线x ＝3对称，应有x 1＋x 22＝3⇒x 1＋x 2＝6. 答案 67．(2014·苏州检测)已知函数y ＝－x 2＋4ax 在区间[1,3]上单调递减，则实数a 的取值范围是________．解析 根据题意，得对称轴x ＝2a ≤1，所以a ≤12. 答案 ⎝ ⎛⎦⎥⎤－∞，128．已知函数f (x )＝⎩⎪⎨⎪⎧2x，x ≥2，(x －1)3，x <2.若关于x 的方程f (x )＝k 有两个不同的实根，则实数k 的取值范围是________．解析 将方程有两个不同的实根转化为两个函数图象有两个不同的交点．作出函数f (x )的图象，如图，由图象可知，当0<k <1时，函数f (x )与y ＝k 的图象有两个不同的交点，所以所求实数k 的取值范围是(0,1)． 答案 (0,1) 二、解答题9．已知二次函数f (x )的二次项系数为a ，且f (x )＞－2x 的解集为{x |1＜x ＜3}，方程f (x )＋6a ＝0有两相等实根，求f (x )的解析式． 解 设f (x )＋2x ＝a (x －1)(x －3) (a ＜0)，则f (x )＝ax 2－4ax ＋3a －2x ， f (x )＋6a ＝ax 2－(4a ＋2)x ＋9a ，Δ＝[－(4a ＋2)]2－36a 2＝0，即(5a ＋1)(a －1)＝0， 解得a ＝－15或a ＝1(舍去)．因此f (x )的解析式为f (x )＝－15x 2－65x －35.10．设函数y ＝x 2－2x ，x ∈[－2，a ]，求函数的最小值g (a )．解 ∵函数y ＝x 2－2x ＝(x －1)2－1，∴对称轴为直线x ＝1，而x ＝1不一定在区间[－2，a ]内，应进行讨论．当－2<a <1时，函数在[－2，a ]上单调递减，则当x ＝a 时，y min ＝a 2－2a ； 当a ≥1时，函数在[－2,1]上单调递减，在[1，a ]上单调递增，则当x ＝1时，y min ＝－1.综上，g (a )＝⎩⎨⎧a 2－2a ，－2<a <1，－1，a ≥1.能力提升题组 (建议用时：25分钟)一、填空题1．(2014·江门、佛山模拟)已知幂函数f (x )＝x α，当x ＞1时，恒有f (x )＜x ，则α的取值范围是________．解析 当x ＞1时，恒有f (x )＜x ，即当x ＞1时，函数f (x )＝x α的图象在y ＝x 的图象的下方，作出幂函数f (x )＝x α在第一象限的图象，由图象可知α＜1时满足题意． 答案 (－∞，1)2．(2014·衡水中学二调)设集合A ＝{}x |x 2＋2x －3＞0，集合B ＝{}x |x 2－2ax －1≤0，a ＞0.若A ∩B 中恰含有一个整数，则实数a 的取值范围是________．解析 A ＝{}x |x 2＋2x －3＞0＝{}x |x ＞1，或x ＜－3，因为函数y ＝f (x )＝x 2－2ax －1的对称轴为x ＝a ＞0，f (0)＝－1＜0，根据对称性可知要使A ∩B 中恰含有一个整数，则这个整数解为2，所以有f (2)≤0且f (3)＞0，即⎩⎨⎧4－4a －1≤0，9－6a －1＞0，所以⎩⎪⎨⎪⎧a ≥34，a ＜43，即34≤a ＜43. 答案 [34，43) 3．已知函数f (x )＝，给出下列四个命题：①若x ＞1，则f (x )＞1；②若0＜x 1＜x 2，则f (x 2)－f (x 1)＞x 2－x 1； ③若0＜x 1＜x 2，则x 2f (x 1)＜x 1f (x 2)； ④若0＜x 1＜x 2，则f (x 1)＋f (x 2)2＜f ⎝⎛⎭⎪⎫x 1＋x 22. 其中，所有正确命题的序号是________． 解析 对于①：∵y ＝在(0，＋∞)上为增函数，∴当x ＞1时，f (x )＞f (1)＝1，①正确；对于②：取x 1＝14，x 2＝4，此时f (x 1)＝12，f (x 2)＝2，但f (x 2)－f (x 1)＜x 2－x 1，②错误；对于③：构造函数g (x )＝f (x )x ＝xx ，则g ′(x )＝x2x －x x 2＝－x 2x 2＜0，所以g (x )在(0，＋∞)上为减函数，当x 2＞x 1＞0时，有f (x 2)x 2＜f (x 1)x 1，即x 1f (x 2)＜x 2f (x 1)，③错误；对于④：画出f (x )＝x 12在(0，＋∞)的图象，可知f (x 1)＋f (x 2)2＜f ⎝⎛⎭⎪⎫x 1＋x 22，④正确． 答案 ①④ 二、解答题4．(2014·辽宁五校联考)已知函数f (x )是定义在R 上的偶函数，且当x ≤0时，f (x )＝x 2＋2x .现已画出函数f (x )在y 轴左侧的图象，如图所示，请根据图象：(1)写出函数f (x )(x ∈R )的增区间； (2)写出函数f (x )(x ∈R )的解析式；(3)若函数g (x )＝f (x )－2ax ＋2(x ∈[1,2])，求函数g (x )的最小值． 解 (1)f (x )在区间(－1,0)，(1，＋∞)上单调递增．(2)设x ＞0，则－x ＜0，函数f (x )是定义在R 上的偶函数，且当x ≤0时，f (x )＝x 2＋2x ，∴f (x )＝f (－x )＝(－x )2＋2×(－x )＝x 2－2x (x ＞0)， ∴f (x )＝⎩⎨⎧x 2－2x (x ＞0)，x 2＋2x (x ≤0).(3)g (x )＝x 2－2x －2ax ＋2，对称轴方程为x ＝a ＋1， 当a ＋1≤1，即a ≤0时，g (1)＝1－2a 为最小值；当1＜a ＋1≤2，即0＜a ≤1时，g (a ＋1)＝－a 2－2a ＋1为最小值；当a ＋1＞2，即a ＞1时，g (2)＝2－4a 为最小值．综上，g (x )min ＝⎩⎨⎧1－2a (a ≤0)，－a 2－2a ＋1(0＜a ≤1)，2－4a (a ＞1).。

高考数学一轮复习 第2章 函数概念与基本初等函数2．7二次函数与幂函数练习（含解析）苏教版一、填空题1．已知幂函数f (x )＝x α的图象经过点⎝ ⎛⎭⎪⎫2，22，则f (4)＝________. 2．幂函数f (x )＝245a a x--(α为常数)为偶函数，且在(0，＋∞)上为减函数，则整数α的值是__________．3．若(a ＋1)12- ＜(3－2a )12-，则a 的取值范围是__________． 4．幂函数y ＝21322p p x -++ (p ∈Z )为偶函数，且f (1)＜f (4)，则实数p ＝__________.5．若函数f (x )＝(x ＋a )(bx ＋2a )(常数a ，b ∈R )是偶函数，且它的值域为(－∞，4]，则该函数的解析式f (x )＝__________.6．已知t 为常数，函数y ＝|x 2－2x －t |在区间[0,3]上的最大值为2，则t ＝__________.7．已知函数f (x )＝⎩⎪⎨⎪⎧ 4x －4，x ≤1，x 2－4x ＋3，x >1，则关于x 的方程f (x )＝log 2x 解的个数为__________．8．(2012江苏四市调研)如图，已知二次函数y ＝ax 2＋bx ＋c (a ，b ，c 为实数，a ≠0)的图象过点C (t,2)，且与x 轴交于A ，B 两点，若AC ⊥BC ，则a 的值为__________．9．设函数f (x )＝1x，g (x )＝－x 2＋bx .若y ＝f (x )的图象与y ＝g (x )的图象有且仅有两个不同的公共点A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2__________0，y 1＋y 2__________0.(填“＞”或“＜”)二、解答题10．已知函数f (x )＝x m －2x 且f (4)＝72. (1)求m 的值；(2)判定f (x )的奇偶性；(3)判断f (x )在(0，＋∞)上的单调性，并给予证明．11．已知f (x )＝2231n n x -++(n ＝2k ，k ∈Z )的图象在[0，＋∞)上是递增的，解不等式f (x 2－x )＞f (x ＋3)．12．(2012江苏南通四校联考)如图所示，图1是定义在R 上的二次函数f (x )的部分图象，图2是函数g (x )＝log a (x ＋b )的部分图象．(1)分别求出函数f (x )和g (x )的解析式；(2)如果函数y ＝g (f (x ))在区间[1，m )上单调递减，求m 的取值范围．参考答案 一、填空题 1.12 解析：22＝2α⇒α＝－12， ∴f (x )＝12x -，f (4)＝1214.2-=. 2．1或3 解析：易知α2－4α－5＜0，∴－1＜α＜5.∴α＝0,1,2,3,4.代入验证，可得α＝1或3.3.⎝ ⎛⎭⎪⎫23，32 解析：∵函数y ＝x －12在定义域(0，＋∞)上递减， ∴⎩⎪⎨⎪⎧ a ＋1>0，3－2a >0，a ＋1>3－2a ，即23＜a ＜32. 4．1 解析：由幂函数性质知，∵f (1)＜f (4)，∴函数f (x )在(0，＋∞)上是增函数．∴－12p 2＋p ＋32＞0， 解得－1＜p ＜3.又∵p ∈Z ，∴p ＝0,1,2.当p ＝0或2时，幂函数y ＝32x 是非奇非偶函数．当p ＝1时，幂函数y ＝x 2是偶函数，故p ＝1.5．－2x 2＋4 解析：f (x )＝bx 2＋(ab ＋2a )x ＋2a 2，由已知条件ab ＋2a ＝0，又f (x )的值域为(－∞，4]，则2a 2＝4， 则⎩⎪⎨⎪⎧a ≠0，ab ＋2a ＝0，2a 2＝4，所以⎩⎪⎨⎪⎧ 2a 2＝4，b ＝－2. 因此f (x )＝－2x 2＋4.6．1 解析：y ＝|(x －1)2－1－t |.∵x ＝1时，(x －1)2最小，x ＝3时，(x －1)2最大，∴可分两种情况讨论．①⎩⎪⎨⎪⎧ 1＋t ≤0，|9－6－t |＝2或②⎩⎪⎨⎪⎧1＋t >0，|1－2－t |＝2. 解①得，解②得t ＝1.7．3 解析：在同一直角坐标系中画出y ＝f (x )与y ＝log 2x 的图象，从图象中可以看出两函数图象有3个交点，故其解有3个．8．－12 解析：设A (x 1,0)，B (x 2,0)，则AC ＝(x 1－t ，－2)，BC ＝(x 2－t ，－2)，所以AC ·BC ＝x 1x 2－t (x 1＋x 2)＋t 2＋4＝0. 又x 1x 2＝c a ，x 1＋x 2＝－b a ， 所以c a ＋bt a＋t 2＋4＝0. 又at 2＋bt ＋c ＝2，所以t 2＋b t a ＋c a ＝2a ，即－4＝2a ，a ＝－12. 9．＞ ＜二、解答题10．解：(1)因为f (4)＝72， 所以4m －24＝72.所以m ＝1. (2)因为f (x )的定义域为{x |x ≠0}，关于原点对称，又f (－x )＝－x －2－x ＝－⎝ ⎛⎭⎪⎫x －2x ＝－f (x )，所以f (x )是奇函数． (3)设x 1＞x 2＞0，则f (x 1)－f (x 2)＝x 1－2x 1－⎝ ⎛⎭⎪⎫x 2－2x 2＝(x 1－x 2)⎝ ⎛⎭⎪⎫1＋2x 1x 2， 因为x 1＞x 2＞0，所以x 1－x 2＞0,1＋2x 1x 2＞0.所以f (x 1)＞f (x 2)．所以f (x )在(0，＋∞)上为单调递增函数．11．解：由条件知1－n 2＋2n ＋3＞0， －n 2＋2n ＋3＞0，解得－1＜n ＜3.又n ＝2k ，k ∈Z ，∴n ＝0,2.当n ＝0,2时，f (x )＝13x ，∴f (x )在R 上单调递增．∴f (x 2－x )＞f (x ＋3)转化为x 2－x ＞x ＋3.解得x ＜－1或x ＞3.∴原不等式的解集为(－∞，－1)∪(3，＋∞)．12．解：(1)由题图1得，二次函数f (x )的顶点坐标为(1,2)，故可设函数f (x )＝a (x －1)2＋2，又函数f (x )的图象过点(0,0)，故a ＝－2，整理得f (x )＝－2x 2＋4x .由题图2得，函数g (x )＝log a (x ＋b )的图象过点(0,0)和(1,1)，故有⎩⎪⎨⎪⎧ log a b ＝0，log a (1＋b )＝1，∴⎩⎪⎨⎪⎧ a ＝2，b ＝1.∴g (x )＝log 2(x ＋1)(x ＞－1)．(2)由(1)得y ＝g (f (x ))＝log 2(－2x 2＋4x ＋1)是由y ＝log 2t 和t ＝－2x 2＋4x ＋1复合而成的函数，而y ＝log 2t 在定义域上单调递增，要使函数y ＝g (f (x ))在区间[1，m )上单调递减，必须t ＝－2x 2＋4x ＋1在区间[1，m )上单调递减，且有t ＞0恒成立．由t ＝0得x ＝2±62， 又t 的图象的对称轴为x ＝1.所以满足条件的m 的取值范围为1＜m ＜2＋62.。

一、填空题1、不等式(13)x 2－8>3－2x 的解集是________。

解析：原不等式为(13)x 2－8>(13)2x ，∴x 2－8<2x ，解之得－2<x <4.答案：{x |－2<x <4}答案：647153、设a ＝40.9，b ＝80.48，c ＝(12)－1.5，则a 、b 、c 从大到小排列的顺序为________。

解析：∵a ＝40.9＝21.8，b ＝80.48＝21.44，c ＝(12)－1.5＝21.5，∴21.8>21.5>21.44，即a >c >b .答案：a >c >b4、已知f (x )＝2x ＋2－x ，若f (a )＝3，则f (2a )等于________。

解析：由f (a )＝3得2a ＋2－a ＝3，∴(2a ＋2－a )2＝9，即22a ＋2－2a ＋2＝9.所以22a ＋2－2a ＝7，故f (2a )＝22a ＋2－2a ＝7.答案：75、若a >1，b <0，且a b ＋a －b ＝22，则a b －a －b 的值等于________。

解析：∵a >1，b <0，∴0<a b <1，a －b >1.又∵(a b ＋a －b )2＝a 2b ＋a －2b ＋2＝8，∴a 2b ＋a －2b ＝6，∴(a b －a －b )2＝a 2b ＋a －2b －2＝4，∴a b －a －b ＝－2.答案：－26、若f (x )＝a －x 与g (x )＝a x －a (a >0且a ≠1)的图象关于直线x ＝1对称，则a ＝________.解析：函数f (x )＝a －x 上任意一点(x 0，y 0)关于直线x ＝1对称的点为(2－x 0，y 0)，即有g (2－x 0)＝a 2－x 0－a ＝f (x 0)＝a －x 0，故a ＝2.答案：27、若直线ax －by ＋2＝0(a >0，b >0)和函数f (x )＝a x ＋1＋1(a >0且a ≠1)的图象恒过同一个定点，则当1a ＋1b 取最小值时，函数f (x )的解析式是________。

高考数学一轮复习第二章函数2.5幂函数与二次函数教学案苏教版[最新考纲] 1.(1)了解幂函数的概念；(2)结合函数y ＝x ，y ＝x 2，y ＝x 3，y ＝x12，y ＝1x的图象，了解它们的变化情况.2.理解二次函数的图象和性质，能用二次函数、方程、不等式之间的关系解决简单问题．1．幂函数 (1)幂函数的定义一般地，形如y ＝x α(α∈R )的函数称为幂函数，其中x 是自变量，α是常数． (2)常见的五种幂函数的图象和性质比较 函数y ＝x y ＝x 2 y ＝x 3y ＝x 12y ＝x －1图象性质定义域 R RR {x |x ≥0} {x |x ≠0} 值域 R {y |y ≥0} R{y |y ≥0} {y |y ≠0} 奇偶性奇函数偶函数 奇函数非奇非偶 函数奇函数单调性在R 上单 调递增 在(－∞，0]上单调递减； 在(0，＋∞) 上单调递增在R 上单调递增在[0，＋∞)上单调递增在(－∞，0)和(0，＋∞)上单调递减公共点(1,1)解析式f (x )＝ax 2＋bx ＋c(a ＞0)f (x )＝ax 2＋bx ＋c(a ＜0)图象定义域R R值域⎝⎛⎦⎥⎤－∞，4ac－b24a单调性在x∈上单调递减；在x∈⎣⎢⎡⎭⎪⎫－b2a，＋∞上单调递增在x∈⎝⎛⎦⎥⎤－∞，－b2a上单调递增；在x∈⎣⎢⎡⎭⎪⎫－b2a，＋∞上单调递减对称性函数的图象关于直线x＝－b2a对称[常用结论]1．幂函数y＝xα性质研究的方法(1)先确定幂函数的定义域(分数指数幂先转化为根式)，若对称，判定其奇偶性；(2)研究幂函数在第一象限的图象与性质：①当α＞0时，函数y＝xα恒经过(0,0)，(1,1)；在[0，＋∞)上为增函数；②当α＜0时，函数恒经过(1,1)；在(0，＋∞)上为减函数；(3)结合函数的奇偶性研究其它象限的图象．(4)当x∈(0,1)时，α越大，函数值越小；当x∈(1，＋∞)时，α越大，函数值越大．2．二次函数解析式的三种形式(1)一般式：f(x)＝ax2＋bx＋c(a≠0)；(2)顶点式：f(x)＝a(x－m)2＋n(a≠0)；(3)零点式：f(x)＝a(x－x1)(x－x2)(a≠0)．3．一元二次不等式恒成立的条件(1)ax2＋bx＋c＞0(a≠0)恒成立的充要条件是“a＞0且Δ＜0”；(2)ax2＋bx＋c＜0(a≠0)恒成立的充要条件是“a＜0且Δ＜0”．一、思考辨析(正确的打“√”，错误的打“×”)(1)函数y＝2x12是幂函数．( )(2)如果幂函数的图象与坐标轴相交，则交点一定是原点．( )(3)当α＜0时，幂函数y＝xα是定义域上的减函数．( )(4)二次函数y ＝ax 2＋bx ＋c ，x ∈[a ，b ]的最值一定是4ac －b24a.( )(5)二次函数y ＝ax 2＋bx ＋c ，x ∈R 不可能是偶函数． ( )(6)在y ＝ax 2＋bx ＋c (a ≠0)中，a 决定了图象的开口方向和在同一直角坐标系中的开口大小．( )[答案](1)× (2)√ (3)× (4)× (5)× (6)√ 二、教材改编1．已知幂函数f (x )＝k ·x α的图象过点⎝ ⎛⎭⎪⎫12，22，则k ＋α＝( )A.12 B ．1 C.32D ．2 C [因为函数f (x )＝k ·x α是幂函数，所以k ＝1，又函数f (x )的图象过点⎝ ⎛⎭⎪⎫12，22，所以⎝ ⎛⎭⎪⎫12a＝22，解得α＝12，则k ＋α＝32.] 2.如图是①y ＝x a；②y ＝x b；③y ＝x c在第一象限的图象，则a ，b ，c 的大小关系为( )A ．c ＜b ＜aB ．a ＜b ＜cC ．b ＜c ＜aD ．a ＜c ＜bD [根据幂函数的性质，可知选D.]3．已知函数f (x )＝x 2＋4ax 在区间(－∞，6)内单调递减，则a 的取值范围是( ) A ．a ≥3 B ．a ≤3 C ．a ＜－3D ．a ≤－3D [函数f (x )＝x 2＋4ax 的图象是开口向上的抛物线，其对称轴是x ＝－2a ，由函数在区间(－∞，6)内单调递减可知，区间(－∞，6)应在直线x ＝－2a 的左侧，所以－2a ≥6，解得a ≤－3，故选D.]4．函数g (x )＝x 2－2x (x ∈[0,3])的值域是________． [－1,3] [∵g (x )＝x 2－2x ＝(x －1)2－1，x ∈[0,3]， ∴当x ＝1时，g (x )min ＝g (1)＝－1，又g (0)＝0，g (3)＝9－6＝3， ∴g (x )max ＝3，即g (x )的值域为[－1,3]．]考点1 幂函数的图象及性质 幂函数的性质与图象特征的关系(1)幂函数的形式是y ＝x α(α∈R )，其中只有一个参数α，因此只需一个条件即可确定其解析式．(2)判断幂函数y ＝x α(α∈R )的奇偶性时，当α是分数时，一般将其先化为根式，再判断．(3)若幂函数y ＝x α在(0，＋∞)上单调递增，则α＞0，若在(0，＋∞)上单调递减，则α＜0.1.幂函数y ＝f (x )的图象经过点(3，3)，则f (x )是( )A ．偶函数，且在(0，＋∞)上是增函数B ．偶函数，且在(0，＋∞)上是减函数C ．奇函数，且在(0，＋∞)上是减函数D ．非奇非偶函数，且在(0，＋∞)上是增函数D [设幂函数f (x )＝x α，则f (3)＝3α＝3，解得α＝12，则f (x )＝x 12＝x ，是非奇非偶函数，且在(0，＋∞)上是增函数．]2．当x ∈(0，＋∞)时，幂函数y ＝(m 2＋m －1)x －5m －3为减函数，则实数m 的值为( )A ．－2B ．1C ．1或－2D ．m ≠－1±52B [因为函数y ＝(m 2＋m －1)x－5m －3既是幂函数又是(0，＋∞)上的减函数，所以⎩⎪⎨⎪⎧m 2＋m －1＝1，－5m －3＜0，解得m ＝1.]3．若a ＝⎝ ⎛⎭⎪⎫1223，b ＝⎝ ⎛⎭⎪⎫1523，c ＝⎝ ⎛⎭⎪⎫1213，则a ，b ，c 的大小关系是( )A ．a ＜b ＜cB ．c ＜a ＜bC ．b ＜c ＜aD ．b ＜a ＜cD [因为y ＝x23在第一象限内是增函数，所以a ＝⎝ ⎛⎭⎪⎫1223＞b ＝⎝ ⎛⎭⎪⎫1523，因为y ＝⎝ ⎛⎭⎪⎫12x 是减函数，所以a ＝⎝ ⎛⎭⎪⎫1223＜c ＝⎝ ⎛⎭⎪⎫1213，所以b ＜a ＜c .]4．若(a ＋1)12＜(3－2a )12，则实数a 的取值范围是________．⎣⎢⎡⎭⎪⎫－1，23 [易知函数y ＝x 12的定义域为[0，＋∞)，在定义域内为增函数， 所以⎩⎪⎨⎪⎧a ＋1≥0，3－2a ≥0，a ＋1＜3－2a ，解得－1≤a ＜23.]在比较幂值的大小时， 必须结合幂值的特点，选择适当的函数，借助其单调性进行比较，如T 3.考点2 求二次函数的解析式 求二次函数解析式的策略[一题多解]已知二次函数f (x )满足f (2)＝－1，f (－1)＝－1，且f (x )的最大值是8，试确定此二次函数的解析式．[解] 法一：(利用二次函数的一般式) 设f (x )＝ax 2＋bx ＋c (a ≠0)． 由题意得⎩⎪⎨⎪⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b 24a ＝8，解得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7.故所求二次函数为f (x )＝－4x 2＋4x ＋7. 法二：(利用二次函数的顶点式) 设f (x )＝a (x －m )2＋n .∵f (2)＝f (－1)，∴抛物线对称轴为x ＝2＋－12＝12.∴m ＝12，又根据题意函数有最大值8，∴n ＝8，∴y ＝f (x )＝a ⎝ ⎛⎭⎪⎫x －122＋8. ∵f (2)＝－1，∴a ⎝ ⎛⎭⎪⎫2－122＋8＝－1，解得a ＝－4， ∴f (x )＝－4⎝ ⎛⎭⎪⎫x －122＋8＝－4x 2＋4x ＋7.法三：(利用零点式)由已知f (x )＋1＝0的两根为x 1＝2，x 2＝－1， 故可设f (x )＋1＝a (x －2)(x ＋1)， 即f (x )＝ax 2－ax －2a －1.又函数有最大值y max ＝8，即4a －2a －1－a24a ＝8.解得a ＝－4或a ＝0(舍去)，故所求函数解析式为f (x )＝－4x 2＋4x ＋7.求二次函数的解析式常利用待定系数法，但由于条件不同，则所选用的解析式不同，其方法也不同．1.已知二次函数f (x )的图象的顶点坐标是(－2，－1)，且图象经过点(1,0)，则函数的解析式为f (x )＝________.19x 2＋49x －59[法一：(一般式)设所求解析式为f (x )＝ax 2＋bx ＋c (a ≠0)． 由已知得⎩⎪⎨⎪⎧ －b2a＝－2，4ac －b24a ＝－1，a ＋b ＋c ＝0，解得⎩⎪⎨⎪⎧a ＝19，b ＝49，c ＝－59，所以所求解析式为f (x )＝19x 2＋49x －59.法二：(顶点式)设所求解析式为f (x )＝a (x －h )2＋k . 由已知得f (x )＝a (x ＋2)2－1，将点(1,0)代入，得a ＝19，所以f (x )＝19(x ＋2)2－1，即f (x )＝19x 2＋49x －59.]2．已知二次函数f(x)的图象经过点(4,3)，它在x轴上截得的线段长为2，并且对任意x∈R，都有f(2－x)＝f(2＋x)，则函数的解析式f(x)＝________.x2－4x＋3[∵f(2－x)＝f(2＋x)对x∈R恒成立，∴f(x)的对称轴为x＝2.又∵f(x)的图象被x轴截得的线段长为2，∴f(x)＝0的两根为1和3.设f(x)的解析式为f(x)＝a(x－1)(x－3)(a≠0)．又∵f(x)的图象经过点(4,3)，∴3a＝3，a＝1.∴所求f(x)的解析式为f(x)＝(x－1)(x－3)，即f(x)＝x2－4x＋3.]考点3 二次函数的图象与性质解决二次函数图象与性质问题时应注意2点(1)抛物线的开口，对称轴位置，定义区间三者相互制约，要注意分类讨论．(2)要注意数形结合思想的应用，尤其是给定区间上的二次函数最值问题，先“定性”(作草图)，再“定量”(看图求解)．二次函数的图象已知abc＞0，则二次函数f(x)＝ax2＋bx＋c的图象可能是( )A BC DD[A项，因为a＜0，－b2a＜0，所以b＜0.又因为abc＞0，所以c＞0，而f(0)＝c＜0，故A错．B项，因为a＜0，－b2a＞0，所以b＞0.又因为abc＞0，所以c＜0，而f(0)＝c＞0，故B错．C项，因为a＞0，－b2a＜0，所以b＞0.又因为abc＞0，所以c＞0，而f(0)＝c＜0，故C错．D项，因为a＞0，－b2a＞0，所以b＜0，因为abc＞0，所以c＜0，而f(0)＝c＜0，故选D.]识别二次函数图象应学会“三看”。

二次函数与幂函数分层训练A 级 基础达标演练 (时间：30分钟 满分：60分)一、填空题(每小题5分，共30分)1．设函数f (x )＝ax 2＋2x －3在区间(－∞，4)上是单调递增函数，则实数a 的取值范围是________．解析 a ＝0显然成立．a ≠0时，二次函数对称轴为x ＝－1a ，所以a ＜0且－1a≥4，解得－14≤a ＜0，综上，得－14≤a ≤0. ★答案★ ⎣⎢⎡⎦⎥⎤－14，02．已知点⎝ ⎛⎭⎪⎫12，2在幂函数y ＝f (x )的图象上，点⎝ ⎛⎭⎪⎫－2，14在幂函数y ＝g (x )的图象上，则f (2)＋g (－1)＝________.解析 设f (x )＝x m ，g (x )＝x n ，则由2＝⎝ ⎛⎭⎪⎫12m 得m ＝－1，由14＝(－2)n，得n ＝－2，所以f (2)＋g (－1)＝2－1＋(－1)－2＝32.★答案★ 323．(2013·泰州测试)当a ＝________时，函数f (x )＝x 2－2ax ＋a 的定义域为[－1,1]，值域为[－2,2]．解析 f (x )＝(x －a )2＋a －a 2.当a ＜－1时，f (x )在[－1,1]上为增函数，所以⎩⎪⎨⎪⎧f －1＝1＋3a ＝－2，f 1＝1－a ＝2⇒a ＝－1(舍去)；当－1≤a ≤0时，⎩⎪⎨⎪⎧f a ＝a －a 2＝－2，f 1＝1－a ＝2⇒a ＝－1；当0＜a ≤1时，⎩⎪⎨⎪⎧fa ＝a －a 2＝－2，f －1＝1＋3a ＝2⇒a 不存在；当a ＞1时，f (x )在[－1,1]上为减函数，所以⎩⎪⎨⎪⎧f －1＝1＋3a ＝2，f 1＝1－a ＝－2⇒a 不存在．综上可得a ＝－1.★答案★ －14．设f (x )＝x 2－2ax ＋2，当x ∈[－1，＋∞)时，f (x )≥a 恒成立，则实数a 的取值范围是________．解析 当a ≤－1时，f (x )min ＝f (－1)＝3＋2a ，于是由a ≤f (x )min ，得a ≤3＋2a ⇒a ≥－3，所以－3≤a ≤－1；当a ＞－1时，f (x )min ＝f (a )＝2－a 2，于是由a ≤f (x )min ，得a ≤2－a 2⇒－2≤a ≤1，所以，－1＜a ≤1. 综上，得－3≤a ≤1. ★答案★ [－3,1]5．(2012·苏州模拟)给出关于幂函数的以下说法：①幂函数的图象都经过(1,1)点；②幂函数的图象都经过(0,0)点；③幂函数不可能既不是奇函数也不是偶函数；④幂函数的图象不可能经过第四象限；⑤幂函数在第一象限内一定有图象；⑥幂函数在(－∞，0)上不可能是递增函数．其中正确的说法有________．解析 命题①显然正确；只有当α>0时幂函数的图象才能经过原点(0,0)，若α<0，则幂函数的图象不过原点，故命题②错误；函数y ＝x 12就是一个非奇非偶函数，故命题③错误；由于在y ＝x α(α∈R )中，只要x >0，必有y >0，所以幂函数的图象不可能在第四象限，故命题④正确，命题⑤也正确；幂函数y ＝x 3在(－∞，0)上是递增函数，故命题⑥错误．因此正确的说法有①④⑤. ★答案★ ①④⑤6.某汽车运输公司，购买了一批豪华大客车投入营运，据市场分析，每辆客车营运的总利润y (单位：万元)与营运年数x (x ∈N *)为二次函数的关系如图所示，则每辆客车营运________年，使其营运年平均利润最大．解析 由题设y ＝a (x －6)2＋11，过点(4,7)，得a ＝－1.∴y ＝－(x －6)2＋11，则每年平均利润为y x＝－⎝ ⎛⎭⎪⎫x ＋25x ＋12≤－10＋12，当且仅当x ＝5时，取“＝”． ★答案★ 5二、解答题(每小题15分，共30分) 7．已知函数f (x )＝x |x －2|. (1)写出f (x )的单调区间； (2)解不等式f (x )＜3；(3)设0＜a ≤2，求f (x )在[0，a ]上的最大值．解 (1)f (x )的图象如图所示，所以f (x )的增区间为(－∞，1)和(2，＋∞)，减区间为[1,2]．(2)当x ＝3时，f (3)＝3，所以f (x )＜3的解集为(－∞，3)． (3)因为0＜a ≤2，所以当0＜a ≤1时，f (x )在[0，a ]上的最大值为f (x )max ＝f (a )＝2a －a 2；当1＜a ≤2时，f (x )在[0，a ]上的最大值为f (x )max ＝1.综上得f (x )max ＝⎩⎪⎨⎪⎧2a －a 2，0<a ≤1，1，1＜a ≤2.8．已知函数f (x )＝x 2，g (x )＝x －1.(1)若存在x ∈R 使f (x )＜b ·g (x )，求实数b 的取值范围；(2)设F (x )＝f (x )－mg (x )＋1－m －m 2，且|F (x )|在[0,1]上单调递增，求实数m 的取值范围．解 (1)∃x ∈R ，f (x )＜bg (x )⇒∃x ∈R ，x 2－bx ＋b ＜0⇒ (－b )2－4b ＞0⇒b ＜0或b ＞4.(2)F (x )＝x 2－mx ＋1－m 2，Δ＝m 2－4(1－m 2)＝5m 2－4. ①当Δ≤0，即－255≤m ≤255时，则必需⎩⎪⎨⎪⎧m2≤0，－255≤m ≤255⇒－255≤m ≤0.②当Δ＞0，即m ＜－255或m ＞255时，设方程F (x )＝0的根为x 1，x 2(x 1＜x 2)．若m2≥1，则x 1≤0，即⎩⎪⎨⎪⎧m 2≥1，F 0＝1－m 2≤0⇒m ≥2；若m2≤0，则x 2≤0，即⎩⎪⎨⎪⎧m 2≤0，F 0＝1－m 2≥0⇒－1≤m ＜－255；综上所述：实数m 的取值范围是[－1,0]∪[2，＋∞)分层训练B 级 创新能力提升1．(2013·徐州模拟)已知函数f (x )＝x 2＋1的定义域为[a ，b ](a <b )，值域为[1,5]，则在平面直角坐标系内点(a ，b )的运动轨迹与两坐标轴围成的图形面积为________．解析 由题意，得⎩⎪⎨⎪⎧a ＝－2，0≤b ≤2或⎩⎪⎨⎪⎧－2<a ≤0，b ＝2，所以动点(a ，b )的轨迹与两坐标轴围成的图形是边长为2的正方形，面积为4. ★答案★ 42．已知二次函数y ＝f (x )的顶点坐标为⎝ ⎛⎭⎪⎫－32，49，且方程f (x )＝0的两个实根之差等于7，则此二次函数的解析式是________． 解析 设二次函数的解析式为：f (x )＝a ⎝⎛⎭⎪⎫x ＋322＋49(a ≠0)，方程a ⎝ ⎛⎭⎪⎫x ＋322＋49＝0的两个根分别为x 1，x 2，则|x 1－x 2|＝2－49a＝7.∴a ＝－4，故f (x )＝－4x 2－12x ＋40. ★答案★ f (x )＝－4x 2－12x ＋403．(2012·苏锡常镇四市调研)如图，已知二次函数y ＝ax 2＋bx ＋c (a ，b ，c 为实数，a ≠0)的图象过点C (t,2)，且与x 轴交于A ，B 两点，若AC ⊥BC ，则a 的值为________．解析 由二次函数的图象可得a <0，设ax 2＋bx ＋c ＝0两根分别为x 1，x 2，则A (x 1,0)，B (x 2,0)．由AC ⊥BC ，可得(x 1－t ，－2)·(x 2－t ，－2)＝(x 1－t )(x 2－t )＋4＝x 1x 2－t (x 1＋x 2)＋t 2＋4＝c a ＋b a t ＋t 2＋4＝at 2＋bt ＋c a＋4＝0.因为at 2＋bt ＋c ＝2，所以2a ＋4＝0，解得a ＝－12.★答案★ －124．(2012·泰州模拟)已知函数f (x )＝|2x －3|，若0＜2a ＜b ＋1，且f (2a )＝f (b ＋3)，则T ＝3a 2＋b 的取值范围为________．解析 由0＜2a ＜b ＋1，且f (2a )＝f (b ＋3)， 得0＜2a ≤32≤b ＋3，于是由|4a －3|＝|2b ＋3|，得3－4a ＝2b ＋3，所以b ＝－2a ，∴2a ＜－2a ＋1，a ＜14，所以T ＝3a 2＋b ＝3a 2－2a ＝3⎝ ⎛⎭⎪⎫a 2－23a ＝3⎝ ⎛⎭⎪⎫a －132－13.又0＜2a ≤32，所以0＜a <14，所以T ∈⎝ ⎛⎭⎪⎫－516，0.★答案★ ⎝ ⎛⎭⎪⎫－516，0 5．(2012·盐城检测)设二次函数f (x )＝ax 2＋bx ＋c (a ≠0)在区间[－2,2]上的最大值、最小值分别是M ，m ，集合A ＝{x |f (x )＝x }．(1)若A ＝{1,2}，且f (0)＝2，求M 和m 的值；(2)若A ＝{1}，且a ≥1，记g (a )＝M ＋m ，求g (a )的最小值． 解 (1)由f (0)＝2可知c ＝2.又A ＝{1,2}， 故1,2是方程ax 2＋(b －1)x ＋2＝0的两实根． 所以⎩⎪⎨⎪⎧1＋2＝1－b a ，2＝2a .解得a ＝1，b ＝－2.所以f (x )＝x 2－2x ＋2＝(x －1)2＋1，x ∈[－2,2]． 当x ＝1时，f (x )min ＝f (1)＝1，即m ＝1. 当x ＝－2时，f (x )max ＝f (－2)＝10，即M ＝10.(2)由题意知，方程ax 2＋(b －1)x ＋c ＝0有两相等实根x ＝1. 所以⎩⎪⎨⎪⎧1＋1＝1－b a ，1＝ca ，即⎩⎪⎨⎪⎧b ＝1－2a ，c ＝a .所以f (x )＝ax 2＋(1－2a )x ＋a ，x ∈[－2,2]，其对称轴方程为x ＝2a －12a ＝1－12a .又a ≥1，故1－12a ∈⎣⎢⎡⎭⎪⎫12，1.所以M ＝f (－2)＝9a －2.m ＝f ⎝⎛⎭⎪⎫2a －12a ＝1－14a .g (a )＝M ＋m ＝9a －14a－1.又g (a )在区间[1，＋∞)上单调递增，所以当a ＝1时，g (a )min ＝314. 6．(2012·无锡调研)已知13≤a ≤1，若f (x )＝ax 2－2x ＋1在区间[1,3]上的最大值为M (a )，最小值为N (a )，令g (a )＝M (a )－N (a )． (1)求g (a )的函数表达式；(2)判断g (a )的单调性，并求出g (a )的最小值． 解 (1)函数f (x )＝ax 2－2x ＋1的对称轴为直线x ＝1a，而13≤a ≤1，所以1≤1a≤3. 所以f (x )在[1,3]上，N (a )＝f ⎝ ⎛⎭⎪⎫1a ＝1－1a.①当1≤1a ≤2时，即12≤a ≤1时，M (a )＝f (3)＝9a －5.②当2＜1a ≤3时，即13≤a ＜12时，M (a )＝f (1)＝a －1.所以g (a )＝M (a )－N (a )＝⎩⎪⎨⎪⎧9a ＋1a －6，12≤a ≤1，a ＋1a －2，13≤a ＜12.(2)g (a )在⎣⎢⎡⎦⎥⎤12，1上单调递增，在⎣⎢⎡⎭⎪⎫13，12上单调递减，故g (a )min ＝g ⎝ ⎛⎭⎪⎫12＝12.。

（江苏专版）高考数学一轮复习第二章函数的概念与基本初等函数Ⅰ课时跟踪检测（八）二次函数与幂函数文课时跟踪检测（八） 二次函数与幂函数一抓基础，多练小题做到眼疾手快1．(2018·清河中学检测)已知幂函数f (x )＝k ·x α的图象过点⎝ ⎛⎭⎪⎫12，22，则k ＋α＝________.解析：由幂函数的定义知k ＝1.又f ⎝ ⎛⎭⎪⎫12＝22，所以⎝ ⎛⎭⎪⎫12α＝22，解得α＝12，从而k ＋α＝32.答案：322. (2018·扬州中学测试)已知二次函数y ＝3x 2＋2(m －1)x ＋n 在区间(－∞，1)上是减函数，在区间[1，＋∞)上是增函数，则实数m ＝________.解析：二次函数y ＝3x 2＋2(m －1)x ＋n 的图象的开口向上，对称轴为直线x ＝－m －13，要使得函数在区间(－∞，1)上是减函数，在区间[1，＋∞)上是增函数，则x ＝－m －13＝1，解得m ＝－2.答案：－23．(2018·淮阴模拟)已知函数f (x )＝x 2－m 是定义在区间[－3－m ，m 2－m ]上的奇函数，则f (m )，f (0)的大小关系为________．解析：因为函数f (x )是奇函数，所以－3－m ＋m 2－m ＝0，解得m ＝3或－1.当m ＝3时，函数f (x )＝x －1，定义域不是[－6,6]，不合题意；当m ＝－1时，函数f (x )＝x 3在定义域[－2,2]上单调递增，又m ＜0，所以f (m )＜f (0)．答案：f (m )＜f (0)4．若函数f (x )＝(x ＋a )(bx ＋2a )(常数a ，b ∈R)是偶函数，且它的值域为(－∞，2]，则该函数的解析式f (x )＝________.解析：由题意知：a ≠0，f (x )＝(x ＋a )(bx ＋2a )＝bx 2＋(2a ＋ab )x ＋2a 2是偶函数，则其图象关于y 轴对称，所以2a ＋ab ＝0，b ＝－2.所以f (x )＝－2x 2＋2a 2，因为它的值域为(－∞，2]，所以2a 2＝2.所以f (x )＝－2x 2＋2.答案：－2x 2＋25．若二次函数f (x )＝－x 2＋4x ＋t 图象的顶点在x 轴上，则t ＝________.解析：由于f (x )＝－x 2＋4x ＋t ＝－(x －2)2＋t ＋4图象的顶点在x 轴上， 所以f (2)＝t ＋4＝0， 所以t ＝－4. 答案：－46．(2018·杭州测试)若函数f (x )＝x 2－2x ＋1在区间[a ，a ＋2]上的最小值为4，则实数a 的取值集合为________．解析：因为函数f (x )＝x 2－2x ＋1＝(x －1)2的图象的对称轴为直线x ＝1，f (x )在区间[a ，a ＋2]上的最小值为4，所以当a ≥1时，f (x )min ＝f (a )＝(a －1)2＝4，a ＝－1(舍去)或a ＝3；当a ＋2≤1，即a ≤－1时，f (x )min ＝f (a ＋2)＝(a ＋1)2＝4，a ＝1(舍去)或a ＝－3； 当a <1<a ＋2，即－1<a <1时，f (x )min ＝f (1)＝0≠4. 故a 的取值集合为{－3,3}． 答案：{－3,3}二保高考，全练题型做到高考达标 1．(2018·海安中学检测)已知幂函数f (x )＝xα，其中α∈⎩⎨⎧⎭⎬⎫－2，－1，12，1，2，3.则使f (x )为奇函数，且在区间(0，＋∞)上是单调增函数的α的取值集合为________．解析：若幂函数f (x )为奇函数，则α＝－1,1,3，又f (x )在区间(0，＋∞)上是单调增函数，所以α的取值集合为{1,3}．答案：{1,3}2．已知函数h (x )＝4x 2－kx －8在[5,20]上是单调函数，则k 的取值范围是________． 解析：函数h (x )的对称轴为x ＝k 8，因为h (x )在[5,20]上是单调函数，所以k 8≤5或k8≥20，即k ≤40或k ≥160.答案：(－∞，40]∪[160，＋∞)3．若函数f (x )＝(1－x 2)(x 2＋ax －5)的图象关于直线x ＝0对称，则f (x )的最大值是________．解析：依题意，函数f (x )是偶函数，则y ＝x 2＋ax －5是偶函数，故a ＝0，f (x )＝(1－x 2)(x 2－5)＝－x 4＋6x 2－5＝－(x 2－3)2＋4，当x 2＝3时，f (x )取得最大值4.答案：44．(2018·泰州中学调研)已知f (x )是定义在R 上的奇函数，当x <0时，f (x )＝x 2－2x ＋1，不等式f (x 2－3)>f (2x )的解集为________．解析：根据题意，f (x )是定义在R 上的奇函数，则有f (0)＝0，当x <0时，f (x )＝x 2－2x ＋1＝(x －1)2为减函数，则当x >0时，f (x )也为减函数，综上可得f (x )在R 上为减函数，若f (x 2－3)>f (2x )，则有x 2－3<2x ，解得－1<x <3，即不等式f (x 2－3)>f (2x )的解集为(－答案：(－1,3)5．(2018·泰州二中测试)若函数f (x )＝xα2－2α－3(常数α∈Z)为偶函数，且在(0，＋∞)上是单调递减函数，则α的值为________．解析：根据幂函数的性质，要使函数f (x )为偶函数，且在(0，＋∞)上是单调递减函数，则α2－2α－3为偶数，且α2－2α－3＜0，解不等式可得－1＜α＜3.因为α∈Z ，所以α＝0,1,2.当α＝0时，α2－2α－3＝－3，不满足条件；当α＝1时，α2－2α－3＝－4，满足条件；当α＝2时，α2－2α－3＝－3，不满足条件，所以α＝1.答案：16．若函数y ＝x 2－3x －4的定义域为[0，m ]，值域为⎣⎢⎡⎦⎥⎤－254，－4，则m 的取值范围是________．解析：二次函数图象的对称轴为x ＝32，且f ⎝ ⎛⎭⎪⎫32＝－254，f (3)＝f (0)＝－4，由图得m ∈⎣⎢⎡⎦⎥⎤32，3.答案：⎣⎢⎡⎦⎥⎤32，3 7．对于任意实数x ，函数f (x )＝(5－a )x 2－6x ＋a ＋5恒为正值，则a 的取值范围是________．解析：由题意可得⎩⎪⎨⎪⎧5－a ＞0，Δ＝36－45－a a ＋5＜0，解得－4＜a ＜4. 答案：(－4,4)8．(2018·南通一调)若函数f (x )＝ax 2＋20x ＋14(a >0)对任意实数t ，在闭区间[t －1，t ＋1]上总存在两实数x 1，x 2，使得|f (x 1)－f (x 2)|≥8成立，则实数a 的最小值为________．解析：由题意可得，当x ∈[t －1，t ＋1]时，[f (x )max －f (x )min ]min ≥8，当[t －1，t ＋1]关于对称轴对称时，f (x )max －f (x )min 取得最小值，即f (t ＋1)－f (t )＝2at ＋a ＋20≥8，f (t －1)－f (t )＝－2at ＋a －20≥8，两式相加，得a ≥8，所以实数a 的最小值为8.答案：89．已知幂函数f (x )＝x (m 2＋m )－1(m ∈N *)．(1)试确定该函数的定义域，并指明该函数在其定义域上的单调性．(2)若该函数f (x )的图象经过点(2，2)，试确定m 的值，并求满足条件f (2－a )>f (a －1)的实数a 的取值范围．解：(1)因为m 2＋m ＝m (m ＋1)(m ∈N *)，而m 与m ＋1中必有一个为偶数，所以m 2＋m 为偶所以函数f (x )＝x (m 2＋m )－1(m ∈N *)的定义域为[0，＋∞)，并且该函数在[0，＋∞)上为增函数．(2)因为函数f (x )的图象经过点(2，2)，所以2＝2(m 2＋m )－1，即212＝2(m 2＋m )－1，所以m 2＋m ＝2，解得m ＝1或m ＝－2. 又因为m ∈N *，所以m ＝1，f (x )＝x 12.又因为f (2－a )>f (a －1)， 所以⎩⎪⎨⎪⎧2－a ≥0，a －1≥0，2－a >a －1，解得1≤a <32，故函数f (x )的图象经过点(2，2)时，m ＝1.满足条件f (2－a )>f (a －1)的实数a 的取值范围为⎣⎢⎡⎭⎪⎫1，32. 10．(2018·上海七校联考)已知a ，b 为实数，函数f (x )＝x 2＋ax ＋1，且函数y ＝f (x ＋1)是偶函数，函数g (x )＝－b ·f (f (x ＋1))＋(3b －1)·f (x ＋1)＋2在区间(－∞，－2]上是减函数，在区间(－2,0)上是增函数．(1)求函数f (x )的解析式； (2)求实数b 的值；(3)设h (x )＝f (x ＋1)－2qx ＋1＋2q ，问是否存在实数q ，使得h (x )在区间[0,2]上有最小值－2？若存在，求出q 的值；若不存在，说明理由．解：(1)因为函数y ＝f (x ＋1)是偶函数，所以(x ＋1)2＋a (x ＋1)＋1＝(－x ＋1)2＋a (－x ＋1)＋1， 所以4x ＋2ax ＝0，所以a ＝－2， 所以f (x )＝(x －1)2.(2)由(1)知，g (x )＝－b ·f (f (x ＋1))＋(3b －1)·f (x ＋1)＋2＝－bx 4＋(5b －1)x 2＋2－b ，令t ＝x 2，则u (t )＝－bt 2＋(5b －1)t －(b －2)，在区间(－∞，－2]上，t ＝x 2是减函数，且t ∈[4，＋∞)，由g (x )是减函数，可知u (t )为增函数；在区间(－2,0)上，t ＝x 2是减函数，且t ∈(0,4)，由g (x )是增函数，可知u (t )为减函数，所以u (t )在(0,4)上是减函数，在(4，＋∞)上是增函数，可得二次函数开口向上，b ＜0且－5b －1－2b ＝4，所以b ＝－13.(3)h (x )＝f (x ＋1)－2qx ＋1＋2q ＝x 2－2qx ＋1＋2q ，x ∈[0,2]．则h (x )的对称轴为直线x ＝q .当q ＜0时，h (x )min ＝h (0)＝1＋2q ＝－2，q ＝－32；当0≤q ≤2时，h (x )min ＝h (q )＝－q 2＋2q ＋1＝－2，所以q ＝3或－1，舍去； 当q ＞2时，h (x )min ＝h (2)＝－2q ＋5＝－2，q ＝72.综上所述，q ＝－32或q ＝72.三上台阶，自主选做志在冲刺名校1．设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y ＝f (x )－g (x )在x ∈[a ，b ]上有两个不同的零点，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )＝x 2－3x ＋4与g (x )＝2x ＋m 在[0,3]上是“关联函数”，则m 的取值范围为________．解析：由题意知，y ＝f (x )－g (x )＝x 2－5x ＋4－m 在[0,3]上有两个不同的零点．在同一直角坐标系下作出函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象如图所示，结合图象可知，当x ∈[2,3]时，y ＝x 2－5x ＋4∈⎣⎢⎡⎦⎥⎤－94，－2，故当m ∈⎝ ⎛⎦⎥⎤－94，－2时，函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象有两个交点．答案：⎝ ⎛⎦⎥⎤－94，－22．(2018·启东检测)已知a ∈R ，函数f (x )＝x 2－2ax ＋5.(1)若a ＞1，且函数f (x )的定义域和值域均为[1，a ]，求实数a 的值；(2)若不等式x |f (x )－x 2|≤1对x ∈⎣⎢⎡⎦⎥⎤13，12恒成立，求实数a 的取值范围．解：(1)因为f (x )＝x 2－2ax ＋5的图象的对称轴为x ＝a (a ＞1)， 所以f (x )在[1，a ]上为减函数， 所以f (x )的值域为[f (a )，f (1)]． 又已知值域为[1，a ]，所以⎩⎪⎨⎪⎧f a ＝a 2－2a 2＋5＝1，f 1＝1－2a ＋5＝a ，解得a ＝2.(2)由x |f (x )－x 2|≤1，得－12x 2＋52x ≤a ≤12x 2＋52x.(*) 令1x＝t ，t ∈[2,3]，则(*)可化为－12t 2＋52t ≤a ≤12t 2＋52t .记g (t )＝－12t 2＋52t ＝－12⎝ ⎛⎭⎪⎫t －522＋258，则g (t )max ＝g ⎝ ⎛⎭⎪⎫52＝258，所以a ≥258；记h (t )＝12t 2＋52t ＝12⎝ ⎛⎭⎪⎫t ＋522－258，则h (t )min ＝h (2)＝7，所以a ≤7， 综上所述，258≤a ≤7.所以实数a 的取值范围是⎣⎢⎡⎦⎥⎤258，7.。

一轮分层练案(九) 幂函数与二次函数A 级——基础达标1．若f(x)是幂函数，且满足f （4）f （2）＝3，则f ⎝⎛⎭⎫12 ＝( ) A ．3 B ．－3 C ．13D ．－13【答案】C 设f(x)＝x α，则4α2α ＝2α＝3，∴f ⎝⎛⎭⎫12 ＝⎝⎛⎭⎫12 α＝13. 2．已知a ，b ，c ∈R ，函数f(x)＝ax 2＋bx ＋c.若f(0)＝f(4)>f(1)，则( ) A ．a>0，4a ＋b ＝0 B ．a<0，4a ＋b ＝0 C ．a>0，2a ＋b ＝0D ．a<0，2a ＋b ＝0【答案】A 由f(0)＝f(4)，得f(x)＝ax 2＋bx ＋c 图象的对称轴为x ＝－b2a ＝2，∴4a ＋b＝0，又f(0)>f(1)，f(4)>f(1)，∴f(x)先减后增，于是a>0，故选A.3.若幂函数y ＝x －1，y ＝x m 与y ＝x n 在第一象限内的图象如图所示，则m 与n 的取值情况为( )A ．－1<m<0<n<1B ．－1<n<0<mC ．－1<m<0<nD ．－1<n<0<m<1【答案】D 对于幂函数y ＝x α，当α>0时，y ＝x α在(0，＋∞)上为增函数，且0<α<1时，图象上凸，∴0<m<1；当α<0 时，y ＝x α在(0，＋∞)上为减函数，不妨令x ＝2，根据图象可得2－1<2n ，∴－1<n<0，综上所述，故选D.4．已知函数f(x)＝－2x 2＋bx ＋c ，不等式f(x)＞0的解集为(－1，3).若对任意的x ∈[－1，0]，f(x)＋m ≥4恒成立，则m 的取值范围是( )A ．(－∞，2]B ．[4，＋∞)C ．[2，＋∞)D ．(－∞，4]【答案】B 因为f(x)＞0的解集为(－1，3)，故－2x 2＋bx ＋c ＝0的两个根为－1，3，所以⎩⎨⎧－c2＝－1×3，b2＝－1＋3，即⎩⎪⎨⎪⎧b ＝4，c ＝6， 令g(x)＝f(x)＋m ，则g(x)＝－2x 2＋4x ＋6＋m ＝－2(x －1)2＋8＋m ，由x ∈[－1，0]可得g(x)min ＝m ，又g(x)≥4在[－1，0]上恒成立，故m ≥4，故选B.5．(多选)设函数f(x)＝ax 2＋bx ＋c(a ≠0)，对任意实数t 都有f(4＋t)＝f(－t)成立，则函数值f(－1)，f(1)，f(2)，f(5)中，最小的可能是( )A ．f(－1)B ．f(1)C ．f(2)D ．f(5)【答案】ACD 因为对任意实数t 都有f(4＋t)＝f(－t)成立，所以函数f(x)＝ax 2＋bx ＋c(a ≠0)的对称轴是x ＝2，当a ＞0时，函数值f(－1)，f(1)，f(2)，f(5)中，最小的是f(2)；当a ＜0时，函数值f(－1)，f(1)，f(2)，f(5)中，最小的是f(－1)和f(5).6．(多选)由于被墨水污染，一道数学题仅能见到如下文字：“已知二次函数y ＝ax 2＋bx ＋c 的图象过点(1，0)，…，求证：这个二次函数的图象关于直线x ＝2对称．”根据现有信息，题中的二次函数可能具有的性质是( )A ．在x 轴上截得的线段的长度是2B ．与y 轴交于点(0，3)C ．顶点是(－2，－2)D ．过点(3，0)【答案】ABD 由已知得⎩⎪⎨⎪⎧a ＋b ＋c ＝0，－b 2a ＝2，解得b ＝－4a ，c ＝3a ，所以二次函数为y ＝a(x 2－4x ＋3)，其顶点的横坐标为2，所以顶点一定不是(－2，－2)，故选A 、B 、D.7．(多选)已知函数f(x)＝|x 2－2ax ＋b|(x ∈R )，给出下列命题，其中是真命题的是( ) A ．若a 2－b ≤0，则f(x)在区间[a ，＋∞)上单调递增 B ．存在a ∈R ，使得f(x)为偶函数C ．若f(0)＝f(2)，则f(x)的图象关于x ＝1对称D ．若a 2－b －2＞0，则函数h(x)＝f(x)－2有2个零点【答案】AB 对于选项A ，若a 2－b ≤0，则f(x)＝|(x －a)2＋b －a 2|＝(x －a)2＋b －a 2在区间[a ，＋∞)上单调递增，正确；对于选项B ，当a ＝0时，f(x)＝|x 2＋b|显然是偶函数，正确；对于选项C ，取a ＝0，b ＝－2，函数f(x)＝|x 2－2ax ＋b|化为f(x)＝|x 2－2|，满足f(0)＝f(2)，但f(x)的图象不关于x ＝1对称，错误；对于选项D ，如图，a 2－b －2＞0，即a 2－b ＞2，则h(x)＝|(x －a)2＋b －a 2|－2有4个零点，错误．8．若二次函数y ＝8x 2－(m －1)x ＋m －7的值域为[0，＋∞)，则m ＝________．解析：y ＝8⎝ ⎛⎭⎪⎫x －m －116 2 ＋m －7－8⎝ ⎛⎭⎪⎫m －116 2，∵值域为[0，＋∞)，∴m －7－8⎝ ⎛⎭⎪⎫m －116 2＝0，∴m ＝9或m ＝25. 【答案】9或259．已知函数f(x)＝⎩⎪⎨⎪⎧x 2＋x ，－2≤x ≤c ，1x ，c<x ≤3. 若c ＝0，则f(x)的值域是________；若f(x)的值域是⎭⎫－14，2 ，则实数c 的取值范围是________．解析：当c ＝0时，即x ∈[－2，0]时，f(x)∈⎣⎡⎦⎤－14，2 ，当x ∈(0，3]时，f(x)∈⎣⎡⎦⎤13，＋∞ ，所以f(x)的值域为⎣⎡⎭⎫－14，＋∞ .作出y ＝x 2＋x 和y ＝1x 的图象如图所示，当f(x)＝－14 时，x ＝－12 ；当x 2＋x ＝2时，x ＝1或x ＝－2；当1x ＝2时，x ＝12 ，由图象可知当f(x)的值域为⎣⎡⎦⎤－14，2 时，需满足12≤c ≤1.【答案】⎣⎡⎭⎫－14，＋∞ ⎣⎡⎦⎤12，1 10．已知函数f(x)＝x 2＋(2a －1)x －3.(1)当a ＝2，x ∈[－2，3]时，求函数f(x)的值域；(2)若函数f(x)在[－1，3]上的最大值为1，求实数a 的值． 解：(1)当a ＝2时，f(x)＝x 2＋3x －3，x ∈[－2，3]，对称轴为x ＝－32∈[－2，3]，∴f(x)min ＝f ⎝⎛⎭⎫－32 ＝94 －92 －3＝－214 ， f(x)max ＝f(3)＝15，∴函数f(x)的值域为⎣⎡⎦⎤－214，15 . (2)∵函数f(x)的对称轴为x ＝－2a －12 .①当－2a －12 ≤1，即a ≥－12 时，f(x)max ＝f(3)＝6a ＋3，∴6a ＋3＝1，即a ＝－13 ，满足题意；②当－2a －12 ＞1，即a ＜－12 时，f(x)max ＝f(－1)＝－2a －1，∴－2a －1＝1，即a ＝－1，满足题意． 综上可知，a ＝－13或a ＝－1.B 级——综合应用11．设函数f(x)＝1x ，g(x)＝ax 2＋bx(a ，b ∈R ，a ≠0).若y ＝f(x)的图象与y ＝g(x)的图象有且仅有两个不同的公共点A(x 1，y 1)，B(x 2，y 2)，则下列判断正确的是( )A ．当a<0时，x 1＋x 2<0，y 1＋y 2>0B ．当a<0时，x 1＋x 2>0，y 1＋y 2<0C ．当a>0时，x 1＋x 2<0，y 1＋y 2<0D ．当a>0时，x 1＋x 2>0，y 1＋y 2>0【答案】B 当a<0时，作出两个函数的图象，如图，由题意不妨记函数f(x)与g(x)的图象在第三象限交于点A(x 1，y 1)，在第一象限相切于点B(x 2，y 2)，因为函数f(x)＝1x 是奇函数，所以设A 关于原点对称的点为A′(－x 1，－y 1)，显然x 2>－x 1>0，即x 1＋x 2>0，－y 1>y 2，即y 1＋y 2<0；当a>0时，由对称性知x 1＋x 2<0，y 1＋y 2>0.故选B.12．幂函数y ＝x α，当α取不同的正数时，在区间[0，1]上它们的图象是一组美丽的曲线(如图)，设点A(1，0)，B(0，1)，连接AB ，线段AB 恰好被其中的两个幂函数y ＝x a ，y ＝x b 的图象三等分，即有BM ＝MN ＝NA ，那么a －1b＝( )A ．0B ．1C ．12D ．2【答案】A 因为BM ＝MN ＝NA ，点A(1，0)，B(0，1)，所以M ⎝⎛⎭⎫13，23 ，N ⎝⎛⎭⎫23，13 ，将两点坐标分别代入y ＝x a ，y ＝x b ，得a ＝log 13 23 ，b ＝log 23 13 ，所以a －1b ＝log 13 23 －1log 2313＝0.13．(多选)已知函数f(x)＝2x ，g(x)＝x 2－ax ，对于不相等的实数x 1，x 2，设m ＝f （x 1）－f （x 2）x 1－x 2 ，n ＝g （x 1）－g （x 2）x 1－x 2，现有如下说法，其中正确的是( )A ．对于不相等的实数x 1，x 2，都有m ＞0B ．对于任意实数a 及不相等的实数x 1，x 2，都有n ＞0C ．对于任意实数a 及不相等的实数x 1，x 2，都有m ＝nD ．存在实数a ，对任意不相等的实数x 1，x 2，都有m ＝n【答案】AD 任取x 1≠x 2，则m ＝f （x 1）－f （x 2）x 1－x 2 ＝2x 1－2x 2x 1－x 2 ＝2＞0，A 正确；由二次函数的单调性可得g(x)在⎝⎛⎭⎫－∞，a 2 上单调递减，在⎝⎛⎭⎫a2，＋∞ 上单调递增，可取x 1＝0，x 2＝a ，则n ＝g （x 1）－g （x 2）x 1－x 2 ＝g （0）－g （a ）0－a ＝0－00－a＝0，B 错误；m ＝2，n ＝g （x 1）－g （x 2）x 1－x 2 ＝x 21 －ax 1－x 22 ＋ax 2x 1－x 2＝（x 1－x 2）（x 1＋x 2－a ）x 1－x 2＝x 1＋x 2－a ，则m ＝n 不恒成立，C 错误； m ＝2，n ＝x 1＋x 2－a ，若m ＝n ，则x 1＋x 2－a ＝2， 只需x 1＋x 2＝a ＋2即可，D 正确． 14．已知幂函数f(x)的部分对应值如表：则不等式f(|x|)≤2的解集是________． 解析：设幂函数为f(x)＝x α，则⎝⎛⎭⎫12 α＝22 ，∴α＝12 ，∴f(x)＝x 12. 不等式f(|x|)≤2等价于|x|12 ≤2，∴|x|≤4，∴－4≤x ≤4.∴不等式f(|x|)≤2的解集是[－4，4]. 【答案】[－4，4]15．已知值域为[－1，＋∞)的二次函数f(x)满足f(－1＋x)＝f(－1－x)，且方程f(x)＝0的两个实根x 1，x 2满足|x 1－x 2|＝2.(1)求f(x)的表达式；(2)函数g(x)＝f(x)－kx 在区间[－1，2]上的最大值为f(2)，最小值f(－1)，求实数k 的取值范围．解：(1)由f(－1＋x)＝f(－1－x)可得f(x)的图象关于直线x ＝－1对称，设f(x)＝a(x ＋1)2＋h ＝ax 2＋2ax ＋a ＋h(a ≠0)，由函数f(x)的值域为[－1，＋∞)，可得h ＝－1，根据根与系数的关系可得x 1＋x 2＝－2，x 1x 2＝1＋ha ，所以|x 1－x 2|＝（x 1＋x 2）2－4x 1x 2 ＝－4ha＝2， 解得a ＝1，所以f(x)＝x 2＋2x.(2)由题意得函数g(x)在区间[－1，2]上单调递增， 又g(x)＝f(x)－kx ＝x 2－(k －2)x. 所以g(x)的对称轴方程为x ＝k －22，则k －22≤－1，即k ≤0，故k 的取值范围为(－∞，0].C 级——迁移创新16．定义：如果在函数y ＝f(x)定义域内的给定区间[a ，b]上存在x 0(a<x 0<b)，满足f(x 0)＝f （b ）－f （a ）b －a ，则称函数y ＝f(x)是[a ，b]上的“平均值函数”，x 0是它的一个均值点，如y ＝x 4是[－1，1]上的平均值函数，0就是它的均值点．现有函数f(x)＝－x 2＋mx ＋1是[－1，1]上的平均值函数，求实数m 的取值范围．解：因为函数f(x)＝－x 2＋mx ＋1是[－1，1]上的平均值函数，设x 0为均值点，所以f （1）－f （－1）1－（－1） ＝m ＝f(x 0)，即关于x 0的方程－x 20 ＋mx 0＋1＝m 在(－1，1)内有实数根，解方程得x 0＝1或x 0＝m －1.所以必有－1<m －1<1，即0<m<2，所以实数m 的取值范围是(0，2).。

§2.5幂函数、函数与方程考纲解读考点内容解读要求五年高考统计常考题型预测热度2013 2014 2015 2016 20171.二次函数与幂函数1.二次函数的图象与性质2.幂函数的概念B13题5分填空题解答题★★★2.函数的零点与方程的根1.求函数零点2.由函数零点求参数B13题5分填空题解答题★★★分析解读二次函数的图象与性质和函数零点问题是某某高考的热点内容,试题一般难度较大,综合性较强.五年高考考点一二次函数与幂函数1.(2016课标全国Ⅲ理改编,6,5分)已知a=,b=,c=2,则a,b,c的大小关系是(用<连接).答案b<a<c2.(2015某某改编,9,5分)如果函数f(x)=(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间上单调递减,那么mn的最大值为.答案183.(2014某某,16,5分)对于c>0,当非零实数a,b满足4a2-2ab+4b2-c=0且使|2a+b|最大时,-+的最小值为. 答案-24.(2013某某理改编,11,5分)已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=.答案-165.(2013某某,13,5分)在平面直角坐标系xOy中,设定点A(a,a),P 是函数y=(x>0)图象上一动点.若点P,A之间的最短距离为2,则满足条件的实数a的所有值为.答案-1,教师用书专用(6—7)6.(2014某某改编,7,5分)在同一直角坐标系中,函数f(x)=x a(x>0),g(x)=log a x的图象可能是(填序号).答案④7.(2015某某,18,15分)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[-1,1]上的最大值.(1)证明:当|a|≥2时,M(a,b)≥2;(2)当a,b满足M(a,b)≤2时,求|a|+|b|的最大值.解析(1)证明:由f(x)=+b-,得f(x)图象的对称轴为直线x=-.由|a|≥2,得≥1,故f(x)在[-1,1]上单调,所以M(a,b)=max{|f(1)|,|f(-1)|}.当a≥2时,由f(1)-f(-1)=2a≥4,得max{f(1),-f(-1)}≥2,即M(a,b)≥2.当a≤-2时,由f(-1)-f(1)=-2a≥4,得max{f(-1),-f(1)}≥2,即M(a,b)≥2.综上,当|a|≥2时,M(a,b)≥2.(2)由M(a,b)≤2得|1+a+b|=|f(1)|≤2,|1-a+b|=|f(-1)|≤2,故|a+b|≤3,|a-b|≤3,由|a|+|b|=得|a|+|b|≤3.当a=2,b=-1时,|a|+|b|=3,且|x2+2x-1|在[-1,1]上的最大值为2,即M(2,-1)=2.所以|a|+|b|的最大值为3.考点二函数的零点与方程的根1.(2017某某理改编,10,5分)已知当x∈[0,1]时,函数y=(mx-1)2的图象与y=+m的图象有且只有一个交点,则正实数m的取值X围是.答案(0,1]∪[3,+∞)2.(2016某某,15,5分)已知函数f(x)=其中m>0.若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值X围是.答案(3,+∞)3.(2016某某,14,5分)已知函数f(x)=(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2-恰有两个不相等的实数解,则a的取值X围是.答案4.(2015,14,5分)设函数f(x)=①若a=1,则f(x)的最小值为;②若f(x)恰有2个零点,则实数a的取值X围是.答案①-1 ②∪[2,+∞)5.(2015某某改编,8,5分)已知函数f(x)=函数g(x)=b-f(2-x),其中b∈R.若函数y=f(x)-g(x)恰有4个零点,则b的取值X围是.答案6.(2015某某,15,5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)-b有两个零点,则a的取值X 围是.答案(-∞,0)∪(1,+∞)7.(2014某某,13,5分)已知f(x)是定义在R上且周期为3的函数,当x∈[0,3)时, f(x)=.若函数y=f(x)-a在区间[-3,4]上有10个零点(互不相同),则实数a的取值X围是.答案8.(2014某某,14,5分)已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值X围为.答案(0,1)∪(9,+∞)9.(2013某某理改编,10,5分)若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数是.答案 3教师用书专用(10—11)10.(2017课标全国Ⅲ理改编,11,5分)已知函数f(x)=x2-2x+a(e x-1+e-x+1)有唯一零点,则a=.答案11.(2013某某理,20,13分)设函数f n(x)=-1+x+++…+(x∈R,n∈N*).证明:(1)对每个n∈N*,存在唯一的x n∈,满足f n(x n)=0;(2)对任意p∈N*,由(1)中x n构成的数列{x n}满足0<x n-x n+p<.证明(1)对每个n∈N*,当x>0时, f 'n(x)=1++…+>0,故f n(x)在(0,+∞)内单调递增. 由于f1(1)=0,当n≥2时, f n(1)=++…+>0,故f n(1)≥0.又f n=-1++≤-+=-+·=-·<0,所以存在唯一的x n∈,满足f n(x n)=0.(2)当x>0时, f n+1(x)=f n(x)+>f n(x),故f n+1(x n)>f n(x n)=f n+1(x n+1)=0.由f n+1(x)在(0,+∞)内单调递增知,x n+1<x n.故{x n}为单调递减数列.从而对任意n,p∈N*,x n+p<x n.对任意p∈N*,由于f n(x n)=-1+x n++…+=0,①f n+p(x n+p)=-1+x n+p++…+++…+=0,②①式减去②式并移项,利用0<x n+p<x n≤1,得x n-x n+p=+≤≤<=-<.因此,对任意p∈N*,都有0<x n-x n+p<.三年模拟A组2016—2018年模拟·基础题组考点一二次函数与幂函数1.(2018某某常熟高三期中调研)已知幂函数y=(m∈N*)在(0,+∞)上是增函数,则实数m的值是.答案 12.(2018某某东台安丰高级中学月考)已知幂函数y=f(x)的图象过点,则log2f(8)=.答案3.(2018某某海安中学阶段测试)若幂函数f(x)=xα的图象经过点,则其单调减区间为.答案(0,+∞)4.(苏教必1,三,3,2,变式)设α∈,则使函数y=xα的定义域为R且为奇函数的所有α值为.答案1,35.(2016某某某某中学期中)下列幂函数:①y=;②y=x-2;③y=;④y=,其中既是偶函数,又在区间(0,+∞)上单调递增的函数是.(填相应函数的序号)答案③考点二函数的零点与方程的根6.(2018某某金陵中学高三月考)记函数y=ln x+2x-6的零点为x0,若k满足k≤x0且k为整数,则k的最大值为.答案 27.(2018某某姜堰中学高三期中)函数f(x)=log2(3x-1)的零点为.答案8.(2018某某东台安丰高级中学月考)若函数f(x)=在其定义域上恰有两个零点,则正实数a的值为.答案 e9.(2018某某某某中学月考)方程xlg(x+2)=1有个不同的实数根.答案 210.(2018某某天一中学调研)已知函数f(x)=若函数g(x)=f(x)-k有三个零点,则k的取值X围是.答案11.(苏教必1,三,4,2,变式)函数f(x)=2x|log0.5 x|-1的零点个数为.答案 212.(苏教必1,三,4,8,变式)若函数f(x)=(m-2)x2+mx+(2m+1)的两个零点分别在区间(-1,0)和区间(1,2)内,则m 的取值X围是.答案13.(2017某某某某期中,9)已知函数f(x)=若函数g(x)=f(x)-m有三个零点,则实数m的取值X围是.答案14.(2016某某某某中学质检,10)关于x的一元二次方程x2+2(m+3)x+2m+14=0有两个不同的实根,且一根大于3,一根小于1,则m的取值X围是.答案B组2016—2018年模拟·提升题组(满分:35分时间:20分钟)一、填空题(每小题5分,共20分)1.(2017某某某某学情调研,11)已知函数f(x)=若关于x的方程f(x)=k(x+1)有两个不同的实数根,则实数k的取值X围是.答案2.(2017某某、某某第二次模拟考试,12)若函数f(x)=x2-mcos x+m2+3m-8有唯一零点,则满足条件的实数m组成的集合为.答案{2}3.(2017某某苏北四市期末,14)已知函数f(x)=若函数f(x)的图象与直线y=x有三个不同的公共点,则实数a的取值X围为.答案{a|-20<a<-16}4.(2016某某某某中学期中,10)已知关于x的一元二次方程x2-2ax+a+2=0的两个实数根是α,β,且有1<α<2<β<3,则实数a的取值X围是.答案二、解答题(共15分)5.(2017某某某某二中期初,20)设函数f(x)=x2+ax+b(a,b∈R).(1)当b=+1时,求函数f(x)在[-1,1]上的最小值g(a)的表达式;(2)已知函数f(x)在[-1,1]上存在零点,0≤b-2a≤1,求b的取值X围.解析(1)当b=+1时,f(x)=+1,图象的对称轴为x=-,当a<-2时,->1,函数f(x)在[-1,1]上递减,则g(a)=f(1)=+a+2;当-2≤a≤2时,-1≤-≤1,g(a)=f=1;当a>2时,-<-1,函数f(x)在[-1,1]上递增,则g(a)=f(-1)=-a+2.综上可得,g(a)=(2)设s,t是方程f(x)=0的解,且-1≤t≤1,则由于0≤b-2a≤1,故≤s≤(-1≤t≤1),当0≤t≤1时,≤st≤.易知-≤≤0,-≤≤9-4,所以-≤b≤9-4;当-1≤t<0时,≤st≤,由于-2≤<0,-3≤<0,所以-3≤b<0,故b的取值X围是[-3,9-4].C组2016—2018年模拟·方法题组方法1 判断函数零点个数的常用方法1.(2016某某某某中学月考)偶函数f(x)满足f(x-1)=f(x+1),且当x∈[0,1]时,f(x)=-x+1,则关于x的方程f(x)=lg(x+1)在x∈[0,9]上解的个数是.答案9方法2 利用函数零点求参数的值或取值X围2.(2018某某某某高三期中)关于x的方程2|x+a|=e x有3个不同的实数解,则实数a的取值X围为.答案(1-ln 2,+∞)3.(2016某某闸北区调研)已知函数f(x)=若函数g(x)=f(x)-m有3个零点,则实数m的取值X围是.答案(0,1)D组2016—2018年模拟·突破题组(2016某某某某调研,14)已知函数f(x)=x3+ax+,g(x)=-ln x,设函数h(x)=min{f(x),g(x)}(x>0),若h(x)有3个零点,则实数a的取值X围是.答案。

一、填空题1．函数f (x )＝x 2－2x ＋c 在[－2,2]上的最大值是________．解析：因为二次函数f (x )的对称轴为x ＝1并且开口向上，所以在区间[－2,2]上的最大值为f (－2)＝8＋c .答案：8＋c2．若f (x )的定义域为[－2,3]，则f (x )＋log 2(x 2－3)的定义域为________． 解析：∵f (x )的定义域为－2≤x ≤3，由log 2(x 2－3)≥0，则x 2－3≥1，x ≥2或x ≤－2.即f (x )＋log 2(x 2－3)的定义域为2≤x ≤3或x ＝－2.答案：{－2}∪{x |2≤x ≤3}3．y ＝133x －9－|x |－2的定义域为________．解析：依题意⎩⎨⎧|x |－2≥03x －9≠0， 由此解得x ≤－2或x ≥2，且x ≠3，即函数的定义域是{x ∈R|x ≤－2或2≤x <3或x >3}．答案：{x ∈R|x ≤－2或2≤x <3或x >3}4．若函数f (x )＝x －4mx 2＋4mx ＋3的定义域为R ，则实数m 的取值范围是________． 解析：若m ＝0，则f (x )＝x －43的定义域为R ；若m ≠0，则Δ＝16m 2－12m <0，得0<m <34，综上可知，所求的实数m 的取值范围为[0，34)．答案：[0，34)5．函数y ＝|x ＋2|＋(x －3)2的值域为________．解析：y ＝|x ＋2|＋(x －3)2＝|x ＋2|＋|x －3| ＝⎩⎨⎧ －2x ＋1 (x ≤－2)，5 (－2<x <3)，2x －1 (x ≥3).当x ≤－2时，－2x ＋1≥－2×(－2)＋1＝5；当x ≥3时， 2x －1≥2×3－1＝5，∴y ≥5.答案：[5，＋∞)6．函数y ＝log 2 (4－x )的定义域是________．解析：由⎩⎨⎧ 4－x >0log 2 (4－x )≥0， 即⎩⎨⎧4－x >04－x ≥1，得x ≤3. 答案：(－∞，3]7．已知函数f (x )＝x ＋p x －1(p 为常数，且p >0)，若f (x )在(1，＋∞)上的最小值为4，则实数p 的值为________．解析：由题意得x －1>0，f (x )＝x －1＋p x －1＋1≥2p ＋1，当且仅当x ＝p ＋1时，取等号，则2p ＋1＝4，解得p ＝94.答案：948．对a ，b ∈R ，记min {a ，b }＝⎩⎨⎧a (a <b )，b (a ≥b )，函数f (x )＝min ⎩⎨⎧⎭⎬⎫12x ，－|x －1|＋2(x ∈R)的最大值为________．解析：y ＝f (x )是y ＝12x 与y ＝－|x －1|＋2两者中的较小者，数形结合可知，函数的最大值为1.答案：19．定义：区间[x 1，x 2](x 1<x 2)的长度为x 2－x 1.已知函数y ＝2|x |的定义域为[a ，b ]，值域为[1,2]，则区间[a ，b ]的长度的最大值与最小值的差为________．解析：[a ，b ]的长度取得最大值时[a ，b ]＝[－1,1]，区间[a ，b ]的长度取得最小值时[a ，b ]可取[0,1]或[－1,0]，因此区间[a ，b ]的长度的最大值与最小值的差为1. 答案：1二、解答题10．已知函数f (x )＝x 2＋4ax ＋2a ＋6.(1)若函数f (x )的值域为[0，＋∞)，求a 的值；(2)若函数f (x )的函数值均为非负数，求g (a )＝2－a |a ＋3|的值域．解析：(1)∵函数的值域为[0，＋∞)，∴Δ＝16a 2－4(2a ＋6)＝0⇒2a 2－a －3＝0⇒a ＝－1或a ＝32.(2)∵对一切x ∈R ，函数值均为非负数，∴Δ＝8(2a 2－a －3)≤0⇒－1≤a ≤32，∴a ＋3>0，∴g (a )＝2－a |a ＋3|＝－a 2－3a ＋2＝－(a ＋32)2＋174(a ∈[－1，32])．∵二次函数g (a )在[－1，32]上单调递减，∴g (32)≤g (a )≤g (－1)，即－194≤g (a )≤4，∴g (a )的值域为[－194，4]．11．已知函数y ＝log a (ax 2＋2x ＋1)．(1)若此函数的定义域为R ，求a 的取值范围；(2)若此函数的定义域为(－∞，－2－2)∪(－2＋2，＋∞)，求a 的值．解析：(1)ax 2＋2x ＋1>0，Δ＝4－4a ，∵定义域为R.∴a >0，Δ<0，∴a >1.(2)由题意，ax 2＋2x ＋1>0的解集为(－∞，－2－2)∪(－2＋2，＋∞)．∴⎩⎪⎨⎪⎧ －2a ＝－4，1a ＝2，∴a ＝12.12．设f (x )＝2x 2x ＋1，g (x )＝ax ＋5－2a (a >0)． (1)求f (x )在x ∈[0,1]上的值域；(2)若对于任意x 1∈[0,1]，总存在x 0∈[0, 1]，使得g (x 0)＝f (x 1)成立，求a 的取值范围．解析：(1)(导数法) f ′(x )＝4x (x ＋1)－2x 2(x ＋1)2＝2x 2＋4x (x ＋1)2≥0在x ∈[0,1]上恒成立． ∴f (x )在[0,1]上单调递增，∴f (x )在[0,1]上的值域为[0,1]．(2)f (x )在[0,1]上的值域为[0,1]，g (x )＝ax ＋5－2a (a >0)在x ∈[0,1]上的值域为[5－2a,5－a ]．由条件，只需[0,1]⊆[5－2a,5－a ]，∴⎩⎨⎧5－2a ≤05－a ≥1⇒52≤a ≤4.。

【优化探究】2017届高考数学一轮复习 第二章 第四节 二次函数与幂函数课时作业 理 新人教A 版A 组 考点能力演练1．当ab >0时，函数y ＝ax 2与f (x )＝ax ＋b 在同一坐标系中的图象可能是下列图象中的( )解析：因为ab >0，所以，当a <0，b <0时，函数y ＝ax 2的图象开口向下，函数f (x )＝ax ＋b 的图象在x ，y 轴上的截距均为负值，显然D 项满足条件；而当a >0，b >0时，函数y ＝ax2的图象开口向上，函数f (x )＝ax ＋b 的图象在x 轴上的截距为负值，在y 轴上的截距为正值，没有符合条件的选项，故选D.答案：D2．(2015·芜湖质检)已知函数f (x )＝x 2＋x ＋c .若f (0)>0，f (p )<0，则必有( ) A ．f (p ＋1)>0 B ．f (p ＋1)<0 C ．f (p ＋1)＝0D ．f (p ＋1)的符号不能确定解析：函数f (x )＝x 2＋x ＋c 的图象的对称轴为直线x ＝－12，又∵f (0)>0，f (p )<0，∴－1<p <0，p ＋1>0，∴f (p ＋1)>0.答案：A3．若幂函数y ＝(m 2－3m ＋3)·xm 2－m －2的图象不过原点，则m 的取值是( ) A ．－1≤m ≤2 B ．m ＝1或m ＝2 C ．m ＝2D ．m ＝1解析：由幂函数性质可知m 2－3m ＋3＝1，∴m ＝2或m ＝1.又幂函数图象不过原点，∴m 2－m －2≤0，即－1≤m ≤2，∴m ＝2或m ＝1.答案：B4．若函数y ＝x 2－3x －4的定义域为[0，m ]，值域为⎣⎢⎡⎦⎥⎤－254，－4，则m 的取值范围是( ) A ．[0,4]B.⎣⎢⎡⎦⎥⎤32，4C.⎣⎢⎡⎭⎪⎫32，＋∞ D.⎣⎢⎡⎦⎥⎤32，3 解析：二次函数图象的对称轴为x ＝32，且f ⎝ ⎛⎭⎪⎫32＝－254，f (3)＝f (0)＝－4，由图得m ∈⎣⎢⎡⎦⎥⎤32，3.答案：D5．(2015·沧州质检)如果函数f (x )＝x 2＋bx ＋c 对任意的x 都有f (x ＋1)＝f (－x )，那么( )A ．f (－2)<f (0)<f (2)B ．f (0)<f (－2)<f (2)C ．f (2)<f (0)<f (－2)D ．f (0)<f (2)<f (－2)解析：由f (1＋x )＝f (－x )知f (x )的图象关于直线x ＝12对称，又抛物线f (x )开口向上，∴f (0)<f (2)<f (－2)．答案：D6．二次函数f (x )＝x 2＋(2－log 2m )x ＋m 是偶函数，则实数m ＝________.解析：利用偶函数性质求解．因为偶函数的图象关于y 轴对称，所以－2－log 2m2＝0，解得m ＝4.答案：47．已知幂函数f (x )＝x 12-，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．解析：∵f (x )＝x12-＝1x(x >0)，易知x ∈(0，＋∞)时为减函数，又f (a ＋1)<f (10－2a )，∴⎩⎪⎨⎪⎧a ＋1>0，10－2a >0，a ＋1>10－2a ，解得⎩⎪⎨⎪⎧a >－1，a <5，a >3，∴3<a <5. 答案：(3,5)8．(2015·济南二模)已知函数f (x )＝x 2－2x ，x ∈[a ，b ]的值域为[－1,3]，则b －a 的取值范围是________．解析：由题意知，f (x )＝x 2－2x ＝(x －1)2－1，因为函数f (x )在[a ，b ]上的值域为[－1,3]，所以当a ＝－1时，1≤b ≤3；当b ＝3时，－1≤a ≤1，所以b －a ∈[2,4]．答案：[2,4]9．已知函数f (x )＝ax 2＋bx ＋1(a ，b 为实数，a ≠0，x ∈R )．(1)若函数f (x )的图象过点(－2,1)，且方程f (x )＝0有且只有一个根，求f (x )的表达式； (2)在(1)的条件下，当x ∈[－1,2]时，g (x )＝f (x )－kx 是单调函数，求实数k 的取值范围．解：(1)因为f (－2)＝1，即4a －2b ＋1＝1，所以b ＝2a . 因为方程f (x )＝0有且只有一个根，所以Δ＝b 2－4a ＝0. 所以4a 2－4a ＝0，所以a ＝1，所以b ＝2. 所以f (x )＝(x ＋1)2.(2)g (x )＝f (x )－kx ＝x 2＋2x ＋1－kx ＝x 2－(k －2)x ＋1＝⎝ ⎛⎭⎪⎫x －k －222＋1－k －224.由g (x )的图象知：要满足题意，则k －22≥2或k －22≤－1，即k ≥6或k ≤0，∴所求实数k 的取值范围为(－∞，0]∪[6，＋∞)．10．已知函数f (x )＝x 2－2ax ＋5(a >1)．(1)若f (x )的定义域和值域均是[1，a ]，求实数a 的值；(2)若f (x )在区间(－∞，2]上是减函数，且对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4，求实数a 的取值范围．解：(1)∵f (x )＝(x －a )2＋5－a 2(a >1)， ∴f (x )在[1，a ]上是减函数． 又定义域和值域均为[1，a ]．∴⎩⎪⎨⎪⎧f1＝a ，f a ＝1，即⎩⎪⎨⎪⎧1－2a ＋5＝a ，a 2－2a 2＋5＝1，解得a ＝2.(2)∵f (x )在区间(－∞，2]上是减函数， ∴a ≥2.又x ＝a ∈[1，a ＋1]，且(a ＋1)－a ≤a －1， ∴f (x )max ＝f (1)＝6－2a ，f (x )min ＝f (a )＝5－a 2.∵对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4，∴f (x )max －f (x )min ≤4，得－1≤a ≤3.又a ≥2，∴2≤a ≤3.故实数a 的取值范围是[2,3]．B 组 高考题型专练1．(2014·高考浙江卷)在同一直角坐标系中，函数f (x )＝x a(x >0)，g (x )＝log a x 的图象可能是( )解析：函数y ＝x a(x ≥0)与y ＝log a x (x >0)，选项A 中没有幂函数图象，不符合；对于选项B ，y ＝x a(x ≥0)中a >1，y ＝log a x (x >0)中0<a <1，不符合；对于选项C ，y ＝x a(x ≥0)中，0<a <1，y ＝log a x (x >0)中a >1，不符合，对于选项D ，y ＝x a (x ≥0)中0<a <1，y ＝log a x (x >0)中，0<a <1，符合，故选D.答案：D2．(2014·高考北京卷)加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”．在特定条件下，可食用率p 与加工时间t (单位：分钟)满足函数关系p ＝at2＋bt ＋c (a ，b ，c 是常数)，如图记录了三次实验的数据．根据上述函数模型和实验数据，可以得到最佳加工时间为( )A ．3.50分钟B ．3.75分钟C ．4.00分钟D ．4.25分钟解析：由已知得⎩⎪⎨⎪⎧9a ＋3b ＋c ＝0.7，16a ＋4b ＋c ＝0.8，25a ＋5b ＋c ＝0.5，解得⎩⎪⎨⎪⎧a ＝－0.2，b ＝1.5，c ＝－2，∴p ＝－0.2t 2＋1.5t －2＝－15⎝⎛⎭⎪⎫t －1542＋1316，∴当t ＝154＝3.75时p 最大，即最佳加工时间为3.75分钟．故选B.答案：B3．(2013·高考辽宁卷)已知函数f (x )＝x 2－2(a ＋2)x ＋a 2，g (x )＝－x 2＋2(a －2)x －a2＋8.设H 1(x )＝max{f (x )，g (x )}，H 2(x )＝min{f (x )，g (x )}(max{p ，q }表示p ，q 中的较大值，min{p ，q }表示p ，q 中的较小值)．记H 1(x )的最小值为A ，H 2(x )的最大值为B ，则A －B ＝( )A ．a 2－2a －16 B ．a 2＋2a －16 C ．－16D ．16解析：f (x )＝g (x )，即x 2－2(a ＋2)x ＋a 2＝－x 2＋(a －2)x －a 2＋8，即x 2－2ax ＋a 2－4＝0，解得x ＝a ＋2或x ＝a －2.f (x )与g (x )的图象如图.由图及H 1(x )的定义知H 1(x )的最小值是f (a ＋2)，H 2(x )的最大值为g (a －2)，A －B ＝f (a ＋2)－g (a －2)＝(a ＋2)2－2(a ＋2)2＋a 2＋(a －2)2－2(a －2)2＋a 2－8＝－16. 答案：C4．(2015·高考福建卷)若a ，b 是函数f (x )＝x 2－px ＋q (p >0，q >0)的两个不同的零点，且a ，b ，－2这三个数可适当排序后成等差数列，也可适当排序后成等比数列，则p ＋q 的值等于________．解析：依题意有a ，b 是方程x 2－px ＋q ＝0的两根，则a ＋b ＝p ，ab ＝q ，由p >0，q >0可知a >0，b >0.由题意可知ab ＝(－2)2＝4＝q ，a －2＝2b 或b －2＝2a ，将a －2＝2b 代入ab ＝4可解得a ＝4，b ＝1，此时a ＋b ＝5，将b －2＝2a 代入ab ＝4可解得a ＝1，b ＝4，此时a ＋b ＝5，则p ＝5，故p ＋q ＝9.答案：9。

第 4 讲幂函数与二次函数基础稳固题组(建议用时： 40 分钟 )一、填空题．幂函数的图象过点 2，1，则它的单一递加区间是 ______．14αα 12分析设幂函数 y＝ x ，则 2 ＝4，解得α＝－ 2，所以 y＝x－，故函数 y＝x－2的单一递加区间是 (－∞， 0)．答案(－∞， 0)．·浙江七校模拟)二次函数2＋4x＋ t 图象的极点在 x 轴上，则 t 的2 (2013y＝－ x值是 ________．分析二次函数图象的极点在x 轴上，所以＝42－×－1)×＝，解得t4 (t0＝－ 4.答案－43．(2014 ·扬州检测 )若函数 f(x)＝x2＋ax＋ b 的图象与 x 轴的交点为 (1,0)和(3,0)，则函数 f(x)的单一递加区间为 ________．分析由已知可得该函数的图象的对称轴为x＝2，又二次项系数为1＞0，所以 f(x)在(－∞，2]上是递减的，在 [2，＋∞ )上是递加的．答案[2，＋∞ )．若＜，则a,a,－a的大小关系是 ________．4a00.555分析5－a＝ 1 a，由于a ＜时，函数y＝xa 单一递减，且1＜＜，所以550.5 5 a a－a5 ＜0.5＜5 .答案a a－a5 ＜0.5 ＜55．(2014 ·南阳一中月考 )函数 f(x)＝log a (6－ ax)在 [0,2] 上为减函数，则 a 的取值范围是 ________．分析若 0＜a＜1，则 f(x)不行能为减函数，当a＞ 1 时，由函数 (f)x＝log a(6－ax)在 [0,2] 上为减函数，知 6－ax＞0 在[0,2] 恒建立，等价于 (6－ax)min＞ 0，即 6－2a＞0，得 a＜3，所以 a 的取值范围是 (1,3)．答案(1,3)6．二次函数 y＝ f(x)知足 f(3＋x)＝ f(3－x)(x∈R)，且 f(x)＝0 有两个实根 x1，x2，则 x1＋x2＝ ________.分析由 f(3＋x)＝f(3 －x)，知函数y＝ f(x)的图象对于直线x＝3 对称，应有x1＋ x2＝3? x1＋x2＝ 6.2答案67．(2014 ·苏州检测 )已知函数 y＝－ x2＋ 4ax 在区间 [1,3] 上单一递减，则实数a 的取值范围是 ________．1分析依据题意，得对称轴x＝2a≤1，所以 a≤2.1答案－∞，22．已知函数x， x≥2，f(x)＝若对于 x 的方程 f(x)＝k 有两个不一样的实根，8x－1 3， x<2.则实数 k 的取值范围是 ________．分析将方程有两个不一样的实根转变为两个函数图象有两个不一样的交点．作出函数 f(x)的图象，如图，由图象可知，当0<k<1 时，函数 f(x)与 y＝k 的图象有两个不一样的交点，所以所务实数k 的取值范围是 (0,1)．答案(0,1)二、解答题9．已知二次函数 f(x)的二次项系数为a，且 f(x)＞－ 2x 的解集为 {x|1＜x＜3} ，方程 f(x)＋6a＝ 0 有两相等实根，求 f(x)的分析式．解设 f(x)＋ 2x＝a(x－1)(x－ 3) (a＜0)，则 f(x)＝ax2－4ax＋3a－2x，f(x)＋6a＝ax2－(4a＋2)x＋9a，＝[－(4a＋2)] 2－36a2＝0，即 (5a＋1)(a－1)＝0，1解得 a＝－5或 a＝ 1(舍去 )．1263所以 f(x)的分析式为 f(x)＝－5x －5x－5.10．设函数 y＝x2－2x，x∈[－ 2， a] ，求函数的最小值g(a)．解∵函数 y＝x2－2x＝(x－1)2－1，∴对称轴为直线 x＝1，而 x＝ 1 不必定在区间 [－ 2， a] 内，应进行议论．当－ 2<a<1 时，函数在 [ －2，a]上单一递减，则当 x＝ a 时， y min＝ a2－2a；当 a≥1 时，函数在 [ －2,1]上单一递减，在 [1， a] 上单一递加，则当 x＝ 1 时，y min＝－ 1.a2－ 2a，－ 2<a<1，综上， g(a)＝－1， a≥ 1.能力提高题组(建议用时： 25 分钟 )一、填空题1．(2014 ·江门、佛山模拟 )已知幂函数 f(x)＝xα，当 x＞1 时，恒有 f(x)＜x，则α的取值范围是 ________．分析当 x＞ 1 时，恒有 f(x)＜ x，即当 x＞1 时，函数 f(x)＝xα的图象在 y＝x的图象的下方，作出幂函数f(x)＝xα在第一象限的图象，由图象可知α＜1时知足题意．答案 (－∞， 1)2．(2014·衡水中学二调)设会合2＋2x－3＞0}，集合B＝A ＝{ x|x{ x|x2－2ax－1≤0，a＞0} .若A∩B中恰含有一个整数，则实数 a 的取值范围是 ________．分析A＝{ x|x2＋ 2x－3＞0}＝{ x|x＞1，或 x＜－ 3}，由于函数y＝ f(x)＝ x2－ 2ax－ 1 的对称轴为 x＝ a＞ 0，f(0)＝－ 1＜0，依据对称性可知要使 A∩B 中恰含有一个整数，则这个整数解为2，所以有f(2)≤0 且f(3) ＞ 0 ，即34－4a－1≤0，a≥4，34所以4即4≤a＜3.9－6a－1＞0，a＜3，3 4答案 [4，3)13．已知函数 f(x)＝x2，给出以下四个命题：①若 x＞1，则 f(x)＞ 1；②若 0＜x1＜ x2，则 f(x2)－f(x1)＞ x2－x1；③若 0＜x1＜ x2，则 x2 f(x1)＜x1f(x2)；④若 0＜x1＜ x2，则f x1＋f x2＜fx1＋x2.22此中，全部正确命题的序号是________．1分析对于①：∵y＝x2在 (0，＋∞ )上为增函数，∴当x ＞112111 时，f(x)＞f(1) ＝1，①正确；对于②：取 x＝4，x＝4，此时 f(x )＝2，f x xf(x2)＝ 2，但 f(x2)－f(x1)＜x2－x1，②错误；对于③：结构函数g(x)＝x＝x，x－x2x x则 g′(x)＝x2＝－2x2＜0，所以g(x)在(0，＋∞)上为减函数，当x2＞x1f x2 f x11＞ 0时，有x2＜x1，即 x1f(x2)＜x2f(x1)，③错误；对于④：画出f(x)＝x2在(0，＋∞)的图象，可知f x1＋f x2＜ f122x＋x，④正确．2答案①④二、解答题4．(2014 ·辽宁五校联考 )已知函数 f(x)是定义在R上的偶函数，且当 x≤ 0 时，f(x)＝ x2＋2x.现已画出函数 f(x)在 y 轴左边的图象，如下图，请依据图象：(1)写出函数 f(x)(x∈R)的增区间；(2)写出函数 f(x)(x∈R)的分析式；(3)若函数 g(x)＝f(x)－ 2ax＋ 2(x∈ [1,2]) ，求函数 g(x)的最小值．解 (1)f(x)在区间 (－1,0)，(1，＋∞ )上单一递加．(2)设 x＞0，则－ x＜ 0，函数 f(x)是定义在R上的偶函数，且当x≤0 时， f(x)＝x2＋2x，∴f(x)＝ f(－ x)＝(－x)2＋ 2× (－x)＝ x2－2x(x＞ 0)，x2－ 2x x＞0 ，∴f(x)＝x2＋2x x≤0 .(3)g(x)＝x2－ 2x－2ax＋2，对称轴方程为x＝a＋1，当 a＋1≤1，即 a≤0 时， g(1)＝1－2a 为最小值；当 1＜a＋1≤ 2，即 0＜a≤1 时， g(a＋1)＝－ a2－2a＋ 1 为最小值；当 a＋ 1＞2，即 a＞1 时，g(2)＝ 2－ 4a 为最小值．1－2a a≤ 0 ，综上， g(x)min＝－a2－2a＋1 0＜a≤1，2－4a a＞ 1 .。

一、填空题1、函数y ＝5x 与函数y ＝－15x 的图象关于________对称。

解析：因y ＝－15x ＝－5－x ，所以关于原点对称。

答案：原点2、为了得到函数y ＝3×(13)x 的图象，可以把函数y ＝(13)x 的图象向________平移________个单位长度。

解析：函数y ＝3×(13)x ＝(13)x －1，∴把函数y ＝(13)x 的图象向右平移一个单位便得到y ＝(13)x －1，即y ＝3×(13)x .答案：右 13.函数y ＝1－1x －1的图象是________。

解析：将函数y ＝1x 的图形变形到y ＝1x －1，即向右平移一个单位，再变形到y ＝－1x －1，即将前面图形沿x 轴翻转，再变形到y ＝－1x －1＋1，从而得到答案②. 答案：②4、设函数f (x )＝|x |x ＋bx ＋c ，则下列命题中正确命题的序号有________。

(请将你认为正确的命题序号都填上)①当b >0时，函数f (x )在R 上是单调增函数；②当b <0时，函数f (x )在R 上有最小值；③函数f (x )的图象关于点(0，c )对称；④方程f (x )＝0可能有三个实数根。

解析：f (x )＝⎩⎨⎧x 2＋bx ＋c ，x ≥0，－x 2＋bx ＋c ，x <0，结合图象可知①正确，②不正确，对于③，因为|x |x ＋bx 是奇函数，其图象关于原点(0,0)对称，所以f (x )的图象关于点(0，c )对称，③正确；当c ＝0，b <0时f (x )＝0有三个实数根，故④正确。

答案：①③④5、已知函数f (x )＝|x －a |x ＋b (a ，b ∈R)，给出下列命题：(1)当a ＝0时，f (x )的图象关于点(0，b )成中心对称；(2)当x >a 时，f (x )是递增函数；(3)当0≤x ≤a 时，f (x )的最大值为a 24＋b .其中正确的序号是________。