指数函数的概率密度函最大似然估计

- 1 - 习题一：

1.1 写出下列随机试验的样本空间：

(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;

解：连续5 次都命中，至少要投5次以上，故,7,6,51；

(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;

解：12,11,4,3,22；

(3) 观察某医院一天内前来就诊的人数;

解：医院一天内前来就诊的人数理论上可以从0到无穷，所以,2,1,03；

(4) 从编号为1，2，3，4，5 的5 件产品中任意取出两件, 观察取出哪两件产品;

解：属于不放回抽样，故两件产品不会相同，编号必是一大一小，故：

;51,4jiji

(5) 检查两件产品是否合格;

解：用0 表示合格, 1 表示不合格，则1,1,0,1,1,0,0,05；

(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2);

解：用x表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间，故：

216,TyxTyx；

(7) 在单位圆内任取两点, 观察这两点的距离;

解：207xx；

(8) 在长为l的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.

解：lyxyxyx,0,0,8；

1.2

(1) A 与B 都发生, 但C 不发生; CAB；

(2) A 发生, 且B 与C 至少有一个发生;)(CBA；

(3) A,B,C 中至少有一个发生; CBA； - 2 - (4) A,B,C 中恰有一个发生;CBACBACBA；

(5) A,B,C 中至少有两个发生; BCACAB；

(6) A,B,C 中至多有一个发生;CBCABA；

(7) A;B;C 中至多有两个发生;ABC

第二章 随机变量

2.1

X 2 3 4 5 6 7 8 9 10 11 12

P 1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36

2.2解：根据1)(0kkXP，得10kkae，即1111eae。

故 1ea

2.3解：用X表示甲在两次投篮中所投中的次数，X~B(2,0.7)

用Y表示乙在两次投篮中所投中的次数, Y~B(2,0.4)

(1) 两人投中的次数相同

P{X=Y}= P{X=0,Y=0}+ P{X=1,Y=1} +P{X=2,Y=2}=

0011220202111120202222220.70.30.40.60.70.30.40.60.70.30.40.60.3124CCCCCC(2)甲比乙投中的次数多

P{X>Y}= P{X=1,Y=0}+ P{X=2,Y=0} +P{X=2,Y=1}=

1020211102200220112222220.70.30.40.60.70.30.40.60.70.30.40.60.5628CCCCCC2.4解:（1）P{1≤X≤3}= P{X=1}+ P{X=2}+ P{X=3}=12321515155

(2) P{0.5

2.5解：（1）P{X=2,4,6,…}=246211112222k=11[1()]1441314kklim （2）P{X≥3}=1―P{X<3}=1―P{X=1}- P{X=2}=1111244

2.6解：设iA表示第i次取出的是次品，X的所有可能取值为0，1，2

12341213124123{0}{}()(|)(|)(|)PXPAAAAPAPAAPAAAPAAAA=18171615122019181719

1123412342341234{1}{}{}{}{}2181716182171618182161817162322019181720191817201918172019181795PXPAAAAPAAAAPAAAAPAAAA

标准正态分布概率密度函数

f(x) = (1 / √(2π)) * exp(-(x^2 / 2))

其中，“f(x)”表示概率密度函数，而“exp”表示自然指数函数，“π”表示圆周率。该概率密度函数的图像呈钟形曲线，中心位于坐标原点(0, 0)，并且在中心处取得最大值。

概率密度函数的性质之一是对称性。对于标准正态分布来说，概率密度函数在均值(μ=0)附近关于y轴对称。这就意味着，当x的取值远离0时，曲线的斜率逐渐减小，即变得越平缓。而在0点两侧，斜率逐渐增加，即变得越陡峭。

正态分布具有中心极限定理的重要性质，意味着当样本容量增加时，样本均值的分布将趋近于正态分布。这是由于标准正态分布是众多独立随机变量的总和的极限分布。

当计算标准正态分布概率密度函数的积分时，往往需要使用查表方法或者计算机软件进行计算。在统计学中，通过积分得到的概率值可以用来进行假设检验、置信区间估计以及统计推断等。

总结来说，标准正态分布的概率密度函数是用来描述服从该分布的随机变量在不同取值处的概率分布情况。它的均值为0，标准差为1，呈现出钟形曲线的形态特征，并具有对称性。概率密度函数在实际应用中被广泛使用，可用于计算区间概率以及进行统计推断等相关分析。

K2MG-E《专业技术人员绩效管理与业务能力提升》练习与答案

- 1 -

习题一：1.1 写出下列随机试验的样本空间：

(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;

解：连续5 次都命中，至少要投5次以上，故；

(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;

解：；

(3) 观察某医院一天内前来就诊的人数;

解：医院一天内前来就诊的人数理论上可以从0到无穷，所以；

(4) 从编号为1，2，3，4，5 的5 件产品中任意取出两件, 观察取出哪两件产品;

解：属于不放回抽样，故两件产品不会相同，编号必是一大一小，故：

(5) 检查两件产品是否合格;

解：用0 表示合格, 1 表示不合格，则；

(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2);

解：用表示最低气温, 表示最高气温;考虑到这是一个二维的样本空间，故：

；

(7) 在单位圆内任取两点, 观察这两点的距离;

解：；

(8) 在长为的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.

解：；

1.2

(1) A 与B 都发生, 但C 不发生; ；

(2) A 发生, 且B 与C 至少有一个发生;；

(3) A,B,C 中至少有一个发生; ；

(4) A,B,C 中恰有一个发生;；

(5) A,B,C 中至少有两个发生; ； K2MG-E《专业技术人员绩效管理与业务能力提升》练习与答案

- 2 - (6) A,B,C 中至多有一个发生;；

(7) A;B;C 中至多有两个发生;

(8) A,B,C 中恰有两个发生. ；

注意：此类题目答案一般不唯一，有不同的表示方式。

1.3 设样本空间, 事件=,

具体写出下列各事件：

(1) ; (2) ; (3) ; (4)

（1）；

(2) =；

指数函数的概念

指数函数是一种常见的数学函数，以指数为自变量，以一个常数(基数)为底数的幂函数为定义。该函数的特点是随着自变量指数的增长或减小，函数值呈现出快速增长或快速衰减的趋势。

指数函数的一般形式可以表示为f(x) = a^x，其中a是一个正常数，且a≠1。指数函数的定义域为实数集R，值域为正实数集R+。

在指数函数中，底数a决定了函数的增长速度。当a>1时，随着指数的增大，函数值呈现出快速增长的趋势；当0

指数函数在实际生活和科学研究中有广泛的应用。下面列举几个常见的应用场景。

1. 经济领域的复利计算

指数函数在经济领域的复利计算中有着重要的应用。当我们将一笔本金以一定的利率投资，利息会按照指数函数的增长趋势不断积累，使得投资额快速增加。复利计算常被应用于银行、保险、投资等金融领域。

2. 自然界中的增长和衰减

指数函数也被广泛地应用于自然界的增长和衰减现象的描述。例如，生物种群的增长、放射性元素的衰变等都可以使用指数函数来描述和预测。在这些情况下，指数函数提供了一个完整的模型，能够准确描述物种的繁衍和元素的衰变过程。 3. 物理学中的衰减和振荡

在物理学中，指数函数也扮演着重要的角色。比如在电路中，电容器或电感器的充放电过程中，电流的变化会随时间按指数函数的规律发生衰减或振荡。指数函数的应用使得物理学家可以更好地研究和理解电路中的现象。

4. 统计学中的概率分布

指数函数在统计学中也有重要的应用。例如，指数分布常用于描述事件发生的时间间隔，如两个红绿灯的间隔时间、地震发生的时间间隔等。指数分布的概率密度函数形式为f(x) =

λe^(-λx)，其中λ为正常数。通过指数函数的应用，可以对这些事件发生的概率进行统计和预测。

总之，指数函数具有快速增长或衰减的特性，在数学和实际应用中都有广泛的应用。通过研究指数函数的性质和应用，我们能更好地理解和解决各种实际问题。

K1+478～K1+5888段左侧片石混凝土挡土墙第1部分- 1 -页脚内容习题一：1.1 写出下列随机试验的样本空间：

(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;

解：连续5 次都命中，至少要投5次以上，故；

(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;

解：；

(3) 观察某医院一天内前来就诊的人数;

解：医院一天内前来就诊的人数理论上可以从0到无穷，所以；

(4) 从编号为1，2，3，4，5 的5 件产品中任意取出两件, 观察取出哪两件产品;

解：属于不放回抽样，故两件产品不会相同，编号必是一大一小，故：

(5) 检查两件产品是否合格;

解：用0 表示合格, 1 表示不合格，则；

(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2);

解：用表示最低气温, 表示最高气温;考虑到这是一个二维的样本空间，故：

；

(7) 在单位圆内任取两点, 观察这两点的距离;

解：；

(8) 在长为的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.

解：；

1.2

(1) A 与B 都发生, 但C 不发生; ；

(2) A 发生, 且B 与C 至少有一个发生;；

(3) A,B,C 中至少有一个发生; ； K1+478～K1+5888段左侧片石混凝土挡土墙第1部分- 2 -页脚内容(4) A,B,C 中恰有一个发生;；

(5) A,B,C 中至少有两个发生; ；

(6) A,B,C 中至多有一个发生;；

(7) A;B;C 中至多有两个发生;

(8) A,B,C 中恰有两个发生. ；

注意：此类题目答案一般不唯一，有不同的表示方式。

1.3 设样本空间, 事件=,

具体写出下列各事件：

(1) ; (2) ; (3) ; (4)

（1）；

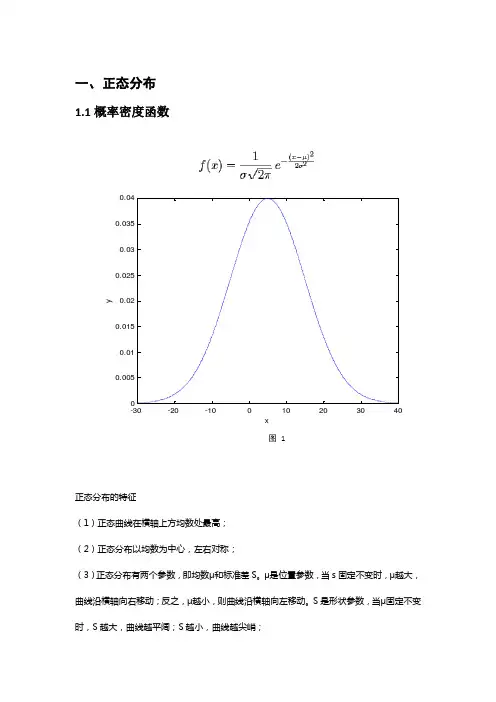
一、 正态分布

1.1概率密度函数

正态分布的特征

（1）正态曲线在横轴上方均数处最高；

（2）正态分布以均数为中心，左右对称；

（3）正态分布有两个参数，即均数μ和标准差S。μ是位置参数，当s固定不变时，μ越大，曲线沿横轴向右移动；反之，μ越小，则曲线沿横轴向左移动。S是形状参数，当μ固定不变时，S越大，曲线越平阔；S越小，曲线越尖峭； -30-20-1001020304000.0050.010.0150.020.0250.030.0350.04xy图 1 （4）正态曲线下面积的分布有一定规律：

①正态分布时区间（μ-1s,μ+1s）的面积占总面积的68.27%；②正态分布时区间（μ-1.96s,μ+1.96s）的面积占总面积的95%；③正态分布时区间（μ-2.58s,μ+2.58s）的面积占总面积的99%。

1.2、分布函数

图-2

正态分布是连续性变数的理论分布，计算其概率的原理和方法不同于二项分布。它不能计算变量取某一定值，即某一点时的概率，而只能计算变量落在某一区间内的概率（即-100-80-60-40-2002040608010000.10.20.30.40.50.60.70.80.91xp概率密度）。

对于任何正态分布随机变量 x 落入任意区间（ a ， b ）的概率可以表示为： P(a

1.3、正态分布可度函数

图 3

-100-80-60-40-2002040608010000.10.20.30.40.50.60.70.80.91by1.4、正态分布失效率函数

(x) =f(x)/R(x)

图

4

1.5、应用、问题、案例

考察某个工程的质量，由于偶然误码差的存在，其实际质量评分是不相同的，如将所有的数值按一定的组距进行大小分组整理，每组的分值个数叫做频率。以频率为纵坐标，数值为横坐标，可求出各组坐标，用线段把这些点连接起来，就可得到“中间高，两边低，左右近似对称”的折线。这折线叫实验分布曲线。由于它近似于理论分布曲线，可根据理论分布曲线的数学表达式，对工程质量的情况进行研究和讨论。

第二章 随机变量 2.1

2.2解：根据1)(0kkXP，得10kkae，即1111eae。

故 1ea

2.3解：用X表示甲在两次投篮中所投中的次数，X~B(2,0.7)

用Y表示乙在两次投篮中所投中的次数, Y~B(2,0.4)

(1) 两人投中的次数相同

P{X=Y}= P{X=0,Y=0}+ P{X=1,Y=1} +P{X=2,Y=2}=

0011220202111120202222220.70.30.40.60.70.30.40.60.70.30.40.60.3124CCCCCC(2)甲比乙投中的次数多

P{X>Y}= P{X=1,Y=0}+ P{X=2,Y=0} +P{X=2,Y=1}=

1020211102200220112222220.70.30.40.60.70.30.40.60.70.30.40.60.5628CCCCCC2.4解:（1）P{1≤X≤3}= P{X=1}+ P{X=2}+ P{X=3}=12321515155

(2) P{0.5

2.5解：（1）P{X=2,4,6,…}=246211112222k=11[1()]1441314kklim

（2）P{X≥3}=1―P{X<3}=1―P{X=1}- P{X=2}=1111244

2.6解：(1)设X表示4次独立试验中A发生的次数，则X~B(4,0.4)

34314044(3)(3)(4)0.40.60.40.60.1792PXPXPXCC X 2 3 4 5 6 7 8 9 10 11 12

P 1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36 (2)设Y表示5次独立试验中A发生的次数，则Y~B(5,0.4)

- 1 - normal函数

normal函数又被称为正态分布函数，是数理统计中用到的概率密度函数。它又称为高斯分布，是描述任何经济学、地理学、天文学以及政治学等具有规律分布的广泛性分布的函数。在计算机科学中，normal函数也被称为高斯函数，它的特点是可以用来模拟出某些随机变量的概率分布。

normal函数的数学表达式是：f(x) = 1/(σ*√2pi) * exp(-x^2/2σ^2) 。其中σ是normal函数的标准差，x是正态分布的函数变量，μ是均值，exp是指数函数。normal函数的密度函数随着x值的变化，分布中心也将移动，因而也会在一定程度上影响normal函数的形状。

normal函数在实际工程中有很多应用。比如在温度传感器测量时，采用normal函数来拟合温度传感器的读数，从而按照传感器的特性来实现准确的读数。此外，normal函数也可以用来模拟不同情况下的信号传输，如模拟噪声信号。

正态分布函数在概率论中也有相应的应用，如显著性检验、极大似然估计等。显著性检验是一种统计检验，它通过使用极大似然函数来测定给定变量的显著性，在极大似然函数中，normal函数可以用来建立变量的概率密度。

正态分布函数由于其容易理解和计算的特点，被经常用于抽样误差的估计、回归分析和推断技术的应用。比如在回归分析中，normal函数可以用来描述观测值的分布特性，而抽样误差的估计可以利用normal函数来估计抽样误差。 - 2 - normal函数也经常用在模式识别中，如计算机视觉和语音识别等。在视觉识别中，通常利用normal函数来拟合图片模型的灰度分布，从而实现对某些图片模型的分析。而在语音识别中，normal函数也可以被用于模拟语谱图的概率分布，从而实现语音识别。

normal函数由于具有广泛性和简便性的特点，在各种领域都有广泛的应用。其应用不仅在计算机科学，经济学、地理学、天文学、政治学以及概率论等多个领域都可以看到它的影子。它是描述不确定性概率关系的重要函数，可以用来描述存在规律性的随机性分布，是一种有用的概率密度函数。

概率密度函数与分布函数的关系

概率密度函数：在数学中，连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

指数分布的概率密度是指数函数是重要的基本初等函数之一。

通常地，y=ax函数(a为常数且以a\ue0，a≠1)叫作指数函数，函数的定义域就是 r 。特别注意，在指数函数的定义表达式中，在ax前的系数必须就是数1，自变量x必须在指数的边线上，且无法就是x的其他表达式，否则，就不是指数函数。

细胞的分裂是一个很有趣的现象，新细胞产生的速度之快是十分惊人的。例如，某种细胞在分裂时，1个分裂成2个，2个分裂成4个，因此，理想条件下第x次分裂得到新细胞数y与分裂次数x的函数关系式即为：这个函数便是指函数的形式，且自变量为幂指数，我们下面来研究这样的函数。

未知驱动探索，专注成就专业

1

Gamma分布密度函数

介绍

Gamma分布是一种概率分布，常用于描述随机事件的持续时间或等待时间。它在统计学、概率论和相关领域中被广泛使用。本文将介绍Gamma分布的数学定义、性质、概率密度函数以及其在实际应用中的一些例子。

数学定义

Gamma分布表现为一个连续概率分布，其函数形式可以表示为：

f(x; k, θ) = 1 / (θ^k * Γ(k)) * x^(k-1) * exp(-x/θ)

其中，k是形状参数(shape parameter)，θ是尺度参数(scale parameter)，exp为指数函数，Γ(k)是Gamma函数。Gamma函数定义为：

Γ(k) = ∫(0, ∞) t^(k-1) * exp(-t) dt

Gamma分布的形状由参数k决定，尺度由参数θ决定。 未知驱动探索，专注成就专业

2

参数选择

在使用Gamma分布时，参数k和θ的选择非常重要。参数k决定了分布的形状，可以用于控制分布的偏度(skewness)和峰度(kurtosis)。参数θ决定了分布的尺度，可以控制分布的变化范围。

性质

Gamma分布有一些重要的性质：

1. 期望值和方差： Gamma分布的期望值和方差分别由参数k和θ决定：

– 期望值: E(x) = k * θ

– 方差: Var(x) = k * θ^2

通过调整参数k和θ，可以改变Gamma分布的期望值和方差。

2. 归一化： Gamma分布的概率密度函数经过归一化处理，总和等于1。 未知驱动探索，专注成就专业

3

3. 累积分布函数： Gamma分布的累积分布函数表示随机变量X小于或等于x的概率，可以表示为：

F(x; k, θ) = ∫[0, x] f(t; k, θ) dt

其中，f(t; k, θ)是Gamma分布的概率密度函数。

4. 最大似然估计： 对于给定的一组观测值，可以使用最大似然估计方法来估计Gamma分布的参数k和θ。最大似然估计是一种常用的统计方法，用于求取使得观测值出现的可能性最大的参数值。

正态分布概率公式

正态分布是一种概率分布，它在许多自然现象中具有重要意义，可以用来提供定量描述。正态分布也被称为钟形曲线，因为一个正态分布的曲线是一个钟形的抛物线。

正态分布用一个函数来描述一个变量的概率分布，它的函数表达式是这样的：

f(x)=1/sqrt(2*pi*σ^2)*exp(-(x-μ)^2/2*σ^2)

其中，f(x)是概率密度函数，x是变量的取值，μ是总体均值，σ是总体标准差，pi是圆周率，2*σ^2表示方差，exp(-(x-μ)^2/2*σ^2)表示指数函数。

正态分布的概率密度函数在总体均值μ的位置取最大值，两边对称地逐渐减小。它的概率密度函数曲线是一个钟状的抛物线，抛物线的两端出现了“尾部”，反映了极端值==出现的可能性越来越小。

正态分布及其变种（比如双正态分布）的累积概率函数可以用来表示一组统计数据的概率分布。举个例子，假设有一组考试分数，均值为75分，标准差为5分。我们可以使用正态分布函数求出每个考试成绩在一个区间中的概率。

例如，求60～90分之间的考试成绩的概率。

此时我们可以使用正态分布概率公式：

概率=累积概率（90分）-累积概率（60分）=F(90）-F(60）

累积概率函数F(x)的表达式为： F(x)=1/2*（1+erf ((x-μ)/σ/sqrt (2))

概率分布函数与随机变量的期望

概率分布函数（Probability Density Function，PDF）和随机变量的期望（Expectation）是概率论与数理统计中常见的概念，它们对于描述和分析随机变量的分布特征具有重要意义。

一、概率分布函数（Probability Density Function）

概率分布函数是描述随机变量取各个取值的概率的函数。在统计学中，常见的概率分布函数有几何分布、泊松分布、正态分布等。以正态分布为例，它的概率分布函数可以表示为：

f(x) = (1 / (σ * √(2π))) * exp(-(x-μ)²/(2σ²))

其中，f(x)为随机变量X取值为x的概率密度，μ为均值，σ为标准差，exp()为指数函数。

二、随机变量的期望（Expectation）

随机变量的期望是指随机变量在大量重复试验中取各个值的平均值。可以用公式来表示，以离散型随机变量为例：

E(X) = ∑(x * P(X = x))

其中，E(X)表示随机变量X的期望，x表示随机变量X的取值，P(X = x)表示随机变量X取值为x的概率。

对于连续型随机变量，期望的计算需要对概率密度函数进行积分：

E(X) = ∫(x * f(x) dx) 其中，f(x)为随机变量X的概率密度函数。

三、应用示例

假设某超市的销售额（单位：万元）服从正态分布，均值为50万元，标准差为10万元。现在我们希望计算超市一天的销售额的期望是多少。

根据正态分布的概率密度函数公式，代入μ和σ的值，我们可以得到超市一天销售额的概率密度函数为：

f(x) = (1 / (10 * √(2π))) * exp(-(x-50)²/(2*10²))

然后，我们可以对概率密度函数进行积分，计算超市一天销售额的期望：

E(X) = ∫(x * (1 / (10 * √(2π))) * exp(-(x-50)²/(2*10²)) dx)

最常见的变量分布类型是

离散型随机变量的常见分布

1、0-1分布

伯努利试验（Bernoulli trial）：在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。

2、二项分布（Binomial distribution）

二项代表它有两种可能的结果，成功或失败。它满足性质：每次试验成功的概率均是相同的，记录为p；失败的概率也相同，为1-p。每次试验必须相互独立，该试验也叫做伯努利试验，重复n次即二项概率分布，它主要用于解决n次试验中成功x次的概率。

掷硬币就是一个典型的二项分布。当我们要计算抛硬币n次，恰巧有x次正面朝上的概率，可以使用二项分布的公式：f(x)=(nx)px(1−p)n−x

数学期望为E(x)=np，方差Var(x)=np(1-p)

【例】假设现在有一个抽奖活动，每位用户拥有10次抽奖机会，中奖概率是5%。老板准备先考虑成本问题，想知道至少有3次以上中奖机会的概率是多少？

思路一：可以拿恰巧3次，恰巧4次直到恰巧10次累加求和，但是这样太麻烦了。

思路二：先计算最多2次的概率是多少，f(0)+f(1)+f(2)，结果是92.98%，利用逆向思维：概率公式1-92.98%，就是至少3次的概率了，为7.02%。

PS：二项分布和泊松分布、正太分布的关系

二项分布是多次伯努利，即扔多次硬币

泊松分布是p很小的二项，即扔好多好多次硬币，且扔出正面概率极小

正态分布是n很大的二项，即扔好多好多次硬币，且硬币是完全相同的

3、泊松分布（Poison distribution）

泊松概率主要用于估计某事件在特定时间或空间中发生的次数。比如一天内中奖的个数，一个月内某机器损坏的次数等。x代表发生x次，u代表发生次数的数学期望，概率函数为：

f(x)=uxe−ux!

【例】现在又举办了一个新的运营活动，这次的中奖概率未知，只知24小时内中奖的平均个数为5个，老板想知道24小时内恰巧中奖次数为7的概率是多少？

2021年大二重点课程概率论与数理统计通用试题及答案（精品）

一、单选题

1、对正态总体的数学期望进行假设检验，如果在显著水平0.05下接受00:H，那么在显著水平0.01下，下列结论中正确的是

（A）必须接受0H （B）可能接受，也可能拒绝0H

（C）必拒绝0H （D）不接受，也不拒绝0H

【答案】A

2、设总体X服从正态分布212,,,,,nNXXX是来自X的样本，则2的最大似然估计为

（A）211niiXXn （B）2111niiXXn （C）211niiXn （D）2X

【答案】A

3、已知nXXX,,,21是来自总体的样本，则下列是统计量的是（ ）

XXA)( +A niiXnB1211)( aXC)( +10 131)(XaXD+5

【答案】B

4、下列二无函数中， 可以作为连续型随机变量的联合概率密度。

A）f(x,y)=cosx,0,x,0y122其他

B) g(x,y)=cosx,0,1x,0y222其他

C) (x,y)=cosx,0,0x,0y1其他

D) h(x,y)=cosx,0,10x,0y2其他

【答案】B 5、设X的密度函数为)(xf，分布函数为)(xF，且)()(xfxf。那么对任意给定的a都有

A）0()1()afafxdx B） 01()()2aFafxdx

C）)()(aFaF D） 1)(2)(aFaF

【答案】B

6、设总体X服从正态分布212,,,,,nNXXX是来自X的样本，则2的最大似然估计为

高斯分布特征函数

高斯分布（Gaussian distribution）是概率论与统计学中常用的一个连续概率分布。它又称为正态分布，是一种对称的钟形曲线，特点是均值和标准差，可以通过概率密度函数来描述。在机器学习中，高斯分布经常被用于对数据的建模。特征函数是将输入空间映射到特征空间的函数，用于提取数据的特征。在高斯分布中，特征函数用于计算每个样本的特征向量。

高斯分布的概率密度函数（Probability Density Function，PDF）可以表示为：

f(x，μ,σ)=(1/(σ*√(2π)))*e^(-((x-μ)^2)/(2σ^2))

其中，μ是均值，σ是标准差，e是自然对数的底。

特征函数是一种从输入空间到特征空间的映射，可以将原始数据转化为可以更容易处理的特征向量。在高斯分布中，特征函数可以是各种形式的函数，用于提取数据的特征。常见的特征函数有多项式函数、高斯函数、指数函数等。

在机器学习中，高斯分布特征函数被广泛应用于分类、回归以及聚类等任务中。对于分类任务，可以使用高斯分布特征函数来构建分类器，通过计算样本在特征空间中的距离或相似度，来判断其属于哪个类别。对于回归任务，可以使用高斯分布特征函数来建立回归模型，通过拟合数据的概率分布来预测输出。对于聚类任务，可以使用高斯分布特征函数来表示每个类别的概率分布，通过最大化概率来将样本划分为不同的簇。

在实际应用中，高斯分布特征函数可以根据具体问题进行选择和设计。常用的特征函数包括多项式特征函数、高斯核函数、拉普拉斯核函数等。多项式特征函数可以通过多项式扩展将低维数据映射到高维特征空间，从而增加模型的表达能力。高斯核函数和拉普拉斯核函数则可以通过非线性映射将样本映射到高维空间，从而更好地建模非线性关系。

总结来说，高斯分布特征函数是一种将输入空间映射到特征空间的函数，用于提取数据的特征。在高斯分布中，特征函数可以是各种形式的函数，用于计算每个样本的特征向量。在机器学习中，高斯分布特征函数被广泛应用于分类、回归、聚类等任务中，通过对数据进行建模和特征提取，来实现模型的训练和预测。