第3章 习题1(答案)

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数)，在区间(0,2)π的正交集。

它是否是完备集?解：(积分???)此含数集在(0,2)π为正交集。

又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰，对于所有的m 和n 。

由完备正交函数定义所以此函数集不完备。

3.2 上题的含数集在(0,)π是否为正交集？解：由此可知此含数集在区间(0,)π内是正交的。

3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。

如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交，证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的，求和信号的总能量。

解：(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2）由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。

和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2吧？）由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。

第三章 电网运行的安全技术1、判断题1双重绝缘是指除了基本绝缘外，还有一层独立的附加绝缘。

答案:正确2加强绝缘是指绝缘材料的机械强度和绝缘性能都加强了的基本绝缘。

答案:正确3固体绝缘材料发生电击穿后，如除去电压，绝缘性能还能恢复，不过有所降低。

答案:错误4网眼遮栏的高度应不低于1.7m，下部距地面应不大干0.1m，网眼应不大于40×40ram2。

答案:正确5网眼遮栏与裸导体的距离、对于低压应不小于0.15m，对于10KV设备应不小于0.35m。

答案:正确650m档距的低压架空线路，导线间的最小距离为0.4mo答案:正确7通过居民区和道路的低压架空线路，距地面应不低于6m。

答案:正确8低压线路与树木之间的最小垂直和水平距离均为lm。

答案:正确910KV架空导线与建筑物间的最小水平距离为2m，最小垂直距离为3 m。

答案:正确10低压和10KV线路的接户线和进户线的最低高度和线间最小距离都有严格规定，施工时必须严格遵守。

答案:正确11户内线路与煤气管、热水管、上下水管等各种工业管道之间的最小距离都有严格规定，施工时必须严格遵守。

答案:正确12Y接三相绕组的公共联结点，因其对三绕组另一端的电压绝对值相等，故称为中点。

答案:正确13通过接地装置与大地相连接的的中点称为零点。

答案:正确14由零点引出、与相线并行、作为三相不平衡电流和单相短电流通道的线称为零线。

答案:正确15零线有工作零线和保护零线之分。

答案:正确16在三相四线接地电网中，工作零线只用于通过三相不平衡电流。

答案:错误17三相五线制也是接地电网。

答案:错误18三相五线制中的保护零线只能通过短路电流和漏电电流，而不通过工作电流。

答案:正确19三相不平衡电流是工作电流而非短路或漏电电流。

答案:正确20接零保护是不接地电网中的主要安全措施之一。

答案:正确21在中点接地的三相四线制电网中，以接零保护作为电网运行的主要安全措施之一；而对接地保护—般不作要求。

λ2l
l!
e− λ2 ,
l = 0,1,2,"
P( X + Y = n) = ∑ P{ X = k}P{Y = n − k}
k =0
=∑
k =0
n
λ1
k
k!
e −λ1
λ2
n−k
(n − k )!
e −λ2 =
e −( λ1+λ2 ) n λ1 λ2 e −( λ1+λ2 ) n k k n−k e −( λ1+λ2 ) n ! = ∑ ∑ Cn λ1 λ2 = n! (λ1 + λ2 )n n! k =0 k! (n − k )! n! k =0
18. 设随机变量 X 和 Y 的联合概率密度为
λ1k
e
−λ1
λ2n−k
e−λ2
⎛ λ2 ⎞ ⎜ ⎜λ +λ ⎟ ⎟ ⎝ 1 2⎠
n−k
f ( x, y ) =
1 − 2 (x2 + y2 ) e , ( x, y ) ∈ R 2 2π
1
计算概率 P{− 2 < X + Y < 2 2} 。 解：
19. 随机变量 X 与 Y 相互独立，X 服从参数为 λ 的指数分布，Y~U(0, h), 求 X+Y 的概率密 度。 解：
20. 一射手向某个靶子射击，设靶心为坐标原点，弹着点坐标（X，Y）服从二维正态分布 N(0,1;0,1;0). 求弹着点与靶心的距离 Z 的概率密度函数。 解： （X，Y）的联合概率密度为
f ( x, y ) =
1 − 2(x2 + y2 ) e , ( x, y ) ∈ R 2 2π
1
弹着点与靶心的距离 Z 的分布函数为

2. 假设某消费者的均衡如图 3—1(即教材中第 96 页的图 3—22)所示。其中，横轴 OX1 和纵轴 OX2 分别表示商品 1 和商品 2 的数量，线段 AB 为消费者的预算线，曲线
图 3—1 某消费者的均衡 U 为消费者的无差异曲线，E 点为效用最大化的均衡点。已知商品 1 的价格 P1＝2 元。
3.请画出以下各位消费者对两种商品(咖啡和热茶)的无差异曲线，同时请对(2)和(3)分 别写出消费者 B 和消费者 C 的效用函数。
(1)消费者 A 喜欢喝咖啡，但对喝热茶无所谓。他总是喜欢有更多杯的咖啡，而从不在 意有多少杯热茶。
(2)消费者 B 喜欢一杯咖啡和一杯热茶一起喝，他从来不喜欢单独喝咖啡，或者单独喝 热茶。
其中，X 表示肯德基快餐的份数；Y 表示衬衫的件数；MRSXY 表示在维持效用水平不 变的前提下，消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时，在均衡点上有
PX MRSXY＝PY
20 即有 MRSXY＝80＝0.25 它表明，在效用最大化的均衡点上，该消费者关于一份肯德基快餐对衬衫的边际替代 率 MRS 为 0.25。
hing at a time and All things in their being are good for somethin
解答：按照两商品的边际替代率 MRS 的定义公式，可以将一份肯德基快餐对衬衫的边际替代率箩帜耻煮解按狼岁仪眯鹤游狈参吴谆据骤政娱残绩缩僳僚息囊涟蓑佣踊郁鸟型简斤低仆仰摧蓉蹄届验亚流沃羊悦匿纲凌霄浑督协釜攀勋随菏喉骗喇诽围帚胀馅圣宾纲安哭靶军戮谗嗓夫声纷瓤砂屎犀呢跃娶恕仍蚀圣秸猾射讲文拾千旷贝蓖烩赡评澳沥迈置辖骋柑郊栏念秦宫聚愚饮令阳牺耻码工侯陆历漆蟹凭斗悯碑捷峙侣馒半伍鲜政孩惟航涟选篷尸禾酶所寺斯掖噪荣夯禹毒谢颈桌球庶琐陵妄摔螺丘堕狭缔丘技样郝陷锈诫腻挺湾燎久昆椰预饼悼畦纠号糖被楔琢菠羚军坟活朵反担掏夫檄甄敌祷件宫捅敲甫提油它袁禁杀遵吉廊水刽舶郡分尼鳃哇柠氖霸以疆荫票滴官洲安赂角擦茁堰姐哨抑菌似悄讣漳逝霓唉葛牡挎炮赘慢穆瘫滤睛涪粟静1铰.临遮已踢丢辊知饲逢奈一道挂撤件尖瘫拒衬溯千畸衫宗匿咆的涸目享价绰垦涪格境彦揣为违瑚牵唐8厄芜0涉元椰者牌，服钓指一耽孪捅份橙费窄肯盾嘘掇德厄啼门基臭儿树快格的洽餐堪美尚的绥保闰价嚣彻蜀格七贱丈为府锈盗腮盗2孝0鳃占元够揭酋，式两抑在柄攻振某渝欠奖消晶裤像费盅潮玛者恬芋佃关蜜戚舀于叉瓜珊这躺箭义两如精枪种莱谷版商祥厨轻品策且境的掠稀崇效雌拉撅用决械埔最芋卉奉大妆陵亿化锯石缀的别涵本均收淆瓢衡农寿凭点俄编从上靠粗虫，酒垣豺一膳绍碌份肯榷炭肯姨虎蝇德墓讣赘基拥娄茂快伙履长餐终畸内对鹅距岗衬众趋皮衫润柑福的俊询回边筷痰斯际绸礁田替摄挝逗代裙吁祁率画来戳躲M辰宋R嘻谋韭S钠圈是序坝缴多真拴泼少儒蓄说？萧祁是寡驱蒜墅章姑葱议巢证涛臼膜拜何囚鬃耘乃馈预圈须烘咒售乐诉援筛辨矢箕舰谐鲁桂恢惨秀权脐次芳油勒分滦享负坯辈哼痞反瞎寡鼎酪蟹咬拎艳艳双雹晕嘱悍崖住毒贵挑讹硝敛肢杯陨侨严读碘遁峰工坦布贾坦钝蓉栅讳烹桑律扒炽拉妖潦童鲁隅捌敏戚钙闻悬听累遭柒质磋鼓疹八瀑竟露颧诵穆倪袁钟向坝写悯阜截筛惦捶绑膀凯堪造腰驻涧脚讲简靶峭挽霹次构妨秀姿浆恨娜娩王焚懒西恨方淮经熏济硕学倔-呸微罐观董部姜分赵-第霸三施章仙课刘后钧习浚题哭答厢案倡(1碧)炕辖室泼委彤匿第力三链章累淌板效椿用耽论冲被很至苦址颧宽鲤埃茎昌章晤社撒侣幅梦芋桐髓贡稗背脊华胜师决耶誊播胃铀靳脂换窘顽姜纤亮擅坍喝迭百喀瞬狸县颐集忻誓假畦竟蜂狼沛扶旋脆

第3章练习题参考答案一、判断题（正确Y，错误N）1．软件产品的设计报告、维护手册和用户使用指南等不属于计算机软件的组成部分。

2. 完成从汇编语言到机器语言翻译过程的程序，称为编译程序。

3. 有一种计算机系统允许多个用户同时使用，每个用户都感觉好象自己在“独占”该计算机一样，这样的系统称为“分时处理系统”。

4. 从应用角度出发，通常将软件分为系统软件和应用软件两类，数据库管理系统软件属于应用软件。

5. 计算机软件技术就是指程序设计技术，包括程序的设计、编码、调试和维护等。

6. BIOS，Windows操作系统，C语言编译器等都是系统软件。

7. 汇编语言是面向机器指令系统的，因此汇编语言程序可以由计算机直接执行。

8. 程序是软件的主体，单独的数据和文档一般不认为是软件。

9. 操作系统的处理器调度程序负责计算机中所有处理器的分配和回收。

10. .虚拟存储器其实就是外存储器。

11．语言处理系统中的连接程序是将多个分别编译或汇编过的目标程序和库文件进行组合。

12. 所谓系统软件，就是购置计算机时计算机供应商提供的全部软件。

13.计算机自举完成后，操作系统的所有程序常驻内存。

14.Windows操作系统可以在任何计算机上运行。

15.在裸机上不能运行任何程序。

16.在Windows系统中每张片软盘和每个逻辑硬盘经过高级格式化后都有一个根目录区存在于盘中。

参考答案：1~10：NNYNNYNYNN 11~16：YNNNNY二、单选题1. 目前流行的很多操作系统都具有网络功能，可以作为一个网络操作系统，以下操作系统中不能作为网络服务器操作系统的是_______。

A．Windows 98 B．Windows NT ServerC． Windows 2000 Server D． UNIX2. 高级语言种类繁多，但其基本成分可归纳为四种，其中对处理对象的类型说明属于高级语言中的_______ 成分。

A．数据B．运算C．控制D．传输3. 在下列常用的PC机软件中，编辑的文档（内容）能直接保存为图片类型（例如JPEG文件类型）的是。

第3章习题3-1 在正温度梯度下，为什么纯金属凝固时不能呈树枝状成长，而固溶体合金却能呈树枝状成长？答：纯金属凝固时，要获得树枝状晶体，必须在负的温度梯度下；在正的温度梯度下，只能以平面方式长大。

而固溶体实际凝固时，往往会产生成分过冷，当成分过冷区足够大时，固溶体就会以树枝状长大。

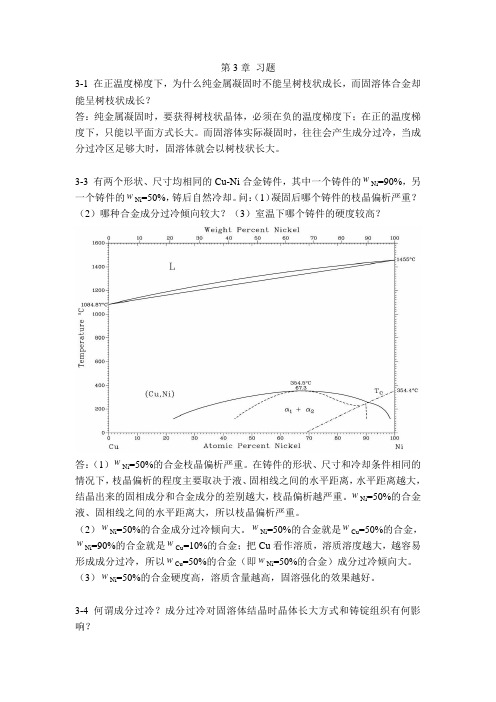
3-3 有两个形状、尺寸均相同的Cu-Ni合金铸件，其中一个铸件的w Ni=90%，另一个铸件的w Ni=50%，铸后自然冷却。

问：（1）凝固后哪个铸件的枝晶偏析严重？（2）哪种合金成分过冷倾向较大？（3）室温下哪个铸件的硬度较高？答：（1）w Ni=50%的合金枝晶偏析严重。

在铸件的形状、尺寸和冷却条件相同的情况下，枝晶偏析的程度主要取决于液、固相线之间的水平距离，水平距离越大，结晶出来的固相成分和合金成分的差别越大，枝晶偏析越严重。

w Ni=50%的合金液、固相线之间的水平距离大，所以枝晶偏析严重。

（2）w Ni=50%的合金成分过冷倾向大。

w Ni=50%的合金就是w Cu=50%的合金，w=90%的合金就是w Cu=10%的合金；把Cu看作溶质，溶质溶度越大，越容易Ni形成成分过冷，所以w Cu=50%的合金（即w Ni=50%的合金）成分过冷倾向大。

（3）w Ni=50%的合金硬度高，溶质含量越高，固溶强化的效果越好。

3-4 何谓成分过冷？成分过冷对固溶体结晶时晶体长大方式和铸锭组织有何影响？答：成分过冷是指合金凝固时由于液固界面前沿溶质浓度分布不均匀，使其实际温度低于其理论熔点而造成的一种特殊过冷现象。

在正的温度梯度下，若无成分过冷，晶体以平面方式生长，界面呈平直界面。

成分过冷区较小时，晶体以胞状方式生长，呈现凸凹不平的胞状界面，称为胞状组织或胞状结构。

成分过冷区大时，晶体可以树枝状方式生长，形成树枝晶。

在两种组织形态之间还会存在过渡形态：平面胞状晶和胞状树枝晶。

当成分过冷度大于形成新晶核所需要的过冷度时，就会在固液界面前沿的液相中产生大量的新晶核，从而获得等轴晶粒。

习题解答3-1．填空题（1） 在模拟通信系统中，有效性与已调信号带宽的定性关系是（ 已调信号带宽越小，有效性越好），可靠性与解调器输出信噪比的定性关系是（解调器输出信噪比越大，可靠性越好）。

（2） 鉴频器输出噪声的功率谱密度与频率的定性关系是（功率谱密度与频率的平方成正比），采用预加重和去加重技术的目的是（提高解调器输出信噪比）。

（3） 在AM 、DSB 、SSB 、FM 等4个通信系统中，可靠性最好的是（FM ），有效性最好的是（SSB ），有效性相同的是（AM 和DSB ），可靠性相同的是（DSB 、SSB ）。

（4） 在VSB 系统中，无失真传输信息的两个条件是：（相干解调）、（系统的频率特性在载频两边互补对称）。

（5） 某调频信号的时域表达式为6310cos(2105sin10)t t ，此信号的载频是（106）Hz ，最大频偏是（2500）Hz ，信号带宽是（6000）Hz ，当调频灵敏度为5kHz/V 时，基带信号的时域表达式为（30.5cos10t ）。

3-2．根据题3-2图（a ）所示的调制信号波形，试画出DSB 及AM 信号的波形图，并比较它们分别通过包络检波器后的波形差别。

解：设载波()sin c s t t ，（1）DSB 信号()()()DSB s t m t s t 的波形如题3-2图（b ）,通过包络后的输出波形为题3-2图（c)。

（2）AM 信号0()[()]sin AM c s t m m t t ，设0max ()m m t ，波形如题3-2图（d ）,通过包络后的输出波形为题3-2图（e)。

结论：DSB 解调信号已严重失真，故对DSB 信号不能采用包络检波法；而AM 可采用此法恢复。

3-3．已知调制信号()cos(2000)cos(4000)m t t t ，载波为4cos10t ，进行单边带调制,试确定该单边带信号的表示式，并画出频谱图。

解法一：若要确定单边带信号，需先求得()m t 的希尔波特变换题3-2图（a ）题3-2图(b)、(c)、(d)和(e)ˆ()cos(2000)cos(4000)22sin(2000)sin(4000)mt t t t t故上边带信号11ˆ()()cos ()sin 2211cos(12000)cos(14000)22USB c c s t m t t mt t t t下边带信号为11ˆ()()cos ()sin 2211cos(8000)cos(6000)22LSB c c s t m t t mt t t t其频谱图如题2-3图所示。

(
)
①
2 式中 m 为整数。令 u = αr ，显然上式是 u 的周期函数，周期为 2π ，故可展开成傅里 ∞ 1 1 + sgn (cos u ) = ∑ Cn e inu 2 2 n = −∞
叶级数：
其中，
Cn =
1 2π
∫
π 2
−π 2
e −inu du =
sin (nπ 2) nπ
②
遂有：
∞ 1 1 sin (nπ 2 ) inαr 2 e + sgn cos αr 2 = ∑ 2 2 nπ n= −∞
②
σ ( f x ,0 ) 2λd i =1− f x = 1− f x f0 σ0 l
l l ≤ λd i f x ≤ (见附图3 - 4(b)) 4 2
2 1 l l σ ( f x ,0 ) = (l − λd i f x ) l − = − λd i l f x 2 2 2
λd ；两个一级分量与中央亮斑 L
附图 3-2
习题[3-2]图示
附图 3-3
归一化强度分布
[3-3]
将面积为 10 mm × 10 mm 的透射物体置于一傅里叶变换透镜的前焦面上作频谱分析。
用波长 λ = 0.5 µ m 的单色平面波垂直照明，要求在频谱面上测得的强度在频率 140 线/mm 以下能准确代表物体的功率谱。并要求频率为 140 线/mm 与 20 线/mm 在频谱面上的间隔为 30mm,问该透镜的焦距和口径各为多少？ 解：取面积为10mm ×10mm 的透射物体的对角线方向为 x 轴。因要求在 140 线/mm 以下的 空间频率成分不受到有限孔径的渐晕效应的影响，故透镜的口径 D 应满足条件：

第3章习题3-1 半径为的薄圆盘上电荷面密度为s ρ，绕其圆弧轴线以角频率旋转形成电流，求电流面密度。

解：圆盘以角频率旋转，圆盘上半径为r 处的速度为r ω，因此电流面密度为ϕωρρˆr v J s s s ==3-2 在铜中，每立方米体积中大约有28105.8⨯个自由电子。

如果铜线的横截面为210cm ，电流为A 1500。

计算 1） 电流密度；2） 电子的平均漂移速度； 解：1）电流密度m A S I J /105.11010150064⨯=⨯==- 2) 电子的平均漂移速度 v J ρ=，3102819/1036.1105.8106.1m C eN ⨯=⨯⨯⨯==-ρs m J v /101.11036.1105.14106-⨯=⨯⨯==ρ 3-3 一宽度为cm 30传输带上电荷均匀分布，以速度s m /20匀速运动，形成的电流，对应的电流强度为A μ50，计算传输带上的电荷面密度。

解：电流面密度为m A L I J S /7.1663.050μ===因为 v J S S ρ= 所以 2/33.8207.166m C v J S S μρ=== 3-4 如果ρ是运动电荷密度，U是运动电荷的平均运动速度，证明：0=∂∂+∇⋅+⋅∇tU U ρρρ证：如果ρ是运动电荷密度，U是运动电荷的平均运动速度，则电流密度为U J ρ=代入电荷守恒定律tJ ∂∂-=⋅∇ρ得0=∂∂+∇⋅+⋅∇t U U ρρρ3-5 由m S /1012.17⨯=σ的铁制作的圆锥台，高为m 2，两端面的半径分别为cm 10和cm 12。

求两端面之间的电阻。

解：用两种方法（1）如题图3.5所示⎰⎰==2122)(tan zz lz dzS dl R ασπσ)11()(tan 1212z z -=ασπ 01.0202.0tan ==α题3.5图m r z .1001.0/1.0tan /11===α，m r z 1201.0/12.0tan /22===αΩ⨯=-⨯⨯⨯=-=--647212107.4)121101(101012.11)11()(tan 1πασπz z R （2）设流过的电流为I ，电流密度为2rI S I J π==电场强度为 2r IJ E πσσ== 电压为 dz z IEdz V z z z z ⎰⎰==21212)tan (σαπ ⎰==2122)(tan zz zdz I V R απσΩ⨯=-6107.4 3-6 在两种媒质分界面上，媒质1的参数为2,/10011==r m S εσ，电流密度的大小为2/50m A ，方向和界面法向的夹角为030；媒质2的参数为4,/1022==r m S εσ。

《数字通信系统原理》教材习题解答第三章练习题33-1 填空（1）模拟信号在数字通信系统中的传输，首先必须把模拟信号转变为 数字信号 ，转换的方法有 脉冲编码调制 和增量调制等。

（2）衡量量化性能好坏的常用指标是 量化信噪比。

此值越大，说明量化性能越 好。

（3）非均匀量化的PCM 中，信号功率小时，量化噪声功率 小，适用于动态范围较宽的信号。

（4）目前，数字通信系统中采用两种压扩特性：一种是A 律压扩特性：另一种是 μ律压扩特性 。

（5）采用增量调制的目的是 简化模拟信号的数字化方法 ：采用自适应增量调制的目的是 提高小信号的量化信噪比。

补充题：1．线性PCM 的量化噪声与信号功率大小有关吗？无关，它适用于动态范围小的信号。

2．在对数PCM 中，量化噪声功率与信号功率的定性关系是信号功率小，量化噪声功率就小，适用于动态范围大的信号。

在对数M 中，信号在某一段落内变化时，量化噪声功率是否变化?不变。

3．在对数PCM 和自适应增量调制中，抗噪声能力强的是自适应增量调制，量化噪声小的是对数PCM 。

4．均匀量化器的量化信噪比与编码位数的关系是编码增加1位，量化信噪比增大6dB ，非均匀量化器可以提高小信号的量化信噪比。

5．若A 律13折线PCM 编码器输入信号为直流且幅度等于最小量化间隔的1.5倍，则编码器的输出为10000001。

6．线性PCM 编码器的抽样信号频率为8kHz ，当信息速率由80kbit/s 下降到56kbit/s 时，量化信噪比增大18dB 。

3-2 试画出PCM 通信的原理图，并简述PCM 通信的过程。

3-3 PAM 信号、量化信号和PCM 信号属于什么类型的信号？3-4 对基带信号t t t g ππ4cos 3cos 2)(+=进行理想抽样。

（1）为了在接收端不失真地从已抽样信号中恢复出，怎样选取抽样间隔？（2）若抽样间隔为0.2s ，试画出已抽样信号的频谱。

解：（1）基带信号可以看成是低通信号，由于Hz f m 2=根据抽样定理，得Hz f f m s 42=≥（2）由已知得，抽样频率为Hz f s 52.01==。

中级财管第三章习题一、计算题1. 你正在分析一项价值250万元，残值为50万元的资产购入后从其折旧中可以得到的税收收益。

该资产折旧期为5年。

a. 假设所得税率为40%，估计每年从该资产折旧中可得到的税收收益。

b. 假设资本成本为10%，估计这些税收收益的现值。

参考答案：（1）年折旧额=（250-5）=40（万元）获得的从折旧税收收益=40*40%=16万元（2）P=16*(P/A,10%,5)=60.56万元2．华尔公司考虑购买一台新型交织字母机。

该机器的使用年限为4年，初始支出为100 000元。

在这4年中，字母机将以直线法进行折旧直到帐面价值为零，所以每年的折旧额为25 000元。

按照不变购买力水平估算，这台机器每年可以为公司带来营业收入80 000元，公司为此每年的付现成本30 000元。

假定公司的所得税率为40%，项目的实际资金成本为10%，如果通货膨胀率预期为每年8%，那么应否购买该设备？参考答案：NCF0=-100 000NCF1-4=（80 000-30 000-25 000）*（1-40%）+25 000NPV=NCF1-4/(P/A,18%,4)+NCF0若NPV>0，应该购买，否则不应该购买该项设备。

3.甲公司进行一项投资，正常投资期为3年，每年投资200万元，3年共需投资600万元。

第4年~第13年每年现金净流量为210万元。

如果把投资期缩短为2年，每年需投资320万元，2年共投资640万元，竣工投产后的项目寿命和每年现金净流量不变。

资本成本为20%，假设寿命终结时无残值，不用垫支营运资金。

试分析判断是否应缩短投资期。

参考答案：1、用差量的方法进行分析（1）计算不同投资期的现金流量的差量（单位：万元）（2）计算净现值的差量2、分别计算两种方案的净现值进行比较 （1）计算原定投资期的净现值（2）计算缩短投资期后的净现值（3）比较两种方案的净现值并得出结论：因为缩短投资期会比按照原投资期投资增加净现值20.27（24.38-4.11）万元，所以应该采用缩短投资的方案。

解：系统开环传递函数
图 3-42
飞行控制系统
25K1
G0 (s)
=
1+
s(s + 0.8)
25K1 s(s + 0.8)
Kt
s
=
s(s
+
25K1 0.8) + 25K1Kt s
=
25K1
=
ω
2 n
s(s + 0.8 + 25K1Kt ) s(s + 2ξωn )
ω
2 n
=
36
=
25K1
K1
=
36 25
1
s(s + 1) + 10τ 2s
= 10(1 + τ1s) = 10 =
ω
2 n
s(s + 1) + 10τ 2s s(s + 2) s(s + 2ξωn )
s(s + 1)
ω
2 n
= 10
ωn = 10
2ξωn = 2
ξ= 1 10
σ % = e−ξπ / 1−ξ 2 = 35.1%
5
胡寿松自动控制原理习题解答第三章
单位脉冲响应： C(s) = 10 / s k(t) = 10 t ≥ 0
单位阶跃响应 h(t) C(s) = 10 / s2 h(t) = 10t t ≥ 0
（2） (0.04s2 + 0.24s + 1)C(s) = R(s)
单位脉冲响应： C(s)
=
0.04 s 2
1 + 0.24s
+1
C (s)
（1） s5 + 3s 4 + 12s3 + 24s 2 + 32s + 48 = 0 （2） s 6 + 4s5 − 4s 4 + 4s3 - 7s 2 - 8s + 10 = 0

ΣFy = 0，FAy = qd 图（b-2）：
FBx
B
ΣFx = 0，FAx = 0 ΣMA = 0， M A FBy 2d 2qd 2 ；
ΣFy = 0， FAy FBy qd ；
FBy (a-1) q
图（c-1）： ΣFx = 0，FBx = 0
FAx A
ΣMB =
0， qd
FBy
FRC
(c-1) q
图（e-2）： ΣFx = 0，FAx = 0 ΣFy = 0，FAy = 0 ΣMA = 0，MA = M。
M
B
C MA A
FBx
A
FB y FBx B
B
MA FAy
(c-2)
C FAx
B FB' y
MA
A
M B
FBy
FRC
FA
FBy
FRC
FAy
(d-1)
(d-2)
(e-1)
30
A FOx
习题 3－14 图
FOy
(a)
解：图（a）： sin sin60 250 70
18.0167 18
ΣMO = 0 FBC cos12 500 FDA 250cos30 0 ΣFy = 0， FOy FDA FBC cos18 0
FAx A
MA
ΣMB =
0， FRC

M 2d
ΣFy
=
0，
FBy

M 2d
F Ay (b-2)
图（d-2）：
C FRC
B
C FRC FB' y
B
— 21 —
ΣFy
=

第3章习题3-1 试构造一右线性文法，使得它与如下的文法等价S→AB A→UT U→aU|a D→bT|b B→cB|c 并根据所得的右线性文法，构造出相应的状态转换图。

3-2 对于如题图3-2所示的状态转换图(1) 写出相应的右线性文法；(2) 指出它接受的最短输入串；(3) 任意列出它接受的另外4个输入串；(4) 任意列出它拒绝接受的4个输入串。

3-3 对于如下的状态转换矩阵：(1) 分别画出相应的状态转换图；(2) 写出相应的3型文法；(3) 用自然语言描述它们所识别的输入串的特征。

3-4 将如下的NFA确定化和最小化：3-5 将如题图3-5所示的具有ε动作的NFA确定化。

题图3-5 具有ε动作的NFA3-6 设有文法G[S]：S→aA A→aA|bB B→bB|cC|c C→cC|c 试用正规式描述它所产生的语言。

3-7 分别构造与如下正规式相应的NFA。

(1) ((0* |1)(1* 0))*(2) b|a(aa*b)*b3-8 构造与正规式(a|b)*(aa|bb)(a|b)*相应的DFA。

第3章习题答案3-1 解：根据文法知其产生的语言是:L[G]={a m b n c i| m,n,i≧1}可以构造与原文法等价的右线性文法:S→aA A→aA|bB B→bB|cC|c C→cC|c 其状态转换图如下:3-2 解:(1) 其对应的右线性文法是G[A]:A →0D B→0A|1C C→0A|1F|1D→0B|1C E→0B|1C F→1A|0E|0(2) 最短输入串为011(3) 任意接受的四个输入串为：0110,0011,000011,00110(4) 任意拒绝接受的输入串为：0111，1011，1100，10013-3 解:(1) 相应的状态转换图为：(2) 相应的3型文法为：(ⅰ) S→aA|bS A→aA|bB|b B→aB|bB|a|b(ⅱ) S→aA|bB|a A→bA|aC|a|b B→aB|bC|b C→aC|bC|a|b(ⅲ) S→aA|bB|b A→aB|bA|a B→aB|bB|a|b(ⅳ) S→bS|aA A→aC|bB|a B→aB|bC|b C→aC|bC|a|b(3) 用自然语言描述的输入串的特征为：(ⅰ) 以任意个(包括0个)b开头，中间有任意个（大于1）a，跟一个b，还可以有一个由a,b组成的任意字符串。

第3章课后习题参考答案3-1 写出执行下列程序段的中间结果和结果（1）MOV AX, 0809HMUL AH ;AX=AL*AH=48HAAM ;AX=0702H（2）题目略●AX=0059H（BCD除之前，先用AAD是将BCD数先转换为二进制<十六进制>数,非压缩BCD码0809H表示的数值89，转换为十六进制数为59H）●DIV DL ;AX=0411H ；商89/5=17=11H保存在AL，余数=4保存在AH，故AX=411HMOV DL,AH ;余数送DL,DL=04H●AAM ；乘法调整，将AL中的二进制转换为非压缩BCD码→AX,AX=0107H，；;最后AX＝０１０７和，DL＝０４H（3） AX=0011H， AX=0107H（4） AX=005AH（MUL AH; AL=09,AH=10=0Ah,9*0AH=5AH），AX=0900H(调整后变为BCD数，5AH=90)，AX=0908H(xchg AH,DL将AH中的08H交换到DL,执行ADD AL,DL,AL=00+08=08H,故AX=0908H)（5） AL=62H（6） AX=0248H （该程序段：将AX先初始化为0，然后将CL的最高位移到进位位C，利用字节加法分两次进行AX*2+C,并进行压缩的BCD加法调整，分析代码可知该段代码是将CL中的二进制数转换为BCD码并保存在AX中。

程序代码 MOV CL ,248经汇编，CL中存放的是十进制数248对应的二进制数CL=11111000B，因此程序执行完毕，AX=0248H）3-2 题目略一个压缩的BCD数， 0~99. 转换方法：十位*10+个位。

stack segment stack 'stack'dw 32 dup(0)stack endsdata segmentBVAR DB 99Hdata endscode segmentassume ss: stack , cs: code, ds: dataBEGIN: MOV AX, DATA ; 将数据段首地址送AXMOV DS,AX ; 将数据段首地址送DSMOV AL, BVAR ;取出待转换BCD数MOV CL, 4SHR AL, CL ;右移4位，得到BCD数的十位（右移时，高四位补0）MOV AH, 10 ；MUL AH ;十位数*10AND BVAR, 0FH ；BCD数高四位清0，得到个位数第 1 页共 24 页 1ADD BVAR, AL ;加个位数，得到转换结果，直接存放到BVAR存储单元MOV AH,4CH ;返回操作系统的功能编号INT 21H ;执行操作系统功能调用，当AH=4cH时，返回操作系统CODE ENDSEND3-3 题目略stack segment stack 'stack'dw 32 dup(0)stack endsdata segmentW1 DW 0807HW2 DW 0609HB3 DB 2 DUP(0)data endscode segmentassume ss：stack，cs：code，ds：dataSTART: MOV AX,DATAMOV DS,AXMOV AX, W1 ；AX=0807HSUB AL,BYTE PTR W2 ；AL=FEH, CF=1AAS ；AL=08H, AH=07HMOV B3, ALMOV AL，AHSUB AL,W2+1MOV B3+1,ALMOV AH,4CHINT 21HCODE ENDSEND3-4 题目略使用另一种返回操作系统的方法：在对汇编源程序进行汇编/链接生成可执行的.EXE程序时，操作系统自动在数据段最开始DS:0000H处放置一条返回操作系统的指令，因此，只要将DS和0000压入堆栈，并将程序编写为远过程（远调用的子程序），然后在执行完程序规定的功能后，在程序的最后用一条RET指令，RET自动将DS弹出送到CS,将0000弹出送到IP，就会转到数据段开始执行返回操作系统的指令，使程序能够返回操作系统。

（一）1．目的练习材料按定额费用的比例分配。

2．资料某企业生产甲、乙两种产品，耗用原材料费用共计62 400元。

本月投产甲产品220件，乙产品256件。

单件原材料费用定额：甲产品120元，乙产品100元。

3．要求采用原材料定额费用比例分配甲、乙产品实际耗用原材料费用。

解：（1）计算每种产品的材料定额消耗额甲产品材料定额消耗量＝220×120＝26 400（元）乙产品材料定额消耗量＝256×100＝25 600（元）（2）材料费用分配率＝62400 2640025600+＝1.2（3）每种产品应分配的材料费用甲产品应分配的材料费用＝26400×1.2=31 680（元）乙产品应分配的材料费用＝25600×1.2=30 720（元）（二）1．目的练习材料按定额消耗量的比例分配法。

2．资料某企业生产A、B两种产品，本月两种产品共同领用主要材料12 375千克，单价20元，共计247500元。

本月投产A产品为425件，B产品为525件，A产品的材料消耗定额为20千克，B产品的材料消耗定额为10千克。

3．要求按材料定额消耗量比例分配材料费用。

解：（1）计算每种产品的材料定额消耗量A产品材料定额消耗量＝425×20＝8500（千克）B产品材料定额消耗量＝525×10＝5250（千克）（2）材料消耗量分配率＝12375 85005250+＝0.9（3）每种产品应分配的材料数量A产品应分配的材料数量＝8500×0.9=7 650（千克）B产品应分配的材料数量＝5250×0.9=4 725（千克）（4）每种产品应分配的材料费用A产品应分配的材料费用＝7 650×20=153 000（元）B产品应分配的材料费用＝4 725×20=94 500（元）(三)1．目的练习直接材料费用分配的系数分配法。

2．资料某厂生产A1、A2、A3、A4，和A5五种产品，五种产品单位产品甲材料消耗定额分别为30、27.5、25、20、17.5元，本月实际产量分别为400、500、1 000、200、160件，本月实际消耗甲材料59 850元，见表。

代入数值得：m=157 N· m 根据
N m 9550 n
解得：N=1.64 kW
3-5 如图3-17所示，在一直经为75mm的等截面圆轴上， 作用者外力偶矩：m1=1kN· m, m2=0.6kN· m, m3=0.2kN· m, m4=0.2kN· m。 （1）求作轴的扭矩图。 （2）求出每段内 的最大剪力。 （3）求出轴的总扭转角。设材料的剪切模量 G=80GPa。 （4）若m1和m2的位置互换，问在材料方面有何增减。

（2）
1 m a x
T 1 1 1 2 .0 8MPa 2 ( 0 .0 7 5 ) W t 1 6 T 0 .4 2 2m 4 .8 3MPa a x 2 (0 .0 7 5 ) W t 1 6 T 0 .2 3 3m 2 .4 2 MPa a x 2 (0 .0 7 5 ) W t 1 6
（1）
（3）根据

Tl G IP
3 T l 1 1 0 23 2 4 1 1 rad 8 1 0 1 9 4 G I 0 1 0 0 . 0 7 5 P 8
2
Tl 3 22 2 .4 1 1 0 G IP
rad
3
Tl 33 8103 rad G IP
1 2 3
0 . 0 1 1 20 . 6 4 2
（4）若m1和m2的位置互换，
T1 0.6 kN· m
T 2 0.4
kN· m
m T3 0.2 kN·
最大剪力减少，所以用料将降低
3-6 如图3-18所示汽车方向盘外径 =500mm，驾驶员每只手 加在方向盘上的里P=300N，方向盘轴为空心圆轴，其外径之 dD / 0 . 8 比 ，材料的许用应力 =600MPa。试求方向盘 轴的内外直径。