2017年春季新版北师大版七年级数学下学期1.1、同底数幂的乘法素材2

北师大版七年级下册数学知识点总结第一章：整式的乘除。

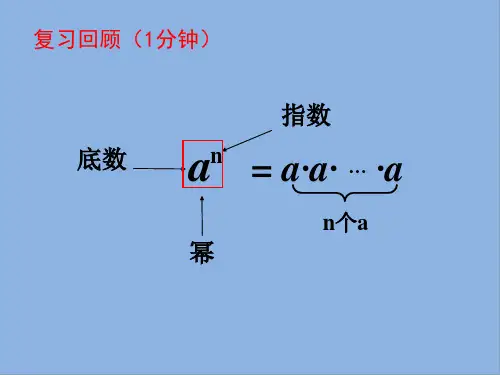
1. 同底数幂的乘法。

- 法则：同底数幂相乘，底数不变，指数相加。

即a^m· a^n=a^m + n（m，n 都是正整数）。

- 例如：2^3×2^4=2^3 + 4=2^7。

2. 幂的乘方与积的乘方。

- 幂的乘方：(a^m)^n=a^mn（m，n都是正整数）。

例如(3^2)^3=3^2×3=3^6。

- 积的乘方：(ab)^n=a^nb^n（n是正整数）。

例如(2×3)^2=2^2×3^2=4×9 = 36。

3. 同底数幂的除法。

- 法则：同底数幂相除，底数不变，指数相减。

即a^m÷ a^n=a^m - n（a≠0，m，n都是正整数，且m>n）。

例如3^5÷3^2=3^5 - 2=3^3。

- 零指数幂：a^0=1(a≠0)。

例如5^0=1。

- 负整数指数幂：a^-p=(1)/(a^p)(a≠0,p是正整数)。

例如2^-3=(1)/(2^3)=(1)/(8)。

4. 整式的乘法。

- 单项式与单项式相乘：把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

例如2x^2·3x^3=(2×3)(x^2·x^3) = 6x^5。

- 单项式与多项式相乘：就是用单项式去乘多项式的每一项，再把所得的积相加。

例如a(b + c)=ab+ac。

- 多项式与多项式相乘：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

例如(a + b)(c + d)=ac+ad+bc+bd。

5. 平方差公式。

- 公式：(a + b)(a - b)=a^2-b^2。

例如(3 + 2)(3 - 2)=3^2-2^2=9 - 4 = 5。

6. 完全平方公式。

- (a + b)^2=a^2+2ab + b^2；(a - b)^2=a^2-2ab + b^2。

北师大版数学七年级下册1.1《同底数幂的乘法》教案一. 教材分析《同底数幂的乘法》是北师大版数学七年级下册第一章《整式的运算》中的第一节内容。

本节内容主要介绍同底数幂的乘法法则，为学生以后学习幂的运算打下基础。

同底数幂的乘法是初中学员比较容易混淆的知识点，因此，在教学过程中，需要通过大量的例子让学生理解和掌握同底数幂的乘法法则。

二. 学情分析七年级的学生已经学习了有理数的乘法、幂的定义等知识，对于幂的运算有一定的基础。

但是，学生对于同底数幂的乘法法则的理解和运用还需要加强。

因此，在教学过程中，需要通过引导、讲解、练习等方式，帮助学生理解和掌握同底数幂的乘法法则。

三. 教学目标1.让学生理解同底数幂的乘法法则，并能熟练运用。

2.培养学生的数学思维能力，提高学生的数学素养。

3.通过对同底数幂的乘法的学习，培养学生解决问题的能力。

四. 教学重难点1.同底数幂的乘法法则的推导和理解。

2.同底数幂的乘法在实际问题中的应用。

五. 教学方法采用讲授法、引导法、练习法、小组合作法等教学方法。

通过讲解、引导、练习等形式，让学生理解和掌握同底数幂的乘法法则。

六. 教学准备1.教案、PPT等教学资料。

2.练习题。

3.黑板、粉笔等教学工具。

七. 教学过程1.导入（5分钟）通过复习幂的定义和有理数的乘法，引导学生思考同底数幂的乘法应该如何计算。

2.呈现（10分钟）利用PPT展示同底数幂的乘法法则，并通过具体的例子进行讲解，让学生理解和掌握同底数幂的乘法法则。

3.操练（10分钟）让学生独立完成一些同底数幂的乘法运算，教师进行个别辅导。

4.巩固（10分钟）通过一些综合性的题目，让学生运用同底数幂的乘法法则进行计算，巩固所学知识。

5.拓展（10分钟）引导学生思考同底数幂的乘法在实际问题中的应用，让学生尝试解决一些实际问题。

6.小结（5分钟）对本节课的主要内容进行小结，让学生巩固所学知识。

7.家庭作业（5分钟）布置一些同底数幂的乘法运算题目，让学生巩固所学知识。

北师大版数学七年级下册1.1《同底数幂的乘法》教学设计一. 教材分析《同底数幂的乘法》是北师大版数学七年级下册第一章“幂的运算”中的第一节内容。

本节内容是在学生已经掌握了有理数的乘法、幂的定义和幂的运算性质等知识的基础上进行学习的，是幂的运算的基础知识，对于学生以后学习幂的其它运算和函数等内容有着重要的影响。

本节课主要让学生掌握同底数幂的乘法法则，并能够运用这些法则进行计算和解决实际问题。

二. 学情分析学生在进入七年级下册之前，已经学习过了有理数的乘法、幂的定义和幂的运算性质等知识，对于这些知识的理解和运用已经有一定的基础。

但是，同底数幂的乘法是一个比较抽象的概念，学生可能对于如何理解和运用这些法则存在一定的困难。

因此，在教学过程中，需要教师通过生动的例子和实际问题，帮助学生理解和掌握同底数幂的乘法法则。

三. 教学目标1.知识与技能目标：让学生掌握同底数幂的乘法法则，能够正确进行计算。

2.过程与方法目标：通过教师的讲解和学生的实践，让学生能够理解和运用同底数幂的乘法法则。

3.情感态度与价值观目标：培养学生对数学的兴趣和热情，让学生感受到数学的美妙和实际应用的价值。

四. 教学重难点1.重点：同底数幂的乘法法则的掌握和运用。

2.难点：对于同底数幂的乘法法则的理解和运用。

五. 教学方法采用讲解法、实践法、问题驱动法等教学方法。

通过教师的讲解，让学生掌握同底数幂的乘法法则；通过学生的实践，让学生理解和运用这些法则；通过问题的提出和解决，激发学生的思考和兴趣。

六. 教学准备1.准备PPT，包括同底数幂的乘法法则的讲解和实际问题的展示。

2.准备一些实际的例子和问题，用于帮助学生理解和掌握同底数幂的乘法法则。

七. 教学过程1.导入（5分钟）通过一个实际问题，如“一个长方体的长、宽、高分别是23、22、2^1，求这个长方体的体积”，引入同底数幂的乘法法则。

2.呈现（15分钟）教师通过PPT讲解同底数幂的乘法法则，包括定义和运算规则。

第一章 整式的乘除1.1 同底数幂的乘法1.掌握同底数幂的乘法法则，并能运用同底数幂的乘法法则进行计算.2.经历探索同底数幂的乘法法则的过程，体会“特殊到一般再特殊”的思想方法.自学指导 阅读教材P2～3，完成下列问题.(一)知识探究a m ·a n ＝a m ＋n (m ，n 都是正整数). 同底数幂相乘，底数不变，指数相加.(二)自学反馈1.计算a 2·a 的结果是( B )A .a 2 B.a 3 C.a 4 D.a 52.已知10m ＝2，10n ＝3，则10m ＋n 的值是( C )A .4 B.5 C.6 D.23活动1 小组讨论例1 计算：(1)(－3)7×(－3)6； (2)(1111)3×1111； (3)－x 3·x 5； (4)b 2m ·b 2m ＋1.解：(1)(－3)7×(－3)6＝(－3)7＋6＝(－3)13.(2)(1111)3×1111＝(1111)3＋1＝(1111)4. (3)－x 3·x 5＝－x 3＋5＝－x 8.(4)b 2m ·b 2m ＋1＝b 2m ＋2m ＋1＝b 4m ＋1.利用同底数幂的乘法法则计算时底数必须相同.例2 光在真空中的速度约为3×108 m/s ，太阳光照射到地球上大约需要5×102 s.地球距离太阳大约有多远？解：3×108×5×102＝15×1010＝1.5×1011(m).答：地球距离太阳大约有1.5×1011 m.活动2 跟踪训练1.计算b 2·(－b)3的结果是( D )A .－2b 6 B.2b 5 C.b 6 D.－b 52.下列各式中，计算正确的是( B )A .m 5·m 5＝2m 10 B.m 4·m 4＝m 8C .m 3·m 3＝m 9 D.m 6＋m 6＝2m 123.写出一个运算结果是a 4的算式：答案不唯一，如：a·a 3.4.一个长方体的长、宽、高分别为a 2，a ，a 3，则这个长方体的体积是a 6.5.已知a 2·a x －3＝a 6，那么x 的值为7.6.计算：(1)x 2·x 5＋(－x 3)·x 4；(2)(x －y)2·(x －y)3·(y －x)4·(y －x)5.解：(1)原式＝x 7－x 7＝0.(2)原式＝－(x －y)14.活动3 课堂小结同底数幂的乘法法则.。