学第一学期理论力学B期末考试题评分标准
- 格式:pptx
- 大小:1.83 MB
- 文档页数:34

B工程力学期末考试题及答案一、选择题(每题3分,共30分)1. 力的合成遵循什么法则?A. 牛顿第一定律B. 牛顿第二定律C. 牛顿第三定律D. 平行四边形法则答案:D2. 以下哪一项是刚体的固有属性?A. 质量B. 体积C. 形状D. 颜色答案:A3. 弹性模量是描述材料的哪种性质?A. 塑性B. 弹性C. 韧性D. 硬度答案:B4. 根据胡克定律,弹簧的伸长量与什么成正比?A. 弹簧的原长B. 弹簧的直径C. 作用力D. 弹簧的刚度系数答案:C5. 以下哪种力是保守力?A. 摩擦力B. 重力C. 空气阻力D. 离心力答案:B6. 材料的屈服强度是指材料在什么条件下的应力?A. 断裂B. 塑性变形C. 弹性变形D. 永久变形答案:B7. 动量守恒定律适用于哪种系统?A. 非惯性参考系B. 有外力作用的系统C. 封闭系统D. 任何系统答案:C8. 以下哪种情况下物体的转动惯量最大?A. 质量分布均匀B. 质量集中在外缘C. 质量集中在中心D. 质量分布不均匀答案:B9. 根据能量守恒定律,以下哪项说法是正确的?A. 能量可以被创造B. 能量可以被消灭C. 能量可以转化为其他形式D. 能量在转化过程中总量不变答案:D10. 流体静力学中,液体的压强与什么成正比?A. 液体的密度B. 液体的深度C. 液体的流速D. 液体的黏度答案:B二、填空题(每题4分,共20分)1. 牛顿第二定律的公式是_______。
答案:F=ma2. 力矩的计算公式是_______。
答案:τ=r×F3. 材料的弹性模量E与杨氏模量Y之间的关系是_______。
答案:E=3Y(1-ν^2)4. 根据能量守恒定律,机械能守恒的条件是_______。
答案:没有非保守力做功5. 流体的连续性方程是_______。
答案:A1v1=A2v2三、简答题(每题10分,共20分)1. 简述达朗贝尔原理及其应用。
答案:达朗贝尔原理是将动力学问题转化为静力学问题来解决的方法。

2011~2012 学年度第 二 学期《 理论力学 》试卷(A 卷)一、填空题(每小题 4 分,共 28 分)1、如图1.1所示结构,已知力F ,AC =BC =AD =a ,则CD 杆所受的力F CD =( ),A 点约束反力F Ax =( )。
2、如图1.2 所示结构,,不计各构件自重,已知力偶矩M ,AC=CE=a ,A B ∥CD 。
则B 处的约束反力F B =( );CD 杆所受的力F CD =( )。
E 1.1 1.23、如图1.3所示,已知杆OA ,以匀角速度ω绕O 轴转动,如以滑块A 为动点,动系建立在BC 杆上,当BO 铅垂、BC 杆处于水平位置时,滑块A 的相对速度v r =( );科氏加速度a C =( )。
4、平面机构在图1.4位置时, AB 杆水平而OA 杆铅直,轮B 在水平面上作纯滚动,已知速度v B ,OA 杆、AB 杆、轮B 的质量均为m 。
则杆AB 的动能T AB =( ),轮B 的动能T B =( )。
C1.3 1.45、如图1.5所示均质杆AB 长为L ,质量为m,其A 端用铰链支承,B 端用细绳悬挂。
当B 端细绳突然剪断瞬时, 杆AB 的角加速度 =( ),当杆AB 转到与水平线成300角时,AB 杆的角速度的平方ω2=( )。
6、图1.6所示机构中,当曲柄OA 铅直向上时,BC 杆也铅直向上,且点B 和点O 在同一水平线上;已知OA=0.3m,BC=1m ,AB=1.2m,当曲柄OA 具有角速度ω=10rad/s 时,则AB 杆的角速度ωAB =( )rad/s,BC 杆的角速度ωBC =( )rad/s 。
AB1.57、图1.7所示结构由平板1、平板2及CD 杆、EF 杆在C 、D 、E 、F 处铰接而成,在力偶M 的作用下,在图上画出固定铰支座A 、B 的约束反力F A 、F B 的作用线方位和箭头指向为( )(要求保留作图过程)。
1.7二、单项选择题(每小题 4 分,共28 分)1、如图2.1所示,四本相同的书,每本重均为P ,设书与书间的摩擦因数为0.1,书与手间的摩擦因数为0.25,欲将四本书一起抱起,则两侧手应加的压力至少大于( )。

海南师范大学物理与电子工程学院09级物理专业《理论力学》2011—2012学年度第一学期期末考试B卷注意事项:1. 考前请将密封线内填写清楚2. 所有答案请直接答在试卷上(或答题纸上)3.考试形式:闭卷4. 本试卷共三大题,满分100分,考试时间100分钟一、填空题(每空3分,共45分)1、在介质中上抛一质量为m的小球,已知小球所受阻力vR k-=,若选择坐标轴x铅直向上,则小球的运动微分方程为。
2、质点在运动过程中,在下列条件下,各作何种运动?①aτ=0,an=0(答):;②aτ≠0, an=0(答):;③aτ=0,an≠0(答):;④aτ≠0,an≠0(答):;3、质量为10kg的质点,受水平力F的作用,在光滑水平面上运动,设tF43+=(t以s计,F以N计),初瞬间(0=t)质点位于坐标原点,且其初速度为零。
则s3=t时,质点的位移等于,速度等于_______________。
4、在南半球地面附近自南向北的气流有朝的偏向;而北半球的河流岸冲刷较为严重。
5、哈密顿正则方程用泊松括号表示为,1、6、质点的质量是1千克,它运动时的速度kjivˆ3ˆ2ˆ3ˆ++=,质点的动能为,当质点以上述速度运动到(1,2,3)点时,它对z轴的动量矩是。
7、在平面极坐标系中,质点的径向加速度为,横向加速度为。
8、质点系内力功等于零的条件是。
二、简答题(本题3小题,每题6分,共18分)1、已知一匀质棒,当它绕过其一端并垂直于棒的轴转动时,转动惯量为231ml,m为棒的质量,l为棒长。
问此棒绕通过离棒端为l41且与上述轴线平行的另一轴线转动时,转动惯量是不是等于224131⎪⎭⎫⎝⎛+lmml?为什么?2、一光滑球A与另一静止的光滑球B发生斜碰。
如两者均为完全弹性体,且两球的质量相等,则两球碰撞后的速度互相垂直,说明其理由。
3、如图所示,质点m作平面曲线运动若分别已知作为时间函数的点M的直角坐标,x y;自然坐标S及极坐标,r,分别用直角坐标、自然坐标、极坐标表示则M的速度。

理论力学期末试题及答案一、选择题(每题2分,共20分)1. 牛顿第一定律描述的是物体在不受外力作用时的运动状态,这种状态被称为:A. 静止状态B. 匀速直线运动状态C. 加速运动状态D. 曲线运动状态答案:B2. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体质量成反比,其数学表达式为:A. \( F = ma \)B. \( F = \frac{m}{a} \)C. \( a = \frac{F}{m} \)D. \( a = \frac{m}{F} \)答案:C3. 动量守恒定律适用于:A. 所有物理过程B. 只有弹性碰撞过程C. 只有非弹性碰撞过程D. 系统受外力为零的情况答案:D4. 角动量守恒的条件是:A. 系统不受外力B. 系统受外力矩为零C. 系统受外力矩不为零D. 系统受外力矩为零且不受外力答案:B5. 简谐运动的周期与振幅无关,而与以下哪个因素有关?A. 质量B. 弹性系数C. 重力加速度D. 以上都不是答案:B6. 刚体的转动惯量与以下哪个因素有关?A. 质量B. 质量分布C. 物体的形状D. 以上都是答案:D7. 根据能量守恒定律,以下哪种情况下机械能守恒?A. 只有重力做功B. 只有弹力做功C. 只有重力和弹力做功D. 以上都是答案:C8. 虚功原理是分析力学中的一个重要概念,它表明:A. 系统在平衡状态下,任何虚位移对应的虚功都为零B. 系统在非平衡状态下,任何虚位移对应的虚功都为零C. 系统在平衡状态下,任何虚位移对应的虚功都不为零D. 系统在非平衡状态下,任何虚位移对应的虚功都不为零答案:A9. 拉格朗日方程是分析力学中描述系统运动的基本方程,它的形式为:A. \( \frac{d}{dt} \left( \frac{\partial L}{\partial\dot{q}_i} \right) - \frac{\partial L}{\partial q_i} = Q_i \) B. \( \frac{d}{dt} \left( \frac{\partial T}{\partial\dot{q}_i} \right) - \frac{\partial T}{\partial q_i} = Q_i \) C. \( \frac{d}{dt} \left( \frac{\partial L}{\partial\dot{q}_i} \right) - \frac{\partial L}{\partial q_i} = 0 \)D. \( \frac{d}{dt} \left( \frac{\partial T}{\partial\dot{q}_i} \right) - \frac{\partial T}{\partial q_i} = 0 \) 答案:A10. 哈密顿原理是分析力学中用于寻找系统运动方程的原理,它表明实际运动路径是使作用量取极值的路径,作用量定义为:A. \( S = \int (T - V) dt \)B. \( S = \int (T + V) dt \)C. \( S = \int L dt \)D. \( S = \int H dt \)答案:C二、填空题(每题2分,共20分)1. 牛顿第三定律指出,对于两个相互作用的物体,它们之间的力大小相等、方向相反、作用在同一直线上,这种力被称为________。
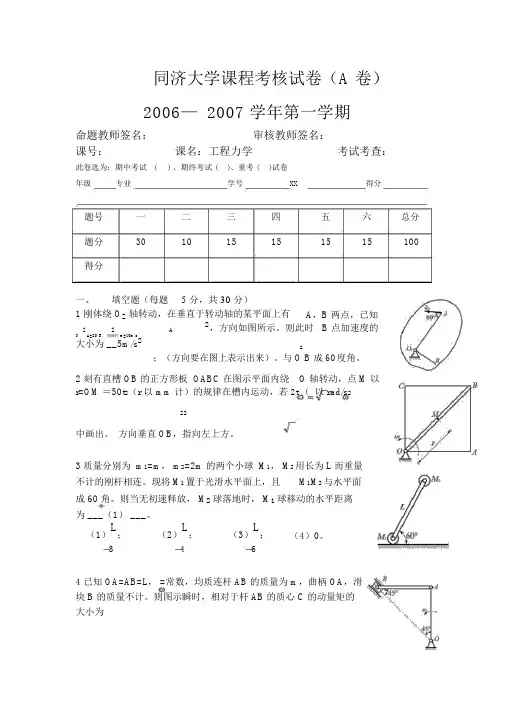
同济大学课程考核试卷(A 卷)2006— 2007 学年第一学期命题教师签名:审核教师签名:课号:课名:工程力学考试考查:此卷选为:期中考试 ( ) 、期终考试 ()、重考 ( )试卷年级专业学号XX得分题号 一二 三 四五 六 总分题分 301015151515100得分一、 填空题(每题 5 分,共 30 分)1 刚体绕 O Z 轴转动,在垂直于转动轴的某平面上有 A ,B 两点,已知Z Z A2,方向如图所示。
则此时 B 点加速度的OA=2O B ,某瞬时 a =10m/s大小为 __5m/s 2z 度角。
;(方向要在图上表示出来)。
与 O B 成 602 刻有直槽 OB 的正方形板 OABC 在图示平面内绕 O 轴转动,点 M 以 r=OM =50t 2(r 以 mm 计)的规律在槽内运动,若2t ( 以rad/s 222中画出。
方向垂直 OB ,指向左上方。
3 质量分别为 m 1=m , m 2=2m 的两个小球 M 1, M 2用长为 L 而重量 不计的刚杆相连。
现将M 1置于光滑水平面上,且 M 1M 2与水平面成 60 角。
则当无初速释放, M 2球落地时, M 1球移动的水平距离为 ___(1) ___。
(1)L;(2)L;(3)L;(4)0。
3464 已知 OA=AB=L , =常数,均质连杆 AB 的质量为 m ,曲柄 OA ,滑块 B 的质量不计。
则图示瞬时,相对于杆 AB 的质心 C 的动量矩的大小为__ L CmL 2,(顺时针方向) ___。
125 均质细杆 AB 重 P ,长 L ,置于水平位置,若在绳 BC 突然剪断瞬时有角加速度 ,则杆上各点惯性力的合力的大小为_ PL,(铅直向上) _,作用点的位置在离 A 端_2L_处,并2g3在图中画出该惯性力。
6 铅垂悬挂的质量-- 弹簧系统,其质量为m ,弹簧刚度系数为k ,若坐标原点分别取在弹簧静伸长处和未伸长处,别写成 _ mx kx 0 _和_ mx kx mg _。

同济大学课程考核试卷(A 卷) 2006— 2007学年第一学期命题教师签名: 审核教师签名:课号: 课名:工程力学 考试考查:此卷选为:期中考试( )、期终考试( )、重考( )试卷年级 专业 学号 姓名 得分题号 一二三四五 六 总分题分 3010151515 15 100得分一、 填空题(每题5分,共30分)1刚体绕O Z 轴转动,在垂直于转动轴的某平面上有A ,B 两点,已知O Z A =2O Z B ,某瞬时a A =10m/s 2,方向如图所示。
则此时B 点加速度的大小为__5m/s 2 ;(方向要在图上表示出来)。
与O z B 成60度角。
2刻有直槽OB 的正方形板OABC 在图示平面内绕O 轴转动,点M 以r =OM =50t 2(r 以mm 计)的规律在槽内运动,若t 2=ω(以rad/s 计),则当t =1s 时,点M 的相对加速度的大小为_0.1m/s 2_;牵连加速度的大小为__1.6248m/s 2__。
科氏加速度为_22.0m/s 2_,方向应在图中画出。
方向垂直OB ,指向左上方。
3质量分别为m 1=m ,m 2=2m 的两个小球M 1,M 2用长为L 而重量不计的刚杆相连。
现将M 1置于光滑水平面上,且M 1M 2与水平面成︒60角。
则当无初速释放,M 2球落地时,M 1球移动的水平距离为___(1)___。
(1)3L ; (2)4L; (3)6L; (4)0。
4已知OA =AB =L ,=常数,均质连杆AB 的质量为m ,曲柄OA ,滑块B 的质量不计。
则图示瞬时,相对于杆AB 的质心C 的动量矩的大小为__122ωmL L C =,(顺时针方向)___。
5均质细杆AB 重P ,长L ,置于水平位置,若在绳BC 突然剪断瞬时有角加速度,则杆上各点惯性力的合力的大小为_g PL 2α,(铅直向上)_,作用点的位置在离A 端_32L_处,并在图中画出该惯性力。
6铅垂悬挂的质量--弹簧系统,其质量为m ,弹簧刚度系数为k ,若坐标原点分别取在弹簧静伸长处和未伸长处,则质点的运动微分方程可分别写成_0=+kx xm _和_mg kx x m =+ _。
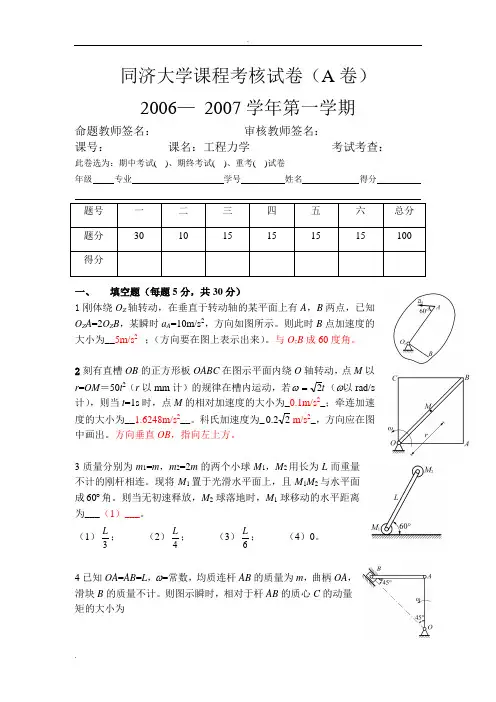
同济大学课程考核试卷(A 卷) 2006— 2007学年第一学期命题教师签名: 审核教师签名:课号: 课名:工程力学 考试考查:此卷选为:期中考试( )、期终考试( )、重考( )试卷年级 专业 学号 姓名 得分一、 填空题(每题5分,共30分)1刚体绕O Z 轴转动,在垂直于转动轴的某平面上有A ,B 两点,已知O Z A =2O Z B ,某瞬时a A =10m/s 2,方向如图所示。
则此时B 点加速度的大小为__5m/s 2 ;(方向要在图上表示出来)。
与O z B 成60度角。
2刻有直槽OB 的正方形板OABC 在图示平面内绕O 轴转动,点M 以r =OM =50t 2(r 以mm 计)的规律在槽内运动,若t 2=ω(ω以rad/s 计),则当t =1s 时,点M 的相对加速度的大小为_0.1m/s 2_;牵连加速度的大小为__1.6248m/s 2__。
科氏加速度为_22.0m/s 2_,方向应在图中画出。
方向垂直OB ,指向左上方。
3质量分别为m1=m ,m 2=2m 的两个小球M 1,M 2用长为L 而重量不计的刚杆相连。
现将M 1置于光滑水平面上,且M 1M 2与水平面成︒60角。
则当无初速释放,M 2球落地时,M 1球移动的水平距离为___(1)___。
(1)3L; (2)4L; (3)6L; (4)0。
4已知OA =AB =L ,ω=常数,均质连杆AB 的质量为m ,曲柄OA ,滑块B 的质量不计。
则图示瞬时,相对于杆AB 的质心C 的动量矩的大小为__122ωmL L C =,(顺时针方向)___。
5均质细杆AB 重P ,长L ,置于水平位置,若在绳BC 突然剪断瞬时有角加速度α,则杆上各点惯性力的合力的大小为_g PL 2α,(铅直向上)_,作用点的位置在离A 端_32L_处,并在图中画出该惯性力。
6铅垂悬挂的质量--弹簧系统,其质量为m ,弹簧刚度系数为k ,若坐标原点分别取在弹簧静伸长处和未伸长处,则质点的运动微分方程可分别写成_0=+kx xm _和_mg kx x m =+ _。