基于MATLAB的牛头刨床传动机构仿真

附录牛头刨床主运动机构MATLAB程序由主程序six」six_bar 两部分组成。

1.主程序six_bar_main文件%1.输入已知数据clear;11=0.125;13=0.600;14=0.150;16=0.275;161=0.575;omega1=1;alpha 仁0;hd=pi/180;du=180/pi;%2.调用子函数six_bar计算牛头刨床机构位移，角速度, for n1=1:459;theta1( n1)=-2*pi+5.8199+( n1-1)*hd; _main 和子函数角加速度II=[I1,I3,I4,I6,I61];[theta,omega,alpha]=six_bar(theta1( n1),omega1,alpha1,ll);s3( n1)=theta(1);theta3( n1)=theta(2);theta4( n1)=theta(3);sE( n1)=theta(4);v2( n1)=omega(1);omega3( n1)=omega(2);omega4 (n 1)=omega(3);vE( n1)=omega(4);a2( n1)=alpha(1);alpha3( n1)=alpha(2);alpha4( n1)=alpha(3);aE( n1)=alpha(4);end%3.位移、角速度、角加速度、和牛头刨床图形输出figure©);n1=1:459;t=( n1-1)*2*pi/360;subplot(2,2,1); %绘角位移及位移线图plot(t,theta3*du,'r-.');grid on;axis auto;[haxes,hli ne1,hli ne2]=plotyy(t,theta4*du,t,sE); grid on;hold on;xlabel('时间/s')axes(haxes(1));ylabel('角位移八circ')axes(haxes(2));ylabel('位移/m')hold on;grid on;text(1.15,-0.15,'\theta_3')text(3.40,0.27,'\theta_4')text(2.25,-0.15,'s_E')subplot(2,2,2); %绘角速度及速度线图plot(t,omega3,'r-.');grid on;hold on;[haxes,hli ne1,hli ne2]=plotyy(t,omega4,t,vE);grid on;hold on;xlabel('时间/s')axes(haxes(1));ylabel('角速度/rad\cdots A{-1}')axes(haxes(2));ylabel('速度/m\cdotsA{-1}')hold on;grid on;text(3.1,0.35,'\omega_3')text(2.1,0.1,'\omega_4')text(5.5,0.45,'v_E')subplot(2,2,3); %绘角加速度及加速度线图plot(t,alpha3,'r-.');grid on;hold on;axis auto;[haxes,hli ne1,hli ne2]=plotyy(t,alpha4,t,aE); grid on; hold on;xlabel('时间/s')axes(haxes(1));ylabel('角加速度/rad\cdots A{-2}')axes(haxes(2));ylabel('加速度/m\cdotsA{-2}')hold on;grid on;text(1.5,0.3,'\alpha_3')text(3.5,0.51,'\alpha_4')text(1.5,-0.11,'a_E')subplot(2,2,4); %牛头刨床机构n1=20;x(1)=0;y(i)=0;x(2)=(s3( n1)*1000-50)*cos(theta3( n1));y(2)=(s3( n1)*1000-50)*si n(theta3( n1));x(3)=0;y(3)=16*1000;x(4)=l1*1000*cos(theta1( n1));y⑷=s3( n1)*1000*si n(theta3( n1));x(5)=(s3( n1)*1000+50)*cos(theta3( n1));y(5)=(s3( n1)*1000+50)*si n(theta3( n1));x(6)=13*1000*cos(theta3( n1));y(6)=13*1000*si n(theta3( n1));x(7)=13*1000*cos(theta3( n1))+14*1000*cos(theta4( n1));y(7)=13*1000*si n(theta3( n1))+14*1000*si n(theta4( n1));x(8)=13*1000*cos(theta3( n1))+14*1000*cos(theta4( n1))-900;y(8)=161*1000;x(9)=13*1000*cos(theta3( n1))+14*1000*cos(theta4( n1))+600;y(9)=161*1000;x(10)=(s3( n1)*1000-50)*cos(theta3( n1));y(10)=(s3( n1)*1000-50)*si n(theta3( n1));x(11)=x(10)+25*cos(pi/2-theta3( n1));y(11)=y(10)-25*si n(pi/2-theta3( n1));x(12)=x(11)+100*cos(theta3( n1));y(12)=y(11)+100*si n(theta3( n1));x(13)=x(12)-50*cos(pi/2-theta3( n1));y(13)=y(12)+50*si n(pi/2-theta3( n1)); x(14)=x(10)-25*cos(pi/2-theta3( n1)); y(14)=y(10)+25*si n(pi/2-theta3( n1)); x(15)=x(10); y(15)=y(10);x(16)=0;y(16)=0;x(17)=0;y(17)=16*1000;k=1:2;plot(x(k),y(k));hold on;k=3:4;plot(x(k),y(k));hold on;k=5:9;plot(x(k),y(k));hold on;k=10:15;plot(x(k),y(k));hold on;k=16:17;plot(x(k),y(k));hold on;grid on;axis([-500 600 0 650]); title('牛头刨床运动仿真'); grid on;xlabel('mm')ylabel('mm') plot(x(1),y(1),'o'); plot(x (3),y (3) ,'o'); plot(x(4),y(4),'o'); plot(x(6),y(6),'o');plot(x ⑺,y(7),'o');hold on;grid on;xlabel('mm')ylabel('mm')axis([-400 600 0 650]);%4牛头刨床机构运动仿真figure(2)m=movie in( 20);j=0；for n仁1:5:360j=j+1；elf;x(1)=0;y(i)=0;x(2)=(s3( n1)*1000-50)*cos(theta3( n1));y(2)=(s3( n1)*1000-50)*si n(theta3( n1));x(3)=0;y(3)=l6*1000x⑷=l1*1000*cos(theta1( n1));y⑷=s3( n1)*1000*si n(theta3( n1));x(5)=(s3( n1)*1000+50)*cos(theta3( n1));y(5)=(s3( n1)*1000+50)*si n(theta3( n1));x(6)=l3*1000*cos(theta3( n1));y(6)=l3*1000*si n(theta3( n1));x(7)=l3*1000*cos(theta3( n1))+l4*1000*cos(theta4( n1));x(7)=l3*1000*cos(theta3( n1))+l4*1000*cos(theta4( n1)); y(7)=l3*1000*si n(theta3( n1))+l4*1000*si n(theta4( n1));x(8)=l3*1000*cos(theta3( n1))+l4*1000*cos(theta4( n1))-900;y(8)=l61*1000;x(9)=l3*1000*cos(theta3( n1))+l4*1000*cos(theta4( n1))+600;y(9)=l61*1000;x(10)=(s3( n1)*1000-50)*cos(theta3( n1));y(10)=(s3( n1)*1000-50)*si n(theta3( n1));x(11)=x(10)+25*cos(pi/2-theta3( n1));y(11)=y(10)-25*si n(pi/2-theta3( n1));x(12)=x(11)+100*cos(theta3( n1));y(12)=y(11)+100*si n(theta3( n1));x(13)=x(12)-50*cos(pi/2-theta3( n1)); y(13)=y(12)+50*si n(pi/2-theta3( n1)); x(14)=x(10)-25*cos(pi/2-theta3( n1)); y(14)=y(10)+25*si n(pi/2-theta3( n1)); x(15)=x(10);y(15)=y(10);x(16)=0;y(16)=0;x(17)=0;y(17)=l6*1000;k=1:2;plot(x(k),y(k));hold on;k=3:4plot(x(k),y(k));hold on;k=5:9;plot(x(k),y(k));hold on;k=10:15;plot(x(k),y(k));hold on;k=16:17;plot(x(k),y(k));hold on;grid on;axis([-500 600 0 650]);title('牛头刨床运动仿真'); grid on; xlabel('mm');ylabel('mm');plot(x(1),y(1),'o');plot(x (3),y (3) ,'o');plot(x(4),y(4),'o');plot(x(6),y(6),'o');plot(x ⑺,y(7),'o');axis equal;m(j)=getframe;endmovie(m)2.子函数six_bar文件fun ctio n[theta,omega,alpha]=six_bar(theta1,omega1,alpha1,ll)11=11(1);l3=ll(2);14=11(3);16=11(4);161=11(5);%1计算角位移和线位移s3=sqrt((l1*cos(theta1))*(l1*cos(theta1))+(l6+l1*si n(theta1))*(l6+l1*si n(t heta1)));theta3=acos((l1*cos(theta1))/s3);theta4=pi-asi n((l61-l3*si n(theta3))/l4);sE=l3*cos(theta3)+l4*cos(theta4);theta(1)=s3;theta(2)=theta3;theta(3)=theta4;theta (4)=sE;%2计算角速度和线速度A=[s in (theta3),s3*cos(theta3),0,0; -cos(theta3),s3*s in (theta3),0,0;0,l3*si n(theta3),l4*(theta4),1;0,l3*cos(theta3),l4*cos(theta4),0];%3计算角加速度和加速度A=[s in (theta3),s3*cos(theta3),0,0; % 从动件位置参数矩阵 cos(theta3),-s3*s in (theta3),0,0;0,l3*si n( theta3),l4*(theta4),1;0,l3*cos(theta3),l4*cos(theta4),0];At=[omega3*cos(theta3),(v2*cos(theta3)-s3*omega3*si n(theta3)),0,0; -omega3*si n( theta3),(-v2*si n(theta3)-s3*omega3*cos(theta3)),0,0; 0,l3*omega3*cos(theta3),l4*omega4*cos(theta4),0;0,-l3*omega3*si n(theta3),-l4*omega4*si n( theta4),0];Bt=[-l1*omega1*si n(theta1);-l1*omega1*cos(theta1);0;0];%从动件位置参数矩阵 B=[l1*cos(theta1);l1*si n(theta1);0;0]% omega=A\(omega1*B);v2=omega(1);omega3=omega(2); omega4=omega(3); vE=omega(4)原动件位置参数矩阵 %滑块2的速度 %构件3的角速度 %构件4的角速度 构件的速度alpha=A\(-At*omega+omega1*Bt); a2=alpha(1);alpha3=alpha (2);alpha4=alpha (3);aE=alpha(4);%机构从动件的加速度矩阵%a2表示滑块2的加速度%alpha3表示杆件3的角加速度%alpha4表示杆件4的角加速度%构件5的加速度。

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构，按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。

许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量，运动参数又是机械动力学分析的依据，所以机构的运动分析是机械设计过程中必不可少的重要环节。

以计算机为手段的解析方法，由于解算速度快，精确度高，程序有一定的通用性，已成为机构运动分析的主要方法。

连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式，同其他型式机构特别是凸轮机构相比具有很多优点。

连杆机构采用低副连接，结构简单，易于加工、安装并能保证精度要求。

连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件，实现间歇运动，满足给定的运动要求，完成机器的工艺操作。

牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。

工作台的纵向往复运动是机床的主运动，实现工件的切削。

工作台的横向运动即是进给运动，实现对切削精度的控制。

本文中只分析纵向运动的运动特性。

牛头刨床有很多机构组成，其中实现刨头切削运动的六连杆机构是一个关键机构。

刨床工作时，通过六杆机构驱动刨刀作往复移动。

刨刀右行时，当刨刀处于工作行程时;要求刨刀的速度较低且平稳，以减小原动机的容量和提高切削质量。

当刨刀处于返回行程时，刨刀不工作，称为空行程，此时要求刨刀的速度较高以提高生产率。

由此可见，牛头刨床的纵向运动特性对机床的性能有决定性的影响。

1 牛头刨床的六连杆机构牛头刨床有很多机构组成，其中实现刨头切削运动的六杆机构是一个关键机构。

图1所示的为一牛头刨床的六连杆机构。

杆1为原动件，刨刀装在C点上。

假设已知各构件的尺寸如表1所示，原动件1以等角速度ω1=1rad/s沿着逆时针方向回转，要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。

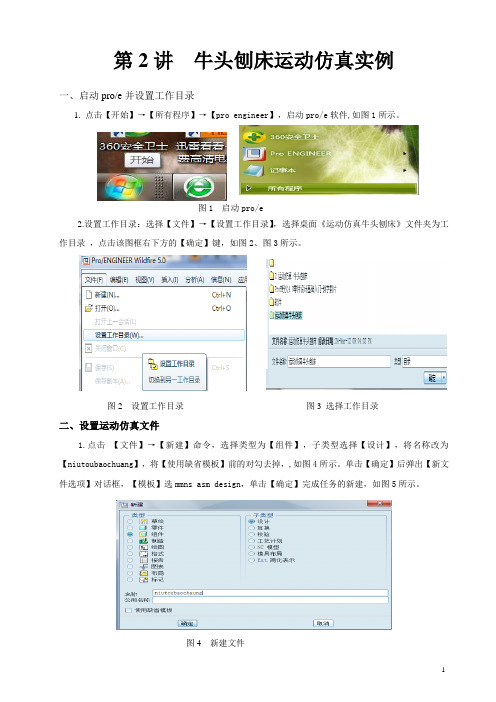
第2讲牛头刨床运动仿真实例一、启动pro/e并设置工作目录1.点击【开始】→【所有程序】→【pro engineer】，启动pro/e软件,如图1所示。

图1 启动pro/e2.设置工作目录：选择【文件】→【设置工作目录】，选择桌面《运动仿真牛头刨床》文件夹为工作目录，点击该图框右下方的【确定】键，如图2、图3所示。

图2 设置工作目录图3 选择工作目录二、设置运动仿真文件1.点击【文件】→【新建】命令，选择类型为【组件】，子类型选择【设计】，将名称改为【niutoubaochuang】，将【使用缺省模板】前的对勾去掉，,如图4所示。

单击【确定】后弹出【新文件选项】对话框，【模板】选mmns asm design，单击【确定】完成任务的新建，如图5所示。

图4 新建文件图5 选择模板三、零件的装配1.预览整个机构效果图单击工作窗口右边工具栏中的【装配】命令，在【打开】命令中单击【niutoubaoch.asm】项。

单击【预览】可在框图中查看整个凸轮机构组装好后的效果图，如图6所示，后面的组装皆可按此标准来进行。

图6 机构效果图2. 安装基座（1）单击工作窗口右边的【装配】命令，在【打开】命令中选择ground.prt文件，即机座（也可以现【预览】确认一下），点击【打开】如图7所示。

图7 选择基座文件（2）导入机座后单击图8中所示【自动】命令右边小三角形，将机座设置为【缺省】模式，再点击面板右端的对勾，完成机座的放置，如图8所示。

图8 设置基座3. 安装圆盘（1）点击【装配】选中并打开打开第二个文件yuanpan.prt，即圆盘机构然后预览并单击【打开】,如图9所示，点击工具栏旁的【用户定义】下拉菜单，选择【销钉】连接类型,如图10所示。

图9 选择圆盘文件图10 设置约束类型（2）先进行轴对齐，即选择机座机架上矮圆柱的中心线A-2，再选择圆盘上圆孔的中心线A-1，完成轴对齐，如图11所示。

图11 轴对齐（3）再面匹配，光标移到圆盘上选中表面，然后选择矮圆柱的表面，点击工具栏上的对勾完成凸轮的装配，如图12所示。

牛头刨床机构运动分析一、设计小组人员构成二、设计任务1、机构结构分析2、机构运动分析建立数学模型，解析法进行运动分析；程序编写；上机调试程序；位移、速度和加速度运动曲线图与分析；三、设计参数四、设计分工五、 设计内容如右图，建立直角坐标系，并标出各杆矢量及方位角。

利用两个封闭图形ABCA 及CDEGC ，由此可得:l 6⃑⃑⃑ +l 3⃑⃑⃑ =s 3⃑⃑⃑ , l 3⃑⃑⃑ +l 4⃑⃑⃑ =l 6′⃑⃑⃑ +S E ⃑⃑⃑⃑投影方程式为:s 3 cos θ3=l 1 cos θ1 s 3sin θ3=l 6+l 1sin θ1 l 3cos θ3+l 4cos θ4−s E =0l 3sin θ3+l 4sin θ4=l 6′有以上各式即可求得s 3 、θ3 、θ4 四个运动那个变量，二滑块2的方位角θ2=θ3。

然后，分别将上式对时间去一次、二次导数，并写成矩阵形式，即得以下速度和加速度方程式：[cos θ3−s 3sin θ3sin θ3s 3cos θ30 00 00 −l 3sin θ30l 3cos θ3−l 4sin θ4−1l 4cos θ40] [s 3ω3ω4v E ]=ω1[−l 1sin θ1l 1cos θ100][cos θ3−s 3sin θ3sin θ3s 3cos θ30 00 00 −l 3sin θ30l 3cos θ3−l 4sin θ4−1l 4cos θ40] [s 3α3α4αE ] =- [−ω3sin θ3 −s 3sin θ3−s 3ω3sin θ3ω3cos θ3 s 3cos θ3−s 3ω3sin θ30 00 00 −l 3ω3cos θ30 −l 3ω3sin θ3−l 4ω4cos θ4 0−l 4ω4sin θ4 0] [s 3ω3ω4v E ]+ ω1[−l 1ω1cos θ1−l 1ω1sin θ100]而ω2=ω3 、α2=α3 。

机械原理课程设计令狐采学计算说明书课题名称：牛头刨床刨刀的往复运动机构姓名：院别：工学院学号：专业：机械设计制造及其自动化班级：机设1201指导教师：2014年6月7日工学院课程设计评审表目录一．设计任务书 (4)1.1 设计题目 (4)1.2 牛头刨床简介 (4)1.3 牛头刨床工作原理 (4)1.4 设计要求及设计参数 (6)1.5 设计任务 (7)二．导杆机构的设计及运动分析 (8)2.1 机构运动简图 (8)2.2 机构运动速度多边形 (9)2.3 机构运动加速度多边形 (11)三．导杆机构动态静力分析 (14)3.1 静态图 (14)3.2 惯性力及惯性力偶矩 (14)3.3 杆组拆分及用力多边形和力矩平衡求各运动反力和曲柄平衡力 (15)心得与体会 (21)参考文献 (22)一、设计任务书1.1 设计题目：牛头刨床刨刀的往复运动机构1.2 牛头刨床简介：牛头刨床是用于加工中小尺寸的平面或直槽的金属切削机床，多用于单件或小批牛头刨床外形图量生产。

为了适用不同材料和不同尺寸工件的粗、精加工，要求主执行构件—刨刀能以数种不同速度、不同行程和不同起始位置作水平往复直线移动，且切削时刨刀的移动速度低于空行程速度，即刨刀具有急回现象。

刨刀可随小刀架作不同进给量的垂直进给；安装工件的工作台应具有不同进给量的横向进给，以完成平面的加工，工作台还应具有升降功能，以适应不同高度的工件加工。

1.3 牛头刨床工作原理：牛头刨床是一种刨削式加工平面的机床，图1所示为较常见的一种机械运动的牛头刨床。

电动机经皮带传动和两对齿轮传动，带动曲柄2和曲柄相固结的凸轮转动，由曲柄2驱动导杆2－3－4－5－6，最后带动刨头和刨刀作往复运动。

当刨头右行时，刨刀进行切削，称为工作行程。

当刨头左行时，刨刀不切削，称为空回行程。

当刨头在工作行程时，为减少电动机容量和提高切削质量，要求刨削速度较低，且接近于匀速切削。

在空回行程中，为节约时间和提高生产效率，采用了具有急回运动特性的导杆机构。

基于matlab的机械结构仿真程序基于Matlab的机械结构仿真程序是一种用于模拟和分析机械系统动态行为的工具。

通过使用Matlab编程语言和Simulink仿真环境，我们可以构建出具有各种结构和运动特性的机械系统，并对其进行仿真和优化。

以下是一个基于Matlab的机械结构仿真程序的探讨：1. 简介在介绍这个仿真程序之前，我们首先明确一下机械结构仿真的定义和意义。

机械结构仿真是指通过建立数学模型和运用仿真技术，对机械系统进行虚拟化，以便通过模拟和分析机械系统的行为，获得系统的性能指标和设计优化。

2. Matlab的仿真环境Matlab是一种强大的科学计算软件，具有丰富的工具箱和编程语言。

Simulink是Matlab的一个附属工具，用于建立、模拟和分析动态系统。

Simulink提供了一个直观的图形化界面，使得机械结构仿真程序的搭建更加便捷。

3. 机械结构建模在进行机械结构仿真前，我们需要首先建立机械系统的数学模型。

这包括建立机械结构的几何模型、物理模型和动力学模型。

通过使用Matlab的数学工具箱，可以方便地表示机械结构的运动学和动力学方程，从而实现仿真程序的搭建。

4. 动力学仿真一旦机械结构的数学模型建立完毕，我们可以使用Matlab的仿真工具对机械系统的动态行为进行仿真。

仿真可以模拟机械结构在不同工况下的运动和响应，例如负载变化、初始条件变化等。

通过对仿真数据的分析，我们可以获得机械系统的性能指标，如速度、加速度、力矩等。

5. 仿真结果分析仿真结果的分析是机械结构仿真程序中非常重要的一环。

通过使用Matlab的数据处理和可视化工具，我们可以对仿真结果进行综合分析。

通过绘制机械系统的运动轨迹图、动力学响应曲线和频谱图，我们可以更直观地理解系统的行为特性，并进一步对机械结构进行优化。

6. 优化设计基于仿真结果的分析，我们可以对机械结构的设计进行优化。

通过改变机械结构的几何参数、材料选择和工艺参数等，可以改善系统的性能和可靠性。

高等机构学题目: 牛头刨床机构运动分析院系名称：机械与动力学院专业班级：机械工程学生姓名：学号：学生姓名：学号：学生姓名：学号：指导教师：2015年12 月17日目录一问题描述................................................................................................................................ - 1 -二运动分析................................................................................................................................ - 1 -2.1矢量法构建机构独立位置方程 ............................................................................. - 1 -2.2机构速度分析 ............................................................................................................. - 2 -2.3机构加速度分析......................................................................................................... - 2 -2.4机构运动线图绘制.................................................................................................... - 3 -三总结......................................................................................................................................... - 4 -附录一：Matlab程序............................................................................................................... - 4 -牛头刨床机构运动分析一 问题描述如图1-1所示的牛头刨床机构中，800h mm =，1360h mm =，2120h mm =，200AB l mm =，960CD l mm =，160DE l mm =。

参数名称L 1L 3L 5H G 准 3P 准 5S n 1准 1转向参数含义原动件 AB 的长度从动件 DE 的长度从动件 EF 的长度 AD 的长度刨头距离底座的竖直高度从动件 DE 的转角滑块 2到底座的距离从动件 EF 的转角滑块 6的位移原动件 AB 的转速原动件 AB 的转角原动件 AB 的转向表 1模型参数含义基于 Matlab 的牛头刨床运动学分析及通用仿真软件开发吴国祥(兰州交通大学教务处, 兰州 7300701引言机构运动分析的任务是在已知机构尺寸及原动件运动规律的情况下, 确定机构中其他构件上某些点的轨迹、位移、速度、加速度和构件的角位移、角速度及角加速度。

上述这些内容, 不论是设计新的机器, 还是为了了解现有机械的运动性能, 都是十分必要的, 而且它还是研究机械动力性能的必要基础和前提 [1]。

对于牛头刨床来说,其刨刀在有效工作行程中应该接近等速运动, 而回程速度却应高于前者速度, 从而提高效率。

为了确定牛头刨床的设计是否满足要求, 就必须对其进行运动分析 [2]。

本文建立了牛头刨床的力学模型,并推导了其运动微分方程,通过数值方法求得了牛头刨床的运动学规律并开发了一款用于牛头刨床的通用运动学分析软件 [3]。

2牛头刨床的数学模型图 1所示为牛头刨床的机构简图, 模型中各参数的物理意义如表 1所示。

设已知结构参数为 :L 1、 L 3、 L 5、 G H , 原动件的转角φ1和转速 n 1。

解:如图 1, 先建立一个直角坐标系, 并标出各杆矢及其方位角。

其中有四个未知变量φ3、φ5, P 及 S 。

为求解需建立两个封闭矢量方程,为此需利用两个封闭图形 ABDA 及 DEFD 。

为求这些未知量可以通过两种方法求解。

2.1用分析力学基础知识求解(1 求准 3、ω3及α3由封闭形 ABDA 可得L 1+H =P(1分别用 i 和 j 点积上式两端, 有L 1cos 准 1=P cos 准 3H +L 1sin 准 1=P sin 准 3联解上面两式可得:准3=arctan[(H +L 1sin 准 1 /L 1cos 准 1]H =L 1cos 准 1/cos准 3式 (1 对时间 t 求导数, 注意 P 为变量, 有准觶 1L 1e t 1=准 3Pe t 3+Pe3(2可用 e 3点积上式两端以消去准觶 3,并利用矢量方程解析法, 有P 觶 =V B 2B 3=-ω1L 1sin (准 1-准 3用 e t 3点积式 (2 两端可消去 P 觶 , 并注意到 e n 1·e t 3=-e 1·e t 3,则准觶3=ω3=ω1L 1cos (准 1-准 3 /P再将式 (2 对时间 t 求导, 则有准觶 21L 1e n 1=准咬 23Pe t 3+准觶 3Pe n 3+2准觶 3P 觶 e t 3+P 咬 e t3可分别用 e 3和 e t 3点积上式两端, 以消去准咬 3和 P 咬 , 注意e n 1·e t 3=-e 1·e t3,则 -准觶 1L 1cos (准 1-准 3 =-准觶 3P +P 咬准觶 21L 1sin(准 3-准 1 =准咬 3P +2准觶 3摘要:文中建立了牛头刨床的力学模型, 基于分析力学原理推导了牛头刨床的运动微分方程。

牛头刨床主传动机构运动简图一、绘制牛头刨床主传动机构运动简图注意事项1.用中心线绘制出机构的两极限位置和曲柄的运动轨迹；2.对机架、原动件、构件编号、运动副进行标示；3.标注曲柄的位置；4.写出比例尺及其单位m/mm；5.在机构运动简图旁写出各构件的长度：l AB ；l CD ；l DE ；l AC ；l A到E 点运动轨迹的距离；θ 或Φ。

二、图解法运动分析注意事项 1.速度多边形图和加速度多边形图分别都画在一个图上，并在相应的图旁写出比例尺及其单位，速度多边形图比例尺单位m/s/mm，加速度多边形图比例尺单位m/s 2 /mm；2.分别写出速度多边形图和加速度多边形图的矢量方程，并分析各矢量的大小和方向，在矢量方程中只写出各矢量的大小和具体方向，分析及计算过程写在设计说明书中。

3.速度多边形图中矢量的起始点和终止点用小写字母p、a、b、c…等表示；加速度多边形图中矢量的起始点和终止点用小写字母、、、等表示。

三、动力分析注意事项 1.绘制等效力矩图：在0~360°内绘制出等效阻力矩和等效驱动力矩图，横坐标为曲柄转角，纵坐标为力矩，并写出横坐标和纵坐标比例尺及其单位，横坐标比例尺单位°/mm，纵坐标比例尺单位N·m /mm。

注意在0~φ 1 和φ 2 ~360°之间的等效阻力矩均为零；2.绘制能量指示图：注意应分别写出各盈亏功和Δ W max 的大小；3.计算飞轮的转动惯量：写出飞轮转动惯量计算公式中各变量的大小并代入公式中计算出飞轮的转动惯量；注意：动力分析的所有分析与计算过程均写在设计说明书中，图纸上只写出结果。

进给凸轮机构简图一、绘制凸轮机构注意事项 1.列表分别计算出推程和回程摆杆至少 6 个位置转角的大小，远休止和近休止摆杆转角分别为最大摆角和零度。

2.写出比例尺及其单位m/mm； 3.摆杆回转中心与凸轮回转中心之间的连线与水平线的夹角为45°（见设计任务书图1）；4.绘制凸轮轮廓线：理论轮廓线为中心线，实际轮廓线以及摆杆和滚子的初始位置均为粗实线，其余辅助线条或圆（圆弧）均为细实线且保留在图纸上，各辅助点用大写字母表示，如：A 1 、A 2 、…，B 1 、B 2 、…，C 1 、C 2 、…等；5.对机架、构件的编号、运动副进行标示； 6.标注项目：基圆半径、运动角度、机架中心距、摆杆长度、凸轮的正转和反转方向。

牛头刨床matlab程序机械原理课程设计第一篇：牛头刨床matlab程序机械原理课程设计clear all;clc;%初始条件theta1=linspace(-18,342,100);%单位度theta1=theta1*pi/180;%转换为弧度制 W1=80*pi/30;%角速度单位rad/s H=0.5;%行程单位m L1=0.1329;%O2A的长度单位m L3=0.8091;%O3B的长度单位m L4=0.2589;%BF的长度单位m L6=0.430;%O2O3的长度单位m L6u=0.7893;%O3D的长度单位m Z=pi/180;%角度与弧度之间的转换dT=(theta1(3)-theta1(2))/W1;%时间间隔for j=1:100 t(j)=dT*(j-1);%时间因素end %求解S3、Theta3、Theta4和SE四个变量theta3(i)=atan((L6+L1*sin(theta1(i)))/L1/cos(theta(i)));fori=1:100 S3=L1*cos(theta1(i))/cos(theta3(i));theta4(i)=asin((L6u-L3*sin(theta3(i)))/L4);SE(i)=L3*cos(theta3(i))+L4*cos(theta4(i));en d%求解完成 %求解完成%求解VS3、W3、W4和VE四个变量for i=1:100 J= inv([cos(theta3(i)),-S3(i)*sin(theta3(i)),0,0;sin(theta3(i)),S3(i)*cos(theta3(i)),0,0;0,-L3*sin(theta3(i)),-L4*sin(theta4(i)),-1;0,L3*cos(theta3(i)),L4*cos(theta4(i)),0]);K=J*W1*[-L1*sin(theta1(i));L1*cos(theta1(i));0;0];VS3(i)=K(1);W3(i)=K(2);W4 (i)=K(3);VE(i)=K(4);end%求解完成%求解aS3、a3、a4、aE四个变量for i=1:100 J= inv([cos(theta3(i)),-S3(i)*sin(theta3(i)),0,0;sin(theta3(i)),S3(i)*cos(theta3(i)),0,0;0,-L3*sin(theta3(i)),-L4*sin(theta4(i)),-1;0,L3*cos(theta3(i)),L4*cos(theta4(i)),0]);P=W1*[-L1*cos(theta1(i));L1*sin(theta1(i));0;0];M=[-W3(i)*sin(theta3(i)),-VS3(i)*sin(theta3(i))-S3(i)*W3(i)*cos(theta3(i)),0,0;W3(i)*cos(theta3(i)),VS3(i)*cos(theta3(i))-S3(i)*W3(i)*sin(theta3(i)),0,0;0,-L3*W3(i)*cos(theta3(i)),-L4*W4(i)*cos(theta4(i)),0;0,-L3*W3(i)*sin(theta3(i)),-L4*W4(i)*sin(theta4(i)),0];N=[VS3(i);W3(i);W4(i);VE(i)];K=J*(-M*N+P);aS3(i)=K(1);a3(i)=K(2);a4(i)=K(3);aE(i)=K(4);end%求解完成%动态静力分析%初始条件M4=20;M5=3;M6=62;Js4=1.2;Js5=0.025;Fc=1500;Ls4=0.5*L3;Ls 5=0.5*L4;%给切削阻力赋值 for i=1:100if((abs(SE(1)-SE(i))>0.05*H&&abs(SE(1)-SE(i))<0.95*H)&&(theta1(i)J4=Js4+M4*(0.5*L3)*(0.5*L3);%导杆对点O3的转动惯量for i=1:100Ekk(i)=(M6*VE(i)*VE(i)+Js5*W4(i)*W4(i)+M5*VE(i)*VE(i)+J4* W3(i)*W3(i))/2;%计算总动能end dEkk(1)=Ekk(1)-Ekk(100);%动能的改变量for i=2:100 dEkk(i)=Ekk(i)-Ekk(i-1);%动能的改变量end for i=1:100 MM(i)=(dEkk(i)+Fc(i)*abs(VE(i)))/W1;%求平衡力矩end %画图%画运动图figure(1);plot(t,theta3,'r');hold on;plotyy(t,theta4,t,SE);grid on;xlabel('时间t/s');ylabel('theta3、theta4(rad)');title('角度Theta3、theta4和位移SE');axis([ 0 , 0.75,-0.2,2]);figure(2);plot(t,W3,'r');hold on;grid on;plotyy(t,W4,t,VE);xlabel('时间t/s');ylabel('W3、W4(rad/s)');title('角度速度W3、W4和速度VE');axis([0 , 0.75,-5,3]);figure(3);plot(t,a3,'r');hold on;plotyy(t,a4,t,aE);grid on;xlabel('时间t/s');ylabel('a3、a4(rad/s/s)');title('角度加速度a3、a4和加速度aE');axis([0 , 0.75,-80,80]);%运动图画完%画反力图figure(4);plotyy(theta1,Fc,theta1,SE);xlabel('Theta1（时间t）');ylabel('Fc');axis([theta1(1),theta1(100),-50,1500]);title('切削阻力Fc与位移SE');grid on;figure(5);plotyy(theta1,MM,theta1,Fc);xlabel('Theta1（时间t）');ylabel('力矩');axis([theta1(1),theta1(100),-50,300]);title('平衡力矩');grid on;figure(6);plotyy(theta1,Ekk,theta1,SE);xlabel('Theta1（时间t）');ylabel('Fc');title('导杆、连杆和刨头的总动能');grid on;theta1(1)theta1(100)第二篇：牛头刨床课程设计matlab程序lo2o3=0.65;l2=0.09250;l4=1.1245;l5=0.281125;lo3d=1.1187 8;w2=8*pi/3;m4=16;m5=4;m6=68;g=9.8;j4=1.6;j5=0.03;k2=-38.18;for i=1:13;k2=k2+30;if k2>90&k2<270 k4=pi+atan((lo2o3+l2*sin(k2*pi/180))/(l2*cos(k2*pi/180)));else k4=atan((lo2o3+l2*sin(k2*pi/180))/(l2*cos(k2*pi/180)));end k5=asin((lo3d-l4*sin(k4))/l5);sf= l4*cos(k4)+l5*cos(k5);%得到牛头刨头的位移l3=l2*cos(k2*pi/180)/cos(k4);B1=[cos(k4),-l3*sin(k4),0,0;sin(k4),l3*cos(k4),0,0;0,-l4*sin(k4),-l5*sin(k5),-1;0,l4*cos(k4),l5*cos(k5),0;];M=inv(B1)*(w2*[-l2*sin(k2*pi/180);l2*cos(k2*pi/180);0;0;]);%求得矩阵，其中M=[v3;w4;w5;vf]B2=[-M(2)*sin(k4),-M(1)*sin(k4)-M(2)*l3*cos(k4),0,0;M(2)*cos(k4),M(1)*cos(k4)-M(2)*l3*cos(k4),0,0;0,-M(2)*l4*cos(k4),-l5*M(3)*cos(k5),0;0,-M(2)*l4*sin(k4),-l5*M(3)*sin(k5),0;];N=inv(B1)*(-B2*M+w2*[-l2*w2*cos(k2*pi/180);-l2*w2*sin(k2*pi/180);0;0;]);%求得加速度矩阵，其中N=[a3;a4;a5;af]vf=M(4);af=N(4);X(i,:)=[k2,sf,vf,af];%收集Φ2与牛头刨头位移，速度，加速度与Φ2的数据a4x=-N(2)*l4*sin(k4)/2-M(2)*M(2)*l4*cos(k4)/2;a4y=N(2)*l4*cos(k4)/2-M(2)*M(2)*l4*sin(k4)/2;a5x=2*a4x-N(3)*l5*sin(k5)/2-M(3)*M(3)*l5*cos(k5)/2;a5y=2*a4y+N(3)*l5*cos(k5)/2-M(3)*M(3)*l5*sin(k5)/2;%求出构件4，5质心的加速度，以便惯性力的计算p4x=-m4*a4x;p4y=-m4*a4y;M4=-j4*N(2);p5x=-m5*a5x;p5y=-m5*a5y;M5=-j5*N(3);p6=-m6*af;%构件4，5，6的惯性力及惯性力矩if sf>(0.03+0.50237-0.6)&sf<(0.50237-0.03)fc=14000;else fc=0;end %判断fc的取值M1=[1,0,1,0,0;0,1,0,0,0;0,0,-1,0,1;0,-1,0,1,0;0,l5*sin(k5)/2,-l5*cos(k5)/2,l5*sin(k5)/2,-l5*cos(k5)/2;];N1=[m6*g;-fc-p6;m5*g-p5y;-p5x;-M5;];F1=inv(M1)*N1;%其中F1对应的量为：F1=[fn;r56x;r56y;r45x;r45y;]M2=[1,0,1,0,0;0,1,0,1,0;cos(k4),sin(k4),0,0,0;(l4/2-l3)*sin(k4),-(l4/2-l3)*cos(k4),l4*sin(k4)/2,-l4*cos(k4)/2,0;l2*sin(k2*pi/180),-l2*cos(k2*pi/180),0,0,1;];N2=[F1(4)-p4x;F1(5)-p4y+m4*g;0;F1(5)*l4*cos(k4)/2-F1(4)*l4*sin(k4)/2-M4;0;];F2=inv(M2)*N2;%其中F2对应的量为：F2=[r34x;r34y;r14x;r14y;Mb;]Y(i,:)=[k2,F2(1), F2(2), F2(3), F2(4), F1(4), F1(5), F1(2), F1(3)];%记录不同角度时反力r34x,r34y,r14x,r14y,r45x,r45y,r56x,r56y的数据Z(i,:)=[k2,F2(5),p4x,p4y,M4,p5x,p5y,M5,p6];%记录Φ2与平衡力矩的关系 enddisp(X);disp(Y);disp(Z);plot(X(:,1),X(:,2),'-')grid on title('s6--Φ2函数')xlabel('变量Φ2（°）')ylabel('变量s6（m）')figure plot(X(:,1),X(:,3),'-')grid on title('v6--Φ2函数')xlabel('变量Φ2（°）')ylabel('变量v6（m/s）')figure plot(X(:,1),X(:,4),'-')grid on title('a6--Φ2函数')xlabel('变量Φ2（°）')ylabel('变量a6（m*m/s）')figure plot(Z(:,1),Z(:,2),'-')grid on title('Mb--Φ2函数')xlabel('变量Φ（2°）')ylabel('变量Mp（N*m）')21.82000.4211-0.6064-8.013051.82000.3698-0.9980-4.405581.82000.3010-1.1660-0.9019111.82000.2286-1.11542.4802141.82000.1661-0.84795.9804171.82000.1273-0.35719.5994201.82000.12570.333912.1179231.82000.17031.078110.6189261.82000.25461.53732.9031291.82000.34951.3924-7.1580321.82000.41800.7490-12.0727 351.82000.4411-0.0000-11.1982 381.82000.4211-0.6064-8.01301.0e+004 *0.0022-2.34530.29430.8812-0.0177 -0.2917-1.4577-0.0136 -1.4545-2.2130 0.1751 0.7778 -0.1467 -1.4317 0.0132 -1.4300 0.0094 0.0082 -2.1335 0.0379 0.7263 0.0064 -1.4065 0.0295 -1.4061 0.0258 0.0112 -2.1010 -0.0982 0.7208 0.1370 -1.3821 0.0239 -1.3831 0.0202 0.0142 -2.1175 -0.21770.2345-1.35690.0011-1.3593-0.00280.0172-2.1882-0.30210.86500.2979-1.3309-0.0209-1.3347-0.02500.0202-0.0257 0.0232-0.0008 0.0262 0.0247 0.0292 0.0169 0.0322-0.0160 0.0352-0.03220.0382-0.01771.0e+003 * 0.0218 0.5449 0.0518 0.2996 0.0818 0.0613 0.1118-0.1687 0.1418-0.4067 0.1718-0.6528 0.2018-0.82400.2318-0.72210.2618-2.3215-2.5278-2.7700-2.8882-2.7690-2.5408-2.34531.0591 1.70921.9584 1.83791.3691 0.5646-0.5201-1.6948-2.5276-0.3238-0.2504-0.06530.17600.3396 0.3653 0.2943 0.0640 0.0351 0.0074-0.0198-0.0481-0.0767-0.0968-0.0853-0.02291.01841.21281.39321.43091.2724 1.0512 0.8812-0.00530.00440.00950.00800.0003-0.0097-0.0127-0.00010.01630.3193 0.2692 0.1076-0.1408-0.3350-0.3763-0.2917-0.0114-0.0062-0.0013 0.0035 0.0085 0.0137 0.0174 0.0151 0.0040-1.3128-1.3235-1.3791-1.4515-1.4869-1.4806-1.4577 0.0320 0.0176 0.0037-0.0099-0.0240-0.0384-0.0484-0.0426-0.0115-0.02150.00310.02820.0205-0.0119-0.0279-0.0136-0.00130.00110.00240.00200.0001-0.0024-0.0032-0.0000 0.0041-1.3176-1.3278-1.3803-1.4487-1.4821-1.4761-1.45450.0001-0.0001-0.0001-0.0001-0.00000.00010.00020.0000-0.0002-0.19740.2918-2.41960.05720.0104-0.01000.02860.48670.3218-1.33630.0964-0.0077-0.01720.04820.82090.35180.00010.0898-0.0129-0.01610.04490.7615 0.38181.05910.0640-0.0053-0.01140.03200.54490.0026-0.0001-0.00190.0001-0.00320.0002-0.00130.0001第三篇：机械原理课程设计牛头刨床机械原理课程设计——牛头刨床设计说明书（3）待续2.6．滑块6的位移，速度，加速度随转角变化曲线§其位移，速度，加速度随转角变化曲线如图所示：三．设计方案和分析§3.1方案一3.1.1方案一的设计图3.1.2方案一的运动分析及评价（1）运动是否具有确定的运动该机构中构件n=5。

牛头刨床主传动机构运动简图一、绘制牛头刨床主传动机构运动简图注意事项1.用中心线绘制出机构的两极限位置和曲柄的运动轨迹；2.对机架、原动件、构件编号、运动副进行标示；3.标注曲柄的位置；4.写出比例尺及其单位m/mm；5.在机构运动简图旁写出各构件的长度：l AB ；l CD ；l DE ；l AC ；l A到E 点运动轨迹的距离；θ 或Φ。

二、图解法运动分析注意事项 1.速度多边形图和加速度多边形图分别都画在一个图上，并在相应的图旁写出比例尺及其单位，速度多边形图比例尺单位m/s/mm，加速度多边形图比例尺单位m/s 2 /mm；2.分别写出速度多边形图和加速度多边形图的矢量方程，并分析各矢量的大小和方向，在矢量方程中只写出各矢量的大小和具体方向，分析及计算过程写在设计说明书中。

3.速度多边形图中矢量的起始点和终止点用小写字母p、a、b、c…等表示；加速度多边形图中矢量的起始点和终止点用小写字母、、、等表示。

三、动力分析注意事项 1.绘制等效力矩图：在0~360°内绘制出等效阻力矩和等效驱动力矩图，横坐标为曲柄转角，纵坐标为力矩，并写出横坐标和纵坐标比例尺及其单位，横坐标比例尺单位°/mm，纵坐标比例尺单位N·m /mm。

注意在0~φ 1 和φ 2 ~360°之间的等效阻力矩均为零；2.绘制能量指示图：注意应分别写出各盈亏功和Δ W max 的大小；3.计算飞轮的转动惯量：写出飞轮转动惯量计算公式中各变量的大小并代入公式中计算出飞轮的转动惯量；注意：动力分析的所有分析与计算过程均写在设计说明书中，图纸上只写出结果。

进给凸轮机构简图一、绘制凸轮机构注意事项 1.列表分别计算出推程和回程摆杆至少 6 个位置转角的大小，远休止和近休止摆杆转角分别为最大摆角和零度。

2.写出比例尺及其单位m/mm； 3.摆杆回转中心与凸轮回转中心之间的连线与水平线的夹角为45°（见设计任务书图1）；4.绘制凸轮轮廓线：理论轮廓线为中心线，实际轮廓线以及摆杆和滚子的初始位置均为粗实线，其余辅助线条或圆（圆弧）均为细实线且保留在图纸上，各辅助点用大写字母表示，如：A 1 、A 2 、…，B 1 、B 2 、…，C 1 、C 2 、…等；5.对机架、构件的编号、运动副进行标示； 6.标注项目：基圆半径、运动角度、机架中心距、摆杆长度、凸轮的正转和反转方向。

基于MATLAB/SIMULINK的牛头刨床导杆机构运动学及动力学分析Kinematics and dynamics analysis of guide-bar mechanism in shaping machine based on MATLAB/SIMULINK钱文婷1，徐承妍2，李滨城1QIAN Wen-ting1, XU Cheng-yan2, LI Bin-cheng1（1. 江苏科技大学机械工程学院，镇江 212003；2. 华东师范大学软件学院，上海 200062）摘 要：本文运用MATLAB/SIMULINK 软件对牛头刨床导杆机构进行了运动学和动力学分析，并通过仿真直观地揭示了机构的运动规律和受力情况，为对其深入研究提供了基础。

另外,在应用SIMULINK进行运动学仿真过程中采用了微分的方法，从而使数学建模过程更为简便。

关键词：牛头刨床导杆机构；运动学分析；动力学分析； MATLAB/SIMULINK中图分类号：TP321 文献标识码：A 文章编号：1009-0134(2011)2(上)-0104-03 Doi: 10.3969/j.issn.1009-0134.2011.2(上).330 引言随着计算机技术的发展，在机构综合中计算机辅助分析得到了迅猛发展，特别为其建模仿真提供了极大的方便[1]，为后续综合出机械最优化设计参数提供了可能。

牛头刨床是一种常见的金属切削机床，其导杆机构作为牛头刨床的主要执行机构，实现将回转运动转变为直线往复运动的重要功能，如图1所示。

本文运用矢量法和矩阵法建立了牛头刨床导杆机构分析的数学模型，在对其进行运动学和动力学分析的基础上，运用MATLAB/SIMULINK进行了运动学和动力学仿真，从而获得了机构的运动曲线图及运动副反力曲线图，为对其进一步深入研究提供了基础。

1 运动学分析1.1 数学模型的建立建立如图1所示的直角坐标系，将各构件视为杆矢量。

方案一clear allclcn = 360fr = 4500l1 = 0.35 * sin(15 / 180 * pi)l3 = 0.7727407l4 = 0.22l6 = 0.35slm = 0.4196m5 = 700/9.8g5 = 700js3 = 1.1g3 = 200m3 = 200/9.8h = 0.76w1 = 72*2*pi/60fi = 75 / 180 * pifi1 = fi:0.0175:(2*pi+fi)fi1t=1:1:360lx = sqrt(l1^2+l6^2-2*l6*l1*cos(fi1))for i=1:1:nlxd1(i) = (l6*l1*w1*sin(fi1(i)))/(sqrt(l1^2+l6^2-2*l6*l1*cos(fi1(i))))lxd2(i) = (l1*l6*w1^2*cos(fi1(i)))/(l1^2 - 2*cos(fi1(i))*l1*l6 + l6^2)^(1/2) - (l1^2*l6^2*w1^2*sin(fi1(i))^2)/(l1^2 - 2*cos(fi1(i))*l1*l6 + l6^2)^(3/2)endfor i=1:1:nfi3(i)=atan((l1*sin(fi1(i)))/(l6-l1*cos(fi1(i))))endfor i=1:1:nfi4(i)=asin((h-l3*cos(fi3(i)))/l4)endfor i=1:1:ns(i) = slm-l4*cos(fi4(i))-l3*sin(fi3(i))endfor i = 1:1:nw3(i) = (l1*w1*cos(fi1(i))-lxd1(i)*sin(fi3(i)))/(lx(i)*cos(fi3(i)))endfor i = 1:1:nw4(i) = (l3*w3(i)*sin(fi3(i)))/(l4*cos(fi4(i)))endfor i=1:1:nv(i)=l4*w4(i)*sin(fi4(i))-l3*w3(i)*cos(fi3(i))endfor i=1:1:ne3(i) = (-l1*w1^2*sin(fi1(i))+lx(i)*w3(i)^2*sin(fi3(i))-lxd1(i)*w3(i)*cos(fi3(i))-lxd1(i)*w3(i)*cos(fi3(i)) -lxd2(i)*sin(fi3(i)))/(lx(i)*cos(fi3(i)))endfor i=1:1:ne4(i) = (l4*w4(i)^2*sin(fi4(i))+l3*e3(i)*sin(fi3(i))+l3*w3(i)^2*cos(fi3(i)))/(l4*cos(fi4(i))) endfor i=1:1:na(i)=l4*e4(i)*sin(fi4(i))+l4*w4(i)^2*cos(fi4(i))-l3*e3(i)*cos(fi3(i))+l3*w3(i)^2*sin(fi3(i)) endfor i=43:1:170,b=1:1:170-43ad(b) = (a(i)-a(i-1))/(2*pi/360)endfor i=1:1:nif v(i)>0&(s(i)<0.36&s(i)>0.04)re45x(i) = m5*a(i)+frelsere45x(i) = m5*a(i)endendfor i=1:1:nre45(i) = re45x(i)/cos(fi4(i))re45y(i) = re45(i)*sin(abs(fi4(i)))r65(i) = g5+re45y(i)endfor i=1:1:nr12(i) = (re45x(i)*l3*cos(fi3(i))+re45y(i)*l3*sin(abs(fi3(i)))+js3*e3(i)+m3*(l3/2*e3(i)*cos(fi3(i))+w3(i)^ 2*l3/2*sin(abs(fi3(i)))+l3/2*e3(i)*sin(abs(fi3(i)))+w3(i)^2*l3/2*cos(fi3(i)))*l3/2+g3*l3/2*sin(fi3 (i)))/lx(i)endfor i=1:1:nmi(i) = r12(i)*sin(fi1(i)+fi3(i)-pi/2)*l1endfor i=1:1:nrc3y(i) = re45y(i)+m3*(l3/2*e3(i)*sin(abs(fi3(i)))+w3(i)^2*l3/2*cos(fi3(i)))+g3-r12(i)*sin(abs(fi3(i))) rc3x(i) = re45x(i)-m3*(l3/2*e3(i)*cos(fi3(i))+w3(i)^2*l3/2*sin(abs(fi3(i))))-r12(i)*cos(fi3(i)) rc3(i) = sqrt(rc3y(i)^2+rc3x(i)^2)endv5max = max(abs(v)) %滑枕最大工作速度a5max = 5.8577 %工作段滑枕最大加速度a5dmax = max(abs(ad)) %工作段滑枕最大加速度最大变化率v5m = 1.1556 %工作段滑枕平均速度mbmax = max(abs(mi)) %最大平衡力矩fi5max = m5*a5max %工作段滑枕最大惯性力rc3max = max(abs(rc3)) %机架对最大摆动件转轴最大反力r12max = max(abs(r12)) %机架对曲柄最大反力gm23 = pi/2 %2、3构件的传动角gm45 = (pi/2-max(abs(fi4))) %4、5构件的最小传动角zdmax = l3*0.4 %最大运动轮廓尺寸gjfz = 35 %机构复杂程度subplot(2,2,1)plot(fi1t,s)subplot(2,2,2)plot(fi1t,v)subplot(2,2,3)plot(fi1t,a)subplot(2,2,4)plot(fi1t,mi)。

第21卷　第3期 2006年9月 西　南　科　技　大　学　学　报 Journal of South west University of Science and Technol ogy Vol .21No .3 Sep t .2006　收稿日期:2006-05-31　基金项目:四川省教育厅资助项目(2005005031)。

　作者简介:张晓勇(1972-),男,硕士,讲师,主要从事计算机图形学及辅助设计、计算机软件的研究与教学。

E_mail:scuxyz@ 。

牛头刨床的机构运动仿真软件模型研究张晓勇　张　莹(西南科技大学制造科学与工程学院　四川绵阳　621010)摘要:对牛头刨床机构动动的特点进行了分析,建立了牛头刨床机构动动仿真软件的运动模型。

在给出系统结构和设计流程的基础上,详细阐述了各个功能模块设计的关键技术。

系统采用OpenG L 技术开发,实现了牛头刨床机构运动分析数字化,具有良好的人机交互界面。

关键词:运动模型　运动仿真　参数化建模　牛头刨床中图分类号:TH139.2 文献标识码:A 文章编号:1671-8755(2006)03-0071-04Research on S i m ul a ti on Software of M echan i ca l M ovem en t M odelof Hor i zon t a l ShaperZHANG Xiao 2yong,ZHANG Ying(School of M anufacturing Science and Engineering,Sou thw est U niversity of Science and Technology,M ianyang 621010,S ichuan,China )Abstract:On detailed analysis of the move ment model of Horiz ontal Shaper,si m ulati on s oft w are is i m p le 2mented under OpenG L.The hierarchy of the syste m and the fl ow chart of the design are given and the key techniques of all the functi on modules are detailed .The hu man 2machine interface of the s oft w are is good and analysis of the mechanical move ment of Horiz ontal Shaper is digitized .Key words:move ment model;move ment si m ulati on;para metric modeling;Horiz ontal Shaper机构运动仿真分析,可以实现机械工程中非常复杂、精确的机构运动分析,在实际制造前利用零件的三维数字模型进行机构运动仿真已成为现代CAD 工程中的一个重要方向及课题。