离散数学复习题(二)

离散数学集合论部分形成性考核书面作业本课程形成性考核书面作业共3次，内容主要分别是集合论部分、图论部分、数理逻辑部分的综合练习，基本上是按照考试的题型（除单项选择题外）安排练习题目，目的是通过综合性书面作业，使同学自己检验学习成果，找出掌握的薄弱知识点，重点复习，争取尽快掌握．本次形考书面作业是第一次作业，大家要认真及时地完成集合论部分的综合练习作业．要求：学生提交作业有以下三种方式可供选择：1. 可将此次作业用A4纸打印出来，手工书写答题，字迹工整，解答题要有解答过程，完成作业后交给辅导教师批阅．2. 在线提交word文档3. 自备答题纸张，将答题过程手工书写，并拍照上传．一、填空题1．设集合{1,2,3},{1,2}A B==，P(A)-P(B )={{3},{1,3},{2,3},{1,2,3}}，A⨯B={<1,1>,<1,2>,<2,1>,<2,2>,<3,1>,<3,2>} ．2．设集合A有10个元素，那么A的幂集合P(A)的元素个数为1024 ．3．设集合A={0, 1, 2, 3}，B={2, 3, 4, 5}，R是A到B的二元关系，∈xyR⋂<且=且>∈∈{B,,xAyAyBx}则R的有序对集合为{<2,2>,<2,3>,<3,2>,<3,3>}．4．设集合A={1, 2, 3, 4 }，B={6, 8, 12}，A到B的二元关系R＝}yyx∈=<那么R－1＝{<6,3>,<8,4>}．>∈A2,x,,xy{B5．设集合A=｛a, b, c, d｝，A上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>}，则R具有的性质是没有任何性质．6．设集合A=｛a, b, c, d｝，A上的二元关系R={<a, a >, <b, b>, <b, c>, <c, d>}，若在R中再增加两个元素<c,b> <d,c> ，则新得到的关系就具有对称性．7．如果R1和R2是A上的自反关系，则R1∪R2，R1∩R2，R1-R2中自反关系有 2 个．8．设A={1, 2}上的二元关系为R={<x, y>|x∈A，y∈A, x+y =10}，则R的自反闭包为<1,1>,<2,2> ．9．设R是集合A上的等价关系，且1 , 2 , 3是A中的元素，则R中至少包含<1,1>,<2,2>,<3,3> 等元素．10．设A ={1，2}，B ={a ，b }，C ={3，4，5}，从A 到B 的函数f ={<1, a >, <2, b >}，从B 到C 的函数g ={< a ，4>, < b ，3>}，则Ran(g ︒ f )= {<1,b>,<2,a>} ．二、判断说明题（判断下列各题，并说明理由．）1．若集合A = {1，2，3}上的二元关系R ={<1, 1>，<2, 2>，<1, 2>}，则 (1) R 是自反的关系； (2) R 是对称的关系．解：（1）错误。

离散数学复习题含答案1. 集合论基础集合A和集合B的交集表示为A∩B，它包含所有既属于A又属于B的元素。

请写出集合{1, 2, 3}和{2, 3, 4}的交集。

答案：{2, 3}2. 逻辑运算设命题p为“今天是周一”，命题q为“明天是周三”。

请判断复合命题“p且q”的真值。

答案：假3. 图论初步在无向图中，若存在一条路径使得起点和终点相同，则称该图为欧拉图。

请判断一个有5个顶点且每个顶点的度均为2的无向图是否一定是欧拉图。

答案：是4. 组合数学从5个不同的球中选取3个，有多少种不同的选取方法？答案：10种5. 布尔代数在布尔代数中，逻辑或运算符表示为∨，逻辑与运算符表示为∧。

请计算表达式(A∨B)∧(¬A∨¬B)的值。

答案：¬(A∧B)6. 归纳与递归给定递归关系式T(n) = 2T(n-1) + 1，初始条件为T(1) = 1，求T(3)的值。

答案：T(3) = 2T(2) + 1 = 2(2T(1) + 1) + 1 = 2(2*1 + 1) + 1 =2(3) + 1 = 77. 有限状态机在有限状态机中，状态转移可以通过一个转移函数来描述。

若状态转移函数定义为δ(q, a) = q'，其中q和q'是状态，a是输入符号，请说明该函数的作用。

答案：该函数定义了在给定当前状态q和输入符号a的情况下，有限状态机将转移到新的状态q'。

8. 正则表达式正则表达式用于描述字符串的模式。

请写出匹配任意长度的数字串的正则表达式。

答案：\d*9. 命题逻辑命题逻辑中的等价关系是指两个命题逻辑表达式在所有可能的真值赋值下具有相同的真值。

请判断命题p∨¬p和命题¬(p∧¬p)是否等价。

答案：是10. 树的遍历在计算机科学中，树的遍历有前序、中序和后序三种方式。

请简述后序遍历的步骤。

答案：后序遍历的步骤是先访问左子树，然后访问右子树，最后访问根节点。

离散数学复习题一、单项选择题1.下列命题公式为重言式的是【 A 】。

A．p→(p∨q) B．(p∨┐p)→qC．q∧┐q D．p→┐q2．下列语句中不是．．命题的是【 A 】。

A．这个语句是假的。

B．1+1=1.0C．飞碟来自地球外的星球。

D．凡石头都可练成金。

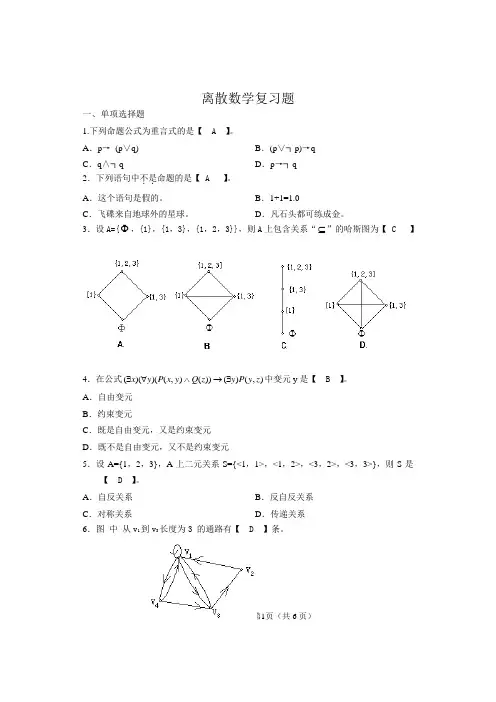
3．设A={Φ，{1}，{1，3}，{1，2，3}}，则A上包含关系“⊆”的哈斯图为【 C 】4．在公式)QyzPyxP∧∀→x∃y∃中变元y是【 B 】。

(z()))y,(()())((,A．自由变元B．约束变元C．既是自由变元，又是约束变元D．既不是自由变元，又不是约束变元5．设A={1，2，3}，A上二元关系S={<1，1>，<1，2>，<3，2>，<3，3>}，则S是【 D 】。

A．自反关系B．反自反关系C．对称关系D．传递关系6．图中从v1到v3长度为3 的通路有【 D 】条。

离散数学试卷（B）第1页（共6页）离散数学试卷（B ）第2页（共6页）A ．0；B ．1；C ．2；D ．3。

7．在下列代数系统中，不是环的只有【 C 】。

A ．<Z ，+，*)，其中Z 为整数集，+，*分别为整数加法和乘法。

B ．(Q ，+，*)，其中Q 为有理数集，+，*分别为有理数加法和乘法。

C ．<R ，+，*>，其中R 为实数集，+为实数加法，a*b=a+2b 。

D ．<M n (R)，+，*>，其中M n (R)为实数集n×n 阶矩阵结合，+，*是矩阵加法和乘法。

8．下列整数集对于整除关系都构成偏序集，而能构成格的是【 B 】。

A ．{l ，2，3，4，5} B ．{1，2，3，6，12} C ．{2，3，7}D ．{l ，2，3，7}9．结点数为奇数且所有结点的度数也为奇数的连通图必定是【 D 】。

A ．欧拉图 B ．汉密尔顿图 C ．非平面图D ．不存在的10．无向图G 是欧拉图当且仅当G 是连通的且【 C 】。

页眉内容《离散数学》试题及答案一、选择或填空（数理逻辑部分）1、下列哪些公式为永真蕴含式？( )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P答：（1），（4）2、下列公式中哪些是永真式？( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答：（2），（3），（4）3、设有下列公式，请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P答：（2），（3），（4），（5），（6）4、公式∀x((A(x)→B(y，x))∧∃z C(y，z))→D(x)中，自由变元是( )，约束变元是( )。

答：x,y, x,z5、判断下列语句是不是命题。

若是，给出命题的真值。

( )(1)北京是中华人民共和国的首都。

(2) 陕西师大是一座工厂。

(3) 你喜欢唱歌吗？ (4) 若7+8＞18，则三角形有4条边。

(5) 前进！ (6) 给我一杯水吧！答：（1）是，T （2）是，F （3）不是（4）是，T （5）不是（6）不是6、命题“存在一些人是大学生”的否定是( )，而命题“所有的人都是要死的”的否定是( )。

答：所有人都不是大学生，有些人不会死7、设P：我生病，Q：我去学校，则下列命题可符号化为( )。

(1) 只有在生病时，我才不去学校 (2) 若我生病，则我不去学校(3) 当且仅当我生病时，我才不去学校(4) 若我不生病，则我一定去学校答：（1）PP⌝P→⌝↔（4）QQ→⌝（2）QP⌝→（3）Q8、设个体域为整数集，则下列公式的意义是( )。

(1) ∀x∃y(x+y=0) (2) ∃y∀x(x+y=0)答：（1）对任一整数x存在整数 y满足x+y=0（2）存在整数y对任一整数x满足x+y=0 9、设全体域D是正整数集合，确定下列命题的真值：(1) ∀x∃y (xy=y) ( ) (2) ∃x∀y(x+y=y) ( )(3) ∃x∀y(x+y=x) ( ) (4) ∀x∃y(y=2x) ( )答：（1） F （2） F （3）F （4）T10、设谓词P(x)：x是奇数，Q(x)：x是偶数，谓词公式∃x(P(x)∨Q(x))在哪个个体域中为真?( )(1) 自然数(2) 实数 (3) 复数(4) (1)--(3)均成立答：（1）11、命题“2是偶数或-3是负数”的否定是（）。

题型一、填空题1、设集合A有n个元素，那么A的幂集P(A)的元素个数为____________。

2、谓词公式∃xF(x)→Q(x,y)中的前束范式为______________。

3、设集合A＝{a,b,{a,b}}，B＝{{a,b}},则B-A=_____________。

4、设集合A＝{0,1}，B＝{1,2},则A×B=_____________________________________。

5．已知图G中有1个1度结点，2个2度结点，3个3度结点，则G的边数是。

二、单项选择题1、下列各命题中真值为真的命题有（）。

A. 2+2=4当且仅当3是奇数B. 2+2=4当且仅当3不是奇数C. 2+2≠4当且仅当3是奇数D. 2+2=4仅当3不是奇数2、设个体域D={a,b}，与公式)∀等价的公式是( )。

xA(xA. )aAA∨ D. ))((b(aA→bA()(bAa(bA→ C. )(A∧ B. ))Aa)(3、令F(x):x是人，G(x):x是犯错误，则命题“没有不犯错误的人”可符号化为（）。

A.))G)x(→(⌝∃x⌝F(x()((xGx∧Fx∀ B.))C.))(x()Gx∧x⌝F(⌝∃()((xGx∧Fx⌝∃ D.))4、下列命题公式不是永真式的是( )。

A. p∨p→q⌝ D. pq(→)p∨→ C. )→)p→q( B . )(pp→q(p5、设X={1,2,3},Y={a,b,c},f={<1,b>,<2,a>,<3,a>},则以下命题正确的是( )。

A．f是从X到Y的二元关系，但不是从X到Y的函数B．f是从X到Y的函数，但不是满射的，也不是单射的C．f是从X到Y的满射，但不是单射D．f是从X到Y的双射6、设集合A={a, b, c}，A上的二元关系R={<a,a>, <a,c>, <c,a>}，则R是( )。

一、选择题：（每题2’）1、下列语句中不是命题的有（）。

A．离散数学是计算机专业的一门必修课。

B．鸡有三只脚。

C．太阳系以外的星球上有生物。

D．你打算考硕士研究生吗?2、命题公式A与B是等价的，是指（）。

A．A与B有相同的原子变元B．A与B都是可满足的C．当A的真值为真时，B的真值也为真D．A与B有相同的真值3、所有使命题公式P∨(Q∧¬R)为真的赋值为（）。

A．010，100，101，110，111 B．010，100，101，111C．全体赋值D．不存在4、合式公式⌝(P∧Q)→R的主析取范式中含极小项的个数为（）。

A．2 B．3 C．5 D．05、一个公式在等价意义下，下面哪个写法是唯一的（）。

A．析取范式B．合取范式C．主析取范式D．以上答案都不对6、下述公式中是重言式的有（）。

A．(P∧Q) → (P∨Q) B．(P↔Q) ↔ (( P→Q)∧(Q→P))C．⌝(P →Q)∧Q D．P →(P∧Q)7、命题公式(⌝P→Q) →(⌝Q∨P)中极小项的个数为（），成真赋值的个数为（）。

A．0 B．1 C．2 D．38、若公式(P∧Q)∨(⌝P∧R) 的主析取范式为m001∨m011∨m110∨m111则它的主合取范式为（）。

A．m001∧m011∧m110∧m111B．M000∧M010∧M100∧M101C．M001∧M011∧M110∧M111D．m000∧m010∧m100∧m1019、下列公式中正确的等价式是（）。

A．⌝(∃x)A(x) ⇔ (∃x)⌝A(x) B．(∀x) (∀y)A(x, y) ⇔ (∃y) (∀x) A(x, y)C．⌝(∀x)A(x) ⇔ (∃x)⌝A(x) D．(∀x) (A(x) ∧B(x)) ⇔ (∀x) A(x) ∨(∀x) B(x)10、下列等价关系正确的是（）。

A．∀x ( P(x) ∨Q(x) ) ⇔∀x P(x) ∨∀x Q(x) B．∃x ( P(x) ∨Q(x) ) ⇔∃x P(x) ∨∃x Q(x)C．∀x ( P(x) →Q ) ⇔∀x P(x) → Q D．∃x ( P(x) →Q ) ⇔∃x P(x) → Q11、设个体域为整数集，下列真值为真的公式是（）。

《离散数学》复习题一、填空题（每小题1分，共10分）1、P ：你努力，Q ：你失败。

“除非你努力，否则你将失败”的翻译为 ；2、一阶逻辑公式()()()()()()x F x G x y F y G y ∀→∧⌝∀→的类型是_______。

3、设个体域为整数集合，命题()0=+∃∀y x y x 的真值为_______。

4、对于任意两个集合A,B,它们有共同的子集_______。

5、 如果关系R 是传递的，则⊆R R _______。

6、集合S={α，β，γ，δ}上的二元运算*为那么，代数系统<S, *>中的幺元是β , α的逆元是 。

7、一个无向图E V G ,=是二部图，当且仅当G 中无__ _____的回路。

8、无向图G 有12条边，6个的3度节点和2个4度节点。

此命题的真值为_______。

9、当3≥n 并且n 为奇数时，无向完全图n k 是欧拉图。

此命题的真值为_______。

10、 设代数系统,*V =，其中Q 是有理数集合，*表示对Q y x ∈∀,有xy y x y x -+=*，则Q 上关于*的幺员（或称单位元）是_______。

二、选择题（每小题1分，共10分）1．设{},(()),A B A ρρ=∅=以下不正确的式子是（ ） A.{{},}B ∅∅∈ B. {{}}B ∅∈ C. B ∅⊆ D. {{{{}},}}B ∅∅⊆2．设E(x)：“x 是偶数”；D （x,y ）：“x 除尽y ”，P(x):“x 是质数”，则公式))),()(()((y x D y E y x P x ∧∃→∀ 正确的翻译是：( )A 、所有质数都能除尽偶数；B 、所有不能除尽偶数的数是质数；C 、对任一质数，都有被它除尽的偶数；D 、对任一偶数，都有被它除尽的质数。

3．下列论述哪个是错误的？（ ）A 、任何一个群，均无零元；B 、任何一个群，其中至少有两个元素是等幂元；C 、任何一个群，其中的二元运算满足消去律；D 、群中每个元素的逆元是唯一的。

离散数学期末复习题第一章集合论一、判断题（1）空集是任何集合的真子集． （ 错 ）（2）{}φ是空集． （ 错 ） （3）{}{}a a a },{∈ （ 对 ） （4）设集合{}{}{}{}AA 22,1,2,1,2,1⊆=则. ( 对 ） （5）如果B A a ⋃∉，则A a ∉或B a ∉． （ 错 ）解 B A a ⋃∉则B A B A a ⋂=⋃∈，即A a ∈且B a ∈，所以A a ∉且B a ∉（6）如果A ∪.,B A B B ⊆=则 （ 对 ）（7）设集合},,{321a a a A =，},,{321b b b B =，则},,,,,{332211><><><=⨯b a b a b a B A （ 错 ）（8）设集合}1,0{=A ，则}1},0{,0},0{,1,,0,{><><><><=φφρ是A2到A 的关系． （ 对 ）解 A 2}},1{},0{,{A φ=， =⨯A A 2}1,,0,,1},1{,0},1{,1},0{,0},0{,1,,0,{><><><><><><><><A A φφ（9）关系的复合运算满足交换律． （ 错 ）（10）.条件具有传递性的充分必要上的关系是集合ρρρρA = （ 错 ）（11）设.~,上的传递关系也是则上的传递关系是集合A A ρρ ( 对 ) （12）集合A 上的对称关系必不是反对称的. （ 错 ）（13）设21,ρρ为集合A 上的等价关系, 则21ρρ⋂也是集合A 上的等价关系( 对 )（14）设ρ是集合A 上的等价关系, 则当ρ>∈<b a ,时， ρρ][][b a = ( 对 )（15）设21,ρρ为集合 A 上的等价关系, 则 ( 错 )二、单项选择题（1）设R 为实数集合，下列集合中哪一个不是空集 （ A ）A. {}R x x x ∈=-且,01|2 B ．{}R x x x ∈=+且,09|2C. {}R x x x x ∈+=且,1|D. {}R x x x ∈-=且,1|2（2）设B A ,为集合，若φ=B A \，则一定有 （ C ）A. φ=B B ．φ≠B C. B A ⊆ D. B A ⊇（3）下列各式中不正确的是 （ C ）A. φφ⊆ B ．{}φφ∈ C. φφ⊂ D. {}}{,φφφ∈ （4）设{}}{,a a A =，则下列各式中错误的是 （ B ）A. {}A a 2∈ B ．{}A a 2⊆ C. {}A a 2}{∈ D. {}Aa 2}{⊆ （5）设{}2,1=A ，{}c b a B ,,=，{}d c C ,=，则)(C B A ⨯为 （ B ） A. {}><><c c ,2,1, B ．{}><><c c ,2,,1C. {}><><2,,,1c cD. {}><><2,,1,c c（6）设{}b A ,0=，{}3,,1b B =，则B A 的恒等关系为 （ A ） A. {}><><><><3,3,,,1,1,0,0b b B ．{}><><><3,3,1,1,0,0C. {}><><><3,3,,,0,0b bD. {}><><><><0,3,3,,,1,1,0b b（7）设{}c b a A ,,=上的二元关系如下，则具有传递性的为 （ D ）A. {}><><><><=a b b a a c c a ,,,,,,,1ρB ． {}><><=a c c a ,,,2ρC. {}><><><><=c b a b c c b a ,,,,,,,3ρD. {}><=a a ,4ρ（8）设ρ为集合A 上的等价关系，对任意A a ∈，其等价类[]ρa 为 （ B ）A. 空集； B ．非空集； C. 是否为空集不能确定； D. }|{A x x ∈.（9）映射的复合运算满足 （ B ）A. 交换律 B ．结合律 C. 幂等律 D. 分配律（10）设A ，B 是集合，则下列说法中（ C ）是正确的.A ．A 到B 的关系都是A 到B 的映射B ．A 到B 的映射都是可逆的C ．A 到B 的双射都是可逆的D ．B A ⊂时必不存在A 到B 的双射（11）设A 是集合，则（ B ）成立.A ．A A #22#=B ．A X X A⊆↔∈2 C ．{}A2∈φ D ．{}AA 2∈ （12）设A 是有限集（n A =#），则A 上既是≤又是～的关系共有（B ）.A ．0个B ．1个C ．2个D ．n 个三、填空题1. 设}}2,1{,2,1{=A ，则=A2____________.填}}},2,1{,2{}},2,1{,1{},2,1{}},2,1{{},2{},1{,{2A A φ=2.设}}{,{φφ=A ，则A 2= . 填}}},{{},{,{2A A φφφ=3.设集合B A ,中元素的个数分别为5#=A ，7#=B ，且9)(#=⋃B A ，则集合B A ⋂中元素的个数=⋂)(#B A .34.设集合}4,1001|{Z x x x x A ∈≤≤=的倍数，是，}5,1001|{Z x x x x B ∈≤≤=的倍数，是，则B A 中元素的个数为 .405.设 },{b a A =, ρ 是 A2 上的包含于关系，,则有ρ= .},,},{,}{},{,},{,}{},{,,,}{,,}{,,,{><><><><><><><><><A A A b b b A a a a A b a φφφφφ6.设21,ρρ为集合 A 上的二元关系, 则=21ρρ .~1~2ρρ7.集合A 上的二元关系ρ为传递的充分必要条件是 ．ρρρ⊆8. 设集合{}{}><><==0,2,2,02,1,01ρ上的关系A 及集合A 到集合{}4,2,0=B 的关系=2ρ｛><b a ,|><b a ,A b a B A ∈⨯∈,且∩}=21,ρρ 则B ___________________. 填 }2,2,0,2,2,0,0,0{><><><><四、解答题1. 设 A d c b a A },,,,{=上的关系 },,,,,,,,,,,,,,,{><><><><><><><><=c d d c a b b a d d c c b b a a ρ（1）写出ρ的关系矩阵；（2）验证ρ是A 上的等价关系；（3）求出A 的各元素的等价类。

离散数学考试试题及答案离散数学考试试题及答案离散数学是计算机科学和数学中的一门重要学科，它研究的是离散的结构和对象。

离散数学的理论和方法在计算机科学、信息科学、通信工程等领域具有广泛的应用。

下面将为大家提供一些离散数学考试试题及答案，希望对大家的学习和复习有所帮助。

1. 集合论题目(1) 设A={1,2,3,4,5}，B={3,4,5,6,7}，求A∪B的结果。

答案：A∪B={1,2,3,4,5,6,7}(2) 设A={1,2,3,4,5}，B={3,4,5,6,7}，求A∩B的结果。

答案：A∩B={3,4,5}(3) 设A={1,2,3,4,5}，B={3,4,5,6,7}，求A-B的结果。

答案：A-B={1,2}2. 图论题目(1) 给定一个无向图G，顶点集为V={A,B,C,D,E}，边集为E={(A,B),(A,C),(B,D),(C,D),(D,E)}，求该图的邻接矩阵。

答案：邻接矩阵为：A B C D EA 0 1 1 0 0B 1 0 0 1 0C 1 0 0 1 0D 0 1 1 0 1E 0 0 0 1 0(2) 给定一个有向图G，顶点集为V={A,B,C,D,E}，边集为E={(A,B),(B,C),(C,D),(D,E),(E,A)}，求该图的邻接表。

答案：邻接表为：A ->B ->C ->D ->E -> AB -> CC -> DD -> EE -> A3. 命题逻辑题目(1) 判断以下命题是否为永真式：(p∨q)∧(¬p∨r)∧(¬q∨¬r)。

答案：是永真式。

(2) 给定命题p：如果天晴，那么我去游泳；命题q：我没有去游泳。

请判断以下命题的真假：(¬p∨q)∧(p∨¬q)。

答案：是真命题。

4. 关系代数题目(1) 给定关系R(A,B,C)和S(B,C,D)，求R⋈S的结果。

离散数学试题带答案 四、证明题 1. 设是群，具有幺元e，如果对G的任意元素a，都有 a²=e, 则是交换群 2. 形式证明qsprsrqp,, 3. 证明：P(QR)PQR. 4．试证明：RSQPSRQP)())((

5．试证明：QRRQQP)()( 6. 证明：)()(xxBxxA))()((xBxAx 7．设G是图，无回路，但若外加任意一条边于G后，就形成一回路. 试证明G必为树. 8. 设B是任意集合，试验证(P(B),)是群. P(B)是集合B的幂集，是集合的对称差运算， 9．给定代数系统(G,+,*), 二元运算见表一，表二. 表一 表二 + a b c D * a b c D A a b c D a a a a a B b a d C b a b c d C c D a B c a c d b D d C b A d a d b c 证明(G,+,*)是域. 10. 证明如果非空集合A上的二元关系R和S是偏序关系，则SR也是A上的偏序关系． 11．试证A－(B－C)＝(A－B)(AC) 12．设非空集合A，验证(AAP,~,,,),()是布尔代数， 13. 试证明属于关系不满足传递性，即对于任意的集合A,B,C若A∈B且B∈C 不一定有 A∈C 14．设 A,B为两个集合，证明 A—B=A当且仅当A∩B= ø 15. 设R,S都是非空集合A上的二元关系，且他们是对称的，证明：RoS具有对称性当且仅当 RoS=SoR. 16. 已知g：A->B,f：B->C 1） 已知fog是单射的且g是满射的，证明f是单射的 2） 已知fog 是满射的且f是单射的，证明g是满射的 17．设A是传递集，证明A+也是传递集。 18．设G是n阶无向简单图，其直径为d(G)=2, ο(G)=n-2，证明G的边数m≥2n-4 19．V=是可交换半群,若a,b ∈S是V中得幂等元，证明a*b也是V中的幂等元 20．设 L是格，证明对于任意a,b,c,d∈L有：( a∧b)∨(c∧d)≤(a∨c)∧(b∨d) 五、计算题 1. 无向树T有2个2度顶点，1个3度顶点，3个4度顶点，其他的都是树叶，问T中有多少片树叶？

离散数学复习资料试卷习题与答案 (离散数学试卷》。 一、选择题（每题3分，共30分）。 1. 设集合A = {1, 2, 3}，B={2, 3, 4}，则A∩ B为（ ）。 A. {1, 2, 3, 4} B. {2, 3} C. {1, 4} D. varnothing 2. 下列命题公式中，为重言式的是（ ）。 A. (pto q)∧(p∧¬ q) B. (pto q)↔(¬ p∨ q) C. (p∧ q)to(p∨ q) D. (pto q)∧(qto p) 3. 设R是集合A上的自反关系，则下列说法正确的是（ ）。 A. R^-1一定是自反关系。 B. R^-1一定不是自反关系。 C. R^-1可能是自反关系。 4. 设G是一个有n个结点，m条边的连通简单平面图，若n≥3，则m与n满足（ ）。 A. m≤3n 6 B. m≥3n 6 C. m = 3n 6 D. 不确定。 5. 下列哪个是群（ ）。 A. (Z, +)，其中Z是整数集，+是普通加法。 B. (Z, ×)，其中Z是整数集，×是普通乘法。 C. (N, +)，其中N是自然数集，+是普通加法。 D. (N, ×)，其中N是自然数集，×是普通乘法。 6. 设A={a,b,c}，A上的关系R={(a,a),(a,b),(b,c)}，则R的传递闭包t(R)为（ ）。

A. {(a,a),(a,b),(b,c),(a,c)} B. {(a,a),(a,b),(b,c)} C. {(a,a),(a,b),(b,c),(b,b)} D. {(a,a),(a,b),(b,c),(a,c),(b,b)} 7. 命题公式¬(pto q)的主析取范式为（ ）。 A. p∧¬ q B. p∨¬ q C. ¬ p∧ q D. ¬ p∨ q 8. 设无向图G有16条边，有3个4度结点，4个3度结点，其余结点的度数均小于3，则G中至少有（ ）个结点。

A. 10. B. 11. C. 12. D. 13. 9. 设G是n阶无向简单图，若G中任意两个不相邻的结点的度数之和（ ），则G是哈密顿图。

离散数学经典测试题及答案第一题: 命题逻辑与真值表根据下列命题符号表示的逻辑表达式，填写真值表。

1. \(p \land q\)2. \((\lnot p \lor q) \land (p \implies q)\)答案1. \(p \land q\)2. \((\lnot p \lor q) \land (p \implies q)\)第二题: 数学归纳法证明使用数学归纳法证明下列等式对于所有\(n \geq 1\)成立。

\(\sum_{i=1}^{n}(2i-1) = n^2\)证明1. 基础步骤：当\(n=1\)时，左边等式为\(1\), 右边等式为\(1^2 = 1\), 成立。

2. 归纳假设：假设当\(n=k\)时等式成立，即\(\sum_{i=1}^{k}(2i-1) = k^2\)。

3. 归纳步骤：考虑\(n=k+1\)的情况，- 左边等式为\(\sum_{i=1}^{k+1}(2i-1) = \sum_{i=1}^{k}(2i-1) + (2(k+1)-1)\)- 右边等式为\((k+1)^2 = k^2 + 2k + 1\)现在我们可以利用归纳假设，将左边等式展开：\(\sum_{i=1}^{k}(2i-1) + (2(k+1)-1) = k^2 + 2k + 1\)然后，化简左边的部分可以得到：\(k^2 + (2k - 1) + (2(k+1) - 1) = k^2 + 2k + 1\)这个等式成立，证明完毕。

第三题: 集合论给定两个集合A和B，证明下列恒等式成立：\(A \cup (B - A) = A \cup B\)证明我们可以使用集合论的定义来证明这个恒等式。

1. 证明\(A \cup (B - A) \subseteq A \cup B\)- 对于任意\(x \in A \cup (B - A)\)，有两种情况：- 如果\(x \in A\)，则\(x \in A \cup B\)，因为\(A \subseteq A \cupB\)。