第四单元同步测试2(北师大版七上)
- 格式:doc
- 大小:51.50 KB
- 文档页数:7

北师大版七年级语文上册第四单元练习题SANY GROUP system office room 【SANYUA16H-第四单元学情调研试题一、积累与运用(20分)1.漂亮的书写能给人以美的享受。
请把下面这句话正确、规范、美观地抄写在方格内。
(2分)寓言是生活的棱镜,寻常现象中折射出深刻哲理。
2.下列加线的字注音有误的一项是( )(2分)A 、怜悯.m ǐn 丑陋.l òu 警惕.t ì 争辩.bi ànB 、纠.缠ji ū 啰.嗦lu ō 更.换g ēng 禽.兽q ínC 、凝.成níng 倒霉.méi 屠.宰tú 蠢.材ch ǔnD 、撬.开qi ào 庞.大p áng 作.揖zu ò 尚.且sh àng3.下列词语中有四个错别字,划出来并在方格中改正。
(4分) 嬉笑颜开 无恶不作 乔妆打扮 忘恩负义自言自语 荣华福贵 张牙舞爪 传宗接代奇形怪状 后患无穷 仙风道骨 衣食住行披头散发 下流无耻 来龙去脉 恩将仇抱4.句中加线的词语解释不当的一项是( )(2分)A 、我因为怜悯恶人,才受到如此的恶报啊!怜悯: 对遭遇不幸的人表示同情。
B 、就劝丈夫放弃报仇的念头,以免毒蛇纠缠。
纠缠:缠绕在一起。
C 、把全世界的地下宝藏都指点给他。
指点:指出来使人知道。
D、我是个堂堂的人。
堂堂:这里形容有志气,有气魄。
5.对本单元课文的分析有误的一项是()(2分)A、《农夫和蛇》选自《伊索寓言》。
《伊索寓言》大多是动物故事,以动物为喻教人处世做人道理。
B、《渔夫的故事》中的渔夫,虽然善良,但毕竟有点胆小,害怕恶势力。
C、《东郭先生与狼》和《渔夫的故事》分别为东、西方文化背景下的经典故事,但异曲同工。
D、《白蛇传》是着名民间传说。
主要描述由白蛇所变的白娘子与青年许仙的恋爱婚姻悲剧。
6.下列词语中的“书”与“大书特书”中的“书”词义相近的一项是()(2分)A、藏书万卷B、一封家书C、挥毫疾书D、楷书行书7.下列各项中不全是反义词的一项是()(2分)A、冷漠—热忱慷慨—吝惜B、墨守—开拓安静—喧闹C、压抑—放纵悲痛—哀痛D、七嘴八舌—异口同声沸沸扬扬—冷冷清清8.根据你对文学名着的了解答题。

最新北师大版七年级数学上册单元测试题全套含答案单元测试(一)丰富的图形世界(时间:120分钟满分:150分)一、选择题(本大题共15小题,每小题3分,共45分)1.下列图形不是立体图形的是( )A.球B.圆柱C.圆锥D.圆2.如图,在下面四个物体中,最接近圆柱的是( )A.烟囱B.弯管C.玩具硬币D.某种饮料瓶3.直棱柱的侧面都是( )A.正方形B.长方形C.五边形D.以上都不对4.下列几何体没有曲面的是( )A.圆锥B.圆柱C.球D.棱柱5.(芦溪县期末)如图所示,用一个平面去截一个圆柱,则截得的形状应为( )A B C D6.一个几何体的展开图如图所示,这个几何体是( )A.圆锥B.圆柱C.四棱柱D.无法确定7.如图中几何体从正面看得到的平面图形是( )A B C D 8.(长沙一模)如图,直角三角形绕直线l旋转一周,得到的立体图形是( )A B C D10.如图的四个几何体,它们各自从正面,上面看得到的形状图不相同的几何体的个数是( )A.1 B.2 C.3 D.411.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )12.下列说法不正确的是( )A.球的截面一定是圆B.组成长方体的各个面中不可能有正方形C.从三个不同的方向看正方体,得到的平面图形都是正方形D.圆锥的截面可能是圆13.将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )A.3 B.9 C.12 D.1814.(深圳期末)用平面去截如图所示的三棱柱,截面形状不可能是( )A.三角形B.四边形C.五边形D.六边形15.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其他空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )A B C D二、填空题(本大题共5小题,每小题5分,共25分)16.飞机表演的“飞机拉线”用数学知识解释为:________________.17.下列图形中,是柱体的有________ .(填序号)20.一个正方体盒子的展开图如图所示,如果要把它粘成一个正方体,那么与点A重合的点是________.三、解答题(本大题共7小题,共80分)21.(12分)将下列几何体与它的名称连接起来.22.(6分)如图,求这个棱柱共有多少个面?多少个顶点?有多少条棱?23.(10分)若要使图中平面图形折叠成正方体后,相对面上的数字相等,求x+y+z的值.24.(10分)如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.25.(12分)如图所示的正方体被竖直截去了一部分,求被截去的那一部分的体积.(棱柱的体积等于底面积乘以高)26.(14分)如图所示,长方形ABCD的长AB为10 cm,宽AD为6 cm,把长方形ABCD绕AB边所在的直线旋转一周,然后用平面沿AB方向去截所得的几何体,求截面的最大面积.27.(16分)根据如图所给出的几何体从三个方向看得到的形状图,试确定几何体中小正方体的数目的范围.参考答案1.D 2.C 3.B 4.D 5.B 6.A 7.D 8.C 9.C 10.C11.C 12.B 13.D 14.D 15.B 16.点动成线 17.②③⑥ 18.答案不唯一,如:球、正方体等 19.8 20.C 、E 21.略.22.这个棱柱共有7个面,10个顶点,15条棱. 23.“2”与“y”相对,“3”与“z”相对,“1”与“x”相对.则x +y +z =1+2+3=6. 24.从正面和从左面看到的形状图如图所示.25.V =12×(5-4)×(5-3)×5=5(cm 3).答:被截去的那一部分体积为5 cm 3.26.由题意得:把长方形ABCD 绕AB 边所在的直线旋转一周,得到的几何体为圆柱,且圆柱的底面半径为6 cm ,高为10 cm .所以截面的最大面积为:6×2×10=120(cm 2).27.根据题意,从上面看,构成几何体所需小正方体最多情况如图1所示,所需小正方体最少情况如图2所示:所以最多需要11个小正方体,最少需要9个小正方体.单元测试(二) 有理数及其运算(时间:120分钟 满分:150分)一、选择题(本大题共15小题,每小题3分,共45分)1.如果用+0.02克表示一只乒乓球质量超出标准质量0.02克,那么一只乒乓球质量低于标准质量0.02克记作( ) A .-0.02克 B .+0.02克 C .0克 D .+0.04克 2.(宁波中考改编)下列各数中,既不是正数也不是负数的是( )A .0B .-1 C.12 D .23.(遂宁中考)在下列各数中,最小的数是( )A .0B .-1 C.32 D .-24.-8的相反数是( )A .-6B .8C .-16 D.185.用四舍五入法得到近似数4.005万,关于这个数有下列说法,其中正确的是( )A .-2B .-8C .8D .27.(盐城中考)2014年5月,中俄两国签署了供气购销合同,从2018年起,俄罗斯开始向我国供气,最终达到每年380亿立方米.380亿这个数据用科学记数法表示为( )A .3.8×109B .3.8×1010C .3.8×1011D .3.8×1012 8.(河北中考)计算:3-2×(-1)=( )A .5B .1C .-1D .6 9.下列计算正确的是( )A .(-14)-(+5)= -9 B. 0-(-3)=0+(-3) C .(-3)×(-3)= -6 D .|3-5|= 5-310.某校小卖铺一周的盈亏情况如下表所示(每天固定成本200元,其中“+”表示盈利,“-”表示亏损)星期 一 二 三 四 五 盈亏+220-30+215-25+225则这个周共盈利( )A .715元B .630元C .635元D .605元 11.下列四个有理数12、0、1、-2,任取两个相乘,积最小为 ( )A.12 B .0 C .-1 D .-212.在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )A .-54B .54C .-558D .55813.如图,四个有理数在数轴上对应点M ,P ,N ,Q ,若点P ,N 表示的有理数互为相反数,则图中表示绝对值最大的数的点是( )A .点MB .点NC .点PD .点Q 14.若(a +3)2+|b -2|=0,则a b 的值是( )A .6B .-6C .9D .-915.观察下列各算式:21=2,22=4,23=8,24=16,25=32,26=64…通过观察,用你所发现的规律确定22 016的个位数字是 ( )A .2B .4C .6D .8 二、填空题(本大题共5小题,每小题5分,共25分) 16.-32的倒数的绝对值为________.17.一种零件的内径尺寸在图纸上是30±0.05(单位:毫米),表示这种零件的标准尺寸是30毫米,加工要求最大不超过________毫米,最小不低于________毫米. 18.大于-1.5小于2.5的整数共有________个.19.一个点从数轴的原点开始,先向右移动5个单位长度,再向左移动8个单位长度,到达的终点表示的数是________________.a -b21.(12分)把下列各数填入相应集合内:+8.5,-312,0.3,0,-3.4,12,-9,413,-1.2,-2.(1)正数集合:{ };(2)整数集合:{ }; (3)负分数集合:{ }.22.(8分)把数-2,1.5,-(-4),-312,(-1)4,-|+0.5|在数轴上表示出来,然后用“<”把它们连接起来.23.(16分)计算:(1)6.8-(-4.2)+(-9); (2)|-2|-(-3)×(-15);(3)(12+56-712)×(-24); (4)-24÷(23)2+312×(-13)-(-0.5)2.24.(8分)已知a 、b 互为相反数,c 、d 互为倒数,x 的绝对值是2,求3x -(a +b +cd )x 的值.25.(10分)已知x 、y 为有理数,现规定一种新运算※,满足x ※y =xy +1. (1)求2※4的值;(2)求(1※4)※(-2)的值;26.(12分)“新春超市”在2015年1~3月平均每月盈利20万元,4~6月平均每月亏损15万元,7~10月平均每月盈利17万元,11~12月平均每月亏损23万元.问“新春超市”2015年总的盈亏情况如何?27.(14分)一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10.(1)守门员最后是否回到了球门线的位置?(2)在练习过程中,守门员离开球门线最远距离是多少米? (3)守门员全部练习结束后,他共跑了多少米?参考答案1.A 2.A 3.D 4.B 5.D 6.B 7.B 8.A 9.D 10.D11.D 12.C 13.A 14.C 15.C 16.23 17.30.05 29.95 18.4 19.-3 20.-7或-17 21.(1)+8.5,0.3,12,413(2)0,12,-9,-2 (3)-312,-3.4,-1.2 22.在数轴上表示数略,-312<-2<-|+0.5|<(-1)4<1.5<-(-4). 23.(1)原式=2. (2)原式=-43. (3)原式=-18. (4)原式=-37512. 24.由题意知,a +b =0,cd =1,x =±2,当x =2时,原式=4;当x =-2时,原式=-4. 25.(1)2※4=2×4+1=9.(2)(1※4)※(-2)=(1×4+1)×(-2)+1=-9. 26.(+20)×3+(-15)×3+(+17)×4+(-23)×2=37(万元).答:“新春超市”2015年总的盈利为37万元. 27.(1)(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)=0.答:守门员最后回到了球门线的位置.(2)由观察可知:5-3+10=12.答:在练习过程中,守门员离开球门线最远距离是12米.(3)|+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|=54(米).答:守门员全部练习结束后,他共跑了54米.单元测试(三) 整式及其加减(时间:120分钟 满分:150分)一、选择题(本大题共15小题,每小题3分,共45分) 1.下列各式中不是单项式的是( )A .-a 3B .-15C .0D .-3a2.单项式-3xy 2z 3的系数是( )A .-1B .5C .6D .-33.某班数学兴趣小组共有a 人,其中女生占30%,那么女生人数是( ) A .30%a B .(1-30%)a C.a 30% D.a 1-30%4.下列各组式子中,为同类项的是( )A .5x 2y 与-2xy 2B .4x 与4x 2C .-3xy 与32yx D .6x 3y 4与-6x 3z 45.当a =-1,b =2时,代数式a 2b 的值是( )A .-2B .1C .2D .-1 6.列式表示“比m 的平方的3倍大1的数”是( )A .(3m )2+1B .3m 2+1C .3(m +1)2D .(3m +1)27.若m ,n 为自然数,多项式x m +y n +4m +n 的次数应是( )A .mB .nC .m ,n 中的较大数D .m +n 8.化简2x -(x -y)-y 的结果是( )A .3xB .xC .x -2yD .2x -2y 9.(玉林中考)下列运算中,正确的是( )A .3a +2b =5abB .2a 3+3a 2=5a 5C .3a 2b -3ba 2=0D .5a 2-4a 2=1 10.一个多项式减去x 2-2y 2等于x 2-2y 2,则这个多项式是( )A .-2x 2+y 2B .x 2-2y 2C .2x 2-4y 2D .-x 2+2y 2 11.下列判断错误的是( )A .多项式5x 2-2x +4是二次三项式B .单项式-a 2b 3c 4的系数是-1,次数是9C .式子m +5,ab ,-2,sv 都是代数式 D .多项式与多项式的和一定是多项式 12.十位数字是x ,个位数字是y 的两位数是 ( )A .xyB .x +10yC .x +yD .10x +y13.(厦门中考)某商店举办促销活动,促销的方法是将原价x 元的衣服以(45x -10)元出售,则下列说法中,能正确表达该商店促销方法的是( )A .原价减去10元后再打8折B .原价打8折后再减去10元C .原价减去10元后再打2折D .原价打2折后再减去10元 14.(湘西中考)已知x -2y =3,则代数式6-2x +4y 的值为( )A .0B .-1C .-3D .3 15.下面一组按规律排列的数:0,2,8,26,80,…,则第2 016个数是( )A .32 016B .32 015C .32 016-1D .32 015-1 二、填空题(本大题共5小题,每小题5分,共25分) 16.去括号:-(3x -2)=________.18.对于有理数a,b,定义a⊙b=3a+2b,则(x+y)⊙(x-y)化简后得________.19.当m=________时,代数式2x2+(m+2)xy-5x不含xy项.20.若用围棋子摆出下列一组图形:…(1)(2)(3)按照这种方法摆下去,第n个图形共用________枚棋子.三、解答题(本大题共7小题,共80分)21.(8分)化简下列各式:(1)a+2b+3a-2b; (2)2(a-1)-(2a-3)+3.22.(8分)先化简,再求值:(2m2-3mn+8)-(5mn-4m2+8),其中m=2,n=1.23.(10分)如图所示:(1) 用代数式表示阴影部分的面积;(2) 当a=10,b=4时,求阴影部分的面积(π取3.14,结果精确到0.01).24.(12分)已知a,b,c在数轴上的位置如图所示,求|b+c|-|a-b|-|c-b|的值.25.(12分)已知长方形的一边长为2a+3b,另一边比它短(b-a),试计算此长方形的周长.26.(14分)已知A=2a2+3ab-2a-1,B=-a2+ab-1.(1)求3A+6B;(2)若3A+6B的值与a的取值无关,求b的值.27.(16分)某农户承包荒山若干亩,种果树2 000棵.今年水果总产量为18 000千克,此水果在市场上每千克售a 元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1 000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.(1)分别用a,b表示两种方式出售水果的收入;(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.参考答案1.D 2.D 3.A 4.C 5.C 6.B 7.C 8.B 9.C 10.C11.D 12.D 13.B 14.A 15.D 16.-3x +2 17.某班级有a 名学生参加考试,30名学生成绩合格,则合格人数占总人数的30a18.5x +y 19.-2 20.3n 21.(1)原式=4a. (2)原式=4. 22.原式=2m 2-3mn +8-5mn +4m 2-8=6m 2-8mn.当m =2,n =1时,原式=6×22-8×2×1=8. 23.(1)ab -12πb 2.(2)当a =10,b =4时,ab -12πb 2≈10×4-12×3.14×42=14.88. 24.由图知:b +c >0,a -b <0,c -b >0,|b +c|-|a -b|-|c -b|=b +c -[-(a -b)]-(c -b)=b +c +a -b -c +b =a +b. 25.长方形的另一边长为3a +2b ,则周长为2[(2a +3b)+(3a +2b)]=2(5a +5b)=10a +10b. 26.(1)3A +6B =3(2a 2+3ab -2a -1)+6(-a 2+ab -1)=6a 2+9ab -6a -3-6a 2+6ab -6=15ab -6a -9.(2)因为15ab -6a -9=a(15b -6)-9,且3A +6B 的值与a 的取值无关,所以15b =6,即b =25. 27.(1)将这批水果拉到市场上出售收入为18 000a -18 0001 000×8×25-18 0001 000×100=18 000a -3 600-1 800=18 000a -5 400(元).在果园直接出售收入为18 000b 元.(2)当a =1.3时,市场收入为18 000a -5 400=18 000×1.3-5 400=18 000(元).当b =1.1时,果园收入为18 000b =18 000×1.1=19 800(元).因为18 000<19 800,所以应选择在果园出售.单元测试(四) 基本平面图形题号一二三总分 合分人 复分人 得分一、选择题(本大题共15题号123456789 10 11 12 13 14 15 选项1.A .线段 B .射线 C .直线 D .弧线 2.下列图形中表示直线AB 的是( )A B C D 3.下面四个图形中,是多边形的是( )4.下列说法正确的是( )A .平角是一条直线B .角的边越长,角越大C .大于直角的角叫做钝角D .把线段AB 向两端无限延伸可得到直线AB 5.木匠在木料上画线,先确定两个点的位置,就能把线画得很准确,其依据是( ) A .两点确定一条直线 B .两点确定一条线段C.过一点有一条直线D.过一点有无数条直线6.如图,若∠AOC=∠BOD,则∠AOD与∠BOC的关系是( )A.∠AOD>∠BOC B.∠AOD<∠BOCC.∠AOD=∠BOC D.无法确定7.如图,点C在线段AB上,则下列说法正确的是( )A.AC=BC B.AC>BCC.图中共有两条线段D.AB=AC+BC8.如图是一块手表早上8时的时针、分针的位置图,那么分针与时针所成的角的度数是( ) A.60°B.80°C.120°D.150°9.下列计算错误的是( )A.0.25°=900″ B.1.5°=90′C.1 000″=(518)°D.125.45°=1 254.5′10.如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方位角是( )A.西偏北60°B.北偏西60°C.北偏东60°D.东偏北60°11.如图,OC是∠AOB的平分线,OD平分∠AOC,若∠COD=25°,则∠AOB的度数为( )A.100°B.80°C.70°D.60°12.已知线段AB=5 cm,在直线AB上画线段BC=2 cm,则AC的长是( )A.3 cm B.7 cmC.3 cm或7 cm D.无法确定13.过多边形的一个顶点可以引出6条对角线,则多边形的边数是( )A.7 B.8 C.9 D.1014.将一个圆分成四个扇形,它们的圆心角的度数比为4∶4∶5∶7,则这四个扇形中,圆心角最大的是( ) A.54°B.72°C.90°D.126°15.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,…那么六条直线最多有( ) A.21个交点B.18个交点C.15个交点D.10个交点二、填空题(本大题共5小题,每小题5分,共25分)16.要在A、B两个村庄之间建一个车站,则当车站建在A、B村庄之间的线段上时,它到两个村庄的路程和最短,理由是________________.17.如图,点A、B、C在直线l上,则图中共有________条线段,有________条射线.18.如图,已知C为线段AB的中点,D在线段CB上.若DA=6,DB=4,则CD=________.19.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB=155°,则∠COD=________,∠BOC =________ .20.若一个多边形截去一个角后,变成六边形,则原来多边形的边数可能是________.三、解答题(本大题共7小题,共80分)21.(8分)如图,直线AB表示一条公路,公路两旁各有一点M、N表示工厂,要在公路旁建一个货场,使它到两个工厂的距离之和最小,问这个货场应建在什么地方.22.(8分)已知四点A、B、C、D.根据下列语句,画出图形.①画直线AB;②连接AC、BD,相交于点O;③画射线AD、BC,交于点P.23.(10分)如图,已知A、B、C三点在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5 cm,CN=3 cm.求线段AB的长.24.(12分)如图,已知∠AOE=∠COD,且射线OC平分∠BOE,∠EOD=30°,求∠AOD的度数.25.(12分)王老师到市场买菜,发现如果把10千克的菜放到秤上,指标盘上的指针转了180°,第二天王老师就给同学们出了两个问题:(1)如果把0.6千克的菜放在秤上,指针转过多少角度? (2)如果指针转了7°12′,这些菜有多少千克?26.(14分)画图并计算:已知线段AB =2 cm ,延长线段AB 至点C ,使得BC =12AB ,再反向延长AC 至点D ,使得AD =AC.(1)准确地画出图形,并标出相应的字母;(2)线段DC 的中点是哪个?线段AB 的长是线段DC 长的几分之几? (3)求出线段BD 的长度.27.(16分)如图,正方形ABCD 内部有若干个点,用这些点以及正方形ABCD 的顶点A 、B 、C 、D 把原正方形分割成一些三角形(互不重叠).(1)填写下表:正方形ABCD 内点的个数1234…n分割成三角形的个数4 6 …(2)参考答案1.B 2.D 3.D 4.D 5.A 6.C 7.D 8.C 9.D 10.B 11.A 12.C 13.C 14.D 15.C 16.两点之间,线段最短 17.3 6 18.1 19.25° 65° 20.5,6,7 21.连接MN 于AB 相交,交点即为所求.22.图略.23.因为AM =5 cm ,CN =3 cm ,且M 是线段AC 的中点,N 是线段BC 的中点,所以AC =10 cm ,CB =6 cm.所以AB =AC +CB =16 cm.24.因为∠AOB =180°,∠EOD =30°,所以∠AOD +∠EOC +∠COB =150°.因为∠AOE =∠COD ,所以∠AO D =∠EOC.因为OC 平分∠EOB ,所以∠EOC =∠COB.所以∠EOC =∠COB =∠AOD =50°. 25.(1)由题意,得(180°÷10)×0.6=10.8°.(2)由题意,得(10÷180°)×7°12′=(10÷180°)×7.2°=0.4(千克). 26.(1)如图所示.(2)线段DC 的中点是点A ,AB =13CD.(3)由BC =12AB =12×2=1(cm),因而AC =AB +BC =2+1=3(cm),而AD =AC =3 cm ,故BD =DA +AB =3+2=5(cm).27.(1)8 10 2n +2 (2)不可以,因为2n +2是偶数,不可能等于2 015,所以不可以.单元测试(五) 一元一次方程 (时间:120分钟 满分:150分)题号一二三总分 合分人 复分人 得分一、选择题(本大题共15小题,每小题3分,共45分)题号1234567 8 9 10 11 12 13 14 15 选项1.下列式子中,是一元一次方程的是( )A .x -7 B.2x =7C .4x -7y =6D .2x -6=0 2.下列方程变形中,属于移项的是( )A .由3x =-2,得x =-23B .由x2=3,得x =6C .由5x -10=0,得5x =10D .由2+3x =0,得3x +2=03.若a =b ,则下列式子不正确的是( )A .a +1=b +1B .a +5=b -5C .-a =-bD .a -b =0 4.解方程-2(x -5)+3(x -1)=0时,去括号正确的是( )A .-2x -10+3x -3=0B .-2x +10+3x -1=0C .-2x +10+3x -3=0D .-2x +5+3x -3=0 5.下列方程中,解是2的方程是( )A.23x =2 B .-14x +12=0 C .3x +6=0 D .5-3x =1 6.方程3-2(x -5)=9的解是( )A .x =-2B .x =2C .x =23D .x =17.解方程x +12-x -14=1有下列四步,其中发生错误的一步是( )A .去分母,得2(x +1)-x -1=4B .去括号,得2x +2-x -1=4C .移项,得2x -x =4-2+1D .合并同类项,得x =3 8.已知x =1是方程x +2a =-1的解,那么a 的值是( ) A .-1 B .0 C .1 D .2 9.如果2x -3与-13互为倒数,那么x 的值为( )A .x =53B .x =43C .x =0D .x =110.设某数为x ,若比它的34大1的数的相反数是6,可列方程为( )A .-34x +1=6B .-(34x +1)=6C.34x -1=6 D .-(34x -1)=6 11.小马虎在计算16-13x 时,不慎将“-”看成了“+”,计算的结果是17,那么正确的计算结果应该是( )A .15B .13C .7D .-112.某班在一次美化校园的劳动中,先安排35人打扫卫生,15人拔草,后又增派10人去支援,结果打扫卫生的人数是拔草人数的2倍,若设支援打扫卫生的同学有x 人,则下列方程正确的是( ) A .35+x =2×10 B .35+x =2×(15+10-x ) C .35+x =2×(15-x ) D .35+x =2×1513.学校组织了一次知识竞赛,共有25道题,每一道题答对得5分,答错或不答都扣3分,小明得了85分,那么他答对的题数是( )A .22B .20C .19D .1814.如果方程6x +3a =22与方程3x +5=11的解相同,那么a 的值为( ) A.310 B.103 C .-310 D .-10315.某品牌商品按标价九折出售,仍可获得20%的利润.若该商品标价为28元,则商品的进价为( ) A .21元 B .19.8元 C .22.4元 D .25.2元 二、填空题(本大题共5小题,每小题5分,共25分)16.若-3x =13,则x =________.17.若(m +1)x |m|=6是关于x 的一元一次方程,则m 等于________.18.若4x 2m y n +1与-3x 4y 3的和是单项式,则m =________,n =________.19.已知A 种品牌的文具比B 种品牌的文具单价少1元,小明买了2个A 种品牌的文具和3个B 种品牌的文具,一共花了28元,那么A 种品牌的文具单价是________元.20.一条山路,某人从山下往山顶走3小时还有1千米才到山顶,若从山顶走到山下只用150分钟,已知下山速度是上山速度的1.5倍,则山下到山顶的路程为________千米. 三、解答题(本大题共7小题,共80分)21.(9分)在下列横线上填上适当的数或整式,使所得结果仍是等式,并说明根据的是等式的哪一条性质. (1)如果x -2=-y ,那么x =________,根据________;(2)如果2x =-2y ,那么x =________,根据等式的性质________; (3)如果-x 10=y5,那么x =________,根据等式的性质________.22.(7分)解方程:x -74-5x +82=1.23.(10分)当x 取何值时,代数式2x -35的值比代数式23x -4的值小1?24.(12分)小明和小刚从学校出发去敬老院送水果,小明带着东西先走了200 m ,小刚才出发.若小明每分钟行80 m ,小刚每分钟行120 m .则小刚用几分钟可以追上小明?25.(12分)对于任意有理数a ,b ,c ,d ,我们规定⎪⎪⎪ ⎪⎪⎪a c b d =ad -bc ,如⎪⎪⎪⎪⎪⎪1234=1×4-2×3.若⎪⎪⎪⎪⎪⎪322x -12x +1=3,求x 的值.26.(14分)某中学组织七年级学生参观,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车恰好坐满.试问:(1)七年级学生人数是多少?(2)原计划租用45座客车多少辆?27.(16分)某织布厂有150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30 m ,或利用所织布制衣4件,制衣一件需要布1.5 m ,将布直接出售,每米布可获利2元,将布制成衣后出售,每件可获利25元,若每名工人每天只能做一项工作,且不计其他因素,设安排x 名工人制衣. (1)一天中制衣所获利润P =________(用含x 的式子表示); (2)一天中剩余布所获利润Q =________(用含x 的式子表示); (3)一天当中安排多少名工人制衣时,所获利润为11 806元?参考答案1.D 2.C 3.B 4.C 5.B 6.B 7.A 8.A 9.C 10.B11.A 12.B 13.B 14.B 15.A 16.-19 17.1 18.2 2 19.5 20.521.(1)2-y 等式的性质1 (2)-y 2 (3)-2y 2 22.x =-3.23.根据题意得:2x -35+1=23x -4,去分母,得6x -9+15=10x -60, 移项合并,得4x =66,解得x =332.24.设小刚用x 分钟可以追上小明.根据题意,得200+80x =120x.解得x =5. 答:小刚用5分钟可以追上小明. 25.因为⎪⎪⎪⎪⎪⎪a cb d =ad -bc ,又⎪⎪⎪⎪⎪⎪322x -12x +1=3,所以3(2x +1)-2(2x -1)=3,解得x =-1.26.(1)设七年级人数是x 人,根据题意得x -1545=x60+1,解得x =240.答:七年级学生人数是240人.(2)原计划租用45座客车:(240-15)÷45=5(辆). 答:原计划租用45座客车5辆.27.(1)100x (2)-72x +9 000 (3)根据题意得100x -72x +9 000=11 800.解得x =100. 答:应安排100名工人制衣.单元测试(六)数据的收集与整理(时间:120分钟满分:150分)一、选择题(本大题共15小题,每小题3分,共45分)1.某同学想了解寿春路与阜阳路交叉路口1分钟内各个方向通行的车辆数量,他应采取的收集数据方法为( ) A.查阅资料B.实验C.问卷调查D.观察2.2015年某市初中毕业升学考试的考生人数约为3.2万名,从中抽取300名考生的数学成绩进行分析,在本次调查中,样本指的是( )A.300名考生的数学成绩B.300C.3.2万名考生的数学成绩D.300名考生3.(佛山中考)下列调查中,适合用普查方式的是( )A.调查佛山市市民的吸烟情况B.调查佛山市电视台某节目的收视率C.调查佛山市市民家庭日常生活支出情况D.调查佛山市某校某班学生对“文明佛山”的知晓率4.扇形统计图中某扇形占圆的30%,则此扇形所对的圆心角是( )A.120°B.108°C.90°D.60°5.某课外兴趣小组为了了解所在地区老年人的健康状况,分别作了四种不同的抽样调查.你认为抽样比较合理的是( )A.在公园调查了1 000名老年人的健康状况B.在医院调查了1 000名老年人的健康状况C.调查了10名老年邻居的健康状况D.利用派出所的户籍网随机调查了该地区10%的老年人的健康状况6.我国五座名山的海拔高度如下表:山名泰山华山黄山庐山峨眉山海拔(m) 1 524 1 997 1 873 1 500 3 099)A.扇形统计图B.条形统计图C.折线统计图D.以上三种都可以7.为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该图中a的值是( )A.28B.26C.24D.228.某人设计了一个游戏,在一网吧征求了三位游戏迷的意见,就宣传“本游戏深受游戏迷欢迎”,这种说法错误的原因是( )A.没有经过专家鉴定B.应调查四位游戏迷C.这三位玩家不具有代表性D.以上都不是9.空气是由多种气体混合而成的,为了简明扼要地介绍空气的组成情况,较好地描述数据,最适合使用的统计图是( )A.扇形统计图B.条形统计图C.折线统计图D.以上都不对10.如图的两个统计图,女生人数较多的学校是( )A.甲校B.乙校C.甲、乙两校女生人数一样多D.无法确定11.小明家下个月的开支预算如图所示,如果用于衣服上的支出是200元,则估计用于食物上的支出是( ) A.200元B.250元C.300元D.35012.对某中学70名女生的身高进行测量,得到一组数据的最大值为169 cm,最小值为143 cm,对这组数据整理时测定它的组距为5 cm,应分成( )A.5组B.6组C.7组D.8组13.某次考试中,某班级的数学成绩被绘制成了如图所示的频数分布直方图.下列说法错误的是( )A.得分在70~80分之间的人数最多B.该班的总人数为40C.得分在90~100分之间的人数占总人数的5% D.及格(不低于60分)的人数为2614.某市股票在七个月之内增长率的变化状况如图所示.从图上看出,下列结论不正确的是( )A.2~6月份股票月增长率逐渐减少B.7月份股票的月增长率开始回升C.这七个月中,每月的股票不断上涨D.这七个月中,股票有涨有跌15.如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形统计图(两图都不完整),则下列结论中错误的是( )A.该班总人数为50 B.骑车人数占总人数的20%C.步行人数为30 D.乘车人数是骑车人数的2.5倍二、填空题(本大题共5小题,每小题5分,共25分)16.要反映一天的气温变化情况用________统计图表示比较合适.17.专家提醒:目前我国从事脑力劳动的人群中,“三高”(高血压、高血脂、高血糖)现象必须引起重视.这个结论是通过________得到的(填“普查”或“抽样调查”).18.学校为了考察我校七年级同学的视力情况,从七年级的10个班共540名学生中,每班抽取了5名进行分析,在这个问题中,总体是________________________,个体是________________________.19.某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示,那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为________.20.(金华中考)小亮对60名同学进行节水方法选择的问卷调查(每人选择一项),人数统计如图,如果绘制成扇形统计图,那么表示“一水多用”的扇形圆心角的度数是________.三、解答题(本大题共7小题,共80分)21.(8分)下面这几个抽样调查选取样本的方法是否合适?并说明理由.(1)为调查全校学生对购买正版书籍、唱片和软件的支持率,在全校所有的班级中,任意抽取8个班级,调查这8个班所有学生对购买正版书籍、唱片和软件的支持率;(2)为调查一个省的环境污染情况,调查省会城市的环境污染情况.22.(8分)为了解某校全体同学喜欢的NBA篮球明星的情况,小明抽取了七年级一班50名同学进行调查,得到最喜欢的NBA篮球明星的调查结果如下:A ABCD A B A A C B A A C B C A A B C A A B A CD B A C D B A C D A A B C D A C B A C A C D C A A其中:A代表姚明,B代表科比,C代表詹姆斯,D代表麦迪.(1)填表:(2)该班同学喜欢最多的是谁?(3)明星划记人数ABCD23.(10分)对某文明小区400户家庭拥有电视机数量情况进行抽样调查,得扇形统计图,根据图中提供的信息回答下列问题:(1)有一台彩电的家庭有多少户?(2)有三台彩电的家庭所在扇形的圆心角是多少度?24.(12分)如图是某班在一次数学小测验中学生考试成绩分布图(满分100分),根据图中提供的信息回答问题:(1)该班共有多少学生?(2)该次测验成绩哪一分数段的人数最多?是多少人?(3)如果80分及以上为优秀,那么优秀率是多少?25.(12分)某家电商场A、B两种品牌彩电2016年5~12月销售量统计如图.(1)有人认为B品牌彩电销售量比A品牌彩电销售量增长快.你同意这种观点吗?(2)根据统计图进行比较、判断时要注意些什么?(3)如果你是商场经理,从上面的统计图中你能得到哪些信息?对你有什么帮助?A品牌彩电月销售量统计图B品牌彩电月销售量统计图26.(14分)(贵阳中考)2014年巴西世界杯足球赛正在如火如荼地进行,小明和喜爱足球的伙伴们一起预测“巴西队”能否获得本届杯赛的冠军,他们分别在3月、4月、5月、6月进行了四次预测,并且每次参加预测的人数相同,小明根据四次预测结果绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:(1)每次有________人参加预测;(2)计算6月份预测“巴西队”夺冠的人数;(3)补全条形统计图和折线统计图.27.(16分)端午节即将来临,某商场对去年端午节这天销售A,B,C三种品牌粽子的情况进行了统计,绘制如图1和图2所示的统计图.根据图中信息解答下列问题:(1)哪一种品牌的粽子的销售量最大?(2)补全图1中的条形统计图;(3)写出A种品牌粽子在图2中所对应的圆心角的度数;(4)根据上述统计信息,今年端午节期间该商场对A、B、C三种品牌的粽子如何进货?请你提一条合理化的建议.。

最新北师大版七年级数学上册第四章同步测试题及答案4.1线段、射线、直线AB,D为AC的中点,DC=2,那么AB的长为.1. 如图,已知线段AB,延长AB到C,使BC=132. 已知点O在直线AB上,且线段OA的长度为4cm,线段OB的长度为6cm,E、F分别为线段OA、OB的中点,则线段EF的长度为_________.3. 小宇同学在一次手工制作活动中,先把一张长方形纸片按如图所示的方式进行折叠,使折痕的左侧部分比右侧部分短1cm;展开后按图的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm,再展开后,在纸上形成的两条折痕之间的距离是______cm.4. 如图,C是AB的中点,D是BC的中点,下列等式不正确的是()ABA. B. C. D. CD=135. 如图,点A、B、C顺次在直线上,M是线段AC的中点,N是线段BC的中点.若想求出MN的长度,则只需条件()A. AB=12B. BC=4C. AM=5D. CN=26. 如图,有a、b、c三户家用电路接人电表,相邻电路的电线等距排列,则三户所用电线()A. a户最长B. b户最长C. c户最长D. 三户一样长7. 已知线段AB=8,直线AB上有一点P(l)若AP=5,求BP的长;(2)若C是AP的中点,D是BP的中点,求CD的长.8. (1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.(2)四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.(3)平面上有n条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的n条直线分一个平面所成的区域最多,记为a n,试研究a n与n之间的关系.思维方法天地9. 如图,B、C、D依次是AE上的三点,已知AE=8.9cm,BD=3cm,则图中以A、B、C、D、E这5个点为端点的所有线段长度的和为_______cm.10. 平面上不重合的两点确定一条直线,不同三点最多可确定3条直线.若平面上不同的n个点最多确定21条直线,则n的值为_______.11. 如图,一根长为30cm、宽3cm的长方形纸条,将它按图所示的过程折叠.为了美观,希望折叠完成后纸条A端到点P的距离等于B端到点M的距离,则最初折叠时,MA的长应为______cm.12. 某班50名同学分别站在公路的A、B两点处,A、B两点相距1000米,A处有30人,B处有20人.要让两处的同学走到一起,并且使所有同学走的路程总和最小,那么集合地点应选在()A. A点处B. 线段AB的中点处米处 D. 线段AB上,距A点400米处C. 线段AB上,距A点1000313. 公园里准备修5条直的通道,并在通道交叉路口处设一个报亭,这样的报亭最多设()A. 9个B. 10个C. 11个D. 12个14. 线段AB上选取3种点,第1种是将AB10等分的点;第2种是将AB12等分的点;第3种是将AB15等分的点,这些点连同线段AB的端点可组成线段的条数是()A. 35B. 595C. 406D. 66615. 电子跳蚤游戏盘为鈻?/m:t>BC.AB=8a,AC=9a,BC=10a,如果电子跳蚤开始时在BC边上P0点,BP0=4a。

新北师大版七年级数学上册第四章基本平面图形同步练习题一、选择题1、在四边形的内角中,直角最多可以有( )A .1个 B .2个 C .3个 D .4个2、如图,下列说法错误的是( )A .∠B 也可以表示为∠ABC B .∠BAC 也可以表示为∠A C.∠1也可以表示为∠C D .以C 为顶点且小于180°的角有3个3、下列说法正确的是( )A.延长直线AB 到C ,使AB BC 21= B .延长线段AB 到C ,使BC =AC C .延长线段AB 到C ,使AB BC 21= D .延长线段BA 到C ,使BC =AB4、两个锐角的和为( )A .锐角 B .直角 C .钝角 D .以上都有可能5、若一个多边形有14条对角线,则这个多边形的边数是( ) A .10 B .7 C .14 D .66、植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中的数学道理是( )A .两点之间线段最短 B .两点之间直线最短 C .两点确定一条射线 D .两点确定一条直线7、如图,能用∠1,∠ACB,∠C 三种方法表示同一个角的是( )A. B . C . D .8、如图,∠1+∠2=( )A .60° B.90° C.110° D .180° 9、一轮船行驶到小岛A 处,同时测得灯塔B 、C 分别在它的北偏西30°和东北方向,则∠BAC=( )A .105°B . 115° C. 75° D.95° 10、同一平面内有四点,过每两点画一条直线,则直线的条数是( )A .1 B .4条 C .6条 D .1条或4条或6条二、填空题11、在飞机飞行时,飞行方向是用飞行路线与实际南或北方向线之间的夹角大小来表示的.如图,用AN (南北线)与飞行线之间顺时针方向的夹角作为飞行方向角,从A 到B 的飞行方向角为35°,从A 到C 的飞行方向角为60°,从A 到D 的飞行方向角为145°,则AB 与AC 之间的夹角是 °,AD 与AC 之间的夹角是 °. 12、如图中射线OA 表示的方位角为_______. 13、三条直线两两相交,交点的个数是______.14、四边形的内角和等于________;四边形的外角和等于______. 15、在直线l 上顺次截取线段AB ,BC ,若AB =6 cm ,AB 的中点与AC 的中点相距2 cm ,则BC =_________.16、已知n(n≥2)个点P 1,P 2,P 3,…,P n 在同一平面内,且其中没有任何三点在同一直线上. 设S n 表示过这n 个点中的任意2个点所作的所有直线的条数,显然,S 2=1,S 3=3,S 4=6,S 5=10,…,由此推断,S n =______________. 三、解答题17. 如图所示,∠AOB︰∠BOC=3︰5.又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOE=60°,求∠AOB和∠BOC的度数.18、如图:∠1=∠2,∠3=∠4.若∠AOE=128°,求∠BOD的度数.19、如何在操场上画出一个很大的圆?说一说你的方法.作图说明:已知点AB=4cm,到点A的距离小于2cm,到点B的距离小于3cm的所有点组成的图形.20.已知两条线段的和是10cm,这两条线段的比是2∶3,求这两条线段的长.21、读出下列语句,并按照这些语句画出图形(1)两条直线a、b,相交于点P.(2)直线l经过A、B、C三点,点C在点A与点B之间.(3)直线a经过点A、B,点P不在直线a上.22.如图,∠1:∠2:∠3:∠4=1:2:3:4,求∠1:∠2:∠3:∠4的度数.23、如图所示,从一点O出发引射线OA、OB、OC、OD,请你数一数图中有多少个角,并把它们表示出来.24、小华从A点出发向北偏东50°方向走了80米到达B地,从B 地他又向西走了100米到达C地. (1)用1:2000的比例尺(即图上1cm等于实际距离20米)画出示意图;(2)用刻度尺和量角器量出AC的距离,以及C点的方向角;(3)回答C点距A点的实际距离是多少(精确到1米),C点的方向角为多少.(精确到1°).试卷答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 D C C D B D C B C D 二、填空题题号11 12 13 14 15 16 答案25,85 北偏西40°1或3个360°360°,4cm三、解答题17. 45°,75° 18. 64°19,解:在操场上用一根很长的绳子,固定一头,拉紧后另一头旋转一周即可得到一个很大的圆.阴影部分就是到点A的距离小于2cm,到点B的距离小于3cm的所有点组成的图形20.,4cm和6cm21.略22,∠1是36°,∠2是72°,∠3是108°,∠4是144°23,解:共6个角,有∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD,共6个角.24,略。

北师大版七年级上册数学第四章试题(含答案)北师大版七年级上册数学第四章试题(含答案)一、选择题(本题共10小题,每小题 3分,共30分)1.平面上有四点,经过其中的两点画直线最多可画出( ).A.三条B.四条C.五条D.六条2.在实际生产和生活中,下列四个现象:①用两个钉子把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设天线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用“两点之间,线段最短”来解释的现象有( ).A.①②B.①③C.②④D.③④3.平面上有三点A,B,C,如果AB=8,AC=5,BC=3,那么( ).A.点C在线段AB上B.点C在线段AB的延长线上C.点C在直线AB外D.点C可能在直线AB上,也可能在直线AB外4.下列各角中,是钝角的是( ).A. 周角B. 周角C. 平角D. 平角5.如图,O为直线AB上一点,∠COB=26°30′,则∠1=( ).A.153°30′B.163°30′C.173°30′D.183°30′6.在下列说法中,正确的个数是( ).①钟表上九点一刻时,时针和分针形成的角是平角;②钟表上六点整时,时针和分针形成的角是平角;③钟表上十二点整时,时针和分针形成的角是周角;④钟表上差一刻六点时,时针和分针形成的角是直角;⑤钟表上九点整时,时针和分针形成的角是直角.A.1B.2C.3D.47.如图,C是AB的中点,D是BC的中点,下面等式不正确的是( ).A.CD=AC-DBB.CD=AD-BCC.CD= AB-BDD.CD= AB8.如图,C,D是线段AB上两点,若CB=4 cm,DB=7 cm,且D是AC的中点,则AC的长等于( ).A.3 cmB.6 cmC.11 cmD.14 cm9.A,B,C,D,E五个景点之间的路线如图所示.若每条路线的里程a(km)及行驶的平均速度b(km/h)用(a,b)表示,则从景点A到景点C用时最少的路线是( ).A.A→E→CB.A→B→CC.A→E→B→CD.A→B→E→C10.如图所示,云泰酒厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在金斗大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在这个路段上只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ).A.点AB.点BC.AB之间D.BC之间二、填空题(本题共4小题,每小题4分,共16分)11.如图所示,线段AB比折线AMB__________,理由是:____________________.12.如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10,AC=6,则CD=__________.13.现在是9点20分,此时钟面上的时针与分针的夹角是_______ ___.14. 如图所示,由泰山到青岛的某一次列车,运行途中停靠的车站依次是:泰山——济南——淄博——潍坊——青岛,那么要为这次列车制作的火车票有__________种.三、解答题(本题共4小题,共54分)15.(12分)计算:(1)将24.29°化为度、分、秒;(2)将36°40′30″化为度.16.(7分)请以给定的图形“ ”(两个圆,两个三角形,两条线段)构思独特而且又有意义的图形,并且写上一句贴切的解说词.17.(8分)已知线段a,b(如图),画出线段x,使x=a+2b.18.(8分)已知在平面内,∠AOB=70°,∠BOC=40°,求∠AOC的度数.19.(9分)如图,已知AB和CD的公共部分BD= AB= CD.线段AB,CD的中点E,F之间的距离是10 cm,求AB,CD的长.20.(10分)某摄制组从A市到B市有一天的路程,由于堵车,中午才赶到一个小镇,只行驶了原计划的三分之一(原计划行驶到C地),过了小镇,汽车赶了400千米,傍晚才停下来休息,司机说,再走从C地到这里路程的二分之一就到达目的地了,问A,B两市相距多少千米?1答案:D2答案:D3答案:A4答案:C 点拨:因为平角= ×180°=120°,所以平角是钝角,故选C.5答案:A 点拨:∠1=180°-26°30′=153°30′.6答案:C 点拨:说法①④错误.7答案:D8答案:B9答案:D 点拨:分别计算各选项中的用时可知,从景点A 到景点C用时最少的线路是A→B→E→C,故选D.10答案:A11答案:短两点之间,线段最短12答案:2 点拨:∵AB=10,AC=6,∴BC=AB-AC=10-6=4.又∵点D是线段BC的中点,∴CD= BC=2.13答案:160° 点拨:可画出钟表的示意图帮助解答(如图).观察图可知,9点20分时,时针和分针的夹角是5个大格加时针从9点开始转过的角度,所以9点20分时,时针和分针的夹角是5×30°+20×0.5°=160°.14答案:10 点拨:由泰山到青岛的某一次列车的车票的种数是:泰山——济南,泰山——淄博,泰山——潍坊,泰山——青岛;济南——淄博,济南——潍坊,济南——青岛;淄博——潍坊,淄博——青岛;潍坊——青岛,共10种.15解:(1)先将0.29°化为17.4′,再将0.4′化为24″.24.29°=24°+0.29×60′=24°+17′+0.4×60″=24°+17′+24″=24°17′24″.(2)先将30″化为0.5′,再将40.5′化为0.675°.∵1′= ,1″= ,∴ 30″= ×30=0.5′,40.5′= ×40.5=0.675°.∴36°40′30″=36.675°.16解:以下答案供参考.17答案:略18解:(1)当∠BOC在∠AOB的外部时,如图1所示,∠AOC=∠AOB+∠BOC=70°+40°=110°;(2)当∠BOC在∠AOB的内部时,如图2所示,∠AOC=∠AOB-∠BOC=70°-40°=30°.故∠AOC的度数为110°或30°.19解:设BD=x cm,则AB=3x cm,CD=4x cm.因为E,F分别是线段AB,CD的中点,所以EB= AB=1.5x,FD= CD=2x.又EF=10 cm,EF=EB+FD-BD,所以1.5x+2x-x=10.解得x=4.所以3x=12,4x=16.所以AB长12 cm ,CD长16 cm.20解:如图,设小镇为D,傍晚汽车在E处休息,由题意知,DE=400千米,AD= DC,EB= CE,AD+EB= (DC+CE)= DE=×400=200(千米).所以AB=AD+EB+DE=600(千米).答:A,B两市相距600千米.北师大版七年级上册数学第四章试题就分享到这里了,更多初中生班级活动请继续关注!各版本初一数学上册第四章试题集浙教版七年级数学上册整式检测题(含答案)。

第四章第三节角一、选择题(共6小题;共30分)1. ∠α和∠β的顶点和一边都重合,另一边都在公共边的同侧,且∠α>∠β,那么∠α的另一边落在∠β的( )A. 另一边上B. 内部C. 外部D. 以上结论都不对2. 如图,从点O出发的五条射线,可以组成( )个角A. 4B. 6C. 8D. 103. 如图,下列说法正确的是( )A. ∠BAC和∠DAE不是同—个角B. ∠ABC和∠ACB是同一个角C. ∠ADE可以用∠D表示D. ∠ABC可以用∠B表示4. 下面等式成立的是( )A. 83.5∘=83∘50ʹB. 37∘12ʹ36ʺ=37.48∘C. 24∘24ʹ24ʺ=24.44∘D. 41.25∘=41∘15ʹ5. 八点三十分这一时刻,分针和时针的夹角是( )A. 70∘B. 75∘C. 80∘D. 85∘6. 用一副三角板不能画出( )A. 15∘角B. 100∘角C. 135∘角D. 75∘角二、填空题(共6小题;共30分)7. 2点30分时,时针与分针所成的角为.8. 将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108∘,则∠COB=.9. 计算72∘35ʹ÷2+18∘33ʹ×4=.10. 如图以AC为一条边的角有.11. 如图,∠AOB=90∘,以O为顶点的锐角共有个.12. 如图中,有个角可以用一个大写字母表示,它们是.三、解答题(共6小题;共90分)13. 已知∠α+∠β=180∘,∠α−∠β=60∘,求∠α,∠β的度数.14. 如图,以B为顶点的角有几个?把它们表示出来.以D为顶点的角有几个(不包括平角)?把它们表示出来.15. 计算:(1)90∘3ʺ−57∘21ʹ44ʺ;(2)38∘24ʹ×4;(3)153∘19ʹ42ʺ+26∘40ʹ28ʺ.16. (1)平面上四条直线最多可以把一个平面分成几部分?(2)平面上n条直线最多可以把一个平面分成几部分?17. 如果两个角的差的绝对值等于90∘,那么称这两个角互为反余角,其中一个角叫做另一个角的反余角.例如:∠1=120∘,∠2=30∘,∣∠1−∠2∣=90∘,则∠1和∠2互为反余角,其中∠1是∠2的反余角,∠2也是∠1的反余角.(1)如图,O为直线AB上一点,OC⊥AB于点O,OE⊥OD于点O,则∠AOE的反余角是,∠BOE的反余角是;,求这个角的度数.(2)若一个角的反余角是它的补角的2318. 在一条笔直的公路L的两侧,分别有A.B两个村庄,如图,现在要在公路上建一个汽车站P,使汽车站P到两村的距离和最小,请在图中画出汽车站P的位置,请说明理由.答案第一部分1. C2. D3. D4. D5. B6. B第二部分7. 105∘8. 72∘【解析】∵∠COD=90∘,∠AOB=90∘,∠AOD=108∘,∴∠AOC=∠AOD−∠COD=108∘−90∘=18∘,∴∠COB=∠AOB−∠AOC=90∘−18∘=72∘.故答案为:72∘.9. 110∘29ʹ30ʺ10. ∠DAC,∠BAC,∠ACB11. 5【解析】以O为顶点的锐角有∠AOD,∠AOC,∠DOC,∠DOB,∠COB,共5个.12. 2,∠B,∠C第三部分13. ∠α=120∘,∠β=60∘14. B为顶点的角有3个,分别是∠ABD,∠CBD,∠ABC.以D为顶点的角有4个,分别是∠ADB,∠ADM,∠BDC,∠MDC.15. (1)90∘3ʺ−57∘21ʹ44ʺ=89∘59ʹ63ʺ−57∘21ʹ44ʺ=(89∘−57∘)+(59ʹ−21ʹ)+(63ʺ−44ʺ)=32∘38ʹ19ʺ.(2)38∘24ʹ×4=38∘×4+24ʹ×4=152∘96ʹ=153∘36ʹ.(3)153∘19ʹ42ʺ+26∘40ʹ28ʺ=(153∘+26∘)+(19ʹ+40ʹ)+(42ʺ+28ʺ)=180∘10ʺ.16. (1)如图:平面上四条直线最多可以把一个平面分成11部分.(2)一条直线把一个平面分成2=1+1部分,两条直线最多可以把一个平面分成4=1+2+1部分,三条直线最多可以把一个平面分成7=1+2+3+1部分,四条直线最多可以把一个平面分成11=1+2+3+4+1部分,所以平面上n条直线最多可以把一个平面分成n(n+1)2+1=n2+n+22部分.17. (1)∠AOD;∠EOC和∠DOB(2)设这个角的度数为x,若这个角是锐角,则它的反余角为(90∘+x),由题意得90∘+x=23(180∘−x),解得x=18∘.若这个角是钝角,则它的反余角为(x−90∘),由题意,得x−90∘=23(180∘−x),解得x=126∘.综上所述,这个角的度数为18∘或126∘.18. 连接AB与L的交点即为P点.。

加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第四章综合测试一、单选题1.以下说法中正确是( )A .延长射线AB B .延长直线ABC .画直线AB 直线等于1cmD .延长线段AB 到C2.“植树时只要确定两棵树的位置,就能确定这一行树所在的直线”,用数学知识解释其道理应是( )A .两点之间,线段最短B .两点确定一条直线C .直线可以向两边延长D .两点之间线段的长度,叫做这两点之间的距离3.如图,在数轴上,点B 在点A 的右侧.已知点A 对应的数为1-,点B 对应的数为m .若在AB 之间有一点C ,点C 到原点的距离为2,且2AC BC -=,则m 的值为( )A .4B .3C .2D .14.下列现象中,用“两点之间,线段最短”来解释的现象是( )A .用两个钉子把木条固定在墙上B .利用圆规可以比较两条线段的大小C .把弯曲的公路改直,就缩短路程D .植树时,只要固定两棵树的位置,就能确定一行树所在的直线5.如图,由A 点测量B 点方向,得到( )A .B 点在A 点北偏西30︒的方向上B .B 点在A 点南偏东30︒的方向上C .B 点在A 点南偏东60︒的方向上D .B 点在A 点北偏西60︒的方向上6.小明妈妈下午下班的时间是5:20分,此时,时钟的分针与时针所夹的角等于( )A .20B .30C .40D .507.从n 边形的一个顶点出发可以连接8条对角线,则n =( )A .8B .9C .10D .11二、填空题8.已知点A ,B ,C 都在直线l 上,点P 是线段AC 的中点.设AB a =,PB b =,则线段BC 的长为________(用含a ,b 的代数式表示).9.如图是时钟的钟面,下午1点30分,时钟的分针与时针所夹的角等于________°.10.如图,已知OB OA ⊥,直线CD 过点O ,且20AOC ︒∠=,那么BOD ∠=________.11.374940α︒'''∠=,521020,β︒'''∠=,βα∠-∠=________.三、解答题12.如图B 、C 两点把线段AD 分成2:3:4三部分,M 是AD 的中点,8CD =,求MC 的长.四、作图题13.如图,在平面内有A ,B ,C 三点.(1)①画直线AC ,线段BC ,射线AB ;②在线段BC 上任取一点D 不同于B ,C ,连接线段AD ;(2)数数看,此时图中线段的条数.第四章综合测试答案解析一、1.【答案】D【解析】A 、射线不能延长,故A 不符合题意;B 、直线不能延长,故B 不符合题意;C 、直线可以向两端无限延伸,不可测量,故不符合题意;D 、线段可以延长,故D 符合题意;故答案为:D .2.【答案】B【解析】“植树时只要确定两棵树的位置,就能确定这一行树所在的直线”,用数学知识解释其道理应是两点确定一条直线.故答案为:B3.【答案】B【解析】 点C 到原点的距离为2,∴设点C 表示的数为c ,则|c |2=,即c 2=±,点B 在点A 的右侧,点C 在点A 的右侧,且点A 表示的数为1-,∴点C 表示的数为2,-= AC BC ,2(1)(2)2m ∴----=,解得:3m =.故答案为:B .4.【答案】C【解析】A .应用的原理为两点确定一条直线;B .为线段长度的比较;C .为两点之间,距离最短;D .为两点确定一条直线.故答案为:C .5.【答案】C【解析】 A 在B 店的北偏西60︒,∴B 点在A 点南偏东60︒的方向上,故答案为:C .6.【答案】C【解析】根据题意可知,5:20时,时针与分针之间相差113大格,∴夹角为°1301403°⨯=答案为:C .7.【答案】D【解析】由题意得:38n -=,解得11n =,故答案为:D二、8.【答案】2b a -或22b b a a +=-【解析】当点B 在A 的右侧,如图,AB a PB b ==AP b a ∴=-点P 是线段AC 的中点PC AP b a ∴==-()()2BC BA AP PC a b a b a b a ∴=++=+-+-=-当点B 在AP 之间,如图,AB a PB b ==AP b a ∴=+点P 是线段AC 的中点PC AP b a ∴==+()2BC BP PC b b a b a ∴=+=++=+当点B 在PC 之间,如图,AB a PB b ==AP a b ∴=-点P 是线段AC 的中点PC AP a b ∴==-,()2BC PC PB a b b a b ∴=-=--=-当点B 在C 的左侧,如图,AB a PB b == ,AP a b ∴=-点P 是线段AC 的中点222AC AP a b ∴==-,(22)2BC AB AC a a b b a ∴=-=--=-综上所述:2BC b a =-或2BC b a =+,或2BC a b =-故答案为:2b a -或22b a a b +=-9.【答案】135【解析】根据钟表的特点,可知钟表的一大格的度数为30︒,而1点30分时共有4个半格,因此可知30 4.5135⨯=︒故答案为:135︒10.【答案】110︒【解析】,20,OB OA AOC ︒⊥∠= ,902070BOC ︒︒︒∴∠=-=,18070110BOD ︒︒︒∴∠=-=,故答案为:110︒11.【答案】142040︒'''【解析】374940α︒'''∠= ,521020β︒'''∠=521020374940142040βα︒'''︒'''︒'''∴∠-∠=-∠=故答案为:142040︒'''三、12.【答案】解:设AB 为2x ,则48CD x ==,得出2x =,再利用MC MD CD =-求解.解:设2,3,4AB x BC x CD x ===,9AD x ∴=,92MD x =, 则48CD x ==,2x =,911421222MC MD CD x x x =-=-==⨯=. 【解析】根据题意,三段线段成比例,可设AB 为2x ,BC 为3x ,CD 为4x ,根据线段中点的性质表示出CD ,根据CD 的长度计算得到x 的值,即可得到MC 的长.四、13.【答案】(1)解:如图,直线AC ,线段BC ,射线AB ,线段AD 即为所求;(2)解:由题可得,图中线段有AC 、AB 、AD 、BD 、DC 、BC 共6条.【解析】(1)依据直线、射线、线段的定义,即可得到直线AC ,线段BC ,射线AB ;依据在线段BC 上任取一点D(不同于B,C),连接线段AD即可;(2)根据图中的线段有AC、AB、AD、BD、DC、BC,即可得到图中线段的条数.。

A DB C七年级(上)第四单元测试题班级 姓名 学号 总分一、填空题:(每小题3分,共39分)1、两条直线相交,只有 个交点。
2、经过两点, 且 一条直线。
3、将弯曲的河道改直,可以缩短航程,是因为:两点之间的所有连线中, 最短。
4、若AB ∥CD ,HG ∥5、若点C 为线段AB 67、右图有 条线段。
8、0.5周角= 平角9、0.15°= ′10、若∠1:∠2:∠3=1:2:3,且∠1+∠2+∠3=180°,则∠2= 度。
11、直线AB 上有一点C ,直线AB 外有一点P ,由A 、B 、C 、P 四点可以确定 条线段。
12、钟表在3点30分(即3点半)时,时针与分针所成的锐角是 度。
13、如右图所示,图中有 个小于平角的角。
二、选择题。
(每小题3分,共21分)1、下列说法正确的是( )A 、过一点P 只能作一条直线。
B 、经过三点只能作三条直线。
C 、直线AB 和直线BA 表示同一条直线D 、直线a 比直线b 短2、下列语句正确的是( )A 、平角就是一条直线;B 、周角就是一条射线C 、小于平角的角是钝角D 、一周角等于四个直角3、下列图形中,无端点的是( )A 、角平分线B 、线段C 、射线D 、直线4、平面内三条两两相交的直线( )A 、有一个交点B 、有一个或三个交点C 、有三个交点D 、上述都不对5、在长方形、长方体、三角形、球、直线、圆中,有( )个平面图形。
A 、3B 、4C 、5D 、6 6、已知AB=10cm ,在AB 的延长线上取一点C ,使AC=16cm , 那么线段AB 的中点与AC 的中点的距离为( ) A 、5cm ; B 、4cm ; C 、3cm ; D 、2cm 7、若点B 在点A 的北偏东30度,则点A 在点B 的( ) A 、南偏西30度;B 、北偏东60度;C 、南偏西60度;D 、西偏南60度三、 作图题(每小题6分,共18分)1、 如图,在同一平面内有四个点A 、B 、C 、D 。

第四章第一节线段、射线、直线一、选择题(共6小题;共30分)1. 下列各直线的表示法中,正确的是( )A. 直线abB. 直线AbC. 直线AD. 直线AB2. 如图,下列说法正确的是( )A. 射线ABB. 延长线段ABC. 反向延长线段BAD. 延长线段BA3. 经过同一平面内A、B、C三点可连接直线的条数为( )A. 只能一条B. 只能三条C. 三条或一条D. 不能确定4. 下列说法正确的是( )A. 线段AB和线段BA表示的不是同一条线段B. 射线AB和射线BA表示的是同一条射线ABC. 若点P是线段AB的中点,则PA=12D. 线段AB叫做A,B两点间的距离5. 以下关于距离的几种说法中,正确的有( )①连接两点间的线段长度叫做这两点的距离;②连接直线外的点和直线上的点的线段叫做点到直线的距离;③从直线外一点所引的这条直线的垂线叫做点到直线的距离;④直线外一点到这条直线的垂线段叫做这点到直线的距离.A. 1个B. 2个C. 3个D. 4个6. 平面上有四个点,经过其中的两点画直线最少可画a条直线,最多可画b条直线,那么a+b的值为( )A. 4B. 5C. 6D. 7二、填空题(共4小题;共20分)7. 如图所示,直线a上有点A,B,C,D,则图中有条直线,条线段.8. 如图,图中有条线段,它们是;图中以点A为端点的射线有条,它们是;图中有条直线,它们是.9. 两两相交的5条直线,最少有个交点,最多有个交点.10. 平面内有若干条直线,在下列情形下,直线最多可将平面分成几部分?(1)画图观察:有1条直线时,最多分成部分;有2条直线时,最多分成部分;有3条直线时,最多分成部分.(2)根据上面的规律,猜想:有n条直线时,最多可将平面分成部分.三、解答题(共8小题;11-14每题各12分,15-18每题各13分,共100分)11. 如图所示,读语句画图(1)连接BC,AD;(2)画直线AB,CD相交于点E;(3)延长线段BC,反向延长线段DA,相交于点F;(4)连接AC,BD,相交于点O.12. 已知A,B,C三点,过其中的每两点画一条直线,能画几条?13. 在如图给出的直线、射线和线段中,找出能相交的图形.14. 如图所示,图中有几条射线?能用图中的字母表示出来的有几条?不再添加新的字母,把它们表示出来.15. 在线段AB上取一点C时,共有几条线段?在线段AB上取两点C,D时,共有几条线段?在线段AB上取三点C,D,E时,共有几条线段?16. 如图,小蚂蚁在点A处,观察从A到B的两条路线,那么这两条路线的距离相同吗?请说明理由.17. 读下列语句,并按照这些语句画出它们的图形:(1)直线l经过点C,D.(2)点P在直线a上,但在直线b外.(3)两条直线a与b相交于点P,P是直线c外的一点,c与a交于点Q,c与b交于点R.18. 解答题:(1)在直线l上任取两个点,最多有几条线段?任取3个点,最多有几条线段?任取n个点呢?(2)如图所示,P为直线l外一点,A,B为直线l上两点,把点P和点A,B连接起来,一共可以得到多少个三角形?若在直线上增加一个点C,一共可以得到多少个三角形?若直线l上有n个点,一共可以得到多少个三角形?(3)当直线l上有两个点时,有几条射线?有n个点时,有几条射线?答案1. D 【解析】根据直线的表示方法可得直线AB正确.2. D 【解析】A选项,图中的射线应该是射线BA,不是射线AB,故A不符合题意;B选项,应该为延长线段BA,故B不符合题意;C选项,反向延长线段BA是不符合图形的,故C不符合题意;D选项,延长线段BA是符合图形的,故D符合题意.3. C4. C5. A6. D 【解析】如图所示:平面上有四个点最少画1条直线,最多画6条直线.故a=1,b=6.则a+b=1+6=7.7. 1,68. 8,AD,AB,DB,AE,AC,EC,DE,BC,2,射线AM,射线AN,1,直线MN9. 1,1010. (1)2,4,7,(2)n2+n+2211.12. 1条或3条13. ①③14. 图中共有6条射线,能用图中的字母表示出来的共有4条,它们是射线AB(或AC),射线BA,射线BC,射线CB(或CA).15. 3条,6条,10条.16. 由A到B的两条路线距离相同.如图,可知AC=MN,DE=NL,FG=LB,CD=AH,EF= HK,GB=KM,则AM+MB=AH+HK+KM+MN+NL+LB=CD+EF+GB+AC+DE+ FG=AC+CD+DE+EF+FG+GB,所以由A到B的两条路线距离相同.17. (1)(2)(3)18. (1)1条;3条;n(n−1)条.2个.(2)1个;3个;n(n−1)2(3)4;2n。

北师大版(2024)七年级上册《4.2角2》2024年同步练习卷一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.若,,,则有()A. B. C. D.2.已知,,则与的大小关系是()A. B. C. D.无法确定3.如图,点C在的OB边上,用尺规作出了,作图痕迹中,是()A.以点C为圆心,OD为半径的弧B.以点C为圆心,DM为半径的弧C.以点E为圆心,OD为半径的弧D.以点E为圆心,DM为半径的弧4.如图,小明将自己用的一副三角板摆成如图形状,如果,那么等于()A. B. C. D.5.如图,用同样大小的三角板比较和的大小,下列判断正确的是()A.无法确定B.C.D.6.,的顶点和一边重合,另一边都在公共边的同侧,且,那么的另一边落在的()A.另一边上B.内部C.外部D.以上结论都不对7.,,关于两个角的大小,下列正确的是()A. B. C. D.无法确定8.点P在内部,现在有四个等式:①;②;③;④其中,能表示OP为的平分线的有()A.1个B.2个C.3个D.4个9.如图.已知O是直线AB上一点,,OD平分,则的度数是()A.B.C.D.10.如图,,以OA为边作,使,则下列结论成立的是()A.B.C.或D.或11.已知,,OD平分,OM平分,则的度数是()A.或B.或C.或D.或12.如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点和点,如图2,设,则的度数为()A. B. C. D.二、填空题:本题共7小题,每小题3分,共21分。
13.如图,BD平分,BE把分成3:7的两部分,,则的度数为______.14.已知,求作:,使作法:以______为圆心,______为半径画弧.分别交OA,OB于点C,画一条射线,以______为圆心,______长为半径画弧,交于点,以点______为圆心______长为半径画弧,与第2步中所画的弧交于点过点______画射线,则15.如图所示的网格是正方形网格,则______填“>”“<”或“=”16.比较角的大小,另一种方法是使两个角的顶点及一条边重合,另一条边放在重合边的______就可以比较大小.17.将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.则______度.18.从一个角的顶点出发,把它分成两个角的直线叫做这个角的平分线.______填“正确”或“错误”19.已知,在其顶点O处引一条射线OC,且,则______.三、解答题:本题共3小题,共24分。

第四章第二节比较线段的长短一、选择题(共7小题;共35分)1. 如图所示,下列各式错误的是( )A. AB=AD+DBB. CB=AB−ACC. CB−DB=CDD. CB−DB=AC2. 宣传委员制作黑板报时,想在黑板上画出一条笔直的参照线,由于尺子不够长,她想出了一个办法,如下:这种画法的数学依据是( )A. 两点之间,线段最短B. 两点确定一条直线C. 线段的中点的定义D. 两点的距离的定义3. 已知线段AB=10cm,PA+PB=20cm,则下列说法正确的是( )A. 点P一定在线段AB的延长线上B. 点P一定在线段BA的延长线上C. 点P一定不在线段AB上D. 点P一定不在直线AB外4. 如图,下列说法中不正确的是( )A. 直线AC经过点AB. 射线DE与直线AC有公共点C. 点B在直线AC上D. 直线AC与线段BD相交于点A5. 如图,AB=CD,则AC与BD的大小关系是( )A. AC>BDB. AC<BDC. AC=BDD. 无法确定6. 如图 1,线段a,b,图 2 中线段AB表示的是( )A. a−bB. a+bC. a−2bD. 2a−b7. 如果线段AB=5cm,BC=4cm,则A,C两点间的距离是( )A. 1cmB. 9cmC. 1cm或9cmD. 以上答案都不对二、填空题(共5小题;共25分)8. 已知线段AB和CD,如果将CD移动到AB的位置,使点C与点A重合,CD与AB叠合,如果点D在AB的延长线上,那么AB CD(填“>”“<”或“=”).9. 已知线段AB=8cm,在直线AB上画线段BC,使BC=3cm,则线段AC=.10. 如果线段AB=2,延长AB到C,使BC=AB,再反向延长BC到D,使BD=2AB,则CD=.11. 直线上有A,B,C三点,已知AB=8cm,BC=5cm,则AC=cm.BC,则线段12. 已知线段AB的长为18cm,点C在线段AB的延长线上,且AC=53 BC=.三、解答题(共6小题;共90分)13. 已知线段a,b(如图),画出线段AB,使AB=2a+b.14. 如图所示,A,B,C,D表示四个村庄,村民们准备合打一口井.(1)水井的位置现有P,Q两种选择方案,点P在线段BD上,点Q在线段AB上.哪一种方案的水井到各村庄的距离总和较小?(2)你能给出一种使水井到各村庄的距离之和最小的方案吗?若能,请标出水井的位置,并说明理由.15. 如图所示,已知线段AB上有两点C,D,AD=35,BC=44,AC=23BD,求线段AB的长.16. 如图,已知线段AB和CD的公共部分BD=13AB=14CD,线段AB,CD的中点E,F之间距离是10cm,求AB,CD的长.17. 如图,比较图中线段AB与CD的大小.18. 如图,已知线段AB和CD的公共部分为BD,且BD=13AB=14CD,线段AB、CD的中点E、F之间距离是20,求AB、CD的长.答案1. D 【解析】点D在线段AB上,AB是线段AD与DB的和,即AB=AD+DB;点C在线段AB 上,CB是线段AB与AC的差,即CB=AB−AC;点D在线段CB上,CD是线段CB与DB的差,即CB−DB=CD.2. B3. C 【解析】∵线段AB=10cm,PA+PB=20cm,∴PA+PB>AB,∴点P一定不在线段AB上.4. C5. C【解析】∵AB=CD,∴AB+BC=CD+BC,即AC=BD.6. D 【解析】由图可得,AB=AC−BC=a+a−b=2a−b.7. D8. <9. 5cm或11cm10. 611. 3或1312. 27cm13. 如图所示:14. (1)可以用测量或比较线段长短的方法得到,选点P,水井到各村庄的距离总和较小;(2)当水井的位置选在AC与BD的交点时,水井到各村庄的距离之和最小;理由:两点之间,线段最短.15. 设CD=x,因为AC=23BD,所以AD−CD=23(BC−CD),即35−x=2(44−x).解这个方程,得x=17.所以AB=AD+CB−CD=35+44−17=62.16. 设BD=x cm,则AB=3x cm,CD=4x cm,AC=6x cm,∵点E,F分别为AB,CD的中点,∴AE=12AB=1.5x cm,CF=12CD=2x cm,∴EF=AC−AE−CF=6x−1.5x−2x=2.5x cm,∵EF=10cm,∴2.5x=10,解得x=4,∴AB=12cm,CD=16cm.17. 略18. 设BD=x,则AB=3x,CD=4x,AC=6x.∵点E、点F分别为AB、CD的中点,∴AE=12AB=1.5x,CF=12CD=2x.∴EF=AC−AE−CF=2.5x ∵EF=20,∴2.5x=20,解得x=8.∴AB=24,CD=32.。
北师大版(2024)七年级上册《4.2角1》2024年同步练习卷一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列说法中正确的是()A.两条射线组成的图形叫做角B.直线是一个平角C.一条射线就是一个周角D.与表示同一个角2.下列四个图中,能用,,三种方法表示同一个角的是()A. B.C. D.3.如图,货轮O在航行过程中,发现灯塔A在它南偏东的方向上,同时,在它的北偏东方向上又发现了客轮B,则的度数为()A. B. C. D.4.如图所示,还可以表示为()A.B. C. D.5.用度、分,秒表示为()A.B. C. D.6.如图,已知,在内逐一画射线,下面三个图中分别有3个、6个、10个角不大于平角的角当内有n 条射线时,角的个数为()A. B. C. D.7.如图,从点O 出发的五条射线,可以组成个角.A.4B.6C.8D.108.钟表在9:10时,时针与分针所成的钝角为()A.B.C.D.二、填空题:本题共6小题,每小题3分,共18分。
9.如图所示,能用一个字母表示的角有______个,图中所有小于平角的角有______个.10.____________'______;______11.____________'____________12.若在传统钟表的表盘上时间显示为7:30,则此时时针与分针所成的角为______度.13.如图所示,射线OP表示的方向是______。
14.角的定义:由两条具有______的射线组成的图形叫作角,也可以看成是由一条射线绕着它的端点______而成的.三、解答题:本题共2小题,共16分。
解答应写出文字说明,证明过程或演算步骤。
15.本小题8分写出如图的符合下列条件的角图中所有的角均指小于平角的角能用一个大写字母表示的角;以点A为顶点的角.16.本小题8分“好奇、发现、质疑、探究”是科学研究的基础与原动力,就像牛顿被苹果砸到后,悟出万有引力,小明就被身边的钟表所吸引.他看到时针,分针,秒针在表盘上有规律的周期性的转动着,就想探究出里面的一些东西.分钟秒针转动1周,因此秒针的转动速度______度/分;分钟分针转动1周,因此分针的转动速度是______度/分;分钟时针转动______周,因此时针的转动速度是______度/分;从中午12点开始,到第一次时针与分针恰好垂直,需要多少分钟?从上午9点开始,到第一次秒针恰好平分时针与分针的夹角小于,需要多少分钟?答案和解析1.【答案】D【解析】解:A、应为有公共端点的两条射线组成的图形叫做角,故本选项错误;B、直线与平角是两个不同的概念,故本选项错误;C、一条射线与一个周角是两个不同的概念,故本选项错误;D、与表示同一个角正确,故本选项正确.故选:根据角的概念对各选项分析判断后利用排除法求解.本题考查了角的概念,是基础题,要注意与直线、射线的区分.2.【答案】B【解析】解:对于选项A,图中的,还可以用表示,不能用表示,故选A不符合题意;对于选项B,图中,还可以,表示,故选B符合题意;对于选项C,图中的,不能用和表示,故选C不符合题意;对于选项D,图中的,能用表示,但不能用表示,故选D不符合题意;故选:结合各选项中的图形,根据角的表示方法即可得出答案.此题主要考查了角的表示方法,准确识图,熟练掌握角的表示方法是解决问题的关键.3.【答案】D【解析】解:故选:首先根据方向角的定义作出图形,根据图形即可求解.本题考查了方向角的定义,正确理解方向角的定义,理解A、B、O的相对位置是关键.4.【答案】B【解析】解:还可以表示为,故选:根据角的表示方法解答即可.本题考查了角的概念,熟练掌握角的表示方法是解题的关键.5.【答案】C【解析】解:,,故选:将化成即可.本题考查度、分、秒的换算,掌握度、分、秒的换算方法以及单位之间的进率是正确解答的前提.6.【答案】D【解析】【分析】本题考查了角的概念的应用,关键是能根据求出结果得出规律.画1条、2条、3条射线时可以数出角的个数分别有3个、6个、10个角,当画n条时,由规律得到角的个数的表达式.【解答】解:画1条、2条、3条射线时可以数出角的个数分别有3个、6个、10个角,当画n条时,角的个数为故选7.【答案】D【解析】解:点O出发的五条射线,可以组成的角有:,,,,,,,,,故选:先以OA为角的一边,依次得到以OB、OC、OD、OE为另一边的五个角,然后利用同样的方法得到其他角.本题考查了角的定义:有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.角的表示方法:角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母如,,、…表示,或用阿拉伯数字…表示.8.【答案】C【解析】解:如图,由钟面角的定义可知,,,,故选:由钟面角的定义可求出,由钟面上时针、分针在转动过程中所成角度的变化关系可求出,进而求出答案.本题考查钟面角,掌握钟面角的定义以及钟面上时针、分针在转动过程中所处角度的变化关系是正确解答的关键.9.【答案】27【解析】解:能用一个字母表示的角有2个:,;小于平角的角有7个:,,,,,,故答案为:2;根据角的概念和角的表示方法,依题意求得答案.本题考查了角的概念:从一点引出两条射线组成的图形就叫做角.角的表示方法一般有以下几种:角个大写英文字母;角个大写英文字母;角+小写希腊字母;角+阿拉伯数字.10.【答案】【解析】解:,,,,,故答案为:26;32;24;,,,,,故答案为:根据度分秒的进制进行计算,即可解答;根据度分秒的进制进行计算,即可解答.本题考查了度分秒的换算,准确熟练地进行计算是解题的关键.11.【答案】【解析】,,;故答案为:34,22,12;,,;故答案为:根据大单位化小单位乘以进率,可得答案.根据小单位化大单位除以进率,可得答案.此题主要考查了度分秒的计算,关键是掌握度、分、秒之间是60进制.12.【答案】45【解析】解:钟面每份是,7:30时时针与分针相距份,此时时针与分针所成的角为故答案为:根据钟面平均分成12份,可得每份的度数;根据时针与分针相距的份数乘以每份的度数,可得答案.本题考查了钟面角,能够利用时针与分针相距的份数乘以每份的度数进行计算是解题的关键.13.【答案】南偏西【解析】【分析】根据余角的性质,可得的度数,根据方向角的表示方法,可得答案。

北师大版七年级上第四单元数学测试卷一.单选题:1.下面表示∠ABC 的图是( ) A B C D2.直线AB 和直线CD 相交于点O,若∠AOC=40o ,则∠BOC 等于( ) A. 140o B. 60o C.40o D. 160o3.同一平面内互不重合的三条直线的交点的个数是( )A.可能是0个,1个,2个B.可能是0个,2个,3个C.可能是0个,1个,2个或3个D.可能是1个或3个4.下列说法正确的是( )A.过一点P 只能作一条直线B.直线AB 和直线BA 表示同一条直线C.射线AB 和射线BA 表示同一条射线D.射线a 比直线b 短5.下列说法正确的是( )A.连接两点的线段叫做两点的距离B.线段的中点到线段两个端点的距离相等C.到线段两个端点距离相等的点叫做线段的中点D.AB=BC,则点B 是线段AC 的中点6.现在的时间是9点30分,时钟面上的时针与分针的夹角度数是( ) A. 90o B.100o C.105o D. 107o7.如图,COLAB,DO 是∠AOC 平分线,EO 是∠BOC 平分线,则∠DOE 度数是( ) A. 89o B.91o C. 92o D. 90o8.如图,点C 是线段AB 上一点,点M 是AC 的中点,点N 是BC 的中点,如果MC 比NC 长2cm,那么AC 比BC 长( )A.2cm B.4cm C.1cm D.6cm9.如图,圆的四条半径分别是OA,OB,OC,OD,其中点O,A,B 在同一条直线上,若∠AOD=90o ,∠AOC=3∠BOC,那么圆被四条半径分成的四个扇形的面积的比是( ) A. 1:2:2:3 B. 3:2:2:3 C. 4:2:2:3 D. 1:2:2:110.已知线段AB=5cm,在直线AB 上画线段AC=3cm,则线段BC 的长为( ) A.8cm B.2cm 或8cm C.2cm D.不能确定11.如图,C 、D 是线段AB 上两点,M 、N 分别是线段AD 、BC 的中点,下列结论:①若AD=BM,则AB=3BD;②若AC=BD,则AM=BN;③AC-BD=2(MC-DN);④2MN=AB-CD.其中正确的结论是( ) A. ①②③ B. ③④ C. ①②④ D. ①②③④二.填空题12.把一条弯曲的公路改为直道,可以缩短路程,其理由是________.13.选定多边形的一个顶点,连接这个顶点和多边形的其余各个顶点,得到了8个三角形,则原多边形的边数是________.14.如图,点A,B,C 在直线1上,则图中共有________条线段,有________条射线.15.在直线AB 上,AB=10,AC=16,那么AB 的中点与AC 的中点的距离为_______.16.如图,AM 、CM 平分∠BAD 和∠BCD,若∠B=34o ,∠D=42o ,则∠M=______.三.解答题17.计算:(1)-14-16×[2-(-3)2]; (2)(-2)4÷(-223)2+512×(-16)-0.25; (3)(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2).18.设A=-12x -4(x-13y)+(-32x+23y).(1)当x=-13,y=1时,求A 的值;(2)若y-3x=2,则A=_____.19.半径为2的圆中扇形AOB圆心角为150o,请在圆内画出这个扇形,并求它的面积.20.如图,已知四点A,B,C,D,请按要求画图:(1)画直线AB,射线CD交于点M;(2)连接 AC,BD交于点N;(3)连接MN,并延长至点E,使NE=NM.21.如图,已知∠AOC=∠BOD=70o,∠BOC=31o,求∠AOD的度数.22.已知,点O为直线AB上一点,∠COD=90o,OE是∠AOD的平分线.(1)如图1,若∠COE=63o,求∠BOD的度数;(2)如图2,OF是∠BOC的平分线,求∠∠BOD,若∠AOC+∠DOF=∠EOF,请直接写出∠FOP的度数.(不用写过程) EOF的度数;(3)如图3,在(2)的条件下,OP是∠BOD的一条三等分线∠DOP=13图1 图2 图323.已知:如图1,点M是线段AB上一定点,AB=12cm,C、D两点分别从M、B出发以 1cm/s、2cm/s 的速度沿直线BA向左运动,运动方向如箭头所示(C 在线段AM上,D在线段BM上).(1)若AM=4cm,当点C、D运动了2s,此时AC=______,DM=______;(直接填空)(2)当点C、D运动了2s,求AC+MD 的值.(3)若点C、D运动时,总有MD=2AC,则AM=_____(填空).(4)在(3)的条件下,N 是直线AB上一点,且AN-BN=MN,求MN的值.AB。

第四章基本平面图形时间:45分钟分值:100分一、选择题(每题4分,共32分)1.下列命题中,正确的有(B)①两点之间线段最短;②连接两点的线段,叫做两点间的距离;③角的大小与角的两边的长短无关;④射线是直线的一部分,所以射线比直线短.A.1个B.2个C.3个D.4个解析:①和③正确,②连接两点的线段的长度叫做两点间的距离;④射线与直线无法比较长短.2.如图,直线AB和CD相交于点O,若∠AOC=125°,则∠AOD等于(B)A.50°B.55°C.60°D.65°3.一个多边形从一个顶点最多能引出三条对角线,这个多边形是(D)A.三角形B.四边形C.五边形D.六边形4.下列计算错误的是(D)A.0.25°=900″B.1.5°=90′C.1 000″=(518)°D.125.45°=1 254.5′5.如图,AB=CD,则下列结论不一定成立的是(D)A.AC>BC B.AC=BDC.AB+BC=BD D.AB+CD=BC解析:A.∵AC=AB+BC,∴AC>BC,故本选项正确;B.∵AB=CD,∴AB +BC=CD+BC,即AC=BD,故本选项正确;C.∵AB=CD,∴AB+BC=CD +BC,即AB+BC=BD,故本选项正确;D.AB,BC,CD是线段AD上的三部分,大小不明确,所以AB +CD 与BC 大小关系不确定,故本选项错误.故选D.6.如图,∠AOB =120°,OC 是∠AOB 内部任意一条射线,OD ,OE 分别是∠AOC ,∠BOC 的平分线,下列叙述正确的是(C)A .∠DOE 的度数不能确定B .∠AOD =12∠EOCC .∠AOD +∠BOE =60° D .∠BOE =2∠COD解:本题是对角的平分线的性质的考查,角平分线将角分成相等的两部分.结合选项得出正确结论.7.一个人从A 点出发向南偏东30°方向走到B 点,再从B 点出发向北偏西45°方向走到C 点,那么∠ABC 等于(D)A .75°B .45°C .30°D .15°8.如图,已知扇形AOB 的半径为2,圆心角为90°,连接AB ,则图中阴影部分的面积是(A)A .π-2B .π-4C .4π-2D .4π-4解:由∠AOB 为90°,得到△OAB 为等腰直角三角形,于是OA =OB ,而S阴影部分=S 扇形OAB -S △OAB .然后根据扇形和直角三角形的面积公式计算即可. 二、填空题(每题4分,共24分)9.C 是线段AB 上一点,D 是BC 的中点,若AB =12 cm ,AC =2 cm ,则BD 的长为5_cm.10.计算:50°-15°30′=34°30′.11.两点半时钟面上时针与分针的夹角为105°.12.如图,C岛在A岛的北偏东60°方向,C岛在B岛的北偏西50°方向,从C岛看A,B两岛的视角∠ACB是110度.13.如图所示的圆面图案是用相同半径的圆与圆弧构成的.若圆的半径为3,则阴影部分的面积为3π.解析:阴影部分的面积占了整个圆面积的13,所以阴影部分的面积为13π×32=3π.14.如图,已知OE是∠BOC的平分线,OD是∠AOC的平分线,且∠AOB =150°,∠DOE的度数是75°.三、解答题(共44分)15.(10分)如图,直线AB,CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.解:因为∠FOC=90°,∠1=40°,且AB为直线,所以∠3=180°-∠FOC-∠1=50°.因为CD为直线,所以∠AOD=180°-∠3=130°,因为OE平分∠AOD,所以∠2=12∠AOD=65°.16.(12分)如图甲所示,将一副三角尺的直角顶点重合在点O处.(1)①∠AOD和∠BOC相等吗?说明理由.②∠AOC和∠BOD在数量上有何关系?说明理由.(2)若将这副三角尺按图乙所示摆放,三角尺的直角顶点重合在点O处.①∠AOD和∠BOC相等吗?说明理由.②∠AOC和∠BOD的以上关系还成立吗?说明理由.甲乙解:(1)①∠AOD=90°+∠BOD,∠BOC=90°+∠BOD,所以∠AOD和∠BOC相等.②∠AOC+90°+∠BOD+90°=360°,所以∠AOC+∠BOD=180°;(2)①∠AOD=90°-∠BOD,∠BOC=90°-∠BOD,所以∠AOD和∠BOC相等.②成立.由∠AOC=90°+90°-∠BOD可知∠AOC+∠BOD=180°.17.(10分)有一个周长为62.8 m的圆形草坪,准备为它安装自动旋转喷灌装置进行喷灌,现有射程为20 m,15 m,10 m的三种装置,你认为应选哪种比较合适?安装在什么地方?解:设圆形草坪的半径为r,则由题意得2πr=62.8,解得r=10(m).所以选射程为10 m的喷灌装置较合适,安装在圆形草坪的中心处.18.(12分)如图,点C在线段AB上,线段AC=15,BC=5,点M,N分别是AC ,BC 的中点.(1)求MN 的长度.(2)根据(1)的计算过程与结果,设AC +BC =a ,其他条件不变,你能猜出MN 的长度吗?请用一句简洁的语言表达你发现的规律.(3)若把(1)中的“点C 在线段AB 上”改为“点C 在直线AB 上”,其他条件不变,结论又如何?请说明你的理由.解:(1)因为点M ,N 分别是AC ,BC 的中点, 所以MC =12AC =12×15=152,NC =12BC =52. 所以MN =MC +NC =10. (2)能,MN 的长度是a2.规律:已知线段被分成两部分,它们的中点之间的距离等于原来线段长度的一半.(3)分情况讨论:当点C 在线段AB 上时, 由(1)得MN =12AB =10;当点C 在线段AB 延长线上时(如图),MN =MC -NC =12AC -12BC =12AB =5.。

第四章测试卷( 时间: 120 分钟 总分: 120 分)一 二 三 总分一、选择题(每小题3分,共30分)1.40°15′的12是 ( )A .20°B .20°7′C .20°8′D .20°7′30″ 2.一轮船航行到B 处测得小岛A 的方向为北偏西30°,那么从A 处观测B 处的方向 为 ( ) A .南偏东30° B .东偏北30° C .南偏东60° D .东偏北60° 3.如图,在此图中小于平角的角有 ( )A .9个B .10个C .11个D .12个4.平面内三条直线两两相交,其交点的个数可能是 ( ) A .1个 B .3个 C .1个或3个 D .不确定5.下列说法中正确的是 ( ) A .一个锐角加上一个锐角还是锐角 B .一个角不是钝角必是锐角C .钝角与锐角的差一定大于锐角D .钝角与直角的差一定小于直角6.如图,点D 、E 、F 是线段AB 上的三点,则图中线段的条数是 ( )A .4B .8C .10D .127.从多边形的一个顶点出发可以引9条对角线,则这个多边形的边数为 ( ) A .9 B .10 C .11 D .128.已知扇形的圆心角为120°,面积为12π,则这个扇形的半径为 ( ) A .6 B .8 C .9 D .129.如图,C 、D 是线段AB 上的任意两点,M 、N 分别是AC 、BD 的中点,若CD =a ,MN =b ,则AB 的长为 ( )A .2b -aB .b -aC .2b +aD .以上均不对 10.已知∠AOC =135°,OB 为∠AOC 内部的一条射线,且∠BOC =90°,以OB 为一条边,以OA 为角平分线的角的另一边是 ( ) A .∠BOC 的平分线 B .射线OCC .射线OC 的延长线D .射线OC 的反向延长线 二、填空题(每小题3分,共30分)11.时针从2点走到5点,则分针转了__ __度. 12.用度、分、秒表示48.26°为_ __. 13.若∠AOB =45°,∠BOC =30°,则∠AOC =_ __.14.如图,AO⊥OC,DO⊥OB,∠AOD=60°,则∠BOC=_ __.第14题图第16题图15.平面内有A、B、C、D四点,过其中任意两点作直线,则一共可以作__ __条直线.16.如图所示,OM平分∠AOB,ON平分∠BOC,已知∠AOB<∠BOC,那么可以确定∠AOM__ __∠CON.(填“>”“=”或“<”)17.如图,若M是AB的中点,C是MB上任意一点,如果AB=a,BC=b,那么MC 可用a、b的式子表示为_ _.18.已知线段AB,在AB的延长线上取一点C,使AC=2BC,在AB的反向延长线上取一点D,使DA=2AB,那么线段AC是线段DB的___ _倍.19.如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB 的度数为_ ___.第19题图第20题图20.如图,把正方形ABCD对折,折痕为MN.把顶点D折到MN上的一点P上,折痕为CE,再把顶点A折到MN上的同一点,折痕为BF,则∠CPB的度数是____度.三、解答题(共60分)21.(5分)如图,按下列语句画出图形:(1)过点A作BC的垂线,垂足为O;(2)度量点A到BC的距离;(3)用量角器画出∠AOC的平分线OD;(4)在OD上取一点E,过E分别画OC,OA边的平行线.22.(6分)计算:(1)35°2′-19°10′+35°47′;(2)(40°40′÷3+10°5′16″)×2.23.(6分)如图,已知C是AB的中点,D是AC的中点,E是BC的中点.(1)若AB=20 cm,求DE的长;(2)若CE=6 cm,求DB的长.24.(6分)如图所示,设∠BOC-∠AOB=20°,∠BOC∶∠COD∶∠DOA=3∶5∶8,求∠COD的度数.25.(7分)如图所示,A,B,C三棵树在同一直线上,量得树A与树B的距离为4 m,树B与树C的距离为3 m,小亮正好在A、C两树的正中间O处,请你计算一下小亮距离树B多远?26.(8分)把书的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数,∠DBM与∠ABC的关系是什么?27.(10分)已知点C在线段AB所在的直线上.(1)请你画图表示出A、B、C三点之间的位置关系.(2)若已知AB=6 cm,BC=2 cm,求AC的长.(3)若点C在A、B两点之外,且M、N分别为AB、AC的中点,已知AB=a,AC=b,求MN的长.28.(12分)(1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;(2)若题(1)中∠AOB=∠α,其他条件不变,求∠MON的度数;(3)若题(1)中∠BOC=∠β(∠β为锐角),其他条件不变,求∠MON的度数.第四章测试卷1.D 2.A 3.C 4.C 5.D 6.C 7.D 8.A 9.A 10.D 11.1 08012.48°15′36″ 13.15°或75°14.120° 15.1或4或6 16.< 17.12a -b18.2319.180° 20.60 21.解:如图所示.(测量结果略)22.解: (1)原式=70°49′-19°10′=51°39′; (2)原式=(13°33′20″+10°5′16″)×2 =23°38′36″×2 =46°76′72″=47°17′12″.23. 解:(1)因为C 是AB 的中点, 所以AC =BC =12AB =10(cm).因为D 是AC 的中点, 所以AD =DC =12AC =5(cm).因为E 是BC 的中点, 所以CE =BE =12BC =5(cm).又因为DE =DC +CE, 所以DE =5+5=10(cm); (2)由(1)知AD =DC =CE =BE, 所以CE =13BD.因为CE =6 cm, 所以BD =18(cm).24.设∠BOC =3x ,则∠COD =5x ,∠DOA =8x , 因为∠BOC -∠AOB =20°, 所以∠AOB =∠BOC -20°=3x -20°.因为∠DOA +∠AOB +∠BOC +∠COD =360°, 所以8x +3x -20°+3x +5x =360°, 所以x =20°.所以∠COD =100°.25.解:因为AB =4,BC =3, 所以AC =7.又因为点O 为AC 的中点, 所以OA =12AC =3.5.因为OB =AB -OA ,所以OB =4-3.5=0.5(米).26.解: 由题意可知BC 平分∠ABE ,而BD 平分∠EBM ,所以∠CBD =12×180°=90°.∠DBM 与∠ABC 为互余关系.27.解:(1)A 、B 、C 三点之间的位置关系有三种,分别如下图所示:(2)若点C 在线段AB 上时,如图甲所示, AC =AB -BC =6-2=4(cm);若点C 在线段AB 的延长线上时,如图乙所示,AC =AB +BC =6+2=8(cm). (3)如图丙所示,MN =AM +AN =12AB +12AC =12(a +b);如图丁所示,MN =AN -AM =12AC -12AB =12(b -a).28.解:(1)因为OM 平分∠AOC ,ON 平分∠BOC , 所以∠MOC =12∠AOC ,∠NOC =12∠BOC ,所以∠MON =∠MOC -∠NOC =12∠AOC -12∠BOC =12(∠AOC -∠BOC) =12∠AOB. 又因为∠AOB =90°, 所以∠MON =12×90°=45°;(2)∠MON =12∠α;(3)∠MON =45°.。

此文档下载后即可编辑北师大版七年级数学上册各单元同步测试题【精品全套】第一章丰富的图形世界------ 第1课时班级姓名1.图形是由________,__________,____________构成的.2.物体的形状似于圆柱的有________________;类似于圆锥的有______________;类似于球的有_________________.3.围成几何体的侧面中,至少有一个是曲面的是有_____________.4.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.5.圆柱,圆锥,球的共同点是_____________________________.6.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.7、一个六棱柱共有条棱,如果六棱柱的底面边长都是2cm,侧棱长都是4cm,那么它所有棱长的和是cm.8、图1-1是由( )图形饶虚线旋转一周形成的9、图1-2绕虚线旋转一周形成的图形是( )1后而形成的,这个几何10、如图所示的几何体是由一个正方体截去4体是由个面围成的,其中正方形有个,长方形有个.11、在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,如图拼成一个长方体,请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色?12、如图,已知一个正方体的六个面上分别写着六个连续的整数,且每两个相对面上的两个数的和都相等,图中所能看到的数是16,19和20,求这6个整数的和.13.如图一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?14、一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形如图,你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形第一章丰富的图形世界------ 第2课时展开与折叠(1)班级姓名1,如图,把左边的图形折叠起来,它会变为()2,下面图形经过折叠不能围成棱柱()3,如图,把左边的图形折叠起来,它会变成()4,一个几何体的边面全部展开后铺在平面上,不可能是()A.一个三角形 B.一个圆C.三个正方形D.一个小圆和半个大圆5、如果有一个正方体,它的展开图可能是下面四个展开图中的()二、填空题:1、侧面可以展开成一长方形的几何体有;圆锥的侧面展开后是一个;各个面都是长方形的几何体是;棱柱两底面的形状,大小,所有侧棱长都.2、用一个边长为4cm的正方形折叠围成一个四棱柱的侧面,若该四棱柱的底面是一个正方形,则此正方形边长为cm.3、这个棱柱的底面是_______边形。
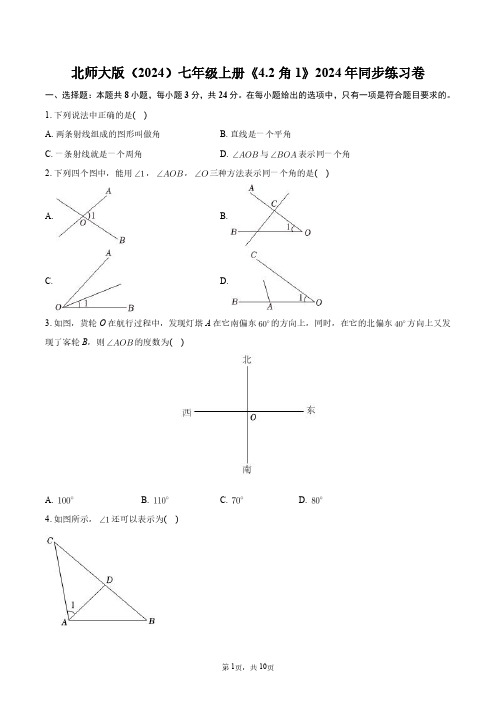
第四单元学情调研试题一、积累与运用(20分)1.漂亮的书写能给人以美的享受。
请把下面这句话正确、规范、美观地抄写在方格内。
(2分)寓言是生活的棱镜,寻常现象中折射出深刻哲理。
2.下列加线的字注音有误的一项是()(2分)A、怜悯.mǐn 丑陋.lîu 警惕.tì争辩.biànB、纠.缠jiū啰.嗦luō更.换gēng 禽.兽qínC、凝.成níng 倒霉.méi 屠.宰tú蠢.材chǔnD、撬.开qiào 庞.大páng 作.揖zuî尚.且shàng3.下列词语中有四个错别字,划出来并在方格中改正。
(4分)嬉笑颜开无恶不作乔妆打扮忘恩负义自言自语荣华福贵张牙舞爪传宗接代奇形怪状后患无穷仙风道骨衣食住行披头散发下流无耻来龙去脉恩将仇抱4.句中加线的词语解释不当的一项是()(2分)A、我因为怜悯恶人,才受到如此的恶报啊!怜悯:对遭遇不幸的人表示同情。
B、就劝丈夫放弃报仇的念头,以免毒蛇纠缠。
纠缠:缠绕在一起。
C、把全世界的地下宝藏都指点给他。
指点:指出来使人知道。
D、我是个堂堂的人。
堂堂:这里形容有志气,有气魄。
5.对本单元课文的分析有误的一项是()(2分)A、《农夫和蛇》选自《伊索寓言》。
《伊索寓言》大多是动物故事,以动物为喻教人处世做人道理。
B、《渔夫的故事》中的渔夫,虽然善良,但毕竟有点胆小,害怕恶势力。
C、《东郭先生与狼》和《渔夫的故事》分别为东、西方文化背景下的经典故事,但异曲同工。
D、《白蛇传》是著名民间传说。
主要描述由白蛇所变的白娘子与青年许仙的恋爱婚姻悲剧。
6.下列词语中的“书”与“大书特书”中的“书”词义相近的一项是()(2分)A、藏书万卷B、一封家书C、挥毫疾书D、楷书行书7.下列各项中不全是反义词的一项是()(2分)A、冷漠—热忱慷慨—吝惜B、墨守—开拓安静—喧闹C、压抑—放纵悲痛—哀痛D、七嘴八舌—异口同声沸沸扬扬—冷冷清清8.根据你对文学名著的了解答题。
(4分)(1)安徒生是世界著名的童话作家。
请写出他的两篇童话的名称:《》《》(2)中国古典文学名著《三国演义》描写了先后发生在官渡、赤壁和夷陵的三个弱军打败强军的故事。
请选择其中的一个故事用一句话写出故事情节。
二、阅读理解(40分)(一)阅读下面课内文字,完成9-12题。
(12分)农夫和蛇有位农夫,是村里村外有名的大善人。
一个隆冬时节,他在村口遇到了一条冻僵了的蛇,他觉得这条蛇挺可怜,就发了善心,把蛇拾起来,放在怀里,用自己的身体去温暖它。
蛇得到了温暖,渐渐的苏醒过来了,等到它恢复了体力,活动自如时,便露出了残忍的本性,在农夫的胸脯上,凶狠地咬了一口。
原来这是一条毒蛇,农夫受了致命的伤害。
蛇毒很快布满了农夫的全身。
当农夫到家时,求医治疗已经来不及了。
农夫在临死的时候对家里人说:“你们要记住我这血的教训,我因为怜悯恶人,才受到如此的恶报啊!”9.《农夫和蛇》选自,相传为希腊被释放的奴隶所作。
(3分)10.文章第一句话“有位农夫,是村里村外有名的大善人”在文中起什么作用?(3分)11.这则寓言的寓意是什么?(3分)12.这则寓言故事与中国的一个成语意思相近,这个成语是什么?(3分)(二)阅读下面文章,完成13-16题。
(14分)蝙蝠的故事很久很久以前,鸟兽间爆发了一场战争,蝙蝠暗自盘算:“现在我究竟是当鸟好,还是当兽好呢?有人说我是兽,有人说我是鸟。
我最好还是观望观望,我要在一旁看一看,哪一边取胜我就属于哪一伙。
”这时,兽类大军和鸟类大军对阵交锋,展开了殊死的战斗。
蝙蝠躲得远远的,他觉得鸟类正占上风,便跑到鸟群一边,但并不参战,他想:“等他们获得全胜,我再参加也不迟。
”过了片刻,战局发生急剧变化,兽类好像已经得胜,这时,他急忙窜到兽类队伍宣布:“我的头和躯干同老鼠一模一样,我用自己的乳汁喂养后代,这些全是鸟类根本不具备的特征,我分明是兽。
请接受我作为你们队伍中的一员吧!我将一生一世地为你们忠诚服务,永不背叛。
”兽类们相信了蝙蝠的话,接受他为队伍中的一员。
但是,这场战争最终还是鸟类取胜了,因为他们有一位勇猛无比的统帅——雄鹰。
这时候蝙蝠已吓得半死。
蝙蝠决定逃跑,他跑进了深山老林,躲藏在树洞里。
直到如今,蝙蝠仍栖息在树洞里,生怕被发现。
白天藏起来,入夜鸟儿归巢之后,他们才敢飞出来觅食。
13.选择正确答案。
()(2分)A、这是一篇神话故事。
B、这是一篇寓言故事。
C、这是一篇民间故事。
D、这是一篇童话故事。
14.鸟兽间爆发了一场战争时,为什么蝙蝠双方都能加入?(2分)15.写战局的部分是按什么顺序安排材料的?在文中的标志性词语有哪些?(3分)16.这篇故事的深刻寓意是什么?(3分)(三)阅读下面文章,完成17-22题。
(14分)地球上还剩一个鸡蛋整个鸡家族都不甘心自己在地球上的地位——任人宰割,供人食用。
从一百年前起,鸡家族的有识之士就试图摆脱鸡家族的困境。
但每次行动都以鸡的失败告终。
人类大获全胜,还不断完善着吃鸡的艺术:现代化养鸡场、填鸡、肯德鸡、扒鸡、烧鸡等等,真是到了炉火纯青的境界。
这还不算,鸡被人类吃得最多,可人类却发明出“黄鼠狼给鸡拜年”的成语嫁祸于黄鼠狼,鸡们确实咽不下这口气。
鸡王决定在本世纪末之前扭转鸡家族的处境,他召集幕僚想办法。
“要想让人类放弃吃鸡很难。
”一位幕僚说。
他曾经用十斤鸡蛋收买了人类中一位写东西的人,让他在报上写文章说,吃鸡容易患癌症,可人类照吃不误。
“依我看,人吃咱们并不是因为恨咱们,而是说明他们离不开咱们。
”另一位年纪大一些的幕僚说,他曾经发明过鸡瘟,但被人类用药物治住了。
“有道理。
”鸡王点头,示意这位幕僚继续往下说。
“大王下一道圣旨,命令所有母鸡停止下蛋。
保准人类不会再像现在这样对待咱们了。
”幕僚建议。
“停止下蛋?”鸡王吃了一惊,这可是断子绝孙的举动呀。
“没有鸡蛋,就不会再有新的鸡出生,光这一点,就够人类伤脑筋的。
”幕僚说。
鸡王点点头。
五分钟后,鸡王向整个鸡家族下达了圣旨:停止下蛋。
当人类发现全世界所有的母鸡都不下蛋了时,地球上只剩下一个鸡蛋了。
人类意识到问题的严重性了,地球上的鸡将吃一只少一只,最终灭绝。
人们将不再有鸡肉吃,不再有鸡蛋吃。
科学家们想尽一切办法动员母鸡们恢复下蛋,什么音乐刺激法,红外线紫外线这线那线照射啦,遗憾的是母鸡们不为所动,不管科学家们想出什么绝活儿,她们就是不下蛋。
人类专门为此召开了一个紧急会议,会议的结果是制定了一部关于保护珍贵动物——鸡的法律。
鸡终于改变了卑微的地位,加入进珍贵动物的行列。
人们以拥有一只鸡为荣,狗和猫的地位一落千丈。
在公园里时常见到牵着鸡散步的达官贵人。
一只鸡的售价已高达上千美元。
科学家们研制的延长鸡的寿命的药物刚一问世就被抢购一空。
有几个国家的国旗上出现了鸡的图案,经营炸鸡的快餐店统统倒闭,老板不是跳楼就是离婚,这一切都因为母鸡不下蛋了。
地球上惟一的那个鸡蛋更是价值连城,光是守护它的军队就有两个旅之多。
这个鸡蛋的妈妈是最后一个听到鸡王的圣旨的,当时她正在下蛋,想把这个蛋退回到肚子里已经不可能了,于是她成了地球上惟一的鸡蛋的母亲。
她因此身价百倍,人们将延续鸡的生命的期望寄托在她身上,人们把最好的食物给她吃,为她建造了超豪华住宅,还让她上报纸上电视上电影。
鸡王的臣民们不再被人类杀戮,不再供人类食用,人类视他们为珍宝。
鸡王满意了。
那个惟一的鸡蛋的母亲的显赫地位渐渐引起了鸡家族成员的注意,他们羡慕她嫉妒她。
同样是鸡,为什么她住的房子比同类的好?为什么她的食谱比同类的高级?为什么她能上电视还享有鸡皇后的称号?就因为她生了地球上最后一个鸡蛋!没人甘心比同类活得差。
于是,在一个上午,一只母鸡违抗鸡王的圣旨,她公然下了一个蛋。
这只母鸡立刻成为全球新闻的焦点,她的待遇立即超过了那只“鸡皇后”。
鸡家族受到了强烈的震动。
第三个鸡蛋__了。
第四个鸡蛋__了。
第五个鸡蛋__了。
鸡王感到大事不妙,他连降圣旨制止母鸡们下蛋,但他已经控制不了他的臣民了。
所有的母鸡都想当鸡皇后,所有的母鸡都想比别的鸡活得好,她们玩命地下蛋。
保护鸡的法律取消了。
鸡又重新出现在餐桌上。
没人牵着鸡逛公园了。
鸡王想再发一道不下蛋的圣旨,幕僚进谏劝住了他。
幕僚告诉鸡王,人类已经有了对付鸡不下蛋的办法:他们留出了一个鸡蛋,只要鸡们再不下蛋,他们就拼命抬举这个鸡蛋和它的妈妈。
鸡家族算是没有出头之日了。
鸡王哀叹。
17.根据下列解释写出在文中出现的成语。
(4分)(1)():明白事理的人。
(2)():学问、技术等达到纯熟完美地步。
(3)():形容地位、声誉等下降很厉害。
(4)():形容物品极其贵重。
18.“这一切都因为母鸡不下蛋了”中的“这一切’指的是什么?(2分)19.文中有三条横线,请在它们上面分别填上三个同义词。
(3分)20. 文章写到倒数第 3自然段,情节已经很完整了。
如果把倒数第 2自然段删除,可不可以?为什么?(2分)21.全文的线索是什么?(2分)22.判断下列表述的对错。
(4分)(l)鸡家族齐心协力是有机会摆脱困境的。
()(2)本文讽刺了那些因顾及私利而遭致更大损失的行为。
()(3)本文中心是再狡猾的动物也必将败在人类面前。
()(4)本文中心可这样概括:“物以稀为贵。
”()三、写作(40分)23.请你以某一小动物为写作对象,模仿本单元几篇文章的写法,试着编写一个美丽的寓言故事。
要求:①想象要合理。
②能表现某一个生活道理。
③语言要生动活泼。
参考答案一、积累与运用1.略2.D点拨:“作揖”的“作”此处应读“zuō”。
3.喜装富报4.B点拨:“纠缠”这里的意思是“找麻烦”。
5.B点拨:故事中的渔夫,是人民善良和智慧的化身。
6.C点拨:A是指书籍,B指书信,D指书法,名词;C和例句的“书”都是指书写的意思,动词。
7.C点拨:“悲痛”和“哀痛”是一对近义词。
8.⑴《丑小鸭》、《皇帝的新装》、《卖火柴的小女孩》等。
⑵例:诸葛亮和周瑜两位军事天才团结协作,以区区数万人在赤壁击败号称拥有八十万大军的曹操,奠定了三国鼎立的局面。
点拨:答案不固定,能写出自己的认识即可。
二、阅读理解(一)9.伊索寓言伊索10.引起下文,为后文写救蛇,被蛇咬死作铺垫。
11.示例:①不要怜悯像蛇一样的恶人。
②恩将仇报(忘恩负义)是蛇一样的恶人的本性。
③不要指望向恶人施善他会还你仁义。
④“善有善报”不一定适用于恶人。
点拨:答案不固定,从不同的角度理解可得出不同的结论。
12.与中国成语“养虎为患”有类似相通意。
(二)13.B14.有人说它是兽,有人说它是鸟,它兼具了双方部分特点。
15.时间顺序这时过了片刻最终16.无论做什么事都要有一个坚定的立场,明确的目标,摇摆不定,脚踏两只船最终会失败的。