解一元一次方程的步骤

一次方程的求解方法一次方程作为方程中最基础的形式，应用广泛，需要熟练掌握。

在管综考试中，涉及到的一次方程包含一元一次方程和二元一次方程组。

一、一元一次方程的求解一元一次方程求解的一般步骤：1、去分母：在方程两边同乘以各分母的最小公倍数，注意每项都要乘。

2、去括号：依据乘法分配律和去括号法则，注意变号，防止漏乘。

3、移项：把含有未知数的项移到方程的一边，常数项移到另一边，注意移项要变号。

5、系数化为1：方程两边同时除以未知数的系数或者乘以系数的倒数。

在求解具体的题目时，上述步骤不一定全部用到，同学们要根据具体的题目进行选择。

二、二元一次方程组的求解消元是解二元一次方程组的基本思路，所谓消元就是减少未知数的个数，使多元方程最终转化为一元方程再进行求解。

常用的消元方法有：代入消元法（简称代入法）和加减消元法（简称加减法）。

一般情况下，当未知数的系数为1时，选择代入消元法更快，同一未知数的系数出现相同或者互为相反数时，选择加减消元法更快。

如果这两种情况都不符合，一般会利用等式的性质，将某一未知数的系数化为相同或者相反数，再用加减消元法进行求解。

三、一次方程的应用在应用题中，利用一次方程求解的一般步骤是：1、审：审题，找准等量关系。

2、设：设未知数，一般求谁设谁。

3、列：根据等量关系列出方程。

4、解：根据前面所学方法求解方程。

在例3中，我们利用了二元一次方程组进行求解，列出方程后，由于方程中系数有分数，可以先去掉分母以后再进行求解。

例4的解题关键在于分析出每个竖式无盖箱子与横式无盖箱子需要几块正方形木板和长方形木板，从而找准等量关系，列出方程组。

在解方程组时，不同于例3，这道题目可以用选项代入验证，同学们可以结合自身掌握程度灵活选取。

解一元一次方程的步骤是什么？
一元一次方程是指只有一个未知数并且该未知数的指数为1的方程。

解一元一次方程的步骤如下：
1. 确定未知数：首先，需要确定方程中的未知数，通常用字母表示，例如x。

2. 整理方程：将方程中的各项按照系数和未知数的次数整理在一起。

将常数项移至方程的另一侧，使方程等号两边的式子成为一个多项式。

3. 消去系数：通过除以系数的方式消去未知数的系数，使未知数的系数化为1。

这样可以简化方程，方便计算。

4. 消去常数：通过减去常数的方式消去方程中的常数项，使方程等号的另一侧成为0。

这样可以将方程变为等式，从而继续进行下一步的计算。

5. 求解未知数：根据已经消去系数和常数的方程，计算出未知
数的值。

这可以通过代入法、配方法或使用计算器等方法来求解。

6. 检验解：将求得的未知数代入原方程中，验证是否满足方程
的等式。

如果方程两边的值相等，则证明求得的解是正确的；如果
不相等，则需要重新检查计算过程或重新求解。

总结起来，解一元一次方程的步骤包括确定未知数、整理方程、消去系数、消去常数、求解未知数和检验解。

这些步骤可以帮助我
们有效地解决一元一次方程的问题。

解一元一次方程的方法
解一元一次方程可以采用以下方法：
1. 两边加减同一个数：对于方程ax + b = c，可以将b的相反
数加到两边，得到ax = c - b。

2. 两边乘除同一个数：对于方程ax = c，可以将方程两边同时
除以a，得到x = c/a。

要注意a不能为零。

3. 移项：对于方程ax + b = c，可以将b移动到等式的另一边，得到ax = c - b。

再根据上述方法继续求解x。

4. 合并同类项：对于方程ax + bx + c = d，可以将同类项ax和bx相加，得到(a + b)x + c = d。

再根据上述方法继续求解x。

5. 解方程应用逆运算：对于方程3x - 5 = 4，可以通过逆运算
来求解。

首先将-5移动到等式的另一边，得到3x = 4 + 5。

然
后再除以3，得到x = 9/3。

所以方程的解为x = 3。

以上是解一元一次方程的一些常用方法，根据具体情况选择合适的方法来解方程。

注意要进行合理的运算步骤，并在求解过程中保持等式的平衡。

解方程的步骤解方程是数学中非常重要的内容之一。

在方程中，我们需要找到一个或多个数值，使得方程两边的值相等。

通过解方程，我们可以解决各种实际问题，例如计算小费，计算利润等。

首先，让我们来看一下一元一次方程。

一元一次方程指的是只有一个未知数（通常用x表示）且次数为一的方程。

一元一次方程的一般形式为ax+b=c，其中a、b、c是已知数。

解一元一次方程的基本步骤如下：1. 将方程的形式转化为 ax=b-c。

这一步可以通过移项来实现，将常数项移动至方程的另一侧。

2. 化简方程，将方程化简为 ax=d的形式，其中d=b-c。

3. 除以系数a，得到 x=d/a。

这一步的目的是消除方程中未知数的系数。

通过这些步骤，我们可以得到方程的解。

下面，我们通过一个具体的例子来说明解一元一次方程的过程。

假设有一个一元一次方程 2x+3=9。

首先，我们需要将方程的形式转化为 ax=b-c。

在这个例子中，我们把方程转化为 2x=9-3。

然后，化简方程，得到 2x=6。

接下来，我们除以系数2，得到 x=3。

所以，方程的解为 x=3。

除了一元一次方程，还有许多其他类型的方程需要解决。

例如，二次方程、多项式方程等。

每种类型的方程都有相应的解法。

对于二次方程，一般形式为 ax^2+bx+c=0。

解二次方程有两种常见的方法：配方法和求根公式。

根据具体的情况选择适合的方法来解决问题。

对于多项式方程，我们可以使用因式分解法来解决。

该方法的目的是将方程分解为一个或多个乘法因子的积。

解方程在数学中起着重要的作用。

通过解方程，我们可以解决各种实际问题，并推导出更复杂的数学概念和定理。

因此，掌握解方程的方法和技巧对于学习数学以及在日常生活中运用数学知识都非常重要。

总结起来，解方程是数学中的重要内容之一。

通过解方程，我们可以找到方程的解，解决实际问题，并推导出更深入的数学概念。

无论是一元一次方程、二次方程还是多项式方程，都有相应的解法。

掌握解方程的方法和技巧对于学习数学和应用数学知识都至关重要。

初中三年级一元一次方程的解法一、一元一次方程的概念和解法一元一次方程是指只含有一个未知数，并且未知数的最高次数是1的方程。

它的一般形式为ax + b = 0，其中a和b是已知的实数，而x 是未知数。

解一元一次方程的基本思路是通过逆运算将方程变换，使得未知数x的系数为1，从而得到方程的解。

下面将介绍两种主要的解法：使用加减法和使用乘除法。

二、使用加减法解一元一次方程使用加减法解一元一次方程的步骤如下：步骤1：将方程两边的常数项（b）移到等号的另一边，得到ax = -b。

步骤2：将方程两边除以未知数的系数a，得到x = -b/a。

这样，我们就得到了一元一次方程的解x。

例如，考虑方程3x + 5 = 2。

按照上述步骤解方程，可以得到3x = -3，进而得到x = -1。

因此，方程的解是x = -1。

三、使用乘除法解一元一次方程使用乘除法解一元一次方程的步骤如下：步骤1：将方程两边除以未知数的系数a，使得未知数系数变为1，得到x + b/a = 0。

步骤2：将方程两边减去常数项b/a，得到x = -b/a。

这样，我们同样得到了一元一次方程的解x。

举个例子，考虑方程2x - 3 = 7。

按照上述步骤解方程，可以得到x - 3/2 = 7/2，进而得到x = 7/2 + 3/2 = 10/2 = 5。

因此，方程的解是x = 5。

四、实际问题中的一元一次方程一元一次方程在实际问题中具有广泛的应用。

我们来看一个例子：例子：小明买了一些苹果和一些橙子，总共花费了30元。

已知苹果的价格是2元/个，橙子的价格是3元/个，问小明买了多少个苹果和橙子？解：设小明买了x个苹果和y个橙子。

根据题目中的信息，我们可以列出一个一元一次方程：2x + 3y = 30。

现在，我们可以使用上述介绍的解法来解这个方程。

首先，我们使用加减法解方程：将方程改写为2x = 30 - 3y。

然后，我们使用乘除法解方程：将方程改写为x = (30 - 3y)/2。

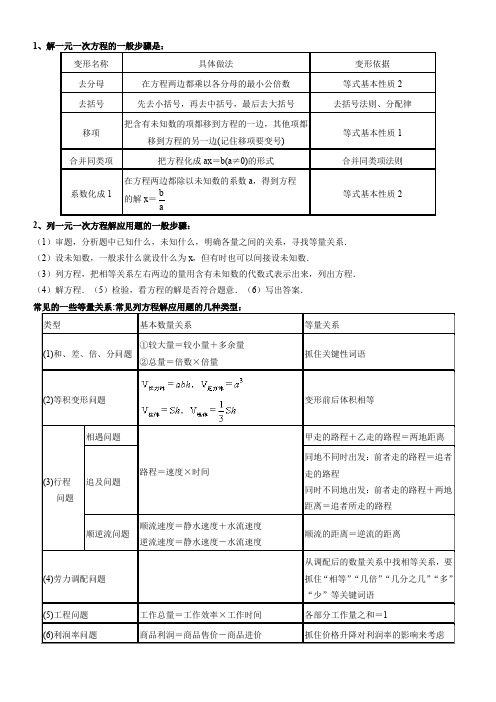
12、列一元一次方程解应用题的一般步骤：（1）审题，分析题中已知什么，未知什么，明确各量之间的关系，寻找等量关系．（2）设未知数，一般求什么就设什么为x，但有时也可以间接设未知数．（3）列方程，把相等关系左右两边的量用含有未知数的代数式表示出来，列出方程．（4）解方程．（5）检验，看方程的解是否符合题意．（6）写出答案．商品利润率＝1.商品销售此类问题主要涉及的关键量：进价，标价，实际售价，利润，利润率。

熟记这些量间的基本关系式：商品的利润=商品的实际售价-商品的进价.（这里不考虑其它因素）商品的利润率=商品打折后的售价=商品的标价÷10×折扣数.另外在解决商品的利润率的问题中，还涉及如下关系式.注意会由基本关系式推出式子的变形，以便于解决问题.例：由×100%=利润率，可得商品的实际售价=商品的进价×(1+利润率).例1、商店里的皮上衣每件标价为2200元，在一次促销活动中，它打八折销售，结果仍获利10%，求此商品的进价.分析：题中的相等关系是商品的进价×(1+利润率)=商品的实际售价.解：设此商品的进价为x元，依题意(1+10%)x=2200×0.8.解这个方程，得x=1600.答：此商品的进价为1600元.例2、以现价销售一件商品的利润率为30%，如果商家在现有的价格基础上先提价40%，后降价50%的方法进行销售，商家还能有利润吗？为什么？依题意其后来折扣后的售价为(1+30%)a×(1+40%)(1-50%)=0.91a.∵0.91a-a=-0.09a,∴×100%=-9%.答：商家不仅没有利润，而且亏损的利润率为9%.2.银行存贷款例3、夏老师欲购买一辆汽车，销售商告诉夏老师，若采取分期付款方式：一种付款方式是第一月付4万元，以后每月付款一万元；另一种付款方式是前一半时间每月付款1万四千元，后一半时间，每月付款1万1千元；两种付款方式中付款钱数和付款时间都相同。

初中解方程步骤范文解方程是数学中很重要的一部分内容，它可以帮助我们求出未知数的值。

初中阶段，我们主要学习一元一次方程和一元二次方程的解法。

下面是解一元一次方程和一元二次方程的详细步骤。

一、解一元一次方程的步骤：1.观察方程，将方程的两边分别记作f(x)和g(x)。

2.如果方程两边都含有未知数，则需要合并同类项。

3.将未知数的系数移到方程的一边并整理方程。

4.将方程两边的常数项合并并整理方程。

5.如果方程的系数是分数，可以通过乘以分母的倒数将其转化为整数。

6.将已知条件代入方程求解。

7.检验解，并写出解答。

如果解满足已知条件，则方程有解，否则无解。

例如：解方程3x-5=71.观察方程，将方程的两边分别记作f(x)=3x-5和g(x)=72.方程两边都含有未知数x，没有同类项需要合并。

3.将未知数x的系数3移到方程的一边，得到3x=7+54.将方程两边的常数项合并，得到3x=125.方程的系数是整数，不需要转化。

6.将已知条件代入方程，得到3x=12，得出未知数x的值为x=47.检验解：将x=4代入方程，得到3*4-5=7，等式两边相等，所以x=4是方程的解。

二、解一元二次方程的步骤：1.观察方程，将方程的两边分别记作f(x)和g(x)。

2.将方程移到一边，使方程等于零，得到一个二次方程。

3.通过配方法将二次方程化简为标准形式(ax^2+bx+c=0)。

4.根据二次方程的计算公式求解，得到两个根。

5.检验解，并写出解答。

如果解满足已知条件，则方程有解，否则无解。

例如：解方程x^2+3x-4=01.观察方程，将方程的两边分别记作f(x)=x^2+3x-4和g(x)=0。

2.将方程移到一边，得到x^2+3x-4=0。

3.通过配方法将二次方程化简为标准形式(x+4)(x-1)=0。

4.根据二次方程的计算公式求解，得到两个根x=-4和x=15.检验解：将x=-4和x=1代入方程，得到(-4)^2+3*(-4)-4=0和1^2+3*1-4=0，等式两边相等，所以x=-4和x=1是方程的解。

列一元一次方程解应用题的步骤
一元一次方程是代数中常见的一种类型的方程，其形式为ax+b=0，其中a和b
是已知数，x是未知数。

解一元一次方程的步骤如下：
1. 理解问题：仔细阅读问题并理解其中给出的条件和要求。

确定问题中未知数
的含义和符号。

2. 设变量：根据问题中给出的条件，设未知数为x，并列出相应的方程。

3. 化简方程：根据方程的形式，进行合并和化简，使方程变为ax + b = 0的标
准形式。

4. 消元：通过一系列代数运算，将方程中的未知数消去，得到解方程的步骤。

5. 解方程：根据方程的标准形式，求得未知数的解x。

这可以通过减法、加法、乘法和除法等运算来实现。

6. 检验解：将求得的解代入原方程中，验证方程的等式成立。

若等式成立，则
解是正确的；若不成立，则需要重新检查步骤。

7. 提出答案：将解写成有意义的句子或符号形式，回答问题所要求的内容。

通过以上步骤，我们可以解决各种应用题，其中包括计算物体运动速度、求解
几何图形的边长或面积、解决货币交换或时间计算问题等。

实践中，我们需要熟悉一元一次方程的基本概念和运算规则，以便准确解答各类应用题。

需要注意的是，解题过程中应仔细审题、灵活运用代数运算法则，并进行适当
的化简和验证，确保所得的解是可信的。

此外，解答过程中应注意单位和符号的一致性，避免因数值计算错误导致解答错误。

通过掌握解一元一次方程的步骤，我们可以更好地应用代数知识解决实际问题，提高数学解题能力。

一元一次方程的解法步骤
一元一次方程指只含有一个未知数、未知数的最高次数为1且两边都为整式的等式。

一元一次方程只有一个根。

一元一次方程的一般形式
只含有一个未知数(又称为一元)，且其次数是1的方程叫作一元一次方程。

任何一个一元一次方程总可以化为ax=b(a≠0)的形式，这是一元一次方程的标准形式。

一元一次方程的解法
1.去分母：在方程两边都乘以各分母的最小公倍数（不含分母的项也要乘）；
2.去括号：先去小括号，再去中括号，最后去大括号；（记住如括号外有减号的话一定要变号）
3.移项：把含有未知数的项都移到方程的一边，其他项都移到方程的另一边；（移项要变号）
4.合并同类项：把方程化成ax=b(a≠0)的形式；
5.系数为成1：在方程两边都除以未知数的系数a，得到方程的解x=b/a。

等式的性质
1.等式两边同时加(或减)同一个数或式子，等式仍是等式。

若a=b，那么a+c=b+c；
2.等式的两边同时乘或除以同一个不为0的数所得的结果仍是等式。

若a=b，那么有a·c=b·c或a÷c=b÷c（c≠0）；
3.等式具有传递性。

初中数学解一元一次方程的基本步骤一、引言解一元一次方程是初中数学中的基本内容之一，也是进一步学习代数和方程的基础。

掌握解一元一次方程的基本步骤对于提高数学解题能力至关重要。

二、方程的定义和基本形式一元一次方程是由一个未知数和系数组成的等式。

其一般形式表示为：ax + b = 0，其中，a和b为已知常数，x为未知数。

三、解一元一次方程的基本步骤解一元一次方程的基本步骤如下：1. 去括号：如果方程中有括号，根据分配律进行去括号运算；2. 合并同类项：合并方程中的同类项，即将具有相同变量的项进行简化；3. 移项：将含有未知数的项移到方程的一边，将常数项移到方程的另一边；4. 化简：对于方程两边进行合并、消去或简化，使方程的形式变为ax = b的形式；5. 求解：根据解一元一次方程的性质，将解代入方程中进行验证；6. 得出结论：根据情况得出方程的解或者无解的结论。

四、实例演示为了更好地理解解一元一次方程的基本步骤，我们来看一个实际的例子：例1：解方程2x + 5 = 11解：第一步，去括号：方程中没有括号，跳过此步骤；第二步，合并同类项：方程中的同类项为2x，简化后方程为2x + 5 = 11；第三步，移项：将常数项5移到方程的另一边，得到2x = 11 - 5；第四步，化简：计算得到2x = 6；第五步，求解：将解x = 3代入方程2x + 5 = 11进行验证，验证结果为2 × 3 + 5 = 11，方程成立；第六步，得出结论：方程的解为x = 3。

五、解一元一次方程的注意事项在解一元一次方程时，还需要注意以下几点：1. 若方程两边是完全相同的多项式，则方程有无穷多个解；2. 若方程两边是完全不同的多项式，则方程没有解；3. 若方程两边是完全相同的非零常数，则方程没有解。

六、解一元一次方程的应用解一元一次方程的方法在日常生活和其他学科中都有广泛的应用。

例如，在商业中解方程可以帮助我们计算商品折扣率、利润和成本；在物理学中解方程可以求解速度和加速度等问题。

一元一次方程应用题解题步骤1.前言解一元一次方程是数学中基础而重要的内容，通过解题可以培养逻辑思维和数学推理能力。

一元一次方程的解题步骤是相对固定的，通过本文的介绍和实例分析，希望能够帮助读者掌握解决这类问题的方法和技巧。

2.解题步骤解一元一次方程的一般步骤如下：步骤一：列出方程根据题目描述，将问题中的条件以等式的形式表示出来，列出方程式。

通常，使用字母来表示未知数，并附上系数。

步骤二：化简方程如果方程中有括号或分数，需要先进行化简，将方程变为正常的形式。

步骤三：移项整理将方程中的项按照未知数所在的位置进行整理，将常数项移到方程的另一侧。

步骤四：合并同类项对方程式中的同类项进行合并，将系数相同的项相加或相减，简化方程。

步骤五：消去系数如果方程中的未知数有系数，可以通过除以系数的方法将系数化简为1，简化方程。

步骤六：求解方程根据方程的形式，进行解方程的运算，得出未知数的值。

步骤七：验证解将求得的未知数代入原方程中进行验证，确认解是否正确。

3.实例分析为了更好地理解解题步骤，我们通过一些实例分析来进行演示。

示例一某商场举办打折促销活动，折后价格为原价的四分之三。

现有一双价值300元的鞋子，打完折后的价格为225元，问原价是多少？解答：首先，我们设原价为x元。

根据题目描述，我们可以列出方程式：x*(3/4)=225接下来，我们进行步骤二至步骤六的计算化简，最后得到：x=300所以，原价为300元。

示例二某数的四分之一与六十的差是六十的一半的两倍，求这个数是多少？解答：设这个数为x。

根据题目描述，我们可以列出方程式：x/4-60=(60/2)*2化简后，得到：x/4-60=120接下来，按照步骤三至步骤六的方法进行整理和合并同类项，最后得到：x=480这个数是480。

4.总结通过本文对一元一次方程应用题的解题步骤进行介绍和实例分析，我们可以总结出解题的一般方法：1.列出方程：根据题目描述，将条件以等式形式表示。

初中数学第一册一元一次方程教案：解方程的步骤详解。

一、解一元一次方程的基本步骤1.将方程化为标准形式：将方程中未知数的系数移到等号的右侧，使未知数的系数为1。

2.消去未知数的系数：通过运用加减乘除法则，将未知数的系数与常数项分别移到等号两侧，逐步将未知数的系数消去。

3.检验解的正确性：将求得的解代入原方程，检验解是否符合原方程的要求。

二、解线性方程的方法1.等式法：即，将未知数移到等号一侧，将常数移到等号另一侧，使等号两侧相等得到解。

例如：2x+3=9 变形为 2x=6，最终解得 x=3。

2.前项合并法：即，通过合并同类项，将未知数的系数与常数项进行运算，化简方程后得到解。

例如：6x+3x+4=2x+10 变形为 7x=6，最终解得 x=6/7。

3.因式分解法：通过将方程两边同乘或同除一同样的式子，使其中一个项相加或相减得到解。

例如：3x+4=7x-8 可以变形为 x=3。

4.代数法：即，通过将方程中的一个数为未知数，代入原方程，得到新的等式，并进行求解得到原方程的解。

例如：3(x+2)=5x-4 可以变形为 x=2。

三、解一元一次方程的常用技巧1.同时乘除法：如果要将方程两边同时乘或除以同一个非零数，可以省略等号和工作过程的某些步骤，直接影响解的速度和准确度。

例如：如果在 7x+8=22 这个方程两侧同时除以7，得到方程x=2。

2.平方恒等式：可以将等式两边同时平方消去方程中的平方根，从而进一步简化方程式。

例如：如果在x+5=±3 这个方程式两侧同时平方，得到方程 x=-8 或 x=-2。

3.按系数查表：如果方程中未知数系数为整数，可以通过查找已知的一元一次方程的解得分类似的解。

例如：在 6x+5=47 这个方程中，未知数系数为6，可以将方程改写为 3x+2.5=23.5，然后查一元一次方程 x+1=3 的解得 x=2，进而推导出原方程的解 x=7。

解一元一次方程是数学学习的重要技能之一，需要灵活运用各种方法和技巧，从而更加高效、准确地解决数学问题。

一、等式：用等号暗示相等关系的式子叫等式.之吉白夕凡创作等式性质1 等式两边加上（或减去）同一个数（或式子）,结果仍相等.等式性质2 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.等式性质3 等式两边同时乘方（或开方）,两边依然相等.等式性质4 等式具有对称性.若a=b,则b=a.等式性质5 等式具有对传递性.如果a=b且b=c,那么a=c.注意：1）等式中一定含有等号；2）等式两边除以一个数时,这个数必须不为0；3）对等式变形必须同时进行,且是同一个数或式.二、一元一次方程的概念：只含有一个未知数（元）且未知数的指数是1（次）的方程叫做一元一次方程.解方程就是求出使方程中等号左右两边相等的未知数的值,能使方程左右两边相等的未知数的值,叫做方程的解1、写出一个满足下列条件的一元一次方程：①某个未知数的系数是2；②方程的解是3；这样的方程是.2、若关于x的方程（k－1）x²+x－1=0是一元一次方程,则k=.三、列一元一次方程解应用题的一般步调：1、审题：弄清题意．2、找出等量关系：找出能够暗示本题含义的相等关系．3、设出未知数,列出方程：设出未知数后,暗示出有关的含字母的式子,然后利用已找出的等量关系列出方程.1）直接设元法,求什么设什么,方程的解就是问题的答案； 2）间接设元法,不是求什么设什么,方程的解其实不是问题的答案,需要按照问题中的数量关系求出最后的答案.4、解方程：解所列的方程,求出未知数的值．5、检验,写答案：检验所求出的未知数的值是否是方程的解,是否合适实际,检验后写出答案.四、解方程的一般步调和注意事项：1、去括号：先去小括号,再去中括号,最后去大括号,注意：括号外面是负号时,去括号后,括号内的每一项都要变号.2、移项：把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(也就是说未知数和常数项各占等号一边,记住：被移项要改动符号.）3、去分母在方程两边都乘分母的最小公倍数.去分母时：1）没有分母的项不要漏乘（尤其整数项）.也可以说方程中的每一项都要乘以分母的最小公分母.2)去分母时,应把份子作为一个整体加上括号.4、合并同类项把方程化成ax=b(a≠0)的形式系数化成1,在方程两边都除以。

一、等式：用等号暗示相等关系的式子叫等式.之杨若古兰创作等式性质1 等式两边加上（或减去）同一个数（或式子），结果仍相等.等式性质2 等式两边乘同一个数，或除以同一个不为0的数，结果仍相等.等式性质3 等式两边同时乘方（或开方），两边仍然相等.等式性质4 等式具有对称性.若a=b,则b=a.等式性质5 等式具有对传递性.如果a=b且b=c,那么a=c.留意：1）等式中必定含有等号；2）等式两边除以一个数时，这个数必须不为0；3）对等式变形必须同时进行，且是同一个数或式.二、一元一次方程的概念：只含有一个未知数（元）且未知数的指数是1（次）的方程叫做一元一次方程.解方程就是求出使方程中等号摆布两边相等的未知数的值，能使方程摆布两边相等的未知数的值，叫做方程的解1、写出一个满足以下条件的一元一次方程：①某个未知数的系数是2；②方程的解是3；如许的方程是.2、若关于x的方程（k－1）x²+x－1=0是一元一次方程，则k=.三、列一元一次方程解利用题的普通步调：1、审题：弄清题意．2、找出等量关系：找出能够暗示本题含义的相等关系．3、设出未知数，列出方程：设出未知数后，暗示出有关的含字母的式子，然后利用已找出的等量关系列出方程.1）直接设元法，求什么设什么，方程的解就是成绩的答案；2）间接设元法，不是求什么设什么，方程的解其实不是成绩的答案，须要根据成绩中的数量关系求出最初的答案.4、解方程：解所列的方程，求出未知数的值．5、检验，写答案：检验所求出的未知数的值是否是方程的解，是否符合实际，检验后写出答案.四、解方程的普通步调和留意事项：1、去括号：先去小括号,再去中括号,最初去大括号，留意：括号里面是负号时，去括号后，括号内的每一项都要变号.2、移项：把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(也就是说未知数和常数项各占等号一边，记住：被移项要改变符号.）3、去分母在方程两边都乘分母的最小公倍数.去分母时：1）没有分母的项不要漏乘（特别整数项）.也能够说方程中的每一项都要乘以分母的最小公分母.2)去分母时，应把分子作为一个全体加上括号.4、合并同类项把方程化成ax=b(a≠0)的方式系数化成1，在方程两边都除以未知数的系数a,得到方程的解x=b/a.。