冀教版数学八年级上册17.2直角三角形综合练习题

直角三角形和勾股定理专题一勾股定理与方程1．如图所示，已知在三角形纸片ABC中，BC=3，AB=6，∠BCA=90°，在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，A与BC延长线上的点D重合，则DE的长度为（）A．6 B．3 C． D．2．一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH的边长为2米，坡角∠A ＝30°,∠B＝90°,BC＝6米. 当正方形DEFH运动到什么位置,即当AE＝米时,有DC2＝AE2＋BC2.专题二构造直角三角形3.如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝23，求AB的长．4．如图，在四边形ABCD中，AB:BC:CD:DA=2:2:3:1，且∠ABC=90°，求∠DAB的度数.专题三勾股定理中的分类讨论思想5.在等腰△ABC中，∠A=30°，AB=8，则AB边上的高CD的长是．6.在△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长为_______.7. 在△ABC中， AB=25，AC=4，BC=2，以AB为边向△ABC外作△ABD，使△ABD为等腰直角三角形，求线段CD的长．参考答案1.C 解析：由折叠可知BC=BA=6，DE=AE，∵BC=3，∴CD=BC=3，∴BE=DE=AE，由勾股定理可得AC=DE=AE=BE=x，在Rt△BCE中，32＋()2x=x2，解得x=DE的长度为.2.143解析：因为∠A＝30°,∠B＝90°,BC＝6米，所以AC ＝12米.设当AE 为 x 时，所以EC ＝ 12－x ，由DC 2＝AE 2＋BC 2及DC 2＝DE 2＋EC 2，所以有22＋（12－x ）2＝x 2＋36，解得x ＝143. 3.解：过C 作CD ⊥AB 于D ，∴∠ADC ＝∠BDC ＝90°，∵∠B ＝45°，∴∠BCD ＝∠B ＝45°，∴CD ＝BD .∵∠A ＝30°，AC ＝CD∴BD ＝CD由勾股定理得：AD 3，∴AB ＝AD ＋BD ＝3答：AB 的长是34．解：连结AC.设AB 、BC 、CD 、DA 分别为2x ，2x ，3x ，x ，则2222228,,9A C x A D x C D x ===，∴222AC AD CD +=，∴∠DAC=90°，∴∠DAB=90°+45°=135°.4解析：（1）如图①，当AB=AC 时，∵∠A=30°，∴CD=12AC=12×8=4；（2）如图②，当AB=BC 时，则∠A=∠ACB=30°，∴∠ACD=60°，∴∠BCD=30°，∴BD=1=42BC ，∴CD =（3）如图③，当AC=BC 时，则AD=4，设CD=x ，则AC=2x. 则2222)4x x -=（，解得4． 6.42或32 解析：当△ABC 是锐角三角形时，如图①，根据勾股定理可得BD=9，DC=5,∴BC=14,此时△ABC 的周长为15+13+14=42；当△ABC 是钝角三角形时，如图②，根据勾股定理可得BD=9，DC=5,∴BC=9-5=4,此时△ABC 的周长为15+13+4=32.8.解：∵AC=4，BC=2，AB=2+BC 2=AB 2，∴△ACB 为直角三角形，∠ACB=90°．分三种情况如图(1)，过点D 作DE⊥CB，垂足为点E ．易证△ACB≌△BED，易求如图(2)，过点D 作DE⊥CA，垂足为点E ．易证△ACB≌△DEA，易求 如图(3)，过点D 作DE⊥CB，垂足为点E ，过点A 作AF⊥DE ，垂足为点F ．易证△AFD≌△DEB，易求.∴CD 的长为.。

专题应用HL解决问题1. 如图，AB=AE，BC=ED，∠B=∠E，AF⊥CD，F为垂足，求证：CF=DF2。

如图（1），A，E，F，C在一条直线上,AE=CF，过E,F分别作DE⊥AC,BF⊥AC，(1)若AB=CD，求证：BD平分EF。

（2）若将△DEC的边EC沿AC方向移动变为图(2)时，其余条件不变,上述结论是否成立，请说明理由。

参考答案1.证明：连结AC、AD，∵AB=AE,∠B=∠E，BC=ED，∴△ABC≌△AED（SAS）。

∴AC=AD。

又∵A F⊥CD，∴∠AFC＝∠AFD＝90°。

又∵AF=AF,∴Rt△ACF≌Rt△ADF（HL）.∴CF=DF.2.解：(1）证明：∵DE⊥AC,B F⊥AC，∴∠DEC＝∠BFA＝90°。

∵AE=CF，∴A E+EF=CF+EF，即:AF=CE。

在Rt△ABF和Rt△CDE中，∵AF=CE，AB=CD,∴Rt△ABF≌Rt△CDE（HL).∴BF=DE在△B FG和△DEG中，∵∠BFG＝∠DEG ，∠BGF＝∠DGE, BF=DE，∴△BFG≌Rt△DEG(AAS）.∴FG=EG,故BD平分EF.（2）成立.理由：∵DE⊥AC,BF⊥AC，∴∠DEC＝∠BFA＝90°.∵AE=CF,∴AE—EF=CF—EF,即:AF=CE,在Rt△ABF和Rt△CDE中，∵AF=CE，AB=CD，∴Rt△ABF≌Rt△CDE(HL)。

∴BF=DE，△BFG和△DEG中，∵∠BFG＝∠DEG ，∠BGF＝∠DGE, BF=DE，∴△BFG≌Rt△DEG（AAS）。

∴FG=EG，故BD平分EF.尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

专题应用HL解决问题1.如图，AE=AE BC=ED / B=Z E, AF丄CD, F为垂足，求证：CF=DF2.如图(1), A, E, F, C在一条直线上，AE=CF过E, F分别作DEL AC, BF丄AC,(1)若AB=CD求证：BD平分EF.(2)若将△ DEC的边EC沿AC方向移动变为图(2)时，其余条件不变，上述结论是否成立，请说明理由•参考答案1. 证明：连结AC AD,•/ AB=AE / B=Z E, BC=ED・」ABC^^ AED(SAS). /• AC=AD.又••• AF丄CDAFC=Z AFD= 90°.又••• AF=AF, A Rt△ ACF^ Rt△ ADF(HL). /• CF=DF.2. 解：(1)证明：•/ DEL AC, BF丄AC, A / DEC=Z BFA= 90° . v AE=CF 二AE+EF=CF+EF 即：AF=CE. 在Rt△ ABF和Rt △ CDE中 , •/ AF=CE AB=CD A Rt△ ABF^ Rt△ CDE( HL).A BF=DE在△ BFG和厶DEG中, v/ BFG=Z DEG , / BGF=Z DGE BF=DE,•••△BFG^ Rt△ DEG( AAS . A FG=EG 故BD平分EF.(2)成立.理由：v DEI AC BF L AC, A/DEC=/ BFA= 90° . v AE=CF, A AE-EF=CF-EF, 即: AF=CE 在Rt△ABF和Rt △CDE中, v AF=CE AB=CD • Rt △ABF^ Rt△CDE( HL).A BF=DE △BFG和厶DEG中, v/ BFG=/ DEG , / BGF=/ DGE BF=DE,•••△BFG^ Rt△ DEG( AAS • • FG=EG 故BD平分EF.2。

专题一勾股定理与方程1．如图所示，已知在三角形纸片ABC中，BC=3，AB=6，∠BCA=90°，在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，A与BC延长线上的点D重合，则DE的长度为（）A．6 B．3 C．23 D．32．一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH的边长为2米，坡角∠A＝30°,∠B ＝90°,BC＝6米. 当正方形DEFH运动到什么位置,即当AE＝米时,有DC2＝AE2＋BC2.专题二构造直角三角形3.如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝23，求AB的长．4．如图，在四边形ABCD中，AB:BC:CD:DA=2:2:3:1，且∠ABC=90°，求∠DAB的度数.专题三勾股定理中的分类讨论思想5.在等腰△ABC中，∠A=30°，AB=8，则AB边上的高CD的长是．6.在△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长为_______.7. 在△ABC中， AB=25，AC=4，BC=2，以AB为边向△ABC外作△ABD，使△ABD为等腰直角三角形，求线段CD的长．参考答案1.C 解析：由折叠可知BC =BA =6，DE =AE ，∵BC =3，∴CD =BC =3，∴BE =DE =AE ，由勾股定理可得AC =33，设DE =AE =BE =x ，在Rt △BCE 中，32＋()233x -=x 2，解得x =23，即DE 的长度为23.2.143解析：因为∠A＝30°,∠B＝90°,BC＝6米，所以AC ＝12米.设当AE 为 x 时，所以EC ＝ 12－x ，由DC 2＝AE 2＋BC 2及DC 2＝DE 2＋EC 2，所以有22＋（12－x ）2＝x 2＋36，解得x ＝143.3.解：过C 作CD ⊥AB 于D ，∴∠ADC ＝∠BDC ＝90°， ∵∠B ＝45°，∴∠BCD ＝∠B ＝45°，∴CD ＝BD . ∵∠A ＝30°，AC ＝23，∴CD ＝3， ∴BD ＝CD ＝3， 由勾股定理得：AD ＝22AC CD -＝3，∴AB ＝AD ＋BD ＝3＋3. 答：AB 的长是3＋3．4．解：连结AC.设AB 、BC 、CD 、DA 分别为2x ，2x ，3x ，x ，则2222228,,9AC x AD x CD x ===，∴222AC AD CD +=，∴∠DAC=90°，∴∠DAB=90°+45°=135°.5.433或43或4 解析：（1）如图①，当AB=AC 时，∵∠A=30°，∴CD=12AC=12×8=4；（2）如图②，当AB=BC 时，则∠A=∠ACB=30°，∴∠ACD=60°，∴∠BCD=30°，∴BD=1=42BC ， ∴CD =22BC BD -=43；（3）如图③，当AC=BC 时，则AD=4，设CD=x ，则AC=2x. 则2222)4x x -=（，解得x=433. 故答案为：433或43或4． 6.42或32 解析：当△ABC 是锐角三角形时，如图①，根据勾股定理可得BD=9，DC=5,∴BC=14,此时△ABC 的周长为15+13+14=42；当△ABC 是钝角三角形时，如图②，根据勾股定理可得BD=9，DC=5,∴BC=9-5=4,此时△ABC 的周长为15+13+4=32.8.解：∵AC=4，BC=2，AB=25，∴AC 2+BC 2=AB 2，∴△ACB 为直角三角形，∠ACB=90°．分三种情况如图(1)，过点D 作DE⊥CB，垂足为点E ．易证△ACB≌△BED，易求CD=210； 如图(2)，过点D 作DE⊥CA，垂足为点E ．易证△ACB≌△DEA，易求13如图(3)，过点D作DE⊥CB，垂足为点E，过点A作AF⊥DE，垂足为点F．易证△AFD≌△DEB，易求CD=32.∴CD的长为210或213或32.。

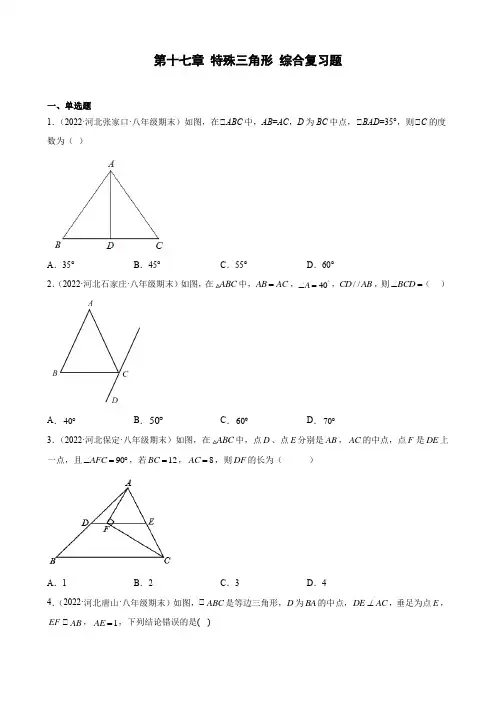
第十七章 特殊三角形 综合复习题一、单选题1．（2022·河北张家口·八年级期末）如图，在△ABC 中，AB =AC ，D 为BC 中点，△BAD =35°，则△C 的度数为（ ）A ．35°B ．45°C ．55°D ．60°2．（2022·河北石家庄·八年级期末）如图，在ABC 中，AB AC =，40A ︒∠=，//CD AB ，则BCD ∠=（ ）A ．40︒B ．50︒C ．60︒D ．70︒3．（2022·河北保定·八年级期末）如图，在ABC 中，点D 、点E 分别是AB ，AC 的中点，点F 是DE 上一点，且90AFC ∠=︒，若12BC =，8AC =，则DF 的长为（ ）A ．1B ．2C ．3D ．44．（2022·河北唐山·八年级期末）如图，△ABC 是等边三角形，D 为BA 的中点，DE AC ⊥，垂足为点E ，EF △AB ，1AE =，下列结论错误的是( )A．ADEAD=∠=30°B．2C．△ABC的周长为10D．△EFC的周长为95．（2022·河北邯郸·八年级期末）如图，在△ABC中，△B＝30°，△C＝45°，AE△BC于点E，AB的垂直平分线交BC于点D，交AB于点F，若BD＝，则CE的长为（）A．B．C．D．∆，不是直角三角形的是（）6．（2022·河北廊坊·八年级期末）满足下列条件的ABCA．222a b c=b c a-=B．::5:12:13∠=∠-∠C．::3:4:5∠∠∠=D．C A BA B C7．（2022·河北秦皇岛·八年级期末）如图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长是（）A．52B．42C．76D．728．（2022·河北邢台·八年级期末）如图，已知AB BD⊥，CD BD⊥，若用“HL”判定Rt ABD和Rt CDB全等，则需要添加的条件是（）A ．AD CB = B ．AC ∠=∠ C ．=BD DB D ．AB CD =9．（2022·河北廊坊·八年级期末）老师在画△AOB 的平分线OP 时，设计了△，△两种做法，这两种做法均可由△OMP △△ONP 得知，其全等的依据分别是（ ）△如图1，在边OA ，OB 上分别取OM ＝ON ，调整角尺，使角尺的顶点到点M ，N 的距离相等，此时，角尺的顶点为P ，画出射线OP ；△如图2，在边OA ，OB 上分别取OM ＝ON ，再分别过点M ，N ，作OA ，OB 的垂线，交点为P ，画出射线OP ．A ．SSS ；HLB ．SAS ；HLC ．SSS ；SASD ．SAS ；SSS10．（2022·河北唐山·八年级期末）用反证法证明“在ABC ∆中，AB AC =，则B ∠是锐角”，应先假设（ ） A ．在ABC ∆中，B ∠一定是直角B ．在ABC ∆中，B ∠是直角或钝角 C ．在ABC ∆中，B ∠是钝角D ．在ABC ∆中，B ∠可能是锐角二、填空题11．（2022·河北唐山·八年级期末）如图，在ABC 中，AB AC ＝，点D 在AC 上，且BD BC AD ＝＝，则A ∠＝_____度．12．（2022·河北保定·八年级期末）如图：点C 在AB 上，DAC ∆、EBC ∆均是等边三角形，AE 、BD 分别与CD 、CE 交于点M 、N ，则下列结论△AE DB = △CM CN = △CMN ∆为等边三角形 △//BC MN 正确的是______（填出所有正确的序号）13．（2022·河北秦皇岛·八年级期末）如图，在△ABC 中，△ACB =90°，D 是AB 的中点，连接CD ．若CD =8，则AB =_______．14．（2022·河北石家庄·八年级期末）如图，在Rt ABC 中，90ABC ∠=︒，斜边上的中线BE 的长为4 cm ，高BD 的长为3 cm ，则ABC 的面积是______2cm ．15．（2022·河北承德·八年级期末）如图，点A 、B 、C 分别在边长为1的正方形网格图顶点，则ABC ∠=______．16．（2022·河北张家口·八年级期末）如图，在△ABC 中，CE 平分△ACB ，CF 平分△ACD ，且EF △BC 交AC 于M ，若CM ＝3，则CE 2+CF 2＝_____．17．（2022·河北邯郸·八年级期末）如图，点D在BC上，DE△AB于点E，DF△BC交AC于点F，BD＝CF，BE＝CD．若△AFD＝145°，则△EDF＝_____．三、解答题18．（2022·河北唐山·八年级期末）如图，已知点D，E分别是ABC的边BA和BC延长线上的点，作△DAC 的平分线AF，若AF△BC．（1）求证：ABC是等腰三角形（2）作△ACE的平分线交AF于点G，若40∠=，求△AGC的度数．B19．（2022·河北石家庄·八年级期末）在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC．（1）当点E为AB的中点时，如图1，确定线段A与DB的大小关系，请你直接写出结论：AE DB（填“＞”，“＜”或“＝”）．（2）当E不是AB的中点时，AE与DB的大小关系是：AE DB（填“＞”，“＜”或“＝”）．理由如下：如图2，过点E作EF△BC，交AC点F．请你接下来按照这种思路完成全部解答过程．（3）在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED＝EC．若△ABC的边长为2，AE＝4，则CD的长为．20．（2022·河北保定·八年级期末）将一个三角形沿着其中一个顶点及其对边上的一点所在的直线折叠，若折叠后原三角形的一边垂直于这条对边，则称这条直线是该三角形的“对垂线”．（1）如图1，AD 是等边△ABC 的对垂线，把△ABC 沿直线AD 折叠后，点B 落在点B '处，求△BAD 的度数；（2）如图2．在△ABC 中，△BAC =90°，点D 在边BC 上，且AB =AD ，若△B =2△DAC ，判断直线AD 是否是△ABC 的对垂线，并说明理由．21．（2022·河北张家口·八年级期末）课外兴趣小组活动时，老师出示了如下问题：如图△，已知在四边形ABCD 中，AC 平分△DAB ，△DAB ＝60°，△B 与△D 互补，求证：AB ＋AD．小敏反复探索，不得其解．她想，可先将四边形ABCD 特殊化，再进一步解决该问题．(1)由特殊情况入手，添加条件：“△B ＝△D”，如图△，可证AB ＋AD．请你完成此证明．(2)受到(1)的启发，在原问题中，添加辅助线：过C 点分别作AB ，AD 的垂线，垂足分别为点E ，F ，如图△.请你补全证明过程．22．（2022·河北廊坊·八年级期末）如图，在ABC 中，90ACB ∠=︒，CD AB ⊥于点D ，DCB ∠的平分线CE 交AB 于点E ．（1）求证：AC AE =；（2）若60A ∠=︒，3AD =，求BD 的长．23．（2022·河北廊坊·八年级期末）如图，在ABC 中，AD BC ⊥，垂足为D ，BD CD =，延长BC 至E ，使得CE CA =，连接AE ．（1）求证：B ACB ∠=∠；（2）若5AB =，4=AD ，求ABE 的周长和面积．24．（2022·河北邢台·八年级期末）如图，在一次地震中，一棵垂直于地面且高度为16米的大树被折断，树的顶部落在离树根8米处，即8BC =，求这棵树在离地面多高处被折断（即求AC 的长度）？25．（2022·河北秦皇岛·八年级期末）如图，小明家在一条东西走向的公路MN 北侧200米的点A 处，小红家位于小明家北500米（500AC =米）、东1200米（1200BC =米）点B 处．（1）求小明家离小红家的距离AB ；（2）现要在公路MN 上的点P 处建一个快递驿站，使PA PB +最小，请确定点P 的位置，并求PA PB +的最小值．26．（2022·河北沧州·八年级期末）如图，在△ABC 中，△C=90°，AD 平分△BAC ，DE△AB 于点E ，点F 在AC 上，且BD=DF ．（1）求证：△DCF△△DEB ；（2）若DE=5，EB=4，AF=8，求AD 的长．27．（2022·河北唐山·八年级期末）已知：如图，在ABC 中，A ABC CB =∠∠，直线l 经过点A ，过B ，C 两点作直线l 的垂线，垂足分别为D ，E ，BD AE =．求证：AB AC ⊥．参考答案：1．C【解析】根据等腰三角形的三线合一的性质可直接得到AD 平分△BAC ，AD △BC ，结合图形，利用各角之间的关系及三角形内角和定理即可得．解：△△ABC 为等腰三角形，△AD 平分△BAC ，AD △BC ，△35DAC BAD ∠=∠=︒，90ADC ∠=︒，△18055C ADC DAC ∠=︒-∠-∠=︒，故选C ．题目主要考查等腰三角形三线合一的性质，三角形内角和定理，理解题意，找准各角之间的数量关系是解题关键．2．D【解析】先根据等腰三角形的性质得到△B 的度数，再根据平行线的性质得到△BCD. 解：△AB=AC ，△A=40°，△△B=△ACB=70°，△CD△AB ，△△BCD=△B=70°，故选D.本题考查了等腰三角形的性质和平行线的性质，掌握等边对等角是关键，难度不大.3．B【解析】根据三角形中位线定理求出DE ，根据直角三角形的性质求出FE ，结合图形计算，得到答案．解：△点D ，点E 分别是AB ，AC 的中点，△DE 是△ABC 的中位线，△DE =12BC =6（cm ），在Rt △AFC 中，点E 是AC 的中点，△FE =12AC =4（cm ），△DF =DE -EF =2（cm ），故选：B ．本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．4．C【解析】根据等边三角形的性质和直角三角形两锐角互余的性质可判断A；根据30°角的直角三角形的性质可判断B；由B的结论结合D为BA的中点可求出AB的长，进而可判断C；由EF△AB可判断△CEF是等边三角形，再求出CE的长即可判断D.解：△△ABC是等边三角形，△AB=AC=BC，△A=△B=△C=60°，，△∠AED=90°，△DE AC△△ADE=90°－△A=30°，所以A正确；△AE=1，△ADE=30°，△AD=2AE=2，所以B正确；△D为BA的中点，△AB=2AD=4，△△ABC的周长为4×3=12，所以C错误；△EF△AB，△△CEF=△A=60°，△CFE=△B=60°，△△CEF是等边三角形，△AE=1，△CE=AC－AE=3，△△EFC的周长为9，所以D正确.故选C.本题考查了等边三角形的性质和30°角的直角三角形的性质，属于基础题型，熟练掌握等边三角形的性质和直角三角形的性质是解题的关键.5．D【解析】根据题意连接AD，由线段的垂直平分线的性质可得AD的长；由等腰三角形的性质及三角形的外角性质可求得△ADE＝60°，从而可求得△DAE＝30°，解直角三角形ADE，可得AE的长度；由△C＝45°，可得△AEC为等腰直角三角形，从而可得EC的长度．解：连接AD，如图：△AB的垂直平分线交BC于点D，△AD＝BD＝△在△ABC中，△B＝30°，△△BAD＝△B＝30°，△△ADE＝△B+△BAD＝60°．△AE△BC于点E，△△AED＝90°，△△DAE＝30°，AD＝，△DE＝12△AE，△△C＝45°，△△AEC为等腰直角三角形，△EC＝AE＝故选：D．本题考查含30度角的直角三角形的性质、线段的垂直平分线的性质、等腰三角形的性质及解直角三角形等知识点，熟练掌握相关性质及定理是解题的关键．6．C【解析】根据三角形内角和定理、勾股定理的逆定理对各个选项分别进行计算即可．A. 222-=,则a2+c2=b2 ,△ABC是直角三角形,故A正确，不符合题意；b c aB. 52+122=132，△ABC是直角三角形，故B正确，不符合题意；C.△A：△B：△C=3：4：5，设△A、△B、△C分别为3x、4x、5x，则3x+4x+5x=180°，解得，x=15°，则△A 、△B 、△C 分别为45°，60°，75°，△ABC 不是直角三角形；故C 选项错误，符合题意；D. △A -△B=△C ，则△A=△B+△C ，△A=90°，△ABC 是直角三角形，故D 正确，不符合题意；故选C ．本题考查的是三角形内角和定理、勾股定理的逆定理的应用，勾股定理的逆定理：如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形就是直角三角形．7．C解：依题意得，设“数学风车”中的四个直角三角形的斜边长为x ，则x 2=122+52=169，解得：x =13．故“数学风车”的周长是：（13+6）×4=76．故选C ．8．A【解析】由图示可知BD 为公共边，若想用“HL ”判定证明Rt ABD 和Rt CDB 全等，必须添加AD =CB ．解：在Rt ABD 和Rt CDB 中BD BD AD CB =⎧⎨=⎩△()Rt ABD Rt CDB HL ≌△△故选A此题主要考查学生对全等三角形判定定理（HL ）的理解和掌握，此题难度不大，属于基础题．9．A【解析】根据作图过程可得MO = NO ，MP = NP ，再利用SSS 可判定△MPO △△PNO ，可得OP 是△AOB 的平分线；根据题意得出Rt △MOP △Rt △NOP (HL )，进而得出射线OP 为△AOB 的角平分线．解：如图△：在△MPO 和△NPO 中OM ON OP OP MP NP =⎧⎪=⎨⎪=⎩，△△MPO △△PNO (SSS )△△AOP =△BOP ，即射线OP 为△AOB 的角平分线；如图△，在Rt △MOP 和Rt △NOP 中，OP OP MO NO=⎧⎨=⎩， △Rt△MOP △Rt△NOP (HL )△△MOP =△NOP ，即射线OP 为△AOB 的角平分线；故选：A ．此题主要考查了基本作图以及全等三角形的判定，关键是掌握判定三角形全等的方法．10．B【解析】假设命题的结论不成立或假设命题的结论的反面成立，然后推出矛盾，说明假设错误，结论成立．解：用反证法证明命题“在ABC ∆中，AB AC =，则B ∠是锐角”时，应先假设在ABC ∆中，B ∠是直角或钝角．故选B ．本题考查反证法，记住反证法的一般步骤是：△假设命题的结论不成立；△从这个假设出发，经过推理论证，得出矛盾；△由矛盾判定假设不正确，从而肯定原命题的结论正确． 11．36【解析】设△A=x ，利用等腰三角形的性质和三角形内角和定理即可求得答案．设△A=x ．△AD=BD ，△△ABD=△A=x ；△BD=BC ，△△BCD=△BDC=△ABD+△A=2x ；△AB=AC ，△△ABC=△BCD=2x ，△△DBC=x ；△x+2x+2x=180°，△x=36°，△△A=36°，故答案为36.本题考查了等腰三角形的性质，涉及了等边对等角、三角形外角的性质，三角形的内角和定理，通过三角形内角和定理列方程求解是正确解答本题的关键．12．△△△△【解析】利用等边三角形的性质得CA＝CD，△ACD＝60°，CE＝CB，△BCE＝60°，所以△DCE ＝60°，△ACE＝△BCD＝120°，则利用“SAS”可判定△ACE△△DCB，所以AE＝DB，△CAE ＝△CDB，则可对△进行判定；再证明△ACM△△DCN得到CM＝CN，则可对△进行判定；然后证明△CMN为等边三角形得到△CMN＝60°，则可对△△进行判定．解：△△DAC、△EBC均是等边三角形，△CA＝CD，△ACD＝60°，CE＝CB，△BCE＝60°，△△DCE＝60°，△ACE＝△BCD＝120°，在△ACE和△DCB中AC CDACE DCB EC BC⎪∠⎪⎩∠⎧⎨＝＝＝，△△ACE△△DCB（SAS），△AE＝DB，所以△正确；△△ACE△△DCB，△△MAC=△NDC，△△ACD=△BCE=60°，△△MCA=△DCN=60°，在△ACM和△DCN中MAC NDC CA CDACM DCN∠∠∠⎧⎪⎪⎩∠⎨＝＝＝，△△ACM△△DCN（ASA），△CM＝CN，所以△正确；△CM＝CN，△MCN＝60°，△△CMN为等边三角形，故△正确，△△CMN＝60°，△△CMN＝△MCA，△MN△BC，所以△正确，故答案为：△△△△．本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具，在判定三角形全等时，关键是选择恰当的判定条件，也考查了等边三角形的判定与性质．13．16【解析】根据直角三角形斜边上的中线等于斜边的一半解答即可．解：△△ACB=90°，D是AB中点，CD=8，△AB=2CD=16，故答案为：16．本题考查的是直角三角形的性质，掌握直角三角形斜边上的中线等于斜边的一半是解题的关键．14．12【解析】根据直角三角形的性质求出AC，根据三角形的面积公式计算，得到答案．解：在Rt△ABC中，BE为斜边上的中线，BE＝4cm，则AC＝2BE＝2×4＝8（cm），△S△ABC＝12AC•BD＝12×8×3＝12（cm2），故答案为：12．本题考查的是直角三角形的性质，在直角三角形中，斜边上的中线等于斜边的一半．15．45°【解析】利用勾股定理可求出AB2，AC2，BC2的长，进而可得出AB2=AC2+BC2，AC=BC，利用勾股定理的逆定理可得出△ABC为等腰直角三角形，再利用等腰直角三角形的性质，可得出△ABC=45°．解：连接AC，根据题意，可知：BC2=12+22=5，AC2=12+22=5，AB2=12+32=10．△AB2=AC2+BC2，AC=BC，△△ABC为等腰直角三角形，△△ABC=45°．故答案为：45°．本题考查了勾股定理的逆定理、勾股定理以及等腰直角三角形的性质，利用勾股定理的逆定理及AC=BC，找出△ABC为等腰直角三角形是解题的关键．16．36【解析】根据角平分线的定义、外角定理推知△ECF＝90°，然后在直角三角形ECF中利用勾股定理求CE2+CF2的值即可．△CE平分△ACB，CF平分△ACD，△△ACE＝12△ACB，△ACF＝12△ACD，△△ECF＝12(△ACB+△ACD)＝90°，又△EF△BC，CE平分△ACB，CF平分△ACD，△△ECB＝△MEC＝△ECM，△DCF＝△CFM＝△MCF，△CM＝EM＝MF＝3，△EF＝6，由勾股定理可知CE2+CF2＝EF2＝36，故答案为36．本题考查了直角三角形的性质-勾股定理，等腰三角形的判定，平行线的性质，以及角平分线的定义，证明出△ECF是直角三角形是解决本题的关键．17．55°##55度【解析】由图示知：△DFC+△AFD=180°，则△DFC=35°．通过全等三角形Rt△BDE△△Rt△CFD （HL）的对应角相等推知△BDE=△CFD．解：△△DFC +△AFD =180°，△AFD =145°，△△CFD =35°．又△DE △AB ，DF △BC ，△△BED =△CDF =90°，在Rt △BDE 与△Rt △CFD 中，BE CD BD CF =⎧⎨=⎩， △Rt △BDE △△Rt △CFD （HL ），△△BDE =△CFD =35°，△△EDF +△BDE =△EDF +△CFD =90°，△△EDF =55°．故答案是：55°．本题考查了全等三角形的判定与性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．18．（1）证明见解析；（2）70AGC ∠=【解析】（1）根据角平分线的定义，得到△DAF =△CAF ，又根据//BC AF ，得到△DAF =△ABC ，△CAG =△ACB ，进一步得到△ABC =△ACB ，即可证明ABC 是等腰三角形；（2）在ACG 中，分别求得ACG ∠和CAG ∠的度数，利用三角形内角和求解即可．（1）证明：△AF 是△DAC 的角平分线△△DAF =△CAF又△//BC AF△△DAF =△ABC ，△CAG =△ACB△△ABC =△ACB∠AB=AC△ABC 是等腰三角形（2）△CG 是△ACE 的角平分线△△ACG =△ECG又△40B ∠=，△ACB =△B△40ACB ∠=△△ACG =△ECG =()118040702⨯-= 又△△CAG =△ACB△△AGC =180407070--=本题考查等腰三角形的判定，平行线的性质，角平分线的定义等相关知识点，牢记知识点是解题关键．19．（1）=，（2）=，理由见解析，（3）2或6．【解析】（1）根据等边三角形的性质得出∠D ＝∠BED ＝30°，证BD ＝BE 即可．（2）结论：AE ＝BD ．如图2中，作EF ∥BC 交AC 于F ．只要证明△DBE ≌△EFC ，推出BD ＝EF ＝AE ，推出BD ＝AE ．（3）分两种情形讨论，类似（2）得出BD ＝AE ，根据线段和差即可解决问题． 解：（1）如图1中，∵△ABC 是等边三角形，AE ＝EB ，∴∠BCE ＝∠ACE ＝30°，∠ABC ＝60°，∵ED ＝EC ，∴∠D ＝∠ECD ＝30°，∵∠EBC ＝∠D +∠BED ，∴∠D ＝∠BED ＝30°，∴BD ＝BE ＝AE ．故答案为：＝．（2）结论：AE ＝BD ．理由如下：如图2中，作EF ∥BC 交AC 于F ．∴∠AEF ＝∠B ＝60°，∠ECB ＝∠CEF ，∵∠A ＝60°，∴△AEF 是等边三角形，∴AE ＝EF ＝AF ，∠AFE ＝60°，∴∠EFC ＝∠DBE ＝120°，∵AB ＝AC ，AE ＝AF ，∴BE ＝CF ，∵ED ＝EC ．∴∠D ＝∠ECD ＝∠CEF ，在△DBE 和△FEC 中，DBE EFC D CEF BE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DBE ≌△EFC ，∴BD ＝EF ＝AE ，∴BD ＝AE ，故答案为：＝．（3）如图，当E 在BA 的延长线上时，作EF ∥BC 交CA 延长线于F ．同理可证△DBE ≌△EFC ，可得BD ＝EF =AE ＝4，CD ＝BD ﹣BC ＝4﹣2＝2．如图，当E在AB的延长线上时，作EF∥BC交AC的延长线于F，同理可证△EBD≌△CFE，可得BD＝EF=AE＝4，CD＝BD+BC＝4+2＝6．综上所述，CD的长为2或6．本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．20．（1）15°；（2）是，理由见解析．【解析】（1）由“对垂线”的定义可得AB'△BC，△ABD△△AB'D，则可得出△BAD=△B'AD，由等边三角形的性质得出△BAB'12=△BAC=30°，则由折叠的性质可得出答案；（2）由等腰三角形的性质得出△B=△BDA，可得出△DAC=△C12=△B，求出△B=60°，证得△AFD=90°，则可得出答案．解：（1）△AD是等边△ABC的对垂线，把△ABC沿直线AD折叠后，点B落在点B'处，△AB'△BC，△ABD△△AB'D，△△BAD =△B 'AD ．△△ABC 是等边三角形，△AB =AC ，△BAC =60°．又△AB '△BC ，△△BAB '12=△BAC =30°， △△BAD 12=△BAB '1302=⨯°=15°； （2）直线AD 是△ABC 的对垂线．理由如下：△AB =AD ，△△B =△BDA ．△△B =2△DAC ，△BDA =△DAC +△C ，△△DAC =△C 12=△B ． △△ABC 中，△BAC =90°，△△B +△C =90°，△△B 12+△B =90°， △△B =60°=△BDA ，△DAC =△C =30°．把△ADC 沿直线AD 折叠，设点C 落在C '处，直线AC '交BC 于点F ，则△ACD △△AC 'D ， △△DAC '=△DAC =30°，△△AFD 中，△AFD =180°﹣30°﹣60°=90°，即AC '△BC ，△AD 是△ABC 的对垂线．本题是几何变换综合题，考查了等腰三角形的性质，等边三角形的性质，三角形“对垂线”的概念，折叠的性质，全等三角形的性质，直角三角形的性质，熟练掌握折叠的性质是解答本题的关键．21．(1)见解析;(2)见解析.【解析】（1）如果：“△B=△D”，根据△B 与△D 互补，那么△B=△D=90°，又因为△DAC=△BAC=30°，因此我们可在直角三角形ADC 和ABC 中得出，那么．（2）按（1）的思路，作好辅助线后，我们只要证明三角形CFD 和BCD 全等即可得到（1）的条件．根据AAS 可证两三角形全等，DF=BE ．然后按照（1）的解法进行计算即可．(1)证明：△△B ＝△D ＝90°，AC 平分△DAB ，△DAB ＝60°，△CD ＝CB ，△CAB ＝△CAD ＝30°.设CD ＝CB ＝x ，则AC ＝2x.由勾股定理，得AD，AB△AD ＋AB＝，即AB ＋AD(2)解：由(1)知，AE ＋AF△AC 为角平分线，CF△AD ，CE△AB ，△CF ＝CE ，△CFD ＝△CEB ＝90°.△△ABC 与△D 互补，△ABC 与△CBE 也互补，△△D ＝△CBE ，△△CDF△△CBE(AAS )．△DF ＝BE.△AB ＋AD ＝AB ＋(AF ＋FD)＝(AB ＋BE)＋AF ＝AE ＋AF本题考查了直角三角形全等的判定及性质；通过辅助线来构建全等三角形是解题的常用方法，也是解决本题的关键．22．（1）证明见解析；（2）9【解析】（1）根据已知条件得到ACD B ∠=∠，再根据角平分线的定义得到BCE DCE ∠=∠，即可得解；（2）根据含30度角的直角三角形的性质计算即可；解：（1）△90ACB ∠=︒，CD AB ⊥，△90ACD A B A ∠+∠=∠+∠=︒，△ACD B ∠=∠，△CE 平分BCD ∠，△BCE DCE ∠=∠，△B BCE ACD DCE ∠+∠=∠+∠，即AEC ACE ∠=∠，△AC AE =．（2）△90ACB ∠=︒，60A ∠=︒，△30ACD ∠=︒，30B ∠=︒，△Rt ACD △中，26AC AD ==，△Rt ABC △中，212AB AC ==，△1239BD AB AD =-=-=．本题主要考查了角平分线的定义、等腰三角形的判定和含30度角的直角三角形，准确计算是解题的关键．23．（1）证明见解析；（2）周长为16+22．【解析】（1）先根据垂直的定义可得90ADB ADC ∠=∠=︒，再根据三角形全等的判定定理与性质即可得证；（2）先根据全等三角形的性质可得5AB AC ==，从而可得5CE =，再利用勾股定理可得3CD BD ==，从而可得11,8BE DE ==，然后利用勾股定理可得AE =形的周长公式和面积公式即可得．（1）证明：AD BC ⊥，90ADB ADC ∴∠=∠=︒，在ABD △和ACD 中，AD AD ADB ADC BD CD =⎧⎪∠=∠⎨⎪=⎩，()ABD ACD SAS ∴≅，B ACB ∴∠=∠；（2）ABD ACD ≅，5AB =，5AB AC ∴==，CE CA =，5CE ∴=，5,4,AB AD AD BC ==⊥，3BD ∴=，BD CD =，3CD ∴=，11,8BE BD CD CE DE CD CE ∴=++==+=，AE ∴则ABE 的周长为51116AB BE AE ++=++=+ ABE 的面积为111142222BE AD ⋅=⨯⨯=． 本题考查了三角形全等的判定定理与性质、勾股定理等知识点，熟练掌握三角形全等的判定定理与性质是解题关键．24．这棵树在离地面6米处被折断【解析】设AC x =，利用勾股定理列方程求解即可.解：设AC x =，△在Rt ABC △中，222AC BC AB +=，△()222816x x +=-，△6x =．答：这棵树在离地面6米处被折断本题考查了勾股定理，熟练掌握勾股定理是解答本题的关键．直角三角形两条直角边的平方和等于斜边的平方． 当题目中出现直角三角形，且该直角三角形的一边为待求量时，常使用勾股定理进行求解．有时也可以利用勾股定理列方程求解．25．（1）1300AB =米；（2）见解析，1500米【解析】（1）如图，连接AB ，根据勾股定理即可得到结论；（2）如图，作点A 关于直线MN 的对称点A '，连接A 'B 交MN 于点P ．驿站到小明家和到小红家距离和的最小值即为A 'B ，根据勾股定理即可得到结论．解：（1）如图，连接AB ，由题意知AC=500，BC=1200，△ACB=90°，在Rt△ABC中，△△ACB=90°，△AB2=AC2+BC2=5002+12002=1690000，△AB＞0△AB=1300米；（2）如图，作点A关于直线MN的对称点A'，连接A'B交MN于点P．驿站到小明家和到小红家距离和的最小值即为A'B，由题意知AD=200米，A'C△MN，△A'C=AC+AD+A'D=500+200+200=900米，在Rt△A'BC中，△△ACB=90°，△A'B2=A'C2+BC2=9002+12002=2250000，△A'B＞0，△A'B=1500米，即从驿站到小明家和到小红家距离和的最小值为1500米．本题考查轴对称-最短问题，勾股定理，题的关键是学会利用轴对称解决最短问题．26．（1）见解析；（2）AD=13．【解析】（1）先利用角平分线的性质定理得到DC=DE，再利用HL定理即可证得结论．（2）由△DCF△△DEB得CD=DE=5，CF=BE=4，进而有AC=12，在Rt△ACD中，利用勾股定理即可解得AD 的长．（1）△AD 平分△BAC ，DE△AB ，△C=90°，△DC=DE ，在Rt△DCF 和Rt△DEB 中，DC DE DF DB=⎧⎨=⎩， △Rt△DCF△Rt△DEB(HL)；（2）△△DCF△△DEB ，△CF=EB=4，△AC=AF+CF=8+4=12，又知DC=DE=5，在Rt△ACD 中，13=．本题考查了角平分线的性质定理、全等三角形的判定与性质、勾股定理，熟练掌握角平分线的性质定理和HL 定理证明三角形全等是解答的关键．27．见解析【解析】由ABC =△ACB ，得AB =AC ，再利用HL 证明R t △ABD △Rt △CAE ，得△DAB =△ECA ，由△ECA +△EAC =90°，等量代换即可证．证明：△BD △l ，CE △l△△ABD 和△CAE 为直角三角形△△ABC =△ACB△AB =AC又△BD =AE△Rt △ABD △Rt △CAE （HL ），△△DAB =△ECA△△ECA +△EAC =90°△△DAB +△EAC =90°△△BAC =90°△AB △AC本题考查了全等三角形的判定与性质，等腰三角形的判定等知识，解题的关键是证Rt△ABD△Rt△CAE。