2020高考数学异构异模复习第十二章概率与统计课时撬分练12-2离散型随机变量及其分布列均值与方差理

2018高考数学异构异模复习考案第十二章概率与统计 12.1.2 古典概型撬题理1.袋中共有15个除了颜色外完全相同的球，其中有10个白球，5个红球．从袋中任取2个球，所取的2个球中恰有1个白球，1个红球的概率为( )A.521B.1021C.1121D．1答案 B解析由题意得基本事件的总数为C215，恰有1个白球与1个红球的基本事件个数为C110C15，所以所求概率P＝C110C15C215＝1021.故选B.2．从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离不小于该正方形边长的概率为( )A.15B.25C.35D.45答案 C解析从5个点取2个共有C25＝10种取法，而不小于正方形边长的只有4条边与2条对角线，共6种，所以P＝610＝35.3．有一个奇数列，1,3,5,7,9，…，现在进行如下分组，第一组有1个数为1，第二组有2个数为3、5，第三组有3个数为7、9、11，…，依此类推，则从第十组中随机抽取一个数恰为3的倍数的概率为( )A.110B.310C.15D.35答案 B解析将数列1,3,5,7,9…记为{a n}，则前九组共有1＋2＋3＋…＋9＝45个奇数，故第十组中第一个数字为a46＝2×46－1＝91，第十组共有10个奇数，分别是91,93,95,97,99,101,103,105,107,109这10个数字，其中为3的倍数的数有93,99,105三个，故所求概率为P＝310.4．从正方体的8个顶点的任意两个所确定的所有直线中取出两条，则这两条直线是异面直线的概率是( )A.29189B.2963C.3463D.47答案 B解析从8个顶点中任选2个共确定直线28条，从中任取两条直线，共有C228种取法；考查异面直线有多少对，可以考虑8个顶点共组成多少个三棱锥：上、下底面各取两点，共面的情形有10个．从而三棱锥共2C14C34＋C 24C 24－10＝58个，每个三棱锥有三对异面直线，故P ＝58×3C 228＝2963.5．从分别写有1,2,3,4,5的五张卡片中任取两张，假设每张卡片被取到的概率相等，且每张卡片上只有一个数字，则取到的两张卡片上的数字之和为偶数的概率为( )A.45 B.1625 C.1325 D.25答案 D解析 解法一：(列举法)从分别写有1,2,3,4,5的五张卡片中任取两张，总的情况为：(1,2)，(1,3)，(1,4)，(1,5)，(2,1)，(2,3)，(2,4)，(2,5)，(3,1)，(3,2)，(3,4)，(3,5)，(4,1)，(4,2)，(4,3)，(4,5)，(5,1)，(5,2)，(5,3)，(5,4)共20种情况．两张卡片上的数字之和为偶数的有：(1,3)，(1,5)，(2,4)，(3,1)，(3,5)，(4,2)，(5,1)，(5,3)共8种情况．∴从分别写有1,2,3,4,5的五张卡片中任取两张，这两张卡片上的数字之和为偶数的概率P ＝820＝25.故选D.解法二：(组合法)由题意知本题是一个古典概率模型，试验发生包含的事件是从5张中随机地抽2张，共C 25＝10种结果．满足条件的事件分两种情况，一种为从1,3,5中任取两张，有C 23＝3种结果，另一种为从2,4中任取两张，有C 22＝1种，所以取到的两张卡片上的数字之和为偶数共有3＋1＝4种结果，∴P ＝410＝25.故选D.6．从0,1,2,3,4,5,6,7,8,9中任取七个不同的数，则这七个数的中位数是6的概率为________． 答案 16解析 从0,1,2,3,4,5,6,7,8,9中任取七个不同的数，共有C 710种不同的取法．当这七个数的中位数是6时，应该有3个比6小的数，还有3个比6大的数，因此一共有C 36·C 33种不同的取法，故所求概率P ＝C 36·C 33C 710＝20120＝16. 7.从1,2,3,6这4个数中一次随机地取2个数，则所取2个数的乘积为6的概率是________． 答案 13解析 从1,2,3,6这4个数中随机地取2个数，不同的取法为{1,2}，{1,3}，{1,6}，{2,3}，{2,6}，{3,6}共6个基本事件，其中乘积为6的有{1,6}，{2,3}两个基本事件，因此所求事件的概率为P ＝26＝13.8．从n 个正整数1,2，…，n 中任意取出两个不同的数，若取出的两数之和等于5的概率为114，则n ＝________.答案 8解析 因为5＝1＋4＝2＋3，所以2C 2n ＝114，即n (n －1)＝56，解得n ＝8或n ＝－7(舍)．。

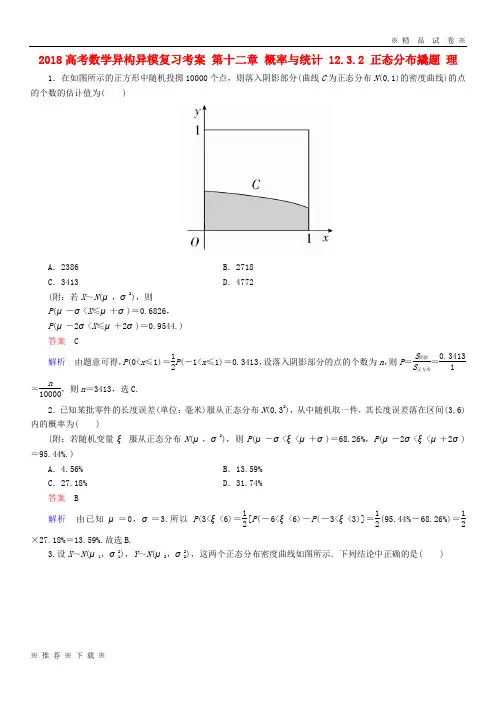
2018高考数学异构异模复习考案 第十二章 概率与统计 12.3.2 正态分布撬题 理1．在如图所示的正方形中随机投掷10000个点，则落入阴影部分(曲线C 为正态分布N (0,1)的密度曲线)的点的个数的估计值为( )A ．2386B ．2718C ．3413D ．4772(附：若X ～N (μ，σ2)，则 P (μ－σ<X ≤μ＋σ)＝0.6826，P (μ－2σ<X ≤μ＋2σ)＝0.9544.)答案 C解析 由题意可得，P (0<x ≤1)＝12P (－1<x ≤1)＝0.3413，设落入阴影部分的点的个数为n ，则P ＝S 阴影S 正方形＝0.34131＝n 10000，则n ＝3413，选C. 2．已知某批零件的长度误差(单位：毫米)服从正态分布N (0,32)，从中随机取一件，其长度误差落在区间(3,6)内的概率为( )(附：若随机变量ξ服从正态分布N (μ，σ2)，则P (μ－σ<ξ<μ＋σ)＝68.26%，P (μ－2σ<ξ<μ＋2σ)＝95.44%.)A ．4.56%B ．13.59%C ．27.18%D ．31.74%答案 B解析 由已知μ＝0，σ＝3.所以P (3<ξ<6)＝12[P (－6<ξ<6)－P (－3<ξ<3)]＝12(95.44%－68.26%)＝12×27.18%＝13.59%.故选B.3.设X ～N (μ1，σ21)，Y ～N (μ2，σ22)，这两个正态分布密度曲线如图所示．下列结论中正确的是( )A ．P (Y ≥μ2)≥P (Y ≥μ1)B ．P (X ≤σ2)≤P (X ≤σ1)C ．对任意正数t ，P (X ≤t )≥P (Y ≤t )D ．对任意正数t ，P (X ≥t )≥P (Y ≥t )答案 C解析 由正态分布密度曲线的性质可知，X ～N (μ1，σ21)，Y ～N (μ2，σ22)的密度曲线分别关于直线x ＝μ1，x ＝μ2对称，因此结合题中所给图象可得，μ1<μ2，所以P (Y ≥μ2)<P (Y ≥μ1)，故A 错误．又X ～N (μ1，σ21)的密度曲线较Y ～N (μ2，σ22)的密度曲线“瘦高”，所以σ1<σ2，所以P (X ≤σ2)>P (X ≤σ1)，B 错误．对任意正数t ，P (X ≤t )≥P (Y ≤t )，P (X ≥t )≤P (Y ≥t )，C 正确，D 错误．4．已知随机变量ξ服从正态分布N (0,1)，若P (ξ>1)＝a ，a 为常数，则P (－1≤ξ≤0)＝________.答案 12－a 解析 由正态曲线的对称轴为ξ＝0，又P (ξ>1)＝a ，故P (ξ<－1)＝a ，所以P (－1≤ξ≤0)＝1－2a 2＝12－a ，即答案为12－a . 5．某班有50名学生，一次考试后数学成绩ξ(ξ∈N )服从正态分布N (100,102)，已知P (90≤ξ≤100)＝0.3，估计该班学生数学成绩在110分以上的人数为________．答案 10解析 由题意，知P (ξ>110)＝1－2P ξ2＝0.2，所以该班学生数学成绩在110分以上的人数为0.2×50＝10.。

2018高考数学异构异模复习考案 第十二章 概率与统计 12.1.1 事件与概率撬题 理1．4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率为( )A.18B.38C.58D.78答案 D解析 由题意知4位同学各自在周六、周日两天中任选一天参加公益活动有24种情况，而4位同学都选周六有1种情况，4位同学都选周日有1种情况，故周六、周日都有同学参加公益活动的概率为P ＝24－1－124＝1416＝78，故选D. 2.袋中有形状、大小都相同的4只球，其中1只白球，1只红球，2只黄球．从中一次随机摸出2只球，则这2只球颜色不同的概率为________．答案 56 解析 从4只球中一次随机摸出2只球，C 24＝6，有6种结果，其中这2只球颜色不同有5种结果，故所求概率为56. 3．现有某类病毒记作X m Y n ，其中正整数m ，n (m ≤7，n ≤9)可以任意选取，则m ，n 都取到奇数的概率为________．答案 2063解析 由题意知m 的可能取值为1,2,3，…，7；n 的可能取值为1,2,3…，9.由于是任取m ，n ：若m ＝1时，n 可取1,2,3，…，9，共9种情况；同理m 取2,3，…，7时，n 也各有9种情况，故m ，n 的取值情况共有7×9＝63种．若m ，n 都取奇数，则m 的取值为1,3,5,7；n的取值为1,3,5,7,9，因此满足条件的情形有4×5＝20种．故所求概率为2063. 4．A ，B 两组各有7位病人，他们服用某种药物后的康复时间(单位：天)记录如下：A 组：10,11,12,13,14,15,16；B 组：12,13,15,16,17,14，a .假设所有病人的康复时间相互独立．从A ，B 两组随机各选1人，A 组选出的人记为甲，B 组选出的人记为乙．(1)求甲的康复时间不少于14天的概率；(2)如果a ＝25, 求甲的康复时间比乙的康复时间长的概率；(3)当a 为何值时，A ，B 两组病人康复时间的方差相等？(结论不要求证明)解 设事件A i 为“甲是A 组的第i 个人”，事件B i 为“乙是B 组的第i 个人”，i ＝1,2， (7)由题意可知P (A i )＝P (B i )＝17，i ＝1,2，…，7. (1)由题意知，事件“甲的康复时间不少于14天”等价于“甲是A 组的第5人，或者第6人，或者第7人”，所以甲的康复时间不少于14天的概率是P (A 5∪A 6∪A 7)＝P (A 5)＋P (A 6)＋P (A 7)＝37.(2)设事件C 为“甲的康复时间比乙的康复时间长”．由题意知， C ＝A 4B 1∪A 5B 1∪A 6B 1∪A 7B 1∪A 5B 2∪A 6B 2∪A 7B 2∪A 7B 3∪A 6B 6∪A 7B 6.因此P (C )＝P (A 4B 1)＋P (A 5B 1)＋P (A 6B 1)＋P (A 7B 1)＋P (A 5B 2)＋P (A 6B 2)＋P (A 7B 2)＋P (A 7B 3)＋P (A 6B 6)＋P (A 7B 6)＝10P (A 4B 1)＝10P (A 4)P (B 1)＝1049.(3)a ＝11或a ＝18.。

高考数学异构异模复习第十二章概率与统计12-2-2离散型随机变量及其分布列均值与方差撬题理1．已知甲盒中仅有1个球且为红球，乙盒中有m个红球和n个蓝球(m≥3，n≥3)，从乙盒中随机抽取i(i＝1,2)个球放入甲盒中．(a)放入i个球后，甲盒中含有红球的个数记为ξi(i＝1,2)；(b)放入i个球后，从甲盒中取1个球是红球的概率记为pi(i＝1,2)．则( )A．p1>p2，E(ξ1)<E(ξ2)B．p1<p2，E(ξ1)>E(ξ2)C．p1>p2，E(ξ1)>E(ξ2)D．p1<p2，E(ξ1)<E(ξ2)答案A解析当i＝1时，若从乙盒中抽取的1个球为红球，记从甲盒中取1个球是红球的事件为A1，则P(A1)＝.若从乙盒中抽取的1个球为蓝球，记从甲盒中取1个球是红球的事件为A2，则P(A2)＝×＝，而A1与A2互斥，则p1＝P(A1＋A2)＝P(A1)＋P(A2)＝.此时，ξ1的取值为1或2，P(ξ1＝1)＝，P(ξ1＝2)＝，则E(ξ1)＝1×＋2×＝.当i＝2时，若从乙盒中抽取的2个球都为红球，记从甲盒中取1个球是红球的事件为B1，则P(B1)＝.若从乙盒中抽取的2个球为1个红球和1个蓝球，记从甲盒中取1个球是红球的事件为B2，则P(B2)＝×.若从乙盒中抽取的2个球都是蓝球，记从甲盒中取1个球是红球的事件为B3，则P(B3)＝×.因为B1，B2，B3互斥，则p2＝P(B1＋B2＋B3)＝P(B1)＋P(B2)＋P(B3)＝＝＝＝.则p1－p2＝>0，即有p1>p2.此时，ξ2的取值为1,2,3.P(ξ2＝1)＝，P(ξ2＝2)＝，P(ξ2＝3)＝，则E(ξ2)＝1×＋2×＋3×＝＝3p2＝，则有E(ξ1)<E(ξ2)，综上，p1>p2，E(ξ1)<E(ξ2)，故选A.2．随机变量ξ的取值为0,1,2.若P(ξ＝0)＝，E(ξ)＝1，则D(ξ)＝________.答案25解析设P(ξ＝1)＝p，则P(ξ＝2)＝－p，从而由E(ξ)＝0×＋1×p＋2×＝1，得p＝.故D(ξ)＝(0－1)2×＋(1－1)2×＋(2－1)2×＝.3．设某校新、老校区之间开车单程所需时间为T，T只与道路畅通状况有关，对其容量为100的样本进行统计，结果如下：(1)求T(2)刘教授驾车从老校区出发，前往新校区做一个50分钟的讲座，结束后立即返回老校区，求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率．解(1)由统计结果可得T的频率分布为从而E(T)32(分钟)．(2)设T1，T2分别表示往、返所需时间，T1，T2的取值相互独立，且与T的分布列相同．设事件A表示“刘教授共用时间不超过120分钟”，由于讲座时间为50分钟，所以事件A对应于“刘教授在路途中的时间不超过70分钟”．解法一：P(A)＝P(T1＋T2≤70)＝P(T1＝25，T2≤45)＋P(T1＝30，T2≤40)＋P(T1＝35，T2≤35)＋P(T1＝40，T2≤30)＝0.2×1＋0.3×1＋0.4×0.9＋0.1×0.5＝0.91.。

2018高考数学异构异模复习考案 第十二章 概率与统计 12.3.1 条件概率、相互独立事件及二项分布撬题 理1．投篮测试中，每人投3次，至少投中2次才能通过测试．已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为( )A ．0.648B ．0.432C ．0.36D ．0.312答案 A解析 根据二项分布，由题意得所求概率P ＝C 23×0.62×(1－0.6)＋C 33×0.63＝0.648.2．某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是( )A ．0.8B ．0.75C ．0.6D ．0.45答案 A解析 设某天空气质量为优良为事件A ，随后一天空气质量为优良为事件B ，由已知得P (A )＝0.75，P (AB )＝0.6，所求事件的概率为P (B |A )＝P AB P A ＝0.60.75＝0.8，故选A.3．已知随机变量X 服从二项分布B (n ，p )．若E (X )＝30，D (X )＝20，则p ＝________. 答案 13解析 根据二项分布的期望与方差． 由题知⎩⎪⎨⎪⎧np ＝30np－p ＝20得p ＝13.4.某高三毕业班甲、乙两名同学在连续的8次数学周练中，统计解答题失分的茎叶图如图所示．(1)比较这两名同学8次周练解答题失分的平均数和方差的大小，并判断哪位同学做解答题相对稳定些； (2)以上述数据统计甲、乙两名同学失分超过15分的频率作为概率，假设甲、乙两名同学在同一次周练中失分多少互不影响，预测在接下来的2次周练中，甲、乙两名同学失分均超过15分的次数X 的分布列和均值．解 (1)x 甲＝18(7＋9＋11＋13＋13＋16＋23＋28)＝15，x 乙＝18(7＋8＋10＋15＋17＋19＋21＋23)＝15，s 2甲＝18[(－8)2＋(－6)2＋(－4)2＋(－2)2＋(－2)2＋12＋82＋132]＝44.75，s 2乙＝18[(－8)2＋(－7)2＋(－5)2＋02＋22＋42＋62＋82]＝32.25.甲、乙两名同学解答题失分的平均数相等；甲同学解答题失分的方差比乙同学解答题失分的方差大． 所以乙同学做解答题相对稳定些．(2)根据统计结果，在一次周练中，甲和乙失分超过15分的概率分别为P 1＝38，P 2＝12，两人失分均超过15分的概率为P 1P 2＝316，X 的所有可能取值为0,1,2.依题意，X ～B ⎝⎛⎭⎪⎫2，316，P (X ＝k )＝C k 2⎝ ⎛⎭⎪⎫316k ⎝ ⎛⎭⎪⎫13162－k，k ＝0,1,2， 则X 的分布列为X 的均值E (X )＝2×316＝38.5．在一块耕地上种植一种作物，每季种植成本为1000元，此作物的市场价格和这块地上的产量均具有随机性，且互不影响，其具体情况如下表：(1)设X (2)若在这块地上连续3季种植此作物，求这3季中至少有2季的利润不少于2000元的概率． 解 (1)设A 表示事件“作物产量为300 kg”，B 表示事件“作物市场价格为6元/kg”， 由题设知P (A )＝0.5，P (B )＝0.4， ∵利润＝产量×市场价格－成本， ∴X 所有可能的取值为500×10－1000＝4000,500×6－1000＝2000， 300×10－1000＝2000,300×6－1000＝800.P (X ＝4000)＝P (A )P (B )＝(1－0.5)×(1－0.4)＝0.3，P (X ＝2000)＝P (A )P (B )＋P (A )P (B )＝(1－0.5)×0.4＋0.5×(1－0.4)＝0.5， P (X ＝800)＝P (A )P (B )＝0.5×0.4＝0.2，所以X 的分布列为(2)设C i 表示事件“第i 由题意知C 1，C 2，C 3相互独立，由(1)知，P (C i )＝P (X ＝4000)＋P (X ＝2000)＝0.3＋0.5＝0.8(i ＝1,2,3)，3季的利润均不少于2000元的概率为P (C 1C 2C 3)＝P (C 1)P (C 2)P (C 3)＝0.83＝0.512；3季中有2季利润不少于2000元的概率为P (C 1C 2C 3)＋P (C 1C 2C 3)＋P (C 1C 2C 3)＝3×0.82×0.2＝0.384，所以，这3季中至少有2季的利润不少于2000元的概率为0.512＋0.384＝0.896.6.一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分(即获得－200分)．设每次击鼓出现音乐的概率为12，且各次击鼓出现音乐相互独立．(1)设每盘游戏获得的分数为X ，求X 的分布列； (2)玩三盘游戏，至少有一盘出现音乐的概率是多少？(3)玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了．请运用概率统计的相关知识分析分数减少的原因．解 (1)X 可能的取值为10,20,100，－200.根据题意，有P (X ＝10)＝C 13×⎝ ⎛⎭⎪⎫121×⎝ ⎛⎭⎪⎫1－122＝38，P (X ＝20)＝C 23×⎝ ⎛⎭⎪⎫122×⎝⎛⎭⎪⎫1－121＝38，P (X ＝100)＝C 33×⎝ ⎛⎭⎪⎫123×⎝⎛⎭⎪⎫1－12＝18，P (X ＝－200)＝C 03×⎝ ⎛⎭⎪⎫120×⎝⎛⎭⎪⎫1－123＝18. 所以X 的分布列为(2)设“第i i 则P (A 1)＝P (A 2)＝P (A 3)＝P (X ＝－200)＝18.所以，“三盘游戏中至少有一次出现音乐”的概率为 1－P (A 1A 2A 3)＝1－⎝ ⎛⎭⎪⎫183＝1－1512＝511512.因此，玩三盘游戏至少有一盘出现音乐的概率是511512.(3)X 的数学期望为E (X )＝10×38＋20×38＋100×18－200×18＝－54.这表明，获得的分数X 的均值为负． 因此，多次游戏之后分数减少的可能性更大．。

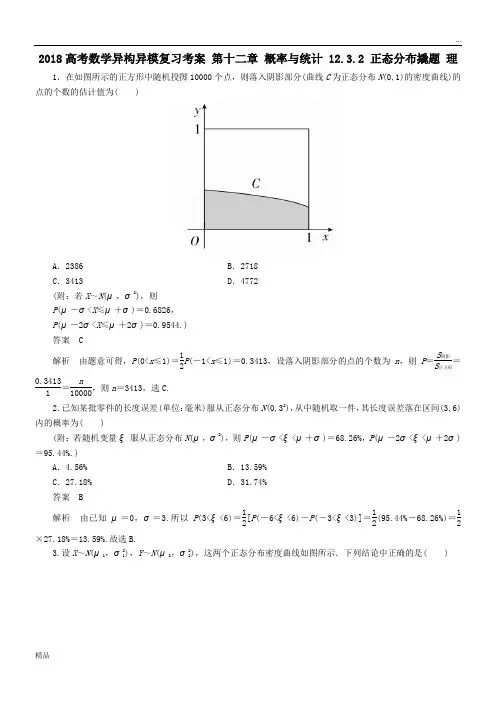
2018高考数学异构异模复习考案 第十二章 概率与统计 12.3.2 正态分布撬题 理1．在如图所示的正方形中随机投掷10000个点，则落入阴影部分(曲线C 为正态分布N (0,1)的密度曲线)的点的个数的估计值为( )A ．2386B ．2718C ．3413D ．4772(附：若X ～N (μ，σ2)，则 P (μ－σ<X ≤μ＋σ)＝0.6826，P (μ－2σ<X ≤μ＋2σ)＝0.9544.)答案 C解析 由题意可得，P (0<x ≤1)＝12P (－1<x ≤1)＝0.3413，设落入阴影部分的点的个数为n ，则P ＝S 阴影S 正方形＝0.34131＝n 10000，则n ＝3413，选C. 2．已知某批零件的长度误差(单位：毫米)服从正态分布N (0,32)，从中随机取一件，其长度误差落在区间(3,6)内的概率为( )(附：若随机变量ξ服从正态分布N (μ，σ2)，则P (μ－σ<ξ<μ＋σ)＝68.26%，P (μ－2σ<ξ<μ＋2σ)＝95.44%.)A ．4.56%B ．13.59%C ．27.18%D ．31.74%答案 B解析 由已知μ＝0，σ＝3.所以P (3<ξ<6)＝12[P (－6<ξ<6)－P (－3<ξ<3)]＝12(95.44%－68.26%)＝12×27.18%＝13.59%.故选B.3.设X ～N (μ1，σ21)，Y ～N (μ2，σ22)，这两个正态分布密度曲线如图所示．下列结论中正确的是( )A ．P (Y ≥μ2)≥P (Y ≥μ1)B ．P (X ≤σ2)≤P (X ≤σ1)C ．对任意正数t ，P (X ≤t )≥P (Y ≤t )D ．对任意正数t ，P (X ≥t )≥P (Y ≥t )答案 C解析 由正态分布密度曲线的性质可知，X ～N (μ1，σ21)，Y ～N (μ2，σ22)的密度曲线分别关于直线x ＝μ1，x ＝μ2对称，因此结合题中所给图象可得，μ1<μ2，所以P (Y ≥μ2)<P (Y ≥μ1)，故A 错误．又X ～N (μ1，σ21)的密度曲线较Y ～N (μ2，σ22)的密度曲线“瘦高”，所以σ1<σ2，所以P (X ≤σ2)>P (X ≤σ1)，B 错误．对任意正数t ，P (X ≤t )≥P (Y ≤t )，P (X ≥t )≤P (Y ≥t )，C 正确，D 错误．4．已知随机变量ξ服从正态分布N (0,1)，若P (ξ>1)＝a ，a 为常数，则P (－1≤ξ≤0)＝________.答案 12－a 解析 由正态曲线的对称轴为ξ＝0，又P (ξ>1)＝a ，故P (ξ<－1)＝a ，所以P (－1≤ξ≤0)＝1－2a 2＝12－a ，即答案为12－a .5．某班有50名学生，一次考试后数学成绩ξ(ξ∈N )服从正态分布N (100,102)，已知P (90≤ξ≤100)＝0.3，估计该班学生数学成绩在110分以上的人数为________．答案 10解析 由题意，知P (ξ>110)＝1－2P ξ2＝0.2，所以该班学生数学成绩在110分以上的人数为0.2×50＝10.。

2018高考数学异构异模复习考案 第十二章 概率与统计 课时撬分练12.3 二项分布及其应用、正态分布 理时间：45分钟基础组1.[2016·冀州中学热身]已知某射击运动员，每次击中目标的概率都是0.8，则该射击运动员射击4次至少击中3次的概率为( )A ．0.85B ．0.8192C ．0.8D ．0.75答案 B解析 由题意知，该射击运动员射击4次击中目标次数X ～B (4,0.8)，P (X ≥3)＝C 34·0.83·0.2＋C 44·0.84＝0.8192，故选B.2．[2016·枣强中学周测]已知盒中装有3只螺口灯泡与7只卡口灯泡，这些灯泡的外形与功率都相同且灯口向下放着，现需要一只卡口灯泡，电工师傅每次从中任取一只并不放回，则在他第1次抽到的是螺口灯泡的条件下，第2次抽到的是卡口灯泡的概率为( )A.310B.29C.78D.79答案 D解析 设事件A 为“第1次抽到的是螺口灯泡”，事件B 为“第2次抽到的是卡口灯泡”，则P (A )＝310，P (AB )＝310×79＝730.则所求概率为P (B |A )＝P ABP A ＝730310＝79.3．[2016·冀州中学预测]已知变量x 服从正态分布N (4，σ2)，且P (x >2)＝0.6，则P (x >6)＝( ) A ．0.4 B ．0.3 C ．0.2 D ．0.1答案 A解析 因为P (x >2)＝0.6，所以P (x <2)＝1－0.6＝0.4，因为N (4，σ2)，所以此正态分布的图象关于x ＝4对称，所以P (x >6)＝P (x <2)＝0.4.故选A.4．[2016·衡水二中期中]已知随机变量ξ服从正态分布N (2，σ2)，且P (ξ<4)＝0.8，则P (0<ξ<2)＝( ) A ．0.6 B ．0.4 C ．0.3 D ．0.2答案 C解析画出正态曲线如图，结合图象知：P (ξ<0)＝P (ξ >4)＝1－P (ξ<4)＝1－0.8＝0.2，P (0<ξ<2)＝12P (0<ξ<4)＝12[1－P (ξ<0)－P (ξ>4)]＝12(1－0.2－0.2)＝0.3.5.[2016·枣强中学模拟]在4次独立重复试验中，事件A 发生的概率相同，若事件A 至少发生1次的概率为6581，则事件A 在1次试验中发生的概率为( ) A.13 B.25 C.56 D.34答案 A解析 设事件A 在1次试验中发生的概率为p ，由题意得1－C 04p 0(1－p )4＝6581，所以1－p ＝23，p ＝13.6．[2016·衡水二中期末]设随机变量δ服从正态分布N (3,7)，若P (δ>a ＋2)＝P (δ<a －2)，则a ＝( ) A ．1 B ．2 C ．3 D ．4 答案 C解析 由P (δ>a ＋2)＝P (δ<a －2)，得a ＋2＋a －22＝3⇒a ＝3.7．[2016·武邑中学猜题]某种元件的使用寿命超过1年的概率为0.6，使用寿命超过2年的概率为0.3，则使用寿命超过1年的元件还能继续使用的概率为( )A ．0.3B ．0.5C ．0.6D ．1答案 B解析 设事件A 为“该元件的使用寿命超过1年”，B 为“该元件的使用寿命超过2年”，则P (A )＝0.6，P (B )＝0.3.因为B ⊆A ，所以P (AB )＝P (B )＝0.3，于是P (B |A )＝P AB P A ＝0.30.6＝0.5.8．[2016·冀州中学仿真]某人从某城市的南郊乘公交车前往北区火车站，由于交通拥挤，所需时间(单位：分)服从X ～N (50,102)，则他在时间段(30,70)内赶到火车站的概率为________．答案 0.9544解析 ∵X ～N (50,102)，∴μ＝50，σ＝10. ∴P (30<X <70)＝P (μ－2σ<X <μ＋2σ)＝0.9544.9．[2016·武邑中学预测]将一枚均匀的硬币抛掷6次，则正面出现的次数比反面出现的次数多的概率为________．答案1132解析 正面出现的次数比反面出现的次数多，则正面可以出现4次，5次或6次，所以概率P ＝C 46⎝ ⎛⎭⎪⎫126＋C 56·⎝ ⎛⎭⎪⎫126＋C 66⎝ ⎛⎭⎪⎫126＝1132.10．[2016·衡水二中模拟]某大街在甲、乙、丙三处设有红、绿灯，汽车在这三处因遇绿灯而通行的概率分别为13、12、23，则汽车在这三处因遇红灯而停车一次的概率为________．答案718解析 设汽车分别在甲、乙、丙三处通行为事件A ，B ，C ，停车为A －，B －，C －，则P (A )＝13，P (B )＝12，P (C )＝23，停车一次即为事件(A －BC )∪(A B －C )∪(AB C －)发生，故概率为P ＝⎝ ⎛⎭⎪⎫1－13×12×23＋13×⎝ ⎛⎭⎪⎫1－12×23＋13×12×⎝ ⎛⎭⎪⎫1－23＝718.11．[2016·枣强中学期末]甲、乙两人轮流投篮，每人每次投一球．约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球3次时投篮结束．设甲每次投篮投中的概率为13，乙每次投篮投中的概率为12，且各次投篮互不影响．(1)求甲获胜的概率；(2)求投篮结束时甲的投球次数ξ的分布列与期望． 解 设A k ，B k 分别表示甲、乙在第k 次投篮投中， 则P (A k )＝13，P (B k )＝12(k ＝1,2,3)．(1)记“甲获胜”为事件C ，由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知P (C )＝P (A 1)＋P (A 1 B 1A 2)＋P (A 1 B 1 A 2 B 2 A 3)＝P(A 1)＋P(A 1)P(B 1)P(A 2)＋P(A 1)P(B 1)P(A 2)·P(B 2)P(A 3)＝13＋23×12×13＋⎝ ⎛⎭⎪⎫232×⎝ ⎛⎭⎪⎫122×13＝13＋19＋127＝1327.(2)ξ的所有可能取值为1,2,3，且 P(ξ＝1)＝P(A 1)＋P(A 1B 1)＝13＋23×12＝23，P(ξ＝2)＝P(A 1 B 1A 2)＋P(A 1 B 1 A 2B 2)＝23×12×13＋⎝ ⎛⎭⎪⎫232×⎝ ⎛⎭⎪⎫122＝29，P(ξ＝3)＝P(A 1 B 1 A 2 B 2)＝⎝ ⎛⎭⎪⎫232×⎝ ⎛⎭⎪⎫122＝19.综上知，ξ的分布列为从而，E(ξ)＝1×3＋2×9＋3×9＝9.12．[2016·衡水二中仿真]某人向一目标射击4次，每次击中目标的概率为13.该目标分为3个不同的部分，第一、二、三部分面积之比为1∶3∶6，击中目标时，击中任何一部分的概率与其面积成正比．(1)设X 表示目标被击中的次数，求X 的分布列；(2)若目标被击中2次，A 表示事件“第一部分至少被击中1次或第二部分被击中2次”，求P(A)．解 (1)依题意知X ～B ⎝ ⎛⎭⎪⎫4，13， P(X ＝0)＝C 04⎝ ⎛⎭⎪⎫130⎝ ⎛⎭⎪⎫1－134＝1681，P(X ＝1)＝C 14⎝ ⎛⎭⎪⎫131⎝ ⎛⎭⎪⎫1－133＝3281，P(X ＝2)＝C 24⎝ ⎛⎭⎪⎫132⎝ ⎛⎭⎪⎫1－132＝2481，P(X ＝3)＝C 34⎝ ⎛⎭⎪⎫133⎝ ⎛⎭⎪⎫1－131＝881，P(X ＝4)＝C 44⎝ ⎛⎭⎪⎫134⎝ ⎛⎭⎪⎫1－130＝181.即X 的分布列为i i 第i 部分”，i ＝1,2.依题意知P(A 1)＝P(B 1)＝0.1， P(A 2)＝P(B 2)＝0.3，A ＝A 1B 1∪A 1B 1∪A 1B 1∪A 2B 2所求概率为P(A)＝P(A 1B 1)＋P(A 1B 1)＋P(A 1B 1)＋P(A 2B 2)＝P(A 1)P(B 1)＋P(A 1)P(B 1)＋P(A 1)P(B 1)＋P(A 2)P(B 2)＝0.1×0.9＋0.9×0.1＋0.1×0.1＋0.3×0.3＝0.28.能力组13.[2016·枣强中学期中]一台机床有13的时间加工零件A ，其余时间加工零件B .加工零件A 时，停机的概率为310，加工零件B 时，停机的概率是25，则这台机床停机的概率为( )A.1130B.730C.710 D.110答案 A解析 加工零件A 停机的概率是13×310＝110，加工零件B 停机的概率是⎝ ⎛⎭⎪⎫1－13×25＝415，所以这台机床停机的概率是110＋415＝1130. 14．[2016·冀州中学猜题]一盒中放有大小相同的10个小球，其中8个黑球、2个红球，现甲、乙二人先后从盒子中无放回地任意抽取2个小球，已知甲取到了2个黑球，则乙也取到2个黑球的概率是________．答案1528解析 记事件“甲取到2个黑球”为A ，“乙取到2个黑球”为B ，则有P (B |A )＝P AB P A ＝C 28·C 26C 28·C 28＝1528，即事件“甲取到2个黑球，乙也取到2个黑球”的概率是1528.15．[2016·武邑中学仿真]设随机变量X ～N (10,1)，P (9≤x <10)＝a ，其中a ＝⎠⎜⎜⎛14191x d x ，则P(X≥11)＝______.答案 16解析 ∵a＝⎠⎜⎜⎛14191xd x ＝2x12⎪⎪⎪⎪1419＝2⎝ ⎛⎭⎪⎫12－13＝13， ∴P(X≥11)＝1－2a 2＝12－13＝16.16.[2016·衡水中学模拟]在一次数学考试中，第22,23,24题为选做题，规定每位考生必须且只须在其中选做一题，设5名考生选做这三题中任意一题的可能性均为13，每位学生对每题的选择是相互独立的，各学生的选择相互之间没有影响．(1)求其中甲、乙两人选做同一题的频率；(2)设选做第23题的人数为ξ，求ξ的分布列及数学期望．解 (1)设事件A 1表示甲选22题，A 2表示甲选23题，A 3表示甲选24题， B 1表示乙选22题，B 2表示乙选23题，B 3表示乙选24题，则甲、乙两人选做同一题的事件为A 1B 1＋A 2B 2＋A 3B 3，且A 1与B 1，A 2与B 2，A 3与B 3相互独立，所以P(A 1B 1＋A 2B 2＋A 3B 3)＝P(A 1)P(B 1)＋P(A 2)P(B 2)＋P(A 3)P(B 3)＝3×19＝13.(2)ξ可能取值为0,1,2,3,4,5，则精品ξ～B ⎝⎛⎭⎪⎫5，13.∴P(ξ＝k)＝C k5⎝ ⎛⎭⎪⎫13k ⎝ ⎛⎭⎪⎫235－k ＝C k 525－k35，k ＝0,1,2,3,4,5.∴ξ的分布列为∴E(ξ)＝np ＝5×3＝3.。

2018高考数学异构异模复习考案 第十二章 概率与统计 课时撬分练12.4 统计与统计案例 理基础组时间：60分钟1.[2016·冀州中学期中]某市共有400所学校，现要用系统抽样的方法抽取20所学校作为样本，调查学生课外阅读的情况．把这400所学校编上1～400的号码，再从1～20中随机抽取一个号码，如果此时抽得的号码是6，则在编号为21到40的学校中，应抽取的学校的编号为( )A ．25B ．26C ．27D ．以上都不是答案 B解析 系统抽样是把个体编号后，先抽取第一个，然后每次间隔相同的数依次抽取，本题中每次间隔20，第一个抽取的是6号，接下来应该抽取的是第26号，故选B.2．[2016·衡水中学仿真]在某次测量中得到的A 样本数据如下：82,84,84,86,86,86,88,88,88,88.若B 样本数据恰好是A 样本数据每个都加2后所得数据，则A ，B 两样本的下列数字特征对应相同的是( )A ．众数B ．平均数C ．中位数D ．标准差 答案 D解析 由题原来众数88变为90，中位数由86变为88，平均数增加2，所以每个数与平均数的差不变，即标准差不变．故选D.3．[2016·枣强中学预测]对具有线性相关关系的变量x ，y 有一组观测数据(x i ，y i )(i ＝1,2，…，8)，其回归直线方程是y ^＝13x ＋a ^，且x 1＋x 2＋x 3＋…＋x 8＝2(y 1＋y 2＋…＋y 8)＝6，则实数a ^的值是( )A.116B.18C.14D.12答案 B解析 依题意可知x ＝68，y ＝38，样本中心点为⎝ ⎛⎭⎪⎫34，38，则38＝13×34＋a ^，解得a ^＝18.4.[2016·冀州中学一轮检测]为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分(十分制)如图所示，假设得分值的中位数为m e ，众数为m o ，平均值为x ，则( )A ．m e ＝m o ＝xB ．m e ＝m o <xC ．m e <m o <xD ．m o <m e <x答案 D解析 由图可知，30名学生的得分情况依次为：2个人得3分，3个人得4分，10个人得5分，6个人得6分，3个人得7分，2个人得8分，2个人得9分，2个人得10分．中位数为第15个数和第16个数(分别为5,6)的平均数，即m e ＝5.5,5出现次数最多，故m o ＝5，x ＝2×3＋3×4＋10×5＋6×6＋3×7＋2×8＋2×9＋2×1030≈5.97.于是得m o <m e <x .故选D.5．[2016·武邑中学一轮检测]某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测．若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是( )A ．4B ．5C ．6D ．7 答案 C解析 四类食品的每一种被抽到的概率为 2040＋10＋30＋20＝15，∴植物油类和果蔬类食品被抽到的种数之和为(10＋20)×15＝6.6．[2016·武邑中学月考]甲、乙两位运动员在5场比赛的得分情况如茎叶图所示，记甲、乙两人的平均得分分别为x －甲，x －乙，则下列判断正确的是( )A.x －甲>x －乙；甲比乙成绩稳定B.x －甲>x －乙；乙比甲成绩稳定C.x －甲<x －乙；甲比乙成绩稳定D.x －甲<x －乙；乙比甲成绩稳定 答案 D解析 由茎叶图可知x －甲＝17＋16＋28＋30＋345＝25，x －乙＝15＋28＋26＋28＋335＝26，∴x －甲<x －乙．又s 2甲＝15[(17－25)2＋(16－25)2＋(28－25)2＋(30－25)2＋(34－25)2]＝52，s 2乙＝15[(15－26)2＋(28－26)2＋(26－26)2＋(28－26)2＋(33－26)2]＝35.6，∴s 2甲>s 2乙，∴乙比甲成绩稳定．7.[2016·衡水中学热身]将参加夏令营的600名学生编号为：001,002，…，600.采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003.这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495在第Ⅱ营区，从496到600在第Ⅲ营区，三个营区被抽中的人数依次为( )A ．26,16,8B ．25,17,8C ．25,16,9D ．24,17,9答案 B解析 依题意及系统抽样可知，将这600名学生按编号依次分成50组，每一组各有12名学生，第k (k ∈N *)组抽中的号码是3＋12(k －1)．令3＋12(k －1)≤300得k ≤1034，因此第Ⅰ营区被抽中的人数是25；令300<3＋12(k－1)≤495得1034<k ≤42，因此第Ⅱ营区被抽中的人数是42－25＝17.所以第Ⅲ营区被抽中的人数为50－25－17＝8(人)．8．[2016·衡水二中热身]在一组样本数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )(n ≥2，x 1，x 2，…，x n 不全相等)的散点图中，若所有样本点(x i ，y i )(i ＝1,2，…，n )都在直线y ＝12x ＋1上，则这组样本数据的样本相关系数为( )A ．－1B ．0 C.12 D ．1答案 D解析 由题设可知这组样本中的数据完全正相关，又都在y ＝12x ＋1上，故相关系数为1，故选D.9．[2016·武邑中学期末]甲、乙两名射击运动员参加某大型运动会的预选赛，他们分别射击了5次，成绩如下表(单位：环)：如果甲、乙两人中只有1答案 甲解析 x 甲＝x 乙＝9环，s 2甲＝15[(9－10)2＋(9－8)2＋(9－9)2＋(9－9)2＋(9－9)2]＝25，s 2乙＝15[(9－10)2＋(9－10)2＋(9－7)2＋(9－9)2＋(9－9)2]＝65>s 2甲，故甲更稳定，故填甲．10．[2016·衡水二中预测]某中学2015年共91人参加高考，统计数据如下：答案 无关解析 2×2列联表如下：统计假设H 0计算K 2＝－255×36×50×41≈0.11.我们接受统计假设，故考生的户口形式对高考录取没有影响．11．[2016·枣强中学月考]某市统计局就本地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图(每个分组包括左端点，不包括右端点，如第一组表示月收入在[1000,1500)(单位：元)．(1)估计居民月收入在[1500,2000)的概率； (2)根据频率分布直方图估计样本数据的中位数．解 (1)由题意知，居民月收入在[1500,2000)的概率约为1－(0.0002＋0.0001＋0.0003＋0.0005×2)×500＝1－0.0016×500 ＝1－0.8＝0.2.(2)由频率分布直方图知，中位数在[2000,2500)中，设中位数为x ，则0.0002×500＋0.2＋0.0005(x －2000)＝0.5，解得x ＝2400.12.[2016·衡水二中猜题]以下茎叶图记录了甲、乙两组各四名同学的植树棵树，乙组记录中有一个数据模糊，无法确认，在图中用X 表示．(1)如果X ＝8，求乙组同学植树棵树的平均数与方差；(2)如果X ＝9，分别从甲、乙两组中随机选取一名同学，求这两名同学植树总棵数为19的概率．解 (1)当X ＝8时，由茎叶图可知，乙组同学的植树棵树是8,8,9,10，所以平均数为x －＝8＋8＋9＋104＝354， 方差为s 2＝14⎣⎢⎡ ⎝⎛⎭⎪⎫8－3542＋⎝ ⎛⎭⎪⎫8－3542＋⎝ ⎛⎭⎪⎫9－3542⎦⎥⎤＋⎝⎛⎭⎪⎫10－3542＝1116.(2)当X ＝9时，记甲组四名同学为A 1，A 2，A 3，A 4，他们植树的棵数依次为9,9,11,11；乙组四名同学为B 1，B 2，B 3，B 4，他们植树的棵数依次为9,8,9,10.分别从甲、乙两组中随机选取一名同学，所有可能的结果有16个，它们是(A 1，B 1)，(A 1，B 2)，(A 1，B 3)，(A 1，B 4)，(A 2，B 1)，(A 2，B 2)，(A 2，B 3)，(A 2，B 4)， (A 3，B 1)，(A 3，B 2)，(A 3，B 3)，(A 3，B 4)， (A 4，B 1)，(A 4，B 2)，(A 4，B 3)，(A 4，B 4)．用C 表示“选出的两名同学的植树总棵树为19”这一事件，则C 中的结果有4个，它们是(A 1，B 4)，(A 2，B 4)，(A 3，B 2)，(A 4，B 2)．由古典概型知，所求概率P (C )＝416＝14. 能力组13.[2016·衡水二中一轮检测]某产品在某零售摊位上的零售价x (单位：元)与每天的销售量y (单位：个)的统计资料如下表所示：由上表可得回归直线方程y ^＝b ^x ＋a ^中的b ＝－4，据此模型预计零售价定为15元时，每天的销售量为( )A ．48个B ．49个C ．50个D ．51个答案 B解析 由题意知x －＝17.5，y －＝39，代入回归直线方程得a ^＝109,109－15×4＝49，故选B.14．[2016·冀州中学周测]某商场调查旅游鞋的销售情况，随机抽取了部分顾客的购鞋尺寸，整理得如下频率分布直方图，其中直方图从左至右的前3个小矩形的面积之比为1∶2∶3，则购鞋尺寸在[39.5,43.5)内的顾客所占百分比为________．答案 55%解析 后两个小组的频率为(0.0375＋0.0875)×2＝0.25， 所以前3个小组的频率为1－0.25＝0.75， 又前3个小组的面积比为1∶2∶3， 即前3个小组的频率比为1∶2∶3.所以第三小组的频率为31＋2＋3×0.75＝0.375，第四小组的频率为0.0875×2＝0.175，所以购鞋尺寸在[39.5,43.5)的频率为0.375＋0.175＝0.55＝55%.15．[2016·冀州中学热身]有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表．已知从全部105人中随机抽取1人为优秀的概率为7.(1)请完成上面的列联表；(2)根据列联表的数据，能否有95%的把握认为“成绩与班级有关系”？(3)按下面的方法从甲班的优秀学生中抽取一人．把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到6号或10号的概率．附：K2＝n ad－bc2a ＋b c＋d a＋c b＋d，其中n＝a＋b＋c＋d.解(1)2×2列联表如下；(2)根据列联表中的数据，得到K2＝－255×50×30×75≈6.109>3.841，因此有95%的把握认为“成绩与班级有关系”．(3)设“抽到6号或10号”为事件A，先后两次抛掷一枚均匀的骰子，出现的点数为(x，y)，则所有的基本事件有(1,1)，(1,2)，(1,3)，…，(6,6)，共36个．事件A包含的基本事件有(1,5)，(2,4)，(3,3)，(4,2)，(5,1)，(4,6)，(5,5)，(6,4)，共8个，∴P(A)＝8 36＝29.16．[2016·枣强中学周测]某百货公司1～6月份的销售量x与利润y的统计数据如下表：(1)根据2至5月份的数据，画出散点图，求出y关于x的回归直线方程y＝b x＋a；(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元，则认为得到的回归直线方程是理想的，试问所得回归直线方程是否理想？解 (1)根据表中2至5月份的数据作出散点图，如图所示：计算得x －＝11，y －＝24，∑5i ＝2x i y i ＝11×25＋13×29＋12×26＋8×16＝1092，∑5i ＝2x 2i ＝112＋132＋122＋82＝498，则b ^＝∑5i ＝2x i y i －4x －y－∑5i ＝2x 2i －4x－2＝1092－4×11×24498－4×112＝187， a ^＝y －－b ^x －＝24－187×11＝－307.故y 关于x 的回归直线方程为y ^＝187x －307. (2)当x ＝10时，y ^＝187×10－307＝1507，此时⎪⎪⎪⎪⎪⎪1507－22<2；当x ＝6时，y ^＝187×6－307＝787，此时⎪⎪⎪⎪⎪⎪787－12<2.故所得的回归直线方程是理想的．。

教学资料范本【2019-2020】高考数学异构异模复习第十二章概率与统计课时撬分练12-2离散型随机变量及其分布列均值与方差理编辑：__________________时间：__________________20xx高考数学异构异模复习考案 第十二章 概率与统计 课时撬分练12.2 离散型随机变量及其分布列、均值与方差 理时间：60分钟基础组1.[20xx·枣强中学模拟]设随机变量的分布列如表所示，且E(ξ)＝1.6，则ab＝()ξ012 3P 0.1 a b 0.1A.0.2 B．0.1C．0.15 D．0.4答案 C解析由分布列的性质，得0.1＋a＋b＋0.1＝1.∴a＋b＝0.8.①又由E(ξ)＝0×0.1＋1×a＋2×b＋3×0.1＝1.6，得a＋2b＝1.3.②由①②解得a＝0.3，b＝0.5，∴ab＝0.3×0.5＝0.15.2．[20xx·衡水二中期末]某运动员投篮命中率为0.6，他重复投篮5次，若他命中一次得10分，没命中不得分；命中次数为X，得分为Y，则E(X)，D(Y)分别为()A．0.6,60 B．3,12C．3,120 D．3,1.2答案 C解析X～B(5,0.6)，Y＝10X，∴E(X)＝5×0.6＝3，D(X)＝5×0.6×0.4＝1.2，D(Y)＝100D(X)＝120.3．[20xx·武邑中学猜题]一个人将编号为1,2,3,4的四个小球随机放入编号为1,2,3,4的四个盒子中，每个盒子放一个小球，球的编号与盒子的编号相同时叫做放对了，否则叫做放错了．设放对的个数为ξ，则ξ的期望值为()A.12B.23C．1 D．2答案 C解析将四个不同小球放入四个不同盒子，每个盒子放一个小球，共有A4种不同放法，放对的个数ξ可取的值有0,1,2,4.其中，P(ξ＝0)＝9 A44＝38，P(ξ＝1)＝C14×2A44＝13，P(ξ＝2)＝C24A44＝14，P(ξ＝4)＝1A44＝124，E(ξ)＝0×38＋1×13＋2×14＋4×124＝1，故选C.4．[20xx·冀州中学仿真]已知ξ～B⎝⎛⎭⎪⎫4，13，并且η＝2ξ＋3，则方差D(η)＝()A.329B.89C.439D.599答案 A解析D(ξ)＝4×13×⎝⎛⎭⎪⎫1－13＝89，∵η＝2ξ＋3，∴D(η)＝4·D(ξ)＝4×89＝329.5．[20xx·武邑中学预测]现有10张奖券，8张2元的，2张5元的，某人从中随机地、无放回地抽取3张，则此人得奖金额的数学期望是() A．6 B．7.8C．9 D．12答案 B解析P(ξ＝6)＝C38C310，P(ξ＝9)＝C28C12C310，P(ξ＝12)＝C18C22 C310，则E(ξ)＝6×C38C310＋9×C28C12C310＋12×C18C22C310＝7.8.6．[20xx·衡水二中模拟]甲乙两人分别独立参加某高校自主招生面试，若甲、乙能通过面试的概率都是23，则面试结束后通过的人数X的数学期望是()A.43B.119C．1 D.8 9答案 A解析依题意，X的取值为0,1,2，且P (X ＝0)＝⎝⎛⎭⎪⎫1－23×⎝ ⎛⎭⎪⎫1－23＝19，P (X ＝1)＝23×⎝ ⎛⎭⎪⎫1－23＋⎝ ⎛⎭⎪⎫1－23×23＝49， P (X ＝2)＝23×23＝49.故X 的数学期望E (X )＝0×19＋1×49＋2×49＝129＝43，故选A.7．[20xx·枣强中学期末]设随机变量ξ的概率分布列如下表所示：x 0 1 2P (ξ＝x )a b c其中a ，b ，c 成等差数列，若随机变量ξ的均值为43，则ξ的方差为________．答案 59解析由题意有a ＋b ＋c ＝1,2b ＝a ＋c ，b ＋2c ＝43，解得a ＝16，b ＝13，c ＝12，则其方差为D (ξ)＝⎝⎛⎭⎪⎫0－432×16＋⎝ ⎛⎭⎪⎫1－432×13＋⎝ ⎛⎭⎪⎫2－432×12＝59.8．[20xx·衡水二中仿真]某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者，若用随机变量ξ表示选出的志愿者中女生的人数，则均值E (ξ)＝________(结果用最简分数表示)．答案 47 解析可以将“从7名学生中选出2名志愿者”看作“从7件产品中抽取2件产品”，将“选出的志愿者中女生的人数”看作“任取2件产品中的次品数”，则随机变量ξ服从参数为N ＝7，M ＝2，n ＝2的超几何分布．ξ的可能取值为0,1,2，因为P (ξ＝0)＝C25C27＝1021，P (ξ＝1)＝C12C15C27＝1021，P (ξ＝2)＝C22C27＝121，故ξ的分布列为ξ0 1 2 P10211021121从而E(ξ)＝0×1021＋1×1021＋2×121＝47.或由超几何分布期望E(ξ)＝nMN＝2×27＝47.9.[20xx·枣强中学期中]一个袋子里装有7个球，其中有红球4个，编号分别为1,2,3,4；白球3个，编号分别为1,2,3.从袋子中任取4个球(假设取到任何一个球的可能性相同)．(1)求取出的4个球中，含有编号为3的球的概率；(2)在取出的4个球中，红球编号的最大值设为X，求随机变量X的分布列和数学期望．解(1)设“取出的4个球中，含有编号为3的球”为事件A，由题意知，取出4个球共有C47种取法，其中含有编号为3的球的取法有C12C35＋C2C25种．则P(A)＝C12C35＋C2C25C47＝67.所以取出的4个球中，含有编号为3的球的概率为6 7 .(2)随机变量X的所有可能取值为1,2,3,4，则P(X＝1)＝C33C47＝135，P(X＝2)＝C34C47＝435，P(X＝3)＝C35C47＝27，P(X＝4)＝C36C47＝47，所以随机变量X的分布列为X 123 4P1354352747随机变量X的数学期望E(X)＝1×135＋2×435＋3×27＋4×47＝175.10．[20xx·衡水二中热身]为振兴旅游业，四川省20xx年面向国内发行总量为20xx万张的熊猫优惠卡，向省外人士发行的是熊猫金卡(简称金卡)，向省内人士发行的是熊猫银卡(简称银卡)．某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游，其中34是省外游客，其余是省内游客．在省外游客中有13持金卡，在省内游客中有23持银卡．(1)在该团中随机采访3名游客，求恰有1人持金卡且持银卡者少于2人的概率；(2)在该团的省内游客中随机采访3名游客，设其中持银卡人数为随机变量ξ，求ξ的分布列．解(1)由题意得，省外游客有27人，其中9人持金卡；省内游客有9人，其中6人持银卡．设事件B为“采访该团3人，恰有1人持金卡且持银卡者少于2人”，事件A1为“采访该团3人，1人持金卡，0人持银卡”，事件A2为“采访该团3人，1人持金卡，1人持银卡”，则P(B)＝P(A1)＋P(A2)＝C19C221C336＋C19C16C121C336＝934＋27170＝3685.所以在该团中随机采访3人，恰有1人持金卡且持银卡者少于2人的概率是36 85 .(2)ξ的可能取值为0,1,2,3，且ξ服从参数为N＝9，M＝6，n＝3的超几何分布，故P(ξ＝0)＝C06C33C39＝184，P(ξ＝1)＝C16C23C39＝314，P(ξ＝2)＝C26C13C39＝1528，P(ξ＝3)＝C36C03C39＝521.所以ξ的分布列为ξ012 3P184314152852111.[20xx·武邑中学期末]袋中有20个大小相同的球，其中记上0号的有10个，记上n号的有n个(n＝1,2,3,4)，现从袋中任取一球，ξ表示所取球的标号．(1)求ξ的分布列、期望和方差；(2)若η＝aξ＋b，E(η)＝1，D(η)＝11，试求a，b的值．解(1)ξ的取值为0,1,2,3,4，其分布列为ξ0123 4P 1212011032015∴E(ξ)＝0×12＋1×120＋2×110＋3×320＋4×15＝1.5，D (ξ)＝(0－1.5)2×12＋(1－1.5)2×120＋(2－1.5)2×110＋(3－1.5)2×320＋(4－1.5)2×15＝2.75.(2)由D (η)＝a 2D (ξ)得2.75a 2＝11，得a ＝±2， 又E (η)＝aE (ξ)＋b ，∴当a ＝2时，由1＝2×1.5＋b ，得b ＝－2； 当a ＝－2时，由1＝－2×1.5＋b ，得b ＝4， ∴⎩⎨⎧a＝2，b＝－2，或⎩⎨⎧a＝－2，b＝4.12．[20xx·衡水二中预测]年龄在60岁(含60岁)以上的人称为老龄人，某地区老龄人共有35万，随机调查了该地区700名老龄人的健康状况，结果如下表：健康指数 2 1 0 －1 60岁至79岁的人数 250 260 6525 80岁及以上的人数20452015其中健康指数的含义是：2表示“健康”，1表示“基本健康”，0表示“不健康，但生活能够自理”，－1表示“生活不能自理”．(1)估计该地区80岁以下老龄人生活能够自理的概率；(2)若一个地区老龄人健康指数的平均值不小于1.2，则该地区可被评为“老龄健康地区”．请写出该地区老龄人健康指数X 的分布列，并判断该地区能否被评为“老龄健康地区”．解 (1)该地区80岁以下老龄人生活能够自理的频率为250＋260＋65250＋260＋65＋25＝2324， 所以该地区80岁以下老龄人生活能够自理的概率约为2324. (2)该地区老龄人健康指数X 的可能取值为2,1,0，－1，其分布列为(用频率估计概率)：X 2 1 0 －1 P2707003057008570040700E (X )＝2×270700＋1×305700＋0×85700＋(－1)×40700＝1.15， 因为E (X )<1.2，所以该地区不能被评为“老龄健康地区”．能力组13.[20xx·枣强中学月考]某种种子每粒发芽的概率都为0.9，现播种了1000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X，则X的数学期望为()A．100 B．200C．300 D．400答案 B解析记“不发芽的种子数为ξ”，则ξ～B(1000,0.1)，所以E(ξ)＝1000×0.1＝100，而X＝2ξ，故E(X)＝E(2ξ)＝2E(ξ)＝200.14．[20xx·衡水二中猜题]若p为非负实数，随机变量ξ的分布列如下表，则E(ξ)的最大值为________，D(ξ)的最大值为________．ξ01 2P 12－p p12答案321解析E(ξ)＝p＋1≤32⎝⎛⎭⎪⎫0≤p≤12；D(ξ)＝－p2－p＋1≤1.15．[20xx·衡水二中一轮检测]某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历．假定该毕业生得到甲公司面试的概率为23，得到乙、丙两公司面试的概率均为p，且三个公司是否让其面试是相互独立的，记X为该毕业生得到面试的公司个数．若P(X＝0)＝112，则随机变量X的数学期望E(X)＝________.答案5 3解析由题意知P(X＝0)＝13(1－p)2＝112，∴p＝12.随机变量X的分布列为X 012 3P1121351216E(X)＝0×112＋1×13＋2×512＋3×16＝53.16.[20xx·冀州中学周测]甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛．假设每局甲获胜的概率为23，乙获胜的概率为13，各局比赛结果相互独立．(1)求甲在4局以内(含4局)赢得比赛的概率；(2)记X 为比赛决出胜负时的总局数，求X 的分布列和均值(数学期望)． 解用A 表示“甲在4局以内(含4局)赢得比赛”，A k 表示“第k 局甲获胜”，B k 表示“第k 局乙获胜”，则P (A k )＝23，P (B k )＝13，k ＝1,2,3,4,5.(1)P (A )＝P (A 1A 2)＋P (B 1A 2A 3)＋P (A 1B 2A 3A 4)＝P (A 1)P (A 2)＋P (B 1)P (A 2)P (A 3)＋P (A 1)P (B 2)P (A 3)P (A 4) ＝⎝ ⎛⎭⎪⎫232＋13×⎝ ⎛⎭⎪⎫232＋23×13×⎝ ⎛⎭⎪⎫232＝5681. 所以甲在4局以内(含4局)赢得比赛的概率为5681. (2)X 的可能取值为2,3,4,5.P (X ＝2)＝P (A 1A 2)＋P (B 1B 2) ＝P (A 1)P (A 2)＋P (B 1)P (B 2)＝59，P (X ＝3)＝P (B 1A 2A 3)＋P (A 1B 2B 3)＝P (B 1)P (A 2)P (A 3)＋P (A 1)P (B 2)P (B 3)＝29，P (X ＝4)＝P (A 1B 2A 3A 4)＋P (B 1A 2B 3B 4)＝P (A 1)P (B 2)P (A 3)P (A 4)＋P (B 1)P (A 2)P (B 3)·P (B 4)＝1081， P (X ＝5)＝1－P (X ＝2)－P (X ＝3)－P (X ＝4)＝881.故X 的分布列为X 2 3 4 5 P 59 29 1081881E (X )＝2×59＋3×29＋4×1081＋5×881＝22481.。