高中数学复习讲义 第一章 集合与简易逻辑

⊂⊂⊂高一数学第一章集合与简易逻辑辅导讲义第一讲集合【辅导内容】 1、集合2、子集、全集、补集3、交集、并集 【学习内容】 一、集合的概念1、常用数集及其记法。

φ空集 N 非负整数集，自然数集 N +或N +正整数集 Z 整数集Q 有理数集 R 实数集 C 复数集 2、集合中元素的特征确定性；互异性；无序性， 会判断一组对象是否组成集合 3、集合的表示方法 ①列举法②描述法{x| p(x)} 4、集合的分类空集，有限集，无限集 二、子集，全集，补集1、掌握子集，真子集，全集，补集的概念及表示方法2、掌握子集，补集的性质①A ⊆B B ⊆C 则A ⊆C A ≠B B ≠C 则A ≠C②A ⊆BB ⊆A则A=B③Cu(CuA)=A ；CuU=φ，Cu φ=U ，CuA ⊆U ④φ⊆A ，A ⊆A三、交集、并集1、掌握交集、并集的概念及表示方法2、结合文氏图，掌握交集并集的性质①A ∩A=A ，A ∩φ=φA ∪A=A ，A ∪φ=A ②(A ∩B)⊆A ，(A ∩B)⊆B(A ∪B)⊇A ，(A ∪B)⊇B③A ∩B=B ∩A A ∪B=B ∪A ④若A ⊆B 则A ∩B=A 反之也其 若A ⊆B 则A ∪B=B 反之也其 ⑤(A ∩B) ⊆(A ∪B)当且仅当A=B 时，A ∩B= A ∪B⊂⊂3、结合文氏图及数轴会求两集合的交集，并集，补集四、1、理解奇数、偶数的定义，会用集合语言表示奇数集，偶数集、整数集之间的关系2、注意a 与{a}的区别，以及φ，0，{0}的区别。

【例题选讲】例1、已知集合A={x|ax 2+2x+1=0,a ∈R}（1）若A 只有一个元素，试求a 的值，并求出这个元素； （2）若A 是空集，求a 的取值范围；（3）若A 中至多有一个元素，求a 取值范围 分析：（1）集合只有一个元素时有两种情形： ①a=0，方程为2x+1=0，只有一个根为21-=x ②当a ≠0时，△=0，即4-4a=0，∴a=1，这时方程有两个相同的实数根x 1=x 2=-1 由①②可知，当a=0或a=1时，A 中只有一个元素，分别为21-或-1 （2）若A 为空集，则必须有⎩⎨⎧<-=∆≠0440a a ，解得a>1。

高中数学核心知识点及基本思想方法总结第一章 集合与简易逻辑¤第一部分·集合与集合运算¤◆内容概述◆集合是现代数学的基本概念，专门研究集合的理论叫做集合论。

“疯人数学家”康托尔(Cantor,G.F.P,1845-1918年，德国人)是集合论的创始者。

目前集合论的基本思想已渗透到现代数学的所有领域。

集合的思想、集合的语言和集合的符号在高中数学的很多章节如函数、数列、方程和不等式、立体几何、解析几何等中都被广泛的使用。

要求理解集合、子集、补集、交集、并集的概念。

了解空集和全集的意义。

了解属于、包含、相等关系的意义。

掌握有关术语和符号，并会用它们正确表示一些简单的集合。

◆知识点拨◆※< 1 >※ 集合与元素。

一般地，某些指定的对象．．．．．集在一起就成为一个集合（确定性）。

集合中每个对象叫做这个集合的元素。

【注意】①集合的确定性如何体现？（例如很高的山，一条快乐的鱼能成为一个集合么） ②元素与集合的关系。

（属于∈、不属于∉）【例题】设集合},12|{},,2|{Z k k x x B Z k k x x A ∈+==∈==，若B b A a ∈∈,，试判断a+b 与A 、B 的关系。

〖分析〗两个集合中的k 不可以理解成是同一个变量，即解作：Z k k b a k b B b k a A a ∈+=+∴+=∴∈=∴∈,14,12,,2,，此法失去任意性。

〖解答〗.,,.1)(2,,12,,,2,21212211A b a B b a Z k k k k b a Z k k b B b Z k k a A a ∉+∈+∴∈+++=+∴∈+=∴∈∈=∴∈ ③集合中元素的三个特征。

（确定性、互异性、无序性） 【例题】已知}1,12,3{2+--=a a a A ，其中R a ∈。

（1）若A ∈-3，求实数a 的值；（2）当a 为何值时，集合A 的表示不正确？〖解答〗.2,,,11213123:,,3,)2(;10,12333,13)1(222-=∴∈+=-+=--=--==-=--=-∴+≠-a R a A a a a a a a A a a a a a 的表示不正确时或或即表示不正确集合个元素有重复情况时当由集合中元素的互异性或解得或显然④集合的表示方法有哪些？（列举法、描述法、图示法、区间法）【思考】各表示方法的特点，比如描述法注意限制决定条件、条件决定元素、元素决定集合。

第一章集合与简易逻辑第一单元集合单元知识要点点击本单元是“集合”.在初中数集(整数的集合、有理数的集合)、点集(直线、圆)等基础上,给出集合与集合元素的概念,并介绍其表示方法.从讨论集合与集合之间包含与相等关系入手,给出了子集的概念,与子集相联系的全集与补集的概念,属于集合运算的交集、并集的初步知识.考虑到集合知识的运用与巩固及下一章的函数的定义域与值域的需要,介绍了含绝对值不等式和一元二次不等式的解法.1.1 集合①课文三点专讲重点:(1)集合的含义集合的概念是数学中最原始的、不加定义的概念，它只是通过一些实例，描述性地说明其含义.(2)集合中元素的特征给定的集合，它的元素必须是确定的，互异的，并且集合与其中元素的排列次序无关，即集合中元素的三个性质：确定性、互异性、无序性.只要构成集合的元素是一样的，这两个集合就是相等的.(3)元素与集合的关系如果a是集合A的元素，就说a属于A，记作：a∈A；如果a不是集合A的元素，就说a不属于A，记作：a A.难点：运用集合的两种常用表示方法——列举法与描述法，正确表示一些简单的集合(1)集合的表示——列举法列举法表示集合就是把集合中的元素一一列举出来，并用花括号“{ }”括起来.(2)集合的表示——描述法有些集合的元素无法用列举法一一列举出来的，我们可以用描述法表示，即在花括号“{ }”内先写上表示这个集合元素的一般符号及取值（或变化）范围，再画一条竖线，在竖线后写出这个集合中元素所具有的共同特征.考点:(1)集合元素的特性:考察集合元素的确定性、互异性、无序性,是高考中常考的内容之一.(2)集合的表示方法:考察集合的列举法和描述法两种表示方法,常用的还有图示法,要分清几种方法能间的相互转化及其关系.②练功篇典型试题分析例1.已知23{3,21,1}a a a -∈--+, 求实数a 的值.分析: -3的值可能有三种可能取值情况,必须分别代入求解,但要注意最后必须要验证所得结果的正确性. 实质上对于集合2{3,21,1}a a a --+均可能是-3 , 考虑集合元素的互异性, 在求得0a =或1a =-后,重新代入集合验证是必要的, 因为求得的值很可能会出现集合中有两个元素相同 , 此时对应的a 的值要舍去.解析: 由23{3,21,1}a a a -∈--+,可得33a -=-,即0a =; 或213a -=-,即1a =-; 或213a +=-(此方程无解). 当0a =时2{3,21,1}{3,1,1}a a a --+=-- ; 当1a =-时, 2{3,21,1}{4,3,2}a a a --+=-- . 所以0a =或1a =- . 例2.用列举法表示下列集合: (1)6{|,}2x Z x Z x ∈∈-; (2)*{|,,,||2,3}a x x a Z a b N b b=∈<∈≤且;(3) {(,)|2,14}x y y x x N x =-∈≤<且; (4) {|}x y x N ∈.分析:上述几题均是用描述法表示集合,列举其元素时一定要注意各自集合中的代表元素.寻找集合中的元素时,先要将其满足条件的集合中的相关数一一列举出来,其关键在于抓住集合中元素的特征,在列举元素时,要注意充分考虑集合中元素的三个特征:确定性、互异性、无序性,如(2)集合中的元素个数只能有7个.解析:(1)∵6,2Z x Z x∈∈- , ∴|2|x -是6的因数 , 即|2|x -的值应取1或2或3或6, 分别解得1,3,4,0,1,5,4,8x =-- , ∴6{|,}{1,3,4,0,1,5,4,8}2x Z x Z x∈∈=--- . (2)由,||2a Z a ∈<知1,0,1a =-; 由*3b N b ∈≤且知1,2,3b = . ∴a b 的值分别为101101101,,,,,,,,111222333--- , 考虑到集合中元素的互异性,故原集合可用列举法表示为:1111{1,0,1,,,,}2233--- . (3)由14x N x ∈≤<且知1,2,3x =, 其对应的y 的值分别为1,0,1y =-, 故原集合用列举法可表示为:{(1,1),(2,0),(3,1)}- .(4) 由已知条件可得20x x N -≥∈且, 即2x x N ≤∈且 , ∴0,1,2x = ,∴{|}{0,1,2}x y x N ∈= .基础知识巩固1.用列举法表示下列集合：(1)｛y ｜y ＝－x 2－2x ＋3，x ∈R ，y ∈N ｝．(2)｛20以内的质数｝．(3)｛(x ，y )｜x ＋y ＝6，x ∈N ，y ∈N ｝．2.用描述法表示下列集合：(1)数轴上离开原点的距离大于3的点的集合.(2)平面直角坐标系中第Ⅱ、Ⅲ象限点的集合．(3)方程组⎩⎨⎧=-=+11y x y x 的解的集合.(4)能被3整除的整数.3.用列举法表示下列集合:(1) {|}y y x N =∈;(2) {(,)|}x y y x N =∈4.方程组⎩⎨⎧=+-=++03062y x y x 的解集是 ( ). A .{(-3,0)} B .{-3,0} C .(-3,0) D .{(0,-3)}5.下列各题中M 与P 表示同一集合的是 ( )A .)},3,1{(-=M )}1,3{(-=PB .}0{,=∅=P MC .22{|1,},{(,)|1,}M y y x x R P x y y x x R ==+∈==+∈D .22{|1,},{|(1)1,}M y y x x R P t t y y R ==+∈==-+∈6.下列四个关系中，正确的是 ( )A .}{a ∈∅B .}0{=∅C .},{}{b a a ∈D .}}{},{{}{b a a ∈7.已知A ＝｛－2，－1，0，1｝，B ＝｛x ｜x ＝｜y ｜y ∈A ｝，求B ．8..将方程组⎩⎨⎧=-=+273223y x y x 的解集用列举法、描述法分别表示． 9..设集合A ＝｛x ｜x ＝2k ，k ∈Z ｝，B ＝｛x ｜x ＝2k ＋1，k ∈Z ｝，C ＝｛x ｜x ＝4k ＋1，k ∈Z ｝，又有a ∈A ，b ∈B ，判断元素a ＋b 与集合A 、B 和C 的关系．10.已知2{|}A x x px q x =++=,2{|(1)(1)1}B x x p x q x =-+-+=+,当{2}A =时,求集合B .③升级篇典型试题分析例3：已知集合{0,2,4}M =，定义集合{|,,}P x x ab a M b M ==∈∈，求集合P . 分析：求集合P ，根据集合P 的定义，集合P 中的代表元素x 满足,,x ab a M b M =∈∈，所以分别取,a M b M ∈∈，求出ab 的所有可能值，用列举法一一列举出来，即得集合P .解析：∵,a M b M ∈∈，∴a =0,2,4, b =0,2,4,a 或b 至少有一个为0时，0x ab ==，a =2且b =2时, 4x ab ==， a =2且b =4时, 8x ab ==，a =4且b =2时, 8x ab ==， a =4且b =4时, 16x ab ==，根据集合中元素的互异性知{0,4,8,16}P =.例4.2008年第29届奥运会将在北京召开，现有三个实数的集合，既可以表示为{a ，a b ，1}，也可表示为{a 2，a ＋b ，0}，请求a 2008＋b 2008的值 ．分析：根据集合中元素的确定性，我们不难得到两集合的元素是相同的，这样需要列方程组分类讨论，显然复杂又烦琐．这时若能发现0这个特殊元素，和ab 中的a 不为0的隐含信息，就能得到如下解法.解析: 由已知得ab ＝0，及a ≠0，所以b ＝0，于是a 2＝1，即a ＝1或a ＝－1，又根据集合中元素的互异性a ＝1应舍去，因而a ＝－1，故a 2008＋b 2008＝(-1) 2008＝1． 知识应用与提升11.已知x 、y 、z 为非零实数，代数式xyzxyz z z y y x x ＋＋＋的值所组成的集合是M ，则下列判断正确的是 （ ）A ．0∉MB ．2∈MC ．－4∉MD ．4∈M12.集合{0,1,2,3,5}A =，当x A ∈时，若1x A -∉，且1x A +∉，则称x 为A 的一个“孤立元素”，则A 中孤立元素的个数为 .13.关于x 的方程0=+b ax ，当实数b a ,满足条件 时，方程的解集是有限集；当实数b a ,满足条件 时，方程的解集是无限集.14.若一数集中的任一元素的倒数仍在该集合中，则称该集合为“可倒数集”，试写出一个含三个元素的可倒数集_____.15.已知},,0,1{2x x ∈ 求实数x 的值.16.已知集合12,6A x x N N x ⎧⎫=∈∈⎨⎬-⎩⎭用列举法表示集合A 为 ④闯关篇典型试题分析例5：集合M 由正整数的平方组成，即{}1,4,9,16,25,...M =，若对某集合中的任意两个元素进行某种运算，运算结果仍在此集合中，则称此集合对该运算是封闭的. M 对下列运算封闭的是（ ）A. 加法B. 减法C. 乘法D. 除法分析：本题定义了集合的封闭运算，要探求集合对哪种运算封闭，一种思路是直接根据定义去探求这种运算，对于选择题，再一种思路就是排除不符合定义的运算，从而得到符合定义的运算.解析：设a b 、表示任意两个正整数，则22a b 、的和不一定是属于M ，如22125M =∉+；22a b 、的差也不一定是属于M ，如22123M =-∉-；22a b 、的商也不一定是属于M ，如2211M 24=∉；因为a b 、表示任意两个正整数， 222()a b ab ⋅= ，ab 为正整数，所以2()ab 属于M ，即22a b 、的积属于M .故选C.例6. 已知集合A ＝{x |x ＝m ＋n 2，m ，n ∈Z}．（1）证明任何整数都是A 的元素；（2）设x 1，x 2∈A ，求证：x 1·x 2∈A ．分析: 转换思维模式可将复杂问题具体化、简略化,本题的实质是证明任意两个A 集合中的元素的乘积运算仍在A 集合中,它反映了集合元素运算封闭性.证明：（1）设a ∈Z ，则a ＝a ＋02 ．∵a ，0∈Z ，∴ a ＝a ＋02∈A ．故任何整数都是A 的元素 ．（2）∵x 1，x 2∈A ，可设x 1＝m 1＋n 12，x 2＝m 2＋n 22，（其中m 1，n 1，m 2，n 2∈Z ）. ∴x 1x 2＝（m 1＋n 12）（m 2＋n 22）＝（m 1m 2＋2n 1n 2）＋（m 1n 2＋m 2n 1）2． ∵m 1，n 1，m 2，n 2∈Z ，∴（m 1m 2＋2n 1n 2）∈Z ，（m 1n 2＋m 2n 1）∈Z ．当m 1n 2＋m 2n 1＝0时，x 1·x 2＝（m 1m 2＋2m 1n 2）∈Z ， ∴x 1·x 2∈A ．知识拔高与创新17.已知A={1，2，3}， B={2，4}，定义集合A 、B 间的运算A*B={|}x x A x B ∈∈且，则集合A*B=（ ）A. {1，2，3}B. {2，4}C. {1，2，3，4}D. {2}18. 已知集合241x A a x a ⎧⎫-⎪⎪==⎨⎬+⎪⎪⎩⎭有惟一解，又列举法表示集合A 为 19.求集合2160{|}3a a Z Z a∈∈-且中所有元素的和. 20.已知集合A ＝{x |x ＝m 2－n 2,m ∈Z ,n ∈Z}求证：（1）3∈A ； （2）偶数4k —2 (k ∈Z)不属于A.⑤行侠篇高考试题点击21.（2005高考湖北）设P 、Q 为两个非空实数集合，定义集合P+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ，则P+Q 中元素的个数是 （ ）A ．9B ．8C ．7D ．622.（2004高考湖南）若集合{}(,)|20A x y x y m =-+>，{}(,)|0B x y x y n =+-≤，若点P （2，3）∈A 且P （2，3）∉B ，则（ ）A. 15m n >-<,B. 15m n <-<,C. 15m n >->,D. 15m n <->,⑥娱乐广场开阔视野、趣味学习为数学而疯的人集合论的创立者是德国数学家康托尔.1845年3月3日，乔治·康托生于俄国的一个丹麦—犹太血统的家庭.1856年康托尔和他的父母一起迁到德国的法兰克福.他在中学阶段就表现出一种对数学的特殊敏感，并不时得出令人惊奇的结论.进入了柏林大学后，康托尔受了外尔斯特拉斯的影响而转到纯粹的数学.他在1869年取得在哈勒大学任教的资格，不久后就升为副教授，并在1879年被升为正教授.由于研究无穷时往往推出一些合乎逻辑的但又荒谬的结果(称为“悖论”)，许多大数学家唯恐陷进去而采取退避三舍的态度1874—1876年期间，不到30岁的年轻德国数学家康托尔向神秘的无穷宣战他靠着辛勤的汗水，成功地证明了一条直线上的点能够和一个平面上的点一一对应，也能和空间中的点一一对与太平洋面上的点，以及整个地球内部的点都应这样看起来，1厘米长的线段内的点“一样多”.后来几年，康托尔对这类“无穷集合”问题发表了一系列文章，通过严格证明得出了许多惊人的结论，轰动了当时数学界. 康托尔的创造性工作与传统的数学观念发生了尖锐冲突，遭到一些人的反对、攻击甚至谩骂，有人说，康托尔的集合论是一种“疾病”，康托尔的概念是“雾中之雾”，甚至说康托尔是“疯子”，康托尔一直在逆境中拼搏着，以致不到40岁就患了神经衰弱和精神抑郁症，就这样他还在奋斗着.真金不怕火炼， 1897年举行的第一次国际数学家会议上，他的成就得到承认，伟大的哲学家、数学家罗素称赞康托尔的工作“可能是这个时代所能夸耀的最巨大的工作”可是这时康托尔仍然神志恍惚，不能从人们的崇敬中得到安慰和喜悦1918年1月6日，康托尔在哈勒大学附属精神病院去世.1.2子集、全集、补集①课文三点专讲重点:(1)子集、全集、补集的概念.集合之间包含与相等的含义,识别给定集合的子集; 在具体情境中,了解全集与空集的含义(2)注意区别区分}0{},{,∅∅间的关系.}{∅表示以空集,∅为元素的单元素集合,当把∅视为集合时, }{∅⊆∅成立;当把∅视为元素时,}{∅∈∅也成立.0表示元素,}0{表示以0为元素的单元素集合,不能混淆它们的含意.难点：(1)弄清元素与子集、属于与包含之间的区别.区分∈与⊆符号: ∈表示元素与集合之间的关系,如:N N ∉-∈1,1; ⊆表示集合与集合之间的关系,如R R N ⊆∅⊆,等.(2) 有限集合的子集个数:n 个元素的集合有n 2个子集;有12-n个非空子集;有12-n 个真子集;有22-n 个非空真子集.考点:(1)求集合的所有子集或子集的个数.此类问题有两种类型:其一是无条件地写出已知集合的所有子集或所有真子集,其解题关键是正确地进行分类,分别写出含有1个元素,2个元素,……,n 个元素的子集;其二是有条件地写出适合某条件的所有子集.(2)集合与集合之间的关系考察.此类问题常以两个集合间元素的属性及它们属性间的共同点及不同的点,来判断元素与集合间的从属关系,然后由子集定义得出其间的包含关系.几何图形可以直观形象地提示集合间的包含关系.(3)补集的求解问题.此类问题需要弄清全集U 及集合A 的元素构成,掌握补集的性质及应用,如(),,.U U U U A A U U ==∅∅=痧痧②练功篇典型试题分析例1.满足∅⊂≠A ⊆},,,{d c b a 的集合A 是什么?共有多少个?分析: ∅⊂≠A ⊆},,,{d c b a 的意义是集合A 为非空集合,且{,,,}A a b c d ≠.解析:由∅⊂≠A 可知,集合A 必为非空集合;又由A ⊆},,,{d c b a 可知,此题即为求集合},,,{d c b a 的所有非空子集。

第一章集合与简易逻辑一、基础知识定义1 一般地，一组确定的、互异的、无序的对象的全体构成集合，简称集，用大写字母来表示；集合中xxx Ax?不属于，记为在集合A中，称，否则称属于的各个对象称为元素，用小写字母来表示，元素A+x?A。

例如，通常用N，Z，Q，B，QA，记作分别表示自然数集、整数集、有理数集、实数集、正有理数?来表示。

集合分有限集和无限集两种。

集，不含任何元素的集合称为空集，用集合的表示方法有列举法：将集合中的元素一一列举出来写在大括号内并用逗号隔开表示集合的方法，如{xx?0}分别表}，；描述法：将集合中的元素的属性写在大括号内表示集合的方法。

例如{有理数{1，2，3}示有理数集和正实数集。

定义2 子集：对于两个集合A与B，如果集合A中的任何一个元素都是集合B中的元素，则A叫做B的子集，A?BN?Z。

规定空集是任何集合的子集，如果A是B的子集，B记为也是A的子集，则称，例如A 与B相等。

如果A是B的子集，而且B中存在元素不属于A，则A叫B的真子集。

A?B?{xx?A且x?B}.交集，定义3A?B?{xx?A或x?B}.定义4 并集，A?I,则CA?{xx?I,且x?A}称为定义5 A补集，若在I 中的补集。

1A\B?{xx?A,且x?B}。

差集，6 定义{xa?x?b,x?R,a?b}(a,b)，集合定义7 记作开区间集合{xa?x?b,x?R,a?b}[a,b](??,??).记作，记作闭区间R定理1 集合的性质：对任意集合A，B，C，有：A?(B?C)?(A?B)?(A?C);A?(B?C)?(A?B)?(A?C)；（2（1））CA?CB?C(A?B);CA?CB?C(A?B). 4（）（3）111111【证明】这里仅证（1）、（3），其余由读者自己完成。

x?A?(B?C)x?(A?B)x?(A?C)Cx?Ax?Bx?，即，且，所以或（1）若或，则x?(A?B)?(A?C)x?(A?B)?(A?C)x?(A?B)x?(A?C)x?A且，即；反之，，则或x?(B?C)x?A?(B?C).ABx?Cx?x?或，即且，即xCACB?x?CBx?(A?B)x?Ix?Ax?B A?Cx?，（，又或，所以，所以3）若或，则1111x?C(A?B)CA?CB?C(A?B)C(A?B)?CA?CB.所以，反之也有，即1111111mmn种不同的加法原理：做一件事有种不同的方法，第二类办法中有类办法，第一类办法中有定理2 21N?m?m???mmn种不同的方类办法中有，第种不同的方法，那么完成这件事一共有方法， (12)法。

2019-2020年高中数学竞赛教材讲义 第一章 集合与简易逻辑一、基础知识定义1 一般地，一组确定的、互异的、无序的对象的全体构成集合，简称集，用大写字母来表示；集合中的各个对象称为元素，用小写字母来表示，元素在集合A 中，称属于A ，记为，否则称不属于A ，记作。

例如，通常用N ，Z ，Q ，B ，Q +分别表示自然数集、整数集、有理数集、实数集、正有理数集，不含任何元素的集合称为空集，用来表示。

集合分有限集和无限集两种。

集合的表示方法有列举法：将集合中的元素一一列举出来写在大括号内并用逗号隔开表示集合的方法，如{1，2，3}；描述法：将集合中的元素的属性写在大括号内表示集合的方法。

例如{有理数}，分别表示有理数集和正实数集。

定义2 子集：对于两个集合A 与B ，如果集合A 中的任何一个元素都是集合B 中的元素，则A 叫做B 的子集，记为，例如。

规定空集是任何集合的子集，如果A 是B 的子集，B 也是A 的子集，则称A 与B 相等。

如果A 是B 的子集，而且B 中存在元素不属于A ，则A 叫B 的真子集。

定义3 交集，}.{B x A x x B A ∈∈=且定义4 并集，}.{B x A x x B A ∈∈=或定义5 补集，若},{,1A x I x x A C I A ∉∈=⊆且则称为A 在I 中的补集。

定义6 差集，},{\B x A x x B A ∉∈=且。

定义7 集合},,{b a R x b x a x <∈<<记作开区间，集合},,{b a R x b x a x <∈≤≤记作闭区间，R 记作定理1 集合的性质：对任意集合A ，B ，C ，有：（1）);()()(C A B A C B A = （2）)()()(C A B A C B A =；（3）);(111B A C B C A C = （4）).(111B A C B C A C =【证明】这里仅证（1）、（3），其余由读者自己完成。

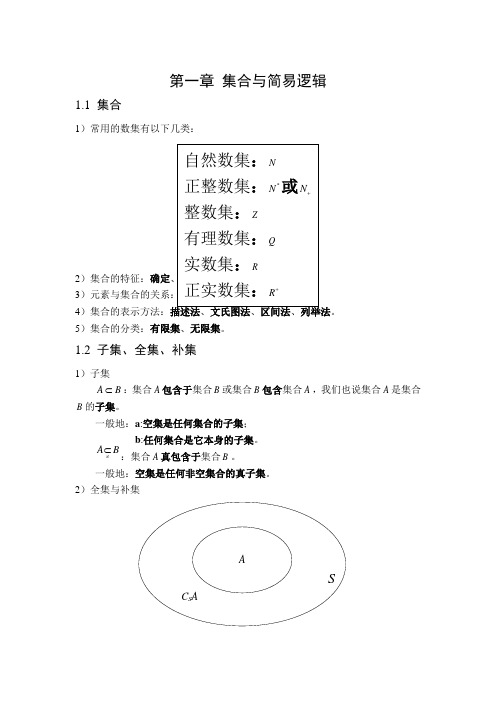
第一章 集合与简易逻辑1.1 集合1）常用的数集有以下几类：2）集合的特征：确定34）集合的表示方法：。

5）集合的分类：有限集、无限集。

1.2 子集、全集、补集1）子集A B ⊂：集合A 包含于集合B 或集合B 包含集合A ，我们也说集合A 是集合B 的子集。

一般地：a :空集是任何集合的子集； b :任何集合是它本身的子集。

B A ≠⊂：集合A 真包含于集合B 。

一般地：空集是任何非空集合的真子集。

2）全集与补集S 是全集，A 是S 的一个子集，S C A 是补集（或余集），{,}S C A x x S x A =∈∉。

1.3 交集、并集交集：{,}A B x A x B ⋂=∈∈且。

并集：{,}A B x A x B ⋃=∈∈或。

交集并集1.4 含绝对值的不等式的解法1）{}(0)x a a x a a <=-<<<， 2）{,}(0)x a x a x a a >=<-><或。

1.5 一元二次不等式解法1）求根； 2）画图。

1.6 逻辑联结词1）与命题：2）或命题3）非命题：1.7 四种命题（1）四种命题的形式：1）原命题：若p 则q ； 2）逆命题：若q 则p ； 3）否命题：p ⌝则q ⌝； 4）逆否命题：若q ⌝则p ⌝； （2）四种命题的相互关系：（3）原命题与其他三个命题的真假关系： 1）原命题为真，它的逆命题不一定为真； 2）原命题为真，它的否命题不一定为真； 3）原命题为真，它的逆否命题一定为真；。

高中数学复习讲义 第一章 集合与简易逻辑第1课时 集合的概念及运算【基础练习】1.集合{(,)02,02,,}x y x y x y Z ≤≤≤<∈用列举法表示{(0,0),(0,1),(1,0),(1,1),(2,0),(2,1)}．2.设集合{21,}A x x k k Z ==-∈，{2,}B x x k k Z ==∈，则A B ⋂=∅．3.已知集合{0,1,2}M =，{2,}N x x a a M ==∈，则集合M N ⋂=_______． 4.设全集{1,3,5,7,9}I =，集合{1,5,9}A a =-，{5,7}I C A =，则实数a 的值为____8或2___．【范例解析】例.已知R 为实数集，集合2{320}A x x x =-+≤.若R B C A R ⋃=，{01R B C A x x ⋂=<<或23}x <<，求集合B.分析：先化简集合A ，由R B C A R ⋃=可以得出A 与B 的关系；最后，由数形结合，利用数轴直观地解决问题.解：（1）{12}A x x =≤≤ ，{1R C A x x ∴=<或2}x >.又R B C A R ⋃=，R A C A R ⋃=， 可得A B ⊆.而{01R B C A x x ⋂=<<或23}x <<，∴{01x x <<或23}x <<.B ⊆借助数轴可得B A =⋃{01x x <<或23}x <<{03}x x =<<.【反馈演练】1．设集合{}2,1=A ，{}3,2,1=B ，{}4,3,2=C ，则()C B A U ⋂=_________． 2．设P ，Q 为两个非空实数集合，定义集合P+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ，则P+Q 中元素的个数是_______个．{0,2}3．设集合2{60}P x x x =--<，{23}Q x a x a =≤≤+. （1）若P Q P ⋃=，求实数a 的取值范围； （2）若P Q ⋂=∅，求实数a 的取值范围； （3）若{03}P Q x x ⋂=≤<，求实数a 的值.解：（1）由题意知：{23}P x x =-<<， P Q P ⋃=，Q P ∴⊆. ①当Q =∅时，得23a a >+，解得3a >．②当Q ≠∅时，得2233a a -<≤+<，解得10a -<<． 综上，(1,0)(3,)a ∈-⋃+∞．（2）①当Q =∅时，得23a a >+，解得3a >；②当Q ≠∅时，得23,3223a a a a ≤+⎧⎨+≤-≥⎩或，解得3532a a ≤-≤≤或．综上，3(,5][,)2a ∈-∞-⋃+∞．（3）由{03}P Q x x ⋂=≤<，则0a =．第2课 命题及逻辑联结词1.下列语句中：①230x -=；②你是高三的学生吗？③315+=；④536x ->． 其中，不是命题的有____①②④_____．2.一般地若用p 和q 分别表示原命题的条件和结论，则它的逆命题可表示为若q 则p ，否命题可表示为 p q ⌝⌝若则，逆否命题可表示为q p ⌝⌝若则；原命题与逆否命题互为逆否命题，否命题与逆命题互为逆否命题．例1. 写出下列命题的逆命题，否命题，逆否命题并判断真假. （1） 平行四边形的对边相等； （2） 菱形的对角线互相垂直平分；（3） 设,,,a b c d R ∈，若,a b c d ==，则a c b d +=+.分析：先将原命题改为“若p 则q ”，在写出其它三种命题. 解：（1）原命题：若一个四边形是平行四边形，则其两组对边相等；真命题；逆命题：若一个四边形的两组对边相等，则这个四边形是平行四边形；真命题； 否命题：若一个四边形不是平行四边形，则其两组对边至少一组不相等；真命题； 逆否命题：若一个四边形的两组对边至少一组不相等，则这个四边形不是平行四边形；真命题.（2）原命题：若一个四边形是菱形，则其对角线互相垂直平分；真命题； 逆命题：若一个四边形的对角线互相垂直平分，则这个四边形是菱形；真命题； 否命题：若一个四边形不是菱形，则其对角线不垂直或不平分；真命题；逆否命题：若一个四边形的对角线不垂直或不平分，则这个四边形不是菱形；真命题. （3）原命题：设,,,a b c d R ∈，若,a b c d ==，则a c b d +=+；真命题； 逆命题：设,,,a b c d R ∈，若a c b d +=+，则,a b c d ==；假命题； 否命题：设,,,a b c d R ∈，若a b ≠或c d ≠，则a c b d +≠+；假命题； 逆否命题：设,,,a b c d R ∈，若a c b d +≠+，则a b ≠或c d ≠；真命题.点例.写出下列命题的否定，并判断真假.（1）p ：所有末位数字是0或5的整数都能被5整除； （2）p ：每一个非负数的平方都是正数；（3）p ：存在一个三角形，它的内角和大于180°； （4）p ：有的四边形没有外接圆； （5）p ：某些梯形的对角线互相平分.分析：全称命题“,()x M p x ∀∈”的否定是“,()x M p x ∃∈⌝”，特称命题“,()x M p x ∃∈”的否定是“,()x M p x ∀∈⌝” . 解：（1）p ⌝：存在末位数字是0或5的整数，但它不能被5整除，假命题； （2）p ⌝：存在一个非负数的平方不是正数，真命题；（3）p ⌝：任意一个三角形，它的内角和都不大于180°，真命题； （4）p ⌝：所有四边形都有外接圆，假命题； （5）p ⌝：任一梯形的对角线都不互相平分，真命题.【反馈演练】1．命题“若a M ∈，则b M ∉”的逆否命题是__________________. 2．已知命题p ：1sin ,≤∈∀x R x ，则:p ⌝,sin 1x R x ∃∈>.3．若命题m 的否命题n ，命题n 的逆命题p ，则p 是m 的____逆否命题____.4．命题“若b a >，则122->b a ”的否命题为________________________．第3 课时 充分条件和必要条件【考点导读】1. 从集合的观点理解充要条件，有以下一些结论： 若集合P Q ⊆，则P 是Q 的充分条件； 若集合P Q ⊇，则P 是Q 的必要条件； 若集合P Q =，则P 是Q 的充要条件． 【基础练习】1.用“充分不必要条件，必要不充分条件，充要条件和既不充分也不必要条件”填空. （1）已知:2p x >，:2q x ≥，那么p 是q 的_____ ___条件．（2）已知:p 两直线平行，:q 内错角相等，那么p 是q 的____ _____条件． （3）已知:p 四边形的四条边相等，:q 四边形是正方形，那么p 是q 的___ __条件． 2.若x R ∈，则1x >的一个必要不充分条件是——————．3．设集合}30|{≤<=x x M ，}20|{≤<=x x N ，则“M a ∈”是“N a ∈”的_ 条件．4．已知p ：1＜x ＜2，q ：x(x －3)＜0，则p 是q 的 条件．若b M ∈，则a M ∉若a b ≤，则221a b ≤-。

第一章 集合与简易逻辑一、基础知识定义1 一般地，一组确定的、互异的、无序的对象的全体构成集合，简称集，用大写字母来表示；集合中的各个对象称为元素，用小写字母来表示，元素x 在集合A 中，称x 属于A ，记为A x ∈，否则称x 不属于A ，记作A x ∉。

例如，通常用N ，Z ，Q ，B ，Q +分别表示自然数集、整数集、有理数集、实数集、正有理数集，不含任何元素的集合称为空集，用∅来表示。

集合分有限集和无限集两种。

集合的表示方法有列举法：将集合中的元素一一列举出来写在大括号内并用逗号隔开表示集合的方法，如{1，2，3}；描述法：将集合中的元素的属性写在大括号内表示集合的方法。

例如{有理数}，}0{>x x 分别表示有理数集和正实数集。

定义2 子集：对于两个集合A 与B ，如果集合A 中的任何一个元素都是集合B 中的元素，则A 叫做B 的子集，记为B A ⊆，例如Z N ⊆。

规定空集是任何集合的子集，如果A 是B 的子集，B 也是A 的子集，则称A 与B 相等。

如果A 是B 的子集，而且B 中存在元素不属于A ，则A 叫B 的真子集。

定义3 交集，}.{B x A x x B A ∈∈=且I定义4 并集，}.{B x A x x B A ∈∈=或Y定义5 补集，若},{,1A x I x x A C I A ∉∈=⊆且则称为A 在I 中的补集。

定义6 差集，},{\B x A x x B A ∉∈=且。

定义7 集合},,{b a R x b x a x <∈<<记作开区间),(b a ，集合},,{b a R x b x a x <∈≤≤记作闭区间],[b a ，R 记作).,(+∞-∞定理1 集合的性质：对任意集合A ，B ，C ，有：（1）);()()(C A B A C B A I Y I Y I = （2）)()()(C A B A C B A Y I Y I Y =；（3）);(111B A C B C A C I Y = （4）).(111B A C B C A C Y I =【证明】这里仅证（1）、（3），其余由读者自己完成。

1．集合、简易逻辑「集合」把某些指定的对象集中在一起就成为一个集合，简称集。

集合中每个对象叫做这个集合的元素。

集合通常用大写拉丁字母 ,,,C B A 表示集合，用小写拉丁字母 ,,,c b a 表示集合的元素。

「集合的特征」集合中的元素具有确定性、互异性、无序性。

「集合的类型」① 有限集：含有有限个元素的集合叫有限集。

② 无限集：含有无限个元素的集合叫无限集。

③ 空集：不含任何元素的集合叫做空集，记作∅。

「集合的表示方法」①列举法 把一个集合的元素逐个列举出来，写在大括号内，这一表示法叫做列举法。

②特征性质描述法 用该集合所含元素的共有特征性质来描述，这一表示法叫做特征性质描述法，具体作法是：在大括号内先写上表示该集合元素的一般符号及其取值范围，再画一条竖线（或一个冒号或分号），再写出这一集合中的元素所具有的一个特征性质。

特征性质必须绝对明确，必须是集合中所有元素共有的特征性质。

「元素与集合的从属关系」如果元素a 是集合A 的元素，就说a 属于集合A ，记作A a ∈；如果元素a 不是集合A 的元素，就说a 不属于集合A ，记作A a ∉或A a ∈或a ∈.A 。

「集合与集合的容量关系」对于两个集合,,B A 如果集合A 的任何一个元素都是集合B 的元素，那么集合A 叫做集合B 的子集，记作B A ⊆或A B ⊇，读作“A 包含于B ”或“B 包含A ”。

如果A 是B 的子集，并且B 中至少有一个元素不属于A ，那么集合A 叫做集合B 的真子集，记作A ØB 或B ÙＡ。

当集合A 不包含于集合B ，或集合B 不包含集合A 时，记作A B ⊂或 .B A ⊃显然，空集是任何集合A 的子集，即A ∅⊆，空集是任何非空集合B 的真子集，即∅ ØB若,,A B B C ⊆⊆则;A C ⊆若,,A B B A ⊆⊆则.A B =「常用数集的符号」 N 非负整数集；自然数集*N 或+N 正整数集Z 整数集-+Z Z 整数集Z 内排除0的集Q 有理数集。

数学一轮总复习 第一章 集合与简易逻辑第一节 集合【考纲要求】【知识网络】【考点梳理】 一．集合的概念：集 合集 合 表 示 法集 合 的 关 系集 合 的 运 算 描 述 法图 示 法列 举 法 相 等 包 含 交 集并 集 补 集子集、真子集1.一般的，我们把研究对象统称为元素，把一些元素组成的总体叫做集合，简称为集。

集合通常用大写的拉丁字母表示，如A 、B 、C 、……元素通常用小写的拉丁字母表示，如a 、b 、c 、…… 2.集合中元素特征（1）确定性：给定一个集合，任何对象是不是这个集合的元素是确定的了. （2）互异性：集合中的元素一定是不同的. （3）无序性：集合中的元素没有固定的顺序. 3.集合的分类：根据集合所含元素个属不同，可把集合分为如下几类： （1）把不含任何元素的集合叫做空集Ф （2）含有有限个元素的集合叫做有限集 （3）含有无穷个元素的集合叫做无限集 注：应区分Φ，}{Φ，}0{，0等符号的含义 4、常用数集（1）非负整数集（自然数集）：全体非负整数的集合.记作N （2）正整数集：非负整数集内排除0的集.记作N *或N + （3）整数集：全体整数的集合.记作Z （4）有理数集：全体有理数的集合.记作Q （5）实数集：全体实数的集合.记作R 注：（1）自然数集包括数0.（2）非负整数集内排除0的集.记作N *或N +，Q 、Z 、R 等其它数集内排除0的集，也这样表示，例如，整数集内排除0的集，表示成Z *二．集合的表示法：1.列举法：用来表示有限集或具有显著规律的无限集，如N +={0，1，2，3，…}；2.描述法：例如，不等式232>-x x 的解集可以表示为：}23|{2>-∈x x R x 或}23|{2>-x x x ， 3.韦恩图： 4.区间法：三．集合间的基本关系：1.元素与集合的关系，用∈或∉表示；属于：如果a 是集合A 的元素，就说a 属于A ，记作a ∈A 不属于：如果a 不是集合A 的元素，就说a 不属于A ，记作A a ∉ 要注意“∈”的方向，不能把a ∈A 颠倒过来写.2.集合与集合的关系，用⊆，≠⊂，=表示，当A ⊆B 时，称A 是B 的子集；当A ≠⊂B 时，称A 是B 的真子集。

XX年高考数学第一轮复习集合与简易逻辑
一、集合的概念与运算
知识梳理
1.集合的有关概念
2.元素与集合、集合与集合之间的关系
（1）元素与集合：“∈”或“ ”.
（2）集合与集合之间的关系：包含关系、相等关系.
3.集合的运算
（1）交集：由所有属于集合A且属于集合B的元素所组成的集合，
叫做集合A与B的交集，记为A∩B，即A∩B={x|x∈A且x∈B}. （2）并集：由所有属于集合A或属于集合B的元素所组成的集合，
叫做集合A与集合B的并集，记为A∪B，即A∪B={x|x∈A或x∈B}. （3）补集：一般地，设S是一个集合，A是S的一个子集（即A S），由S中所有不属于A的元素组成的集合，叫做子集A在全集S
中的补集（或余集），记为 S A，即S A={x|x∈S且x A}.
点击双基
1.集合M={x|x2＜4}，N={x|x2－2x－3＜0}，那么集合M∩N等于
A.{x|x＜－2}
B.{x|x＞3}
C.{x|－1＜x＜2}
D.{x|2＜x＜3}
解析：M={x|x2＜4}={x|－2＜x＜2}，N={x|x2－2x－3＜0}={x|－1
＜x＜3}，结合数轴，
∴M∩N={x|－1＜x＜2}.
答案：C
2.集合A={x∈R|x＜5－ }，B={1，2，3，4}，那么（ RA）∩B等于
A.{1，2，3，4}
B.{2，3，4}
C.{3，4}
D.{4}
解析：RA={x∈R|x≥5－ }，而5－∈（3，4），∴（ RA）∩B={4}.。

高中数学基础知识整理§01. 集合与简易逻辑1. 元素与集合的关系U x A x C A ∈⇔∉,U x C A x A ∈⇔∉.2．集合运算 全集U ：如U=R交集：}{B x A x x B A ∈∈=且 并集：}{B x A x x B A ∈∈=⋃或 补集：}{A x U x x A C U ∉∈=且 3．集合关系 空集A ⊆φ子集B A ⊆:任意B x A x ∈⇒∈ B A B B A BA AB A ⊆⇔=⊆⇔=4. 包含关系A B A A B B =⇔=U U A B C B C A ⇔⊆⇔⊆U A C B ⇔=ΦU C A B R ⇔=5．集合12{,,,}n a a a 的子集个数共有2n 个；真子集有2n –1个；非空子集有2n –1个；非空的真子集有2n –2个.6. 常见结论的否定形式7. 四种命题原命题：若p 则q 逆命题：若q 则p 否命题：若p ⌝则q ⌝ 逆否命题：若q ⌝则p ⌝原命题与逆否命题真假相同 否命题与逆命题真假相同8. 充要条件（1）充分条件：若p q ⇒，则p 是q 充分条件.（2）必要条件：若q p ⇒，则p 是q 必要条件.（3）充要条件：若p q ⇒，且q p ⇒，则p 是q 充要条件. 注：如果甲是乙的充分条件，则乙是甲的必要条件；反之亦然.§02. 函数1. 函数的单调性设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数；[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数.对于复合函数的单调性：()f g x ⎡⎤⎣⎦ 同增异减（即()f x 与()g x 的增减性相同，那么复合函数就是增函数（同增）； ()f x 与()g x 的增减性相反，那么符合函数就是减函数（异减）） 2．函数的奇偶性判断奇偶性的前提是定义域关于原点对称。

2012高中数学复习讲义 第一章 集合与简易逻辑第1课时 集合的概念及运算【考点导读】了解集合的含义，体会元素与集合的属于关系；能选择自然语言，图形语言，集合语言描述不同的具体问题，感受集合语言的意义和作用．理解集合之间包含与相等的含义，能识别给定集合的子集；了解全集与空集的含义．理解两个集合的交集与并集的含义，会求两个集合的交集与并集；理解在给定集合中一个子集补集的含义，会求给定子集的补集；能使用文氏图表达集合的关系及运算，体会直观图示对理解抽象概念的作用．集合问题常与函数，方程，不等式有关，其中字母系数的函数，方程，不等式要复杂一些，综合性较强，往往渗透数形思想和分类讨论思想．【基础练习】1.集合{(,)02,02,,}x y x y x y Z ≤≤≤<∈用列举法表示{(0,0),(0,1),(1,0),(1,1),(2,0),(2,1)}．2.设集合{21,}A x x k k Z ==-∈，{2,}B x x k k Z ==∈，则A B ⋂=∅．3.已知集合{0,1,2}M =，{2,}N x x a a M ==∈，则集合M N ⋂=_______． 4.设全集{1,3,5,7,9}I =，集合{1,5,9}A a =-，{5,7}I C A =，则实数a 的值为____8或2___．【范例解析】例.已知R 为实数集，集合2{320}A x x x =-+≤.若R B C A R ⋃=，{01R B C A x x ⋂=<<或23}x <<，求集合B .分析：先化简集合A ，由R B C A R ⋃=可以得出A 与B 的关系；最后，由数形结合，利用数轴直观地解决问题.解：（1）{12}A x x =≤≤，{1R C A x x ∴=<或2}x >.又R B C A R ⋃=，R A C A R ⋃=，可得A B ⊆.而{01R B C A x x ⋂=<<或23}x <<，∴{01x x <<或23}x <<.B ⊆{0,2}借助数轴可得B A =⋃{01x x <<或23}x <<{03}x x =<<.【反馈演练】1．设集合{}2,1=A ，{}3,2,1=B ，{}4,3,2=C ，则()C B A U ⋂=_________． 2．设P ，Q 为两个非空实数集合，定义集合P +Q =},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ，则P +Q 中元素的个数是____8___个．3．设集合2{60}P x x x =--<，{23}Q x a x a =≤≤+.（1）若P Q P ⋃=，求实数a 的取值范围；（2）若P Q ⋂=∅，求实数a 的取值范围；（3）若{03}P Q x x ⋂=≤<，求实数a 的值.解：（1）由题意知：{23}P x x =-<<，P Q P ⋃=，Q P ∴⊆.①当Q =∅时，得23a a >+，解得3a >．②当Q ≠∅时，得2233a a -<≤+<，解得10a -<<．综上，(1,0)(3,)a ∈-⋃+∞．（2）①当Q =∅时，得23a a >+，解得3a >；②当Q ≠∅时，得23,3223a a a a ≤+⎧⎨+≤-≥⎩或，解得3532a a ≤-≤≤或． 综上，3(,5][,)2a ∈-∞-⋃+∞． （3）由{03}P Q x x ⋂=≤<，则0a =．第2课 命题及逻辑联结词【考点导读】了解命题的逆命题，否命题与逆否命题的意义；会分析四种命题的相互关系．了解逻辑联结词“或”，“且”，“非”的含义；能用“或”，“且”，“非”表述相关的数学内容．理解全称量词与存在量词的意义；能用全称量词与存在量词叙述简单的数学内容．理解对含有一个量词的命题的否定的意义；能正确地对含有一个量词的命题进行否定．【基础练习】1.下列语句中：①230x -=；②你是高三的学生吗？③315+=；④536x ->．其中，不是命题的有____①②④_____．2.一般地若用p 和q 分别表示原命题的条件和结论，则它的逆命题可表示为若q 则p ，否命题可表示为 p q ⌝⌝若则，逆否命题可表示为q p ⌝⌝若则；原命题与逆否命题互为逆否命题，否命题与逆命题互为逆否命题．【范例解析】例1. 写出下列命题的逆命题，否命题，逆否命题并判断真假.（1） 平行四边形的对边相等；（2） 菱形的对角线互相垂直平分；（3） 设,,,a b c d R ∈，若,a b c d ==，则a c b d +=+.分析：先将原命题改为“若p 则q ”，在写出其它三种命题.解：（1）原命题：若一个四边形是平行四边形，则其两组对边相等；真命题；逆命题：若一个四边形的两组对边相等，则这个四边形是平行四边形；真命题；否命题：若一个四边形不是平行四边形，则其两组对边至少一组不相等；真命题；逆否命题：若一个四边形的两组对边至少一组不相等，则这个四边形不是平行四边形；真命题.（2）原命题：若一个四边形是菱形，则其对角线互相垂直平分；真命题；逆命题：若一个四边形的对角线互相垂直平分，则这个四边形是菱形；真命题；否命题：若一个四边形不是菱形，则其对角线不垂直或不平分；真命题；逆否命题：若一个四边形的对角线不垂直或不平分，则这个四边形不是菱形；真命题.（3）原命题：设,,,a b c d R ∈，若,a b c d ==，则a c b d +=+；真命题；逆命题：设,,,a b c d R ∈，若a c b d +=+，则,a b c d ==；假命题；否命题：设,,,a b c d R ∈，若a b ≠或c d ≠，则a c b d +≠+；假命题；逆否命题：设,,,a b c d R ∈，若a c b d +≠+，则a b ≠或c d ≠；真命题.点评：已知原命题写出其它的三种命题首先应把命题写成“若p 则q ”的形式，找出其条件p 和结论q ，再根据四种命题的定义写出其它命题；对于含大前提的命题，在改写命题时大前提不要动；在写命题p 的否定即p ⌝时，要注意对p 中的关键词的否定，如“且”的否定为“或”，“或”的否定为“且”，“都是”的否定为“不都是”等.例2.写出由下列各组命题构成的“p 或q ”，“p 且q ”，“非p ”形式的命题，并判断真假.（1）p ：2是4的约数，q ：2是6的约数；（2）p ：矩形的对角线相等，q ：矩形的对角线互相平分；（3）p ：方程210x x -+=的两实根的符号相同，q ：方程210x x -+=的两实根的绝对值相等.分析：先写出三种形式命题，根据真值表判断真假.解：（1）p 或q ：2是4的约数或2是6的约数，真命题；p 且q ：2是4的约数且2是6的约数，真命题；非p ：2不是4的约数，假命题.（2）p 或q ：矩形的对角线相等或互相平分，真命题；p 且q ：矩形的对角线相等且互相平分，真命题；非p ：矩形的对角线不相等，假命题.（3）p 或q ：方程210x x -+=的两实根的符号相同或绝对值相等，假命题；p 且q ：方程210x x -+=的两实根的符号相同且绝对值相等，假命题；非p ：方程210x x -+=的两实根的符号不同，真命题.点评：判断含有逻辑联结词“或”，“且”，“非”的命题的真假，先要把结构弄清楚，确定命题构成的形式以及构成它们的命题p ，q 的真假然后根据真值表判断构成新命题的真假.例3.写出下列命题的否定，并判断真假.（1）p ：所有末位数字是0或5的整数都能被5整除；（2）p ：每一个非负数的平方都是正数；（3）p ：存在一个三角形，它的内角和大于180°；（4）p ：有的四边形没有外接圆；（5）p ：某些梯形的对角线互相平分.分析：全称命题“,()x M p x ∀∈”的否定是“,()x M p x ∃∈⌝”，特称命题“,()x M p x ∃∈”的否定是“,()x M p x ∀∈⌝” .解：（1）p ⌝：存在末位数字是0或5的整数，但它不能被5整除，假命题；（2）p ⌝：存在一个非负数的平方不是正数，真命题；（3）p ⌝：任意一个三角形，它的内角和都不大于180°，真命题；（4）p ⌝：所有四边形都有外接圆，假命题；（5）p ⌝：任一梯形的对角线都不互相平分，真命题.点评：一些常用正面叙述的词语及它的否定词语列表如下：【反馈演练】1．命题“若a M ∈，则b M ∉”的逆否命题是__________________.2．已知命题p ：1sin ,≤∈∀x R x ，则:p ⌝,sin 1x R x ∃∈>.3．若命题m 的否命题n ，命题n 的逆命题p ，则p 是m 的____逆否命题____. 4．命题“若b a >，则122->b a ”的否命题为________________________．5．分别写出下列命题的逆命题，否命题，逆否命题，并判断它们的真假．若b M ∈，则a M ∉ 若a b ≤，则221a b ≤-（1）设,a b R ∈，若0ab =，则0a =或0b =；（2）设,a b R ∈，若0,0a b >>，则0ab >．解：（1）逆命题：设,a b R ∈，若0a =或0b =，则0ab =；真命题；否命题：设,a b R ∈，若0ab ≠，则0a ≠且0b ≠；真命题；逆否命题：设,a b R ∈，若0a ≠且0b ≠，则0ab ≠；真命题；（2）逆命题：设,a b R ∈，若0ab >，则0,0a b >>；假命题；否命题：设,a b R ∈，若0a ≤或0b ≤，则0ab ≤；假命题；逆否命题：设,a b R ∈，若0ab ≤，则0a ≤或0b ≤；真命题．第3 课时 充分条件和必要条件【考点导读】理解充分条件，必要条件和充要条件的意义；会判断充分条件，必要条件和充要条件．2. 从集合的观点理解充要条件，有以下一些结论：若集合P Q ⊆，则P 是Q 的充分条件；若集合P Q ⊇，则P 是Q 的必要条件；若集合P Q =，则P 是Q 的充要条件．3. 会证明简单的充要条件的命题，进一步增强逻辑思维能力．【基础练习】1.若p q ⇒，则p 是q 的充分条件．若q p ⇒，则p 是q 的必要条件．若p q ⇔，则p 是q 的充要条件．2.用“充分不必要条件，必要不充分条件，充要条件和既不充分也不必要条件”填空.（1）已知:2p x >，:2q x ≥，那么p 是q 的_____充分不必要___条件．（2）已知:p 两直线平行，:q 内错角相等，那么p 是q 的____充要_____条件．（3）已知:p 四边形的四条边相等，:q 四边形是正方形，那么p 是q 的___必要不充分__条件．3.若x R ∈，则1x >的一个必要不充分条件是0x >．【范例解析】例.用“充分不必要条件，必要不充分条件，充要条件和既不充分也不必要条件”填空.（1）2,2.x y >⎧⎨>⎩是4,4.x y xy +>⎧⎨>⎩的___________________条件；（2）(4)(1)0x x -+≥是401x x -≥+的___________________条件； （3）αβ=是tan tan αβ=的___________________条件；（4）3x y +≠是1x ≠或2y ≠的___________________条件.分析：从集合观点“小范围⇒大范围”进行理解判断，注意特殊值的使用.解：（1）因为2,2.x y >⎧⎨>⎩结合不等式性质易得4,4.x y xy +>⎧⎨>⎩，反之不成立，若12x =，10y =，有4,4.x y xy +>⎧⎨>⎩，但2,2.x y >⎧⎨>⎩不成立，所以2,2.x y >⎧⎨>⎩是4,4.x y xy +>⎧⎨>⎩的充分不必要条件.（2）因为(4)(1)0x x -+≥的解集为[1,4]-，401x x -≥+的解集为(1,4]-，故(4)(1)0x x -+≥是401x x -≥+的必要不充分条件. （3）当2παβ==时，tan ,tan αβ均不存在；当tan tan αβ=时，取4πα=，54πβ=，但αβ≠，所以αβ=是tan tan αβ=的既不充分也不必要条件.（4）原问题等价其逆否形式，即判断“1x =且2y =是3x y +=的____条件”，故3x y +≠是1x ≠或2y ≠的充分不必要条件.点评：①判断p 是q 的什么条件，实际上是判断“若p 则q ”和它的逆命题“若q 则p ”的真假，若原命题为真，逆命题为假，则p 为q 的充分不必要条件；若原命题为假，逆命题为真，则p 为q 的必要不充分条件；若原命题为真，逆命题为真，则p 为q 的充要条件；若原命题，逆命题均为假，则p 为q 的既不充分也不必要条件.②在判断时注意反例法的应用.③在判断“若p 则q ”的真假困难时，则可以判断它的逆否命题“若⌝q 则⌝p ”的真假.【反馈演练】1．设集合}30|{≤<=x x M ，}20|{≤<=x x N ，则“M a ∈”是“N a ∈”的_必要不充分 条件．2．已知p ：1＜x ＜2，q ：x (x －3)＜0，则p 是q 的 条件．3．已知条件2:{10}p A x R x ax =∈++≤，条件2:{320}q B x R x x =∈-+≤．若q ⌝是p ⌝的充分不必要条件，求实数a 的取值范围．解：:{12}q B x R x =∈≤≤，若q ⌝是p ⌝的充分不必要条件，则A B ⊆． 若A =∅，则240a -<，即22a -<<；若A ≠∅，则240,a x ⎧-≥≤≤解得522a -≤≤-． 综上所述，522a -≤<．充分不必要。