29正多边形扇形和圆锥侧面展开图.docx

圆柱和圆锥的侧面展开图（四）2006-8-1 13:35页面功能【字体：大中小】【打印】【关闭】圆锥侧面展开图(扇形)中的各元素与圆锥的各元素之间的关系极为密切，即扇形的半径是圆锥的母线，扇形的弧长是圆锥底面圆的周长。

因此我们要重视空间图形与平面图形的互相转化。

教学步骤（一）明确目标在小学，同学们除了学习圆柱之外还学习了一个几何体——圆锥，在生活中我们也常常遇到圆锥形的物体，涉及到这些物体表面积的计算．这些圆锥形物体的表面积是怎样计算出来的？这就是本节课“7.21圆锥的侧面展开图”所要研究的内容。

（二）整体感如和圆柱一样，圆锥也是日常生活或实践活动中常见物体，在学生学过圆柱的有关计算后，进一步学习圆锥的有关计算，不仅对培养学生的空间观念有好处，而且能使学生体会到用平面几何知识可以解决立体图形的计算，为学习立体几何打基础。

圆锥的侧面展开图不仅用于圆锥表面积的计算，而且在生产中常用于画图下料上，因此圆锥侧面展开图是本课的重点。

本课首先在小学已具有圆锥直观感知的基础上，用直角三角形旋转运动的观点给出圆锥的一系列概念，然后利用圆锥的模型，把其侧面展开，使学生认识到圆锥的侧面展开图是一个扇形，并能将圆锥的有关元素与展开图扇形的有关元素进行相互间的转化，最后应用圆锥及其侧面展开图之间对应关系进行计算。

（三）教学过程［幻灯展示生活中常遇的圆锥形物体，如：铅锤、粮堆、烟囱帽］前面屏幕上展示的物体都是什么几何体？［安排回忆起的学生回答：圆锥］在小学我们已学过圆锥，哪位同学能说出圆锥有哪些特征？安排举手的学生回答：圆锥是由一个底面和一个侧面围成的，圆锥的底面是一个圆，侧面是一个曲面，从圆锥的顶点到底面圆的距离是圆锥的高。

［教师边演示模型，边讲解］：大家观察Rt，绕直线SO旋转一周得到的图形是什么？［安排中下生回答：圆锥］大家观察圆锥的底面，它是Rt 的哪条边旋转而成的？［安排中下生回答：OA］圆锥的侧面是Rt的什么边旋转而得的？［安排中下生回答，斜边］，因圆锥是Rt绕直线SO旋转一周得到的，与圆柱相类似，直线SO应叫做圆锥的什么？［安排中下生回答：轴］大家观察圆锥的轴SO应具有什么性质？［安排学生稍加讨论，举手发言：圆锥的轴过底面圆的圆心，且与底面圆垂直，轴上连接圆锥顶点与底面圆心的线段就是圆锥的高。

正多边形、扇形和圆锥侧面展开图一、选择题1、（2012年浙江金华五模）一把大遮阳伞，伞面撑开时可近似地看成是圆锥形，如图，它的母线长是2. 5米，底面半径为2米，则做这把遮阳伞需用布料的面积是（ ▲ ）平方米（接缝不计） A ． π3 B ．π4 C ．π5 D ．π425答案：C2、（浙江金华一模）一个长方形的长与宽分别为和16cm ，绕它的对称中心旋转一周所扫过的面积是 2cm ；旋转90度时，扫过的面积是 2cm ． 答案：256π,6401283π+ 3、（2012年上海青浦二模）如果⊙1O 的半径是 5，⊙2O 的半径为 8，124O O =，那么⊙1O 与⊙2O 的位置关系是（ ）A ．内含；B ．内切；C ．相交；D ．外离． 答案：C4、如图，已知圆锥的高为8，底面圆的直径为则此圆锥的侧面积是（ ） A 、24∏B 、30∏C 、48∏D 、60∏5、已知圆柱的底面直径为4cm ，高为5cm ，则圆柱的侧面积是 ( ) A ．10cm 2 B ．10兀cm 2 C ．20兀cm 2 D ．40 兀cm 2 答案：C6、（2012山东省德州四模）已知⊙O 1和⊙O 2外切，它们的半径分别为2cm 和5cm ，则O 1O 2的长（ ） （A ）2cm （B ）3cm （C ）5cm （D ）7cm 答案：D7（2012山东省德州一模） 以O 为圆心的两个同心圆的半径分别为9cm 和5 cm ，若⊙P 与这两个圆都相切，则下列说法中正确的是( )．(A)⊙P 的半径一定是2cm (B)⊙P 的半径一定是7 cm (C) 符合条件的点P 有2个 (D) ⊙P 的半径是2 cm 或7cm 答案：D 8、（2012江苏无锡前洲中学模拟）已知圆锥的底面直径是12cm ，母线长为8cm ，则这个圆锥的侧面积是（ ）A ．48πcm 2B ．48cm 2C ．96π cm 2D ．96 cm 2答案：A 9、（2012荆门东宝区模拟）在综合实践活动课上，小明同学用纸板制作了一个圆锥形漏斗模型．如图所示，它的底面半径OB ＝6cm ，高OC ＝8cm ．则这个圆锥漏斗的侧面积是（ ）． A ．30cm 2 B ．30πcm 2 C ．60πcm 2 D ．120cm210、（2012兴仁中学一模）如图，在Rt △ABC 中，∠C =90°，CA=CB=4，分别以A 、B 、C 为圆心，以21AC 为半径画弧，三条弧与边AB 所围成的阴影部分的面积是． 答案π28-11.(2012年春期福集镇青龙中学中考模拟)已知圆锥的底面半径为4cm ，高为3cm ，则这个圆锥的侧面积为__________cm 2． 答案20π12、(2012温州市泰顺九校模拟) 在R t △ABC 中，∠C=90°，AC=8，BC=6，两等圆⊙A ，⊙B外切，那么图中两个扇形（即阴影部分）的面积之和为（ ） A ．258πB ． 254πC ．2516πD ．2532π答案B13、(2012石家庄市42中二模)如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为（ ）A ．π B.1 C.2 D.23π答案：C14、(2012温州市泰顺九校模拟)在R t △ABC 中，∠C=90°，AC=8，BC=6，两等圆⊙A ，⊙B 外切，那么图中两个扇形（即阴影部分）的面积之和为（ ）A ．π825 B ．π425C ．π1625 D ．π3225 第1７题图 （第9题）答案：B15（2012荆州中考模拟）如图1，现有一个圆心角为90°，半径为8cm 的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为（ ）A ．4cmB ．3cmC ．2cmD ．1cm答案：C16、（2012双柏县学业水平模拟考试）已知圆锥的母线长为4，底面半径为2，则圆锥的侧面积等于【 】A ．11πB ．10πC ． 9πD ． 8π 答案：D17、（2012深圳市龙城中学质量检测）露露从纸上剪下一个圆形和一个扇形的纸片（如图），用它们恰好 能围成一个圆锥模型，若圆的半径为1．扇形的圆心角等于120°， 则此扇形的半径为A 、3B 、6错误！未找到引用源。

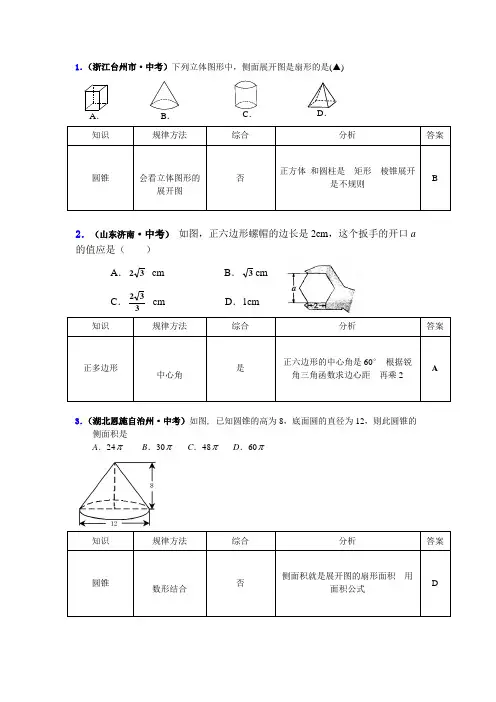
1．（浙江台州市·中考）下列立体图形中，侧面展开图是扇形的是(▲)知识规律方法 综合分析答案圆锥会看立体图形的展开图否正方体 和圆柱是 矩形 棱锥展开是不规则B2．（山东济南·中考） 如图，正六边形螺帽的边长是2cm ，这个扳手的开口a 的值应是（ ）A ．32 cmB ．3cmC ．332 cm D ．1cm 知识规律方法综合分析答案正多边形中心角是正六边形的中心角是60°根据锐角三角函数求边心距 再乘2A3．（湖北恩施自治州·中考）如图, 已知圆锥的高为8，底面圆的直径为12，则此圆锥的侧面积是A ．24πB ．30πC ．48πD ．60π知识规律方法综合 分析 答案圆锥数形结合否侧面积就是展开图的扇形面积 用面积公式DA ．B ．C ．D ．4．（泸州·期中）已知O 为圆锥的顶点，M 为底面圆周上一点，点P 在OM 上，一只蚂蚁从点P 出发绕圆锥侧面爬行回到P 时，所经过的最短路径的痕迹如图2，若沿OM 将圆锥侧面剪开并展平，所得侧面展开图是（ ）知识规律方法综合分析答案圆锥数形结合否 两点之间线段最短 D5．（荷泽·期末） 如图，在正方形铁皮中，剪下一个圆和一个扇形，使余料尽量少，用圆做圆锥的底面，用扇形做圆锥的侧面，正好围成一个圆锥，若圆的半径记为r ，扇形的半径记为R ，那么 A ．R ＝2r B ．R ＝r C ．R ＝3r D ．R ＝4r知识规律方法综合分析答案扇形数形结合是根据扇形面积公式 扇形的弧长和圆的周长相等D6．（湖北宜昌·中考）如图,在圆心角为90°的扇形MNK 中，动点P 从点M 出发，沿MN ⌒NKAB C EFGD→KM 运动，最后回到点M 的位置。

设点P 运动的路程为x ，P 与M 两点之间的距离为y ，其图象可能是（ ）。

知识规律方法综合分析答案扇形数形结合是 从M 到N 和K 到M 这两个过程正好相反 在弧KN 上 到M 的距离一直不变B7．（四川凉山·中考）如第15题图，如果从半径为3cm 的圆形纸片剪去13圆周的一个扇形，将留下在扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的体积是 。

九年级数学扇形面积公式、圆柱、圆锥侧面展开图人教版【本讲教育信息】一. 教学内容：扇形面积公式、圆柱、圆锥侧面展开图［学习目标］1. 掌握基本概念：正多边形，正多边形的中心角、半径、边心距以及平面镶嵌等。

2. 扇形面积公式：S n R lR 扇==π236012n 是圆心角度数，R 是扇形半径，l 是扇形中弧长。

3. 圆柱是由矩形绕一边旋转360°形成的几何体，侧面展开是矩形，长为底面圆周长，宽为圆柱的高S rh 圆柱侧=2π r 底面半径 h 圆柱高4. 圆锥侧面积圆锥是由直角三角形绕一直角边旋转360°形成的几何体。

侧面展开是扇形，扇形半径是圆锥的母线，弧长是底面圆周长。

5. 了解圆柱由两平行圆面和一曲面围成，明确圆柱的高和母线，它们相等。

6. 了解圆锥由一个曲面和一个底面圆围成，明确圆锥的高和母线，知道可以通过解高、母线、底面半径所围直角三角形，解决圆锥的有关问题。

7. 圆柱圆柱的侧面展开图是两邻边分别为圆柱的高和圆柱底面周长的矩形。

圆柱的侧面积等于底面周长乘以圆柱的高。

如图所示，若圆柱的底面半径为r ，高为h ，则：S rh 侧=2π，S S S rh r r h r 表侧底=+=+=+22222πππ()。

8. 圆锥圆锥是由一个底面和一个侧面组成的。

圆锥的底面是一个圆，侧面是一个曲面，这个曲面在一个平面上展开后是一个扇形，这个扇形的半径是圆锥的母线，扇形的弧长是圆锥底面的周长。

因此，圆锥的侧面积是圆锥的母线与底面周长积的一半。

如图所示，若圆锥的底面半径为r ，母线长为l ，则S l r rl 侧·，==122ππ S S S rl r r l r 表侧底=+=+=+πππ2()。

［重点、难点］扇形面积公式及圆柱、圆锥侧面积公式的理解和灵活应用。

【典型例题】例1. 已知如图1，矩形ABCD 中，AB ＝1cm ，BC ＝2cm ，以B 为圆心，BC 为半径作14圆弧交AD 于F ，交BA 延长线于E ，求扇形BCE 被矩形所截剩余部分的面积。

有关圆锥展开图计算的两个重要公式⼤家在解决有关圆锥侧⾯展开图的计算问题时，通常利⽤了两个等量关系，第⼀个是=×底⾯圆周长(或侧⾯的弧长)×母线长，第⼆个就是侧⾯的弧长等于底⾯的周长，但每次都直接利⽤这两个等量关系来计算还是很⿇烦，特别是同学们往往容易忘记乘以系数，基于此我们不妨把这两个等量关系进⼀步推导，得出实质性的乘积、⽐例公式。

我相信同学们在理解并运⽤这两个公式后，解题的思路可以变得清晰，速度和准确度也可以得到很⼤的提⾼。

⼀、推导公式：1.乘积式：侧⾯积：全⾯积：2.⽐例式：弧长等于⊙O1的周长∵∴⼜∵即：这两组公式的优点是避开了求底⾯圆周长，⽽直接建⽴了S侧与R、r的乘积关系，以及圆⼼⾓n与R、r的⽐例关系，减少了许多中间过程，特别是⽐例式给我们的计算带来了极⼤的便利。

⼆、运⽤乘积式：类型⼀：顺向使⽤公式【问题】（2009济南）在综合实践活动课上，⼩明同学⽤纸板制作了⼀个圆锥形漏⽃模型．如图所⽰，它的底⾯半径⾼则这个圆锥漏⽃的侧⾯积是（）A．　B． C． D．分析：从刚才推导出的可以看出，只与圆锥的母线长度以及底⾯圆半径有关，若题⽬没有直接给出母线长度以及底⾯圆半径，往往还可以利⽤R、r和h组成的直⾓三⾓形，求出未知的R 或r来，从⽽计算出侧⾯积。

结论：要求,就求R、r。

解答：此题由底⾯半径⾼可以求出母线BC为10cm，即R=10cm，r=6cm，再由，选C。

【练习】1. （2009铁岭）⼩丽想⽤⼀张半径为5cm的扇形纸⽚围成⼀个底⾯半径为4cm的圆锥，接缝忽略不计，则扇形纸⽚的⾯积是cm2．（结果⽤表⽰）202.（2009南昌）⼀个圆锥的底⾯直径是80cm,母线长是90cm,则它的侧⾯积是____ 。

3600cm23. （2008成都）⼩红同学要⽤纸板制作⼀个⾼4cm，底⾯周长是6πcm的圆锥形漏⽃模型，若不计接缝和损耗，则她所需纸板的⾯积是（）BA．12πcm2 B．15πcm2 C．18πcm2 D．24πcm2类型⼆：逆向使⽤公式【问题】（2009义乌）如图，圆锥的侧⾯积为，底⾯半径为3，则圆锥的⾼AO为 .分析：从刚才推导出的可以看出，已知、R、r中任意两个量可以求出余下未知的量，若题⽬要求求出圆锥的⾼h，往往还可以利⽤R、r和h组成的直⾓三⾓形，从⽽求出。

2016届中考复习29：（正多边形.扇形.圆锥侧⾯展开图）⼀、选择题1.（2015⼭东省青岛市，6，3分）如图，正六边形ABCDEF内接于⊙O，若直线PA与相切与点A，则∠PAB=（）A.30°B.35°C.45°D.60°【答案】A2.（2015浙江省湖州市，3，分）若⼀个圆锥的侧⾯展开图是半径为18cm，圆⼼⾓为240°的扇形，则这个圆锥的底⾯半径长是( )．A．6cm B．9cm C．12cm D．18cm【答案】C【解析】扇形弧长：，设底⾯圆的半径为r，则，得r＝12．3.（2015⼭东省德州市，9，3分）如图，要制作⼀个圆锥形的烟囱帽，使底⾯圆的半径与母线长的⽐是4：5，那么所需扇形铁⽪的圆⼼⾓应为A.288°B.144°C.216°D.120°第9题图【答案】A4.（2015四川省凉⼭州市，8，4分）将圆⼼⾓为90°，⾯积为4πcm2的扇形围成⼀个圆锥的侧⾯，则所围成的圆锥的底⾯半径为（）A.1cmB.2cmC.3cmD.4cm【答案】D.【解析】由侧⾯积公式，得r=4，故选D.5.（2015上海市，4，4分）如果⼀个正多边形的中⼼⾓为72多边形的边数是（A）4；（B）5；（C）6；（D）7【答案】B【解析】直接⽤周⾓360=56.（2015江苏泰州，4，3分）⼀个⼏何体的表⾯展开图如图所⽰，则这个⼏何体是A．四棱锥 B．四棱柱 C．三棱锥 D．三棱柱（第4题图）【答案】A7.（2015⼭东省威海市，８，３分）若⽤⼀张直径为20cm的半圆做成⼀个圆锥的侧⾯，接缝忽略不计，则所得圆锥的⾼为（）A. B. C. D.【答案】A【解析】先利⽤弧长公式直径为20cm的半圆的弧长10π，根据圆锥的侧⾯展开图为扇形，扇形的弧长等于圆锥的底⾯圆的周长，则可计算出圆锥的底⾯圆的半径，然后根据勾股定理可计算出圆锥的⾼．∵直径为20cm的半圆的弧长=10π，∴圆锥的底⾯圆的周长为10π，∴圆锥的底⾯圆的半径为5，∴这个纸帽的⾼=（cm）．故选A．8.（2015⼭东省威海市，12，3分）如图，正六边形的边长为2，正六边形的外接圆与正六边形的各边相切，正六边形的外接圆与正六边形的的各边相切，·······按这样的规律进⾏下去，正⼗边形的边长为（）A. B. C. D.【答案】D【解析】设正六边形相邻连边和与⊙O的切点分别为和，连接，，，与的交点为M，则，，由题意知∠=30°,,,所以，所以,根据这个规律.故选D.9.（2015浙江宁波，9，4分）如图，⽤⼀个半径为 30cm，⾯积为300πcm2的扇形铁⽪，制作⼀个⽆底的圆锥(不计损耗)，则圆锥的底⾯半径r为( )A.5cmB.10cmC.20cmD.5πcm【答案】B10. (2015年⼭东省济宁市)只⽤下列哪⼀种正多边形，可以进⾏平⾯镶嵌（）A. 正五边形B. 正六边形C. 正⼋边形D.正⼗边形【答案】B11.（2015⼭东⽇照市，8，3分）如右图，等腰直⾓△ＡＢＣ中，ＡＢ＝AC=8，以ＡＢ为直径的半圆O交斜边ＢＣ于D，则阴影部分⾯积为（结果保留）（）（A） (B) (C) (D)【答案】A【解析】解：（1）如图连接AD、OD。