(苏锡常镇连徐六市)2014届高三3月教学情况调研(一)

苏锡常镇四市2014届高三3月教学情况调研（一）数学Ⅰ试题 2014．3参考公式：柱体的体积公式：V 柱体=Sh ，其中S 是柱体的底面积，h 是高． 直棱柱的侧面积公式：S 直棱柱侧=ch ，其中c 是直棱柱的底面周长，h 是高．一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1．已知集合{}1,2,3,4A =，{},4,7B m =，若{}1,4A B =，则AB = ▲ ．2．若复数z =13i1i+-（i 为虚数单位），则 | z | = ▲ ． 3．已知双曲线2218x y m -=m 的值为 ▲ ．4．一个容量为20的样本数据分组后，分组与频数分别如下：(]10,20，2；(]20,30，3；(]30,40，4；(]40,50，5；(]50,60，4；(]60,70，2．则样本在(]10,50上的频率是 ▲ ． 5．执行如图所示的算法流程图，则最后输出的y 等于 ▲ ．6．设函数2()sin f x a x x =+，若(1)0f =，则(1)f -的值为 ▲ ． 7． 四棱锥P ? ABCD 的底面ABCD 是边长为2的正方形，PA ⊥底面ABCD 且PA = 4，则PC 与底面ABCD 所成角的正切值为 ▲ ．8．从甲，乙，丙，丁4个人中随机选取两人，则甲乙两人中有且只有一个被选取的概率为 ▲ ． 9．已知2tan()5a b +=，1tan 3b =，则tan +4p a ⎛⎫ ⎪⎝⎭的值为 ▲ ．（第5题）10．设等差数列{}n a 的前n 项和为n S ，若13a =-，132k a +=，12k S =-，则正整数k = ▲ ． 11．已知正数,x y 满足22x y +=，则8x yxy+的最小值为 ▲ ． 12．如图，在△ABC 中，BO 为边AC 上的中线，2BG GO =，设CD ∥AG ，若15AD AB AC =+λ()∈R λ，则λ的值为 ▲ ． 13．已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+，若函数()g x 恰有两个不同的零点，则实数k 的取值范围为 ▲ ．14．在平面直角坐标系xOy 中，已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内，动直线AB 过点P 且交圆C 于,A B 两点，若△ABC 的面积的最大值为16，则实数m 的取值范围为 ▲ ．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分14分）设函数2()6cos cos f x x x x =-． （1）求()f x 的最小正周期和值域；（2）在锐角△ABC 中，角,,A B C 的对边分别为,,a b c ，若()0f B =且2b =，4cos 5A =，求a 和sin C ． 16．（本小题满分14分）如图，在三棱柱111ABC A B C -中，侧面11AA B B 为菱形， 且160A AB ∠=︒，AC BC =，D 是AB 的中点． （1）求证：平面1A DC ⊥平面ABC ； （2）求证：1BC ∥平面1A DC ． 17．（本小题满分14分）一个圆柱形圆木的底面半径为1m ，长为10m ，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD （如图所示，其中O 为圆心，,C D 在半圆上），设BOC q ∠=，木梁的体积为V （单位：m 3），表面积为S（单位：m 2）．（1）求V 关于θ的函数表达式； （2）求q 的值，使体积V 最大；（3）问当木梁的体积V 最大时，其表面积S 是否也最大请说明理由．111DC B CBA （第16题）（第12题）ABCDOG18．（本小题满分16分）如图，在平面直角坐标系xOy 中，已知A ，B ，C 是椭圆22221(0)x y a b a b +=>>上不同的三点，A ，(3,3)B --，C 在第三象限，线段BC 的中点在直线OA 上．（1）求椭圆的标准方程； （2）求点C 的坐标；（3）设动点P 在椭圆上（异于点A ，B ，C ）且直线PB ，PC 分别交直线OA 于M ，N 两点，证明OM ON ⋅为定值并求出该定值．19．（本小题满分16分）设各项均为正数的数列{}n a 的前n 项和为S n ，已知11a =，且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立．（1）若λ = 1，求数列{}n a 的通项公式； （2）求λ的值，使数列{}n a 是等差数列． 20．（本小题满分16分）已知函数e ()ln ,()e xxf x mx a x mg x =--=，其中m ，a 均为实数． （1）求()g x 的极值；（2）设1,0m a =<，若对任意的12,[3,4]x x ∈12()x x ≠，212111()()()()f x f xg x g x -<-恒成立，求a 的最小值；（3）设2a =，若对任意给定的0(0,e]x ∈，在区间(0,e]上总存在1212,()t t t t ≠，使得120()()()f t f t g x == 成立，求m 的取值范围．苏锡常镇连徐四市2014届高三3月教学情况调研（一）θD CBAO（第17题）（第18题）数学Ⅱ（附加题） 2014．321．【选做题】在A 、B 、C 、D 四小题中只能选做两题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤． A ．选修4—1：几何证明选讲如图，⊙O 为四边形ABCD 的外接圆，且AB AD =，E 是CB 延 长线上一点，直线EA 与圆O 相切．求证：CD ABAB BE=． B ．选修4—2：矩阵与变换 已知矩阵1221⎡⎤=⎢⎥⎣⎦M ，17⎡⎤=⎢⎥⎣⎦β，计算6M β． C ．选修4—4：坐标系与参数方程 在平面直角坐标系xOy 中，圆的参数方程为22cos ,()2sin x y a a a =+⎧⎨=⎩为参数，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．求：（1）圆的直角坐标方程；（2）圆的极坐标方程． D ．选修4—5：不等式选讲已知函数2()122f x x x a a =++---，若函数()f x 的图象恒在x 轴上方，求实数a 的取值范围．【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）甲乙两个同学进行定点投篮游戏，已知他们每一次投篮投中的概率均为23，且各次投篮的结果互不影响．甲同学决定投5次，乙同学决定投中1次就停止，否则就继续投下去，但投篮次数不超过5次． （1）求甲同学至少有4次投中的概率；（2）求乙同学投篮次数x 的分布列和数学期望． 23．（本小题满分10分）（第21-A 题）设01212(1)m mn n n n n m S C C C C ---=-+-+-，*,m n ∈N 且m n <，其中当n 为偶数时，2nm =；当n 为奇数时，12n m -=． （1）证明：当*n ∈N ，2n ≥时，11n n n S S S +-=-； （2）记01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，求S 的值． 苏锡常镇连徐四市2014届高三3月教学情况调研（一）数学Ⅰ试题参考答案 2014．3一、填空题：本大题共14小题，每小题5分，共70分． 1．{}1,2,3,4,7 2 3. 4 4.7105．63 6．2 7 8. 23 9． 9810．13 11．9 12．65 13. 27321,{0,22e +⎛⎫-- ⎪⎝⎭14. [3(327,3++--二、解答题：本大题共6小题，共计90分．解答时应写出文字说明、证明过程或演算步骤． 15. 解：（1）1+cos2()622xf x x =⨯=3cos223x x + =)36x p++． …………………3分 所以()f x 的最小正周期为22T pp ==，…………………4分 值域为[3-+． …………………6分（2）由()0f B =，得πcos(2)6B +=． B 为锐角，∴ππ7π2666B <+<，π5π266B +=，∴π3B =． …………………9分∵4cos 5A =，(0,)A p ∈，∴3sin 5A ．…………………10分在△ABC 中，由正弦定理得32sin sin b A a B⨯===…………………12分∴21sin sin()=sin()sin 32C A B A A A p p =---=+=． …………………14分 16．（1）证明：∵ 11ABB A 为菱形，且160A AB ∠=︒，∴△1A AB 为正三角形． …………………2分D 是AB 的中点，∴1AB A D ⊥．∵AC BC =，D 是AB 的中点，∴ AB CD ⊥． …………………4分1A D CD D =，∴AB ⊥平面1A DC ． …………………6分∵AB ⊂平面ABC ，∴平面1A DC ⊥平面ABC ． …………………8分（2）证明：连结1C A ，设11AC AC E =，连结DE ． ∵三棱柱的侧面11AA C C 是平行四边形，∴E 为1AC 中点． …………………10分 在△1ABC 中，又∵D 是AB 的中点，∴DE ∥1BC ． …………………12分 ∵DE ⊂平面1A DC ，1BC ⊄平面1A DC ，∴ 1BC ∥平面1A DC ． …………………14分 17．解：（1）梯形ABCD 的面积2cos 2sin 2ABCD S q q +=⋅=sin cos sin q q q +，(0,)2pq ∈． …………………2分 体积()10(sin cos sin ),(0,)2V pq q q q q =+∈． …………………3分 （2）2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+． 令()0V q '=，得1cos 2q =，或cos 1q =-（舍）． ∵(0,)2p q ∈，∴3pq =． …………………5分 当(0,)3p q ∈时，1cos 12q <<，()0,()V V q q '>为增函数； 当(,)32p p q ∈时，10cos 2q <<，()0,()V V q q '<为减函数． …………………7分 ∴当3pq =时，体积V 最大． …………………8分 （3）木梁的侧面积210S AB BC CD =++⋅侧（）=20(cos 2sin 1)2q q ++，(0,)2pq ∈． 2ABCD S S S =+侧=2(sin cos sin )20(cos 2sin 1)2q q q q q ++++，(0,)2pq ∈．…………………10分设()cos 2sin 12g q q q =++，(0,)2p q ∈．∵2()2sin 2sin 222g q qq =-++， ∴当1sin22q =，即3pq =时，()g q 最大． …………………12分 又由（2）知3pq =时，sin cos sin q q q +取得最大值， 所以3pq =时，木梁的表面积S 最大． …………………13分 综上，当木梁的体积V 最大时，其表面积S 也最大． …………………14分18．解：（1）由已知，得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩ …………………2分所以椭圆的标准方程为22127272x y +=． …………………3分 （2）设点(,)C m n (0,0)m n <<，则BC 中点为33(,)22m n --． 由已知，求得直线OA 的方程为20x y -=，从而23m n =-．① 又∵点C 在椭圆上，∴22227m n +=．②由①②，解得3n =（舍），1n =-，从而5m =-． …………………5分 所以点C 的坐标为(5,1)--． …………………6分 （3）设00(,)P x y ，11(2,)M y y ，22(2,)N y y ． ∵,,P B M 三点共线，∴011033233y y y x ++=++，整理，得001003()23y x y x y -=--．…………………8分 ∵,,P C N 三点共线，∴22011255y y y x ++=++，整理，得00200523y x y x y -=-+．…………………10分 ∵点C 在椭圆上，∴2200227x y +=，2200272x y =-．从而22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+． …………………14分 所以124552OM ON y y ⋅==． …………………15分 ∴OM ON ⋅为定值，定值为452． …………………16分 19．解：（1）若λ = 1，则11(1)(1)n n n n S a S a +++=+，111a S ==．又∵00n n a S >>，， ∴1111n n n nS a S a +++=+， ………………… 2分 ∴3131221212111111n n n nS S a a S a S S S a a a +++++⋅⋅⋅=⋅⋅⋅+++， 化简，得1112n n S a +++=．① ………………… 4分 ∴当2n ≥时，12n n S a +=．②② ? ①，得12n n a a +=， ∴12n na a +=（2n ≥）． ………………… 6分 ∵当n = 1时， 22a =，∴n = 1时上式也成立，∴数列{a n }是首项为1，公比为2的等比数列， a n = 2n ?1（*n ∈N ）． …………………8分（2）令n = 1，得21a λ=+．令n = 2，得23(1)a λ=+． ………………… 10分要使数列{}n a 是等差数列，必须有2132a a a =+，解得λ = 0． ………………… 11分 当λ = 0时，11(1)n n n n S a S a ++=+，且211a a ==． 当n ≥2时，111()(1)()n n n n n n S S S S S S +-+-=+-， 整理，得2111n n n n n S S S S S +-++=+，1111n n n nS S S S +-+=+， ………………… 13分 从而3312412123111111n n n nS S S S S S S S S S S S +-+++⋅⋅⋅=⋅⋅⋅+++， 化简，得11n n S S ++=，所以11n a +=． ……………… 15分 综上所述，1n a =（*n ∈N ），所以λ = 0时，数列{}n a 是等差数列． ………………… 16分 20．解：（1）e(1)()e xx g x -'=，令()0g x '=，得x = 1． ………………… 1分 列表如下：∵g (1) = 1，∴y =()g x 的极大值为1，无极小值． …………………3分（2）当1,0m a =<时，()ln 1f x x a x =--，(0,)x ∈+∞．∵()0x af x x -'=>在[3,4]恒成立，∴()f x 在[3,4]上为增函数． …………………4分 设1e ()()e x h x g x x ==，∵12e (1)()x x h x x --'=> 0在[3,4]恒成立， ∴()h x 在[3,4]上为增函数． …………………5分设21x x >，则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-， 即2211()()()()f x h x f x h x -<-．设1e ()()()ln 1e xu x f x h x x a x x=-=---⋅，则u (x )在[3,4]为减函数．∴21e (1)()10e x a x u x x x -'=--⋅≤在（3，4）上恒成立． …………………6分∴11e ex x a x x---+≥恒成立．设11e ()e x x v x x x --=-+，∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+，x ?[3，4]， ∴1221133e [()]e 1244x x --+>>，∴()v x '< 0，()v x 为减函数．∴()v x 在[3，4]上的最大值为v (3) = 3 ?22e 3． ………………… 8分 ∴a ≥3 ?22e 3，∴a 的最小值为3 ?22e 3． …………………9分 （3）由（1）知()g x 在(0,e]上的值域为(0,1]． …………………10分 ∵()2ln f x mx x m =--，(0,)x ∈+∞，当0m =时，()2ln f x x =-在(0,e]为减函数，不合题意． ………………… 11分当0m ≠时，2()()m x m f x x-'=，由题意知()f x 在(0,e]不单调，所以20e m <<，即2em >．① …………………12分 此时()f x 在2(0,)m 上递减，在2(,e)m上递增， ∴(e)1f ≥，即(e)e 21f m m =--≥，解得3e 1m -≥．② 由①②，得3e 1m -≥． …………………13分 ∵1(0,e]∈，∴2()(1)0f f m=≤成立． …………………14分 下证存在2(0,]t m∈，使得()f t ≥1． 取emt -=，先证e2mm-<，即证2e 0mm ->．③ 设()2e xw x x =-，则()2e 10xw x '=->在3[,)e 1+∞-时恒成立． ∴()w x 在3[,)e 1+∞-时为增函数．∴3e ))01((w x w ->≥，∴③成立． 再证()e mf -≥1．∵ee 3()1e 1m mf m m m --+=>>-≥，∴3e 1m -≥时，命题成立． 综上所述，m 的取值范围为3[,)e 1+∞-． …………………16分 苏锡常镇连徐四市2014届高三3月教学情况调研（一）数学Ⅱ（附加题） 参考答案 2014．321、【选做题】在A 、B 、C 、D 四小题中只能选做两题．．．．．．，每小题10分，共计20分． A ．选修4—1：几何证明选讲证明：连结AC ．EA 是圆O 的切线，∴EAB ACB ∠=∠． …………………2分AB AD =，∴ACD ACB ∠=∠． ∴ACD EAB ∠=∠． …………………4分圆O 是四边形ABCD 的外接圆，∴D ABE ∠=∠． …………………6分∴CDA ∆∽ABE ∆． …………………8分 ∴CD DAAB BE=， AB AD =，∴CD ABAB BE=． …………………10分 B ．选修4—2：矩阵与变换解：矩阵M 的特征多项式为212()2321f λλλλλ--==----． 令12()031f λλλ===-，解得，，对应的一个特征向量分别为111⎡⎤=⎢⎥⎣⎦α，211⎡⎤=⎢⎥-⎣⎦α． …5分 令12m n =+βαα，得4,3m n ==-．6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α．……………10分C ．选修4—4：坐标系与参数方程解：（1）圆的直角坐标方程为22(2)4x y -+=． …………………5分（2）把cos ,sin ,x y ρθρθ=⎧⎨=⎩代入上述方程，得圆的极坐标方程为4cos ρθ=．…………………10分D ．选修4—5：不等式选讲解：()f x 的最小值为232a a --， …………………5分由题设，得223a a -<，解得(1,3)a ∈-． …………………10分【必做题】第22题、第23题，每题10分，共计20分．22．解：（1）设甲同学在5次投篮中，有x 次投中，“至少有4次投中”的概率为P ，则(4)(5)P P x P x ==+= …………………2分=44155552222()(1)()(1)3333C C -+-=112243． …………………4分 （2）由题意1,2,3,4,5=x ．2(1)3P ==x ，122(2)339P ==⨯=x ，1122(3)33327P ==⨯⨯=x ，3122(4)3381P x ⎛⎫==⨯= ⎪⎝⎭， 411(5)381P x ⎛⎫=== ⎪⎝⎭．x 的分布表为…………………8分x 的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=x ． …………………10分 23．解：（1）当n 为奇数时，1n +为偶数，1n -为偶数，∵1101221112(1)n n n n nn S CC C+++++=-++-，110122112(1)n n n n n n S C C C---+=-++-， 11012211212(1)n n n n n n S C CC------=-++-，∴1111110011222221111111222()()(1)()(1)n n n n n n n n nnn n n n S S C C C C CCC-+-++-++-++++-=---++--+-=11012212112((1))n n n n n n CCCS --------++-=-．∴当n 为奇数时，11n n n S S S +-=-成立． …………………5分 同理可证，当n 为偶数时， 11n n n S S S +-=-也成立． …………………6分 （2）由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，得 =0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -． …………………9分 又由11n n n S S S +-=-，得6n n S S +=，所以20142012421S S S S -=-=-，12014S =-．………10分。

苏锡常镇四市2014届高三教学情况调研 (一)政 治 2014．3第Ⅰ卷（选择题 共66分）一、单项选择题：本大题共33小题，每小题2分，共66分。

在每题给出的四个选项中，只有一个选项是最符合题意的。

1．2014年2月，中国人民银行表示，将保持适度流动性，实现货币信贷及社会融资规模合理增长。

这意味着今后央行货币供应既不会大开闸门放水，也不会紧缩以致闹“钱荒”。

保持适度流动性A.可以避免通货膨胀的出现B.是纸币流通规律的客观要求C.会直接影响商业银行利润D.是国家运用财政政策的表现2．在不考虑其它因素的情况下，下列选项中与图1需求曲线变化 相吻合的是A.汽油价格上调后，新能源汽车需求量的变化B.政府取消汽车购置税优惠后，汽车需求量的变化C.人民币汇率下降后，进口汽车需求量的变化D.政府优先发展公共交通后，汽车需求量的变化图13. 随着消费者对移动网络宽带化需求的日益迫切，第四代移动通信技术（4G）应运而生。

4G能够快速传输高质量视频图像，更好地满足用户对于无线服务的要求。

这表明①消费对生产的调整和升级起导向作用 ②消费是经济增长的根本动力③企业要坚持“高精尖”的战略定位 ④生产决定消费的质量和水平A.①②B.①④C.②③D.③④4．《中国劳动力动态调研：2013年报告》显示，有38.42%的职工在调查的上个月加过班，但其中只有45.57%拿到了加班工资。

劳动者因担心“不加班、或者要加班工资可能丢饭碗”而选择忍气吞声。

解决这一问题需要A.完善市场机制，改善就业结构B.加强劳动保护，改善劳动条件C.规范劳动制度，加强监管力度D.健全社会保障，依法维护权利5. 赵某花5万元在银行购买了一款理财产品，工作人员称收益率在5.5%，而且无风险。

产品到期后，赵某只获得300多元收益。

银行解释说，这款理财产品收益率是0.36%—5.5%。

经消协调解，银行以高于当前的银行定期利率补偿了赵某损失。

这说明①存款业务是商业银行的基础业务 ②诚实守信是规范市场秩序的治本之策③市场调节存在自发性的固有缺陷 ④银行理财产品的收益与风险是并存的A.①②B. ②③C. ②④D.③④2014年中央一号文件——《关于全面深化农村改革加快推进农业现代化的若干意见》全面定调2014年及今后一个时期农业农村工作。

注意事项 2014．3考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共6页，满分为160分，考试时间为150分钟。

2. 答题前，务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在答题卡的规定位置，考试结束后，请将答题卡交回，在本试卷上答题无效。

一、语言文字运用（15分）1．下列各组词语中，没有错别字．．．．．的一组是（3分） A ．耄耋 钟灵毓秀 德高望众 筚路蓝缕B ．朔源 切磋琢磨 平心而论 金碧辉煌C ．甄别 蓬荜生辉 喧宾夺主 以逸代劳D ．暮霭 涸泽而渔 韬光养晦 急流勇退2．下列各句中，没有语病．．．．的一句是（3分） A ．这家公司的利润近三个季度来一直下滑，根本原因是公司经营理念落后，产品质量下降造成的。

B ．大范围的雾霾使长三角地区变得“灰头土脸”，南京、无锡等地空气质量达重度污染程度。

C ．虽然情感生活不是我们生命的全部，但谁又能否认它不是我们整个生命中的重要组成部分呢？D ．《时代周刊》认为曼德拉是这个世界最接近圣人、最具有宽恕美德，这种宽恕无论在哪个时代都极其珍贵。

3．钱钟书对翻译有如下形象的表述：翻译的最高境界是让原作“投胎转世”，躯壳换了一个，而精神姿致依然故我。

请你将钱钟书的话用平实的语言重新表述。

（不超过30个字）（4分）4．仿照例句再写两个句子。

（5分）例句：（1）尘土受到损辱，却以花朵来报答。

（2）白云谦逊地站在天之一隅，晨光给它带上霞彩。

二、文言文阅读（19分）2013~2014学年苏锡常镇四市高三教学情况调研（一）语 文 Ⅰ阅读下面的文言文，完成5～8题。

贺齐字公苗，会稽山阴人也。

少为郡吏，守剡长。

县吏斯从轻侠为奸，齐欲治之，主簿谏曰：“从，县大族，山越所附，今日治之，明日寇至。

”齐闻大怒，立斩从。

从族党遂相纠合，众千余人，举兵攻县。

齐率吏民，开城门突击，大破之，威震山越。

后太末、丰浦民反，转守太末长，诛恶养善，期月尽平。

建安元年，孙策临郡，察齐孝廉。

【名师综述】1.本试卷难度适中，知识点单一的小题较多,如前十题，也有拉开档次的题目（如,13,14,19，20)，考查知识点和能力点基本到位。

其中，第14题将圆中弦长问题和最值问题交汇在一起，试题的选拔性和交汇性极高。

挖掘“圆心到直线距离不大于CP ”这一隐含条件是确保解题正确关键.第13题，容易在研究“-∞→x 时，函数)(x f 恒小于零”上出错。

运用数学结合解题应严格分析图形在各单调区间趋势范围。

第18题求椭圆定值问题，有一定运算量.学生失分原因:除去畏难心理外，还有忽略整体感知，导致方向性错误的因素。

建议考生:多练、多思。

2.本套试题题型稳中有变，内容鲜活,富有时代气息.第19题数列题，一改其常规面目，以“类等比”给出n S 与na 关系式,将“叠乘法” 化简数列 “隐身”其中,试题的交汇天衣无缝！第20题是导数题，是对恒成立的考查，以两种不同说法的形式，给出了问题，动中有静，静中有动，动静结合,命题者独具匠心!恒成立问题关键在于等价转化不等式。

第20题第(2）小题设计两道坎，一是绝对值，二是两个变量依存关系。

第20题第（3)小题，难度上升一个层次，设计三个参量，重点考查学生思维能力。

【易错题解读】1.【理科试卷第13题】已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点，则实数k 的取值范围为 ．【原创题解读】1。

【理科试卷第14 题】在平面直角坐标系xOy中，已知点(3,0)P在圆222+--+-=内，动直线AB过点P且交圆C于,A B两点，若△ABC :24280C x y mx y m的面积的最大值为16，则实数m的取值范围为．【举一反三】在平面直角坐标系xOy中，过点O作直线l与圆。

江苏省苏锡常镇四市2014届高三3月教学情况调研生物卷（带解析）1．下列各种化合物中，不直接参与线粒体内有关代谢反应的是0B．有氧呼吸酶C．葡萄糖D．丙酮酸A．H2【答案】C【解析】试题分析：水分子在线粒体基质与丙酮酸反应生成二氧化碳和{H}，故A正确。

有氧呼吸2、3阶段在线粒体进行，线粒体分布大量与有氧呼吸相关的酶，故B正确。

葡萄糖不能进入线粒体反应，先在细胞质基质分解为丙酮酸，再进入线粒体反应，故C错，D正确。

考点：本题考查有氧呼吸相关知识，意在考查考生能理解所学知识的要点，把握知识间的内在联系，形成知识的网络结构能力。

2．下列关于现代生物进化理论的叙述中。

正确的是A．共同进化与生态系统的信息传递密切相关B．无法进行基因交流的生物之间一定存在生殖隔离C．生物进化过程的实质在于保存对环境更适应的性状D．某种群的数量长期维持稳定，说明该种群的基因频率保持不变【答案】A【解析】试题分析：生态系统的信息能够调节种间关系，与共同进化相关，故A正确。

同一种群个体由于地理隔离会导致生物无法进行基因交流，一旦相遇，还是可以进行基因交流，不存在生殖隔离，故B错。

生物进化过程的实质是正确基因频率的定向改变，故C错。

某种群的数量长期维持稳定，该种群的基因频率可能改变，故D错。

考点：本题考查生物进化相关知识，意在考查考生能理解所学知识的要点，把握知识间的内在联系，形成知识的网络结构能力。

3．下列关于人体内环境及稳态调节的叙述中，正确的是A．毛细血管壁细胞生活的内环境是血浆和淋巴B．甲状腺激素和尿素等物质均可能存在于内环境中C．血浆中的蛋白质均会透过毛细血管壁到达组织液中D．细胞外液渗透压升高时，机体释放的抗利尿激素减少【答案】B【解析】试题分析：毛细血管壁细胞内环境是血浆和组织液，故A错。

激素分泌后进入血浆运输，细胞代谢产生的尿素进入血浆运输，故B正确。

由于细胞膜的选择透过性，血浆中的蛋白质一般不会透过毛细血管壁到达组织液中，故C错。

江苏省苏、锡、常、镇四市2014届高三教学情况调查一3高考英语2014-03-25 2047()第五部分书面表达(满分25分)2014年央视春晚的广告收入创新高，但节目中的植入广告引发了热议。

最近，某网站举行了一次题为“对今年春晚植入广告的态度”的调查，请根据以下饼图(pie chart)所示信息用英语写一篇短文，并提出你自己的看法。

注意：1. 对所给提示，不要简单翻译，可适当增加细节，使行文连贯。

2. 词数150左右。

开头已给出，不计入总词数。

3. 植入广告 product placementThe 2014 Spring Festival Gala has set records for TV commercial rates, which accordingly has caused heated discussions due to product placement in the programmes.参考答案听力1-5 ACABC 6-2014 BCCAB 11-15BCAAC 16-20 BCABC单选21-25 CCABD 26-30 BADAB 31-35 CCDBD完形36-40 DCABA 41-45 CBDDA 46-50ADCBC 51-55 ABBDC阅读56-60 BCDBD 61-65 ACCBA 66-70 DACBC任务型阅读71. origin/beginning/start 72.display/show 73. being/existence74. differed 75.cultural 76. Although/Though/While77. images/brands 78.participating/joining 79. Besides80. Future/Upcoming书面表达：(满分25分)One possible versionThe 2014 Spring Festival Gala has set records for TV commercial rates, which accordingly has caused heated discussions due to product placement in the programmes.As is shown in the pie chart, 20% of the people surveyed think it acceptable, for the product placement appears in the programmes naturally. And 15% of them consider it necessary for CCTV to make money from product placement, which is of great benefit to the development of CCTV itself.However, among the people surveyed, more than one third of them complain that the product placement has nothing to do with the programmes. 25% of them even feel hurt seeing so much of it. Furthermore, the rest 2014% hold the view that great harm has been done to the image of CCTV.From the chart we can draw a conclusion that most of the people surveyed are against product placement in the programmes. In my opinion, product placement nowadays is almost unavoidable, but itshould not damage the art of the show and should take the audience’s feelings into account. (151 words)听力录音稿(Text 1)W Flight 331 is being announced. I’d better be on my way. Goodbye. Thanks for your help.M You’re welcome. Have a good trip.(Text 2)M Did the Johnsons come to your party?W Yes, they did. They also brought two strangers with them.(Text 3)M Have you read the research report?W Yes, but it wasn’t well written. I sent it back to the department with some suggestions.M Good. I couldn’t understand it either, but I thought it was just me!(Text 4)M What’s your present job?W I’m a secretary in a computer company.M That sounds like a good job. Why do you want to change it?W It’s hard to say, but I want more challenges.(Text 5)M Are you sure you have corrected all the typing errors in this paper? W Perhaps I’d better read it through again.M I hope there are no more mistakes.(Text 6）M Excuse me. Could you tell me the way to Dobson’s bookstore?W Yes. Go two blocks, and then turn left. It’s on the corner opposite the post office.M Thanks. I’ve only been in the city for a few days, so I reall y don’t know my way around yet.W Oh, I know how you feel. We moved here a year ago, and I still don’t know where everything is.(Text 7)W Do you think that climate change is responsible for the recent floods?M It could be. There are floods in this country every year, but in recent years they have been more widespread and more frequent.W It seems that the climate in this country is changing.M The summers are hotter. The last three summers have been thehottest for the past 200 years. There have also been stronger winds.W I think that the changing climate is a sign that we’re causing too much damage to the environment.M I think you’re right. Climate changes naturally over time, but I think that human activities are speeding up the change. I wish that governments would join together and try to resolve the problem.W I agree. If we don’t do something soon, it might be too late.(Text 8)M I visited some friends in a small town—Clinton Rex.W That must have been very interesting! I’ve never been to a smal l town—I just stay in big cities. And…what did you do?M Well, on Saturday we went to a potluck supper.W A potluck supper? What’s that?M The whole neighborhood has a party. Everybody brings something. We put them on the table and you can eat whatever you like.W It’s something like a picnic, isn’t it? That must be so much fun.M Well, yes. It was warm, so we had it outdoors.W That sounds great! What else did you do?M On Sunday we went out for a swim in the sea. Then we had lunch on the seaside.W That sounds like a pleasant trip. I wish I had been there.(Text 9)M Good morning, Mrs. Adams. How are you today?W Oh. Not very well. I’ve caught a bad cold.M Have you taken your temperature?W Yes, I’ve got a fever.M Are you coughing?W Yes, especial ly at night. It’s quite bad then. And I can’t go to sleep.M Oh, I see. I can understand that. Um, I think you’ve got the flu.I suggest you should not goto work, and take this medicine every four hours.W What else should I do?M Drink more water and have a good rest.W OK. Thanks. Goodbye!M Goodbye!(Text 2014)The day after Christmas or the first weekday, if December 26 falls on the weekend, is a legal holiday known as Boxing Day in the United Kingdom, Canada, and several other countries. It is possible that Boxing Day received its name because churches often open the boxes of money, food, and other items donated by church goers during the Christmas season and deliver it to the poor on this day. Another explanation is that the name arose from the old custom of noblemen giving their servants boxes with gifts on this day. Likewise, people who performed public services, such as lamplighters or postal workers, often carried around boxes on the 26th to receive tips from thepeople who benefited from their work. Although employees and public workers continue to receive Christmas gifts or money in modern times, the exchange often occurs before Christmas.In some parts of the Bahamas people hold parades on Boxing Day. In Ireland people may mark the occasion by making a type of potato bread known as boxty. For most people, the holiday is used to spend timewith family, rest after the many activities of Christmas, and get rid of boxes from Christmas presents.。

江苏省苏、锡、常、镇四市2014届高三教学情况调查（一）理科数学试卷（带解析）1．已知集合{}1,2,3,4A =，{},4,7B m =，若{}1,4A B =，则AB = ．【答案】{}1,2,3,4,7 【解析】 试题分析：因为{}1,4AB =，所以B ∈1,.1=m 因此AB ={}1,2,3,4,7.考点：集合运算 2．若复数z =13i1i+-（i 为虚数单位），则|z |= ．【解析】试题分析：因为13i 1i +-,21242i i +-=+-=所以.5||=z 也可利用复数模的性质求解，即.5210|1||31|||==-+=i i z考点：复数的模3．已知双曲线2218x y m -=m 的值为 ．【答案】4 【解析】试题分析：由题意得：,38=+mm 解得.4=m 解答此类问题，要明确对应关系，一是,8,22==b m a 二是双曲线中.222b a c +=考点：双曲线离心率4．一个容量为20的样本数据分组后，分组与频数分别如下：(]10,20，2；(]20,30，3；(]30,40，4；(]40,50，5；(]50,60，4；(]60,70，2．则样本在(]10,50上的频率是 ． 【答案】710【解析】试题分析：因为样本在(]10,50上的频数共有 145432=+++，所以样本在(]10,50上的频率是1072014=.也可从反面求解，即样本不在(]10,50上的频数共有 624=+，所以样本在(]10,50上的频率是107206-1=.考点：样本频率5．执行如图所示的算法流程图，则最后输出的y 等于 ．【答案】63 【解析】试题分析：第一次循环，,2,3==x y 第二次循环，,3,7==x y 第三次循环，,4,15==x y 第四次循环，,5,31==x y 第六次循环，,56,63>==x y 终止循环，输出63=y . 考点：流程图6．设函数2()sin f x a x x =+，若(1)0f =，则(1)f -的值为 ． 【答案】2 【解析】试题分析：因为(1)0f =，所以1sin 1-=a .因此(1)f -.211sin =+-=a 本题也可应用函数性质求解，因为2)()(=-+x f x f ，所以,2)1()1(=-+f f .2)1(=-f考点：函数性质 7．四棱锥P - ABCD 的底面ABCD 是边长为2的正方形，PA ⊥底面ABCD 且PA =4，则PC 与底面ABCD 所成角的正切值为 ．【解析】试题分析：因为PA ⊥底面ABCD ，所以PC 与底面ABCD 所成角的为.PCA ∠，因此.2224tan ===∠AC PA PCA考点：直线与平面所成角8．从甲，乙，丙，丁4个人中随机选取两人，则甲乙两人中有且只有一个被选取的概率为 ． 【答案】23【解析】试题分析：从甲，乙，丙，丁4个人中随机选取两人共有624=C 种基本事件，而甲乙两人中有且只有一个被选取包含41212=C C 种基本事件，所以所求概率为3264=.考点：古典概型概率9．已知2tan()5a b +=，1tan 3b =，则tan +4p a ⎛⎫ ⎪⎝⎭的值为 ．【答案】98【解析】试题分析：因为171315213152tan )tan(1tan )tan()tan(tan =⋅+-=++-+=-+=bb a b b a b b a a ，所以8917111711tan 1tan 1)4tan(=-+=-+=+aa a π. 考点：两角和与差正切10．设等差数列{}n a 的前n 项和为n S ，若13a =-，132k a +=，12k S =-，则正整数k = ． 【答案】13 【解析】试题分析：设等差数列{}n a 公差为d ，则12)1(213,233-=-+-=+-d k k k kd ，消去d得：.13=k考点：等差数列通项公式及前n 项和公式11．已知正数,x y 满足22x y +=，则8x yxy +的最小值为 ．【答案】9 【解析】 试题分析：因为9)16210(21)1610(21)22)(81(818=+≥++=++=+=+x y y x y x x y x y xy y x ，当且仅当22,16=+=y x x y y x 即31,34==y x 时取等号，所以8x y xy +的最小值为9. 考点：基本不等式求最值12．如图，在△ABC 中，BO 为边AC 上的中线，2BG GO =，设CD ∥AG ，若15A D AB A C=+λ()∈R λ，则λ的值为 ．【答案】65【解析】试题分析：因为,2=所以31313231+=+=.又CD ∥AG ，可设,AG m CD =从而mm m m 3)31(33++=++=+=.因为15A D A B A C =+λ，所以5631,513=+==m m λ. 考点：向量共线表示13．已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+，若函数()g x 恰有两个不同的零点，则实数k 的取值范围为 ． 【答案】27321,{0,22e +⎛⎫-- ⎪⎝⎭ 【解析】试题分析：由2(2)(0)x y x x e x =-≤求导得2(2)x y x e '=-，故2(2)(0)xy x x e x =-≤在(上单调增，在(,-∞上单调减,且当0x <时，恒有2(2)0xy x x e =-<.又243(0)y x x x =-++>在(0,2)上单调增，在(2,)+∞上单调减,所以可作出函数()y f x =的图像，如图.由图可知，要使函数()g x 恰有两个不同的零点，需20k -=或2k -=327k <-<,即实数k 的取值范围为27321,{0,22e +⎛⎫-- ⎪⎝⎭.考点：利用导数研究函数图像14．在平面直角坐标系xOy 中，已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内，动直线AB 过点P 且交圆C 于,A B 两点，若△ABC 的面积的最大值为16，则实数m 的取值范围为 ．【答案】[3(327,3++-- 【解析】试题分析：由题意得圆心(,2),C m 半径.r =因为点(3,0)P 在圆222:24280C x y m x y m +--+-=内，所以223060280m m +--+-<，解得3727.m-<<设C 到直线距离为d,则.d CP ≤又222211162222ABCd r d r S d AB d ∆+-=⋅=⋅==，当且仅当222d r d =-，即216,4d d ==时取等号，因此4CP ≥≥，即3m ≥+3m ≤-综上实数m 的取值范围为[3(327,3++--. 考点：直线与圆位置关系15．设函数2()6cos cos f x x x x =-．（1）求()f x 的最小正周期和值域；（2）在锐角△ABC 中，角,,A B C 的对边分别为,,a b c ，若()0f B =且2b =，4cos 5A =，求a 和sin C ．【答案】（1） π,[3-+,（2）534,10343+.【解析】试题分析：（1）要研究三角函数的性质，首先先将三角函数化为B x A y ++=)sin(ϕω型.利用降幂公式22cos 1cos 2x x +=及倍角公式xx x 2sin 21cos sin =可将函数次数化为一次，再利用配角公式)sin(cos sin 22ϕ++=+x b a x b x a 化为3)62s i n (32++=πx y ，然后利用基本三角函数图像求其最小正周期和值域，（2）解三角形问题，一般利用正余弦定理解决.本题为已知两角及一对边，选用正弦定理.由于是锐角△ABC ，开方时取正.试题解析：（1）1+cos2()622xf x x =⨯=3cos223x x +=)36x p++． 3分 所以()f x 的最小正周期为22T pp ==， 4分值域为[3-+． 6分（2）由()0f B =，得πcos(2)6B +=． B 为锐角，∴ππ7π2666B <+<，π5π266B +=，∴π3B =． 9分 ∵4cos 5A =，(0,)A p ∈，∴3sin 5A ==． 10分 在△ABC中，由正弦定理得32sin sin b A a B⨯===． 12分∴21sin sin()=sin()sin 32C A B A A A p p =---=+= 14分考点：倍角公式，正余弦定理16．如图，在三棱柱111ABC A B C -中，侧面11AA B B 为菱形， 且160A AB ∠=︒，AC BC =，D 是AB 的中点．（1）求证：平面1A DC ⊥平面ABC ； （2）求证：1BC ∥平面1A DC ． 【答案】（1）详见解析，（2）详见解析. 【解析】试题分析：（1）证明面面垂直，关键找出线面垂直.因为侧面11AA B B 为菱形， 且160A AB ∠=︒,所以△1A AB 为正三角形，因而有1AB A D ⊥.又AC BC =，D 是AB 的中点，所以有A B C D ⊥，这样就可得到AB ⊥平面1A DC ，进而可证平面1A DC ⊥平面ABC .（2）证明线面平行，关键找出线线平行. 条件“D 是AB 的中点”,提示找中位线.取1AC 中点E ，就可得DE ∥1BC ，利用线面平行判断定理即可.解决此类问题，需注意写全定理成立的所有条件，不可省略.试题解析：（1）证明：∵ 11ABB A 为菱形，且160A AB ∠=︒， ∴△1A AB 为正三角形． 2分D 是AB 的中点，∴1AB A D ⊥．∵AC BC =，D 是AB 的中点，∴ AB CD ⊥． 4分 1A DCD D =，∴AB ⊥平面1A DC ． 6分∵AB ⊂平面ABC ，∴平面1A DC ⊥平面ABC ． 8分 （2）证明：连结1C A ，设11AC AC E =，连结DE ．∵三棱柱的侧面11AA C C 是平行四边形，∴E 为1AC 中点． 10分 在△1ABC 中，又∵D 是AB 的中点，∴DE ∥1BC ．12分∵DE ⊂平面1A DC ，1BC ⊄平面1A DC ，∴ 1BC ∥平面1A DC ． 14分考点：面面垂直判定定理，线面平行判定定理 17．一个圆柱形圆木的底面半径为1m ，长为10m ，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD （如图所示，其中O 为圆心，,C D 在半圆上），设BOC q ∠=，木梁的体积为V （单位：m 3），表面积为S （单位：m 2）．（1）求V 关于θ的函数表达式； （2）求q 的值，使体积V 最大；（3）问当木梁的体积V 最大时，其表面积S 是否也最大？请说明理由．【答案】（1）()10(sin cos sin ),(0,)2V p q q q q q =+∈，（2）3pq =，（3）当木梁的体积V 最大时，其表面积S 也最大．【解析】 试题分析：（1）解答实际问题关键读懂题意.本题所求体积为直四棱柱体积，体积为高与底面积的乘积.高为圆木的长，底面积为梯形ABCD 的面积.利用角BOC q ∠=表示出梯形上下底及高，就可得到所求关系式. （2）先求出函数的导数2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+，再根据导数为零时，定义区间导数值的正负讨论其单调性，研究其图像变化规律，确定其极值、最值.本题函数先增后减，在3pq =时，取极大值，也是最大值.（3）本题实质是求表面积的最大值，并判断取最大值时3p q =是否成立.首先先建立表面积的函数关系式.表面积由两部分组成，一是底面积，二是侧面积. 底面积为梯形ABCD 的面积，有两个. 侧面积为梯形ABCD 周长与圆木的长的乘积.再利用导数求出其最大值及取最大值时角的取值. 试题解析：（1）梯形ABCD 的面积 2cos 2sin 2ABCD S q q +=⋅=sin cos sin q q q +，(0,)2pq ∈． 2分 体积()10(sin cos sin ),(0,)2V pq q q q q =+∈． 3分 （2）2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+．令()0V q '=，得1cos 2q =，或cos 1q =-（舍）．∵(0,)2p q ∈，∴3pq =． 5分 当(0,)3p q ∈时，1cos 12q <<，()0,()V V q q '>为增函数；当(,)32p p q ∈时，10cos 2q <<，()0,()V V q q '<为减函数． 7分 ∴当3pq =时，体积V 最大． 8分（3）木梁的侧面积210S AB BC CD =++⋅侧（）=20(cos 2sin 1)2q q ++，(0,)2pq ∈．2ABCD S S S =+侧=2(sin cos sin )20(cos 2sin 1)2q q q q q ++++，(0,)2pq ∈． 10分 设()cos 2sin 12g q q q =++，(0,)2p q ∈．∵2()2sin 2sin 222g q qq =-++，∴当1sin22q =，即3pq =时，()g q 最大． 12分又由（2）知3pq =时，sin cos sin q q q +取得最大值，所以3p q =时，木梁的表面积S 最大． 13分 综上，当木梁的体积V 最大时，其表面积S 也最大． 14分 考点：利用导数求函数最值18．如图，在平面直角坐标系xOy 中，已知A ，B ，C 是椭圆22221(0)x y a b a b+=>>上不同的三点，A ，(3,3)B --，C 在第三象限，线段BC 的中点在直线OA 上．（1）求椭圆的标准方程； （2）求点C 的坐标；（3）设动点P 在椭圆上（异于点A ，B ，C ）且直线PB ，PC 分别交直线OA 于M ，N 两点，证明OM ON ⋅为定值并求出该定值．【答案】（1）求椭圆方程一般用待定系数法.本题已知椭圆过两点，列两个方程222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩，解出b a ,的值,（2）求点(,)C m n 的坐标，需列出两个方程.一是点C 在椭圆上，即22227m n +=，二是BC 的中点在直线OA 上，即23m n =-.注意到C 在第三象限，舍去正值.（3）题意明确，思路简洁，就是求出点N M ,的坐标，算出OM 为定值.难点是如何消去参数.因为点N M ,在直线OA ： 20x y -=上，所以可设11(2,)M y y ，22(2,)N y y ．选择00(,)P x y 作为参数，即用00(,)P x y 表示点N M ,的坐标.由,,P B M 三点共线，解得001003()23y x y x y -=--，同理解得00200523y x y x y -=-+.从而有2220000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+，这里主要用到2200227x y +=代入化简.本题也可利用椭圆参数方程或三角表示揭示21y y 为定值. 【解析】试题分析：（1）22127272x y +=,（2）(5,1)--,（3）452.试题解析：（1）由已知，得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩2分 所以椭圆的标准方程为22127272x y +=． 3分（2）设点(,)C m n (0,0)m n <<，则BC 中点为33(,)22m n --．由已知，求得直线OA 的方程为20x y -=，从而23m n =-．①又∵点C 在椭圆上，∴22227m n +=．②由①②，解得3n =（舍），1n =-，从而5m =-． 5分 所以点C 的坐标为(5,1)--． 6分（3）设00(,)P x y ，11(2,)M y y ，22(2,)N y y ．∵,,P B M 三点共线，∴11033233y y y x ++=++，整理，得001003()23y x y x y -=--． 8分∵,,P C N 三点共线，∴22011255y y y x ++=++，整理，得00200523y x y x y -=-+． 10分∵点C 在椭圆上，∴2200227x y +=，2200272x y =-．从而22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+． 14分所以124552OM ON y y ⋅==15分∴OM ON ⋅为定值，定值为452． 16分考点：椭圆标准方程，直线与椭圆位置关系19．设各项均为正数的数列{}n a 的前n 项和为S n ,已知11a =，且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立．（1）若λ=1，求数列{}n a 的通项公式； （2）求λ的值，使数列{}n a 是等差数列． 【答案】（1）an = 2n -1（2）λ = 0. 【解析】试题分析：（1）本题属于“已知n S 求n a ”,利用)2(1≥-=-n S S a n n n 化简关系式. 因为11(1)(1)n n n n S a S a +++=+，所以先分离n S 与n a ，即1111n n n nS a S a +++=+，这是类等比，利用叠乘法得到1112n n S a +++=，再利用)2(1≥-=-n S S a n n n ，消去n S 得12n n a a +=.求数列{an}通项公式时，需讨论当n = 1时是否满足2n ≥的情形.（2）解答本题需注意逻辑关系，由数列{}n a 是等差数列得λ= 0，这是一个必要条件，还需验证其充分性，即λ = 0时，数列{}n a 是等差数列.这可类似（1）的解答过程.试题解析：解：（1）若λ = 1，则11(1)(1)n n n n S a S a +++=+，111a S ==．又∵00n n a S >>，， ∴1111n n n nS a S a +++=+， 2分 ∴3131221212111111n n n nS S a a S a S S S a a a +++++⋅⋅⋅=⋅⋅⋅+++，化简，得1112n n S a +++=．①4分∴当2n ≥时，12n n S a +=．②② - ①，得12n n a a +=，∴12n na a +=（2n ≥）．6分∵当n = 1时， 22a =，∴n = 1时上式也成立，∴数列{an}是首项为1，公比为2的等比数列， an = 2n -1（*n ∈N ）．8分（2）令n = 1，得21a λ=+．令n = 2，得23(1)a λ=+． 10分要使数列{}n a是等差数列，必须有2132a a a =+，解得λ = 0． 11分当λ = 0时，11(1)n n n n S a S a ++=+，且211a a ==． 当n ≥2时，111()(1)()n n n n n n S S S S S S +-+-=+-，整理，得2111n n n n n S S S S S +-++=+，1111n n n nS S S S +-+=+， 13分从而3312412123111111n n n nS S S S S S S S S S S S +-+++⋅⋅⋅=⋅⋅⋅+++，化简，得11n n S S ++=，所以11n a +=． 15分 综上所述，1n a =（*n ∈N ）， 所以λ = 0时，数列{}n a 是等差数列． 16分考点：已知n S 求n a20．已知函数e ()ln ,()e xxf x mx a x mg x =--=，其中m ，a 均为实数． （1）求()g x 的极值；（2）设1,0m a =<，若对任意的12,[3,4]x x ∈12()x x ≠，212111()()()()f x f xg x g x -<-恒成立，求a 的最小值；（3）设2a =，若对任意给定的0(0,e ]x ∈，在区间(0,e ]上总存在1212,()t t t t ≠，使得120()()()f t f t g x == 成立，求m 的取值范围．【答案】（1）极大值为1，无极小值．（2）3 -22e 3．（3）3[,)e 1+∞-．【解析】试题分析：（1）求函数极值，先明确定义域为,R 再求其导数为e(1)()e x x g x -'=．由()0g x '=，得x = 1.分析导数在定义区间符号正负，确定函数先增后减，所以y =()g x 有极大值为1，无极小值．（2）不等式恒成立问题，先化简不等式212111()()()()f x f xg x g x -<-．化简不等式的难点有两个，一是绝对值，二是两个参量12,.x x 可从函数单调性去绝对值，分析两个函数，一是()y f x =，二是1()y g x =.利用导数可知两者都是增函数，故原不等式等价于21212111()(),()()()f x f x x xg x g x -<->，变量分离调整为21212111()(),()()()f x f x x x g x g x -<->,这又等价转化为函数1()()()u x f x g x =-在区间[3,4]上为减函数，即21e (1)()10e x a x u x x x -'=--⋅≤在[3,4]上恒成立．继续变量分离得11e ex x a x x ---+≥恒成立，即11m a xe (e )x x a x x---+≥.最后只需求函数11e ex x y x x --=-+在[3,4]上最大值,就为a 的最小值.（3）本题含义为：对于函数()y g x =在(0,e]上值域中每一个值，函数()y f x =在(0,e]上总有两个不同自变量与之对应相等．首先求出函数()y g x =在(0,e]上值域(0,1]，然后根据函数()y f x =在(0,e]上必须不为单调函数且每段单调区间对应的值域都需包含(0,1].由()f x 在(0,e]不单调得2e m >，由每段单调区间对应的值域都需包含(0,1]得(e)1f ≥，3e 1m -≥. 试题解析：（1）e(1)()e x x g x -'=，令()0g x '=，得x = 1． 1分列表如下：∵g(1) = 1，∴y =()g x 的极大值为1，无极小值． 3分 （2）当1,0m a =<时，()ln 1f x x a x =--，(0,)x ∈+∞． ∵()0x af x x -'=>在[3,4]恒成立，∴()f x 在[3,4]上为增函数． 4分设1e ()()e x h x g x x ==，∵12e (1)()x x h x x --'=> 0在[3,4]恒成立，∴()h x 在[3,4]上为增函数． 5分设21x x >，则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-，即2211()()()()f x h x f x h x -<-．设1e ()()()ln 1e xu x f x h x x a x x =-=---⋅，则u(x)在[3,4]为减函数． ∴21e (1)()10e x a x u x x x -'=--⋅≤在（3，4）上恒成立． 6分∴11e ex x a x x---+≥恒成立．设11e ()ex x v x x x--=-+，∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+，x ∈[3，4]， ∴1221133e [()]e 1244x x --+>>，∴()v x '< 0，()v x 为减函数．∴()v x 在[3，4]上的最大值为v(3) = 3 -22e3． 8分∴a ≥3 -22e 3，∴a 的最小值为3 -22e3． 9分（3）由（1）知()g x 在(0,e]上的值域为(0,1]． 10分 ∵()2ln f x mx x m =--，(0,)x ∈+∞，当0m =时，()2ln f x x =-在(0,e]为减函数，不合题意． 11分当0m ≠时，2()()m x mf x x-'=，由题意知()f x 在(0,e]不单调，所以20e m <<，即2e m >．①12分 此时()f x 在2(0,)m 上递减，在2(,e)m 上递增，∴(e)1f ≥，即(e)e 21f m m =--≥，解得3e 1m -≥．②由①②，得3e 1m -≥． 13分 ∵1(0,e]∈，∴2()(1)0f f m =≤成立． 14分下证存在2(0,]t m ∈，使得()f t ≥1． 取emt -=，先证e 2m m -<，即证2e 0mm ->．③设()2e xw x x =-，则()2e 10xw x '=->在3[,)e 1+∞-时恒成立．∴()w x 在3[,)e 1+∞-时为增函数．∴3e ))01((w x w ->≥，∴③成立．再证()e mf -≥1．∵e e 3()1e 1m mf m m m --+=>>-≥，∴3e 1m -≥时，命题成立． 综上所述，m 的取值范围为3[,)e 1+∞-． 16分考点：函数极值，不等式恒成立21．如图，⊙O 为四边形ABCD 的外接圆，且AB AD =，E 是CB 延长线上一点，直线EA 与圆O 相切．求证：CD ABAB BE=． 【答案】详见解析 【解析】试题分析：要证明CD ABAB BE =，主要利用相似三角形.难点在找出对应的两个三角形.由AB AD =，可证CDA ∆与ABE ∆相似.利用圆内接四边形性质得D ABE ∠=∠，再由等弦对等角得EAB ACB ∠=∠，ACD ACB ∠=∠，从而ACD EAB ∠=∠.试题解析：证明：连结AC ．EA 是圆O 的切线，∴EAB ACB ∠=∠． 2分AB AD =，∴ACD ACB ∠=∠． ∴ACD EAB ∠=∠ 4分圆O 是四边形ABCD 的外接圆，∴D ABE ∠=∠． 6分 ∴CDA ∆∽ABE ∆． 8分 ∴CD DAAB BE =，AB AD =，∴CD ABAB BE =． 10分考点：圆内接四边形性质22．已知矩阵1221⎡⎤=⎢⎥⎣⎦M ，17⎡⎤=⎢⎥⎣⎦β，计算6M β． 【答案】29132919⎡⎤⎢⎥⎣⎦【解析】试题分析：利用矩阵特征值λ及其对应特征向量α性质：n nM αλα=进行化简.先根据矩阵M 的特征多项式求出其特征值123,1λλ==-，进而求出对应的特征向量111⎡⎤=⎢⎥⎣⎦α，211⎡⎤=⎢⎥-⎣⎦α.再将17⎡⎤=⎢⎥⎣⎦β分解成特征向量，即1243=-βαα，最后利用性质求结果，即6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α试题解析：解：矩阵M 的特征多项式为212()2321f λλλλλ--==----．令12()031f λλλ===-，解得，，对应的一个特征向量分别为111⎡⎤=⎢⎥⎣⎦α，211⎡⎤=⎢⎥-⎣⎦α． 5分 令12m n =+βαα，得4,3m n ==-．6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α． 10分考点：：矩阵特征值、特征向量及其应用23．在平面直角坐标系xOy 中，圆的参数方程为22cos ,()2sin x y a a a =+⎧⎨=⎩为参数，以坐标原点O为极点，x 轴的正半轴为极轴建立极坐标系．求：（1）圆的直角坐标方程； （2）圆的极坐标方程．【答案】（1）22(2)4x y -+=．（2）4cos ρθ=．【解析】试题分析：（1）根据22sin cos 1αα+=消去参数α得圆的直角坐标方程：22(2)4x y -+=.（2）利用cos ,sin ,x y ρθρθ=⎧⎨=⎩代入22(2)4x y -+=，可得圆的极坐标方程为4cos ρθ=．试题解析：解：（1）圆的直角坐标方程为22(2)4x y -+=． 5分 （2）把cos ,sin ,x y ρθρθ=⎧⎨=⎩代入上述方程，得圆的极坐标方程为4cos ρθ=． 10分考点：参数方程、极坐标方程、直角坐标方程之间互化24．已知函数2()122f x x x a a =++---，若函数()f x 的图象恒在x 轴上方，求实数a 的取值范围． 【答案】(1,3)- 【解析】 试题分析：因为12|(1)(2)|3x x x x ++-≥+--=，所以()f x 的最小值为232a a --.因为函数()f x 的图象恒在x 轴上方，所以min ()0.f x ≥因此有223a a -<，解得(1,3)a ∈-．试题解析：解：()f x 的最小值为232a a --， 5分由题设，得223a a -<，解得(1,3)a ∈-． 10分考点：绝对值不等式的应用25．甲乙两个同学进行定点投篮游戏，已知他们每一次投篮投中的概率均为23，且各次投篮的结果互不影响．甲同学决定投5次，乙同学决定投中1次就停止，否则就继续投下去，但投篮次数不超过5次．（1）求甲同学至少有4次投中的概率；（2）求乙同学投篮次数x 的分布列和数学期望． 【答案】（1）112，（2）12181E =x，.【解析】 试题分析：（1）求概率问题关键在于明确题意，即事件是什么. 甲同学至少有4次投中，指甲同学在5次投篮中“恰投中4次”及“恰投中5次”这两个互斥事件.其概率为441550552222()(1)()(1)3333C C -+-=112243．（2）求概率分布，首先正确确定随机变量取值情况，本题1,2,3,4,5=x ，其次要正确确定随机变量对应各个概率，本题中5=x 的概率，直接求时要注意，第5次乙同学不论是否投中都停止，即第5次不考虑乙同学是否投中.也可间接求,利用各概率和为1，即(5)1(1)(2)(3)(4)P PP P P ==-=-=-=-=x x x x x ，这也是一种验证方法.试题解析：解：（1）设甲同学在5次投篮中，有x 次投中，“至少有4次投中”的概率为P ，则(4)(5)P P x P x ==+= 2分=441550552222()(1)()(1)3333C C -+-=112243 4分 （2）由题意1,2,3,4,5=x ．2(1)3P ==x ，122(2)339P ==⨯=x ，1122(3)33327P ==⨯⨯=x ，3122(4)3381P x ⎛⎫==⨯= ⎪⎝⎭， 411(5)381P x ⎛⎫===⎪⎝⎭． x 的分布表为8分x 的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=x ． 10分 考点：概率分布，数学期望值26．设01212(1)m m n n n n n m S C C C C ---=-+-+-，*,m n ∈N 且m n <，其中当n 为偶数时，2nm =；当n 为奇数时，12n m -=． （1）证明：当*n ∈N ，2n ≥时，11n n n S S S +-=-；（2）记01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，求S 的值． 【答案】（1）详见解析，（2）12014S =-. 【解析】试题分析：（1）利用组合数性质111r r r n n n C C C +++=+进行化简.根据奇偶性，对n 进行分类讨论，这不增加难度，仅是便于表示.00112211112()()()n n n n n n n n S S C C C C C C ++----=---+-=01120n n C C ---+-,规律清晰，易于归纳（2）利用组合数性质11k k n n kC nC --=进行化简.123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C =-+++-++-+010213210071006201420132012201220112011201010071006()()()()C C C C C C C C C =-+++-++-+=20142012S S -．再根据11n n n S S S +-=-得周期6T =，从而20142012421S S S S -=-=-，12014S =-．试题解析：解：（1）当n 为奇数时，1n +为偶数，1n -为偶数， ∵1101221112(1)n n n n nn S CC C+++++=-++-，110122112(1)n n n n n n S C C C---+=-++-，11012211212(1)n n n n n n S CCC------=-++-，∴1111110011222221111111222()()(1)()(1)n n n n n n n n n n n n n n S S C C C C CCC-+-++-++-++++-=---++--+-=11012212112((1))n n n n n n CCCS --------++-=-．∴当n 为奇数时，11n n n S S S +-=-成立 5分同理可证，当n 为偶数时， 11n n n S S S +-=-也成立． 6分（2）由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，得123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+- =0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -． 9分又由11n n n S S S +-=-，得6n n S S +=， 所以20142012421S S S S -=-=-，12014S =-． 10分考点：组合数性质。

江苏省苏锡常镇徐连六市高三教学情况调研（一）化 学注意事项：1.本卷满分120分，考试时间 100分钟。

2.请将答案填写到答题卡上，凡填写在试卷上一律无效；交卷只需交答题卡可能用到的相对原子质量： H 1 C 12 N 14 O 16 Na 23 Si 28 Mn 55 Fe 56选择题单项选择题：本题包括10小题，每小题2分，共计20分。

每小题只有一个选项符合题意。

1．化学与社会可持续发展密切相关。

下列做法不合理的是 A ．CO 2合成可降解的聚碳酸酯类塑料，实现“碳循环” B ．提倡步行、骑自行车、乘公交车等“低碳”出行方式 C ．将废电池深埋，防止重金属污染D ．开发利用各种新能源，减少对化石燃料的依赖，可以降低空气中PM2.5的含量 2．下列有关化学用语表示正确的是A ．Cl －的结构示意图：287+17B ．次氯酸的结构式：C ．CH 3F 的电子式：F H:C H:H ⋅⋅⋅⋅ D ．CO 23．常温下，下列溶液中各组离子一定能够大量共存的是 A ．加入苯酚显紫色的溶液：K ＋、NH 4＋、Cl －、I －B ．使紫色石蕊试液变红的溶液：Fe 2+、Mg 2+、NO 3－、Cl －C ．)H (+c K w ＝0.1 mol ·L －1的溶液：Na ＋、K ＋、SiO 32—、NO 3—D ．通入足量SO 2后的溶液：Na ＋、NH 4＋、ClO －、CH 3COO －4．下列关于反应过程中能量变化的说法正确的是 A ．图1中a 、b 曲线可分别表示反应CH 2＝CH 2(g)＋H 2(g)→CH 3CH 3(g) ΔH ＜0 使用和未使用催化剂时，反应过程中的能量变化B ．己知2C(s)＋2O 2(g)＝2CO 2(g) ΔH 1；2C(s)＋O 2(g)＝2CO(g) ΔH 2。

则ΔH 1＞ΔH 2C ．同温同压下，反应H 2(g)＋Cl 2(g)＝2HCl(g)在光照和点燃条件下的 ΔH 不同D ．在一定条件下，某可逆反应的ΔH ＝＋100kJ ·mol －1，则该反应正反应活化能比逆反应活化能大100kJ ·mol －15．下列有关物质性质或应用的说法正确的是HOClA ．制水泥和玻璃都用石灰石作原料B ．利用Al 2O 3制作的坩埚，可用于熔融烧碱C ．Si 可用作太阳能电池和光导纤维的材料D ．铜的金属活泼性比铁的弱，可在海轮外壳上装若干铜块以减缓其腐蚀 6．用下列实验装置进行相应实验，能达到实验目的的是A ．用图2所示装置（正放）可收集NO 气体B ．用图3所示装置可吸收多余氨气且能防止倒吸C ．用图4所示装置可实现反应：Cu ＋2H 2O ══通电Cu(OH)2＋H 2↑D ．用图5所示装置可分离乙醇（沸点78.4℃）与二甲醚（沸点24.9℃）的混合物 7．下列物质的转化在给定条件下能实现的是①氯化钠饱和溶液 NaHCO 3(s)②N 2 NO 2 HNO 3③海水 Mg(OH)2 MgCl 2(aq) MgCl 2(s)④Al 2O 3 AlCl 3(aq) Al(OH)3 ⑤重晶石(BaSO 4) BaCO 3 BaCl 2(aq)A ．①③⑤B ．②③④C ．②④⑤D ．①④⑤ 8．用N A 表示阿伏加德罗常数的值。

苏锡常镇四市2014届高三3月教学情况调研（一）生物 2014．3本试卷分第1卷(选择题)和第ll卷(非选择题)两部分，第1卷l～5页，第II卷6～I0页。

满分共120分．考试时间为100分钟。

注意事项：1.答第I卷前，考生务必在答题卡上写清白己的姓名、准考证号(或考试号)，并用2B铅笔涂写在答题卡上2．答第I卷时，在答题卡的对应题号后，用2B铅笔把正确答案的字母涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

答第II卷时，答案要填写在答题卡的对应题号后的指定位置。

3．考试结束后，将答题卡交回。

第I卷(选择题55分)一、单项选择题：本题包括20小题，每小题2分，共40分。

每小题只有一个选项最符合题意。

1．下列各种化合物中，不直接参与线粒体内有关代谢反应的是A．H20 B．有氧呼吸酶 C．葡萄糖 D．丙酮酸2．下列关于现代生物进化理论的叙述中。

正确的是A．共同进化与生态系统的信息传递密切相关B．无法进行基因交流的生物之间一定存在生殖隔离C．生物进化过程的实质在于保存对环境更适应的性状D．某种群的数量长期维持稳定，说明该种群的基因频率保持不变3．下列关于人体内环境及稳态调节的叙述中，正确的是A．毛细血管壁细胞生活的内环境是血浆和淋巴B．甲状腺激素和尿素等物质均可能存在于内环境中C．血浆中的蛋白质均会透过毛细血管壁到达组织液中D．细胞外液渗透压升高时，机体释放的抗利尿激素减少4．下图l表示已知的染色体，图2表示该染色体在自然状态下发生的几种变异。

上面的字母表示有关的基因。

其中不属于染色体变异的是A．① B．② C．③ D．④5．下列有关“探究酶的特性”系列实验的叙述中，正确的是A．在“探究酶的高效性”实验中，自变量是酶的种类B．在“探究酶的专一性”实验中，自变量一定是酶的种类C．在“探究温度对酶活性的影响”实验中，自变量不止一种D．在“探究pH对酶活性的影响”实验中，无关变量不止一种6．现有2个取自同一个紫色洋葱鳞片叶外表皮的大小相同、生理状态相似的成熟细胞，将它们分别浸没在甲、乙两种溶液中，测得液泡直径的变化情况如右图所示。

苏锡常镇四市高三教学情况调研（一）数学Ⅰ试题一、填空题：本大题共14个小题，每小题5分，共70分.请把答案填写在答题卡相应位置上．．．．．．．．.1. 已知集合，，则集合__________．2. 已知复数满足（为虚数单位），则__________．3. 双曲线的渐近线方程为__________．4. 某中学共有人，其中高二年级的人数为.现用分层抽样的方法在全校抽取人，其中高二年级被抽取的人数为，则__________．5. 将一颗质地均匀的正四面体骰子（每个面上分别写有数字，，，）先后抛掷次，观察其朝下一面的数字，则两次数字之和等于的概率为__________．6. 如图是一个算法的流程图，则输出的值是__________．7. 若正四棱锥的底面边长为，侧面积为，则它的体积为__________．8. 设是等差数列的前项和，若，，则__________．9. 已知，，且，则的最小值是__________．10. 设三角形的内角，，的对边分别为，，，已知，则__________．11. 已知函数（是自然对数的底）.若函数的最小值是，则实数的取值范围为__________．12. 在中，点是边的中点，已知，，，则__________．13. 已知直线：与轴交于点，点在直线上，圆：上有且仅有一个点满足，则点的横坐标的取值集合为__________．14. 若二次函数在区间上有两个不同的零点，则的取值范围为_____．二、解答题：本大题共6小题，共计90分.请在答题卡指定区域．．．．．．．内作答，解答应写出文字说明、证明过程或演算步骤.15. 已知向量，.（1）若角的终边过点，求的值；（2）若，求锐角的大小.16. 如图，正三棱柱的高为，其底面边长为.已知点，分别是棱，的中点，点是棱上靠近的三等分点.求证：（1）平面；（2）平面.17. 已知椭圆：经过点，，点是椭圆的下顶点.（1）求椭圆的标准方程；（2）过点且互相垂直的两直线，与直线分别相交于，两点，已知，求直线的斜率.18. 如图，某景区内有一半圆形花圃，其直径为，是圆心，且.在上有一座观赏亭，其中.计划在上再建一座观赏亭，记.（1）当时，求的大小；（2）当越大，游客在观赏亭处的观赏效果越佳，求游客在观赏亭处的观赏效果最佳时，角的正弦值.19. 已知函数，.（1）若，，且恒成立，求实数的取值范围；（2）若，且函数在区间上是单调递减函数.①求实数的值；②当时，求函数的值域.20. 已知是数列的前项和，，且.（1）求数列的通项公式；（2）对于正整数，，，已知，，成等差数列，求正整数，的值；（3）设数列前项和是，且满足：对任意的正整数，都有等式成立.求满足等式的所有正整数.苏锡常镇四市高三教学情况调研（一）数学Ⅰ试题一、填空题：本大题共14个小题，每小题5分，共70分.请把答案填写在答题卡相应位置上．．．．．．．．.1. 已知集合，，则集合__________．【答案】【解析】2. 已知复数满足（为虚数单位），则__________．【答案】5【解析】因为，所以，即，.3. 双曲线的渐近线方程为__________．【答案】【解析】双曲线的渐近线方程为,即.4. 某中学共有人，其中高二年级的人数为.现用分层抽样的方法在全校抽取人，其中高二年级被抽取的人数为，则__________．【答案】63【解析】5. 将一颗质地均匀的正四面体骰子（每个面上分别写有数字，，，）先后抛掷次，观察其朝下一面的数字，则两次数字之和等于的概率为__________．【答案】【解析】两次数字之和等于有三种基本事件，所以概率为点睛：古典概型中基本事件数的探求方法(1)列举法.(2)树状图法：适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目，常采用树状图法.(3)列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法：适用于限制条件较多且元素数目较多的题目.6. 如图是一个算法的流程图，则输出的值是__________．【答案】25【解析】执行循环得：结束循环，输出25.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.7. 若正四棱锥的底面边长为，侧面积为，则它的体积为__________．【答案】【解析】设侧面斜高为，则，因此高为8. 设是等差数列的前项和，若，，则__________．【答案】8【解析】因为，，所以，因此9. 已知，，且，则的最小值是__________．【答案】【解析】因为，当且仅当时取等号.因此的最小值是点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.10. 设三角形的内角，，的对边分别为，，，已知，则__________．【答案】【解析】因为，所以11. 已知函数（是自然对数的底）.若函数的最小值是，则实数的取值范围为__________．【答案】【解析】当时，（当且仅当时取等号），当时，，因此12. 在中，点是边的中点，已知，，，则__________．【答案】6【解析】,所以点睛：根据定义计算数量积的两种思路(1)若两个向量共起点，则两向量的夹角直接可得，根据定义即可求得数量积；若两向量的起点不同，需要通过平移使它们的起点重合，然后再计算．(2)根据图形之间的关系，用长度和相互之间的夹角都已知的向量分别表示出要求数量积的两个向量，然后再根据平面向量数量积的定义和性质进行计算求解．13. 已知直线：与轴交于点，点在直线上，圆：上有且仅有一个点满足，则点的横坐标的取值集合为__________．【答案】【解析】以AP为直径的圆与圆C相切，设，所以以AP为直径的圆圆心为，半径为，因此外切时：，内切时：，即点的横坐标的取值集合为点睛：研究直线与圆位置关系时，要注意隐圆，即利用直接法或转移法求轨迹方程，最后根据直线与圆或圆与圆位置关系求解参数取值范围.14. 若二次函数在区间上有两个不同的零点，则的取值范围为_____．【答案】【解析】设，则点睛：已知函数零点求参数的范围的常用方法，(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围．(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决．(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，作出函数的图象，然后数形结合求解．二、解答题：本大题共6小题，共计90分.请在答题卡指定区域．．．．．．．内作答，解答应写出文字说明、证明过程或演算步骤.15. 已知向量，.（1）若角的终边过点，求的值；（2）若，求锐角的大小.【答案】（1）；（2）【解析】试题分析：（1）先根据三角函数定义得，，再根据向量数量积得结果，（2）由向量平行得，再利用两角和正弦公式以及同角三角函数关系得，即得锐角的大小试题解析：（1）由题意，，所以.（2）因为，所以，即，所以，则，对锐角有，所以，所以锐角.16. 如图，正三棱柱的高为，其底面边长为.已知点，分别是棱，的中点，点是棱上靠近的三等分点.求证：（1）平面；（2）平面.【答案】（1）见解析；（2）见解析【解析】试题分析：（1）根据平行四边形性质得，再根据线面平行判定定理得结论，（2）根据平几知识得，再根据线面垂直性质定理得，最后根据线面垂直判定定理得结论.试题解析：（1）连结，正三棱柱中，且，则四边形是平行四边形，因为点、分别是棱，的中点，所以且，又正三棱柱中且，所以且，所以四边形是平行四边形，所以，又平面，平面，所以平面；（2）正三棱柱中，平面，平面，所以，正中，是的中点，所以，又、平面，，所以平面，又平面，所以，由题意，，，，，所以，又，所以与相似，则，所以，则，又，，平面，所以平面.点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.(1)证明线面、面面平行，需转化为证明线线平行.(2)证明线面垂直，需转化为证明线线垂直.(3)证明线线垂直，需转化为证明线面垂直.17. 已知椭圆：经过点，，点是椭圆的下顶点.（1）求椭圆的标准方程；（2）过点且互相垂直的两直线，与直线分别相交于，两点，已知，求直线的斜率. 【答案】（1）；（2）【解析】试题分析：（1）将两点坐标代入椭圆方程，解方程组得a,b,（2）设直线斜率，根据方程组解得E,F,再根据解得斜率.试题解析：（1）由题意得，解得，所以椭圆的标准方程为；（2）由题意知，直线，的斜率存在且不为零，设直线：，与直线联立方程有，得，设直线：，同理，因为，所以，①，无实数解；②，，，解得，综上可得，直线的斜率为.18. 如图，某景区内有一半圆形花圃，其直径为，是圆心，且.在上有一座观赏亭，其中.计划在上再建一座观赏亭，记.（1）当时，求的大小；（2）当越大，游客在观赏亭处的观赏效果越佳，求游客在观赏亭处的观赏效果最佳时，角的正弦值.【答案】（1）；（2）【解析】试题分析：（1）先根据直角三角形解得，再根据正弦定理列关于三角方程，根据同角三角函数关系得，即得的大小；（2）根据正弦定理列关于的函数关系，利用导数求最值，即得结果.试题解析：（1）设，由题，中，， ，所以，在中，，，由正弦定理得，即，所以 ，则 ，所以，因为为锐角，所以，所以，得；（2）设，在中，，，由正弦定理得，即，所以，从而，其中，，所以，记，，；令，，存在唯一使得，当时，单调增，当时，单调减，所以当时，最大，即最大，又为锐角，从而最大，此时.答：观赏效果达到最佳时，的正弦值为.19. 已知函数，.（1）若，，且恒成立，求实数的取值范围；（2）若，且函数在区间上是单调递减函数.①求实数的值；②当时，求函数的值域.【答案】（1）；（2）【解析】试题分析：（1）先利用参变分离将不等式化为函数最值：的最大值，再利用导数求函数最值，即得实数的取值范围；（2）①将单调性条件转化为对恒成立，再根据二次函数恒成立条件得不等式，解不等式可得实数的值；②先利用导数研究函数单调性，确定函数值域，再结合图像确定，根据图像确定值域.试题解析：（1）函数的定义域为.当，，，∵恒成立，∴恒成立，即.令，则，令，得，∴在上单调递增，令，得，∴在上单调递减，∴当时，，∴.（2）①当时，，.由题意，对恒成立，∴，∴，即实数的值为.②函数的定义域为.当，，时，.，令，得.∴当时，，当时，，当时，.对于，当时，，当时，，当时，.∴当时，，当时，，当时，.故函数的值域为.点睛：对于求不等式成立时的参数范围问题，在可能的情况下把参数分离出来，使不等式一端是含有参数的不等式，另一端是一个区间上具体的函数，这样就把问题转化为一端是函数，另一端是参数的不等式，便于问题的解决.但要注意分离参数法不是万能的，如果分离参数后，得出的函数解析式较为复杂，性质很难研究，就不要使用分离参数法.20. 已知是数列的前项和，，且.（1）求数列的通项公式；（2）对于正整数，，，已知，，成等差数列，求正整数，的值；（3）设数列前项和是，且满足：对任意的正整数，都有等式成立.求满足等式的所有正整数.【答案】（1）；（2）和【解析】试题分析：（1）先根据和项与通项关系得项之间递推关系，再根据等比数列定义判断，最后根据等比数列通项公式求结果，（2）根据等差数列化简得，再根据正整数限制条件以及指数性质确定不定方程正整数解，（3）先根据定义求数列通项公式，再根据等差数列求和公式求，根据数列相邻项关系确定递减，最后根据单调性求正整数解.试题解析：（1）由得，两式作差得，即.，，所以，，则，所以数列是首项为公比为的等比数列，所以；（2）由题意，即，所以，其中，，所以，，，所以，，；（3）由得，，，，所以，即，所以，又因为，得，所以，从而，，当时；当时；当时；下面证明：对任意正整数都有，，当时，，即，所以当时，递减，所以对任意正整数都有；综上可得，满足等式的正整数的值为和.。

高中化学学习材料金戈铁骑整理制作注意事项：1.本卷满分120分，考试时间100分钟。

2.请将答案填写到答题卡上，凡填写在试卷上一律无效；交卷只需交答题卡可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 Si 28 Mn 55 Fe 56选择题单项选择题：本题包括10小题，每小题2分，共计20分。

每小题只有一个选项符合题意。

1．化学与社会可持续发展密切相关。

下列做法不合理的是A．CO2合成可降解的聚碳酸酯类塑料，实现“碳循环”B．提倡步行、骑自行车、乘公交车等“低碳”出行方式C．将废电池深埋，防止重金属污染D．开发利用各种新能源，减少对化石燃料的依赖，可以降低空气中PM2.5的含量2．下列有关化学用语表示正确的是A ．Cl －的结构示意图：287+17B ．次氯酸的结构式：C ．CH 3F 的电子式：F H:C H:H ⋅⋅⋅⋅ D ．CO 2的分子比例模型：【答案】B 【解析】试题分析：A 、Cl －质子数为17、电子数为18，错误；B 、次氯酸结构式为H-O-Cl ，正确；C 、CH 3F 中F周围应有8个电子，错误；D 、碳原子半径大于氧原子半径，中间的球比两边的球大，错误。

考点： 微粒结构示意图 结构式 电子式 比例模型 3．常温下，下列溶液中各组离子一定能够大量共存的是A ．加入苯酚显紫色的溶液：K ＋、NH 4＋、Cl －、I －B ．使紫色石蕊试液变红的溶液：Fe 2+、Mg 2+、NO 3－、Cl －C ．)H (+c K w ＝0.1 mol ·L －1的溶液：Na ＋、K ＋、SiO 32—、NO 3—D ．通入足量SO 2后的溶液：Na ＋、NH 4＋、ClO －、CH 3COO －4．下列关于反应过程中能量变化的说法正确的是A ．图1中a 、b 曲线可分别表示反应CH 2＝CH 2(g)＋H 2(g)→CH 3CH 3(g) ΔH ＜0 使用和未使用催化剂时，反应过程中的能量变化B ．己知2C(s)＋2O 2(g)＝2CO 2(g) ΔH 1；2C(s)＋O 2(g)＝2CO(g) ΔH 2。

江苏省苏、锡、常、镇四市2014届高三教学情况调查一1高考英语2014-03-25 2029()江苏省苏、锡、常、镇四市2014届高三教学情况调查（一）英语注意：本试卷分第一卷(选择题)和第二卷(非选择题)两部分。

两部分答案都做在答题纸上。

总分为120分。

考试时间120分钟。

第一卷（选择题共85分）第一部分：听力（共两节，满分20分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题纸上。

第一节 (共5小题；每小题1分，满分5分)听下面5段对话。

每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。

听完每段对话后, 你都有2014秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. Where are the two speakers?A. At the airport.B. In a school.C. At the railway station.2. What can we know about the Johnsons?A. They didn’t come.B. They came asexpected. C. They came with others.3. How did the woman try to improve the report?A. By making suggestions on it.B. By asking the man to rewrite it.C. By getting someone else to read it.4. Why does the woman want to change her job?A. To make more money.B. To have more challenges.C. To get a better office environment.5. What is the woman going to do?A. Do the typing again.B. Read the paper aloud.C. Check for typing errors.第二节 (共15小题；每小题1分，满分15分)听下面5段对话或独白。

2013—2014学年度苏锡常镇四市高三教学情况调研（一）物理2014. 3注意事项：考生在答题前请认真阅读本注意事项1 •本试卷包含选择题和非选择题两部分•考生答题全部答在答题卡上，答在本试卷上无效•本次考试时间为100分钟，满分值为120分.2 •答题前，请务必将自己的姓名、准考证号（考试号）刚书写黑色字迹的0.5毫米签字笔填写在答题卡上，并用2B铅笔将对应的数字标号涂黑.3. 答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑. 如需改动，请用橡皮擦干净后，再选涂其它答案.答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其它位置答题一律无效.一、单项选择题：本大题共5小题，每小题3分，共计15分•每小题只有一个选项符合题意.1. 关丁物理学研究方法，下列叙述中正确的是A •伽利略研究自由落体运动运用了微小量放大法B •用点电荷来代替实际带电体运用了理想模型法C .探究求合力的方法实验运用了控制变量法D •法拉第在研究电磁感应现象用了理想实验法2. 如图是带电粒子在气泡室中运动径迹的照片及其中某条径迹的放大图。

匀强磁场与带电粒子运动径迹垂直，A、B、C是该条径迹上的三点。

若该粒子在运动过程中质量和电量保持不变，不断克服阻力做功，则关丁此径迹下列说法正确的是A .粒子由A经B向C的方向运动B .粒子由C经B向A的方向运动C .粒子一定带正电，磁场方向垂直纸面向里D .粒子一定带负电，磁场方向垂直纸面向外3 .在t=0时，甲乙两质点从相距70m的两地开始相向运动，它们的v—t图象如图所示.贝UA .第1s末，乙质点改变运动方向B .第2s木，甲乙两质点相遇C .前4s内，乙质点运动的加速度先比甲质点的小后比甲质点的大D .第4s末，甲乙两质点相距20m4. 如图为某位移式传感器的原理示意图，平行金属板A、B和介质P构成电容器.则A. A向上移电容器的电容变大B. P向左移电容器的电容变大C. A向上移流过电阻R的电流方向从N到MD. P向左移流过电阻R的电流方向从M到N5. 如图所示，水平面上质量相等的两木块A、B用一轻弹簧相连，整个系统处于静止状态. t=0时刻起用一竖直向上的力F拉动木块，使A向上做匀加速直线运动. 打时刻弹簧恰好恢复原长，t2时刻木块B恰好要离开水平面.以下说法正确的是A .在0-t 2时间内，拉力F与时间t成正比B .在0-t2时间内，拉力F与A位移成正比C .在0-t2时间内，拉力F做的功等于A的机械能增量D .在O-t i时间内，拉力F做的功等于A的动能增量二、多项选择题：本大题共4小题，每小题4分，共计16分•每小题有多个选项符合题意•全部选对的得4分，选对但不全的得2分，错选或不选的得0分。

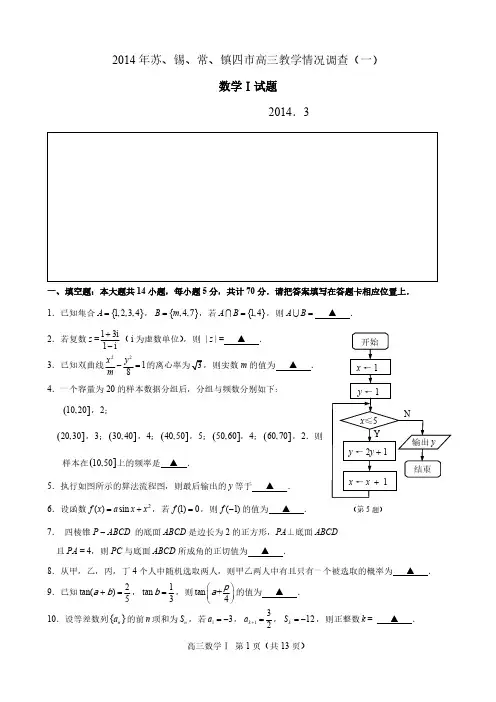
苏锡常镇四市2014届高三3月教学情况调研（一）数学Ⅰ试题 2014．3参考公式：柱体的体积公式：V 柱体=Sh ，其中S 是柱体的底面积，h 是高． 直棱柱的侧面积公式：S 直棱柱侧=ch ，其中c 是直棱柱的底面周长，h 是高．一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1．已知集合{}1,2,3,4A =，{},4,7B m =，若{}1,4A B =，则AB = ▲ ．2．若复数z =13i1i+-（i 为虚数单位），则 | z | = ▲ ． 3．已知双曲线2218x y m -=m 的值为 ▲ ．4．一个容量为20的样本数据分组后，分组与频数分别如下：(]10,20，2；(]20,30，3；(]30,40，4；(]40,50，5；(]50,60，4；(]60,70，2．则样本在(]10,50上的频率是 ▲ ．5．执行如图所示的算法流程图，则最后输出的y 等于 ▲ ．6．设函数2()sin f x a x x =+，若(1)0f =，则(1)f -的值为 ▲ ． 7． 四棱锥P - ABCD 的底面ABCD 是边长为2的正方形，P A ⊥底面ABCD 且P A = 4，则PC 与底面ABCD 所成角的正切值为 ▲ ．8．从甲，乙，丙，丁4个人中随机选取两人，则甲乙两人中有且只有一个被选取的概率为 ▲ ．9．已知2tan()5+=，1tan 3=，则tan +4⎛⎫⎪⎝⎭的值为 ▲ ．10．设等差数列{}n a 的前n 项和为n S ，若13a =-，132k a +=，12k S =-，则正整数k = ▲．（第5题）11．已知正数,x y 满足22x y +=，则8x yxy+的最小值为 ▲ ． 12．如图，在△ABC 中，BO 为边AC 上的中线，2BG GO =，设CD ∥AG ，若15AD AB AC =+λ()∈R λ，则λ的值为 ▲ ． 13．已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+，若函数()g x 恰有两个不同的零点，则实数k 的取值范围为 ▲ ．14．在平面直角坐标系xOy 中，已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内，动直线AB 过点P 且交圆C 于,A B 两点，若△ABC 的面积的最大值为16，则实数m 的取值范围为 ▲ ．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）设函数2()6cos cos f x x x x =-． （1）求()f x 的最小正周期和值域；（2）在锐角△ABC 中，角,,A B C 的对边分别为,,a b c ，若()0f B =且2b =，4cos 5A =，求a 和sin C ．16．（本小题满分14分）如图，在三棱柱111ABC A B C -中，侧面11AA B B 为菱形， 且160A AB ∠=︒，AC BC =，D 是AB 的中点．111DC B ACBA （第16题）（第12题）ABCDOG（1）求证：平面1A DC ⊥平面ABC ； （2）求证：1BC ∥平面1A DC ．17．（本小题满分14分）一个圆柱形圆木的底面半径为1m ，长为10m ，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD （如图所示，其中O 为圆心，,C D 在半圆上），设BOC ∠=，木梁的体积为V（单位：m3），表面积为S（单位：m2）．（1）求V关于θ的函数表达式；（2）求的值，使体积V最大；（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．18．（本小题满分16分）如图，在平面直角坐标系xOy中，已知A，B，C是椭圆22221(0)x ya ba b+=>>上不同的三点，A，(3,3)B--，C在第三象限，线段BC的中点在直线OA上．（1）求椭圆的标准方程；θD CB A O（第17题）（2）求点C 的坐标；（3）设动点P 在椭圆上（异于点A ，B ，C ）且直线PB ，PC 分别交直线OA 于M ，N 两点，证明OM ON ⋅为定值并求出该定值．19．（本小题满分16分）设各项均为正数的数列{}n a 的前n 项和为S n ，已知11a =，且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立． （1）若λ = 1，求数列{}n a 的通项公式； （2）求λ的值，使数列{}n a 是等差数列．（第18题）20．（本小题满分16分）已知函数e ()ln ,()e xxf x mx a x mg x =--=，其中m ，a 均为实数． （1）求()g x 的极值；（2）设1,0m a =<，若对任意的12,[3,4]x x ∈12()x x ≠，212111()()()()f x f xg x g x -<-恒成立，求a 的最小值；（3）设2a =，若对任意给定的0(0,e]x ∈，在区间(0,e]上总存在1212,()t t t t ≠，使得120()()()f t f t g x == 成立，求m 的取值范围．苏锡常镇连徐四市2014届高三3月教学情况调研（一）数学Ⅱ（附加题）2014．321．【选做题】在A 、B 、C 、D 四小题中只能选做两题．．．．．．，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． A ．选修4—1：几何证明选讲如图，⊙O 为四边形ABCD 的外接圆，且AB AD =，E 是CB 延 长线上一点，直线EA 与圆O 相切．求证：CD ABAB BE=．B ．选修4—2：矩阵与变换 已知矩阵1221⎡⎤=⎢⎥⎣⎦M ，17⎡⎤=⎢⎥⎣⎦β，计算6M β．C ．选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，圆的参数方程为22cos ,()2sin x y =+⎧⎨=⎩为参数，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．求：（1）圆的直角坐标方程；（2）圆的极坐标方程．D ．选修4—5：不等式选讲已知函数2()122f x x x a a =++---，若函数()f x 的图象恒在x 轴上方，求实数a 的取值范围．【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）甲乙两个同学进行定点投篮游戏，已知他们每一次投篮投中的概率均为23，且各次投篮的结果互不影响．甲同学决定投5次，乙同学决定投中1次就停止，否则就继续投下去，但投篮次数不超过5次． （1）求甲同学至少有4次投中的概率； （2）求乙同学投篮次数的分布列和数学期望．E（第21-A 题）23．（本小题满分10分）设01212(1)m m n n n n n m S C C C C ---=-+-+-，*,m n ∈N 且m n <，其中当n 为偶数时，2nm =；当n 为奇数时，12n m -=． （1）证明：当*n ∈N ，2n ≥时，11n n n S S S +-=-； （2）记01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，求S 的值．苏锡常镇连徐四市2014届高三3月教学情况调研（一）数学Ⅰ试题参考答案 2014．3一、填空题：本大题共14小题，每小题5分，共70分．1．{}1,2,3,4,7 2 3. 4 4.710 5．63 6．2 7 8. 23 9． 9810．13 11．9 12．65 13. 27321,{0,22e+⎛⎫-- ⎪⎝⎭ 14. [3(327,3++--二、解答题：本大题共6小题，共计90分．解答时应写出文字说明、证明过程或演算步骤．15. 解：（1）1+cos2()622xf x x =⨯=3cos223x x +=)36x ++． …………………3分所以()f x 的最小正周期为22T ==， …………………4分值域为[3-+． …………………6分（2）由()0f B =，得πcos(2)6B +=． B 为锐角，∴ππ7π2666B <+<，π5π266B +=，∴π3B =． …………………9分 ∵4cos 5A =，(0,)A ∈，∴3sin 5A =． …………………10分在△ABC中，由正弦定理得32sin sin b A a B⨯===． …………………12分∴21sin sin()=sin()sin 322C A B A A A =---=+=． …………………14分 16．（1）证明：∵ 11ABB A 为菱形，且160A AB ∠=︒，∴△1A AB 为正三角形．…………………2分D 是AB 的中点，∴1AB A D ⊥．∵AC BC =，D 是AB 的中点，∴ AB CD⊥． …………………4分1A D CD D =，∴AB ⊥平面1A DC ． …………………6分∵AB ⊂平面ABC ，∴平面1A DC ⊥平面ABC ． …………………8分（2）证明：连结1C A ，设11AC AC E =，连结DE ． ∵三棱柱的侧面11AA C C 是平行四边形，∴E 为1AC 中点． …………………10分 在△1ABC 中，又∵D 是AB 的中点，∴DE ∥1BC ． …………………12分 ∵DE ⊂平面1A DC ，1BC ⊄平面1A DC ，∴ 1BC ∥平面1A DC ． …………………14分 17．解：（1）梯形ABCD 的面积2cos 2sin 2ABCD S +=⋅=sin cos sin +，(0,)2∈． …………………2分 体积()10(sin cos sin ),(0,)2V =+∈． …………………3分 （2）2()10(2coscos 1)10(2cos 1)(cos 1)V '=+-=-+．令()0V '=，得1cos 2=，或cos 1=-（舍）． ∵(0,)2∈，∴3=． …………………5分当(0,)3∈时，1cos 12<<，()0,()V V '>为增函数； 当(,)32∈时，10cos 2<<，()0,()V V '<为减函数． …………………7分∴当3=时，体积V 最大． …………………8分（3）木梁的侧面积210S AB BC CD =++⋅侧（）=20(cos 2sin 1)2++，(0,)2∈．2ABCD S S S =+侧=2(sin cos sin )20(cos 2sin 1)2++++，(0,)2∈．…………………10分设()cos 2sin 12g =++，(0,)2∈．∵2()2sin 2sin 222g =-++，∴当1sin22=，即3=时，()g 最大． …………………12分 又由（2）知3=时，sin cos sin +取得最大值，所以3=时，木梁的表面积S 最大． …………………13分综上，当木梁的体积V 最大时，其表面积S 也最大． …………………14分18．解：（1）由已知，得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩ …………………2分所以椭圆的标准方程为22127272x y +=． …………………3分 （2）设点(,)C m n (0,0)m n <<，则BC 中点为33(,)22m n --． 由已知，求得直线OA 的方程为20x y -=，从而23m n =-．① 又∵点C 在椭圆上，∴22227m n +=．②由①②，解得3n =（舍），1n =-，从而5m =-． …………………5分 所以点C 的坐标为(5,1)--． …………………6分 （3）设00(,)P x y ，11(2,)M y y ，22(2,)N y y ． ∵,,P B M 三点共线，∴011033233y y y x ++=++，整理，得001003()23y x y x y -=--．…………………8分 ∵,,P C N 三点共线，∴22011255y y y x ++=++，整理，得00200523y x y x y -=-+．…………………10分 ∵点C 在椭圆上，∴2200227x y +=，2200272x y =-．从而22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+． …………………14分 所以124552OM ON y y ⋅==． …………………15分 ∴OM ON ⋅为定值，定值为452． …………………16分19．解：（1）若λ = 1，则11(1)(1)n n n n S a S a +++=+，111a S ==．又∵00n n a S >>，， ∴1111n n n nS a S a +++=+， ………………… 2分 ∴3131221212111111n n n nS S a a S a S S S a a a +++++⋅⋅⋅=⋅⋅⋅+++， 化简，得1112n n S a +++=．① ………………… 4分 ∴当2n ≥时，12n n S a +=．②② - ①，得12n n a a +=， ∴12n na a +=（2n ≥）． ………………… 6分 ∵当n = 1时， 22a =，∴n = 1时上式也成立，∴数列{a n }是首项为1，公比为2的等比数列， a n = 2n -1（*n ∈N ）． …………………8分 （2）令n = 1，得21a λ=+．令n = 2，得23(1)a λ=+． ………………… 10分要使数列{}n a 是等差数列，必须有2132a a a =+，解得λ = 0． ………………… 11分 当λ = 0时，11(1)n n n n S a S a ++=+，且211a a ==． 当n ≥2时，111()(1)()n n n n n n S S S S S S +-+-=+-， 整理，得2111n n n n n S S S S S +-++=+，1111n n n nS S S S +-+=+， ………………… 13分 从而3312412123111111n n n nS S S S S S S S S S S S +-+++⋅⋅⋅=⋅⋅⋅+++， 化简，得11n n S S ++=，所以11n a +=． ……………… 15分 综上所述，1n a =（*n ∈N ），所以λ = 0时，数列{}n a 是等差数列． ………………… 16分 20．解：（1）e(1)()exx g x -'=，令()0g x '=，得x = 1． ………………… 1分 列表如下：∵g (1) = 1，∴y =()g x 的极大值为1，无极小值． …………………3分 （2）当1,0m a =<时，()ln 1f x x a x =--，(0,)x ∈+∞．∵()0x af x x -'=>在[3,4]恒成立，∴()f x 在[3,4]上为增函数． …………………4分 设1e ()()e x h x g x x ==，∵12e (1)()x x h x x --'=> 0在[3,4]恒成立， ∴()h x 在[3,4]上为增函数． …………………5分设21x x >，则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-， 即2211()()()()f x h x f x h x -<-．设1e ()()()ln 1e xu x f x h x x a x x=-=---⋅，则u (x )在[3,4]为减函数．∴21e (1)()10e x a x u x x x -'=--⋅≤在（3，4）上恒成立． …………………6分∴11e ex x a x x---+≥恒成立． 设11e ()e x x v x x x --=-+，∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+，x ∈[3，4]， ∴1221133e [()]e 1244x x --+>>，∴()v x '< 0，()v x 为减函数．∴()v x 在[3，4]上的最大值为v (3) = 3 -22e 3． ………………… 8分 ∴a ≥3 -22e 3，∴a 的最小值为3 -22e 3． …………………9分 （3）由（1）知()g x 在(0,e]上的值域为(0,1]． …………………10分 ∵()2ln f x mx x m =--，(0,)x ∈+∞，当0m =时，()2ln f x x =-在(0,e]为减函数，不合题意． ………………… 11分当0m ≠时，2()()m x m f x x-'=，由题意知()f x 在(0,e]不单调，所以20e m <<，即2em >．① …………………12分 此时()f x 在2(0,)m 上递减，在2(,e)m上递增， ∴(e)1f ≥，即(e)e 21f m m =--≥，解得3e 1m -≥．② 由①②，得3e 1m -≥． …………………13分 ∵1(0,e]∈，∴2()(1)0f f m=≤成立． …………………14分 下证存在2(0,]t m∈，使得()f t ≥1． 取emt -=，先证e 2mm-<，即证2e 0mm ->．③设()2e x w x x =-，则()2e 10xw x '=->在3[,)e 1+∞-时恒成立． ∴()w x 在3[,)e 1+∞-时为增函数．∴3e ))01((w x w ->≥，∴③成立． 再证()emf -≥1．∵e e 3()1e 1m m f m m m --+=>>-≥，∴3e 1m -≥时，命题成立． 综上所述，m 的取值范围为3[,)e 1+∞-． …………………16分苏锡常镇连徐四市2014届高三3月教学情况调研（一）数学Ⅱ（附加题） 参考答案 2014．321、【选做题】在A 、B 、C 、D 四小题中只能选做两题．．．．．．，每小题10分，共计20分． A ．选修4—1：几何证明选讲 证明：连结AC ．EA 是圆O 的切线，∴EAB ACB ∠=∠． …………………2分AB AD =，∴ACD ACB ∠=∠． ∴ACD EAB ∠=∠． …………………4分圆O 是四边形ABCD 的外接圆，∴D ABE ∠=∠． …………………6分∴CDA ∆∽ABE ∆． …………………8分 ∴CD DAAB BE=， AB AD =，∴CD ABAB BE=． …………………10分 B ．选修4—2：矩阵与变换解：矩阵M 的特征多项式为212()2321f λλλλλ--==----． 令12()031f λλλ===-，解得，，对应的一个特征向量分别为111⎡⎤=⎢⎥⎣⎦α，211⎡⎤=⎢⎥-⎣⎦α． …5分 令12m n =+βαα，得4,3m n ==-．6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α．……………10分C ．选修4—4：坐标系与参数方程解：（1）圆的直角坐标方程为22(2)4x y -+=． …………………5分（2）把cos ,sin ,x y ρθρθ=⎧⎨=⎩代入上述方程，得圆的极坐标方程为4cos ρθ=．…………………10分D ．选修4—5：不等式选讲解：()f x 的最小值为232a a --， …………………5分由题设，得223a a -<，解得(1,3)a ∈-． …………………10分【必做题】第22题、第23题，每题10分，共计20分．22．解：（1）设甲同学在5次投篮中，有x 次投中，“至少有4次投中”的概率为P ，则(4)(5)P P x P x ==+= …………………2分=441550552222()(1)()(1)3333C C -+-=112243． …………………4分 （2）由题意1,2,3,4,5=．2(1)3P ==，122(2)339P ==⨯=，1122(3)33327P ==⨯⨯=，3122(4)3381P ⎛⎫==⨯= ⎪⎝⎭， 411(5)381P ⎛⎫=== ⎪⎝⎭．的分布表为…………………8分的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=． …………………10分 23．解：（1）当n 为奇数时，1n +为偶数，1n -为偶数，∵1101221112(1)n n n n nn S CC C+++++=-++-，110122112(1)n n n n n n S C CC---+=-++-， 11012211212(1)n n n n n n S C CC------=-++-，∴1111110011222221111111222()()(1)()(1)n n n n n n n n nnn n n n S S C C C C CCC-+-++-++-++++-=---++--+-=11012212112((1))n n n n n n CCCS --------++-=-．∴当n 为奇数时，11n n n S S S +-=-成立． …………………5分 同理可证，当n 为偶数时， 11n n n S S S +-=-也成立． …………………6分（2）由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-，得 0123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-=0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -． …………………9分 又由11n n n S S S +-=-，得6n n S S +=，所以20142012421S S S S -=-=-，12014S =-．………10分。

苏锡常镇四市2014 届高三 3 月教课状况调研（一）英语2014年 3月第一卷（选择题共85 分）第一部分：听力（共两节，满分20 分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题纸上。

第一节（共 5 小题；每题 1 分，满分 5 分）听下边 5 段对话。

每段对话后有一个小题，从题中所给的A,B,C 三个选项中选出最佳选项，并标在试卷的相应地点。

听完每段对话后，你都有10 秒钟的时间往返答相关小题和阅读下一小题。

每段对话仅读一遍。

1 ． Where will the woman most probably go?A. To a theatre.B. To a restaurant.C. To a bookstore.2. When will Lucy arrive here?A. 4:30.B. 5:10.C. 5:30.3 ． What's the woman ，s opinion about the bridge?A. It needn't be built.B. It will be a better one.C. It should have been built earlier.4. What does the man think of the woman’ s choice of clothing?A. He doesn't think her choice is suitable.B. He thinks her choice shows her good taste.C. He thinks the skirt is nicer than her red dress.5 ． How much does the woman have to pay?A. $70.B. $105.C. $140.第二节（共15 小题：每题 1 分，满分15 分）听下边 5 段对话或独白。

B．在绕地球飞行的宇宙飞船中，自由飘浮的水滴呈球形，这是外表X力作用的结果C．液晶显示器是利用了液晶对光具有各向同性的特点D ．当两分子间距离大于平衡位置的间距r0时，分子间的距离越大，分子势能越小(2)一定质量的理想气体由状态 A经过程 I变至状态 B时，内能增加 120 J．当气体从状态 B经过程 II回到状态 A时，外界压缩气体做功200 J，那么 II 过程中气体▲(填“吸热〞缄“放热〞)，热量为▲J(3) 一定质量的理想气体状态变化如下列图，其中 AB段与 t轴平行．在状态 A时气体的体积为 1.0L ，那么变到状态B时气体的体积为多少?从状态 A变到状态 C的过程中气体对外做功为多少?B． (选修模块 3-4)(12 分 )(1) 如下列图为两列简谐横波在同一绳上传播时某时刻的波形图，甲波的速度为v1，乙波的速度为 v2，质点 M的平衡位置为 x=0.2m．那么以下说法中正确的选项是▲A ．这两列波发生干预现象，且质点M的振动始终加强B ．由图示时刻开场，再经过1／ 4甲波周期， M将位于波峰D．因波的周期未知，故两列波波速的大小无法比较(2)相对论认为时间和空间与物体的速度有关．在高速前进中的列车的中点处，某乘客突然按亮电灯，使其发出一道闪光，该乘客认为闪光向前、向后传播的速度相等，都为c；站在铁轨旁边地面上的观察者认为闪光向前、向后传播的速度▲(选填“相等〞或“不等〞)．车上的乘客认为，电灯的闪光同时到达列车的前、后壁：地面上的观察者认为电灯的闪光先到达列车的▲(选填“前〞或“后〞)壁．(3)如下列图，折射率为 2 的两面平行的玻璃砖，下外表涂有反射物质，右端垂直地放置一标尺MN ．一细束光以 450角度入射到玻璃砖的上外表，会在标尺上的两个位置出现光点，假设两光点之间的距离为 a(图中未画出 ) ，那么光通过玻璃砖的时间是多少 ?(设光在真空中的速度为 c)C． (选修模块 3-5)(12 分 )(1) 以下说法正确的选项是▲A．原子核发生衰变时要遵守电荷守恒和质量守恒的规律B．α粒子散射实验能提醒原子具有核式构造C．发生光电效应时光电子的动能只与入射光的强度有关D．氢原子从激发态向基态跃迁只能辐射特定频率的光子(2) 在光电效应试验中，某金属的截止频率相应的波长为λ0，该金属的逸出功为▲．假设用波长为λ(兄λ<λ▲．(电子的电荷量、真空0)单色光做实验，那么其截止电压为中的光速和普朗克常量分别为e、 c和h)(3)光滑水平轨道上有三个木块 A、B、C，质量分别为 m A =3m、m B=m C=m，开场时木块 B、 C均静止，木块 A以初速度 v0向右运动， A与B碰撞后分开，B又与 C发生碰撞并粘在一起，此后 A与 B间的距离保持不变．求B与C碰撞前 B的速度大小．四、计算题：此题共 3小题，共计 47分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题，答案中必须明确写出数值和单位．13．(15分 )如下列图，质量 m1=0.1kg ，电阻 R l=0.3Ω，长度 l=0.4m 的导体棒 ab横放在 U 型金属框架上．框架质量m2=0.2kg ，放在绝缘水平面上，与水平面间的动摩擦因数μ=0.2 ，相距 0.4m的MM ’、NN’相互平行，电阻不计且足够长． MN 电阻 R2=0.1Ω且垂直于 MM ’．整个装置处于竖直向上的磁感应强度 B=0.5T 的匀强磁场中．垂直于 ab施加 F=2N 的水平恒力， ab从静止开场无摩擦地运动，始终与 MM ’、NN’保持良好接触．当 ab运动到某处时，框架开场运动．设框架与水平面间的最大静摩擦力等于滑动摩擦力，g取10m/s2．求：(1)框架开场运动时导体棒ab的加速度 a的大小；(2)框架开场运动时导体棒ab的速度 v的大小；(3)从导体棒 ab开场运动到框架开场运动的过程中，MN上产生的热量 Q=0.1J，该过程通过导体棒ab的电量的大小．14．(16分 )如下列图，倾角为θ的斜面上只有AB段粗糙，其余局部都光滑，AB段长为 3L．有假设干个一样的小方块沿斜面靠在一起，但不粘接，总长为L ．现将它们由静止释放，释放时下端距 A为 2L．当下端运动到 A下面距 A 为L/2时物块运动的速度到达最大．求：(1)物块与粗糙斜面的动摩擦因数(2)最后一个木块运动过 A时的速度(3) 假设小方块的总质量为m，那么物块下滑过程中产生的热量15．(16分 )如图 a所示，两竖直线所夹区域内存在周期性变化的匀强电场与匀强磁场，变化情况如图 b、c所示，电场强度方向以y轴负方向为正，磁感应强度方向以垂直纸面向外为正． t=0时刻，一质量为 m、电量为 q的带正电粒子从坐标原点 O开场以速度 v0沿 x轴正方向运动，粒子重力忽略不计，图 b、c中E03B00，t0m，B0．要4qB0使带电粒子在 0～ 4nt0(n∈N)时间内一直在场区运动，求：(1) 在 t0时刻粒子速度方向与x轴的夹角；(2)右边界到 O的最小距离；(3)场区的最小宽度。

高中化学学习材料江苏省苏锡常镇四市2014届高三教学情况调研（一）化学 2014年3月注意事项：1．本试卷分为选择题和非选择题两部分，共120分，考试时间100分钟。

2．请把选择题和非选择题的答案均填写在答题卷的指定栏目内。

可能用到的相对原子质量：N-14 O-16 S-32 K-39 Cr-52 Fe-56 Cu-64 Ba-137第Ⅰ卷（选择题共40分）单项选择题：本题包括10 小题，每小题2 分，共计20 分。

每小题只有一个选项符合题意。

1．天宫一号与神舟九号载人飞船的交会对接，标志着我国具备了建设空间站的基本能力。

下列有关说法正确的是A．天宫一号利用太阳能将水加热分解为氢气和氧气B．天宫一号使用的碳纤维是一种新型有机高分子材料C．神舟九号中的氢氧燃料电池将电能转换为化学能D．神舟九号升空时火箭发射的动力主要来源于化学能2．下列有关化学用语表示错误的是A．HCN的结构式：H－C≡NB．HClO的电子式为：H O ClC．CH4分子的球棍模型：D．2-氯甲苯的结构简式：CH3 Cl【答案】C【解析】试题分析：A、正确；B、HClO分子中氧原子分别与氢原子和氯原子形成公用电子对，形成8电子稳定结构，正确；C、该模型是比例模型，错误；D、正确。

考点：考查化学用语有关问题。

3．下列离子组在指定溶液中能大量共存的是A．中性溶液：Cu2+、Al3+、NO3－、SO42－B．加入苯酚显紫色的溶液：K+、NH4+、Cl－、I－C．加入Al能放出大量H2的溶液中：NH4+、Fe2+、NO3－、SO42－D．常温下，c(H+)/c(OH一)＝1×10－12的溶液：K+、AlO2－、CO32－、Na+【答案】D【解析】试题分析：A、Cu2+、Al3+只存在于酸性溶液中，错误；B、该溶液中含有Fe3+，I－与其发生氧化还原反应而不能共存，错误；C、该溶液可能为酸性或碱性溶液，酸性条件下Fe2+与NO3－发生氧化还原反应不能共存，碱性条件下NH4+、Fe2+不能共存，错误；D、该溶液为碱性溶液，离子能大量共存，正确。