布拉菲点阵
- 格式:docx
- 大小:10.28 KB
- 文档页数:4


第一章晶体结构1 布喇菲点阵和初基矢量晶体结构的特点在于原子排列的周期性质。
布喇菲点阵是平移操作112233R n a n a n a =++所联系的诸点的列阵。
布喇菲点阵是晶体结构周期性的数学抽象。
点阵矢量112233R n a n a n a =++,其中,1n ,2n 和3n 均为整数,1a ,2a 和3a 是不在同一平面内的三个矢量,叫做布喇菲点阵的初基矢量,简称基矢。
初基矢量所构成的平行六面体是布喇菲点阵的最小重复单元。
布喇菲点阵是一个无限的分立点的列阵,无论从这个列阵中的哪个点去观察,周围点的分布和排列方位都是完全相同的。
对一个给定的布喇菲点阵,初级矢量可以有多种取法。
2 初基晶胞(原胞)初基晶胞是布喇菲点阵的最小重复单元。
初基晶胞必定正好包含布喇菲点阵的一个阵点。
对于一个给定的布喇菲点阵,初基晶胞的选取方式可以不只一种,但不论初基晶胞的形状如何,初基晶胞的体积是唯一的,()123c V a a a =⋅⨯。
3 惯用晶胞(单饱)惯用晶胞是为了反映点阵的对称性而选用的晶胞。
惯用晶胞可以是初基的或非初基的。
惯用晶胞的体积是初基晶胞体积的整数倍,c V nV =。
其中,n 是惯用晶胞所包含的阵点数。
确定惯用晶胞几何尺寸的数字叫做点阵常数。
4 维格纳—赛兹晶胞(W-S 晶胞)维格纳—赛兹晶胞是另一种能够反映晶体宏观对称性的晶胞,它是某一阵点与相邻阵点连线的中垂面(或中垂线)所围成的最小体积。
维格纳—赛兹晶胞是初基晶胞。
5 晶体结构当我们强调一个实际的晶体与布喇菲点阵的抽象几何图案的区别时,我们用“晶体结构”这个名词[1]。
理想的晶体结构是由相同的物理单元放置在布喇菲点阵的阵点上构成的。
这些物理单元称为基元,它可以是原子、分子或分子团(有时也可以指一组抽象的几何点)。
将基元平移布喇菲点阵的所有点阵矢量,就得到晶体结构,或等价地表示为基元十点阵=晶体结构[2]当选用非初基的惯用晶胞时,一个布喇菲点阵可以用带有基元的点阵去描写。

关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中,布拉菲晶格(又译布拉菲点阵)是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲(A.Bravais)于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于七个晶系。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。

关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中,布拉菲晶格(又译布拉菲点阵)是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲(A.Bravais)于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于七个晶系。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。



布拉菲点阵名词解释
布拉菲点阵是一种在计算机图形学中使用的数据结构,它与普通的网格和网格数据的结构不同。
布拉菲点阵是一种二叉树数据结构,它由一个节点数组和一些指针组成,每个节点数组都是指针到下一个节点的指针。
在布拉菲点阵中,每个节点数组都有一个指向下一个节点的指针,但最后一个节点的指针指向一个空指针,表示没有下一个节点。
这种结构使得布拉菲点阵可以在一个很小的空间内表示一个较大的网格,并且可以方便地进行插入、删除和查找等操作。
布拉菲点阵可以被分为两种类型:满布拉菲点阵和空布拉菲点阵。
在满布拉菲点阵中,每个节点数组都有一个指向下一个节点的指针,而在空布拉菲点阵中,每个节点数组都有两个指针,分别指向下一个节点和空指针。
布拉菲点阵在计算机图形学中应用广泛,例如在3D图形中,可以使用布拉菲点阵来表示一个网格,然后通过遍历这个网格来渲染出图
形。
此外,布拉菲点阵还可以用于一些其他领域,例如信号处理和图像处理等。
总之,布拉菲点阵是一种非常有用的数据结构,它在计算机图形学和许多其他领域中都可以被广泛应用。


关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中,布拉菲晶格(又译布拉菲点阵)是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲(A.Bravais)于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于七个晶系。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲( A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。

关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在以及中,布拉菲晶格(又译布拉菲点阵)是为了纪念在固态物理学的贡献命名的。
法国晶体学家()于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。


Catio3离子晶体的布拉菲点阵离子晶体是由正离子和负离子通过离子键相互结合而形成的无机晶体。
其中,Catio3离子晶体是一种重要的离子晶体,它由钙离子(Ca2+)和氧离子(O2-)组成。
布拉菲点阵是描述离子晶体晶格结构的一种方式,下面将详细介绍Catio3离子晶体的布拉菲点阵。
1. 什么是离子晶体的布拉菲点阵?布拉菲点阵(Bravais lattice)是描述晶体的周期性结构的一种数学模型。
它由一些特殊位置的晶胞以及晶胞间的平移操作构成。
布拉菲点阵的性质决定了晶体的一些基本特征,如晶格常数、晶胞体积等。
2. Catio3离子晶体的结构Catio3离子晶体是由正离子钙离子(Ca2+)和负离子氧离子(O2-)通过离子键相互结合而形成的。
它的结构可以通过布拉菲点阵来描述。
2.1 布拉菲点阵类型Catio3离子晶体的布拉菲点阵属于立方晶系。
在立方晶系中,常见的布拉菲点阵有简单立方点阵、面心立方点阵和体心立方点阵。
Catio3离子晶体的布拉菲点阵属于面心立方点阵。
2.2 布拉菲点阵参数对于Catio3离子晶体的面心立方点阵,它的晶格常数为a,晶胞的共有八个角点,每个角点上有一个离子;此外,每个面心位置处也有一个离子。
因此,Catio3离子晶体的布拉菲点阵参数可以表示为:a = 2r,其中r为钙离子半径,假设钙离子和氧离子半径相等。
3. Catio3离子晶体的布拉菲点阵示意图O O O O/ // /O Ca O O\ \\ \O O O O上述示意图展示了Catio3离子晶体的布拉菲点阵。
其中,大圆球表示钙离子(Ca2+),小圆球表示氧离子(O2-)。
需要注意的是,实际的晶格结构比此示意图更加复杂,但此示意图可以帮助我们了解离子在晶格中的排列方式。
4. 小结Catio3离子晶体是由钙离子和氧离子通过离子键相互结合而形成的。
它的布拉菲点阵属于面心立方点阵,晶格常数为a,晶胞包含八个角点和一个面心位置。
Catio3离子晶体的布拉菲点阵描述了离子在晶格中的周期性排列方式,对于研究其物理、化学性质具有重要意义。


关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中,布拉菲晶格(又译布拉菲点阵)是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲(A.Bravais)于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于七个晶系。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。




1.2布喇菲空间点阵原胞晶胞
1.2.1布喇菲空间点阵
晶体内部结构可以看成是由一些相同的点子在空间作规则的周期性无限分布,这些点子的总体称为布喇菲点阵。
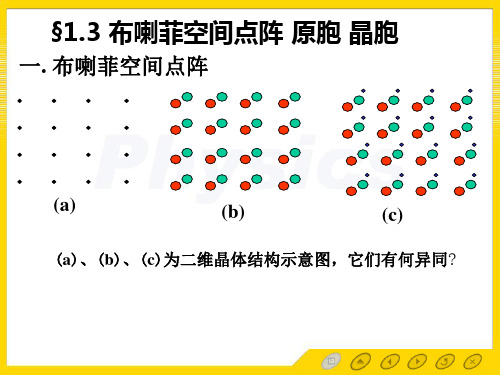
二维晶体结构,基元及其点阵:
沿三个不同方向通过点阵中的结点作平行的直线族,把结点包括无遗,点阵便构成一个三维网格.这种三维格子称为晶格,又称为布喇菲格子,结点又称格点.
1.2.2 原胞
以一结点为顶点,以三个不同方向的周期为边长的平行六面体可作为晶格的一个重复单元.体积最小的重复单元,称为原胞或固体物理学原胞.它能反映晶格的周期性.原胞的选取不是惟一的,但它们
的体积都相等.
下图示出了原胞与基矢.
原胞与基矢
原胞选取的任意性
1.2.3 晶胞
为了同时反映晶体对称的特征,结晶学上所取的重复单元,体积不一定最小,结点不仅在顶角上,还可以是体心或面心.这种重复单元称作晶胞、惯用晶胞或布喇菲原胞.
我们称重复单元的边长矢量为基矢.若以a1、a2和a3表示原胞的基矢。
简立方
原胞基矢与晶胞基矢的关系:
简立方晶胞
体心立方
原胞基矢
体积:
面心立方
原胞基矢
体积:
立方晶系中几种实际晶体结构:氯化铯:
氯化钠:
金刚石:
钙钛矿:。

1说明布拉菲点阵和晶体结构的关系答:晶体的原子或分子在空间的分布具有周期性,这种分布可看成是由若干个原子或离子构成的重复单元(即基元)在三维空间的周期性的分布,把基元抽象为一个空间几何点,称之为阵点。
阵点在空间的周期性分布构成布拉菲点阵。
晶体结构=基元+布拉菲点阵2原胞:整个晶体可以通过由结点构成的某一单元沿空间三个不同方向各按一定的距离作周期性地平移而构成,这个重复单元就称为原胞或晶胞,平移一定的距离称为晶格的周期。
说明原胞和晶胞的关系答:构成布拉菲点阵的最小的平行六面体称为原胞。
能充分体现布拉菲点阵的对称性的重复单元称为晶胞热缺陷:当温度T不等于0K时,晶体中格点上原子发生热振动有几率离开格点位置而成为间隙原子和空位,即缺陷。
热缺陷为点缺陷,包括:弗仑克尔缺陷-原子脱离格点后,同时形成空格点和间隙原子,空格点等于间隙原子数。
肖脱基缺陷-晶体内部格点上的原子跑到晶体表面,形成空格点。
间隙原子-晶体表面原子跑到晶体内部晶格间隙位置,形成间隙原子。
离子晶体正负离子交替排列在晶格格点上,依靠离子键原子晶体原子共价键金属失去价电子的离子实金属键分子分子和饱和原子范德瓦尔斯力晶面与晶列指数2.电子有效质量的意义是什么?它与能带有什么关系?答:有效质量概括了晶体中电子的质量以及内部周期势场对电子的作用,引入有效质量后,晶体中电子的运动可用类似于自由电子运动来描述。
有效质量与电子所处的状态有关,与能带结构有关:(1)、有效质量反比于能谱曲线的曲率;(2)、有效质量是k的函数,在能带底附近为正值,能带顶附近为负值。
(3)、具有方向性---沿晶体不同方向的有效质量不同。
只有当等能面是球面时,有效质量各向同性。
导体半导体绝缘体能带结构的差异导体:有未被填满的价带。
绝缘体:价带全部被电子填满,禁带上面的导带是空带,且禁带宽度较大。
半导体:价带全部被电子填满,禁带上面的导带是空带,但禁带宽度相对较小。
施主杂质:V A族杂质在硅、锗中电离时,能够释放电子而产生导电电子并形成正电中心施主能级Ed:被施主杂质束缚的多余的一个价电子状态对应的能量。
关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲
在以及中,布拉菲晶格(又译布拉菲点阵)是为了纪念在固态物理学的贡献命名的。
法国晶体学家()于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:
其选取方式有,
1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:
①要能充分反映整个空间点阵的周期性和对称性;
②在满足①的基础上,单胞要具有尽可能多的直角;
③在满足①、②的基础上,所选取单胞的体积要最小。
根据以上原则,所选出的14种布拉菲点阵的单胞(见表1)可以分为两大类。
一类为简单单胞,即只在平行六面体的 8个顶点上有结点,而每个顶点处的结点又分属于 8个相邻单胞,故一个简单单胞只含有一个结点。
另一类为复合单胞(或称复杂单胞),除在平行六面体顶点位置含有结点之外,尚在体心、面心、底心等位置上存在结点,整个单胞含有一个以上的结点。
14种布拉菲点阵中包括7个简单单胞,7个复合单胞。
布拉维晶格
P
P C
P C I F
(正交晶系)
P I
P
(棱方晶系)
A
P I F
(立方晶系)
表1 14种布拉菲点阵
晶体根据其对称程度的高低和对称特点可以分为七大晶系,所有晶体
均可归纳在这七个晶系中,而晶体的七大晶系是和14种布拉菲点阵相对应的,如表1和表2所示。
所有空间点阵类型均包括在这14种之中,不存在这14种布拉菲点阵外的其它任何形式的空间点阵。
底心正方点阵可以用简单正方点阵来表示,面心正方可以用体心正方来表示。
如果在单胞的结点位置上放置一个结构基元,则此平行六面体就成为晶体结构中的一个基本单元,称之为晶胞。
在实际应用中我们常将单胞与晶胞的概念混淆起来用而没有加以细致的区分。
表2 七大晶系和14种布拉菲点阵
对称性是晶体最重要的基本特征之一,也是研究晶体结构的重要基础。
点阵所表达的晶体平移对称性包括晶体内每一个原子的平移对称性,也包括各原子间每个空隙位置的平移对称性。
因此,点阵是实际晶体所具备的平移对称性的高度抽象和概括,点阵内阵点与阵点之间的关系等同于实际晶体内所具有的相应平移对称几何点之间的关系。
切忌把阵点简单地理解成真实晶体中原子的位置。
有很多种晶体单胞在其所对应的点阵单胞的阵点位置上并没有原子。