【名师一号】2016-2017学年高一人教版物理必修1同步学习方略典型分析：2-2 Word版含解析

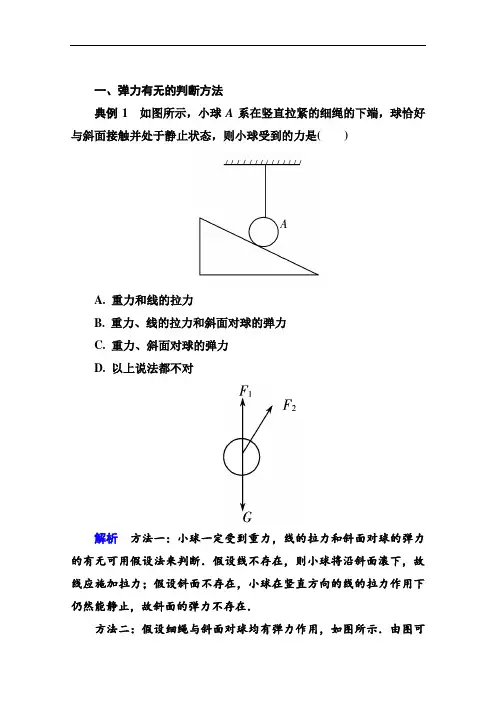
一、弹力有无的判断方法典例1如图所示，小球A系在竖直拉紧的细绳的下端，球恰好与斜面接触并处于静止状态，则小球受到的力是()A. 重力和线的拉力B. 重力、线的拉力和斜面对球的弹力C. 重力、斜面对球的弹力D. 以上说法都不对解析方法一：小球一定受到重力，线的拉力和斜面对球的弹力的有无可用假设法来判断．假设线不存在，则小球将沿斜面滚下，故线应施加拉力；假设斜面不存在，小球在竖直方向的线的拉力作用下仍然能静止，故斜面的弹力不存在．方法二：假设细绳与斜面对球均有弹力作用，如图所示．由图可知，F2的存在破坏了小球的静止状态，与题意矛盾，故斜面的弹力不存在．答案 A巩固练习1判断图中小球是否受到A、B两个接触面的弹力作用．解析题图①中将接触面B去掉，球仍能处于平衡，故球不受B 面的弹力作用，而受到A面的弹力作用．题图②中小球同时受到A、B 两面的弹力作用．答案见解析二、弹力方向的判断典例2如图①、②、③所示，画出物体A受到的弹力示意图．解析图①中，A球与容器壁及容器底部是球面与平面接触，弹力方向分别垂直于容器壁、底部指向A球(必通过球心)；A和B是球面与球面接触，弹力方向垂直于过接触点的切面，在两球连线上，如图①所示．②图中，杆下端与球面接触点与球面接触，弹力方向垂直于球面过接触点的切面，即沿半径方向指向球心；杆与碗边接触为点与直线(平面)接触，故弹力垂直于杆斜向上，如图②所示．③图中，两绳对A产生的弹力为拉力，由绳子形变而产生，故弹力必沿绳子且指向绳子收缩方向．如图③所示．答案见解析图巩固练习2画出图①、②中物体A受到的弹力的示意图．解析弹力是一种接触力，弹力的方向垂直于接触点处的切面，方向跟施力物体恢复原状的趋势一致，指向被支持物体，如图．答案见解析图三、弹力大小的计算典例3竖直悬挂的弹簧下端，挂一重为4 N的物体时，弹簧长度为12 cm；挂重为6 N的物体时，弹簧长度为13 cm，则弹簧原长为________ cm，劲度系数为________ N/m.解析弹簧上悬挂重物时弹簧要伸长，由胡克定律知：弹簧上的弹力与弹簧的伸长量成正比，即F＝kx，其中k为劲度系数，x为弹簧伸长量，数值上等于伸长后的总长度减去原长L0，即x＝L－L0.改变悬挂重物的重量，伸长量变化，这样可以列出两个方程，可通过方程组求出弹簧原长和劲度系数．设弹簧的原长为L0，劲度系数为k，设挂G1＝4 N重物时弹簧的长度为L1，挂G2＝6 N的重物时弹簧的长度为L2，则L1＝12 cm，L2＝13 cm，由胡克定律得G1＝k(L1－L0)G2＝k(L2－L0)代入数据解得L0＝10 cm，k＝200 N/m.即弹簧原长为10 cm，劲度系数为200 N/m.答案10200名师点拨(1)弹力的大小与形变程度有关，具体问题中可由物理规律求解.如静止在桌面上的物体受到桌面向上的弹力和自身的重力作用，由二力平衡知，弹力的大小等于物体重力的大小.(2)对弹簧的弹力有胡克定律：发生弹性形变的弹簧在弹性限度内，弹力的大小与弹簧的长度变化量成正比，即F＝kx.式中F表示弹力，k表示劲度系数，与弹簧自身性质有关，由弹簧的材料、长度、粗细、匝数决定，与F或x的大小无关，单位符号是N/m；x表示弹簧长度的变化量，单位符号是m.注意：若x的给出单位为“cm”时，要先化为“m”才能代入公式计算．巩固练习3量得一只弹簧测力计3 N和5 N两刻线之间的距离为2.5 cm，求：(1)弹簧测力计3 N刻线与零刻线之间的距离；(2)测力计所用弹簧的劲度系数．解析设3 N刻线到零刻线之间的距离为x，劲度系数为k.(1)根据胡克定律有F1＝kx，F2＝k(x＋2.5)由题意知F1＝3 N F2＝5 N解得x＝3.75 cm.(2)k＝F1x＝33.75×10－2N/m＝80 N/m.答案(1)3.75 cm (2)80 N/m。

一、位移公式x ＝v 0t ＋12at 2的应用 典例1 自行车以4 m/s 的初速度匀减速地上一个斜坡，加速度大小为0.2 m/s 2，斜坡长20 m ，则自行车通过斜坡所需的时间为多少？解析 选取初速度v 0＝4 m/s 的方向为正方向，a ＝－0.2 m/s 2，x ＝20 m ，由公式x ＝v 0t ＋12at 2，得 20＝4t ＋12(－0.2)×t 2. 解得t 1＝(20＋102) s ≈34.14 s ，t 2＝(20－102) s ≈5.86 s当t ＝34.14 s 时，末速度v ＝v 0＋at ≈－2.828 m/s ，这说明此时自行车的速度沿斜坡向下，故不合题意应舍去t 1，即所需时间为5.86 s.答案 5.86 s名师点拨 对于实际物体的运动由运动学公式求的结果，一定要与实际情况相符，经过讨论得出符合实际情况的结论．巩固练习1 一小球沿斜面由静止开始匀加速滚下(斜面足够长)，已知小球在第4 s 末的速度为4 m/s.求：(1)第6 s 末的速度；(2)前6 s 内的位移；(3)第6 s 内的位移．解析 a ＝v －v 0t ＝4－04m/s 2＝1 m/s 2 (1)第6 s 末的速度：v ′＝at ′＝1×6 m/s ＝6 m/s.(2)前6 s 内的位移：x ＝12at ′2＝12×1×62 m ＝18 m.(3)第6 s 内的位移：Δx ＝x －12a (t ′－1)2＝[18－12×1×(6－1)2] m ＝5.5 m. 答案 (1)6 m/s (2)18 m (3)5.5 m二、v －t 图象的应用典例2 某一做直线运动的物体的v －t 图象如图所示，根据图象求(1)物体距出发点的最远距离；(2)前4 s 物体的位移；(3)前4 s 物体通过的路程．解析 (1)由题意可知物体0～3 s 速度方向与规定正方向相同．即3 s 末物体距出发点最远x m ＝12v 1t 1＝12×4×3 m ＝6 m. (2)前4 s 内的位移x ＝|x 1|－|x 2|＝|12v 1t 1|－|12v 2t 2| ＝|12×4×3| m －|12×(－2)×1| m ＝5 m. (3)前4 s 内物体通过的路程s ＝|x 1|＋|x 2|＝|12v 1t 1|＋|12v 2t 2|＝7 m. 答案 (1)6 m (2)5 m (3)7 m名师点拨 离出发点远近涉及位移在v －t 图象中位移，的判断可利用图线与坐标轴围成的面积表示，但要注意，当所围图形在t 轴的下方时，表示此位移为负方向上的位移．巩固练习2 如图所示为某物体做直线运动的v －t 图象，下列有关物体运动情况判断正确的是( )A. 前2 s 加速度为5 m/s 2B. 4 s 末物体返回到出发点C. 6 s 末物体距出发点最远D. 8 s 末物体距出发点最远解析 前2 s 内加速度a ＝Δv Δt ＝102m/s 2＝5 m/s 2，故A 选项正确；由图象可知前2 s 内加速运动，2～4 s 物体做减速运动，4 s 末速度为零，前4 s 物体沿正方向运动，后4 s 物体沿负方向运动，故4 s 末物体离出发点最远，B 、C 、D 选项错误．答案 A三、刹车问题典例3 一辆汽车以20 m/s 的速度行驶，现因故刹车，并最终停止运动．已知汽车刹车过程中加速度大小为5 m/s 2，则汽车刹车经过5 s 所通过的距离是多少？解析 此问题是生活中的实际问题．汽车刹车的阻力来自于地面的摩擦力，汽车停止运动后，不可能再向相反方向运动，由运动学公式，当汽车速度减小到零时所需要的时间t ＝v －v 0a ＝0－20－5s ＝4 s 即汽车经过4 s 就已经停止下来，最后1 s 处于静止状态，5 s 所通过的距离就应该是4 s 内通过的距离，由位移公式x ＝v 0t ＋12at 2 得x ＝[20×4＋12×(－5)×42] m ＝40 m. 答案 40 m名师点拨 此类问题称为刹车问题，在解决此类问题时应注意所给定的时间内物体是否已经停下来，如已经停下来，在使用公式x ＝v 0t ＋12at 2时要注意时间的选取． 巩固练习3 以12 m/s 的速度行驶的汽车，紧急刹车后加速度大小为5 m/s 2，求刹车后6 s 内的位移．解析 根据条件，如果用公式x ＝v 0t ＋12at 2来求位移，x ＝12×6＋12×(－5)×62＝－18 m. 位移为负值表示汽车倒退，这是不合理的，原因是汽车从刹车开始经过时间t ＝0－v 0a ＝0－12－5s ＝2.4 s 后就停下来了．即在6 s 时间内汽车只在前2.4 s 内做减速运动，以后就处于静止状态了．正确解法：由v＝v0＋at，得t＝0－v0a＝2.4 s.x＝v0t＋12at2＝12×2.4＋12×(－5)×2.42＝14.4 m.答案14.4 m。

一、速度典例1 (多选题)汽车以36 km/h 的速度从甲地匀速直线运动到乙地用了2 h ，若汽车从乙地返回甲地仍做匀速直线运动用了2.5 h ，则汽车返回时的速度为(设甲、乙两地在同一条直线上)( )A. －8 m/sB. 8 m/sC. －28.8 km/hD. 28.8 km/h解析 由第一次运动情况可求得汽车从甲地至乙地的位移大小，结合第二次运动时间可求得第二次运动的速度大小．又因为第一次速度36 km/h 为正值，隐含了从甲地到乙地方向为正，所以返回时速度为负，可淘汰B 、D.甲、乙两地间距Δx＝v 1t 1＝36 km/h×2 h＝72 km.返回速度v 2＝－Δx Δt 2＝－72 km 2.5 h＝－28.8 km/h ＝－8 m/s 故A 、C 正确．答案 AC名师点拨 由v ＝Δx Δt可得时间Δt 内发生的位移Δx＝vΔt，发生位移Δx 的时间Δt＝Δx v. 巩固练习1 天狼星发出的光到达地球要2.5×108 s ，即大约8年的时间，求天狼星与地球的距离．(光在真空中传播速率v ＝3.0×108 m/s)解析 根据v ＝Δx Δt知Δx＝v×Δt＝3.0×108×2.5×108 m ＝7.5×1016 m. 答案 7.5×1016m二、平均速度、瞬时速度典例2 一辆汽车沿平直的公路行驶，第1 s 内通过5 m 的距离，第2 s内和第3 s 内各通过20 m 的距离，第4 s 内又通过了15 m 的距离．求汽车在最初2 s 内的平均速度和这4 s 内的平均速度各是多少？解析 最初2 s 内的时间为2 s ，位移为(5＋20) m ＝25 m ；前4 s 的时间间隔为4 s ，位移为(5＋20＋20＋15) m ＝60 m. 根据平均速度的定义公式v ＝x t 得 最初2 s 内的平均速度是v －1＝x 1＋x 2t 1＋t 2＝5＋201＋1m/s ＝12.5 m/s ， 4 s 内的平均速度是v －2＝x 1＋x 2＋x 3＋x 4t 1＋t 2＋t 3＋t 4＝5＋20＋20＋151＋1＋1＋1m/s ＝15 m/s. 答案 12.5 m/s 15 m/s名师点拨 在变速直线运动中，不同时间内的平均速度一般不同．因此说平均速度必须指明是哪段位移或哪段时间内的平均速度．巩固练习2 某汽车沿直线由甲地驶向乙地，前一半时间的平均速度为40 km/h ，后一半时间的平均速度为60 km/h.求汽车在甲、乙两地之间行驶的平均速度．解析 设汽车在甲、乙两地间运动的时间为t ，前一半时间发生的位移为s 1＝v 1t 2，后一半时间发生的位移为s 2＝v 2t 2.则甲、乙两地间全程的平均速度 v ＝s 1＋s 2t ＝v 1＋v 2t 2t ＝v 1＋v 22＝50 km/h. 答案 50 km/h三、x －t 图象典例3 (多选题)如图所示为甲、乙两物体相对于同一参考系的x －t 图象，下列说法中正确的是( )A. 甲、乙两物体出发点相距x0B. 甲、乙两物体都做匀速直线运动C. 甲物体比乙物体早出发的时间为t1D. 甲、乙两物体同方向运动解析本题考查x－t图象的特点，由题意可知甲物体在t＝0时的位移为x0.而乙物体在t＝0时的位移为0，则两物体最初相距x0，故A选项正确；由x －t图象可知，两物体的x－t图象均为倾斜直线，所以两物体都做匀速直线运动，B选项正确；甲物体的位移随时间越来越小，其x－t图象斜率为负值，而乙物体的x－t图象的斜率为正值，说明两物体，速度方向相反，D选项错误；甲物体t＝0时开始沿与规定正方向相反的方向做匀速运动，而乙物体从t＝t1时刻开始沿与规定正方向相同的方向做匀速直线运动，故C选项正确．答案ABC名师点拨x－t图象中的倾斜直线表示物体做匀速直线运动，斜率的大小表示速度大小，斜率为正表示速度方向与正方向相同，斜率为负表示速度方向与规定正方向相反，图线在x轴的截距表示初始时刻物体初始位置距坐标原点的距离大小和方向．巩固练习3 如图所示的位移—时间图象中，均表示物体做直线运动，其中描述物体做匀速直线运动的速度为2 m/s的图象是( )解析x－t图象中直线斜率表示做匀速直线运动的速度，故B选项正确．答案 B高考理综物理模拟试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

一、时刻和时间问题典例1 (多选题)关于时间和时刻，下列说法正确的是( )A. 电台报时时说：“现在是北京时间8点整”，这里实际上指的是时刻B. 物体在3 s时在什么位置指的是3 s末这一时刻C. 物体在第3 s内的运动情况，这里指的是时刻D. 第3 s末就是第4 s初，指的是时刻解析时刻是一个状态量，时间是一个过程量，区分二者的关系关键是看它们对应的是一个状态还是一个过程，北京时间8点整，指的是状态，即为时刻，故A选项正确；物体在3 s时在什么位置，对应的也是状态，即指3 s末这一时刻，故B选项正确；第3 s内对应的是一个过程，即第3个1 s这一过程，物体怎样运动，所以指的是时间，C选项错误；在时间坐标轴上第3 s末和第4 s初是同一时刻，故D选项正确．答案ABD名师点拨时间间隔在时间坐标轴上对应一段线段，表示一个过程，即时间间隔为过程量；时刻在时间坐标轴上对应一个点，即时刻为状态量．巩固练习1 在五四青年节，某校高一和高二学生组织了一场足球友谊比赛，下列关于比赛的表述中涉及的计时数据指时间的是( )A．比赛于2020年5月4日下午2点30分开始B．开场20 min时，红队率先进球C．比赛第30 min，蓝队换人D．整场比赛共进行了90 min解析时刻指的是某一瞬间，时间指的是两个时刻之间的间隔．选项A、B、C中涉及的计时数据都指的是时刻，D中的“90 min”指的是一段时间，D对．答案 D二、路程和位移典例2 一质点绕半径为R 的圆圈运动了一周，如图所示，则其位移大小为________，路程是________．若质点运动了134周，则其位移大小为________，路程是________，此运动过程中最大位移是________，最大路程是________．解析 质点绕半径为R 的圆圈运动一周，位置没有变化，位移是0，走过的路程是2πR；质点运动134周，设从A 点开始逆时针运动，则末位置为C ，如题中图所示，其位移为由A 指向C 的有向线段，大小为2R ，路程即轨迹的总长为134个周长，即72πR；运动过程中位移最大是由A 到B 点时，最大位移是2R ，最大路程即为72πR. 答案 0 2πR2R 72πR 2R 72πR 巩固练习2如图所示，一质点沿两个半径为R的半圆弧从A运动到C，则它的位移和路程分别是( )A. 4R，由A指向C；2RB. 4R，由A指向C；2πRC. 2πR，由A指向C；4RD. 4πR，由A指向C；2πR，由A指向C解析质点的位移大小等于初位置A与末位置C之间的距离，方向由A指向C；路程等于从A到C轨迹的长度，即弧长，故B选项正确．答案 B三、参量和标量典例3 一质点由位置A向北运动了4 m又转弯向东运动了3 m到达B点．在这个过程中质点运动的路程是多少？运动的位移是多少？方向如何？解析如图所示路程为7 m，位移大小x＝42＋32 m＝5 m.tanθ＝34＝0.75θ＝37°，即北偏东37°.答案7 m 5 m 北偏东37°名师点拨路程是标量，位移是矢量，不仅有大小，而且还有方向，其运算法则与标量的运算法则是不同的．巩固练习3 (多选题)关于矢量和标量，下列说法中正确的是( )A．矢量是既有大小又有方向的物理量B．标量是既有大小又有方向的物理量C．位移－10 m比5 m小D．－10 ℃比5 ℃的温度低解析由矢量的定义可知，A正确，B错；关于位移的正、负号只表示方向，不表示大小，其大小由数值和单位决定，所以－10 m的位移比5 m的位移大，故C错；温度的正、负表示比0 ℃高还是低，所以－10 ℃比5 ℃的温度低，故D正确．答案AD高考理综物理模拟试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

一、加速度的理解典例1 关于加速度，下列说法中正确的是( )A. 速度变化越大，加速度一定越大B. 速度变化所用时间越短，加速度一定越大C. 速度变化越快，加速度一定越大D. 速度为零，加速度一定为零解析由加速度的定义式a＝ΔvΔt可知，加速度是由速度的变化和所用时间两个因素共同决定，速度变化越大，加速度不一定越大；速度变化所用时间越短，但速度变化量的大小没有确定，也不能确定加速度一定越大；加速度是描述速度变化快慢的物理量，速度变化越快，加速度一定越大；速度为零，并不是速度的变化量为零，故加速度不一定为零．综上所述选C.答案 C名师点拨加速度是描述物体速度变化快慢的物理量，与速度v、速度变化量Δv、时间Δt无必然联系，加速度等于ΔvΔt，即加速度等于速度的变化率．加速度是矢量，其方向与Δv的方向相同．巩固练习1 甲、乙两个物体沿同一直线向同一方向运动时，取物体的初速度方向为正，甲的加速度恒为2 m/s2，乙的加速度恒为－3 m/s2，则下列说法正确的是( )A. 两物体都做加速运动，乙的速度变化快B. 甲做加速直线运动，它的速度变化快C. 乙做减速运动，它的速度变化率大D. 甲的加速度比乙的加速度大解析物体做加速运动还是做减速运动，取决于速度方向和加速度方向是否相同，比较加速度大小时，只比较它们的绝对值，加速度的正负号表示的是方向，故C选项正确．答案 C二、加速度的计算典例2 足球以8 m/s的速度飞来，运动员在0.2 s的时间内将足球以12 m/s 的速度反向踢出．足球在这段时间内的平均加速度大小为________ m/s2，方向与______ m/s的速度方向相反．解析以12 m/s速度方向为正方向，足球飞来速度为－8 m/s，速度改变量Δv＝12 m/s－(－8) m/s＝20 m/s，所用时间Δt＝0.2 s，其加速度为a＝Δv Δt ＝200.2m/s2＝100 m/s2，加速度的方向与8 m/s的速度方向相反．答案100 8名师点拨a＝ΔvΔt是加速度的定义式，因此，公式只能求得一段时间内的平均加速度大小．在计算速度变化量Δv时，应先确定正方向，与规定方向相同的速度取正值，与规定方向相反的速度取负值，最后求得加速度的正负也表示方向，加速度为正时，说明加速度方向与规定的正方向相同，反之，说明与规定正方向相反．巩固练习2 (多选题)一物体做匀变速直线运动，某时刻速度的大小为4 m/s,1 s后速度的大小变为10 m/s，在这1 s内该物体的( )A. 速度变化的大小可能小于4 m/sB. 速度变化的大小可能大于10 m/sC. 加速度的大小可能小于4 m/s2D. 加速度的大小可能大于10 m/s2解析本题只给出了1 s初、末速度的大小，而不知方向，若方向相同，a＝v t－v0t＝10－41m/s2＝6 m/s2，Δv＝6 m/s，若方向相反a＝－10－41m/s2＝－14 m/s2，Δv＝－14 m/s，负号说明方向与初速度方向相反．故B、D正确．答案BD三、v－t图象典例3 如图所示是一个物体向东运动的速度图象．由图象可知在0～10 s内物体的加速度大小是__________，方向是________；在10～40 s内物体的加速度为________；在40～60 s内物体的加速度大小是__________，方向是________．解析在0～10 s内由图象可以看出速度是增加的：由0增至30 m/s，因此其加速度大小为3010m/s2＝3 m/s2，这段运动是加速运动，故加速度与速度同向，向东；在10～40 s，速度为30 m/s不变，故其加速度为0；在40～60 s 内，速度由30 m/s变为0，是匀减速运动，其加速度大小为1.5 m/s2，方向与速度方向相反．答案 3 m/s2与速度方向相同0 1.5 m/s2与速度方向相反名师点拨判断物体做加速运动还是减速运动时，在v－t图象中，就讨论速度随时间是增加还是减小，物体加速时，加速度与速度方向相同，减速时，速度方向与加速度方向相反．巩固练习3 质点做直线运动的v－t图象如图所示，质点在0～t1内速度、加速度如何变化？在t1～t2内质点的速度、加速度分别是多少？解析由题中图可知，0～t1时间内，质点的速度逐渐增大，且不是匀变速直线运动．在非匀变速直线运动的v－t图象中，图象上任一点的切线的斜率等于该时刻质点的加速度．由图可知，切线的斜率逐渐减小，即加速度逐渐减小，速度增加得越来越慢．在t1～t2时间内，质点的速度v1保持恒定，加速度为零．答案见解析高考理综物理模拟试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

一、速度－位移关系式典例1 汽车以10 m/s的速度行驶，刹车后的加速度大小为3 m/s2.求它向前滑行12.5 m后的瞬时速度．解析本题中只有初速度、加速度、位移三个已知量，求末速度，可直接应用位移和速度关系求解．选取汽车的初速度方向为正，则v0＝10 m/s，a＝－3 m/s2，x＝12.5 m由公式v2－v20＝2ax，得v2＝v20＋2ax＝102＋2×(－3)×12.5.解得v1＝5 m/s，v2＝－5 m/s(负号说明汽车刹车后又反向运动与实际不符，故舍去)．答案 5 m/s名师点拨公式v2－v20＝2ax中均是矢量，在应用时需规定统一的正方向，与之相同为正，相反为负．解二次方程得出两个结果，要根据实际情况取舍．巩固练习1 一物体以初速度v0从斜面上滑下，滑到斜面底端时速度为v，求它滑到斜面中点时的速度．解析设斜面长为x，物体的加速度a，中点的速度v′，则有v2－v20＝2ax，v′2－v20＝2a x 2联立解得v′＝v20＋v22.答案v20＋v22二、匀变速直线运动的几个重要推论典例2 一物体做匀加速直线运动，第5 s内的位移为10 m，第7 s内的位移为20 m，求物体的加速度大小？解析方法一：第5 s内和第7 s内的平均速度分别等于第4.5 s和6.5 s的瞬时速度，即v 4.5＝x 5t ＝101 m/s ＝10 m/sv 6.5＝x 7t ＝201m/s ＝20 m/s所以a ＝v 6.5－v 4.5t′＝20－102 m/s 2＝5 m/s 2.方法二：由公式Δx＝aT 2 得a ＝ΔxT2.设第5 s 内的位移为x 5，第6 s 内的位移为x 6，第7 s 内的位移为x 7，则x 6－x 5＝aT 2①x 7－x 6＝aT 2② 由①②得x 7－x 5＝2aT 2a ＝x 7－x 52T 2＝20－102×12 m/s 2＝5 m/s 2.答案 5 m/s 2名师点拨 匀变速直线运动的基本公式和推论较多，在应用时要灵活应用，并注意一题多解或一题多法；根据Δx＝aT 2可以得出另一个较为常用的推论：在连续相等的n 段时间间隔T 内的位移分别为x 1、x 2、x 3……x m ……x n ，则x n －x m ＝(n －m)aT 2.巩固练习2 物体从静止开始做匀加速直线运动，第3 s 内通过的位移是3 m ，则以下说法错误的是( )A ．第3 s 内的平均速度是3 m/sB ．物体的加速度是1.2 m/s 2C ．前3 s 内的位移是6 mD ．3 s 末的速度是3.6 m/s解析 前2 s 位移x 1＝12at 21，前3 s 内位移x 2＝12at 22，则第3 s 内位移x 3＝x 2－x 1＝12at 22－12at 21，可得加速度a ＝1.2 m/s 2，则前3 s 内的位移x 2＝12at 22＝5.4 m；3 s末的速度是v3＝1.2×3 m/s＝3.6 m/s，第3 s内的平均速度是3 m 1 s＝3 m/s，故A、B、D正确．答案 C高考理综物理模拟试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

一、物体和质点典例1 (多选题)在下列各运动的物体中，可视为质点的有( )A. 做高低杠表演的体操运动员B. 沿斜槽下滑的木块，研究它沿斜槽下滑的速度C. 人造卫星，研究它绕地球的转动D. 列车通过南京长江大桥，研究它通过大桥的时间解析A选项中运动员做体操表演时，人们要欣赏运动员力和美的统一，研究运动员的各种花样动作，若视为质点，又欣赏什么？研究什么呢？故A选项错误；沿斜槽下滑的木块上各点的运动情况是相同的，研究它下滑的速度与木块的形状和大小无关，故B选项正确；研究人造卫星绕地球转动时，由于卫星的大小比卫星距地心的距离小得多，所以卫星的形状和大小可以不考虑，即可视为质点，故C选项正确；研究列车通过南京长江大桥的时间，由于大桥的长度和列车的长度差不多，列车的长度不能忽略不计，不能把列车看成质点，故D 选项错误．答案BC名师点拨物体能否被看成质点模型，关键是看物体的形状和大小在研究的问题中所起的作用，是不是达到可以忽略的程度．通过质点模型的建立，要注意学习和体会理想化方法的应用，这是一种科学的方法，在物理学的研究中经常采用理想化模型的方法．巩固练习1 (多选题)下列关于质点的说法中正确的是( )A. 质点就是质量很小的物体B. 质点就是体积很小的物体C. 质点是一种理想化模型，实际上并不存在D. 当物体的形状和大小对所研究的问题是无关紧要的因素时，即可把物体视为质点解析能否被看成质点是由所研究问题的性质决定的，与物体质量和体积无关，故A、B选项错误；质点是代替物体的有质量的点，是对实际物体的近似，是一种科学的抽象，实际上并不存在，是理想化模型，故C、D选项正确．答案CD二、参考系与物体的运动典例2 (多选题)甲、乙两人坐在同一辆沿水平直公路行驶的汽车上，以下有关的叙述中正确的是( )A. 以乙为参考系，甲是静止的B. 以地面为参考系，甲是运动的C. 以汽车为参考系，路边的树是运动的D. 以汽车为参考系，路边的树是静止的解析因为甲、乙两人具有相同的运动状态，所以甲以乙为参考系时，他们之间的位置没有变动，故甲相对乙是静止的，故A选项正确；汽车本身相对地面在运动，甲选地面为参考系时，自己本身是运动的，所以B选项正确；当选运动的汽车为参考系时，即假定汽车不动，则汽车周边的树木都向汽车运动的反方向运动，故C选项正确，D选项错误．答案ABC名师点拨描述物体的运动，一定要明确参考系，参考系的选择原则上是任意的，但选不同的参考系，对同一运动的描述可能有很大的差异，在对运动的研究上也有简繁之分．巩固练习2 如图所示，下雨天，地面观察者看到雨滴竖直下落时，坐在匀速行驶的车厢里的乘客看到的雨滴是( )A．向前运动B．向后运动C．倾斜落向前方D．倾斜落向后方解析选择不同的参考系来观察同一物体的运动，得到的结果不同，因车厢向前运动，所以车中的乘客看到的雨滴是倾斜落向后方的．答案 D三、坐标系典例3 质点由西向东运动，从A点出发到达C点再返回B点静止．如下图，若AC＝100 m，BC＝30 m，以B点为原点，向东为正方向建立直线坐标系，则出发点A点位置为________，B点的位置为________，C点的位置为________．解析以B为坐标原点，以向东为正方向建立直线坐标系如图所示A、C在坐标系中的位置如图所示，x A＝－70 m，x C＝30 m，x B＝0.答案－70 m 0 30 m名师点拨建立了坐标系后，物体的位置就是物体在坐标系中的坐标值．建立坐标系应确定正方向和坐标原点．巩固练习3 一个小球从距地面4 m处落下，到达地面并被弹回，在距地面1 m处被接住．以抛出点正下方2 m处为坐标原点，向下的方向为正方向，则球的抛出点，落地点，接住点的位置坐标分别为( )A. 2 m、－2 m、－1 mB. －2 m、2 m、1 mC. 4 m、0 m、1 mD. －4 m、0 m、－1 m解析根据题意，建立如图所示的坐标系．A为抛出点其坐标为x A＝－2 m，B为坐标原点，D为地面坐标为x D＝2 m，C 为接住点，其坐标为x C＝1 m，所以B选项正确．答案 B高考理综物理模拟试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。