(精品)2008年数学中考试题分类汇编(平面直角坐标系)(独家首发含参考答案)

2008年北京市高级中等学校招生考试数学试卷答案及评分参考阅卷须知：1．一律用红钢笔或红圆珠笔批阅，按要求签名．2．第Ⅰ卷是选择题，机读阅卷．3．第Ⅱ卷包括填空题和解答题．为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可．若考生的解法与本解法不同，正确者可参照评分参考给分．解答右端所注分数，表示考生正确做到这一步应得的累加分数．第Ⅰ卷（机读卷共32分）一、选择题（共8道小题，每小题4分，共32分）题号 1 2 3 4 5 6 7 8 答案ADCCBBBD第Ⅱ卷（非机读卷共88分）二、填空题（共4道小题，每小题4分，共16分）题号9101112答案12x()()a ab a b 4207ba31(1)n nnba三、解答题（共5道小题，共25分）13．（本小题满分5分）解：1182sin 45(2π)32222132··················································································· 4分22． ································································································· 5分14．（本小题满分5分）解：去括号，得51286x x ≤．···································································· 1分移项，得58612x x ≤．··········································································· 2分合并，得36x ≤． ······················································································ 3分系数化为1，得2x ≥．················································································· 4分不等式的解集在数轴上表示如下：················································································································· 5分15．（本小题满分5分）证明：AB ED ∥，B E ． ····························································································· 2分在ABC △和CED △中，1 2 30 123AB CE B E BCED ，，，ABC CED △≌△．···················································································· 4分AC CD ． ····························································································· 5分16．（本小题满分5分）解：由图象可知，点(21)M ，在直线3y kx 上， ············································· 1分231k ．解得2k ． ······························································································· 2分直线的解析式为23y x ．······································································· 3分令0y，可得32x．直线与x 轴的交点坐标为302，． ······························································ 4分令0x ，可得3y．直线与y 轴的交点坐标为(03)，． ······························································· 5分17．（本小题满分5分）解：222()2x y x y xxy y22()()x y x y x y ························································································ 2分2x yxy ． ································································································· 3分当30xy时，3x y ．·············································································· 4分原式677322y y y yyy．··············································································· 5分四、解答题（共2道小题，共10分）18．（本小题满分5分）解法一：如图1，分别过点A D ，作AEBC 于点E ，DF BC 于点F ．······································1分AE DF ∥．又AD BC ∥，四边形AEFD 是矩形．2EF AD ．······································2分ABCDFE 图1AB AC ，45B，42BC ，AB AC ．1222AEECBC ．22DF AE ，2CFECEF···················································································· 4分在Rt DFC △中，90DFC ，2222(22)(2)10DC DFCF． ··········································· 5分解法二：如图2，过点D 作DF AB ∥，分别交AC BC ，于点E F ，．···················· 1分ABAC ，90AEDBAC．AD BC ∥，18045DAEB BAC ．在Rt ABC △中，90BAC，45B，42BC，2sin 454242AC BC ································································· 2分在Rt ADE △中，90AED ，45DAE，2AD ，1DEAE ．3CE AC AE．·················································································· 4分在Rt DEC △中，90CED，22221310DC DECE．························································· 5分19．（本小题满分5分）解：（1）直线BD 与O 相切． ······································································· 1分证明：如图1，连结OD ．OA OD ，A ADO ．90C，90CBD CDB ．又CBDA ，90ADO CDB ．90ODB．直线BD 与O 相切．················································································· 2分DCOABE图1ABCDFE图2（2）解法一：如图1，连结DE ．AE 是O 的直径，90ADE ．:8:5AD AO ，4cos 5AD A AE ． ···················································································· 3分90C，CBD A ，4cos 5BC CBD BD． ············································································· 4分2BC，52BD．······································································ 5分解法二：如图2，过点O 作OH AD 于点H ．12AH DHAD ．:8:5AD AO ，4cos 5AH A AO ． ···················3分90C，CBD A ，4cos 5BC CBD BD． ································4分2BC ，52BD．································································································· 5分五、解答题（本题满分6分）解：（1）补全图1见下图． ············································································· 1分9137226311410546373003100100（个）．这100位顾客平均一次购物使用塑料购物袋的平均数为3个．································· 3分200036000．估计这个超市每天需要为顾客提供6000个塑料购物袋． ········································ 4分（2）图2中，使用收费塑料购物袋的人数所占百分比为25%． ······························ 5分根据图表回答正确给1分，例如：由图2和统计表可知，购物时应尽量使用自备袋和押金式环保袋，少用塑料购物袋；塑料购物袋应尽量循环使用，以便减少塑料购物袋的使用量，为环保做贡献．6分D COABH图240 35 30 25 20 15 10 5 0图1123 4 567 4311 26379 塑料袋数／个人数／位“限塑令”实施前，平均一次购物使用不同数量塑料．．购物袋的人数统计图10六、解答题（共2道小题，共9分）21．解：设这次试车时，由北京到天津的平均速度是每小时x 千米，则由天津返回北京的平均速度是每小时(40)x千米． ·························································································· 1分依题意，得3061(40)602xx ． ··································································· 3分解得200x．······························································································ 4分答：这次试车时，由北京到天津的平均速度是每小时200千米．······························ 5分22．解：（1）重叠三角形A B C 的面积为3． ·················································· 1分（2）用含m 的代数式表示重叠三角形A B C 的面积为23(4)m ； ····················· 2分m 的取值范围为843m ≤．··········································································· 4分七、解答题（本题满分7分）23．（1）证明：2(32)220mxm x m 是关于x 的一元二次方程，222[(32)]4(22)44(2)m m m mm m ．当0m时，2(2)0m ，即0．方程有两个不相等的实数根．········································································ 2分（2）解：由求根公式，得(32)(2)2m m xm．22m x m 或1x ． ················································································· 3分0m ，222(1)1mm mm．12x x ，11x ，222m x m ． ··············································································· 4分21222221m yx x m m．即2(0)ymm 为所求． ·······················5分（3）解：在同一平面直角坐标系中分别画出2(0)y mm与2(0)y m m 的图象．····························································6分由图象可得，当1m ≥时，2y m ≤． ··········7分八、解答题（本题满分7分）24．解：（1）ykx 沿y 轴向上平移3个单位长度后经过y 轴上的点C ，1 2 3 44 3 21xy O -1 -2 -3 -4 -4-3 -2-1 2(0)ymm 2(0)ym m(03)C ，．设直线BC 的解析式为3ykx ．(30)B ，在直线BC 上，330k．解得1k．直线BC 的解析式为3yx． ································································· 1分抛物线2y xbx c 过点B C ，，9303b c c，．解得43b c，．抛物线的解析式为243yxx ． ······························································ 2分（2）由243y xx ．可得(21)(10)D A ，，，．3OB ，3OC ，1OA ，2AB．可得OBC △是等腰直角三角形．45OBC，32CB．如图1，设抛物线对称轴与x 轴交于点F ，112AF AB ．过点A 作AEBC 于点E ．90AEB．可得2BE AE ，22CE ．在AEC △与AFP △中，90AECAFP，ACEAPF ，AEC AFP △∽△．AE CE AFPF，2221PF．解得2PF．点P 在抛物线的对称轴上，点P 的坐标为(22)，或(22)，． ··································································· 5分1 Oy x2 344 3 2 1-1 -2 -2-1P EBD P ACF 图1（3）解法一：如图2，作点(10)A ，关于y 轴的对称点A ，则(10)A ，．连结A C A D ，，可得10A C AC，OCAOCA ．由勾股定理可得220CD，210A D ．又210A C，222A DA CCD ．A DC △是等腰直角三角形，90CA D，45DCA ．45OCA OCD ．45OCAOCD．即OCA 与OCD 两角和的度数为45． ························································ 7分解法二：如图3，连结BD ．同解法一可得20CD ，10AC．在Rt DBF △中，90DFB，1BFDF，222DB DFBF．在CBD △和COA △中，221DB AO ，3223BC OC，20210CD CA．DBBCCDAO OC CA ．CBD COA △∽△．BCD OCA ．45OCB ，45OCAOCD．即OCA 与OCD 两角和的度数为45． ························································ 7分九、解答题（本题满分8分）25．解：（1）线段PG 与PC 的位置关系是PG PC ；1 O yx2 3 4 43 2 1-1 -2-1BDA C F 图2A 1 O y x2 3 443 2 1-1 -2 -2-1BDA C F 图3PG PC3．································································································· 2分（2）猜想：（1）中的结论没有发生变化．证明：如图，延长GP 交AD 于点H ，连结CH CG ，．P 是线段DF 的中点，FP DP ．由题意可知AD FG ∥．GFP HDP ．GPF HPD ，GFP HDP △≌△．GPHP ，GF HD ．四边形ABCD 是菱形，CDCB ，60HDC ABC．由60ABC BEF ，且菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上，可得60GBC ．HDCGBC ．四边形BEFG 是菱形，GF GB ．HD GB ．HDC GBC △≌△．CH CG ，DCH BCG ．120DCHHCB BCGHCB．即120HCG ．CH CG ，PH PG ，PG PC ，60GCPHCP．3PG PC．······························································································· 6分（3）PG PCtan(90)． ············································································ 8分D CG P ABEFH。

．在下列图形中，既是轴对称图形又是中心对称图形的是（）．．右图是某一几何体的三视图，则这个几何体是（）．A．圆柱体B．圆锥体C．正方体D．球体④正六边形．若，则这样的烟囱帽的侧面）．．如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，则线段CN的长是（）．A．3cm B．4cmC．5cm D．6cm千个白球，这些球除颜色外，形状、大小、质地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出一个球为白球它们是按一定规律排列的，依照此规律，第20个图形共有．己知菱形ABCD的边长是6，点E在直线AD上，DE＝3，连接于点M，则MC的值是．222222小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S （单位：平方米）随矩形（单位：米）的变化而变化．之间的函数关系式，并写出自变量x 的取值范围； 是多少时，矩形场地面积S 最大？最大面积是多少？（参考公式：二次函数y ＝a x 2＋b x ＋c ＝0，当x ＝2b a -时，y 最大（小）值第 4 页 共 13 页已知：如图，B 、E 、F 、C 四点在同一条直线上，AB ＝DC ，BE ＝CF ，∠B ＝∠C ． 求证：OA ＝OD ．23．（本题 6分）如图，一艘轮船位于灯塔P 的北偏东60°方向，与灯塔P 的距离为80海里的A 处，它沿正南方向航行一段时间后，到达位于灯塔P 的南偏东45°方向上的B 处．求此时轮船所在的B 处与灯塔P 的距离（结果保留根号）． 24．（本题6分）哈市某中学为了解该校学生对四种国家一级保护动物的喜爱情况，围绕“在丹顶鹤、大熊猫、滇金丝猴、藏羚羊四种国家一级保护动物中，你最喜欢哪一种动物？（只写一种）”这一问题，在全校范围内随机抽取部分同学进行问卷调查．甲同学根据调查结果计算得知：最喜欢丹顶鹤的学生人数占被抽取人数的 16％；乙同学根据调查结果绘制成如下不完整的条形统计图．请你根据甲、乙两位同学提供的信息解答下列问题：（1）在这次调查中，一共抽取了多少名学生？ （2）补全条形统计图的空缺部分；（3）如果全校有1200名学生，请你估计全校最喜欢滇金丝猴的学生有多少名？25．（本题6分）8分）荣昌公司要将本公司100吨货物运往某地销售，经与春晨运输公司协商，计划租用甲、乙两种型号的汽车共6辆，用这6辆汽车一次将货物全部运走，其中每辆甲型汽车最多能装16吨，每辆乙型汽车最多能装该种货物18吨．已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元；租用2辆甲型汽车和1辆乙型汽车共需费用2450元，且同一种型号汽车每辆租车费用相同．）求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元？）若荣昌公司计划此次租车费用不超过5000元．通过计算求出该公司有几种租车方案？请你设计出来,并求出最低的租车费用．（本题10分）如图，在平面直角坐标系中，直线y＝152x+与x轴、y轴分别交于A、B两点，ABO绕原点O顺时针旋转得到△A′B′O，并使OA′⊥AB，垂足为D，直线AB与线′B′相交于点G．动点E从原点O出发，以1个单位/秒的速度沿x轴正方向运动，设（图a）（图b）（图c））设租用一辆甲型汽车的费用是x元，租用一辆乙型汽车的费用是y元．+=y22500························································································。

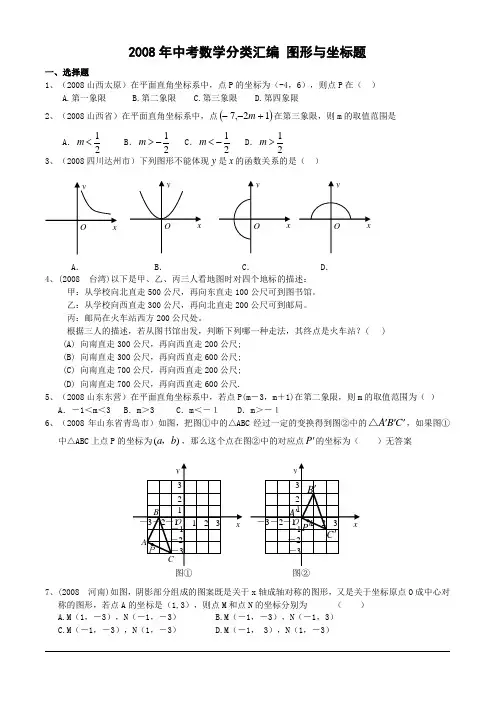
2008年中考数学分类汇编 图形与坐标题一、选择题1、（2008山西太原）在平面直角坐标系中，点P 的坐标为（-4，6），则点P 在（ ）A.第一象限B.第二象限C.第三象限D.第四象限 2、（2008山西省）在平面直角坐标系中，点()12,7+--m 在第三象限，则m 的取值范围是A ．21<m B ．21->m C ．21-<m D ．21>m3、（2008四川达州市）下列图形不能体现y 是x 的函数关系的是（ ）A ．B ．C ．D ． 4、(2008 台湾)以下是甲、乙、丙三人看地图时对四个地标的描述： 甲：从学校向北直走500公尺，再向东直走100公尺可到图书馆。

乙：从学校向西直走300公尺，再向北直走200公尺可到邮局。

丙：邮局在火车站西方200公尺处。

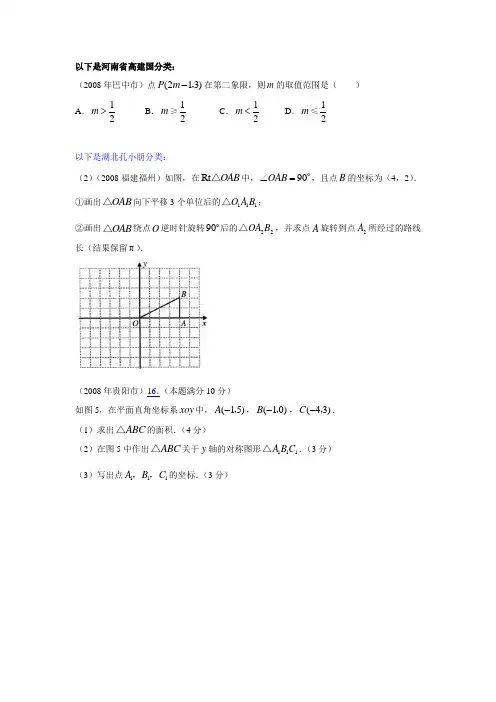
根据三人的描述，若从图书馆出发，判断下列哪一种走法，其终点是火车站？( )(A) 向南直走300公尺，再向西直走200公尺; (B) 向南直走300公尺，再向西直走600公尺; (C) 向南直走700公尺，再向西直走200公尺; (D) 向南直走700公尺，再向西直走600公尺.5、（2008山东东营）在平面直角坐标系中，若点P(m －3，m ＋1)在第二象限，则m 的取值范围为（ ） A ．－1＜m ＜3 B ．m ＞3 C ．m ＜－１ D ．m ＞－１6、（2008年山东省青岛市）如图，把图①中的△ABC 经过一定的变换得到图②中的A B C '''△，如果图①中△ABC 上点P 的坐标为()a b ，，那么这个点在图②中的对应点P '的坐标为（ ）无答案7、(2008 河南)如图，阴影部分组成的图案既是关于x 轴成轴对称的图形，又是关于坐标原点O 成中心对称的图形，若点A 的坐标是（1,3），则点M 和点N 的坐标分别为 （ ） A.M （1，－3），N （－1，－3） B.M （－1，－3），N （－1，3） C.M （－1，－3），N （1，－3） D.M （－1， 3），N （1，－3）图①图②8、(2008 湖北 十堰)如图，将ΔPQR 向右平移2个单位长度，再向下平移3个单位长度，则顶点P 平移后的坐标是( )A ． (-2,-4)B ． (-2,4)C ．(2,-3)D ．(-1,-3)9、（2008山东济南）已知△ABC 在平面直角坐标系的位置如图所示，将△ABC 向右平移6个单位，则平移后A 点的坐标是（ ）A.（－2，1）B.（2，1）C.（2，－1）D.（－2，－1）10、（2008年云南省双柏县）如图，小明从点O 出发，先向西走40米，再向南走30米到达点M ，如果点M 的位置用(－40，－30)表示，那么(10，20)表示的位置是（ ） A ．点A B ．点B C ．点C D ．点D11、(2008年镇江)如下图，把矩形OABC 放在直角坐标系中，OC 在x 轴上，OA 在y 轴上，且2OC ，4OA =，把矩形OABC 绕着原点顺时针旋转90 得到矩形OA B C '''，则点B '的坐标为（ ）A ．(24)，B ．(24)-，C ．(42)，D ．(24)-，12、（2008年荆州）如图，在平面直角坐标系中，点A 在第一象限，⊙A 与轴相切于B ，与轴交于C （0，1），D （0，4）两点，则点A 的坐标是 （ ） A.35(,22 B.3(,2)2 C.5(2,2 D.53(,2213、(2008年宁波市)在平面直角坐标系中，点(32)-，关于原点对称的点是（ ） A ．(23)-，B ．(32)--，C ．(32)，D ．(32)-，14、(2008年宁波市)如图，某电信公司提供了A B ，两种方案的移动通讯费用y （元）与通话时间x （元）之间的关系，则以下说法错误．．的是（ ） A ．若通话时间少于120分，则A 方案比B 方案便宜20元 B ．若通话时间超过200分，则B 方案比A 方案便宜12元 C ．若通讯费用为60元，则B 方案比A 方案的通话时间多D ．若两种方案通讯费用相差10元，则通话时间是145分或185分15、（2008海南省）如图4，直线l 1和l 2的交点坐标为（ ）A.(4,-2)B. (2,-4)C. (-4,2)D. (3,-1)120 170 20016.(2008湖北天门)如图，在平面直角坐标系中，OABC 是正方形，点A 的坐标是(4，0)，点P 为边AB 上一点，∠CPB ＝60°，沿CP 折叠正方形，折叠后，点B 落在平面内点B ’处，则B ’点的坐标为（ ）．A 、(2，32) B 、(23，32-) C 、(2，324-) D 、(23，324-)17. (2008年广东湛江市) 函数12y x =-的自变量x 的取值范围是（ ） A ． 2x = B ． 2x ≠ C ． 2x ≠- D ． 2x > 18、（无省份）对任意实数x ，点2(2)P x x x -，一定不在．．（ ） A.第一象限B ．第二象限C ．第三象限D ．第四象限19.（2008山东烟台）正方形ABCD 在坐标系中的位置如图所示，将正方形ABCD绕D 点顺时针旋转90°后，B 点的坐标为（ ）A 、（－2，2）B 、（4，1）C 、（3，1）D 、（4，0）20.(2008年宁波市)在平面直角坐标系中，点(32)-，关于原点对称的点是（ ） A ．(23)-，B ．(32)--，C ．(32)，D ．(32)-，21. （2008扬州市）在平面直角坐标系中，将点A （1，2）的横坐标乘以-1，纵坐标不变，得到点A ’,则点A 和点A ’的关系是( )A 、关于x 轴对称B 、关于y 轴对称C 、关于原点对称D 、将点A 向x 轴负方向平移一个单位得点A ’ 22．（2008四川内江）下列图形中，既是中心对称图形又是轴对称图形的是（） A ．等边三角形 B ．平行四边形 C ．抛物线 D ．双曲线 23.(2008年广东梅州市)一列货运火车从梅州站出发，匀加速行驶一段时间后开始匀速行驶，过了一段时间，火车到达下一个车站停下，装完货以后，火车又匀加速行驶，一段时间后再次开始匀速行驶，那么可以近似地刻画出火车在这段时间内的速度变化情况的是（ ）图424．（2008扬州市）在平面直角坐标系中，点P （-1，2）的位置在（ ）A.第一象限B.第二象限C. 第三象限D.第四象限25.（2008年辽宁大连）如图，下列各点在阴影区域内的是 ( )A ．(3，2)B ．(－3，2)C ．(3，－2)D ．(－3，－2)26.（2008年福建宁德）如图，点A 的坐标是（1，1），若点B 在x 轴上，且△ABO 是等腰三角形，则点B 的坐标不可能．．．是（ ）． A.（2，0） B.（21，0） C.（2-，0） D.（1，0）27.（2008年山东滨州）在平面直角坐标系中，若点()13-+，m m P 在第四象限，则m 的取值范围为（ ） A 、－3＜m ＜1 B 、m ＞1 C 、m ＜－3 D 、m ＞－328、（2008浙江湖州）已知A 的坐标为（a ，b ）O 为坐标原点，连结OA ，将线段OA 绕O 按逆时针方向旋转90得OA 1，则点A 1的坐标为（ ）A 、（－a ，b ）B 、（a ，－b ）C 、（－b ，a ）D 、（b ，－a ） （无答案）29.(2008 湖北 荆门)如图，将三角形向右平移2个单位长度，再向上平移3个单位长度，则平移后三个顶点的坐标是( )(A) (1, 7) , (－2, 2),(3, 4)． (B) (1, 7) , (-2, 2),(4, 3)． (C) (1, 7) , (2, 2),(3, 4)． (D) (1, 7) , (2,－2),(3, 3)．二、填空题 1. (08仙桃等)如图，ABC ∆中，点A 的坐标为（0，1），点C 的坐标为（4，3），如果要使ABD ∆与ABC ∆ 全等，那么点D 的坐标是 .2.（2008四川内江）如图，当四边形PABN 的周长最小时，a = ．（无答案）3．（2008山西省）在方格纸上建立如图所示的平面直角坐标系，将△ABO 绕点O 按顺时针方向旋转90 o,得△A ’B ’O ，则点A 的对应点A ’的坐标为 。

以下是河南省高建国分类：（2008年巴中市）点(213)P m -，在第二象限，则m 的取值范围是（ ） A ．12m >B ．12m ≥C ．12m <D ．12m ≤以下是湖北孔小朋分类：（2）（2008福建福州）如图，在Rt OAB △中，90OAB ∠=，且点B 的坐标为（4，2）． ①画出OAB △向下平移3个单位后的111O A B △；②画出OAB △绕点O 逆时针旋转90后的22OA B △，并求点A 旋转到点2A 所经过的路线长（结果保留π）．（2008年贵阳市）16．（本题满分10分）如图5，在平面直角坐标系xoy 中，(15)A -，，(10)B -，，(43)C -，． （1）求出ABC △的面积．（4分）（2）在图5中作出ABC △关于y 轴的对称图形111A B C △．（3分） （3）写出点111A B C ，，的坐标．（3分）（2008年贵阳市）9．对任意实数x ，点2(2)P x x x -，一定不在．．（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限答案：B.本题主要考查平面直角坐标系内点的坐标的特征. 坐标轴把坐标平面分成四个象限，各象限内点的符号特征如图所示，即象限以坐标轴为界限，按逆时针方向依次为：第一象限、第二象限、第三象限、第四象限，坐标轴上的点不属于任何限象.因为22(2)x x x x -=-，可知当0x <时，一定有(2)0x x -<，所以这个点一定不在第二象限.（2008年遵义市）10．如图，如果A B C '''△与ABC △关于y 轴对称，那么点A 的对应点A '的坐标为 ．（10题图）第四象限 第三象限 第二象限 第一象限xyO （－，－）（+，－）（－，+）（+，+）图（图5）（图5）以下是江西康海芯的分类:1. （2008年郴州市）如果点M 在直线1y x =-上，则M 点的坐标可以是（ ）A ．（－1，0）B ．（0，1）C ．（1，0）D ．（1，－1）3. ( 2008年杭州市) 在直角坐标系xOy 中, 点),4(y P 在第一象限内, 且OP 与x 轴正半轴的夹角为60, 则y 的值是( B ) (A)334 (B) 34 (C) 8 (D) 28．(2008年双柏县) 如图，小明从点O 出发，先向西走40米，再向南走30米到达点M ，如果点M 的位置用(－40，－30)表示，那么(10，20)表示的位置是（ ）A ．点AB ．点BC ．点CD ．点D以下是辽宁省高希斌的分类1．（2008年湖北省咸宁市）如图，在平面直角坐标系中，直线l 是第一、三象限的角平分线． 实验与探究：(1) 由图观察易知A （0，2）关于直线l 的对称点A '的坐标为（2，0），请在图中分别标明 B (5,3) 、C (-2,5) 关于直线l 的对称点B '、C '的位置，并写出他们的坐标:B ' 、C ' ； 归纳与发现：(2) 结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P (a ,b )关于第一、三象限的角平分线l 的对称点P '的坐标为 （不必证明）； 运用与拓广：(3) 已知两点D (1,-3)、E (-1,-4)，试在直线l 上确定一点Q ，使点Q 到D 、E 两点的距离之和最小，并求出Q 点坐标．说明：由点E 关于直线l 的对称点也可完成求解．2．（2008年荆州市）如图，在平面直角坐标系中，点A 在第一象限，⊙A 与轴相切于B ，与轴交于C （0，1），D （0，4）两点，则点A 的坐标是 （ ）A.35(,)22B.3(,2)2C.5(2,)2D.53(,)223．（2008年荆州市）已知点P （a+1，2a-1）关于x 轴的对称点在第一象限，求a 的取值范围. 4．（2008年湖北省鞥仙桃市潜江市江汉油田）ABC ∆中，点A 的坐标为（0，1），点C 的坐标为（4，3），如果要使ABD ∆与ABC ∆ 全等，那么点D 的坐标是 .1．（2008年龙岩市）函数3-=x y 的自变量x 的取值范围是 .2．（2008年龙岩市）（13分）如图，在平面直角坐标系xOy 中，⊙O 交x 轴于A 、B 两点，直线F A ⊥x 轴于点A ，点D 在F A 上，且DO 平行⊙O 的弦MB ，连DM 并延长交x 轴于点C .（1）判断直线DC 与⊙O 的位置关系，并给出证明； （2）设点D 的坐标为（-2，4），试求MC 的长及直线DC 的解析式.8（2008乌鲁木齐）．将点(12)，向左平移1个单位，再向下平移2个单位后得到对应点的坐标是 ．(00)，以下是山东任梦送的分类(梅州)如图6，已知ABC △: （1） AC 的长等于_______．（2）若将ABC △向右平移2个单位得到A B C '''△，则A 点的对应点A '的坐标是______；（3） 若将ABC △绕点C 按顺时针方向旋转90后得到∆A 1B 1C 1，则A 点对应点A 1的坐标是_________．（1）在同一方格纸中，画出将小金鱼图案绕原点O 旋转180°后得到的图案；（4分）（2）在同一方格纸中，并在y 轴的右侧，将原小金鱼图案以原点O 为位似中心放大，使它们的位似比为1：2，画出放大后小金鱼的图案．（4分）以下是江苏省赣榆县罗阳中学李金光分类:1．（2008年大连市）如图，下列各点在阴影区域内的是 ( )A ．(3，2)B ．(－3，2)C ．(3，－2)D ．(－3，－2)2．（2008年沈阳市）在平面直角坐标系中，点A 的坐标为(11)，，点B 的坐标为(111)，，点C 到直线AB 的距离为4，且ABC △是直角三角形，则满足条件的点C 有 个．3．（2008年南昌市）在平面直角坐标系中，以点（2，3）为圆心，2为半径的圆必定（ ） A ．与x 轴相离、与y 轴相切 B ．与x 轴、y 轴都相离 C ．与x 轴相切、与y 轴相离 D ．与x 轴、y 轴都相切22．（2008年义乌市）已知：等腰三角形OAB 在直角坐标系中的位置如图，点A 的坐标为（-），点B 的坐标为（－6，0）.（1）若三角形OAB 关于y 轴的轴对称图形是三角形O A B ''，请直接写出A 、B 的对称点A 'B '、的坐标；（2）若将三角形OAB 沿x 轴向右平移a 个单位，此时点A恰好落在反比例函数y =a 的值； （3）若三角形OAB 绕点O 按逆时针方向旋转α度（090α<<）.①当α=30时点B 恰好落在反比例函数ky x=的图像上，求k 的值． ②问点A 、B 能否同时落在①中的反比例函数的图像上，若能，求出α 的值；若不能，请说明理由.24. （2008年义乌市）如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴x负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积； ②当42<<t 时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直．线．AB ．．上是否存在点P ，使PDE ∆为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由．24．（2008嘉兴市）如图，直角坐标系中，已知两点(00)(20)O A ，，，，点B 在第一象限且OAB △为正三角形，OAB △的外接圆交y 轴的正半轴于点C ，过点C 的圆的切线交x 轴于点D ．（1）求B C ，两点的坐标； （2）求直线CD 的函数解析式；（3）设E F ，分别是线段AB AD ，上的两个动点，且EF 平分四边形ABCD 的周长． 试探究：AEF △的最大面积？(2008年安徽省) 如图，在平面直角坐标系中，一颗棋子从点P 处开始依次关于点A 、B 、C 作循环对称跳动，即第一次跳到点P 关于点A 的对称点M 处，接着跳到点M 关于点B 的对称点N 处，第三次再跳到点N 关于C 的对称点处，…．如此下去。

10、平面直角坐标系要点一：位置的确定及平面直角坐标系一、选择题1、（2010·金华中考）在平面直角坐标系中，点P（－1，3）位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限【解析】选B.点P横坐标小于0，纵坐标大于0，故点P（－1，3）位于第二象限。

2、（2009·杭州中考）有以下三个说法：①坐标的思想是法国数学家笛卡儿首先建立的；②除了平面直角坐标系外，我们也可以用方向和距离来确定物体的位置；③平面直角坐标系内的所有点都分别属于四个象限．其中错误的是（）A．只有① B．只有② C．只有③ D．①②③答案：选C3、(2009·宁波中考)以方程组21y xy x=-+⎧⎨=-⎩的解为坐标的点(,)x y在平面直角坐标系中的位置是（）A．第一象限B．第二象限C．第三象限D．第四象限【解析】选A. 方程组21y xy x=-+⎧⎨=-⎩的解为1.50.5xy=⎧⎨=⎩，（1.5，0.5）在第一象限.4、(2009黄石中考)已知点A（m2－5，2m+3）在第三象限角平分线上，则m=（）A 、4B 、－2C 、4或－2D 、－1【解析】选B.由点A （m 2－5，2m+3）在第三象限角平分线上知：m 2－5=2m+3，将选择项代入方程检验可得 答案：5、(2009济南中考)在平面直角坐标系中，对于平面内任一点()a b ，，若规定以下三种变换：()()()()1313;f a b a b f -=-如①，=，．，，， ()()()()1331;g a b b a g =如②，=，．，，， ()()()()1313h a b a b h --=--如③，=，．，，，．按照以上变换有：(())()()233232f g f -=-=，，，，那么()()53f h -，等于（ ）A ．()53--，B ．()53，C ．()53-，D ．()53-，【解析】选B. ()()()535,3(5,3)f h f -=-=，. 6、（2008·金华中考）2008年5月12日，在四川省汶川县发生8.0级特大地震，能够准确表示汶川这个地点位置的是（ D ）A.北纬31oB.东经103.5oC.金华的西北方向上D.北纬31o ，东经103.5o 答案：选D7、（2008·大连中考）在平面直角坐标系中，点P (2，3)在 ( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 答案：选A8、（2007·杭州中考）点P 在第二象限内，P 到x 轴的距离是4，到y 轴的距离是3，那么点P 的坐标为（ ）（A ）()4,3- （B ）()3,4-- （C ）()3,4- （D ）()3,4-【解析】选C.到x轴的距离描述的是纵坐标的绝对值，到y轴的距离是横坐标的绝对值.根据其在第二象限确定横坐标为负，纵坐标为正.9、（2007·盐城中考）如图，已知棋子“车”的坐标为（－2，3），棋子“马”的坐标为（1，3），则棋子“炮”的坐标为（）（A）（3，2）（B）（3，1）（C）（2，2）（D）（－2，2）【解析】选A.. 棋子“车”的坐标为（－2，3）确定x轴为棋盘下边缘所在的直线，y轴为棋盘左右的中轴线，棋盘中小方格的长度为单位1，从而确定棋子“炮”的坐标为（3，2）.10、（2007·宜昌中考）如图，小明从点O出发，先向西走40米，再向南走30米到达点M，如果点M的位置用(－40，－30)表示，那么(10，20)表示的位置是（）.(A)点A(B)点B (C)点C(D)点D答案：选B.二、填空题11、（2010·嘉兴中考）在直角坐标系中，横坐标和纵坐标都是整数的点称为格点．已知一个圆的圆心在原点，半径等于5，那么这个圆上的格点有个．【解析】因为222543=+，点（3，4），（4，3）符合要求，由对称性可知（3，－4），（－3，4），（－3，－4），（4，－3），（－4，3），（－4，－3）也符合要求，所以共8个点符合要求. 答案：812、（2010·宿迁中考）在平面直角坐标系中，线段AB 的端点A 的坐标为)2,3(-，将其先向右平移4个单位，再向下平移3个单位，得到线段B A ''，则点A 对应点A '的坐标为______．【解析】根据平移的规律得坐标为（1，－1） 答案：（1，－1）13．（2009·绍兴中考）如图是绍兴市行政区域图，若上虞市区所在地用坐标表示为(12)，，诸暨市区所在地用坐标表示为(52)--，，那么嵊州市区所在地用坐标可表示为__________．【解析】建立如图所示的坐标系，每个小正方形的边长为单位长度1.答案：（0，－3）14、（2009·乌鲁木齐中考）在平面直角坐标系中，点(12)A x x--，在第四象限，则实数x的取值范围是．【解析】由题知10. 2. 20xxx->⎧>⎨-<⎩解得答案：2x>15、(2008·益阳中考)如图是益阳市行政区域图，图中益阳市区所在地用坐标表示为(1,0)，安化县城所在地用坐标表示为(－3，－1)，那么南县县城所在地用坐标表示为 .答案：（2,4）16、（2008·邵阳中考）2008年奥运火炬于6月3日至5日在我省传递（传递路线为：岳阳—汩罗—长沙—湘潭—韶山）．如图，学生小华在地图上设定汩罗市位置点的坐标为(02)-，，长沙市位置点的坐标为(04)-，，请帮助小华确定韶山市位置点的坐标为．答案：(15)--，三、解答题17、（2007·泸州中考）如图是某市市区四个旅游景点的示意图(图中每个小正方形的边长为1 个单位长度)，请以某景点为原点，建立平面直角坐标系(保留坐标系的痕迹)，并用坐标表示下列景点的位置：①动物园_____________________②烈士陵园____________________【解析】答案不唯一，坐标系建立不同则结果不同，建立如图所示的坐标系①（3，5），②（0，0） ∴︒=∠70A ，︒=∠90B ，︒=∠140C 要点二、坐标与轴对称 一、选择题1. (2009·南充中考)在平面直角坐标系中，点(25)A ，与点B 关于y 轴对称，则点B 的坐标是（ ） A ．(52)--，B ．(25)--，C ．(25)-，D ．(25)-，【解析】选C. 由关于y 轴对称点的纵坐标相同，横坐标相反得点B 的坐标是(25)-，.2、（2010·綦江中考）直角坐标系内点P(－2,3)关于原点的对称点Q 的坐标为（ ）A ． （2，－3）B ． （2,3）C ．（－2,3）D ． （－2，－3）【解析】选A ，关于原点对称的点的坐标，横、纵坐标均互为相反数。

一、选择题1．A2．B3．C4．B5．B6．C7．C8．A9．B10．D11．B12．C 二、填空题13．914．(3)(1)x x+-15．BD=CD，OE=OF，DE∥AC等16．417．15 三、解答题18．（1）解：2210x-+= ................................................................................................. 1分21x=............................................................................................................. 2分12x= ............................................................................................................... 3分（2）解：解①得x＞－2 ................................................................................................ 4分解②得x＜3 .................................................................................................... 5分∴此不等式组的解集是－2＜x＜3 ...................................................................... 6分解集在数轴上表示正确............................................................................................ 7分19．（1）证明：∵AB∥DE，∴∠B=∠DEF∵AC∥DF，∴∠F=∠ACB................................................................................... 1分∵BE=CF，∴BE+EC= CF + EC即BC=EF ....................................................... 2分∴△ABC≌△DEF∴AB=DE ....................................................... 3分（2）解：过点O作OG⊥AP于点G连接OF ..................................................... 4分∵DB=10，∴OD=5∴AO=AD+OD=3+5=8∵∠PAC=30°∴OG=12AO=1842⨯=cm ........................... 5分∵OG⊥EF，∴EG=GF∵GF =2222543OF OG-=-=∴EF=6cm ................................................. 7分20．解：组成的所有坐标列树状图为：第19题图2OAD B CEFPＧ........................................ 5分或列表为：........................................ 5分 方法一：根据已知的数据，点(,)m n 不在第二象限的概率为123164=方法二：1－43164= .................................................................................................... 8分 21．解：设康乃馨每支x 元，水仙花每支y 元 ........................................................... 1分 由题意得：3192218x y x y +=⎧⎨+=⎩ ................................................................................... 4分解得：54x y =⎧⎨=⎩......................................................................................................... 6分第三束花的价格为353417x y +=+⨯= ............................................................... 7分 答：第三束花的价格是17元． ........... ............................................................... 8分22．解:（1）设CD 为x 千米，由题意得，∠CBD =30°，∠CAD =45° ∴AD =CD =x ..................................... 1分11 －12 －2(1，1)(1，－1)(1，2)(1，－2) －11 －12 －2(－1，1)(－1，－1)(－1，2) (－1，－2)2 1 －1 2 －2 (2，1)(2，－1)(2，2)(2，－2)－21 －12 －2(－2，1)(－2，－1)(－2，2) (－2，－2)第一次第二次第一次第二次第一次第二次1 -12 -2 1 (1，1) (-1，1) (2，1) (-2，1) -1 (1，-1) (-1，-1) (2，-1) (-2，-1) 2 (1，2) (-1，2) (2，2) (-2，2) -2(1，-2)(-1，-2)(2，-2)(-2，-2)在Rt △BCD 中，tan30°=xBD∴ BD =3x ...................................... 2分 AD +DB =AB =40∴ 340x x += ................................3分解得 x ≈14.7∴ 牧民区到公路的最短距离CD 为14.7千米． ................................................ 4分 （若用分母有理化得到CD=14.6千米，可得4分）（2）设汽车在草地上行驶的速度为v ，则在公路上行驶的速度为3v ，在Rt △ADC 中，∠CAD =45°，∴ AC =2CD 方案I 用的时间134333AD CD AD CD CDt v v v v +=+==............................................... . 5分 方案II 用的时间22ACCDt vv== .......................................................................... . 6分 ∴ 21243CD CDt t v v-=- =(324)3CDv- ....................................................................................................... . 7分∵ 324-＞0∴ 21t t -＞0 .......................................................................................................... . 8分 ∴方案I 用的时间少，方案I 比较合理 ............................................................. . 9分23．解：（1）3433y x y x⎧=-+⎪⎨=⎪⎩ ................................................................................... 1分解得：223x y =⎧⎪⎨=⎪⎩.................................................................................................... 2分∴点P 的坐标为(2，23) ....................................................................................... 3分 （2）将0y =代入343y x =-+ 3430x -+=∴ 4x =，即OA =4 ..................................................................................................... 4分 做PD ⊥OA 于D ，则OD =2，PD =23 ∵ tan ∠POA =2332= ∴ ∠POA =60° ........................................................................................................ 5分 ∵ OP =222(23)4+=ADＢC45°60°第22题图∴△POA 是等边三角形． ....................... 6分（3）① 当0<t ≤4时，如图1在Rt △EOF 中，∵∠EOF =60°，OE =t∴EF =23t ，OF =21t∴S =21·OF ·EF =283t .............................. 7分 当4<t <8时，如图2 设EB 与OP 相交于点C易知：CE =PE =t －4，AE =8－t ∴AF =4－t 21，EF =23(8－t) ∴OF =OA －AF =4－（4－21t ）=21t ∴S =21(CE +OF )·EF =12(t －4+12t )×32(8－t ） =－3832t +43t －83.................................. 8分 ② 当0<t ≤4时，S =382t ， t =4时，S 最大=23 当4<t <8时，S =－3832t +43t －83=－383(t －316)2+338 t =316时，S 最大=338 ∵338>23，∴当t =316时，S 最大=338 ...................................................... 9分 24．解：(1)设抛物线的解析式为2(1)3y a x =-- .................................................... 1分 将A (－1，0)代入: 20(11)3a =--- ∴ 34a =.......................................... 2分 ∴ 抛物线的解析式为23(1)34y x =--，即：2339424y x x =-- ............................ 3分（2）是定值，1PM PNBE AD+= ...................................................................................... 4分 ∵ AB 为直径，∴ ∠AEB =90°，∵ PM ⊥AE ，∴ PM ∥BEF第23题图2PxOBCEAyF第23题图1yOA xPEBD∴ △APM ∽△ABE ，∴ PM APBE AB=① 同理:PN PBAD AB=② .............................................................................................. 5分 ① + ②:1PM PN AP PBBE AD AB AB+=+=............................................................................ 6分 （3）∵ 直线EC 为抛物线对称轴，∴ EC 垂直平分AB∴ EA =EB ∵ ∠AEB =90°∴ △AEB 为等腰直角三角形． ∴ ∠EAB =∠EBA =45° ...................... 7分如图，过点P 作PH ⊥BE 于H ，由已知及作法可知，四边形PHEM 是矩形， ∴PH =ME 且PH ∥ME 在△APM 和△PBH 中 ∵∠AMP =∠PHB =90°， ∠EAB =∠BPH =45° ∴ PH =BH且△APM ∽△PBH∴ PA PM PB BH=∴PA PM PMPB PH ME==① .................... 8分 在△MEP 和△EGF 中，∵ PE ⊥FG ， ∴ ∠FGE +∠SEG =90° ∵∠MEP +∠SEG =90° ∴ ∠FGE =∠MEP ∵ ∠PME =∠FEG =90° ∴△MEP ∽△EGF ∴PM EF ME EG = ② 由①、②知：PA EFPB EG=............................................................................................. 9分 （本题若按分类证明，只要合理，可给满分）。

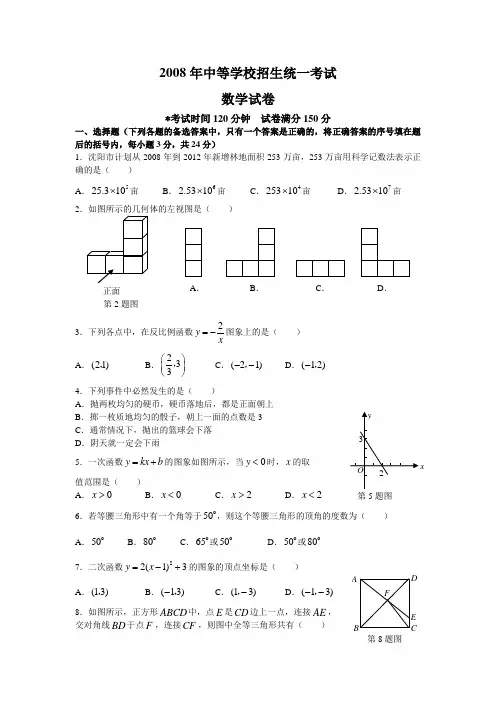
2008年中等学校招生统一考试数学试卷*考试时间120分钟 试卷满分150分一、选择题（下列各题的备选答案中，只有一个答案是正确的，将正确答案的序号填在题后的括号内，每小题3分，共24分）1．沈阳市计划从2008年到2012年新增林地面积253万亩，253万亩用科学记数法表示正确的是（ ） A ．525.310⨯亩B ．62.5310⨯亩C ．425310⨯亩D ．72.5310⨯亩2）3．下列各点中，在反比例函数2y x=-图象上的是（）A ．(21)，B ．233⎛⎫⎪⎝⎭，C ．(21)--，D ．(12)-，4．下列事件中必然发生的是（ ）A ．抛两枚均匀的硬币，硬币落地后，都是正面朝上B ．掷一枚质地均匀的骰子，朝上一面的点数是3C ．通常情况下，抛出的篮球会下落D ．阴天就一定会下雨5．一次函数y kx b =+的图象如图所示，当0y <时，x 的取 值范围是（ ） A ．0x > B ．0x <C ．2x >D ．2x <6．若等腰三角形中有一个角等于50，则这个等腰三角形的顶角的度数为（ ） A ．50B ．80C ．65或50D ．50或807．二次函数22(1)3y x =-+的图象的顶点坐标是（ ）A ．(13)，B ．(13)-，C ．(13)-，D ．(13)--， 8．如图所示，正方形ABCD 中，点E 是CD 边上一点，连接AE ， 交对角线BD 于点F ，连接CF ，则图中全等三角形共有（ ）正面第2题图A ．B ．C ．D ．第5题图xADCEFB第8题图A ．1对B ．2对C ．3对D ．4对二、填空题（每小题3分，共24分）9．已知A ∠与B ∠互余，若70A ∠=，则B ∠的度数为 ． 10．分解因式：328m m -= ．11．已知ABC △中，60A ∠=，ABC ∠，ACB ∠的平分线交于点O ，则BOC ∠的度数为 ．12．如图所示，菱形ABCD 中，对角线AC BD ，相交于点O ，若再补 充一个条件能使菱形ABCD 成为正方形，则这个条件是 （只填一个条件即可）． 13．不等式26x x -<-的解集为 ．14．如图所示，某河堤的横断面是梯形ABCD ，BC AD ∥，迎水坡AB 长13米，且12tan 5BAE ∠=，则河堤的高BE 为 米．15．观察下列图形的构成规律，根据此规律，第8第15题图16．在平面直角坐标系中，点A 的坐标为(11)，，点B 的坐标为(111)，，点C 到直线AB 的距离为4，且ABC △是直角三角形，则满足条件的点C 有 个．三、（第17小题6分，第18，19小题各8分，第20小题10分，共32分）17．计算：101(1)52-⎛⎫π-+-+- ⎪⎝⎭18．解分式方程：1233xx x=+--．19．先化简，再求值：222()()2y x y x y x y ++---，其中13x =-，3y =．第1个 ……第2个 第3个 第4个ADC BO 第12题图 B C DA 第14题图20．如图所示，在66⨯的方格纸中，每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形，如图①中的三角形是格点三角形． （1）请你在图①中画一条直线将格点三角形分割成两部分，将这两部分重新拼成两个不同的格点四边形，并将这两个格点四边形分别画在图②，图③中； （2）直接写出这两个格点四边形的周长．四、（每小题10分，共20分）21．如图所示，AB 是O 的一条弦，OD AB ⊥，垂足为C ，交O 于点D ，点E 在O 上．（1）若52AOD ∠=，求DEB ∠的度数；（2）若3OC =，5OA =，求AB 的长．22．小刚和小明两位同学玩一种游戏．游戏规则为：两人各执“象、虎、鼠”三张牌，同时各出一张牌定胜负，其中象胜虎、虎胜鼠、鼠胜象，若两人所出牌相同，则为平局．例如，小刚出象牌，小明出虎牌，则小刚胜；又如，两人同时出象牌，则两人平局． （1）一次出牌小刚出“象”牌的概率是多少？（2）如果用A B C ，，分别表示小刚的象、虎、鼠三张牌，用1A ，1B ，1C 分别表示小明的象、虎、鼠三张牌，那么一次出牌小刚胜小明的概率是多少？用列表法或画树状图（树形图）法加以说明．图① 第20题图图②图③第21题图 小刚 小明A 1B 1C 1A B C 第22题图23．在学校组织的“喜迎奥运，知荣明耻，文明出行”的知识竞赛中，每班参加比赛的人数相同，成绩分为A B C D ，，，四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：请你根据以上提供的信息解答下列问题：（1）此次竞赛中二班成绩在C 级以上（包括C 级）的人数为 ； （2）请你将表格补充完整：（3）请从下列不同角度对这次竞赛成绩的结果进行分析：①从平均数和中位数的角度来比较一班和二班的成绩； ②从平均数和众数的角度来比较一班和二班的成绩；③从B 级以上（包括B 级）的人数的角度来比较一班和二班的成绩． 六、（本题12分）24．一辆经营长途运输的货车在高速公路的A 处加满油后，以每小时80千米的速度匀速行驶，前往与A 处相距636千米的B 地，下表记录的是货车一次加满油后油箱内余油量y （升）与行驶时间x （1）请你认真分析上表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示y 与x 之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式；（不要求写出自变量的取值范围）（2）按照（1）中的变化规律，货车从A 处出发行驶4.2小时到达C 处，求此时油箱内余油多少升？（3）在（2）的前提下，C 处前方18千米的D 处有一加油站，根据实际经验此货车在行驶中油箱内至少保证有10升油，如果货车的速度和每小时的耗油量不变，那么在D处至少加多少升油，才能使货车到达B 地．（货车在D 处加油过程中的时间和路程忽略不计）第23题图 一班竞赛成绩统计图 二班竞赛成绩统计图25．已知：如图①所示，在ABC △和ADE △中，AB AC =，AD AE =，BAC DAE ∠=∠，且点B A D ，，在一条直线上，连接BE CD M N ，，，分别为BE CD ，的中点． （1）求证：①BE CD =；②AMN △是等腰三角形．（2）在图①的基础上，将ADE △绕点A 按顺时针方向旋转180，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立； （3）在（2）的条件下，请你在图②中延长ED 交线段BC 于点P ．求证：PBD AMN △∽△．八、（本题14分） 26．如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，． （1）判断点E 是否在y 轴上，并说明理由； （2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．2008年沈阳市中等学校招生统一考试C E ND A BM图① C A EM B D N图② 第25题图第26题图数学试题参考答案及评分标准一、选择题（每小题3分，共24分） 1．B 2．A 3．D 4．C 5．C 6．D7．A8．C二、填空题（每小题3分，共24分） 9．2010．2(2)(2)m m m +-11．12012．90BAD ∠=（或AD AB ⊥，AC BD =等）13．4x >14．1215．65 16．8 三、（第17小题6分，第18，19小题各8分，第20小题10分，共32分）17．解：原式1(2)5=+-+- ···························································· 4分125=-+- ··················································································· 5分6= ······································································································ 6分18．解：12(3)x x =-- ·················································································· 2分126x x =--7x = ··········································································································· 5分 检验：将7x =代入原方程，左边14==右边 ························································ 7分所以7x =是原方程的根 ·················································································· 8分 （将7x =代入最简公分母检验同样给分）19．解：原式2222222xy y x xy y x y =++-+-- ················································ 4分 xy =- ········································································································· 6分 当13x =-，3y =时，原式1313⎛⎫=--⨯= ⎪⎝⎭······················································································ 8分 20．解：（1）答案不唯一，如分割线为三角形的三条中位线中任意一条所在的直线等．································· 2分拼接的图形不唯一，例如下面给出的三种情况：图① 图② 图③ 图④图①~图④，图⑤~图⑦，图⑧~图⑨，画出其中一组图中的两个图形． ······················ 6分 （2）对应（1）中所给图①~图④的周长分别为4+8，4+4+ 图⑤~图⑦的周长分别为10，8+8+图⑧~图⑨的周长分别为2+4+ ···································· 10分 四、（每小题10分，共20分） 21．解：（1）OD AB ⊥，AD DB ∴= ··························································· 3分 11522622DEB AOD ∴∠=∠=⨯= ································································· 5分 （2）OD AB ⊥，AC BC ∴=，AOC △为直角三角形， 3OC =，5OA =，由勾股定理可得4AC == ·············································· 8分 28AB AC ∴== ························································································· 10分 22．解：（1）1()3P =一次出牌小刚出象牌“” ··················································· 4分（2）树状图（树形图）：·············································································· 8分图⑤ 图⑥图⑦图⑧ 图⑨A 1B 1C 1 AA 1B 1C 1 BA 1B 1C 1C开始小刚 小明或列表···························································· 8分 由树状图（树形图）或列表可知，可能出现的结果有9种，而且每种结果出现的可能性相同，其中小刚胜小明的结果有3种． ········································································ 9分1()3P ∴=一次出牌小刚胜小明． ····································································· 10分 五、（本题12分） 23．解：（1）21······························································································ 2分 （2）一班众数为90，二班中位数为80 ······························································· 6分 （3）①从平均数的角度看两班成绩一样，从中位数的角度看一班比二班的成绩好，所以一班成绩好； ···································································································· 8分 ②从平均数的角度看两班成绩一样，从众数的角度看二班比一班的成绩好，所以二班成绩好； ················································································································· 10分 ③从B 级以上（包括B 级）的人数的角度看，一班人数是18人，二班人数是12人，所以一班成绩好． ······························································································· 12分 六、（本题12分） 24．解：（1）设y 与x 之间的关系为一次函数，其函数表达式为y kx b =+ ················ 1分将(0100)，，(180)，代入上式得， 10080b k b =⎧⎨+=⎩ 解得20100k b =-⎧⎨=⎩20100y x ∴=-+ ·························································································· 4分验证：当2x =时，20210060y =-⨯+=，符合一次函数； 当 2.5x =时，20 2.510050y =-⨯+=，也符合一次函数．∴可用一次函数20100y x =-+表示其变化规律，而不用反比例函数、二次函数表示其变化规律． ··················································· 5分 y ∴与x 之间的关系是一次函数，其函数表达式为20100y x =-+ ··························· 6分 （2）当 4.2x =时，由20100y x =-+可得16y =即货车行驶到C 处时油箱内余油16升． ····························································· 8分 （3）方法不唯一，如：方法一：由（1）得，货车行驶中每小时耗油20升， ············································· 9分 设在D 处至少加油a 升，货车才能到达B 地．依题意得，63680 4.220101680a -⨯⨯+=+， ··················································· 11分 解得，69a =（升） ····················································································· 12分方法二：由（1）得，货车行驶中每小时耗油20升， ············································· 9分 汽车行驶18千米的耗油量：1820 4.580⨯=（升） D B ，之间路程为：63680 4.218282-⨯-=（千米）汽车行驶282千米的耗油量：2822070.580⨯=（升） ················································································· 11分 70.510(16 4.5)69+--=（升） ···································································· 12分 方法三：由（1）得，货车行驶中每小时耗油20升， ············································· 9分设在D 处加油a 升，货车才能到达B 地．依题意得，63680 4.220101680a -⨯⨯++≤，解得，69a ≥ ····························································································· 11分 ∴在D 处至少加油69升，货车才能到达B 地． ················································· 12分七、（本题12分） 25．证明：（1）①BAC DAE ∠=∠ BAE CAD ∴∠=∠AB AC =，AD AE = ABE ACD ∴△≌△BE CD ∴= ·································································································· 3分 ②由ABE ACD △≌△得ABE ACD ∠=∠，BE CD =M N ，分别是BE CD ，的中点，BM CN ∴= ················································· 4分 又AB AC = ABM ACN ∴△≌△AM AN ∴=，即AMN △为等腰三角形 ···························································· 6分 （2）（1）中的两个结论仍然成立． ···································································· 8分 （3）在图②中正确画出线段PD由（1）同理可证ABM ACN △≌△ CAN BAM ∴∠=∠ BAC MAN ∴∠=∠ 又BAC DAE ∠=∠MAN DAE BAC ∴∠=∠=∠AMN ∴△，ADE △和ABC △都是顶角相等的等腰三角形 ································· 10分 PBD AMN ∴∠=∠，PDB ADE ANM ∠=∠=∠PBD AMN ∴△∽△ ···················································································· 12分 八、（本题14分）26．解：（1）点E 在y 轴上 ·············································································· 1分 理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，BO =2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上，∴点E 在y 轴上． ································································· 3分 （2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，2OM =点D 在第一象限，∴点D 的坐标为12⎫⎪⎪⎝⎭， ················································································ 5分 由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A的坐标为( ·················································································· 6分抛物线2y ax bx c =++经过点E ，2c ∴=由题意，将(A ，12D ⎫⎪⎪⎝⎭，代入22y ax bx =++中得32131242a a ⎧+=⎪⎨+=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为：2829y x x =--+ ·················································· 9分（3）存在符合条件的点P ，点Q ． ································································· 10分。

中考数学平面直角坐标系训练题库（含答案）（102页）一、选择题1. 在平面直角坐标系中，点P(2, 3)位于（）。

A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案：D2. 已知点A(3, 4)和点B(2, 1)，则线段AB的中点坐标为（）。

A. (1/2, 3/2)B. (1/2, 7/2)C. (1/2, 3/2)D. (1/2, 3/2)答案：B3. 在平面直角坐标系中，点(3, 3)关于原点对称的点的坐标是（）。

A. (3, 3)B. (3, 3)C. (3, 3)D. (3, 3)答案：C4. 已知点A(2, 3)和点B(2, 3)，则线段AB的长度为（）。

A. 4B. 6C. 8D. 10答案：A5. 在平面直角坐标系中，点(4, 5)关于x轴对称的点的坐标是（）。

A. (4, 5)B. (4, 5)C. (4, 5)D. (4, 5)答案：A二、填空题6. 在平面直角坐标系中，点P在第二象限，且到x轴的距离是4，到y轴的距离是3，则点P的坐标是______。

答案：(3, 4)7. 已知点A(0, 2)和点B(4, 0)，则线段AB的斜率为______。

答案：1/28. 在平面直角坐标系中，点(5, 0)关于原点对称的点的坐标是______。

答案：(5, 0)9. 已知点A(2, 1)和点B(4, 3)，则线段AB的中点坐标为______。

答案：(1, 2)10. 在平面直角坐标系中，点(0, 3)关于y轴对称的点的坐标是______。

答案：(0, 3)（后续题目及答案请见完整题库）三、解答题11. 在平面直角坐标系中，有一矩形ABCD，顶点A的坐标为(1, 2)，顶点C的坐标为(3, 1)。

求矩形对角线AC的长度。

解：我们可以通过坐标计算出对角线AC的长度。

设点B的坐标为(x, y)，则点D的坐标为(3, y)。

由于ABCD是矩形，所以AB和CD平行且等长，AD和BC平行且等长。

以下是河北省柳超的分类（2008年贵阳市）13．符号“f ”表示一种运算，它对一些数的运算结果如下： （1）(1)0f =，(2)1f =，(3)2f =，(4)3f =，…（2）122f ⎛⎫=⎪⎝⎭，133f ⎛⎫= ⎪⎝⎭，144f ⎛⎫= ⎪⎝⎭，155f ⎛⎫= ⎪⎝⎭，…利用以上规律计算：1(2008)2008f f ⎛⎫-= ⎪⎝⎭．（2008年贵阳市）10．根据如图2所示的（1），（2），（3）三个图所表示的规律，依次下去第n个图中平行四边形的个数是（ ）A ．3nB ．3(1)n n +C ．6nD ．6(1)n n +（2008年遵义市）16．如图是与杨辉三角形有类似性质的三角形数垒，a b ，是某行的前两个数，当7a =时，b = ．以下是江西康海芯的分类:1. （2008年郴州市）因式分解：24x -=____________ ()()22x x +-辽宁省 岳伟 分类2008年桂林市（图2）……（1）（2） （3）1 2 2 3 4 3 4 7 7 4 5 11 14 11 5· · · · · · · · · a b · · · · · · · · （16题图）如图，矩形1111ＡＢＣＤ的面积为４，顺次连结各边中点得到四边形2222ＡＢＣＤ，再顺次连结四边形2222ＡＢＣＤ四边中点得到四边形3333ＡＢＣＤ，依此类推，求四边形n n n n ＡＢＣＤ的面积是 。

18．(2008年湖州市)将自然数按以下规律排列，则2008所在的位置是第 行第 列．10. ( 2008年杭州市) 如图, 记抛物线12+-=x y 的图象与x 正半轴的交点为A , 将线段OA 分成n 等份, 设分点分别为121,,,-n P P P , 过每个分点作x 轴的垂线, 分别与抛物线交于点121,,,-n Q Q Q , 再记直角三角形 ,,22111Q P P Q OP 的面积分别为 ,,21S S ,这样就有,24,21322321nn S n n S -=-=… ; 记21S S W += 1-++n S , 当n 越来越大时, 你猜想W 最接近的常数是( C ) (A) 32 (B)21 (C)31(D) 41(第10题)16. ( 2008年杭州市) 如图, 一个4×2的矩形可以用3种不同的方式分割成2或5或8个小正方形, 那么一个5×3的矩形用不同的方式分割后, 小正方形的个数可以是 ________________ .以下是安徽省马鞍山市成功中学的汪宗兴老师的分类1．(2008年·东莞市)（本题满分9分）（1）解方程求出两个解1x 、2x ，并计算两个解的写出你的结论.24．(2008年双柏县)（本小题9分）依法纳税是每个公民应尽的义务．从2008年3月1日起，新修改后的《中华人民共和国个人所得税法》规定，公民每月收入不超过2000元，不需交税；超过2000元的部分为全月应纳税所得额，都应纳税，且根据超过部分的多少按不同的税率纳税，详细的税率如下表：（1）某工厂一名工人2008年3月的收入为2 400元，问他应交税款多少元？ （2）设x 表示公民每月收入（单位：元），y 表示应交税款（单位：元），(第16题)当2500≤x ≤4000时，请写出y 关于x 的函数关系式；（3）某公司一名职员2008年4月应交税款120元，问该月他的收入是多少元？(08年宁夏回族自治区)商场为了促销，推出两种促销方式：方式①：所有商品打7.5折销售： 方式②：一次购物满200元送60元现金．（1）杨老师要购买标价为628元和788元的商品各一件，现有四种购买方案：方案一：628元和788元的商品均按促销方式①购买； 方案二：628元的商品按促销方式①购买，788元的商品按促销方式②购买； 方案三：628元的商品按促销方式②购买，788元的商品按促销方式①购买； 方案四：628元和788元的商品均按促销方式②购买． 你给杨老师提出的最合理购买方案是 ．（2）通过计算下表中标价在600元到800元之间商品的付款金额，你总结出商品的购买规律是 。

2008年北京市高级中等学校招生考试数 学 试 卷下列各题均有四个选项，其中只有一个是符合题意的．用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑．1．6-的绝对值等于（ ）A ．6B ．16C ．16- D ．6- 2．截止到2008年5月19日，已有21 600名中外记者成为北京奥运会的注册记者，创历届奥运会之最．将21 600用科学记数法表示应为（ ）A ．50.21610⨯B ．321.610⨯C ．32.1610⨯D ．42.1610⨯3．若两圆的半径分别是1cm 和5cm ，圆心距为6cm ，则这两圆的位置关系是（ ）A ．内切B ．相交C ．外切D ．外离4．众志成城，抗震救灾．某小组7名同学积极捐出自己的零花钱支援灾区，他们捐款的数额分别是（单位：元）：50，20，50，30，50，25，135．这组数据的众数和中位数分别是（ ）A ．50，20B ．50，30C ．50，50D ．135，505．若一个多边形的内角和等于720，则这个多边形的边数是（ ）A ．5B ．6C ．7D ．86．如图，有5张形状、大小、质地均相同的卡片，正面分别印有北京奥运会的会徽、吉祥物（福娃）、火炬和奖牌等四种不同的图案，背面完全相同．现将这5张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片正面图案恰好是吉祥物（福娃）的概率是（ ）A ．15B ．25C ．12D ．357．若20x +=，则xy 的值为（ ）A ．8-B ．6-C ．5D ．68．已知O 为圆锥的顶点，M 为圆锥底面上一点，点P 在OM 上．一只蜗牛从P 点出发，绕圆锥侧面爬行，回到P 点时所爬过的最短路线的痕迹如右图所示．若沿OM 将圆锥侧面剪开并展开，所得侧面展开图是（ ）2008年北京市高级中等学校招生考试数 学 试 卷二、填空题（共4道小题，每小题4分，共16分）9．在函数121y x =-中，自变量x 的取值范围是 ． 10．分解因式：32a ab -= ． 11．如图，在ABC △中，D E ，分别是AB AC ，的中点，若2cm DE =，则BC = cm ． 12．一组按规律排列的式子：2b a -，53b a ，83b a-，114b a ，…（0ab ≠），其中第7个式子是 ，第n 个式子是 （n 为正整数）．三、解答题（共5道小题，共25分）13．（本小题满分5分）1012sin 45(2)3-⎛⎫+-π- ⎪⎝⎭． 解：CAE DB OP M O M ' M P A ． O M ' M P B ． O M 'M P C ．O M ' M P D ．14．（本小题满分5分）解不等式5122(43)x x --≤，并把它的解集在数轴上表示出来．解：15．（本小题满分5分）已知：如图，C 为BE 上一点，点A D ，分别在BE 两侧．AB ED ∥，AB CE =，BC ED =．求证：AC CD =． 证明：16．（本小题满分5分）如图，已知直线3y kx =-经过点M ，求此直线与x 轴，y 轴的交点坐标．解：17．（本小题满分5分）已知30x y -=，求222()2x y x y x xy y +--+的值． 解：四、解答题（共2道小题，共10分）18．（本小题满分5分）如图，在梯形ABCD 中，AD BC ∥，AB AC ⊥，45B ∠=，AD =BC =求DC 的长．解： A C E D B y xA D19．（本小题满分5分）已知：如图，在Rt ABC △中，90C ∠=，点O 在AB 上，以O 为圆心，OA 长为半径的圆与AC AB ，分别交于点D E ，，且CBD A ∠=∠．（1）判断直线BD 与O（2）若:8:5AD AO =，2BC =，求解：（1）（2）五、解答题（本题满分6分）20．为减少环境污染，自2008年6月1日起，全国的商品零售场所开始实行“塑料购物袋有偿使用制度”（以下简称“限塑令”）．某班同学于6月上旬的一天，在某超市门口采用问卷调查的方式，随机调查了“限塑令”实施前后，顾客在该超市用购物袋的情况，以下是根据100位顾客的100份有效答卷画出的统计图表的一部分：B 图1 “限塑令”实施前，平均一次购物使用不同数量塑料购物袋的人“限塑令”实施后，使用各种 购物袋的人数分布统计图 其它 _______％ 24%（1）补全图1，“限塑令”实施前，如果每天约有2 000人次到该超市购物．根据这100位顾客平均一次购物使用塑料购物袋的平均数，估计这个超市每天需要为顾客提供多少个塑料购物袋？（2）补全图2，并根据统计图和统计表说明，购物时怎样选用购物袋，塑料购物袋使用后怎样处理，能对环境保护带来积极的影响．解：（1）（2）六、解答题（共2道小题，共9分）21．（本小题满分5分）列方程或方程组解应用题：京津城际铁路将于2008年8月1日开通运营，预计高速列车在北京、天津间单程直达运行时间为半小时．某次试车时，试验列车由北京到天津的行驶时间比预计时间多用了6分钟，由天津返回北京的行驶时间与预计时间相同．如果这次试车时，由天津返回北京比去天津时平均每小时多行驶40千米，那么这次试车时由北京到天津的平均速度是每小时多少千米？解：22．（本小题满分4分）已知等边三角形纸片ABC的边长为8，D为AB边上的点，过点D作DG BC∥交AC于点G．DE BC⊥于点E，过点G作GF BC⊥于点F，把三角形纸片ABC 分别沿DG DE GF，，按图1所示方式折叠，点A B C，，分别落在点A'，B'，C'处．若点A'，B'，C'在矩形DEFG内或其边上，且互不重合，此时我们称A B C'''△（1）若把三角形纸片ABC放在等边三角形网格中（图中每个小三角形都是边长为1的等边三角形），点A B C D，，，恰好落在网格图中的格点上．如图2所示，请直接写出此时重叠三角形A B C'''的面积；（2）实验探究：设AD的长为m，若重叠三角形A B C'''存在．试用含m的代数式表示重叠三角形A B C'''的面积，并写出m的取值范围（直接写出结果，备用图供实验，探究使用）．图1图2A A解：（1）重叠三角形A B C '''的面积为 ；（2）用含m 的代数式表示重叠三角形A B C '''的面积为 ；m 的取值范围为 ．七、解答题（本题满分7分）23．已知：关于x 的一元二次方程2(32)220(0)mx m x m m -+++=>．（1）求证：方程有两个不相等的实数根；（2）设方程的两个实数根分别为1x ，2x （其中12x x <）．若y 是关于m 的函数，且212y x x =-，求这个函数的解析式；（3）在（2）的条件下，结合函数的图象回答：当自变量m 的取值范围满足什么条件时，2y m ≤．（1）证明：（2）解：（3八、解答题（本题满分7分）24．在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A B ，两点（点A在点B 的左侧），与y 轴交于点C ，点B 的坐标为(30)，，将直线y kx =沿y 轴向上平移3个单位长度后恰好经过B C ，两点．（1）求直线BC 及抛物线的解析式；x（2）设抛物线的顶点为D ，点P 在抛物线的对称轴上，且APD ACB ∠=∠，求点P 的坐标；（3）连结CD ，求OCA ∠与OCD ∠解：（1）（2）（3）九、解答题（本题满分8分）25．请阅读下列材料：问题：如图1，在菱形ABCD 和菱形BEFG 中，点A B E ，，在同一条直线上，P 是线段DF 的中点，连结PG PC ，．若60ABC BEF ∠=∠=，探究PG 与PC 的位置关系及PG PC的值． 小聪同学的思路是：延长GP 交DC 于点H ，构造全等三角形，经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决下列问题：（1）写出上面问题中线段PG 与PC 的位置关系及PG PC的值； （2）将图1中的菱形BEFG 绕点B 顺时针旋转，使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上，原问题中的其他条件不变（如图2）．你在（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明． x D A B E F C P G 图1 D C G P A B F 图2（3）若图1中2(090)ABC BEFαα∠=∠=<<，将菱形BEFG绕点B顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出PGPC的值（用含α的式子表示）．解：（1）线段PG与PC的位置关系是；PGPC=．（2）2008年北京市高级中等学校招生考试数学试卷答案及评分参考阅卷须知：1．一律用红钢笔或红圆珠笔批阅，按要求签名．2．第Ⅰ卷是选择题，机读阅卷．3．第Ⅱ卷包括填空题和解答题．为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可．若考生的解法与本解法不同，正确者可参照评分参考给分．解答右端所注分数，表示考生正确做到这一步应得的累加分数．第Ⅰ卷（机读卷共32分）第Ⅱ卷（非机读卷共88分）13．（本小题满分5分）112sin45(2π)3-⎛⎫+-- ⎪⎝⎭2132=⨯+-········································································· 4分2=． ····················································································· 5分14．（本小题满分5分）解：去括号，得51286x x --≤． ························································ 1分 移项，得58612x x --+≤． ······························································· 2分 合并，得36x -≤． ·········································································· 3分 系数化为1，得2x -≥． ··································································· 4分···································································································· 5分15．（本小题满分5分）证明：AB ED ∥，B E ∴∠=∠． ·················································································· 2分 在ABC △和CED △中，AB CE B E BC ED =⎧⎪∠=∠⎨⎪=⎩，，， ABC CED ∴△≌△．········································································· 4分 AC CD ∴=． ·················································································· 5分 16．（本小题满分5分）解：由图象可知，点(21)M -，在直线3y kx =-上， ·································· 1分 231k ∴--=．解得2k =-． ·················································································· 2分 ∴直线的解析式为23y x =--． ······································································· 3分令0y =，可得32x =-． ∴直线与x 轴的交点坐标为302⎛⎫- ⎪⎝⎭，． ··················································· 4分 令0x =，可得3y =-．∴直线与y 轴的交点坐标为(03)-，． ···················································· 5分17．（本小题满分5分）解：222()2x y x y x xy y+--+ 22()()x y x y x y +=-- ·············································································· 2分2x y x y +=-． ····················································································· 3分 当30x y -=时，3x y =． ·································································· 4分 原式677322y y y y y y +===-． ··································································· 5分 四、解答题（共2道小题，共10分）18．（本小题满分5分）解法一：如图1，分别过点A D ，作AE BC ⊥于点E ，DF BC ⊥于点F ． ······························· 1分 ∴AE DF ∥．又AD BC ∥，∴四边形AEFD 是矩形．EF AD ∴==． ································ 2分 AB AC ⊥，45B ∠=，BC =AB AC ∴=．12AE EC BC ∴===DF AE ∴==CF EC EF =-=········································································· 4分在Rt DFC △中，90DFC ∠=，DC ∴=== ······································ 5分 解法二：如图2，过点D 作DF AB ∥，分别交AC BC ，于点E F ，． ·········· 1分AB AC ⊥，90AED BAC ∴∠=∠=． AD BC ∥， 18045DAE B BAC ∴∠=-∠-∠=． 在Rt ABC △中，90BAC ∠=，45B ∠=，BC =sin 454242AC BC ∴=== ························································ 2分 在Rt ADE △中，90AED ∠=，45DAE ∠=，AD =AB CD F E2 A B C D F E 图11DE AE ∴==．3CE AC AE ∴=-=． ······································································· 4分 在Rt DEC △中，90CED ∠=，DC ∴===． ················································· 5分 19． （本小题满分5分）解：（1）直线BD 与O 相切． ························································· 1分证明：如图1，连结OD ．OA OD =，A ADO ∴∠=∠．90C ∠=，CBD ∴∠+∠又CBD A ∠=∠，90ADO CDB ∴∠+∠=．90ODB ∴∠=． ∴直线BD 与O 相切． ···································································· 2分（2）解法一：如图1，连结DE ．AE 是O 的直径， 90ADE ∴∠=．:8:5AD AO =，4cos 5AD A AE ∴==． ·········································································· 3分 90C ∠=，CBD A ∠=∠，4cos 5BC CBD BD ∴∠==． ···································································· 4分 2BC =， 52BD ∴=． ·························································· 5分 解法二：如图2，过点O 作OH AD ⊥于点H ． 12A H D H A D ∴==． :8:5AD AO =， 4cos 5AH A AO ∴==．················· 3分 90C ∠=，CBD A ∠=∠， 4cos 5BC CBD BD ∴∠==． ························2BC =，BB52BD ∴=． ···················································································· 5分 五、解答题（本题满分6分）解：（1）补全图1见下图． ······························································ 1分913723100100⨯+⨯+==（个）． 这100位顾客平均一次购物使用塑料购物袋的平均数为3个． ·················· 3分200036000⨯=．估计这个超市每天需要为顾客提供6000个塑料购物袋． ·························· 4分（2）图2中，使用收费塑料购物袋的人数所占百分比为25%． ················· 5分 根据图表回答正确给1分，例如：由图2和统计表可知，购物时应尽量使用自备袋和押金式环保袋，少用塑料购物袋；塑料购物袋应尽量循环使用，以便减少塑料购物袋的使用量，为环保做贡献． ··················································· 6分六、解答题（共2道小题，共9分）21．解：设这次试车时，由北京到天津的平均速度是每小时x 千米，则由天津返回北京的平均速度是每小时(40)x +千米． ············································ 1分依题意，得3061(40)602x x +=+． ························································ 3分 解得200x =． ················································································· 4分 答：这次试车时，由北京到天津的平均速度是每小时200千米． ··············· 5分 22．解：（1）重叠三角形A B C '''． ···································· 1分（2）用含m 的代数式表示重叠三角形A B C '''2)m -； ··········· 2分m 的取值范围为843m <≤． ······························································ 4分 七、解答题（本题满分7分）23．（1）证明：2(32)220mx m x m -+++=是关于x 的一元二次方程，222[(32)]4(22)44(2)m m m m m m ∴∆=-+-+=++=+．当0m >时，2(2)0m +>，即0∆>．∴方程有两个不相等的实数根． ·························································· 2分 图1 塑料袋数／个 “限塑令”实施前，平均一次购物使用不同数量塑料购物袋的人（2）解：由求根公式，得(32)(2)2m m x m+±+=． 22m x m+∴=或1x =． ······································································· 3分 0m >，222(1)1m m m m++∴=>． 12x x <，11x ∴=，222m x m+=． ····································································· 4分 21222221m y x x m m+∴=-=-⨯=． 即2(0)y m m =>为所求． ·····（32(0)y m m =>与2(y m m => ·······································由图象可得，当1m ≥时，y ≤八、解答题（本题满分24．解：（1）y kx =沿y 轴向上平移3个单位长度后经过y 轴上的点C ，(03)C ∴，．设直线BC 的解析式为3y kx =+．(30)B ，在直线BC 上，330k ∴+=．解得1k =-．∴直线BC 的解析式为3y x =-+． ······················································· 1分抛物线2y x bx c =++过点B C ，，9303b c c ++=⎧∴⎨=⎩，．解得43b c =-⎧⎨=⎩，． ∴抛物线的解析式为243y x x =-+． ··················································· 2分 x 0)（2）由24y x x =-+可得(21)(1D A -，，3OB ∴=，3OC =，1OA =可得OBC △45OBC ∴∠=，CB =如图1，设抛物线对称轴与x 112AF AB ∴==过点A 作AE BC ⊥于点E ．90AEB ∴∠=． 可得BE AE ==CE =在AEC △与AFP △中，90AEC AFP ∠=∠=，ACE APF ∠=∠，AEC AFP ∴△∽△．AE CE AF PF∴=，1PF =． 解得2PF =．点P 在抛物线的对称轴上，∴点P 的坐标为(22)，或(22)-，． ························································· 5分（3）解法一：如图2，作点(10)A ，关于y 轴的对称点A '，则(10)A '-，． 连结A C A D ''，，可得A C AC '==OCA '∠=由勾股定理可得220CD =，2A D '又210A C '=， 222A D A C CD ''∴+=． A DC '∴△是等腰直角三角形，CA '∠45DCA '∴∠=． 45OCA OCD '∴∠+∠=．45OCA OCD ∴∠+∠=．x图1 x图2即OCA∠与OCD∠两角和的度数为45．·············································· 7分解法二：如图3同解法一可得CD=在Rt DBF△中，90DFB∠=DB∴==在CBD△和COA△1DBAO==3BCOC==DB BC CDAO OC CA∴==．CBD COA∴△∽△．BCD OCA∴∠=∠．45OCB∠=，45OCA OCD∴∠+∠=．即OCA∠与OCD∠两角和的度数为45．·············································· 7分九、解答题（本题满分8分）25．解：（1）线段PG与PC的位置关系是PG PC⊥；PGPC= ···················································································· 2分（2）猜想：（1）中的结论没有发生变化．证明：如图，延长GP交AD于点H，连结CH CG，．P是线段DF的中点，FP DP∴=．由题意可知AD FG∥．GFP HDP∴∠=∠．GPF HPD∠=∠，GFP HDP∴△≌△．GP HP∴=，GF HD=．四边形ABCD是菱形，CD CB∴=，60HDC ABC∠=∠=．由60ABC BEF∠=∠=，且菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上，可得60GBC∠=．xD CGPA BEFH。

2008年中考试卷分类---函数与几何图形1. 如图，在直角梯形ABCD 中，DC ∥AB ，∠A=90°，AB=28cm ，DC=24cm ，AD=4cm ，点M 从点D 出发，以1cm/s 的速度向点C 运动，点N 从点B 同时出发，以2cm/s 的速度向点A 运动，当其中一个动点到达端点停止运动时，另一个动点也随之停止运动.则四边形AMND 的面积y （cm 2）与两动点运动的时间t （s ）的函数图象大致是（ D ）2. 如图，已知正三角形ABC 的边长为1，E 、F 、G 分别是AB 、BC 、CA 上的点，且AE ＝BF ＝CG ，设△EFG 的面积为y ，AE 的长为x ，则y 关于x 的函数的图象大致是（ C ）3. （潍坊）如图，圆B 切y 轴于原点O ，过定点(A -作圆B 切线交圆于点P ．已知tan PAB =∠，抛物线C 经过A ，P 两点．（1）求圆B 的半径；（2）若抛物线C 经过点B ，求其解析式；（3）投抛物线C 交y 轴于点M ，若三角形APM 为直角三角形，求点M 的坐标．4. （威海）如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积； （2）求四边形MEFN 面积的最大值． （3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由． 解：（1）分别过D ，C 两点作DG ⊥AB 于点G ，CH ⊥AB 于点H ． ∵ AB ∥CD ， ∴ DG ＝CH ，DG ∥CH ． ∴ 四边形DGHC 为矩形，GH ＝CD ＝1．∵ DG ＝CH ，AD ＝BC ，∠AGD ＝∠BHC ＝90°，∴ △AGD ≌△BHC （HL ）．∴ AG ＝BH ＝2172-=-GH AB ＝3． ………2分∵ 在Rt △AGD 中，AG ＝3，AD ＝5， ∴ DG ＝4．∴ ()174162ABCD S +⨯==梯形．（2）∵ MN ∥AB ，ME ⊥AB ，NF ⊥AB ，∴ ME ＝NF ，ME ∥NF ． ∴ 四边形MEFN 为矩形． ∵ AB ∥CD ，AD ＝BC ， ∴ ∠A ＝∠B ． ∵ ME ＝NF ，∠MEA ＝∠NFB ＝90°， ∴ △MEA ≌△NFB （AAS ）．∴ AE ＝BF ． 设AE ＝x ，则EF ＝7－2x ． ∵ ∠A ＝∠A ，∠MEA ＝∠DGA ＝90°， ∴ △MEA ∽△DGA ．∴DG ME AG AE =．∴ ME ＝x 34． ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN 矩形．当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．（3）能． 由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ． 即 =34x 7－2x ．解，得 1021=x ．∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFN S 正方形．5. （青岛）已知：如图①，在Rt ΔABC 中，∠C=900，AC=4cm ，BC=3cm ，点P 由B 出发沿BA 方向向点A 匀速运动，速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为t （s ）（0<t <2），解答下列问题：（1）当t 为何值时，PQ ∥BC ？（2）设ΔAQP 的面积为y （cm 2），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使线段PQ 恰好把Rt ΔABC 的周长和面积同时平分？若存在，求出此时t 的值；若不存在，说明理由；（4）如图②，连接PC ，并把ΔPQC 沿QC 翻折，得到四边形PQP ′C ，那么是否存在某一时刻t ，使四边形PQP ′C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由． 解：（1）在Rt △ABC 中，522=+=AC BC AB ，由题意知：AP = 5－t ，AQ = 2t ，若PQ ∥BC ，则△APQ ∽△ABC ，∴=AC AQ AB AP ，∴52t t -=，∴10=t ． （2）过点P 作PH ⊥AC 于H ． ∵△APH ∽△ABC ，A BE F G H B∴=BC PH AB AP ，∴=3PH 55t -，∴t PH 533-=，∴t t t t PH AQ y 353)533(221212+-=-⨯⨯=⨯⨯=．（3）若PQ 把△ABC 周长平分，则AP+AQ=BP+BC+CQ ．∴)24(32)5(t t t t -++=+-， 解得：1=t ．若PQ 把△ABC 面积平分，则ABC APQ S S ∆∆=21， 即－253t ＋3t =3．∵ t =1代入上面方程不成立，∴不存在这一时刻t ，使线段PQ 把Rt △ACB 的周长和面积同时平分． （4）过点P 作PM ⊥AC 于Ｍ，PN ⊥BC 于N ，若四边形PQP ′ C 是菱形，那么PQ ＝PC ． ∵PM ⊥AC 于M ，∴QM=CM ． ∵PN ⊥BC 于N ，易知△PBN ∽△ABC ． ∴AB BP AC PN =， ∴54tPN =， ∴54t PN =， ∴54tCM QM ==，∴425454=++t t t ，解得：910=t ． ∴当910=t 时，四边形PQP ′ C 是菱形．此时37533=-=t PM ， 9854==t CM ， 在Rt △PMC 中，9505816494922=+=+=CM PM PC ， ∴菱形PQP ′ C 边长为9505．6. （温州）如图，在Rt △ABC 中，∠A ＝90º，AB ＝6，AC ＝8，D ，E分别是边AB ，AC 的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ ⊥BC 于Q ，过点Q 作QR ∥BA 交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ ＝x ，QR ＝y ．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使△PQR 为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．解：（1） Rt A ∠=∠，6AB =，8AC =，10BC ∴=． 点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠= ，B B ∠=∠．BHD BAC ∴△∽△，BNAC BC ∴=，8105DH AC BC ∴==⨯= ． （2）QR AB ∥，90QRC A ∴∠=∠= ．C C ∠=∠ ，RQC ABC ∴△∽△， RQ QC AB BC ∴=，10610y x -∴=，即y 关于x 的函数关系式为：365y x =-+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠= ，290C ∠+∠= ， 1C ∴∠=∠． 84cos 1cos 105C ∴∠===，45QM QP ∴=，1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=，6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BAC CR CA == ， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △为等腰三角形．7. （义乌）如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积；②当2<t <4时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使ΔPDE 为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由。

中考数学总复习《平面直角坐标系》专题训练(附带答案)学校:___________班级：___________姓名：___________考号：___________一、单选题1．若点A到x轴的距离为2，到y轴的距离为5，且点A在第四象限，则点A的坐标是（）A．(2,−5)B．(5,−2)C．(−2,5)D．(−5,2)2．若点P(m+5,m−3)在x轴上，则点P的坐标为（）A．(8,0)B．(0,−8)C．(4,0)D．(0,−4)3．在平面直角坐标系中，若直线AB经过点(3，−4)和(−3，4)，则直线AB() A．平行于x轴B．平行于y轴C．经过原点D．无法确定4．在平面直角坐标系中，将点P(−1,5)绕原点O顺时针旋转90°得到P′，则点P′的坐标为（）A．(1,5)B．(5,1)C．(−1,−5)D．(−5,−1) 5．点P坐标为(6−3a,a+2)，且点P到两坐标轴的距离相等，则点P的坐标是（）A．(3,3)B．(3,−3)C．(3,3)或(−6,6)D．(3,−3)或(6,−6)6．在平面直角坐标系中，点A(3,4)，B(−1,b)，当线段AB最短时，b的值为（）A．5B．4C．3D．07．如图，雷达探测器测得六个目标A，B，C，D，E，F，目标E，F的位置分别表示为E(3,330°),F(2,30°)按照此方法，目标A，B，C，D的位置表示不正确的是（）A．A(5,60°)B．B(3,120°)C．C(3,210°)D．D(5,270°) 8．如图A1(1,0)，A2(1,1)，A3(−1,1)，A4(−1,−1)，A5(2,−1)…按此规律，点A2022的坐标为（）A．(505,505)B．(−506,506)C．(506,506)D．(−505,−505)二、填空题9．电影票上“10排8号”记作(10,8)，那么(15,9)表示的意义是10．已知A(a，−4)与B(3，4)两点关于x轴对称，则a的值为11．已知点A(m+1,2)和点B(3,m−1)，若直线AB∥x轴，则A的坐标为．12．如图，在平面直角坐标系xOy中，Rt△OAB的斜边OB在x轴上∠ABO=30°，若点A的横坐标为1，则点B的坐标为．13．如图，△ABC为等腰直角三角形∠ABC=90°，点B、C在坐标轴上，已知点A坐标为(3,4)，则△ABC的面积为．14．在平面直角坐标系中，用大小、形状完全相同的长方形纸片摆放成如图所示的图案，已知点A的坐标为(−1,3)，则点B的坐标为．15．如图所示，在平面直角坐标系xOy中，点A的坐标是(2,0)，点B的坐标是(0,4)，点C 在x轴上运动（不与点A重合），点D在y轴上运动（不与点B重合），当点C的坐标为时，以点C，O，D为顶点的三角形与△AOB全等．16．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到(1,1)，第2次接着运动到点(2,0)，第3次接着运动到点(3,2)，按这样的运动规律，经过第2023次运动后，动点P的坐标是．三、解答题17．为了更好的开展古树名木的系统保护工作，某公园对园内的4棵百年古树都利用坐标确定了位置，并且定期巡视．(1)请在如图所示的正方形网格中建立平面直角坐标系xOy，使得古树A，B的位置分别表示为A(2,1)，B(5,5)；(2)在（1）建立的平面直角坐标系xOy中．①表示古树C的位置的坐标为______，并在网格中标出古树E(4,−1)的位置；②现需要在沿y轴的道路某处P点向古树A，B修建两条步道，使得点P到古树A，B的距离和最小．请在网格中画出点P（保留作图痕迹，不写作图过程）；该距离和的最小值为______．18．已知平面直角坐标系中有一点M(m−1,2m+3)．(1)当点M到x轴的距离为1时，求点M的坐标；(2)当点M到两坐标轴的距离相等时，求点M的坐标．19．如图，已知△ABC的三个顶点的坐标分别为A(−6，0),B(−2，3),C(−1，0)．(1)将△ABC绕坐标原点O逆时针旋转90°．画出对应的△A′B′C′图形，直接写出点A的对应点A′的坐标；(2)在格点图内，若四边形A′B′C′D′为平行四边形，请直接写出第四个顶点D′的坐标．20．如图，在直角坐标系中A(0,1)，B(2,0)，C(4,3)．(1)在平面直角坐标系中描点，画出△ABC；并作出△ABC关于y轴对称的图形△A1B1C1；(2)求△ABC的面积；(3)设点P在y轴上，且△ABP与△ABC的面积相等，直接写出点P的坐标．21．如图，已知△ABC的顶点分别为A(−2,2)，B(−4,5)，C(−5,1)．(1)作出△ABC关于x轴对称的图形△A1B1C1(2)写出点C1的坐标(3)在x轴上找一点P，使得AP+CP最小（画出图形，找到点P的位置）．22．如图，在平面直角坐标系中，设一点M自P0(1，0)处向上运动1个单位长度至P1(1，1)，然后向左运动2个单位长度至P2处，再向下运动3个单位长度至P3处，再向右运动4个单位长度至P4处，再向上运动5个单位长度至P5处…如此继续运动下去，设P n(x n，y n)，n=1，2，3，……．(1)计算x1+x2+x3+x4．(2)计算x1+x2+⋅⋅⋅+x2023+x2024的值．参考答案1．解：设A(x,y)∵点A到x轴的距离为2，到y轴的距离为5∴x=±5,y=±2∵点A在第四象限∴x>0,y<0∴x=5,y=−2∴A(5,−2)故选：B．2．解：依题意得：m−3=0，即：m=3∴m+5=3+5=8∴点P的坐标为(8,0)故选A．3．解：点(3，−4)和(−3，4)的横纵坐标互为相反数故点(3，−4)和(−3，4)关于原点对称故直线AB经过原点．故选：C．4．解：如图，过P、P′分别向x轴作垂交于H、K根据旋转的定义可知OP=OP′，∠POP′=90°∴∠POH+∠P′OK=90°，∠P′OK+∠P′=90°∴∠POH=∠P′∴∠PHO=∠P′KO=90°∴△PHO≌△P′OK(AAS)．∴PH=OK=5，OH=P′K=1即P′(5,1)．故选B．5．解：由点(6−3a,a+2)到两坐标轴的距离相等，得6−3a=a+2，或6−3a+a+2=0解得a=1，或a=4则该点的坐标为(3,3)或(−6,6)故选：C．6．解：由题意知，点B(−1,b)在直线x=−1上运动∴当AB⊥直线x=−1时，线段AB最短此时b=4．故选：B．7．解：∴E(3,330°)，F(2,30°)∴A(5,60°)，B(3,120°)，C(4,210°)，D(5,270°)故选：C8．解：由题可知第一象限的点：A2,A6,A10，……角标除以4余数为2；第二象限的点：A3,A7,A11……角标除以4余数为3；第三象限的点：A4,A8,A12……角标除以4余数为0；第四象限的点：A5,A9,A13……角标除以4余数为1；由上规律可知：2022÷4=505⋯2∴点A2022在第一象限．观察图形，得：点A2的坐标为(1,1)，点A6的坐标为(2,2)，点A10的坐标为(3,3)，……∴第一象限点的横纵坐标数字隐含规律：点的横纵坐标=n+2（n为角标）4∴点A2022的坐标为(506,506)．故选：C．9．解：∴“10排8号”记为(10,8)∴(15,9)表示的意义是15排9号．故答案为：15排9号．10．解：∴A(a，−4)与B(3，4)两点关于x轴对称∴a=3故答案为：3．11．解：∴直线AB∥x轴∴m−1=2∴m=3∴m+1=4即点A坐标：A(4,2)故答案为：(4,2)．12．解：过点A作x轴的垂线，垂足为点C ∴Rt△OAB中∠ABO=30°∴∠AOB=60°∴AC⊥OB∴∠OAC=30°∴点A的横坐标为1∴OC=1∴OA=2OC=2∴∠ABO=30°∴OB=2OA=4∴点B的坐标为(4,0)故答案为：(4,0)．13．解：如图所示，过点A作AD⊥y轴于点D∴△ABC是等腰直角三角形∴AB =BC ，∠ABC=90°∴∠ABD =90°−∠OBC =∠OCB又∠ADB =∠BOC =90°∴△ADB ≌△BOC (AAS)∴AD =OB,DB =OC∴点A 坐标为(3,4)∴AD =OB =3∴S △ABC =S 梯形−S △ABD −S △OBC =12(1+3)×4−12×1×3−12×1×3=5 故答案为：5．14．解：设每个长方形纸片的宽为x ，长为y由题意可得：{2y −x −y =12x +y =3解得{x =23y =53∴点B 的到x 轴的距离为x +y =73，到y 轴的距离为2y −x =83 ∴点B 的坐标为(−83,73)． 故答案为：(−83,73)．15．解：如图（1）所示当点C 在x 轴负半轴上，点D 在y 轴负半轴上时若△AOB ≌△COD ，则CO =AO =2∴点C 的坐标为(−2,0)；若△AOB ≌△DOC ，则OC =OB =4∴点C 的坐标为(−4,0)；如图（2）所示当点C在x轴负半轴上，点D在y轴正半轴上时若△AOB≌△DOC，则CO=BO=4∴点C的坐标为(−4,0)．若△AOB≌△COD，则CO=AO=2∴点C的坐标为(−2,0)；如图（3）所示当点C在x轴正半轴上，点D在y轴正半轴上时同理可得C的坐标为(4,0)；如图（4）所示当点C在x轴正半轴上，点D在y轴负半轴上时，同理可得点C的坐标为(4,0)；综上所述，点C的坐标为(−4,0)或(−2,0)或(4,0)故答案为：(−4,0)或(−2,0)或(4,0)．16．解：由图可得，动点P的横坐标和运动的次数相同，纵坐标以1，0，2，0为一个循环组依次循环∴经过第2023次运动后，动点P的横坐标为2023∴2023÷4=505 (3)∴经过第2023次运动后，动点P的纵坐标为2∴动点P的坐标是(2023,2)故答案为：(2023,2)．17．解：（1）如图所示（2）①点C(−2,2)，点E(4,−1)的位置如图所示；②过点A作关于y轴的对称点为A′，则A′(−2,1)，连接A′B与y轴交于点P，此时PA+PB最小等于A′B的长度；A′B=√[5−(−2)]2+(5−1)2=√72+42=√65∴点P到古树A，B的距离和的最小值为√65；故答案为：√6518．解：（1）∵|2m+3|=1∴2m+3=1或2m+3=−1解得：m=−1或m=−2∴点M的坐标是(−2,1)或(−3,−1)；（2）∵|m−1|=|2m+3|∴m−1=2m+3或m−1=−2m−3解得：m=−4或m=−23∴点M的坐标是：(−5,−5)或(−53,5 3 ).19．（1）解：△A′B′C′如图所示∴A′(0,−6)；（2）解：如图平行四边形A′B′C′D′即为所求：根据平行四边形性质可得D′(3,−5)故答案为：D′(3,−5)．20．（1）解：如图所示，△ABC即为所求；△A1B1C1即为所求．（2）S△ABC=3×4−12×1×2−12×2×4−12×2×3=4；（3）当点P在y轴上时，△ABP的面积=12AP×|x B|=4即12AP×2=4解得：AP=4．∴点P的坐标为(0,5)或(0,−3)．21．解：（1）如图1所示，△A1B1C1即为所求；（2）点C1的坐标为(−5,−1)；（3）如图2所示，点P即为所求．22．（1）解：由题意可知P1(1，1)，P2(−1，1)，P3(−1，−2)，P4(3，−2)，P5(3，3)，P6(−3，3)，P7(−3，−4)，P8(5，−4)，……于是得到x1，x2，x3，x4的值为1，-1，-1，3∴x1+x2+x3+x4=1−1−1+3=2（2）解：∴x5，x6，x7，x8的值分别为3，-3，-3，5∴x5+x6+x7+x8=3−3−3+5=2；∴x1+x2+x3+x4=1−1−1+3=2x5+x6+x7+x8=3−3−3+5=2…x2021+x2022+x2023+x2024=2∴2024÷4=506∴x1220232024。

常州市二00六年初中毕业、升学统一考试数 学注意事项：1、全卷共8页，满分120分，考试时间120分钟。

2、答卷前将密封线内的项目填写清楚，并将座位号填写在试卷规定的位置上。

3、用蓝色或黑色钢笔、圆珠笔将答案直接填写在试卷上。

4、考生在答题过程中，可以使用CZ1206、HY82型函数计算器，若试题计算结果没有要求取近似值，则计算结果取精确值（保留根号和π）。

一、填空题（本大题每个空格1分，共18分，把答案填写在题中横线上） 1．3的相反数是 ，5-的绝对值是 ，9的平方根是 。

2．在函数1-=xy 中，自变量x 的取值范围是 ；若分式12--x x 的值为零，则=x 。

3．若α∠的补角是120°，则α∠＝ °，=αcos 。

4．某校高一新生参加军训，一学生进行五次实弹射击的成绩（单位：环）如下：8，6，10，7，9，则这五次射击的平均成绩是 环，中位数 环，方差是 环2。

5．已知扇形的圆心角为120°，半径为2cm ，则扇形的弧长是 cm ，扇形的面积是 2cm 。

6．已知反比例函数()0≠=k xky 的图像经过点（1，2-），则这个函数的表达式是 。

当0 x 时，y 的值随自变量x 值的增大而 （填“增大”或“减小”）7、如图，在△ABC 中，D 、E 分别是AB 和AC 的中点，F 是BC 延长线上的一点，DF 平分CE 于点G ，1=CF ，则 =BC ，△ADE 与△ABC 的周长之比为 ，△CFG 与△BFD 的面积之比为 。

8．如图，小亮从A 点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……照这样走下去，他第一次回到出发地A 点时，一共走了 米。

二、选择题（下列各题都给出代号为A 、B 、C 、D 的四个答案，其中有且只有一个是正确的，把正确答案的代号填在题后【 】内，每小题2分，共18分） 9．下列计算正确的是 【 】 A ．123=-x x B ．2x x x =∙ C ．2222x x x =+ D ．()423a a -=-第7题B第8题10．如图，已知⊙O 的半径为5mm ，弦mm AB 8=，则圆心O 到AB 的距离是 【 】A ．1 mmB ．2 mmC ．3 mmD ．4 mm 11．小刘同学用10元钱买两种不同的贺卡共8张，单价分别是1元与2元，设1元的贺卡为x 张，2元的贺卡为y 张，那么x 、y 所适合的一个方程组是 【 】A ．⎪⎩⎪⎨⎧=+=+8102y x y xB ．⎪⎩⎪⎨⎧=+=+1028102y x y x C ．⎩⎨⎧=+=+8210y x y x D ．⎩⎨⎧=+=+1028y x y x 12．刘翔为了备战2008年奥运会，刻苦进行110米跨栏训练，为判断他的成绩是否稳定，教练对他10次训练的成绩进行统计分析，则教练需了解刘翔这10次成绩的【 】 A ．众数 B ．方差 C ．平均数 D ．频数 13、图1表示正六棱柱形状的高大建筑物，图2中的阴影部分表示该建筑物的俯视图，P 、Q 、M 、N 表示小明在地面上的活动区域，小明想同时看到该建筑物的三个侧面，他应在【 】A ．P 区域B ．Q 区域C ．M 区域D ．N 区域14、下列左图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，则该几何体的主视图为 【 】224113第14题ABCD15．锐角三角形的三个内角是∠A 、∠B 、∠C ，如果B A ∠+∠=∠α，C B ∠+∠=∠β，A C ∠+∠=∠γ，那么α∠、β∠、γ∠这三个角中 【 】A ．没有锐角B ．有1个锐角C ．有2个锐角D ．有3个锐角 16、如果0,0,0 b a b a +，那么下列关系式中正确的是 【 】 A ．a b b a -- B ．b b a a -- C ．a b a b -- D ．a b b a --17．已知：如图1，点G 是BC 的中点，点H 在AF 上，动点P 以每秒2cm 的速度沿图1的边线运动，运动路径为：H F E D C G →→→→→，相应的△ABP 的面积)(2cm y 关于运动时间)(s t 的函数图像如图2，若cm AB 6=，则下列四个结论中正确的个数有第10题第13题图2图1【 】图1F C①图1中的BC 长是8cm ②图2中的M 点表示第4秒时y 的值为242cm ③图1中的CD 长是4cm ④图2中的N 点表示第12秒时y 的值为182cm A ．1个 B ．2个 C ．3个 D ．4个三、解答题（本大题共2小题，共20分，解答应写出演算步骤） 18．（本小题满分10分）计算或化简：（1）03260tan 33⎪⎭⎫⎝⎛-+︒+ （2）2422---m m m19．（本小题满分10分）解方程或解不等式组： （1）x x 211=- （2）⎩⎨⎧-≥+≤-1)1(212x x x四、解答题（本大题共2小题，共12分，解答应写出证明过程） 20．（本小题满分5分）已知：如图，在四边形ABCD 中，AC 与BD 相交与点O ，AB ∥CD ，CO AO =， 求证：四边形ABCD 是平行四边形。

2008年中考试卷分类—函数与几何图形（2）1. 如图4，正方形ABCD 的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上，且它们的各边与正方形ABCD 各边平行或垂直．若小正方形的边长为x ，且0<x ≤10，阴影部分的面积为y ，则能反映y 与x 之间函数关系的大致图象是（ D ）2. （连云港）如图，现有两块全等的直角三角形纸板Ⅰ，Ⅱ，它们两直角边的长分别为1和2．将它们分别放置于平面直角坐标系中的ΔAOB ，ΔCOD 处，直角边OB ，OD 在x 轴上．一直尺从上方紧靠两纸板放置，让纸板Ⅰ沿直尺边缘平行移动．当纸板Ⅰ移动至ΔPEF 处时，设PE ，PF 与OC 分别交于点M ，N ，与x 轴分别交于点G ，H ．（1）求直线AC 所对应的函数关系式；（2）当点P 是线段AC （端点除外）上的动点时，试探究：①点M 到x 轴的距离h 与线段BH 的长是否总相等？请说明理由；②两块纸板重叠部分（图中的阴影部分）的面积S 是否存在最大值？若存在，求出这个最大值及S 取最大值时点P 的坐标；若不存在，请说明理由． 解：（1）由直角三角形纸板的两直角边的长为1和2， 知A C ，两点的坐标分别为(12)(21)，，，．设直线AC 所对应的函数关系式为y kx b =+． ··················································· 2分有221k b k b +=⎧⎨+=⎩，．解得13k b =-⎧⎨=⎩，． 所以，直线AC 所对应的函数关系式为3y x =-+． ············································· 4分 （2）①点M 到x 轴距离h 与线段BH 的长总相等． 因为点C 的坐标为(21)，，所以，直线OC 所对应的函数关系式为12y x =． 又因为点P 在直线AC 上， 所以可设点P 的坐标为(3)a a -，．过点M 作x 轴的垂线，设垂足为点K ，则有MK h =．因为点M 在直线OC 上，所以有(2)M h h ，． ··················· 6分 因为纸板为平行移动，故有EF OB ∥，即EF GH ∥．又EF PF ⊥，所以PH GH ⊥．法一：故Rt Rt Rt MKG PHG PFE △∽△∽△，（第24题答图）从而有12GK GH EF MK PH PF ===． 得1122GK MK h ==，11(3)22GH PH a ==-．所以13222OG OK GK h h h =-=-=．又有13(3)(1)22OG OH GH a a a =-=--=-． ················································ 8分所以33(1)22h a =-，得1h a =-，而1BH OH OB a =-=-，从而总有h BH =． ······················································································· 10分法二：故Rt Rt PHG PFE △∽△，可得12GH EF PH PF =-． 故11(3)22GH PH a ==-．所以13(3)(1)22OG OH GH a a a =-=--=-．故G 点坐标为3(1)02a ⎛⎫-⎪⎝⎭，． 设直线PG 所对应的函数关系式为y cx d =+，则有330(1)2a ca d c a d -=+⎧⎪⎨=-+⎪⎩，．解得233c d a =⎧⎨=-⎩ 所以，直线PG 所对的函数关系式为2(33)y x a =+-． ······································· 8分 将点M 的坐标代入，可得4(33)h h a =+-．解得1h a =-．而1BH OH OB a --=-，从而总有h BH =． ················································· 10分 ②由①知，点M 的坐标为(221)a a --，，点N 的坐标为12a a ⎛⎫ ⎪⎝⎭，．ONH ONG S S S =-△△1111133(1)222222a NH OH OG h a a a -=⨯-⨯=⨯⨯-⨯⨯- 22133133224228a a a ⎛⎫=-+-=--+ ⎪⎝⎭． ···························································· 12分 当32a =时，S 有最大值，最大值为38． S 取最大值时点P 的坐标为3322⎛⎫ ⎪⎝⎭，．3. （沈阳）如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且AB=1，OB=3，矩形ABOC 绕点O 按顺时针方向旋转600后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线y=ax 2+bx+c 过点A ，E ，D ．（1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O ，B ，P ，Q 为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．解：（1）点E 在y 轴上 ··············································································· 1分 理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，BO =，2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上，∴点E 在y 轴上． ································································· 3分 （2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，2OM = 点D 在第一象限，∴点D 的坐标为12⎫⎪⎪⎝⎭， ··············································································· 5分 由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A 的坐标为( ················································································· 6分 抛物线2y ax bx c =++经过点E ，2c ∴=由题意，将()A ，12D ⎫⎪⎪⎝⎭，代入22y ax bx =++中得32131242a a ⎧-+=⎪⎨++=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为：28299y x x =--+ ·················································· 9分 （3）存在符合条件的点P ，点Q ． ·································································· 10分 理由如下：矩形ABOC 的面积3AB BO ==∴以O B P Q ，，，为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边， 又3OB =OB ∴边上的高为2························································································ 11分依题意设点P 的坐标为(2)m ，点P在抛物线28299y x x =--+上282299m m ∴--+=解得，10m =，2m = 1(02)P ∴，，22P ⎛⎫ ⎪ ⎪⎝⎭以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，PQ OB =， ∴当点1P 的坐标为(02)，时， 点Q 的坐标分别为1(Q，2Q ；当点2P的坐标为2⎛⎫⎪ ⎪⎝⎭时，点Q 的坐标分别为328Q ⎛⎫-⎪ ⎪⎝⎭，428Q ⎛⎫⎪ ⎪⎝⎭．x4. （徐州）如图1，一副直角三角板满足AB ＝BC ，AC ＝DE ，∠ABC ＝∠DEF ＝90°，∠EDF ＝30°【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板．．．．DEF ．．．绕．点．E ．旋转．．，并使边DE 与边AB 交于点P ，边EF 与边BC 于点Q 【探究一】在旋转过程中， （1） 如图2，当CE1EA＝时，EP 与EQ 满足怎样的数量关系？并给出证明. （2） 如图3，当CE2EA＝时EP 与EQ 满足怎样的数量关系？，并说明理由. （3） 根据你对（1）、（2）的探究结果，试写出当CEEA＝m 时，EP 与EQ 满足的数量关系式 为_________,其中m 的取值范围是_______(直接写出结论，不必证明)【探究二】若，AC ＝30cm ，连续PQ ，设△EPQ 的面积为S(cm 2)，在旋转过程中： （1） S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由.（2） 随着S 取不同的值，对应△EPQ 的个数有哪些变化？不出相应S 值的取值范围.5. （河南）如图，直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ，点A 的坐标是（-2，0）．（1）试说明△ABC 是等腰三角形；（2）动点M 从A 出发沿x 轴向点B 运动，同时动点N 从点B 出发沿线段BC 向点C 运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，△MON 的面积为S ．① 求S 与t 的函数关系式；② 设点M 在线段OB 上运动时，是否存在S =4的情形？若存在，求出对应的t 值；若不存在请说明理由；③在运动过程中，当△MON 为直角三角形时，求t 的值．6. 如图20，在平面直角坐标系中，四边形OABC 是矩形，点B 的坐标为（4，3）．平行于对角线AC 的直线m 从原点O 出发，沿x 轴正方向以每秒1个单位长度的速度运动，设直线m 与矩形OABC 的两边．．分别交于点M 、N ，直线m 运动的时间为t （秒）．(1) 点A 的坐标是__________，点C 的坐标是__________； (2) 当t= 秒或 秒时，MN=21AC ；(3) 设△OMN 的面积为S ，求S 与t 的函数关系式；(4) 探求(3)中得到的函数S 有没有最大值？若有，求出最大值；若没有，要说明理由．解：(1)（4，0），（0，3）； ··································································· 2分 (2) 2，6； ··························································································· 4分 (3) 当0＜t ≤4时，OM =t ．由△OMN ∽△OAC ，得OCONOA OM =， ∴ ON =t 43，S=283t ． ······························ 6分 当4＜t ＜8时，如图，∵ OD =t ，∴ AD = t-4． 方法一：由△DAM ∽△AOC ，可得AM =)4(43-t ，∴ BM =6-t 43． ······················· 7分 由△BMN ∽△BAC ，可得BN =BM 34=8-t ，∴ CN =t-4． ····························· 8分S=矩形OABC 的面积-Rt △OAM 的面积- Rt △MBN 的面积- Rt △NCO 的面积=12-)4(23-t -21（8-t ）（6-t 43）-)4(23-t =t t 3832+-． ··············································································· 10分方法二：易知四边形ADNC 是平行四边形，∴ CN =AD =t-4，BN =8-t ． ···························· 7分 由△BMN ∽△BAC ，可得BM =BN 43=6-t 43，∴ AM =)4(43-t ． ············· 8分 以下同方法一． (4) 有最大值． 方法一： 当0＜t ≤4时，∵ 抛物线S=283t 的开口向上，在对称轴t=0的右边， S 随t 的增大而增大， ∴ 当t=4时，S 可取到最大值2483⨯=6； ················································ 11分当4＜t ＜8时， ∵ 抛物线S=t t 3832+-的开口向下，它的顶点是（4，6），∴ S ＜6． 综上，当t=4时，S 有最大值6． ···························································· 12分方法二：∵ S=22304833488t t t t t ⎧<⎪⎪⎨⎪-+<<⎪⎩，≤，∴ 当0＜t ＜8时，画出S 与t 的函数关系图像，如图所示． ························· 11分 显然，当t=4时，S 有最大值6．7. （郴州）如图10，平行四边形ABCD 中，AB ＝5，BC ＝10，BC 边上的高AM =4，E 为 BC 边上的一个动点（不与B 、C 重合）．过E 作直线AB 的垂线，垂足为F ． FE 与DC 的延长线相交于点G ，连结DE ，DF ．．（1） 求证：ΔBEF ∽ΔCEG ．（2） 当点E 在线段BC 上运动时，△BEF 和△CEG 的周长之间有什么关系？并说明你的理由．（3）设BE ＝x ，△DEF 的面积为 y ，请你求出y 和x 之间的函数关系式，并求出当x 为何值时,y 有最大值，最大值是多少？（1） 因为四边形ABCD 是平行四边形， 所以AB DG ································································································· 1分 所以,B GCE G BFE ∠=∠∠=∠所以BEF CEG △∽△ ·············································································· 3分 （2）BEF CEG △与△的周长之和为定值． ···················································· 4分 理由一：过点C 作FG 的平行线交直线AB 于H ，因为GF ⊥AB ，所以四边形FHCG 为矩形．所以 FH ＝CG ，FG ＝CH 因此，BEF CEG △与△的周长之和等于BC ＋CH ＋BH由 BC ＝10，AB ＝5，AM ＝4，可得CH ＝8，BH ＝6， 所以BC ＋CH ＋BH ＝24 ··············································································· 6分 理由二：由AB ＝5，AM ＝4，可知在Rt △BEF 与Rt △GCE 中，有：4343,,,5555EF BE BF BE GE EC GC CE ====，所以，△BEF 的周长是125BE ， △ECG 的周长是125CE 又BE ＋CE ＝10，因此BEF CEG 与的周长之和是24． ··································· 6分（3）设BE ＝x ，则43,(10)55EF x GC x ==- 所以21143622[(10)5]2255255y EF DG x x x x ==-+=-- ······························ 8分A M xH GFED CB配方得：2655121()2566y x =--+． 所以，当556x =时，y 有最大值． ·································································· 9分最大值为1216．8. （镇江）如图，在直角坐标系xoy 中，点P 为函数214y x =在第一象限内的图象上的任一点，点A 的坐标为（0，1），直线l 过B （0，-1）且与x 轴平行，过P 作y 轴的平行线分别交x 轴，l 于C ，Q ，连结AQ 交x 轴于H ，直线PH 交y 轴于R ．（1）求证：H 点为线段AQ 的中点；（2）求证：①四边形APQR 为平行四边形；②平行四边形APQR 为菱形；（3）除P 点外，直线PH 与抛物线214y x =有无其它公共点？并说明理由．（1）法一：由题可知1AO CQ ==．90AOH QCH ∠=∠=，AHO QHC ∠=∠，AOH QCH ∴△≌△． ············································································ （1分） OH CH ∴=，即H 为AQ 的中点． ··························································· （2分）法二：(01)A ，，(01)B -，，OA OB ∴=． ················································· （1分） 又BQ x ∥轴，HA HQ ∴=． ··································································· （2分） （2）①由（1）可知AH QH =，AHR QHP ∠=∠，AR PQ ∥，RAH PQH ∴∠=∠，RAH PQH ∴△≌△． ············································································· （3分） AR PQ ∴=，又AR PQ ∥，∴四边形APQR 为平行四边形． ············································ （4分） ②设214P m m ⎛⎫ ⎪⎝⎭，，PQ y ∥轴，则(1)Q m -，，则2114PQ m =+．过P 作PG y ⊥轴，垂足为G ，在Rt APG △中，2114AP m PQ ====+=．∴平行四边形APQR 为菱形． ··································································· （6分） （3）设直线PR 为y kx b =+，由OH CH =，得22m H ⎛⎫⎪⎝⎭，，214P m m ⎛⎫ ⎪⎝⎭，代入得： 2021.4m k b km b m ⎧+=⎪⎪⎨⎪+=⎪⎩， 221.4m k b m ⎧=⎪⎪∴⎨⎪=-⎪⎩，∴直线PR 为2124m y x m =-． ···················· （7分） 设直线PR 与抛物线的公共点为214x x ⎛⎫ ⎪⎝⎭，，代入直线PR 关系式得：22110424m x x m -+=，21()04x m -=，解得x m =．得公共点为214m m ⎛⎫ ⎪⎝⎭，． 所以直线PH 与抛物线214y x =只有一个公共点P ． 9. （无锡）如图，已知点A 从（1，0）出发，以1个单位长度/秒的速度沿x 轴向正方向运动，以O ，A 为顶点作菱形OABC ，使点B ，C 在第一象限内，且∠AOC=600，；以P （0，3）为圆心，PC 为半径作圆．设点A 运动了t 秒，求：（1）点C 的坐标（用含t 的代数式表示）；（2）当点A 在运动过程中，所有使⊙P 与菱形OABC 的边所在直线相切的t 的值． 解：（1）过C 作CD x ⊥轴于D ， 1OA t =+，1OC t ∴=+，1cos 602t OD OC +∴==，3(1sin 60DC OC ==， ∴点C 的坐标为12t ⎛+ ⎝⎭． ············ （2分） （2）①当P 与OC 相切时（如图1），切点为C ，此时PC OC ⊥，cos30OC OP ∴=，3132t ∴+=，1t ∴=． ················ （4分） ②当P 与OA ，即与x 轴相切时（如图2），则切点为O ，PC OP =，过P 作PE OC ⊥于E ，则12OE OC =， ···················································· （5分） 133cos302t OP+∴==，1t ∴=． ··············································· （7分） ③当P 与AB 所在直线相切时（如图3），设切点为F ，PF 交OC 于G，则PF OC ⊥，FG CD ∴==3(1sin 30PC PF OP ∴==+······················································· （8分） 过C 作CH y ⊥轴于H ，则222PH CH PC +=，2221)3)32222t t t ⎛⎫⎛⎫+++⎛⎫∴+-=+ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭， 化简，得2(1)1)270t t +-++=， 解得1t+=9310t =-<， 1t∴=．∴所求t的值是12-，1和1．10. (辽宁)如图14，在Rt ΔABC 中，∠A=900,AB=AC,BC=42，另有一等腰梯形DEFG （GF ∥DE ）的底边DE 与BC 重合，两腰分别落在AB,AC 上，且G,F 分别是AB,AC 的中点．（1）求等腰梯形DEFG 的面积；（2）操作：固定ΔABC ，将等腰梯形DEFG 以每秒1个单位的速度沿BC 方向向右运动，直到点D 与点C 重合时停止．设运动时间为x 秒，运动后的等腰梯形为DEF ′G ′（如图15）．探究1：在运动过程中，四边形BDG ′G 能否是菱形？若能，请求出此时x 的值；若不能，请说明理由．探究2：设在运动过程中ΔABC 与等腰梯形DEFG 重叠部分的面积为y ，求y 与x 的函数关系式．解：如图6，（1）过点G作GM BC ⊥于M ．AB AC =，90BAC ∠=，BC =G 为AB 中点GM ∴=．又G F ，分别为AB AC ，的中点12GF BC ∴==······························· 2分162DEFG S ∴==梯形 ∴等腰梯形DEFG 的面积为6． ······································································· 3分 （2）能为菱形 如图7，由BG DG '∥，GG BC '∥∴四边形BDG G '是平行四边形当122BD BG AB ===时，四边形BDG G '为菱形，此时可求得2x =∴当2x =秒时，四边形BDG G '为菱形． （3）分两种情况：①当0x <≤时， 方法一：GM =，BDG GS'∴=∴重叠部分的面积为：6y =∴当0x <≤y 与x 的函数关系式为6y = ··································· 10分 ②当x ≤设FC 与DG '交于点P ，则45PDC PCD ∠=∠= 90CPD ∴∠=，PC PD =作PQ DC ⊥于Q ，则1)2PQ DQ QC x ===∴重叠部分的面积为：221111)))82244y x x x x =⨯==-+11. 如图14，已知半径为1的⊙O1与x 轴交于A ，B 两点，OM 为⊙O1的切线，切点为M ，圆心O1的坐标为（2，0），二次函数y=-x 2+bx+c 的图象经过A ，B 两点．（1）求二次函数的解析式；（2）求切线OM 的函数解析式；（3）线段OM 上是否存在一点P ，使得以P ，O ，A 为顶点的三角形与ΔOO 1M 相似．若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由． 解：（1）圆心1O 的坐标为(20)，，1O 半径为1，(10)A ∴，，(30)B ， ·············· 1分 二次函数2y x bx c =-++的图象经过点A B ，，AFG (D )B C (E ) 图6M F G A F 'G ' BD CE图7MF GAF 'G 'BCE图8Q D P∴可得方程组10930b c b c -++=⎧⎨-++=⎩········································································· 2分 解得：43b c =⎧⎨=-⎩∴二次函数解析式为243y x x =-+- ··········································· 3分 （2）过点M 作MF x ⊥轴，垂足为F ． ··························································· 4分OM 是1O 的切线，M 为切点，1O M OM ∴⊥（圆的切线垂直于经过切点的半径）．在1Rt OO M △中，1111sin 2O M O OM OO ∠== 1O OM ∠为锐角，130O OM ∴∠=····························· 5分1cos302OM OO ∴===在Rt MOF △中，3cos3032OF OM ===． 1sin 30322MF OM ===． ∴点M 坐标为322⎛ ⎝⎭，·················································································· 6分 设切线OM 的函数解析式为(0)y kx k =≠32k =，k ∴=········· 7分 ∴切线OM 的函数解析式为y =······························································· 8分 （3）存在． ·································································································· 9分①过点A 作1AP x ⊥轴，与OM 交于点1P ．可得11Rt Rt APO MO O △∽△（两角对应相等两三角形相似） 113tan tan 303P A OA AOP =∠==，11P ⎛∴ ⎝⎭··········································· 10分 ②过点A 作2AP OM ⊥，垂足为2P ，过2P 点作2P H OA ⊥，垂足为H ． 可得21Rt Rt APO O MO △∽△（两角对应相等两三角开相似） 在2Rt OP A △中，1OA =，23cos30OP OA ∴==，。

2008年中考数学分类汇编二次函数（2）1、(2008 福建龙岩)如图，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中一个动点到达端点时，另一个动点也随之停止运动.（1）求AD的长；（2）设CP=x，问当x为何值时△PD Q的面积达到最大，并求出最大值；（3）探究：在BC边上是否存在点M使得四边形PD Q M是菱形？若存在，请找出点M，并求出BM 的长；不存在，请说明理由.2、（2008 四川凉山州）我州有一种可食用的野生菌，上市时，外商李经理按市场价格20元/千克收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将以每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这类野生菌在冷库中最多保存160元，同时，平均每天有3千克的野生菌损坏不能出售．（1）设x到后每千克该野生菌的市场价格为y元，试写出y与x之间的函数关系式．（2）若存放x天后，将这批野生菌一次性出售，设这批野生菌的销售总额为P元，试写出P与x之间的函数关系式．（3）李经理将这批野生茵存放多少天后出售可获得最大利润W元？（利润＝销售总额－收购成本－各种费用）3、(2008 青海)王亮同学善于改进学习方法，他发现对解题过程进行回顾反思，效果会更好．某一天他利用30分钟时间进行自主学习．假设他用于解题的时间x （单位：分钟）与学习收益量y 的关系如图甲所示，用于回顾反思的时间x （单位：分钟）与学习收益量y 的关系如图乙所示（其中OA 是抛物线的一部分，A 为抛物线的顶点），且用于回顾反思的时间不超过用于解题的时间．（1）求王亮解题的学习收益量y 与用于解题的时间x 之间的函数关系式，并写出自变量x 的取值范围；（2）求王亮回顾反思的学习收益量y 与用于回顾反思的时间x 之间的函数关系式； （3）王亮如何分配解题和回顾反思的时间，才能使这30分钟的学习收益总量最大？ （学习收益总量=解题的学习收益量+回顾反思的学习收益量）4、（2008 山东 临沂）如图，已知抛物线与x 轴交于A （－1，0）、B （3，0）两点，与y 轴交于点C （0，3）。