(完整版)几何模型截长补短模型
- 格式:doc
- 大小:57.01 KB
- 文档页数:4

中考数学几何模型1:截长补短模型有一类几何题其命题主要是证明三条线段长度的“和”或"差”及其比例关系. 这一类题目一般可以采取“截长”或“补短”的方法来进行求解. 所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系. 所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等. 然后求出延长后的线段与最长的已知线段的关系. 有的是采取截长补短后,使之构成某种特定的三角形进行求解.例题1. 如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,若E在AD上.求证:(1)BE⊥CE;(2)BC=AB+CD.变式练习>>>1. 已知△ABC的内角平分线AD交BC于D,∠B=2∠C. 求证:AB+BD=AC.例题2. 已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC的数量关系,并说明理由.变式练习>>>2. 已知:△ABC中,AB=AC,D为△ABC外一点,且∠ABD=60°,∠ADB=90°﹣∠BDC.试判断线段CD、BD与AB之间有怎样的数量关系?并证明你的结论.例题3. 如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.变式练习>>>3. 如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探究BM、MN、CN之间的数量关系,并给出证明.例题4. 在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为;(直接写出答案)(2)如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;(3)如图(3),BD=8,AB=2,DE=8,若ACE=135°,求线段AE长度的最大值.例题5.在△ABC中,∠BAC=90°.(1)如图1,直线l是BC的垂直平分线,请在图1中画出点A关于直线l的对称点A′,连接A′C,A′B,A′C与AB交于点E;(2)将图1中的直线A′B沿着EC方向平移,与直线EC交于点D,与直线BC交于点F,过点F作直线AB的垂线,垂足为点H.①如图2,若点D在线段EC上,请猜想线段FH,DF,AC之间的数量关系,并证明;②若点D在线段EC的延长线上,直接写出线段FH,DF,AC之间的数量关系.例题6. 如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.(1)当直线l经过点C时(如图2),求证:BN=CD;(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;(3)请直接写出BN、CE、CD之间的等量关系.达标检测领悟提升强化落实1. 如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC=AB+BD,求∠ABC的度数.2. 如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并证明你的结论.3. 如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.4. 如图,▱ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DF A=2∠BAE.(1)若∠D=105°,∠DAF=35°.求∠F AE的度数;(2)求证:AF=CD+CF.5. 如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.(1)若正方形ABCD的边长为4,且AB=2FB,求FG的长;(2)求证:AE+BF=AF.6. 如图,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,连接AC,BD交于点E.(1)若BC=CD=2,M为线段AC上一点,且AM:CM=1:2,连接BM,求点C到BM的距离.(2)证明:BC+CD=AC.7. 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过点A作AF⊥AE交DP于点F,连接BF.(1)若AE=2,求EF的长;(2)求证:PF=EP+EB.答案例题1. 如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,若E在AD上.求证:(1)BE⊥CE;(2)BC=AB+CD.【解答】证明:如图所示:(1)∵BE、CE分别是∠ABC和∠BCD的平分线,∴∠1=∠2,∠3=∠4,又∵AB∥CD,∴∠1+∠2+∠3+∠4=180°,∴∠2+∠3=90°,∴∠BEC=90°,∴BE⊥CE.(2)在BC上取点F,使BF=BA,连接EF.在△ABE和△FBE中,,∴△ABE≌△FBE(SAS),∴∠A=∠5.∵AB∥CD,∴∠A+∠D=180°,∴∠5+∠D=180,∵∠5+∠6=180°,∴∠6=∠D,在△CDE和△CFE中,,∴△CDE≌△CFE(AAS),∴CF=CD.∵BC=BF+CF,∴BC=AB+CD,变式练习>>>1. 已知△ABC的内角平分线AD交BC于D,∠B=2∠C. 求证:AB+BD=AC.答案:略例题2. 已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC 的数量关系,并说明理由.【解答】解:在BC上取点G使得CG=CD,∵∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣60°)=120°,∴∠BOE=∠COD=60°,∵在△COD和△COG中,,∴△COD≌△COG(SAS),∴∠COG=∠COD=60°,∴∠BOG=120°﹣60°=60°=∠BOE,∵在△BOE和△BOG中,,∴△BOE≌△BOG(ASA),∴BE=BG,∴BE+CD=BG+CG=BC.变式练习>>>2. 已知:△ABC中,AB=AC,D为△ABC外一点,且∠ABD=60°,∠ADB=90°﹣∠BDC.试判断线段CD、BD与AB之间有怎样的数量关系?并证明你的结论.【解答】解:AB=BD+CD,理由是:延长CD到E,使DE=BD,连接AE,∵∠ADB=90°﹣∠BDC,∴∠ADE=180°﹣(90°﹣)﹣∠BDC=90°﹣,∴∠ADB=∠ADE,在△ABD和△AED中∴△ABD≌△AED(SAS),∴∠E=∠ABD=60°,AB=AE,∵AB=AC,∴AE=AC,∴△ACE是等边三角形,∴AB=CE=CD+DE=BD+CD.例题3. 如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.【解答】解:连接AC,延长DE到F,使EF=BC,连接AF,∵BC+DE=CD,EF+DE=DF,∴CD=FD,∵∠ABC+∠AED=180°,∠AEF+∠AED=180°,∴∠ABC=∠AEF,在△ABC和△AEF中,,∴△ABC≌△AEF(SAS),∴AC=AF,在△ACD和△AFD中,,∴△ACD≌△AFD(SSS)∴∠ADC=∠ADF,即AD平分∠CDE.变式练习>>>3. 如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探究BM、MN、CN之间的数量关系,并给出证明.【解答】解:CN=MN+BM证明:在CN上截取点E,使CE=BM,连接DE,∵△ABC为等边三角形,∴∠ACB=∠ABC=60°,又△BDC为等腰三角形,且∠BDC=120°,∴BD=DC,∠DBC=∠BCD=30°,∴∠ABD=∠ABC+∠DBC=∠ACB+∠BCD=∠ECD=90°,在△MBD和△ECD中,,∴△MBD≌△ECD(SAS),∴MD=DE,∠MDB=∠EDC,又∵∠MDN=60°,∠BDC=120°,∴∠EDN=∠BDC﹣(∠BDN+∠EDC)=∠BDC﹣(∠BDN+∠MDB)=∠BDC﹣∠MDN=120°﹣60°=60°,∴∠MDN=∠EDN,在△MND与△END中,,∴△MND≌△END(SAS),∴MN=NE,∴CN=NE+CE=MN+BM.例题4. 在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为AE=AB+DE;(直接写出答案)(2)如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;(3)如图(3),BD=8,AB=2,DE=8,若ACE=135°,则线段AE长度的最大值是10+4.(直接写出答案).【解答】解:(1)AE=AB+DE;(2)猜想:AE=AB+DE+BD.证明:在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.∵C是BD边的中点,∴CB=CD=BD.∵AC平分∠BAE,∴∠BAC=∠FAC.在△ACB和△ACF中,,∴△ACB≌△ACF(SAS),∴CF=CB,∴∠BCA=∠FCA.同理可证:CD=CG,∴∠DCE=∠GCE.∵CB=CD,∴CG=CF∵∠ACE=120°,∴∠BCA+∠DCE=180°﹣120°=60°.∴∠FCA+∠GCE=60°.∴∠FCG=60°.∴△FGC是等边三角形.∴FG=FC=BD.∵AE=AF+EG+FG.∴AE=AB+DE+BD.(3)作B关于AC的对称点F,D关于EC的对称点G,连接AF,FC,CG,EG,FG.∵C是BD边的中点,∴CB=CD=BD.∵△ACB≌△ACF(SAS),∴CF=CB,∴∠BCA=∠FCA.同理可证:CD=CG,∴∠DCE=∠GCE∵CB=CD,∴CG=CF∵∠ACE=135°,∴∠BCA+∠DCE=180°﹣135°=45°.∴∠FCA+∠GCE=45°.∴∠FCG=90°.∴△FGC是等腰直角三角形.∴FC=BD.∵BD=8,∴FC=4,∴FG=4.∵AE=AB+4+DE.∵AB=2,DE=8,∴AE≤AF+FG+EG=10+4.∴当A、F、G、E共线时AE的值最大2,最大值为10+4.故答案为:10+4.例题5.在△ABC中,∠BAC=90°.(1)如图1,直线l是BC的垂直平分线,请在图1中画出点A关于直线l的对称点A′,连接A′C,A′B,A′C与AB交于点E;(2)将图1中的直线A′B沿着EC方向平移,与直线EC交于点D,与直线BC交于点F,过点F作直线AB 的垂线,垂足为点H.①如图2,若点D在线段EC上,请猜想线段FH,DF,AC之间的数量关系,并证明;②若点D在线段EC的延长线上,直接写出线段FH,DF,AC之间的数量关系.【解答】解:(1)如图1:;(2)①DF+FH=CA,证明:如图2,过点F作FG⊥CA于点G,∵FH⊥BA于H,∠A=90°,FG⊥CA,∴∠A=∠FGA=∠FHA=90°,∴四边形HFGA为矩形.∴FH=AG,FG∥AB,∴∠GFC=∠EBC,∵直线l是BC的垂直平分线,∴BE=EC,∴∠EBC=∠ECB,由(1)和平移可知,∠ECB=∠EBC=∠GFC,∠FDC=∠A=90°,∴∠FDC=∠FGC=90°.∵在△FGC和△CDF中∴△FGC≌△CDF,∴CG=FD,∴DF+FH=GC+AG,即DF+FH=AC;②解:FH﹣DF=AC,理由是:过F作FH⊥BA于H,过点C作CG⊥FH于G,∵FH⊥BA于H,∠BAC=90°,CG⊥FH,∴∠CAH=∠CGH=∠FHA=90°,∴四边形ACGH为矩形.∴AC=GH,CG∥AB,∴∠GCF=∠EBC,∵直线l是BC的垂直平分线,∴BE=EC,∴∠EBC=∠ECB=∠FCD,∴∠GCF=∠FCD,由(1)和平移可知,∠FDC=∠A=90°,∴∠FDC=∠FGC=90°.∵在△FGC和△CDF中∴△FGC≌△CDF,∴FG=FD,∵FH﹣FG=GH,∴FH﹣DF=AC.例题6. 如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H 作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.(1)当直线l经过点C时(如图2),求证:BN=CD;(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;(3)请直接写出BN、CE、CD之间的等量关系.【解答】(1)证明:连接ND,如图2所示:∵AO平分∠BAC,∴∠BAD=∠CAD,∵直线l⊥AO于H,∴∠AHN=∠AHE=90°,∴∠ANH=∠AEH,∴AN=AC,∴NH=CH,∴AH是线段NC的中垂线,∴DN=DC,∴∠DNH=∠DCH,∴∠AND=∠ACB,∵∠AND=∠B+∠BDN,∠ACB=2∠B,∴∠B=∠BDN,∴BN=DN,∴BN=DC;(2)解:当M是BC中点时,CE和CD之间的等量关系为CD=2CE,理由如下:过点C作CN'⊥AO交AB于N',过点C作CG∥AB交直线l于点G,如图3所示:由(1)得:BN'=CD,AN'=AC,AN=AE,∴∠ANE=∠AEN,NN'=CE,∴∠ANE=∠CGE,∠B=∠BCG,∴∠CGE=∠AEN,∴CG=CE,∵M是BC中点,∴BM=CM,在△BNM和△CGM中,,∴△BNM≌△CGM(ASA),∴BN=CG,∴BN=CE,∴CD=BN'=NN'+BN=2CE;(3)解:BN、CE、CD之间的等量关系:当点M在线段BC上时,CD=BN+CE;理由如下:过点C作CN'⊥AO交AB于N',如图3所示:由(2)得:NN'=CE,CD=BN'=BN+CE;当点M在BC的延长线上时,CD=BN﹣CE;理由如下:过点C作CN'⊥AO交AB于N',如图4所示:同(2)得:NN'=CE,CD=BN'=BN﹣CE;当点M在CB的延长线上时,CD=CE﹣BN;理由如下:过点C作CN'⊥AO交AB于N',如图5所示:同(2)得:NN'=CE,CD=BN'=CE﹣BN.达标检测领悟提升强化落实1. 如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC=AB+BD,求∠ABC的度数.【解答】解:如图,在AC上截取AE=AB,∵AD平分∠BAC,∴∠BAD=∠CAD,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴BD=DE,∠B=∠AED,∵AC=AE+CE,AC=AB+BD,∴CE=BD,∴CE=DE,∴∠C=∠CDE,即∠B=2∠C,在△ABC中,∠BAC+∠B+∠C=180°,∴60°+2∠C+∠C=180°,解得∠C=40°,∴∠ABC=2×40°=80°.2. 如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并证明你的结论.3. 如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.【解答】解:探究结论:BM+CN=NM.证明:延长AC至E,使CE=BM,连接DE,∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,∴∠BCD=30°,∴∠ABD=∠ACD=90°,即∠ABD=∠DCE=90°,∴在△DCE和△DBM中,∴Rt△DCE≌Rt△DBM(SAS),∴∠BDM=∠CDE,又∵∠BDC=120°,∠MDN=60°,∴∠BDM+∠NDC=∠BDC﹣∠MDN=60°,∴∠CDE+∠NDC=60°,即∠NDE=60°,∴∠MDN=∠NDE=60°∴DM=DE(上面已经全等)在△DMN和△DEN中∵∴△DMN≌△DEN(SAS),∴BM+CN=NM.4. 如图,▱ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;(2)求证:AF=CD+CF.【解答】(1)解:∵∠D=105°,∠DAF=35°,∴∠DFA=180°﹣∠D﹣∠DAF=40°(三角形内角和定理).∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD(平行四边形对边平行且相等).∴∠DFA=∠FAB=40°(两直线平行,内错角相等);∵∠DFA=2∠BAE(已知),∴∠FAB=2∠BAE(等量代换).即∠FAE+∠BAE=2∠BAE.∴∠FAE=∠BAE;∴2∠FAE=40°,∴∠FAE=20°;(2)证明:在AF上截取AG=AB,连接EG,CG.∵∠FAE=∠BAE,AE=AE,∴△AEG≌△AEB.∴EG=BE,∠B=∠AGE;又∵E为BC中点,∴CE=BE.∴EG=EC,∴∠EGC=∠ECG;∵AB∥CD,∴∠B+∠BCD=180°.又∵∠AGE+∠EGF=180°,∠AGE=∠B,∴∠BCF=∠EGF;又∵∠EGC=∠ECG,∴∠FGC=∠FCG,∴FG=FC;又∵AG=AB,AB=CD,∴AF=AG+GF=AB+FC=CD+FC.5. 如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.(1)若正方形ABCD的边长为4,且AB=2FB,求FG的长;(2)求证:AE+BF=AF.【解答】解:(1)∵四边形ABCD是正方形,且边长为4,∴∠ABF=90°,AB=AD=4,∵在Rt△ABF中,AB=2FB,∴FB=×4=2,∴AF==2,∵AG=AD=4,∴FG=AF﹣AG=2﹣4;(2)证明:在BC上截取BM=AE,连接AM,∵AG=AD,AB=AD,∴AG=AB,∵AE⊥AF,∴∠EAG=∠ABM=90°,在△AGE和△BAM中,,∴△AGE≌△BAM(SAS),∴∠AMB=∠AEG,∠BAM=∠AGD,∵AG=AD,∴∠AGD=∠ADG,∴∠BAM=∠ADG,∵∠BAD=90°,∴∠FAB+∠BAE=∠BAE+∠EAD=90°,∴∠FAB=∠EAD,∴∠AEG=∠EAD+∠ADG=∠FAB+∠BAM=∠FAM,∴∠FAM=∠AMB,∴AF=FM=BF+BM=BF+AE.6. 如图,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,连接AC,BD交于点E.(1)若BC=CD=2,M为线段AC上一点,且AM:CM=1:2,连接BM,求点C到BM的距离.(2)证明:BC+CD=AC.【解答】解:(1)∵AB=AD,∠BAD=60°,∴△ABD是等边三角形,∴∠ABD=∠ADB=60°.∵BC=CD,∴△ABC≌△ADC,∴∠BAC=∠DAC=30°,∠ACB=∠ACD=60°.∴∠AEB=∠BEC=90°,∠ABC=90°,∴CE=BC=1,BE=,AC=2BC=4.∵AM:CM=1:2,∴AM=,CM=,∴EM=,在Rt△BEM中由勾股定理得BM==.过点C作CF⊥BM于点F.∴.∴,∴CF=.即点C到BM的距离.(2)证明:延长BC到点F,使CF=CB,连接DF,∵AB=AD,∠ABD=60°,∴△ABD是等边三角形,∴∠ADB=60°,AD=BD,∴BC=CD,∴CF=CD.∵∠BCD=120°,∴∠DCF=180°﹣∠BCD=60°,∴△DCF是等边三角形,∴∠CDF=∠ADB=60°,DC=DF,∴∠ADC=∠BDF,又∵AD=BD,∴△ACD≌△BDF,∴AC=BF=BC+CF,即AC=BC+CD.7. 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过点A作AF⊥AE交DP于点F,连接BF.(1)若AE=2,求EF的长;(2)求证:PF=EP+EB.【解答】解:(1)∵四边形ABCD是正方形,且BE⊥DP,AF⊥AE,∴AB=AD,∠BAD=∠EAF=∠BEF=90°,∴∠1+∠FAB=∠2+∠FAB=90°,∴∠1=∠2.∵∠3+∠5=∠4+∠6,且∠5=∠6,∴∠3=∠4.在△AEB和△AFD中,∵,∴△AEB≌△AFD,∴AE=AF=2,在Rt△EAF中,由勾股定理,得EF==2.(2)过点A作AM⊥EF于M,且∠EAF=90°,AE=AF,∴△EAF为等腰直角三角形.∴AM=MF=EM.∠AME=∠BEF=90°.∵点P是AB的中点,∴AP=BP.在△AMP和△BEP中,∵,∴△AMP≌△BEP,∴BE=AM,EP=MP,∴MF=BE,∴PF=PM+FM=EP+BE.。


全等模型-倍长中线与截长补短模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(倍长中线模型、截长补短模型)进行梳理及对应试题分析,方便掌握。
模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.(注:一般都是原题已经有中线时用,不太会有自己画中线的时候)。
【常见模型及证法】1、基本型:如图1,在三角形ABC 中,AD 为BC 边上的中线.证明思路:延长AD 至点E ,使得AD =DE . 若连结BE ,则BDE CDA ∆≅∆;若连结EC ,则ABD ECD ∆≅∆;2、中点型:如图2,C 为AB证明思路:若延长EC 至点F ,使得CF EC =,连结AF ,则BCE ACF ∆≅∆;若延长DC 至点G ,使得CG DC =,连结BG ,则ACD BCG ∆≅∆.3、中点+平行线型:如图3, //AB CD ,点E 为线段AD 的中点.证明思路:延长CE 交AB 于点F (或交BA 延长线于点F ),则EDC EAF ∆≅∆.例1.(2023·江苏徐州·模拟预测)(1)阅读理解:如图①,在ABC 中,若8AB =,5AC =,求BC 边上的中线AD 的取值范围.可以用如下方法:将ACD △绕着点D 逆时针旋转180︒得到EBD △,在ABE △中,利用三角形三边的关系即可判断中线AD 的取值范围是______;(2)问题解决:如图②,在ABC 中,D 是BC 边上的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,求证:BE CF EF +>;(3)问题拓展:如图③,在四边形ABCD 中,180B D ∠+∠=︒,CB CD =,100BCD ∠=︒,以C 为顶点作一个50︒的角,角的两边分别交AB 、AD 于E 、F 两点,连接EF ,探索线段BE ,DF ,EF 之间的数量关系,并说明理由.【答案】(1)31322AD <<;(2)见详解;(3)EF BE DF =+,理由见详解【分析】(1)根据旋转的性质可证明ADC EDB ≅,6,AC BE AD ED ===,在ABE △中根据三角形三边关系即可得出答案;(2)延长FD 至M ,使DF=DM ,连接BM ,EM ,可得出CF BM =,根据垂直平分线的性质可得出EF EM =,利用三角形三边关系即可得出结论;(3)延长AB 至N ,使BN=DF ,连接CN ,可得NBC D ∠=∠,证明NBC FDC ≅,得出,CN CF NCB FCD =∠=∠,利用角的和差关系可推出50ECN ECF ∠=︒=,再证明NCE FCE ≅,得出EN EF =,即可得出结论.【详解】解:(1)∵,,AD ED CD BD ADC BDE ==∠=∠∴ADC EDB ≅∴5,AC BE AD ED ===在ABE △中根据三角形三边关系可得出:AB BE AE AB BE −<<+,即3213AD << ∴31322AD <<故答案为:31322AD <<; (2)延长FD 至M ,使DF=DM ,连接BM ,EM ,同(1)可得出CF BM =,∵,FD MD FD DE =⊥∴EF EM =在BEM △中,BE BM EM +>∴BE CF EF +>;(3)EF BE DF =+,理由如下:延长AB 至N ,使BN=DF ,连接CN ,∵180,180ABC D ABC NBC ∠+∠=︒∠+∠=︒∴NBC D ∠=∠∴NBC FDC ≅∴,CF CN NCB FCD =∠=∠∵100,50BCD FCE ∠=︒∠=︒∴50ECN ECF ∠=︒=∴NCE FCE ≅(SAS )∴EN EF =∴EF EN BE BN BE DF ==+=+∴EF BE DF =+.【点睛】本题考查的知识点有旋转的性质、全等三角形的判定及性质、线段垂直平分线的性质、三角形三边关系、角的和差等,解答此题的关键是作出辅助线,构造出与图①中结构相关的图形.此题结构精巧,考查范围广,综合性强.例2.(2023·贵州毕节·二模)课外兴趣小组活动时,老师提出了如下问题:(1)如图1,△ABC 中,若AB =5,AC =3,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到点E ,使DE =AD ,请根据小明的方法思考帮小明完成解答过程.(2)如图2,AD 是△ABC 的中线,BE 交AC 干E ,交AD 于F ,且AE =EF .请判昕AC 与BF 的数量关系,并说明理由.【答案】(1)见解析(2)AC=BF ,理由见解析【解析】(1)解:如图,延长AD 到点E ,使DE=AD ,连接BE ,在△ADC 和△EDB 中∵AD DE ADC EDB CD DB =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△EDB (SAS ).∴BE=AC=3.∵AB -BE<AE<AB+BE ∵2<AE<8.∵AE=2AD ∴1<AD<4.(2)AC=BF ,理由如下:延长AD 至点G ,使GD=AD ,连接BG ,在△ADC 和△GDB 中,AD DG ADC GDB BD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△GDB (SAS ).∴BG=AC ,∠G=∠DAC ..∵AE=EF ∴∠AFE=∠FAE . ∴∠DAC=∠AFE=∠BFG ∴∠G=∠BFG ∴BG=BF ∴AC=BF .【点睛】本题考查全等三角形判定与性质,三角形三边的关系,作辅助线:延长AD 到点E ,使DE=AD ,构造全等三角形是解题的关键.例3.(2022·山东·安丘市一模)阅读材料:如图1,在ABC 中,D ,E 分别是边AB ,AC 的中点,小亮在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,通过延长DE 到点F ,使EF DE =,连接CF ,证明ADE CFE ≌,再证四边形DBCF 是平行四边形即得证.类比迁移:(1)如图2,AD 是ABC 的中线,E 是AC 上的一点,BE 交AD 于点F ,且AE EF =,求证:AC BF =. 小亮发现可以类比材料中的思路进行证明.证明:如图2,延长AD 至点M ,使MD FD =,连接MC ,……请根据小亮的思路完成证明过程.方法运用:(2)如图3,在等边ABC 中,D 是射线BC 上一动点(点D 在点C 的右侧),连接AD .把线段CD 绕点D 逆时针旋转120°得到线段DE ,F 是线段BE 的中点,连接DF 、CF .请你判断线段DF 与AD 的数量关系,并给出证明.【答案】(1)证明见解析;(2)2AD DF =,证明见解析【分析】(1) 延长AD 至M ,使MD FD =,连接MC ,证明BDF CDM △≌△,结合等角对等边证明即可. (2) 延长DF 至点M ,使DF FM =,连接BM 、AM ,证明(SAS)ABM ACD △≌△,△ABM 是等边三角形,代换后得证.【详解】(1)证明:延长AD 至M ,使MD FD =,连接MC .在BDF 和CDM V 中,BD CD BDF CDM DF DM =⎧⎪∠=∠⎨⎪=⎩,∴BDF CDM △≌△,∴MC BF =,M BFM ∠=∠, ∵AE EF =,∴EAF EFA ∠=∠,∵EFA BFM ∠=∠,∴M MAC ∠=∠,∴AC MC =,∴AC BF =.(2)线段DF 与AD 的数量关系为:2AD DF =.证明如下:延长DF 至点M ,使DF FM =,连接BM 、AM ,如图2所示:∵点F 为BE 的中点,∴BF EF =在BFM 和EFD △中,∵BF EF BFM EFD FM DF =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)BFM EFD △≌△∴BM DE =,MBF DEF ∠=∠,∴BM DE ∥ ∵线段CD 绕点D 逆时针旋转120°得到线段DE∴CD DE BM ==,120∠=︒BDE ,∴18012060MBD ∠=−=︒︒︒∵ABC 是等边三角形∵AB AC =,60ABC ACB ∠=∠=︒,∴6060120ABM ABC MBD ∠∠∠︒︒=+=+=︒ ∵180********ACD ACB ∠=︒−∠=︒−︒=︒,∴ABM ACD ∠=∠在ABM 和ACD △中,∵AB AC ABM ACD BM CD =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)ABM ACD △≌△∴AM AD =,BAM CAD ∠=∠,∴60MAD MAC CAD MAC BAM BAC ∠∠∠∠∠∠=+=+==︒∴AMD 是等边三角形,∴2==AD DM DF .【点睛】本题考查了等边三角形的判定和性质,三角形全等的判定和性质,熟练掌握等边三角形的判定和性质,三角形全等的判定和性质是解题的关键.例4.(2022·河南商丘·一模)阅读材料如图1,在△ABC 中,D ,E 分别是边AB ,AC 的中点,小明在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,通过延长DE 到点F ,使EF =DE ,连接CF ,证明△ADE ≌△CFE ,再证四边形DBCF 是平行四边形即得证.(1)类比迁移:如图2,AD 是△ABC 的中线,BE 交AC 于点E ,交AD 于点F ,且AE =EF ,求证:AC =BF . 小明发现可以类比材料中的思路进行证明.证明:如图2,延长AD 至点M ,使MD =FD ,连接MC ,……请根据小明的思路完成证明过程.(2)方法运用:如图3,在等边△ABC 中,D 是射线BC 上一动点(点D 在点C 的右侧),连接AD .把线段CD 绕点D 逆时针旋转120°得到线段DE .F 是线段BE 的中点,连接DF ,CF .请你判断线段DF 与AD 的数量关系,并给出证明;【答案】(1)见解析(2)线段DF 与AD 的数量关系为:AD =2DF ,证明见解析;【分析】(1)类比材料,运用倍长中线辅助线作法,证得结论.(2)运用倍长中线辅助线作法,结合三角形全等证明及等边三角形性质,得出结论.(1)证明:如图,延长AD 至M ,使MD =FD ,连接MC ,在△BDF 和△CDM 中,∵BD CD BDF CDM DF DM =⎧⎪∠=∠⎨⎪=⎩,∴△BDF ≌△CDM (SAS ),∴MC =BF ,∠M =∠BFM ,∵AE =EF ,∴∠EAF =∠EFA ,∵∠EFA=∠BFM,∴∠M=∠MAC,∴AC=MC,∴AC=BF;(2)解:线段DF与AD的数量关系为:AD=2DF,证明如下:延长DF至点M,使DF=FM,连接BM、AM,如图所示:∵点F为BE的中点,∴BF=EF,在△BFM和△EFD中,∵BF EFBFM EFDFM DF=⎧⎪∠=∠⎨⎪=⎩,∴△BFM≌△EFD(SAS),∴BM=DE,∠MBF=∠DEF,∴BM∥DE,∵线段CD绕点D逆时针旋转120°得到线段DE,∴CD=DE=BM,∠BDE=120°,∴∠MBD=180°﹣120°=60°,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,∴∠ABM=∠ABC+∠MBD=60°+60°=120°,∵∠ACD=180°﹣∠ACB=180°﹣60°=120°,∴∠ABM=∠ACD,在△ABM和△ACD中,∵AB ACABM ACDBM CD=⎧⎪∠=∠⎨⎪=⎩,∴△ABM≌△ACD(SAS),∴AM=AD,∠BAM=∠CAD,∴∠MAD=∠MAC+∠CAD=∠MAC+∠BAM=∠BAC=60°,∴△AMD是等边三角形,∴AD=DM=2DF;综合运用相关知识是解题的关键.模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。

132HABFE1GEFDCB ADCBA OGABCD第三章截长补短模型截长补短如图①,若证明线段AB、CD、EF之间EF=AB+CD,可以考虑截长补短法。
截长法:如图②,在EF上截取EG=AB,再GF=CD即可。
补短法:如图③,延长AB至H点,使BH=C再证明AH模型分析截长补短的方法适用于求证线段的和差倍分关系。
截长,指在长线段中截取一段等于已知线段;补短,指将短线段延长,延长部分等于已知线段。
该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程。
模型实例例1.如图,已知在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D。
求证:AB=AC+CD。
例2.如图,已知OD平分∠AOB,DC⊥OA于点C,∠A=∠GBD。
求证:AO+BO=2CO。
2ABC DOEABCD热搜精练1.如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC=AB+BD。
求∠ABC的度数。
2.如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB。
求证:AC=AE+CD。
3EABC D EABCD3.如图,∠ABC+∠BCD=180°,BE、CE分别平分∠ABC、∠BCD。
求证:AB+CD=BC。
4.如图,在△ABC中,∠ABC=90°,AD平分∠BAC交BC于点D,∠C=30°,BE⊥AD于点E。
求证:AC-AB=2BE。
4FABCD EABCD5.如图,Rt△ABC中,AC=BC,AD平分∠BAC交BC于点D,CE⊥AD交AD于F点,交AB于点E。
求证:AD=2DF+CE。
6.如图,五边形ABCDE中,AB=AC,BC+DE=CD,∠B+∠E=180°。
求证:AD平分∠CDE。

模型介绍有一类几何题其命题主要是证明三条线段长度的“和”或"差”及其比例关系.这一类题目一般可以采取“截长”或“补短”的方法来进行求解.所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系.所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等.然后求出延长后的线段与最长的已知线段的关系.有的是采取截长补短后,使之构成某种特定的三角形进行求解.①截长:在较长的线段上截取另外两条较短的线段.如图所示,在BF上截取BM=DF,易证△BMC≌△DFC(SAS).②补短:选取两条较短线段中的一条进行延长,使得较短的两条线段共线并寻求解题突破.如图所示,延长GC至N,使CN=DF,易证△CDF≌△BCN(SAS).例题精讲考点一:截长型【例1】.如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C等于_______.解:在DC上截取DE=DB,连接AE.设∠BCA=α,∵AB+BD=DC,DE=DB,∴CE=AB.∵AD⊥BC,DB=DE,∴直线AD是BE的垂直平分线,∴AB=AE,∴CE=AE,∴∠BCA=∠CAE.∵AB=AE,∴∠CBA=∠AEB.∵∠AEB是△CAE的一个外角,∴∠AEB=∠BCA+∠CAE,∴∠CBA=∠AEB=2α,∴∠CBA+∠BCA=3α=180°﹣120°=60°,∴α=20°,∴∠BCA=20°.变式训练【变式1-1】.如图,△ABC中,AC=BC,AD平分∠BAC,若AC+CD=AB,求∠C的度数.解:在AB上截取AC=AE,设∠B=x°,∵AC=BC,∴∠BAC=∠B=x°∵AD平分∠BAC,∴∠EAD=∠CAD,在△EAD和△CAD中,∴△EAD≌△CAD,∴∠C=∠AED,CD=DE,∵AC+CD=AB,AB﹣BE+AE,AE=AC,∴BE=DE=DC,∴∠B=∠BDE=x°,∴∠C=∠AED=∠B+∠BDE°,在△ABC中,x+x+2x=180°,∴x=45,即∠C=2x°=90°.【变式1-2】.如图,四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且∠B+∠D=180°,若BE=3,CE=4,S△ACE=14,则S△ACD=________.解:在AE 上截取AM =AD ,连接CM ,∵AC 平分∠BAD ,∴∠1=∠2,在△AMC 和△ADC 中,12AC AC AD AM =⎧⎪∠=∠⎨⎪=⎩,∴△AMC ≌△ADC (SAS ),∴3D ∠=∠,∵∠B +∠D =180°,43=180∠+∠︒,∴4=B ∠∠,∵CE ⊥AB ,∴90CEM CEB ∠=∠=︒,在EMC △和EBC 中,4B CEM CEB CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EMC ≌△EBC (AAS ),∴ME =EB =3,∵CE =4,S △ACE =14,∴21474AE ⨯==,∴AM =AE -EM =7-3=4,∴1144822AMC S AM CE =⨯=⨯⨯= ,∴8ADC AMC S S ==.故答案为:8.【变式1-3】.已知在△ABC 中,∠B =2∠C ,∠BAC 的平分线AD 交BC 边于点D .求证:AC =AB +BD.证明:在AC 上截取AE =AB ,连接DE .∵∠BAC 的平分线AD 交BC 边于点D ,∴∠BAD =∠DAC ,在△ABD 与△AED中,,∴△ABD≌△AED(SAS),∴BD=DE,∠B=∠AED,∵∠B=2∠C,∠AED=∠C+∠EDC,∴∠AED=2∠C,∴∠C=∠EDC,∴CE=DE,∴CE=BD,∴AC=AE+EC=AB+BD.考点二:补短型【例2】.已知:如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°求证:BD+DC=AB.证明:延长BD到F,使BF=BA,连接AF,CF,∵∠ABD=60度,∴△ABF为等边三角形,∴AF=AB=AC=BF,∠AFB=60°,∴∠ACF=∠AFC,又∵∠ACD=60°,∴∠AFB=∠ACD=60°∴∠DFC=∠DCF,∴DC=DF.∴BD+DC=BD+DF=BF=AB,即BD+DC=AB.变式训练【变式2-1】.如图,四边形ABCD中,AB∥DC,点E为AD上一点,连接BE,CE,且BE、CE 分别平分∠ABC 、∠BCD .求证:BC =AB +DC .证明:延长BE 交CD 的延长线于点F ,∵BE 平分∠ABC ,∴∠ABE =∠CBE ,∵AB ∥CD ,∴∠F =∠ABE ,∠A =∠FDA ,∴∠F =∠CBE ,∴CF =BC ,∵CE 平分∠BCD ,∴BE =EF (三线合一),在△ABE 和△DFE 中,,∴△ABE ≌△FDE (ASA ),∴FD =AB ,∵CF =DF +CD ,∴CF =AB +CD ,∴BC =AB +CD .【变式2-2】.【问题背景】如图1:在四边形ABCD 中,AB AD =,120BAD ∠=︒,E 、F 分别是BC 、CD 上的点,且60EAF ∠=︒,小王同学探究此问题的方法是:延长FD 到点G ,使DG BE =,连接AG ,再证明AEF AGF ≅△△,可得出结论.【探索延伸】如图2,若在四边形ABCD 中,AB AD =,E 、F 分别是BC ,CD 上的点12BAD ,上述结论是否仍然成立【学以致用】如图3,四边形ABCD 是边长为5的正方形,45EBF ∠=︒,求DEF 的周长.解:(1)【问题背景】如图1在ABE △和ADG 中,∵DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴()ABE ADG SAS ≅△△,∴AE AG =,BAE DAG ∠=∠,∵18EAF BAD ∠=∠,∴GAF DAG DAF BAE DAF BAD EAF EAF ∠=∠+∠=∠+∠=∠-∠=∠,∴EAF GAF ∠=∠,在AEF 和GAF 中,∵AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()AEF AGF SAS ≅△△,∴EF FG =,∵FG DG DF BE DF =+=+,∴EF BE DF =+;故答案为:EF BE DF =+.(2)【探索延伸】解:结论EF BE DF =+仍然成立;理由:如图2,延长FD 到点G .连接AG ,在ABE △和ADG 中,∵DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴()ABE ADG SAS ≅△△,∴AE AG =,BAE DAG ∠=∠,∵13EAF BAD ∠=∠,∴GAF DAG DAF BAE DAF BAD EAF EAF ∠=∠+∠=∠+∠=∠-∠=∠,∴EAF GAF ∠=∠,在AEF 和GAF 中,∵AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()AEF AGF SAS ≅△△,∴EF FG =,∵FG DG DF BE DF =+=+,∴EF BE DF =+;(3)【学以致用】解:如图3,延长DC 到点G ,连接BG ,在AEB △与CGB △中,∵AE CG A BCG AB BC =⎧⎪∠=∠⎨⎪=⎩,∴()AEB CGB SAS ≅△△,∴BE BG =,ABE CBG ∠=∠.∵45EBF ∠=︒,90ABC ∠=︒,∴45ABE CBF ∠+∠=︒,∴45CBF CBG ∠+∠=︒,在EBF △与GBF 中,∵BE BG EBF GBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴()EBF GBF SAS ≅△△,∴EF GF =,∴DEF 的周长5510EF ED DF AE CF DE DF AD CD =++=+++=+=+=.实战演练1.如图,在△ABC 中,BD 平分∠ABC ,∠C =2∠CDB ,AB =12,CD =3,则△ABC 的周长为()A .21B .24C .27D .30解:如图,在AB 上截取BE =BC ,连接DE,∵BD 平分∠ABC ,∴∠ABD =∠CBD ,在△CBD 和△EBD 中,CB BE CBD DBE BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△CBD ≌△EBD (SAS ),∴∠CDB =∠BDE ,∠C =∠DEB ,∵∠C =2∠CDB ,∴∠CDE =∠DEB ,∴∠ADE =∠AED ,∴AD =AE ,∴△ABC 的周长=AD +AE +BE +BC +CD =AB +AB +CD =27,故选C .2.如图,AD ⊥BC ,AB +BD =DC ,∠B =54°,则∠C =27°.解:在DC 上截取DE =BD ,连接AE,∵AD ⊥BC ,DE =BD ,∴AD 是BE 的垂直平分线,∴AB =AE ,∴∠B =∠AEB =54°,∵AB +BD =DC ,DE +EC =DC ,∴AB =EC ,∴AE =EC ,∴∠C =∠EAC ,∵∠C+∠EAC=∠AEB=54°,∴∠C=∠EAC=∠AEB=27°,故答案为:27°.3.已知:如图,在△ABC中,AC=BC,∠C=100°,AD平分∠CAB.求证:AD+CD=AB.证明:如图,在AB上截取AE=AC,延长AD到F使AF=AB,连接DE、BF.又∵∠1=∠2,AD是公共边BE,在△ADC和△ADE中,,∴△ADC≌△ADE,∴∠AED=∠C=100°,则得∠DEB=80°∵CA=CB,AD平分∠BAC,∴∠1=∠2=20°,∠3=40°∵AF=AB,∠2=20°,∴∠F=∠ABF=1/2(180°﹣∠2)=80°则∠F=∠DEB∴∠4=80°﹣∠3=40°,∴∠3=∠4,∠F=∠DEC,在△BDF和△BDE中,,∴△DBE≌△DBF(AAS)∴DF=DE=CD∴AB=AF=AD+DF=AD+DC.4.如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.证明:延长OE至点M,使OM=OC,连接CM,∵∠BCD=∠CBE=30°,∴OB=OC,∠MOC=30°+30°=60°,∵OM=OC,∴△OMC为等边三角形,∴CM=OC=OB,∠M=60°,∴∠DBO=∠MCE,在△BOD和△CME中,,∴△BOD≌△MCE,∴DO=EM,∴OE+OD=OM=OB,在Rt△OBG中,∠OBG=30°,OG⊥BC,∴2OG=OB,∴OE+OD=2OG.5.如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别是∠BAC、∠ABC的角平分线.求证:(1)BQ=CQ;(2)BQ+AQ=AB+BP.证明:(1)∵BQ是∠ABC的角平分线,∴∠QBC=∠ABC.∵∠ABC+∠ACB+∠BAC=180°,且∠BAC=60°,∠ACB=40°,∴∠ABC=80°,∴∠QBC==40°,∴∠QBC=∠C,∴BQ=CQ;(2)延长AB至M,使得BM=BP,连接MP.∴∠M=∠BPM,∵△ABC中∠BAC=60°,∠C=40°,∴∠ABC=80°,∵BQ平分∠ABC,∴∠QBC=40°=∠C,∴BQ=CQ,∵∠ABC=∠M+∠BPM,∴∠M=∠BPM=40°=∠C,∵AP平分∠BAC,∴∠MAP=∠CAP,在△AMP和△ACP中,∵∴△AMP≌△ACP,∴AM=AC,∵AM=AB+BM=AB+BP,AC=AQ+QC=AQ+BQ,∴AB+BP=AQ+BQ.6.如图,△ABC两条角平分线BD,CE相交于点O,∠A=60°,求证:CD+BE=BC.证明:在BC上找到F使得BF=BE,,∵∠A=60°,BD、CE是△ABC的角平分线,∴∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=120°,∴∠BOE=∠COD=60°,在△BOE和△BOF中,,∴△BOE≌△BOF,(SAS)∴∠BOF=∠BOE=60°,∴∠COF=∠BOC﹣∠BOF=60°,在△OCF和△OCD中,,∴△OCF≌△OCD(ASA),∴CF=CD,∵BC=BF+CF,∴BC=BE+CD.7.如图,梯形ABCD中,AB∥CD,∠ABC和∠BCD的平分线的交点E在AD上.求证:(1)点E是AD的中点;(2)BC=AB+CD.证明:延长CE交BA的延长线于点F.∵CE和BE分别是∠ABC和∠BCD的平分线,即∠ECB=∠DCB,∠EBC=∠CBA,又∵AB∥CD,∴∠DCB+∠CBA=180°,∴∠ECB+∠EBC=90°,∴∠CEB=90°,即BE⊥EC,∵AB∥CD∴∠DCE=∠F,又∵∠DCE=∠ECB,∴∠F=∠ECB∴BF=BC,EC=EF.在△DCE和△AFE中,,∴△DCE≌△AFE,∴DE=AE,即E是AD的中点,DC=AF,∴BC=BF=AB+CD.8.已知,如图,BD是△ABC的角平分线,AB=AC,(1)若BC=AB+AD,请你猜想∠A的度数,并证明;(2)若BC=BA+CD,求∠A的度数?(3)若∠A=100°,求证:BC=BD+DA.解:(1)答:∠A=90°.理由如下:在BC上截取BE=BA,连接DE.∵BC=AB+AD,∴CE=AD,∵BD是△ABC的角平分线,∴∠ABD=∠EBD,∵AB=BE,BD=BD,∴△ABD≌△EBD,∴AD=DE=CE,∠A=∠DEB∴∠C=∠EDC,∴∠A=∠DEB=∠C+∠EDC=2∠C,∵AB=AC,∴∠C=∠B,∵∠A+∠ABC+∠C=180°,∴4∠C=180°,∴∠C=45°,∠A=2∠C=90°,即∠A=90°;(2)解:在BC上截取CF=CD,连接DF.∵BC=BA+CD,∴BF=BA,∵∠ABD=∠FBD,BD=BD,∴△ABD≌△FBD,∴∠A=∠DFB,∵CD=CF,∴∠CDF=∠CFD,∴∠C+2∠DFC=180°,∵∠A+∠DFC=180°,∴2∠A﹣∠C=180°,∵∠A+2∠C=180°,解得:∠A=108°,答:∠A的度数是108°.(3)证明:在BC上截取BQ=BD,连接DQ,延长BA到W使BW=BQ,连接DW.∵∠A=100°,AC=AB,∴∠C=∠ABC=40°,∵BD平分∠ABC,∴∠DBQ=20°,∵BD=BQ,∴∠DQB=∠BDQ=(180°﹣∠DBQ)=80°,∴∠CDQ=∠DQB﹣∠C=40°=∠C,∴DQ=CQ,∵在△WBD和△QBD中,∴△WBD≌△QBD,∴∠W=∠DQB=80°,DW=DQ=CQ,∵∠BAC=100°,∴∠WAD=180°﹣∠BAC=180°﹣100°=80°,即∠WAD=∠W,∴AD=DW=DQ=CQ,∴BC=BD+DA.9.阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.(1)请完成下题的证明过程:如图1,在△ABC中,∠B=2∠C,AD平分∠BAC.求证:AB+BD=AC.证明:在AC上截取AE=AB,连接DE(2)如图2,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.证明:在AC上截取AE=AB,连接DE,如图1:∵AD平分∠BAC,∴∠BAD=∠DAC,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴∠B=∠AED,BD=DE,又∠B=2∠C,∴∠AED=2∠C,而∠AED=∠C+∠EDC=2∠C,∴∠C=∠EDC,∴DE=CE,∴AB+BD=AE+CE=AC;(2)延长AE、BC交于F,∵AB=BF,BE平分∠ABF,∴AE=EF,在△ADE和△FCE中,,∴△ADE≌△FCE(ASA),∴AD=CF,∴AB=BF=BC+CF=BC+AD.10.在菱形ABCD中,∠BAD=60°,点E、F分别在边AB、AD上,且AE=DF,BF与DE交于点G.(1)如图①,连接BD.求证:△ADE≌△DBF;(2)如图②,连接CG.求证:BG+DG=CG.证明:(1)∵四边形ABCD是菱形,∠BAD=60°,∴AB=BC=CD=AD,∠C=∠BAD=60°,∴△ABD和△CBD都是等边三角形,∴AD=DB,∠BDF=∠DAE=60°,在△ADE和△DBF中,,∴△ADE≌△DBF(SAS);(2)如图②,延长GB到点H,使BH=DG,连接CH、BD,由(1)知△ADE≌△DBF,△CBD是等边三角形,∴∠ADE=∠DBF,∠CBD=∠BCD=60°,∴∠DBF+∠CBH=180°﹣∠CBD=120°,∵四边形ABCD是菱形,∠BAD=60°,∴BC=CD,∠ADC=180°﹣∠BAD=120°,∴∠ADE+∠CDG=120°,∴∠CBH=∠CDG,在△CBH和△CDG中,,∴△CBH≌△CDG(SAS),∴CH=CG,∠BCH=∠DCG,∵∠BCD=∠DCG+∠BCG=60°,∴∠BCH+∠BCG=60°,即∠GCH=60°,∴△CGH是等边三角形,∴GH=CG,∵GH=BG+BH=BG+DG,∴BG+DG=CG.11.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=∠BAD.(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由;(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.解:(1)EF=BE+DF,理由:延长EB至G,使BG=DF,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,∴∠ADC=∠ABG,在△ABG和△ADF中,,∴△ABG≌△ADF(SAS),∴AG=AF,∠BAG=∠DAF,∵∠EAF=∠BAD,∴∠BAE+∠DAF=∠BAE+∠BAG=∠EAF,即∠EAG=∠EAF,在△EAG和△EAF中,,∴△EAG≌△EAF(SAS),∴GE=EF,∴EF=BE+DF;(2)(1)中结论不成立,EF=BE﹣FD,在BE上截取BM=DF,连接AM,∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,∴∠ABC=∠ADF,在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∵∠BAM+∠MAD=∠DAF+∠MAD,∴∠BAD=∠MAF,∵∠EAF=∠BAD,∴∠EAF=∠MAF,∴∠EAF=∠EAM,在△AME和△AFE中,,∴△AME≌△AFE(SAS),∴ME=EF,∴ME=BE﹣BM=BE﹣DF,∴EF=BE﹣FD.12.如图,在锐角△ABC中,∠A=60°,点D,E分别是边AB,AC上一动点,连接BE 交直线CD于点F.(1)如图1,若AB>AC,且BD=CE,∠BCD=∠CBE,求∠CFE的度数;(2)如图2,若AB=AC,且BD=AE,在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM,连接MF,点N是MF的中点,连接CN.在点D,E运动过程中,猜想线段BF,CF,CN之间存在的数量关系,并证明你的猜想.解:(1)如图1中,在射线CD上取一点K,使得CK=BE,在△BCE和△CBK中,,∴△BCE≌△CBK(SAS),∴BK=CE,∠BEC=∠BKD,∵CE=BD,∴BD=BK,∴∠BKD=∠BDK=∠ADC=∠CEB,∵∠BEC+∠AEF=180°,∴∠ADF+∠AEF=180°,∴∠A+∠EFD=180°,∵∠A=60°,∴∠EFD=120°,∴∠CFE=180°﹣120°=60°;(2)结论:BF+CF=2CN.理由:如图2中,∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴AB=CB,∠A=∠CBD=60°,∵AE=BD,∴△ABE≌△BCD(SAS),∴∠BCF=∠ABE,∴∠FBC+∠BCF=60°,∴∠BFC=120°,如图2中,延长CN到Q,使得NQ=CN,连接FQ,∵NM=NF,∠CNM=∠FNQ,CN=NQ,∴△CNM≌△QNF(SAS),∴FQ=CM=BC,延长CF到P,使得PF=BF,则△PBF是等边三角形,∴∠PBC+∠PCB=∠PCB+∠FCM=120°,∴∠PFQ=∠FCM=∠PBC,∵PB=PF,∴△PFQ≌△PBC(SAS),∴PQ=PC,∠CPB=∠QPF=60°,∴△PCQ是等边三角形,∴BF+CF=PC=QC=2CN.13.如图1,点A和点B分别在y轴正半轴和x轴正半轴上,且OA=OB,点C和点D分别在第三象限和第二象限上,且OC⊥OD,OC=OD,点C的坐标为(m,n),且满足(m﹣2n)2+|n+2|=0.(1)求点C坐标;(2)求证:AC=BD,AC⊥BD;(3)求∠BEO度数;(4)如图2,点P在OA上,点Q在OB上且OP=OQ,直线ON⊥BP,交AB于点N,MN⊥AQ交BP延长线于点M,请猜想ON,MN,BM的数量关系并证明.解:(1)∵(m﹣2n)2+|n+2|=0又∵(m﹣2n)2≥0,|n+2|≥0,∴n=﹣2,m=﹣4,∴点C坐标为(﹣4,﹣2);(2)如图1中,作OH⊥BD于H,OF⊥AC于F.∵OA=OB,OD=OC,∠AOB=∠COD=90°,∴∠BOD=∠AOC,∴△BOD≌△AOC(SAS),∴BD=AC,∴HO=OF(全等三角形对应边上的高相等),∴OE平分∠BEC,∵△BOD≌△AOC,∴∠OBD=∠OAC,设BD交y轴于点R,则∠ARE=∠BRO,∴∠AEB=∠BOA=90°,即AC⊥BD;(3)由(2)知,AC⊥BD,则∠FEH=90°,∴∠OHE=∠OFE=∠FEH=90°,故四边形OHEF为矩形,而HO=OF,故四边形OHEF为正方形,而OE为该正方形的对角线,∴∠BEO=45°;(4)结论:BM=MN+ON.理由:如图2中,过点B作BH∥y轴交MN的延长线于H.∵OQ=OP,OA=OB,∠AOQ=∠BOP=90°,∴△AOQ≌△BOP(SAS),∴∠OBP=∠OAQ,∵∠OBA=∠OAB=45°,∴∠ABP=∠BAQ,∵NM⊥AQ,BM⊥ON,∴∠ANM+∠BAQ=90°,∠BNO+∠ABP=90°,∴∠ANM=∠BNO=∠HNB,∵∠HBN=∠OBN=45°,BN=BN,∴△BNH≌△BNO(ASA),∴HN=NO,∠H=∠BON,∵∠HBM+∠MBO=90°,∠BON+∠MBO=90°,∴∠HBM=∠BON=∠H,∴MH=MB,∴BM=MN+NH=MN+ON.14.如图所示:△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B 在y轴上(1)如图1所示,若C的坐标是(2,0),点A的坐标是(﹣2,﹣2),求:点B的坐标;(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由;(3)如图3角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①为定值;②为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.解:(1)过点A作AD垂直OC于D.∵∠DAC+∠ACD=90°,∠ACD+∠BCD=90°,∴∠BCD=∠DAC,在△ADC和△COB中,,∴△ADC≌△COB(AAS),∴AD=OC,CD=OB,∴点B坐标为(0,4);(2)延长BC,AE交于点F,∵AC=BC,AC⊥BC,∴∠BAC=∠ABC=45°,∵BD平分∠ABC,∴∠COD=22.5°,∠DAE=90°﹣∠ABD﹣∠BAD=22.5°,在△ACF和△BCD中,,∴△ACF≌△BCD(ASA),∴AF=BD,在△ABE和△FBE中,,∴△ABE≌△FBE(ASA),∴AE=EF,∴BD=2AE;(3)作AE⊥OC,则AF=OE,∵∠CBO+∠OCB=90°,∠OCB+∠ACO=90°,∴∠ACO=∠CBO,在△BCO和△ACE中,,∴△BCO≌△ACE(AAS),∴CE=OB,∴OB+AF=OC.∴=1.。

中考必考几何模型(猿辅导)最新讲义截长补短辅助线模型模型:截长补短如图①,若证明线段AB、CD、EF之间存在EF=AB+CD,可以考虑截长补短法.截长法:如图②,在EF上截取EG=AB,再证明GF=CD即可.补短法:如图③,延长AB至H点,使BH=CD,再证明AH=EF即可.模型分析截长补短的方法适用于求证线段的和差倍分关系. 截长,指在长线端中截取一段等于已知的线段;补短,指将一条短线端延长,延长部分等于已知线段. 该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程.模型实例例1:如图,已知在△ABC中,∠C=2∠B,∠1=∠2 .求证:AB=AC+CD .证法一,截长法:如图①,在AB上取一点E,使AE=AC,连接DE.∵AE=AC,∠1=∠2,AD=AD,∴△ACD≌△AED ,∴CD=DE,∠C=∠3 .∵∠C=2∠B,∴∠3=2∠B=∠4+∠B ,∴∠4=∠B ,∴DE=BE ,∴CD=BE.∵AB=AE+BE,∴AB=AC+CD .证法二,补短法:如图②,延长AC到点E,使CE=CD,连接DE .∵CE=CD,∴∠4=∠E .∵∠3=∠4+∠E,∴∠3=2∠E .∵∠3=2∠B,∴∠E=∠B .∵∠1=∠2,AD=AD,∴△EAD≌△BAD,∴AE=AB.又∵AE=AC+CE,∴∴AB=AC+CD .例2:如图,已知OD平分∠AOB,DC⊥OA于点C,∠A=∠GBD . 求证:AO+BO=2CO .证明:在线段AO上取一点E,使CE=AC,连接DE .∵CD=CD,DC⊥OA,∴△ACD≌△ECD,∴∠A=∠CED .∵∠A=∠GBD ,∴∠CED=∠GBD ,∴1800-∠CED=1800-∠GBD ,∴∠OED=∠OBD .∵OD平分∠AOB,∴∠AOD=∠BOD .∵OD=OD,∴△OED≌△OBD ,∴OB=OE,∴AO+BO=AO+OE=OE+2CE+OE=OE+CE+OE+CE=2(CE+OE)=2CO .跟踪练习1. 如图,在△ABC中,∠BAC=600,AD是∠BAC的平分线,且AC=AB+BD .求∠ABC 的度数 .【答案】证法一:补短延长AB 到点E ,使BE =BD . 在△BDE 中, ∵BE =BD ,∴∠E =∠BDE , ∴∠ABC =∠BDE +∠E =2∠E . 又∵AC =AB +BD ,∴AC =AB +BE ,∴AC =AE .∵AD 是∠BAC 的平分线,∠BAC =600, ∴∠EAD =∠CAD =600÷2=300 . ∵AD =AD ,∴△AED ≌△ACD ,∴∠E =∠C . ∵∠ABC =2∠E ,∴∠ABC =2∠C . ∵∠BAC =600,∴∠ABC +∠C =1800-600=1200,∴32∠ABC =1200,∴∠ABC =800 . 证法二:在AC 上取一点F ,使AF =AB ,连接DF. ∵AD 是∠BAC 的平分线, ∴∠BAD =∠FAD . ∵AD =AD ,∴△BAD ≌△FAD ,∴∠B =∠AFD ,BD =FD .∵AC =AB +BD ,AC =AF +FC ∴FD =FC ,∴∠FDC =∠C . ∵∠AFD =∠FDC +∠C , ∴∠B =∠FDC +∠C =2∠C . ∵∠BAC +∠B +∠C =1800, ∴32∠ABC =1200,∴∠ABC =800 .2. 如图,在△ABC 中,∠ABC =600,AD 、CE 分别平分∠BAC 、∠ACB . 求证:AC =AE +CD .【答案】如图,在AC 边上取点F ,使AE =AF ,连接OF . ∵∠ABC =600,∴∠BAC +∠ACB =1800-∠ABC =1200 . ∵AD 、CE 分别平分∠BAC 、∠ACB , ∴∠OAC =∠OAB =2BAC Ð,∠OCA =∠OCB =2ACBÐ, ∴∠AOE =∠COD =∠OAC +∠OCA =2BAC ACB??=600,∴∠AOC=1800-∠AOE=1200 .∵AE=AF,∠EAO=∠FAO,AO=AO,∴△AOE≌△AOF(SAS),∴∠AOF=∠AOE=600,∴∠COF=∠AOC-∠AOF=600,∴∠COF=∠COD .∵CO=CO,CE平分∠ACB,∴△COD≌△COF(ASA),∴CD=CF .∵AC=AF+CF,∴AC=AE+CD,3. 如图,∠ABC+∠BCD=1800,BE、CE分别平分∠ABC、∠DCB .求证:AB+CD=BC .【答案】证法一:截长如图①,在BC上取一点F,使BF=AB,连接EF .∵∠1=∠ABE,BE=BE,∴△ABE≌△FBE,∴∠3=∠4 .∵∠ABC+∠BCD=1800,BE、CE分别平分∠ABC、∠DCB,∴∠1+∠2=12∠ABC+12∠DCB=12×1800=900,∴∠BEC=900,∴∠4+∠5=900,∠3+∠6=900 .∵∠3=∠4 ,∴∠5=∠6 .∵CE=CE,∠2=∠DCE ,∴△CEF≌△CED,∴CF=CD .∵BC=BF+CF,AB=BF,∴AB+CD=BC证法二:补短如图②,延长BA到点F,使BF=BC,连接EF .∵∠1=∠ABE,BE=BE,∴△BEF≌△BEC,∴EF=EC,∠BEC=∠BEF .∵∠ABC+∠BCD=1800,BE、CE分别平分∠ABC、∠DCB,∴∠1+∠2=12∠ABC+12∠DCB=12×1800=900,∴∠BEC=900,∴∠BEF=∠BEC=900,∴∠BEF+∠BEC=1800,∴C、E、F三点共线 .∵AB∥CD,∴∠F=∠FCD .∵EF=EC,∠FEA=∠DEC,∴△AEF≌△DEC,∴AF=CD .∵BF=AB+AF,∴BC=AB+CD .4.如图,在△ABC中,∠ABC=900,AD平分∠BAC交BC于D,∠C=300,BE⊥AD于点E .求证:AC-AB=2BE .【答案】延长BE交AC于点M .∵BE⊥AD,∴∠AEB=∠AEM=900.∵∠3=900-∠1,∠4=900-∠2,∠1=∠2,∴∠3=∠4,∴AB=AM .∵BE⊥AE,∴BM=2BE .∵∠ABC=900,∠C=300,∴∠BAC=600.∵AB=AM,∴∠3=∠4=600,∴∠5=900-∠3=300,∴∠5=∠C,∴CM=BM,∴AC-AB=CM=BM=2BE .5. 如图,Rt△ACB中,A=BC,AD平分∠BAC交BC于点D,CE⊥AD交AD于点F,交AB于点E .求证:AD=2DF+CE .【答案】在AD上取一点G,使AG=CE,连接CG .∵CE⊥AD,∴∠AFC=900,∠1+∠ACF=900.∵∠2+∠ACF=900,∴∠1=∠2 .∵AC=BC,AG=CE,∴△ACG≌△CBE,∴∠3=∠B=450,∴∠2+∠4=900-∠3=450.∵∠2=∠1=12∠BAC=22.50,∴∠4=450-∠2=22.50,∴∠4=∠2=22.50.又∵CF=CF,DG⊥CF,∴△CDF≌△CGF,∴DF=GF .∵AD=AG+DG,∴AD=CE+2DF .6. 如图,五边形ABCDE中,AB=AE,BC+DE=CD,∠B+∠E=1800.求证:AD平分∠CDE.【答案】如图,延长CB到点F,使BF=DE,连接AF、AC .∵∠1+∠2=1800,∠E+∠1=1800,∴∠2=∠E .∵AB=AE,∠2=∠E,BF=DE,∴△ABF≌△AED,∴∠F=∠4,AF=AD .∵BC+DE=CD,∴BC+BF=CD,即FC=CD .又∵AC=AC,∴△ACF≌△ACD,∴∠F=∠3 .∵∠F=∠4,∴∠3=∠4,∴AD平分∠CDE .。

全等三角形模型——截长补短与倍长中线截长补短截长:即在一条较长的线段上截取一段较短的线段在线段AB 上截取AD AC=补短:即在较短的线段上补一段线段使其和较长的线段相等延长AC ,使得AD AB =1.ABC D 中,AD 是BAC Ð的平分线,且AB AC CD =+.若60BCA Ð=°,则ABC Ð的大小为( )A .30°B .60°C .80°D .100°【分析】可在AB 上取AC AC ¢=,则由题中条件可得BC C D ¢=¢,即2C AC D B Ð=Т=Ð,再由三角形的外角性质即可求得B Ð的大小.【解答】解:如图,在AB 上取AC AC ¢=,AD Q 是角平分线,DAC DAC ¢\Ð=Ð,ACD \D @△()AC D SAS ¢,CD C D ¢\=,又AB AC CD =+Q ,AB AC C B ¢¢=+,BC C D \¢=¢,DCBAAB CD260C AC D B ¢\Ð=Ð=Ð=°,30B \Ð=°.故选:A .2.阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.(1)请完成下题的证明过程:如图1,在ABC D 中,2B C Ð=Ð,AD 平分BAC Ð.求证:AB BD AC +=.证明:在AC 上截取AE AB =,连接DE(2)如图2,//AD BC ,EA ,EB 分别平分DAB Ð,CBA Ð,CD 过点E ,求证:AB AD BC =+.【分析】(1)在AC 上截取AE AB =,连接DE ,证明ABD AED D @D ,得到B AED Ð=Ð,再证明ED EC =即可;(2)由等腰三角形的性质知AE FE =,再证明ADE FCE D @D 即可解决本题.【解答】证明:在AC 上截取AE AB =,连接DE ,如图1:AD Q 平分BAC Ð,BAD DAC \Ð=Ð,在ABD D 和AED D 中,AE AB BAD DAC AD AD =ìïÐ=Ðíï=î,()ABD AED SAS \D @D ,B AED \Ð=Ð,BD DE =,又2BC Ð=Ð,2AED C \Ð=Ð,而2AED C EDC C Ð=Ð+Ð=Ð,C EDC \Ð=Ð,DE CE \=,AB BD AE CE AC \+=+=;(2)延长AE 、BC 交于F ,AB BF =Q ,BE 平分ABF Ð,AE EF \=,在ADE D 和FCE D 中,DAE F AE EFAED CEF Ð=Ðìï=íïÐ=Ðî,()ADE FCE ASA \D @D ,AD CF \=,AB BF BC CF BC AD \==+=+.3.如图,在ABC D 中,AD 平分BAC Ð交BC 于D ,在AB 上截取AE AC =.(1)求证:ADE ADC D @D ;(2)若6AB =,5BC =,4AC =,求BDE D的周长.【分析】(1)根据SAS 证明ADE ADC D @D 即可;(2)根据全等三角形的性质和线段之间的关系进行解答即可.【解答】证明:(1)AD Q 平分BAC Ð,EAD CDA \Ð=Ð,在ADE D 与ADC D 中,AE AC EAD CDA AD AD =ìïÐ=Ðíï=î,()ADE ADC SAS \D @D ,(2)ADE ADC D @D Q ,ED DC \=,BDE \D 的周长6457BE BD DE AB AE BC DC DC AB AC BC DC DC AB AC BC =++=-+-+=-+-+=-+=-+=4.(2020秋•武昌区期中)如图,ABC D 中,60ABC Ð=°,AD 、CE 分别平分BAC Ð、ACB Ð,AD 、CE 相交于点P(1)求CPD Ð的度数;(2)若3AE =,7CD =,求线段AC 的长.【分析】(1)利用60ABC Ð=°,AD 、CE 分别平分BAC Ð,ACB Ð,即可得出答案;(2)由题中条件可得APE APF D @D ,进而得出APE APF Ð=Ð,通过角之间的转化可得出CPF CPD D @D ,进而可得出线段之间的关系,即可得出结论.【解答】解:(1)60ABC Ð=°Q ,AD 、CE 分别平分BAC Ð,ACB Ð,120BAC BCA \Ð+Ð=°,1()602PAC PCA BAC BCA Ð+Ð=Ð+Ð=°,120APC \Ð=°,60CPD \Ð=°.(2)如图,在AC 上截取AF AE =,连接PF .AD Q 平分BAC Ð,BAD CAD \Ð=Ð,在APE D 和APF D 中AE AF EAP FAP AP AP =ìïÐ=Ðíï=î,()APE APF SAS \D @D ,APE APF \Ð=Ð,120APC Ð=°Q ,60APE \Ð=°,60APF CPD CPF \Ð=Ð=°=Ð,在CPF D 和CPD D 中,FPC DPC CP CPFCP DCP Ð=Ðìï=íïÐ=Ðî,()CPF CPD ASA \D @D CF CD \=,3710AC AF CF AE CD \=+=+=+=.5.如图,在ABC D 中,60BAC Ð=°,AD 是BAC Ð的平分线,且AC AB BD =+,求ABC Ð的度数.【分析】在AC上截取AE AB=,根据角平分线的定义可得BAD CADÐ=Ð,然后利用“边角边”证明ABDD和AEDD全等,根据全等三角形对应边相等可得BD DE=,全等三角形对应角相等可得B AEDÐ=Ð,再求出CE BD=,从而得到CE DE=,根据等边对等角可得C CDEÐ=Ð,根据三角形的一个外角等于与它不相邻的两个内角的和可得2AED CÐ=Ð,然后根据三角形的内角和定理列方程求出CÐ,即可得解.【解答】解:如图,在AC上截取AE AB=,ADQ平分BACÐ,BAD CAD\Ð=Ð,在ABDD和AEDD中,AE ABBAD CAD AD AD=ìïÐ=Ðíï=î,()ABD AED SAS\D@D,BD DE\=,B AEDÐ=Ð,AC AE CE=+Q,AC AB BD=+,CE BD\=,CE DE\=,C CDE\Ð=Ð,即2B CÐ=Ð,在ABCD中,180BAC B CÐ+Ð+Ð=°,602180C C\°+Ð+Ð=°,解得40CÐ=°,24080ABC\Ð=´°=°.6.如图,五边形ABCDE 中,AB AE =,BC DE CD +=,120BAE BCD Ð=Ð=°,180ABC AED Ð+Ð=°,连接AD .求证:AD 平分CDE Ð.【分析】连接AC ,将ABC D 绕A 点旋转120°到AEF D ,由AB AE =,120BAE Ð=°,得到AB 与AE 重合,并且AC AF =,又由180ABC AED Ð+Ð=°,得到180AEF AED Ð+Ð=°,即D ,E ,F 在一条直线上,而BC DE CD +=,得CD DF =,则易证ACD AFD D @D ,于是ADC ADF Ð=Ð.【解答】证明:如图,连接AC ,将ABC D 绕A 点旋转120°到AEF D ,AB AE =Q ,120BAE Ð=°,AB \与AE 重合,并且AC AF =,又180ABC AED Ð+Ð=°Q ,而ABC AEF Ð=Ð,180AEF AED Ð+Ð=°Q ,D \,E ,F 在一条直线上,而BC EF =,BC DE CD +=,CD DF \=,又AC AF =Q ,ACD AFD \D @D ,ADC ADF \Ð=Ð,即AD 平分CDE Ð.7.已知:如图,在ABC D 中,D 是BA 延长线上一点,AE 是DAC Ð的平分线,P 是AE 上的一点(点P 不与点A 重合),连接PB ,PC .通过观察,测量,猜想PB PC +与AB AC +之间的大小关系,并加以证明.【分析】根据全等三角形的判定与性质,可得FP CP =,根据三角形的两边之和大于第三边,可得答案.【解答】解:PB PC AB AC +>+,理由如下:在BA 的延长线上截取AF AC =,连接PF ,在FAP D 和CAP D 中,AF AC FAP CAP AP AP =ìïÐ=Ðíï=î,()FAP CAP SAS \D @D ,FP CP \=.在FPB D 中,FP BP FA AB +>+,即PB PC AB AC +>+.8.已知ABC D 中,AB AC =,BE 平分ABC Ð交边AC 于E .(1)如图(1),当108BAC Ð=°时,证明:BC AB CE =+;(2)如图(2),当100BAC Ð=°时,(1)中的结论还成立吗?若不成立,是否有其他两条线段之和等于BC,若有请写出结论并完成证明.【分析】(1)如图1中,在BC 上截取BD BA =.只要证明BEA BED D @D ,CE CD =即可解决问题;(2)结论:BC BE AE =+.如图2中,在BA 、BC 上分别截取BF BE =,BH BE =.则EBH EBF D @D ,再证明EA EH EF CF ===即可解决问题;【解答】解:(1)如图1中,在BC 上截取BD BA =.BA BD =Q ,EBA EBD Ð=Ð,BE BE =,BEA BED \D @D ,BA BD \=,108A BDE Ð=Ð=°,AB AC =Q ,36C ABC \Ð=Ð=°,72EDC Ð=°,72CED \Ð=°,CE CD \=,BC BD CD AB CE \=+=+.(2)结论:BC BE AE =+.理由:如图2中,在BA 、BC 上分别截取BF BE =,BH BE =.则EBH EBF D @D ,EF EH \=,100BAC Ð=°Q ,AB AC =,40ABC C \Ð=Ð=°,20EBA EBC \Ð=Ð=°,80BFE H EAH \Ð=Ð=Ð=°,AE EH \=,BFE C FEC Ð=Ð+ÐQ ,40CEF C \Ð=Ð=°,EF CF \=,BC BF CF BE AE \=+=+.9.(2020秋•建华区期末)阅读下面文字并填空:数学习题课上李老师出了这样一道题:“如图1,在ABC D 中,AD 平分BAC Ð,2B C Ð=Ð.求证:AB BD AC +=.”李老师给出了如下简要分析:要证AB BD AC +=,就是要证线段的和差问题,所以有两个方法:方法一:“截长法”.如图2,在AC 上截取AE AB =,连接DE ,只要证BD = EC 即可,这就将证明线段和差问题 为证明线段相等问题,只要证出△ @△ ,得出B AED Ð=Ð及BD = ,再证出Ð = ,进而得出ED EC =,则结论成立.此种证法的基础是“已知AD 平分BAC Ð,将ABD D 沿直线AD 对折,使点B 落在AC 边上的点E 处”成为可能.方法二:“补短法”.如图3,延长AB 至点F ,使BF BD =.只要证AF AC =即可,此时先证Ð C =Ð,再证出△ @△ ,则结论成立.“截长补短法”是我们今后证明线段或角的“和差倍分”问题常用的方法.【分析】方法一、如图2,在AC 上截取AE AB =,由“SAS ”可证ABD AED D @D ,可得B AED Ð=Ð,BD DE =,由角的数量关系可求DE CE =,即可求解;方法二、如图3,延长AB 至点F ,使BF BD =,由“AAS ”可证AFD ACD D @D ,可得AC AF =,可得结论.【解答】解:方法一、在AC 上截取AE AB =,连接DE ,如图2:AD Q 平分BAC Ð,BAD DAC \Ð=Ð,在ABD D 和AED D 中,AE AB BAD DAC AD AD =ìïÐ=Ðíï=î,()ABD AED SAS \D @D ,B AED \Ð=Ð,BD DE =,又2B C Ð=ÐQ ,2AED C \Ð=Ð,而2AED C EDC C Ð=Ð+Ð=Ð,C EDC \Ð=Ð,DE CE \=,AB BD AE CE AC \+=+=,故答案为:EC ,转化,ABD ,AED ,DE ,EDC ,C Ð;方法二、如图3,延长AB 至点F ,使BF BD =,F BDF \Ð=Ð,2ABD F BDF F \Ð=Ð+Ð=Ð,2ABD C Ð=ÐQ ,F C \Ð=Ð,在AFD D 和ACD D 中,FAD CAD F CAD AD Ð=ÐìïÐ=Ðíï=î,()AFD ACD AAS \D @D ,AC AF \=,AC AB BF AB BD \=+=+,故答案为F ,AFD ,ACD .倍长中线倍长中线:即延长三角形的中线,使得延长后的线段是原中线的两倍.其目的是构造一对对顶的全等三角形;其本质是转移边和角.其中BD CD =,延长AD 使得DE AD =,则BDE CDA △≌△.10.三角形ABC 中,AD 是中线,且4AB =,6AC =,求AD 的取值范围是 .【分析】延长AD 到E ,使AD DE =,连接BE ,证ADC EDB D @D ,推出8AC BE ==,在ABE D 中,根据三角形三边关系定理得出AB BE AE AB BE -<<+,代入求出即可.【解答】解:延长AD 到E ,使AD DE =,连接BE ,AD Q 是BC 边上的中线,BD CD \=,在ADC D 和EDB D 中,Q AD DE ADC EDB DC BD =ìïÐ=Ðíï=î,()ADC EDB SAS \D @D ,4AC BE \==,在ABE D 中,AB BE AE AB BE -<<+,64264AD \-<<+,15AD \<<,故答案为:15AD <<.11.(2021春•碑林区校级期中)问题背景:课外兴趣小组活动时,老师提出了如下问题:如图1,ABCD 中,若4AB =,3AC =,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下ED ABC的解决方法:延长AD 到点E ,使DE AD =,则得到ADC EDB D @D ,小明证明BED CAD D @D 用到的判定定理是: (用字母表示);问题解决:小明发现:解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.请写出小明解决问题的完整过程;拓展应用:以ABC D 的边AB ,AC 为边向外作ABE D 和ACD D ,AB AE =,AC AD =,90BAE CAD Ð=Ð=°,M 是BC 中点,连接AM ,DE .当3AM =时,求DE 的长.【分析】问题背景:先判断出BD CD =,由对顶角相等BDE CDA Ð=Ð,进而得出()ADC EDB SAS D @D ;问题解决:先证明()ADC EDB SAS D @D ,得出3BE AC ==,最后用三角形三边关系即可得出结论;拓展应用:如图2,延长AM 到N ,使得MN AM =,连接BN ,同(1)的方法得出()BMN CMA SAS D @D ,则BN AC =,进而判断出ABN EAD Ð=Ð,进而判断出ABN EAD D @D ,得出AN ED =,即可求解.【解答】解:问题背景:如图1,延长AD 到点E ,使DE AD =,连接BE ,AD Q 是ABC D 的中线,BD CD \=,在ADC D 和EDB D 中,AD ED CDA BDE CD BD =ìïÐ=Ðíï=î,()ADC EDB SAS \D @D ,故答案为:SAS;问题解决:如图1,延长AD 到点E ,使DE AD =,连接BE ,AD Q 是ABC D 的中线,BD CD \=,在ADC EDB D @D 中,AD ED CDA BDE CD BD =ìïÐ=Ðíï=î,()ADC EDB SAS \D @D ,BE AC \=,在ABE D 中,AB BE AE AB BE -<<+,4AB =Q ,3AC =,4343AE \-<<+,即17AE <<,DE AD =Q ,12AD AE \=,\1722AD <<;拓展应用:如图2,延长AM 到N ,使得MN AM =,连接BN ,由问题背景知,()BMN CMA SAS D @D ,BN AC \=,CAM BNM Ð=Ð,AC AD =Q ,//AC BN ,BN AD \=,//AC BN Q ,180BAC ABN \Ð+Ð=°,90BAE CAD Ð=Ð=°Q ,180BAC EAD \Ð+Ð=°,ABN EAD \Ð=Ð,在ABN D 和EAD D 中,AB EA ABN EAD BN AD =ìïÐ=Ðíï=î,()ABN EAD SAS \D @D ,AN DE \=,MN AM =Q ,2DE AN AM \==,3AM =Q ,6DE \=.12.如图,ABC D 中,D 为BC 的中点.(1)求证:2AB AC AD +>;(2)若5AB =,3AC =,求AD 的取值范围.【分析】(1)再延长AD 至E ,使DE AD =,构造ADC EDB D @D ,再根据三角形的三边关系可得2AB AC AD +>;(2)直接利用三角形的三边关系:三角形两边之和大于第三边,三角形的两边差小于第三边可得53253AD -<<+,再计算即可.【解答】(1)证明:由BD CD =,再延长AD 至E ,使DE AD =,D Q 为BC 的中点,DB CD \=,在ADC D 和EDB D 中AD DE ADC BDE DB CD =ìïÐ=Ðíï=î,BE AC \=,在ABE D 中,AB BE AE +>Q ,2AB AC AD \+>;(2)5AB =Q ,3AC =,53253AD \-<<+,14AD \<<.13.如图,平面直角坐标系中,A 为y 轴正半轴上一点,B 、C 分别为x 轴负半轴,x 轴正半轴上的点,AB AD =,AC AE =,90BAD CAE Ð=Ð=°,连DE .如图,F 为BC 的中点,求证:2DE AF =.【分析】延长AF 至点N ,使FN AF =,连接BN ,证明BFN CFA D @D ,根据全等三角形的性质得到BN AC =,FBN FCA Ð=Ð,证明ABN DAE D @D ,根据全等三角形的性质证明;【解答】证明:延长AF 至点N ,使FN AF =,连接BN ,在BFN D 和CFA D 中,FB FC BFN CFA FN AF =ìïÐ=Ðíï=î,BN AC \=,FBN FCA Ð=Ð,BN AE \=,ABN DAE Ð=Ð,在ABN D 和DAE D 中,AB AD ABN DAE BN AE =ìïÐ=Ðíï=î,()ABN DAE SAS \D @D ,AN DE \=,2DE AF \=.14.如图,AD 是ABC D 的边BC 上的中线,CD AB =,AE 是ABD D 的边BD 上的中线.求证:2AC AE =.【分析】延长AE 至点F ,使EF AE =,连接DF ,由SAS 证得ABE FDE D @D ,得出DF AB CD ==,EDF B Ð=Ð,易证AB BD =,得出ADB BAD Ð=Ð,证明ADC ADF Ð=Ð,由SAS 证得ADF ADC D @D ,即可得出结论.【解答】证明:延长AE 至点F ,使EF AE =,连接DF ,如图所示:AE Q 是ABD D 的边BD 上的中线,BE DE \=,在ABE D 与FDE D 中,AE EF AEB FED BE DE =ìïÐ=Ðíï=î,()ABE FDE SAS \D @D ,DF AB CD \==,EDF B Ð=Ð,AD Q 是ABC D 的边BC 上的中线,CD AB =,AB BD \=,ADB BAD \Ð=Ð,ADC B BAD BDA EDF ADF \Ð=Ð+Ð=Ð+Ð=Ð,在ADF D 与ADC D 中,AD AD ADF ADC DF DC =ìïÐ=Ðíï=î,()ADF ADC SAS \D @D ,2AC AF AE \==.15.如图,在ABC D 中,D ,E 是AB 边上的两点,AD EB =,CF 是AB 边上的中线,则求证AC BC CD CE +>+.【分析】如图,延长CF 至H ,使FH CF =,连接AH ,DH ,延长CD 交AH 于点G ,通过证明AFH BFC D @D ,BCE AHD D @D ,可得BC AH =,CE DH =,利用三角形的三边关系可求解.【解答】证明:如图,延长CF 至H ,使FH CF =,连接AH ,DH ,延长CD 交AH 于点G,Q是AB边上的中线,CF\=,且CFB AFHAF BF=,Ð=Ð,CF FH()\D@DAFH BFC SAS=,Ð=Ð,且AD BE\=,CBE HADBC AH\D@D()BCE AHD SAS\=,CE DH在AGC+>+,D中,AC AG DC DG在GDH+>,D中,DG GH DHAC AG DG GH DC DG DH\+++>++,\+>+,AC AH DC DH\+>+.AC BC CD CE16.如图1,ABCÐ=Ð.D中,CD为ABCD的中线,点E在CD上,且AED BCD(1)求证:AE BC=.(2)如图2,连接BE,若2CBEÐ的度数为 (直接写出结果),Ð=°,则ACDAB AC DE==,14【分析】(1)如图1,延长CD到F,使DF CDD@D,可得=,连接AF,由“SAS”可证ADF BDCAF BC=,F BCDÐ=Ð,由等腰三角形的性质可得结论;(2)由等腰三角形的性质可得DEB DBEÐ=Ð,可得14DCB DEBÐ=Ð-°,14ACB ABC DEBÐ=Ð=Ð+°,即可求解.【解答】证明:(1)如图1,延长CD到F,使DF CD=,连接AF,CDQ为ABCD的中线,AD BD\=,且ADF BDCÐ=Ð,且CD DF=,()ADF BDC SAS\D@D,AF BC\=,F BCDÐ=Ð,AED BCDÐ=ÐQ,AED F\Ð=Ð,AE AF\=,AE BC\=;(2)12DE AB=Q,CD为ABCD的中线,DE AD DB\==,DEB DBE\Ð=Ð,14 ABC DBE CBE DEB\Ð=Ð+Ð=Ð+°,DEB DCB CBEÐ=Ð+ÐQ,14DCB DEB\Ð=Ð-°,AC AB=Q,14ACB ABC DEB\Ð=Ð=Ð+°28ACD ACB DCB\=Ð-Ð=°,故答案为:28°.17.如图,ABC D 中,点D 是BC 中点,连接AD 并延长到点E ,连接BE .(1)若要使ACD EBD D @D ,应添上条件: ;(2)证明上题:(3)在ABC D 中,若5AB =.3AC =,可以求得BC 边上的中线AD 的取值范围4AD <.请看解题过程:由ACD EBD D @D 得:AD ED =,3BE AC ==,因此AE AB BE <+,即8AE <,而12AD AE =,则4AD <请参考上述解题方法,可求得AD m >,则m 的值为 .(4)证明:直角三角形斜边上的中线等于斜边的一半.(提示:画出图形,写出已知,求证,并加以证明)【分析】(1)根据“边角边”求证三角形全等的方法可以添加条件AD DE =;(2)易证BD CD =,根据“边角边”求证三角形全等的方法即可解题;(3)根据三角形三边关系即可解题;(4)已知RT ABC D 中90BAC Ð=°,AD 是斜边中线,求证12AD BC =;证明:延长AD 到点E 使得DE AD =,连接BE ,易证ACD EBD D @D ,可得C DBE Ð=Ð,AC BE =,即可证明BAC ABE D @D ,可得BC AE =,即可解题.【解答】解:(1)应添上条件:AD DE =,故答案为AD DE =;(2)Q 点D 是BC 中点,BD CD \=,Q 在ACD D 和EBD D 中,BD CD ADC BDE AD DE =ìïÐ=Ðíï=î,()ACD EBD SAS \D @D ;(3)Q 三角形两边之差小于第三边,AE AB BE \>-,即2AE >,12AD AE =Q ,1AD \>,故答案为 1;(4)已知RT ABC D 中90BAC Ð=°,AD 是斜边中线,求证12AD BC =,证明:延长AD 到点E 使得DE AD =,连接BE ,Q 点D 是BC 中点,BD CD \=,Q 在ACD D 和EBD D 中,BD CD ADC BDE AD DE =ìïÐ=Ðíï=î,()ACD EBD SAS \D @D ;C DBE \Ð=Ð,AC BE =,90ABC C Ð+Ð=°Q ,90ABC DBE \Ð+Ð=°,即90ABE Ð=°,Q 在BAC D 和ABE D 中,90AB BA ABE BAC AC BE =ìïÐ=Ð=°íï=î,()BAC ABE SAS \D @D ;BC AE \=,12AD BC \=.。
初中几何模型5(截长补短)例题:如图,△ABC中,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于点N,求证:AE=CN+EN角度1:直接截长法证明:在AE上截取一段AF等于短边CN,连接CF,再证EF=EN即可,先证△AFC≌△CNB(SAS),再证△CFE≌△BNE(SAS).思考:这里能否在EA上截取一段EF等于短边等于EN,为什么?你试一试角度2:间接截长法证明:作∠ACB的平分线CF交AE于点F,先证△ACF≌△CBN(ASA),再证△CFE≌△BNE(SAS),此法本质上是通过全等对应边相等间接地在AE上截取AF=CN.角度3:直接补短法证明:延长CN至点F,使CF=AE,再证EN=NF,先证△CFB≌△AEC(SAS),再证△BNF≌△BNE(SAS).思考:这里能否直接延长CN至点F,使得NF=NE,为什么?你试一试角度4:间接补短法证明:作BF⊥BC交CN的延长线于F,先通过△CFB≌△AEC(ASA)证CF=AE,再通过△BNF≌△BNE(SAS)证NF=NE.此法本质上是间接地在CN后面补上NF=EN.1、如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.(1)如图1,连接EC,求证:△EBC是等边三角形;(2)如图2,点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG 交DE延长线于点G. 求证:AD=DG+MD;(3)如图3,点M是线段AD上的一点,以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G. 探究MD,DG与AD数量之间的关系.2.如图,在等腰R t△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角形内部作R t△ABE,且∠AEB=90°,连接EO.求证:(1)∠OAE=∠OBE;(2)AE=BE+2OE.3. 如图,在ABC ∆中,︒=∠45ACB ,AD 是ABC ∆的BC 边上的高,在AD 上取点E ,使得DB DE =,连接CE 并延长,交边AB 于点F ,连接DF . 求证:(1)CE AB =;(2)FD EF BF 2=+.4.如图所示,△ABC 是边长为1的正三角形,△BDC 是顶角为120°的等腰三角形,以D 为顶点作一个60°的∠MDN ,点M 、N 分别在AB 、AC 上,则△AMN 的周长多少?5.如图,在△ABC 中,AB=AC ,∠ABC=40°,BD 是∠ABC 的平分线,延长BD 至E ,是DE=AD ,则∠ECA 的度数为多少?6、如图, ABCD 中,AB ∥CD ,AD=DC=BC ,∠DAB=60°,E 是对角线AC 延长线上一点,F 是AD 延长线上的一点,且EB ⊥AB ,EF ⊥AF .(1)当CE=1时,求△BCE 的面积;(2)求证:BD=EF+CE .7、如图,△ABC 中,∠ABC=45°,过点C 作CD ⊥AB 于点D ,过点B 作BM ⊥AC 于点M ,BM 交CD 于点E ,且点E 为CD 的中点,连接MD ,过点D 作ND ⊥MD 于点D ,DN 交BM 于点N .的周长; 2)求证:NE -ME=CM .8、如图,在△ABC 中,∠ACB=45°,AD 是△ABC 的高,在AD 上取点E ,使得DE=DB ,连接CE 并延长,交边AB 于点F ,连接DF.(1)求证:AB=CE ;(2)求证:BF+EF=2FD.9.在△ABC 中,∠ACB =90°,AC =BC ,过C 作CD ∥AB 交∠ABC 的平分线于点D ,∠ACB 的平分线交BD 于点E 。

第三章截长补短模型截长补短如图①,若证明线段 AB CD EF 之间存在 EF=AB+CD 可以考虑截长补短法。
截长法:如图②,在 EF 上截取EG=AB 再证明 GF=C[即卩可。
补短法:如图③,延长 AB 至H 点,使BH=CD 再证明AH=EF 即卩可。
B © 模型分析截长补短的方法适用于求证线段的和差倍分关系。
截长,指在长线段中截取一段等 于已知线段;补短,指将短线段延长,延长部分等于已知线段。
该类题目中常出现等腰 三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程。
模型实例例1.如图,已知在^ ABC 中,/ C=2/ B, AD 平分/ BAC 交BC 于点D 。
求证:AB=AC+CD例2.如图,已知 OD 平分/ AOB DCL OA 于点C,/ A=/ GBD 求证:AO+BO=2CO.1 HB热搜精练1.如图,在△ ABC中,/ BAC=60 , AD是/ BAC的平分线,且AC=AB+BD 求/ ABC勺度数。
C2 .如图,在△ ABC中,/ ABC=60 , AD CE分别平分/ BAG / ACB 求证:AC=AE+C 。
CD3 .如图,/ ABCf BCD=180 , BE CE分别平分/ ABC / BCD 求证:AB+CD=B。
4 .如图,在△ ABC中,/ ABC=90 , AD平分/ BAC交BC于点D,/ C=30°, BE丄AD于点E。
求证:AC-AB=2BEC5 .如图,Rt△ ABC中, AC=BC AD平分/ BAC交BC于点D, CE!AD交AD于F 点,交AB于点E。
求证:AD=2DF+CE6 .如图,五边形ABCDEK AB=AC BC+DE=C,D/ B+/ E=18O°。
求证:AD平分/ CDEC E。

专题01 全等模型--倍长中线与截长补短全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(倍长中线模型、截长补短模型)进行梳理及对应试题分析,方便掌握。
模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.(注:一般都是原题已经有中线时用,不太会有自己画中线的时候)。
【常见模型及证法】1、基本型:如图1,在三角形ABC 中,AD 为BC 边上的中线.证明思路:延长AD 至点E ,使得AD =DE . 若连结BE ,则BDE CDA ∆≅∆;若连结EC ,则ABD ECD ∆≅∆;2、中点型:如图2,C 为AB 的中点.证明思路:若延长EC 至点F ,使得CF EC =,连结AF ,则BCE ACF ∆≅∆;若延长DC 至点G ,使得CG DC =,连结BG ,则ACD BCG ∆≅∆.3、中点+平行线型:如图3, //AB CD ,点E 为线段AD 的中点.证明思路:延长CE 交AB 于点F (或交BA 延长线于点F ),则EDC EAF ∆≅∆.1.(2022·山东烟台·一模)(1)方法呈现:如图①:在ABC 中,若6AB =,4AC =,点D 为BC 边的中点,求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法:延长AD 到点E 使DE AD =,再连接BE ,可证ACD EBD △≌△,从而把AB 、AC ,2AD 集中在ABE △中,利用三角形三边的关系即可判断中线AD 的取值范围是_______________,这种解决问题的方法我们称为倍长中线法;(2)探究应用:如图②,在ABC 中,点D 是BC 的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,判断BE CF +与EF 的大小关系并证明;(3)问题拓展:如图③,在四边形ABCD 中,//AB CD ,AF 与DC 的延长线交于点F 、点E 是BC 的中点,若AE 是BAF ∠的角平分线.试探究线段AB ,AF ,CF 之间的数量关系,并加以证明.2.(2022·河南南阳·中考模拟)【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:如图,在ABC 中,D 是边BC 的中点,过点C 画直线CE ,使//CE AB ,交AD 的延长线于点E ,求证:AD ED=证明∵//CE AB (已知)∴ABD ECD ∠=∠,BAD CED ∠=∠(两直线平行,内错角相等).在ABD △与ECD 中,∵ABD ECD ∠=∠,BAD CED ∠=∠(已证),BD CD =(已知),∴()A.A.S ABD ECD △△≌,∴AD ED =(全等三角形的对应边相等).(1)【方法应用】如图①,在ABC 中,6AB =,4AC =,则BC 边上的中线AD 长度的取值范围是______.(2)【猜想证明】如图②,在四边形ABCD 中,//AB CD ,点E 是BC 的中点,若AE 是BAD ∠的平分线,试猜想线段AB 、AD 、DC 之间的数量关系,并证明你的猜想;(3)【拓展延伸】如图③,已知//AB CF ,点E 是BC 的中点,点D 在线段AE 上,EDF BAE ∠=∠,若5AB =,2CF =,求出线段DF 的长.3.(2022·河北·中考模拟)倍长中线的思想在丁倍长某条线段(被延长的线段a 要满足两个条件:①线段a 一个端点是图中一条线段b 的中点;②线段a 与这条线段b 不共线),然后进行连接,构造三角形全等,再进一步将某些线段进行等量代换,再证明全等或其他的结论,从而解决问题.【应用举例】如图(1),已知:AD 为ABC ∆的中线,求证:2AB AC AD +>.简证:如图(2),延长AD 到E ,使得DE AD =,连接CE ,易证ABD ECD ∆≅∆,得AB = ,在ACE ∆中,AC CE +> ,2AB AC AD +>.【问题解决】(1)如图(3),在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,求证:AF EF =.(2)如图(4),在ABC ∆中,90,A D ∠=︒是BC 边的中点,E F 、分别在边AB AC 、上,DE DF ⊥,若3,4BE CF ==,求EF 的长.(3)如图(5),AD 是ABC ∆的中线,,AB AE AC AF ==,且90BAE FAC ∠=∠=︒,请直接写出AD 与EF 的数量关系_ 及位置关系_ .模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。

截长补短模型证三角形全等一、截长补短法:包含截长法和补短法,即a=b+c 和a=b-c截长补短法适用于求证线段的和差倍分关系。
截长,指在长线段中截取一段等于已知线段;补短,指将短线段延长,延长部分等于已知线段。
当出现等腰三角形、角平分线等关键词句时,常采用截长补短法构造全等三角形来完成证明过程。
如图①,若证明线段AB 、CD 、EF 之间存在EF =AB +CD ,可以考虑截长补短法。
截长法:如图②,在EF 上截取EG =AB ,再证明GF =CD 即可。
补短法:如图③,延长AB 至H 点,使BH =CD ,再证明AH =EF 即可。
二、模型实例例1:在△ABC 中,∠C=2∠B ,∠1=∠2,试说明AB=AC+CD .例2:如图1,△ABC 是正三角形,△BDC 是等腰三角形,BD=CD ,∠BDC=120°,以D 为顶点作一个60°角,角的两边分别交AB 、AC 边于M 、N 两点,连接MN . (1)探究BM 、MN 、NC 之间的关系,并说明理由; (2)若△ABC 的边长为2,求△AMN 的周长;(3)若点M 、N 分别是线段AB 、CA 延长线上的点,其他条件不变,此时(1)中的结论是否还成立,在图2中画出图形,并说明理由.例3:已知:如图,ABCD 是正方形,∠FAD=∠FAE .求证:BE+DF=AE .32HA B FE1G E F D C B A截长补短模型演练题1、如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于D,CE⊥BD的延长线于点E.求证: CE=BD.2、已知,如图AB//CD,BE、CE分别是∠ABC、∠BCD的平分线,点E在AD上,求证:BC=AB+CD。
3、如图,五边形ABCDE中,AB=AE,BC+DE=CD,∠BAE=∠BCD=120°,∠ABC+∠AED=180°,连接AD.求证:AD平分∠CDE.。
FA B C12几何模型01——截长补短法在平面几何当中,证明一条线段与线段的和、差、倍数(特别是2倍)相等,其他常规方法不好用的时候,“截长补短法”是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗! 例1.已知:如图,在△ABC 中,△1=△2,△B =2△C .求证:AC =AB +BD . 分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AB 至E 使BE =BD ,或在AC 上截取AF =AB .证明:补短法:证明:如图,延长AB 到E ,使BE =BD ,连接DE .∵∵ABD 是∵BDE 的一个外角 ∵∵ABD =∵E +∵BDE ∵BE =BD∵∵E =∵BDE ∵∵ABD =2∵E ∵∵ABD =2∵C ∵∵E =∵C在∵ADE 和∵ADC 中12E C AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∵∵ADE ∵∵ADC (AAS )∵AE =AC ∵AC =AB +BE=AB +BD 截长法:证明:如图,在AC 上截取AF =AB ,连接DF . 在∵ABD 和∵AFD 中12AB AF AD AD =⎧⎪∠=∠⎨⎪=⎩∵∵ABD ∵∵AFD (SAS )∵∵B =∵AFD ,BD =FD ∵∵B =2∵C ∵∵AFD =2∵C∵∵AFD 是∵DFC 的一个外角∵∵AFD =∵C +∵FDC∵∵FDC =∵C ∵DF =FC ∵BD =FC ∵AC =AF +FC =AB +BD练习1.如图,在∵ABC 中,∵BAC =60°,∵ABC =80°,AD 是∵BAC 的平分线.求证:AC =AB +BD .引例:如图,四边形ABCD 中,∵A+∵C=180°E21D CB A 21DCB A AB C D(1)∵B 与∵D 有什么关系? (2)延长AD 至E ,∵B 与∵CDE 有什么关系?例2.已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD . 求证:∠BAP +∠BCP =180°. 分析:证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造. 证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ∴PE =PD ,在Rt △BPE 与Rt △BPD 中,∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD . ∵AB +BC =2BD ,∴AB +BD +DC =BD +BE , ∴AB +DC =BE 即DC =BE -AB =AE . 在Rt △APE 与Rt △CPD 中,∴Rt △APE ≌Rt △CPD (SAS), ∴∠PAE =∠PCD又∵∠BAP +∠PAE =180°. ∴∠BAP +∠BCP =180° 练习2.已知:如图,∵1=∵2,P 为BN 上一点,且PD ∵BC 于点D ,∵A +∵C =180°.求证:BD =AB +CD .21N PD CBA练习3.已知:如图,在四边形ABCD 中,BC >AB ,AD =DC ,∵C =60°,BD 平分∵ABC .求证:BC =AB +AD .练习4.如图,AC 平分∵BAD ,CE ∵AB 于E ,∵B +∵D =180°.求证:AE =AD +BE .练习5.如图,四边形ABCD 中,∵B+∵D=180°,CB=CD ,点E 为AB 上一点,点F 为AD 上一点,∵BCD=2∵ECF ,求证:EF=BE+DFDC BACDB A E87654321FO CDBE A 练习6.如图,四边形ABCD 中,∵B+∵D=180°,CB=CD ,点E 为AB 上一点,点F 为AD 上一点,∵BCD=2∵ECF ,求证:EF=BE -DF例3.已知:如图,在△AB C 中,△ABC =60°,△ABC 的角平分线AD ,CE 交于点O .求证:AC =AE +CD .证明:如图,在AC 上截取AF =AE ,连接OF .∵AD ,CE 为∵ABC 的角平分线 ∵∵1=∵2,∵3=∵4 在∵AEO 和∵AFO 中12AE AF AO AO =⎧⎪∠=∠⎨⎪=⎩∵∵AEO ∵∵AFO (SAS )∵∵5=∵6∵∵ABC =60° ∵∵1+∵2+∵3+∵4=180∵B=18060=120∵∵2+∵3=60∵∵AOC =180°60 =120° ∵∵5=∵6=∵7=∵8=60° 在∵OFC 和∵ODC 中8734OC OC =⎧⎪=⎨⎪=⎩∠∠∠∠ ∵∵OFC ∵∵ODC (ASA )∵CF =CD ∵AC =AF +FC =AE +CD练习7.如图所示,在∆ ABC 是边长为1的正三角形,∆BDC 是顶角为120︒的等腰三角形, ∠ MDN=60°,点M 、N 分别在AB 、AC 上,求的∆AMN 的周长。
截长补短法的20种模型
截长补短法是一种用于数据处理和建模的技术,它可以帮助我们处理数据中的缺失值或者异常值,从而提高模型的准确性和可靠性。
以下是一些常见的截长补短法模型:
1. 线性回归模型。
2. 逻辑回归模型。
3. 决策树模型。
4. 随机森林模型。
5. 支持向量机模型。
6. 朴素贝叶斯模型。
7. K近邻模型。
8. 主成分分析模型。
9. 神经网络模型。
10. 集成学习模型。
11. 贝叶斯网络模型。
12. 马尔可夫模型。
13. 隐马尔可夫模型。
14. 马尔可夫链模型。
15. 马尔可夫决策过程模型。
16. 马尔可夫随机场模型。
17. 因子分析模型。
18. 混合模型。
19. 时间序列模型。
20. 非参数模型。
这些模型涵盖了监督学习、无监督学习、半监督学习和强化学习等多种机器学习方法,可以根据不同的数据特点和建模需求选择合适的模型进行截长补短,以提高建模效果。
在实际应用中,根据数据的特点和问题的复杂程度,可以选择其中的一种或多种模型进行组合使用,以达到更好的建模效果。
同时,还可以根据具体情况对模型进行调参和优化,以进一步提升模型的性能。
模型介绍有一类几何题其命题主要是证明三条线段长度的“和”或"差”及其比例关系.这一类题目一般可以采取“截长”或“补短”的方法来进行求解.所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系.所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等.然后求出延长后的线段与最长的已知线段的关系.有的是采取截长补短后,使之构成某种特定的三角形进行求解.①截长:在较长的线段上截取另外两条较短的线段.如图所示,在BF上截取BM=DF,易证△BMC≌△DFC(SAS).②补短:选取两条较短线段中的一条进行延长,使得较短的两条线段共线并寻求解题突破.如图所示,延长GC至N,使CN=DF,易证△CDF≌△BCN(SAS).例题精讲考点一:截长型【例1】.如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C等于_______.变式训练【变式1-1】.如图,△ABC中,AC=BC,AD平分∠BAC,若AC+CD=AB,求∠C的度数.【变式1-2】.如图,四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且∠B+∠D=180°,若BE=3,CE=4,S△ACE=14,则S△ACD=________.【变式1-3】.已知在△ABC中,∠B=2∠C,∠BAC的平分线AD交BC边于点D.求证:AC =AB +BD .考点二:补短型【例2】.已知:如图,在△ABC 中,AB =AC ,D 是△ABC 外一点,且∠ABD =60°,∠ACD =60°求证:BD +DC =AB .变式训练【变式2-1】.如图,四边形ABCD 中,AB ∥DC ,点E 为AD 上一点,连接BE ,CE ,且BE 、CE 分别平分∠ABC 、∠BCD .求证:BC =AB +DC .【变式2-2】.【问题背景】如图1:在四边形ABCD 中,AB AD =,120BAD ∠=︒,E 、F 分别是BC 、CD 上的点,且60EAF ∠=︒,小王同学探究此问题的方法是:延长FD 到点G ,使DG BE =,连接AG ,再证明AEF AGF ≅△△,可得出结论.【探索延伸】如图2,若在四边形ABCD 中,AB AD =,E 、F 分别是BC ,CD 上的点12BAD ,上述结论是否仍然成立【学以致用】如图3,四边形ABCD 是边长为5的正方形,45EBF ∠=︒,求DEF 的周长.实战演练1.如图,在△ABC中,BD平分∠ABC,∠C=2∠CDB,AB=12,CD=3,则△ABC的周长为()A.21B.24C.27D.302.如图,AD⊥BC,AB+BD=DC,∠B=54°,则∠C=.3.已知:如图,在△ABC中,=BC,∠C=100°,AD平分∠CAB.求证:AD+CD=AB.4.如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.5.如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别是∠BAC、∠ABC的角平分线.求证:(1)BQ=CQ;(2)BQ+AQ=AB+BP.6.如图,△ABC两条角平分线BD,CE相交于点O,∠A=60°,求证:CD+BE=BC.7.如图,梯形ABCD中,AB∥CD,∠ABC和∠BCD的平分线的交点E在AD上.求证:(1)点E是AD的中点;(2)BC=AB+CD.8.已知,如图,BD是△ABC的角平分线,AB=AC,(1)若BC=AB+AD,请你猜想∠A的度数,并证明;(2)若BC=BA+CD,求∠A的度数?(3)若∠A=100°,求证:BC=BD+DA.9.阅读:探究线段的和.差.倍.分关系是几何中常见的问题,解决此类问题通常会用截长法或补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.(1)请完成下题的证明过程:如图1,在△ABC中,∠B=2∠C,AD平分∠BAC.求证:AB+BD=AC.证明:在AC上截取AE=AB,连接DE(2)如图2,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.10.在菱形ABCD中,∠BAD=60°,点E、F分别在边AB、AD上,且AE=DF,BF与DE交于点G.(1)如图①,连接BD.求证:△ADE≌△DBF;(2)如图②,连接CG.求证:BG+DG=CG.11.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=∠BAD.(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由;(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.12.如图,在锐角△ABC中,∠A=60°,点D,E分别是边AB,AC上一动点,连接BE 交直线CD于点F.(1)如图1,若AB>AC,且BD=CE,∠BCD=∠CBE,求∠CFE的度数;(2)如图2,若AB=AC,且BD=AE,在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM,连接MF,点N是MF的中点,连接CN.在点D,E运动过程中,猜想线段BF,CF,CN之间存在的数量关系,并证明你的猜想.13.如图1,点A和点B分别在y轴正半轴和x轴正半轴上,且OA=OB,点C和点D分别在第三象限和第二象限上,且OC⊥OD,OC=OD,点C的坐标为(m,n),且满足(m﹣2n)2+|n+2|=0.(1)求点C坐标;(2)求证:AC=BD,AC⊥BD;(3)求∠BEO度数;(4)如图2,点P在OA上,点Q在OB上且OP=OQ,直线ON⊥BP,交AB于点N,MN⊥AQ交BP延长线于点M,请猜想ON,MN,BM的数量关系并证明.14.如图所示:△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B 在y轴上(1)如图1所示,若C的坐标是(2,0),点A的坐标是(﹣2,﹣2),求:点B的坐标;(2)如图2,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由;(3)如图3角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①为定值;②为定值,只有一个结论成立,请你判断正确的结论加以证明,并求出定值.。
截长补短模型截长补短如图①,若证明线段AB、CD、EF之间存在EF=AB+CD,可以考虑截长补短法。
截长法:如图②,在EF上截取EG=AB,再证明GF=CD即可。
补短法:如图③,延长AB至H点,使BH=CD,再证明AH=EF即可。
模型分析截长补短的方法适用于求证线段的和差倍分关系。
截长,指在长线段中截取一段等于已知线段;补短,指将短线段延长,延长部分等于已知线段。
该类题目中常出现等腰三角形、角平分线等关键字句,可以采用截长补短法构造全等三角形来完成证明过程。
模型实例例1.如图,已知在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D。
求证:AB=AC+CD。
证明:如图在AB上取一点E使AE=AC∵AD平分∠BAC∴∠CAD=∠DAE,AD=AD∴△CAD≌△EAD∴CD=ED,∠C=∠AED=∠B+∠EDB又∠C=2∠B∴∠B=∠EDB∴ED=EB∴AB=AE+EB=AC+CD∴AB=AC+CD例2.如图,已知OD平分∠AOB,DC⊥OA于点C,∠A=∠GBD。
求证:AO+BO=2CO。
证明:如图过D点作DE垂直BG交于点E∵OD平分∠AOB,DC⊥OA于点C∴DC=DE,∠COD=∠DOE,OD=OD∴△OCD≌△OED∴OC=OE又∠A=∠GBD,DC=DE∴RT△DCA≌RT△DEB∴AC=BE∴AO+BO=AC+CO+EO-BE=CO+OE=2OC∴AO+BO=2CO模型练习1.如图,已知点C是∠MAN的平分在线一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=1 2(AD+AB).问:∠1和∠2有何关系.2.如图,已知△ABC中,∠A=90°,AB=AC,BE平分∠ABC,CE⊥BD于E,求证:CE=12BD.3.如图,已知正方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE=DF.4.如图,已知四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE恰好平分∠ABC,判断AB的长与AD+BC的大小关系并证明.。
截长补短辅助线模型模型:截长补短如图①,假设证明线段AB 、CD、EF 之间存在EF=AB+CD,可以考虑截长补短法.截长法:如图②,在EF 上截取EG=AB ,再证明GF=CD 即可.补短法:如图③,延长AB 至H 点,使 BH =CD,再证明 AH =EF 即可.模型解析截长补短的方法适用于求证线段的和差倍分关系. 截长,指在长线端中截取一段等于已知的线段;补短,指将一条短线端延长,延长局部等于线段. 该类题目中常出现等腰三角形、角均分线等要点词句,可以采用截长补短法构造全等三角形来完成证明过程.模型实例例 1:如图,在△ABC 中,∠ C=2∠B,∠1=∠2 . 求证:AB =AC +CD .证法一,截长法:如图①,在AB 上取一点E,使 AE=A C,连接 DE.∵AE =AC ,∠1=∠2,AD =AD ,∴△ACD ≌△AED ,∴CD=DE,∠C=∠3 .∵∠C=2∠B,∴∠3=2∠B=∠4+∠B ,∴∠4=∠B ,∴DE=BE ,∴CD=BE .∵AB =AE +BE,∴AB =AC +CD .1证法二,补短法:如图②,延长AC 到点 E,使 CE=CD,连接DE .∵CE=CD,∴∠4=∠E .∵∠3=∠4+∠E,∴∠3=2∠E .∵∠3=2∠B,∴∠E=∠B .∵∠1=∠2,AD =AD ,∴△EAD ≌△BAD ,∴AE =AB.又∵AE=AC +CE,∴∴AB =AC +CD .例 2:如图, OD均分∠ AOB ,DC⊥OA 于点 C,∠A =∠GBD . 求证:AO +BO=2CO .证明:在线段AO 上取一点E,使 CE=AC ,连接DE .∵CD=CD,DC⊥OA,∴△ACD ≌△ECD,∴∠A=∠CED .∵∠A=∠GBD ,∴∠CED=∠GBD ,∴1800-∠CED=1800-∠GBD ,∴∠OED=∠OBD .∵OD 均分∠ AOB ,∴∠AOD =∠BOD .∵OD=OD,∴△OED≌△OBD ,∴OB=OE,∴AO +BO=AO+OE=OE+2CE+OE=OE+CE+OE+CE=2〔CE+OE〕=2CO .追踪练习0,AD 是∠BAC 的均分线,且 AC=AB +BD . 求∠ABC 1. 如图,在△ABC 中,∠BAC =60的度数 .【答案】2证法一:补短延长 AB 到点 E,使 BE=BD . 在△BDE 中,∵BE =BD ,∴∠E=∠BDE,∴∠ABC =∠BDE +∠E=2∠E .又∵AC=AB +BD ,∴AC =AB +BE,∴AC=AE .∵AD 是∠BAC 的均分线,∠BAC =600,∴∠EAD =∠CAD =600÷2=300 .∵AD =AD ,∴△AED ≌△ACD ,∴∠E=∠C .∵∠ABC =2∠E,∴∠ABC =2∠C .∵∠BAC =600,∴∠ABC +∠C=1800-600=1200,∴32∠ABC =1200,∴∠ ABC =800 .证法二:在AC 上取一点F,使 AF =AB ,连接DF.∵AD 是∠BAC 的均分线,∴∠BAD =∠FAD .∵AD =AD ,∴△BAD ≌△FAD ,∴∠B=∠AFD ,BD =FD .∵AC =AB +BD ,AC=AF +FC∴FD=FC ,∴∠ FDC=∠C .∵∠AFD =∠FDC+∠C,∴∠B=∠FDC+∠C=2∠C .∵∠BAC +∠B+∠C=1800,∴ 32∠ABC =1200,∴∠ ABC =800 .0,AD 、CE 分别均分∠BAC 、∠ACB . 求证:AC =AE 2. 如图,在△ABC 中,∠ ABC =60+CD .【答案】如图,在AC 边上取点F,使 AE=AF ,连接OF .∵∠ABC =600,∴∠BAC +∠ACB =1800-∠ABC =1200 .∵AD 、CE 分别均分∠BAC 、∠ACB ,∴∠OAC=∠OAB =D BAC ,∠OCA =∠OCB=2D ACB ,23∴∠AOE =∠COD =∠OAC +∠ OCA =∴∠AOC =1800-∠AOE =1200 .? BAC ? ACB =60 0, 2∵AE =AF ,∠EAO =∠ FAO ,AO =AO ,∴△AOE ≌△AOF 〔SAS 〕,∴∠AOF =∠AOE =600,∴∠COF =∠AOC -∠AOF =600,∴∠COF =∠COD .∵CO =CO ,CE 均分∠ ACB ,∴△COD ≌△COF 〔ASA 〕,∴CD =CF .∵AC =AF +CF ,∴AC =AE +CD , 0,BE 、CE 分别均分∠ ABC 、∠DCB . 求证:AB +CD =BC .3. 如图, ∠ABC +∠BCD =180【答案】证法一:截长如图①,在 BC 上取一点 F ,使 BF =AB ,连接 EF .∵∠1=∠ABE ,BE =BE ,∴△ABE ≌△FBE ,∴∠ 3=∠ 4 .∵∠ABC +∠BCD =1800,BE 、CE 分别均分∠ ABC 、∠DCB ,∴∠1+∠2= 1 2 ∠ABC + 1 2∠DCB =1 2×1800=900 , ∴∠BEC =900, ∴∠4+∠5=900,∠3+∠6=900 .∵∠3=∠4 ,∴∠ 5=∠6 .∵CE =CE , ∠2=∠DCE ,∴△CEF ≌△CED ,∴ CF =CD .∵BC =BF +CF ,AB =BF ,∴ AB +CD =BC证法二:补短如图②,延长 BA 到点 F ,使 BF =BC ,连接 EF .∵∠1=∠ABE ,BE =BE ,∴△BEF ≌△BEC ,∴EF =EC ,∠BEC =∠BEF .∵∠ABC +∠BCD =1800,BE 、CE 分别均分∠ ABC 、∠DCB ,4∴∠1+∠2= 1 2 ∠ABC + 1 2∠DCB =1 2 0=900 , ×180 ∴∠BEC =900, ∴∠BEF =∠BEC =900,∴∠BEF +∠BEC =1800,∴C 、E 、F 三点共线 .∵AB ∥CD ,∴∠ F =∠FCD .∵EF =EC ,∠FEA =∠DEC ,∴△AEF ≌△DEC ,∴AF =CD .∵BF =AB +AF ,∴BC =AB +CD .4. 如图,在△ ABC 中,∠ABC =900,AD 均分∠ BAC 交 BC 于 D ,∠C =300,BE ⊥AD 于 点 E . 求证: AC -AB =2BE . 【答案】延长 BE 交 AC 于点 M .∵BE ⊥AD ,∴∠ AEB =∠AEM =900 .∵∠3=900-∠1,∠4=900-∠ 2,∠1=∠2,∴∠3=∠4,∴AB =AM .∵BE ⊥AE ,∴BM =2BE .∵∠ABC =900,∠C =300,∴∠BAC =600 .∵AB =AM ,∴∠ 3=∠4=600,∴∠5=900-∠3=300,∴∠5=∠C ,∴ CM =BM ,∴AC -AB =CM =BM =2BE .5. 如图, Rt △ACB 中,A =BC ,AD 均分∠ BAC 交 BC 于点 D ,CE ⊥AD 交 AD 于点 F , 交 AB 于点 E . 求证: AD =2DF +CE . 5【答案】在AD 上取一点G,使 AG=CE,连接CG .∵CE⊥AD ,∴∠AFC =900,∠1+∠ACF =900 .∵∠2+∠ACF =900,∴∠ 1=∠2 .∵AC =BC,AG =CE,∴△ACG≌△CBE,∴∠ 3=∠B=450,∴∠2+∠4=900-∠3=450 .1∵∠2=∠1=∠BAC =0,2∴∠4=450-∠2=0,∴∠4=∠2=0 .又∵CF=CF,DG⊥CF,∴△CDF≌△CGF,∴DF=GF .∵AD =AG +DG ,∴AD =CE+2DF .6. 如图,五边形ABCDE 中,AB =AE,BC+DE=CD,∠B+∠E=1800 . 求证:AD 均分∠CDE .【答案】如图,延长CB 到点 F,使 BF=DE,连接 AF 、AC .∵∠1+∠2=1800,∠E+∠1=1800,∴∠ 2=∠E .∵AB =AE ,∠2=∠E,BF=DE,∴△ABF ≌△AED ,∴∠F=∠4,AF=AD .∵BC+DE=CD,∴BC+BF=CD,即 FC=CD .又∵AC=AC ,∴△ACF ≌△ACD ,∴∠F=∠3 .∵∠F=∠4,∴∠3=∠4,∴AD 均分∠ CDE .6。
初中数学几何模型(三)线段间的关系模型(一)截长补短模型:遇到求线段和差、倍数(含分数)关系时,可以尝试截长补短模型。
截长是指在长线段中截取一段等于较短的已知线段;补短是指延长较短线段,延长部分等于已知线段。
常见的条件有等腰三角形、角平分线和对角互补等关键词,通过截长或补短,并连接一些点,构造全等得出结论。
典型例题:1、已知:如图,在△ABC中,∠C=2∠B,∠1=∠2。
求证:AB=AC+CD.方法1:在AB上截取AE,使AE=AC,连接DE。
(截长)。
易证,△ACD≌△AED,∴∠ACB=∠AED,CD=DE;再证,△BDE是等腰三角形,则DE=BE。
∵AB=AE+BE,∴AB=AC+CD方法2:延长AC到F,使CF=CD,连接DF。
(补短)2、如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE。
略证:延长CB到N,使BN=ED,连接AN、AC。
∵∠ABC+∠AED=180°,∠ABC+∠ABN=180°,∴∠AED=∠ABN;在△AED与△ABN中,∵AE=AB,∠AED=∠ABN,ED=BN,∴△AED ≌△ABN ,∴∠ADE=∠N ,AD=AN ;用SSS 易证△ACD ≌△ACN ,∴∠ADC=∠N ;∴∠ADE=∠ADC , ∴DA 平分∠CDE 。
3、如图,已知四边形ABCD 是矩形,点E 在BA 的延长线上,AE=AD ,EC 与BD 相较于点G ,与AD 相较于点F ,AF=AB 。
(1)求证:BD ⊥EC ;(2)若AB=1,求AE 的长;(3)连接AG ,求证:EG -DG=√2 AG (1)证明:∵AE=AD ,∠EAF=∠DAB ,AF=AB ,∴△AEF ≌△ADB ,∴∠E=∠ADB ;∵四边形ABCD 是矩形,∴∠DAB=90°,∴∠ADB+∠ABD=90°, ∴∠E+∠ABD=90°,∴BD ⊥EC ;(2)解:∵四边形ABCD 是矩形,点E 在BA 的延长线上,∴AE//CD ,∴△AEF ∽△DCF ,∴AEDC =AFDF; 设AE 的长为x ,则DF 的长为x -1,x1=1x−1; 整理,得:x 2−x −1=0,解,得:x 1=1+√52,x 2=1−√52(不合题意,舍去) ∴AE 的长为1+√52。
32
H A B F E 1G
E
F D C B A
D C B A O G A B
C D 第三章 截长补短
模型 截长补短 如图①,若证明线段AB 、CD 、EF 之间存在 EF=AB+CD ,可以考虑截长补短法。
截长法:如图②,在EF 上截取EG=AB ,再证明 GF=CD 即可。
补短法:如图③,延长AB 至H 点,使BH=CD , 再证明AH=EF 即可。
模型分析
截长补短的方法适用于求证线段的和差倍分关系。
截长,指在长线段中截取一段等于已知线段;补短,指将短线段延长,延长部分等于已知线段。
该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程。
模型实例
例1.如图,已知在△ABC 中,∠C=2∠B ,AD 平分∠BAC 交BC 于点D 。
求证:AB=AC+CD 。
例2.如图,已知OD 平分∠AOB ,DC ⊥OA 于点C ,∠A=∠GBD 。
求证:AO+BO=2CO 。
A B C D O E A B C
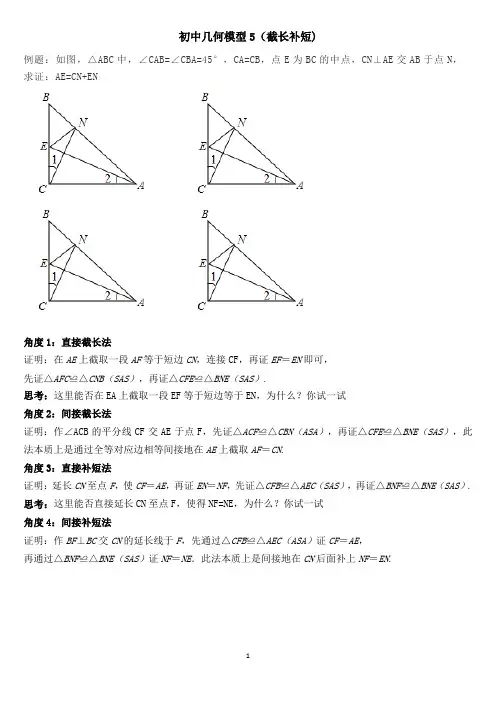
D 热搜精练
1.如图,在△ABC 中,∠BAC=60°,AD 是∠BAC 的平分线,且AC=AB+BD 。
求∠ABC 的度数。
2.如图,在△ABC 中,∠ABC=60°,AD 、CE 分别平分∠BAC 、∠ACB 。
求证:AC=AE+CD 。
E A
B
C D E A B C D 3.如图,∠ABC+∠BCD=180°,BE 、CE 分别平分∠ABC 、∠BCD 。
求证:AB+CD=BC 。
4.如图,在△ABC 中,∠ABC=90°,AD 平分∠BAC 交BC 于点D ,∠C=30°, BE ⊥AD 于点E 。
求证:AC-AB=2BE 。
F E A B C D
E
A
B
C D
5.如图,Rt △ABC 中,AC=BC ,AD 平分∠BAC 交BC 于点D ,CE ⊥AD 交AD 于F 点,交AB
于点E 。
求证:AD=2DF+CE 。
6.如图,五边形ABCDE 中,AB=AC ,BC+DE=CD ,∠B+∠E=180°。
求证:AD 平分∠CDE 。