江苏省南京市高一上学期期末考试数学试题

2019-2020学年江苏省南京市高一上学期期末数学试题一、单选题1．已知集合A ＝{1，2，3}，集合B ＝{x |x 2≤4，x ∈R }，则A ∩B ＝（ ） A ．∅ B ．{1}C ．{1，2}D ．{1，2，3}【答案】C【解析】解一元二次不等式求得集合B ，由此求得A B .【详解】由24x ≤，解得22x -≤≤，故{}2B x x =|-2≤≤，所以{}1,2A B =.故选：C 【点睛】本小题主要考查集合交集，考查一元二次不等式的解法，属于基础题. 2．已知向量(1,2)OA =-，(1,1)OB =-，则向量AB 的坐标为（ ） A ．（－2，3） B ．（0，1）C ．（－1，2）D ．（2，－3）【答案】D【解析】利用向量减法运算，求得AB . 【详解】依题意()()()1,11,22,3AB OB OA =-=---=-. 故选：D 【点睛】本小题主要考查平面向量减法的坐标运算，属于基础题.3．已知a ＝log 0.81.2，b ＝1.20.8，c ＝sin 1.2，则a ，b ，c 的大小关系是（ ） A ．a ＜b ＜c B ．a ＜c ＜bC ．c ＜a ＜bD ．c ＜b ＜a【答案】B【解析】利用0,1分段法，判断出,,a b c 的大小关系. 【详解】0.80.8log 1.2log 10a =<=，0.801.2 1.21b =>=，由于ππ1.232<<，所以0sin1.21c <=<，所以a c b <<.故选：B 【点睛】本小题主要考查指数式、对数式和三角函数比较大小，属于基础题. 4．函数()tan 24f x x π⎛⎫=+⎪⎝⎭的定义域为（ ） A ．,2x x k k ππ⎧⎫≠+∈⎨⎬⎩⎭Z B ．2,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭C ．,28k x x k Z ππ⎧⎫≠+∈⎨⎬⎩⎭D ．,8x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭【答案】C【解析】根据正切型三角函数定义域的求法，求得()f x 的定义域. 【详解】 由ππ2π42x k +≠+，解得ππ28k x ≠+，所以()f x 的定义域为,28k x x k Z ππ⎧⎫≠+∈⎨⎬⎩⎭.故选：C 【点睛】本小题主要考查正切型三角函数定义域的求法，属于基础题.5．已知扇形OAB 的面积为4，圆心角为2弧度，则AB 的长为（ ） A ．2 B ．4C ．2πD ．4π【答案】B【解析】利用扇形面积公式求得扇形的半径，进而求得AB 的长. 【详解】设扇形的半径为r ，依题意2124,22r r ⋅⋅==.所以AB 224r α=⋅=⋅=. 故选：B 【点睛】本小题主要考查扇形面积公式，考查扇形弧长计算，属于基础题.6．若向量,a b 满足：()()1,,2a a b a a b b =+⊥+⊥，则a b -=（ ）A ．1B ．2C ．5D 【答案】D【解析】利用已知条件求得2,a b b ⋅，由此求得a b -r r的值.【详解】由()()1,,2a a b a a b b =+⊥+⊥得()()222102220a b a a a b a b a b b a b b a b b ⎧+⋅=+⋅=+⋅=⎪⎨+⋅=⋅+=⋅+=⎪⎩，化简得212a b b ⎧⋅=-⎨=⎩.所以()22221225a b a ba ab b -=-=-⋅+=++=.故选：D 【点睛】本小题主要考查平面向量数量积运算，考查两个向量垂直的表示，考查向量模的运算，考查运算求解能力，属于基础题. 7．函数212ln ||()x f x x ⋅=图象的大致为（ ） A ． B ．C ．D ．【答案】A【解析】根据函数的奇偶性和单调性，选出正确选项. 【详解】由于函数()f x 的定义域为{}|0x x ≠，且()()f x f x -=，所以函数()f x 为偶函数，由此排除B,C 选项.由于()()222221212212,f e f e e e e e ==⋅<，所以当0x >时，()f x 存在减区间，由此排除D 选项. 故选：A 【点睛】本小题主要考查函数图像的识别，考查函数的奇偶性和单调性，属于基础题.8．安装了某种特殊装置的容器内有细沙10cm 3，容器倒置后，细沙从容器内流出，tmin 后容器内剩余的细沙量为y ＝101+at（单位：cm 3），其中a 为常数．经过4min 后发现容器内还剩余5cm 3的沙子，再经过xmin 后，容器中的沙子剩余量为1.25cm 3，则x ＝（ ） A ．4 B ．6C ．8D ．12【答案】C【解析】根据已知条件求得a 的值，由此列方程，求得x 的值.【详解】当4t =时5y =，所以14510a +=，即11114lg5,4lg51lg,lg 242a a a +==-==⋅.设经过min y 后，剩余沙子为111lg 425104y +⋅=，即1411l g 1011241lg 421510101024yy y ⎡⎤⎛⎫⎢⎥⋅ ⎪⎢⎥⎝⎭+⋅⎢⎥⎣⎦⎛⎫==⋅=⎪⎝⎭，即1341122y ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，13,124y y ==.所以再经过的时间1248x =-=. 故选：C 【点睛】本小题主要考查待定系数法求函数解析式，考查对数运算，考查运算求解能力，属于中档题.二、多选题9．下列各选项中，值为1的是（ ） A ．log 26·log 62 B ．log 62＋log 64C ．()()112222⋅D．((112222+-【答案】AC【解析】对选项逐一化简，由此确定符合题意的选项. 【详解】对于A 选项，根据log log 1a b b a ⋅=可知，A 选项符合题意. 对于B 选项，原式()66log 24log 81=⨯=≠，B 选项不符合题意. 对于C选项，原式((11222211⎡⎤==⎣⎦⋅=+，C 选项符合题意.对于D选项，由于(()((1111222222222222-+⎡⎤=⎣⋅⎢⎥⎦4221=-=≠，D 选项不符合题意. 故选：AC 【点睛】本小题主要考查对数、根式运算，属于基础题. 10．记函数()sin 23f x x π⎛⎫=-⎪⎝⎭的图象为G ，则下列结论正确的是（ ）A ．函数f （x ）的最小正周期为πB ．函数f （x ）在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递增 C ．直线12x π=-是图象G 的一条对称轴D ．将函数y ＝sin 2x 的图象向右平移3π个单位长度，得到图象G 【答案】ABC【解析】根据三角函数的图像与性质，对选项逐一分析，由此得出正确选项. 【详解】函数()f x 的最小正周期为2ππ2=，故A 选项正确. 由πππ2232x -≤-≤，解得π5π1212x -≤≤，所以函数f （x ）在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递增，故B 选项正确. 由于ππππsin 2sin 1121232f ⎡⎤⎛⎫⎛⎫⎛⎫-=--=-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以直线12x π=-是图象G 的一条对称轴，故C 选项正确.sin 2y x =向右平移π3得到π2πsin 2sin 233y x x ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，故D 选项错误.故选：ABC 【点睛】本小题主要考查三角函数图像与性质，包括周期性、单调性、对称性和图像变换等知识，属于基础题.11．已知函数f （x ）＝x ，g （x ）＝x －4，则下列结论正确的是（ ） A ．若h （x ）＝f （x ）g （x ），则函数h （x ）的最小值为4 B ．若h （x ）＝f （x ）|g （x ）|，则函数h （x ）的值域为RC ．若h （x ）＝|f （x ）|－|g （x ）|，则函数h （x ）有且仅有一个零点D ．若h （x ）＝|f （x ）|－|g （x ）|，则|h （x ）|≤4恒成立 【答案】BCD【解析】对选项逐一分析，由此确定结论正确的选项. 【详解】对于A 选项，()()()224424h x x x x x x =-=-=--，当2x =时，函数()h x 的最小值为4-，所以A 选项错误.对于B 选项，()224,444,4x x x h x x x x x x ⎧-≥=-=⎨-+<⎩，画出()h x 图像如下图所示，由图可知，()h x 的值域为R ，故B 选项正确.对于C 选项，()4,0424,044,4x h x x x x x x -<⎧⎪=--=-≤≤⎨⎪>⎩，画出()h x 图像如下图所示，由图可知，()h x 有唯一零点2，故C 选项正确.对于D 选项，由C 选项的分析，结合()h x 图像可知()4h x ≤恒成立，故D 选项正确. 故选：BCD 【点睛】本小题主要考查函数的最值、值域和零点，考查分段函数，考查数形结合的思想方法，属于基础题.12．已知向量,a b 是同一平面α内的两个向量，则下列结论正确的是（ ） A ．若存在实数λ，使得b a λ=，则a 与b 共线 B ．若a 与b 共线，则存在实数λ，使得b a λ=C ．若a 与b 不共线，则对平面α内的任一向量c ，均存在实数,λμ，使得c a b λμ=+r r rD ．若对平面α内的任一向量c ，均存在实数,λμ，使得c a b λμ=+r r r，则a 与b 不共线【答案】ACD【解析】根据平面向量共线、平面向量的基本定理判断出正确选项. 【详解】根据平面向量共线的知识可知A 选项正确.对于B 选项，若a 与b 共线，可能0a =，当b 为非零向量时，不存在实数λ，使得b a λ=，所以B 选项错误.根据平面向量的基本定理可知C 、D 选项正确. 故选：ACD 【点睛】本小题主要考查平面向量共线、平面向量的基本定理，属于基础题.三、填空题13．已知a 和b 都是单位向量，且0,2a b c a b ⋅==+，则向量b 与c 的夹角的余弦值是____．【解析】利用cos ,b c b c b c⋅=⋅求得向量b 与c 的夹角的余弦值.【详解】依题意cos ,b c b c b c⋅=⋅()2222442b a ba b a b ⋅+====+⋅+.【点睛】本小题主要考查平面向量数量积、模的运算，考查向量夹角的计算，考查化归与转化的数学思想方法，属于基础题.14．在△ABC 中，已知7sin cos 13A A ＋＝，则sinAcosA 的值为____，tanA 的值为____．【答案】60169-125- 【解析】利用同角三角函数的基本关系式，求得sin cos ,tan A a A 的值. 【详解】 由7sin cos =13A A +两边平方得496012sin cos ,sin cos 169169A A A A +==-.由于A 是三角形的内角，故A 为钝角，所以sin cos 0A A ->，而()2289sin cos 12sin cos 169A A A A -=-=，所以17sin cos 13A A -=.由17sin cos 137sin cos 13A A A A ⎧-=⎪⎪⎨⎪⎪⎩＋＝解得125sin ,cos 1313A A ==-，所以sin 12tan cos 5A A A ==-. 故答案为：（1）60169-（2）125-【点睛】本小题主要考查利用同角三角函数的基本关系式进行化简求值，考查化归与转化的数学思想方法，属于中档题.15．已知函数f （x ）（x ∈R ）是周期为4的奇函数，且当0≤x ≤2时，(1),01()sin ,12x x x f x x x π-⎧=⎨<⎩剟…则376f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭______． 【答案】14【解析】根据函数()f x 的周期性、奇偶性和分段函数解析式，求得所求表达式的值. 【详解】 依题意3711111111π42sin66666f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=⨯-=-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ππ1sin 2πsin 662⎛⎫=--== ⎪⎝⎭.371111162224f f f ⎛⎫⎛⎫⎛⎫⎛⎫==-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 故答案为：14【点睛】本小题主要考查分段函数求函数值，考查函数的奇偶性和周期性，属于基础题. 16．已知A ，B 是函数()sin 2xf x π=的图象与函数()cos2xg x π=的图象的两个不同的交点，则线段AB 长度的最小值是______．【解析】求得()(),f x g x 在一个周期内的两个交点坐标，由此求得AB 长度的最小值. 【详解】()f x 和()g x 的周期为2π4π2T ==，由()()f x g x =得ππsin cos 22x x =，在[]0,4x ∈时，有ππ24x =或π5π24x =，记得12x =或52x =，不妨设15,,,2222A B ⎛⎫⎛- ⎪ ⎪ ⎝⎭⎝⎭，所以AB 长度的最小值为AB ==.【点睛】本小题主要考查正弦函数与余弦函数，考查两点间的距离公式.四、解答题17．已知向量()()2,,1,6a m b m ==-． （1）若//a b ，求实数m 的值； （2）若a b a b +=-，求实数m 的值． 【答案】（1）3-或4；（2）14【解析】（1）利用两个向量平行的条件列方程，解方程求得m 的值；（2）将a b a b +=-两边平方，求得0a b ⋅=，根据向量数量积的坐标运算列方程，解方程求得m 的值.【详解】（1）由于//a b ，所以()2610m m ⋅--=，解得3m =-或4m =.（2）将a b a b +=-两边平方得222222a a b b a a b b +⋅+=-⋅+r r r r r r r r ，所以0a b ⋅=，即()2160m m -+=，解得14m =.【点睛】本小题主要考查两个向量平行的坐标表示，考查向量模的运算、数量积的运算，考查方程的思想，属于基础题.18．在平面直角坐标系xOy 中，角α的顶点为O ，始边为x 轴的正半轴，终边经过点P （－3，m ），且4sin 5α=． （1）求实数m 的值；（2）求sin(2)cos()3sin cos 22παππααπα-++⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭的值．【答案】（1）4；（2）17【解析】（1）根据三角函数的定义列方程，解方程求得m 的值. （2）由（1）求得cos α的值，利用诱导公式化简求得表达式的值. 【详解】（1）由于角α的终边经过点()3,P m -，且4sin 05α=>，所以0m>，且4sin 5α==，从而()2225169m m =+，即216m =，解得4m =. （2）由（1）知()4,3,4m P =-，所以3cos 5α==-，所以sin(2)cos()sin cos 13cos sin 7sin cos 22ππααππαααααα-++--==-⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭. 【点睛】本小题主要考查三角函数的定义，考查诱导公式和同角三角函数的基本关系式，属于基础题.19．已知函数()2x x e ae f x --=是奇函数，其中e 是自然对数的底数．（1）求实数a 的值；（2）若f （lgx ）＋f （－1）＜0，求x 的取值范围． 【答案】（1）1；（2）()0,10【解析】（1）根据奇函数的性质，利用()00f =列方程，解方程求得a 的值. （2）利用函数的奇偶性和单调性化简不等式，并由此求得不等式的解集. 【详解】（1）函数()f x 的定义域为R ，且为奇函数，所以()1002af -==，解得1a =. （2）由（1）得()122x x e f x e=-，由于1,2xx e e -都在R 上递增，所以函数()122x x e f x e=-在R 上递增，根据()f x 为奇函数得()()()lg 11f x f f <--=，所以lg 1x <，解得010x <<.即不等式的解集为()0,10. 【点睛】本小题主要考查函数的奇偶性，考查函数的单调性，考查化归与转化的数学思想方法，属于基础题.20．如图，摩天轮的半径为50m ，圆心O 距地面的高度为65m ．已知摩天轮按逆时针方向匀速转动，每30min 转动一圈．游客在摩天轮的舱位转到距离地面最近的位置进舱．（1）游客进入摩天轮的舱位，开始转动tmin 后，他距离地面的高度为h ，求h 关于t 的函数解析式；（2）已知在距离地面超过40m 的高度，游客可以观看到游乐场全景，那么在摩天轮转动一圈的过程中，游客可以观看到游乐场全景的时间是多少？ 【答案】（1）π6550cos ,015t h t ⎛⎫=-≥⎪⎝⎭；（2）20min 【解析】（1）建立平面直角坐标系，根据摩天轮的转动速度，结合三角函数的知识，求得h 关于t 的解析式.（2）由40h >列不等式，解不等式求得距离地面超过40m 的时间范围，由此求得游客可以观看到游乐场全景的时间. 【详解】（1）如图以摩天轮的圆心为坐标原点，水平方向为x 周，建立平面直角坐标系.设游客的位置为点P .因为摩天轮按逆时针方向匀速转动，且每30min 转动一圈，所以OP 在min t 内所转过的角为2πt πt3015=.因为游客是从摩天轮的最低点进入摩天轮的舱位，所以，以x 轴正半轴为始边，以OP 为终边的角为πt π152-，因此P 点的纵坐标为ππ50sin 152t ⎛⎫- ⎪⎝⎭.从而游客距离地面的高度πππ50sin 656550cos 15215t t h ⎛⎫⎛⎫=-+=- ⎪ ⎪⎝⎭⎝⎭，0t ≥.（2）令π6550c o s 4015t h ⎛⎫=-> ⎪⎝⎭，得π1co s 152t ⎛⎫< ⎪⎝⎭，所以ππt 5π2π2π3153k k +<<+，即3053025k t k +<<+，k ∈N ，令0k =，则525t <<.由于在距离地面超过40m 的高度，游客可以观看到游乐场全景，因此，在转动一圈的过程中，游客可以观看到游乐场全景的时间为25520min -=.【点睛】本小题主要考查三角函数在实际生活中的应用，考查三角不等式的解法，属于中档题. 21．在△ABC 中，AB ＝6，AC ＝3，D 为BC 中点，2AE EB =,12AF FC =．（1）若3A π∠=，求AD EF ⋅的值；（2）若0DE DF ⋅=，求AB AC ⋅uu u r uuu r的值． 【答案】（1）12-；（2）818【解析】（1）利用向量加法、减法和数量积运算，化简求得AD EF ⋅的值.（2）利用向量加法、减法和数量积运算，结合0DE DF ⋅=，化简求得AB AC ⋅uu u r uuu r的值. 【详解】（1）由于D 是BC 的中点，所以()12AD AB AC =+，由于2AE EB =,12AF FC =，所以21,33AE AB AF AC ==.所以AD EF ⋅()112233AB AC AC AB ⎛⎫=+⋅- ⎪⎝⎭2212112333AB AB AC AC ⎛⎫=--⋅+ ⎪⎝⎭22111366AB AB AC AC =--⋅+22111166333626-⨯-⨯⨯⨯+⨯33121222=--+=-.（2）()21113262DE AE AD AB AB AC AB AC =-=-+=-， ()11113226DF AF AD AC AB AC AB AC =-=-+=--，所以11116226DE DF AB AC AB AC ⎛⎫⎛⎫⋅=-⋅-- ⎪ ⎪⎝⎭⎝⎭2211212129AB AC AB AC=-++⋅323049AB AC =-++⋅=,解得818AB AC ⋅=.【点睛】本小题主要考查向量加法、减法和数量积的运算，考查化归与转化的数学思想方法，属于中档题.22．已知函数f （x ）＝sinx ，g （x ）＝lnx ． （1）求方程()2f x f x π⎛⎫=-⎪⎝⎭在[0，2π]上的解； （2）求证：对任意的a ∈R ，方程f （x ）＝ag （x ）都有解；（3）设M 为实数，对区间[0，2π]内的满足x 1＜x 2＜x 3＜x 4的任意实数x i （1≤i ≤4），不等式()()()()()()122334M f x f x f x f x f x f x -+-+-…成立，求M 的最小值． 【答案】（1）π4或5π4；（2）详见解析；（2）4【解析】（1）利用诱导公式化简()2f x f x π⎛⎫=- ⎪⎝⎭，结合同角三角函数的基本关系式求得tan x 的值，由此求得方程的解.（2）将a 分成0a =和0a ≠两种情况，结合零点存在性证得结论成立.（3）先证得4M ≥，再证得()()()()()()1223344f x f x f x f x f x f x ≥-+-+-，由此求得M 的最小值为4. 【详解】（1）因为，()()πsin ,2f x x f x f x ⎛⎫==-⎪⎝⎭，所以πsin sin 2x x ⎛⎫=- ⎪⎝⎭，即sin cos x x =，且[]0,2πx ∈.若cos 0x =，则sin 0x =，与22sin cos 1x +=矛盾.所以cos 0x ≠，从而tan 1x =.又[]0,2πx ∈，所以π4x =或5π4x =. （2）当0a =时，由()()f x ag x =得sin 0x =，即πx =是该方程的一个解；当0a ≠时，令()1ln sin h x x x a =-.因为()h x 的图像在区间22,a ae e -⎡⎤⎢⎥⎢⎥⎣⎦上连续不断，且2221211sin 0a a h ee a a a a a --⎛⎫⎛⎫=--≤-+=-< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，2221211sin 0a a h e e a a a a a -⎛⎫⎛⎫=-≥-=> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，根据零点存在性定理可知，存在220,aax e e-⎛⎫∈⎪ ⎪⎝⎭，使得()00h x =.因此，当0a ≠时，方程()()f x ag x =有解0x x =. 综上所述，对任意a R ∈，方程()()f x ag x =都有解. （3）先证：4M ≥. 取1234π3π0,,,2π22x x x x ====，122334sin sin sin sin sin sin 1214M x x x x x x ≥-+-+-=++=.再证：当123402πx x x x ≤<<<≤时，都有()()()()()()1223344f x f x f x f x f x f x ≥-+-+-，即1223344sin sin sin sin sin sin x x x x x x --≥+-+.①若2πx ≤，因为234π2πx x x ≤<<≤，于是2341sin ,sin ,sin 0x x x -≤≤，所以2334sin sin 1,sin sin 1x x x x -≤-≤，而12sin sin 2x x -≤，所以122334sin sin sin sin sin sin 4x x x x x x --+-+≤.②若3πx ≤，1223sin sin 1,sin sin 1x x x x -≤-≤，34sin sin 2x x -≤，所以122334sin sin sin sin sin sin 4x x x x x x --+-+≤；③若23πx x <<，1223sin sin 1,sin sin 2x x x x -≤-≤，34sin sin 1x x -≤，所以122334sin sin sin sin sin sin 4x x x x x x --+-+≤，于是对任意满足条件的1234x x x x <<<，都有1223344sin sin sin sin sin sin x x x x x x --≥+-+.综上所述，M 的最小值为4. 【点睛】本小题主要考查诱导公式、同角三角函数的基本关系式，考查零点存在性定理，考查分类讨论的数学思想方法，考查化归与转化的数学思想方法，考查分析、思考与解决问题的能力，属于难题.。

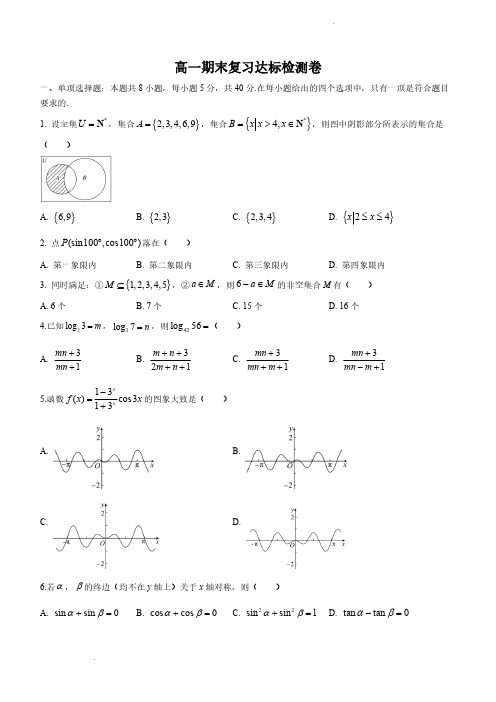
高一期末复习达标检测卷一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设全集，集合，集合，则图中阴影部分所表示的集合是*N U ={}2,3,4,6,9A ={}*4,NB x x x =>∈（ ）A. B.C.D.{}6,9{}2,3{}2,3,4{}24x x ≤≤2. 点落在（ ）(sin100,cos100)P ︒︒A. 第一象限内B. 第二象限内C. 第三象限内D. 第四象限内3. 同时满足：①，②，则的非空集合M 有（ ）{}1,2,3,4,5M ⊆a M ∈6a M -∈A. 6个B. 7个C. 15个D. 16个4.已知，，则（ ）2log 3m =3log 7n =42log 56=A.B.C.D.31mn mn ++321m n m n ++++31mn mn m +++31mn mn m +-+5.函数的图象大致是（ ） 13()cos313xxf x x -=+A.B.C.D.6.若，的终边（均不在y 轴上）关于x 轴对称，则（ ）αβA.B.C. D.sin sin 0αβ+=cos cos 0αβ+=22sin sin 1αβ+=tan tan 0αβ-=7.已知函数的部分图象如图所示，若存在，满足()sin()(0,||)f x x ωϕωϕπ=+><120x x π<……，则（ ） 123()()4f x f x ==12cos()x x -=A. B.C.D.3434-8.已知函数的定义域为，且函数的图象关于点对称，对于任意的x ，总有()y f x =R ()1y f x =-()1,0成立，当时，，函数，对任意()()22f x f x -=+()0,2x ∈2()21f x x x =-+2()()R g x mx x x =+∈，存在，使得成立，则满足条件的实数m 构成的集合为（ ）R x ∈R t ∈()()f x g t >A. B. C. D. 14m m ⎧⎫≤⎨⎬⎩⎭14m m ⎧⎫<⎨⎬⎩⎭104m m ⎧⎫<≤⎨⎬⎩⎭14m m ⎧⎫>⎨⎬⎩⎭二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分. 9.关于x 的不等式的解集可以是（ ）230ax x ++>A.B. C.D. {}3x x >R ∅312x x ⎧⎫-<<⎨⎬⎩⎭10.已知点是角终边上一点，则（）(,2)(0)P m m m ≠αA.B. C.D.tan 2α=sin α=sin()2sin 2παπα-=⎛⎫+ ⎪⎝⎭223sin cos 5αα-=11.已知函数的图象如图所示，则（ ） ()sin()0,2f x A x πωϕωϕ⎛⎫=+><⎪⎝⎭A. 函数解析式 ()2sin 23f x x π⎛⎫=+⎪⎝⎭B. 将函数的图象向左平移个单位长度可得函数的图象2sin 26y x π⎛⎫=-⎪⎝⎭4π()f x C. 直线是函数图象的一条对称轴 1112x π=-()f x D. 函数在区间上的最大值为2 ()f x ,02π⎡⎤-⎢⎥⎣⎦12.设函数，，下列正确的是（ ）ln(2),2()1,2x x f x x x ->⎧=⎨+≤⎩22()(1)2g x x m x m =-++-A. 当时，有5个不相等的实根 3m >()f f x m =⎡⎤⎣⎦B. 当时，有4个不相等的实根 0m =()g g x m =⎡⎤⎣⎦C. 当时，有6个不相等的实根 01m <<()f g x m =⎡⎤⎣⎦D. 当时，有5个不相等的实根 2m =()g f x m =⎡⎤⎣⎦三、填空题：本题共4小题，每小题5分，共20分. 13.函数的最小正周期是______. tan 23y x π⎛⎫=-⎪⎝⎭14.设：，：若是的必要条件，则m 的取值范围是______.α13x ≤≤β124().m x m m ++∈R ……βα15.数学中处处存在着美，机械学家莱洛沷现的莱洛三角形就给人以对称的美感.莱洛三角形的画法：先画等边三角形ABC ，再分别以点A ，B ，C 为圆心，线段AB 长为半径画圆弧，便得到莱洛三角形.若线段AB 长为2，则莱洛三角形的面积是__________.16.已知a 为正数，函数在区间和上的最大值分别记为和，若()sin f x x =[0,]a [,2]a a 1M 2M，则______，a 的取值范围为______.122M ≥1M =四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17.（本小题10.0分）设全集，已知集合 U R ={|228}.{|xA xB x y ===……（1）求A B,().UB A ð（2）已知非空集合，求实数a 的取值范围. {}|1,C x x a C A C =<<= 且18.（本小题12.0分）（1）已知角的终边经过点，求的值；α(4,3)P -2sin cos αα+（2）已知角终边上一点P 与x 轴的距离与y 轴的距离之比为，求的值. α3:42sin cos αα+19.（本小题12.0分） 已知函数图象的相邻两条对称轴间的距离为.()2sin()(0)3f x x πωω=->2π（1）求函数的单调递增区间和其图象的对称轴方程；()f x （2）先将函数的图象各点的横坐标向左平移个单位长度，纵坐标不变得到曲线C ，再把C 上()y f x =12π各点的横坐标保持不变，纵坐标变为原来的，得到的图象，若，求x 的取值范围. 12()g x 1()2g x …20.（本小题12.0分） 已知函数，. 22()log (1)1f x x =+-1()2xg x +=-（1）求证：为奇函数；()f x （2）若恒成立，求实数k 的取值范围； (2)2()xf kg x -≥（3）解关于a 的不等式. ()(2)22g a g a a --≤-21.（本小题12.0分）已知函数（且）.41()log 2x a xf x +=0a >1a ≠（1）试判断函数的奇偶性； ()f x （2）当时，求函数的值域；2a =()f x（3）已知，若，，使得，求实数a 的取值范()g x x =-[]14,4x ∀∈-[]20,4x ∃∈()()122f x g x -≥围.22.（本小题12.0分）设函数（，且）.()x x f x a a -=-R x ∈0a >1a ≠（1）若，证明是奇函数，并判断单调性（不需要证明）；01a <<()y f x =（2）若，求使不等式恒成立时，实数t 的取值范围；()10f <()2(4)0f x tx f x ++-<（3）若，，且在上的最小值为－2，求实数m 的值. ()312f =22()2()x xg x a a mf x -=+-()g x [)1,+∞参考答案1.【答案】C 【解答】解：由题意知图中阴影部分对应的集合为， ()U A B ð因为全集，所以，*N U ={}{}*4,1,2,3,4U N B x x x =≤∈=ð所以图中阴影部分表示 (){}2,3,4U A C B = 故选：C. 2.【答案】D 【解答】解：，，sin1000︒>cos1000︒<在第四象限，(sin100,cos100)P ︒︒故选D. 3.【答案】B 【解答】解：∵①； ②若，则， {1,2,3,4,5}M ⊆a M ∈(6)a M -∈当时，， 1a =65a -=当时，， 2a =64a -=当时，，3a =63a -=所以集合M 中，若有1、5，则成对出现，有2、4，则成对出现.∴满足题意点的集合M 有：、、、、、、共7个. {1,5}{2,4}{3}{1,5,2,4}{1,5,3}{2,4,3}{1,5,2,4,3}故选B. 4.【答案】C【解答】解：因为，， 2log 3m =3log 7n =所以， 232lg3lg 7log 3log 7log 7lg 2lg3mn ⋅=⋅==所以2422log 56log 56log 42=. 332222222log (72)log 7log 23log (723)log 7log 2log 31mn mn m⨯++===⨯⨯++++故选C. 5.【答案】A 【解答】解：因为， 1331()cos(3)cos3()1331x x x x f x x x f x -----=⋅-=⋅=-++所以函数为奇函数，排除C ，D ；()f x 又，排除B ， 13()cos3013f ππππ-=>+故选：A. 6.【答案】A 【解答】解：因为，的终边（均不在y 轴上）关于x 轴对称， αβ则，，2k αβπ+=k Z ∈选项A ：，故A 正确， sin sin sin sin(2)sin sin 0k αβαπααα+=+-=-=选项B ：，故B 错误， cos cos cos cos(2)2cos 0k αβαπαα+=+-=≠选项C ：，故C 错误，22222sinsin sin sin (2)2sin 0k αβαπαα+=+-=≠选项D ：，故D 错误， tan tan tan tan(2)tan tan 2tan 0k αβαπαααα-=--=+=≠故选A. 7.【答案】C 【解答】解：由图象知函数的周期，即，得， 13762(2121212T ππππ=⨯-=⨯=2ππω=2ω=，71310101212()()sin(2)121212f f ππππϕ+==⨯+=-即，即，， 53232k ππϕπ+=+26k πϕπ=-k Z ∈，当时，，即， ϕπ<0k =6πϕ=-()sin 26f x x π⎛⎫=-⎪⎝⎭∵存在，满足， 120x x π≤<≤123()()4f x f x ==当，，[0,]x π∈112[,666x πππ-∈-∴，得，且，12226622x x πππ-+-=2123x x π=-13sin(2)64x π-=则， 1212cos()cos(23x x x π-=-设，则，即， 126x πα-=126x πα=+3sin 4α=则. 121223cos()cos(2)cos()cos(sin 36324x x x ππππααα-=-=+-=-==故选：C. 8.【答案】A 【解答】解：由函数的图象关于点对称知函数的图象关于原点对称，即函数()1y f x =-()1,0()y f x =()y f x =是奇函数，由任意的 x ，总有成立，即恒成立，于是得函数的周期是()()22f x f x -=+()()4f x f x +=()y f x =4，又当时，，则当时，，(0,2)x ∈2()21f x x x =-+(0,2)x ∈()01f x ≤<而是奇函数，当时，，()y f x =()2,0x ∈-()10f x -<≤又，，从而得，即时，()()22f f -=()()22f f -=-()()()2200f f f -===[)2,2x ∈-，()11f x -<<而函数的周期是4，于是得函数在R 上的值域是，()y f x =()y f x =()1,1-因为对任意，存在，使得成立，从而得不等式，即在Rx R ∈t R ∈()()f x g t >()1g x ≤-210mx x ++≤上有解，当时，取，成立，即得， 0m ≤2x =-4221m -≤-<-0m ≤当时，在R 上有解，必有，解得，则有， 0m >210mx x ++≤140m ∆=-≥14m ≤104m <≤综上得， 14m ≤所以满足条件的实数m 构成的集合为. 14m m ⎧⎫≤⎨⎬⎩⎭故选A. 9.【答案】BD 【解答】解：对于A ，若不等式的解集为， 230ax x ++>{|3}x x >若，此时，解得显然不符合题意， 0a =30x +> 3.x >-∴不等式的解集不会是.故A 错误；230ax x ++>{|3}x x >对于B ，当， 21120a a >⎧⎨∆=-<⎩即时，不等式的解集是R ，故B 正确；112a >230ax x ++>对于C ，若不等式的解集为，230ax x ++>∅则有，00a <⎧⎨∆≤⎩，与矛盾，21121(12)0a a ∆=-=+->0∆≤∴不等式的解集不可以是故C 错误； 230ax x ++>.∅对于D ，若不等式的解集是，230ax x ++>3{|1}2x x -<<则方程的两个实数根分别为和，此时符合题意，故D 正确. 230ax x ++=1-3220a =-<故选：BD. 10.【答案】ACD 【解答】解：因为点是角终边上一点，(,2)(0)P m m m ≠α所以，故A 正确， 2tan 2mmα==因为当时，，故B 错误；0m<sin 0α=<因为，故C 正确； sin()sin tan 2cos sin()2παααπαα-===+因为，故D 正确.2222222222sin cos tan 1213sin cos sin cos tan 1215αααααααα----====+++故选：ACD. 11.【答案】ABC 【解答】解：由题图知：函数的最小正周期， ()f x 453612T πππ⎛⎫=⨯-= ⎪⎝⎭则，，所以函数.22πωπ==2A =()()2sin 2f x x ϕ=+将点代入解析式中可得， ,212π⎛⎫⎪⎝⎭22sin 6πϕ⎛⎫=+ ⎪⎝⎭则，得，2()62k k Z ππϕπ+=+∈2()3k k Z πϕπ=+∈因为，所以，2πϕ<3πϕ=因此，故A 正确. ()2sin 23f x x π⎛⎫=+⎪⎝⎭将函数的图像向左平移个单位长度可得函数的图像，故B 正确. 2sin 26y x π⎛⎫=-⎪⎝⎭4π()2sin 23f x x π⎛⎫=+ ⎪⎝⎭，当时，，故C 正确.()2sin 23f x x π⎛⎫=+ ⎪⎝⎭1112x π=-()2f x =当时，，所以， ,02x π⎡⎤∈-⎢⎥⎣⎦22,333x πππ⎡⎤+∈-⎢⎥⎣⎦()f x ⎡∈-⎣故D 错误. 故选：ABC. 12.【答案】BCD 【解答】解：由题意，作出的图象，如图所示：ln(2),2()1,2x x f x x x ->⎧=⎨+≤⎩对于A 选项，令，得 ()f x t =()()f f x f t m ==⎡⎤⎣⎦当时，有两个根：，，3m >()f t m =14t <-322t e >+方程有1个根，方程有2个根，故A 错误； 1()f x t =2()f x t =对于B 选项，当时，， 0m =2()2g x x x =--令，由，得， ()g x a =()0g a =122,1a a ==-当，即时，解得， 12a =222x x --=12x x ==当，即时，解得，故B 正确； 21a =-221x x --=-34x x ==对于C 选项，令，则，()g x a =()f a m =由题可知若有6个不相等的实根，则应有3个根，由图可得①， ()f g x m =⎡⎤⎣⎦()f a m =03m <≤设为的3个根，123a a a <<()f a m =所以， 1231,1,ln (2)a m a m a m --=+=-=由图可知最小根应大于的最小值， ()f a m =1a ()g x 即，解得②， 221min14(2)(1)1()(24m m m a m g x g +--+=-->==513m -<<由①②得，故C 正确；01m <<对于D 选项，令，()f x t =当时，方程，即，解得；2m =()2g t =230t t -=120,3t t ==当时，得；10()t f x ==121,3x x =-=当时，得，符合题意，故D 正确，23()t f x ==33454,2,2e x x x =-==+故选BCD.13.【答案】2π【解答】解：根据题意，结合正切函数图像性质，易知函数的最小正周期. tan 23y x π⎛⎫=- ⎪⎝⎭2T ππω==14.【答案】 1,02⎡⎤-⎢⎥⎣⎦【解析】【解答】 解：记的解集为A ，的解集为 B ，13x ……124m x m ++……因为是的必要条件，所以，βαA B ⊆当时，即，不满足；B =∅3m <-A B ⊆当时，要使得，则，解得， B ≠∅A B ⊆12411243m m m m +≤+⎧⎪+≤⎨⎪+≥⎩102m -≤≤故答案为：. 1,02⎡⎤-⎢⎥⎣⎦15.【答案】2π-【解析】【分析】本题考查了三角形中的几何计算，属于基础题.由题设可得，求出一个扇形的面积并乘以3，减去三角形面积的2倍即可.2AB BC AC ===【解答】解：由已知得， 23AB BC AC π===则，故扇形的面积为， 2AB BC AC ===23π的高为， ABC△2=莱洛三角形的面积扇形面积的3倍减去三角形面积的2倍，∴所求面积为21322232ππ⨯-⨯⨯=-故答案为： 2π-16.【答案】127,36ππ⎡⎤⎢⎥⎣⎦【解答】解：如图是函数，的图象，sin y x =[]0,3x π∈若，在上单调递增，所以，此时，，02a π<<sin y x =[]0,a 1sin M a =21sin M a M >=这与已知矛盾，故，所以，2a π≥11M =当时，矛盾，所以，即， 522a π≥21M =122M≥522a π<54a π<所以，即 524a ππ≤<122M ≥2M ≤又因为当时，，或， 524a ππ≤<522a ππ≤<2sin M a =sin 2a ，即. sin sin 2a a ⎧≤⎪⎪⎨⎪≤⎪⎩2534723a a ππππ⎧≤<⎪⎪⎨⎪≤≤⎪⎩2736a ππ≤≤17.【答案】解：（1）∵， {|228}[1,3]xA x ≤=≤=， {|{|20}(2,)B x y x x ===->=+∞∴，U (,2]B =-∞ð∴，.[)1,A B =+∞ ()[]1,2U C B A = （2）∵，C A C = ∴，且C 为非空集合.C A ⊆故，解得， 13a a >⎧⎨≤⎩13a <≤∴实数a 的取值范围为.(]1,318.【答案】解：（1）∵角的终边经过点，α()4,3P -∴， 5OP ==∴，， 3sin 5α-=4cos 5α=∴； 22sin cos 5αα+=-（2）∵角终边上一点P 与x 轴的距离与y 轴的距离之比为，α3:4∴，(4,3)(0)P a a a ±±≠当角终边在第一象限时，，，； α4cos 5α=3sin 5α=2sin cos 2αα+=当角终边在第二象限时，，，； α4cos 5α=-3sin 5α=22sin cos 5αα+=当角终边在第三象限时，，，； α4cos 5α=-3sin 5α=-2sin cos 2αα+=-当角终边在第四象限时，，，. α4cos 5α=3sin 5α=-22sin cos 5αα+=-19.【答案】解：（1）因为图象的相邻两条对称轴间的距离为，所以的最小正周期为 ()f x 2π()f x .π所以，，所以，2ππω=2ω=()2sin(2)3f x x π=-由，可得，， 222232k x k πππππ--+……51212k x k ππππ-+……()k Z ∈所以函数的单调递增区间为， ()f x 5[,)1212k k k Z ππππ-+∈由得， 232x k πππ-=+5()212k x k Z ππ=+∈所以所求对称轴方程为 5().212k x k Z ππ=+∈（2）将函数的图象向左平移个单位长度得到曲线， ()y f x =12π:2sin(2)6C y x π=-把C 上各点的横坐标保持不变，纵坐标变为原来的得到的图象， 12()sin(26g x x π=-由得，所以， 1()2g x …1sin(2)62x π-…5222666k x k πππππ+-+……所以，62k x k ππππ++……所以x 的取值范围为[,).62k k k Z ππππ++∈【解析】本题主要考查了正弦型函数的周期性，单调性以及对称性，考查了正弦性函数的图象变换以及利用正弦函数的单调性解不等式，考查了运算能力以及推理能力，属于中档题.20.【答案】解：（1）证明：函数，即， 22()log 11f x x ⎛⎫=+ ⎪-⎝⎭21()log 1x f x x +=-可得，解得或，可得定义域为，关于原点对称， 101x x +>-1x >1x <-{}11x x x <->或，则为奇函数； 2211()log log ()11x x f x f x x x -+-==-=-+-()f x （2）由或，解得，21x >21x <-0x >所以恒成立，即，()22()(0)x f k g x x -≥>221log 12122x x x k ++--≥-化为，即对恒成立， 121221x x x k ++-≥--()1212232212121x x x x x k ++≤+=++---0x >由，当且仅当即时，取得等号， ()23221322721x x ++-≥+⨯=-()222121x x =--1x =所以，即k 的取值范围是；7k ≤(],7-∞（3）不等式，即为，()(2)22g a g a a --≤-()(2)(2)g a a g a a -≤---设，即，可得在R 上递减，()()h x g x x =-1()2x h x x +=--()h x 所以，所以，解得，()(2)h a h a -…2a a -…1a …所以原不等式的解集为.[1,)+∞21.【答案】解：（1）因为（且，所以其定义域为R ，又41()log 2x a x f x +=0a >1)a ≠，所以函数是偶函数； 4114()log log ()22x xa a x x f x f x --++-===()f x （2）当时，，因为，当且仅当，即时取等，所以2a =241()log 2x x f x +=4+120,22x x x >≥21x =0x =，2241()log log 212x x f x +=≥=所以函数的值域为；()f x [1,+)∞（3），，使得，等价于. []14,4x ∀∈-[]20,4x ∃∈()()122f x g x -≥min min [()][()2]f x g x +≥令，，，t =[0,4]x ∈[0,2]t ∈令，则在上的最小值等于在上的最小值， ()222h t t t =-+()2g x +[]0,4()h t [0,2]在上的单调递减，在上的单调递增，所以在上的最小值为，所以()h t [0,1][1,2]()h t [0,2]()11h =.()min 1f x ≥⎡⎤⎣⎦当，因为当且仅当，即时取等，所以，01a <<4120,2,2x xx +>…21x =0x =41()log log 22x a a x f x +=…所以函数无最小值，此时实数a 不存在，()f x当，因为当且仅当，即时取等，所以，函数1a >4120,2,2x xx +>…21x =0x =41()log log 22x a a x f x +=≥的最小值为，，.()f x log 2a log 21a ≥2a ≤综上得：实数a 的取值范围为.(]1,222.【答案】（1）证明：的定义域为，关于原点对称， ()f x R 且，()()x x f x a a f x --=-=-∴为奇函数，()f x ∵，01a <<∴递减，递减，x y a =x y a -=-故是减函数；()f x （2）（且，()x x f x a a -=-0a >1)a ≠∵，()10f <∴， 10a a-<又，且，0a >1a ≠∴，01a <<故在上单调递减，()f x R 不等式化为，()2(4)f x tx f x +<-∴，即恒成立，24x tx x +>-2(1)40x t x +-+>∴，2(1)160t ∆=--<解得；35t -<<（3）∵， ()312f =∴，即， 132a a -=22320a a --=解得或（舍去）， 2a =12a =-∴，()()222()2()222222x x x x x x g x a a mf x m ---=+-=---+令，()22x x t f x -==-由（1）可知为增函数，()22x x f x -=-∵，1x ≥∴， 3(1)2t f ≥=令， 2223()22()22h t t mt t m m t ⎛⎫=-+=-+-≥⎪⎝⎭若，当时，，∴； 32m ≥t m =2min ()22h t m =-=-2m =若时，当时，，解得，无解； 32m <32t =()min 2h t =-253122m =>综上，.2m =。

2023-2024学年江苏省南京市高一（上）期末数学试卷一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符 1．已知集合M ＝{﹣1，0，1}，N ＝{0，1，2}，则M ∪N ＝（ ） A ．{﹣1，0，1，2} B ．{﹣1，0，1} C ．{﹣1，0，2}D ．{0，1}2．命题“∀x ∈R ，x +2≤0”的否定是（ ） A ．∃x ∈R ，x +2＞0 B ．∃x ∈R ，x +2≤0 C ．∀x ∈R ，x +2＞0D ．∀x ∉R ，x +2＞0 3．若函数f （x ）＝x 2﹣mx +3在区间（﹣∞，2）上单调递减，则实数m 的取值范围是（ ） A ．（﹣∞，2]B ．[2，+∞）C ．（﹣∞，4]D ．[4，+∞）4．已知角θ的终边经过点P （x ，﹣5），且tanθ=512，则x 的值是（ ） A ．﹣13B ．﹣12C ．12D ．135．已知a ＝log 0.32，b ＝log 0.33，c ＝log 32，则下列结论正确的是（ ） A ．a ＜b ＜cB ．a ＜c ＜bC ．c ＜a ＜bD ．b ＜a ＜c6．北京时间2023年5月10日21时22分，搭载天舟六号货运飞船的长征七号遥七运载火箭，在我国文昌航天发射场点火发射，约10分钟后，天舟六号货运飞船与火箭成功分离并进入预定轨道，发射取得圆满成功．在不考虑空气阻力的情况下，火箭的最大速度v （km /s ）和燃料的质量M （kg ）、火箭（除燃料外）的质量m （kg ）的函数关系的表达式为v =2ln(1+Mm )，若火箭的最大速度v 达到10km /s ，则M m的值是（ ） A ．5e ﹣1B ．e 5﹣1C ．510﹣1D ．105﹣17．已知定义在R 上的函数f （x ）={cosx ，x ≤0f(x −π)，x ＞0，则f(113π)的值是（ ）A ．−√32B ．−12C ．12D ．√328．在等式a b ＝N 中，如果只给定a ，b ，N 三个数中的一个数，那么a b ＝N 就成为另两个数之间的“函数关系”．如果N 为常数10，将a 视为自变量x （x ＞0且x ≠1），则b 为x 的函数，记为y ，那么x y ＝10，现将y 关于x 的函数记为y ＝f （x ）．若f （m 2）＞f （2m ），则实数m 的取值范围是（ ） A ．（0，2）B ．（1，2）C ．（0，1）∪（1，2）D ．(0，12)∪（1，2）二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题 9．若a ＜b ＜0，c ∈R ，则（ ）A ．a +c ＜b +cB ．ab ＜b 2C ．1a ＜1bD ．b a ＜ab10．已知关于x 的不等式ax 2+bx +c ＞0的解集是{x |1＜x ＜3}，则（ ） A ．a ＜0B ．a +b +c ＝0C ．4a +2b +c ＜0D ．不等式cx 2﹣bx +a ＜0的解集是{x |x ＜﹣1或x ＞−13}11．古人立杆测日影以定时间，后来逐步形成了正切和余切的概念．余切函数可以用符号表示为f （x ）＝cot x ，其中cotx =tan(π2−x)，则下列关于余切函数的说法正确的是（ ）A ．定义域为{x |x ≠k π，k ∈Z }B ．在区间(π2，π)上单调递增C ．与正切函数有相同的对称中心D ．将函数y ＝﹣tan x 的图象向右平移π2个单位可得到函数y ＝cot x 的图象12．已知扇形的半径为r ，弧长为l ．若其周长的数值为面积的数值的2倍，则下列说法正确的是（ ） A ．该扇形面积的最小值为8 B ．当扇形周长最小时，其圆心角为2 C ．r +2l 的最小值为9D ．1r 2+4l 2的最小值为12三、填空题：本大题共4小题，每小题5分，共20分.请把答案填写在答题卡相应位置上 13．已知幂函数f （x ）＝x α的图象经过点（9，3），则f （8）的值是 ． 14．已知sin(x +π6)=13，则sin 2(π3−x)的值是 ．15．已知定义在实数集R 上的偶函数f （x ）在区间[0，+∞）上是单调增函数，若f （lgx ）＜f （1），则实数x 的取值范围是 ．16．已知函数f(x)=log 9x +12x −1的零点为x 1．若x 1∈（k ，k +1）（k ∈Z ），则k 的值是 ；若函数g （x ）＝3x +x ﹣2的零点为x 2，则x 1+x 2的值是 ．四、解答题：本大题共6小题，共70分.请在答题卡指定区域内作答，解答时应写出必要的文字说明， 17．（10分）（1）已知a +a﹣1＝3，求a 12+a−12的值；（2）求值：e ln 2+（lg 5）2+lg 5lg 2+lg 20．18．（12分）设全集U ＝R ，已知集合A ＝{x |x 2﹣5x +4≤0}，B ＝{x |m ≤x ≤m +1}． （1）若A ∩B ＝∅，求实数m 的取值范围；（2）若“x ∈B ”是“x ∈A ”的充分条件，求实数m 的取值范围．19．（12分）已知函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，0＜φ＜π）的部分图象如图所示． （1）求函数f （x ）的解析式；（2）求函数y ＝f （x ）在区间[﹣π，0]上的单调减区间．20．（12分）已知函数f(x)=a⋅2x−12x +1(a ∈R)．（1）若函数f （x ）为奇函数，求a 的值；（2）当a ＝3时，用函数单调性的定义证明：函数f(x)=a⋅2x−12x +1在R 上单调递增；（3）若函数y ＝f （x ）﹣2x 有两个不同的零点，求a 的取值范围．21．（12分）如图，有一条宽为30m 的笔直的河道（假设河道足够长），规划在河道内围出一块直角三角形区域（图中△ABC ）种植荷花用于观赏，C ，B 两点分别在两岸l 1，l 2上，AB ⊥AC ，顶点A 到河两岸的距离AE ＝h 1，AD ＝h 2，设∠ABD ＝α．（1）若α＝30°，求荷花种植面积（单位：m 2）的最大值； （2）若h 2＝4h 1，且荷花的种植面积为150m 2，求sin α．22．（12分）若存在实数对（a ，b ），使等式f （x ）•f （2a ﹣x ）＝b 对定义域中每一个实数x 都成立，则称函数f （x ）为（a ，b ）型函数．（1）若函数f （x ）＝2x 是（a ，1）型函数，求a 的值； （2）若函数g(x)=e 1x 是（a ，b ）型函数，求a 和b 的值；（3）已知函数h （x ）定义在[﹣2，4]上，h （x ）恒大于0，且为（1，4）型函数，当x ∈（1，4]时，ℎ(x)=−(log 2x)2+m ⋅log 2x +2．若h （x ）≥1在[﹣2，4]恒成立，求实数m 的取值范围．2023-2024学年江苏省南京市高一（上）期末数学试卷参考答案与试题解析一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符1．已知集合M＝{﹣1，0，1}，N＝{0，1，2}，则M∪N＝（）A．{﹣1，0，1，2}B．{﹣1，0，1}C．{﹣1，0，2}D．{0，1}解：因为集合M＝{﹣1，0，1}，N＝{0，1，2}，所以M∪N＝{﹣1，0，1，2}，故选：A．2．命题“∀x∈R，x+2≤0”的否定是（）A．∃x∈R，x+2＞0B．∃x∈R，x+2≤0C．∀x∈R，x+2＞0D．∀x∉R，x+2＞0解：命题为全称命题，则命题的否定为“∃x∈R，x+2＞0”．故选：A．3．若函数f（x）＝x2﹣mx+3在区间（﹣∞，2）上单调递减，则实数m的取值范围是（）A．（﹣∞，2]B．[2，+∞）C．（﹣∞，4]D．[4，+∞）解：函数f（x）＝x2﹣mx+3开口向上，对称轴方程为x=m 2，所以函数的单调递减区间为（﹣∞，m2 ]，要使在区间（﹣∞，2）上单调递减，则m2≥2，解得m≥4．即m的范围为[4，+∞）．故选：D．4．已知角θ的终边经过点P（x，﹣5），且tanθ=512，则x的值是（）A．﹣13B．﹣12C．12D．13解：由题意得，tanθ=512=−5x，故x＝﹣12．故选：B．5．已知a＝log0.32，b＝log0.33，c＝log32，则下列结论正确的是（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．b＜a＜c解：∵log0.33＜log0.32＜log0.31＝0，∴b＜a＜0，∵log32＞log31＝0，∴c＞0，∴b＜a＜c．故选：D．6．北京时间2023年5月10日21时22分，搭载天舟六号货运飞船的长征七号遥七运载火箭，在我国文昌航天发射场点火发射，约10分钟后，天舟六号货运飞船与火箭成功分离并进入预定轨道，发射取得圆满成功．在不考虑空气阻力的情况下，火箭的最大速度v （km /s ）和燃料的质量M （kg ）、火箭（除燃料外）的质量m （kg ）的函数关系的表达式为v =2ln(1+Mm )，若火箭的最大速度v 达到10km /s ，则M m的值是（ ） A ．5e ﹣1B ．e 5﹣1C ．510﹣1D ．105﹣1解：由题意知火箭的最大速度v 达到10km /s ，故10=2ln(1+M m )，即1+Mm =e 5，∴M m =e 5−1． 故选：B ．7．已知定义在R 上的函数f （x ）={cosx ，x ≤0f(x −π)，x ＞0，则f(113π)的值是（ ）A ．−√32B ．−12C ．12D ．√32解：定义在R 上的函数f （x ）={cosx ，x ≤0f(x −π)，x ＞0，则f(113π)=f(83π)=f(5π3)=f(2π3)=f(−π3)=cos(−π3)=12． 故选：C ．8．在等式a b ＝N 中，如果只给定a ，b ，N 三个数中的一个数，那么a b ＝N 就成为另两个数之间的“函数关系”．如果N 为常数10，将a 视为自变量x （x ＞0且x ≠1），则b 为x 的函数，记为y ，那么x y ＝10，现将y 关于x 的函数记为y ＝f （x ）．若f （m 2）＞f （2m ），则实数m 的取值范围是（ ） A ．（0，2）B ．（1，2）C ．（0，1）∪（1，2）D ．(0，12)∪（1，2）解：因为x y ＝10，（x ＞0且x ≠1），所以lgx y ＝lg 10＝1，即ylgx ＝1， 所以y ＝f （x ）=1lgx，所以函数f （x ）在（0，1），（1，+∞）上单调递减， 若f （m 2）＞f （2m ），则0＜m 2＜2m ＜1，或1＜m 2＜2m ，解得0＜m ＜12或1＜m ＜2．故选：D ．二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题 9．若a ＜b ＜0，c ∈R ，则（ ） A ．a +c ＜b +cB ．ab ＜b 2C ．1a ＜1bD ．b a ＜ab解：对于A ，由a ＜b ，两边都加上c ，可得a +c ＜b +c ，故A 正确； 对于B ，a ＜b ＜0，两边都乘以b ，可得ab ＞b 2，故B 不正确； 对于C ，a ＜b ＜0，则1a −1b =b−a ab ＞0，可知1a ＞1b，故C 不正确；对于D，a＜b＜0，则ba −ab=b2−a2ab=(b+a)(b−a)ab＜0，可得ba＜ab，故D正确．故选：AD．10．已知关于x的不等式ax2+bx+c＞0的解集是{x|1＜x＜3}，则（）A．a＜0B．a+b+c＝0C．4a+2b+c＜0D．不等式cx2﹣bx+a＜0的解集是{x|x＜﹣1或x＞−13}解：因为不等式ax2+bx+c＞0的解集是{x|1＜x＜3}，所以a＜0且1，3为方程ax2+bx+c＝0的两根，A正确；故{1+3=−ba1×3=ca，所以b＝﹣4a，c＝3a，所以a+b+c＝a﹣4a+3a＝0，B正确；4a+2b+c＝4a﹣8a+3a＝﹣a＞0，C错误；由不等式cx2﹣bx+a＝3ax2+4ax+a＜0可得3x2+4x+1＞0，解得x＜﹣1或x＞−13，D正确．故选：ABD．11．古人立杆测日影以定时间，后来逐步形成了正切和余切的概念．余切函数可以用符号表示为f（x）＝cot x，其中cotx=tan(π2−x)，则下列关于余切函数的说法正确的是（）A．定义域为{x|x≠kπ，k∈Z}B．在区间(π2，π)上单调递增C．与正切函数有相同的对称中心D．将函数y＝﹣tan x的图象向右平移π2个单位可得到函数y＝cot x的图象解：根据cotx=tan(π2−x)，所以余切函数的图象如图所示：对于A：函数的定义域为{x|x≠kπ，k∈Z}，故A正确；对于B：在区间(π2，π)上单调递减，故B错误；对于C ：与正切函数有相同的对称中心，都为（kπ2，0）（k ∈Z ），故C 正确；对于D ：将函数y ＝﹣tan x 的图象向右平移π2个单位可得到函数y ＝﹣tan （x −π2）＝cot x 的图象，故D 正确． 故选：ACD ．12．已知扇形的半径为r ，弧长为l ．若其周长的数值为面积的数值的2倍，则下列说法正确的是（ ） A ．该扇形面积的最小值为8 B ．当扇形周长最小时，其圆心角为2 C ．r +2l 的最小值为9D ．1r 2+4l 2的最小值为12解：因为扇形的半径为r ，弧长为l ，所以扇形的周长为2r +l ，面积为12lr ；因为2r +l ＝2×12lr ，所以l =2rr−1，且r ＞1；所以扇形的面积为S =12×2r r−1×r =r 2r−1=(r−1)2+2(r−1)+1r−1=（r ﹣1）+1r−1+2≥2√(r −1)⋅1r−1+2＝4，当且仅当r ﹣1=1r−1，即r ＝2时取等号，所以选项A 错误； 扇形的周长为L ＝2r +2r r−1=2（r ﹣1）+2r−1+4≥2√2(r −1)⋅2r−1+4＝8， 当且仅当2（r ﹣1）=2r−1，即r ＝2时取等号，此时圆心角为|α|=l r =42=2，α＝±2，选项B 错误； r +2l ＝r +4r r−1=r +4+4r−1=（r ﹣1）+4r−1+5≥2√(r −1)⋅4r−1+5＝9， 当且仅当r ﹣1=4r−1，即r ＝3时取等号，选项C 正确； 1r 2+4l 2=1r 2+(r−1)2r 2=1−2r +2r 2=2(1r −12)2+14]≥12，当r ＝2时取等号，所以选项D 正确．故选：CD ．三、填空题：本大题共4小题，每小题5分，共20分.请把答案填写在答题卡相应位置上 13．已知幂函数f （x ）＝x α的图象经过点（9，3），则f （8）的值是 2√2 ． 解：根据幂函数f （x ）＝x α的图象经过点（9，3），可得9α＝3，求得α=12，故f （x ）=x 12=√x ．故f （8）=√8=2√2．故答案为：2√2．14．已知sin(x +π6)=13，则sin 2(π3−x)的值是 89 ．解：∵cos （π3−x ）=sin(x +π6)=13，∴sin2(π3−x)=1﹣cos2（π3−x）＝1−19=89．故答案为：8 9．15．已知定义在实数集R上的偶函数f（x）在区间[0，+∞）上是单调增函数，若f（lgx）＜f（1），则实数x的取值范围是110＜x＜10．解：∵f（x）定义在实数集R上的偶函数，在区间[0，+∞）上是单调增函数∴f（x）中（﹣∞，0）上是减函数又f（lgx）＜f（1）∴﹣1＜lgx＜1∴110＜x＜10故答案为：110＜x＜1016．已知函数f(x)=log9x+12x−1的零点为x1．若x1∈（k，k+1）（k∈Z），则k的值是1；若函数g （x）＝3x+x﹣2的零点为x2，则x1+x2的值是2．解：函数f(x)=log9x+12x−1是增函数，f（1）=−12＜0，f（2）＝log92＞0，满足f（1）f（2）＜0，所以函数的零点x1∈（1，2），所以k的值为1．函数f(x)=log9x+12x−1=12（log3x+x﹣2），函数的零点是y＝log3x与y＝2﹣x两个函数的图象的交点的横坐标x1，函数g（x）＝3x+x﹣2的零点为x2，是函数y＝3x与y＝2﹣x图象交点的横坐标，由于y＝log3x与y＝3x是反函数，关于y＝x对称，并且y＝2﹣x与y＝x垂直，交点坐标（1，1），所以x1+x2的值是2．故答案为：1；2．四、解答题：本大题共6小题，共70分.请在答题卡指定区域内作答，解答时应写出必要的文字说明，17．（10分）（1）已知a+a﹣1＝3，求a 12+a−12的值；（2）求值：e ln2+（lg5）2+lg5lg2+lg20．解：（1）因为（a 12+a−12）2＝a+a﹣1+2＝3+2＝5，又因为a 12+a−12＞0，所以a12+a−12=√5；（2）e ln2+（lg5）2+lg5lg2+lg20＝2+1g5（lg5+1g2）+1g2+1＝2+1g5+1g2+1＝2+1+1＝4．18．（12分）设全集U＝R，已知集合A＝{x|x2﹣5x+4≤0}，B＝{x|m≤x≤m+1}．（1）若A∩B＝∅，求实数m的取值范围；（2）若“x∈B”是“x∈A”的充分条件，求实数m的取值范围．解：（1）由x 2﹣5x +4≤0，解得1≤x ≤4，所以A ＝{x |1≤x ≤4}． 因为A ∩B ＝∅，且B ≠∅，所以m +1＜1或m ＞4，得m ＜0或m ＞4， 所以实数m 的取值范围是{m |m ＜0或m ＞4}．（2）因为“x ∈B ”是“x ∈A ”的充分条件，所以B ⊆A ， 所以{m ≥1m +1≤4，解得1≤m ≤3，所以实数m 的取值范围是{m |1≤m ≤3}．19．（12分）已知函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，0＜φ＜π）的部分图象如图所示． （1）求函数f （x ）的解析式；（2）求函数y ＝f （x ）在区间[﹣π，0]上的单调减区间．解：（1）由图可知A ＝2，T =4×(π3−π12)=π，所以ω=2πT=2．∵f （x ）＝2sin （2x +φ）的图象经过点(π12，2)， ∴π6+φ=π2+2kπ，k ∈Z ，即φ=π3+2kπ，k ∈Z ．∵0＜φ＜π，所以φ=π3，∴f(x)=2sin(2x +π3)．（2）令π2+2kπ≤2x +π3≤3π2+2kπ，k ∈Z ，解得π12+kπ≤x ≤7π12+kπ，k ∈Z ，∴f(x)=2sin(2x +π3)的减区间为[π12+kπ，7π12+kπ]，k ∈Z ，∴f(x)=2sin(2x +π3)在[﹣π，0]上的减区间为[−11π12，−5π12]．20．（12分）已知函数f(x)=a⋅2x−12x +1(a ∈R)．（1）若函数f （x ）为奇函数，求a 的值；（2）当a ＝3时，用函数单调性的定义证明：函数f(x)=a⋅2x−12x +1在R 上单调递增；（3）若函数y ＝f （x ）﹣2x 有两个不同的零点，求a 的取值范围．解：（1）由 f （0）＝0，得a ＝1，此时f(x)=2x−12x +1．因为f(−x)=2−x−12−x +1=1−2x1+2x =−f(x)，所以f （x ）为奇函数，故a ＝1． 证明：（2）当a ＝3时，f(x)=3⋅2x−12x +1=3−42x +1．任取x 1，x 2∈R ，且x 1＜x 2，则f(x 1)−f(x 2)=42x 2+1−42x 1+1=4(2x1−2x2)(1+2x 1)(1+2x 2)， 因为x 1＜x 2，所以2x 1＜2x 2，2x 1+1＞0，2x 2+1＞0， 所以4(2x 1−2x 2)(1+2x 1)(1+2x 2)＜0，即f （x 1）＜f （x 2），所以函数f(x)=a⋅2x−12x +1在R 上单调递增．解：（3）y ＝f （x ）﹣2x 有两个不同的零点，等价于（2x ）2+（1﹣a ）2x +1＝0有两个不同的实数解． 令t ＝2x （t ＞0），则t 2+（1﹣a ）t +1＝0在（0，+∞）有两个不同的实数解， 所以{(1−a)2−4＞0a −1＞0，解得a ＞3．所以a 的取值范围为（3，+∞）．21．（12分）如图，有一条宽为30m 的笔直的河道（假设河道足够长），规划在河道内围出一块直角三角形区域（图中△ABC ）种植荷花用于观赏，C ，B 两点分别在两岸l 1，l 2上，AB ⊥AC ，顶点A 到河两岸的距离AE ＝h 1，AD ＝h 2，设∠ABD ＝α．（1）若α＝30°，求荷花种植面积（单位：m 2）的最大值； （2）若h 2＝4h 1，且荷花的种植面积为150m 2，求sin α．解：由题可得，AB =ℎ2sinα，AC =ℎ1cosα． （1）当α＝30°时，AB ＝2h 2，AC =2√31， 所以S △ABC =12AB ⋅AC =2√31ℎ2，又因为h 1+h 2＝30，h 1，h 2≥0， 所以S △ABC =√31ℎ2≤√3(ℎ1+ℎ22)2=150√3，当且仅当h 1＝h 2＝15时取等号．所以荷花种植区域面积的最大值为150√3m 2．（2）因为h 1+h 2＝30，h 2＝4h 1，所以h 1＝6，h 2＝24，故AB =24sinα，AC =6cosα，α∈(0，π2)， 从而S △ABC =12AB ⋅AC =72sinαcosα=150， 所以sinαcosα=1225，① 所以(sinα+cosα)2=1+2sinαcosα=4925． 又因为α∈[0，π2]，所以sinα+cosα=75，② 由①②解得：sinα=35或45． 22．（12分）若存在实数对（a ，b ），使等式f （x ）•f （2a ﹣x ）＝b 对定义域中每一个实数x 都成立，则称函数f （x ）为（a ，b ）型函数．（1）若函数f （x ）＝2x 是（a ，1）型函数，求a 的值；（2）若函数g(x)=e 1x 是（a ，b ）型函数，求a 和b 的值；（3）已知函数h （x ）定义在[﹣2，4]上，h （x ）恒大于0，且为（1，4）型函数，当x ∈（1，4]时，ℎ(x)=−(log 2x)2+m ⋅log 2x +2．若h （x ）≥1在[﹣2，4]恒成立，求实数m 的取值范围．解：（1）由f （x ）＝2x 是（a ，1）型函数，得f （x ）•f （2a ﹣x ）＝2x •22a ﹣x ＝1，即22a ＝1，所以a ＝0． （2）由g(x)=e 1x是（a ，b ）型函数，得g(x)⋅g(2a −x)=e 1x ⋅e 12ax −x =b ，则1x +12a−x =lnb ，因此x 2lnb ﹣2axlnb +2a ＝0对定义域{x |x ≠0}内任意x 恒成立，于是{lnb =02alnb =02a =0，解得a ＝0，b ＝1，所以a ＝0，b ＝1．（3）由h （x ）是（1，4）型函数，得h （x ）•h （2﹣x ）＝4，（1）当x ＝1时，h （1）•h （1）＝4，而h （x ）＞0，则h （1）＝2，满足h （x ）≥1；（2）当x ∈（1，4]时，ℎ(x)=−(log 2x)2+m ⋅log 2x +2≥1恒成立，令log 2x ＝t ，则当t ∈（0，2]时，﹣t 2+mt +2≥1恒成立，于是m ≥t −1t 恒成立，而函数y =t −1t在（0，2]单调递增，则t −1t ≤32，当且仅当t ＝2时取等号，因此m ≥32； （3）当x ∈[﹣2，1）时，2﹣x ∈（1，4]，则ℎ(x)=4ℎ(2−x)=4−[log 2(2−x)]2+m⋅log 2(2−x)+2，由h （x ）≥1，得0＜−[log 2(2−x)]2+m ⋅log 2(2−x)+2≤4，令log 2（2﹣x ）＝u ，则当u ∈（0，2]时，0＜﹣u 2+mu +2≤4，由（2）知﹣u 2+mu +2≥1，则只需u ∈（0，2]时，﹣u 2+mu +2≤4恒成立，即m ≤2u +u 恒成立，又u +2u≥2√u ⋅2u =2√2，当且仅当u =√2时取等号，因此m ≤2√2， 所以实数m 的取值范围是：[32，2√2]．。

南京市第一中学2022-2023学年高一上学期期末考试数学卷一、单项选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合，，则( )R A B ⋃= A．B．C．D ．2．函数的定义域为．( )()lg(2)f x x =+-A ．B ．C ．D ．1[,)3+∞1[,2]31[,2)3[2,)+∞3．设，，，则a ，b ，c 的大小关系为．( )0.73a =0.81(3b -=0.7log 0.8c =A ．B ．a b c <<b a c <<C ．D ．b c a<<c a b<<4．圆心在原点，半径为10的圆上的两个动点M ，N 同时从点出发，沿圆周运动，点M 按(10,0)P 逆时针方向旋转，速度为弧度/秒，点N 按顺时针方向旋转，速度为弧度/秒，则它们第三次相6π3π遇时点M 转过的弧度数为( )A ．B ．C ．D ．2ππ2π3π5．设，则( )0.311531log 3,log 5,()5a b c ===A ．B ．C ．D ．a b c<<a c b<<b c a<<b a c<<6．设函数，则( )()ln |21|ln |21|f x x x =+--()f x A ．是偶函数，且在单调递增B ．是奇函数，且在单调递减1(,)2+∞11(,)22-C ．是偶函数，且在单调递增D ．是奇函数，且在单调递减1(,2-∞-1(,2-∞-7．中国早在八千多年前就有了玉器，古人视玉为宝，佩玉不再是简单的装饰，而有着表达身份、感情、风度以及语言交流的作用．不同形状、不同图案的玉佩又代表不同的寓意．如图1所示的扇形玉佩，其形状具体说来应该是扇形的一部分如图，经测量知，，(2)4AB CD ==3BC =，则该玉佩的面积为( )7AD =A ．B ．C ．D ．496π-493π-496π493π8．已知函数的表达式为，若且，则的取值()y f x =2()|log |f x x =0m n <<()()f m f n =2m n +范围为( )A ．B ．C ．D ．二、多项选择题：本题共4小题，每小题5分，共20分。

江苏省南京市2019-2020学年上学期期末考试高一数学试题注意事项：1．本试卷共4页，包括填空题（第1题~第14题）、解答题（第15题~第20题）两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校、班级、学号写在答题卡的密封线内．试题的答案写在答题卡．．．上对应题目的答案空格内．考试结束后，交回答题卡．一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置．．．．．．．上． 1．已知集合M ＝{x |0≤x ＜2}，N ＝{－1，0，1，2}，则M ∩ N ＝ ▲ ． 2．计算：lg4＋lg 52的值是 ▲ ．3．函数 f (x )＝(x －2)12的定义域是 ▲ ． 4．已知 tan α＝2，则 tan(α＋π4) 的值是 ▲ ．5．若函数 f (x )＝cos x ＋|2x －a | 为偶函数，则实数a 的值是 ▲ ．6．已知向量a ＝(1，2)，b ＝(－2，1)．若向量a －b 与向量k a ＋b 共线，则实数k 的值是 ▲ ． 7．已知角α的终边经过点P (12，5)，则sin(π＋α)＋cos(－α) 的值是 ▲ ．8．已知函数 f (x )＝⎩⎪⎨⎪⎧log 2(2－x )，x ＜1，2x ，x ≥1，则 f (－2)＋f (log 23) 的值是 ▲ ．9．在△ABC 中，若 tan A ＞1，则角A 的取值范围是 ▲ ．10．在平行四边形ABCD 中，AB →＝a ，AD →＝b ．若|a |＝2，|b |＝3，a 与b 的夹角为 π3，则线段BD 的长度为 ▲ ．11．已知α∈(0，π2)，且满足 sin 2α_x001F_－3cos 2α_x001F_sin αcos α ＝2，则tan α 的值是 ▲ ．12．已知函数 f (x )＝sin(ωx －π3) (ω＞0)，将函数 y ＝f (x ) 的图象向左平移 π个单位长度后，所得图象与原函数图象重合，则ω的最小值是 ▲ ．13．如图，已知函数f (x )的图象为折线ACB (含端点A ，B )，其中A (－4，0)，B (4，0)，C (0，4)，则不等式 f (x )＞log 2(x ＋2) 的解集是 ▲ ．14．若m ＞0，且关于x 的方程 (mx －1)2－m ＝x 在区间 [0，1] 上有且只有一个实数解，则实数m 的取值范围是 ▲ ．二、解答题：本大题共6小题，共90分．请在答题卡指定区域内．．．．．．．．作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）已知向量a ＝(1，2)，b ＝(－3，4)． （1）求向量a ＋b 与向量a 夹角的大小； （2）若a ⊥(a ＋λb )，求实数λ的值．16．（本小题满分14分）已知函数 f (x )＝A sin(ωx ＋φ) ( A ＞0，ω＞0，0＜φ＜π) 的图象如图所示． （1）求A ，ω，φ的值；（2）若x ∈[－π2，π12]，求f (x )的值域．(第16题图)已知sin α＝－437，α∈(－π2，0)．（1）求cos(π4＋α)的值；（2）若sin(α＋β)＝－3314，β∈(0，π2)，求β的值．18．（本小题满分16分）如图，已知OPQ 是半径为1，圆心角为 π3的扇形，点A 在弧 ⌒PQ 上(异于点P ，Q )，过点A 作AB ⊥OP ，AC ⊥OQ ，垂足分别为B ，C ．记∠AOB ＝θ，四边形ACOB 的周长为l ．（1）求l 关于θ的函数关系式；（2）当θ为何值时，l 有最大值，并求出l 的最大值．19．（本小题满分16分）如图，在矩形ABCD 中，点E 在边AB 上，且AE →＝2EB →．M 是线段CE 上一动点． （1）若M 是线段CE 的中点，AM →＝m AB →＋n AD →，求m ＋n 的值； （2）若AB ＝9，CA →·CE →＝43，求 (MA →＋2MB →)·MC →的最小值．P（第18题图）MEDCBA(第19题图)如果函数f(x)在定义域内存在区间[a，b]，使得该函数在区间[a，b]上的值域为[a2，b2]，则称函数f(x)是该定义域上的“和谐函数”．（1）求证：函数f(x)＝log2(x＋1)是“和谐函数”；（2）若函数g(x)＝x2－1＋t (x≥1)是“和谐函数”，求实数t的取值范围．江苏省南京市2019-2020学年上学期期末考试高一数学试题参考答案说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，填空题不给中间分数．一、填空题：本大题共14小题，每小题5分，共70分．1．{0，1} 2．1 3．[2，＋∞) 4．－3 5．06．－1 7．713 8．5 9．(π4，π2) 10．711．3 12．2 13．(－2，2) 14．(0，1]∪[3，＋∞)注：第1、3、13题的答案必须是集合或区间形式，第9、14题可以用不等式表示；其它题严格按标准执行。

2019~2020学年江苏南京高一上学期期末数学试卷(详解)一、单项选择题（本大题共8题，每小题5分，共计40分。

）2.A.B.C.D.【答案】【解析】已知向量，，则向量的坐标为（ ）．D ∵向量，，∴，选项正确．故选．3.A.B.C.D.【答案】已知，，，则，，的大小关系是（ ）．B1.A.B.C.D.【答案】【解析】已知集合，集合，则（ ）．C ∵集合，集合，∴．故选．【解析】，，∵，∴，∴．故选．4.A. B.C.D.【答案】【解析】函数的定义域为（ ）．C ∵函数，则，，即，，∴函数的定义域为．故选．5.A.B.C.D.【答案】【解析】已知扇形的面积为，圆心角为弧度，则的长为（ ）．B∵扇形面积为，圆心角又为，∴，则，由，则．即，，解得．故的长为．故选．6.A.B.C.D.【答案】【解析】若向量，满足：，，，则（ ）．D 依题意，，，∴，，∴，∴，，∴，∴．故选．7.A.B.C. D.【答案】【解析】函数图象的大致为（ ）．A 的定义域为，故排除选项；，所以函数是偶函数，图象关于轴对称，故排除选项；又当时，，，令，得，当时，，单调递增，当时，，单调递减，故排除选项．故选．8.A.B.C.D.【答案】【解析】安装了某种特殊装置的容器内有细沙，容器倒置后，细沙从容器内流出，后容器内剩余的细沙量为（单位：），其中为常数．经过后发现容器内还剩余的沙子，再经过后，容器中的沙子剩余量为，则（ ）．C由题意可知，后，剩沙子，则，∴，又∵再过剩沙子，∴，∴，∴．故选．二、多项选择题（本大题共4题，每小题5分，共计20分。

）9.A. B.C.D.【答案】A 选项：【解析】下列各选中，值为的是（ ）．AC根据换底公式有：，故正确；B 选项：C 选项：D 选项：，故错误；，故正确；原式的平方可得：，∴原式，故错误．故选 A C .10.A.B.C.D.【答案】A 选项：B 选项：C 选项：D 选项：【解析】记函数的图象为，则下列结论正确的是（ ）．函数的最小正周期为函数在区间上单调递增直线是图象的一条对称轴将函数的图象向右平移个单位长度，得到图象ABC∵函数，∴函数的最小正周期为，故正确；令，，，，则函数在上单调递增，当时，在上单调递增，故正确；令，，则，，函数的对称轴为，，当时，函数的一对称轴为，故正确；将函数的图象向右平移个单位长度，得到，故错误．故选 A B C .11.A.B.C.D.【答案】【解析】已知函数，，则下列结论正确的是（ ）．若，则函数的最小值为若，则函数的值域为若，则函数有且仅有一个零点若，则恒成立BCD 若，则，故取得的最小值．所以选项错误．若，则当时，，当时，．所以当时，，当时，．故的值域为．所以选项正确．若，当时，，当时，，当时，．故当时，解得，只有一个零点．所以选项正确．当时，单调递增，此时有，所以恒成立．故选项正确．一综上所述，结论正确的有、、．故选、、．12.A.B.C.D.【答案】A 选项：B 选项：C 选项：D 选项：【解析】已知向量，是同一平面内的两个向量，则下列结论正确的是（ ）．若存在实数，使得，则与共线若与共线，则存在实数，使得若与不共线，则对平面内的任一向量，均存在实数，，使得若对平面内的任一向量，均存在实数，，使得，则与不共线ACD若存在实数，使得，则不可能为零向量，所以与共线，故正确；若与共线，当为零向量时，不为零向量时，不存在实数，使得，故错误；若与不共线，则与可作为平面内一组基底，则存在实数，，使得平面内的任一向量，都可以表示成，故正确；若对平面内的任一向量，均存在实数，，使得，则与为平面内的一组基底，故与不共线，故正确．故选 A C D .三、填空题（本大题共4题，每小题5分，共计20分。

江苏省南京市高一上学期期末考试数学试题一、填空题：本大题共14小题，每小题3分，共42分． 1．函数f (x )＝1x – 3的定义域是 ▲ ． 2．集合{0，1}的子集的个数为 ▲ ． 3．求值：log 345－log 35＝ ▲ ．4．已知角α 的终边经过点P (2，－1)，则sin α 的值为 ▲ ．5．已知扇形的半径为3cm ，圆心角为2弧度，则扇形的面积为 ▲ cm 2． 6．函数f (x )＝cos (x －π3)，x ∈[0，π2]的值域是 ▲ ．7．三个数a ＝0.32，b ＝log 20.3，c ＝20.3之间的大小关系是 ▲ （用a ，b ，c 表示，并用“＜”连结）．8．将函数y ＝sin2x 的图象向右平移π6个单位长度，所得图象的函数解析式是 ▲ ． 9．如图，在矩形ABCD 中，已知AB ＝3，AD ＝2，且BE →＝EC →，DF →＝12FC →，则AE →·BF →＝ ▲ ．10．已知函数f (x )＝3x －log 2x 的零点为x 0，若x 0∈(k ，k ＋1)，其中k 为整数，则k ＝ ▲ ． 11．已知函数f (x )＝⎩⎪⎨⎪⎧e x ， x ≤0，ln x ，x ＞0，其中e 为自然对数的底数，则f [f (12)]＝ ▲ ．12．已知定义在实数集R 上的偶函数f (x )在区间[0，＋∞)上是单调增函数，且f (lg x )＜f (1)，则x 的取值范围是 ▲ ．C E （第9题）13．若函数f (x )＝m ·4x －3×2x ＋1－2的图象与x 轴有交点，则实数m 的取值范围是▲ ．14．若函数f (x )＝sin(ωx ＋π3) (ω＞0)在区间[0，2π]上取得最大值1和最小值－1的x 的值均唯一，则ω的取值范围是 ▲ ．二、解答题：本大题共6小题，共58分．请在答题卡指定区域内．．．．．．．．作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分8分）已知sin x ＝45，其中0≤x ≤π2． （1）求cos x 的值；（2）求cos(－x )sin(π2－x ) －sin(2π － x )的值．17．（本小题满分10分）经市场调查，某商品在过去20天的日销售量和日销售价格均为销售时间t (天)的函数，日销售量(单位：件)近似地满足：f (t )＝－t ＋30(1≤t ≤20，t ∈N *)，日销售价格(单位：元)近似地满足：g (t )＝⎩⎪⎨⎪⎧2t + 40，1≤t ≤10，t ∈N *，15， 11≤t ≤20，t ∈N *．（1）写出该商品的日销售额S 关于时间t 的函数关系； （2）当t 等于多少时，日销售额S 最大？并求出最大值．18．（本小题满分10分）已知函数f (x )＝A sin(ωx ＋ϕ)（A ＞0，ω＞0，0＜ϕ＜2π）的部分图象如图所示，且f (0)＝f（1）求函数f (x )（2）求f (x ) 参考答案一、填空题：本大题共14小题，每小题3分，共42分．1． (3，＋∞) 2．4 3．2 4．－55 5． 9 6．[12，1] 7．b ＜a ＜c8． y ＝sin(2x －π3) 9． －4 10．2 11．12 12．(110，10)13． (0，＋∞) 14．[712，1312)二、解答题：本大题共6小题，共58分．15．解（1）因为sin 2x ＋cos 2 x ＝1，所以cos 2x ＝1－sin 2 x ＝1－(45)2＝925．…… 2分 又因为0≤x ≤π2，故cos x ≥≤0，所以cos x ＝35． ………… 4分（2）原式＝cos x cos x ―(―sin x ) ＝cos x cos x ＋sin x…… 7分 ＝3535＋45＝37．………… 8分（第18题）17．解（1）由题意知，S ＝f (t )·g (t )＝⎩⎪⎨⎪⎧(2t ＋40)(－t ＋30)，1≤t ≤10，t ∈N *，15(－t ＋30)， 11≤t ≤20，t ∈N *． ………… 4分（2）当1≤t ≤10，t ∈N *时，S ＝(2t ＋40)(－t ＋30)＝－2 t 2＋20t ＋1200＝－2 (t －5)2＋1250．因此，当t ＝5时，S 最大值为1250； ……………………… 7分 当11≤t ≤20，t ∈N *时，S ＝15(－t ＋30)＝－15t ＋450为减函数，因此，当t ＝11时，S 最大值为285． ……………………… 9分综上，S 的最大值为1250．答：当t ＝5 时，日销售额S 最大，最大值为1250元． …………… 10分18．解（1）由题意知，函数图象的一条对称轴为x ＝0＋5π62＝5π12， ………… 2分则 T 4＝5π12－π6＝π4， 即T ＝π．所以函数的最小正周期是π．…………… 4分（2）由图可知，A ＝2，因为T ＝π，所以ω＝2πT ＝2． ……………………… 6分 又f (5π12)＝－2，所以2 sin(5π6＋ϕ)＝－2，即sin(5π6＋ϕ)＝－1，因此5π6＋ϕ＝2k π－π2，即ϕ＝2k π－4π3，k ∈Z ．因为0＜ϕ＜2π，所以ϕ＝2π3．所以函数的解析式为f (x )＝2sin(2x ＋2π3)．… 8分由2k π－π2≤2x ＋2π3≤2k π＋π2，k ∈Z ，解得k π－7π12≤x ≤k π－π12，k ∈Z ，所以函数的单调增区间为[k π－7π12， k π－π12]，k ∈Z ．……………… 10分。

一、单选题1．已知，则（ ）{}R,{13},2U A x x B x x ==-<<=≤∣∣()U A B ⋃=ðA ． B ． (](),12,-∞-+∞ ()[),12,-∞-⋃+∞C ． D ．[)3,+∞()3,+∞【答案】C【分析】由并集和补集的概念即可得出结果.【详解】∵ {}R,{13},2U A xx B x x ==-<<=≤∣∣∴，则， ),3(A B ⋃=-∞,()[)3U A B ⋃=+∞ð故选：C.2．已知，则（ ） 22log 3,log 5a b ==18log 15=A ．B ．21a ba +-12a ba++C ． D ．1a b -+-1a b +-【答案】B【分析】利用对数的换底公式和对数的运算性质进行运算求解即可． 【详解】，2221822log 15log 3log 5log 15log 1812log 312a ba++===++故选：B ．3．设为实数，且，则“”是“的（ ） a b c d ,,,c d <a b <”a c b d -<-A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B【分析】根据充分条件、必要条件的定义判断即可.【详解】解：由不能推出，如，，，， a b <a c b d -<-2a =3b =0c =1d =满足，但是，故充分性不成立；a b <a c b d -=-当时，又，可得，即，故必要性成立； a c b d -<-c d <a c c b d d -+<-+a b <所以“”是“的必要不充分条件. a b <”a c b d -<-故选：B.4．函数的零点所在的大致区间为（ ）()3ln f x x x=-A ． B ． C ． D ．()0,1()1,2()2,e ()e,3【答案】D【分析】由题意可知在递增，且，由零点存在性定理即可得出答案. ()f x ()0,∞+()()e 0,30f f 【详解】易判断在递增，. ()f x ()0,∞+()()3e lne 0,3ln310ef f =-=-由零点存在性定理知，函数的零点所在的大致区间为.()3ln f x x x=-()e,3故选:D.5．已知，则的值是（ ）π1sin 63x ⎛⎫+= ⎪⎝⎭25πsin()2cos (6π3x x -+-A ．B ．C ．D 59-1959【答案】C 【分析】令，代入所求式子，结合诱导公式化简即可得出结果. π6t x =+【详解】令，则，， π6t x =+π6=-x t 1sin 3t =则. 2225π125sin()2cos ()sin(π)2cos ()sin 2sin 63399ππ2x x t t t t -+-=-+-=+=+=故选：C.6．将函数的图象向右平移个单位长度，在纵坐标不变的情况下，再把平移()π2sin 43⎛⎫=- ⎪⎝⎭f x x π3后的函数图象上每个点的横坐标变为原来的2倍，得到函数的图象，则函数所具有的性()g x ()g x 质是（ ） A ．图象关于直线对称3x π=B ．图象关于点成中心对称π,06⎛⎫⎪⎝⎭C ．的一个单调递增区间为()g x 5ππ,44⎡⎤-⎢⎥⎣⎦D ．曲线与直线 ()g x y =π6【答案】D【分析】先利用题意得到，然后利用正弦函数的性质对每个选项进行判断即可()π2sin 23⎛⎫=+ ⎪⎝⎭g x x 【详解】函数的图象向右平移个单位长度得到()f x π3，ππ5ππ2sin 42sin 42sin 43333⎛⎫⎛⎫⎛⎫⎛⎫=--=-=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭y x x x 纵坐标不变，横坐标变为原来的2倍得到，()π2sin 23⎛⎫=+ ⎪⎝⎭g x x对于A ，因为ππsin 2sin π01,33⎛⎫⨯+==≠± ⎪⎝⎭所以直线不是的对称轴，故错误；3x π=()g x A对于B ， ππ2πsin 2sin0,633⎛⎫⨯+==≠ ⎪⎝⎭所以图象不关于点成中心对称，故错误；π,06⎛⎫⎪⎝⎭B 对于C ，当，则， 5ππ,44⎡⎤∈-⎢⎥⎣⎦x π13π5π2,366⎡⎤+∈-⎢⎥⎣⎦x 因为正弦函数在不单调，故不是的一个单调递增区间，故错sin y x =13π5π,66⎡⎤-⎢⎥⎣⎦5ππ,44⎡⎤-⎢⎥⎣⎦()g x C 误；对于D ，当则或， ()g x =sin 23⎛⎫+=⎪⎝⎭x πππ22π33+=+x k 2π2π,Z 3+∈k k 则或，则相邻交点距离最小值为，故D 正确πx k =Z π6,+∈k k ππ6故选：D. 7．函数的图象大致为（ ） ()22cos 1x xf x x =+A ． B ．C ．D ．【答案】D【分析】利用函数的奇偶性及在上的函数值正负逐个选项判断即可．()f x π0,2⎛⎫⎪⎝⎭【详解】因为，定义域为R ， ()22cos 1x xf x x =+所以， ()222()cos()2cos ()()11x x x xf x f x x x ---==-=--++所以为奇函数，又因为时，所以由图象知D 选项正确，()f x π0,2x ⎛⎫∈ ⎪⎝⎭()0f x >故选D ．8．高斯是德国著名的数学家，近代数学奠基者之一，用其名字命名的“高斯函数”为：设，用x ∈R 表示不超过的最大整数，则称为高斯函数.例如：.已知函数[]x x []y x =][3.64,3.63⎡⎤-=-=⎣⎦，则函数的值域是（ ） ()1e 21e xxf x =-+()()y f x f x =+⎡⎤⎣-⎡⎤⎦⎣⎦A ． B ．C ．D ．{}1,0-{}0{}0,1{}1,0,1-【答案】A【分析】依题意可得，再根据指数函数的性质讨论，和时，函数()1121e x f x =-++0x >0x =0x <的单调性与值域，即可得出答案.【详解】因为，定义域为， ()1e 11e 11111121e 21e 21e 21e x x x x xx f x +-⎛⎫=-=-=--=-+⎪++++⎝⎭R 因为在定义域上单调递增，则在定义域上单调递减， 1e x y =+11e xy =+所以在定义域上单调递减，()1121e xf x =-++R 时，， 0x <()()()111e 0,1,,1,0,,01e 22xx f x f x ⎛⎫⎛⎫⎡⎤∈∈∈= ⎪ ⎪⎣⎦+⎝⎭⎝⎭()00f ⎡⎤=⎣⎦时，； 0x >()()()111e 1,,0,,,0,11e 22xx f x f x ∞⎛⎫⎛⎫⎡⎤∈+∈∈-=- ⎪ ⎪⎣⎦+⎝⎭⎝⎭则时，0x >()()101,f x f x ⎡⎤⎡⎤+-=-+=-⎣⎦⎣⎦时，，0x <()()()011f x f x ⎡⎤⎡⎤+-=+-=-⎣⎦⎣⎦时，.0x =()()000f x f x ⎡⎤⎡⎤+-=+=⎣⎦⎣⎦故选：A.【点睛】关键点睛：本题解题关键在于理解题中高斯函数的定义，才能通过研究的性质来研()f x 究的值域，突破难点. ()()y f x f x =+⎡⎤⎣-⎡⎤⎦⎣⎦二、多选题9．下列说法正确的是（ ） A ．若为正整数，则 ,a b n >n n a b >B ．若，则0,0b a m >>>a m ab m b+>+C ．22222a ba b++≥D ．若，则0απ<<0sin 1α<<【分析】利用不等式性质、基本不等式及正弦函数的图象性质逐个选项判断即可得到答案． 【详解】对于A ，若，则，故A 错误； 1,1,2a b n ==-=n n a b =对于B ，时，，故B 正确； 0,0b a m >>>a m aab bm ab am b a b m b+>⇔+>+⇔>+对于C ，由，则，当且仅当时取等号，故C 正确；20,20a b >>22222a b a b ++≥=⨯a b =对于D ，当时，，故D 错误； π2α=πsin 12=故选：BC ．10．设为实数，已知关于的方程，则下列说法正确的是（ ）m x ()2310mx m x +-+=A ．当时，方程的两个实数根之和为0 3m =B ．方程无实数根的一个必要条件是1m >C ．方程有两个不相等的正根的充要条件是 01m <<D ．方程有一个正根和一个负根的充要条件是 0m <【答案】BCD【分析】逐项分析每个选项方程根的情况对应的参数m 满足的不等式，解出m 的范围，判断正误. 【详解】对于A 选项，时无实根，A 错误；3m =2310x +=对于B 选项，当时方程有实根，当时，方程无实根则，解得0m =0m ≠2(3)40m m --<19m <<，一个必要条件是，B 正确；1m >对于C 选项，方程有两个不等正根，则，，，，解得； 0m ≠0∆>30mm ->10m>01m <<对于D 选项，方程有一个正根和一个负根，则，，解得，D 正确； 0m ≠10m<0m <故选：BCD.11．设，已知 ） 0,0a b >>22,a b M N ab +=A ．有最小值 B ．没有最大值M MC ．D ．N N 【答案】ABD【分析】由均值不等式分别求出的最值，即可得出答案. ,M N 【详解】时正确， ,0a b >()[)10,,2,AB b b a t M t a a b t∞∞=∈+=+=+∈+，时错误，D 正确； 0,0a b >>2a b +C ≥12．设为正实数，为实数，已知函数，则下列结论正确的是（ ） ωa ()()4sin f x x a ωϕ=++A ．若函数的最大值为2，则()f x 2a =-B ．若对于任意的，都有成立，则 x ∈R ()()πf x f x +=2ω=C ．当时，若在区间上单调递增，则的取值范围是 π3ϕ=()f x ππ,62⎡⎤-⎢⎥⎣⎦ω10,3⎛⎤ ⎥⎝⎦D ．当，函数在区间上至少有两个零点，则的取值a =-ϕ∈R ()f x π0,2⎡⎤⎢⎥⎣⎦ω范围是 [)4,+∞【答案】ACD【分析】对A ：根据正弦函数的有界性分析判断；对B ：利用函数的周期的定义分析判断；对C ：以为整体，结合正弦函数的单调性分析判断；对D ：以为整体，结合正弦函数的性质x ωϕ+x ωϕ+分析判断.【详解】A 选项，由题意，则，A 正确； 42a +=2a =-B 选项，若，则的周期为， ()()πf x f x +=()f x π设的最小正周期为，则， ()f x T ()*2π=πkT kk ωN =Î解得，B 错误；()*2ωk k N =ÎC 选项，当时， π3ϕ=∵，则，ππ,62x ⎡⎤∈-⎢⎥⎣⎦πππππ,36323x ωωω⎡⎤+∈-++⎢⎥⎣⎦若在区间上单调递增，则，()f x ππ,62⎡⎤-⎢⎥⎣⎦0πππ632πππ232ωωω⎧⎪>⎪⎪-+≥-⎨⎪⎪+≤⎪⎩解得，C 正确；10,3ω⎛⎤∈ ⎥⎝⎦选项，由题意可得，对，在上至少两个零点，D ()sin x ωϕ+=ϕ∀∈R π0,2⎡⎤⎢⎥⎣⎦∵，则，π0,2x ⎡⎤∈⎢⎥⎣⎦π,2x ωϕϕωϕ⎡⎤+∈+⎢⎥⎣⎦若对，在上至少两个零点，则，解得，D 正确；ϕ∀∈R π0,2⎡⎤⎢⎥⎣⎦π2π2ωϕϕ⎛⎫+-≥ ⎪⎝⎭4ω≥【点睛】方法点睛：求解函数y ＝A sin(ωx ＋φ)的性质问题的三种意识(1)转化意识：利用三角恒等变换将所求函数转化为f (x )＝A sin(ωx ＋φ)的形式．(2)整体意识：类比y ＝sin x 的性质，只需将y ＝A sin(ωx ＋φ)中的“ωx ＋φ”看成y ＝sin x 中的“x ”，采用整体代入求解． ①令ωx ＋φ＝k π＋(k ∈Z )，可求得对称轴方程． π2②令ωx ＋φ＝k π(k ∈Z )，可求得对称中心的横坐标．③将ωx ＋φ看作整体，可求得y ＝A sin(ωx ＋φ)的单调区间，注意ω的符号． (3)讨论意识：当A 为参数时，求最值应分情况讨论A >0，A <0.三、填空题13．命题“”的否定是__________. 21,20x x ∃≥-<【答案】21,20x x ∀≥-≥【分析】根据特称命题的否定，可得答案. 【详解】由题意，则其否定为. 21,20x x ∀≥-≥故答案为：. 21,20x x ∀≥-≥14．已知，则__________.2212sin cos 2sin cos θθθθ+=-tan θ=【答案】3【分析】将已知式中分子，再分子分母同时除以，解方程即可得出答案.221sin cos θθ=+2cos θ【详解】由题意，222222sin 2sin cos cos tan 2tan 12sin cos tan 1θθθθθθθθθ++++==--即，则. tan 12tan 1θθ+=-tan 3θ=故答案为：3.15．设函数，则满足的的取值范围是__________.21,0()3,0x x x f x x +≤⎧=⎨>⎩3()()32f x f x +->x 【答案】()1,+∞【分析】结合函数解析式，对分三种情况讨论，分别计算可得.x 【详解】当时，，则在0x ≤()33212141122f x f x x x x ⎛⎫⎛⎫+-=++-+=-≤- ⎪ ⎪⎝⎭⎝⎭()332f x f x ⎛⎫+-> ⎪⎝⎭当时，，在单调递增，时302x <≤()3332132222x x f x f x x x ⎛⎫⎛⎫+-=+-+=+- ⎪ ⎪⎝⎭⎝⎭R 1x =，则的解集为；132123+⨯-=()332f x f x ⎛⎫+-> ⎪⎝⎭31,2⎛⎤⎥⎝⎦当时，，则在时恒成立；32x >()33022*******x x f x f x -⎛⎫+-=+>+> ⎪⎝⎭()332f x f x ⎛⎫+-> ⎪⎝⎭32x >综上，的解集为.()332f x f x ⎛⎫+-> ⎪⎝⎭()1,+∞故答案为：．()1,+∞16．已知函数是定义在上不恒为零的偶函数，且对于任意实数都有()f x R x ()1()(1)x f x xf x -=-成立，则__________.7(())2f f =【答案】0【分析】根据解析式求出，进而得到若，则，从而求出.102f ⎛⎫= ⎪⎝⎭()10f x -=()0f x =7(())02f f =【详解】由，令可得，今可得，()1()(1)x f x xf x -=-0x =()00f =12x =11112222f f ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭由是偶函数可得，则， ()f x 1122f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭102f ⎛⎫= ⎪⎝⎭时，若，则，0,1x ≠()10f x -=()0f x =则，135702222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭则.7(((0)02f f f ==故答案为：0.四、解答题17．设，已知集合. m ∈R (){}2321,2201x A xB x x m x m x +⎧⎫=<=+--<⎨⎬-⎩⎭∣∣(1)当时，求；1m =A B ⋃(2)若“”是“”的必要条件，求的取值范围.x B ∈x A ∈m 【答案】(1)3,12⎛⎫- ⎪⎝⎭(2) [)3,+∞【分析】（1）求出集合，由并集的定义即可得出答案.,A B（2）由“”是“”的必要条件可得，则，解不等式即可得出答案. x B ∈x A ∈A B ⊆322m -≤-【详解】（1）由可得，即，则， 3211x x +<-2301x x +<-()()1230x x -+<3,12A ⎛⎫=- ⎪⎝⎭时，.()(){210},1B x x m x m =+-<=∣13,1,,122B A B ⎛⎫⎛⎫=-⋃=- ⎪ ⎪⎝⎭⎝⎭（2）由“”是“”的必要条件可得， x B ∈x A ∈A B ⊆则，则，实数的取值范围是. 322m -≤-3m ≥m [)3,+∞18．设，计算下列各式的值： tan 2α=(1)；2sin cos 3sin cos αααα+-(2).22sin sin cos ααα-【答案】(1)1 (2)5【分析】（1）所求表达式分子分母同时除以，代入求解即可；cos α（2）将分子看成，所求表达式分子分母同时除以，代入求解即可；2()222sin cos αα+2cos α【详解】（1）原式；2tan 122113tan 1321αα+⨯+===-⨯-（2）原式. ()22222222sin cos 2tan 22225sin sin cos tan tan 22αααααααα++⨯+====---19．设函数和的定义域为，若是偶函数，是奇函数，且()f x ()g x ()1,1-()f x ()g x .()()2lg(1)f x g x x -=-(1)求函数和的解析式；()f x ()g x (2)判断在上的单调性，并给出证明.()f x ()0,1【答案】(1)， ()lg(1)lg(1)f x x x =-++()()()lg 1lg 1g x x x =+--(2)单调递减，证明见解析【分析】（1）根据函数奇偶性构造关于和得方程组，进而求出它们的解析式； ()f x ()g x （2）根据函数单调性定义进行证明.【详解】（1）由，可得，()()2lg(1)f x g x x -=-()()2lg(1)f x g x x ---=+由为偶函数，为奇函数，可得， ()f x ()g x ()()2lg(1)f x g x x +=+则，；()lg(1)lg(1)f x x x =-++()()()lg 1lg 1g x x x =+--（2）由（1）得()2lg(1)f x x =-在单调递减，证明如下： ()f x ()0,1取任意，1212,(0,1),x x x x Î< ()()22211212221lg(1)lg(1)lg 1x f x f x x x x --=---=-由，可得，则， 1201x x <<<2212110x x ->->2122111x x ->-则， ()()2112221lg 01x f x f x x --=>-则，则在单调递减.()()12fx f x >()f x ()0,120．如图所示，有一条“L ”，河道均足够长.现过点修建一条长为的栈道，开辟出直角三角形区域（图中）养殖观赏鱼，且D m l ABOAB A .点在线段上，且.线段将养殖区域分为两部分，其中上方养殖金OAB θ∠=H AB OH AB ⊥OH OH 鱼，下方养殖锦鲤.OH(1)当养殖观赏鱼的面积最小时，求的长度；l (2)若游客可以在河岸与栈道上投喂金鱼，在栈道上投喂锦鲤，且希望投喂锦鲤的道路OA AH HB ，求的取值范围. 1θ【答案】(1)(2). ππ,42⎡⎫⎪⎢⎣⎭【分析】（1）过作垂直于，求得，从而得出养殖观赏D ,DM DN ,OAOB AM BN θ=鱼的面积，利用基本不等式可求得最小时的值，进而113tan 2tan OAB S OA OB θθ=⋅=+A OAB S A θ求得的长度；l （2）由，可得，则，由题意π2AOB OHA ∠=∠=BOH θ∠=,,tan sin tan OH OH OA AH BH OH θθθ===，则，化切为弦可得即可求得1BH OA AH -+tan 111sin tan θθθ≥+1cos θ≥π0,2θ⎛⎫∈ ⎪⎝⎭结果.【详解】（1）过作垂直于，垂足分别为，D,DM DN ,OA OB ,M N则DM ON DN OM ====，tan tan DM AMBN DN θθθ====养殖观赏鱼的面积， )1113tan 22tan OAB S OA OB θθθ=⋅==+A 由可得，则，当且仅当时取等号， π0,2θ⎛⎫∈ ⎪⎝⎭tan 0θ>13tan tanθθ+≥tanθ=π6θ=则最小时，，此时l 的长度为； OAB S A π6θ=sin cos DM DN l θθ=+==（2）由，可得，π2AOB OHA ∠=∠=BOH θ∠=则，,,tan sin tan OH OH OA AH BH OH θθθ===由题意，则， 1BH OA AH ≥+tan 111sin tan θθθ≥-+而， ()()22sin tan sin 1cos 1cos 1111cos cos 1cos cos 1cos cos sin tan sin θθθθθθθθθθθθθθ-====-++++则可得，则. 1cos θ≥π0,2θ⎛⎫∈ ⎪⎝⎭cos 0θ>cos θ≤ππ,42θ⎡⎫∈⎪⎢⎣⎭21．设为实数，已知函数，. a ()122x x f x =-()()ln ln 2g x x x a =⋅-+(1)若函数和的定义域为，记的最小值为，的最小值为.当()f x ()g x [)1,+∞()f x 1M ()g x 2M 时，求的取值范围；21M M ≤a (2)设为正实数，当恒成立时，关于的方程是否存在实数解？若存在，x ()0g x >x ()()0f g x a +=求出此方程的解；若不存在，请说明理由.【答案】(1) 5,2⎛⎤-∞ ⎥⎝⎦(2)不存在，理由见解析【分析】（1）利用指数函数的单调性及二次函数的性质，分别求出和的最小值，()f x ()g x 12,M M 然后解不等式即可；（2）利用二次函数的性质，求得的最小值为，由题意可得，当时,()g x 1a -1a >()0g x >()21g x >，，可得，即可得出结论. ()112g x <()()0f g x a +>【详解】（1）当时，函数和均单调递增，所以函数单调递增，故1x ≥2x y =12x y =-()122x x f x =-当时，取最小值，则； 1x =()f x 32132M =当时，，，1x ≥ln 0x ≥()()2ln 11g x x a =-+-则当，即时，取最小值，即，ln 10x -=e x =()g x 1a -21M a =-由题意得，则，即的取值范围是； 312a -≤52a ≤a 5,2⎛⎤-∞ ⎥⎝⎦（2）当时，，，0x >ln R x ∈()()2ln 11g x x a =-+-则当，即时，取最小值为，ln 10x -=e x =()g x 1a -则恒成立时，有，即，()0g x >10a ->1a >当时，，， ()0g x >()21g x >()112g x <则，则，()()()()1202g x g x f g x =->()()0f g x a +>故关于的方程不存在实数解.x ()()0f g x a +=22．设，函数. a ∈R ()2πsin cos ,,π2f x x x a x ⎛⎫=-+∈ ⎪⎝⎭(1)讨论函数的零点个数；()f x (2)若函数有两个零点，求证：. ()f x 12,x x 123π2x x +<【答案】(1)答案见解析(2)证明见解析【分析】（1）利用分离参数法分类讨论函数的零点个数；()f x （2）利用根与系数关系和三角函数单调性证明. 123π2x x +<【详解】（1）， ()2cos cos 1f x x x a =--++令，即，()0f x =2cos cos 1x x a +=+时，即， π,π2x ⎛⎫∈ ⎪⎝⎭()()21cos 1,0,,0,04t x t t f x ⎡⎫=∈-+∈-=⎪⎢⎣⎭21t t a +=+或即时，无解； 10a +≥114a +<-[)5,1,4a ∞∞⎛⎫∈--⋃-+ ⎪⎝⎭21t t a +=+即时，仅有一解，此时仅有一解； 114a +=-54a =-21t t a +=+12t =-x 2π3即时，有两解， 1104a -<+<514a -<<-21t t a +=+12t =-有两个零点； 1cos 2x =-()f x 综上，时，无零点， [)5,1,4a ∞∞⎛⎫∈--⋃-+ ⎪⎝⎭()f x 时，有一个零点， 54a =-()f x 时，有两个零点； 5,14a ⎛⎫∈-- ⎪⎝⎭()f x （2）有两个零点时，令，则为两解，()f x 1122cos ,cos t x t x ==12,t t 21t t a +=+则，则，121t t +=-12cos cos 1x x +=-则，221122cos 2cos cos cos 1x x x x ++=由可得， 12π,,π2x x ⎛⎫∈ ⎪⎝⎭12cos 0,cos 0x x <<则，则，122cos cos 0x x >2212cos cos 1x x +<则， 2221223πcos sin cos 2x x x ⎛⎫<=- ⎪⎝⎭由可得， 2π,π2x ⎛⎫∈ ⎪⎝⎭223ππ3π,π,cos 0222x x ⎛⎫⎛⎫-∈-< ⎪ ⎪⎝⎭⎝⎭则，由在递减， 123πcos cos 2x x ⎛⎫>- ⎪⎝⎭cos y x =π,π2⎛⎫ ⎪⎝⎭可得，则. 123π2x x <-123π2x x +<【点睛】函数零点的求解与判断方法：(1)直接求零点：令f (x )＝0，如果能求出解，则有几个解就有几个零点．(2)零点存在性定理：利用定理不仅要函数在区间[a ，b ]上是连续不断的曲线，且f (a )·f (b )＜0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．(3)利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其交点的横坐标有几个不同的值，就有几个不同的零点．。

高一（上）期末(qī mò)数学试卷一、选择题（本大题为单项选择题，共10小题(xiǎo tí)，每小题5分）1．满足(mǎnzú){1，3}∪A={1，3，5}的所有(suǒyǒu)集合A的个数（）A．1个B．2个C．3个D．4个2．直线(zhíxiàn)=1的斜率是（）A．B．﹣C．D．﹣3．一水平放置的平面图形的直观图如图所示，则此平面图形的形状是（）A．B．C．D．4．空间直角坐标系中点P（1，3，5）关于原点对称的点P′的坐标是（）A．（﹣1，﹣3，﹣5）B．（﹣1，﹣3，5）C．（1，﹣3，5）D．（﹣1，3，5）5．函数f（x）=log2x﹣的一个零点落在下列哪个区间（）A．（0，1）B．（1，2）C．（2，3）D．（3，4）6．如图，在正方体ABCD﹣A1B1C1D1中，E为A1C1的中点，则异面直线CE与BD所成的角为（）A．30° B．45°C．60°D．90°7．今有一组数据(shùjù)如下：t 1.99 3.0 4.0 5.1 6.12v 1.5 4.04 7.5 12 18.01在以下四个模拟(mónǐ)函数中，最合适这组数据的函数是（）A．v=log2t B．C．D．v=2t﹣28．已知lga+lgb=0（a＞0，b＞0且a≠1，b≠1），则函数(hánshù)f（x）=a x与函数(hánshù)g（x）=﹣log b x的图象(tú xiànɡ)可能是（）A．B．C．D．9．点P（2，﹣1）为圆（x﹣1）2+y2=25的弦AB的中点，则直线AB的方程为（）A．x+y﹣1=0 B．2x+y﹣3=0 C．x﹣y﹣3=0 D．2x﹣y﹣5=010．把正方形ABCD沿对角线AC折起，当以A、B、C、D四点为顶点的三棱锥体积(tǐjī)最大时，直线BD和平面ABC所成的角的大小为（）A．90° B．60°C．45°D．30°二、填空题（本大题共5小题(xiǎo tí)，每小题5分，共25分）11．幂函数的图象(tú xiànɡ)经过点（4，2），那么的值是．12．经过(jīngguò)（3，4），且与圆x2+y2=25相切的直线(zhíxiàn)的方程为．13．某几何体的三视图如图，其中正视图与侧视图上半部分为半圆，则该几何体的表面积为．14．若奇函数y=f（x）的定义域为[﹣4，4]，其部分图象如图所示，则不等式f（x）ln（2x﹣1）＜0的解集是．15．已知直线a、b、c以及平面α、β，给出下列(xiàliè)命题：①若a∥α且b∥α，则a∥b；②若α∥β，c⊥α，则c⊥β；③若a⊥b，a⊥α，则b∥α；④若α⊥β，a∥α，则a⊥β⑤若a⊥c，b⊥c，则a∥b或a、b异面或a、b相交(xiāngjiāo)其中(qízhōng)正确命题的序号是（把所有正确(zhèngquè)命题的序号都填上）．三、解答题（本大题共6小题(xiǎo tí)，总分75分，请把解答写在指定方框内，否则不记分）16．分别求满足下列条件的直线方程．（Ⅰ）过点（0，1），且平行于l1：4x+2y﹣1=0的直线；（Ⅱ）与l2：x+y+1=0垂直，且过点P（﹣1，0）的直线．17．已知：函数f（x）=+lg（3x﹣9）的定义域为A，集合B={x|x﹣a＜0，a∈R}．（1）求：集合A；（2）求：A∩B．18．某校办工厂生产学生校服的固定成本为20000元，每生产一件需要(xūyào)增加投入100元，已知总收益R（x）满足函数R（x）=，其中(qízhōng)x是校服的月产量，问：（1）将利润表示为关于月产量(chǎnliàng)x的函数f（x）；（2）当月产量为何(wèihé)值时，工厂所获利润最大？最大利润为多少元？（总收益=总成本+利润(lìrùn)）．19．长方体ABCD﹣A1B1C1D1中，，AB=BC=2，O是底面对角线的交点．（Ⅰ）求证：B1D1∥平面BC1D；（Ⅱ）求证：A1O⊥平面BC1D；（Ⅲ）求三棱锥A1﹣DBC1的体积．20．已知圆C1的方程为x2+y2﹣4x+2my+2m2﹣2m+1=0．（1）求当圆的面积最大时圆C1的标准方程；（2）求（1）中求得的圆C1关于直线l：x﹣y+1=0对称的圆C2的方程．21．已知函数f（x）满足f（log a x）=（x﹣x﹣1），其中a＞0，a≠1，（1）讨论(tǎolùn)f（x）的奇偶性和单调性；（2）对于(duìyú)函数f（x），当x∈（﹣1，1）时，f（1﹣m）+f（﹣2m）＜0，求实数(shìshù)m取值的集合；（3）是否存在实数(shìshù)a，使得当x∈（﹣∞，2）时f（x）的值恒为负数(fùshù)？，若存在，求a的取值范围，若不存在，说明理由．2021-2021学年(xuénián)湖南省衡阳市常宁市高一（上）期末数学试卷参考答案与试题(shìtí)解析一、选择题（本大题为单项选择题，共10小题(xiǎo tí)，每小题5分）1．满足(mǎnzú){1，3}∪A={1，3，5}的所有(suǒyǒu)集合A的个数（）A．1个B．2个C．3个D．4个【考点】并集及其运算．【分析】由题意得1，3和5可能是集合B的元素，把集合B所有的情况写出来．【解答】解：∵{1，3}∪A={1，3，5}，∴1和2和3可能是集合B的元素，则集合B可能是：{5}，{1，5}，{3，5}，{1，5，3}共4个．故选D．2．直线=1的斜率是（）A．B．﹣C．D．﹣【考点】直线的斜率．【分析(fēnxī)】把直线(zhíxiàn)的方程化为斜截式，从而求得它的斜率．【解答(jiědá)】解：直线(zhíxiàn)=1 即 y=x﹣2，故直线(zhíxiàn)的斜率等于，故选 A．3．一水平放置的平面图形的直观图如图所示，则此平面图形的形状是（）A．B．C．D．【考点】平面图形的直观图．【分析】本选择题，可以用选择题的特殊方法来解，观察直观图右边的边与纵轴平行，与x轴垂直，这样只有C符合题意，从而得出正确答案．【解答】解：根据平面图形水平放置的直观图可知，右边的边与纵轴平行，与x轴垂直，这样此平面图形中有一个内角是直角，只有C符合题意，故选C．4．空间直角坐标系中点P（1，3，5）关于原点对称的点P′的坐标是（）A．（﹣1，﹣3，﹣5）B．（﹣1，﹣3，5）C．（1，﹣3，5）D．（﹣1，3，5）【考点(kǎo diǎn)】空间(kōngjiān)中的点的坐标．【分析(fēnxī)】根据空间坐标关于点的对称的结论(jiélùn)进行求解即可．【解答(jiědá)】解：空间直角坐标系中点P（1，3，5）关于原点对称的点的坐标都有相应的相反数，即（﹣1，﹣3，﹣5），故选：A5．函数f（x）=log2x﹣的一个零点落在下列哪个区间（）A．（0，1）B．（1，2）C．（2，3）D．（3，4）【考点】函数零点的判定定理．【分析】根据函数的实根存在定理，要验证函数的零点的位置，只要求出函数在区间的两个端点上的函数值，即可得到结论．【解答】解：∵f（1）=﹣1＜0．f（2）=1﹣=∴f（1）•f（2）＜0．根据函数的实根存在定理得到函数的一个零点落在（1，2）上故选B．6．如图，在正方体ABCD﹣A1B1C1D1中，E为A1C1的中点(zhōnɡ diǎn)，则异面直线CE 与BD所成的角为（）A．30° B．45°C．60°D．90°【考点(kǎo diǎn)】异面直线及其所成的角；直线与平面(píngmiàn)垂直的判定．【分析(fēnxī)】连接(liánjiē)AC，BD，则AC⊥BD，证明AC⊥平面BDD1，可得AC⊥BD1，利用EF∥AC，即可得出结论．【解答】解：连接AC，底面是正方形，则AC⊥BD，几何体是正方体，可知∴BD⊥AA1，AC∩AA1=A，∴BD⊥平面CC1AA1，∵CE⊂平面CC1AA1，∴BD⊥CE，∴异面直线BD、CE所成角是90°．故选：D．7．今有一组数据(shùjù)如下：t 1.99 3.0 4.0 5.1 6.12v 1.5 4.04 7.5 12 18.01在以下(yǐxià)四个模拟函数中，最合适这组数据的函数是（）A．v=log2t B．C．D．v=2t﹣2【考点(kǎo diǎn)】变量间的相关(xiāngguān)关系．【分析(fēnxī)】观察表中的数据发现随着t的增加，数据v的递增速度越来越快，可以从此变化趋势上选择恰当的函数关系．【解答】解：把t看作自变量，v看作其函数值，从表中数据的变化趋势看，函数递增的速度不断加快对照四个选项，A选项是对数型函数，其递增速度不断变慢B选项随着t的增大v变小，故不能选D选项以一个恒定的幅度变化，其图象是直线型的，符合本题的变化规律C选项是二次型，对比数据知，其最接近实验数据的变化趋势故应选(yīnɡ xuǎn)C．8．已知lga+lgb=0（a＞0，b＞0且a≠1，b≠1），则函数(hánshù)f（x）=a x与函数(hánshù)g（x）=﹣log b x的图象(tú xiànɡ)可能是（）A．B．C．D．【考点(kǎo diǎn)】对数函数的图象与性质；指数函数的图象与性质．【分析】由lga+lgb=0（a＞0，b＞0且a≠1，b≠1），得ab=1，从而得到g（x）=log a x，与f（x）=a x互为反函数，从而得到答案．【解答】解：∵lga+lgb=0（a＞0，b＞0且a≠1，b≠1），∴ab=1，∴b=，∴g（x）=﹣log b x的=﹣=log a x，函数f（x）=a x与函数g（x）=﹣log b x互为反函数，∴二者的图象关于直线y=x对称，故选B．9．点P（2，﹣1）为圆（x﹣1）2+y2=25的弦AB的中点(zhōnɡ diǎn)，则直线AB的方程为（）A．x+y﹣1=0 B．2x+y﹣3=0 C．x﹣y﹣3=0 D．2x﹣y﹣5=0【考点(kǎo diǎn)】直线与圆相交(xiāngjiāo)的性质．【分析(fēnxī)】由垂径定理，得AB中点与圆心C的连线与AB互相(hù xiāng)垂直，由此算出AB的斜率k=1，结合直线方程的点斜式列式，即可得到直线AB的方程．【解答】解：∵AB是圆（x﹣1）2+y2=25的弦，圆心为C（1，0）∴设AB的中点是P（2，﹣1）满足AB⊥CP因此，PQ的斜率k===1可得直线PQ的方程是y+1=x﹣2，化简得x﹣y﹣3=0故选：C10．把正方形ABCD沿对角线AC折起，当以A、B、C、D四点为顶点的三棱锥体积最大时，直线BD和平面ABC所成的角的大小为（）A．90° B．60°C．45°D．30°【考点】空间中直线与平面之间的位置关系．【分析(fēnxī)】欲使得(shǐ de)三棱锥体积最大，因为三棱锥底面积一定，只须三棱锥的高最大即可，即当平面BAC⊥平面DAC时，三棱锥体积最大，计算(jì suàn)可得答案．【解答(jiědá)】解：如图，当平面(píngmiàn)BAC⊥平面DAC时，三棱锥体积最大取AC的中点E，则BE⊥平面DAC，故直线BD和平面ABC所成的角为∠DBEcos∠DBE=，∴∠DBE=45°．故选C．二、填空题（本大题共5小题，每小题5分，共25分）11．幂函数的图象经过点（4，2），那么的值是．【考点】幂函数的概念、解析式、定义域、值域．【分析】先设出幂函数解析式来，再通过经过点（4，2），解得参数，从而求得其解析式，再代入求值．【解答】解：设幂函数为：y=xα∵幂函数的图象(tú xiànɡ)经过点（4，2），∴2=4α∴α=∴∴=故答案(dáàn)为：12．经过(jīngguò)（3，4），且与圆x2+y2=25相切的直线(zhíxiàn)的方程为3x+4y﹣25=0．【考点(kǎo diǎn)】直线与圆的位置关系．【分析】由点在圆上，设过该点与圆相切的直线方程的斜率为k，利用点到直线的距离公式，由直线与圆相切时，圆心到直线的距离等于圆的半径列出关于k的方程，求出方程的解得到k的值，由k的值写出切线方程即可．【解答】解：因为点（3，4）在圆x2+y2=25上，设切线方程的斜率为k，则切线方程为y﹣4=k（x﹣3），即kx﹣y﹣3k+4=0，则圆心（0，0）到切线的距离为d==5，解得k=﹣，则切线方程为﹣x﹣y++4=0，即3x+4y﹣25=0．故答案为：3x+4y﹣25=0．13．某几何体的三视图如图，其中(qízhōng)正视图与侧视图上半部分为半圆，则该几何体的表面积为7π．【考点(kǎo diǎn)】由三视图求面积(miàn jī)、体积．【分析(fēnxī)】由三视图知几何体上部是半球，下部是圆柱(yuánzhù)，且圆柱的底面圆的直径为2，圆柱的高为2，半球的半径为1，把数据代入面积公式计算可得答案．【解答】解：由三视图知几何体上部是半球，下部是圆柱，且圆柱的底面圆的直径为2，圆柱的高为2；半球的半径为1，∴几何体的表面积S=π×12+2π×1×2+2π×12=π+4π+2π=7π．故答案是7π．14．若奇函数y=f（x）的定义域为[﹣4，4]，其部分图象如图所示，则不等式f（x）ln（2x﹣1）＜0的解集是（1，2）．【考点(kǎo diǎn)】其他不等式的解法；奇偶(qíǒu)函数图象的对称性．【分析(fēnxī)】结合图象利用奇函数的图象关于(guānyú)原点对称可得f（x）＞0的解集、f（x）＜0的解集，再求出ln（2x﹣1）＞0的解集以及(yǐjí) ln（2x﹣1）＜0的解集，不等式即或，由此求得原不等式的解集．【解答】解：由图象并利用奇函数的图象关于原点对称的性质可得，f（x）＞0的解集为（﹣2，0）∪（2，4），f（x）＜0的解集为（﹣4，﹣2）∪（0，2）．由于不等式ln（2x﹣1）＞0的解集为（1，+∞），不等式ln（2x﹣1）＜0的解集为（0，1）．由f（x）ln（2x﹣1）＜0可得或．解得 x∈∅，或 1＜x＜2，故不等式f（x）ln（2x﹣1）＜0的解集是（1，2），故答案为（1，2）．15．已知直线a、b、c以及平面α、β，给出下列命题：①若a∥α且b∥α，则a∥b；②若α∥β，c⊥α，则c⊥β；③若a⊥b，a⊥α，则b∥α；④若α⊥β，a∥α，则a⊥β⑤若a⊥c，b⊥c，则a∥b或a、b异面或a、b相交(xiāngjiāo)其中正确(zhèngquè)命题的序号是②⑤（把所有(suǒyǒu)正确命题的序号都填上）．【考点(kǎo diǎn)】命题的真假判断与应用；空间中直线(zhíxiàn)与直线之间的位置关系；空间中直线与平面之间的位置关系；平面与平面之间的位置关系．【分析】根据线面平行的几何特征及线线位置关系的定义，可判断①，根据一条直线垂直于两个平行平面中的一个，也垂直于另一个，可判断②；根据a⊥b，a⊥α时，可能b⊂α，可判断③；根据面面垂直及线面平行的几何特征及线面垂直的判定方法，可判断④；根据线线垂直的几何特征，及空间中直线与直线位置关系的定义，可判断⑤．【解答】解：若a∥α且b∥α，则a与b可能平行，可能相交，也可能异面，故①错误；若α∥β，c⊥α，因为一条直线垂直于两个平行平面中的一个，也垂直于另一个，则c⊥β，故②正确；若a⊥b，a⊥α，则b∥α或b⊂α，故③错误；若α⊥β，a∥α，则a与β可能平行，可能相交（包括垂直），也可能线在面内，故④错误；若a⊥c，b⊥c，则a∥b或a、b异面或a、b相交(xiāngjiāo)，故⑤正确；故答案(dáàn)为：②⑤三、解答(jiědá)题（本大题共6小题，总分75分，请把解答写在指定方框内，否则不记分）16．分别求满足(mǎnzú)下列条件的直线方程．（Ⅰ）过点（0，1），且平行(píngxíng)于l1：4x+2y﹣1=0的直线；（Ⅱ）与l2：x+y+1=0垂直，且过点P（﹣1，0）的直线．【考点】直线的一般式方程与直线的垂直关系；直线的一般式方程与直线的平行关系．【分析】（Ⅰ）根据直线的平行关系代入点斜式方程即可；（Ⅱ）根据直线的垂直关系设出直线方程，求出即可．【解答】解：（Ⅰ）所求直线行于l1，∴所求直线的斜率为﹣2，又过点为（0，﹣1），∴由点斜式可得直线方程为y+1=﹣2（x﹣0），即2x+y+1=0；（Ⅱ）所求直线直线与l2垂直，可设直线方程为x﹣y+m=0，过点P（﹣1，0），则m=1，故所求直线方程为x﹣y+1=0．17．已知：函数(hánshù)f（x）=+lg（3x﹣9）的定义域为A，集合(jíhé)B={x|x﹣a ＜0，a∈R}．（1）求：集合(jíhé)A；（2）求：A∩B．【考点(kǎo diǎn)】交集及其运算(yùn suàn)；函数的定义域及其求法．【分析】（1）根据负数没有算术平方根，对数函数性质求出f（x）定义域A即可；（2）表示出B中不等式的解集确定出B，根据a的范围分类讨论求出A∩B即可．【解答】解：（1）由题意得：，即，解得：2＜x≤4，则A=（2，4]；（2）由B中不等式解得：x＜a，a∈R，即B=（﹣∞，a），①当a≤2时，A∩B=∅；②当2＜a≤4时，A∩B=（2，a）；③当a＞4时，A∩B=（2，4]．18．某校办工厂生产学生(xué sheng)校服的固定成本为20000元，每生产一件需要增加投入100元，已知总收益R（x）满足函数R（x）=，其中x是校服(xiào fú)的月产量，问：（1）将利润表示(biǎoshì)为关于月产量x的函数f（x）；（2）当月产量(chǎnliàng)为何值时，工厂所获利润最大？最大利润为多少元？（总收益=总成本+利润(lìrùn)）．【考点】函数模型的选择与应用．【分析】（1）由题意，由总收益=总成本+利润可知，分0≤x≤400及x＞400求利润，利用分段函数表示；（2）在0≤x≤400及x＞400分别求函数的最大值或取值范围，从而确定函数的最大值．从而得到最大利润．【解答】解：（1）由题意，当0≤x≤400时，f（x）=400x﹣0.5x2﹣20000﹣100x=300x﹣0.5x2﹣20000；当x＞400时，f（x）=80000﹣100x﹣20000=60000﹣100x；故f（x）=；（2）当0≤x≤400时，f（x）=300x﹣0.5x2﹣20000；当x==300时，f（x）max=25000；当x＞400时，f（x）=60000﹣100x＜60000﹣40000=20000；故当月产量为300件时，工厂(gōngchǎng)所获利润最大，最大利润为25000元．19．长方体ABCD﹣A1B1C1D1中，，AB=BC=2，O是底面对角线的交点(jiāodiǎn)．（Ⅰ）求证(qiúzhèng)：B1D1∥平面(píngmiàn)BC1D；（Ⅱ）求证(qiúzhèng)：A1O⊥平面BC1D；（Ⅲ）求三棱锥A1﹣DBC1的体积．【考点】直线与平面平行的判定；棱柱、棱锥、棱台的体积；直线与平面垂直的判定．【分析】（Ⅰ）直接根据B1D1∥BD，以及B1D1在平面BC1D外，即可得到结论；（Ⅱ）先根据(gēnjù)条件得到BD⊥平面(píngmiàn)ACC1A1⇒A1O⊥BD；再通过求先线段(xiànduàn)的长度推出A1O⊥OC1，即可证明(zhèngmíng)A1O⊥平面(píngmiàn)BC1D；（Ⅲ）结合上面的结论，直接代入体积计算公式即可．【解答】解：（Ⅰ）证明：依题意：B1D1∥BD，且B1D1在平面BC1D外．∴B1D1∥平面BC1D（Ⅱ）证明：连接OC1∵BD⊥AC，AA1⊥BD∴BD⊥平面ACC1A1又∵O在AC上，∴A1O在平面ACC1A1上∴A1O⊥BD∵AB=BC=2∴∴∴Rt△AA1O中，同理：OC1=2∵△A1OC1中，A1O2+OC12=A1C12∴A1O⊥OC1∴A1O⊥平面BC1D（Ⅲ）解：∵A1O⊥平面BC1D∴所求体积(tǐjī)=20．已知圆C1的方程(fāngchéng)为x2+y2﹣4x+2my+2m2﹣2m+1=0．（1）求当圆的面积(miàn jī)最大时圆C1的标准(biāozhǔn)方程；（2）求（1）中求得的圆C1关于(guānyú)直线l：x﹣y+1=0对称的圆C2的方程．【考点】直线与圆的位置关系；圆的标准方程．【分析】（1）根据圆的面积最大时半径最大，写出圆C1半径r的解析式，求出半径最大值以及对应的圆C1的方程，再化为标准方程；（2）求出圆C1的圆心坐标关于直线l的对称点，即可写出对称圆圆C2的方程．【解答】解：（1）圆C1的面积最大，即圆的半径最大，则圆C1的半径为，即，因此当m=1时圆C1的半径最大，最大值为2，…此时圆C1的方程为x2+y2﹣4x+2y+1=0，化为标准(biāozhǔn)方程是（x﹣2）2+（y+1）2=4；…（2）由（1）知圆C1的圆心坐标(zuòbiāo)是（2，﹣1），半径为2，设圆C2的圆心(yuánxīn)为（a，b），则C1C2的中点(zhōnɡ diǎn)坐标为，直线(zhíxiàn)C1C2的斜率为，…..由题意，直线l垂直平分线段C1C2，∴，解得；…所以，所求圆C2的方程为（x+2）2+（y﹣3）2=4．…21．已知函数f（x）满足f（log a x）=（x﹣x﹣1），其中a＞0，a≠1，（1）讨论f（x）的奇偶性和单调性；（2）对于函数f（x），当x∈（﹣1，1）时，f（1﹣m）+f（﹣2m）＜0，求实数m取值的集合；（3）是否存在实数a，使得当x∈（﹣∞，2）时f（x）的值恒为负数？，若存在，求a的取值范围，若不存在，说明理由．【考点】函数奇偶性的判断；函数单调性的判断与证明；函数恒成立问题．【分析】（1）利用换元法，求出函数的解析式，再讨论f（x）的奇偶性和单调性；（2）由f（x）是R上的奇函数，增函数，f（1﹣m）+f（﹣2m）＜0有﹣1＜1﹣m＜2m＜1，即可求实数(shìshù)m取值的集合；（3）由x＜2，得f（x）＜f（2），要使f（x）的值恒为负数(fùshù)，则f（2）≤0，求出a的范围(fànwéi)，可得结论．【解答(jiědá)】解：（1）令log a x=t，则x=a t，∴f（t）=（a t﹣a﹣t），∴f（x）=（a x﹣a﹣x），…因为(yīn wèi)f（﹣x）=（a﹣x﹣a x）=﹣f（x），所以f（x）是R上的奇函数；…当a＞1时，＞0，a x是增函数，﹣a﹣x是增函数所以f（x）是R上的增函数；当0＜a＜1时，＜0，a x是减函数，﹣a﹣x是减函数，所以f（x）是R上的增函数；综上所述，a＞0，a≠1，f（x）是R上的增函数…（2）由f（x）是R上的奇函数，增函数，f（1﹣m）+f（﹣2m）＜0有﹣1＜1﹣m＜2m＜1，解得＜m＜…（3）因为f（x）是R上的增函数，由x＜2，得f（x）＜f（2），要使f（x）的值恒为负数(fùshù)，则f（2）≤0，即f（2）=（a2﹣a﹣2）≤0解得 a＜0，与a＞0，a≠1矛盾(máodùn)，所以满足条件的实数(shìshù)a不存在．…内容总结（1）（Ⅱ）先根据条件得到BD⊥平面ACC1A1⇒A1O⊥BD。

江苏省南京市高一（上）期末数学试卷一、填空题（共14小题，每小题5分，共70分）1．（5分）若集合A={﹣1，0，1，2}，B={x|x+1＞0}，则A∩B= ．（1﹣x）的定义域为．2．（5分）函数f（x）=log23．（5分）函数f（x）=3sin（3x+）的最小正周期为．4．（5分）已知角α的终边过点P（﹣5，12），则cosα= ．5．（5分）若幂函数y=x a（a∈R）的图象经过点（4，2），则a的值为．6．（5分）若扇形的弧长为6cm，圆心角为2弧度，则扇形的面积为cm2．7．（5分）设，是不共线向量，﹣4与k+共线，则实数k的值为．8．（5分）定义在区间[0，5π]上的函数y=2sinx的图象与y=cosx的图象的交点个数为．2，b=20.3，c=log2，则a，b，c的大小关系用“＜”表示9．（5分）若a=log3为．10．（5分）函数f（x）=2x+a•2﹣x是偶函数，则a的值为_．11．（5分）如图，点E是正方形ABCD的边CD的中点，若•=﹣2，则•的值为12．（5分）已知函数f（x）对任意实数x∈R，f（x+2）=f（x）恒成立，且当x ∈[﹣1，1]时，f（x）=2x+a，若点P（2017，8）是该函数图象上一点，则实数a 的值为．x）成立的x取13．（5分）设函数f（x）=﹣3x2+2，则使得f（1）＞f（log3值范围为．14．（5分）已知函数f（x）=，其中m＞0，若对任意实数x，都有f（x）＜f（x+1）成立，则实数m的取值范围为．二、解答题（共6题，90分）15．（14分）已知=2．（1）求tanα；（2）求cos（﹣α）•cos（﹣π+α）的值．16．（14分）已知向量=（﹣2，1），=（3，﹣4）．（1）求（+）•（2﹣）的值；（2）求向量与+的夹角．17．（14分）如图，在一张长为2a米，宽为a米（a＞2）的矩形铁皮的四个角上，各剪去一个边长是x米（0＜x≤1）的小正方形，折成一个无盖的长方体铁盒，设V（x）表示铁盒的容积．（1）试写出V（x）的解析式；（2）记y=，当x为何值时，y最小？并求出最小值．18．（16分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的最下正周期为π，且点P（，2）是该函数图象的一个人最高点．（1）求函数f（x）的解析式；（2）若x∈[﹣，0]，求函数y=f（x）的值域；（3）把函数y=f（x）的图线向右平移θ（0＜θ＜）个单位，得到函数y=g （x）在[0，]上是单调增函数，求θ的取值范围．19．（16分）如图，在△ABC中，已知CA=1，CB=2，∠ACB=60°．（1）求||；（2）已知点D是AB上一点，满足=λ，点E是边CB上一点，满足=λ．①当λ=时，求•；②是否存在非零实数λ，使得⊥？若存在，求出的λ值；若不存在，请说明理由．20．（16分）已知函数f（x）=x﹣a，g（x）=a|x|，a∈R．（1）设F（x）=f（x）﹣g（x）．①若a=，求函数y=F（x）的零点；②若函数y=F（x）存在零点，求a的取值范围．（2）设h（x）=f（x）+g（x），x∈[﹣2，2]，若对任意x1，x2∈[﹣2，2]，|h（x1）﹣h（x2）|≤6恒成立，试求a的取值范围．2016-2017学年江苏省南京市高一（上）期末数学试卷参考答案与试题解析一、填空题（共14小题，每小题5分，共70分）1．（5分）若集合A={﹣1，0，1，2}，B={x|x+1＞0}，则A∩B= {0，1，2} ．【解答】解：∵集合A={﹣1，0，1，2}，B={x|x+1＞0}={x|x＞﹣1}，∴A∩B={0，1，2}．故答案为：{0，1，2}．（1﹣x）的定义域为{x|x＜1} ．2．（5分）函数f（x）=log2（1﹣x）有意义【解答】解：要使函数f（x）=log2则1﹣x＞0即x＜1（1﹣x）的定义域为{x|x＜1}∴函数f（x）=log2故答案为：{x|x＜1}3．（5分）函数f（x）=3sin（3x+）的最小正周期为．【解答】解：函数f（x）=3sin（3x+）的最小正周期为，故答案为：．4．（5分）已知角α的终边过点P（﹣5，12），则cosα= ．【解答】解：角α的终边上的点P（﹣5，12）到原点的距离为 r=13，由任意角的三角函数的定义得 cosα==﹣．故答案为﹣．5．（5分）若幂函数y=x a（a∈R）的图象经过点（4，2），则a的值为．【解答】解：幂函数y=x a（a∈R）的图象经过点（4，2），所以4a=2，解得a=．故答案为：．6．（5分）若扇形的弧长为6cm，圆心角为2弧度，则扇形的面积为9 cm2．【解答】解：因为：扇形的弧长为6cm，圆心角为2弧度，所以：圆的半径为：3，所以：扇形的面积为：6×3=9．故答案为：9．7．（5分）设，是不共线向量，﹣4与k+共线，则实数k的值为﹣．【解答】解：∵e1﹣4e2与ke1+e2共线，∴，∴λk=1，λ=﹣4，∴，故答案为﹣．8．（5分）定义在区间[0，5π]上的函数y=2sinx的图象与y=cosx的图象的交点个数为 5 ．【解答】解：画出函数y=2sinx与y=cosx在一个周期[0，2π]上的图象如图实数：由图可知，在一个周期内，两函数图象在[0，π]上有1个交点，在（π，2π]上有1个交点，所以函数y=2sinx与y=cosx在区间[0，5π]上图象共有5个交点．故答案为：5．9．（5分）若a=log2，b=20.3，c=log2，则a，b，c的大小关系用“＜”表示3为c＜a＜b ．2∈（0，1），b=20.3＞1，c=log2＜0，【解答】解：∵a=log3∴c＜a＜b．故答案为：c＜a＜b．10．（5分）函数f（x）=2x+a•2﹣x是偶函数，则a的值为 1 _．【解答】解：∵f（x）=2x+a•2﹣x是偶函数，∴f（﹣x）=f（x），即f（﹣x）=2﹣x+a•2x=2x+a•2﹣x，则（2﹣x﹣2x）=a（2﹣x﹣2x），即a=1，故答案为：111．（5分）如图，点E是正方形ABCD的边CD的中点，若•=﹣2，则•的值为 3【解答】解：以A为坐标原点，AB为x轴，AD为y轴，设正方形的边长为2a，则：E（a，2a），B（2a，0），D（0，2a）可得：=（a，2a），=（2a，﹣2a）．若•=﹣2，可得2a2﹣4a2=﹣2，解得a=1，=（﹣1，2），=（1，2），则•的值：﹣1+4=3．故答案为：3．12．（5分）已知函数f（x）对任意实数x∈R，f（x+2）=f（x）恒成立，且当x ∈[﹣1，1]时，f（x）=2x+a，若点P（2017，8）是该函数图象上一点，则实数a 的值为 2 ．【解答】解：函数f（x）对任意实数x∈R，f（x+2）=f（x）恒成立，可得函数的周期为：2，f（2017）=f（2×1008+1）=f（1）．且当x∈[﹣1，1]时，f（x）=2x+a，点P（2017，8）是该函数图象上一点，可得21+a=8，解得a=2．故答案为：2．13．（5分）设函数f（x）=﹣3x2+2，则使得f（1）＞f（logx）成立的x取3值范围为（0，）∪（3，+∞）．【解答】解：由题意，f（﹣x）=f（x），函数是偶函数，f′（x）=﹣﹣6x，f（x）在（0，+∞）递减，x）∵f（1）＞f（log3∴|logx|＞1，3∴0＜x＜或x＞3，x）成立的x取值范围为（0，）∪（3，+∞），∴使得f（1）＞f（log3故答案为（0，）∪（3，+∞）．14．（5分）已知函数f（x）=，其中m＞0，若对任意实数x，都有f（x）＜f（x+1）成立，则实数m的取值范围为（0，）．【解答】解：由函数f（x）=，其中m＞0，可得f（x+1）=，作出y=f（x）的简图，向左平移1个单位，可得y=f（x+1），由对任意实数x，都有f（x）＜f（x+1）成立，只要f（x）的图象恒在f（x+1）的图象上，由x≤﹣m，f（x）的图象与x≥m﹣1的图象重合，可得2m=1﹣2m，解得m=，通过图象平移，可得m的范围为0＜m＜．故答案为：（0，）．二、解答题（共6题，90分）15．（14分）已知=2．（1）求tanα；（2）求cos（﹣α）•cos（﹣π+α）的值．【解答】解：（1）∵已知=2=，∴tanα=5．（2）cos（﹣α）•cos（﹣π+α）=sinα•（﹣cosα）===﹣．16．（14分）已知向量=（﹣2，1），=（3，﹣4）．（1）求（+）•（2﹣）的值；（2）求向量与+的夹角．【解答】解：（1）向量=（﹣2，1），=（3，﹣4）．（+）=（1，﹣3），（2﹣）=（﹣7，6）．所以（+）•（2﹣）=﹣7﹣18=﹣25．（2）+=（1，﹣3），cos＜，+＞===﹣．向量与+的夹角为135°．17．（14分）如图，在一张长为2a米，宽为a米（a＞2）的矩形铁皮的四个角上，各剪去一个边长是x米（0＜x≤1）的小正方形，折成一个无盖的长方体铁盒，设V（x）表示铁盒的容积．（1）试写出V（x）的解析式；（2）记y=，当x为何值时，y最小？并求出最小值．【解答】解：（1）由题意，V（x）=（2a﹣2x）（a﹣2x）x（0＜x≤1）；（2）y==（2a﹣2x）（a﹣2x）=，∵a＞2，0＜x≤1，∴x=1时，y最小，最小值为2（a﹣1）（a﹣2）．18．（16分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）的最下正周期为π，且点P（，2）是该函数图象的一个人最高点．（1）求函数f（x）的解析式；（2）若x∈[﹣，0]，求函数y=f（x）的值域；（3）把函数y=f（x）的图线向右平移θ（0＜θ＜）个单位，得到函数y=g （x）在[0，]上是单调增函数，求θ的取值范围．【解答】解：（1）∵由题意可得，A=2，=π，∴ω=2．∵再根据函数的图象经过点P（，2），可得2sin（2×+φ）=2，结合|φ|＜，可得φ=，∴f（x）=2sin（2x+）．（2）∵x∈[﹣，0]，∴2x+∈[﹣，]，∴sin（2x+）∈[﹣1，]，可得：f（x）=2sin（2x+）∈[﹣2，1]．（3）把函数y=f（x）的图线向右平移θ（0＜θ＜）个单位，得到函数y=g（x）=2sin[2（x﹣θ）+]=2sin（2x﹣2θ+），∴令2kπ﹣≤2x﹣2θ+≤2kπ+，k∈Z，解得：kπ+θ﹣≤x≤kπ+θ+，k∈Z，可得函数的单调递增区间为：[kπ+θ﹣，kπ+θ+]，k∈Z，∵函数y=g（x）在[0，]上是单调增函数，∴，∴解得：，k∈Z，∵0＜θ＜，∴当k=0时，θ∈[，]．19．（16分）如图，在△ABC中，已知CA=1，CB=2，∠ACB=60°．（1）求||；（2）已知点D是AB上一点，满足=λ，点E是边CB上一点，满足=λ．①当λ=时，求•；②是否存在非零实数λ，使得⊥？若存在，求出的λ值；若不存在，请说明理由．【解答】解：（1）△ABC中，CA=1，CB=2，∠ACB=60°，由余弦定理得，AB2=CA2+CB2﹣2CA•CB•cos∠ACB=12+22﹣2×1×2×cos60°=3，∴AB=，即||=；（2）①λ=时，=，=，∴D、E分别是BC，AB的中点，∴=+=+，=（+），∴•=（+）•（+）=•+•+•+=﹣×12+×1×2×cos120°+×2×1×cos60°+×22=；②假设存在非零实数λ，使得⊥，由=λ，得=λ（﹣），∴=+=+λ（﹣）=λ+（1﹣λ）；又=λ，∴=+=（﹣）+λ（﹣）=（1﹣λ）﹣；∴•=λ（1﹣λ）﹣λ•+（1﹣λ）2•﹣（1﹣λ）=4λ（1﹣λ）﹣λ+（1﹣λ）2﹣（1﹣λ）=﹣3λ2+2λ=0，解得λ=或λ=0（不合题意，舍去）；即存在非零实数λ=，使得⊥．20．（16分）已知函数f（x）=x﹣a，g（x）=a|x|，a∈R．（1）设F（x）=f（x）﹣g（x）．①若a=，求函数y=F（x）的零点；②若函数y=F（x）存在零点，求a的取值范围．（2）设h（x）=f（x）+g（x），x∈[﹣2，2]，若对任意x1，x2∈[﹣2，2]，|h（x1）﹣h（x2）|≤6恒成立，试求a的取值范围．【解答】解：（1）F（x）=f（x）﹣g（x）=x﹣a﹣a|x|，①若a=，则由F（x）=x﹣|x|﹣=0得：|x|=x﹣，当x≥0时，解得：x=1；当x＜0时，解得：x=（舍去）；综上可知，a=时，函数y=F（x）的零点为1；②若函数y=F（x）存在零点，则x﹣a=a|x|，当a＞0时，作图如下：由图可知，当0＜a＜1时，折线y=a|x|与直线y=x﹣a有交点，即函数y=F（x）存在零点；同理可得，当﹣1＜a＜0时，求数y=F（x）存在零点；又当a=0时，y=x与y=0有交点（0，0），函数y=F（x）存在零点；综上所述，a的取值范围为（﹣1，1）．（2）∵h（x）=f（x）+g（x）=x﹣a+a|x|，x∈[﹣2，2]，∴当﹣2≤x＜0时，h（x）=（1﹣a）x﹣a；当0≤x≤2时，h（x）=（1+a）x﹣a；又对任意x1，x2∈[﹣2，2]，|h（x1）﹣h（x2）|≤6恒成立，则h（x1）max﹣h（x2）min≤6，①当a≤﹣1时，1﹣a＞0，1+a≤0，h（x）=（1﹣a）x﹣a在区间[﹣2，0）上单调递增；h（x）=（1+a）x﹣a在区间[0，2]上单调递减（当a=﹣1时，h（x）=﹣a）；∴h（x）max=h（0）=﹣a，又h（﹣2）=a﹣2，h（2）=2+a，∴h（x2）min=h（﹣2）=a﹣2，∴﹣a﹣（a﹣2）=2﹣2a≤6，解得a≥﹣2，综上，﹣2≤a≤﹣1；②当﹣1＜a＜1时，1﹣a＞0，1﹣a＞0，∴h（x）=（1﹣a）x﹣a在区间[﹣2，0）上单调递增，且h（x）=（1+a）x﹣a在区间[0，2]上也单调递增，∴h（x）max =h（2）=2+a，h（x2）min=h（﹣2）=a﹣2，由a+2﹣（a﹣2）=4≤6恒成立，即﹣1＜a＜1适合题意；③当a≥1时，1﹣a≤0，1+a＞0，h（x）=（1﹣a）x﹣a在区间[﹣2，0）上单调递减（当a=1时，h（x）=﹣a），h（x）=（1+a）x﹣a在区间[0，2]上单调递增；∴h（x）min=h（0）=﹣a；又h（2）=2+a＞a﹣2=h（﹣2），∴h（x）max=h（2）=2+a，∴2+a﹣（﹣a）=2+2a≤6，解得a≤2，又a≥1，∴1≤a≤2；综上所述，﹣2≤a≤2．。

2023-2024学年江苏省南京市高一上册期末学情自测数学试题一、单选题1．已知集合A ={1，2，3}，B ={x ∈N |x ≤2}，则A ∪B =（）A ．{2，3}B ．{0，1，2，3}C ．{1，2}D ．{1，2，3}【正确答案】B【分析】先求出集合B ，再求A ∪B.【详解】因为{1,2,3},{0,1,2}A B ==，所以0,1,3}2,{A B = .故选：B2．命题“(0,)sin 2x x x π∀∈≤，”的否定是（）A ．(0,)sin 2x x x π∀∈≥，B ．(0,sin 2x x xπ∀∈>，C ．(0,)sin 2x x xπ∃∈≤，D ．(0,sin 2x x xπ∃∈>，【正确答案】D【分析】直接利用全称命题的否定为特称命题进行求解.【详解】命题“(0,)sin 2x x x π∀∈≤，”为全称命题，按照改量词否结论的法则，所以否定为：(0,)sin 2x x x π∃∈>，，故选：D 3．已知弧长为3π的弧所对的圆心角为6π，则该弧所在的扇形面积为（）AB ．1π3C ．2π3D ．4π3【正确答案】B【分析】先求得扇形的半径，由此求得扇形面积.【详解】依题意，扇形的半径为π32π6=，所以扇形面积为1ππ2233⋅⋅=.故选：B4．,x R ∀∈不等式2410ax x +-<恒成立，则a 的取值范围为（）A ．4a <-B ．4a <-或0a =C ．4a ≤-D ．40a -<<【正确答案】A【分析】先讨论系数为0的情况，再结合二次函数的图像特征列不等式即可.【详解】,x R ∀∈不等式2410ax x +-<恒成立，当0a =时，显然不恒成立，所以0Δ1640a a <⎧⎨=+<⎩，解得.4a <-故选：A.5．已知0.50.5e ,ln 5,log e a b c -===，则（）A ．c<a<bB ．c b a <<C ．b a c <<D ．a b c<<【正确答案】A【分析】借助指对函数的单调性，利用中间量0或1比较即可.【详解】因为0.500=e <e 1a -<=，ln 5ln e=1b =>，0.50.5=log e<log 1=0c ，所以c<a<b ，故选：A.6．已知函数()f x 是定义在R 上的奇函数，()(4)f x f x =+，且(1)1f -=-，则(2020)(2021)f f +=（）A ．1-B ．0C ．1D ．2【正确答案】C【分析】由()(4)f x f x =+得函数的周期性，由周期性变形自变量的值，最后由奇函数性质求得值．【详解】∵()f x 是奇函数，∴(0)0,(1)(1)1f f f ==--=，又()(4)f x f x =+，∴()f x 是周期函数，周期为4．∴(2020)(2021)(0)(1)011f f f f +=+=+=．故选：C ．7．已知函数()e xf x x =+，()lng x x x =+，()sinh x x x =+的零点分别为,,,a b c 则,,a b c 的大小顺序为（）A ．c b a <<B ．b a c <<C ．a c b <<D ．c<a<b【正确答案】C【分析】利用数形结合，画出函数的图象，判断函数的零点的大小即可．【详解】函数()e xf x x =+，()lng x x x =+，()sinh x x x =+的零点转化为e x y =，ln y x =，sin y x =与y x =-的图象的交点的横坐标，因为零点分别为,,,a b c 在坐标系中画出e x y =，ln y x =，sin y x =与y x =-的图象如图：可知a<0，0b >，0c =，满足a c b <<．故选：C ．8．已知函数()()sin f x A x ωϕ=+的图象的一部分如图1所示，则图2中的函数图象对应的函数解析式为（）A ．1(2)2y f x =+B ．(21)y f x =+C ．1(22x y f =+D ．(1)2xy f =+【正确答案】B【分析】利用三角函数的图象变换规律可求得结果.【详解】观察图象可知，右方图象是由左方图象向左移动一个长度单位后得到()1y f x =+的图象，再把(1)=-y f x 的图象上所有点的横坐标缩小为原来的12（纵坐标不变）得到的，所以右图的图象所对应的解析式为(21)y f x =+.故选：B二、多选题9．下列函数中，既是偶函数又在区间()0,∞+上是增函数的是（）A ．21y x =+B ．3y x =C ．23y x=D ．3xy -=【正确答案】AC【分析】利用函数的奇偶性和单调性的概念进行判断.【详解】对于A ：()2211=-+=+ y x x ∴函数21y x =+是偶函数，在()0,∞+上是增函数，故A 正确；对于B ：()33=-=- y x x ∴函数3y x =是奇函数，故B 错误；对于C ：()2233=-= y x x23y x ∴=是偶函数，在()0,∞+上是增函数，故C 正确；对于D ：33---== xxy 3-∴=xy 是偶函数，在()0,∞+上是减函数，故D 错误.故选：AC10．若110a b<<，则下列不等式正确的是（）A ．a b <B ．a b <C ．a b ab +<D ．2b a a b+>【正确答案】BCD【分析】利用不等式的基本性质求解即可【详解】由于110a b<<，则0b a <<，故a b <错误；0a b ab +<<正确；||||a b <正确；2222a b a b abb a ab ab++=>=，∴2b a a b +>，正确故选：BCD ．11．若函数()tan(2)3f x x π=+，则下列选项正确的是（）A ．最小正周期是πB ．图象关于点(,0)3π对称C ．在区间7(,)1212ππ上单调递增D ．图象关于直线12x π=对称【正确答案】BC【分析】利用正切函数的周期，对称中心，函数的单调性，判断选项即可．【详解】函数tan(2)3y x π=+，函数的最小正周期为：2π，A 错误；令23246k k x x k Z ππππ+=⇒=-∈，，当2k =时，3x π=，所以图象关于点(,0)3π对称，B 正确；因为2232k x k πππππ-<+<+，Z k ∈，解得5(212k x ππ∈-，)212k ππ+，当1k =时，7(,1212x ππ∈,所以在区间7(,)1212ππ上单调递增，C 正确；又正切函数不具有对称轴，所以D 错误故选：B C ．12．设x R ∈，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，也叫取整函数.令[]()22f x x x =-，以下结论正确的是（）A ．()1.10.8f -=B ．()f x 为偶函数C ．()f x 最小正周期为12D ．()f x 的值域为[]0,1【正确答案】AC【分析】根据高斯函数的定义逐项检验即可，对于A ，直接求解即可，对于B ，取 1.1x =-，检验可得反例，对于C ，直接求解()12f x f x ⎛⎫+= ⎪⎝⎭即可；对于D ，要求()f x 的值域，只需求102x ≤<时()f x 的值域即可.【详解】对于A ，()[]2.21 2.230..8.122f --=-+=-=-，故A 正确.对于B ，取 1.1x =-，则()1.10.8f -=，而()[]2.2 2.2 2.221021..f --===，故()()1.1 1.1f f -≠-，所以函数()f x 不为偶函数，故B 错误.对于C ，则[][]()1212121212f x x x x x f x ⎛⎫+=+-+=+--= ⎪⎝⎭，故C 正确.对于D ，由C 的判断可知，()f x 为周期函数，且周期为12，要求()f x 的值域，只需求102x ≤<时()f x 的值域即可.当0x =时，则()[]0000f =-=，当102x <<时，()[]22202(0,1)f x x x x x =-=-=∈，故当102x ≤<时，则有()01f x ≤<，故函数()f x 的值域为[)0,1，故D 错误.故选：AC ．三、填空题135log 25=_____．【正确答案】6【分析】利用根式性质与对数运算进行化简.5log 25426=+=，故614．请写出一个同时满足下列两个条件的函数：____________.（1）12x x R ∀∈，，若12x x >则12()()f x f x >（2）121212,,()()()x x R f x x f x f x ∀∈+=【正确答案】()2x f x =，答案不唯一【分析】由条件（1）12x x R ∀∈，，若12x x >则12()()f x f x >.可知函数()f x 为R 上增函数；由条件（2）121212,,()()()x x R f x x f x f x ∀∈+=.可知函数()f x 可能为指数型函数.【详解】令()2x f x =，则()2x f x =为R 上增函数，满足条件（1）.又1212()2x x f x x ++=，121212()()222x x x xf x f x +=⨯=故12()f x x +=12()()f x f x 即121212,,()()()x x R f x x f x f x ∀∈+=成立.故()2x f x =，（()3x f x =，()4x f x =等均满足题意）15．在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于P ，Q 两点，P ，Q 的纵坐标分别为35，45．则αβ+的终边与单位圆交点的纵坐标为_____________.【正确答案】1【分析】根据任意角三角函数的定义可得3sin 5α=，4cos 5α=，4sin 5β=，3cos 5β=，再由()sin αβ+展开求解即可.【详解】以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于P ，Q 两点，P ，Q 的纵坐标分别为35，45所以3sin 5α=，α是锐角，可得4cos 5α=，因为锐角β的终边与单位圆相交于Q 点，且纵坐标为45，所以4sin 5β=，β是锐角，可得3cos 5β=，所以()3344sin sin cos cos sin 15555αβαβαβ+=+=⨯+⨯=，所以αβ+的终边与单位圆交点的纵坐标为1.故答案为.1四、双空题16．已知函数()2log ,042,482x x f x cos x x π⎧<<⎪=⎨≤≤⎪⎩，,t R ∃∈使方程()f x t =有4个不同的解：1234,,,x x x x ，则1234x x x x 的取值范围是_________;1234x x x x +++的取值范围是________.【正确答案】(32,35)65(14,4【分析】先画出分段函数()f x 的图像，依据图像得到12,x x 之间的关系式以及34,x x 之间的关系式，分别把1234x x x x +++和1234x x x x 转化成只有一个自变量的代数式，再去求取值范围即可.【详解】做出函数()2log ,042,482x x f x cos x x π⎧<<⎪=⎨≤≤⎪⎩的图像如下：()f x 在](0,1单调递减：最小值0；()f x 在[]1,4单调递增：最小值0，最大值2；()f x 在[]4,8上是部分余弦型曲线：最小值2-，最大值2.若方程()f x t =有4个不同的解：1234,,,x x x x ，则02t <<不妨设四个解依次增大，则12341145,784x x x x <<<<<<<<12,x x 是方程2log x t =(04)x <<的解，则2122log log x x =-，即121=x x ；34,x x 是方程2cos2x t π=(48)x ≤≤的解，则由余弦型函数的对称性可知3412x x +=.故2123434333(12)(6)36x x x x x x x x x ==-=--+，由345x <<得2332(6)3635x <--+<即12343235x x x x <<1234121111212x x x x x x x x +++=++=++当1114x <<时，1()12m x x x=++单调递减，则1116514124x x <++<故①(32,35)；②65(14,4五、解答题17．求值：(1)22log 33582lg 2lg 22+--(2)25π10π13πsincos tan 634⎛⎫-+- ⎪⎝⎭【正确答案】(1)6(2)0【分析】(1)根据指数运算公式和对数运算公式求解即可；(2)根据诱导公式化简求值即可.【详解】（1）22log 33582lg 2lg 22+--()()2lo 23g 3322lg5lg 22lg 2=+---223lg 5lg 22lg 2=+-+-7(lg 5lg 2)=-+71=-6=；（2）25π10π13πsincos tan 634⎛⎫-+- ⎪⎝⎭πππsin 4πcos 3πtan 3π634⎛⎫⎛⎫⎛⎫=+-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭πππsin cos tan634=+-11122=+-0=．18．已知全集U =R ，集合{}2120A x x x =--≤，集合{}11B x m x m =-≤≤+.(1)当4m =时，求()U A B ⋃ð；(2)若()U B A ⊆ð，求实数m 的取值范围.【正确答案】(1){4x x ≤或5}x >；(2)4m <-或5m >.【分析】（1）确定集合A ，B ，求出集合B 的补集，根据集合的并集运算，即可求得答案.（2）求出集合A 的补集，根据()U B A ⊆ð，列出相应不等式，求得答案.【详解】（1）集合{}{}212034A x x x x x =--≤=-≤≤，当4m =时，{}35B x x =≤≤，则{3U B x x =<ð或5}x >，故()U A B = ð{4x x ≤或5}x >；（2）由题意可知{3U A x x =<-ð或4}x >，{}11B x m x m =-≤≤+≠∅,由U B A ⊆ð，则13m +<-或14m ->，解得4m <-或5m >.19．已知函数()()sin (0,0,)2f x A x A πωϕωϕ=+>><的部分图象如图.(1)求函数()f x 的解析式;(2)将函数()f x 的图象上所有点的横坐标变为原来的2倍，纵坐标不变，再将所得图象向左平移6π个单位，得到函数()g x 的图象，当,6x ππ⎡⎤∈-⎢⎥⎣⎦时，求()g x 值域.【正确答案】(1)()2sin 23f x x π⎛⎫=- ⎪⎝⎭；(2)[2].【分析】（1）根据图象由函数最值求得A ，由函数周期求得ω，由特殊点求得ϕ，即可求得解析式；（2）根据三角函数图象的变换求得()g x 的解析式，再利用整体法求函数值域即可.【详解】（1）由图象可知，()f x 的最大值为2，最小值为2-，又0A >，故2A =，周期453123T πππ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦，2||ππω∴=，0ω>，则2ω=，从而()2sin(2)f x x ϕ=+，代入点5,212π⎛⎫ ⎪⎝⎭，得5sin 16⎛⎫+= ⎪⎝⎭πϕ，则5262k ππϕπ+=+，Z k ∈，即23k πϕπ=-+，Z k ∈，又||2ϕπ<，则3πϕ=-.()2sin 23f x x π⎛⎫∴=- ⎪⎝⎭.（2）将函数()f x 的图象上所有点的横坐标变为原来的2倍，纵坐标不变，故可得2sin 3y x π⎛⎫=- ⎪⎝⎭；再将所得图象向左平移6π个单位，得到函数()g x 的图象故可得()2sin()6g x x π=-；[,]6x ππ∈- 5[,]636x πππ∴-∈-，sin 6x π⎡⎤⎛⎫-∈⎢⎥ ⎪⎝⎭⎣⎦，2sin 26x π⎛⎫⎡⎤-∈ ⎪⎣⎦⎝⎭，()[2]g x ∴的值域为.20．已知函数sin()cos sin()cos(2)()cos tan()sin 2f πααπαπααπααα-+-=-⎛⎫- ⎪⎝⎭（1）化简()f α；（2）若1(),052f παα=-<<，求sin cos ,s cos in αααα⋅-的值.【正确答案】（1）()sin cos f ααα=+；（2）75-【分析】（1）利用诱导公式进行化简即可；（2）由（1）结果两边平方，再利用同角三角函数的基本关系联立解方程组即可得出结果.【详解】解：（1）sin()cos sin()cos(2)sin cos (sin )cos ()cos tan()cos cos tan sin 2f πααπαπααααααπαααααα-+--==+--⎛⎫- ⎪⎝⎭所以()sin cos f ααα=+.（2）由1()sin cos 5f ααα=+=，平方可得221sin 2sin cos cos 25αααα++=，即242sin cos 25αα⋅=-.所以12sin cos 25αα⋅=-，因为249 (sin cos )12sin cos 25αααα-=-=，又02πα-<<，所以sin 0α<，cos 0α>，所以sin cos 0αα-<,所以7sin cos 5αα-=-.本题考查了诱导公式、同角三角函数的化简与求值，属于基础题.21．某市城郊有一块大约500m 500m ⨯的接近正方形的荒地，地方政府准备在此建一个综合性休闲广场，首先要建设如图所示的一个矩形体育活动场地，其中总面积为3000平方米，其中阴影部分为通道，通道宽度为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为S 平方米.（1）分别用x 表示y 及S 的函数关系式，并给出定义域；（2）请你设计规划该体育活动场地，使得该塑胶运动场地占地面积S 最大，并求出最大值【正确答案】（1）1500030306S x x=--，定义域是(6，500)；（2）设计50m 60m x y ，==时，运动场地面积最大，最大值为2430平方米.【分析】（1）总面积为3000xy =，且26a y +=，可得3000y x=，15003a x =-（其中6500)x <<，从而运动场占地面积为(4)(6)S x a x a =-+-，代入整理即得；（2）由（1）知，占地面积150003030(6)S x x =-+，由基本不等式可得函数的最大值，以及对应的x 的值．【详解】解：（1）由已知30003000,,xy y x=∴=其定义域是(6,500).(4)(6)(210),S x a x a x a =-+-=-26a y += ，∴1500332y a x =-=-，150015000(210)(3)30306S x x x x∴=--=--，其定义域是(6,500).（2）150003030(6)3030303023002430,S x x =-+≤-=-⨯=当且仅当150006x x=，即50(6,500)x =∈时，上述不等式等号成立，此时，50x =，60y =，2430max S =．答：设计50m 60m x y ，==时，运动场地面积最大，最大值为2430平方米.22．已知函数1()ln 1x f x x -=+.(1)求证：()f x 是奇函数；(2)若对于任意[]3,5x ∈都有()3f x t >-成立，求t 的取值范围；(3)若存在,(1,)αβ∈+∞，且αβ<，使得函数()f x 在区间[],αβ上的值域为ln ,ln 22m m m m αβ⎡⎤⎛⎫⎛⎫-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，求实数m 的取值范围.【正确答案】(1)证明见解析(2)(,3ln 2)-∞-(3)209m <<【分析】（1）利用奇偶性的定义求解即可；（2）对于任意[]3,5x ∈都有()3f x t >-成立，仅需min ()3f x t >-即可；（3）由()f x 单调性可得,αβ是方程112x m mx x -=-+，即22(2)20mx m x m +-+-=的两实数根，根据一元二次函数的图像和性质求解即可.【详解】（1）又101x x ->+即(1)(1)0x x -+>解得(,1)(1,)x ∈-∞-⋃+∞，所以()f x 的定义域为(,1)(1,)x ∈-∞-⋃+∞，关于原点对称，又因为1111()ln ln ln ()111x x x f x f x x x x -+--⎛⎫-===-=- ⎪-++⎝⎭，所以()f x 是奇函数.（2）由题意2()ln 11f x x ⎛⎫=- ⎪+⎝⎭，令2()11u x x =-+(()0)u x >，因为()u x 在(1,)+∞上为增函数，ln u 在(0,)+∞上为增函数，所以()f x 在(1,)+∞上为增函数，当[]3,5x ∈时，ln 2()ln 2ln 3f x -≤≤-，对于任意[]3,5x ∈都有()3f x t >-成立，仅需min ()3f x t >-即可，所以ln 23t ->-，解得3ln 2t <-.（3）由（2）可知()f x 在(1,)+∞上为增函数，又因为()f x 在区间[],αβ上的值域为ln ,ln 22m m m m αβ⎡⎤⎛⎫⎛⎫-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以0m >且1ln ln 121ln ln 12m m m m αααβββ⎧-⎛⎫=- ⎪⎪+⎝⎭⎪⎨-⎛⎫⎪=- ⎪⎪+⎝⎭⎩，所以112112m m m m αααβββ-⎧=-⎪+⎪⎨-⎪=-+⎪⎩，则,αβ是方程112x m mx x -=-+，即22(2)20mx m x m +-+-=的两实数根，令2()2(2)2h x mx m x m =+-+-，则由题意对称轴214m x m -=>，2(2)42(2)0m m m ∆=--⨯⨯->，(1)0h m =>，解得209m <<.。