信号的采样与恢复、采样定理的仿真设计

*****************实践教学*******************计算机与通信学院2013年春季学期信号处理课程设计题目：正弦信号的采样与恢复专业班级：姓名：学号：指导教师：成绩：摘要通过对信号取样定理与信号恢复知识认识的学习，了解到数字信号处理的理论之后，了解到数字信号处理技术相对于模拟信号处理技术有许多优点，因此人们希望将模拟信号经过采样和量化编码形成数字信号，在采用数字信号处理技术进行处理。

数字信号处理是一门理论与实践紧密结合的课程,而本课程设计是对正弦信号进行采样与恢复，通过产生一个连续时间信号并生成其频谱，然后对该连续信号抽样，并对采样后的频谱进行分析，最后通过设计低通滤波器滤出抽样所得频谱中的多个周期中的一个周期频谱，并显示恢复后的时域连续信号，采用MATLAB软件进行一些仿真和设计，并对所得到的MATLAB图形进行分析和比较。

最后总结。

关键字：采样、恢复、 MATLAB、仿真目录前言 (1)一、设计任务 (2)二、低通滤波器 (3)1、概念 (3)2、工作原理 (3)3、特点 (3)三、设计原理 (4)1、采样定理的原理 (4)2、信号的恢复 (4)四、设计流程图 (6)五、设计内容与步骤 (7)1、正弦信号的采样 (7)1.1连续信号y=sin(t)和其对应的频谱 (7)1.2 对连续信号y=sin(t)进行抽样并产生其频谱 (7)2、通过低通滤波恢复原连续信号 (10)总结 (13)参考文献 (14)致谢 (15)附录 (16)前言随着信息科学和计算机技术的迅速发展，数字信号处理的理论与应用得到飞跃的发展，形成了一门及其重要的学科。

数字信号处理是一门理论与实践紧密结合的课程。

做大量的习题和上机实验，有助于进一步理解和巩固理论知识，还有助于提高分析和解决实际问题的能力。

过去用其他算法语言，实验程序复杂，在有限的实验课时内所做的实验内容少。

MATLAB 强大的运算和图形显示功能，可使数字信号处理上机实验效率大大提高。

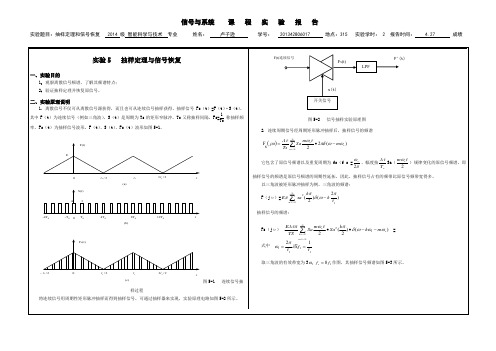
(a) 三角波频谱fE/2F(f)13f -1f -1f 13ffFs(f)fs 2fs(b) 抽样信号频谙1f图5-3 抽样信号频谱图如果离散信号是由周期连续信号抽样而得，则其频谱的测量与周期连续信号方法相同，但应注意频谱的周期性延拓。

3. 抽样信号在一定条件下可以恢复出原信号，其条件是fs ≥2B f ，其中fs 为抽样频率，B f 为原信号占有频带宽度。

由于抽样信号频谱是原信号频谱的周期性延拓，因此，只要通过一截止频率为fc （fm ≤fc ≤fs-fm ，fm 是原信号频谱中的最高频率）的低通滤波器就能恢复出原信号。

如果fs ＜2B f ，则抽样信号的频谱将出现混迭，此时将无法通过低通滤波器获得原信号。

在实际信号中，仅含有有限频率成分的信号是极少的，大多数信号的频率成分是无限的，并且实际低通滤波器在截止频率附近频率特性曲线不够陡峭（如图4-4所示），若使fs=2Bf ，fc=fm=Bf ，恢复出的信号难免有失真。

为了减小失真，应将抽样频率fs 取高（fs ＞2Bf ），低通滤波器满足fm ＜fc ＜fs-fm 。

为了防止原信号的频带过宽而造成抽样后频谱混迭，实验中常采用前置低通滤波器滤除高频分量，如图5-5所示。

若实验中选用原信号频带较窄，则不必设置前置低通滤波器。

本实验采用有源低通滤波器，如图4-6所示。

若给定截止频率fc ，并取Q=12（为避免幅频特性出现峰值），R1=R2=R ，则:C1=Rf Qc π （4-1） C2=QRf 41c π （4-2）图5-5 信号抽样流程图前置低通滤波器抽样 频率低 通 滤波器抽样器F(t)F S (t)F ’(t)S(t) 图5-4 实际低通滤波器在截止频率附近频率特性曲线+-C 1+15VF ’(t)R 1R 2C 2F S (t)12367TP603TP604三、实验内容1. 观察抽样信号波形。

① 调整信号源，使DDS1输出1KHZ 的三角波，调节电位器1W1，使输出信号幅度为1V ； ② 连接DDS1与1P01，输入抽样原始信号；③ 改变抽样脉冲的频率，用示波器观察1TP03（Fs （t ））的波形，此时需把拨动开关1K1拨到“空”位置进行观察；④ 使用不同的抽样脉冲频率，观察信号的变化。

采样定理的原理仿真
一、仿真原理：
采样定理表明，如果以不小于2B次/秒的速率对基带模拟信号均匀采样，那么就可以通过该序列可以无失真地重建对应的基带模拟信号。

如果采样率低于基带信号最高频率的2倍，那么采样输出序列的频谱就会发生交叠，从而无法恢复原基带模拟信号。

设模拟基带信号的频带为(0,200)Hz，对其进行采样的序列为均匀间隔的窄脉冲串，为保证无失真采样，最低采样率设计为400次/秒。

二、Simulink仿真模型：
三、采样与恢复结果：
1.当输入模拟信号频带为$(0,100)$Hz时的仿真结果如图（1）所示。

显然，采样之后频谱产生了周期为采样率（400Hz）的延拓。

只要周期延拓的频谱和原信号频谱不发生交叠，那么就可通过低通滤波器将采样输出信号中的频率延拓部分滤除，也就无失真地恢复了原信号。

从时域仿真结果看，恢复波形与原信号波形之间的区别仅仅是幅度比例和一定的延时，波形形状是无失真的。

图（1）
2.如果基带信号最高频率超过200Hz，则以400次/秒采样后频谱产生交叠，这时将不能够无失真还原信号如图（2）。

图（2）。

《信号与系统实验》信号的采样与恢复（抽样定理）实验一、实验目的1、了解电信号的采样方法与过程以及信号恢复的方法。

2、验证抽样定理。

二、实验设备1、信号与系统实验箱2、双踪示波器三、原理说明1、离散时间信号可以从离散信号源获得，也可以从连续时间信号抽样而得。

抽样信号f s(t)可以看成连续f(t)和一组开关函数s (t)的乘积。

s (t)是一组周期性窄脉冲，见实验图5-1，T s(t)称为抽样周期，其倒数f s(t)= 1/T s称为抽样频率。

图5-1 矩形抽样脉冲对抽样信号进行傅立叶分析可知，抽样信号的频率包括了原连续信号以及无限个经过平移的信号频率。

平移的频率等于抽样频率f s(t)及其谐波频率2f s、3f s》》》》》》。

当抽样信号是周期性窄脉冲时，平移后的频率幅度(sinx)/x规律衰减。

抽样信号的频谱是原信号频谱周期的延拓，它占有的频带要比原信号频谱宽得多。

2、正如测得了足够的实验数据以后，我们可以在坐标纸上把一系列数据点连起来，得到一条光滑的曲线一样，抽样信号在一定条件下也可以恢复到原信号。

只要用一截止频率等于原信号频谱中最高频率f n的低通滤波器，滤除高频分量，经滤波后得到的信号包含了原信号频谱的全部内容，故在低通滤波器输出可以得到恢复后的原信号。

3、但原信号得以恢复的条件是f s 2，其中f s为抽样频率，为原信号占有的频带宽度。

而f min=2 为最低抽样频率又称“柰奎斯特抽样率”。

当f s<2 时，抽样信号的频谱会发生混迭，从发生混迭后的频谱中我们无法用低通滤波器获得原信号频谱的全部内容。

在实际使用中，仅包含有限频率的信号是及少的，因此即使f s=2 ，恢复后的信号失真还是难免的。

图5-2画出了当抽样频率f s>2 （不混叠时）f s<2 （混叠时）两种情况下冲激抽样信号的频谱。

t f(t)0F()t 0m ωm ω-(a)连续信号的频谱Ts t 0f s (t)F()t0m ωm ω-s ω-s ω（）(b)高抽样频率时的抽样信号及频谱 不混叠图5-2 冲激抽样信号的频谱实验中f s >2 、f s =2 、f s <2 三种抽样频率对连续信号进行抽样，以验证抽样定理——要使信号采样后能不失真地还原，抽样频率f s 必须大于信号频率中最高频率的两倍。

中北大学课程设计说明书学生姓名：学号：学院：信息与通信工程专业：电子信息工程题目：信息处理综合实践:信号的采样与恢复、采样定理的仿真指导教师：职称:2014 年 6 月 26 日中北大学课程设计任务书2013/2014 学年第二学期学院：信息与通信工程专业：电子信息工程学生姓名：学号：学生姓名：学号：学生姓名：学号：课程设计题目：信息处理综合实践:信号的采样与恢复、采样定理的仿真起迄日期：2014年6月9日～2012年6月27日课程设计地点：学院楼201实验室、510实验室、608实验室指导教师：负责人：下达任务书日期: 2014 年6月9 日课程设计任务书1．设计目的：运用数字信号处理的理论知识进行频谱分析和滤波器设计，通过理论推导得出相应结论，再利用MATLAB 或C 语言作为编程工具进行计算机仿真实现，从而加深对所学理论知识的理解，培养解决实际问题的能力。

2．设计内容和要求（包括原始数据、技术参数、条件、设计要求等）：课程设计内容（1）掌握USB总线或PCI总线的基本结构，了解基于USB总线或PCI总线A/D卡的通用结构。

（2）通过A/D卡，编写信号的采集、存储和显示程序。

（3）对连续信号进行采样，在满足采样定理和不满足采样定理情况下对连续信号和采样信号进行频谱分析；（4）分析采样结果；（5）根据信号频谱特点，自定义性能指标，设计IIR数字低通滤波器设计。

滤波器的类型可以从巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器、贝塞尔滤波器中任选其中的三种。

分别给出所设计滤波器的频率响应；（6）用所设计的滤波器对采样信号进行恢复，对不同采样频率下的恢复信号进行比较分析；课程设计基本要求（1）掌握数字信号处理的基本概念、基本理论和基本方法；（2）学会用MATLAB 对信号进行分析和处理；（3）要求两位同学各负责一种方法，第三位同学分析运算效率，共同完成任务；3．设计工作任务及工作量的要求〔包括课程设计计算说明书(论文)、图纸、实物样品等〕：（1）课程设计说明书（2）关于基于USB总线或PCI总线A/D卡的报告。

信号的抽样与恢复（抽样定理）信号的抽样和恢复是数字信号处理中的基本操作。

它是将连续时间信号（模拟信号）转化为离散时间信号（数字信号）的过程，也是将数字信号转化为连续时间信号的过程。

抽样定理是信号的抽样和恢复中一个十分重要的定理，它的证明也是数字信号处理中的一个重要课题。

一、信号的抽样在信号处理中，可以通过对连续时间信号进行离散化处理，使其转化为离散时间信号，便于数字处理。

抽样是指在每隔一定的时间间隔内对连续时间信号进行采样，得到一系列离散的采样值。

抽样操作可以用如下公式进行表示：x(nT) = x(t)|t=nT其中，x(t)是原始连续时间信号，x(nT)是在时刻nT处采样得到的值，T为采样周期。

具体来说，采样过程可以通过模拟信号经过一个采样和保持电路，将连续时间信号转换为离散信号的形式。

这里的采样周期越小，采样得到的离散信号的数量就越多，离散信号在时间轴的表示就越密集。

抽样后得到的信号形式如下：二、抽样定理抽样定理又称为奈奎斯特定理，是数字信号处理中的基础理论之一。

它指出，如果连续时间信号x(t)的带宽为B，则在抽样周期为T时，可以恰好通过抽样重建出原始信号x(t)，当且仅当：T ≤ 1/(2B)即抽样周期T应小于等于原始信号的最大频率的倒数的一半。

这个定理的物理意义是，需要对至少每个周期内的信号进行采样，才能够恢复出连续信号。

如果采样周期过大，将会丢失信号的高频成分，从而无法准确重建原始信号。

抽样定理说明了作为采样频率的一个下限值2B，因为将采样频率设置为低于此值会失去信号的唯一信息（高频成分）。

当采样频率等于2B时，可以从这些采样值恢复出信号的完整频率谱，即避免了信息损失。

三、信号的恢复当原始信号被采样后，需要对采样得到的离散信号进行恢复，以便生成一个趋近于原始信号的连续信号。

采样定理的证明告诉了我们如何确保在扫描连续信号的采样点时，可以正确地还原其原始形式。

例如，可以通过插值的方式将采样点之间的值计算出来，从而恢复出连续时间信号。

一、设计目的与要求1、设计目的通过本课程设计，主要训练和培养学生综合应用所学过的信号及信息处理等课程的相关知识，独立完成信号仿真及信号处理的能力。

包括：查阅资料、合理性的设计、分析和解决实际问题的能力，数学仿真软件Matlab和C语言程序设计的学习和应用，培养规范化书写说明书的能力。

2、设计要求设有一信号Xa(t)=EXP-1000|t|,计算傅立叶变换，分析其频谱，并在精度为1/1000的条件下，分别取采样频率为F=5000Hz,F=1000Hz,绘出对应的采样信号的时域信号波形频谱图。

（1）实现信号时域分析和频谱分析以及滤波器等有关Matlab函数。

（2）写好总结、程序、图表、原理、结果分析。

二、设计原理框图三、设计原理本次课程设计主要涉及采样定理、傅里叶变换、信号时域分析和频谱分析的相关内容的相关知识。

1.采样定理设连续信号)(t x a 属带限信号，最高截止频率为c Ω，如果采样角频率c s Ω≥Ω2，那么让采样性信号)(t x a ∧通过一个增益为T 、截止频率为2/s Ω的理想低通滤波器，可以唯一地恢复出原连续信号)(t x a 。

否则，c s Ω<Ω2会造成采样信号中的频谱混叠现象，不可能无失真地恢复原连续信号。

对连续信号进行等间隔采样形成采样信号，对其进行傅里叶变换可以发现采样信号的频谱是原连续信号的频谱以采样频率s Ω为周期进行周期性的延拓形成的。

对模拟信号进行采样可以看做一个模拟信号通过一个电子开关S ，设电子开关每隔周期T 和上一次，每次和上的时间为τ，在电子开关的输出端得到采样信号x^a(t)。

图1 对模拟信号进行采样2、傅里叶变换(1)对于一个非周期函数f（t），如果在（－∞，＋∞）满足下列条件：①、f（t）在任一有限区间上满足狄利克雷条件；②、f（t）在（－∞，＋∞）上绝对可积（如下积分收敛），即：（1）则有下式的傅立叶积分成立：（2）(2)f(t)满足傅立叶积分定理条件时，下图①式的积分运算称为f(t)的傅立叶变换，②式的积分运算叫做F(ω)的傅立叶逆变换。

抽样定理与信号恢复实验报告抽样定理与信号恢复实验报告引言：信号恢复是数字信号处理中的一个重要问题，其目标是通过采样和重构技术来恢复原始信号。

在实际应用中，由于各种原因，我们往往无法直接获得完整的信号，而只能通过采样来获取信号的部分信息。

因此，如何有效地从有限的采样数据中恢复原始信号成为一个关键问题。

本实验旨在通过抽样定理来解决信号恢复问题，并通过实验验证其有效性。

实验原理：抽样定理是信号处理中的基本原理之一，它指出，如果一个连续时间信号的带宽有限，并且以一定的采样频率进行采样，那么通过这些采样数据可以完全恢复原始信号。

具体而言，抽样定理要求采样频率至少是信号带宽的两倍，即Nyquist采样定理。

实验步骤：1. 准备信号源：我们选择了一个正弦信号作为原始信号源，其频率为f0，幅度为A。

通过函数生成器产生该信号，并连接到示波器上。

2. 采样：根据抽样定理，我们选择了采样频率为2f0，即原始信号频率的两倍。

通过示波器的采样功能，将信号进行采样，并记录采样数据。

3. 信号恢复：根据采样数据，我们使用重构算法对信号进行恢复。

在本实验中，我们选择了最常用的插值法进行信号恢复。

通过对采样数据进行插值处理，可以得到连续时间的信号。

4. 重构信号验证：将恢复的信号与原始信号进行对比，验证重构的准确性。

通过示波器将原始信号和恢复信号进行叠加显示，观察它们的相似程度。

实验结果与分析：在本实验中，我们选择了一个频率为1kHz的正弦信号作为原始信号源，采样频率选择为2kHz。

通过示波器进行采样，并得到了采样数据。

接下来，我们使用插值法对采样数据进行信号恢复，并将恢复的信号与原始信号进行对比。

通过观察示波器显示的结果，我们可以明显看到恢复的信号与原始信号非常接近，几乎无法区分它们之间的差异。

这表明，通过抽样定理和插值法，我们成功地从有限的采样数据中恢复了原始信号。

结论：本实验通过采样定理与信号恢复技术，成功地实现了从有限采样数据中恢复原始信号的目标。

实验一信号的采样与恢复（采样定理）一、实验目的1、了解信号的采样方法与过程以及信号恢复的方法。

2、验证采样定理。

二、实验设备1、Dais－XTB信号与系统实验箱一台2、双踪示波器一台3、任意函数发生器一台三、实验原理1、离散时间信号可以从离散信号源获得，也可以从连续时间信号采样而得。

采样信号x s（t）可以看成连续信号x（t）和一组开关函数s（t）的乘积。

s（t）是一组周期性窄脉冲，如图2－5－1，T s称为采样周期，其倒数f s＝1/T s称采样频率。

图2－5－1 矩形采样信号对采样信号进行傅里叶分析可知，采样信号的频率包括了原连续信号以及无限个经过平移的原信号频率。

平移的频率等于采样频率f s及其谐波频率2f s、3f s……。

当采样信号是周期性窄脉冲时，平移后的频率幅度按sinx/x规律衰减。

采样信号的频谱是原信号频谱周期的延拓，它占有的频带要比原信号频谱宽得多。

2、采样信号在一定条件下可以恢复到原信号。

只要用一截止频率等于原信号频谱中最高频率f n的低通滤波器，滤除高频分量，经滤波后得到的信号包含了原信号频谱的全部内容，故在低通滤波器输出端可以得到恢复后的原信号。

3、原信号得以恢复的条件是f s≥2f max，f s为采样频率，f max为原信号的最高频率。

当fs ＜2f max时，采样信号的频谱会发生混迭，从发生混迭后的频谱中无法用低通滤波器获得原信号频谱的全部内容。

在实际使用中，仅包含有限频率的信号是极少的，因此即使f s＝2 f max，恢复后的信号失真还是难免的。

实验中选用f s＜2 f max、f s＝2 f max、f s＞2 f max三种采样频率对连续信号进行采样，以验证采样定理：要使信号采样后能不失真地还原，采样频率f s必须大于信号最高频率的两倍。

4、连续信号的采样和采样信号的复原原理框图如图2－5－2所示。

除选用足够高的采样频率外，常采用前置低通滤波器来防止原信号频谱过宽而造成采样后信号频谱的混迭，但这也会造成失真。

实验三 信号的采样与恢复一、实验目的1、了解电信号的采样方法与过程以及信号恢复的方法。

2、验证抽样定理。

二、实验仪器1、信号与系统实验箱一台（主板）。

2、系统时域与频域分析模块一块。

3、20M 双踪示波器一台。

三、实验内容、过程及结果1)实验内容：观察低中高三种频率下不混叠时（即f ≥2B ）原信号与抽样信号以及抽样恢复信号的波形然后进行对比。

2)实验步骤：1、把系统时域与频域分析模块插在主板上，用导线接通此模块“电源接入”和主板上的电源（看清标识，防止接错，带保护电路），并打开此模块的电源开关。

2、将函数信号发生器产生一正弦波（幅度（峰值）为2V 左右，为便于观察，抽样信号频率一般选择50HZ ～400HZ 的范围，抽样脉冲的频段由开关SK1000进行选择，有“高”“中”“低”档，频率则是通过电位器“频率调节”来调节的，抽样脉冲的脉宽则是由电位器“脉宽调节”进行调节的（一般取30％）），将其送入抽样器，即用导线将函数信号发生器的输出端与本实验模块的输入端相连，用示波器测试“抽样信号”的波形，观察经抽样后的正弦波。

3、改变抽样脉冲的频率为B f s 2 ，用导线将“抽样信号”和“低通输入”相连，用示波器测试测试钩“抽样恢复”，观察复原后的信号，比较其失真程度。

3)实验结果：①低频下：原信号与抽样信号 原信号与抽样恢复信号②中频下：原信号与抽样信号原信号与抽样恢复信号③高频下：原信号与抽样信号原信号与抽样恢复信号四、实验结果分析1）由原信号、抽样信号以及复原信号的波形，能得出什么结论？答：抽样信号是从原信号中获得的离散周期性的信号，其包含了部分乃至绝大部分的原信号内容，通过对这些抽样信号内容进行还原，就可以得到近似原信号波形的结果，但是不能得到跟原信号完全一致的波形，因为失真无法完全避免，只能调试到最佳结果。

2）比较三种不同抽样频率下的fs(t)的波形，能得出什么结论？答：当fs<2B时，抽样信号的频谱会发生混叠，从发生混叠后的频谱中无法用低通滤波器获得原信号频谱的全部内容，即使fs=2B，复原后的信号失真还是难免的。

《信号与系统》课程设计——信号的采样与重建【设计题目】信号的采样与重建 【设计要求】(1) 理解并掌握采样定理。

(2) 分别给定的带限信号进行临界采样、欠采样、过采样，观察采样前后信号的时域波形及频谱特点。

(3) 分别对临界采样、欠采样、过采样后的信号进行重构，设计合理的滤波器，完成信号的重建。

【设计工具】MATLAB 【设计原理】1 采样定理取样定理论述了在一定条件下，一个连续时间信号完全可以用该信号在等时间间隔上的瞬时值（或称样本值）表示，这些样本值包含了连续时间信号的全部信息，利用这些样本值可以恢复原信号。

可以说取样定理在连续时间信号与离散时间信号中架起了一座桥梁。

其具体内容如下：取样定理：设为带限信号，带宽为0F ，则当取样频率02F F s ≥时，可从取样序列)()(s a nT x n x =中重构，否则将导致)(n x 的混叠现象。

带限信号的最低取样频率称为Nyquist （奈奎斯特）速率。

图1给出信号采样原理图图1 信号采样原理图由图1可见，)()()(t t f t f Ts s δ⋅=，其中，冲激采样信号)(t Ts δ的表达式为：∑∞-∞=-=n sT nT t t s)()(δδ （1）其傅立叶变换为∑∞-∞=-n s s n )(ωωδω，其中ss T πω2=。

设)(ωj F ，)(ωj F s 分别为)(t f ，)(t f s 的傅立叶变换，由傅立叶变换的频域卷积定理，可得：∑∑∞-∞=∞-∞=-=-=n ssn s s s n j F T n j F j F )]([1)(*)(21)(ωωωωδωωπω （2）若设)(t f 是带限信号，带宽为m ω如图（2），由式（2）可见，)(t f 经过采样后的频谱)(ωj F s 就是将)(ωj F 在频率轴上搬移至 ,,,,,02ns s s ωωω±±±处（幅度为原频谱的s 1倍）。

因此，当m s ωω2≥时如图（4），频谱不发生混叠；而当m s ωω2<时如图（5），频谱发生混叠。

信号采样与恢复仿真实验的实现与分析信号采样与恢复仿真实验的实现与分析摘要Systemview是一个完整的动态系统设计、分析和仿真的可视化开发环境。

它是一个信号级的系统仿真软件，主要用于电路与通信系统的设计和仿真，是一个强有力的动态系统分析工具，能满足从数字信号处理，滤波器设计，直到复杂的通信系统等不同层次的设计、仿真要求，也是分析处理信号的一个工具。

Systemview是基于windows环境的应用软件，它对硬件的性能要求适中，在CPU为486/66，16M 以上内存的普通PC机上就能运行，应用起来很方便，。

因此，这次课程设计就利用Systemview软件来进行仿真。

在本次课程设计中，通过利用Systemview软件对信号采样和恢复进行的设计及仿真，我不仅加深了对Systemview软件的认识和了解，更加深了对信号采样与恢复原理的了解，而且还懂得了如何利用软件对信号进行分析和仿真，体会了软件仿真的基本过程，从而提高了理论水平和动手能力。

关键词:Systemview仿真，信号的采样，信号的恢复目录1 课题描述 ..................................................................... (1)1.1 Systemview仿真概述 (1)1.2课程设计的目的及意义 ........................................................... 1 2 抽样定理 ..................................................................... (2)2.1 信号的抽样定理 (2)2.2 抽样定理的证明 ................................................................ 3 3 信号的采样与恢复 (4)3.1 采样器 ..................................................................... .. 43.2 保持器 ..................................................................... .. 7 4 信号的采样与恢复原理 ............................................................... 9 5信号的采样与恢复仿真电路图 ......................................................... 9 6 仿真结果分析 ......................................................................106.1 500Hz的抽样频率 (10)6.2 100Hz的抽样频率 (11)6.3 200Hz的抽样频率 ............................................................. 12 总结 ..................................................................... ............ 13 参考文献 ..................................................................... .. (14)权王鹏现代通讯原理课程设计说明1 课题描述1.1 Systemview仿真概述Systemview是一个完整的动态系统设计、分析和仿真的可视化开发环境。

安徽工业大学信号与系统实验指导书实验三抽样定理与信号恢复一.实验目的1.观察离散信号频谱，了解其频谱特点。

2.验证抽样定理并恢复原信号。

二.实验原理1、由于离散时间信号处理更为灵活，所以工程中将连续信号转化为离散信号进行处理，然后再将处理后的离散信号转化为连续信号。

离散信号不仅可从离散信号源获得，而且也可从连续信号抽样获得。

抽样信号fs(t)= f(t)·S(t)。

其中f(t)为连续信号（例如三角波），S(t)是周期为Ts的矩形窄脉冲。

Ts又称抽样间隔，fs=1Ts称抽样频率，fs(t)为抽样信号波形。

f(t)、S(t)、fs(t)波形如图1。

图1 连续信号抽样过程图2 信号的频谱对抽样信号进行傅立叶分析可知，抽样信号的频率包括了原连续信号以及无限个经过平移的原信号频率。

平移的频率等于抽样频率fs 及其谐波频率2 fs、3 fs······。

如图2所示，抽样信号的频谱是原信号频谱周期的延拓，它占有的频带要比原信号频谱宽得多。

2、正如测得了足够的实验数据以后，我们可以在坐标纸上把一系列数据点连起来，得到一条光滑的曲线一样，抽样信号在一定条件下也可以恢复到原信号。

只要用一截止频率等于原信号频谱中最高频率fn 的低通滤波器，滤除高频分量，经滤波后得到的信号包含了原信号频谱的全部内容，故在低通滤波器输出可以得到恢复后的原信号。

3、由抽样定理可知，当抽样信号频率fs>=2fm(原信号最高频率)时，Fs(w)是F(w)的无限个振幅按变化的“重复平移”，因此可以通过低通滤波器(截止频率=fm)从抽样信号fs(t)中恢复原信号f(t)。

fmin＝2 fm为最低抽样频率又称“奈奎斯特抽样率”。

当fs＜2 fm时，抽样信号的频谱会发生混迭，从发生混迭后的频谱中我们无法用低通滤波器获得原信号频谱的全部内容。

在实际使用中，仅包含有限频率的信号是极少的，因此即使fs＝2 fm，恢复后的信号失真还是难免的。

基于MATLAB抽样定理及其信号恢复的仿真基于MATLAB抽样定理及其信号恢复的仿真摘要本设计是运用MATLAB编程来实现抽样定理及其信号恢复的仿真并能在建立的图形用户界面上显示出相应的仿真结果。

目的在于能够熟练的应用MATLAB软件来建立友好的用户界面，通过界面来显示原始信号、抽样信号以及恢复后仿真的信号。

通过编写程序来完成用户界面上各个按钮的功能，通过MATLAB软件中的信号分析的方法来验证抽样定理的正确性。

论文包括用MATLAB语言进行图形用户界面编程的相关知识，如何新建一个图形用户界面，如何添加各种控件，如何更改各种控件的属性，如何使通过编写程序使各种控件实现相应的功能等问题，通过一些有关MATLAB软件的学习来建立一个完整的抽样定理图形用户界面，用户可以利用鼠标或键盘来完成模拟信号的抽样定理及其信号的恢复的全过程，论文中介绍了用MATLAB语言的基本用法和进行信号分析的方法，用户可以选择不同的波形来实现相应的抽样定理并能在图形用户界面上显示相应的波形，在形用户界面上，通过原始信号与恢复信号及其仿真的对比可得出抽样定理的结论。

从而验证抽样的正确性。

关键词MATLAB；抽样定理；仿真AbstractThe design is to use MATLAB programming to achieve sampling theorem and its signal the resumption of the simulation and be able to establish the graphical user interface displayed on the corresponding simulation results. The aim is to skillfully use MATLAB software to create a friendly user interface, through the interface to display the original signal, the sampling signal and the restoration of the signal after the simulation. Through the preparation process to complete the user interface on the various button functions, through the MATLAB software in signal analysis methods to verify the accuracy of sampling theorem.Papers including the use of MATLAB language programming graphical user interface of knowledge, how to create a new graphical user interface, how to add all kinds of controls, how to change the control of various attributes, how to make through the preparation process so that all kinds of controls to achieve the corresponding The functions and so on, through the study of the MATLAB software to create a complete sampling theorem graphical user interface, users can use the mouse or keyboard to complete the analog signal sampling theorem and the restoration of the entire process, the paper introduced by MATLAB language usage and the basic signal analysis method, the user can select a different wave to achieve the appropriate sampling theory and in the graphical user interface displayed on the corresponding waveform, in the form user interface, through the restoration of the original signal and the signal and Simulation The contrast can be drawn to the conclusion sampling theorem. To verify the accuracy of sampling.Keywords MATLAB；sample theory; simulation目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 MATLAB语言的特点 (1)1.2 MATLAB产品主要的应用领域 (1)1.3 抽样定理简介 (1)第2章抽样信号 (3)2.1 抽样信号原理 (3)2.2 模拟信号算法 (4)2.2.1 模拟信号频率计算. (4)2.2.2 采样信号频率计算. (4)2.2.3 模拟信号实现 (5)2.3 本章小结 (7)第3章GUI界面的介绍及设计 (8)3.1 图形用户界面的设计原则 (8)3.2 图形用户界面设计过程 (8)3.2.1 界面设计初步规划 (8)3.2.2 设计MATLAB的GUI (9)3.2.3 创建菜单 (9)3.2.4 控件的设计 (9)3.2.5 对象属性编辑器 (10)3.2.6 回调函数的编写 (10)3.3 算法实现 (11)分析控制系统建模 (11)3.4 信号恢复设计 (11)3.5 GUI界面实现及动态数字调节器软模块的设计 (12)3.6 信号恢复 (14)第4章MATLAB程序仿真 (19)4.1 概述 (19)4.2 程序框图 (19)4.3 恢复原理及其程序设计思想 (20)4.3.1 从冲激抽样信号恢复连续时间信号的时域分析 (20)4.3.2 设计思想 (21)4.3.3 程序框图 (22)结论 (24)致谢 (25)参考文献 (26)附录A (27)附录B (35)第1章绪论MATLAB 是矩阵实验室（点阵式实验室）之意。

matlab信号抽样与恢复信号抽样与恢复是数字信号处理中的基本概念，也是数字信号处理应用中常常涉及到的一个环节。

本文将介绍抽样定理、抽样的操作方法以及抽样信号的信号恢复。

一、抽样定理抽样定理是数字信号处理中一个基本且重要的定理，又称为奈奎斯特抽样定理。

它给出了信号在模拟域和数字域之间的对应关系。

其表述为：在对模拟信号f(t)进行采样时，采样频率F_s必须大于等于信号带宽2B，即F_s≥2B，采样出的数字信号才不会产生混叠现象，即在恢复信号时不会产生失真。

其中，Fs为采样频率，B为信号带宽。

对于一个连续的信号f(t)，在进行采样时，需要首先将其通过一个称为采样保持电路的设备进行采样。

该设备会按照一定的时间间隔Ts （也称采样周期）对信号f(t)进行采样，并将采样结果以数字信号的形式输出。

输出的数字信号可以看作是在时间上离散化、幅度上量化了的原信号f(t)。

二、抽样的操作方法抽样的操作方法是指在进行抽样时需要满足的一些条件。

在实际的数字信号处理中，通常采用交织抽样方式对信号进行抽样。

交织抽样即将原信号采样的时间间隔与采样保持电路采样的时间间隔错开一定的时间（通常为半个采样周期），使得采样时的信号可以有效地避免失真。

具体而言，交织抽样的操作方法如下：首先确定采样频率Fs，以及采样点数n。

采样频率Fs应该满足抽样定理的要求，即Fs≥2B。

采样点数n由采样的时间长度T和采样频率Fs决定，即n=T*Fs。

计算采样周期Ts，即Ts=1/Fs。

在采样时，一般采用一个称为采样保持电路的设备对信号进行采样。

采样保持电路包含一个开关和一个电容，当开关处于闭合状态时，电容开始充电，并将信号的幅度存储在电容中；当开关处于断开状态时，电容被断开，信号的幅度得到保持并输出。

根据交织抽样的操作方法进行采样，并将采样结果存储在计算机中。

三、信号恢复在进行数字信号处理时，需要对数字信号进行重构和恢复。

重构指的是将数字信号重新合成为与原信号类似的模拟信号的过程，而恢复则是在数字信号的基础之上还原原信号的过程。

实验7连续信号的采样与重构一、实验目的1.加深理解采样对信号的时域和频域特性的影响；2.加深对采样定理的理解和掌握，以及对信号恢复的必要性；3.掌握对连续信号在时域的采样与重构的方法。

二、实验内容1.选取信号()()=作为被采样的信号，请绘制出其在欠采样、临界采样、f t Sa t过采样三种情况下的采样信号和重构信号，比较这三种情况下重构信号与原信号的绝对误差，并将绝对误差绘制出来，方便比较说明。

t =-20:0.01:20;w = -20:0.01:20;subplot(4,1,1);plot(t,sinc(t/pi),'linewidth', 2);%取样函数grid on ;axis([-20,20,-0.2,1]);title('源信号，105082009043林裕丰');%采样n = -40:1:40;w = -40:1:40;Ts = 0.5;Wc = 4;f1 = sinc(n*Ts/pi) ;%采样subplot(4,1,2);stem(n*Ts,f1,'.'); %离散点，画图函数axis([-40,40,-0.2,1]);grid on;title('欠采样');y = zeros(1,length(t));for k = -10:10 y = y + Ts*Wc/pi*sinc(k*Ts)*sinc(Wc/pi*(t-k*Ts));end;subplot(4,1,3);plot(t,y,'linewidth', 2);grid on;axis([-20,20,-0.2,1]);title('重构信号');y3 = abs(sinc(t/pi) - y);subplot(4,1,4);plot(t,y3);grid on ; axis([-20,20,-0.2,2]); title('绝对误差');不知道为什么我的软件的那个sinc 函数说找不到。