机器人matlab仿真函数比对结果

选择MATLAB2016a版，高版本不能安装。

安装好按照下面的操作做出来，然后截图做成Word文档发给我。

MATLAB2016a版同学们网上下载安装，安装方法网上随便可找到。

机器人工具箱我发给你们。

一、将文件夹放到MATLAB安装文件夹指定目录下放到安装目录的toolbox文件夹下，如下图是笔者的电脑的位置，其中那个installation address是我自己取得名字，英语不好，不要见怪。

三、打开MATLAB软件，进行手动启动（1）打开matlab，依次点击file（文件）-setpath（设置路径）-add with subfolder （添加子文件夹），然后选择这个rvctools文件夹就好了，然后save（保存）-close （关闭）（2）在命令行窗口输入startup_rvc，回车，如图，显示了一段英语，我恩可以看到，版本是9.10。

本文主要是给大家一个系统的概念，如何用Matlab实现六轴机器人的建模和实现轨迹规划。

以后将会给大家讲解如何手写正逆解以及轨迹插补的程序。

程序是基于Matlab2016a，工具箱版本为Robotic Toolbox 9.10。

1.D-H建模三个两两相互垂直的XYZ轴构成欧几里得空间，存在六个自由度：沿XYZ 平移的三个自由度，绕XYZ旋转的三个自由度。

在欧几里得空间中任意线性变换都可以通过这六个自由度完成。

Denavit-Hartenberg提出的D-H参数模型能满足机器人学中的最小线性表示约定，用4个参数就能描述坐标变换：绕X轴平移距离a；绕X轴旋转角度alpha；绕Z轴平移距离d；绕Z轴旋转角度theta。

2.标准D-H模型和改进D-H模型对比来看参数并没有改变，标准的D-H 模型是将连杆的坐标系固定在该连杆的输出端（下一关节），也即坐标系i-1与关节i对齐；改进的D-H模型则是将坐标系固定在该连杆的输入端（上一关节），也即坐标系i-1与关节对齐i-1。

第1章任务描述及需求分析1.1任务描述本文选用雅马哈公司SCARA(Selective Compliance Assembly Robot Arm) 机器人作为该系统机器人主体，同时结合所选用的工控机、雅马哈SCARA机器人控制器RXC340等控制设备，还采用红外光栅以及光栅控制器构成安全保护装置，同时选用伺服驱动器、电机、震荡送料机、DDC工业摄像机、气动夹爪和气缸等相关设备共同组成了该自动插件机器人系统，在保证产品合格率达标、操作人员安全、经济效益高的条件下，将保险片插接速度提升至每分钟20个以上，良好的满足生产工艺的需要。

本次实践主要包括两个部分，第一部分为了解自动插件机器人原理，相关硬件选型，最终绘制电气原理图。

第二部分为利用MATLAB软件进行SCARA机器人基于D-H 法建模仿真，然后进行该机器人的正逆运动学分析并绘制相关位置、速度、加速度还有轨迹规划曲线。

1.2需求分析1.2.1性能指标分析（1）生产线插接速度>=20个/min,且插接速度可调。

（2）具有1-8种颜色的保险片识别功能，并能根据保险片的颜色进行1-6工位保险盒定位插接。

（3）控制系统具有手动和半自动运行模式功能。

（4）控制系统具有启动，停止，暂停等功能。

（5）控制系统具有防触碰安全报警指示及复位功能。

（6）储料区容量满时具有暂停供料功能。

（7）控制系统可以实现脱机运行。

1.2.2功能需求目前，工业上的自动插件技术主要包括一下这几种，分别为人工插件技术，半自动插件技术和全自动插件技术。

自动插件技术的发展主要是由于，传统的人工插件工艺已经无法满足现代工业的发展需求了，而且由于人工插件需要大量人工，随着社会的发展人工成本不断上升，并且人工插件的生产效率低、且生产质量得不到有效保障，这些问题都严重制约了企业的发展。

所以设计出一款能够代替人工进行自动化插装的插件机器人是非常有必要的。

在这次实践过程中，我们设计所采用的日本雅马哈公司生产的SCARA机器人，利用该机器人分别实现硬件设备的选型，电气原理图的绘制，还有基于MATLAB软件实现该机器人的仿真、D-H法以及正逆运动学分析。

要建立PUMA560的机器人对象，首先我们要了解PUMA560的D-H参数，之后我们可以利用Robotics Toolbox工具箱中的link和robot函数来建立PUMA560的机器人对象。

其中link函数的调用格式：L = LINK([alpha A theta D])L =LINK([alpha A theta D sigma])L =LINK([alpha A theta D sigma offset])L =LINK([alpha A theta D], CONVENTION)L =LINK([alpha A theta D sigma], CONVENTION)L =LINK([alpha A theta D sigma offset], CONVENTION)参数CONVENTION可以取‘standard’和‘modified’，其中‘standard’代表采用标准的D-H参数，‘modified’代表采用改进的D-H参数。

参数‘alpha’代表扭转角，参数‘A’代表杆件长度，参数‘theta’代表关节角，参数‘D’代表横距，参数‘sigma’代表关节类型：0代表旋转关节，非0代表移动关节。

另外LINK还有一些数据域：LINK.alpha %返回扭转角LINK.A %返回杆件长度LINK.theta %返回关节角LINK.D %返回横距LINK.sigma %返回关节类型LINK.RP %返回‘R’(旋转)或‘P’(移动)LINK.mdh %若为标准D-H参数返回0，否则返回1LINK.offset %返回关节变量偏移LINK.qlim %返回关节变量的上下限 [min max]LINK.islimit(q) %如果关节变量超限，返回 -1, 0, +1LINK.I %返回一个3×3对称惯性矩阵LINK.m %返回关节质量LINK.r %返回3×1的关节齿轮向量LINK.G %返回齿轮的传动比LINK.Jm %返回电机惯性LINK.B %返回粘性摩擦LINK.Tc %返回库仑摩擦LINK.dh return legacy DH rowLINK.dyn return legacy DYN row其中robot函数的调用格式：ROBOT %创建一个空的机器人对象ROBOT(robot) %创建robot的一个副本ROBOT(robot, LINK) %用LINK来创建新机器人对象来代替robotROBOT(LINK, ...) %用LINK来创建一个机器人对象ROBOT(DH, ...) %用D-H矩阵来创建一个机器人对象ROBOT(DYN, ...) %用DYN矩阵来创建一个机器人对象利用MATLAB中Robotics Toolbox工具箱中的transl、rotx、roty和rotz可以实现用齐次变换矩阵表示平移变换和旋转变换。

关节型机器人仿真软件
杨涛（sc11010039）2011.12.10
一、开发环境：matlab2008及以上版本（要求带机器人学工具箱）
二、功能：
1．按照DH矩阵建立图形化的关节型机器人对象
2．对生成的机器人进行正逆运动学的位置和速度进行分析和图形仿真
3．对机器人进行轨迹规划，并在轨迹规划的基础上对其做出动力学的分析。

计算机器人在负载情况下的各个关机所需提供
的力向量。

三、本软件的使用方法：
1.启动：如下图在将matlab的工作目录调整为本软件所在的
work目录，在matlab命令界面中输入maininterface命令；
的参数点击完成并返回即可生成相应机器人对象
3.点击文件菜单的显示子菜单即可显示如下的机器人对象
4.点击运动学分析菜单即可弹出如下运动学分析界面
5.在运动学位置分析的基础上选择进行运动学速度分析即可
弹出以下界面，利用雅克比矩阵对当前位置的速度向量进行正逆分析
6.点击轨迹规划菜单即可弹出以下界面，分别输入初始位置的
空间参数（位置参数和RPY参数）点击轨迹规划即可查看关机空间的轨迹规划的结果曲线和方程（五次多项式插值法）
7.在轨迹规划得到一系列位置、速度、加速度向量的基础上可
以对机器人进行动力学分析，计算完成以下动作机器人各个关节所需提供的力向量；。

基于MATLAB的六⾃由度⼯业机器⼈运动分析和仿真基于MATLAB 的六⾃由度⼯业机器⼈运动分析及仿真摘要：以FANUC ARC mate100⼯业机器⼈为研究对象，对其机构和连杆参数进⾏分析，采⽤D-H 法对机器⼈进⾏正运动学和逆运动学分析，建⽴运动学⽅程。

在MATLAB 环境下，运⽤机器⼈⼯具箱进⾏建模仿真，仿真结果证明了所建⽴的运动学正、逆解模型的合理性和正确性。

关键词:FANUC ARC mate100⼯业机器⼈; 运动学; MATLAB 建模仿真 1引⾔⼯业机器⼈技术是在控制⼯程、⼈⼯智能、计算机科学和机构学等多种学科的基础上发展起来的⼀种综合性技术。

经过多年的发展，该项技术已经取得了实质性的进步[1]。

⼯业机器⼈的发展⽔平随着科技的进步和⼯业⾃动化的需求有了很⼤的提⾼，同时⼯业机器⼈技术也得到了进⼀步的完善。

⼯业机器⼈的运动学分析主要是通过⼯业机器⼈各个连杆和机构参数，以确定末端执⾏器的位姿。

⼯业机器⼈的运动学分析包括正运动学分析和逆运动学分析。

随着对焊接件要求的提⾼，弧焊等机器⼈的需求越来越多。

本⽂就以FANUC ARC mate100机器⼈为研究对象，通过分析机构和连杆参数，运⽤D-H 参数法建⽴坐标系，求出连杆之间的位姿矩阵，建⽴⼯业机器⼈运动学⽅程。

并在MATLAB 环境下，利⽤RoboticsToolbox 进⾏建模仿真。

2 FANUC ARC mate100 D-H 坐标系的建⽴mate100是FANUC 公司⽣产的6⾃由度⼯业机器⼈，包括底座、机⾝、臂、⼿腕和末端执⾏器，每个⾃由度对应⼀个旋转关节，如图1所⽰。

图1FANUC ARC mate 100机器⼈三维模型DENAVIT 和HARTENBERG 于1955年提出了⼀种为关节链中的每⼀个杆件建⽴坐标系的矩阵⽅法，即D-H 参数法，在机器⼈运动学分析得到了⼴泛运⽤。

采⽤这种⽅法建⽴坐标系:(1) Z i 轴沿关节i +1的轴线⽅向。

基于MATLAB Robotics Toolbox 的机器人学仿真实验教学机器人学是一门高度交叉的前沿学科方向, 也是自动化和机电工程等相关专业的一门重要专业基础课。

在机器人学的教学和培训中, 实验内容一直是授课的重点和难点。

实物机器人通常是比较昂贵的设备, 这就决定了在实验教学中不可能运用许多实际的机器人来作为教学和培训的试验设备。

由于操作不方便、体积庞大等原因, 往往也限制了实物机器人在课堂授课时的应用。

此外, 由于计算量、空间结构等问题,当前大多数机器人教材只能以简单的两连杆机械手为例进行讲解,而对于更加实际的 6 连杆机械手通常无法讲解得很清楚。

因此, 各式各样的机器人仿真系统应运而生。

经过反复的比较,我们选择了MATLAB RoboticsToolbox [1] 来进行机器人学的仿真实验教学。

MATLABRobotics Toolbox 是由澳大利亚科学家Peter Corke开发和维护的一套基于MATLAB勺机器人学工具箱，当前最新版本为第8版,可在该工具箱的主页上免费下载提供了机器人学研究(petercorke/robot/) 。

Robotics Toolbox中的许多重要功能函数, 包括机器人运动学、动力学、轨迹规划等。

该工具箱可以对机器人进行图形仿真, 并能分析真实机器人控制时的实验数据结果, 因此非常适宜于机器人学的教学和研究。

本文简要介绍了Robotics Toolbox 在机器人学仿真实验教学中的一些应用, 具体内容包括齐次坐标变换、机器人对象构建、机器人运动学求解以及轨迹规划等。

1坐标变换机器人学中关于运动学和动力学最常用的描述方法是矩阵法, 这种数学描述是以四阶方阵变换三维空间点的齐次坐标为基础的[2] 。

如已知直角坐标系{A} 中的某点坐标,那么该点在另一直角坐标系{B} 中的坐标可通过齐次坐标变换求得。

一般而言齐次变换矩阵是4X4的方阵,具有如下形式: 和分别表示{A}{B} 两坐标系之间的旋转变换和平移变换。

matlab仿真实验总结摘要：本文旨在介绍基于Matlab的仿真实验，从基本的Matlab 代码编写开始，到分析参数变化的影响，再到定量分析实验结果。

实验结果表明，通过Matlab的仿真实验，可以很容易地理解模型的参数变化对模型性能的影响，并对模型调整做出科学决策。

关键词：Matlab；仿真实验；参数变化；定量分析Matlab仿真实验总结一、实验目标1、掌握Matlab基本的语法、操作和使用；2、掌握利用Matlab进行模型仿真及参数调优的基本方法；3、熟悉Matlab程序运行过程，熟悉Matlab调试程序的基本方法；4、通过程序仿真实验，了解系统及模型的基本特性，定性分析及定量分析系统特性；二、实验内容1、基于Matlab的程序编写：（1）建立Matlab编辑器环境，熟悉编辑环境基本操作；（2）了解Matlab程序编写的基本方法，熟悉调试Matlab程序的基本方法；（3）编写模型仿真程序。

2、Matlab仿真实验：（1）分析仿真实验结果，收集数据；（2）定性分析实验结果，观察参数变化对结果的影响；（3）计算参数变化后的结果，定量分析实验结果；（4）将实验结果以图形的形式展示，完成Matlab仿真实验报告。

三、实验结果通过本次Matlab仿真实验，可以得出：1、通过Matlab的仿真实验，可以很容易地理解模型的参数变化对模型性能的影响，从而有效地进行模型调整；2、可以定量分析实验结果，从而更好地进行科学决策；3、Matlab操作安全，程序编写简单实用，可以有效地减少实验工时。

四、实验总结本次Matlab仿真实验对于掌握Matlab程序编写及仿真实验的基本方法，了解实验结果的定性及定量分析等方面有着很大的帮助，为今后更深入的Matlab程序及仿真研究打下了基础。

利用MATLAB进行机器人控制引言：机器人已经成为现代社会中不可或缺的一部分。

它们可以在各种环境下完成各种任务，从简单的装配到复杂的手术。

为了实现精确的机器人控制，工程师们使用了各种工具和软件。

其中，MATLAB是一个非常强大且广泛使用的工具，它可以帮助工程师们设计和调试机器人控制系统。

一、MATLAB基础知识在开始探讨如何利用MATLAB进行机器人控制之前，我们先了解一些MATLAB的基础知识。

MATLAB是一种高级的数值计算和数据分析软件，它专门用于快速开发和执行科学和工程项目。

它提供了许多功能和工具，可以帮助工程师们建立复杂的控制算法。

MATLAB具有强大的数值计算能力，可以执行计算，绘图和数据分析等任务。

它还提供了大量的内置函数，可以简化编程和算法设计过程。

使用MATLAB，用户可以轻松处理矩阵和矢量操作，进行符号计算，拟合曲线和解决微分方程等。

二、机器人动力学建模在进行机器人控制之前，我们需要建立机器人的动力学模型。

动力学模型描述了机器人在给定输入和外部力的情况下如何运动。

利用MATLAB，我们可以快速准确地建立机器人的动力学模型。

建立机器人动力学模型的第一步是定义机器人的几何参数和质量参数。

这些参数包括机器人的连杆长度，连杆质量和连接点位置等。

通过这些参数，我们可以计算机器人的动力学参数，如惯性矩阵，质心位置和关节摩擦力等。

在MATLAB中，我们可以使用符号计算工具箱来定义和操作符号变量。

符号变量可以用于表示机器人的几何和质量参数。

通过定义这些符号变量，我们可以快速地计算机器人的动力学参数。

三、控制算法设计在建立机器人的动力学模型后，我们需要设计适当的控制算法来实现所需的运动。

MATLAB提供了许多功能和工具，可以帮助我们进行控制算法设计和分析。

在MATLAB中，我们可以使用控制系统工具箱来设计和分析控制系统。

控制系统工具箱提供了各种函数和工具，例如PID控制器，状态空间模型和频域分析等。

附录MATLAB 机器人工具箱仿真程序:1)运动学仿真模型程序(Rob1、m)L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})r、name=’MOTOMAN-UP6’ % 模型的名称>>drivebot(r)2）正运动学仿真程序(Rob2、m)L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})r、name=’MOTOMAN-UP6’t=[0:0、01:10];%产生时间向量qA=[0 0 0 0 0 0 ]; %机械手初始关节角度qAB=[-pi/2 -pi/3 0 pi/6 pi/3 pi/2 ];%机械手终止关节角度figure('Name','up6机器人正运动学仿真演示');%给仿真图像命名q=jtraj(qA,qAB,t);%生成关节运动轨迹T=fkine(r,q);%正向运动学仿真函数plot(r,q);%生成机器人的运动figure('Name','up6机器人末端位移图')subplot(3,1,1);plot(t, squeeze(T(1,4,:)));xlabel('Time (s)');ylabel('X (m)');subplot(3,1,2);plot(t, squeeze(T(2,4,:)));xlabel('Time (s)');ylabel('Y (m)');subplot(3,1,3);plot(t, squeeze(T(3,4,:)));xlabel('Time (s)');ylabel('Z (m)');x=squeeze(T(1,4,:));y=squeeze(T(2,4,:));z=squeeze(T(3,4,:));figure('Name','up6机器人末端轨迹图'); plot3(x,y,z);3)机器人各关节转动角度仿真程序:(Rob3、m)L1=link([pi/2 150 0 0 ])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0 ])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})r、name='motoman-up6't=[0:0、01:10];qA=[0 0 0 0 0 0 ];qAB=[ pi/6 pi/6 pi/6 pi/6 pi/6 pi/6]; q=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,q(:,1));title('转动关节1'); xlabel('时间/s'); ylabel('角度/rad'); subplot(6,1,2);plot(t,q(:,2));title('转动关节2'); xlabel('时间/s'); ylabel('角度/rad'); subplot(6,1,3);plot(t,q(:,3));title('转动关节3'); xlabel('时间/s'); ylabel('角度/rad'); subplot(6,1,4);plot(t,q(:,4));title('转动关节4'); xlabel('时间/s'); ylabel('角度/rad' ); subplot(6,1,5);plot(t,q(:,5));title('转动关节5'); xlabel('时间/s'); ylabel('角度/rad'); subplot(6,1,6);plot(t,q(:,6));title('转动关节6'); xlabel('时间/s');ylabel('角度/rad');4)机器人各关节转动角速度仿真程序:(Rob4、m)t=[0:0、01:10];qA=[0 0 0 0 0 0 ];%机械手初始关节量qAB=[ 1、5709 -0、8902 -0、0481 -0、5178 1、0645 -1、0201]; [q,qd,qdd]=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,qd(:,1));title('转动关节1');xlabel('时间/s');ylabel('rad/s');subplot(6,1,2);plot(t,qd(:,2));title('转动关节2');xlabel('时间/s');ylabel('rad/s');subplot(6,1,3);plot(t,qd(:,3));title('转动关节3');xlabel('时间/s');ylabel('rad/s');subplot(6,1,4);plot(t,qd(:,4));title('转动关节4');xlabel('时间/s');ylabel('rad/s' );subplot(6,1,5);plot(t,qd(:,5));title('转动关节5');xlabel('时间/s');ylabel('rad/s');subplot(6,1,6);plot(t,qd(:,6));title('转动关节6');xlabel('时间/s');ylabel('rad/s');5)机器人各关节转动角加速度仿真程序:(Rob5、m)t=[0:0、01:10];%产生时间向量qA=[0 0 0 0 0 0]qAB =[1、5709 -0、8902 -0、0481 -0、5178 1、0645 -1、0201]; [q,qd,qdd]=jtraj(qA,qAB,t);figure('name','up6机器人机械手各关节加速度曲线');subplot(6,1,1);plot(t,qdd(:,1));title('关节1');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,2);plot(t,qdd(:,2));title('关节2');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,3);plot(t,qdd(:,3));title('关节3');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')subplot(6,1,4);plot(t,qdd(:,4));title('关节4');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)') subplot(6,1,5);plot(t,qdd(:,5));title('关节5');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)') subplot(6,1,6);plot(t,qdd(:,6));title('关节6');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')。

基于MAT LAB ΠSimulink 的机器人运动学仿真张晓超　董玉红(哈尔滨理工大学,哈尔滨150080)摘要　利用M AT LAB ΠS imulink 仿真软件对机器人的运动学仿真进行研究,提出基于机构仿真工具S imMechanics 的运动学仿真和基于M AT LAB 函数的运动学仿真,并以平面两关节机器人为例比较了各自的特点。

这两种仿真方法对于复杂多关节机器人也同样适用。

关键词:MAT LAB ΠSimulink SimMech anics 运动学　仿真中图分类号:TP 39119　文献标识码:A 文章编号:1671—3133(2005)增—0061—02K inematics simulation of robots based on MAT LAB ΠSimulinkZhang Xiaochao ,Dong Yuhong(College of Mechanical and Pow er E ngineering ,H aerbin U niversity ofScience and T echnology ,H aerbin 150080,CHN )Abstract K inematics simulations of robots were studied by M AT LAB ΠS imulink simulation s oftware.K inematics simulations based on mechanism simulation tool S imMechanics and on M AT LAB function were put forward ,and their features compared for tw o joints robot as an example.The tw o methods can als o be used in application to multiple joints robots.K ey w ords :MAT LAB ΠSimulink SimMech anics K inem atics Simulation 本文利用M AT LAB ΠSimulink 仿真软件对机器人的运动学仿真进行研究,提出基于机构仿真工具Sim Me 2chanics 的运动学仿真和基于M A T LAB 的函数的运动学仿真,并以平面两关节机器人为例比较了各自的特点。

机器人学课程设计基于Matlab的签名机器人建模与仿真一、课程设计问题描述 (1)1.基本要求 (1)2.实现正运动学与工作空间 (1)3.实现逆运动学轨迹规划 (1)4.自由发挥项 (1)5.附录要求 (1)二、六自由度机器人设计 (1)1.机器人的基本构型设计 (1)2.机器人的关节与连杆参数设计 (1)三、正运动学实现与工作空间 (2)1. 建立坐标系 (2)2. 建立D-H 表 (3)3.分析正运动 (3)4.按摩机器人正运动学仿真结果与工作空间 (4)四、机器人逆解与奇异型分析 (5)1. 机器人逆运动学与微分运动学分析 (5)2. 机器人轨迹规划仿真结果 (6)五、机器人数值解法改进 (6)1. 逆运动的数值解法 (6)六、心得体会 (9)七、程序流程与代码附录 (9)一、课程设计问题描述1. 基本要求①设计一款六自由度机器人，要求2,3,4,5关节中有一个是滑动关节，其余关节应为转动关节。

试构想该机器人的功能，并根据功能设定机器人的介绍参数（杆件长及关节极限）；②建立机器人的正运动学模型，进行Matlab运动仿真。

（分析机器人的工作空间，制作机器人的各个运动的动画）。

2.实现正运动学与工作空间①自行设计一个六自由度机器人，对其关节建立坐标系，注意包含滑动关节；②给出所设计的六自由度机器人的D-H 参数表；③推导所设计的六自由度机器人的正运动学，写出各个齐次变换矩阵；④使用MATLAB 编程，得出机器人工作空间，包含立体图和剖面图、机器人工作动画；⑤对设计的六自由度机器人机器的工作空间进行简单分析。

3.实现逆运动学轨迹规划①这里特征机器人末端的轨迹规划，不是关节空间的轨迹规划；②要实现控制机器人末端在空间完成某种轨迹（如直线、圆弧、写字、画图等）；③可以采用求解逆运动的方程或者是利用微分运动；④写出详细的推导过程（公式）；⑤使用MATLAB 编程仿真，得到仿真动画和图片。

4.自由发挥项①机器人完整逆解（数值解）；②寻找奇异点，分析奇异位型；5.附录要求①附程序流程图；②附代码。

第44卷　第5期厦门大学学报(自然科学版)Vol.44　No.5　2005年9月Journal of Xiamen University(Nat ural Science)Sep.2005　基于MA TL AB的机器人运动仿真研究收稿日期:2004210211基金项目:福建省重点科技项目(982H236)资助作者简介:罗家佳(1981-),男,硕士研究生.罗家佳,胡国清(厦门大学机电工程系,福建厦门361005)摘要:按照一定的要求对一种柱面坐标机器人进行了参数设计,讨论了该机器人的运动学问题,然后在MA TL AB环境下,用Robotics Toolbox对该机器人的正运动学、逆运动学、轨迹规划进行了仿真.通过仿真,观察到了机器人各个关节的运动,并得到了所需的数据,说明了所设计的参数是正确的,从而能够达到预定的目标.关键词:机器人;柱面坐标;轨迹规划;仿真;MA TL AB;Robotics Toolbox中图分类号:TP24 文献标识码:A 文章编号:043820479(2005)0520640205 随着科技的发展,机器人与人类的联系日益密切.出于对机器人的兴趣和关注,人们更加想了解机器人,学习机器人,因此,进行机器人的教学和培训就显得尤为重要.然而,机器人是一个比较昂贵的设备,在进行机器人教学时,不可能用许多实际的机器人来作为教学和培训的试验设备.这时,就有必要用到机器人仿真系统,它可为此提供一个方便、灵活的试验工具和手段[1～3].对机器人进行图形仿真,可以将机器人仿真的结果以图形的形式表示出来,从而直观地显示出机器人的运动情况,得到从数据曲线或数据本身难以分析出来的许多重要信息[3],还可以从图形上看到机器人在一定控制条件下的运动规律.对于机器人运动学,在国内的相关著作[4,5]中,讨论较多的是PUMA和斯坦福机器人.本文则讨论一种柱面坐标机器人,同时选用MA TL AB语言进行仿真.目前MA TL AB已经成为控制界上最流行的软件之一,它除了传统的交互式编程之外,还提供了丰富可靠的矩阵运算、图形绘制、数据处理、图像处理、Win2 dows编程等便利工具[6,7].随着MA TL AB在中国逐渐流行,它将成为在PC机上进行机器人仿真的理想方式.基于以上叙述,本文首先设计了柱面坐标机器人的各连杆参数,然后详细讨论了正、逆运动学算法,轨迹规划问题,最后在MA TL AB环境下,运用Robotics Toolbox[8],编制简单的程序语句,快速完成了运动学仿真.在仿真过程中,不仅直观地观测到了机器人的运动情况,还得到了所需的数据,且以图形的形式显示了出来.1　柱面坐标机器人参数设计1.1　D2H变换为描述相邻杆件间平移和转动的关系,Denavit和Hartenberg(1955)提出了一种为关节链中的每一杆件建立附体坐标系的矩阵方法.D2H方法是为每个关节处的杆件坐标系建立4×4齐次变换矩阵,表示它与前一杆件坐标系的关系,其原理[4,5]如下:O X Y Z:与固定坐标相连的固定参考坐标系,称为基坐标系.O i X i Y i Z i:与机器人的第i个杆件相固连,坐标原点在第i+1关节的中心点处.确定和建立每个坐标系遵循以下三条规则:1)Z i-1轴沿着第i关节的运动轴;2)X i轴垂直于Z i-1轴及Z i轴并指向离开Z i-1轴的方向;3)Y i轴按右手坐标系的要求建立.同时,刚性杆件的D2H表示法取决于连杆的以下四个参数:θi:两连杆的夹角;d i:两连杆的距离;a i:连杆的长度(即Z i-1轴和Z i轴间的最小距离);αi:连杆的扭转角.对于转动关节,θi是关节变量,其余为关节参数(保持不变);对于移动关节,d i是关节变量,其余为关节参数.1.2　机器人参数设计柱面坐标机器人主要由垂直柱子、水平手臂(或机械手)和底座构成.水平机械手装在垂直柱子上,能自由伸缩,并可沿垂直柱子上下运动.垂直柱子安装在底座上,并与水平机械手一起能在底座上移动.因此,这种机器人的工作区间就形成一段段圆柱面.通常的柱面坐标机器人有三个自由度.对于本文叙述的柱坐标机器人(参见图1(a );图1中关节2和关节3位移量分别为180.0mm 和185.0mm ),为了能够满足更多的任务需求,设计为六自由度机器人,共有六个关节.它的第一个关节为转动关节,第二、三个关节均为移动关节,最后三个关节均为转动关节.前三个关节确定手臂的位置,后三个关节确定手臂的姿态.我们为该柱坐标机器人取名为“robot001”,具体参数见表1.下面,我们对该机器人参数设计所要达到的目标及设计情况进行简要的叙述.文中设计的柱坐标机器人用于作为搬运机器人或装配机器人,要求能够实现水平机械手在水平方向上的自由伸缩,绕垂直柱子转动和沿垂直柱子上下运动,最后三个关节确定多种方位的姿态,进而完成预定的任务.而具体的参数如d 2和d 3以及d 4则是由预定的工作任务来决定的.对于参数设计而言,并没有严格的要求.连杆长度a i 是由工作任务要求的工作空间的形状和体积来决定的,按上文D 2H 变换的叙述,结合该机器人的结构及它将完成的任务,所设计的a i 均为零,其余均按D 2H 变换的定义进行设计.表1　机器人“robot001”的连杆参数Tab.1　The link parameters of “robot001”连杆iαi /(°)a i /mm θi /(°)d i /mm 变量范围10000-160°～160°2-9000d 2(180.0)0～600mm 3000d 3(185.0)0～560mm 49000431.8-110°～170°5-90000-100°～100°6-266°～266°2　机器人运动学仿真算法2.1　机器人运动学正问题所谓运动学正问题[4,5],就是对于一机器人,给定杆件的几何参数和关节的位移,求解末端连杆坐标系相对于基坐标系的位姿.为求解运动学方程式,我们用齐次变换矩阵i-1A i来描述第i 坐标系相对于(i -1)坐标系的位置和方位,记作:　图1　“robot001”的实体模型及其连杆坐标系　Fig.1　The solid modeling and coordinate f rames of “ro 2bot001”i-1A i =　co s θi -cos αi sin θi sin αi sin θiαi co s θisin θi co s αi cos θi-sin αi cos θi αi sin θi0sin αi cos αid i1(1)现在,将机器人的参数代入式(1),得到第i 坐标系相对于机座坐标系位姿的齐次变换矩阵0T i ,表示为:T i =0A 11A 2…i-1A i(2)特别地,当i =6时,可求得T =0T 6,它确定了机器人的末端相对于基坐标系的位置和姿态,可以把T 矩阵表示为:T =0T 6=0A 11A 22A 33A 44A 55A 6=n xs x a x p x n y s y a y p y n zs za zp z0001(3)其中:A 1=cos θ1-sin θ100sin θ1co s θ1000010001;1A 2=100000100-10d 20001;2A 3=10000100001d 3001;・146・第5期 罗家佳等:基于MA TL AB 的机器人运动仿真研究3A4=co sθ40sinθ40sinθ40-co sθ40 0100.4318 0001;4A5=co sθ50-sinθ50 sinθ50co sθ50 0100 0001;5A6=co sθ6-sinθ600 sinθ6cosθ600 0010 0001.2.2　机器人运动学逆问题机器人运动学逆问题就是已知末端连杆的位置和方位(可表示为位姿矩阵T,即式(3)),求得机器人的各个关节变量.对于上述的“robot001”,需要求解的变量为θ1,d2,d3,θ4,θ5,θ6.机器人运动学逆问题的求解方法是:将运动方程式(3)的两端依次左乘各A矩阵的逆矩阵,并使两端相等矩阵的对应元素相等,即可求得各关节变量.先用i-1T6表示连杆6的坐标系与连杆i-1坐标系的关系[4,5]:i-1T6=Ai A i+1…5A6(4)求解关节变量的方程式如下:A1-1T=1T6(5) A2-1A1-1T=2T6(6) A3-1A2-1A1-1T=3T6(7) A4-1A3-1A2-1A1-1T=4T6(8) A5-1A4-1A3-1A2-1A1-1T=5T6(9) 3　轨迹规划机器人轨迹规划是根据机器人要完成的任务设计机器人各关节的运动规律.轨迹规划主要有两种方案[4,5]:i)点到点运动(P TP,point2to2point motion)的轨迹规划;ii)连续路径运动(CP,continuous2pat h motion)的轨迹规划.对于连续路径运动,不仅要规定机械手的起始点和终止点,而且要指明两点之间的若干中间点(称路径点),必须沿特定的路径运动(路径约束).本文设计的柱坐标机器人,采用了点到点运动的轨迹规划.设它的起始点为A,运动到B点完成一定任务后,再将B点视为起始点,运动到C点完成了预定工作任务,然后又将C点视为起始点,继续运动.这里,对于形如A点到B点,B点到C点的运动,它们之间不存在任何的中间点,并且对于运动的路径也没有设置要求.因而,可以将上述规划视为P TP规划.4　MA TL AB运动仿真4.1　运动仿真(i)在对上述规划轨迹进行仿真前,先输入机器人的参数,并命名“robot001”.命令如下:%连杆的前四个元素依次为α、a、θ、d,最后%一个为0(转动关节)或1(移动关节)>>L1=link([0　0　0　0　0]);L2=link([-pi/2　0　0　0　1]);%移动关节L3=link([0　0　0　0　1]);%移动关节L4=link([pi/2　0　0　0.4318　0]);L5=link([-pi/2　0　0　0　0]);L6=link([0　0　0　0　0]);r=robot({L1　L2　L3　L4　L5　L6});%构建机器人=′robot001′;%命名(ii)运用命令drivebot(),可以立刻看到该机器人的三维图,并且,可以用手动的方式,通过驱动图中的滑块,来驱使机器人运动,就像实际控制着机器人一样[8],见图2所示,对机器人的教学和培训带来了极大方便.>>drivebot(r);%驱动机器人r.(iii)按预定轨迹进行仿真(由于篇幅有限,仅对A到B,B到C进行仿真示例).对于A、B、C三点,A 点处于起始位置,可表示为qA=[0　0　0　0　0　0],即表示机器人的各个关节都处于图2(a)示的零位置处.机械手在B点和C点相对于基坐标系的位姿可用齐次变换矩阵TB和T C表示.然后,按运动学逆问题的解决方法,可以求得A到B,B到C的各个关节变量.下面,用Ro botics Toolbox的逆运动学命令ikine()来求解:>>qA=0　0　0　0　0　0;%定义所有关节变量的初值;TB=-0.65330.2706-0.7071-0.63180.4571-0.6036-0.65330.0000-0.6036-0.75000.27060.1500000 1.0000;qA B=ikine(r,TB);%对TB进行运动学逆问题求解;qA B=1.5708　0.1500　0.2000　0.3927・246・厦门大学学报(自然科学版) 2005年　图2　“robot001”的三维图及滑块控制图　Fig.2　The three2dimension image and slider2controlling picture of“robot001”　0.7854　0.3927%qA B=[1.5708　0.1500　0.2000　0.3927%0.7854　0.3927];%它说明机械手由A到B,关节1需%正向转动1.5708rad,关节2和3需向前移%动0.1500m和0.2000m,最后三个关节需各%自正向转动0.3927,0.7854,0.3927rad.T C=0.3361-0.2075-0.9187-0.48210.8669-0.31310.38790.4821-0.3681-0.92680.07470.1800000 1.0000;qB C=ikine(r,T C)-ikine(r,TB);qB C=-0.7854　0.0300　0.0500　-0.1963　-0.3927　-0.1963%说明机械手由B到C,关节1需逆向转动%0.7854rad,关节2和3需向前移动0.0300m %和0.0500m,最后三个关节需各自逆向%转动0.1963,0.3927,0.1963rad.(iv)用命令plot()对机器人由A到B的运动进行仿真(取仿真时间为2s,采样间隔时间为0.056s),这时就可以看到机器人各关节的具体运动情况.命令如下:>>t=[0:.056:2]′;%产生时间向量qA=[0　0　0　0　0　0];qA B=[1.5708　0.1500　0.2000　0.39270.7854　0.3927];q=jt raj(qA,qA B,t);%jt raj()为构建轨迹命令plot(r,q);%图3给出了机器人运动到B时的三维图　图3　“robot001”运动到B点的三维图　Fig.3　The three2dimension image of“robot001”at point B(v)由于篇幅限制,下面只给出机器人由A运动到B,转动关节1与移动关节2的位移随时间变换的仿真图象(见图4),以及末端关节沿x,y,z方向的运动轨迹(见图5).取仿真时间为2s,采样间隔时间为0.056s.4.2　仿真结果分析从图2可以看出(通过驱动滑块使机器人运动),机器人前三个关节的运动可以满足通常三自由度柱面坐标机器人的运动要求,即机械手可以实现水平方向上的自由伸缩,绕垂直柱子的转动和沿垂直柱子的上下运动,从而验证了连杆1,2,3的连杆参数设计的合理性.机器人后三个关节的运动可以使末端关节具有不同的姿态,也说明了设计的参数是合理的.在运动仿真的第(iv)步,我们观察到机器人由A 运动到B时各个关节的运动情况(文中无法显示这一运动过程),且各个关节运动情况均为正常,各连杆没・346・第5期 罗家佳等:基于MA TL AB的机器人运动仿真研究　图4　位移2时间曲线(a )转动关节1;(b )移动关节2　Fig.4　Displacement 2time curve　图5　末端关节的运动轨迹　Fig.5　The trajectory of the last link有运动错位的情况,从而验证了所有连杆参数的合理性,且说明了各参数的设计能够实现预定的目标.Study on the Simulation of R obot Motion B ased on MAT LABL UO Jia 2jia ,HU Guo 2qing(Department of Mechanical and Electrical Engineering ,Xiamen University ,Xiamen 361005,China )Abstract :The parameters of a kind of cylindrical coordinate robot were designed in this paper ,according to some qualification.Inthe same time ,the problem of the kinematics of the robot was discussed.Then the kinematics ,inverse kinematics and the trajectory planning are simulated with the Robotics Toolbox of the Matlab computer program language.Based on the simulation ,we observe the motion of the robot ’s joints and obtain the data that we need.This process proves that all the parameters we design are right and they can satisfy the goal that we expect.In conclusion ,writing some simple program sentences with the Matlab computer program lan 2guage ,we can carry on the simulation of robot motion conveniently ,in order to check the correctness and the rationality of the param 2eters.K ey w ords :robot ;cylindrical coordinate ;trajectory planning ;simulation ;MA TL AB ;Robotics Toolbox从图4还可以看出:在所取的仿真时间内,转动关节1的位移由零逐渐变化到1.5708rad ;移动关节2的位移由零逐渐变化到0.1500m.图5说明机器人由A 运动到B ,末端关节沿x ,y ,z 方向的位移由初始位置分别变化到-0.6318m ,0,0.1500m.由末端关节的位姿变化也可以看出,机器人后三个关节的运动可以实现不同方位的姿态,即再次说明了其参数的合理性.5　结束语本文对一柱面坐标机器人进行了参数设计,分析了它的运动学问题和轨迹规划问题.在MA TL AB 环境下,编制简单的程序语句,对该机器人已规划好的轨迹进行了运动学仿真,验证了参数的合理性,达到了良好的效果.参考文献:[1]　Dollarhide Robert L ,Agah Arvin.Simulation and controlof distributed robot search teams [J ].Computers and E 2lectrical Engineering ,2003,29(5):625-642.[2]　Zhao Qingjie ,Sun Zengqi.Image 2based robot motion sim 2ulation[J ].Optics Communications ,2002,205(4-6):257-263.[3]　孙增圻.机器人系统仿真及应用[J ].系统仿真学报,1995,7(3):23-29.[4]　蒋新松,主编.机器人学导论[M ].沈阳:辽宁科学技术出版社,1994.[5]　蔡自兴.机器人学[M ].北京:清华大学出版社,2000.[6]　薛定宇,陈阳泉.基于MA TL AB/Simulink 的系统仿真技术与应用[M ].北京:清华大学出版社,2002.[7]　Hanselman D ,Littlefield B.精通Matlab6[M ].张航,黄攀,译.北京:清华大学出版社,2002.[8]　Corke P I.A Robotics Toolbox for MA TL AB [J ].IEEERobotics and Automation Magazine ,1996,3(1):24-32.・446・厦门大学学报(自然科学版) 2005年。

附录MATLAB 机器人工具箱仿真程序：1）运动学仿真模型程序（Rob1.m）L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})=’MOTOMAN-UP6’ % 模型的名称>>drivebot(r)2）正运动学仿真程序（Rob2.m）L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})=’MOTOMAN-UP6’t=[0:0.01:10];%产生时间向量qA=[0 0 0 0 0 0 ]; %机械手初始关节角度qAB=[-pi/2 -pi/3 0 pi/6 pi/3 pi/2 ];%机械手终止关节角度figure('Name','up6机器人正运动学仿真演示');%给仿真图像命名q=jtraj(qA,qAB,t);%生成关节运动轨迹T=fkine(r,q);%正向运动学仿真函数plot(r,q);%生成机器人的运动figure('Name','up6机器人末端位移图'）subplot(3,1,1);plot(t, squeeze(T(1,4,:)));xlabel('Time (s)');ylabel('X (m)');subplot(3,1,2);plot(t, squeeze(T(2,4,:)));xlabel('Time (s)');ylabel('Y (m)');subplot(3,1,3);plot(t, squeeze(T(3,4,:)));xlabel('Time (s)');ylabel('Z (m)');x=squeeze(T(1,4,:));y=squeeze(T(2,4,:));z=squeeze(T(3,4,:));figure('Name','up6机器人末端轨迹图'); plot3(x,y,z);3）机器人各关节转动角度仿真程序：（Rob3.m）L1=link([pi/2 150 0 0 ])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0 ])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})='motoman-up6't=[0:0.01:10];qA=[0 0 0 0 0 0 ];qAB=[ pi/6 pi/6 pi/6 pi/6 pi/6 pi/6]; q=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,q(:,1));title('转动关节1');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,2);plot(t,q(:,2));title('转动关节2');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,3);plot(t,q(:,3));title('转动关节3');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,4);plot(t,q(:,4));title('转动关节4');xlabel('时间/s');ylabel('角度/rad' );subplot(6,1,5);plot(t,q(:,5));title('转动关节5');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,6);plot(t,q(:,6));title('转动关节6');xlabel('时间/s');ylabel('角度/rad');4）机器人各关节转动角速度仿真程序：（Rob4.m）t=[0:0.01:10];qA=[0 0 0 0 0 0 ];%机械手初始关节量qAB=[ 1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,qd(:,1));title('转动关节1');xlabel('时间/s');ylabel('rad/s');subplot(6,1,2);plot(t,qd(:,2));title('转动关节2');xlabel('时间/s');ylabel('rad/s');subplot(6,1,3);plot(t,qd(:,3));title('转动关节3');xlabel('时间/s');ylabel('rad/s');subplot(6,1,4);plot(t,qd(:,4));title('转动关节4');xlabel('时间/s');ylabel('rad/s' );subplot(6,1,5);plot(t,qd(:,5));title('转动关节5');xlabel('时间/s');ylabel('rad/s');subplot(6,1,6);plot(t,qd(:,6));title('转动关节6');xlabel('时间/s');ylabel('rad/s');5）机器人各关节转动角加速度仿真程序：（Rob5.m）t=[0:0.01:10];%产生时间向量qA=[0 0 0 0 0 0]qAB =[1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);figure('name','up6机器人机械手各关节加速度曲线');subplot(6,1,1);plot(t,qdd(:,1));title('关节1');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,2);plot(t,qdd(:,2));title('关节2');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,3);plot(t,qdd(:,3));title('关节3');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)') subplot(6,1,4);plot(t,qdd(:,4));title('关节4');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)') subplot(6,1,5);plot(t,qdd(:,5));title('关节5');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)') subplot(6,1,6);plot(t,qdd(:,6));title('关节6');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')。

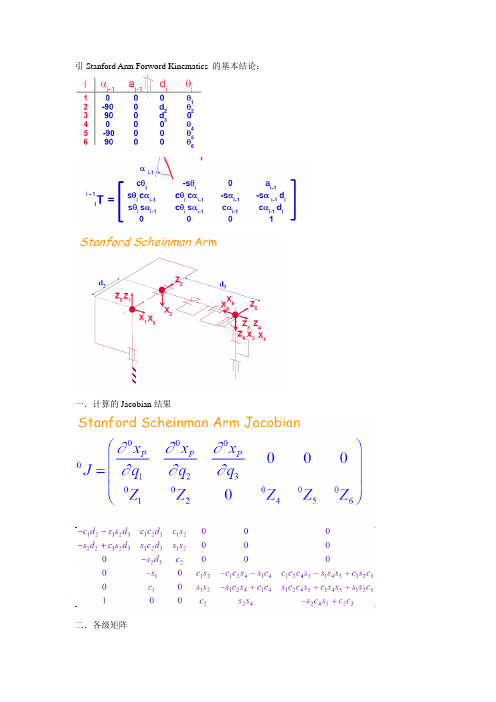
引Stanford Arm Forword Kinematics 的基本结论：一．计算的Jacobian结果二．各级矩阵三．矢量叉积法J=[J1 J2 J3 J4 J5 J6]四．验证直接微分法和矢量叉积法的结果一致： 1.J1111110161;0101321212123[]1001321212123000320001V W V W J J J c d s s d c d s s d J Z P s d s c d s d c s d d c J ⎡⎤=⎢⎥⎣⎦----⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⨯=⋅-+=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与直接求导比较：…………………….. 2.J222220202266223456345622620022626;01[]001110456364564645056565345646456464500001030V W V J J J c J Z P s P c s c c c s s c c s s c c s s c s s c d T T T T T s c c c s s c s c c s s P d P R P ⎡⎤=⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥=⨯=⋅⎢⎥⎢⎥--⎣⎦---⎡⎤⎢⎥---⎢⎥==⎢⎥+-+⎢⎥⎣⎦⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦=⋅=202022662121210123121213123220023001[]001110001w c C c S S c s d s c s s c d s s d s c c d c V Z P s P c s J --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⋅-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⨯=⋅=⎢⎥⎢⎥--⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦带入：matlab 的计算验证过程：>> syms c6 s6 c5 s5 c4 s4>> T65=[c6 -1*s6 0 0;0 0 -1 0;s6 c6 0 0;0 0 0 1]>> T54=[c5 -1*s5 0 0;0 0 1 0;-1*s5 -1*c5 0 0;0 0 0 1] >> T43=[c4 -1*s4 0 0;s4 c4 0 0 ;0 0 1 0;0 0 0 1] >> T63=T43*T54*T65 T63 =[ c4*c5*c6-s4*s6, -c4*c5*s6-s4*c6, c4*s5, 0] [ s4*c5*c6+c4*s6, -s4*c5*s6+c4*c6, s4*s5, 0] [ -s5*c6, s5*s6, c5, 0] [ 0, 0, 0, 1] >> syms d3>> T32=[1 0 0 0; 0 0 -1 -1*d3;0 1 0 0;0 0 0 1] >> T62=T32*T63 T62 =[ c4*c5*c6-s4*s6, -c4*c5*s6-s4*c6, c4*s5, 0] [ s5*c6, -s5*s6, -c5, -d3][ s4*c5*c6+c4*s6, -s4*c5*s6+c4*c6, s4*s5, 0][ 0, 0, 0, 1]>> syms c1 c2 s1 s2>> R20=[c1*c2 -1*c1*s2 -1*s1;s1*c2 -1*s1*s2 c1;-1*s2 -1*c2 0]>> p622=[0;-1*d3;0]p622 =-d3>> p620=R20*p622p620 =c1*s2*d3s1*s2*d3c2*d3>> z2=[0 0 c1;0 0 s1;-1*c1 -1*s1 0]z2 =[ 0, 0, c1][ 0, 0, s1][ -c1, -s1, 0]>> v2=z2*p620v2 =c1*c2*d3s1*c2*d3-c1^2*s2*d3-s1^2*s2*d3与直接求导比较：……………………..在matlab中用B=jacobian(f,v)方法直接求导获取雅可比矩阵>> clear>> syms theta1 d3 d2 theta2>>F=[cos(theta1)*d3*sin(theta2)-sin(theta1)*d2;sin(theta1)*d3*sin(theta2)+cos(theta1)*d2;d3*cos(t heta2)]F =cos(theta1)*d3*sin(theta2)-sin(theta1)*d2sin(theta1)*d3*sin(theta2)+cos(theta1)*d2d3*cos(theta2)>> syms theta4 theta5 theta6>> v=[theta1;theta2;d3;theta4;theta5;theta6]v =theta1theta2d3theta4theta5theta6>> jacob=jacobian(F,v)jacob =[ -sin(theta1)*d3*sin(theta2)-cos(theta1)*d2, cos(theta1)*d3*cos(theta2), cos(theta1)*sin(theta2), 0, 0, 0] [ cos(theta1)*d3*sin(theta2)-sin(theta1)*d2, sin(theta1)*d3*cos(theta2), sin(theta1)*sin(theta2), 0, 0, 0] [ 0, -d3*sin(theta2), cos(theta2), 0, 0, 0]直接求偏导：>> syms theta1 d3 d2 theta2 theta4 theta5 theta6>>F1=cos(theta1)*d3*sin(theta2)-sin(theta1)*d2>> dif(F1,theta1)补充对教材雅可比矩阵逆矩阵的求解：>> syms l1 theta1 l2 theta2>>J=[-l1*sin(theta1)-l2*sin(theta1+theta2)-l2*sin(theta1+theta2);l1*cos(theta1)+l2*cos(theta1+theta2) l2*cos(theta1+theta2)]J =[ -l1*sin(theta1)-l2*sin(theta1+theta2), -l2*sin(theta1+theta2)][ l1*cos(theta1)+l2*cos(theta1+theta2), l2*cos(theta1+theta2)]>> inv(J)ans =[ -cos(theta1+theta2)/l1/(cos(theta1+theta2)*sin(theta1)-sin(theta1+theta2)*cos(theta1)),-sin(theta1+theta2)/l1/(cos(theta1+theta2)*sin(theta1)-sin(theta1+theta2)*cos(theta1))][ (l1*cos(theta1)+l2*cos(theta1+theta2))/l2/l1/(cos(theta1+theta2)*sin(theta1)-sin(theta1+theta2)*cos(theta1)),(l1*sin(theta1)+l2*sin(theta1+theta2))/l2/l1/(cos(theta1+theta2)*sin(theta1)-sin(theta1+theta2)*cos(theta1))] >>J11=simple(-cos(theta1+theta2)/l1/(cos(theta1+theta2)*sin(theta1)-sin(theta1+theta2)*cos(theta1))) J11 =cos(theta1+theta2)/l1/sin(theta2)02R T 02对应前3行3列。

matlab机器人运动学正解-回复Matlab机器人运动学正解引言：在现代制造业和工业自动化中，机器人已经成为非常重要的工具和设备。

机器人运动学解决了机器人如何在三维空间中移动和操作的问题。

Matlab 作为一种强大的计算工具，可以极大地简化机器人运动学分析过程。

本文将一步一步回答机器人运动学正解问题，以帮助读者理解和使用Matlab 进行机器人运动学分析。

第一步：机器人建模为了进行机器人运动学分析，首先需要一个机器人模型。

机器人模型包含机器人的结构，关节，连杆长度和连接方式等信息。

可以使用Matlab的工具，如Robotics System Toolbox来创建机器人模型。

此工具箱提供了一系列函数和类来定义机器人的各个部分和连接方式。

第二步：关节变量和末端执行器坐标系机器人运动学分析的核心是找到机器人各个关节的变量和末端执行器的坐标系。

机器人的关节变量是描述机器人关节位置和角度的参数。

末端执行器的坐标系是描述机器人末端位置和姿态的坐标系。

可以使用Matlab 的机器人模型对象提供的函数来获取关节变量和末端执行器的坐标系。

第三步：正解算法机器人运动学正解问题是寻找机器人末端执行器的位置和姿态。

正解算法的目标是计算机器人末端执行器的位置矢量和旋转矩阵。

该算法依赖于机器人的关节变量和连杆长度。

可以使用Matlab提供的机器人模型对象的函数来实现机器人运动学正解算法。

第四步：编写Matlab代码编写Matlab代码来实现机器人运动学正解算法。

首先，创建机器人模型对象并定义机器人结构和参数。

然后，使用机器人模型对象的函数来获取关节变量和末端执行器的坐标系。

最后，使用正解算法计算机器人末端执行器的位置和姿态。

第五步：实际应用利用Matlab进行机器人运动学正解的结果可以应用于许多实际问题和应用中。

例如，可以使用机器人运动学正解来规划机器人的路径和轨迹，以达到期望的位置和姿态。

此外，还可以分析机器人的工作空间和约束，以优化机器人的运动。

matlab求解机器人的hessian矩阵算法机器人的Hessian矩阵是一个重要的数学工具，用于描述机器人运动学和动力学问题的特征，例如机器人姿态的稳定性、动态参数的优化等。

在机器人控制和路径规划中，了解Hessian矩阵的性质和计算方法是非常重要的。

Hessian矩阵是一个二阶偏导数矩阵，用于描述函数的局部曲率和形状。

对于机器人运动学和动力学模型，可以将机器人的状态（位置、速度、加速度等）表示为一个多变量函数，并利用Hessian矩阵来分析这个函数的二阶导数信息。

机器人的Hessian矩阵可以用于判断机器人姿态的稳定性。

当机器人处于一个平衡点附近时，通过计算Hessian矩阵的特征值，可以确定该平衡点的稳定性。

如果Hessian矩阵的特征值都为负值，则该平衡点是一个稳定点；如果存在正的特征值，则说明该平衡点是不稳定的。

这个判断方法可以用于机器人控制中，设计合适的控制策略来保持机器人的稳定性。

另外，Hessian矩阵还可以用于优化机器人动力学参数。

在机器人动力学建模中，通常需要确定机器人的质量、惯性参数等。

通过最小化机器人模型预测值和实际观测值之间的差异，并利用Hessian矩阵的逆来更新动力学参数，可以优化机器人模型，提高动力学参数的精确性和性能。

计算机算法用于求解机器人的Hessian矩阵。

常见的算法包括数值方法和解析方法。

在数值方法中，可以使用有限差分法或自动微分法来近似计算Hessian矩阵的元素。

有限差分法通过计算函数在不同状态下的一阶导数差值和二阶导数差值来近似计算Hessian矩阵。

自动微分法则基于计算图和链式法则，通过反向传播计算函数的一阶和二阶导数，并构建Hessian矩阵。

解析方法通过计算机代数的方法直接求解机器人模型的Hessian矩阵。

对于一些简单的机器人模型，可以通过手动计算偏导数和二阶偏导数来获得Hessian矩阵。

对于复杂的机器人模型，可以使用符号计算软件，如MATLAB的符号计算工具箱，通过符号表达式计算Hessian矩阵。

MATLAB机器人仿真程序随着机器人技术的不断发展，机器人仿真技术变得越来越重要。

MATLAB是一款强大的数学计算软件，也被广泛应用于机器人仿真领域。

本文将介绍MATLAB在机器人仿真程序中的应用。

一、MATLAB简介MATLAB是MathWorks公司开发的一款商业数学软件，主要用于算法开发、数据可视化、数据分析以及数值计算等。

MATLAB具有丰富的工具箱，包括信号处理、控制系统、神经网络、图像处理等，可以方便地实现各种复杂的计算和分析。

二、MATLAB机器人仿真程序在机器人仿真领域，MATLAB可以通过Robotics System Toolbox实现各种机器人的仿真。

该工具箱包含了机器人运动学、动力学、控制等方面的函数库，可以方便地实现机器人的建模、控制和可视化。

下面是一个简单的MATLAB机器人仿真程序示例：1、建立机器人模型首先需要定义机器人的几何参数、连杆长度、质量等参数，并使用Robotics System Toolbox中的函数建立机器人的运动学模型。

例如，可以使用robotics.RigidBodyTree函数来建立机器人的刚体模型。

2、机器人运动学仿真在建立机器人模型后，可以使用Robotics System Toolbox中的函数进行机器人的运动学仿真。

例如，可以使用robotics.Kinematics函数计算机器人的位姿，并使用robotics.Plot函数将机器人的运动轨迹可视化。

3、机器人动力学仿真除了运动学仿真外，还可以使用Robotics System Toolbox中的函数进行机器人的动力学仿真。

例如，可以使用robotics.Dynamic函数计算机器人在给定速度下的加速度和力矩，并使用robotics.Plot函数将机器人的运动轨迹可视化。

4、机器人控制仿真可以使用Robotics System Toolbox中的函数进行机器人的控制仿真。

例如，可以使用robotics.Controller函数设计机器人的控制器，并使用robotics.Plot函数将机器人的运动轨迹可视化。

MATLAB是一种功能强大的数学软件，它提供了各种各样的数学和工程计算功能，包括不同的算法。

在实际应用中，我们经常需要根据具体的情况选择合适的算法来进行计算，以获得最优的结果。

本文将介绍MATLAB中四种不同的算法，并通过比较它们的计算结果，以帮助读者更好地选择合适的算法来解决实际问题。

二、算法介绍1. 算法A算法A是一种基于数学模型的算法，它通过建立数学方程来描述问题，并使用数值方法进行求解。

算法A适用于一般的数学和工程计算问题，可以在较短的时间内获得结果。

2. 算法B算法B是一种优化算法，它通过迭代计算的方式寻找问题的最优解。

算法B适用于需要求解最优化问题的情况，可以找到全局最优解或局部最优解。

3. 算法C算法C是一种统计算法，它通过对数据进行分析和建模来进行计算。

算法C适用于需要对大量数据进行分析和预测的情况，可以得到数据的统计特性和趋势。

算法D是一种机器学习算法，它通过对已有数据进行学习和训练来进行计算。

算法D适用于需要进行模式识别和预测的情况，可以根据已有数据来预测未来的结果。

三、算法比较在实际应用中，我们经常需要根据具体的情况选择合适的算法来进行计算。

下面将通过一个实际的案例来比较四种不同算法的计算结果。

案例背景：假设有一组数据，需要对其进行分析和预测。

1. 算法A的计算结果通过算法A的计算，得到数据的统计特性和趋势，进而进行预测和分析。

2. 算法B的计算结果通过算法B的计算，得到数据的最优解，进而进行优化和规划。

3. 算法C的计算结果通过算法C的计算，得到数据的统计特性和趋势，进而进行预测和分析。

4. 算法D的计算结果通过算法D的计算，得到数据的模式和规律，进而进行模式识别和预测。

四、结果分析根据对四种不同算法的计算结果进行分析和比较，可以得出以下结论：1. 算法A适用于对数据进行分析和预测，能够获得数据的统计特性和趋势。

2. 算法B适用于对问题进行优化和规划，能够得到问题的最优解。

Matlab技术机器人控制方法详解引言:近年来，机器人技术在工业领域得到了广泛应用。

而机器人的控制方法也是实现机器人运动和任务的关键技术之一。

其中，Matlab技术无疑是现代机器人控制领域中使用最广泛的工具之一。

本文将为大家详细介绍Matlab在机器人控制中的应用方法。

一、Matlab在机器人运动学控制中的应用1.1正向运动学分析机器人的正向运动学是指已知机器人各关节角度，确定机器人末端执行器的位置姿态。

Matlab提供了一系列的工具箱，如Robotics System Toolbox，可以非常方便地实现机器人正向运动学分析。

通过调用相应的函数和工具，可以获得机器人末端执行器在笛卡尔坐标系下的位置和姿态信息，为机器人的路径规划和运动控制提供支持。

1.2逆向运动学分析机器人的逆向运动学是指已知机器人末端执行器的位置姿态，计算出机器人各关节角度。

逆向运动学分析是机器人控制中的一个复杂问题，通常需要使用数值计算方法来求解。

Matlab提供了强大的数值计算能力，可以通过数值求解的方法得到机器人的逆向运动学解。

此外，Matlab还提供了一些逆向运动学求解算法的工具箱，如Inverse Kinematic Toolbox，可以进一步简化逆向运动学分析的过程。

二、Matlab在机器人动力学控制中的应用2.1机器人运动学模型的建立在机器人动力学控制中，首先需要建立机器人的运动学模型。

机器人的运动学模型可以用来描述机器人各关节之间的约束关系，从而计算机器人在特定位姿下的速度和加速度。

Matlab提供了各种符号运算工具和函数，非常方便地实现机器人运动学模型的建立。

通过建立机器人的运动学模型，可以为机器人的动力学控制提供基础。

2.2机器人动力学建模与仿真机器人动力学建模是机器人动力学控制的关键一步。

Matlab提供了多种方法来实现机器人的动力学建模和仿真。

通过调用相应的函数和工具箱，可以实现机器人的动力学建模，并模拟机器人在不同控制输入下的运动轨迹。