必修二立体几何单元测试题(详细答案)[1]

高一数学（必修二）立体几何初步单元测试卷及答案一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.如图所示，己知正方形O A B C ''''的边长为1，它是水平放置的一个平面图形的直观图，则其原图形的周长为( )A.8B.22C.4D.223+2.下列说法正确的是( ) A.三点确定一个平面B.圆心和圆上两个点确定一个平面C.如果两个平面相交有一个交点，则必有无数个公共点D.如果两条直线没有交点，则这两条直线平行3.正方体1111ABCD A B C D -中，P ，Q ，R 分别是AB ，AD ，11B C 的中点，那么正方体中过P ，Q ，R 的截面图形是( ) A.三角形B.四边形C.五边形D.六边形4.某圆柱的高为2，其正视图如图所示，圆柱上下底面圆周及侧面上的点A ，B ，D ，F ，C 在正视图中分别对应点A ，B ，E ，F ，C ，且3AE EF =，2BF BC =，异面直线AB ，CD 所成角的正弦值为45，则该圆柱的外接球的表面积为( )A.20πB.16πC.12πD.10π5.在《九章算术·商功》中将正四面形棱台体（棱台的上、下底面均为正方形）称为方亭.在方亭1111ABCD A B C D -中，1124AB A B ==，四个侧面均为全等的等腰梯形且面积之和为122( ) 282B.283142D.1436.异面直线是指( ) A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线7.如图，在正方体1111ABCD A B C D -中，E ，F 分别是11A D ，11B C 的中点，则与直线CF 互为异面直线的是( )A.1CCB.11B CC.DED.AE8.下列说法中正确的是( ) A.三点确定一个平面 B.四边形一定是平面图形 C.梯形一定是平面图形D.两个不同平面α和β有不在同一条直线上的三个公共点二、多选题（本题共4小题，每小题5分，共20分。

第二章测试时间120分钟 满分150分一、选择题(本大题共10小题，每小题5分，共50分．在下列四个选项中，只有一项是符合题意的)1．已知点P (－3，1)，点Q 在y 轴上，且直线PQ 的倾斜角为120° ，则Q 点的坐标为( )A ．(0,2)B ．(0，－2)C ．(2,0)D ．(－2,0)解析 设Q (0，y )，由k ＝y －13＝－3，得y ＝－2.答案 B2．已知两条直线y ＝ax －2和y ＝(a ＋2)x ＋1互相垂直，则a 等于( )A ．2B ．1C ．0D ．－1解析 由题意，得a (a ＋2)＝－1，得a ＝－1. 答案 D3．已知过点A (－2，m )和B (m,4)的直线与直线2x ＋y －1＝0平行，则m 的值为( )A ．0B ．－8C ．2D ．10解析 由4－mm ＋2＝－2，得m ＝－8.答案 B4．若点A 是点B (1,2,3)关于x 轴对称的点，点C 是点D (2，－2,5)关于y 轴对称的点，则|AC |＝( )A ．5 B.13 C ．10D.10解析 A (1，－2，－3)，C (－2，－2，－5)代两点间距离公式即可．答案 B5．直线y ＋4＝0与圆x 2＋y 2－4x ＋2y －4＝0的位置关系是( ) A ．相切B ．相交，但直线不经过圆心C ．相离D ．相交且直线经过圆心 答案 A6．已知M (－2,0)，N (2,0)，则以MN 为斜边的直角三角形直角顶点P 的轨迹方程是( )A ．x 2＋y 2＝4(x ≠±2)B ．x 2＋y 2＝4C ．x 2＋y 2＝2(x ≠±2)D ．x 2＋y 2＝2解析 由题可知，点P 的轨迹是以MN 为直径的圆(除去M 、N 两点)，∴点P 的轨迹方程是x 2＋y 2＝4(x ≠±2)．答案 A7．若直线3x ＋2y －2m －1＝0与直线2x ＋4y －m ＝0的交点在第四象限，则实数m 的取值范围是( )A ．(－∞，－2)B ．(－2，＋∞)C.⎝⎛⎭⎪⎫－∞，－23D.⎝⎛⎭⎪⎫－23，＋∞解析 由⎩⎪⎨⎪⎧3x ＋2y －2m －1＝0，2x ＋4y －m ＝0，得⎩⎨⎧x ＝3m ＋24，y ＝－m －28.由题意，得⎩⎨⎧3m ＋24＞0，－m ＋28＜0，得m ＞－23.答案 D8．已知圆C 的方程为x 2＋y 2－4x ＝0，若圆C 被直线l ：x ＋y ＋a ＝0截得的弦长为23，则a ＝( )A ．2＋ 2 B.2 C ．2± 2D ．－2±2解析 由弦长公式，得3＝4－⎝ ⎛⎭⎪⎪⎫2＋a 12＋122， 得a ＝－2± 2. 答案 D9．将直线2x －y ＋λ＝0沿x 轴向左平移1个单位，所得直线与x 2＋y 2＋2x －4y ＝0相切，则实数λ的值为( )A ．－3或7B ．－2或8C ．0或10D ．1或11解析 将直线平移后得到y ＝2(x ＋1)＋λ＝2x ＋2＋λ， 由题可知，|－2－2＋2＋λ|22＋(－1)2＝5， 得λ＝－3，或λ＝7，故选A. 答案 A10．若圆x 2＋y 2－2x －4y ＝0的圆心到直线x －y ＋a ＝0的距离为22，则a 的值为( )A ．－2或2 B.12或32 C ．2或0D ．－2或0解析 圆的圆心(1,2)，∴d ＝|1－2＋a |2＝22，得a ＝0，或a ＝2.答案 C二、填空题(本大题共5小题，每小题5分，共25分．把答案填在题中横线上)11．当a 为任意实数时，直线ax －y ＋1－3a ＝0恒过定点________． 解析 原方程可化为a (x －3)－(y －1)＝0，∴直线l 过(3,1)． 答案 (3,1)12．直线x －2y ＋5＝0与圆x 2＋y 2＝8相交于A ，B 两点，则|AB |＝________.解析 圆心到该直线的距离d ＝55＝5，∴弦长＝2(22)2－(5)2＝2 3. 答案 2313．两圆相交于两点(1,3)和(m ，－1)，两圆圆心都在直线x －y ＋c ＝0上，且m 、c 均为实数，则m ＋c ＝________.解析 根据两圆相交的性质可知，两点(1,3)和(m ，－1)的中点⎝ ⎛⎭⎪⎫1＋m 2，1在直线x －y ＋c ＝0上，并且过两点的直线与x －y ＋c ＝0垂直，故有⎩⎨⎧1＋m2－1＋c ＝0，3－(－1)1－m ×1＝－1，∴m ＝5，c ＝－2，∴m ＋c ＝3. 答案 314．若不同两点P ，Q 的坐标分别为(a ，b )，(3－b,3－a )，则线段PQ 的垂直平分线l 的斜率为________；圆(x －2)2＋(y －3)2＝1关于直线l 对称的圆的方程为________．解析 ∵k PQ ＝3－a －b3－b －a ＝1，又k l ·k PQ ＝－1∴k l ＝－1，又(2,3)关于l 的对称点为(0,1)， 故所求的圆的方程为x 2＋(y －1)2＝1. 答案 －1 x 2＋(y －1)2＝115．过圆x 2＋y 2－x ＋y －2＝0与x 2＋y 2＝5的交点，且圆心在直线3x －4y －1＝0上的圆的方程为________．解析 设所求的圆的方程为x 2＋y 2－x ＋y －2＋ λ(x 2＋y 2－5)＝0，即(1＋λ)x 2＋(1＋λ)y 2－x ＋y －2－5λ＝0.∴圆心为⎝ ⎛⎭⎪⎫12(1＋λ)，－12(1＋λ). 由32(1＋λ)－42(1＋λ)－1＝0，得λ＝－32 故所求的圆的方程为(x ＋1)2＋(y －1)2＝13. 答案 (x ＋1)2＋(y －1)2＝13三、解答题(本大题共有6小题，共75分．解答时应写出必要的文字说明，证明过程或演算步骤)16．(12分)已知两条直线l 1：mx ＋8y ＋n ＝0和l 2：2x ＋my －1＝0.试确定m ，n 的值，使(1)l 1和l 2相交于点(m ，－1)；(2)l 1∥l 2；(3)l 1⊥l 2，且l 1在y 轴上的截距为－1. 解 (1)∵m 2－8＋n ＝0，且2m －m －1＝0， ∴m ＝1，n ＝7.(2)由m ·m －8×2＝0，得m ＝±4， 由8×(－1)－n ·m ≠0，得n ≠±2，即m ＝4，n ≠－2时，或m ＝－4，n ≠2时，l 1∥l 2. (3)当且仅当m ·2＋8·m ＝0，即m ＝0时，l 1⊥l 2，又－n8＝－1，∴n ＝8. 即m ＝0，n ＝8时，l 1⊥l 2，且l 1在y 轴上的截距为－1.17．(12分)△ABC 中，顶点A 的坐标为(1,2)，高BE ，CF 所在直线的方程分别为2x －3y ＋1＝0，x ＋y ＝0，求这个三角形三条边所在直线的方程．解 由已知，直线AC 的斜率为－32， 直线AB 的斜率为1.∴直线AC 的方程为3x ＋2y －7＝0， 直线AB 的方程为x －y ＋1＝0.再由⎩⎪⎨⎪⎧x ＋y ＝0，3x ＋2y －7＝0，可解得C 点坐标为(7，－7)．由⎩⎪⎨⎪⎧2x －3y ＋1＝0，x －y ＋1＝0，可解得B 点坐标为(－2，－1) . 于是直线BC 的方程为2x ＋3y ＋7＝0.18．(12分)已知圆x 2＋y 2－12x ＝0的圆心为Q ，过点P (0,2)且斜率为k 的直线与圆Q 相交于不同两点A ，B ，求实数k 的取值范围．解 x 2＋y 2－12x ＝0可化为(x －6)2＋y 2＝36，又直线过点P (0,2)，斜率为k ，故l 的方程为y ＝kx ＋2，即kx －y ＋2＝0，由题意，得|6k ＋2|k 2＋1＜6，得k ＜43.∴k 的取值范围是⎝⎛⎭⎪⎫－∞，43.19．(13分)已知P (1,2)为圆x 2＋y 2＝9内一定点，过P 点任作直线，与圆相交，求弦的中点的轨迹方程．解 设过P 点的直线与圆相交于A ，B 两点，C 为AB 的中点，设C (x ，y )，由题意，得当P 与C 不重合时，△OPC 为直角三角形，∴C 点在以OP 为直径的圆上，又OP 的中点⎝ ⎛⎭⎪⎫12，1，|OP |＝12＋22＝5，∴点C 的轨迹方程为⎝ ⎛⎭⎪⎫x －122＋(y －1)2＝54(除去P 点)．又当x ＝1，y ＝2时上式仍成立，∴点C 的轨迹方程为⎝ ⎛⎭⎪⎫x －122＋(y －1)2＝54.20．(13分)已知方程x 2＋y 2－2x －4y ＋m ＝0. (1)若此方程表示圆，求m 的取值范围；(2)若(1)中的圆与直线x ＋2y －4＝0相交于M ，N 两点，且OM ⊥ON (O 为坐标原点)，求m ；(3)在(2)的条件下，求以MN 为直径的圆的方程． 解 (1)原方程化为(x －1)2＋(y －2)2＝5－m . ∵此方程表示圆， ∴5－m >0. ∴m <5.(2)设M (x 1，y 1)，N (x 2，y 2)， 则x 1＝4－2y 1，x 2＝4－2y 2， 得x 1x 2＝16－8(y 1＋y 2)＋4y 1y 2. ∵OM ⊥ON ， ∴x 1x 2＋y 1y 2＝0.∴16－8(y 1＋y 2)＋5y 1y 2＝0.①由⎩⎪⎨⎪⎧x ＝4－2y ，x 2＋y 2－2x －4y ＋m ＝0，得 5y 2－16y ＋m ＋8＝0. ∴y 1＋y 2＝165，y 1y 2＝8＋m 5. 代入①得m ＝85.(3)以MN 为直径的圆的方程为 (x －x 1)(x －x 2)＋(y －y 1)(y －y 2)＝0， 即x 2＋y 2－(x 1＋x 2)x －(y 1＋y 2)y ＝0.∴所求圆的方程为x 2＋y 2－85x －165y ＝0.21．(13分)已知圆C ：x 2＋y 2＋2x －4y ＋1＝0，O 为坐标原点，动点P 在圆外，过点P 作圆C 的切线，设切点为M .(1)若点P 运动到(1,3)处，求此时切线l 的方程； (2)求满足|PM |＝|PO |的点P 的轨迹方程．解 (1)把圆C 的方程化为标准方程为(x ＋1)2＋(y －2)2＝4，∴圆心为(－1,2)，半径为2.①当l 的斜率不存在时，l 的方程为x ＝1满足条件．②当l 的斜率存在时，设斜率为k ，则l ：y －3＝k (x －1)，即kx －y ＋3－k ＝0.由题意，得|－k －2＋3－k |1＋k 2＝2，得k ＝－34. ∴l 的方程为3x ＋4y －15＝0.综上得，满足条件的切线l 的方程为x ＝1，或3x ＋4y －15＝0. (2)设P (x ，y )，∵|PM |＝|PO |， ∴(x ＋1)2＋(y －2)2－4＝x 2＋y 2. 整理得2x －4y ＋1＝0.即点P 的轨迹方程为2x －4y ＋1＝0.。

高中数学立体几何测试题（理科）一、选择题：1．下列说法不正确的是A 圆柱的侧面展开图是一个矩形B 圆锥中过轴的截面是一个等腰三角形C 直角三角形绕它的一边旋转一周形成的曲面围成的几何体是圆锥D 圆台平行于底面的截面是圆面2、下面表述正确的是A、空间任意三点确定一个平面B、分别在不同的三条直线上的三点确定一个平面C、直线上的两点和直线外的一点确定一个平面D、不共线的四点确定一个平面3、“a、b是异面直线”是指①a∩b=∅，且a和b不平行；②a⊂平面α，b⊂平面β，且α∩β=∅；③a⊂平面α，b⊂平面β，且a∩b=∅；④a⊂平面α，b ⊄平面α；⑤不存在平面α，使得a⊂平面α，且b⊂平面α都成立。

上述说法正确的是A ①④⑤B ①③④C ②④D ①⑤4、一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是A、垂直B、平行C、相交不垂直D、不确定5、下列命题中正确命题的个数是①一条直线和另一条直线平行，那么它和经过另一条直线的任何平面平行；②一条直线平行于一个平面，则这条直线与这个平面内所有直线都没有公共点，因此这条直线与这个平面内的所有直线都平行；③若直线与平面不平行，则直线与平面内任一直线都不平行；④与一平面内无数条直线都平行的直线必与此平面平行。

A 、0B 、1C 、2D 、36、一条直线若同时平行于两个相交平面，则这条直线与这两个平面交线的位置关系是A 、异面B 、相交C 、平行D 、不确定 7、直线a 与b 垂直，b 又垂直于平面α，则a 与α的位置关系是A 、a α⊥B 、//a αC 、a α⊆D 、a α⊆或//a α 8、如果在两个平面内分别有一条直线，这两条直线互相平行，那么这两个平面的位置关系一定是A 、平行B 、相交C 、平行或相交D 、无法确定 9．已知二面角α－AB －β为︒30，P 是平面α内的一点，P 到β的距离为1．则P 在β内的射影到AB 的距离为（ ）． A ．23B ．3C ．43 D ．2110、若,m n 表示直线，α表示平面，则下列命题中，正确命题的个数为 ①//m n n m αα⎫⇒⊥⎬⊥⎭；②//m m n n αα⊥⎫⇒⎬⊥⎭；③//m m n n αα⊥⎫⇒⊥⎬⎭；④//m n m n αα⎫⇒⊥⎬⊥⎭A 、1个B 、2个C 、3个D 、4个 二、填空题：11、三条两两相交的直线可确定12．水平放置的△ABC 的斜二测直观图如图所示，已知A′C′=3，B′C′=2。

一、选择题1．在下列四个正方体中，能得出直线AB 与CD 所成角为90︒的是（ ）A ．B ．C ．D ．2．球面上有,,,A B C D 四个点，若,,AB AC AD 两两垂直，且4AB AC AD ===，则该球的表面积为（ ）A ．803πB ．32πC ．42πD ．48π3．如图，在长方体1111ABCD A B C D -中，13,2,4AA AB AD ===，点M 是棱AD 的中点，点N 在棱1AA 上，且满足12AN NA =，P 是侧面四边形11ADD A 内的一动点（含边界），若1//C P 平面CMN ，则线段1C P 长度的取值范围是（ ）A ．17]B ．[2,3]C ．6,22]D ．[17,5] 4．如图，在棱长为1的正方体1111ABCD A B C D -中，点E ，F 分别是棱BC ，1CC 的中点，P 是侧面11BCC B 内一点，若1//A P 平面AEF ，则线段1A P 长度的取值范围是（ ）A ．[2,3]B ．5,22⎡⎤⎢⎥⎣⎦C ．325,42⎡⎤⎢⎥⎣⎦D ．51,2⎡⎤⎢⎥⎣⎦ 5．如图所示，在棱长为a 的正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 是侧面11CDD C 上的动点，且1//B F 面1A BE ，则F 在侧面11CDD C 上的轨迹的长度是（ ）A ．aB ．2aC ．2aD ．22a 6．如图，在长方体1111ABCD A B C D -中，若,,,E F G H 分别是棱111111,,,A B BB CC C D 的中点，则必有（ ）A ．1//BD GHB ．//BD EFC ．平面//EFGH 平面ABCDD ．平面//EFGH 平面11A BCD7．菱形ABCD 的边长为3，60B ∠=，沿对角线AC 折成一个四面体，使得平面ACD ⊥平面ABC ，则经过这个四面体所有顶点的球的表面积为（ ）A ．15πB ．12πC ．8πD ．6π8．鲁班锁运用了中国古代建筑中首创的榫卯结构，相传由春秋时代各国工匠鲁班所作，是由六根内部有槽的长方形木条，按横竖立三方向各两根凹凸相对咬合一起，形成的一个内部卯榫的结构体.鲁班锁的种类各式各样，千奇百怪.其中以最常见的六根和九根的鲁班锁最为著名.下图1是经典的六根鲁班锁及六个构件的图片，下图2是其中的一个构件的三视图（图中单位：mm ），则此构件的表面积为（ ）A ．27600mmB ．28400mmC ．29200mmD ．210000mm 9．将表面积为36π的圆锥沿母线将其侧面展开，得到一个圆心角为23π的扇形，则该圆锥的轴截面的面积为（ ）A ．3B ．2C ．3D ．310．在长方体1111ABCD A B C D -中，23AB AD ==12CC =1C BD C --的大小是（ ）A ．30ºB ．45ºC ．60ºD ．90º 11．αβ、是两个不同的平面，m n 、是平面α及β之外的两条不同直线，给出四个论断：①m n ⊥；②αβ⊥；③n β⊥；④.m α⊥以其中三个论断作为条件，余下一个作为结论，其中正确命题的个数是（ ）A ．1个B ．2个C ．3个D ．4个12．已知四棱锥的各个顶点都在同一个球的球面上，且侧棱长都相等，高为4，底面是边长为32 ）A ．75518πB ．62516πC ．36πD ．34π13．长方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E 为AB 的中点，3CE =，53cos 9ACE ∠=，且四边形11ABB A 为正方形，则球O 的直径为（ ） A ．4 B 51C ．451D ．4或514．垂直于同一条直线的两条直线的位置关系是（ ）A ．平行B ．相交C ．异面D ．A 、B 、C 均有可能二、解答题15．如图，在三棱锥V-ABC 中，VC ⊥底面ABC ，AC BC ⊥，D 是棱AB 的中点，且AC BC VC ==.（1）证明：平面VAB ⊥平面VCD ；（2）若22AC =，且棱AB 上有一点E ，使得线VD 与平面VCE 所成角的正弦值为1515，试确定点E 的位置，并求三棱锥C-VDE 的体积. 16．如图所示，在四棱锥P ABCD -中，90CAD ABC ∠=∠=，30BAC ADC ∠=∠=，PA ⊥平面ABCD ，E 为PD 中点，2AC =.（1）求证：//AE 平面PBC .（2）若四面体PABC 的体积为33，求PCD 的面积. 17．如图三棱柱111ABC A B C －中，11,,60CA CB AB AA BAA ∠︒＝＝＝，（1）证明1AB A C ⊥；（2）若16AC ＝，2ABCB ＝＝，求三棱柱111ABC A B C －的体积S .18．如图甲，平面四边形ABCD 中，已知45A ︒∠=，90︒∠=C ，105ADC ︒∠=，2AB BD ==，现将四边形ABCD 沿BD 折起，使得平面ABD ⊥平面BDC (如图乙)，设点E ，F 分别是棱AC ，AD 的中点.（1）求证：DC ⊥平面ABC ；（2）求三棱锥A BEF -的体积.19．如图，在底面半径为2、母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的体积及表面积．20．在四棱锥P ABCD -中，//AD BC ，BC CD ⊥，120ABC ∠=︒，4=AD ，3BC =，=2AB ，3=CD CE ，⊥AP ED ．（1）求证：DE ⊥面PEA ；（2）已知点F 为AB 中点，点P 在底面ABCD 上的射影为点Q ，直线AP 与平面ABCD 所成角的余弦值为3，当三棱锥-P QDE 的体积最大时，求异面直线PB 与QF 所成角的余弦值．21．如图，在正三棱柱111ABC A B C -（侧棱垂直于底面，且底面是正三角形）中，16AC CC ==，M 是棱1CC 的中点.（1）求证：平面1AB M ⊥平面11ABB A ；（2）求1A M 与平面1AB M 所成角的正弦值.22．如图，在直三棱柱111ABC A B C -中，1AC CC =，AC BC ⊥，D 为1BC 中点，1AC 与1A C 交于点O .（1）求证：//OD 平面111A B C ；（2）求证：平面1AC B ⊥平面1A BC .23．如图，AB 是圆O 的直径，CA 垂直圆O 所在的平面，D 是圆周上一点.（1）求证：平面ADC ⊥平面CDB ；（2）若1AC =，12AD =，BD AD =，求二面角A BC D --的余弦值. 24．如图，四面体ABCD 中，点E ，F 分别为线段AC ，AD 的中点，平面EFNM ⋂平面BCD MN =，90CDA CDB ∠=∠=︒，DH AB ⊥，垂足为H .（1）求证：//EF MN ；（2）求证：平面CDH ⊥平面ABC .25．如图，在四棱锥P ABCD -中，PA ⊥平面ABC ，//,90AD BC ABC ︒∠=，2AD =，23AB =，6BC =．（1）求证：平面PBD ⊥平面PAC ；（2）PA 长为何值时，直线PC 与平面PBD 所成角最大？并求此时该角的正弦值． 26．如图所示，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD DC =，E 是PC 的中点，过E 点作EF PB ⊥交PB 于点F .求证：（1）//PA 平面EDB ；（2）PB ⊥平面EFD .【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】根据线面垂直的性质以及判定定理判断A ，平移直线结合异面直线的定义，判断BCD.【详解】对于A ，如下图所示，连接,AE GB由于,CD BE CD BG ⊥⊥，根据线面垂直判定定理得CD ⊥平面AEBG ，再由线面垂直的性质得出AB CD ⊥，则A 正确；对于B ，如下图所示，连接,BF AF因为ABF 为正三角形，//CD AF ，所以直线AB 与CD 所成角为60︒，则B 错误； 对于C ，如图所示，连接HD因为在CDH △中，45HDC ∠=︒，//AB HD ，所以直线AB 与CD 所成角为45︒，则C 错误；对于D ，如下图所示，连接GB因为//AG CD ，所以直线AB 与CD 所成角为90GAB ∠≠︒，则D 错误；故选：A【点睛】本题主要考查了求异面直线的夹角，属于中档题.2．D解析：D【分析】分析：首先求得外接球半径，然后求解其表面积即可.详解：由题意可知，该球是一个棱长为4的正方体的外接球，设球的半径为R ，由题意可得：()22222444R =++,据此可得：212R =，外接球的表面积为：2441248S R πππ==⨯=.本题选择D 选项.点睛：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径. 3．C解析：C【分析】首先找出过点1C 且与平面CMN 平行的平面，然后可知点P 的轨迹即为该平面与侧面四边形11ADD A 的交线段，进而可以利用解三角形的知识求出线段1C P 长度的取值范围．【详解】 如图所示：，取11A D 的中点G ，取MD 的中点E ，1A G 的中点F ，1D D 的三等分点H 靠近D ，并连接起来．由题意可知1//C G CM ，//GH MN ，所以平面1//C GH 平面CMN ．即当点P 在线段GH 上时，1//C P 平面CMN ．在1H C G 中，2212222C G =+=2212222C H =+=22GH =， 所以1H C G 为等边三角形，取GH 的中点O ，1226C O ==故线段1C P 长度的取值范围是6,22]．故选：C ．【点睛】本题主要考查线面平行，面面平行的判定定理和性质定理的应用，以及解三角形，意在考查学生的逻辑推理能力和数学运算能力，属于中档题．4．C解析：C【分析】分别取111,BB B C 的中点,N M ,可得平面1//A MN 平面AEF ，从而点P 的轨迹为线段MN ，然后计算出线段1A P 的范围.【详解】分别取111,BB B C 的中点,N M ,则1//A M AE ,1A M ⊄平面AEF ，AE ⊂平面AEF ，则1//A M 平面AEF . //EF NM ,MN ⊄平面AEF ，EF ⊂平面AEF ，则//MN 平面AEF又1MN A M M ⋂=,所以平面1//A MN 平面AEF又平面1A MN ⋂面11BCC B MN =所以点P 的轨迹为线段MN当P 为线段MN 的端点M （或N ）时，1A P 最长，此时1122111522P M A B A BB A ⎛⎫==+= ⎪⎝⎭当P 为线段MN 的中点时，1A P 最短，此时22111322P A N MN A ⎛⎫=-= ⎪⎝⎭所以325,42AP ⎡⎤∈⎢⎥⎣⎦， 故选：C ．【点睛】本题考查利用向量法解决线面平面的探索问题，本题也可以构造面面平面得出动点的轨迹，从而求解，属于中档题.5．D解析：D【分析】解：设G ，H ，I 分别为CD 、1CC 、11C D 边上的中点，证明平面1//A BGE 平面1B HI ， 得到1//B F 面1A BE ，则F 落在线段HI 上，求出1122HI CD ==【详解】解：设G ，H ，I 分别为CD 、1CC 、11C D 边上的中点，1//A B EG ,则1A BEG 四点共面，11//,//EG HI B H A E , 平面1//A BGE 平面1B HI ，又1//B F 面1A BE ，F ∴落在线段HI 上，正方体1111ABCD A B C D -中的棱长为a ，1122HI CD a ∴==， 即F 在侧面11CDD C 上的轨迹的长度是22a ． 故选：D ．【点睛】本题考查利用线面平行求线段长度，找到动点的运动轨迹是解题的关键，属于基础题. 6．D解析：D【分析】根据“过直线外一点有且只有一条直线与已知直线平行”来判断AB 选项的正确性，根据平行直线的性质判断C 选项的正确性，根据面面平行的判定定理判断D 选项的正确性.【详解】选项A:由中位线定理可知：1//GH D C ，因为过直线外一点有且只有一条直线与已知直线平行，所以1,BD GH 不可能互相平行，故A 选项是错误的；选项B: 由中位线定理可知：1//EF A B ，因为过直线外一点有且只有一条直线与已知直线平行，所以,BD EF 不可能互相平行，故B 选项是错误的；选项C: 由中位线定理可知：1//EF A B ，而直线1A B 与平面ABCD 相交，故直线EF 与平面ABCD 也相交，故平面EFGH 与平面ABCD 相交，故C 选项是错误的；选项D:由三角形中位线定理可知：111//,//EF A B EH A D ，EF ⊄平面11A BCD ，1A B ⊂平面11A BCD ，EH ⊄平面11A BCD ，11A D ⊂平面11A BCD ,所以有//EF 平面11A BCD ，//EH 平面11A BCD ，而EF EH E =，因此平面//EFGH 平面11A BCD .所以D 选项正确.故本选：D【点睛】本小题主要考查面面平行的判定定理，考查线线平行的性质，属于中档题.7．A解析：A【分析】首先根据已知条件找到四面体外接球的球心，再求出半径，即可得到球体的表面积.【详解】如图所示，1O ，2O 分别为ABC 和DAC △的外接圆圆心，因为菱形ABCD ，60B ∠=，所以ABC 和DAC △为等边三角形.设E 为AC 的中点，连接DE ，BE ，则DE AC ⊥，BE AC ⊥，又因为平面ACD ⊥平面ABC AC =，所以DE ⊥平面ABC .分别过1O ，2O 作垂直平面ABC 和平面ACD 的直线，则交点O 为四面体ABCD 外接球的球心.因为2233332⎛⎫==-= ⎪⎝⎭EB DE ，四边形12OO EO 为矩形， 所以123==O B DO ，1213===O E O E OO . 所以外接圆半径为()223153=22⎛⎫+⎪ ⎪⎝⎭，表面积为15π. 故选：A【点睛】 本题主要考查四面体外接球的表面积，根据题意确定外接球的球心为解题关键，属于中档题.8．B解析：B【分析】由三视图可知，该构件是长为100，宽为20，高为20的长方体的上面的中间部分去掉一个长为40，宽为20，高为10的小长方体的一个几何体，进而求出表面积即可.【详解】由三视图可知，该构件是长为100，宽为20，高为20的长方体的上面的中间部分去掉一个长为40，宽为20，高为10的小长方体的一个几何体，如下图所示，其表面积为：()210020220202100204010210202840m 0m S =⨯⨯+⨯⨯+⨯-⨯⨯+⨯⨯=.故选：B.【点睛】本题考查几何体的表面积的求法，考查三视图，考查学生的空间想象能力与计算求解能力，属于中档题.9．B解析：B【分析】如图所示，设此圆锥的底面半径为r ，高为h ，母线长为l .可得πr 2+πrl ＝36π，2πr ＝l •23π，联立解得：r ，l ，h 22l r =-即可得出该圆锥的轴截面的面积S 12=•2r •h ＝rh . 【详解】如图所示，设此圆锥的底面半径为r ，高为h ，母线长为l .则πr 2+πrl ＝36π，化为：r 2+rl ＝36，2πr ＝l •23π，可得l ＝3r . 解得：r ＝3，l ＝9，h 22l r =-=2.该圆锥的轴截面的面积S 12=•2r •h ＝rh ＝2=2. 故选：B.【点睛】本题考查了圆锥的表面积、弧长的计算公式，考查了推理能力与计算能力，属于中档题. 10．A解析：A【分析】取BD 中点为O ，1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，易知CO BD ⊥，再利用线面垂直证明1BD C O ⊥，得到1COC ∠即二面角1C BD C --，再计算二面角大小即可.【详解】由题意，作出长方体1111ABCD A B C D -的图象，取BD 中点为O ，连接CE 、1C E ，因为1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，又BD ⊂平面ABCD ，所以1CC BD ⊥， 因为23AB AD ==ABCD 是正方形，O 为BD 中点，所以CO BD ⊥，又1CO CC C =，所以BD ⊥平面1COC ，又1C O ⊂平面1COC ，所以1BD C O ⊥，1COC ∠即二面角1C BD C --， 又12CC =()()2223236CO +==所以123tan 36COC ∠==，130COC ∠=.故选：A【点睛】本题主要考查二面角的求法和线面垂直的判定定理和性质，考查学生空间想象能力，属于中档题.11．B解析：B【分析】分别以①②③④作为结论，另外三个作条件，根据线面垂直和面面垂直的判定定理依次判断真假.【详解】若m n ⊥，αβ⊥，n β⊥，则m 与α可能平行可能相交，即①②③不能推出④； 同理①②④不能推出③；若m n ⊥，n β⊥，m α⊥，两个平面的垂线互相垂直则这两个平面垂直，则αβ⊥，即①③④能够推出②；若αβ⊥，n β⊥，m α⊥，两个平面互相垂直，则这两个平面的垂线互相垂直，即m n ⊥，所以②③④能够推出①.所以一共两个命题正确.故选：B【点睛】此题考查空间直线与平面位置关系的辨析，根据选择的条件推出结论，关键在于熟练掌握空间垂直关系的判定和证明.12．B解析：B【分析】如图所示，设四棱锥P ABCD -中，球的半径为R ，底面中心为O '且球心为O ，可得OP ⊥底面ABCD ．3AO '=，4PO '=，在Rt AOO ∆'中，利用勾股定理解得R ，即可得出球的表面积．【详解】如图所示，设球的半径为R ，底面中心为O '且球心为O .∵四棱锥P ABCD -中，32AB =， ∴3AO '=.∵4PO '=，∴Rt AOO ∆'中，|4|OO R '=-，222AO AO OO ''=+，∴2223(4)R R =+-，解得258R =， ∴该球的表面积为222562544816R πππ⎛⎫=⨯= ⎪⎝⎭.故选：B .【点睛】本题考查几何体的外接球问题，此类问题常常构造直角三角形利用勾股定理进行求解，属于中等题.13．C解析：C【分析】设2AB x =，则AE x =，29BC x =-，由余弦定理可得222539392393x x x =++-⨯⨯+⨯，求出x ，即可求出球O 的直径. 【详解】 根据题意，长方体内接于球O 内，则球的直径为长方体的体对角线，如图作出长方体1111ABCD A B C D -：设2AB x =，则AE x =，29BC x =-，由余弦定理可得：222539392393x x x =++-⨯+，∴1x =6，∴2AB =，22BC =，球O 的直径为4484++=；或26AB =，3BC =，球O 的直径为2424351++=.故选：C ．【点睛】本题考查球的直径的计算方法，考查余弦定理，考查计算能力和分析能力，属于常考题. 14．D解析：D【分析】结合公理及正方体模型可以判断：A ，B ，C 均有可能，可以利用反证法证明结论，也可以从具体的实物模型中去寻找反例证明．【详解】解：如图，在正方体1AC 中，1A A ⊥平面ABCD ，1A AAD ，1A A BC ⊥， 又//AD BC ，∴选项A 有可能； 1A A ⊥平面ABCD ，1A A AD ，1A A AB ⊥，又AD AB A =，∴选项B 有可能；1A A ⊥平面ABCD ，1A A ⊥平面1111D C B A ，AC ⊂平面ABCD ，11A D ⊂平面1111D C B A ，1A A AC ∴⊥，111A A A D ⊥，又AC 与11A D 不在同一平面内，∴选项C 有可能．故选：D ．【点睛】本题主要考查了空间中直线与直线之间的位置关系，考查空间想象能力和思维能力，属于中档题．二、解答题15．（1）证明见解析；（2）点E 位于线段AD 的中点或线段BD 22. 【分析】（1）易得CD AB ⊥，再根据VC ⊥底面ABC ，得到 VC AB ⊥，进而AB ⊥平面VCD ，再利用面面垂直的判定定理证明.（2）过点D 在平面ABC 内作DF CE ⊥于F ，DF ⊥平面VCE ，则DVF ∠就是直线VD 与平面VCE 所成的角，在Rt VFD 中，由15sin DF DVF VD ∠==，求得DF ，然后在Rt DCE 中，求出1DE =，然后由三棱锥C-VDE 的体积为13CDE V S VC =⋅⋅求解. 【详解】（1）因为AC BC =，D 是AB 的中点，所以CD AB ⊥.又VC ⊥底面ABC ，AB 平面ABC ，所以VC AB ⊥，而VC CD C ⋂=，所以AB ⊥平面VCD .又AB 平面VAB ，所以平面VAB ⊥平面VCD .（2）过点D 在平面ABC 内作DF CE ⊥于F ，则由题意知DF ⊥平面VCE .，连接VF ，于是DVF ∠就是直线VD 与平面VCE 所成的角.在Rt VFD 中，1515DF VD =. 又因为3VD =55DF =. 在Rt DCE 中，1DE =.故知点E 位于线段AD 的中点或线段BD 的中点，三棱锥C-VDE 的体积为1112221223323CDE S VC ⋅⋅=⨯⨯⨯⨯=. 【点睛】方法点睛：(1)证明平面和平面垂直的方法：①面面垂直的定义；②面面垂直的判定定理(a ⊥β，a ⊂α⇒α⊥β)．(2)已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．16．（1）证明见解析；（2）7【分析】（1）取CD 中点F ，连接EF ，AF ，利用面面平行的判定定理证明平面//AEF 平面PBC ，再用面面平行的性质可得//AE 平面PBC ；（2）根据体积求出PA ，过A 作AQ CD ⊥于Q ，连接PQ ，AQ ，求出PQ 和CD 后，根据三角形面积公式可求得结果.【详解】（1）取CD 中点F ，连接EF ，AF ，则//EF PC ，又120BCD AFD ∠=∠=︒，∴//BC AF ，∴平面//AEF 平面PBC ，∴//AE 平面PBC .（2）因为90CAD ABC ∠=∠=，30BAC ADC ∠=∠=，2AC =， 所以1,3BC AB == 由已知得：113323P ABC V AB BC PA -=⋅⋅⋅=，即11331323PA ⨯⨯⨯⨯=， 可得2PA =.过A 作AQ CD ⊥于Q ，连接PQ ，AQ ，∵PA ⊥平面ABCD ，∴PA AQ ⊥，PA CD ⊥，∴CD PQ ⊥，ACD △中，2AC =，90CAD ∠=，30ADC ∠=，∴4CD =，23AD =22334AC AD AQ CD ⋅⨯===， 222237PQ PA AQ =+=+=，∴11742722PCD S PQ CD =⋅=⨯⨯=△. 【点睛】 关键点点睛：掌握面面平行的判定定理和面面平行的性质是解题关键.17．（1）证明见解析；（2）3.【分析】（1）取AB 中点E ，连接11,,CE A B A E ，根据已知条件，利用等腰三角形的性质得到1A E AB ⊥，,CE AB ⊥利用线面垂直的判定定理证得AB ⊥面1,CEA 即可得到1AB A C ⊥ ；（2） 在1CEA 中可以证明1A E CE ⊥，结合1A E AB ⊥，利用线面垂直判定定理得到1A E ⊥平面ABC ,作为三棱柱的高，进而计算体积.【详解】(1)取AB 中点E ，连接11,,CE A B A E ，11,60AB AA BAA ∠︒＝＝，1BAA ∴是等边三角形，1A E AB ∴⊥，CA CB ＝，,CE AB ∴⊥1,CE A E E ⋂＝AB ∴⊥面1,CEA 1AB A C ∴⊥.(2)由于CAB ∆为等边三角形，3CE ∴＝1123322S AB CE ⨯⨯⨯=底面积＝＝1CEA 中，3CE ＝13EA ＝16AC =1A E CE ∴⊥，结合1A E AB ⊥，又,,AB CE E AB CE ⋂=⊂平面ABC ,1A E ∴⊥平面ABC ,13h A E ∴＝＝3V Sh =＝.【点睛】本题考查线面垂直的判定与证明，考查棱柱的体积计算，属基础题，为证明线线垂直，常常先证线面垂直，为证明线面垂直，又常常需要先证明线线垂直，这是线面垂直关系常用的证明与判定方式，要熟练掌握.18．（1）证明见解析；（2. 【分析】（1）在图甲中先证AB BD ⊥，在图乙中由面面垂直的性质定理先证AB CD ⊥，由条件可得DC BC ⊥，进而可判定DC ⊥平面AB C ；（2）利用等体积法进行转化计算即可.【详解】（1）图甲中，∵AB BD =且45A ︒∠=，45ADB ︒∴∠=， ()()180180454590ABD ADB A ︒︒︒︒︒∴∠=-∠+∠=-+=，即AB BD ⊥， 图乙中，∵平面ABD ⊥平面BDC ，且平面ABD 平面BDC BD =，∴AB ⊥平面BDC ，又CD ⊂平面BDC ，∴AB CD ⊥，又90DCB ︒∠=，∴DC BC ⊥，且AB BC B ⋂=，又AB ，BC ⊂平面AB C ，∴DC ⊥平面AB C ；（2）因为点E ，F 分别是棱AC ，AD 的中点，所以//EF DC ，且12EF DC =，所以EF ⊥平面ABC ， 由（1）知，AB ⊥平面BDC ，又BC ⊂平面BDC ，所以AB BC ⊥，105ADC ︒∠=，45ADB ︒∠=，1054560CDB ADC ADB ︒︒︒∴∠=∠-∠=-=， 90906030CBD CDB ︒︒︒︒∴∠=-∠=-=，cos3022BC BD ︒∴=⋅=⨯=1sin 30212DC BD ︒=⋅=⨯=，所以12ABC S AB BC =⨯⨯△12ABE ABC S S ==△△1122EF DC ==，所以111332A BEF F ABE ABE V V EF S --==⋅⋅=⋅=△ 【点睛】方法点睛：计算三棱锥体积时，常用等体积法进行转化，具体的方法为：①换顶点，换底面；②换顶点，不换底面；③不换顶点，换底面.19．体积V ；表面积(21π+．【分析】由已知计算出圆柱的底面半径，代入圆柱表面积和体积公式，即可得到答案.【详解】解：设圆柱的底面半径为r ，高为'h ，圆锥的高h ='3h ＝，1'2h h ∴＝，则122r =，1r ∴＝． ∴圆柱的体积2V r h π'=＝；表面积(22221S r rh πππ=+='． 【点睛】本题考查的知识点求圆柱的表面积和体积，其中根据已知条件，求出圆柱的底面半径，是解答本题的关键.20．（1）证明见解析；（2． 【分析】（1）在直角梯形ABCD 中先求出,,CD CE BE ，然后可求得,DE AE ，从而可证明DE AE ⊥，由线面垂直判定定理证明线面垂直；（2）由（1）得面面垂直，知Q 在AE 上，PAQ ∠为直线AP 与平面ABCD 所成的角，cos AQ PAQ AP ∠==AQ x =（0x <≤-P QDE 的体积，由二次函数知识求得最大值，及此时x 的值，得Q 为AE 中点，从而有//FQ BE ，PBE ∠为异面直线PB 与QF 所成角（或补角），由余弦定理可得．【详解】（1）证明：//AD BC ，BC CD ⊥，120ABC ∠=︒，4=AD ，3BC =，=2AB ，∴CD ===CD ，∴1CE =，CD =2BE =， 由余弦定理得AE ===又2DE ===，∴222DE AE AD ，∴AD DE ⊥，∵AP DE ⊥，又AP AE A =，AP AE ⊂、平面APE ，∴DE ⊥平面APE ．（2）由（1）DE ⊥平面APE ．DE ⊂平面ABCD ，∴平面ABCD ⊥平面PAE ，∴Q 点在AE 上，PAQ ∠为直线AP 与平面ABCD 所成的角，cos 3AQ PAQ AP ∠==，设AQ x =（0x <≤PQ =，QE x =，12(23)232QDE S x x =⨯⨯-=-△， 212(23)33P QDE QDE V PQ S x x -=⋅=--△22(3)223x =--+≤，当且仅当3x =时等号成立，则当P QDE V -最大时，3AQ =，∴Q 为AE 中点，∵F 为AB 中点，∴//FQ BC ，∴PBE ∠为异面直线PB 与QF 所成角（或补角），1,3QB QE ==，则由PQ ⊥平面ABCD 得3,7PE PB ==，又2BE =，则2227cos 2PB BE PE PBE PB BE +-∠==⋅， ∴异面直线PB 与QF 所成角的余弦值为714．【点睛】本题考查线面垂直的判定定理，考查直线与平面所成的角，异面直线所成的角，三棱锥的体积等，旨在考查学生的空间想象能力，运算求解能力，逻辑推理能力．属于中档题． 21．（1）证明见解析；（210 【分析】（1）连接1A B 交1AB 于O ，连接MO ，证明1MO AB ⊥，1MO A B ⊥，然后得到MO ⊥平面11ABB A 即可；（2）首先证明1A O ⊥平面1AB M ，然后可得1A MO ∠即为1A M 与平面1AB M 所成的角，然后利用111sin A O MO MA A ∠=算出答案即可. 【详解】（1）证明：连接1A B 交1AB 于O ，连接MO ，易得O 为1A B ，1AB 的中点∵1CC ⊥平面ABC ，AC ⊂平面ABC∴1CC AC ⊥又M 为1CC 中点，16AC CC == ∴223635AM =+=同理可得135B M =∴1MO AB ⊥连接MB ，同理可得135A M BM ==1MO A B ∴⊥又11AB A B O ⋂=，1AB ，1A B ⊂平面11ABB A∴MO ⊥平面11ABB A又MO ⊂平面1AB M∴平面1AB M ⊥平面11ABB A（2）解：易得11A O AB ⊥又由（1）平面1AB M ⊥平面1ABB A平面1AB M 平面111ABB A AB =，1AO ⊂平面11ABB A ∴1A O ⊥平面1AB M∴1A MO ∠即为1A M 与平面1AB M 所成的角在11Rt AA B △中，22111663222AB AO ==+=在1Rt AOM 中，1113210sin 35AO MO A A M ∠=== 故1A M 与平面1AB M 10【点睛】方法点睛：几何法求线面角的步骤：（1）作：作出辅助线，构成三角形；（2）证：利用线面角的定义证明作出的角即为所求角；（3）求：在直角三角形中求解即可. 22．（1）证明见解析；（2）证明见解析.（1）连接1B C ，可知点D 为1B C 的中点，利用中位线的性质可得出11//OD A B ，利用线面平行的判定定理可证得结论成立；（2）证明出四边形11AAC C 为菱形，可得出11AC AC ⊥，证明出BC ⊥平面11AAC C ，可得出1AC BC ⊥，利用线面垂直和面面垂直的判定定理可证得结论成立.【详解】（1）如下图所示，连接1B C ，在三棱柱111ABC A B C -中，11//BB CC 且11BB CC =，则四边形11BB C C 为平行四边形， D 为1BC 的中点，则D 为1B C 的中点，同理可知，点O 为1A C 的中点，11//OD A B ∴， OD ⊄平面111A B C ，11A B ⊂平面111A B C ，因此，//OD 平面111A B C ；（2）在直三棱柱111ABC A B C -中，1CC ⊥平面ABC ，11//AA CC 且11AA CC =， 所以四边形11AAC C 为平行四边形，1AC CC =，所以，平行四边形11AAC C 为菱形，则11AC AC ⊥，1CC ⊥平面ABC ，BC ⊂平面ABC ，1BC CC ∴⊥，BC AC ⊥，1AC CC C =，BC ∴⊥平面11AAC C ，1AC ⊂平面11AAC C ，1AC BC ∴⊥，1AC BC C =，1AC ∴⊥平面1A BC ，1AC ⊂平面1AC B ，因此，平面1AC B ⊥平面1A BC .【点睛】方法点睛：证明面面垂直的常用方法：（1）面面垂直的定义；（2）面面垂直的判定定理.在证明面面垂直时，可假设两个平面垂直成立，利用面面垂直的性质定理转化为线面垂直，即可找到所要证的线面垂直，然后组织论据证明即可.23．（1）证明见解析；（2）105.（1）证明,BD AC BD AD ⊥⊥后得BD ⊥平面ADC ，然后可得面面垂直；（2）连结OD ，作OE BC ⊥于E ，连结DE ，证得OED ∠为二面角A BC D --的平面角，在三角形中可得其余弦值．【详解】证明：（1）∵CA ⊥平面ADB ，BD ⊂平面ADB ，∴CA BD ⊥，.又D 是圆周上一点，AB 是圆O 的直径，DA DB ⊥，又CA ⊂平面CAD ，DA ⊂平面CAD ，ADCA A =，∴BD ⊥平面CAD ，而BD ⊂平面ACD ，∴平面ADC ⊥平面CDB ；（2）连结OD ，作OE BC ⊥于E ，连结DE ，∵CA ⊥平面ADB ，CA ⊂平面ABC ，∵平面ABC ⊥平面ADB ，∵BD AD =，∴⊥OD AB ，又∵OD ⊂平面ADB ，∵平面ABC平面ADB AB =， ∴OD ⊥平面ABC ，∵BC ⊂面ABC ，∴BC OD ⊥.又∵BC OE ⊥，OE DE E =，∴BC ⊥平面ODE ，∴BC DE ⊥，∴OED ∠为二面角A BC D --的平面角.又1AC =，12AD =，BD AD =， ∴2OD =，3OE =，30DE =，所以cos OE OED DE ∠==10所以二面角A BC D --的余弦值为105. 【点睛】方法点睛：本题考查证明面面垂直，求二面角．求二面角的方法：（1）定义法：根据定义作出二面角的平面角（并证明）然后在相应三角形中求角．（2）向量法：建立空间直角坐标系，用二面角的两个面的法向量的夹角与二面角相等或互补计算．24．（1）证明见解析；（2）证明见解析.【分析】本题考查线面平行与线面垂直的判定，难度不大.（1）利用线面平行的判定定理证得//EF 平面BCD ，进而利用线面平行的性质定理证得； （2）利用线面垂直的判定定理证得CD ⊥平面ADB ，进而证得AB ⊥平面CDH ，然后由面面垂直判定定理证得结论.【详解】证明：（1）因为点E 、F 分别为线段AC 、AD 的中点，EF ∴为ACD △的中位线，则//EF CD ，CD ⊂平面BCD ，EF ⊄平面BCD ，//EF ∴平面BCD ，又EF ⊂平面EFNM ，平面EFNM ⋂平面BCD MN =，//EF MN ∴；（2）90CDA CDB ∠=∠=︒，CD DA ∴⊥，CD DB ⊥，DA DB D ⋂=，DA ⊂平面ADB ，DB ⊂平面ADB ， CD 平面ADB ，CD AB ∴⊥又DH AB ⊥，DH CD D ⋂=，DC ⊂平面DCH ，DH ⊂平面DCH ，AB ∴⊥平面CDH ，AB ⊂平面ABC ，∴平面CDH ⊥平面ABC.【点睛】要证线线平行，常常先证线面平行，综合利用线面平行的判定与性质进行证明；要证面面垂直，常常先证线面垂直，而要证线面垂直，又常常先证另一个线面垂直.25．（1）证明见解析；（2）PA =PC 与平面PBD 所成角最大，此时该角的正弦值为35. 【分析】 （1）根据已知条件，得到BD PA ⊥，再利用正切函数的性质，求得0030,BAC 60ABD ∠=∠=，得到BD AC ⊥，进而可证得平面PBD ⊥平面PAC ；（2）建立空间坐标系，得到()BD =-，()0,2,DP t =-，()2PC t =-，进而得到平面PBD 的一个法向量为1,3,n ⎛= ⎝⎭，进而可利用向量的公式求解 【详解】（1）∵PA ⊥平面,ABCD BD ⊂平面ABCD ，∴BD PA ⊥，又3tan ,tan 33AD BC ABD BAC AB AB ∠==∠==， ∴0030,BAC 60ABD ∠=∠=，∴090AEB ∠=，即BD AC ⊥（E 为AC 与BD 交点）．又PA AC ，∴BD ⊥平面PAC ，又因为BD ⊂平面PBD ，所以，平面PAC ⊥平面PBD（2）如图，以AB 为x 轴，以AD 为y 轴，以AP 为z 轴，建立空间坐标系，如图， 设AP t =，则()()()()23,0,0,23,6,0,0,2,0,0,0,B C D P t ，则()23,2,0BD =-，()0,2,t DP =-，()23,6,PC t =-，设平面PBD 法向量为(),,n x y z =，则00n BD n DP ⎧⋅=⎨⋅=⎩，即232020x y y tz ⎧-+=⎪⎨-+=⎪⎩，取1x =，得平面PBD 的一个法向量为231,3,n t ⎛⎫= ⎪ ⎪⎝⎭， 所以22226333cos ,1214448451PC nPC n PC n t t t t ⋅===++++， 因为22221441445151275t t t t +++=≥，当且仅当23t =时等号成立， 所以5c 33353os ,PC n ≤=，记直线PC 与平面PBD 所成角为θ，则sin cos ,PC n θ=，故3sin 5θ≤，即23t =时，直线PC 与平面PBD 所成角最大，此时该角的正弦值为35． 【点睛】关键点睛：解题关键在于利用定义和正切函数的性质，得到BD ⊥平面PAC ，进而证明平面PAC ⊥平面PBD ；以及建立空间直角坐标系，求出法向量，进行求解直线PC 与平面PBD 所成角的最大值，难度属于中档题26．（1）证明见解析；（2）证明见解析.【分析】（1）连结AC 、BD ，交于点O ，连结OE ，通过//OE PA 即可证明；（2）通过PD BC ⊥， CD BC ⊥可证BC ⊥平面PDC ，即得DE BC ⊥，进而通过DE ⊥平面PBC 得DE PB ⊥，结合EF PB ⊥即证.【详解】证明：（1）连结AC 、BD ，交于点O ，连结OE ，底面ABCD 是正方形，∴O 是AC 中点，点E 是PC 的中点，//OE PA ∴.OE ⊂平面EDB ， PA ⊄平面EDB ，∴//PA 平面EDB .（2）PD DC =，点E 是PC 的中点，DE PC ∴⊥.底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，∴PD BC ⊥， CD BC ⊥，且 PD DC D ⋂=，∴BC ⊥平面PDC ，∴DE BC ⊥，又PC BC C ⋂=，∴DE ⊥平面PBC ，∴DE PB ⊥，EF PB ⊥，EF DE E ⋂=，PB ∴⊥平面EFD .【点睛】本题考查线面平行和线面垂直的证明，属于基础题.。

高中数学必修2立体几何考题13．如图所示，正方体ABCD－A1B1C1D1中，M、N分别是A1B1，B1C1的中点．问：(1)AM和CN是否是异面直线？说明理由；(2)D1B和CC1是否是异面直线？说明理由．解析：(1)由于M、N分别是A1B1和B1C1的中点，可证明MN∥AC，因此AM与CN不是异面直线．(2)由空间图形可感知D1B和CC1为异面直线的可能性较大，判断的方法可用反证法．探究拓展：解决这类开放型问题常用的方法有直接法(即由条件入手，经过推理、演算、变形等)，如第(1)问，还有假设法，特例法，有时证明两直线异面用直线法较难说明问题，这时可用反证法，即假设两直线共面，由这个假设出发，来推证错误，从而否定假设，则两直线是异面的．解：(1)不是异面直线．理由如下：∵M、N分别是A1B1、B1C1的中点，∴MN∥A1C1.又∵A1A∥D1D，而D1D綊C1C，∴A1A綊C1C，∴四边形A1ACC1为平行四边形．∴A1A∥AC，得到MN∥AC，∴A、M、N、C在同一个平面内，故AM和CN不是异面直线．(2)是异面直线．理由如下：假设D1B与CC1在同一个平面CC1D1内，则B∈平面CC1D1，C∈平面CC1D1.∴BC⊂平面CC1D1，这与在正方体中BC⊥平面CC1D1相矛盾，∴假设不成立，故D1B与CC1是异面直线．14．如下图所示，在棱长为1的正方体ABCD－A1B1C1D1中，M为AB的中点，N为BB1的中点，O为面BCC1B1的中心．(1)过O作一直线与AN交于P，与CM交于Q(只写作法，不必证明)；(2)求PQ的长(不必证明)．解析：(1)由ON∥AD知，AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如下图所示)．∵三个平面α，β和ABCD两两相交，有三条交线OP、CM、DA，其中交线DA与交线CM不平行且共面．∴DA与CM必相交，记交点为Q.∴OQ是α与β的交线．连结OQ与AN交于P，与CM交于Q，故OPQ即为所作的直线．(2)解三角形APQ可得PQ＝14 3.15．如图，在直三棱柱ABC－A1B1C1中，AB＝BC＝B1B＝a，∠ABC＝90°，D、E分别为BB1、AC1的中点．(1)求异面直线BB1与AC1所成的角的正切值；(2)证明：DE为异面直线BB1与AC1的公垂线；(3)求异面直线BB1与AC1的距离．解析：(1)由于直三棱柱ABC－A 1B1C1中，AA1∥BB1，所以∠A1AC1就是异面直线BB1与AC1所成的角．又AB＝BC＝B1B＝a，∠ABC＝90°，所以A1C1＝2a，tan∠A1AC1＝2，即异面直线BB1与AC1所成的角的正切值为 2.(2)证明：解法一：如图，在矩形ACC1A1中，过点E作AA1的平行线MM1分别交AC、A1C1于点M、M1，连结BM，B1M1，则BB1綊MM1.又D、E分别是BB1、MM1的中点，可得DE綊BM.在直三棱柱ABC－A1B1C1中，由条件AB＝BC得BM⊥AC，所以BM⊥平面ACC1A1，故DE⊥平面ACC1A1，所以DE⊥AC1，DE⊥BB1，即DE为异面直线BB1与AC1的公垂线．解法二：如图，延长C1D、CB交于点F，连结AF，由条件易证D是C1F的中点，B是CF的中点，又E是AC1的中点，所以DE∥AF.在△ACF中，由AB＝BC＝BF知AF⊥AC.在直三棱柱ABC－A1B1C1中，AA1⊥平面ABC，所以AF⊥AA1，故AF⊥平面ACC1A1，故DE⊥平面ACC1A1，所以DE⊥AC1，DE⊥BB1，即DE为异面直线BB1与AC1的公垂线．(3)由(2)知线段DE的长就是异面直线BB1与AC1的距离，由于AB＝BC＝a，∠ABC＝90°，所以DE＝2 2a.反思归纳：两条异面直线的公垂线是指与两条异面直线既垂直又相交的直线，两条异面直线的公垂线是惟一的，两条异面直线的公垂线夹在两条异面直线之间的线段的长度就是两条异面直线的距离．证明一直线是某两条异面直线的公垂线，可以分别证明这条直线与两条异面直线垂直．本题的思路是证明这条直线与一个平面垂直，而这一平面与两条异面直线的位置关系是一条直线在平面内，另一条直线与这个平面平行．16．如图所示，在正方体ABCD－A1B1C1D1中，O，M分别是BD1，AA1的中点．(1)求证：MO是异面直线AA1和BD1的公垂线；(2)求异面直线AA1与BD1所成的角的余弦值；(3)若正方体的棱长为a，求异面直线AA1与BD1的距离．解析：(1)证明：∵O是BD1的中点，∴O是正方体的中心，∴OA＝OA 1，又M为AA1的中点，即OM是线段AA1的垂直平分线，故OM⊥AA1.连结MD1、BM，则可得MB＝MD1.同理由点O为BD1的中点知MO⊥BD1，即MO 是异面直线AA 1和BD 1的公垂线． (2)由于AA 1∥BB 1，所以∠B 1BD 1就是异面直线AA 1和BD 1所成的角． 在Rt △BB 1D 1中，设BB 1＝1，则BD 1＝3，所以cos ∠B 1BD 1＝33，故异面直线AA 1与BD 1所成的角的余弦值等于33.(3)由(1)知，所求距离即为线段MO 的长，由于OA ＝12AC 1＝32a ，AM ＝a 2，且OM ⊥AM ，所以OM ＝22a .13．如图所示，正方体ABCD －A 1B 1C 1D 1中，侧面对角线AB 1，BC 1上分别有两点E 、F ，且B 1E ＝C 1F ，求证：EF ∥ABCD .证明：解法一：分别过E 、F 作EM ⊥AB 于M ，FN ⊥BC 于N ，连结MN .∵BB 1⊥平面ABCD ， ∴BB 1⊥AB ，BB 1⊥BC ， ∴EM ∥BB 1，FN ∥BB 1， ∴EM ∥FN .又B 1E ＝C 1F ，∴EM ＝FN ，故四边形MNFE 是平行四边形， ∴EF ∥MN ，又MN 在平面ABCD 中， 所以EF ∥平面ABCD .解法二：过E 作EG ∥AB 交BB 1于G ，连结GF ，则B 1E B 1A ＝B 1GB 1B，∵B 1E ＝C 1F ，B 1A ＝C 1B ， ∴C 1F C 1B ＝B 1G B 1B，∴FG ∥B 1C 1∥BC . 又EG ∩FG ＝G ，AB ∩BC ＝B ， ∴平面EFG ∥平面ABCD ， 而EF ⊂平面EFG ， ∴EF ∥平面ABCD .14．如下图，在四棱锥P －ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD ＝DC .过BD 作与P A 平行的平面，交侧棱PC 于点E ，又作DF ⊥PB ，交PB 于点F .(1)求证：点E 是PC 的中点； (2)求证：PB ⊥平面EFD .证明：(1)连结AC ，交BD 于O ，则O 为AC 的中点，连结EO . ∵P A ∥平面BDE ，平面P AC ∩平面BDE ＝OE ，∴P A ∥OE . ∴点E 是PC 的中点；(2)∵PD ⊥底面ABCD 且DC ⊂底面ABCD ，∴PD ⊥DC ，△PDC 是等腰直角三角形，而DE 是斜边PC 的中线， ∴DE ⊥PC ，①又由PD ⊥平面ABCD ，得PD ⊥BC .∵底面ABCD 是正方形，CD ⊥BC ，∴BC ⊥平面PDC .而DE ⊂平面PDC .∴BC ⊥DE .②由①和②推得DE ⊥平面PBC .而PB ⊂平面PBC ， ∴DE ⊥PB ，又DF ⊥PB 且DE ∩DF ＝D ， 所以PB ⊥平面EFD .15．如图，l 1、l 2是互相垂直的异面直线，MN 是它们的公垂线段．点A 、B 在l 1上，C 在l 2上，AM ＝MB ＝MN .(1)求证AC ⊥NB ； (2)若∠ACB ＝60°，求NB 与平面ABC 所成角的余弦值．证明：(1)如图由已知l 2⊥MN ，l 2⊥l 1，MN ∩l 1＝M ，可得l 2⊥平面ABN .由已知MN ⊥l 1，AM ＝MB ＝MN ，可知AN ＝NB 且AN ⊥NB . 又AN 为AC 在平面ABN 内的射影， ∴AC ⊥NB .(2)∵Rt △CNA ≌Rt △CNB ，∴AC ＝BC ，又已知∠ACB ＝60°，因此△ABC 为正三角形． ∵Rt △ANB ≌Rt △CNB ，∴NC ＝NA ＝NB ，因此N 在平面ABC 内的射影H 是正三角形ABC 的中心．连结BH ，∠NBH 为NB 与平面ABC 所成的角．在Rt △NHB 中，cos ∠NBH ＝HB NB ＝33AB22AB ＝63.16．如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，点E 、F 分别是AB 、BD 的中点．求证：(1)直线EF ∥平面ACD ； (2)平面EFC ⊥平面BCD .命题意图：本小题主要考查直线与平面、平面与平面的位置关系，考查空间想象能力、推理论证能力．证明：(1)在△ABD 中，∵E 、F 分别是AB 、BD 的中点，所以EF ∥AD . 又AD ⊂平面ACD ，EF ⊄平面ACD ，∴直线EF ∥平面ACD . (2)在△ABD 中，∵AD ⊥BD ，EF ∥AD ，∴EF ⊥BD .在△BCD 中，∵CD ＝CB ，F 为BD 的中点，∴CF ⊥BD .∵EF ⊂平面EFC ，CF ⊂平面EFC ，EF 与CF 交于点F ，∴BD ⊥平面EFC . 又∵BD ⊂平面BCD ，∴平面EFC ⊥平面BCD .13．如图，在四棱锥P －ABCD 中，底面ABCD 是边长为a 的正方形，P A ⊥平面ABCD ，且P A ＝2AB .(1)求证：平面P AC ⊥平面PBD ； (2)求二面角B －PC －D 的余弦值． 解析：(1)证明：∵P A ⊥平面ABCD ， ∴P A ⊥BD .∵ABCD 为正方形，∴AC ⊥BD .∴BD ⊥平面P AC ，又BD 在平面BPD 内，∴平面P AC ⊥平面BPD . (2)在平面BCP 内作BN ⊥PC ，垂足为N ，连结DN ， ∵Rt △PBC ≌Rt △PDC ， 由BN ⊥PC 得DN ⊥PC ；∴∠BND 为二面角B －PC －D 的平面角，在△BND 中，BN ＝DN ＝56a ，BD ＝2a ，∴cos ∠BND ＝56a 2＋56a 2－2a 253a 2＝－15.14．如图，已知ABCD －A 1B 1C 1D 1是棱长为3的正方体，点E 在AA 1上，点F 在CC 1上，G 在BB 1上，且AE ＝FC 1＝B 1G ＝1，H 是B 1C 1的中点．(1)求证：E 、B 、F 、D 1四点共面； (2)求证：平面A 1GH ∥平面BED 1F . 证明：(1)连结FG .∵AE ＝B 1G ＝1，∴BG ＝A 1E ＝2， ∴BG 綊A 1E ，∴A 1G 綊BE . ∵C 1F 綊B 1G ，∴四边形C 1FGB 1是平行四边形． ∴FG 綊C 1B 1綊D 1A 1，∴四边形A 1GFD 1是平行四边形． ∴A 1G 綊D 1F ，∴D 1F 綊EB ， 故E 、B 、F 、D 1四点共面．(2)∵H 是B 1C 1的中点，∴B 1H ＝32.又B 1G ＝1，∴B 1G B 1H ＝32.又FC BC ＝23，且∠FCB ＝∠GB 1H ＝90°， ∴△B 1HG ∽△CBF ，∴∠B 1GH ＝∠CFB ＝∠FBG ， ∴HG ∥FB .又由(1)知A 1G ∥BE ，且HG ∩A 1G ＝G ， FB ∩BE ＝B ，∴平面A 1GH ∥平面BED 1F .15．在三棱锥P －ABC 中，P A ⊥面ABC ，△ABC 为正三角形，D 、E 分别为BC 、AC 的中点，设AB ＝P A ＝2.(1)求证：平面PBE ⊥平面P AC ；(2)如何在BC 上找一点F ，使AD ∥平面PEF ，请说明理由； (3)对于(2)中的点F ，求三棱锥B －PEF 的体积． 解析：(1)证明：∵P A ⊥面ABC ，BE ⊂面ABC ， ∴P A ⊥BE .∵△ABC 是正三角形，E 为AC 的中点， ∴BE ⊥AC ，又P A 与AC 相交， ∴BE ⊥平面P AC ，∴平面PBE ⊥平面P AC .(2)解：取DC 的中点F ，则点F 即为所求． ∵E ，F 分别是AC ，DC 的中点， ∴EF ∥AD ，又AD ⊄平面PEF ，EF ⊂平面PEF ， ∴AD ∥平面PEF .(3)解：V B －PEF ＝V P －BEF ＝13S △BEF ·P A ＝13×12×32×32×2＝34.16．(2009·天津，19)如图所示，在五面体ABCDEF 中，F A ⊥平面ABCD ，AD ∥BC ∥FE ，AB ⊥AD ，M 为CE 的中点，AF ＝AB ＝BC ＝FE ＝12AD .(1)求异面直线BF 与DE 所成的角的大小； (2)求证：平面AMD ⊥平面CDE ； (3)求二面角A －CD －E 的余弦值．解答：(1)解：由题设知，BF ∥CE ，所以∠CED (或其补角)为异面直线BF 与DE 所成的角．设P 为AD 的中点，连结EP ，PC .因为FE 綊AP ，所以F A 綊EP .同理，AB 綊PC .又F A ⊥平面ABCD ，所以EP ⊥平面ABCD .而PC ，AD 都在平面ABCD 内，故EP ⊥PC ，EP ⊥AD .由AB ⊥AD ，可得PC ⊥AD .设F A ＝a ，则EP ＝PC ＝PD ＝a ，CD ＝DE ＝EC ＝2a .故∠CED ＝60°.所以异面直线BF 与DE 所成的角的大小为60°.(2)证明：因为DC ＝DE 且M 为CE 的中点，所以DM ⊥CE .连结MP ，则MP ⊥CE .又MP ∩DM ＝M ，故CE ⊥平面AMD .而CE ⊂平面CDE ，所以平面AMD ⊥平面CDE .(3)设Q 为CD 的中点，连结PQ ，EQ .因为CE ＝DE ，所以EQ ⊥CD .因为PC ＝PD ，所以PQ ⊥CD ，故∠EQP 为二面角A －CD －E 的平面角．由(1)可得，EP ⊥PQ ，EQ ＝62a ，PQ ＝22a .于是在Rt △EPQ 中，cos ∠EQP ＝PQ EQ ＝33.所以二面角A －CD －E 的余弦值为33.13．(2009·重庆)如图所示，四棱锥P －ABCD 中，AB ⊥AD ，AD ⊥DC ，P A ⊥底面ABCD ，P A ＝AD ＝DC ＝12AB ＝1，M 为PC 的中点，N 点在AB 上且AN ＝13NB .(1)求证：MN ∥平面P AD ；(2)求直线MN 与平面PCB 所成的角．解析：(1)证明：过点M 作ME ∥CD 交PD 于E 点，连结AE .∵AN ＝13NB ，∴AN ＝14AB ＝12DC ＝EM .又EM ∥DC ∥AB ，∴EM 綊AN ， ∴AEMN 为平行四边形，∴MN ∥AE ，∴MN ∥平面P AD .(2)解：过N 点作NQ ∥AP 交BP 于点Q ，NF ⊥CB 于点F . 连结QF ，过N 点作NH ⊥QF 于H ，连结MH ， 易知QN ⊥面ABCD ，∴QN ⊥BC ，而NF ⊥BC ， ∴BC ⊥面QNF ，∵BC ⊥NH ，而NH ⊥QF ，∴NH ⊥平面PBC ，∴∠NMH 为直线MN 与平面PCB 所成的角．通过计算可得MN ＝AE ＝22，QN ＝34，NF ＝342，∴NH ＝QN ·NF QF ＝ON ·NF QN 2＋NF 2＝64，∴sin ∠NMH ＝NH MN ＝32，∴∠NMH ＝60°，∴直线MN 与平面PCB 所成的角为60°. 14．(2009·广西柳州三模)如图所示，已知直平行六面体ABCD －A 1B 1C 1D 1中，AD ⊥BD ，AD ＝BD ＝a ，E 是CC 1的中点，A 1D ⊥BE .(1)求证：A 1D ⊥平面BDE ；(2)求二面角B －DE －C 的大小．解析：(1)证明：在直平行六面体ABCD －A 1B 1C 1D 1中， ∵AA 1⊥平面ABCD ，∴AA 1⊥BD . 又∵BD ⊥AD ，∴BD ⊥平面ADD 1A 1，即BD ⊥A 1D . 又∵A 1D ⊥BE 且BE ∩BD ＝B ， ∴A 1D ⊥平面BDE .(2)解：如图，连B 1C ，则B 1C ⊥BE ， 易证Rt △BCE ∽Rt △B 1BC ，∴CE BC ＝BC B 1B，又∵E 为CC 1中点， ∴BC 2＝12BB 21.BB 1＝2BC ＝2a .取CD 中点M ，连结BM ，则BM ⊥平面CC 1D 1C ， 作MN ⊥DE 于N ，连NB ，由三垂线定理知：BN ⊥DE ，则∠BNM 是二面角B －DE －C 的平面角．在Rt △BDC 中，BM ＝BD ·BC DC ＝22a ，Rt △CED 中，易求得MN ＝1010a ，Rt △BMN 中，tan ∠BNM ＝BMMN＝5，则二面角B －DE －C 的大小为arctan 5.15．如图，已知正方体ABCD －A 1B 1C 1D 1中，E 为AB 的中点．(1)求直线B 1C 与DE 所成的角的余弦值； (2)求证：平面EB 1D ⊥平面B 1CD ； (3)求二面角E －B 1C －D 的余弦值．解析：(1)连结A 1D ，则由A 1D ∥B 1C 知，B 1C 与DE 所成的角即为A 1D 与DE 所成的角．连结A 1E ，由正方体ABCD －A 1B 1C 1D 1，可设其棱长为a ，则A 1D ＝2a ，A 1E ＝DE ＝52a ，∴cos ∠A 1DE＝A 1D 2＋DE 2－A 1E 22·A 1D ·DE ＝105.∴直线B 1C 与DE 所成角的余弦值是105. (2)证明取B 1C 的中点F ，B 1D 的中点G ，连结BF ，EG ，GF . ∵CD ⊥平面BCC 1B 1，且BF ⊂平面BCC 1B 1，∴DC ⊥BF . 又∵BF ⊥B 1C ，CD ∩B 1C ＝C ， ∴BF ⊥平面B 1CD .又∵GF 綊12CD ，BE 綊12CD ，∴GF 綊BE ，∴四边形BFGE 是平行四边形， ∴BF ∥GE ，∴GE ⊥平面B 1CD . ∵GE ⊂平面EB 1D ，∴平面EB 1D ⊥平面B 1CD . (3)连结EF .∵CD ⊥B 1C ，GF ∥CD ，∴GF ⊥B 1C . 又∵GE ⊥平面B 1CD ，∴EF ⊥B 1C ，∴∠EFG 是二面角E －B 1C －D 的平面角． 设正方体的棱长为a ，则在△EFG 中，GF ＝12a ，EF ＝32a ，∴cos ∠EFG ＝FG EF ＝33，∴二面角E －B 1C －D 的余弦值为33.16．(2009·全国Ⅱ，18)如图所示，直三棱柱ABC －A 1B 1C 1中，AB ⊥AC ，D 、E 分别为AA 1、B 1C 的中点，DE ⊥平面BCC 1.(1)求证：AB ＝AC ；(2)设二面角A －BD －C 为60°，求B 1C 与平面BCD 所成的角的大小． 解析：(1)证明：取BC 中点F ，连结EF ，则EF 綊12B 1B ，从而EF 綊DA .连结AF ，则ADEF 为平行四边形，从而AF ∥DE .又DE ⊥平面BCC 1，故AF ⊥平面BCC 1，从而AF ⊥BC ，即AF 为BC 的垂直平分线，所以AB ＝AC .(2)解：作AG ⊥BD ，垂足为G ，连结CG .由三垂线定理知CG ⊥BD ，故∠AGC 为二面角A －BD －C 的平面角．由题设知，∠AGC ＝60°.设AC ＝2，则AG ＝23.又AB ＝2，BC ＝22，故AF ＝ 2.由AB ·AD ＝AG ·BD 得2AD ＝23·AD 2＋22，解得AD ＝2，故AD ＝AF .又AD ⊥AF ，所以四边形ADEF 为正方形．因为BC ⊥AF ，BC ⊥AD ，AF ∩AD ＝A ，故BC ⊥平面DEF ，因此平面BCD ⊥平面DEF . 连结AE 、DF ，设AE ∩DF ＝H ，则EH ⊥DF ，EH ⊥平面BCD .连结CH ，则∠ECH 为B 1C 与平面BCD 所成的角．因ADEF 为正方形，AD ＝2，故EH ＝1，又EC ＝12B 1C ＝2，所以∠ECH ＝30°，即B 1C 与平面BCD 所成的角为30°.13．在正四棱柱ABCD －A 1B 1C 1D 1中，底面边长为22，侧棱长为4，E 、F 分别为棱AB 、BC 的中点．(1)求证：平面B 1EF ⊥平面BDD 1B 1； (2)求点D 1到平面B 1EF 的距离d .分析：(1)可先证EF ⊥平面BDD 1B 1.(2)用几何法或等积法求距离时，可由B 1D 1∥BD ，将点进行转移：D 1点到平面B 1EF 的距离是B 点到它的距离的4倍，先求B 点到平面B 1EF 的距离即可．解答：(1)证明：⎭⎪⎬⎪⎫EF ⊥BD EF ⊥B 1B ⇒EF ⊥平面BDD 1B 1⇒平面B 1EF ⊥平面BDD 1B 1.(2)解：解法一：连结EF 交BD 于G 点． ∵B 1D 1＝4BG ，且B 1D 1∥BG ，∴D 1点到平面B 1EF 的距离是B 点到它的距离的4倍． 利用等积法可求．由题意可知，EF ＝12AC ＝2，B 1G ＝17.S △B 1EF ＝12EF ·B 1G ＝12×2×17＝17，S △BEF ＝12BE ·BF ＝12×2×2＝1.∵VB －B 1EF ＝VB 1－BEF ，设B 到面B 1EF 的距离为h 1，则13×17×h 1＝13×1×4，∴h 1＝41717.∴点D 1到平面B 1EF 的距离为h ＝4h 1＝161717.解法二：如图，在正方形BDD 1B 1的边BD 上取一点G ，使BG ＝14BD ，连结B 1G ，过点D 1作D 1H ⊥B 1G 于H ，则D 1H 即为所求距离．可求得D 1H ＝161717(直接法)．14．如图直三棱柱ABC －A 1B 1C 1中，侧棱CC 1＝2，∠BAC ＝90°，AB ＝AC ＝2，M 是棱BC 的中点，N 是CC 1中点．求：(1)二面角B 1－AN －M 的大小； (2)C 1到平面AMN 的距离． 解析：(1)∵∠BAC ＝90°，AB ＝AC ＝2，M 是棱BC 的中点， ∴AM ⊥BC ，BC ＝2，AM ＝1. ∴AM ⊥平面BCC 1B 1.∴平面AMN ⊥平面BCC 1B 1.作B 1H ⊥MN 于H ，HR ⊥AN 于R ，连结B 1R ， ∴B 1H ⊥平面AMN .又由三垂线定理知，B 1R ⊥AN .∴∠B 1RH 是二面角B 1－AN －M 的平面角． 由已知得AN ＝3，MN ＝2，B 1M ＝5＝B 1N ，则B 1H ＝322，又Rt △AMN ∽Rt △HRN ，RH AM ＝HN AN ，∴RH ＝66.∴B 1R ＝143，∴cos ∠B 1RH ＝RH B 1R ＝714.∴二面角B 1－AN －M 的大小为arccos 714.(2)∵N 是CC 1中点，∴C 1到平面AMN 的距离等于C 到平面AMN 的距离． 设C 到平面AMN 的距离为h ， 由V C －AMN ＝V N －AMC 得13×12·MN ·h ＝13×12AM ·MC . ∴h ＝22.15．(2009·北京海淀一模)如图所示，四棱锥P －ABCD 中，P A ⊥平面ABCD ，底面ABCD 为直角梯形，且AB ∥CD ，∠BAD ＝90°，P A ＝AD ＝DC ＝2，AB ＝4.(1)求证：BC ⊥PC ；(2)求PB 与平面P AC 所成的角的正弦值； (3)求点A 到平面PBC 的距离．解析：(1)证明：如图，在直角梯形ABCD 中， ∵AB ∥CD ，∠BAD ＝90°，AD ＝DC ＝2， ∴∠ADC ＝90°，且AC ＝2 2. 取AB 的中点E ，连结CE ，由题意可知，四边形ABCD 为正方形， ∴AE ＝CE ＝2.又∵BE ＝12AB ＝2.∴CE ＝12AB ，∴△ABC 为等腰直角三角形， ∴AC ⊥BC .又∵P A ⊥平面ABCD ，且AC 为PC 在平面ABCD 内的射影， BC ⊂平面ABCD ，由三垂线定理得， BC ⊥PC .(2)由(1)可知，BC ⊥PC ，BC ⊥AC ，PC ∩AC ＝C ， ∴BC ⊥平面P AC .PC 是PB 在平面P AC 内的射影，∴∠CPB 是PB 与平面P AC 所成的角．又CB ＝22， PB 2＝P A 2＋AB 2＝20，PB ＝25，∴sin ∠CPB ＝BC PB ＝105，即PB 与平面P AC 所成角的正弦值为105.(3)由(2)可知，BC ⊥平面P AC ，BC ⊂平面PBC ， ∴平面PBC ⊥平面P AC .过A 点在平面P AC 内作AF ⊥PC 于F ， ∴AF ⊥平面PBC ，∴AF 的长即为点A 到平面PBC 的距离．在直角三角形P AC 中， P A ＝2，AC ＝22，PC ＝23，∴AF ＝263.即点A 到平面PBC 的距离为263.16．(2009·吉林长春一模)如图所示，四棱锥P －ABCD 的底面是正方形，P A ⊥底面ABCD ，P A ＝2，∠PDA ＝45°，点E 、F 分别为棱AB 、PD 的中点．(1)求证：AF ∥平面PCE ；(2)求二面角E －PD －C 的大小； (3)求点A 到平面PCE 的距离．解析：(1)证明：如图取PC 的中点G ，连结FG 、EG ， ∴FG 为△PCD 的中位线，∴FG ＝12CD 且FG ∥CD .又∵底面四边形ABCD 是正方形，E 为棱AB 的中点，∴AE ＝12CD 且AE ∥CD ，∴AE ＝FG 且AE ∥FG .∴四边形AEGF 是平行四边形， ∴AF ∥EG .又EG ⊂平面PCE ，AF ⊄平面PCE ， ∴AF ∥平面PCE .(2)解：∵P A ⊥底面ABCD ， ∴P A ⊥AD ，P A ⊥CD . 又AD ⊥CD ， P A ∩AD ＝A ， ∴CD ⊥平面P AD . 又∵AF ⊂平面P AD ， ∴CD ⊥AF .又P A ＝2，∠PDA ＝45°， ∴P A ＝AD ＝2.∵F 是PD 的中点，∴AF ⊥PD . 又∵CD ∩PD ＝D ， ∴AF ⊥平面PCD .∵AF ∥EG ，∴EG ⊥平面PCD . 又GF ⊥PD ，连结EF ，则∠GFE 是二面角E －PD －C 的平面角． 在Rt △EGF 中，EG ＝AF ＝2，GF ＝1，∴tan ∠GFE ＝GEGF＝ 2.∴二面角E －PD －C 的大小为arctan 2. (3)设A 到平面PCE 的距离为h ，由V A －PCE ＝V P －ACE ，即13×12PC ·EG ·h ＝13P A ·12AE ·CB ，得h ＝63，∴点A 到平面PCE 的距离为63.13．(2009·陕西，18)如图所示，在直三棱柱ABC －A 1B 1C 1中，AB ＝1，AC ＝AA 1＝3，∠ABC ＝60°.(1)求证：AB ⊥A 1C ；(2)求二面角A －A 1C －B 的大小．解析：(1)证明：∵三棱柱ABC －A 1B 1C 1为直三棱柱， ∴AB ⊥AA 1，在△ABC 中，AB ＝1，AC ＝3，∠ABC ＝60°，由正弦定理得∠ACB ＝30°， ∴∠BAC ＝90°，即AB ⊥AC .∴AB ⊥平面ACC 1A 1，又A 1C ⊂平面ACC 1A 1，∴AB ⊥A 1C .(2)解：如图，作AD ⊥A 1C 交A 1C 于D 点，连结BD ，由三垂线定理知BD ⊥A 1C ，∴∠ADB 为二面角A －A 1C －B 的平面角．在Rt △AA 1C 中，AD ＝AA 1·AC A 1C ＝3×36＝62，在Rt △BAD 中，tan ∠ADB ＝AB AD ＝63， ∴∠ADB ＝arctan63，即二面角A －A 1C －B 的大小为arctan 63. 14．如图，三棱柱ABC －A 1B 1C 1的底面是边长为a 的正三角形，侧面ABB 1A 1是菱形且垂直于底面，∠A 1AB ＝60°，M 是A 1B 1的中点．(1)求证：BM ⊥AC ；(2)求二面角B －B 1C 1－A 1的正切值； (3)求三棱锥M －A 1CB 的体积．解析：(1)证明：∵ABB 1A 1是菱形，∠A 1AB ＝60°⇒△A 1B 1B 是正三角形， ⎭⎪⎬⎪⎫∵M 是A 1B 1的中点，∴BM ⊥A 1B 又∵平面AA 1B 1B ⊥平面A 1B 1C 1 ⇒BM ⊥平面A 1B 1C 1. ⎭⎪⎬⎪⎫∴BM ⊥A 1C 1又∵AC ∥A 1C 1⇒BM ⊥AC .⎭⎪⎬⎪⎫(2)过M 作ME ⊥B 1C 1且交于点E ，∵BM ⊥平面A 1B 1C 1，⇒BE ⊥B 1C 1，∴∠BEM 为所求二面角的平面角， △A 1B 1C 1中，ME ＝MB 1·sin60°＝34a ，Rt △BMB 1中，MB ＝MB 1·tan60°＝32a ， ∴tan ∠BEM ＝MBME＝2，∴所求二面角的正切值是2.(3)VM －A 1CB ＝12VB 1－A 1CB ＝12VA －A 1CB ＝12VA 1－ABC ＝12×13×34a 2·32a ＝116a 3.15．(2009·广东汕头一模)如图所示，已知△BCD 中，∠BCD ＝90°，BC ＝CD ＝1，AB ⊥平面BCD ，∠ADB ＝60°，E 、F 分别是AC 、AD 上的动点，且AE AC ＝AFAD＝λ(0<λ<1)．(1)求证：不论λ为何值，总有EF ⊥平面ABC ；(2)若λ＝12，求三棱锥A －BEF 的体积．解析：(1)证明：∵AB ⊥平面BCD ， ∴AB ⊥CD .又∵在△BCD 中，∠BCD ＝90°， ∴BC ⊥CD .∵又AB ∩BC ＝B ，∴CD ⊥平面ABC .又∵在△ACD 中，E 、F 分别是AC 、AD 上的动点，且AE AC ＝AFAD＝λ(0<λ<1)，∴不论λ为何值，都有EF ∥CD ， ∴EF ⊥平面ABC .(2)在△BCD 中，∠BCD ＝90°，BC ＝CD ＝1， ∴BD ＝ 2.又∵AB ⊥平面BCD ， ∴AB ⊥BC ，AB ⊥BD .又∵在Rt △ABD 中，∠ADB ＝60°， ∴AB ＝BD ·tan60°＝6， 由(1)知EF ⊥平面ABC ， ∴V A －BEF ＝V F －ABE ＝13S △ABE ·EF ＝13×12S △ABC ·EF ＝16×12×1×6×12＝624. 故三棱锥A －BEF 的体积是624.16．在四棱锥P －ABCD 中，侧面PDC 是边长为2的正三角形，且与底面垂直，底面ABCD 是面积为23的菱形，∠ADC 为菱形的锐角．(1)求证：P A ⊥CD ；(2)求二面角P －AB －D 的大小； (3)求棱锥P －ABCD 的侧面积；解析：(1)证明：如图所示，取CD 的中点E ，由PE ⊥CD ，得PE ⊥平面ABCD ，连结AC 、AE .∵AD ·CD ·sin ∠ADC ＝23， AD ＝CD ＝2，∴sin ∠ADC ＝32，即∠ADC ＝60°，∴△ADC 为正三角形，∴CD ⊥AE . ∴CD ⊥P A (三垂线定理)．(2)解：∵AB ∥CD ，∴AB ⊥P A ，AB ⊥AE ， ∴∠P AE 为二面角P －AB －D 的平面角． 在Rt △PEA 中，PE ＝AE ，∴∠P AE ＝45°. 即二面角P －AB －D 的大小为45°. (3)分别计算各侧面的面积： ∵PD ＝DA ＝2，P A ＝6，∴cos ∠PDA ＝14，sin ∠PDA ＝154.S △PCD ＝3，S △P AB ＝12AB ·P A ＝12·2·2·3＝6，S △P AD ＝S △PBC ＝12PD ·DA ·sin ∠PDA ＝152.∴S P －ABCD 侧＝3＋6＋15.13．把地球当作半径为R 的球，地球上A 、B 两地都在北纬45°，A 、B 两点的球面距离是π3R ，A 点在东经20°，求B 点的位置． 解析：如图，求B 点的位置即求B 点的经度，设B 点在东经α，∵A 、B 两点的球面距离是π3R .∴∠AOB ＝π3，因此三角形AOB 是等边三角形，∴AB ＝R ，又∵∠AO 1B ＝α－20°(经度差)问题转化为在△AO 1B 中借助AO 1＝BO 1＝AO cos45°＝22R ，求出∠AO 1B ＝90°，则α＝110°，同理：B 点也可在西经70°，即B 点在北纬45°东经110°或西经70°.14．在球心同侧有相距9cm 的两个平行截面，它们的面积分别为49πcm 2和400πcm 2，求球的表面积和体积．解析：如图，两平行截面被球大圆所在平面截得的交线分别为AO 1、BO 2，则AO 1∥BO 2. 若O 1、O 2分别为两截面圆的圆心，则由等腰三角形性质易知OO 1⊥AO 1，OO 2⊥BO 2， 设球半径为R ，∵πO 2B 2＝49π， ∴O 2B ＝7cm ，同理O 1A ＝20cm. 设OO 1＝x cm ，则OO 2＝(x ＋9)cm. 在Rt △OO 1A 中，R 2＝x 2＋202， 在Rt △OO 2B 中，R 2＝(x ＋9)2＋72， ∴x 2＋202＝72＋(x ＋9)2，解得x ＝15cm. ∴R ＝25cm ，∴S 球＝2500πcm 2，V 球＝43πR 3＝625003πcm 3.15．设A 、B 、C 是半径为1的球面上的三点，B 、C 两点间的球面距离为π3，点A 与B 、C 两点间的球面距离均为π2，O 为球心，求：(1)∠AOB 、∠BOC 的大小； (2)球心O 到截面ABC 的距离．解析：(1)如图，因为球O 的半径为1，B 、C 两点间的球面距离为π3，点A 与B 、C 两点间的球面距离均为π2，所以∠BOC ＝π3，∠AOB ＝∠AOC ＝π2， (2)因为BC ＝1，AC ＝AB ＝2，所以由余弦定理得cos ∠BAC ＝34，sin ∠BAC ＝74，设截面圆的圆心为O 1，连结AO 1，则截面圆的半径r ＝AO 1，由正弦定理得r ＝BC 2sin ∠BAC＝277，所以OO 1＝OA 2－r 2＝217.16．如图四棱锥A －BCDE 中，AD ⊥底面BCDE ，AC ⊥BC ，AE ⊥BE . (1)求证：A 、B 、C 、D 、E 五点共球； (2)若∠CBE ＝90°，CE ＝3，AD ＝1，求B 、D 两点的球面距离． 解析：(1)证明：取AB 的中点P ，连结PE ，PC ，PD ，由题设条件知△AEB 、△ADB 、△ABC 都是直角三角形．故PE ＝PD ＝PC ＝12AB ＝P A ＝PB .所以A 、B 、C 、D 、E 五点在同一球面上． (2)解：由题意知四边形BCDE 为矩形， 所以BD ＝CE ＝3，在Rt △ADB 中，AB ＝2，AD ＝1，∴∠DPB ＝120°，D 、B 的球面距离为23π.17．(本小题满分10分)如图，四棱锥S —ABCD 的底面是正方形，SA ⊥底面ABCD ，E 是SC 上一点．(1)求证：平面EBD ⊥平面SAC ；(2)假设SA ＝4，AB ＝2，求点A 到平面SBD 的距离；解析：(1)∵正方形ABCD ，∴BD ⊥AC ，又∵SA ⊥平面ABCD ，∴SA ⊥BD ，则BD ⊥平面SAC ，又BD ⊂平面BED ，∴平面BED ⊥平面SAC .(2)设AC ∩BD ＝O ，由三垂线定理得BD ⊥SO .AO ＝12AC ＝122AB ＝12·2·2＝2，SA ＝4，则SO ＝SA 2＋AO 2＝16＋2＝32，S △BSD ＝12BD ·SO ＝12·22·32＝6.设A 到面BSD 的距离为h ，则V S －ABD ＝V A －BSD ，即13S △ABD ·SA ＝13S △BSD ·h ，解得h ＝43，即点A 到平面SBD 的距离为43. 18．(本小题满分12分)如图，正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ＝4，点E 在C 1C 上且C 1E ＝3EC .(1)证明A 1C ⊥平面BED ；(2)求二面角A 1－DE －B 的大小． 解析：依题设知AB ＝2，CE ＝1，(1)证明：连结AC 交BD 于点F ，则BD ⊥AC . 由三垂线定理知，BD ⊥A 1C .在平面A 1CA 内，连结EF 交A 1C 于点G ，由于AA 1FC ＝AC CE＝22，故Rt △A 1AC ∽Rt △FCE ，∠AA 1C ＝∠CFE ，∠CFE 与∠FCA 1互余． 于是A 1C ⊥EF .A 1C 与平面BED 内两条相交直线BD 、EF 都垂直． 所以A 1C ⊥平面BED .(2)作GH ⊥DE ，垂足为H ，连结A 1H . 由三垂线定理知A 1H ⊥DE ，故∠A 1HG 是二面角A 1－DE －B 的平面角． EF ＝CF 2＋CE 2＝3，CG ＝CE ×CF EF ＝23.EG ＝CE 2－CG 2＝33.EG EF ＝13，GH ＝13×EF ×FD DE ＝215. 又A 1C ＝AA 21＋AC 2＝26，A 1G ＝A 1C －CG ＝563， tan ∠A 1HG ＝A 1GHG＝5 5.所以二面角A 1－DE －B 的大小为arctan5 5.19．(本小题满分12分)如图，四棱锥S －ABCD 的底面是直角梯形，∠ABC ＝∠BCD ＝90°，AB ＝BC ＝SB ＝SC ＝2CD ＝2，侧面SBC ⊥底面ABCD .(1)由SA 的中点E 作底面的垂线EH ，试确定垂足H 的位置； (2)求二面角E －BC －A 的大小．解析：(1)作SO ⊥BC 于O ，则SO ⊂平面SBC ， 又面SBC ⊥底面ABCD ， 面SBC ∩面ABCD ＝BC ， ∴SO ⊥底面ABCD ①又SO ⊂平面SAO ，∴面SAO ⊥底面ABCD ， 作EH ⊥AO ，∴EH ⊥底面ABCD ② 即H 为垂足，由①②知，EH ∥SO ， 又E 为SA 的中点，∴H 是AO 的中点． (2)过H 作HF ⊥BC 于F ，连结EF ， 由(1)知EH ⊥平面ABCD ，∴EH ⊥BC ，又EH ∩HF ＝H ，∴BC ⊥平面EFH ，∴BC ⊥EF ，∴∠HFE 为面EBC 和底面ABCD 所成二面角的平面角． 在等边三角形SBC 中，∵SO ⊥BC ， ∴O 为BC 中点，又BC ＝2.∴SO ＝22－12＝3，EH ＝12SO ＝32，又HF ＝12AB ＝1，∴在Rt △EHF 中，tan ∠HFE ＝EH HF ＝321＝32，∴∠HFE ＝arctan 32.即二面角E －BC －A 的大小为arctan 32.20．(本小题满分12分)(2010·唐山市高三摸底考试)如图，在正四棱柱ABCD －A 1B 1C 1D 1中，AB ＝1，AA 1＝2，N 是A 1D 的中点，M ∈BB 1，异面直线MN 与A 1A 所成的角为90°.(1)求证：点M 是BB 1的中点；(2)求直线MN 与平面ADD 1A 1所成角的大小；(3)求二面角A －MN －A 1的大小．解析：(1)取AA 1的中点P ，连结PM ，PN .∵N 是A 1D 的中点，∴AA 1⊥PN ，又∵AA 1⊥MN ，MN ∩PN ＝N ， ∴AA 1⊥面PMN .∵PM ⊂面PMN ，∴AA 1⊥PM ，∴PM ∥AB ， ∴点M 是BB 1的中点．(2)由(1)知∠PNM 即为MN 与平面ADD 1A 1所成的角．在Rt △PMN 中，易知PM ＝1，PN ＝12，∴tan ∠PNM ＝PMPN＝2，∠PNM ＝arctan2.故MN 与平面ADD 1A 1所成的角为arctan2.(3)∵N 是A 1D 的中点，M 是BB 1的中点，∴A 1N ＝AN ，A 1M ＝AM ， 又MN 为公共边，∴△A 1MN ≌△AMN .在△AMN 中，作AG ⊥MN 交MN 于G ，连结A 1G ，则∠A 1GA 即为二面角A －MN －A 1的平面角．在△A 1GA 中，AA 1＝2，A 1G ＝GA ＝305，∴cos ∠A 1GA ＝A 1G 2＋GA 2－AA 212A 1G ·GA ＝－23，∴∠A 1GA ＝arccos(－23)，故二面角A －MN －A 1的大小为arccos(－23)．21．(2009·安徽，18)(本小题满分12分)如图所示，四棱锥F －ABCD 的底面ABCD 是菱形，其对角线AC ＝2，BD ＝ 2.AE 、CF 都与平面ABCD 垂直，AE ＝1，CF ＝2.(1)求二面角B －AF －D 的大小；(2)求四棱锥E －ABCD 与四棱锥F －ABCD 公共部分的体积． 命题意图：本题考查空间位置关系，二面角平面角的作法以及空间几何体的体积计算等知识．考查利用综合法或向量法解决立体几何问题的能力．解答：(1)解：连接AC 、BD 交于菱形的中心O ，过O 作OG ⊥AF ，G 为垂足，连接BG 、DG .由BD ⊥AC ，BD ⊥CF 得BD ⊥平面ACF ，故BD ⊥AF .于是AF ⊥平面BGD ，所以BG ⊥AF ，DG ⊥AF ，∠BGD 为二面角B －AF －D 的平面角．由FC ⊥AC ，FC ＝AC ＝2，得∠F AC ＝π4，OG ＝22.由OB ⊥OG ，OB ＝OD ＝22，得∠BGD ＝2∠BGO ＝π2.(2)解：连接EB 、EC 、ED ，设直线AF 与直线CE 相交于点H ，则四棱锥E －ABCD 与四棱锥F －ABCD 的公共部分为四棱锥H －ABCD .过H 作HP ⊥平面ABCD ，P 为垂足． 因为EA ⊥平面ABCD ，FC ⊥平面ABCD ，所以平面ACEF ⊥平面ABCD ，从而P ∈AC ，HP ⊥AC . 由HP CF ＋HP AE ＝AP AC ＋PC AC ＝1，得HP ＝23. 又因为S 菱形ABCD ＝12AC ·BD ＝2，故四棱锥H －ABCD 的体积V ＝13S 菱形ABCD ·HP ＝229.22．(2009·深圳调考一)(本小题满分12分)如图所示，AB 为圆O 的直径，点E 、F 在圆O 上，AB ∥EF ，矩形ABCD 所在平面和圆O 所在的平面互相垂直．已知AB ＝2，EF ＝1.(1)求证：平面DAF ⊥平面CBF ；(2)求直线AB 与平面CBF 所成角的大小；(3)当AD 的长为何值时，二面角D －FE －B 的大小为60°？ 解析：(1)证明：∵平面ABCD ⊥平面ABEF ，CB ⊥AB ， 平面ABCD ∩平面ABEF ＝AB ， ∴CB ⊥平面ABEF .∵AF ⊂平面ABEF ，∴AF ⊥CB ， 又∵AB 为圆O 的直径，∴AF ⊥BF ， ∴AF ⊥平面CBF .∵AF ⊂平面DAF ，∴平面DAF ⊥平面CBF . (2)解：根据(1)的证明，有AF ⊥平面CBF ， ∴FB 为AB 在平面CBF 上的射影，因此，∠ABF 为直线AB 与平面CBF 所成的角． ∵AB ∥EF ，∴四边形ABEF 为等腰梯形， 过点F 作FH ⊥AB ，交AB 于H .AB ＝2，EF ＝1，则AH ＝AB －EF 2＝12.在Rt △AFB 中，根据射影定理AF 2＝AH ·AB ，得AF ＝1，sin ∠ABF ＝AF AB ＝12，∴∠ABF ＝30°，∴直线AB 与平面CBF 所成角的大小为30°.(3)解：过点A 作AM ⊥EF ，交EF 的延长线于点M ，连结DM . 根据(1)的证明，DA ⊥平面ABEF ，则DM ⊥EF ， ∴∠DMA 为二面角D －FE －B 的平面角， ∠DMA ＝60°.在Rt △AFH 中，∵AH ＝12，AF ＝1，∴FH ＝32. 又∵四边形AMFH 为矩形，∴MA ＝FH ＝32. ∵AD ＝MA ·tan ∠DMA ＝32·3＝32. 因此，当AD 的长为32时，二面角D －FE －B 的大小为60°.。

一、选择题1．如下图所示，在正方体1111ABCD A B C D -中，E 是平面11ADD A 的中心，M 、N 、F 分别是11B C 、1CC 、AB 的中点，则下列说法正确的是（ ）A ．12MN EF =，且MN 与EF 平行 B ．12MN EF ≠，且MN 与EF 平行 C ．12MN EF =，且MN 与EF 异面 D ．12MN EF ≠，且MN 与EF 异面 2．《九章算术》与《几何原本》并称现代数学的两大源泉.在《九章算术》卷五商功篇中介绍了羡除（此处是指三面为等腰梯形，其他两侧面为直角三角形的五面体）体积的求法.在如图所示的羡除中，平面ABDA '是铅垂面，下宽3m AA '=，上宽4m BD =，深3m ，平面BDEC 是水平面，末端宽5m CE =，无深，长6m （直线CE 到BD 的距离），则该羡除的体积为（ ）A ．324mB ．330mC ．336mD ．342m 3．已知正方体1111ABCD A B C D -的棱长为2，E 为棱1AA 的中点，截面1CD E 交棱AB 于点F ，则四面体1CDFD 的外接球表面积为（ ）A ．394π B ．414π C ．12π D ．434π 4．已知α、β是平面，m 、n 是直线，下列命题中不正确的是（ ） A ．若//m α，n αβ=，则//m n B ．若//m n ，m α⊥，则n α⊥C ．若m α⊥，m β⊥，则//αβD ．若m α⊥，m β⊂，则αβ⊥5．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（ ）A ．24B ．30C ．47D ．676．如图所示，A ，B 为正方体的两个顶点，M ，N 为其所在棱的中点，则异面直线AB 与MN 所成角的大小为（ ）A ．30°B ．45°C ．60°D ．90°7．如图，在四棱锥P ABCD -中，底面ABCD 是矩形.其中3AB =，2AD =，PAD △是以A ∠为直角的等腰直角三角形，若60PAB ∠=︒，则异面直线PC 与AD 所成角的余弦值是（ ）A 22B ．22C 27D 211 8．设有直线m ，n ，l 和平面α，β，下列四个命题中，正确的是（ ） A ．若//,//m n αα，则//m nB ．若//,//,//l m αβαβ，则//l mC ．若,m αβα⊥⊂，则m β⊥D ．若,,m m αββα⊥⊥⊄，则//m α 9．某三棱锥的三视图如图所示，已知网格纸上小正方形的边长为1，则该三棱锥的体积为（ ）A ．43B ．83C ．3D ．4 10．在正方体1111ABCD A B C D -中，三棱锥11A B CD -的表面积为43，则正方体外接球的体积为（ ）A ．43πB ．6πC ．323πD ．86π 11．如果一个水平放置的平面图形的斜二测直观图是如图所示的直角梯形，其中2O A ''=，45B A O '''∠=,//B C O A ''''.则原平面图形的面积为（ ）A ．32B ．62C 322D ．3412．已知在底面为菱形的直四棱柱1111ABCD A B C D -中，14,42AB BD ==60BAD ︒∠=，则异面直线1B C 与1AD 所成的角为（ ）A ．90︒B ．60︒C ．45︒D ．30︒二、填空题13．四棱锥V ABCD -中，底面ABCD 是正方形，各条棱长均为2.则异面直线VC 与AB 所成角的大小为______.14．已知H 是球O 的直径AB 上一点，:1:3AH HB =，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为__________.15．如图，在三棱台111ABC A B C -中，11190,4,22ACB AC BC A B CC ∠=︒====，平面11AA B B ⊥平面ABC ，则该三棱台外接球的表面积为___________.16．如图，在一个底面面积为4，侧棱长为10的正四棱锥P ABCD -中，大球1O 内切于该四棱锥，小球2O 与大球1O 及四棱锥的四个侧面相切，则小球2O 的体积为___________.17．如图，已知一个八面体的各条棱长均为2，四边形ABCD 为正方形，给出下列说法：①该八面体的体积为83；②该八面体的外接球的表面积为8π； ③E 到平面ADF 的距离为3；④EC 与BF 所成角为60°.其中正确的说法为__________.（填序号）18．表面积为16π的球与一个正三棱柱各个面都相切，则这个正三棱柱的体积为___________.19．如图，在长方体1111ABCDA B C D ﹣中，O 是11B D 的中点，P 是线段AC 上一点，且直线1PA 交平面11AB D 于点M ．给出下列结论：①A ，M ，O 三点共线；②A ，M ，O ，1A 不共面；③A ，M ，C ，O 共面；④B ，1B ，O ，M 共面．其中正确结论的序号为______．20．将半径为3，圆心角为23π的扇形围成一个圆锥，则该圆锥内切球的体积为________． 三、解答题21．如图所示，四棱锥P ABCD -的底面ABCD 是平行四边形，90DBA ∠=︒，2BA BD ==，10,,PA PD E F ==分别是棱,AD PC 的中点.（1）证明：//EF 平面PAB ；（2）若二面角P AD B --为60︒，求点B 到平面PAD 的距离.22．如图所示，在四棱锥P ABCD -中，底面ABCD 是60DAB ∠=且边长为a 的菱形，侧面PAD 为正三角形，其所在平面垂直于底面ABCD ，若G 为AD 的中点，E 为BC 的中点．（1）求证：//BG 平面PDE ；（2）在棱PC 上是否存在一点F ，使平面DEF ⊥平面ABCD ，若存在，确定点F 的位置；若不存在，说明理出．23．已知圆锥的侧面展开图为半圆，母线长为23.（1）求圆锥的底面积；（2）在该圆锥内按如图所示放置一个圆柱，当圆柱的侧面积最大时，求圆柱的体积. 24．如图，已知在三棱锥P ABC -中，ABC 是边长为2的正三角形，PAC △是以AC 为斜边的等腰直角三角形，若直线PB 与平面ABC 所成的角为6π．（Ⅰ）若PB PC >，求证：平面PAC ⊥平面ABC ；（Ⅱ）若PB PC <，求直线AB 与平面PAC 所成角的正弦值．25．如图，四棱锥P ABCD -中，底面ABCD 是正方形，PD ⊥平面ABCD ，226AB PD ==，，O 为AC 与BD 的交点，E 为棱PB 上一点.（1）证明：平面EAC ⊥平面PBD ；（2）若//PD 平面EAC ，求三棱锥B AEC -的体积.26．在三棱锥P ABC -中，G 是底面ABC 的重心，D 是线段PC 上的点，且2PD DC =.（1）求证：DG//平面PAB ；（2）若PAB △是以PB 为斜边的等腰直角三角形，求异面直线DG 与PB 所成角的余弦值.【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】设正方体1111ABCD A B C D -的棱长为2，利用正方体性质可求得2MN =，3EF =，知12MN EF ≠，再利用三角形中位线性质知1//MN B C ，从而//MN ED ，又EF 与ED 相交，可知MN 与EF 异面，即可选出答案.【详解】设正方体1111ABCD A B C D -的棱长为2，则22112MN MC C N =+=作E 点在平面ABCD 的投影点G ，即EG ⊥平面ABCD ，连接,EG GF ，在直角EGF △中，1EG =，222GF AG AF =+=，则2222123EF EG GF =+=+=，所以12MN EF ≠，故排除A 、C 连接DE ，由E 是平面11ADD A 的中心，得112DE A D = 又M N 、分别是11B C 、1CC 的中点，所以1//MN B C又11//A D B C ，所以//MN ED ，又EF ED E ⋂=，所以MN 与EF 异面故选：D.【点睛】关键点睛：本题考查正方体中的线面关系，线线平行的关系，及判断异面直线，解题的关键是熟记正方体的性质，考查学生的逻辑推理能力，属于基础题.2．C解析：C【分析】在BD ，CF 上分别取点B '，C '，使得3m BB CC ''==，连接A B ''，A C ''，B C ''，把几何体分割成一个三棱柱和一个四棱锥，然后由棱柱、棱锥体积公式计算．【详解】如图，在BD ，CF 上分别取点B '，C '，使得3m BB CC ''==，连接A B ''，A C ''，B C ''，则三棱柱ABC A B C '''-是斜三棱柱，该羡除的体积V V =三棱柱ABC A B C '''-V +四棱锥A B DEC '''-()311123636336m 232+⎛⎫⎛⎫=⨯⨯⨯+⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭. 故选：C ．【点睛】思路点睛：本题考查求空间几何体的体积，解题思路是观察几何体的结构特征，合理分割，将不规则几何体体积的计算转化为锥体、柱体体积的计算．考查了空间想象能力、逻辑思维能力、运算求解能力．3．B解析：B【分析】可证F 为AB 的中点，设1DD 的中点为G ，DFC △的外接圆的球心为1O ，四面体1CDFD 的外接球的球心为O ，连接11,,,OG OF OO A B ，利用解三角形的方法可求DFC △的外接圆的半径，从而可求四面体1CDFD 的外接球的半径.【详解】设1DD 的中点为G ，DFC △的外接圆的圆心为1O ，四面体1CDFD 的外接球的球心为O ，连接11,,,OG OF OO A B ，因为平面11//A ABB 平面11D DCC ，平面1CD E ⋂平面11A ABB EF =，平面1CD E ⋂平面111D DCC D C =，故1//EF D C ，而11//A B D C ，故1//EF A B ，故F 为AB 的中点， 所以145DF CF ==+=，故3cos 5255DFC ∠==⨯⨯， 因为DFC ∠为三角形的内角，故4sin 5DFC ∠=，故DFC △的外接圆的半径为1254245⨯=，1OO ⊥平面ABCD ，1DD ⊥平面ABCD ，故11//OO DD ，在平面1GDO O 中，111,OG DD O D DD ⊥⊥，故1//OG O D ，故四边形1GDO O 为平行四边形，故1//OO GD ，1OO GD =，所以四面体1CDFD 2541116+= 故四面体1CDFD 的外接球表面积为41414164ππ⨯=， 故选：B.【点睛】方法点睛：三棱锥的外接球的球的半径，关键是球心位置的确定，通常利用“球心在过底面外接圆的圆心且垂直于底面的直线上”来确定. 4．A解析：A【分析】根据已知条件判断直线m 、n 的位置关系，可判断A 选项的正误；利用线面垂直的性质可判断BC 选项的正误；利用面面垂直的判定定理可判断D 选项的正误. 【详解】对于A 选项，若//m α，则直线m 与平面α内的直线平行或异面， 由于n αβ=，则直线m 、n 平行或异面，A 选项错误；对于B 选项，若//m n ，m α⊥，则n α⊥，B 选项正确； 对于C 选项，若m α⊥，m β⊥，则//αβ，C 选项正确；对于D 选项，若m α⊥，m β⊂，由面面垂直的判定定理可知αβ⊥，D 选项正确. 故选：A. 【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．5．D解析：D 【分析】先找到几何体的原图，再求出几何体的高，再求几何体的体积得解. 【详解】由三视图可知几何体为图中的四棱锥1P CDD E -， 由题得22437AD =-7 所以几何体的体积为11(24)676732⋅+⋅=. 故选：D 【点睛】方法点睛：通过三视图找几何体原图常用的方法有：（1）直接法；（2）拼凑法；（3）模型法.本题利用的就是模型法.要根据已知条件灵活选择方法求解.6．C解析：C 【分析】由MN 与正方体的面对角线平行，可得异面直线所成的角，此角是正三角形的内角，由此可得． 【详解】作如图所示的辅助线，由于M ，N 为其所在棱的中点，所以//MN PQ ，又因为//AC PQ ，所以//AC MN ，所以CAB ∠即为异面直线AB 与MN 所成的角（或补角），易得AB AC BC ==，所以60CAB ∠=︒. 故选：C ．7．D解析：D 【分析】在图形中找到（并证明）异面直线所成的角，然后在三角形中计算． 【详解】因为//AD BC ，所以PCB ∠是异面直线PC 与AD 所成角（或其补角）， 又PA AD ⊥，所以PA BC ⊥，因为AB BC ⊥，AB PA A ⋂=，,AB PA ⊂平面PAB ，所以BC ⊥平面PAB ， 又PB ⊂平面PAB ，所以PB BC ⊥． 由已知2PA AD ==，所以22222cos 23223cos607PB PA AB PA AB PAB =+-⋅∠=+-⨯⨯︒=22211cos 11(7)2BC PCB PC ∠===+， 所以异面直线PC 与AD 211． 故选：D ． 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．8．D解析：D 【分析】在A 中，m 与n 相交、平行或异面； 在B 中，l 与m 不一定平行，有可能相交； 在C 中，m ⊥β或m ∥β或m 与β相交；在D 中，由直线与平面垂直的性质与判定定理可得m ∥α．【详解】由直线m 、n ，和平面α、β，知：对于A ，若m ∥α，n ∥α，则m 与n 相交、平行或异面，故A 错误； 对于B ，若//,//,//l m αβαβ，l 与m 不一定平行，有可能相交，故B 错误； 对于C ，若α⊥β，m ⊂α，则m ⊥β或m ∥β或m 与β相交，故C 错误；对于D ，若α⊥β，m ⊥β，m ⊄α，则由直线与平面垂直的性质与判定定理得m ∥α，故D 正确．故选：D ． 【点睛】本题考查了命题真假的判断问题，考查了空间线线、线面、面面的位置关系的判定定理及推论的应用，体现符号语言与图形语言的相互转化，是中档题．9．A解析：A 【分析】首先由三视图还原几何体，然后由几何体的空间结构特征求解三棱锥的体积即可. 【详解】由三视图可知，在棱长为2的正方体中，其对应的几何体为棱锥P ABC -，该棱锥的体积：11142223323V Sh ⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭. 故选：A. 【点睛】方法点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．10．B解析：B 【分析】根据三棱锥的表面积进一步求出正方体的棱长，最后求出正方体的外接球的半径，进一步求出结果． 【详解】解：设正方体的棱长为a ，则1111112B D AC AB AD B C D C a ======， 由于三棱锥11A B CD -的表面积为43， 所以()12133442242AB CS S a==⨯⨯=所以2a =所以正方体的外接球的半径为()()()2222226++=， 所以正方体的外接球的体积为34663ππ⎛⎫= ⎪ ⎪⎝⎭故选：B ． 【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.11．A解析：A 【分析】作出原平面图形，然后求出面积即可． 【详解】45B A O '''∠=B O A '''=∠，则O A B '''△是等腰直角三角形，∴2A B OB '''==，又O C C B ''''⊥，45C O B '''∠=︒，∴1B C ''=， 在直角坐标系中作出原图形为：梯形OABC ，//OA BC ，2,1OA BC ==，高22OB = ∴其面积为1(21)22322S =+⨯= 故选：A 【点睛】方法点睛：本题考查斜二测法画平面图形直观图，求原图形的面积，可能通过还原出原平面图形求得面积，也可以通过直观图到原图形面积的关系求解：直观图面积为S '，原图形面积为S ，则24S S '=． 12．A解析：A 【分析】把1AD 平移到1BC ，把异面直线所成的角转化为相交直线的夹角． 【详解】 连接1,BD BC ，∵四边形ABCD 为菱形， 60,4BAD AB ︒∠==，4BD ∴=.又1BDD 为直角三角形，22211BD BD DD ∴=+，得14DD =，∴四边形11BCC B 为正方形.连接1BC 交1B C 于点O 11//BC AD ，BOC ∴∠（或其补角)为异面直线1B C 与1AD 所成的角，由于11BCC B 为正方形， 90BOC ︒∴∠=，故异面直线1B C 与1AD 所成的角为90°. 故选：A. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．二、填空题13．60°【分析】根据AB ∥CD 得到异面直线与所成角即为∠VCD 由△VCD 为等边三角形即可求解【详解】如图示因为是正方形所以AB ∥CD 所以异面直线与所成角即为∠VCD 又各条棱长均为2所以△VCD 为等边三解析：60°【分析】根据AB ∥CD ,得到异面直线VC 与AB 所成角即为∠VCD ,由△ VCD 为等边三角形，即可求解. 【详解】如图示，因为ABCD 是正方形，所以AB ∥CD , 所以异面直线VC 与AB 所成角即为∠VCD. 又各条棱长均为2，所以△ VCD 为等边三角形， 所以∠VCD =60°，异面直线VC 与AB 所成角的大小为60°. 故答案为：60° 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： (1)平移：平移异面直线中的一条或两条，作出异面直线所成的角； (2)认定：证明作出的角就是所求异面直线所成的角； (3)计算：求该角的值，常利用解三角形； (4)取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．14．【分析】求出截面圆的半径设可得出从而可知球的半径为根据勾股定理求出的值可得出球的半径进而可求得球的表面积【详解】如下图所示设可得出则球的直径为球的半径为设截面圆的半径为可得由勾股定理可得即即所以球的解析：163π【分析】求出截面圆H 的半径，设AH x =，可得出3HB x =，从而可知，球O 的半径为2x ，根据勾股定理求出x 的值，可得出球O 的半径，进而可求得球O 的表面积. 【详解】如下图所示，设AH x =，可得出3HB x =，则球O 的直径为4AB x =，球O 的半径为2x ，设截面圆H 的半径为r ，可得2r ππ=，1r ∴=，由勾股定理可得()2222OH r x +=，即()22214x AH x -+=，即2214x x +=，3x ∴=， 所以，球O 的半径为232x =，则球O 的表面积为22316433S ππ⎛⎫=⨯= ⎪ ⎪⎝⎭. 故答案为：163π. 【点睛】方法点睛：在求解有关球的截面圆的问题时，一般利用球的半径、截面圆的半径以及球心到截面圆的距离三者之间满足勾股定理来求解.15．【分析】取与中点根据平面平面可知平面球心必在直线上设球心为D 则可求得球心恰好为点O 从而求得外接球的半径代入球的表面积公式计算【详解】在三棱台中可得都是等腰三角形四边形为等腰梯形即如图取与中点连接则可 解析：32π【分析】取AB 与11A B 中点,O O '，根据平面11AA B B ⊥平面ABC ，可知'⊥O O 平面ABC ，球心必在直线O O '上，设球心为D ，则()22221O D O O OC O D O C ''''-+=+，可求得球心恰好为点O ，从而求得外接球的半径R ，代入球的表面积公式计算. 【详解】在三棱台111ABC A B C -中，11190,4,22ACB AC BC A B CC ∠=︒====111,A A C C B B 都是等腰三角形，11112A C B C ==，四边形11A ABB 为等腰梯形即11AA BB =，如图，取AB 与11A B 中点,O O '，连接1,,CO OO C O ''，则可得122,2CO C O '==O O AB '⊥，又平面11AA B B ⊥平面ABC ，两面交线为AB ，所以'⊥O O 平面ABC .因为OA OB OC ==,111O A O B O C '''==,面//ABC 面111A B C ,所以球心必在直线O O '上.所以在直角梯形1C O OC '中可求得6O O '=，由题意可知，该三棱台外接球的外接球的球心必在直线O O '上，设球的半径为R ，球心为D ，则()22221O D O O OC O D O C ''''-+=+，得6O D '=，所以球心恰好为点O ，所以球的半径为22，所以该三棱台外接球的表面积为24(22)32ππ=. 故答案为：32π【点睛】方法点睛：定义法：到各个顶点距离均相等的点为外接球的球心，借助面面垂直的性质，找到线面垂直，则球心一定在垂线上，再根据到其他顶点距离也是半径，列关系求解即可.16．【分析】设为正方形的中心的中点为连接求出如图分别可求得大球与小球半径分别为和进而可得小球的体积【详解】解：由题中条件知底面四边形是边长为2的正方形设O 为正方形的中心的中点为M 连接则如图在截面中设N 为 解析：224【分析】设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，求出OM ，PM ，PO ，如图，分别可求得大球1O 与小球2O 半径分别为22和24，进而可得小球的体积． 【详解】解：由题中条件知底面四边形ABCD 是边长为2的正方形.设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，则1OM =，221013PM PA AM =-=-=，9122PO =-=，如图，在截面PMO 中，设N为球1O 与平面PAB 的切点，则N 在PM 上，且1O N PM ⊥，设球1O 的半径为R ，则1O N R =，∵1sin 3OM MPO PM ∠==，∴1113NO PO =，则13PO R =，11422PO PO OO R =+==∴22R =，设球1O 与球2O 相切于点Q ，则22PQ PO R R =-=，设球2O 的半径为r ，同理可得4PQ r =，∴224R r ==，故小球2O 的体积342324V r ππ==.故答案为：224π．【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.17．②④【分析】①求出该八面体的体积即可判断；②可得球心为正方形ABCD 对角线交点即可得出半径求出表面积；③取AD 的中点G 连接EGFGEF 过E 作求出即可；④可得为所成角【详解】①八面体的体积为；②八面体解析：②④ 【分析】①求出该八面体的体积即可判断；②可得球心为正方形ABCD 对角线交点，即可得出半径求出表面积；③取AD 的中点G ，连接EG ，FG ，EF ，过E 作EH FG ⊥，求出EH 即可；④可得DEC ∠为所成角. 【详解】①八面体的体积为2122(22)33⨯⨯=②八面体的外接球球心为正方形ABCD 2，表面积为8π；③取AD 的中点G ，连接EG ，FG ，EF ，易得3EG FG ==AD ⊥平面EGF ，过E 作EH FG ⊥，交FG 的延长线于H ，又EH AD ⊥，AD FG G ⋂=，故EH ⊥平面ADF ， 解得26EH =，所以E 到平面ADF 26； ④因为//ED BF ，所以EC 与BF 所成角为60︒.故答案为：②④.【点睛】解本题的关键是正确理解正八面体的性质，根据线面垂直关系得到点到平面的垂线段. 18．【分析】求出正三棱柱的高底面三角形的边长和高即可求出正三棱柱的体积【详解】设球的半径为r 由得则球的半径为2正三棱柱的高为正三棱柱底面正三角形的内切圆的半径是2所以正三角形的边长是高是6正三棱柱的体积 解析：3【分析】求出正三棱柱的高、底面三角形的边长和高，即可求出正三棱柱的体积.【详解】设球的半径为r ，由2416r π=π，得2r ，则球的半径为2，正三棱柱的高为24r =， 正三棱柱底面正三角形的内切圆的半径是2，所以正三角形的边长是36， 正三棱柱的体积为143644832⨯⨯= 故答案为：3【点睛】本题考查正三棱柱的内切球、正三棱柱的体积，考查空间想象能力与计算能力. 19．①③【分析】由公理1判断①正确；由公理2判断②错误③正确用反证法可得④错误【详解】∵连接∵是的中点∴平面与平面有公共点与则平面平面对于①平面则平面又平面则即三点共线故①正确；对于②在平面内由①知∴平解析：①③【分析】由公理1判断①正确；由公理2判断②错误③正确，用反证法可得④错误.【详解】∵连接11A C ，∵O 是11B D 的中点，∴11O A C ∈．平面11AB D 与平面11AAC C 有公共点A 与O ，则平面11AAC C 平面11AB D AO =．对于①，1M PA ∈，1PA ⊂平面11AAC C ，则M ∈平面11AAC C ，又M ∈平面11AB D ，则M AO ∈，即A ，M ，O 三点共线，故①正确；对于②，A ，O ，1A 在平面11AAC C 内，由①知M AO ∈，∴O ∈平面11AAC C ， 即A ，M ，O ，1A 共面，故②错误；对于③，A ，O ，C 在平面11AAC C 内，由①知M AO ∈，∴O ∈平面11AA C CA ， 则A ，M ，C ，O 共面11AAC C ，故③正确；对于④，连接BD ，则B ，1B ，O 都在平面11BB D D 上，若M ∈平面11BB D D ，则直线OM ⊂平面11BB D D ，∴A ∈面11BB D D ，显然A ∉面11BB D D 的，故④错误．∴正确命题的序号是①③．故答案为：①③．【点睛】本题考查命题的真假判断与应用，考查空间中的直线与平面、平面与平面的位置关系，考查空间想象能力与思维能力，是中档题.20．【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径设内切球半径为r ﹐圆锥高为h 结合轴截面图形计算得最后计算体积即可【详解】解：设圆锥底面半径为R 则所以设内切球半径为r ﹐圆锥高为h 则如图是圆锥轴截面三 解析：23π 【分析】根据圆锥底面圆周长为扇形弧长得圆锥底面半径1R =，设内切球半径为r ﹐圆锥高为h ，结合轴截面图形计算得2r ，最后计算体积即可. 【详解】 解：设圆锥底面半径为R ，则2233R ππ=⨯，所以1R =． 设内切球半径为r ﹐圆锥高为h ，则9122h =-=，如图，是圆锥轴截面三角形图，所以3r R h r =-，解得：2r ， 故3442223383r V πππ==⨯=． 故答案为：23π【点睛】本题考查圆锥的侧面展开图，圆锥的内切球的体积，考查空间想象能力，是中档题.三、解答题21．（1）证明见解析；（2）62 【分析】（1）取PB 中点M ，连接,MF AM ，证出四边形AMFE 为平行四边形，利用线面平行的判定定理即可证明.（2）连接,PE BE ，可得PEB ∠为二面角P AD B --的平面角，求出22PE =，再利用余弦定理可得PB ，再利用面面垂直的判定定理证明平面PBE ⊥平面PDA ，点B 作BO PE ⊥交PE 于点O ，在PEB △中即可求解.【详解】解：（1）证明：取PB 中点M ，连接,MF AM ，由F 为PC 中点，则//MF BC 且12MF BC =. 由已知有//,BC AD BC AD =， 又由于E 为AD 中点，从而//,MF AE MF AE =，故四边形AMFE 为平行四边形，所以//EF AM .又AM ⊂平面PAB ，而EF ⊂/平面PAB ，则//EF 平面PAB .（2）证明：连接,PE BE .由,PA PD BA BD ==，而E 为AD 中点，所以,PE AD BE AD ⊥⊥，所以PEB ∠为二面角P AD B --的平面角，60PEB ∴∠=︒.又2,90,22BA BD DBA AD ==∠=︒∴=.∴在PAD △中，由10,22PA PD AD ===，可解得22PE =.在Rt ABD △中，由22,AD E =为AD 的中点，可得122BE AD ==. ∴在PEB △中，2222cos PB PE EB PE EB PEB =+-⋅∠，2182222262PB ∴=+-⨯⨯⨯=， 2226,,PB PB EB PE PB EB ∴=∴+=∴⊥.又,,,PE AD BE AD PE BE E AD ⊥⊥⋂=∴⊥平面PBE ，AD ⊂平面PAD ，∴平面PBE ⊥平面PDA .过点B 作BO PE ⊥交PE 于点,O OB ∴⊥平面PDA .∴在PEB △中，OB PE PB EB ⋅=⋅，从而626222PB EB OB PE ⋅⨯===. ∴点B 到平面PAD 的距离为62.【点睛】关键点点睛：本题考查了面面垂直的判定定理，求点到面的距离，解题的关键是求出6PB =，证出平面PBE ⊥平面PDA ，作出点到面的距离，考查了计算能力.22．（1）证明见解析；（2）点F 为PC 的中点，证明见解析.【分析】（1）连接,DE PE ，可证明四边形DGBE 是平行四边形，得出//BG DE ，利用线面平行的判断定理即可证明；（2）猜想点F 为PC 的中点时，平面DEF ⊥平面ABCD ，再利用面面垂直的性质定理证明PG ⊥平面ABCD ，//OF PG ，可得OF ⊥平面ABCD ，利用面面垂直的判定定理即可证明.【详解】（1）连接,DE PE ，因为G 为AD 的中点，E 为BC 的中点， 所以12DG DA =，12BE BC =， 因为底面ABCD 是菱形，所以AD BC ∥， 所以DG BE ，所以四边形DGBE 是平行四边形，所以//BG DE ，又因为BG ⊄平面PDE ，DE ⊂平面PDE ，所以//BG 平面PDE ，（2）点F 为PC 的中点时，平面DEF ⊥平面ABCD ，证明如下：因为侧面PAD 为正三角形，G 为AD 的中点，所以PG AD ⊥，因为平面PAD ⊥平面ABCD ， 平面PAD 平面ABCD AD =，PG AD ⊥，PG ⊂平面PAD ，所以PG ⊥平面ABCD ，连接CG 交DE 于点O ，则点O 是CG 的中点，所以//OF PG ，所以OF ⊥平面ABCD ，又因为OF ⊂平面DEF ，所以平面DEF ⊥平面ABCD .【点睛】方法点睛：证明面面垂直的方法（1）利用面面垂直的判定定理，先找到其中一个平面的一条垂线，再证明这条垂线在另外一个平面内或与另外一个平面内的一条直线平行即可；（2）利用性质：//,αββγαγ⊥⇒⊥（客观题常用）；（3）面面垂直的定义（不常用）；（4）向量方法：证明两个平面的法向量垂直，即法向量数量积等于0.23．（1）3π；（2）98π.【分析】（1）先由圆的周长公式求出圆锥的底面圆的半径，再求圆锥的底面积；（2）圆柱的高1OO h =，OD r =，再由11AO D △AOB 求出,h r 的关系式，进而得出圆柱的侧面积，再结合二次函数的性质以及圆柱的体积公式求解即可.【详解】解：（1）沿母线AB 剪开，侧展图如图所示：设OB R =，在半圆⊙A 中，23AB = 弧长'23BB π=，这是圆锥的底面周长，所以223R ππ=，所以3R ，故圆锥的底面积为23S R ππ==圆锥；（2）设圆柱的高1OO h =，OD r =，在Rt AOB 中，223AO AB OB -=，11AO D △AOB ，所以111AO O D AO OB =， 即333h -=33h r =， 222(33)23(3)S rh r r r r πππ===-圆柱侧面积，23333r π⎛=--+ ⎝⎭， 所以，当32r =，32h =时，圆柱的侧面积最大，此时298Vr h ππ==圆柱. 【点睛】关键点睛：在第一问中，关键是由圆锥底面圆的周长与侧面展开扇形的弧长相等，从而求出圆锥底面圆的半径.24．（Ⅰ）证明见解析；（Ⅱ）3 【分析】（Ⅰ）取AC 中点M ，连接PM ，BM ，可得P 在平面ABC 的投影在直线BM 上，即6PBM π∠=，由余弦定理求出2PB =，即可由勾股定理判断PM BM ⊥，结合PM AC ⊥即可证明； （Ⅱ）取BM 中点O ，连接PO ，可得PO ⊥平面ABC ，利用等体积法求出点B 到平面PAC 的距离，即可求出直线AB 与平面PAC 所成角的正弦值.【详解】 （Ⅰ）取AC 中点M ，连接PM ，BM ，,BC BA PA PC ==，,BM AC PM AC ∴⊥⊥， PM BM M =，AC ∴⊥平面PMB ，AC ⊂平面ABC ，∴平面ABC ⊥平面PMB ，P ∴在平面ABC 的投影在直线BM 上，则PBM ∠即为直线PB 与平面ABC 所成的角，6PBM π∴∠=，11,32PM AC BM === 由余弦定理可得22231cos 623PB PBπ+-=⋅，解得1PB =或2，PB PC >，2PC =2PB ∴=，则满足222PM BM PB +=，PM BM ∴⊥，,PM AC AC BM M ⊥⋂=，PM ∴⊥平面ABC ，PM ⊂平面PAC ，∴平面PAC ⊥平面ABC ；（Ⅱ）若PB PC <，则由（Ⅰ）可得1PB =，取BM 中点O ，连接PO ，1PM =，PO BM ∴⊥，由（Ⅰ）AC ⊥平面PMB ，AC ⊂平面ABC ，∴平面ABC ⊥平面PMB ，平面ABC 平面PMB BM =，PO ∴⊥平面ABC ，且2231122PO ⎛⎫=-= ⎪ ⎪⎝⎭， 设点B 到平面PAC 的距离为d ，则由P ABC B PAC V V --=可得1133ABC PAC S PO S d ⋅=⋅， 即11111232132232d ⨯⨯=⨯⨯⨯⨯，解得32d =， 设直线AB 与平面PAC 所成角为θ，则3sin 4d AB θ==. 【点睛】本题考查线面角的求解，解题的关键是利用等体积法求出点B 到平面PAC 的距离，即可建立关系求出正弦值. 25．（1）证明见解析；（2）263. 【分析】（1）证明出AC ⊥平面PBD ，利用面面垂直的判定定理可证得结论成立；（2）连接OE ，推导出点E 为PB 的中点，利用等体积法可得出B AEC E ABC V V --=，利用锥体的体积公式即可得解.【详解】 （1）因为四边形ABCD 为正方形，则AC BD ⊥， PD ⊥底面ABCD ，AC ⊂平面ABCD ，AC PD ∴⊥，PD BD D ⋂=，AC ∴⊥平面PBD ，AC ⊂平面EAC ，∴平面EAC ⊥平面PBD ；（2）如下图所示，连接OE ，。

一、选择题1．在空间四边形ABCD 中，AB BC =，AD DC =，则对角线AC 与BD 所成角的大小是（ ） A ．90︒B ．60︒C ．45︒D ．302．已知三棱锥A BCD -的各棱长都相等，E 为BC 中点，则异面直线AB 与DE 所成角的余弦值为（ ） A ．136B ．36C ．336D ．1163．如图，正三棱柱111ABC A B C -的高为4，底面边长为43，D 是11B C 的中点，P 是线段1A D 上的动点，过BC 作截面AP α⊥于E ，则三棱锥P BCE -体积的最小值为（ ）A ．3B ．23C ．43D ．124．下图中小正方形的边长为1，粗线画出的是某四棱锥的三视图，则该四棱锥的体积为（ ）A ．64B ．48C ．32D ．165．已知球O 的半径为5，球面上有,,A B C 三点，满足214,27AB AC BC ===，则三棱锥O ABC -的体积为（ ） A ．77B ．142C ．714D ．1476．已知一个正三棱锥的四个顶点都在一个球的球面上，且这个正三棱锥的所有棱长都为22，求这个球的表面积（ ） A ．4π B ．8πC ．12πD ．24π7．在正方体1111ABCD A BC D -中，M 是棱1CC 的中点．则下列说法正确的是（ ） A ．异面直线AM 与BC 所成角的余弦值为53B ．BDM 为等腰直角三角形C ．直线BM 与平面11BDD B 所成角的正弦值等于105D ．直线1AC 与平面BDM 相交8．如图，正方形ABCD 的边长为4，点E ，F 分别是AB ，B C 的中点，将ADE ，EBF △，FCD 分别沿DE ，EF ，FD 折起，使得A ，B ，C 三点重合于点A '，若点G 及四面体A DEF '的四个顶点都在同一个球面上，则以FDE 为底面的三棱锥G -DEF 的高h 的最大值为（ ）A ．263+B ．463+C ．4263-D ．2263-9．如下图所示是一个正方体的平面展开图，在这个正方体中①//BM 平面ADE ；②D E BM ⊥；③平面//BDM 平面AFN ；④AM ⊥平面BDE ．以上四个命题中，真命题的序号是（ ）A ．①②③④B ．①②③C ．①②④D ．②③④10．某三棱锥的三视图如图所示， 则该三棱锥的体积为（ ）A ．16B ．13C ．23D ．211．空间四边形PABC 的各边及对角线长度都相等，D 、E 、F 外别是AB 、BC 、CA 的中点，下列四个结论中不成立的是（ ） A ．//BC 平面PDF B ．DF ⊥平面PAE C ．平面PDE ⊥平面ABCD ．平面PAE ⊥平面ABC12．已知三棱锥D ABC -，记二面角C AB D --的平面角是θ，直线DA 与平面ABC 所成的角是1θ，直线DA 与BC 所成的角是2θ，则（ ） A ．1θθ≥B ．1θθ≤C ．2θθ≥D ．2θθ≤二、填空题13．已知ABC 三个顶点都在球O 的表面上，且1AC BC ==，2AB =，S 是球面上异于A ､B ､C 的一点，且SA ⊥平面ABC ，若球O 的表面积为16π，则球心O 到平面ABC 的距离为____________.14．已知正四棱锥的体积为18，侧棱与底面所成的角为45，则该正四棱锥外接球的表面积为___________.15．已知三棱锥P ABC -的外接球O 的表面积为12π，PA ⊥平面ABC ，BA AC ⊥，2PA =，则ABC 面积的最大值为__________．16．如图，在矩形ABCD 中，2AB =，1AD =，点E 为CD 的中点，F 为线段CE （端点除外）上一动点．现将DAF △沿AF 折起，使得平面ABD ⊥平面ABC ．设直线FD 与平面ABCF 所成角为θ，θ的取值范围为__________．17．如图，在三棱台111ABC A B C -中，11190,4,22ACB AC BC A B CC ∠=︒====，平面11AA B B ⊥平面ABC ，则该三棱台外接球的表面积为___________.18．如图，在直角梯形ABCD 中，//,,2,3,60AB CD AB AD CD AB ABC ⊥==∠=°，将此梯形以AD 所在直线为轴旋转一周，所得几何体的表面积是_________________．19．在三棱锥-P ABC 中，侧面PBC 和底面ABC 都是边长为2的正三角形，若3PA =，则侧棱PA 与底面ABC 所成的角的大小是___________．20．水平放置的ABC ∆的斜二测直观图如图所示,已知''4,''3B C A C ==,则ABC ∆中AB 边上的中线的长度为_______ .三、解答题21．如图，在四棱锥M ABCD -中，四边形ABCD 为梯形，90ABC BAD ∠=∠=，//BC AD ，22AD AB BC ==（1）若E 为MA 中点，证明：BE //面MCD（2）若点M 在面ABCD 上投影在线段AC 上，1AB =，证明：CD ⊥面MAC . 22．如图，四面体ABCD 中，O 是BD 的中点，点G 、E 分别在线段AO 和BC 上，2BE EC =，2AG GO =，2CA CB CD BD ====，2AB AD ==.（1）求证：//GE 平面ACD ； （2）求证：平面ABD ⊥平面BCD .23．如图，在三棱柱111ABC A B C -中，1B C ⊥平面ABC ，侧面11ABB A 为矩形，11,2AB AA AC ===.（1）证明：平面11ABB A ⊥平面1BB C ； （2）求四棱锥11C ABB A -的体积.24．如图，三棱锥V —ABC 中， VA=VB ＝AC=BC=2，AB ＝23，VC=1．（1）证明： AB ⊥VC ； （2）求三棱锥V —ABC 的体积．25．如图，在直角梯形ABED 中，//BE AD ，DE AD ⊥，BC AD ⊥，4AB =，23BE =将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE .（1）若BC BE =，证明：平面ABD ⊥平面ACE ；（2）当三棱锥A BCE -的体积最大时，求平面ADE 与平面ABC 所成的锐二面角的余弦值.26．如图，四棱锥P ABCD -中，底面ABCD 是正方形，PD ⊥平面ABCD ，226AB PD ==，，O 为AC 与BD 的交点，E 为棱PB 上一点.（1）证明：平面EAC ⊥平面PBD ；（2）若//PD 平面EAC ，求三棱锥B AEC -的体积.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】取AC 中点O ，根据条件分析AC 与平面BOD 的位置关系，由此得到异面直线AC 与BD 所成角的大小.【详解】取AC 中点O ，连接,,BO DO BD ，如图所示：因为AB BC =，AD DC =，所以,BO AC DO AC ⊥⊥，且BO DO O =，所以AC ⊥平面BOD ，又BD ⊂平面BOD ，所以AC BD ⊥，所以AC 与BD 所成角为90︒， 故选：A.【点睛】关键点点睛：解答问题的关键是通过找AC 中点证明线面垂直，从而确定出线线垂直关系，和常规的求解异面直线所成角的方法不同.2．B解析：B 【分析】取AC 中点F ，连接,EF DF ，证明FED ∠是异面直线AB 与DE 所成角（或其补角），然后在三角形中求得其余弦值即可得． 【详解】取AC 中点F ，连接,EF DF ，∵E 是BC 中点，∴//EF AB ，12EF AB =， 则FED ∠是异面直线AB 与DE 所成角（或其补角）， 设1AB =，则12EF =，32DE DF ==， ∴在等腰三角形DEF 中，11324cos 63EFFED DE ∠===．所以异面直线AB 与DE 3 故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．3．C解析：C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时，三棱锥P BCE -体积有最小值，建立坐标系求得当点E 的高为3时，问题得解. 【详解】以点O 为原点，,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系，如图所示：设点(),0,E x z ，依题意得()6,0,0A ，则()6,0,AE x z =- ，(),0,OE x z = 因为过BC 作截面AP α⊥于E ，所以AE OE ⊥则0AE OE ⋅=，故()2600x x z -++= 所以()6z x x =-，当3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅⋅= 故选：C 【点睛】关键点点晴：本题的解题关键是将问题转化为求E ABC V -的最大值，通过建系求得三棱锥E ABC -的高的最大值即可.4．C解析：C 【分析】在长方体中还原三视图后，利用体积公式求体积. 【详解】根据三视图还原后可知，该四棱锥为镶嵌在长方体中的四棱锥P -ABCD （补形法） 且该长方体的长、宽、高分别为6、4、4， 故该四棱锥的体积为1(64)4323V =⨯⨯⨯=. 故选C ． 【点睛】(1)根据三视图画直观图，可以按下面步骤进行：①、首先看俯视图，根据俯视图画出几何体地面的直观图 ；②、观察正视图和侧视图找到几何体前、后、左、右的高度；③、画出整体，让后再根据三视图进行调整；(2)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解．5．A解析：A 【分析】利用正弦定理求出ABC 的外接圆半径，则可求出三棱锥的高，进而求出三棱锥体积. 【详解】设ABC 的外接圆的圆心为D ，半径为r ， 在ABC 中，72cos 4214ABC ∠==，14sin ABC ∴∠=， 由正弦定理可得28sin ACr ABC==∠，即4r =，则22543OD =-=，11114214273773324O ABC ABCV SOD -∴=⨯⨯=⨯⨯⨯⨯⨯=. 故选：A.【点睛】本题考查球内三棱锥的相关计算，解题的关键是利用正弦定理求出ABC 的外接圆半径，利用勾股关系求出高.6．C解析：C 【分析】将正三棱锥补成一个正方体，计算出正方体的棱长，可得出正方体的体对角线长，即为外接球的直径，进而可求得这个球的表面积. 【详解】设该正三棱锥为A BCD -，将三棱锥A BCD -补成正方体AEBF GCHD -，如下图所示：则正方体AEBF GCHD -2222=，该正方体的体对角线长为23 所以，正三棱锥A BCD -的外接球直径为223R =3R该球的表面积为2412S R ππ==.故选：C.【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可. 7．C解析：C【分析】A 通过平移，找出异面直线所成角，利用直角三角形求余弦即可.B.求出三角形的三边，通过勾股定理说明是不是直角三角形.C.求出点M 到面11BB D D 的距离，再求直线BM 与平面11BDD B 所成角的正弦.D.可通过线线平行证明线面平行.【详解】设正方体棱长为2A. 取1BB 的中点为N ，则//BC MN ，则AM 与BC 所成角为AMN ∠由BC ⊥面11ABB A ，故MN ⊥面11ABB A ，故MN AN ⊥，在Rt ANM △中，5tan AMN ∠=，故2cos 3AMN ∠=B. BDM 中，5BM =，22BD =，5DM =，不满足勾股定理，不是直角三角形C. AC BD ⊥，1AC BB ⊥，故AC ⊥面11BB D D ，1//CC 面11BB D D ，故M 到面11BB D D 的距离等于C 到面11BB D D 的距离，即为122d AC ==直线BM 与平面11BDD B 所成角为θ 210sin 55d BM θ=== 直线BM 与平面11BDD B 所成角的正弦值等于10 D.如图AC BD O =OM 为1ACC △的中位线，有1//OM AC故直线1AC 与平面BDM 平行故选：C【点睛】本题考查了空间几何体的线面位置关系判定与证明：（1）对于异面直线的判定要熟记异面直线的概念：把既不平行也不相交的两条直线称为异面直线；（2）对于线面位置关系的判定中，熟记线面平行与垂直、面面平行与垂直的定理是关键. 8．A解析：A【分析】先求出'A FDE -外接球的半径和外接圆的半径，再利用勾股定理求出外接球的球心到外接圆的圆心的距离，可得高h 的最大值.【详解】因为A ，B ，C 三点重合于点A '，原来A B C ∠∠∠、、都是直角，所以折起后三条棱'''A F A D A E 、、互相垂直，所以三棱锥'A FDE -可以看作一个长方体的一个角，它们有相同的外接球，外接球的直径就是长方体的体对角线，即为'2'2'22441626R AF AD AE =++=++6R =，2241625DE DF AD AE ==+=+=2222EF BE BF =+在DFE △中，22210cos 21022522DE EF DF DEF DE EF +-∠===⨯⨯⨯， 所以DEF ∠为锐角，所以2310sin 1cos DEF DEF ∠=-∠=， DEF 的外接圆的半径为5522sin 310DF r DEF ===∠则球心到DEF 2223R r -，以FDE 为底面的三棱锥G -DEF 的高h 的最大值为1R OO +263. 故选：A.【点睛】 本题考查了翻折问题和外接球的问题，关键点翻折前后量的变化及理解外接球和三棱锥的关系，考查了学生的空间想象力和计算能力.9．A解析：A【分析】把正方体的平面展开图还原成正方体ABCA ﹣EFMN ，得出BM ∥平面ADNE ，判断①正确；由连接AN ，则AN ∥BM ，又ED AN ⊥，判断②正确；由BD ∥FN ，得出BD ∥平面AFN ，同理BM ∥平面AFN ，证明平面BDM ∥平面AFN ，判断③正确；由MC BD ⊥，ED ⊥AM ，根据线面垂直的判定，判断④正确．【详解】把正方体的平面展开图还原成正方体ABCA ﹣EFMN ，如图1所示；对于①，平面BCMF ∥平面ADNE ，BM ⊂平面BCMF ，∴BM ∥平面ADNE ，①正确；对于②，如图2所示，连接AN ，则AN ∥BM ，又ED AN ⊥，所以D E BM ⊥，②正确； 对于③，如图2所示，BD ∥FN ，BD ⊄平面AFN ，FN ⊂平面AFN ，∴BD ∥平面AFN ；同理BM ∥平面AFN ，且BD ∩BM ＝B ，∴平面BDM ∥平面AFN ，③正确；对于④，如图3所示，连接AC ，则BD AC ⊥，又MC ⊥平面ABCD ，BD ⊂平面ABCD ，所以MC BD ⊥，又ACMC C ，所以BD ⊥平面ACM ，所以BD ⊥AM ， 同理得ED ⊥AM ，EDBD D =，所以AM ⊥平面BDE ，∴④正确．故选：A ．【点睛】关键点点睛：解决本题的关键在于展开空间想象，将正方体的平面展开图还原，再由空间的线线，线面，面面关系及平行，垂直的判定定理去判断命题的正确性．10．C解析：C【分析】根据题中所给的几何体的三视图还原几何体，得到相应的三棱锥，之后利用椎体体积公式求得结果.【详解】根据题中所给的几何体的三视图还原几何体如图所示：该三棱锥满足底面BCD △是等腰三角形，且底边和底边上的高线都是2；且侧棱AD ⊥底面BCD ，1AD =， 所以112=221=323V ⨯⨯⨯⨯， 故选：C.【点睛】方法点睛：该题考查的是有关根据所给几何体三视图求几何体体积的问题，解题方法如下：（1）应注意把握三个视图的尺寸关系：主视图与俯视图长应对正（简称长对正），主视图与左视图高度保持平齐（简称高平齐），左视图与俯视图宽度应相等（简称宽相等），若不按顺序放置和不全时，则应注意三个视图名称；（2）根据三视图还原几何体；（3）利用椎体体积公式求解即可. 11．C解析：C【分析】由线面平行的判定定理可判断A ；由线面垂直的判定定理可判断B ；反证法可说明C ；由面面垂直的判定定理可判断D.【详解】对于A ，D ，F 外别是AB ，CA 的中点，//BC DF ∴，DF ⊂平面PDF ，∴//BC 平面PDF ，故A 正确，不符合题意；对于B ，各棱长相等，E 为BC 中点，,BC AE BC PE ∴⊥⊥，PE AE E =， BC ∴⊥平面PAE ，//BC DF ，∴DF ⊥平面PAE ，故B 正确，不符合题意；对于C ，假设平面PDE ⊥平面ABC ，设DE BF O ⋂=，连接PO ，则O 是DE 中点，PO DE ∴⊥，平面PDE 平面ABC DE =，PO ∴⊥平面ABC ，BF ⊂平面ABC ，PO BF ∴⊥，则PB PF =，与PB PF ≠矛盾，故C 错误，符合题意；对于D ，由B 选项DF ⊥平面PAE ， DF ⊂平面ABC ，∴平面PAE ⊥平面ABC ，故D 正确，不符合题意.故选：C.【点睛】本题考查线面关系和面面关系的判定，解题的关键是正确理解判断定理，正确理解垂直平行关系.12．A解析：A【分析】设三棱锥D -ABC 是棱长为2的正四面体，取AB 中点E ，DC 中点M ，AC 中点M ，连结DE 、CE 、MN 、EN ，过D 作DO CE ⊥，交CE 于O ，连结AO ，则DEC θ∠=，1DAO θ∠=，2MNE θ∠=，排除B ，C ．当二面角C AB D --是直二面角时，2θθ≥，排除D ．由此能求出结果．【详解】设三棱锥D -ABC 是棱长为2的正四面体，取AB 中点E ，DC 中点M ，AC 中点M ，连结DE 、CE 、MN 、EN ，过D 作DO ⊥CE ，交CE 于O ，连结AO ，则DEC θ∠=，1DAO θ∠=，2MNE θ∠=，413DE CE ==-2DC =， ∴1cos 3233θ==⨯⨯，2233AO CO CE === ∴12333cos 3AO AD θ===， 取BC 中点F ，连结DF 、AF ，则DF BC ⊥，AF BC ⊥，又DF AF F ⋂=，∴BC ⊥平面AFD ，∴BC AD ⊥，∴290θ=︒， ∴21θθθ≥≥，排除B ，C ，当二面角C AB D --是直二面角时，2θθ≥，排除D ，故选：A .【点睛】关键点点睛：将三棱锥看成特殊的正四面体，采用排除法，充分理解线线角、线面角以及面面的概念是解题的关键.二、填空题13．【分析】根据题中的垂直关系确定球心再根据球的表面积公式计算再求点到平面的距离【详解】由并且平面平面且平面是直角三角形和的公共斜边取的中点根据直角三角形的性质可知所以点是三棱锥外接球的球心设则则三棱锥解析：2 【分析】根据题中的垂直关系，确定球心O ，再根据球的表面积公式计算SA ，再求点O 到平面ABC 的距离.【详解】由222AC BC AB +=，AC BC ∴⊥，并且SA ⊥平面ABC ，BC ⊂平面ABC ，SA BC ∴⊥，且AC SA A ⋂=BC ∴⊥平面SAC ，BC SC ∴⊥，SB ∴是直角三角形SBC 和SAB 的公共斜边，取SB 的中点O ，根据直角三角形的性质可知OA OB OC OS ===，所以点O 是三棱锥S ABC -外接球的球心，设SA x =，则12r SB ==则三棱锥S ABC -外接球的表面积2416S r ππ==，()21264x +=，解得：x =,点O 到平面ABC 的距离122d SA ==.故答案为：142【点睛】 方法点睛：本题考查了球与几何体的综合问题，考查空间想象能力以及化归和计算能力，（1）当三棱锥的三条侧棱两两垂直时，并且侧棱长为,,a b c ，那么外接球的直径2222R a b c =++，（2）当有一条侧棱垂直于底面时，先找底面外接圆的圆心，过圆心做底面的垂线，球心在垂线上，根据垂直关系建立R 的方程.（3）而本题类型，是两个直角三角形的公共斜边的中点是外接球的球心.14．【分析】作出图形计算出正四棱锥的高与底面边长设底面的中心为计算得出为正四棱锥的外接球球心可求得该正四棱锥的外接球半径即可得解【详解】如下图所示设正四棱锥的底面的中心为连接设正四棱锥的底面边长为则由于 解析：36π【分析】作出图形，计算出正四棱锥P ABCD -的高与底面边长，设底面ABCD 的中心为E ，计算得出E 为正四棱锥P ABCD -的外接球球心，可求得该正四棱锥的外接球半径，即可得解.【详解】如下图所示，设正四棱锥P ABCD -的底面ABCD 的中心为E ，连接PE 、AC 、BD ，设正四棱锥P ABCD -的底面边长为a ，则2AC BD a ==，由于E 为正四棱锥P ABCD -的底面ABCD 的中心，则PE ⊥平面ABCD ，由于正四棱锥P ABCD -的侧棱与底面所成的角为45，则45PAC PCA ∠=∠=， 所以，PAC △是以APC ∠为直角的等腰直角三角形，同理可知，PBD △是以BPD ∠为直角的等腰直角三角形，E 为AC 的中点，122PE AC a ==，2ABCD S a =正方形，2311183326P ABCD ABCD V S PE a a a -=⋅=⨯⨯==正方形，解得a = 232PE a ==，由直角三角形的性质可得1122PE AC BD ==， 即PE AE BE CE DE ====，所以，E 为正四棱锥P ABCD -外接球的球心， 球E 的半径为3r PE ==，该球的表面积为2436r ππ=.故答案为：36π.【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可. 15．2【分析】由球的表面积可求出半径取的中点可得设由基本不等式可得即可求出面积的最大值【详解】因为球的表面积为所以球的半径取的中点则为的外接圆圆心平面设由得因为所以当且仅当时取等因为的面积为所以面积的最 解析：2【分析】由球的表面积可求出半径R BC 的中点D ，可得1OD =，设AB x =，AC y =，由基本不等式可得4xy ≤，即可求出ABC 面积的最大值.【详解】因为球O 的表面积为12π，所以球O 的半径R = 取BC 的中点D ，则D 为ABC 的外接圆圆心，PA ⊥平面ABC ，112OD PA ∴==，设AB x =，AC y =，由===R OC 228x y +=． 因为222x y xy +≥，所以4xy ≤，当且仅当2x y ==时取等．因为ABC 的面积为1122⋅=AB AC xy ，所以ABC 面积的最大值为2． 故答案为：2.【点睛】本题考查几何体的外接球问题，解题的关键是是建立勾股关系，利用基本不等式求出4xy ≤.16．【分析】在矩形中作交于交于在翻折后的几何体中证得平面平面从而平面得是直线与平面所成的角设C 求得的范围后可得范围【详解】在矩形中作交于交于设由图易知∴即∴则在翻折后的几何体中又平面∴平面又平面∴平面平 解析：(0,]6π 【分析】在矩形ABCD 中作DO AF ⊥，交AF 于O ，交AB 于M ，在翻折后的几何体中，证得平面ODM ⊥平面ABCF ，从而DM ⊥平面ABCF ，得DFM ∠是直线FD 与平面ABCF 所成的角．设(01)CF x x =<<C ，求得sin θ的范围后可得θ范围．【详解】在矩形ABCD 中作DO AF ⊥，交AF 于O ，交AB 于M ，设(01)CF x x =<<，AM t =，由图易知DAM FDA △△， ∴AM AD DA DF =，即112t x =-，∴12t x=-，01x <<，则112t <<． 在翻折后的几何体中，AF OD ⊥，AF OM ⊥，又ODOM O =，,OD OM ⊂平面ODM ，∴AF ⊥平面ODM ，又AF ⊂平面ABCF ，∴平面ODM ⊥平面ABCF ，又平面ABD ⊥平面ABC AB =．平面ODM 平面ABD DM =，∴DM ⊥平面ABCF ，连接MF ，则DFM ∠是直线FD 与平面ABCF 所成的角．DFM θ∠=， 而21DM t -12DF x t =-=， ∴2422211sin 1()24DM t t t t DF θ==-=-+=--+，∵112t <<，∴2114t <<，∴10sin 2θ<≤，即06πθ<≤． 故答案为：(0,]6π．【点睛】方法点睛：本题考查求直线与平面所成的角，求线面角常用方法：（1）定义法：作出直线与平面所成的角并证明，然后在直角三角形中计算可得；（2）向量法：建立空间直角坐标系，由直线的方向向量与平面的法向量夹角的余弦的绝对值等于直线与平面所成角的正弦值计算．17．【分析】取与中点根据平面平面可知平面球心必在直线上设球心为D 则可求得球心恰好为点O 从而求得外接球的半径代入球的表面积公式计算【详解】在三棱台中可得都是等腰三角形四边形为等腰梯形即如图取与中点连接则可 解析：32π【分析】取AB 与11A B 中点,O O '，根据平面11AA B B ⊥平面ABC ，可知'⊥O O 平面ABC ，球心必在直线O O '上，设球心为D ，则()22221O D O O OC O D O C ''''-+=+，可求得球心恰好为点O ，从而求得外接球的半径R ，代入球的表面积公式计算.【详解】在三棱台111ABC A B C -中，11190,4,22ACB AC BC A B CC ∠=︒====111,A A C C B B 都是等腰三角形，11112AC B C ==，四边形11A ABB 为等腰梯形即11AA BB =，如图，取AB 与11A B 中点,O O '，连接1,,CO OO C O ''，则可得122,2CO C O '=，O O AB '⊥，又平面11AA B B ⊥平面ABC ，两面交线为AB ，所以'⊥O O 平面ABC .因为OA OB OC ==,111O A O BO C '''==,面//ABC 面111A B C , 所以球心必在直线O O '上.所以在直角梯形1C O OC '中可求得6O O '=由题意可知，该三棱台外接球的外接球的球心必在直线O O '上，设球的半径为R ，球心为D ，则()22221O D O O OC O D O C ''''-+=+，得6O D '=，所以球心恰好为点O ， 所以球的半径为22，所以该三棱台外接球的表面积为24(22)32ππ=.故答案为：32π【点睛】方法点睛：定义法：到各个顶点距离均相等的点为外接球的球心，借助面面垂直的性质，找到线面垂直，则球心一定在垂线上，再根据到其他顶点距离也是半径，列关系求解即可. 18．【分析】此梯形以AD 所在直线为轴旋转一周得到的是圆台然后根据圆台的侧面积和表面积公式进行计算【详解】将此梯形以AD 所在直线为轴旋转一周得到的是圆台其中圆台的上底半径为r ＝CD ＝2下底半径为R ＝AB ＝ 解析：23π【分析】此梯形以AD 所在直线为轴旋转一周，得到的是圆台，然后根据圆台的侧面积和表面积公式进行计算．【详解】将此梯形以AD 所在直线为轴旋转一周，得到的是圆台，其中圆台的上底半径为r ＝CD ＝2，下底半径为R ＝AB ＝3，母线BC ＝2，∴圆台的上底面积为πr 2＝4π，下底面积为πR 2＝9π，圆台的侧面积为（πr +πR ）•BC ＝π（2+3）×2＝10π，∴圆台的表面积为4π+9π+10π＝23π，故答案为23π．【点睛】本题考查圆台表面积的计算，利用旋转体的定义确定该几何体是圆台是解决本题的关键． 19．【分析】先画出直观图证明平面平面然后侧棱与底面ABC 所成的角即为根据题目中的数据算出即可【详解】如图作的中点连结因为侧面PBC 和底面ABC 都是边长为2的正三角形而为的中点所以又所以平面同时平面所以平 解析：o 60.【分析】先画出直观图，证明平面PAD ⊥平面ABC ，然后侧棱PA 与底面ABC 所成的角即为PAD ∠，根据题目中的数据算出即可.【详解】如图，作BC 的中点D ，连结AD 、PD因为侧面PBC 和底面ABC 都是边长为2的正三角形而D 为BC 的中点，所以BC PD ⊥，BC AD ⊥，又PD AD D ⋂=，所以BC ⊥平面PAD ，同时BC ⊂平面ABC所以平面PAD ⊥平面ABC ，所以PAD ∠即为侧棱PA 与底面ABC 所成的角由侧面PBC 和底面ABC 都是边长为2的正三角形得 3AD PD ==，又已知3PA =所以PAD ∆为等边三角形，则=PAD ∠o 60即侧棱PA 与底面ABC 所成的角为o 60故答案为：o 60【点睛】本题主要考查空间直线与平面所成角的计算，较简单.20．【分析】首先根据直观图可知其平面图形为直角三角形且两条直线边长为长接下来利用勾股定理即可求出AB 的长然后利用直角三角形的性质进行解答即可【详解】把直观图还原成平面图形如图所示：得为直角三角形且两条直 解析：73 【分析】首先根据直观图可知其平面图形为直角三角形，且两条直线边长为长3,8AC BC ==，接下来利用勾股定理即可求出AB 的长，然后利用直角三角形的性质进行解答即可.【详解】把直观图还原成平面图形如图所示：得ABC ∆为直角三角形，且两条直角边的长3,8AC BC ==，由勾股定理可得73AB =，故三角形AB 边上的中线长为73， 故答案是732. 【点睛】 本题是一道关于平面几何图形的直观图的题目，解答本题的关键是熟练掌握斜二测画法的相关知识.三、解答题21．（1）证明见解析；（2）证明见解析.【分析】（1）取MD 中点为F ，连接EF ，CF ，四边形BCFE 为平行四边形，所以//BE CF ，利用线面平行的性质定理即可证明；（2）利用勾股定理证明AC CD ⊥，设点M 在面ABCD 上投影在线段AC 上设为点H ，再利用已知条件证明MH CD ⊥，利用线面垂直的判断定理即可证明.【详解】（1）取MD 中点为F ，连接EF ，CF ， 则EF 为△MAD 中位线，∴ 1//2EF AD 且1=2EF AD ， 又四边形ABCD 是直角梯形，22AD AB BC ==1//2BC AD ∴，1=2BC AD //BC EF ∴且=BC EF ，∴四边形BCFE 为平行四边形，所以//BE CF ，因为BE ⊄面MCD ，CF ⊂面 MCD ，所以//BE 面MCD .（2）在四棱锥M ABCD -中，四边形ABCD 是直角梯形，222AD AB BC ===，90ABC BAD ∠=∠=，22112AC CD ∴==+=222AC CD AD ∴+=，AC CD ∴⊥，设点M 在面ABCD 上投影在线段AC 上，设为点H ，MH ∴⊥面ABCD ，CD ⊂面ABCD ， MH CD ∴⊥，又AC CD ⊥，AC MH H ⋂=，CD 面MAC .【点睛】方法点睛：证明直线与平面平行的常用方法（1）定义法：证明直线与平面没有公共点，通常要借助于反证法来证明；（2）判定定理：在利用判断定理时，关键找到平面内与已知直线平行的直线，常考虑利用三角形中位线、平行四边形的对边平行或过已知直线作一平面，找其交线进行证明； 22．（1）证明见解析；（2）证明见解析.【分析】（1）先依题意得到G 为ABD △的重心，即得到21BG BE GM EC ==，证得//GE MC ，再利用线面平行的判定定理即证结论；（2）先在ABD △中，证得AO BD ⊥，求得1AO =，在BCD △中，求得3OC =，结合勾股定理证得AO OC ⊥，再利用线面垂直的判定定理证明AO ⊥平面BCD ，即证平面ABD ⊥平面BCD .【详解】证明：（1）连接BG 并延长，交AD 于M ，连接MC ，在ABD △中，O 为BD 中点，G 在AO 上，2AG GO =，∴G 为ABD △的重心∴21BG GM =， 又21BE EC =∴BG BE GM EC=∴//GE MC ， ∵GE ⊄平面ACD ，AC ⊂平面ACD ，∴//GE 平面ACD ；（2）在ABD △中，O 为BD 中点，2BD =，2AB AD ==∴AO BD ⊥∴221AO AB BO -=，在BCD △中，2BC CD BD ===，O 为BD 中点，连接OC ，则OC = 又2CA =，∴222OA OC CA +=，∴AO OC ⊥由AO OC ⊥，AO BD ⊥，OCBD O =，,OC BD ⊂平面BCD ， 得AO ⊥平面BCD ，又AO ⊂平面ABD ，∴平面ABD ⊥平面BCD .【点睛】思路点睛：证明线面平行时运用线面平行的判定定理证得，或者利用面面平行的性质证得；证明线面垂直时，运用其判定定理需要证明一条直线与相交的两条直线垂直，当题目条件中给出长度时可以采用勾股定理逆定理证得线线垂直，或者运用面面垂直的性质定理证得线面垂直．23．（1）证明见解析；（2 【分析】（1）根据线面垂直的判定定理，先证明AB ⊥平面1BB C ，再由面面垂直的判定定理，即可证明结论成立；（2）先由（1）得到AB BC ⊥，求出BC 和1BC ，过点C 作1CD BB ⊥于点D ，求出CD ，再由棱锥的体积公式，即可求出结果.【详解】（1）∵1B C ⊥平面ABC ，AB 平面ABC ，∴1B C AB ⊥，又四边形11ABB A 为矩形，∴1AB BB ⊥. 又∵111B B BC B ⋂=，1B B ⊂平面1BB C ，1B C ⊂平面1BB C ，∴AB ⊥平面1BB C ， 又AB 平面11ABB A ，∴平面11ABB A ⊥平面1BB C .（2）由（1）知AB ⊥平面1BB C ，∴AB BC ⊥，则BC 11B C ==，在1BB C △中，过点C 作1CD BB ⊥于点D ，由于平面11ABB A ⊥平面1BB C ，平面11ABB A 平面11BB C BB =， ∴CD ⊥平面11ABB A ，由1111122BC B S B C BC BB CD =⋅=⋅可得2CD =，∴四棱锥11C ABB A -的体积为11111233ABB A V S CD =⋅=⨯⨯=.。

立体几何单元测验题一、选择题：把每小题的正确答案填在第二页的答题卡中，每小题4分，共60分 1．一个圆锥的底面圆半径为3，高为4，则这个圆锥的侧面积为A ．152πB ．10πC ．15πD ．20π 2．C B A ,,表示不同的点，l a ,表示不同的直线，βα,表示不同的平面，下列推理错误的是A ．ααα⊂⇒∈∈∈∈lB l B A l A ,,, B ．,,,AB l l AB l αβαβαβ=⊥⊂⊥⇒⊥IC ．,l A l A αα⊄∈⇒∉D ．βαβα与不共线，，且⇒∈∈C B A C B A C B A ,,,,,,重合 3．直线c b a ,,相交于一点，经过这3条直线的平面有A ．0个B ．1个C ．3个D ．0个或1个 4．下列说法正确的是A ．平面α和平面β只有一个公共点B ．两两相交的三条直线共面C ．不共面的四点中，任何三点不共线D ．有三个公共点的两平面必重合5． 直线b a 与是一对异面直线，a B A 是直线,上的两点，b D C 是直线,上的两点，N M ，分别是BD AC 和的中点，则a MN 和的位置关系为A ．异面直线B ．平行直线C ．相交直线D ．平行直线或异面直线6．已知正方形ABCD ，沿对角线ABC AC ∆将折起，设AD 与平面ABC 所成的角为α，当α最大时，二面角D AC B --等于（ ）A ．090 B ．060 C ．045 D ．030 7．已知异面直线b a ,分别在平面βα,内，且βαI c =，直线c A ．同时与b a ,相交 B ．至少与b a ,中的一条相交 C ．至多与b a ,中的一条相交 D ．只能与b a ,中的一条相交 8．一个平面多边形的斜二侧图形的面积是S ，则这个多边形的面积是A B ．2S C ． D ．4SMD'DCBA1A 9．直线l 在平面α外，则A ．α//lB ．α与l 相交C ．α与l 至少有一个公共点D ．α与l 至多有一个公共点10．如图，BD AB BD M AC M AB BD AC AB ，，平面，平面，⊥⊥⊂===1与平面M 成030角，则D C 、间的距离为（ ） A ．1 B ．2 C ．2 D ．311．如果在两个平面内分别有一条直线，这两条直线互相平行，那么这两个平面的位置关系一定是A ．平行B ．相交C ．平行或相交D ．垂直相交 12．已知平面α及α外一条直线l ，下列命题中 （1）若l 垂直于α内的两条平行线，则α⊥l ；（2）若l 垂直于α内的所有直线，则α⊥l ；（3）若l 垂直于α内的两条相交直线，则α⊥l ；（4）若l 垂直于α内的任意一条直线，则α⊥l ；正确的有A ．0 个B ．1 个C ．2个D ．3个 13．与空间四点等距离的平面有A ．7个B ．2个C ．9个D ．7个或无穷多个 14．如果球的内接正方体的表面积为24，那么球的体积等于 A． B．C ．D ．315．直三棱柱111111ABC A B C AC AB AA AC A B-==中，，异面直线与 060所成的角为，则CAB ∠等于A ． 090 B ． 060 C ．045 D ．030姓名 班级 座位号二、解答题：（本大题共三个小题，共40分，要求写出求解过程） 16．（12分）在空间四边形ABCD 中，F E 、分别为BC AB 、中点。

一、选择题1．设m ，n 是两条异面直线，下列命题中正确的是（ ） A ．过m 且与n 平行的平面有且只有一个 B ．过m 且与n 垂直的平面有且只有一个C ．m 与n 所成的角的范围是()0,πD ．过空间一点P 与m 、n 均平行的平面有且只有一个2．平面α⊥平面 β，A ∈α，B ∈β，AB 与两平面α，β所成的角分别为4π和6π，过 A 、B 分别作两平面交线的垂线，垂足为 ,A B ''，则:AB A B ''等于( )．A ．3∶2B ．3∶1C ．2∶1D ．4∶33．设m ，n 是两条不同直线，α，β是两个不同的平面，下列命题正确的是( ) A ．//m α，//n β且//αβ，则//m nB ．m α⊂，n α⊂，//m β，//n β，则//αβ C ．m α⊥，n β⊂，m n ⊥，则αβ⊥ D ．m α⊥，n β⊥且αβ⊥，则m n ⊥4．在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，15AA =，则V 的最大值是（ ）A ．4πB ．92πC ．1256πD ．323π5．如图，梯形ABCD 中，AD ∥BC ，1AD AB ==，AD AB ⊥，45BCD ∠= ，将ABD ∆沿对角线BD 折起．设折起后点A 的位置为A '，并且平面A BD '⊥平面BCD .给出下面四个命题： ①A D BC '⊥；②三棱锥A BCD '-的体积为22； ③CD ⊥平面A BD '；④平面A BC '⊥平面A DC '.其中正确命题的序号是（ ）A ．①②B ．③④C ．①③D ．②④6．已知四棱锥S ABCD -的底面为矩形，SA ⊥底面ABCD ，点E 在线段BC 上，以AD 为直径的圆过点E .若33SA AB ==，则SED ∆的面积的最小值为（ ） A ．9B ．7C ．92D ．727．如图所示，AB 是⊙O 的直径，VA 垂直于⊙O 所在的平面，点C 是圆周上不同于A ，B 的任意一点，M ，N 分别为VA ，VC 的中点，则下列结论正确的是（ ）A ．MN //AB B ．MN 与BC 所成的角为45° C ．OC ⊥平面VACD ．平面VAC ⊥平面VBC 8．设l 是直线，α，β是两个不同的平面，则正确的结论是（ ）A ．若l ∥α，l ∥β，则α∥βB ．若l ∥α，l ⊥β，则α⊥βC ．若α⊥β，l ⊥α，则l ⊥βD ．若α⊥β，l ∥α，则l ⊥β9．半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形为面的多面体，体现了数学的对称美.如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，得到一个有十四个面的半正多面体，它们的棱长都相等，其中八个为正三角形，六个为正方形，称这样的半正多面体为二十四等边体.一个二十四等边体的各个顶点都在同一个球面上，若该球的表面积为16π，则该二十四等边体的表面积为（ ）A ．123+B ．183+C ．2483+D ．363+10．在长方体1111ABCD A B C D -中，23AB AD ==12CC =1C BD C --的大小是（ ）A ．30ºB ．45ºC ．60ºD ．90º11．设α、β是两个不同的平面，m 、n 是两条不同的直线，下列说法正确的是（ ） A ．若α⊥β，α∩β＝m ，m ⊥n ，则n ⊥β B ．若α⊥β，n ∥α，则n ⊥βC ．若m ∥α，m ∥β，则α∥βD ．若m ⊥α，m ⊥β，n ⊥α，则n ⊥β12．设,m n 是两条不同的直线，,αβ是两个不同的平面，则下列命题正确的是（ ） A ．若m n ⊥，//n α，则m α⊥B ．若//m β，βα⊥，则m α⊥C ．若m β⊥，n β⊥，n α⊥，则m α⊥D ．若m n ⊥，n β⊥，βα⊥，则m α⊥ 13．一个几何体的三视图如图所示，则该几何体的表面积为（ ）A ．186+B ．206+C ．2010+D ．1810+ 14．垂直于同一条直线的两条直线的位置关系是（ ）A ．平行B ．相交C ．异面D ．A 、B 、C 均有可能二、解答题15．在如图所示的几何体中，侧面CDEF 为正方形，底面ABCD 中，//AB CD ，222AB BC DC ===，30BAC ∠=，AC FB ⊥.（1）求证：AC ⊥平面FBC ；（2）线段AC 上是否存在点M ，使//EA 平面FDM ？证明你的结论. 16．如图，已知三棱锥A BCD -中，点M 在BD 上，2BAD BDC π∠=∠=，BM MD DC ==，且ACD 为正三角形.（1）证明：CM AD ⊥；（2）求直线CM 与平面ACD 所成角的正弦值.17．如图所示的几何体ABCDEF 中，四边形ABCD 为菱形，//AF DE ，AF ⊥平面ABCD ，BAD ∠=α.（1）求证：//BF 平面CDE ； （2）若60α=︒，12AF AD DE ==，求直线AE 与平面CDE 所成角的正弦值. 18．如图所示，在四棱锥P ABCD -中，90CAD ABC ∠=∠=，30BAC ADC ∠=∠=，PA ⊥平面ABCD ，E 为PD 中点，2AC =.（1）求证：//AE 平面PBC . （2）若四面体PABC 3PCD 的面积.19．如图三棱柱111ABC A B C －中，11,,60CA CB AB AA BAA ∠︒＝＝＝，（1）证明1AB A C ⊥；（2）若16AC ＝，2AB CB ＝＝，求三棱柱111ABC A B C －的体积S . 20．如图，在三棱柱111ABC A B C -中，1CC ⊥面ABC ，2AC BC ==，22AB =，14CC =，M 是棱1CC 上一点．（1）若,M N 分别是1CC ，AB 的中点，求证：//CN 面1AB M ； （2）若132C M =，求二面角1A B M C --的大小． 21．如图所示正四棱锥S ABCD -，2,2SA SB SC SD AB =====，P 为侧棱SD 上的点.（1）求证：AC SD ⊥； （2）若3SAPAPDSS=，侧棱SC 上是否存在一点E ，使得BE ∥ 平面PAC .若存在，求SEEC的值；若不存在，试说明理由. 22．如图，在长方形ABCD 中，4AB =，2AD =，点E 是DC 的中点.将ADE 沿AE折起，使平面ADE ⊥平面ABCE ，连结DB 、DC 、EB .（1）求证：AD ⊥平面BDE ；（2）点M 是线段DA 的中点，求三棱锥D MEC -的体积.23．如图，在直三棱柱111ABC A B C -中，1AC CC =，AC BC ⊥，D 为1BC 中点，1AC 与1A C 交于点O .（1）求证：//OD 平面111A B C ； （2）求证：平面1AC B ⊥平面1A BC .24．如图，在平行四边形ABCD 中，4AB =，60DAB ∠=︒．点G ，H 分别在边CD ，CB 上，点G 与点C ，D 不重合，GH AC ⊥，GH 与AC 相交于点O ，沿GH 将CGH 翻折到EGH 的位置，使二面角E GH B --为90°，F 是AE 的中点．（1）请在下面两个条件：①AB AD =，②AB BD ⊥中选择一个填在横线处，使命题P ：若________，则BD ⊥平面EOA 成立，并证明．（2）在（1）的前提下，当EB 取最小值时，求直线BF 与平面EBD 所成角的正弦值． 25．如图，ABCD 是边长为2的正方形，ED ⊥平面ABCD ，1ED =，//EF BD .（1）设EF BD λ=，是否存在实数λ，使//BF 平面ACE ； （2）证明：平面EAC ⊥平面BDEF ； （3）当12EF BD =时，求几何体ABCDEF 的体积. 26．如图所示，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD DC =，E 是PC 的中点，过E 点作EF PB ⊥交PB 于点F .求证：（1）//PA 平面EDB ； （2）PB ⊥平面EFD .【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】在A 中，过m 上一点作n 的平行线，只能作一条l ，l 与m 是相交关系，故确定一平面与n 平行；在B 中，只有当m 与n 垂直时才能；在C 中，两异面直线所成的角的范围是0,2π⎛⎫⎪⎝⎭； 在D 中，当点P 与m ，n 中一条确定的平面与另一条直线平行时，满足条件的平面就不存在． 【详解】在A 中，过m 上一点P 作n 的平行直线l ，m l P ⋂=，由公理三的推论可得m 与l 确定唯一的平面α，l ⊂α，n ⊄α，故//n α．故A 正确．在B 中，设过m 的平面为β，若n ⊥β，则n ⊥m ，故若m 与n 不垂直，则不存在过m 的平面β与n 垂直，故B 不正确．在C 中，根据异面直线所成角的定义可知，两异面直线所成的角的范围是0,2π⎛⎫⎪⎝⎭，故C 不正确．在D 中，当点P 与m ，n 中一条确定的平面与另一条直线平行时，满足条件的平面就不存在，故D 不正确． 故选：A ． 【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，属于中档题．2．C解析：C 【分析】结合题意分别在直角三角形中求出各边之间的数量关系，从而计算出结果 【详解】在Rt ABB '∆中，cos 42AB AB AB π'=⋅=在Rt ABA '∆中，1sin 62AA AB AB π'=⋅=,在Rt AA B ''∆中，12A B AB ''==, 所以:2:1AB A B ''= 故选C 【点睛】本题运用线面角来解三角形的边长关系，较为基础3．D解析：D 【分析】对每一个命题逐一判断得解.【详解】对于A ，若m ∥α，n ∥β且α∥β，说明m 、n 是分别在平行平面内的直线，它们的位置关 系应该是平行或异面或相交，故A 不正确；对于B ，若“m ⊂α，n ⊂α，m ∥β，n ∥β”，则“α∥β”也可能α∩β＝l ，所以B 不成立． 对于C ，根据面面垂直的性质，可知m ⊥α，n ⊂β，m ⊥n ，∴n ∥α，∴α∥β也可能α∩β＝l ，也可能α⊥β，故C 不正确；对于D ，由m ⊥α，n ⊥β且α⊥β，则m 与n 一定不平行，否则有α∥β，与已知α⊥β矛盾，通过平移使得m 与n 相交，且设m 与n 确定的平面为γ，则γ与α和β的交线所成的角即 为α与β所成的角，因为α⊥β，所以m 与n 所成的角为90°，故命题D 正确． 故答案为D 【点睛】本题考查直线与平面平行与垂直，面面垂直的性质和判断的应用，考查逻辑推理能力和空间 想象能力.4．D解析：D 【分析】先保证截面圆与ABC 内切，记圆O 的半径为r ，由等面积法得()68AC AB BC r ++=⨯，解得2r．由于三棱柱高为5，此时可以保证球在三棱柱内部，球的最大半径为2，由此能求出结果．【详解】解：如图，由题意可知，球的体积要尽可能大时，球需与三棱柱内切． 先保证截面圆与ABC 内切，记圆O 的半径为r ， 则由等面积法得1111 (682222)ABC S AC r AB r BC r =++=⨯⨯△， 所以()68AC AB BC r ++=⨯，又因为6AB =，8BC =，所以10AC =，所以2r．由于三棱柱高为5，此时可以保证球在三棱柱内部，若r 增大，则无法保证球在三棱柱内，故球的最大半径为2，所以3344322333V r πππ==⋅=．故选：D ．【点评】本题考查球的最大体积的求法，考查空间想象能力，属于中档题.5．B解析：B 【分析】利用折叠前四边形ABCD 中的性质与数量关系，可证出BD DC ⊥，然后结合平面A BD '⊥平面BCD ，可得CD ⊥平面A BD '，从而可判断①③；三棱锥'A BCD -的体积为1122223226⋅=，可判断②；因为CD ⊥平面A BD '，从而证明CD A B '⊥，再证明'A B ⊥平面A DC '，然后利用线面垂直证明面面垂直. 【详解】 ①90,BAD AD AB ︒∠==，45ADB ABD ︒∴∠=∠=，//,45AD BC BCD ︒∠=，BD DC ∴⊥，平面A BD ' ⊥平面BCD ，且平面A BD'平面BCD BD =，CD 平面A BD '，A D '⊂平面A BD '，CD A D '∴⊥，若A D BC '⊥则A D '⊥面BCD ，则A D '⊥BD ，显然不成立， 故A D BC '⊥不成立，故①错误；②棱锥'A BCD -的体积为11222232⋅=，故②错误； ③由①知CD ⊥平面A BD '，故③正确； ④由①知CD ⊥平面A BD '，又A B '⊂平面A BD '，CD A B '∴⊥，又A B A D ''⊥，且'A D 、CD ⊂平面A DC '，A DCD D '=，A B '∴⊥平面A DC '，又A B '⊂平面'A BC ， ∴平面'A BC ⊥平面A DC '，故④正确.故选：B .【点睛】本题通过折叠性问题，考查了面面垂直的性质，面面垂直的判定，考查了体积的计算，关键是利用好直线与平面、平面与平面垂直关系的转化，也要注意利用折叠前后四边形ABCD 中的性质与数量关系.6．C解析：C【分析】根据线面垂直的性质以及线面垂直的判定，根据勾股定理，得到,BE EC 之间的等量关系，再用,BE EC 表示出SED 的面积，利用均值不等式即可容易求得.【详解】设BE x =，EC y =，则BC AD x y ==+.因为SA ⊥平面ABCD ，ED ⊂平面ABCD ，所以SA ED ⊥.又AE ED ⊥，SA AE A ⋂=，所以ED ⊥平面SAE ，则ED SE ⊥.易知AE =ED = 在Rt AED ∆中，222AE ED AD +=，即22233()x y x y +++=+，化简得3xy =.在Rt SED ∆中，SE =ED ==.所以12SED S SE ED ∆=⋅=.因为22108336x x +≥=，当且仅当x =2y =时等号成立，所以92SED S ∆≥=. 故选：C.【点睛】 本题考查空间几何体的线面位置关系及基本不等式的应用，考查空间想象能力以及数形结合思想，涉及线面垂直的判定和性质，属中档题.7．D解析：D【分析】由中位线性质，平移异面直线即可判断MN 不与AB 平行，根据异面直线平面角知MN 与BC 所成的角为90°，应用反证知OC 不与平面VAC 垂直，由面面垂直的判定知面VAC ⊥面VBC ，即可知正确选项.【详解】M ，N 分别为VA ，VC 的中点，在△VAC 中有//MN AC ，在面ABC 中AB AC A =，MN 不与AB 平行；AC BC C =，知：MN 与BC 所成的角为90BCA ∠=︒；因为OC ⋂面VAC C =，OC 与平面内交线,AC VC 都不垂直，OC 不与平面VAC 垂直； 由VA ⊥面ABC ，BC ⊂面ABC 即VA BC ⊥，而90BCA ∠=︒知AC BC ⊥，AC VA A ⋂=有BC ⊥面VAC ，又BC ⊂面VBC ，所以面VAC ⊥面VBC ； 故选：D【点睛】本题考查了异面直线的位置关系、夹角，以及线面垂直的性质，面面垂直判定的应用，属于基础题.8．B解析：B【分析】根据直线、平面间平行、垂直的位置关系判断．【详解】若l ∥α，l ∥β，则α∥β或,αβ相交，A 错；若l ∥α，由线面平行的性质得，知α内存在直线b 使得//l b （过l 作平面与α相交，交线即是平行线），又l ⊥β，∴b β⊥，∴α⊥β，B 正确；若α⊥β，l ⊥α，则不可能有l ⊥β，否则由l ⊥α，l ⊥β，得//αβ，矛盾，C 错； 若α⊥β，l ∥α，则l 与β可能平行，可能在平面内，可能相交也可能垂直，D 错． 故选：B ．【点睛】本题考查空间直线、平面间平行与垂直关系的判断，掌握直线、平面间位置关系是解题关键．9．C解析：C【分析】通过二十四等边体的外接球表面积求得半径，进而计算出二十四等边体的边长，进而计算出二十四等边体的表面积.【详解】由于二十四等边体的外接球表面积为16π，设其半径为r ，则2416r π=π，解得2r .设O 为球心，依题意可知四边形,,,A B C D 分别为正方体侧棱的中点，所以ABCD 正方形，由于2OA OB OC OD ====，所以四边形ABCD 是正方形，AB ==所以二十四等边体的边长为2. 所以二十四等边体的边长的表面积为122622sin 823π⨯⨯+⨯⨯⨯⨯24=+.【点睛】本小题主要考查几何体外接球有关计算，考查空间想象能力，属于中档题.10．A解析：A【分析】取BD 中点为O ，1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，易知CO BD ⊥，再利用线面垂直证明1BD C O ⊥，得到1COC ∠即二面角1C BD C --，再计算二面角大小即可.【详解】由题意，作出长方体1111ABCD A B C D -的图象，取BD 中点为O ，连接CE 、1C E ，因为1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，又BD ⊂平面ABCD ，所以1CC BD ⊥， 因为23AB AD ==，所以四边形ABCD 是正方形，O 为BD 中点，所以CO BD ⊥，又1CO CC C =，所以BD ⊥平面1COC ，又1C O ⊂平面1COC ，所以1BD C O ⊥，1COC ∠即二面角1C BD C --，又12CC =，()()2223236CO +==，所以123tan 6COC ∠==，130COC ∠=.【点睛】本题主要考查二面角的求法和线面垂直的判定定理和性质，考查学生空间想象能力，属于中档题.11．D解析：D【分析】根据直线、平面平行垂直的关系进行判断．【详解】由α、β是两个不同的平面，m 、n 是两条不同的直线，知：在A 中，若α⊥β，α∩β＝m ，m ⊥n ，则n 与β相交、平行或n ⊂β，故A 错误； 在B 中，若α⊥β，n ∥α，则n 与β相交、平行或n ⊂β，故B 错误； 在C 中，若m ∥α，m ∥β，则α与β相交或平行，故C 错误；在D 中，若m ⊥α，m ⊥β，则α∥β，∴若n ⊥α，则n ⊥β，故D 正确.故选：D.【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的益关系等基础知识，考查运算求解能力，是中档题.12．C解析：C【分析】根据空间中直线与平面、平面与平面位置关系相关定理依次判断各个选项可得结果.【详解】对于A ，当m 为α内与n 垂直的直线时，不满足m α⊥，A 错误；对于B ，设l αβ=，则当m 为α内与l 平行的直线时，//m β，但m α⊂，B 错误； 对于C ，由m β⊥，n β⊥知：//m n ，又n α⊥，m α∴⊥，C 正确； 对于D ，设l αβ=，则当m 为β内与l 平行的直线时，//m α，D 错误.故选：C .【点睛】本题考查立体几何中线面关系、面面关系有关命题的辨析，考查学生对于平行与垂直相关定理的掌握情况，属于基础题. 13．B解析：B【分析】根据所给三视图，还原出空间几何体，即可求得几何体的表面积.【详解】根据三视图，还原空间几何体如下图所示：在正方体中，去掉三棱锥111B A C M -，正方体的棱长为2，M 为1BB 的中点，则111111111B MC A B C A B M A C M S S S S S S =---+正方体 ()()22211116212221222522222=⨯-⨯⨯-⨯⨯-⨯⨯+⨯- 206=+故选：B.【点睛】本题考查了空间几何体三视图的简单应用，关键是能够正确还原出空间几何体，属于中档题.14．D解析：D【分析】结合公理及正方体模型可以判断：A ，B ，C 均有可能，可以利用反证法证明结论，也可以从具体的实物模型中去寻找反例证明．【详解】解：如图，在正方体1AC 中，1A A ⊥平面ABCD ，1A AAD ，1A A BC ⊥， 又//AD BC ，∴选项A 有可能； 1A A ⊥平面ABCD ，1A A AD ，1A A AB ⊥，又AD AB A =，∴选项B 有可能；1A A ⊥平面ABCD ，1A A ⊥平面1111D C B A ，AC ⊂平面ABCD ，11A D ⊂平面1111D C B A ，1A A AC ∴⊥，111A A A D ⊥，又AC 与11A D 不在同一平面内，∴选项C 有可能．故选：D ．【点睛】本题主要考查了空间中直线与直线之间的位置关系，考查空间想象能力和思维能力，属于中档题．二、解答题15．（1）证明见解析；（2）M 为AC 的中点，证明见解析.【分析】（1）本题首先可通过正弦定理得出90ACB ∠=以及AC BC ⊥，然后根据AC FB ⊥以及线面垂直的判定即可证得结果；（2）本题首先可取AC 的中点M ，连接CE 、MN ，然后通过三角形中位线的性质得出//EA MN ，最后通过线面平行的判定即可得出结果.【详解】（1）因为30BAC ∠=，2AB =，1BC =， 所以sin sin AB BC ACB BAC =∠∠，即211sin 2ACB ，解得sin 1ACB ∠=，90ACB ∠=，AC BC ⊥，因为AC FB ⊥，BC FB B ⋂=，所以AC ⊥平面FBC .（2）当M 为AC 的中点时，//EA 平面FDM .证明如下：如图，取AC 的中点M ，连接CE ，与DF 交于点N ，连接MN ，因为四边形CDEF 为正方形，所以N 为CE 的中点，因为M 是AC 的中点，所以//EA MN ，因为MN ⊆平面FDM ，EA ⊄平面FDM ，所以//EA 平面FDM .【点睛】关键点点睛：本题考查线面垂直与线面平行的判定，若直线与平面内的两条相交直线都垂直，则线面垂直，若平面外一条直线平行平面内一条直线，则线面平行，考查数形结合思想，是中档题.16．（1）证明见解析 ；（2【分析】（1）取AD 中点P ，连结MP ，CP ，推导出CP AD ⊥，MP AD ⊥，从而AD ⊥面CMP ，由此能证明CM AD ⊥．（2）过M 作MH CP ⊥于点H ，则MH ⊥面ACD ，MCP ∠即为直线CM 与面ACD 所成的角，由此能求出直线CM 与平面ACD 所成角的正弦值．【详解】（1）取AD 中点P ，连结,MP CP ，由ACD 为正三角形可得CP AD ⊥， 又由,//2BAD MP AB π∠=得MP AD MP CP P ⊥⋂=，， ∴AD ⊥面CMP ，又∵CM ⊂面MPC ，∴CM AD ⊥；（2）过M 作MH CP ⊥于点H ，由（1）可知，,AD MH CP AD P ⊥⋂=， ∴MH ⊥面ACD ，∴MCP ∠即为直线CM 与面ACD 所成的角，不妨设1CD =，则22CM MP CP ===，∴cos MCP ∠==∴sin 3MCP ∠=所以直线CM 与平面ACD【点睛】求直线与平面所成的角有两种方法：一是传统法，证明线面垂直找到直线与平面所成的角，利用平面几何知识解答；二是利用空间向量，求出直线的方向向量以及平面的方向向量，利用空间向量夹角余弦公式求解即可.17．（1）证明见解析；（2）15. 【分析】（1）根据四边形ABCD 是菱形得到//AB CD ，再由//AF DE ，证得平面//ABF 平面CDE 即可.（2）当60α=︒，即60BAD ∠=︒，过A 作AM CD ⊥，交CD 延长线于M ，连结AM ，EM ，易知AM ⊥平面CDE ，则AEM ∠为AE 与平面CDE 所成的角，然后由sin AM AEM AE ∠=求解. 【详解】（1）∵四边形ABCD 是菱形，∴//AB CD ，又//AF DE ，ABAF A =，CD DE D =，∴平面//ABF 平面CDE ，又BF ⊂平面ABF ，∴//BF 平面CDE .（2）当60α=︒，即60BAD ∠=︒，如图所示：过A 作AM CD ⊥，交CD 延长线于M ，连结AM ，EM ，而AF ⊥平面ABCD ，又AF DE ∥，∴DE ⊥平面ABCD ，∴DE AM ⊥，又AM CD ⊥，CDDE D =，∴AM ⊥平面CDE ，∴AEM ∠为AE 与平面CDE 所成的角， ∴cos303sin 3sin 515AM AD AEM AED AE AE ⋅=︒∠===∠=. ∴直线AE 与平面CDE 所成角的正弦值为15. 【点睛】 方法点睛：判断或证明线面平行的常用方法：(1)利用线面平行的定义，一般用反证法；(2)利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；(3)利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)；(4)利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)． 18．（1）证明见解析；（2）27.【分析】（1）取CD 中点F ，连接EF ，AF ，利用面面平行的判定定理证明平面//AEF 平面PBC ，再用面面平行的性质可得//AE 平面PBC ；（2）根据体积求出PA ，过A 作AQ CD ⊥于Q ，连接PQ ，AQ ，求出PQ 和CD 后，根据三角形面积公式可求得结果.【详解】（1）取CD 中点F ，连接EF ，AF ，则//EF PC ，又120BCD AFD ∠=∠=︒，∴//BC AF ，∴平面//AEF 平面PBC ，∴//AE 平面PBC .（2）因为90CAD ABC ∠=∠=，30BAC ADC ∠=∠=，2AC =，所以1,3BC AB ==由已知得：113323P ABC V AB BC PA -=⋅⋅⋅=，即1133132PA ⨯⨯=， 可得2PA =.过A 作AQ CD ⊥于Q ，连接PQ ，AQ ，∵PA ⊥平面ABCD ，∴PA AQ ⊥，PA CD ⊥，∴CD PQ ⊥， ACD △中，2AC =，90CAD ∠=，30ADC ∠=，∴4CD =，23AD =，2233AC AD AQ CD ⋅⨯===， 222237PQ PA AQ =+=+=，∴11742722PCD S PQ CD =⋅=⨯⨯=△. 【点睛】关键点点睛：掌握面面平行的判定定理和面面平行的性质是解题关键. 19．（1）证明见解析；（2）3.【分析】（1）取AB 中点E ，连接11,,CE A B A E ，根据已知条件，利用等腰三角形的性质得到1A E AB ⊥，,CE AB ⊥利用线面垂直的判定定理证得AB ⊥面1,CEA 即可得到1AB A C ⊥ ；（2） 在1CEA 中可以证明1A E CE ⊥，结合1A E AB ⊥，利用线面垂直判定定理得到1A E ⊥平面ABC ,作为三棱柱的高，进而计算体积.【详解】(1)取AB 中点E ，连接11,,CE A B A E ，11,60AB AA BAA ∠︒＝＝，1BAA ∴是等边三角形，1A E AB ∴⊥，CA CB ＝，,CE AB ∴⊥1,CE A E E ⋂＝AB ∴⊥面1,CEA1AB A C ∴⊥.(2)由于CAB ∆为等边三角形，CE ∴11222S AB CE ⨯⨯⨯=底面积＝＝1CEA 中，CE 1EA 1AC =1A E CE ∴⊥，结合1A E AB ⊥，又,,AB CE E AB CE ⋂=⊂平面ABC ,1A E ∴⊥平面ABC ,1h A E ∴＝3V Sh =＝.【点睛】本题考查线面垂直的判定与证明，考查棱柱的体积计算，属基础题，为证明线线垂直，常常先证线面垂直，为证明线面垂直，又常常需要先证明线线垂直，这是线面垂直关系常用的证明与判定方式，要熟练掌握.20．（1）证明见解析；（2）4π. 【分析】（1）连接A 1B 交AB 1于P ，根据平行四边形AA 1B 1B 的性质，结合三角形中位线定理，可得NP 与CM 平行且相等，从而四边形MCNP 是平行四边形，可得CN ∥MP ，再结合线面平行的判定定理，得到CN ∥平面AB 1M ；（2）以C 为原点，CA ，CB ，CC 1分别为x 轴，y 轴，z 轴建立空间直角坐标系如图，根据题意得到C 、A 、、B 1、M 各点的坐标，从而得到向量AB 、1B M 的坐标，再利用垂直向量数量积为零的方法，列方程组可求出平面AMB 1的法向量n =（5，﹣3，4），结合平面MB 1C 的一个法向量CA =（2，0，0），利用空间两个向量的夹角公式，得到n 与CA 的夹角，即得二面角A ﹣MB 1﹣C 的大小．【详解】（1）连结A 1B 交AB 1于P ．因为三棱柱ABC -A 1B 1C 1，所以P 是A 1B 的中点．因为M ，N 分别是CC 1，AB 的中点，所以NP // CM ，且NP = CM ，所以四边形MCNP 是平行四边形，所以CN //MP ．因为CN ⊄平面AB 1M ，MP ⊂平面AB 1M ，所以CN //平面AB 1M ．（2）因为AC =BC =2，AB = 所以由勾股定理的逆定理知BC ⊥AC ．又因为CC 1⊥平面ABC ，以C 为原点，CA ，CB ，CC 1分别为x 轴，y 轴，z 轴建立空间直角坐标系C-xyz ．因为132C M =，所以C (0,0,0)，A (2,0,0)，B 1(0,2,4)，5(0,0,)2M ，5(2,0,)2AM =-，13(0,2,)2BM =--． 设平面1AMB 的法向量(,,)n x y z =，则0n AM ⋅=，10n B M ⋅=． 即5(2,0,)(,,)=023(0,2,)(,,)=0.2x y z x y z ⎧-⋅⎪⎪⎨⎪--⋅⎪⎩，，令5x =，则3,4y z =-=，即(5,3,4)n =-． 又平面MB 1C 的一个法向量是=(2,0,0)CA ，所以2cos ,>=||||n CA n CA n CA ⋅<=． 由图可知二面角A-MB 1-C 为锐角，所以二面角A-MB 1-C 的大小为4π．【点睛】关键点睛：解题关键在于由勾股定理的逆定理知BC ⊥AC ．又因为CC 1⊥平面ABC ，进而 以C 为原点，CA ，CB ，CC 1分别为x 轴，y 轴，z 轴建立空间直角坐标系，进而利用法向量计算二面角，难度属于中档题21．(1)证明见解析.(2) 侧棱SC 上存在一点E ，当满足2SE EC =时，//BE 平面PAC . 【分析】（1）连结,AC BD 相交于点O ，可得AC ⊥平面BSD ，从而可证.（2）取点F 为SD 的中点，可得//BF OP ，过点F 作//FE PC ，交SC 于点E ，连结BE ，可得平面//BEF 平面ACP ，可得//BE 平面PAC ，从而得出答案.【详解】连结,AC BD 相交于点O , 由棱锥S ABCD -为正四棱锥则SO ⊥平面ABCD ，AC ⊂平面ABCD ,所以SO AC ⊥又棱锥S ABCD -为正四棱锥，则四边形ABCD 为正方形，所以BD AC ⊥由BD SO O ⋂=,所以AC ⊥平面BSDSD ⊂平面BSD ，所以AC SD ⊥（2）侧棱SC 上存在一点E ，当满足2SE EC =时，//BE 平面PAC . 由3SAP APD S S =，可得3SP PD =取点F 为SD 的中点，则点P 为FD 的中点,又O 为BD 的中点所以在BFD △中，//BF OP .BF ⊄平面ACP ，OP ⊂平面ACP ，则//BF 平面ACP过点F 作//FE PC ，交SC 于点E ，连结BE由EF ⊄平面ACP ，PC ⊂平面ACP ，则//EF 平面ACP又EF BE E =，所以平面//BEF 平面ACP又BE ⊂平面BEF ,则//BE 平面PAC . 由//FE PC ，则SE SF EC FP=, 由3SP PD =，F 为SD 的中点，则2SF FP =，所以2SE EC= 所以侧棱SC 上存在一点E ，当满足2SE EC =时，//BE 平面PAC .【点睛】关键点睛：本题考查线线垂直的证明和平行线性的探索性问题，解答的关键是过点B 构造一个平面使之与平面ACP 平行，则所构造的平面与SC 的交点即为所求，即取点F 为SD 的中点，可得//BF OP ，过点F 作//FE PC ，交SC 于点E ，连结BE ，可得平面//BEF 平面ACP ，构造出所需的平面，本题还可以建立空间坐标系利用向量方法求解，属于中档题.22．（1）证明见解析；（2）23. 【分析】（1）先利用勾股定理得出AE BE ⊥，再利用面面垂直的性质定理得到BE ⊥平面ADE ，进而得到AD BE ⊥，利用线面垂直的判定定理即可得证；（2）利用1122D MEC M DEC A DEC D AEC V V V V ----===，取AE 的中点O ，连接DO ，用面面垂直的性质定理得到DO ⊥平面ABCE ，利用体积公式求解即可.【详解】（1）证明：∵2AD DE ==，90ADE ∠=︒，∴22AE BE ==，4AB =，∴222AE BE AB +=，∴AE BE ⊥，又平面ADE ⊥平面ABCE ， 平面ADE平面ABCE AE =， ∴BE ⊥平面ADE ，又AD ⊂平面ADE ，所以AD BE ⊥，又AD DE ⊥，DE BE E ⋂=，所以AD ⊥平面BDE.（2）∵M 是线段DA 的中点，∴1122D MEC M DEC A DEC D AEC V V V V ----===， 取AE 的中点O ，连接DO ，∵DA DE =∴DO AE ⊥，又平面DAE ⊥平面ABCE ，∴DO ⊥平面ABCE ， 又2DO =， 1sin13522AEC S AE EC =⨯⨯⨯︒=， ∴1222233D AEC V -=⨯⨯=， ∴23D MEC V -=. 【点睛】方法点睛：证明线面垂直的常用方法：利用线面垂直的判定定理；利用面面垂直的性质定理；利用面面平行的性质；利用垂直于平面的传递性.23．（1）证明见解析；（2）证明见解析.【分析】（1）连接1B C ，可知点D 为1B C 的中点，利用中位线的性质可得出11//OD A B ，利用线面平行的判定定理可证得结论成立；（2）证明出四边形11AAC C 为菱形，可得出11AC AC ⊥，证明出BC ⊥平面11AAC C ，可得出1AC BC ⊥，利用线面垂直和面面垂直的判定定理可证得结论成立.【详解】（1）如下图所示，连接1B C ，在三棱柱111ABC A B C -中，11//BB CC 且11BB CC =，则四边形11BB C C 为平行四边形， D 为1BC 的中点，则D 为1B C 的中点，同理可知，点O 为1A C 的中点，11//OD A B ∴， OD ⊄平面111A B C ，11A B ⊂平面111A B C ，因此，//OD 平面111A B C ；（2）在直三棱柱111ABC A B C -中，1CC ⊥平面ABC ，11//AA CC 且11AA CC =，所以四边形11AAC C 为平行四边形，1AC CC =，所以，平行四边形11AAC C 为菱形，则11AC AC ⊥，1CC ⊥平面ABC ，BC ⊂平面ABC ，1BC CC ∴⊥，BC AC ⊥，1AC CC C =，BC ∴⊥平面11AAC C ，1AC ⊂平面11AAC C ，1AC BC ∴⊥，1AC BC C =，1AC ∴⊥平面1A BC ，1AC ⊂平面1AC B ，因此，平面1AC B ⊥平面1A BC .【点睛】方法点睛：证明面面垂直的常用方法：（1）面面垂直的定义；（2）面面垂直的判定定理.在证明面面垂直时，可假设两个平面垂直成立，利用面面垂直的性质定理转化为线面垂直，即可找到所要证的线面垂直，然后组织论据证明即可.24．（1）答案见解析；（2. 【分析】（1）选择①，结合直二面角的定义，证明BD ⊥平面EOA 内的两条相交直线,EO AO ；（2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则AC =CO x =，可得EB 关于x 的函数，求出EB 取得最小值时x 的值，连结EM ，作QF EM ⊥于F ，连结BF ，求出sin QBF ∠的值，即可得答案；【详解】解：（1）命题P ：若AB AD =，则BD ⊥平面EOA .∵AC GH ⊥，∴AO GH ⊥，EO GH ⊥，又二面角E GH B --的大小为90°，∴90AOE ∠=︒，即EO AO ⊥，∴EO ⊥平面ABCD ，∴EO BD ⊥，又AB BC =，∴AO BD ⊥， AO EO O =，∴BD ⊥平面EOA .（2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则AC =设CO x =，OM x =，222216OB OM MB x =+=-+，2222216EB EO OB x =+=-+，当x =min EB =连结EM ，作QF EM ⊥于F ，连结BF ，由（1）知BD ⊥平面EOA ，∴BD QF ⊥，∴QF ⊥平面EBD ，∴QBF ∠即为QB 与平面EBD 所成角，在Rt EMB 中，10EB =，2BM =，6EM=，30AE =， 由()222222(2)22QB AE AB BE QB +=+⇒=， 6QF =， ∴33sin 11QF QBF QB ∠==，即QB 与平面EBD 所成角得正弦值为33.【点睛】求线面角首先要根据一作、二证、三求找出线面角，然后利用三角函数的知识，求出角的三角函数值即可.25．（1）存在；（2）证明见解析；（3）2.【分析】（1）存在12λ=满足题意，设AC 与BD 的交点为O ，连接EO ，由平面几何的知识可得//BF EO ，再由线面平行的判定即可得证；（2）由线面垂直的性质与判定可得AC ⊥平面BDEF ，再由面面垂直的判定即可得证； （3）结合（2）可得AC ⊥平面BDEF 、2ABCDEF A BDEF V V -=，再由棱锥的体积公式即可得解.【详解】（1）存在12λ=满足题意，理由如下： 设AC 与BD 的交点为O ，则12DO BO BD ==，连接EO ，如图，∵//EF BD ，当12λ=时，12EF BD BO ==， ∴四边形EFBO 是平行四边形，∴//BF EO ，又EO ⊂平面ACE ，BF ⊄平面ACE ，∴//BF 平面ACE ；（2）证明：ED ⊥平面ABCD ，AC ⊂平面ABCD ，∴ED AC ⊥，∵ABCD 为正方形，∴BD AC ⊥，又ED BD D =，∴AC ⊥平面BDEF ，又AC ⊂平面EAC ，∴平面EAC ⊥平面BDEF ；（3）∵ED ⊥平面ABCD ，∴ED BD ⊥，又∵//EF BD 且12EF BD =，∴BDEF 是直角梯形， 又∵ABCD 是边长为2的正方形，22BD =，2EF =∴1222322BDEF S ⨯==， 由（2）知AC ⊥平面BDEF ， ∴12322222332ABCDEF A BDEF BDEF V V S AO -==⨯⋅=⨯=. 【点睛】本题考查了线面平行、面面垂直的判定及几何体体积的求解，考查了空间思维能力与运算求解能力，属于中档题.26．（1）证明见解析；（2）证明见解析.【分析】（1）连结AC 、BD ，交于点O ，连结OE ，通过//OE PA 即可证明；（2）通过PD BC ⊥， CD BC ⊥可证BC ⊥平面PDC ，即得DE BC ⊥，进而通过DE ⊥平面PBC 得DE PB ⊥，结合EF PB ⊥即证.【详解】证明：（1）连结AC 、BD ，交于点O ，连结OE ，底面ABCD 是正方形，∴O 是AC 中点， 点E 是PC 的中点，//OE PA ∴.OE ⊂平面EDB ， PA ⊄平面EDB ，∴//PA 平面EDB .（2）PD DC =，点E 是PC 的中点，DE PC ∴⊥. 底面ABCD 是正方形，侧棱PD ⊥底面ABCD ， ∴PD BC ⊥， CD BC ⊥，且 PD DC D ⋂=， ∴BC ⊥平面PDC ，∴DE BC ⊥，又PC BC C ⋂=，∴DE ⊥平面PBC ，∴DE PB ⊥，EF PB ⊥，EF DE E ⋂=，PB ∴⊥平面EFD .【点睛】本题考查线面平行和线面垂直的证明，属于基础题.。

高一数学必修2立体几何初步单元测试题（修改）高一数学必修2立体几何初步单元测试题班级：姓名：学号：一、选择题：1、线段AB 在平面α内，则直线AB 与平面α的位置关系是（）A 、AB α? B 、AB α?C 、由线段AB 的长短而定D 、以上都不对2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点3、垂直于同一条直线的两条直线一定（）A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A BC D -中，下列几种说法正确的是（）A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角 D 、11AC 与1BC成60角 5、若直线l ∥平面α，直线a α?，则l 与a 的位置关系是（）A 、l ∥aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点6、下列命题中：（1）平行于同一直线的两个平面平行；（2）平行于同一平面的两个平面平行；（3）垂直于同一直线的两直线平行；（4）垂直于同一平面的两直线平行。

其中正确的个数有（）A 、1B 、2C 、3D 、47、a ，b ，c 表示直线，M 表示平面，给出下列四个命题：①若a ∥M ，b ∥M ，则a ∥b ；②若b íM ，a ∥b ，则a ∥M ；③若a ⊥c ，b ⊥c ，则a ∥b ；④若a ⊥M ，b ⊥M ，则a ∥b .其中正确命题的个数有（）A 、0个B 、1个C 、2个D 、3个8、如图:直三棱柱ABC —A 1B 1C 1的体积为V ，点P 、Q 分别在侧棱AA 1和CC 1上，AP=C 1Q ，则四棱锥B —APQC 的体积为（）A 、2VB 、3VC 、4VD 、5V二、填空题：9、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).10、正方体1111ABCD A BC D -中，平面11AB D 和平面1BCD 的位置关系为QC'B'A'CBAB1C 1A 1D 1BAC D11、已知PA 垂直平行四边形ABCD 所在平面，若PC BD ⊥，则平行四边形ABCD 一定是 .12、如图，在直四棱柱A 1B 1C 1 D 1－ABCD 中，当底面四边形ABCD满足条件_________时，有A 1 B ⊥B 1 D 1．(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形.)三、解答题：13、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.14、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且ＥＨ∥ＦＧ．求证：EH ∥BD .15、已知ABC ?中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ．H G FE D B A CSDBA16、已知正方体1111ABCD A BC D -，O 是底ABCD 对角线的交点.,求证：(１) C 1O ∥面11AB D ；(2)面1BDC //面11AB D ．17、已知△BCD 中，∠BCD =90°，BC =CD =1，AB ⊥平面BCD ，∠ADB =60°，E 、F 分别是AC 、AD 上的动点，且ADAFAC AE = 求证：平面BEF ⊥平面ABC .D 1ODB AC 1B 1A 1CFEDBAC高一数学必修2立体几何测试题参考答案一、选择题 ACDDD BBB 二、填空题11、小于 12、平行 13、菱形 14、对角线A 1C 1与B 1D 1互相垂直三、解答题15、解:设圆台的母线长为l ,则圆台的上底面面积为224S ππ=?=上圆台的上底面面积为2525S ππ=?=下，所以圆台的底面面积为29S S S π=+=下上又圆台的侧面积(25)7S l l ππ=+=侧于是725l ππ= 即297l =为所求. 16、证明：,EH FG EH ? 面BCD ，FG ?面BCD∴EH ∥面BCD又EH ? 面BCD ，面BCD 面ABD BD =，∴EH ∥BD17、证明：90ACB ∠=BC AC ∴⊥又SA ⊥面ABC SA BC ∴⊥ BC ∴⊥面SAC BC AD ∴⊥ 又,SC AD SC BC C ⊥=AD ∴⊥面SBC19、证明：（1）连结11AC ，设11111ACB D O = 连结1AO ， 1111ABCD A BCD -是正方体11A ACC ∴是平行四边形∴A 1C 1∥AC 11AC AC = 又1,O O 分别是11,AC AC 的中点，∴O 1C 1∥AO 且11OC AO = 11AOC O ∴是平行四边形111,C O AO AO ∴? 面11ABD ，1C O ?面11AB D∴C 1O ∥面11AB D（2）1CC ⊥ 面1111A B C D 11!CC B D ∴⊥又1111AC B D ⊥ ，1111B D AC C ∴⊥面 111AC B D ⊥即同理可证11AC AB ⊥，又1111D B AB B =∴1AC ⊥面11AB D 20、证明：（Ⅰ）∵AB ⊥平面BCD ，∴AB ⊥CD ，∵CD ⊥BC 且AB ∩BC=B ，∴CD ⊥平面ABC.又ADAFAC AE = ∴EF ∥CD ，∴EF ⊥平面ABC ，EF ?平面BEF,∴平面BEF ⊥平面ABC.。

一、选择题1．已知正三棱柱111ABC A B C -，底面正三角形ABC 的边长为2，侧棱1AA 长为2，则点1B 到平面1A BC 的距离为（ ） A ．2217B ．22121C．477D ．47212．现有一个三棱锥形状的工艺品P ABC -，点P 在底面ABC 的投影为Q ，满足12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，22222213QA QB QC AB BC CA ++=++，93ABCS =，若要将此工艺品放入一个球形容器（不计此球形容器的厚度）中，则该球形容器的表面积的最小值为（ ）A ．42πB ．44πC ．48πD ．49π3．正方体1111ABCD A B C D -的棱长为2，E 是1CC 的中点，则点1C 到平面EBD 的距离为（ ） A ．34B ．63C ．5 D ．2234．已知正三棱柱111ABC A B C -中，1AB AA =，M 是1CC 的中点，则异面直线AM 与1A B 所成角的大小为（ ）A ．π6B ．π4C ．π3D ．π25．如图为某几何体的三视图，正视图、左视图和俯视图均为等腰直角三角形，则该几何体的表面积是（ ）A ．23+B ．223+C ．63D ．66．设有直线m ，n ，l 和平面α，β，下列四个命题中，正确的是（ ）A ．若//,//m n αα，则//m nB ．若//,//,//l m αβαβ，则//l mC ．若,m αβα⊥⊂，则m β⊥D ．若,,m m αββα⊥⊥⊄，则//m α7．某三棱锥的三视图如图所示， 则该三棱锥的体积为（ ）A ．16B ．13C ．23D ．28．在正方体1111ABCD A B C D -中，三棱锥11A B CD -的表面积为43，则正方体外接球的体积为（ ） A ．43πB ．6πC ．323πD ．86π9．我国古代数学名著《九章算术》中“开立圆术”曰：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径意思是：球的体积V 乘16，除以9，再开立方，即为球的直径d ，由此我们可以推测当时球的表面积S 计算公式为（ ）A ．2278S d =B ．2272S d =C ．292S d =D ．21114S d = 10．设m 、n 是两条不同的直线，α是平面，m 、n 不在α内，下列结论中错误的是（ ）A ．m α⊥，//n α，则m n ⊥B ．m α⊥，n α⊥，则//m nC ．m α⊥，m n ⊥，则//n αD ．m n ⊥，//n α，则m α⊥11．已知三棱锥D ABC -，记二面角C AB D --的平面角是θ，直线DA 与平面ABC 所成的角是1θ，直线DA 与BC 所成的角是2θ，则（ ） A ．1θθ≥B ．1θθ≤C ．2θθ≥D ．2θθ≤12．如果一个水平放置的平面图形的斜二测直观图是如图所示的直角梯形，其中2O A ''=，45B A O '''∠=,//B C O A ''''.则原平面图形的面积为（ ）A ．32B ．62C ．322D ．34二、填空题13．已知直三棱柱111ABC A B C -，14AB BC AA ===，42AC =，若点P 是上底面111 A B C 所在平面内一动点，若三棱锥P ABC -的外接球表面积恰为41π，则此时点P 构成的图形面积为________．14．如图所示，Rt A B C '''∆为水平放置的ABC ∆的直观图，其中A C B C ''''⊥，2B O O C ''''==，则ABC ∆的面积是________________.15．如图，在四棱锥P ABCD -中，底面ABCD 为菱形，PD ⊥底面ABCD ，O 为对角线AC 与BD 的交点，若2PD =，3APD BAD π∠=∠=，则三棱锥P AOD -的外接球表面积为_________．16．已知一个圆锥内接于球O （圆锥的底面圆周及顶点均在同一球面上），圆锥的高是底面半径的3倍，圆锥的侧面积为910π，则球O 的表面积为________．17．世界四大历史博物馆之首卢浮宫博物馆始建于1204年，原是法国的王宫，是法国文艺复兴时期最珍贵的建筑物之一，以收藏丰富的古典绘画和雕刻而闻名于世，卢浮宫玻璃金字塔为正四棱锥，且该正四棱锥的高为21米，底面边长为30米，是华人建筑大师贝聿铭设计的.若玻璃金字塔五个顶点恰好在一个球面上，则该球的半径为______米.18．如图，在长方体1111ABCDA B C D ﹣中，O 是11B D 的中点，P 是线段AC 上一点，且直线1PA 交平面11AB D 于点M ．给出下列结论：①A ，M ，O 三点共线；②A ，M ，O ，1A 不共面；③A ，M ，C ，O 共面；④B ，1B ，O ，M 共面．其中正确结论的序号为______．19．如图①，一个圆锥形容器的高为2a ，内装有一定量的水.如果将容器倒置，这时水面的高恰为a （如图②），则图①中的水面高度为_________．20．将底面直径为8，高为23的圆锥体石块打磨成一个圆柱，则该圆柱侧面积的最大值为______.三、解答题21．在如图所示几何体中，平面PAC ⊥平面ABC ，//PM BC ，PA PC =，1AC =，22BC PM ==，5AB =．若该几何体左视图（侧视图）的面积为3．（1）画出该几何体的主视图（正视图）并求其面积S ； （2）求出多面体PMABC 的体积V ．22．如图，在四棱锥P ABCD -中，底面ABCD 是边长为1的正方形，PA ⊥底面ABCD ，PA AB =，点M 是棱PD 的中点.（1）求证：//PB 平面ACM ； （2）求三棱锥P ACM -的体积.23．如图，平行四边形ABCD 中，45DAB ∠=，PD ⊥平面ABCD ，PA BD ⊥，BD PD =，4AB =.（1）求证：平面PBC ⊥平面PBD ；（2）若点,M N 分别是,PA PC 的中点，求三棱锥P MBN -的体积.24．将棱长为2的正方体1111ABCD A B C D -沿平面11A BCD 截去一半（如图1所示）得到如图2所示的几何体，点E ，F 分别是BC ，DC 的中点.（Ⅰ）证明：EF ⊥平面1A AC ； （Ⅱ）求三棱锥1A D EF -的体积.25．如图，在四棱锥C ﹣ABDE 中，F 为CD 的中点，DB ⊥平面ABC ，BD ∥AE ，BD =2AE ．（1）求证：EF ∥平面ABC ；（2）若AB =BC =CA=BD =6，求点A 到平面ECD 的距离26．如图，在矩形ABCD 中，2AB AD =，M 为DC 的中点，将ADM △沿AM 折起使平面ADM ⊥平面ABCM .（1）求证：BM AD ⊥；（2）求直线DC 与平面DAB 所成角的正弦值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】根据题意，将点1B 到平面1A BC 的距离转化为点A 到平面1A BC 的距离，然后再利用等体积法11A A BC A ABC V V --=代入求解点A 到平面1A BC 的距离. 【详解】已知正三棱柱111ABC A B C -，底面正三角形ABC 的边长为2，侧棱1AA 长为2，所以可得1122==A B AC ，1A BC为等腰三角形，所以1A BC 的高为7，由对称性可知，111--=B A BC A A BC V V ，所以点1B 到平面1A BC 的距离等于点A 到平面1A BC 的距离，所以11A A BC A ABC V V --=，又因为112772=⨯⨯=A BC S △，12332ABCS =⨯⨯=，所以111233⨯⨯=⨯⨯A BC ABC S h S △△，即2322177h ==. 故选：A.【点睛】一般关于点到面的距离的计算，一是可以考虑通过空间向量的方法，写出点的坐标，计算平面的法向量，然后代入数量积的夹角公式计算即可，二是可以通过等体积法，通过换底换高代入利用体积相等计算.2．D解析：D 【分析】作QM AB ⊥，连接PM ，易证AB PM ⊥，由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM =，再根据12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，由对称性得到AB BC AC ==，然后根据22222213QA QB QC AB BC CA ++=++，93ABCS =，求得6,23AB AQ ==，在AOQ△中，由222AO OQ AQ =+求解半径即可.【详解】 如图所示：作QM AB ⊥与M ，连接PM ， 因为PQ ⊥平面ABC ，所以PQ AB ⊥，又QM PQ Q ⋂=， 所以AB ⊥平面PQM ， 所以AB PM ⊥，所以112122QAB PABAB QM S S AB PM ⨯⨯==⨯⨯△△, 2PM QM =,因为12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△， 由对称性得AB BC AC ==,又因为22222213QA QB QC AB BC CA ++=++，93ABCS=所以21sin 60932ABCSAB =⨯⨯= 解得6,3AB AQ == 所以3,23,3QM PM PQ ===，设外接球的半径为r ，在AOQ △中，222AO OQ AQ =+，即()(222323r r =-+，解得72r=，所以外接球的表面积为2449S rππ==，即该球形容器的表面积的最小值为49π.故选：D【点睛】关键点点睛：本题关键是由12QAB QAC QBCPAB PAC PBCS S SS S S===△△△△△△得到三棱锥是正棱锥，从而找到外接球球心的位置而得解..3．B解析：B【分析】利用等体积法11C EBD D C EBV V--=，设点1C到平面EBD的距离为d，利用三棱锥的体积公式代入面积即求得d.【详解】如图，利用等体积法，11C EBD D C EBV V--=，设点1C到平面EBD的距离为d，正方体1111ABCD A B C D-的棱长为2，故22,5BD BE ED===，如图，2215232h ED BD⎛⎫=-=-=⎪⎝⎭11223622EBDS BD h=⨯⨯=⨯=又点D到平面1C EB的距离，即D到平面11C CBB的距离，为CD=2，111212EBCS=⨯⨯=，由11C EBD D C EB V V --=得，111233d =⨯⨯，故d ==. 故选：B. 【点睛】 方法点睛：空间中求点到平面的距离的常见方法： （1）定义法：直接作垂线，求垂线段长；（2）等体积法：利用三棱锥换底求体积，结合两个面积和另一个高求未知高，即得距离； （3）向量法：过点的一个斜线段对应的向量a ，平面法向量n ，则a n d n⋅=.4．D解析：D 【分析】取AC 中点E ，连接1,A E BE ，先通过BE ⊥平面11ACC A 可得BE AM ⊥，再由1ACM A AE ≅可得1AM A E ⊥，即可得出AM ⊥平面1A BE ，即1AM A B ⊥.【详解】取AC 中点E ，连接1,A E BE ，ABC 为正三角形，BE AC ∴⊥，正三棱柱111ABC A B C -中，1CC ⊥平面ABC ，BE ⊂平面ABC ，1CC BE ∴⊥，1ACCC C =，BE ∴⊥平面11ACC A ，AM ⊂平面11ACC A ，BE AM ∴⊥，在直角三角形ACM 和直角三角形1A AE 中，1,AC A A CM AE ==,1ACM A AE ∴≅， 1CAM AA E ∴∠=∠，12CAM A EA π∴∴∠+∠=，则1AM A E ⊥，1BE A E E ⋂=，AM ∴⊥平面1A BE ，1A B ⊂平面1A BE ，1AM A B ∴⊥，故异面直线AM 与1A B 所成角的大小为2π.【点睛】本题考查异面直线所成角的求解，解题的关键是通过证明AM ⊥平面1A BE 判断出1AM A B ⊥.5．A解析：A【分析】由三视图可知原几何体是三棱锥，平面ACD ⊥平面ABC ，ACD ACB ≅底面是等腰直角三角形，底为2AC =，高为1BE =，ABD BCD ≅是边长为2的等边三角形，计算四个三角形面积之和即可求解.【详解】由三视图可知原几何体是三棱锥：底面ACB △是等腰直角三角形，底2AC =，高1BE =，平面ACD ⊥平面ABC ，ACD ACB ≅，由三视图知ACB △中，2AC =，ACB △是等腰直角三角形，所以2AB BC == ACD △是等腰直角三角形，2AD CD ==，2AC =，222BD BE DE =+=所以等腰直角三角形ACB △的面积为12112⨯⨯=， 等腰直角三角形ACD △的面积为12112⨯⨯=，等边ABD △的面积为()233242⨯=， 等边BCD △的面积为()2332⨯=， 所以该几何体的表面积是331123+++=+， 故选：A. 6．D解析：D【分析】在A 中，m 与n 相交、平行或异面；在B 中，l 与m 不一定平行，有可能相交；在C 中，m ⊥β或m ∥β或m 与β相交； 在D 中，由直线与平面垂直的性质与判定定理可得m ∥α．【详解】由直线m 、n ，和平面α、β，知：对于A ，若m ∥α，n ∥α，则m 与n 相交、平行或异面，故A 错误；对于B ，若//,//,//l m αβαβ，l 与m 不一定平行，有可能相交，故B 错误；对于C ，若α⊥β，m ⊂α，则m ⊥β或m ∥β或m 与β相交，故C 错误； 对于D ，若α⊥β，m ⊥β，m ⊄α，则由直线与平面垂直的性质与判定定理得m ∥α，故D 正确．故选：D ．【点睛】本题考查了命题真假的判断问题，考查了空间线线、线面、面面的位置关系的判定定理及推论的应用，体现符号语言与图形语言的相互转化，是中档题．7．C解析：C【分析】根据题中所给的几何体的三视图还原几何体，得到相应的三棱锥，之后利用椎体体积公式求得结果.【详解】根据题中所给的几何体的三视图还原几何体如图所示：该三棱锥满足底面BCD △是等腰三角形，且底边和底边上的高线都是2；且侧棱AD ⊥底面BCD ，1AD =， 所以112=221=323V ⨯⨯⨯⨯， 故选：C.【点睛】方法点睛：该题考查的是有关根据所给几何体三视图求几何体体积的问题，解题方法如下： （1）应注意把握三个视图的尺寸关系：主视图与俯视图长应对正（简称长对正），主视图与左视图高度保持平齐（简称高平齐），左视图与俯视图宽度应相等（简称宽相等），若不按顺序放置和不全时，则应注意三个视图名称；（2）根据三视图还原几何体；（3）利用椎体体积公式求解即可.8．B解析：B【分析】根据三棱锥的表面积进一步求出正方体的棱长，最后求出正方体的外接球的半径，进一步求出结果．【详解】解：设正方体的棱长为a ，则1111112B D AC AB AD B C D C a ======，由于三棱锥11A B CD -的表面积为3 所以)1213344224AB C S Sa ==⨯=所以2a =()()()2222226++=， 所以正方体的外接球的体积为34663ππ⎛⎫= ⎪ ⎪⎝⎭ 故选：B ．【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.9．A解析：A【分析】根据已知条件结合球的体积公式3432d π⎛⎫ ⎪⎝⎭求解出π的值，然后根据球的表面积公式242d π⎛⎫ ⎪⎝⎭求解出S 的表示，即可得到结果. 【详解】3169V d =，所以33941632d d V π⎛⎫== ⎪⎝⎭，所以278π=， 所以2222727442848d d S d π⎛⎫==⨯⨯= ⎪⎝⎭， 故选：A.【点睛】关键点点睛：解答本题的关键是根据球的体积公式得到π的表示，再将π带入到球的表面积公式即可完成求解. 10．D解析：D【分析】利用线面平行的性质定理和线面垂直的定义可判断A 选项的正误；由线面垂直的性质定理可判断B 选项的正误；根据已知条件判断直线n 与平面α的位置关系，可判断C 选项的正误；根据已知条件判断直线m 与平面α的位置关系，可判断D 选项的正误.【详解】对于A ，//n α，由线面平行的性质定理可知，过直线n 的平面β与平面α的交线l 平行于n ， m α⊥，l α⊂，m l ∴⊥，m n ∴⊥，故A 正确；对于B ，若m α⊥，n α⊥，由直线与平面垂直的性质，可得//m n ，故B 正确； 对于C ，若m α⊥，m n ⊥，则//n α或n ⊂α，又n α⊄，//n α∴，故C 正确； 对于D ，若m n ⊥，//n α，则//m α或m 与α相交或m α⊂，而m α⊄，则//m α或m 与α相交，故D 错误．故选：D ．【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．11．A解析：A【分析】设三棱锥D -ABC 是棱长为2的正四面体，取AB 中点E ，DC 中点M ，AC 中点M ，连结DE 、CE 、MN 、EN ，过D 作DO CE ⊥，交CE 于O ，连结AO ，则DEC θ∠=，1DAO θ∠=，2MNE θ∠=，排除B ，C ．当二面角C AB D --是直二面角时，2θθ≥，排除D ．由此能求出结果．【详解】设三棱锥D -ABC 是棱长为2的正四面体，取AB 中点E ，DC 中点M ，AC 中点M ，连结DE 、CE 、MN 、EN ，过D 作DO ⊥CE ，交CE 于O ，连结AO ，则DEC θ∠=，1DAO θ∠=，2MNE θ∠=，413DE CE ==-=2DC =，∴1 cos3233θ==⨯⨯，22333AO CO CE===，∴12333cos3AOADθ===，取BC中点F，连结DF、AF，则DF BC⊥，AF BC⊥，又DF AF F⋂=，∴BC⊥平面AFD，∴BC AD⊥，∴290θ=︒，∴21θθθ≥≥，排除B，C，当二面角C AB D--是直二面角时，2θθ≥，排除D，故选：A.【点睛】关键点点睛：将三棱锥看成特殊的正四面体，采用排除法，充分理解线线角、线面角以及面面的概念是解题的关键.12．A解析：A【分析】作出原平面图形，然后求出面积即可．【详解】45B A O'''∠=B O A'''=∠，则O A B'''△是等腰直角三角形，∴2A B OB'''==，又O C C B''''⊥，45C O B'''∠=︒，∴1B C''=，在直角坐标系中作出原图形为：梯形OABC，//OA BC，2,1OA BC==，高22OB=∴其面积为1(21)22322S=+⨯=故选：A【点睛】方法点睛：本题考查斜二测法画平面图形直观图，求原图形的面积，可能通过还原出原平面图形求得面积，也可以通过直观图到原图形面积的关系求解：直观图面积为S '，原图形面积为S ，则4S S '= 二、填空题13．【分析】确定是等腰直角三角形的中点分别是和的外心由直棱柱性质得的外接球的球心在上外接球面与平面的交线是圆是以为圆心为半径的圆求出可得面积【详解】则设分别是的中点则分别是和的外心由直三棱柱的性质得平面 解析：4π【分析】确定ABC 是等腰直角三角形，11,AC A C 的中点1,D D 分别是ABC 和111A B C △的外心，由直棱柱性质得P ABC -的外接球的球心O 在1DD 上，外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆，求出1PD 可得面积．【详解】4,AB BC AC ===90ABC ∠=︒，设1,D D 分别是11,AC A C 的中点，则1,D D 分别是ABC 和111A B C △的外心，由直三棱柱的性质得1DD ⊥平面ABC ，所以P ABC -的外接球的球心O 在1DD 上，如图，24()41OA ππ=，则2OP OA ==，32OD ===， 所以11135422OD DD OD AA OD =-=-=-=，12PD ===， P ABC -的外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆， 其面积为224S ππ=⨯=．故答案为：4π．【点睛】关键点点睛：本题考查立体几何中动点轨迹问题的求解，重点考查了几何体的外接球的有关问题的求解，关键是根据外接球的性质确定球心位置，结合勾股定理得出动点所满足的具体条件，结论：三棱锥的外接球的球心在过各面外心且与此面垂直的直线上． 14．【分析】根据直观图和原图的之间的关系由直观图画法规则将还原为如图所示是一个等腰三角形直接求解其面积即可【详解】由直观图画法规则将还原为如图所示是一个等腰三角形则有所以故答案为：【点睛】关键点点睛：根 解析：82【分析】 根据直观图和原图的之间的关系，由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形，直接求解其面积即可．【详解】由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形,则有2BO OC B O O C ''''====，242AO A O ''==所以114428222ABC S BC AO =⋅=⨯⨯= 故答案为：2【点睛】关键点点睛：根据斜二测画法的规则，可得出三角形的直观图，并求出对应边长，根据面积公式求解．15．【分析】根据棱锥的性质证明的中点就是三棱锥的外接球球心得出半径后可求表面积【详解】取中点中点连接则因为底面所以平面是菱形则所以是的外心又底面平面所以所以到四点距离相等即为三棱锥的外接球球心又所以所以解析：16π．【分析】根据棱锥的性质，证明PA 的中点就是三棱锥P AOD -的外接球球心，得出半径后可求表面积．【详解】取PA 中点M ，DA 中点E ，连接,ME EO ，则//ME PD ，因为PD ⊥底面ABCD ，所以ME ⊥平面ABCD ，ABCD 是菱形，则AO OD ⊥，所以E 是AOD △的外心，又PD ⊥底面ABCD ，AD ⊂平面ABCD ，所以PD AD ⊥，所以M 到,,,P A D O 四点距离相等，即为三棱锥P AOD -的外接球球心．又2PD =，3APDπ∠=，所以24cos 3PA π==，所以2MA MP ==， 所以三棱锥P AOD -的外接球表面积为24216S ππ=⨯=．故答案为：16π．【点睛】结论点睛：本题考查求三棱锥外接球表面积，解题关键是求出外接球球心．三棱锥的外接球球心一定在过各面外心且与此面垂直的直线上．16．【分析】设圆锥的底面半径为球的半径为根据勾股定理可得根据圆锥的侧面积公式可得再根据球的表面积公式可得结果【详解】设圆锥的底面半径为球的半径为则圆锥的高为则球心到圆锥的底面的距离为根据勾股定理可得化简 解析：100π【分析】设圆锥的底面半径为r ，球O 的半径为R ，根据勾股定理可得53R r =，根据圆锥的侧面积公式可得3,5r R ==，再根据球的表面积公式可得结果.【详解】设圆锥的底面半径为r ，球O 的半径为R ，则圆锥的高为3r ，则球心O 到圆锥的底面的距离为3r R -，根据勾股定理可得()2223R r r R =+-，化简得53R r =， 因为圆锥的高为3r ，母线长为()22310r r r +=， 所以圆锥的侧面积为21010r r r ππ⨯=，所以210910r ππ=，解得r =3，所以5353R =⨯=， 所以球O 的表面积为24425100R πππ=⨯=.故答案为：100π【点睛】关键点点睛：利用圆锥的侧面积公式和球的表面积公式求解是解题关键. 17．【分析】作出图形设球体的半径为根据几何关系可得出关于的等式进而可解得的值【详解】如下图所示：在正四棱锥中设为底面正方形的对角线的交点则底面由题意可得则设该球的半径为设球心为则由勾股定理可得即解得故答 解析：29714【分析】作出图形，设球体的半径为R ，根据几何关系可得出关于R 的等式，进而可解得R 的值.【详解】如下图所示：在正四棱锥P ABCD -中，设M 为底面正方形ABCD 的对角线的交点，则PM ⊥底面ABCD ，由题意可得21PM =，30AB =，2302BD ==，则152BM = 设该球的半径为R ，设球心为O ，则O PM ∈，由勾股定理可得222OB OM BM =+，即()(22221152R R =-+，解得29714R =. 故答案为：29714. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.18．①③【分析】由公理1判断①正确；由公理2判断②错误③正确用反证法可得④错误【详解】∵连接∵是的中点∴平面与平面有公共点与则平面平面对于①平面则平面又平面则即三点共线故①正确；对于②在平面内由①知∴平解析：①③ 【分析】由公理1判断①正确；由公理2判断②错误③正确，用反证法可得④错误. 【详解】∵连接11A C ，∵O 是11B D 的中点，∴11O A C ∈． 平面11AB D 与平面11AAC C 有公共点A 与O ， 则平面11AAC C平面11AB D AO =．对于①，1M PA ∈，1PA ⊂平面11AAC C ，则M ∈平面11AAC C ， 又M ∈平面11AB D ，则M AO ∈，即A ，M ，O 三点共线，故①正确； 对于②，A ，O ，1A 在平面11AAC C 内，由①知M AO ∈，∴O ∈平面11AAC C ， 即A ，M ，O ，1A 共面，故②错误；对于③，A ，O ，C 在平面11AAC C 内，由①知M AO ∈，∴O ∈平面11AA C CA ， 则A ，M ，C ，O 共面11AAC C ，故③正确；对于④，连接BD ，则B ，1B ，O 都在平面11BB D D 上，若M ∈平面11BB D D ，则直线OM ⊂平面11BB D D ，∴A ∈面11BB D D ，显然A ∉面11BB D D 的，故④错误． ∴正确命题的序号是①③． 故答案为：①③．【点睛】本题考查命题的真假判断与应用，考查空间中的直线与平面、平面与平面的位置关系，考查空间想象能力与思维能力，是中档题.19．【分析】由第二个图可知水的体积占整个圆锥体积的在第一个图中水的体积占圆锥的上面小圆锥体积占大圆锥体积的根据小圆锥体积与大圆锥体积比是其高的三次方的比即可解得a 的值【详解】在图②中水形成的小圆锥和大圆解析：(2a【分析】由第二个图可知，水的体积占整个圆锥体积的18，在第一个图中，水的体积占圆锥的18，上面小圆锥体积占大圆锥体积的78，根据小圆锥体积与大圆锥体积比是其高的三次方的比，即可解得a 的值. 【详解】在图②中，水形成的小“圆锥”和大圆锥形容器高的比为12，底面半径比为12，故其底面积的比为14，所以体积比为18，则在图①中，无水部分形成的小“圆锥”和大圆锥形容器的体积比为78，设水面高度为h ，则小“圆锥”和大圆锥形容器的高的比为22a h a-，体积比为327(=28a h a -），解的h =(2a .故答案为: (2a 【点睛】本题考查了圆锥的体积的计算，属于中档题目，解题中的关键是要准确利用圆锥体积公式得到大小圆锥体积比与大小圆锥的高比的关系.20．【分析】欲使圆柱侧面积最大需使圆柱内接于圆锥设圆柱的高为h 底面半径为r 用r 表示h 从而求出圆柱侧面积的最大值【详解】欲使圆柱侧面积最大需使圆柱内接于圆锥；设圆柱的高为h 底面半径为r 则解得；所以；当时取解析：【分析】欲使圆柱侧面积最大，需使圆柱内接于圆锥，设圆柱的高为h ，底面半径为r ，用r 表示h ，从而求出圆柱侧面积的最大值. 【详解】欲使圆柱侧面积最大，需使圆柱内接于圆锥； 设圆柱的高为h ，底面半径为r ， 23423r =，解得33h r =； 所以()23222334S rh r r r πππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧； 当2r时，S 圆柱侧取得最大值为43π故答案为：3π. 【点睛】本题考查了求圆柱侧面积的最值，考查空间想象能力，将问题转化为函数求最值，属于中档题.三、解答题21．（1）主视图（正视图）见解析，334S =；（2）34V =. 【分析】（1）根据侧视图计算出PAC △的边AC 上的高，进而可作出几何体PMABC 的主视图，利用梯形的面积公式可求得几何体的主视图的面积；（2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，推导出AN ⊥平面BCPM ，计算出AN 和梯形BCPM 的面积，利用锥体的体积公式可求得多面体PMABC 的体积V . 【详解】（1）在几何体PMABC 中，平面PAC ⊥平面ABC ， 设PAC △的边AC 上的高为h ，则该几何体的侧视图的面积为1324AC h ⋅=，得32h =， 又因为22BC PM ==，所以，该几何体的主视图（正视图）如下图所示：由图可知，该几何体的主视图为直角梯形，其面积为()1233322S +⨯==⨯； （2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，如下图所示：PA PC =，O 为AC 的中点，所以，PO AC ⊥，由（1）可知，32PO h ==，1122AO CO AC ===，由勾股定理可得221PC PA AO PO ==+=，所以，PAC △为等边三角形，N 为PC 的中点，AN PC ∴⊥，且3sin 602AN AC ==. 1AC =，2BC =，5AB =222AC BC AB ∴+=，BC AC ∴⊥，平面PAC ⊥平面ABC ，平面PAC平面ABC AC =，BC ⊂平面ABC ，BC ∴⊥平面PAC ，AN 、PC ⊂平面PAC ，BC AN ∴⊥，BC PC ⊥， PC BC C =，AN ∴⊥平面BCPM ， //PM BC ，PM PC ∴⊥，所以，梯形BCPM 的面积为()322BCPM BC PM PC S +⋅==梯形，因此，1133333224BCPM V S AN =⋅=⨯⨯=梯形. 【点睛】方法点睛：求空间几何体体积的方法如下：（1）求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．22．（1）证明见解析；（2）23． 【分析】（1）连接BD 交AC 于点O ，由中位线定理得//OM PB ，从而得证线面平行； （2）由M 是PD 中点，得12M ACD P ACD V V --=，求出三棱锥P ACD -的体积后可得． 【详解】（1）如图，连接BD 交AC 于点O ，连接OM ，则O 是BD 中点，又M 是PD 中点， ∴//OM PB ，又PB ⊄平面ACM ，OM ⊂平面ACM ， 所以//PB 平面ACM ； （2）由已知12222ACDS=⨯⨯=，11422333P ACD ACD V S PA -=⋅=⨯⨯=△，又M 是PD 中点，所以1223M ACD P ACD V V --==， 所以23P ACM P ACD M ACD V V V ---=-=．【点睛】思路点睛：本题考查证明线面平行，求三棱锥的体积．求三棱锥的体积除掌握体积公式外，还需要注意割补法，不易求体积的三棱锥（或一个不规则的几何体）的体积可通过几个规则的几何体（柱、锥、台等）的体积加减求得．三棱锥的体积还可通过转化顶点，转移底面利用等体积法转化为求其他三棱锥的体积，从而得出结论． 23．（1）证明见解析；（2）223. 【分析】（1）可由PD BD ⊥，PA BD ⊥证得BD ⊥平面PAD ，故BD AD ⊥，再由BD BC ⊥和PD BC ⊥可得BC ⊥平面PBD ，从而面PBC ⊥面PBD （2）可利用1144P MBN B PMN B PAC P ABC V V V V ----===，进行转化求体积. 【详解】解：（1）因为PD ⊥平面ABCD ，BD ⊂平面ABCD ，所以PD BD ⊥.又PA BD ⊥，PA PD P =，平面PD ⊂平面PAD ，PA ⊂平面PAD ，所以BD ⊥平面PAD ，而AD ⊂平面PAD ，所以BD AD ⊥.在平行四边形ABCD 中，//AD BC ，所以BD BC ⊥.由PD ⊥平面ABCD ，BC ⊂平面ABCD ，所以PD BC ⊥， 而BDPD D =，PD ⊂平面PBD ，BD ⊂平面PBD ，所以BC ⊥平面PBD .又BC ⊂平面PBC ，所以平面PBC ⊥平面PBD .（2）由（1）可知，BD AD ⊥，而45DAB ∠=，则ADB △为等腰直角三角形，又4AB =，所以22PD BD AD ===，连接AC ，由点,M N 分别是,PA PC 的中点，所以PMN PAC 且12MN AC =， 所以14PMNPAC SS =，则1144P MBN B PMN B PAC P ABC V V V V ----===， 在平行四边形ABCD 中，1222242ABCABDSS==⨯=， PD 为三棱锥P ABC -的高，所以1182422333P ABC ABCV SPD -=⨯=⨯⨯=， 所以三棱锥P MBN -的体积为12243P MBN P ABC V V --==. 【点睛】求三棱锥的体积时要注意三棱锥的每个面都可以作为底面，例如三棱锥的三条侧棱两两垂直，我们就选择其中的一个侧面作为底面，另一条侧棱作为高来求体积． 24．（Ⅰ）证明见解析；（Ⅱ）1. 【分析】（Ⅰ）由BD AC ⊥和1A A BD ⊥，利用线面垂直的判定定理证得BD ⊥平面1A AC ，然后再由//BD EF 证明.（Ⅱ）由1D D ⊥平面ABCD ，则1D D 是三棱锥1D AEF -在平面AEF 上的高，然后利用等体积法11A D EF D AEF V V --=求解.【详解】 （Ⅰ）如图所示：连接BD ，易知BD AC ⊥，因为1A A ⊥平面ABCD ，BD ⊂平面ABCD ， 所以1A A BD ⊥，又1A A AC A =，所以BD ⊥平面1A AC .在CBD 中，点E ，F 分别是BC ，DC 的中点， 所以//BD EF . 所以EF ⊥平面1A AC . （Ⅱ）∵1D D ⊥平面ABCD ，∴1D D 是三棱锥1D AEF -在平面AEF 上的高，且12D D =. ∵点E ，F 分别是BC ，DC 的中点， ∴1DF CF CE BE ====. ∴2111322222AEF S AD DF CF CE AB BE =-⋅⋅-⋅⋅-⋅⋅=△. ∴11111321332A D EF D AEF AEF V V S D D --==⋅⋅=⨯⨯=△.【点睛】方法点睛：(1)证明直线和平面垂直的常用方法：①线面垂直的定义；②判定定理；③垂直于平面的传递性(a ∥b ，a ⊥α⇒b ⊥α)；④面面平行的性质(a ⊥α，α∥β⇒a ⊥β)；⑤面面垂直的性质．(2)证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想． 25．（1）证明见解析（232【分析】（1）取CB 的中点M ，连,MF AM ，可证四边形AMFE 为平行四边形，从而可得//EF AM ，再根据直线与平面平行的判定定理可证结论；（2）根据A ECD D ACE B ACE E ACB V V V V ----===可求得结果. 【详解】。

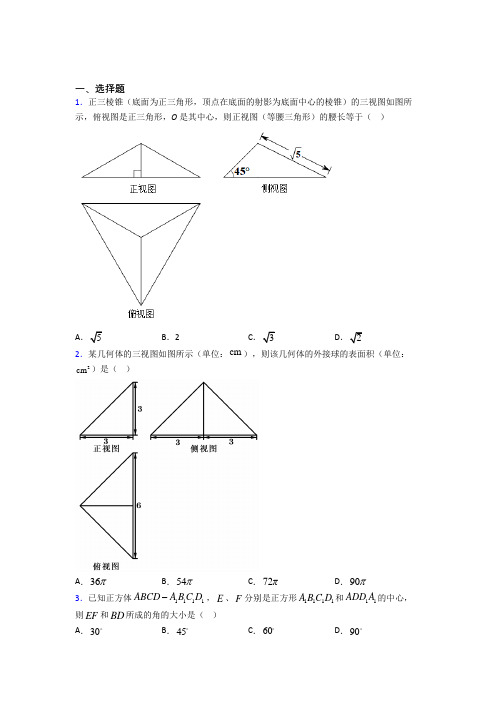
一、选择题1．正三棱锥（底面为正三角形，顶点在底面的射影为底面中心的棱锥）的三视图如图所示，俯视图是正三角形，O 是其中心，则正视图（等腰三角形）的腰长等于（ ）A ．5B ．2C ．3D ．22．某几何体的三视图如图所示（单位：cm ），则该几何体的外接球的表面积（单位：2cm ）是（ ）A ．36πB ．54πC ．72πD ．90π3．已知正方体1111ABCD A B C D -，E 、F 分别是正方形1111D C B A 和11ADD A 的中心，则EF 和BD 所成的角的大小是（ ） A ．30B ．45C ．60D ．904．已知平面,αβ，直线l ，记l 与,αβ所成的角分别为1θ，2θ，若αβ⊥，则（ ） A ．12sin sin 1θθ+≤B ．12sin sin 1θθ+≥C ．122πθθ+≤D ．122πθθ+≥5．现有一个三棱锥形状的工艺品P ABC -，点P 在底面ABC 的投影为Q ，满足12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，22222213QA QB QC AB BC CA ++=++，93ABCS =，若要将此工艺品放入一个球形容器（不计此球形容器的厚度）中，则该球形容器的表面积的最小值为（ ）A ．42πB ．44πC ．48πD ．49π6．已知三棱锥P ABC -的三条侧棱两两垂直，且,,PA PB PC 的长分别为,,a b c ，又2()162a b c +=，侧面PAB 与底面ABC 成45︒角，当三棱锥体积最大时，其外接球的表面积为（ ） A ．10πB ．40πC ．20πD ．18π7．如图，四棱柱ABCD A B C D ''''-中，底面ABCD 为正方形，侧棱AA '⊥底面ABCD ，32AB =，6AA '=，以D 为圆心，DC '为半径在侧面BCC B ''上画弧，当半径的端点完整地划过C E '时，半径扫过的轨迹形成的曲面面积为（ ）A ．964π B ．934π C ．962π D ．93π 8．如图，在正四棱锥P ABCD -中，设直线PB 与直线DC 、平面ABCD 所成的角分别为α、β，二面角P CD B --的大小为γ，则（ ）A ．,αβγβ>>B ．,αβγβ><C ．,αβγβ<>D ．,αβγβ<<9．在正方体1111ABCD A B C D -，中，M ，N ，P ，Q 分别为1A B ，1B D ，1A D ，1CD 的中点，则异面直线MN 与PQ 所成角的大小是（ ） A ．6π B ．4π C ．3π D ．2π 10．在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中，点E ，F 分别是棱C 1D 1，B 1C 1的中点，P 是上底面A 1B 1C 1D 1内一点，若AP ∥平面BDEF ，则线段AP 长度的取值范围是（ ） A ．[322，5] B ．[5，22]C ．[324，6] D ．[6，22]11．《九章算术》是古代中国乃至东方的第一步自成体系的数学专著，书中记载了一种名为“刍甍”的五面体（如图），其中四边形ABCD 为矩形，//EF AB ，若3AB EF =，ADE 和BCF △都是正三角形，且2AD EF =，则异面直线AE 与CF 所成角的大小为（ ）A ．6π B ．4π C ．3π D ．2π 12．在正方体1111ABCD A B C D -中，M 和N 分别为11A B ，和1BB 的中点．，那么直线AM 与CN 所成角的余弦值是（ ）A ．25B ．1010C ．35D ．32二、填空题13．如图，在三棱锥P ABC -中，点B 在以AC 为直径的圆上运动，PA ⊥平面,ABC AD PB ⊥，垂足为,D DE PC ⊥，垂足为E ，若3,2PA AC ==，则三棱锥P ADE -体积的最大值是_________．14．如图，已知直四棱柱1111ABCD A B C D -的所有棱长均相等，3BAD π∠=，E 是棱AB的中点，设平面α经过直线1A E ，且α平面111,B BCC l α=⋂平面112C CDD l =，若α⊥平面11A ACC ，则异面直线1l 与2l 所成的角的余弦值为_______．15．在边长为3的菱形ABCD 中，对角线3AC =，将三角形ABC 沿AC 折起，使得二面角B AC D --的大小为2π，则三棱锥B ACD -外接球的体积是_________________．16．如图，四边形ABCD 是矩形，且有2AB BC =，沿AC 将ADC 翻折成AD C '，当二面角D AC B '--的大小为3π时，则异面直线D C '与AB 所成角余弦值是______.17．已知长方体1234ABCD A B C D -，底面是边长为4的正方形，高为2，点O 是底面ABCD 的中心，点P 在以O 为球心，半径为1的球面上，设二面角111P A B C --的平面角为θ，则tan θ的取值范围是________.18．日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球（球心记为O ），地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40︒，则晷针与点A 处的水平面所成角的大小为_________.19．如图，已知正四面体D ABC -，P 为线段AB 上的动点（端点除外），则二面角D PC B --的平面角的余弦值的取值范围是___________．20．在矩形ABCD 中，1AB =，3AD =.将BCD 沿对角线BD 翻折，得到三棱锥A BCD -，则该三棱锥外接球的表面积为________. 三、解答题21．如图所示，在四棱锥P ABCD -中，//AD BC ，3AD =，4BC =，M 为线段AD 上点，且满足2AM MD =，N 为PC 的中点.（Ⅰ）证明：//MN 平面PAB ；（Ⅱ）设三棱锥N BCM -的体积为1V ，四棱锥P ABCD -的体积为2V ，求12V V . 22．如图，四棱锥P ABCD -的底面为正方形，PA ⊥底面ABCD ，E ，F ，H 分别为AB ，PC ，BC 的中点.（1）求证：DE ⊥平面PAH ；（2）若2PA AD ==，求直线PD 与平面PAH 所成线面角的正弦值.23．如图，四棱锥P ABCD -的底面ABCD 是边长为2的菱形，60BCD ∠=，已知2PB PD ==，6PA =，E 为PA 的中点.（1）求证：PC BD ⊥；（2）求二面角B PC E --的余弦值； （3）求三棱锥P BCE -的体积.24．如图，三枝锥D ABC -中，90ABC ∠=︒，1AB =，2BC CD DB ===.（1）若平面BCD ⊥平面ABC .求证：AB CD ⊥； （2）若1AD =，求CD 与平面ABC 所成的角.25．在四棱锥P ABCD -中，四边形ABCD 为正方形，平面PAB ⊥平面,ABCD PAB 为等腰直角三角形，,2PA PB AB ⊥=．（1）求证：平面PBC ⊥平面PAC ；（2）设E 为CD 的中点，求点E 到平面PBC 的距离．26．在三棱锥A BCD -中，E 、F 分别为AD 、DC 的中点，且BA BD =，平面ABD ⊥平面ADC .（1）证明：//EF 平面ABC ； （2）证明：BE CD ⊥.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】可得原几何体如图所示正三棱锥A BCD -，取BD 中点E ，连接,AE CE ，设底面边长为2x ，表示出2522x AO OE -===133xOE CE ==x ，进而求出腰长. 【详解】根据三视图可得原几何体如图所示正三棱锥A BCD -，取BD 中点E ，连接,AE CE ，则底面中心O 在CE 上，连接AO ，可得AO ⊥平面ABC ，由三视图可知5AB AC AD ===45AEC ∠=，设底面边长为2x ，则DE x =，则25AE x =-，则在等腰直角三角形AOE 中，2522x AO OE -===， O 是底面中心，则133xOE CE ==， 则25323x x-=，解得3x =， 则1AO =，底面边长为23， 则正视图（等腰三角形）的腰长为()22312+=.故选：B.【点睛】本题考查根据三视图计算原几何体的相关量，解题的关键是根据正三棱锥中的关系求出底面边长.2．A解析：A 【分析】由三视图知该几何体是底面为等腰直角三角形，且侧面垂直于底面的三棱锥，由题意画出图形，结合图形求出外接球的半径，再计算外接球的表面积． 【详解】解：由几何体的三视图知，该几何体是三棱锥P ABC -，底面为等腰ABC ∆， 且侧面PAB ⊥底面ABC ，如图所示；设D 为AB 的中点，又3DA DB DC DP ====，且PD ⊥平面ABC ，∴三棱锥P ABC -的外接球的球心O 在PD 上，设OP R =，则OA R =，3OD R =-，222(3)3R R ∴=-+， 解得3R =，∴该几何体外接球的表面积是32436R cm ππ=．故选：A ． 【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.3．C解析：C 【分析】作出图形，连接1AD 、11B D 、1AB ，推导出1//EF AB ，11//BD B D ，可得出异面直线EF 和BD 所成的角为11AB D ∠，分析11AB D 的形状，即可得出结果. 【详解】如下图所示，连接1AD 、11B D 、1AB ，设正方体1111ABCD A B C D -的棱长为1，则11112AD AB B D === 所以，11AB D 为等边三角形，则1160AB D ∠=，因为E 、F 分别是正方形1111D C B A 和11ADD A 的中心，则E 、F 分别是11B D 、1AD 的中点，所以，1//EF AB ，在正方体1111ABCD A B C D -中，11//BB DD 且11BB DD =， 所以，四边形11BB D D 为平行四边形，则11//BD B D ， 所以，异面直线EF 和BD 所成的角为1160AB D ∠=. 故选：C. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．4．C解析：C 【分析】如图，作出1θ和2θ，再由线面角推得12sin sin 2πθθ⎛⎫≤- ⎪⎝⎭，利用三角函数的单调性判断选项. 【详解】设直线l 为直线AB ，m αβ=，AD m ⊥，BC m ⊥，连结BD ，AC ，1ABD θ=∠，2BAC θ=∠，12sin sin 2AD AC AB AB πθθ⎛⎫=≤=- ⎪⎝⎭，12,2πθθ-都是锐角，122πθθ∴≤-，即122πθθ+≤故选：C 【点睛】关键点点睛：本题的关键是作图，并利用线段AD AC ≤，传递不等式，12sin sin 2AD AC AB AB πθθ⎛⎫=≤=- ⎪⎝⎭. 5．D解析：D 【分析】作QM AB ⊥，连接PM ，易证AB PM ⊥，由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM =，再根据12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，由对称性得到AB BC AC ==，然后根据22222213QA QB QC AB BC CA ++=++，93ABCS =，求得6,23AB AQ ==，在AOQ△中，由222AO OQ AQ =+求解半径即可.【详解】 如图所示：作QM AB ⊥与M ，连接PM ， 因为PQ ⊥平面ABC ，所以PQ AB ⊥，又QM PQ Q ⋂=， 所以AB ⊥平面PQM ， 所以AB PM ⊥，所以112122QAB PABAB QM S S AB PM ⨯⨯==⨯⨯△△, 2PM QM =,因为12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△， 由对称性得AB BC AC ==,又因为22222213QA QB QC AB BC CA ++=++，ABCS =所以21sin 60932ABCSAB =⨯⨯= 解得6,ABAQ ==所以3QM PM PQ ===，设外接球的半径为r ，在AOQ △中，222AOOQ AQ =+，即()(2223r r =-+，解得72r =， 所以外接球的表面积为2449S r ππ==， 即该球形容器的表面积的最小值为49π. 故选：D 【点睛】关键点点睛：本题关键是由12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△得到三棱锥是正棱锥，从而找到外接球球心的位置而得解..6．A解析：A 【分析】将三棱锥体积用公式表示出来，结合均值不等式和2()a b c+=a b =，进而得到2c a =，带入体积公式求得2,a b c ===24S R π=求出外接球的表面积.【详解】解：211166()643V abc ab ab a b ab ==⋅⋅=+，当且仅当a b =时取等号， 因为侧面PAB 与底面ABC 成45︒角，则PC c ==，216V a ∴==2,a b c ∴===所以2222410R a b c =++=， 故外接球的表面积为10π. 故选：A. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.7．A解析：A 【分析】先确定曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，利用圆锥的侧面积S rl π=即可得出结论. 【详解】由题意 6,CE CC AA BC AB ''=====BE ==，所以45BCE ∠=， 45ECC '∠=， 所以曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，所以圆锥的侧面积 6S rl CC DC πππ'==⨯⨯=⨯⨯=，所以曲面面积为18⨯=. 故选：A. 【点睛】方法点睛：本题考查曲面面积，考查圆锥的侧面积，确定曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18是关键，考查系数的空间想象力. 8．A解析：A 【分析】连接AC 、BD 交于O ，连PO ，取CD 的中点E ，连,OE PE ，根据正棱锥的性质可知，PCE α∠=，PCO β∠=，PEO γ∠=，再比较三个角的正弦值可得结果. 【详解】连接AC 、BD 交于O ，连PO ，取CD 的中点E ，连,OE PE ，如图：因为//AB CD ，所以PBA α∠=，又因为四棱锥P ABCD -为正四棱锥，所以PCE α∠=，由正四棱锥的性质可知，PO ⊥平面ABCD ，所以PCO β∠=， 易得OE CD ⊥，PE CD ⊥，所以PEO γ∠=， 因为sin PE PC α=，sin POPCβ=，且PE PO >，所以sin sin αβ>，又,αβ都是锐角，所以αβ>，因为sin PO PE γ=，sin POPCβ=，且PC PE >，所以sin sin γβ>，因为,βγ都是锐角，所以γβ>.故选：A 【点睛】关键点点睛：根据正棱锥的性质，利用异面直线所成角、直线与平面所成角、二面角的平面角的定义得到这三个角是解题关键，属于中档题.9．B解析：B 【分析】由M 也是1A B 的中点，P 也是1AD 中点，得平行线，从而找到异面直线MN 与PQ 所成角，在三角形中可得其大小． 【详解】如图，连接1AD ，1AB ，显然M 也是1A B 的中点，P 也是1AD 中点，又N 是1B D 中点，Q 是1CD 中点，所以//MN AD ，//PQ AC ， 所以CAD ∠是异面直线MN 与PQ 所成角（或补角），大小为4π． 故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．10．A解析：A 【分析】分别取棱A 1B 1、A 1D 1的中点M 、N ，连接MN ，可证平面AMN ∥平面BDEF ，得P 点在线段MN 上．由此可判断当P 在MN 的中点时，AP 最小；当P 与M 或N 重合时，AP 最大．然后求解直角三角形得答案． 【详解】如图所示，分别取棱A 1B 1、A 1D 1的中点M 、N ，连接MN ，连接B 1D 1， ∵M 、N 、E 、F 为所在棱的中点，∴MN ∥B 1D 1，EF ∥B 1D 1， ∴MN ∥EF ，又MN ⊄平面BDEF ，EF ⊂平面BDEF ，∴MN ∥平面BDEF ； 连接NF ，由NF ∥A 1B 1，NF ＝A 1B 1，A 1B 1∥AB ，A 1B 1＝AB ， 可得NF ∥AB ，NF ＝AB ，则四边形ANFB 为平行四边形，则AN ∥FB ，而AN ⊄平面BDEF ，FB ⊂平面BDEF ，则AN ∥平面BDEF ． 又AN ∩NM ＝N ，∴平面AMN ∥平面BDEF ．又P 是上底面A 1B 1C 1D 1内一点，且AP ∥平面BDEF ，∴P 点在线段MN 上．在Rt △AA 1M 中，AM 222211215AA A M =+=+=，同理，在Rt △AA 1N 中，求得AN 5=，则△AMN 为等腰三角形．当P 在MN 的中点时，AP 最小为222322()2+=， 当P 与M 或N 重合时，AP 最大为5． ∴线段AP 长度的取值范围是32,5⎡⎤⎢⎥⎣． 故选：A ．【点睛】本题主要考查了空间中点、线、面间的距离问题，其中解答中通过构造平行平面寻找得到点P 的位置是解答的关键，意在考查空间想象能力与运算能力，属于中档试题.11．D解析：D 【分析】过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，然后在CFG △中求解. 【详解】如下图所示，在平面ABFE 中，过点F 作//FG AE 交AB 于点G ，连接CG ， 则异面直线AE 与CF 所成角为CFG ∠或其补角，设1EF =，则3AB =，2BC CF AE ===，因为//EF AB ，//FG AE ，所以，四边形AEFG 为平行四边形， 所以，2FG AE ==，1AG =，2BG =，由于2ABC π∠=，由勾股定理可得2222CG BC BG =+=，所以，222CG CF FG =+，则2CFG π∠=.故选：D. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．12．A解析：A 【分析】作出异面直线AM 和CN 所成的角，然后解三角形求出两条异面直线所成角的余弦值. 【详解】设,E F 分别是1,AB CC 的中点，由于,M N 分别是111,A B BB 的中点，结合正方体的性质可知11//,//B E AM B F CN ，所以1EB F ∠是异面直线AM 和CN 所成的角或其补角， 设异面直线AM 和CN 所成的角为θ，设正方体的边长为2，2211125B E B F ==+=，2221216EF =++=，则1cos cos EB F θ=∠=55625255+-=⨯⨯.故选：A.【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．二、填空题13．【分析】由已知证明再由三角形相似列比例式可得证明利用基本不等式求得的最大值可得三棱锥体积的最大值【详解】由平面得又平面得又平面得而平面可得在中由得由得则由得又得即（当且仅当时等号成立）三棱锥体积的最解析：34【分析】由已知证明AE PC ⊥，再由三角形相似列比例式可得PE ，证明AD DE ⊥，利用基本不等式求得AD DE ⋅的最大值，可得三棱锥P ADE -体积的最大值． 【详解】由PA ⊥平面ABC ，得PA BC ⊥，又BC AB ⊥，PAAB A =，BC ∴⊥平面PAB ，得BC AD ⊥，又AD PB ⊥，PB BC B ⋂=，AD ∴⊥平面PBC ，得AD PC ⊥，而DE PC ⊥，AD DE D ⋂=， PC ∴⊥平面ADE ，可得AE PC ⊥．在Rt PAC △中，由2PA AC ==，得4PC =．由Rt PEA Rt PAC ∽，得PE PA PA PC =，则21234PA PE PC ===，由3PE =，PA =23AE =，又AD DE ⊥，2223AD DE AE ∴+==，得2232AD DE AD DE =+≥⋅， 即32AD DE⋅（当且仅当AD DE =时等号成立）， ∴三棱锥P ADE -体积的最大值是1111333323224AD DE PE ⨯⨯⨯=⨯⨯⨯=．故答案为：34． 【点睛】方法点睛：解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理．14．【分析】取的中点连接证明平面平面平面即平面然后分别取的中点证明平面平面可得可得异面直线与所成的角即与所成的角由余弦定理可得答案【详解】由直四棱柱的所有棱长均相等所以是菱形连接且所以因为平面平面所以且解析：910【分析】取AD 的中点F ，连接1A F ，证明平面1A EF ⊥平面11A ACC ，平面1A EF 即平面α，然后分别取1111B C D C 、的中点M N 、，证明平面1//A EF 平面MNC ，可得//CM 1l ，//CN 2l ，可得异面直线1l 与2l 所成的角即CM 与CN 所成的角，由余弦定理可得答案.【详解】由直四棱柱1111ABCD A B C D -的所有棱长均相等，3BAD π∠=，所以ABCD 是菱形，连接AC BD 、，1111AC B D 、，且ACBD O =，11111A C B D O ⋂=，所以BD AC ⊥，1111B D A C ⊥，因为1AA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以1AA BD ⊥，且1AA AC A =，所以BD ⊥平面11A ACC ，取AD 的中点F ，连接1A F ，连接EF 交AC 与G ，所以//EF BD ，且G 是AO 的中点，所以EF ⊥平面11A ACC ，所以平面1A EF ⊥平面11A ACC ， 又1A E ⊂平面1A EF ，所以平面1A EF 即平面α，分别取1111B C D C 、的中点M N 、，连接MN 交11A C 与H 点，H 即为11O C 的中点， 所以1A H GC =，且1//A H GC ，所以四边形1A HCG 是平行四边形，所以1//A G HC ，1AG ⊄平面CMN ，CH ⊂平面CMN ，所以//A G 平面CMN ， 又因为11//////EF BD B D MN ，EF ⊄平面CMN ，MN ⊂平面CMN ， 所以//MN 平面CMN ，又1AG EF G =，所以平面1//A EF 平面MNC ，且平面11B C CB ⋂平面MNC MC =， 平面11D C CD平面MNC NC =，所以//CM 1l ，//CN 2l ，所以异面直线1l 与2l 所成的角即CM 与CN 所成的角，设2AB =， 则直四棱柱1111ABCD A B C D -的所有棱长均为2，由3BAD π∠=，所以112BD AB B D ===，11112MN D B ==，且CM CN ====，由余弦定理得222551922510CM CN MN MCN CM CN +-+-∠===⨯⨯.故答案为：910.【点睛】本题考查了异面直线所成的角，关键点是作出平面α及找出异面直线所成的角，考查了学生分析问题、解决问题的能力及空间想象力.15．；【分析】分析菱形的特点结合其翻折的程度判断其外接球球心的位置放到相应三角形中利用勾股定理求得半径利用球的体积公式求得外接球的体积【详解】根据题意画出图形根据长为的菱形中对角线所以和都是正三角形又因解析：556π； 【分析】分析菱形的特点，结合其翻折的程度，判断其外接球球心的位置，放到相应三角形中，利用勾股定理求得半径，利用球的体积公式求得外接球的体积. 【详解】根据题意，画出图形，3的菱形ABCD 中，对角线3AC = 所以ABC 和DBC △都是正三角形， 又因为二面角B AC D --的大小为2π， 所以分别从两个正三角形的中心做面的垂线，交于O ，则O 是棱锥B ACD -外接球的球心，且11,2GD OG GE ===，所以球的半径2R ==，所以其体积为3344(3326V R ππ==⋅=，故答案为：6. 【点睛】思路点睛：该题考查的是有关几何体外接球的问题，解题思路如下： （1）根据题中所给的条件，判断菱形的特征，得到两个三角形的形状；（2）根据直二面角，得到两面垂直，近一倍可以确定其外接球的球心所在的位置； （3）利用勾股定理求得半径； （4）利用球的体积公式求得结果；（5）要熟知常见几何体的外接球的半径的求解方法.16．【分析】作于于可得等于二面角的平面角从而可得然后求得而因此可得是异面直线与所成角（或补角）这样在求解可得【详解】如图作于于则连接根据二面角平面角的定义知与的夹角等于二面角的平面角所以因为所以设则在矩解析：12． 【分析】作DM AC ⊥于M ，BN AC ⊥于N ，可得,MD NB '<>等于二面角D AC B '--的平面角，从而可得DMD '∠，然后求得DD '，而//AB CD ，因此可得D CD '∠是异面直线D C '与AB 所成角（或补角）．这样在DCD '求解可得．【详解】如图，作DM AC ⊥于M ，BN AC ⊥于N ，则//DM BN ，连接,D M DD ''， 根据二面角平面角的定义知MD '与NB 的夹角等于二面角D AC B '--的平面角， 所以,3MD NB π'<>=，因为//DM BN ，所以23DMD π'∠=，设1BC =，则AB ==ABCD 中，AC =3DM ==，D M DM '==， 则22222212cos 2232DD DM D M DM D M π⎛⎫'''=+-⋅=+--= ⎪⎝⎭⎝⎭⎝⎭， 所以2DD '=，因为//AB CD ，所以D CD '∠是异面直线D C '与AB 所成角（或补角）．DCD '是正三角形，3D CD π'∠=，1cos 2D CD '∠=． 所以异面直线D C '与AB 所成角余弦值是12． 故答案为：12．【点睛】关键点点睛：本题考查求异面直线所成的角，解题方法根据异面直线所成角定义作出它们所成的角，然后解三角形可得，解题关键是利用图中MD '与NB 的夹角等于二面角D AC B '--的平面角，从而求得DMD '∠，只要设1BC =，可求得DD '，从而求得结论．17．【分析】根据题意画出相应的图形结合题意找出什么情况下取最大值什么情况下取最小值利用和差角正切公式求得最值得到结果【详解】根据题意如图所示：取的中点过点作球的切线切点分别为可以判断为的最小值为的最大值解析：4747-+⎣⎦【分析】根据题意，画出相应的图形，结合题意，找出什么情况下取最大值，什么情况下取最小值，利用和差角正切公式求得最值，得到结果. 【详解】根据题意，如图所示：取11A B 的中点H ，过H 点作球O 的切线，切点分别为,M N ， 可以判断1O HN ∠为θ的最小值，1O HM ∠为θ的最大值， 且1112tan 12OO O HO HO ∠===， 22,1OH OM ON ===，所以7HM HN ==tan tan 7NHO OHM ∠=∠=， 1117827477tan tan()1637117O HN O HO NHO ---∠=∠-∠====++ 1117827477tan tan()1637117O HM O HO OHM ++∠=∠+∠====-， 所以tan θ的取值范围是4747-+⎣⎦，故答案为：4747-+⎣⎦. 【点睛】方法点睛：该题考查的是有关二面角的求解问题，解题方法如下： （1）先根据题意画图；（2）结合题意，找出在什么情况下取最大值和最小值； （3）结合图形求得相应角的正切值； （4）利用和差角正切公式求得结果.18．40°【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图根据面面平行的性质定理和线面垂直的定义判定有关截线的关系根据点处的纬度计算出晷针与点处的水平面所成角【详解】画出截面图如下图所示其中是赤解析：40° 【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图，根据面面平行的性质定理和线面垂直的定义判定有关截线的关系，根据点A 处的纬度，计算出晷针与点A 处的水平面所成角. 【详解】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥.. 由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒， 由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒. 故答案为：40°.【点睛】本小题主要考查中国古代数学文化，解题的关键是将稳文中的数据建立平面图形，属于中档题.19．【分析】当点从点运动到点时二面角的平面角逐渐增大二面角的平面角最小趋于二面角的平面角最大趋于二面角的平面角的补角求出二面角的平面角和二面角的平面角即可【详解】当点从点运动到点时二面角的平面角逐渐增大解析：11,33⎛⎫- ⎪⎝⎭【分析】当点P 从点A 运动到点B 时，二面角D PC B --的平面角逐渐增大，二面角D PC B --的平面角最小趋于二面角D AC B --的平面角，最大趋于二面角D BC A --的平面角的补角，求出二面角D AC B --的平面角和二面角D BC A --的平面角即可. 【详解】当点P 从点A 运动到点B 时，二面角D PC B --的平面角逐渐增大，二面角D PC B --的平面角最小趋于D AC B --的平面角，最大趋于二面角D BC A --的平面角的补角，设正四面体的棱长为2a ，如图所示，取AC 的中点E ，连接DE 、BE ， 易知DEB ∠为二面角D AC B --的平面角，3DE BE a ==，所以((()()()2223321cos 3233a a a DEB a a+-∠==⨯⨯， 同理可得：二面角D BC A --的平面角的补角的余弦值为13-， 故二面角D PC B --的平面角的余弦值的取值范围是11,33⎛⎫- ⎪⎝⎭， 故答案为：11,33⎛⎫- ⎪⎝⎭【点睛】本题主要考查了二面角的平面角的求解，考查空间想象能力，属于中档题.20．【分析】作出图示求得外接球的半径由球的表面积可求得答案【详解】作出图示因为在矩形ABCD 中则连接交于点则设该三棱锥外接球的半径为则所以该三棱锥外接球的表面积故答案为：【点睛】本题考查三棱锥的外接球的 解析：4π【分析】作出图示，求得外接球的半径，由球的表面积可求得答案. 【详解】作出图示，因为在矩形ABCD 中，1AB =，3AD =.则2==AC BD ，连接AC BD，交于点O ，则1AO BO CO DO ====，设该三棱锥外接球的半径为R ，则1R =， 所以该三棱锥外接球的表面积244S R ππ==， 故答案为：4π.【点睛】本题考查三棱锥的外接球的表面积计算，关键在于求得外接球的球心位置和半径，属于中档题.三、解答题21．（Ⅰ）证明见解析；（Ⅱ）1227V V =. 【分析】（Ⅰ）要证明线面平行，需证明线线平行，取BP 的中点T ，连接AT ，TN ，证明//MN AT ；（Ⅱ）利用锥体体积公式，分别求两个锥体底面积和高的比值，表示体积比值.【详解】（Ⅰ）如图，取BP 的中点T ，连接AT ，TN .因为N 为PC 的中点，所以TN //BC ，且122TN BC ==.又因为223AM AD ==，且//AD BC ，所以TN //AM ，TN AM =，即四边形AMNT 为平行四边形， 所以MN //AT ，因为AT ⊂平面PAB ，MN ⊄平面PAB ，所以//MN 平面PAB .（Ⅱ）设四棱锥P ABCD -的高为h ，AD 与BC 间的距离为d . 则()21117343326ABCD V h S h d hd =⨯⨯=⨯+=梯形， 11114323223BCM h h hd V S d =⨯⨯=⨯⨯⨯=△因此1227V V =. 【点睛】方法点睛：本题考查了线面平行的判断定理，意在考查转化与化归和计算求解能力，不管是证明面面平行，还是证明线面平行，都需要证明线线平行，证明线线平行的几种常见形式，1.利用三角形中位线得到线线平行；2.构造平行四边形；3.构造面面平行. 22．（1）证明见解析；（2）5. 【分析】（1）由PA ⊥底面ABCD ，得PA DE ⊥，由Rt ABH Rt DAE ≌△△，得DE AH ⊥，可得答案.（2）由可知DE ⊥平面PAH ，连接PG ，则DPG ∠即为直线PD 与平面PAH 所成线面角，在Rt PDG △中，由sin DPG ∠可得答案. 【详解】（1）因为PA ⊥底面ABCD ，DE ⊂底面ABCD ，所以PA DE ⊥，因为E ，H 分别为正方形ABCD 的边AB ，BC 的中点，,,AB DA BH AE HBAEAD ，所以Rt ABH Rt DAE ≌△△，所以BAH ADE ∠=∠，由90AED ADE ∠+∠= 所以90BAH AED ∠+∠=，所以DE AH ⊥， 因为PA ⊂平面PAH ，AH ⊂平面PAH ，PA AH A ⋂=，所以DE ⊥平面PAH .（2）由（1）可知DE ⊥平面PAH ，设AH DE G ⋂=，如图，连接PG ，则DPG ∠即为直线PD 与平面PAH 所成线面角， 因为2PA AD ==，所以PD =DE = 在Rt DAE 中，由于AG DE ⊥，所以2AD DG DE =⋅，所以4DG =DG =所以在Rt PDG △中，sin DG DPG PD ∠===PD 与平面PAH 所成线面角的正弦值为5.。

高中数学必修2立体几何部分试卷试卷满分100分。

时间70分钟考号 班级 姓名第Ⅰ卷（选择题共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、垂直于同一条直线的两条直线一定 （ ）A 、平行B 、相交C 、异面D 、以上都有可能 2、过直线l 外两点作与直线l 平行的平面，可以作（ ）A ．1个B ．1个或无数个C ．0个或无数个D ．0个、1个或无数个 3、正三棱锥底面三角形的边长为3，侧棱长为2，则其体积为 （ ）A ．41 B ．21 C ．43 D ．49 4、右图是一个实物图形，则它的左视图大致为 （ ）5、已知正四棱台的上、下底面边长分别为3和6，其侧面积等于两底面积之和，则该正四棱台的高是 （ ）A ．2B ．25C ．3D ．27 6、已知α、β是平面，m 、n 是直线，则下列命题不正确．．．的是 （ ） A ．若//,m n m α⊥，则n α⊥ B ．若,m m αβ⊥⊥，则//αβ C ．若,//,m m n n αβ⊥⊂，则αβ⊥ D ．若//,m n ααβ=I，则//m n7、正六棱柱ABCDEF －A 1B 1C 1D 1E 1F 1的侧面是正方形，若底面的边长为a ，则该正六棱柱的外接球的表面积是 ( )A ．4πa 2 B.5 πa 2 C. 8πa 2 D.10πa 28、如右下图，在ABC ∆中，2AB =，BC=1.5，120ABC ∠=o，如图所示。

若将ABC ∆绕BC 旋转一周，则所形成的旋转体的体积是（ ） （A ）92π （B ）72π （C ）52π （D ）32π（第8题图）9、如左上图是由单位立方体构成的积木垛的三视图，据此三视图可知，构成这堆积木垛的单 位正方体共有 （ ） A ．6块 B ．7块 C ．8块 D ．9块10、给出下列命题①过平面外一点有且仅有一个平面与已知平面垂直 ②过直线外一点有且仅有一个平面与已知直线平行 ③过直线外一点有且仅有一条直线与已知直线垂直 ④过平面外一点有且仅有一条直线与已知平面垂直 其中正确命题的个数为（ ） A ．0个 B ．1个C ．2个D ．3个第Ⅱ卷（非选择题 共60分）二、填空题（每小题4分，共16分）11、已知直线m 、n 及平面α，其中m ∥n ，那么在平面α内到两条直线m 、n 距离相等的点的集合可能是：①一条直线；②一个平面；③一个点；④空集。

一、选择题1．在四面体S ABC -中，SA ⊥平面ABC ，901ABC SA AC AB ︒∠====,，则该四面体的外接球的表面积为（ ）A ．23πB ．43π C ．4π D ．5π 2．设m ，n 是两条不同直线，α，β是两个不同的平面，下列命题正确的是( ) A ．//m α，//n β且//αβ，则//m nB ．m α⊂，n α⊂，//m β，//n β，则//αβ C ．m α⊥，n β⊂，m n ⊥，则αβ⊥D ．m α⊥，n β⊥且αβ⊥，则m n ⊥3．在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，15AA =，则V 的最大值是（ ）A ．4πB ．92πC ．1256πD ．323π 4．点A ，B ，C 在球O 表面上，2AB =，4BC =，60ABC ∠=︒，若球心O 到截面ABC 的距离为 ）A ．323π B ． C ．36π D ． 5．已知四棱锥S ABCD -的底面为矩形，SA ⊥底面ABCD ，点E 在线段BC 上，以AD为直径的圆过点E .若3SA ==，则SED ∆的面积的最小值为（ ）A ．9B ．7C ．92D ．726．的内切球，则此棱柱的体积是（ ）.A ．3B ．354cmC ．327cmD ．3 7．在棱长为a 的正方体1111ABCD A B C D －中，M 为AB 的中点， 则点C 到平面1A DM 的距离为（ ）A ．3aB ．6aC ．2aD ．12a 8．已知三棱锥A BCD -中，侧面ABC ⊥底面BCD ，ABC 是边长为3的正三角形，BCD 是直角三角形，且90BCD ∠=︒，2CD =，则此三棱锥外接球的体积等于()A ．B ．323πC ．12πD ．643π 9．半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形为面的多面体，体现了数学的对称美.如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，得到一个有十四个面的半正多面体，它们的棱长都相等，其中八个为正三角形，六个为正方形，称这样的半正多面体为二十四等边体.一个二十四等边体的各个顶点都在同一个球面上，若该球的表面积为16π，则该二十四等边体的表面积为（ ）A ．1243+B ．1863+C ．2483+D ．36123+ 10．如图，三棱柱111ABC A B C -中，侧棱1AA ⊥底面111A B C ，底面三角形111A B C 是正三角形，E 是BC 中点，则下列叙述正确的是（ ）A ．1CC 与1B E 是异面直线B ．AC ⊥平面11ABB A C ．AE ，11B C 为异面直线，且11AE B C ⊥D ．11//A C 平面1AB E11．α，β是两个平面，m ，n 是两条直线，有下列四个命题；①如果m n ⊥，m α⊥，//n β，那么αβ⊥.②如果m α⊥，//n α，那么m n ⊥.③如果//αβ，m α⊂，那么//m β.④如果//m n ，//αβ，那么m 与α所成的角和n 与β所成的角相等.其中正确的命题的个数为（ ）A ．1B ．2C ．3D ．4 12．αβ、是两个不同的平面，m n 、是平面α及β之外的两条不同直线，给出四个论断： ①m n ⊥；②αβ⊥；③n β⊥；④.m α⊥ 以其中三个论断作为条件，余下一个作为结论，其中正确命题的个数是（ ）A ．1个B ．2个C ．3个D ．4个13．在正方体1111ABCD A B C D -中，E ，F 分别为1CC ，1DD 的中点，则异面直线AF ，DE 所成角的余弦值为（ ）A ．14B ．154C ．65D ．1514．设l 是直线，α，β是两个不同的平面，下列命题正确的是（ ）A ．若//l α，//l β，则//αβB ．若αβ⊥，//l α，则l β⊥C ．若αβ⊥，l α⊥，则//l βD ．若//l α，l β⊥，则αβ⊥二、解答题15．如图，直三棱柱ABC －A 1B 1C 1中，AA 1＝2，A 1C ＝25，AB ＝2，∠BAC ＝60°.（1）求三棱锥A 1－ABC 的表面积；（2）证明：在线段A 1C 上存在点M ，使得AC ⊥BM ，并求1A M MC的值. 16．如图所示的四棱锥E -ABCD 中，底面ABCD 为矩形，AE ＝EB ＝BC ＝2，AD ⊥平面ABE ，且CE 上的点F 满足BF ⊥平面ACE .（1）求证：AE ∥平面BFD ；（2）求三棱锥C -AEB 的体积.17．如图，在三棱锥V-ABC 中，VC ⊥底面ABC ，AC BC ⊥，D 是棱AB 的中点，且AC BC VC ==.（1）证明：平面VAB ⊥平面VCD ；（2）若22AC =AB 上有一点E ，使得线VD 与平面VCE 所成角的正弦值为1515，试确定点E 的位置，并求三棱锥C-VDE 的体积. 18．如图，已知三棱柱111ABC A B C -的所有棱长都相等，侧棱1AA ⊥底面ABC ，,E F 分别是1111,A B AC 的中点.（1）求证:11B F AC ⊥ ；（2）求平面EFCB 与底面ABC 所成二面角的正切值.19．如图三棱柱111ABC A B C －中，11,,60CA CB AB AA BAA ∠︒＝＝＝，（1）证明1AB A C ⊥；（2）若16AC ＝，2AB CB ＝＝，求三棱柱111ABC A B C －的体积S . 20．如图，已知AF ⊥平面ABCD ，四边形ABEF 为矩形，四边形ABCD 为直角梯形，90DAB ∠=︒，//AB CD ，2AD AF CD ===，4AB =.（1）求证：AC ⊥平面BCE ；（2）求三棱锥E BCF -的体积.21．如图，在三棱柱111ABC A B C -中，侧棱垂直于底面，AC BC ⊥，1AC BC CC ==，E ，F 分别为11A B ，BC 的中点．（Ⅰ）求证：1AC C F ⊥；（Ⅱ）求证：BE ∥平面11AC F ；（Ⅲ）在棱1CC 上是否存在一点G ，使得平面1B EG ⊥平面11AC F ？说明理由． 22．如图，在斜三棱柱111ABC A B C -中，点O .E 分别是11A C 、11A B 的中点，1A C 与1AC 交于点F ，AO ⊥平111A B C .已知90BCA ∠=︒，12AA AC BC ===.（1）求证：//EF 平面11BB C C ；（2）求11A C 与平面11AA B 所成角的正弦值.23．如图，在平行四边形ABCD 中，4AB =，60DAB ∠=︒．点G ，H 分别在边CD ，CB 上，点G 与点C ，D 不重合，GH AC ⊥，GH 与AC 相交于点O ，沿GH 将CGH 翻折到EGH 的位置，使二面角E GH B --为90°，F 是AE 的中点．（1）请在下面两个条件：①AB AD =，②AB BD ⊥中选择一个填在横线处，使命题P ：若________，则BD ⊥平面EOA 成立，并证明．（2）在（1）的前提下，当EB 取最小值时，求直线BF 与平面EBD 所成角的正弦值．24．如图，在梯形ABCD 中，//BC AD ，E 在AD 上，且2BC BE ED ===．沿BE 将ABE △折起，使得AB CE ．（1）证明：AD CE ⊥；（2）若在梯形ABCD 中，π3ADC ∠=，折起后π3ABD ∠=，点A 在平面BCDE 内的射影H 为线段BD 的一个四等分点（靠近点B ），求三棱锥D ABC -的体积． 25．如图，在五面体ABCDEF 中，FA ⊥平面ABCD ，AD //BC //FE ，AB ⊥AD ，M 为EC 的中点，AF ＝AB ＝BC ＝FE ＝12AD .（I ）证明：平面AMD ⊥平面CDE ；（II ）求二面角A ﹣CD ﹣E 的余弦值.26．如图所示，四棱锥P －ABCD 的底面是边长为8的正方形，四条侧棱长均为217.点G ，E ，F ，H 分别是棱PB ，AB ，CD ，PC 上共面的四点，平面GEFH ⊥平面ABCD ，BC ∥平面GEFH .（1）证明：GH ∥EF ；（2）若EB ＝2，求四边形GEFH 的面积.【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据题目条件先确定出外接球的球心，得出外接球半径，然后计算表面积.【详解】因为SA ⊥平面ABC ，BC ⊂平面ABC ，所以SA ⊥BC ，又90ABC ∠=，SA AB A ⋂=，且AB平面SAB ，SA ⊂平面SAB ， 所以BC ⊥平面ABC ，所以BC SB ⊥. 因为21SA AC AB ===,，所以2SC =，3SB =，1BC =，根据该几何体的特点可知，该四面体的外接球球心位于SC 的中点，则外接球半径112R SC ==， 故该四面体的外接球的表面积为244R ππ=.故选：C.,【点睛】本题考查棱锥的外接球问题，难度一般，根据几何条件确定出球心是关键.2．D解析：D【分析】对每一个命题逐一判断得解.【详解】对于A ，若m ∥α，n ∥β且α∥β，说明m 、n 是分别在平行平面内的直线，它们的位置关 系应该是平行或异面或相交，故A 不正确；对于B ，若“m ⊂α，n ⊂α，m ∥β，n ∥β”，则“α∥β”也可能α∩β＝l ，所以B 不成立． 对于C ，根据面面垂直的性质，可知m ⊥α，n ⊂β，m ⊥n ，∴n ∥α，∴α∥β也可能α∩β＝l ，也可能α⊥β，故C 不正确；对于D ，由m ⊥α，n ⊥β且α⊥β，则m 与n 一定不平行，否则有α∥β，与已知α⊥β矛盾，通过平移使得m 与n 相交，且设m 与n 确定的平面为γ，则γ与α和β的交线所成的角即 为α与β所成的角，因为α⊥β，所以m 与n 所成的角为90°，故命题D 正确． 故答案为D【点睛】本题考查直线与平面平行与垂直，面面垂直的性质和判断的应用，考查逻辑推理能力和空间想象能力.3．D解析：D【分析】先保证截面圆与ABC 内切，记圆O 的半径为r ，由等面积法得()68AC AB BC r ++=⨯，解得2r．由于三棱柱高为5，此时可以保证球在三棱柱内部，球的最大半径为2，由此能求出结果．【详解】 解：如图，由题意可知，球的体积要尽可能大时，球需与三棱柱内切．先保证截面圆与ABC 内切，记圆O 的半径为r ， 则由等面积法得1111 (682222)ABC S AC r AB r BC r =++=⨯⨯△， 所以()68AC AB BC r ++=⨯，又因为6AB =，8BC =，所以10AC =，所以2r．由于三棱柱高为5，此时可以保证球在三棱柱内部，若r 增大，则无法保证球在三棱柱内，故球的最大半径为2，所以3344322333V r πππ==⋅=． 故选：D ．【点评】本题考查球的最大体积的求法，考查空间想象能力，属于中档题.4．D解析：D【分析】先判断出底面三角形的形状，然后从球心作截面的垂足，确定垂足的位置后，再利用勾股定理得到半径，再求体积即可.【详解】由2AB =，4BC =，60ABC ∠=︒及余弦定理得，2222cos 416224cos6012AC AB BC AB BC ABC =+-⋅∠=+-⨯⨯︒=，所以222BC AB AC =+，即A 是直角，BC 是底面圆的直径，过球心O 作OD ⊥平面ABC ，D 即为BC 的中点，所以22OD =，122BD BC == 连接OB ，OB 即为半径，由勾股定理得2223OB OD BD =+=，所以球的体积为34(23)3233V ππ==， 故选：D.【点睛】本题考查了球的外接问题，确定球心在截面上的射影的位置是关键，属于基础题. 5．C解析：C【分析】根据线面垂直的性质以及线面垂直的判定，根据勾股定理，得到,BE EC 之间的等量关系，再用,BE EC 表示出SED 的面积，利用均值不等式即可容易求得.【详解】设BE x =，EC y =，则BC AD x y ==+.因为SA ⊥平面ABCD ，ED ⊂平面ABCD ，所以SA ED ⊥.又AE ED ⊥，SA AE A ⋂=，所以ED ⊥平面SAE ，则ED SE ⊥.易知23AE x =+23ED y =+ 在Rt AED ∆中，222AE ED AD +=，即22233()x y x y +++=+，化简得3xy =.在Rt SED ∆中，SE =ED ==.所以12SED S SE ED ∆=⋅=.因为22108336x x +≥=，当且仅当x =2y =时等号成立，所以92SED S ∆≥=. 故选：C.【点睛】 本题考查空间几何体的线面位置关系及基本不等式的应用，考查空间想象能力以及数形结合思想，涉及线面垂直的判定和性质，属中档题.6．B解析：B【分析】由题意知正三棱柱的高为，可得底面正三角形的边长为6cm ，即得到底面三角形的面积，代入棱柱的体积公式求解即可．【详解】∵的内切球，则正三棱柱的高为，，设底面正三角形的边长为a cm,则123a ⨯=6a =cm ，∴正三棱柱的底面面积为16622⨯⨯⨯=2，故此正三棱柱的体积V ＝54=cm 3．故选：B ．【点睛】本题考查棱柱的体积的求法，考查几何体的内切球的性质，属于基础题.7．A解析：A【分析】根据等体积法有11A CDM C A DM V V --=得解.【详解】画出图形如下图所示，设C 到平面1A DM 的距离为h ，在△1A DM 中11,,2A M DM a A D ===1A ∴到DM 的距离为32a 则根据等体积法有11A CDM C A DM V V --=，即11113232322a a a a a h ⋅⋅⋅⋅=⋅⋅⋅⋅，解得63h a =， 故选:A.【点睛】本题考查利用等体积法求距离，属于基础题.8．B 解析：B【分析】把三棱锥放入长方体中，根据长方体的结构特征求出三棱锥外接球的半径，再计算三棱锥外接球的体积．【详解】三棱锥A BCD -中，侧面ABC ⊥底面BCD ，把该三棱锥放入长方体中，如图所示；且333AM AB == 设三棱锥外接球的球心为O ，则2233333AG AM ===112OG CD ==， 所以三棱锥外接球的半径为22221(3)2R OA OG AG =+=+=，所以三棱锥外接球的体积为3344232333R V πππ===． 故选：B ．【点睛】本题考查了三棱锥外接球的体积计算问题，也考查了数形结合与转化思想，是中档题． 9．C解析：C【分析】通过二十四等边体的外接球表面积求得半径，进而计算出二十四等边体的边长，进而计算出二十四等边体的表面积.【详解】由于二十四等边体的外接球表面积为16π，设其半径为r ，则2416r π=π，解得2r .设O 为球心，依题意可知四边形,,,A B C D 分别为正方体侧棱的中点，所以ABCD 正方形，由于2OA OB OC OD ====，所以四边形ABCD 是正方形，2222AB OA OB =+=.所以二十四等边体的边长为2.所以二十四等边体的边长的表面积为122622sin 823π⨯⨯+⨯⨯⨯⨯ 2483=+.故选：C【点睛】本小题主要考查几何体外接球有关计算，考查空间想象能力，属于中档题.10．C解析：C【分析】根据异面直线定义可判断A ；由线面垂直的性质即可判断B ；由异面直线的位置关系并得11AE B C ⊥可判断C ；根据线面平行的判定定理可判断D.【详解】对于A 项，1CC 与1B E 在同一个侧面中，故不是异面直线，所以A 错；对于B 项，由题意知，上底面是一个正三角形，故AC ⊥平面11ABB A 不可能，所以B 错；对于C 项，因为AE ，11B C 为在两个平行平面中且不平行的两条直线，故它们是异面直线，由底面111A B C 是正三角形，E 是BC 中点，根据等腰三角形三线合一可知AE BC ⊥，结合棱柱性质可知11//B C BC ，则11AE B C ⊥，所以C 正确；对于D 项，因为11A C 所在的平面与平面1AB E 相交，且11A C 与交线有公共点，故11//A C 平面1AB E 不正确，所以D 项不正确.故选C.【点睛】该题考查的是有关立体几何中空间关系的问题，在解题的过程中，需要对其相关的判定定理和性质定理的条件和结论熟练掌握，注意理清其关系，属于中档题11．C解析：C【分析】对①，运用长方体模型，找出符合条件的直线和平面，即可判断；对②，运用线面平行的性质定理和线面垂直的性质定理，即可判断；对③，运用面面平行的性质定理，即可判断；对④，由平行的传递性及线面角的定义，即可判断④．【详解】对于命题①，可运用长方体举反例证明其错误：如图，不妨设AA '为直线m ，CD 为直线n ，ABCD 所在的平面为α，ABC D ''所在的平面为β，显然这些直线和平面满足题目条件，但αβ⊥不成立；命题②正确，证明如下：设过直线n 的某平面与平面α相交于直线l ，则//l n ，由m α⊥知m l ⊥，从而m n ⊥，结论正确；由平面与平面平行的定义知命题如果//αβ，m α⊂，那么//m β.③正确；由平行的传递性及线面角的定义知命题：如果//m n ，//αβ，那么m 与α所成的角和n 与β所成的角相等，④正确.故选：C .【点睛】本题考查命题的真假判断，考查空间线面、面面平行和垂直的位置关系，注意运用判定定理和性质定理，考查推理能力，属于中档题．12．B解析：B【分析】分别以①②③④作为结论，另外三个作条件，根据线面垂直和面面垂直的判定定理依次判断真假.【详解】若m n ⊥，αβ⊥，n β⊥，则m 与α可能平行可能相交，即①②③不能推出④； 同理①②④不能推出③；若m n ⊥，n β⊥，m α⊥，两个平面的垂线互相垂直则这两个平面垂直，则αβ⊥，即①③④能够推出②；若αβ⊥，n β⊥，m α⊥，两个平面互相垂直，则这两个平面的垂线互相垂直，即m n ⊥，所以②③④能够推出①.所以一共两个命题正确.故选：B【点睛】此题考查空间直线与平面位置关系的辨析，根据选择的条件推出结论，关键在于熟练掌握空间垂直关系的判定和证明.13．D解析：D【分析】连接BE ，BD ，因为//BE AF ，所以BED ∠为异面直线AF 与DE 所成的角（或补角），不妨设正方体的棱长为2，取BD 的中点为G ，连接EG ，在等腰BED ∆中，求出cosEG BEG BE ∠==cos BED ∠，即可得出答案. 【详解】 连接BE ，BD ，因为//BE AF ，所以BED ∠为异面直线AF 与DE 所成的角（或补角），不妨设正方体的棱长为2，则BE DE ==BD =，在等腰BED ∆中，取BD 的中点为G ，连接EG ，则EG ==cos EG BEG BE ∠== 所以2cos cos 22cos 1BED BEG BEG ∠=∠=∠-， 即：31cos 2155BED ∠=⨯-=， 所以异面直线AF ，DE 所成角的余弦值为15.故选：D.【点睛】本题考查空间异面直线的夹角余弦值，利用了正方体的性质和二倍角公式，还考查空间思维和计算能力.14．D解析：D【分析】利用空间线线、线面、面面的位置关系对选项进行逐一判断，即可得到答案.【详解】A.若//l α，//l β，则α与β可能平行，也可能相交，所以不正确.B.若αβ⊥，//l α，则l 与β可能的位置关系有相交、平行或l β⊆,所以不正确.C.若αβ⊥，l α⊥，则可能l β⊆，所以不正确.D.若//l α，l β⊥，由线面平行的性质过l 的平面与α相交于l '，则ll '，又l β⊥.所以l β'⊥，所以有αβ⊥，所以正确.故选：D【点睛】本题考查面面平行、垂直的判断，线面平行和垂直的判断,属于基础题. 二、解答题15．（1）6+23+26；（2）证明见解析；13. 【分析】（1）可先证明1A B ⊂平面1A AB 得出1BC A B ⊥，即可求出三棱锥A 1－ABC 各个面的面积，得出表面积；（2）在平面ABC 内，过点B 作BN AC ⊥，垂足为N ，过N 作1//MN A A 交1A A 于M ，连接BM ，即可得出.【详解】（1）2,4,=60=23AB AC BAC BC BC AB ==∠∴∴⊥，，，1A A ⊥平面ABC ，BC ⊆平面ABC ，1BC AA ∴⊥，1A A AB A =，BC ∴⊥平面1A AB ，1A B ⊂平面1A AB ，1BC A B ∴⊥，112223262A BC S∴=⨯⨯=， 1=232ABC S AB BC ∴⋅⋅=，111==22A AB S A A AB ⋅，111=42A AC S A A AC =⋅， 则表面积=6+23+26S ；（2）证明：在平面ABC 内，过点B 作BN AC ⊥，垂足为N ，过N 作1//MN A A 交1A A 于M ，连接BM ，1A A ⊥AC ，1//MN A A ，AC MN ∴⊥，MN BN N =，∴AC ⊥平面MBN .又BM ⊂平面MBN ，∴AC BM ⊥.在直角BAN 中，cos 1, 3.=∠==-=AN AB BAC NC AC AN111//.3，∴==A M AN MN A A MC NC 【点睛】 本题考查三棱柱表面积的求解，解题的关键是得出1BC A B ⊥以便求出各个面的面积，考查点的存在性问题，解题关键是正确利用线面垂直关系作出辅助线.16．（1）证明见解析；（2）43. 【分析】（1）由ABCD 为矩形，易得G 是AC 的中点，又BF ⊥平面ACE ，BC ＝BE ，则F 是EC 的中点，从而FG ∥AE ，再利用线面平行的判定定理证明.（2）根据AD ⊥平面ABE ，易得AE ⊥BC ，再由BF ⊥平面ACE ，得到AE ⊥BF ，进而得到AE ⊥平面BCE ，然后由C AEB A BCE V V --=求解.【详解】（1）如图所示：因为底面ABCD 为矩形，所以AC ，BD 的交点G 是AC 的中点，连接FG ，∵BF ⊥平面ACE ，则CE ⊥BF ，而BC ＝BE ，∴F 是EC 的中点，∴FG ∥AE .又AE ⊄平面BFD ，FG ⊂平面BFD ，∴AE ∥平面BFD .（2）∵AD ⊥平面ABE ，AD ∥BC ，∴BC ⊥平面ABE ，则AE ⊥BC .又BF ⊥平面ACE ，则AE ⊥BF ，∴AE ⊥平面BCE .∴三棱锥C -AEB 的体积11142223323C AEB A BCE BCE V V S AE --⎛⎫==⋅=⨯⨯⨯⨯= ⎪⎝⎭△. 【点睛】方法点睛：1、判断或证明线面平行的常用方法：（1）利用线面平行的定义，一般用反证法；（2）利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；（3）利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)；（4）利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)．17．（1）证明见解析；（2）点E 位于线段AD 的中点或线段BD 的中点；223. 【分析】（1）易得CD AB ⊥，再根据VC ⊥底面ABC ，得到 VC AB ⊥，进而AB ⊥平面VCD ，再利用面面垂直的判定定理证明.（2）过点D 在平面ABC 内作DF CE ⊥于F ，DF ⊥平面VCE ，则DVF ∠就是直线VD 与平面VCE 所成的角，在Rt VFD 中，由15sin 15DF DVF VD ∠==，求得DF ，然后在Rt DCE 中，求出1DE =，然后由三棱锥C-VDE 的体积为13CDE V S VC =⋅⋅求解. 【详解】（1）因为AC BC =，D 是AB 的中点，所以CD AB ⊥.又VC ⊥底面ABC ，AB 平面ABC ，所以VC AB ⊥，而VC CD C ⋂=，所以AB ⊥平面VCD .又AB 平面VAB ，所以平面VAB ⊥平面VCD .（2）过点D 在平面ABC 内作DF CE ⊥于F ，则由题意知DF ⊥平面VCE .，连接VF ，于是DVF ∠就是直线VD 与平面VCE 所成的角.在Rt VFD 中，15DF VD =. 又因为3VD =25DF =. 在Rt DCE 中，1DE =.故知点E 位于线段AD 的中点或线段BD 的中点，三棱锥C-VDE 的体积为111222122332CDE S VC ⋅⋅=⨯⨯⨯⨯=. 【点睛】方法点睛：(1)证明平面和平面垂直的方法：①面面垂直的定义；②面面垂直的判定定理(a ⊥β，a ⊂α⇒α⊥β)．(2)已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．18．（1）证明见解析；（243 【分析】（1）由线面垂直得到线线垂直，再由线线垂直得到线面垂直；（2）取EF 中点P ，BC 中点K ，找到二面角，再在三角形中计算就可以了.【详解】（1）证明：1AA ⊥平面11,ABC B F AA ∴⊥ ， 又111A B C 为正三角形，F 为11A C 中点，111B F AC ∴⊥得1B F ⊥平面11ACC A .又因为1AC ⊂平面11ACC A ，所以11B F AC ⊥；（2）设所有棱长都为2，取EF中点P，BC中点K，连,,PK AK PA. 易知,PK BC AK BC⊥⊥，则PKA∠为平面EFCB的与底面ABC所成二面角的平面角，在PKA中，取AK中点O，连PO，有PO⊥平面ABC，则PO AK⊥，且32,POOK==，43tan33POPKAOK∠===,【点睛】第二问的关键点是由线面垂直找到线线垂直，求出二面角，然后在三角形中计算就可以了. 19．（1）证明见解析；（2）3.【分析】（1）取AB中点E，连接11,,CE A B A E，根据已知条件，利用等腰三角形的性质得到1A E AB⊥，,CE AB⊥利用线面垂直的判定定理证得AB⊥面1,CEA即可得到1AB A C⊥；（2）在1CEA中可以证明1AE CE⊥，结合1A E AB⊥，利用线面垂直判定定理得到1A E⊥平面ABC,作为三棱柱的高，进而计算体积.【详解】(1)取AB中点E，连接11,,CE A B A E，11,60AB AA BAA∠︒＝＝，1BAA∴是等边三角形，1A E AB∴⊥，CA CB ＝，,CE AB ∴⊥1,CE A E E ⋂＝AB ∴⊥面1,CEA1AB A C ∴⊥.(2)由于CAB ∆为等边三角形， 3CE ∴＝，1123322S AB CE ⨯⨯⨯⨯=底面积＝＝ 1CEA 中，3CE ＝，13EA ＝，16AC =1A E CE ∴⊥，结合1A E AB ⊥，又,,AB CE E AB CE ⋂=⊂平面ABC ,1A E ∴⊥平面ABC ,13h A E ∴＝＝，333V Sh ⨯=＝＝.【点睛】本题考查线面垂直的判定与证明，考查棱柱的体积计算，属基础题，为证明线线垂直，常常先证线面垂直，为证明线面垂直，又常常需要先证明线线垂直，这是线面垂直关系常用的证明与判定方式，要熟练掌握.20．（1）证明见解析；（2）83. 【分析】（1）先证明AC ⊥BE ,再取AB 的中点M ，连接CM ，经计算，利用勾股定理逆定理得到AC ⊥BC ,然后利用线面垂直的判定定理证得结论；（2）利用线面垂直的判定定理证得CM ⊥平面BEF ,即为所求三棱锥的高，进而计算得到其体积.【详解】解：（1）证明：∵四边形ABEF 为矩形∴//AF BE∵AF ⊥平面ABCD ∴BE ⊥平面ABCD∵AC ⊂平面ABCD ∴AC BE ⊥.如图，取AB 的中点M ，连接CM ，∴122AM AB DC === ∵//AM DC ，90MAD ∠=︒，2AM DC AD === ∴四边形ADCM 是正方形.∴90ADC ∠=︒∴222448C AD DC =+=+=，222448BC CM BM =+=+= ∵4AB =∴222AC BC AB +=∴ABC 是直角三角形∴AC BC ⊥. ∵BCBE B =，BC 、BE ⊂平面BCE ∴AC ⊥平面BCE（2）由（1）知：CM AB ⊥∵AF ⊥平面ABCD ，CM ⊂平面ABCD ∴AF CM ⊥∵AF AB A ⋂=，AF 、AB 平面ABEF∴CM ⊥平面ABEF ，∴CM ⊥平面BEF即：CM 是三棱锥C BEF -的高 ∴11182243323E BCF C BEF BEF V V CM S --==⋅=⨯⨯⨯⨯=△ 【点睛】本题考查线面垂直的证明，棱锥的体积的计算，属基础题.在利用线面垂直的判定定理证明线面垂直时一定要将条件表述全面，“两个垂直，一个相交”不可缺少.21．（Ⅰ）证明见解析；（Ⅱ）证明见解析；（Ⅲ）在棱1CC 上存在点G ，且G 为1CC 的中点．理由见解析.【分析】（Ⅰ）在三棱柱111ABC A B C -中，由侧棱垂直于底面，可得1CC ⊥平面ABC ，则1CC AC ⊥，再由AC BC ⊥，结合线面垂直的判定可得AC ⊥平面11BCC B ．从而得到1AC C F ⊥；（Ⅱ）取11A C 的中点H ，连结EH ，FH ．可得//EH BF ，且EH BF =．则四边形BEHF 为平行四边形，则//BE FH ．再由线面平行的判定可得//BE 平面11AC F ； （Ⅲ）在棱1CC 上存在点G ，且G 为1CC 的中点．连接EG ，1GB ．首先证明△11B C G ≅△1C CF ．可得11190C CF B GC ∠+∠=︒，则11B G C F ⊥．由（Ⅰ）可得AC ⊥平面11BB C C ，得到11A C ⊥平面11BB C C ．即111AC B G ⊥．由线面垂直的判定可得1B G ⊥平面11AC F ．进一步得到平面1B EG ⊥平面11AC F ．【详解】解：（Ⅰ）在三棱柱111ABC A B C -中，因为侧棱垂直于底面，所以1CC ⊥平面ABC ． 又AC ⊂平面ABC所以1CC AC ⊥．因为AC BC ⊥，1CC BC C ⋂=，1CC ⊥平面11BCC B ，BC ⊂平面11BCC B 所以AC ⊥平面11BCC B ．因为1C F ⊂平面11BCC B ，所以1AC C F ⊥．（Ⅱ）取11A C 中点H ，连结EH ，FH ．则EH //11B C ，且1112EH B C =， 又因为BF //11B C ，且1112BF B C =， 所以EH //BF ，且EH BF =．所四边形BEHF 为平行四边形．所以BE //FH ．又BE ⊄平面11AC F ，FH⊂平面11AC F ，所以BE //平面11AC F（Ⅲ）在棱1CC 上存在点G ，且G 为1CC 的中点．连接1,EG GB ．在正方形11BB C C 中，因为F 为BC 中点，所以△11B C G ≌△1C CF ．所以11190C CF B GC ∠+∠=︒．所以11B G C F ⊥．由（Ⅰ）可得AC ⊥平面11BB C C ，因为11AC//A C ，所以11A C ⊥平面11BB C C ．因为1B G ⊂平面11BB C C ，所以111AC B G ⊥．因为1111AC C F C =，11A C ⊂平面11AC F ，1C F ⊂平面11AC F ．所以1B G ⊥平面11AC F ．因为1B G ⊂平面1B EG ，所以平面1B EG ⊥平面11AC F ．【点睛】本题考查直线与平面、平面与平面垂直的判定，考查空间想象能力与思维能力，考查数学转化思想方法与数形结合的解题思想方法．22．（1）证明见解析；（2）217. 【分析】（1）由题意可得11//OE B C ，1//OF C C ，利用面面平行的判定定理可得平面//OEF 平面11BB C C ，由面面平行的性质定理即可证明. （2）利用等体法111112A A B C C AA B V V --=，求出点1C 到平面11AA B 的距离2217d =，由11sin d A C θ=即可求解. 【详解】证明：（1）∵O ，E 分别是11A C 、11A B 的中点，1A C 与1AC 交于点F ，∴11//OE B C ，1//OF C C ，1111B C C C C ⋂=，//OE ∴平面11B C C ，//OF ∴平面11B C C ，又OE OF O ⋂=，∴平面//OEF 平面11BB C C ，∵EF ⊂平面OEF ，∴//EF 平面11BB C C .（2）解：设点1C 到平面11AA B 的距离为d ，∵111112A A B C C AA B V V --=， ∴111111111323AA B AC B C AO S d ⨯⨯⨯⨯=⨯⨯，AO ==1OB ==1AB ==，∵11AA B中，111A B AB ==，12AA =，∴11AA B S =∴11122323d ⨯⨯⨯=，解得7d =， 设11A C 与平面11AA B 所成角为θ，∴11A C 与平面11AA B所成角的正弦值为：11sin 7d AC θ==. 【点睛】方法点睛：证明线面平行的常用方法：（1）利用线面平行的定义（无公共点）.（2）利用线面平行的判定定理.（3）利用面面平行的性质.23．（1）答案见解析；（2. 【分析】（1）选择①，结合直二面角的定义，证明BD ⊥平面EOA 内的两条相交直线,EO AO ； （2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则AC =CO x =，可得EB 关于x 的函数，求出EB 取得最小值时x 的值，连结EM ，作QF EM ⊥于F ，连结BF ，求出sin QBF ∠的值，即可得答案；【详解】解：（1）命题P ：若AB AD =，则BD ⊥平面EOA .∵AC GH ⊥，∴AO GH ⊥，EO GH ⊥，又二面角E GH B --的大小为90°，∴90AOE ∠=︒，即EO AO ⊥，∴EO ⊥平面ABCD ，∴EO BD ⊥，又AB BC =，∴AO BD ⊥， AO EO O =，∴BD ⊥平面EOA .（2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则43AC =， 设CO x =，23OM x =-，22224316OB OM MB x x =+=-+，222224316EB EO OB x x =+=-+，当3x =，min 10EB =，连结EM ，作QF EM ⊥于F ，连结BF ，由（1）知BD ⊥平面EOA ，∴BD QF ⊥，∴QF ⊥平面EBD ，∴QBF ∠即为QB 与平面EBD 所成角，在Rt EMB 中，10EB =，2BM =，6EM=，30AE =， 由()222222(2)22QB AE AB BE QB +=+⇒=， 6QF =， ∴33sin 11QF QBF QB ∠==，即QB 与平面EBD 所成角得正弦值为3311.【点睛】求线面角首先要根据一作、二证、三求找出线面角，然后利用三角函数的知识，求出角的三角函数值即可.24．（1）证明见解析；（2）3V =. 【分析】（1）设BD 与EC 交于点O ，连接AO ，由四边形BCDE 为菱形，可得BD EC ⊥，再利用线面垂直的判定定理即可证明.（2）求出四棱锥A BCDE -的高为32，即三棱锥A BCD -的高，再利用等体积法即可求解.【详解】（1）设BD 与EC 交于点O ，连接AO ．因为BC BE ED ==，//BC DE ，所以四边形BCDE 为菱形，所以BD EC ⊥，又AB EC ⊥，AB BD B =，所以EC ⊥平面ABD ，因为AD ⊂平面ABD ，所以EC AD ⊥． （2）因为在菱形BCDE 中，π3EDC ∠=，2BC BE ==， 所以2CE =，23BD =因为H 为线段BD 的一个四等分点（靠近点B ），所以134BH BD ==． 因为AH ⊥平面BCDE ，所以AH ⊥ BD ， 又π3ABD ∠=，所以3tan 2AH BH ABD =∠=，所以四棱锥A BCDE -的高为32． 即三棱锥D ABC -的高为32. 易得BCD 的面积11231322BCD S BD OC =⋅=⨯=， 所以三棱锥D ABC -的体积133332A BCD D ABC V V --=== 【点睛】方法点睛：本题考查了证明异面直线垂直以及求三棱锥的体积，常用方法如下：（1）证明线线垂直的常法：①利用特殊图形中的垂直关系；②利用等腰三角形底边中线的性质；③利用勾股定理的逆应用；④利用直线与平面垂直的性质.（2）求体积的常用方法：①直接法；②割补法；③等体积法.25．(I)证明见解析；3 【分析】（I ）取AD 的中点P ，连结EP PC ，，MP ，利用平行四边形及线面垂直的性质定理证明,,PE PC AD 相互垂直，从而可证明EC 与,MP MD 垂直，然后可得线面垂直，面面垂直；（II ）取Q CD 为的中点，连结,PQ EQ ，可得EQP ∠为二面角A CD E --的平面角，在Rt EPQ △中求得其余弦值．【详解】（Ⅰ）证明：取AD 的中点P ，连结EP PC ，．则EF AP =，∵//FE AP =，∴四边形FAPE 是平行四边形，∴//FA EP =，同理，//AB PC =.又∵FA ⊥平面ABCD ，∴EP ⊥平面ABCD ，而PC AD ，都在平面ABCD 内，∴.EP PC EP AD ⊥⊥，由AB AD ⊥，可得PC AD ⊥，设FA a =，则2.EP PC PD a CD DE EC a ======，所以△ECD 为正三角形.∵DC DE =且M 为CE 的中点，∴DM CE ⊥.连结MP ，则.MP CE ⊥PM ∩MD =M ，而PM ，MD 在平面AMD 内 ，∴CE ⊥平面AMD而CE ⊂平面CDE ，所以平面AMD ⊥CDE .（Ⅱ）解：取Q CD 为的中点，连结,PQ EQ ，∵CE DE =，∴.EQ CD ⊥∵PC PD =，∴PQ CD ⊥∴EQP ∠为二面角A CD E --的平面角.由(Ⅰ)可得， 622EP PQ EQ a PQ a ==⊥，，． 于是在Rt EPQ △中，3cos PQ EQP EQ ∠==． ∴二面角A CD E --3. 【点睛】 方法点睛：本题考查证明面面垂直，考查求二面角．求二面角的几何方法：一作二证三计算，一作：作出二面角的平面角；二证：证明所作的角是二面角的平面角；三计算：在三角形中求出这个角（这个角的余弦值）．26．（1）证明见解析；（2）18.【分析】（1）利用线面直线与平面平行的性质定理，分别证得GH ∥BC 和EF ∥BC ，即可证得GH ∥EF .（2）连接AC ，BD 交于点O ，BD 交EF 于点K ，连接OP ，GK ，分别证得PO ⊥AC 和PO ⊥BD ，进而得到GK 是梯形GEFH 的高，结合梯形的面积，即可求解.【详解】（1）因为BC ∥平面GEFH ，BC ⊂平面PBC ，且平面PBC ∩平面GEFH ＝GH ，所以GH ∥BC ， 又因为BC ∥平面GEFH ，BC ⊂平面ABCD ，且平面ABCD ∩平面GEFH ＝EF ，所以EF ∥BC ， 所以GH ∥EF .（2）如图所示，连接AC ，BD 交于点O ，BD 交EF 于点K ，连接OP ，GK .因为PA ＝PC ，O 是AC 的中点，所以PO ⊥AC ，同理可得PO ⊥BD ，又BD ∩AC ＝O ，且AC ，BD 都在底面内，所以PO ⊥底面ABCD ，又因为平面GEFH ⊥平面ABCD ，且PO ⊄平面GEFH ，所以PO ∥平面GEFH ，因为平面PBD ∩平面GEFH ＝GK ，所以PO ∥GK ，且GK ⊥底面ABCD .从而GK ⊥EF .所以GK 是梯形GEFH 的高，由AB ＝8，EB ＝2，得EB ∶AB ＝KB ∶DB ＝1:4，从而KB ＝14DB ＝12OB ，即K 为OB 的中点， 再由PO ∥GK ，得GK ＝12PO ，即G 是PB 的中点，且GH ＝12BC ＝4， 由已知可得OB ＝42，PO ＝2268326PB OB -=-=，所以GK ＝3，故四边形GEFH 的面积S ＝2GH EF +·GK ＝482+×3＝18.【点睛】本题主要考查了线面平行的判定与性质定理，以及正棱锥的结构特征和截面面积的计算，其中解答中熟记线面平行的判定定理和性质定理，以及正棱锥的结构特征，结合梯形的面积公式求解是解答的关键，着重考查推理与运算能力.。

一、选择题1．在正方体1111ABCD A B C D -中，点,E F 分别是梭BC ，CD 的中点，则1A F 与1C E所成角的余弦值为（ ） A ．5 B ．25C ．5 D ．252．大摆锤是一种大型游乐设备(如图)，游客坐在圆形的座舱中，面向外，通常大摆锤以压肩作为安全束缚，配以安全带作为二次保险，座舱旋转的同时，悬挂座舱的主轴在电机的驱动下做单摆运动.假设小明坐在点A 处，“大摆锤”启动后，主轴OB 在平面α内绕点O 左右摆动，平面α与水平地面垂直，OB 摆动的过程中，点A 在平面β内绕点B 作圆周运动，并且始终保持OB β⊥，B β∈.设4OB AB =，在“大摆锤”启动后，下列结论错误的是（ ）A ．点A 在某个定球面上运动；B ．β与水平地面所成锐角记为θ，直线OB 与水平地面所成角记为δ，则θδ+为定值；C ．可能在某个时刻，AB//α；D ．直线OA 与平面α所成角的正弦值的最大值为1717. 3．已知m ，n 是两条直线，α，β是两个平面，则下列命题中错误的是（ ） A ．若m n ⊥，m α⊥，n β⊥，则αβ⊥ B ．若m α⊂，//αβ，则//m βC ．若m n ⊥，m α⊥，βn//，则αβ⊥D ．若l αβ=，//m α，//m β，则//m l4．已知正方体1111ABCD A B C D -，点,E F 分别是棱11B C ，11A D 的中点，则异面直线BE ，DF 所成角的余弦值为（ ） A 5B ．35C ．45D 255．在长方体1111ABCD A B C D -中，12,3AB BC AA ===，E 是BC 的中点，则直线1ED 与直线BD 所成角的余弦值是（ ） A ．728B ．728-C ．3714D ．3714-6．已知球O 的半径为5，球面上有,,A B C 三点，满足214,27AB AC BC ===，则三棱锥O ABC -的体积为（ ） A ．77B ．142C ．714D ．1477．如图，在正方体1111ABCD A B C D -中，点F 是线段1BC 上的动点，则下列说法错误的是（ ）A ．无论点F 在上1BC 怎么移动，都有11A FB D ⊥B ．当点F 移动至1BC 中点时，才有1A F 与1BD 相交于一点，记为点E ，且12A EEF= C ．当点F 移动至1BC 中点时，直线1A F 与平面1BDC 所成角最大且为60° D ．无论点F 在1BC 上怎么移动，异面直线1A F 与CD 所成角都不可能是30° 8．如下图所示是一个正方体的平面展开图，在这个正方体中①//BM 平面ADE ；②DE BM ⊥；③平面//BDM 平面AFN ；④AM ⊥平面BDE ．以上四个命题中，真命题的序号是（ ）A ．①②③④B ．①②③C ．①②④D ．②③④9．在四棱锥P -ABCD 中，//AD BC ，2AD BC =，E 为PD 中点，平面ABE 交PC 于F ，则PFFC=（ ） A ．1B ．32C ．2D ．310．某三棱锥的三视图如图所示，已知网格纸上小正方形的边长为1，则该三棱锥的体积为（ ）A ．43 B ．83C ．3D ．411．在正方体1111ABCD A B C D -中，三棱锥11A B CD -的表面积为3球的体积为（ ） A ．3πB 6πC ．3πD ．86π12．空间四边形PABC 的各边及对角线长度都相等，D 、E 、F 外别是AB 、BC 、CA 的中点，下列四个结论中不成立的是（ ） A ．//BC 平面PDF B ． DF ⊥平面PAE C ．平面PDE ⊥平面ABCD ．平面PAE ⊥平面ABC二、填空题13．如图，在一个底面面积为410的正四棱锥P ABCD -中，大球1O 内切于该四棱锥，小球2O 与大球1O 及四棱锥的四个侧面相切，则小球2O 的体积为___________.14．如图，已知ABC 的顶点C ∈平面α，点,A B 在平面α的同一侧，且||23,||2AC BC ==．若,AC BC 与平面α所成的角分别为5,124ππ，则ABC 面积的取值范围是_____15．在棱长为2的正方体1111ABCD A B C D -中，P 是11A B 的中点，过点1A 作与平面1PBC 平行的截面，则此截面的面积是_______________．16．在三棱锥P ABC -中，P 在底面ABC 的射影为ABC 的重心，点M 为棱PA 的中点，记二面角P BC M --的平面角为α，则tan α的最大值为___________.17．祖恒是我国南北朝时代的伟大科学家，他总结了刘徽的有关工作，提出来体积计算的原理“幂势既同，则积不容异”，称为祖恒原理，意思是底面处于同一平面上的两个同高的几何体，若在等高处 的截面面积始终相等，则它们的体积相等，利用这个原理求半球O 的体积时，需要构造一个几何体，该几何体的三视图如图所示，则该几何体的体积为_________________18．如下图所示，三棱锥P ABC -外接球的半径为1，且PA 过球心，PAB △围绕棱PA 旋转60︒后恰好与PAC △重合.若3PB =，则三棱锥P ABC -的体积为_____________.19．若三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形，23AB =，7SA SB SC ===，则该三棱锥的外接球的表面积为__________．20．在三棱锥P ABC -中，PA ⊥平面ABC ，60BAC ∠=︒，23AB AC ==，2PA =，则三棱锥P ABC -外接球的半径为____________.三、解答题21．如图，四边形ABCD 为正方形，QA ⊥平面ABCD ，PD//QA ，112QA AB PD ===.（1）证明：直线PQ ⊥平面DCQ ；（2）求二面角D QB A --的余弦值.22．在如图所示几何体中，平面PAC ⊥平面ABC ，//PM BC ，PA PC =，1AC =，22BC PM ==，5AB =．若该几何体左视图（侧视图）的面积为34．（1）画出该几何体的主视图（正视图）并求其面积S ； （2）求出多面体PMABC 的体积V ．23．在棱长为2的正方体1111ABCD A B C D -中，O 是底面ABCD 的中心.（1）求证:1B O//平面11DA C ; （2）求点O 到平面11DA C 的距离.24．如图，在三棱锥P ABC -中，1,2,135AB AC BAC ︒==∠=，1cos ,3BAP AP BC ∠=-⊥．（1）若23BM MC =，求证：PM BC ⊥； （2）当3AP =，且N 为BC 中点时，求AN 与平面PBC 所成角的正弦值． 25．如图，在五面体ABCDEF 中，四边形ABCD 是平行四边形.（1）求证：//AB EF ；（2）若CF AE ⊥，AB AE ⊥，求证：平面ABFE ⊥平面CDEF . 26．如图，正三棱柱111ABC A B C -的棱长均为2，M 是侧棱1AA 的中点．（1）在图中作出平面ABC 与平面1MBC 的交线l （简要说明），并证明l ⊥平面11CBB C ；（2）求点C 到平面1MBC 的距离．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】延长DA 至G ，使AG CE =，可证11//A G C E ，得1GA F ∠是异面直线1A F 与1C E 所成的角（或其补角）．在1AGF △中，由余弦定理可得结论． 【详解】延长DA 至G ，使AG CE =，连接1,GE GA ,GF ，11,AC A C ， 又//AG CE 所以AGEC 是平行四边形，//,GE AC GE AC =， 又正方体中1111//,AC AC AC AC =， 所以1111//,AC DE AC DE =，所以11AC EG 是平行四边形，则11//A G C E ，所以1GA F ∠是异面直线1A F 与1C E 所成的角（或其补角）． 设正方体棱长为2，在正方体中易得15AG =10GF =22222112(21)3A F AA AF=+=++=，1AGF△中，2221111125cos2253AG A F GFGA FAG A F+-∠===⋅⨯⨯．故选：D．【点睛】方法点睛：本题考查空间向量法求异面直线所成的角，求异面直线所成角的方法：（1）定义法：根据定义作出异面直线所成的角并证明，然后解三角形得结论；（2）建立空间直角坐标系，由两异面直线的方向向量的夹角得异面直线所成的角．2．C解析：C【分析】利用已知条件确定OA是定值，即得A选项正确；作模型的简图，即得B正确；依题意点B在平面α内，不可能AB//α，得C错误；设AB a，结合题意知ABα⊥时，直线OA 与平面α所成角最大，计算此时正弦值，即得D正确.【详解】因为点A在平面β内绕点B作圆周运动，并且始终保持OBβ⊥，所22OA OB AB=+，又因为OB，AB为定值，所以OA也是定值，所以点A在某个定球面上运动，故A正确；作出简图如下，OB l⊥，所以2πδθ+=，故B正确；因为B α∈，所以不可能有AB//α，故C 不正确； 设AB a ，则4OB a =，2217OA AB OB a =+，当AB α⊥时，直线OA 与平面α所成角最大，此时直线OA 与平面α171717a =，故D 正确. 故选:C. 【点睛】本题解题关键在于认真读题、通过直观想象，以实际问题为背景构建立体几何关系，再运用立体几何知识突破难点.3．C解析：C 【分析】利用直二面角可判断A 的正误，利用面面平行或线面平行性质定理即判断定理可判断BD 的正误，从而可得正确的选项，利用反例可判断C 是错误的. 【详解】 对于A ，如图，设l αβ=，空间中取一点O （O 不在平面,αβ内，也不在直线,m n上），过O 作直线,a b ，使得,////a m b n ，且,a A b B αβ⋂=⋂=，故a b ⊥. 因为m α⊥，故a α⊥，而l α⊂，故a l ⊥，同理b l ⊥, 因为a b O ⋂=，故l ⊥平面OAB . 设平面OAB 交l 与C ，连接,AC BC ，因为,AC BC ⊂平面OAB ，故,,l AC l BC ⊥⊥所以ACB ∠为l αβ--的平面角. 因为a α⊥，AC α⊂，故OA AC ⊥，同理OB BC ⊥，而OA OB ⊥， 故在四边形OACB 中，90ACB ∠=︒即αβ⊥，故A 正确.对于B ，由面面平行的性质可得若m α⊂，//αβ，则//m β，故B 正确. 对于D ，如图，过m 作平面γ，使得a γα=，过m 作平面η，使得b ηβ⋂=，因为//m α，m γ⊂，故//a m ，同理//b m ，故//a b ， 而a β⊄，b β⊂，故//a β，而a α⊂，l αβ=，故//a l ，所以//m l ，故D 正确.对于C ，在如图所示的正方体中，//AD 平面11A D CB ，1AA ⊥平面ABCD ，1AD AA ⊥，但是平面11A D CB 与平面ABCD 不垂直，故C 错误.故选：C. 【点睛】思路点睛：对于立体几何中与位置有关的命题的真假判断，一般根据性质定理和判定定理来处理，反例一般可得正方体中寻找.4．B解析：B 【分析】证明//BE AF ，得AFD ∠是异面直线BE ，DF 所成角或其补角，在三角形中求解即可． 【详解】连接,AF EF ，∵,E F 分别是棱11B C ，11A D 的中点，∴//EF AB ，EF AB =， ∴ABEF 是平行四边形，∴//BE AF ，∴AFD ∠是异面直线BE ，DF 所成角或其补角， 设正方体的棱长为2，则111A F D F ==，22215AF DF ==+=，2223cos 25255AF DF AD AFD AF DF +-∠===⋅⨯⨯，异面直线BE ，DF 所成角的余弦值为35． 故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．5．C解析：C 【分析】连接11D B 、1D E 、DE ，先证明四边形11BB D D 为平行四边形，得到11//B D BD ，故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角，由余弦定理可得答案. 【详解】连接11D B 、1D E 、DE ，因为棱11//BB DD ，11BB DD =，所以四边形11BB D D 为平行四边形，所以11//B D BD ，故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角11B D E ∠，因为12,3AB AD AA ===,1BE CE ==，所以2211111122B D D C B C =+=213110B E =+=222415ED CE DC +=+==，所以222115914D E ED D D ==+=+，由余弦定理得，从而22211111111137cos 2144214B D D E B E B D E B D D E +-∠===⨯⨯. 故选：C 【点睛】本题考查异面直线所成角的余弦值的求法，关键点是找到异面直线所成的角，考查空间中线线的位置关系等基础知识，考查运算求解能力，是中档题．6．A解析：A 【分析】利用正弦定理求出ABC 的外接圆半径，则可求出三棱锥的高，进而求出三棱锥体积. 【详解】设ABC 的外接圆的圆心为D ，半径为r ，在ABC 中，72cos 4214ABC ∠==，14sin 4ABC ∴∠=， 由正弦定理可得28sin ACr ABC==∠，即4r =，则22543OD =-=，11114214273773324O ABC ABCV SOD -∴=⨯⨯=⨯⨯⨯⨯⨯=. 故选：A.【点睛】本题考查球内三棱锥的相关计算，解题的关键是利用正弦定理求出ABC 的外接圆半径，利用勾股关系求出高.7．C解析：C 【分析】A.通过证明线面垂直，证得线线垂直；B.利用相似三角形，求1A EEF的值；C.首先构造直线1A F 与平面1BDC 所成角，再通过数形结合分析最大角，以及最大角的余弦值，判选项；D.将异面直线所成角转化为相交直线所成角，求解判断. 【详解】A.AC BD ⊥，1AC BB ⊥，AC ∴⊥平面1BB D ，1AC B D ∴⊥，11//AC AC ，111B D AC ∴⊥，同理11B D BC ⊥，1111A C BC C ，1B D ∴⊥平面11A BC ，1A F ⊂平面11A BC ，11B D A F ∴⊥，故A 正确；B.连结1A D ，1B C 交1BC 于点F ，11//A B DC ,且11A B DC =，∴四边形11A DCB 是平行四边形，所以11//A D B C ，∴11A DEFB E，得1112A E A DEF B F==，故B 正确；C.1A O ⊥平面1BDC ，1111A B AC A D ==，∴点O1BDC 是等边三角形的中心，11A BC 是等边三角形，111A BC BDC ≅ 当点F 是1BC 的中点时，11A F BC ⊥，此时1A F 是点1A 和1BC 上的点连线的最短距离，设直线1A F 与平面1BDC 所成角为θ，此时11sin A O A F θ=最大，所以此时θ最大，所以111cos 32OF A F θ==<,最大角大于60，故C 不正确；D.11//A B CD ，CD ∴与1A F 所成的角，转化为11B A F ∠的大小，11B A F ∠的最小角是11B A 与平面11A BC 所成的角，即11B A F ∠，此时1111123tan 2FB B A F A B ∠==>，所以11B A F ∠的最小角大于30，故D 正确.故选：C 【点睛】关键点点睛：本题考查利用几何的综合应用，包含线线，线面角，垂直关系，首先会作图，关键选项是C 和D ，C 选项的关键是1A O ⊥平面1BDC ，点O1BDC 是等边三角形的中心，D 选项的关键是知道先与平面中线所成角中，其中线面角是其中的最小角.8．A解析：A 【分析】把正方体的平面展开图还原成正方体ABCA ﹣EFMN ，得出BM ∥平面ADNE ，判断①正确；由连接AN ，则AN ∥BM ，又ED AN ⊥，判断②正确；由BD ∥FN ，得出BD ∥平面AFN ，同理BM ∥平面AFN ，证明平面BDM ∥平面AFN ，判断③正确；由MC BD ⊥，ED ⊥AM ，根据线面垂直的判定，判断④正确．【详解】把正方体的平面展开图还原成正方体ABCA ﹣EFMN ，如图1所示； 对于①，平面BCMF ∥平面ADNE ，BM ⊂平面BCMF ， ∴BM ∥平面ADNE ，①正确；对于②，如图2所示，连接AN ，则AN ∥BM ，又ED AN ⊥，所以DE BM ⊥，②正确； 对于③，如图2所示，BD ∥FN ，BD ⊄平面AFN ，FN ⊂平面AFN ，∴BD ∥平面AFN ；同理BM ∥平面AFN ，且BD ∩BM ＝B ，∴平面BDM ∥平面AFN ，③正确； 对于④，如图3所示，连接AC ，则BD AC ⊥，又MC ⊥平面ABCD ，BD ⊂平面ABCD ，所以MC BD ⊥，又AC MC C ，所以BD ⊥平面ACM ，所以BD ⊥AM ， 同理得ED ⊥AM ，ED BD D =，所以AM ⊥平面BDE ，∴④正确．故选：A ．【点睛】关键点点睛：解决本题的关键在于展开空间想象，将正方体的平面展开图还原，再由空间的线线，线面，面面关系及平行，垂直的判定定理去判断命题的正确性．9．C解析：C 【分析】首先通过延长直线,DC AB ，交于点G ，平面BAE 变为GAE ，连结PG ，EG 交于点F ，再根据三角形中线的性质，求PFFC的值. 【详解】延长,DC AB ，交于点G ，连结PG ，EG 交PC 于点F ，//AD BC ，且2AD BC =，可得点,B C 分别是,AG DG 的中点，又点E 是PD 的中点，PC ∴和GE 是△PGD 的中线，∴点F 是重心，得2PFFC=故选：C 【点睛】关键点点睛：本题的关键是找到PC 与平面BAE 的交点，即将平面BAE 转化为平面GAE 是关键. 10．A解析：A 【分析】首先由三视图还原几何体，然后由几何体的空间结构特征求解三棱锥的体积即可. 【详解】由三视图可知，在棱长为2的正方体中，其对应的几何体为棱锥P ABC -，该棱锥的体积：11142223323V Sh ⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭. 故选：A. 【点睛】方法点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．11．B解析：B 【分析】根据三棱锥的表面积进一步求出正方体的棱长，最后求出正方体的外接球的半径，进一步求出结果． 【详解】解：设正方体的棱长为a ，则1111112B D AC AB AD B C D C a ======， 由于三棱锥11A B CD -的表面积为43， 所以()1213344224AB CS S a==⨯⨯=所以2a =()()()2222226++=， 所以正方体的外接球的体积为34663ππ⎛⎫= ⎪ ⎪⎝⎭故选：B ． 【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.12．C解析：C 【分析】由线面平行的判定定理可判断A ；由线面垂直的判定定理可判断B ；反证法可说明C ；由面面垂直的判定定理可判断D.【详解】对于A ，D ，F 外别是AB ，CA 的中点，//BC DF ∴，DF ⊂平面PDF ，∴//BC 平面PDF ，故A 正确，不符合题意；对于B ，各棱长相等，E 为BC 中点，,BC AE BC PE ∴⊥⊥，PEAE E =，BC ∴⊥平面PAE ，//BC DF ，∴DF ⊥平面PAE ，故B 正确，不符合题意；对于C ，假设平面PDE ⊥平面ABC ，设DE BF O ⋂=，连接PO ，则O 是DE 中点，PO DE ∴⊥，平面PDE平面ABC DE =，PO ∴⊥平面ABC ，BF ⊂平面ABC ，PO BF ∴⊥，则PB PF =，与PB PF ≠矛盾，故C 错误，符合题意；对于D ，由B 选项 DF ⊥平面PAE ， DF ⊂平面ABC ，∴平面PAE ⊥平面ABC ，故D 正确，不符合题意. 故选：C. 【点睛】本题考查线面关系和面面关系的判定，解题的关键是正确理解判断定理，正确理解垂直平行关系.二、填空题13．【分析】设为正方形的中心的中点为连接求出如图分别可求得大球与小球半径分别为和进而可得小球的体积【详解】解：由题中条件知底面四边形是边长为2的正方形设O 为正方形的中心的中点为M 连接则如图在截面中设N 为 解析：2π 【分析】设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，求出OM ，PM ，PO ，如图，分别可求得大球1O 与小球2O 半径分别为22和24，进而可得小球的体积． 【详解】解：由题中条件知底面四边形ABCD 是边长为2的正方形.设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ，则1OM =，221013PM PA AM =-=-=，9122PO =-=，如图，在截面PMO 中，设N为球1O 与平面PAB 的切点，则N 在PM 上，且1O N PM ⊥，设球1O 的半径为R ，则1O N R =，∵1sin 3OM MPO PM ∠==，∴1113NO PO =，则13PO R =，11422PO PO OO R =+==，∴22R =，设球1O 与球2O 相切于点Q ，则22PQ PO R R =-=，设球2O 的半径为r ，同理可得4PQ r =，∴224R r ==，故小球2O 的体积3423V r ππ==.故答案为：224π．【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.14．【分析】由题意可得AB 的轨迹得到当ACBC 与轴l 共面时∠ACB 取到最大值和最小值求得sin ∠ACB 的范围代入三角形面积公式得答案【详解】∵ACBC 与平面α所成的角分别为且|AC|＝2|BC|＝2则A 解析：[3,3]【分析】由题意可得A ，B 的轨迹，得到当AC 、BC 与轴l 共面时，∠ACB 取到最大值和最小值，求得sin ∠ACB 的范围，代入三角形面积公式得答案． 【详解】∵AC ，BC 与平面α所成的角分别为512π，4π，且|AC |＝23，|BC |＝2， 则A ，B 分别在如图所示的两个不同的圆周上运动，当直线AC ，BC 与轴l 在同一平面内时，∠ACB 取到最大值和最小值， 于是，有63ACB ππ≤∠≤，∴sin6π≤sin ∠ACB ≤sin 3π，即12≤sin ∠ACB ≤3而ABC 的面积S ＝12|AC |⋅|BC |⋅sin ∠ACB ＝3∠ACB ． ∴33S ≤≤．故答案为：[3,3] 【点睛】关键点睛：根据题意得到A ，B 的轨迹，利用几何直观和空间想象进行分析是解题的关键.15．【分析】取的中点分别为连接先证明四边形是平行四边形再利用面面平行的判断定理证明平面平面可得平行四边形即为所求的截面再计算其面积即可【详解】取的中点分别为连接因为所以四边形是平行四边形所以因为所以四边 解析：6【分析】取AB ，11D C 的中点分别为,M N ，连接11,,,,A M MC CN A N PM ，先证明四边形1A MCN 是平行四边形，再利用面面平行的判断定理证明平面1//PBC 平面1A MCN ，可得平行四边形1A MCN 即为所求的截面，再计算其面积即可. 【详解】取AB ，11D C 的中点分别为,M N ，连接11,,,,A M MC CN A N PM ，因为11A P NC ，所以四边形11A PC N 是平行四边形，所以11A N PC ， 因为1PM CC 所以四边形1PMCC 是平行四边形，所以1MC PC ， 所以1A N MC ，所以四边形1A MCN 是平行四边形， 因为11//PC A N ，1PC ⊄平面1A MCN ，1A N ⊂平面1A MCN ， 所以1//PC 平面1A MCN ， 同理可证//PB 平面1A MCN ， 因为1PC PB P ⋂=，所以平面1//PBC 平面1A MCN ，因此过点1A 作与平面1PBC 平行的截面，即是平行四边形1A MCN ， 连接MN ，作1A H MN ⊥于点H ， 由115AM A N ==，22MN = 可得()()221523A H =-=所以1111223622A MNSMN A H =⨯⨯=⨯=， 所以平行四边形1A MCN 的面积为1226A MNS =故答案为：26【点睛】关键点点睛：本题的关键点是找出过点1A 与平面1PBC 平行的截面，所以想到作平行线，利用面面平行的判断定理证明所求的截面即是平行四边形1A MCN ，先求四边形一半的面积，乘以2即可得所求平行四边形的面积，也可以直接求菱形的面积.16．【分析】取中点为过分别作底面的垂线根据题中条件得到；过分别作的垂线连接由二面角的定义结合线面垂直的判定定理及性质得到为二面角的平面角；为二面角的平面角得出令进而可求出最值【详解】取中点为过分别作底面解析：34【分析】取BC 中点为E ，过P 、M 分别作底面的垂线PO 、MN ，根据题中条件，得到AN NO OE ==，2PO MN =；过O 、N 分别作BC 的垂线OG 、NH ，连接MH ，PG ，由二面角的定义，结合线面垂直的判定定理及性质，得到MHN ∠为二面角MBC A--的平面角；PGO ∠为二面角A BC P --的平面角，得出tan 4tan PGO MHN ∠=∠，()23tan tan tan 14tan MHNPGO MHN MHNα∠=∠-∠=+∠，令tan 0x MHN =∠>，进而可求出最值. 【详解】取BC 中点为E ，过P 、M 分别作底面的垂线PO 、MN ， 则O 为ABC 的重心，MN ⊥平面ABC ；PO ⊥平面ABC ； 由于点M 为棱PA 的中点，所以有AN NO OE ==，2PO MN =； 过O 、N 分别作BC 的垂线OG 、NH ，连接MH ，PG ， 因为BC ⊂平面ABC ，所以MN BC ⊥，同理PO BC ⊥； 又MN NH N ⋂=，MN ⊂平面MNH ，NH ⊂平面MNH ， 所以BC ⊥平面MNH ；因为MH ⊂平面MNH ，所以BC MH ⊥， 所以MHN ∠为二面角MBC A --的平面角；同理BC PG ⊥，所以PGO ∠为二面角A BC P --的平面角，所以tan PO PGO OG ∠=，tan MNMHN HN∠=， 因为NO OE =，//OG NH ，所以12OG NH =； 因此2tan 4tan 12PO MNPGO MHNOG HN∠===∠， 所以()2tan tan 3tan tan tan 1tan tan 14tan PGO MHN MHNPGO MHN PGO MHN MHNα∠-∠∠=∠-∠==+∠⋅∠+∠，令tan 0x MHN =∠>，则2333tan 1444x x x x α=≤=+， 当且仅当214x =，即12x =时，等号成立. 故答案为：34. 【点睛】 关键点点睛：求解本题的关键在于确定二面角MBC A --、A BC P --以及P BC M --三者之间的关系，由题中条件得出二面角A BC P --是二面角M BC A --的4倍，进而可求得结果.17．【分析】根据给定的几何体的三视图得到该几何体为一个圆柱挖去一个圆锥得出圆柱的底面半径和高利用圆柱和圆锥的体积以及圆的公式即可求解【详解】解：根据给定的几何体的三视图可得该几何体表示一个圆柱挖去一个圆 解析：23π 【分析】根据给定的几何体的三视图，得到该几何体为一个圆柱挖去一个圆锥，得出圆柱的底面半径和高，利用圆柱和圆锥的体积以及圆的公式，即可求解． 【详解】解：根据给定的几何体的三视图，可得该几何体表示一个圆柱挖去一个圆锥， 且底面半径1，高为1的组合体，所以几何体的体积为：2221311113πππ⨯⨯⨯=⨯-⨯． 故答案为：23π.【点睛】关键点点睛：本题考查了几何体的三视图及体积的计算，在由三视图还原为空间几何体的实际形状时，要根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线，求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应公式求解．18．【分析】作于可证得平面得得等边三角形利用是球的直径得然后计算出再应用棱锥体积公式计算体积【详解】∵围绕棱旋转后恰好与重合∴作于连接则∴又过球心∴而∴同理由得平面∴故答案为：【点睛】易错点睛：本题考查 解析：3 【分析】作BH PA ⊥于H ，可证得PA ⊥平面BCH ，得60BHC ∠=︒，得等边三角形BCH ，利用PA 是球的直径，得PB AB ⊥，然后计算出BH ，再应用棱锥体积公式计算体积． 【详解】∵PAB △围绕棱PA 旋转60︒后恰好与PAC △重合， ∴PAB PAC ≅△△，作BH PA ⊥于H ，连接CH ，则,CH PA CH BH ⊥=，60BHC ∠=︒， ∴BC BH CH ==．又PA 过球心，∴PB AB ⊥，而2,3PA PB ==，∴1AB =，同理1AC =，313PB AB BH PA ⋅⨯===，223333344216BCH S BH ⎛⎫=⨯=⨯= ⎪ ⎪⎝⎭△， 由BH PA ⊥，CH PA ⊥，CH BH H =，得PA ⊥平面BCH ，∴11333233168P ABC BCH V S PA -=⋅=⨯⨯=△． 故答案为：38．【点睛】易错点睛：本题考查求棱锥的体积，解题关键是作BH PA ⊥于H ，利用旋转重合，得PA ⊥平面BCH ，这样只要计算出BCH 的面积，即可得体积，这样作图可以得出60BHC ∠=︒，为旋转所形成的二面角的平面角，这里容易出错在误认为旋转60︒，即为60CAB ∠=︒．旋转60︒是旋转形成的二面角为60︒．应用作出二面角的平面角． 19．【详解】取的中点由题意可得：所以面ABC 所以球心在直线上所以得所以 解析：494π【详解】取AB 的中点，由题意可得：2222,3,SD DC SD DC SC ==+=，所以,SD AB SD DC ⊥⊥，SD ⊥面ABC.所以球心在直线SD 上，所以()2232R R =+-，得74R =， 所以24944S R ππ==． 20．【分析】先在等边三角形中求出外接圆半径从而可求该三棱锥的外接球的半径【详解】详解：因为所以为等边三角形所以等边外接圆的半径为如图三棱锥外接球球心为半径为设球心到平面的距离为外接圆圆心为连接则平面取中 5【分析】先在等边三角形ABC 中求出23BC =，外接圆半径2r ，从而可求该三棱锥的外接球的半径. 【详解】详解：因为023,60AB AC BAC ==∠=，所以ABC 为等边三角形， 所以23BC =ABC 外接圆的半径为23r，如图，三棱锥P ABC -外接球球心为O ，半径为R ，设球心O 到平面ABC 的距离为d ，ABC 外接圆圆心为'O ， 连接,','AO AO OO ，则'OO ⊥平面ABC ， 取PA 中点,D OP OA =，所以OD PA ⊥，又PA ⊥平面ABC ，所以//PA OO '，则四边形'ADOO 是矩形， 所以在PDO △和'OAO △中，由勾股定理可得()222222222R d R d ⎧=+⎪⎨=+-⎪⎩，解得：1,5d R ==. 故答案为：5.【点睛】本题主要考查了三棱锥外接球的表面积，其中根据几何体的结构特征和球的性质，求得三棱锥的外接球的半径是解答的关键，着重考查了空间想象能力，以及推理与运算能力.三、解答题21．（1）证明见解析（23【分析】（1）由CD PQ ⊥，PQ DQ ⊥可证得结论成立；（2）取BQ 的中点E ，连DE 、AE ，则AED ∠是二面角D QB A --的平面角，在Rt ADE △中，通过计算可得结果. 【详解】（1）因为QA ⊥平面ABCD ，∴QA CD ⊥，又四边形ABCD 为正方形，∴CD AD ⊥， 又因为QAAD A =，∴CD ⊥平面AQPD ，则CD PQ ⊥，因为1AQ AD ==，AQ AD ⊥，∴2DQ =，因为4PDQ π∠=，2PD =，∴2DQP π∠=，即PQ DQ ⊥，因为CD DQ D =，所以PQ ⊥平面DCQ .（2）取BQ 的中点E ，连DE 、AE ，如图：因为2BD DQ ==BE EQ =，∴DE BQ ⊥，AE BQ ⊥，所以AED ∠是二面角D QB A --的平面角，因为QA ⊥平面ABCD ，所以QA AD ⊥，又AD AB ⊥，AB AQ A =，∴AD ⊥平面BAQ ，∴AD AE ⊥，因为1AB AQ ==，所以2BQ =2AE =， 在Rt ADE △中，221612DE AD AE =+=+=所以232cos 36AE ADE DE ∠===. 所以二面角D QB A --3 【点睛】关键点点睛：根据二面角的平面角的定义作出平面角是本题解题关键. 22．（1）主视图（正视图）见解析，33S =；（2）3V =. 【分析】（1）根据侧视图计算出PAC △的边AC 上的高，进而可作出几何体PMABC 的主视图，利用梯形的面积公式可求得几何体的主视图的面积；（2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，推导出AN ⊥平面BCPM ，计算出AN 和梯形BCPM 的面积，利用锥体的体积公式可求得多面体PMABC 的体积V . 【详解】（1）在几何体PMABC 中，平面PAC ⊥平面ABC ， 设PAC △的边AC 上的高为h ，则该几何体的侧视图的面积为1324AC h ⋅=，得32h =， 又因为22BC PM ==，所以，该几何体的主视图（正视图）如下图所示：由图可知，该几何体的主视图为直角梯形，其面积为()1233322S +⨯==⨯； （2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，如下图所示：PA PC =，O 为AC 的中点，所以，PO AC ⊥，由（1）可知，3PO h ==1122AO CO AC ===，由勾股定理可得221PC PA AO PO ==+=，所以，PAC △为等边三角形，N 为PC 的中点，AN PC ∴⊥，且3sin 602AN AC ==. 1AC =，2BC =，5AB =222AC BC AB ∴+=，BC AC ∴⊥，平面PAC ⊥平面ABC ，平面PAC平面ABC AC =，BC ⊂平面ABC ，BC ∴⊥平面PAC ，AN 、PC ⊂平面PAC ，BC AN ∴⊥，BC PC ⊥， PC BC C =，AN ∴⊥平面BCPM ， //PM BC ，PM PC ∴⊥，所以，梯形BCPM 的面积为()322BCPM BC PM PC S +⋅==梯形，因此，1133333224BCPM V S AN =⋅=⨯⨯=梯形. 【点睛】方法点睛：求空间几何体体积的方法如下：（1）求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．23．（1）证明见解析；（2）23. 【分析】（1）连接11B D ，设11111B D AC O ⋂=，连接1DO ，证明11B O DO 是平行四边形，再利用线面平行的判定定理即可证明.（2）由题意可得平面11DA C ⊥平面11B D DB ，过点O 作1OH DO ⊥于H ，在矩形11B D DB 中，连接1OO ，可得1O OD OHD ∽△△，由三角形相似，对应边成比例即可求解. 【详解】（1）证明：连接11B D ，设11111B D AC O ⋂=，连接1DO .11//O B DO 且11O B DO =， 11B O DO ∴是平行四边形.11//B O DO ∴.又1DO ⊂平面11DA C ，1B O ⊂/平面11DA C ，1//B O ∴平面11DA C .（2）1111A C B D ⊥，111AC BB ⊥，且1111BB B D B ⋂=，11A C ∴⊥平面11B D DB .∴平面11DA C ⊥平面11B D DB ，且交线为1DO .。

一、选择题1．已知AB 是平面α外的一条直线，则下列命题中真命题的个数是（ ）①在α内存在无数多条直线与直线AB 平行；②在α内存在无数多条直线与直线AB 垂直；③在α内存在无数多条直线与直线AB 异面；④一定存在过AB 且与α垂直的平面β.A ．1个B ．2个C ．3个D ．4个2．在底面为正方形的四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ，PA AD ⊥，PA AD =，则异面直线PB 与AC 所成的角为（ ）A ．30B ．45︒C ．60︒D ．90︒3．如图，四棱柱ABCD A B C D ''''-中，底面ABCD 为正方形，侧棱AA '⊥底面ABCD ，32AB =，6AA '=，以D 为圆心，DC '为半径在侧面BCC B ''上画弧，当半径的端点完整地划过C E '时，半径扫过的轨迹形成的曲面面积为（ ）A 96B 93C 96D 93 4．如图正三棱柱111ABC A B C -的所有棱长均相等，O 是1AA 中点，P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ，则直线OP 与平面ABC 所成角正弦值的最大值为（ ）A ．22B ．255C ．32D ．2775．如图为某几何体的三视图，正视图、左视图和俯视图均为等腰直角三角形，则该几何体的表面积是（ ）A ．23+B ．223+C ．63+D ．6 6．三个平面将空间分成n 个部分，则n 不可能是（ ）A ．5B ．6C ．7D ．8 7．《九章算术》是古代中国乃至东方的第一步自成体系的数学专著，书中记载了一种名为“刍甍”的五面体（如图），其中四边形ABCD 为矩形，//EF AB ，若3AB EF =，ADE 和BCF △都是正三角形，且2AD EF =，则异面直线AE 与CF 所成角的大小为（ ）A ．6πB ．4πC ．3πD ．2π 8．在三棱锥S ABC -中，SA ⊥底面ABC ，且22AB AC ==，30C ∠=，2SA =，则该三棱锥外接球的表面积为（ ）A ．20πB ．12πC ．8πD ．4π 9．某三棱锥的三视图如图所示，已知网格纸上小正方形的边长为1，则该三棱锥的体积为（ ）A ．43B ．83C ．3D ．410．αβ是两个不重合的平面，在下列条件中，可判定平面α与β平行的是（ ） A ．m 、n 是α内的两条直线，且//m β，βn//B ．α、β都垂直于平面γC ．α内不共线三点到β的距离相D ．m 、n 是两条异面直线，m α⊂，n β⊂，且//m β，//n α11．已知三棱锥D ABC -，记二面角C AB D --的平面角是θ，直线DA 与平面ABC 所成的角是1θ，直线DA 与BC 所成的角是2θ，则（ ）A ．1θθ≥B ．1θθ≤C ．2θθ≥D ．2θθ≤ 12．已知在底面为菱形的直四棱柱1111ABCD A B C D -中，14,42AB BD ==60BAD ︒∠=，则异面直线1B C 与1AD 所成的角为（ ）A ．90︒B ．60︒C ．45︒D ．30︒二、填空题13．在边长为3的菱形ABCD 中，对角线3AC =，将三角形ABC 沿AC 折起，使得二面角B AC D --的大小为2π，则三棱锥B ACD -外接球的体积是_________________．14．如图所示，Rt A B C '''∆为水平放置的ABC ∆的直观图，其中A C B C ''''⊥，2B O O C ''''==，则ABC ∆的面积是________________.15．已知H 是球O 的直径AB 上一点，:1:3AH HB =，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为__________.16．如图①，矩形ABCD 中，2AB =，4=AD ，E 是BC 的中点，将三角形ABE 沿AE 翻折，使得平面ABE 和平面AECD 垂直，如图②，连接BD ，则异面直线BD 和AE 所成角的余弦值为______.17．如图，在四棱柱1111ABCD A B C D -中，底面ABCD 是正方形，1AA ⊥平面ABCD ，且2AB BC ==，13AA =，经过顶点A 作一个平面α，使得//α平面11CB D ，若α平面1ABCD l =，α平面112ABB A l =，则异面直线1l 与2l 所成的角的余弦值为___________.18．在棱长为2的正方体1111ABCD A B C D -中，P 是11A B 的中点，过点1A 作与平面1PBC 平行的截面，则此截面的面积是_______________．19．已知扇形的面积为56π，圆心角为63π，则由该扇形围成的圆锥的外接球的表面积为_________．20．将底面直径为8，高为23的圆锥体石块打磨成一个圆柱，则该圆柱侧面积的最大值为______. 三、解答题21．如图，该多面体由底面为正方形ABCD 的直四棱柱被截面AEFG 所截而成，其中正方形ABCD 的边长为4，H 是线段EF 上（不含端点）的动点，36==FC EB ．（1）证明：//GH 平面ABCD ；（2）求H 到平面AEC 的距离．22．如图，在直四棱柱1111ABCD A B C D -中，底面ABCD 是梯形，,//AB CD AB AD ⊥，22CD AB AD ==．（1）求证：BD ⊥平面1BCC ；（2）在线段11C D 上是否存在一点E ，使//AE 面1BC D ．若存在，确定点E 的位置并证明；若不存在，请说明理由．23．在如图所示的几何体中，四边形BCED 为直角梯形，//DE CB ，BC EC ⊥，90AED ∠=︒.（1）证明：平面ABC ⊥平面ACE .（2）若P ，Q 分别是AE ，CD 的中点，证明：//PQ 平面ABC .24．如图，在三棱锥A BCD -中，2,22,23,BC BD AB CD AC AB BD =====⊥（1）证明：平面ABC ⊥平面ABD ．（2）在侧面ACD 内求作一点H ，使得BH ⊥平面ACD ，写出作法（无需证明），并求线段AH 的长．25．如图，在三棱柱ABC －A 1B 1C 1中，F 为AC 中点.（1）若此三棱柱为正三棱柱，且1112A A AC =，求异面直线1AB 与BF 所成角的大小； （2）求证：1AB //平面1BFC .26．如图，在三棱柱111ABC A B C -中，平面11A ACC ⊥平面ABC ，2,AB BC == 30ACB ∠=，13AA =，11BC A C ，E 为AC 的中点.（1）求证：1//AB 平面1C EB ；（2）求证：1A C ⊥平面1C EB .【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据线面平行，线面垂直，异面直线等有关结论和定义即可判断．【详解】对于A ，若直线AB 与平面α相交，则在α内不存在直线与直线AB 平行，错误；对于B ，若直线AB 与平面α相交且不垂直，设AB M α=，过平面α外直线AB 上一点⊥，垂足为C，则在平面α内过点C一定可以作一条直线CD，使得P作PCα⊥，而在平面α内，与直线CD平行的直线有无数条，所以在⊥，所以CD ABCD CMα内存在无数多条直线与直线AB垂直，若直线AB与平面α垂直，显然在α内存在无数多条直线与直线AB垂直，当直线AB与平面α平行时，显然可知在α内存在无数多条直线与直线AB垂直，正确；α=，根据异面直线的判定定理，在平面α对于C，若直线AB与平面α相交，设AB M内，不过点M的直线与直线AB异面，所以在α内存在无数多条直线与直线AB异面，当直线AB与平面α平行时，显然可知在α内存在无数多条直线与直线AB异面，正确；α=，过平面α外直线AB上一点对于D，若直线AB与平面α相交且不垂直，设AB M⊥，垂足为C，所以平面ABC与平面α垂直，若直线AB与平面α垂直，则P作PCα过直线AB的所有平面都与平面α垂直，当直线AB与平面α平行时，在直线AB上取一⊥，垂足为C，所以平面ABC与平面α垂直，正确．点P作PCα故真命题的个数是3个．故选：C．【点睛】本题主要考查线面平行，线面垂直，异面直线等有关结论和定义的理解和应用，熟记定义，定理和有关结论是解题的关键，属于中档题．2．C解析：C【分析】由已知可得PA⊥平面ABCD，底面ABCD为正方形，分别过P，D点作AD，AP的平行线交于M，连接CM，AM，因为PB∥CM，所以ACM就是异面直线PB与AC所成的角,再求解即可.【详解】由题意：底面ABCD为正方形，⊥，侧面PAD⊥底面ABCD，PA AD=，面PAD面ABCD ADPA⊥平面ABCD，分别过P，D点作AD，AP的平行线交于M，连接CM，AM，∵PM∥AD，AD∥BC，PM ＝AD ，AD ＝BC ．∴ PBCM 是平行四边形，∴ PB ∥CM ，所以∠ACM 就是异面直线PB 与AC 所成的角．设PA ＝AB ＝a ，在三角形ACM 中，,,AM AC CM ===， ∴三角形ACM 是等边三角形．所以∠ACM 等于60°，即异面直线PB 与AC 所成的角为60°．故选：C.【点睛】思路点睛：先利用面面垂直得到PA ⊥平面ABCD ，分别过P ，D 点作AD ，AP 的平行线交于M ，连接CM ，AM ，得到∠ACM 就是异面直线PB 与AC 所成的角． 3．A解析：A【分析】先确定曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，利用圆锥的侧面积S rl π=即可得出结论. 【详解】由题意 6,CE CC AA BC AB ''=====BE ==，所以45BCE ∠=， 45ECC '∠=， 所以曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，所以圆锥的侧面积 6S rl CC DC πππ'==⨯⨯=⨯⨯=，所以曲面面积为18⨯=. 故选：A.【点睛】方法点睛：本题考查曲面面积，考查圆锥的侧面积，确定曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18是关键，考查系数的空间想象力. 4．D解析：D【分析】先找到与平面11A BC 平行的平面OEFG ,确定点P 在直线FG 上，作出线面角，求出正弦，转化为求AP 的最小值.【详解】分别取1,,CC BC BA 的中点，连接,,,OE EF FG GO ,并延长FG ，如图，由中位线性质可知11//OE A C , 1//EF BC ,且OE EF E =, 故平面11//A BC 平面OGFE ， 又P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC 则点P 在直线FG 上，OA ⊥平面ABC ,OPA ∴∠是直线OP 与平面ABC 所成角， sin OA OPA OP∴∠=, OA 为定值， ∴当OP 最小时，正弦值最大， 而22OP OA AP +所以当AP 最小时，sin OPA ∠最大， 故当AP FG ⊥时，sin OPA ∠最大， 设棱长为2， 则1212AG =⨯=，而30GAP ∠=︒, 3AP ∴=, 又1212OA =⨯=, 222sin 773()12OA OPA OP∴∠===+故选：D【点睛】关键点点睛：由P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ，转化为找过O 的平面与平面11A BC 平行，P 在所找平面与平面ABC 的交线上，从而容易确定出线面角，是本题解题的关键所在.5．A解析：A 【分析】由三视图可知原几何体是三棱锥，平面ACD ⊥平面ABC ，ACD ACB ≅底面是等腰直角三角形，底为2AC =，高为1BE =，ABD BCD ≅是边长为2的等边三角形，计算四个三角形面积之和即可求解. 【详解】由三视图可知原几何体是三棱锥：底面ACB △是等腰直角三角形，底2AC =，高1BE =，平面ACD ⊥平面ABC ，ACD ACB ≅，由三视图知ACB △中，2AC =，ACB △是等腰直角三角形，所以2AB BC ==ACD △是等腰直角三角形，2AD CD ==，2AC =，222BD BE DE =+=所以等腰直角三角形ACB △的面积为12112⨯⨯=， 等腰直角三角形ACD △的面积为12112⨯⨯=， 等边ABD △的面积为233242=， 等边BCD △2332=， 所以该几何体的表面积是33112322+++=+， 故选：A.6．A解析：A【分析】三个平面不重合，先按其中平行的平面的个数分类：三个平面两两平行，两个平面平行，没有平行的平面(两两相交)，对两两相交的情况，再根据三条交线互相平行，重合，交于一点，分别讨论.【详解】按照三个平面中平行的个数来分类：（1）三个平面两两平行，如图1，可将空间分成4部分；（2）两个平面平行，第三个平面与这两个平行平面相交，如图2，可将空间分成6部分；（3）三个平面中没有平行的平面：（i）三个平面两两相交且交线互相平行，如图3，可将空间分成7部分；（ii）三个平面两两相交且三条交线交于一点，如图4，可将空间分成8部分.（iii）三个平面两两相交且交线重合，如图5，可将空间分成6部分；综上，可以为4，6，7，8部分，不能为5部分， 故选：A.7．D解析：D 【分析】过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，然后在CFG △中求解. 【详解】如下图所示，在平面ABFE 中，过点F 作//FG AE 交AB 于点G ，连接CG ， 则异面直线AE 与CF 所成角为CFG ∠或其补角，设1EF =，则3AB =，2BC CF AE ===，因为//EF AB ，//FG AE ，所以，四边形AEFG 为平行四边形， 所以，2FG AE ==，1AG =，2BG =， 由于2ABC π∠=，由勾股定理可得2222CG BC BG =+=所以，222CG CF FG =+，则2CFG π∠=.故选：D. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．8．A解析：A 【分析】利用正弦定理求出ABC 的外接圆直径2r ，利用公式()2222R r SA =+可计算得出三棱锥S ABC -的外接球直径，然后利用球体的表面积公式可求得结果. 【详解】如下图所示，设圆柱的底面半径为r ，母线长为h ，圆柱的外接球半径为R ，取圆柱的轴截面，则该圆柱的轴截面矩形的对角线的中点O 到圆柱底面圆上每个点的距离都等于R ，则O 为圆柱的外接球球心，由勾股定理可得()()22222r h R +=.本题中，SA ⊥平面ABC ，设ABC 的外接圆为圆1O ，可将三棱锥S ABC -内接于圆柱12O O ，如下图所示：设ABC 的外接圆直径为2r ，2SA h ==，由正弦定理可得24sin ABr C==∠，，该三棱锥的外接球直径为2R ，则()222225R r h =+=.因此，三棱锥S ABC -的外接球的表面积为()224220R R πππ=⨯=. 故选：A. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.9．A解析：A 【分析】首先由三视图还原几何体，然后由几何体的空间结构特征求解三棱锥的体积即可. 【详解】由三视图可知，在棱长为2的正方体中，其对应的几何体为棱锥P ABC -，该棱锥的体积：11142223323V Sh ⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭. 故选：A. 【点睛】方法点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．10．D解析：D 【分析】取a αβ⋂=，且//m a ，//n a ，利用线面平行的判定定理可判断A 选项；根据αγ⊥，βγ⊥判断平面α与β的位置关系，可判断B 选项；设AB 、AC 的中点D 、E 在平面β内，记平面ABC 为平面α，判断出A 、B 、C 三点到平面β的距离相等，可判断C选项；过直线n 作平面γ，使得a αγ⋂=，利用线面平行、面面平行的判定定理可判断D 选项. 【详解】对于A 选项，若a αβ⋂=，且//m a ，//n a ，m β⊄,n β⊄,则//m β，βn//，但α与β相交；对于B 选项，若αγ⊥，βγ⊥，则α与β平行或相交；对于C 选项，设AB 、AC 的中点D 、E 在平面β内，记平面ABC 为平面α，如下图所示：D 、E 分别为AB 、AC 的中点，则//DE BC ，DE β⊂，BC β⊄，//BC β∴，所以，点B 、C 到平面β的距离相等，由于D 为AB 的中点，则点A 、B 到平面β的距离相等，所以，点A 、B 、C 三点到平面β的距离相等，但平面α与平面β相交； 对于D 选项，如下图所示：由于//n α，过直线n 作平面γ，使得a αγ⋂=，则//a n ，//n a ，a β⊄，n β⊂，//a β∴，//m β，m a A =，m α⊂，a α⊂，//αβ∴.故选：D. 【点睛】方法点睛：证明或判断两个平面平行的方法有： ①用定义，此类题目常用反证法来完成证明；②用判定定理或推论（即“线线平行”⇒“面面平行”），通过线面平行来完成证明； ③根据“垂直于同一条直线的两个平面平行”这一性质进行证明； ④借助“传递性”来完成．11．A解析：A 【分析】设三棱锥D -ABC 是棱长为2的正四面体，取AB 中点E ，DC 中点M ，AC 中点M ，连结DE 、CE 、MN 、EN ，过D 作DO CE ⊥，交CE 于O ，连结AO ，则DEC θ∠=，1DAO θ∠=，2MNE θ∠=，排除B ，C ．当二面角C AB D --是直二面角时，2θθ≥，排除D ．由此能求出结果． 【详解】设三棱锥D -ABC 是棱长为2的正四面体，取AB 中点E ，DC 中点M ，AC 中点M ，连结DE 、CE 、MN 、EN ， 过D 作DO ⊥CE ，交CE 于O ，连结AO ，则DEC θ∠=，1DAO θ∠=，2MNE θ∠=，413DE CE ==-=2DC =，∴1 cos3233θ==⨯⨯，22333AO CO CE===，∴12333cos3AOADθ===，取BC中点F，连结DF、AF，则DF BC⊥，AF BC⊥，又DF AF F⋂=，∴BC⊥平面AFD，∴BC AD⊥，∴290θ=︒，∴21θθθ≥≥，排除B，C，当二面角C AB D--是直二面角时，2θθ≥，排除D，故选：A.【点睛】关键点点睛：将三棱锥看成特殊的正四面体，采用排除法，充分理解线线角、线面角以及面面的概念是解题的关键.12．A解析：A【分析】把1AD平移到1BC，把异面直线所成的角转化为相交直线的夹角．【详解】连接1,BD BC，∵四边形ABCD为菱形，60,4BAD AB︒∠==，4BD∴=.又1BDD为直角三角形，22211BD BD DD∴=+，得14DD=，∴四边形11BCC B为正方形.连接1BC交1B C于点O11//BC AD，BOC∴∠（或其补角)为异面直线1B C与1AD所成的角，由于11BCC B为正方形，90BOC︒∴∠=，故异面直线1B C与1AD所成的角为90°.故选：A.【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．二、填空题13．；【分析】分析菱形的特点结合其翻折的程度判断其外接球球心的位置放到相应三角形中利用勾股定理求得半径利用球的体积公式求得外接球的体积【详解】根据题意画出图形根据长为的菱形中对角线所以和都是正三角形又因解析：55π； 【分析】分析菱形的特点，结合其翻折的程度，判断其外接球球心的位置，放到相应三角形中，利用勾股定理求得半径，利用球的体积公式求得外接球的体积. 【详解】根据题意，画出图形，3的菱形ABCD 中，对角线3AC = 所以ABC 和DBC △都是正三角形， 又因为二面角B AC D --的大小为2π， 所以分别从两个正三角形的中心做面的垂线，交于O ， 则O 是棱锥B ACD -外接球的球心，且11,2GD OG GE ===， 所以球的半径225R GD OG =+=，所以其体积为3344555()3326V R πππ==⋅=， 故答案为：556π. 【点睛】思路点睛：该题考查的是有关几何体外接球的问题，解题思路如下： （1）根据题中所给的条件，判断菱形的特征，得到两个三角形的形状；（2）根据直二面角，得到两面垂直，近一倍可以确定其外接球的球心所在的位置； （3）利用勾股定理求得半径； （4）利用球的体积公式求得结果；（5）要熟知常见几何体的外接球的半径的求解方法.14．【分析】根据直观图和原图的之间的关系由直观图画法规则将还原为如图所示是一个等腰三角形直接求解其面积即可【详解】由直观图画法规则将还原为如图所示是一个等腰三角形则有所以故答案为：【点睛】关键点点睛：根 解析：82【分析】根据直观图和原图的之间的关系，由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形，直接求解其面积即可． 【详解】由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形,则有2BO OC B O O C ''''====，242AO A O ''==所以114428222ABCSBC AO =⋅=⨯⨯= 故答案为：2【点睛】关键点点睛：根据斜二测画法的规则，可得出三角形的直观图，并求出对应边长，根据面积公式求解．15．【分析】求出截面圆的半径设可得出从而可知球的半径为根据勾股定理求出的值可得出球的半径进而可求得球的表面积【详解】如下图所示设可得出则球的直径为球的半径为设截面圆的半径为可得由勾股定理可得即即所以球的 解析：163π【分析】求出截面圆H 的半径，设AH x =，可得出3HB x =，从而可知，球O 的半径为2x ，根据勾股定理求出x 的值，可得出球O 的半径，进而可求得球O 的表面积. 【详解】如下图所示，设AH x =，可得出3HB x =，则球O 的直径为4AB x =，球O 的半径为2x ，设截面圆H 的半径为r ，可得2r ππ=，1r ∴=，由勾股定理可得()2222OH r x +=，即()22214x AH x -+=，即2214x x +=，3x ∴=， 所以，球O 的半径为232x =，则球O 的表面积为22316433S ππ⎛⎫=⨯= ⎪ ⎪⎝⎭. 故答案为：163π. 【点睛】方法点睛：在求解有关球的截面圆的问题时，一般利用球的半径、截面圆的半径以及球心到截面圆的距离三者之间满足勾股定理来求解.16．【分析】取的中点作交延长线于则是异面直线和所成角或其补角可结合原矩形求出然后由直角三角形得出再用余弦定理求得结论【详解】取的中点作交延长线于则是异面直线和所成角或其补角连接∵所以又平面平面平面平面平 6【分析】取AE 的中点O ，作//DF AE 交EC 延长线于F ，则BDF ∠是异面直线BD 和AE 所成角或其补角，可结合原矩形求出,OD OF ，然后由直角三角形得出,BD BF ，再用余弦定理求得结论． 【详解】取AE 的中点O ，作//DF AE 交EC 延长线于F ，则BDF ∠是异面直线BD 和AE 所成角或其补角，连接,OB OF ，OD ， ∵AB BE =，所以BO AE ⊥， 又平面ABE ⊥平面ECDA ，平面ABE 平面ECDA AE =，BO ⊂平面ABE ，∴BO ⊥平面ECDA ，而,OD OF ⊂平面ECDA ，所以BO OF ⊥，BO OD ⊥， 又∵90ABE ∠=︒，2AB BE ==，所以2BO =，2AO EO ==，22AE =，//DF AE ,//AD EF ，则ADFE 是平行四边形，4,22EF AD DF AE ====，在原矩形中45BAE BEA ∠=∠=︒，则45,135DAE CEA ∠=︒∠=︒，22222cos 4542242102OD AD AO AD AO =+-⋅︒=+-⨯⨯⨯=， 22222cos135********OF EF EO EF EO =+-⋅︒=++⨯⨯⨯=， 22212BD BO OD =+=，22228BF BO OF =+=，在BDF 中，222cos 2BD DF BF BDF BD DF +-∠=⋅6621222==-⨯⨯， 所以异面直线BD 和AE 所成角的余弦为6． 故答案为：66.【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下： （1）平移：平移异面直线中的一条或两条，作出异面直线所成的角； （2）认定：证明作出的角就是所求异面直线所成的角； （3）计算：求该角的值，常利用解三角形； （4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．17．【分析】先利用线面平行的性质定理和平面扩展得到异面直线所成角即BD 与所成的角再结合长方体棱长的条件在中求其余弦值即可【详解】如图设平面平面平面平面因为平面所以故异面直线与所成的角即与所成的角延长AD 解析：2613【分析】先利用线面平行的性质定理和平面扩展，得到异面直线所成角即BD 与1A B 所成的角1A BD ∠，再结合长方体棱长的条件在1A BD 中求其余弦值即可.【详解】如图，设平面11CB D ⋂平面1ABCD l '=，平面11CB D ⋂平面112ABB A l '=，因为//α平面11CB D ，所以1122//,//l l l l ''，故异面直线1l 与2l 所成的角，即1l '与2l '所成的角.延长AD 至E ，使AD DE =，连接CE ，则易见BD 与CE 平行且相等，又BD 与11B D 平行且相等，故BD 与11B D 平行且相等，即四边形11D B CE 是平行四边形，CE 就是交线1l '. 同理可知1B F 就是交线2l '.又知BD //CE ，11//B F A B ，故1l '与2l '所成的角，即BD 与1A B 所成的角1A BD ∠，依题意可知，2AB BC ==，13AA =，故1A BD 中，1113,22A B A D BD ===故1112262cos13BDA BD AB ∠===. 故答案为：2613. 【点睛】 方法点睛：求空间角的常用方法：（1）定义法，由异面直线所成角、线面角、二面角的定义，结合图形，作出所求空间角，再结合题中条件，解对应三角形，即可求出结果；（2）向量法：建立适当的空间直角坐标系，通过计算向量夹角（直线方向向量与直线方向向量、直线方向向量与平面法向量，平面法向量与平面法向量）余弦值，即可求出结果.18．【分析】取的中点分别为连接先证明四边形是平行四边形再利用面面平行的判断定理证明平面平面可得平行四边形即为所求的截面再计算其面积即可【详解】取的中点分别为连接因为所以四边形是平行四边形所以因为所以四边 解析：26【分析】取AB ，11D C 的中点分别为,M N ，连接11,,,,A M MC CN A N PM ，先证明四边形1A MCN 是平行四边形，再利用面面平行的判断定理证明平面1//PBC 平面1A MCN ，可得平行四边形1A MCN 即为所求的截面，再计算其面积即可. 【详解】取AB ，11D C 的中点分别为,M N ，连接11,,,,A M MC CN A N PM ，因为11A P NC ，所以四边形11A PC N 是平行四边形，所以11A N PC ， 因为1PM CC 所以四边形1PMCC 是平行四边形，所以1MC PC ， 所以1A N MC ，所以四边形1A MCN 是平行四边形， 因为11//PC A N ，1PC ⊄平面1A MCN ，1A N ⊂平面1A MCN ，所以1//PC 平面1A MCN ， 同理可证//PB 平面1A MCN ， 因为1PC PB P ⋂=，所以平面1//PBC 平面1A MCN ，因此过点1A 作与平面1PBC 平行的截面，即是平行四边形1A MCN ， 连接MN ，作1A H MN ⊥于点H ，由11AM A N ==，MN =可得1A H ==所以111122A MNSMN A H =⨯⨯=⨯=，所以平行四边形1A MCN 的面积为12A MNS =故答案为：【点睛】关键点点睛：本题的关键点是找出过点1A 与平面1PBC 平行的截面，所以想到作平行线，利用面面平行的判断定理证明所求的截面即是平行四边形1A MCN ，先求四边形一半的面积，乘以2即可得所求平行四边形的面积，也可以直接求菱形的面积.19．【分析】由扇形的面积及圆心角可得扇形的半径再由扇形的弧长等于圆锥的底面周长可得底面半径再由外接球的半径与圆锥的高和底面半径的关系求出外接球的半径进而求出球的表面积【详解】设扇形的长为l 半径为R 则解得 解析：36π【分析】由扇形的面积及圆心角可得扇形的半径，再由扇形的弧长等于圆锥的底面周长可得底面半径，再由外接球的半径与圆锥的高和底面半径的关系求出外接球的半径，进而求出球的表面积. 【详解】设扇形的长为l ，半径为R ，则221112223S lR R R α===⨯=，解得R =l 为锥底面周长2r π，∴底面的半径r =∴5=．设外接球的半径为1R ，∴()222115R R =-+，解得13R =，∴该外接球的表面积为21436R ππ=，故答案为：36π. 【点睛】本题考查扇形的弧长与圆锥的底面周长的关系及外接球的半径和圆锥的高及底面半径的关系，和球的表面积公式的应用，属于中档题.20．【分析】欲使圆柱侧面积最大需使圆柱内接于圆锥设圆柱的高为h 底面半径为r 用r 表示h 从而求出圆柱侧面积的最大值【详解】欲使圆柱侧面积最大需使圆柱内接于圆锥；设圆柱的高为h 底面半径为r 则解得；所以；当时取 解析：43π【分析】欲使圆柱侧面积最大，需使圆柱内接于圆锥，设圆柱的高为h ，底面半径为r ，用r 表示h ，从而求出圆柱侧面积的最大值. 【详解】欲使圆柱侧面积最大，需使圆柱内接于圆锥； 设圆柱的高为h ，底面半径为r ， 23423h r -=，解得33h r =； 所以()232223342S rh r r r r πππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧； 当2r时，S 圆柱侧取得最大值为43π故答案为：3π. 【点睛】本题考查了求圆柱侧面积的最值，考查空间想象能力，将问题转化为函数求最值，属于中档题.三、解答题21．（1）证明见解析；（26． 【分析】（1）取BC 的中点M ，连接HM ，DM ．证明四边形DGHM 是平行四边形，可得线面平行；（2）由H 到平面AEC 的距离为F 到平面AEC 的距离的一半，先求出F 到平面AEC 的距离，用体积法可求得F 到平面AEC 的距离． 【详解】（1）证明：取BC 的中点M ，连接HM ，DM ．因为该多面体由底面为正方形ABCD 的直四棱柱被截面AEFG 所截而成， 所以截面AEFG 是平行四边形， 则4=-=DG CF EB ． 因为36==FC EB ， 所以1(26)42=⨯+=HM ，且DG//FC//HM ， 所以四边形DGHM 是平行四边形，所以GH //DM ． 因为DM ⊂平面ABCD ，GH ⊄平面ABCD ， 所以//GH 平面ABCD ．（2）解：连接HA ，HC ，AF ，记F 到平面ACE 的距离为d ， 则H 到平面ACE 的距离为2d ． 在CEF △中，6EF =，高为4，所以CEF △的面积为164122⨯⨯=． 因为三棱锥A CEF -的高为4，所以A CEF -的体积为1124163⨯⨯=． 在ACE 中，42AC =，25AE CE ==， 所以ACE 的面积为22142(25)(22)462⨯⨯-=． 因为A CEF -的体积与F ACE -的体积相等， 所以146163⨯⨯=d ，所以26d =． 故H 到平面ACE 的距离为6．【点睛】方法点睛：本题考查证明线面平行，考查求点到平面的距离．求点到平面的距离的常用方法：（1）定义法：作出点到平面的垂线段，求出垂线段的长；。

一、选择题1．点A ，B ，C 在球O 表面上，2AB =，4BC =，60ABC ∠=︒，若球心O 到截面ABC 的距离为22，则该球的体积为（ ） A ．323π B ．86π C ．36π D ．323π 2．在正四面体ABCD 中，异面直线AB 与CD 所成的角为α，直线AB 与平面BCD 所成的角为β，二面角C AB D --的平面角为γ，则α，β，γ的大小关系为（ ） A ．βαγ<< B ．αβγ<< C ．γβα<< D ．βγα<< 3．正三棱锥底面边长为a ，高为66a ，则此正三棱锥的侧面积为（ ） A ．234a B ．232a C ．233a D ．233a 4．已知l ，m 是两条不同的直线，α是一个平面，且//l α，则下列选项正确的是（ ） A ．若//l m ，则//m αB ．若//m α，则//l mC ．若l m ⊥，则m α⊥D ．若m α⊥，则l m ⊥5．用长度分别是2，3，5，6，9（单位：cm ）的五根木棒连接（只允许连接，不允许折断），组成共顶点的长方体的三条棱，则能够得到的长方体的最大表面积为（ ） A ．2258cm B ．2414cm C ．2416cm D ．2418cm 6．如图，在长方体1111ABCD A B C D -中，若,,,E F G H 分别是棱111111,,,A B BB CC C D 的中点，则必有（ ）A ．1//BD GHB ．//BD EFC ．平面//EFGH 平面ABCDD ．平面//EFGH 平面11A BCD7．下列说法正确的是（ ）A ．直线l 平行于平面α内的无数条直线，则l ∥αB ．若直线a 在平面α外，则a ∥αC ．若直线a b φ⋂=，直线b α⊂，则a ∥αD ．若直线a ∥b ，b α⊂，那么直线a 就平行于平面α内的无数条直线8．鲁班锁运用了中国古代建筑中首创的榫卯结构，相传由春秋时代各国工匠鲁班所作，是由六根内部有槽的长方形木条，按横竖立三方向各两根凹凸相对咬合一起，形成的一个内部卯榫的结构体.鲁班锁的种类各式各样，千奇百怪.其中以最常见的六根和九根的鲁班锁最为著名.下图1是经典的六根鲁班锁及六个构件的图片，下图2是其中的一个构件的三视图（图中单位：mm ），则此构件的表面积为（ ）A ．27600mmB ．28400mmC ．29200mmD ．210000mm 9．在长方体1111ABCD A B C D -中，P 为BD 上任意一点，则一定有（ ）A ．1PC 与1AA 异面B ．1PC 与1A C 垂直 C ．1PC 与平面11ABD 相交 D ．1PC 与平面11AB D 平行10．在长方体1111ABCD A B C D -中，23AB AD ==，12CC =，则二面角1C BD C --的大小是（ ）A ．30ºB ．45ºC ．60ºD ．90º11．设,m n 是两条不同的直线，,αβ是两个不同的平面，则下列命题正确的是（ ） A ．若m n ⊥，//n α，则m α⊥ B ．若//m β，βα⊥，则m α⊥ C ．若m β⊥，n β⊥，n α⊥，则m α⊥ D ．若m n ⊥，n β⊥，βα⊥，则m α⊥ 12．已知平面α，直线m ，n 满足m ⊄a ，n ⊂α，则“m ∥n ”是“m ∥α”的（ ）A ．充要条件B ．既不充分也不必要条件C ．必要不充分条件D ．充分不必要条件13．一个几何体的三视图如图所示，则该几何体的表面积为（ ）A ．186+B ．206+C ．2010+D ．1810+ 14．已知,m n 是两条不同的直线，,αβ为两个不同的平面，有下列四个命题： ①若m α⊥，n β⊥，m n ⊥，则a β⊥；②若//m α，//n β，m n ⊥，则//a β；③若m α⊥，//n β，m n ⊥，则//αβ；④若m α⊥，//n β，//αβ，则m n ⊥.其中所有正确的命题是（ ）A ．①④B ．②④C ．①D ．④二、解答题15．如图，在三棱锥V-ABC 中，VC ⊥底面ABC ，AC BC ⊥，D 是棱AB 的中点，且AC BC VC ==.（1）证明：平面VAB ⊥平面VCD ；（2）若22AC =，且棱AB 上有一点E ，使得线VD 与平面VCE 所成角的正弦值为1515，试确定点E 的位置，并求三棱锥C-VDE 的体积. 16．如图，已知三棱柱111ABC A B C -的所有棱长都相等，侧棱1AA ⊥底面ABC ，,E F 分别是1111,A B AC 的中点.（1）求证:11B F AC ⊥ ；（2）求平面EFCB 与底面ABC 所成二面角的正切值.17．如图，在长方形ABCD 中，4AB =，2AD =，点E 是DC 的中点.将ADE 沿AE 折起，使平面ADE ⊥平面ABCE ，连结DB 、DC 、EB .（1）求证：AD ⊥平面BDE ；（2）点M 是线段DA 的中点，求三棱锥D MEC -的体积.18．如图，四面体ABCD 中，点E ，F 分别为线段AC ，AD 的中点，平面EFNM ⋂平面BCD MN =，90CDA CDB ∠=∠=︒，DH AB ⊥，垂足为H .（1）求证：//EF MN ；（2）求证：平面CDH ⊥平面ABC .19．如图，在四棱锥P ABCD -中，平面PCD ⊥平面ABCD ，且PCD 是边长为2的等边三角形，四边形ABCD 是矩形，22BC =，M 为BC 的中点.（1）证明：AM PM ⊥；（2）求二面角P AM D --的大小；（3）求点D 到平面APM 的距离.20．如图，在四棱锥P ABCD -中，ABCD 为菱形，PA ⊥平面ABCD ，连接AC ，BD 交于点O ，6AC =，8BD =，E 是棱PC 上的动点，连接DE ．（1）求证：平面BDE ⊥平面PAC ；（2）当BED 面积的最小值是6时，求此时点E 到底面ABCD 的距离．21．如图，在四棱锥P ABCD -中，四边形ABCD 为菱形，60BAD ︒∠=，PAD △为正三角形，且E ，F 分别为AD ，PC 的中点．（Ⅰ）求证：//DF 平面PEB ；（Ⅱ）求证：BC ⊥平面PEB ．22．如图，在平行四边形ABCD 中，4AB =，60DAB ∠=︒．点G ，H 分别在边CD ，CB 上，点G 与点C ，D 不重合，GH AC ⊥，GH 与AC 相交于点O ，沿GH 将CGH 翻折到EGH 的位置，使二面角E GH B --为90°，F 是AE 的中点．（1）请在下面两个条件：①AB AD =，②AB BD ⊥中选择一个填在横线处，使命题P ：若________，则BD ⊥平面EOA 成立，并证明．（2）在（1）的前提下，当EB 取最小值时，求直线BF 与平面EBD 所成角的正弦值． 23．如图，ABCD 是边长为2的正方形，ED ⊥平面ABCD ，1ED =，//EF BD .（1）设EF BD λ=，是否存在实数λ，使//BF 平面ACE ；（2）证明：平面EAC ⊥平面BDEF ；（3）当12EF BD =时，求几何体ABCDEF 的体积. 24．如图，在四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，PB PA ⊥，PB PA =，90DAB ABC ∠=∠=，435AB BC CD ===，，，M 是PA 的中点.（1）求证：BM //平面PCD ；（2）求三棱锥B CDM -的体积.25．如图，四棱锥P ABCD -的底面是边长为2的菱形，PD ⊥底面ABCD .（1）求证：AC ⊥平面PBD ；（2）若2PD =，直线45DBP ∠=，求四棱锥P ABCD -的体积.26．如图，已知三棱柱111ABC A B C -中，AB AC =，D 为BC 上一点，1A B 平面1AC D ．（1）求证：D 为BC 的中点;（2）若平面ABC ⊥平面11BCC B ，求证：1AC D ∆为直角三角形.【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】先判断出底面三角形的形状，然后从球心作截面的垂足，确定垂足的位置后，再利用勾股定理得到半径，再求体积即可.【详解】由2AB =，4BC =，60ABC ∠=︒及余弦定理得，2222cos 416224cos6012AC AB BC AB BC ABC =+-⋅∠=+-⨯⨯︒=，所以222BC AB AC =+，即A 是直角，BC 是底面圆的直径，过球心O 作OD ⊥平面ABC ，D 即为BC 的中点，所以22OD =，122BD BC == 连接OB ，OB 即为半径，由勾股定理得2223OB OD BD =+=，所以球的体积为34(23)3233V ππ==， 故选：D.【点睛】本题考查了球的外接问题，确定球心在截面上的射影的位置是关键，属于基础题. 2．D解析：D【分析】在正四面体ABCD 中易证AB CD ⊥,即90α=，然后作出直线AB 与平面BCD 所成的角，二面角C AB D --的平面角，在将之放到三角形中求解比较其大小.【详解】在正四面体ABCD 中,设棱长为2,设O 为底面三角形BCD 是中心，则AO ⊥平面BCD .取CD 边的中点E ，连结,AE BE , 如图.则易证,AE CD BE CD ⊥⊥,又AE BE E =.所以CD ⊥平面ABE ,又AB ⊆平面ABE ，所以AB CD ⊥.所以异面直线AB 与CD 所成的角为90α=.又AO ⊥平面BCD .所以直线AB 与平面BCD 所成的角为β=ABO ∠在ABO 中,2233BO BE ==,2AB = 所以3cos BO ABO AB ∠==. 取边AB 的中点F ，连结,CF FD ，则有,CF AB FD AB ⊥⊥，所以二面角C AB D --的平面角为CFD γ=∠, 在CFD △中，3,2CF FD CD === 由余弦定理有：2221cos 23CF FD CD CFD CF FD +-∠==⨯⨯, 即31=90cos cos =33αβγ=>，， 所以βγα<<，故选：D.【点睛】本题考查异面直线成角，线面角，二面角的求法，关键是在立体图中作出相应的角，也可以用向量法，属于中档题.3．A解析：A【分析】根据条件，可计算正三棱锥的斜高，利用侧面积公式计算即可求出.【详解】23⨯=，且棱锥高22632632a a a，斜高2221222aa a，所以侧面积为21133224S a a a.选A.【点睛】本题主要考查了正三棱锥的性质，侧面积公式，属于中档题.4．D解析：D【分析】根据空间中直线与平面平行与垂直的相关性质依次判断各个选项可得结果.【详解】对于A，若//l m，此时//mα或mα⊂，A错误；对于B，若//mα，此时l与m可能平行、相交或异面，B错误；对于C，若l m⊥，此时m与平面α可能平行或相交，C错误；对于D，若mα⊥，则m垂直于α内任意直线，必垂直于l的平行线，则l m⊥，D正确.故选：D.【点睛】本题考查空间中线线关系、线面关系相关命题的辨析，考查学生对于平行与垂直相关性质和定理掌握的熟练程度，属于基础题.5．C解析：C【分析】设出长方体的三条棱的长度为,,a b c，根据表面积公式()2S ab bc ac=++求解出,,a b c 在何种条件下取得最大值，由此考虑长方体棱的长度，并计算出对应的长方体的最大表面积.【详解】设长方体的三条棱的长度为,,a b c，所以长方体表面积()()()()2222S ab bc ac a b b c a c=++≤+++++，取等号时有a b c==，又由题意可知a b c==不可能成立，所以考虑当,,a b c 的长度最接近时，此时对应的表面积最大，此时三边长：8,8,9， 用2和6连接在一起形成8，用3和5连接在一起形成8，剩余一条棱长为9，所以最大表面积为：()22888989416cm ⨯+⨯+⨯=. 故选C.【点睛】本题考查基本不等式与长方体表面积最大值的综合，难度一般.求解()0,0ab a b >>的最2a b +≤可知最大值为2a b +⎛⎫ ⎪⎝⎭，此时要注意取等号的条件a b =是否成立，若取等号的条件不成立，则满足条件的,a b 相差最小时可取得最大值.6．D解析：D【分析】根据“过直线外一点有且只有一条直线与已知直线平行”来判断AB 选项的正确性，根据平行直线的性质判断C 选项的正确性，根据面面平行的判定定理判断D 选项的正确性.【详解】选项A:由中位线定理可知：1//GH D C ，因为过直线外一点有且只有一条直线与已知直线平行，所以1,BD GH 不可能互相平行，故A 选项是错误的；选项B: 由中位线定理可知：1//EF A B ，因为过直线外一点有且只有一条直线与已知直线平行，所以,BD EF 不可能互相平行，故B 选项是错误的；选项C: 由中位线定理可知：1//EF A B ，而直线1A B 与平面ABCD 相交，故直线EF 与平面ABCD 也相交，故平面EFGH 与平面ABCD 相交，故C 选项是错误的；选项D:由三角形中位线定理可知：111//,//EF A B EH A D ，EF ⊄平面11A BCD ，1A B ⊂平面11A BCD ，EH ⊄平面11A BCD ，11A D ⊂平面11A BCD ,所以有//EF 平面11A BCD ，//EH 平面11A BCD ，而EF EH E =，因此平面//EFGH 平面11A BCD .所以D 选项正确.故本选：D【点睛】本小题主要考查面面平行的判定定理，考查线线平行的性质，属于中档题.7．D解析：D【分析】根据直线与平面平行的判定及相关性质，一一验证各选项即可得出答案.【详解】解：A 项，若直线l 平行于平面α内的无数条直线，则l 可能平行于平面α，也可能位于平面α内，故A 项错误；B 项，直线a 在平面α外，则直线a 与平面α可能平行，也可能相交，故B 错误；C 项，直线,a b b φα⋂=⊂，所以a 可能与平面α相交或与平面α平行,故C 项错误；D 项，直线a ∥b ,b α⊂,当a ∥α时,直线a 与平面α内所有与直线b 平行的直线平行；当a α⊂时,除了直线a 本身,直线a 与平面α内所有与直线b 平行的直线平行,因此直线a 平行于平面α内的无数条直线,故D 项正确.故选：D.【点睛】本题主要考查直线与平面平行的判定及相关性质，属于基础题型.8．B解析：B【分析】由三视图可知，该构件是长为100，宽为20，高为20的长方体的上面的中间部分去掉一个长为40，宽为20，高为10的小长方体的一个几何体，进而求出表面积即可.【详解】由三视图可知，该构件是长为100，宽为20，高为20的长方体的上面的中间部分去掉一个长为40，宽为20，高为10的小长方体的一个几何体，如下图所示，其表面积为：()210020220202100204010210202840m 0m S =⨯⨯+⨯⨯+⨯-⨯⨯+⨯⨯=.故选：B.【点睛】本题考查几何体的表面积的求法，考查三视图，考查学生的空间想象能力与计算求解能力，属于中档题.9．D解析：D【分析】取P 为BD 的中点可判断A 、B 、C 选项的正误；证明平面1//BC D 平面11AB D ，可判断D 选项的正误.【详解】如下图所示：对于A 选项，当点P 为BD 的中点时，1PC ⊂平面11AAC C ，则直线1PC 与1AA 相交，A 选项错误；对于B 选项，当点P 为BD 的中点时，1AC P ∠为锐角，1PC 与1A C 不垂直，B 选项错误；对于C 选项，当点P 为BD 的中点时，连接11A C 、11B D 交于点O ，则O 为11A C 的中点， 在长方体1111ABCD A B C D -中，11//AA CC 且11AA CC =，则四边形11AAC C 为平行四边形，11//AC AC ∴且11AC A C =， O 、P 分别为11A C 、AC 的中点，则1//AP OC 且1AP OC =，∴四边形1OAPC 为平行四边形，1//PC AO ∴，AO ⊂平面11AB D ，1PC ⊄平面11AB D ，1//PC ∴平面11AB D ，C 选项错误；对于D 选项，在长方体1111ABCD A B C D -中，11//BB DD 且11BB DD =，则四边形11BB D D 为平行四边形，11//BD B D ∴，BD ∴⊄平面11AB D ，11B D ⊂平面11AB D ，//BD ∴平面11AB D ，同理可证1//BC 平面11AB D ，1BD BC B ⋂=，∴平面1//BC D 平面11AB D ，1PC ⊂平面1BC D ，1//PC ∴平面11AB D .D 选项正确.故选：D.【点睛】本题考查空间中直线与直线、直线与平面位置关系的判断，考查推理能力，属于中等题. 10．A解析：A【分析】取BD 中点为O ，1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，易知CO BD ⊥，再利用线面垂直证明1BD C O ⊥，得到1COC ∠即二面角1C BD C --，再计算二面角大小即可.【详解】由题意，作出长方体1111ABCD A B C D -的图象，取BD 中点为O ，连接CE 、1C E ，因为1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，又BD ⊂平面ABCD ，所以1CC BD ⊥，因为AB AD ==ABCD 是正方形，O 为BD 中点，所以CO BD ⊥，又1CO CC C =，所以BD ⊥平面1COC ，又1C O ⊂平面1COC ，所以1BD C O ⊥，1COC ∠即二面角1C BD C --，又1CC =CO ==所以1tan 3COC ∠==，130COC ∠=.故选：A【点睛】本题主要考查二面角的求法和线面垂直的判定定理和性质，考查学生空间想象能力，属于中档题.11．C解析：C【分析】根据空间中直线与平面、平面与平面位置关系相关定理依次判断各个选项可得结果.【详解】对于A ，当m 为α内与n 垂直的直线时，不满足m α⊥，A 错误；对于B ，设l αβ=，则当m 为α内与l 平行的直线时，//m β，但m α⊂，B 错误； 对于C ，由m β⊥，n β⊥知：//m n ，又n α⊥，m α∴⊥，C 正确；对于D ，设l αβ=，则当m 为β内与l 平行的直线时，//m α，D 错误. 故选：C .【点睛】本题考查立体几何中线面关系、面面关系有关命题的辨析，考查学生对于平行与垂直相关定理的掌握情况，属于基础题. 12．D解析：D【分析】根据线面平行的判定定理以及充分条件和必要条件的定义进行判断即可．【详解】若“//m n ”则“//m α”成立，即充分性成立，//m α，m ∴不一定平行n ，因为m 还有可能和n 异面.即“//m n ”是“//m α”的充分不必要条件，故选：D ．【点睛】本题主要考查充分条件和必要条件的判断，结合线面平行的判断和性质是解决本题的关键．13．B解析：B【分析】根据所给三视图，还原出空间几何体，即可求得几何体的表面积.【详解】根据三视图，还原空间几何体如下图所示：在正方体中，去掉三棱锥111B A C M -，正方体的棱长为2，M 为1BB 的中点，则111111111B MC A B C A B M A C M S S S S S S =---+正方体 ()()22211116212221222522222=⨯-⨯⨯-⨯⨯-⨯⨯+⨯- 206=+故选：B.【点睛】本题考查了空间几何体三视图的简单应用，关键是能够正确还原出空间几何体，属于中档题.14．A解析：A【分析】①若m α⊥，m n ⊥，∴n ⊂α或//n α再由面面垂直的判定定理得到结论．②根据面面平行的判定定理判断．③若m α⊥，m n ⊥，则n ⊂α或//n α，再由面面平行的判定定理判断．④若m α⊥，//αβ，由面面平行的性质定理可得m β⊥，再由//n β得到结论．【详解】①若m α⊥，m n ⊥，∴n ⊂α或//n α，又∵n β⊥，∴a β⊥,故正确．②若//m α，//n β，由面面平行的判定定理可知，若m 与n 相交才平行，故不正确． ③若m α⊥，m n ⊥，则n ⊂α或//n α，又//n β，两平面不一定平行，故不正确． ④若m α⊥，//αβ，则m β⊥，又∵//n β，则m n ⊥．故正确．故选：A【点睛】本题主要考查线与线，线与面，面与面的位置关系及垂直与平行的判定定理和性质定理，综合性强，方法灵活，属中档题．二、解答题15．（1）证明见解析；（2）点E 位于线段AD 的中点或线段BD 的中点；22. 【分析】（1）易得CD AB ⊥，再根据VC ⊥底面ABC ，得到 VC AB ⊥，进而AB ⊥平面VCD ，再利用面面垂直的判定定理证明.（2）过点D 在平面ABC 内作DF CE ⊥于F ，DF ⊥平面VCE ，则DVF ∠就是直线VD 与平面VCE 所成的角，在Rt VFD 中，由15sin DF DVF VD ∠==，求得DF ，然后在Rt DCE 中，求出1DE =，然后由三棱锥C-VDE 的体积为13CDE V S VC =⋅⋅求解. 【详解】（1）因为AC BC =，D 是AB 的中点，所以CD AB ⊥.又VC ⊥底面ABC ，AB平面ABC ， 所以VC AB ⊥，而VC CD C ⋂=，所以AB ⊥平面VCD .又AB 平面VAB ，所以平面VAB ⊥平面VCD .（2）过点D 在平面ABC 内作DF CE ⊥于F ，则由题意知DF ⊥平面VCE .，连接VF ，于是DVF ∠就是直线VD 与平面VCE 所成的角.在Rt VFD 中，15DF VD =. 又因为3VD =55DF =. 在Rt DCE 中，1DE =.故知点E 位于线段AD 的中点或线段BD 的中点，三棱锥C-VDE 的体积为1112221223323CDES VC⋅⋅=⨯⨯⨯⨯=.【点睛】方法点睛：(1)证明平面和平面垂直的方法：①面面垂直的定义；②面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．(2)已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．16．（1）证明见解析；（2）43.【分析】（1）由线面垂直得到线线垂直，再由线线垂直得到线面垂直；（2）取EF中点P，BC中点K，找到二面角，再在三角形中计算就可以了.【详解】（1）证明：1AA⊥平面11,ABC B F AA∴⊥，又111A B C为正三角形，F为11A C中点，111B F AC∴⊥得1B F⊥平面11ACC A.又因为1AC⊂平面11ACC A，所以11B F AC⊥；（2）设所有棱长都为2，取EF中点P，BC中点K，连,,PK AK PA. 易知,PK BC AK BC⊥⊥，则PKA∠为平面EFCB的与底面ABC所成二面角的平面角，在PKA中，取AK中点O，连PO，有PO⊥平面ABC，则PO AK⊥，且32,PO OK==，43tan332POPKAOK∠===,【点睛】第二问的关键点是由线面垂直找到线线垂直，求出二面角，然后在三角形中计算就可以了.17．（1）证明见解析；（2）23. 【分析】 （1）先利用勾股定理得出AE BE ⊥，再利用面面垂直的性质定理得到BE ⊥平面ADE ，进而得到AD BE ⊥，利用线面垂直的判定定理即可得证；（2）利用1122D MEC M DEC A DEC D AEC V V V V ----===，取AE 的中点O ，连接DO ，用面面垂直的性质定理得到DO ⊥平面ABCE ，利用体积公式求解即可.【详解】（1）证明：∵2AD DE ==，90ADE ∠=︒，∴22AE BE ==，4AB =，∴222AE BE AB +=，∴AE BE ⊥，又平面ADE ⊥平面ABCE ， 平面ADE平面ABCE AE =， ∴BE ⊥平面ADE ，又AD ⊂平面ADE ，所以AD BE ⊥，又AD DE ⊥，DE BE E ⋂=，所以AD ⊥平面BDE.（2）∵M 是线段DA 的中点，∴1122D MEC M DEC A DEC D AEC V V V V ----===， 取AE 的中点O ，连接DO ，∵DA DE =∴DO AE ⊥，又平面DAE ⊥平面ABCE ，∴DO ⊥平面ABCE ，又2DO =，1sin13522AEC S AE EC =⨯⨯⨯︒=，∴123D AEC V -=⨯=∴3D MEC V -=. 【点睛】方法点睛：证明线面垂直的常用方法：利用线面垂直的判定定理；利用面面垂直的性质定理；利用面面平行的性质；利用垂直于平面的传递性.18．（1）证明见解析；（2）证明见解析.【分析】本题考查线面平行与线面垂直的判定，难度不大.（1）利用线面平行的判定定理证得//EF 平面BCD ，进而利用线面平行的性质定理证得； （2）利用线面垂直的判定定理证得CD ⊥平面ADB ，进而证得AB ⊥平面CDH ，然后由面面垂直判定定理证得结论.【详解】证明：（1）因为点E 、F 分别为线段AC 、AD 的中点，EF ∴为ACD △的中位线，则//EF CD ，CD ⊂平面BCD ，EF ⊄平面BCD ，//EF ∴平面BCD ，又EF ⊂平面EFNM ，平面EFNM ⋂平面BCD MN =，//EF MN ∴；（2）90CDA CDB ∠=∠=︒，CD DA ∴⊥，CD DB ⊥，DA DB D ⋂=，DA ⊂平面ADB ，DB ⊂平面ADB ， CD 平面ADB ，CD AB ∴⊥又DH AB ⊥，DH CD D ⋂=，DC ⊂平面DCH ，DH ⊂平面DCH ，AB ∴⊥平面CDH ，AB ⊂平面ABC ，∴平面CDH ⊥平面ABC.【点睛】要证线线平行，常常先证线面平行，综合利用线面平行的判定与性质进行证明；要证面面垂直，常常先证线面垂直，而要证线面垂直，又常常先证另一个线面垂直.19．（1）证明见解析；（2）45；（3）3. 【分析】（1）取CD 的中点E ，连接PE 、EM 、EA ，根据面面垂直的性质可知PE ⊥平面ABCD ，从而AM PE ⊥，由勾股定理可求得AM EM ⊥，又PE EM E =，满足线面垂直的判定定理则AM ⊥平面PEM ，根据线面垂直的性质可知AM PM ⊥；（2）由（Ⅰ）可知EM AM ⊥，PM AM ⊥，根据二面角平面角的定义可知PME ∠是二面角P AM D --的平面角，然后在三角形PME 中求出此角即可；（3）设D 点到平面PAM 的距离为d ，连接DM ，则根据等体积得P ADM D PAM V V --=，建立关于d 的等式解之即可得到点D 到平面PAM 的距离．【详解】（1）取CD 的中点E ，连接PE 、EM 、EA ．PCD 为正三角形，PE CD ∴⊥，平面PCD ⊥平面ABCD ，PE ∴⊥平面ABCDAM PE ∴⊥四边形ABCD 是矩形ADE ∴、ECM 、ABM 均为直角三角形 由勾股定理可求得：3EM =，6AM =3AE =222EM AM AE ∴+=AM EM ∴⊥又PE EM E AM =∴⊥平面PEMAM PM ∴⊥（2）由（1）可知EM AM ⊥，PM AM ⊥PME ∴∠是二面角P AM D --的平面角3tan 13PE PME EM ∴∠=== 45PME ∴∠=︒∴二面角P AM D --为45︒（3）设D 点到平面PAM 的距离为d ，连接DM ，则P ADM D PAM V V --=，∴11··33ADM PAM S PE S d =而1·2ADMSAD CD ==在Rt PEM 中，由勾股定理可求得PM =1·32PAMSAM PM ∴==，所以：11333d ⨯=⨯⨯d ∴即点D 到平面PAM 的距离为3. 【点睛】方法点睛：求点到平面的距离常用的方法有：（1）几何法：找→作→证→指→求；（2）向量法：利用向量中点到平面的距离公式求解；（3）等体积法：根据体积相等求出点到平面的距离.20．（1）证明见解析；（2）4． 【分析】（1）根据线面垂直的判定定理可证得BD ⊥平面PAC ，再由面面垂直的判定定理可得证．（2）由（1）知BD ⊥平面PAC ，根据三角形的面积公式求得()min 32OE =，作//EH PA 交AC 于H ，可得EH ⊥平面ABCD ，从而求得点E 到底面ABCD 的距离． 【详解】（1）证明：∵四边形ABCD 是菱形，∴AC BD ⊥．PA ⊥平面ABCD ，BD ⊂平面ABCD ，∴PA BD ⊥．又PA AC A =，∴BD ⊥平面PAC ，又BD ⊂平面BDE ，∴平面BDE ⊥平面PAC ．（2）解：如图（1），连接OE ，由（1）知BD ⊥平面PAC ，OE ⊂平面PAC ．BD OE ∴⊥．∵8BD =，由()min 162BDE S BD OE =⋅⋅=△，得()min 32OE =，∵当OE PC ⊥时，OE 取到最小值32，此时2CE ===． 作//EH PA 交AC 于H ，∵PA ⊥平面ABCD ，∴EH ⊥平面ABCD ，如图（2），由OE CE EH OC ⋅==E 到底面ABCD【点睛】本题考查线面垂直的判定和面面垂直的判定定理，以及求点到面的距离，关键在于逐一满足判定定理所需的条件，在求点到面的距离时，可以采用几何法，由题目的条件直接过已知点作出面的垂线，运用求解三角形的知识，求点到面的距离，属于中档题. 21．（Ⅰ）证明见解析；（Ⅱ）证明见解析. 【分析】（Ⅰ）取PB 中点G ，可证得四边形DEGF 是平行四边形，进而可得//DF EG ，最后可证//DF 平面PEB ；（Ⅱ）由条件可得PE AD ⊥，BE AD ⊥，进而由线面垂直的判定定理得出结论. 【详解】（Ⅰ）取PB 中点G ，因为F 是PC 中点，∴//FG BC ，且12FG BC =， ∵E 是AD 的中点，则//DE BC ，且12DE BC =，∴//FG DE ，且FG DE =， ∴四边形DEGF 是平行四边形，∴//DF EG ，又∵DF ⊄平面PEB ，EG ⊂平面PEB ，∴//DF 平面PEB ；（Ⅱ）因为E 是正三角形PAD 边为AD 的中点，则PE AD ⊥， ∵四边形ABCD 为菱形，60BAD ︒∠=，∴正三角形BAD 中，BE AD ⊥，∵PE BE E ⋂=，∴AD ⊥平面PEB ，∵//AD BC ，∴BC ⊥平面PEB ．【点睛】方法点睛：本题考查线面平行、线面垂直的判定，解题关键是熟记线面平行和线面垂直的判定定理，以及定理成立时的条件，考查空间想象能力，属于常考题. 22．（1）答案见解析；（233. 【分析】（1）选择①，结合直二面角的定义，证明BD ⊥平面EOA 内的两条相交直线,EO AO ；（2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则AC =CO x =，可得EB 关于x 的函数，求出EB 取得最小值时x 的值，连结EM ，作QF EM ⊥于F ，连结BF ，求出sin QBF ∠的值，即可得答案； 【详解】解：（1）命题P ：若AB AD =，则BD ⊥平面EOA . ∵AC GH ⊥，∴AO GH ⊥，EO GH ⊥， 又二面角E GH B --的大小为90°， ∴90AOE ∠=︒，即EO AO ⊥， ∴EO ⊥平面ABCD ， ∴EO BD ⊥，又AB BC =，∴AO BD ⊥，AO EO O =，∴BD ⊥平面EOA .（2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则AC =设CO x =，OM x =，222216OB OM MB x =+=-+，2222216EB EO OB x =+=-+，当x =min EB =连结EM ，作QF EM ⊥于F ，连结BF ， 由（1）知BD ⊥平面EOA ， ∴BD QF ⊥，∴QF ⊥平面EBD ， ∴QBF ∠即为QB 与平面EBD 所成角，在Rt EMB 中，EB =2BM =，EM =AE =，由()2222(2)22QB AE AB BE QB +=+⇒=，2QF =∴sin QF QBF QB ∠==，即QB 与平面EBD .【点睛】求线面角首先要根据一作、二证、三求找出线面角，然后利用三角函数的知识，求出角的三角函数值即可.23．（1）存在；（2）证明见解析；（3）2. 【分析】 （1）存在12λ=满足题意，设AC 与BD 的交点为O ，连接EO ，由平面几何的知识可得//BF EO ，再由线面平行的判定即可得证；（2）由线面垂直的性质与判定可得AC ⊥平面BDEF ，再由面面垂直的判定即可得证；（3）结合（2）可得AC ⊥平面BDEF 、2ABCDEF A BDEF V V -=，再由棱锥的体积公式即可得解. 【详解】 （1）存在12λ=满足题意，理由如下： 设AC 与BD 的交点为O ，则12DO BO BD ==，连接EO ，如图，∵//EF BD ，当12λ=时，12EF BD BO ==， ∴四边形EFBO 是平行四边形，∴//BF EO ，又EO ⊂平面ACE ，BF ⊄平面ACE ，∴//BF 平面ACE ；（2）证明：ED ⊥平面ABCD ，AC ⊂平面ABCD ，∴ED AC ⊥， ∵ABCD 为正方形，∴BD AC ⊥， 又EDBD D =，∴AC ⊥平面BDEF ，又AC ⊂平面EAC ，∴平面EAC ⊥平面BDEF ； （3）∵ED ⊥平面ABCD ，∴ED BD ⊥， 又∵//EF BD 且12EF BD =，∴BDEF 是直角梯形，又∵ABCD 是边长为2的正方形，BD =，EF =∴122BDEF S⨯==，由（2）知AC ⊥平面BDEF ，∴12222332ABCDEF A BDEF BDEF V V S AO -==⨯⋅=⨯=. 【点睛】本题考查了线面平行、面面垂直的判定及几何体体积的求解，考查了空间思维能力与运算求解能力，属于中档题. 24．（1）证明见解析；（2）2. 【分析】（1）取PD 中点N ，证明BMNC 为平行四边形，得到//BM NC ，从而得到//BM 平面PCD ．（2）对三棱锥B CDM -进行等体积转化，转化为求P BCD -的体积的一半．取AB 中点O ，连PO ，可证PO 为三棱锥P BCD -的高并求出其长度，求出BCD △的面积，得到三棱锥P BCD -的体积，即可求出三棱锥B CDM -的体积． 【详解】证明：（1）取PD 中点N ，连接MN ，NC , MN 为PAD △的中位线，//MN AD ∴，且12MN AD =， 又//BC AD ，且12BC AD =，//MN BC ∴，且MN BC =， 则BMNC 为平行四边形，//BM NC ∴，又NC ⊂平面PCD ，MB ⊂/平面PCD ， //BM ∴平面PCD ．（2）取AB 中点O ，连PO ，,PB PA PO AB =∴⊥，又平面PAB ⊥平面ABCD ，平面PAB ⋂平面ABCD AB =，PO ⊂平面PAB ，PO ∴⊥平面ABCD ． PO ∴为三棱锥P BCD -的高， PA PB =，4AB =，PB PA ⊥， PAB ∴为等腰直角三角形，2PO =，90DAB ABC，//AD BC ，1134622BCDSBC AB =⨯⨯=⨯⨯=， M 是PA 的中点，∴三棱锥B CDM -的体积为：11162223126P B CDM M BCD BCD BCDV V V SPO ---==⨯=⨯=⨯⨯=．【点睛】本题考查通过线线平行证明线面平行，通过面面垂直证明线面垂直，变换顶点和底面进行等体积转化，求三棱锥的体积，属于中档题． 25．（1）证明见解析；（2）33. 【分析】（1）证明AC BD ⊥，PD AC ⊥，结合线面垂直的判定定理得出AC ⊥平面PBD ； （2）求出菱形ABCD 的面积，结合PD ⊥平面ABCD ，利用棱锥的体积公式得出四棱锥P ABCD -的体积. 【详解】（1）证明：因为四边形ABCD 是菱形，所以AC BD ⊥. 又因为PD ⊥平面ABCD ，AC ⊂平面ABCD ， 所以PD AC ⊥.又PD BD D ⋂=，PD ⊂平面PBD ，BD ⊂平面PBD ， 故AC ⊥平面PBD ；（2）因为45DBP ∠=，PD ⊥平面ABCD 因此2BD PD ==. 又2AB AD ==所以菱形ABCD 的面积为sin6023S AB AD =⋅⋅= 故四棱锥P ABCD -的体积1433V S PD =⋅=. 【点睛】本题主要考查了证明线面垂直以及求棱锥的体积，属于中档题. 26．(1)见解析(2)见解析【分析】（1）连接A 1C 交AC 1于O ，连接OD ，利用线面平行的性质定理和中位线的定义，即可证明D 为BC 的中点；（2）由等腰三角形的性质和面面垂直的性质定理，证明AD ⊥C 1D 即可． 【详解】证明:(1) 联结1A C 交1AC 于O ，联结OD .∵四边形11ACC A 是棱柱的侧面， ∴四边形11ACC A 是平行四边形.∵O 为平行四边形11ACC A 对角线的交点， ∴O 为1A C 的中点. ∵1A B 平面1AC D ，平面1A BC ⋂平面1AC D OD =，1A B ⊂平面1A BC ，∴1A B OD∴OD 为1A BC ∆的中位线， ∴D 为BC 的中点. （2）∵AB AC =，D 为BC 的中点， ∴AD BC ⊥.∵平面ABC ⊥平面11BCC B ,AD ⊂平面ABC ，平面ABC 平面11BCC B BC =，∴AD ⊥平面11BCC B .∵1C D ⊂平面11BCC B ，∴AD ⊥ 1C D ， ∴1AC D ∆为直角三角形. 【点睛】本题考查线面平行的性质定理和面面垂直的性质定理的应用.。