【解析版】广东省肇庆市2013届高三第一次模拟数学理试题

2013广东各地高考 一模 理数 打包：广州 佛山 深圳 揭阳 肇庆 梅州 东莞广州市2013届普通高中毕业班综合测试（一）数学（理科）本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1.答卷前，考生务必用2B 铅笔在“考生号”处填涂考生号。

用黑色字迹的钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题 卡上。

用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上。

2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑； 如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域 内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔 和涂改液。

不按以上要求作答的答案无效。

4.作答选做题时，请先用2B 铅笔填涂选做题题号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5.考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

参考公式：如果事件A ，B 相互独立，那么)()()(B P A P B A P ∙=∙.线性回归方程a x b yˆˆˆ+=中系数计算公式x b y ax x y y x x b ni i ni ii-=---=∑∑==ˆ,)())((ˆ121， 其中y x ,表示样本均值。

一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设全集}6,5,4,3,2,1{=U ，集合}5,3,1{=A ，}4,2{=B ，则 A.B A U ⋃= B.B A C U U ⋃=)( C.)(B C A U U ⋃= D.)()(B C A C U U U ⋃=2.已知bi ia+=-11，其中a,b 是实数，i 是虚数单位，则a+bi= A.1+2i B.2+i C.2-i D.1-2i3.已知变量x,y 满足约束条件⎪⎩⎪⎨⎧≤-≤-≥+.01,1,12y y x y x ，则y x z 2-=的最大值为A.-3 B .0 C.1 D.34.直线03==y x 截圆4)2(22=+-y x 所得劣弧所对的圆心角是A.6π B.3π C.2π D.32π5.某空间几何体的三视图及尺寸如图1，则该几何体的体积是A.2B.1C.32D.316.函数)cos )(sin cos (sin x x x x y -+=是A.奇函数且在]2,0[π上单调递增 B.奇函数且在],2[ππ上单调递增C.偶函数且在]2,0[π上单调递增 D.偶函数且在],2[ππ上单调递增7.已知e 是自然对数的底数，函数2)(-+=x e x f x 的零点为a ，函数2ln )(-+=x x x g 的零点为b ，则下列不等式中成立的是A.)()1()(b f f a f <<B.)1()()(f b f a f <<C.)()()1(b f a f f << D.)()1()(a f f b f <<8.如图2，一条河的两岸平行，河的宽度d=600m ，一艘客船从码头A 出发匀速驶往 河对岸的码头B.已知km AB 1=，水流速度为2km/h ，若客船行驶完航程所用最短时间为6分钟，则客船在静水中的速度大小为A.8km/hB.h km /26C.h km /342D.10km/h二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分. （一）必做题（9-13题） 9.不等式x x ≤-1的解集是_________.10.⎰=1._______cos xdx11.某工厂的某种型号机器的使用年限x 和所支出的维修费用y （万元）有下表的统计资料：x 2 3 4 5 6 y2.23.85.56.57.0根据上表可得回归方程a x yˆ23.1ˆ+=，据此模型估计，该型号机器使用所限为10年维修费用约______万元（结果保留两位小数）.12.已知1,0≠>a a ，函数⎩⎨⎧>+-≤=1,1,)(x a x x a x f x ，若函数)(x f 在区间[0,2]上的最大值比最小值大25，则a 的值为________. 13.已知经过同一点的)3*,(≥∈n N n n 个平面，任意三个平面不经过同一条直线，若这n 个平面将空间分成)(n f 个部分，则.________)(______,)3(n f f =（二）选做题（14-15题，考生只能从中选做一题）14.（坐标系与参数方程选做题）在极坐标系中，定点)23,2(πA ，点B 在直线0sin 3cos =+θρθρ上 运动，当线段AB 最短时，点B 的极坐标为______.15.（几何证明选讲选做题）如图3，AB 是⊙O 的直径，BC 是⊙O 的切线，AC 与⊙O交于点D ，若BC=3，516=AD ，则AB 的长为______.三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤. 16.（本小题满分12分） 已知函)4sin()(πω+=x A x f （其中0,0,>>∈ωA R x ）的最大值为2，最小正周期为8．(1)求函数)(x f 的解析式；(2)若函数)(x f 图象上的两点P ，Q 的横坐标依次为2，4，O 坐标原点，求POQ ∆的面积.17.（本小题满分12分）甲、乙、丙三位学生独立地解同一道题，甲做对的概率为,21乙，丙做对的概率分别为m,n(m>n)，且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数，其分布列为：ξ0 1 2 3P41 a b241 (1)求至少有一位学生做对该题的概率； (2)求m,n 的值； (3)求ξ的数学期望.18.（本小题满分14分）如图4，在三棱柱ABC-A 1B 1C 1中，ABC ∆是边长为2的等边三角形，⊥1AA 平面ABC ，D ，E 分别是CC 1，AB 的中点.(1)求证：CE//平面A 1BD ；(2)若H 为A 1B 上的动点，当CH 为平面A 1AB 所成最大角的正切值为215时，求平面A 1BD 与平面ABC 所成二面角（锐角）的余弦值.19.（本小题满分14分）已知数列}{n a 的前n 项和为S n ，且nna a a a ++++ 32132*)(2)1(N n n S n n ∈+-=.(1)求数列}{n a 的通项公式；(2)若p,q,r 是三个互不相等的正整数，且p,q,r 成等差数列，试判断1,1,1---r q p a a a是否成等比数列？并说明理由.20.（本小题满分14分）已知椭圆C 1的中心在坐标原点，两个焦点分别为)0,2(),0,2(21F F -，点A （2，3）在椭圆C 1上，过点A 的直线L 与抛物线y x C 4:22=交于B ，C 两点，抛物线C 2在点B ，C处的切线分别为21,l l ，且1l 与2l 交于点P.(1)求椭圆C 1的方程； (2)是否存在满足||2121AF AF PF PF +=+的点P ？若存在，指出这样的点P 有几个（不必求出点P 的坐标）；若不存在，说明理由.21.（本小题满分14分）已知二次函数1)(2+++=m ax x x f ，关于x 的不等式21)12()(m x m x f -+-<的解集为)1,(+m m ，其中m 为非零常数.设1)()(-=x x f x g . (1)求a 的值；(2))(R k k ∈如何取值时，函数)1ln()()(--=x k x g x φ存在极值点，并求出极值点；(3)若m=1，且x>0，求证：*)(22)1()]1([N n x g x g n n n ∈-≥+-+参考答案说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力对照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．一、选择题：本大题考查基本知识和基本运算．共8小题，每小题5分，满分40分．题号 1 2 3 4 5 6 7 8 答案DBCDACAB二、填空题：本大题考查基本知识和基本运算，体现选择性．共7小题，每小题5分，满分30分．其中14~15题是选做题，考生只能选做一题．9．1,2⎡⎫+∞⎪⎢⎣⎭ 10．1sin 11．12.38 12．12或27 13．8，22n n -+14．1116,π⎛⎫⎪⎝⎭15．4 说明：① 第13题第一个空填对给2分，第二个空填对给3分． ② 第14题的正确答案可以是：11126k k ,(ππ⎛⎫+∈ ⎪⎝⎭Z ).三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分）（本小题主要考查三角函数的图象与性质、诱导公式、余弦定理、正弦定理、两点间距离公式等知识，考查化归与转化的数学思想方法，以及运算求解能力） （1）解：∵()f x 的最大值为2，且0A >， ∴2A =. ……………1分∵()f x 的最小正周期为8， ∴28T πω==，得4πω=. ……………2分∴()2sin()44f x x ππ=+. ……………3分（2）解法1：∵(2)2sin 2cos 2244f πππ⎛⎫=+== ⎪⎝⎭， ……………4分(4)2sin 2sin 244f πππ⎛⎫=+=-=- ⎪⎝⎭， …………5分∴(2,2),(4,2)P Q -. ∴6,23,32OP PQ OQ ===. ……………8分∴()()()222222632233cos 232632OP OQ PQPOQ OP OQ+-+-∠===⨯.…10分 ∴21POQ POQ sin cos ∠=-∠=63. ……………11分 ∴△POQ 的面积为116632223S OP OQ POQ sin =∠=⨯⨯⨯32=. ………12分解法2：∵(2)2sin 2cos 2244f πππ⎛⎫=+== ⎪⎝⎭， ……………4分(4)2sin 2sin 244f πππ⎛⎫=+=-=- ⎪⎝⎭， ……………5分∴(2,2),(4,2)P Q -.∴(2,2),(4,2)OP OQ ==-. ……………8分∴63cos cos ,3632OP OQ POQ OP OQ OP OQ⋅∠=<>===⨯. ……………10分 ∴21POQ POQ sin cos ∠=-∠=63. ……………11分 ∴△POQ 的面积为116632223S OP OQ POQ sin =∠=⨯⨯⨯32=. ………12分解法3：∵(2)2sin 2cos 2244f πππ⎛⎫=+== ⎪⎝⎭， ………4分(4)2sin 2sin 244f πππ⎛⎫=+=-=- ⎪⎝⎭， ……………5分∴(2,2),(4,2)P Q -.∴直线OP 的方程为22y x =，即20x y -=. ……………7分∴点Q 到直线OP 的距离为42233d +==. ……………9分∵6OP =， ……………11分∴△POQ 的面积为1162322SOP d =⋅=⨯⨯32=.……………12分 17．（本小题满分12分）（本小题主要考查相互独立事件的概率、离散型随机变量的均值等基础知识，考查数据处理、推理论证、运算求解能力和应用意识，以及或然与必然的数学思想）解：设“甲做对”为事件A ，“乙做对”为事件B ，“丙做对”为事件C ，由题意知， ()()()12PA PB m PC n ,,===. ……………1分 （1）由于事件“至少有一位学生做对该题”与事件“0ξ=”是对立的，所以至少有一位学生做对该题的概率是()1310144P ξ-==-=.…………3分 （2）由题意知()()()()1101124PP ABC m n ξ===--=， ……………4分 ()()113224P P ABC mn ξ====， ……………5分 整理得 112mn=，712m n +=. 由mn >，解得13m =，14n =. ……………7分 （3）由题意知()()()()1aP P ABC P ABC P ABC ξ===++()()()()11111111122224m n m n m n =--+-+-=， …9分 (2)1(0)(1)(3)b P P P P ξξξξ===-=-=-==14， ……………10分∴ξ的数学期望为0(0)1(1)2(2)3(3)E P P P P ξξξξξ=⨯=+⨯=+=+==1312. …………12分H FABCA 1C 1B 1DE18．（本小题满分14分）（本小题主要考查空间线面位置关系、直线与平面所成的角、二面角等基础知识，考查空间想象、推理论证、抽象概括和运算求解能力，以及化归与转化的数学思想方法） 解法一：（1）证明：延长1A D 交AC 的延长线于点F ，连接BF .∵CD ∥1AA ，且CD 12=1AA ， ∴C 为AF 的中点. ……………2分 ∵E 为AB 的中点，∴CE ∥BF . ……………3分 ∵BF⊂平面1ABD ，CE ⊄平面1ABD ， ∴CE ∥平面1ABD . ……………4分 （2）解：∵1AA ⊥平面ABC ，CE ⊂平面ABC ，∴1AA ⊥CE . ……………5分∵△ABC 是边长为2的等边三角形，E 是AB 的中点， ∴CE AB ⊥，332CE AB ==.∵AB⊂平面1A AB ，1AA ⊂平面1A AB ，1AB AA A = ，∴CE⊥平面1A AB . ……………6分∴EHC ∠为CH 与平面1A AB 所成的角. ……………7分 ∵3CE =，在R t △CEH 中，tan 3CE EHC EH EH∠==， ∴当EH 最短时，tan EHC ∠的值最大，则EHC ∠最大. ……………8分∴当1EHAB ⊥时，EHC ∠最大. 此时，tan 3CE EHC EH EH∠===152.∴255EH =. ……………9分 ∵CE ∥BF ，CE⊥平面1A AB ，z yxH ABCA 1C 1B 1DE F∴BF ⊥平面1A AB . ……………10分∵AB ⊂平面1A AB ，1AB ⊂平面1A AB ， ∴BF⊥AB ，BF ⊥1AB . ……………11分∴1ABA ∠为平面1ABD 与平面ABC 所成二面角（锐角）. ……………12分 在R t △EHB 中，22BH EB EH =-=55，cos 1ABA ∠55BH EB ==.…13分 ∴平面1ABD 与平面ABC 所成二面角（锐角）的余弦值为55. ……………14分 解法二：（1）证明：取1AB 的中点F ，连接DF 、EF .∵E 为AB 的中点， ∴EF ∥1AA ，且112EFAA =. ……………1分 ∵CD ∥1AA ，且CD 12=1AA ， ∴EF ∥CD ，EF =CD . ……………2分 ∴四边形EFDC 是平行四边形.∴CE ∥DF . ……………3分 ∵DF⊂平面1ABD ，CE ⊄平面1ABD ， ∴CE ∥平面1ABD . ……………4分 （2）解：∵1AA ⊥平面ABC ，CE ⊂平面ABC ，∴1AA ⊥CE . ……………5分∵△ABC 是边长为2的等边三角形，E 是AB 的中点， ∴CE AB ⊥，332CE AB ==.∵AB⊂平面1A AB ，1AA ⊂平面1A AB ，1AB AA A = ，∴CE⊥平面1A AB . ……………6分∴EHC ∠为CH 与平面1A AB 所成的角. ……………7分∵3CE =，在R t △CEH 中，tan 3CE EHC EH EH∠==， ∴当EH 最短时，tan EHC ∠的值最大，则EHC ∠最大. ……………8分∴当1EHAB ⊥时，EHC ∠最大. 此时，tan 3CE EHC EH EH∠===152.∴255EH =. ……………9分 在R t △EHB 中，2255BHEB EH =-=. ∵R t △EHB ～R t △1A AB ，∴1EH BHAA AB=，即1255552AA =. ∴14AA =. ……………10分以A 为原点，与AC 垂直的直线为x 轴，AC 所在的直线为y 轴，1AA 所在的直线为z 轴，建立空间直角坐标系A xyz -.则()000A,,，1A ()004,,，B ()310,,，D ()02,,2.∴1AA = ()004,,，1AB =()314,,-，1AD =()02,,-2. 设平面ABD 1的法向量为n =()x y z ,,， 由n B A 1⋅，n 01=⋅D A ，得340220x y z y z .ìï+-=ïíï-=ïî 令1y=，则13z x ==,.∴平面ABD 1的一个法向量为n =()311,,. ……………12分∵1AA ⊥平面ABC ， ∴1AA=()004,,是平面ABC 的一个法向量.∴cos 111,⋅==n AA n AA n AA 55. ……………13分 ∴平面1ABD 与平面ABC 所成二面角（锐角）的余弦值为55. ……………14分 19．（本小题满分14分）（本小题主要考查等比数列的通项公式、数列的前n 项和等基础知识，考查合情推理、化归与转化、特殊与一般的数学思想方法，以及抽象概括能力、推理论证能力、运算求解能力） (1) 解：12323(1)2nn a a a na n S n ++++=-+ ，∴ 当1n=时，有 11(11)2,a S =-+ 解得 12a =. ……………1分由12323(1)2nn a a a na n S n ++++=-+ , ①得1231123(1)2(1)n n n a a a na n a nS n ++++++++=++ , ② ……………2分 ② - ①得: 11(1)(1)2n n n n a nS n S +++=--+. ③ ……………3分 以下提供两种方法：法1：由③式得：11(1)()(1)2n n n n n S S nS n S +++-=--+，即122n n S S +=+; ……………4分∴122(2)n n S S ++=+， ……………5分∵112240S a +=+=≠，∴数列{2}n S +是以4为首项,2为公比的等比数列. ∴1242n n S -+=⨯,即1142222n n n S -+=⨯-=-. ……………6分 当2n≥时, 11(22)(22)2n n n n n n a S S +-=-=---=， ……………7分又12a =也满足上式,∴2nn a =. ……………8分法2：由③式得：()111(1)(1)22n n n n n n n a nS n S nS S S ++++=--+=-++，得12n n a S +=+. ④ ……………4分当2n≥时,12n n a S -=+, ⑤ ……………5分⑤-④得：12n n a a +=. ……………6分 由12224a a S +=+，得24a =， ∴212a a =. ……………7分∴数列{}n a 是以12a =为首项，2为公比的等比数列. ∴2n n a =. …………8分 （2）解：∵p q r ,,成等差数列，∴2p r q +=. …………9分假设111p q r a a a ,,---成等比数列，则()()()2111p r q a a a --=-， …………10分即()()()2212121prq--=-，化简得：2222p r q +=⨯. （*） ……………11分∵p r ≠，∴2222222p r p r q +>⨯=⨯，这与(*)式矛盾，故假设不成立.…13分 ∴111pq r a a a ,,---不是等比数列. ……………14分20．（本小题满分14分）（本小题主要考查椭圆、抛物线、曲线的切线等基础知识，考查数形结合、函数与方程、化归与转化的数学思想方法，以及推理论证能力、运算求解能力、创新意识）(1) 解法1：设椭圆1C 的方程为22221x y a b+=()0a b >>,依题意: 222222231,4.a b a b ⎧+=⎪⎨⎪=+⎩解得:2216,12.a b ⎧=⎪⎨=⎪⎩ ……………2分 ∴ 椭圆1C 的方程为2211612x y +=. ……………3分 解法2：设椭圆1C 的方程为22221x y a b+=()0a b >>，根据椭圆的定义得1228a AF AF =+=，即4a =， ……………1分∵2c =， ∴22212b a c =-=. ……………2分∴ 椭圆1C 的方程为2211612x y +=. ……………3分 (2)解法1：设点)41,(211x x B ,)41,(222x x C ，则))(41,(212212x x x x BC --=， )413,2(211x x BA --=，∵C B A ,,三点共线,∴BC BA //. ……………4分∴()()()222211211113244xx x x x x ⎛⎫--=-- ⎪⎝⎭,化简得：1212212x x x x ()+-=. ① ……………5分 由24x y =,即214yx ,=得y '=12x . ……………6分 ∴抛物线2C 在点B 处的切线1l 的方程为)(2411121x x x x y -=-，即211412x x x y -=. ② 同理，抛物线2C 在点C 处的切线2l 的方程为222412x x x y -=. ③ ………8分 设点),(y x P ，由②③得：=-211412x x x 222412x x x -， 而21x x ≠，则 )(2121x x x +=. ……………9分代入②得 2141x x y =， ……………10分则212x x x +=，214x x y =代入 ① 得 1244=-y x ，即点P 的轨迹方程为3-=x y .……………11分若1212PF PF AF AF +=+ ，则点P 在椭圆1C 上，而点P 又在直线3-=x y 上，……………12分∵直线3-=x y 经过椭圆1C 内一点(3,0),∴直线3-=x y 与椭圆1C 交于两点. ……………13分∴满足条件1212PF PF AF AF +=+ 的点P 有两个. ……………14分解法2：设点),(11y x B ,),(22y x C ，),(00y x P ，由24x y =,即214yx ,=得y '=12x . ……………4分 ∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-， 即2111212x y x x y -+=. ……………5分 ∵21141x y =， ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① ……………6分 同理，20202y x x y -=. ② ……………7分 综合①、②得，点),(),,(2211y x C y x B 的坐标都满足方程y x xy -=002. ………8分 ∵经过),(),,(2211y x C y x B 的直线是唯一的， ∴直线L 的方程为y x xy -=2， ……………9分 ∵点)3,2(A 在直线L 上， ∴300-=x y . ……………10分∴点P 的轨迹方程为3-=x y . ……………11分 若1212PF PF AF AF +=+ ，则点P 在椭圆1C 上，又在直线3-=x y 上，…12分∵直线3-=x y 经过椭圆1C 内一点(3,0),∴直线3-=x y 与椭圆1C 交于两点. ……………13分 ∴满足条件1212PF PF AF AF +=+ 的点P 有两个. ……………14分解法3：显然直线L 的斜率存在，设直线L 的方程为()23y k x =-+，由()2234y k x x y ,,⎧=-+⎪⎨=⎪⎩消去y ，得248120x kx k -+-=. ……………4分设()()1122B x y C x y ,,,,则12124812x x k x x k ,+==-. ……………5分 由24x y =,即214yx ,=得y '=12x . ……………6分 ∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-，即2111212x y x x y -+=.…7分 ∵21141x y =， ∴211124x y x x =-. 同理,得抛物线2C 在点C 处的切线2l 的方程为222124x yx x =-. ……………8分 由211222124124x y x x x y x x ,,⎧=-⎪⎪⎨⎪=-⎪⎩解得121222234x x x k x x y k ,.⎧+==⎪⎪⎨⎪==-⎪⎩ ∴()223P k k ,-. ……………10分 ∵1212PF PF AF AF +=+,∴点P 在椭圆22111612x y C :+=上. ……………11分 ∴()()2222311612k k -+=. 化简得271230kk --=.(*) ……………12分由()2124732280Δ=-⨯⨯-=>, ……………13分可得方程(*)有两个不等的实数根. ∴满足条件的点P 有两个. ……………14分 21．（本小题满分14分）（本小题主要考查二次函数、一元二次不等式、一元二次方程、函数应用、均值不等式等基础知识，考查数形结合、函数与方程、分类与整合、化归与转化的数学思想方法，以及抽象概括能力、推理论证能力、运算求解能力、创新意识） （1）解：∵关于x 的不等式()()2211fx m x m <-+-的解集为()1m m ,+，即不等式()22120x a m x m m ++-++<的解集为()1m m ,+，∴()2212x a m x m m ++-++=()()1x mx m ---.∴()2212x a m x m m ++-++=()()2211x m x m m -+++. ∴()1221a m m +-=-+. ∴2a=-. ……………2分(2)解法1:由(1)得()()1f xg x x =-()221111x x m mx x x -++==-+--.∴()()x g x ϕ=-()1k x ln -()11mx x =-+-()1k x ln --的定义域为()1,+∞.∴()1x ϕ'=-()211mkx x ---()()22211x k x k m x -++-+=-. ……………3分 方程()2210x k x k m -++-+=（*）的判别式()()222414Δk k m k m =+--+=+. ……………4分①当0m >时，0Δ>，方程（*）的两个实根为212412k k mx ,+-+=<222412k k m x ,+++=> ……………5分则()21x x ,∈时，()0x ϕ'<；()2x x ,∈+∞时，()0x ϕ'>. ∴函数()x ϕ在()21x ,上单调递减，在()2x ,+∞上单调递增.∴函数()x ϕ有极小值点2x . ……………6分 ②当0m<时，由0Δ>,得2k m <--或2k m >-，若2k m <--，则212412k k m x ,+-+=<222412k k mx ,+++=<故x∈()1,+∞时，()0x ϕ'>，∴函数()x ϕ在()1,+∞上单调递增.∴函数()x ϕ没有极值点. ……………7分若2k m >-时，212412k k m x ,+-+=>222412k k mx ,+++=>则()11x x ,∈时，()0x ϕ'>；()12x x x ,∈时，()0x ϕ'<；()2x x ,∈+∞时，()0x ϕ'>.∴函数()x ϕ在()11x ,上单调递增，在()12x x ,上单调递减，在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x ，有极大值点1x . ……………8分 综上所述, 当0m >时，k 取任意实数, 函数()x ϕ有极小值点2x ；当0m<时，2k m >-，函数()x ϕ有极小值点2x ，有极大值点1x .…9分(其中21242k k m x +-+=, 22242k k mx +++=)解法2:由(1)得()()1f xg x x =-()221111x x m m x x x -++==-+--.∴()()x g x ϕ=-()1k x ln -()11mx x =-+-()1k x ln --的定义域为()1,+∞. ∴()1x ϕ'=-()211mkx x ---()()22211x k x k m x -++-+=-. ……………3分 若函数()()x g x ϕ=-()1k x ln -存在极值点等价于函数()x ϕ'有两个不等的零点，且至少有一个零点在()1,+∞上. ……………4分令()x ϕ'()()22211x k x k m x -++-+=-0=, 得()221x k x k m -++-+0=, (*)则()()2224140Δk k m k m =+--+=+>,(**) ……………5分方程（*）的两个实根为21242k k m x +-+=, 22242k k mx +++=.设()h x =()221x k x k m -++-+,①若1211x x ,<>,则()10h m =-<,得0m>,此时,k 取任意实数, (**)成立.则()21x x ,∈时，()0x ϕ'<；()2x x ,∈+∞时，()0x ϕ'>. ∴函数()x ϕ在()21x ,上单调递减，在()2x ,+∞上单调递增.∴函数()x ϕ有极小值点2x . ……………6分②若1211x x ,>>,则()10212h m k ,.⎧=->⎪⎨+>⎪⎩得00m k ,.⎧<⎨>⎩又由(**)解得2k m >-或2k m <--,故2k m >-. ……………7分 则()11x x ,∈时，()0x ϕ'>；()12x x x ,∈时，()0x ϕ'<；()2x x ,∈+∞时，()0x ϕ'>.∴函数()x ϕ在()11x ,上单调递增，在()12x x ,上单调递减，在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x ，有极大值点1x . ……………8分 综上所述, 当0m >时，k 取任何实数, 函数()x ϕ有极小值点2x ；当0m<时，2k m >-，函数()x ϕ有极小值点2x ，有极大值点1x .…9分(其中21242k k m x +-+=, 22242k k mx +++=)(2)证法1：∵1m=， ∴()g x =()111x x -+-. ∴()()1111nnnn n g x g x x x x x ⎛⎫⎛⎫⎡⎤+-+=+-+ ⎪ ⎪⎣⎦⎝⎭⎝⎭112212111111n n n n n n n n n n n n n x C x C x C x C x x x x x x ----⎛⎫=+⋅+⋅++⋅+-+ ⎪⎝⎭ 122412n n n nn n n C x C x C x ----=+++ . ……………10分令T 122412n n n n n n n C x C x C x ----=+++ ， 则T122412n n n n n n n n C x C x C x -----=+++122412n n n n n n n C x C x C x ----=+++ .∵x0>，∴2T()()()122244122n n n n n n n n n n C x x C x x C x x -------=++++++ …11分≥122244122222n n n n n n n n n n C x x C x x C x x -------⋅⋅+⋅⋅++⋅⋅ …12分()1212n n n n C C C -=+++()12102n n n nn n n n n n C C C C C C C -=+++++--()222n=-. ……………13分∴22n T≥-，即()()1122nn n g x g x ⎡⎤+-+≥-⎣⎦. ……………14分 证法2：下面用数学归纳法证明不等式11nn n x x x x ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭22n ≥-.① 当1n=时，左边110x x x x ⎛⎫⎛⎫=+-+= ⎪ ⎪⎝⎭⎝⎭，右边1220=-=，不等式成立；……………10分② 假设当n k =k (∈N *)时，不等式成立，即11kk k x x x x ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭22k ≥-，则 11111k k k x x x x +++⎛⎫⎛⎫+-+ ⎪⎪⎝⎭⎝⎭11111111kk k k k k k x x x x x x x x x x x x ++⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥=++-++++-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦111kk k x x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=++-++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦111k k x x --⎛⎫+ ⎪⎝⎭ ……………11分()11112222k k k x x x x--≥⋅⋅-+⋅ ……………12分 122k +=-. ……………13分也就是说，当1n k =+时，不等式也成立.由①②可得，对∀n ∈N*，()()1122nn n gx g x ⎡⎤+-+≥-⎣⎦都成立. ………14分2013年佛山市普通高中高三教学质量检测（一）数 学（理科）本试卷共4页，21小题，满分150分．考试用时120分钟． 注意事项：1．答卷前，考生要务必填写答题卷上密封线内的有关项目．2．选择题每小题选出答案后，用铅笔把答案代号填在答题卷对应的空格内．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．请考生保持答题卷的整洁．考试结束后，将答题卷和答题卡交回． 参考公式：①柱体的体积公式V Sh =，其中S 为柱体的底面积，h 为柱体的高．②锥体的体积公式13V Sh =，其中S 为柱体的底面积，h 为锥体的高．2013-1-25 ③标准差222121[()()()]n s x x x x x x n=-+-++- ，其中x 为样本12,,,n x x x 的平均数．一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设i 为虚数单位，则复数i2i+等于 A ．12i 55+ B ． 12i 55-+ C ．12i 55- D ．12i 55--2．命题:p 2,11x x ∀∈+≥R ，则p ⌝是A ．2,11x x ∀∈+<R B ．2,11x x ∃∈+≤R C ．2,11x x ∃∈+<R D ．2,11x x ∃∈+≥R3．已知(1,2)=a ，(0,1)=b ，(,2)k =-c ，若(2)+⊥a b c ，则k = A ．2 B ．8 C ．2- D ．8-4．一个直棱柱被一个平面截去一部分后所剩几何体的 三视图如图所示，则该几何体的体积为 A ．9 B ．10C ．11D ．232221 31 正视图侧视图俯视图第4题图5．为了从甲乙两人中选一人参加数学竞赛，老师将两人最近的6次数学测试的分数进行统计，甲乙两人的得分情况如茎叶图所示，若甲乙两人的平均成绩分别是x 甲，x 乙，则下列说法正确的是A ．x x >甲乙，乙比甲成绩稳定，应该选乙参加比赛B ．x x >甲乙，甲比乙成绩稳定，应该选甲参加比赛C ．x x <甲乙，甲比乙成绩稳定，应该选甲参加比赛D ．x x <甲乙，乙比甲成绩稳定，应该选乙参加比赛6．已知实数,x y 满足11y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则目标函数2z x y =-的最大值为A ．3-B ．12C ．5D ．67．已知集合{}|4||1|5Mx x x =-+-<，{}6N x a x =<< ,且()2,M N b = ,则a b +=A ．6B ．7C ．8D ．9 8．对于函数()y f x =，如果存在区间[,]m n ，同时满足下列条件：①()f x 在[,]m n 内是单调的；②当定义域是[,]m n 时，()f x 的值域也是[,]m n ，则称[,]m n 是该函数的“和谐区间”．若函数11()(0)a f x a a x+=->存在“和谐区间”，则a 的取值范围是 A ．(0,1) B ． (0,2) C ．15(,)22D ．(1,3)二、填空题：本大共7小题，考生作答6小题，每小题5分，满分30分． (一)必做题(9～13题) 9．已知函数()y f x =是奇函数，当0x >时，()f x =2log x ，则1(())4f f 的值等于 ．10．已知抛物线24x y =上一点P 到焦点F 的距离是5，则点P 的横坐标是_____．11．函数sin sin 3y x x π⎛⎫=+-⎪⎝⎭的最小正周期为 ，最大值是 ．12．某学生在参加政、史、地 三门课程的学业水平考试中，取得ξ0 1 2 3 P6125ab24125第5题图A 等级的概率分别为54、53、52，且三门课程的成绩是否取得A 等级相互独立.记ξ为该生取得A 等级的课程数，其分布列如表所示，则数学期望ξE 的值为______________. 13．观察下列不等式： ①112<；②11226+<；③11132612++<；… 则第5个不等式为 ．(二)选做题(14～15题，考生只能从中选做一题)14．（坐标系与参数方程）在极坐标系中，直线l 过点(1,0)且与直线3πθ=（ρ∈R ）垂直，则直线l 极坐标方程为 ． 15．（几何证明选讲）如图，M 是平行四边形ABCD 的边AB 的 中点，直线l 过点M 分别交,AD AC 于点,E F ．若3AD AE =，则:AF FC = ．三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤． 16．（本题满分12分）如图，在△ABC 中，45C ∠=，D 为BC 中点，2BC =. 记锐角ADB α∠=．且满足7cos225α=-． （1）求cos α；（2）求BC 边上高的值．第15题图F ABCD E Ml第16题图CBD A17．（本题满分12分）数列{}n a 的前n 项和为122n n S +=-，数列{}n b 是首项为1a ，公差为(0)d d ≠的等差数列，且1311,,b b b 成等比数列． （1）求数列{}n a 与{}n b 的通项公式；（2）设nnnb c a =，求数列{}n c 的前n 项和n T ． 18．（本题满分14分）如图所示，已知AB 为圆O 的直径，点D 为线段AB 上一点，且13AD DB =，点C 为圆O 上一点，且3BC AC =． 点P 在圆O 所在平面上的正投影为点D ，PD DB =．PABDO（1）求证：PA CD ⊥；（2）求二面角C PB A --的余弦值．19．（本题满分14分）某工厂生产某种产品，每日的成本C （单位：万元）与日产量x （单位：吨）满足函数关系式3C x =+，每日的销售额S （单位：万元）与日产量x 的函数关系式35, (06)814, (6)k x x S x x ⎧++<<⎪=-⎨⎪≥⎩ 已知每日的利润L S C =-，且当2x =时，3L =．（1）求k 的值；（2）当日产量为多少吨时，每日的利润可以达到最大，并求出最大值． 20．（本题满分14分）设椭圆22221(0)x y a b a b +=>>的左右顶点分别为(2,0),(2,0)A B -，离心率32e =．过该椭圆上任一点P 作PQ x ⊥轴，垂足为Q ，点C 在QP 的延长线上，且||||QP PC =． （1）求椭圆的方程；（2）求动点C 的轨迹E 的方程；（3）设直线AC （C 点不同于,A B ）与直线2x =交于点R ，D 为线段RB 的中点，试判断直线CD 与曲线E 的位置关系，并证明你的结论． 21．（本题满分14分）设()xg x e =，()[(1)]()f x g x a g x =λ+-λ-λ，其中,a λ是常数，且01λ<<．（1）求函数()f x 的极值；（2）证明：对任意正数a ，存在正数x ，使不等式11x e a x--<成立； （3）设12,λλ∈+R ，且121λλ+=，证明：对任意正数21,a a 都有：12121122a a a a λλ≤λ+λ．2013年佛山市普通高中高三教学质量检测（一）数学试题（理科）参考答案和评分标准一、选择题：本大题共8小题，每小题5分，满分40分． 题号 1 2 3 4567 8 答案A CBCD C BA二、填空题：本大共7小题，考生作答6小题，每小题5分，满分30分． 9．1- 10．4± 11．2π（2分），3 （3分） 12．5913．11111526122030++++< 14．2sin()16πρθ+=（或2cos()13πρθ-=、cos 3sin 1ρθρθ+=） 15．1:4 三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤．16．（本题满分12分） 解析：（1）∵27cos22cos 125αα=-=-，∴29cos 25α=， ∵(0,)2πα∈，∴3c o s 5α=． -----------------5分（2）方法一、由（1）得24sin 1cos 5αα=-=，∵45CAD ADB C α∠=∠-∠=-，∴2sin sin()sin cos cos sin 44410CAD πππααα∠=-=-=，-----------------9分在ACD ∆中，由正弦定理得：sin sin CD ADCAD C=∠∠，∴21sin 25sin 210CD C AD CAD ⨯⋅∠===∠，-----------------11分则高4sin 545h AD ADB =⋅∠=⨯=． -----------------12分方法二、如图，作BC 边上的高为AH在直角△ADH 中，由（1）可得3cos 5DB AD α==， 则不妨设5,AD m = 则3,4DH m AH m ==-----------------8分注意到=45C ∠，则AHC ∆为等腰直角三角形，所以CD DH AH += ，则134m m +=-----------------10分 所以1m =，即4AH =-----------------12分 17．（本题满分12分） 解析：（1）当2n ≥，时11222n nn n n n a S S +-=-=-=， -----------------2分又111112222a S +==-==，也满足上式，所以数列{na }的通项公式为2n n a =． -----------------3分112b a ==，设公差为d ，则由1311,,b b b 成等比数列，得2(22)2(210)d d +=⨯+，第16题图 C BD AH-----------------4分 解得d =（舍去）或3d =，----------------5分 所以数列}{n b 的通项公式为31n b n =-． -----------------6分（2）由（1）可得312123n n nb b b b T a a a a =++++ 123258312222nn -=++++ ， -----------------7分121583122222n n n T --=++++ ，-----------------8分两式式相减得1213333122222n n n n T --=++++- ，-----------------11分131(1)3135222512212n n n n n n T ---+=+-=--，-----------------12分 18．（本题满分14分） 解析：（Ⅰ）法1：连接CO ，由3AD DB =知，点D 为AO 的中点， 又∵AB 为圆O 的直径，∴AC CB ⊥， 由3AC BC =知，60CAB ∠= ，∴ACO ∆为等边三角形，从而CD AO ⊥．-----------------3分 ∵点P 在圆O 所在平面上的正投影为点D ， ∴PD ⊥平面ABC ，又CD ⊂平面ABC ， ∴PD CD ⊥，-----------------5分由PD AO D = 得，CD ⊥平面PAB ，又PA ⊂平面PAB ，∴PA CD ⊥． -----------------6分（注：证明CD ⊥平面PAB 时，也可以由平面PAB ⊥平面ACB 得到，酌情给分．） 法2：∵AB 为圆O 的直径，∴AC CB ⊥，在Rt ABC ∆中设1AD =，由3A D D B=，3AC BC =得，3DB =，4AB =，23BC =，PA BDCO∴32BD BC BC AB ==，则BDC BCA ∆∆∽， ∴BCA BDC∠=∠，即C ⊥． -----------------3分∵点P 在圆O 所在平面上的正投影为点D ， ∴PD ⊥平面ABC ，又CD ⊂平面ABC ， ∴PD CD⊥，-----------------5分由PD AO D = 得，CD ⊥平面PAB ，又PA ⊂平面PAB ，∴PA CD ⊥． -----------------6分 法3：∵AB 为圆O 的直径，∴AC CB ⊥， 在Rt ABC ∆中由3AC BC =得，30ABC ∠= ，设1AD =，由3AD DB =得，3DB =，23BC =，由余弦定理得，2222cos303CD DB BC DB BC =+-⋅= ， ∴222CD DB BC +=，即C ⊥． -----------------3分∵点P 在圆O 所在平面上的正投影为点D ， ∴PD ⊥平面ABC ，又CD ⊂平面ABC ， ∴PD CD⊥，-----------------5分由PD AO D = 得，CD ⊥平面PAB ，又PA ⊂平面PAB，∴PA CD ⊥． -----------------6分（Ⅱ）法1：（综合法）过点D 作DE PB ⊥，垂足为E ，连接CE ． -----------------7分由（1）知CD ⊥平面PAB ，又PB ⊂平面PAB ， ∴CD PB ⊥，又DE CD D = ， ∴PB ⊥平面CDE ，又CE ⊂平面CDE ， ∴CE PB ⊥，-----------------9分∴DEC ∠为二面角C PB A --的平面角． -----------------10分 由（Ⅰ）可知3CD =，3PD DB ==，PABDCOE（注：在第（Ⅰ）问中使用方法1时，此处需要设出线段的长度，酌情给分．） ∴32PB =，则932232PD DB DE PB ⋅===， ∴在Rt CDE ∆中，36tan 3322CD DEC DE ∠===， ∴15cos 5DEC ∠=，即二面角C P B --的余弦值为155． -----------------14分 法2：（坐标法）以D 为原点，DC 、DB 和DP的方向分别为x 轴、y 轴和z 轴的正向，建立如图所示的空间直角坐标系． -----------------8分 （注：如果第（Ⅰ）问就使用“坐标法”时，建系之前先要证明CD AB ⊥，酌情给分．） 设1AD =，由3AD DB =，3AC BC =得，3PD DB ==，3CD =，∴(0,0,0)D ，(3,0,0)C ，(0,3,0)B ，(0,0,3)P ，∴(3,0,3)PC =- ，(0,3,3)PB =- ，(3,0,0)CD =-，由CD ⊥平面PAB ，知平面PAB 的一个法向量为(3,0,0)CD =-． -----------------10分设平面PBC 的一个法向量为(,,)x y z =n ，则00PC PB ⎧⋅=⎪⎨⋅=⎪⎩ n n ，即330330x y y z ⎧-=⎪⎨-=⎪⎩，令1y =，则3x =，1z =， ∴(3,1,1)=n ，-----------------12分设二面角C PB A --的平面角的大小为θ，则315cos 5||53CD CD θ⋅-===-⋅⨯ n |n|，-----------------13分 ∴二面角C PB A --的余弦值为155．-----------------14分19．（本题满分14分）解析：（Ⅰ）由题意可得：22,06811,6k x x L x x x ⎧++<<⎪=-⎨⎪-≥⎩，PABDCOyz x-----------------2分 因为2x =时，3L =，所以322228k =⨯++-.-----------------4分解得18k =.-----------------5分（Ⅱ）当06x <<时，18228L x x =++-，所以 1818182818=[2(8)]182********L x x x x x x=-++--++--⋅+=---≤（）（）．-----------------8分 当且仅当182(8)8x x-=-，即5x =时取得等号． -----------------10分 当6x ≥时，1L x =-≤． -----------------12分 所以当5x =时，L 取得最大值6．所以当日产量为5吨时，每日的利润可以达到最大值6万元． -----------------14分 20．（本题满分14分） 解析：（1）由题意可得2a =，32c e a ==，∴3c =， -----------------2分 ∴2221b a c =-=，所以椭圆的方程为2214x y +=． -----------------4分 （2）设(,)C x y ，00(,)P x y ，由题意得002x x y y =⎧⎨=⎩，即0012x xy x =⎧⎪⎨=⎪⎩， -----------------6分又220014x y +=，代入得221()142x y +=，即224x y +=． 即动点C的轨迹E的方程为224x y +=． -----------------8分（3）设(,)C m n ，点R 的坐标为(2,)t ，∵,,A C R 三点共线，∴//AC AR，而(2,)AC m n =+ ，(4,)AR t =，则4(2)n t m =+，∴42nt m =+， ∴点R 的坐标为4(2,)2nm +，点D 的坐标为2(2,)2nm +，-----------------10分∴直线CD 的斜率为222(2)22244nn m n n mn m k m m m -+-+===---， 而224m n +=，∴224m n -=-，∴2mn mk n n==--，-----------------12分∴直线CD 的方程为()my n x m n-=--，化简得40mx ny +-=， ∴圆心O 到直线CD 的距离224424dr m n====+， 所以直线CD 与圆O相切． -----------------14分 21．（本题满分14分）解析：（1）∵()[(1f x g x a g x λλλλ'''=+--，-----------------1分 由()0f x '>得，[(1)]()g x a g x λλ''+->，∴(1)x a x λλ+->，即(1)()0x a λ--<，解得x a <，-----------------3分 故当x a <时，()0f x '>；当x a >时，()0f x '<；∴当x a =时，()f x 取极大值，但()f x 没有极小值．-----------------4分（2）∵111x x e e x x x----=， 又当0x >时，令()1x h x e x =--，则()10x h x e '=->， 故()(0)0h x h >=， 因此原不等式化为1x e x a x--<，即(1)1x e a x -+-<， -----------------6分令()(1)1x g x e a x =-+-，则()(1)x g x e a '=-+， 由()0g x '=得：1xe a =+，解得ln(1)x a =+，当0ln(1)x a <<+时，()0g x '<；当ln(1)x a >+时，()0g x '>． 故当l n (1x a =+时，()g x 取最小值[ln(1)](1)ln(1)g a a a a +=-++，-----------------8分令()ln(1),01a s a a a a =-+>+，则2211()0(1)1(1)as a a a a '=-=-<+++． 故()(0)0s a s <=，即[ln(1)](1)ln(1)0g a a a a +=-++<． 因此，存在正数ln(1)x a =+，使原不等式成立． -----------------10分 （3）对任意正数12,a a ，存在实数12,x x 使11xa e =，22x a e =，则121122112212x x x x a a e e e λλλλλλ+=⋅=，12112212x x a a e e λλλλ+=+，原不等式12121122a a a a λλλλ≤+11221212x x x x e e e λλλλ+⇔≤+，11221122()()()g x x g x g x λλλλ⇔+≤+-----------------14分 由（1）()(1)()f x g a λ≤-恒成立，故[(1)]()(1)()g x a g x g a λλλλ+-≤+-， 取1212,,,1x x a x λλλλ===-=， 即得11221122()()()g x x g x g x λλλλ+≤+， 即11221212x x x x e e e λλλλ+≤+，故所证不等式成立． -----------------14分。

广东省肇庆市中小学教学质量评估2013届第一学期高三统一检测理科数学试题详细解析一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1．设1z i =-（i 是虚数单位），则2z z+= ( ) A ．2 B ．3 C ．22i - D ． 22i +2．已知集合{}1,2,A m =，{}3,4B =，{}1,2,3,4AB =则m =（ ）A. 0B. 3C. 4D. 3或43．已知向量(1,cos ),(1,2cos )θθ=-=a b 且⊥a b ，则cos2θ等于 （ ）A.1-B. 0 C .12D.224．已知变量,x y 满足约束条件1101x y x x y +≤⎧⎪+≥⎨⎪-≤⎩，则23z x y =+的取值范围是（ ）A. [8,4]-B.[8,2]- C. [4,2]-D. [4,8]-- 5．图1是某算法的程序框图，则程序运行后输出的结果是27，则判断框①处应填入的条件是 ( )A.2n >B. 3n >C. 4n >D. 5n >6．已知某个几何体的三视图如图2所示，根据图中标出的尺寸（单位：cm ），则这个几何体的体积是( ). A. 38cm B. 312cm C. 324cm D. 372cm7．101x x ⎛⎫- ⎪⎝⎭的展开式中含x 的正整数指数幂的项数是( )A. 0B. 2C. 4D. 68.定义空间两个向量的一种运算sin ,⊗=⋅<>a b a b a b ，则关于空间向量上述运算的以下结论中，①⊗=⊗a b b a ，②()()λλ⊗=⊗a b a b ，③()()()+⊗=⊗+⊗a b c a c b c ， ④若1122(,),(,)x y x y ==a b ，则1221x y x y ⊗=-a b . 恒成立的有A ．1个 B. 2个 C. 3个 D. 4个二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分. （一）必做题（9～13题）9．不等式3|52|9x <-≤的解集是 .10．等比数列{n a }中，123420,40a a a a +=+=，则56a a +等于 11．函数321()2323f x x x x =-+-在区间[0,2]上最大值为 12．圆心在直线270x y -+=上的圆C 与x 轴交于两点(2,0)A -、(4,0)B -，则圆C 的方程为__________.13．某班有学生40人，将其数学期中考试成绩平均分为两组，第一组的平均分为80分，标准差为4，第二组的平均分为90分，标准差为6， 则此班40名学生的数学期中考试成绩平均分 方差为（ ） ▲14．（坐标系与参数方程选做题）在极坐标系(),ρθ（0,02πρθ>≤<）中，曲线2sin ρθ=与2cos ρθ=的交点的极坐标为_____15.（几何证明选讲选做题）如图3,△ABC 的外角平分线AD 交外接圆于D,4BD =，则CD = .三、解答题:本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. 16.（本小题满分12分） 已知向量sin ,cos ,cos ,sin 3366x x A A ππ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭a b ，函数()f x =a b （0,A x R >∈），且(2)2f π=.（1）求函数()y f x =的表达式；（2）设,[0,]2παβ∈， 16(3),5f απ+=5203213f πβ⎛⎫+=- ⎪⎝⎭；求cos()αβ+的值。

本卷共12小题，满分100分，考试用时50分钟。

可能用到的相对原子质量：H-1 C-12 O-16 Mg-24 Fe-56第一部分选择题一、单项选择题：本大题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一个选项符合题目要求，选对的得4分，选错或不答的得0分。

7．下列说法正确的是A．氨基酸和蛋白质既能与酸反应又能与碱反应B．在米汤中加入食盐，可以检验食盐中是否加碘C．“酸雨”是由大气中的碳、硫、氮的氧化物溶于雨水造成D．蔗糖、麦芽糖、淀粉和纤维素都能水解，最终水解产物都为葡萄糖【答案】A【解析】氨基和羧基既是氨基酸的官能团，也是蛋白质的官能团，氨基能与酸反应，羧基能与碱反应，故A正确；米汤的主要成分是淀粉，遇I2变蓝，加碘食盐中无I2，只有KIO3，因此米汤遇加碘食盐也不能变蓝，故B错误；酸雨是大气中硫、氮的氧化物溶于水造成，与二氧化碳无关，因为饱和碳酸的pH约为5.6，pH<5.6的雨才能称为酸雨，故C错误；淀粉和纤维素属于多糖，它们水解的最终产物都是葡萄糖，蔗糖水解产物是葡萄糖和果糖，麦芽糖水解产物是葡萄糖，故D错误。

8．下列离子方程式正确的是A．氨水吸收足量的SO2气体：OH－+SO2===HSO3－B．稀硝酸中加入过量铁粉：Fe + 4H＋+ NO3－===Fe3＋+ NO↑+ 2H2OC．用NaOH溶液吸收废气中氮氧化物：NO+NO2+OH－==NO2－+H2OD．苯酚钠溶液中通入少量CO2：9．设N A为阿伏加德罗常数的数值，则下列叙述正确的是A．1 mol氨基（—NH2）中含电子数为10N AB．标准状况下，2.24 L 18O2中所含中子的数目是2N AC．标准状况下，22.4 L C8H18中含有的共价键键数为25N AD．在反应CaO + 3C = CaC2 + CO↑中，每生成1 mol CO，转移的电子数为3N A【答案】B【解析】1个氨基由1个氮原子和2个氢原子构成，氮原子含有7个电子，氢原子含有O+CO2 + H2O OH+ HCO310．下列陈述I、II均正确并且有因果关系的是选项陈述I 陈述IIA Fe3+有氧化性铁盐可用作净水剂B SiO2是两性氧化物SiO2可和HF反应C Al2O3的熔点很高Al2O3可用作耐火材料D SO2有漂白性SO2可使高锰酸钾溶液褪色10．关于常温下pH = 12的NaOH溶液，下列说法错误．．的是A．c(OH－) =c(Na+) + c(H+)B．由水电离出的c(OH－) = 1.0×10－12 mol·L－1C．与等体积pH = 2的醋酸混合后所得溶液显碱性D．与等体积0.01 mol·L－1氯化铵溶液混合后所得溶液中：c(Na+)> c(NH4+) 【答案】C11．下图是部分短周期主族元素原子半径与原子序数的关系图。

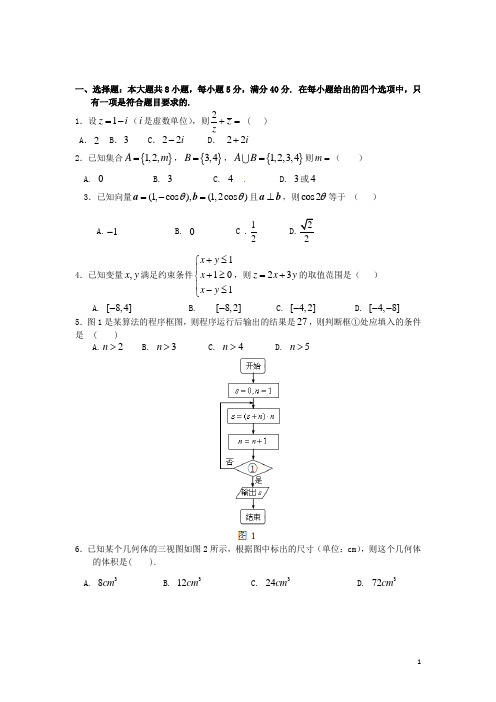
一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1．设1z i =-（i 是虚数单位），则2z z+= ( ) A ．2 B ．3 C ．22i - D ． 22i +2．已知集合{}1,2,A m =，{}3,4B =，{}1,2,3,4AB =则m =（ ）A. 0B. 3C. 4D. 3或43．已知向量(1,cos ),(1,2cos )θθ=-=a b 且⊥a b ，则cos2θ等于 （ ）A.1-B. 0 C .12D.224．已知变量,x y 满足约束条件1101x y x x y +≤⎧⎪+≥⎨⎪-≤⎩，则23z x y =+的取值范围是（ ）A. [8,4]-B.[8,2]- C. [4,2]-D. [4,8]-- 5．图1是某算法的程序框图，则程序运行后输出的结果是27，则判断框①处应填入的条件是 ( )A.2n >B. 3n >C. 4n >D. 5n >6．已知某个几何体的三视图如图2所示，根据图中标出的尺寸（单位：cm ），则这个几何体的体积是( ). A. 38cm B. 312cm C. 324cm D. 372cm7．101x x ⎛⎫- ⎪⎝⎭的展开式中含x 的正整数指数幂的项数是( )A. 0B. 2C. 4D. 68.定义空间两个向量的一种运算sin ,⊗=⋅<>a b a b a b ，则关于空间向量上述运算的以下结论中，①⊗=⊗a b b a ，②()()λλ⊗=⊗a b a b ，③()()()+⊗=⊗+⊗a b c a c b c ， ④若1122(,),(,)x y x y ==a b ，则1221x y x y ⊗=-a b . 恒成立的有A ．1个 B. 2个 C. 3个 D. 4个二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分. （一）必做题（9～13题）9．不等式3|52|9x <-≤的解集是 .10．等比数列{n a }中，123420,40a a a a +=+=，则56a a +等于 11．函数321()2323f x x x x =-+-在区间[0,2]上最大值为 12．圆心在直线270x y -+=上的圆C 与x 轴交于两点(2,0)A -、(4,0)B -，则圆C 的方程为__________.13．某班有学生40人，将其数学期中考试成绩平均分为两组，第一组的平均分为80分，标准差为4，第二组的平均分为90分，标准差为6， 则此班40名学生的数学期中考试成绩平均分 方差为（ ） ▲14．（坐标系与参数方程选做题）在极坐标系(),ρθ（0,02πρθ>≤<）中，曲线2sin ρθ=与2cos ρθ=的交点的极坐标为_____15.（几何证明选讲选做题）如图3,△ABC 的外角平分线AD 交外接圆于D,4BD =，则CD = .三、解答题:本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. 16.（本小题满分12分） 已知向量sin ,cos ,cos ,sin 3366x x A A ππ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭a b ，函数()f x =a b （0,A x R >∈），且(2)2f π=.（1）求函数()y f x =的表达式；（2）设,[0,]2παβ∈， 16(3),5f απ+=5203213f πβ⎛⎫+=- ⎪⎝⎭；求cos()αβ+的值。

肇庆市中小学教学质量评估2013—2014学年第一学期统一检测题高三数学（理科）注意事项：1. 答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的所在县（市、区）、姓名、试室号、座位号填写在答题卷上对应位置，再用2B 铅笔将准考证号涂黑.2. 选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需要改动，用橡皮擦干净后，再选涂其它答案，答案不能写在试卷上.3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在另发的答题卷各题目指定区域内相应的位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.参考公式：1、锥体的体积公式13V Sh =，其中S 为锥体的底面积，h 为锥体的高。

一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知集合2{|30}M x x x =-=，集合{|21,}N x x n n Z ==-∈，则M N =( )A. {3}B.{0}C.{0,3}D. {3}- 2．设复数31iz i-=-（i 是虚数单位），则复数z 的共轭复数z = A ．12i - B. i 21+ C. 2i - D. 2i + 3．下列四个函数中,既是奇函数又在定义域上单调递增的是（ ）A.()ln f x x =B.()2sin f x x x =+C.1()f x x x=+D.()x xe f e x -=+ 4．已知实数x y ，满足2201x y x y x +≤⎧⎪-≤⎨⎪≤≤⎩，，，则23z x y =-的最大值是( )．A.6-B.1-C.4D.65．执行如图1所示的程序框图,输出的z 值为（ ）A ．3B ．4C ．5D ．66．某几何体的三视图如图2所示(单位：cm), 则其体积和表面积分别是（ ） A. 6π3cm 和12(1)π+2cm B. 6π3cm 和12π2cm C. 12π3cm 和12(1)π+2cm D. 12π3cm 和12π2cm7．平面内有4个红点,6个蓝点,其中只有一个红点和两个蓝点共线,其余任三点不共线,过这十个点中的任两点所确定的直线中,至少过一红点的直线的条数是( ) A.28 B.29 C.30 D.27 8．已知集合{1,3,7,,(21)}()n n A n N *=-∈，若从集合n A 中任取(1,2,3,,)k k n =个数，其所有可能的k 个数的乘积的和为k T （若只取一个数，规定乘积为此数本身），记123n n S T T T T =++++．例如当1n =时，1{1}A =，111,1T S ==；当2n =时，212{1,3},13,13A T T ==+=⨯，213137S =++⨯=.则n S =（ ）． A.21n- B. 2121n -- C.(1)121n n -+- D.(1)221n n +-二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分. （一）必做题（9～13题）9．函数()f x =的定义域为10．若等比数列{}n a 满足243520,40a a a a +=+=，则3a =11．在1041x x ⎛⎫+ ⎪⎝⎭的展开式中常数项是____________.（用数字作答）12．曲线32361y x x x =++-的切线中,斜率最小的切线方程为___________.13．在平面直角坐标系xoy 中，已知点A 是半圆2240x y x +-=(24)x ≤≤ 上的一个动点，点C 在线段OA 的延长线上．当20OA OC ∙=时，则点C 的纵坐标的取值范围是 ．（ ） ▲14．（坐标系与参数方程选做题）在极坐标系中，曲线(0)4πθρ=≥与4cos ρθ=的交点的极坐标为 .15.（几何证明选讲选做题）如图3，在ABC ∆中，90o ACB ∠=，CE AB ⊥于点E ,以AE为直径的圆与AC 交于点D ，若24BE AE ==，3CD =，则______AC =三、解答题:本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. 16.（本小题满分12分）已知函数()sin 6f x A x π⎛⎫=+ ⎪⎝⎭,(0,R)A x >∈的最大值为2.(1) 求()fπ的值； (2) 若3sin 5θ=-,,02πθ⎛⎫∈- ⎪⎝⎭,求26f πθ⎛⎫+ ⎪⎝⎭．17.（本小题满分12分）一次考试中，5名同学的语文、英语成绩如下表所示：（1） 根据表中数据，求英语分y 对语文分x 的线性回归方程；（2） 要从4名语文成绩在90分（含90分）以上的同学中选出2名参加一项活动，以ξ表示选中的同学的英语成绩高于90分的人数，求随机变量ξ的分布列及数学期望.E ξ（附:线性回归方程y bx a =+中，121()(),,()niii nii x x y y b a y bx x x ==--==--∑∑其中,x y 为样本平均值，ˆˆ,ba 的值的结果保留二位小数.）18. （本题满分14分）如图4，在四棱锥P ABCD -，PA ⊥平面ABCD ，12PA AB BC AD ===，四边形ABCD 是直角梯形中，90ABC BAD ∠=∠=︒．（1）求证: CD ⊥平面PAC ；（2）求二面角A PD C --的余弦值．19.（本小题满分14分） 已知数列{}n a 满足11a =,11n n n a a n a ++-=,n N *∈（1）求数列{}n a 的通项公式；（2）设2nn nb a =，数列{}n b 的前n 项和为n T ，求n T .(3)证明：22221232n a a a a ++++<.20. （本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12,椭圆短轴的一个端点与两个焦点构C 的右焦点的动直线l 与椭圆C 相交于A 、B 两点.(1)求椭圆C 的方程; (2)若线段AB 中点的横坐标为12,求直线l 的方程;(3) 若线段AB 的垂直平分线与x 轴相交于点D .设弦AB 的中点为P ,试求DP AB的取值范围.21．（本小题满分14分）已知函数2()ln 21)f x x ax x a -+=+（(其中常数0a ≠). (1) 当1a =时，求()f x 的单调区间；(2) 若()f x 在 1x =处取得极值，且在(]0,e 上的最大值为1，求a 的值.肇庆市中小学教学质量评估2012—2013学年第一学期统一检测题高三数学（理科）参考答案一、选择题：二、填空题：9．(,3][1,)-∞-+∞ 10. 8 11. 45 12. 320x y --= 13. [5,5]-14. (0,0),,4π⎛ ⎝ 15.831【解析】{0,3}M =，{,1,1,3,}N =-,M N ={3}2【解析】 223(3)(1)324221(1)(1)12i i i i i iz i i i i i --++-+=====+--+-, 2z i =-.3【解析】()()2sin 2cos 0f x x x x ''=+=+>,()2sin()()f x x x f x -=-+-=-4【解析】画图可知，四个角点分别是(0,2),(1,1),(1,1),(0,2)A B C D --，可知max 6A z z ==5【解析】1:1,1;2:2;2;3:8,3S s a S s a S s a ======，4:64,4S s a ==62log 26z ==，结束。

市2013届高中毕业班第一次模拟考试数 学（文科）本试卷共4页，21小题，满分150分. 考试用时120分钟.注意事项：1. 答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的班别、、考号填写在答题卡的密封线.2. 选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需要改动，用橡皮擦干净后，再选涂其它答案，答案不能写在试卷上.3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在另发的答题卷各题目指定区域相应的位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效. 参考公式：锥体的体积公式13V Sh =其中S 为锥体的底面积，h 为锥体的高一、选择题：本大题共10小题，每小题5分，满分50分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1．设i 为虚数单位，复数i a z 31-=，bi z +=22，其中a 、b ∈R. 若12z z =，则ab =A ．1-B ．5C ．6-D ．62．已知全集{2,1,0,1,2,3,4,5,6}U =--，集合M ={大于2-且小于5的整数}，则=M C UA ．∅B ．{6}C ．{2,6}-D ．{2,5,6}- 3．命题“∃x ∈R ，12<x”的否定是A ．,21xx ∀∈≥R B ．,21xx ∀∈<RC ．,21x x ∃∈≥RD ．12,>∈∃xR x4．甲、乙两种水稻试验品种连续5年的单位面积平均产量如下（单位：t/hm 2），根据这组数据下列说确的是A ．甲品种的样本平均数大于乙品种的样本平均数B ．甲品种的样本平均数小于乙品种的样本平均数 C. 甲品种的样本方差大于乙品种的样本方差 D. 甲品种的样本方差小于乙品种的样本方差5．已知等差数列{na}，满足398a a+=，则此数列的前11项的和11S= A．44 B．33 C．22 D．116．平面上有三个点A（2，2）、M（1，3）、N（7，k），若向量AM与AN垂直，则k= A．6 B．7 C．8 D．97．阅读如图1的程序框，并判断运行结果为A．55 B．-55 C．5 D．-58．设变量,x y满足20403x yx yy-≤⎧⎪≤+≤⎨⎪≤≤⎩，则32z x y=+的最大值为A．1 B．9 C．11 D．139．△ABC中，3,13,4AB BC AC===，则△ABC的面积是A．23B．33C．3 D．3310．设集合{}012345,,,,,M A A A A A A=，在M上定义运算“⊗”为：i j kA A A⊗=，其中k为i j+被4除的余数，,0,1,2,3,4,5i j=．则满足关系式20()a a A A⊗⊗=的()a a M∈的个数为A．2 B．3 C．4 D．5二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分.（一）必做题（11～13题）11．函数()1lnf x x x=-+的定义域为__▲__.12．若圆心在直线y x=上、半径为2的圆M与直线4x y+=相切，则圆M的方程是__▲__.13．若一个底面是正三角形的三棱柱的正视图如图2所示，则其表面积．．．等于__▲__.14．（坐标系与参数方程选做题）在极坐标系中，圆2ρ=上的点到直线()6sin3cos=+θθρ的距离的最小值为__▲__.15．（几何证明选讲选做题）如图3，D 是⊙O 的直径AB 延长线上一点，PD 是⊙O 的切线，P 是切点，∠D =30°，4,2AB BD ==，则PA =__▲__.三、解答题：本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. 16．（本小题满分12分）已知函数1cos 2)62cos()32sin()(2-+-+-=x x x x f ππ，x ∈R ．（1）求函数)(x f 的最小正周期； （2）求函数)(x f 在区间]4,4[ππ-上的最大值和最小值． 17．（本小题满分13分）某市电视台为了宣传举办问答活动，随机对该市15～65岁的人群抽样了n 人，回答问题统计结果如下图表所示：（1）分别求出a ，b ，x ，y 的值；（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组各抽取多少人?（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率．如图4，PA 垂直于⊙O 所在平面ABC ，AB 为⊙O 的直径，PA =AB =2，14BF BP =，C 是弧AB 的中点.（1）证明：BC ⊥平面PAC ； （2）证明：CF ⊥BP ；（3）求四棱锥C —AOFP 的体积.19．（本小题满分14分）已知S n 是数列{}n a 的前n 项和，且11=a ，)(2*1N n S na n n ∈=+.（1）求234,,a a a 的值； （2）求数列{}n a 的通项n a ； （3）设数列{}n b 满足2(2)n nb n a =+，求数列{}n b 的前n 项和n T .已知圆C 的方程为22270x y x ++-=，圆心C 关于原点对称的点为A ，P 是圆上任一点，线段AP 的垂直平分线l 交PC 于点Q .（1）当点P 在圆上运动时，求点Q 的轨迹L 方程； （2）过点B （1，21）能否作出直线2l ，使2l 与轨迹L 交于M 、N 两点，且点B 是线段MN 的中点，若这样的直线2l 存在，请求出它的方程和M 、N 两点的坐标；若不存在，请说明理由. 21．（本小题满分14分）。

肇庆市中小学教学质量评估 2013届高中毕业班第一次模拟试题数 学（理科）一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1．设1z i =-（i 是虚数单位），则2z z+=A ．2 B ．2i + C ．2i - D ．22i +2．集合{|lg 0}M x x =>，2{|9}N x x =≤，则M N =A ．(1,3)B ．[1,3)C ．(1,3]D ．[1,3] 3．已知向量(1,2),(1,0),(3,4)===a b c ．若λ为实数，()λ+⊥b a c ，则λ=A ．311-B ．113- C ．12 D ．354．公比为2的等比数列{n a } 的各项都是正数，且 41016a a =，则6a =A ．1B ．2C ．4D ．8 5．某程序框图如图1所示，则输出的结果S =A ．26B ．57C ．120D ．2476．下列函数中，既是偶函数又在区间0,+∞（）上单调递增的函数为A ．1y x -= B ．2log y x = C ．||y x = D ．2y x =- 7．已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图2所示，则其侧视图的面积为AC D8．在实数集R 中定义一种运算“⊕”，具有性质： ①对任意,,a b R a b b a ∈⊕=⊕； ②对任意,0a R a a ∈⊕=；③对任意,,,()()()()2a b c R a b c c ab a c b c c ∈⊕⊕=⊕+⊕+⊕-； 函数1()(0)f x x x x=⊕>的最小值为A ．4B ．3C ．．1二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分. （一）必做题（9～13题）9．不等式4|||2|≥++x x 的解集是 ______. 10. 2个好朋友一起去一家公司应聘，公司人事主管通知他们面试时间时说：“我们公司要从面试的人中招3个人，你们都被招聘进来的概率是701” .根据他的话可推断去面试的人有______个（用数字作答）. 11．若圆2210x y mx ++-=与直线1y =-相切，其圆心在y 轴的左侧，则m =______.12．在ABC ∆中，AC =，BC =2，︒=∠60B ，则ABC ∆的面积等于_____.13．已知不等式组⎪⎪⎩⎪⎪⎨⎧≥-≤+≥≥ay x y x y x ,2,0,0表示一个三角形区域（包括三角形的内部及边界），则实数a 的取值范围为______.14．（坐标系与参数方程选做题） 已知直线113:(24x tl t y t =+⎧⎨=-⎩为参数）与直线2:245l x y -=相交于点B ，又点(1,2)A ，则AB =______.15．（几何证明选讲选做题）如图4，已知圆O 的半径为2，从圆O 外一点A 引切线AB 和割线，C 为AD 与圆O 的交点，圆心O 到AD 的距AB =，则AC 的长为______.三、解答题:本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. 16.（本小题满分12分）已知函数)0,0)(4sin()(πϕϕ<<>+=A x A x f 在16x π=时取得最大值2.（1）求()f x 的最小正周期； （2）求()f x 的解析式； （3）若,02πα⎡⎤∈-⎢⎥⎣⎦，164165f πα⎛⎫+= ⎪⎝⎭，求sin 24πα⎛⎫- ⎪⎝⎭的值.17.（本小题满分13分）因台风灾害，我省某水果基地龙眼树严重受损，为此有关专家提出两种拯救龙眼树的方案，每种方案都需分四年实施．若实施方案1，预计第三年可以使龙眼产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第四年可以使龙眼产量为第三年产量的1.25倍、1.0倍的概率分别是0.5、0.5．若实施方案2，预计第三年可以使龙眼产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第四年可以使龙眼产量为第三年产量的1.2倍、1.0倍的概率分别是0.4、0.6．实施每种方案第三年与第四年相互独立，令()1,2i i ξ=表示方案i 实施后第四年龙眼产量达到灾前产量的倍数．（1）写出ξ1、ξ2的分布列；（2）实施哪种方案，第四年龙眼产量超过灾前产量的概率更大?（3）不管哪种方案，如果实施后第四年龙眼产量达不到、恰好达到、超过灾前产量，预计利润分别为10万元、15万元、20万元．问实施哪种方案的平均利润更大?如图5，PA 垂直⊙O 所在平面ABC ，AB 为⊙O 的直径，PA =AB ，14BF BP =，C 是弧AB 的中点.（1）证明：BC ⊥平面PAC ； （2）证明：CF ⊥BP ；（3）求二面角F —OC —B 的平面角的正弦值.19. （本小题满分14分）已知椭圆22122:1(0)x y C a b a b+=>>的离心率为e =，直线:2l y x =+与以原点为圆心、以椭圆1C 的短半轴长为半径的圆O 相切.（1）求椭圆C 1的方程；（2）设椭圆1C 的左焦点为1F ，右焦点为2F ，直线1l 过点1F ，且垂直于椭圆的长轴，动直线2l 垂直于1l ，垂足为点P ，线段2PF 的垂直平分线交2l 于点M ，求点M 的轨迹2C 的方程； （3）设2C 与x 轴交于点Q ，不同的两点R 、S 在2C 上，且满足0=⋅，求||QS的取值范围.20.（本小题满分14分）已知S n 是数列{}n a 的前n 项和，且11=a ，)(2*1N n S na n n ∈=+. （1）求234,,a a a 的值； （2）求数列{}n a 的通项n a ； （3）设数列{}n b 满足21111,2n n n kb b b b a +==+，求证：当n k ≤时有1n b <.以其面积为12S ==8B 解析：根据条件③，对于任意的,,a b c 有()()()()2a b c c ab a c b c c ⊕⊕=⊕+⊕+⊕-，∴取0c =得()00()(0)(0)20a b ab a b ⊕⊕=⊕+⊕+⊕-⋅得①②得00a a a ⊕=⊕=对任意实数a 都成立，代入上式得：a b ab a b ⊕=++这就是运算⊕的定义,将其代入题目检验符合①②③，∴1111()113f x x x x x x x x x =⊕=⋅++=++≥=，当且仅当1x =时“=”成立，即函数1()(0)f x x x x=⊕>的最小值为3.二、填空题9. (][)+∞-∞-,13, 13. (,2][0,2)-∞- 14.5215. 3 三、解答题 16．（本小题满分12分）解：（1）()f x 的最小正周期为242T ππ== （2分） （2）由()f x 的最大值是2知，2A =， （3分）又()2sin 421616max f x f ππϕ⎛⎫⎛⎫==⨯+= ⎪ ⎪⎝⎭⎝⎭，即sin 14πϕ⎛⎫+= ⎪⎝⎭， （4分）∵0ϕπ<<，∴5444πππϕ<+<，∴42ππϕ+=，∴4πϕ= （5分）∴()2sin(4)4f x x π=+（6分）（3）由（2）得1162sin 441641645f πππαα⎡⎤⎛⎫⎛⎫+=++= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 即3sin()25πα+=，∴3cos 5α=， （7分）∵,02πα⎡⎤∈-⎢⎥⎣⎦，∴4sin 5α===- （8分）∴4324sin 22sin cos 25525ααα⎛⎫==⨯-⨯=- ⎪⎝⎭ （9分）2237cos 22cos 121525αα⎛⎫=-=⨯-=- ⎪⎝⎭（10分）∴sin 2sin 2cos cos 2sin 444πππααα⎛⎫-=- ⎪⎝⎭2472525=-+=（12分）17．（本小题满分13分） 解：（1（3分）（6分）（2）由（1）可得ξ1＞1的概率P （ξ1＞1）= 0.15 + 0.15 = 0.3， （7分） ξ2＞1的概率P （ξ2＞1）= 0.24 + 0.08 = 0.32， （8分） ∵P （ξ2＞1）＞P （ξ1＞1），∴实施方案2，第四年产量超过灾前概率更大. （9分） （3）设实施方案1、2的平均利润分别为利润A 、利润B ，根据题意，利润A =（0.2 +0.15）×10 + 0.35×15 +（0.15 + 0.15）×20 = 14.75（万元） （10分） 利润B =（0.3 + 0.2）×10 + 0.18×15 + （0.24 + 0.08）×20 = 14.1（万元） （11分） ∵利润A ＞利润B ，∴实施方案1平均利润更大. （13分） 18．（本小题满分13分）（1）证明：∵PA ⊥平面ABC ，BC ⊂平面ABC ，∴BC ⊥PA . （1分） ∵∠ACB 是直径所对的圆周角，∴90o ACB ∠=，即BC ⊥AC . （2分） 又∵PA AC A = ，∴BC ⊥平面PAC . （3分） （2）证明：∵PA ⊥平面ABC ，OC ⊂平面ABC ，∴OC ⊥PA . （4分） ∵C 是弧AB 的中点， ∴∆ABC 是等腰三角形，AC =BC ， 又O 是AB 的中点，∴OC ⊥AB . （5分）又∵PA AB A = ，∴OC ⊥平面PAB ，又PB ⊂平面PAB ， ∴BP OC ⊥. （6分） 设BP 的中点为E ，连结AE ，则//OF AE ，AE BP ⊥ ∴BP OF ⊥. （7分）∵OC OF O = ，∴BP ⊥平面CFO . 又CF ⊂平面CFO ，∴CF BP ⊥. （8分） （3）解：由（2）知OC ⊥平面PAB ，∴OF OC ⊥，OC OB ⊥， （9分） ∴BOF ∠是二面角F OC B --的平面角. （10分） 又∵BP OF ⊥，045FBO ∠=，∴045FOB ∠=， （12分）∴sin FOB ∠=，即二面角F OC B --. （13分） 19．（本小题满分14分）解：（1）由直线:2l y x =+与圆222x y b +=b =，即b =. （2分）由3e =，得222213b e a =-=，所以a = （3分）所以椭圆的方程是221:132x y C +=. （4分） （2）由条件，知2||||MF MP =，即动点M 到定点2F 的距离等于它到直线1:1l x =-的距离，由抛物线的定义得点M 的轨迹2C 的方程是x y 42=. （7分）（3）由（2），知(0,0)Q ，设221212,,,44y y R y S y ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，∴222121,,,y y y QR y RS y y ⎛⎫⎛⎫-==- （8分）由0=⋅，得()()222121121016y y y y y y -+-= （9分）∵12y y ≠，∴21116y y y ⎛⎫=-+ ⎪⎝⎭，∴222121256323264y y y =++≥=，当且仅当2121256y y =，即14y =±时等号成立. （11分）又||QS == （12分）∵2264y ≥，∴当2264y =，即28y =±时，min ||QS =（13分）故||QS的取值范围是)⎡+∞⎣. （14分）20．（本小题满分14分）解：（1）由111,2()n n a na S n N *+==∈得 2122a a == ， （1分）32123a S a a ==+=， （2分）由43123322()a S a a a ==++得44a = （3分） （2）当1>n 时，由12n n na S += ① ，得1(1)2n n n a S --= ② （4分） ①－②得11(1)2()n n n n na n a S S +---=-，化简得1(1)n n na n a +=+，∴11n n a n a n++=（1>n ）. （5 分） ∴22=a ，3232a a =，……，11n n a na n -=- （6 分）以上（1n -）个式子相乘得n n na n =-⨯⨯⨯=1232 （1>n ） （7 分）又11=a ，∴()n a n n N *=∈ （8 分）（3）∵0>=n a n ，0211>=b ，n n k n b b a b +=+211， ∴{}n b 是单调递增数列，故要证：当n k ≤时，1n b <，只需证1k b <. （9分）（i ）当1k =时 ，1112b =<，显然成立； （10分）（ii ）当2k ≥时，∵01>>+n n b b ，n n kn b b a b +=+211， ∴n n n n b b b kb +<++111，∴1111n n b b k +->-. （11分） ∴112232111111111111k k k k k k k b b b b b b b b b b -----⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 112k k k k -+>-+= （12分）∴11k kb k <<+. （13分） 综上，当n k ≤时有1n b <. （14分）。

2013年广东省肇庆市高考数学一模试卷（文科）参考答案与试题解析一、选择题本大题共10小题，每小题5分，满分50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）（2013•肇庆一模）设i为虚数单位，复数z1=a﹣3i，z2=2+bi，其中a、b∈R．若z1=z2，则ab=（）A．﹣1 B．5C．﹣6 D．6考点：复数相等的充要条件．专题：计算题．分析：利用复数相等的条件即可得出所求参数的方程，解之即可．解答：解：∵复数z1=a﹣3i，z2=2+bi，其中a、b∈R，z1=z2，∴，∴ab=2×（﹣3）=﹣6．故选C．点评：熟练掌握复数相等的定义是解题的关键．2．（5分）（2013•肇庆一模）已知全集U={﹣2，﹣1，0，1，2，3，4，5，6}，集合M={大于﹣2且小于5的整数}，则∁U M=（）A．∅B．{6} C．{﹣2，6} D．{﹣2，5，6}考点：补集及其运算．专题：计算题．分析：利用列举法化简集合M，然后直接利用补集运算求解．解答：解：由M={大于﹣2且小于5的整数}={﹣1，0，1，2，3，4}，而U={﹣2，﹣1，0，1，2，3，4，5，6}，所以∁U M={﹣2，5，6}．故选D．点评：本题考查了补集及其运算，是基础的会考题型．3．（5分）（2013•肇庆一模）命题“∂x∈R，2x＜1”的否定是（）A．∀x∈R，2x≥1 B．∀x∈R，2x＜1 C．∂x∈R，2x≥1 D．∂x∈R，2x＞1考点：特称命题；命题的否定．专题：规律型．分析：利用特称命题的否定是全称命题写出结果即可判断选项．解答：解：因为特称命题的否定是全称命题，所以命题“∂x∈R，2x＜1”的否定：∀x∈R，2x≥1；故选A．点评：本题考查特称命题与全称命题的否定关系的应用，基本知识的考查．4．（5分）（2013•肇庆一模）甲、乙两种水稻试验品种连续5年的单位面积平均产量如下（单位：t/hm2），根据这组数据下列说法正确的是（）品种第1年第2年第3年第4年第5年甲9.8 9.9 10.1 10 10.2乙9.4 10.3 10.8 9.7 9.8A．甲品种的样本平均数大于乙品种的样本平均数B．甲品种的样本平均数小于乙品种的样本平均数C．甲品种的样本方差大于乙品种的样本方差D．甲品种的样本方差小于乙品种的样本方差考点：极差、方差与标准差．专题：计算题；概率与统计．分析：由平均数计算公式，算出甲=乙=10，从而排除A、B两项；再由方差计算公式算出即可得到甲品种的样本方差小于乙品种的样本方差，从而得到D项是正确答案．解答：解：根据题意，得甲品种的样本平均数为甲=（9.8+9.9+10.1+10+10.2）=10；乙品种的样本平均数为乙=（9.4+10.3+10.8+9.7+9.8）=10∴甲品种的样本平均数与乙品种的样本平均数相等甲品种的样本方差为s2甲=[（9.8﹣10）2+（9.9﹣10）2+（10.1﹣10）2+（10﹣10）2+（10.2﹣10）2]=0.020；乙品种的样本方差为s2乙=[（9.4﹣10）2+（10.3﹣10）2+（10.8﹣10）2+（9.7﹣10）2+（9.8﹣10）2]=0.244∵0.020＜0.244，∴甲品种的样本方差小于乙品种的样本方差故选：D点评：本题给出两组数据，要求我们比较它们的平均数与方差的大小，着重考查了平均数、方差、标准差等样本特殊数的计算公式的知识，属于基础题．做统计题目时，请同学们注意所得结果应该保持同样的精确度，如本题的方差写成s2甲=0.02而s2乙=0.244，就不太规范了．5．（5分）（2013•肇庆一模）已知等差数列{a n}，满足a3+a9=8，则此数列的前11项的和S11=（）A．44 B．33 C．22 D．11考点：等差数列的前n项和；等差关系的确定．专题：等差数列与等比数列．分析：由等差数列的性质可得a1+a11=a3+a9=8，代入求和公式可得答案．解答：解：由等差数列的性质可得a1+a11=a3+a9=8，故S11===44故选A点评：本题考查等差数列的性质和求和公式，属基础题．6．（5分）（2013•肇庆一模）平面上有三个点A（2，2）、M（1，3）、N（7，k），若向量与垂直，则k=（）A．6B．7C．8D．9考点：数量积判断两个平面向量的垂直关系．专题：平面向量及应用．分析：利用向量⊥⇔=0即可得出．解答：解：∵=（﹣1，1），=（5，K﹣2），．∴=﹣5+K﹣2=0，解得k=7．故选B．点评：熟练掌握向量⊥⇔=0是解题的关键．7．（5分）（2013•肇庆一模）阅读如图的程序框，并判断运行结果为（）A．55 B．﹣55 C．5D．﹣5考点：程序框图．专题：图表型．分析：框图首先给变量S和变量i赋值，然后对i是否大于10进行判断，不大于10，继续判断i是否为偶数，是执行路径S=S﹣i，否执行路径S=S+i，再执行i=i+1，依次循环执行，当i大于10时跳出循环，输出S的值．解答：解：框图首先给变量S和变量i赋值，S=0，i=1．判断i＞10不成立，判断1是偶数不成立，执行S=0+1=1，i=1+1=2；判断i＞10不成立，判断2是偶数成立，执行S=1﹣2=﹣1，i=2+1=3；判断i＞10不成立，判断3是偶数不成立，执行S=﹣1+3=2，i=3+1=4；判断i＞10不成立，判断4是偶数成立，执行S=2﹣4=﹣2，i=4+1=5；判断i＞10不成立，判断5是偶数不成立，执行S=﹣2+5=3，i=5+1=6；判断i＞10不成立，判断6是偶数成立，执行S=3﹣6=﹣3，i=6+1=7；。

2013届高考理科数学第一次模拟试题（附答案）江门市2013年高考模拟考试数学（理科）本试卷共4页，21题，满分150分，测试用时120分钟．参考公式：锥体的体积公式，其中是锥体的底面积，是锥体的高．如果事件、互斥，那么．一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．⒈已知函数定义域为，定义域为，则A．B．C．D．⒉在复平面内，是原点，向量对应的复数是（其中，是虚数单位），如果点关于实轴的对称点为点，则向量对应的复数是A．B．C．D．⒊采用系统抽样方法从1000人中抽取50人做问卷调查，为此将他们随机编号为1，2，…，1000，适当分组后在第一组采用简单随机抽样的方法抽到的号码为8．抽到的50人中，编号落入区间1，400]的人做问卷A，编号落入区间401，750]的人做问卷B，其余的人做问卷C．则抽到的人中，做问卷C的人数为A．12B．13C．14D．15⒋右图是某个四面体的三视图，该四面体的体积为A．72B．36C．24D．12⒌在中，若，，，则A．B．C．D．⒍若、，则是的A．充分非必要条件B．必要非充分条件C．充要条件D．非充分非必要条件⒎已知、满足，则的取值范围是A．B．C．D．⒏设是定义在上的周期为2的偶函数，当时，，则在区间内零点的个数为A．2013B．2014C．3020D．3024二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．(一)必做题（9～13题）⒐已知数列的首项，若，，则．⒑执行程序框图，如果输入，那么输出．⒒如图，在棱长为2的正方体内（含正方体表面）任取一点，则的概率．⒓在平面直角坐标系中，若双曲线的焦距为，则．⒔在平面直角坐标系中，直线（）与抛物线所围成的封闭图形的面积为，则．(二)选做题（14、15题，考生只能从中选做一题）⒕（坐标系与参数方程选做题）在极坐标系（）中，曲线与的交点的极坐标为．⒖（几何证明选讲选做题）如图，圆内的两条弦、相交于，，．若到的距离为，则到的距离为．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．⒗（本小题满分12分）已知函数（，）的最小值为．⑴求；⑵若函数的图象向左平移（）个单位长度，得到的曲线关于轴对称，求的最小值．⒘（本小题满分14分）春节期间，某商场决定从3种服装、2种家电、3种日用品中，选出3种商品进行促销活动。

2013年广东省肇庆市高考数学一模试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，满分40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设z=1﹣i（i是虚数单位），则=（）A．2B．2+i C．2﹣i D．2+2i考点：复数代数形式的乘除运算．专题：计算题．分析：利用复数的运算法则和共轭复数的定义即可得出．解答：解：∵z=1﹣i，∴，==．∴==1+i+1+i=2+2i．故选D．点评：熟练掌握复数的运算法则和共轭复数的定义是解题的关键．2．（5分）（2013•肇庆一模）集合M={x|lgx＞0}，N={x|x2≤9}，则M∩N=（）A．（1，3）B．[1，3）C．（1，3]D．[1，3]考点：交集及其运算．分析：根据对数函数的单调性求出集合M，解不等式x2≤9求出集合N，再进行交集运算．解答：解：∵M={x|lgx＞0}={x|x＞1}，N={x|x2≤9}={x|﹣3≤x≤3}，∴M∩N={x|1＜x≤3}，故选C．点评：本题主要考查对数函数的单调性和特殊点，两个集合的交集的定义和求法，属于基础题．3．（5分）（2013•菏泽二模）已知向量=（1，2），=（1，0），=（3，4）．若λ为实数，（+λ）⊥，则λ=（）A．B．C．D．考点：平面向量数量积的运算；数量积判断两个平面向量的垂直关系．专题：平面向量及应用．分析：由向量的运算可得的坐标，由向量的垂直可得关于λ的方程，解之可得答案．解答：解：由题意可知：=（1，0）+λ（1，2）=（1+λ，2λ）由（）⊥可得：3（1+λ）+4×2λ=0，解之可得λ=故选A点评：本题考查平面向量数量积的运算以及向量的垂直与数量积的关系，属中档题．4．（5分）（2013•肇庆一模）公比为2的等比数列{a n} 的各项都是正数，且a4a10=16，则a6=（）A．1B．2C．4D．8考点：等比数列的通项公式．专题：等差数列与等比数列．分析：由题意结合等比数列的性质可得a7=4，由通项公式可得a6．解答：解：由题意可得=a4a10=16，又数列的各项都是正数，故a7=4，故a6===2故选B点评：本题考查等比数列的通项公式，属基础题．5．（5分）（2013•肇庆一模）某程序框图如图所示，则输出的结果S=（）A．26 B．57 C．120 D．247考点：程序框图．专题：图表型．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算变量S的值，并输出K＞4时，变量S的值，模拟程序的运行，用表格对程序运行过程中各变量的值进行分析，不难得到输出结果．解答：解：程序在运行过程中各变量的值如下表示：是否继续循环k S循环前/1 1第一圈是 2 4第二圈是 3 11第三圈是 4 26第四圈是 5 57第五圈否故选B．点评：根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．6．（5分）（2013•肇庆一模）下列函数中，既是偶函数又在区间（0，+∞）上单调递增的函数为（）A．y=x﹣1B．y=log2x C．y=|x| D．y=﹣x2考点：奇偶性与单调性的综合．专题：计算题；函数的性质及应用．分析：根据y=x﹣1=在区间（0，+∞）上单调递减，得A项不符合题意；根据y=log2x的定义域不关于原点对称，得y=log2x不是偶函数，得B项不符合题意；根据y=﹣x2的图象是开口向下且关于x=0对称的抛物线，得y=﹣x2的在区间（0，+∞）上为减函数，得D项不符合题意．再根据函数单调性与奇偶性的定义，可得出只有C项符合题意．解答：解：对于A，因为函数y=x﹣1=，在区间（0，+∞）上是减函数不满足在区间（0，+∞）上单调递增，故A不符合题意；对于B，函数y=log2x的定义域为（0，+∞），不关于原点对称故函数y=log2x是非奇非偶函数，故B不符合题意；对于C，因为函数y=|x|的定义域为R，且满足f（﹣x）=f（x），所以函数y=|x|是偶函数，而且当x∈（0，+∞）时y=|x|=x，是单调递增的函数，故C符合题意；对于D，因为函数y=﹣x2的图象是开口向下的抛物线，关于直线x=0对称所以函数y=﹣x2的在区间（0，+∞）上为减函数，故D不符合题意故选：C点评：本题给出几个基本初等函数，要求我们找出其中的偶函数且在区间（0，+∞）上单调递增的函数，着重考查了基本初等函数的单调性与奇偶性等知识，属于基础题．7．（5分）（2013•肇庆一模）已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为（）A．B．C．D．考点：简单空间图形的三视图；由三视图求面积、体积．专题：计算题．分析：由题意可得侧视图为三角形，且边长为边长为1的正三角形的高线，高等于正视图的高，分别求解代入三角形的面积公式可得答案．解答：解：∵边长为1的正三角形的高为=，∴侧视图的底边长为，又侧视图的高等于正视图的高，故所求的面积为：S==故选A点评：本题考查简单空间图形的三视图，涉及三角形面积的求解，属基础题．8．（5分）（2013•肇庆一模）在实数集R中定义一种运算“⊕”，具有性质：①对任意a，b∈R，a⊕b=b⊕a；②对任意a∈R，a⊕0=a；③对任意a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c．函数f（x）=x⊕（x＞0）的最小值为（）A．4B．3C．2D．1考点：进行简单的合情推理；函数的值域．专题：计算题；新定义．分析：根据题中给出的对应法则，可得f（x）=（x⊕）⊕0=1+x+，利用基本不等式求最值可得x+≥2，当且仅当x=1时等号成立，由此可得函数f（x）的最小值为f（1）=3．解答：解：根据题意，得f（x）=x⊕=（x⊕）⊕0=0⊕（x•）+（x⊕0）+（⊕0 ）﹣2×0=1+x+即f（x）=1+x+∵x＞0，可得x+≥2，当且仅当x==1，即x=1时等号成立∴1+x+≥2+1=3，可得函数f（x）=x⊕（x＞0）的最小值为f（1）=3故选：B点评：本题给出新定义，求函数f（x）的最小值．着重考查了利用基本不等式求最值、函数的解析式求法和简单的合情推理等知识，属于中档题．二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分.必做题（9～13题），选做题（14、15题）9．（5分）（2013•肇庆一模）不等式|x+2|+|x|≥4的解集是（﹣∞，﹣3]∪[1，+∞）．考点：绝对值不等式的解法．专题：不等式的解法及应用．分析：利用绝对值的几何意义直接求解即可．解答：解：不等式|x+2|+|x|≥4，由绝对值的几何意义可知，数轴上的点到0与﹣2点距离之和大于等于4的实数，所以不等式的解集为：（﹣∞，﹣3]∪[1，+∞）．故答案为：（﹣∞，﹣3]∪[1，+∞）．点评：本题考查绝对值不等式的解法，绝对值的几何意义的应用，考查计算能力．10．（5分）（2013•肇庆一模）2个好朋友一起去一家公司应聘，公司人事主管通知他们面试时间时说：“我们公司要从面试的人中招3个人，你们都被招聘进来的概率是”．根据他的话可推断去面试的人有21个（用数字作答）．ξ0 1 2 3P6125 a b24125考点：等可能事件．专题：概率与统计．分析：设出去公司面试的人数n，从面试的人数中任取3人的方法种数是，两人都被聘用的方法种数是．则两人都被聘用的概率即为．解答：解：设去面试的人数为n，则2人都被招聘的概率为．整理得n2﹣n﹣420=0．解得n=﹣20（舍）或n=21．所以，去面试的是21人．故答案为21．点评：本题考查了等可能事件的概率，解答的关键是正确理解题意，求出从面试人数中任取3人的事件数及两人都被聘用的基本事件个数，是基础题．11．（5分）（2013•肇庆一模）若圆x2+y2+mx﹣=0与直线y=﹣1相切，且其圆心在y轴的左侧，则m的值为考点：直线与圆的位置关系．专题：计算题．分析：将圆的方程配方后求出圆心，据圆x2+y2+mx﹣=0与直线y=﹣1相切求出m的值．解答：解：圆方程配方得（x+）2+y2=，圆心为（﹣，0）．由条件知﹣＜0，即m＞0．又圆与直线y=﹣1相切，则0﹣（﹣1）=，即m2=3，∴m=．点评：本题考查直线和圆的位置关系．12．（5分）（2013•肇庆一模）在△ABC中，AC=，BC=2，B=60°，则△ABC的面积等于．考点：余弦定理；三角形的面积公式．专题：计算题；解三角形．分析：通过余弦定理求出AB的长，然后利用三角形的面积公式求解即可．解答：解：设AB=c，在△ABC中，由余弦定理知AC2=AB2+BC2﹣2AB•BCcosB，即7=c2+4﹣2×2×c×cos60°，c2﹣2c﹣3=0，又c＞0，∴c=3．S△ABC=AB•BCsinB=BC•h可知S△ABC==．故答案为：点评：本题考查三角形的面积求法，余弦定理的应用，考查计算能力．13．（5分）（2013•肇庆一模）已知不等式组表示一个三角形区域（包括三角形的内部及边界），则实数a的取值范围为（﹣∞，﹣2]∪[0，2）．考点：二元一次不等式（组）与平面区域．专题：不等式的解法及应用．分析：本题考查的是简单线性规划问题．线性规划要注意数形结合，要综合运用多方面的知识．特别要注意区域的边界．因此在解答此题时应先根据先行约束条件画出可行域，然后根据可行域的特点及条件：表示的平面区域是一个三角形及其内部，找出不等关系即可．解答：解：由题意可知：画可行域如图：不等式组表示的平面区域是一个三角形及其内部，且当直线x﹣y=a过A（2，0）点时，a=2；当直线x﹣y=a过O（0，0）点时，a=0；当直线x﹣y=a过B（0，2）点时，a=﹣2．结合图形得，所以a的取值范围是：a≤﹣2或0≤a＜2．故答案为：（﹣∞，﹣2]∪[0，2）．点评：本题考查的是简单线性规划问题．在解答的过程当中成分体现了数形结合的思想和构成三角形的相关知识．特别是对线性规划中的区域边界考查得到了充分的体现．值得同学们体会反思．14．（5分）（2013•肇庆一模）（坐标系与参数方程选做题）已知直线（t为参数）与直线l2：2x﹣4y=5相交于点B，又点A（1，2），则|AB|=．考点：参数方程化成普通方程；两点间的距离公式．专题：计算题；直线与圆．分析：先把直线l1的方程化为普通方程，与直线l2的方程联立可求得点B的坐标，然后由两点间距离公式可求得|AB|．解答：解：由，得4x+3y﹣10=0，由解得，即B（，0），所以|AB|==，故答案为：．点评：本题考查参数方程与普通方程的互化、两点间距离公式，属基础题．15．（2013•肇庆一模）（几何证明选讲选做题）如图所示，已知圆O的半径为2，从圆O外一点A引切线AB和割线AD，C为AD与圆O的交点，圆心O到AD的距离为，，则AC的长为3．考点：与圆有关的比例线段；圆的切线的性质定理的证明．专题：计算题．分析：利用圆心到直线的距离，求出CD的值，然后利用圆的切割线定理求解即可．解答：解：因为圆O的切线AB和割线AD，所以由切割线定理可知AB2=AC•AD，圆心O到AD的距离为，圆O的半径为2，所以CD=2=2，，所以AB2=AC•（AC+CD），即15=AC•（AC+2），解得AC=3，故答案为：3．点评：本题考查弦心距、半径、半弦长满足的勾股定理以及切割线定理的应用，考查计算能力．三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.16．（12分）（2013•肇庆一模）已知函数f（x）=Asin（4x+φ）（A＞0，0＜φ＜π）在时取得最大值2．（1）求f（x）的最小正周期；（2）求f（x）的解析式；（3）若，，求的值．考点：三角函数的周期性及其求法；两角和与差的正弦函数；由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题；三角函数的图像与性质．分析：（1）根据函数表达得ω=4，结合三角函数的周期公式即可得出f（x）的最小正周期的值；（2）由函数f（x）在时取得最大值2，得+φ=+2kπ（k∈Z），结合0＜φ＜π取k=0得，从而得到f（x）的解析式；（3）由（2）求出的解析式代入，结合诱导公式化简得，由同角三角函数的关系结合算出sinα=﹣，用二倍角的三角公式算出sin2α、cos2α之值，代入的展开式，即可得到的值．解答：解：（1）∵函数表达式为：f（x）=Asin（4x+φ），∴ω=4，可得f（x）的最小正周期为（2分）（2）∵f（x）在时取得最大值2，∴A=2，且时4x+φ=+2kπ（k∈Z），即+φ=+2kπ（k∈Z），（4分）∵0＜φ＜π，∴取k=0，得（5分）∴f（x）的解析式是；（6分）（3）由（2）得，即，可得，（7分）∵，∴，（8分）∴，（9分），（10分）∴=．（12分）点评：本题给出y=Asin（ωx+φ）中的部分参数，根据函数的最大值及其相应的x值求函数的表达式，并依此求特殊的三角函数的值．着重考查了三角函数的图象与性质、三角恒等变换、诱导公式和同角三角函数基本关系等知识，属于中档题．17．（13分）（2013•肇庆一模）因台风灾害，我省某水果基地龙眼树严重受损，为此有关专家提出两种拯救龙眼树的方案，每种方案都需分四年实施．若实施方案1，预计第三年可以使龙眼产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第四年可以使龙眼产量为第三年产量的1.25倍、1.0倍的概率分别是0.5、0.5．若实施方案2，预计第三年可以使龙眼产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第四年可以使龙眼产量为第三年产量的1.2倍、1.0倍的概率分别是0.4、0.6．实施每种方案第三年与第四年相互独立，令ξi（i=1，2）表示方案i 实施后第四年龙眼产量达到灾前产量的倍数．（1）写出ξ1、ξ2的分布列；（2）实施哪种方案，第四年龙眼产量超过灾前产量的概率更大？（3）不管哪种方案，如果实施后第四年龙眼产量达不到、恰好达到、超过灾前产量，预计利润分别为10万元、15万元、20万元．问实施哪种方案的平均利润更大？考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分析：（1）根据题意得到两个变量的可能取值，根据条件中所给的方案一和方案二的两年龙眼产量的变化有关数据写出两个变量的分布列．（2）根据两种方案对应的数据，做出方案一、方案二两年后龙眼产量超过灾前产量的概率，得到结论：方案二两年后龙眼产量超过灾前产量的概率更大．（3）根据两年后龙眼产量和灾前产量的比较，做出达不到灾前产量，达到灾前产量，超过灾前产量的概率，列出龙眼带来效益的分布列，做出期望．解答：解：（1）ξ1的分布列为：ξ10.8 0.9 1.0 1.125 1.25P10.2 0.15 0.35 0.15 0.15（3分）ξ2的分布列为ξ20.8 0.96 1.0 1.2 1.44P20.3 0.2 0.18 0.24 0.08（6分）（2）由（1）可得ξ1＞1的概率P（ξ1＞1）=0.15+0.15=0.3，（7分）ξ2＞1的概率P（ξ2＞1）=0.24+0.08=0.32，（8分）∵P（ξ2＞1）＞P（ξ1＞1），∴实施方案2，第四年产量超过灾前概率更大．（9分）（3）设实施方案1、2的平均利润分别为利润A、利润B，根据题意，利润A=（0.2+0.15）×10+0.35×15+（0.15+0.15）×20=14.75（万元）（10分）利润B=（0.3+0.2）×10+0.18×15+（0.24+0.08）×20=14.1（万元）（11分）∵利润A＞利润B，∴实施方案1平均利润更大．（13分）点评：本题考查离散型随机变量的分布列和期望，考查解决实际问题的能力，考查对题干较长的应用题的理解，是一个综合题．18．（13分）（2013•肇庆一模）如图，PA垂直⊙O所在平面ABC，AB为⊙O的直径，PA=AB，BF=，C是弧AB的中点．（1）证明：BC⊥平面PAC；（2）证明：CF⊥BP；（3）求二面角F﹣OC﹣B的平面角的正弦值．考点：二面角的平面角及求法；直线与平面垂直的判定；直线与平面垂直的性质．专题：空间位置关系与距离；空间角．分析：（1）利用线面垂直的性质及已知PA⊥平面ABC，可得BC⊥PA．再利用∠ACB是直径所对的圆周角，可得BC⊥AC．再利用线面垂直的判定定理即可证明结论；（2）由于PA⊥平面ABC，利用线面垂直的性质即可得到OC⊥PA．再利用等腰三角形的性质可得OC⊥AB，得到OC⊥平面PAB，取BP的中点为E，连接AE，可得OF∥AE，AE⊥BP，进而得到BP⊥平面CFO即可．（3）利用（2）知OC⊥平面PAB，可得OF⊥OC，OC⊥OB，于是∠BOF是二面角F﹣OC ﹣B的平面角．由已知可得∠FOB=45°即可得出．解答：（1）证明：∵PA⊥平面ABC，BC⊂平面ABC，∴BC⊥PA．∵∠ACB是直径所对的圆周角，∴∠ACB=90°，即BC⊥AC．又∵PA∩AC=A，∴BC⊥平面PAC．（2）∵PA⊥平面ABC，OC⊂平面ABC，∴OC⊥PA．∵C是弧AB的中点，∴△ABC是等腰三角形，AC=BC，又O是AB的中点，∴OC⊥AB．又∵PA∩AB=A，∴OC⊥平面PAB，又PB⊂平面PAB，∴BP⊥OC．设BP的中点为E，连接AE，则OF∥AE，AE⊥BP，∴BP⊥OF．∵OC∩OF=O，∴BP⊥平面CFO．又CF⊂平面CFO，∴CF⊥BP．（3）解：由（2）知OC⊥平面PAB，∴OF⊥OC，OC⊥OB，∴∠BOF是二面角F﹣OC﹣B的平面角．又∵BP⊥OF，∠FBO=45°，∴∠FOB=45°，∴，即二面角FOOC﹣B的平面角的正弦值为．点评：本题综合考查了线面垂直的判定与性质定理、圆的性质、三角形的中位线定理、等腰三角形的性质、二面角等基础知识与基本技能，考查了空间想象能力、推理能力和计算能力．19．（14分）（2013•梅州二模）已知椭圆的离心率为，直线l：y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆相切．（1）求椭圆C1的方程；（2）设椭圆C1的左焦点为F1，右焦点为F2，直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直于直线l1，垂足为点P，线段PF2的垂直平分线交l2于点M，求点M的轨迹C2的方程；（3）设C2与x轴交于点Q，不同的两点R，S在C2上，且满足，求的取值范围．考点：圆与圆锥曲线的综合；平面向量数量积的运算；轨迹方程；椭圆的标准方程．专题：计算题；压轴题．分析：（1）先由离心率为，求出a，b，c的关系，再利用直线l：y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆相切，求出b即可求椭圆C1的方程；（2）把题中条件转化为动点M的轨迹是以l1：x=﹣1为准线，F2为焦点的抛物线，即可求点M的轨迹C2的方程；（3）先设出点R，S的坐标，利用求出点R，S的坐标之间的关系，再用点R，S 的坐标表示出，利用函数求最值的方法即可求的取值范围．解答：解：（1）由得2a2=3b2，又由直线l：y=x+2与圆x2+y2=b2相切，得，，∴椭圆C1的方程为：．（4分）（2）由MP=MF2得动点M的轨迹是以l1：x=﹣1为准线，F2为焦点的抛物线，∴点M的轨迹C2的方程为y2=4x．（8分）（3）Q（0，0），设，∴，由，得，∵y1≠y2∴化简得，（10分）∴（当且仅当y1=±4时等号成立），∵，又∵y22≥64，∴当y22=64，即y2=±8时，∴的取值范围是．（13分）点评：本题是对圆与椭圆知识的综合考查．当直线与圆相切时，可以利用圆心到直线的距离等于半径求解．，也可以把直线与圆的方程联立让对应方程的判别式为0求解．20．（14分）（2013•肇庆一模）已知S n是数列{a n}的前n项和，且a1=1，．（1）求a2，a3，a4的值；（2）求数列{a n}的通项a n；（3）设数列{b n}满足，求证：当n≤k时有b n＜1．考点：数列递推式；等差数列的通项公式；数列的求和．专题：等差数列与等比数列．分析：（1）由a1=1，．可得a2=2a1=2；及a3=S2=a1+a2=3可得a4=4；（2）当n＞1时，由na n+1=2S n，再构造一式：（n﹣1）a n=2S n﹣1，两式相减可化得，从而有a2=2，，…，以上（n﹣1）个式子相乘得数列{a n}的通项a n（3）分析可得{b n}是单调递增数列，故要证：当n≤k时，b n＜1，只需证b k＜1．下面分（i）当k=1时和（ii）当k≥2时，结合裂项法等求数列的前n项和可得当n≤k时有b n＜1．解答：解：（1）由a1=1，．得a2=2a1=2，（1分）a3=S2=a1+a2=3，（2分）由3a4=2S3=2（a1+a2+a3），得a4=4 （3分）（2）当n＞1时，由na n+1=2S n①，得（n﹣1）a n=2S n﹣1②（4分）①﹣②得na n+1﹣（n﹣1）a n=2（S n﹣S n﹣1），化简得na n+1=（n+1）a n，∴（n＞1）．（5 分）∴a2=2，，…，（6 分）以上（n﹣1）个式子相乘得a n=2×…×（n＞1）（7 分）又a1=1，∴a n=n（n∈N+）（8 分）（3）∵a n=n＞0，b1=＞0，b n+1=b+b n，∴{b n}是单调递增数列，故要证：当n≤k时，b n＜1，只需证b k＜1．（9分）（i）当k=1时，b1=＜1，显然成立；（10分）（ii）当k≥2时，∵b n+1＞b n＞0，，∴，∴．（11分）∴…+＞﹣（12分）∴b k＜＜1．（13分）综上，当n≤k时有b n＜1．（14分）点评：本题是数列问题比较经典的考题，是高考试卷考查数列的常见题型，首先要根据定义法，迭代法、构造数列法等求出数列的通项公式，再利用裂项法等求数列的前n项和．21．（14分）（2013•肇庆一模）若f（x）=其中a∈R（1）当a=﹣2时，求函数y（x）在区间[e，e2]上的最大值；（2）当a＞0，时，若x∈[1，+∞），恒成立，求a的取值范围．考点：利用导数求闭区间上函数的最值；导数在最大值、最小值问题中的应用．专题：压轴题；导数的综合应用．分析：（1）当a=﹣2，x∈[e，e2]时，f（x）=x2﹣2lnx+2，求其导数可判函数在在[e，e2]上单调递增，进而可得其最大值；（2）分类讨论可得函数y=f（x）在[1，+∞）上的最小值为，分段令其，解之可得a的取值范围．解答：解：（1）当a=﹣2，x∈[e，e2]时，f（x）=x2﹣2lnx+2，（1分）∵，∴当x∈[e，e2]时，f'（x）＞0，（2分）∴函数f（x）=x2﹣2lnx+2在[e，e2]上单调递增，（3分）故+2=e4﹣2（4分）（2）①当x≥e时，f（x）=x2+alnx﹣a，，∵a＞0，∴f'（x）＞0，∴f（x）在[e，+∞）上单调递增，（5分）故当x=e时，；（6分）②当1≤x≤e时，f（x）=x2﹣alnx+a，f′（x）=2x﹣=（x+）（x﹣），（7分）（i）当≤1，即0＜a≤2时，f（x）在区间[1，e）上为增函数，当x=1时，f（x）min=f（1）=1+a，且此时f（1）＜f（e）=e2；（8分）（ii）当，即2＜a≤2e2时，f（x）在区间上为减函数，在区间上为增函数，（9分）故当x=时，，且此时f（）＜f（e）=e2；（10分）（iii）当，即a＞2e2时，f（x）=x2﹣alnx+a在区间[1，e]上为减函数，故当x=e时，．（11分）综上所述，函数y=f（x）在[1，+∞）上的最小值为（12分）由得0＜a≤2；由得无解；由得无解；（13分）故所求a的取值范围是（0，2]．（14分）点评：本题考查利用导数求闭区间的最值，涉及分类讨论的思想，属难题．。

图1乙甲7518736247954368534321高三六校第一次联考 理科数学 试题命题学校：珠海一中第一部分 选择题（共40分）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的1．若集合M 是函数lg y x =的定义域，N是函数y =M N 等于( ) A ．(0,1] B ．(0,)+∞ C ．φ D ．[1,)+∞ 2．在复平面内，复数311i i+-对应的点位于 （ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3．下列命题正确的是（ ）A ．2000,230x R x x ∃∈++= B ．32,x N x x ∀∈> C ．1x >是21x >的充分不必要条件 D ．若a b >,则22a b >4．已知向量a =（x ，1），b =（3，6），a ⊥b ，则实数x 的值为（ ） A ．12 B ．2- C ．2 D ．21- 5．经过圆:C 22(1)(2)4x y ++-=的圆心且斜率为1的直线方程为（ ）A ．30x y -+=B ．30x y --= C.10x y +-= D ．30x y ++=6. 图1是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图， 则甲、乙两人这几场比赛得分的中位数之和是（ ） A ．65 B ．64C ．63D ．627．已知等比数列{}n a 中，各项都是正数，且2312,21,a a a 成等差数列，则8967a a a a ++等于（ ）A ．21+ B. 21- C. 223+ D. 223-8. 在约束条件53,420≤≤⎪⎪⎩⎪⎪⎨⎧≤+≤+≥≥s x y s y x y x 当下时，目标函数y x z 23+=的最大值的变化范围是（ ）()A ．[6，15]()B ．[7，15] ()C [6，8] ()D ．[7，8]图4P第二部分 非选择题（共110分）二、填空题: 本大题共7小题，考生作答6小题，每小题5分，满分30分 （一）必做题（9～13题） 9．(ax －x1)8的展开式中2x 的系数为70，则a 的值为；10.下面是一个算法的程序框图，当输入的值x 为5时，则其输出的结果是 ； 11. 若axdx =1⎰，则实数a 的值是_________.12.已知双曲线22221(0b 0)x y a a b -=＞，＞和椭圆22x y =1169+有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为 .13．已知函数⎩⎨⎧≥+-<=)0(4)3(),0()(x a x a x a x f x 满足对任意0)()(,212121<--≠x x x f x f x x 都有成立，则a 的取值范围是 .（二）选做题（14～15题，考生只能从中选做一题） 14. (坐标系与参数方程选做题) 在极坐标系中，直线ρsin(θ+π4)=2被圆ρ=4截得的弦长为 ． 15．（几何证明选讲选做题）如图4，P 是圆O 外一点，过P 引圆O 的两条割线PAB 、PCD ，5==AB PA ，3=CD ，则=PC ____________．三、解答题：本大题共6小题，满分80分.16. （本小题满分12分） 已知函数()2sin cos cos2f x x x x =+(x ∈R ). (1) 求()f x 的最小正周期和最大值；若θ为锐角，且83f πθ⎛⎫+= ⎪⎝⎭，求tan 2θ的值.17．（本小题满分12分）设函数x x f a log )(=（1,0≠>a a a 为常数且），已知数列),(1x f ),(2x f ),(n x f 是公差为2的等差数列，且21a x =.（Ⅰ）求数列}{n x 的通项公式；（Ⅱ）当21=a 时，求证：3121<+++n x x x .18．(本小题满分14分)为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为35． （1）请将上面的列联表补充完整(不用写计算过程)；（2）能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关？说明你的理由； （3）现从女生中抽取2人进一步调查，设其中喜爱打篮球的女生人数为ξ，求ξ的分布列与期望.(参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++)19．（本小题满分14分）一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.（Ⅰ）请画出该几何体的直观图，并求出它的体积；（Ⅱ）用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼？试证明你的结论；（Ⅲ）在（Ⅱ）的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.正视图侧视图俯视图20．（本小题满分14分）已知点()0,1F ，直线l ：1y =-，P 为平面上的动点，过点P 作直线l 的垂线，垂足为Q ，且FQ FP QF QP ∙=∙．（1）求动点P 的轨迹C 的方程；（2）已知圆M 过定点()0,2D ，圆心M 在轨迹C 上运动，且圆M 与x 轴交于A 、B 两点，设1DA l =，2DB l =，求1221l l l l +的最大值．21.（本小题满分14分）已知函数2()(0)f x x ax a =-≠，()ln g x x =，()f x 图象与x 轴异于原点的交点M 处的切线为1l ，(1)g x -与x 轴的交点N 处的切线为2l ， 并且1l 与2l 平行.（1）求(2)f 的值；（2）已知实数t∈R，求函数[][()+],1,y f xg x t x e =∈的最小值；（3）令()()'()F x g x g x =+，给定1212,(1,),x x x x ∈+∞<，对于两个大于1的正数βα,，存在实数m 满足：21)1(x m mx -+=α，21)1(mx x m +-=β，并且使得不等式12|()()||()()|F F F x F x αβ-<-恒成立，求实数m 的取值范围.2013届高三六校第一次联考 理科数学参考答案及评分标准10小题，每小题5分，满分50分．二、填空题：本大题主要考查基本知识和基本运算．本大题共5小题，考生作答4小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题．9．1或-110．2 11．2 12.22143x y -= 13.⎥⎦⎤ ⎝⎛41.0 14．34 15．2 三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(1) 解: ()2sin coscos2f x x x x =+ sin 2cos 2x x =+…… 2分2222x x ⎫=+⎪⎪⎭…… 3分 24x π⎛⎫=+ ⎪⎝⎭. …… 4分 ∴()f x 的最小正周期为22ππ=,…… 6分 (2) 解:∵83f πθ⎛⎫+= ⎪⎝⎭, 223πθ⎛⎫+= ⎪⎝⎭. …… 7分 ∴1cos 23θ=. …… 8分 ∵θ为锐角，即02πθ<<, ∴02θπ<<.∴sin 23θ==. …… 10分 ∴sin 2tan 2cos 2θθθ==… 12分 17．（本小题满分12分）解：（Ⅰ）n n x f d a x f n a 22)1(2)(22log )(21=⋅-+=∴===n n n a a x nx 22log :==即 --------6分（Ⅱ）当21=a 时，nn x ⎪⎭⎫⎝⎛=41314113141141414121<⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=-⋅⎪⎭⎫ ⎝⎛-=+++nnn x x x ---12分18．(本小题满分14分)解：（2）∵2250(2015105)8.3337.87930202525K ⨯⨯-⨯=≈>⨯⨯⨯------------------------6分 ∴在犯错误的概率不超过0.005的前提下，认为喜爱打篮球与性别有关.---------------------7分（3）喜爱打篮球的女生人数ξ的可能取值为0,1,2.-------------------------9分其概率分别为021*******(0)20C C P C ξ===,1110152251(1)2C C P C ξ===,2010152253(2)20C C P C ξ=== --------------------------12分故ξ的分布列为:--------------------------13分ξ的期望值为:7134012202205E ξ=⨯+⨯+⨯= ---------------------14分19．（本小题满分14分）解：（Ⅰ）该几何体的直观图如图1所示，它是有一条 侧棱垂直于底面的四棱锥. 其中底面ABCD 是边长为6的 正方形，高为CC 1=6，故所求体积是 7266312=⨯⨯=V ------------------------4分 （Ⅱ）依题意，正方体的体积是原四棱锥体积的3倍， 故用3个这样的四棱锥可以拼成一个棱长为6的正方体， 其拼法如图2所示. ------------------------6分 证明:∵面ABCD 、面ABB1A 1、面AA 1D 1D 为全等的 正方形，于是D D AA C A ABB C ABCD C V V V 1111111---== 故所拼图形成立.---8分（Ⅲ）方法一：设B 1E ，BC 的延长线交于点G ， 连结GA ，在底面ABC 内作BH ⊥AG ，垂足为H ， 连结HB 1，则B 1H ⊥AG ，故∠B 1HB 为平面AB 1E 与 平面ABC 所成二面角或其补角的平面角. --------10分 在R t △ABG 中，180=AG ，则512180126=⨯=BH ，5182121=+=BB BH H B ，BC D C 1图1BC DD 1A 1B 1C 1 图232cos 11==∠HB HB HB B ，故平面AB 1E 与平面ABC 所成二面角的余弦值为32±.---14分方法二：以C 为原点，CD 、CB 、CC 1所在直线分别为x 、y 、z 轴建立直角坐标系（如图3），∵正方体棱长为6，则E （0，0，3），B 1（0，6，6），A （6，6，0）. 设向量n =（x ，y ，z ），满足n ⊥1EB ，n ⊥1AB ，于是⎩⎨⎧=+-=+066036z x z y ，解得⎪⎩⎪⎨⎧-==z y zx 21. --------------------12分取z =2，得n =（2，-1，2）. 又=1BB （0，0，6），321812||||,cos 111==>=<BB n BB 故平面AB 1E 与平面ABC 所成二面角的余弦值为32±. ----------------14分20、（本小题满分14分）（1）解：设(),P x y ，则(),1Q x -，∵QP QF FP FQ = ，∴()()()()0,1,2,1,2y x x y x +-=-- ． --------------------2分 即()()22121y x y +=--，即24x y =，所以动点P 的轨迹C 的方程24x y =． --------------------4分 （2）解：设圆M 的圆心坐标为(),M a b ，则24a b =． ①圆M 的半径为MD =．圆M 的方程为()()()22222x a y b a b -+-=+-． 令0y =，则()()22222x a b a b -+=+-，整理得，22440x ax b -+-=． ②由①、②解得，2x a =±． --------------------6分 不妨设()2,0A a -，()2,0B a +， ∴1l =2l =--------------------8分∴22212122112l l l l l l l l ++==== ③ 当0a ≠时，由③得，1221l l l l +=．当且仅当a =±--------------------12分 当0a =时，由③得，12212l l l l +=．--------------------13分 故当a =±1221l ll l +的最大值为 --------------------14分 21、（本小题满分14分）解: ()y f x =图象与x 轴异于原点的交点(,0)M a ，'()2f x x a =-(1)ln(1)y g x x =-=-图象与x 轴的交点(2,0)N ，1'(1)1g x x -=- 由题意可得12l l k k =，即1a =， ………………………………………………2分 ∴2(),f x x x =-，2(2)222f =-= …………………………………………3分2[()+][ln +](ln +)y f xg x t x x t x x t ==-=22(ln )(21)(ln )x x t x x t t +-+-…………………4分令ln u x x =，在 []1,x e ∈时，'ln 10u x =+>，∴ln u x x =在[]1,e 单调递增，0,u e ≤≤ …………5分22(21)y u t u t t =+-+-图象的对称轴122tu -=，抛物线开口向上 ①当1202t u -=≤即12t ≥时，2min 0|u y y t t ===- …………………………………6分 ②当122t u e -=≥即122e t -≤时，22min |(21)u e y y e t e t t ===+-+- ……………………7分 ③当1202t e -<<即12122e t -<<时， 22min 12212121|()(21)224tu t t y y t t t -=--==+-+-=- ……………… …………………8分 1(3)()()'()ln F x g x g x x x =+=+,22111'()0x F x x x x-=-=≥1x ≥得11 所以()F x 在区间(1,)+∞上单调递增………………………………………………9分∴1x ≥当时，F F x ≥>（）（1）0 ①当(0,1)m ∈时，有12111(1)(1)mx m x mx m x x α=+->+-=，12222(1)(1)mx m x mx m x x α=+-<+-=，得12(,)x x α∈，同理12(,)x x β∈，…………………………………１０分∴ 由)(x f 的单调性知 0<1()()F x F α<、2()()F F x β<从而有12|()()||()()|F F F x F x αβ-<-，符合题设. ………………………………11分 ②当0m ≤时，12222(1)(1)mx m x mx m x x α=+-≥+-=，12111(1)(1)m x mx m x mx x β=-+≤-+=，由)(x f 的单调性知 0<12()()()()F F x F x F βα≤<≤，∴12|()()||()()|F F F x F x αβ-≥-，与题设不符 ……………………………………12分③当1m ≥时，同理可得12,x x αβ≤≥，得12|()()||()()|F F F x F x αβ-≥-，与题设不符. ……………………………………13分 ∴综合①、②、③得(0,1)m ∈ ……………………………………14分 说明：各题如有其它解法，按照相应的步骤给分.。

广东省肇庆市2013届高三3月第一次模拟考试物理13．下列说法正确的是A ．在完全失重的情况下，密闭容器内的气体对器壁的顶部没有作用力B ．分子间存在相互作用的斥力和引力，它们都随分子间距离的减小而增大C ．布朗运动是悬浮在液体中的固体分子所做的无规则运动D ．相同质量的0℃的水和冰，水的分子势能比冰的分子势能小 14．空气压缩机在一次压缩过程中，活塞对空气做了2.0×105J 的功，同时空气的内能增加了1.5×105J 。

下列说法正确的是A ．空气从外界吸收的热量是0.5×105JB ．空气对外界放出的热量是0.5×105JC ．空气从外界吸收的热量是3.5×105JD ．空气对外界放出的热量是3.5×105J 15．如右图所示，在水平地面上放着斜面体B ，物体A 置于斜面体B 上，一水平向右的力F 作用于物体A 。

在力F 变大的过程中，两物体相对地面始终保持静止，则地面对斜面体B 的支持力N 和摩擦力f 的变化情况是A ．N 变大，f 不变B ．N 变大，f 变小C ．N 不变，f 变大D ．N 不变，f 不变16．一匀强磁场的边界是MN ，MN 左侧是无场区，右侧是匀强磁场区域，如图（甲）所示，现有一个金属线框以恒定速度从MN 左侧进入匀强磁场区域。

线框中的电流随时间变化的I-t二、双项选择题：17．以下是有关近代物理内容的若干叙述，其中正确的是A ．原子核发生一次β衰变,该原子外层就失去一个电子B ．一束频率不变的光照射到某种金属上不能发生光电效应，可能是因为这束光的光强太小C ．按照玻尔理论，氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时，电子的动能减小，但原子的能量增大D ．天然放射现象中发出的三种射线是从原子核内放出的看不见的射线18．如图所示，一只理想变压器原线圈与频率为50 Hz 的正弦交流电源相连，两个阻值均为20Ω的电阻串联后接在副线圈的两端.线圈匝数分别为200匝和100匝，电压表的示数为5V 。

肇庆市2020届高中毕业班第一次统一检测理科数学一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合{}|10A x x =-<，{}2|20B x x x =-<，则AB =( )A. {}|0x x <B. {}|1x x <C. {}1|0x x <<D. {}|12x x <<2.“a=1”是“函数()f x x a =-在区间[1, +∞)上为增函数”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件D. 既不充分也不必要条件3.设x R ∈，向量(,1)a x =，(1,2)b =-，且a b ⊥，则a b +=( )C. D. 104.已知sin 2cos αα=，则sin cos αα=( ) A. 25-B. 15-C.25D.155.下面是关于复数21z i=-+的四个命题：其中的真命题为( ) 1:2p z =22:2p z i =3:p z 的共轭复数为1i +4:p z 的虚部为1-A. 23,p pB. 12,p pC. 24,p pD. 34,p p6.设变量x, y 满足约束条件360,{20,30,x y x y y +-≥--≤-≤则目标函数z = y －2x 的最小值为( )A. －7B. －4C. 1D. 27.若01x y <<<，则 A. 33y x < B. log 3log 3x y < C. 44log log x y <D. 11()()44xy<8. 执行如图所示的程序框图，如果输入n=3，中输入的S=( )A.67B.37C.89D.499.由函数f (x )＝sin 2x 的图象平移得到g (x )＝cos (ax 6π-)，(其中a 为常数且a ＞0)的图象，需要将f (x )的图象( )A. 向左平移3π个单位 B. 向左平移6π个单位 C. 向右平移3π个单位D. 向右平移6π个单位10.已知函数()sin f x x x =⋅的图象是下列两个图象中的一个，如图，请你选择后再根据图象作出下面的判断：若12,,22x x ππ⎛⎫∈-⎪⎝⎭，且()()12f x f x <，则( )A. 12x x >B. 120x x +>C. 12x x <D. 2212x x < 11.已知函数()()f x x R ∈图象上任一点00,x y 处的切线方程为()()200021y y x x -=--()0x x -，那么函数()f x 的单调减区间是( ) A. [)1,-+∞B. (],2-∞C. (),1-∞-和1,2D. [)2,+∞12.已知函数()()()1ln 1f x x x t x =++-(t R ∈，且0t ≠)有3个零点1x ，2x ，3x ，则123x x x ++的取值范围是( ) A . [)2,+∞B. [)3,+∞C. ()3,+∞D. ()0,3二、填空题：本题共4小题，每小题5分，共20分．13.若等差数列{}n a 和等比数列{}n b 满足111a b ==-，448a b ==，则22a b =_______.14.在ABC ∆中，已知D 是AB 边上一点，若2AD DB =，13CD CA CB λ=+，则λ=_____． 15.已知等差数列的前n 项和为n S ，且12130,0S S ><，则使n S 取得最大值的n 为_______.16.定义在R 上的函数()f x 满足()()()()2log 1,012,0x x f x f x f x x ⎧-≤⎪=⎨--->⎪⎩，则()2020f 的值为_____．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.17.已知f (x)=﹣2sin 22xω(ω＞0)的最小正周期为3π．(1)求ω的值； (2)当x ∈[324ππ，]时，求函数f (x )的最小值． 18.已知△ABC 内角A ，B ，C 的对边分别为a ，b ，c，sin cos )A A =-． (1)求A ；(2)若7a =，sin sin 14B C +=，求△ABC 的面积． 19.已知数列{a n }中，a 1＝1，a n ＞0，前n 项和为S n，若n a =n ∈N *，且n ≥2)．(1)求数列{a n }通项公式；(2)记2n an n c a =⋅，求数列{c n }的前n 项和T n ．20.已知在ABC ∆中，角A ，B ，C 对应的边分别为a ，b ，c ，若b 是a 与c 的等比中项，sin A 是()sin B A -与sin C 的等差中项．(1)证明ABC∆直角三角形；(2)求cos B 的值． 21.已知函数()()1ln 1a x f x x x -=-+，a R ∈． (1)若2x =是函数()f x 的极值点，求曲线()y f x =在点()()1,1f 处的切线方程； (2)设m ，n 为正实数且m n ≠，求证：ln ln 2m n m nm n -+<-．22.设函数()()31sin 6f x x ax x a R =-+∈． (1)讨论()f x 的导函数()'f x 零点的个数；(2)若对任意的0x ≥，()0f x ≥成立，求a 的取值范围．。

2013年广东省揭阳市高考数学一模试卷（理科）参考答案与试题解析一．选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）（2013•揭阳一模）已知复数z1，z2在复平面内对应的点分别为A（0，1），B（﹣1，3），则=（）A．﹣1+3i B．﹣3﹣i C．3+i D．3﹣i考点：复数代数形式的乘除运算．专题：计算题．分析：利用复数的运算法则和复数的几何意义即可得出．解答：解：由题意可得z1=i，z2=﹣1+3i．∴==i+3．故选C．点评：熟练掌握复数的运算法则和复数的几何意义是解题的关键．2．（5分）（2013•揭阳一模）已知集合A={x|y=log2（x+1）}，集合，则A∩B=（）A．（1，+∞）B．（﹣1，1）C．（0，+∞）D．（0，1）考点：交集及其运算．专题：计算题．分析：求对数型函数的定义域化简集合A，求解指数函数的值域化简集合B，然后直接利用交集的运算求解．解答：解：由A={x|y=log2（x+1）}={x|x＞﹣1}=（﹣1，+∞），={y|0＜y＜1}=（0，1），所以A∩B=（﹣1，+∞）∩（0，1）=（0，1）．故选D．点评：本题考查了交集及其运算，考查了对数型函数定义域的求法及指数函数值域的求法，是基础题．3．（5分）（2013•揭阳一模）在四边形ABCD中，“，且”是“四边形ABCD是菱形”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：平面向量及应用．分析：根据，以及共线向量定理可得AB∥CD，且AB=CD，从而可知在四边形ABCD是平行四边形，又由，得四边形ABCD的对角线互相垂直，因此得到四边形ABCD为菱形．反之也成立．再根据充要条件进行判断即得．解答：解：由可得四边形ABCD是平行四边形，由得四边形ABCD的对角线互相垂直，∴对角线互相垂直的平行四边形是菱形．反之也成立．∴“，且”是“四边形ABCD是菱形”的充要条件．故选C．点评：此题是个基础题．考查必要条件、充分条件与充要条件的判断、共线向量定理以及向量在几何中的应用，考查学生利用知识分析解决问题的能力．4．（5分）（2013•泰安一模）当时，函数f（x）=Asin（x+φ）（A＞0）取得最小值，则函数是（）A．奇函数且图象关于点对称B．偶函数且图象关于点（π，0）对称C．奇函数且图象关于直线对称D．偶函数且图象关于点对称考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题．分析：由f（）=sin（+φ）=﹣1可求得φ=2kπ﹣（k∈Z），从而可求得y=f（﹣x）的解析式，利用正弦函数的奇偶性与对称性判断即可．解答：解：∵f（）=sin（+φ）=﹣1，∴+φ=2kπ﹣，∴φ=2kπ﹣（k∈Z），∴y=f（﹣x）=Asin（﹣x+2kπ﹣）=﹣Asinx，令y=g（x）=﹣Asinx，则g（﹣x）=﹣Asin（﹣x）=Asinx=﹣g（x），∴y=g（x）是奇函数，可排除B，D；其对称轴为x=kπ+，k∈Z，对称中心为（kπ，0）k∈Z，可排除A；令k=0，x=为一条对称轴，故选C．点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求φ是难点，考查正弦函数的奇偶性与对称性，属于中档题．5．（5分）（2013•揭阳一模）一简单组合体的三视图及尺寸如图（1）示（单位：cm）则该组合体的体积为．（）A．72000cm3B．64000cm3C．56000cm3D．44000cm3考点：由三视图求面积、体积．专题：计算题．分析：利用三视图复原的几何体以及三视图的数据，求出几何体的体积即可．解答：解：由三视图知，该组合体由两个直棱柱组合而成，上部长方体三度为：40，20，50；下部长方体三度为：60，40，10；故组合体的体积V=60×40×10+20×40×50=64000（cm3），故选B．点评：本题考查三视图与几何体的直观图的关系，正确判断几何体是特征与形状是解题的关键．6．（5分）（2013•揭阳一模）已知等差数列{a n}满足，a1＞0，5a8=8a13，则前n项和S n取最大值时，n的值为（）A．20 B．21 C．22 D．23考点：等差数列的前n项和；数列的函数特性．专题：等差数列与等比数列．分析：由条件可得，代入通项公式令其≥0可得，可得数列{a n}前21项都是正数，以后各项都是负数，可得答案．解答：解：设数列的公差为d，由5a8=8a13得5（a1+7d）=8（a1+12d），解得，由a n=a1+（n﹣1）d=，可得，所以数列{a n}前21项都是正数，以后各项都是负数，故S n取最大值时，n的值为21，故选B．点评：本题考查等差数列的前n项和公式，从数列的项的正负入手是解决问题的关键，属基础题．7．（5分）（2013•揭阳一模）如图，阅读程序框图，任意输入一次x（0≤x≤1）与y（0≤y≤1），则能输出数对（x，y）的概率为（）A．B．C．D．考点：几何概型．专题：计算题．分析：据程序框图得到事件“能输出数对（x，y）”满足的条件，求出所有基本事件构成的区域面积；利用定积分求出事件A构成的区域面积，据几何概型求出事件的概率．解答：解：是几何概型所有的基本事件Ω=设能输出数对（x，y）为事件A，则A=S（Ω）=1S（A）=∫01x2dx==故选A点评：本题考查程序框图与概率结合，由程序框图得到事件满足的条件、考查利用定积分求曲边图象的面积；利用几何概型概率公式求出事件的概率．8．（5分）（2013•揭阳一模）已知方程在（0，+∞）有两个不同的解α，β（α＜β），则下面结论正确的是（）A ．B．C．D．考点：根的存在性及根的个数判断；两角和与差的正切函数．专题：计算题．分析：利用x的范围化简方程，通过方程的解转化为函数的图象的交点问题，利用相切求出β的正切值，通过两角和的正切函数求解即可．解答：解：，要使方程在（0，+∞）有两个不同的解，则y=|sinx|的图象与直线y=kx（k＞0）有且仅有三个公共点，所以直线y=kx与y=|sinx|在内相切，且切于点（β，﹣sinβ），由，，故选C．点评：本题考查函数的零点与方程根的关系，直线与曲线相切的转化，两角和的正切函数的应用，考查计算能力．二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（9-13题）（二）选做题（14、15题，考生只能从中选做一题）9．（5分）（2013•揭阳一模）计算：= 2 ．考点：对数的运算性质；二倍角的正弦．专题：函数的性质及应用．分析：利用对数的运算性质和倍角公式即可得出．解答：解：原式====2．故答案为2．点评：熟练掌握对数的运算性质和倍角公式是解题的关键．10．（5分）（2013•揭阳一模）若二项式的展开式中，第4项与第7项的二项式系数相等，则展开式中x6的系数为9 ．（用数字作答）考点：二项式系数的性质．专题：计算题．分析：由题意可得，，可求n，然后写出展开式的通项，令x的次方为6求出r，即可求解解答：解：由题意可得，，解得n=9∵的展开式的通项为=令9﹣=6，解得r=2此时的系数为=9故答案为：9点评：本题主要考查了二项式系数的性质及二项展开式的通项的应用，解题的关键是熟练掌握基本公式11．（5分）（2013•揭阳一模）x 20 21 22 23 24 25 26 27 28 29y 141 146 154 160 169 176 181 188 197 203一般来说，一个人脚掌越长，他的身高就越高，现对10名成年人的脚掌长x与身高y进行测量，得到数据（单位均为cm）如上表，作出散点图后，发现散点在一条直线附近，经计算得到一些数据：，；某刑侦人员在某案发现场发现一对裸脚印，量得每个脚印长为26.5cm，则估计案发嫌疑人的身高为185.5 cm．考点：线性回归方程．专题：应用题．分析：根据所给的数据，求得回归方程的斜率b的值，代入样本中心点求出a的值，得到线性回归方程，把所给的x的值代入预报出身高．解答：解：∵经计算得到一些数据：，；∴回归方程的斜率，，，截距，即回归方程为=7x，当x=26.5，，则估计案发嫌疑人的身高为 185.5 cm．故答案为：185.5．点评：本题考查回归分析的初步应用，本题解题的关键是正确运算出横标和纵标的平均数，写出线性回归方程，再者注意根据所给的自变量的值和线性回归方程得到的结果是一个预报值，而不是准确值，本题是一个中档题目．12．（5分）（2013•揭阳一模）已知圆C经过直线2x﹣y+2=0与坐标轴的两个交点，又经过抛物线y2=8x的焦点，则圆C的方程为．考点：抛物线的简单性质；圆的标准方程．专题：计算题．分析：求出抛物线的焦点坐标，设出圆的一般方程为x2+y2+Dx+Ey+F=0，把三个点的坐标分别代入即可得到关于D，E及F的三元一次方程组，求出方程组的解即可得到D，E及F的值，进而确定出圆的方程．解答：解：抛物线y2=8x的焦点为F（2，0），直线2x﹣y+2=0与坐标轴的两个交点坐标分别为A（﹣1，0），B（0，2），设所求圆的方程为x2+y2+Dx+Ey+F=0．将A、B、F三点的坐标代入圆的方程得：，解得于是所求圆的方程为x2+y2﹣x﹣y﹣2=0．即．（12分）故答案为：；点评：本题考查圆的方程，考查抛物线的简单性质，解题的关键是利用待定系数法求圆的方程，属于中档题．13．（5分）（2013•揭阳一模）函数f（x）的定义域为D，若对任意的x1、x2∈D，当x1＜x2时，都有f（x1）≤f（x2），则称函数f（x）在D上为“非减函数”．设函数g（x）在[0，1]上为“非减函数”，且满足以下三个条件：（1）g（0）=0；（2）；（3）g（1﹣x）=1﹣g（x），则g（1）= 1 、= ．考点：函数的值；抽象函数及其应用．专题：新定义．分析：①在（3）中令x=0即可得出g（1）；②在（2）中令x=1得，在（3）中令得，再利用函数g（x）在[0，1]上为“非减函数”即可得出．解答：解：①在（3）中令x=0得g（1）=1﹣g（0）=1，∴g（1）=1；②在（2）中令x=1得，在（3）中令得，故，∵，∴，故．故答案分别为1，．点评：恰当对函数g（x）的x赋值及利用函数g（x）在[0，1]上为“非减函数”是解题的关键．14．（2013•东莞二模）（坐标系与参数方程选做题）已知曲线C1：和曲线C2：，则C1上到C2的距离等于的点的个数为 3 ．考点：直线与圆的位置关系；点的极坐标和直角坐标的互化．专题：直线与圆．分析：把极坐标方程化为直角坐标方程，求出圆心到直线的距离等于半径的一半，可得圆上到直线的距离等于的点的个数．解答：解：将方程与化为直角坐标方程得与x﹣y﹣2=0，可知C1为圆心在坐标原点，半径为r=的圆，C2为直线，因圆心到直线x﹣y﹣2=0的距离为=，故满足条件的点的个数n=3，故答案为 3．点评：本题主要考查把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，直线和圆的位置关系，属于中档题．15．（5分）（2013•揭阳一模）如图所示，AB是⊙O的直径，过圆上一点E作切线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C．若CB=2，CE=4，则⊙O 的半径长为 3 ；AD的长为．考点：相似三角形的性质．专题：计算题．分析：设出圆的半径直接利用切割线定理求出圆的半径，通过三角形相似列出比例关系求出AD即可．解答：解：设r是⊙O的半径．由切割线定理可知：CE2=C A•CB，即42=（2r+2）×2，解得r=3．因为EC是圆的切线，所以OE⊥EC，AD⊥DC，所以△ADC∽△OEC，所以，，解得．故答案为：3；．点评：本题考查圆的切割线定理的应用，三角形相似的证明以及应用，考查计算能力．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（12分）（2013•揭阳一模）在△ABC中，角A，B，C所对的边分别为a，b，c，且满足．（1）求角C的大小；（2）求的最大值，并求取得最大值时角A，B的大小．考点：正弦定理；两角和与差的正弦函数．专题：解三角形．分析：（1）已知等式变形后利用正弦定理化简，整理后再利用同角三角函数间的基本关系求出tanC的值，由C为三角形的内角，利用特殊角的三角函数值即可求出C的度数；（2）由C的度数及内角和定理，用A表示出B，代入所求式子中，利用诱导公式化简，再利用两角和与差的余弦函数公式及特殊角的三角函数值化简，整理后利用两角和与差的正弦函数公式化为一个角的正弦函数，由A的范围求出这个角的范围，利用正弦函数的图象与性质求出最大值及此时A与B的度数即可．解答：解：（1）由csinA=acosC，结合正弦定理得，==，∴sinC=cosC，即tanC=，∵0＜C＜π，∴C=；（2）由（1）知B=﹣A，∴sinA﹣sin（B+）=sinA﹣cosB=sinA﹣cos（﹣A）=sinA﹣cos cosA﹣sin sinA=sinA+cosA=sin（A+），∵0＜A＜，∴＜A+＜，当A+=时，sinA﹣sin（B+）取得最大值1，此时A=，B=．点评：此题考查了正弦定理，两角和与差的正弦、余弦函数公式，诱导公式，同角三角函数间的基本关系，以及特殊角的三角函数值，熟练掌握定理及公式是解本题的关键．17．（12分）（2013•揭阳一模）根据公安部最新修订的《机动车驾驶证申领和使用规定》：每位驾驶证申领者必须通过《科目一》（理论科目）、《综合科》（驾驶技能加科目一的部分理论）的考试．已知李先生已通过《科目一》的考试，且《科目一》的成绩不受《综合科》的影响，《综合科》三年内有5次预约考试的机会，一旦某次考试通过，便可领取驾驶证，不再参加以后的考试，否则就一直考到第5次为止．设李先生《综合科》每次参加考试通过的概率依次为0.5，0.6，0.7，0.8，0.9．（1）求在三年内李先生参加驾驶证考试次数ξ的分布列和数学期望；（2）求李先生在三年内领到驾驶证的概率．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分析：（1）可知ξ的取值为1，2，3，4，5，分别可得所对应的概率，可得分布列，进而可得期望Eξ；（2）李先生在三年内领到驾照的对立事件为5次考试全不过，由对立事件的概率可得结果．解答：解：（1）由题意可知ξ的取值为1，2，3，4，5．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（1分）P（ξ=1）=0.5，P（ξ=2）=（1﹣0.5）×0.6=0.3，P（ξ=3）=（1﹣0.5）×（1﹣0.6）×0.7=0.14，P（ξ=4）=（1﹣0.5）×（1﹣0.6）×（1﹣0.7）×0.8=0.048，P（ξ=5）=（1﹣0.5）×（1﹣0.6）×（1﹣0.7）×（1﹣0.8）=0.012﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）∴ξ的分布列为：ξ 1 2 3 4 5P 0.5 0.3 0.14 0.048 0.012﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）∴Eξ=1×0.5+2×0.3+3×0.14+4×0.048+5×0.012=1.772﹣﹣﹣﹣﹣﹣﹣﹣（10分）（2）李先生在三年内领到驾照的概率为：P=1﹣（1﹣0.5）×（1﹣0.6）×（1﹣0.7）×（1﹣0.8）×（1﹣0.9）=0.9988﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）点评：本题考查离散型随机变量及其分布列，涉及数学期望的求解，属中档题．18．（14分）（2013•揭阳一模）如图（1），在等腰梯形CDEF中，CB、DA是梯形的高，AE=BF=2，，现将梯形沿CB、DA折起，使EF∥AB且EF=2AB，得一简单组合体ABCDEF如图（2）示，已知M，N，P分别为AF，BD，EF的中点．（1）求证：MN∥平面BCF；（2）求证：AP⊥DE；（3）当AD多长时，平面CDEF与平面ADE所成的锐二面角为60°？考点：直线与平面平行的判定；直线与平面垂直的性质；二面角的平面角及求法．专题：空间位置关系与距离；空间角．分析：（1）如图1，连接AC．利用矩形的性质可得N为AC的中点，利用三角形的中位线定理可得MN∥CF，再利用线面平行的判定定理即可证明；（2）利用线面垂直的判定定理可得AD⊥平面ABFE，得到AD⊥AP；利用平行四边形的判定和性质可得AP=BF，利用勾股定理的逆定理可得AP⊥AE，利用线面垂直的判定定理可得AP⊥平面ADE．进而得到结论．（3）解法一：如图所示，通过建立空间直角坐标系，利用两个平面的法向量的夹角公式即可得出二面角，解出即可；解法二：点A作AK⊥DE交DE于K点，连结PK，则DE⊥PK，可得∠AKP为二面角A﹣DE﹣F的平面角，利用直角三角形的边角关系即可得出．解（1）证明：如图1，连接AC，∵四边形ABCD是矩形，N为BD中点，答：∴N为AC中点，在△ACF中，M为AF中点，故MN∥CF．∵CF⊂平面BCF，MN⊄平面BCF，∴MN∥平面BCF；（2）证明：由题意知DA⊥AB，DA⊥AE 且AB∩AE=A，∴AD⊥平面ABFE，∵AP⊂平面ABFE，∴AP⊥AD，∵P为EF中点，∴，又AB∥EF，可得四边形ABFP是平行四边形．∴AP∥BF，AP=BF=2．∴AP2+AE2=PE2，∴∠PAE=90°，∴PA⊥AE．又AD∩AE=A，∴AP⊥平面ADE．∵DE⊂平面ADE，∴AP⊥DE．（3）解法一：如图2，分别以AP，AE，AD所在的直线为x，y，z轴建立空间直角坐标系设AD=m（m＞0），则A（0，0，0），D（0，0，m），E（0，2，0），P（2，0，0）．∴，．可知平面ADE的一个法向量为，设平面DEF的一个法向量为，则，令x=1，则y=1，．故．∴，由题意得，=cos60°，解得，即时，平面CDEF与平面ADE所成的锐二面角为60°．解法二：过点A作AK⊥DE交DE于K点，连结PK，则DE⊥PK，∴∠AKP为二面角A﹣DE﹣F的平面角，由∠AKP=60°，AP=BF=2得AK=，又AD•AE=AK•DE得，解得，即时，平面CDEF与平面ADE所成的锐二面角为60°．点评：熟练掌握利用矩形的性质、三角形的中位线定理、线面平行的判定定理、线面垂直的判定和性质定理、平行四边形的判定和性质、勾股定理的逆定理、通过建立空间直角坐标系利用两个平面的法向量的夹角公式得出二面角的方法、利用二面角的定义作出二面角、直角三角形的边角关系等是解题的关键．19．（14分）（2013•揭阳一模）如图，设点F1（﹣c，0）、F2（c，0）分别是椭圆的左、右焦点，P为椭圆C上任意一点，且最小值为0．（1）求椭圆C的方程；（2）若动直线l1，l2均与椭圆C相切，且l1∥l2，试探究在x轴上是否存在定点B，点B到l1，l2的距离之积恒为1？若存在，请求出点B坐标；若不存在，请说明理由．考点：直线与圆锥曲线的关系；椭圆的标准方程．专题：计算题；圆锥曲线的定义、性质与方程．分析：（1）设P（x，y），可得向量坐标关于x、y的形式，从而得到，结合点P为椭圆C上的点，化简得，说明最小值为1﹣c2=0，从而解出a2=2且b2=1，得到椭圆C的方程．（2）当直线l1，l2斜率存在时，设它们的方程为y=kx+m与y=kx+n，与椭圆方程联解并利用根的判别式列式，化简得m2=1+2k2且n2=1+2k2，从而得到m=﹣n．再假设x轴上存在B（t，0），使点B到直线l1，l2的距离之积为1，由点到直线的距离公式列式，并化简去绝对值整理得k2（t2﹣3）=2或k2（t2﹣1）=0，再经讨论可得t=±1，得B（1，0）或B（﹣1，0）．最后检验当直线l1，l2斜率不存在时，（1，0）或（﹣1，0）到直线l1，l2的距离之积与等于1，从而得到存在点B（1，0）或B（﹣1，0），满足点B到l1，l2的距离之积恒为1．解解：（1）设P（x，y），则有，﹣﹣﹣﹣﹣答：﹣﹣﹣﹣﹣﹣﹣﹣（1分）∴∵点P在椭圆C上，可得，可得y2=x2，∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）因此，最小值为1﹣c2=0，解之得c=1，可得a2=2，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（3分）∴椭圆C的方程为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）（2）①当直线l1，l2斜率存在时，设其方程为y=kx+m，y=kx+n﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）把l1的方程代入椭圆方程，得（1+2k2）x2+4mkx+2m2﹣2=0∵直线l1与椭圆C相切，∴△=16k2m2﹣4（1+2k2）（2m2﹣2）=0，化简得m2=1+2k2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（7分）同理可得n2=1+2k2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）∴m2=n2，而若m=n则l1，l2重合，不合题意，因此m=﹣n﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）设在x轴上存在点B（t，0），点B到直线l1，l2的距离之积为1，则，即|k2t2﹣m2|=k2+1，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）把1+2k2=m2代入，并去绝对值整理，可得k2（t2﹣3）=2或k2（t2﹣1）=0，而前式显然不能恒成立；因而要使得后式对任意的k∈R恒成立必须t2﹣1=0，解之得t=±1，得B（1，0）或B（﹣1，0）；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）②当直线l1，l2斜率不存在时，其方程为和，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）定点（﹣1，0）到直线l1，l2的距离之积为；定点（1，0）到直线l1，l2的距离之积为，也符合题意．综上所述，满足题意的定点B为（﹣1，0）或（1，0）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）点评：本题给出椭圆上一点P ，在最小值为0的情况下求椭圆的方程，并讨论x 轴上存在定点B到l1，l2的距离之积恒为1的问题，着重考查了椭圆的标准方程与简单几何性质、点到直线的距离公式、向量数量积运算和直线与圆锥曲线的位置关系等知识点，属于中档题．20．（14分）（2013•揭阳一模）已知函数为常数），数列{a n}满足：，a n+1=f（a n），n∈N*．（1）当α=1时，求数列{a n}的通项公式；（2）在（1）的条件下，证明对∀n∈N*有：；（3）若α=2，且对∀n∈N*，有0＜a n＜1，证明：．考点：数列与函数的综合；不等式的证明；数学归纳法．专题：计算题；证明题；等差数列与等比数列；点列、递归数列与数学归纳法．分析：（1）当α=1时，说明数列是以为首项，1为公差的等差数列，然后求数列{a n}的通项公式；（2）法一：在（1）的条件下，化简数列的通项公式，利用裂项法：证明对∀n∈N*有：；法二：直接利用数学归纳法的证明步骤证明即可．（3）法一：通过α=2，化简a n+1﹣a n 的表达式为，利用基本不等式直接证明．法二：通过，以及0＜a n＜1，说明，a n∈[，1），n∈N*，构造函数，利用函数的导数，求出函数的最大值即可证明结果．解解：（1）当α=1时，，两边取倒数，得，﹣﹣﹣答：﹣（2分）故数列是以为首项，1为公差的等差数列，，，n∈N*．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）（2）证法1：由（1）知，故对k=1，2，3…=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）∴a1a2a3+a2a3a4+…+a n a n+1a n+2===．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）．[证法2：①当n=1时，等式左边=，等式右边=，左边=右边，等式成立；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）②假设当n=k（k≥1）时等式成立，即，则当n=k+1时==这就是说当n=k+1时，等式成立，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）综①②知对于∀n∈N*有：．﹣﹣﹣﹣（9分）] （3）当α=2时，则，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）∵0＜a n＜1，∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（11分）===．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）∵a n=1﹣a n与不能同时成立，∴上式“=”不成立，即对∀n∈N*，．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）证法二：当α=2时，，则﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）又0＜a n＜1，∴，∴a n+1＞a n，∴a n∈[，1），n∈N*﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（11分）令，则，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）当，所以函数g（x）在单调递减，故当，所以命题得证﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）所以命题得证﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）点评：本题考查数列与函数的综合应用，数学归纳法的证明方法，构造法以及函数的导数求解函数的最大值证明不等式，基本不等式的应用，考查分析问题解决问题的能力，转化思想的应用．21．（14分）（2013•揭阳一模）已知函数f（x）=lnx，g（x）=f（x）+ax2+bx，函数g（x）的图象在点（1，g（1））处的切线平行于x轴．（1）确定a与b的关系；（2）试讨论函数g（x）的单调性；（3）证明：对任意n∈N*，都有ln（1+n ）＞成立．考点：利用导数研究函数的单调性；利用导数研究曲线上某点切线方程；不等式的证明．专题：导数的综合应用．分析：（1）求导得到g′（x），利用导数的几何意义即可得出；（2）利用（1）用a表示b，得到g′（x），通过对a分类讨论即可得到其单调性；（3）证法一：由（2）知当a=1时，函数g（x）=lnx+x2﹣3x在（1，+∞）单调递增，可得lnx+x2﹣3x≥g（1）=﹣2，即lnx≥﹣x2+3x﹣2=﹣（x﹣1）（x﹣2），令，则，利用“累加求和”及对数的运算法则即可得出；证法二：通过构造数列{a n}，使其前n项和T n=ln（1+n），则当n≥2时，，显然a1=ln2也满足该式，故只需证，令，即证ln（1+x）﹣x+x2＞0，记h（x）=ln（1+x）﹣x+x2，x＞0，再利用（2）的结论即可；证法三：令φ（n）=ln（1+n ）﹣，则=，令，则x∈（1，2]，，记h（x）=lnx﹣（x﹣1）+（x﹣1）2=lnx+x2﹣3x+2，利用（2）的结论即可．解答：解：（1）依题意得g（x）=lnx+ax2+bx，则，由函数g（x）的图象在点（1，g（1））处的切线平行于x轴得：g'（1）=1+2a+b=0，∴b=﹣2a﹣1．（2）由（1）得=，∵函数g（x）的定义域为（0，+∞），∴①当a≤0时，2ax﹣1＜0在（0，+∞）上恒成立，由g'（x）＞0得0＜x＜1，由g'（x）＜0得x＞1，即函数g（x）在（0，1）上单调递增，在（1，+∞）单调递减；②当a＞0时，令g'（x）=0得x=1或，若，即时，由g'（x）＞0得x＞1或，由g'（x）＜0得，即函数g（x ）在，（1，+∞）上单调递增，在单调递减；若，即时，由g'（x）＞0得或0＜x＜1，由g'（x）＜0得，即函数g（x）在（0，1），上单调递增，在单调递减；若，即时，在（0，+∞）上恒有g'（x）≥0，即函数g（x）在（0，+∞）上单调递增，综上得：当a≤0时，函数g（x）在（0，1）上单调递增，在（1，+∞）单调递减；当时，函数g（x）在（0，1）单调递增，在单调递减；在上单调递增；当时，函数g（x）在（0，+∞）上单调递增，当时，函数g（x）在上单调递增，在单调递减；在（1，+∞）上单调递增．（3）证法一：由（2）知当a=1时，函数g（x）=lnx+x2﹣3x在（1，+∞）单调递增，∴lnx+x2﹣3x≥g（1）=﹣2，即lnx≥﹣x2+3x﹣2=﹣（x﹣1）（x﹣2），令，则，∴+…+＞+…+，∴，即．证法二：构造数列{a n}，使其前n项和T n=ln（1+n），则当n≥2时，，显然a1=ln2也满足该式，故只需证，令，即证ln（1+x）﹣x+x2＞0，记h（x）=ln（1+x）﹣x+x2，x＞0，则，h（x）在（0，+∞）上单调递增，故h（x）＞h（0）=0，∴成立，以下同证法一．证法三：令φ（n）=ln（1+n）﹣，则=，令，则x∈（1，2]，，记h（x）=lnx﹣（x﹣1）+（x﹣1）2=lnx+x2﹣3x+2，∵∴函数h（x）在（1，2]单调递增，又h（1）=0，∴当x∈（1，2]时，h（x）＞0，即φ（n+1）﹣φ（n）＞0，∴数列φ（n）单调递增，又φ（1）=ln2＞0，∴即．点评：熟练掌握导数的几何意义、分类讨论、利用导数研究函数的单调性、善于利用已经证明的结论、“累加求和”及对数的运算法则、“分析法”、“构造法”等是解题的关键．。

广东省11大市2013年高三数学（理）一模试题分类汇编 平面向量 一、选择、填空题 1、（肇庆市2013届高三3月第一次模拟考试）已知向量．若为实数，，则A． B． C．D． ，，，若，则 A． B． C． D． 答案：C 3、（江门市2013届高三2月高考模拟）在复平面内，是原点，向量对应的复数是（其中，是虚数单位），如果点关于实轴的对称点为点，则向量对应的复数是 A．B．C．D． 在四边形ABCD中，，且四边形ABCD是 A． B． C． D． 6、（韶关市2013届高三调研考试）若向量满足条件＝30，则x＝＿＿＿ 答案：4 7、（茂名市2013届高三第一次高考模拟考试）已知向量,则的充要条件是（ ） A．B．C．D． ，｜x＋1｜＋｜x－2｜＞a，则a＜3”；命题q：“设M为平面内任意一点，则A、B、C三点共线的充要条件是存在角，使”，则A、为真命题B、为假命题C、为假命题D、为真命题 答案：C 解析：P正确，q错误：，BA=MA-MB=(cosa)^2*(MC-MB)=(cosa)^2*BC,==>A,B,C三点共线。

反之，不成立。

例如，A(0,0),B(1,0),C(2,0),BA=(-1,0),BC=(1,0),不存在角a,使向量MA=(sina)^2*向量MB+(cosa)^2*向量 MC。

所以这个命题是假的。

， ，且。

（I）求角A的大小； （II）若且△ABC的面积为，求b十c的值。

解：（1） …………………… …（2分） ……………… ………（4分） 又 ………………………………………………（6分） （2） …………………………………（8分） ……………………………………………………………………（9分） 由余弦定理得：………………………………………（10分） …………………………………………………………（11分） …………………………………………………………………（12分） 2、（梅州市2013届高三3月总复习质检）已知△ABC的内角A，B，C的对边分别为a，b，c，满足。

广东省11大市2013年高三数学（理）一模试题分类汇编 排列组合二项式定理 1、（揭阳市2013届高三3月第一次高考模拟）若二项式的展开式中，第4项与第7项的二项式系数相等，则展开式中的系数为 ．展开式中的常数项为＿＿＿＿ 答案：－672 3、（汕头市2013届高三3月教学质量测评）给一个正方体的六个面涂上四种不同颜色（红、黄、绿、兰），要求相邻两个面涂不同的颜色，则共有涂色方法（涂色后，任意翻转正方体，能使正方体各面颜色一致，我们认为是同一种涂色方法（ ）A. 6种B. 12种C. 24种D. 48种 答案：A 4、（韶关市2013届高三调研考试）在实验员进行一项实验中，先后要实施5个程序，其中程度A只能出现在第一步或最后一步，程序C或D实施时必须相邻，请问实验顺序的编排方法共有（ ）A、15种B、18种C、24种D、44种 答案：C 5、（深圳市2013届高三2月第一次调研考试）我们把各位数字之和为6 的四位数称为“六合数”（如2013 是“六合数”），则“六合数”中首位为2 的“六合数”共有 A．个 B．个 C．个 D． 个 答案：B 【解析】设满足条件的“六合数”为，则于是满足条件的可分以下几种情形： （1）一个为，两个为，共有种； （2）一个为，一个为，一个为，共有种； （3）两个为，一个为，共有种； （4）一个为，两个为，共有种. 6、（茂名市2013届高三第一次高考模拟考试末）若n的展开式中所有二项式系数之和为64，则展开式的常数项为 . 7、（湛江市2013届高三高考测试（一）） 若，则＝A、1B、32C、－1D、－32 答案：B 8、（深圳市2013届高三2月第一次调研考试） 若，则 答案： 【解析】所以。