第7章-3 收敛性稳定性

《机械工程控制基础》教案学时分配总学时：32学时授课学时：28学时实验：4学时。

基础课程先修课：大学物理、理论力学、工程数学、电工学、高等数学、机械原理。

课程性质《机械工程控制基础》是高等工业院校机械类专业普遍开设的一门重要的技术基础课，在整个教学计划中，以主干课程的角色，起着承上启下的作用，具有十分重要的地位。

本课程是一门专业基础理论课程,详述了研究对象的建模方法、系统响应分析方法，系统介绍了单输入单输出线性定常系统的时域性能分析、频域性能分析、系统的稳定性分析方法，介绍系统性能校正方法，为《机电一体化系统设计》、《机电传动控制》、《计算机控制技术》等机械电子工程专业的后续课程打下基础。

课程的主要任务通过本课程的学习，使学生掌握经典控制理论的基本概念和基础知识, 掌握机械工程中的研究对象的建模方法；掌握一阶、二阶系统的时域性能分析和频域性能分析方法；能熟练地根据Nyquist图、Bode图判断系统的稳定性；掌握系统性能校正方法；使学生能分析系统的性能,能改进或设计简单的控制系统。

第一次课第1章绪论1.1机械控制基础的研究对象、课程的基本任务、控制系统的基本要求一、机械控制基础的研究对象：系统、输入、输出2、典型闭环控制系统的框图的构成输入信号输出量给定值偏差控制器执行机构被控对象-测量变送器给定环节：给出与系统输出量希望值相对应的系统输入量。

测量环节：测量系统输出量的实际值，并把输出量的量纲转化成与输入量相同。

比较环节：比较系统的输入量和主反馈信号，并给出两者之间的偏差。

放大环节：对微弱的偏差信号进行放大和变换，使之具有足够的幅值和功率，以适应执行元件动作的要求。

执行环节：根据放大后的偏差信号产生控制、动作，操作系统的输出量，使之按照输入量的变化规律而变化。

二、课程的基本任务研究系统、输入、输出之间的动态关系三、控制系统的基本要求：稳、快、准1.2 控制理论的研究内容、发展、应用、学习方法。

控制理论研究五方面的内容系统分析问题当系统已定、输入(或激励)已知时,求出系统的输出（或响应）,并通过输出来研究系统本身的有关问题。

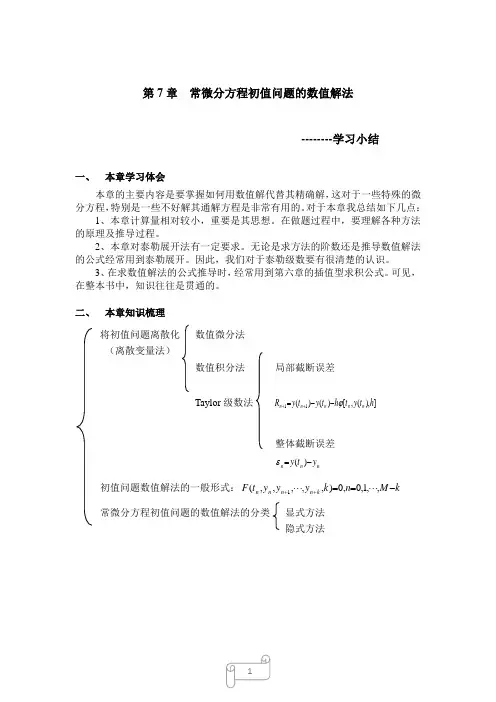
第7章 常微分方程初值问题的数值解法--------学习小结一、 本章学习体会本章的主要内容是要掌握如何用数值解代替其精确解，这对于一些特殊的微分方程，特别是一些不好解其通解方程是非常有用的。

对于本章我总结如下几点：1、本章计算量相对较小，重要是其思想。

在做题过程中，要理解各种方法的原理及推导过程。

2、本章对泰勒展开法有一定要求。

无论是求方法的阶数还是推导数值解法的公式经常用到泰勒展开。

因此，我们对于泰勒级数要有很清楚的认识。

3、在求数值解法的公式推导时，经常用到第六章的插值型求积公式。

可见，在整本书中，知识往往是贯通的。

二、 本章知识梳理将初值问题离散化 数值微分法（离散变量法）数值积分法 局部截断误差Taylor 级数法 ]),(,[)()(11h t y t h t y t y R n n n n n ϕ--=++整体截断误差n n n y t y -=)(ε初值问题数值解法的一般形式：k M n k y y y t F k n n n n -==++,,1,0,0),,,,,(1 常微分方程初值问题的数值解法的分类 显式方法隐式方法一般形式 ,2,1,0),,,(1=+=+n h y t h y y n n n n ϕ局部截断误差 ),,(11h y t h y y R n n n n n ϕ--=++整体截断误差 n n n y t y -=)(ε显示单步法 局部截断误差与整体截断误差的关系若)(11++=p n h O R ，则)(1p n h O =+ε若数值方法的局部截断误差为)(1+p h O ，则称这种数值方法的阶数是p显式欧拉公式),,(1n n n n y t h y y ϕ+=+欧拉法隐式欧拉公式),(111++++=n n n n y t h y y ϕ基本思想⎩⎨⎧=≤≤='000)(),,(y t y T t t y t f y等价于10)],(,[)())(,()()(11<<+++=+=⎰++θθθh t y h t hf t y dt t y t f t y t y n n n t t n n n n ),(y x f龙格-库塔法不同点的数值解加权平均代替)](,[h t y h t f n n θθ++而使得截断误差的阶数尽可能高N 级R-K 方法的形式,2,1,0),,,(1=+=+n h y t h y y n n n n ϕ，∑==Ni i i n n k c h y t 1),,(ϕ相容性，收敛性和绝对稳定性1、相容性：设增量函数),,(h y t ϕ在区域}0,,|),,{(00h h y T t t h y t D ≤≤<∞≤≤=上连续，且对h 满足Lipschitz 条件，则单步法与微分方程相容的充要条件是单步法至少是一阶的方法2、收敛性;（1）定义：若对任意的0y 及任意的),(0T t t ∈，极限)(lim )0(t y y n tt n h n ==∞→→则称单步法是收敛的（2）单步法的收敛的充要条件：)(0∞→→n n ε（3）收敛与相容的关系:设增量函数),,(h y t ϕ在区域}0,,|),,{(00h h y T t t h y t D ≤≤<∞≤≤=上连续，且对y 满足Lipschitz 条件，则单步法与微分方程相容的充要条件是单步法是收敛的3、稳定性（描述初始值的误差对计算结果的影响）4、绝对稳定性：线性多步法的基本思想线性多步法的一般形式∑∑==--++=r i ri i n i i n i n f h y y 011βα线性多步法 Simpson 公式Admas 公式 基于数值积分方法Milne 公式线性多步法的构造基于泰勒展开的待定系数法∑∑=-=--++'--=r i ri i n i i n i n n x y h x y x y R 0111)()()(βα三、 本章思考题试用数值积分法建立常微分方程的初值问题：),()(00y x f dxdy y x y =⎪⎩⎪⎨⎧=的数值求解公式：)(211n n n n f f h y y ++=++ 解：由),(y x f dxdy =得：dx y x f dy ),(= （1） 对于（1）式。

第七章非线性方程求根一、重点内容提要 （一）问题简介 求单变量函数方程()0f x = (7.1)的根是指求*x （实数或复数），使得(*)0f x =.称*x 为方程(7.1)的根,也称*x 为函数()f x 的零点.若()f x 可以分解为()(*)()mf x x xg x =- 其中m 为正整数,()g x 满足()0g x ≠,则*x 是方程(7.1)的根.当m=1时,称*x 为单根;当m>1时,称*x 为m 重根.若()g x 充分光滑,*x 是方程(7.1)的m 重根,则有(1)()(*)'(*)...(*)0,(*)m m f x f x f x f x -====≠ 若()f x 在[a,b]上连续且()()0f a f b <,则方程(7.1)在(a,b)内至少有一个实根,称[a,b]为方程(7.1)的有根区间.有根区间可通过函数作图法或逐次搜索法求得. (二)方程求根的几种常用方法 1.二分法设()f x 在[a,b]上连续,()()0f a f b <,则()0f x =在(a,b)内有根*x .再设()0f x =在(a,b)内仅有一个根.令00,a a b b ==,计算0001()2x a b =+和0()f x .若0()0f x =则*x x =,结束计算;若00()()0f a f x >,则令10,1a x b b ==,得新的有根区间11[,]a b ;若00()()0f a f x <,则令10,a a bx ==,得新的有根区间11[,]a b .0011[,][,]a b a b ⊂,11001()2b a b a -=-.再令1111()2x a b =+计算1()f x ,同上法得出新的有根区间22[,]a b ,如此反复进行,可得一有根区间套1100...[,][,]...[,]n n n n a b a b a b --⊂⊂⊂⊂且110011*,0,1,2,...,()...()22n n n n n n a x b n b a b a b a --<<=-=-==-.故1l i m ()0,l i m l i m ()*2n n n n n n n nb a x a b x →∞→∞→∞-==+=因此,1()2n n n x a b =+可作为()0f x =的近似根,且有误差估计11|*|()2n n x x b a +-≤- (7.2)2.迭代法将方程式(7.1)等价变形为 ()x x ϕ= (7.3)若要求*x 满足(*)0f x =则*(*)x x ϕ=;反之亦然.称*x 为函数()x ϕ的一个不动点.求方程(7.1)的根等价于求()x ϕ的不动点由式(7.3)产生的不动点迭代关系式(也称简单迭代法)为1(),0,1,2...k k x x k ϕ+== (7.4)函数()x ϕ称为迭代函数.如果对任意1(),0,1,2...k k x x k ϕ+==,由式(7.4)产生的序列{}k x 有极限 l i m *k k x x →∞=则称不动点迭代法(7.4)收敛.定理7.1(不动点存在性定理)设()[,]x C a b ϕ∈满足以下两个条件: 1.对任意[,]x a b ∈有();a x b ϕ≤≤2.存在正常数1L <,使对任意,[,]x y a b ∈,都有|()()|||x y x y ϕϕ-≤- (7.5) 则()x ϕ在[,]a b 上存在惟一的不动点*x .定理7.2(不动点迭代法的全局收敛性定理)设()[,]x C a b ϕ∈满足定理7.1中的两个条件,则对任意0[,]x a b ∈,由(7.4)式得到的迭代序列{}k x 收敛.到()x ϕ的不动点,并有误差估计式1|*|||1k k k Lx x x x L --≤-- (7.6) 和 1|*|||1kk k k L x x x x L --≤-- (7.7)定理7.3(不动点迭代法的局部收敛性定理)设*x 为()x ϕ的不动点,'()x ϕ在*x 的某个邻域连续,且|'()|1x ϕ<,则迭代法(7.4)局部收敛.收敛阶的概念 设迭代过程(7.4)收敛于方程()x x ϕ=的根*x ,如果迭代误差*k k e x x =-当k →∞时成产下列渐近关系式1(0)k k e C C e +→≠常数 (7.8) 则称该迭代过程是p 阶收敛的.特别地,p=1时称线性收敛,p>1时称超线性收敛,p=2时称平方收敛.定理7.4(收敛阶定理)对于迭代过程(7.4),如果()()K x ϕ在所求根*x 的邻近连续,并且(1)()'(*)''(*)...(*)0(*)0p p x x x x ϕϕϕϕ-====≠ (7.9)则该迭代过程在点*x 的邻近是收敛的,并有()11lim(*)!p k p k ke x e p ϕ+→∞= (7.10)斯蒂芬森(Steffensen)迭代法 当不动点迭代法(7.4)只有线性收敛阶,甚至于不收敛时,可用斯蒂芬森迭代法进行加速.具体公式为21(),()()20,1,2,...k k k k k k k k k k ky x z y y x x x z y x k ϕϕ+==-=--+= (7.11)此法也可写成如下不动点迭代式12(),0,1,2,...(())()(())2()k k x x k x x x x x x x ψϕψϕϕϕ+==-=--+ (7.12)定理7.5(斯蒂芬森迭代收敛定理) 设*x 为式(7.12)中()x ψ的不动点,则*x 是()x ϕ的不动点;设''()x ϕ存在,'(*)1x ϕ≠,则*x 是()x ψ的不动点,则斯蒂芬森迭代法(7.11)是2阶收敛的. 3.牛顿迭代法牛顿迭代法是一种特殊的不动点迭代法,其计算公式为其迭代函数为1(),0,1,2,...'()k k k k f x x x k f x +=-= (7.13)()()'()f x x x f x ϕ=-牛顿迭代法的收敛速度 当(*)0,'(*)0,''(*)0f x f x f x =≠≠时,容易证明,'(*)0f x ≠,''(*)''(*)0'(*)f x x f x ϕ=≠,由定理7.4知,牛顿迭代法是平方收敛的,且12''(*)l i m 2'(*)k k k e f x e f x +→∞= (7.14) 重根情形的牛顿迭代法 当*x 是()0f x =的m 重根(2)m ≥时,迭代函数()()'()f x x x f x ϕ=-在*x 处的导数1'(*)10x m ϕ=-≠,且|'(*)|1x ϕ<.所以牛顿迭代法求重根只是线性收敛.若*x 的重数m 知道,则迭代式1(),0,1,2,...'()k k k k f x x x mk f x +==-= (7.15)求重根二阶收敛.当m 未知时,*x 一定是函数()()'()f x x f x μ=的单重零点,此时迭代式1()()'()'()['()]()''()0,1,2,...k k kk k k k kk k x f x f x x x x x f x f x f x k μμ+=-=--= (7.16)也是二阶收敛的.简化牛顿法 如下迭代法10(),0,1,2,...'()k k k f x x x k f x +=-=称为简化牛顿法或平行弦法.牛顿下山法 为防止迭代不收敛,可采用牛顿下山法.具体方法见教材. 4.弦截法将牛顿迭代法(7.13)中的'()k f x 用()f x 在1k x -,k x 处的一阶差商来代替,即可得弦截法111()()()()k k k k k k k f x x x x x f x f x ++-=--- (7.17)定理7.6假设()f x 在其零点*x 的邻域:|*|x x δ∆-≤内具有二阶连续导数,且对任意x ∈∆有'()0f x ≠,又初值01,x x ∈∆,,则当邻域∆充分小时,弦截法(7.17)将按阶151.6182p +=≈收敛到*x .这里p 是方程210λλ--=的正根.5.抛物线法弦截法可以理解为用过11(,()),(())k k k k x f x x f x ---两点的直线方程的根近似替()0f x =的根.若已知()0f x =的三个近似根k x ,1k x -,2k x -用过1122(,()),(,()),(,())k k k k kk x f x x f x x f x ----的抛物线方程的根近似代替()0f x =的根,所得的迭代法称为抛物线法,也称密勒(Muller)法.当()f x 在*x 的邻近有三阶连续导数,'(*)0f x ≠,则抛物线法局部收敛,且收敛阶为 1.839 1.84p =≈.二、知识结构图10[1,2]1x x --=≤≤--∈3-3-6k k 32三、常考题型及典型题精解例7-1 证明方程x 在上有一个实根x*,并用二分法求这个根,要求|x -x*|10.若要求|x -x*|10,需二分区间[1,2]多少次?解 设f(x)=x ,则f(1)=-1<0,f(2)=5>0,故方程f(x)=0在[1,2]上有根x*.又因f'(x)=3x -1,所以当x [1,2]时,f'(x)>0,即f (x)=0在[1,2]上有惟一实根x*.用二分法计算结果如表7-1所示.表7-1k k ak b k x ()k f x 的符号0 1 2 3 4 5 6 7 81 1 1.25 1.25 1.3125 1.3125 1.3125 1.3204 1.32432 1.5 1.5 1.375 1.375 1.13438 1.3282 1.32821.5 1.25 1.375 1.3125 1.3438 1.3282 1.3204 1.3243 1.3263+ - + - + + - - +9 1.3243 1.3282 1.32631.3253 +610x e -≤≤⨯≤≤≤≤≥∈-3-39910-6k k k+101此时x =1.3253满足|x -x*|0.9771010,可以作为x*的近2似值.1若要求|x -x*|,只需|x -x*|10即可,解得k+119.932,2即只需把[1,2]二分20次就能满足精度要求.例7-2 已知函数方程(x-2)=1,(1)确定有根区间[a,b];(2)构造不动点迭代公式使之对任意初始近似x [a,b],31|10.k x ---<k 迭代方法均收敛;(3)用所构造的公式计算根的近似值,要求|x1lim lim x x x x x e e e e →+∞→-∞∞∞∞∈解 (1)令f(x)=(x-2)-1,由于f(2)=-1<0,f(3)=-1>0,因此区间[2,3]是方程f(x)=0的一个有根区间.又因f'(x)=(x-1),f(x)=+,f(x)=-1,f'(1)=--1<0,当x>1时f(x)单增,x<1时f(x)单减,故f(x)=0在(-,+)内有且仅有一根x*,即x*[2,3].2'k k x x x x x x e e e e e e e ϕϕϕ-----∈∈≤≤≤∀∈k+100k+1(2)将(x-2)=1等价变形为x=2+,x [2,3].则(x)=2+.由于当x [2,3]时2(x)3,|(x)|=|-|<1故不动点迭代法x =2+,k=0,1,2,...,对x [2,3]均收敛.(3)取x =2.5,利用x =2+进行迭代计算,结果如表7-2所示.表7-2k k x 1||k k x x --0 1 2 3 42.5 2.082084999 2.124670004 2.119472387 2.1200949760.417915001 0.042585005 0.0005197617 0.0006225894 2.120094976.73cos 3120cos c k x x x x ϕ≈=--+=∈≤4k+10-30k+1k+1k 此时x 已满足误差要求,即x*例 考虑求解方程2的迭代公式2x =4+,k=0,1,2,...3(1)试证:对任意初始近似x R,该方法收敛;(2)取x =4,求根的近似值x ,要求|x -x |10;(3)所给方法的收敛阶是多少?2解 (1)由迭代公式知,迭代函数(x)=4+3{}os ,(,).|'sin |1(,)x x x ϕϕϕ∈-∞+∞≤<-∞+∞∀∈0k 022由于(x)的值域介于(4-)与(4+)之间,且3322(x)|=|-33故根据定理7.1,7.2知,(x)在内存在惟一的不动点x*,且对x R,迭代公式得到的序列x 收敛于x*.(2) 取x =4,迭代计算结果如表7-3所示.表7-3k k x 1||k k x x --0 1 2 3 4 54 3.564237587 3.391995168 3.354124827 3.348333384 3.3475299030.435762413 0.172242419 0.037870341 0.005791443 0.000803481此时5x 已满足误差要求，即5* 3.347529903x x ≈=（3）由于'(*)0.1363231290x ϕ≈≠，故根据定理7 .4知方法是线性收敛的，并且有1lim'(*)k k k e x e ϕ+→∞=。