9.1.2不等式的性质(修改过好用)课件PPT

盘点收获 承上启下
凯旋归来话收获
性质1： 不等式两边加上（或减去）同一个数 （或式子），不等号的方向不变；
性质2：不等式两边乘以（或除以）同一个正数， 不等号的方向不变；
性质3：不等式两边乘以（或除以）同一个负数， 不等号的方向改变
盘点收获 承上启下
凯旋归来话收获
三种思想：
类比的思想； 数形结合的思想； 分类讨论的思想
拓展训练
若x ≠2，（x-2)a>（x-2)b，比较a和b大小。
十五岁那年我第一次收到了男孩的情书，那时的我青涩懵懂，根本不知何为爱情。只知道打开情书的那一瞬间我的心跳加速，脸红的像滴血的玫瑰一般，生怕被其他同学知道班上的男同学暗恋我。于是又偷偷的把那封情书夹在我的作文本里带回家再次拿来阅读，一边读还一边红着脸偷偷的抿嘴微笑。自己心中思虑着原来被人喜欢的感觉是这样的。 时间让我的思想日渐成熟起来，慢慢的我也长成了一个亭亭玉立的大姑娘。我开始从书中寻找爱情，那时的我总是把那些书写美好爱情的诗词歌赋一遍一遍的读着，我爱读诗也爱写诗，看着柳永——衣带渐宽终不悔，为伊消得人憔悴时，他对爱情的执着让我真的敬佩；看着徐再思在《折桂令》中写到平生不会相思，才会相思，便害相思，我总是在思考者相思的滋味到底如何；在看着《红楼梦》中是一个阆苑奇葩，一个是美玉无瑕，有情却终究虚无一场空而感到忧伤，我感叹为何他俩不能长相见兮呢！ 当然我也在很多戏曲中看到很多爱情故事，但是这些终究是艺术传达出，而不是我自己真心体会的爱情，我渴望爱情，但是没有面包的爱情真的能够执子之手天长地久吗？但是，大学二年级的我看着喜欢自己的男生千里迢迢下着雨赶来看我时，心里怎能不会有些感动。 当我见到他的一瞬间我真的好紧张，我好像拥抱他。可是我是一个传统而矜持的女孩子，即使见到再喜欢的男孩子我都会克制自己的情绪，当我俩走在大学的校园里，两人记在小小的雨伞下面，两只手随着步伐时不时碰在一起时，彼此的心跳声呼吸声都能听见，听着不远处时不时传来萨克斯吹奏的曲子《罗密欧与朱丽叶》时，真是别有一番风味。在这样的情境下我们这对互相暗恋的年轻人始终两只手没有牵在一起，他的眼神时如此的温柔，回到寝室后我一夜未眠写下了这首简单的小诗： 今忆梦 雨夜魂牵梦几回。 烟雨袅袅， 心语徘徊， 七个雨夜，七种相思。 倒是花无人红， 情无依倚。 今雨期欲子青， 七日相许期期相依。 原来思念一个人是这样的滋味。可是一个对自己未来都如此懵懂的我怎么能真正对爱情负责人呢，当我拒绝他时，我眼睛有了泪花了；原来离开一个自己喜欢的人时这样的痛苦。当我看见不久后他牵着一个女孩的手自然都走在街上时，我的心流血了；原来看着自己爱恋的对象爱上别人的那种滋味，简直比咖啡更苦！ 我将这份苦涩的校园之恋深藏心底，当成是一种回忆。我无法左右我的爱情，但我可以左右的我的人生。当我成功的走近了我所规划的职业生涯时，我已经到了谈婚论嫁的年纪，这几年间不乏追求者，可我一再拒绝。 因为我再也找不到当初一见倾心的感觉了，我听不到紧凑的呼吸声、看不到温柔的眼神、也没有一句句关切的问候，有的只是百无聊赖的比较，学历、单位、家境，这样的相亲让我机器厌倦，我真的很 怀念大学的生活，怀念大学时间那一段段纯纯的山楂树之恋，而社会如此现实，看着街上的小情侣如此开放时，我始终坚持我医生一次的恋爱准则。 缘分真的是一件很奇怪的东西，在你不经意间偷偷的溜走了，又悄悄的像你走来。我仍然那般强淡定的面对我的爱情，似乎对一切异性都是那么不屑一顾，而我那一天的那一个眼神如此灼热的看着我，而这双囧囧有神的眼睛看着我一看就是一生。 当我被一个异性第一次十指相扣握住我的手时，我好有安全感，心里一股暖流划过我的心房，几年未曾有过的急促的心跳再一次频率如此之快，我对这个男人有一种直觉，总觉得我们之间会发生什么，结果一年之后我和这个男人就走进了婚姻的殿堂。我曾经许诺的唯一的爱情我终于做到了，我把我女人最美好的东西留给了这个男人，当在新婚之夜落在床单上的那一抹殷红时，他向我曾诺“我将一生对你不离不弃”。 当时的我处在24岁这样的年纪里对于不离不弃这个概念尚且模糊不清，我只知道这个男人让我有心动的感觉，他很执着的追求我，他很浪漫，他曾经单膝跪下求我做她的恋人，曾经捧着一大束玫瑰带给我惊喜，曾经脱下他的外套披在我的身上、曾经无数次容忍我的坏脾气、曾经给我冬日里送来一碗碗鲜美的汤汁、曾经生病时一口一口喂我吃药——太多的小事情发生在我的身上。当时的我没有所谓的两情若是久长时的概念，有的只是只争朝夕。 一年之后我们可爱的宝贝也出生了，可是我们的婚姻并不是一帆风顺的，我是一个爱美的女孩，我喜欢漂亮的包包，喜欢好看的裙子、喜欢香水化妆品。但是孩子的出生打乱了我们的生活节奏，也让我们的经济压力越发的大，我们的争吵声越来越多，我开始排斥他，我甚至后悔当初为什么没有选择那些经济能力强的男人结婚生孩子，我开始胡思乱想。我讨厌他给我带来的枯燥的奶妈生活、我讨厌他让我过早的走近的婚姻生活、我讨厌他给我买不起我想要的物质用品，我甚至有了放弃这段婚姻的念头，我不想把一生都献给这样一个平凡的男人身上、我讨厌他每天只知道洗床单洗被套、讨厌他整天唠唠叨叨。我要的丈夫是一个思想前进、事业心强的男人，而不是一个过

。
1 4 5 1 1 2 2 3 3 4 4 5 5
-3 -2 -1 0
。
-3 -2 -1 0 -3 -2 -1 0
.
育才初一数学备课组
发挥集体的智慧,让我们共同努力
求不等式1 求不等式1-2x < 6的负整数解
思考：要知道x的负整数解，首先应该求出一 元一次此不等式x的解集. 1-2x < 6
−2 x < 6 − 1
根据以下图形， 写出不等式的解集： 根据以下图形 ， 写出不等式的解集 ：
(1) (2) (3) ( ( (
x≤4 x>2
) )
x≥- 2 )
育才初一数学备课组
大于向右， 大于向右，小于 向左， 向左，有等号为实 心，无等号为空心
育才初一数学备课组
.
在数轴上表示下列不等式的解集： 在数轴上表示下列不等式的解集： (1)x≤-1 )x≤(3)x＜2 )x＜ (2)x≥-3 )x≥(4)-3≤x＜2 ≤x＜
育才初一数学备课组
：解不等式： 解不等式： •（1）x－7<8 （
解： x-7+7 <8+7 移 x <8+7 x <15 解：
这两小题中不等式的 变形与方程的什么变 形相类似？ 形相类似？
3x<2x（2）3x<2x-3
3x-2x <2x-3-2x 2x-
移
3x-2x <-3 x <-3
这里的变形与方程中的移项相类似： 注意：移项要变号
> > > ＝
4×3 4×2 × 4×1 × 4×0 ×
负数： × 负数：7×（-1） ）
< 7 ×（-2） < ） 7 × （-3） < ）

【例】利用不等式的性质解下列不等式：
(3) 2 x﹥50；
3
不等式的两边都除以
2
，不等号的方向不变，得
3
x﹥75
这个不等式的解集在数轴上的表示如图所示:
０
75
【例】利用不等式的性质解下列不等式： (4)-4x﹥3.
不等式两边都除以_-_4__，不等号的方向_改__变___，得
x﹤－ 3 4
这个不等式的解集在数轴上的表示如图所示：
B
C
D
E
三、巩固提高
一、平面上利用有序数对确定物体位置的方法
• 1、行列定位法： 例如： 座位
• 2、方格纸定位法： 例如： 棋盘
• 3、经纬定位法 例如：地图
• 4、区域定位法 例如：探究四的简图
四、概括整合
生活中还有哪些确定位置的其他方法？
（1）如果全班同学站成一列做早操，现在教师 想找某个同学，是否还需要用2个数据呢？
根据发现的规律填空:当不等式两边加或减 同一个数(正数或负数）时,不等号的方向_不__变___.
(3) 6＞2, 6×5__﹥__2×5 , 6×（-5）_﹤___2×（-5） ;
(4)–2<3, (-2)×6_﹤__3×6 , (-2) ×（-6）_﹥__3×（-6 ） 当不等式两边乘同一个正数时,不等号的方向_不__变__; 而乘同一个负数时,不等号的方向_改__变__;
这个不等式的解集在数轴上的表示为：
0
33
【例】利用不等式的性质解下列不等式： (2)3x<2x+1； 解：不等式两边都减去_2_x__，不等号的方向_不__变__，得
3x-2x﹤2x+1-2x x﹤1
这个不等式的解集在数轴上的表示如图所示：

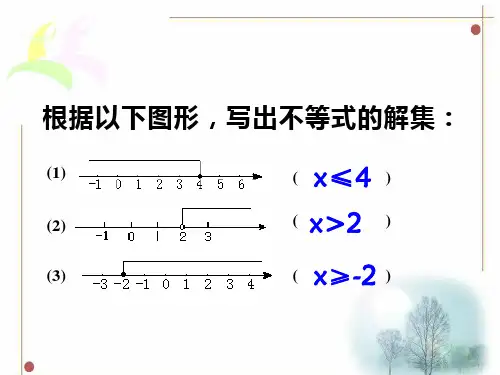
例 1 根据不等式的性质，把下列 不等式化成 x＜a 或 x＞a的形式： （ 1） x － 7 ＞ 2 （ 2） 6 x ＜ 5 x － 1
（3）4x-5＜ 5x
1 （4） － x ＜ -1 4
变 式 训 练，培 养 能 力
解下列不等式,并把解集在数 轴上表示出来.
（1） x-7 > 26
（2） 3x<5x+1 （ 3） （4） –4x>3
＞4 7＿＿ ＞ 4+(-1) 7+(-1)＿＿
7-(-1)＿＿ ＞ 4-(-1)
若a＜b,那么a+c＿＿ ＜ b+c, a-c＿＿ ＜ b-c.
＞ b+c, a-c＿＿ ＞ b-c. 若a＞b,那么a+c＿＿
对于上面数的比较,你发现了什么?
不等式的基本性质1:
不等式的两边都加上(或减去)同一 个数, 不等号方向不变，所得到的不 等式仍成立.
>
b c
不等式的基本性把不等号的方向改变, 所得的不等式成立.
如果a＞b,且c＜0, a b 那么ac ＜ bc, ＜ c c
尝 试 反 馈，巩 固 知 识
设a b, 用" "或" "填空 : > 3b; (1) 3a ___ ( 2) a 7 ___ > b 7; (3) 5a ___ < 5b; ( 4) (5) 2a 5 ___ > 2b 5; 3.5a 1 ___ 3 . 5 b 1 . <
2 3
x>50
课堂小结
1、谈一谈这节课的收获。 2、在解不等式时我们应该 注意哪些地方？ 3、对于哪些地方还存在疑问？ 互相交流一下。

如果关于x的不等式 (1-a)x>1-a 的解 集为 x<1 ,那么请给出一个符合题意a
的值
解：由(1-a)x>1-a ，不等式两边同 时除以 1-a ，得到 x<1
不等号方向改变了，由不等式的性 质3可知
1-a<0,a>1
可以取a=2
作 业: P128-----3,6
1 不等关系 不相等 处处可见
在古代，我们的祖先就懂得了翘翘板的工作原理， 并且根据这一原理设计出了一些简单机械， 并把它们用到了生活实践当中．
由此可见，“不相等”处处可见。 从今天起，我们开始学习一类新的数学知识：不等式．
不等式
７＞４ －3＜４
...ቤተ መጻሕፍቲ ባይዱ
两边都加（或减去） 同一个数
7+5＞4+5 -3-7 ＜4－7
－8＜４ -8÷（-2）>4÷（-2）
...
...
不等号 的方向
改变
改变
...
不等式性质3：
不等式两边乘( 或)除同以一个负数，不等号的方向改变。
类比推导
不等式的性质 3 不等式的两边乘（或除以）同 一个负数，不等号的方向改变
必须把不等号的方向改变
字母表示为：
﹤ ﹤ 如果a＞b，c＜0那么ac
bc，(或
(2)如果在-7<8的两边都加上9可得到 2 < 17
(3)如果在5>-2的两边都加上a+2可得到a+7 > a
(4)如果在-3>-4的两边都乘以7可得到 -21>-28
(5)如果在8>0的两边都乘以8可得到 64 > 0
(6)如果在 X >2+的两X 边都乘以14

2、将不等式2x-5 > -1化为x > 2
a是一个实数，比较a与3a的大小。
作业: 教科书第119页第4、6题
初中数学资源网
数，不等号的方向改变。就是说，如果
a b a ＞b，c <0 ,那么 ac<bc(或 c c
)
加减都用性质1 乘除正数性质2
不等号方向不改变 不等号方向还不变
乘除负数性质3
不等号方向必改变
1、 判断下列各题是否正确？为什 么(学生口答) (1)因为4a＞4b， 所以a＞b （ ） (2)因为a+8＞4， 所以a＞-4 （ ） (3)如果a＞b， 那么ac＞bc （ ） (4)如果a＞b， 那么ac2＞bc2 （ ）
1.说出下面结论的依据。 如果a＞b， 那么a-8 > b-8 （ ） 如果a-1＞0 那么a-1+1 > 1 （ ） 2. 设a＞b，用“＜”或“＞”填空并说明 理由。 （1）a - 3____b - 3； （2）a- b____0 3.如果x+5＞4，那么两边都减去5， 可得x ____ -1
a b <bc (或 c c ) 如果a>b ________, ______________ ，c<0 那么ac
1、由不等式2a<8，得a<4,是在不等 式的两边都 （ ） 2、已知x>y,那x/2 y/2 3、在不等式a>b的两边都乘以-1， 可得 ，根据是（ ） 4、若-2x>10，则x -5 5、如果a>0,那么5a 7a
不等式的性质1：不等式两边都加上 (或减去）同一 个数(或式子),不等号方向不变。
就是说，如果a ＞b，那么a±c＞b±c. 不等式性质2：不等式的两边都乘以（或除以） 同一个正

课外作业：

课本128页5、7
拓展延伸：1、将下列不等式化成x > a或 x < a 的形式 (1) x-5 > -1 (2) -2x > 4 (3) 7x < 6x －6
2、已知不等式2a＋3b＞3a＋ 2b,试比较a、b 的大小。
初中数学资源网
6 ×(-5)____2×(-5), <
如果-2< 3, 那么-2×2____3×2, <
Байду номын сангаас
-2÷2____3÷2, <
-2×(- 4)____3×( - 4), -2÷ (- 4)____3÷ ( - 4) ＞ ＞
试一试，你能行： 判断下列各题的推导是否正确？为什么(学生口答) (1)因为7.5＞5.7，所以-7.5＜-5.7； (2)因为a+8＞4，所以a＞-4； (3)因为4a＞4b，所以a＞b； (4)因为-1＞-2，所以-a-1＞-a-2； (5)因为3＞2，所以3a＞2a．
＞ (4)-a/4______0 (6)a3______0 ＜
我会填:
正 (1) ∵ 2a < 3a , ∴a是____数
a a 正 (2) ∵ , ∴a是____数 2 3
(3) ∵ ax < a 且 x > 1 , 负 ∴a是____数
盘点收获： 通过本节的学习你有哪些收获？还有哪些疑 惑？
滨州市里则树人学校
周玉玲
如果 5 ＞ 3 那么 5+2 ____ 3+ 2, ＞ 如果-1< 3, 那么-1+2____3+2, <
＞ 5 -2____3-2
< -1- 4____3 - 4

x＜10 － 3
8x－2≤7x＋3 8x－7x≤3＋2
再说一遍：移项要变号,不影 响不等号的方向
填 空：
解不等式：－2x＋1＞3－3x 解： －2x＋1＞ 3 － 3x
移项，得 －2x +3x ＞3 －1
合并，得
x＞ 2
例3 解不等式
3（1－x）＞2（1－2x）
解: 去括号,得 3-3 x ＞2-4x 移项,得 -3 x +4x ＞-3+2 合并同类项,得 x ＞-1
∴原不等式的解集是x ＞-1
比一比，谁做得又快又好！
解下列不等式，并把它们的解集在数轴上 表示出来。
（1）x＋4＞3 （2）7x＋6 ≥ 6x＋3 （3）7x－1 ≤ 6x＋1 （4）3－5x < 2（2－3x）
例
例如 解不等式3＋3x＞2＋4x
解：移项，得 3－2＞ 4x－3x
合并同类项，得
1＞x
的解是非正数.
4 24
从中你得到什么规律？
例2 三角形中任意两边之差
与第三边有怎样的大小关系？ a
b
解：如图，设a,b,c为任意一个三角
形的三条边的长，则
c
a＋b＞c, b＋c＞a, c＋a＞b.
由式子a＋b＞c 移项可得 a＞c－b, b＞c－a . 类似地，由式子b+c＞a及c+a＞b移项可得 c＞a-b, b＞a-c 及 c＞b-a, a＞b-c
三角形中任意两边之差小于第三边
1、不等式性质1：不等式的两边＿都＿加上 或＿都＿减去＿同＿一个数或式，所得到的不等式 仍＿＿成＿立＿.
2、不等式移项法则：把不等式的任何一项 的＿符＿号＿改＿变＿后，从_不__等__号__的＿一＿边＿移到_＿ _另__一＿边＿，所得到的不等式仍成立。

第十一页，编辑于星期三：二十二点 二十分。
x ＋ 33 < 10 －3
x＜10 － 3
8x－2≤7x＋3 8x－－7x ≤3＋＋2
再说一遍：移项要变号,不影 响不等号的方向
第十二页，编辑于星期三：二十二点 二十分。
填 空：
解不等式：1－2x＞ － 3x + 3 解： 1－2x＞ － 3x + 3
10x – 5(20 – x) ≥ 80
解这个不等式，得: x ≥ 12
答：……
第二十一页，编辑于星期三：二十二点 二十分 。
1、不等式性质1：不等式的两边＿＿都加上或＿ ＿减都去＿＿一同个数或式，所得到的不等式＿＿＿＿. 仍成立
2、不等式移项法那么：把不等式的任何一 项的符＿号＿改＿变＿＿后，从不_等__号____的一＿边＿＿移到_ ＿另_一__边＿＿，所得到的不等式仍成立。
移项，得 －2x +3x ＞3 －1
合并，得
x＞ 2
第十三页，编辑于星期三：二十二点 二十分。
例3 解不等式
3〔1－x〕＞2〔1－2x〕
解: 去括号,得 3-3 x ＞2-4x 移项,得 -3x +4x ＞-3+2
合并同类项,得 x ＞-1
∴原不等式的解集是x ＞-1
第十四页，编辑于星期三：二十二点 二十分。
从中你得到什么规律？
例2 三角形中任意两边之差
与第三边有怎样的大小关系？
a
b
解：如图，设a,b,c为任意一个三角
形的三条边的长，那么
c
a＋b＞c, b＋c＞a, c＋a＞b.由式子a＋b＞c 移项可得
a＞c－b, b＞c－a . 类似地，由式子b+c＞a及c+a＞b移项可得

课堂练习
1、（2010鄂州）根据下图所示，对a、b、c 三种物体的质量判断正确的是（ ）
A、a<c B、Biblioteka <bC、a>c
D、b<c
2．(2012广州)若a>b，c是任意实数，则下列 不等式中总成立的是（ ） A．a＋c＜b＋c B．a－c ＜b－c C．ac＜bc D．ac>bc
课堂练习
3.（2013广东）已知实数 a、b ，若a >b ，则 下列结论正确的是( ) A. a-5<b-5 B. 2+a<2+b C.a b D.3a>3b
3 3
4.（2014汕尾）若 x>y，则下列式子中错误的 是（ ） x y A．x-3>y-3 B． 3 3 C．x+3>y+3 D．-3x>-3y
5.（2013德宏）如果a＜0，则下列式子错误的 是（ ） A. 5+a＞3+a B.5﹣a＞3﹣a a a C．5a＞3a D．
5 3
感悟与反思
性质1
性质2
2．探究新知
问题2 研究等式性质的基本思路是什么？
等式的性质就是从加减乘除运算的角度研 究运算的不变性.
(1) 5>3,
5+2____3+2 ,
5－2____3－2 ; -1－3____3－3 ;
(2) –1<3 , -1+2____3+2 , (3) a>b, a+c____b+c 根据发现的规律填空:
不等式的基本性质３ 不等式的两边都乘 （或除以）同一个负数，不等号的方向改变.
ab 如果 a b , c 0 , 那么 ac bc （或 ) ． cc

是的在 你不数 怎是学 么你的 知知天 道道地
什里 么， ，重 而要
毕达哥拉斯 (约前580年—前500年) 古希腊哲学家、数学家和音乐理论家。
夯实基础 巩固提高
如果a>b，用“>”，“<”填空 （1）a-3 _____ b-3 （不等式性质 ___） （2）2+a _____ 2+b （不等式性质____） （3）-3a _____ -3b （不等式性质____） （4）6a_____6b （不等式性质____）
夯实基础 巩固提高
加减都用性质1，不等号方向不改变 乘除正数性质2，不等号方向还不变 乘除负数性质3，不等号方向要改变
夯实基础 巩固提高
把下列不等式化成 x>a或x<a的形式. 例1：-x+3>5 解：根据不等式的性质1， 将解集用数轴表示为：
两边同时加上-3得： -x+3-3>5-3 -x>2
拓展训练
若x ≠2，（x-2)a>（x-2)b，比较a和b大小。
不等式性质2：不等式两边乘以（或除 以）同一个正数，不等号的方向不变；
数学语言：若a>b，c>0则a·c>b·c，
或a÷c>b÷c
先学后教 循序渐进
不等式性质3 ： 不等式两边乘以（或除 以）同一个负数，不等号的方向改变。
数学语言：若a>b，c<0则a·c<b·c，
或a÷c<b÷c
先学后教 循序渐进
不访设c>0，则
c
c
a+c>b+c
b b+c a a+c
c
b-c b
c
a-c a