材料力学习题第12章资料
- 格式：doc
- 大小：648.00 KB
- 文档页数：8
下载文档原格式
合集下载
材料力学课件(哈工大)第12章杆件的强度与刚度计算
12-1 强度计算与刚度计算1）构件的失效模式若载荷过大，超出了构件的承载能力，构件将失去某些功能而不能正常工作，称为构件失效。
工程中，构件的失效模式主要有：•强度失效——构件的材料断裂或屈服。
•刚度失效——构件的弹性变形过大，超出规定范围。
•疲劳失效——构件在交变应力作用下的强度失效。
•稳定失效——构件丧失了原有的平衡形态。
本章只研究杆件强度失效与刚度失效的计算问题。
12-1 强度计算与刚度计算首先根据内力分析方法，对受力杆件进行内力分析（画出内力图），确定可能最先发生强度失效的横截面（危险截面）。
[]()4 , 3 , 2 , 1 之一=≤i ri σσ根据强度条件，即上面不等式，强度计算可解决三类问题：•校核强度•设计截面•计算许可载荷1）构件的失效模式2）杆件的强度计算其次根据杆件横截面上应力分析方法，确定危险截面上可能最先发生强度失效的点（危险点），并确定出危险点的应力状态。
最后根据材料性能（脆性或塑性）和应力状态，判断危险点的强度失效形式（断裂或屈服），选择相应的强度理论，建立强度条件：12-1 强度计算与刚度计算3）杆件的刚度计算除了要求满足强度条件之外，对其刚度也要有一定要求。
即要求工作时杆件的变形或某一截面的位移（最大位移或指定截面处的位移）不能超过规定的数值，即∆为计算得到的变形或位移；[∆]为许用（即人为规定的）变形或位移。
对轴向拉压杆，∆是指轴向变形或位移u ；对受扭的杆件，∆是指两指定截面的相对扭转角φ或单位长度扭转角ϕ；对于梁，∆是指挠度v 或转角θ。
根据刚度条件，即上面不等式，刚度计算可解决三类问题：•校核刚度•设计截面•计算许可载荷][ΔΔ≤刚度条件1）构件的失效模式2）杆件的强度计算12-2 轴向拉压杆件的强度计算轴向拉压杆横截面上正应力是均匀分布的，各点均处于单向应力状态。
因此，无论选用哪个强度理论，强度条件表达式均演化为][m axσσ≤例1螺旋压力机的立柱如图所示。
材料力学第十二章
A
i
写成
r Ai Ai
i
（12-10）
例 12-1 设曲杆的截面为梯形（见图 12-6），尺寸 b1 40 mm ，b2 60 mm ， h 140 mm ， R1 260 mm ， R2 120 mm 。试确定曲杆中性层的曲率半径 r ， 并计算截面对中性轴的静矩 S 。若截面上的弯矩 M 18.53 kN m ，试求最大
与 M 对应的弯曲正应力已于例 12-1 中算出。将弯曲正应力与均布的正应
力 FN 叠加，得出截面内侧边缘处的最大拉应力为 A
l
M (R2 r) SR2
FN A
143.5
100 103 7 000 106
MPa
158 MPa
截面外侧边缘处的最大压应力为
y
M (R1 r) SR1
FN A
第四节 曲杆的强度计算
图 12-12（a）所示曲杆的纵向对称面内作用载荷时，将在其横截面上引起内 力，这些内力包括弯矩、轴力和剪力。用截面 m m 将曲杆截开，取出右半部分来
研究，如图 12-12（b）所示，把截 面 m m 上的内力和曲杆右半部 分上的外力分别向 m m 截面的 法线方向和切线方向投影。再对截 面的形心取矩，由平衡条件不难求 得
设 R0 为轴线的曲率半径，e 为截面形心到中性轴的距离，由图 12-2 可 知
e R0 r 将式（12-1）代入式（d），得
M y
E (d) d
yz dA 0
A
由于 y 轴是横截面的对称轴，有
（12-3）
yz
A dA 0
所以式（d）便自动满足了。
将式（12-1）代入式（e），得
M
A
图12-9
浙江工业大学材料力学第12章答案
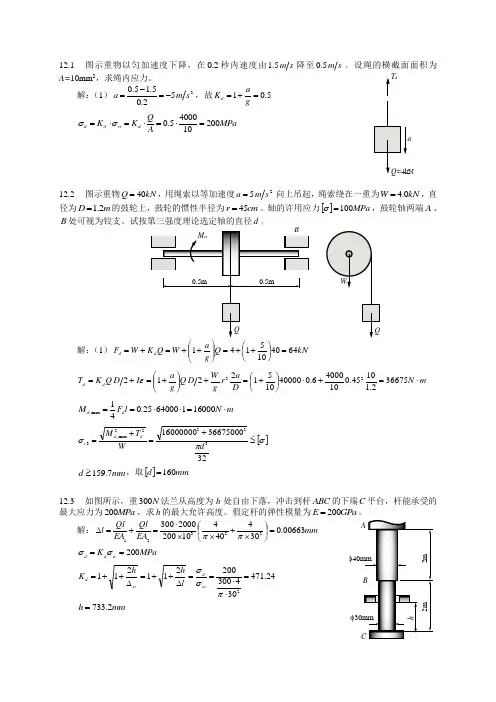
12.1 图示重物以匀加速度下降，在2.0秒内速度由s m 5.1降至s m 5.0。
设绳的横截面面积为A=10mm 2，求绳内应力。
解：（1）252.05.15.0s m a -=-=，故5.01=+=g a K dMPa A Q K K d st d d 2001040005.0=⋅=⋅=⋅=σσ12.2 图示重物kN Q 40=，用绳索以等加速度25s m a =向上吊起，绳索绕在一重为kN W 0.4=，直径为m D 2.1=的鼓轮上，鼓轮的惯性半径为cm r 45=。
轴的许用应力[]MPa 100=σ，鼓轮轴两端A 、B解：（1）kN Q g a W Q K W F d d 6440105141=⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛++=+= m N D a r g W D Q g a I D Q K T d d ⋅=+⋅⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛+=+=366752.11045.01040006.0400001051221222ε m N l F M d d ⋅=⋅⋅==1600016400025.041max , []σπσ≤+=+=32366750001600000032222max ,3d WT M d d rmm d 7.159≥，取[]mm d 160=12.3 如图所示，重N 300法兰从高度为h 处自由下落，冲击到杆ABC 的下端C 平台，杆能承受的最大应力为MPa 200，求h 的最大允许高度。
假定杆的弹性模量为E 200=解：mm EA Ql EA Ql l 00663.030440410200200030022321=⎪⎭⎫ ⎝⎛⨯+⨯⨯⋅=+=∆ππ MPa K st d d 200==σσ24.4713043002002112112=⋅⋅==∆++=∆++=πσσst d st d l h h K mm h 2.733=12.4 如图所示，重N 100物体从mm h 500=位置自由下落到铝制梁AB 上的C 点，求截面C 的位移和梁上的最大应力。
材料力学第十二章
寸系数。 1.弯曲时的有效应力集中系数和尺寸系数
D 50 1.25 d 40
f50
f40
r 5 0.125 d 40
由图表查有效应力集中系数 r=5
当 : b 1000 MPa 时 ,K 1.55
当 : b 900MPa 时 ,K 1.55
当 : b 920MPa 时 ,K 1.55
的有效应力集中系数和尺寸系数。
10、简述影响构件持久极限的主要因素
11、交变应力的平均应力为σm＝20MPa，应力 幅为σa＝50MPa，其循环特性中的 最大应力 σmax ＝ ，最小应力σmin＝ ，循环特性r ＝ 。
12、最大弯曲正应力相等的三根材料相同的梁，承受交变应力。 （A）是对称循环；
（B）是脉动循环；
（C）是∣σmin∣<∣σmax∣的不对称循环。 则以 种循环的梁的疲劳强度最低。
α B
18、 火车轮轴受力情况如图所示。a=500mm，
l=1435mm，轮轴中段直径d=15cm。若P=50kN， 试求轮轴中段截面边缘上任一点的最大应力，最 小应力，循环特征，并作出曲线。
19、阶梯轴如图所示。材料为铬镍合 b 920MPa 金， 1 420MPa ， 1 250MPa 。轴的尺寸是： d=40mm，D=50mm，r=5mm。求弯曲和扭转时
③ 强度校核
0 1 1
max 1
安全
1、构件在临近疲劳断裂时，其内部： A：无应力集中；
。
B：无明显的塑性变形；
C：不存在裂纹； D：不存在应力；
2、塑性较好的材料在交变应力的作用下，当危险点的最 大应力低于屈服极限时： A：既不可能有明显的塑性变形，也不可能发生断裂； B：虽可能有明显的塑性变形，但不可能发生断裂； C：不仅可能有明显的塑性变形，而且可能发生断裂；
D 50 1.25 d 40
f50
f40
r 5 0.125 d 40
由图表查有效应力集中系数 r=5
当 : b 1000 MPa 时 ,K 1.55
当 : b 900MPa 时 ,K 1.55
当 : b 920MPa 时 ,K 1.55
的有效应力集中系数和尺寸系数。
10、简述影响构件持久极限的主要因素
11、交变应力的平均应力为σm＝20MPa，应力 幅为σa＝50MPa，其循环特性中的 最大应力 σmax ＝ ，最小应力σmin＝ ，循环特性r ＝ 。
12、最大弯曲正应力相等的三根材料相同的梁，承受交变应力。 （A）是对称循环；
（B）是脉动循环；
（C）是∣σmin∣<∣σmax∣的不对称循环。 则以 种循环的梁的疲劳强度最低。
α B
18、 火车轮轴受力情况如图所示。a=500mm，
l=1435mm，轮轴中段直径d=15cm。若P=50kN， 试求轮轴中段截面边缘上任一点的最大应力，最 小应力，循环特征，并作出曲线。
19、阶梯轴如图所示。材料为铬镍合 b 920MPa 金， 1 420MPa ， 1 250MPa 。轴的尺寸是： d=40mm，D=50mm，r=5mm。求弯曲和扭转时
③ 强度校核
0 1 1
max 1
安全
1、构件在临近疲劳断裂时，其内部： A：无应力集中；
。
B：无明显的塑性变形；
C：不存在裂纹； D：不存在应力；
2、塑性较好的材料在交变应力的作用下，当危险点的最 大应力低于屈服极限时： A：既不可能有明显的塑性变形，也不可能发生断裂； B：虽可能有明显的塑性变形，但不可能发生断裂； C：不仅可能有明显的塑性变形，而且可能发生断裂；
工程力学-材料力学-第12章动量矩定理
•注意：内力不能改变质点系的动量矩。
•
例12-3 •已知：m1，r，k ，m2 ，R，
•求：弹簧被拉长s时，重物m2的加速度a2 。 •解 •选系统为研究对象,受力分析如图 •设：塔轮该瞬时的角速度为ω，则
•解得：
•
3．动量矩守恒定律
•若
，则 常矢量；
•若
，则 常量。
•
§12-3 刚体绕定轴转动的微分方程 •主动力： •约束力：
•
例12-8 •已知：l，m，θ=60°。求：1. αAB；2. FA • 解：绳子刚被剪断，杆AB作平面运
动，受力如图，根据平面运动微分 方程
• 补充运动学方 程
• 在y轴方向 投影
•
例12-9 •已知：如图r，m， m1。求：1. aA；2. FAB ；3. FS2 • 解：分别以A、B、C为研究对象
•其中： • (O为定点)
•
质点的动量矩定理
•因此 •称为质点的动量矩定理：质点对某定点的动量矩 对时间的一阶导数，等于作用力对同一点的矩。
•投影式：
•
2. 质点系的动量矩定理 •对第i个质点有 ： •对n个质点有：
• 由于
•得
•
2. 质点系的动量矩定理
•称为质点系的动量矩定理：质点系对某定点O的动量 矩对时间的一阶导数，等于作用于质点系的外力对于 同一点之矩的矢量和。 •投影式：
•2. 选轮2为研究对象
•积分
•
§12-4 质点系相对于质心的动量矩定理 •1．对质心的动量矩 •如图，以质心C为原点，取平移坐标系Cx’y’z’。 •质点系相对质心C为的动量矩为：
•由于 •得 • 质点系相对质心的动量矩，无论是以相对速度计算还是
以绝对速度计算，其结果都相同。
•
例12-3 •已知：m1，r，k ，m2 ，R，
•求：弹簧被拉长s时，重物m2的加速度a2 。 •解 •选系统为研究对象,受力分析如图 •设：塔轮该瞬时的角速度为ω，则
•解得：
•
3．动量矩守恒定律
•若
，则 常矢量；
•若
，则 常量。
•
§12-3 刚体绕定轴转动的微分方程 •主动力： •约束力：
•
例12-8 •已知：l，m，θ=60°。求：1. αAB；2. FA • 解：绳子刚被剪断，杆AB作平面运
动，受力如图，根据平面运动微分 方程
• 补充运动学方 程
• 在y轴方向 投影
•
例12-9 •已知：如图r，m， m1。求：1. aA；2. FAB ；3. FS2 • 解：分别以A、B、C为研究对象
•其中： • (O为定点)
•
质点的动量矩定理
•因此 •称为质点的动量矩定理：质点对某定点的动量矩 对时间的一阶导数，等于作用力对同一点的矩。
•投影式：
•
2. 质点系的动量矩定理 •对第i个质点有 ： •对n个质点有：
• 由于
•得
•
2. 质点系的动量矩定理
•称为质点系的动量矩定理：质点系对某定点O的动量 矩对时间的一阶导数，等于作用于质点系的外力对于 同一点之矩的矢量和。 •投影式：
•2. 选轮2为研究对象
•积分
•
§12-4 质点系相对于质心的动量矩定理 •1．对质心的动量矩 •如图，以质心C为原点，取平移坐标系Cx’y’z’。 •质点系相对质心C为的动量矩为：
•由于 •得 • 质点系相对质心的动量矩，无论是以相对速度计算还是
以绝对速度计算，其结果都相同。
材料力学12
max m min
r
min 0 max
max
2
a m
a
t
3）静循环
m max min
min r 1 max
t
a 0
m max min
§12-2 循环特性、平均应力和应力幅度 二、几种特殊循环应力 1）对称循环应力
max1 max 2
r
N0—循环基数
S-N曲线
r—材料持久限
r—循环特性 1 —对称循环持久极限应力
N
N0 107
—钢材的循环基数
N1 N2
N0
钢材达到 N0 107 而未疲劳的 最大应力值为钢材的疲劳极限
§12-3 疲劳极限
二、疲劳极限(材料持久极限) 3）“条件”持久极限 有色金属没有明显趋于水平直线部分，通常规定循 环基数为 N0 108 对应且不引起疲劳的最大应力。
1）对称循环应力
max
min
M y Iz
max
M Wz
§12-2 循环特性、平均应力和应力幅度 二、几种特殊循环应力
1）对称循环应力
min r 1 max
max m min
a max
m 0
t
a
T
§12-2 循环特性、平均应力和应力幅度 二、几种特殊循环应力 2）脉动循环应力
max2 b 60%
. . . .
N1
N2
. . . .
. .
. .
max n
. .
Nn
第n根试件
§12-3 疲劳极限
一、疲劳试验 光滑小试件的弯曲疲劳试验 max1 max 2 2）疲劳试件 3）疲劳试验 一组光滑小试件（6~10根） 第一根试件 第二根试件
材料力学第2版 课后习题答案 第12章 变形能法
3 d1 ； 2
(b) 梁的抗弯刚度EI，略去剪切变形的影响。 解： （a） M n1 = m
M n2 = m U2 = J P2 =
9.6m 2 l Gπd14
U1 = J P1 =
m 2l 4GJ P1 π 4 d1 32
m 2l 4GJ P2 π 4 5.06π 4 d2 = d1 32 32
故
U a 16 = Ub 7
11-3 图示桁架各杆材料相同，截面面积相等，试求在 P 力作用下，桁架的变形能。 解：
支反力
R Ax = P R Ay = R B =
各杆的轴力和变形能如表所示 杆号 1 内力 Ni 杆长 各杆的变形能 Ui
P 2
2P 2
2l
2 P 2 l (4 EA)
2
− 2P 2
求 θA
M 0 ( x1 ) = −1 M 0 ( x 2 ) = −1
θA =
1 EJ
⎡ ⎛L ⎤ 1 ⎞ − P⎜ + x2 ⎟(− 1)⎥ dx 2 ∫0 (− Px1 )(− 1)dx1 + 2EJ ∫0 2 ⎢ ⎠ ⎣ ⎝2 ⎦
2
L
L
1 L2 1 = ⋅P⋅ + EJ 8 2 EJ =
求 δB
0
2l
l l l
2 P 2 l (4 EA)
0
3 4 5ຫໍສະໝຸດ P 2 P 2P 2 l (8EA) P 2l (8 EA)
故珩架的变形能为
5
U = ∑ Ui =
i =1
2 2 + 1 P 2l P 2l = 0.957 4 EA EA
11-4 试计算图示各杆的变形能。 (a) 轴材料的剪切弹性模量为G， d 2 =
材料力学第12章 能量法
范围内工作时，其轴线弯曲成为一段圆弧，如图12.5（a）所示。两端横截
面有相对转动，其夹角为θ ，由第7章求弯曲变形的方法可以求出
图12.5 与前面的情况相似，在线弹性范围内，当弯曲外力偶矩由零逐渐增加到M0时
，梁两端截面相对于转动产生的夹角也从零逐渐增加到θ ，M0与θ 的关系也
是斜直线，如图12.5（b）所示，所以杆件纯弯曲变形时的应变能为
dW在图12.2（a）中以阴影面积来表示。拉力从零增加到FP的整个加载过程
中所做的总功则为这种单元面积的总和，也就是说是△OAB的面积，即
可以将以上的分析推广到其他受力情况，因而静载荷下外力功的计算式可以
写为 式中的 F是广义力，它可以是集中力或集中力偶；Δ 是与广义力F相对应的
位移，称为广义位移，它可以是线位移或角位移。式（12.2）表明，当外力
在工程实际中，最常遇到的是横力弯曲的梁。这时梁横截面上同时有剪力和
弯矩，所以梁的应变能应包括两部分：弯矩产生的应变能和剪力产生的应变 能。在细长梁的情况下，剪切应变能与弯曲应变能相比，一般很小，可以不
计，常只计算弯曲应变能。另外，此时弯矩通常均随着截面位置的不同而变
化，类似于式（12.5）与式（12.9），梁的弯曲应变能为
表面上的剪力与相应的位移方向垂直，没有做功。因此，单元体各表面上的 剪切力在单元体变形过程中所做的功为
故单元体内积蓄的应变能为
则单元体内积蓄的应变比能为
下
这表明，vε 等于γ 直线
的面积。由剪切胡克定律=Gγ ,比能又可以写成下列形式
（3）扭转 如图12.4（a）所示的受扭圆轴，若扭转力偶矩由零开始缓慢增加到最终值T
，积蓄在弹性体内的应变能Vε 及能量耗损Δ E在数值上应等于载荷所做的功 ，既 如果在加载过程中动能和其他形式的能量耗损不计，应有
材料力学 第12章
集中质量势能
由静态量与冲击动态量之关系 得杆件变形能为 由能量守恒 于是冲击应力为
静载Q作用于C端，可求得C点的静位移 最大静应力发生在B截面，其表达式为 综合以上结果，可求出B截面处的最大冲击应力为
P=5kN
1m
6m
已知
木柱：E＝10GPa 橡皮：E＝8MPa
计算： 1. 木柱最大正应力？ 2. 在木柱上端垫20mm的橡皮 300mm ，木柱最大正应力为多少？
§12-3 构件受冲击载荷作用时的动应力计算
1. 工程中的冲击问题 锻锤与锻件的撞击，重锤打桩，用铆钉枪进行铆接，高速转 动的飞轮突然刹车等均为冲击问题，其特点是冲击物在极短 瞬间速度剧变为零，被冲击物在此瞬间经受很大的 和
2. 求解冲击问题的能量法
基本假定 ① 不计冲击物的变形；
② 冲击物与构件（被冲击物）接触后无回弹，二者合为一个运动系统； ③ 构件的质量（惯性）与冲击物相比很小，可略去不计，冲击应力 瞬时传遍整个构件； ④ 材料服从虎克定律； ⑤ 冲击过程中，声、热等能量损耗很小，可略去不计。
【解】以叶根为起始点建坐标x。设处横截面的面积为A(x) ，由 于横截面面积沿轴线按线性规律变化，故有：
这个表达式满足 处任取一微段 ，有
该点向心加速度为 惯性力为
截面以上部分杆件的惯性力是
设作用在截面上的轴力为 Nx，由平衡方程
最大轴力发生在叶根横截面上
处任取一微段 ，有 积分可求出叶片的总伸长
解得 从而可求得钢索横截面上的动应力为
其中
是P作为静载荷作用时钢索横 截面上的应力
是动荷系数
ห้องสมุดไป่ตู้
3. 等角速转动构件内的动应力分析
【例13-2】 图中一平均直径为D，壁厚为t的薄壁圆环，绕通过 其圆心且垂直于环平面的轴作均速转动。已知环的角速度 ， 环的横截面积A和材料的容重 ，求此环横截面上的正应力
由静态量与冲击动态量之关系 得杆件变形能为 由能量守恒 于是冲击应力为
静载Q作用于C端，可求得C点的静位移 最大静应力发生在B截面，其表达式为 综合以上结果，可求出B截面处的最大冲击应力为
P=5kN
1m
6m
已知
木柱：E＝10GPa 橡皮：E＝8MPa
计算： 1. 木柱最大正应力？ 2. 在木柱上端垫20mm的橡皮 300mm ，木柱最大正应力为多少？
§12-3 构件受冲击载荷作用时的动应力计算
1. 工程中的冲击问题 锻锤与锻件的撞击，重锤打桩，用铆钉枪进行铆接，高速转 动的飞轮突然刹车等均为冲击问题，其特点是冲击物在极短 瞬间速度剧变为零，被冲击物在此瞬间经受很大的 和
2. 求解冲击问题的能量法
基本假定 ① 不计冲击物的变形；
② 冲击物与构件（被冲击物）接触后无回弹，二者合为一个运动系统； ③ 构件的质量（惯性）与冲击物相比很小，可略去不计，冲击应力 瞬时传遍整个构件； ④ 材料服从虎克定律； ⑤ 冲击过程中，声、热等能量损耗很小，可略去不计。
【解】以叶根为起始点建坐标x。设处横截面的面积为A(x) ，由 于横截面面积沿轴线按线性规律变化，故有：
这个表达式满足 处任取一微段 ，有
该点向心加速度为 惯性力为
截面以上部分杆件的惯性力是
设作用在截面上的轴力为 Nx，由平衡方程
最大轴力发生在叶根横截面上
处任取一微段 ，有 积分可求出叶片的总伸长
解得 从而可求得钢索横截面上的动应力为
其中
是P作为静载荷作用时钢索横 截面上的应力
是动荷系数
ห้องสมุดไป่ตู้
3. 等角速转动构件内的动应力分析
【例13-2】 图中一平均直径为D，壁厚为t的薄壁圆环，绕通过 其圆心且垂直于环平面的轴作均速转动。已知环的角速度 ， 环的横截面积A和材料的容重 ，求此环横截面上的正应力
材料力学——第12章(压杆稳定计算)
情况(b)： I z =hb3 /12
FPcrb2
l/2
z x
b h x
h b
2 EI z
2 l 2 10 10 9 0.2 0.12 3 44.4kN 2 12 8 FPcrb2 / FPcrb1 44.4 / 493.5 9% FPcra 2 / FPcra1 123.4 / 177.6 70%
32
②S< 时：
cr
S
P
0 的杆为小柔度杆，其临 界应力为屈服极限。
cr s
cr a b
③临界应力总图
2E cr 2
l
i
33
0 s a b
P 2E P
2.抛物线型经验公式 对于由结构钢、低合金结构钢等材料制成的非细长杆， 可采用抛物线型经验公式计算其临界应力
E cr 2 P
2
2E P
令
P
E
P
P
29
满足
P
压杆
细长杆（大柔度杆）
即只有当压杆为细长杆时，才能用欧拉公式计算其临界应 力和临界力。 λ P 值仅与材料的弹性模量 E 及比例极限σ P 有关，所 以，λ P值仅随材料而异。例如，对于 Q235 钢（ E = 206 GPa ，σ P＝200 MPa ) ，λ P的理论值为
35
36
37
[例12-2] Q235钢制成的矩形截面压杆，受力及两端约 束情况如图所示，在A、B两处为销钉连接。若已知l=2300mm, , b=40mm,h=60mm，材料的弹性模量E=206GPa,λ P=101。试求此 杆的临界力。
解：⑴确定压杆将首 先在哪个平面内屈曲。
材料力学-第12章动载荷与疲劳强度概述(A)
FN FT T st I ＝ v 2 A A
可见，由于飞轮以等角速度转动，其轮缘中的正应力与 轮缘上点的速度平方成正比。 设计时必须使总应力满足强度条件。
第12章 动载荷与疲劳强度概述
旋转构件的受力分析与动应力计算
FN FT T st I v2 A A
第12章 动载荷与疲劳强度概述
旋转构件的受力分析与动应力计算
考察以等角速度旋转的飞轮。飞轮材料密 度为 ，轮缘平均半径为 R，轮缘部分的横 截面积为A。 设计轮缘部分的截面尺寸时，为简单 起见，可以不考虑轮辐的影响，从而将飞 轮简化为平均半径等于R的圆环。 由于飞轮作等角速度转动，其上各点 均只有向心加速度，故惯性力均沿着半径 方向、背向旋转中心，且为沿圆周方向连 续均匀分布的力。
第12章 动载荷与疲劳强度概述
等加速度直线运动构件的动应力分析
W FT FI Fst ma W a W g
单向拉伸时杆件横截面上的总正应力为
FN FT T st I A A
其中
W st , A
W I a Ag
分别称为静应力(statics stress)和动应力(dynamics stress)。
第12章
动载荷与疲劳强度概述(A)
工程结构中还有一些构件或零部件中的应力虽然与加速 度无关，但是，这些应力的大小或方向却随着时间而变化， 这种应力称为交变应力 （alternative stress）。在交变应力作 。 用下发生的失效，称为疲劳失效，简称为疲劳（fatigue）。
本章将首先应用达朗贝尔原理和机械能守恒定律，分析 两类动载荷和动应力，然后将简要介绍疲劳失效的主要特征 与失效原因，以及影响疲劳强度的主要因素。
材料力学习题及答案
材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。
解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。
1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量，并确定其大小。
图中之C点为截面形心。
解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。
解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。
材料力学答案第十二章
56 第十二章 动载荷第十二章 动载荷第十二章答案12.1 吊索以匀加速度a = 4.9m/s 2提升重F = 20kN 的重物，吊索的许用应力〔σ〕= 80MPa ，试求吊索的最小横截面面积。
N F F ma -=， 4.92020309.8N F =+⨯=kN []NF Aσσ=≤ 3463010 3.75108010A -⨯≥=⨯⨯m 2.12.2 用两根平行钢索，以匀加速度a =9.8m/s 2提升图示工字钢梁（型号：32c ），试求梁的最大动应力。
由惯性力引起的载荷密度：q 2=ma /l=62.765la lq =62.765g +62.765a 666262.7659.81090.9081.210M W σ--⨯⨯⨯==⨯=⨯MPa.12.3 直径d 1=30cm ，长l =6m 弹性模量E 1 = 10GPa 的二相同木杆。
重W =5kN 的重锤从杆的上部H =1m 高度处自由落下，其中杆b 顶端放一直径d =15cm ，厚h =20mm ，弹性模量E 2 = 8 MPa 的橡皮垫。
试求二杆的应力。
(1) 3592510644.2441010100.3st Pl EA π-⨯⨯⨯∆===⨯⨯⨯⨯m 1511093.0d F P ⎛⎛=== ⎝⎝kN 36210931041015.460.3d d F A σπ-⨯⨯==⨯=⨯MPa. (2) 橡皮垫的静位移：342625100.0247.0736108100.15st π-⨯⨯⨯∆==⨯⨯⨯⨯m 总的静位移：5444.244107.0736107.49810st ---∆=⨯+⨯=⨯maF( a )( b )第十二章 动载荷 5751260d F ⎛== ⎝kN 362260.710410 3.690.3d σπ-⨯⨯=⨯=⨯MPa. 12.4 图示装置,直径d = 4cm ,长l = 4m 的钢杆,上端固定,下端有一托盘,钢杆的弹性模量 E = 200GPa,许用应力〔σ〕=120MPa,弹簧刚度k =160kN/cm,自由落体重P = 20kN,试求容许高度h 为多少。
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-能量法(圣才出品)
第12章能量法12.1 复习笔记由于弹性体的变形具有可逆性，因此外力在相应位移上做功在数值上等于在物体内积蓄的应变能。
利用功和能的概念求解可变形固体的位移、变形和内力等的方法，称为能量法。
能量法是有限元法求解固体力学问题的基础。
本章首先介绍了应变能和余能的概念及计算方法，在此基础上讨论了卡氏定理，最后介绍了能量法在求解超静定问题中的应用。
本章应重点掌握卡氏定理内容及能量法求解超静定问题的应用。
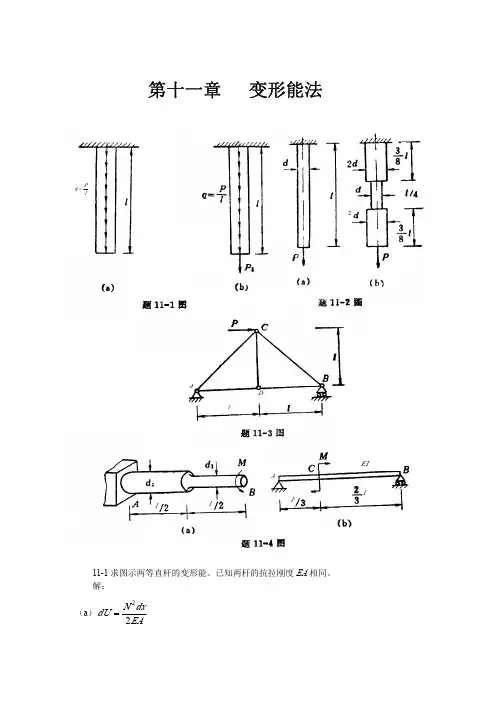
一、应变能和余能（见表12-1-1）表12-1-1 应变能和余能二、卡氏定理（见表12-1-2）表12-1-2 卡氏定理三、能量法求解超静定系统（见表12-1-3）表12-1-3 能量法求解超静定系统12.2 课后习题详解12-1 图12-2-1（a）、（b）所示各杆均由同一种材料制成，材料为线弹性，弹性模量为E。
各杆的长度相同。
试求各杆的应变能。
图12-2-1（a）图12-2-1（b ）解：（1）图12-2-1中（a ）杆的应变能为：222112212222222222231842112(2)24478Ni i i F l F l F l V EA EA EA l F F lE d E dF l Ed ==⨯+⎛⎫⋅⋅ ⎪⎝⎭=⨯+⋅⋅=∑επππ（2）图12-2-1中（b ）杆上距离下端x 处截面上的轴力为：F N （x ）＝F ＋fx ＝F ＋（F/l ）x ，故杆件的应变能为：2002220()d d 214d 23llN l F x V V xEAF F x F l l x EA Ed ==⎛⎫+ ⎪⎝⎭==⎰⎰⎰εεπ12-2 拉、压刚度为EA的等截面直杆，上端固定、下端与刚性支承面之间留有空隙Δ，在中间截面B处承受轴向力F作用，如图12-2-2所示。
杆材料为线弹性，当F＞EAΔ/l时，下端支承面的反力为：F C＝F/2－（Δ/l）（EA/2）。
于是，力F作用点的铅垂位移为：ΔB＝（F－F C）l/EA＝Fl/（2EA）＋Δ/2。
材料力学习题第12章
材料力学习题第１2章12－1一桅杆起重机，起重杆ＡB得横截面积如图所示。
钢丝绳得横截面面积为1０mm2。
起重杆与钢丝得许用力均为，试校核二者得强度。
1２－2重物Ｆ=130kＮ悬挂在由两根圆杆组成得吊架上。
ＡC就是钢杆,直径ｄ1=30ｍｍ,许用应力[σ]sｔ=160M Ｐa。
BC就是铝杆，直径ｄ2=40mm，许用应力[σ］al= ６０MＰa。
已知ＡＢC为正三角形,试校核吊架得强度。
12-３图示结构中,钢索BC由一组直径d =2ｍｍ得钢丝组成。
若钢丝得许用应力[σ］=１60MPa,横梁AＣ单位长度上受均匀分布载荷q=30kN/m作用,试求所需钢丝得根数n。
若将AＣ改用由两根等边角钢形成得组合杆,角钢得许用应力为［σ] =1６０MPa,试选定所需角钢得型号。
12-4图示结构中AＣ为钢杆,横截面面积A1=２ｃm2;ＢC杆为铜杆，横截面面积A2=3cm2。
[σ]ｓｔ= 160ＭＰａ,[σ]ｃop =100MPa，试求许用载荷。
１2-5图示结构,杆AB为5号槽钢,许用应力［σ］＝1６0ＭPａ,杆ＢC为= 2得矩形截面木杆,其截面尺寸为ｂ＝5ｃｍ, h= 10cｍ,许用应力[σ] ＝8MPａ,承受载荷F =128ｋN，试求:（1)校核结构强度;(２)若要求两杆得应力同时达到各自得许用应力,两杆得截面应取多大？12-6图示螺栓，拧紧时产生∆l = 0、１0ｍm得轴向变形,试求预紧力Ｆ,并校核螺栓强度。
已知d1=8mm, d2=6、８mm, d3=7mm,l1=6mｍ, l2=29mｍ,l3=8mm; E=21０GPa, ［σ]=500ＭPa。
12-7图示传动轴得转速为n=５０0r／ｍｉn,主动轮1输入功率P1=368kW,从动轮2与３分别输出功率Ｐ2=１4７kW与P3=２21kW。
已知［σ]＝212MPａ,[ϕ]=1︒／m,G =8０GPa。
（1)试按第四强度理论与刚度条件确定AB段得直径ｄ1与BＣ段得直径d2。
材料力学习题第12章.pptx
39 图示圆截面钢杆，承受载荷F1，F2与力矩M 作用。试根据第三强度理论校核杆的强度。已知载荷F1=
500N，F2 = 15kN，力矩M = 1.2kN·m，许用应力[] = 160MPa。
12-40 图示圆截面钢轴，由电机带动。在斜齿轮的齿面上，作用有切向力Ft= 1.9kN、径向力Fr = 740N 以及
26 图示承受均布载荷的简支梁由两根竖向放置普通槽钢组成。已知 q = 10kN/m, l = 4m，材料的[] = 100MPa，许用挠度[v] = l/1000,E = 200GPa。试确定槽钢型号。
27 图示三根压杆，它们的最小横截面面积相等，材料相同，许用应力[]= 120MPa，试校核三杆的强度。 28 矩形截面杆在自由端承受位于纵向对称面内的纵向载荷F，若已知F = 60kN，试求： 1 横截面上点A 的正应力取最小值的截面高度h； 2 在上述h 值下点B 的正应力值。
7 图示传动轴的转速为n=500r/min，主动轮1 输入功率P1=368kW，从动轮2 和 3 分别输出功率P2=147kW
和 P3=221kW。已知[]=212MPa，[ ]=1/m,G =80GPa。
（1）试按第四强度理论和刚度条件确定AB 段的直径d1和 BC 段的直径d2。 1
学海无 涯
15 矩形截面简支梁由圆形木料制成，已知F = 5kN, a = 1.5m,[] = 10MPa。若要求在圆木中所截取的梁抗 弯截面 系数具有最大值，试确定此矩形截面h b 的值及所需木料的最小上径d。
16 如图所示支承楼板的木梁，其两端支承可视为铰支，跨度l = 6m, 两木梁的间距a = 1m,楼板受均布载荷 q=3.5kN/m2的作用。若[] = 100MPa,[] = 10MPa，木梁截面为矩形，b/h = 2/3，试选定其尺寸。
500N，F2 = 15kN，力矩M = 1.2kN·m，许用应力[] = 160MPa。
12-40 图示圆截面钢轴，由电机带动。在斜齿轮的齿面上，作用有切向力Ft= 1.9kN、径向力Fr = 740N 以及
26 图示承受均布载荷的简支梁由两根竖向放置普通槽钢组成。已知 q = 10kN/m, l = 4m，材料的[] = 100MPa，许用挠度[v] = l/1000,E = 200GPa。试确定槽钢型号。
27 图示三根压杆，它们的最小横截面面积相等，材料相同，许用应力[]= 120MPa，试校核三杆的强度。 28 矩形截面杆在自由端承受位于纵向对称面内的纵向载荷F，若已知F = 60kN，试求： 1 横截面上点A 的正应力取最小值的截面高度h； 2 在上述h 值下点B 的正应力值。
7 图示传动轴的转速为n=500r/min，主动轮1 输入功率P1=368kW，从动轮2 和 3 分别输出功率P2=147kW
和 P3=221kW。已知[]=212MPa，[ ]=1/m,G =80GPa。
（1）试按第四强度理论和刚度条件确定AB 段的直径d1和 BC 段的直径d2。 1
学海无 涯
15 矩形截面简支梁由圆形木料制成，已知F = 5kN, a = 1.5m,[] = 10MPa。若要求在圆木中所截取的梁抗 弯截面 系数具有最大值，试确定此矩形截面h b 的值及所需木料的最小上径d。
16 如图所示支承楼板的木梁，其两端支承可视为铰支，跨度l = 6m, 两木梁的间距a = 1m,楼板受均布载荷 q=3.5kN/m2的作用。若[] = 100MPa,[] = 10MPa，木梁截面为矩形，b/h = 2/3，试选定其尺寸。
材料力学12-5
y
z
x
面内失稳近似两端固定, 在 xz 面内失稳近似两端固定, 长度 l 1=880 .
hb Iy 12 = b = 0.722cm = iy = A bh 2 3
3
λy =
l 0.5×88
iy = 0.722
= 61> λz = 54.3
面内先失稳, 计算临界力. 杆在 xz 面内先失稳,应用 λy 计算临界力.
l
i
=125>123
用欧拉公式计算
Pcr
π 2 EI = 397KN =
l
2
Pcr = 397 = 2.2 < 2.5 P 180
稳定性不足, 稳定性不足,再选 20a 工字截面 查表: 查表:A = 35.5cm2 , imin = 2.12cm
λ=
用经验公式
l
i
=118<123
λ=
l
i
P
A ≈ 2π r t
t ≥ 5.6mm
取壁厚 t =6mm,此时 ,
l
r
t = 0.1 r
不超过10%,可按薄环处理. ,可按薄环处理. 不超过
P
t
例题4 例题
压杆的约束情况,轴向压力,材料均同上例, 压杆的约束情况,轴向压力,材料均同上例,
试选择工字型截面. 试选择工字型截面.已知材料的 E = 206GPa,强度 , 许用应力 [σ] = 140MPa. σ . 解:用试算法 先根据 A3 钢的强度许用应力求一截面作参考
根据λ=97,查表得φ=0.575,代 ,查表得 根据 , 入公式可得压杆的稳定许用应力为
x
[σ ]st = φ [σ ] = 97.8 MPa
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
材料力学习题第12章12-1一桅杆起重机，起重杆AB的横截面积如图所示。
钢丝绳的横截面面积为10mm2。
起重杆与钢丝的许用σ，试校核二者的强度。
力均为MPa[=]12012-2重物F=130kN悬挂在由两根圆杆组成的吊架上。
AC是钢杆，直径d1=30mm，许用应力[σ]st=160MPa。
BC是铝杆，直径d2= 40mm, 许用应力[σ]al= 60MPa。
已知ABC为正三角形，试校核吊架的强度。
12-3图示结构中，钢索BC由一组直径d =2mm的钢丝组成。
若钢丝的许用应力[σ]=160MPa,横梁AC单位长度上受均匀分布载荷q =30kN/m作用，试求所需钢丝的根数n。
若将AC改用由两根等边角钢形成的组合杆，角钢的许用应力为[σ] =160MPa，试选定所需角钢的型号。
12-4图示结构中AC为钢杆，横截面面积A1=2cm2；BC杆为铜杆，横截面面积A2=3cm2。
[σ]st = 160MPa，[σ]cop [F。
= 100MPa，试求许用载荷]12-5图示结构，杆AB为5号槽钢，许用应力[σ] = 160MPa，杆BC为bh= 2的矩形截面木杆，其截面尺寸为b = 5cm, h = 10cm,许用应力[σ] = 8MPa，承受载荷F = 128kN，试求：（1）校核结构强度；（2）若要求两杆的应力同时达到各自的许用应力，两杆的截面应取多大？12-6图示螺栓，拧紧时产生∆l = 0.10mm的轴向变形，试求预紧力F，并校核螺栓强度。
已知d1=8mm, d2=6.8mm, d3=7mm, l1=6mm, l2=29mm, l3=8mm; E=210GPa, [σ]=500MPa。
12-7图示传动轴的转速为n=500r/min，主动轮1输入功率P1=368kW，从动轮2和3分别输出功率P2=147kW 和P3=221kW。
已知[σ]=212MPa，[ ϕ]=1︒/m, G =80GPa。
（1）试按第四强度理论和刚度条件确定AB段的直径d1和BC段的直径d2。
（2）若AB段和BC段选用同一直径，试确定直径d。
（3）主动轮和从动轮的位置如可以重新安排，试问怎样安排才比较合理？12-8图示钢轴，d1 = 4d2/3, M=1kN·m，许用应力[σ]=160MPa，[ϕ ]=0.5︒/m, G=80GPa，试按第三强度理论和刚度条件设计轴径d1与d2。
12-9 图示钢轴所受扭转力偶矩分别为M1=0.8kN·m，M2=1.2kN·m及M3=0.4kN·m。
已知：l1=0.3m,l2=0.7m, [σ]=100MPa, [ϕ]=0.25︒/m, G=80GPa。
试按第三强度理论和刚度条件求轴的直径。
12-10图示组合轴，套筒和芯轴借两端刚性平板牢固地连接在一起。
设作用在刚性平板上的力矩M=2kN·m，套筒和芯轴的切变模量分别为G1=40GPa，G2=80GPa。
许用应力分别为[σ]1=85MPa，[σ]2=110MPa。
试按第三强度理论分别校核套筒与芯轴的强度。
12-11图示槽形截面悬臂梁，F=10kN, M=70kN·m, [σt]=35MPa, [σc]=120MPa，试校核其强度。
12-12图示简支梁，由四块尺寸相同的木板胶合而成，试校核其强度。
已知：F =4kN, l = 400mm, b = 50mm, h = 80mm,板的许用应力[σ]=7MPa，胶缝的许用应力[τ]=5MPa。
12-13图示外伸梁由25a工字钢制成，其跨度l=6m, 全梁上受均布载荷q作用，为使支座处截面A、B上及跨度中央截面C上的最大正应力均为140MPa，试求外伸部分的长度a及载荷集度q。
12-14某四轮吊车之轨道为两工字形截面梁，设吊车重力W=50kN，最大起重量F=10kN，工字钢的许用应力为[σ] = 160MPa，[τ] = 80MPa，试选择吊车梁的工字钢型号。
12-15矩形截面简支梁由圆形木料制成，已知F = 5kN, a = 1.5m, [σ] = 10MPa。
若要求在圆木中所截取的梁抗弯截面系数具有最大值，试确定此矩形截面bh的值及所需木料的最小上径d。
12-16如图所示支承楼板的木梁，其两端支承可视为铰支，跨度l = 6m, 两木梁的间距a = 1m,楼板受均布载荷q=3.5kN/m2的作用。
若[σ] = 100MPa, [τ] = 10MPa，木梁截面为矩形，b/h = 2/3，试选定其尺寸。
12-17图示为一承受纯弯曲的铸铁梁，其截面为⊥形，材料的拉伸和压缩的许用应力之比[σt]/[σc]=1/4,求水平翼板的合理宽度b。
12-18图示轧辊轴直径D = 280mm,l = 450mm, b = 100mm，轧辊材料的许用应力[σ] = 100MPa。
试根据轧辊轴的强度求轧辊能承受的最大轧制力F（F = qb）。
12-19某操纵系统中的摇臂，右端所受的力F1=8.5kN，截面1-1和2-2均为高宽比h/b=3的矩形，材料的许用应力[σ] = 50MPa。
试确定1-1及2-2两个横截面的尺寸。
12-20为了起吊W = 300kN的大型设备，采用一台150kN和一台200kN的吊车及一根辅助梁AB，如图所示。
已知钢材的许用应力[σ] = 160MPa，l = 4m。
试分析和计算：（1）设备吊在AB的什么位置（以到150kN吊车的间距a表示），才能保证两台吊车都不会超载？（2）若以普通热轧工字型钢作为辅梁，确定工字钢型号。
12-21图示结构中，ABC为No10普通热轧工字型钢梁，钢梁在A处为铰链支承，B处用圆截面钢杆悬吊。
已知梁与杆的许用应力均为[σ] = 160MPa。
试求：（1）许可分布载荷集度q；（2）圆杆直径d。
12-22组合梁如图所示，已知q = 40kN/m, F = 48kN，梁材料的许用应力[σ] = 160MPa。
试根据形变应变能强度理论对梁的强度作全面校核。
12-23梁受力如图所示，已知F = 1.6kN, d = 32mm, E = 200GPa。
若要求加力点的挠度不大于许用挠度[v] = 0.05mm，试校核梁的刚度。
12-24一端外伸的轴在飞轮重力作用下发生变形，已知飞轮重W = 20kN，轴材料的E = 200GPa。
轴承B处的许用转角[θ] = 0.5︒。
试设计轴径d。
12-25简易桥式起重机的最大载荷F = 20kN，起重机梁为32a工字钢，E = 210GPa, l = 8.76m，规定许用挠度[v] = l/500。
试校核梁的刚度。
12-26图示承受均布载荷的简支梁由两根竖向放置普通槽钢组成。
已知q = 10kN/m, l= 4m，材料的[σ] = 100MPa，许用挠度[v] = l/1000, E = 200GPa。
试确定槽钢型号。
12-27图示三根压杆，它们的最小横截面面积相等，材料相同，许用应力[σ] = 120MPa，试校核三杆的强度。
12-28矩形截面杆在自由端承受位于纵向对称面内的纵向载荷F，若已知F = 60kN，试求：（1）横截面上点A的正应力取最小值的截面高度h；（2）在上述h值下点B的正应力值。
12-29已知木质简支梁，横截面为矩形，l = 1m, h = 200mm, b = 100mm。
受力情况如图所示，F = 4kN。
[σ] = 20MPa。
校核强度。
12-30有一用10号工字钢制造的悬臂梁，长度为l，端面处承受通过截面形心且与z轴夹角为α的集中力F作用。
试求当α为何值时，截面上危险点的应力值为最大。
12-31两槽钢一端固定，另一端装一定滑轮，拉力F可通过定滑轮与拉力为40kN的W力平衡，构件的主要尺寸见图，[σ] = 80MPa，试选择适当的槽钢型号。
12-32由三根木条胶合而成的悬臂梁的如图所示，跨长l = 1m，若胶合面上的许用切应力为0.34MPa，木材的许用弯曲正应力为[σ] = 10MPa，许用切应力[τ] = 1MPa，试求许可载荷F。
12-33手摇式提升机如图所示，最大提升力为W = 1kN，提升机轴的许用应力[σ] = 80MPa。
试按第三及第四强度理论设计轴的直径。
12-34图示一齿轮传动轴，齿轮A上作用铅垂力F1= 5kN，齿轮B上作用水平方向力F2= 10kN。
若[σ] = 100MPa，齿轮A的直径为300mm，齿轮B的直径为150mm，试用第四强度理论计算轴的直径。
12-35电动机功率P = 9kW，转速n = 715rpm，皮带轮直径D = 250mm，电动机轴外伸长度l = 120mm，轴的直径d = 40mm, 轴材料的许用应力[σ] = 60MPa。
试按最大切应力理论校核轴的强度。
12-36图示传动轴，传递的功率P = 7kW，转速n = 200rpm。
齿轮A上作用的力F与水平切线夹角20︒（即压力角）。
皮带轮B上的拉力F1和F2为水平方向，且F1 = 2F2。
若轴的[σ] = 80MPa，试对下列两种情况，按最大切应力理论设计轴的直径。
（1）忽略皮带轮的重力W。
（2）考虑皮带轮的自重W = 1.8kN 。
12-37 圆截面等直杆受横向力F 和绕轴线的外力偶M 作用。
由实验测得杆表面A 点处沿轴线方向的线应变40104-⨯=οε，杆表面B 点处沿与母线成45︒方向的线应变4451075.3-⨯=οε。
并知杆的抗弯截面系数W = 6000mm 3，弹性模量E = 200GPa ，泊松比v = 0.25，许用应力[σ] = 140MPa 。
试按第三强度理论校核杆的强度。
12-38 图示圆截面杆，直径为d ，承受轴向力F N 与扭力矩T 作用，杆用塑性材料制成，许用应力为[σ]。
试画出危险点处微体的应力状态图，并根据第四强度理建立杆的强度条件。
12-39 图示圆截面钢杆，承受载荷F 1，F 2与力矩M 作用。
试根据第三强度理论校核杆的强度。
已知载荷F 1 = 500N ，F 2 = 15kN ，力矩M = 1.2kN ·m ，许用应力[σ] = 160MPa 。
12-40 图示圆截面钢轴，由电机带动。
在斜齿轮的齿面上，作用有切向力F t = 1.9kN 、径向力F r = 740N 以及 平行于轴线的外力F = 660N 。
若许用应力[σ] = 160MPa ，试根据第四强度理论校核轴的强度。
12-41图示简支梁，跨度中点承受集中载荷F作用。
若横截面的宽b保持不变，试根据等强度观点确定截面高度h (x)的变化规律。
许用应力[σ]与许用切应力[τ]均为已知。